Chuyên Đề Hệ Thức Lượng Trong Tam Giác Vuông Ôn Thi Vào 10 Giải Chi Tiết
Sử dụng đinh nghĩa tỉ số lượng giác của góc nhọn vào tam giác vuông. Sử dụng tỉ số lượng giác của hai góc phụ nhau. Cho tam giác ABC vuông tại C có BC = 4cm, AC = 3cm. Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc A. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Chương 1: Hệ thức lượng trong tam giác vuông 33 tài liệu
Môn: Toán 9 2.7 K tài liệu
Tác giả:
Preview text:
CHUYÊN ĐỀ 16: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
CHỦ ĐỀ 1: TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
DẠNG 1: TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN.
A. KIẾN THỨC CẦN NHỚ 1. Định nghĩa
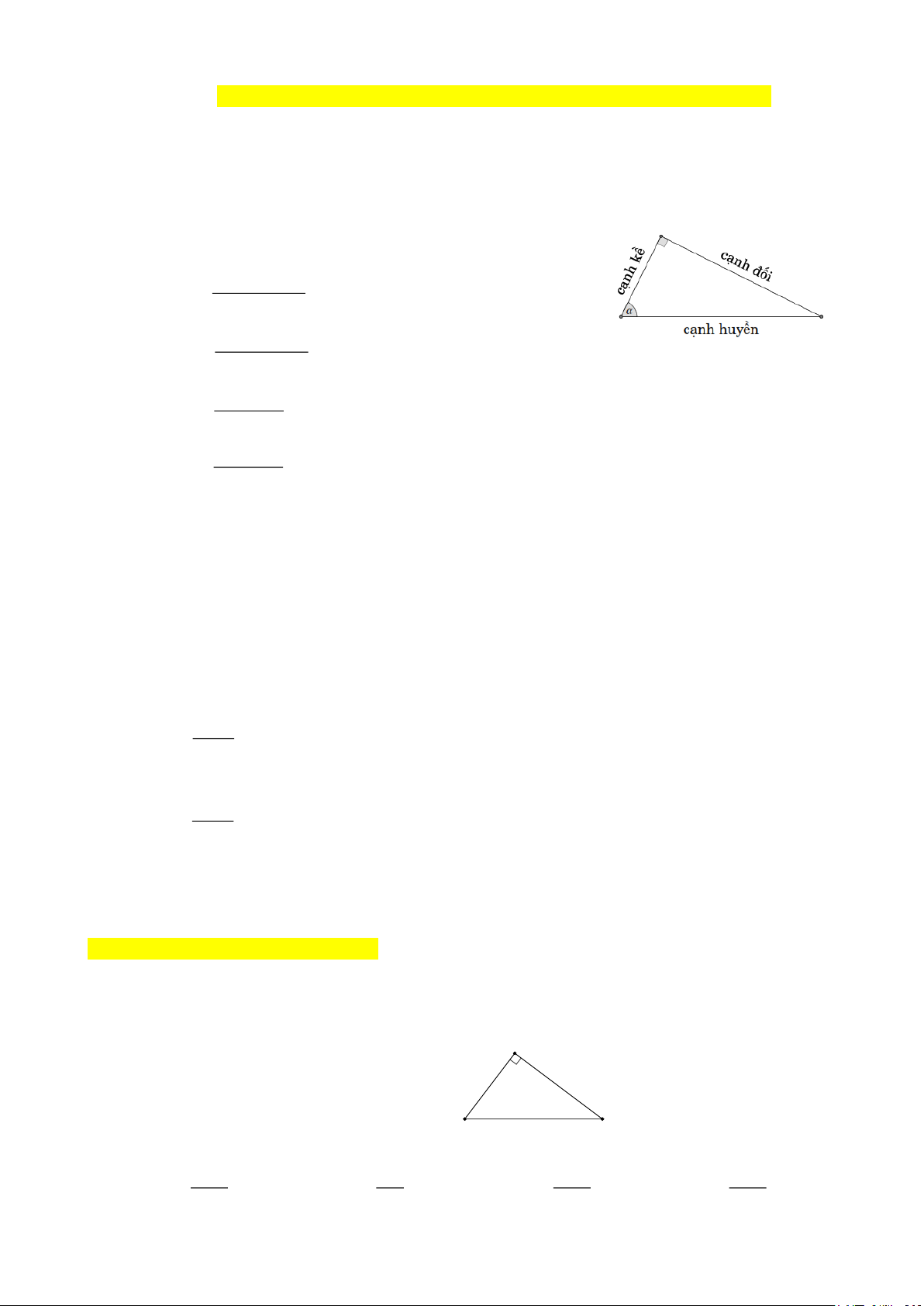
▪ Với là góc nhọn trong tam giác vuông ta có ▪ sin = caïnh ñoái ; caïnh huyeàn ▪ cos = caïnh keà ; caïnh huyeàn ▪ tan = caïnh ñoái; caïnh keà ▪ cot = caïnh keà. caïnh ñoái
2. Một số hệ thức và tính chất cơ bản
▪ Với hai góc nhọn , và + = 90 thì
sin = cos ; cos = sin ; tan = tan ; cot = cot .
Với góc nhọn (0 90) , ta có
▪ 0 sin 1;0 cos 1 .
▪ Nếu tăng thì sin và tan tăng; còn cos và cot giảm.
3. Một số công thức lượng giác sin ▪ tan = ; cos ▪ tan cot = 1; cos ▪ cot = ; sin ▪ 2 2 sin + cos = 1 B. BÀI TẬP
DẠNG 1.1: TÍNH TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN.
PHẦN I. BÀI TẬP TRẮC NGHIỆM
1. TRẮC NGHIỆM CHỌN ĐÁP ÁN ·
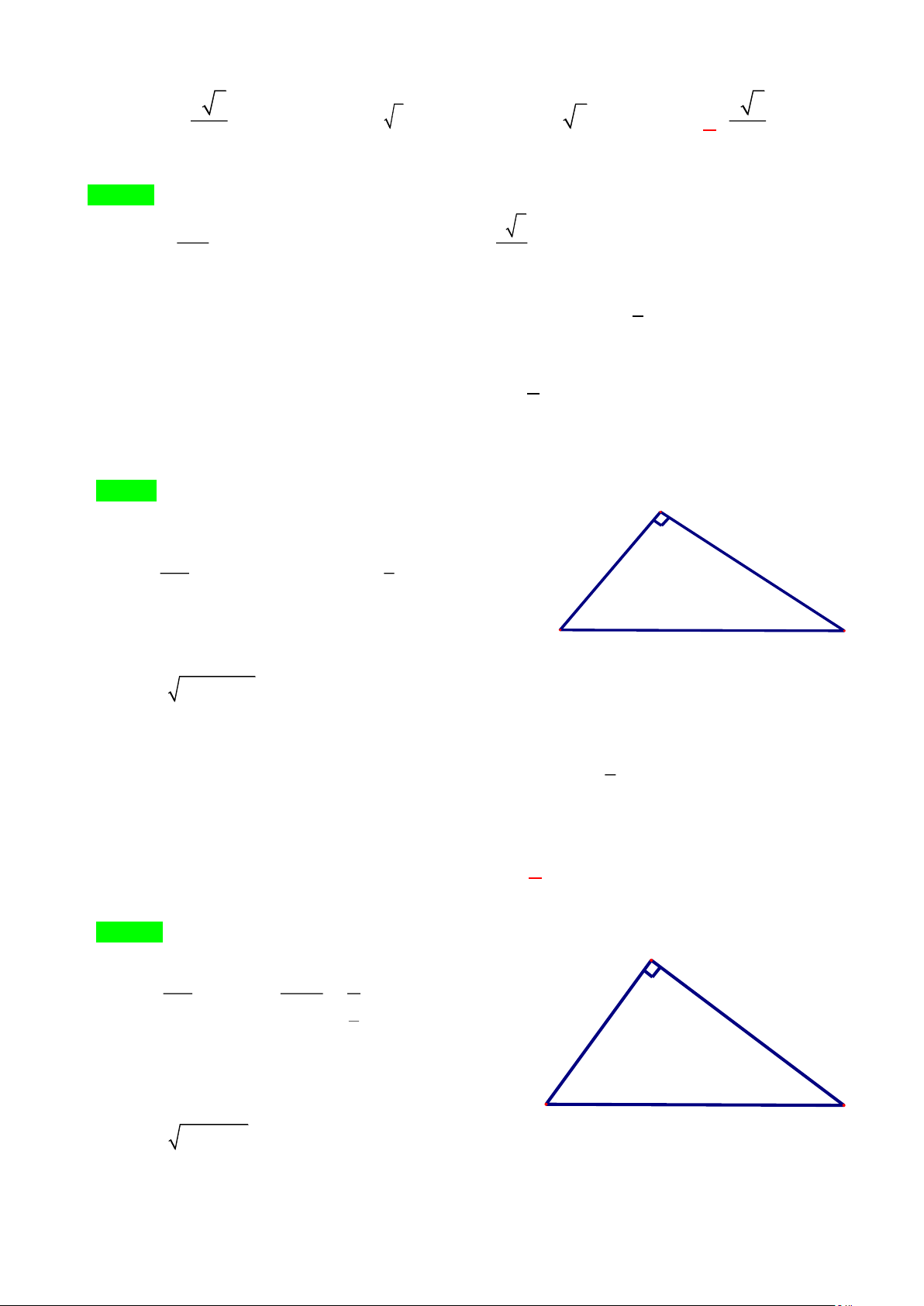
Câu 1. [NB] Cho tam giác MNP vuông tại M . Khi đó sin MNP bằng M N P MN MP MN MP A. . B. . C. . D. . NP NP MP MN Lời giải Trang 1 · MP ·
Chọn B sin MNP =
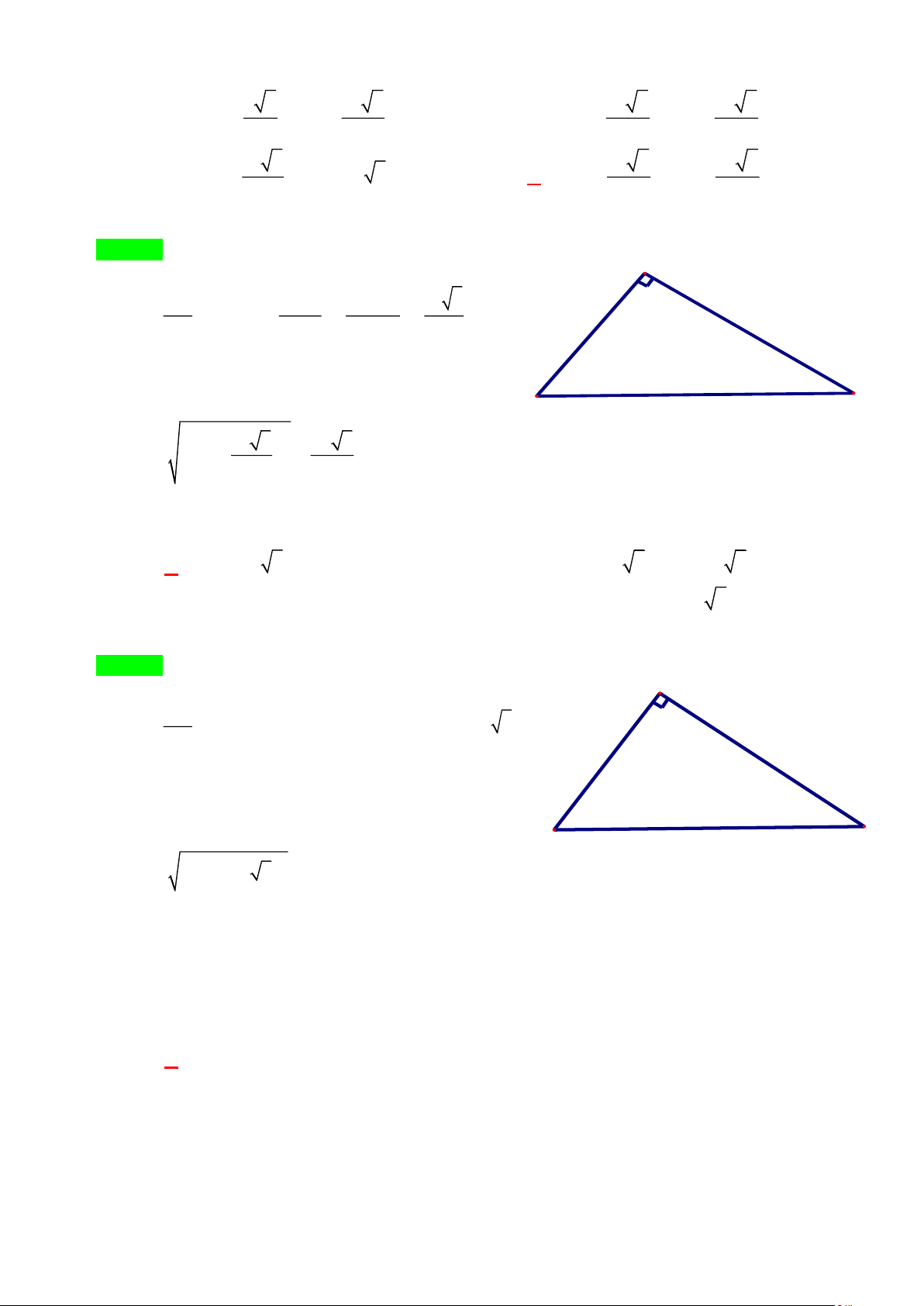
Câu 2. [NB] Cho tam giác MNP vuông tại M . Khi đó cos MNP bằng NP M N P MN MP MN MP A. . B. . C. . D. . NP NP MP MN Lời giải · MN
Chọn A cos MNP = NP ·
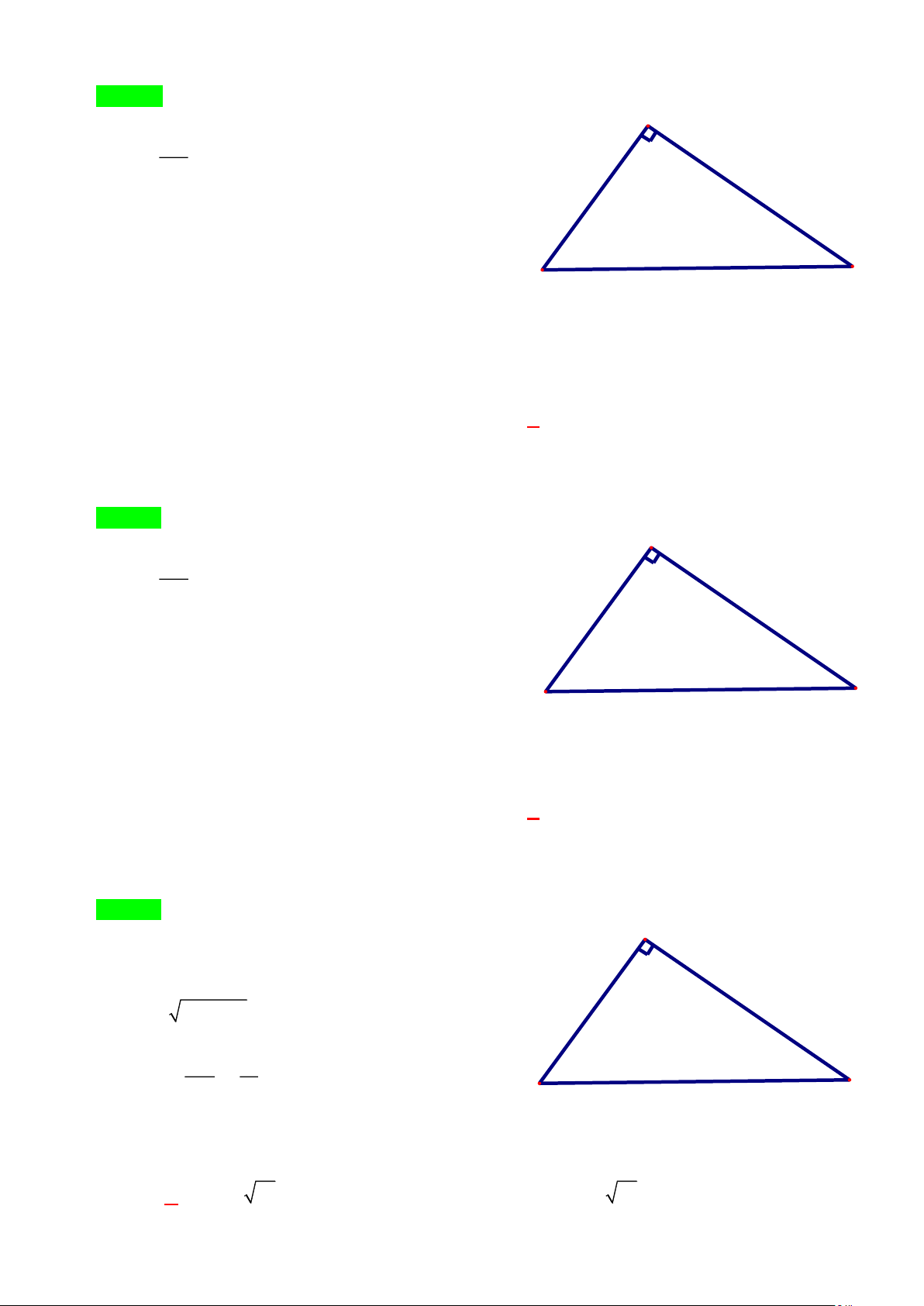
Câu 3. [NB] Cho tam giác MNP vuông tại M . Khi đó tan MNP bằng: M N P MN MP MN MP A. . B. . C. . D. . NP NP MP MN Lời giải · MP
Chọn D tan MNP = MN ·
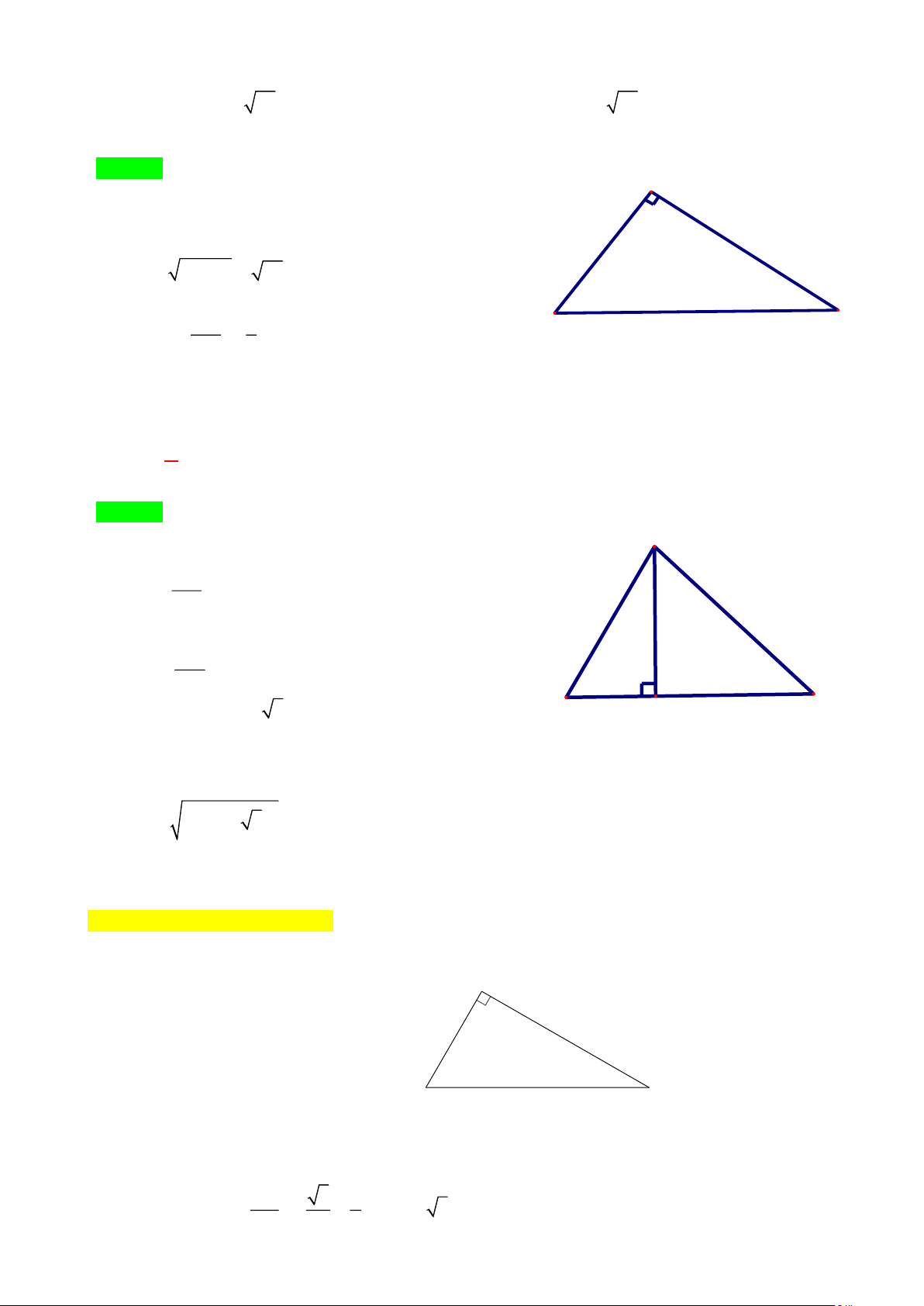
Câu 4. [NB] Cho tam giác MNP vuông tại M . Khi đó co t MNP bằng: M N P MN MP MN MP A. . B. . C. . D. . NP NP MP MN Lời giải · MN
Chọn C co t MNP = MP
Câu 5. [TH] Cho tam giác A BC vuông tại C có BC = 1, 2cm, A C = 0, 9cm . Tính các tỉ số lượng giác
sin B ; cos B .
A. sin B = 0, 6;cos B = 0, 8 .
B. sin B = 0, 8;cos B = 0, 6 . Trang 2
C. sin B = 0, 4;cos B = 0, 8 .
D. sin B = 0, 6;cos B = 0, 4 . Lời giải Chọn A
Xét tam giác ABC vuông tại C có: C 2 2 2 2 2
AB = BC + AC = 1, 2 + 0,9 = 2, 25 AB = 1,5cm . A C 0, 9 sin B = = = 0, 6 Khi đó: A B 1, 5 . 0,9 1,2 BC 1, 2 cosB = = = 0, 8 A B 1, 5 A B
Câu 6. [TH] Cho tam giác A BC vuông tại A có BC = 8cm, A C = 6cm . Tính tỉ số lượng giác tanC
(làm tròn đến chữ số thập phân thứ 2).
A. t anC » 0, 87 .
B. t anC » 0, 86 .
C. t anC » 0, 88 .
D. t anC » 0, 89 . Lời giải Chọn C
Xét tam giác ABC vuông tại A có: A 2 2 2 2 2
AB = BC − AC = 8 − 6 = 28 AB = 2 7 cm . 6 Khi đó: A B 2 7 t anC = = » 0, 88 . A C 6 B 8 C
Câu 7. [TH] Cho tam giác A BC vuông tại A , đường cao A H có A B = 13cm, BH = 0, 5dm . Tính tỉ
số lượng giác sinC (làm tròn đến chữ số thập phân thứ 2)
A. sinC » 0, 35 .
B. sinC » 0, 37 .
C. sinC » 0, 39 .
D. sinC » 0, 38 . Lời giải Chọn D
Xét tam giác ABC vuông tại A, đường cao AH có: A 2 2 AB 13 2
AB = BH.BC = BC = = = 33,8 . BH 5 13 Khi đó: A B 13 si nC = = » 0, 38 . BC 33, 8 B 5 H C
Câu 8. [TH] Cho tam giác A BC vuông tại A , đường cao A H có CH = 4cm, BH = 3cm . Tính tỉ số
lượng giác cosC (làm tròn đến chữ số thập phân thứ 2).
A. cosC » 0, 76 .
B. cosC » 0, 77 .
C. cosC » 0, 75 .
D. cosC » 0, 78 . Trang 3 Lời giải Chọn A
Xét tam giác ABC vuông tại A, đường cao AH có: A 2
AC = CH.BC = AC = 4.7 = 2 7 cm .
Xét tam giác AHC vuông tại H có: HC 4 cosC = = » 0, 76 . A C 2 7 3 B H 4 C
Câu 9. [VD] Cho tam giác A BC vuông tại A . Hãy tính tanC biết rằng t an B = 4 . 1 1 A. tanC = .
B. t anC = 4 .
C. t anC = 2 . D. t anC = . 4 2 Lời giải Chọn A
Xét tam giác ABC vuông tại A có: A AC AB 1 tan B = = 4 = = . AB AC 4 Khi đó: A B 1 t anC = = . A C 4 B C 3
Câu 10. [VD] Tính sin a, tan a biết cos a = . 4 4 3 7 3 A. sin a = ; tan a = . B. sin a = ; tan a = . 7 4 4 7 7 7 7 7 C. sin a = ; tan a = . D. sin a = ; tan a = . 4 3 3 4 Lời giải Chọn C µ A
Đặt B = a
Xét tam giác ABC vuông tại A có: AB 3 os c = cos B = = BC 4 . = AB = 3 ;
x BC = 4x (x 0)
AC = BC − AB = ( x)2 − ( x)2 2 2 2 2 4 3 = 7x AC = x 7 B C Trang 4 A C 7 sin a = sin B = = Khi đó: B C 4 . A C 7
t an a = t an B = = A B 3 5
Câu 11. [VD] Cho a là góc nhọn bất kỳ. Tính cot a biết sin a = . 13 12 11 5 13 A. cot a = . B. cot a = . C. cot a = . D. cot a = . 5 5 12 5 Lời giải Chọn A µ A Đặt B = a
Xét tam giác ABC vuông tại A có: AC 5 sin = sin B = = BC 13 . = AC = 5 ;
x BC = 13x (x 0)
AB = BC − AC = ( x)2 − ( x)2 2 2 2 2 13 5 =144x AB =12x B C Khi đó: A B 12x 12
co t a = co t B = = = . A C 5x 5
Câu 12. [VDC] Cho tam giác nhọn A BC hai đường cao A D và BE cắt nhau tại H . Biết HD : HA = 3 : 2 · ·
. Khi đó t an A BC . t an A CB bằng: 3 5 A. 3 . B. 5 . C. . D. . 5 3 Lời giải Chọn D Ta có: ABC = D A ACB = D A tan ; tan D B D C 2 ABC ACB = D A tan .tan (1) D B . D C
HBD = CAD (cùng phụ với ACB ), HDB = D A C = 90 Do đó AHB ADC (g.g), suy ra: DH = D B D
B .DC = DH. D A (2) DC D A 2 D A AD
Từ (1) và (2) suy ra: tan ABC.tan ACB = = (3) DH. D A DH HD 3 HD 3 HD 3 Theo giả thiết: = = = = HA 2 AH + HD 2 + 3 AD 5 AD = 5 . HD 3
Thay vào (3), ta được: ABC ACB = 5 tan .tan . 3 Trang 5
2. TRẮC NGHIỆM ĐÚNG SAI (Soạn khoảng 4 câu): Các khẳng định đúng sai được sắp xếp theo
thứ tự từ dễ đến khó, các khẳng định về cùng một nội dung hỏi.
Trong mỗi ý a), b), c), d) ở mỗi câu, em chọn đúng hoặc sai
Câu 1. Cho tam giác ABC vuông tại A.
A. sin B = cos C. B. cot B = cot C . C. tan B = cot C . D. 2 2
si n B + cos C = 1. Lời giải A. Đ B. S C. S D. Đ
- Tam giác ABC vuông tại A thì góc B và góc C phụ nhau nên sin B = cos C.
- Góc B và góc C chưa cho bằng nhau nên cot B = cot C là sai.
- Tam giác ABC vuông tại A thì góc B và góc C phụ nhau nên tan B = cot C .
- Vì sin B = cos C nên 2 2
si n B + cos C = 1là khẳng định đúng.
Câu 2. Cho ABC vuông tại A có AB = 3cm và BC = 5cm. Khẳng định nào đúng, sai? 3 3 4 4
A. cos B = B. sin C = C. sin B = D. co t C = 4 5 5 5 Lời giải A 3 5 C B A. S B. Đ C. S D. S - Theo đ/l Pytago: 2 2 2 2 2 2
AC = BC − AB = 5 − 3 = 4 AC = 4cm AB 3
- Theo định nghĩa tỉ số lượng giác: cos B = = nên đáp án A sai BC 5 AB 3
- Đáp án B đúng vì sin C = = BC 5 AC 4
- Đáp án C đúng vì sin B = = BC 5 AC 4
- Đáp án D sai vì cot C = = AB 3 5
Câu 3. Cho tam giác ABC vuông tại C có AC = AB 13 Trang 6 5 12 17 37 A. cos A = B. tan B =
C. sin A + sin B =
D. co t A + cot B = 13 5 13 60 Lời giải C A B A. Đ B. S C. Đ D. S 5 AC 5
Từ giả thiết: AC = AB = = 13 AB 13 AC 5
- Đáp án A đúng vì ta có cos A = = AB 13
- Đặt AC = 5x; AB = 13x( x > 0) . Theo đ/l Pytago:
BC = AB − AC = ( x)2 − ( x)2 2 2 2 2 13 5
=144x BC =12x AC 5x 5
Đáp án sai vì tan B = = = BC 12x 12 5 12 17
- Ta có: sin A + sin B = + = => đáp án C đúng 13 13 13 5 12 169
- Ta có: cot A + cot B = + = => đáp án D sai. 12 5 60
Câu 4. Khẳng định nào đúng, sai? 1
A. sin 20° < sin 70° . B. cot 40° < cot 50° . C. t an 20°. t an 70° = 2 . D. 2 2 sin 10° + sin 80° = 2 Lời giải
- Vì góc tăng thì tỉ số sin tăng nên đáp án A đúng
- Vì góc tăng thì cot giảm nên đáp án B sai
- Ta có t an 70° = cot 20° nên t an 20°. t an 70° = t an 20°. cot 20° = 1 nên đáp án C sai
- Do hai góc phụ nhau nên sin 10° = cos80° nên 2 2 2 2
sin 10° + sin 80° = co s 10° + sin 80° = 1. Nên đáp án D sai
3. TRẮC NGHIỆM TRẢ LỜI NGẮN ( soạn khoảng 6 câu)
Câu 1. [NB] Cho tam giác ABC vuông tại A. Khi đó cosC bằng tỉ số…. Lời giải Trang 7
Theo định nghĩa tỉ số lượng giác ta có: A AC cosC = BC C B
Câu 2. [NB] Cho a và b là hai góc nhọn bất kỳ thoả mãn a + b = 90° . Khi đó tan a = ..... Lời giải
Vì a + b = 90° nên t an a = cot b.
Câu 3. [TH] Cho a là góc nhọn bất kỳ. Giá trị của 2 2
sin a + cos a bằng….. Lời giải µ AC AB
Đặt B = a . Khi đó: sin = ; cos = BC BC 2 2 2 2 2 AC AB AC AB BC 2 2 = sin + cos + = + = = =1 2 2 BC BC BC BC
Câu 4. [TH] Cho tam giác A BC vuông tại A , đường cao A H cóA C = 15cm,CH = 6cm . Tỉ số lượng
giác cos B là……. Lời giải
Xét tam giác ABC vuông tại A, đường cao AH có: 2 2 AC 15 2
AC = CH.BC = BC = = = 37,5cm . CH 6
Lại có: AB = BC − AC = ( )2 −( )2 2 2 2 37,5
15 = 1181, 25 AB 34,37cm A B 34, 37 có: cosB = = » 0, 92 . BC 37, 5 A 15 6 B H C
Câu 5. [VD] Cho tam giác A BC vuông tại A , đường cao A H có CH = 11cm, BH = 12cm . Tỉ số
lượng giác sin B (làm tròn đến chữ số thập phân thứ 2) là…… Trang 8 A C 11 12 H B
Xét tam giác ABC vuông tại A
Xét tam giác ABC vuông tại A, đường cao AH có: 2
AC = CH.BC = AC = 11.(11+12) 15,91cm . A C 15, 91 có: sinB = » » 0, 69 BC 23
PHẦN II. BÀI TẬP TỰ LUẬN Phương pháp giải:
☑️ Sử dụng đinh nghĩa tỉ số lượng giác của góc nhọn vào tam giác vuông
☑️ Sử dụng tỉ số lượng giác của hai góc phụ nhau BÀI TẬP MẪU
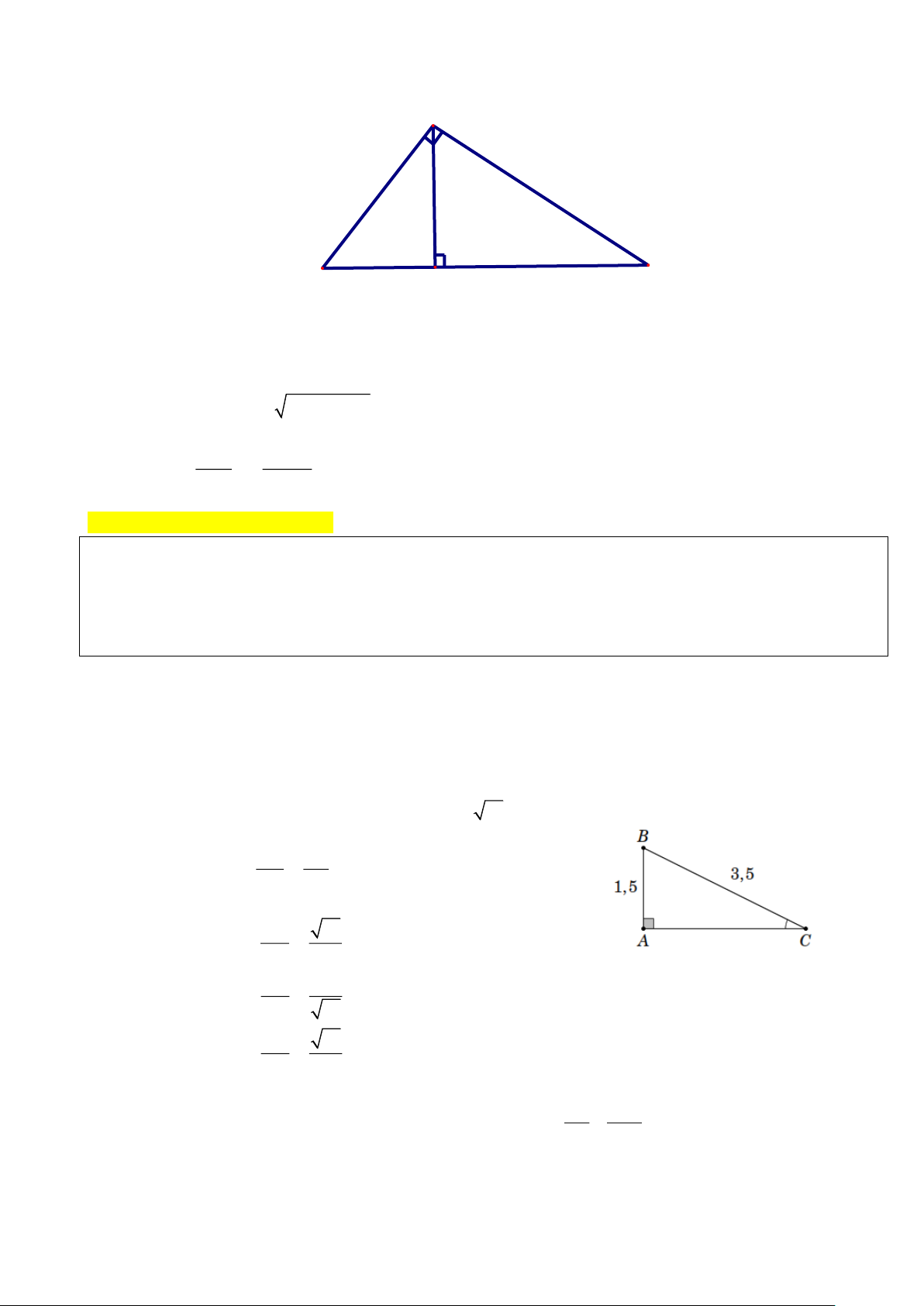
Ví dụ 1 [NB]: Tam giác ABC vuông tại A , AB = 1,5 ; BC = 3,5 . Tính tỉ số lượng giác của góc C rồi
suy ra các tỉ số lượng giác của góc B . Lời giải Ta có 2 2 2 2 2
AC = BC − AB = 3,5 −1,5 = 10 AC = 10 . AB 1,5
Do đó cos B = sin C = = 0,4286 BC 3,5 AC 10 sin B = cos C = = 0,9035 BC 3,5 AB 1,5 cot B = tan C = = 0, 4743 AC 10 AC 10 tan B = cot C = = 2,1082 AB 1,5
Ví dụ 2 [TH]: Cho ABC vuông tại A, Chứng minh rằng: AC sin B = . AB sin C Lời giải Trang 9
Xét ABC vuông tại A có A AC AB sin B = ; sinC = BC BC sin B AC AB AC = : = sin C BC BC AB B C
Ví dụ 3 [TH]: ABC vuông tại A có BC = 2AB . Tính các tỉ số lượng giác của góc C . Lời giải
Ta đặt AB = m thì BC = 2m , suy ra 2 2 2 2 2 2
AC = BC − AB = 4m − m = 3m AC = m 3 . AB m 1 AC m 3 3 Ta có sin C = = = ;cosC = = = ; BC 2m 2 BC 2m 2 AB m 1 AC m 3 tan C = = = ;cot C = = = 3 . AC m 3 3 AB m
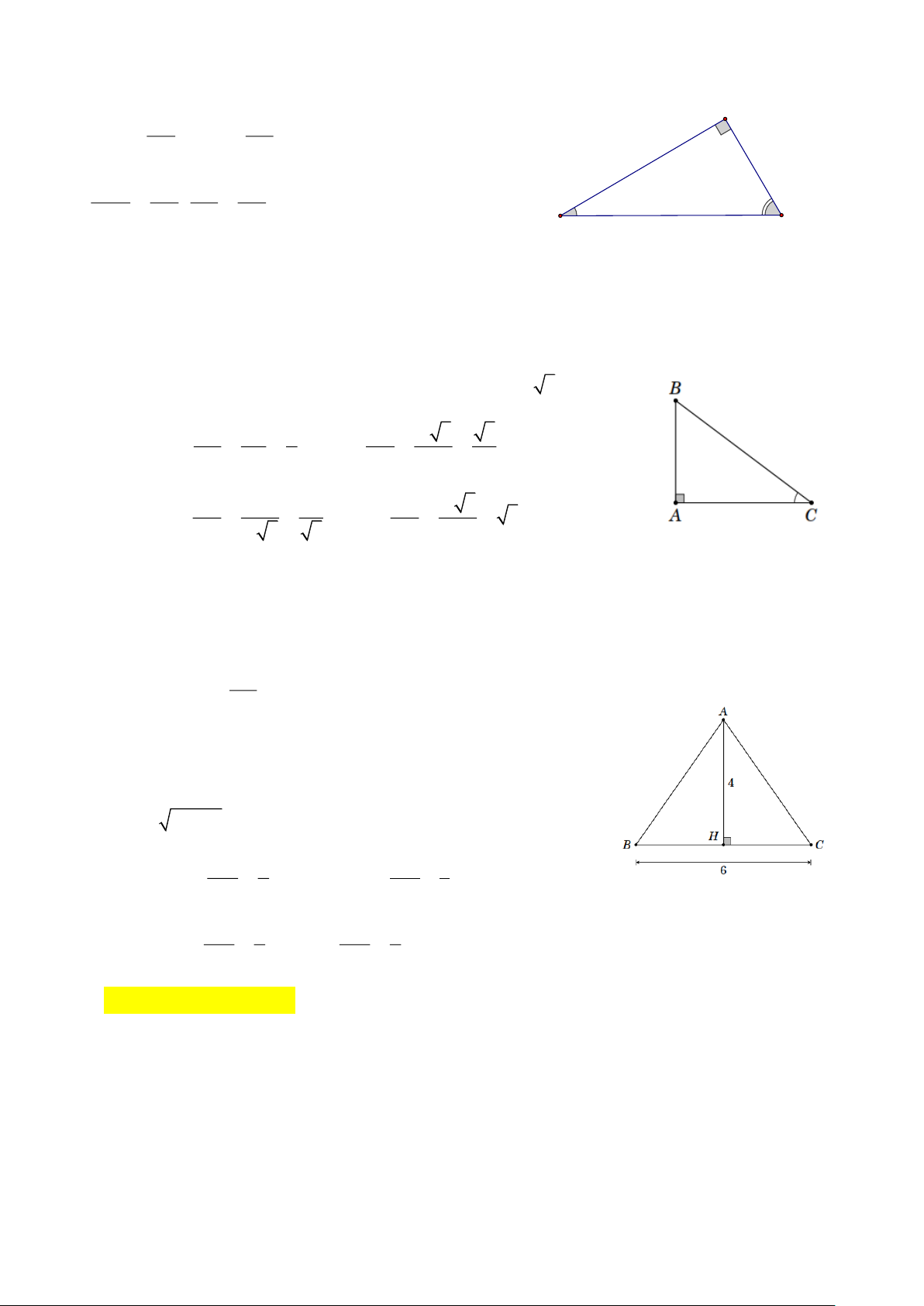
Ví dụ 4 [VD]: Tam giác ABC cân tại A , có BC = 6 , đường cao AH = 4 . Tính các tỉ số lượng giác của góc B . Lời giải BC Ta có BH = HC = = 6 : 2 = 3; 2
Xét tam giác AHB vuông tại H có 2 2 2
AB = AH + HB . 2 2 = AB = 4 + 3 = 5 AH 4 BH 3 Do đó: sin B = = = 0,8; cos B = = = 0,6; AB 5 AB 5 AH 4 BH 3 tan B = = ; cot B = = = 0,75. AB 3 AH 4
✔️BÀI TẬP TỰ LUYỆN
Bài 1. [NB] Cho tam giác ABC vuông tại C có BC = 4cm, AC = 3cm. Tính các tỉ số lượng giác của
góc B. Từ đó suy ra tỉ số lượng giác của góc A. Hướng dẫn
Áp dụng định lý Pytago và tam giác vuông ABC
Ta có: AB2 = AC2 + BC2 => AB = 5
Áp dụng tỉ số lượng giác, tính được: Trang 10 3 4 3 4
sin B = ,cos B = , tan B = ,cot B = 5 5 4 3 4 3 4 3
sinA = ,cosA = , tanA = và cotA = 5 5 3 4
Bài 2. [TH] Cho tam giác ABC vuông ở A, đường cao AH. Biết AB = 7,5cm; AH = 6cm. a) Tính AC, BC; b) Tính cosB, cosC. Hướng dẫn
a) Tam giác ABH vuông ở H, theo định lí Py-ta- go, ta có: A 2 2 2 2 2
BH = AB − AH = (7,5) − 6 = 20, 25
= AC = 20,25 = 4,5c . m 7,5 6
Tam giác ABC vuông ở A, có AH ⊥ BC, theo hệ
thức lượng trong tam giác vuông, ta có: B C H 2
AB = BH.BC 2 2 AB 7,5 = BC = = = 12,5(cm). BH 4,5
Lại áp dụng định lý Py-ta-go với tam giác vuông ABC, ta có: 2 2 2 2 2
AC = BC − AB = (12,5) − (7,5) =156, 25 − 56, 25 = 100 = AC = 0 10 = 10c . m
Vậy AC = 10cm, BC = 12,5cm.
b) Trong tam giác vuông ABC, ta có: AB 7,5 AC 10 cos B = = = 0,6 cosC = = = 0,8. BC 12,5 BC 12,5 Vậy cosB = 0,6; cosC = 0,8.
Bài 3. [VD] Cho tam giác ABC, đường cao AH, trung tuyến AM. Biết AH = 12 cm, BH = 9 cm,
CH = 16 cm. Tính các tỉ số lượng giác của góc HAM. Hướng dẫn
Chứng minh được tam giác ABC vuông tại A Trang 11 BC 25 => AM = = (cm) A 2 2
Từ đó tính được tỉ số lượng giác của góc HAM 7 24 sin HAM = ;cos HAM = ; 25 25 7 24 tan HAM = ;cot HAM = C 24 7 B H M
Bài 4. [VD] Cho tam giác ABC vuông tại A. Chứng minh rằng: cot B + cot C 2 Hướng dẫn A H M C B 1
Kẻ đường cao AH và trung tuyến AM thì AH AM =
BC BC 2AH; 2 BH CH BH CH BC cot B = ;cot C =
cot B + cot C = + = 2 AH AH AH AH AH
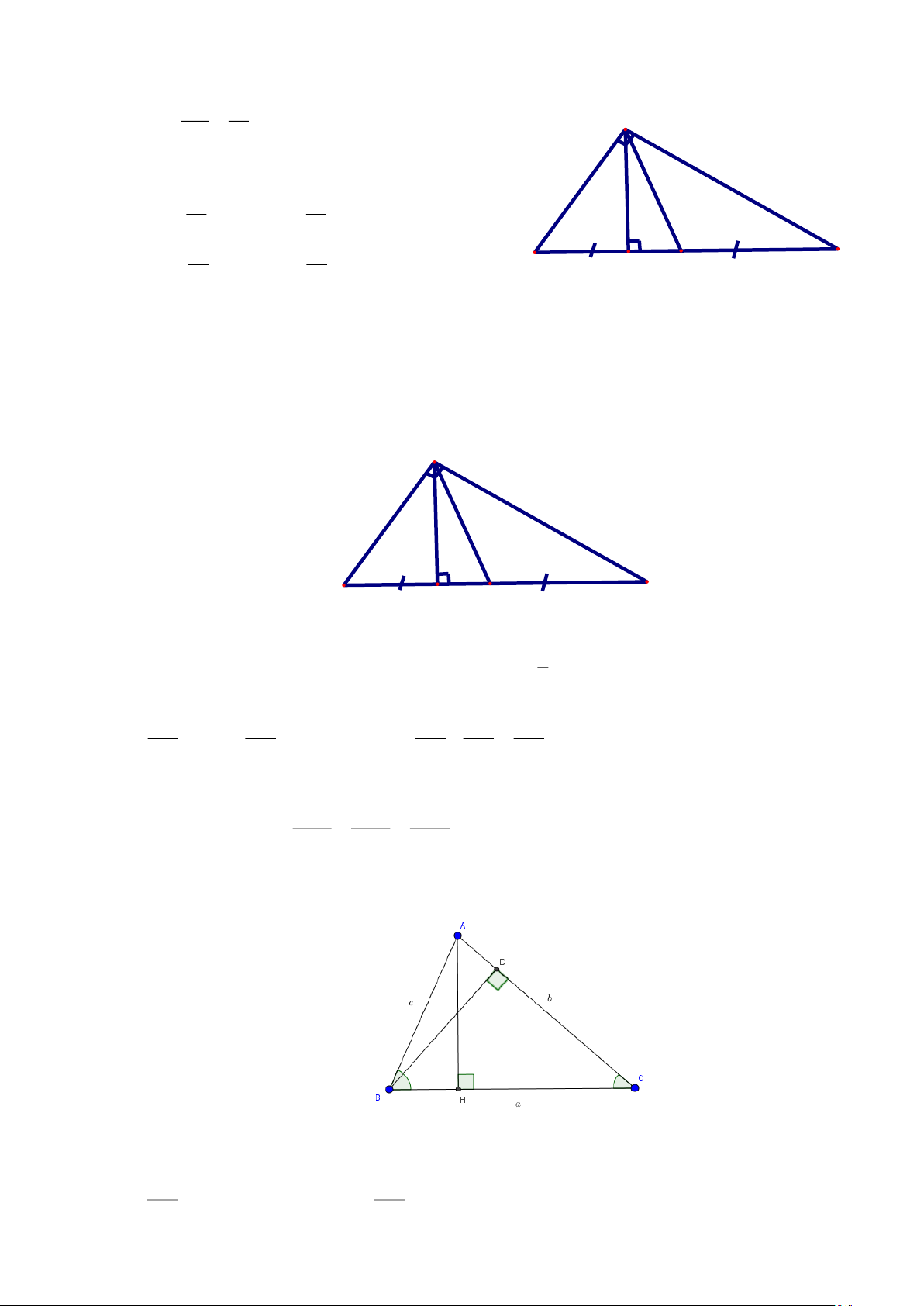
Bài 5. [VD] Cho tam giác ABC nhọn, gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, a b c B , C. Chứng minh rằng: = = sin A sin B sin C Hướng dẫn
Kẻ AH ⊥ BC (H BC) . Khi đó : AH AH sin B = sin .
B c = AH và sin C =
sin C .b = AH c b Trang 12 b c
Từ đó ta có: sinB . c = sinC . b = . sin B sin C
Tương tự kẻ đường cao BD của tam giác ABC (D AC) sẽ chứng minh được: a b a b c = = = sin A sin B sin A sin B sin C
DẠNG 1.2: TÍNH CẠNH VÀ GÓC NHỌN CHƯA BIẾT TRONG TAM GIÁC VUÔNG.
PHẦN I. BÀI TẬP TRẮC NGHIỆM
1. TRẮC NGHIỆM CHỌN ĐÁP ÁN (soạn khoảng 12 câu theo các mức độ
NB: 4 câu; TH: 4 câu; VD: 3 câu; VDC: 1 câu) · 1
Câu 1. [NB] Cho tam giác MNP vuông tại M , MN = 6cm và cos MNP = . Khi đó NP bằng 2 M N P A. 6cm .
B. 12cm. . C. 9cm . D. 15cm . Lời giải · MN MN 6
Chọn B Xét tam giác MNP vuông tại M có: co s MNP = = > NP = = = 12cm · NP 1 co s MNP 2 · 1
Câu 2. [NB] Cho tam giác MNP vuông tại M , NP = 14cm và sin MPN = . Khi đó MN bằng: 4 M N P
A. 3, 5cm .
B. 7cm. .
C. 10cm . D. 28cm . Lời giải · MN · 1
Chọn A Xét tam giác MNP vuông tại M có: sin MPN =
= > MN = NP.sin MPN = 14. = 3, 5cm NP 4 ·
Câu 3. [NB] Cho tam giác MNP vuông tại M , NP = 9cm và 0
MNP = 30 . Khi đó MN bằng: M N P Trang 13 9 3 9 3 A. cm.
B. 6 3cm. .
C. 9 3cm . D. cm. 4 2 Lời giải
Chọn D Xét tam giác MNP vuông tại M có: · MN · 9 3 0 cosMNP =
= > MN = NP.cosMNP = 9.cos30 = cm. NP 2 7
Câu 4. [TH] Cho tam giác A BC vuông tại A có A B = 5cm, cotC =
. Tính độ dài các đoạn thẳng 8
A C và BC (làm tròn đến chữ số thập phân thứ 2)
A. A C » 4, 39(cm );BC » 6, 66(cm ) .
B. A C » 4, 38(cm );BC » 6, 65(cm ) .
C. A C » 4, 38(cm );BC » 6, 64(cm ) .
D. A C » 4, 37(cm );BC » 6, 67(cm ) . Lời giải Chọn B A
Xét tam giác ABC vuông tại A có: A C 7 cotC =
= > A C = A B.cotC = 5. » 4, 38cm. 5 A B 8
Áp dụng định lý Pytago ta có: B C 2 2 2
BC = AB + AC 2 2
= BC = 5 + 4,38 6,65c . m 5
Câu 5. [TH] Cho tam giác A BC vuông tại A có A B = 9, tanC =
. Tính độ dài các đoạn thẳng A C 4
và BC . (làm tròn đến chữ số thập phân thứ 2).
A. A C = 11, 53;BC = 7, 2 .
B. A C = 7;BC » 11, 53 .
C. A C = 5, 2;BC » 11. D. A C = 7, 2;BC » 11, 53 . Lời giải Chọn D. A
Xét tam giác ABC vuông tại A có: A B A B 9 tanC = = > A C = = = 7,2. A C tanC 5 9 4
Áp dụng định lý Pytago ta có: 2 2 2
BC = AB + AC B C 2 2
= BC = 9 + 7,2 11,53. µ
Câu 6. [TH] Cho tam giác A BC vuông tại A có A C = 10,C = 30° . Tính A B ;BC . Trang 14 5 3 20 3 10 3 14 3 A. A B = ;BC = . B. A B = ;BC = . 3 3 3 3 10 3 10 3 20 3 C. A B = ;BC = 20 3 . D. A B = ;BC = . 3 3 3 Lời giải Chọn D. A
Xét tam giác ABC vuông tại A có: A B A C 10 10 3 tanC = = > A B = = = . 0 A C tanC tan 30 3 10
Áp dụng định lý Pytago ta có: 30° 2 2 2
BC = AB + AC B C 2 2 10 3 20 3 = BC = 10 + = . 3 3 µ
Câu 7. [TH] Cho tam giác A BC vuông tại A có A C = 20,C = 60° . Tính A B ;BC .
A. A B = 20 3;BC = 40 .
B. A B = 20 3;BC = 40 3 .
C. A B = 20;BC = 40 . D. A B = 20;BC = 20 3 . Lời giải Chọn A.
Xét tam giác ABC vuông tại A có: A A B 0 tanC =
= > A B = A C . tanC = 20. tan 60 = 20 3. A C 20
Áp dụng định lý Pytago ta có: 60° 2 2 2
BC = AB + AC C B 2 2
= BC = 20 + (20 3) = 40. µ
Câu 8. [TH] Cho tam giác A BC vuông tại A có BC = 12;B = 40° . Tính µ
A C ;C (làm tròn đến chữ
số thập phân thứ hai) A. µ
A C » 7, 71;C = 40° . B. µ
A C » 7, 72;C = 50° . C. µ
A C » 7, 71;C = 50° . D. µ
A C » 7, 73;C = 50° . Lời giải Trang 15 Chọn C.
Xét tam giác ABC vuông tại A có: A A C 0 sin B =
= > A C = BC .sin B = 12.sin 40 » 7, 71. BC Ta có: µ µ B + C = 90° 40° µ
= > C = 90° - 40° = 50° 12 C B µ
Câu 9. [TH] Cho tam giác A BC vuông tại A có BC = 15, B = 55° . Tính µ
A C ;C (làm tròn đến chữ
số thập phân thứ hai). A. µ
A C » 12, 29;C = 45° . B. µ
A C » 12, 29;C = 35° . C. µ
A C » 12, 2;C = 35° . D. µ
A C » 12, 92;C = 40°. Lời giải Chọn B.
Xét tam giác ABC vuông tại A có: A A C 0 sin B =
= > A C = BC .sin B = 15.si n 55 » 12,29. BC Ta có: µ µ B + C = 90° 55° µ
= > C = 90° - 55° = 35° 15 C B
Câu 10. [VD] Cho tam giác A BC vuông tại A có BC = 15cm, A B = 12cm . Tính µ A C ;B . A. µ
A C = 8(cm );B » 36°52¢. B. µ
A C = 9(cm );B » 36°52¢. C. µ
A C = 9(cm );B » 37°52¢. D. µ
A C = 9(cm );B » 36°55¢. Lời giải Chọn B.
Xét tam giác ABC vuông tại A có: A
Áp dụng định lý Pytago ta có: 2 2 2
AC = BC − AB 2 2 = AC = 15 −12 = 9 . cm ? 12 Ta có: µ A C 9 sin B = = = 0, 6 ? BC 15 µ 15 C B = > B » 36°52 '
Câu 11. [VD] Cho tam giác A BC vuông tại A có A C = 7cm, A B = 5cm . Tính µ BC ;C . A. µ BC =
74(cm );C » 35°32¢. B. µ BC =
74(cm );C » 36°32¢. Trang 16 C. µ BC =
74(cm );C » 35°33¢. D. µ BC =
75(cm );C » 35°32¢. Lời giải Chọn A. A
Xét tam giác ABC vuông tại A có:
Áp dụng định lý Pytago ta có: 2 2 2
BC = AB + AC 7 5 2 2
= BC = 5 + 7 = 74c . m Ta có: ? A B 5 ta nC = = ? C B A C 7 µ = > C » 35°32 ' µ
Câu 12. [VDC] Cho tam giác A BC có A B = 16, A C = 14 và B = 60° . Tính BC .
A. BC » 17cm .
B. BC » 19cm .
C. BC » 15cm .
D. BC » 12cm . Lời giải Chọn A. Kẻ AH vuông góc với BC. A
Xét tam giác ABH vuông tại H có: BH +) os c B = = BH = . AB cos B AB 16 0 = BH = 14. os c 60 = 7c . m 14 AH +)sin B = = AH = . AB sin B AB 60° 0 = AH = 7sin 60 = 7 3 B C H
Xét tam giác AHC vuông tại H có:
Áp dụng định lý Pytago ta có: 2 2 2
HC = AC − AH = HC = 16 − (7 3)2 2 10 . cm
= > BC = BH + HC » 7 + 10 » 17cm.
PHẦN II. BÀI TẬP TỰ LUẬN
Ví dụ 1 [NB]: Cho Hình 3. a) Tìm x . A b) Tính cạnh AB . x 600 B C 8 cm Hình 3 Lời giải AC 3 x
a) Ta có sin B = = x = 4 3 c m BC 2 8 Trang 17 AB 1 AB
b) Ta có cos B = = AB = 4 c m BC 2 8
Ví dụ 2 [TH]: Cho Hình 4. A
a) Tính cạnh AC và BC b) Chứng minh rằng 2 0 2 0 sin 3 0 + cos 3 0 = 1. 4 cm Lời giải 300 AC 3 AC 4 3 B C
a) Ta có tan B = = AC = c m Hình 4 AB 3 4 3 AB 3 4 8
Ta có cos B = = BC = c m BC 2 BC 3 2 2 2 2 2 AC AB AC + AB BC b) Ta có 2 0 2 0 sin 3 0 + cos 3 0 = + = = =1 2 2 BC BC BC BC 3
Ví dụ 3 [TH]: Cho ΔABC vuông tại A có AB = 12 c
m và tan B = ( Hình 6). 4
a) Tính AC và BC .
b) Tính số đo góc B . Lời giải AC 3 AC
a) Ta có tan B = = AC = 9 c m A AB 4 12
Áp dụng định lý Pythagore ta có: 12 cm 2 2 2 2
BC = AB + AC = 12 + 9 = 15 c m AC 9 b) Ta có 0 sin B = =
B 36,8 . B C BC 15 Hình 6
Ví dụ 4 [VD]: Cho Hình 17.
a) Tính các góc của ΔABC
b) Tính chu vi và diện tích của ΔABC Lời giải
a) ΔAHB vuông tại H , ta có A BH 4 0 cos B =
= B 36,8 AB 5 Khi đó 0 0 0 0
C = 90 − B 90 − 36,8 = 53, 2 5 cm
b) Ta có BC = BH + HC = 9 c m
Áp dụng định lý Pythagore ta có: B C 4 cm H 5 cm 2 2 2 2 2
AC = BC − AB = 9 − 5 = 56 AC = 56 c m Hình 17
Khi đó chu vi ΔABC là: AB + BC + AC = 5 + 9 + 56 = 14 + 56 ( c m) 1 1
Diện tích ΔABC là A .
B AC = .5 . 56 ( 2 cm ) 2 2 Trang 18
BÀI TẬP TỰ LUYỆN Bài 1. [NB] 5
Cho ΔABC vuông tại A có AB = 15 c
m . Biết cot B =
( Hình 8). Tính AC 13 Hướng dẫn AB 5 15 A
Ta có cot B = = AC = 39 c m AC 13 AC 15 cm B C Hình 8
Bài 2. [TH] Cho tam giác ABC vuông tại A biết 0
B = 50 , AC = 5cm . Tính . AB Hướng dẫn A
Ta có tam giác ABC vuông tại A nên AC 5 5cm AC = A .
B tan B AB = = 4,2 (cm) 0 tan B tan 50 50 B C
Bài 3. [VD] : Cho tam giác ABC vuông tại A , đường cao AH , biết AC = 16 cm và 4 sin CAH = . 5
Tính độ dài các cạnh BC , AB . Hướng dẫn
Trong AHC vuông tại H ta có HC 4 sin CAH =
HC = AC sin CAH =16 =12,8 cm. AC 5
Xét ABC vuông tại A ta có 2 2 AC
AC = BC HC BC = = 20 cm. HC Trong ABC ta có 2 2
AB = BC − AC = 12 cm.
Vậy AB = 12 cm, BC = 20 cm.
Bài 4 [VD] Cho tam giác ABC vuông tại A , đường cao AH , biết AB = 5 cm và BC = 13 cm . Từ
H kẻ HK vuông góc với AB (K AB) . Tính AC , BH và cos HBK . Hướng dẫn
Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có 2 2 2
BC = AB + AC 2 2 2 2
AC = BC − AB = 13 − 5 = 12 cm. Trang 19
Áp dụng hệ thức lượng cho tam giác ABC vuông tại A có đường cao AH ta được 2 2 AB 25
BA = BH BC hay BH = = cm BC 13 Ta có: AB 5
cos HBK = cos ABC = = . BC 13 Vậy AC = 12cm, 25 BH = cm và 5 cos HBK = . 13 13 µ µ
Bài 5 [VD] Cho tam giác A BC có B = 60 ,°C = 50 ,°CA = 3, 5cm . Tính diện tích tam giác A BC Hướng dẫn
Kẻ AH vuông góc BC tại H A
Xét tam giác AHC vuông tại H có: HC cos HCA =
= HC = AC.cos HCA AC = HC = 3,5. os50 c 2, 25 . cm 3,5 AH sin HCA =
= HA = AC.sin HCA Lại có: C A = HA = 3,5 si . n50 2,68 . cm 500 600
Xét tam giác AHB vuông tại H có: B H C AH AH tan ABH = = HB = BH tan ABH 2,68 = B H = 1,55c . m tan 60
BC = HB + HC 1,55 + 2, 25 3,8 . cm
Diện tích tam giác ABC là: 1 1 S
= .AH.BC .2,68.3,8 5,092 ABC ( 2 cm ) 2 2
CHỦ ĐỀ 1: TỈ SỐ LƯỢNG GIÁC VÀ GÓC NHỌN
DẠNG 2: TỈ SỐ LƯỢNG GIÁC CỦA HAI GÓC PHỤ NHAU – SỬ DỤNG MÁY TÍNH CẦM TAY
PHẦN I. BÀI TẬP TRẮC NGHIỆM
1. TRẮC NGHIỆM CHỌN ĐÁP ÁN
Câu 1. [NB] Trong các đẳng thức sau. Đẳng thức nào đúng A. sin 60 = 60 os c .
B. sin 60 = tan 60
C. sin 60 = tan 30 D. sin 60 = o c s 0 3 . Câu 2. [NB] Biết 1 60 os c
= . Đẳng thức nào sau đây đúng 2 Trang 20