Chuyên đề hệ thức lượng trong tam giác vuông Toán 9 KNTTVCS

BÀI 11. TỈ SỐ LƯỢNG GIÁC GÓC NHỌN
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. KHÁI NIỆM TỈ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN
Khái niệm sin, côsin, tang, côtang của góc nhọn α
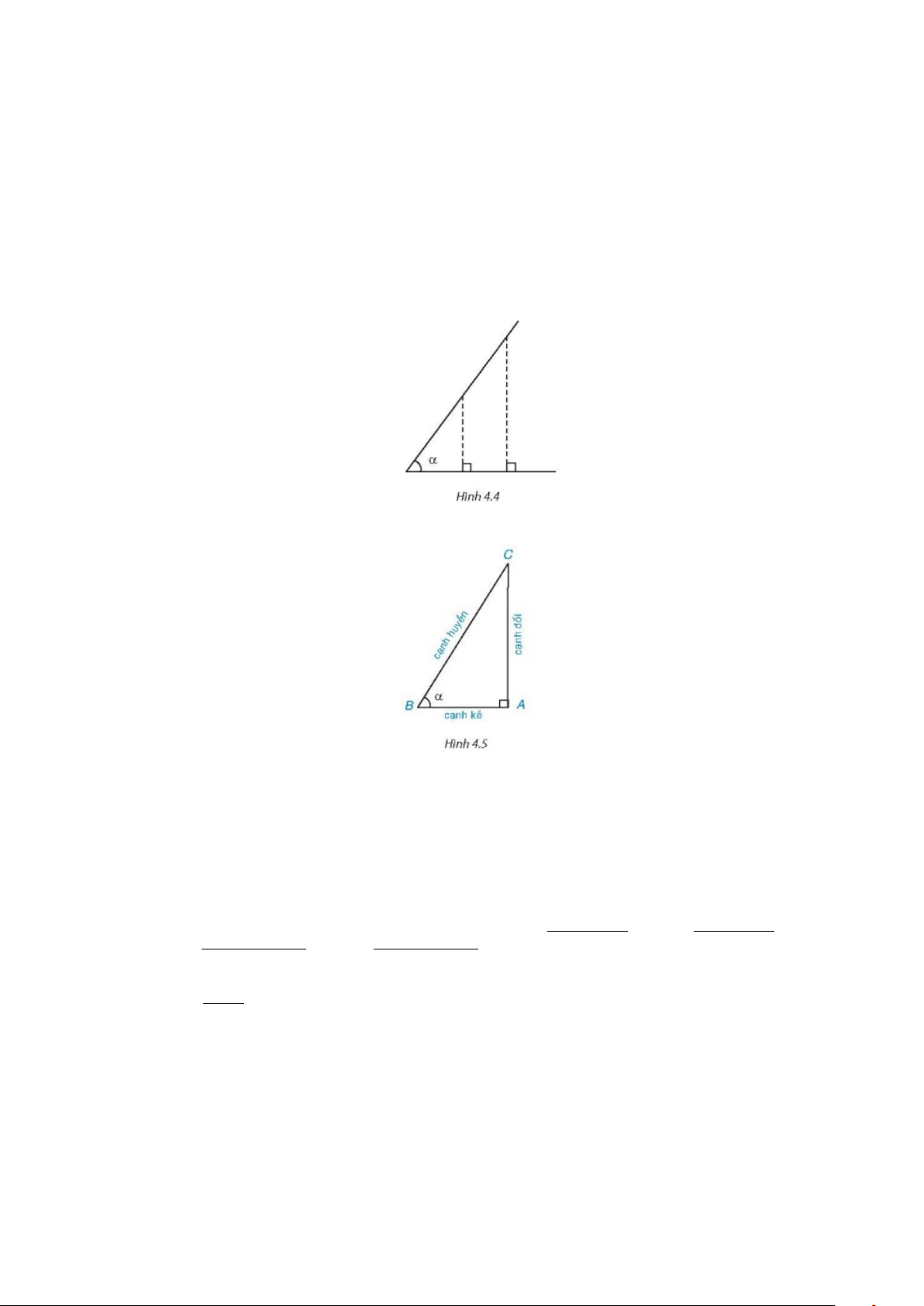
Nhận xét. Trong Hình 4.4 , các tam giác vuông có cùng một góc nhọn α là đồng dạng với nhau. Vì
vậy các tỉ số giữa cạnh đối và cạnh huyền (cạnh kề và cạnh huyền), cạnh đối và cạnh kề (cạnh kề và
cạnh đối) của góc nhọn α là như nhau, cho dù độ dài các cạnh đối (các cạnh kề) của góc α và các
cạnh huyền có thể khác nhau với từng tam giác.
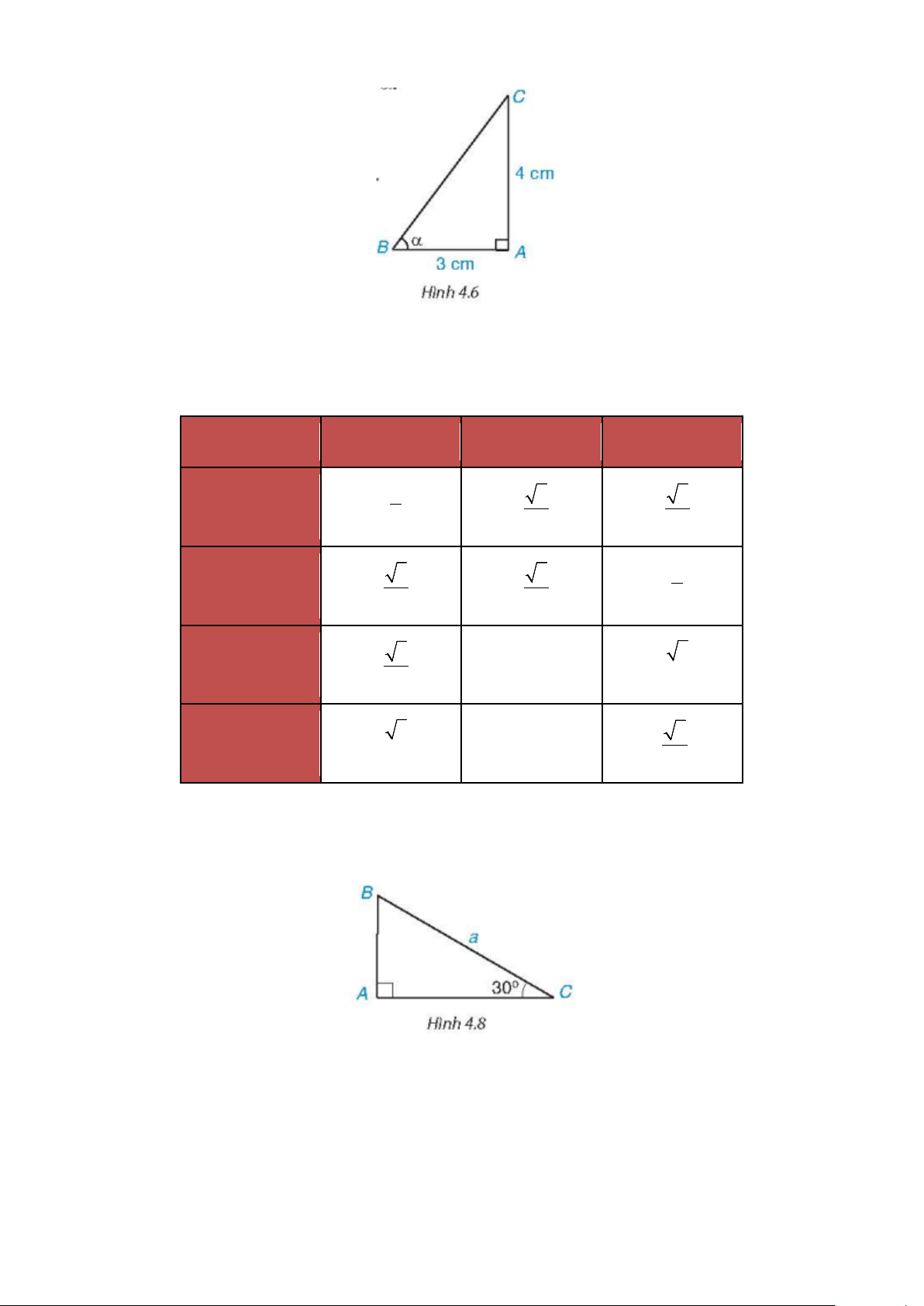
Cho góc nhọn α . Xét tam giác ABC vuông tại A có góc nhọn B bằng α . (H.4.5). Ta có:
- Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của α , kí hiệu sinα .
- Tỉ số giữa cạnh kề và cạnh huyền gọi là côsin của α , kí hiệu cosα .
- Tỉ số giửa cạnh đối và cạnh kề của góc α gọi là tang của α , kí hiệu tan α .
- Tỉ số giữa cạnh kề và cạnh đối của góc α gọi là côtang của α , kí hiệu cotα . Chú ý. Ta có: caïnh ñoái caïnh keà caïnh ñoái caïnh keà tanα = ;cotα = • sinα = ;cosα = ; caïnh keà caïnh ñoái ; caïnh huyeàn caïnh huyeàn 1 cotα = tanα .
• sinα,cosα, tanα,cotα gọi là các tỉ số lượng giác của góc nhọn α . Chú ý:
sin, côsin của góc nhọn luôn dương và bé hơn 1 vì trong tam giác vuông, cạnh huyền dài nhất
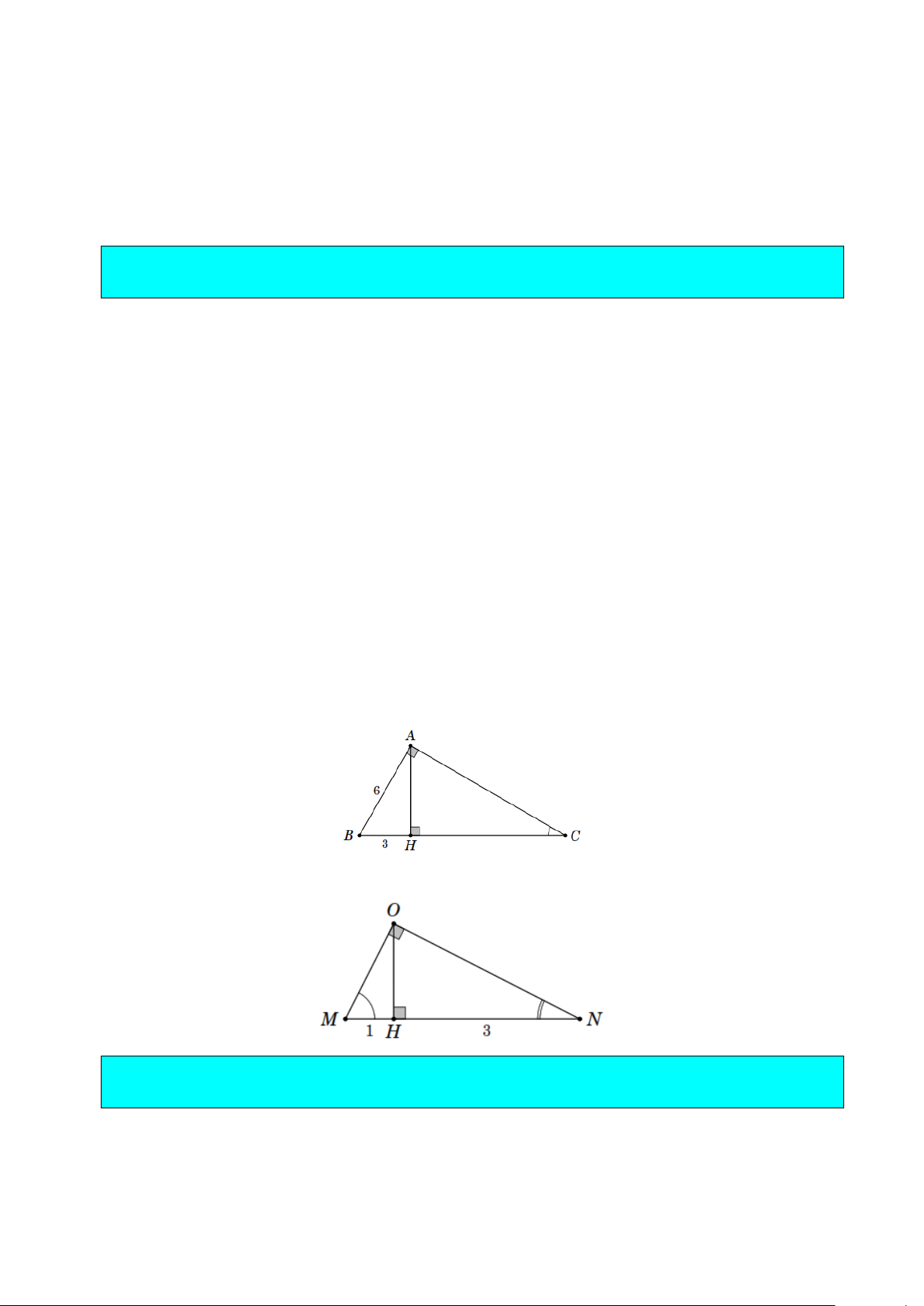
Ví dụ 1. Cho tam giác ABC vuông tại A , có AB = 3 cm, AC = 4 cm(H.4.6) . Hãy tính các tỉ số lượng
giác sinα,cosα, tanα với α = ˆB .
Chú ý: sinα còn được viết là sin ˆB hay sin B . Tương tự cho cosα, tanα và cotα .
Giá trị lượng giác sin, côsin, tang, côtang của các góc 30°,45°,60° Ta có bảng sau: α 30 45 60 sinα 1 2 2 3 2 2 cosα 3 1 2 2 2 2 tanα 3 1 3 3 cotα 3 1 3 . 3
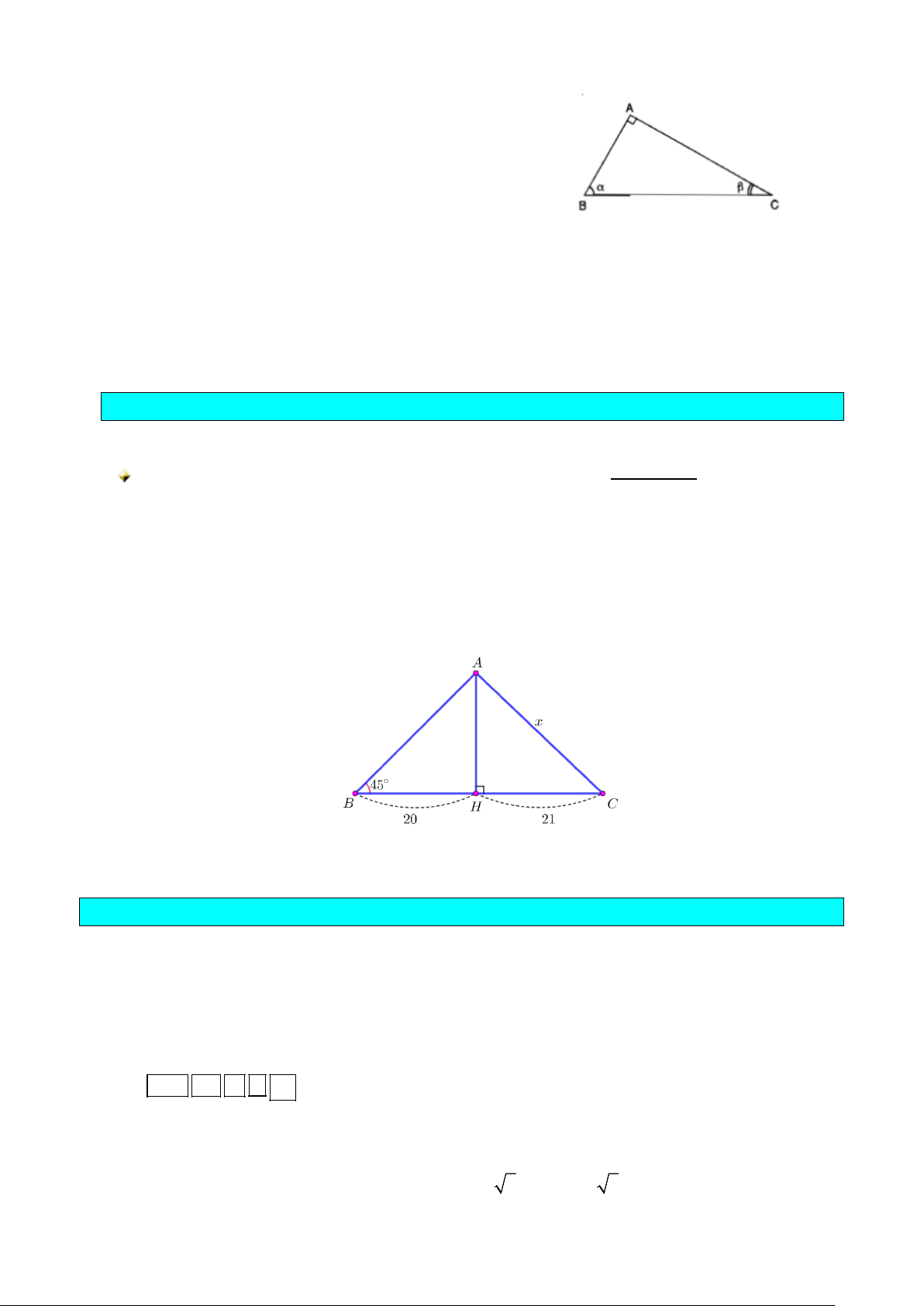
Ví dụ 2. Cho tam giác ABC vuông tại A có ˆC 30° =
và BC = a (H.4.8). Tính các cạnh AB, AC theo a .
2. TỈ SỐ LƯỢNG GIÁC CỦA HAI GÓC PHỤ NHAU
a) Tỉ số lượng giác của hai góc phụ nhau
Định lí: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Chú ý. Cho α và β là hai góc phụ nhau (H.4.9), khi đó
sinα = cos β,cosα = sin β, tanα = cot β,cotα = tan β.
- Vẽ số đo, hai góc phụ nhau có thể coi là hai góc nhọn của một tam giác vuông.
Ví dụ 3. Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn 45° :
sin 60°,cos75°,sin 52°30′, tan80°,cot82 . °
3. SỬ DỤNG MÁY TÍNH CẦM TAY TÍNH TỈ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN
Chú ý: Về số đo góc, dưới đơn vị độ ( 0 ) còn có các đơn vị phút (") và giây (") với 1° = 60 ,′1′ = 60′ . Ví dụ 4. 1° = 60 ,1′
′ = 60′ . Dùng MTCT, tính sin 27°,cos32 15 ° , tan 52 12 ° ′
′ và cot 35°23′ (làm tròn đến
chữ số thập phân thứ ba). Lưu ý: ° 1 cot 35 23′ = . tan 35°23′
Nhận xét. Để tính cot 35°23′ , ta có thể tính trực tiếp như trên, hoặc có thể tìm góc phụ với góc
35°23′ là 54°37′ rồi dùng MTCT tính tan 54°37′ và suy ra kết quả.
Ví dụ 5. Dùng MTCT, tìm các góc (làm tròn đến phút) biết sinα = 0,3214,cosα = 0,4321, 1 2
tanα =1,2742 và cotα =1,5384 . 3 4
Chú ý. Để tìm góc α khi biết cot α , ta có thể tìm góc (90° −α ) (vì tan(90° −α ) = cotα ) rồi suy ra α .
B. GIẢI BÀI TẬP SÁCH GIÁO KHOA
4.1. Cho tam giác ABC vuông tại A . Tính các tỉ số lượng giác sin, côsin, tang, côtang của các góc
nhọn B và C khi biết:
a) AB = 8 cm, BC =17 cm ;
b) AC = 0,9 cm, AB =1,2 cm .
4.2. Cho tam giác vuông có một góc nhọn 60° và cạnh kể với góc 60° bằng 3 cm . Hãy tính cạnh đối của góc này.
4.3. Cho tam giác vuông có một góc nhọn bằng 30° và cạnh đối với góc này bằng 5 cm . Tính độ dài
cạnh huyền của tam giác.
4.4. Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và 3 . Tính góc giữa đường chéo và
cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69).
4.5. a) Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45° :
sin 55°,cos62°, tan 57°,cot 64° . °
b) Tính tan 25 , tan 34° − cot 56° . cot 65°
4.6. Dùng MTCT , tính (làm tròn đến chữ số thập phân thứ ba): a) sin 40 12 ° ;′ b) cos52°54′; c) tan 63°36 ;′ d) cot 25 18 ° ′ .
4.7. Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút), biết rẳng: a) sin x = 0,2368 ; b) cos x = 0,6224 ; c) tan x =1,236 ; d) cot x = 2,154. C. CÁC DẠNG TOÁN
Dạng 1. Tính các tỉ số lượng giác của các góc nhọn trong một tam giác vuông biết độ dài các cạnh
1. Phương pháp giải
Dựng một tam giác có hai cạnh là m và n ( m và n là hai cạnh góc vuông hoặc một cạnh góc vuông
và cạnh huyền ) rồi vận dụng định nghĩa của các tỉ số lượng giác để nhận ra góc α 2. Ví dụ minh họa
Ví dụ 1: Cho tam giác ABC vuông tai C , trong đó BC =1,2 m và AB =1,5m Tính các tỉ số
lượng giác cua góc B , từ đó suy ra các tỉ số lượng giác của góc A .
Ví dụ 2. Cho tam giác ABC vuông tại A . Biết AB = 3cm, AC = 4cm . Tính tỉ số lượng giác của góc nhọn B
Ví dụ 3. Tam giác ABC vuông tại A , AB =1,5; BC = 3,5. Tính tỉ số lượng giác của góc C rồi suy
ra các tỉ số lượng giác của góc B .
Ví dụ 4. Tính tỉ số lượng giác của góc B trong hình bên. Ví dụ 5. A
∆ BC vuông tại A có BC = 2AB . Tính các tỉ số lượng giác của góc C .
Ví dụ 6. Tam giác ABC cân tại A , có BC = 6 , đường cao AH = 4. Tính các tỉ số lượng giác của góc B .
Ví dụ 7. Tính tan C trong hình bên.
Ví dụ 8. Tính sin M + cos N trong hình bên.
Dạng 2. Biến đổi tỉ số lượng giác của một góc nhọn thành tỉ số lượng giác của một góc nhỏ
hơn ( hoặc lớn hơn 45 độ)
1. Phương pháp giải
Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tan góc này bằng cotang góc kia. sinB = cosC ; cosB = sinC tanB = cotC ; cotB = tanC. 2. Ví dụ minh họa
Ví dụ 1. Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45° : ° ° ° '
sin 60 ;cos75 ;sin 52 30 ;cot82°;tan80°
Ví dụ 2. Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45° : cos32° ; 7 sin 42°; cot 27°36'
Dạng 3. Tính độ dài một cạnh trong tam giác vuông biết một góc và một cạnh
1. Phương pháp giải
Sử dụng định nghĩa của các tỉ số lượng giác, chẳng hạn sin canh doi α = canh huyen
⇒ cạnh đối = cạnh huyền .sinα . 2. Ví dụ minh họa
Ví dụ 1. Cho tam giác vuông có một góc 60° và cạnh huyền có độ dài là 8. Hãy tìm độ dài của cạnh đối diện với góc 60 . °
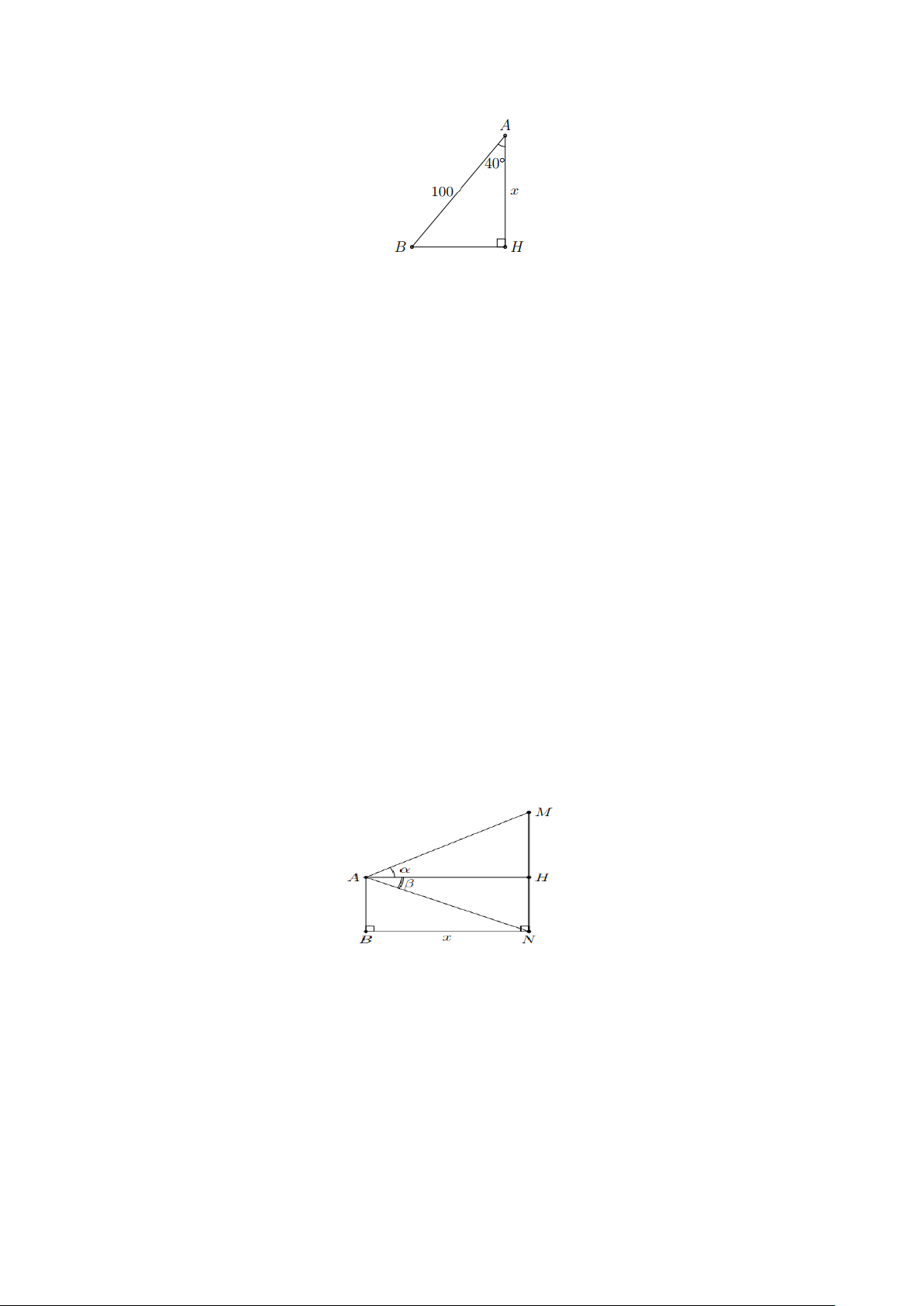
Ví dụ 2. Tìm x trong Hình 25. Hình 25
Ví dụ 3. Cho tam giác ABC vuông tại A có ˆB 60° =
và BC =10 . Tính độ dài cạnh AB và BC .
Dạng 4: Tìm góc nhọn α thỏa đẳng thức cho trước 1. Phương pháp
 Sử dụng các hệ thức lượng giác cơ bản để biến đổi về dạng cơ bản
 Dùng MTBT hoặc bảng giá trị lượng giác các góc đặc biệt để tìm.
Cách dùng MTBT tìm α khi biết sinα (tương tự đối với cosα và tanα )
Nếu sinα = m thì bấm các phím sau shift sin m = °''' . 2. Ví dụ
Ví dụ 1. Tìm góc nhọn x , biết a) 4sin x −1 =1;
b) 2 3 − 3tan x = 3 . Lời giải
a) 4sin x −1 =1
b) 2 3 − 3tan x = 3 1 3
⇔ 4sin x = 2 ⇔ sin x = ⇔ 3
− tan x = 3 − 2 3 ⇔ tan x = 2 3
⇔ sin x = sin 30° ⇔ x = 30 .° ° °
⇔ tan x = tan 30 ⇔ x = 30 .
Dạng 5: Một số bài toán thực tế
Câu 1: Treo quả cầu kim loại nhỏ vào giá thí nghiệm bằng sợi dây mảnh nhẹ không dãn. Khi quả
cầu đứng yên tại vị trí cân bằng, dây treo có phương thẳng đứng. Kéo quả cầu khỏi vị trí
cân bằng một đoạn nhỏ rồi buông ra thì quả cầu sẽ chuyển động qua lại quanh vị trí cân
bằng. Khi kéo quả cầu khỏi vị trí cân bằng, giả sử tâm 𝐴𝐴 của quả cầu cách 𝐵𝐵 một khoảng
𝐴𝐴𝐵𝐵 = 60 cm và cách vị trí cân bằng một khoảng 𝐴𝐴𝐴𝐴 = 20 cm (Hình 9). Tính số đo góc
𝛼𝛼 tạo bởi sợi dây 𝐵𝐵𝐴𝐴 và vị trí cân bằng (làm tròn kết quả đến hàng đơn vị của độ).
Câu 2: Hình 10 mô tả một chiếc thang có chiều dài 𝐴𝐴𝐵𝐵 = 4 m được đặt dựa vào tường, khoảng
cách từ chân thang đến chân tường là 𝐵𝐵𝐴𝐴 = 1,5 m. Tính góc tạo bởi cạnh 𝐴𝐴𝐵𝐵 và phương
nằm ngang trên mặt đất (làm tròn kết quả đến hàng đơn vị của độ). Hình 10 D. BÀI TẬP TỰ LUYỆN
Câu 1. Hãy viết tỉ số lượng giác của các góc sau thành tỉ số lượng giác của các góc nhỏ hơn 45°
sin 75°,cos60°,tan80°,cot 50°
Câu 2. Cho tam giác ABC vuông tại A có AB = 6 cm, ˆB = α . Biết 5 tanα = . Hãy tìm độ dài 12 cạnh AB, BC .
Câu 3. Tính giá trị của các biểu thức sin 32° 1. A = cos58° 2. B tan 76° cot14° = − .
Câu 4. Cho tam giác ABC có  BAC 60° = . Chứng minh rằng 2 2 2
BC = AB + AC − AB⋅ AC .
Câu 5. Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo. Chứng minh rằng 1 S = AC ⋅ BC ⋅ α ABCD sin 2
Câu 6. Cho tam giác nhọn ABC . Gọi a,b,c là độ dài các cạnh đối diện với các đỉnh , A B,C .
a) Chứng minh rằng: a b c = = .
sin A sin B sin C
b) Có thể sảy ra đẳng thức: sin A = sin B + sin C không?
Câu 7. Cho tam giác nhọn ABC , A = 30° . Hai đường cao CH và BK . Chứng minh rằng: S = S . AHK 3 BCHK
BÀI 12. MỘT SỐ HỆ THỨC GIỮA CẠNH, GÓC TRONG TAM GIÁC VUÔNG VÀ ỨNG DỤNG
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. HỆ THỨC GIỮA CẠNH HUYỀN VÀ CẠNH GÓC VUÔNG
Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn
Định lí 1. Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc
nhân với côsin góc kề.
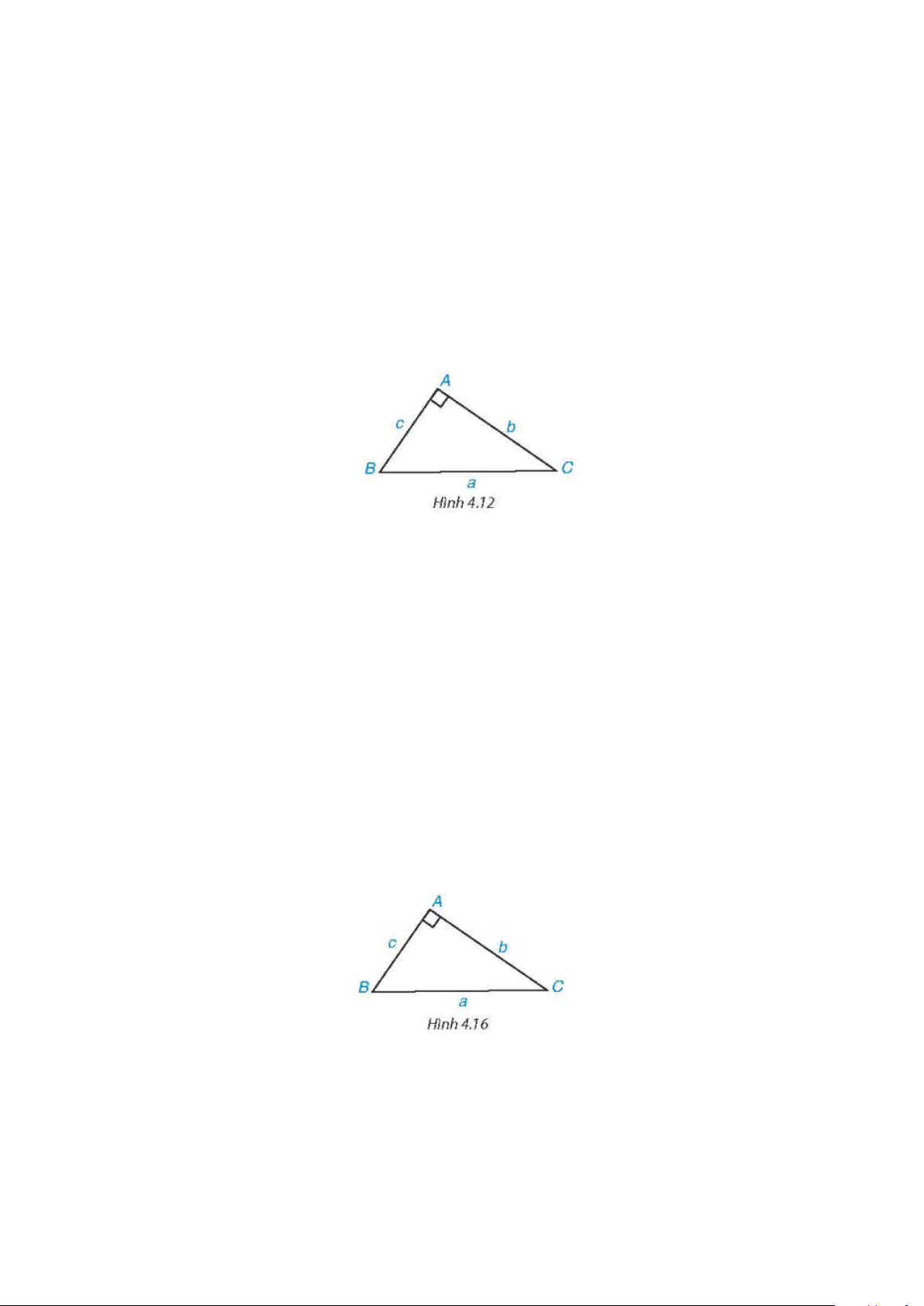
Chú ý. Trong tam giác ABC vuông tại A (H .4 .12), ta có:
b = a ⋅sin B = a ⋅cosC; c = a ⋅sin C = a ⋅cos . B
Ví dụ 1. Một chiếc máy bay bay lên với vận tốc 500 km / h . Đường bay lên tạo với phương nẳm
ngang một góc 30° (H.4.13). Hỏi sau 1,2 phút, máy bay lên cao được bao nhiêu kilômét theo phương thẳng đứng?
2. HỆ THỨC GIỮA HAI CẠNH GÓC VUÔNG
Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn
Định lí 2. Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc
đối hoặc nhân với côtang góc kề.
Chú ý. Trong tam giác ABC vuông tại A (H.4.16), ta có:
b = c⋅ tan B = c⋅cot C;c = b⋅ tan C = b⋅cot B ⋅
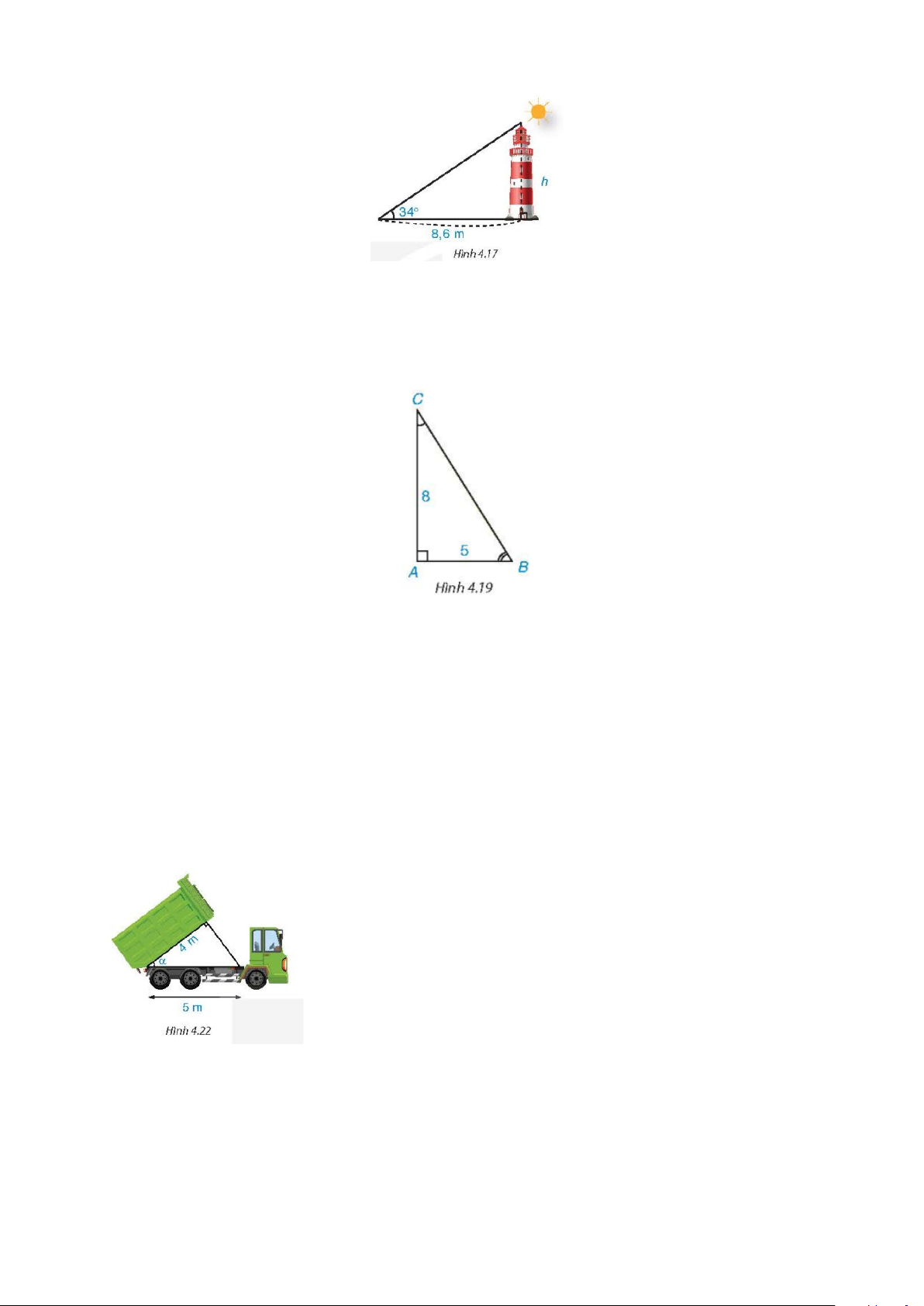
Ví dụ 2. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 34° và bóng của một toà tháp trên
mặt đất dài 8,6 m(H.4.17) . Tính chiều cao của toà tháp đó (làm tròn đến mét).
3. GIẢI TAM GIÁC VUÔNG
Ví dụ 3. Cho tam giác vuông ABC với các cạnh góc vuông AB = 5, AC = 8 (H.4.19). Hãy tính cạnh
BC (làm tròn đến chữ số thập phân thứ nhất) và các góc B, C (làm tròn đến độ).
Ví dụ 4. Cho tam giác ABC vuông tại A có AB 3, ˆB 42° = =
(H.4.20). Tính góc C và các cạnh AC,
BC (làm tròn đến chữ số thập phân thứ ba).
B. GIẢI BÀI TẬP SÁCH GIÁO KHOA
4.8. Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c , trong các trường hợp:
a) a = 21,b =18 ; b) ˆ b 10,C 30° = = ; c) c = 5,b = 3.
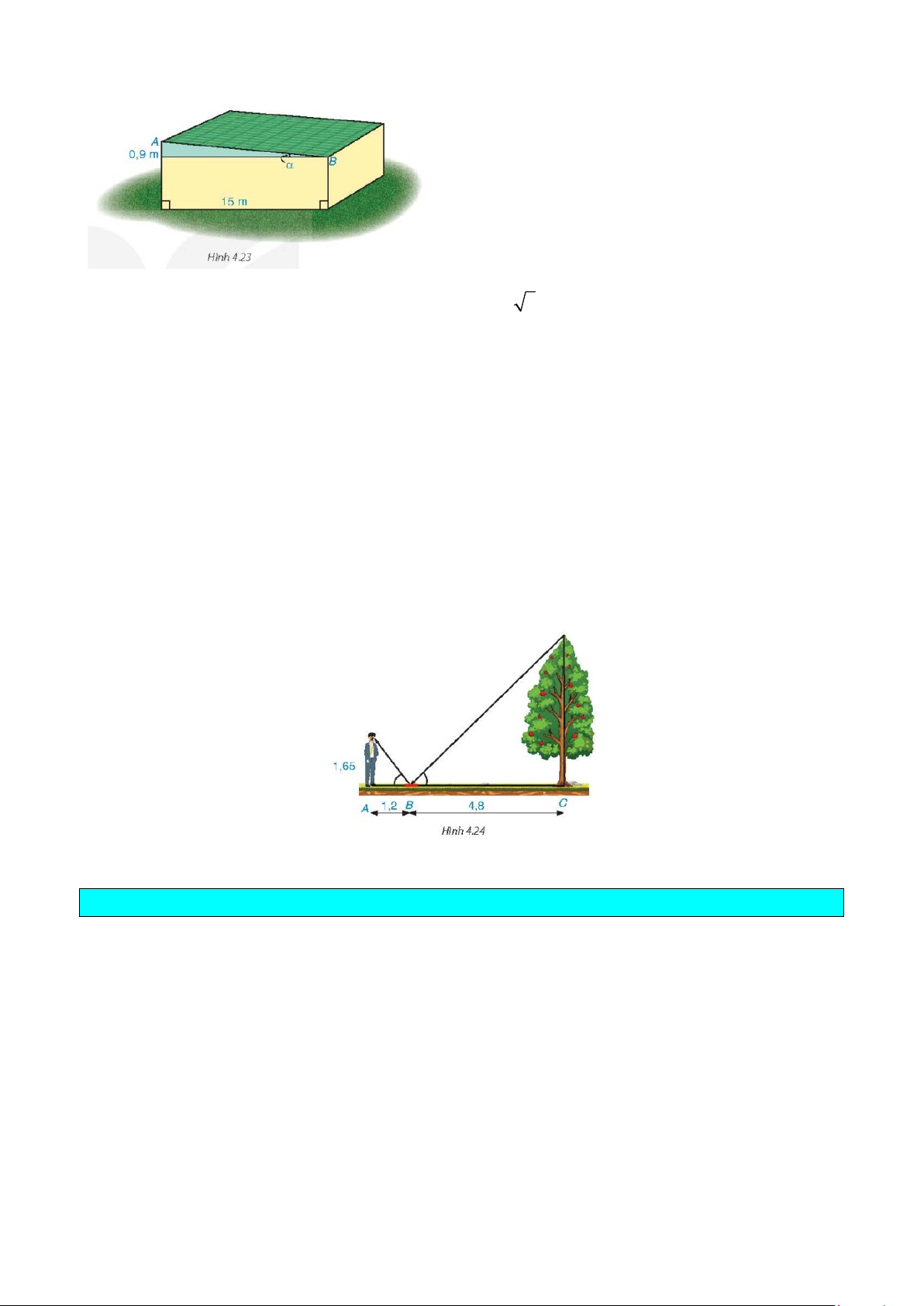
4.9. Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22.
4.10. Tìm góc nghiêng α và chiều rộng A B của mái nhà kho trong Hình 4.23.
4.11. Tính các góc của hình thoi có hai đường chéo dài 2 3 và 2 .
4.12. Cho hình thang ABCD(AD / /BC) có AD =16 cm, BC = 4 cm và ˆA ˆ  B ACD 90° = = = .
a) Kẻ đường cao CE của tam giác ACD. Chứng minh  = 
ADC ACE . Tính sin của các góc  
ADC, ACE và suy ra 2
AC = AE ⋅ AD . Từ đó tính AC.
b) Tính góc D của hình thang.
4.13. Một người đứng tại điểm A , cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m , nhìn
thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm
giữa A và C ). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m . Tính chiều cao của cây (H.4.24). C. CÁC DẠNG TOÁN
DẠNG 1. GIẢI TAM GIÁC VUÔNG 1. Phương pháp
 Vận dụng các công thức liên hệ giữa cạnh và góc trong tam giác vuông để tìm cạnh.
 Vận dụng công thức liên hệ giữa cạnh và đường cao trong tam giác vuông để tìm cạnh.
 Vận dụng các tỉ số lượng giác của góc nhọn để tính góc. Lưu ý:
 Nếu cho trước 1 góc nhọn thì nên tìm góc nhọn còn lại.
 Nếu cho trước hai cạnh thì dùng định lý Py-ta-go tìm cạnh thứ hai. 2. Ví dụ
Ví dụ 1. Giải tam giác ABC vuông tại A, biết rằng: a) b =  10cm, C = 30 ;° b) c =  10cm, C = 45 ;° c)  a 20 cm,B 35° = = ; d) c = 21cm,b =18 cm .
Ví dụ 2. Giải tam giác ABC vuông tại A , biết AB = 3,5 và AC = 4,2 .
Ví dụ 3. Giải tam giác ABC vuông tại A , biết AB = 3,0 và BC = 4,5 .
Ví dụ 4. Giải tam giác ABC vuông tại A , biết ˆB 50° = và AB = 3,7 .
Ví dụ 5. Giải tam giác ABC vuông tại A , biết ˆB 57° = và BC = 4,5 .
Ví dụ 6. Cho tam giác ABC vuông tại A , đường cao AH . Biết AB = 2,5, BH =1,5. Tính ˆB , ˆC và AC DẠNG 2.
TÍNH CẠNH, TÍNH GÓC CỦA TAM GIÁC 1. Phương pháp
Vẽ thêm một đường cao để vận dụng hệ thức giữa các cạnh và các góc của một tam giác vuông. 2. Ví dụ
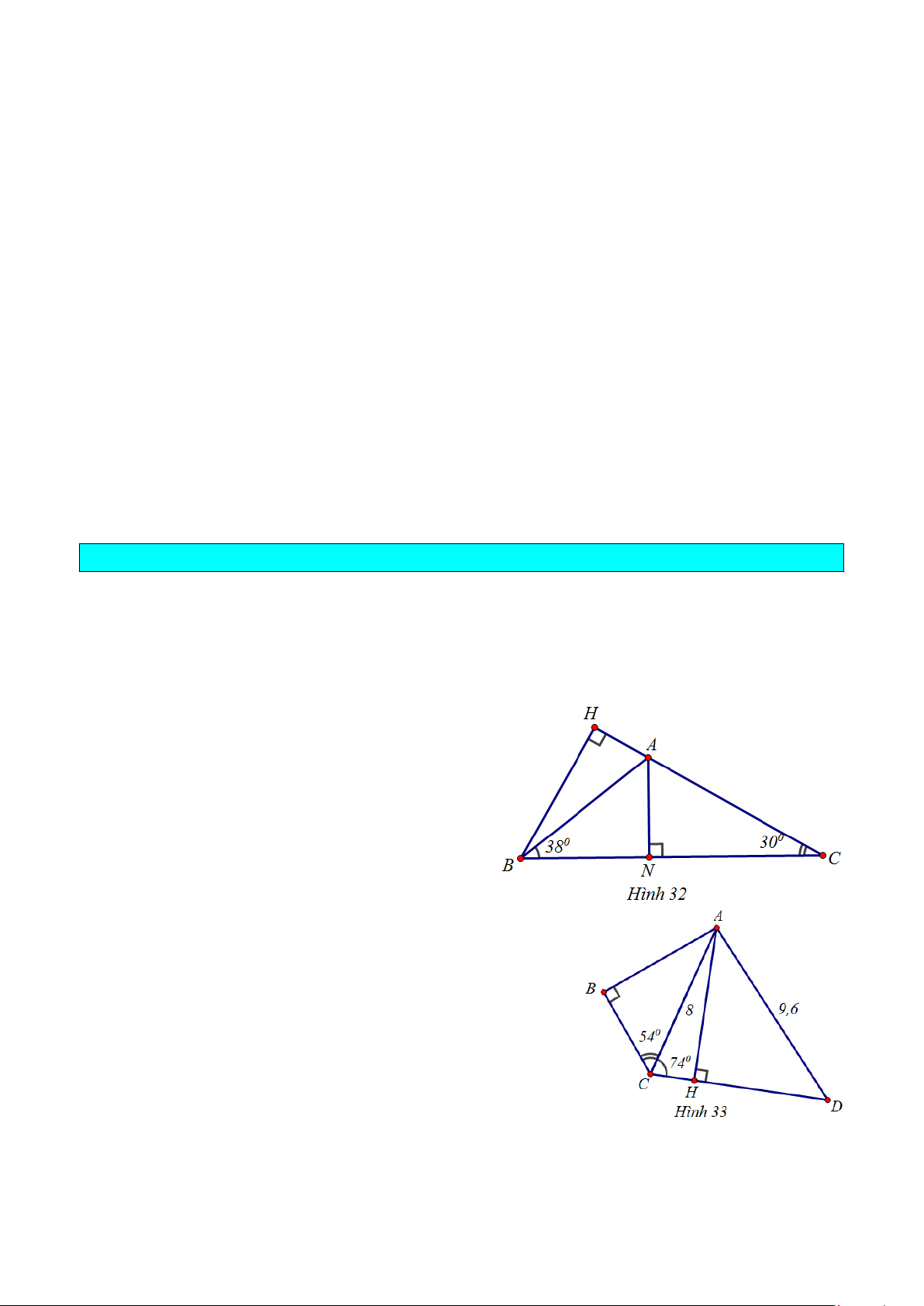
Ví dụ 1. Cho tam giác ABC, trong đó =  BC 11c ,
m ABC = 38 ,°  ACB = 30 .°
Gọi điểm N là chân đường vuông góc kẻ
từ A đến cạnh BC. Hãy tính: a) Đoạn thẳng AN; b) Cạnh AC.
Ví dụ 2. Trong hình 33: = =  = °  AC 8c , m AD 9,6c ,
m ABC 90 , ACB = 54° và 
ACD = 74 .°Hãy tính: a) Đoạn thẳng A ; B b)  ADC.
Ví dụ 3. Cho tam giác ABC có ˆB 65° = , ˆC 45° = và
AB = 2,8cm . Tính các góc và cạnh còn lại của tam giác đó (gọi là giải tam giác ABC ).
Ví dụ 4. Giải tam giác ABC biết ˆB 65° = , ˆC 40° = và BC = 4,2cm .
Ví dụ 5. Giải tam giác nhọn ABC biết AB = 2,1, AC = 3,8 và ˆB 70° = .
DẠNG 3: CÁC BÀI TOÁN THỰC TẾ 1. Phương pháp
Dùng hệ thức giữa các cạnh và các góc của một tam giác vuông. 2. Ví dụ
Ví dụ 1: Các tia nắng Mặt Trời tạo với mặt đất một góc xấp xĩ bằng 34° và bóng của một tháp trên
mật đất dài 86 m . Tính chiều cao của tháp (làm tròn đến mét).
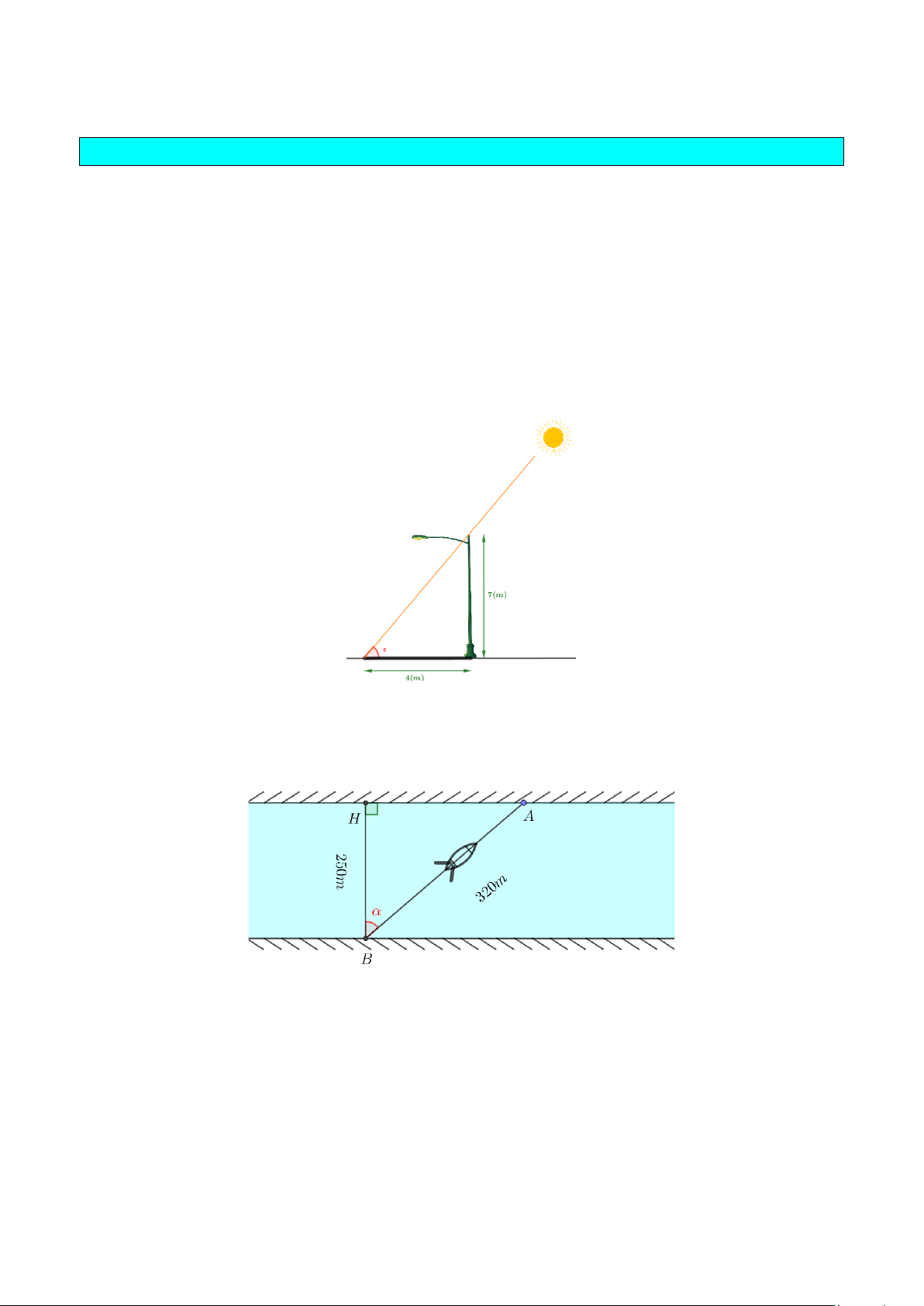
Ví dụ 2: Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến phút) mà tia
sáng Mặt Trời tạo với mặt đất (góc α như trong hình 35).
Ví dụ 3: Một khúc sông rộng khoảng 250m. Một chiếc đò chéo qua sông bị dòng nước đẩy xiên
nên phải chèo khoảng 320m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy đò lệch đi một góc
bao nhiêu độ? (góc α trong hình 36).
Ví dụ 4: Một con thuyền với vận tốc 2km/h vượt qua một khúc sông nước chảy mạnh mất 5
phút.Biết rằng đường đi của con thuyền tạo với bờ một góc 0
70 .Từ đó ta đã tính được chiều rộng
của khúc sông chưa? Nếu có hãy tính kết quả (làm tròn đến mét).
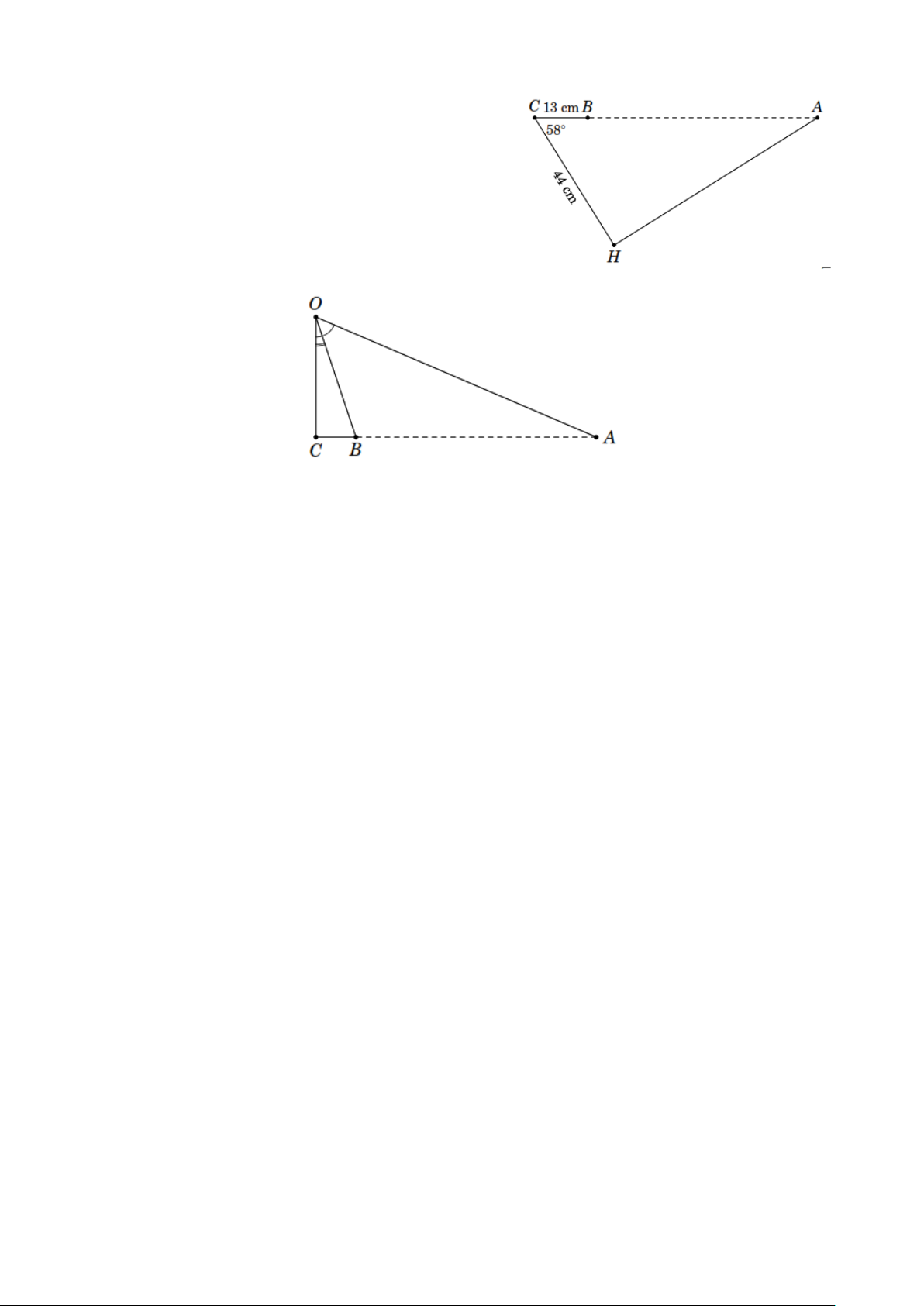
Ví dụ 5. Tính khoảng cách giữa hai điểm A và B trên
một bờ hồ nước sâu, biết ˆC 58° = , CB =13m ,
CH = 44m như hình bên.
Ví dụ 6. Trong hình vẽ bên dưới, tính chiều rộng AB
của con sông, biết OC = 47m ,  AOC 74° = ,  BOC 23° = .
Ví dụ 7. Khoảng cách giữa hai chân tháp AB và MN là a như hình vẽ bên dưới. Từ đỉnh A của
tháp AB nhìn lên đỉnh M của tháp MN ta được góc α . Từ đỉnh A nhìn xuống chân N của tháp
MN ta được góc β (so với phương nằm ngang AH ). Hãy tìm chiều cao MN nếu a =120m , α 30° = , β 20° = . D. BÀI TẬP TỰ LUYỆN
Câu 1. Giải tam giác vuông ABC, biết  = 90 A và: a) a =15c ; m b =10c . m b) b =12c ; m c = 7c . m
Câu 2. Tam giác ABC có  =   60 ; = 50 B C
và AC= 35cm. Tính diện tích tam giác ABC ( làm tròn đến hàng đơn vị).
Câu 3. Tứ giác ABCD có  =  = 90 A D ,  = 40 C
. Cho biết AB = 4cm; AD = 3cm, tính diện tích tứ giác ABCD.
Câu 4. Cho tam giác 𝐴𝐴𝐴𝐴𝐴𝐴 vuông tại A , có BC = a, AC = b, AB = c. Giải tam giác ABC , biết rằng = 
b 10 cm,C = 30 .
Câu 5. Một cột đèn có bóng trên mặt đất dài 7,5m. Các tia nắng mặt trời tạo với mặt đất một góc
xấp xỉ bằng 42° . Tính chiều cao của cột đèn .
Câu 6. Một chiếc diều với đoạn dây thả diều AB dài 100m , dây thả diều tạo với phương thẳng
đứng một góc 40° (hình bên). Tính chiều cao của diều. Câu 7. Cho A
∆ BC có BC =15cm ,  ABC 42° = và  ACB 30° =
. Gọi H là chân đường cao hạ từ
đỉnh A xuống BC . Hãy tính
a) Độ dài đoạn thẳng AH
b) Độ dài đoạn thẳng AC
Câu 8. Cho tam giác ABC vuôag tai A .Biêt AB = 3 cm, BC = 5 cm .
a) Giải tam giác vuông ABC .
b) Từ B kẻ đường thẳng vuông góc với BC , đường thẳng này cắt đường thẳng AC tại D
Tính độ dài các đoạn thẳng AD và BD .
Câu 9. Cho ABD vuông tại ˆ ,
A AB 21 cm,C 40° = =
. Tính độ dài đường phân giác BD .
Câu 10. Tinh diện tich A ∆ BC có  °  BC 2c , m B 45 ,C 30° = = = .
Câu 11. Khoảng cách giữa hai chân tháp AB và MN là x ( như hình vẽ ). Từ đỉnh A của tháp AB
nhìn lên đinh M của tháp MN ta được góc α . Từ đỉnh A nhìn xuống chân N của tháp MN ta
được góc β (so với phương nầm ngang AH . Hãy tìm chiều cao MN nếu x 120 m,α 30° = = và β 20° =
Câu 12. Cho hình thang ABCD có AB //CD ,  °  D 90 ,C 38° = =
, AB = 3,5và AD = 3,1.
Tinh diên tich hình thang ABCD .
Câu 13. Cho hình thang cân ABCD(AB //CD), AB = 2 cm,CD = 6 cm , chiều cao bằng 4 cm. Tính
góc nhọn tạo bởi hai đường thẳng chứa cạnh bên hình thang. Câu 14. Cho A ∆ BC có ˆ ° ˆ B 40 ,C 60° = =
, đường trung tuyến AM .Tính số đo góc AMC
Câu 15. Tính diện tích tam giác ABC biết ˆ ° ˆ B 30 ,C 135° = = , BC = 2 cm .
Câu 16. Tứ giác ABCD có các đường chéo cắt nhau tại O. Cho biết AC = 4c ; m BD = 5cm và  = 50 AOB
. Tính diện tích tam giác ABCD.
Câu 17. Một cầu trượt trong công viên có độ dốc là 0
28 và có độ cao là 2,1m. Tính độ dài của mặt
cầu trượt ( làm tròn đến chữ số thập phân thứ nhất ).
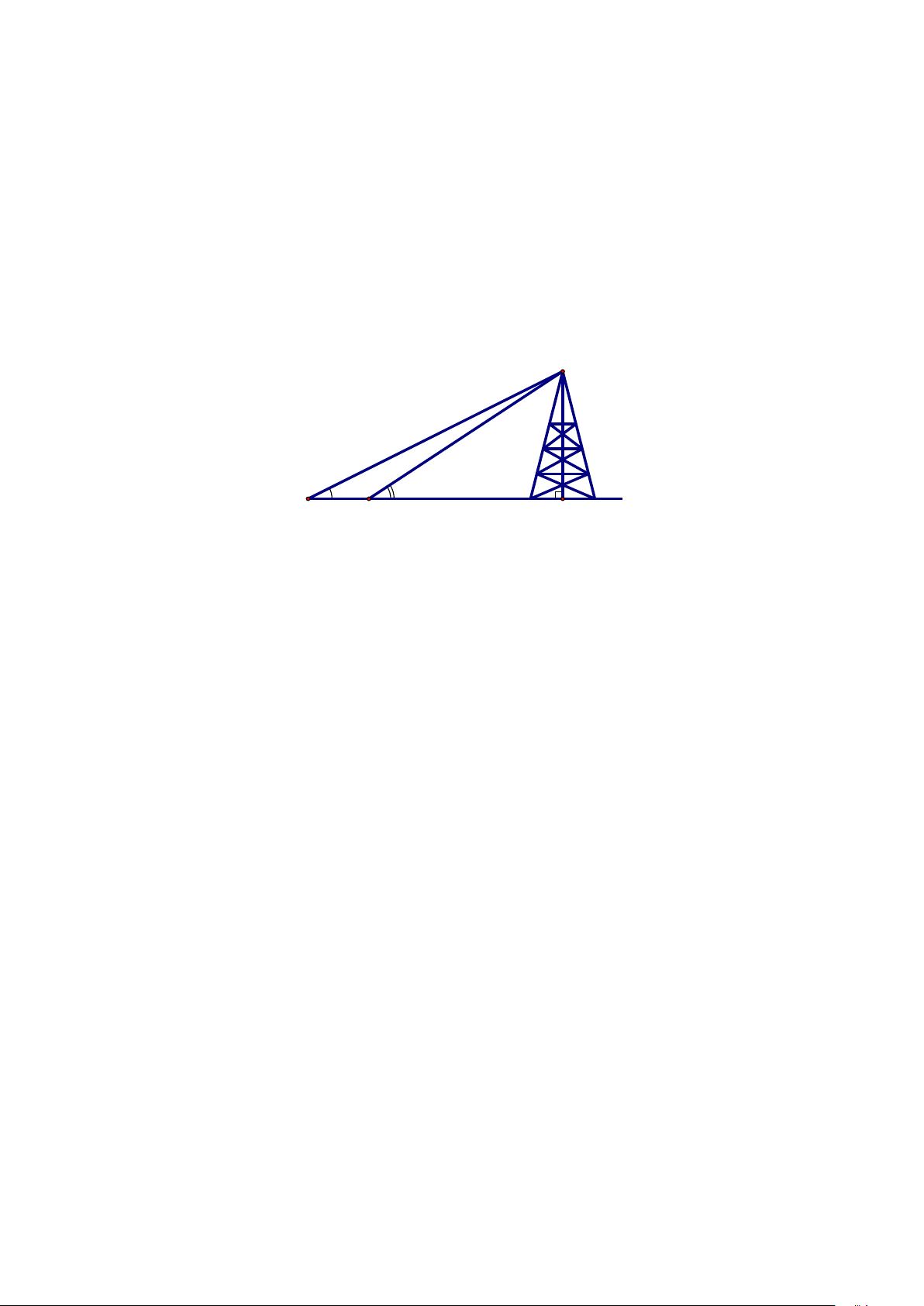
Câu 18. Hãy xác định độ cao của cột ăng- ten CH trong hình 38 với a = 8,5m ; 0 0 α = 20 ;β = 24
(làm tròn đến hàng đơn vị ) C α β A a B H Hình 38 LUYỆN TẬP CHUNG
PHẦN 1. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Ví dụ 1. Cho tam giác ABC vuông tại A , AB = 5 cm, AC =12 cm .
a) Tính các tỉ số lượng giác của góc B .
b) Từ kết quả câu a) suy ra các tỉ số lượng giác của góc C .
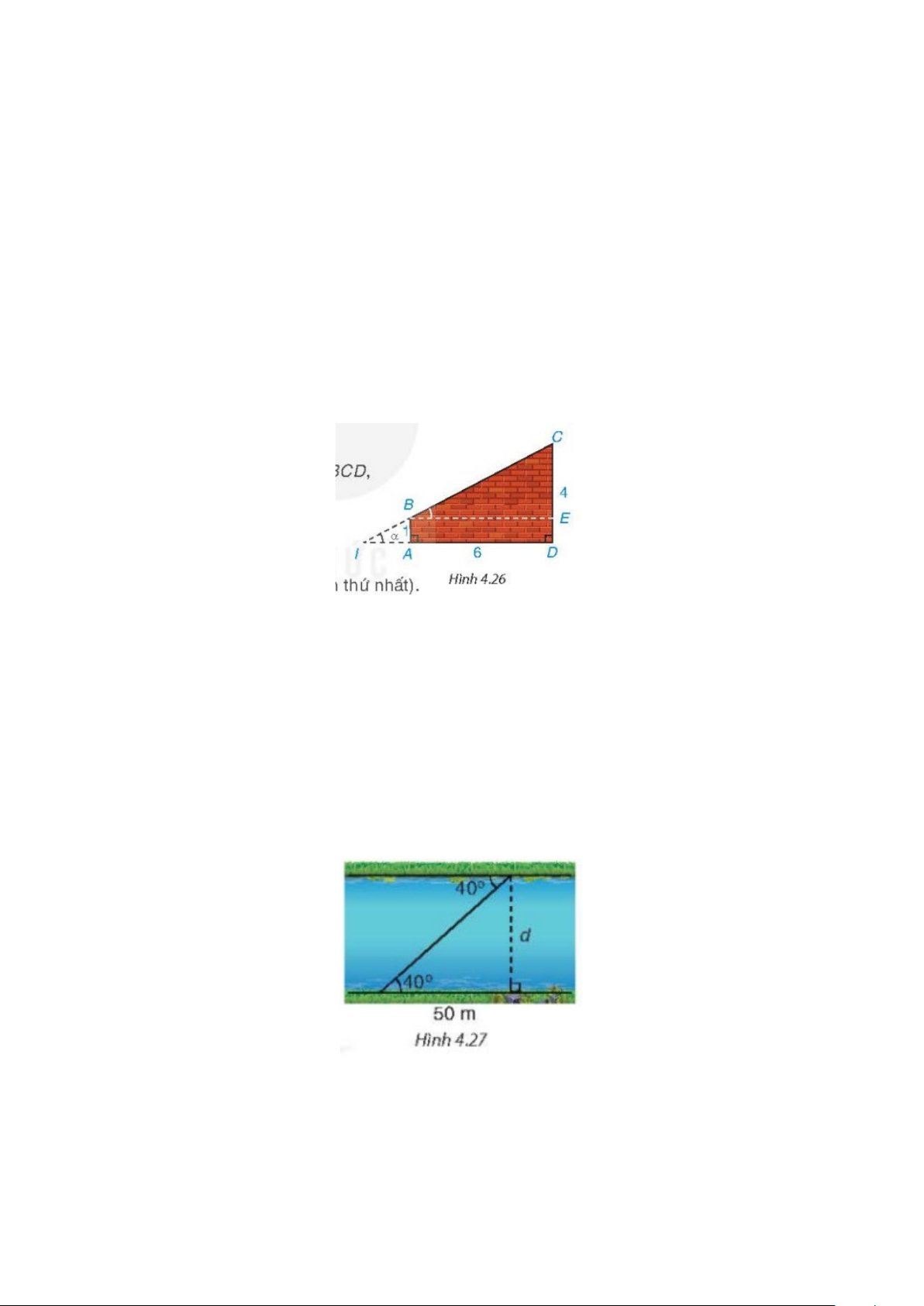
Ví dụ 2. Một bức tường đang xây dở có dạng hình thang vuông ABCD, vuông góc ở A và D ,
AB =1 m,CD = 4 m, AD = 6 m .
a) Hỏi góc α tạo bởi đường thẳng BC và mặt đất AD có số đo xấp xỉ bằng bao nhiêu (làm tròn đến phút)?
b) Tính độ dài cạnh BC (làm tròn đến chữ số thập phân thứ nhất). B. BÀI TẬP
4.14. Một cuốn sách khổ 17× 24 cm , tức là chiều rộng 17 cm , chiều dài 24 cm . Gọi α là góc giữa
đường chéo và cạnh 17 cm . Tính sinα,cosα (làm tròn đến chữ số thập phân thứ hai) và tính số đo α (làm tròn đến độ).
4.15. Cho tam giác ABC có chân đường cao AH nằm giữa B và C . Biết HB = 3 cm , 
HC 6 cm, HAC 60° = =
. Hãy tính độ dài các cạnh (làm tròn đến cm ), số đo các góc của tam giác
ABC (làm tròn đến độ).
4.16. Tìm chiều rộng d của dòng sông trong Hình 4.27 (làm tròn đến m ).
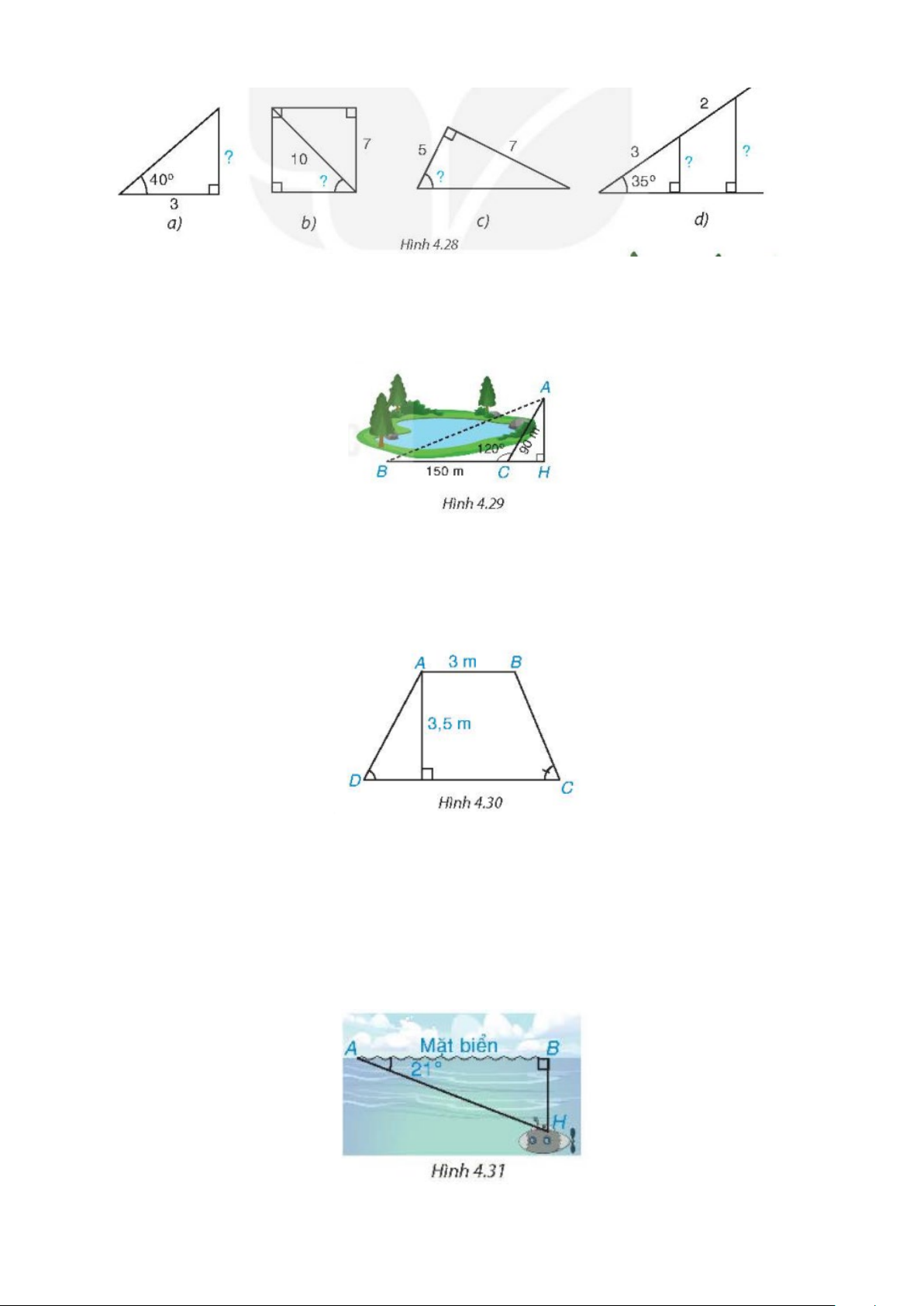
4.17. Tính các số liệu còn thiếu (dấu "?") ở Hình 4.28 với góc làm tròn đến độ, với độ dài làm tròn
đến chữ số thập phân thứ nhất.
4.18. Một bạn muốn tính khoảng cách giữa hai địa điểm A , B ở hai bên hồ nước. Biết rằng các
khoảng cách từ một điểm C đến A và đến B là CA = 90 m,CB =150 m và  ACB 120° = (H.4.29). Hãy tính AB giúp bạn.
4.19. Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD(H.4.30) . Chiều rộng của mặt
trên AB của đập là 3 m . Độ dốc của sườn AD, tức là tan D =1,25 . Độ dốc của sườn BC, tức là tan
C =1,5 . Chiều cao của đập là 3,5 m . Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn
AD và BC (làm tròn đến dm ).
4.20. Trong một buổi tập trận, một tàu ngẩm đang ở trên mặt biển bắt đẩu đi chuyển theo đường
thẳng tạo với mặt nước biển một góc 21° để lặn xuống (H.4.31).
a) Khi tàu chuyển động theo hướng đó và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước
biển? (làm tròn đến m ).
b) Giả sử tốc độ của tàu là 9 km / h thì sau bao lâu (tính từ lúc bắt đẩu lặn) tàu ở độ sâu 200 m (tức là
cách mặt nước biển 200 m )?
PHẦN 2. BÀI TẬP THÊM
Bài 1. Giải tam giác ABC vuông tại A , biết
a) AB = 2,7 và AC = 4,5 ;
b) AC = 4,0 và BC = 4,8 .
Bài 2. Giải tam giác ABC vuông tại A , biết
a) BC = 4,5 và ˆC 35° = ;
b) AB = 3,1 và ˆB 65° = .
Bài 3. Cho tam giác ABC cân tại A , đường cao BH . Biết ˆA 50° =
, BH = 2,3. Tính chu vi của A ∆ BC .
Bài 4. Hình thang ABCD có ˆ ˆ A D 90° = =
. Biết AB = 2,6 , CD = 4,7 và ˆC 35° = . Tính diện tích hình thang.
Bài 5. Cho tam giác nhọn ABC , AB > AC , đường cao AH và đường trung tuyến AM . Gọi α là số đo góc  HAM .
a) Chứng minh rằng HB − HC = 2HM ; b) Chứng minh rằng cot B cot tan C α − = . 2
Bài 6. Giải tam giác nhọn ABC biết ˆB 60° =
, AB = 3,0 và BC = 4,5 .
Bài 7. Hình thang ABCD ( AB  CD ) có ˆD 90° = , ˆC 38° =
, AB = 3,5 , AD = 3,1. Tính diện tích hình thang đó.
BÀI TẬP CUỐI CHƯƠNG IV
PHẦN 1. GIẢI BÀI TẬP SÁCH GIÁO KHOA A. TRẮC NGHIỆM
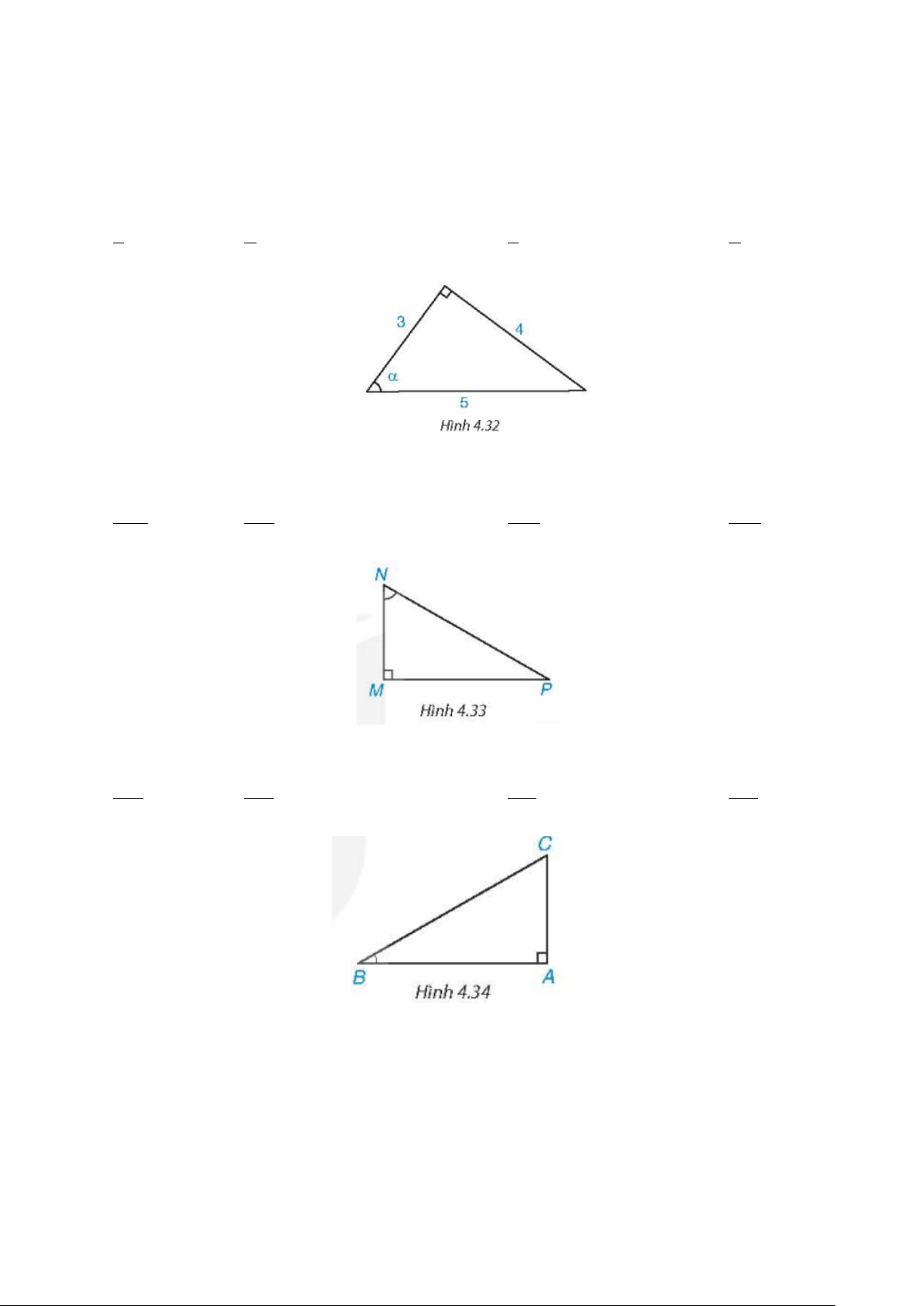
4.21. Trong Hình 4.32, cosα bằng A. 5 . B. 3 . C. 3 . D. 4 . 3 4 5 5
4.22. Trong tam giác MNP vuông tại M (H.4.33),  sin MNP bằng A. PN . B. MP . C. MN . D. MN . NM PN PN MP
4.23. Trong tam giác ABC vuông tại A (H.4.34), tan B bằng A. AB . B. AC . C. AB . D. BC . AC AB BC AC
4.24. Với mọi góc nhọn α , ta có
A. sin (90° −α ) = cosα .
B. tan (90° −α ) = cosα .
C. cot (90° −α ) =1− tanα .
D. cot (90° −α ) = sinα .
4.25. Giá trị tan 30° bằng A. 3 . B. 3 . C. 1 . D. 1 . 2 3 B. TỰ LUẬN
4.26. Xét các tam giác vuông có một góc nhọn bằng hai lần góc nhọn còn lại. Hỏi các tam giác đó có
đồng dạng với nhau không? Tính sin và côsin của góc nhọn lớn hơn.
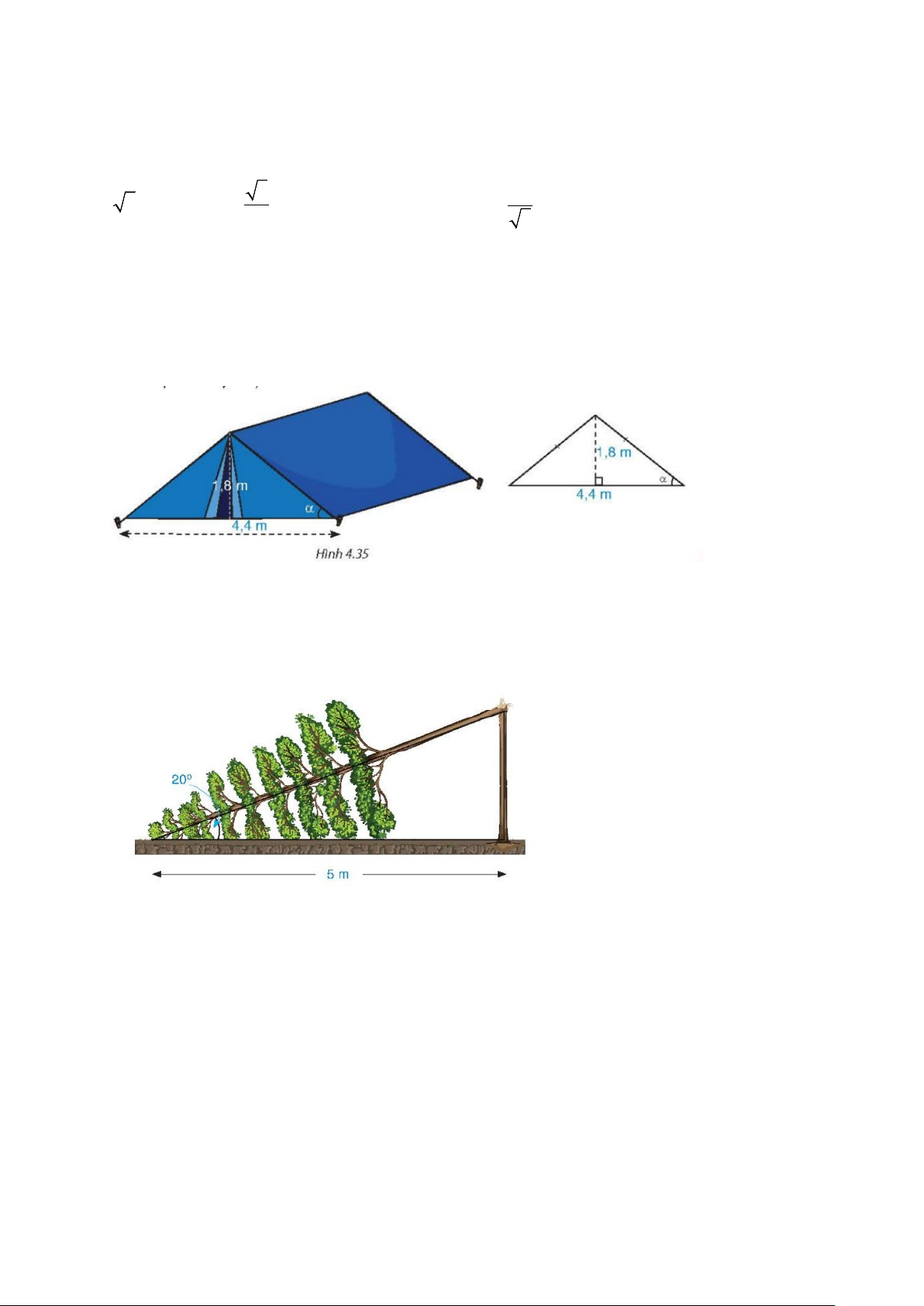
4.27. Hình 4.35 là mô hình của một túp lểu. Tìm góc α giữa cạnh mái lều và mặt đất (làm tròn kết quả đến phút).
4.28. Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo
thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc 20° và chắn ngang lối đi một đoạn 5 m
(H.4.36). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
4.29. Cho tam giác ABC vuông tại A , có ˆB = α (H.4.37).
a) Hãy viết các tỉ số lượng giác sinα,cosα .
b) Sử dụng định lí Pythagore, chứng minh rằng 2 2 sin α + cos α =1.