Chuyên đề khảo sát hàm số – Lưu Huy Thưởng Toán 12

Chuyên đề khảo sát hàm số – Lưu Huy Thưởng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

112 56 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC

2013 - 2014

KHẢO SÁT HÀM SỐ

BIÊN SOẠN: LƯU HUY THƯỞNG

HÀ N

ỘI, 8/2013

HỌ VÀ TÊN: …………………………………………………………………

LỚP :………………………………………………………………….

TRƯỜNG :…………………………………………………………………

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 1

CHUYÊN ĐỀ:

KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ

CÁC BÀI TOÁN LIÊN QUAN ĐẾN KHẢO SÁT HÀM SỐ

VẤN ĐỀ 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

1. Đinh nghĩa:

 



1 2 1 2 1 2

( , , ( ) ( ))

K x x K x x f x f x

⇔ ∀ ∈ < ⇒ <



 



1 2 1 2 1 2

( , , ( ) ( ))

K x x K x x f x f x

⇔ ∀ ∈ < ⇒ >



2. Điều kiện cần:

 

I

 

I 

'( ) 0,

f x x I

≥ ∀ ∈



 

I  

'( ) 0,

f x x I

≤ ∀ ∈



3.Điều kiện đủ:

 

I.

 

'( ) 0,

f x x I

≥ ∀ ∈

!

'( ) 0

f x

"#$ 

%

 

'( ) 0,

f x x I

≤ ∀ ∈

!

'( ) 0

f x

"#$ 

%

 

'( ) 0,

f x x I

= ∀ ∈

&∀'∈% 

()%

Chú ý: Nếu khoảng I được thay bởi đoạn hoặc nửa khoảng thì f phải liên tục trên đó.

Dạng toán 1: Xét tính đơn điệu của hàm số

Phương pháp: Để xét chiều biến thiên của hàm số y = f(x), ta thực hiện các bước như sau:

– Tìm tập xác định của hàm số.

– Tính y

′

. Tìm các điểm mà tại đó y

′

= 0 hoặc y

′

không tồn tại (gọi là các điểm tới hạn)

– Lập bảng xét dấu y

′

(bảng biến thiên). Từ đó kết luận các khoảng đồng biến, nghịch biến của hàm số.

Bài tập cơ bản

HT 1. *+,-./01

 2

3 2

2 2

y x x x

= − + −

  3

(4 )( 1)

y x x

= − −

  4

3 2

3 4 1

y x x x

= − + −



 5

4 2

2 1

y x x

= − −

  6

4 2

2 3

y x x

= − − +

  7

4 2

1 1

10 10

y x x

= + −



 8

2 1

−

   9

−

   :

= −

−



 2;

3 2 2

y x x

= + + −

  22

2 1 3

y x x

= − − −

 23

y x x

= −

  

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 2

Dạng toán2: Tìm điều kiện để hàm số luôn đồng biến hoặc nghịch biến trên tập xác định

(hoặc trên từng khoảng xác định)

Cho hàm số

( , )

y f x m

, m là tham số, có tập xác định D.

•

Hàm số f đồng biến trên D

⇔

′≥

∀

∈

•

Hàm số f nghịch biến trên D

⇔

′≤

∀

∈

Từ đó suy ra điều kiện của m.

Chú ý:

1) y

′

= 0 chỉ xảy ra tại một số hữu hạn điểm.

2) Nếu

y ax bx c

= + +

thì:

•

••

•

' 0,

a b

y x R







= =













≥







≥ ∀ ∈ ⇔



















∆ ≤











•

' 0,

a b

y x R







= =













≤







≤ ∀ ∈ ⇔



















∆ ≤











3) Định lí về dấu của tam thức bậc hai

( )

g x ax bx c

= + +

•

Nếu

∆

< 0 thì g(x) luôn cùng dấu với a.

•

Nếu

∆

= 0 thì g(x) luôn cùng dấu với a (trừ x =

−

)

•

Nếu

∆

> 0 thì g(x) có hai nghiệm x

, x

và trong khoảng hai nghiệm thì g(x) khác dấu với a, ngoài khoảng hai nghiệm

thì g(x) cùng dấu với a.

4) So sánh các nghiệm

1 2

x x

của tam thức bậc hai

( )

g x ax bx c

= + +

với số 0:

•

1 2

0 0

x x P





∆ >



< < ⇔ >







•

1 2

0 0

x x P





∆ >



< < ⇔ >







•

1 2

0 0

x x P

< < ⇔ <

5) Để hàm số

3 2

y ax bx cx d

= + + +

có độ dài khoảng đồng biến (nghịch biến)

1 2

( ; )

x x

bằng d thì ta thực hiện các bước

•

Tính y

′

•

Tìm điều kiện để hàm số có khoảng đồng biến và nghịch biến:





≠







∆ >





(1)

•

Biến đổi

1 2

x x d

− =

thành

2 2

1 2 1 2

( ) 4

x x x x d

+ − =

(2)

•

Sử dụng định lí Viet đưa (2) thành phương trình theo m.

•

Giải phương trình, so với điều kiện (1) để chọn nghiệm.

Bài tập cơ bản

HT 2. < 

$0=(>?'0!@A'0/1

 2

3 2

3 ( 2)

y x mx m x m

= − + + −

  3

3 2

2 1

3 2

x mx

y x

= − − +

 

4

x m

−

    5

x m

    

HT 3. < 

$1

 2

3 2

y x x mx m

= + + +

""BC2 

 3

3 2

1 1

2 3 1

3 2

y x mx mx m

= − + − +

""BC4

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 3

 4

3 2

( 1) ( 3) 4

y x m x m x

= − + − + + −

""BC5 

HT 4. < 

$1

 2

( 1) ( 1) 1

y m x m x

= + + − + +

!2DE∞ 

 3

3 2

3(2 1) (12 5) 2

y x m x m x

= − + + + +

!3DE∞

 4

( 2)

y m

x m

= ≠ ±

!2DE∞ 

 5

x m

−

!F2DE∞



BÀI TẬP TỔNG HỢP – NÂNG CAO

HT 5. G !2< H00/m$!2

 Đ/s: 

HT 6. G !G



< m$

 Đ/s: 

HT 7. G < m$ 

Đ/s:

≤



HT 8. G !2&!m=<  m$!2

(1;2).

Đ/s:

[

;1)

∈ − ∞



HT 9. G

3 2

3(2 1) (12 5) 2

y x m x m x

= − + + + +



( ; 1)

−∞ −

I

(2; )

+∞



Đ/s:

7 5

12 12

m− ≤ ≤



HT 10. G

3 2 2

(2 7 7) 2( 1)(2 3)

y x mx m m x m m

= − − − + + − −

< m$

[

2; ).

+∞

Đ/s:

− ≤ ≤



JJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJ 

3 2

3 4

y x x mx

= + − −

( ;0)

−∞

≤ −

3 2

2 3(2 1) 6 ( 1) 1

y m x m m x

= − + + + +

(2; )

+∞

≤

3 2

(1 2 ) (2 ) 2

y x m x m x m

= + − + − + +

(

)

+∞

4 2

2 3 1

y x mx m

= − − +

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 4

VẤN ĐỀ 2: CỰC TRỊ CỦA HÀM SỐ

I. KIẾN THỨC CẦN NHỚ

I.Khái niệm cực trị của hàm số

 

'0>?

( )

D D

⊂

ℝ

I

x D

∈



 2

F$K/



( ; )

a b D

⊂

I

( ; )

x a b

∈



    

( ) ( )

f x f x

&

{ }

( ; ) \

x a b x

∀ ∈



 L

( )

f x

MNO=0K!K/



 3

F$K$/



( ; )

a b D

⊂

I

( ; )

x a b

∈



    

( ) ( )

f x f x

&

{ }

( ; ) \

x a b x

∀ ∈



 L

( )

f x

MNO=0K$!K$/



 4

=$K/

 $

0 0

( ; ( ))

x f x

MNO=$K/



II. Điều kiện cần để hàm số có cực trị





IK$ 

'( ) 0

f x



Chú ý: Hàm số

chỉ có thể đạt cực trị tại những điểm mà tại đó đạo hàm bằng 0 hoặc không có đạo hàm.

III. Điểu kiện đủ để hàm số có cực trị

1. Định lí 1: 

=P

( ; )

a b

Q$

I

{ }

( ; ) \

a b x



 2

'( )

f x

)BHAâmdương

R

 

cực tiểu



 3

'( )

f x

)BHAdươngâm

R

 

cực đại



2. Định lí 2:



( ; )

a b

Q$

&

'( ) 0

f x

IH?0;

$



 2

"( ) 0

f x

 

K



 3

"( ) 0

f x

 SK$



II. CÁC DẠNG TOÁN

Dạng toán 1: Tìm cực trị của hàm số

Qui tắc 1: Dùng định lí 1.

•

Tìm

'( )

f x

•

Tìm các điểm

( 1, 2,...)

x i =

mà tại đó đạo hàm bằng 0 hoặc không có đạo hàm.

•

Xét dấu

'( )

f x

. Nếu

'( )

f x

đổi dấu khi

đi qua

thì hàm số đạt cực trị tại

Qui tắc 2: Dùng định lí 2.

•

Tính

'( )

f x

•

Giải phương trình

'( ) 0

f x

tìm các nghiệm

( 1, 2,...)

x i =

•

Tính

"( )

f x

và

"( ) ( 1, 2,...)

f x i

Nếu

"( ) 0

f x

thì hàm số đạt cực đại tại

. Nếu

"( ) 0

f x

thì hàm số đạt cực tiểu tại

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 5

Bài tập cơ bản

HT 11. < K/0:

2

2 3

3 2

y x x

= −

   3

3 2

2 2 1

y x x x

= − + −

 4

3 2

4 15

y x x x

= − + −



 5

y x

= − +

  6

4 2

4 5

y x x

= − +

  7

2 2

y x

= − + +



 8

3 6

x x

− + +

  9

3 4 5

x x

+ +

  :

2 15

x x

− −

−



 2;

3 4

( 2) ( 1)

y x x

= − +

  22

4 2 1

2 3

x x

+ −

  23

3 4 4

x x

+ +



 24

y x x

= −

   25

2 5

y x x

= − +

  26

y x x x

= + −



Dạng toán 2: Tìm điều kiện để hàm số có cực trị

1. Nếu hàm số

( )

y f x

đạt cực trị tại điểm

thì

'( ) 0

f x

hoặc tại

không có đạo hàm.

2. Để hàm số

( )

y f x

) đạt cực trị tại điểm

thì

'( )

f x

đổi dấu khi

đi qua

Chú ý:

•

Hàm số bậc ba

3 2

y ax bx cx d

= + + +

có cực trị

⇔

Phương trình

' 0

có hai nghiệm phân biệt.

Khi đó nếu x

là điểm cực trị thì ta có thể tính giá trị cực trị y(x

) bằng hai cách:

3 2

0 0 0 0

( )

y x ax bx cx d

= + + +

0 0

( )

y x Ax B

= +

, trong đó Ax + B là phần dư trong phép chia y cho y

′

Bài tập cơ bản

HT 12. < 

$1

 2

3 2

( 2) 3 5

y m x x mx

= + + + −

K&K$

 3

3 2 2

3( 1) (2 3 2) ( 1)

y x m x m m x m m

= − − + − + − −

K&K$

 4

3 2 2 3

3 3( 1)

y x mx m x m

= − + − −



 5



3 2

2 3(2 1) 6 ( 1) 1

y x m x m m x

= − + + + +





6



3 2 2

3 ( 1) 2

y x mx m x

= − + − +

K

7



4 2

2( 2) 5

y mx m x m

= − + − + −

"K

x =



GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 6

HT 13. < 

, , ,

a b c d

$1

 2

3 2

y ax bx cx d

= + + +

K$C;

IKC





 3

4 2

y ax bx c

= + +

R"OIKCF:



HT 14. < 

$0(K1

 2

3 2

3 3 3 4

y x x mx m

= − + + +

  3

3 2

3 ( 1) 1

y mx mx m x

= + − − −



HT 15. < 

$1

 2

3 2 2 2

2( 1) ( 4 1) 2( 1)

y x m x m m x m

= + − + − + − +

K$

1 2

x x

1



1 2

1 1 1

( )

x x

+ = +



 3

3 2

y x mx mx

= − + −

K$

1 2

x x

1

1 2

x x

− ≥



 4

3 2

1 1

( 1) 3( 2)

3 3

y mx m x m x

= − − + − +

K$

1 2

x x

1

1 2

2 1

x x

+ =



HT 16. < 

$1

 2

3 2

y x mx

= − + −

$K=A, BI

900

729

AB =



 3

4 2

y x mx x m

= − + +

4$K=A, B, CI0TUG>"V=OW

BÀI TẬP TỔNG HỢP VÀ NÂNG CAO

HT 17. < 

$1

 2

3 2

2 12 13

y x mx x

= + − −

$K0XPĐ/s:

 3

3 2 3

3 4

y x mx m

= − +

0$K&K$'QRMY?W0QH

Đ/s:

m = ±



 4

3 2 3

3 4

y x mx m

= − +

0$K&K$ZIX"?,I[MY\

: 3 2 8 0

d x y

− + =



Đ/s:

{

;1 \ 0}

 







∈ −











 



HT 18. < 

$1

2

3 2

y x x m

= + +

3$KA, B



120

AOB



Đ/s:

12 132

m m

− +

= =

4 2

2 2

y x mx

= − +

4$K20MY]?R

3 9

;

5 5

 

















 

Đ/s:

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 7

4

4 2 2

y x mx m m

= + + +

4$K20"C

120 .



Đ/s:

m = −

5

4 2 4

2 2

y x mx m m

= − + +

4$K20B.,C5

Đ/s:

HT 19. < 

$1

2

3 2

y x mx

= − +

$KIMY]R3$K^MY]W

(1;1)

0,

C2$A, BB.,0

IAB

=[HĐ/s:

2 3

3

3 2

4 3

y x mx x

= + −

$K

1 2

x x

_`1

1 2

4 0

x x

+ =

Đ/s:

= ±

HT 20. < 

$1

 2

3 2

2 3( 1) 6( 2) 1

y x m x m x

= + − + − −

  MY \  R  $ K    I[ MY \

4 1

y x

= − −

 Đ/s:



 3

3 2

2 3( 1) 6 (1 2 )

y x m x m m x

= + − + −

0$K&K$/CMY\

y x

= −



Đ/s:



 4

3 2

7 3

y x mx x

= + + +

  MY \  R 0 $ K & K $ I(  I[ MY \

3 7

y x

= −

 Đ/s:

3 10

m = ±



 5

3 2 2

y x x m x m

= − + +

0$K  IK$'Q R MY \!∆1

1 5

2 2

y x

= −



Đ/s:



JJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJ

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 8

VẤN ĐỀ 3: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ

I. KIẾN THỨC CẦN NHỚ

1. Các bước khảo sát sự biến thiên và vẽ đồ thị của hàm số

 •< >?'0/

 •*+K/1

  E< 0[I(K&[I(KI .>!

E<,



  E< 0$

' 0y =

@('0

  Ea>?bBH/&X&K/

 •cd/1

  E< $/!I[>Ie?M-

  Ecd0MY.>!/

  E*0"$@./M$/I[0P"!MYN?

(^0P"@I. "$?Q? $_RG$ "

$"$$Id,'0-



2. Khảo sát sự biến thiên và vẽ đồ thị hàm bậc ba

3 2

( 0)y ax bx cx d a= + + + ≠



 •<>?'0

D = ℝ



 •f=("$I>$=W'Q

 •G0B1

 a > 0 a < 0

' 0

3.?W.

⇔

' 3 0b ac∆ = − >



 

' 0

.+?

⇔

' 3 0b ac∆ = − =



' 0

I(.

⇔

' 3 0b ac∆ = − <



 



GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 9

3. Hàm số trùng phương

4 2

( 0)

y ax bx c a= + + ≠

 •<>?'0

ℝ



 •f=(>P=P'Q

•G0B1



4. Hàm số nhất biến

( 0; 0)

ax b

y c ad bc

cx d

= ≠ − ≠



 •<>?'0gh

 

 

−

 

 

 

ℝ



 •f".>Q= I".>= $/.>=W

'Q/

 •G0B1



Bài tập cơ bản

HT 21. L0KIId01

2

3 2

3 1

y x x

= − + −

  3

y x x

= − + −

  4

2 1

y x x

= − + − +



5

4 2

2 2

y x x

= − +

  6

4 2

y x x

= − − +

  7

−



8

2 1

−

   9

2 1

−

− +



JJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJ

= −

a > 0 a < 0

có 3 nghiệm phân biệt

⇔

chỉ có 1 nghiệm

⇔

–

bc >

–

bc <

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 10

VẤN ĐỀ 4: SỰ TƯƠNG GIAO CỦA CÁC ĐỒ THỊ

Dạng toán 1: Dùng đồ thị hàm số biện luận số nghiệm phương trình

•G-Z/?M-?0?1Xét phương trình:

( ) ( )

f x g x

(1)

Số nghiệm của phương trình (1) = Số giao điểm của

( ) : ( )

C y f x

và

( ) : ( )

C y g x

Nghiệm của phương trình (1) là hoành độ giao điểm của

( ) : ( )

C y f x

và

( ) : ( )

C y g x



•f$.=>./?M- 

( , ) 0

F x m

!iC)!iIXB1

( , ) 0 ( ) ( )

F x m f x g m

= ⇔ =

 !2

 L!2$'j=?M- "

 $/MY1

  

( ) : ( )

C y f x

I

: ( )

d y g m

•

=MY\e?M-I[P

 •gKI(C).=>$

 /(CI

<Ak./!2

Bài tập cơ bản

HT 22. L0KIId(C)/ge(C).=>jm./?M-

 1

 2

3 3

3 1; 3 1 0

y x x x x m

= − + − + − =

  3

3 3

3 1; 3 1 0

y x x x x m

= − + − − + + =



 4

3 3 2

3 1; 3 2 2 0

y x x x x m m

= − + − − − − =

 5

3 3

3 1; 3 4 0

y x x x x m

= − + − − + + =



 6

2 4 2

2 2; 4 4 2 0

y x x x m

= − + + − − + =

 7

4 2 4 2

2 2; 2 2 0

y x x x x m

= − + − − + =



HT 23. L0KIId(C)/ge(C).=>jm./?M-

 1

2

3 2 3 2

( ) : 3 6; 3 6 3 0

C y x x x x m

= − + − + − + =



3

3 2 2

( ) : 2 9 12 4; 2 9 12 0

C y x x x x x x m

= − + − − + + =



4

2 2 2

( ) : ( 1) (2 ); ( 1) 2 ( 1) (2 )

C y x x x x m m

= + − + − = + −



5

1 1

1 1 1

( ) : ; ; ;

1 1 1

1 1

x x

x x x

C y m m m m

x x x

x x

− −

− − −

= = = = =

+ + +

+ +



JJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJ

g(m

(C)

(4) : y =

g(m)

CĐ

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 11

Dạng toán 2: Tìm điều kiện tương giao giữa các đồ thị

1.G

( ) : ( )

C y f x

và

( ) : ( )

C y g x

f$ "$/

( )

I

( )

?M- 1

( ) ( )

f x g x

!i!O=?M- "$

 l./?M- !iC$/

2.f>

3 2

( 0)

y ax bx cx d a= + + + ≠

^P4$?W.

 ⇔mM- 

3 2

ax bx cx d

+ + + =

4.?W.

Bài tập cơ bản

HT 24. < "$/0/01

 2

2 2

y x





= − + −







= +





  3

2 4

y x x





−



−





= − + +





  4

4 3

y x x

y x





= −







= − +







HT 25. < 

$01

 2

2 2

( 1)( 3)

y x x mx m

= − − + −

^P$?W.

 3

3 2

3 (1 2 ) 1

y mx mx m x

= + − − −

^P$?W.

 4

3 2

2 2 ; 2

y x x mx m y x

= + + + = +

^$?W.

 5

3 2 2

2 2 2 1; 2 2

y x x x m y x x

= + − + − = − +

^$?W.

HT 26. < 

$01

 2

4 2

2 1;

y x x y m

= − − =

^$?W.

 3

4 2 3

( 1)

y x m m x m

= − + +

^P$?W.

 4

4 2 2

(2 3) 3

y x m x m m

= − − + −

^P$?W.

HT 27. U.=>j

$/0/01

 2

3 2

( 2)

y x x

y m x





= − −







= −





 3

( 3)

y x

y m x





= − +







= −







HT 28. < 

$/01

2

3 1

; 2

y y x m

= = +

−

^$?W.A, BL 

$AB^H

3

4 1

;

y y x m

−

= = − +

−

^$?W.A, BL 

$AB^H

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 12

BÀI TẬP TỔNG HỢP VÀ NÂNG CAO

HT 29. < 

$1

2

2 1

( )

y C

−

^MY\

y x m

∆ = +

$?W.A, B

2 2

Đ/s:

1; 7

m m

= − =

3

( )

y C

−

^MY\

y x m

∆ = − +

$?W.A, BA, B"B_H

Đ/s:

4

2 1

( )

y C

−

^MY\

y x m

∆ = +

$?W.A, B0

OAB

I(O.

Đ/s:

= −

5

2 2 3

( )

mx m

y C

− −

^MY\

: 2

y x

∆ = −

$?W.A, B



AOB



6

(1 ) 2(1 )

m x m

+ + −

^MY\

y x

∆ =

$?W.A, B1

OA OB

OB OA

+ =



7

3 1

−

^MY\

: ( 1) 2

y m x m

∆ = + + −

$?W.A, B0

OAB

B.,

C



8

( )

2 1

y C

^MY\

: 2 2 1 0,

mx y m

∆ − + + =

^(C)$?W.A, B$

Q

2 2

P OA OB

= +

0_H

HT 30. G

( )

y C

−

OI=$/.>< (C)$A, B0

IAB>

(4; 2)

−

=KWĐ/s:

(2; 4),( 2; 0)

−



HT 31. G

( )

2 1

y C

− +

−

*0

$MY\

y x m

∆ = +

^(C)$?W.

"

1 2

x x

)

1 2

'( ) '( )

f x f x

0=[H

HT 32. G

( )

2 1

y C

−

*0

$MY\

y x m

∆ = +

^(C)$?W.

"

1 2

x x

)

1 2

'( ) '( )

f x f x

0_H

HT 33. G

3 4

( )

2 3

y C

−

*0O"0$(C))0A$

PH?3=n0A$.>Q

JJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJ

 

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 13

VẤN ĐỀ 5: SỰ TIẾP XÚC CỦA HAI ĐƯỜNG CONG

1.op O/1f/

( )

y f x

$

=./?kI[(C)/

$

(

)

0 0 0

; ( )

M x f x



L?M- ?k/(C)$

(

)

0 0 0

; ( )

M x f x

=1

   

0 0 0

'( )( )

y y f x x x

− = −

 

0 0

( ( ))

y f x



2.fX.nI/$MY

( ) : ( )

C y f x

và

( ) : ( )

C y g x

?'q=.?M- .1

   

( ) ( )

'( ) '( )

f x g x











 !i

 ./.!i="/?$/MY

3.

( ) :

C y px q

= +

I

( ) :

C y ax bx c

= + +

 (C

)I(C

)?'q

⇔?M- 

ax bx c px q

+ + = +

.+?

Dạng toán 1: Lập phương trình tiếp tuyến của đường cong (C): y = f(x)

Bài toán 1: Viết phương trình tiếp tuyến

∆

của

( ) : ( )

C y f x

tại điểm

(

)

0 0 0

;

M x y

•

Nếu cho

thì tìm

0 0

( )

y f x

Nếu cho

thì tìm

là nghiệm của phương trình

( )

f x y

•

Tính

' '( )

y f x

. Suy ra

0 0

'( ) '( )

y x f x

•

Phương trình tiếp tuyến

∆

là:

0 0 0

'( )( )

y y f x x x

− = −

Bài toán 2: Viết phương trình tiếp tuyến

∆

của

( ) : ( )

C y f x

biết

∆

có hệ số góc k cho trước.

Cách 1: Tìm toạ độ tiếp điểm.

•

Gọi M(x

; y

) là tiếp điểm. Tính f

′

•∆

có hệ số góc k

⇒

′

) = k (1)

•

Giải phương trình (1), tìm được x

và tính y

= f(x

). Từ đó viết phương trình của

∆

Cách 2: Dùng điều kiện tiếp xúc.

•

Phương trình đường thẳng

∆

có dạng: y = kx + m.

•∆

tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:

( )

'( )

f x kx m

f x k





= +









(*)

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 14

•

Giải hệ (*), tìm được m. Từ đó viết phương trình của

∆

Chú ý: Hệ số góc k của tiếp tuyến

∆

có thể được cho gián tiếp như sau:

∆

tạo với chiều dương trục hoành góc

thì k = tan

∆

song song với đường thẳng d: y = ax + b thì k = a

∆

vuông góc với đường thẳng d: y = ax + b (a

≠

0) thì k =

−

∆

tạo với đường thẳng d: y = ax + b một góc

thì

tan

k a

−

Bài toán 3: Viết phương trình tiếp tuyến

∆

của (C): y = f(x), biết

∆

đi qua điểm

( ; )

A A

A x y

Cách 1:Tìm toạ độ tiếp điểm.

•

Gọi M(x

; y

) là tiếp điểm. Khi đó: y

= f(x

), y

′

= f

′

•

Phương trình tiếp tuyến

∆

tại M: y – y

= f

′

).(x – x

)

•∆

đi qua

( ; )

A A

A x y

nên: y

– y

= f

′

).(x

– x

) (2)

•

Giải phương trình (2), tìm được x

. Từ đó viết phương trình của

∆

Cách 2: Dùng điều kiện tiếp xúc.

•

Phương trình đường thẳng

∆

đi qua

( ; )

A A

A x y

và có hệ số góc k: y – y

= k(x – x

•∆

tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:

( ) ( )

'( )

A A

f x k x x y

f x k





= − +









(*)

•

Giải hệ (*), tìm được x (suy ra k). Từ đó viết phương trình tiếp tuyến

∆

Bài tập cơ bản

HT 34. c?M- ?k/(C)$MNr1

2

3 2

( ) : 3 7 1

C y x x x

= − − +

T!;D2  3

( ) :

4 2

2 1

y x x

= − +

U!2D;

4(C):

3 4

2 3

−

G!2DF8   

5(C):

−

0$/!GI[P&P

6(C):

2 2 1

y x x

= − +

0$/!GI[P&P 

7(C):

3 1

y x x

= − +

$/!G

HT 35. c?M- ?k/!G0$/!GI[MYMNr1

2!G1

3 2

2 3 9 4

y x x x

= − + −

IB1

7 4

y x

= +



GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 15

3!G1

3 2

2 3 9 4

y x x x

= − + −

I!m1

8 3

y x x

= − + −



HT 36. <,B.,0^P"Z?k/!G$MNr1

!G1

5 11

2 3

−

$T'

h3 

HT 37. < $?k/!G$MNr^P""0B.,Cl

M[1

2!G1

x m

−

$T'

h3 I



3!G1

x m

−

$U'

hF2Ilh



4!G1

1 ( 1)

y x m x

= + − +

$G'

h;Ilh9

HT 38. c?M- ?k∆/!G&∆.MNr1

2!G1

3 2

2 3 5

y x x

= − +

Dh23  3!G1

2 1

−

DhF4

HT 39. c?M- ?k∆/!G&∆I[MY\BM[1

2!G1

2 3 1

y x x

= − + +

DB1kh4'E3 3!G1

2 1

−

DB1

y x

= − +



HT 40. c?M- ?k∆/!G&∆I(I[MY\BM[1

2!G1

2 3 1

y x x

= − + +

DB1

= − +

 3!G1

2 1

−

DB1

y x



HT 41. < $?k∆/!G$MNrI[MY\BM[1

2!G1

(3 1)

( 0)

m x m m

y m

x m

+ − +

= ≠

$Tk

h;IB1

y x

= −



HT 42. c?M- ?k∆/!G&∆đi qua$MNr1

2!G1

3 2

y x x

= − + −

DT!3DF5  3!G1

3 1

y x x

= − +

DU!2DF7

4!G1

(

)

y x

= −

DG!;D5   5!G1

4 2

1 3

2 2

y x x

= − +

D

 













 



6!G1

−

Ds!F7D6   7!G1

3 4

−

Dt!3D4

HT 43. < $MY!G

&!G

?'q1

 2

3 2

1 2

( ) : (3 ) 2; ( ) :

C y x m x mx C= + + + −

P 

 3

3 2

1 2

( ) : 2 ( 1) ; ( ) :

C y x x m x m C= − − − +

P

 4

1 2

( ) : ( 1) 1; ( ) : 1

C y x m x C y x

= + + + = +



 5

3 2

1 2

( ) : 2 2 1; ( ) :

C y x x x C y x m

= + + − = +



HT 44. < $MY!G

&!G

?'q1

 2

4 2 2

1 2

( ) : 2 1; ( ) : 2

C y x x C y mx m

= + + = +



GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 16

 3

4 2 2

1 2

( ) : 1; ( ) :

C y x x C y x m

= − + − = − +



 4

4 2 2

1 2

1 9

( ) : 2 ; ( ) :

4 4

C y x x C y x m

= − + + = − +



 5

2 2 2

1 2

( ) : ( 1) ( 1) ; ( ) : 2

C y x x C y x m

= + − = +



 6

1 2

(2 1)

( ) : ; ( ) :

m x m

C y C y x

− −

= =

−



Dạng toán 2: Tìm những điểm trên đường thẳng d mà từ đó có thể vẽ được 1, 2, 3, … tiếp tuyến với đồ thị (C):

( )

y f x

Giả sử d: ax + by +c = 0. M(x

; y

)

∈

•

Phương trình đường thẳng

∆

qua M có hệ số góc k: y = k(x – x

) + y

•∆

tiếp xúc với (C) khi hệ sau có nghiệm:

( ) ( ) (1)

'( ) (2)

M M

f x k x x y

f x k





= − +









•

Thế k từ (2) vào (1) ta được: f(x) = (x – x

).f

′

(x) + y

(C)

•

Số tiếp tuyến của (C) vẽ từ M = Số nghiệm x của (C)

Bài tập cơ bản

HT 45. < 0$!GAIdMNđúng một?kI[!G1

2

3 2

( ) : 3 2

C y x x

= − + −

   3

( ) : 3 1

C y x x

= − +



HT 46. < 0$MY\BAIdMNđúng một?kI[!G1

2

( ) :

C y

−

DB=P   3

( ) :

C y

−

DB1kh3'E2

HT 47. < 0$MY\BAIdMNít nhất một?kI[!G1

2

2 1

( ) :

C y

−

DB1'h4   3

3 4

( ) :

4 3

C y

−

DB1kh3

HT 48. < 0$MY\BAIdMNba?kI[!G1

2

3 2

( ) : 3 2

C y x x

= − + −

DB1kh3  3

( ) : 3

C y x x

= −

DB1'h3

4

( ) : 3 2

C y x x

= − + +

DB=P 5

( ) : 12 12

C y x x

= − +

DB1khF5

HT 49. <A$T$uMN?kI[!G1

2

3 2

( ) : 9 17 2

C y x x x

= − + +

DT!F3D6 3

3 2

1 4 4

( ) : 2 3 4; ;

3 9 3

C y x x x A

 







= − + +







 



HT 50. <A"$H MY\d$uMN?kI[!G1

2

3 2

( ) : 6 9 1

C y x x x

= − + −

D

: 2

d x

  3

( ) : 3

C y x x

= −

D

: 2

d x



GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 17

Dạng toán 3: Tìm những điểm mà từ đó có thể vẽ được 2 tiếp tuyến với đồ thị (C): y = f(x) và 2 tiếp tuyến đó

vuông góc với nhau

Gọi M(x

; y

•

Phương trình đường thẳng

∆

qua M có hệ số góc k: y = k(x – x

) + y

•∆

tiếp xúc với (C) khi hệ sau có nghiệm:

( ) ( ) (1)

'( ) (2)

M M

f x k x x y

f x k





= − +









•

Thế k từ (2) vào (1) ta được: f(x) = (x – x

).f

′

(x) + y

(C)

•

Qua M vẽ được 2 tiếp tuyến với (C)

⇔

, x

•

Hai tiếp tuyến đó vuông góc với nhau

⇔

′

).f

′

) = –1

Từ đó tìm được M.

Chú ý: Qua M vẽ được 2 tiếp tuyến với (C) sao cho 2 tiếp điểm nằm về hai phía với trục hoành thì

1 2

(3) 2

( ). ( ) 0

coù nghieäm phaân bieät

f x f x











Bài tập cơ bản

HT 51. GQCA$T=(uMN?kI[!GI(I[c?M- 0?

k1

( ) : 2 3 1; 0;

C y x x A

 







= − + −







 



HT 52. < 0$MY\BA$IdMN?kI[!GI(I[1

2

3 2

( ) : 3 2

C y x x

= − +

DB1khF3  3

3 2

( ) : 3

C y x x

= +

DB=P

Dạng toán 4: Các bài toán khác về tiếp tuyến

HT 53. Gk?j=!I$vH "!O%=$/.><?kv^3.>

TIU

 2GQv=$/TU

 3GQB.,/∆%TU="C

 4< $v$I∆%TU=_H

5< v$0,&I&B.,MY]?0%TU0_H

6< v$0,&I&B.,MY]"?0%TU0=[H

7< v$0A%?k==[H

2

2 1

( ) :

H y

−

 3

( ) :

H y

−

  4

4 5

( ) :

2 3

H y

−

− +



HT 54. < $?k$vH "k?j=!^MY.>"0B.

,Cl1

2

2 3

( ) : ; 8

H y S

x m

= =

−



GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 18

VẤN ĐỀ 7: KHOẢNG CÁCH

Kiến thức cơ bản:

1) Khoảng cách giữa hai điểm A, B: AB =

2 2

( ) ( )

B A B A

x x y y− + −

2) Khoảng cách từ điểm M(x

; y

) đến đường thẳng

∆

: ax + by + c = 0:

d(M,

∆

) =

0 0

2 2

ax by c

a b

+ +

3) Diện tích tam giác ABC:

S =

( )

2 2

1 1

. . sin . .

2 2

AB AC A AB AC AB AC

= −

 

Bài tập cơ bản

HT 55. < 0$v"k?j=!)00A.>=_H

2

( ) :

H y

−

   3

2 1

( ) :

H y

−

  4

4 9

( ) :

H y

−

 

HT 56. < 0$v"k?j=!)00AP"=_H

2

( ) :

H y

−

   3

2 1

( ) :

H y

−

  4

4 9

( ) :

H y

−



HT 57. Gk?j=!< $T&U"00/!"BTU=_H

2

( ) :

H y

−

   3

2 3

( ) :

H y

−

  4

4 9

( ) :

H y

−

 

HT 58. G!GIMY\B< $B^!G3$T&U"BTU=_H

( ) : ; : 2 0

H y d x y m

= − + =

−

 

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 19

ÔN TẬP TỔNG HỢP

PHẦN I: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

HT 1. G

3 2

( 1) (3 2)

y m x mx m x

= − + + −

!2< H00/m$!2

>?'0/Đ/s:

≥

HT 2. G  

3 2

3 4

y x x mx

= + − −

 !2<  H  0 0  /    $   !2   



( ; 0)

−∞

 Đ/s:

≤ −

HT 3. G

3 2

2 3(2 1) 6 ( 1) 1

y m x m m x

= − + + + +

!G



< m$

(2; )

+∞

Đ/s:

≤

HT 4. G

3 2

(1 2 ) (2 ) 2

y x m x m x m

= + − + − + +

< m$

(

)

+∞

 Đ/s:

≥



HT 5. G

4 2

2 3 1

y x mx m

= − − +

!2&!m=< m$!2!2D3

Đ/s:

(



∈ −∞





HT 6. G

x m

 !2 <  H  0 0  /   m $   !2    

( ;1)

−∞

Đ/s:

2 1

− < ≤ −

HT 7. G

3 2

y x x mx m

= + + +

< $"BC2Đ/s:

⇔

PHẦN II: CỰC TRỊ CỦA HÀM SỐ

HT 8. G

3 2

(1 – 2 ) (2 – ) 2

y x m x m x m

= + + + +

!m=!2< 00/m$

!2$K&$K$&Y"/$K$_-2Đ/s:

5 7

4 5

< <

HT 9. G

3 2

( 2) 3 5

y m x x mx

= + + + −

&m=< 00/m$0$K&K$/

`"=0BM- Đ/s:

3 2

− < < −

HT 10. G

3 2 3

2 3( 2) 6(5 1) (4 2).

y x m x m x m

= − + + + − +

< 

$K$

(

1;2



∈





Đ/s:

− ≤ <

HT 11. G

4 2

1 3

2 2

y x mx

= − +

!2*0m$/!2K$(K

Đ/s:

≤

HT 12. G

4 2

2 4 ( ).

y x mx C= − + −

< 00/$H0$K/

( )

XC

0PO" Đ/s:

2; 0

m m

= ≤

HT 13. G

3 2 2

(2 1) ( 3 2) 4

y x m x m m x

= − + + − − + −

!m==!G

*0m$!G



0$KIK$CIX?,/P Đ/s:

1 2

< <

HT 14. G

3 2

(2 1) 3

y x mx m x

= − + − −

!m==!G

*0m$!G

0$

K&K$CIXe"?,I[P Đ/s:





≠









HT 15. G

3 2

3 – 2

y x x mx m

= + + +

!m==!G

*0m$!G

0$K

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 20

IK$CIX?,I[P Đ/s:

HT 16. G

3 2 3

1 4

( 1) ( 1) ( ).

3 3

y x m x m C

= − + + +

< 

$0$K/(C) CIX?,

!?,I?,/MY]?M- 1

2 2

4 3 0.

x y x

+ − + =

Đ/s:

HT 17. G

3 2 3

3 4

y x mx m

= − +

!m==!G

*0m$!G

0$KI

K$'QRMY\yhx Đ/s:

m = ±

HT 18. G

3 2

3 3 1

y x mx m

= − + − −

c[0/m $KI$K$

'QI[RMY\

: 8 74 0

d x y

+ − =

 Đ/s:

HT 19. G

3 2 2 3 2

3 3(1 )

y x mx m x m m

= − + + − + −

!2c?M- MY\R$K

/!2 Đ/s:

y x m m

= − +

HT 20. G

3 2

3 2 ( ).

y x x mx C= − + +

< 

$

( )

KIK$&Y0$K

/0XMY\

: 1 0.

d x y

− − =

Đ/s:

HT 21. G

3 2

y x x mx

= − − +

!m==!G

*0m$!G

0$KI

K$0XMY\

y x

= −

 Đ/s:

 

 

= −

 

 

 

HT 22. G

3 2

y x x mx

= − +

 !2c[0/m !20$KI$

K$'QI[RMY\

: – 2 – 5 0

d x y

 Đ/s:

HT 23. G

3 2

3( 1) 9 2

y x m x x m

= − + + + −

!2=!G



c[0/m 

$KI$K$'QI[RMY\

d y x

 Đ/s:

HT 24. G

3 2

1 1

( 1) 3( 2)

3 3

y x m x m x

= − − + − +

&I[

=K*0

$`

K

1 2

x x



1 2

2 1

x x

+ =

 Đ/s:

4 34

− ±

HT 25. G

3 2

3( 1) 9

y x m x x m

= − + + −

&I[

=K*0

$`K

1 2

x x



1 2

x x

− ≤

Đ/s:

3 1 3

− ≤ < − −

và

1 3 1.

− + < ≤

HT 26. G

3 2

(1 2 ) (2 ) 2

y x m x m x m

= + − + − + +

&I[

=K*0

$`

K

1 2

x x



1 2

x x

− >

Đ/s:

3 29

m m

> ∨ < −

HT 27. G

3 2

4 – 3

y x mx x

= +

< m$$K

1 2

x x

_

1 2

x x

= −

 Đ/s:

= ±

HT 28. < 00/$

3 2 2

1 1

( 3)

3 2

y x mx m x

= − + −

K

, K$

Y

D

=

"B0I(/"0I("BkXC

Đ/s:

m =

HT 29. G

3 2 2

( 1) ( 4 3) 1.

y x m x m m x

= + + + + + +

< 

$K< 0=[H/

$Q

1 2 1 2

2( )

A x x x x

= − +

I[

1 2

x x

=0$K

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 21

Đ/s:

≤

khi

= −

HT 30. G

3 2

3( 1) 9 (1)

y x m x x m= − + + −

I[

=K*0

$!2K&

K$

CD CT

y y

+ =

Đ/s:





= −





HT 31. G

3 2 2

( 1) 1 ).

y x mx m x= − + − +

< $KK$I1

C CT

y y

+ >

Đ/s:

1 0



− < <







HT 32. G

3 2

– 3 2

y x x

= +

!2< $v"MY\

: 3 2

d y x

= −

)0Av

[$K_H Đ/s:

4 2

;

5 5

 

















 

HT 33. G

3 2 2 3

3 3( 1)

y x mx m x m m

= − + − − +

!2< m$!2KY

0A$K/O"VC

=n0A$K$/

O"VĐ/s:

3 2 2



= − +



= − −



HT 34. G

3 2

3( 1) 3 ( 2) 2 ( )

y x m x m m x m C

= − + + + − +

< 

$(C)KY

0A$K/(C) [P

C0A$K$/(C)

[P

Đ/s:

2; 1; 1; 0

m m m m

= = = − =

HT 35. G 

3 2

y x x mx

= − − +

 = !G

<  m $ !G

 0 $K &K $I MY

\R0$KI[MY\

: 4 3

d y x

= − +

Đ/s:

HT 36. G 

3 2

y x x mx

= − − +

 = !G

<  m $ !G

 0 $K &K $I MY

\R0$KI[MY\

: 4 – 5 0

d x y

+ =

"

 Đ/s:

= −

HT 37. G   

3 2

y x x m

= + +

  !2*0  m $   /   !2  $ K  A& B 



120

AOB

 Đ/s:

12 2 3

− +

HT 38. G

3 2 2 3

3 3( 1) 4 1 (1),

y x mx m x m m m

= − + − − + −

=K< 00/

$

!2$K

A B

0

OAB

I(

I[

=O" Đ/s:

1; 2

m m

= − =

HT 39. G

3 2 3 2

3( 1) 3 ( 2) 3 .

y x m x m m x m m

= + + + + + +

GQCI[O=(3K

I0#$k(?P"II,/

HT 40. G

3 2

y x x mx

= − − +

!2I[m=Kfm$!2K&Y

MY\R$K/I[PO""0W Đ/s:

= −

HT 41. G

4 2 2

( ) 2( 2) 5 5

y f x x m x m m

= = + − + − +

( )

< 00/m$

( )

/

0$K&K$20I(W Đ/s:

HT 42. G 

(

)

4 2 2

2( 2) 5 5 .

y x m x m m C= + − + − +

c[ # 0   / m   !G





$K  I $ K $&  Y 0 $ K  I $ K $ =>?  "  0 X Đ/s:

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 22

2 3

= −

HT 43. G

4 2 2

y x mx m m

= + + +

!G



c[#0/m !G



$

K&Y$K=>?"0"C

120

 Đ/s:

m = −

HT 44. G

4 2

2 1

y x mx m

= − + −

!G



c[#0/m !G



$K

&Y$K=>?"00,MY]?C



Đ/s:

5 1

m m

−

= =

HT 45. G

4 2 4

2 2

y x mx m m

= − + +

!G



c[#0/m !G



$

K&Y$K=>?"0B.,C5 Đ/s:

HT 46. G

4 2

2 2

x mx

− +



( )

< H00/$

( )

$K

"0MY]?R$g

3 9

;

5 5

 

















 



Đ/s: m = 1

PHẦN 3: SỰ TƯƠNG GIAO

HT 47. G

3 2

6 9 6

y x x x

= − + −

=!Gfm$MY\

( ) : 2 4

d y mx m

= − −

^!G

$?W. Đ/s:

> −

HT 48. G

3 2

y x m x m

= − −

!G

< m$!G

IPq3$?W.

Đ/s:

= ±



HT 49. G

3 2

2 6 1

y x x

= − + +

< $MY\

y mx

= +

^!G4$?W.T&U&G

T!;D2IU=$/TG Đ/s:m = 4

HT 50. G

3 2

1 2

3 3

y x mx x m

= − − + +

w xy

( )

<z{mj|

( )

}P{y4j|?~j~yw|

z{?M-w{~y=-w -26 Đ/s:

HT 51. G1

3 2

2 3 1 (1)

y x x= − +

< (C) #$M?k/(C) M^P

$"C9 Đ/s:

( 1; 4)

− −



HT 52. G

3 2

2 ( 3) 4

y x mx m x

= + + + +

=!G



!m=GMY\!B1

y x

= +

I

$L!2D4< 00/m$!B^!G



$?W.T!;D5&U&G0LUGB.,

C

8 2

 Đ/s:

1 137

HT 53. G

3 2

3 4

y x x

= − +

=!GO

=MY\R$

( 1; 0)

−

I[.

( )

∈

ℝ

< 

$MY\

^!G$?W.T&U&GI3$U&GeI["



"0B.,C

 Đ/s:

HT 54. G

3 2

y x x

= − +

=!GOs=W'Q/!Gc?M- MY

\RsI^!G$s&T&U?W.B.,0VTUC



Đ/s:

(

)

1; 1 3 ( 1)

y x y x

= − + = − ± −

HT 55. G  

3 2

4 1

(2 1) ( 2)

3 3

y x m x m x

= − + + + +

  

( ),

C m

 =   O

 =  $ /

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 23

( )

I[P< 

?k/

( )



I[PO""0B.,C

Đ/s:

13 11

;

6 6

m m= − = −

HT 56. G

y x mx

= + +

!G



< m$!G



^P"$BkH

Đ/s:

> −

HT 57. G

3 2

2 3( 1) 6 2

y x m x mx

= − + + −

!G



< m$!G



^P"$

BkHĐ/s:

1 3 1 3

− < < +

HT 58. G

3 2

– 3 1

y x x

= +

< m$MY\!∆1

(

2 1) – 4 – 1

y m x m

= −

^!Gq

$?W. Đ/s:

= −

;

HT 59. G  

3 2

3 ( 1) 1

y x mx m x m

= − + − + +

   =

( )

 <  H  0 0  /  $

: 2 1

d y x m

= − −

^

( )

$?W."=[-@C2

Đ/s: không có giá trị m

HT 60. G

3 2

y x x

= − +

!Gc?M- MY\^!G4$?W.T&U&G



I

2 2

Đ/s:

: 2

d y x

= +

HT 61. G

3 2

4 6 1

y x mx

= − +

!G&=< $MY\

: 1

d y x

= − +

^

4$T!;D2&U&GI[U&G'QRMY?W0QH Đ/s:

HT 62. G

3 2

3 1

y x x mx

= + + +

!m=!2< m$MY\

: 1

d y

^!2

$?W.A!;D2&B&C0?k/!2BICI(I[

Đ/s:

9 65 9 65

8 8

m m

− +

= ∨ =

HT 63. G  

– 3 1

y x x

= +

    !GI MY \ !B1

y mx m

= + +

 <  m $!B ^ !G 

(1; 3)

&&m?k/!GImI(I[ Đ/s:

3 2 2 3 2 2

3 3

m m

− + − −

= ∨ =

HT 64. G

3 2

3 4

y x x

= − +

!GO!d=MY\R$T!3D;.k< k$!d^

!G$?W.T&v&?k/!GvII(I[

Đ/s:

3 2 2

− ±

HT 65. G

1 ( ).

y x mx m C= − + −

< $?k/`$

= −



^MY]!G1

2 2

( 2) ( 3) 4

x y

− + − =

j"BWk"B_H Đ/s:



HT 66. G

(

)

3 2 .

y x mx C= − +

< 

$MY\R$K&K$/

(

)

^MY

]W

(

)

1;1 ,

0,C2$?W.A, BB.,0IAB0=[H

Đ/s:

2 3



HT 67. G

4 2

y x mx m

= − + −

=

(

)

f$

(

)

^PP$

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 24

?W. Đ/s:









≠







HT 68. G

4 2

2( 1) 2 1 ( ).

y x m x m C= − + + +

< H00/

∈

ℝ

$`

^P5$?W.

, , ,

A B C D

=n=MN"

1 2 3 4

, , ,

x x x x

1 2 3 4

( )

x x x x

< < <



0

ACK

B.,C5

(3; 2).

−

Đ/s:

HT 69. G

(

)

4 2

2 1 2 1

y x m x m

= − + + +

=

(

)

f

$

(

)

^P5$

?W."=>?H?" Đ/s:

 

 

= −

 

 

 

HT 70. G

4 2

– (3 2) 3

y x m x m

= + +

=!G



&m=< m$MY\

= −

^

!G



5$?W.X"_-3 Đ/s:





− < <







≠





HT 71. G

(

)

4 2

2 1 2 1

y x m x m

= − + + +

=!G



&m=< m$!G



^P

4$?W.X"_-4 Đ/s:

m m

= − ∨ ≥

.

HT 72. G1

4 2

5 4

y x x

= − +

< H0$M(C)/?k/ (C)

M^(C)$?W.0M. Đ/s:

10 10

2 2





− < <







≠ ±







HT 73. G

2 1

=(C).GQCMY\

d y x m

= − +

=(^(C)

$?W.A, B< m$AB"B_H Đ/s:

HT 74. G

−

!Gc?M- MY\dR$

( 1;1)

−

I^!C$

M&NI =$/MN Đ/s:

y kx k

= + +

với

HT 75. G

2 4

−

!GO!d=MY\RA!2D2I.k< k$!d^!C

$M, N

3 10

 Đ/s:

3 41 3 41

3; ;

16 16

k k k

− + − −

= − = =

HT 76. G

2 2

−

!G< m$MY\!d1

y x m

= +

^!C$?W.T, U

Đ/s:

10; 2

m m

= = −

HT 77. G

x m

−

!2< 00/mMY\!d1

y x

= +

^

!2$A IB

2 2

 Đ/s:



HT 78. G

( ).

2 2

y C

−

< H00/

∈

ℝ

$MY\

d y x m

= +

^

A B



2 2

OA OB+ =

Đ/s:

m m

= − ∨ =

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 25

HT 79. G

( ).

y C

−

< H00/

∈

ℝ

$MY\

: 1

d y mx m

= − −

^

(C) $?W.

A B



2 2

MA MB

0_HĐ/s:

= −

HT 80. G

( ).

y C

−

Od=MY\R

(2; 0)

I.=

< 

$d ^(C) 

$?W.

A B

1

MA MB

= −

 

Đ/s:

HT 81. G

!< m$MY\d :y = 2x + 3m ^!$?W.



. 4

OAOB

= −

 

I[V=O" Đ/s:

m =

HT 82. < !1

− +

−

0$T&U"B\TUC5IMY\TUI(I[

MY\

y x



Đ/s:

(3 2; 2); (3 2; 2) (3 2; 2); (3 2; 2)

+ − − + − −

A B hoaëc A B

(1 2; 2 2); (1 2; 2 2) (1 2; 2 2); (1 2; 2 2)

+ − − − − + − − + + − −

A B hoaëc A B

HT 83. G

−

!< $MY\

: 1

d y x m

= − + +

$?W.T&U





AOB

OĐ/s:

> −

HT 84. G  

3 2

( )

y C

 fMY \

y x

^ !G   $ T& U <   $ MY \

y x m

= +

^!G$G&gTUGg=   Đ/s:

HT 85. G

2 1

−

!G< m$MY\B1

y x m

= +

^!G$?W.T&U

∆VTUI(V Đ/s:

= −



HT 86. G

x m

−

!2GQCI[O

≠

!2^!B1

2 2

y x m

= −



$?W.T&U""MY!fMY\!B^PV'&Vk=n=MN0$v&< $

OAB OMN

S S=



HT 87. G

2 1

( ).

y C

−

OI=$/.>/!Gc[0/

 MY\

y x m

= − +

^!G$?W.A, BI0IABX Đ/s:

3 6

= ±

HT 88. G

( )

y C

−

< 00/

$MY\

y x m

= − +

^!G$?W

.

A B



OA OB

C

60 .

c[

=O" Đ/s:

2 6

m m

= − ∨ =

PHẦN 4: TIẾP TUYẾN

HT 89. G{•

2 1

−

c?M- ?k/!G&0A$

(1;2)

?k

C

 Đ/s:

1 0

x y

+ − =

và

5 0

x y

+ − =

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 26

HT 90. G

3 2

(1 2 ) (2 ) 2

y x m x m x m

= + − + − + +

!2!m=< m$/

!2?kI[MY\B1

7 0

x y

+ + =



&

cos

α =

Đ/s:

≤ −

hoặc

≥

HT 91. G

3 2

2 ( ).

y x x x C

= − + −

< O"0$PR$uMN?

kI[!GI#?kkC

45 .

Đ/s:

;

M O

≡

; 0

 

















 

HT 92. G

3 2

3 1

y x x

= − +

!G< $T&U"!G?k/!GT

IUI[I"BTUh

4 2

 Đ/s:

(3;1), ( 1; 3)

A B

− −

HT 93. G

−

!G< VyH0$AuMNBkH"?k[!G

Đ/s:

(0;1); (0; 1)

M M

−



HT 94. G

y x x

= −

!G< MY\

d y x

= −

0$AuMNq3?k

?W.I[!GĐ/s:

(2; 2); ( 2;2)

A B

− −



HT 95. G1

3 2

y x x

= − +

< H$MY\

&AuMNq3?

k[!G Đ/s:

( 1; 4); ; 4 ;(2; 4)

 







− −











 

HT 96. G

3 2

y x x

= − + −

!G< MY\

: 2

d y

0$AuMN4?k

?W.I[!G Đ/s:







< −























≠





HT 97. G

(

)

(

)

2 2

1 . 1

y x x

= + −

!GG$

( ; 0)

A a

< a$ATuMN4?k?W.I[

!G Đ/s:

3 3

1 1

2 2

− ≠ < − ≠ >

a hoaëc a

HT 98. G

3 2

3 2.

y x x

= − +

< MY\

0$A$uMN3?k[

I3?kI(I[ Đ/s:

 







−











 

HT 99. G

3 2

( ) ( 1) (4 3 ) 1

y f x mx m x m x

= = + − + − +

=!G



< 00m

!G



"$BkH"W?kI(I[MY\

: 2 3 0

d x y

+ − =



Đ/s:

hay

m m

< >

HT 100. < H00

( )

3 2

( 1) (4 3) 1

y mx m x m x

= + − + − +

q

$"BM-?kI(I[MY\!a1

2 3 0

x y

+ − =

Đ/s:

1 1 2

0; ;

2 2 3

   

 

 

 

∈ ∪

 

 

 

 

 

   

HT 101. G

!Gc?M- ?k/!G&C0AW

'Q/!G?k==[H Đ/s:

y x

và

y x

= +

HT 102. G

2 3

 !2c?M- ?k/!2&?k^

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 27

P&P=n=MN$?W.T&UI0VTUWO"V Đ/s:

y x

= − −

HT 103. Gkh

2 1

−

a>??M- ?k/!G?kk^0PVx&Vy

=n=MN0$TIU`VTh5VU Đ/s:

1 5

4 4

1 13

4 4

y x





= − +



= − +





HT 104. c?M- ?k/

−

?k^V'&Vk=n=MNTIU

0VTU_`1

AB OA

Đ/s:

y x

= − +

HT 105. G

2 3

−

!G< !G#$v?kv/!G^.

>/!GT&UTU^HĐ/s:

(3; 3)

hoặc

(1;1)

HT 106. G

2 3

−

GM =$H !C<?k/!C)M ^0MY.>/!C

AIB.OI =$/0MY.>< "$MMY]?0IAB 

B.,_H Đ/s:

(1;1); (3; 3)

M M

HT 107. G

3 2 2

2 1 ( ).

y x mx m x m C= − + − +

< 

$?'qI[P

Đ/s:

1 3

m m m

= ∨ = − ∨ =

HT 108. G

2 1

−

!GO%=$/.>< $v"!G?

k/!Gv^3.>TIUI[I0%TU0_H

Đ/s:

(

)

1 3; 2 3

M + +

(

)

1 3;2 3

M − −

HT 109. G1

−

!GG$

(0; )

A a

< a$ATuMN3?k[!G3

?$M-QCIX3?,/P Đ/s:





> −







≠





HT 110. Gkh

O%=$/3MY.>&

∆

="?kH€/!GB

=0A%

∆

< 0=[H/B Đ/s:GTLN của d bằng

khi





= −





HT 111. G

2 1

c?M- ?k/!G&C?k0X$

A!3D5&B!−5D−3 Đ/s:

1 5

; 1; 5

4 4

y x y x y x

= + = + = +

HT 112. G

2 3

−

!Gc?M- ?k$v"!G?k^.

>QI.>=n=MNT&U(



ABI

C

&I[%=3.>

Đ/s: Tại

 













 

1 3

4 2

y x

= − +

; Tại

 













 

1 7

4 2

y x

= − +

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 28

HT 113. G

2 1

−

!G< 0_H/,H"$v

∈

!G?k

v/!GI[PO""0OWCMY\

2 1

y m

= −

Đ/s:

≥

HT 114. G

2 1

( ).

y C

−

< 00/

$(C)?'qI[MY\

y mx

= +

Đ/s:

= −

hoặc

= −

PHẦN 5: BIỆN LUẬN SỐ NGHIỆM CỦA PHƯƠNG TRÌNH

HT 115. G

3 2

3 1

y x x

= − + +



 2L0KIId!G/

 3< m$?M- 

3 2 3 2

3 3

x x m m

− = −

.?W.

Đ/s:

{

( 1; 3) \ 0;2}

∈ −

HT 116. G

4 2

5 4

y x x

= − +

!G

 2L0KIId!G/

 3< m$?M- 

4 2

| 5 4 | log

x x m

− + =

7.

•

Dựa vào đồ thị ta có PT có 6 nghiệm

⇔

log 12 144 12

m m= ⇔ = =

HT 117. G1

4 2

2 1

y x x

= − +



 2L0KIId!G/

 3U.=>jm./?M- 1

4 2

2 1 log 0

x x m

− + + =

 !m•;

< <

2 nghiệm 3 nghiệm 4 nghiệm 2 nghiệm vô nghiệm



HT 118. G

4 2

( ) 8 9 1

y f x x x

= = − +



 2L0KIId!G/

 3gKI!G`k.=>j./?M- 1

   

4 2

8 cos 9 cos 0

x x m

− + =

I[

[0; ]

∈



Đ/s:

0 1

< <

m≤ <

m =

m >

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 29

vô nghiệm 1 nghiệm 2 nghiệm 4 nghiệm 2 nghiệm vô nghiệm

HT 119. G

−



 2L0KIId!G/

 3U.=>jm./?M- 

−



1; 1

m m

< − >

= −

1 1

− < ≤

2 nghiệm 1 nghiệm vô nghiệm



PHẦN 6: ĐIỂM ĐẶC BIỆT CỦA ĐỒ THỊ

HT 120. G 

3 2

y x x

= − + +

!G < 3$     q'Q R W

( 1; 3)

−

 Đ/s:

(

)

1; 0

−

và

(

)

1;6

−

HT 121. G

3 2

y x x

= − + +

!G< !G$'QRMY\

: 2 – 2 0

d x y

+ =



Đ/s:

7 1 7 7 1 7

;2 ; ;2

2 2 2 2 2 2

   

 

 

 

 

− − +

 

 

 

 

 

 

   

HT 122. G

3 3

y x= − + + −

< (C)$?W.M, N 'QRP

Đ/s:

16 16

3; , 3;

3 3

M N

   

 

 

 

−

 

 

 

   

HT 123. G

2 1

−

(C)< $v"(C) $?k/(C) MI[MY\RM

I$MY.>,0.CF:

Đ/s:

(0; 3); ( 2; 5)

M M

− −

HT 124. G

2 1

 (C).< (C)#$)0.>/(C)_H

Đ/s:

(0;1);( 2; 3)

−

HT 125. G

3 4

−

(C).< 0$"(C)0X3.>

Đ/s:

1 2

(1;1); (4; 6)

M M

HT 126. G

4 2

1 1

1 ( ).

4 2

y x x C

= − +

< $M"(C))0A$MP

O"=_HĐ/s:

(0;1)

HT 127. G

4 2

0 0 0 0

2 3 2 1

y x x x

= − + +

=(C)IMY\

( ) 2 1

∆ = −

< (C)$

A0

( )

∆

=_H Đ/s:

3 1

; 3

2 8

 









− − −













 

3 1

; ; 3

2 8

 









− +













 

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 30

HT 128. G

−

< $M0AMPO"=

_H Đ/s:

 







−











 

HT 129. G    

2 4

−

 <   (C)  $  'Q  R MY \ MN 

( 3; 0); ( 1; 1)

M N

− − −

Đ/s:A(0; –4), B(2; 0).

HT 130. G

−

< (C)$B, C"00ABCI(W

rAI[A(2; 0). Đ/s:

( 1;1), (3; 3)

B C

−

HT 131. G

2 1

−

< O"$M

∈

(C)0A$

( 1; 2)

−

[?k/(C)

M==[H Đ/s:

(

)

1 3 ; 2 3

M − + −

hoặc

(

)

1 3 ;2 3

M − − +

HT 132. G

2 1

−

< #$(C)0X$

(2; 0), (0;2)

A B

Đ/s:

1 5 1 5 1 5 1 5

, ; ,

2 2 2 2

   

 

− − + +

 

 

 

 

 

 

 

 

 

   

HT 133. G   

−

  <    0 /   (C)  $ A I B   AB ^ HĐ/s:

(

)

(

)

4 4 4 4

1 4;1 64 , 1 4;1 64

A B− − + − + −

HT 134. G

4 2

2 1

y x x

= − +

< O"$m‚"!GMY\m‚I[P

I0A$K/!GMY\m‚C9

Đ/s:Vậy, P(-2;9), Q(2;9) hoặc P(2;9); Q(-2;9)

HT 135. G

(3 1)

m x m m

x m

+ − +

< 0$"MY\

(R

Đ/s:Tập hợp các điểm thuộc đường thẳng

có tung độ bằng a với a thỏa mãn :

2 10

< <

HT 136. G

2 1

( ).

y C

−

< (C) $

A B

?W.$

, , (0; 1)

A B I

−

\

Y_`1

. 4.

IAIB



Đ/s:

(

)

(

)

2 2;1 2 ; 2 2;1 2

A B− − + +

@

(

)

(

)

1 3; 2 3 ; 1 3; 2 3

A B− − + + − −



PHẦN 7: CÁC BÀI TỔNG HỢP

HT 137. G

2 3

( ).

y C

−

< 

$MY\

: 2

d y x m

= +

^$?W.

?k$/I[ Đ/s:

= −

HT 138. G

3 2

2 2 1 ( ).

y x mx mx C

= − + −

< 

$(C)^P4$?W.

(1; 0),

A B

I



1 2

. 5

k k BC+ =



1 2

k k

=n=MN=.?kB, C /(C).

Đ/s:

1; 2

m m

= − =

HT 139. G

3 2

3 2 ( ).

y x x mx m C= − + + −

< 

$

( )

^P4$?W.

, ,

A B C



GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 31

)0./?k/

( )



, ,

A B C

C4Đ/s:

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 32

PHẦN 8: TUYỂN TẬP ĐỀ THI ĐẠI HỌC TỪ NĂM 2009

HT 140. (ĐH A – 2009)G

(1)

2 3

c?M- ?k/!2&?k

^P&P=n=MN$?W.A, B0OABWO"O

Đ/s:

y x

= − −



HT 141. (ĐH B – 2009) G1

4 2

2 4 (1)

y x x= −

c[0/

?M- 

2 2

x x m

− =

q7

.K?W.Đ/s:

0 1

< <

HT 142. (ĐH D – 2009) G

4 2

(3 2) 3

y x m x m

= − + +

=

( )

I[

=< 

$MY

\

= −

^

( )

5$?W.X"_-3

Đ/s:

1, 0

m m

− < < ≠



HT 143. (ĐH A – 2010) G

3 2

2 (1 ) (1),

y x x m x m= − + − +

I[

=K< 

$!2^

P4$?W."

1 2 3

, ,

x x x

_`X.1

2 2 2

1 2 3

x x x

+ + <

Đ/s:

− < <

I

≠



HT 144. (ĐH B – 2010) G 

2 1

( )

y C

< 

$MY \

y x m

= − +

^  

( )



$A IB0OABB.,C

!O=O"Đ/s:

= ±



HT 145. (D – 2010)G

4 2

6 ( )

y x x C

= − − +

c?M- ?k/!G?k

I(I[MY\

y x

= −

Đ/s:

6 10

y x

= − +



HT 146. (A – 2011)G

( )

2 1

y C

− +

−

GQCI[O

MY\

y x m

= +

=(^



( )

$?W.AIBO

1 2

k k

=n=MN=./?kI[

( )

AIB< 

$)

1 2

k k

0=[H Đ/s:

1 2

k k

=[HC

−

&Ir

= −



HT 147. (B – 2011) G

4 2

2( 1) (1)

y x m x m= − + +

!I[

=< 

$!2

$KA, B, COA = BCDO=O"&A=$K"P&BIC=$K

]= Đ/s:

2 2 2

= ±



HT 148. (D – 2011)G

2 1

( )

y C

< 

$MY\

2 1

y kx k

= + +

^

( )

$

?W.

A B

0AAIBPCĐ/s: 

HT 149. (A,A1 – 2012) G

4 2 2

2( 1) (1)

y x m x m= − + +

&I[

=K< 

$

!24$K4r/"0I(Đ/s:



HT 150. (B – 2012) G

3 2 3

3 3 (1),

y x mx m= − +

=K< 

$!2

$KAIB0OABB.,C59Đ/s:

= ±



HT 151. (D – 2012) G

3 2 2

2 2

2(3 1) (1),

3 3

y x mx m x m

= − − − +

=K< 

$!2

$K

1 2

;

x x

1

1 2 1 2

2( ) 1.

x x x x

+ + =

Đ/s:



HT 152. (A,A1 – 2013) G  

3 2

3 3 1 (1)

y x x mx= − + + −

& I[

=   K < 

$   !2

= −

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 33



(0; )

+∞

Đ/s:

≤ −



HT 153. (B – 2013) G

3 2

2 3( 1) 6 (1),

y x m x mx= − + +

I[

=K< 

$!2

$KA, BMY\ABI(I[MY\

y x

= +

Đ/s:

0; 2

m m

= =



HT 154. (D – 2013) G

3 2

2 3 ( 1) 1 (1),

y x mx m x= − + − +

I[

=K< 

$MY\

y x

= − +

^!2$?W.fƒ1

m m

< >



-----------------------------------------------------------HẾT-----------------------------------------------------------



 

Bấm Tải xuống để xem toàn bộ.

| 1/34

| | Tải xuống

Preview text:

CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC 2013 - 2014 KHẢO SÁT HÀM SỐ
BIÊN SOẠN: LƯU HUY THƯỞNG
HỌ VÀ TÊN: ………………………………………………………………… LỚP
:………………………………………………………………….
TRƯỜNG :………………………………………………………………… HÀ NỘI, 8/2013
GV.Lưu Huy Thưởng 0968.393.899 CHUYÊN ĐỀ:
KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ
CÁC BÀI TOÁN LIÊN QUAN ĐẾN KHẢO SÁT HÀM SỐ
VẤN ĐỀ 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ 1. Đinh nghĩa:
Hàm số f đồng biến trên K ⇔ (∀x , x ∈ K, x < x ⇒ f (x ) < f (x )) 1 2 1 2 1 2
Hàm số f nghịch biến trên K ⇔ (∀x , x ∈ K, x < x ⇒ f (x ) > f (x )) 1 2 1 2 1 2
2. Điều kiện cần:
Giả sử f có đạo hàm trên khoảng I.
a) Nếu f đồng biến trên khoảng I thì f '(x) ≥ 0, ∀x ∈ I
b) Nếu f nghịch biến trên khoảng I thì f '(x) ≤ 0, ∀x ∈ I
3.Điều kiện đủ:
Giả sử f có đạo hàm trên khoảng I.
a) Nếu f '(x) ≥ 0, ∀x ∈ I ( f '(x) = 0 tại một số hữu hạn điểm) thì f đồng biến trên I.
b) Nếu f '(x) ≤ 0, ∀x ∈ I ( f '(x) = 0 tại một số hữu hạn điểm) thì f nghịch biến trên I.
c) Nếu f '(x) = 0, ∀x ∈ I , ∀x ∈ I thì f không đổi trên I.
Chú ý: Nếu khoảng I được thay bởi đoạn hoặc nửa khoảng thì f phải liên tục trên đó.
Dạng toán 1: Xét tính đơn điệu của hàm số
Phương pháp: Để xét chiều biến thiên của hàm số y = f(x), ta thực hiện các bước như sau:
– Tìm tập xác định của hàm số.
– Tính y′. Tìm các điểm mà tại đó y′ = 0 hoặc y′ không tồn tại (gọi là các điểm tới hạn)
– Lập bảng xét dấu y′ (bảng biến thiên). Từ đó kết luận các khoảng đồng biến, nghịch biến của hàm số.
Bài tập cơ bản
HT 1. Xét tính đơn điệu của các hàm số sau: 1) 3 2
y = x − 2x + x − 2 2) 2
y = (4 − x)(x − 1) 3) 3 2
y = x − 3x + 4x − 1 1 1 1 4) 4 2 y = x − 2x − 1 5) 4 2 y = x − − 2x + 3 6) 4 2 y = x + x − 2 4 10 10 x − 1 1 7) 2x − 1 y = 8) y = 9) y = 1 − x + 5 2 − x 1 − x
10) y = x + 3 + 2 2 − x
11) y = 2x − 1 − 3 − x 12) 2
y = x 2 − x
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 1
GV.Lưu Huy Thưởng 0968.393.899
Dạng toán2: Tìm điều kiện để hàm số luôn đồng biến hoặc nghịch biến trên tập xác định
(hoặc trên từng khoảng xác định)
Cho hàm số y = f (x, m) , m là tham số, có tập xác định D.
• Hàm số f đồng biến trên D ⇔ y′≥ 0, ∀x ∈ D.
• Hàm số f nghịch biến trên D ⇔ y′≤ 0, ∀x ∈ D.
Từ đó suy ra điều kiện của m. Chú ý:
1) y′ = 0 chỉ xảy ra tại một số hữu hạn điểm. 2) Nếu 2
y ' = ax + bx + c thì:  a  = b = 0      a = b = 0      c  ≥ 0   c  ≤ 0  •   y ' 0, x R  ≥ ∀ ∈ ⇔  •y ' 0, x R  ≤ ∀ ∈ ⇔   a  > 0      a < 0     ∆ ≤ 0  ∆ ≤ 0     
3) Định lí về dấu của tam thức bậc hai 2
g(x) = ax + bx + c :
• Nếu ∆< 0 thì g(x) luôn cùng dấu với a. b
• Nếu ∆ = 0 thì g(x) luôn cùng dấu với a (trừ x = − ) 2a
• Nếu ∆> 0 thì g(x) có hai nghiệm x1, x2 và trong khoảng hai nghiệm thì g(x) khác dấu với a, ngoài khoảng hai nghiệm
thì g(x) cùng dấu với a.
4) So sánh các nghiệm x , x của tam thức bậc hai 2
g(x) = ax + bx + c với số 0: 1 2 ∆ > 0   ∆ > 0   •x x 0 P  < < ⇔   > 0
• 0 < x < x ⇔ P 
> 0 • x < 0 < x ⇔ P < 0 1 2  1 2  1 2 S  < 0   S  > 0   5) Để hàm số 3 2
y = ax + bx + cx + d có độ dài khoảng đồng biến (nghịch biến) (x ; x ) bằng d thì ta thực hiện các bước 1 2 sau: • Tính y′.
• Tìm điều kiện để hàm số có khoảng đồng biến và nghịch biến: a  ≠ 0   (1) ∆ > 0 
• Biến đổi x − x = d thành 2 2
(x + x ) − 4x x = d (2) 1 2 1 2 1 2
• Sử dụng định lí Viet đưa (2) thành phương trình theo m.
• Giải phương trình, so với điều kiện (1) để chọn nghiệm. Bài tập cơ bản
HT 2. Tìm m để các hàm số sau luôn đồng biến trên tập xác định (hoặc từng khoảng xác định) của nó: 3 2 1) 3 2 x mx
y = x − 3mx + (m + 2)x − m 2) y = − − 2x + 1 3 2 x + m 3) mx + y = 4) 4 y = x − m x + m
HT 3. Tìm m để hàm số: 1) 3 2
y = x + 3x + mx + m nghịch biến trên một khoảng có độ dài bằng 1. 1 1 2) 3 2 y =
x − mx + 2mx − 3m + 1 nghịch biến trên một khoảng có độ dài bằng 3. 3 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 2
GV.Lưu Huy Thưởng 0968.393.899 1 3) 3 2
y = − x + (m − 1)x + (m + 3)x − 4 đồng biến trên một khoảng có độ dài bằng 4. 3
HT 4. Tìm m để hàm số: 3 1) x 2 y =
+ (m + 1)x − (m + 1)x + 1 đồng biến trên khoảng (1; +∞). 3 2) 3 2
y = x − 3(2m + 1)x + (12m + 5)x + 2 đồng biến trên khoảng (2; +∞). 3) mx + 4 y =
(m ≠ ±2) đồng biến trên khoảng (1; +∞). x + m x + m 4) y =
đồng biến trong khoảng (–1; +∞). x − m
BÀI TẬP TỔNG HỢP – NÂNG CAO 3 2
HT 5. Cho hàm số y = x + 3x − mx − 4 (1).Tìm tất cả các giá trị của tham số m để hàm số (1) đồng biến trên khoảng (− ;
∞ 0) . Đ/s: m ≤ −3
HT 6. Cho hàm số y = x3 2 2
− 3(2m + 1)x + 6m(m + 1)x + 1 có đồ thị (Cm).Tìm m để hàm số đồng biến trên khoảng (2; + )
∞ Đ/s: m ≤ 1 3 2
HT 7. Cho hàm số y = x + (1 − 2m)x + (2 − m)x + m + 2 . Tìm m để hàm đồng biến trên (0;+∞) . Đ/s: 5 m ≤ 4 4 2
HT 8. Cho hàm số y = x − 2mx − 3m + 1 (1), (m là tham số).Tìm m để hàm số (1) đồng biến trên khoảng
(1; 2). Đ/s: m ∈ [ − ; ∞ 1) HT 9. Cho hàm số 3 2
y = x − 3(2m + 1)x + (12m + 5)x + 2 đồng biến trên khoảng (− ; ∞ −1) và (2; + ) ∞ Đ/s: 7 5 − ≤ m ≤ 12 12 HT 10. Cho hàm số 3 2 2
y = x − mx − (2m − 7m + 7)x + 2(m − 1)(2m − 3) . Tìm mđể hàm số đồng biến trên [2; + ) ∞ . Đ/s: 5 1 − ≤ m ≤ 2
---------------------------------------------------------
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 3
GV.Lưu Huy Thưởng 0968.393.899
VẤN ĐỀ 2: CỰC TRỊ CỦA HÀM SỐ
I. KIẾN THỨC CẦN NHỚ
I.Khái niệm cực trị của hàm số
Giả sử hàm số f xác định trên tập D (D ⊂ ℝ) và x ∈ D 0
1) x – điểm cực đại của f nếu tồn tại khoảng (a;b) ⊂ D và x ∈ (a;b) sao cho 0 0
f (x) < f (x ) , ∀x ∈ (a;b) \ {x }. 0 0
Khi đó f (x ) được gọi là giá trị cực đại (cực đại) của f . 0
2) x – điểm cực tiểu của f nếu tồn tại khoảng (a;b) ⊂ D và x ∈ (a;b) sao cho 0 0
f (x) > f (x ) , ∀x ∈ (a;b) \ {x }. 0 0
Khi đó f (x ) được gọi là giá trị cực tiểu (cực tiểu) của f . 0
3) Nếu x là điểm cực trị của f thì điểm (x ; f (x )) được gọi là điểm cực trị của đồ thị hàm số f . 0 0 0
II. Điều kiện cần để hàm số có cực trị
Nếu hàm số f có đạo hàm tại x và đạt cực trị tại điểm đó thì f '(x ) = 0 . 0 0
Chú ý: Hàm số f chỉ có thể đạt cực trị tại những điểm mà tại đó đạo hàm bằng 0 hoặc không có đạo hàm.
III. Điểu kiện đủ để hàm số có cực trị
1. Định lí 1: Giả sử hàm số f liên tục trên khoảng (a;b) chứa điểm x và có đạo hàm trên (a;b) \ {x } 0 o
1) Nếu f '(x) đổi dấu từ âm sang dương khi x đi qua x thì f đạt cực tiểu tại x . 0 0
2) Nếu f '(x) đổi dấu từ dương sang âm khi x đi qua x thì f đạt cực đại tại x 0 0
2. Định lí 2: Giả sử hàm số f có đạo hàm trên khoảng (a;b) chứa điểm x , f '(x ) = 0 và có đạo hàm cấp hai khác 0 tại 0 0 điểm x . 0
1) Nếu f "(x ) < 0 thì f đạt cực đại tại x . 0 0
2) Nếu f "(x ) > 0 thì f đạt cực tiểu tại x . 0 0 II. CÁC DẠNG TOÁN
Dạng toán 1: Tìm cực trị của hàm số
Qui tắc 1: Dùng định lí 1.
• Tìm f '(x) .
• Tìm các điểm x (i = 1,2,...) mà tại đó đạo hàm bằng 0 hoặc không có đạo hàm. i
• Xét dấu f '(x) . Nếu f '(x) đổi dấu khi x đi qua x thì hàm số đạt cực trị tại x . i i
Qui tắc 2: Dùng định lí 2.
• Tính f '(x)
• Giải phương trình f '(x) = 0 tìm các nghiệm x (i = 1,2,...) i
• Tính f "(x) và f "(x ) (i = 1,2,...). i
Nếu f "(x ) < 0 thì hàm số đạt cực đại tại x .
Nếu f "(x ) > 0 thì hàm số đạt cực tiểu tại x i i i i
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 4
GV.Lưu Huy Thưởng 0968.393.899 Bài tập cơ bản
HT 11. Tìm cực trị của các hàm số sau: 1 1) 2 3
y = 3x − 2x 2) 3 2
y = x − 2x + 2x − 1 3) 3 2
y = − x + 4x − 15x 3 4 4 4) x 2 x y = − x + 3 5) 4 2
y = x − 4x + 5 6) 2 3 y = − + x + 2 2 2 2 2 2 7) x − + 3x + 6 3x + 4x + 5 x − 2x − 15 y = 8) y = 9) y = x + 2 x + 1 x − 3 2 4x + 2x − 1 2 3x + 4x + 4 10) 3 4
y = (x − 2) (x + 1) 11) y = 12) y = 2 2x + x − 3 2 x + x + 1 13) 2 y = x x − 4 14) 2
y = x − 2x + 5 15) 2
y = x + 2x − x
Dạng toán 2: Tìm điều kiện để hàm số có cực trị
1. Nếu hàm số y = f (x) đạt cực trị tại điểm x thì f '(x ) = 0 hoặc tại x không có đạo hàm. 0 0 0
2. Để hàm số y = f (x) ) đạt cực trị tại điểm x thì f '(x) đổi dấu khi x đi qua x . 0 0 Chú ý: • Hàm số bậc ba 3 2
y = ax + bx + cx + d có cực trị ⇔ Phương trình y ' = 0 có hai nghiệm phân biệt.
Khi đó nếu x0 là điểm cực trị thì ta có thể tính giá trị cực trị y(x0) bằng hai cách: + 3 2
y(x ) = ax +bx + cx + d 0 0 0 0
+ y(x ) = Ax + B , trong đó Ax + B là phần dư trong phép chia y cho y′. 0 0 Bài tập cơ bản
HT 12. Tìm m để hàm số: 1) 3 2
y = (m + 2)x + 3x + mx − 5 có cực đại, cực tiểu. 2) 3 2 2
y = x − 3(m − 1)x + (2m − 3m + 2)x − m(m − 1) có cực đại, cực tiểu. 3) 3 2 2 3
y = x − 3mx + 3(m − 1)x − m 4) 3 2
y = 2x − 3(2m + 1)x + 6m(m + 1)x + 1 x = 2 5) 3 2 2
y = x − 3mx + (m − 1)x + 2 đạt cực đại tại 1 6) 4 2 y = m
− x + 2(m − 2)x + m − 5 có một cực đại x = . 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 5
GV.Lưu Huy Thưởng 0968.393.899 HT 13. Tìm , a , b , c d để hàm số: 1 1) 3 2
y = ax + bx + cx + d đạt cực tiểu bằng 0 tại x = 0 và đạt cực đại bằng 4 tại x = 27 3 2) 4 2
y = ax + bx + c có đồ thị đi qua gốc toạ độ O và đạt cực trị bằng –9 tại x = 3 .
HT 14. Tìm m để các hàm số sau không có cực trị: 1) 3 2
y = x − 3x + 3mx + 3m + 4 2) 3 2
y = mx + 3mx − (m − 1)x − 1
HT 15. Tìm m để hàm số : 1) 3 2 2 2
y = x + 2(m − 1)x + (m − 4m + 1)x − 2(m + 1) đạt cực trị tại hai điểm x , x sao cho: 1 2 1 1 1 + = (x + x ) . 1 2 x x 2 1 2 1 2) 3 2 y =
x − mx + mx − 1 đạt cực trị tại hai điểm x , x 2 sao cho: x − x ≥ 8 . 3 1 2 1 2 1 1 3) 3 2 y =
mx − (m − 1)x + 3(m − 2)x +
đạt cực trị tại hai điểm x , x sao cho: x + 2x = 1 . 3 3 1 2 1 2
HT 16. Tìm m để đồ thị hàm số : 2 1) 3 2 m y = x −
+ mx − 4 có hai điểm cực trị là A, B và 2 900 AB = . 729 2) 4 2
y = x − mx + 4x + m có 3 điểm cực trị là A, B, C và tam giác ABC nhận gốc toạ độ O làm trọng tâm.
BÀI TẬP TỔNG HỢP VÀ NÂNG CAO
HT 17. Tìm m để đồ thị hàm số : 1) 3 2
y = 2x + mx − 12x − 13 có hai điểm cực trị cách đều trục tung. Đ/s: m = 0 2) 3 2 3
y = x − 3mx + 4m có các điểm cực đại, cực tiểu đối xứng nhau qua đường phân giác thứ nhất. Đ/s: 1 m = ± 2 3) 3 2 3
y = x − 3mx + 4m có các điểm cực đại, cực tiểu ở về một phía đối với đường thẳng d : 3x − 2y + 8 = 0 .   Đ/s: 4 m  ∈ −  ;1 \ {0}  3 
HT 18. Tìm m để đồ thị hàm số: 1) 3 2
y = x + 3x + m có 2 điểm cực trị tại A, B sao cho 0 AOB = 120 Đ/s: 1 − 2 + 132 m = 0, m = 3   2) 4 2 3 9
y = x − 2mx + 2 có 3 điểm cực trị tạo thành 1 tam giác có đường tròn ngoại tiếp đi qua D  ;  Đ/s:  m = 1 5 5
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 6
GV.Lưu Huy Thưởng 0968.393.899 3) 4 2 2
y = x + 2mx + m + m có 3 điểm cực trị tạo thành 1 tam giác có một góc bằng 0 120 . Đ/s: 1 m = − 3 3 4) 4 2 4
y = x − 2mx + 2m + m có 3 điểm cực trị tạo thành 1 tam giác có diện tích bằng 4. Đ/s: 3 m = 2
HT 19. Tìm m để hàm số: 1) 3
y = x − 3mx + 2 có hai điểm cực trị và đường tròn qua 2 điểm cực trị cắt đường tròn tâm I (1;1) bán kính ±
bằng 1 tại hai điểm A, B sao cho diện tích tam giác IAB lớn nhất. Đ/s: 2 3 m = 2 2) 3 2
y = 4x + mx − 3x có hai điểm cực trị x , x thỏa mãn: x 4 + x = 0 Đ/s: 9 m = ± 1 2 1 2 2
HT 20. Tìm m để hàm số: 1) 3 2
y = 2x + 3(m − 1)x + 6(m − 2)x − 1 có đường thẳng đi qua hai điểm cực trị song song với đường thẳng y = 4
− x −1 . Đ/s: m = 5 2) 3 2
y = 2x + 3(m − 1)x + 6m(1 − 2m)x có các điểm cực đại, cực tiểu của đồ thị nằm trên đường thẳng y = 4 − x . Đ/s: m = 1 3) 3 2
y = x + mx + 7x + 3 có đường thẳng đi qua các điểm cực đại, cực tiểu vuông góc với đường thẳng
y = 3x − 7 . Đ/s: 3 10 m = ± 2 1 5 4) 3 2 2
y = x − 3x + m x + m có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng (∆): y = x − . 2 2 Đ/s: m = 0
-------------------------------------------------------
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 7
GV.Lưu Huy Thưởng 0968.393.899
VẤN ĐỀ 3: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ
I. KIẾN THỨC CẦN NHỚ
1. Các bước khảo sát sự biến thiên và vẽ đồ thị của hàm số
• Tìm tập xác định của hàm số.
• Xét sự biến thiên của hàm số:
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận (nếu có). + Tính y ' .
+ Tìm các điểm tại đó đạo hàm y ' = 0 hoặc không xác định.
+ Lập bảng biến thiên ghi rõ dấu của đạo hàm, chiều biến thiên, cực trị của hàm số.
• Vẽ đồ thị của hàm số:
+ Tìm điểm uốn của đồ thị (đối với hàm số bậc ba và hàm số trùng phương).
+ Vẽ các đường tiệm cận (nếu có) của đồ thị.
+ Xác định một số điểm đặc biệt của đồ thị như giao điểm của đồ thị với các trục toạ độ (trong trường hợp đồ
thị không cắt các trục toạ độ hoặc việc tìm toạ độ giao điểm phức tạp thì có thể bỏ qua). Có thể tìm thêm một số
điểm thuộc đồ thị để có thể vẽ chính xác hơn.
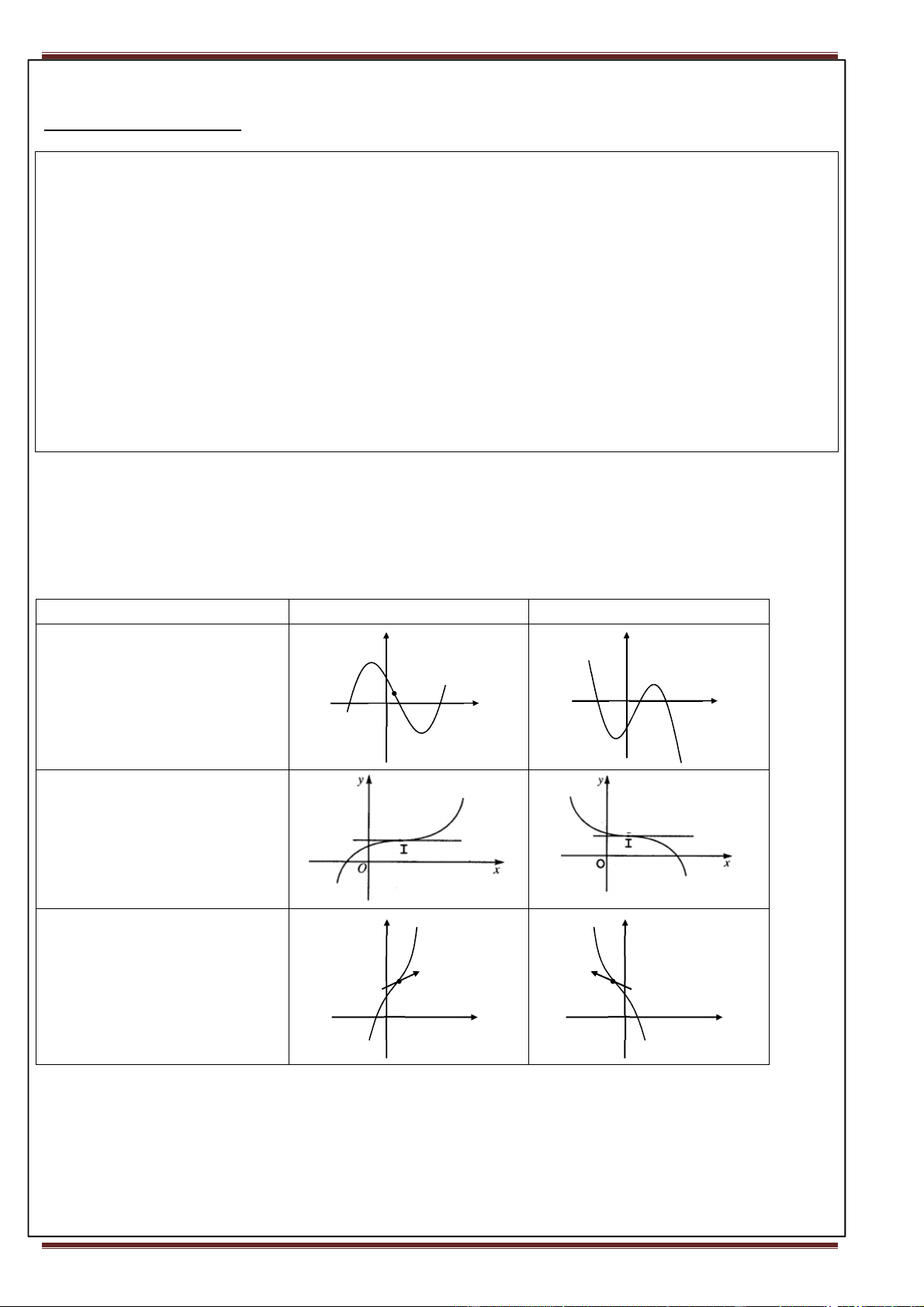
2. Khảo sát sự biến thiên và vẽ đồ thị hàm bậc ba 3 2
y = ax + bx + cx + d (a ≠ 0)
• Tập xác định D = ℝ .
• Đồ thị luôn có một điểm uốn và nhận điểm uốn làm tâm đối xứng. • Các dạng đồ thị: a > 0 a < 0
y ' = 0 có 2 nghiệm phân biệt y y ⇔ 2
∆ ' = b − 3ac > 0 I 0 x 0 x I
y ' = 0 có nghiệm kép ⇔ 2
∆ ' = b − 3ac = 0 y ' = 0 vô nghiệm y y ⇔ 2
∆ ' = b − 3ac < 0 I I 0 x 0 x
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 8
GV.Lưu Huy Thưởng 0968.393.899
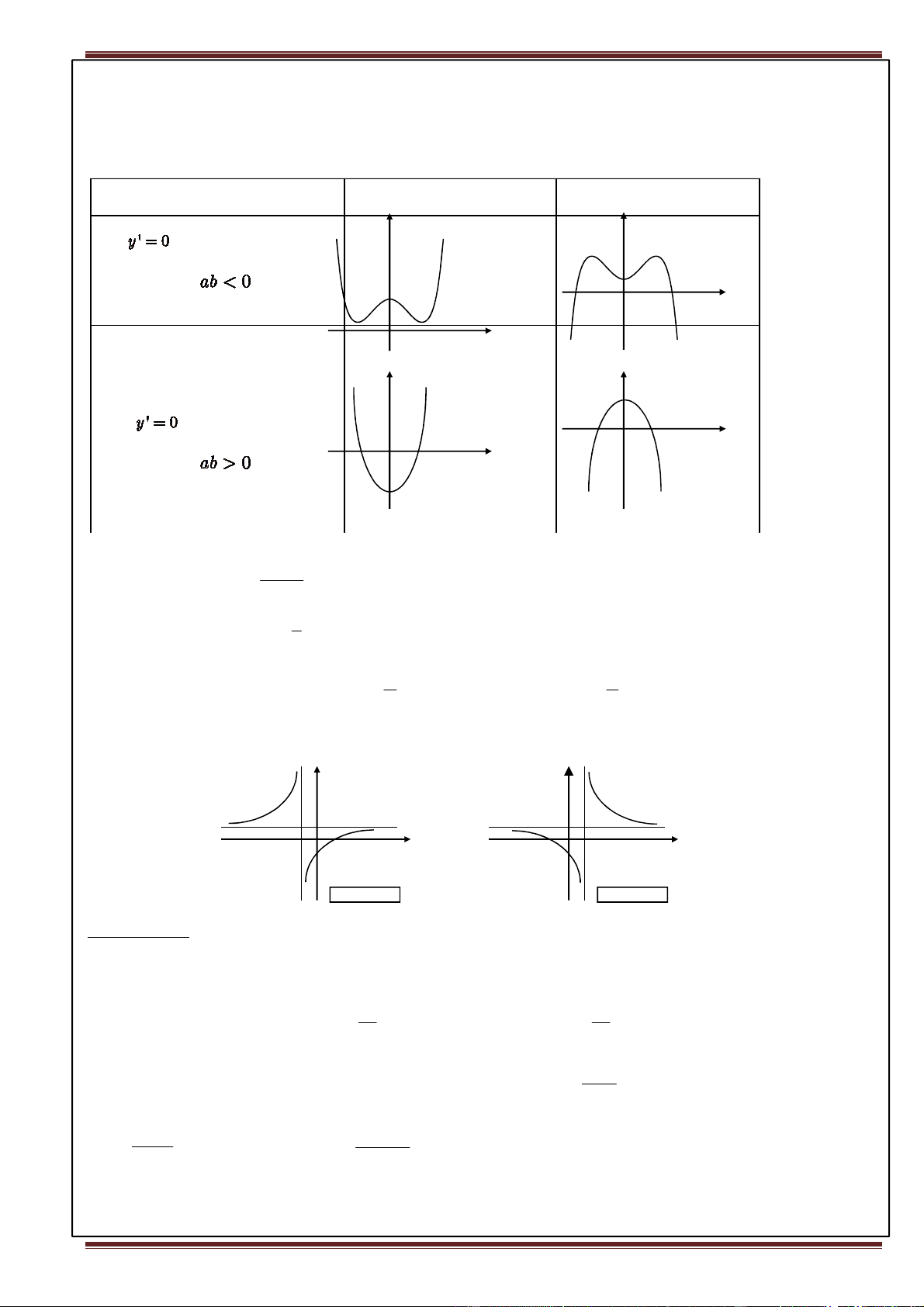
3. Hàm số trùng phương 4 2
y = ax + bx + c (a ≠ 0)
• Tập xác định D = ℝ
• Đồ thị luôn nhận trục tung làm trục đối xứng. • Các dạng đồ thị: a > 0 a < 0 y y có 3 nghiệm phân biệt ⇔ 0 x 0 x y y chỉ có 1 nghiệm 0 x ⇔ 0 x
4. Hàm số nhất biến ax + b y =
(c ≠ 0;ad −bc ≠ 0) cx + d  d 
• Tập xác định D = ℝ \   −    c    d
• Đồ thị có một tiệm cận đứng là x = − a
và một tiệm cận ngang là y =
. Giao điểm của hai tiệm cận là tâm đối c c
xứng của đồ thị hàm số. • Các dạng đồ thị: y y 0 x 0 x ad – bc > ad – bc < Bài tập cơ bản
HT 21. Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau: 3 3 1. 3 2 x x y = x − + 3x − 1 2. 2 y = − x + x − 1 3. 2 y = − + x − 2x + 1 3 3 4. 4 2 x −
y = x − 2x + 2 5. 4 2 y = x − − x + 1 6. 1 y = x + 1 2x − 1 7. x − y = 8. 1 y = x − 1 −2x + 1
----------------------------------------------------
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 9
GV.Lưu Huy Thưởng 0968.393.899
VẤN ĐỀ 4: SỰ TƯƠNG GIAO CỦA CÁC ĐỒ THỊ
Dạng toán 1: Dùng đồ thị hàm số biện luận số nghiệm phương trình
• Cơ sở của phương pháp: Xét phương trình:
f (x) = g(x) (1)
Số nghiệm của phương trình (1) = Số giao điểm của (C ) : y = f (x) và (C ) : y = g(x) 1 2
Nghiệm của phương trình (1) là hoành độ giao điểm của (C ) : y = f (x) và (C ) : y = g(x) 1 2
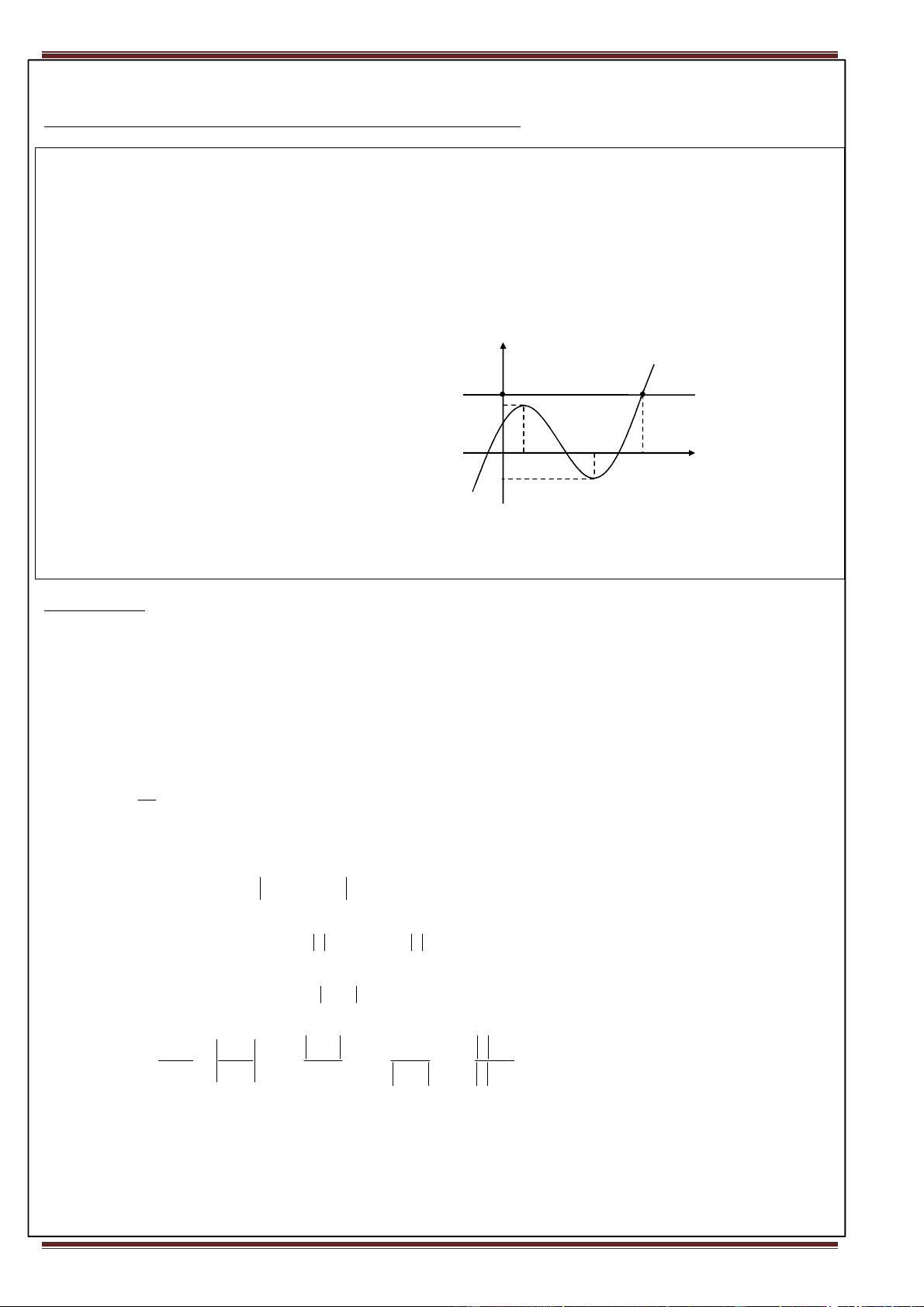
• Để biện luận số nghiệm của phương trình F(x,m) = 0 (*) bằng đồ thị ta biến đổi (*) về dạng sau:
F(x, m) = 0 ⇔ f (x) = g(m) (1) y (C)
Khi đó (1) có thể xem là phương trình hoành độ g(m A (4) : y = yCĐ g(m)
giao điểm của hai đường:
(C ) : y = f (x) và d : y = g(m) xA x yCT
•d là đường thẳng cùng phương với trục hoành.
• Dựa vào đồ thị (C) ta biện luận số giao điểm
của (C) và d . Từ đó suy ra số nghiệm của (1) Bài tập cơ bản
HT 22. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. Dùng đồ thị (C) biện luận theo m số nghiệm của phương trình: 1) 3 3
y = x − 3x + 1; x − 3x + 1 − m = 0 2) 3 3 y = x −
+ 3x − 1; x − 3x + m + 1 = 0 3) 3 3 2
y = x − 3x + 1; x − 3x − m − 2m − 2 = 0 4) 3 3 y = x −
+ 3x − 1; x − 3x + m + 4 = 0 4 5) x 2 4 2 y = −
+ 2x + 2; x − 4x − 4 + 2m = 0 6) 4 2 4 2
y = x − 2x + 2; x − 2x − m + 2 = 0 2
HT 23. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. Dùng đồ thị (C) biện luận theo m số nghiệm của phương trình: 1) 3 2 3 2
(C ) : y = x − 3x + 6;
x − 3x + 6 − m + 3 = 0 3 2) 3 2 2
(C ) : y = 2x − 9x + 12x − 4; 2 x − 9x + 12 x + m = 0 3) 2 2 2
(C ) : y = (x + 1) (2 − x); (x + 1) 2 − x = (m + 1) (2 − m) x − 1 x − 1 4) x − 1 x − 1 x − 1 (C ) : y = = m; = m; = m; = m x + 1 x + 1 x + 1 x + 1 x + 1
------------------------------------------------
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 10
GV.Lưu Huy Thưởng 0968.393.899
Dạng toán 2: Tìm điều kiện tương giao giữa các đồ thị
1.Cho hai đồ thị (C ) : y = f (x) và (C ) : y = g(x). Để tìm hoành độ giao điểm của (C ) và (C ) ta giải phương trình: 1 2 1 2
f (x) = g(x) (*) (gọi là phương trình hoành độ giao điểm).
Số nghiệm của phương trình (*) bằng số giao điểm của hai đồ thị.
2. Đồ thị hàm số bậc ba 3 2
y = ax + bx + cx + d (a ≠ 0) cắt trục hoành tại 3 điểm phân biệt ⇔ Phương trình 3 2
ax + bx + cx + d = 0 có 3 nghiệm phân biệt. Bài tập cơ bản
HT 24. Tìm toạ độ giao điểm của các đồ thị của các hàm số sau:  2  x 3  x y  = − + 3x − 2 − 4  y  =  3 1)  2 2 y  = 4x − 3x  2)  x − 1 3)   x 1  2 y  = x − + 2 y  = + y  = x − + 2x + 4      2 2 
HT 25. Tìm m để đồ thị các hàm số: 1) 2 2
y = (x − 1)(x − mx + m − 3) cắt trục hoành tại ba điểm phân biệt. 2) 3 2
y = mx + 3mx − (1 − 2m)x − 1 cắt trục hoành tại ba điểm phân biệt. 3) 3 2
y = x + 2x + mx + 2m; y = x + 2 cắt nhau tại ba điểm phân biệt. 4) 3 2 2
y = x + 2x − 2x + 2m − 1; y = 2x − x + 2 cắt nhau tại ba điểm phân biệt.
HT 26. Tìm m để đồ thị các hàm số: 1) 4 2
y = x − 2x − 1; y = m cắt nhau tại bốn điểm phân biệt. 2) 4 2 3
y = x − m(m + 1)x + m cắt trục hoành tại bốn điểm phân biệt. 3) 4 2 2
y = x − (2m − 3)x + m − 3m cắt trục hoành tại bốn điểm phân biệt.
HT 27. Biện luận theo m số giao điểm của các đồ thị của các hàm số sau:    3  3  x  1) y
 = x − 3x − 2  y  = − + 3x  2)  3 y  = m(x − 2)    y  = m(x − 3) 
HT 28. Tìm m để đồ thị của các hàm số: 3x + 1 1) y =
; y = x + 2m cắt nhau tại hai điểm phân biệt A, B. Khi đó tìm m để đoạn AB ngắn nhất. x − 4 4x − 1 2) y = ;y = x
− + m cắt nhau tại hai điểm phân biệt A, B. Khi đó tìm m để đoạn AB ngắn nhất. 2 − x
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 11
GV.Lưu Huy Thưởng 0968.393.899
BÀI TẬP TỔNG HỢP VÀ NÂNG CAO
HT 29. Tìm m để hàm số: 1) 2x − 1 y =
(C ) cắt đường thẳng ∆ : y = x + m tại hai điểm phân biệt A, B sao cho AB = 2 2 Đ/s: m = 1 − ;m = 7 x + 1 x − 1 2) y =
(C ) cắt đường thẳng ∆ : y = x
− + m tại hai điểm phân biệt A, B sao cho A, B có độ dài nhỏ nhất. 2x Đ/s: 1 m = 2 2x − 1 3) y =
(C ) cắt đường thẳng ∆ : y = x + m tại hai điểm phân biệt A, B sao cho tam giác OAB vuông tại O. x − 1 Đ/s: m = 2 − 4) 2mx − 2m − 3 y =
(C ) cắt đường thẳng ∆ : y = x − 2 tại hai điểm phân biệt A, B sao cho 0 AOB = 45 x + 2
(1 + m)x + 2(1 − m) OA OB 5) y =
cắt đường thẳng ∆ : y = x tại hai điểm phân biệt A, B sao cho: + = 4 x OB OA 3x + 1 6) y =
cắt đường thẳng ∆ : y = (m + 1)x + m − 2 tại hai điểm phân biệt A, B sao cho tam giác OAB có diện tích x − 1 3 bằng . 2 7) x + 1 y =
(C ) cắt đường thẳng ∆ : 2mx − 2y + m + 1 = 0, cắt đồ thị (C) tại hai điểm phân biệt A, B sao cho biểu 2x + 1 thức 2 2
P = OA +OB đạt giá trị nhỏ nhất. x + 2
HT 30. Cho hàm số y =
(C ) Gọi I là giao điểm của hai tiệm cận. Tìm trên đồ thị (C) hai điểm A, B sao cho tam giác x − 1
IAB nhận H (4;−2) làm trực tâm. Đ/s: (2; 4),( 2 − ; 0) x − + 1
HT 31. Cho hàm số y =
(C ) Xác định m để đường thẳng ∆ : y = x + m cắt đồ thị (C) tại hai điểm phân biệt 2x − 1
có hoành độ x , x sao cho tổng f '(x ) + f '(x ) đạt giá trị lớn nhất. 1 2 1 2 x − HT 32. Cho hàm số 1 y =
(C ) Xác định m để đường thẳng ∆ : y = x + m cắt đồ thị (C) tại hai điểm phân biệt có 2x + 1
hoành độ x , x sao cho tổng f '(x ) + f '(x ) đạt giá trị nhỏ nhất. 1 2 1 2 3x − 4
HT 33. Cho hàm số y =
(C ) Xác định tọa độ các điểm trên đồ thị (C) sao cho tổng khoảng cách từ điểm đó đến 2x − 3
trục hoành gấp 2 lần khoảng cách từ điểm đó đến tiệm cận đứng.
-----------------------------------------------------
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 12
GV.Lưu Huy Thưởng 0968.393.899
VẤN ĐỀ 5: SỰ TIẾP XÚC CỦA HAI ĐƯỜNG CONG
1. Ý nghĩa hình học của đạo hàm: Đạo hàm của hàm số y = f (x) tại điểm x là hệ số góc của tiếp tuyến với đồ thị (C) của 0
hàm số tại điểm M x ; f (x ) . 0 ( 0 0 )
Khi đó phương trình tiếp tuyến của (C) tại điểm M x ; f (x ) là: 0 ( 0 0 )
y − y = f '(x )(x − x )
(y = f (x )) 0 0 0 0 0
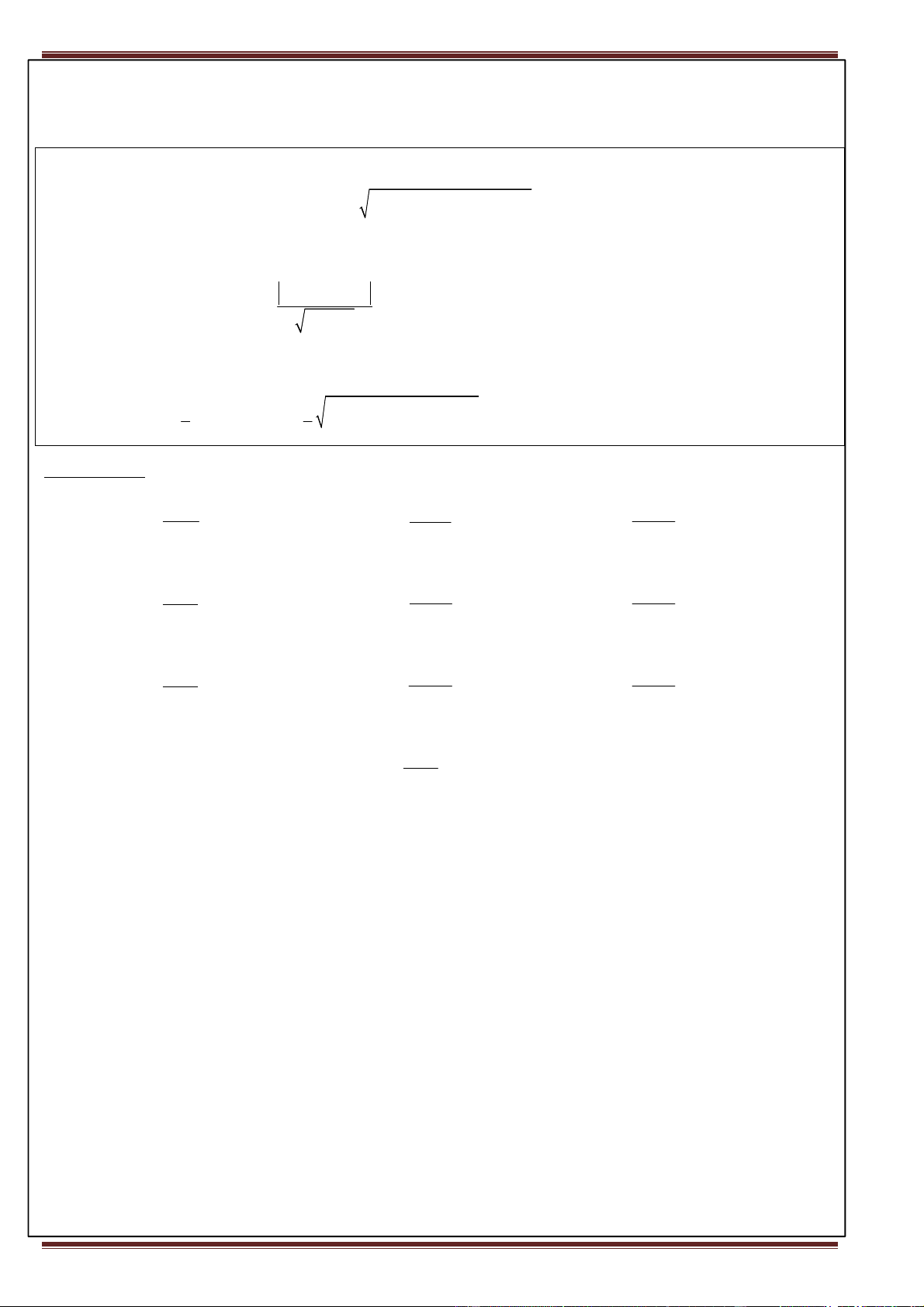
2. Điều kiện cần và đủ để hai đường (C ) : y = f (x) và (C ) : y = g(x)tiếp xúc nhau là hệ phương trình sau có nghiệm: 1 2
 f (x) = g(x)   (*)
f '(x) = g '(x) 
Nghiệm của hệ (*) là hoành độ của tiếp điểm của hai đường đó.
3. Nếu (C ) : y = px + q và 2
(C ) : y = ax +bx + c thì (C 1 2
1) và (C2) tiếp xúc nhau ⇔ phương trình 2
ax + bx + c = px + q có nghiệm kép.
Dạng toán 1: Lập phương trình tiếp tuyến của đường cong (C): y = f(x)
Bài toán 1: Viết phương trình tiếp tuyến ∆ của (C ) : y = f (x) tại điểm M x ;y : 0 ( 0 0 )
• Nếu cho x thì tìm y = f(x ) 0 0 0
Nếu cho y thì tìm x là nghiệm của phương trình f (x) = y . 0 0 0
• Tính y ' = f '(x). Suy ra y '(x ) = f '(x ) . 0 0
• Phương trình tiếp tuyến ∆ là: y −y = f '(x )(x − x ) 0 0 0
Bài toán 2: Viết phương trình tiếp tuyến ∆ của (C ) : y = f (x) biết ∆ có hệ số góc k cho trước.
Cách 1: Tìm toạ độ tiếp điểm.
• Gọi M(x0; y0) là tiếp điểm. Tính f′ (x0).
•∆ có hệ số góc k ⇒ f′ (x0) = k (1)
• Giải phương trình (1), tìm được x0 và tính y0 = f(x0). Từ đó viết phương trình của ∆.
Cách 2: Dùng điều kiện tiếp xúc.
• Phương trình đường thẳng ∆ có dạng: y = kx + m.
•∆ tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:
f (x) = kx + m   (*)
f '(x) = k 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 13
GV.Lưu Huy Thưởng 0968.393.899
• Giải hệ (*), tìm được m. Từ đó viết phương trình của ∆.
Chú ý: Hệ số góc k của tiếp tuyến ∆ có thể được cho gián tiếp như sau:
+ ∆ tạo với chiều dương trục hoành góc α thì k = tanα
+ ∆ song song với đường thẳng d: y = ax + b thì k = a 1
+ ∆ vuông góc với đường thẳng d: y = ax + b (a ≠ 0) thì k = − a k −a
+ ∆ tạo với đường thẳng d: y = ax + b một góc α thì = tan α 1 + ka
Bài toán 3: Viết phương trình tiếp tuyến ∆ của (C): y = f(x), biết ∆ đi qua điểm (
A x ; y ) . A A
Cách 1:Tìm toạ độ tiếp điểm.
• Gọi M(x0; y0) là tiếp điểm. Khi đó: y0 = f(x0), y′0 = f′ (x0).
• Phương trình tiếp tuyến ∆ tại M: y – y0 = f′ (x0).(x – x0) •∆ đi qua (
A x ; y ) nên: y A A
A – y0 = f′ (x0).(xA – x0) (2)
• Giải phương trình (2), tìm được x0. Từ đó viết phương trình của ∆.
Cách 2: Dùng điều kiện tiếp xúc.
• Phương trình đường thẳng ∆ đi qua (
A x ; y ) và có hệ số góc k: y – y A A A = k(x – x1)
•∆ tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:
f (x) = k(x − x ) + y  A A  (*)
f '(x) = k 
• Giải hệ (*), tìm được x (suy ra k). Từ đó viết phương trình tiếp tuyến ∆. Bài tập cơ bản
HT 34. Viết phương trình tiếp tuyến của (C) tại điểm được chỉ ra: 1) 3 2
(C ) : y = 3x − x − 7x + 1 tại A(0; 1) 2) (C ) : 4 2
y = x − 2x + 1 tại B(1; 0) 3x + 4 3) (C): y = tại C(1; –7) 2x − 3 x + 1 4) (C): y =
tại các giao điểm của (C) với trục hoành, trục tung. x − 2 5) (C): 2
y = 2x − 2x + 1 tại các giao điểm của (C) với trục hoành, trục tung. 6) (C): 3
y = x − 3x + 1 tại điểm uốn của (C).
HT 35. Viết phương trình tiếp tuyến của (C) tại các giao điểm của (C) với đường được chỉ ra: 1) (C): 3 2
y = 2x − 3x + 9x − 4 và d: y = 7x + 4 .
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 14
GV.Lưu Huy Thưởng 0968.393.899 2) (C): 3 2
y = 2x − 3x + 9x − 4 và (P): 2 y = x − + 8x − 3 .
HT 36. Tính diện tích tam giác chắn hai trục toạ độ bởi tiếp tuyến của đồ thị (C) tại điểm được chỉ ra: 5x + 11 (C): y = tại điểm A có xA = 2 . 2x − 3
HT 37. Tìm m để tiếp tuyến của đồ thị (C) tại điểm được chỉ ra chắn hai trục toạ độ một tam giác có diện tích bằng S cho trước: 2x + m 1 1) (C): y =
tại điểm A có xA = 2 và S = . x − 1 2 9 2) (C): x − 3m y =
tại điểm B có xB = –1 và S = . x + 2 2 3) (C): 3
y = x + 1 − m(x + 1) tại điểm C có xC = 0 và S = 8.
HT 38. Viết phương trình tiếp tuyến ∆ của (C), biết ∆ có hệ số góc k được chỉ ra: 2x − 1 1) (C): 3 2
y = 2x − 3x + 5 ; k = 12 2) (C): y = ; k = –3 x − 2
HT 39. Viết phương trình tiếp tuyến ∆ của (C), biết ∆ song song với đường thẳng d cho trước: 3 2x − 1 3 1) (C): x 2 y =
− 2x + 3x + 1 ; d: y = 3x + 2 2) (C): y =
; d: y = − x + 2 3 x − 2 4
HT 40. Viết phương trình tiếp tuyến ∆ của (C), biết ∆ vuông góc với đường thẳng d cho trước: 3 x 2x − 1 1) (C): x 2 y =
− 2x + 3x + 1 ; d: y = − + 2 2) (C): y = ; d: y = x 3 8 x − 2
HT 41. Tìm m để tiếp tuyến ∆ của (C) tại điểm được chỉ ra song song với đường thẳng d cho trước: 2 1) (C):
(3m + 1)x − m + m y =
(m ≠ 0) tại điểm A có yA = 0 và d: y = x −10 . x + m
HT 42. Viết phương trình tiếp tuyến ∆ của (C), biết ∆đi qua điểm được chỉ ra: 1) (C): 3 y = x −
+ 3x − 2 ; A(2; –4) 2) (C): 3
y = x − 3x + 1 ; B(1; –6) 1 3  3
3) (C): y = ( − x )2 2 2 ; C(0; 4) 4) (C): 4 2 y = x − 3x + ; D 0;  2 2  2 x + 2 3x + 4 5) (C): y = ; E(–6; 5) 6) (C): y = ; F(2; 3) x − 2 x − 1
HT 43. Tìm m để hai đường (C1), (C2) tiếp xúc nhau: 1) 3 2
(C ) : y = x + (3 + m)x + mx − 2; (C ) : trục hoành 1 2 2) 3 2
(C ) : y = x − 2x − (m − 1)x + m; (C ) : trục hoành 1 2 3) 3
(C ) : y = x + m(x + 1) + 1; (C ) : y = x + 1 1 2 4) 3 2
(C ) : y = x + 2x + 2x − 1; (C ) : y = x + m 1 2
HT 44. Tìm m để hai đường (C1), (C2) tiếp xúc nhau: 1) 4 2 2
(C ) : y = x + 2x + 1; (C ) : y = 2mx + m 1 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 15
GV.Lưu Huy Thưởng 0968.393.899 2) 4 2 2
(C ) : y = x −
+ x − 1; (C ) : y = x − + m 1 2 1 9 3) 4 2 2
(C ) : y = − x + 2x + ; (C ) : y = x − + m 1 2 4 4 4) 2 2 2
(C ) : y = (x + 1) (x − 1) ; (C ) : y = 2x + m 1 2 2 5)
(2m − 1)x − m (C ) : y =
; (C ) : y = x 1 2 x − 1
Dạng toán 2: Tìm những điểm trên đường thẳng d mà từ đó có thể vẽ được 1, 2, 3, … tiếp tuyến với đồ thị (C):
y = f (x)
Giả sử d: ax + by +c = 0. M(xM; yM) ∈ d.
• Phương trình đường thẳng ∆ qua M có hệ số góc k: y = k(x – xM) + yM
•∆ tiếp xúc với (C) khi hệ sau có nghiệm:
f (x) = k(x − x ) + y (1)  M M 
f '(x) = k (2) 
• Thế k từ (2) vào (1) ta được:
f(x) = (x – xM).f′ (x) + yM (C)
• Số tiếp tuyến của (C) vẽ từ M = Số nghiệm x của (C) Bài tập cơ bản
HT 45. Tìm các điểm trên đồ thị (C) mà từ đó vẽ được đúng một tiếp tuyến với (C): 1) 3 2
(C ) : y = x − + 3x − 2 2) 3
(C ) : y = x − 3x + 1
HT 46. Tìm các điểm trên đường thẳng d mà từ đó vẽ được đúng một tiếp tuyến với (C): x + 1 x + 3 1) (C ) : y = ; d là trục tung 2) (C ) : y = ; d: y = 2x + 1 x − 1 x − 1
HT 47. Tìm các điểm trên đường thẳng d mà từ đó vẽ được ít nhất một tiếp tuyến với (C): 2x + 1 3x + 4 1) (C ) : y = ; d: x = 3 2) (C ) : y = ; d: y = 2 x − 2 4x − 3
HT 48. Tìm các điểm trên đường thẳng d mà từ đó vẽ được ba tiếp tuyến với (C): 1) 3 2
(C ) : y = x − + 3x − 2 ; d: y = 2 2) 3
(C ) : y = x − 3x ; d: x = 2 3) 3
(C ) : y = x −
+ 3x + 2 ; d là trục hoành 4) 3
(C ) : y = x − 12x + 12 ; d: y = –4
HT 49. Từ điểm A có thể kẻ được bao nhiêu tiếp tuyến với (C): 1 4 4 1) 3 2
(C ) : y = x − 9x + 17x + 2 ; A(–2; 5) 2) 3 2 (C ) : y =
x − 2x + 3x + 4; A ;  3 9 3
HT 50. Từ một điểm bất kì trên đường thẳng d có thể kẻ được bao nhiêu tiếp tuyến với (C): 1) 3 2
(C ) : y = x − 6x + 9x − 1 ; d : x = 2 2) 3
(C ) : y = x − 3x ; d : x = 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 16
GV.Lưu Huy Thưởng 0968.393.899
Dạng toán 3: Tìm những điểm mà từ đó có thể vẽ được 2 tiếp tuyến với đồ thị (C): y = f(x) và 2 tiếp tuyến đó vuông góc với nhau Gọi M(xM; yM).
• Phương trình đường thẳng ∆ qua M có hệ số góc k: y = k(x – xM) + yM
•∆ tiếp xúc với (C) khi hệ sau có nghiệm:
f (x) = k(x − x ) + y (1)  M M 
f '(x) = k (2) 
• Thế k từ (2) vào (1) ta được:
f(x) = (x – xM).f′ (x) + yM (C)
• Qua M vẽ được 2 tiếp tuyến với (C) ⇔ (C) có 2 nghiệm phân biệt x1, x2.
• Hai tiếp tuyến đó vuông góc với nhau ⇔ f′ (x1).f′ (x2) = –1
Từ đó tìm được M.
Chú ý: Qua M vẽ được 2 tiếp tuyến với (C) sao cho 2 tiếp điểm nằm về hai phía với trục hoành thì (
 3) coù 2 nghieäm phaân bieät  
f (x ).f (x ) < 0  1 2  Bài tập cơ bản
HT 51. Chứng minh rằng từ điểm A luôn kẻ được hai tiếp tuyến với (C) vuông góc với nhau. Viết phương trình các tiếp tuyến đó:   2 1
(C ) : y = 2x − 3x + 1; A0;  −    4
HT 52. Tìm các điểm trên đường thẳng d mà từ đó có thể vẽ được hai tiếp tuyến với (C) vuông góc với nhau: 1) 3 2
(C ) : y = x − 3x + 2 ; d: y = –2 2) 3 2
(C ) : y = x + 3x ; d là trục hoành
Dạng toán 4: Các bài toán khác về tiếp tuyến
HT 53. Cho hypebol (H) và điểm M bất kì thuộc (H). Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến tại M cắt 2 tiệm cận tại A và B.
1) Chứng minh M là trung điểm của đoạn AB.
2) Chứng minh diện tích của ∆IAB là một hằng số.
3) Tìm điểm M để chu vi ∆IAB là nhỏ nhất.
4) Tìm M để bán kính, chu vi, diện tích đường tròn ngoại tiếp tam giác IAB đạt giá trị nhỏ nhất.
5) Tìm M để bán kính, chu vi, diện tích đường tròn nội tiếp tam giác IAB đạt giá trị lớn nhất.
6) Tìm M để khoảng cách từ I đến tiếp tuyến là lớn nhất. 2x − 1 x + 1 1) x − (H ) : y = 2) (H ) : y = 3) 4 5 (H ) : y = x − 1 x − 1 −2x + 3
HT 54. Tìm m để tiếp tuyến tại điểm M bất kì thuộc hypebol (H) cắt hai đường tiệm cận tạo thành một tam giác có diện tích bằng S: 2mx + 3 1) (H ) : y = ; S = 8 x − m
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 17
GV.Lưu Huy Thưởng 0968.393.899
VẤN ĐỀ 7: KHOẢNG CÁCH
Kiến thức cơ bản:
1) Khoảng cách giữa hai điểm A, B: AB = 2 2
(x − x ) + (y − y ) B A B A
2) Khoảng cách từ điểm M(x0; y0) đến đường thẳng ∆: ax + by + c = 0:
ax + by + c d(M, ∆) = 0 0 2 2 a + b
3) Diện tích tam giác ABC: 1 1
S = AB.AC. sin A =
AB .AC − (AB.AC )2 2 2 2 2 Bài tập cơ bản
HT 55. Tìm các điểm M thuộc hypebol (H) sao cho tổng các khoảng cách từ đó đến hai tiệm cận là nhỏ nhất. x + 2 4x − 9 1) x − (H ) : y = 2) 2 1 (H ) : y = 3) (H ) : y = x − 2 x + 1 x − 3
HT 56. Tìm các điểm M thuộc hypebol (H) sao cho tổng các khoảng cách từ đó đến hai trục toạ độ là nhỏ nhất. 2x + 1 4x − 9 1) x − 1 (H ) : y = 2) (H ) : y = 3) (H ) : y = x + 1 x − 2 x − 3
HT 57. Cho hypebol (H). Tìm hai điểm A, B thuộc hai nhánh khác nhau của (H) sao cho độ dài AB là nhỏ nhất. 2x + 3 4x − 9 1) x − 1 (H ) : y = 2) (H ) : y = 3) (H ) : y = x + 1 2 − x x − 3
HT 58. Cho (C) và đường thẳng d. Tìm m để d cắt (C) tại 2 điểm A, B sao cho độ dài AB là nhỏ nhất. x + 1 (H ) : y =
; d : 2x − y + m = 0 x − 1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 18
GV.Lưu Huy Thưởng 0968.393.899 ÔN TẬP TỔNG HỢP
PHẦN I: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ 1 HT 1. Cho hàm số 3 2 y =
(m − 1)x + mx + (3m − 2)x (1).Tìm tất cả các giá trị của tham số m để hàm số (1) đồng 3
biến trên tập xác định của nó. Đ/s: m ≥ 2 HT 2. Cho hàm số 3 2
y = x + 3x − mx − 4 (1).Tìm tất cả các giá trị của tham số m để hàm số (1) đồng biến trên khoảng (− ;
∞ 0) . Đ/s: m ≤ 3 −
HT 3. Cho hàm số y = x3 2 2
− 3(2m + 1)x + 6m(m + 1)x + 1 có đồ thị (Cm).Tìm m để hàm số đồng biến trên khoảng (2; + )
∞ Đ/s: m ≤ 1 HT 4. Cho hàm số 3 2
y = x + (1 − 2m)x + (2 − m)x + m + 2 . Tìm m để hàm đồng biến trên (0; + )
∞ . Đ/s: 5 ≥ m 4 HT 5. Cho hàm số 4 2
y = x − 2mx − 3m + 1 (1), (m là tham số).Tìm m để hàm số (1) đồng biến trên khoảng (1; 2). Đ/s: m ( ;1 ∈ −∞  .  mx + HT 6. Cho hàm số 4 y =
(1). Tìm tất cả các giá trị của tham số m để hàm số (1) nghịch biến trên khoảng x + m (− ; ∞ 1) .Đ/s: 2 − < m ≤ 1 − . HT 7. Cho hàm số 3 2
y = x + 3x + mx + m . Tìm m để hàm số nghịch biến trên đoạn có độ dài bằng 1. Đ/s:⇔ 9 m = 4
PHẦN II: CỰC TRỊ CỦA HÀM SỐ HT 8. Cho hàm số 3 2
y = x + (1 – 2m)x + (2 – m)x + m + 2 (m là tham số) (1). Tìm các giá trị của m để đồ thị hàm số
(1) có điểm cực đại, điểm cực tiểu, đồng thời hoành độ của điểm cực tiểu nhỏ hơn 1. Đ/s: 5 7 < m < . 4 5 HT 9. Cho hàm số 3 2
y = (m + 2)x + 3x + mx − 5 , m là tham số.Tìm các giá trị của m để các điểm cực đại, cực tiểu của
đồ thị hàm số đã cho có hoành độ là các số dương. Đ/s:
−3 < m < −2 HT 10. Cho hàm số 3 2 3
y = 2x − 3(m + 2)x + 6(5m + 1)x − (4m + 2). Tìm m để hàm số đạt cực tiểu tại x 1; 2 ∈ 0 (  Đ/s: 1 − ≤ m < 0 3 1 3 HT 11. Cho hàm số 4 2 y = x − mx +
(1).Xác định m để đồ thị của hàm số (1) có cực tiểu mà không có cực đại. 2 2
Đ/s: m ≤ 0 HT 12. Cho hàm số 4 2 y = x − + 2mx − 4
(C ). Tìm các giá trị của m để tất cả các điểm cực trị của (C ) đều nằm m m
trên các trục tọa độ. Đ/s: m = 2;m ≤ 0 HT 13. Cho hàm số 3 2 2 y = x −
+ (2m + 1)x − (m − 3m + 2)x − 4 (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có
các điểm cực đại và cực tiểu nằm về hai phía của trục tung. Đ/s: 1 < m < 2 . 1 HT 14. Cho hàm số 3 2 y =
x − mx + (2m − 1)x − 3 (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm 3 m  ≠ 1 
cực đại, cực tiểu nằm về cùng một phía đối với trục tung. Đ/s:  1 m  >  2 HT 15. Cho hàm số 3 2
y = x + 3x + mx + m – 2 (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 19
GV.Lưu Huy Thưởng 0968.393.899
và cực tiểu nằm về hai phía đối với trục hoành. Đ/s: m < 3 1 4 HT 16. Cho hàm số 3 2 3 y =
x − (m + 1)x + (m + 1) (C ). Tìm m để các điểm cực trị của hàm số (C) nằm về hai phía 3 3
(phía trong và phía ngoài) của đường tròn có phương trình: 2 2
x + y − 4x + 3 = 0. Đ/s: 1 m < 2 HT 17. Cho hàm số 3 2 3
y = x − 3mx + 4m (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và
cực tiểu đối xứng nhau qua đường thẳng y = x. Đ/s: 2 m = ± 2 HT 18. Cho hàm số 3 2 y = x −
+ 3mx − 3m − 1 . Với giá trị nào của m thì đồ thị hàm số có điểm cực đại và điểm cực tiểu
đối xứng với nhau qua đường thẳng d : x + 8y − 74 = 0 . Đ/s: m = 2 HT 19. Cho hàm số 3 2 2 3 2 y = x −
+ 3mx + 3(1 − m )x + m − m (1).Viết phương trình đường thẳng qua hai điểm cực trị
của đồ thị hàm số (1). Đ/s: 2
y = 2x − m + m . HT 20. Cho hàm số 3 2
y = x − 3x + mx + 2 (C ). Tìm m để (C ) có cực đại và cực tiểu, đồng thời các điểm cực trị m m
của hàm số cách đều đường thẳng d : x −y −1 = 0. Đ/s: m = 0 HT 21. Cho hàm số 3 2
y = x − 3x − mx + 2 (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và  3
cực tiểu cách đều đường thẳng y = x −1. Đ/s: m 0  ;  = −   2   HT 22. Cho hàm số 3 2
y = x − 3x + mx (1). Với giá trị nào của m thì đồ thị hàm số (1) có các điểm cực đại và điểm
cực tiểu đối xứng với nhau qua đường thẳng d : x – 2y – 5 = 0 . Đ/s: m = 0 HT 23. Cho hàm số 3 2
y = x − 3(m + 1)x + 9x + m − 2 (1) có đồ thị là (Cm). Với giá trị nào của m thì đồ thị hàm số có 1
điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường thẳng d : y = x . Đ/s: m = 1 . 2 1 1 HT 24. Cho hàm số 3 2 y =
x − (m − 1)x + 3(m − 2)x +
, với m là tham số thực. Xác định m để hàm số đã cho đạt 3 3 − ±
cực trị tại x , x sao cho x + 2x = 1 . Đ/s: 4 34 m = . 1 2 1 2 4 HT 25. Cho hàm số 3 2
y = x − 3(m + 1)x + 9x − m , với m là tham số thực. Xác định m để hàm số đã cho đạt cực trị tại
x , x sao cho x − x ≤ 2 .Đ/s: 3 − ≤ m < 1 − − 3 và 1
− + 3 < m ≤ 1. 1 2 1 2 HT 26. Cho hàm số 3 2
y = x + (1 − 2m)x + (2 − m)x + m + 2 , với m là tham số thực. Xác định m để hàm số đã cho đạt 1 3 + 29
cực trị tại x , x sao cho x − x > .Đ/s: m > ∨ m < 1 − 1 2 1 2 3 8 HT 27. Cho hàm số 3 2
y = 4x + mx – 3x . Tìm m để hàm số có hai điểm cực trị x , x thỏa x = −4x . Đ/s: 9 m = ± 1 2 1 2 2 1 1
HT 28. Tìm các giá trị của m để hàm số 3 2 2 y =
x − mx + (m − 3)x có cực đại x , cực tiểu x đồng thời x ; x là 3 2 1 2 1 2
độ dài các cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5 Đ/s: 14 m = 2 2 2 HT 29. Cho hàm số 3 2 2 y =
x + (m + 1)x + (m + 4m + 3)x + 1. Tìm m để hàm số có cực trị. Tìm giá trị lớn nhất của 3
biểu thức A = x x − 2(x + x ) với x , x là các điểm cực trị cửa hàm số. 1 2 1 2 1 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 20
GV.Lưu Huy Thưởng 0968.393.899 Đ/s: 9 A ≤ khi m = 4 − 2 HT 30. Cho hàm số 3 2
y = x − 3(m + 1)x + 9x − m (1) với m là tham số thực. Xác định m để hàm số (1) đạt cực đại , m  = 1 cực tiểu sao cho y + y = 2 Đ/s:  CD CT m  = 3 −  1 3 2 2
HT 31. Cho hàm số y =
x − mx + (m − 1)x + 1 (C ). Tìm m để hàm số có cực đại cực tiểu và: y + y > 3 m D 2 C CT − < m < Đ/s: 1 0  m  > 1  HT 32. Cho hàm số 3 2
y = x – 3x + 2 (1). Tìm điểm M thuộc đường thẳng d : y = 3x − 2 sao tổng khoảng cách từ M  
tới hai điểm cực trị nhỏ nhất. Đ/s: 4 2 M  ;   5 5 HT 33. Cho hàm số 3 2 2 3
y = x − 3mx + 3(m − 1)x − m + m (1). Tìm m để hàm số (1) có cực trị đồng thời khoảng
cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số m  = 3 − + 2 2
đến gốc tọa độ O. Đ/s:  . m  = 3 − − 2 2  HT 34. Cho hàm số 3 2
y = x − 3(m + 1)x + 3m(m + 2)x − 2 + m (C ) .Tìm m để đồ thị hàm số (C) có cực trị đồng thời
khoảng cách từ điểm cực đại của đồ thị hàm số (C) tới trục Ox bằng khoảng cách từ điểm cực tiểu của đồ thị hàm số (C) tới trục O .
y Đ/s: m = 2;m = 1;m = 1 − ;m = 0 HT 35. Cho hàm số 3 2
y = x − 3x − mx + 2 có đồ thị là (Cm). Tìm m để (Cm) có các điểm cực đại, cực tiểu và đường
thẳng đi qua các điểm cực trị song song với đường thẳng d : y = 4
− x + 3 .Đ/s: m = 3 HT 36. Cho hàm số 3 2
y = x − 3x − mx + 2 có đồ thị là (Cm). Tìm m để (Cm) có các điểm cực đại, cực tiểu và đường
thẳng đi qua các điểm cực trị tạo với đường thẳng d : x + 4y – 5 = 0 một góc 0 45 . Đ/s: 1 m = − 2 HT 37. Cho hàm số 3 2
y = x + 3x + m (1).Xác định m để đồ thị của hàm số (1) có hai điểm cực trị A, B sao cho 0 − +
AOB = 120 . Đ/s: 12 2 3 m = 3 HT 38. Cho hàm số 3 2 2 3
y = x − 3mx + 3(m − 1)x − m + 4m − 1 (1), m là tham số thực. Tìm các giá trị của m để đồ thị
hàm số (1) có hai điểm cực trị ,
A B sao cho tam giác OAB vuông tại O, với O là gốc tọa độ. Đ/s: m = 1 − ;m = 2 HT 39. Cho hàm số 3 2 3 2
y = x + 3(m + 1)x + 3m(m + 2)x + m + 3m . Chứng minh rằng với mọi m hàm số luôn có 2 cực
trị và khoảng cách giữa hai điểm này không phụ thuộc vào vị trí của m. HT 40. Cho hàm số 3 2
y = x − 3x − mx + 2 (1) với m là tham số thực. Định m để hàm số (1) có cực trị, đồng thời
đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với hai trục tọa độ một tam giác cân. Đ/s: 3 m = − 2 HT 41. Cho hàm số 4 2 2
y = f (x) = x + 2(m − 2)x + m − 5m + 5 (C ) . Tìm các giá trị của m để đồ thị (C ) của hàm số m m
có các điểm cực đại, cực tiểu tạo thành 1 tam giác vuông cân. Đ/s: m = 1 HT 42. Cho hàm số 4 2 2
y = x + 2(m − 2)x + m − 5m + 5
(C ). Với những giá trị nào của m thì đồ thị (C m m) có
điểm cực đại và điểm cực tiểu, đồng thời các điểm cực đại và điểm cực tiểu lập thành một tam giác đều. Đ/s:
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 21
GV.Lưu Huy Thưởng 0968.393.899 3 m = 2 − 3 . HT 43. Cho hàm số 4 2 2
y = x + 2mx + m + m có đồ thị (Cm) . Với những giá trị nào của m thì đồ thị (Cm) có ba điểm
cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có một góc bằng 0 1
120 . Đ/s: m = − . 3 3 HT 44. Cho hàm số 4 2
y = x − 2mx + m − 1 có đồ thị (Cm) . Với những giá trị nào của m thì đồ thị (Cm) có ba điểm cực
trị, đồng thời ba điểm cực trị đó lập thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1 . Đ/s: 5 − 1 m = 1;m = 2 HT 45. Cho hàm số 4 2 4
y = x − 2mx + 2m + m có đồ thị (Cm) . Với những giá trị nào của m thì đồ thị (Cm) có ba điểm
cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có diện tích bằng 4. Đ/s: 5 m = 16 . HT 46. Cho hàm số 4 2
x − 2mx + 2 có đồ thị (C ) . Tìm tất cả các giá trị của tham số m để đồ thị (C ) có ba điểm cực m m 3 9
trị tạo thành một tam giác có đường tròn ngoại tiếp đi qua điểm D  ;   5 5 Đ/s: m = 1
PHẦN 3: SỰ TƯƠNG GIAO HT 47. Cho hàm số 3 2
y = x − 6x + 9x − 6 có đồ thị là (C). Định m để đường thẳng (d) : y = mx − 2m − 4 cắt đồ thị (C)
tại ba điểm phân biệt. Đ/s: m > 3 − HT 48. Cho hàm số 3 2
y = x − 3m x − 2m (Cm). Tìm m để (Cm) và trục hoành có đúng 2 điểm chung phân biệt. Đ/s: m = 1 ± HT 49. Cho hàm số 3 2 y = 2
− x + 6x + 1 . Tìm m để đường thẳng y = mx + 1 cắt (C) tại 3 điểm phân biệt A, B, C sao cho
A(0;1) và B là trung điểm của AC. Đ/s:m = 4 1 2 HT 50. Cho hàm số 3 2 y =
x − mx − x + m + có đox thị
(C ) . Tı̀m m đe| (C ) ca}t trục hoành tại 3 đie|m phân biệ t có to|ng 3 3 m m
bı̀nh phương các hoành độ lớn hơn 15. Đ/s: m > 1 HT 51. Cho hàm số: 3 2
y = 2x − 3x + 1 (1) . Tìm trên (C) những điểm M sao cho tiếp tuyến của (C) tại M cắt trục tung tại
điểm có tung độ bằng 8. Đ/s: M(−1;−4) HT 52. Cho hàm số 3 2
y = x + 2mx + (m + 3)x + 4 có đồ thị là (Cm) (m là tham số).Cho đường thẳng (d): y = x + 4 và
điểm K(1; 3). Tìm các giá trị của m để (d) cắt (Cm) tại ba điểm phân biệt A(0; 4), B, C sao cho tam giác KBC có diện tích ± bằng 8 2 . Đ/s: 1 137 m = . 2 HT 53. Cho hàm số 3 2
y = x − 3x + 4 có đồ thị là (C). Gọi d là đường thẳng đi qua điểm ( A 1
− ; 0) với hệ số góc k k
(k ∈ ℝ) . Tìm k để đường thẳng d cắt đồ thị (C) tại ba điểm phân biệt A, B, C và 2 giao điểm B, C cùng với gốc toạ độ O k
tạo thành một tam giác có diện tích bằng 1 . Đ/s: k = 1 HT 54. Cho hàm số 3 2
y = x − 3x + 2 có đồ thị là (C). Gọi E là tâm đối xứng của đồ thị (C). Viết phương trình đường
thẳng qua E và cắt (C) tại ba điểm E, A, B phân biệt sao cho diện tích tam giác OAB bằng 2 .
Đ/s: y = x − + 1; y = ( 1
− ± 3)(x −1) . 4 1 HT 55. Cho hàm số 3 2 y =
x − (2m + 1)x + (m + 2)x +
có đồ thị (C ), m là tham số. Gọi A là giao điểm của 3 3 m
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 22
GV.Lưu Huy Thưởng 0968.393.899 1
(C ) với trục tung. Tìm m sao cho tiếp tuyến của (C ) tại A tạo với hai trục tọa độ một tam giác có diện tích bằng . m m 3 Đ/s: 13 11 m = − ; m = − 6 6 HT 56. Cho hàm số 3
y = x + mx + 2 có đồ thị (Cm). Tìm m để đồ thị (Cm) cắt trục hoành tại một điểm duy nhất. Đ/s: m > 3 − . HT 57. Cho hàm số 3 2
y = 2x − 3(m + 1)x + 6mx − 2 có đồ thị (Cm).Tìm m để đồ thị (Cm) cắt trục hoành tại một điểm
duy nhất. Đ/s: 1 − 3 < m < 1 + 3 HT 58. Cho hàm số 3 2
y = x – 3x + 1 . Tìm m để đường thẳng (∆): y = (2m − 1)x – 4m – 1 cắt đồ thị (C) tại đúng hai 1
điểm phân biệt. Đ/s: 5 m = − ; m = . 8 2 HT 59. Cho hàm số 3 2
y = x − 3mx + (m − 1)x + m + 1 có đồ thị là (C ) . Tìm tất cả các giá trị của m để m
d : y = 2x − m −1 cắt đồ thị (C ) tại ba điểm phân biệt có hoành độ lớn hơn hoặc bằng 1. m
Đ/s: không có giá trị m HT 60. Cho hàm số 3
y = x − 3x + 2 (C). Viết phương trình đường thẳng cắt đồ thị (C) tại 3 điểm phân biệt A, B, C sao
cho x = 2 và BC = 2 2 Đ/s: d : y = x + 2 A HT 61. Cho hàm số 3 2
y = 4x − 6mx + 1 (C), m là tham số. Tìm m để đường thẳng d : y = x
− + 1 cắt đồ thị hàm số tại
3 điểm A(0;1), B, C với B, C đối xứng nhau qua đường phân giác thứ nhất. Đ/s: 2 m = 3 HT 62. Cho hàm số 3 2
y = x + 3x + mx + 1 (m là tham số) (1).Tìm m để đường thẳng d : y = 1 cắt đồ thị hàm số (1)
tại ba điểm phân biệt A(0; 1), B, C sao cho các tiếp tuyến của đồ thị hàm số (1) tại B và C vuông góc với nhau. Đ/s: 9 − 65 9 + 65 m = ∨ m = 8 8 HT 63. Cho hàm số 3
y = x – 3x + 1 có đồ thị (C) và đường thẳng (d): y = mx + m + 3 . Tìm m để (d) cắt (C) tại − + − −
M (1; 3) , N, P sao cho tiếp tuyến của (C) tại N và P vuông góc với nhau. Đ/s: 3 2 2 3 2 2 m = ∨ m = 3 3 HT 64. Cho hàm số 3 2
y = x − 3x + 4 (C). Gọi (d) là đường thẳng đi qua điểm A(2; 0) có hệ số góc k. Tìm k để (d) cắt
(C) tại ba điểm phân biệt A, M, N sao cho hai tiếp tuyến của (C) tại M và N vuông góc với nhau. Đ/s: −3 ± 2 2 k = 3 HT 65. Cho hàm số 3
y = x − mx + m − 1
(C ). Tìm m để tiếp tuyến của đồ thị hàm số đã cho tại điểm x = 1 − m cắt đường tròn (C): 2 2
(x − 2) + (y − 3) = 4 theo một dây cung có độ dài nhỏ nhất. Đ/s: m = 2 HT 66. Cho hàm số 3
y = x − 3mx + 2 (C ). Tìm m để đường thẳng đi qua điểm cực đại, cực tiểu của(C cắt đường m ) m tròn tâm I (1; )
1 , bán kính bằng 1 tại hai điểm phân biệt A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất Đ/s: 2 ± 3 m = 2 HT 67. Cho hàm số 4 2
y = x − mx + m − 1 có đồ thị là (C
Định m để đồ thị (C
cắt trục trục hoành tại bốn điểm m ) m )
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 23
GV.Lưu Huy Thưởng 0968.393.899 m  > 1
phân biệt. Đ/s:  m  ≠ 2  HT 68. Cho hàm số 4 2
y = x − 2(m + 1)x + 2m + 1 (C ). Tìm tất cả các giá trị của tham số m ∈ ℝ để đồ thị hàm số đã m
cho cắt trục hoành tại 4 điểm phân biệt ,
A B,C, D lần lượt có hoành độ x , x , x , x (x < x < x < x ) sao cho tam 1 2 3 4 1 2 3 4
giác ACK có diện tích bằng 4 biết K(3; 2
− ). Đ/s: m = 4 HT 69. Cho hàm số 4
y = x − (m + ) 2 2
1 x + 2m + 1 có đồ thị là (C
. Định m để đồ thị (C
cắt trục hoành tại 4 điểm m ) m )  
phân biệt có hoành độ lập thành cấp số cộng. Đ/s: 4 m 4  ;  = −   9   HT 70. Cho hàm số 4 2
y = x – (3m + 2)x + 3m có đồ thị là (Cm), m là tham số. Tìm m để đường thẳng y = 1 − cắt đồ  1 −  < m < 1 thị (C 
m) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2. Đ/s: 3  m  ≠ 0  HT 71. Cho hàm số 4
y = x − (m + ) 2 2
1 x + 2m + 1 có đồ thị là (Cm), m là tham số. Tìm m để đồ thị (Cm) cắt trục hoành 1
tại 3 điểm phân biệt đều có hoành độ nhỏ hơn 3. Đ/s:
m = − ∨ m ≥ 1 . 2 HT 72. Cho hàm số: 4 2
y = x − 5x + 4 . Tìm tất cả các điểm M trên đồ thị (C) của hàm số sao cho tiếp tuyến của (C) tại  10 10 − < m < 
M cắt (C) tại hai điểm phân biệt khác M. Đ/s:  2 2   30 m  ≠ ±  6 x + HT 73. Cho hàm số 2 1 y =
có đồ thị là (C). Chứng minh rằng đường thẳng d : y = x
− + m luôn cắt đồ thị (C) tại x + 2
hai điểm phân biệt A, B. Tìm m để đoạn AB có độ dài nhỏ nhất. Đ/s: m = 0 . x − 3
HT 74. Cho hàm số y =
(C). Viết phương trình đường thẳng d qua điểm I( 1
− ;1) và cắt đồ thị (C) tại hai điểm x + 1
M, N sao cho I là trung điểm của đoạn MN. Đ/s: y = kx + k + 1 với k < 0 . 2x + 4
HT 75. Cho hàm số y =
(C). Gọi (d) là đường thẳng qua A(1; 1) và có hệ số góc k. Tìm k để (d) cắt (C) tại hai 1 − x − + − −
điểm M, N sao cho MN = 3 10 . Đ/s: 3 41 3 41 k = 3 − ; k = ; k = 16 16 x − HT 76. Cho hàm số 2 2 y =
(C). Tìm m để đường thẳng (d): y = 2x + m cắt (C) tại hai điểm phân biệt A, B sao cho x + 1 AB =
5 .Đ/s: m = 10; m = −2 . x − HT 77. Cho hàm số 1 y =
(1). Tìm các giá trị của tham số m sao cho đường thẳng (d): y = x + 2 cắt đồ thị hàm x + m
số (1) tại hai điểm A và B sao cho AB = 2 2 . Đ/s: m = 7 x + 2
HT 78. Cho hàm số y =
(C ). Tìm tất cả các giá trị của tham số m ∈ ℝ để đường thẳng d : y = x + m cắt đồ thị 2x − 2
(C) tại hai điểm phân biệt , A B sao cho 2 2 37 OA +OB = 2 Đ/s: 5
m = − ∨ m = 2 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 24
GV.Lưu Huy Thưởng 0968.393.899 x
HT 79. Cho hàm số y =
(C ). Tìm tất cả các giá trị của tham số m ∈ ℝ để đường thẳng d : y = mx − m −1 cắt 1 − x
đồ thị (C) tại hai điểm phân biệt , A B sao cho 2 2
MA + MB đạt giá trị nhỏ nhất.Đ/s: m = 1 − x + 1
HT 80. Cho hàm số y =
(C ). Gọi d là đường thẳng qua M (2; 0) và có hệ số góc là k . Tìm k để d cắt (C) tại hai x − 2 điểm phân biệt ,
A B sao cho : MA = 2 − MB Đ/s: 2 k = 3 x + HT 81. Cho hàm số 3 y =
có đồ thị (H). Tìm m để đường thẳng d :y = 2x + 3m cắt (H) tại hai điểm phân biệt sao x + 2 cho O . AOB = 4
− với O là gốc tọa độ. Đ/s: 7 m = 12 x − + 1
HT 82. Tìm trên (H) : y =
các điểm A, B sao cho độ dài đoạn thẳng AB bằng 4 và đường thẳng AB vuông góc với x − 2
đường thẳng y = x. Đ/s: ( A 3 + 2; − 2); (
B 3 − 2; 2) hoaëc ( A 3 + 2; − 2); ( B 3 − 2; 2) ( A 1 + 2;−2 − 2); (
B 1 − 2;−2 + 2) hoaëc ( A 1 − 2; −2 + 2); (
B 1 + 2;−2 − 2) x + 3
HT 83. Cho hàm số y =
có đồ thị (H). Tìm m để đường thẳng d : y = x
− + m + 1 tại hai điểm phân biệt A, B sao x − 2
cho AOB nhọn.Đ/s: m > 3 − x + HT 84. Cho hàm số 3 2 y =
(C ) . Đường thẳng y = x cắt (C) tại hai điểm A, B. Tìm m để đường thẳng x + 2
y = x + m cắt (C) tại hai điểm C, D sao cho ABCD là hình bình hành. Đ/s: m = 10 2x − 1
HT 85. Cho hàm số y =
(C). Tìm m để đường thẳng d: y = x + m cắt (C) tại hai điểm phân biệt A, B sao cho x − 1
∆OAB vuông tại O. Đ/s: m = 2 − x − m HT 86. Cho hàm số 2 y =
(1). Chứng minh rằng với mọi m ≠ 0 đồ thị hàm số (1) cắt (d) : y = 2x − 2m tại hai mx + 1
điểm phân biệt A, B thuộc một đường (H) cố định. Đường thẳng (d) cắt trục Ox, Oy lần lượt tại các điểm M, N. Tìm m để S = 3S OAB OMN x − HT 87. Cho hàm số 2 1 y =
(C ). Gọi I là giao điểm của hai tiệm cận của (C). Với giá trị nào của m thì đường thẳng x − 1 y = x
− + m cắt đồ thị (C) tại hai điểm phân biệt A, B và tam giác IAB đều. Đ/s: m = 3 ± 6 x
HT 88. Cho hàm số y =
(C ) . Tìm các giá trị của m để đường thẳng y = x
− + m cắt đồ thị (C) tại hai điểm phân x − 1 biệt , A B sao cho O , A OB bằng 0
60 . Với O là gốc tọa độ. Đ/s: m = 2 − ∨ m = 6
PHẦN 4: TIẾP TUYẾN 2x − 1
HT 89. Cho hàm so• y =
. Viết phương trình tiếp tuyến của (C), biết khoảng cách từ điểm I(1; 2) đến tiếp tuyến x − 1
bằng 2 . Đ/s: x + y −1 = 0 và x + y − 5 = 0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 25
GV.Lưu Huy Thưởng 0968.393.899 HT 90. Cho hàm số 3 2
y = x + (1 − 2m)x + (2 − m)x + m + 2
(1) (m là tham số).Tìm tham số m để đồ thị của hàm 1
số (1) có tiếp tuyến tạo với đường thẳng d: x + y + 7 = 0 góc α , biết 1 cos α = .Đ/s: 1 m ≤ − hoặc m ≥ 26 4 2 HT 91. Cho hàm số 3 2 y = x −
+ 2x − x (C ). Tìm tọa độ các điểm trên trục hoành sao cho qua điểm đó kẻ được hai tiếp 32 
tuyến với đồ thị (C) và góc giữa hai tiếp tuyến này bằng 0
45 . Đ/s: M ≡ ; O M  ; 0  27  HT 92. Cho hàm số 3 2
y = x − 3x + 1 có đồ thị (C). Tìm hai điểm A, B thuộc đồ thị (C) sao cho tiếp tuyến của (C) tại A
và B song song với nhau và độ dài đoạn AB = 4 2 . Đ/s: (
A 3;1), B(−1; 3 − ) . x + 1
HT 93. Cho hàm số y =
(C). Tìm trên Oy tất cả các điểm từ đó kẻ được duy nhất một tiếp tuyến tới (C). x − 1
Đ/s: M(0;1);M(0; 1 − ) HT 94. Cho hàm số 3
y = 3x − x (C). Tìm trên đường thẳng d : y = x
− các điểm mà từ đó kẻ được đúng 2 tiếp tuyến
phân biệt với đồ thị (C).Đ/s: ( A 2; 2 − ); B( 2 − ; 2) HT 95. Cho hàm số: 3
y = x − 3x + 2 . Tìm tất cả điểm trên đường thẳng y = 4 , sao cho từ đó kẻ được đúng 2 tiếp  
tuyến tới đồ thị (C). Đ/s: 2 ( 1 − ; 4);−  ; 4;(2; 4)   3  HT 96. Cho hàm số 3 2 y = x −
+ 3x − 2 (C). Tìm trên đường thẳng d : y = 2 các điểm mà từ đó kẻ được 3 tiếp tuyến  m  < −1  
phân biệt với đồ thị (C). Đ/s:  5 m   >   3  m ≠ 2  2 2
HT 97. Cho hàm số y = ( x + ) 1 .( x − ) 1 (C). Cho điểm (
A a; 0) . Tìm a để từ A kẻ được 3 tiếp tuyến phân biệt với đồ 3 3 thị (C). Đ/s: 1 − ≠ a < −
hoaëc 1 ≠ a > 2 2 HT 98. Cho hàm số 3 2
y = x − 3x + 2. Tìm trên đường thẳng y = 2 các điểm mà từ đó có thể kẻ được 2 tiếp tuyến tới  
đồ thị hàm số và 2 tiếp tuyến đó vuông góc với nhau. Đ/s: 1 M 2  ;  −    27 1 HT 99. Cho hàm số 3 2
y = f (x) =
mx + (m − 1)x + (4 − 3m)x + 1 có đồ thị là (Cm). Tìm các giá trị m sao cho trên đồ 3
thị (Cm) tồn tại một điểm duy nhất có hoành độ âm mà tiếp tuyến tại đó vuông góc với đường thẳng d : x + 2y − 3 = 0 . Đ/s: m < hay 2 0 m > . 3 1
HT 100. Tìm tất cả các giá trị m sao cho trên đồ thị (C ) : 3 2 y =
mx + (m − 1)x + (4m − 3)x + 1 tồn tại đúng hai m 3    
điểm có hoành độ dương mà tiếp tuyến tại đó vuông góc với đường thẳng (L): x + 2y − 3 = 0 Đ/s: 1   1 2 m ∈ 0  ;   ∪  ;    2    2 3 x HT 101. Cho hàm số 2 y =
(C). Viết phương trình tiếp tuyến của đồ thị (C), biết rằng khoảng cách từ tâm đối x + 2
xứng của đồ thị (C) đến tiếp tuyến là lớn nhất. Đ/s: y = x và y = x + 8 . x + HT 102. Cho hàm số 2 y =
(1). Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt 2x + 3
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 26
GV.Lưu Huy Thưởng 0968.393.899
trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. Đ/s: y = x − − 2 . 2x −1
HT 103. Cho hàm số y =
. Lập phương trình tiếp tuyến của đồ thị (C) sao cho tiếp tuyến này cắt các trục Ox, Oy x − 1  1 5 y  = − x +
lần lượt tại các điểm A và B thoả mãn OA = 4OB. Đ/s:  4 4  .  1 13 y = − x +   4 4 2x
HT 104. Viết phương trình tiếp tuyến của đồ thị hàm số y =
biết tiếp tuyến cắt Ox, Oy lần lượt tại A và B mà tam x − 2
giác OAB thỏa mãn: AB = OA 2 Đ/s: y = x − + 8 2x − 3
HT 105. Cho hàm số y =
có đồ thị (C). Tìm trên (C) những điểm M sao cho tiếp tuyến tại M của (C) cắt hai tiệm x − 2
cận của (C) tại A, B sao cho AB ngắn nhất. Đ/s: M(3; 3) hoặc M(1;1) 2x − 3
HT 106. Cho hàm số y =
.Cho M là điểm bất kì trên (C). Tiếp tuyến của (C) tại M cắt các đường tiệm cận của (C) x − 2
tại A và B. Gọi I là giao điểm của các đường tiệm cận. Tìm toạ độ điểm M sao cho đường tròn ngoại tiếp tam giác IAB có
diện tích nhỏ nhất. Đ/s: M(1;1);M(3; 3) HT 107. Cho hàm số 3 2 2
y = x − 2mx + m x − m + 1 (C ). Tìm m để đồ thị hàm số tiếp xúc với trục hoành. m Đ/s: 3 m = 1 ∨ m = 3 − ∨ m = 2 2x + 1
HT 108. Cho hàm số y =
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận. Tìm điểm M thuộc (C) sao cho tiếp x − 1
tuyến của (C) tại M cắt 2 tiệm cận tại A và B với chu vi tam giác IAB đạt giá trị nhỏ nhất.
Đ/s: M (1 + 3;2 + 3) , M (1 − 3;2 − 3) 1 2 x + 2 HT 109. Cho hàm số: y = (C). Cho điểm (
A 0;a) . Tìm a để từ A kẻ được 2 tiếp tuyến tới đồ thị (C) sao cho 2 x − 1  2 a  > −
tiếp điểm tương ứng nằm về 2 phía của trục hoành. Đ/s:  3 . a  ≠ 1  x + HT 110. Cho hàm số y =
2 . Gọi I là giao điểm của 2 đường tiệm cận, ∆ là một tiếp tuyến bất kỳ của đồ thị (C). d x + 1 x = 0
là khoảng cách từ I đến ∆ . Tìm giá trị lớn nhất của d. Đ/s:GTLN của d bằng 2 khi  0  x = 2 −  0  x + HT 111. Cho hàm số 2 1 y =
. Viết phương trình tiếp tuyến của đồ thị (C), biết rằng tiếp tuyến cách đều hai điểm x + 1 1 5
A(2; 4), B(−4; −2). Đ/s: y =
x + ; y = x + 1; y = x + 5 4 4 2x − 3
HT 112. Cho hàm số y =
(C). Viết phương trình tiếp tuyến tại điểm M thuộc (C) biết tiếp tuyến đó cắt tiệm x − 2
cận đứng và tiệm cận ngang lần lượt tại A, B sao cho côsin góc ABI bằng 4 , với I là giao 2 tiệm cận. 17     Đ/s: 3 1 3 5 1 7
Tại M 0;     : y = − x +
; Tại M 4;  : y = − x +  2 4 2  3 4 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 27
GV.Lưu Huy Thưởng 0968.393.899 x + 1
HT 113. Cho hàm số y =
(C). Tìm giá trị nhỏ nhất của m sao cho tồn tại ít nhất một điểm M ∈(C) mà tiếp tuyến 2x − 1
tại M của (C) tạo với hai trục tọa độ một tam giác có trọng tâm nằm trên đường thẳng y = 2m −1 Đ/s: 1 m ≥ 3 x − HT 114. Cho hàm số 2 1 y =
(C ). Tìm các giá trị của m để đồ thị hàm số (C) tiếp xúc với đường thẳng x − 1
y = mx + 5. Đ/s: m = 1 − hoặc m = 9 −
PHẦN 5: BIỆN LUẬN SỐ NGHIỆM CỦA PHƯƠNG TRÌNH HT 115. Cho hàm số 3 2 y = x − + 3x + 1 .
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Tìm m để phương trình 3 2 x − x = 3 2 3
m − 3m có ba nghiệm phân biệt. Đ/s: m ∈ ( 1 − ; 3) \ {0; 2} HT 116. Cho hàm số 4 2
y = x − 5x + 4 có đồ thị (C).
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Tìm m để phương trình 4 2
| x − 5x + 4 |= log m có 6 nghiệm. 2 9 9
• Dựa vào đồ thị ta có PT có 6 nghiệm ⇔ 4 4 log m =
⇔ m = 12 = 144 12 . 12 4 HT 117. Cho hàm số: 4 2
y = x − 2x + 1 .
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Biện luận theo m số nghiệm của phương trình: 4 2
x − 2x + 1 + log m = 0 (m> 0) 2 1 1 1 0 < m < m =
< m < 1 m = 1
m > 1 2 2 2 2 nghiệm 3 nghiệm 4 nghiệm 2 nghiệm vô nghiệm HT 118. Cho hàm số 4 2
y = f (x) = 8x − 9x + 1 .
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Dựa vào đồ thị (C) hãy biện luận theo m số nghiệm của phương trình: 4 2
8 cos x − 9 cos x + m = 0 với x [0; π ∈ ] Đ/s: 81 81
m < 0 m = 0
0 < m < 1 81 1 ≤ m < m = m > 32 32 32
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 28
GV.Lưu Huy Thưởng 0968.393.899 vô nghiệm 1 nghiệm 2 nghiệm 4 nghiệm 2 nghiệm vô nghiệm x + 1
HT 119. Cho hàm số y = . x − 1
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. x + 1
2) Biện luận theo m số nghiệm của phương trình = m. x − 1 m < 1 − ;m > 1 m = 1 − 1
− < m ≤ 1 2 nghiệm 1 nghiệm vô nghiệm
PHẦN 6: ĐIỂM ĐẶC BIỆT CỦA ĐỒ THỊ HT 120. Cho hàm số 3 y = x −
+ 3x + 2 (C). Tìm 2 điểm trên đồ thị hàm số sao cho chúng đối xứng nhau qua tâm
M(−1; 3) . Đ/s: ( 1 − ; ) 0 và ( 1 − ; ) 6 HT 121. Cho hàm số 3 y = x −
+ 3x + 2 (C). Tìm trên (C) hai điểm đối xứng nhau qua đường thẳng d : 2x – y + 2 = 0 .     Đ/s:  7 1 7   7 1 7   ; 2  −  ;− ; 2  +     2 2 2   2 2 2         3 x 11 HT 122. Cho hàm số 2 y = − + x + 3x −
. Tìm trên đồ thị (C) hai điểm phân biệt M, N đối xứng nhau qua trục tung. 3 3     Đ/s: 16 16 M 3  ; , N    3 − ;   . 3      3  x − HT 123. Cho hàm số 2 1 y =
(C).Tìm điểm M thuộc đồ thị (C) để tiếp tuyến của (C) tại M với đường thẳng đi qua M x + 1
và giao điểm hai đường tiệm cận có tích các hệ số góc bằng –9. Đ/s: M(0; 3 − ); M( 2 − ; 5) x + HT 124. Cho hàm số 2 1 y =
(C). Tìm trên (C) những điểm có tổng khoảng cách đến hai tiệm cận của (C) nhỏ nhất. x + 1 Đ/s: (0;1);( 2 − ; 3) 3x − 4 HT 125. Cho hàm số y =
(C). Tìm các điểm thuộc (C) cách đều 2 tiệm cận. x − 2
Đ/s: M (1;1);M (4; 6) 1 2 1 1 HT 126. Cho hàm số 4 2 y =
x − x + 1 (C ). Tìm điểm M thuộc (C) sao cho tổng khoảng cách từ điểm M đến hai trục 4 2
tọa độ là nhỏ nhất. Đ/s: M(0;1) HT 127. Cho hàm số 4 2
y = 2x − 3x + 2x + 1 có đồ thị là (C) và đường thẳng ( )
∆ = 2x − 1 .Tìm trên đồ thị (C) điểm 0 0 0 0     3 1   3 1 
A có khoảng cách đến ( )
∆ là nhỏ nhất Đ/s: A − ; − − 3 ; A  ;− + 3 1      2 8    2     2 8   
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 29
GV.Lưu Huy Thưởng 0968.393.899 x + 1 HT 128. Cho hàm số y =
. Tìm trên đồ thị hàm số điểm M sao cho tồng khoảng cách từ M đến hai trục tọa độ là x − 2   nhỏ nhất. Đ/s: 1 M 0  ;  −    2 x − HT 129. Cho hàm số 2 4 y =
. Tìm trên (C) hai điểm đối xứng nhau qua đường thẳng MN biết x + 1 M( 3
− ; 0); N (−1;−1) Đ/s:A(0; –4), B(2; 0). 2x HT 130. Cho hàm số y =
. Tìm trên đồ thị (C) hai điểm B, C thuộc hai nhánh sao cho tam giác ABC vuông cân tại x − 1
đỉnh A với A(2; 0). Đ/s: B( 1
− ;1), C(3; 3) x − HT 131. Cho hàm số 2 1 y =
. Tìm tọa độ điểm M ∈ (C) sao cho khoảng cách từ điểm I( 1
− ; 2) tới tiếp tuyến của (C) x + 1
tại M là lớn nhất. Đ/s: M (−1 + 3;2 − 3) hoặc M (−1− 3;2 + 3) x + 2
HT 132. Cho hàm số y =
. Tìm những điểm trên đồ thị (C) cách đều hai điểm (
A 2; 0), B(0; 2) . 2x −1    
Đ/s: 1 − 5 1 − 5  1 + 5 1 + 5   ,  ;    ,      2 2   2 2         x − HT 133. Cho hàm số 3 y =
. Tìm trên hai nhánh của đồ thị (C) hai điểm A và B sao cho AB ngắn nhất.Đ/s: x + 1 A( 4 4 − − + ) B ( 4 4 1 4;1 64 , 1 − + 4;1 − 64) . HT 134. Cho hàm số 4 2
y = x − 2x + 1 Tìm tọa độ hai điểm P. Q thuộc (C) sao cho đường thẳng PQ song song với trục
hoành và khoảng cách từ điểm cực đại của (C) đến đường thẳng PQ bằng 8
Đ/s:Vậy, P(-2;9), Q(2;9) hoặc P(2;9); Q(-2;9) 2
(3m + 1)x − m + m
HT 135. Cho hàm số y =
. Tìm các điểm thuộc đường thẳng x = 1 mà không có đồ thị đi qua. x + m
Đ/s:Tập hợp các điểm thuộc đường thẳng x = 1 có tung độ bằng a với a thỏa mãn : 2 < a < 10 2x − 1
HT 136. Cho hàm số y =
(C ). Tìm trên đồ thị (C) hai điểm ,
A B phân biệt sao cho ba điểm , A , B I (0;−1) thẳng x − 1
hàng đồng thời thỏa mãn: I . A IB = 4.
Đ/s: A(2 − 2;1− 2);B (2 + 2;1 + 2)hoặc A(1− 3;−2 + 3);B (1 + 3;−2 − 3)
PHẦN 7: CÁC BÀI TỔNG HỢP 2x + 3
HT 137. Cho hàm số y =
(C ). Tìm m để đường thẳng d : y = 2x + m cắt đồ thị tại hai điểm phân biệt sao cho x − 2
tiếp tuyến tại hai điểm đó của đồ thị hàm số song song với nhau. Đ/s: m = 2 − HT 138. Cho hàm số 3 2
y = x − 2mx + 2mx − 1 (C ). Tìm m để đồ thị hàm số (C) cắt trục hoành tại 3 điểm phân biệt (
A 1; 0), B và C sao cho k + k = BC. 5 trong đó k ,k lần lượt là hệ số góc tiếp tuyến tại B, C của đồ thị hàm số (C). 1 2 1 2 Đ/s: m = 1 − ;m = 2 HT 139. Cho hàm số 3 2
y = x − 3x + mx + 2 − m (C ). Tìm m để (C ) cắt trục hoành tại 3 điểm phân biệt , A B,C m m
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 30
GV.Lưu Huy Thưởng 0968.393.899
sao cho tổng các hệ số góc của tiếp tuyến của (C ) tại ,
A B,C bằng 3.Đ/s: m = 2 m
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 31
GV.Lưu Huy Thưởng 0968.393.899
PHẦN 8: TUYỂN TẬP ĐỀ THI ĐẠI HỌC TỪ NĂM 2009 x +
HT 140. (ĐH A – 2009) Cho hàm số 2 y =
(1) . Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến 2x + 3
đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B sao cho tam giác OAB cân tại gốc tọa độ O.
Đ/s: y = x − − 2
HT 141. (ĐH B – 2009) Cho hàm số: 4 2
y = 2x − 4x (1) .Với giá trị nào của , m phương trình 2 2
x x − 2 = m có đúng 6
nghiệm thực phân biệt. Đ/s: 0 < m < 1
HT 142. (ĐH D – 2009) Cho hàm số 4 2
y = x − (3m + 2)x + 3m có đồ thị là (C ) với m là tham số. Tìm m để đường m thẳng y = 1
− cắt đồ thị (C ) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2. m Đ/s: 1 −
< m < 1, m ≠ 0 3
HT 143. (ĐH A – 2010) Cho hàm số 3 2
y = x − 2x + (1 − m)x + m (1), với m là tham số thực. Tìm m để đồ thị (1) cắt
trục hoành tại 3 điểm phân biệt có hoành độ x , x , x thỏa mãn điều kiện: 2 2 2
x + x + x < 4 1 2 3 1 2 3 Đ/s: 1 −
< m < 1 và m ≠ 0 4 x +
HT 144. (ĐH B – 2010) Cho hàm số 2 1 y =
(C ) . Tìm m để đường thẳng y = 2
− x + m cắt đồ thị (C)tại hai x + 1
điểm A và B sao cho tam giác OAB có diện tích bằng 3 (O là gốc tọa độ). Đ/s: m = 2 ±
HT 145. (D – 2010) Cho hàm số 4 2 y = x −
− x + 6 (C ) . Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến 1
vuông góc với đường thẳng y = x −1Đ/s: y = 6 − x + 10 6 x − + 1
HT 146. (A – 2011)Cho hàm số y =
(C ) . Chứng minh rằng với mọi m đường thẳng y = x + m luôn cắt đồ 2x − 1
thị (C)tại hai điểm phân biệt A và B. Gọi k ,k lần lượt là hệ số góc của tiếp tuyến với (C)tại A và B. Tìm m để tổng 1 2
k + k đạt giá trị lớn nhất. Đ/s: k + k lớn nhất bằng −2 , khi và chỉ khi m = 1 − . 1 2 1 2
HT 147. (B – 2011) Cho hàm số 4 2
y = x − 2(m + 1)x + m (1) (với m là tham số). Tìm m để đồ thị hàm số (1) có ba
điểm cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị
còn lại. Đ/s: m = 2 ± 2 2 x +
HT 148. (D – 2011) Cho hàm số 2 1 y =
(C ) . Tìm k để đường thẳng y = kx + 2k + 1 cắt đồ thị (C) tại hai điểm x + 1 phân biệt ,
A B sao cho khoảng cách từ A và B đến trục hoành bằng nhau. Đ/s: k = 3 −
HT 149. (A,A1 – 2012) Cho hàm số 4 2 2
y = x − 2(m + 1)x + m (1) , với m là tham số thực. Tìm m để đồ thị hàm số
(1) có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác vuông. Đ/s: m = 0
HT 150. (B – 2012) Cho hàm số 3 2 3
y = x − 3mx + 3m (1), m là tham số thực. Tìm m để đồ thị hàm số (1) có hai
điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48. Đ/s: m = 2 ± 2 2
HT 151. (D – 2012) Cho hàm số 3 2 2 y =
x − mx − 2(3m − 1)x +
(1), m là tham số thực. Tìm m để hàm số (1) có 3 3 2
hai điểm cực trị x ;x sao cho: x x + 2(x + x ) = 1. Đ/s: m = 1 2 1 2 1 2 3
HT 152. (A,A1 – 2013) Cho hàm số 3 2 y = x −
+ 3x + 3mx − 1 (1) , với m là tham số thực. Tìm m để hàm số (1)
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 32
GV.Lưu Huy Thưởng 0968.393.899
nghịch biến trên khoảng (0;+ )
∞ Đ/s: m ≤ 1 −
HT 153. (B – 2013) Cho hàm số 3 2
y = 2x − 3(m + 1)x + 6mx (1), với m là tham số thực. Tìm m để đồ thị hàm số (1)
có hai điểm cực trị A, B sao cho đường thẳng AB vuông góc với đường thẳng y = x + 2. Đ/s: m = 0;m = 2
HT 154. (D – 2013) Cho hàm số 3 2
y = 2x − 3mx + (m − 1)x + 1 (1), với m là tham số thực. Tìm m để đường thẳng y = x
− + 1 cắt đồ thị hàm số (1) tại ba điểm phân biệt. Đ/s: 8 m < 0;m > 9
-----------------------------------------------------------HẾT-----------------------------------------------------------
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 33

Chuyên đề khảo sát hàm số – Lưu Huy Thưởng Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số