57 trang 33 lượt tải

Chuyên đề khảo sát hàm số Toán 12: Nhận dạng đồ thị hàm số

65

Chuyên đề khảo sát hàm số Toán 12: Nhận dạng đồ thị hàm số được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 375 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 năm trước
Danh sách Quiz
1/57
KHẢO SÁT HÀM SỐ
TOÁN 12
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
NHẬN DẠNG ĐỒ THỊ HÀM SỐ
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
I. TÓM TẮT LÝ THUYẾT
1 - SƠ ĐỒ KHẢO SÁT HÀM SỐ
Cho hàm số
y f x
.
1. Tìm tập xác định của hàm số.
2. Sự biến thiên
a) Chiều biến thiên.
i. Tính
'y
.
ii. Tìm các nghiệm của phương trình
'0y
và các điểm tại đó
'y
không xác
định.
iii. Xét dấu
'y
và suy ra các khoảng biến thiên của hàm số.
b) Tìm cực trị (nếu có).
c) Tìm các giới vô cực; các giới hạn tại
,
và tại các điểm mà hàm số không xác
định.
d) Tìm các đường tiệm cận của hàm số (nếu có).
e) Lập bảng biến thiên.
3. Đồ thị.
a) Liệt kê các điểm đặc biệt ( điểm cực đại, điểm cực tiểu, tâm đối xứng,…)
b) Xác định giao điểm của (C) với Ox, Oy (nếu có).
c) Vẽ đồ thị.
2- KHẢO SÁT MỘT SỐ HÀM ĐA THỨC VÀ PHÂN THỨC:
a- HÀM SỐ BẬC BA
32
0y ax bx cx d a
TRƯỜNG HỢP
0a
0a
Phương trình
/
0y
có
2 nghiệm phân biệt
x
y
1
O
1
x
y
1
O
1
Phương trình
/
0y
có
nghiệm kép
x
y
1
O
1
x
y
1
O
1
7
VẤN ĐỀ
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Phương trình
/
0y
vô
nghiệm
x
y
1
O
1
x
y
1
O
1
b- HÀM SỐ TRÙNG PHƯƠNG
42
0y ax bx c a
TRƯỜNG HỢP
0a
0a
Phương trình
/
0y
có
3 nghiệm phân biệt
x
y
O
1
1
x
y
1
O
1
Phương trình
/
0y
có
1 nghiệm.
x
y
1
O
1
x
y
O
1
1
c- HÀM SỐ NHẤT BIẾN
0, 0
ax b
y c ad bc
cx d
0D ad bc
0D ad bc
x
y
O
1
1
x
y
1
O
1
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
KỸ NĂNG: NHẬN BIẾT ĐỒ THỊ VÀ BẢNG BIẾN THIÊN
Câu 1: Đồ thị hàm số trong hình vẽ sau là đồ thị của hàm số nào trong các hàm số dưới đây
A.
1
2
x
y
x

. B.
3
2
x
y
x
. C.
13
2
x
y
x
. D.
1
2
x
y
x
.
Câu 2: Hàm số nào dưới đây có bảng biến thiên như sau:
x


y
y


5
1
1
A.
7
5
x
y
x
. B.
5
1
x
y
x
. C.
5
1
x
y
x
. D.
3
5
x
y
x
.
Câu 3: Đồ thị hàm số nào dưới đây có dạng như hình vẽ?
A.
1
1
x
y
x
. B.
1
1
x
y
x
. C.
2
1
x
y
x
. D.
21
1
x
y
x

.
Câu 4: Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên dưới. Hỏi hàm số
y f x
là hàm
số nào trong các hàm số cho dưới đây?
A.
32
31y x x
. B.
32
31y x x
. C.
2
1
x
y
x
. D.
42
21y x x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 5: Đường cong hình bên là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm
số nào?
A.
21
1
x
y
x
. B.
32
31y x x
. C.
42
21y x x
. D.
42
21y x x
.
Câu 6: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số có bảng biến thiên như trên là
A.
42
2y x x
. B.
42
3 6 3y x x
. C.
3
y x x
. D.
3
3y x x
.
Câu 7: Hàm số nào dưới đây có đồ thị như đường cong trong hình bên dưới?
A.
32
31y x x
. B.
42
31y x x
. C.
42
21y x x
. D.
32
21y x x
.
Câu 8: Bảng biến thiên dưới đây của hàm số nào?
A.
1
1
x
y
x
. B.
42
23y x x
. C.
3
34y x x
. D.
3
34y x x
.
Câu 9: Đồ thị sau đây là của hàm số nào?
A.
3
31y x x
. B.
3
31y x x
. C.
32
31y x x
. D.
32
31y x x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 10: Cho hàm số
()y f x
có bảng biến thiên như hình dưới đây. Hàm số
()y f x
là hàm số nào
trong các hàm số sau đây?
A.
42
23y x x
. B.
42
23y x x
. C.
42
1
33
4
y x x
.D.
42
23y x x
.
Câu 11: Đồ thị dưới đây là đồ thị của hàm số nào?
A.
3
y x x
. B.
3
y x x
. C.
3
y x x
. D.
yx
.
Câu 12: Hàm số nào trong các hàm số sau mà đồ thị có dạng hình vẽ dưới đây?
A.
3
31y x x
. B.
32
31y x x
. C.
32
31y x x
. D.
3
31y x x
.
Câu 13: Hàm số
32
31y x x
có đồ thị nào sau đây?
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 14: Cho hàm số
y f x
có đồ thị
C
như hình vẽ. Hỏi
C
là đồ thị của hàm số nào?
A.
3
1yx
. B.
3
1yx
. C.
3
1yx
. D.
3
1yx
.
Câu 15: Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây?
A.
32
1y x x x
. B.
yx
. C.
1
2
x
y
x
. D.
4
.yx
Câu 16: Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây, hàm số nào có bảng
biến thiên như sau?
A.
32
3 9 2y x x x
. B.
32
12
3
33
y x x x
.
C.
32
3 9 2y x x x
. D.
32
12
3
33
y x x x
.
Câu 17: Hàm số
32
3 3 1y x x x
có đồ thị là hình nào sau đây?
A. . B. . C. . D. .
Câu 18: Hàm số nào có đồ thị là hình vẽ sau đây?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
32
34y x x
. B.
42
34y x x
. C.
32
34y x x
. D.
21
35
x
y
x
.
Câu 19: Đường cong trong hình vẽ bên là đồ thị của một hàm số nào?
A.
3
32y x x
. B.
3
32y x x
. C.
42
2y x x
. D.
3
32y x x
.
Câu 20: Hàm số nào dưới đây có bảng biến thiên như hình bên dưới?
A.
3
.
1
x
y
x

B.
3
.
1
x
y
x
C.
2
.
1
x
y
x

D.
3
.
1
x
y
x

Câu 21: Hàm số nào có đồ thị là đường cong trong hình vẽ bên dưới?
A.
42
41y x x
. B.
1
2
x
y
x
. C.
32
41y x x
. D.
2
21yx
.
Câu 22: Đồ thị của hàm số nào dưới đây có dạng như đường cong hình dưới đây?
x
y
1
1
A.
3
31y x x
. B.
3
31y x x
. C.
3
31y x x
. D.
3
31y x x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 23: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số có bảng biến thiên như trên là
A.
42
3 6 3y x x
. B.
42
2y x x
. C.
3
y x x
. D.
3
3y x x
.
Câu 24: Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên dưới:
A.
3
3y x x
. B.
3
3y x x
. C.
32
3y x x
. D.
32
3y x x
.
Câu 25: Bảng biến thiên sau đây là của hàm số nào?
A.
3
2
x
fx
x
. B.
3
2
x
fx
x
C.
3
2
x
fx
x
. D.
23
2
x
fx
x
Câu 26: Đường cong của hình vẽ là đồ thị của hàm số nào trong các hàm số sau?
A.
2
1
x
y
x
. B.
42
22y x x
. C.
42
22y x x
. D.
32
22y x x
Câu 27: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
32
31y x x
. B.
42
21y x x
. C.
42
21y x x
. D.
32
31y x x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 28: Hàm số
2
1
x
y
x
có đồ thị là hình vẽ nào sau đây?
A.
x
y
-2
2
1
-1
0
1
. B.
x
y
-2
1
-1
0
1
.C
.
x
y
-2
3
1
-1
0
1
.D.
x
y
-2
2
1
-1
0
1
.
Câu 29: Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới?
A.
42
31y x x
. B.
42
31y x x
. C.
42
1y x x
. D.
42
1y x x
.
Câu 30: Hàm số nào dưới đây có đồ thị dạng như đường cong trong hình vẽ bên dưới?
x
y
O
1
1
A.
1
1
x
y
x
. B.
21
1
x
y
x
. C.
21
1
x
y
x
. D.
1
1
x
y
x
.
Câu 31: Đồ thị hàm số
3
32y x x
là hình nào trong 4 hình dưới đây?
A. . B. . C. . D. .
Câu 32: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
A.
22
1
x
y
x
. B.
3
21y x x
. C.
21
2
x
y
x

. D.
42
22y x x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 33: Đồ thị hàm số
32
32y x x
là đường cong trong hình nào dưới đây?
A. B. C. D.
Câu 34: Đồ thị hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
2
12y x x
. B.
2
12y x x
. C.
32
32y x x
. D.
42
32y x x
.
Câu 35: Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?
A.
3
32y x x
. B.
32
31y x x
. C.
32
32y x x
. D.
42
31y x x
.
Câu 36: Cho hàm số
32
y f x ax bx cx d
có bảng biến thiên sau:
Đồ thị nào thể hiện hàm số
y f x
?
A.
.I
B.
.II
C.
.III
D.
.IV
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 37: Đồ thị trong hình vẽ sau là đồ thị của hàm số nào trong các hàm số dưới đây.
A.
42
81y x x
. B.
32
31y x x
. C.
42
21y x x
. D.
3
2
31y x x
.
MỘT SỐ BÀI TOÁN LIÊN QUAN
Câu 38: Cho đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
với
, , ,a b c d
là các số thực.
Mệnh đề nào dưới đây đúng?
A.
0,yx
. B.
0, 1yx
. C.
0, 1yx
. D.
0,yx
.
Câu 39: Biết hàm số
1
xa
y
x
(
a
là số thực cho trước,
1a
) có đồ thị như hình vẽ sau:
Mệnh đề nào dưới đây đúng?
A.
' 0, 1yx
. B.
' 0, 1yx
. C.
' 0,yx
. D.
' 0,yx
.
Câu 40: Cho hàm số
1
xm
y
x
, có đồ thị như hình vẽ bên dưới:
Khẳng định nào sau đây đúng?
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 41: Cho hàm số
1
xa
y
x
có đồ thị như hình vẽ bên dưới:
Mệnh đề nào dưới đây đúng?
A.
1a
. B.
3a 
. C.
1a 
. D.
1a
.
Câu 42: Biết hàm số
32
a ( 0)y x bx cx d a
có đồ thị như hình vẽ sau:
x
2
1
y
-1
O
1
Mệnh đề nào dưới đây đúng?
A.
' 0,yx
. B.
' 0,yx
. C.
' 0,yx
. D.
' 0,yx
.
Câu 43: Hàm số
32
y ax bx cx d
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Câu 44: Cho hàm số
1
, ,
ax
f x a b c
bx c

có bảng biến thiên như sau:
Trong các số
,,abc
có bao nhiêu số dương?
A.
3
. B.
2
. C.
1
. D.
0
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 45: Cho hàm số
ax b
y
xc
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
2, 1a b c
. B.
2, 1a b c
.
C.
2, 1, 1a b c
. D.
2, 1a b c
.
Câu 46: Cho hàm số
3
3 , ;y ax x d a d
có đồ thị như hình vẽ bên dưới:
Mệnh đề nào dưới đây đúng?
A.
0, 0ad
. B.
0, 0ad
. C.
0, 0ad
. D.
0, 0ad
.
Câu 47: Cho hàm số
42
,0y ax bx c a
có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
. D.
0, 0, 0abc
.
Câu 48: Cho hàm số
32
y ax bx cx d
có đồ thị như hình vẽ sau:
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 49: Cho hàm số
2ax
fx
bx c
,
,,abc
có đồ thị như sau:
Khẳng định nào dưới đây đúng?
A.
0a b c
. B.
0b a c
. C.
0b c a
. D.
0b a c
.
Câu 50: Cho hàm số
42
y ax bx c
0a
có đồ thị như hình vẽ dưới đây:
Mệnh đề nào dưới đây đúng?
A.
0a
,
0b
,
0c
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
. D.
0, 0, 0abc
.
Câu 51: Cho hàm số
1
ax b
y
cx
có bảng biến thiên như hình vẽ dưới đây:
Xét các mệnh đề sau:
(1)
1c
.
(2)
2a
.
(3) Hàm số đồng biến trên
; 1 1; 
.
(4) Nếu
2
1
1
y
x
thì
1b
.
Số mệnh đề đúng trong các mệnh đề trên là
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 52: Cho hàm số
2ax
y
xb
( với
a
,
b
là các số thực) có đồ thị như hình sau:
Giá trị
ab
bằng
A.
0
. B.
3
. C.
3
. D.
4
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 53: Cho hàm số
32
y ax bx cx d
có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
C.
0, 0, 0, 0a b c d
D.
0, 0, 0, 0a b c d
.
Câu 54: Cho hàm số
32
y ax bx cx d
có đồ thị như hình vẽ bên dưới:
Mệnh đề nào sau đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Câu 55: Cho hàm số
42
y ax bx cx d
có đồ thị như hình vẽ dưới đây, mệnh đề nào sau đây đúng?
A.
0; 0; 0; 0a b c d
. B.
0; 0; 0; 0a b c d
.
C.
0; 0; 0; 0a b c d
. D.
0; 0; 0; 0a b c d
.
Câu 56: Cho hàm số
42
0y ax bx c a
có đồ thị như hình bên. Xác định dấu của
,,abc
.
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
. D.
0, 0, 0abc
.
Câu 57: Hàm số
42
y ax bx c
có đồ thị như hình vẽ bên dưới:
Mệnh đề nào sau đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0abc
. C.
0, 0, 0abc
. D.
0, 0, 0a b c
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 58: Cho hàm số
42
y ax bx c
, với
, , , 0a b c a
, có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
.
C.
0, 0, 0a b c
. D.
0, 0, 0a b c
.
Câu 59: Cho hàm số
ax b
y
xc
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
2, 1a b c
. B.
2, 1a b c
. C.
2, 1, 1a b c
. D.
2, 1a b c
.
Câu 60: Cho hàm số
32
y ax bx cx d
có đồ thị như hình bên. Mệnh đề nào sau đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Câu 61: Hàm số bậc 4 trùng phương
42
..y a x b x c
có đồ thị như hình vẽ. Dấu của các hệ số
,,abc
là
A.
0; 0; 0abc
. B.
0; 0; 0a b c
. C.
0; 0; 0a b c
. D.
0; 0; 0abc
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 62: Xác định các hệ số
a
,
b
,
c
để hàm số
42
y ax bx c
có đồ thị như hình bên dưới:
A.
1
4
a
;
2b 
;
2c
. B.
4a
;
2b
;
2c
.
C.
1
4
a
;
2b 
;
2c 
. D.
4a
;
2b 
;
2c
.
Câu 63: Cho hàm số
1ax
y
bx c
có đồ thị như hình bên dưới:
Giá trị
abc
bằng
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 64: Cho hàm số
32
y ax bx cx d
có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Câu 65: Cho hàm số
32
0 y ax bx cx d a
có đồ thị như hình vẽ dưới đây:
Mệnh đề nào sau đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 66: Cho hàm số
4ax b
y
cx b

có đồ thị là đường cong trong hình bên. Mệnh đề nào dưới đây
đúng?
A.
0,0 4, 0a b c
. B.
0, 0, 0abc
.
C.
0, 4, 0a b c
. D.
0,0 4, 0a b c
.
Câu 67: Cho hàm số
2
ax b
y
cx
,,abc
có đồ thị như sau:
Trong các số
a
,
b
và
c
có bao nhiêu số dương?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 68: Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ bên dưới:
Mệnh đề nào dưới đây đúng?
A.
ab
. B.
0ab
. C.
0ab
. D.
0ba
.
Câu 69: Cho hàm số
0
2
xb
yc
cx

có đồ thị như sau:
Mệnh đề nào sau đây đúng?
A.
0; 0.bc
B.
0; 0.bc
C.
0; 0.bc
D.
0; 0.bc
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 70: Cho hàm số
( , , )
xb
y b c d
cx d

có đồ thị như hình vẽ. Giá trị của biểu thức
2 3 4T b c d
bằng
A. 1. B.
8
. C. 6. D. 0.
Câu 71: Cho hàm số
,,
2
ax b
y a b c
cx

có đồ thị như hình vẽ bên dưới:
Trong các số
,ab
và
c
có bao nhiêu số dương?
A.
2
. B.
0.
C.
1
. D.
3
.
Câu 72: Cho hàm số
3ax
y
xc
có đồ thị như hình vẽ bên dưới:
1
2
x
y
O
3
2
Tính giá trị của
2ac
.
A.
22ac
. B.
23ac
. C.
23ac
. D.
21ac
.
Câu 73:
Đường cong ở hình dưới đây là đồ thị của hàm số
xa
y
bx c
,
( , , )abc
.
Trong các số
a
,
b
và
c
có bao nhiêu số dương?
A.
0
. B.
1.
C.
2.
D.
3.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 74: Cho hàm số
42
y ax bx c
có đồ thị như hình bên dưới:
Khẳng định nào sau đây đúng?
A.
0; 0; 0a b c
. B.
0; 0; 0a b c
. C.
0; 0; 0abc
. D.
0; 0; 0a b c
.
Câu 75: Cho hàm số
32
y ax bx cx d
có đồ thị là đường cong trong hình dưới đây:
Trong các hệ số
, , ,a b c d
có bao nhiêu số âm ?
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 76: Cho hàm số
ax b
y
cx d
có đồ thị như sau:
Mệnh đề nào sau đây đúng?
A.
0; 0ac bd
. B.
0; 0ab cd
. C.
0; 0bc ad
. D.
0; 0ad bd
.
Câu 77: Cho hàm số
3
,0
ax
y b b
bx c
có bảng biến thiên như sau:
Tính tổng
S a b c
.
A.
2
. B.
2
. C.
0
. D.
1
.
Câu 78: Cho hàm số
32
, , ,f x ax bx cx d a b c d
có bảng biến thiên như sau:
Có bao nhiêu số dương trong các số
, , , ?a b c d
A.
3.
B.
4.
C.
2.
D.
1.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 79: Cho hàm số
32
y ax bx cx d
có đồ thị như hình vẽ dưới đây:
Số lớn nhất trong các số
, , ,a b c d
là:
A.
c
. B.
a
. C.
b
. D.
d
.
Câu 80: Hàm số
y f x
thỏa mãn
2021 2021ff
có đồ thị là hình nào trong bốn đồ thị sau:
A. Hình 4. B. Hình 3. C. Hình 1. D. Hình 2.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
LỜI GIẢI CHI TIẾT
Câu 1: Đồ thị hàm số trong hình vẽ sau là đồ thị của hàm số nào trong các hàm số dưới đây
A.
1
2
x
y
x

. B.
3
2
x
y
x
. C.
13
2
x
y
x
. D.
1
2
x
y
x
.
Lời giải:
Dựa vào đồ thị ta thấy hai đường tiệm cận đứng
2x
, tiệm cận ngang
1y
và giao với trục
Oy
tại tung độ bằng
3
2
nên Chọn B thỏa.
Câu 2: Hàm số nào dưới đây có bảng biến thiên như sau:
x


y
y


5
1
1
A.
7
5
x
y
x
. B.
5
1
x
y
x
. C.
5
1
x
y
x
. D.
3
5
x
y
x
.
Lời giải:
Theo bảng biến thiên ta có: Tiệm cận đứng
5x
, tiệm cận ngang
1y
và
0 \ 5yx
nên ta chọn hàm số
3
5
x
y
x
.
Câu 3: Đồ thị hàm số nào dưới đây có dạng như hình vẽ?
A.
1
1
x
y
x
. B.
1
1
x
y
x
. C.
2
1
x
y
x
. D.
21
1
x
y
x

.
Lời giải:
Từ hình vẽ, suy ra đồ thị hàm số có tiệm cận đứng là đường thẳng
1x
, do đó ta loại hai
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chọn A và C.
Mặt khác đồ thị hàm số có tiệm cận ngang là đường thẳng
1y
, nên ta loại Chọn D Vậy đáp
án đúng là Chọn B
Câu 4: Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên dưới. Hỏi hàm số
y f x
là hàm
số nào trong các hàm số cho dưới đây?
A.
32
31y x x
. B.
32
31y x x
. C.
2
1
x
y
x
. D.
42
21y x x
.
Câu 5: Đường cong hình bên là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm
số nào?
A.
21
1
x
y
x
. B.
32
31y x x
. C.
42
21y x x
. D.
42
21y x x
.
Lời giải:
Đồ thị đã cho là đồ thị của hàm số bậc
4
42
y ax bx c
có hệ số
0a
và có
3
điểm cực trị.
Câu 6: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số có bảng biến thiên như trên là
A.
42
2y x x
. B.
42
3 6 3y x x
. C.
3
y x x
. D.
3
3y x x
.
Câu 7: Hàm số nào dưới đây có đồ thị như đường cong trong hình bên dưới?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
32
31y x x
. B.
42
31y x x
. C.
42
21y x x
. D.
32
21y x x
.
Lời giải:
Dựa vào hình dạng của đường cong, ta nhận thấy đó là đồ thị của hàm số bậc 4 trùng
phương có hệ số của
4
x
âm. Vậy Chọn C.
Câu 8: Bảng biến thiên dưới đây của hàm số nào?
A.
1
1
x
y
x
. B.
42
23y x x
. C.
3
34y x x
. D.
3
34y x x
.
Lời giải:
Ta loại phương án A và B vì khi lấy đạo hàm không phù hợp bảng biến thiên.
Còn lại phương án C và D. Dựa vào bảng biến thiên ta có hệ số
0a
.
Do đó, ta chọn hàm số
3
34y x x
.
Câu 9: Đồ thị sau đây là của hàm số nào?
A.
3
31y x x
. B.
3
31y x x
. C.
32
31y x x
. D.
32
31y x x
.
Lời giải:
Hàm số
32
y ax bx cx d
với
0a
và cắt
Oy
tại
0;1
.
Câu 10: Cho hàm số
()y f x
có bảng biến thiên như hình dưới đây. Hàm số
()y f x
là hàm số nào
trong các hàm số sau đây?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
42
23y x x
. B.
42
23y x x
. C.
42
1
33
4
y x x
.D.
42
23y x x
.
Lời giải:
Dựa vào bảng biến thiên ta có
0a
và hàm số có ba điểm cực trị do hàm số có dạng
42
ax bx c
có
.0ab
Câu 11: Đồ thị dưới đây là đồ thị của hàm số nào?
A.
3
y x x
. B.
3
y x x
. C.
3
y x x
. D.
yx
.
Lời giải:
Từ đồ thị ta thấy hàm số luôn nghịch biến, không có cực trị và là hàm bậc ba nên ta
chọn
3
y x x
.
Câu 12: Hàm số nào trong các hàm số sau mà đồ thị có dạng hình vẽ dưới đây?
A.
3
31y x x
. B.
32
31y x x
. C.
32
31y x x
. D.
3
31y x x
.
Lời giải:
Đồ thị hàm số trên là đồ thị hàm số bậc ba
32
y ax bx cx d
Nhìn vào nhánh phải của đồ thị ta thấy đồ thị có hướng đi lên suy ra
0a
Ta thấy đồ thị cắt trục tung tại điểm có tung độ dương suy ra
0d
Nhìn vào đồ thị ta thấy hàm số có hai điểm cực trị
1x
và
1x 
Vậy hàm số thỏa đề là
3
31y x x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 13: Hàm số
32
31y x x
có đồ thị nào sau đây?
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Lời giải:
Đồ thị hàm số
32
31y x x
cắt trục tung tại điểm
0; 1A
nên loại phương án A, C, D.
Vậy Chọn B.
Câu 14: Cho hàm số
y f x
có đồ thị
C
như hình vẽ. Hỏi
C
là đồ thị của hàm số nào?
A.
3
1yx
. B.
3
1yx
. C.
3
1yx
. D.
3
1yx
.
Lời giải:
Dựa vào đồ thị ta có:
+)
01xy
suy ra phương án:
3
1yx
,
3
1yx
không thoả mãn.
+)
01yx
suy ra phương án
3
1yx
không thoả mãn.
+) Do đó phương án
3
1yx
thoả mãn.
Câu 15: Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
32
1y x x x
. B.
yx
. C.
1
2
x
y
x
. D.
4
.yx
Lời giải:
Dễ nhận thấy dạng đồ thị cho trong bài là của hàm số dạng
ax b
y
cx d
.
Câu 16: Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây, hàm số nào có bảng
biến thiên như sau?
A.
32
3 9 2y x x x
. B.
32
12
3
33
y x x x
.
C.
32
3 9 2y x x x
. D.
32
12
3
33
y x x x
.
Lời giải:
Vì
lim
x
y


nên loại A, D.
Xét Chọn B, thay
29
3
3
xy
.
Xét Chọn C, thay
3 29xy
(không thoả mãn bảng biến thiên).
Vậy chọn phương án B.
Câu 17: Hàm số
32
3 3 1y x x x
có đồ thị là hình nào sau đây?
A. . B. . C. . D. .
Lời giải:
Vì
lim ; lim
xx
yy
 
 
nên loại C và D.
Vì
01y
nên Chọn B
Câu 18: Hàm số nào có đồ thị là hình vẽ sau đây?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
32
34y x x
. B.
42
34y x x
. C.
32
34y x x
. D.
21
35
x
y
x
.
Lời giải:
Dựa vào hình dạng đồ thị, ta thấy đây là đồ thị của hàm số bậc 3, với hệ số
0 lim
x
ay


. Nên loại Chọn B và D.
Khi
04xy
nên Chọn C
Câu 19: Đường cong trong hình vẽ bên là đồ thị của một hàm số nào?
A.
3
32y x x
. B.
3
32y x x
. C.
42
2y x x
. D.
3
32y x x
.
Lời giải:
Nhánh cuối của đồ thị đi xuống nên
0a
, đồ thị có hai điểm cực trị nên
.0ac
.
Câu 20: Hàm số nào dưới đây có bảng biến thiên như hình bên dưới?
A.
3
.
1
x
y
x

B.
3
.
1
x
y
x
C.
2
.
1
x
y
x

D.
3
.
1
x
y
x

Lời giải:
Dựa vào bảng biến thiên, ta thấy:
Hàm số có tiệm cận ngang
1y 
. (Loại B)
Hàm số nghịch biến trên
;1
và
1; 
nên
0, 1.yx
Câu 21: Hàm số nào có đồ thị là đường cong trong hình vẽ bên dưới?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
42
41y x x
. B.
1
2
x
y
x
. C.
32
41y x x
. D.
2
21yx
.
Lời giải:
Từ đồ thị ta thấy hàm số có 3 điểm cực trị, suy ra hình vẽ là đồ thị hàm số
42
41y x x
.
Câu 22: Đồ thị của hàm số nào dưới đây có dạng như đường cong hình dưới đây?
x
y
1
1
A.
3
31y x x
. B.
3
31y x x
. C.
3
31y x x
. D.
3
31y x x
.
Lời giải:
Đồ thị có nhánh ngoài cùng đi lên nên
0a
, suy ra lại hàm số
3
31y x x
và
3
31y x x
.
Đồ thị cắt trục tung tại điểm có tung độ dương nên loại hàm số
3
31y x x
.
Câu 23: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số có bảng biến thiên như trên là
A.
42
3 6 3y x x
. B.
42
2y x x
. C.
3
y x x
. D.
3
3y x x
.
Lời giải:
Xét
0fx
có 3 nghiệm phân biệt, loại Chọn C và D.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Hàm số đồng biến trên khoảng
1; 
, loại Chọn B
Câu 24: Đồ thị hàm số nào sau đây có hình dạng như hình vẽ
A.
3
3y x x
. B.
3
3y x x
. C.
32
3y x x
. D.
32
3y x x
.
Câu 25: Bảng biến thiên sau đây là của hàm số nào
A.
3
2
x
fx
x
. B.
3
2
x
fx
x
C.
3
2
x
fx
x
. D.
23
2
x
fx
x
Lời giải:
Ta có
lim 1
x
fx

suy ra đồ thị hàm số có một tiệm cận ngang là
1y
.
2
lim
x
fx

2x
mà một tiệm cận đứng của đồ thị hàm số.
Từ đó ta dễ dàng loại hai phương án B và D.
Dựa vào bảng biến thiên, nhận thấy hàm số đồng biến trên từng khoảng xác định nên Chọn
A có
2
1
0
2
fx
x

thỏa mãn, Chọn C có
2
5
0
2
fx
x

không thỏa mãn.
Câu 26: Đường cong của hình vẽ bên là đồ thị của hàm số nào trong các hàm số sau.
A.
2
1
x
y
x
. B.
42
22y x x
. C.
42
22y x x
. D.
32
22y x x
Câu 27: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
32
31y x x
. B.
42
21y x x
. C.
42
21y x x
. D.
32
31y x x
.
Lời giải:
Từ đồ thị ta thấy:
Đây là đồ thị của hàm bậc ba nên loại B, C
Nhánh cuối của đồ thị đi xuống, suy ra hệ số
0a
nên loại A
Đồ thị trên là đồ thị của hàm số
32
31y x x
.
Câu 28: Hàm số
2
1
x
y
x
có đồ thị là hình vẽ nào sau đây?
A.
x
y
-2
2
1
-1
0
1
. B.
x
y
-2
1
-1
0
1
.C
.
x
y
-2
3
1
-1
0
1
.D.
x
y
-2
2
1
-1
0
1
.
Lời giải:
Đồ thị hàm số có tiệm cận ngang là:
1y
, tiệm cận đứng là
1x
, cắt trục
Ox
tại
2;0
, cắt
Oy
tại
0;2
Câu 29: Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới?
A.
42
31y x x
. B.
42
31y x x
. C.
42
1y x x
. D.
42
1y x x
.
Lời giải:
Đường cong trong hình vẽ là đồ thị của hàm số
42
0y ax bx c a
.
Dựa vào đồ thị, ta thấy:
+)
lim 0
x
ya


.
+) Đồ thị giao với
Oy
tại điểm có tung độ dương
0c
.
+) Hàm số có ba điểm cực trị
0ab
.
Câu 30: Hàm số nào dưới đây có đồ thị dạng như đường cong trong hình vẽ bên dưới?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
x
y
O
1
1
A.
1
1
x
y
x
. B.
21
1
x
y
x
. C.
21
1
x
y
x
. D.
1
1
x
y
x
.
Lời giải:
Dựa vào đồ thị ta thấy đồ thị hàm số có phương trình tiệm cận đứng là
1x
, tiệm cận ngang
1y
. Chỉ có hàm số ở Chọn A là thỏa mãn.
Câu 31: Đồ thị hàm số
3
32y x x
là hình nào trong 4 hình dưới đây?
A. . B. . C. . D. .
Lời giải:
▪ Ta có:
lim
x
y


Loại câu C, D.
▪ Với
02xy
nên ta Chọn A
Câu 32: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
A.
22
1
x
y
x
. B.
3
21y x x
. C.
21
2
x
y
x

. D.
42
22y x x
.
Lời giải:
Ta có đây là đồ thị của hàm số dạng
ax b
y
cx d
Mặt khác đồ thị hàm số đã cho có tiệm cận đứng
1x 
.
Câu 33: Đồ thị hàm số
32
32y x x
là đường cong trong hình nào dưới đây?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A. B. C. D.
Lời giải:
Ta có
32
32y x x
2
36y x x

2
0
0 3 6 0
2
x
y x x
x
nên loại Chọn A và B
Mặt khác
10a 
nên Chọn C
Câu 34: Đồ thị hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
2
12y x x
. B.
2
12y x x
. C.
32
32y x x
. D.
42
32y x x
.
Lời giải:
Dựa vào đồ thị, ta thấy đồ thị hàm số là hàm đa thức bậc ba nên loại D
Do
lim
x
y


nên hệ số
0a
, loại C
Đồ thị hàm số cắt trục hoành Ox tại ba điểm có hoành độ
1
1
2
x
x
x

nên chỉ có Chọn B thỏa khi lập phương trình hoành độ giao điểm.
Câu 35: Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?
A.
3
32y x x
. B.
32
31y x x
. C.
32
32y x x
. D.
42
31y x x
.
Lời giải:
Từ BBT ta thấy: đây là BBT của một hàm số bậc ba, có hệ số của
3
x
là
0a
.
Do đó, đáp án A, D, C sai. Đáp án đúng là B.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 36: Cho hàm số
32
y f x ax bx cx d
có bảng biến thiên sau:
Đồ thị nào thể hiện hàm số
y f x
?
A.
.I
B.
.II
C.
.III
D.
.IV
Lời giải:
Dựa vào bảng biến thiên, ta thấy:
• Hàm số có giá trị cực đại bằng
2
và giá trị cực tiểu bằng
2.
Loại Chọn B và C.
• Khi
x
thì
y 
nên chỉ có Chọn A là phù hợp.
Câu 37: Đồ thị trong hình vẽ sau là đồ thị của hàm số nào trong các hàm số dưới đây.
A.
42
81y x x
. B.
32
31y x x
. C.
42
21y x x
. D.
3
2
31y x x
.
Lời giải:
Chọn B có
0y 
loại.
Chọn C đồ thị tiếp xúc với trục hoành nên loại C.
Chọn A có
2 15xy
nên loạiA.
MỘT SỐ BÀI TOÁN LIÊN QUAN
Câu 38: Cho đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
với
, , ,a b c d
là các số thực.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Mệnh đề nào dưới đây đúng?
A.
0,yx
. B.
0, 1yx
. C.
0, 1yx
. D.
0,yx
.
Lời giải:
Tiệm cận đứng
1x
. Hàm số nghịch biến.
Câu 39: Biết hàm số
1
xa
y
x
(
a
là số thực cho trước,
1a
) có đồ thị như hình vẽ sau:
Mệnh đề nào dưới đây đúng?
A.
' 0, 1yx
. B.
' 0, 1yx
. C.
' 0,yx
. D.
' 0,yx
.
Lời giải:
Ta có tập xác định của hàm số là
\1D
và hàm số nghịch biến trên từng khoảng xác
định.
Vậy
' 0, 1yx
.
Câu 40: Cho hàm số
1
xm
y
x
, có đồ thị như hình vẽ bên dưới:
Khẳng định nào sau đây đúng?
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Câu 41: Cho hàm số
1
xa
y
x
có đồ thị như hình vẽ bên dưới:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Mệnh đề nào dưới đây đúng?
A.
1a
. B.
3a 
. C.
1a 
. D.
1a
.
Lời giải:
Tập xác định:
\1D
.
Ta có:
2
1
1
a
y
x

.
Từ hình vẽ ta thấy:
0, 1 1 0 1y x a a
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2. Do đó
22 aa
.
Câu 42: Biết hàm số
32
a ( 0)y x bx cx d a
có đồ thị như hình vẽ sau:
x
2
1
y
-1
O
1
Mệnh đề nào dưới đây đúng?
A.
' 0,yx
. B.
' 0,yx
. C.
' 0,yx
. D.
' 0,yx
.
Câu 43: Hàm số
32
y ax bx cx d
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Lời giải:
Nhìn vào nhánh phải của đồ thị ta thấy đồ thị có hướng đi lên suy ra
0a
Nhìn vào giao điểm của đồ thị với trục tung ta thấy đồ thị cắt trục tung tại điểm có tung độ
dương suy ra
0d
.
Ta có
2
32y ax bx c
Hàm số đã cho có hai điểm cực trị
1
x
,
2
x
với
12
. 0 0 0
3
c
x x c
a
(vì
0a
)
Vì
1
10x
và
2
1x
nên
12
2
0 0 2 0 0
3
b
x x b b
a
(vì
0a
)
Vậy
0a
,
0b
,
0c
,
0d
.
Câu 44: Cho hàm số
1
, ,
ax
f x a b c
bx c

có bảng biến thiên như sau:
Trong các số
,,abc
có bao nhiêu số dương?
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải:
Từ BBT suy ra
+) Với
1
0 0 0.x f x c
c
+) Với
1
0 0 0.f x x a
a
+) Tiệm cận đứng
2 2 0.
c
x c b b
b
Vậy trong các số
,,abc
có duy nhất một số dương.
Câu 45: Cho hàm số
ax b
y
xc
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
2, 1a b c
. B.
2, 1a b c
.
C.
2, 1, 1a b c
. D.
2, 1a b c
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Lời giải:
Đồ thị hàm số có:
Tiệm cận đứng:
1 1.x c c
Tiệm cận ngang:
2.ya
Giao điểm với trục tung:
0 1 1
b
x y b
c
.
Câu 46: Cho hàm số
3
3 , ;y ax x d a d
có đồ thị như hình vẽ bên dưới:
Mệnh đề nào dưới đây đúng?
A.
0, 0ad
. B.
0, 0ad
. C.
0, 0ad
. D.
0, 0ad
.
Lời giải:
Dựa vào đồ thị, ta có
0, 0ad
.
Câu 47: Cho hàm số
42
,0y ax bx c a
có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
. D.
0, 0, 0abc
.
Lời giải:
Dựa vào đồ thị ta thấy hàm số có 3 điểm cực trị trong đó có hai điểm cực đại và một điểm cực
tiểu nên
0, 0ab
.
Đồ thị hàm số đi qua điểm
0;c
nằm dưới trục hoành nên
0c
.
Vậy
0, 0, 0a b c
.
Câu 48: Cho hàm số
32
y ax bx cx d
có đồ thị như hình vẽ sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Lời giải:
+ Ta có
lim
x
y


0a
.
+ Đồ thị hàm số cắt
Oy
tại điểm có tọa độ
0;d
suy ra
0d
.
+ Ta có
2
32y ax bx c
.
Gọi
1
x
,
2
x
là các điểm cực trị của hàm số.
Dựa vào đồ thị ta có
12
12
2
0
3
0
3
b
xx
a
c
xx
a

, mà
0a
, suy ra
0b
,
0c
.
Vậy
0a
,
0b
,
0c
,
0d
.
Câu 49: Cho hàm số
2ax
fx
bx c
,
,,abc
có đồ thị như sau:
Khẳng định nào dưới đây đúng?
A.
0a b c
. B.
0b a c
. C.
0b c a
. D.
0b a c
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Lời giải:
Dựa vào đồ thị ta có
2
0 1 1 2x y c
c
.
Tiệm cận đứng
1 1 2
c
xb
b
.
Tiệm cận ngang
2 2 4
a
ya
b
.
Vậy
0a b c
.
Câu 50: Cho hàm số
42
y ax bx c
0a
có đồ thị như hình vẽ dưới đây:
Mệnh đề nào dưới đây đúng?
A.
0a
,
0b
,
0c
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
. D.
0, 0, 0abc
.
Câu 51: Cho hàm số
1
ax b
y
cx
có bảng biến thiên như hình vẽ dưới đây:
Xét các mệnh đề sau:
(1)
1c
.
(2)
2a
.
(3) Hàm số đồng biến trên
; 1 1; 
.
(4) Nếu
2
1
1
y
x
thì
1b
.
Số mệnh đề đúng trong các mệnh đề trên là
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải:
Ta có
1
1
lim 1 1
1
x
ax b
xc
cx c



suy ra (1) đúng
lim 2
1
x
ax b a
cx c


22ac
suy ra (2) đúng
Theo bảng biến thiên thì trên khoảng
; 1 1; 
ta thấy
0y
nên (3) đúng.
22
2
1
11
a bc b
y
cx x


1b
suy ra (4) đúng
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 52: Cho hàm số
2ax
y
xb
( với
a
,
b
là các số thực) có đồ thị như hình sau:
Giá trị
ab
bằng
A.
0
. B.
3
. C.
3
. D.
4
.
Lời giải:
Tập xác định
\2D
.
Ta có
1y
là tiệm cận ngang của đồ thị hàm số nên
1a
.
Ta có
2x
là tiệm cận đứng của đồ thị hàm số nên
2b 
.
Suy ra
1 2 3ab
.
Câu 53: Cho hàm số
32
y ax bx cx d
có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
C.
0, 0, 0, 0a b c d
D.
0, 0, 0, 0a b c d
.
Lời giải:
Quan sát đồ thị hàm số ta thấy:
0a
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương
0d
.
Hàm số có hai điểm cực trị
12
;xx
thỏa mãn:
12
12
2
00
3
0; 0
00
3
bb
xx
aa
bc
cc
xx
aa







.
Câu 54: Cho hàm số
32
y ax bx cx d
có đồ thị như hình vẽ bên dưới:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Mệnh đề nào sau đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Lời giải:
Do nhánh bên phải của đồ thị đi xuống nên
0a
.
Đồ thị cắt trục tung ở phần dương nên
0.d
Đồ thị có 2 cực trị tại hai giá trị
x
dương nên phương trình
0y
có
2
nghiệm dương phân
biệt
2
3 2 0ax bx c
có 2 nghiệm dương phân biệt.
2
30
0
0
2
00
0
3
0
0
3
b ac
b
b
S
c
a
P
c
a




.
Câu 55: Cho hàm số
42
y ax bx cx d
có đồ thị như hình vẽ dưới đây, mệnh đề nào sau đây đúng?
A.
0; 0; 0; 0a b c d
. B.
0; 0; 0; 0a b c d
.
C.
0; 0; 0; 0a b c d
. D.
0; 0; 0; 0a b c d
.
Lời giải:
+ Từ ĐTHS
0
0
a
d
+ Do ĐTHS nhận trục
oy
làm trục đối xứng
y f x
là hàm số chẵn nên
0c
+ Ta có:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
,
,
3
4 2 .
0
0
2
y ax bx
x
y
b
x
a


.
+ Hàm số có ba điểm cực trị
0 0 0.
2
bb
yb
aa
Vậy đáp án đúng là D.
Câu 56: Cho hàm số
42
0y ax bx c a
có đồ thị như hình bên. Xác định dấu của
,,abc
.
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
. D.
0, 0, 0abc
.
Lời giải:
Dựa vào hình dạng đồ thị hàm số ta nhận thấy :
Hệ số
0a
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm
0c
.
Đồ thị hàm số có 3 điểm cực trị
00ab b
.
Vậy
0a
,
0b
,
0c
.
Câu 57: Hàm số
42
y ax bx c
có đồ thị như hình vẽ bên dưới:
Mệnh đề nào sau đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0abc
. C.
0, 0, 0abc
. D.
0, 0, 0a b c
.
Lời giải:
Dựa vào đồ thị hàm số, ta thấy:
+
lim 0
x
ya


.
+ Hàm số có 3 cực trị nên
. 0 0a b b
.
+ Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên
0c
.
Câu 58: Cho hàm số
42
y ax bx c
, với
, , , 0a b c a
, có đồ thị như hình vẽ dưới đây.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
.
C.
0, 0, 0a b c
. D.
0, 0, 0a b c
.
Lời giải:
Dựa vào hình dáng đồ thị hàm số ta có
0a
. Loại Chọn B
Vì hàm số có ba cực trị nên
0ab
suy ra
0b
. Loại Chọn C
Đồ thị hàm số cắt trục
Oy
tại điểm nằm trên trục hoành nên
0c
. Loại Chọn D
Câu 59: Cho hàm số
ax b
y
xc
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
2, 1a b c
. B.
2, 1a b c
. C.
2, 1, 1a b c
. D.
2, 1a b c
.
Lời giải:
Từ đồ thị hàm số ta thấy
lim 2
x
y


và
1
lim
x
y


suy ra tiệm cận ngang:
2y 
, tiệm cận
đứng:
1x 
Mặt khác đồ thị hàm số
ax b
y
xc
có tiệm cận ngang
ya
và tiệm cận đứng
xc
Do đó ta có
2a 
và
1c
Đồ thị hàm số cắt trục tung tại điểm có tung độ
1y
nên
11
b
b
c
Câu 60: Cho hàm số
32
y ax bx cx d
có đồ thị như hình bên. Mệnh đề nào sau đây đúng?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Lời giải:
Dựa vào đồ thị suy ra
0a
.
Giao điểm của đồ thị với trục
Oy
suy ra
0d
.
Dựa vào cực trị ta có
12
. 0 0.
c
x x c
a
12
00
b
x x b
a
.
Câu 61: Hàm số bậc 4 trùng phương
42
..y a x b x c
có đồ thị như hình vẽ. Dấu của các hệ số
,,abc
là
A.
0; 0; 0abc
. B.
0; 0; 0a b c
. C.
0; 0; 0a b c
. D.
0; 0; 0abc
.
Lời giải:
Quan sát đồ thị ta thấy:
lim lim
xx
yy
 

suy ra:
0a
Hàm số có 1 điểm cực trị,
a
và
b
cùng dấu hoặc
0b
suy ra:
0b
Đồ thị hàm số cắt
Oy
tại điểm có tung độ dương suy ra:
0c
. Vậy Chọn D
Câu 62: Xác định các hệ số
a
,
b
,
c
để hàm số
42
y ax bx c
có đồ thị như hình bên dưới:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
1
4
a
;
2b 
;
2c
. B.
4a
;
2b
;
2c
.
C.
1
4
a
;
2b 
;
2c 
. D.
4a
;
2b 
;
2c
.
Lời giải:
Đồ thị hàm số đi qua điểm
(0;2)
nên
2c
.
Ta có
3
42y ax bx

nên
2
0
.
0
2
x
b
x
a
y

Dựa vào đồ thị thì hàm số đạt cực trị tại
2x 
nên
48
2
b
ba
a
.
Vậy chỉ có đáp án
1
4
a
;
2b 
;
2c
thỏa mãn.
Câu 63: Cho hàm số
1ax
y
bx c
có đồ thị như hình bên dưới:
Giá trị
abc
bằng
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải:
Vì đồ thị hàm số qua điểm
1
0;
2
M



nên ta có:
11
2
2
c
c
.
Tiệm cận đứng của đồ thị:
21
c
xb
b
.
Tiệm cận ngang của đồ thị:
22
a
ya
b
.
Vậy
1abc
.
Câu 64: Cho hàm số
32
y ax bx cx d
có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Lời giải:
Dựa vào đồ thị hàm bậc ba ta nhận xét:
Nhánh cuối đồ thị hàm số đồng biến nên
0a
.
Đồ thị hàm số cắt Oy tại điểm có tung độ dương nên
0d
.
Đồ thị hàm số có hai điểm cực trị nằm về 2 phía trục tung nên
00ac c
.
Đồ thị hàm số có hoành độ điểm uốn dương nên
00ab b
.
Câu 65: Cho hàm số
32
0 y ax bx cx d a
có đồ thị như hình vẽ dưới đây:
Mệnh đề nào sau đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Lời giải:
Ta có
2
32y ax bx c
theo hình vẽ:
- đồ thị cắt trục tung tại điểm
0,d
nằm phía trên trục hoành nên
0d
;
- hàm số có hai điểm cực trị trái dấu nên
0ac
mà
0a
, do đó
0c
.
- Điểm uốn của đồ thị có hoành độ dương nên
12
2
00
26
xx
b
ab
a
. Do
0a
nên
0b
.
Câu 66: Cho hàm số
4ax b
y
cx b

có đồ thị là đường cong trong hình bên. Mệnh đề nào dưới đây
đúng?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A.
0,0 4, 0a b c
. B.
0, 0, 0abc
.
C.
0, 4, 0a b c
. D.
0,0 4, 0a b c
.
Lời giải:
Từ
4ax b
y
cx b

suy ra dồ thị hàm số có TCĐ:
b
x
c

, TCN:
a
y
c
, giao điểm của đồ thị với
trục tung và trục hoành lần lượt có tọa độ
44
0; ; ;0
bb
ba

.
Từ đồ thị ta thấy
01
02
4
0 3 .
a
c
b
c
b
b

Từ ta có
04b
, từ ta suy ra
0c
, từ suy ra
0a
.
Câu 67: Cho hàm số
2
ax b
y
cx
,,abc
có đồ thị như sau:
Trong các số
a
,
b
và
c
có bao nhiêu số dương?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải:
Đồ thị hàm số có: Tiệm cận đứng:
2
x
c
, tiệm cận ngang:
a
y
c
, giao điểm với Oy:
0;
2
b



.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Từ đồ thị hàm số ta có:
2
0
0
00
0
0
2
c
c
a
a
c
b
b



.
Vậy trong các số
a
,
b
và
c
có
1
số dương.
Câu 68: Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ bên dưới:
Mệnh đề nào dưới đây đúng?
A.
ab
. B.
0ab
. C.
0ab
. D.
0ba
.
Lời giải:
Ta có
lim lim
1
1
1
 

xx
b
a
ax b
x
a
x
x
và
lim lim
1
1
1
 

xx
b
a
ax b
x
a
x
x
nên
ya
là phương trình
đường tiệm cận ngang của đồ thị hàm số.
Dựa vào hình vẽ ta thấy đồ thị có phương trình đường tiệm cận ngang
2y
nên
2a
.
Đồ thị đi qua điểm
0;1
nên thay
0; 1xy
vào hàm số ta được:
.0
11
01
ab
b
Vậy
20ab 
.
Câu 69: Cho hàm số
0
2
xb
yc
cx

có đồ thị như sau:
Mệnh đề nào sau đây đúng?
A.
0; 0.bc
B.
0; 0.bc
C.
0; 0.bc
D.
0; 0.bc
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Theo đồ thị, tiệm cận ngang:
1
0 0.yc
c
0 0 0.y x b b
Vậy
0b
,
0c
.
Câu 70: Cho hàm số
( , , )
xb
y b c d
cx d

có đồ thị như hình vẽ. Giá trị của biểu thức
2 3 4T b c d
bằng
A. 1. B.
8
. C. 6. D. 0.
Lời giải:
Đồ thị hàm số cắt trục
Ox
0
xb
xb
cx d
.
Quan sát đồ thị ta thấy đồ thị hám số cắ trục hoành tại
1 1 1x b b
.
Đồ thị hàm số có tiệm cận ngang là
1
11yc
c
.
Đồ thị hàm số có tiệm cận đứng là:
1 1 1
d
x d c d d
c
.
Vậy:
2 3 4 2.1 3.1 4. 1 1T b c d
.
Câu 71: Cho hàm số
,,
2
ax b
y a b c
cx

có đồ thị như hình vẽ bên dưới:
Trong các số
,ab
và
c
có bao nhiêu số dương?
A.
2
. B.
0.
C.
1
. D.
3
.
Lời giải:
+) Tiệm cận đứng của đồ thị hàm số:
2
00xc
c
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
+) Ta có tiệm cận ngang của đồ thị hàm số
00
a
ya
c
.
+)
0 0 0
2
b
x y b
.
Vậy
0b
.
Câu 72: Cho hàm số
3ax
y
xc
có đồ thị như hình vẽ bên dưới:
1
2
x
y
O
3
2
Tính giá trị của
2ac
.
A.
22ac
. B.
23ac
. C.
23ac
. D.
21ac
.
Lời giải:
Ta có: Đồ thị hàm số
3ax
y
xc
có tiệm cận đứng là
xc
và tiệm cận ngang là
ya
.
Theo đồ thị ta có
22x c c
.
1ya
.
Vậy
23ac
.
Câu 73:
Đường cong ở hình dưới đây là đồ thị của hàm số
xa
y
bx c
,
( , , )abc
.
Trong các số
a
,
b
và
c
có bao nhiêu số dương?
A.
0
. B.
1.
C.
2.
D.
3.
Lời giải:
Dựa vào đồ thị, ta có các nhận xét sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
ĐTHS có TCN:
1
11yb
b
.
ĐTHS có TCĐ:
11
c
x c b c
b
.
ĐTHS đi qua điểm
0;2
, nên
22
a
a
c
.
Vậy trong các số
a
,
b
và
c
có 1 số dương.
Câu 74: Cho hàm số
42
y ax bx c
có đồ thị như hình bên dưới:
Khẳng định nào sau đây đúng?
A.
0; 0; 0a b c
. B.
0; 0; 0a b c
. C.
0; 0; 0abc
. D.
0; 0; 0a b c
.
Lời giải:
Dựa vào đồ thị hàm số
42
0y ax bx c a
ta có
lim 0
x
ya


.
Đồ thị hàm số có 3 cực trị
32
' 4 2 2 2 0y ax bx x ax b
có 3 nghiệm phân biệt nên
00ab b
.
Đồ thị hàm số cắt trục Oy tại điểm có tung độ dương nên
0c
.
Vậy
0; 0; 0a b c
.
Câu 75: Cho hàm số
32
y ax bx cx d
có đồ thị là đường cong trong hình dưới đây:
Trong các hệ số
, , ,a b c d
có bao nhiêu số âm ?
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Dựa vào hình dạng đồ thị: đồ thị hàm bậc ba có hệ số
0a
, đồ thị cắt trục tung tại điểm có
tung độ dương nên
0d
.
Ta có:
2
32y ax bx c
. Đồ thị có hai điểm cực trị cùng nằm bên phải trục tung nên
0y
có
hai nghiệm dương phân biệt
12
,xx
.
Ta có
12
12
2
0
0
3
0
.0
3
b
xx
b
a
cc
xx
a


.
Vậy
0, 0ac
.
Câu 76: Cho hàm số
ax b
y
cx d
có đồ thị như sau:
Mệnh đề nào sau đây đúng?
A.
0; 0ac bd
. B.
0; 0ab cd
. C.
0; 0bc ad
. D.
0; 0ad bd
.
Lời giải:
Theo đồ thị:
Tiệm cận ngang:
0
a
y
c
0ac
. Do đó
,ac
cùng dấu (1)
Tiệm cận đứng
00
dd
x
cc
0cd
. Do đó
,cd
trái dấu (2)
Cho
0y
0
b
x
a
0
b
a

0.ab
Do đó
,ab
cùng dấu (3)
Từ (1) và (2) suy ra
,ad
trái dấu nên
0ad
.
Từ (1) và (3) suy ra
,bc
cùng dấu nên
0bc
.
Câu 77: Cho hàm số
3
,0
ax
y b b
bx c
có bảng biến thiên như sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Tính tổng
S a b c
.
A.
2
. B.
2
. C.
0
. D.
1
.
Lời giải:
3ax
y
bx c
2
3ac b
y
bx c

Kết hợp với bảng biến thiên của hàm số
3
,0
ax
y b b
bx c
ta có:
0,
1
2
30
bb
c
b
a
b
ac b



2
0,
2
2 3 0
bb
cb
ab
bb




1
2
1
c
a
b

. Vậy
2S a b c
.
Câu 78: Cho hàm số
32
, , ,f x ax bx cx d a b c d
có bảng biến thiên như sau:
Có bao nhiêu số dương trong các số
, , , ?a b c d
A.
3.
B.
4.
C.
2.
D.
1.
Lời giải:
lim 0.
x
f x a


0 1 1 0.fd
2
3 2 .f x ax bx c
Ta có
12
12
2
2
2
30
3
.
00
0
3
b
xx
ba
a
x x c c
a



Câu 79: Cho hàm số
32
y ax bx cx d
có đồ thị như hình vẽ dưới đây:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Số lớn nhất trong các số
, , ,a b c d
là:
A.
c
. B.
a
. C.
b
. D.
d
.
Lời giải:
+
2
32y ax bx c
+ Đồ thị ham số có hai điểm cực trị là
1;2M
và
3; 2N
nên:
32
32
2
2
.1 .1 .1 2
.3 .3 .3 2
3 .1 2 .1 0
3 .3 2 .3 0
a b c d
a b c d
a b c
a b c
2
27 9 3 2
3 2 0
27 6 0
a b c d
a b c d
a b c
a b c
1
6
9
2
a
b
c
d


Vậy
9c
là số lớn nhất.
Câu 80: Hàm số
y f x
thỏa mãn
2021 2021ff
có đồ thị là hình nào trong bốn đồ thị sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
A. Hình 4. B. Hình 3. C. Hình 1. D. Hình 2.
Lời giải:
Dựa vào đồ thị các hàm số đã cho, ta chọn đồ thị hàm số ở hình 4 là đồ thị của hàm số chẵn
thỏa mãn
2021 2021ff
.
_______________________HẾT_______________________
Huế,20h30’ Ngày 26 tháng 5 năm 2023

Tài liệu khác của Toán 12

Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 12 KHẢO SÁT HÀM SỐ
NHẬN DẠNG ĐỒ THỊ HÀM SỐ
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia VẤN ĐỀ 7
KHẢO SÁT SỰ BIẾN THIÊN
VÀ VẼ ĐỒ THỊ HÀM SỐ I. TÓM TẮT LÝ THUYẾT
1 - SƠ ĐỒ KHẢO SÁT HÀM SỐ
Cho hàm số y f x .
1. Tìm tập xác định của hàm số. 2. Sự biến thiên a) Chiều biến thiên. i. Tính y ' .
ii. Tìm các nghiệm của phương trình y '  0 và các điểm tại đó y ' không xác định.
iii. Xét dấu y ' và suy ra các khoảng biến thiên của hàm số.
b) Tìm cực trị (nếu có).
c) Tìm các giới vô cực; các giới hạn tại ,   và tại các điểm mà hàm số không xác định.
d) Tìm các đường tiệm cận của hàm số (nếu có).
e) Lập bảng biến thiên. 3. Đồ thị.
a) Liệt kê các điểm đặc biệt ( điểm cực đại, điểm cực tiểu, tâm đối xứng,…)
b) Xác định giao điểm của (C) với Ox, Oy (nếu có). c) Vẽ đồ thị.
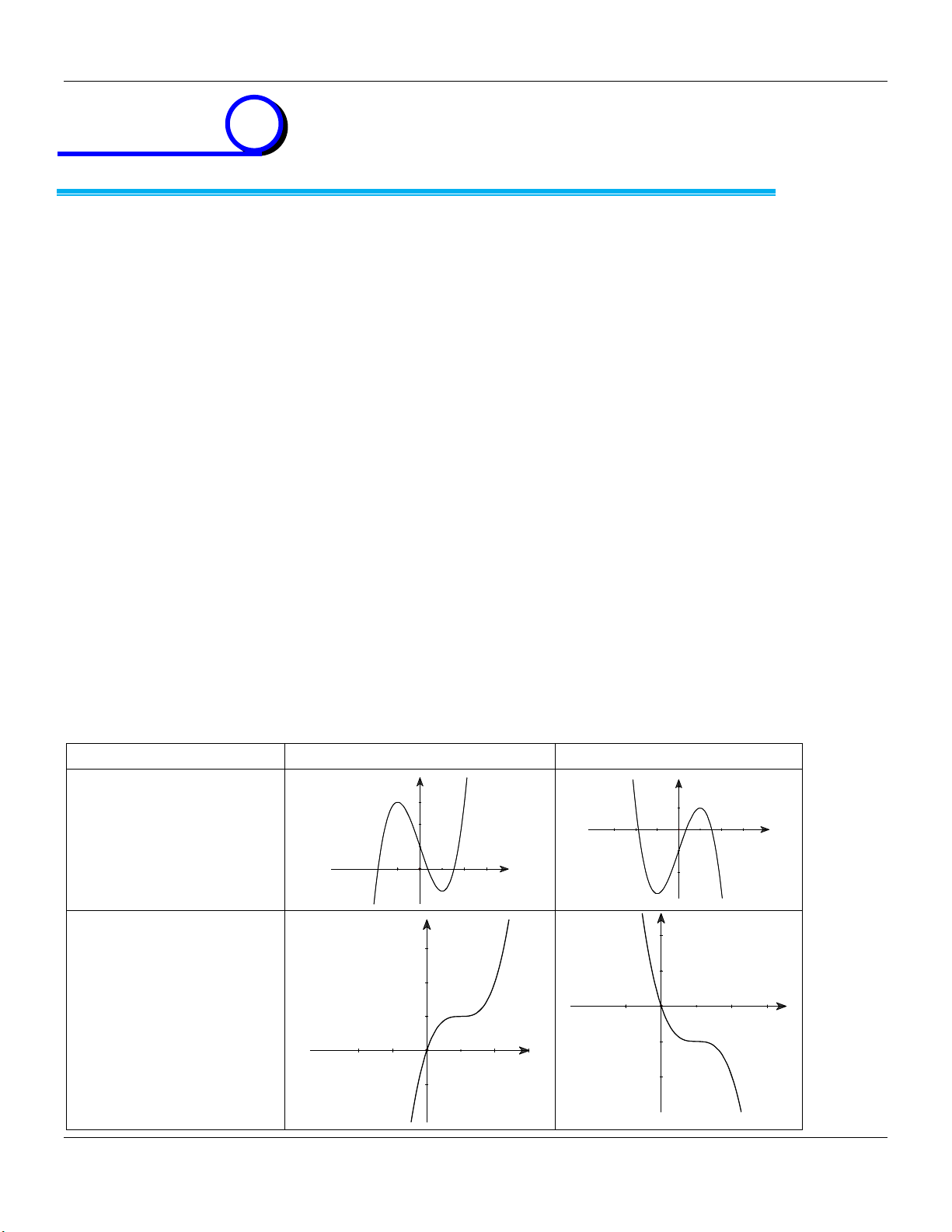
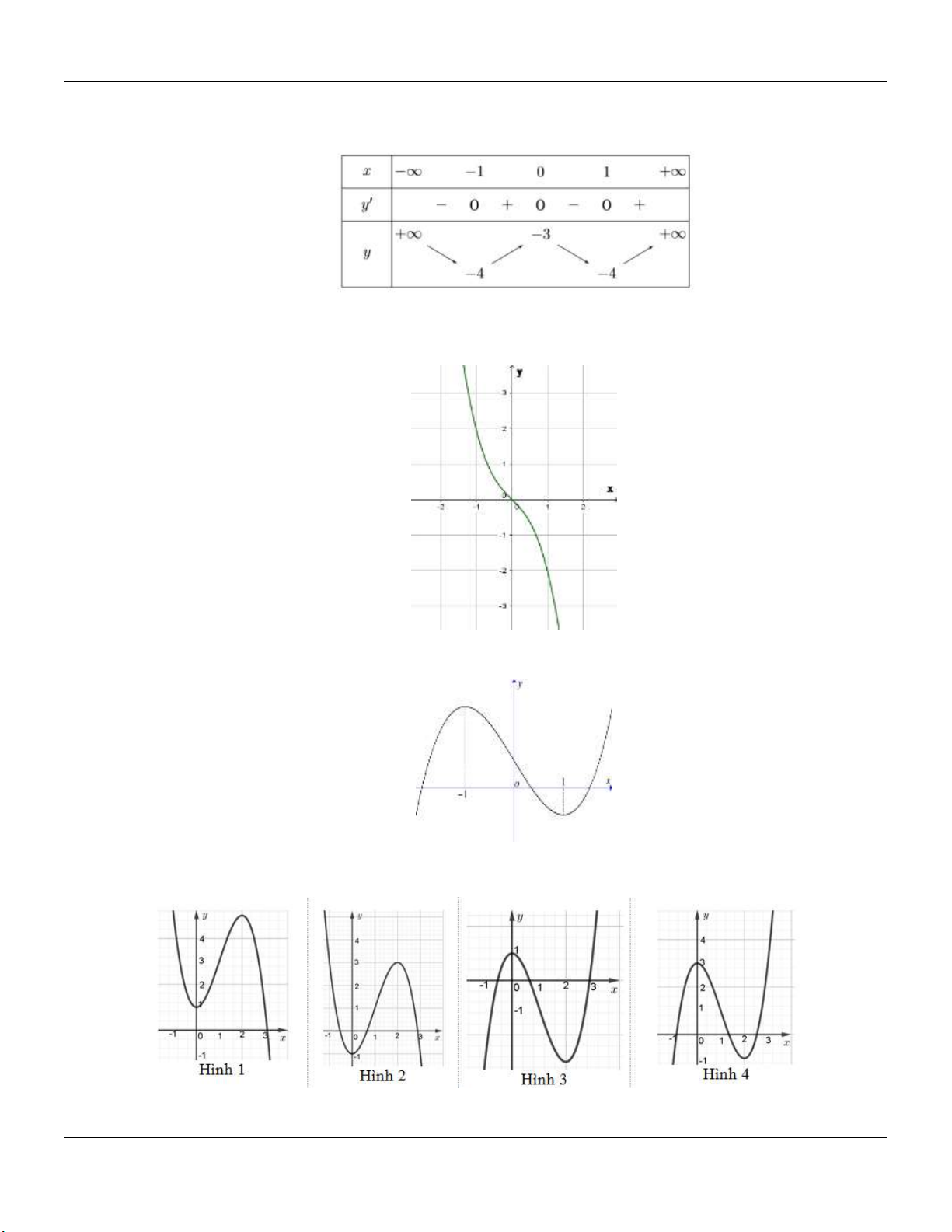
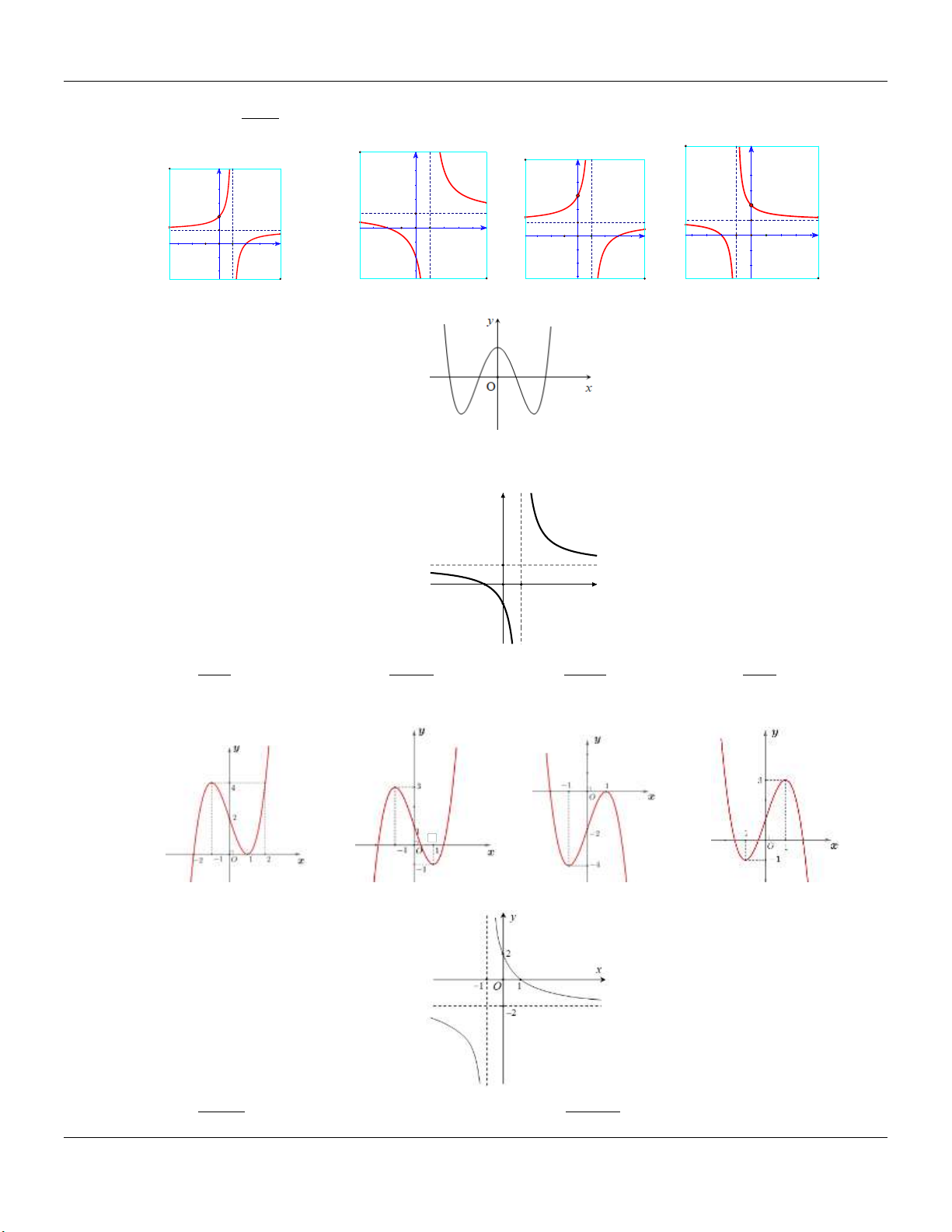
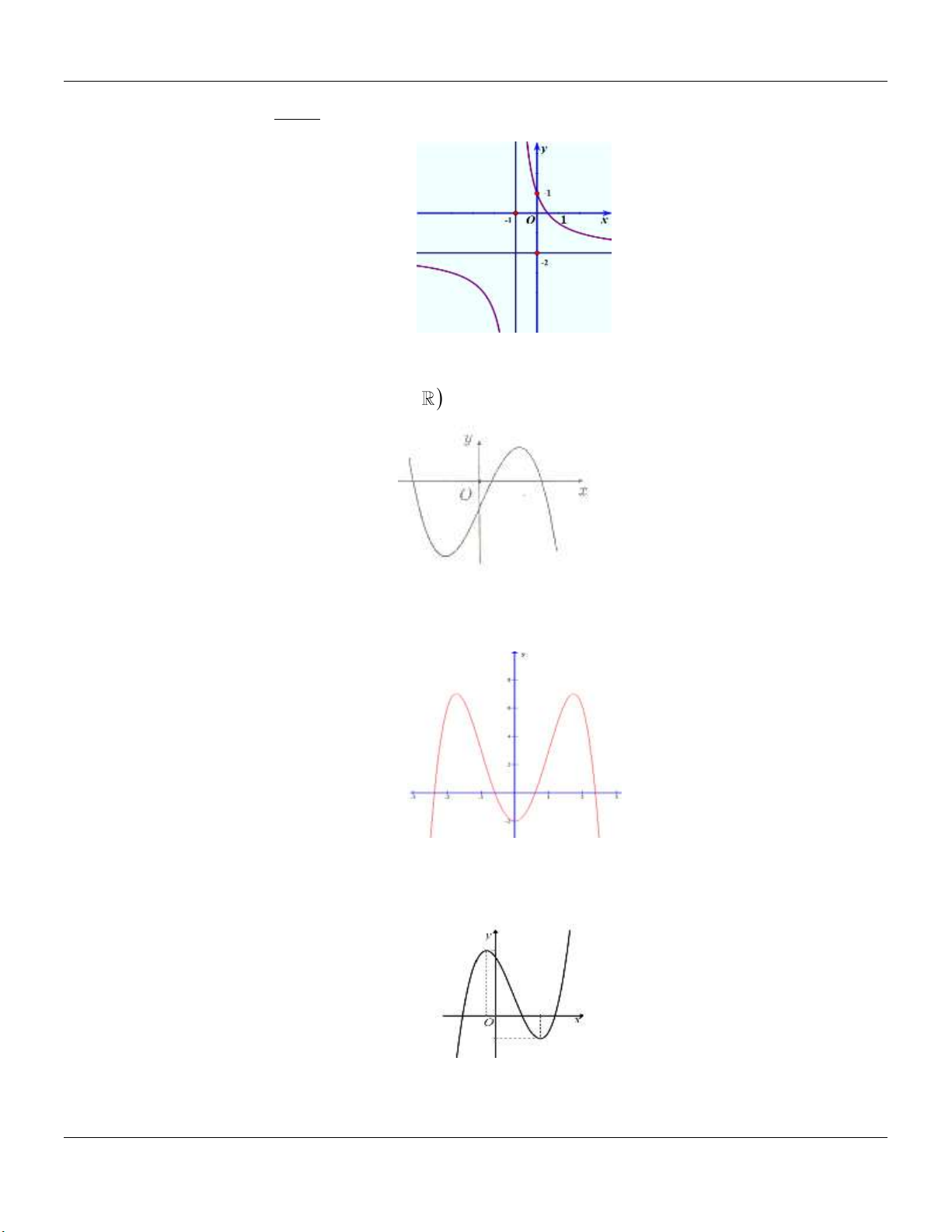
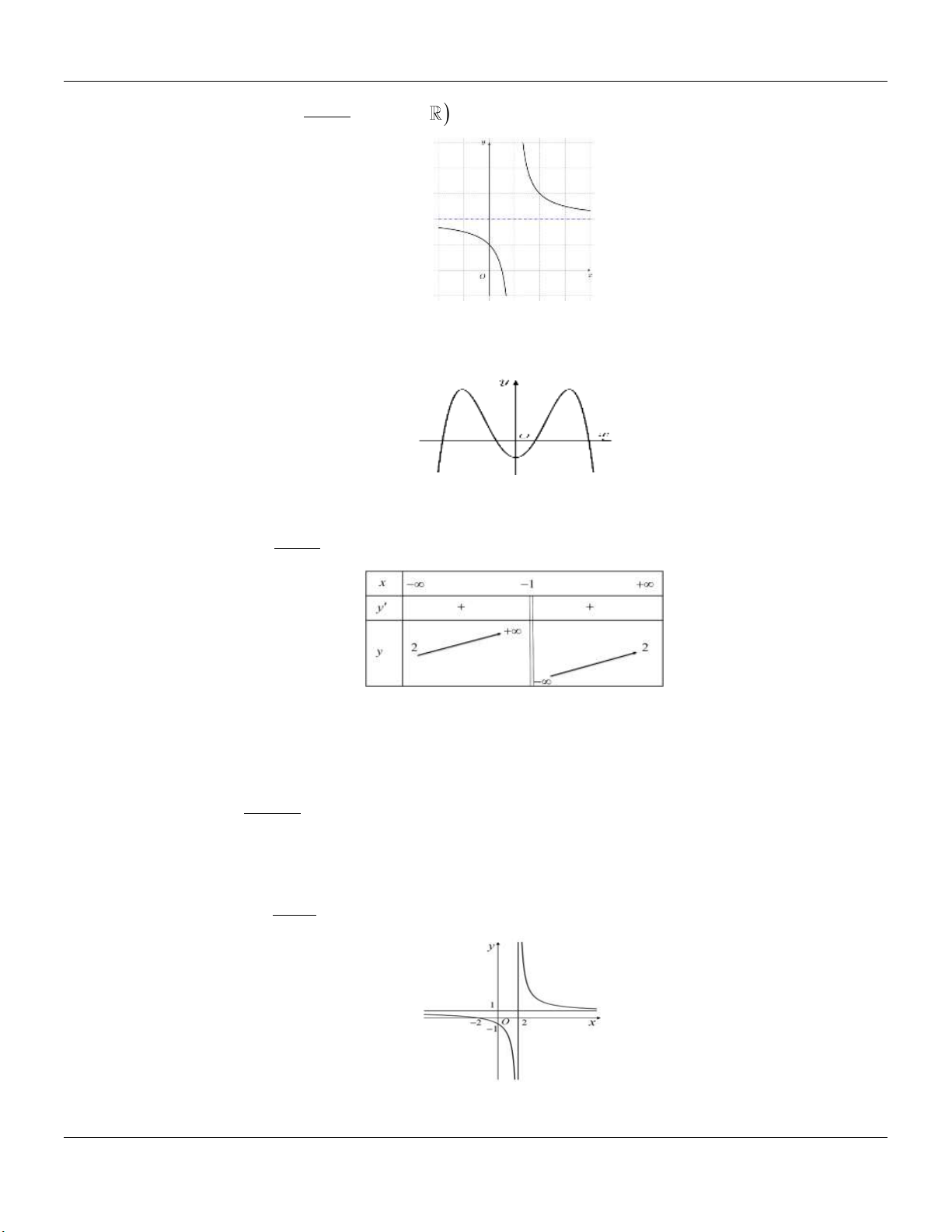
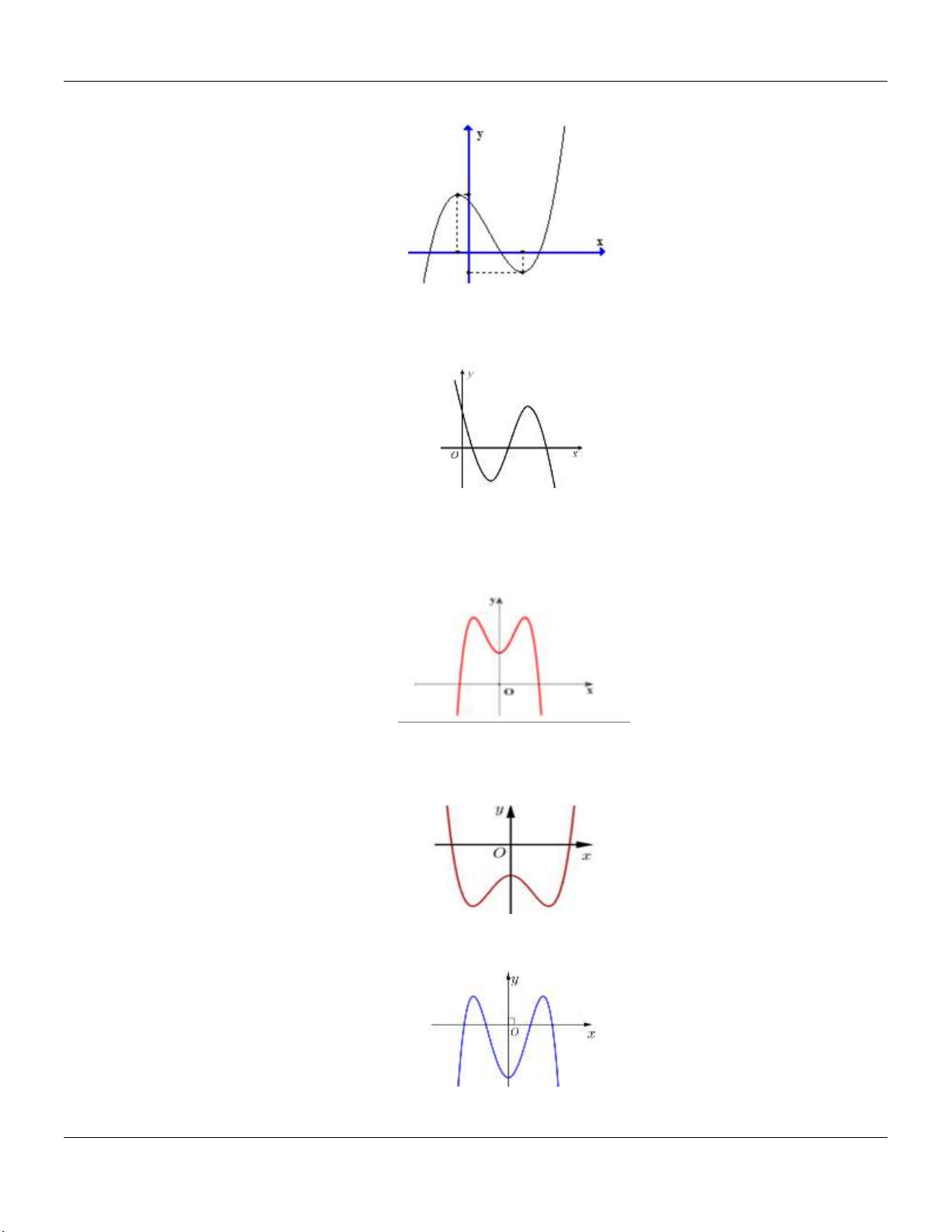
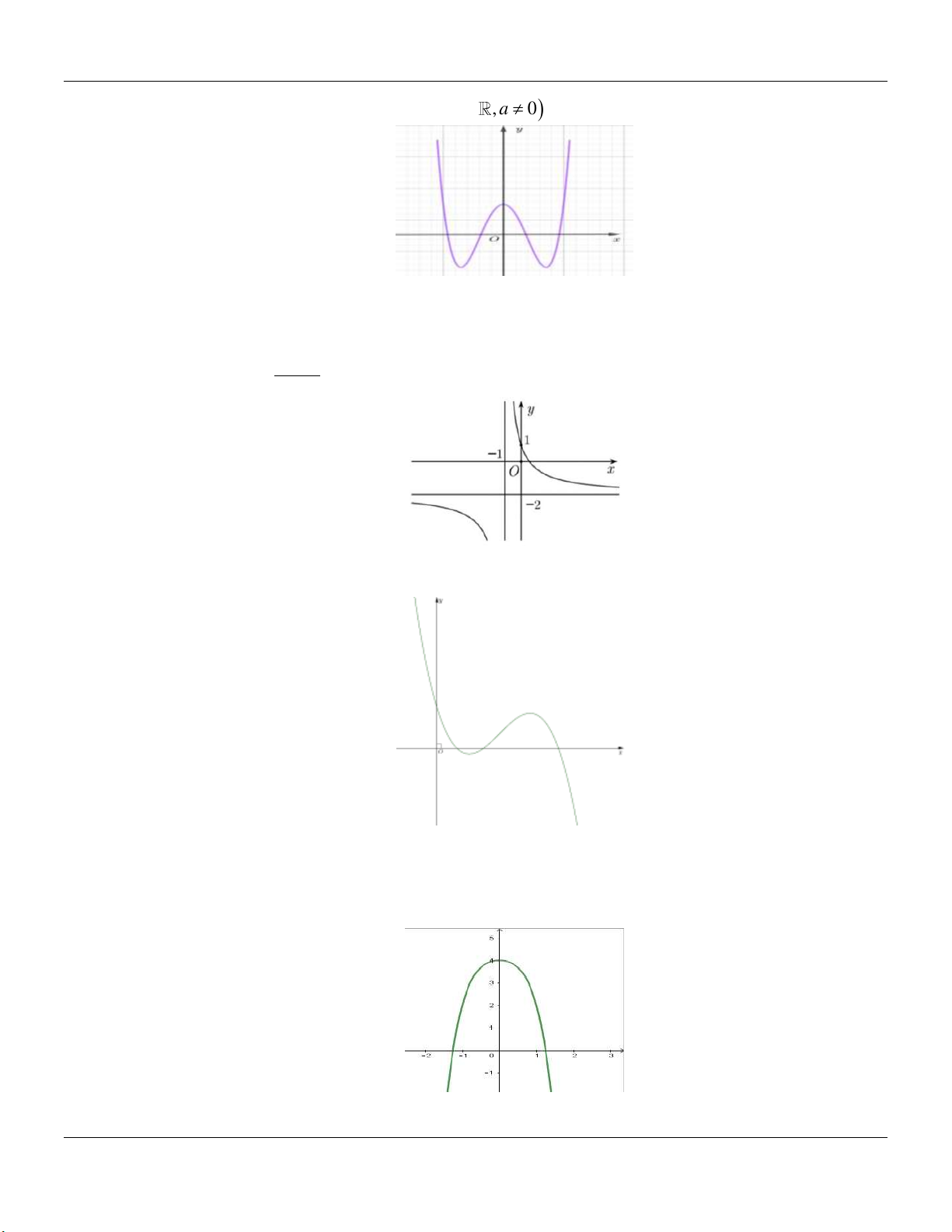
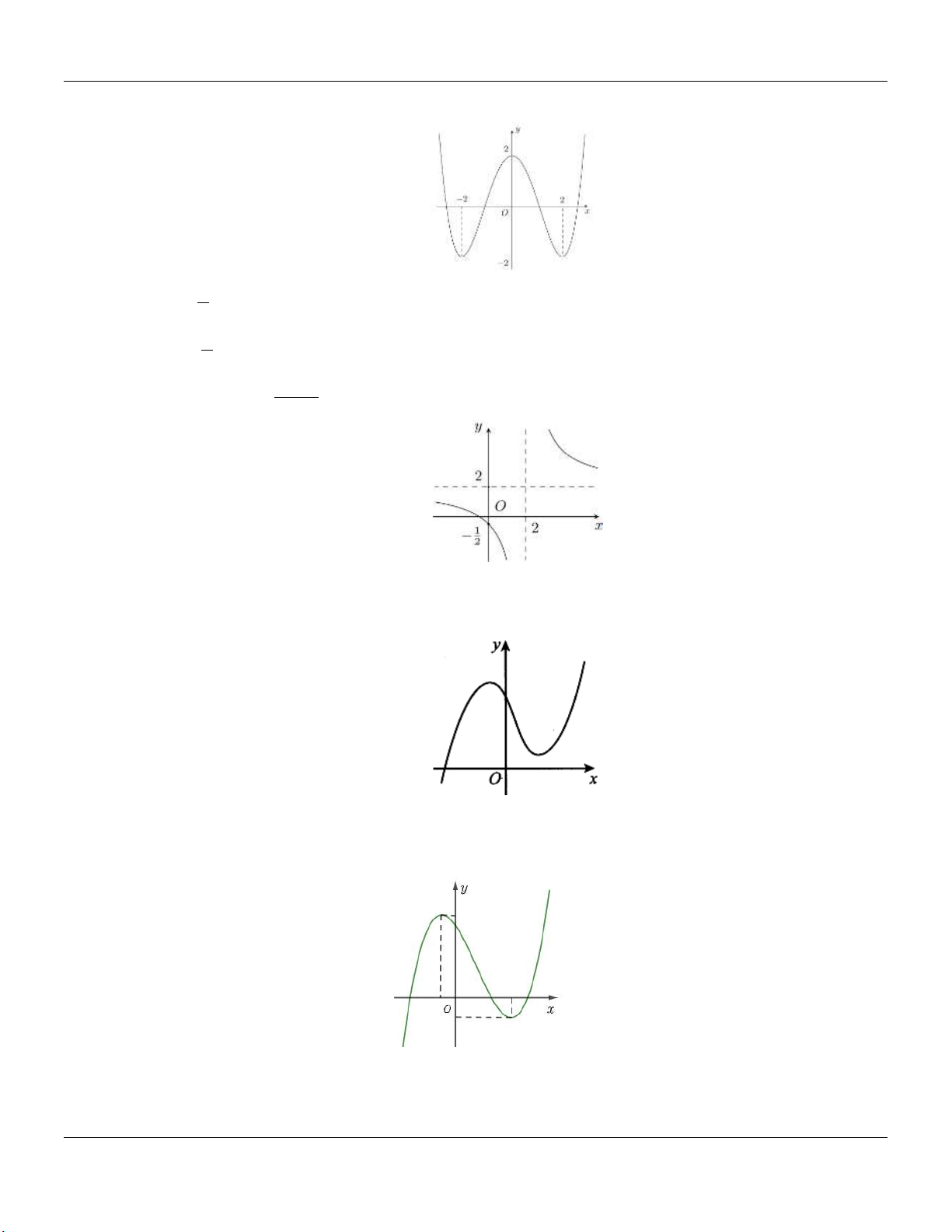
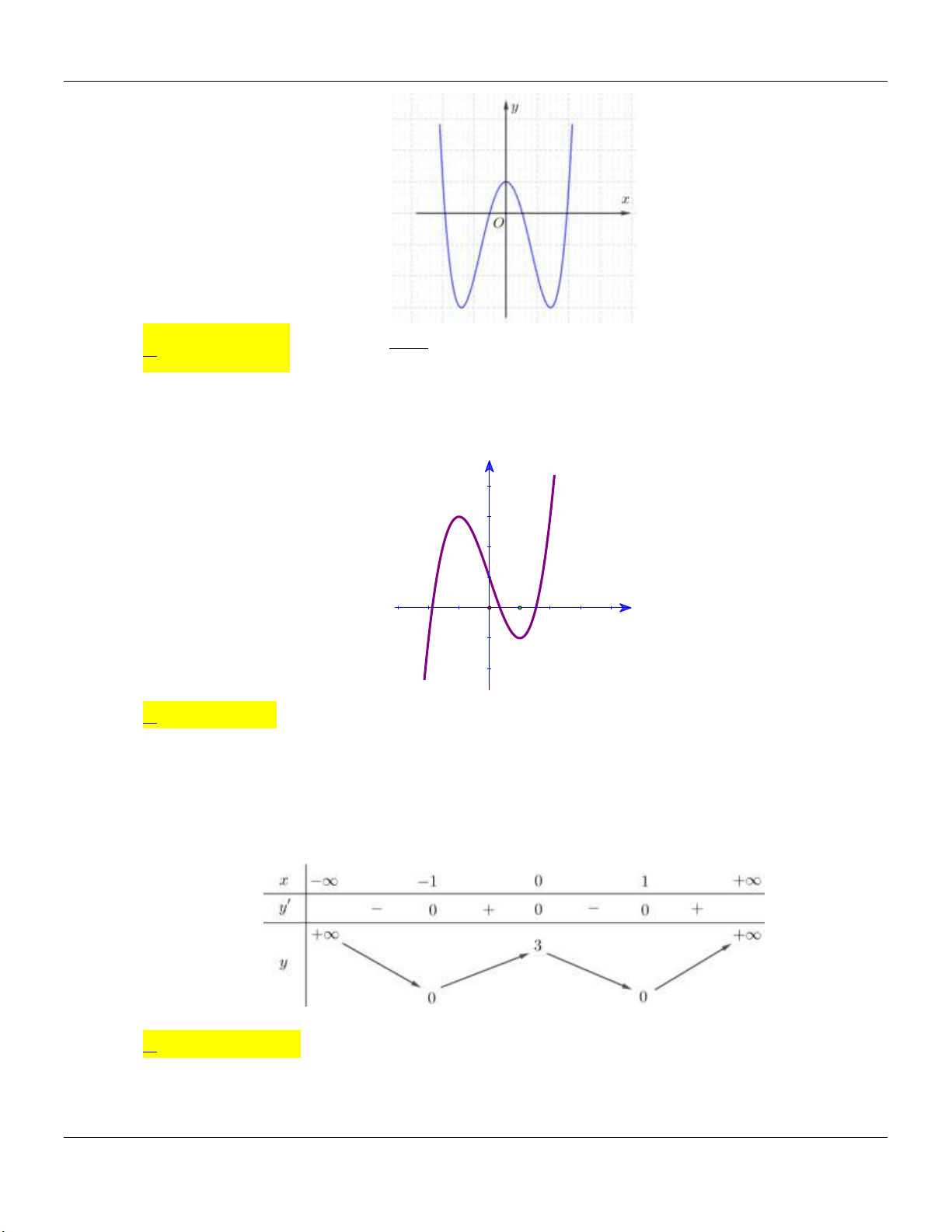
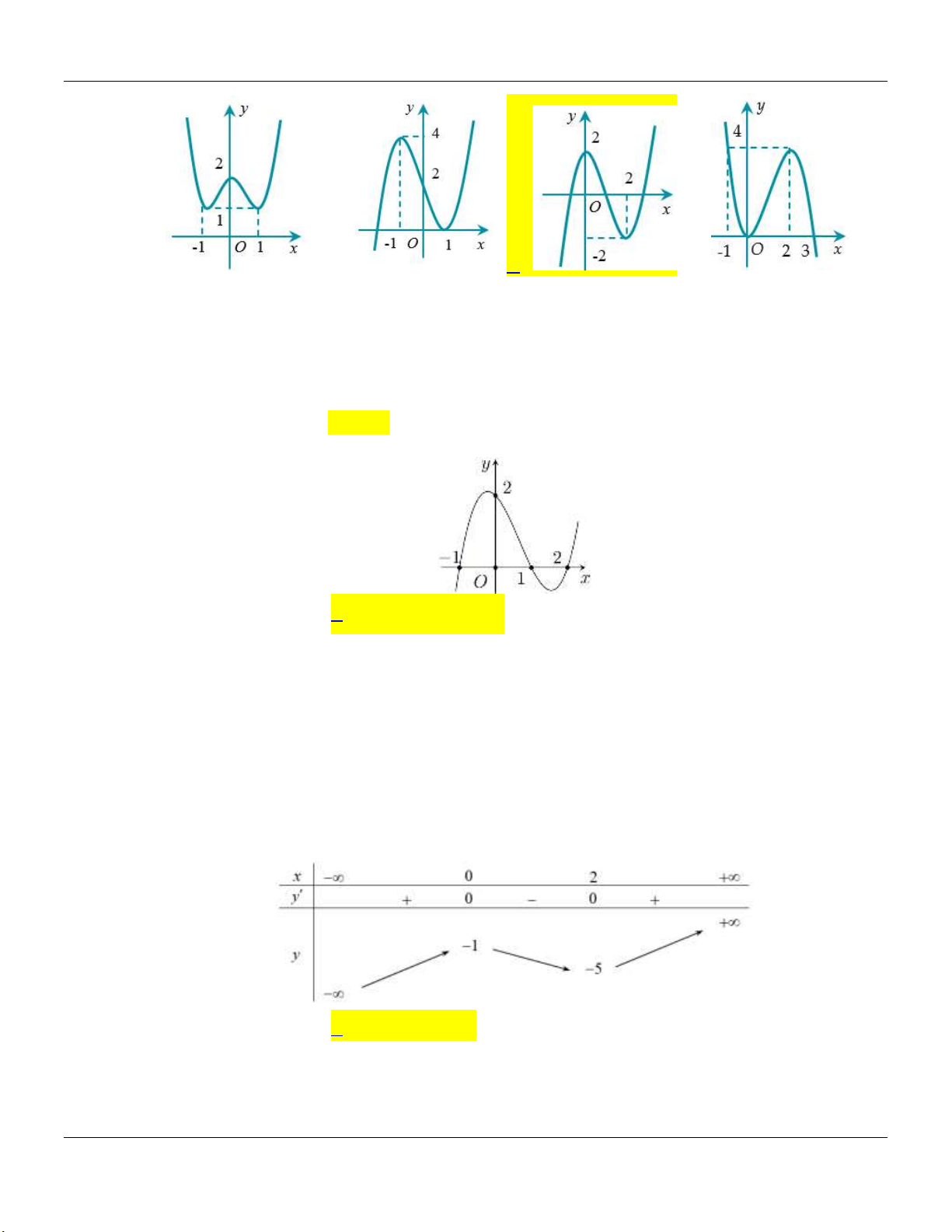
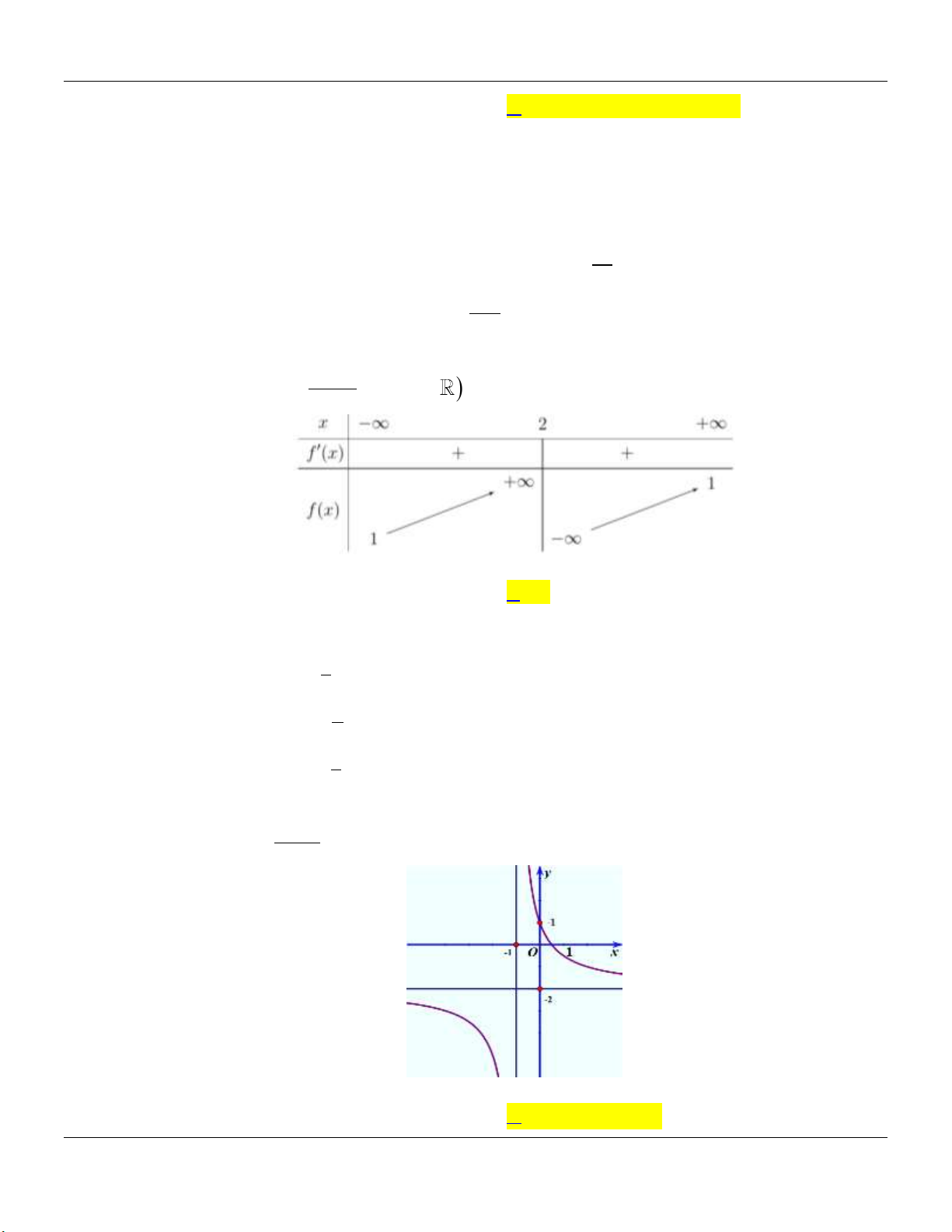
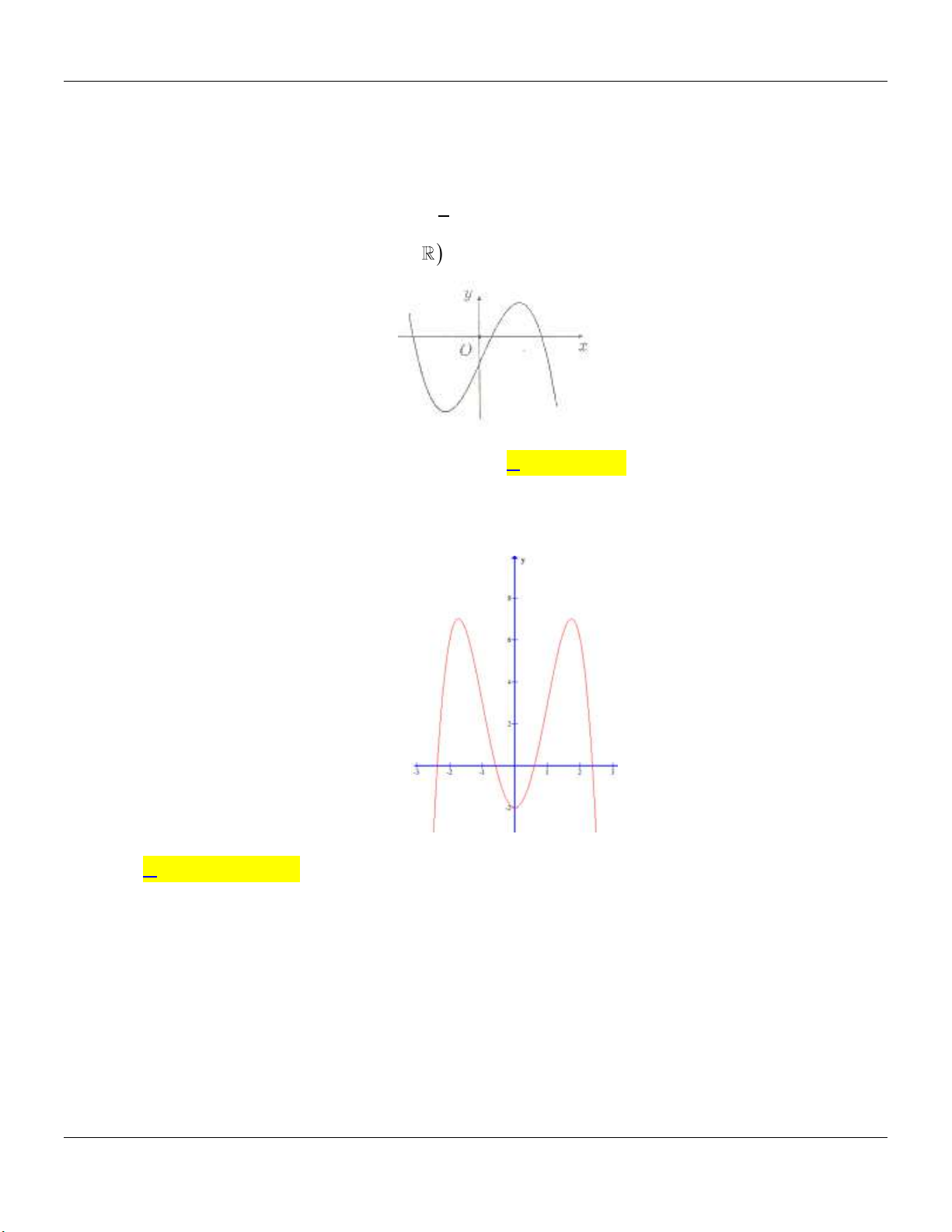
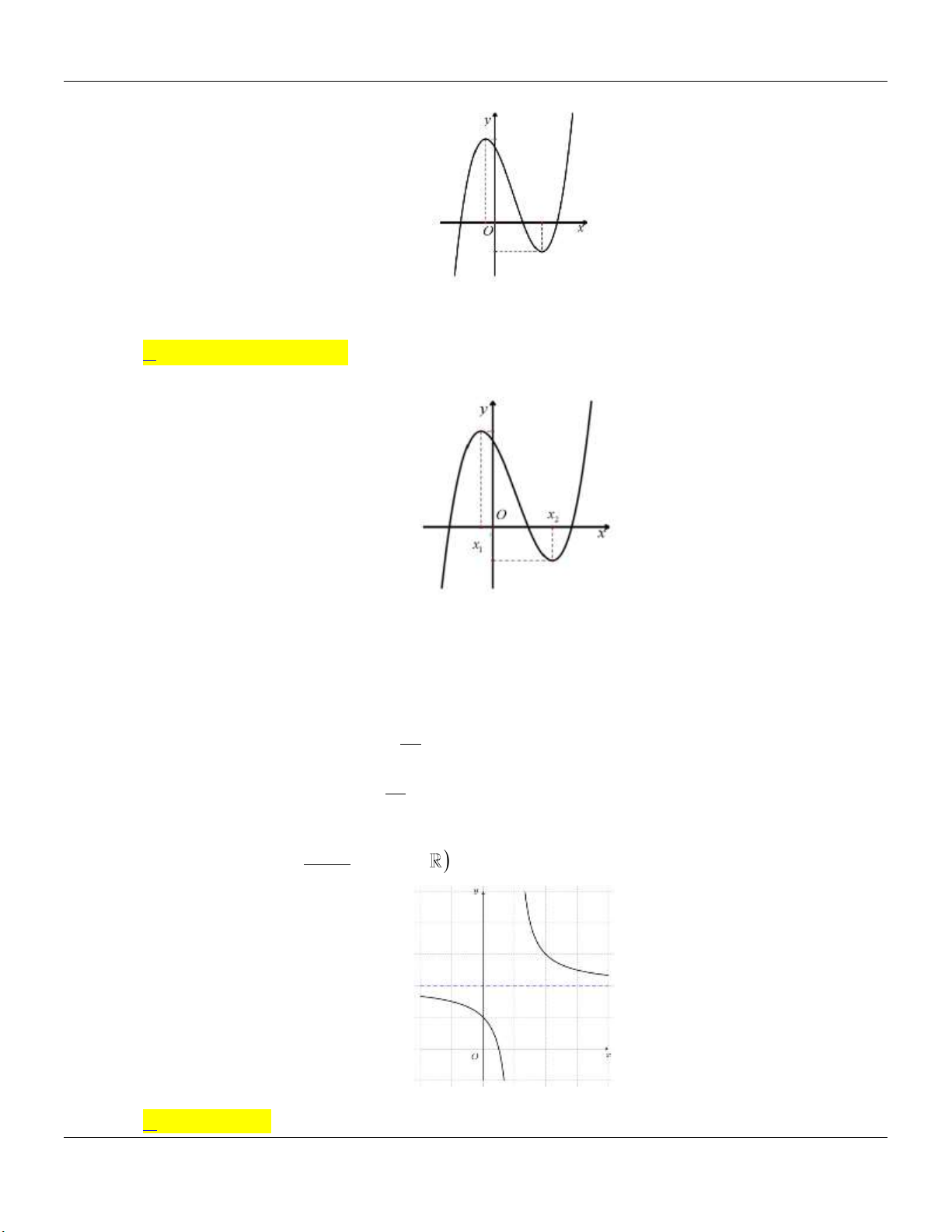
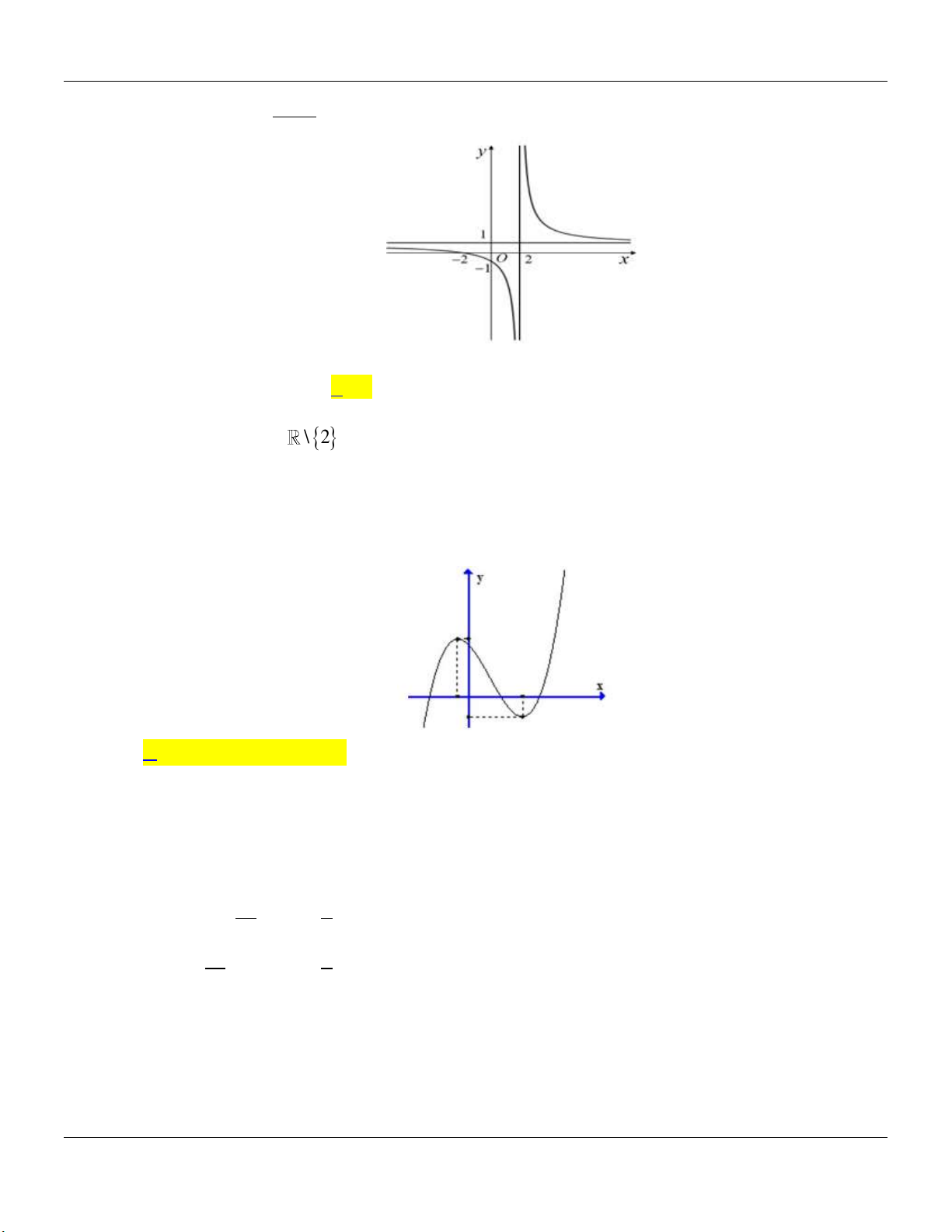
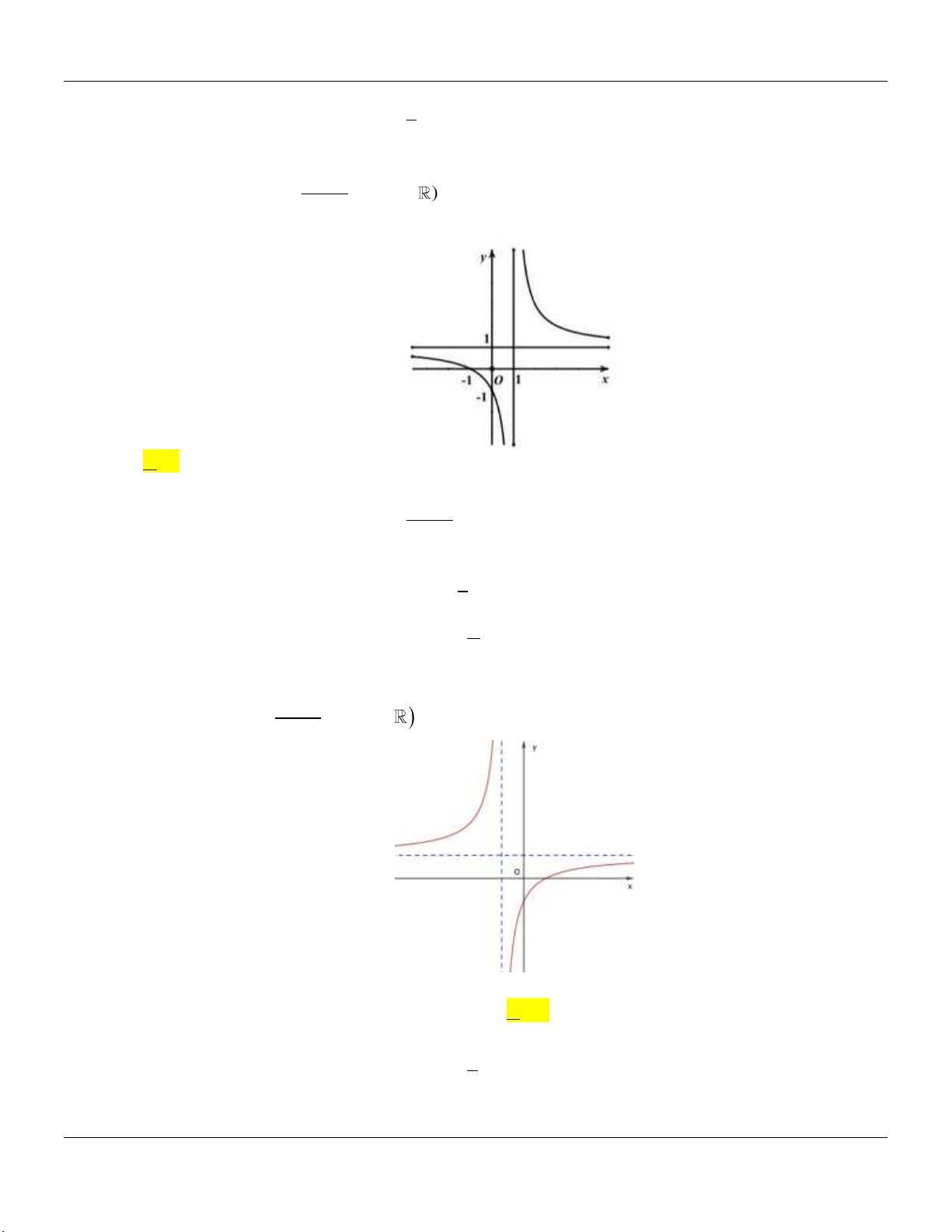
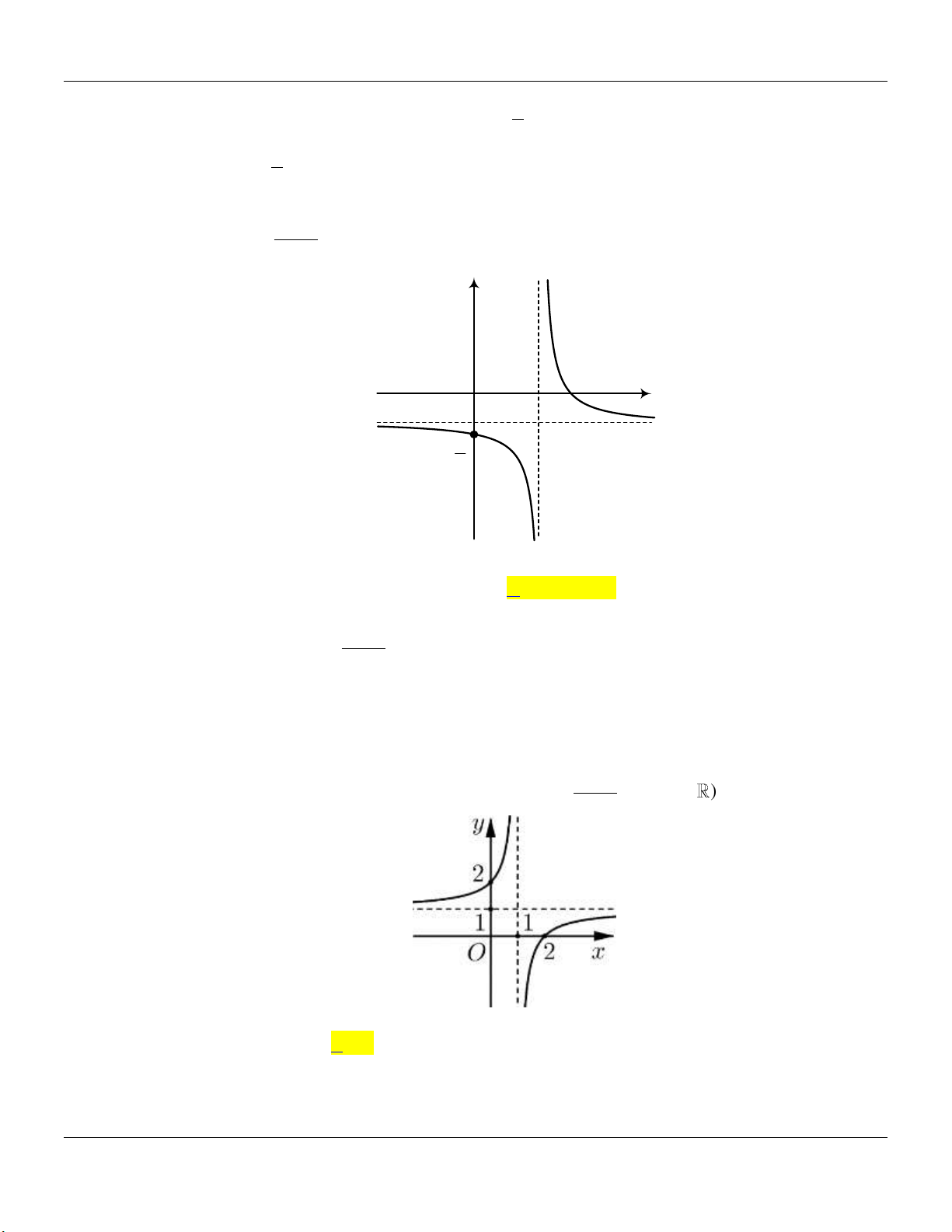
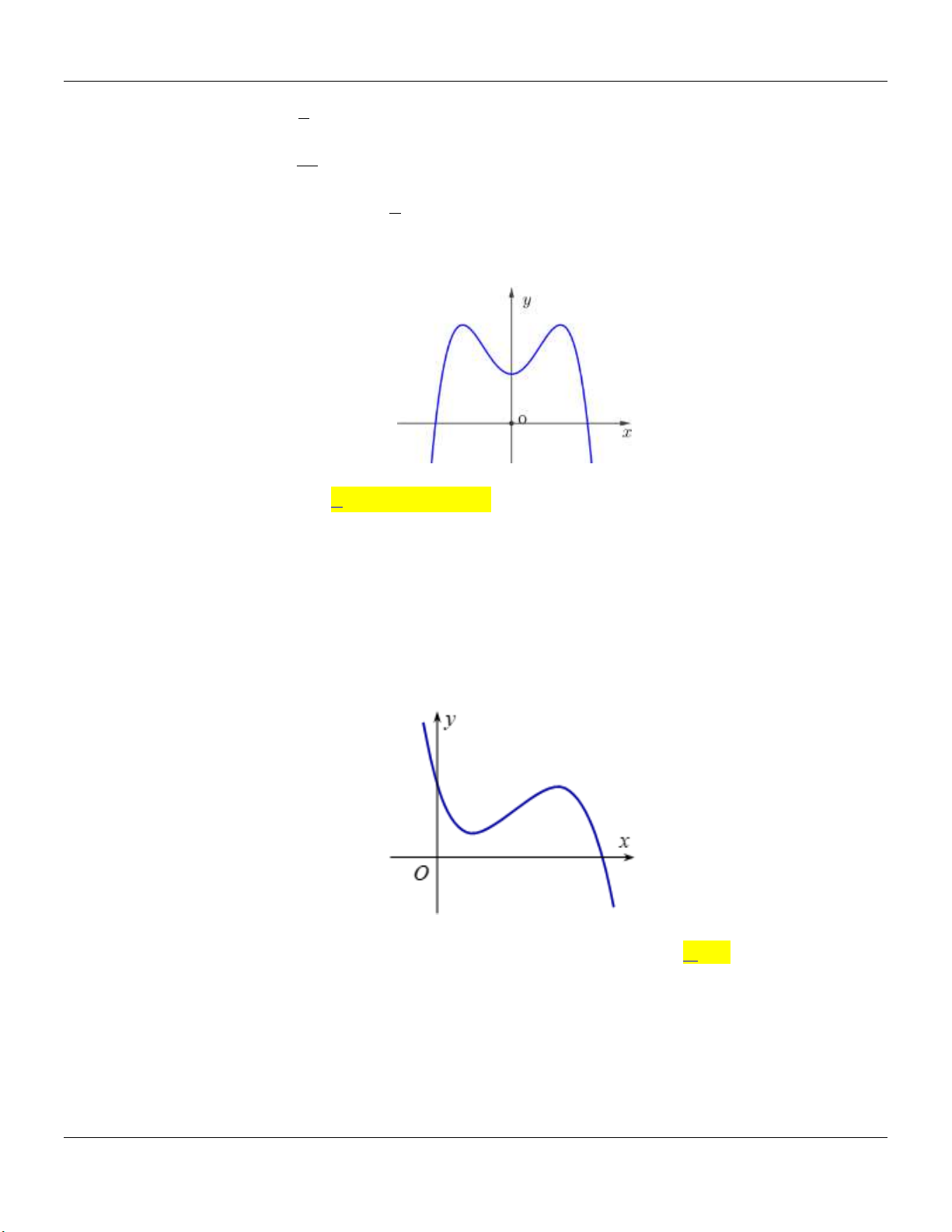
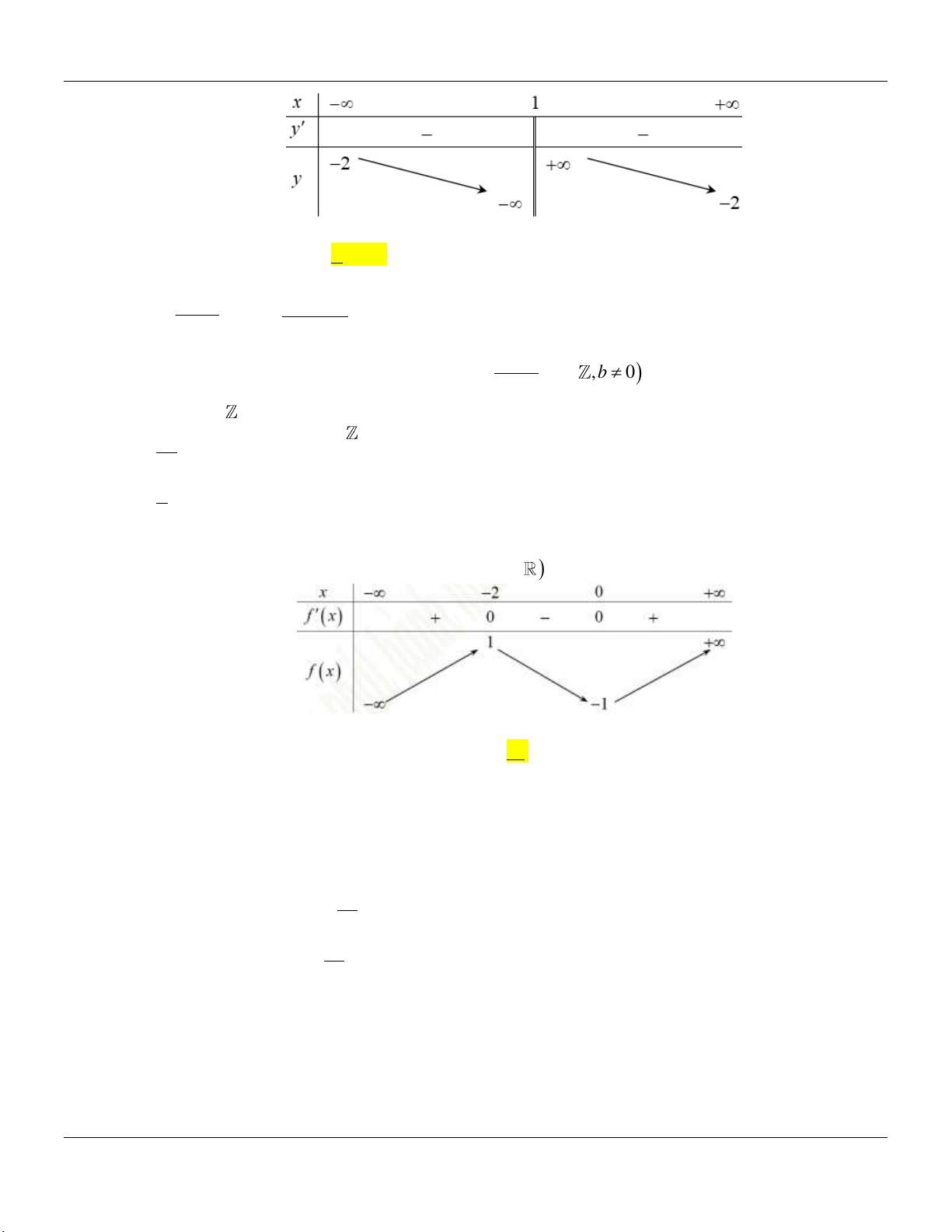
2- KHẢO SÁT MỘT SỐ HÀM ĐA THỨC VÀ PHÂN THỨC: a- HÀM SỐ BẬC BA 3 2
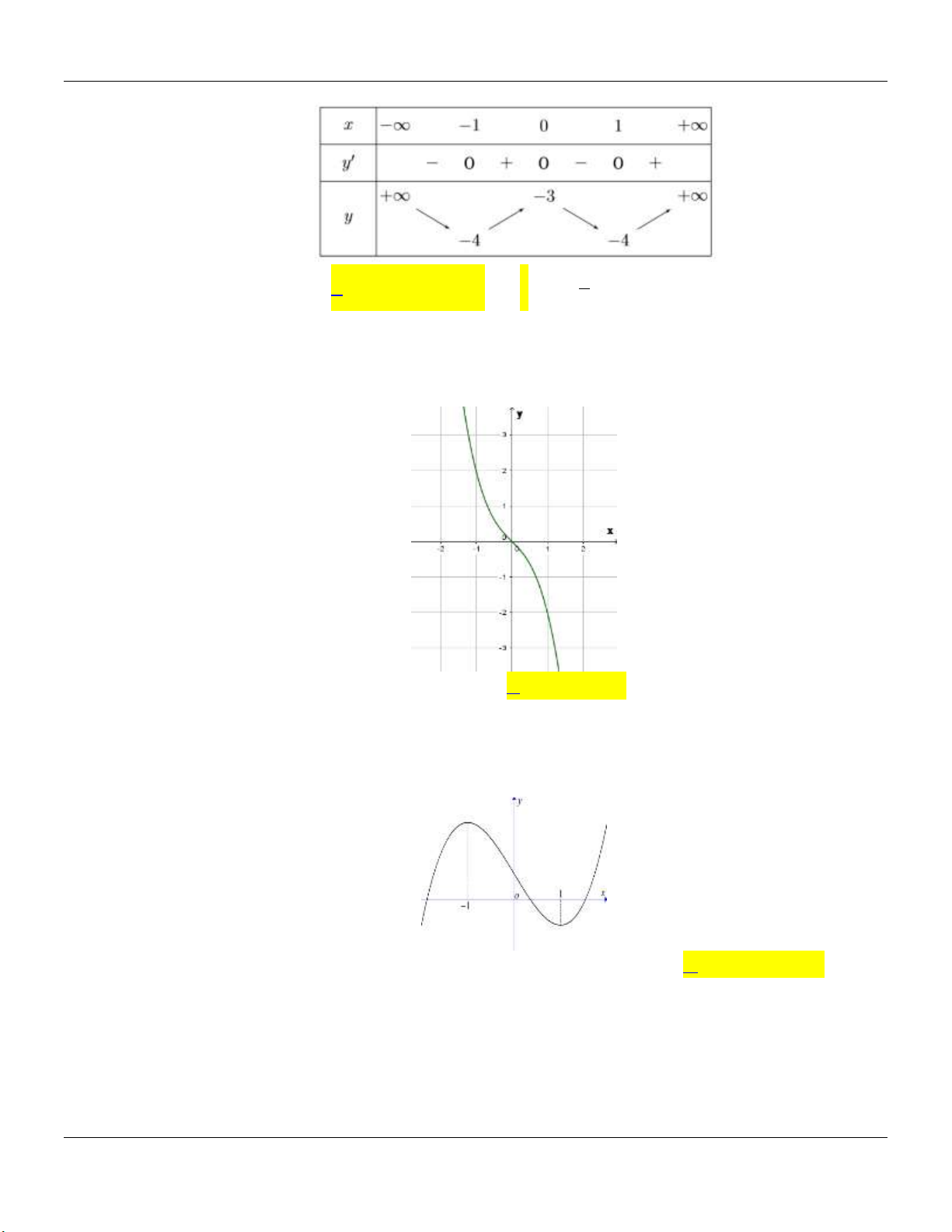
y ax bx cx da  0 TRƯỜNG HỢP a  0 a  0 Phương trình / y  0 có y y 1
2 nghiệm phân biệt 1 1 O x 1 O x y Phương trình / y  0 có y nghiệm kép 1 1 1 O x 1 O x
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Phương trình / y  0 vô y y nghiệm 1 O 1 1 x 1 O x
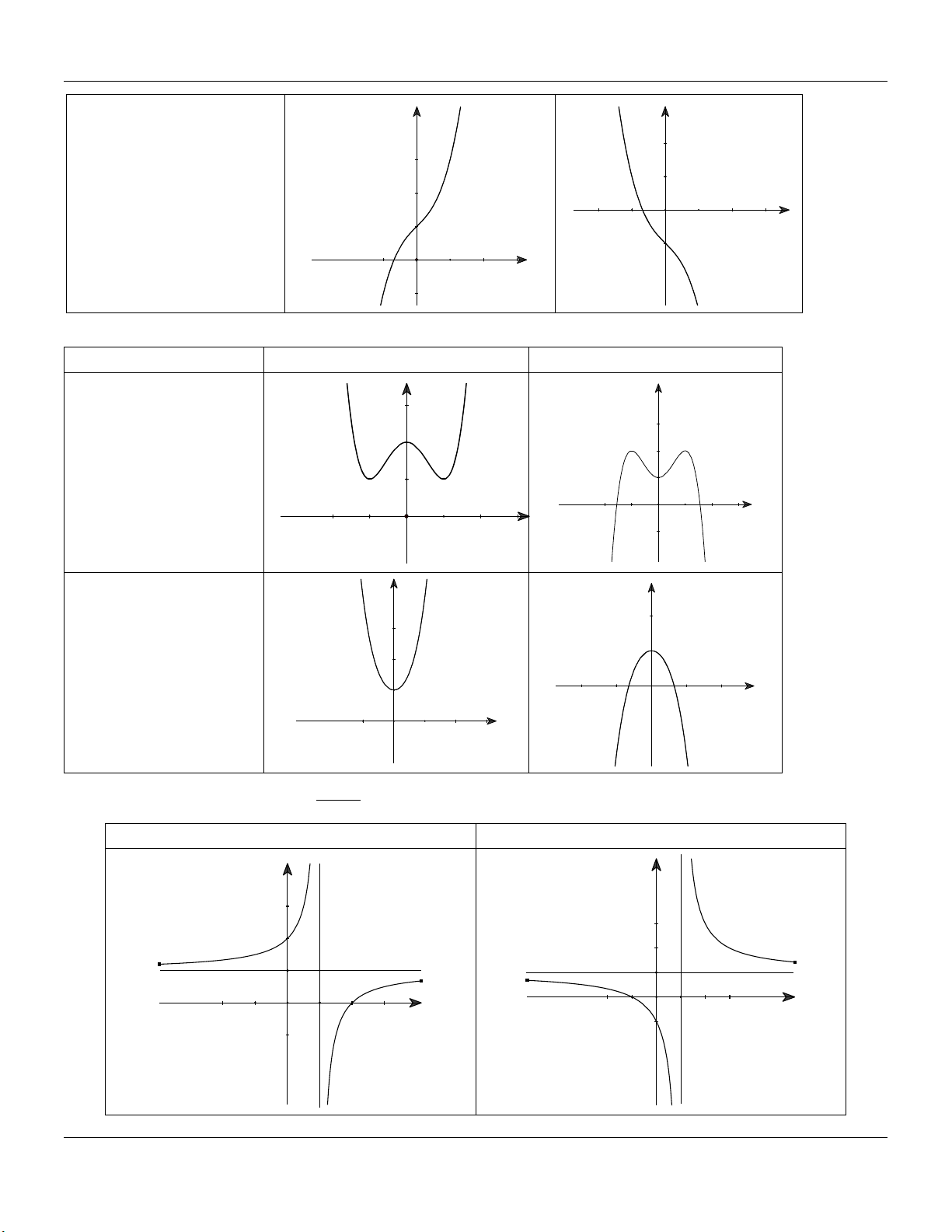
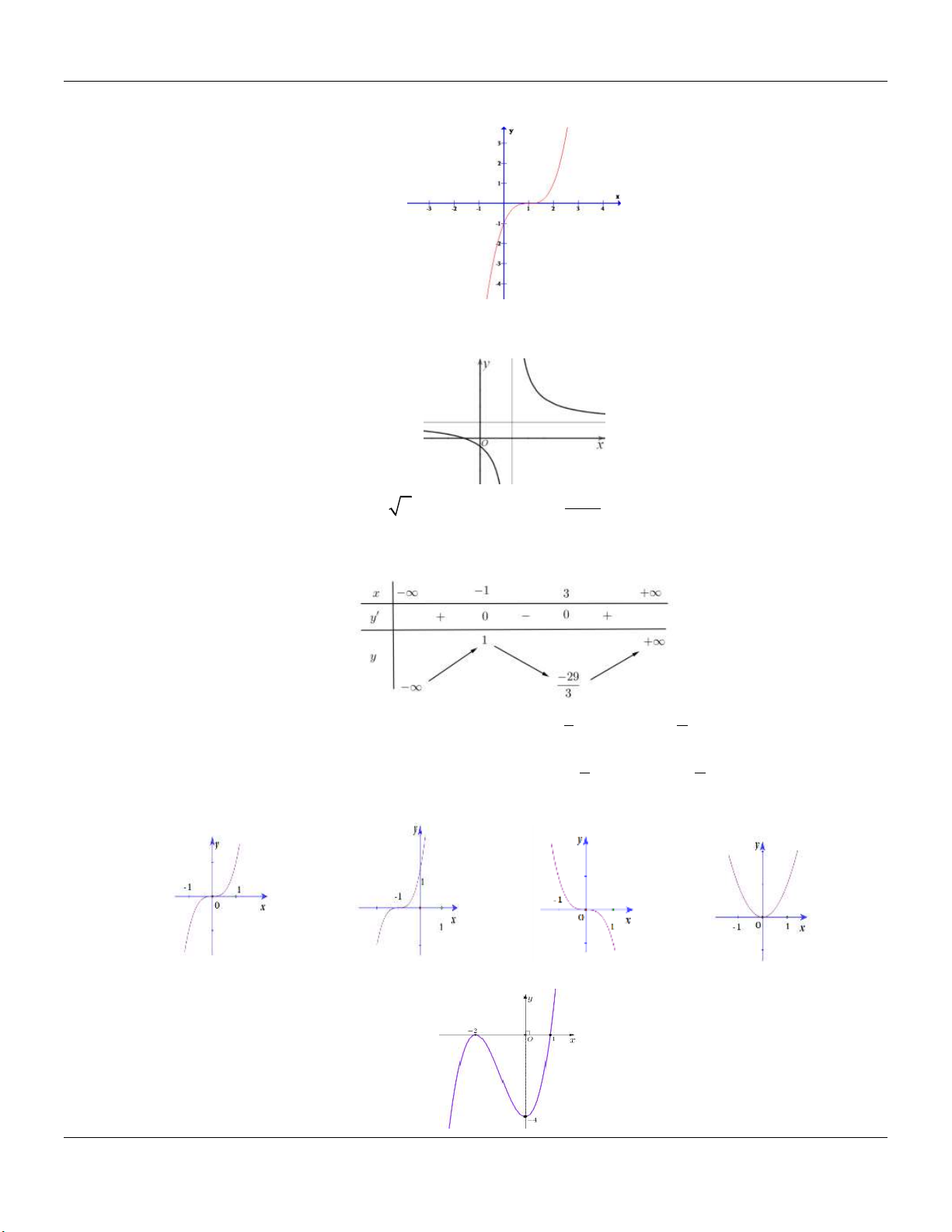
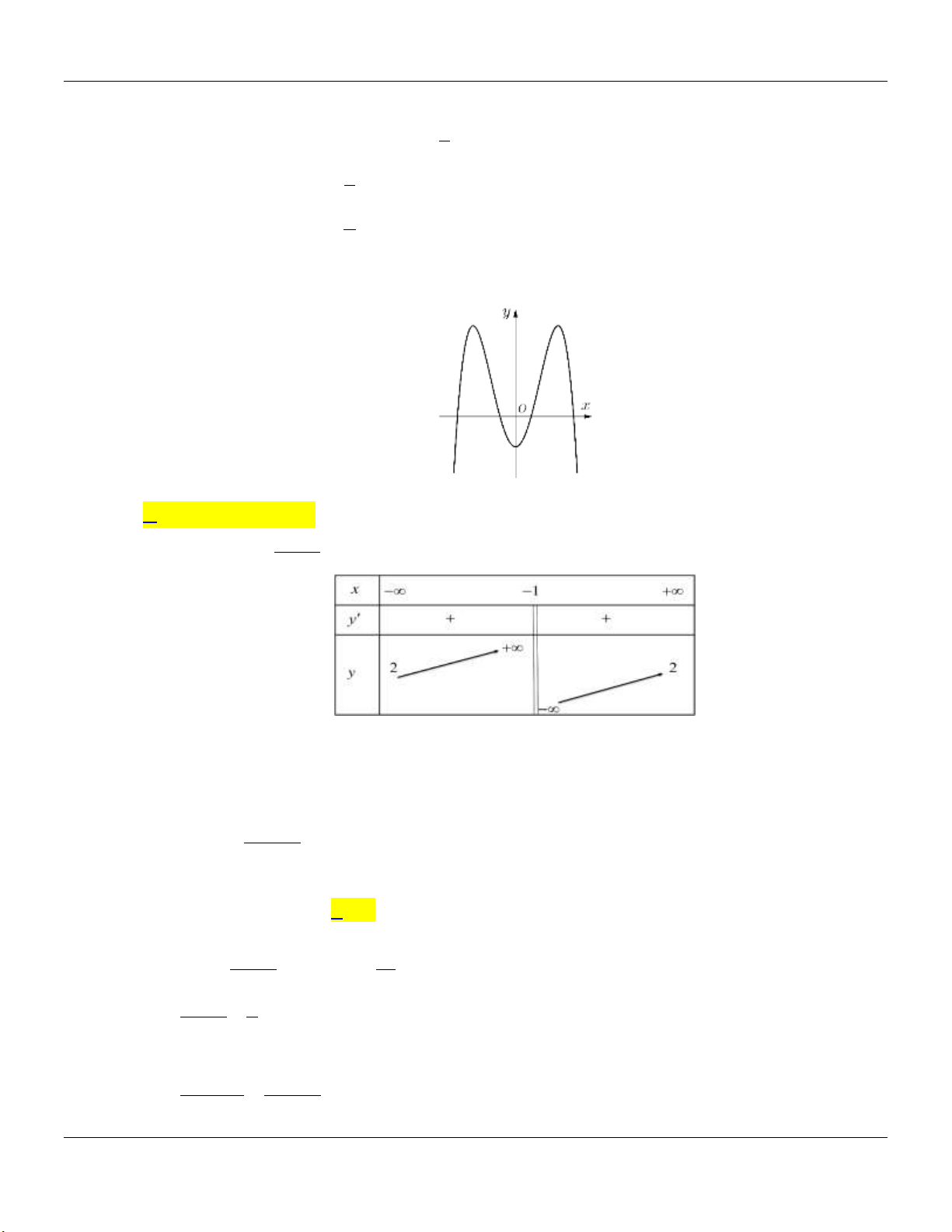
b- HÀM SỐ TRÙNG PHƯƠNG 4 2
y ax bx ca  0 TRƯỜNG HỢP a  0 a  0 Phương trình / y  0 có y y 3 nghiệm phân biệt 1 1 1 1 O x O x Phương trình / y  0 có y y 1 nghiệm. 1 1 1 O x 1 O x ax b
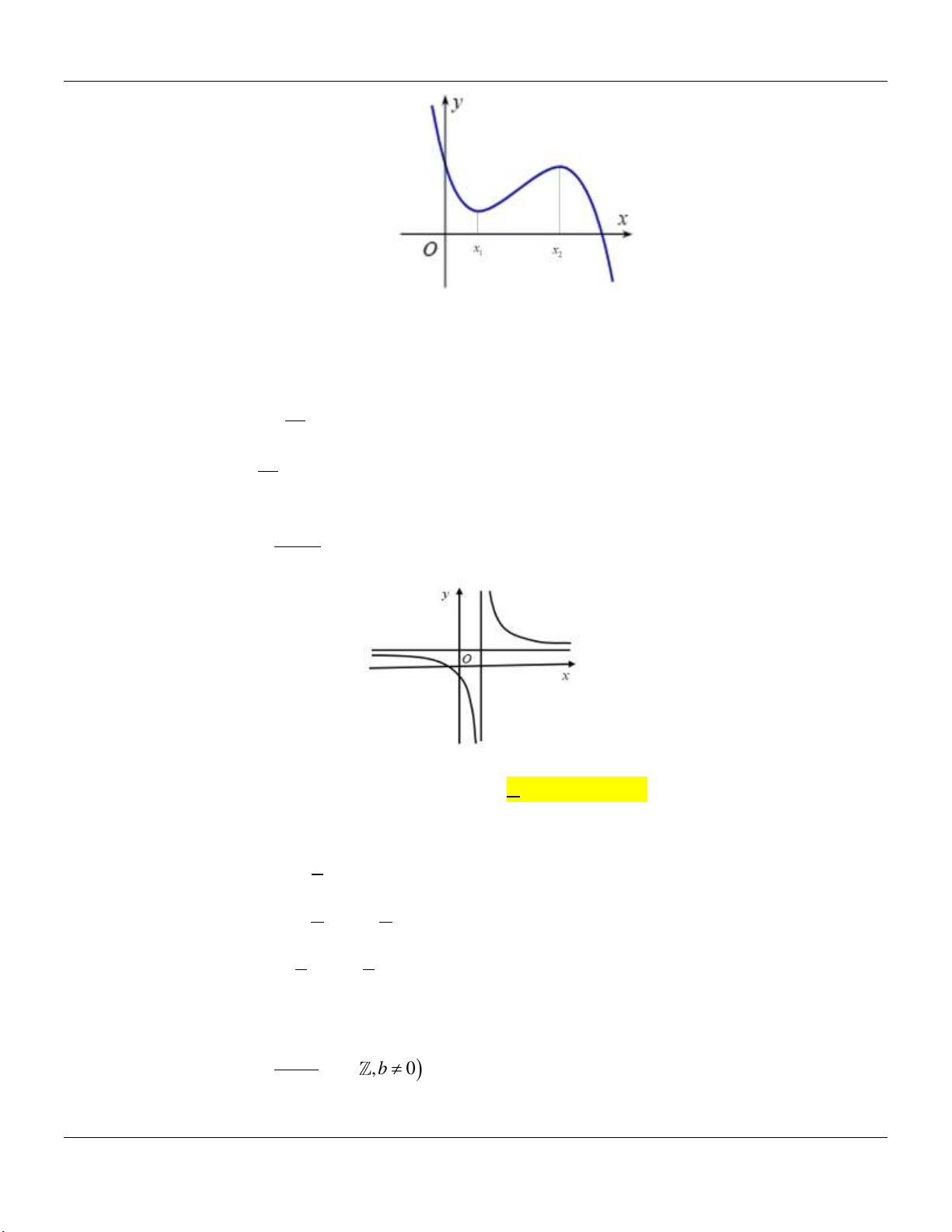
c- HÀM SỐ NHẤT BIẾN y
c  0, ad bc  0 cx d
D ad bc  0
D ad bc  0 y y 1 1 O O 1 1 x x
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
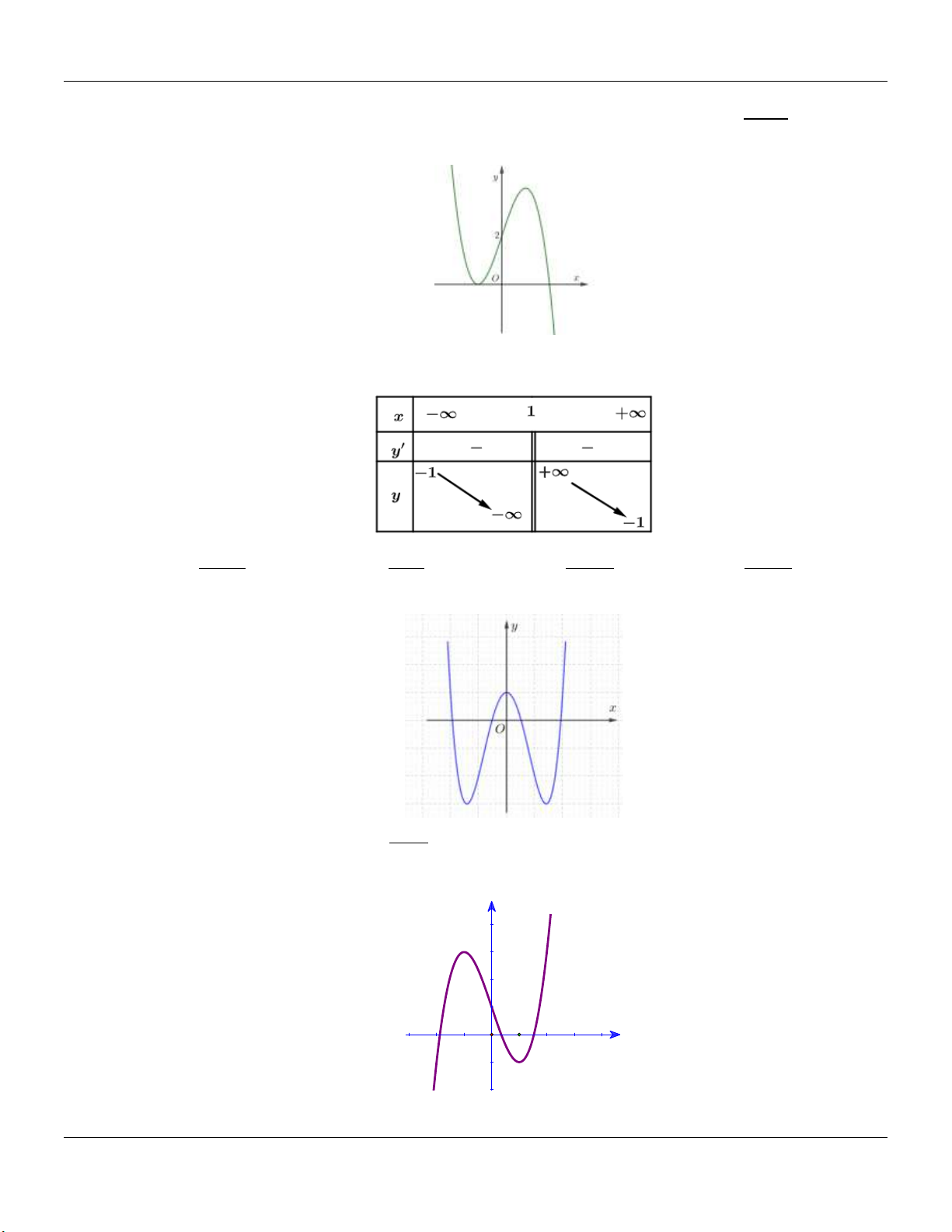
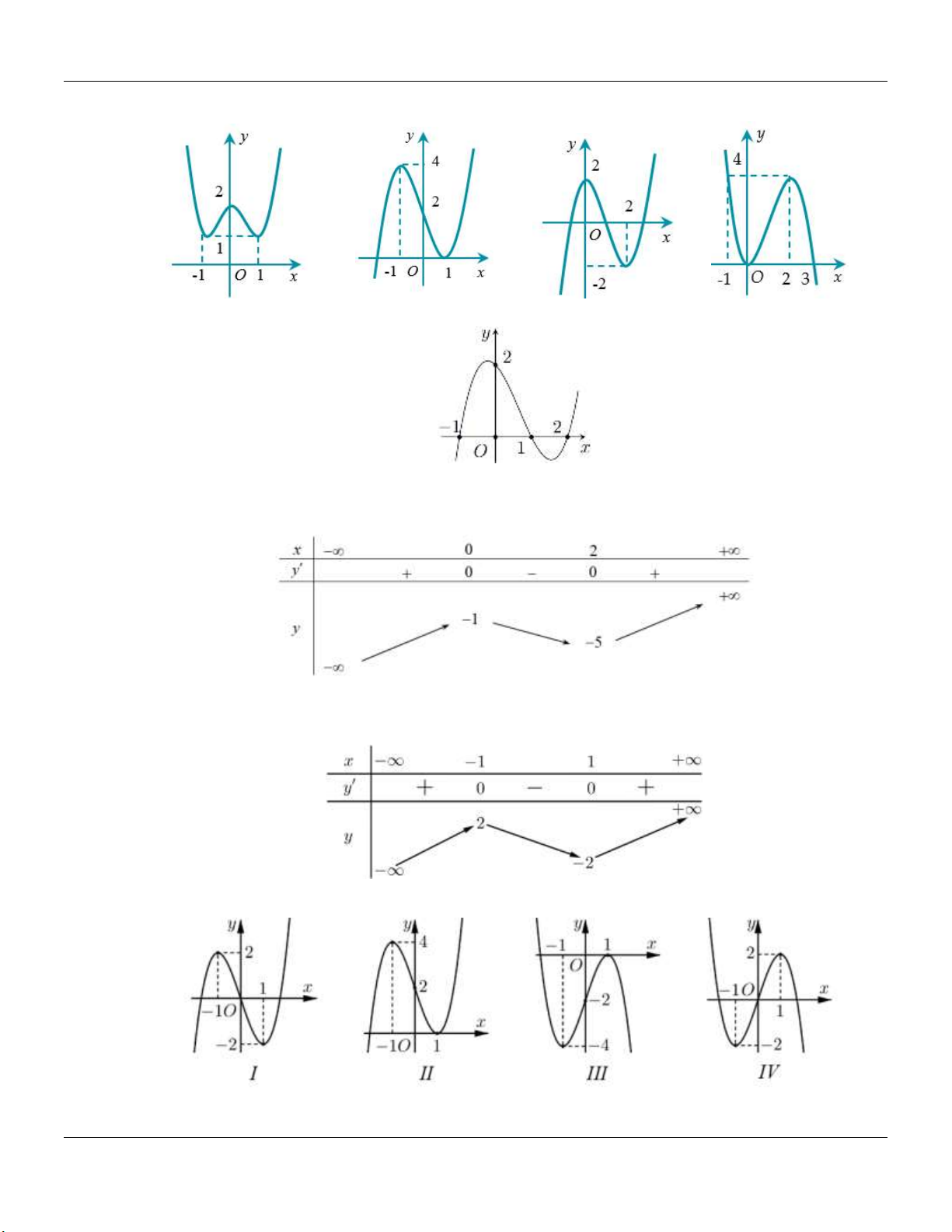
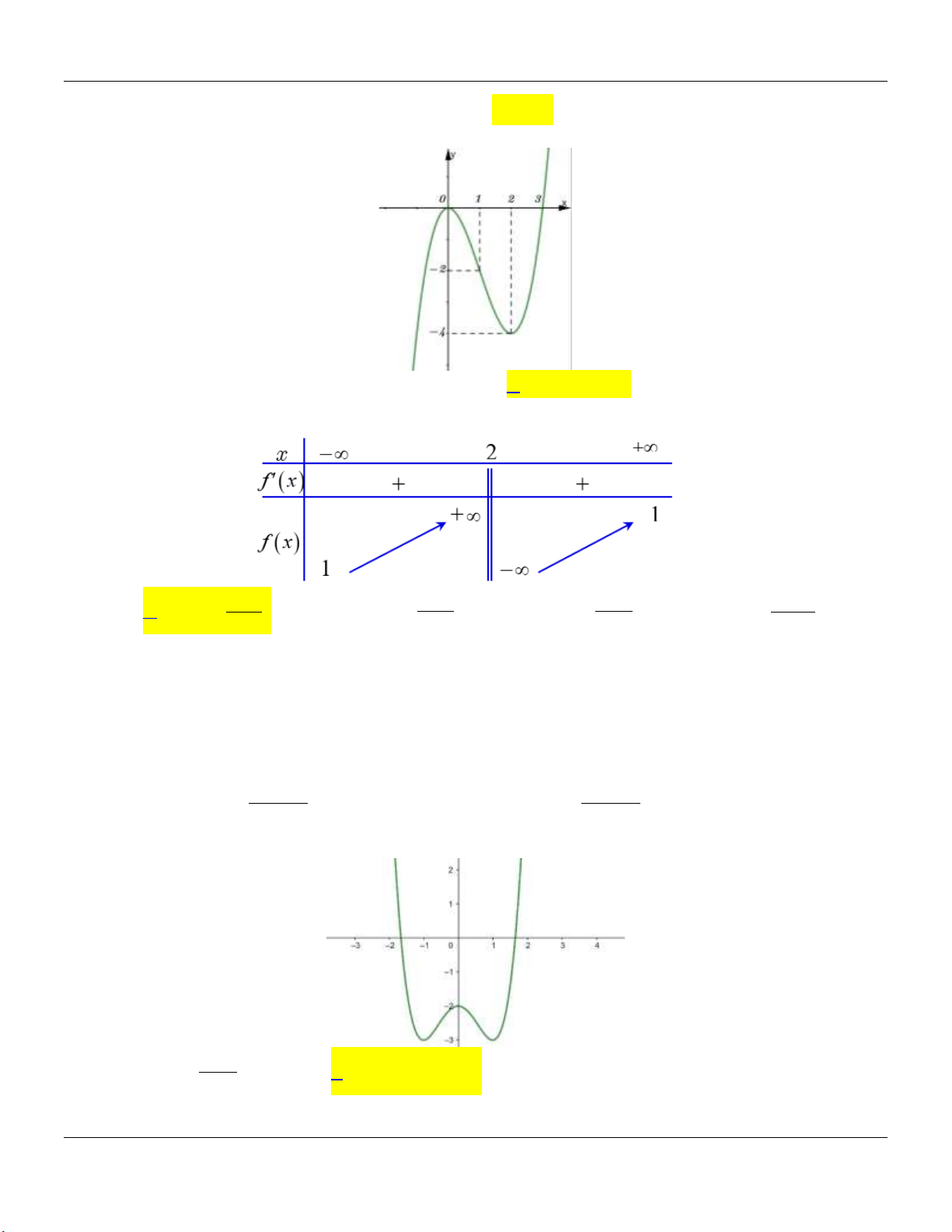
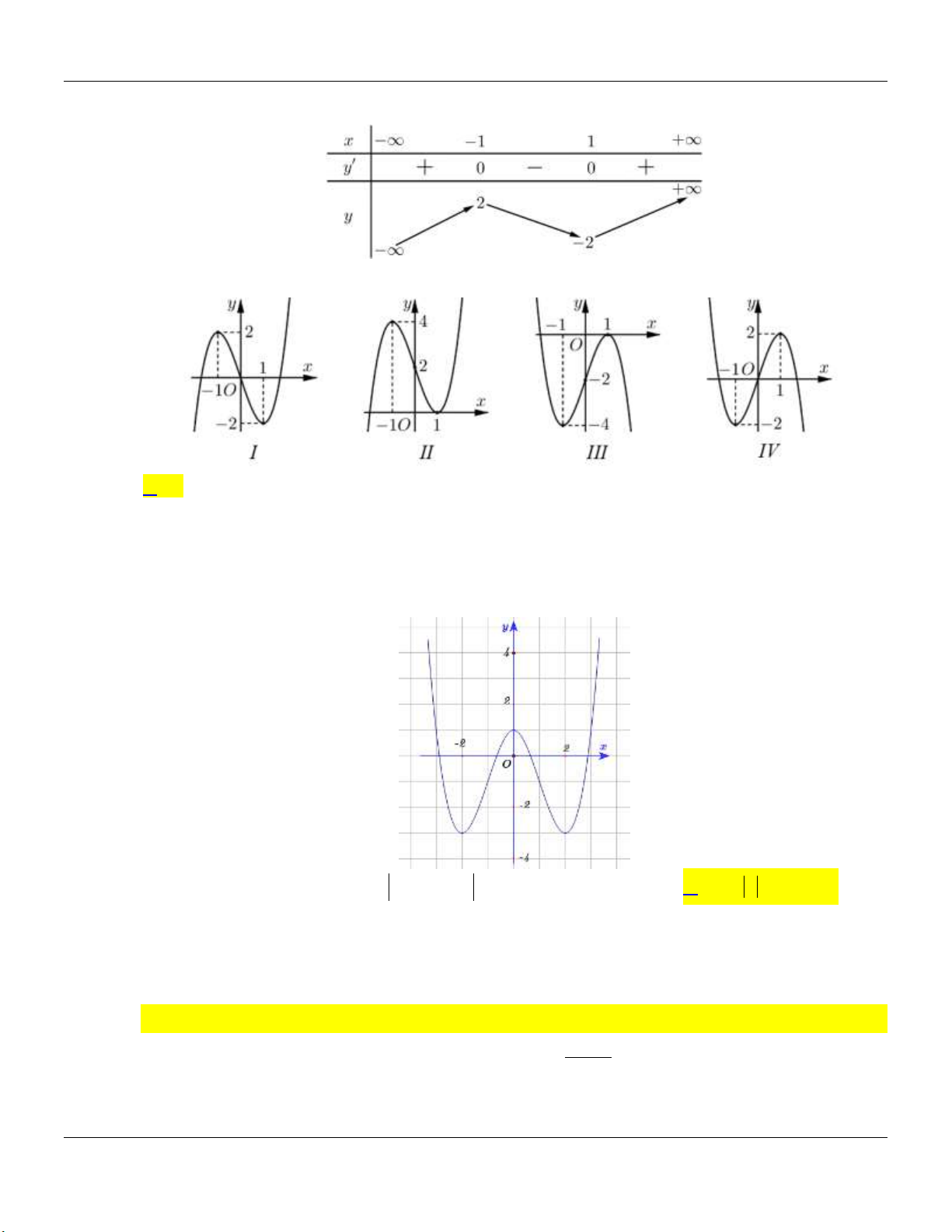
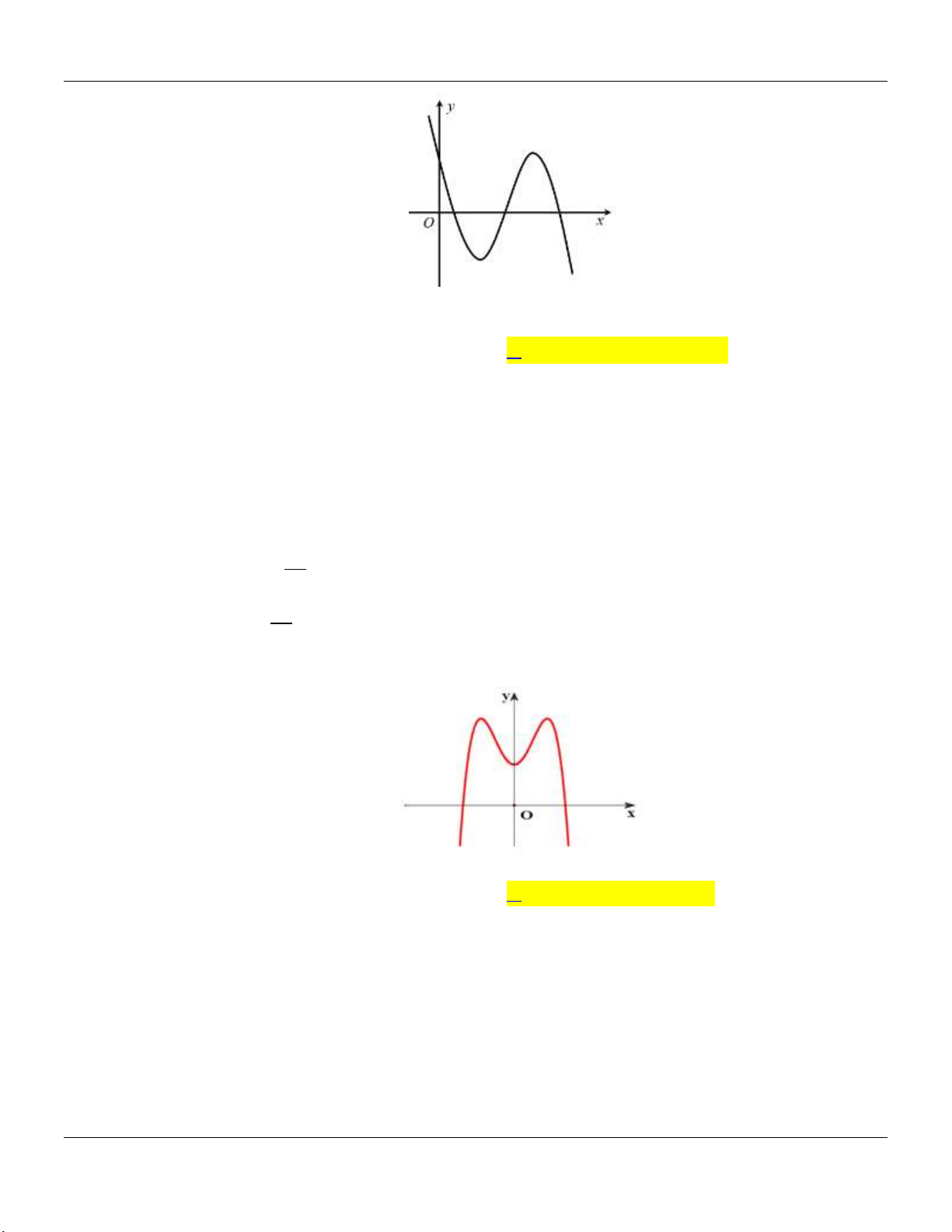
KỸ NĂNG: NHẬN BIẾT ĐỒ THỊ VÀ BẢNG BIẾN THIÊN Câu 1:
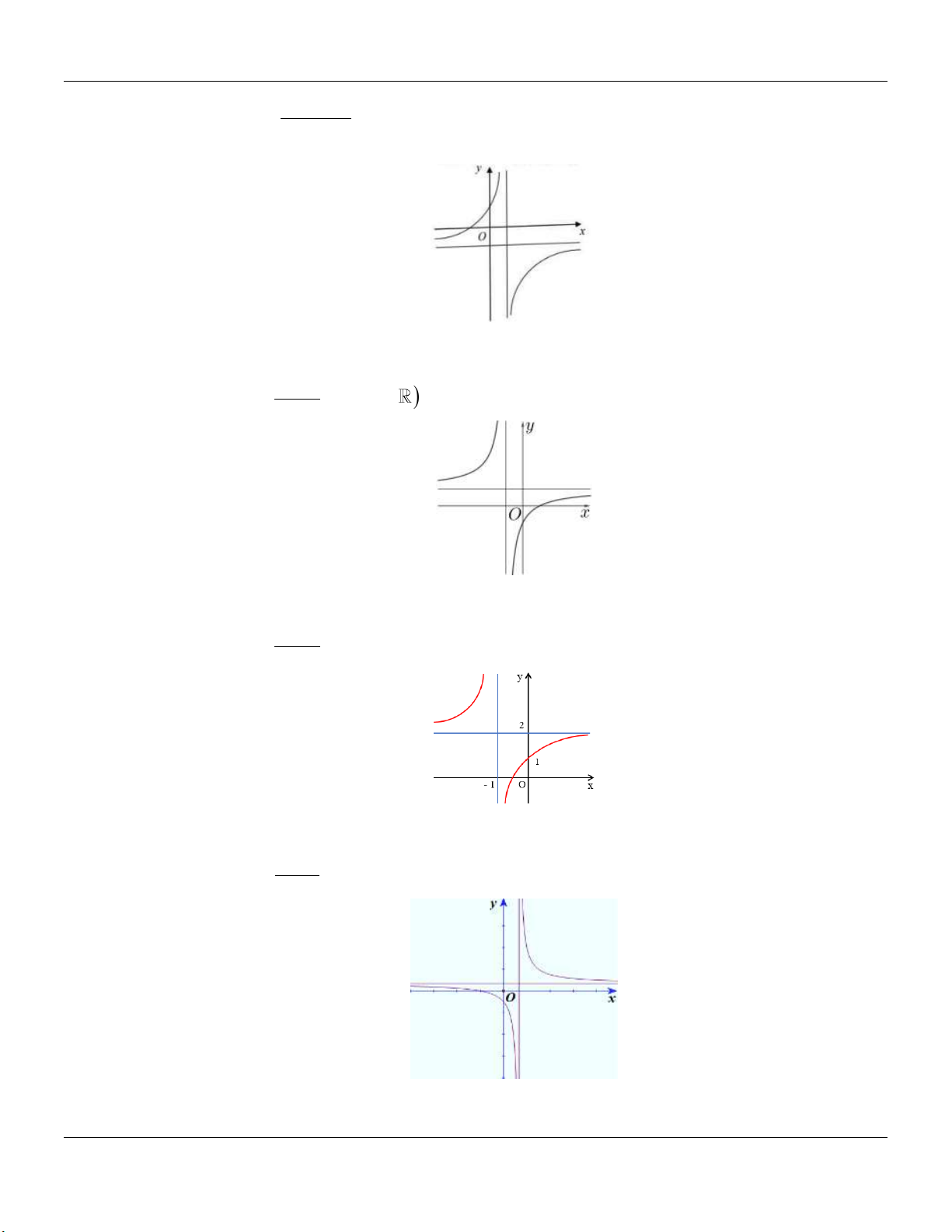
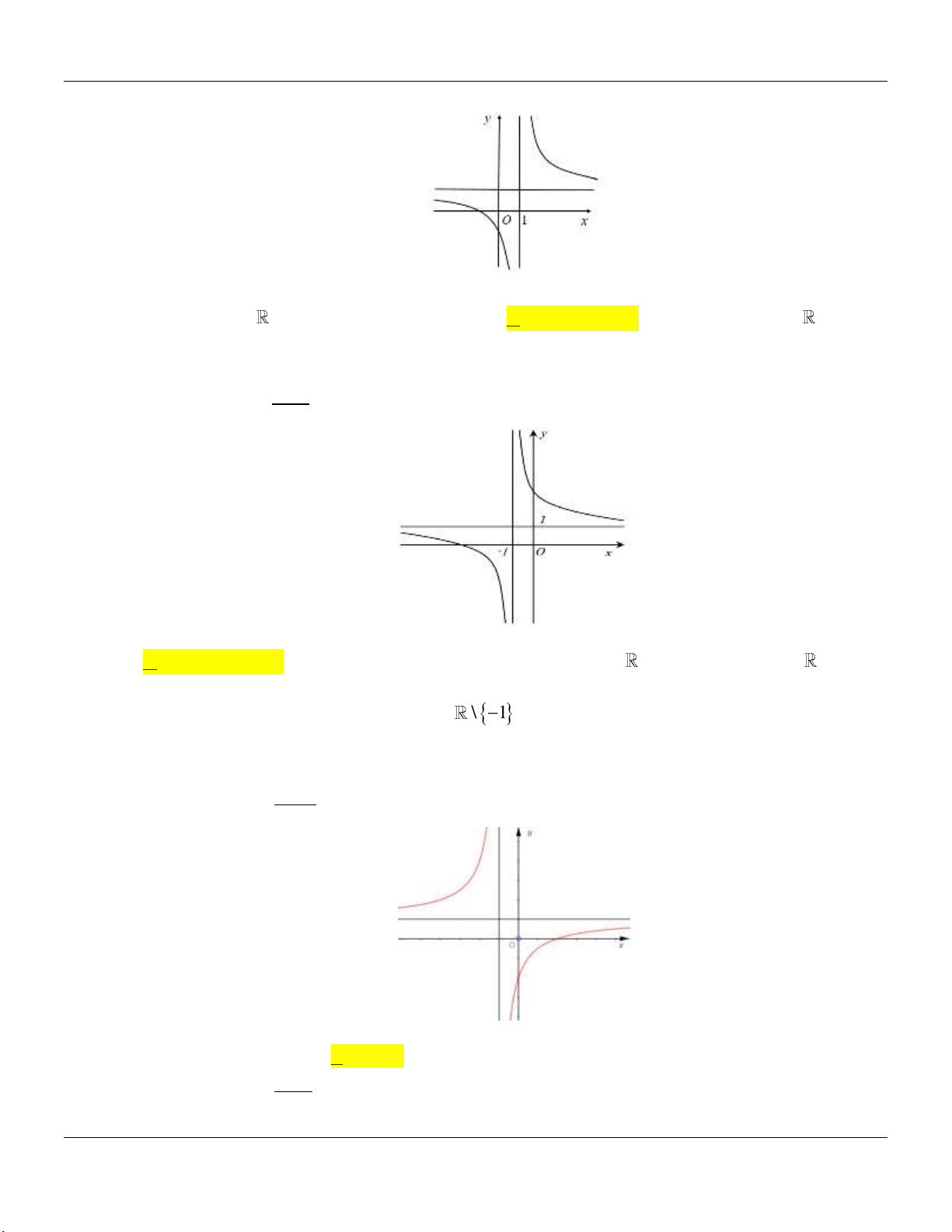
Đồ thị hàm số trong hình vẽ sau là đồ thị của hàm số nào trong các hàm số dưới đây x 1 x  3 1 3x x 1 A. y  . B. y  . C. y  . D. y  . x  2 x  2 x  2 x  2 Câu 2:
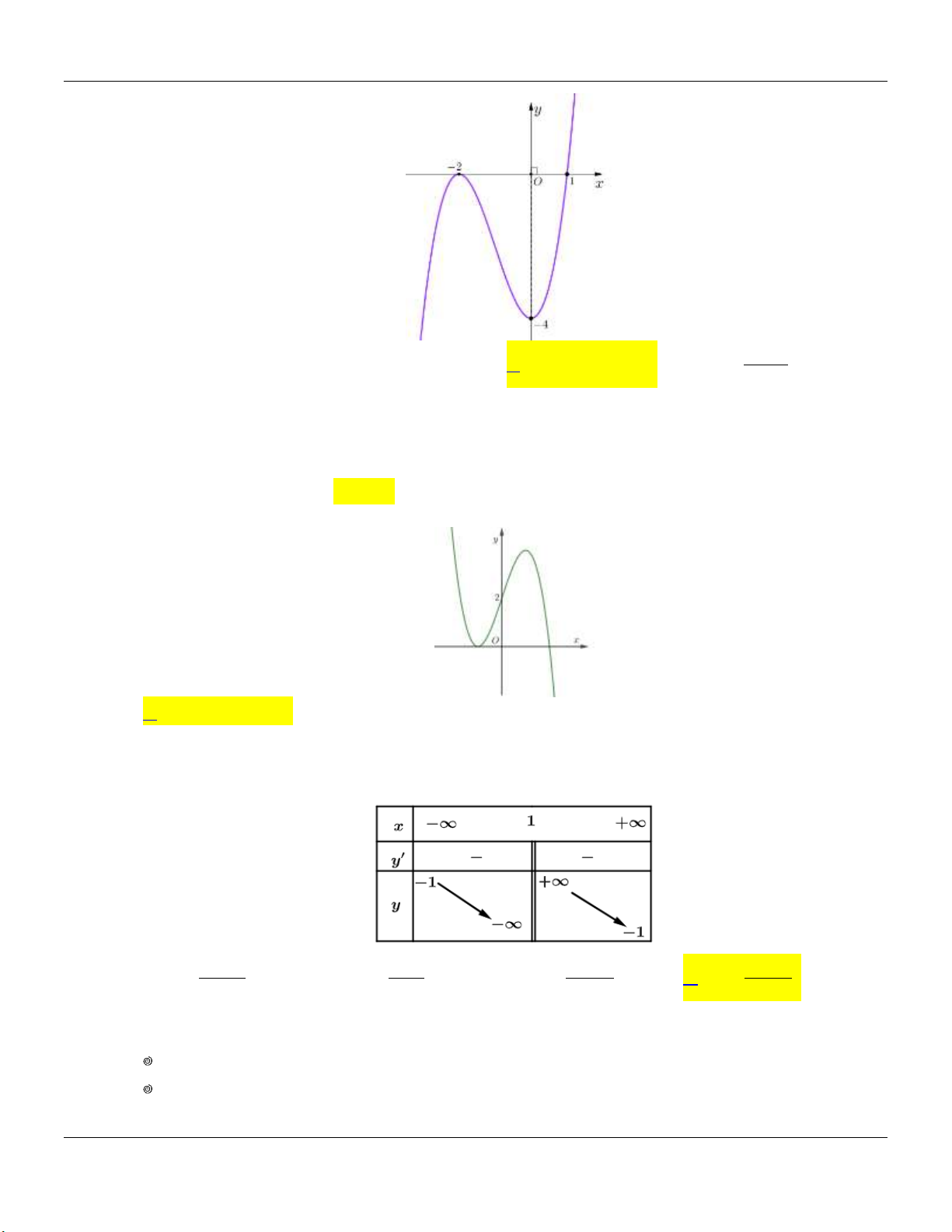
Hàm số nào dưới đây có bảng biến thiên như sau: x  5  y   1  y  1 x  7 x  5 5x x  3 A. y  . B. y  . C. y  . D. y  . x  5 x 1 x 1 x  5 Câu 3:
Đồ thị hàm số nào dưới đây có dạng như hình vẽ? x 1 x 1 x  2 2  x 1 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1 Câu 4:
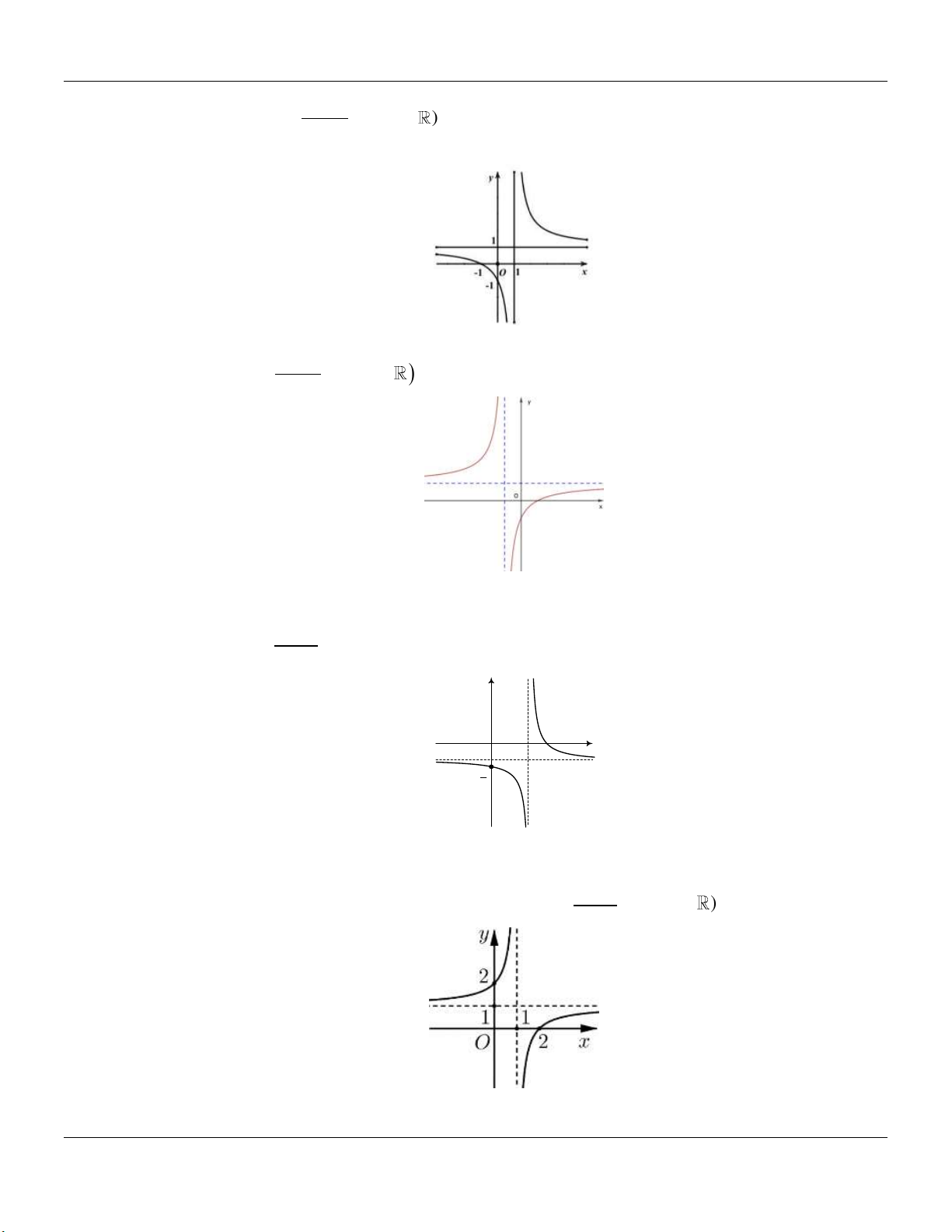
Cho hàm số y f x có bảng biến thiên như hình vẽ bên dưới. Hỏi hàm số y f x là hàm
số nào trong các hàm số cho dưới đây? x  2 A. 3 2
y  x  3x 1. B. 3 2
y x  3x 1. C. y  . D. 4 2
y x  2x 1. x 1
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 5:
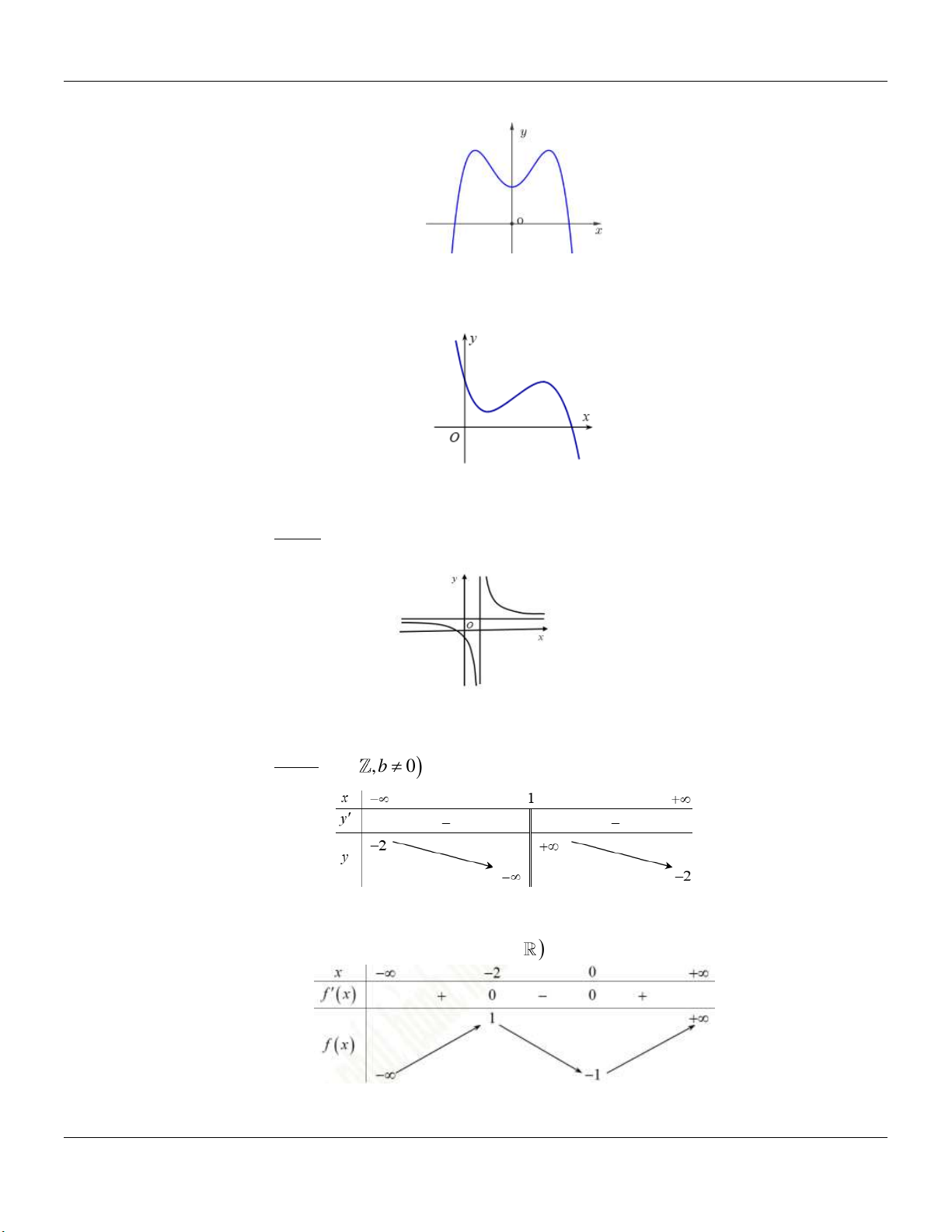
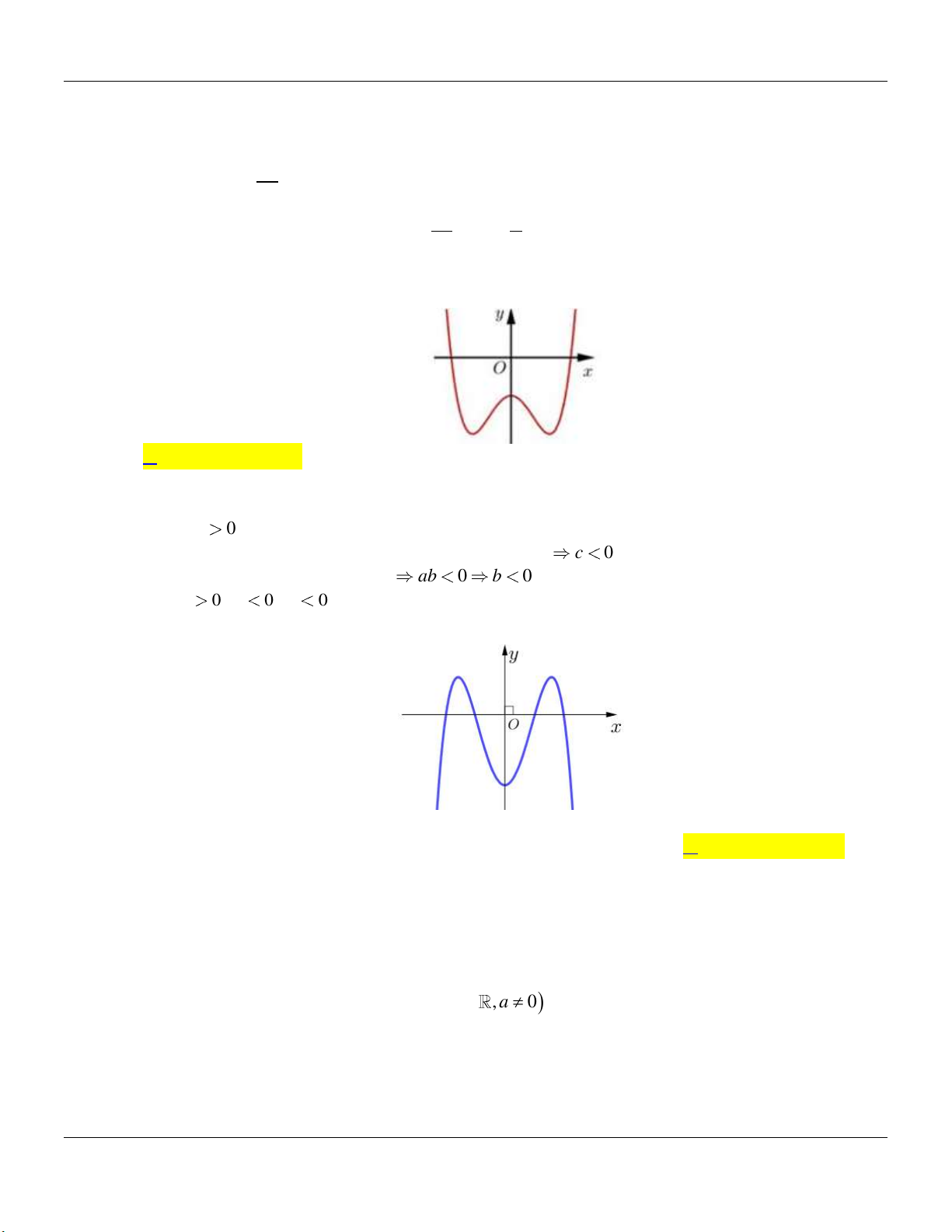
Đường cong hình bên là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm số nào?  3 2 4 2 4 2 A. 2x 1           y  . B. y x 3x 1. C. y x 2x 1. D. y x 2x 1. x 1 Câu 6:
Cho hàm số y f (x) có bảng biến thiên như sau:
Hàm số có bảng biến thiên như trên là A. 4 2
y  x  2x . B. 4 2
y  3x  6x  3 . C. 3
y x x . D. 3
y x x  3 . Câu 7:
Hàm số nào dưới đây có đồ thị như đường cong trong hình bên dưới? A. 3 2
y x  3x 1. B. 4 2
y x  3x 1. C. 4 2
y  x  2x 1. D. 3 2
y x  2x 1. Câu 8:
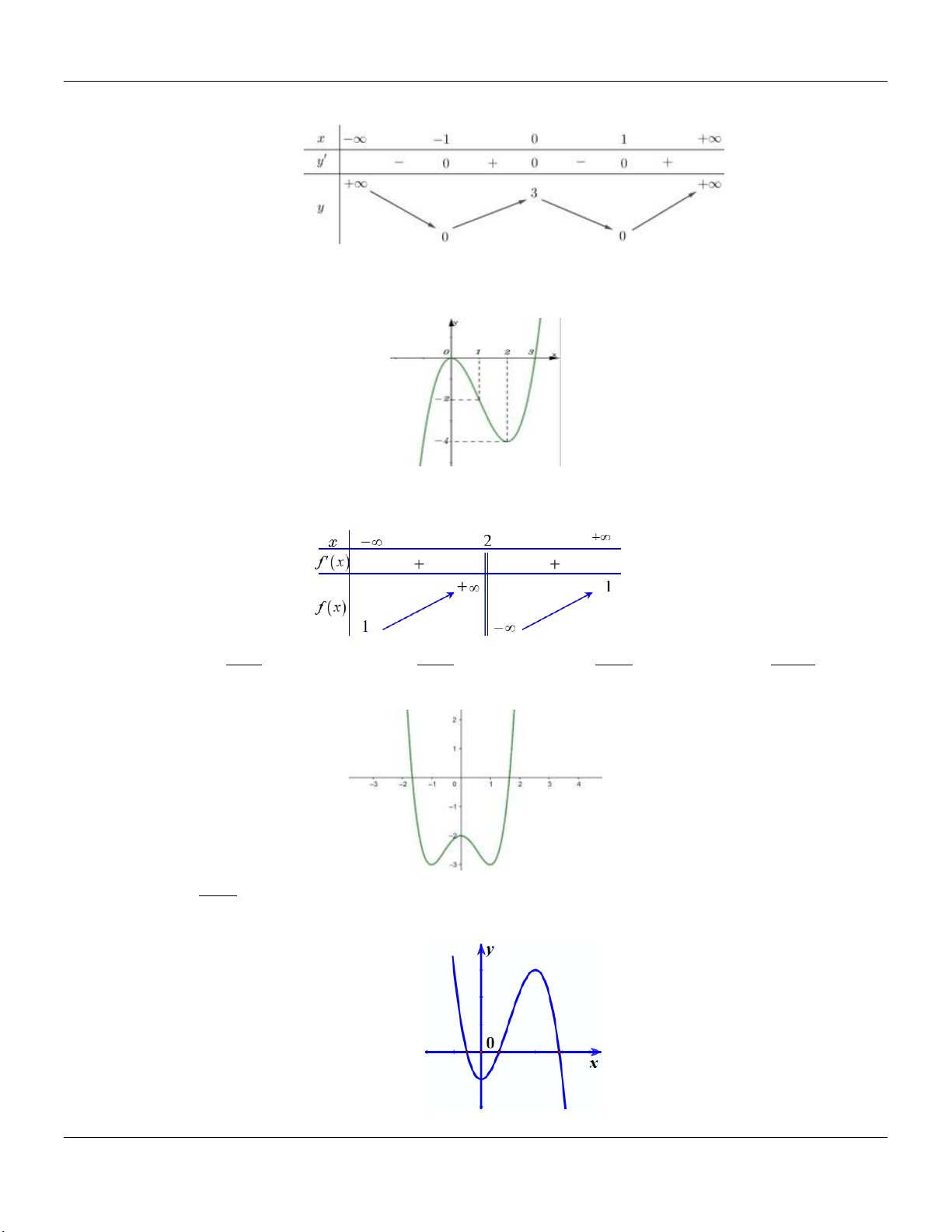
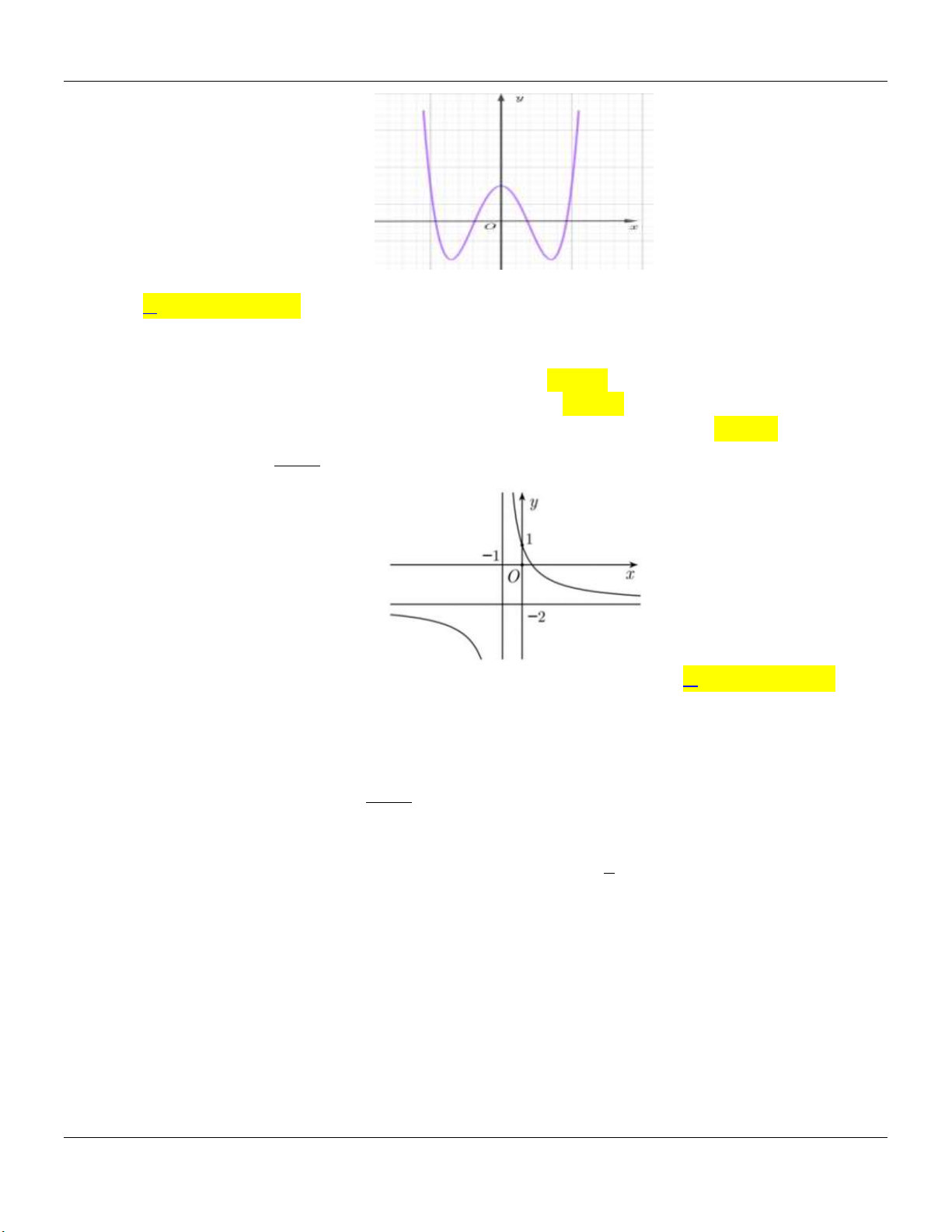
Bảng biến thiên dưới đây của hàm số nào? x 1 A. y . B. 4 2 y x 2x 3 . C. 3 y x 3x 4 . D. 3 y x 3x 4 . x 1 Câu 9:
Đồ thị sau đây là của hàm số nào? A. 3
y x  3x 1. B. 3
y x  3x 1. C. 3 2
y  x  3x 1 . D. 3 2
y  x  3x 1.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 10: Cho hàm số y f (x) có bảng biến thiên như hình dưới đây. Hàm số y f (x) là hàm số nào
trong các hàm số sau đây? 1 A. 4 2
y  x  2x  3 . B. 4 2
y x  2x  3 . C. 4 2 y  
x  3x  3 .D. 4 2
y x  2x  3 . 4
Câu 11: Đồ thị dưới đây là đồ thị của hàm số nào? A. 3
y  x x . B. 3
y x x . C. 3
y  x x .
D. y  x .
Câu 12: Hàm số nào trong các hàm số sau mà đồ thị có dạng hình vẽ dưới đây? A. 3
y x  3x 1. B. 3 2
y x  3x 1. C. 3 2
y x  3x 1. D. 3
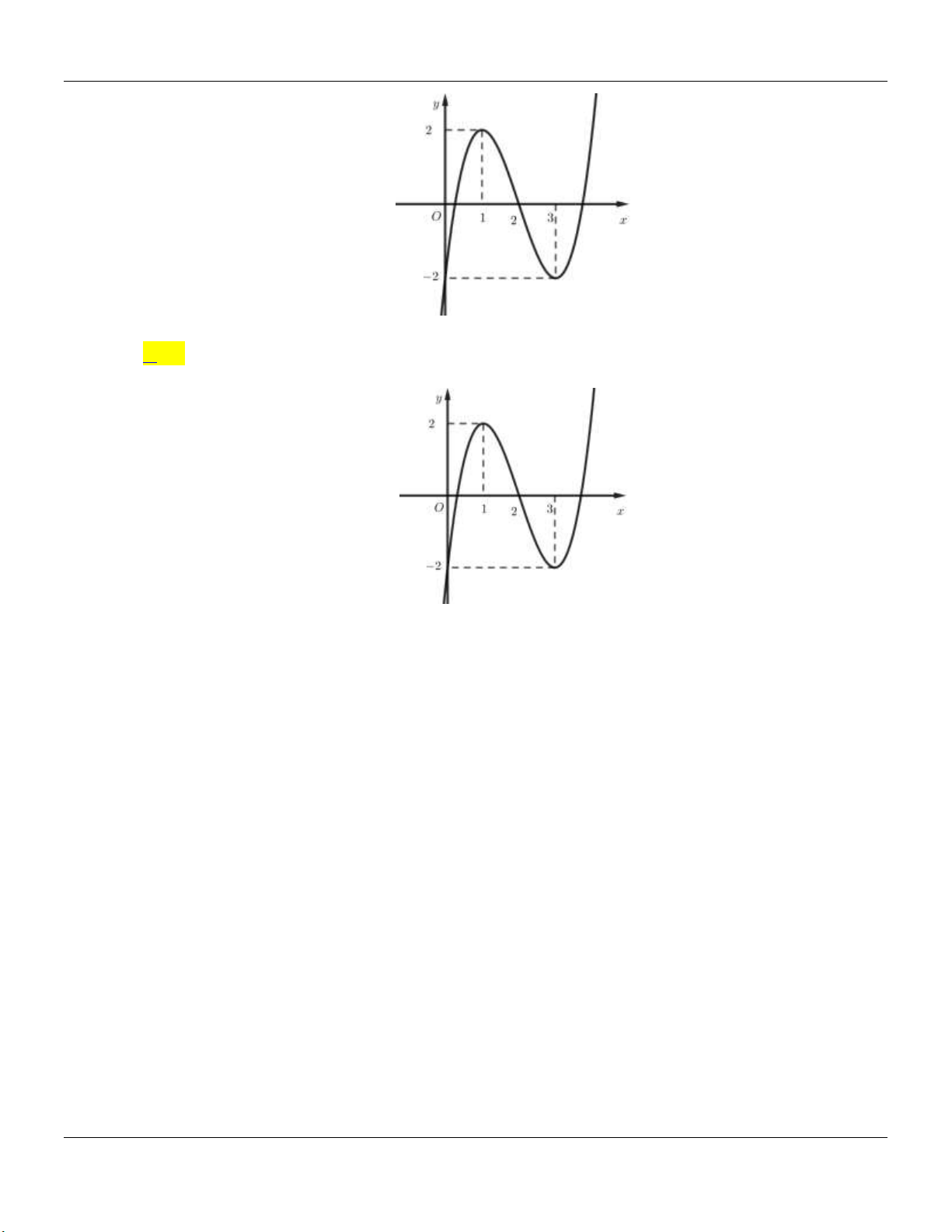
y x  3x 1. Câu 13: Hàm số 3 2
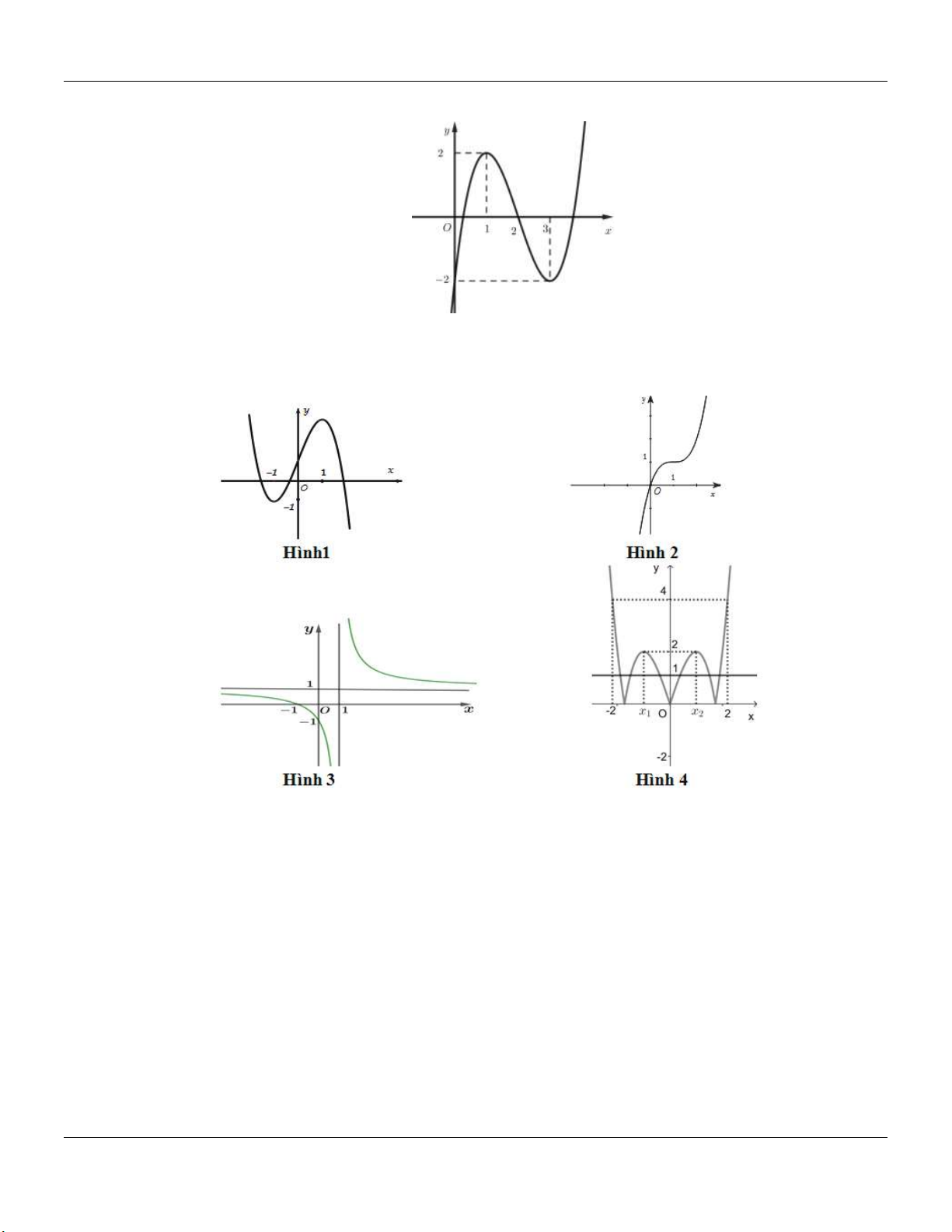
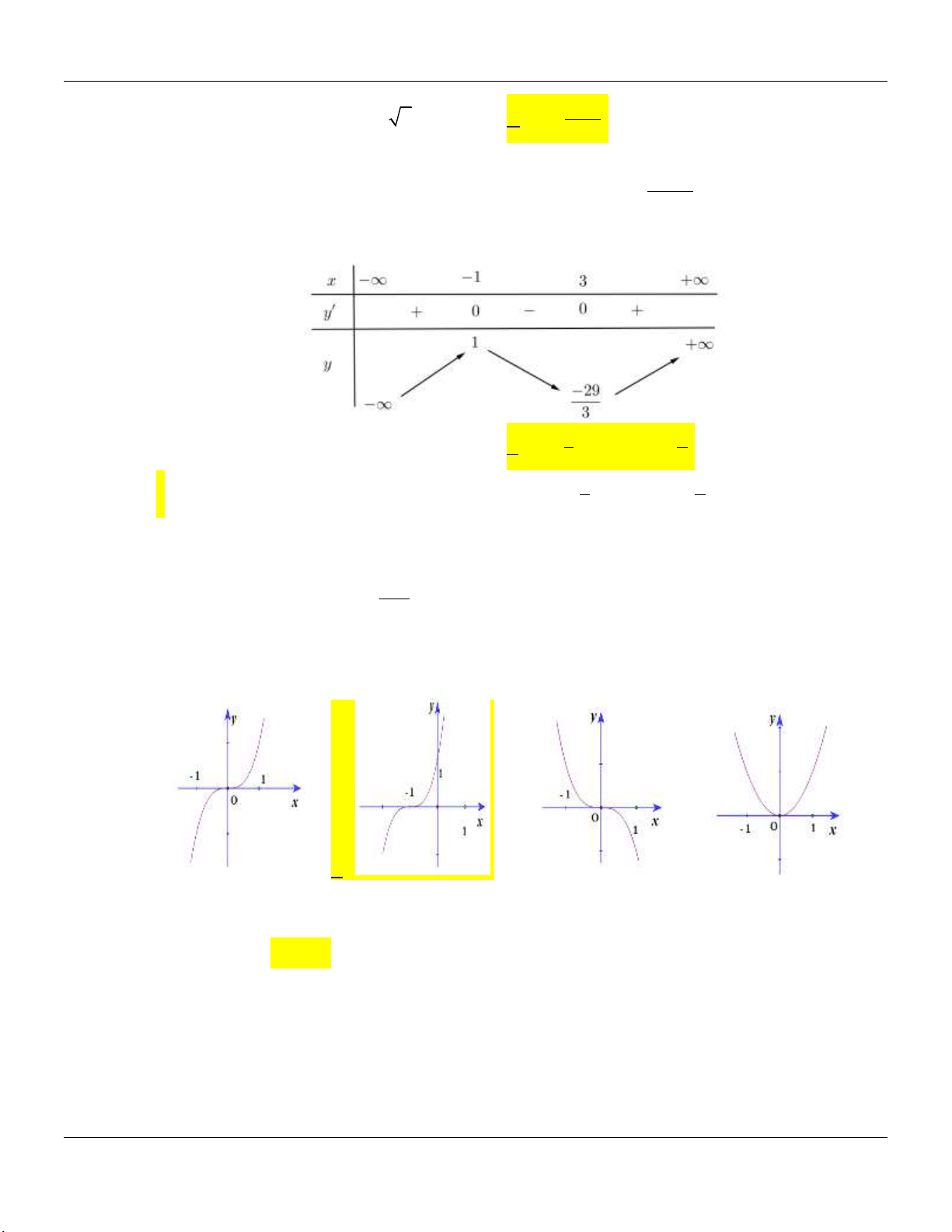
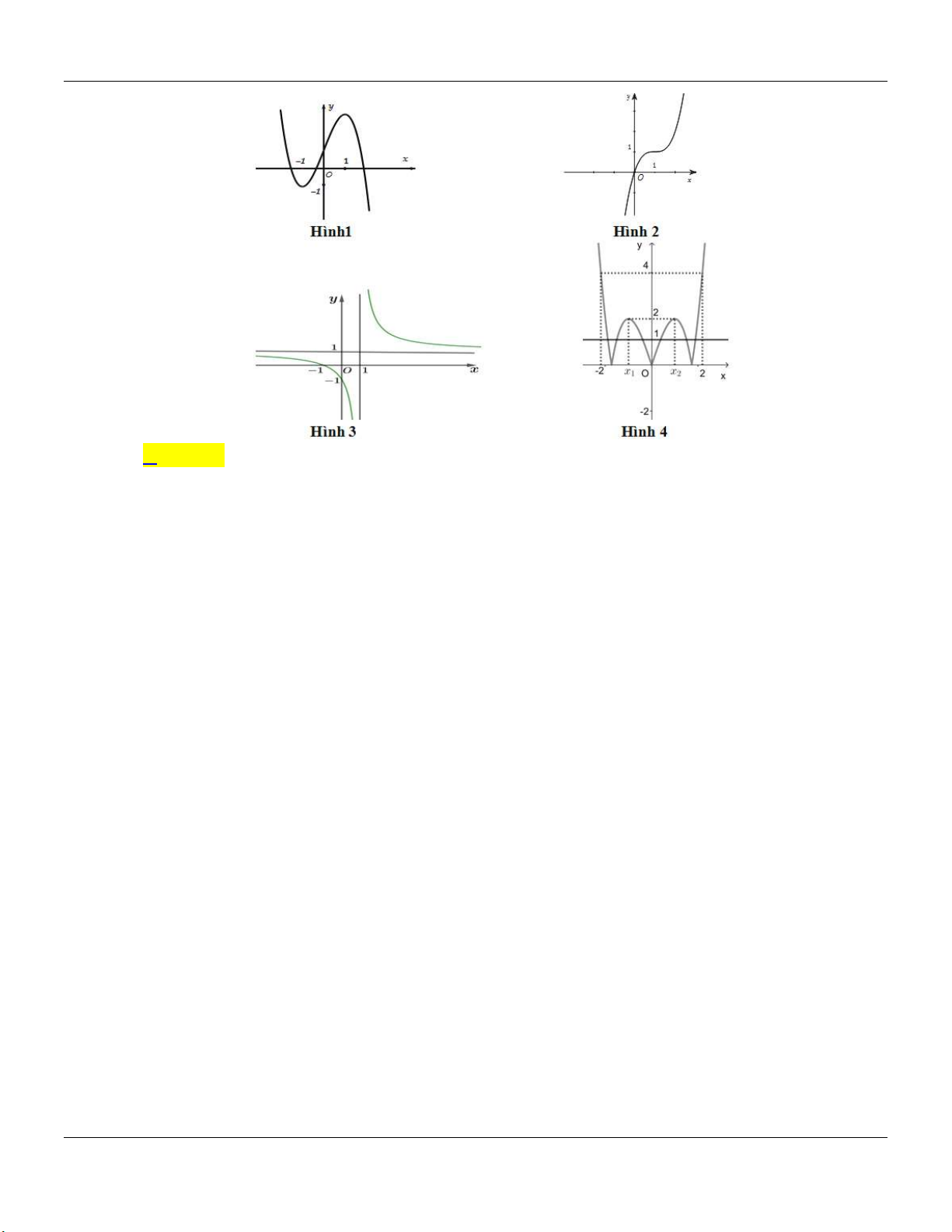
y  x  3x 1 có đồ thị nào sau đây? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 14: Cho hàm số y f x có đồ thị C  như hình vẽ. Hỏi C  là đồ thị của hàm số nào? 3 3
A. y x 1 .
B. y x 1 .
C. y   x  3 1 .
D. y   x  3 1 .
Câu 15: Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây? x 1 A. 3 2
y x x x 1 .
B. y x . C. y y x x  . D. 4 . 2
Câu 16: Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây, hàm số nào có bảng biến thiên như sau? 1 2 A. 3 2
y  x  3x  9x  2 . B. 3 2 y
x x  3x  . 3 3 1 2 C. 3 2
y x  3x  9x  2 . D. 3 2
y   x x  3x  . 3 3 Câu 17: Hàm số 3 2
y x  3x  3x 1 có đồ thị là hình nào sau đây? A. . B. . C. . D. .
Câu 18: Hàm số nào có đồ thị là hình vẽ sau đây?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2x 1 A. 3 2
y x  3x  4 . B. 4 2
y x  3x  4 . C. 3 2
y x  3x  4 . D. y  . 3x  5
Câu 19: Đường cong trong hình vẽ bên là đồ thị của một hàm số nào? A. 3
y  x  3x  2 . B. 3
y  x  3x  2 . C. 4 2
y x x  2 . D. 3
y x  3x  2 .
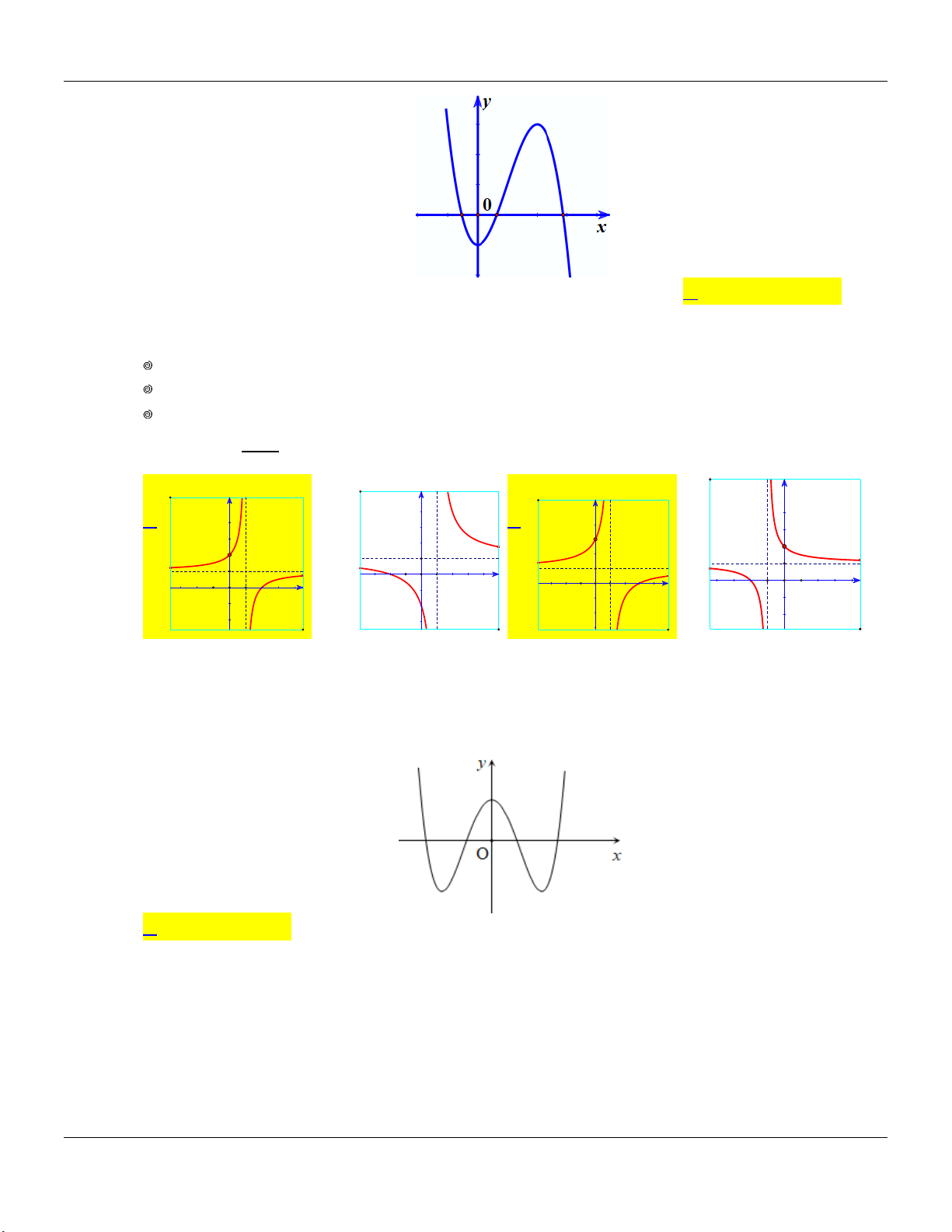
Câu 20: Hàm số nào dưới đây có bảng biến thiên như hình bên dưới? x  3 x  3 x  2 x  3 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1
Câu 21: Hàm số nào có đồ thị là đường cong trong hình vẽ bên dưới? x 1 A. 4 2
y x  4x 1. B. y
y x x  . D. 2 y  2x 1 . x  . C. 3 2 4 1 2
Câu 22: Đồ thị của hàm số nào dưới đây có dạng như đường cong hình dưới đây? y 1 1 x A. 3
y x  3x 1. B. 3
y  x  3x 1. C. 3
y  x  3x 1. D. 3
y x  3x 1.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 23: Cho hàm số y f x có bảng biến thiên như sau:
Hàm số có bảng biến thiên như trên là A. 4 2
y  3x  6x  3 . B. 4 2
y  x  2x . C. 3
y x x . D. 3
y x x  3 .
Câu 24: Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên dưới: A. 3
y x  3x . B. 3
y x  3x . C. 3 2
y x  3x . D. 3 2
y x  3x .
Câu 25: Bảng biến thiên sau đây là của hàm số nào? x x x x
A. f x 3  .
B. f x 3 
C. f x 3  .
D. f x 2 3  x  2 2  x x  2 x  2
Câu 26: Đường cong của hình vẽ là đồ thị của hàm số nào trong các hàm số sau? x  2 A. y
y x x  . C. 4 2
y  x  2x  2 . D. 3 2
y x  2x  2 x  . B. 4 2 2 2 1
Câu 27: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 2
y x  3x 1. B. 4 2
y  x  2x 1. C. 4 2
y x  2x 1. D. 3 2
y  x  3x 1.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x  2
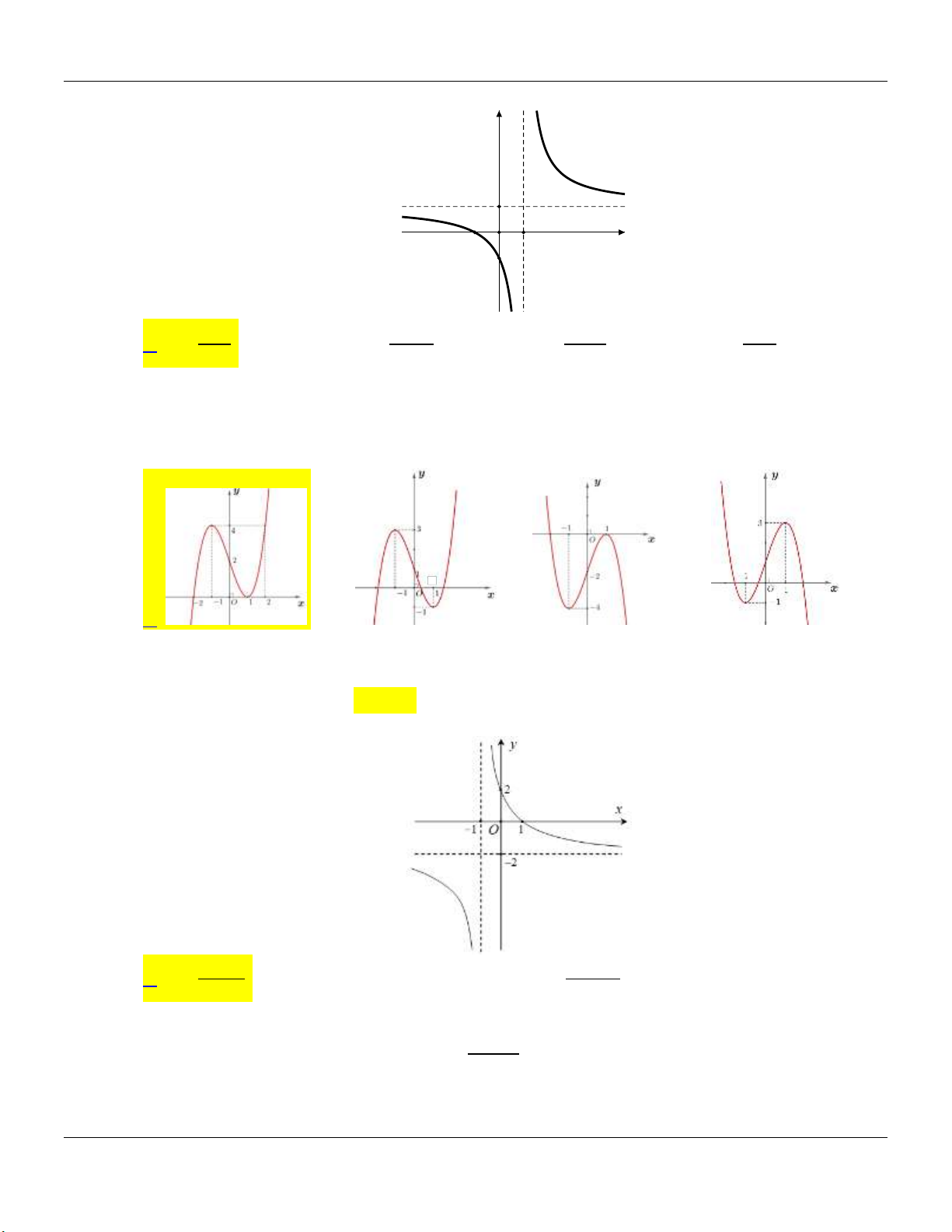
Câu 28: Hàm số y
có đồ thị là hình vẽ nào sau đây? x 1 y y A. y y . B. .C .D. . 3 2 2 1 1 1 -1 1 -2 0 1 x -2 -1 0 1 x -2 -1 0 1 x -2 -1 0 1 x .
Câu 29: Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới? A. 4 2
y x  3x  1. B. 4 2
y x  3x  1. C. 4 2
y x x  1. D. 4 2
y  x x  1 .
Câu 30: Hàm số nào dưới đây có đồ thị dạng như đường cong trong hình vẽ bên dưới? y 1 x O 1 x 1 2x 1 2x 1 x 1 A. y y y y x  . B. 1 x  . C. 1 x  . D. 1 x  . 1
Câu 31: Đồ thị hàm số 3
y x  3x  2 là hình nào trong 4 hình dưới đây? A. . B. . C. . D. .
Câu 32: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây? 2  2x 2  x 1 A. y
y x x . C. y
y x x  . x  . B. 3 2 1 1 x  . D. 4 2 2 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 33: Đồ thị hàm số 3 2
y x  3x  2 là đường cong trong hình nào dưới đây? A. B. C. D.
Câu 34: Đồ thị hình bên là đồ thị của hàm số nào trong các hàm số dưới đây? A. y   2 x  
1  x  2 . B. y   2 x  
1  x  2 . C. 3 2
y  x  3x  2 . D. 4 2
y x  3x  2 .
Câu 35: Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây? 3 3 2 3 2 4 2
A. y  x  3x  2 .
B. y x  3x 1.
C. y  x  3x  2 .
D. y x  3x 1 .
Câu 36: Cho hàm số    3 2 y
f x ax bx cx d có bảng biến thiên sau:
Đồ thị nào thể hiện hàm số y f x ? A. I . B. II.
C. III. D. IV .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 37: Đồ thị trong hình vẽ sau là đồ thị của hàm số nào trong các hàm số dưới đây. 3 A. 4 2
y x  8x 1 . B. 3 2
y x  3x 1 . C. 4 2
y x  2x 1. D. 2
y x  3x 1 .
MỘT SỐ BÀI TOÁN LIÊN QUAN ax b
Câu 38: Cho đường cong ở hình bên là đồ thị của hàm số y
với a,b, c, d là các số thực. cx d
Mệnh đề nào dưới đây đúng?
A. y  0, x   .
B. y  0, x   1.
C. y  0, x   1.
D. y  0, x   . x a
Câu 39: Biết hàm số y
a  ) có đồ thị như hình vẽ sau:
x  ( a là số thực cho trước, 1 1
Mệnh đề nào dưới đây đúng?
A. y '  0, x   1.
B. y '  0, x   1.
C. y '  0, x   .
D. y '  0, x   . x m
Câu 40: Cho hàm số y x  , có đồ thị như hình vẽ bên dưới: 1
Khẳng định nào sau đây đúng? A. m  1.
B. m  1.
C. m  1.
D. m  1.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x a
Câu 41: Cho hàm số y
có đồ thị như hình vẽ bên dưới: x 1
Mệnh đề nào dưới đây đúng?
A. a  1 .
B. a  3 .
C. a  1 . D. a  1 .
Câu 42: Biết hàm số 3 2
y  ax bx cx d (a  0) có đồ thị như hình vẽ sau: y 1 -1 x O 1 2
Mệnh đề nào dưới đây đúng?
A. y '  0, x   .
B. y '  0, x   .
C. y '  0, x   .
D. y '  0, x   . Câu 43: Hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
A. a  0 , b  0 , c  0 , d  0 .
B. a  0 , b  0 , c  0 , d  0 .
C. a  0 , b  0 , c  0 , d  0 .
D. a  0 , b  0 , c  0 , d  0 . ax 1
Câu 44: Cho hàm số f x  a, , b c   bx
có bảng biến thiên như sau: c
Trong các số a,b, c có bao nhiêu số dương? A. 3 . B. 2 . C. 1 . D. 0 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia ax b
Câu 45: Cho hàm số y
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? x c
A. a  2, b c  1.
B. a b  2, c  1.
C. a  2, b  1, c  1. D. a  2
 , b c 1. Câu 46: Cho hàm số 3
y ax  3x d , a; d   có đồ thị như hình vẽ bên dưới:
Mệnh đề nào dưới đây đúng?
A. a  0, d  0 .
B. a  0, d  0 .
C. a  0, d  0 .
D. a  0, d  0 . Câu 47: Cho hàm số 4 2
y ax bx c,a  0 có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 . C. a  0,b  0, c  0 . D. a  0,b  0, c  0 . Câu 48: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ sau:
Mệnh đề nào dưới đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia ax
Câu 49: Cho hàm số f x 2  , a, ,
b c   có đồ thị như sau: bx c
Khẳng định nào dưới đây đúng?
A. a b  0  c .
B. b a  0  c .
C. b  0  c a .
D. b  0  a c . Câu 50: Cho hàm số 4 2
y ax bx c a  0 có đồ thị như hình vẽ dưới đây:
Mệnh đề nào dưới đây đúng?
A. a  0 , b  0 , c  0 . B. a  0, b  0, c  0 . C. a  0, b  0, c  0 . D. a  0, b  0, c  0 . ax b
Câu 51: Cho hàm số y
có bảng biến thiên như hình vẽ dưới đây: cx 1 Xét các mệnh đề sau: (1) c  1. (2) a  2 .
(3) Hàm số đồng biến trên  ;    1   1  ;. 1 (4) Nếu y   thì b  1. x  2 1
Số mệnh đề đúng trong các mệnh đề trên là A. 1. B. 4 . C. 2 . D. 3 . ax  2
Câu 52: Cho hàm số y
( với a , b là các số thực) có đồ thị như hình sau: x b
Giá trị a b bằng A. 0 . B. 3 . C. 3  . D. 4  .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 53: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0
C. a  0,b  0, c  0, d  0
D. a  0,b  0, c  0, d  0 . Câu 54: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên dưới:
Mệnh đề nào sau đây đúng?
A. a  0,b  0,c  0, d  0 .
B. a  0,b  0,c  0, d  0 .
C. a  0,b  0,c  0, d  0 .
D. a  0,b  0,c  0, d  0 . Câu 55: Cho hàm số 4 2
y ax bx cx d có đồ thị như hình vẽ dưới đây, mệnh đề nào sau đây đúng?
A. a  0;b  0;c  0; d  0 .
B. a  0;b  0;c  0; d  0 .
C. a  0;b  0;c  0; d  0 .
D. a  0;b  0;c  0; d  0 . Câu 56: Cho hàm số 4 2
y ax bx ca  0 có đồ thị như hình bên. Xác định dấu của a ,b ,c .
A. a  0,b  0,c  0 .
B. a  0,b  0,c  0 . C. a  0,b  0,c  0 . D. a  0,b  0,c  0 . Câu 57: Hàm số 4 2
y ax bx c có đồ thị như hình vẽ bên dưới:
Mệnh đề nào sau đây đúng?
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 . C. a  0,b  0, c  0 . D. a  0,b  0, c  0 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 58: Cho hàm số 4 2
y ax bx c , với a, ,
b c  , a  0 , có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 .
C. a  0,b  0, c  0 .
D. a  0,b  0, c  0 . ax b
Câu 59: Cho hàm số y
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? x c
A. a  2,b c  1  .
B. a b  2, c  1
 . C. a  2,b  1,c  1. D. a  2
 ,b c  1. Câu 60: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình bên. Mệnh đề nào sau đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 .
Câu 61: Hàm số bậc 4 trùng phương 4 2 y  . a x  .
b x c có đồ thị như hình vẽ. Dấu của các hệ số a, b, c là
A. a  0;b  0;c  0 .
B. a  0;b  0;c  0 . C. a  0;b  0;c  0 . D. a  0;b  0;c  0 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 62: Xác định các hệ số a , b , c để hàm số 4 2
y ax bx c có đồ thị như hình bên dưới: 1 A. a
; b  2 ; c  2 .
B. a  4 ; b  2 ; c  2 . 4 1 C. a
; b  2 ; c  2 .
D. a  4 ; b  2 ; c  2 . 4 ax 1
Câu 63: Cho hàm số y bx  có đồ thị như hình bên dưới: c
Giá trị a b c bằng A. 1. B. 4 . C. 2 . D. 3 . Câu 64: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 . Câu 65: Cho hàm số 3 2
y ax bx cx d a  0 có đồ thị như hình vẽ dưới đây:
Mệnh đề nào sau đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia ax  4  b
Câu 66: Cho hàm số y
có đồ thị là đường cong trong hình bên. Mệnh đề nào dưới đây cx b đúng?
A. a  0, 0  b  4, c  0 .
B. a  0,b  0, c  0 .
C. a  0,b  4, c  0 .
D. a  0, 0  b  4, c  0 . ax b
Câu 67: Cho hàm số y  a, ,
b c   có đồ thị như sau: cx  2
Trong các số a , b và c có bao nhiêu số dương? A. 0 . B. 1. C. 2 . D. 3 . ax b
Câu 68: Cho hàm số y
có đồ thị như hình vẽ bên dưới: x 1
Mệnh đề nào dưới đây đúng?
A. a b .
B. ab  0 .
C. ab  0 .
D. b a  0 . x b
Câu 69: Cho hàm số y  c  0 cx  có đồ thị như sau: 2
Mệnh đề nào sau đây đúng?
A. b  0; c  0.
B. b  0; c  0.
C. b  0; c  0.
D. b  0; c  0.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x b
Câu 70: Cho hàm số y  ( ,
b c, d  ) có đồ thị như hình vẽ. Giá trị của biểu thức cx d
T  2b  3c  4d bằng A. 1. B. 8  . C. 6. D. 0. ax b
Câu 71: Cho hàm số y  a, ,bc  cx
có đồ thị như hình vẽ bên dưới: 2
Trong các số a,b và c có bao nhiêu số dương? A. 2 . B. 0. C. 1. D. 3 . ax  3
Câu 72: Cho hàm số y x  có đồ thị như hình vẽ bên dưới: c y O 2 x 1  3  2
Tính giá trị của a  2c .
A. a  2c  2 .
B. a  2c  3 .
C. a  2c  3 .
D. a  2c  1 . x a
Câu 73: Đường cong ở hình dưới đây là đồ thị của hàm số y
, (a,b, c  ) . bx c
Trong các số a , b và c có bao nhiêu số dương? A. 0 . B. 1. C. 2. D. 3.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 74: Cho hàm số 4 2
y ax bx c có đồ thị như hình bên dưới:
Khẳng định nào sau đây đúng?
A. a  0;b  0;c  0 .
B. a  0;b  0;c  0 . C. a  0;b  0;c  0 . D. a  0;b  0;c  0 . Câu 75: Cho hàm số 3 2
y ax bx cx d có đồ thị là đường cong trong hình dưới đây:
Trong các hệ số a,b, c, d có bao nhiêu số âm ? A. 3 . B. 0 . C. 1. D. 2 . ax b
Câu 76: Cho hàm số y  có đồ thị như sau: cx d
Mệnh đề nào sau đây đúng?
A. ac  0; bd  0 .
B. ab  0; cd  0 .
C. bc  0; ad  0 .
D. ad  0; bd  0 . ax  3
Câu 77: Cho hàm số y
b ,b  0 bx
có bảng biến thiên như sau: c
Tính tổng S a b c . A. 2 . B. 2  . C. 0 . D. 1  .
Câu 78: Cho hàm số f x 3 2
ax bx cx d a, b, c, d   có bảng biến thiên như sau:
Có bao nhiêu số dương trong các số a, b, c, d ? A. 3. B. 4. C. 2. D. 1.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 79: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ dưới đây:
Số lớn nhất trong các số a, b, c, d là: A. c . B. a . C. b . D. d .
Câu 80: Hàm số y f x thỏa mãn f 2021  f  202 
1 có đồ thị là hình nào trong bốn đồ thị sau: A. Hình 4. B. Hình 3. C. Hình 1. D. Hình 2.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
LỜI GIẢI CHI TIẾT Câu 1:
Đồ thị hàm số trong hình vẽ sau là đồ thị của hàm số nào trong các hàm số dưới đây x 1 x  3 1 3x x 1 A. y  . B. y  . C. y  . D. y  . x  2 x  2 x  2 x  2 Lời giải:
Dựa vào đồ thị ta thấy hai đường tiệm cận đứng x  2 , tiệm cận ngang y  1 và giao với trục 3
Oy tại tung độ bằng nên Chọn B thỏa. 2 Câu 2:
Hàm số nào dưới đây có bảng biến thiên như sau: x  5  y   1  y  1 x  7 x  5 5x x  3 A. y  . B. y  . C. y  . D. y  . x  5 x 1 x 1 x  5 Lời giải:
Theo bảng biến thiên ta có: Tiệm cận đứng x  5 , tiệm cận ngang y  1 và y  0 x   \  5 x  3
nên ta chọn hàm số y  . x  5 Câu 3:
Đồ thị hàm số nào dưới đây có dạng như hình vẽ? x 1 x 1 x  2 2  x 1 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1 Lời giải:
Từ hình vẽ, suy ra đồ thị hàm số có tiệm cận đứng là đường thẳng x  1 , do đó ta loại hai
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Chọn A và C.
Mặt khác đồ thị hàm số có tiệm cận ngang là đường thẳng y  1, nên ta loại Chọn D Vậy đáp
án đúng là Chọn B Câu 4:
Cho hàm số y f x có bảng biến thiên như hình vẽ bên dưới. Hỏi hàm số y f x là hàm
số nào trong các hàm số cho dưới đây? x  2 A. 3 2
y  x  3x 1. B. 3 2
y x  3x 1. C. y  . D. 4 2
y x  2x 1. x 1 Câu 5:
Đường cong hình bên là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm số nào?  3 2 4 2 4 2 A. 2x 1           y  . B. y x 3x 1. C. y x 2x 1. D. y x 2x 1. x 1 Lời giải: 4 2
Đồ thị đã cho là đồ thị của hàm số bậc 4 y ax bx c có hệ số a  0 và có 3 điểm cực trị. Câu 6:
Cho hàm số y f (x) có bảng biến thiên như sau:
Hàm số có bảng biến thiên như trên là A. 4 2
y  x  2x . B. 4 2
y  3x  6x  3 . C. 3
y x x . D. 3
y x x  3 . Câu 7:
Hàm số nào dưới đây có đồ thị như đường cong trong hình bên dưới?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. 3 2
y x  3x 1. B. 4 2
y x  3x 1. C. 4 2
y  x  2x 1. D. 3 2
y x  2x 1. Lời giải:
Dựa vào hình dạng của đường cong, ta nhận thấy đó là đồ thị của hàm số bậc 4 trùng phương có hệ số của 4
x âm. Vậy Chọn C. Câu 8:
Bảng biến thiên dưới đây của hàm số nào? x 1 A. y . B. 4 2 y x 2x 3 . C. 3 y x 3x 4 . D. 3 y x 3x 4 . x 1 Lời giải:
Ta loại phương án A và B vì khi lấy đạo hàm không phù hợp bảng biến thiên.
Còn lại phương án C và
D. Dựa vào bảng biến thiên ta có hệ số a  0 .
Do đó, ta chọn hàm số 3 y x 3x 4 . Câu 9:
Đồ thị sau đây là của hàm số nào? A. 3
y x  3x 1. B. 3
y x  3x 1. C. 3 2
y  x  3x 1 . D. 3 2
y  x  3x 1. Lời giải: Hàm số 3 2
y ax bx cx d với a  0 và cắt Oy tại 0;  1 .
Câu 10: Cho hàm số y f (x) có bảng biến thiên như hình dưới đây. Hàm số y f (x) là hàm số nào
trong các hàm số sau đây?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1 A. 4 2
y  x  2x  3 . B. 4 2
y x  2x  3 . C. 4 2 y  
x  3x  3 .D. 4 2
y x  2x  3 . 4 Lời giải:
Dựa vào bảng biến thiên ta có a  0 và hàm số có ba điểm cực trị do hàm số có dạng 4 2
ax bx c có . a b  0
Câu 11: Đồ thị dưới đây là đồ thị của hàm số nào? A. 3
y  x x . B. 3
y x x . C. 3
y  x x .
D. y  x . Lời giải:
Từ đồ thị ta thấy hàm số luôn nghịch biến, không có cực trị và là hàm bậc ba nên ta chọn 3
y  x x .
Câu 12: Hàm số nào trong các hàm số sau mà đồ thị có dạng hình vẽ dưới đây? A. 3
y x  3x 1. B. 3 2
y x  3x 1. C. 3 2
y x  3x 1. D. 3
y x  3x 1. Lời giải:
Đồ thị hàm số trên là đồ thị hàm số bậc ba 3 2
y ax bx cx d
Nhìn vào nhánh phải của đồ thị ta thấy đồ thị có hướng đi lên suy ra a  0
Ta thấy đồ thị cắt trục tung tại điểm có tung độ dương suy ra d  0
Nhìn vào đồ thị ta thấy hàm số có hai điểm cực trị x  1 và x  1
Vậy hàm số thỏa đề là 3
y x  3x 1.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 13: Hàm số 3 2
y  x  3x 1 có đồ thị nào sau đây? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. Lời giải: Đồ thị hàm số 3 2
y  x  3x 1 cắt trục tung tại điểm A0;  
1 nên loại phương án A, C, D. Vậy Chọn B.
Câu 14: Cho hàm số y f x có đồ thị C  như hình vẽ. Hỏi C  là đồ thị của hàm số nào? 3 3
A. y x 1 .
B. y x 1 .
C. y   x  3 1 .
D. y   x  3 1 . Lời giải:
Dựa vào đồ thị ta có: 3 +)  
x  0  y  1suy ra phương án: y x
1, y   x  3 1 không thoả mãn. 3 +)  
y  0  x  1 suy ra phương án y x 1 không thoả mãn.
+) Do đó phương án y   x  3 1 thoả mãn.
Câu 15: Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x 1 A. 3 2
y x x x 1 .
B. y x . C. y y x x  . D. 4 . 2 Lời giải: ax b
Dễ nhận thấy dạng đồ thị cho trong bài là của hàm số dạng y cx  . d
Câu 16: Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây, hàm số nào có bảng biến thiên như sau? 1 2 A. 3 2
y  x  3x  9x  2 . B. 3 2 y
x x  3x  . 3 3 1 2 C. 3 2
y x  3x  9x  2 . D. 3 2
y   x x  3x  . 3 3 Lời giải:
Vì lim y   nên loại A, D. x 29 
Xét Chọn B, thay x  3  y  . 3
Xét Chọn C, thay x  3  y  29 
(không thoả mãn bảng biến thiên).
Vậy chọn phương án B. Câu 17: Hàm số 3 2
y x  3x  3x 1 có đồ thị là hình nào sau đây? A. . B. . C. . D. . Lời giải: Vì lim y   ;
 lim y   nên loại C và D. x x
Vì y 0  1 nên Chọn B
Câu 18: Hàm số nào có đồ thị là hình vẽ sau đây?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2x 1 A. 3 2
y x  3x  4 . B. 4 2
y x  3x  4 . C. 3 2
y x  3x  4 . D. y  . 3x  5 Lời giải:
Dựa vào hình dạng đồ thị, ta thấy đây là đồ thị của hàm số bậc 3, với hệ số
a  0 lim y   . Nên loại Chọn B và D. x 
Khi x  0  y  4 nên Chọn C
Câu 19: Đường cong trong hình vẽ bên là đồ thị của một hàm số nào? A. 3
y  x  3x  2 . B. 3
y  x  3x  2 . C. 4 2
y x x  2 . D. 3
y x  3x  2 . Lời giải:
Nhánh cuối của đồ thị đi xuống nên a  0 , đồ thị có hai điểm cực trị nên . a c  0 .
Câu 20: Hàm số nào dưới đây có bảng biến thiên như hình bên dưới? x  3 x  3 x  2 x  3 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1 Lời giải:
Dựa vào bảng biến thiên, ta thấy:
Hàm số có tiệm cận ngang y  1. (Loại B)
Hàm số nghịch biến trên   ;1 
và 1;  nên y  0, x   1.
Câu 21: Hàm số nào có đồ thị là đường cong trong hình vẽ bên dưới?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x 1 A. 4 2
y x  4x 1. B. y
y x x  . D. 2 y  2x 1 . x  . C. 3 2 4 1 2 Lời giải:
Từ đồ thị ta thấy hàm số có 3 điểm cực trị, suy ra hình vẽ là đồ thị hàm số 4 2
y x  4x 1.
Câu 22: Đồ thị của hàm số nào dưới đây có dạng như đường cong hình dưới đây? y 1 1 x A. 3
y x  3x 1. B. 3
y  x  3x 1. C. 3
y  x  3x 1. D. 3
y x  3x 1. Lời giải:
Đồ thị có nhánh ngoài cùng đi lên nên a  0 , suy ra lại hàm số 3
y  x  3x 1 và 3
y  x  3x 1.
Đồ thị cắt trục tung tại điểm có tung độ dương nên loại hàm số 3
y x  3x 1.
Câu 23: Cho hàm số y f x có bảng biến thiên như sau:
Hàm số có bảng biến thiên như trên là A. 4 2
y  3x  6x  3 . B. 4 2
y  x  2x . C. 3
y x x . D. 3
y x x  3 . Lời giải:
Xét f  x  0 có 3 nghiệm phân biệt, loại Chọn C và D.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Hàm số đồng biến trên khoảng 1;  , loại Chọn B
Câu 24: Đồ thị hàm số nào sau đây có hình dạng như hình vẽ A. 3
y x  3x . B. 3
y x  3x . C. 3 2
y x  3x . D. 3 2
y x  3x .
Câu 25: Bảng biến thiên sau đây là của hàm số nào x x x x
A. f x 3  .
B. f x 3 
C. f x 3  .
D. f x 2 3  x  2 2  x x  2 x  2 Lời giải:
Ta có lim f x  1 suy ra đồ thị hàm số có một tiệm cận ngang là y  1. x
lim f x    x  2 mà một tiệm cận đứng của đồ thị hàm số.  x2
Từ đó ta dễ dàng loại hai phương án B và D.
Dựa vào bảng biến thiên, nhận thấy hàm số đồng biến trên từng khoảng xác định nên Chọn 1 5 
A có f  x      
thỏa mãn, Chọn C có f x 0 không thỏa mãn. x  2 0 2 x  22
Câu 26: Đường cong của hình vẽ bên là đồ thị của hàm số nào trong các hàm số sau. x  2 A. y
y x x  . C. 4 2
y  x  2x  2 . D. 3 2
y x  2x  2 x  . B. 4 2 2 2 1
Câu 27: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. 3 2
y x  3x 1. B. 4 2
y  x  2x 1. C. 4 2
y x  2x 1. D. 3 2
y  x  3x 1. Lời giải:
Từ đồ thị ta thấy:
Đây là đồ thị của hàm bậc ba nên loại B, C
Nhánh cuối của đồ thị đi xuống, suy ra hệ số a  0 nên loại A
Đồ thị trên là đồ thị của hàm số 3 2
y  x  3x 1. x  2
Câu 28: Hàm số y
có đồ thị là hình vẽ nào sau đây? x 1 y y y y A. . B. .C .D. . 3 2 2 1 1 1 1 -2 -1 0 1 x -2 -1 0 -1 1 x -2 0 1 x -2 -1 0 1 x . Lời giải:
Đồ thị hàm số có tiệm cận ngang là: y  1, tiệm cận đứng là x  1 , cắt trục Ox tại 2;0 , cắt
Oy tại 0; 2
Câu 29: Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới? A. 4 2
y x  3x  1. B. 4 2
y x  3x  1. C. 4 2
y x x  1. D. 4 2
y  x x  1 . Lời giải:
Đường cong trong hình vẽ là đồ thị của hàm số 4 2
y ax bx c a  0 .
Dựa vào đồ thị, ta thấy:
+) lim y    a  0 . x 
+) Đồ thị giao với Oy tại điểm có tung độ dương  c  0 .
+) Hàm số có ba điểm cực trị  ab  0 .
Câu 30: Hàm số nào dưới đây có đồ thị dạng như đường cong trong hình vẽ bên dưới?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia y 1 x O 1 x 1 2x 1 2x 1 x 1 A. y y y y x  . B. 1 x  . C. 1 x  . D. 1 x  . 1 Lời giải:
Dựa vào đồ thị ta thấy đồ thị hàm số có phương trình tiệm cận đứng là x  1 , tiệm cận ngang
y  1. Chỉ có hàm số ở Chọn A là thỏa mãn.
Câu 31: Đồ thị hàm số 3
y x  3x  2 là hình nào trong 4 hình dưới đây? A. . B. . C. . D. . Lời giải:
▪ Ta có: lim y    Loại câu C, D. x
▪ Với x  0  y  2 nên ta Chọn A
Câu 32: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây? 2  2x 2  x 1 A. y
y x x . C. y
y x x  . x  . B. 3 2 1 1 x  . D. 4 2 2 2 2 Lời giải: ax b
Ta có đây là đồ thị của hàm số dạng y cx d
Mặt khác đồ thị hàm số đã cho có tiệm cận đứng x  1.
Câu 33: Đồ thị hàm số 3 2
y x  3x  2 là đường cong trong hình nào dưới đây?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. B. C. D. Lời giải: Ta có 3 2
y x  3x  2 2
y  3x  6x x  0 2
y  0  3x  6x  0  
nên loại Chọn A và B x  2
Mặt khác a  1  0 nên Chọn C
Câu 34: Đồ thị hình bên là đồ thị của hàm số nào trong các hàm số dưới đây? A. y   2 x  
1  x  2 . B. y   2 x  
1  x  2 . C. 3 2
y  x  3x  2 . D. 4 2
y x  3x  2 . Lời giải:
Dựa vào đồ thị, ta thấy đồ thị hàm số là hàm đa thức bậc ba nên loại D
Do lim y   nên hệ số a  0 , loại C x x  1 
Đồ thị hàm số cắt trục hoành Ox tại ba điểm có hoành độ x  1  x  2 
nên chỉ có Chọn B thỏa khi lập phương trình hoành độ giao điểm.
Câu 35: Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây? 3 3 2 3 2 4 2
A. y  x  3x  2 .
B. y x  3x 1.
C. y  x  3x  2 .
D. y x  3x 1 . Lời giải:
Từ BBT ta thấy: đây là BBT của một hàm số bậc ba, có hệ số của 3
x là a  0 .
Do đó, đáp án A, D, C sai. Đáp án đúng là B.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 36: Cho hàm số    3 2 y
f x ax bx cx d có bảng biến thiên sau:
Đồ thị nào thể hiện hàm số y f x ? A. I . B. II.
C. III. D. IV . Lời giải:
Dựa vào bảng biến thiên, ta thấy:
• Hàm số có giá trị cực đại bằng 2 và giá trị cực tiểu bằng 2. Loại Chọn B và C.
• Khi x   thì y   nên chỉ có Chọn A là phù hợp.
Câu 37: Đồ thị trong hình vẽ sau là đồ thị của hàm số nào trong các hàm số dưới đây. 3 A. 4 2
y x  8x 1 . B. 3 2
y x  3x 1 . C. 4 2
y x  2x 1. D. 2
y x  3x 1 . Lời giải:
Chọn B có y  0  loại.
Chọn C đồ thị tiếp xúc với trục hoành nên loại C.
Chọn A có x  2  y  15  nên loạiA.
MỘT SỐ BÀI TOÁN LIÊN QUAN ax b
Câu 38: Cho đường cong ở hình bên là đồ thị của hàm số y
với a,b, c, d là các số thực. cx d
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Mệnh đề nào dưới đây đúng?
A. y  0, x   .
B. y  0, x   1.
C. y  0, x   1.
D. y  0, x   . Lời giải:
Tiệm cận đứng x  1 . Hàm số nghịch biến. x a
Câu 39: Biết hàm số y
a  ) có đồ thị như hình vẽ sau:
x  ( a là số thực cho trước, 1 1
Mệnh đề nào dưới đây đúng?
A. y '  0, x   1.
B. y '  0, x   1.
C. y '  0, x   .
D. y '  0, x   . Lời giải:
Ta có tập xác định của hàm số là D  \  
1 và hàm số nghịch biến trên từng khoảng xác định.
Vậy y '  0, x   1  . x m
Câu 40: Cho hàm số y x  , có đồ thị như hình vẽ bên dưới: 1
Khẳng định nào sau đây đúng? A. m  1.
B. m  1.
C. m  1.
D. m  1. x a
Câu 41: Cho hàm số y
có đồ thị như hình vẽ bên dưới: x 1
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Mệnh đề nào dưới đây đúng?
A. a  1 .
B. a  3 .
C. a  1 . D. a  1 . Lời giải:
Tập xác định: D  \   1 . 1   a Ta có: y   . x  2 1
Từ hình vẽ ta thấy: y  0, x   1  1
  a  0  a  1 .
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2. Do đó a  2  a  2 .
Câu 42: Biết hàm số 3 2
y  ax bx cx d (a  0) có đồ thị như hình vẽ sau: y 1 -1 x O 1 2
Mệnh đề nào dưới đây đúng?
A. y '  0, x   .
B. y '  0, x   .
C. y '  0, x   .
D. y '  0, x   . Câu 43: Hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
A. a  0 , b  0 , c  0 , d  0 .
B. a  0 , b  0 , c  0 , d  0 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
C. a  0 , b  0 , c  0 , d  0 .
D. a  0 , b  0 , c  0 , d  0 . Lời giải:
Nhìn vào nhánh phải của đồ thị ta thấy đồ thị có hướng đi lên suy ra a  0
Nhìn vào giao điểm của đồ thị với trục tung ta thấy đồ thị cắt trục tung tại điểm có tung độ
dương suy ra d  0 . Ta có 2
y  3ax  2bx c c
Hàm số đã cho có hai điểm cực trị x , x với x .x  0 
 0  c  0 (vì a  0 ) 1 2 1 2 3a 2  b Vì 1
  x  0 và x  1 nên x x  0   0  2
b  0  b  0 (vì a  0 ) 1 2 1 2 3a
Vậy a  0 , b  0 , c  0 , d  0 . ax 1
Câu 44: Cho hàm số f x  a, , b c   bx
có bảng biến thiên như sau: c
Trong các số a,b, c có bao nhiêu số dương? A. 3 . B. 2 . C. 1 . D. 0 . Lời giải: Từ BBT suy ra
+) Với x   f x 1 0   0  c  0. c
+) Với f x 1
 0  x    0  a  0. a c
+) Tiệm cận đứng x    2  c  2
b b  0. b
Vậy trong các số a,b, c có duy nhất một số dương. ax b
Câu 45: Cho hàm số y x  có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? c
A. a  2, b c  1.
B. a b  2, c  1.
C. a  2, b  1, c  1. D. a  2
 , b c 1.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải:
Đồ thị hàm số có:
Tiệm cận đứng: x  c  1  c  1.
Tiệm cận ngang: y a  2. b
Giao điểm với trục tung: x  0  y  1  b 1. c Câu 46: Cho hàm số 3
y ax  3x d , a; d   có đồ thị như hình vẽ bên dưới:
Mệnh đề nào dưới đây đúng?
A. a  0, d  0 .
B. a  0, d  0 .
C. a  0, d  0 .
D. a  0, d  0 . Lời giải:
Dựa vào đồ thị, ta có a  0, d  0 . Câu 47: Cho hàm số 4 2
y ax bx c,a  0 có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 . C. a  0,b  0, c  0 . D. a  0,b  0, c  0 . Lời giải:
Dựa vào đồ thị ta thấy hàm số có 3 điểm cực trị trong đó có hai điểm cực đại và một điểm cực
tiểu nên a  0,b  0 .
Đồ thị hàm số đi qua điểm 0;c nằm dưới trục hoành nên c  0 .
Vậy a  0,b  0, c  0 . Câu 48: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ sau:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Mệnh đề nào dưới đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 . Lời giải:
+ Ta có lim y    a  0 . x
+ Đồ thị hàm số cắt Oy tại điểm có tọa độ 0; d  suy ra d  0 . + Ta có 2
y  3ax  2bx c .
Gọi x , x là các điểm cực trị của hàm số. 1 2  2b x x    0  1 2  Dựa vào đồ thị ta có 3a
, mà a  0 , suy ra b  0 , c  0 . cx x   0 1 2  3a
Vậy a  0 , b  0 , c  0 , d  0 . ax
Câu 49: Cho hàm số f x 2  , a, ,
b c   có đồ thị như sau: bx c
Khẳng định nào dưới đây đúng?
A. a b  0  c .
B. b a  0  c .
C. b  0  c a .
D. b  0  a c .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải: 2
Dựa vào đồ thị ta có x  0  y  1   1 c  2 . c c
Tiệm cận đứng x  1    1 b  2  . b a
Tiệm cận ngang y  2   2  a  4  . b
Vậy a b  0  c . Câu 50: Cho hàm số 4 2
y ax bx c a  0 có đồ thị như hình vẽ dưới đây:
Mệnh đề nào dưới đây đúng?
A. a  0 , b  0 , c  0 . B. a  0, b  0, c  0 . C. a  0, b  0, c  0 . D. a  0, b  0, c  0 . ax b
Câu 51: Cho hàm số y
có bảng biến thiên như hình vẽ dưới đây: cx 1 Xét các mệnh đề sau: (1) c  1. (2) a  2 .
(3) Hàm số đồng biến trên  ;    1   1  ;. 1 (4) Nếu y   thì b  1. x  2 1
Số mệnh đề đúng trong các mệnh đề trên là A. 1. B. 4 . C. 2 . D. 3 . Lời giải: ax b 1  Ta có lim    x   1
  c  1 suy ra (1) đúng  x 1  cx  1 c ax b a lim
  2  a  2c  2 suy ra (2) đúng
x cx  1 c
Theo bảng biến thiên thì trên khoảng  ;    1   1
 ; ta thấy y  0 nên (3) đúng. a bc 2  b y       b 1 suy ra (4) đúng cx   1 2 1 x  2 1
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia ax  2
Câu 52: Cho hàm số y
( với a , b là các số thực) có đồ thị như hình sau: x b
Giá trị a b bằng A. 0 . B. 3 . C. 3  . D. 4  . Lời giải:
Tập xác định D  \   2 .
Ta có y  1 là tiệm cận ngang của đồ thị hàm số nên a  1 .
Ta có x  2 là tiệm cận đứng của đồ thị hàm số nên b  2 .
Suy ra a b  1  2    3 . Câu 53: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0
C. a  0,b  0, c  0, d  0
D. a  0,b  0, c  0, d  0 . Lời giải:
Quan sát đồ thị hàm số ta thấy: a  0
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương  d  0 .
Hàm số có hai điểm cực trị x ; x thỏa mãn: 1 2  2bb x x    0  0  1 2   3aa   
b  0;c  0. c cx x 0     0 1 2  3a a Câu 54: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên dưới:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Mệnh đề nào sau đây đúng?
A. a  0,b  0,c  0, d  0 .
B. a  0,b  0,c  0, d  0 .
C. a  0,b  0,c  0, d  0 .
D. a  0,b  0,c  0, d  0 . Lời giải:
Do nhánh bên phải của đồ thị đi xuống nên a  0 .
Đồ thị cắt trục tung ở phần dương nên d  0.
Đồ thị có 2 cực trị tại hai giá trị x dương nên phương trình y  0 có 2 nghiệm dương phân biệt 2
 3ax  2bx c  0 có 2 nghiệm dương phân biệt.  2b   3ac  0   0    2b b   0
 S  0    0   . 3a   c  0 P  0   c  0 3a Câu 55: Cho hàm số 4 2
y ax bx cx d có đồ thị như hình vẽ dưới đây, mệnh đề nào sau đây đúng?
A. a  0;b  0;c  0; d  0 .
B. a  0;b  0;c  0; d  0 .
C. a  0;b  0;c  0; d  0 .
D. a  0;b  0;c  0; d  0 . Lời giải: a  0
+ Từ ĐTHS   d  0
+ Do ĐTHS nhận trục oy làm trục đối xứng  y f x là hàm số chẵn nên c  0 + Ta có:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia , 3 y  4ax  2 . bxx  0 . ,  y  0  b  x   2a b b
+ Hàm số có ba điểm cực trị  y  
 0   0  b  0. 2a a
Vậy đáp án đúng là D. Câu 56: Cho hàm số 4 2
y ax bx ca  0 có đồ thị như hình bên. Xác định dấu của a ,b ,c .
A. a  0,b  0,c  0 .
B. a  0,b  0,c  0 . C. a  0,b  0,c  0 . D. a  0,b  0,c  0 . Lời giải:
Dựa vào hình dạng đồ thị hàm số ta nhận thấy : Hệ số a 0
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm c 0 .
Đồ thị hàm số có 3 điểm cực trị ab 0 b 0 . Vậy a 0 , b 0 , c 0 . Câu 57: Hàm số 4 2
y ax bx c có đồ thị như hình vẽ bên dưới:
Mệnh đề nào sau đây đúng?
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 . C. a  0,b  0, c  0 . D. a  0,b  0, c  0 . Lời giải:
Dựa vào đồ thị hàm số, ta thấy:
+ lim y    a  0 . x
+ Hàm số có 3 cực trị nên .
a b  0  b  0 .
+ Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên c  0 . Câu 58: Cho hàm số 4 2
y ax bx c , với a, ,
b c  , a  0 , có đồ thị như hình vẽ dưới đây.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Mệnh đề nào dưới đây đúng?
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 .
C. a  0,b  0, c  0 .
D. a  0,b  0, c  0 . Lời giải:
Dựa vào hình dáng đồ thị hàm số ta có a  0 . Loại Chọn B
Vì hàm số có ba cực trị nên ab  0 suy ra b  0 . Loại Chọn C
Đồ thị hàm số cắt trục Oy tại điểm nằm trên trục hoành nên c  0 . Loại Chọn D ax b
Câu 59: Cho hàm số y
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? x c
A. a  2,b c  1  .
B. a b  2, c  1
 . C. a  2,b  1,c  1. D. a  2
 ,b c  1. Lời giải:
Từ đồ thị hàm số ta thấy lim y  2
 và lim y   suy ra tiệm cận ngang: y  2 , tiệm cận x  x  1 đứng: x  1 ax b
Mặt khác đồ thị hàm số y
có tiệm cận ngang y a và tiệm cận đứng x cx c
Do đó ta có a  2 và c  1 b
Đồ thị hàm số cắt trục tung tại điểm có tung độ y  1 nên 1 b  1 c Câu 60: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình bên. Mệnh đề nào sau đây đúng?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 . Lời giải:
Dựa vào đồ thị suy ra a  0 .
Giao điểm của đồ thị với trục Oy suy ra d  0 . c
Dựa vào cực trị ta có x .x   0  c  0. 1 2 a bx x   0  b  0 . 1 2 a
Câu 61: Hàm số bậc 4 trùng phương 4 2 y  . a x  .
b x c có đồ thị như hình vẽ. Dấu của các hệ số a, b, c là
A. a  0;b  0;c  0 .
B. a  0;b  0;c  0 . C. a  0;b  0;c  0 . D. a  0;b  0;c  0 . Lời giải:
Quan sát đồ thị ta thấy: lim y  lim y   suy ra: a  0 x x
Hàm số có 1 điểm cực trị, a và b cùng dấu hoặc b  0 suy ra: b  0
Đồ thị hàm số cắt Oy tại điểm có tung độ dương suy ra: c  0 . Vậy Chọn D
Câu 62: Xác định các hệ số a , b , c để hàm số 4 2
y ax bx c có đồ thị như hình bên dưới:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1 A. a
; b  2 ; c  2 .
B. a  4 ; b  2 ; c  2 . 4 1 C. a
; b  2 ; c  2 .
D. a  4 ; b  2 ; c  2 . 4 Lời giải:
Đồ thị hàm số đi qua điểm (0; 2) nên c  2 . x  0 Ta có 3
y  4ax  2bx nên   y  0  b 2 x   .  2a b
Dựa vào đồ thị thì hàm số đạt cực trị tại x  2 nên   4  b  8  a . 2a 1
Vậy chỉ có đáp án a
; b  2 ; c  2 thỏa mãn. 4 ax 1
Câu 63: Cho hàm số y bx  có đồ thị như hình bên dưới: c
Giá trị a b c bằng A. 1. B. 4 . C. 2 . D. 3 . Lời giải:  1   1 1 
Vì đồ thị hàm số qua điểm M 0;   nên ta có:   c  2  .  2  c 2 c
Tiệm cận đứng của đồ thị: x   2  b 1. b a
Tiệm cận ngang của đồ thị: y   2  a  2 . b
Vậy a b c  1. Câu 64: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 . Lời giải:
Dựa vào đồ thị hàm bậc ba ta nhận xét:
Nhánh cuối đồ thị hàm số đồng biến nên a  0 .
Đồ thị hàm số cắt Oy tại điểm có tung độ dương nên d  0 .
Đồ thị hàm số có hai điểm cực trị nằm về 2 phía trục tung nên ac  0  c  0 .
Đồ thị hàm số có hoành độ điểm uốn dương nên ab  0  b  0 . Câu 65: Cho hàm số 3 2
y ax bx cx d a  0 có đồ thị như hình vẽ dưới đây:
Mệnh đề nào sau đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 . Lời giải: Ta có 2
y  3ax  2bx c theo hình vẽ:
- đồ thị cắt trục tung tại điểm 0, d  nằm phía trên trục hoành nên d  0 ;
- hàm số có hai điểm cực trị trái dấu nên ac  0 mà a  0 , do đó c  0 . x x 2b
- Điểm uốn của đồ thị có hoành độ dương nên 1 2  
 0  ab  0 . Do a  0 nên 2 6a b  0 . ax  4  b
Câu 66: Cho hàm số y
có đồ thị là đường cong trong hình bên. Mệnh đề nào dưới đây cx b đúng?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
A. a  0, 0  b  4, c  0 .
B. a  0,b  0, c  0 .
C. a  0,b  4, c  0 .
D. a  0, 0  b  4, c  0 . Lời giải: ax  4  b b a Từ y
suy ra dồ thị hàm số có TCĐ: x   , TCN: y
, giao điểm của đồ thị với cx b c c
 4  b   b  4 
trục tung và trục hoành lần lượt có tọa độ 0; ; ; 0     .  b   a  a  0 1  c   b
Từ đồ thị ta thấy   02 c  4  b  0  3.  b
Từ ta có 0  b  4 , từ ta suy ra c  0 , từ suy ra a  0 . ax b
Câu 67: Cho hàm số y  a, ,
b c   có đồ thị như sau: cx  2
Trong các số a , b và c có bao nhiêu số dương? A. 0 . B. 1. C. 2 . D. 3 . Lời giải: 2 ab  
Đồ thị hàm số có: Tiệm cận đứng: x
, tiệm cận ngang: y  , giao điểm với Oy: 0;   . c c  2 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2  0 c  c  0 a
Từ đồ thị hàm số ta có:   0  a  0 . c  b  0  b  0  2
Vậy trong các số a , b và c có 1 số dương. ax b
Câu 68: Cho hàm số y
có đồ thị như hình vẽ bên dưới: x 1
Mệnh đề nào dưới đây đúng?
A. a b .
B. ab  0 .
C. ab  0 .
D. b a  0 . Lời giải: b a b a ax b ax b Ta có lim  lim x a và lim  lim
x a nên y a x x 1 x 1 x x 1 x 1 là phương trình 1 1 x x
đường tiệm cận ngang của đồ thị hàm số.
Dựa vào hình vẽ ta thấy đồ thị có phương trình đường tiệm cận ngang y  2 nên a  2 . .0 ab
Đồ thị đi qua điểm 0; 
1 nên thay x  0; y  1 vào hàm số ta được: 1   b 1 0 1 Vậy ab  2  0 . x b
Câu 69: Cho hàm số y  c  0 cx  có đồ thị như sau: 2
Mệnh đề nào sau đây đúng?
A. b  0; c  0.
B. b  0; c  0.
C. b  0; c  0.
D. b  0; c  0. Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1
Theo đồ thị, tiệm cận ngang:     y 0 c 0. c
y  0  x b
  0  b  0. Vậy b  0 , c  0 . x b
Câu 70: Cho hàm số y  ( ,
b c, d  ) có đồ thị như hình vẽ. Giá trị của biểu thức cx d
T  2b  3c  4d bằng A. 1. B. 8  . C. 6. D. 0. Lời giải: x b
Đồ thị hàm số cắt trục Ox  0   x b  . cx d
Quan sát đồ thị ta thấy đồ thị hám số cắ trục hoành tại x  1 b  1 b  1 . 1
Đồ thị hàm số có tiệm cận ngang là y  1  c 1. c d
Đồ thị hàm số có tiệm cận đứng là: x  
1  d c  d  1  d  1. c
Vậy: T  2b  3c  4d  2.1 3.1 4.  1  1 . ax b
Câu 71: Cho hàm số y  a, ,bc  cx
có đồ thị như hình vẽ bên dưới: 2
Trong các số a,b và c có bao nhiêu số dương? A. 2 . B. 0. C. 1. D. 3 . Lời giải: 2
+) Tiệm cận đứng của đồ thị hàm số: x   0  c  0 c
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia a
+) Ta có tiệm cận ngang của đồ thị hàm số y   0  a  0 . c b
+) x  0  y    0  b  0 . 2 Vậy b  0 . ax  3
Câu 72: Cho hàm số y x  có đồ thị như hình vẽ bên dưới: c y O 2 x 1  3  2
Tính giá trị của a  2c .
A. a  2c  2 .
B. a  2c  3 .
C. a  2c  3 .
D. a  2c  1 . Lời giải: ax  3
Ta có: Đồ thị hàm số y
  và tiệm cận ngang là y a . x
có tiệm cận đứng là x c c Theo đồ thị ta có
x  c  2  c  2 .
y a  1  .
Vậy a  2c  3 . x a
Câu 73: Đường cong ở hình dưới đây là đồ thị của hàm số y
, (a,b, c  ) . bx c
Trong các số a , b và c có bao nhiêu số dương? A. 0 . B. 1. C. 2. D. 3. Lời giải:
Dựa vào đồ thị, ta có các nhận xét sau:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1
ĐTHS có TCN: y  1  b 1. bc ĐTHS có TCĐ: x  1  c b   c  1. b a
ĐTHS đi qua điểm 0; 2 , nên  2  a  2  . c
Vậy trong các số a , b và c có 1 số dương. Câu 74: Cho hàm số 4 2
y ax bx c có đồ thị như hình bên dưới:
Khẳng định nào sau đây đúng?
A. a  0;b  0;c  0 .
B. a  0;b  0;c  0 . C. a  0;b  0;c  0 . D. a  0;b  0;c  0 . Lời giải:
Dựa vào đồ thị hàm số 4 2
y ax bx c a  0 ta có lim y    a  0 . x
Đồ thị hàm số có 3 cực trị 3
y ax bx x 2 ' 4 2 2
2ax b  0 có 3 nghiệm phân biệt nên
ab  0  b  0 .
Đồ thị hàm số cắt trục Oy tại điểm có tung độ dương nên c  0 .
Vậy a  0;b  0;c  0 . Câu 75: Cho hàm số 3 2
y ax bx cx d có đồ thị là đường cong trong hình dưới đây:
Trong các hệ số a,b, c, d có bao nhiêu số âm ? A. 3 . B. 0 . C. 1. D. 2 . Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Dựa vào hình dạng đồ thị: đồ thị hàm bậc ba có hệ số a  0 , đồ thị cắt trục tung tại điểm có
tung độ dương nên d  0 . Ta có: 2
y  3ax  2bx c . Đồ thị có hai điểm cực trị cùng nằm bên phải trục tung nên y  0 có
hai nghiệm dương phân biệt x , x . 1 2  2b x x    0  1 2  b   0 3a Ta có    . c  c  0 x .x   0 1 2  3a
Vậy a  0, c  0 . ax b
Câu 76: Cho hàm số y  có đồ thị như sau: cx d
Mệnh đề nào sau đây đúng?
A. ac  0; bd  0 .
B. ab  0; cd  0 .
C. bc  0; ad  0 .
D. ad  0; bd  0 . Lời giải: Theo đồ thị: a
Tiệm cận ngang: y     0 ac
0 . Do đó a, c cùng dấu (1) c d d
Tiệm cận đứng x  
 0   0  cd  0 . Do đó c,d trái dấu (2) c c b b
Cho y  0  x  
 0   0  ab  0. Do đó a,b cùng dấu (3) a a
Từ (1) và (2) suy ra a, d trái dấu nên ad  0 .
Từ (1) và (3) suy ra b, c cùng dấu nên bc  0 . ax  3
Câu 77: Cho hàm số y
b ,b  0 bx
có bảng biến thiên như sau: c
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Tính tổng S a b c . A. 2 . B. 2  . C. 0 . D. 1  . Lời giải: ax  3 ac  3b y   y  bx cbx c2 ax  3
Kết hợp với bảng biến thiên của hàm số y
b ,b  0 bx  ta có: c b   0,b      c b 0, b   1  c  1   bc b       a  2
 . Vậy S a b c  2 . a      a 2b 2    b  1  b 2     2b 3b 0
ac  3b  0
Câu 78: Cho hàm số f x 3 2
ax bx cx d a, b, c, d   có bảng biến thiên như sau:
Có bao nhiêu số dương trong các số a, b, c, d ? A. 3. B. 4. C. 2. D. 1. Lời giải:
 lim f x    a  0. x  f 0  1   d  1   0.
f  x 2
 3ax  2bx  . c  2b   2  x x  2   b   3a  0 3a Ta có 1 2      . x x  0 c   c  0 1 2  0 3a Câu 79: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ dưới đây:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Số lớn nhất trong các số a, b, c, d là: A. c . B. a . C. b . D. d . Lời giải: + 2
y  3ax  2bx c
+ Đồ thị ham số có hai điểm cực trị là M 1; 2 và N 3; 2 nên: 3 2  .1 a  .1 b  .1 c d  2 
a b c d  2  a  1    3 2  .3 a  .3 b  .3 c d  2
27a  9b  3c d  2 b  6      2 3 .1 a  2 .1 b c  0 
3a  2b c  0  c  9  2  3 .3 a  2 .3 b c  0
 27a  6b c  0 d  2
Vậy c  9 là số lớn nhất.
Câu 80: Hàm số y f x thỏa mãn f   2021  f  
2021 có đồ thị là hình nào trong bốn đồ thị sau:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. Hình 4. B. Hình 3. C. Hình 1. D. Hình 2. Lời giải:
Dựa vào đồ thị các hàm số đã cho, ta chọn đồ thị hàm số ở hình 4 là đồ thị của hàm số chẵn thỏa mãn f   2021  f   2021 .
_______________________HẾT_______________________
Huế,20h30’ Ngày 26 tháng 5 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115

| 1/57
Tài liệu liên quan: