Chuyên đề khảo sát hàm số Toán 12: Sự tương giao của hai đồ thị hàm số

Chuyên đề khảo sát hàm số Toán 12: Sự tương giao của hai đồ thị hàm số được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Môn:

Toán 12 3.9 K tài liệu

Thông tin:
110 trang 1 năm trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chuyên đề khảo sát hàm số Toán 12: Sự tương giao của hai đồ thị hàm số

Chuyên đề khảo sát hàm số Toán 12: Sự tương giao của hai đồ thị hàm số được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

62 31 lượt tải Tải xuống

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 375 tài liệu

Môn: Toán 12 3.9 K tài liệu

Thông tin:

110 trang 1 năm trước

Tác giả:

Profile Mai Nguyệt
KHẢO SÁT HÀM SỐ
TOÁN 12
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
SỰ TƯƠNG GIAO
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
1
Chủ đề 7: SỰ TƯƠNG GIAO CỦA HAI ĐỒ THỊ
I- LÝ THUYẾT
Giả sử (C) và (C’) là đồ thị của hai hàm số:
.
Hoành độ giao điểm của (C) và (C’), nếu có, là nghiệm của phương trình
( ) ( )f x g x
(1)
Lưu ý:
Phương trình
( ) ( )f x g x
là phương trình hoành độ giao điểm
của (C) và (C’).
Đảo lại, nếu
0
x
là nghiệm của (1), tức là:
00
( ) ( )f x g x
thì điểm
hay
0 0 0 0
; ( ) ; ( )M x f x M x g x
là điểm chung của (C) và (C’).
Kết quả:
+ Nếu phương trình (1) vô nghiệm thì (C) và (C’) không có điểm chung.
+ Nếu phương trình (1) có
n
nghiệm thì (C) cắt (C’) tại
n
điểm phân biệt (
n
không là nghiệm bội)
II-BÀI TẬP MINH HỌA
DẠNG 1: XÁC ĐỊNH TOẠ ĐỘ GIAO ĐIỂM CỦA 2 ĐỒ THỊ
Bài tập 1: (ĐHVH-98) Tìm toạ độ giao điểm của đường thẳng
d: 25yx
với đồ thị hàm số (C):
32
31y x x
.
Lời giải:
TXĐ:
D
. Xét phương trình hoành độ giao điểm của d và (C):
3 2 3 2
2
2
3 1 2 5 3 2 4 0
1
1 2 4 0
15
2 4 0
15
x x x x x x
x
x x x
x
xx
x

* Với
1 2.( 1) 5 3xy
.
* Với
1 5 2 1 5 5 3 2 5xy
.
* Với
1 5 2 1 5 5 3 2 5xy
.
Kết luận:
Vậy các giao điểm cần tìm là
1 2 3
1;3 , 1 5;3 2 5 , 1 5;3 2 5M M M
Nhận xét: Khi xác định tung độ giao điểm, ta đã sử dụng hàm số
25yx
để đơn giản hơn.
Bài tập 2: (Đề 105) Chỉ rõ các giao điểm của đồ thị (C):
1
3
1
yx
x
với trục hoành.
Lời giải:
TXĐ:
\1D
.
Xét phương trình hoành độ giao điểm của (C) và Ox:
1
30
1
x
x
(1)
TH 1:
31x
, phương trình (1) trở thành:
x
y
M
y
0
x
0
O
(C)
(C')
1
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
2
2
1
3 0 3 1 1 0 4 4 0 2
1
x x x x x x
x
(nhËn)
TH 2:
3x 
, phương trình (1) trở thành:
(lo¹i)
(nhËn)
2
22
1
3 0 3 1 1 0 4 2 0
1
22
x
x x x x x
x
x
Kết luận: Vậy giao điểm cần tìm là
12
2;0 , 2 2;0MM
.
DẠNG 2: BIỆN LUẬN SỐ GIAO ĐIỂM CỦA 2 HỌ ĐỒ THỊ
Bài tập 1: (Đề 29) Xác định tất cả các giá trị của
a
để đường thẳng
d: 3y ax
không cắt đồ thị hàm số
(C):
34
1
x
y
x
.
Lời giải:
TXĐ:
\1D
.
Xét phương trình hoành độ giao điểm của d và (C):
34
3 3 4 3 1 1
1
x
ax x ax x x
x
2
7 0 1ax ax x
(1)
Để đường thẳng d không cắt (C)
Phương trình (1) vô nghiệm hoặc có nghiệm kép
1x
.
TH 1: Xét
0a
, phương trình (1) trở thành:
70
. Vậy
0a
thỏa.
TH 2: Y.c.b.t
(v« nghiÖm)
2
2
0
0
28;0
28 0
28 0
0
28
28 0
1
2
1
2
a
a
a
a
aa
a
a
aa
a
b
a
a






Kết luận: Vậy các giá trị cần tìm là
28;0a

.
Bài tập 2: (Đề 34) Xác định tất cả các giá trị của
k
để đồ thị hàm số (C):
2
43
2
xx
y
x

cắt đường thẳng
d: 1y kx
tại 2 điểm phân biệt.
Lời giải:
TXĐ:
\2D
.
Xét phương trình hoành độ giao điểm của d và (C):
,
2
2
43
1 4 3 2 1 2
2
xx
kx x x x kx x
x

2
( ) 1 2 3 1 0 2g x k x k x x
(1)
Để d cắt (C) tại 2 điểm phân biệt
Phương trình (1) có 2 nghiệm phân biệt
2
.
2
2
1
10
1
( 2) 0 4 1 2 2 3 1 0 1
4 8 5 0,
0
2 3 4 1 0
g
k
k
k
g k k k k
k k k
kk




.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
3
Kết luận: Vậy các giá trị cần tìm là
;1 1; .k  
Bài tập 3: (ĐHSPII-97) Tìm
m
để hàm số (C):
42
1 2 1y m x mx m
cắt Ox tại 4 điểm phân biệt.
Lời giải:
TXĐ:
D
.
Xét phương trình hoành độ giao điểm của (C) và Ox:
(1)
42
1 2 1 0m x mx m
Đặt
2
0tx
, (1) trở thành:
(2)
2
1 2 1 0m t mt m
Để (C) cắt Ox tại 4 điểm phân biệt
Phương trình (1) có 4 nghiệm phân biệt
Phương trình (2) có 2 nghiệm dương phân biệt, tức là:
12
0 tt
.
Y.c.b.t
2
2
2
1
1
4 2 1 1 0
2
9 12 4 3 2 0
3
0
01
1
1
21
1
0
2
1
m
m
m m m
m m m m
m
S
m
m
m
m
P
m









12
;1 \
23
m



Kết luận: Vậy các giá trị cần tìm là
12
;1 \
23
m


.
CHÚ Ý: Mối quan hệ về số nghiệm của phương trình
42
00ax bx c a
(1) và
2
00at bt c a
(2)
thông qua phép đặt ẩn phụ:
2
0tx
.
TH1: Phương trình (2) có duy nhất 1 nghiệm
0t 
Phương trình (2) không có nghiệm
x
.
TH2: Phương trình (2) có duy nhất 1 nghiệm
0t 
Phương trình (2) có nghiệm
0x
.
TH3: Phương trình (2) có duy nhất 1 nghiệm
0t 
Phương trình (2) có 2 nghiệm
xt
xt

.
Vậy có thể mở rộng yêu cầu của bài toán thành các dạng sau:
3-1) Tìm
m
để hàm số (C) cắt Ox tại 3 điểm phân biệt
Phương trình (2) có nghiệm
12
0
0 (0) 0
0
t t g
S

3-2) Tìm
m
để hàm số (C) cắt Ox tại 2 điểm phân biệt
Phương trình (2) có nghiệm
12
12
00
0
0
0
t t P
tt
S

3-2) Tìm
m
để hàm số (C) cắt Ox tại 1 điểm
Phương trình (2) có nghiệm
12
12
0
0
0
0
0
0
tt
S
tt
S


Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
4
Trên đây là sự mở rộng bài toán cùng hướng giải quyết theo lý thuyết “ Tam thức bậc hai và ứng
dụng”. Chúng ta sẽ bàn lại bàn toán này cùng các phương pháp đặc sắc hơn như “ Ứng dụng tính
biến thiên”, “Phương pháp cực trị hàm số”…trong các bài viết tiếp theo.
Bài tập 4: (Đề dự bị 2003) Tìm
m
để đồ thị hàm số
2
( ) : 1C y x x mx m
cắt Ox tại 3 điểm phân
biệt.
Lời giải:
TXĐ:
D
.
Xét phương trình hoành độ giao điểm của (C) và Ox:
(1)
(2)
2
2
1
10
0
x
x x mx m
g x x mx m
Để (C) cắt Ox tại 3 điểm phân biệt
Phương trình (1) có 3 nghiệm phân biệt
Phương trình (2) có 2 nghiệm phân biệt khác 1.
Y.c.b.t
2
1
1 1 2 0
1
;0 4; \
2
2
40
04
g
gm
m
m
mm
mm



 


Kết luận: Vậy các giá trị cần tìm là
1
;0 4; \
2
m

 


.
Trong bài tập trên, đề bài đã “trình bày” tương đối …dễ thương (!!!) vì đã có dạng
.0AB
. Chúng ta
thử qua bài tập với một sự thay đổi nhẹ nhàng xem sao:
Bài tập 5: (ĐHKT-98) Cho hàm số
(C)
32
31y x x
. Đường thẳng đi qua
3;1A
và có hệ số góc bằng
k
. Xác định
k
để đường thẳng đó cắt đồ thị tại 3 điểm phân biệt.
Lời giải:
TXĐ:
D
.
Đường thẳng d đi qua
3;1A
và có hệ số góc
k
có phương trình:
: 1 3 3 1d y k x y k x
Xét phương trình hoành độ giao điểm của (C) và d:
(1)
(2)
3 2 3 2 2
2
2
3 1 3 1 3 3 3 3
3
30
x x k x x x k x x x k x
x
x x k
xk

Để d cắt (C) tại 3 điểm phân biệt
Phương trình (1) có 3 nghiệm phân biệt
Phương trình (2) có 2 nghiệm phân biệt khác
3
.
Y.c.b.t
0
0; \ 9
9
k
k
k
Kết luận: Vậy các giá trị cần tìm là
0; \ 9k 
.
Các em chú ý, kỹ thuật phân tích
(1)
3 2 3 2
3 1 3 1 3 3x x k x x x k x
, tạo ra được sự
thuận lợi trong quá trình phân tích. Còn không, chúng ta phải đoán được nghiệm và phân tích theo sơ
đồ Hoc-ner. Đoán không được nghiệm thì sao nhỉ???
Chúng ta xét tiếp bài tập sau:
Bài tập 6: Tìm
m
để đồ thị hàm số (C):
3
1
3
y x x m
cắt trục hoành tại 3 điểm phân biệt.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
5
Lời giải:
TXĐ:
D
.
Xét phương trình hoành độ giao điểm của (C) và Ox:
(1)
33
11
0
33
x x m x x m
Để (C) cắt Ox tại 3 điểm phân biệt
Đồ thị
3
1
':
3
C y x x
cắt
: / /d y m Ox
tại 3 điểm
phân biệt.
Xét
3
1
()
3
g x x x
. Ta có:
/ 2 /
2
1
3
( ) 1 ( ) 0
2
1
3
xy
g x x g x
xy
Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy để d cắt (C) tại 3 điểm phân biệt
22
33
m
.
Kết luận: Vậy các giá trị cần tìm là:
22
;
33
m




.
Bài tập 7: (ĐH A-2003) Tìm
m
để đồ thị hàm số
2
1
mx x m
y
x

cắt trục hoành tại hai điểm phân biệt và
hai điểm đó có hoành độ dương.
Lời giải:
TXĐ:
\1D
Đồ thị hàm số
2
1
mx x m
y
x

cắt trục hoành tại 2 điểm phân biệt có hoành độ dương
Phương trình
2
0g x mx x m
có 2 nghiệm dương phân biệt
1
Y.c.b.t
2
0
0
1
1 4 0
1
2
1 2 1 0 0
1
2
1
2
0
0
0
m
m
m
m
g m m
m
S
m
m
m
P
m






Vậy các giá trị
m
cần tìm là:
1
0
2
m
.
Bài tập 8: (ĐH D-2009) Tìm
m
để d:
1y 
cắt
m
C
:
42
– 3 2 3y x m x m
tại 4 điểm phân biệt đều
có hoành độ nhỏ hơn 2.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
6
Lời giải:
TXĐ:
D
Phương trình hoành độ giao điểm của
m
C
và đường thẳng
1y 
là:
42
– 3 2 3 1x m x m
Đặt
2
0t x t
, phương trình trở thành
2
1
3 2 3 1 0
31
t
t m t m
tm

Yêu cầu bài toán tương đương
0 3 1 4
1
;1 \ 0
3 1 1
3
m
m
m




DẠNG 3: SỐ GIAO ĐIỂM VÀ TÍNH CHẤT GIAO ĐIỂM CỦA HAI HỌ ĐỒ THỊ
Phương pháp:
Bước 1: Thiết lập phương trình hoành độ giao điểm của (C) và (C’):
f x g x
(1)
Bước 2: Biện luận số nghiệm và tính chất nghiệm của (1).
Nhận xét: Rõ ràng hoành độ giao điểm của (C) và (C’) là nghiệm của (1) nên số giao điểm và
tính chất giao điểm cũng là số nghiệm và tính chất nghiệm của (1). Điều này, đưa yêu cầu từ
Giải tích sang việc biện luận phương trình sơ cấp mà chúng ta đã biết.
Bài tập 1: Cho hàm số
24
1
x
y
x
. Gọi (d) là đường thẳng qua
1;1A
và có hệ số góc k. Tìm k sao cho (d)
cắt ( C ) tại hai điểm M, N và
3 10MN
.
Lời giải:
TXĐ:
\1D
.
Từ giả thiết ta có:
Bài toán trở thành: Tìm k để hệ phương trình sau có hai
nghiệm
1 1 2 2
; , ;x y x y
phân biệt sao cho
22
2 1 2 1
90 (*)x x y y
(I)
24
11
1
11
x
kx
x
y k x

. Ta có:
(I)
2
2 3 3 0
11
kx k x k
y k x
Dễ có (I) có hai nghiệm phân biệt khi và chỉ khi phương trình
2
2 3 3 0 (**)kx k x k
có
hai nghiệm phân biệt. Khi đó dễ có được
3
0, .
8
kk
Ta biến đổi (*) trở thành:
22
22
2 1 2 1 2 1
1 90 1 4 90 (* * *)k x x k x x x x



Theo định lí Viet cho (**) ta có:
12
12
23
3
k
xx
k
k
xx
k

thế vào (***) ta có phương trình:
3 2 2
8 27 8 3 0 3 8 3 1 0k k k k k k
3 41 3 41
3
16 16
k k k
.
Kết luận: Vậy các giá trị của
k
cần tìm là:
3 41 3 41
3, ,
16 16
k k k
.
Bài tập 2: Cho hàm số
22
1
x
y
x
(C). Tìm
m
để đường thẳng d:
2y x m
cắt đồ thị (C) tại 2 điểm
phân biệt A, B sao cho
5AB
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
7
Lời giải:
TXĐ:
\1D
.
Xét phương trình hoành độ giao điểm:
2
22
2 2 2 0, 1
1
x
x m g x x mx m x
x
(1)
Để d cắt (C) tại 2 điểm phân biệt Phương trình (1) có 2 nghiệm phân biệt khác
1
Y.c.b.t
2
2
8 2 0
8 16 0
1 2 2 0
g
mm
mm
g m m m
;4 4 2 4 4 2;m  
(2)
Lúc đó, gọi A
;2
AA
x x m
; B
;2
BB
x x m
, với
A
x
và
B
x
là các nghiệm của phương trình (1).
Theo định lý Viet ta có:
2
2
.
2
AB
AB
m
xx
m
xx
(*)
Ta có:
22
2
5 4 5
B A B A
AB x x x x
2
41
A B A B
x x x x
(**)
Thay (*) vào (**) ta được:
(tháa ®k (2))
(tháa ®k (2))
2
10
8 20 0
2
m
mm
m

Kết luận: Vậy các giá trị cần tìm là:
2;10 .m
Bài tập 3: Cho hàm số:
2
1
x
y
x
(C). Chứng minh rằng: Với mọi giá trị của
m
, đường thẳng
d
:
y x m
luôn cắt đồ thị (C) tại hai điểm A, B phân biệt. Tìm giá trị nhỏ nhất của độ dài đoạn thẳng
AB.
Lời giải:
TXĐ:
\1D
.
* Phương trình hoành độ giao điểm của d
()C
là:
2
2 0 1x mx m x
(1)
Vì
2
4 8 0
1 1 0
mm
f
m
, nên phương trình (1) có 2 nghiệm phân biệt khác 1 với
m
.
Suy ra d cắt
()C
tại hai điểm phân biệt với
m
.
* Gọi các giao điểm của d
()C
là
;
AA
A x x m
;
;
BB
B x x m
, với
A
x
và
B
x
là các nghiệm
của phương trình (1). Theo định lý Viet ta có:
.2
AB
AB
x x m
x x m


(*)
Ta có:
2
2
2
2 2 4 .
A B A B A B
AB x x x x x x
(**)
Thay (*) vào (**) ta được:
2 2 2
2
2 4 2 2 2 4 2 2 8 8AB m m m m
Vậy
min
22AB
, đạt được khi
2m
.
Bài tập 4: Xác định
m
để đường thẳng
:2d y mx
cắt
1
:
3
x
Hy
x
tại hai điểm phân biệt
,MN
sao
cho độ dài đoạn thẳng
MN
nhỏ nhất.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
8
TXĐ:
\3D
.
Phương trình hoành độ giao điểm của đường thẳng và đồ thị:
2
1
2 3 1 7, 3 *
3
x
mx mx m x x
x
Nhận thấy
3x
không phải là nghiệm của phương trình
*
.
Đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt
Phương trình
*
có hai nghiệm
phân biệt
2
0
0
9 1 28 0
m
m
mm
.
Gọi
11
;M x y
và
22
;N x y
là tọa độ giao điểm của đường thẳng và đồ thị. Khi đó
11
22
2
2
y mx
y mx


và
12
,xx
là nghiệm của phương trình
*
nên
1 2 1 2
31
7
,.
m
x x x x
mm
.
Ta có:
2 2 2 2
2
2 1 2 1 2 1 2 1
MN x x y y x x m x x
22
22
2 1 2 1 1 2
1 1 4m x x m x x x x



2
22
22
91
7 1 1
1 4. 9 10 18
m
m m m
mm
mm




Đặt
1
tm
m

(điều kiện
2t
), suy ra
22
2
1
2mt
m
. Khi đó
2
9 10MN t t
.
Dùng đạo hàm tìm GTNN của hàm số
2
9 10f t t t
trên các nửa khoảng
;2

và
2;

. Ta tìm được
min 2 4f t f
khi
2t
.
Với
1
2 2 1t m m
m
.
Vậy
MN
nhỏ nhất bằng 4 khi
1m
.
Bài tập 5: Cho hàm số
32
12
33
m
y x mx x m C
. Tìm
m
để (Cm) cắt trục hoành tại ba điểm phân
biệt có hoành độ
1 2 3
,,x x x
thỏa mãn điều kiện
222
1 2 3
15xxx
.
Lời giải:
TXĐ:
D
.
Xét phương trình hoành độ giao điểm:
3 2 3 2
12
0 3 3 3 2 0
33
x mx x m x mx x m
2
1 1 3 3 2 0 (1)x x m x m


2
1
1 3 3 2 0 (2)
x
g x x m x m
Để (Cm) cắt trục Ox tại ba điểm phân biệt
Phương trình (1) có ba nghiệm phân biệt
(2) có hai ngiệm phân biệt khác 1.
Y.c.b.t
22
(1 3 ) 4(3 2) 0 3 2 3 0,
0 (*)
(1) 6 0 0
m m m m m
m
g m m





Giả sử
3
1x
, lúc đó
12
,xx
là nghiệm của phương trình (2).
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
9
Theo định lý Viet, ta có:
12
12
31
. 3 2
x x m
x x m
(3)
Khi đó:
(4)
2
2 2 2 2 2
1 2 3 1 2 1 2 1 2
1 15 2 14 0x x x x x x x x x
Thay (3) vào (4) ta được:
22
(3 1) 2(3 2) 14 0 1 0 1 1m m m m m
Đối chiếu với điều kiện (*) suy ra tập các giá trị cần tìm là:
; 1 1;m  
.
Bài tập 6: (Khối A-2011) Cho hàm số
1
21
x
y
x

. Chứng minh rằng với mọi giá trị của
m
thì đường
thẳng
:d y x m
luôn cắt (C) tại hai điểm phân biệt A và B. Gọi
12
,kk
lần lượt là hệ số góc của các tiếp
tuyến tại A và B. Tìm m để tổng
12
kk
đạt giá trị lớn nhất.
Lời giải:
TXĐ:
1
\
2
D



Xét phương trình hoành độ giao điểm của (C) và
d
:
(*)
2
11
2 2 1 0
2 1 2
x
x m g x x mx m x
x




Để
d
cắt (C) tại 2 điểm phân biệt
( ) 0gx
có 2 nghiệm phân biệt
1
2
/
2
0
10
1
1
0
10
2
2
g
m m m
g
m m m







Suy ra
d
luôn cắt (C) tại 2 điểm A, B phân biệt.
Gọi
12
,xx
là 2 nghiệm của phương trình (*). Áp dụng định lí Vi-et:
Hệ số góc của tiếp tuyến với (C) tại
1
x
là:
/
11
2
1
1
1
k f x
x
Hệ số góc của tiếp tuyến với (C) tại
2
x
là:
/
22
2
2
1
1
k f x
x
Cách 1: CHUẨN_ ĐƠN GIẢN_ DỄ HIỂU
Ta có:
(**)
2
1 2 1 2 1 2
12
2 2 2
12
1 2 1 2
4 8 4 2
11
2 1 2 1
4 2 1
x x x x x x
kk
xx
x x x x



Thay (*) vào (**) ta được:
2
2
12
4 8 6 4 1 2 2k k m m m
.
Suy ra
12
kk
lớn nhất bằng
2
, đạt được khi chỉ khi
1.m 
Cách 2: ĐẶC SẮC
Ta có:
12
22
12
11
2 1 2 1
kk
xx

(1)
Áp dụng Bất đẳng thức Cauchy, ta có:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
10
22
22
12
12
12
1 1 2 2
2 1 . 2 1
2 1 2 1
2 1 2 1
xx
xx
xx



nên (1) trở thành:
12
22
12
12
12
1 1 2 2
2 1 . 2 1
2 1 2 1
2 1 2 1
kk
xx
xx
xx







1 2 1 2
12
2
1
4 2 1
4 2( ) 1
2
m
x x x x
m




Suy ra
12
kk
lớn nhất bằng
2
, đạt được khi chỉ khi
( lo¹i do )
1 2 1 2
22
1 2 1 2
12
2 1 2 1
11
2 1 2 1 1 1
2 1 2 1
x x x x
x x x x m
xx


Cách 3: CẦN CÙ VÀ CHÍNH XÁC
Theo trên,
d
luôn cắt (C) tại 2 điểm A, B phân biệt.
Lúc đó:
2
1
2
2
2
22
2
2 2 1 0
22
2
m m m
x
x mx m
m m m
x
Ta có:
12
2 2 2 2
22
12
1 1 1 1
2 1 2 1
2 2 1 2 2 1
kk
xx
m m m m m m

22
22
11
2 2 1 2 2 1m m m m m m
22
22
22
22
2 2 1 2 2 1
2 2 1 2 2 1
m m m m m m
m m m m m m

22
2
2
2
2
2
2
2 2 2 2 2 1
4 8 6 4 1 2 2
2 2 1
m m m m
m m m
m m m



Suy ra
12
kk
lớn nhất bằng
2
, đạt được khi chỉ khi
1.m 
Bài tập 7: Cho hàm số
2
mx
y
x
có đồ thị là
()
m
H
. Tìm m để
: 2 2 1 0d x y
cắt
()
m
H
tại hai điểm
cùng với gốc tọa độ tạo thành một tam giác có diện tích là
3
.
8
S
Lời giải:
TXĐ:
\2D
.
Hoành độ giao điểm A, B của d và
()
m
H
là các nghiệm của phương trình:
1
22
xm
x
x

2
2 2 1 0, 2x x m x
(1)
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
11
Để d cắt
()
m
H
tại 2 điểm phân biệt
Phương trình(1) có 2 nghiệm
12
,xx
phân biệt khác
2
Y.c.b.t
2
17
17 16 0
16
2. 2 2 2 1 0
2
m
m
m
m





(*)
Ta có:
2 2 2
2 1 2 1 2 1
2.AB x x y y x x
2
2 1 1 2
2
2. 4 . 17 16 .
2
x x x x m
Khoảng cách từ gốc tọa độ O đến d là
1
.
22
h
Suy ra
1 1 1 2 3 1
. . . . . 17 16 ,
2 2 2 8 2
22
OAB
S h AB m m
thỏa mãn (*)
Kết luận: Vậy
1
2
m
là giá trị cần tìm.
Bài tập 8: Cho hàm số
2
2
x
y
x
(C). Tìm
m
để đường thẳng (d ):
y x m
cắt đồ thị (C) tại 2 điểm phân
biệt thuộc 2 nhánh khác nhau của đồ thị sao cho khoảng cách giữa 2 điểm đó là nhỏ nhất. Tìm giá trị nhỏ
nhất đó.
Lời giải:
TXĐ:
\2D
.
Xét phương trình hoành độ giao điểm của d và (C):
2
2
4 2 0, 2
2
x
x m x m x m x
x
(1)
Để (d) cắt (C) tại 2 điểm phân biệt
Phương trình (1) có 2 nghiệm phân biệt khác 2.
Y.c.b.t
2
16
40
m
m

(2).
Lúc đó, gọi
1 1 2 2
; , ;A x x m B x x m
là 2 giao điểm của d và (C), với
12
,xx
là 2 nghiệm của
phương trình (1). Theo định lí viet ta có
12
12
4
(3)
2
x x m
x x m

* Để A, B thuộc 2 nhánh khác nhau của đồ thị thì A, B nằm khác phía đối với TCĐ:
20x 
.
Suy ra:
1 2 1 2 1 2
2 2 0 2 4 0x x x x x x
(4)
Thay (3) vào 4 ta được : – 4 < 0 luôn đúng (5)
* Mặt khác ta lại có
2 2 2
1 2 1 2 1 2 1 2
28AB x x y y x x x x
(6)
Thay (3) vào (6) ta được
2
2 32 32AB m
. Suy ra:
min
32AB
khi
0m
.
Kết luận: Vậy
0m
thoả mãn.
Bài tập 9:Tìm
a
và
b
để đường thẳng d:
y ax b
cắt đồ thị (C):
1
1
x
y
x
tại hai điểm phân biệt đối
xứng nhau qua đường thẳng
: 2 3 0xy
.
Lời giải:
TXĐ:
\1D
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
12
Phương trình
: 2 3 0xy
được viết lại:
13
:
22
yx
. Để thỏa mãn đề bài thì trước hết
2a 
. Vậy d:
2y x b
.
Xét phương trình hoành độ giao điểm của d và (C):
2
1
2 2 3 1 0 1
1
x
x b g x x b x b x
x
(1)
Để (d) cắt (C) tại 2 điểm phân biệt
Phương trình (1) có 2 nghiệm phân biệt khác
1
.
Y.c.b.t
2
2
3 8 1 0
2 17 0
1 2 3 1 0
g
bb
b b b
g b b b
(2).
Lúc đó, gọi
1 1 2 2
; 2 , ; 2A x x b B x x b
là 2 giao điểm của d và (C), với
12
,xx
là 2 nghiệm
của phương trình (1). Theo định lí viet ta có
12
12
3
2
(3)
1
2
b
xx
b
xx

Gọi I là trung điểm của AB, ta có:
12
3
33
24
;
42
3
2
2
I
II
xx
b
x
bb
I
b
y x b





.
Lúc đó, yêu cầu bài toán:
Tån t¹i A, B.
AB
2
2
2.
3
1
2 3 0
2 3 0
4
II
b
a
a
a
b
b
b
I x y





Kết luận: Vậy các giá trị cần tìm là
2a 
và
1.b 
Bài tập 10: Cho hàm số:
1
1
x
y
x
(C). Một nhánh của đồ thị (C) cắt Ox, Oy lần lượt tại A, B. Tìm điểm C
thuộc nhánh còn lại sao cho diện tích tam giác ABC bằng 3.
Lời giải:
TXĐ:
\1D
.
Tìm được tọa độ của
1;0 , 0; 1AB
Phương trình của AB:
10xy
.
Do
MC
nên tọa độ
1
; , 1
1
x
M x x
x




và A, B thuộc nhánh các điểm có hoành độ lớn
hơn
1
nên M thuộc nhánh đồ thị có các điểm có hoành độ
1x 
.
Ta có :
d
2
1
1
1
1 1 1
. ; . 2 3
2 2 2 1
2
MAB
x
x
x
xx
S AB M AB
x

(loai)
2
1
2
2
2
2;3
5 6 0 2 3
61
32
3;2
7 6 0
M
x x x y
x x x
xy
M
xx
.
Vậy các điểm cần tìm là
12
2;3 , 3;2 .MM
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
13
Bài tập 11: Tìm
m
để
: 2 2d y x m
cắt
2
:
1
x
Cy
x
tại 2 điểm phân biệt
,AB
sao cho tứ giác
AMBN
có diện tích bằng
5 17
4
, biết
1; 2 , 3; 3MN
.
Lời giải:
TXĐ:
\1D
.
Ta có phương trình đường thẳng
1
:3
2
MN y x
nên
d MN
tại
I
.
I
có tọa độ là nghiệm
của hệ
22
1
3
2
y x m
yx
nên
1 2 8
;
55
mm
I




.
Vì
AMBN
là tứ giác lồi nên
I
thuộc đoạn thẳng
MN
tức là
12
13
5
m

và
8
32
5
m
,
nghĩa là
72ma
, đường thẳng
d
cắt
H
tại hai điểm
,AB
phân biệt khi phương
trình:
2
22
1
x
xm
x
có hai nghiệm phân biệt, nghĩa là:
2
2 5 4 0 1x m x m
có hai
nghiệm phân biệt khác
1 1 2 2m
hoặc
1 2 2m 
và
1 2 2m 
không thỏa
a
.
Gọi
,
AB
xx
là hoành độ của
,AB
thì chúng là hai nghiệm của phương trình
1
.
Nên
54
;.
22
A B A B
mm
x x x x

, do đó:
22
22
51
4
4 . 4. 2
4 2 4
B A A B A B
mm
m
x x x x x x

1 1 1 1
1 ; 1
1 1 1 1
.
BA
A B B A
A B A B
A B A B
xx
y y y y
x x x x
x x x x

Ta có:
2
2
22
2
2
1
2
1
4
2
4
45
22
B A B A
m
m
AB x x y y
mm




2
22
18
4
1*
4
4 2 4 5 5
m
m m m m






Ta có:
5 17 1 1
. 5.
4 2 2
AMBN
S MN AB AB
, tức là:
2
5.17
**
4
AB
.
Từ
* , * *
ta được
2
1 8 17 4mm
hoặc
6m
.
Vậy
4m 
là giá trị cần tìm.
Bài tập 12*: Tìm giá trị tham số
m
sao cho đồ thị
3
: 3 2C y x x
và đường thẳng
2y m x
giới hạn hai hình phẳng có cùng diện tích.
Lời giải:
TXĐ:
D
.
Phương trình hoành độ giao điểm:
3
3 2 2 2x x m x x
hoặc
1 , 0x m m
. Điều
kiện
d
và
C
giới hạn 2 hình phẳng:
09m
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
14
Gọi
1
S
và
2
S
lần lượt là diện tích các hình phẳng nhận được theo thứ tự từ trái sang phải.
d
qua
A
khi
1m
(tức là
d
qua điểm uốn).
Khi đó,
12
4SS
.
+ Nếu
12
0 1: 4m S S
.
+ Nếu
12
1 9 : 4m S S
.
+ Nếu
9 1 2;1 4m m m
.
Khi đó:
2
3
1
1
3 2 2
m
S x x m x dx
;
1
3
2
2
3 2 2
m
S x x m x dx
.
Suy ra
21
20S S m m
.
Vậy
1m
thỏa yêu cầu bài toán.
Bài tập 13: Tìm
m
để
9
:3
4
d y x
cắt đồ thị (C)
32
6 9 3y mx x mx
tại 3 điểm phân biệt
0; 3 , ,A B C
thỏa mãn điều kiện
B
nằm giữa
A
và
C
đồng thời
3AC AB
.
Lời giải:
TXĐ:
D
.
Số giao điểm của đồ thị đã cho với đường thẳng
d
là số nghiệm của phương trình:
3 2 2
99
6 9 3 3 6 9 0 1
44
mx x mx x x mx x m



2
0
9
6 9 0 2
4
x
mx x m
Đường thẳng
d
và đồ thị đã cho cắt nhau tại 3 điểm phân biệt
0; 3 , ,A B C
khi và chỉ khi
phương trình
1
có 3 nghiệm phân biệt
0; 3 , ,A B C
, tức là
2
phải có hai nghiệm phân
biệt khác 0.
Y.c.b.t
2
0
0
0
9 1 65 1 65
' 9 9 0 1 0
4 4 8 8
1
1
9
90
4
4
4
m
m
m
m
m m m m
m
m
m





.
1 65 1 65 1
; \ 0,
8 8 4
m









(*)
Gọi
1 1 2 2
; , ;B x y C x y
với
1 1 2 2
99
3, 3
44
y x y x
, trong đó
12
,xx
là 2 nghiệm của
2
.
Ta có
1 1 2 2
; 3 , ; 3AB x y AC x y
và
21
21
21
3
33
3 3 3
xx
AC AB x x
yy
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
15
Ta có hệ:
11
21
1 2 2 2
2
1 2 1 2
33
3
22
1
6 9 9
3
22
4
99
4 3 0
99
44
xx
xx
mm
m
x x x x
m m m
m
mm
x x x x
mm












thỏa (*)
Vậy
3
4
m 
;
1m
thỏa mãn bài toán.
Bài tập 14: Tìm các giá trị
0m
để đồ thị
m
C
:
42
3 1 3 2y x m x m
cắt trục hoành tại 4 điểm
phân biệt và tiếp tuyến tại điểm có hoành độ lớn nhất cùng với 2 trục tọa độ tạo thành tam giác có diện
tích bằng 24.
Lời giải:
TXĐ:
D
.
Phương trình hoành độ giao điểm của
m
C
và trục hoành:
4 2 2 2
3 1 3 2 0 1 3 2 0 *x m x m x x m


Với
0m
thì
m
C
cắt trục hoành tại 4 điểm phân biệt và
32xm
là hoành độ lớn nhất.
Giả sử
3 2;0Am
là giao điểm có hoành độ lớn nhất và tiếp tuyến
d
tại
A
có phương
trình:
2 3 1 3 2. 2 3 1 3 2y m m x m m
.
Gọi
B
là giao điểm của
d
với
Oy
, suy ra
0; 2 3 1 3 2B m m
.
Theo giả thiết, tam giác
OAB
vuông tại
O
và
24 . 48
OAB
S OA OB
hay
2
3 2 18 22 4 48 *m m m
.
Xét
2
3 2 18 22 4 48, 0f m m m m m
.
Ta có
'0fm
với mọi
0m
, suy ra
fm
đồng biến với mọi
0m
và
2
0
3
f



. Do đó
phương trình
*
có nghiệm duy nhất
2
3
m
.
Vậy
2
3
m
thỏa mãn đề bài.
Bài tập 15: Tìm
m
để đường thẳng
1
:2
2
d y x
cắt
25
:
m
mx
Cy
xm
tại hai điểm phân biệt
,AB
có
hoành độ
12
,xx
thỏa mãn
2
112
98x x x
.
Lời giải:
TXĐ:
\Dm
.
Hoành độ giao điểm của đường thẳng
d
và
m
C
là nghiệm của phương trình
2
2 5 1
2 4 10 0
2
mx
x x x m x m
xm
.
Đặt
2
4 10g x x x m
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
16
Để
d
cắt
m
C
tại hai điểm phân biệt
,AB
Phương trình
0gx
có 2 nghiệm phân biệt
khác
m
, tức là phải có:
2
161
0
16 161 0
16
0
2 5 0
10
2
m
m
gm
mm
m






Áp dụng định lý Viet cho
12
,xx
, ta có:
12
12
1
4
10
4
b
xx
a
cm
xx
a
Xét điều kiện bài toán
22
1 1 2 1 1 1
1
9 8 9 8
4
x x x x x x



2
1
11
1
1
20
2
x
xx
x

+) Với
12
5
1 5.
4
x x m
+) Với
12
7
2 4.
4
x x m
Kết hợp với điều kiện
161
16
m 
và
10
2
m 
.
Vậy
5m 
hoặc
4m
thỏa mãn yêu cầu bài toán.
Bài tập 16: Tìm
m
để
32
: 2 1 5 2 2 4
m
C y x m x m x m
cắt trục hoành tại ba điểm phân biệt
,,A B C
sao cho
,BC
có hoành độ nhỏ hơn 1.
Lời giải:
TXĐ:
D
.
Cách 1: Gọi
12
,xx
là hoành độ của
12
,,B C x x
cũng là nghiệm của phương trình
0gx
.
Theo bài toán ta có:
1 2 1 2
11
1 2 1 2 1 2
22
1 1 0 2
1 1 0
22
1 1 0 1 0
1 1 0 2 2 1 0
x x x x
xx
m
x x x x x x
x x m m






1
1
1
m
m
m

Vậy
1m 
là giá trị cần tìm.
Cách 2: Hoành độ của 3 điểm
,,A B C
là nghiệm của phương trình:
32
2 1 5 2 2 4 0x m x m x m
2
2 2 2 0x x mx m
2
2
2 2 0
x
g x x mx m
Vì hoành độ của
,BC
nhỏ hơn 1 nên giả sử hai nghiệm của
0gx
là
2
1
2x m m m
,
2
2
2x m m m
.
Vì
12
xx
nên
22
1
2
2
1
1 2 1 2 1
1
x
x m m m m m m
x
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
17
2
22
2 0 0
1 0 1 1
1
2 2 1
m m m
m m m
m
m m m m



.
KỸ THUẬT: Vận dụng Cực trị để giải quyết bài toán sự tương giao
của các đồ thị hàm số và trục Ox.
Hàm số bậc ba
32
y f x ax bx cx d
,
0a
có đồ thị (C).
Xét phương trình hoành độ giao điểm:
32
0ax bx cx d
TH 1: (C) cắt Ox tại 3 điểm phân biệt
C§ CT
Hµm sè cã 2 cùc trÞ
.0yy
Minh họa đồ thị:
TH 2: (C) cắt Ox tại 2 điểm
C§ CT
Hµm sè cã 2 cùc trÞ
.0yy
Minh họa đồ thị:
TH 3: (C) cắt Ox tại 1 điểm
C§ CT
Hµm sè kh«ng cã cùc trÞ
Hµm sè cã 2 cùc trÞ
.0yy
Minh họa đồ thị:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
18
x
y
O
(C)
x
y
(C)
O
Nhận xét:
+ Việc xử lí các biểu thức cực trị thì quí độc giả xem lại bài viết cực trị;
+ Với hàm số trùng phương
42
y f x ax bx c
,
0a
thì hoàn toàn biện luận sơ cấp cho đơn
giản;
Tất nhiên việc giải quyết một bài toán tương giao của hai đồ thị thì có nhiều phương pháp, nhưng theo
tinh thần đổi mới của chương trình SGK, cũng như mức độ đề thi Quốc gia, chúng tôi cho rằng,
phương pháp này chỉ mang tính chất tham khảo thêm! Các phương pháp cơ bản và sơ cấp đã hoàn toàn
giải quyết được các đề thi mức độ thi THPT Quốc gia!
Ta xét một số bài tập minh họa cho phương pháp này!
Bài tập 17: Tìm
m
để đồ thị hàm số
3
2y x mx
cắt trục hoành tại điểm duy nhất.
Lời giải:
TXĐ:
D
.
Cách 1: Phương trình hoành độ giao điểm của đồ thị hàm số đã cho với trục
Ox
:
32
2
20x mx x m
x
.
Xét hàm số
2 / /
2
22
2 0 1f x x f x x f x x
x
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy yêu cầu bài toán
33mm
.
Cách 2: Để đồ thị hàm số đã cho cắt
Ox
tại duy nhất một điểm ta có các trường hợp sau:
TH 1: Đồ thị hàm số đã cho không có cực trị hay là hàm số luôn đồng biến (do
10a 
) trên
2
' 3 0, 0y x m x m
.
TH 2: Đồ thị hàm số có hai cực trị cùng dấu
/2
0
33
mm
y x x
với
0m
.
Hai giá trị cực trị là:
12
22
2 ; 2
3 3 3 3
m m m m
yy
3
12
4
. 4 0 3 0
27
m
y y m
.
Vậy
3m 
là những giá trị cần tìm.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
19
Bài tập 18: Tìm
m
để đồ thị (C):
3
1
3
y x x m
cắt trục hoành tại 3 điểm phân biệt.
Lời giải:
TXĐ:
D
.
Cách 1: (Đã trình bày ở bài tập 6)
Cách 2:
Ta có:
/2
2
1
3
10
2
1
3
x y m
yx
x y m
.
Lúc đó, hàm số có 2 cực trị với các giá trị cực trị tương ứng là
2
3
m
và
2
3
m
.
Để (C) cắt Ox tại 3 điểm phân biệt thì
22
0
33
mm
2
4 2 2
0 ; .
9 3 3
mm



Bài tập 19: Tìm
m
để đồ thị
m
C
:
32
12
33
y x mx x m
cắt trục hoành tại 3 điểm phân biệt.
Lời giải:
TXĐ:
D
.
Cách 1: (Đã trình bày ở bài tập 5- Dạng 3)
Cách 2:
Ta có:
/2
21y x mx
.
Để hàm số có hai cực trị
Phương trình
/
0y
có hai nghiệm phân biệt
12
,xx
2
4 4 0,mm
.
Lúc đó, ta viết:
2
/
1 2 2 2 2
3 3 3 3 3
m m m
y y x x







.
Suy ra:
2
11
2
22
2 2 2 2
3 3 3
2 2 2 2
3 3 3
mm
yx
mm
yx








.
Để đồ thị (C) cắt Ox tại 3 điểm phân biệt thì
22
1 2 1 2
2 2 2 2 2 2 2 2
. 0 0
3 3 3 3 3 3
m m m m
y y x x
2
2
22
1 2 1 2
2 2 2 2 2 2 2 2
0
3 3 3 3 3 3
m m m m
x x x x
2
2
22
2 2 2 2 2
22
22
.0
9 3 3 9
m m m
m
m




2 4 3 2
4 8 4 4 4 2 2 4 8 4 0m m m m m m m
4 3 2 2 2
12 8 12 0 4 3 3 0 0m m m m m m m
Do
2
3 3 0,m m m
Vậy
0m
là yêu cầu bài toán.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
20
CHÚ Ý: MỘT SỐ BÀI TOÁN QUAN TRỌNG
Bài toán 1: Xác định tham số để đồ thị hàm số
32
( ) : ( 0)C y ax bx cx d a
cắt trục hoành tại ba điểm
phân biệt có hoành độ lập thành cấp số cộng.
Phương pháp:
Sử dụng: Điều kiện cần và đủ đối với phương trình:
32
0ax bx cx d
(1)
Bước 1: Điều kiện cần:
+ Giải sử phương trình (1) có 3 nghiệm
1 2 3 1 2 3
,,x x x x x x
. Khi đó, theo định lý Viet đối
với phương trình (1):
1 2 3
1 2 2 3 3 1
1 2 3
b
x x x
a
c
x x x x x x
a
d
x x x
a

+ Để
1 2 3 1 2 3
,,x x x x x x
lập thành CSC thì
1 3 2 2
23
b
x x x x
a
2
3
b
x
a
.
Thay vào (1)
m
Bước 2: Điều kiện đủ: Với
m
tìm được giải phương trình (1) và kết luận.
Lưu ý: Tư duy thuật toán còn áp dụng cho bài toán: 3 nghiệm lập thành cấp số nhân. Tất nhiên,
phương pháp nêu trên chỉ mang tính gợi ý, còn trong rất nhiều TH khác thì sẽ có các cách khác tốt
hơn.
Bài tâp 1: (ĐHYHCM-98) Xác định
m
để đồ thị (C):
32
39y x x x m
cắt trục hoành tại 3 điểm phân
biệt với hoành độ lập thành một cấp số cộng.
Lời giải:
TXĐ:
D
.
Xét phương trình hoành độ giao điểm của (C) và Ox:
32
3 9 0x x x m
(1)
+ Giả sử (1) có ba nghiệm phân biệt
1 2 3
,,x x x
, khi đó ta phân tích được:
32
1 2 3
39x x x m x x x x x x
32
1 2 3 1 2 2 3 3 1 1 2 3
x x x x x x x x x x x x x x x
(2)
Đồng nhất hệ số của
2
x
trong phương trình (2), ta được:
1 2 3
3x x x
(3)
Mặt khác, do
1 2 3
,,x x x
theo thứ tự đó lập thành một cấp số công nên ta có:
1 3 2
2x x x
(4)
Từ (3) và (4) suy ra:
2
1x
. Thay
2
1x
vào (1) ta được:
11m
.
+ Kiểm tra với
11m
, ta có:
3 2 2
3 9 11 0 1 2 11 0x x x x x x
1 1 2 3 1 2 3.x x x
Dễ thấy 3 nghiệm vừa tìm được lập thành một cấp số cộng.
Vậy
11m
là yêu cầu bài toán.
Bài tập tương tự:
Bài tập 2: (ĐHYHCM-96) Tìm
a
để d:
yx
cắt đồ thị
3 2 3
( ) : 3 4C y x ax a
tại 3 điểm phân biệt A, B,
C với
AB BC
.
Bài toán 2: Xác định tham số để đồ thị hàm số
42
( ) : ( 0)C y ax bx c a
cắt trục hoành tại 4 điểm
phân biệt có hoành độ lập thành cấp số cộng.
Phương pháp:
Lập phương trình hoành độ giao điểm:
42
0ax bx c
(2)
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
21
Đặt
2
0tx
: (2) có dạng:
2
0at bt c
(3).
Để (2) có 4 nghiệm phân biệt khi chỉ khi (3) có 2 nghiệm phân biệt:
1 2 1 2
, : 0t t t t
(4)
Lúc đó (2) có 4 nghiệm:
2 1 1 2
, , ,t t t t
.
Các nghiệm này lập thành CSC khi:
2 1 1
2 1 2 1
1 2 1
2
39
2
t t t
t t t t
t t t
.
+ Áp dụng định lý Viet đối với phương trình (3):
vµ . Tõ ®©y:(*) hay
2
1
12
21
12
2
9
10
9
(*) 9
100
10
S
t
t t S
S
t t P
t t P S
t



2
9 100SP
(5)
+ Kết hợp (4) và (5) nhận được điều kiện của tham số.
BÀI TẬP:
Bài tập: (ĐHY-D-HCM-98) Xác định
m
để đồ thị
42
( ) : 2 1 2 1C y x m x m
cắt trục hoành tại 4
điểm phân biệt có hoành độ lập thành cấp số cộng.
Lời giải:
TXĐ:
D
.
Xét phương trình hoành độ giao điểm của (C) và Ox:
42
2 1 2 1 0x m x m
(1)
Cách 1: Đặt
2
0tx
. Khi đó, (1) trở thành:
2
2 1 2 1 0t m t m
(2)
Để (C) cắt Ox tại 4 điểm phân biệt
Phương trình (1) có 4 nghiệm phân biệt
Phương trình (2) có 2 nghiệm dương phân biệt
2
4 1 4 2 1 0
1
2 1 0 0.
2
2 1 0
mm
S m m
Pm
(3)
+ Với điều kiện (3), ta tìm được hai nghiệm của (2) là
12
1 ; 1t m t m
Như vậy, 4 giao điểm của (C) và Ox lần lượt là
21
;0 , ;0 ,A t B t
1
;0 ,Ct
2
;0Dt
. Để 4 điểm này có hoành độ lập thành 1 cấp số cộng thì chúng phải chắn trên Ox
thành 3 đoạn thẳng bằng nhau, tức là:
2 1 2
2 1 2 1
2 1 1
2
39
2
t t t
AB BC CD t t t t
t t t

. (4)
Mặt khác, áp dụng định lí Viet với phương trình (2) ta có:
(5)
(6)
12
12
21
21
t t m
t t m
(5)
Từ (4) và (5) suy ra:
12
2 1 9 1
1
10 5 5
mm
m
tt

thay vào (6) ta được:
4
91
1
. 2 1
4
55
9
m
m
m
m
m

. Vậy
4
4;
9
mm
là yêu cầu bài toán.
Cách 2: Ta có (1)
1
21
t
tm

.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
22
Để (C) cắt Ox tại 4 điểm phân biệt
2 1 0
1
0
2 1 1
2
m
m
m


.
Lúc đó, ta tìm được hoành độ của 4 giao điểm lần lượt là
2 1, 2 1, 1, 1mm
.
TH 1:
0m
, thứ tự 4 hoành độ giao điểm là
2 1, 1, 1, 2 1mm
.
Điều kiện để 4 hoành độ giao điểm này tạo thành 1 cấp số cộng là:
2 1 1 2. 1
2 1 3 4
1 2 1 2.1
m
mm
m
.
TH 2:
1
0
2
m
, thứ tự 4 hoành độ giao điểm là
1, 2 1, 2 1, 1mm
.
Điều kiện để 4 hoành độ giao điểm này tạo thành 1 cấp số cộng là:
2 1 1 2. 2 1
4
3 2 1 31
9
1 2 1 2. 2 1
mm
mm
mm
.
Vậy
4
4;
9
mm
là yêu cầu bài toán.
III- BÀI TẬP TỰ LUYỆN
1) Tìm tọa độ giao điểm của các đồ thị sau:
a)
2
3
3
22
1
22
x
yx
x
y

b)
2
24
1
24
x
y
x
y x x
c)
3
43
2
y x x
yx

d)
42
2
1
45
y x x
yx

e)
32
2
5 10 5
1
y x x x
y x x
f)
2
1
31
x
y
x
yx

2) Biện luận số giao điểm của các đồ thị sau:
a)
3
32
2
y x x
y m x

b)
c)
3
3
3
3
x
yx
y m x

d)
21
2
2
x
y
x
y x m

e)
1
1
2
x
y
x
y x m
f)
2
63
2
xx
y
x
y x m



g)
1
3
1
3
yx
x
y mx

h)
2
33
2
41
xx
y
x
y mx m


i)
3
2
21
1
y x x
y m x

3) (Đề 34) Xác định tất cả các giá trị của
k
để đồ thị hàm số
2
43
2
xx
y
x

cắt đường thẳng
d: 1y kx
tại 2 điểm phân biệt.
4) (ĐHKT-98) Cho hàm số
(C)
32
31y x x
. Đường thẳng đi qua
3;1A
và có hệ số góc bằng
k
. Xác
định
k
để đường thẳng đó cắt đồ thị tại 3 điểm phân biệt.
5) (ĐHSPII-97) Tìm
m
để hàm số
42
1 2 1y m x mx m
cắt Ox tại 4 điểm phân biệt.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
23
6) (Đề 148) Tìm
m
để đường thẳng
d: ym
cắt đồ thị hàm số
2
1
1
x mx
y
x

tại 2 điểm A, B với
OA OB
.
7) (ĐH A-03) Tìm
m
để đồ thị hàm số
2
( ) :
1
mx x m
Cy
x

cắt Ox tại 2 điểm phân biệt và 2 điểm đó có
hoành độ dương.
8) (ĐH D-03) Tìm
m
để đường thẳng
: 2 2
m
d y mx m
cắt
2
4
( ) :
2
xx
Cy
x

tại 2 điểm phân biệt.
9)(Dự bị 02) Tìm
m
để đồ thị hàm số
42
( ) : 1C y x mx m
cắt Ox tại 4 điểm phân biệt.
10) (Đề dự bị 2003) Tìm
m
để đồ thị hàm số
2
( ) : 1C y x x mx m
cắt Ox tại 3 điểm phân biệt.
11) (ĐH A-2004) Tìm
m
để đường thẳng
ym
cắt đồ thị hàm số
2
33
( ) :
2( 1)
xx
Cy
x
tại 2 điểm A, B sao cho
1AB
.
12) (ĐH A-06) Gọi
d
là đường thẳng đi qua điểm
3;20A
và có hệ số góc là
m
. Tìm
m
để
d
cắt đồ thị
3
( ) : 3 2C y x x
tại 3 điểm phân biệt.
13) (ĐHBK A-01) Viết phương trình đường thẳng
d
đi qua điểm
2
2;
5
M



sao cho
d
cắt đồ thị
2
3
( ) :
1
x
Cy
x
tại hai điểm A, B phân biệt và M là trung điểm của AB.
14) Tìm các giá trị của
m
sao cho trên
2
1
( ) :
1
xx
Cy
x

có hai điểm khác nhau
;
AA
A x y
,
;
BB
B x y
thoả mãn điều kiện:
AA
BB
x y m
x y m


.
15) CMR: Đường thẳng
1
2
y x m
luôn cắt đồ thị hàm số
3
2
x
y
x
tại hai điểm phân biệt A, B. Tìm
m
sao cho độ dài đoạn AB là nhỏ nhất.
16) (ĐHCĐ- 98) Tìm các giá trị của
m
để đường thẳng
d :2
m
y mx m
cắt đồ thị hàm số
2
41
( ) :
2
xx
Cy
x

tại hai điểm phân biệt cùng thuộc một nhánh của đồ thị (C).
17) Cho hàm số
3 2 2 2
2 2 1 1
m
y x mx m x m m C
. Tìm
m
để đường cong
m
C
cắt trục hoành
tại 3 điểm phân biệt có hoành độ dương.
18)* Cho hàm số
32
3 3 1 1 3
m
y x x m x m C
. Tìm
m
để đường cong
m
C
cắt trục hoành tại 3
điểm phân biệt.
19) Cho hàm số
32
3 3 3 2
m
y x mx x m C
. Tìm
m
để đường cong
m
C
cắt trục hoành
tại 3 điểm phân biệt có hoành độ
1 2 3
,,x x x
sao cho:
222
1 2 3
15xxx
.
20) CMR: Với mọi
m
đường thẳng
2:0x y m
luôn cắt đồ thị
1
( ) :
1
x
Cy
x
tại hai điểm phân biệt
thuộc hai nhánh khác nhau của (C).
21) CMR: Với mọi
m
đường thẳng
: 2 0y x m
luôn cắt
3
( ) : 3
1
C y x
x
tại hai điểm A, B
phân biệt có hoành độ
12
,.xx
Lúc đó, xác định
m
sao cho:
2
12
xx
min.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
24
22) Tìm
m
để đường thẳng
: ( 5) 10
m
d y m x
cắt
2
29
( ) :
2
xx
Cy
x

tại 2 điểm A, B phân biệt và nhận
(5;10)M
làm trung điểm.
23) (ĐH A-2010) Tìm
m
để
32
: 2 (1 )C y x x m x m
cắt trục hoành tại 3 điểm phân biệt có hoành
độ
1 2 3
,,x x x
sao cho:
222
1 2 3
4xxx
.
24) (ĐH B- 2010) Tìm
m
để đường thẳng
2y x m
cắt
21
( ) :
1
x
Cy
x
tại 2 điểm A, B phân biệt sao
cho tam giác OAB có diện tích bằng
3
.
25) (ĐH A-2011) Chứng minh rằng với mọi
m
đường thẳng
y x m
luôn cắt đồ thị hàm số
1
:
21
x
Cy
x

tại hai điểm phân biệt A và B. Gọi
12
,kk
lần lượt là hệ số góc của các tiếp tuyến của (C)
tại A, B. Tìm
m
để
12
kk
đạt giá trị lớn nhất.
26) (ĐH D-2011) Tìm
k
để đường thẳng
21y kx k
cắt đồ thị hàm số
21
1
x
y
x
tại hai điểm A, B sao
cho khoảng cách từ A, B đến trục hoành bằng nhau.
27) Cho hàm số
1
1
x
y
x
(1) có đồ thị
()C
.Chứng minh rằng đường thẳng
( ) : 2d y x m
luôn cắt (C) tại
hai điểm phân biệt A, B thuộc hai nhánh khác nhau. Xác định m để đoạn AB có độ dài ngắn nhất.
------------------------------------------------------------------------
HỆ THỐNG VÀ KHÁI QUÁT:
SỰ TƯƠNG GIAO CỦA HAI ĐỒ THỊ
HÀM BẬC BA:
32
,0y ax bx cx d a
1) Cho hàm số
32
36y x x x
, (C) và đường thẳng d đi qua gốc tọa độ O và có hệ số góc
k
. Tìm
k
để d cắt (C) tại 3 điểm phân biệt O, A, B sao cho
17AB
.
2) Tìm
m
để đường thẳng d :
4yx
cắt (C):
32
2 4 4y x mx m x
tại ba điểm
0;4A
, B, C
sao cho tam giác IBC có diện tích bằng
82
với
3;1I
.
3) Tìm
m
để đường thẳng d :
2yx
cắt (C):
32
2 3 1 2y x mx m x
tại ba điểm
0;2A
, B,
C sao cho tam giác IBC có diện tích bằng
26
với
1;3I
.
4) Tìm
m
để (C):
32
3 1 3 1y x m x mx m
cắt trục hoành tại ba điểm phân biết trong đó có ít
nhất một điểm có hoành độ âm.
5) Cho hàm số
32
6 9 6y x x x
, (C). Tìm
m
để (d):
24y mx m
cắt (C) tại 3 điểm phân biệt.
6) Cho hàm số
32
()
m
y x mx m C
. Tìm
m
để
()
m
C
cắt trục hoành tại 3 điểm phân biệt.
7) Cho hàm số:
32
( 1) 1y x m x x m
()
m
C
. Tìm
m
để
()
m
C
cắt trục hoành tại 3 điểm phân
biệt có hoành độ dương.
8) Cho hàm số
,
3 2 2 2
3 3 1 1 ( )
m
y x mx m x m C
. Tìm
m
để
()
m
C
cắt trục hoành tại 3 điểm
phân biệt có hoành độ dương.
9) Cho hàm số
32
18 2 ( )
m
y x x mx m C
. Tìm m để
()
m
C
cắt trục hoành tại 3 điểm phân biệt có
hoành độ dương.
10) Cho hàm số
3 2 2 2
2 3 1 3 1 1y x m x m x m
()
m
C
. Tìm
m
để
()
m
C
cắt trục hoành tại 3
điểm phân biệt có hoành độ âm.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
25
11) Cho hàm số
3 2 2 3
3 3( 1)y x mx m x m
,
()
m
C
. Tìm
m
để
()
m
C
cắt trục hoành tại 3 điểm phân
biệt trong đó có đúng hai điểm có hoành độ âm.
12) Cho hàm số
32
2 3 1 6 2y x m x mx
()
m
C
. Tìm
m
để
()
m
C
cắt trục hoành tại duy nhất 1
điểm.
13) Cho hàm số
3 2 2
3 1 2 4 1 4 1y x m x m m x m m
()
m
C
. Tìm
m
để
()
m
C
cắt trục hoành
tại 3 điểm phân biệt trong đó có hoành độ lớn hơn 1.
14) Cho hàm số
32
3 9 , ( )
m
y x x x m C
. Xác định
m
để
()
m
C
cắt trục hoành tại 3 điểm có hoành
độ lập thành cấp số cộng.
15) Tìm m để đồ thị hàm số
32
3 3 1 6 6y x mx m x m
cắt trục hoành tại ba điểm phân biệt có
hoành độ
222
1 2 3 1 2 3 1 2 3
, , : 20x x x x x x x x x
.
16) Cho hàm số
32
12
33
y x mx x m
. Tìm
m
để đồ thị hàm số cắt trục hoành tại ba điểm phân
biệt
222
1 2 3 1 2 3
, , : 15x x x x x x
.
17) Tìm
m
để d:
(1 ) 5y m x m
cắt (C):
32
2 (3 1) 3y x x m x m
tại 3 điểm phân biệt có
hoành độ
1 2, 3 1 2 3
, : 1x x x x x x
.
18) Cho hàm số
32
2 1 2y x mx m x m
. Chứng minh rằng đồ thị hàm số luôn đi qua điểm
cố định A trên trục hoành. Tìm
m
để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt A, B, C
thỏa mãn:
22
19
48
OA OA
OB OC

.
19) Cho (C):
2
34y x x
và d là đường thẳng đi qua
1;0A
và có hệ số góc bằng
k
. Tìm
k
để
d cắt (C) tại ba điểm phân biệt. Trong trường hợp này, tìm tập hợp trung điểm M của đoạn
thẳng nối hai giao điểm lưu động khi
k
thay đổi.
20) Cho (C):
32
34y x x
và đường thẳng d đi qua
3;4A
và có hệ số góc
m
. Tìm
m
để đường
thẳng d cắt (C) tại 3 điểm phân biệt A, M, N sao cho hai tiếp tuyến của (C) tại M và N vuông góc
nhau.
21) Cho hàm số
32
31y x x mx
. Tìm
m
để đường thẳng
1y
cắt đồ thị hàm số tại ba điểm
phân biệt
0;1I
, A và B. Với giá trị nào của
m
, các tiếp tuyến của đồ thị hàm số các điểm A, B
vuông góc nhau.
22) Cho hàm số
32
y x mx x m
. Tìm
m
để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt
sao hoành độ của chúng lập thành cấp số cộng.
HÀM TRÙNG PHƯƠNG:
42
,0y ax bx c a
1) Cho hàm số
42
1y x mx m
. Tìm
m
để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt.
2) Tìm
m
để đồ thị hàm số
4 2 2
21y x mx m
. Tìm
m
để đồ thị cắt trục hoành tại bốn điểm
phân biệt có hoành độ nhỏ hơn 2.
3) Cho hàm số
42
3 2 3y x m x m
. Tìm
m
để đường thẳng
1y 
cắt đồ thị hàm số tại 4 điểm
phân biệt đều có hoành độ nhỏ hơn 2.
4) Cho hàm số
42
33y mx m x m
. Tìm
m
để đồ thị hàm số cắt Ox tại 4 điểm phân biệt với
một điểm có hoành độ nhỏ hơn – 2 và 3 điểm kia có hoành độ lớn hơn – 1.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
26
5) Cho hàm số
42
2 2 2 3y x m x m
. Tìm m để đồ thị hàm số cắt Ox tại 4 điểm phân biệt có
hoành độ lập thành một cấp số cộng.
6) Tìm
m
để (C):
42
3 2 3y x m x m
cắt đường thẳng
1y 
tại 4 điểm phân biệt có hoành độ
2222
1 2 3 4 1 2 3 4 1 2 3 4
, , , : 4x x x x x x x x x x x x
.
7) Tìm điều kiện đối với
a
và
b
để (C):
42
y x ax
cắt đường thẳng
yb
tại 4 điểm phân biệt có
hoành độ
1 2 3 4
, , ,x x x x
(
1 2 3 4
x x x x
). Trong trường hợp này, tính tổng:
2222
1 2 3 4
xxxx
.
8) Cho hàm số
42
1 3 5
2 2 2
y x x
, (C). Tìm
m
để tiếp tuyến của (C) tại điểm M có hoành độ
0
xm
còn cắt đồ thị hàm số tại hai điểm phân biệt A, B khác M.
9) Cho hàm số
42
3 2 1 3 3y x m x m
, (C). Tìm
m
sao cho đồ thị (C):
a) Không cắt trục hoành.
b) Cắt trục hoành tại đúng hai điểm A, B sao cho
2AB
.
HÀM NHẤT BIẾN:
,0
ax b
y ad bc
cx d
1) Cho hàm số
21
2
x
y
x
, (C) và đường thẳng d:
y x m
. Tìm
m
để d cắt (C) tại hai điểm phân
biệt AB sao cho AB ngắn nhất.
2) Cho hàm số
24
1
x
y
x
, (C). Tìm
m
để đường thẳng d:
2y x m
cắt (C) tại hai điểm A, B. Khi
đó hãy tìm tập hợp trung điểm I của đoạn thẳng AB.
3) Cho hàm số
2
1
xm
y
x
, (C) và đường thẳng d:
2y mx
.
a) Tìm
m
để (C) và d cắt nhau tại hai điểm A, B phân biệt có khoảng cách đến trục hoành
bằng nhau.
b) Tính diện tích hình chữ nhật nhận A, B (ở câu a) là các đỉnh đối diện và các cạnh song
song với hai trục tọa độ. Tính diện tích hình chữ nhật này. Xác định
m
để diện tích hình
chữ nhật bằng 10.
4) Tìm
m
để đường thẳng
1
:
2
y x m
cắt đồ thị (C):
2
1
x
y
x
tại hai điểm phân biệt A, B sao
cho trung điểm của đoạn AB nằm trên đường thẳng d:
2 4 0xy
.
5) Cho hàm số
32
2
x
y
x
, (C).
a) Tìm
,ab
để đường thẳng
: 2 4y ax b
cắt (C) tại hai điểm phân biệt M, N sao cho M,
N đối xứng nhau qua O.
b) Đường thẳng
yx
cắt đồ thị (C) tại hai điểm A, B. Tìm
m
để đường thẳng
y x m
cắt
(C) tại hai điểm C, D sao cho ABCD là hình bình hành.
6) Cho hàm số
1
1
x
y
x
, (C). Xác định
m
để đường thẳng
2y x m
cắt (C) tại hai điểm phân biệt
A, B sao cho tiếp tuyến của (C) tại A và B song song nhau.
7) Cho hàm số
2
1
x
y
x
, (C). Tìm
()MC
, biết rằng tiếp tuyến với (C) tại M cắt
,Ox Oy
lần lượt tại
A và B tạo thành tam giác OAB có diện tích bằng
1
4
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế
27
8) Cho hàm số
2
22
x
y
x
, (C). Xác định
m
để đường thẳng
y x m
cắt (C) tại hai điểm phân biệt
A, B sao cho
22
37
2
OA OB
(O là gốc tọa độ).
9) Cho hàm số
1
1
x
y
x
, (C). Xác định
,ab
để đường thẳng
y ax b
cắt (C) tại hai điểm phân biệt
A, B đối xứng nhau đường thẳng
: 2 3 0xy
.
IV- TÀI LIỆU THAM KHẢO
1) Tuyển tập đề thi ĐH - CĐ toàn quốc Bộ giáo dục và đào tạo
2) Phương pháp hàm số Lê Hồng Đức
3) Tuyển tập đề thi thử ĐH trên toàn quốc
4) Tạp chí Toán học và Tuổi trẻ NXB Giáo dục Việt Nam
5) Các bài viết chuyên đề từ các website Toán học
P/S: Các bài tập trong tài liệu chưa nhận được sự cho phép của quí thầy cô và các cơ quan liên quan,
nhưng tài liệu biên soạn chỉ với mục đích chia sẽ cho đồng nghiệp và tặng cho các em học sinh có
nguồn tư liệu quí để phục vụ khả năng tự học nên chúng tôi xin phép các tác giả, xin cảm ơn các tác
giả!
Trong quá trình biên soạn không thể tránh khỏi sai sót, kính mong quí thầy cô và các em học sinh đóng
góp để các bản update tiếp theo được hoàn thiện hơn! Xin chân thành cám ơn!
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 1
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
Chuyên đề: KH¶O S¸T HµM Sè
Chủ đề 5: Sù T¦¥NG GIAO
Môn: TOÁN 12 _GIẢI TÍCH
I- LÝ THUYẾT
Giả sử (C) và (C’) là đồ thị của hai hàm số:
vµ y f x y g x
.
Hoành độ giao điểm của (C) và (C’), nếu có,
là nghiệm của phương trình
f x g x
(1)
Lưu ý: Phương trình
f x g x
là phương trình hoành độ
giao điểm của (C) và (C’).
Đảo lại, nếu
0
x
là nghiệm của (1), tức là:
00
f x g x
thì điểm
hay
0 0 0 0
;;M x f x M x g x
là điểm chung của (C) và (C’).
Kết quả:
- Nếu (1) vô nghiệm thì (C) và (C’) không có điểm chung.
- Nếu (1) có
n
nghiệm thì (C) cắt (C’) tại
n
điểm phân biệt (
n
không là nghiệm bội).
Dạng toán: Tìm giao điểm và tính chất giao điểm của hai đồ thị
vµ y f x y g x
Phương pháp:
Bước 1: Thiết lập phương trình hoành độ giao điểm của (C) và (C’):
f x g x
(1)
Bước 2: Biện luận số nghiệm và tính chất nghiệm của (1).
Nhận xét: Rõ ràng hoành độ giao điểm của (C) và (C’) là nghiệm của (1) nên số giao điểm và tính chất
giao điểm cũng là số nghiệm và tính chất nghiệm của (1). Điều này, đưa yêu cầu từ tính chất đồ thị sang
việc biện luận phương trình sơ cấp mà chúng ta đã biết.
II. BÀI TẬP TRẮC NGHIỆM
DẠNG 1: TÌM GIAO ĐIỂM – SỐ GIAO ĐIỂM – TÍNH CHẤT GIAO ĐIỂM
Câu 1: Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm của phương trình
20fx
là
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 2: Cho hàm số
y f x
liên tục trên đoạn
2;2


và có đồ thị như hình vẽ bên dưới:
O
x
y
1
1
1
3
1
2
2
x
y
M
y
0
x
0
O
(C)
(C')
1
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 2
Số nghiệm của phương trình
3 4 0fx
trên đoạn
2;2


là
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 3: Số giao điểm của đồ thị hàm số
22
.4y x x
với đường thẳng
3y
là
A.
8
. B.
2
. C.
4
. D.
6
.
Câu 4: Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm của phương trình
2 3 0fx
là
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 5: Biết rằng đường thẳng
22yx
cắt đồ thị hàm số
3
2y x x
tại một điểm duy nhất, ký
hiệu
00
;xy
là tọa độ điểm đó. Tìm
0
y
.
A.
0
4y
. B.
0
0y
. C.
0
2y
. D.
0
1y
.
Câu 6: Đồ thị hàm số
3
32y x x
cắt trục tung tại điểm có tọa độ là
A.
1;0
. B.
0; 2
. C.
0;2
. D.
2;0
.
Câu 7: Biết đường thẳng
2yx
cắt đồ thị hàm số
21
1
x
y
x
tại hai điểm phân biệt
,AB
có hoành độ
lần lượt
,
AB
xx
. Khi đó giá trị của
AB
xx
bằng
A.
5
. B.
3
. C.
1
. D.
2
.
Câu 8: Đồ thị của hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
A.
23
.
1
x
y
x

B.
23
.
31
x
y
x
C.
41
.
2
x
y
x
D.
4
.
1
x
y
x

Câu 9: Biết rằng đường thẳng
45yx
cắt đồ thị hàm số
3
21y x x
tại điểm duy nhất; kí hiệu
00
;xy
là tọa độ của điểm đó. Tìm
0
y
.
A.
0
10y
. B.
0
13y
. C.
0
11y
. D.
0
12y
.
Câu 10: Đồ thị hàm số
32
22y x x x
cắt parabol
2
6 4 4y x x
tại một điểm duy nhất. Kí hiệu
00
;xy
là tọa độ điểm đó. Tính giá trị của biểu thức
00
xy
.
A.
1.
B.
1.
C.
22.
D.
4.
Câu 11: Đường thẳng
có phương trình
21yx
cắt đồ thị của hàm số
3
3y x x
tại hai điểm
A
và
B
với tọa độ được kí hiệu lần lượt là
;
AA
A x y
và
;
BB
B x y
trong đó
BA
xx
. Tính
.
BB
xy
A.
5.
BB
xy
B.
2.
BB
xy
C.
4.
BB
xy
D.
7.
BB
xy
Câu 12: Tính tổng hoành độ của các giao điểm của đồ thị hàm số
56
2
x
y
x
và đường thẳng
yx
.
A.
7
. B.
5
. C.
5
. D.
7
.
Câu 13: Cho hàm số
3
3y x x
có đồ thị hàm số là
C
. Tìm số giao điểm của
C
và trục hoành.
A.
2.
B.
3.
C.
1
. D.
0
.
Câu 14: Cho hàm số
2
21y x x
có đồ thị
C
. Mệnh đề nào dưới đây đúng?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 3
A.
C
cắt trục hoành tại hai điểm. B.
C
cắt trục hoành tại một điểm.
C.
C
không cắt trục hoành. D.
C
cắt trục hoành tại ba điểm.
Câu 15: Đồ thị của hàm số
42
22y x x
và đồ thị của hàm số
2
4yx
có tất cả bao nhiêu điểm
chung?
A.
0
. B.
4
. C.
1
. D.
2
.
Câu 16: Tìm số giao điểm
n
của đồ thị hàm số
42
83y x x
và đường thẳng
10y
.
A.
0n
. B.
4n
. C.
2n
. D.
3n
.
Câu 17: Tọa độ tất cả các giao điểm của đồ thị hàm số
42
1y x x
và đường thẳng
1y 
là
A.
0; 1 , 1; 1
. B.
1; 1 ; 1; 1
.
C.
0; 1 , 1;1
. D.
0; 1 , 1; 1 , 1; 1
.
Câu 18: Cho hàm số
()y f x
có bảng biến thiên như hình vẽ sau:
Số nghiệm của phương trình
( ) 1fx
là
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 19: Cho hàm số
3
31f x x x
. Tìm số nghiệm của phương trình
0f f x
.
A.
5
. B.
9
. C.
4
. D.
7
.
Câu 20: Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ. Tập hợp nghiệm của phương
trình
10f f x 
có bao nhiêu phần tử?
A.
4
. B.
7
. C.
6
. D.
9
.
Câu 21: Cho hàm số
y f x
liên tục trên các khoảng
( ; 2); 2; 
và có bảng biến thiên như sau:
Số nghiệm thực của phương trình
2
2 3 0f x f x
là
A.
2
. B.
1
. C.
0
. D.
4
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 4
Câu 22: Cho hàm số
32
()y f x ax bx cx d
có đồ thị như hình vẽ bên dưới.
Tập nghiệm của phương trình
( ) ( ) 4 0f x f x



là
A.
{ 1;0;1;2;3}
. B.
{ 1;2}
. C.
{0;3}
. D.
{ 1;0;2;3}
.
Câu 23: Cho hàm số
32
( ) , ( 0)y f x ax bx cx d a
có đồ thị như hình vẽ bên dưới:
Phương trình
0f f x
có bao nhiêu nghiệm thực?
A.
3
. B.
7
. C.
9
. D.
5
.
Câu 24: Cho hàm số
y f x
liên tục trên có đồ thị như hình vẽ bên dưới:
Phương trình
3 2 1f f x
có tất cả bao nhiêu nghiệm thực phân biệt?
A.
6
. B.
5
. C.
7
. D.
4
.
Câu 25: Cho hàm số
y f x
liên tục trên có đồ thị như hình bên dưới:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 5
Phương trình
10f f x 
có tất cả bao nhiêu nghiệm thực phân biệt?
A. 6. B. 5. C. 7. D. 4.
Câu 26: Cho hàm số
y f x
xác định trên và có bảng biến thiên như sau:
x

-1 1

y
0
0
y
1


-1
Số nghiệm của phương trình
2
22f x x
là
A.
4
. B.
2
. C.
3
. D.
8
.
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình
3
1
3
2
f x x
là
A.
6
. B.
10
. C.
12
. D.
3
.
Câu 28: Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình
42
22f x x
là
A.
8
. B.
9
. C.
7
. D.
10
.
Câu 29: Cho hàm số
fx
có bảng biến thiên như sau:
Số nghiệm của phương trình
là
A.
4
. B.
5
. C.
6
. D.
3
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 6
Câu 30: Cho hàm số
y f x
có đồ thị như hình vẽ:
Khi đó phương trình
4
4 3 3 0fx
có bao nhiêu nghiệm dương?
A. 2. B. 4. C. 5. D. 1.
Câu 31: Cho hàm số
y f x
có đồ thị như hình vẽ sau:
Số nghiệm của phương trình
2 sin 1 0fx
trên đoạn
5
;
22




là
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 32: Cho hàm số
fx
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
7
0;
3



của phương trình
2. cos 5 0fx
là
A.
8
. B.
7
. C.
5
. D.
6
.
Câu 33: Cho hàm số
y f x
có đồ thị như hình vẽ.
Số nghiệm thuộc đoạn
0;5


của phương trình
cos 1fx
A.
3
. B.
4
. C.
5
. D.
6
.
O
1
1
1
1
x
y
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 7
Câu 34: Cho hàm số
fx
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;5


của phương trình
sin 1fx
là
A.
6
. B.
4
. C.
10
. D.
8
.
Câu 35: Cho hàm số
y f x
có bảng biến thiên như hình vẽ sau:
x

0
1
2

fx
0
0
0
fx

0
3
1

Số nghiệm của phương trình
sin 1 2fx
trên
;2



là
A. 6. B. 7. C. 5. D. 4.
Câu 36: Cho hàm số
y f x
có bảng biến thiên như hình vẽ dưới đây:
x

1
1
2

fx
0
0
0
fx

1
1
2

Số nghiệm thuộc đoạn
3
;
22




của phương trình
cot 1 1fx
là
A. 7. B. 6. C. 8. D. 5.
Câu 37: Cho hàm số
y f x
có đồ thị như hình vẽ sau:
Số nghiệm thuộc đoạn
0;3


của phương trình
2 cos 1 0fx
là
A.
12
. B.
6
. C.
10
. D.
8
.
Câu 38: Cho hàm số
fx
có bảng biến thiên như sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 8
Số nghiệm thuộc khoảng
;

của phương trình
2
cos cos 2f x f x
là
A.
5
. B.
6
. C.
7
. D.
9
.
Câu 39: Cho hàm số
fx
liên tục trên có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
;



của phương trình
2
2cos 3 3fx
là
A.
8
. B.
2
. C.
6
. D.
4
.
Câu 40: Cho hàm số
fx
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
5
;3
6



của phương trình
cos24 1 0fx
là
A.
5
. B.
9
. C.
4
. D.
10
.
Câu 41: Cho hàm số trùng phương
y f x
có đồ thị như hình vẽ bên dưới:
Số nghiệm thuộc
0;2
của phương trình
cos2 1fx
bằng
A.
4
. B.
6
. C.
3
. D.
8
.
Câu 42: Cho hàm số
y f x
xác định trên và có bảng biến thiên như sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 9
Số nghiệm thuộc đoạn
0;


của phương trình
cos2 0f f x
là
A.
4
. B.
2.
C.
3.
D.
8.
Câu 43: Cho hàm số
42
, ; ; , 0y ax bx c a b c a
có bảng biến thiên như hình vẽ:
x

2
0
2

y
0
0
0
y

2
2
2

Số nghiệm của phương trình
42
0a f x b f x c
là
A.
11.
B.
10.
C.
9.
D.
12.
Câu 44: Cho hàm số
y f x
xác định, liên tục trên và có bảng biến thiên như hình vẽ:
x

1
4
0
2

y
0
0
0
y

2
2
4

Số nghiệm thuộc đoạn
5
;
22




của phương trình
2
5 cos cos 1f x x
là
A.
11.
B.
10.
C.
9.
D.
12.
Câu 45: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ sau:
Số nghiệm của phương trình
sin cos 2 0f x x
trên đoạn
0;2


là
A.
5.
B.
4.
C.
3.
D.
2.
Câu 46: Cho hàm số
32
f x ax bx bx c
có đồ thị như hình vẽ:
x
–∞
1
0
1
+∞
y
+
0
–
0
+
0
–
y

1
0
1

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 10
Số nghiệm nằm trong
;3
2



của phương trình
cos 1 cos 1f x x
là
A.
2
. B.
3
. C. 5. D. 4.
Câu 47: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt
của phương trình
3
10f x f x 
là
A.
8
. B.
5
. C.
6
. D.
4
.
Câu 48: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình
3
10f x f x 
là
A.
6
. B.
4
. C.
5
. D.
8
.
Câu 49: Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân
biệt của phương trình
2
2f x f x
là
A.
8
. B.
12
. C.
6
. D.
9
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 11
Câu 50: Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình
2
20f x f x 
là
A.
6
. B.
12
. C.
8
. D.
9
.
Câu 51: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt
của phương trình
5
20f x f x 
là
A.
8
. B.
5
. C.
6
. D.
4
.
Câu 52: Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt
của phương trình
2
2 3 0f x f x
là
A.
8
. B.
6
. C.
9
. D.
12
.
Câu 53: Cho hàm số
y f x
có đồ thị như hình vẽ sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 12
Số nghiệm thực của phương trình
0f f x f x
là
A.
20
. B.
24
. C.
10
. D.
4
.
DẠNG 2: BÀI TOÁN THAM SỐ
Câu 54: Cho hàm số
y f x
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
Tìm tập hợp tất cả các giá trị của tham số thực
m
sao cho phương trình
f x m
có ba nghiệm
thực phân biệt.
A.
1;2


. B.
1;2
. C.
1;2
. D.
;2

.
Câu 55: Cho hàm số
42
2y x x
có đồ thị như hình bên dưới:
Tìm tất cả các giá trị thực của tham số
m
để phương trình
42
2x x m
có bốn nghiệm thực
phân biệt
A.
0m
. B.
01m
. C.
01m
. D.
1m
.
Câu 56: Cho hàm số
()y f x
có bảng biến thiên như sau:
Tập tất cả các giá trị của tham số m để phương trình
()f x m
có ba nghiệm phân biệt là
A.
(4; )
. B.
( ; 2)
. C.
2;4 .


D.
( 2;4)
.
Câu 57: Tìm tất cả các giá trị của tham số
m
để phương trình
32
32x x m
có ba nghiệm phân biệt.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 13
A.
2;m

. B.
;2m

. C.
2;2m
. D.
2;2m



.
Câu 58: Tìm
m
để đồ thị hàm số
4 2 2
21y x mx m
cắt trục hoành tại
4
điểm phân biệt.
A.
1m
. B.
11m
. C.
1m 
. D.
1
1
m
m

.
Câu 59: Cho hàm số
42
23y x x
có đồ thị hàm số như hình bên dưới. Với giá trị nào của tham số
m
phương trình
42
2 3 2 4x x m
có hai nghiệm phân biệt?
A.
0
1
2
m
m
. B.
1
0
2
m
. C.
0
1
2
m
m
. D.
1
2
m
.
Câu 60: Hàm số
,,a b c
có bảng biến thiên
Có bao nhiêu số nguyên
m
để phương trình
3f x m
có đúng 8 nghiệm phân biệt?
A. Vô số. B. 1. C. 4. D. 2.
Câu 61: Cho hàm số
y f x
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
Tất cả giá trị của tham số thực
m
sao cho đồ thị của hàm số
y f x m
cắt trục
Ox
tại ba
điểm phân biệt là
A.
2;1
. B.
1;2
. C.
1;2
. D.
2;1
.
Câu 62: Cho hàm số
()y f x
xác định, liên tục trên và có bảng biến thiên như sau:
Tìm tất cả các giá trị thực của
m
để phương trình
( ) 1f x m
có đúng hai nghiệm.
A.
0, 1mm
. B.
21m
. C.
1, 2mm
. D.
1, 2mm
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 14
Câu 63: Đường cong trong hình vẽ là đồ thị của hàm số
42
22y x x
. Tìm tất cả các giá trị thực của
tham số
m
để phương trình
42
2x x m
có 4 nghiệm phân biệt.
A.
2m 
. B.
10m
. C.
3m 
. D.
32m
.
Câu 64: Cho hàm số
y f x
xác định trên
\1
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình vẽ sau:
Số giá trị nguyên của tham số
m
để phương trình
f x m
có 3 nghiệm phân biệt là
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 65: Cho hàm số
y f x
có bảng biến thiên như sau:
Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
0f x m
có hai nghiệm phân
biệt là
A.
;2
. B.
1;2
. C.
1;2
. D.
2;
.
Câu 66: Cho hàm số
3
32y x x
có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị thực của tham số m để phương trình
có ba nghiệm
thực phân biệt.
A.
04m
. B.
02m
. C.
04m
. D.
02m
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 15
Câu 67: Cho hàm số
32
3f x x x
. Tính tổng tất cả các giá trị nguyên của
m
để đồ thị hàm số
g x f x m
cắt trục hoành tại 4 điểm phân biệt.
A. 3. B. 10. C. 4. D. 6.
Câu 68: Cho hàm số
y f x
có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên
m
để phương trình
3
3f x x m
có
6
nghiệm phân biệt thuộc đoạn
[ 1;2]
?
A.
3
. B.
2
. C.
6
. D.
7
.
Câu 69: Tìm tất cả các giá trị của tham số
m
để phương trình
32
1
cos 3cos 5 cos 3 2 0
3
x x x m
có
đúng bốn nghiệm thuộc đoạn
0;2 .


A.
31
.
23
m
B.
13
.
32
m
C.
13
.
32
m
D.
31
.
23
m
Câu 70: Cho đồ thị của hàm số
32
6 9 2y x x x
như hình vẽ.
Khi đó phương trình
32
6 9 2x x x m
(
m
là tham số) có 6 nghiệm phân biệt khi và chỉ khi.
A.
22m
. B.
02m
. C.
02m
. D.
22m
.
Câu 71: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ.
y
=
f
(
x
)
-4
y
x
O
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
3sin cos 1
44
2cos sin 4
xx
f f m m
xx





1
có nghiệm?
A.
3
. B.
4
. C.
5
. D. Vô số.
O
x
y
3
2
1
2
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 16
Câu 72: Cho hàm số
y f x
liên tục trên có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của
n
để phương trình
2
16cos 6sin2 8 1f x x f n n
có
nghiệm
x
?
A.
10
. B.
4
. C.
8
. D.
6
.
Câu 73: Cho hàm số
y f x
có đồ thị như hình vẽ.
Có bao nhiêu số nguyên
m
để phương trình
1
1
32
x
f x m



có nghiệm thuộc đoạn
2;2


?
A.
11
. B.
9
. C.
8
. D.
10
.
Câu 74: Cho hàm số
y f x
có bảng biến thiên dưới đây:
Để phương trình
3 2 1 2f x m
có 3 nghiệm phân biệt thuộc
0;1


thì giá trị của tham số m
thuộc khoảng nào dưới đây?
A.
;3
. B.
1;6
. C.
6;
. D.
3;1
.
Câu 75: Cho hàm số
()fx
liên tục trên và có đồ thị như hình vẽ. Số giá trị nguyên của tham số
m
để
phương trình
22
3 4 6 9 1 0f x x m
có nghiệm là
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 17
A.
6
. B.
4
. C.
5
. D.
7
.
Câu 76: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ. Tập hợp các giá trị thực của
tham số
m
để phương trình
2
41f x m
có nghiệm là
A.
2;0 .


B.
4; 2 .



C.
4;0 .


D.
1;1 .


Câu 77: Cho hàm số bậc ba
32
y f x ax bx cx d
có đồ thị như hình bên dưới.
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
5 4 4 0f x m f x m
có
7 nghiệm phân biệt?
A. 1. B. 2. C. 3. D. 4.
Câu 78: Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
( ) :d y x m
cắt đồ thị
1
(C) :
1
x
y
x
tại 2 điểm phân biệt
,AB
sao cho
2 6.AB
A.
2; 2mm
. B.
4; 4mm
. C.
2m
. D.
4m
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 18
Câu 79: Có bao nhiêu giá trị nguyên của tham số
m
để đường thẳng
y x m
cắt đồ thị hàm số
2
1
x
y
x
tại hai điểm phân biệt
A
,
B
sao cho
4?OA OB
A. 2. B. 1. C. 0. D. 3.
Câu 80: Tìm giá trị thực của tham số
m
để đường thẳng
:2d y x m
cắt đồ thị hàm số
2
1
x
y
x
C
tại hai điểm phân biệt
A
và
B
sao cho độ dài
AB
ngắn nhất.
A.
3.m 
B.
3.m
C.
1.m
D.
1.m 
Câu 81: Cho hàm số
32
3 1.f x x x mx
Gọi
S
là tổng tất cả giá trị của tham số
m
để đồ thị hàm số
y f x
cắt đường thẳng
1y
tại ba điểm phân biệt
0;1 ,A
,B
C
sao cho các tiếp tuyến của
đồ thị hàm số
y f x
tại
,B
C
vuông góc với nhau. Gía trị của
S
bằng
A.
9
.
2
B.
9
.
5
C.
9
.
4
D.
11
.
5
Câu 82: Có bao nhiêu giá trị nguyên của tham số
2018;2019m



để đồ thị hàm số
3
33y x mx
và
đường thẳng
31yx
có duy nhất một điểm chung?
A.
1
. B.
2019
. C.
4038
. D.
2018
.
Câu 83: Có bao nhiêu giá trị thực của tham số
m
để phương trình
1 2 0x x x m
có
3
nghiệm
phân biệt lập thành cấp số nhân tăng?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 84: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để phương trình
32
2 3 2 1x x m
có đúng
hai nghiệm phân biệt. Tổng các phần tử của
S
bằng
A.
1
2
. B.
3
2
. C.
5
2
. D.
1
2
.
Câu 85: Giá trị
k
thỏa mãn đường thẳng
:d y kx k
cắt đồ thị
H
:
4
y
22
x
x
tại 2 điểm phân biệt
A
và
B
cùng cách đều đường thẳng
0y
. Khi đó
k
thuộc khoảng
A.
2; 1
. B.
1;2
. C.
1;0
. D
0;1
.
Câu 86: Cho hàm số
1
x
y
x
C
và đường thẳng
:d y x m
. Gọi
S
là tập hợp các số thực
m
để
đường thẳng
d
cắt đồ thị
C
tại hai điểm phân biệt
,AB
sao cho tam giác
OAB
(
O
là gốc tọa
độ) có bán kính đường tròn ngoại tiếp bằng
22
. Tổng các phần tử của
S
bằng
A. 8. B.
4
. C.
1
. D.
2
.
Câu 87: Cho hàm số
42
3 2 3y x m x m
có đồ thị là
()
m
C
. Tìm
m
để đường thẳng
:1dy
cắt đồ
thị
()
m
C
tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2.
A.
1
1
3
m
và
0m
B.
1
1
2
m
và
0m
C.
11
22
m
và
0m
D.
11
32
m
và
0m
Câu 88: Cho hai hàm số
2
1y x x
và
32
23y x x mx
. Giá trị của tham số
m
để đồ thị của hai
hàm số có
3
giao điểm phân biệt và
3
giao điểm đó nằm trên đường tròn bán kính bằng
3
thuộc vào khoảng nào dưới đây?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 19
A.
;4
. B.
4; 2
. C.
0;
. D.
2;0
.
Câu 89: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá
trị thực của tham số
m
để phương trình
sinf x m
có nghiệm thuộc khoảng
0;
là
A.
1;3
. B.
1;1
. C.
1;3
. D.
1;1
.
Câu 90: Cho hàm số
y f x
liên tục trên và có bảng biến thiên như hình vẽ sau:
Tập hợp các giá trị
m
để phương trình
cos2 2 1 0f x m
có nghiệm thuộc
;
34




là
A.
1
0; .
2



B.
1
0; .
2


C.
11
;.
42


D.
2 2 1
;.
44





Câu 91: Cho hàm số
()y f x
xác định, liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của
m
để phương trình
2
2. 3 4 6 9 3f x x m
có nghiệm.
A.
13
. B.
12
. C.
8
. D.
10
.
Câu 92: Cho hàm số
y f x
xác định trên và có đồ thị như hình bên. Có bao nhiêu giá trị nguyên
của tham số
m
để phương trình:
44
4 sin cosf x x m



có nghiệm.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 20
A.
2
. B.
4
. C.
3
. D.
5
.
Câu 93: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
tham số
m
để phương trình
sinf f x m
có nghiệm thuộc khoảng
0;
.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 94: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ. Gọi
S
là tập hợp tất cả các giá
trị nguyên của tham số
m
để phương trình
sin 3sinf x x m
có nghiệm thuộc khoảng
0;
. Tổng các phần tử của
S
bằng
A.
8
. B.
10
. C.
6
. D.
5
.
Câu 95: Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 21
Tìm số giá trị nguyên của
m
để phương trình
2
2f x x m
có đúng
4
nghiệm thực phân biệt
thuộc đoạn
37
;
22



.
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 96: Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây:
Tồn tại bao nhiêu giá trị nguyên của tham số
m
để phương trình
sinf x m
có đúng hai
nghiệm thuộc đoạn
0;


?
A.
4
. B.
7
. C.
5
. D.
6
.
Câu 97: Cho hàm số
fx
là đa thức và có đồ thị như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
sin 2
4 8 17
x
f f m m
có
nghiệm?
A.
3.
B.
4.
C.
5.
D.
6.
Câu 98: Cho hàm số
y f x
liên tục trên có đồ thị như hình vẽ bên dưới.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 22
Tìm
m
để phương trình

2
2f x x m
có đúng
6
nghiệm thực phân biệt thuộc đoạn



37
;
22
?
A.
23m
hoặc
45fm
. B.
23m
hoặc
45fm
.
C.
23m
hoặc
45fm
. D.
23m
hoặc
45fm
.
Câu 99: Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
1y mx m
cắt đồ thị của hàm số
32
32y x x x
tại ba điểm
A
,
B
,
C
phân biệt sao cho
.AB BC
A.
[( ;0) 4; ).m  
B.
.m
C.
5
;.
4
m




D.
( 2; ).m 
Câu 100: Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
y mx
cắt đồ thị của hàm số
32
32y x x m
tại ba điểm phân biệt A, B, C sao cho
AB BC
.
A.
;3m 
. B.
;1m 
. C.
;m  
. D.
1;m 
.
Câu 101: Cho hàm số
4 3 2
f x mx nx px qx r
, (với
, , , ,m n p q r
). Hàm số
y f x
có đồ thị như
hình vẽ bên dưới:
Tập nghiệm của phương trình
f x r
có số phần tử là
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 102: Cho hàm số
4 3 2
f x ax bx cx dx m
, (với
, , , ,a b c d m
). Hàm số
y f x
có đồ thị như
hình vẽ bên dưới:
Tập nghiệm của phương trình
f x m
có số phần tử là
A.
1
. B.
2
. C.
3
. D.
4
.
__________________________HẾT__________________________
Huế, ngày 16 tháng 7 năm 2023
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 23
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
Chuyên đề: KH¶O S¸T HµM Sè
Chủ đề 5: Sù T¦¥NG GIAO
Môn: TOÁN 12 _GIẢI TÍCH
LỜI GIẢI CHI TIẾT
DẠNG 1: TÌM GIAO ĐIỂM – SỐ GIAO ĐIỂM – TÍNH CHẤT GIAO ĐIỂM
Câu 1: Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm của phương trình
20fx
là
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải:
Ta có:
2 0 2f x f x
. Do
2 2;4
nên phương trình đã cho có
3
nghiệm phân biệt.
Chọn đáp án B.
Câu 2: Cho hàm số
y f x
liên tục trên đoạn
2;2


và có đồ thị như hình vẽ bên dưới:
Số nghiệm của phương trình
3 4 0fx
trên đoạn
2;2


là
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải:
y
x
y=
4
3
3
-1
-2
-1
2
1
O
Ta có:
4
3 4 0
3
f x f x
.
O
x
y
1
1
1
3
1
2
2
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 24
Suy ra số nghiệm của phương trình trên đoạn
2;2


bằng số giao điểm của đồ thị
y f x
với đường thẳng
4
3
y
trên đoạn
2;2


.
Dựa vào đồ thị ta thấy số giao điểm của đồ thị
y f x
với đường thẳng
4
3
y
trên đoạn
2;2


là 3 điểm. Vậy số nghiệm của phương trình
3 4 0fx
trên đoạn
2;2


là 3 nghiệm.
Chọn đáp án A.
Câu 3: Số giao điểm của đồ thị hàm số
22
.4y x x
với đường thẳng
3y
là
A.
8
. B.
2
. C.
4
. D.
6
.
Lời giải:
Dựa vào đồ thị ở hình vẽ trên ta thấy, số giao điểm của đồ thị hàm số
22
.4y x x
với đường
thẳng
3y
là
6
.
Chọn đáp án D.
Câu 4: Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm của phương trình
2 3 0fx
là
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải:
Ta có
2 3 0fx
3
2
fx
.
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số
y f x
và đường
thẳng
3
2
y 
.
Dựa vào bảng biến thiên ta thấy
3
21
2
C CĐT
yy
.
Vậy phương trình
2 3 0fx
có 4 nghiệm phân biệt.
Chọn đáp án A.
Câu 5: Biết rằng đường thẳng
22yx
cắt đồ thị hàm số
3
2y x x
tại một điểm duy nhất, ký
hiệu
00
;xy
là tọa độ điểm đó. Tìm
0
y
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 25
A.
0
4y
. B.
0
0y
. C.
0
2y
. D.
0
1y
.
Lời giải:
Phương trình hoành độ giao điểm là:
33
2 2 2 3 0x x x x x
2
3 0 0.x x x
Do
00
02xy
.
Chọn đáp án C.
Câu 6: Đồ thị hàm số
3
32y x x
cắt trục tung tại điểm có tọa độ là
A.
1;0
. B.
0; 2
. C.
0;2
. D.
2;0
.
Lời giải:
Thế
0x
vào hàm số
3
32y x x
ta được
2y 
.
Vậy đồ thị hàm số
3
32y x x
cắt trục tung tại điểm có tọa độ là
0; 2
.
Chọn đáp án B.
Câu 7: Biết đường thẳng
2yx
cắt đồ thị hàm số
21
1
x
y
x
tại hai điểm phân biệt
,AB
có hoành độ
lần lượt
,
AB
xx
. Khi đó giá trị của
AB
xx
bằng
A.
5
. B.
3
. C.
1
. D.
2
.
Lời giải:
Phương trình hoành độ giao điểm của đường thẳng
2yx
và đồ thị hàm số
21
1
x
y
x
là
21
2 2 1 2 1
1
x
x x x x
x
22
3 2 2 1 5 1 0 (*)x x x x x
Ta có
,
AB
xx
là nghiệm của phương trình (*), theo định lí Viét ta có
5.
AB
xx
Chọn đáp án A.
Câu 8: Đồ thị của hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
A.
23
.
1
x
y
x

B.
23
.
31
x
y
x
C.
41
.
2
x
y
x
D.
4
.
1
x
y
x

Lời giải:
Cho
0x
thay vào các hàm số trên ta thấy chỉ có hàm số ở đáp án D là được
40y
.
Chọn đáp án D.
Câu 9: Biết rằng đường thẳng
45yx
cắt đồ thị hàm số
3
21y x x
tại điểm duy nhất; kí hiệu
00
;xy
là tọa độ của điểm đó. Tìm
0
y
.
A.
0
10y
. B.
0
13y
. C.
0
11y
. D.
0
12y
.
Lời giải:
Phương trình hoành độ giao điểm là
33
2 1 4 5 2 4 0 2x x x x x x
Với
2 13xy
. Vậy
0
13y
.
Chọn đáp án B.
Câu 10: Đồ thị hàm số
32
22y x x x
cắt parabol
2
6 4 4y x x
tại một điểm duy nhất. Kí hiệu
00
;xy
là tọa độ điểm đó. Tính giá trị của biểu thức
00
xy
.
A.
1.
B.
1.
C.
22.
D.
4.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 26
Ta có
0
x
là nghiệm của phương trình:
3 2 2
2 2 6 4 4x x x x x
3 2 2
2 5 5 6 0 ( 2)(2 3) 0x x x x x x
0
2x
.
Với
0
2x 
0
20y
. Vậy
00
22xy
.
Chọn đáp án C.
Câu 11: Đường thẳng
có phương trình
21yx
cắt đồ thị của hàm số
3
3y x x
tại hai điểm
A
và
B
với tọa độ được kí hiệu lần lượt là
;
AA
A x y
và
;
BB
B x y
trong đó
BA
xx
. Tính
.
BB
xy
A.
5.
BB
xy
B.
2.
BB
xy
C.
4.
BB
xy
D.
7.
BB
xy
Lời giải:
Hoành độ giao điểm là nghiệm của phương trình:
3
3 2 1x x x
Giải phương trình ta được
1
.
2
x
x
Vì
BA
xx
Vậy
1; 3
BB
xy
4.
BB
xy
Chọn đáp án C.
Câu 12: Tính tổng hoành độ của các giao điểm của đồ thị hàm số
56
2
x
y
x
và đường thẳng
yx
.
A.
7
. B.
5
. C.
5
. D.
7
.
Lời giải:
Xét phương trình hoành độ giao điểm:
56
2
x
x
x

(với
2x 
)
5 6 2x x x
2
7 6 0xx
1
6
x
x


.
Khi đó tổng hoành độ của các giao điểm là:
7
.
Chọn đáp án A.
Câu 13: Cho hàm số
3
3y x x
có đồ thị hàm số là
C
. Tìm số giao điểm của
C
và trục hoành.
A.
2.
B.
3.
C.
1
. D.
0
.
Lời giải:
Xét phương trình hoành độ giao điểm:
3
30xx
2
30xx
0
3
3
x
x
x

`
Vậy có ba giao điểm.
Chọn đáp án B.
Câu 14: Cho hàm số
2
21y x x
có đồ thị
C
. Mệnh đề nào dưới đây đúng?
A.
C
cắt trục hoành tại hai điểm. B.
C
cắt trục hoành tại một điểm.
C.
C
không cắt trục hoành. D.
C
cắt trục hoành tại ba điểm.
Lời giải:
Ta có:
2
2 1 0 2 0x x x
(vì
2
1 0;xx
)
2x
.
C
cắt trục hoành tại một điểm.
Chọn đáp án B.
Câu 15: Đồ thị của hàm số
42
22y x x
và đồ thị của hàm số
2
4yx
có tất cả bao nhiêu điểm
chung?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 27
A.
0
. B.
4
. C.
1
. D.
2
.
Lời giải:
Xét phương trình hoành độ giao điểm:
4 2 2 4 2
2
2 2 4 2 0
2
x
x x x x x
x

.
Vậy hai đồ thị có tất cả 2 giao điểm.
Chọn đáp án D.
Câu 16: Tìm số giao điểm
n
của đồ thị hàm số
42
83y x x
và đường thẳng
10y
.
A.
0n
. B.
4n
. C.
2n
. D.
3n
.
Lời giải:
Xét phương trình hoành độ giao điểm:
4 2 4 2
8 3 10 8 7 0 4 23x x x x x
.
Vậy hai đồ thị có hai giao điểm.
Chọn đáp án C.
Câu 17: Tọa độ tất cả các giao điểm của đồ thị hàm số
42
1y x x
và đường thẳng
1y 
là
A.
0; 1 , 1; 1
. B.
1; 1 ; 1; 1
.
C.
0; 1 , 1;1
. D.
0; 1 , 1; 1 , 1; 1
.
Lời giải:
Phương trình hoành độ giao điểm:
42
11xx
42
0xx
2
0x
,
2
1x
0, 1xx
.
Suy ra toạ độ các giao điểm là
0; 1 , 1; 1 , 1; 1
.
Chọn đáp án D.
Câu 18: Cho hàm số
()y f x
có bảng biến thiên như hình vẽ sau:
Số nghiệm của phương trình
( ) 1fx
là
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải:
Số nghiệm của phương trình
( ) 1fx
chính là số giao điểm của đồ thị hàm số
()y f x
và
đường thẳng
1y 
. Nhìn BBT trên ta thấy đường thẳng
1y 
cắt đồ thị hàm số
()y f x
tại 2
điểm. Vậy phương trình đã cho có 2 nghiệm.
Chọn đáp án B.
Câu 19: Cho hàm số
3
31f x x x
. Tìm số nghiệm của phương trình
0f f x
.
A.
5
. B.
9
. C.
4
. D.
7
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 28
Xét phương trình
3
0 3 1 0f x x x
dùng máy tính cầm tay ta ước lượng được phương
trình có ba nghiệm và
1
2
3
1,879
1,532
0,347
x
x
x

.
Xét hàm số
3
31f x x x
, ta có bảng biến thiên của
fx
như sau:
Xét phương trình
01f f x
ta ước lượng được
1,879
1,532
0,347
fx
fx
fx

.
Dựa vào bảng biến thiên của hàm số
fx
ta có:
+ Với
1,879fx
phương trình
1
có
1
nghiệm.
+ Với
1,532fx
phương trình
1
có
3
nghiệm.
+ Với
0,347fx
phương trình
1
có
3
nghiệm.
Chọn đáp án D.
Câu 20: Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ. Tập hợp nghiệm của phương
trình
10f f x 
có bao nhiêu phần tử?
A.
4
. B.
7
. C.
6
. D.
9
.
Lời giải:
Dựa vào đồ thị ta có
10f f x 
1f f x 
2
2; 1
0
2
f x a
f x b
fx
f x c

.
+ Với
2f x a
1
2
2
2
xx
xx

.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 29
+ Với
2; 1f x b
3
4
5
6
2
2; 1
1;0
2
xx
xx
xx
xx

.
+ Với
0fx
7
8
9
2
0;1
2;3
xx
xx
xx

.
+ Với
2f x c
vô nghiệm.
Ta thấy hàm số
y f x
đơn điệu trên
;2
,
13
f x a b f x
nên
13
xx
.
Hàm số
y f x
đơn điệu trên
2;
,
69
0f x b f x
nên
69
xx
.
Vậy phương trình đã cho có 9 nghiệm phân biệt.
Chọn đáp án D.
Câu 21: Cho hàm số
y f x
liên tục trên các khoảng
( ; 2); 2; 
và có bảng biến thiên như sau:
Số nghiệm thực của phương trình
2
2 3 0f x f x
là
A.
2
. B.
1
. C.
0
. D.
4
.
Lời giải:
Điều kiện:
2x 
. Xét phương trình:
2
1
2 3 0
3
fx
f x f x
fx

Từ bảng biến thiên ta có: phương trình
1fx
có hai nghiệm phân biệt thỏa điều kiện:
12
32xx
và phương trình
3fx
có hai nghiệm phân biệt thỏa mãn điều
kiện
34
21xx
. Vậy phương trình có bốn nghiệm thực phân biệt.
Chọn đáp án D.
Câu 22: Cho hàm số
32
()y f x ax bx cx d
có đồ thị như hình vẽ bên dưới.
Tập nghiệm của phương trình
( ) ( ) 4 0f x f x



là
A.
{ 1;0;1;2;3}
. B.
{ 1;2}
. C.
{0;3}
. D.
{ 1;0;2;3}
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 30
Ta có:
( ) ( ) 4 0 ( ) 0f x f x f x


hoặc
( ) 4fx
.
Từ đồ thị, ta thấy:
( ) 0fx
có hai nghiệm là
1x 
và
2x
vì đồ thị của hàm số cắt trục
hoành tại hai điểm có hoành độ lần lượt là
1x 
và
2x
;
Mặt khác, đồ thị hàm số cắt đường
4y
tại hai điểm có hoành độ là
0x
và
3x
nên
( ) 4fx
có hai nghiệm là
0x
và
3x
.
Vậy phương trình đã cho có tập nghiệm là
{ 1;0;2;3}
.
Chọn đáp án D.
Câu 23: Cho hàm số
32
( ) , ( 0)y f x ax bx cx d a
có đồ thị như hình vẽ bên dưới:
Phương trình
0f f x
có bao nhiêu nghiệm thực?
A.
3
. B.
7
. C.
9
. D.
5
.
Lời giải:
Đặt
t f x
, phương trình
0f f x
trở thành
0*ft
(số nghiệm phương trình
*
là
số giao điểm của đồ thị
fx
với trục
Ox
) . Nhìn vào đồ thị ta thấy phương trình
*
có 3
nghiệm
t
thuộc khoảng
2;2
, với mỗi giá trị
t
như vậy phương trình
f x t
có 3 nghiệm
phân biệt. Vậy phương trình
0f f x
có 9 nghiệm.
Chọn đáp án C.
Câu 24: Cho hàm số
y f x
liên tục trên có đồ thị như hình vẽ bên dưới:
Phương trình
3 2 1f f x
có tất cả bao nhiêu nghiệm thực phân biệt?
A.
6
. B.
5
. C.
7
. D.
4
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 31
Dựa vào đồ thị ta có:
3 2 1f f x
2
3 2 1
1
3 2 2
2
fx
fx
fx
fx


.
Mà
2fx
có 1 nghiệm duy nhất lớn hơn
2
.
Và
1
2
fx
có 3 nghiệm phân biệt
1
2; 1x
,
2
1;0x 
,
3
1;2 .x
Vậy phương trình có 4 nghiệm thực phân biệt.
Chọn đáp án D.
Câu 25: Cho hàm số
y f x
liên tục trên có đồ thị như hình bên dưới:
Phương trình
10f f x 
có tất cả bao nhiêu nghiệm thực phân biệt?
A. 6. B. 5. C. 7. D. 4.
Lời giải:
Từ đồ thị hàm số
y f x
ta có:
0fx
2; 1
1;0
0;2
xa
xb
xc

Do đó
10f f x 
11
12
13
f x a
f x b
f x c


1 1 1;0f x a
pt
1f x a
có 3 nghiệm
1 2 3
,,x x x
thỏa mãn
1 2 3
10x a b x x c
2 1 0;1f x b
pt
1f x b
có 3 nghiệm
4 5 6
,,x x x
thỏa mãn
1 4 5 2 3 6
10x a x x b x x c x
3 1 1;3f x c
pt
1f x c
có nghiệm duy nhất
76
xx
Vậy phương trình
10f f x 
có 7 nghiệm phân biệt.
Chọn đáp án C.
Câu 26: Cho hàm số
y f x
xác định trên và có bảng biến thiên như sau:
x

-1 1

y
0
0
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 32
y
1


-1
Số nghiệm của phương trình
2
22f x x
là
A.
4
. B.
2
. C.
3
. D.
8
.
Lời giải:
BBT của hàm số
2
2:y x x
x

1

y

1

Phương trình
2
23f x x
2
2
22
22
f x x
f x x

+)
22
2 2 2 1f x x x x a
Có hai nghiệm phân biệt.
+)
22
2 2 2 1f x x x x b 
Vô nghiệm.
Vậy phương trình
2
22f x x
có 2 nghiệm phân biệt.
Chọn đáp án B.
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình
3
1
3
2
f x x
là
A.
6
. B.
10
. C.
12
. D.
3
.
Lời giải:
Xét
3
1
3
2
f x x
3
3
1
3
2
1
3
2
f x x
f x x

Xét
3
3g x x x
,
2
' 3 3 0 1g x x x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 33
x
'gx
gx
1
1
0
0




2
2
Quan sát đồ thị:
+ Xét
3
1
3
2
f x x
3
3
3
3 2;0
3 0;2
3 2;
x x a
x x b
x x c

( có lần lượt 3, 3, 1 nên có tất cả 7 nghiệm).
+ Xet
3
1
3
2
f x x
( có 3 nghiệm).
Rõ ràng 10 nghiệm này phân biệt. Vậy phương trình đã cho có tất cả 10 nghiệm.
Chọn đáp án B.
Câu 28: Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình
42
22f x x
là
A.
8
. B.
9
. C.
7
. D.
10
.
Lời giải:
Phương trình
42
42
42
22
22
22
f x x
f x x
f x x

.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 34
* Phương trình
42
4 2 4 2
42
2 , 1 0
2 2 2 , 0 1
2 , 2 3
x x b b
f x x x x c c
x x d d
.
* Phương trình
4 2 4 2
2 2 2 , 2 1f x x x x a a
.
Bảng biến thiên của hàm số
42
2y x x
như sau:
x

1
0
1

y
0
0
0
y

1
0
1

Dựa vào BBT trên ta có:
- Phương trình
42
2 , 2 1x x a a
không có nghiệm thực.
- Phương trình
42
2 , 1 0x x b b
có 4 nghiệm thực phân biệt.
- Phương trình
42
2 , 0 1x x c c
có 2 nghiệm thực phân biệt.
- Phương trình
42
2 , 2 3x x d d
có 2 nghiệm thực phân biệt.
Vậy phương trình
42
22f x x
có 8 nghiệm thực phân biệt.
Chọn đáp án A.
Câu 29: Cho hàm số
fx
có bảng biến thiên như sau:
Số nghiệm của phương trình
là
A.
4
. B.
5
. C.
6
. D.
3
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 35
Dựa vào bảng biến thiên, ta có
;2
1 2;1
1;
xa
f x x b
xc


.
Do đó
( )
( )
( )
42
4 2 4 2
42
3 6 1 1
3 6 1 1 3 6 1 2
3 6 1 3
x x a
f x x x x b
x x c
Xét hàm số
42
3 6 1g x x x
. Ta có:
3
1
12 12 0 0
1
x
g x x x x
x

.
Bảng biến thiên:
Dựa vào bảng biến thiên, có:
- Phương trình (1) vô nghiệm.
- Phương trình (2) có đúng 4 nghiệm phân biệt.
- Phương trình (3) có đúng 2 nghiệm phân biệt.
Vậy phương trình đã cho có tất cả 6 nghiệm.
Chọn đáp án C.
Câu 30: Cho hàm số
y f x
có đồ thị như hình vẽ:
Khi đó phương trình
4
4 3 3 0fx
có bao nhiêu nghiệm dương?
A. 2. B. 4. C. 5. D. 1.
Lời giải:
Bảng biến thiên của hàm số
4
3yx
:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 36
Ta có:
4
11
4 4 4
22
4
33
3 , 1;0
3
4 3 3 0 3 3 , 0;1
4
3 , 1;2
x x x
f x f x x x x
x x x

.
Dựa vào bảng biến thiên ta có
4
1
3xx
vô nghiệm;
4
2
3xx
có một nghiệm âm một nghiệm
dương;
4
3
3xx
có một nghiệm âm một nghiệm dương.
Vậy phương trình
4
4 3 3 0fx
có 2 nghiệm dương.
Chọn đáp án A.
Câu 31: Cho hàm số
y f x
có đồ thị như hình vẽ sau:
Số nghiệm của phương trình
2 sin 1 0fx
trên đoạn
5
;
22




là
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải:
Đặt
sintx
,
1;1t



ta được:
1
2
ft
. Dựa vào đồ thị ta có
,( 1 0)
, 0 1
t a a
t b b
Xét hàm số
sing x x
trên đoạn
5
;
22




Đồ thị của hàm số
sing x x
tên đoạn
5
;
22




là
Dựa vào đồ thị ta có
sin xa
có
3
nghiệm trên
5
;
22




,
sin xb
có
3
nghiệm trên
5
;
22




.
Vậy phương trình
2 sin 1 0fx
có
6
nghiệm trên
5
;
22




.
Chọn đáp án D.
Câu 32: Cho hàm số
fx
có bảng biến thiên như sau:
O
1
1
1
1
x
y
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 37
Số nghiệm thuộc đoạn
7
0;
3



của phương trình
2. cos 5 0fx
là
A.
8
. B.
7
. C.
5
. D.
6
.
Lời giải:
Xét phương trình
5
2. 5 0
2
f x f x
.
Dựa vào bảng biến thiên, ta có
1;0
1
0;
2
5
2
1
;1
2
1;
xa
xb
fx
xc
xd










.
Do đó
cos 1;0 (1)
1
cos 0; (2)
2
5
2. cos 5 0 cos
2
1
cos ;1 (3)
2
cos 1; (4)
xa
xb
f x f x
xc
xd









.
Dựa vào đường tròn lượng giác, trên đoạn
7
0;
3



ta có:
- Phương trình (1) có đúng 2 nghiệm phân biệt.
- Phương trình (2) có đúng 2 nghiệm phân biệt.
- Phương trình (3) có đúng 3 nghiệm phân biệt.
- Phương trình (4) vô nghiệm.
Vậy phương trình đã cho có tất cả 7 nghiệm.
Chọn đáp án B.
Câu 33: Cho hàm số
y f x
có đồ thị như hình vẽ.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 38
Số nghiệm thuộc đoạn
0;5


của phương trình
cos 1fx
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải:
Đặt
costx
,
1;1t



ta được
1ft
ta
với
0;1a
Xét hàm số
cosg x x
trên đoạn
0;5


Đồ thị của hàm số
cosg x x
tên đoạn
0;5


là
Dựa vào đồ thị ta có
cosxa
có
5
nghiệm trên
0;5


Vậy phương trình
cos 1fx
có
5
nghiệm trên
0;5


.
Chọn đáp án C.
Câu 34: Cho hàm số
fx
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;5


của phương trình
sin 1fx
là
A.
6
. B.
4
. C.
10
. D.
8
.
Lời giải:
Từ bảng biến thiên ta được
1
22
3
sin ; 1 ( )
sin 1 sin 1;0 sin 1;0 (1)
sin 1; ( )
x t VN
f x x t x t
x t VN

.
Dựa vào đường tròn lượng giác, phương trình (1) có 4 nghiệm nằm trong đoạn
0;5


.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 39
4
55
6
sin ; 1 ( )
sin 1 sin 0;1 sin 0;1 (2)
sin 1; ( )
x t VN
f x x t x t
x t VN

.
Dựa vào đường tròn lượng giác, ta được phương trình (2) có
6
nghiệm nằm trong đoạn
0;5


.
Vậy phương trình ban đầu có tất cả
10
nghiệm.
Chọn đáp án C.
Câu 35: Cho hàm số
y f x
có bảng biến thiên như hình vẽ sau:
x

0
1
2

fx
0
0
0
fx

0
3
1

Số nghiệm của phương trình
sin 1 2fx
trên
;2



là
A. 6. B. 7. C. 5. D. 4.
Lời giải:
Dựa vào bảng biến thiên hàm số
,fx
ta thấy
0
01
2.
12
2
x a a
x b b
fx
x c c
x d d



Đặt
sin 1.tx
Phương trình đã cho tương đương với
1
2
2
3
4
ta
tb
ft
tc
td

Ta có:
cos 0 .
2
t x x t x x k k

Ta có bảng biến thiên hàm số
tx
trên
;2



là:
x
2
2
3
2
2
tx
0
0
0
tx
1
0
2
0
1
Từ bảng biến thiên này, ta thấy các phương trình
1
và
4
vô nghiệm, phương trình
2
có 4
nghiệm và phương trình
3
có đúng 2 nghiệm. Vậy phương trình đã cho có 6 nghiệm phân
biệt.
Chọn đáp án A.
Câu 36: Cho hàm số
y f x
có bảng biến thiên như hình vẽ dưới đây:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 40
x

1
1
2

fx
0
0
0
fx

1
1
2

Số nghiệm thuộc đoạn
3
;
22




của phương trình
cot 1 1fx
là
A. 7. B. 6. C. 8. D. 5.
Lời giải:
Đặt
cot 1,tx
phương trình tương đương với
1.ft
Dựa vào bảng biến thiên, ta thấy
1
cot 1 cot 1 0
1 1 cot 1 cot 1 0
cot 1 1 cot 0
2
t a a
x a x a
f t t x b x b
xx
t b b






Xét
2
1
0
sin
t
x
nên ta có bảng biến thiên hàm
tx
trên
3
;
22




như sau
x
2
0
3
2
t
t
0




0
Từ đó, phương trình
cot 1xa
có đúng 2 nghiệm, phương trình
cot 1xb
có đúng 2
nghiệm và phương trình
cot 0x
có đúng 3 nghiệm thuộc
3
;
22




nên phương trình đã cho
có
7
nghiệm.
Chọn đáp án A.
Câu 37: Cho hàm số
y f x
có đồ thị như hình vẽ sau:
Số nghiệm thuộc đoạn
0;3


của phương trình
2 cos 1 0fx
là
A.
12
. B.
6
. C.
10
. D.
8
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 41
1
cos
2
2 cos 1 0
1
cos
2
fx
fx
fx

Căn cứ vào đồ thị ta thấy:
1
cos , 1 1
2
11
cos cos , 0 2
22
cos , 1 3
x a a
f x x b b
x c c

cos , 1 4
11
cos cos ,0 5
22
1
cos , 1 6
2
x d d
f x x e e
x g g
Các phương trình
3 , 4
đều vô nghiệm.
Xét đồ thị hàm số
cosyx
trên đoạn
0;3


4
3
2
1
1
2
3
4
5
y
5
π
4
π
3
π
2
π π π
2
π
3
π
4
π
5
O
x
Ta thấy các phương trình
1 , 2 , 5 , 6
lần lượt có
3
nghiệm phân biệt và trong số chúng
không có
2
nghiệm nào trùng nhau. Vậy phương trình ban đầu có
12
nghiệm.
Chọn đáp án A.
Câu 38: Cho hàm số
fx
có bảng biến thiên như sau:
Số nghiệm thuộc khoảng
;

của phương trình
2
cos cos 2f x f x
là
A.
5
. B.
6
. C.
7
. D.
9
.
Lời giải:
Đặt
cos ,tx
;.x


Ta có bảng biến thiên (*)
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 42
1;1 .t
Phương trình đã cho trở thành
2
2 (1)
2 0 .
1 (2)
ft
f t f t
ft

Từ bảng biến thiên của đề bài, với
1;1t

ta có nghiệm của phương trình (1) là
1;0ta
hay
0;1tb
và nghiệm của phương trình (2) là
1t
.
Từ bảng biến thiên (*), ta có:
1;0ta
1
2
;0
.
0;
xx
xx

0;1tb
3
4
;0
.
0;
xx
xx

1t 
0.x
Vậy, phương trình đã cho có 5 nghiệm phân biệt thuộc khoảng
;.

Chọn đáp án A.
Câu 39: Cho hàm số
fx
liên tục trên có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
;



của phương trình
2
2cos 3 3fx
là
A.
8
. B.
2
. C.
6
. D.
4
.
Lời giải:
Đặt
2
2cos 3tx
, vì
;x




nên
3; 1 .t


Ta có phương trình
3 , 3; 1f t t


Dựa vào BBT ta có:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 43
Vậy
3ft
, 3, 2t a a
Ta có:
2
2cos 3 , 3, 2x a a
. Suy ra
2
1
cos , 0; .
2
x b b




Suy ra
cos
cos
xb
xb

với
2
0,
2
b




Với mọi
;x




thì phương trình
cosxb
có 2 nghiệm và phương trình
cosxb
có 2
nghiệm. ( Dựa vào đường tròn lượng giác hoặc đồ thị hàm số
cosyx
để kiểm tra nghiệm)
Vậy có 4 nghiệm thỏa yêu cầu bài toán.
Chọn đáp án D.
Câu 40: Cho hàm số
fx
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
5
;3
6



của phương trình
cos24 1 0fx
là
A.
5
. B.
9
. C.
4
. D.
10
.
Lời giải:
Đặt
cos2tx
, ta có
4 1 0ft
1
4
ft
, ; 1
1
, 1;
2
1
, ;1
2
, 1;
t a a
t b b
t c c
t d d








Khảo sát hàm số
cos2tx
trên
5
;3
6



. Ta có
sin22tx

Cho
0t
sin2 0x
2
k
x

,
k
. Vì
5
;3
6
x



35
; ;2 ; ;3
22
x





.
Ta có BBT của hàm
cos2tx
như sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 44
Từ BBT trên ta thấy:
Với
, ; 1t a a 
phương trình vô nghiệm.
Với
1
, 1;
2
t b b



phương trình có
4
nghiệm.
Với
1
, ;1
2
t c c




phương trình có
5
nghiệm.
Với
, 1;t d d
phương trình vô nghiệm.
Vậy phương trình ban đầu có
9
nghiệm.
Chọn đáp án B.
Câu 41: Cho hàm số trùng phương
y f x
có đồ thị như hình vẽ bên dưới:
Số nghiệm thuộc
0;2
của phương trình
cos2 1fx
bằng
A.
4
. B.
6
. C.
3
. D.
8
.
Lời giải:
Ta có
cos2 1fx
cos2 1
cos2 1
fx
fx

cos2 0
cos2 1
cos2 0
sin4 0
sin2 0
cos2 1
cos2 1
x
x a VN
x
x
x
x b VN
x


Phương trình
sin4 0x
có 8 nghiệm thuộc
0;2
.
Chọn đáp án D.
Câu 42: Cho hàm số
y f x
xác định trên và có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
0;


của phương trình
cos2 0f f x
là
A.
4
. B.
2.
C.
3.
D.
8.
x
–∞
1
0
1
+∞
y
+
0
–
0
+
0
–
y

1
0
1

Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 45
Lời giải:
Dựa và bảng biến thiên ta có
1,f x x
và
os20f f c x
os
os
os
2
2
20
f c x a
f c x a
f c x
với
1.a
Với
os2f c x a
thì phương trình vô nghiệm.
Với
os2f c x a
cos2xb
với
1b
nên phương trình vô nghiệm.
Với
os20f c x
0;
3
cos2 0 2 ; .
2 4 2 4 4
x
x x k x k x x



Vậy phương trình
cos2 0f f x
có 2 nghiệm thuộc đoạn
0;


.
Chọn đáp án B.
Câu 43: Cho hàm số
42
, ; ; , 0y ax bx c a b c a
có bảng biến thiên như hình vẽ:
x

2
0
2

y
0
0
0
y

2
2
2

Số nghiệm của phương trình
42
0a f x b f x c
là
A.
11.
B.
10.
C.
9.
D.
12.
Lời giải:
d
c
b
a
Ta có:
Dùa vµo t¬ng giao
Dùa vµo t¬ng giao
Dùa vµo t¬ng giao
Kh«ng cã nghiÖm.
Cã 4 nghiÖm ph©n biÖt.
Cã 4 nghiÖm ph©n
42
;2
2;0
0
0;2
f x m
f x m
f x m
f x a
f x b
a f x b f x c
f x c
 


Dùa vµo t¬ng giao
biÖt.
Cã 2 nghiÖm ph©n biÖt.2;
f x m
f x d
 
Rõ ràng 10 nghiệm này phân biệt.
Chọn đáp án B.
Câu 44: Cho hàm số
y f x
xác định, liên tục trên và có bảng biến thiên như hình vẽ:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 46
x

1
4
0
2

y
0
0
0
y

2
2
4

Số nghiệm thuộc đoạn
5
;
22




của phương trình
2
5 cos cos 1f x x
là
A.
11.
B.
10.
C.
9.
D.
12.
Lời giải:
Đặt
2
cos cos .u x x
Với
5
;
22
x





thì
1
;2
4
u




(Lập bảng biến thiên hoặc sử dụng
MTCT)
Lúc đó:
v« nghiÖm
v« nghiÖm
1
;
4
1
1
;0
5 1 .
4
5
0;2
2;
ua
ub
f u f u
uc
ud









Chọn giá trị để tính!
+)
Dïng ®êng trßn lîng gi¸c
Dïng ®êng trßn lîng gi¸c
nghiÖm ph©n biÖt
nghiÖm ph©n biÖt
2
5
cos 0,78 4 ;
22
11
cos cos ;0
64
5
cos 0,21 4 ;
22
x
u x x
x













Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 47
+)
Dïng ®êng trßn lîng gi¸c
v« nghiÖm
nghiÖm ph©n biÖt
2
cos 1,6
cos cos 1 0;2
5
cos 0,6 2 ;
22
x
u x x
x





Rõ ràng 10 nghiệm này phân biệt.
Chọn đáp án B.
Câu 45: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ sau:
Số nghiệm của phương trình
sin cos 2 0f x x
trên đoạn
0;2


là
A.
5.
B.
4.
C.
3.
D.
2.
Lời giải:
Ta có:
sin cos 2 0 sin cos 2f x x f x x
V« nghiÖmsin cos 2 sin 2
4
2 sin 1 .
4
2 sin 0;1
4
x x x a
x
xb









Với
0;2x


thì
9
;.
4 4 4
x




Lúc đó:
Dïng ®êng trßn lîng gi¸c
1
sin
2 sin 1
4
4
2
1
2 sin 0;1 sin 0;
44
22
x
x
b
x b x











4 nghiệm phân
biệt trên
9
;.
44




Chọn đáp án B.
Câu 46: Cho hàm số
32
f x ax bx bx c
có đồ thị như hình vẽ:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 48
Số nghiệm nằm trong
;3
2



của phương trình
cos 1 cos 1f x x
là
A.
2
. B.
3
. C. 5. D. 4.
Lời giải:
Từ đồ thị ta có
;0
0;1
2
xa
f x x x b
x

Do đó
cos 1 ;0
cos 1 cos 1 cos 1 0;1
cos 1 2
xa
f x x x b
x


1
2
cos 1 ; 1 ( )
cos 1 1;0 (1)
cos 1 (2)
x a t VN
x b t
x

Dựa vào đường tròn lượng giác, phương trình (1) có 3 nghiệm nằm trong
;3
2



.
Phương trình (2) có
2
nghiệm nằm trong
;3
2



.
Vậy phương trình ban đầu có tất cả 5 nghiệm nằm trong
;3
2



.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 49
Chọn đáp án C.
Câu 47: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt
của phương trình
3
10f x f x 
là
A.
8
. B.
5
. C.
6
. D.
4
.
Lời giải:
3
10f x f x 
3
1f x f x
*
Dựa vào đồ thị,
3
3
3
01
* 2 2 3
3 5 6
x f x
x f x a a
x f x b b
.
11
00
1
0 5 6
xx
f x x x x






.
Xét
2
: dễ thấy
0x
không là nghiệm. Với
0x
,
3
2
a
fx
x

.
Vẽ đồ thị hàm số
3
23
a
f x a
x
và hàm số
y f x
trên cùng hệ trục tọa độ suy ra
phương trình có
2
nghiệm.
Tương tự xét phương trình
3
phương trình có
2
nghiệm.
Vậy phương trình đã cho có
6
nghiệm.
Chọn đáp án C.
Câu 48: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình
3
10f x f x 
là
A.
6
. B.
4
. C.
5
. D.
8
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 50
Ta có
3
3 3 3
3
3 1 1
1 0 1 5 3 2
03
x f x a a
f x f x f x f x x f x b b
x f x
, với
,0ab
.
+ Với
0m
, xét phương trình
3
3
m
x f x m f x
x
.
Đặt
3
m
gx
x
,
4
3
0, 0
m
g x x
x
.
lim lim 0
xx
g x g x
 

,
0
lim
x
gx

,
0
lim
x
gx

.
Ta có bảng biến thiên:
Dựa vào bảng biến thiên và đề bài, suy ra trong mỗi khoảng
;0
và
0;
phương trình
f x g x
có đúng một nghiệm.
Suy ra mỗi phương trình
1
và
2
có
2
nghiệm.
+ Xét
3
0
0
3 : 0
0
0
x
x
x f x
fx
xc

, với
c
khác các nghiệm của
1
và
2
.
Vậy phương trình
3
10f x f x 
có đúng
6
nghiệm.
Chọn đáp án A.
Câu 49: Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân
biệt của phương trình
2
2f x f x
là
A.
8
. B.
12
. C.
6
. D.
9
.
Lời giải:
Ta có
2
2
22
2
2
1
2
2 0 2
3
04
x f x a
x f x b
f x f x f x f x
x f x c
x f x
, với
, , 0a b c
.
+ Với
0m
, xét phương trình
2
2
*
m
x f x m f x
x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 51
Xét hàm số
2
,0
m
g x m
x

, ta có
3
2
,0
m
g x x
x
.
00
lim lim 0; lim ;lim
xx
xx
g x g x g x g x

 

 
.
Bảng biến thiên:
Dựa vào bảng biến thiên và hình vẽ, suy ra trong mỗi khoảng
;0
và khoảng
0;
phương trình
f x g x
có đúng một nghiệm. Do đó phương trình
*
có đúng
2
nghiệm.
Chọn đáp án D.
Câu 50: Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình
2
20f x f x 
là
A.
6
. B.
12
. C.
8
. D.
9
.
Lời giải:
Ta có
22
2 0 2f x f x f x f x
.
Dựa vào đồ thị ta thấy:
2
2
2
2
01
1 0 2
3 2 3
4 3 4
x f x
x f x a a
x f x b b
x f x c c
.
Giải
1
2
0
0
1
0
x
x
xx
fx
xx
(có 3 nghiệm phân biệt).
Giải
2
2
a
fx
x

.
Vẽ đồ thị hàm số
2
a
y
x
lên cùng hệ tọa độ
Oxy
. Ta thấy đồ thị hàm số
2
a
y
x
cắt đồ thị hàm
số
y f x
tại
2
nghiệm phân biệt.
Tương tự với
3
và
4
đều có
2
nghiệm phân biệt.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 52
Vậy có phương trình
2
2f x f x
có
9
nghiệm phân biệt.
Chọn đáp án D.
Câu 51: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt
của phương trình
5
20f x f x 
là
A.
8
. B.
5
. C.
6
. D.
4
.
Lời giải:
5
20f x f x 
5
2f x f x
*
Dựa vào đồ thị,
5
5
5
01
* 2 1 0
3 3 2
x f x
x f x a a
x f x b b
.
11
00
1
0 3 2
xx
f x x x x






.
Xét
2
: dễ thấy
0x
không là nghiệm. Với
0x
,
5
2
a
fx
x

.
Vẽ đồ thị hàm số
5
10
a
f x a
x
và hàm số
y f x
trên cùng hệ trục tọa độ suy ra
phương trình có
2
nghiệm. Tương tự xét phương trình
3
phương trình có
2
nghiệm.
Vậy phương trình đã cho có
6
nghiệm.
Chọn đáp án C.
Câu 52: Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt
của phương trình
2
2 3 0f x f x
là
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 53
A.
8
. B.
6
. C.
9
. D.
12
.
Lời giải:
2
2 3 0f x f x
2
23f x f x
*
Ta có:
2
23f x f x
2
2
2
2
20
20
20
20
x f x
x f x a
x f x b
x f x c

.
Xét phương trình:
2
20x f x
2
0
x
fx

mà
0fx
có hai nghiệm
2
2 . 0x f x
có ba nghiệm.
Xét phương trình:
2
20x f x a
Do
2
20x 
;
2x 
không là nghiệm của phương trình
2
0
2
a
fx
x
Xét
23
2
22
aa
g x g x
xx

Bảng biến thiên:
Từ bảng biến thiên với
0fx
2
2
a
fx
x

có 2 nghiệm.
Tương tự:
2
2x f x b
và
2
2x f x c
,0bc
mỗi phương trình cũng có hai nghiệm.
Vậy số nghiệm của phương trình
2
23f x f x
là 9 nghiệm.
Chọn đáp án C.
Câu 53: Cho hàm số
y f x
có đồ thị như hình vẽ sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 54
Số nghiệm thực của phương trình
0f f x f x
là
A.
20
. B.
24
. C.
10
. D.
4
.
Lời giải:
Đặt
0f x t
. Khi đó phương trình trở thành:
,1f t t
.
Từ đồ thị hàm số ta có:
Phương trình
1
có 4 nghiệm

, 0 1
,1
, 1 2
,2
t a a
t b a b
t c c
t d d
Khi đó các phương trình
f x a
,
f x b
,
f x c
mỗi phương trình có 6 nghiệm phân biệt
không trùng nhau. Phương trình
f x d
có 2 nghiệm phân biệt không trùng với nghiệm của
3 phương trình trên.
Vậy phương trình đã cho có 20 nghiệm phân biệt.
Chọn đáp án A.
DẠNG 2: BÀI TOÁN THAM SỐ
Câu 54: Cho hàm số
y f x
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
Tìm tập hợp tất cả các giá trị của tham số thực
m
sao cho phương trình
f x m
có ba nghiệm
thực phân biệt.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 55
A.
1;2


. B.
1;2
. C.
1;2
. D.
;2

.
Lời giải:
Dựa vào bảng biến thiên đã cho, phương trình
f x m
có ba nghiệm phân biệt khi và chỉ
khi
12m
hay
1;2m
vì lúc đó, đường thẳng
ym
cắt đồ thị hàm số
y f x
tại ba
điểm phân biệt.
Chọn đáp án B.
Câu 55: Cho hàm số
42
2y x x
có đồ thị như hình bên dưới:
Tìm tất cả các giá trị thực của tham số
m
để phương trình
42
2x x m
có bốn nghiệm thực
phân biệt
A.
0m
. B.
01m
. C.
01m
. D.
1m
.
Lời giải:
Số nghiệm thực của phương trình
42
2x x m
chính là số giao điểm của đồ thị hàm số
42
2y x x
và đường thẳng
ym
. Dựa vào đồ thị suy ra
42
2x x m
có bốn nghiệm thực
phân biệt khi
0 1.m
Chọn đáp án B.
Câu 56: Cho hàm số
()y f x
có bảng biến thiên như sau:
Tập tất cả các giá trị của tham số m để phương trình
()f x m
có ba nghiệm phân biệt là
A.
(4; )
. B.
( ; 2)
. C.
[-2;4]
. D.
( 2;4)
.
Lời giải:
+) Số nghiệm của phương trình
()f x m
bằng số giao điểm của đồ thị hàm số
(x)yf
và
đường thẳng
.ym
+) Dựa vào bảng biến thiên của hàm số
(x)yf
suy ra
(x) mf
có 3 nghiệm phân biệt
2;4 .m
Chọn đáp án D.
Câu 57: Tìm tất cả các giá trị của tham số
m
để phương trình
32
32x x m
có ba nghiệm phân biệt.
A.
2;m

. B.
;2m

. C.
2;2m
. D.
2;2m



.
Lời giải:
Xét hàm số
32
32y x x
,
2
36y x x

.
Lập bảng biến thiên:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 56
Số nghiệm của phương trình
32
3 2 *x x m
bằng số giao điểm của đồ thị hàm số
32
32y x x
và đường thẳng
ym
.
Dựa vào bảng biến thiên suy ra PT (*) có 3 nghiệm phân biệt khi
22m
.
Chọn đáp án C.
Câu 58: Tìm
m
để đồ thị hàm số
4 2 2
21y x mx m
cắt trục hoành tại
4
điểm phân biệt.
A.
1m
. B.
11m
. C.
1m 
. D.
1
1
m
m

.
Lời giải:
Xét phương trình:
4 2 2
2 1 0 *x mx m
Đặt
2
0x t t
. Khi đó phương trình (*) trở thành
22
2 1 0 * *t mt m
Để đồ thị hàm số
4 2 2
21y x mx m
cắt trục hoành tại
4
điểm phân biệt
Phương trình (*) có 4 nghiệm phân biệt
phương trình (**) có hai nghiệm phân biệt
dương
0
0
0
S
P

2
10
20
10
m
m


0
1
1
m
m
m

1m
.
Chọn đáp án A.
Câu 59: Cho hàm số
42
23y x x
có đồ thị hàm số như hình bên dưới. Với giá trị nào của tham số
m
phương trình
42
2 3 2 4x x m
có hai nghiệm phân biệt?
A.
0
1
2
m
m
. B.
1
0
2
m
. C.
0
1
2
m
m
. D.
1
2
m
.
Lời giải:
Số nghiệm của phương trình
42
2 3 2 4x x m
bằng số giao điểm của đường thẳng
24ym
và đồ thị hàm số
42
23y x x
.
Dựa vào đồ thị ta có phương trình
42
2 3 2 4x x m
có hai nghiệm phân biệt khi và chỉ khi
0
2 4 4
1
2 4 3
2
m
m
m
m
.
Chọn đáp án A.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 57
Câu 60: Hàm số
,,a b c
có bảng biến thiên
Có bao nhiêu số nguyên
m
để phương trình
3f x m
có đúng 8 nghiệm phân biệt?
A. Vô số. B. 1. C. 4. D. 2.
Lời giải:
+) Lấy đối xứng phần đồ đồ thị phía dưới
Ox
của hàm số
y f x
qua trục
Ox
.
+) Bỏ phần đồ thị
y f x
phía dưới
Ox
.
Khi đó ta có đồ thị hàm số
y f x
.
Số nghiệm của phương trình
3f x m
là số giao điểm của 2 đồ thị
y f x
và
ym
.
Dựa vào bảng biến thiên, ta thấy đồ thị
y f x
cắt đường thẳng
ym
tại 8 điểm phân biệt
khi và chỉ khi
02m
. Vì
m
nên
1m
.
Chọn đáp án B.
Câu 61: Cho hàm số
y f x
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau
Tất cả giá trị của tham số thực
m
sao cho đồ thị của hàm số
y f x m
cắt trục
Ox
tại ba
điểm phân biệt là
A.
2;1
. B.
1;2
. C.
1;2
. D.
2;1
.
Lời giải:
Xét phương trình hoành độ giao điểm:
0f x m
*f x m
.
Số giao điểm giữa đường thẳng
ym
và đồ thị
y f x
cũng chính là số nghiệm của phương
trình
*
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 58
Dựa vào bảng biến thiên ta thấy đường thẳng
ym
cắt đồ thị
y f x
tại ba điểm phân biệt
khi và chỉ khi
12m
hay
21m
. Vậy
21m
.
Chọn đáp án D.
Câu 62: Cho hàm số
()y f x
xác định, liên tục trên và có bảng biến thiên như sau:
Tìm tất cả các giá trị thực của
m
để phương trình
( ) 1f x m
có đúng hai nghiệm.
A.
0, 1mm
. B.
21m
. C.
1, 2mm
. D.
1, 2mm
.
Lời giải:
Ta có
( ) 1 ( ) 1 .f x m f x m
Để phương trình có hai nghiệm thì
1 1 2
.
1 0 1
mm
mm



Chọn đáp án D.
Câu 63: Đường cong trong hình vẽ là đồ thị của hàm số
42
22y x x
. Tìm tất cả các giá trị thực của
tham số
m
để phương trình
42
2x x m
có 4 nghiệm phân biệt.
A.
2m 
. B.
10m
. C.
3m 
. D.
32m
.
Lời giải:
Phương trình đã cho tương đương
42
2 2 2x x m
1
.
Số nghiệm của phương trình
1
chính là số giao điểm của đường thẳng
:2d y m
(song
song hoặc trùng với trục hoành) và đồ thị hàm số
42
( ) : 2 2C y x x
.
Do đó
1
có 4 nghiệm phân biệt khi
d
cắt
C
tại 4 điểm phân biệt.
Dựa vào đồ thị suy ra
3 2 2 1 0mm
.
Chọn đáp án B.
Câu 64: Cho hàm số
y f x
xác định trên
\1
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình vẽ sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 59
Số giá trị nguyên của tham số
m
để phương trình
f x m
có 3 nghiệm phân biệt là
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải:
Ta có số nghiệm của phương trình
f x m
bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
ym
.
Do đó, dựa vào bảng biến thiên ta thấy, phương trình
f x m
có ba nghiệm phân biệt khi và
chỉ khi
03m
. Kết hợp điều kiện
m
suy ra
1;2m
.
Vậy có
2
giá trị nguyên của tham số
m
thỏa mãn yêu cầu bài toán.
Chọn đáp án D.
Câu 65: Cho hàm số
y f x
có bảng biến thiên như sau:
Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
0f x m
có hai nghiệm phân
biệt là
A.
;2
. B.
1;2
. C.
1;2
. D.
2;
.
Lời giải:
0f x m f x m
Phương trình
f x m
có hai nghiệm phân biệt
đồ thị hàm số
ym
cắt đồ thị hàm số
y f x
tại hai điểm phân biệt
2 1 1 2mm
. Vậy
1;2m
.
Chọn đáp án B.
Câu 66: Cho hàm số
3
32y x x
có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị thực của tham số m để phương trình
có ba nghiệm
thực phân biệt.
A.
04m
. B.
02m
. C.
04m
. D.
02m
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 60
Số nghiệm của phương trình
là số giao điểm của đồ thị
3
32y x x
và
đường thẳng
2ym
.
Nhìn vào đồ thị suy ra phương trình có 3 nghiệm phân biệt
0 2 4 0 2mm
.
Chọn đáp án B.
Câu 67: Cho hàm số
32
3f x x x
. Tính tổng tất cả các giá trị nguyên của
m
để đồ thị hàm số
g x f x m
cắt trục hoành tại 4 điểm phân biệt.
A. 3. B. 10. C. 4. D. 6.
Lời giải:
Xét hàm số
32
3f x x x
. Ta có đồ thị hàm số
y f x
như sau:
Như ta đã biết: để vẽ đồ thị hàm số
y f x
từ đồ thị
y f x
ta thực hiện:
Bước 1: Giữ nguyên phần đồ thị
y f x
gồm các điểm bên phải và các điểm nằm trên trục
Oy
; bỏ phần đồ thị bên trái trục
Oy
.Ta được phần đồ thị
1
P
Bước 2: Lấy đối xứng phần đồ thị
1
P
qua trục
Oy
ta được phần đồ thị
2
P
Khi đó: Đồ thị
y f x
bao gồm đồ thị
1
P
và
2
P
.
Từ đó ta có đồ thị hàm số
32
3y f x x x
như sau:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 61
Để đồ thị hàm số
g x f x m
cắt trục hoành tại 4 điểm phân biệt thì phương trình
0gx
có 4 nghiệm phân biệt. Do đó phương trình
f x m
có 4 nghiệm phân biệt hay đường
thẳng
ym
cắt đồ thị hàm số
32
3y f x x x
tại 4 điểm phân biệt.
Dựa vào đồ thị hàm số
y f x
suy ra bài toán thỏa mãn khi và chỉ khi
4 0 0 4mm
. Kết hợp yêu cầu đề bài
m
, do đó
1;2;3m
.
Chọn đáp án D.
Câu 68: Cho hàm số
y f x
có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên
m
để phương trình
3
3f x x m
có
6
nghiệm phân biệt thuộc đoạn
[ 1;2]
?
A.
3
. B.
2
. C.
6
. D.
7
.
Lời giải:
Đặt
3
3t x x
, với
[ 1;2]x
ta có bảng biến thiên
Với
( 2;2]t 
thì có 2 nghiêm
[ 1;2]x
Để phương trình có 6 nghiệm thì phương trình
f t m
có 3 nghiệm
( 2;2]t 
Dựa vao đồ thị ta có
0; 1mm
.
Chọn đáp án B.
Câu 69: Tìm tất cả các giá trị của tham số
m
để phương trình
32
1
cos 3cos 5 cos 3 2 0
3
x x x m
có
đúng bốn nghiệm thuộc đoạn
0;2 .


A.
31
.
23
m
B.
13
.
32
m
C.
13
.
32
m
D.
31
.
23
m
Lời giải:
Đặt
cos 0xt
Phương trình:
32
1
cos 3cos 5 cos 3 2 0
3
x x x m
có đúng bốn nghiệm thuộc đoạn
0;2


32
1
3 5 3 2 0
3
t t t m
có 1 nghiệm
0;1t
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 62
32
1
3 5 3 2
3
t t t m
có 1 nghiệm
0;1t
Xét hàm số
32
1
3 5 3
3
f t t t t
với
0;1t
. Ta có
2
1
6 5 0
5
t
f t t t
t
Bảng biến thiên:
3
3
2
0
5
1
y
y'
x
+
Vậy
2 3 1
32
3 2 3
mm
.
Chọn đáp án C.
Câu 70: Cho đồ thị của hàm số
32
6 9 2y x x x
như hình vẽ.
Khi đó phương trình
32
6 9 2x x x m
(
m
là tham số) có 6 nghiệm phân biệt khi và chỉ khi.
A.
22m
. B.
02m
. C.
02m
. D.
22m
.
Lời giải:
+) Đồ thị hàm số
32
6 9 2y x x x
có được bằng cách biến đổi đồ thị
C
hàm số
32
6 9 2y x x x
:
- Giữ nguyên phần đồ thị
C
nằm trên trục hoành.
- Lấy đối xứng phần đồ thị của
C
phần dưới trục hoành qua trục hoành.
- Xóa phần đồ thị còn lại của
C
phía dưới trục hoành.
y
=
m
x
y
2
y
x
=
x
3
6
∙
x
2
+ 9
∙
x
2
1
O
x
y
3
2
1
2
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 63
+) Số nghiệm của phương trình
32
6 9 2x x x m
là số giao điểm của đồ thị hàm số
32
6 9 2y x x x
và đồ thị hàm số
ym
. Để phương trình có 6 nghiệm phân biệt thì điều
kiện cần và đủ là
02m
.
Chọn đáp án B.
Câu 71: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ.
y
=
f
(
x
)
-4
y
x
O
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
3sin cos 1
44
2cos sin 4
xx
f f m m
xx





1
có nghiệm?
A.
3
. B.
4
. C.
5
. D. Vô số.
Lời giải:
Đặt
3sin cos 1
2cos sin 4
xx
t
xx


2 1 cos 3 sin 1 4t x t x t
*
.
Phương trình
*
có nghiệm
2 2 2
2 1 3 4 1t t t
9
1
11
t
.
Suy ra
01t
.
Từ đồ thị
y f x
ta có
*
y f x
đồng biến trên
0;

*
2
2
4 4 2 0;m m m

.
*
0;t

Nên
2
3sin cos 1
44
2cos sin 4
xx
f f m m
xx





2
44f t f m m
2
44t m m
Phương
trình
1
có nghiệm
2
0 4 4 1mm
2
4 4 1mm
31m
.
Do
3; 2; 1mm
.
Chọn đáp án A.
Câu 72: Cho hàm số
y f x
liên tục trên có đồ thị như hình vẽ.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 64
Có bao nhiêu giá trị nguyên của
n
để phương trình
2
16cos 6sin2 8 1f x x f n n
có
nghiệm
x
?
A.
10
. B.
4
. C.
8
. D.
6
.
Lời giải:
Dựa vào đồ thị hàm số ta thấy hàm số
y f x
đồng biến trên .
Do đó:
22
16cos 6sin2 8 1 16cos 6sin2 8 1f x x f n n x x n n
1 cos2
16. 6sin2 8 1 8cos2 6sin2 1
2
x
x n n x x n n
Phương trình có nghiệm
x
22
2 2 2 2
8 6 1 1 100n n n n
2
2
2
1 10
10 0
1 41 1 41
10 0
22
1 10
10 0
nn
nn
n n n
nn
nn



.
Vì
n
nên
3; 2; 1;0;1;2n
.
Chọn đáp án D.
Câu 73: Cho hàm số
y f x
có đồ thị như hình vẽ.
Có bao nhiêu số nguyên
m
để phương trình
1
1
32
x
f x m



có nghiệm thuộc đoạn
2;2


?
A.
11
. B.
9
. C.
8
. D.
10
.
Lời giải:
Đặt
1
2
x
t 
, khi
22x
thì
02t
.
Phương trình đã cho trở thành
1
22
3
f t t m
6 6 3f t t m
.
Xét hàm số
66g t f t t
trên đoạn
0;2


.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 65
Ta có
6g t f t


. Từ đồ thị hàm số
y f x
suy ra hàm số
ft
đồng biến trên khoảng
0;2
nên
0, 0;2g t t
và
0 10g 
;
2 12g
.
Bảng biến thiên của hàm số
gt
trên đoạn
0;2


Phương trình đã cho có nghiệm thuộc đoạn
2;2


khi và chỉ khi phương trình
3g t m
có
nghiệm thuộc đoạn
0;2


hay
10 3 12m
10
4
3
m
.
Mặt khác
m
nguyên nên
3; 2; 1;0;1;2;3;4m
. Vậy có 8 giá trị
m
thoả mãn bài toán.
Chọn đáp án C.
Câu 74: Cho hàm số
y f x
có bảng biến thiên dưới đây:
Để phương trình
3 2 1 2f x m
có 3 nghiệm phân biệt thuộc
0;1


thì giá trị của tham số m
thuộc khoảng nào dưới đây?
A.
;3
. B.
1;6
. C.
6;
. D.
3;1
.
Lời giải:
Đặt
21tx
. Ta thấy
t
là hàm đồng biến theo
x
và
0;1 1;1xt
.
Do đó phương trình
3 2 1 2f x m
có 3 nghiệm phân biệt thuộc
0;1
2
()
3
m
ft

có 3
nghiệm phân biệt thuộc
1;1
.
Dựa vào bảng biến thiên suy ra
2
1 5.
3
m
m
Chọn đáp án B.
Câu 75: Cho hàm số
()fx
liên tục trên và có đồ thị như hình vẽ. Số giá trị nguyên của tham số
m
để
phương trình
22
3 4 6 9 1 0f x x m
có nghiệm là
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 66
A.
6
. B.
4
. C.
5
. D.
7
.
Lời giải:
Đặt
2
2
3 4 6 9 3 4 1 3 1 1;3t x x x t


.
Dựa vào đồ thị ta có khi
1;3t



thì
1
5;
2
ft



.
Khi đó phương trình
22
3 4 6 9 1 0f x x m
có nghiệm khi và chỉ khi phương trình
2
1f t m
có nghiệm thuộc
1;3


22
11
5 1 4 2 2
22
m m m
.
Kết hợp điều kiện
2; 1; 0; 1; 2mm
.
Chọn đáp án C.
Câu 76: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ. Tập hợp các giá trị thực của
tham số
m
để phương trình
2
41f x m
có nghiệm là
A.
2;0 .


B.
4; 2 .



C.
4;0 .


D.
1;1 .


Lời giải:
Đặt
2
41tx
với
2;2x



2
' ; ' 0 0
4
x
t t x
x
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 67
Khi đó ta đi tìm
m
để phương trình
f t m
có nghiệm trên
1;1


Dựa vào đồ thị trên
1;1


, để phương trình có nghiệm
4 0.m
Chọn đáp án C.
Câu 77: Cho hàm số bậc ba
32
y f x ax bx cx d
có đồ thị như hình bên dưới.
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
5 4 4 0f x m f x m
có
7 nghiệm phân biệt?
A. 1. B. 2. C. 3. D. 4.
Lời giải:
Từ đồ thị hàm số
y f x
, vẽ được đồ thị hàm số
y f x
như sau:
Ta có
2
41
5 4 4 0
12
fx
f x m f x m
f x m

Từ đồ thị hàm số
y f x
suy ra phương trình (1) có 3 nghiệm phân biệt.
Vậy để phương trình đã cho có 7 nghiệm phân biệt thì (2) có 4 nghiệm phân biệt và khác với
các nghiệm của (1)
0 1 4 1 3mm
. Do đó có 3 giá trị nguyên của
m
.
Chọn đáp án C.
Câu 78: Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
( ) :d y x m
cắt đồ thị
1
(C) :
1
x
y
x
tại 2 điểm phân biệt
,AB
sao cho
2 6.AB
A.
2; 2mm
. B.
4; 4mm
. C.
2m
. D.
4m
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 68
Lời giải:
Xét phương trình:
1
1
x
mx
x

1 ( )(1 )x m x x
.
2
1x m mx x x
2
( 2) 1 0(1)x m x m
.
Để đường thẳng
()d
cắt đồ thị
(C)
tại 2 điểm phân biệt
,AB
.
(1)
có 2 nghiệm phân biệt khác 1
2
4 4 4( 1 ) 0
1 ( 2) 1 0
m m m
mm
2
80
20
m


luôn đúng với mọi
.m
Gọi
2
2
2
; ; ; ; 2.
A A B B B A A B B A
A x m x B x m x AB x x x x AB AB x x
.
,
AB
xx
là nghiệm của (1). Nên theo hệ thức viét ta có
2
.1
AB
AB
x x m
x x m
Ta có:
2
2
24 2. 24
BA
AB x x
2
2 4 24
B A A B
x x x x



.
2
4 12
B A A B
x x x x
2
2 4 1 12mm
2
40m
2m
.
Chọn đáp án A.
Câu 79: Có bao nhiêu giá trị nguyên của tham số
m
để đường thẳng
y x m
cắt đồ thị hàm số
2
1
x
y
x
tại hai điểm phân biệt
A
,
B
sao cho
4?OA OB
A. 2. B. 1. C. 0. D. 3.
Lời giải:
Ta có:
2
1
2
2 0 1
1
x
x
xm
x mx m
x
Đường thẳng
y x m
cắt đồ thị hàm số
2
1
x
y
x
tại hai điểm phân biệt
A
,
B
phương trình (1) có hai nghiệm phân biệt khác 1
2
10
4 8 0mm


thỏa mãn với mọi số thực
.m
Với mọi số thực
m
đường thẳng
y x m
cắt đồ thị hàm số
2
1
x
y
x
tại hai điểm phân biệt
11
;A x x m
,
22
;xB x m
, trong đó
12
,xx
là hai nghiệm phân biệt của (1).
Ta có:
2
2 2 2 2 2
1 1 1 1
2 2 2 2 4OA x x m x mx m m m m m
.
Tương tự ta được:
2
24OB m m
.
Do đó:
2
0
4 2 0
2
m
OA OB m m
m
. Vậy có 2 giá trị thỏa mãn yêu cầu đề bài.
Chọn đáp án A.
Câu 80: Tìm giá trị thực của tham số
m
để đường thẳng
:2d y x m
cắt đồ thị hàm số
2
1
x
y
x
C
tại hai điểm phân biệt
A
và
B
sao cho độ dài
AB
ngắn nhất.
A.
3.m 
B.
3.m
C.
1.m
D.
1.m 
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 69
Lời giải:
Tập xác định:
\1D
.
Xét phương trình:
2
21
1
x
x m x
x
2
( ) 1 2 0 1g x x m x m
.
Để
d
cắt
C
tại hai điểm phân biệt
A
và
B
thì (1) có hai nghiệm phân biệt
1x
22
2 1 4 2 2 9 0
.
1 2 0
m m m m m
m
g
Gọi
12
,xx
là hai nghiệm của
1
thì
11
;2A x x m
,
22
;2A x x m
.
Khi đó
22
2
1 2 1 2 1 2
2 2 4AB x x x x x x



22
2 1 4 2 2 1 8 16.m m m
Vậy
AB
ngắn nhất khi
1m
.
Chọn đáp án C.
Câu 81: Cho hàm số
32
3 1.f x x x mx
Gọi
S
là tổng tất cả giá trị của tham số
m
để đồ thị hàm số
y f x
cắt đường thẳng
1y
tại ba điểm phân biệt
0;1 ,A
,B
C
sao cho các tiếp tuyến của
đồ thị hàm số
y f x
tại
,B
C
vuông góc với nhau. Gía trị của
S
bằng
A.
9
.
2
B.
9
.
5
C.
9
.
4
D.
11
.
5
Lời giải:
Xét phương trình:
3 2 2
2
0
3 1 1 6 0
6 0 *
x
x x mx x x x m
x x m
Để đồ thị hàm số
y f x
cắt đồ thị hàm số
1y
tại ba điểm phân biệt
0;1 ,A
11
;,B x y
22
;C x y
thì phương trình
*
có hai nghiệm phân biệt khác
0
0
0
9
9 4 0
4
m
m
m
m


.
Theo hệ thức Viet, ta có
12
12
3
.
.
xx
x x m
Để tiếp tuyến của đồ thị hàm số
y f x
tại
,B
C
vuông góc với nhau thì
22
1 2 1 1 2 2
. 1 3 6 . 3 6 1f x f x x x m x x m

2 2 2 2 2
1 2 1 2 1 2 1 2 1 2 1 2
9 18 3 6 36 1 0x x x x x x m x x m x x x x m
2
9 65
9 65 9 65 9
8
4 9 1 0 .
8 8 4
9 65
8
m
m m S
m

Chọn đáp án C.
Câu 82: Có bao nhiêu giá trị nguyên của tham số
2018;2019m



để đồ thị hàm số
3
33y x mx
và
đường thẳng
31yx
có duy nhất một điểm chung?
A.
1
. B.
2019
. C.
4038
. D.
2018
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 70
Xét phương trình:
3
3 3 3 1x mx x
3
3 2 3x x mx
(1).
Xét hàm
3
2
3 2 2
3
xx
f x x
xx

;
3
22
2 2 2
2
x
f x x
xx
;
01f x x
.
Bảng biến thiên:
Yêu cầu bài toán
0m
. Mà
m
và
2018;2019m



nên có
2018
giá trị thỏa mãn.
Chọn đáp án D.
Câu 83: Có bao nhiêu giá trị thực của tham số
m
để phương trình
1 2 0x x x m
có
3
nghiệm
phân biệt lập thành cấp số nhân tăng?
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải:
Ta có:
1
1 2 0 2
x
x x x m x
xm
Phương trình có
3
nghiệm phân biệt lập thành cấp số nhân tăng khi và chỉ khi
2
2
2
2 1; 2;2
1.2
2 1; 2;2
1. 2 .
4 1;2;4
2. 1
11
;1;2
22
m
m
ml
m
m
m
m




Vậy có
3
giá trị
m
thỏa mãn.
Chọn đáp án B.
Câu 84: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để phương trình
32
2 3 2 1x x m
có đúng
hai nghiệm phân biệt. Tổng các phần tử của
S
bằng
A.
1
2
. B.
3
2
. C.
5
2
. D.
1
2
.
Lời giải:
Xét hàm số:
32
23y x x
2
6 6 0 0 1y x x y x x

.
Bảng biến thiên:
Số nghiệm của phương trình đã cho bằng số giao điểm của hai đồ thị:
32
: 2 3
: 2 1
C y x x
d y m


Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 71
Phương trình đã cho có hai nghiệm phân biệt
1
2 1 1
1
2 1 0
2
m
m
m
m




1
1;
2
S



.
Chọn đáp án B.
Câu 85: Giá trị
k
thỏa mãn đường thẳng
:d y kx k
cắt đồ thị
H
:
4
y
22
x
x
tại 2 điểm phân biệt
A
và
B
cùng cách đều đường thẳng
0y
. Khi đó
k
thuộc khoảng
A.
2; 1
. B.
1;2
. C.
1;0
. D
0;1
.
Lời giải:
Xét phương trình:
4
22
x
kx k
x

x1
2
2 2 4 0kx x k
x1
Đường thẳng
d
cắt
H
tại 2 điểm phân biệt
A
,
B
khi và chỉ khi phương trình có 2 nghiệm
phân biệt khác 1
22
23
( 1) 2 (2 4) 0 4 8 1 0
2
2 1 2 4 0 3 0
23
2
x
k k k k
kk
x



Gọi
A
x
,
B
x
là 2 nghiệm phương trình ta có
;
AA
A x kx k
và
;
BB
B x kx k
vì
A
,
B
cùng cách
đều đường thẳng
0y
nên
( ) 2.
A B A B
kx k kx k x x
Mà
1 1 1
2 1;0
2 2 4
AB
x x k
kk
.
Chọn đáp án C.
Câu 86: Cho hàm số
1
x
y
x
C
và đường thẳng
:d y x m
. Gọi
S
là tập hợp các số thực
m
để
đường thẳng
d
cắt đồ thị
C
tại hai điểm phân biệt
,AB
sao cho tam giác
OAB
(
O
là gốc tọa
độ) có bán kính đường tròn ngoại tiếp bằng
22
. Tổng các phần tử của
S
bằng
A. 8. B.
4
. C.
1
. D.
2
.
Lời giải:
Xét phương trình:
2
0 (*)
.
1
1
x mx m
x
xm
x
x
Để
đường thẳng
d
cắt đồ thị
C
tại hai điểm phân biệt
,AB
thì phương trình
*
phải có hai
nghiệm phân biệt khác
1
nên ta có
2
4
40
0.
10
m
mm
m
Gọi
12
,xx
là hai nghiệm của phương trình
*
, ta có
12
x x m
.
Do đó
1 1 1 2
;;A x x m A x x
,
2 2 2 1
;;B x x m B x x
+)
2
2 2 2
1 2 1 2 1 2
2 2 .OA OB x x x x x x m m
+)
,.
2
O
m
h d O d
Ta có
1 . .
. 2 . .
24
OAB O O
OA OB AB
S AB h R h OA OB
R
2
6
24
2.
m
m m m
m

Vậy tổng các phần tử của tập
S
bằng 4 .
Chọn đáp án B.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 72
Câu 87: Cho hàm số
42
3 2 3y x m x m
có đồ thị là
()
m
C
. Tìm
m
để đường thẳng
:1dy
cắt đồ
thị
()
m
C
tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2.
A.
1
1
3
m
và
0m
B.
1
1
2
m
và
0m
C.
11
22
m
và
0m
D.
11
32
m
và
0m
Lời giải:
Xét phương trình:
42
3 2 3 1x m x m
42
3 2 3 1 0x m x m
Đặt
2
tx
,
0t
, phương trình trở thành
2
3 2 3 1 0t m t m
2
1
31
t
tm

Đường thẳng
:1dy
cắt đồ thị
()
m
C
tại
4
điểm phân biệt đều có hoành độ nhỏ hơn
2
khi và
chỉ khi phương trình
2
có hai nghiệm dương phân biệt
1
t
,
2
t
thỏa mãn
12
04tt
0
3 1 1
.
1
0 3 1 4
1
3
m
m
m
m



Chọn đáp án A.
Câu 88: Cho hai hàm số
2
1y x x
và
32
23y x x mx
. Giá trị của tham số
m
để đồ thị của hai
hàm số có
3
giao điểm phân biệt và
3
giao điểm đó nằm trên đường tròn bán kính bằng
3
thuộc vào khoảng nào dưới đây?
A.
;4
. B.
4; 2
. C.
0;
. D.
2;0
.
Lời giải:
Giả sử
m
là số thực thỏa mãn bài toán.
Xét phương trình:
2 3 2 3 2
1 2 3 1 2 0 1 .x x x x mx x x m x
Gọi
00
;M x y
là một trong
3
giao điểm.
Ta có:
2 4 3 2
2
0 0 0 0 0
0 0 0
32
32
0 0 0
0 0 0
2 2 1 2
1
1 2 0
1 2 0 3
y x x x x
y x x
x x m x
x x m x


.
Từ
2
và
3
suy ra
2 3 2 2 2
0 0 0 0 0 0 0 0 0
1 1 2 1 1 3 1 1 3y x x x m x m x m x m x m x


.
Hay
2 2 2
0 0 0 0 0 0 0
1 3 1 1 3y x mx m x m y x m x
.
Rút gọn ta được
22
0 0 0 0
3 0 4x y x my m
. Đây là phương trình đường tròn khi
22
1
3 0 *
22
m
m
.
Với điều kiện
*
thì
00
;M x y
thuộc đường tròn có bán kính
22
1
3
22
m
Rm
.
Theo đề bài
2
2
2 3 3
1
3 3 9 4 23 0
4
2 3 3
m
m
R m m m
m


.
Thử lại.
Với
2 3 3m 
thì phương trình
1
có
1
nghiệm. Do đó,
2 3 3m 
không thỏa mãn.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 73
Với
2 3 3m 
thì phương trình
1
có
3
nghiệm và cũng thỏa mãn
*
.
Vậy giá trị
m
cần tìm là
2 3 3 4; 2m
.
Chọn đáp án B.
Câu 89: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá
trị thực của tham số
m
để phương trình
sinf x m
có nghiệm thuộc khoảng
0;
là
A.
1;3
. B.
1;1
. C.
1;3
. D.
1;1
.
Lời giải:
Đặt
sintx
. Với
0;x
thì
0;1t
.
Do đó phương trình
sinf x m
có nghiệm thuộc khoảng
0;
khi và chỉ khi phương trình
f t m
có nghiệm thuộc nửa khoảng
0;1
.
Quan sát đồ thị ta suy ra điều kiện của tham số
m
là
1;1m

.
Chọn đáp án D.
Câu 90: Cho hàm số
y f x
liên tục trên và có bảng biến thiên như hình vẽ sau:
Tập hợp các giá trị
m
để phương trình
cos2 2 1 0f x m
có nghiệm thuộc khoảng
;
34




là
A.
1
0; .
2



B.
1
0; .
2


C.
11
;.
42


D.
2 2 1
;.
44





Lời giải:
Đặt
1
cos2 , ; ;1
3 4 2
x t x t

.
Yêu cầu đề bài tương đương với phương trình
21f t m
có nghiệm
1
;1
2
t



.
Từ bảng biến thiên suy ra yêu cầu
1
1 2 1 2 0
2
mm
.
Chọn đáp án A.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 74
Câu 91: Cho hàm số
()y f x
xác định, liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của
m
để phương trình
2
2. 3 4 6 9 3f x x m
có nghiệm.
A.
13
. B.
12
. C.
8
. D.
10
.
Lời giải:
Với
2
0;
3
x



, ta có
22
0 6 9 1 (1 3 ) 1x x x
2
0 4 6 9 4xx
2
3 3 4 6 9 1xx
. Dựa vào đồ thị đã cho suy ra
2
3 4 6 9 5;1f x x


.
Khi đó phương trình
2
2. 3 4 6 9 3f x x m
có nghiệm
3
51
2
m
75m
.
Do
m
nên
7; 6; 5; 4; 3; 2; 1; 0; 1; 2; 3; 4; 5m
, có
13
giá trị của
m
thỏa đề.
Chọn đáp án A.
Câu 92: Cho hàm số
y f x
xác định trên và có đồ thị như hình bên. Có bao nhiêu giá trị nguyên
của tham số
m
để phương trình:
44
4 sin cosf x x m



có nghiệm.
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải:
Đặt
t
4 4 2
4 sin cos 4 2sin 2 2;4x x x t


.
Do đó phương trình
44
4 sin cosf x x m



có nghiệm
phương trình
f t m
có nghiệm
trên đoạn
2;4


.
Dựa vào đồ thị đã cho ta thấy: phương trình
f t m
có nghiệm
t
với
2;4t


15m
.
Vậy
1;2;3;4;5m
.
Chọn đáp án D.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 75
Câu 93: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
tham số
m
để phương trình
sinf f x m
có nghiệm thuộc khoảng
0;
.
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
Đặt
sint f x
, do
0; sin 0;1 1;1x x t


.
Do đó phương trình
sinf f x m
có nghiệm thuộc khoảng
0;
khi và chỉ khi phương
trình
f t m
có nghiệm thuộc nửa khoảng
1;1
.
Quan sát đồ thị đã cho: yêu cầu bài toán
1;3m
.
Chọn đáp án D.
Câu 94: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ. Gọi
S
là tập hợp tất cả các giá
trị nguyên của tham số
m
để phương trình
sin 3sinf x x m
có nghiệm thuộc khoảng
0;
. Tổng các phần tử của
S
bằng
A.
8
. B.
10
. C.
6
. D.
5
.
Lời giải:
Đặt
sintx
, do
0; sin 0;1 0;1x x t


.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 76
Gọi
1
là đường thẳng qua điểm
1; 1
và song song với đường thẳng
3yx
có phương trình
34yx
.
Gọi
2
là đường thẳng qua điểm
0;1
và song song với đường thẳng
3yx
có phương trình
31yx
.
Do đó phương trình
sin 3sinf x x m
có nghiệm thuộc khoảng
0;
khi và chỉ khi phương
trình
3f t t m
có nghiệm thuộc nửa khoảng
0;1
41m
.
Chọn đáp án B.
Câu 95: Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây:
Tìm số giá trị nguyên của
m
để phương trình
2
2f x x m
có đúng
4
nghiệm thực phân biệt
thuộc đoạn
37
;
22



.
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải:
Đặt
2
2t x x
,
37
;
22
x




Bảng biến thiên:
Dựa vào bảng biến thiên
21
1;
4
t



. Ta có:
2
2f x x m
1
f t m
2
.
Ta thấy, với mỗi giá trị
21
1;
4
t



ta tìm được hai giá trị của
37
;
22
x




.
Do đó, phương trình
1
có
4
nghiệm thực phân biệt thuộc
37
;
22



Phương trình
2
có hai nghiệm thực phân biệt thuộc
21
1;
4


Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 77
Đường thẳng
ym
cắt đồ thị hàm số
y f t
tại hai điểm phân biệt có hoành độ thuộc
21
1;
4


.
Dựa vào đồ thị ta thấy có hai giá trị nguyên của
m
thỏa yêu cầu là
3m
và
5m
.
Chọn đáp án C.
Câu 96: Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây:
Tồn tại bao nhiêu giá trị nguyên của tham số
m
để phương trình
sinf x m
có đúng hai
nghiệm thuộc đoạn
0;


?
A.
4
. B.
7
. C.
5
. D.
6
.
Lời giải:
Đặt
sintx
,
0;x


thì
0;1t


. Để phương trình
sinf x m
có đúng hai nghiệm
0;x


thì phương trình
f t m
có đúng một nghiệm
0;1t
. Dựa vào đồ thị ta có
7; 2m
, do
m
nguyên nên
7; 6; 5; 4; 3m
. Vậy có
5
giá trị.
Chọn đáp án C.
Câu 97: Cho hàm số
fx
là đa thức và có đồ thị như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
sin 2
4 8 17
x
f f m m
có
nghiệm?
A.
3.
B.
4.
C.
5.
D.
6.
Lời giải:
Ta có:
sin
2
2
1
4 ;4 ,
4
.
8 17 4 1 1,
x
x
m m m m



Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 78
Để ý rằng trên
0; ,
fx
đồng biến nên
sin 2 sin 2
4 8 17 4 8 17
xx
f f m m m m
(*)
Phương trình (*) có nghiệm
2
1
8 17 ;4 5; 4; 3 .
4
m m m



Chọn đáp án A.
Câu 98: Cho hàm số
y f x
liên tục trên có đồ thị như hình vẽ bên dưới.
Tìm
m
để phương trình

2
2f x x m
có đúng
6
nghiệm thực phân biệt thuộc đoạn



37
;
22
?
A.
23m
hoặc
45fm
. B.
23m
hoặc
45fm
.
C.
23m
hoặc
45fm
. D.
23m
hoặc
45fm
.
Lời giải:
Đặt

2
2t x x
, với




37
;
22
x
.
Ta thấy hàm số

2
2u x x x
liên tục trên đoạn



37
;
22
và
22ux
;
01u x x
.
Bảng biến thiên:
Nhận xétrằng với
0t
hoặc

21
1
4
t
thì phương trình

2
2t x x
có
2
nghiệm phân biệt;
với
1t
thì phương trình

2
2t x x
có
3
nghiệm phân biệt; với mỗi
0;1t
thì phương trình

2
2t x x
có
4
nghiệm phân biệt.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 79
Với

2
2t x x
phương trình

2
2f x x m
thành







21
, 0;
4
f t m t
Dựa vào đồ thị
f
ta biện luận số nghiệm của phương trình







21
, 0;
4
f t m t
trong các
trường hợp sau
TH1:
2m
21f t t
. Khi đó phương trình

2
2f x x m
có
3
nghiệm phân biệt.
TH2:
23m



0;1
1;3
ta
f t m
tb
. Khi đó phương trình

2
2f x x m
có
6
nghiệm phân biệt.
TH3:
3m


0
1;3
t
f t m
tb
. Khi đó phương trình

2
2f x x m
có
4
nghiệm phân biệt.
TH4:
34mf
1;4f t m t a
. Khi đó phương trình

2
2f x x m
có
2
nghiệm phân biệt.
TH5:
4mf


4
1;4
t
f t m
tb
. Khi đó phương trình

2
2f x x m
có
4
nghiệm phân biệt.
TH6:
45fm
f t m
có
3
nghiệm phân biệt thuộc
1;5
. Khi đó phương trình

2
2f x x m
có
6
nghiệm
phân biệt.
TH7:
5m
f t m
có
2
nghiệm phân biệt thuộc
1;5
. Khi đó phương trình

2
2f x x m
có
4
nghiệm
phân biệt.
TH8:




21
5
4
mf
f t m
có
1
nghiệm thuộc



21
1;
4
. Khi đó phương trình

2
2f x x m
có
2
nghiệm phân
biệt.
Vậy phương trình

2
2f x x m
có đúng
6
nghiệm thực phân biệt thuộc đoạn



37
;
22
khi
và chỉ khi
23m
hoặc
45fm
.
Chọn đáp án A.
Câu 99: Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
1y mx m
cắt đồ thị của hàm số
32
32y x x x
tại ba điểm
A
,
B
,
C
phân biệt sao cho
.AB BC
A.
[( ;0) 4; ).m  
B.
.m
C.
5
;.
4
m




D.
( 2; ).m 
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 80
Ta có
32
: 3 2C y x x x
và
:1d y mx m
.
Xét phương trình:
3 2 3 2
3 2 1 3 1 1 0x x x mx m x x m x m
2
2
1
1 2 1 0
2 1 0 1
x
x x x m
x x m
Đồ thị
C
cắt đường thẳng
d
tại ba điểm
A
,
B
,
C
phân biệt
phương trình
1
có hai
nghiệm phân biệt khác 1
1 1 0
2
1 2 *
10
2
m
m
m
g
m



Cách 1: Đường thẳng
d
cắt đồ thị
C
tại ba điểm phân biệt sao cho
AB BC
điểm
B
chính
là điểm uốn của đồ thị
C
.
Ta có
66yx


,
01yx

,
1y 
điểm uốn
1;1Bd
,
2m
.
Vậy với
2;m
thì yêu cầu bài toán được thỏa mãn.
Chú ý. Hàm số bậc ba
32
0y ax bx cx d a
có hoành độ điểm uốn là nghiệm của phương
trình
0y

và điểm uốn chính là tâm đối xứng của đồ thị hàm bậc ba.
Cách 2: Với
2m 
, phương trình
12
1
12
xm
xm
. Ta gán
12
1
12
A
B
C
xm
x
xm
, với cách gán
như vậy, rõ ràng
,2
B A C B
x x x x m
. Suy ra
AB BC
với mọi
2m 
.
Chọn đáp án D.
Câu 100: Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
y mx
cắt đồ thị của hàm số
32
32y x x m
tại ba điểm phân biệt A, B, C sao cho
AB BC
.
A.
;3m 
. B.
;1m 
. C.
;m  
. D.
1;m 
.
Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số
32
32y x x m C
và đường thẳng
y mx d
là:
32
32x x m mx
2
1 2 2 0x x x m
2
1
2 2 0 (*)
x
x x m
Để đường thẳng
y mx
cắt đồ thị của hàm số
32
32y x x m
tại ba điểm phân biệt
,,A B C
(*) có ba nghiệm phân biệt khác 1
3
3
m
m
3m
.
Đường thẳng
d
cắt đồ thị
C
tại ba điểm
,,A B C
phân biệt sao cho
AB BC
thì điểm
B
chính là điểm uốn của đồ thị
C
.
Ta có :
2
36y x x

66yx


,
01yx

.
y

đổi dấu khi
x
đi qua
1x
. Điểm uốn của
đồ thị
C
là
1;Bm
. Mặt khác điểm
1;Bm
thuộc đường thẳng
d
y mx
với mọi
m
.
Vậy với
3m
thì yêu cầu bài toán thỏa mãn.
Chọn đáp án A.
Câu 101: Cho hàm số
4 3 2
f x mx nx px qx r
, (với
, , , ,m n p q r
). Hàm số
y f x
có đồ thị như
hình vẽ bên dưới:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 81
Tập nghiệm của phương trình
f x r
có số phần tử là
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải:
Ta có
32
4 3 2f x mx nx px q
1
Dựa vào đồ thị
y f x
ta thấy phương trình
0fx
có ba nghiệm đơn là
1
,
5
4
,
3
.
Do đó
1 4 5 3f x m x x x
và
0m
. Hay
32
4 13 2 15f x mx mx mx m
2
.
Từ
1
và
2
suy ra
13
3
nm
,
pm
và
15qm
.
Khi đó phương trình
f x r
4 3 2
0mx nx px qx
4 3 2
13
15 0
3
m x x x x



4 3 2
3 13 3 45 0x x x x
2
3 5 3 0x x x
5
03
3
x x x
( nghiệm kép).
Vậy tập nghiệm của phương trình
f x r
là
5
;0;3
3
S




.
Chọn đáp án B.
Câu 102: Cho hàm số
4 3 2
f x ax bx cx dx m
, (với
, , , ,a b c d m
). Hàm số
y f x
có đồ thị như
hình vẽ bên dưới:
Tập nghiệm của phương trình
f x m
có số phần tử là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
Cách 1: Ta có
32
4 3 2f x ax bx cx d
1
.
Dựa vào đồ thị ta có
1 4 5 3f x a x x x
32
4 13 2 15ax ax ax a
2
và
0a
.
Từ
1
và
2
suy ra
13
3
ba
,
ca
và
15da
.
Khi đó:
f x m
4 3 2
0ax bx cx dx
4 3 2
13
15 0
3
a x x x x



Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 82
4 3 2
3 13 3 45 0x x x x
0
5
3
3
x
x
x


. Vậy tập nghiệm của phương trình là
5
;0; 3
3
S




.
Cách 2: Từ đồ thị ta có
0a
.
4 3 2
f x m ax bx cx dx m m
32
0
02
x
ax bx cx d
.
Ta có
32
' 4 3 2f x ax bx cx d
có 3 nghiệm
1 2 3
5
3; ; 1
4
x x x
.
Áp dụng định lý Viet ta có:
1 2 3
1 2 2 3 1 3
1 2 3
3
4
2
4
4
b
x x x
a
c
x x x x x x
a
d
x x x
a

13 3
44
12
24
15
44
b
a
c
a
d
a

13
3
15
ba
ca
da

.
Thế vào
2
ta có:
32
3
13
15 0
5
3
3
x
a x x x
x




.
Vậy tập nghiệm của phương trình là
5
;0; 3
3
S




.
Chọn đáp án C.
__________________________HẾT__________________________
Huế, ngày 16 tháng 7 năm 2023
| 1/110

Tài liệu khác của Toán 12

Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 12 KHẢO SÁT HÀM SỐ SỰ TƯƠNG GIAO
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Chủ đề 7: SỰ TƯƠNG GIAO CỦA HAI ĐỒ THỊ I- LÝ THUYẾT
Giả sử (C) và (C’) là đồ thị của hai hàm số: y (C)
y f (x) vµ y  ( g x) .
Hoành độ giao điểm của (C) và (C’), nếu có, là nghiệm của phương trình
f (x)  g(x) (1) (C') Lưu ý: M
Phương trình f (x)  (
g x) là phương trình hoành độ giao điểm y0 của (C) và (C’). O 1 x0 x
Đảo lại, nếu x là nghiệm của (1), tức là: f (x )  g(x ) 0 0 0
thì điểm M x ; f (x ) hay M x ; (
g x ) là điểm chung của (C) và (C’). 0 0  0 0  Kết quả:
+ Nếu phương trình (1) vô nghiệm thì (C) và (C’) không có điểm chung.
+ Nếu phương trình (1) có n nghiệm thì (C) cắt (C’) tại n điểm phân biệt ( n không là nghiệm bội) II-BÀI TẬP MINH HỌA DẠNG 1:
XÁC ĐỊNH TOẠ ĐỘ GIAO ĐIỂM CỦA 2 ĐỒ THỊ
Bài tập 1: (ĐHVH-98) Tìm toạ độ giao điểm của đường thẳng d: y  2x  5 với đồ thị hàm số (C): 3 2
y x  3x  1 . Lời giải: TXĐ: D
. Xét phương trình hoành độ giao điểm của d và (C): 3 2 3 2
x  3x  1  2x  5  x  3x  2x  4  0 x  1     x  1 2
x  2x  4  0    x  1   5 2
x  2x  4  0      x  1   5 * Với x  1   y  2.( 1  )  5  3 . * Với x  1
  5  y  2 1
  5  5  3  2 5 . * Với x  1
  5  y  2 1
  5   5  3  2 5 . Kết luận:
Vậy các giao điểm cần tìm là M  1  ;3, M  1
  5;3  2 5 , M 1   5;3  2 5 1 2 3  
Nhận xét: Khi xác định tung độ giao điểm, ta đã sử dụng hàm số y  2x  5 để đơn giản hơn. 1
Bài tập 2: (Đề 105) Chỉ rõ các giao điểm của đồ thị (C): y x  3  với trục hoành. x  1 Lời giải: TXĐ: D   \   1 . 1
Xét phương trình hoành độ giao điểm của (C) và Ox: x  3   0 (1) x  1
TH 1: 3  x  1 , phương trình (1) trở thành:
Giáo viên: LÊ BÁ BẢO...0935.785.115... 1
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x   1 3 
 0  x  3x   2
1  1  0  x  4x  4  0  x  2  (nhËn) x  1
TH 2: x  3 , phương trình (1) trở thành:    1 x     x 3 
 0  x  3x  1 2 2 (lo¹i) 2
 1  0  x  4x  2  0   x  1 x  2   2 (nhËn)
Kết luận: Vậy giao điểm cần tìm là M  2  ;0, M 2   2;0 . 1 2  
DẠNG 2: BIỆN LUẬN SỐ GIAO ĐIỂM CỦA 2 HỌ ĐỒ THỊ
Bài tập 1: (Đề 29) Xác định tất cả các giá trị của a để đường thẳng d: y ax  3 không cắt đồ thị hàm số 3x  4 (C): y  . x  1 Lời giải: TXĐ: D   \  1 .
Xét phương trình hoành độ giao điểm của d và (C):
3x  4  ax  3  3x  4  ax  3x 1 x  1 2
ax ax  7  0 x  1 (1) x  1
Để đường thẳng d không cắt (C)  Phương trình (1) vô nghiệm hoặc có nghiệm kép x  1 .
TH 1: Xét a  0 , phương trình (1) trở thành: 7  0 . Vậy a  0 thỏa. a  0 a  0     a 28;0 2      a  28a  0  28   a  0  
TH 2: Y.c.b.t  a  0  a  28    2
  a  28a  0    (v« nghiÖm) a      1  b  2a   1  2a
Kết luận: Vậy các giá trị cần tìm là a  2  8;0 . 2 x  4x  3
Bài tập 2: (Đề 34) Xác định tất cả các giá trị của k để đồ thị hàm số (C): y  cắt đường thẳng x  2
d: y kx  1 tại 2 điểm phân biệt. Lời giải: TXĐ: D   \   2 .
Xét phương trình hoành độ giao điểm của d và (C): 2 x  4x  3 2
kx  1  x  4x  3  x  2kx   1 , x  2   x  2
g x  k   2 ( )
1 x  2k  3x  1  0 x  2   (1)
Để d cắt (C) tại 2 điểm phân biệt  Phương trình (1) có 2 nghiệm phân biệt  2 .  k 1  0 k  1     
 g     k     k   k 1 ( 2) 0 4 1 2 2 3  1  0 k     k  1. 2  
 k k   k     0  g 2k 3   4 8 5 0, 2  4k 1  0
Giáo viên: LÊ BÁ BẢO...0935.785.115... 2
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Kết luận: Vậy các giá trị cần tìm là k ;1  1; .
Bài tập 3: (ĐHSPII-97) Tìm m để hàm số (C): y    m 4 2 1
x mx  2m  1 cắt Ox tại 4 điểm phân biệt. Lời giải: TXĐ: D  .
Xét phương trình hoành độ giao điểm của (C) và Ox:   m 4 2 1
x mx  2m  1  0 (1) Đặt 2
t x  0 , (1) trở thành:   m 2 1
t mt  2m  1  0 (2)
Để (C) cắt Ox tại 4 điểm phân biệt  Phương trình (1) có 4 nghiệm phân biệt
 Phương trình (2) có 2 nghiệm dương phân biệt, tức là: 0  t t . 1 2 m  1 m  1   2
  m  42m  11 m   0
m m    m  2 2 2 9 12 4 3 2  0  m    Y.c.b.t  m 3   S   0  0  m  1  1  m   2m 1   1 P   0   m  1  1  m 2  1  2
m ;1\   2  3  1  2
Kết luận: Vậy các giá trị cần tìm là m ;1\  .  2  3
CHÚ Ý: Mối quan hệ về số nghiệm của phương trình 4 2
ax bx c  0 a  0 (1) và 2
at bt c  0 a  0 (2)
thông qua phép đặt ẩn phụ: 2
t x  0 .
TH1: Phương trình (2) có duy nhất 1 nghiệm t  0  Phương trình (2) không có nghiệm x .
TH2: Phương trình (2) có duy nhất 1 nghiệm t  0  Phương trình (2) có nghiệm x  0 . x t
TH3: Phương trình (2) có duy nhất 1 nghiệm t  0  Phương trình (2) có 2 nghiệm  . x    t
Vậy có thể mở rộng yêu cầu của bài toán thành các dạng sau:
3-1) Tìm m để hàm số (C) cắt Ox tại 3 điểm phân biệt   0  
Phương trình (2) có nghiệm 0  t t  g(0)  0 1 2 S  0 
3-2) Tìm m để hàm số (C) cắt Ox tại 2 điểm phân biệt
t  0  t P  0 1 2  
Phương trình (2) có nghiệm    0
0  t t   1 2  S    0
3-2) Tìm m để hàm số (C) cắt Ox tại 1 điểm    0
t  0  t   1 2 S    0
 Phương trình (2) có nghiệm    0
0  t t   1 2  S    0
Giáo viên: LÊ BÁ BẢO...0935.785.115... 3
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Trên đây là sự mở rộng bài toán cùng hướng giải quyết theo lý thuyết “ Tam thức bậc hai và ứng
dụng”. Chúng ta sẽ bàn lại bàn toán này cùng các phương pháp đặc sắc hơn như “ Ứng dụng tính
biến thiên”, “Phương pháp cực trị hàm số”…trong các bài viết tiếp theo.
Bài tập 4: (Đề dự bị 2003) Tìm m để đồ thị hàm số C y  x   2 ( ) :
1 x mx m cắt Ox tại 3 điểm phân biệt. Lời giải: TXĐ: D  .
Xét phương trình hoành độ giao điểm của (C) và Ox:    x x 1  1 2
x mx m  0 (1)   g  x 2
x mx m   0 (2)
Để (C) cắt Ox tại 3 điểm phân biệt  Phương trình (1) có 3 nghiệm phân biệt
 Phương trình (2) có 2 nghiệm phân biệt khác 1.  g  1 1  1  2m  0 m    1 Y.c.b.t     2
m;0  4;\  2    m  4m  0    2  g
m  0  m   4  
Kết luận: Vậy các giá trị cần tìm là m     1 ; 0 4; \  .  2 
Trong bài tập trên, đề bài đã “trình bày” tương đối …dễ thương (!!!) vì đã có dạng .
A B  0 . Chúng ta
thử qua bài tập với một sự thay đổi nhẹ nhàng xem sao:
Bài tập 5: (ĐHKT-98) Cho hàm số 3 2
y x  3x  (
1 C) . Đường thẳng đi qua A3;1 và có hệ số góc bằng
k . Xác định k để đường thẳng đó cắt đồ thị tại 3 điểm phân biệt. Lời giải: TXĐ: D  .
Đường thẳng d đi qua A3;1 và có hệ số góc k có phương trình:
d : y  1  k x  3  y k x  3  1
Xét phương trình hoành độ giao điểm của (C) và d: 3 2
x  3x  1  k x  3  ( 1 1) 3 2
x  3x kx  3 2
x x  3  kx  3  x    x  3 3 2
x k  0   2 x   k (2)
Để d cắt (C) tại 3 điểm phân biệt  Phương trình (1) có 3 nghiệm phân biệt
 Phương trình (2) có 2 nghiệm phân biệt khác 3  . k  0 Y.c.b.t  
k 0;  \  9 k   9
Kết luận: Vậy các giá trị cần tìm là k 0;   \  9 .
Các em chú ý, kỹ thuật phân tích 3 2
x x   k x    (1) 3 2 3 1 3 1
x  3x kx  3 , tạo ra được sự
thuận lợi trong quá trình phân tích. Còn không, chúng ta phải đoán được nghiệm và phân tích theo sơ
đồ Hoc-ner. Đoán không được nghiệm thì sao nhỉ???
Chúng ta xét tiếp bài tập sau: 1
Bài tập 6: Tìm m để đồ thị hàm số (C): 3
y x x m cắt trục hoành tại 3 điểm phân biệt. 3
Giáo viên: LÊ BÁ BẢO...0935.785.115... 4
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải: TXĐ: D  . 1 1
Xét phương trình hoành độ giao điểm của (C) và Ox: 3 3
x x m  0  x x m (1) 3 3 1
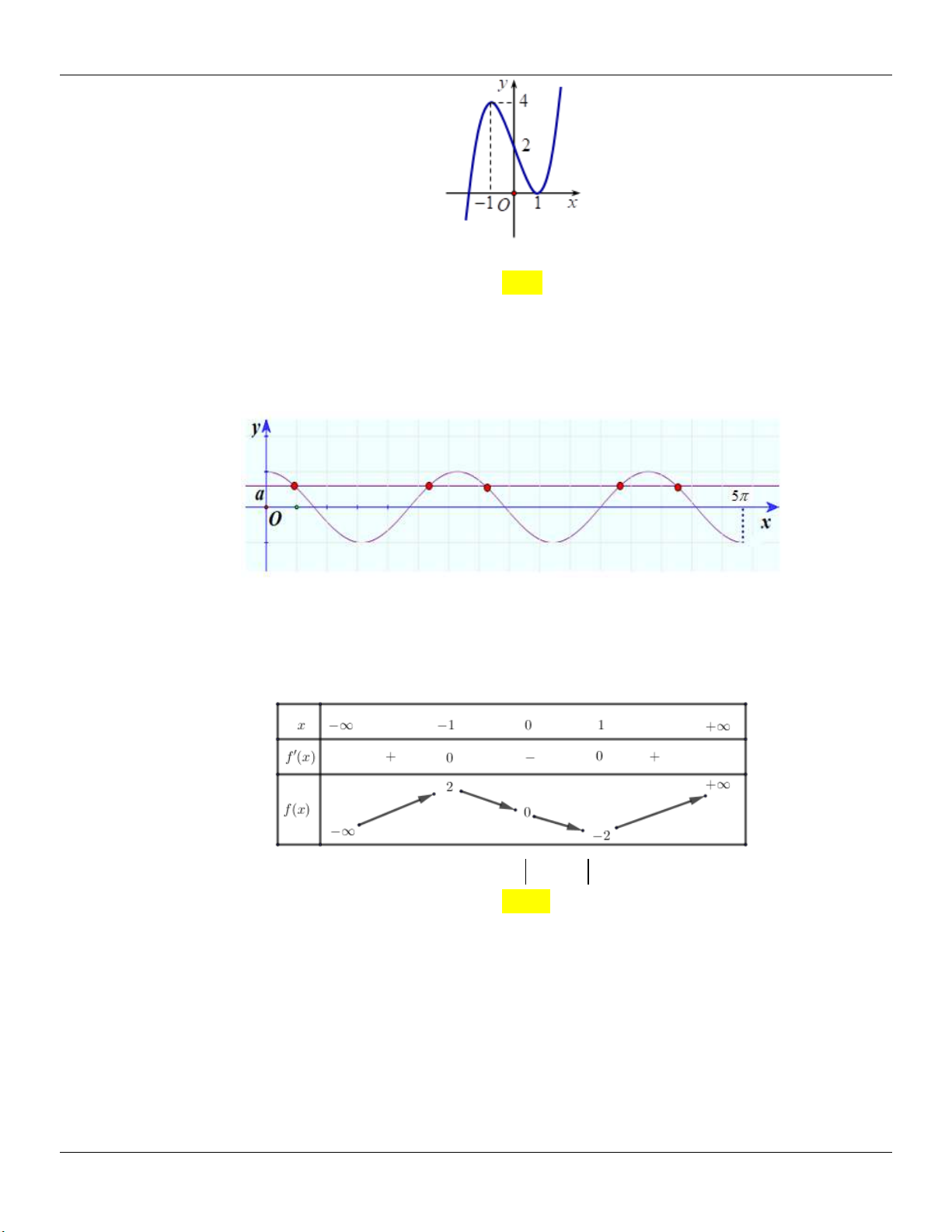
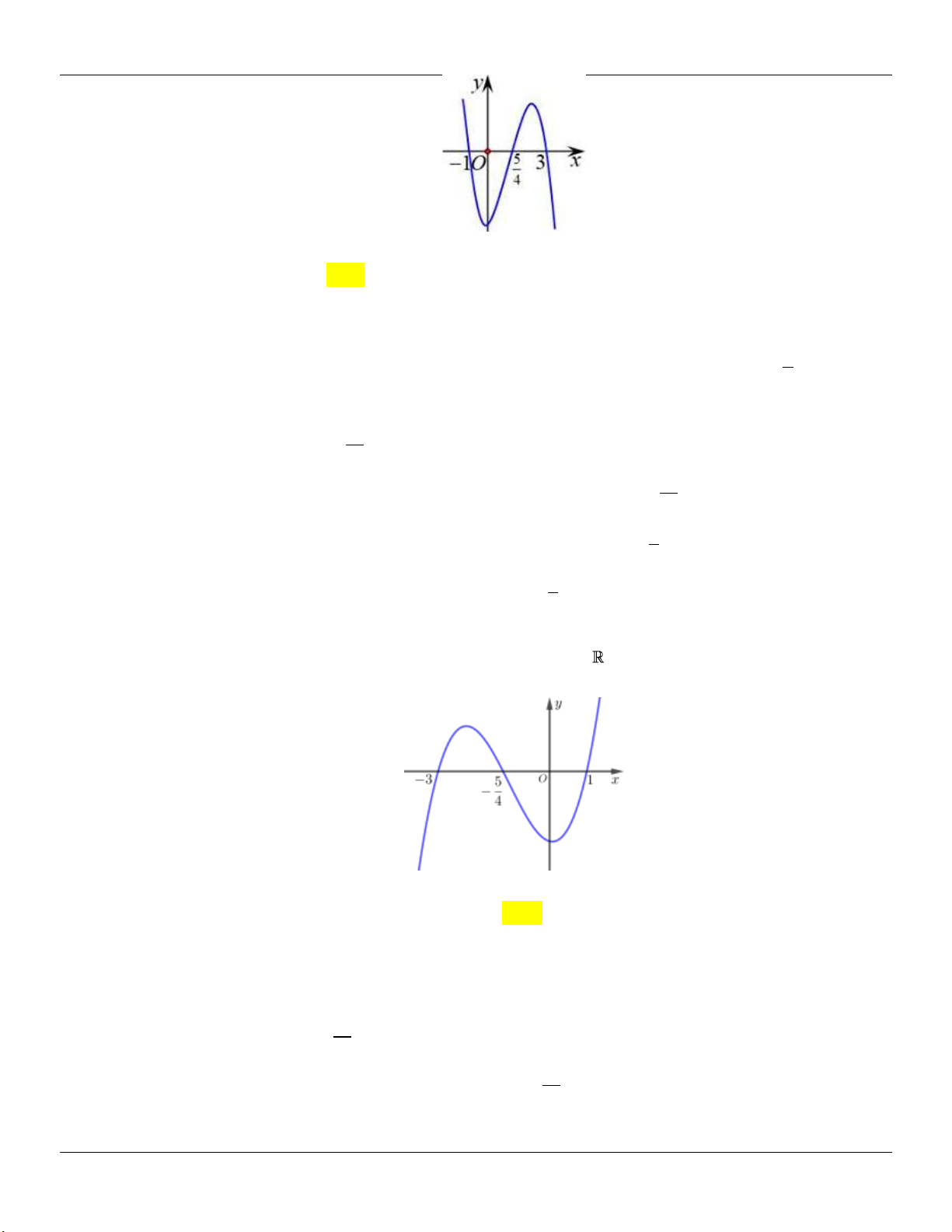
Để (C) cắt Ox tại 3 điểm phân biệt  Đồ thị C' 3
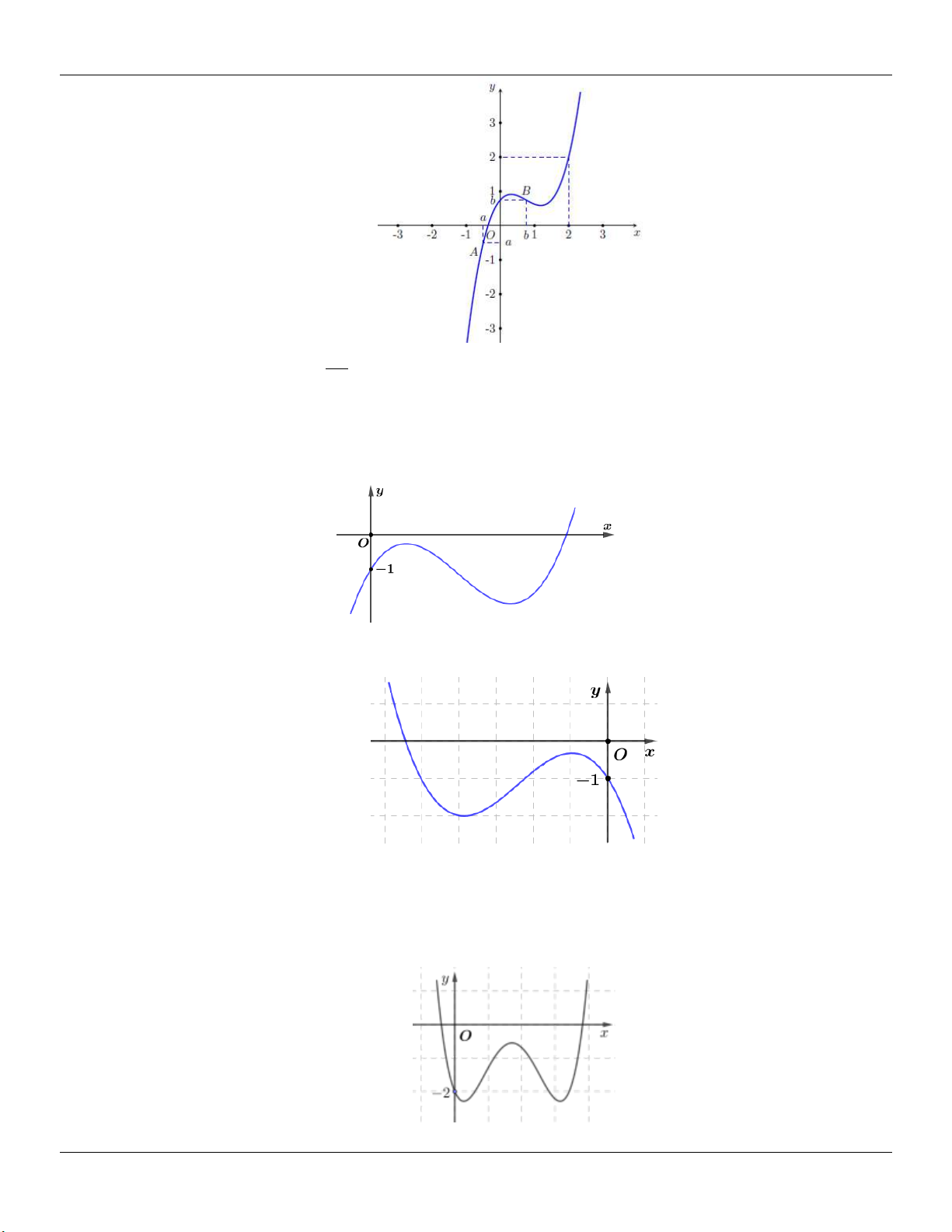
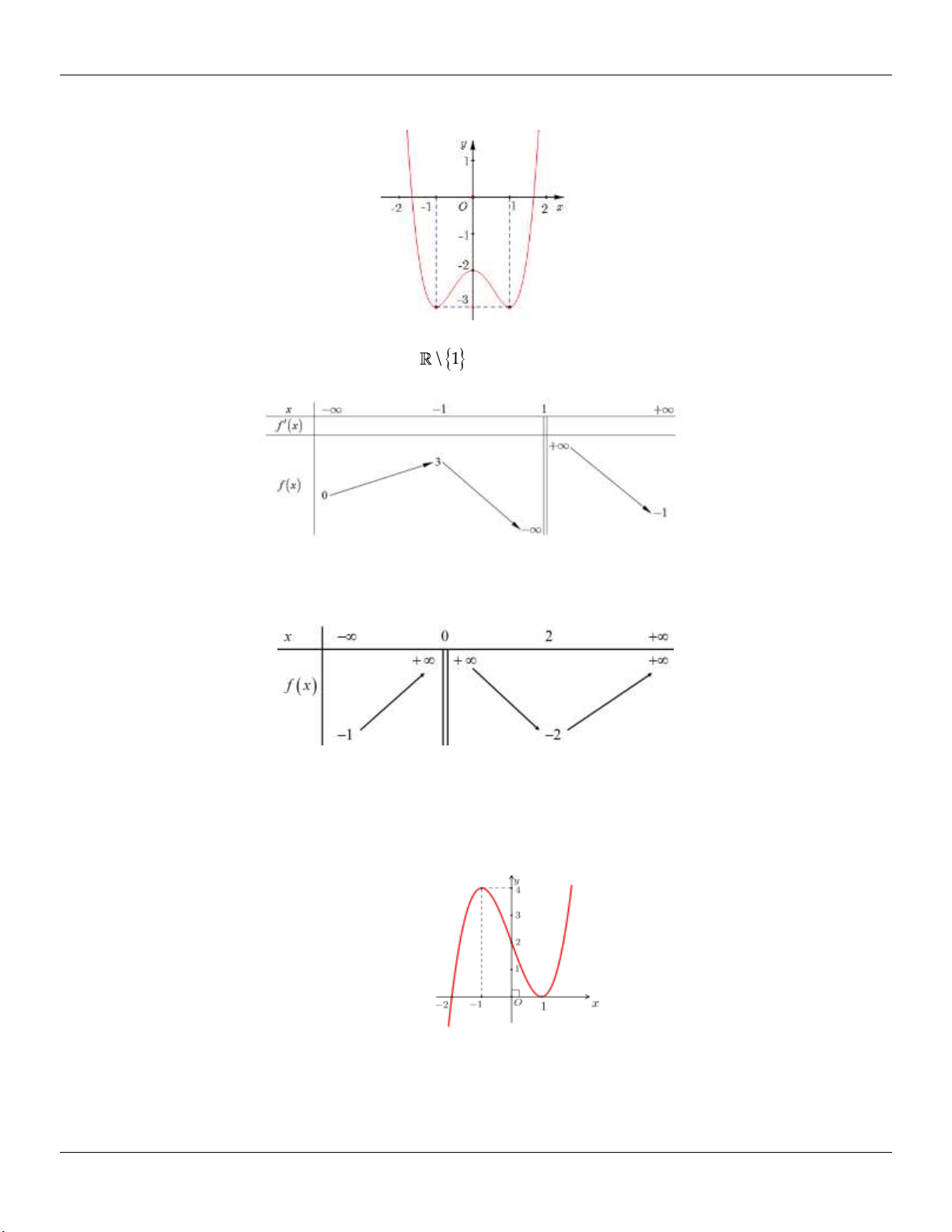
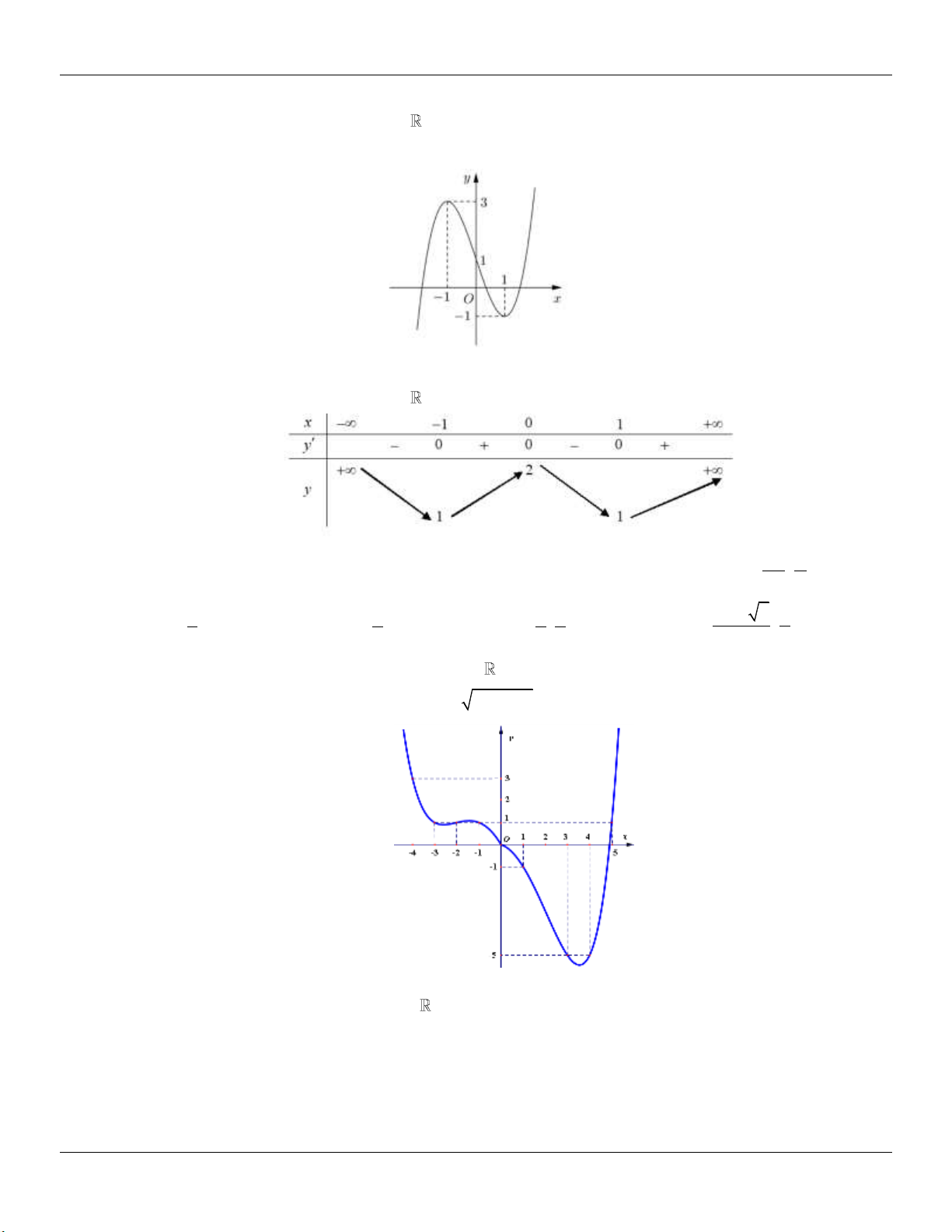
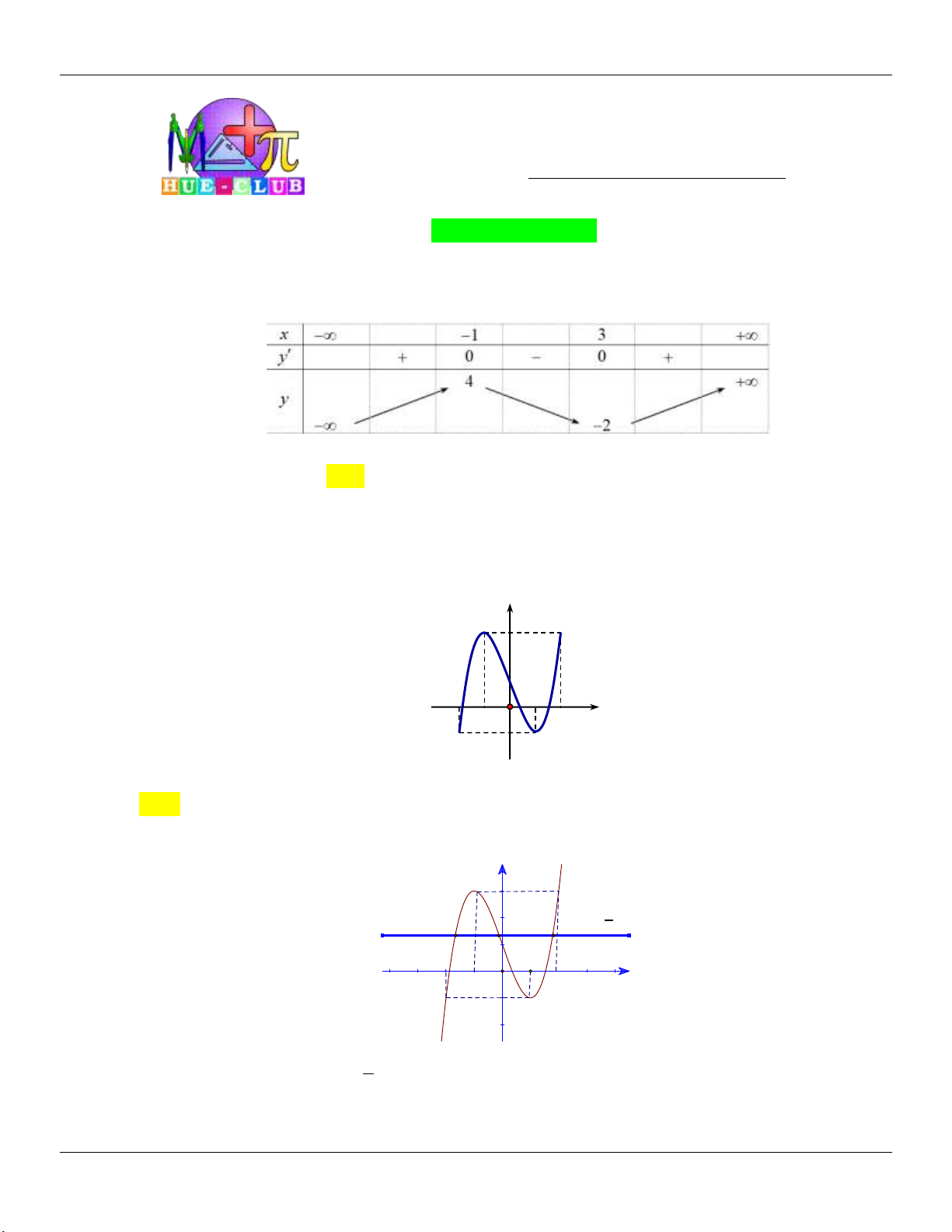
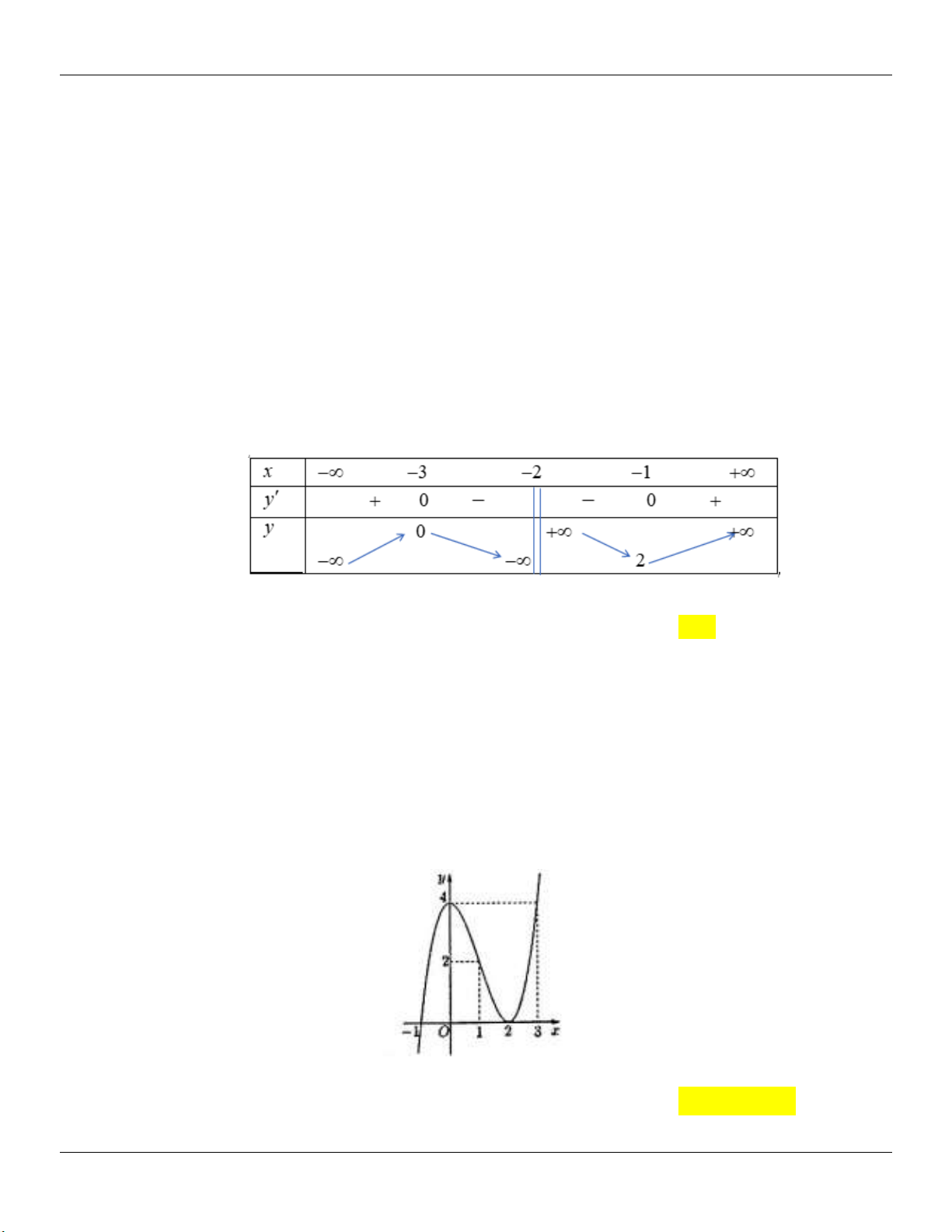
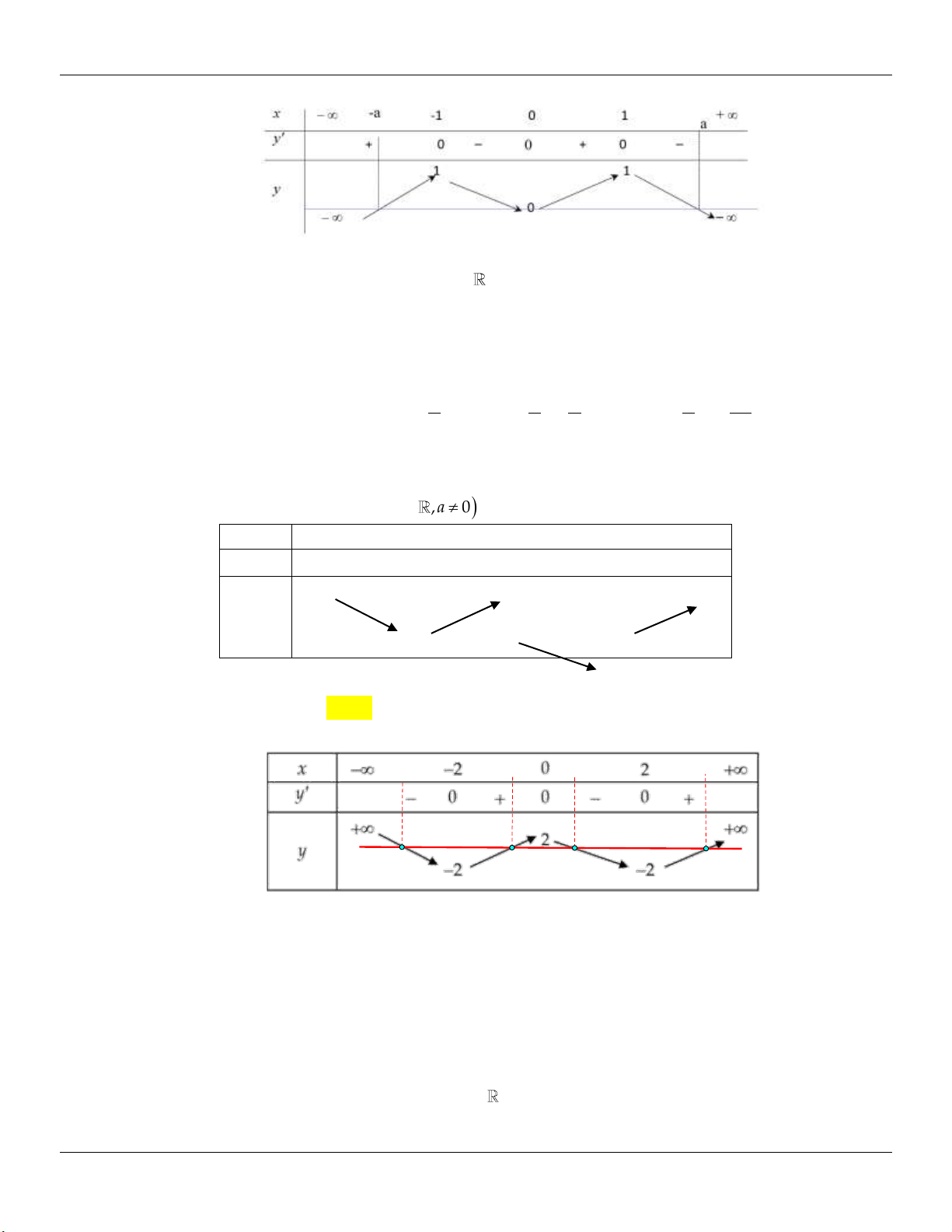
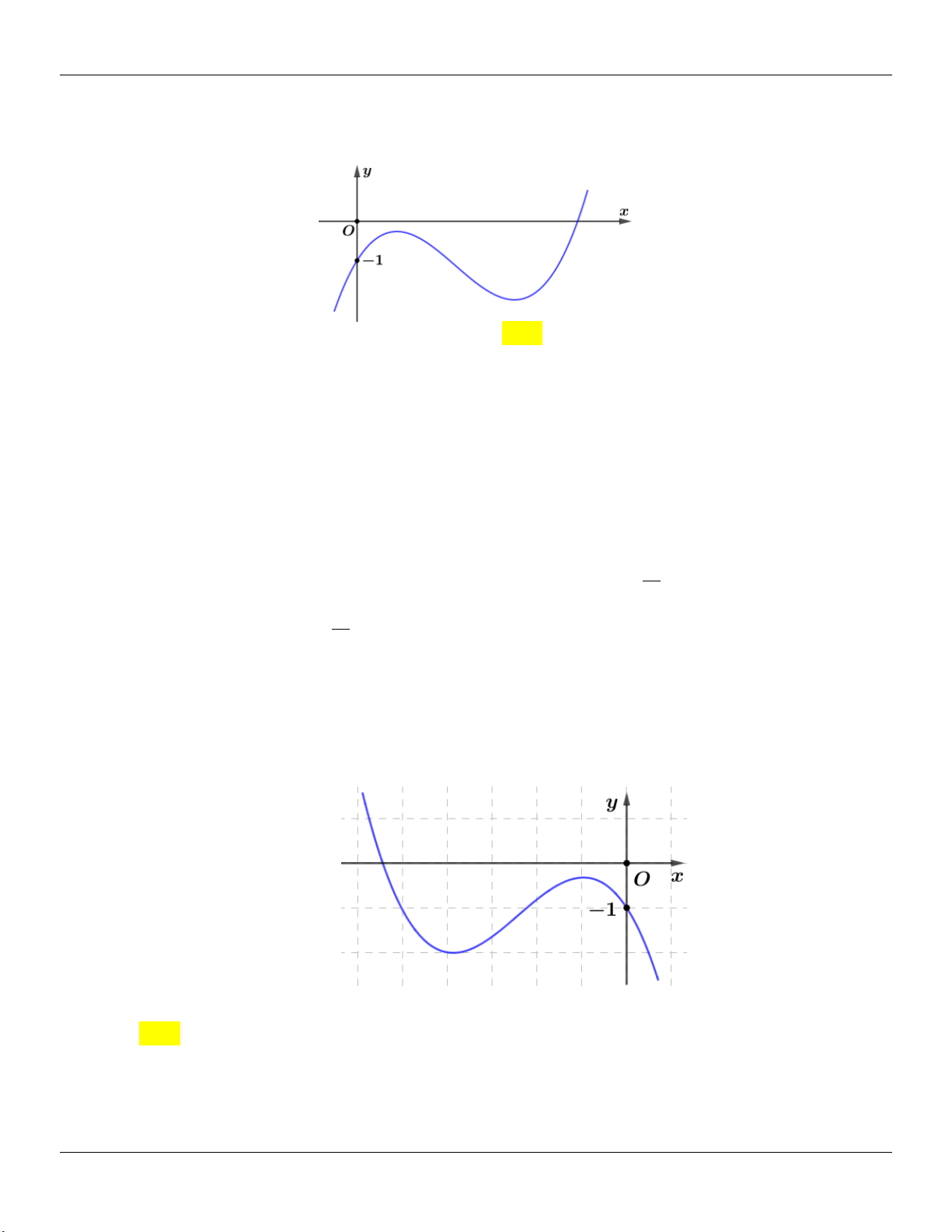
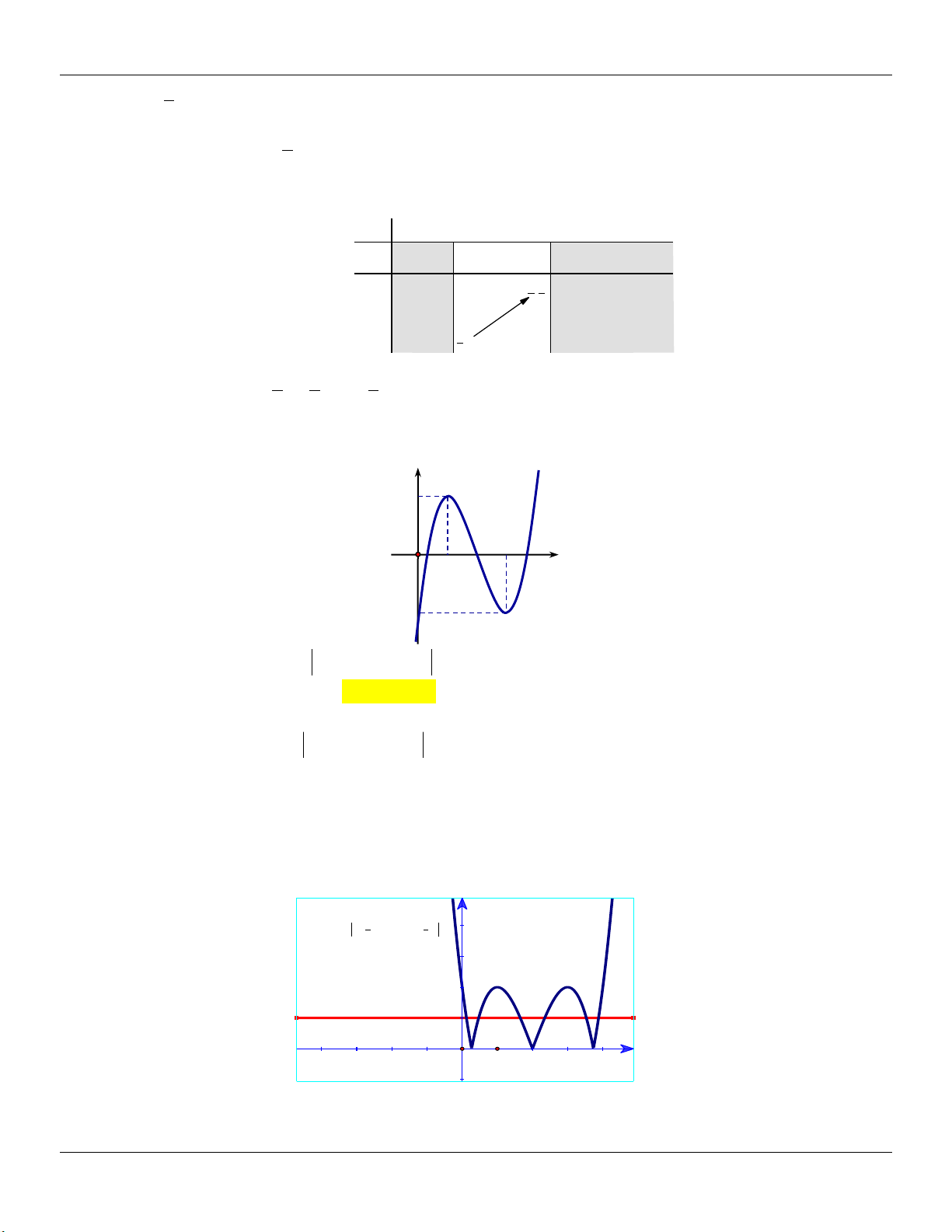
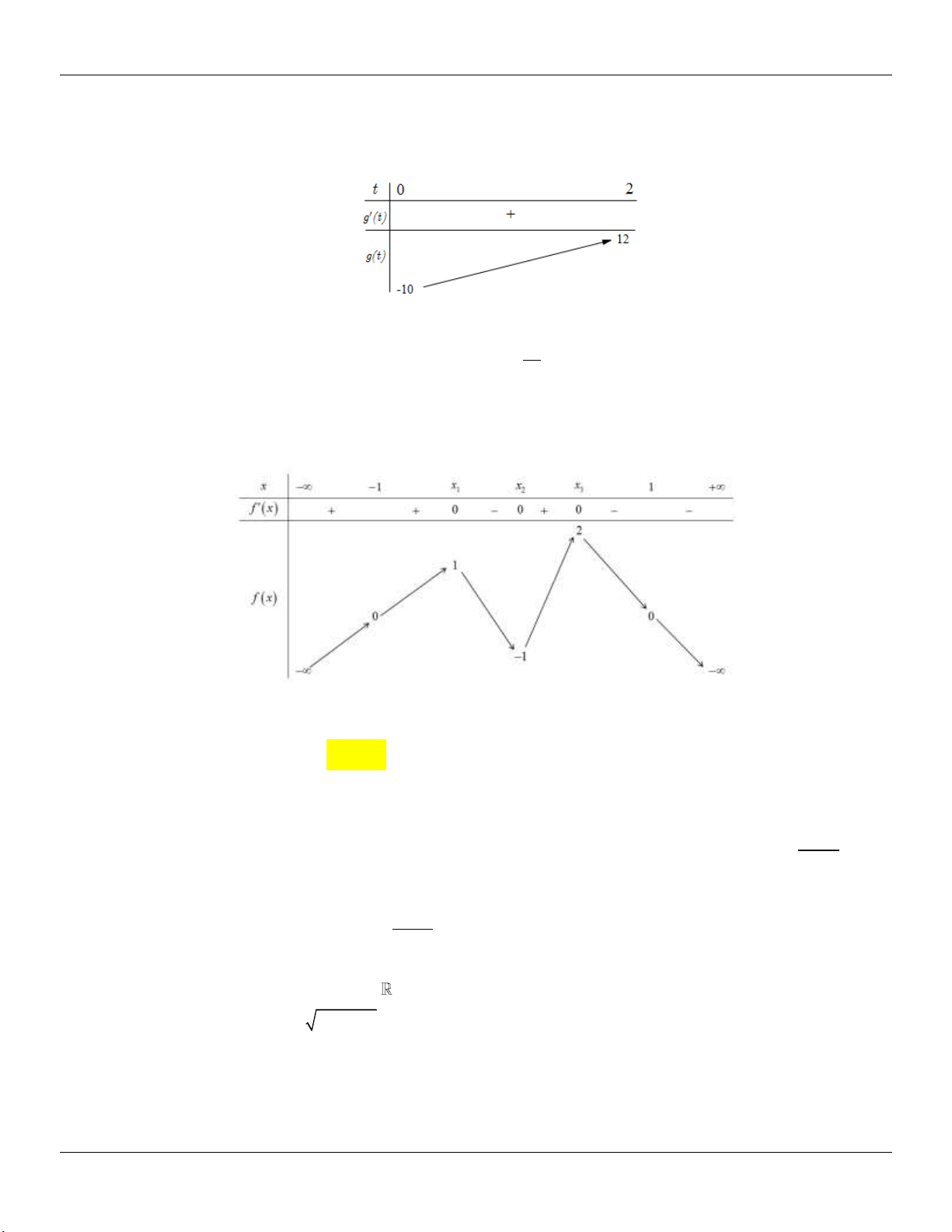
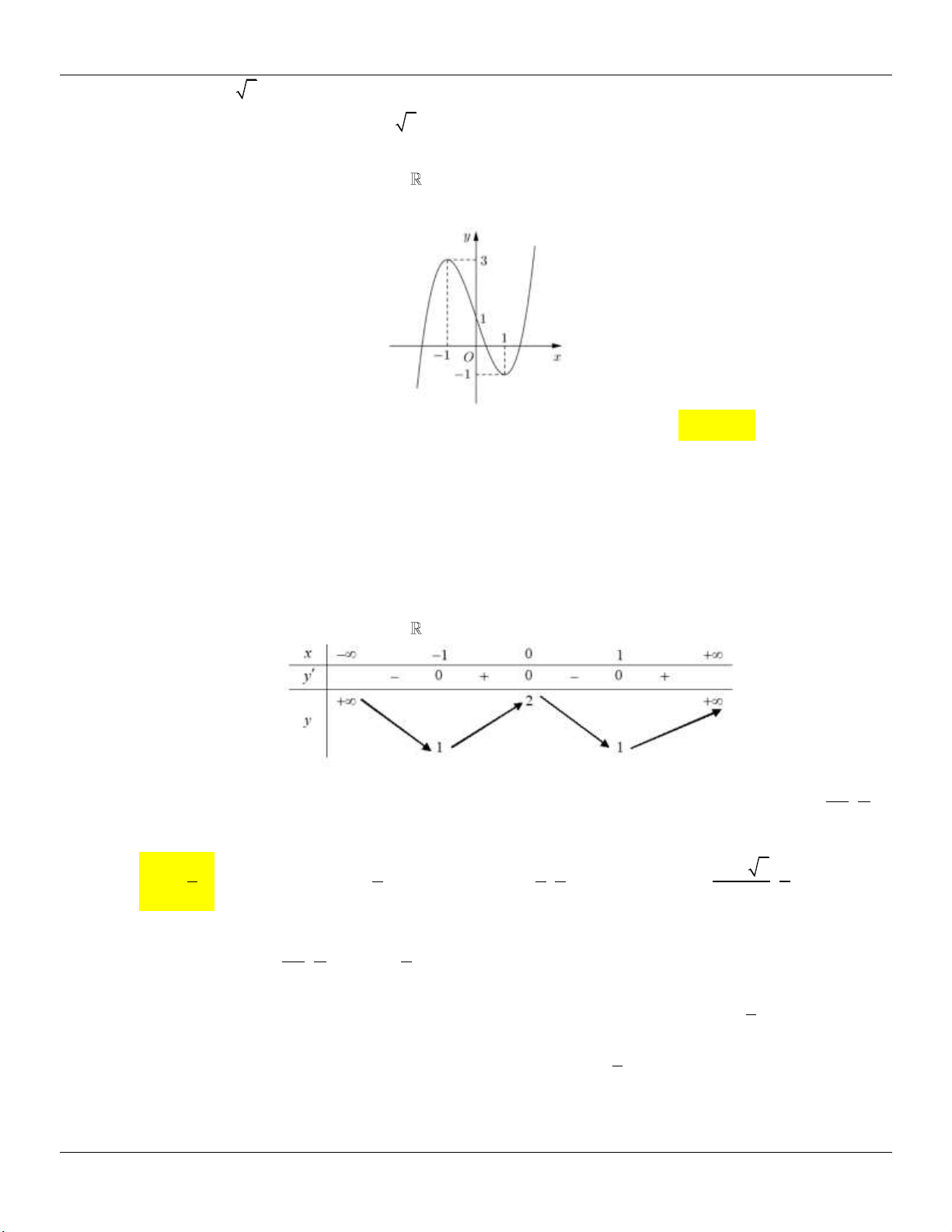
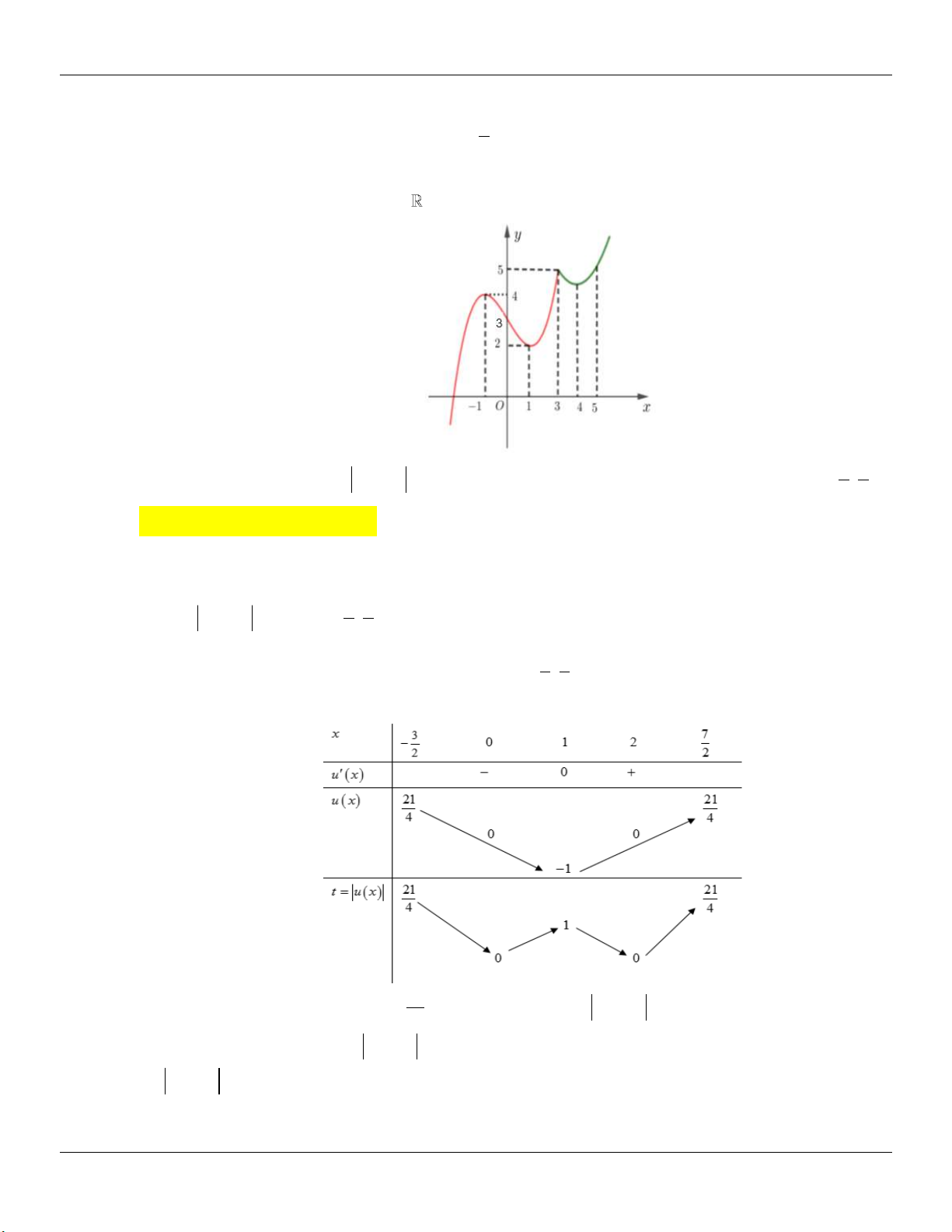
: y x x cắt d : y m / /Ox tại 3 điểm 3 phân biệt.  2
x  1  y   1  Xét 3 (
g x)  x x . Ta có: / 2 / 3
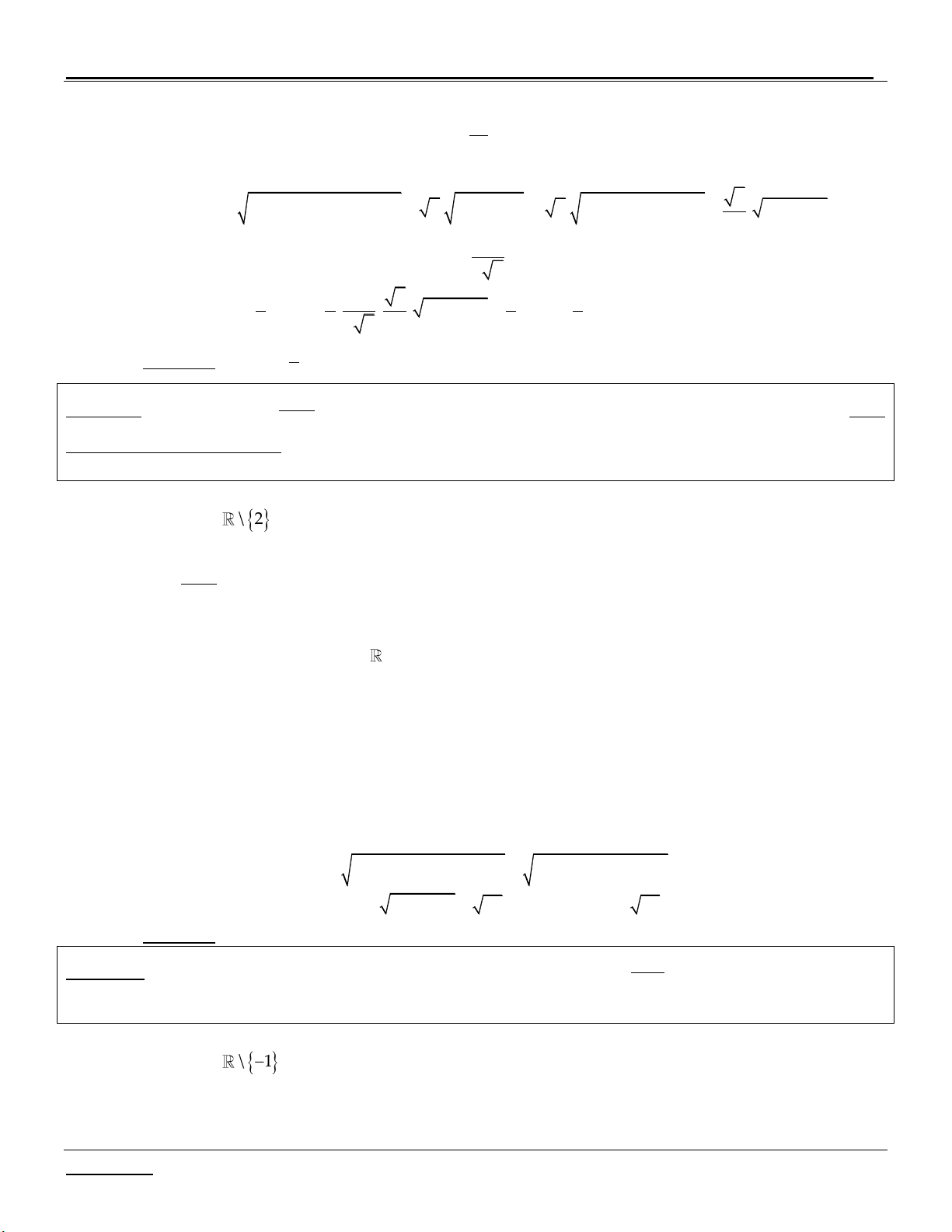
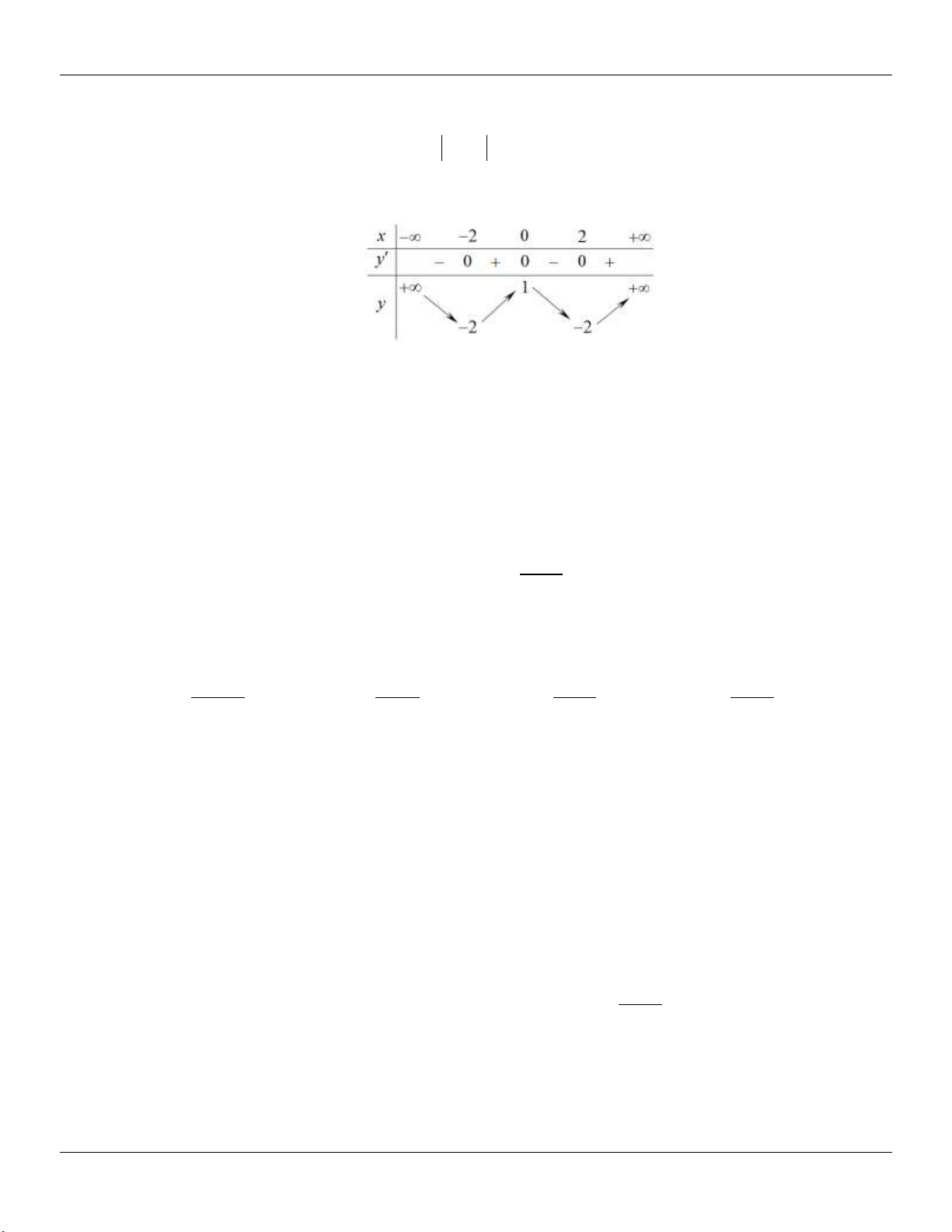
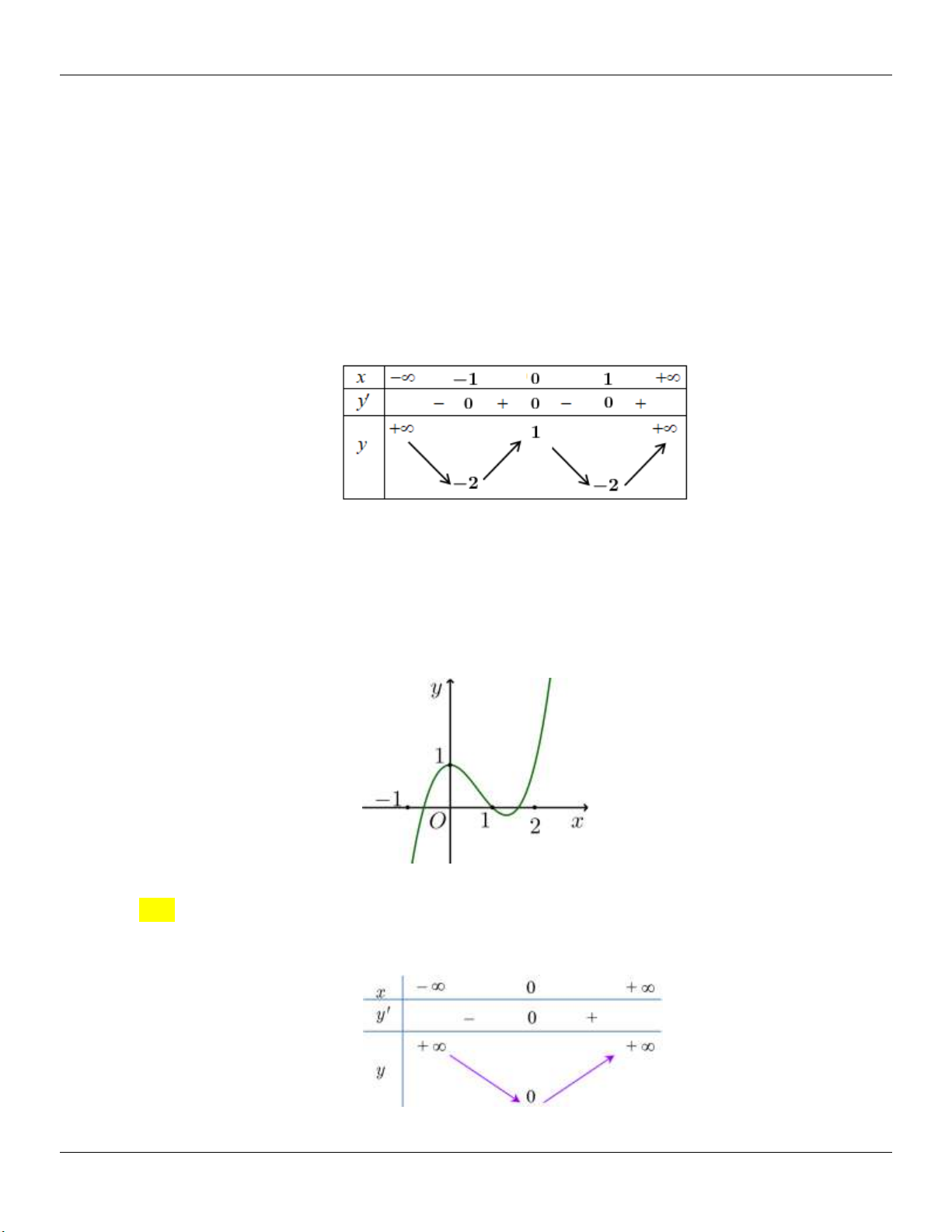
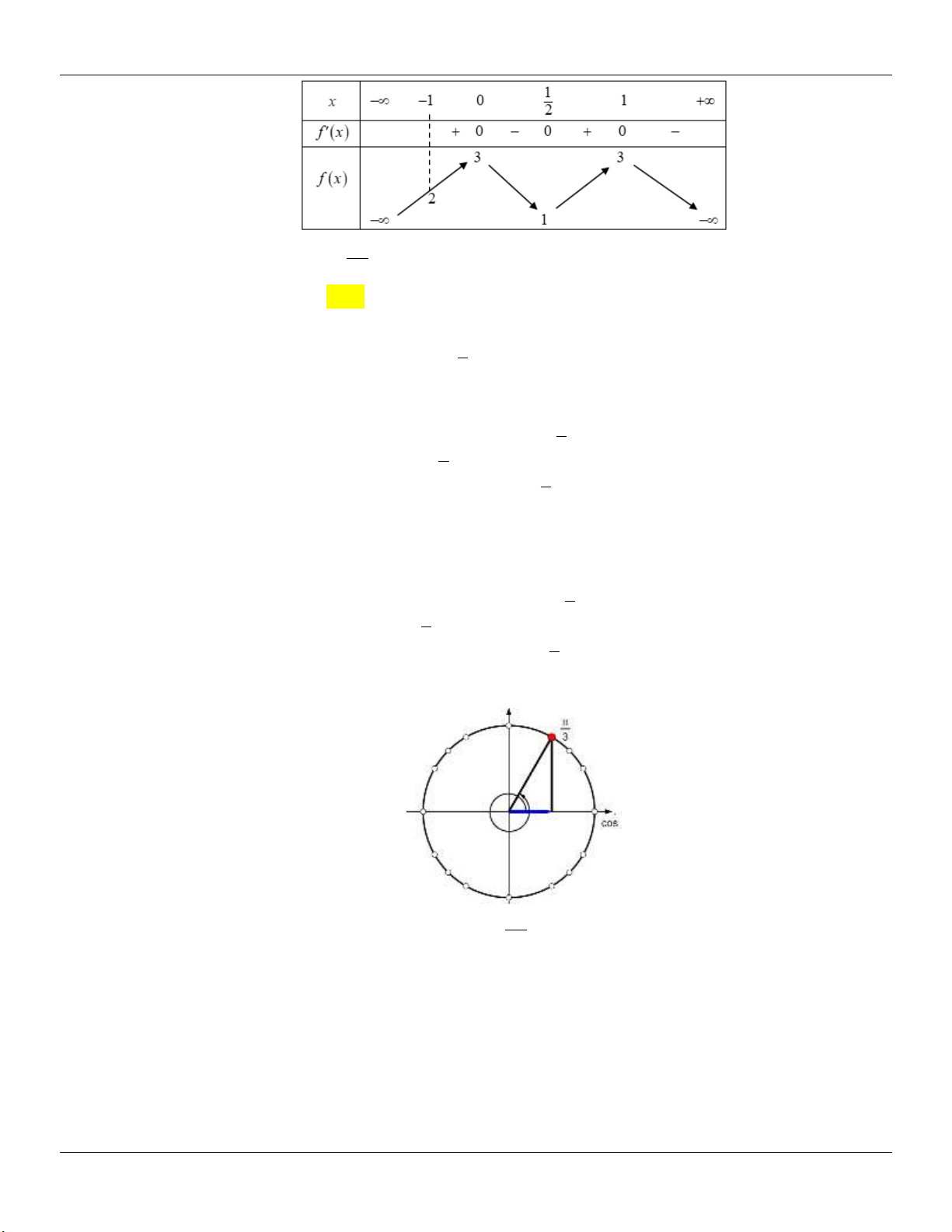
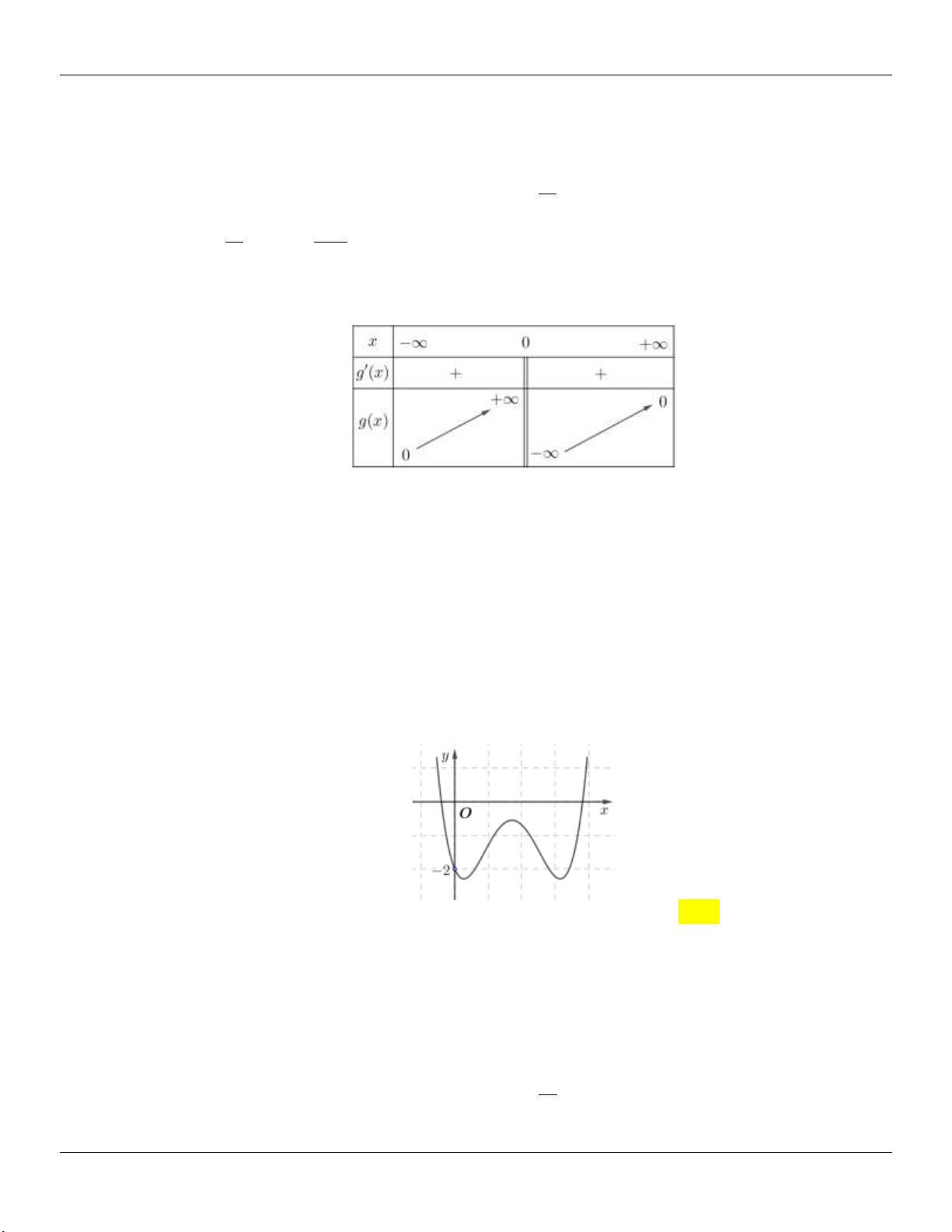
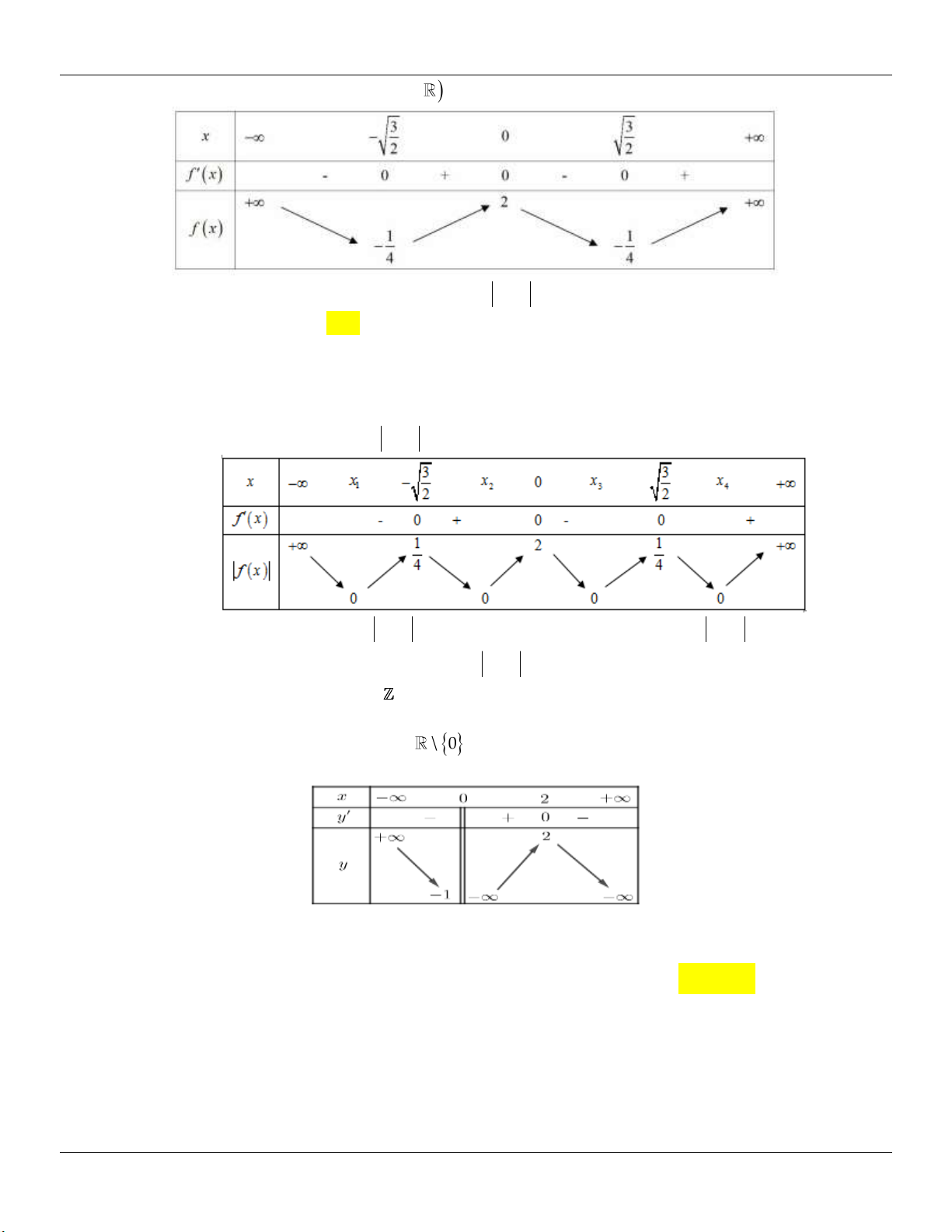
g (x)  x  1  g (x)  0   3  2 x  1   y   3 Bảng biến thiên: 2 2
Dựa vào bảng biến thiên, ta thấy để d cắt (C) tại 3 điểm phân biệt    m  . 3 3  2 2 
Kết luận: Vậy các giá trị cần tìm là: m   ;  .  3 3  2
mx x m
Bài tập 7: (ĐH A-2003) Tìm m để đồ thị hàm số y
cắt trục hoành tại hai điểm phân biệt và x  1
hai điểm đó có hoành độ dương. Lời giải: TXĐ: D   \  1 2
mx x m
Đồ thị hàm số y
cắt trục hoành tại 2 điểm phân biệt có hoành độ dương x  1
 Phương trình gx 2
mx x m  0 có 2 nghiệm dương phân biệt  1   m  0 m  0   2     1 1 4m 0  m    1 Y.c.b.t  g  2
1  2m  1  0      m  0 1 2   1 m   S     0  2  mm   0  mP   0  m 1
Vậy các giá trị m cần tìm là:   m  0 . 2
Bài tập 8: (ĐH D-2009) Tìm m để d: y  1 cắt C : 4 y xm  2 – 3
2 x  3m tại 4 điểm phân biệt đều m
có hoành độ nhỏ hơn 2.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 5
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải: TXĐ: D
Phương trình hoành độ giao điểm của C
và đường thẳng y  1 là: m  4 xm  2 – 3 2 x  3m  1  t  1 Đặt 2
t x t  0 , phương trình trở thành 2
t  3m  2t  3m  1  0   t  3m   1 0  3m  1  4  1 
Yêu cầu bài toán tương đương   m   ;1  \  0 3m  1  1  3 
DẠNG 3: SỐ GIAO ĐIỂM VÀ TÍNH CHẤT GIAO ĐIỂM CỦA HAI HỌ ĐỒ THỊ Phương pháp:
Bước 1: Thiết lập phương trình hoành độ giao điểm của (C) và (C’): f x  gx (1)
Bước 2: Biện luận số nghiệm và tính chất nghiệm của (1).
Nhận xét: Rõ ràng hoành độ giao điểm của (C) và (C’) là nghiệm của (1) nên số giao điểm và
tính chất giao điểm cũng là số nghiệm và tính chất nghiệm của (1). Điều này, đưa yêu cầu từ
Giải tích sang việc biện luận phương trình sơ cấp mà chúng ta đã biết. 2x  4
Bài tập 1: Cho hàm số y
. Gọi (d) là đường thẳng qua A1;1 và có hệ số góc k. Tìm k sao cho (d) 1  x
cắt ( C ) tại hai điểm M, N và MN  3 10 . Lời giải: TXĐ: D   \  1 .
Từ giả thiết ta có: (d) : y k x  1  1. Bài toán trở thành: Tìm k để hệ phương trình sau có hai 2 2
nghiệm x ; y , x ; y phân biệt sao cho x xy y  90 (*) 2 1   2 1 1 1   2 2  2x  4 
kx 1  1 2
kx 2k  3x k  3  0  x  1 (I) . Ta có: (I)     y k  x   y k 1 1  x 11
Dễ có (I) có hai nghiệm phân biệt khi và chỉ khi phương trình 2
kx  2k  3 x k  3  0 (**) có 3
hai nghiệm phân biệt. Khi đó dễ có được k  0, k  . 8 2 2
Ta biến đổi (*) trở thành:  2 1 k x x  90  2 1 k x x 4x x          90 (* * *) 2 1   2 1 2 1    2k  3 x x   1 2 
Theo định lí Viet cho (**) ta có: k
thế vào (***) ta có phương trình: k  3 x x  1 2  k     3 2 k
k k    k   2 8 27 8 3 0
3 8k  3k  1  3 41 3 41 0  k  3   k   k  . 16 16 3   41 3   41
Kết luận: Vậy các giá trị của k cần tìm là: k  3  , k  , k  . 16 16 2x  2
Bài tập 2: Cho hàm số y
(C). Tìm m để đường thẳng d: y  2x m cắt đồ thị (C) tại 2 điểm x  1
phân biệt A, B sao cho AB  5 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... 6
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải: TXĐ: D   \   1 . 2x  2
Xét phương trình hoành độ giao điểm:
 2x m gx 2
 2x mx m  2  0, x  1   (1) x  1
Để d cắt (C) tại 2 điểm phân biệt  Phương trình (1) có 2 nghiệm phân biệt khác 1  2
  m  8 m    g  2 0 Y.c.b.t 2      g    m 8m 16 0
1  2  m m  2  0 m
m;4  4 2   4  4 2; (2)
Lúc đó, gọi A x ; 2x m ; B x ; 2x m , với x và x là các nghiệm của phương trình (1). B BA AA Bm x x    A B  Theo định lý Viet ta có: 2  (*) m  2 x .x A B  2 2 2 Ta có: 2
AB  5  x x   4x x   5  x xx x  (**) A B 2 4 1 B A B A A B
m  10 (tháa ®k (2))
Thay (*) vào (**) ta được: 2
m  8m  20  0   m  2  (tháa ®k (2))
Kết luận: Vậy các giá trị cần tìm là: m 2  ;  10 . x  2
Bài tập 3: Cho hàm số: y
(C). Chứng minh rằng: Với mọi giá trị của m , đường thẳng d : x  1
y  x m luôn cắt đồ thị (C) tại hai điểm A, B phân biệt. Tìm giá trị nhỏ nhất của độ dài đoạn thẳng AB. Lời giải: TXĐ: D   \  1 .
* Phương trình hoành độ giao điểm của d (  C) là: 2
x mx m  2  0 x  1 (1) 2
  m  4m  8  0 Vì 
m  , nên phương trình (1) có 2 nghiệm phân biệt khác 1 với m  . f    1  1    0
Suy ra d cắt (C) tại hai điểm phân biệt với m  .
* Gọi các giao điểm của d (C) là Ax ; x m ; Bx ; x m , với x và x là các nghiệm B BA AA B
x x m
của phương trình (1). Theo định lý Viet ta có: A B  (*)
x .x m  2 A B 2  Ta có: 2
AB  2x x   2 x x 2  4x .x A B A B A B  (**) 2 2 2
Thay (*) vào (**) ta được: 2 AB  2 m  4 
m2  2m 2  4 
 2m  2  8  8    Vậy AB
 2 2 , đạt được khi m  2 . min x
Bài tập 4: Xác định m để đường thẳng d : y mx  2 cắt H 1 : y
tại hai điểm phân biệt M, N sao x  3
cho độ dài đoạn thẳng MN nhỏ nhất. Lời giải:
Giáo viên: LÊ BÁ BẢO...0935.785.115... 7
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia TXĐ: D   \  3 .
Phương trình hoành độ giao điểm của đường thẳng và đồ thị: x  1 2
mx  2  mx  3m  
1 x  7, x  3 * x  3
Nhận thấy x  3 không phải là nghiệm của phương trình * .
Đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt  Phương trình * có hai nghiệm m  0  phân biệt   .       m  2 m 0 9 1  28m   0
Gọi M x ; y và N x ; y là tọa độ giao điểm của đường thẳng và đồ thị. Khi đó 2 2  1 1 
y mx  2 3m   1 7 1 1 
và x , x là nghiệm của phương trình * nên x x  , x .x  .
y mx  2 1 2 1 2 1 2 m m 2 2 2 2 2 2
Ta có: MN  x x   y y   x x  2  m x x 2 1 2 1 2 1  2 1
1 m x x 2 1 m x x 2 2 2 4x x         2 1 2 1 1 2   9 m 1   7  1   1            1 m   2 2 2 4. 9 m  10 m  18 2 2  m m   m   m    1 1
Đặt t m
(điều kiện t  2 ), suy ra 2 2 m   t  2 . Khi đó 2
MN  9t  10t . m 2 m
Dùng đạo hàm tìm GTNN của hàm số f t 2
 9t  10t trê
n các nửa khoảng ; 2 và 2; 
 . Ta tìm được min f t  f 2  4 khi t  2 . 1
Với t  2  m   2  m  1. m
Vậy MN nhỏ nhất bằng 4 khi m  1 . 1 2
Bài tập 5: Cho hàm số 3 2
y x mx x m
C . Tìm m để (Cm) cắt trục hoành tại ba điểm phân 3 3 m
biệt có hoành độ x , x , x thỏa mãn điều kiện 2 2 2
x x x  15 . 1 2 3 1 2 3 Lời giải: TXĐ: D  .
Xét phương trình hoành độ giao điểm: 1 3 2 2 3 2
x mx x m
 0  x  3mx  3x  3m  2  0 3 3 x  1  x   2 1 x  
1 3mx  3m 2  0 (1)    g  x 2
x  1 3mx  3m  2   0 (2)
Để (Cm) cắt trục Ox tại ba điểm phân biệt  Phương trình (1) có ba nghiệm phân biệt
 (2) có hai ngiệm phân biệt khác 1. 2 2   (1 3 )
m  4(3m  2)  0
3m  2m  3  0, m  Y.c.b.t      m  0 (*)  ( g 1)  6  m  0 m  0
Giả sử x  1, lúc đó x , x là nghiệm của phương trình (2). 3 1 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... 8
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
x x  3m 1
Theo định lý Viet, ta có: 1 2  (3) x .x  3  m  2 1 2 2 Khi đó: 2 2 2 2 2
x x x x x  1  15  x x  2x x  14  0 1 2 3 1 2  1 2 (4) 1 2
Thay (3) vào (4) ta được: 2 2
(3m  1)  2(3m  2)  14  0  m  1  0  m  1   m  1
Đối chiếu với điều kiện (*) suy ra tập các giá trị cần tìm là: m; 1    1;. x  1
Bài tập 6: (Khối A-2011) Cho hàm số y
. Chứng minh rằng với mọi giá trị của m thì đường 2x  1
thẳng d : y x m luôn cắt (C) tại hai điểm phân biệt A và B. Gọi k , k lần lượt là hệ số góc của các tiếp 1 2
tuyến tại A và B. Tìm m để tổng k k đạt giá trị lớn nhất. 1 2 Lời giải: 1 TXĐ: D  \  2 
Xét phương trình hoành độ giao điểm của (C) và d : x  1  1 
x m gx 2
 2x  2mx m  1  0 (*) x    2x  1  2  1
Để d cắt (C) tại 2 điểm phân biệt  g(x)  0 có 2 nghiệm phân biệt  2 /   2 0      g m m 1 0 m      1   1 g    0
  m m  1  0 m    2  2
Suy ra d luôn cắt (C) tại 2 điểm A, B phân biệt.
x x  m 1 2 
Gọi x , x là 2 nghiệm của phương trình (*). Áp dụng định lí Vi-et:    (*) 1 2 m 1 x .x   1 2  2 1
Hệ số góc của tiếp tuyến với (C) tại x là: / k f x   1  1 1 x  2 1 1 1
Hệ số góc của tiếp tuyến với (C) tại x là: / k f x   2  2 2 x  2 1 2
Cách 1: CHUẨN_ ĐƠN GIẢN_ DỄ HIỂU 1 1
4x x 2  8x x  4 x x  2 1 2 1 2  1 2 
Ta có: k k      1 2
2x 12 2x 12 4x x  2  x x  (**) 2  1 1 2 1 2 1 2 
Thay (*) vào (**) ta được: k k  4
m  8m  6  4m  12 2  2  2 . 1 2
Suy ra k k lớn nhất bằng 2
 , đạt được khi chỉ khi m  1. 1 2 Cách 2: ĐẶC SẮC 1 1
Ta có: k k    (1) 1 2 2x  2 1 2x  2 1 1 2
Áp dụng Bất đẳng thức Cauchy, ta có:
Giáo viên: LÊ BÁ BẢO...0935.785.115... 9
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1 1 2 2     x  2  x  2   
2x  12 2x  12 2x 1 . 2x 1 2 1 2 1 1 2 1 2 1 2 nên (1) trở thành:   1 1 2 2
k k          1 2     
2x  1 . 2x  1 2x 1 2x 1
2x  1 2x  1 1 2  2 2 1 2  1  2   1 2      2
4x x  2 x x  1  m  1   1 2  1 2  4  2( ) m  1    2 
Suy ra k k lớn nhất bằng 2
 , đạt được khi chỉ khi 1 2 1 1
2x 1  2x
1 ( lo¹i do x x ) 1 2 1 2     x 2  x 2 2x  1  2
x  1  x x  1  m  1 2 1 2 1     1 2 1 2 1 2
Cách 3: CẦN CÙ VÀ CHÍNH XÁC
Theo trên, d luôn cắt (C) tại 2 điểm A, B phân biệt.  2
m m  2m  2 x  1 Lúc đó: 2  2
2x  2mx m  1  0   2
m m  2m  2 x  2  2 1 1 1 1
Ta có: k k        2x  1 2x 1
mm 2m2 1 mm 2m2 1 1 2 2 2 2 2 2 2 1 2 1 1   
m 2m 2 1 m 2  m 2m 2 1 m 2 2 2             
m 2m 2 1 m 2  m 2m 2 1 m 2 2 2              
   m 2m 2 1 m 2 m 2m 2 1 m 2 2 2              2 2
m  2m  2  2 2
m  2m  1    4
m  8m  6  4  m  1  2  2  2  2 2   
m  2m  2 2  1 m2 2   
Suy ra k k lớn nhất bằng 2
 , đạt được khi chỉ khi m  1. 1 2 m x
Bài tập 7: Cho hàm số y
có đồ thị là (H ) . Tìm m để d : 2x  2y  1  0 cắt (H ) tại hai điểm x  2 m m 3
cùng với gốc tọa độ tạo thành một tam giác có diện tích là S  . 8 Lời giải: TXĐ: D   \   2 . x m 1
Hoành độ giao điểm A, B của d và (H ) là các nghiệm của phương trình:  x m x  2 2 2
 2x x  2m 1  0, x  2  (1)
Giáo viên: LÊ BÁ BẢO...0935.785.115... 10
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Để d cắt (H ) tại 2 điểm phân biệt  Phương trình(1) có 2 nghiệm x , x phân biệt khác 2  m 1 2  17
  17  16m  0  m  Y.c.b.t   (*)     2      m   16 2. 2 2 2 1   0 m  2   2 2 2 2
Ta có: AB  x xy y  2. x x
 2. x x  4x x  . 17  16m. 2 1 2 2 1   2 1  2 1 1 2 2 1
Khoảng cách từ gốc tọa độ O đến d là h  . 2 2 1 1 1 2 3 1 Suy ra S  . . h AB  . . . 17  16m
m  , thỏa mãn (*) OAB 2 2 2 2 2 8 2 1
Kết luận: Vậy m  là giá trị cần tìm. 2 2x
Bài tập 8: Cho hàm số y
(C). Tìm m để đường thẳng (d ): y x m cắt đồ thị (C) tại 2 điểm phân x  2
biệt thuộc 2 nhánh khác nhau của đồ thị sao cho khoảng cách giữa 2 điểm đó là nhỏ nhất. Tìm giá trị nhỏ nhất đó. Lời giải: TXĐ: D   \  2 .
Xét phương trình hoành độ giao điểm của d và (C): 2x 2
x m x  m  4x  2m  0, x  2 (1) x  2
Để (d) cắt (C) tại 2 điểm phân biệt  Phương trình (1) có 2 nghiệm phân biệt khác 2. 2   m  16 Y.c.b.t    m   (2).  4   0
Lúc đó, gọi Ax ; x m , B x ; x m là 2 giao điểm của d và (C), với x , x là 2 nghiệm của 1 1  2 2  1 2
x x  4  m
phương trình (1). Theo định lí viet ta có 1 2  (3) x x  2  m 1 2
* Để A, B thuộc 2 nhánh khác nhau của đồ thị thì A, B nằm khác phía đối với TCĐ: x  2  0 .
Suy ra: x  2 x  2  0  x x  2 x x  4  0 (4) 1  2  1 2  1 2
Thay (3) vào 4 ta được : – 4 < 0 luôn đúng (5) 2 2 2
* Mặt khác ta lại có AB  x xy y  2 x x  8x x (6) 1 2   1 2  1 2 1 2 Thay (3) vào (6) ta được 2
AB  2m  32  32 . Suy ra: AB  32 khi m  0 . min
Kết luận: Vậy m  0 thoả mãn. x  1
Bài tập 9:Tìm a và b để đường thẳng d: y ax b cắt đồ thị (C): y
tại hai điểm phân biệt đối x  1
xứng nhau qua đường thẳng  : x  2y  3  0 . Lời giải: TXĐ: D   \   1 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... 11
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1 3
Phương trình  : x  2y  3  0 được viết lại:  : y x  . Để thỏa mãn đề bài thì trước hết 2 2
a  2 . Vậy d: y  2  x b .
Xét phương trình hoành độ giao điểm của d và (C): x  1  2
x b gx 2
 2x  b  3x  b  
1  0 x    1 (1) x  1
Để (d) cắt (C) tại 2 điểm phân biệt  Phương trình (1) có 2 nghiệm phân biệt khác 1  .
  b   b   g  32 8 1 0 Y.c.b.t 2          (2).   b b b g 1
   2  b  3  b  1 2 17 0  0 b
Lúc đó, gọi Ax ; 2
x b, B x ; 2
x b là 2 giao điểm của d và (C), với x , x là 2 nghiệm 1 1  2 2  1 2  b  3 x x   1 2 
của phương trình (1). Theo định lí viet ta có 2  (3) b  1 x x  1 2  2  x x b  3 1 2 x    I
b  3 b  3 
Gọi I là trung điểm của AB, ta có: 2 4   I  ;  . b  3   4 2  y  2  x b I I  2
Lúc đó, yêu cầu bài toán: Tån t¹i A, B.  b  a  2     a  2   AB    a  2  b         b  2 . 3  3  0 b  1  I   
x  2y  3  0    I I 4
Kết luận: Vậy các giá trị cần tìm là a  2 và b  1. x  1
Bài tập 10: Cho hàm số: y
(C). Một nhánh của đồ thị (C) cắt Ox, Oy lần lượt tại A, B. Tìm điểm C x  1
thuộc nhánh còn lại sao cho diện tích tam giác ABC bằng 3. Lời giải: TXĐ: D   \   1 .
Tìm được tọa độ của A1;0 , B0; 1
   Phương trình của AB: x y  1  0 .  x  1 
Do M C nên tọa độ M x; , x  1   
 và A, B thuộc nhánh các điểm có hoành độ lớn  x  1 hơn 1
 nên M thuộc nhánh đồ thị có các điểm có hoành độ x  1. x  1 x   1 2 1 1 x  1 1 x x Ta có : SAB d . M AB    MAB  ;  . 2 3 2 2 2 2 x  1 2
x  5x  6  0 x  2   y  3 M 2  ;3 2 1  
x x  6 x  1       . 2
x  7x  6  0 (loai) x  3   y  2 M 3  ;2  2  
Vậy các điểm cần tìm là M  2  ;3, M 3;  2 . 1 2  
Giáo viên: LÊ BÁ BẢO...0935.785.115... 12
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x
Bài tập 11: Tìm m để d : y  2x m  2 cắt C 2 : y
tại 2 điểm phân biệt A, B sao cho tứ giác AMBN x  1 5 17 có diện tích bằng , biết M 1; 2  , N3; 3   . 4 Lời giải: TXĐ: D   \   1 . 1
Ta có phương trình đường thẳng MN : y   x  3 nên d MN tại I . I có tọa độ là nghiệm 2
y  2x m  2   1 2m m  8  của hệ  1 nên I  ;  . y   x   3  5 5   2 1  2m m  8
Vì AMBN là tứ giác lồi nên I thuộc đoạn thẳng MN tức là 1   3 và 3    2  , 5 5 nghĩa là 7   m  2 
a , đường thẳng d cắt H tại hai điểm A,B phân biệt khi phương x  2
trình: 2x m  2 
có hai nghiệm phân biệt, nghĩa là: 2
2x  m  5 x  4  m  0 1 có hai x  1
nghiệm phân biệt khác 1  m  1  2 2 hoặc m  1  2 2 và m  1  2 2 không thỏa a .
Gọi x , x là hoành độ của A, B thì chúng là hai nghiệm của phương trình 1 . A B 5  m 4  m Nên x x  ; x .x  , do đó: A B 2 A B 2 2 2   mm m x xx xx x     B A 2  A B2 5  4  1 4 . 4. 2 A B 4 2 4 1 1 1 1 x x y  1  ; y  1 B A   y y    A x  1 B x  1 B A x  1 x  1
x .x x x A B A B A BA B m12 2  2  2 2 m 1 Ta có: 2
AB  x xy y    B A   B A   4 2 2 4
 4  m 5  m      2 2  m 12 8     4  1    * 2 2   4 
4 m 24 m5 m 5 m          5 17 1 1 Ta có:  SMN.AB  5.AB , tức là: 2 5.17 AB  * *. 4 AMBN 2 2 4
Từ * ,* * ta được m  2
1  8  17  m  4  hoặc m  6 .
Vậy m  4 là giá trị cần tìm.
Bài tập 12*: Tìm giá trị tham số m
sao cho đồ thị C 3
: y x  3x  2 và đường thẳng y mx  2
giới hạn hai hình phẳng có cùng diện tích. Lời giải: TXĐ: D  .
Phương trình hoành độ giao điểm: 3
x  3x  2  mx  2  x  2
 hoặc x  1 m,m  0 . Điều
kiện d và C giới hạn 2 hình phẳng: 0  m  9 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... 13
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Gọi S và S lần lượt là diện tích các hình phẳng nhận được theo thứ tự từ trái sang phải. 1 2
d qua A khi m  1 (tức là d qua điểm uốn).
Khi đó, S S  4 . 1 2
+ Nếu 0  m  1 : S  4  S . 1 2
+ Nếu 1  m  9 : S  4  S . 1 2
+ Nếu m  9  1  m  2  ;1  m  4 . 2  1 m Khi đó: 3 S
x  3x  2  m x  2 dx  ; 3 S
x  3x  2  m x  2 dx  . 2   1   1 m 2 
Suy ra S S  2m m  0 . 2 1
Vậy m  1 thỏa yêu cầu bài toán.
Bài tập 13: Tìm m để d 9 : y
x  3 cắt đồ thị (C) 3 2
y mx  6x  9mx  3 tại 3 điểm phân biệt 4 A0; 3
 , B, C thỏa mãn điều kiện B nằm giữa A và C đồng thời AC  3AB . Lời giải: TXĐ: D  .
Số giao điểm của đồ thị đã cho với đường thẳng d là số nghiệm của phương trình:   3 2 9 2 9
mx  6x  9mx  3  x  3  x mx  6x  9m     0 1 4  4  x  0   2 9
mx  6x  9m   0 2  4
Đường thẳng d và đồ thị đã cho cắt nhau tại 3 điểm phân biệt A0; 3
 ,B,C khi và chỉ khi
phương trình 1 có 3 nghiệm phân biệt A0; 3
 ,B,C , tức là 2 phải có hai nghiệm phân biệt khác 0.    m  0   m  0 m 0      9   m 1  65 1  65 Y.c.b.t 2
 '  9  m9m    0  m   1  0    m    4  4 8 8     1  1 9 9 0 m m m       4   4 4 .
 1 65 1 65   1  m ; \0,   (*) 8 8     4  9 9
Gọi Bx ; y ,C x ; y với y x  3,y x  3 , trong đó x ,x là 2 nghiệm của 2 . 1 1   2 2 1 1 2 2 4 4 1 2 x   3x
Ta có AB  x ; y  3 , AC x ; y  3 và 2 1
AC  3AB    x  3x . 1 1   2 2  y  3  3  y   3 2 1 2 1
Giáo viên: LÊ BÁ BẢO...0935.785.115... 14
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia   3  3 x x     1  1 x 3x 2 1 2m 2m    m  1  6  9  9 Ta có hệ:  x x   x   x   thỏa (*) 1 2 2 2 3 m 2m 2mm       2  4  9  9
4m m  3  0 x x  9  x x  9   1 2  1 2   4m  4m  3
Vậy m   ; m  1 thỏa mãn bài toán. 4
Bài tập 14: Tìm các giá trị m  0 để đồ thị C : 4
y x  m   2 3
1 x  3m  2 cắt trục hoành tại 4 điểm m
phân biệt và tiếp tuyến tại điểm có hoành độ lớn nhất cùng với 2 trục tọa độ tạo thành tam giác có diện tích bằng 24. Lời giải: TXĐ: D  .
Phương trình hoành độ giao điểm của C
và trục hoành: m  4
x  m   2
x m     2 x   2 3 1 3 2 0 1 x   3m 2  0  *
Với m  0 thì C
cắt trục hoành tại 4 điểm phân biệt và x  3m  2 là hoành độ lớn nhất. m
Giả sử A 3m  2;0 là giao điểm có hoành độ lớn nhất và tiếp tuyến d tại A có phương
trình: y  23m  1 3m  2.x  23m  13m  2 .
Gọi B là giao điểm của d với Oy , suy ra B0; 2
 3m  13m  2 .
Theo giả thiết, tam giác OAB vuông tại O và S  24  . OA OB  48 OAB hay m   2 3
2 18m  22m  4  48 * .
Xét f m  m   2 3
2 18m  22m  4  48, m  0 .  2 
Ta có f 'm  0 với mọi m  0 , suy ra f m đồng biến với mọi m  0 và f    0 . Do đó  3  2
phương trình * có nghiệm duy nhất m  . 3 2 Vậy m  thỏa mãn đề bài. 3 mx
Bài tập 15: Tìm m để đường thẳng d 1
: y  2x  cắt C y
tại hai điểm phân biệt A, B có m  2 5 : 2 x m
hoành độ x , x thỏa mãn 2
x  9x  8x . 1 2 1 1 2 Lời giải: TXĐ: D   \   m .
Hoành độ giao điểm của đường thẳng d và C
là nghiệm của phương trình m  2mx  5 1 2
 2x   4x x m  10  0  x   m . x m 2 Đặt g x 2
 4x x m  10 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... 15
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Để d cắt C
tại hai điểm phân biệt A, B  Phương trình g x  0 có 2 nghiệm phân biệt m   161     0 m 1  6m  161  0  khác 16 m
 , tức là phải có:      g  m 2  0
2m  5m  0  10 m    2  b 1
x x     1 2 
Áp dụng định lý Viet cho x , x , ta có: a 4  1 2 c m  10 x x    1 2  a 4  1  x  1 
Xét điều kiện bài toán 2 2
x  9x  8x x  9x  8   x  2 1
x x  2  0   1 1 2 1 1 1  4  1 1 x   2 1 5 +) Với x  1
  x   m  5  . 1 2 4 7
+) Với x  2  x    m  4. 1 2 4 161 10
Kết hợp với điều kiện m   và m   . 16 2
Vậy m  5 hoặc m  4 thỏa mãn yêu cầu bài toán.
Bài tập 16: Tìm m để C  3
y x  m   2 : 2
1 x  5m  2 x  2m  4 cắt trục hoành tại ba điểm phân biệt m
A, B, C sao cho B, C có hoành độ nhỏ hơn 1. Lời giải: TXĐ: D  .
Cách 1: Gọi x , x là hoành độ của B,C x ,x cũng là nghiệm của phương trình g x  0 . 1 2 1 2 Theo bài toán ta có: x  1 x 1  0
x 1 x 1 0
x x  2 2m  2 1 1 1 2 1 2          x  1 x 1  0
x  1 x  1  0 
x x x x  1  0 
m  2  2m  1  0 2 2  1  2  1 2  1 2 m  1    m  1  m  1  
Vậy m  1 là giá trị cần tìm.
Cách 2: Hoành độ của 3 điểm A, B,C là nghiệm của phương trình: 3
x  m   2 2
1 x  5m  2 x  2m  4  0  x   2
2 x  2mx m  2  0 x  2   g  x 2
x  2mx m  2   0
Vì hoành độ của B,C nhỏ hơn 1 nên giả sử hai nghiệm của g x  0 là 2
x m m m  2 , 1 2
x m m m  2 . 2 x  1
Vì x x nên 1 2 2 
x  1  m m m  2  1  m m  2  1 m 1 2 2 x  1 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... 16
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2
m m  2  0  0  m      1   m  0
 m  1  m  1  .  2 2 
m m  2  m  2m  1 m  1   
KỸ THUẬT: Vận dụng Cực trị để giải quyết bài toán sự tương giao
của các đồ thị hàm số và trục Ox. Hàm số bậc ba    3 2 y
f x ax bx cx d , a  0 có đồ thị (C).
Xét phương trình hoành độ giao điểm: 3 2
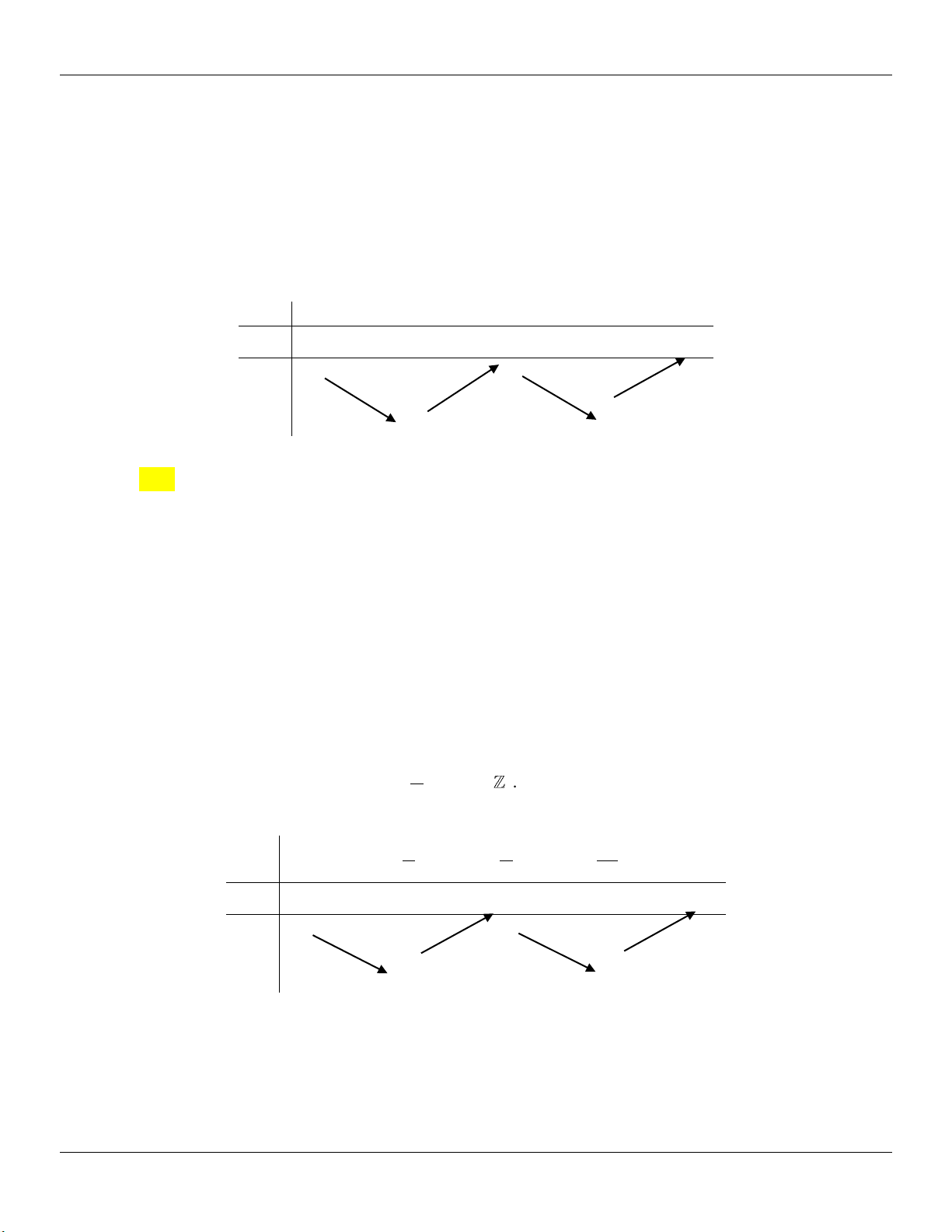
ax bx cx d  0 Hµm sè cã 2 cùc trÞ
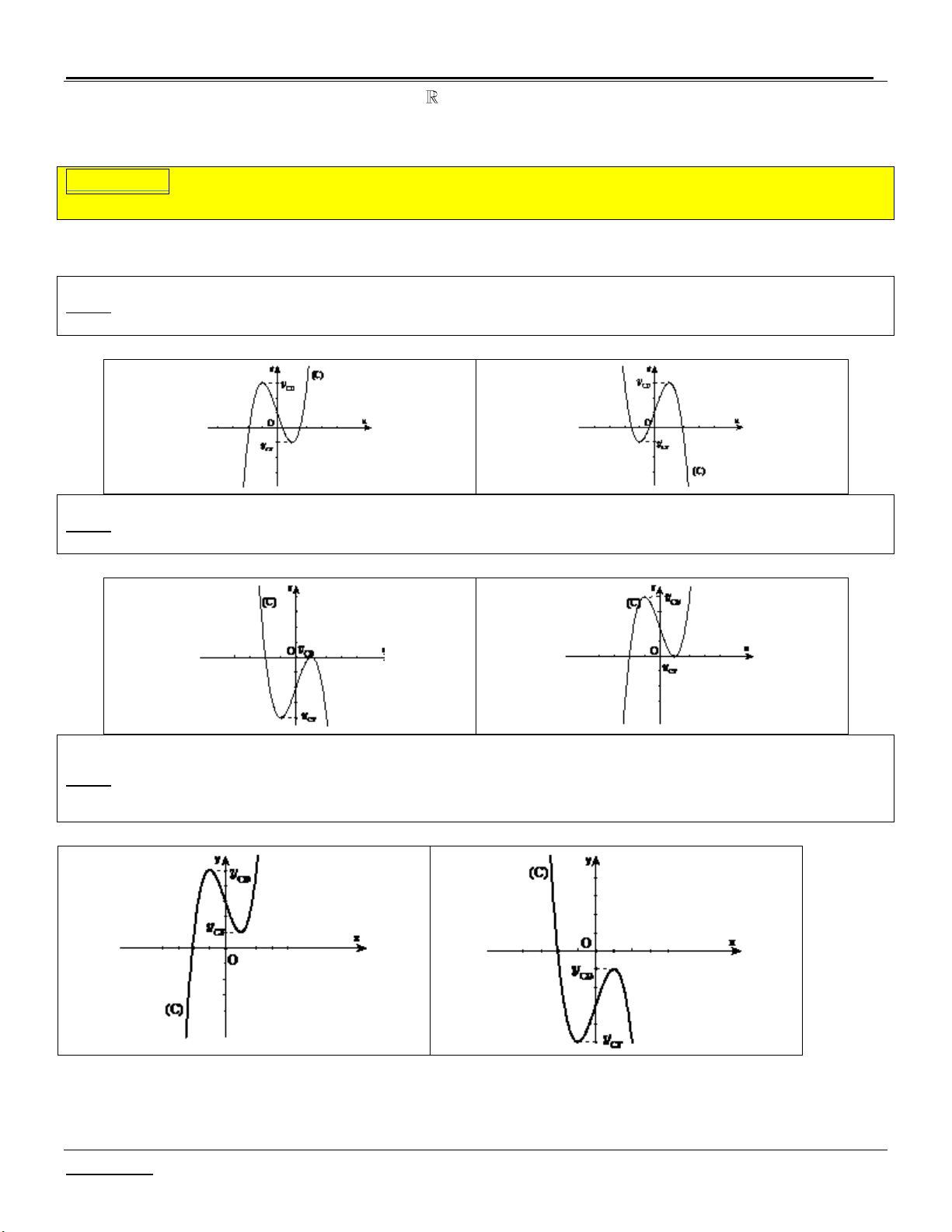
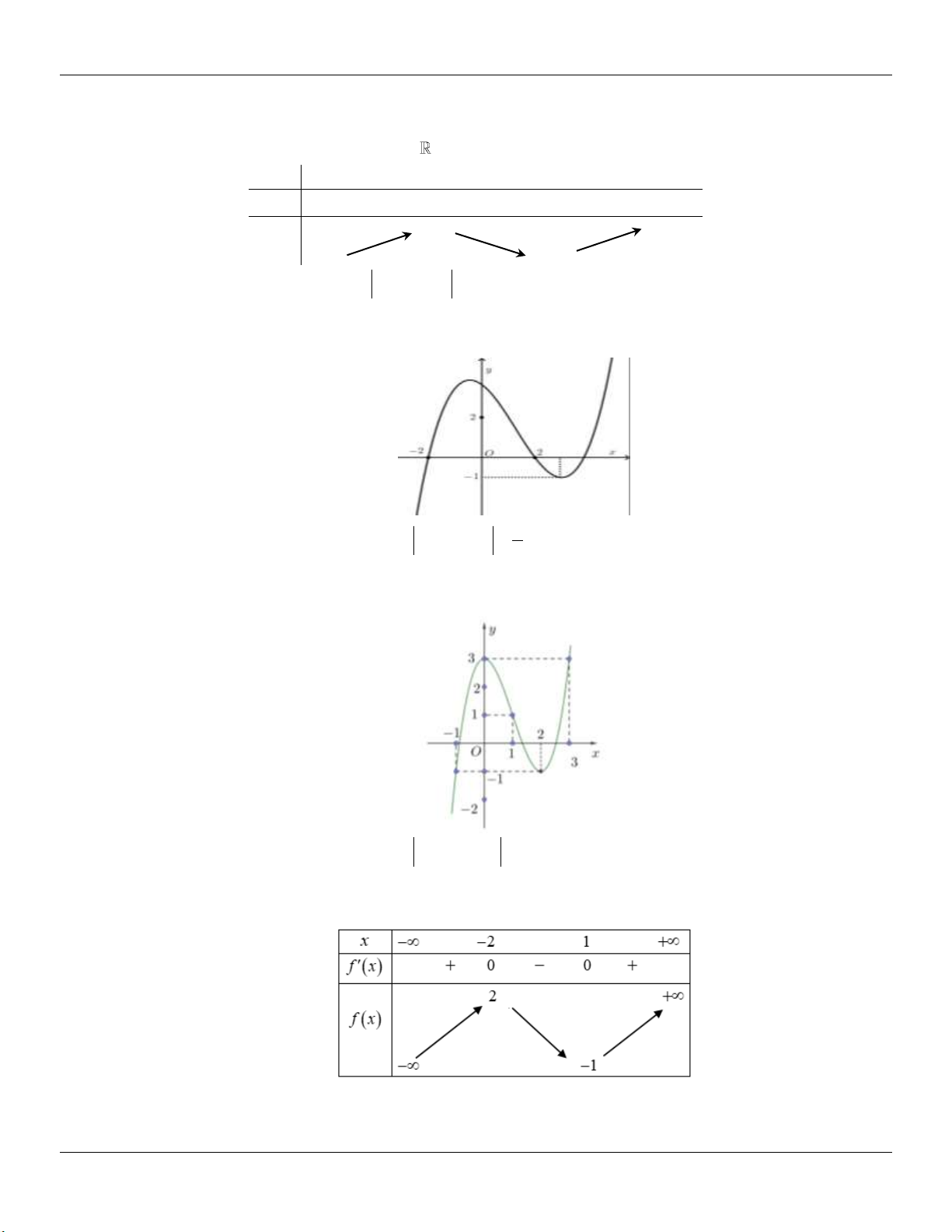
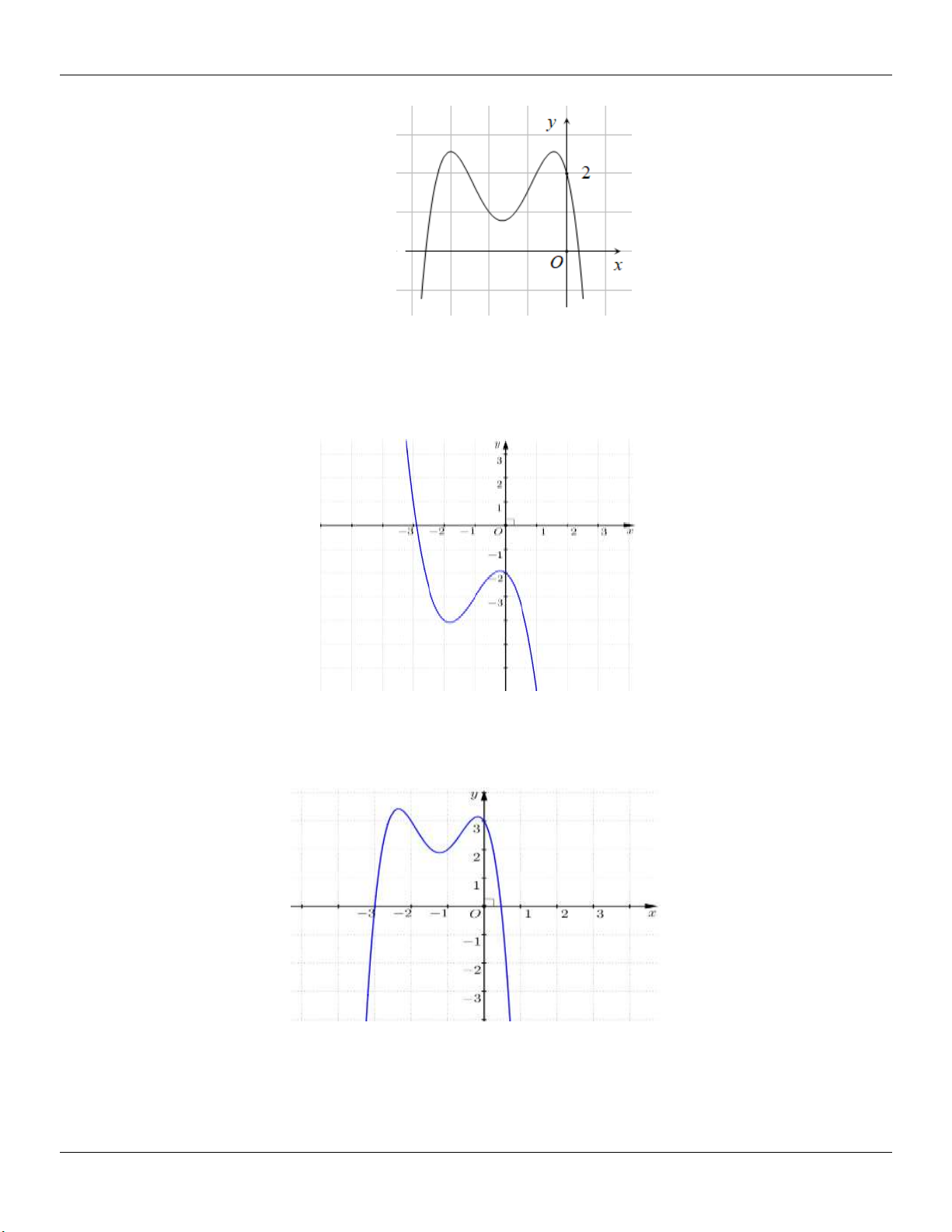
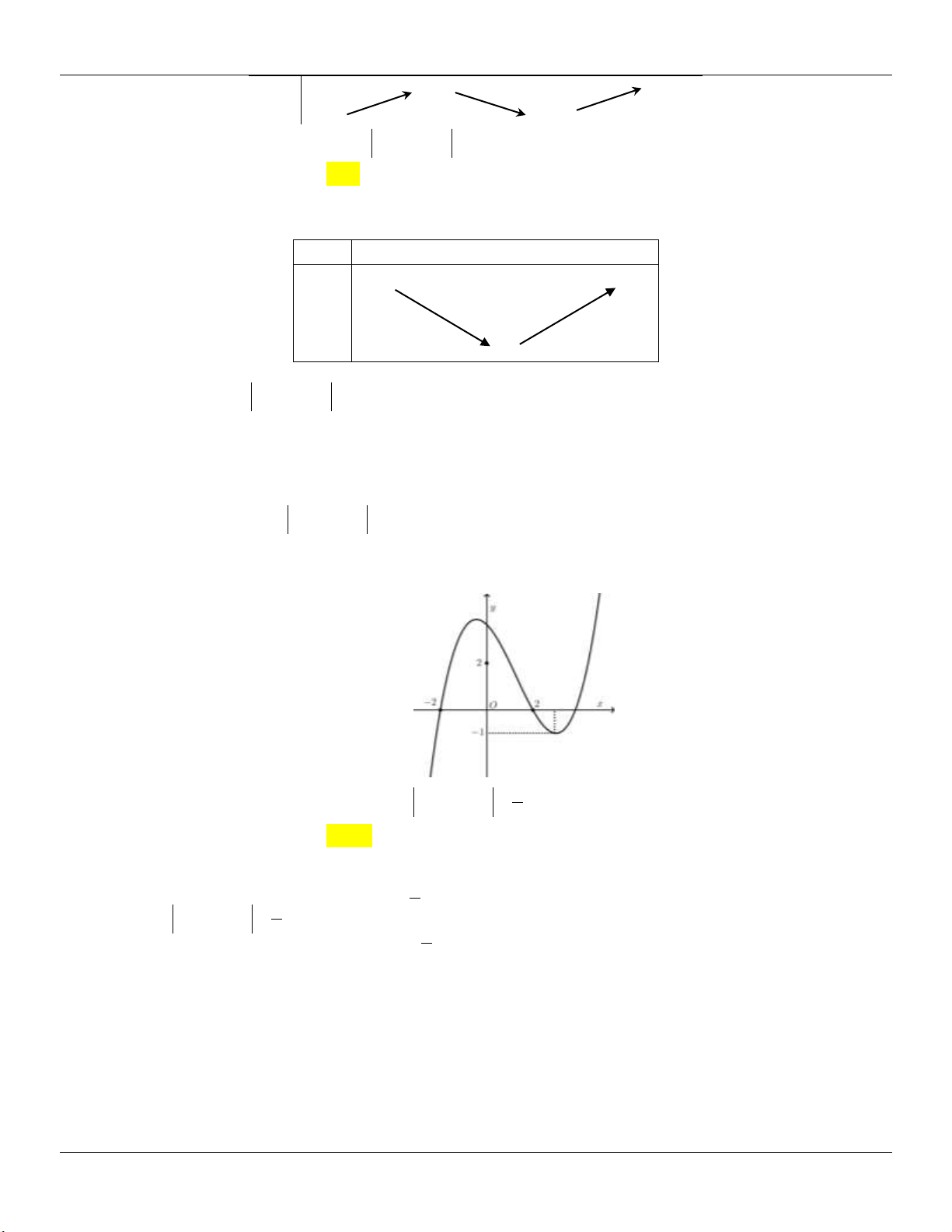
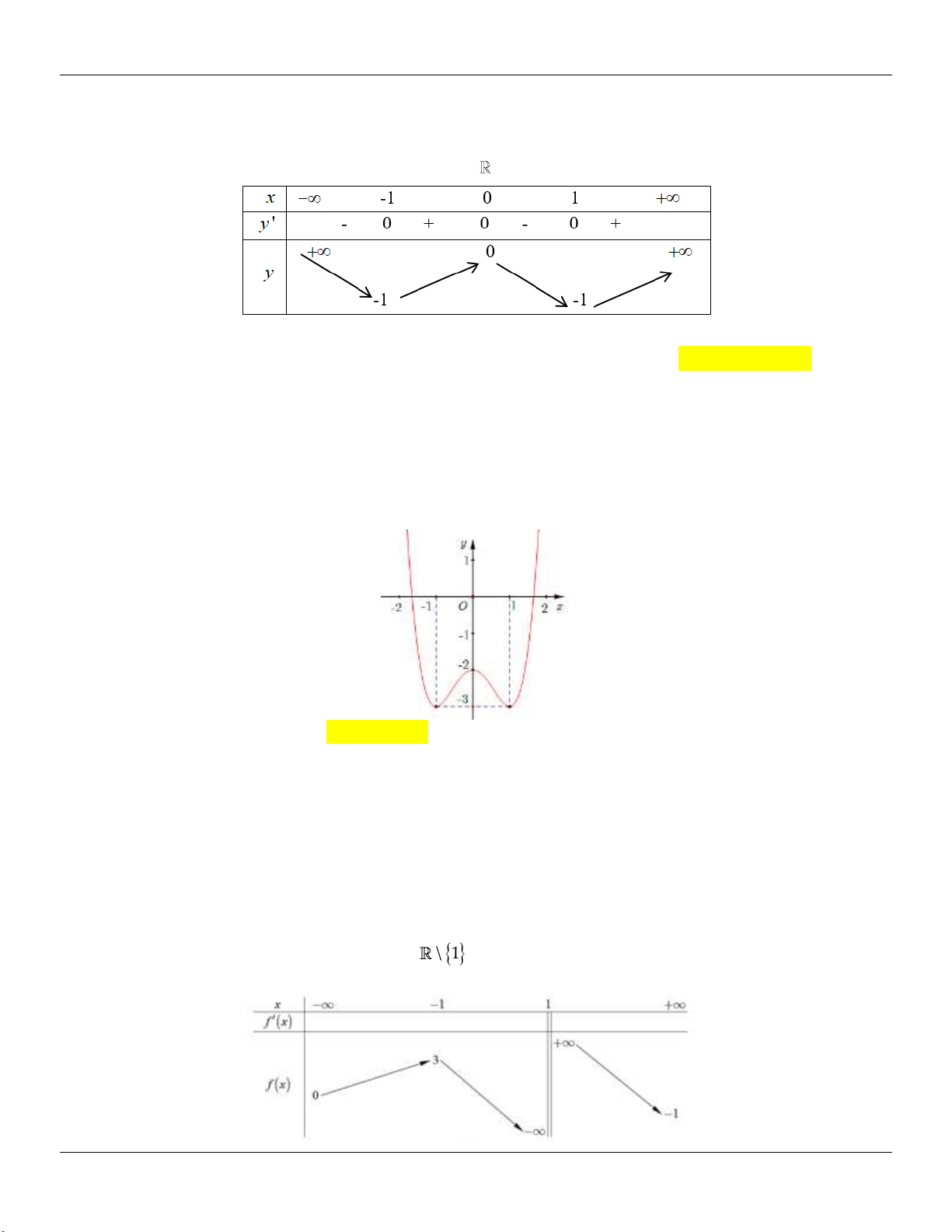
TH 1: (C) cắt Ox tại 3 điểm phân biệt   y .y   0 C§ CT
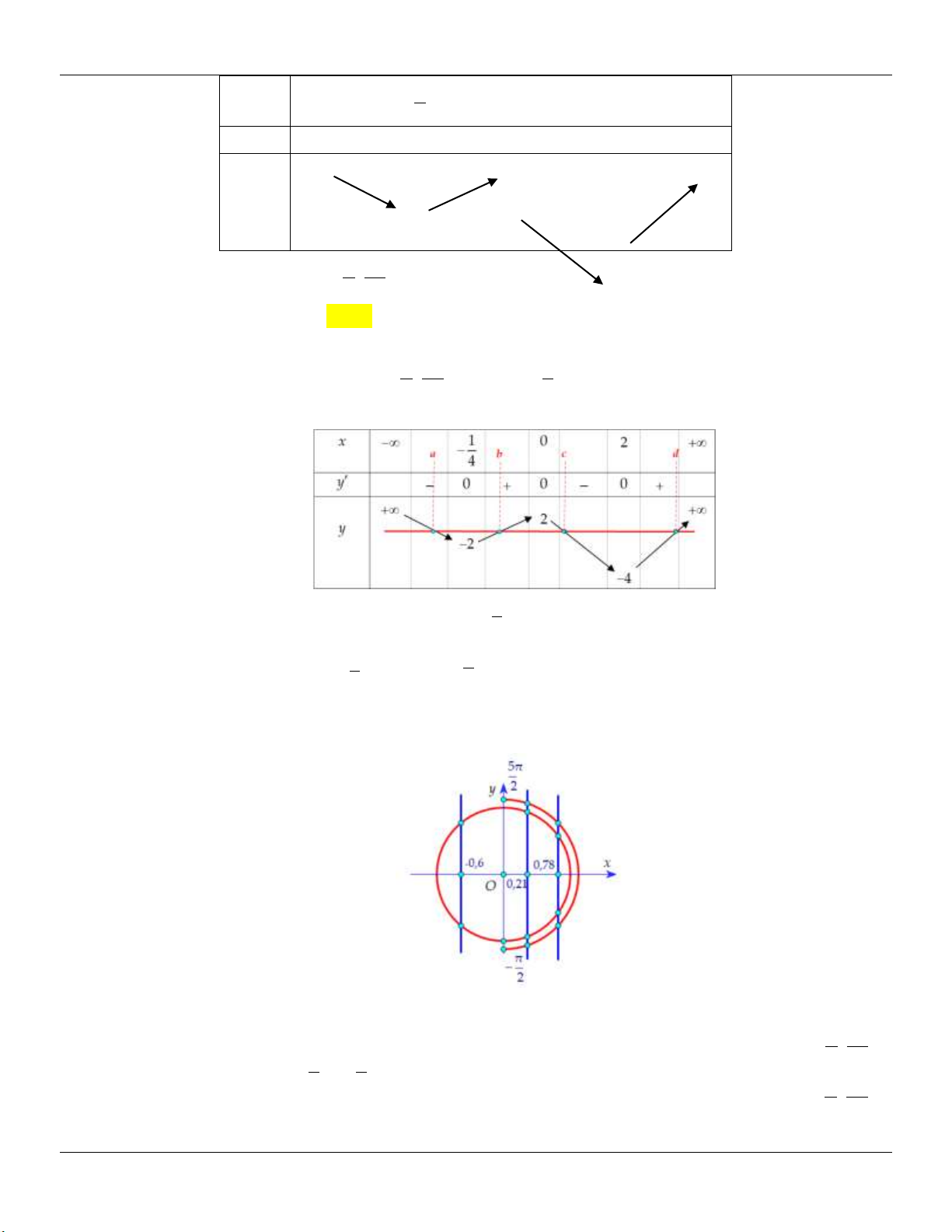
Minh họa đồ thị: Hµm sè cã 2 cùc trÞ
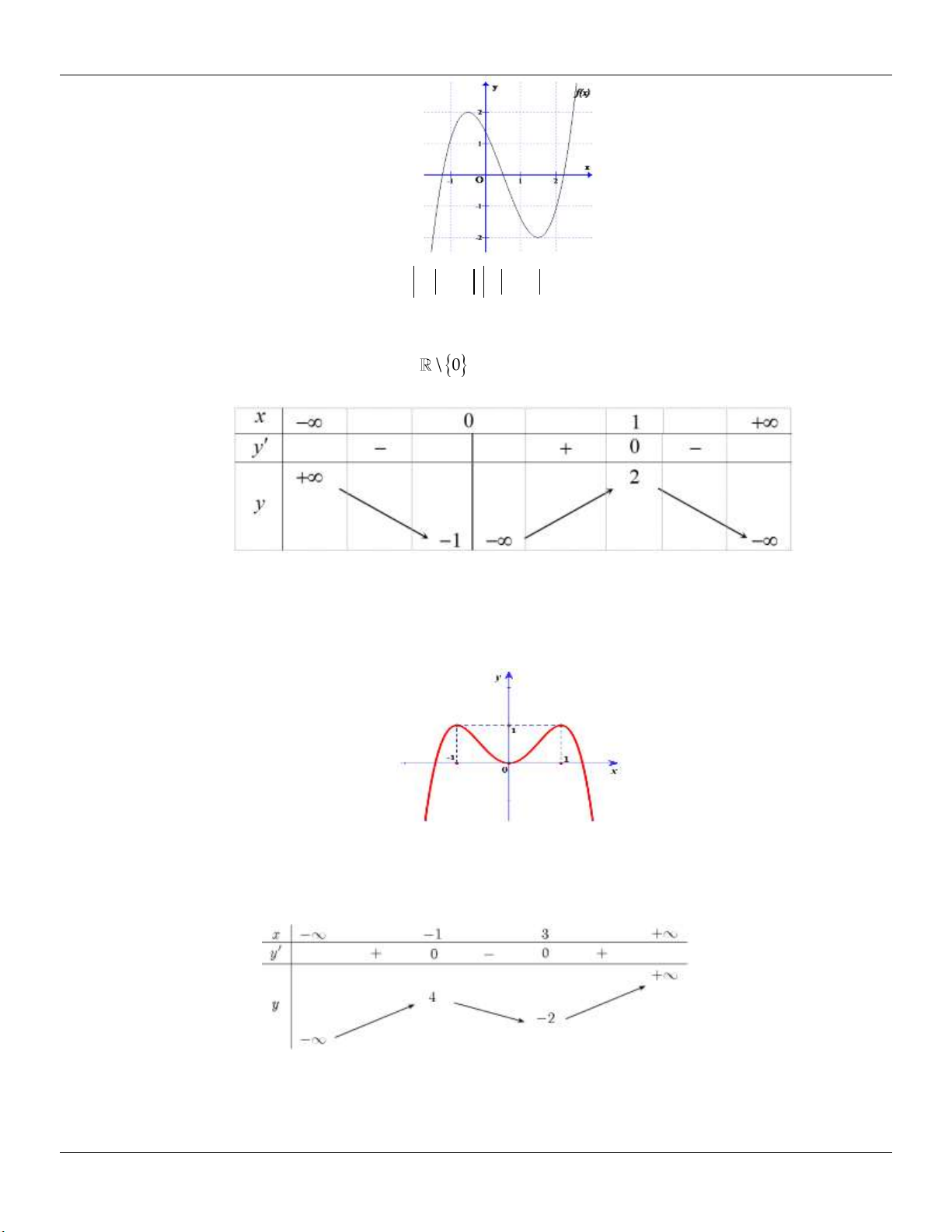
TH 2: (C) cắt Ox tại 2 điểm   y .y   0 C§ CT
Minh họa đồ thị:
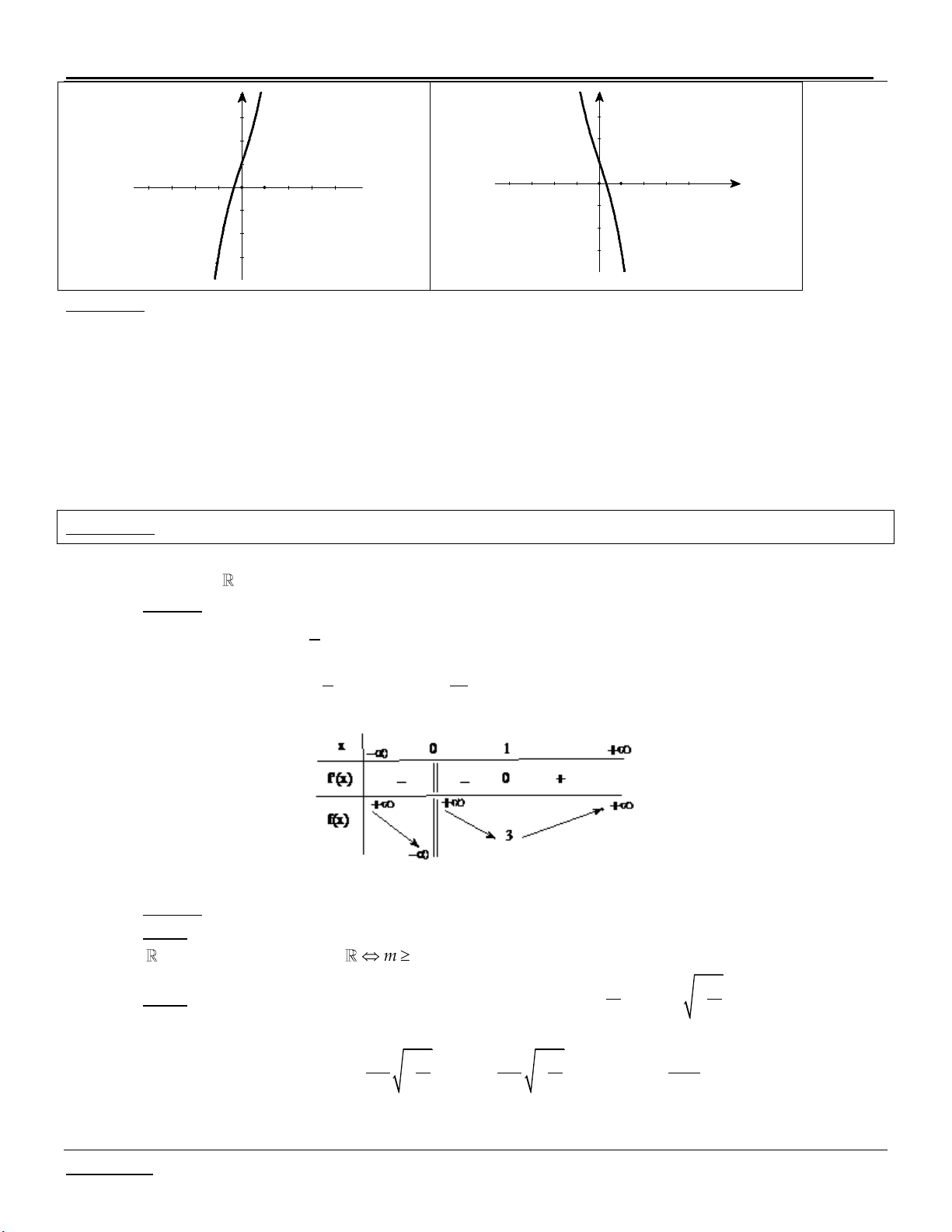
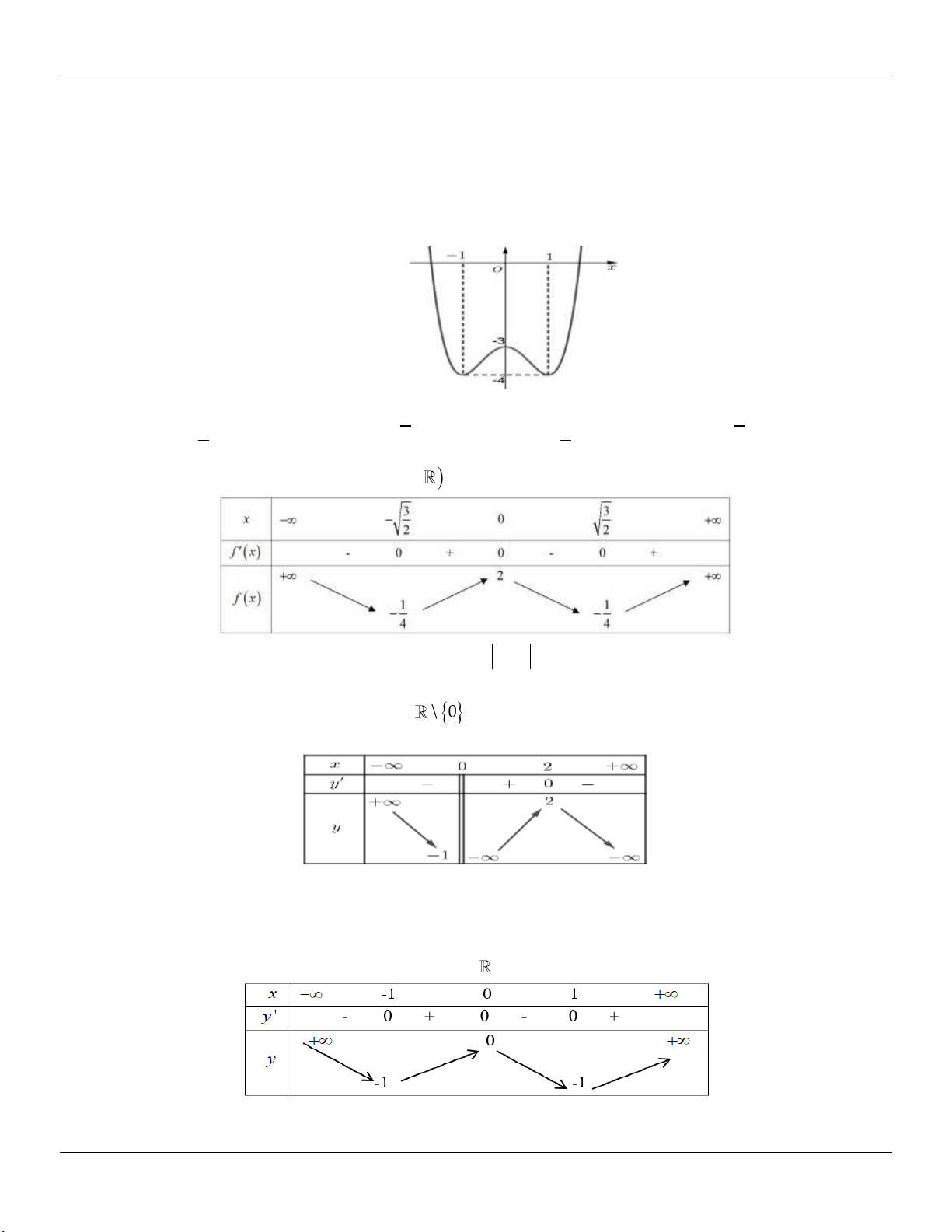
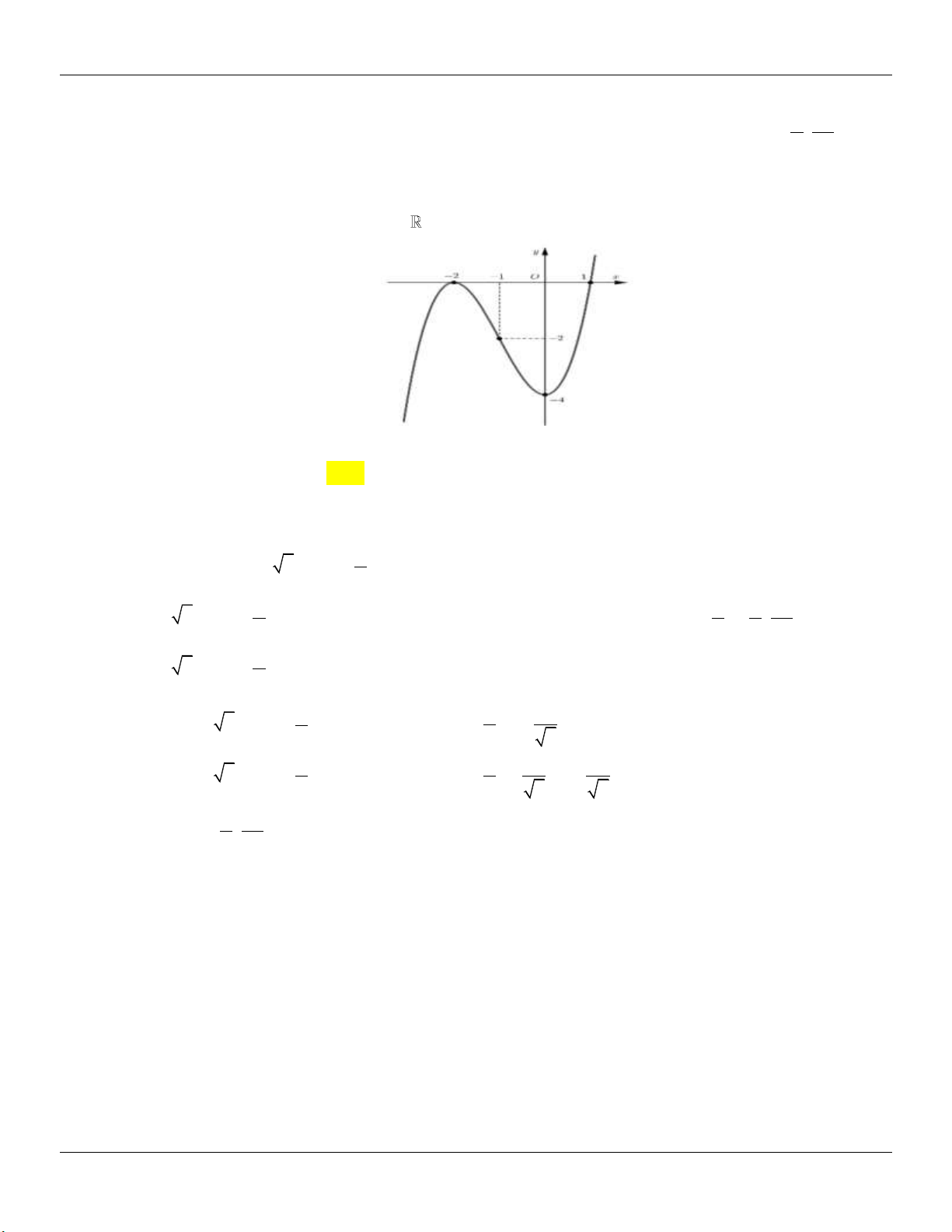
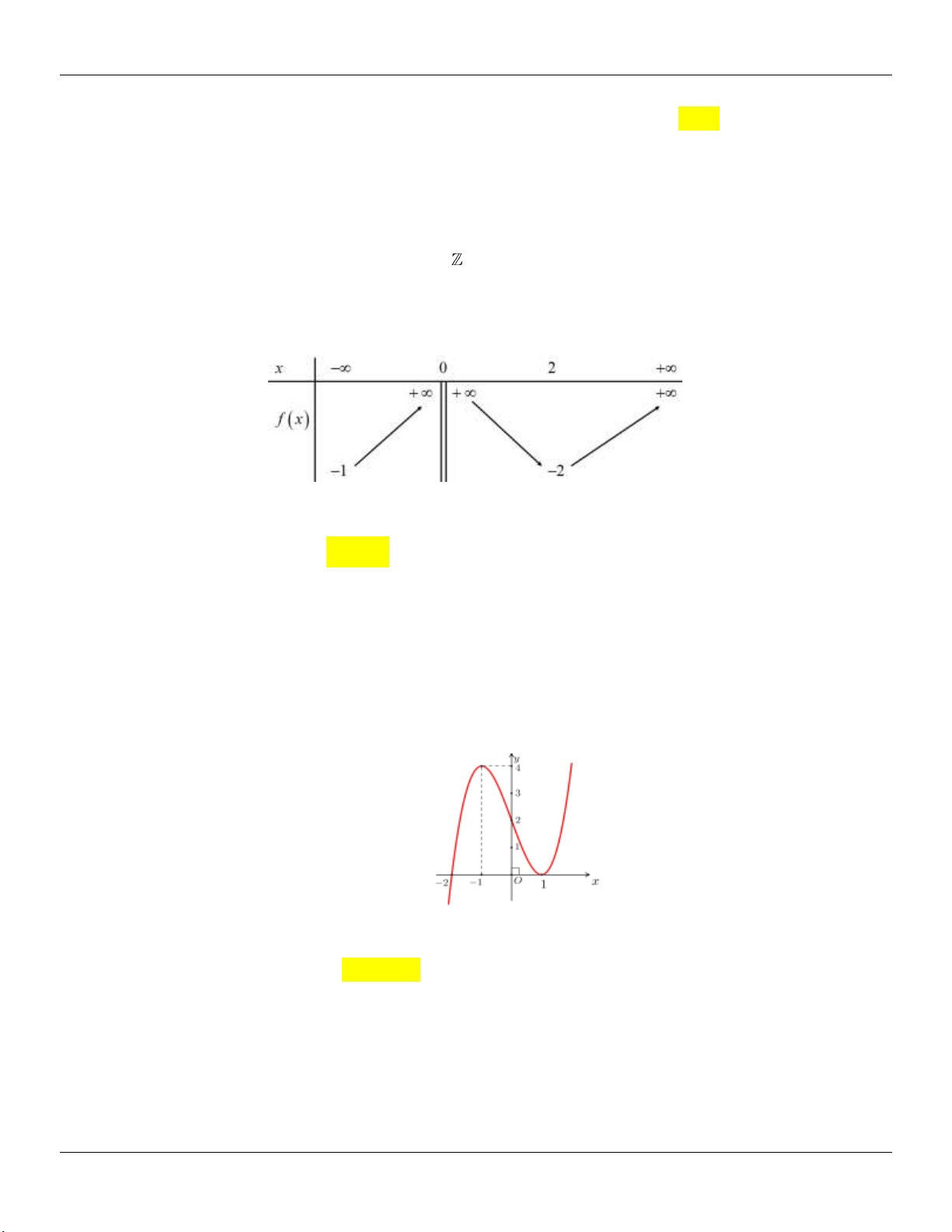
Hµm sè kh«ng cã cùc trÞ 
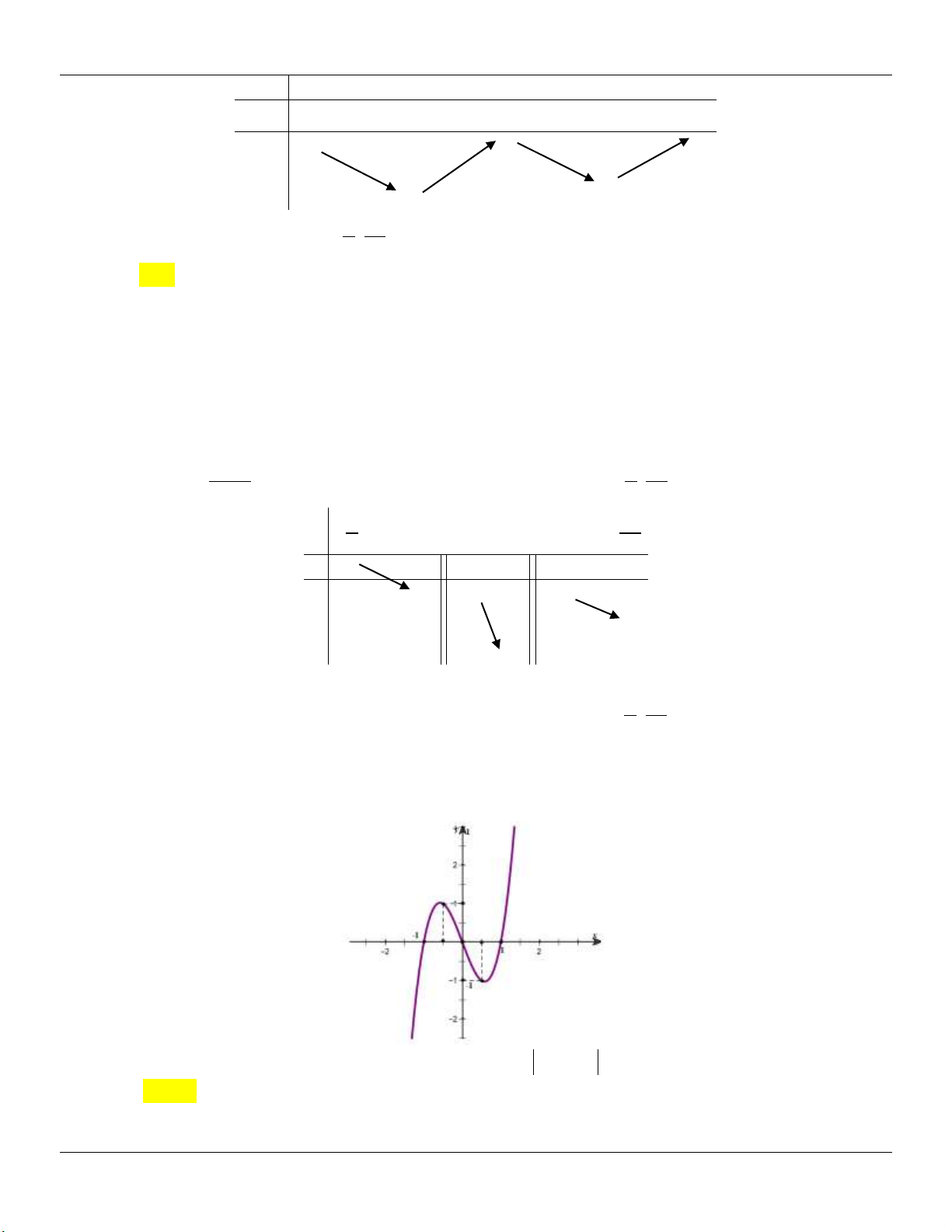
TH 3: (C) cắt Ox tại 1 điểm  Hµm sè cã 2 cùc trÞ    y .y   0 C§ CT
Minh họa đồ thị:
Giáo viên: LÊ BÁ BẢO...0935.785.115... 17
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia y y (C) x O x O (C) Nhận xét:
+ Việc xử lí các biểu thức cực trị thì quí độc giả xem lại bài viết cực trị;
+ Với hàm số trùng phương    4 2 y
f x ax bx c , a  0 thì hoàn toàn biện luận sơ cấp cho đơn giản;
Tất nhiên việc giải quyết một bài toán tương giao của hai đồ thị thì có nhiều phương pháp, nhưng theo
tinh thần đổi mới của chương trình SGK, cũng như mức độ đề thi Quốc gia, chúng tôi cho rằng,
phương pháp này chỉ mang tính chất tham khảo thêm! Các phương pháp cơ bản và sơ cấp đã hoàn toàn
giải quyết được các đề thi mức độ thi THPT Quốc gia!
Ta xét một số bài tập minh họa cho phương pháp này!
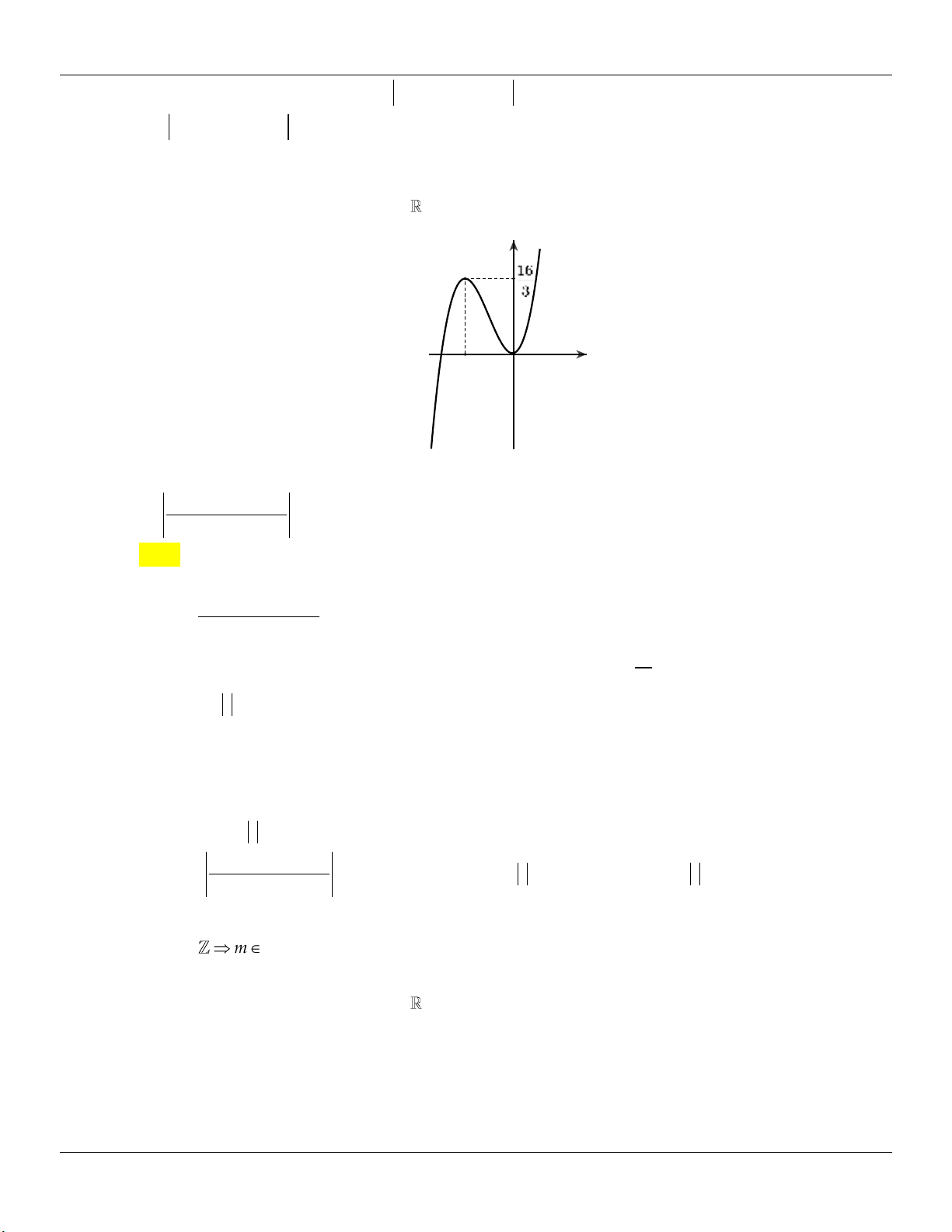
Bài tập 17: Tìm m để đồ thị hàm số 3
y x mx  2 cắt trục hoành tại điểm duy nhất. Lời giải: TXĐ: D  .
Cách 1: Phương trình hoành độ giao điểm của đồ thị hàm số đã cho với trục Ox : 3 2 2
x mx  2  0  x
 m . x 2 2
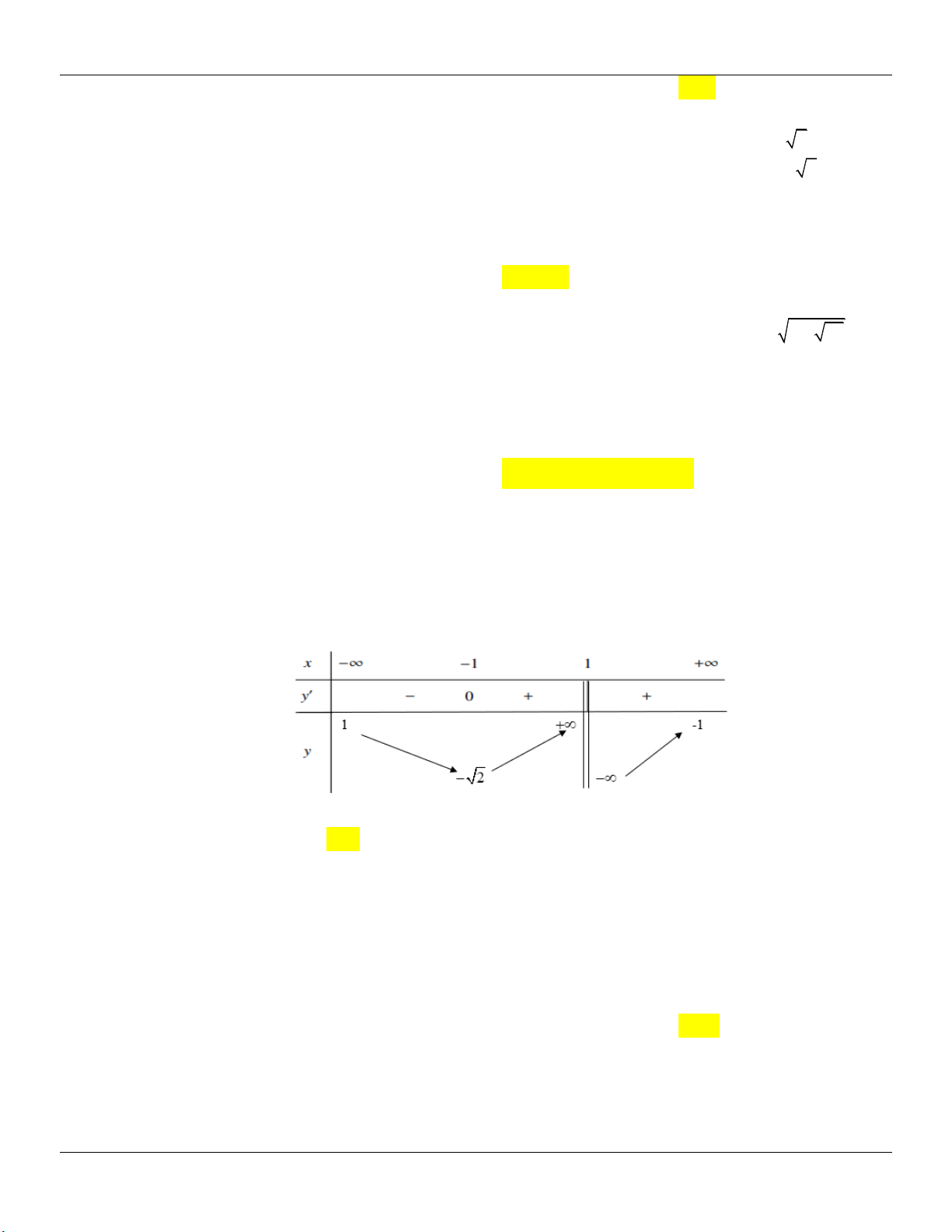
Xét hàm số f x 2 /
x   f x /  2x
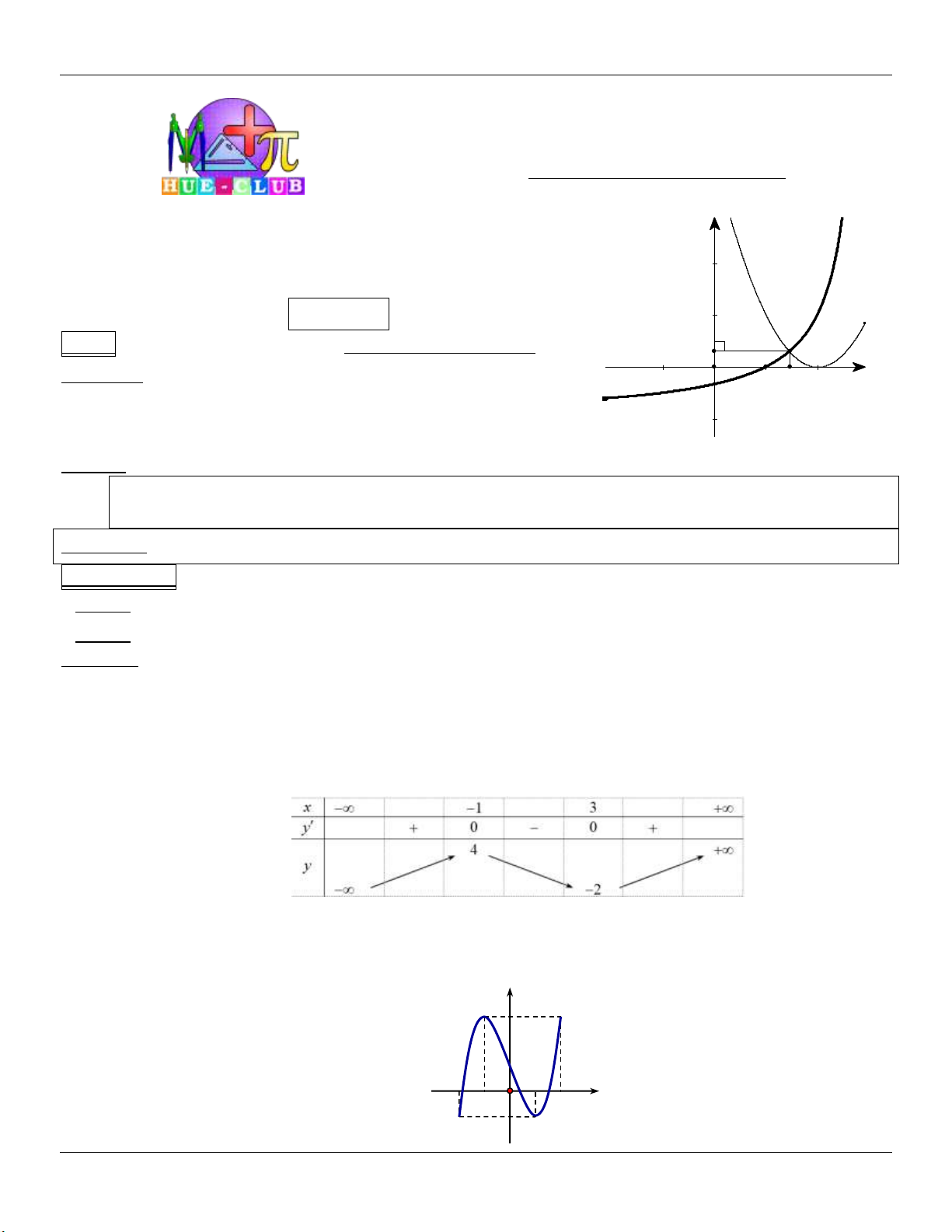
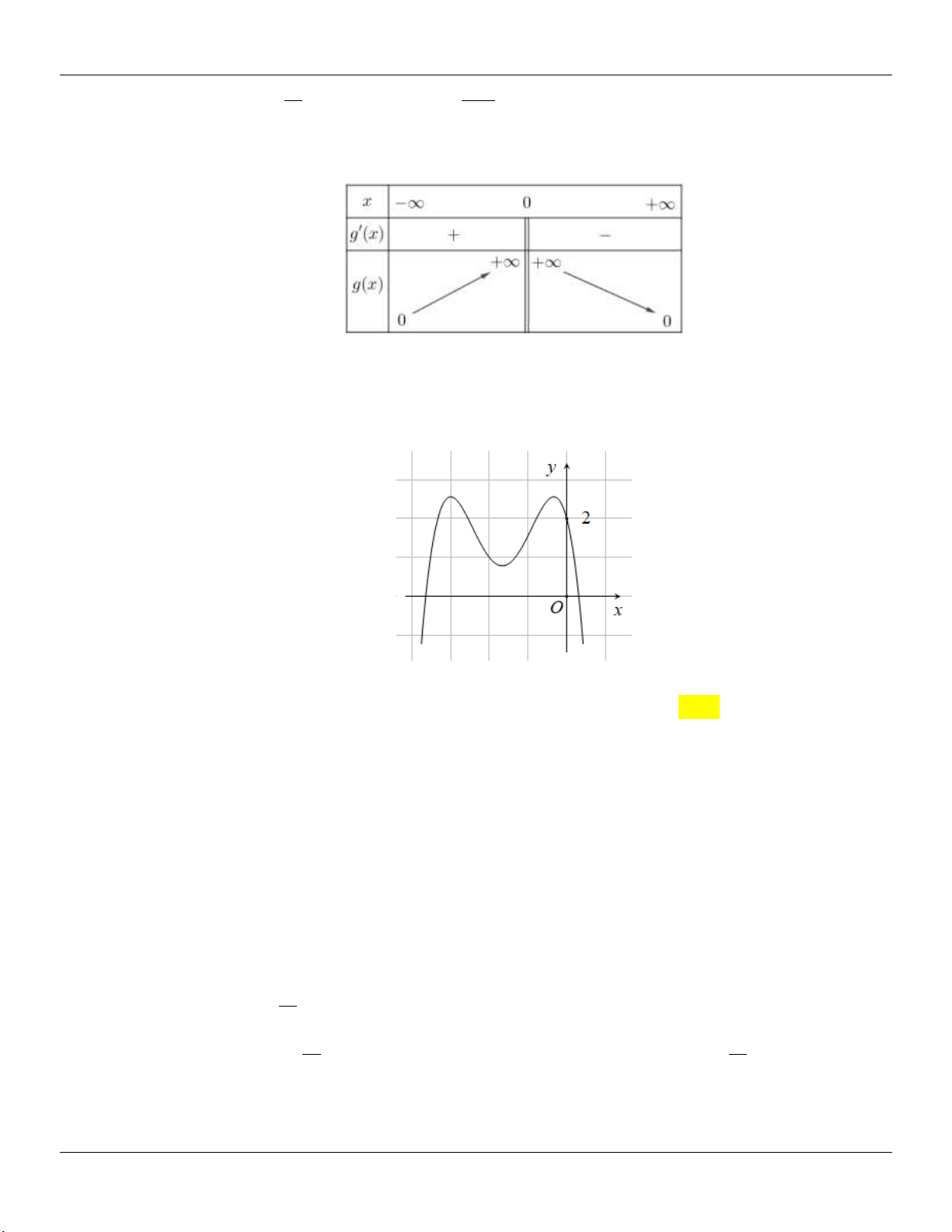
f x  0  x  1 . 2   x x Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy yêu cầu bài toán  m  3  m  3 .
Cách 2: Để đồ thị hàm số đã cho cắt Ox tại duy nhất một điểm ta có các trường hợp sau:
TH 1: Đồ thị hàm số đã cho không có cực trị hay là hàm số luôn đồng biến (do a  1  0 ) trên 2
y'  3x m  0, x    m  0 . m m
TH 2: Đồ thị hàm số có hai cực trị cùng dấu / 2
y  0  x    x    3 3 với m  0 . 2m m 2m m 3 4m
Hai giá trị cực trị là: y  2   ; y  2  
y .y  4   0  3   m  0 . 1 2 3 3 3 3 1 2 27
Vậy m  3 là những giá trị cần tìm.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 18
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1
Bài tập 18: Tìm m để đồ thị (C): 3
y x x m cắt trục hoành tại 3 điểm phân biệt. 3 Lời giải: TXĐ: D  .
Cách 1: (Đã trình bày ở bài tập 6) Cách 2:  2
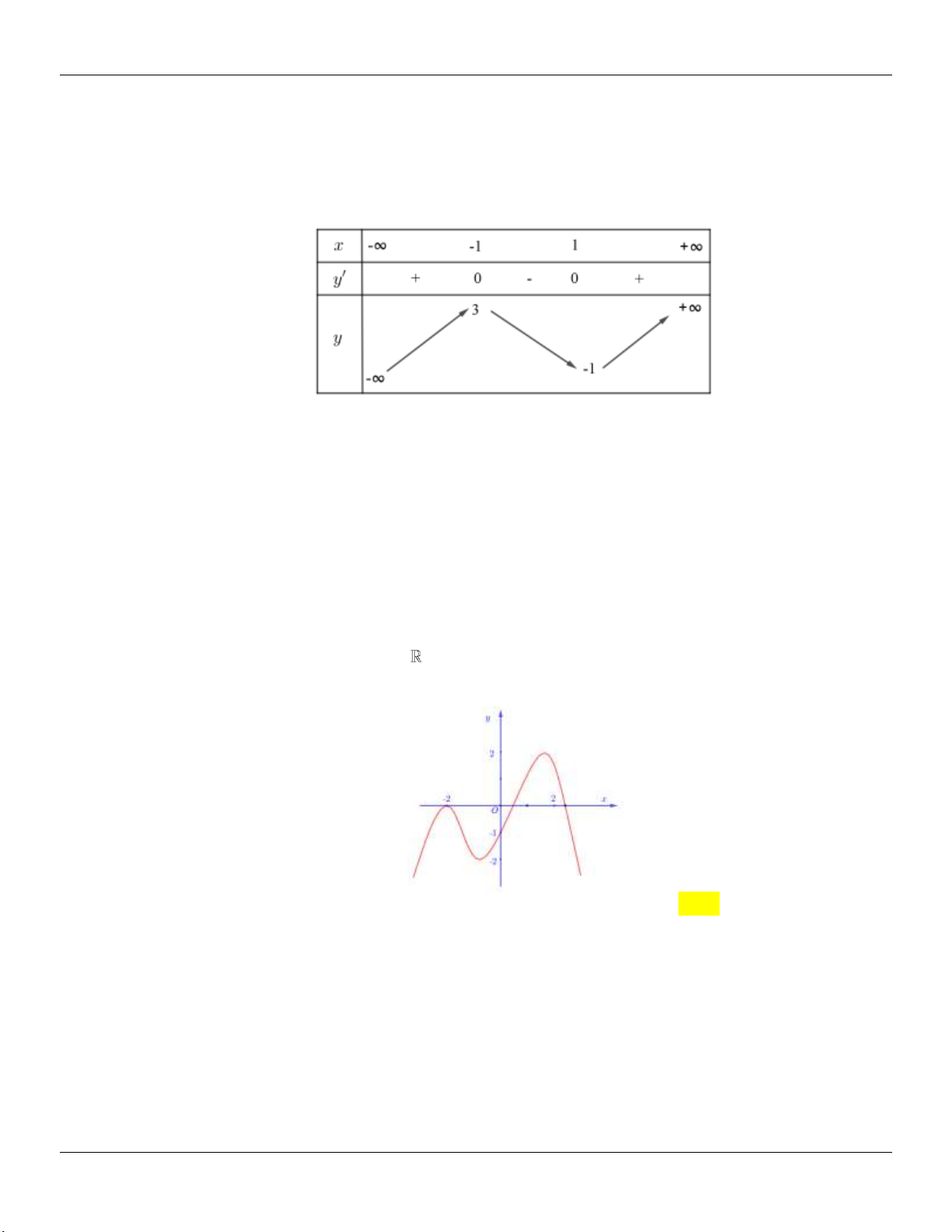
x  1  y    m  Ta có: / 2 3
y x  1  0   .  2 x  1
  y   m  3 2 2
Lúc đó, hàm số có 2 cực trị với các giá trị cực trị tương ứng là   m và  m . 3 3  2  2   
Để (C) cắt Ox tại 3 điểm phân biệt thì   mm     0 2 4 2 2
m   0  m   ; .  3  3  9  3 3  1 2
Bài tập 19: Tìm m để đồ thị C : 3 2
y x mx x m
cắt trục hoành tại 3 điểm phân biệt. m  3 3 Lời giải: TXĐ: D  .
Cách 1: (Đã trình bày ở bài tập 5- Dạng 3) Cách 2: Ta có: / 2
y x  2mx  1.
Để hàm số có hai cực trị  Phương trình /
y  0 có hai nghiệm phân biệt x , x 1 2 2
 4m  4  0, m   . 2 
m     m m Lúc đó, ta viết: / 1 2 2 2 2
y y x     x   .  3 3   3  3 3 2   2  2m  2m 2 y    x   1 1   3  3 3 Suy ra:  . 2   2  2m  2m 2 y    x    2 2   3  3 3
Để đồ thị (C) cắt Ox tại 3 điểm phân biệt thì 2 2  2   2m  2m 2   2   2m  2m 2 
y .y  0   x      x     0 1 2 1 2  3  3 3   3  3 3  2 2 2 2  2   2m   2
  2m  2m 2   2m 2     x x       x x      0 1 2  1 2  3   3  3 3   3 3 
  m 2   m m  2m2  m 2 2 2 2 2 2 2 2 2 2    .     0 9 3  3  9   2 4
m m    3
m m  m     2 4 8 4 4 4 2 2
4m  8m  4  0 4 3 2 2
  m m m    m  2 12 8 12 0 4
3m m  3  0  m  0 Do 2
3m m  3  0, m  
Vậy m  0 là yêu cầu bài toán.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 19
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia CHÚ Ý:
MỘT SỐ BÀI TOÁN QUAN TRỌNG
Bài toán 1: Xác định tham số để đồ thị hàm số 3 2
(C) : y ax bx cx d (a  0) cắt trục hoành tại ba điểm
phân biệt có hoành độ lập thành cấp số cộng. Phương pháp:
Sử dụng: Điều kiện cần và đủ đối với phương trình: 3 2
ax bx cx d  0 (1)
Bước 1: Điều kiện cần:
+ Giải sử phương trình (1) có 3 nghiệm x , x , x x x x . Khi đó, theo định lý Viet đối 1 2 3  1 2 3       b x x x 1 2 3  a  với phương trình (1):     c x x x x x x 1 2 2 3 3 1 a     d x x x 1 2 3  a
+ Để x , x , x x x x lập thành CSC thì   2  3   b x x x x    b x . 1 2 3  1 2 3  1 3 2 2 a 2 3a Thay vào (1)  m
Bước 2: Điều kiện đủ: Với m tìm được giải phương trình (1) và kết luận.
Lưu ý: Tư duy thuật toán còn áp dụng cho bài toán: 3 nghiệm lập thành cấp số nhân. Tất nhiên,
phương pháp nêu trên chỉ mang tính gợi ý, còn trong rất nhiều TH khác thì sẽ có các cách khác tốt hơn.
Bài tâp 1: (ĐHYHCM-98) Xác định m để đồ thị (C): 3 2
y x  3x  9x m cắt trục hoành tại 3 điểm phân
biệt với hoành độ lập thành một cấp số cộng. Lời giải: TXĐ: D  .
Xét phương trình hoành độ giao điểm của (C) và Ox: 3 2
x  3x  9x m  0 (1)
+ Giả sử (1) có ba nghiệm phân biệt x , x , x , khi đó ta phân tích được: 1 2 3 3 2
x  3x  9x m  x x x x x x 1   2   3  3
x  x x x  2
x x x x x x x x x x x (2) 1 2 3  1 2 2 3 3 1 1 2 3
Đồng nhất hệ số của 2
x trong phương trình (2), ta được: x x x  3 (3) 1 2 3
Mặt khác, do x , x , x theo thứ tự đó lập thành một cấp số công nên ta có: x x  2x (4) 1 2 3 1 3 2
Từ (3) và (4) suy ra: x  1. Thay x  1 vào (1) ta được: m  11 . 2 2
+ Kiểm tra với m  11 , ta có: 3 2
x x x
  x   2 3 9 11 0
1 x  2x  11  0
x  1 x  1  2 3  x  1  2 3.
Dễ thấy 3 nghiệm vừa tìm được lập thành một cấp số cộng.
Vậy m  11 là yêu cầu bài toán.
Bài tập tương tự:
Bài tập 2: (ĐHYHCM-96) Tìm a để d: y x cắt đồ thị 3 2 3
(C) : y x  3ax  4a tại 3 điểm phân biệt A, B,
C với AB BC .
Bài toán 2: Xác định tham số để đồ thị hàm số 4 2
(C) : y ax bx c (a  0) cắt trục hoành tại 4 điểm
phân biệt có hoành độ lập thành cấp số cộng. Phương pháp:
Lập phương trình hoành độ giao điểm: 4 2
ax bx c  0 (2)
Giáo viên: LÊ BÁ BẢO...0935.785.115... 20
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Đặt 2
t x  0 : (2) có dạng: 2
at bt c  0 (3).
Để (2) có 4 nghiệm phân biệt khi chỉ khi (3) có 2 nghiệm phân biệt: t , t : 0  t t (4) 1 2 1 2
Lúc đó (2) có 4 nghiệm:  t ,  t , t , t . 2 1 1 2
 t t  2 t
Các nghiệm này lập thành CSC khi: 2 1 1 
t  3 t t  9t . 2 1 2 1
 t t  2 t  1 2 1
+ Áp dụng định lý Viet đối với phương trình (3):   S    t 2 t t S  1 10 9S 1 2 
vµ t  9t   . Tõ ®©y:(*)   P hay 2
9S  100P (5) t  t P 2 1 (*)   9S 100 1 2 t2  10
+ Kết hợp (4) và (5) nhận được điều kiện của tham số. BÀI TẬP:
Bài tập: (ĐHY-D-HCM-98) Xác định m để đồ thị 4
C y x  m   2 ( ) : 2
1 x  2m  1 cắt trục hoành tại 4
điểm phân biệt có hoành độ lập thành cấp số cộng. Lời giải: TXĐ: D  .
Xét phương trình hoành độ giao điểm của (C) và Ox: 4
x  m   2 2
1 x  2m  1  0 (1) Cách 1: Đặt 2
t x  0 . Khi đó, (1) trở thành: 2
t  2m  1t  2m  1  0 (2)
Để (C) cắt Ox tại 4 điểm phân biệt  Phương trình (1) có 4 nghiệm phân biệt
 Phương trình (2) có 2 nghiệm dương phân biệt   m 2 4
1  42m  1  0   S   m   1 2 1  0
   m  0. (3) 2
P  2m1 0 
+ Với điều kiện (3), ta tìm được hai nghiệm của (2) là t m  1  ;t m  1   1 2
Như vậy, 4 giao điểm của (C) và Ox lần lượt là A t ;0, B t ;0, Ct ;0 , 1  2 1
Dt ;0 . Để 4 điểm này có hoành độ lập thành 1 cấp số cộng thì chúng phải chắn trên Ox 2 
thành 3 đoạn thẳng bằng nhau, tức là:
 t t  2 t 2 1 2
AB BC CD  
t  3 t t  9t . (4) 2 1 2 1
 t t  2 t  2 1 1 t
  t  2 m  1 1 2   (5)
Mặt khác, áp dụng định lí Viet với phương trình (2) ta có:  (5) t    t  2m  1 (6) 1 2
2m  1 m  1 9m  1
Từ (4) và (5) suy ra: t    t  thay vào (6) ta được: 1 2 10 5 5 m m  1 m   4 9 1  4 .  2m  1 
4 . Vậy m  4; m   là yêu cầu bài toán. 5 5 m    9  9 t  1
Cách 2: Ta có (1)   . t  2m   1
Giáo viên: LÊ BÁ BẢO...0935.785.115... 21
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2m  1  0 1
Để (C) cắt Ox tại 4 điểm phân biệt      m  0 . 2m  1   1 2
Lúc đó, ta tìm được hoành độ của 4 giao điểm lần lượt là  2m  1, 2m  1,  1, 1 .
TH 1: m  0 , thứ tự 4 hoành độ giao điểm là  2m  1,  1, 1, 2m  1 .
Điều kiện để 4 hoành độ giao điểm này tạo thành 1 cấp số cộng là:
 2m112. 1          .     2m 1 3 m 4 1  2m  1  2.1 1
TH 2:   m  0 , thứ tự 4 hoành độ giao điểm là 1
 ,  2m  1, 2m  1, 1. 2
Điều kiện để 4 hoành độ giao điểm này tạo thành 1 cấp số cộng là:  2m1 
12. 2m1 4         .     m   
 m  3 2m 1 31 m 9 1 2 1 2. 2 1 4
Vậy m  4; m   là yêu cầu bài toán. 9
III- BÀI TẬP TỰ LUYỆN
1) Tìm tọa độ giao điểm của các đồ thị sau: 2  x 3 y    3x     2x 4 y  3
y  4x  3x a) 2 2  b)  x  1 c)   x 1 
y  x  2 y   2      y x 2x 4  2 2 2  4 2  x
y x x  1 3 2
y x  5x  10x  5 y  d)  e)  f)  x  1 2
y  4x  5 2
y x x  1 y  3  x   1
2) Biện luận số giao điểm của các đồ thị sau: 3 2  x x 3  3       x
y x  3x  2 y 2x  y    3x a)  b) 3 2  c)  3 y m  x   2  1   13 
y mx    y m  x  3   2  12  2x  1   2     x 1 x 6x 3 y  y  y  d)  x  2 e)  x  1 f)  x  2 y  2x   m
y  2x   my x   m  1 2     x 3x 3 3
y  x  3    y
y  2x x   1 g)  1  x h)  x  2 i)   y m   2x 1 y mx   3
y mx  4m   1 2 x  4x  3
3) (Đề 34) Xác định tất cả các giá trị của k để đồ thị hàm số y  cắt đường thẳng x  2
d: y kx  1 tại 2 điểm phân biệt.
4) (ĐHKT-98) Cho hàm số 3 2
y x  3x  (
1 C) . Đường thẳng đi qua A3;1 và có hệ số góc bằng k . Xác
định k để đường thẳng đó cắt đồ thị tại 3 điểm phân biệt.
5) (ĐHSPII-97) Tìm m để hàm số y    m 4 2 1
x mx  2m  1 cắt Ox tại 4 điểm phân biệt.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 22
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2 x mx  1
6) (Đề 148) Tìm m để đường thẳng d: y m cắt đồ thị hàm số y
tại 2 điểm A, B với x  1 OA OB . 2
mx x m
7) (ĐH A-03) Tìm m để đồ thị hàm số (C) : y
cắt Ox tại 2 điểm phân biệt và 2 điểm đó có x  1 hoành độ dương. 2 x x  4
8) (ĐH D-03) Tìm m để đường thẳng d : y mx  2  2m cắt (C) : y
tại 2 điểm phân biệt. m x  2
9)(Dự bị 02) Tìm m để đồ thị hàm số 4 2
(C) : y x mx m  1 cắt Ox tại 4 điểm phân biệt.
10) (Đề dự bị 2003) Tìm m để đồ thị hàm số C y  x   2 ( ) :
1 x mx m cắt Ox tại 3 điểm phân biệt. 2
x  3x  3
11) (ĐH A-2004) Tìm m để đường thẳng y m cắt đồ thị hàm số (C) : y  2(x  1)
tại 2 điểm A, B sao cho AB  1.
12) (ĐH A-06) Gọi d là đường thẳng đi qua điểm A3; 20 và có hệ số góc là m . Tìm m để d cắt đồ thị 3
(C) : y x  3x  2 tại 3 điểm phân biệt.  2 
13) (ĐHBK A-01) Viết phương trình đường thẳng d đi qua điểm M  2;  sao cho d cắt đồ thị  5  2 x  3 (C) : y
tại hai điểm A, B phân biệt và M là trung điểm của AB. x  1 2 x x  1
14) Tìm các giá trị của m sao cho trên (C) : y
có hai điểm khác nhau Ax ; y
, Bx ; y B B A A x  1
x y m thoả mãn điều kiện: A A  .
x y m B B 1 x  3
15) CMR: Đường thẳng y x m luôn cắt đồ thị hàm số y
tại hai điểm phân biệt A, B. Tìm m 2 x  2
sao cho độ dài đoạn AB là nhỏ nhất.
16) (ĐHCĐ- 98) Tìm các giá trị của m để đường thẳng d : y mx  2  m cắt đồ thị hàm số m 2 x  4x  1 (C) : y
tại hai điểm phân biệt cùng thuộc một nhánh của đồ thị (C). x  2 17) Cho hàm số 3 2
y x mx   2
m  x m 2 2 2 1
1  m  C . Tìm m để đường cong C cắt trục hoành m m
tại 3 điểm phân biệt có hoành độ dương. 18)* Cho hàm số 3 2
y x  3x  31  mx  1  3mC
. Tìm m để đường cong C cắt trục hoành tại 3 m m  điểm phân biệt. 19) Cho hàm số 3 2
y x  3mx  3x  3m  2 C
. Tìm m để đường cong C cắt trục hoành m m
tại 3 điểm phân biệt có hoành độ x , x , x sao cho: 2 2 2
x x x  15 . 1 2 3 1 2 3 x  1
20) CMR: Với mọi m đường thẳng  : 2x y m  0 luôn cắt đồ thị (C) : y
tại hai điểm phân biệt x  1
thuộc hai nhánh khác nhau của (C). 3
21) CMR: Với mọi m đường thẳng  : y  2x m  0 luôn cắt (C) : y  x  3  tại hai điểm A, B x  1
phân biệt có hoành độ x , x . Lúc đó, xác định m sao cho: x x min. 1 2 2 1 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... 23
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2 x  2x  9
22) Tìm m để đường thẳng d : y  (
m x  5)  10 cắt (C) : y
tại 2 điểm A, B phân biệt và nhận m x  2
M(5;10) làm trung điểm.
23) (ĐH A-2010) Tìm m để C 3 2
: y x  2x  (1  )
m x m cắt trục hoành tại 3 điểm phân biệt có hoành
độ x , x , x sao cho: 2 2 2
x x x  4 . 1 2 3 1 2 3 2x  1
24) (ĐH B- 2010) Tìm m để đường thẳng y  2x m cắt (C) : y
tại 2 điểm A, B phân biệt sao x  1
cho tam giác OAB có diện tích bằng 3 .
25) (ĐH A-2011) Chứng minh rằng với mọi m đường thẳng y x m luôn cắt đồ thị hàm số    Cx 1 : y
tại hai điểm phân biệt A và B. Gọi k , k lần lượt là hệ số góc của các tiếp tuyến của (C) 2x  1 1 2
tại A, B. Tìm m để k k đạt giá trị lớn nhất. 1 2 2x  1
26) (ĐH D-2011) Tìm k để đường thẳng y kx  2k  1 cắt đồ thị hàm số y  tại hai điểm A, B sao x  1
cho khoảng cách từ A, B đến trục hoành bằng nhau. x  1
27) Cho hàm số y
(1) có đồ thị (C) .Chứng minh rằng đường thẳng (d) : y  2x m luôn cắt (C) tại x  1
hai điểm phân biệt A, B thuộc hai nhánh khác nhau. Xác định m để đoạn AB có độ dài ngắn nhất.
------------------------------------------------------------------------
HỆ THỐNG VÀ KHÁI QUÁT:
SỰ TƯƠNG GIAO CỦA HAI ĐỒ THỊ HÀM BẬC BA: 3 2
y ax bx cx d, a  0 1) Cho hàm số 3 2
y x  3x  6x , (C) và đường thẳng d đi qua gốc tọa độ O và có hệ số góc k . Tìm
k để d cắt (C) tại 3 điểm phân biệt O, A, B sao cho AB  17 .
2) Tìm m để đường thẳng d : y x  4 cắt (C): 3 2
y x  2mx  m  4 x  4 tại ba điểm A0; 4 , B, C
sao cho tam giác IBC có diện tích bằng 8 2 với I 3;1 .
3) Tìm m để đường thẳng d : y  x  2 cắt (C): 3 2
y x  2mx  3m  1 x  2 tại ba điểm A0; 2 , B,
C sao cho tam giác IBC có diện tích bằng 2 6 với I 1; 3 .
4) Tìm m để (C): 3
y x  m   2 3
1 x  3mx m  1 cắt trục hoành tại ba điểm phân biết trong đó có ít
nhất một điểm có hoành độ âm. 5) Cho hàm số 3 2
y x  6x  9x  6 , (C). Tìm m để (d): y mx  2m  4 cắt (C) tại 3 điểm phân biệt. 6) Cho hàm số 3 2
y  x mx m (C ) . Tìm m để (C ) cắt trục hoành tại 3 điểm phân biệt. m m 7) Cho hàm số: 3 2
y x  (m  1)x x m  1 (C ) . Tìm m để (C ) cắt trục hoành tại 3 điểm phân m m
biệt có hoành độ dương. 8) Cho hàm số 3 2
y x mx   2
m  x   2 3 3 1
m  1, (C ) . Tìm m để (C ) cắt trục hoành tại 3 điểm m m
phân biệt có hoành độ dương. 9) Cho hàm số 3 2
y x x  18mx  2m (C ) . Tìm m để (C ) cắt trục hoành tại 3 điểm phân biệt có m m hoành độ dương. 10) Cho hàm số 3
y x  m   2 x   2 m   2 2 3 1 3
1 x m  1 (C ) . Tìm m để (C ) cắt trục hoành tại 3 m m
điểm phân biệt có hoành độ âm.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 24
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 11) Cho hàm số 3 2 2 3
y x  3mx  3(m  1)x m , (C ) . Tìm m để (C ) cắt trục hoành tại 3 điểm phân m m
biệt trong đó có đúng hai điểm có hoành độ âm. 12) Cho hàm số 3
y x  m   2 2 3
1 x  6mx  2 (C ) . Tìm m để (C ) cắt trục hoành tại duy nhất 1 m m điểm. 13) Cho hàm số 3
y x  m   2 x   2 3 1
2 m  4m  1x  4mm  1 (C ) . Tìm m để (C ) cắt trục hoành m m
tại 3 điểm phân biệt trong đó có hoành độ lớn hơn 1. 14) Cho hàm số 3 2
y x  3x  9x m, (C ) . Xác định m để (C ) cắt trục hoành tại 3 điểm có hoành m m
độ lập thành cấp số cộng.
15) Tìm m để đồ thị hàm số 3 2
y x  3mx  3m  1x  6m  6 cắt trục hoành tại ba điểm phân biệt có
hoành độ x , x , 2 2 2
x : x x x x x x  20 . 1 2 3 1 2 3 1 2 3 1 2 16) Cho hàm số 3 2
y x mx x m
. Tìm m để đồ thị hàm số cắt trục hoành tại ba điểm phân 3 3 biệt x , x , 2 2 2
x : x x x  15 . 1 2 3 1 2 3
17) Tìm m để d: y  (1  m)x m  5 cắt (C): 3 2
y x  2x  (3m  1)x m  3 tại 3 điểm phân biệt có
hoành độ x , x x : x x  1  x . 1 2, 3 1 2 3 18) Cho hàm số 3 2
y x mx  2m  1 x m  2 . Chứng minh rằng đồ thị hàm số luôn đi qua điểm
cố định A trên trục hoành. Tìm m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt A, B, C 2 2  OA   OA  19 thỏa mãn:       .  OB   OC  48
19) Cho (C): y xx  2
3  4 và d là đường thẳng đi qua A1;0 và có hệ số góc bằng k . Tìm k để
d cắt (C) tại ba điểm phân biệt. Trong trường hợp này, tìm tập hợp trung điểm M của đoạn
thẳng nối hai giao điểm lưu động khi k thay đổi. 20) Cho (C): 3 2
y x  3x  4 và đường thẳng d đi qua A3; 4 và có hệ số góc m . Tìm m để đường
thẳng d cắt (C) tại 3 điểm phân biệt A, M, N sao cho hai tiếp tuyến của (C) tại M và N vuông góc nhau. 21) Cho hàm số 3 2
y x  3x mx  1. Tìm m để đường thẳng y  1 cắt đồ thị hàm số tại ba điểm
phân biệt I 0;1 , A và B. Với giá trị nào của m , các tiếp tuyến của đồ thị hàm số các điểm A, B vuông góc nhau. 22) Cho hàm số 3 2
y x mx x m . Tìm m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt
sao hoành độ của chúng lập thành cấp số cộng. HÀM TRÙNG PHƯƠNG: 4 2
y ax bx c, a  0 1) Cho hàm số 4 2
y x mx m  1 . Tìm m để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt.
2) Tìm m để đồ thị hàm số 4 2 2
y x  2mx m  1 . Tìm m để đồ thị cắt trục hoành tại bốn điểm
phân biệt có hoành độ nhỏ hơn 2. 3) Cho hàm số 4
y x   m   2 3
2 x  3m . Tìm m để đường thẳng y  1 cắt đồ thị hàm số tại 4 điểm
phân biệt đều có hoành độ nhỏ hơn 2. 4) Cho hàm số 4
y mx  m   2
3 x  3m . Tìm m để đồ thị hàm số cắt Ox tại 4 điểm phân biệt với
một điểm có hoành độ nhỏ hơn – 2 và 3 điểm kia có hoành độ lớn hơn – 1.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 25
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 5) Cho hàm số 4
y  x  m   2 2
2 x  2m  3 . Tìm m để đồ thị hàm số cắt Ox tại 4 điểm phân biệt có
hoành độ lập thành một cấp số cộng.
6) Tìm m để (C): 4
y x   m   2 3
2 x  3m cắt đường thẳng y  1 tại 4 điểm phân biệt có hoành độ
x , x , x , 2 2 2 2
x : x x x x x x x x  4 . 1 2 3 4 1 2 3 4 1 2 3 4
7) Tìm điều kiện đối với a và b để (C): 4 2
y x ax cắt đường thẳng y b tại 4 điểm phân biệt có
hoành độ x , x , x , x ( x x x x ). Trong trường hợp này, tính tổng: 2 2 2 2
x x x x . 1 2 3 4 1 2 3 4 1 2 3 4 1 3 5 8) Cho hàm số 4 2
y x x
, (C). Tìm m để tiếp tuyến của (C) tại điểm M có hoành độ x m 2 2 2 0
còn cắt đồ thị hàm số tại hai điểm phân biệt A, B khác M. 9) Cho hàm số 4
y x  m   2 3 2
1 x  3m  3 , (C). Tìm m sao cho đồ thị (C):
a) Không cắt trục hoành.
b) Cắt trục hoành tại đúng hai điểm A, B sao cho AB  2 . ax b
HÀM NHẤT BIẾN: y
, ad bc  0 cx d 2x  1 1) Cho hàm số y
, (C) và đường thẳng d: y  x m . Tìm m để d cắt (C) tại hai điểm phân x  2
biệt AB sao cho AB ngắn nhất. 2x  4 2) Cho hàm số y
, (C). Tìm m để đường thẳng d: y  2x m cắt (C) tại hai điểm A, B. Khi x  1
đó hãy tìm tập hợp trung điểm I của đoạn thẳng AB. 2x m 3) Cho hàm số y
, (C) và đường thẳng d: y mx  2 . x  1
a) Tìm m để (C) và d cắt nhau tại hai điểm A, B phân biệt có khoảng cách đến trục hoành bằng nhau.
b) Tính diện tích hình chữ nhật nhận A, B (ở câu a) là các đỉnh đối diện và các cạnh song
song với hai trục tọa độ. Tính diện tích hình chữ nhật này. Xác định m để diện tích hình chữ nhật bằng 10. 1 2x
4) Tìm m để đường thẳng  : y x m cắt đồ thị (C): y
tại hai điểm phân biệt A, B sao 2 x  1
cho trung điểm của đoạn AB nằm trên đường thẳng d: 2x y  4  0 . 3x  2 5) Cho hàm số y  , (C). x  2
a) Tìm a, b để đường thẳng  : y ax  2b  4 cắt (C) tại hai điểm phân biệt M, N sao cho M,
N đối xứng nhau qua O.
b) Đường thẳng y x cắt đồ thị (C) tại hai điểm A, B. Tìm m để đường thẳng y x m cắt
(C) tại hai điểm C, D sao cho ABCD là hình bình hành. x  1 6) Cho hàm số y
, (C). Xác định m để đường thẳng y  2x m cắt (C) tại hai điểm phân biệt x  1
A, B sao cho tiếp tuyến của (C) tại A và B song song nhau. 2x 7) Cho hàm số y
, (C). Tìm M (C) , biết rằng tiếp tuyến với (C) tại M cắt Ox, Oy lần lượt tại x  1 1
A và B tạo thành tam giác OAB có diện tích bằng . 4
Giáo viên: LÊ BÁ BẢO...0935.785.115... 26
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x  2 8) Cho hàm số y
, (C). Xác định m để đường thẳng y x m cắt (C) tại hai điểm phân biệt 2x  2 A, B sao cho 2 2 37 OA OB
(O là gốc tọa độ). 2 x  1 9) Cho hàm số y
, (C). Xác định a,b để đường thẳng y ax b cắt (C) tại hai điểm phân biệt x  1
A, B đối xứng nhau đường thẳng  : x  2y  3  0 .
IV- TÀI LIỆU THAM KHẢO
1) Tuyển tập đề thi ĐH - CĐ toàn quốc
Bộ giáo dục và đào tạo
2) Phương pháp hàm số Lê Hồng Đức
3) Tuyển tập đề thi thử ĐH trên toàn quốc
4) Tạp chí Toán học và Tuổi trẻ
NXB Giáo dục Việt Nam
5) Các bài viết chuyên đề từ các website Toán học
P/S: Các bài tập trong tài liệu chưa nhận được sự cho phép của quí thầy cô và các cơ quan liên quan,
nhưng tài liệu biên soạn chỉ với mục đích chia sẽ cho đồng nghiệp và tặng cho các em học sinh có
nguồn tư liệu quí để phục vụ khả năng tự học nên chúng tôi xin phép các tác giả, xin cảm ơn các tác giả!
Trong quá trình biên soạn không thể tránh khỏi sai sót, kính mong quí thầy cô và các em học sinh đóng
góp để các bản update tiếp theo được hoàn thiện hơn! Xin chân thành cám ơn!
Giáo viên: LÊ BÁ BẢO...0935.785.115... 27
CLB Giáo viên trẻ TP Huế
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
Chuyên đề: KH¶O S¸T HµM Sè
Chủ đề 5: Sù T¦¥NG GIAO
Môn: TOÁN 12 _GIẢI TÍCH I- LÝ THUYẾT
Giả sử (C) và (C’) là đồ thị của hai hàm số: y (C)
y f x vµ y gx .
Hoành độ giao điểm của (C) và (C’), nếu có,
là nghiệm của phương trình f x  gx (1) (C') M
Lưu ý: Phương trình f x  gx là phương trình hoành độ y0
giao điểm của (C) và (C’). O 1 x0 x
Đảo lại, nếu x là nghiệm của (1), tức là: f x g x 0   0 0
thì điểm M x ; f x  hay M x ; g x
là điểm chung của (C) và (C’). 0 0  0  0 Kết quả: -
Nếu (1) vô nghiệm thì (C) và (C’) không có điểm chung. -
Nếu (1) có n nghiệm thì (C) cắt (C’) tại n điểm phân biệt ( n không là nghiệm bội).
Dạng toán: Tìm giao điểm và tính chất giao điểm của hai đồ thị y f x vµ y gx Phương pháp:
Bước 1: Thiết lập phương trình hoành độ giao điểm của (C) và (C’): f x  gx (1)
Bước 2: Biện luận số nghiệm và tính chất nghiệm của (1).
Nhận xét: Rõ ràng hoành độ giao điểm của (C) và (C’) là nghiệm của (1) nên số giao điểm và tính chất
giao điểm cũng là số nghiệm và tính chất nghiệm của (1). Điều này, đưa yêu cầu từ tính chất đồ thị sang
việc biện luận phương trình sơ cấp mà chúng ta đã biết.
II. BÀI TẬP TRẮC NGHIỆM DẠNG 1:
TÌM GIAO ĐIỂM – SỐ GIAO ĐIỂM – TÍNH CHẤT GIAO ĐIỂM Câu 1:
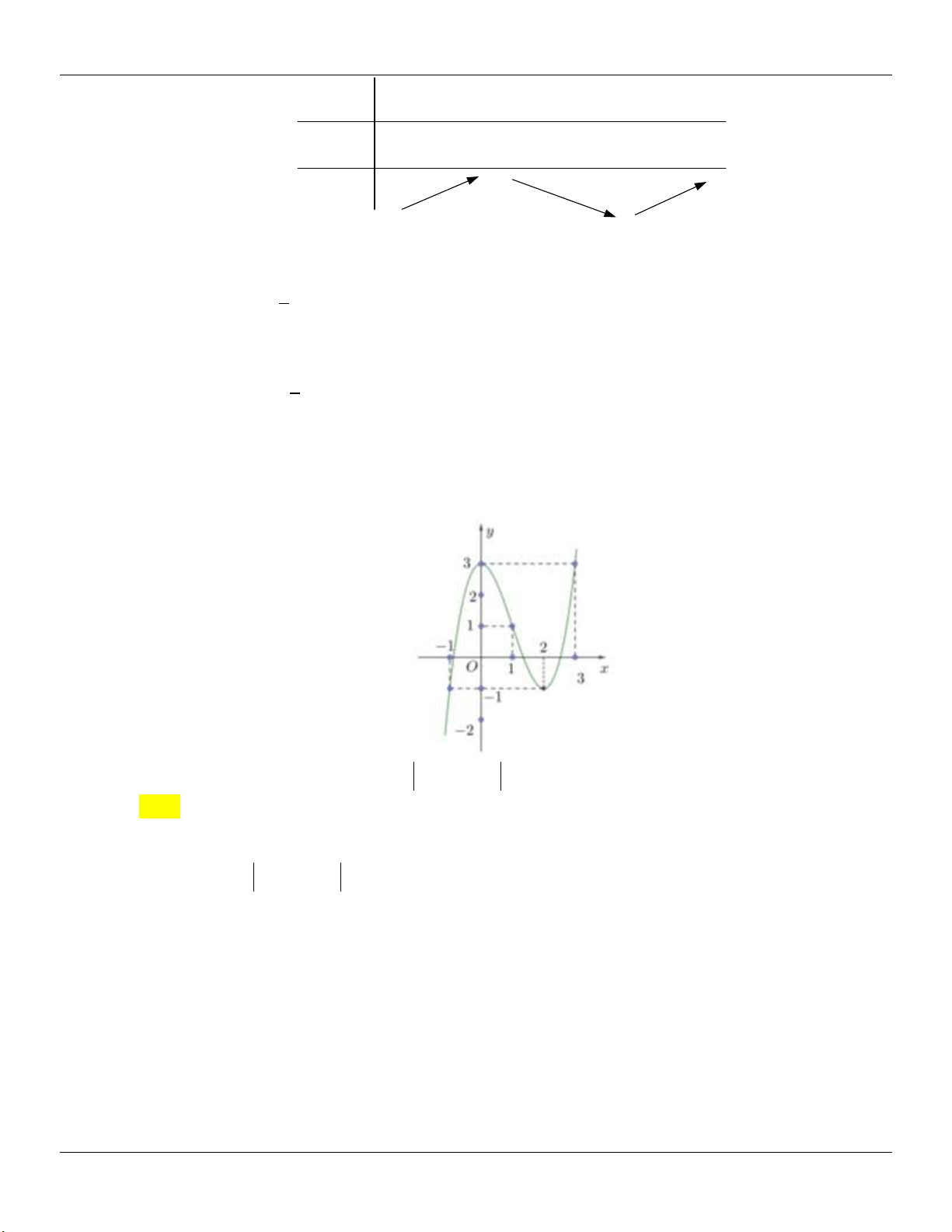
Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm của phương trình f x  2  0 là A. 0 . B. 3 . C. 1 . D. 2 . Câu 2:
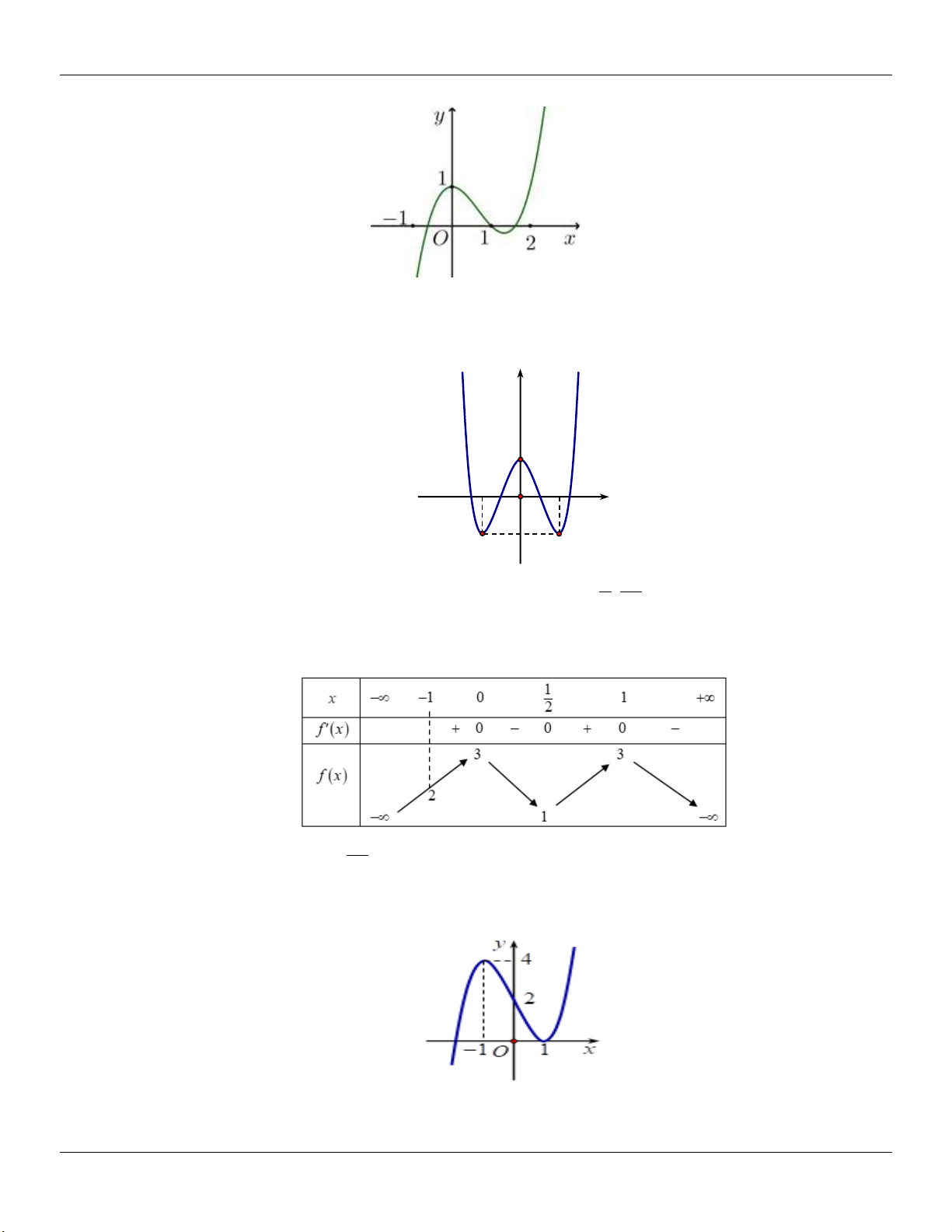
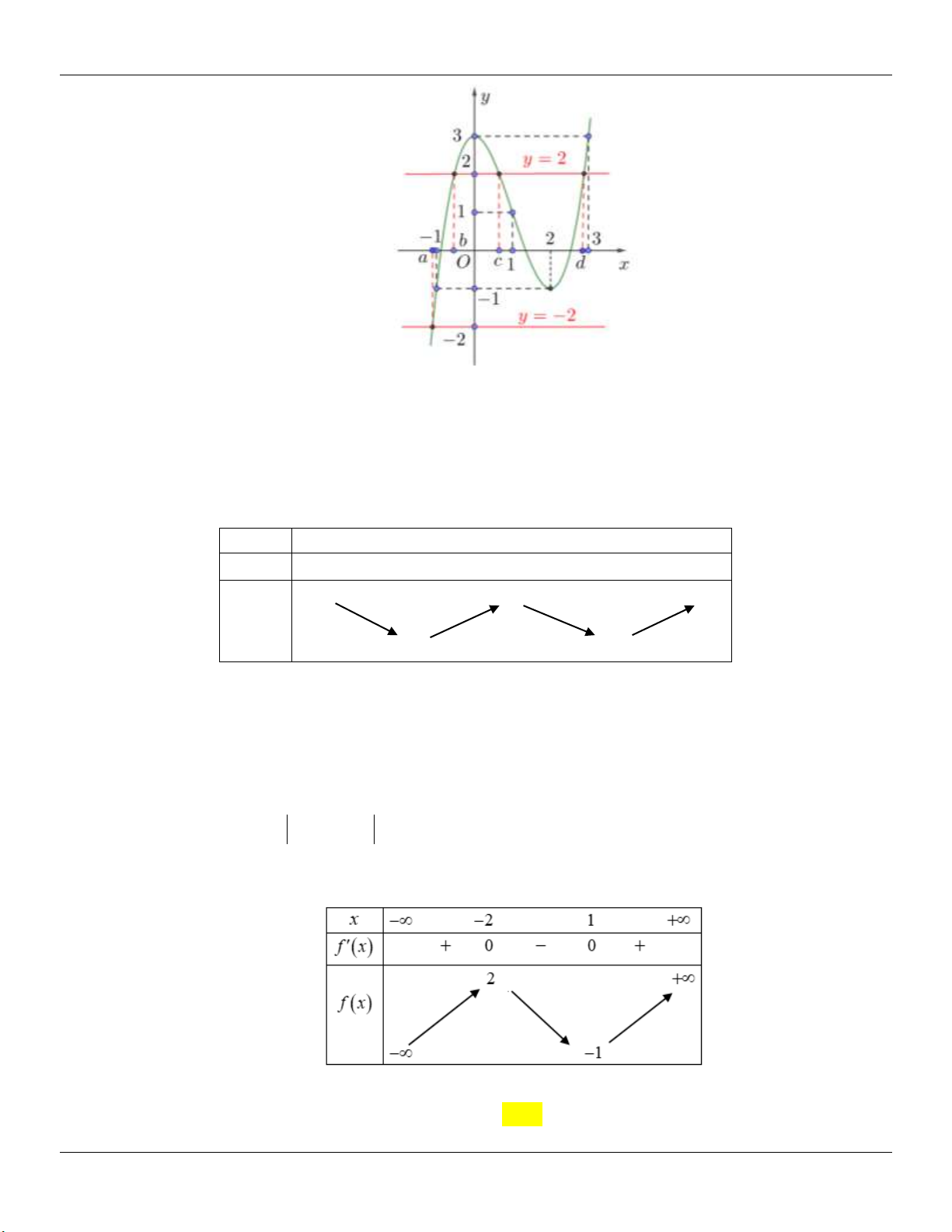
Cho hàm số y f x liên tục trên đoạn 2; 2 
 và có đồ thị như hình vẽ bên dưới: y 3 1 1 2 1  O 2 x 1 
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 1
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Số nghiệm của phương trình 3 f x  4  0 trên đoạn 2; 2   là A. 3 . B. 4 . C. 2 . D. 1 . Câu 3:
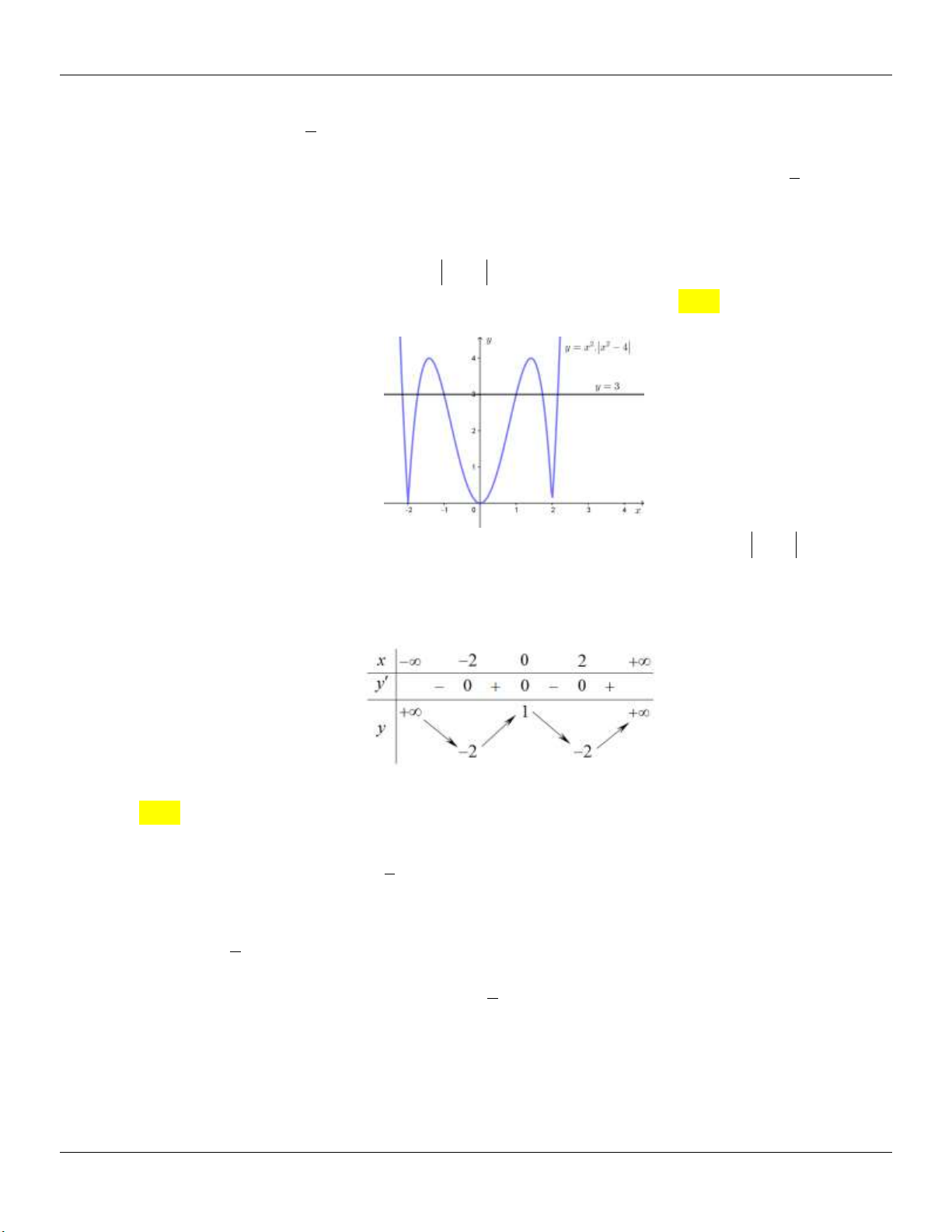
Số giao điểm của đồ thị hàm số 2 2
y x . x  4 với đường thẳng y  3 là A. 8 . B. 2 . C. 4 . D. 6 . Câu 4:
Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm của phương trình 2 f x  3  0 là A. 4 . B. 3 . C. 2 . D. 1 . Câu 5:
Biết rằng đường thẳng y  2
x  2 cắt đồ thị hàm số 3
y x x  2 tại một điểm duy nhất, ký
hiệu x ; y là tọa độ điểm đó. Tìm y . 0 0  0 A. y  4 . B. y  0 . C. y  2 . D. y  1 . 0 0 0 0 Câu 6: Đồ thị hàm số 3
y x  3x  2 cắt trục tung tại điểm có tọa độ là A.  1  ;0 . B. 0;  2 . C. 0; 2 . D. 2;0 . 2x  1 Câu 7:
Biết đường thẳng y x  2 cắt đồ thị hàm số y
tại hai điểm phân biệt A, B có hoành độ x  1
lần lượt x , x . Khi đó giá trị của x x bằng A B A B A. 5 . B. 3 . C. 1 . D. 2 . Câu 8:
Đồ thị của hàm số nào sau đây cắt trục tung tại điểm có tung độ âm? 2  x  3 2x  3 4x  1 x   4 A. y  . B. y  . C. y  . D. y  . x  1 3x  1 x  2 x  1 Câu 9:
Biết rằng đường thẳng y  4x  5 cắt đồ thị hàm số 3
y x  2x  1 tại điểm duy nhất; kí hiệu
x ; y là tọa độ của điểm đó. Tìm y . 0 0  0 A. y  10 . B. y  13 . C. y  11 . D. y  12 . 0 0 0 0
Câu 10: Đồ thị hàm số 3 2
y  2x x x  2 cắt parabol 2 y  6
x  4x  4 tại một điểm duy nhất. Kí hiệu
x ;y là tọa độ điểm đó. Tính giá trị của biểu thức x y . 0 0  0 0 A. 1. B. 1. C. 22. D. 4.
Câu 11: Đường thẳng  có phương trình y  2x  1 cắt đồ thị của hàm số 3
y x x  3 tại hai điểm A
và B với tọa độ được kí hiệu lần lượt là Ax ; y
và Bx ; y trong đó x x . Tính x y . B B A A B A B B
A. x y  5. 
B. x y  2. 
C. x y  4.
D. x y  7. B B B B B B B B 5x  6
Câu 12: Tính tổng hoành độ của các giao điểm của đồ thị hàm số y
và đường thẳng y  x . x  2 A. 7 . B. 5  . C. 5 . D. 7 . Câu 13: Cho hàm số 3
y x  3x có đồ thị hàm số là C . Tìm số giao điểm của C và trục hoành. A. 2. B. 3. C. 1 . D. 0 .
Câu 14: Cho hàm số y  x   2
2 x  1 có đồ thị C . Mệnh đề nào dưới đây đúng?
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 2
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
A. C cắt trục hoành tại hai điểm.
B. C cắt trục hoành tại một điểm.
C. C không cắt trục hoành.
D. C cắt trục hoành tại ba điểm.
Câu 15: Đồ thị của hàm số 4 2
y x  2x  2 và đồ thị của hàm số 2
y  x  4 có tất cả bao nhiêu điểm chung? A. 0 . B. 4 . C. 1 . D. 2 .
Câu 16: Tìm số giao điểm n của đồ thị hàm số 4 2
y x  8x  3 và đường thẳng y  10 . A. n  0 . B. n  4 . C. n  2 . D. n  3 .
Câu 17: Tọa độ tất cả các giao điểm của đồ thị hàm số 4 2
y x x  1 và đường thẳng y  1 là A. 0; 1  , 1  ; 1  . B. 1; 1  ; 1  ; 1  . C. 0; 1  ,1;1 . D. 0; 1  ,1; 1  , 1  ; 1   .
Câu 18: Cho hàm số y f (x) có bảng biến thiên như hình vẽ sau:
Số nghiệm của phương trình f (x)  1 là A. 1 . B. 2 . C. 4 . D. 3 .
Câu 19: Cho hàm số f x 3
x  3x  1 . Tìm số nghiệm của phương trình f f x  0 . A. 5 . B. 9 . C. 4 . D. 7 .
Câu 20: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. Tập hợp nghiệm của phương
trình f f x  1  0 có bao nhiêu phần tử? A. 4 . B. 7 . C. 6 . D. 9 .
Câu 21: Cho hàm số y f x liên tục trên các khoảng (; 2  ); 2
 ; và có bảng biến thiên như sau: 2
Số nghiệm thực của phương trình  f x  2 f x  3  0 là A. 2 . B. 1 . C. 0 . D. 4 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 3
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 22: Cho hàm số 3 2
y f (x)  ax bx cx d có đồ thị như hình vẽ bên dưới.
Tập nghiệm của phương trình f (x)  f (x)  4  0   là A. { 1; 0 ;1; 2 ; 3} . B. { 1; 2} . C. {0 ; 3} . D. { 1; 0 ; 2 ; 3} . Câu 23: Cho hàm số 3 2
y f (x)  ax bx cx d, (a  0) có đồ thị như hình vẽ bên dưới:
Phương trình f f x  0 có bao nhiêu nghiệm thực? A. 3 . B. 7 . C. 9 . D. 5 .
Câu 24: Cho hàm số y f x liên tục trên
có đồ thị như hình vẽ bên dưới:
Phương trình f 3  2 f x  1 có tất cả bao nhiêu nghiệm thực phân biệt? A. 6 . B. 5 . C. 7 . D. 4 .
Câu 25: Cho hàm số y f x liên tục trên có đồ thị như hình bên dưới:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 4
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Phương trình f f x  1  0 có tất cả bao nhiêu nghiệm thực phân biệt? A. 6. B. 5. C. 7. D. 4.
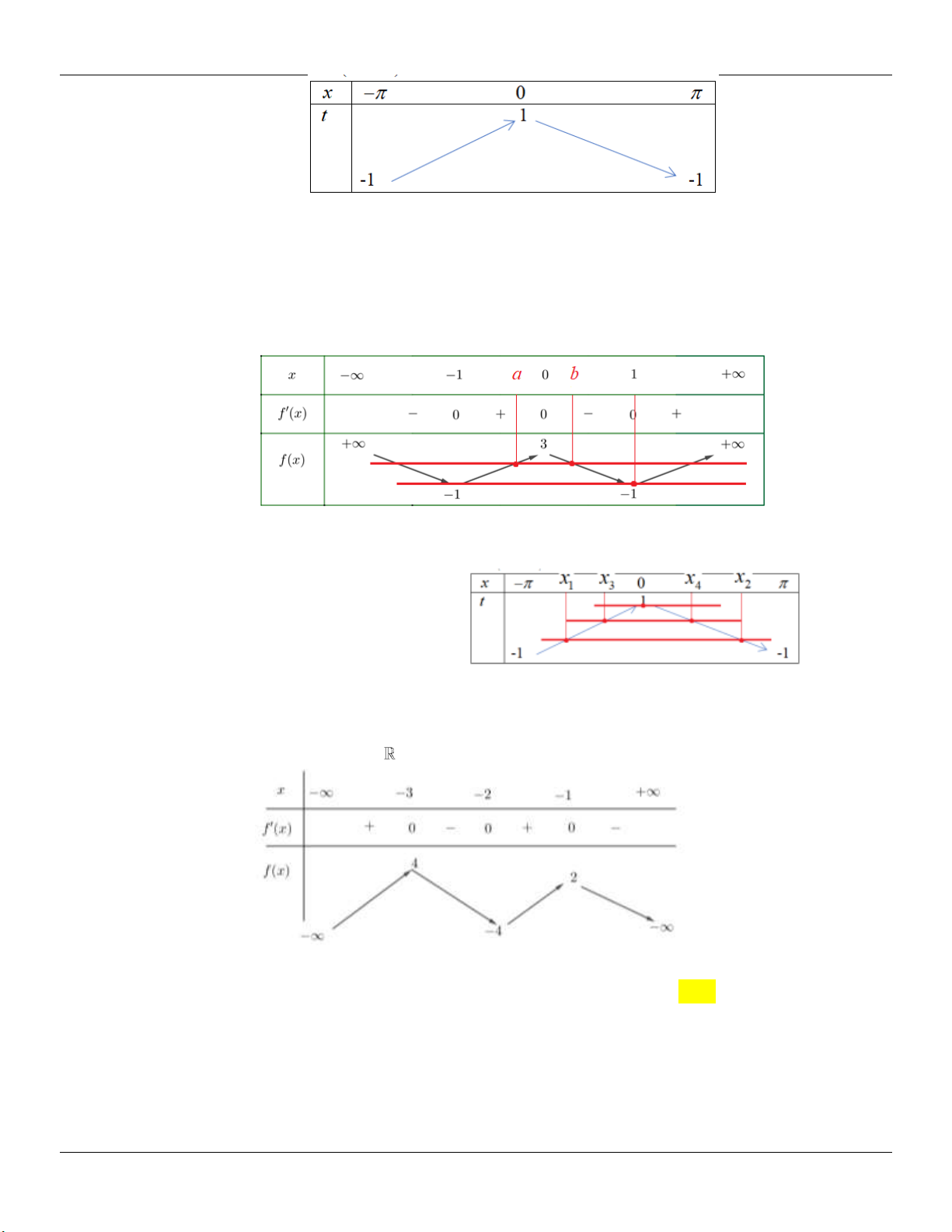
Câu 26: Cho hàm số y f x xác định trên và có bảng biến thiên như sau: x  -1 1  y  0  0  y 1   -1
Số nghiệm của phương trình f  2
x  2x  2 là A. 4 . B. 2 . C. 3 . D. 8 .
Câu 27: Cho hàm số bậc ba y f x có đồ thị như hình vẽ bên dưới: 1
Số nghiệm thực của phương trình f  3
x  3x  là 2 A. 6 . B. 10 . C. 12 . D. 3 .
Câu 28: Cho hàm số bậc ba y f x có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình f  4 2
x  2x   2 là A. 8 . B. 9 . C. 7 . D. 10 .
Câu 29: Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm của phương trình f  4 2
3x  6x  1  1 là A. 4 . B. 5 . C. 6 . D. 3 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 5
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
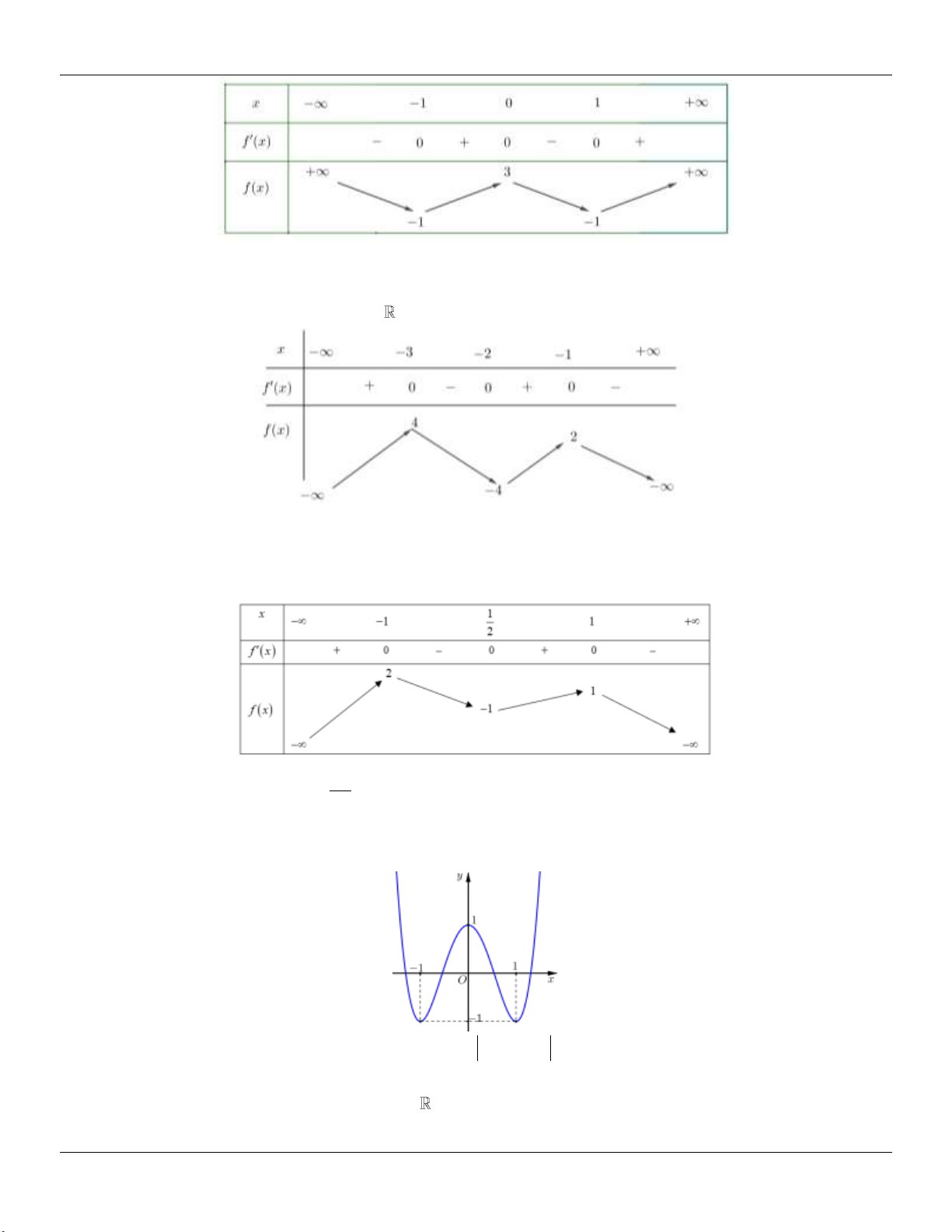
Câu 30: Cho hàm số y f x có đồ thị như hình vẽ:
Khi đó phương trình f  4 4
3x   3  0 có bao nhiêu nghiệm dương? A. 2. B. 4. C. 5. D. 1.
Câu 31: Cho hàm số y f x có đồ thị như hình vẽ sau: y 1 1 1 O x 1   5 
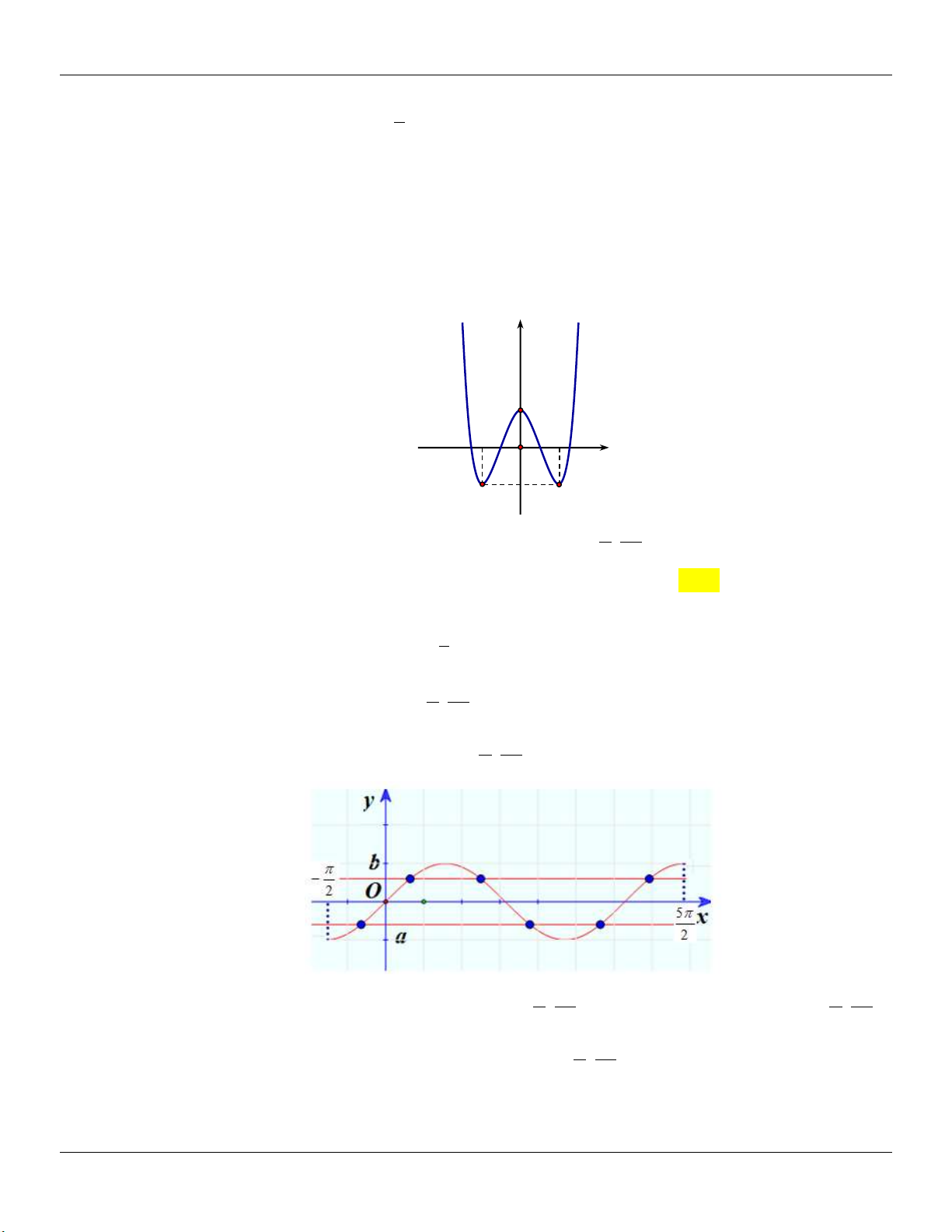
Số nghiệm của phương trình 2 f sin x  1  0 trên đoạn  ;   là  2 2  A. 3 . B. 4 . C. 5 . D. 6 .
Câu 32: Cho hàm số f x có bảng biến thiên như sau:  7 
Số nghiệm thuộc đoạn 0; 
 của phương trình 2. f cos x  5  0 là  3  A. 8 . B. 7 . C. 5 . D. 6 .
Câu 33: Cho hàm số y f x có đồ thị như hình vẽ.
Số nghiệm thuộc đoạn 0; 5  
 của phương trình f cos x  1 A. 3 . B. 4 . C. 5 . D. 6 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 6
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 34: Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn 0; 5  
 của phương trình f sin x  1 là A. 6 . B. 4 . C. 10 . D. 8 .
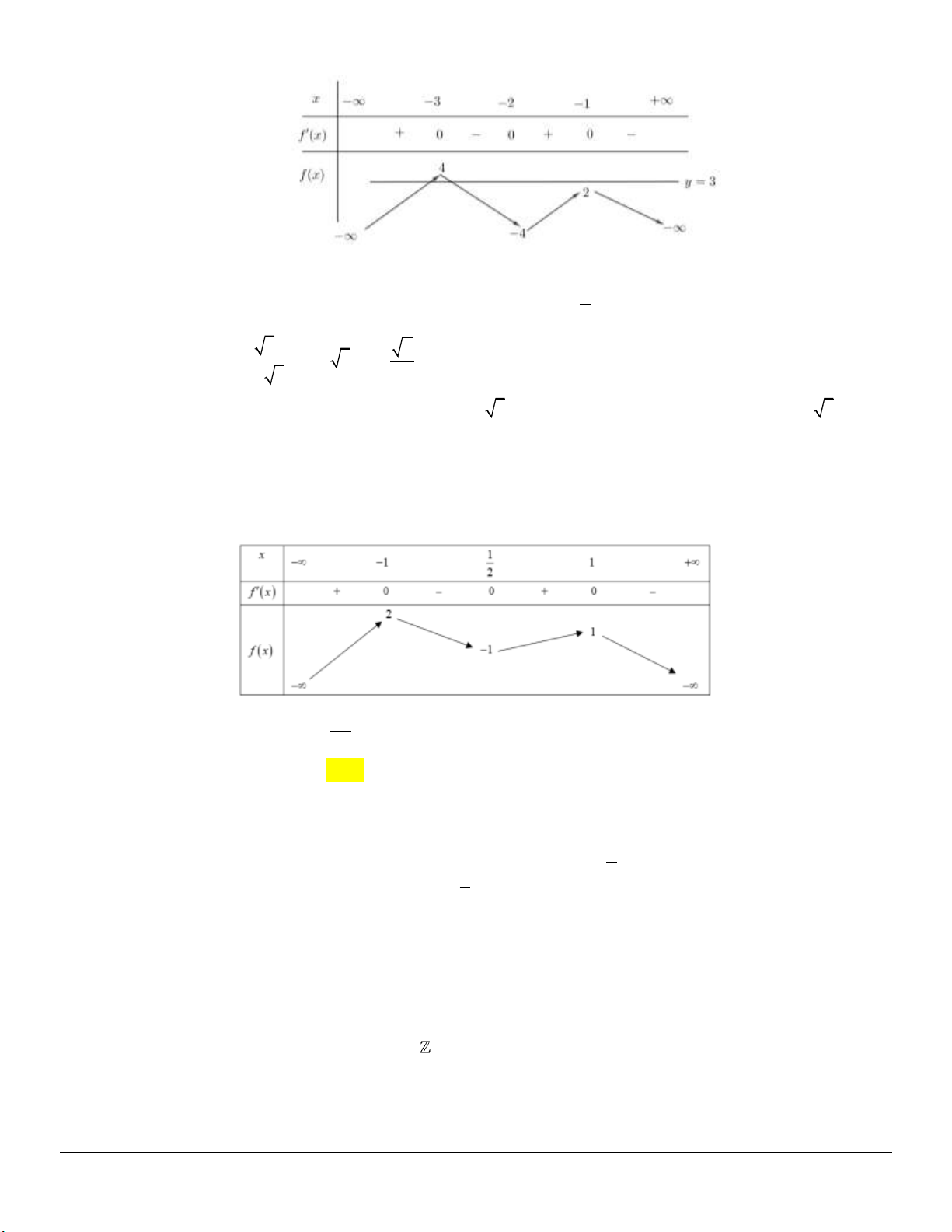
Câu 35: Cho hàm số y f x có bảng biến thiên như hình vẽ sau: x  0 1 2  f x  0  0  0   3  f x 0 1
Số nghiệm của phương trình f sin x  1  2 trên    ;2    là A. 6. B. 7. C. 5. D. 4.
Câu 36: Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây: x  1  1 2  f x  0  0  0   1  f x 1  2    3 
Số nghiệm thuộc đoạn  ; 
 của phương trình f cot x  1  1 là  2 2  A. 7. B. 6. C. 8. D. 5.
Câu 37: Cho hàm số y f x có đồ thị như hình vẽ sau:
Số nghiệm thuộc đoạn 0 ; 3  
 của phương trình 2 f cos x  1  0 là A. 12 . B. 6 . C. 10 . D. 8 .
Câu 38: Cho hàm số f x có bảng biến thiên như sau:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 7
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Số nghiệm thuộc khoảng  
 ;  của phương trình 2
f cos x  f cos x  2 là A. 5 . B. 6 . C. 7 . D. 9 .
Câu 39: Cho hàm số f x liên tục trên có bảng biến thiên như sau:
Số nghiệm thuộc đoạn    ;  
 của phương trình f  2
2 cos x  3  3 là A. 8 . B. 2 . C. 6 . D. 4 .
Câu 40: Cho hàm số f x có bảng biến thiên như sau:  5  Số nghiệm thuộc đoạn ; 3 
 của phương trình 4 f cos2x  1  0 là  6  A. 5 . B. 9 . C. 4 . D. 10 .
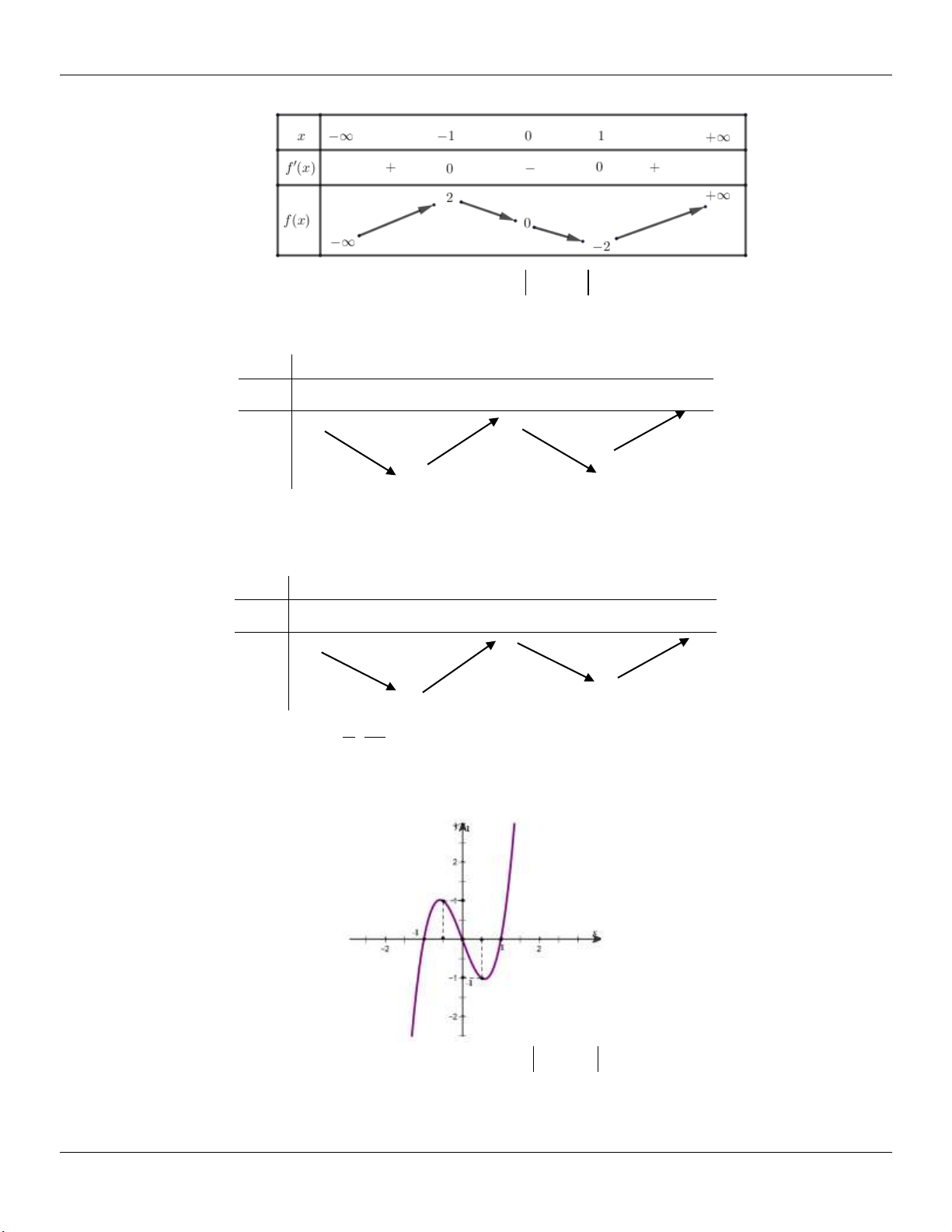
Câu 41: Cho hàm số trùng phương y f x có đồ thị như hình vẽ bên dưới:
Số nghiệm thuộc 0; 2 
của phương trình f cos2x 1 bằng A. 4 . B. 6 . C. 3 . D. 8 .
Câu 42: Cho hàm số y f x xác định trên và có bảng biến thiên như sau:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 8
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x –∞ 1  0 1 +∞ y + 0 – 0 + 0 – 1 1 y  0 
Số nghiệm thuộc đoạn 0;  
 của phương trình f f cos2x  0 là A. 4 . B. 2. C. 3. D. 8. Câu 43: Cho hàm số 4 2
y ax bx c,a;b;c  ,a  0 có bảng biến thiên như hình vẽ: x  2 0 2  y  0  0  0    y 2 2 2 4 2
Số nghiệm của phương trình a f
 x  bf
 x  c  0  là A. 11. B. 10. C. 9. D. 12.
Câu 44: Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên như hình vẽ: x  1  0 2  4 y  0  0  0    y 2 2 4   5 
Số nghiệm thuộc đoạn  ; 
 của phương trình f  2 5
cos x  cos x  1 là  2 2  A. 11. B. 10. C. 9. D. 12.
Câu 45: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ sau:
Số nghiệm của phương trình f sin x  cos x  2  0 trên đoạn 0; 2    là A. 5. B. 4. C. 3. D. 2.
Câu 46: Cho hàm số   3 2
f x ax bx bx c có đồ thị như hình vẽ:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 9
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia     Số nghiệm nằm trong 
; 3  của phương trình f cos x  1  cos x  1 là  2  A. 2 . B. 3 . C. 5. D. 4.
Câu 47: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt
của phương trình f  3
x f x  1  0 là A. 8 . B. 5 . C. 6 . D. 4 .
Câu 48: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình f  3
x f x  1  0 là A. 6 . B. 4 . C. 5 . D. 8 .
Câu 49: Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình bên. Số nghiệm thực phân
biệt của phương trình f  2
x f x  2 là A. 8 . B. 12 . C. 6 . D. 9 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 10
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 50: Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình f  2
x f x  2  0 là A. 6 . B. 12 . C. 8 . D. 9 .
Câu 51: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt
của phương trình f  5
x f x  2  0 là A. 8 . B. 5 . C. 6 . D. 4 .
Câu 52: Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt 2
của phương trình f x  2 f x  3  0 là A. 8 . B. 6 . C. 9 . D. 12 .
Câu 53: Cho hàm số y f x có đồ thị như hình vẽ sau:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 11
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Số nghiệm thực của phương trình f f x   f x  0 là A. 20 . B. 24 . C. 10 . D. 4 . DẠNG 2: BÀI TOÁN THAM SỐ
Câu 54: Cho hàm số y f x xác định trên  \ 
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f x  m có ba nghiệm thực phân biệt. A. 1; 2   . B.  1  ;2 . C.  1  ;2 . D. ; 2 . Câu 55: Cho hàm số 4 2
y  x  2x có đồ thị như hình bên dưới:
Tìm tất cả các giá trị thực của tham số m để phương trình 4 2
x  2x m có bốn nghiệm thực phân biệt A. m  0 . B. 0  m  1 . C. 0  m  1 . D. m  1.
Câu 56: Cho hàm số y f (x) có bảng biến thiên như sau:
Tập tất cả các giá trị của tham số m để phương trình f (x)  m có ba nghiệm phân biệt là A. (4; ) . B. (; 2) . C. 2;4.   D. (2; 4) .
Câu 57: Tìm tất cả các giá trị của tham số m để phương trình 3 2
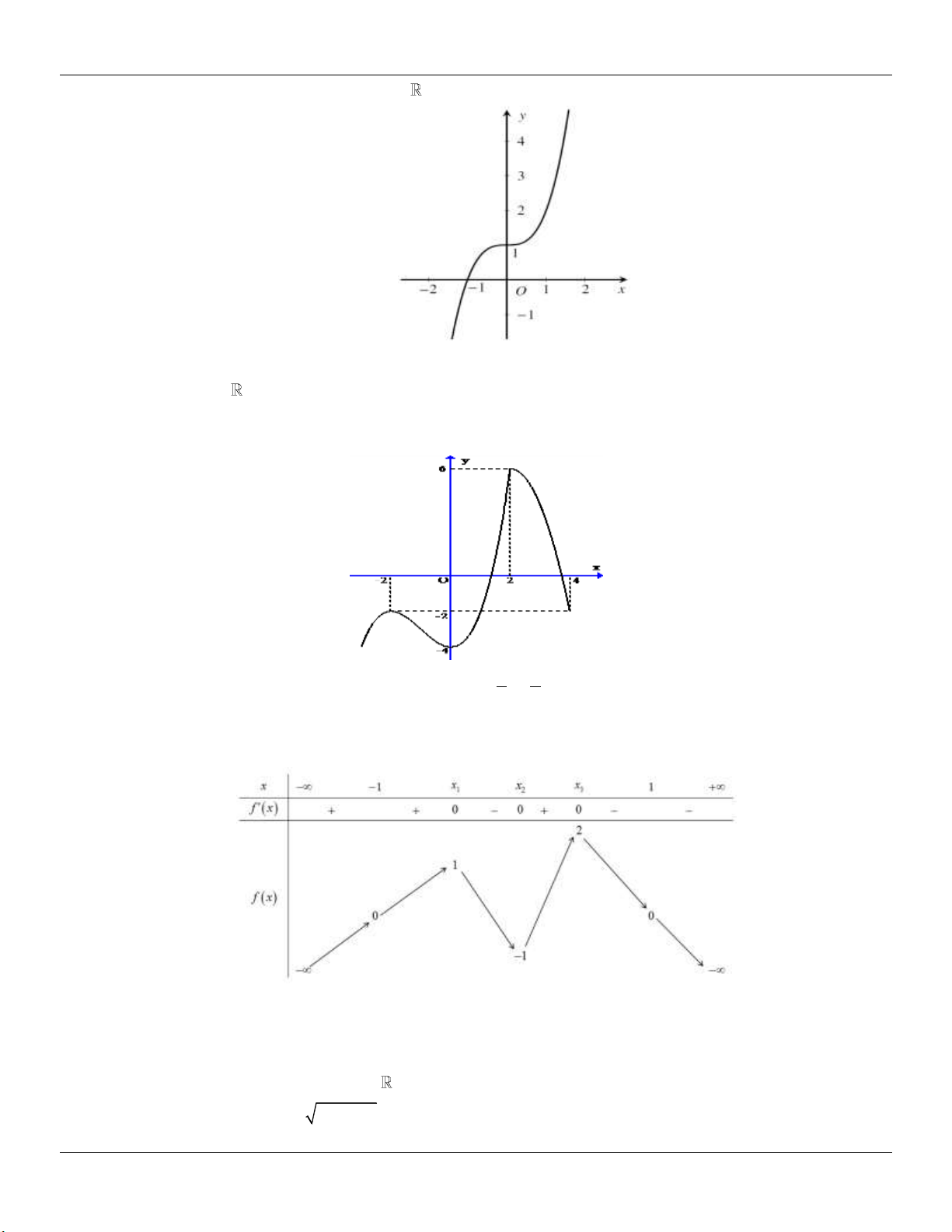
x  3x  2  m có ba nghiệm phân biệt.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 12
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
A. m2;  . B. m; 2   . C. m 2  ;2 . D. m  2  ;2   .
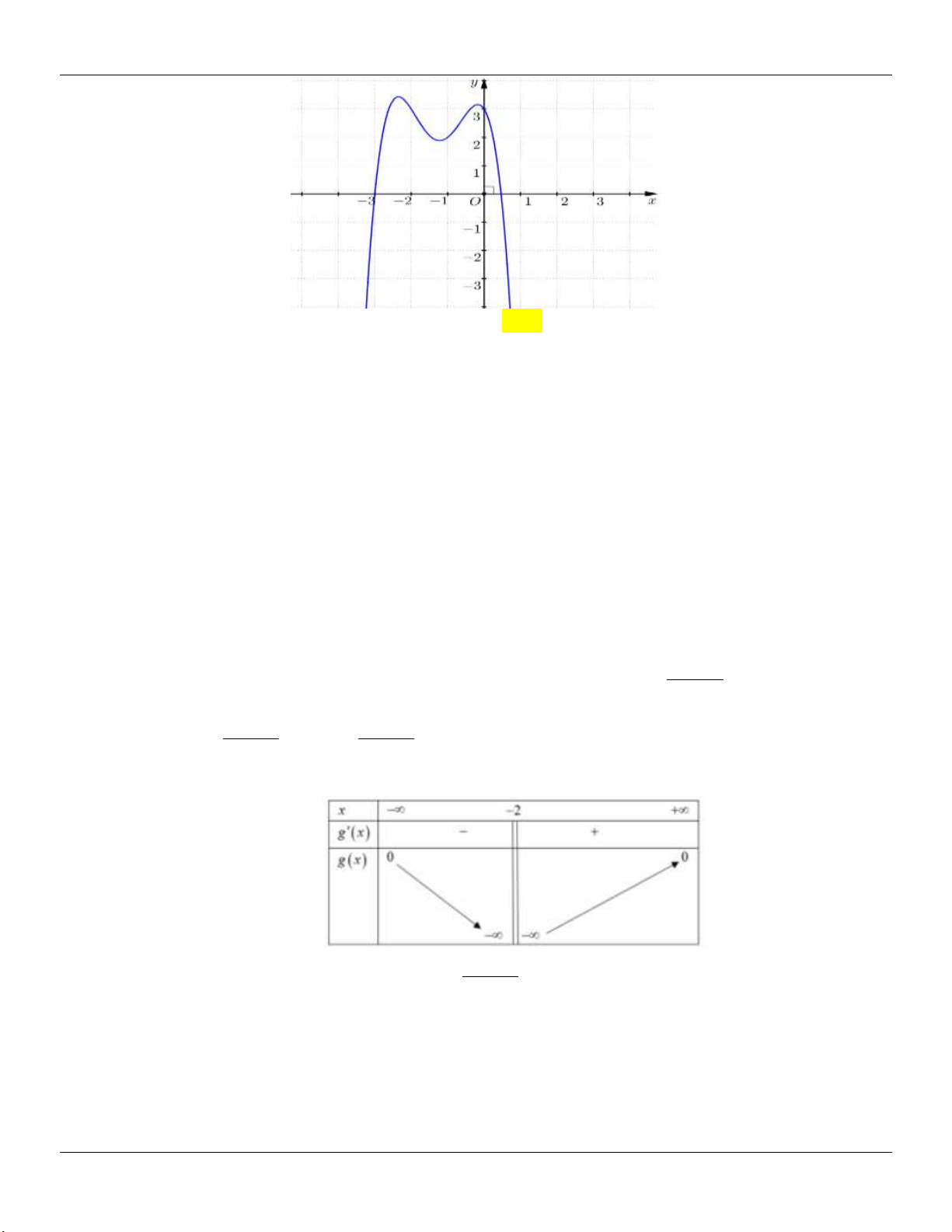
Câu 58: Tìm m để đồ thị hàm số 4 2 2
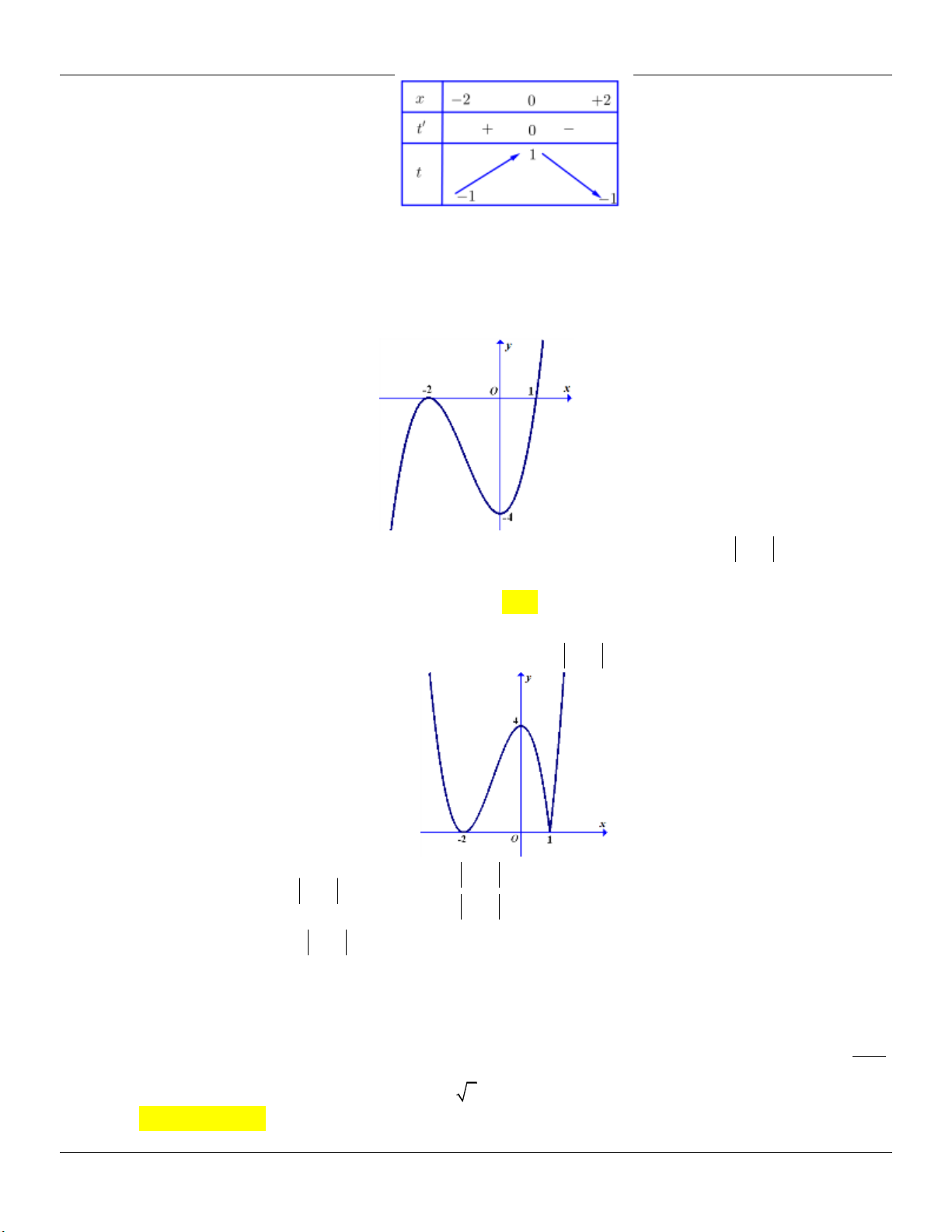
y x  2mx m  1 cắt trục hoành tại 4 điểm phân biệt. m  1  A. m  1 . B. 1  m  1 . C. m  1 . D.  . m   1 Câu 59: Cho hàm số 4 2
y x  2x  3 có đồ thị hàm số như hình bên dưới. Với giá trị nào của tham số m phương trình 4 2
x  2x  3  2m  4 có hai nghiệm phân biệt? m  0 m  0 1 1 A.   1  . B. 0  m  . C. 1 . D. m  . m     2 m 2  2  2
Câu 60: Hàm số   4 2
f x ax bx c a, b, c   có bảng biến thiên
Có bao nhiêu số nguyên m để phương trình f x  3m có đúng 8 nghiệm phân biệt? A. Vô số. B. 1. C. 4. D. 2.
Câu 61: Cho hàm số y f x xác định trên \ 
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Tất cả giá trị của tham số thực m sao cho đồ thị của hàm số y f x  m cắt trục Ox tại ba điểm phân biệt là A.  2  ;1 . B.  1  ;2 . C. 1; 2   . D.  2  ;1.
Câu 62: Cho hàm số y f (x) xác định, liên tục trên
và có bảng biến thiên như sau:
Tìm tất cả các giá trị thực của m để phương trình f (x)  1  m có đúng hai nghiệm.
A. m  0, m  1 . B. 2   m  1  .
C. m  1, m  2 .
D. m  1, m  2 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 13
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 63: Đường cong trong hình vẽ là đồ thị của hàm số 4 2
y x  2x  2 . Tìm tất cả các giá trị thực của
tham số m để phương trình 4 2
x  2x m có 4 nghiệm phân biệt. A. m  2 . B. 1  m  0 . C. m  3 .
D. 3  m  2 .
Câu 64: Cho hàm số y f x xác định trên  \ 
1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:
Số giá trị nguyên của tham số m để phương trình f x  m có 3 nghiệm phân biệt là A. 1 . B. 0 . C. 3 . D. 2 .
Câu 65: Cho hàm số y f x có bảng biến thiên như sau:
Tập hợp tất cả các giá trị thực của tham số m để phương trình f x  m  0 có hai nghiệm phân biệt là A.  ; 2 . B. 1  ;2  . C. 1; 2 . D. 2;   . Câu 66: Cho hàm số 3
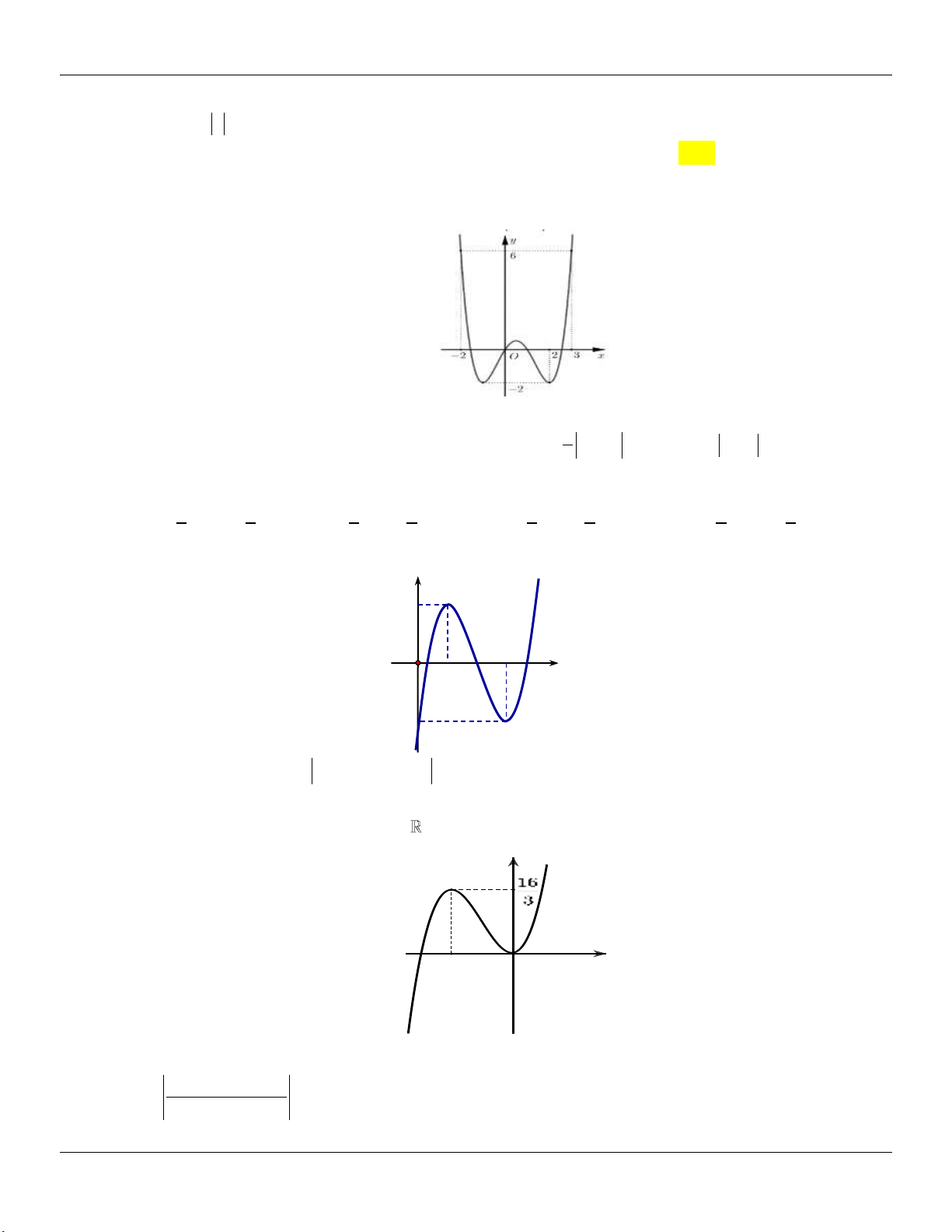
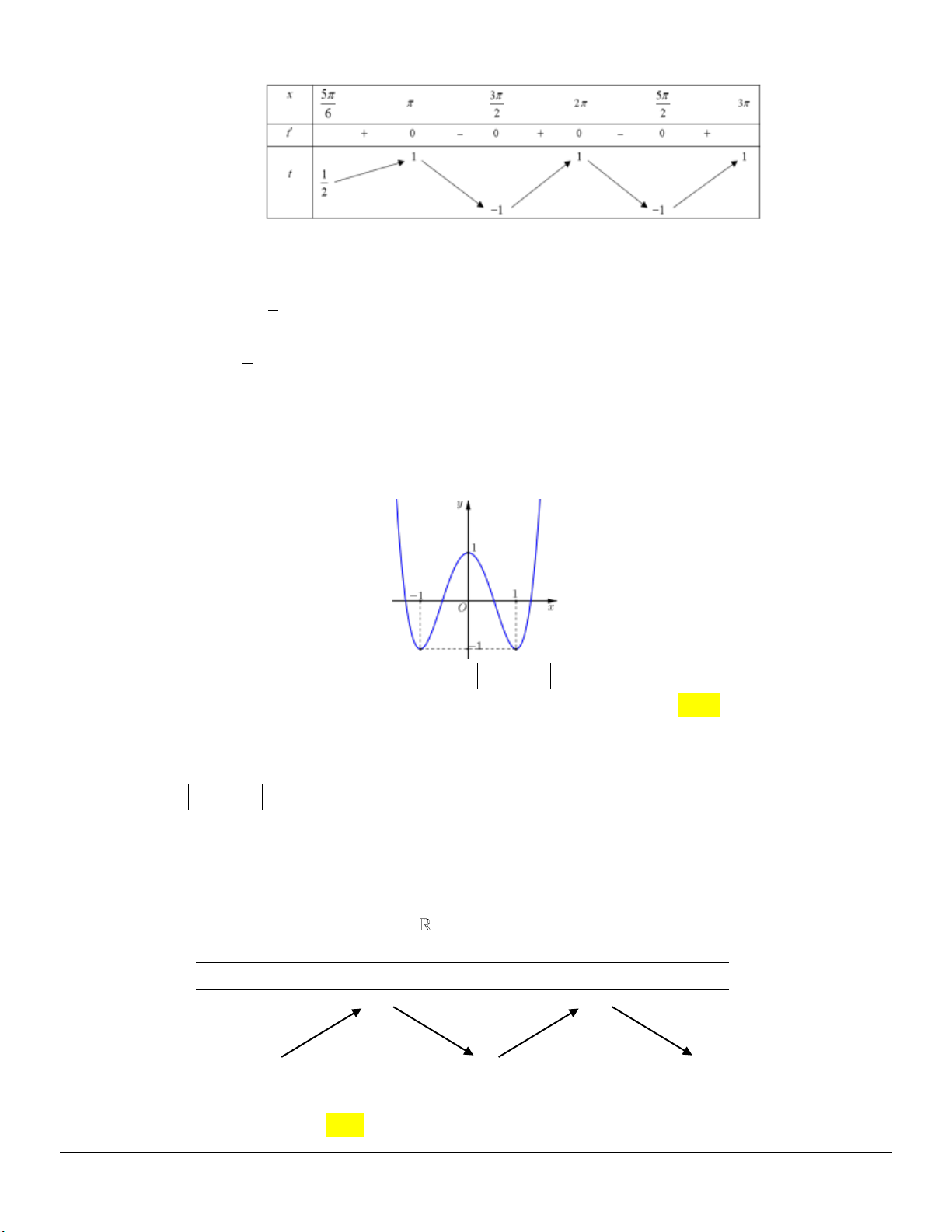
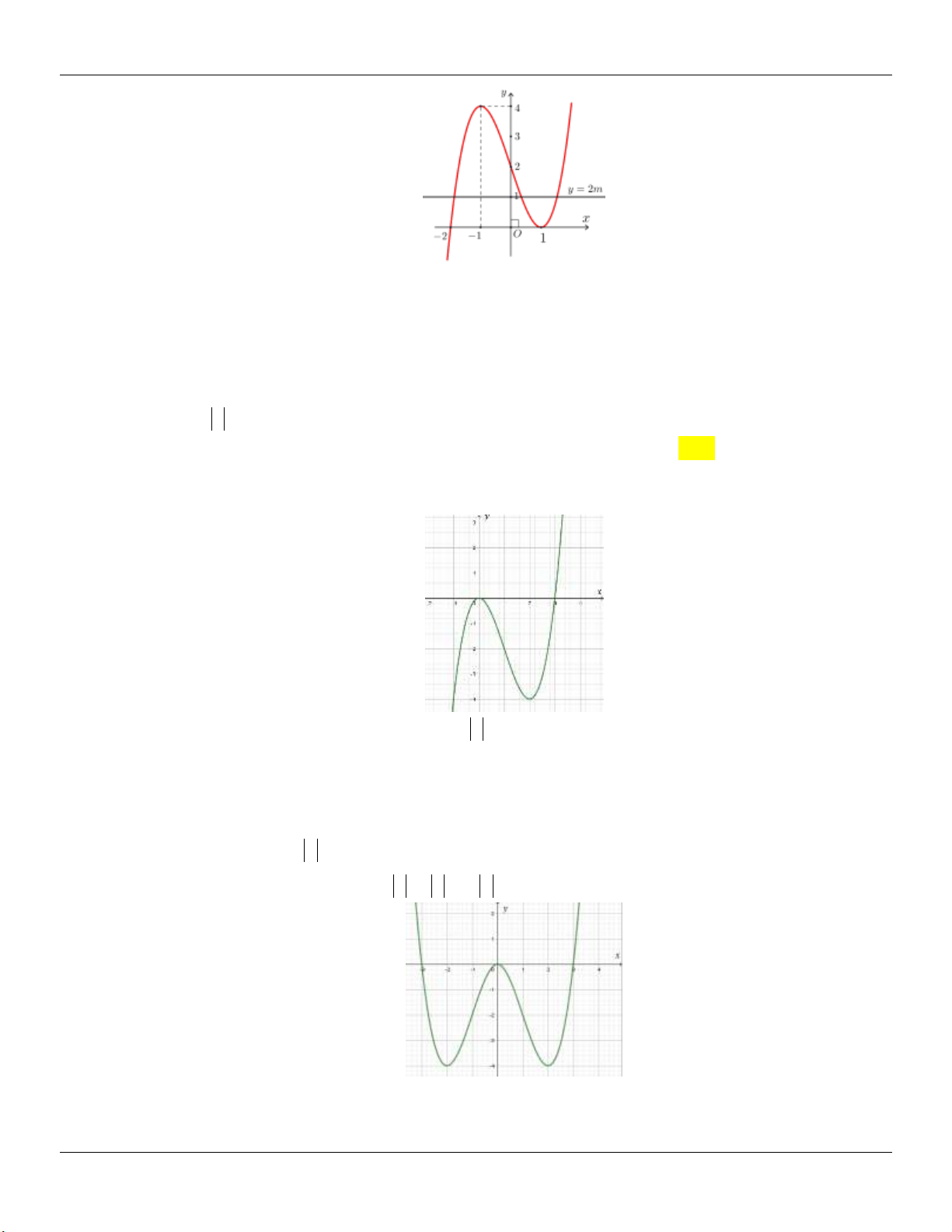
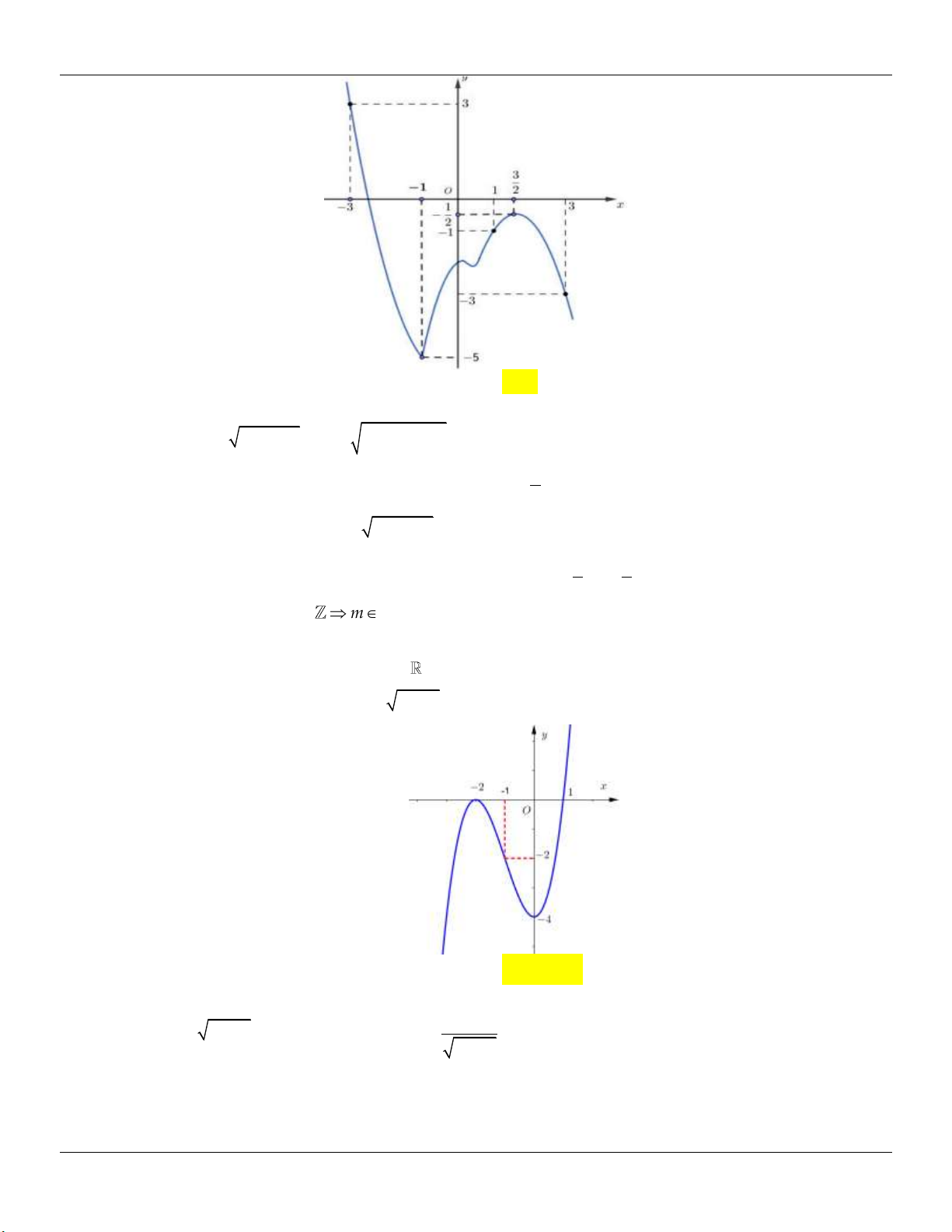
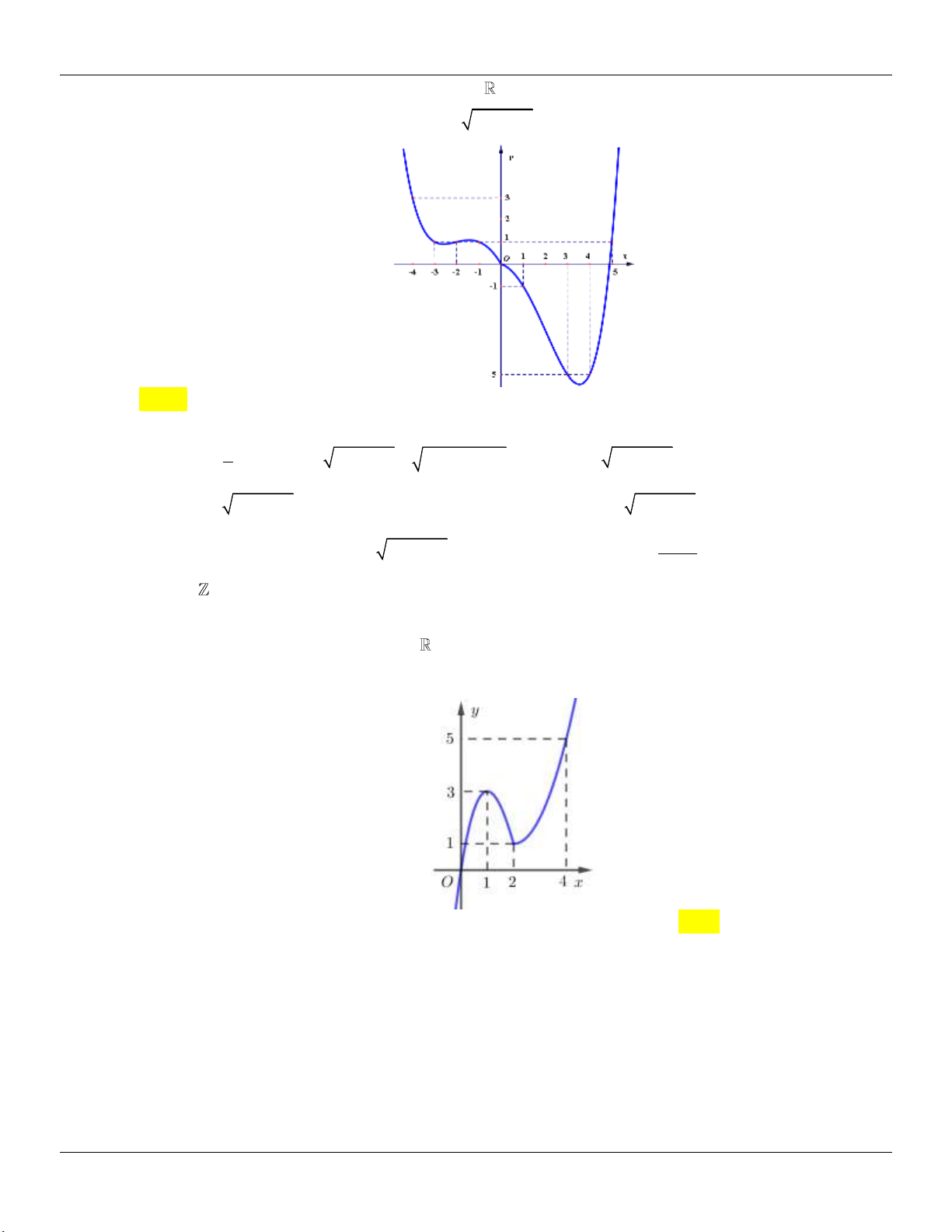
y x  3x  2 có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị thực của tham số m để phương trình 3
x  3x  2  2m  0 có ba nghiệm thực phân biệt. A. 0  m  4 . B. 0  m  2 . C. 0  m  4 . D. 0  m  2 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 14
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 67: Cho hàm số f x 3 2
x  3x . Tính tổng tất cả các giá trị nguyên của m để đồ thị hàm số
g x  f x   m cắt trục hoành tại 4 điểm phân biệt. A. 3. B. 10. C. 4. D. 6.
Câu 68: Cho hàm số y f x có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để phương trình f  3
x  3x  m có 6 nghiệm phân biệt thuộc đoạn [  1; 2]? A. 3 . B. 2 . C. 6 . D. 7 . 1
Câu 69: Tìm tất cả các giá trị của tham số m để phương trình 3 2
cos x  3cos x  5 cos x  3  2m  0 có 3
đúng bốn nghiệm thuộc đoạn 0 ; 2 .   3 1 1 3 1 3 3 1 A.   m   . B.  m  . C.  m  . D.   m   . 2 3 3 2 3 2 2 3
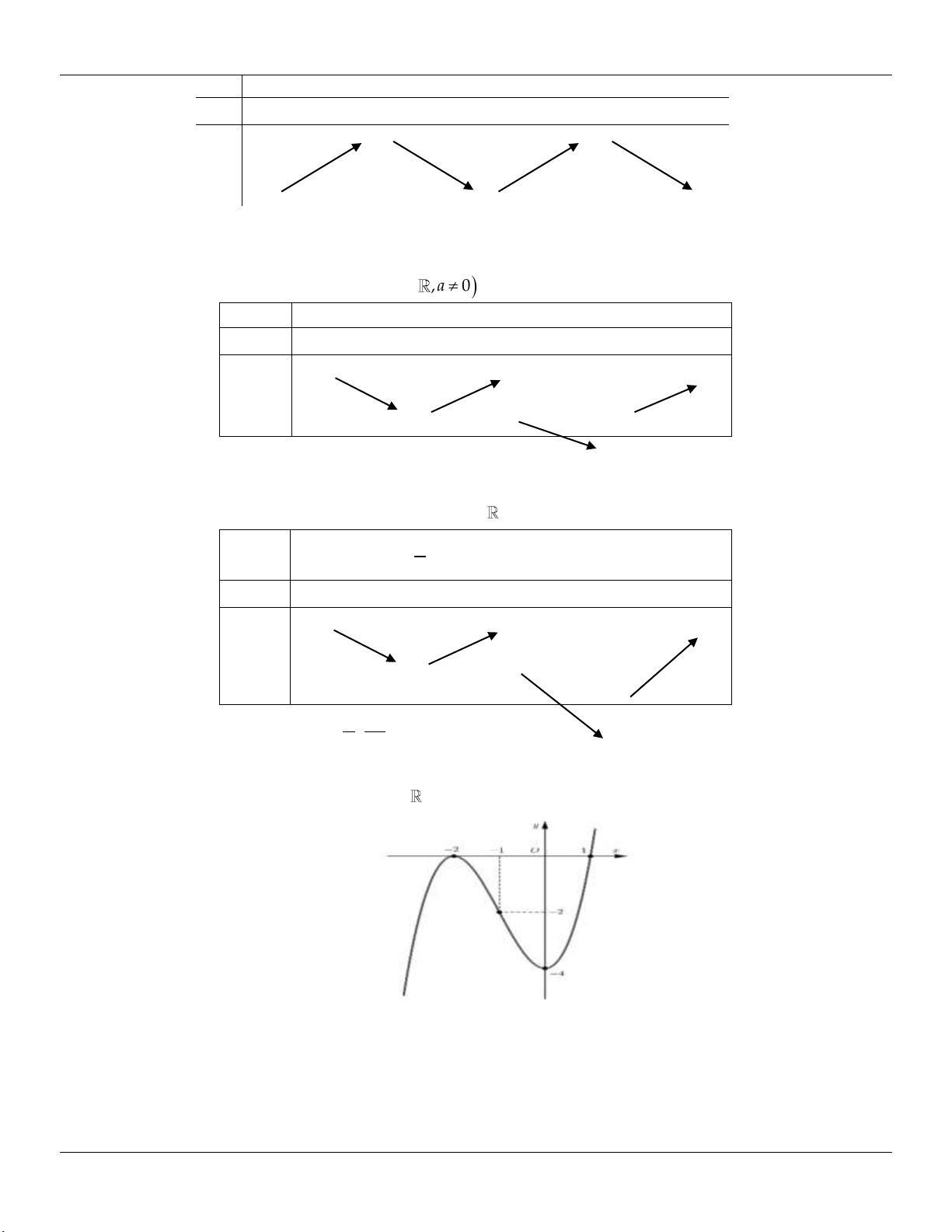
Câu 70: Cho đồ thị của hàm số 3 2
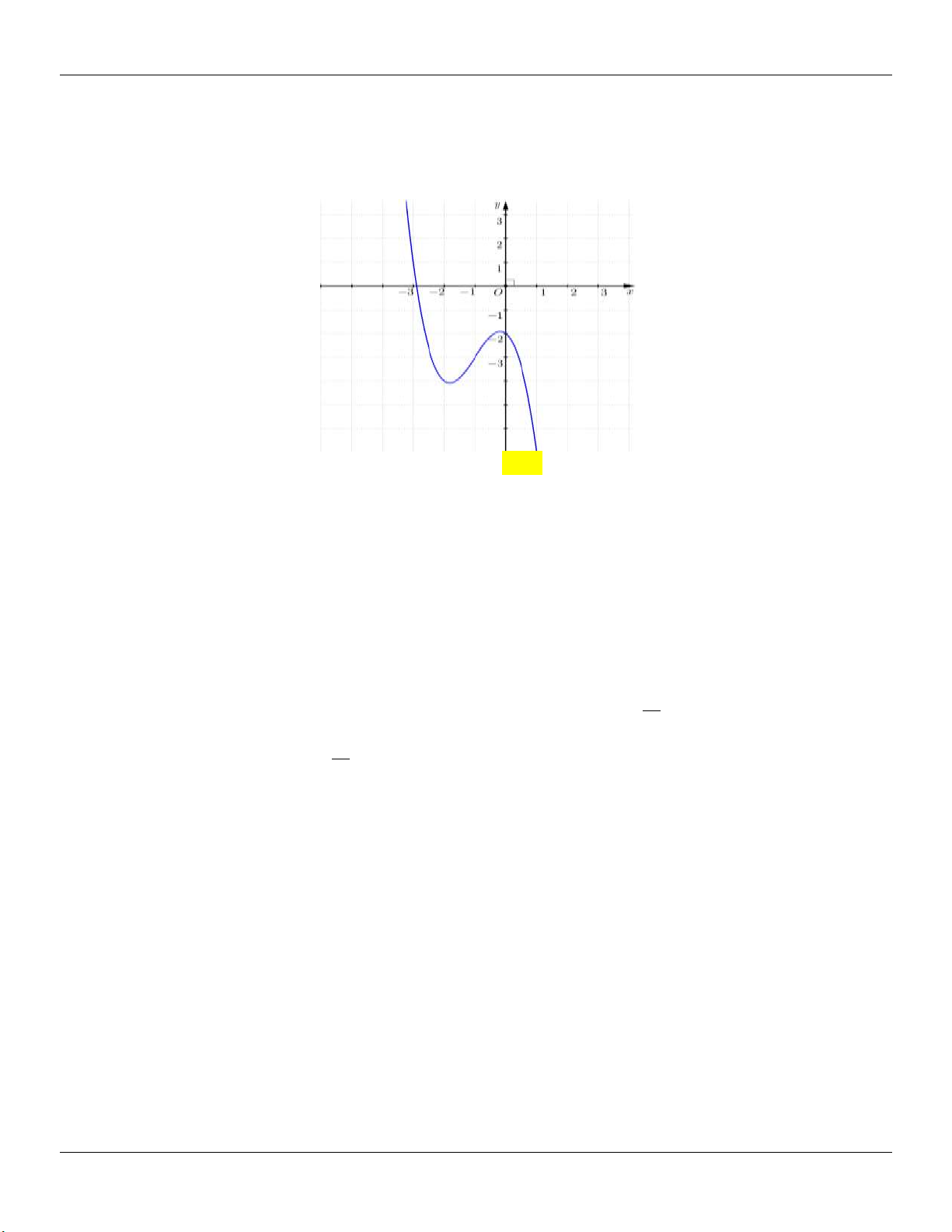
y x  6x  9x  2 như hình vẽ. y 2 3 O 1 x 2 Khi đó phương trình 3 2
x  6x  9x  2  m ( m là tham số) có 6 nghiệm phân biệt khi và chỉ khi. A. 2  m  2 . B. 0  m  2 . C. 0  m  2 . D. 2  m  2 .
Câu 71: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. y y = f(x) -4 O x Có bao nhiêu giá trị nguyên của tham số m để phương trình
 3sin x  cosx 1  f    f  2
m  4m  4 1 có nghiệm?
2cos x  sin x   4  A. 3 . B. 4 . C. 5 . D. Vô số.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 15
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 72: Cho hàm số y f x liên tục trên có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của n để phương trình f  2
16 cos x  6 sin 2x  8  f nn  1 có nghiệm x  ? A. 10 . B. 4 . C. 8 . D. 6 .
Câu 73: Cho hàm số y f x có đồ thị như hình vẽ. 1  x
Có bao nhiêu số nguyên m để phương trình f  1  x   
m có nghiệm thuộc đoạn 2 ; 2   ? 3  2  A. 11 . B. 9 . C. 8 . D. 10 .
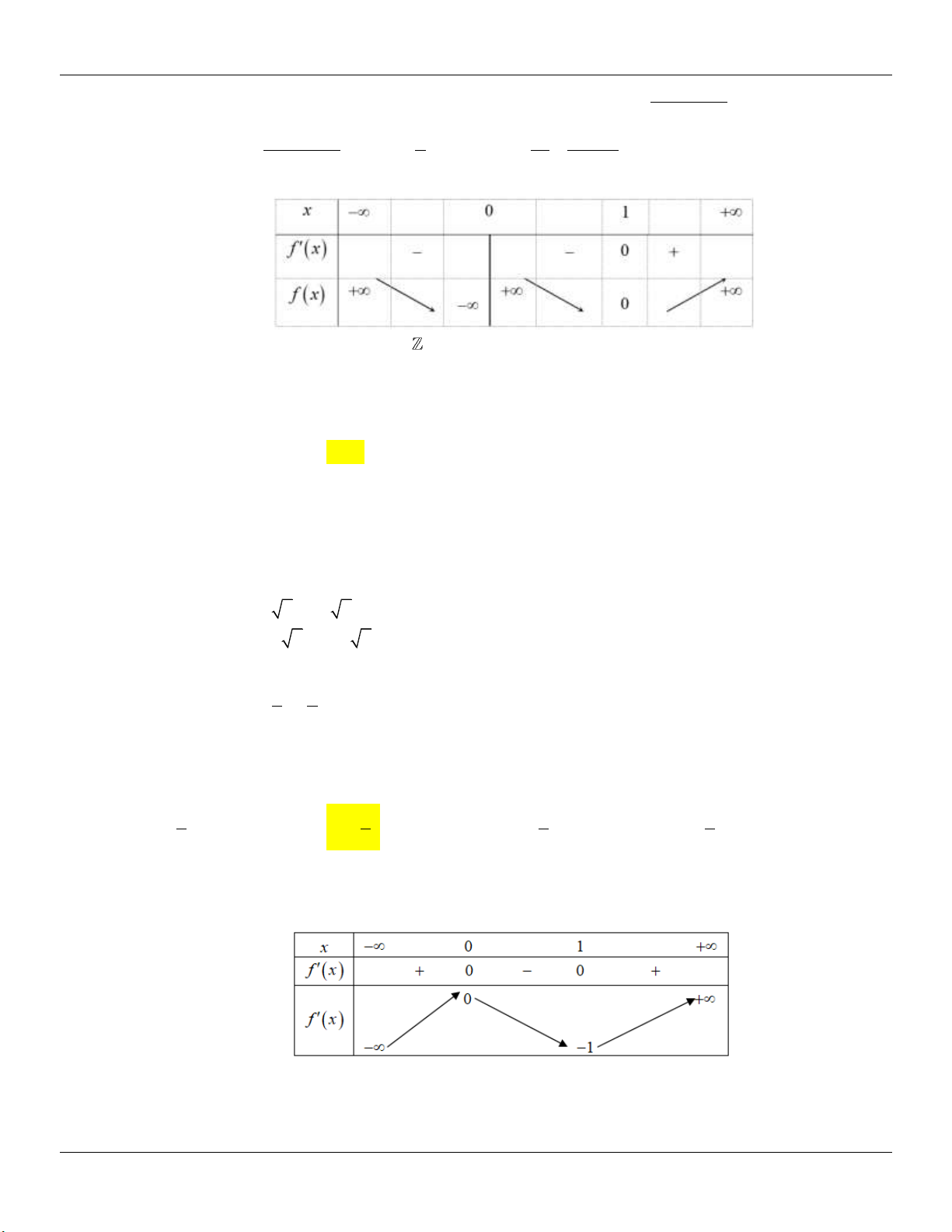
Câu 74: Cho hàm số y f x có bảng biến thiên dưới đây:
Để phương trình 3 f 2x  1  m  2 có 3 nghiệm phân biệt thuộc 0;1 
 thì giá trị của tham số m
thuộc khoảng nào dưới đây? A. ; 3 . B. 1;6 . C. 6;  . D.  3;  1 .
Câu 75: Cho hàm số f (x) liên tục trên
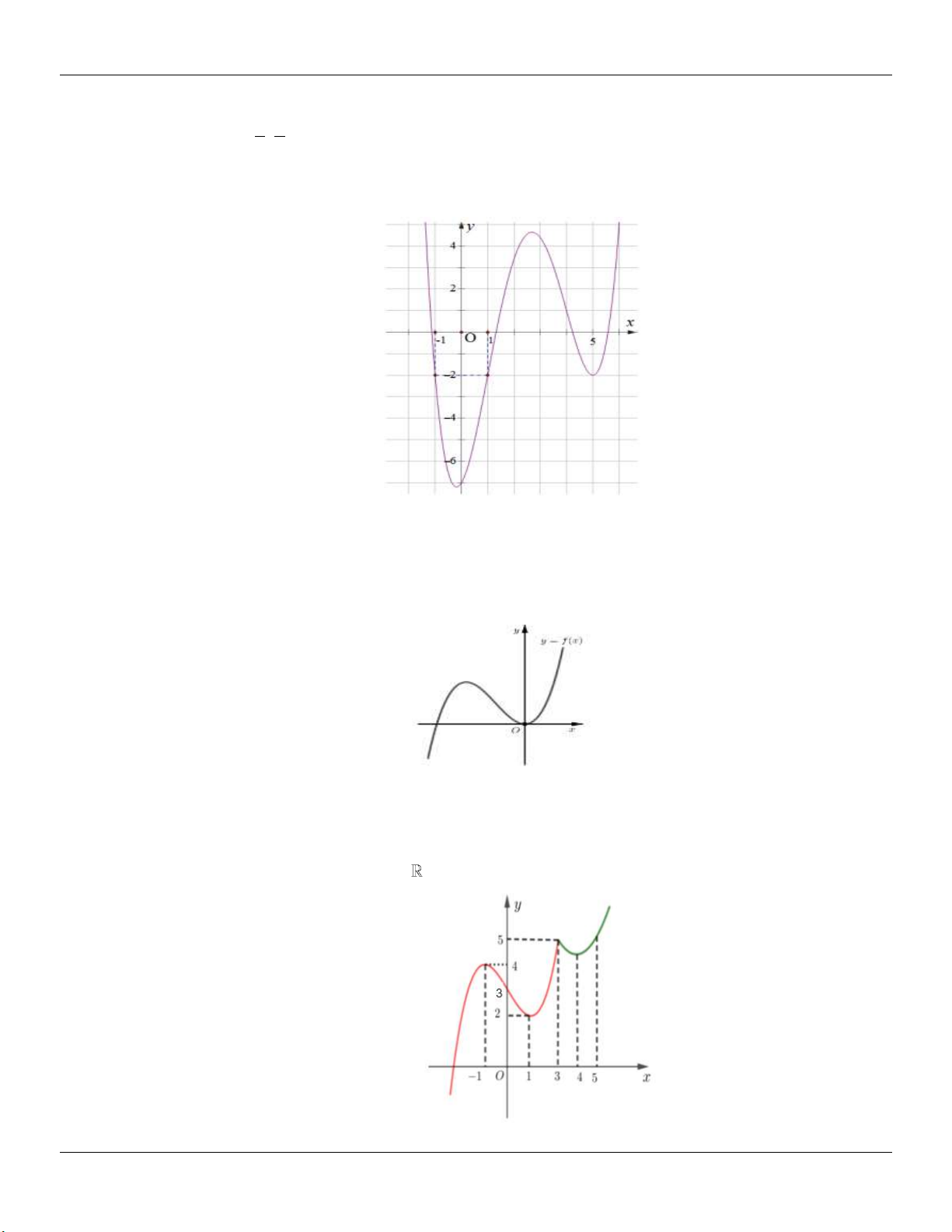
và có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để phương trình f  2  x x  2 3 4 6 9
 1 m  0 có nghiệm là
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 16
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. 6 . B. 4 . C. 5 . D. 7 .
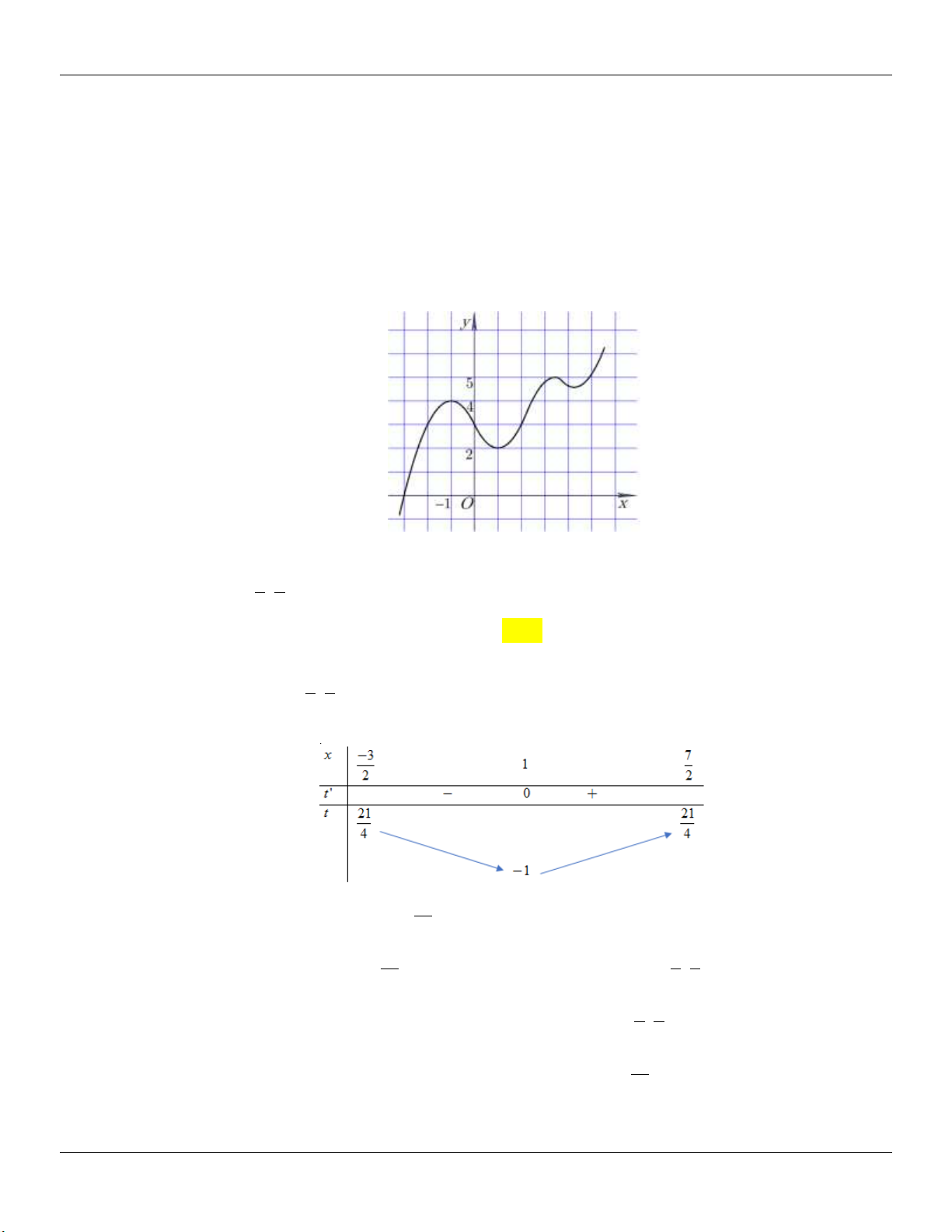
Câu 76: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. Tập hợp các giá trị thực của
tham số m để phương trình f  2 4  x  
1  m có nghiệm là A. 2; 0.   B. 4; 2  .   C. 4; 0.   D. 1;1.  
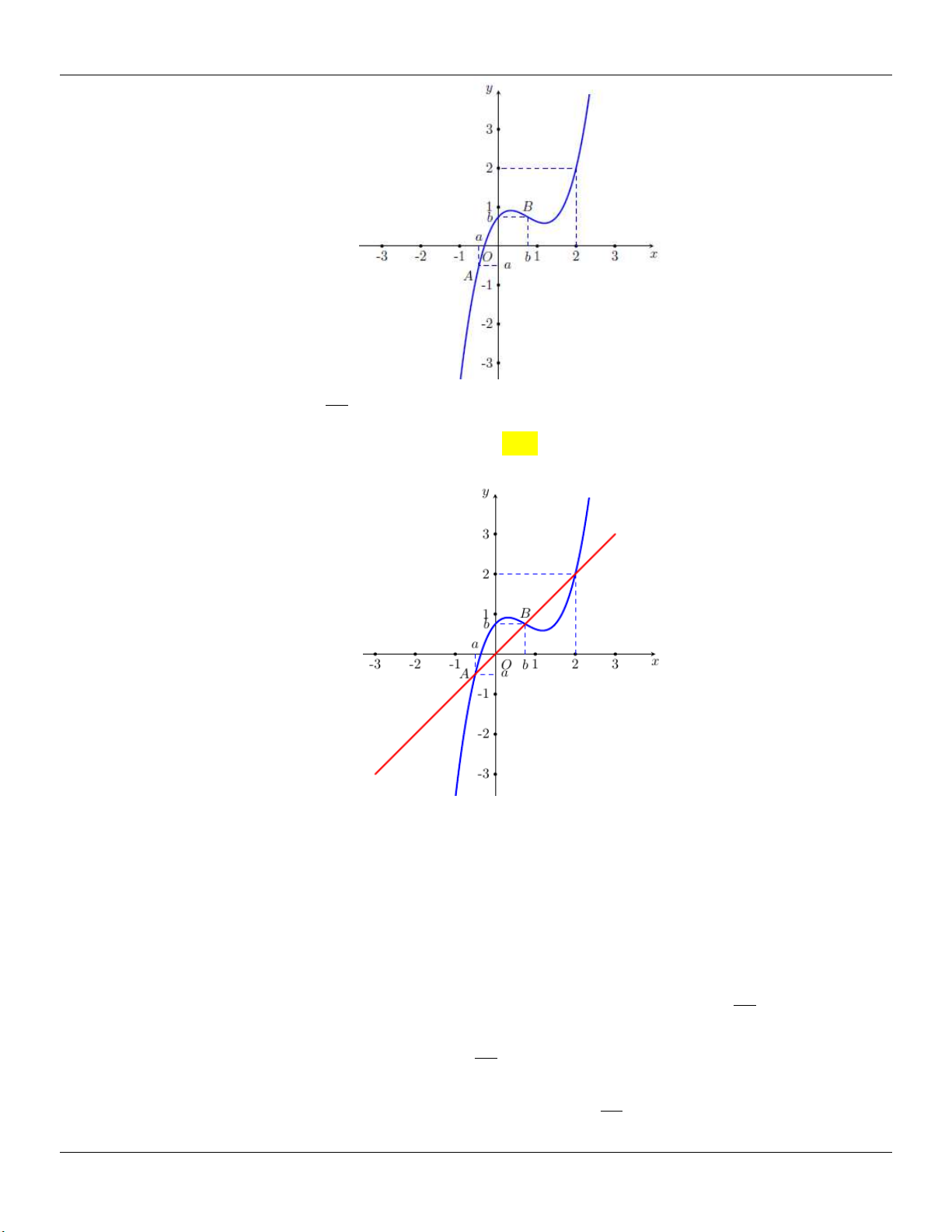
Câu 77: Cho hàm số bậc ba    3 2 y
f x ax bx cx d có đồ thị như hình bên dưới.
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
f x  m  5 f x  4m  4  0 có 7 nghiệm phân biệt? A. 1. B. 2. C. 3. D. 4. x  1
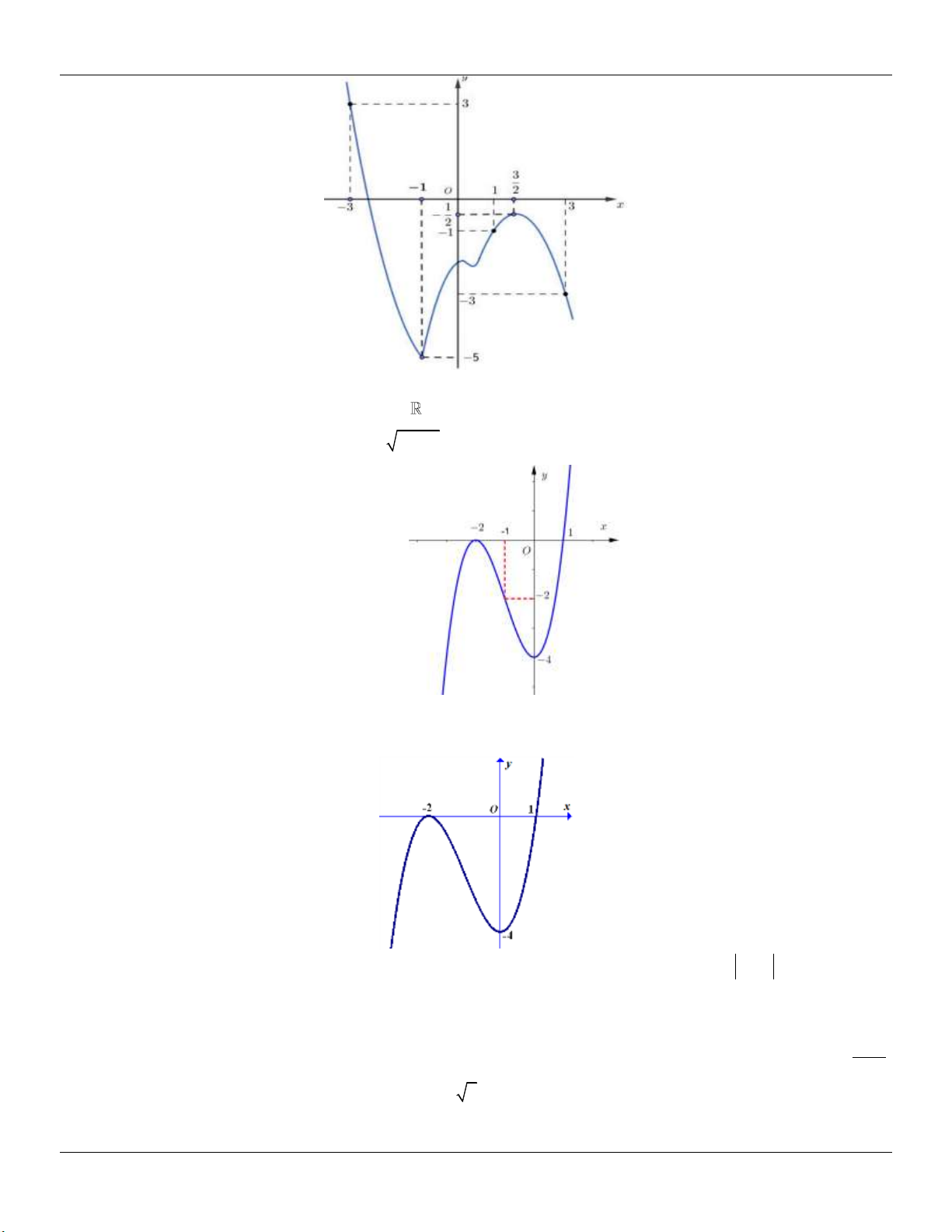
Câu 78: Tìm tất cả các giá trị thực của tham số m để đường thẳng (d) : y  x m cắt đồ thị (C) : y  1  x
tại 2 điểm phân biệt A, B sao cho AB  2 6.
A. m  2; m  2 .
B. m  4; m  4 . C. m  2 . D. m  4 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 17
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 79: Có bao nhiêu giá trị nguyên của tham số m để đường thẳng y  x m cắt đồ thị hàm số x  2 y
tại hai điểm phân biệt A , B sao cho OA OB  4? x  1 A. 2. B. 1. C. 0. D. 3. 2x
Câu 80: Tìm giá trị thực của tham số m để đường thẳng d : y x m  2 cắt đồ thị hàm số y  Cx  1
tại hai điểm phân biệt A và B sao cho độ dài AB ngắn nhất. A. m  3. B. m  3. C. m  1. D. m  1.
Câu 81: Cho hàm số f x 3 2
x  3x mx  1. Gọi S là tổng tất cả giá trị của tham số m để đồ thị hàm số
y f x cắt đường thẳng y  1 tại ba điểm phân biệt A0; 
1 , B, C sao cho các tiếp tuyến của
đồ thị hàm số y f x tại B, C vuông góc với nhau. Gía trị của S bằng 9 9 9 11 A. . B. . C. . D. . 2 5 4 5
Câu 82: Có bao nhiêu giá trị nguyên của tham số m  2  018;2019 
 để đồ thị hàm số 3
y x  3mx  3 và
đường thẳng y  3x  1 có duy nhất một điểm chung? A. 1 . B. 2019 . C. 4038 . D. 2018 .
Câu 83: Có bao nhiêu giá trị thực của tham số m để phương trình x  1x  2x m  0 có 3 nghiệm
phân biệt lập thành cấp số nhân tăng? A. 4 . B. 3 . C. 2 . D. 1 .
Câu 84: Gọi S là tập tất cả các giá trị thực của tham số m để phương trình 3 2
2x  3x  2m  1 có đúng
hai nghiệm phân biệt. Tổng các phần tử của S bằng 1 3 5 1 A.  . B.  . C.  . D. . 2 2 2 2 x  4
Câu 85: Giá trị k thỏa mãn đường thẳng d : y kx k cắt đồ thị H : y 
tại 2 điểm phân biệt A 2x  2
và B cùng cách đều đường thẳng y  0 . Khi đó k thuộc khoảng A. 2;  1 . B. 1; 2 . C.  1  ;0 . D 0;1 . x
Câu 86: Cho hàm số y
C và đường thẳng d : y  x m . Gọi S là tập hợp các số thực m để x  1
đường thẳng d cắt đồ thị C tại hai điểm phân biệt A,B sao cho tam giác OAB (O là gốc tọa
độ) có bán kính đường tròn ngoại tiếp bằng 2 2 . Tổng các phần tử của S bằng A. 8. B. 4 . C. 1 . D. 2 . Câu 87: Cho hàm số 4
y x   m   2 3
2 x  3m có đồ thị là (C ) . Tìm m để đường thẳng d : y  1 cắt đồ m
thị (C ) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2. m 1 1
A.   m  1 và m  0
B.   m  1 và m  0 3 2 1 1 1 1 C.   m
và m  0 D.   m  và m  0 2 2 3 2
Câu 88: Cho hai hàm số 2
y x x  1 và 3 2
y x  2x mx  3 . Giá trị của tham số m để đồ thị của hai
hàm số có 3 giao điểm phân biệt và 3 giao điểm đó nằm trên đường tròn bán kính bằng 3
thuộc vào khoảng nào dưới đây?
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 18
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. ;  4 . B. 4;  2 . C. 0;   . D.  2  ;0.
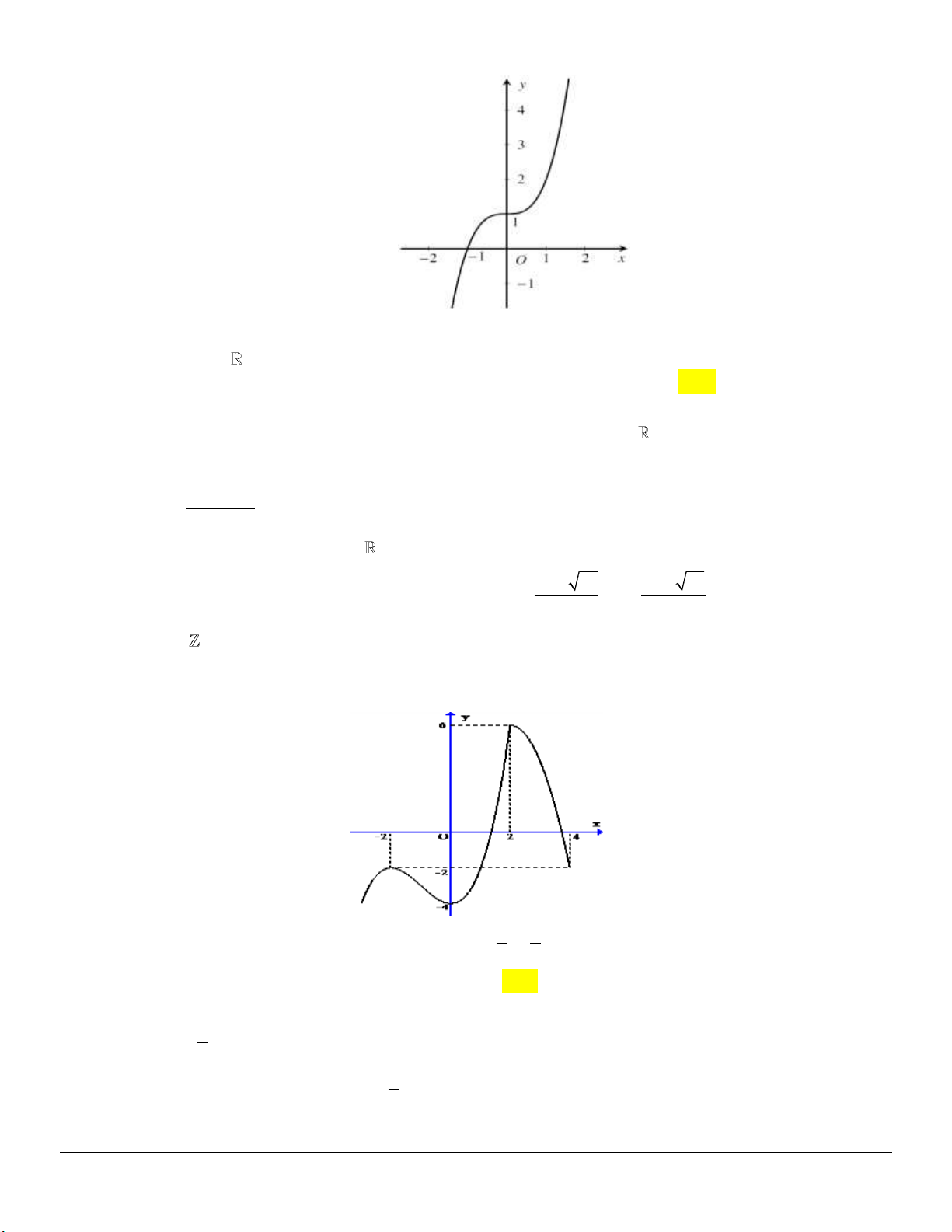
Câu 89: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá
trị thực của tham số m để phương trình f sin x  m có nghiệm thuộc khoảng 0;  là A. 1; 3  . B.  1  ;1 . C.  1  ;3 . D.  1  ;1  .
Câu 90: Cho hàm số y f x liên tục trên và có bảng biến thiên như hình vẽ sau:     
Tập hợp các giá trị m để phương trình f cos 2x  2m  1  0 có nghiệm thuộc  ;  là  3 4   1  1  1 1  2   2 1  A. 0; .   B. 0; .  C.  ; .  D.  ; .  2   2   4 2   4 4   
Câu 91: Cho hàm số y f (x) xác định, liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của m để phương trình f  2 2.
3  4 6x  9x   m  3 có nghiệm. A. 13 . B. 12 . C. 8 . D. 10 .
Câu 92: Cho hàm số y f x xác định trên và có đồ thị như hình bên. Có bao nhiêu giá trị nguyên
của tham số m để phương trình: f   4 4
4 sin x  cos x  m  có nghiệm.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 19
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. 2 . B. 4 . C. 3 . D. 5 .
Câu 93: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
tham số m để phương trình f f sin x  m có nghiệm thuộc khoảng 0;  . A. 1 . B. 2 . C. 3 . D. 4 .
Câu 94: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá
trị nguyên của tham số m để phương trình f sin x  3sin x m có nghiệm thuộc khoảng
0;  . Tổng các phần tử của S bằng A. 8  . B. 10 . C. 6  . D. 5  .
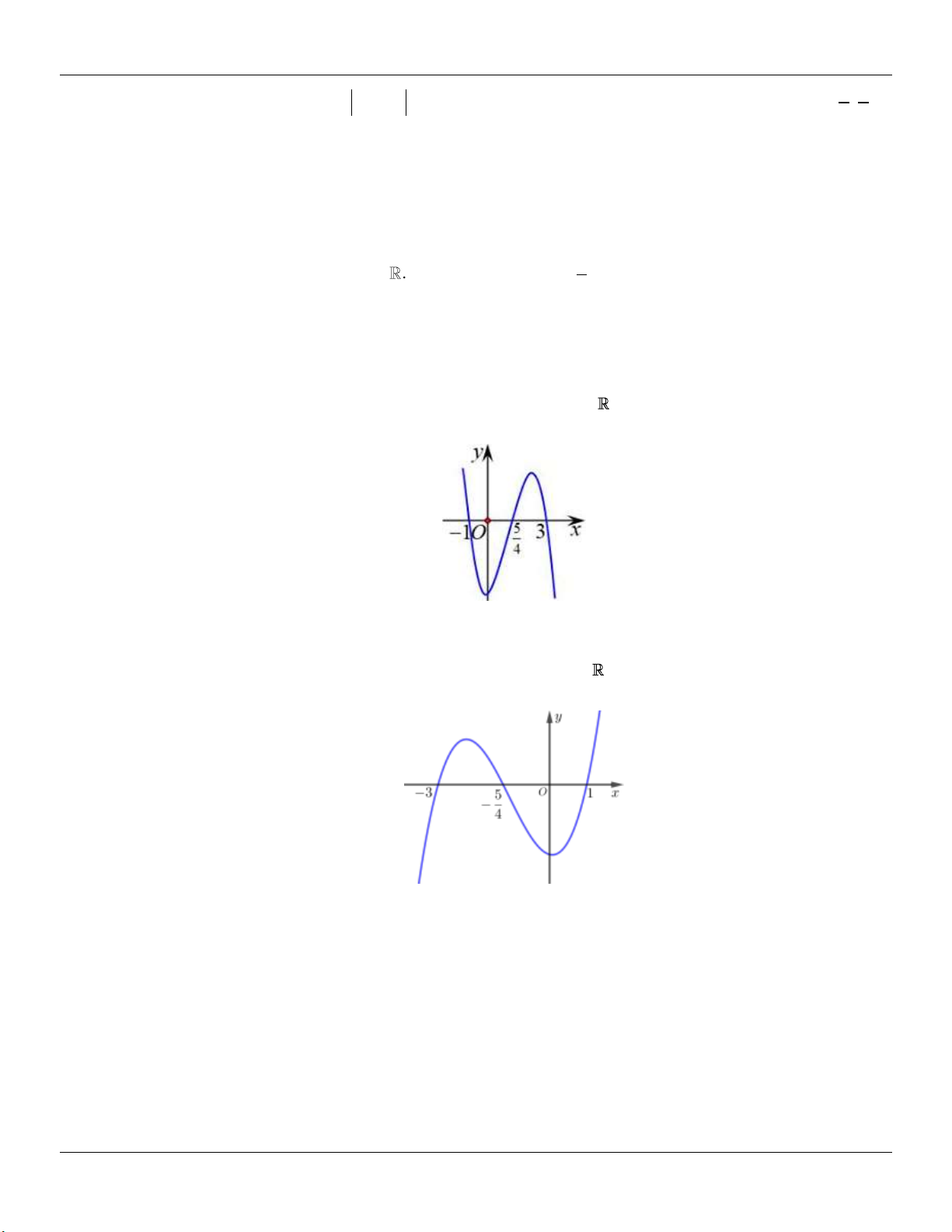
Câu 95: Cho hàm số y f x có đồ thị như hình vẽ dưới đây:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 20
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
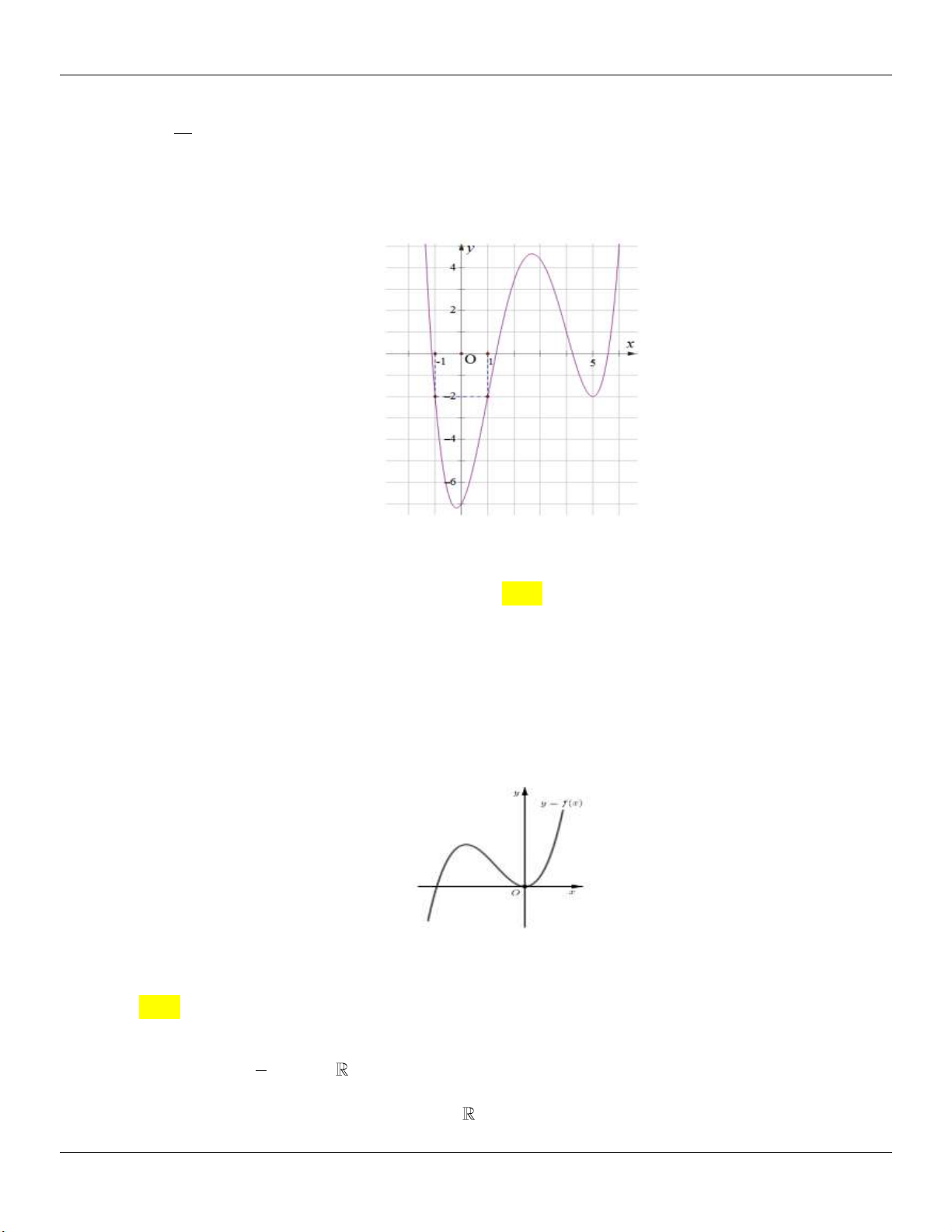
Tìm số giá trị nguyên của m để phương trình f  2
x  2x  m có đúng 4 nghiệm thực phân biệt  3 7  thuộc đoạn  ;   .  2 2  A. 1 . B. 4 . C. 2 . D. 3 .
Câu 96: Cho hàm số y f x có đồ thị như hình vẽ dưới đây:
Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình f sin x  m có đúng hai
nghiệm thuộc đoạn 0;    ? A. 4 . B. 7 . C. 5 . D. 6 .
Câu 97: Cho hàm số f x là đa thức và có đồ thị như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số m để phương trình  sinx f   f  2 4
m  8m  17 có nghiệm? A. 3. B. 4. C. 5. D. 6.
Câu 98: Cho hàm số y f x liên tục trên có đồ thị như hình vẽ bên dưới.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 21
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia  3 7 
Tìm m để phương trình f  2
x  2x   m có đúng 6 nghiệm thực phân biệt thuộc đoạn   ;  ?  2 2 
A. 2  m  3 hoặc f 4  m  5 .
B. 2  m  3 hoặc f 4  m  5 .
C. 2  m  3 hoặc f 4  m  5 .
D. 2  m  3 hoặc f 4  m  5 .
Câu 99: Tìm tất cả các giá trị thực của tham số m để đường thẳng y mx m  1 cắt đồ thị của hàm số 3 2
y x  3x x  2 tại ba điểm A , B , C phân biệt sao cho AB BC.  5 
A. m (; 0) [4; ). B. m  . C. m  ;   .
D. m (2; ).  4 
Câu 100: Tìm tất cả các giá trị thực của tham số m để đường thẳng y  mx cắt đồ thị của hàm số 3 2
y x  3x m  2 tại ba điểm phân biệt A, B, C sao cho AB BC .
A. m; 3 . B. m; 1   .
C. m;  .
D. m1;  .
Câu 101: Cho hàm số   4 3 2
f x mx nx px qx r , (với m,n, p,q,r
). Hàm số y f x có đồ thị như hình vẽ bên dưới:
Tập nghiệm của phương trình f x  r có số phần tử là A. 4 . B. 3 . C. 1 . D. 2 .
Câu 102: Cho hàm số   4 3 2
f x ax bx cx dx m , (với a,b,c,d,m
). Hàm số y f x có đồ thị như hình vẽ bên dưới:
Tập nghiệm của phương trình f x  m có số phần tử là A. 1 . B. 2 . C. 3 . D. 4 .
__________________________HẾT__________________________
Huế, ngày 16 tháng 7 năm 2023
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 22
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
Chuyên đề: KH¶O S¸T HµM Sè
Chủ đề 5: Sù T¦¥NG GIAO
Môn: TOÁN 12 _GIẢI TÍCH
LỜI GIẢI CHI TIẾT DẠNG 1:
TÌM GIAO ĐIỂM – SỐ GIAO ĐIỂM – TÍNH CHẤT GIAO ĐIỂM Câu 1:
Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm của phương trình f x  2  0 là A. 0 . B. 3 . C. 1 . D. 2 . Lời giải:
Ta có: f x  2  0  f x  2 . Do 2 2
 ;4 nên phương trình đã cho có 3 nghiệm phân biệt.
Chọn đáp án B. Câu 2:
Cho hàm số y f x liên tục trên đoạn 2; 2 
 và có đồ thị như hình vẽ bên dưới: y 3 1 1 2 1  O 2 x 1 
Số nghiệm của phương trình 3 f x  4  0 trên đoạn 2; 2   là A. 3 . B. 4 . C. 2 . D. 1 . Lời giải: y 3 4 y= 3 x -2 -1 O 1 2 -1
Ta có: f x    f x 4 3 4 0  . 3
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 23
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Suy ra số nghiệm của phương trình trên đoạn 2; 2 
 bằng số giao điểm của đồ thị y f x 4
với đường thẳng y  trên đoạn 2; 2   . 3 4
Dựa vào đồ thị ta thấy số giao điểm của đồ thị y f x với đường thẳng y  trên đoạn 3 2;2 
 là 3 điểm. Vậy số nghiệm của phương trình 3 f x  4  0 trên đoạn 2; 2   là 3 nghiệm.
Chọn đáp án A. Câu 3:
Số giao điểm của đồ thị hàm số 2 2
y x . x  4 với đường thẳng y  3 là A. 8 . B. 2 . C. 4 . D. 6 . Lời giải:
Dựa vào đồ thị ở hình vẽ trên ta thấy, số giao điểm của đồ thị hàm số 2 2
y x . x  4 với đường
thẳng y  3 là 6 .
Chọn đáp án D. Câu 4:
Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm của phương trình 2 f x  3  0 là A. 4 . B. 3 . C. 2 . D. 1 . Lời giải:
Ta có 2 f x  3  0  f x 3   . 2
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số y f x và đường 3 thẳng y   . 2 3
Dựa vào bảng biến thiên ta thấy y  2
    1  y . CT 2 CĐ
Vậy phương trình 2 f x  3  0 có 4 nghiệm phân biệt.
Chọn đáp án A. Câu 5:
Biết rằng đường thẳng y  2
x  2 cắt đồ thị hàm số 3
y x x  2 tại một điểm duy nhất, ký
hiệu x ; y là tọa độ điểm đó. Tìm y . 0 0  0
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 24
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. y  4 . B. y  0 . C. y  2 . D. y  1 . 0 0 0 0 Lời giải:
Phương trình hoành độ giao điểm là: 3 3
x x  2  2
x  2  x  3x  0  x 2
x  3  0  x  0. Do x  0  y  2 . 0 0
Chọn đáp án C. Câu 6: Đồ thị hàm số 3
y x  3x  2 cắt trục tung tại điểm có tọa độ là A.  1  ;0 . B. 0;  2 . C. 0; 2 . D. 2;0 . Lời giải:
Thế x  0 vào hàm số 3
y x  3x  2 ta được y  2 . Vậy đồ thị hàm số 3
y x  3x  2 cắt trục tung tại điểm có tọa độ là 0;  2 .
Chọn đáp án B. 2x  1 Câu 7:
Biết đường thẳng y x  2 cắt đồ thị hàm số y
tại hai điểm phân biệt A, B có hoành độ x  1
lần lượt x , x . Khi đó giá trị của x x bằng A B A B A. 5 . B. 3 . C. 1 . D. 2 . Lời giải: 2x  1
Phương trình hoành độ giao điểm của đường thẳng y x  2 và đồ thị hàm số y  là x  1 2x  1 x  2 
 x  2x   1  2x  1 x  1 2 2
x  3x  2  2x  1  x  5x  1  0 (*)
Ta có x , x là nghiệm của phương trình (*), theo định lí Viét ta có x x  5. A B A B
Chọn đáp án A. Câu 8:
Đồ thị của hàm số nào sau đây cắt trục tung tại điểm có tung độ âm? 2  x  3 2x  3 4x  1 x   4 A. y  . B. y  . C. y  . D. y  . x  1 3x  1 x  2 x  1 Lời giải:
Cho x  0 thay vào các hàm số trên ta thấy chỉ có hàm số ở đáp án D là được y  4   0 .
Chọn đáp án D. Câu 9:
Biết rằng đường thẳng y  4x  5 cắt đồ thị hàm số 3
y x  2x  1 tại điểm duy nhất; kí hiệu
x ; y là tọa độ của điểm đó. Tìm y . 0 0  0 A. y  10 . B. y  13 . C. y  11 . D. y  12 . 0 0 0 0 Lời giải:
Phương trình hoành độ giao điểm là 3 3
x  2x  1  4x  5  x  2x  4  0  x  2
Với x  2  y  13 . Vậy y  13 . 0
Chọn đáp án B.
Câu 10: Đồ thị hàm số 3 2
y  2x x x  2 cắt parabol 2 y  6
x  4x  4 tại một điểm duy nhất. Kí hiệu
x ;y là tọa độ điểm đó. Tính giá trị của biểu thức x y . 0 0  0 0 A. 1. B. 1. C. 22. D. 4. Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 25
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Ta có x là nghiệm của phương trình: 3 2 2
2x x x  2  6x  4x  4 0 3 2 2
 2x  5x  5x  6  0  (x  2)(2x x  3)  0  x  2  . 0
Với x  2  y  20 . Vậy x y  22 . 0 0 0 0
Chọn đáp án C.
Câu 11: Đường thẳng  có phương trình y  2x  1 cắt đồ thị của hàm số 3
y x x  3 tại hai điểm A
và B với tọa độ được kí hiệu lần lượt là Ax ; y
và Bx ; y trong đó x x . Tính x y . B B A A B A B B
A. x y  5. 
B. x y  2. 
C. x y  4.
D. x y  7. B B B B B B B B Lời giải:
Hoành độ giao điểm là nghiệm của phương trình: 3
x x  3  2x  1 x  1
Giải phương trình ta được 
. Vì x x Vậy x  1; y  3  x y  4. x   2 B A B B B B
Chọn đáp án C. 5x  6
Câu 12: Tính tổng hoành độ của các giao điểm của đồ thị hàm số y
và đường thẳng y  x . x  2 A. 7 . B. 5  . C. 5 . D. 7 . Lời giải: 5x  6
Xét phương trình hoành độ giao điểm:
 x (với x  2 ) x  2     x
5x  6  xx  2 2
x  7x  6  1 0   . x  6  
Khi đó tổng hoành độ của các giao điểm là: 7 .
Chọn đáp án A. Câu 13: Cho hàm số 3
y x  3x có đồ thị hàm số là C . Tìm số giao điểm của C và trục hoành. A. 2. B. 3. C. 1 . D. 0 . Lời giải: x  0 
Xét phương trình hoành độ giao điểm: 3
x  3x  0  x 2
x  3  0  x  3 ` x   3  Vậy có ba giao điểm.
Chọn đáp án B.
Câu 14: Cho hàm số y  x   2
2 x  1 có đồ thị C . Mệnh đề nào dưới đây đúng?
A. C cắt trục hoành tại hai điểm.
B. C cắt trục hoành tại một điểm.
C. C không cắt trục hoành.
D. C cắt trục hoành tại ba điểm. Lời giải:
Ta có: x   2
2 x  1  0  x  2  0 (vì 2 x  1  0; x
  )  x  2 .
 C cắt trục hoành tại một điểm.
Chọn đáp án B.
Câu 15: Đồ thị của hàm số 4 2
y x  2x  2 và đồ thị của hàm số 2
y  x  4 có tất cả bao nhiêu điểm chung?
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 26
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. 0 . B. 4 . C. 1 . D. 2 . Lời giải: x  2
Xét phương trình hoành độ giao điểm: 4 2 2 4 2
x  2x  2  x  4  x x  2  0   . x    2
Vậy hai đồ thị có tất cả 2 giao điểm.
Chọn đáp án D.
Câu 16: Tìm số giao điểm n của đồ thị hàm số 4 2
y x  8x  3 và đường thẳng y  10 . A. n  0 . B. n  4 . C. n  2 . D. n  3 . Lời giải:
Xét phương trình hoành độ giao điểm: 4 2 4 2
x  8x  3  10  x  8x  7  0  x   4  23 .
Vậy hai đồ thị có hai giao điểm.
Chọn đáp án C.
Câu 17: Tọa độ tất cả các giao điểm của đồ thị hàm số 4 2
y x x  1 và đường thẳng y  1 là A. 0; 1  , 1  ; 1  . B. 1; 1  ; 1  ; 1  . C. 0; 1  ,1;1 . D. 0; 1  ,1; 1  , 1  ; 1   . Lời giải:
Phương trình hoành độ giao điểm: 4 2
x x  1  1  4 2
x x  0  2 x  0 , 2 x  1 
x  0 , x  1 .
Suy ra toạ độ các giao điểm là 0; 1  ,1; 1  , 1  ; 1   .
Chọn đáp án D.
Câu 18: Cho hàm số y f (x) có bảng biến thiên như hình vẽ sau:
Số nghiệm của phương trình f (x)  1 là A. 1 . B. 2 . C. 4 . D. 3 . Lời giải:
Số nghiệm của phương trình f (x)  1 chính là số giao điểm của đồ thị hàm số y f (x) và
đường thẳng y  1 . Nhìn BBT trên ta thấy đường thẳng y  1 cắt đồ thị hàm số y f (x) tại 2
điểm. Vậy phương trình đã cho có 2 nghiệm.
Chọn đáp án B.
Câu 19: Cho hàm số f x 3
x  3x  1 . Tìm số nghiệm của phương trình f f x  0 . A. 5 . B. 9 . C. 4 . D. 7 . Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 27
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Xét phương trình f x 3
 0  x  3x  1  0 dùng máy tính cầm tay ta ước lượng được phương x  1  ,879 1 
trình có ba nghiệm và x  1,532  . 2 x  0,347  3
Xét hàm số f x 3
x  3x  1 , ta có bảng biến thiên của f x như sau:
f x  1  ,879 
Xét phương trình f f x  0 1 ta ước lượng được  f x  1,532 .
f x  0,347
Dựa vào bảng biến thiên của hàm số f x ta có:
+ Với f x  1
 ,879 phương trình 1 có 1 nghiệm.
+ Với f x  1,532 phương trình 1 có 3 nghiệm.
+ Với f x  0,347 phương trình 1 có 3 nghiệm.
Chọn đáp án D.
Câu 20: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. Tập hợp nghiệm của phương
trình f f x  1  0 có bao nhiêu phần tử? A. 4 . B. 7 . C. 6 . D. 9 . Lời giải:
f x  a  2 
f x  b2;1
Dựa vào đồ thị ta có f f x  1  0 f f x  1
   f x0 .  f
 x  c  2 x x  2 
+ Với f x  a  2  1   . x x   2 2
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 28
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x x  2  3 x x  2  ; 1   4  
+ Với f x  b 2  ; 1     . x x  1  ;0 5    x x  2  6 x x  2  7 
+ Với f x  0  x x  0;1 . 8   x x   2; 3  9  
+ Với f x  c  2 vô nghiệm.
Ta thấy hàm số y f x đơn điệu trên ; 2 , f x a b f x nên x x . 1   3 1 3
Hàm số y f x đơn điệu trên 2;  , f x b  0  f x nên x x . 6   9 6 9
Vậy phương trình đã cho có 9 nghiệm phân biệt.
Chọn đáp án D.
Câu 21: Cho hàm số y f x liên tục trên các khoảng (; 2  ); 2
 ; và có bảng biến thiên như sau: 2
Số nghiệm thực của phương trình  f x  2 f x  3  0 là A. 2 . B. 1 . C. 0 . D. 4 . Lời giải:    2 f x 1
Điều kiện: x  2 . Xét phương trình:  f x  2 f x    3  0   f  x  3
Từ bảng biến thiên ta có: phương trình f x  1
 có hai nghiệm phân biệt thỏa điều kiện: x  3   x  2 
và phương trình f x  3 có hai nghiệm phân biệt thỏa mãn điều 1 2 kiện 2   x  1
  x . Vậy phương trình có bốn nghiệm thực phân biệt. 3 4
Chọn đáp án D. Câu 22: Cho hàm số 3 2
y f (x)  ax bx cx d có đồ thị như hình vẽ bên dưới.
Tập nghiệm của phương trình f (x)  f (x)  4  0   là A. { 1; 0 ;1; 2 ; 3} . B. { 1; 2} . C. {0 ; 3} . D. { 1; 0 ; 2 ; 3} . Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 29
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Ta có: f (x)  f (x)  4  0  f (x)  0  
hoặc f (x)  4 .
Từ đồ thị, ta thấy: f (x)  0 có hai nghiệm là x  1và x  2 vì đồ thị của hàm số cắt trục
hoành tại hai điểm có hoành độ lần lượt là x  1và x  2 ;
Mặt khác, đồ thị hàm số cắt đường y  4 tại hai điểm có hoành độ là x  0 và x  3 nên
f (x)  4 có hai nghiệm là x  0 và x  3 .
Vậy phương trình đã cho có tập nghiệm là { 1; 0 ; 2 ; 3} .
Chọn đáp án D. Câu 23: Cho hàm số 3 2
y f (x)  ax bx cx d, (a  0) có đồ thị như hình vẽ bên dưới:
Phương trình f f x  0 có bao nhiêu nghiệm thực? A. 3 . B. 7 . C. 9 . D. 5 . Lời giải:
Đặt t f x , phương trình f f x  0 trở thành f t  0 * (số nghiệm phương trình * là
số giao điểm của đồ thị f x với trục Ox ) . Nhìn vào đồ thị ta thấy phương trình * có 3
nghiệm t thuộc khoảng  2
 ;2 , với mỗi giá trị t như vậy phương trình f x  t có 3 nghiệm
phân biệt. Vậy phương trình f f x  0 có 9 nghiệm.
Chọn đáp án C.
Câu 24: Cho hàm số y f x liên tục trên
có đồ thị như hình vẽ bên dưới:
Phương trình f 3  2 f x  1 có tất cả bao nhiêu nghiệm thực phân biệt? A. 6 . B. 5 . C. 7 . D. 4 . Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 30
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia  
  f xf x 2 3 2  1  
Dựa vào đồ thị ta có: f 3  2 f x  1     .   f  x  f x 1 3 2 2   2
Mà f x  2 có 1 nghiệm duy nhất lớn hơn 2 . Và f x 1
 có 3 nghiệm phân biệt x  2  ; 1  , x  1  ;0 , x  1;2 . 3   2   1   2
Vậy phương trình có 4 nghiệm thực phân biệt.
Chọn đáp án D.
Câu 25: Cho hàm số y f x liên tục trên có đồ thị như hình bên dưới:
Phương trình f f x  1  0 có tất cả bao nhiêu nghiệm thực phân biệt? A. 6. B. 5. C. 7. D. 4. Lời giải:
x a2;1 
Từ đồ thị hàm số y f x ta có: f x  0  x b1;0 x c  0;2
f x 1  a1 
Do đó f f x  1  0   f x  1  b2
f x1  c 3
1  f x  a 1 1  ;0
pt f x  a  1 có 3 nghiệm x ,x ,x thỏa mãn x a  1  b x  0  x c 1 2 3 1 2 3
2  f x  b 10;1 pt f x  b 1 có 3 nghiệm x ,x ,x thỏa mãn 4 5 6
x a x  1
  x b x  0  x c x 1 4 5 2 3 6
3  f x  c 11;3  pt f x  c 1 có nghiệm duy nhất x x 7 6
Vậy phương trình f f x  1  0 có 7 nghiệm phân biệt.
Chọn đáp án C.
Câu 26: Cho hàm số y f x xác định trên và có bảng biến thiên như sau: x  -1 1  y  0  0 
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 31
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia y 1   -1
Số nghiệm của phương trình f  2
x  2x  2 là A. 4 . B. 2 . C. 3 . D. 8 . Lời giải: BBT của hàm số 2
y x  2x : x  1    y 1
f  2x  2x  2 Phương trình f  2
x  2x  3   f   2
x  2x  2 +) f  2 x x 2 2
 2  x  2x a  1
 Có hai nghiệm phân biệt. +) f  2 x x 2 2  2
  x  2x b  1    Vô nghiệm.
Vậy phương trình f  2
x  2x  2 có 2 nghiệm phân biệt.
Chọn đáp án B.
Câu 27: Cho hàm số bậc ba y f x có đồ thị như hình vẽ bên dưới: 1
Số nghiệm thực của phương trình f  3
x  3x  là 2 A. 6 . B. 10 . C. 12 . D. 3 . Lời giải:
f  3x x 1 3  1 Xét f  3 x  3x  2   2
f  3x x 1 3    2 Xét g x 3
x  3x , g x 2 '
 3x  3  0  x  1  .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 32
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x  1  1     g ' x 0 0  2 g x  2  Quan sát đồ thị: 3
x  3x a 2  ;0 1  + Xét f  3 x  3x  3
 x  3x b0;2 ( có lần lượt 3, 3, 1 nên có tất cả 7 nghiệm). 2  3
x  3x c 2;    3
x  3x c  2 1  + Xet f  3
x  3x   3
 x  3x d  2 ( có 3 nghiệm). 2  3
x  3x c  2  
Rõ ràng 10 nghiệm này phân biệt. Vậy phương trình đã cho có tất cả 10 nghiệm.
Chọn đáp án B.
Câu 28: Cho hàm số bậc ba y f x có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình f  4 2
x  2x   2 là A. 8 . B. 9 . C. 7 . D. 10 . Lời giải: 4 2
f x  2x  2 Phương trình f  4 2 x  2x     2   . f   4 2
x  2x   2
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 33
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 4 2
x  2x b, 1   b  0 
* Phương trình f  4 2 x  2x  4 2
 2  x  2x c,0  c  1 .  4 2
x  2x d,  2  d   3
* Phương trình f  4 2 x x  4 2 2  2
  x  2x a, 2   a  1   .
Bảng biến thiên của hàm số 4 2
y x  2x như sau: x  1  0 1  y  0  0  0    y 1  0 1  Dựa vào BBT trên ta có: - Phương trình 4 2
x  2x a, 2   a  1
  không có nghiệm thực. - Phương trình 4 2
x  2x b, 1
  b  0 có 4 nghiệm thực phân biệt. - Phương trình 4 2
x  2x c,0  c  1 có 2 nghiệm thực phân biệt. - Phương trình 4 2
x  2x d,2  d  3 có 2 nghiệm thực phân biệt.
Vậy phương trình f  4 2
x  2x   2 có 8 nghiệm thực phân biệt.
Chọn đáp án A.
Câu 29: Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm của phương trình f  4 2
3x  6x  1  1 là A. 4 . B. 5 . C. 6 . D. 3 . Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 34
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
x a; 2   
Dựa vào bảng biến thiên, ta có f x  1  x b 2  ;1 .
x c1;   4 2
3x  6x  1  a ( ) 1  Do đó f  4 2
3x  6x  1 4 2
 1  3x  6x  1  b (2)  4 2
3x  6x  1  c ( ) 3  x  1  
Xét hàm số gx 4 2
 3x  6x  1 . Ta có: gx 3
 12x  12x  0  x  0  . x  1  Bảng biến thiên:
Dựa vào bảng biến thiên, có:
- Phương trình (1) vô nghiệm.
- Phương trình (2) có đúng 4 nghiệm phân biệt.
- Phương trình (3) có đúng 2 nghiệm phân biệt.
Vậy phương trình đã cho có tất cả 6 nghiệm.
Chọn đáp án C.
Câu 30: Cho hàm số y f x có đồ thị như hình vẽ:
Khi đó phương trình f  4 4
3x   3  0 có bao nhiêu nghiệm dương? A. 2. B. 4. C. 5. D. 1. Lời giải:
Bảng biến thiên của hàm số 4 y  3x :
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 35
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 4
3x x , x  1  ;0 1 1   3  Ta có: 4 f  4
3x   3  0  f  4 3x  4
  3x x , x  0;1 . 2 2   4  4
3x x , x   1; 2  3 3  
Dựa vào bảng biến thiên ta có 4
3x x vô nghiệm; 4
3x x có một nghiệm âm một nghiệm 1 2 dương; 4
3x x có một nghiệm âm một nghiệm dương. 3
Vậy phương trình f  4 4
3x   3  0 có 2 nghiệm dương.
Chọn đáp án A.
Câu 31: Cho hàm số y f x có đồ thị như hình vẽ sau: y 1 1 1 O x 1   5 
Số nghiệm của phương trình 2 f sin x  1  0 trên đoạn  ;   là  2 2  A. 3 . B. 4 . C. 5 . D. 6 . Lời giải: t a,( 1   a  0)
Đặt t  sin x , t   1  ;1 
 ta được: f t 1
 . Dựa vào đồ thị ta có  2
t b,0  b   1   5 
Xét hàm số gx  sin x trên đoạn  ;    2 2    5 
Đồ thị của hàm số gx  sin x tên đoạn  ;   là  2 2    5    5 
Dựa vào đồ thị ta có sin x a có 3 nghiệm trên  ; 
 , sin x b có 3 nghiệm trên  ;   .  2 2   2 2    5 
Vậy phương trình 2 f sin x  1  0 có 6 nghiệm trên  ;   .  2 2 
Chọn đáp án D.
Câu 32: Cho hàm số f x có bảng biến thiên như sau:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 36
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia  7 
Số nghiệm thuộc đoạn 0; 
 của phương trình 2. f cos x  5  0 là  3  A. 8 . B. 7 . C. 5 . D. 6 . Lời giải: Xét phương trình
f x    f x 5 2. 5 0  . 2
x a1;0    1  x b    0;  5  2 
Dựa vào bảng biến thiên, ta có f x    . 2   1  x c    ;1  2  
x d1;  
cosx a 1  ;0 (1)    1  cos x b   0;  (2) 5  2 
Do đó 2. f cos x  5  0  f cos x    . 2   1  cos x c    ;1  (3)  2  
cosx d1;   (4)  7 
Dựa vào đường tròn lượng giác, trên đoạn 0;   ta có:  3 
- Phương trình (1) có đúng 2 nghiệm phân biệt.
- Phương trình (2) có đúng 2 nghiệm phân biệt.
- Phương trình (3) có đúng 3 nghiệm phân biệt.
- Phương trình (4) vô nghiệm.
Vậy phương trình đã cho có tất cả 7 nghiệm.
Chọn đáp án B.
Câu 33: Cho hàm số y f x có đồ thị như hình vẽ.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 37
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Số nghiệm thuộc đoạn 0; 5  
 của phương trình f cos x  1 A. 3 . B. 4 . C. 5 . D. 6 . Lời giải:
Đặt t  cos x , t   1  ;1 
 ta được f t  1  t a với a0;1
Xét hàm số gx  cos x trên đoạn 0; 5   
Đồ thị của hàm số gx  cos x tên đoạn 0; 5    là
Dựa vào đồ thị ta có cos x a có 5 nghiệm trên 0; 5   
Vậy phương trình f cos x  1 có 5 nghiệm trên 0; 5    .
Chọn đáp án C.
Câu 34: Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn 0; 5  
 của phương trình f sin x  1 là A. 6 . B. 4 . C. 10 . D. 8 . Lời giải:
Từ bảng biến thiên ta được
sin x t  ; 1  (VN) 1   
f sin x  1  sin x t  1  ;0
 sin x t  1  ;0 (1) . 2   2  
sinx t  1;  (VN)  3  
Dựa vào đường tròn lượng giác, phương trình (1) có 4 nghiệm nằm trong đoạn 0; 5    .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 38
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
sin x t  ; 1  (VN) 4   
f sin x  1
  sin x t  0;1
 sin x t  0;1 (2) . 5   5  
sinx t  1;  (VN)  6  
Dựa vào đường tròn lượng giác, ta được phương trình (2) có 6 nghiệm nằm trong đoạn 0; 5    .
Vậy phương trình ban đầu có tất cả 10 nghiệm.
Chọn đáp án C.
Câu 35: Cho hàm số y f x có bảng biến thiên như hình vẽ sau: x  0 1 2  f x  0  0  0   3  f x 0 1
Số nghiệm của phương trình f sin x  1  2 trên    ;2    là A. 6. B. 7. C. 5. D. 4. Lời giải:
x a a  0 
x b 0  b  1
Dựa vào bảng biến thiên hàm số f x , ta thấy f x  2  
x c   c   . 1 2 x d  d  2
t a 1 
t b 2
Đặt t  sin x  1. Phương trình đã cho tương đương với f t  2   t c  3 t d  4 
Ta có: tx  cos x tx  0  x   k k  . 2
Ta có bảng biến thiên hàm số t x trên    ;2    là:   3 x    2 2 2 2 tx  0  0  0  1 2 1 t x 0 0
Từ bảng biến thiên này, ta thấy các phương trình 1 và 4 vô nghiệm, phương trình 2 có 4
nghiệm và phương trình 3 có đúng 2 nghiệm. Vậy phương trình đã cho có 6 nghiệm phân biệt.
Chọn đáp án A.
Câu 36: Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 39
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x  1  1 2  f x  0  0  0   1  f x 1  2    3 
Số nghiệm thuộc đoạn  ; 
 của phương trình f cot x  1  1 là  2 2  A. 7. B. 6. C. 8. D. 5. Lời giải:
Đặt t  cot x  1, phương trình tương đương với f t  1.
Dựa vào bảng biến thiên, ta thấy
t a a  1  
cot x  1  a
cot x a  1  0   
f t  1  t  1
 cot x  1  b  cot x b  1  0  
t b b  2 cot x  1  1 cot x  0    1   3  Xét t  
 0 nên ta có bảng biến thiên hàm tx trên  ;   như sau 2 sin x  2 2   3 x  0  2 2 t       t 0 0 
Từ đó, phương trình cot x a  1 có đúng 2 nghiệm, phương trình cot x b  1 có đúng 2   3 
nghiệm và phương trình cot x  0 có đúng 3 nghiệm thuộc  ; 
 nên phương trình đã cho  2 2  có 7 nghiệm.
Chọn đáp án A.
Câu 37: Cho hàm số y f x có đồ thị như hình vẽ sau:
Số nghiệm thuộc đoạn 0 ; 3  
 của phương trình 2 f cos x  1  0 là A. 12 . B. 6 . C. 10 . D. 8 . Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 40
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia f x 1 cos   f x 2 2 cos  1  0   f x 1 cos    2  1 cos x a , 1   a    1 2  1  1
Căn cứ vào đồ thị ta thấy: f cos x   cos x b ,  b  02 2  2
cosx c,c 1  3  
cos x d ,d  1  4  1 1
f cos x    cos x e ,0  e  5 2  2  1
cos x g ,  g  16 4  2
Các phương trình 3 , 4 đều vô nghiệm. Xét đồ thị hàm số 3
y  cos x trên đoạn 0 ; 3    y 2 1 O 5π 4π 3π 2π π π 2π 3π x 4π 5 1
Ta thấy các phương trình 1 ,2 ,5,6 lần lượt có 3 nghiệm phân biệt và trong số chúng 2
không có 2 nghiệm nào trùng nhau. Vậy phương trình ban đầu có 12 nghiệm.
Chọn đáp án A. 3
Câu 38: Cho hàm số f x có bảng biến thiên như sau: 4 5
Số nghiệm thuộc khoảng  
 ;  của phương trình 2
f cos x  f cos x  2 là A. 5 . B. 6 . C. 7 . D. 9 . Lời giải:
Đặt t  cos x, x  
 ; . Ta có bảng biến thiên (*)
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 41
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia t  1  ;1.   f t  2 (1)
Phương trình đã cho trở thành 2
f t  f t    2  0    f  t .  1  (2)
Từ bảng biến thiên của đề bài, với t  1
 ;1 ta có nghiệm của phương trình (1) là t a 1  ;0
hay t b0;1 và nghiệm của phương trình (2) là t  1 .
Từ bảng biến thiên (*), ta có:
x x    ;0 1  
t a 1;0   .
x x  0;  2  
x x    ;0 3  
t b 0;1   .
x x  0;  4  
t  1  x  0.
Vậy, phương trình đã cho có 5 nghiệm phân biệt thuộc khoảng    ; .
Chọn đáp án A.
Câu 39: Cho hàm số f x liên tục trên có bảng biến thiên như sau:
Số nghiệm thuộc đoạn    ;  
 của phương trình f  2
2 cos x  3  3 là A. 8 . B. 2 . C. 6 . D. 4 . Lời giải: Đặt 2
t  2 cos x  3 , vì x     ;    nên t   3;  1  . 
 Ta có phương trình f t  3 , t   3;  1     Dựa vào BBT ta có:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 42
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Vậy f t  3  t a, a 3  , 2     Ta có: 2
2 cos x  3  a , a  3  , 2   . Suy ra 2 1
cos x b , b0; .  2  cosx b  2  Suy ra  với b  0,     cos x    b 2  
Với mọi x     ;  
 thì phương trình cos x b có 2 nghiệm và phương trình cos x   b có 2
nghiệm. ( Dựa vào đường tròn lượng giác hoặc đồ thị hàm số y  cos x để kiểm tra nghiệm)
Vậy có 4 nghiệm thỏa yêu cầu bài toán.
Chọn đáp án D.
Câu 40: Cho hàm số f x có bảng biến thiên như sau:  5  Số nghiệm thuộc đoạn ; 3 
 của phương trình 4 f cos2x  1  0 là  6  A. 5 . B. 9 . C. 4 . D. 10 . Lời giải:
t a,a;1    1 
t b ,b     1;   2 
Đặt t  cos2x , ta có 4 f t  1  0  f t 1    4   1 
t c ,c    ;1  2  
t d ,d1;     5 
Khảo sát hàm số t  cos2x trên ; 3   . Ta có t  2  sin2x  6  k 5   3 5 
Cho t  0  sin2x  0  x
, k  . Vì x  ; 3    x   ; ; 2 ; ; 3  . 2  6   2 2 
Ta có BBT của hàm t  cos2x như sau:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 43
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Từ BBT trên ta thấy:
Với t a ,a ;  1  phương trình vô nghiệm.  1 
Với t b ,b 1 
 ;   phương trình có 4 nghiệm.  2   1 
Với t c ,c  ;1  phương trình có 5 nghiệm.  2 
Với t d ,d 1;    phương trình vô nghiệm.
Vậy phương trình ban đầu có 9 nghiệm.
Chọn đáp án B.
Câu 41: Cho hàm số trùng phương y f x có đồ thị như hình vẽ bên dưới:
Số nghiệm thuộc 0; 2 
của phương trình f cos2x 1 bằng A. 4 . B. 6 . C. 3 . D. 8 . Lời giải: cos2x  0  
f cos2x  1
cos 2x a  1  VN cos2x  0
Ta có f cos 2x  1        sin 4x  0  f  cos2x  1 
cos 2x b  1  VN sin 2x  0  cos2x  1  
Phương trình sin 4x  0 có 8 nghiệm thuộc 0; 2  .
Chọn đáp án D.
Câu 42: Cho hàm số y f x xác định trên và có bảng biến thiên như sau: x –∞ 1  0 1 +∞ y + 0 – 0 + 0 – 1 1 y  0 
Số nghiệm thuộc đoạn 0;  
 của phương trình f f cos2x  0 là A. 4 . B. 2. C. 3. D. 8.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 44
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải: f  os
c 2x  a
Dựa và bảng biến thiên ta có f x  1, x  
và f f  os
c 2x  0   f  os
c 2x  a với a  1.  f   os c 2x  0
Với f cos2x  a thì phương trình vô nghiệm.
Với f cos2x  a  cos 2x  b với b  1 nên phương trình vô nghiệm.      
Với f cos2x  0 x 0;   3
 cos2x 0  2x   k  
x   k  x  ;x  . 2 4 2 4 4
Vậy phương trình f f cos2x  0 có 2 nghiệm thuộc đoạn 0;    .
Chọn đáp án B. Câu 43: Cho hàm số 4 2
y ax bx c,a;b;c  ,a  0 có bảng biến thiên như hình vẽ: x  2 0 2  y  0  0  0    y 2 2 2 4 2
Số nghiệm của phương trình a f
 x  bf
 x  c  0  là A. 11. B. 10. C. 9. D. 12. Lời giải: b d c a
f x  a; 2
  Dùa vµo t­¬ng giao fxm
Kh«ng cã nghiÖm.  f x m      4 2
f xb  2;0 Dùa vµo t­¬ng giao   Cã 4 nghiÖm ph©n biÖt.
Ta có: a f x  b f x  c  0       
f x  c0;2 Dùa vµo t­¬ng giao fxm
Cã 4 nghiÖm ph©n biÖt.        2; 
Dùa vµo t­¬ng giao f xm f x d
Cã 2 nghiÖm ph©n biÖt.
Rõ ràng 10 nghiệm này phân biệt.
Chọn đáp án B.
Câu 44: Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên như hình vẽ:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 45
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x  1  0 2  4 y  0  0  0    y 2 2 4   5 
Số nghiệm thuộc đoạn  ; 
 của phương trình f  2 5
cos x  cos x  1 là  2 2  A. 11. B. 10. C. 9. D. 12. Lời giải:   5   1  Đặt 2
u  cos x  cos x. Với x   ;   thì u  ;2 
 (Lập bảng biến thiên hoặc sử dụng  2 2   4  MTCT)   1 
u a   ;  v« nghiÖm   4    1 1 
Lúc đó: f u   f u   u b   ; 0 5 1  .   4 5 
u c0;2 
u d2;  v« nghiÖm
Chọn giá trị để tính!    5 
Dïng ®­êng trßn l­îng gi¸c
cos x  0,78 
 4 nghiÖm ph©n biÖt   ;   1  1    2 2  +) 2
u  cos x  cos x     ; 0    6  4     5 
Dïng ®­êng trßn l­îng gi¸c
cos x  0,21 
 4nghiÖm ph©n biÖt   ;     2 2 
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 46
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
cosx  1,6v« nghiÖm  +) 2
u  cos x  cos x  10; 2     5 
Dïng ®­êng trßn l­îng gi¸c cos x  0
 ,6 
2nghiÖm ph©n biÖt   ;      2 2 
Rõ ràng 10 nghiệm này phân biệt.
Chọn đáp án B.
Câu 45: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ sau:
Số nghiệm của phương trình f sin x  cos x  2  0 trên đoạn 0; 2    là A. 5. B. 4. C. 3. D. 2. Lời giải:
Ta có: f sin x  cos x  2  0  f sin x  cos x  2     
sin x  cos x  2 sin x    a  2  V« nghiÖm   4            9 2 sin  x    1 
. Với x  0; 2    thì x   ; .     4  4  4 4       2 sin x   b   0;1   4          1  2 sin x    1  sin x       4    4  2 Lúc đó:
Dïng ®­êng trßn l­îng gi¸c     4 nghiệm phân            x    b  b 1 2 sin 0;1 sin x     0;    4    4  2  2   9  biệt trên ; .    4 4 
Chọn đáp án B.
Câu 46: Cho hàm số   3 2
f x ax bx bx c có đồ thị như hình vẽ:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 47
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia     Số nghiệm nằm trong 
; 3  của phương trình f cos x  1  cos x  1 là  2  A. 2 . B. 3 . C. 5. D. 4. Lời giải:
x a;0 
Từ đồ thị ta có f x  x  x b0;1 x  2 
cosx  1  a;0
cosx a  1  t  ; 1  (VN) 1    
Do đó f cos x  1  cos x  1  cos x  1  b0;1
 cos x b  1  t  1  ;0 (1) 2     cos x  1  2  cos x  1 (2)     
Dựa vào đường tròn lượng giác, phương trình (1) có 3 nghiệm nằm trong  ; 3  .  2     
Phương trình (2) có 2 nghiệm nằm trong  ; 3  .  2     
Vậy phương trình ban đầu có tất cả 5 nghiệm nằm trong  ; 3  .  2 
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 48
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Chọn đáp án C.
Câu 47: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt
của phương trình f  3
x f x  1  0 là A. 8 . B. 5 . C. 6 . D. 4 . Lời giải: f  3
x f x  1  0  f  3
x f x  1  * 3
x f x  0 1 
Dựa vào đồ thị, * 3
 x f x  a 2 2  a  3 .  3 x f
x  b 3 5  b   6   x  0 x  0 1     . f  x  0 x x 5  x    6  1  1  a
Xét 2 : dễ thấy x  0 không là nghiệm. Với x  0 , 2  f x  . 3 x a
Vẽ đồ thị hàm số f x 
2  a  3 và hàm số y f x trên cùng hệ trục tọa độ suy ra 3   x
phương trình có 2 nghiệm.
Tương tự xét phương trình 3 phương trình có 2 nghiệm.
Vậy phương trình đã cho có 6 nghiệm.
Chọn đáp án C.
Câu 48: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình f  3
x f x  1  0 là A. 6 . B. 4 . C. 5 . D. 8 . Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 49
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 3
x f x  a  3   a  1   1  Ta có f  3
x f x  1  0  f  3 x f x 3  1
  x f x  b  5   b  3  
2 , với a,b  0 .  3 x f  x   0 3 m
+ Với m  0 , xét phương trình 3
x f x  m f x  . 3 x m 3  m
Đặt gx 
, gx   0, x   0 . 3 x 4 x
lim g x  lim gx  0 , lim gx   , lim gx   .     x x x0 x0 Ta có bảng biến thiên:
Dựa vào bảng biến thiên và đề bài, suy ra trong mỗi khoảng ;0 và 0;  phương trình
f x  gx có đúng một nghiệm.
Suy ra mỗi phương trình 1 và 2 có 2 nghiệm. x  0 x  0 + Xét 3 3
: x f x  0    
, với c khác các nghiệm của 1 và 2 .  f  x  0 x c  0
Vậy phương trình f  3
x f x  1  0 có đúng 6 nghiệm.
Chọn đáp án A.
Câu 49: Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình bên. Số nghiệm thực phân
biệt của phương trình f  2
x f x  2 là A. 8 . B. 12 . C. 6 . D. 9 . Lời giải: 2
x f x  a 1  2
x f x  b 2 Ta có f  2
x f x  2  0  f  2
x f x  2   
, với a,b,c  0 . 2 x f x   c 3  2 x f  x  0 4 m
+ Với m  0 , xét phương trình 2
x f x  m f x  * . 2   x
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 50
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia m 2  m
Xét hàm số gx 
,m  0 , ta có gx  , x   0 . 2 x 3 x
lim g x  lim gx  0; lim gx  ; lim gx   .    x x x0 x0 Bảng biến thiên:
Dựa vào bảng biến thiên và hình vẽ, suy ra trong mỗi khoảng ;0 và khoảng 0; 
phương trình f x  gx có đúng một nghiệm. Do đó phương trình * có đúng 2 nghiệm.
Chọn đáp án D.
Câu 50: Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình f  2
x f x  2  0 là A. 6 . B. 12 . C. 8 . D. 9 . Lời giải: Ta có f  2
x f x    f  2 2 0
x f x  2 . 2
x f x  0 1  2
x f x  a 1
  a  0 2
Dựa vào đồ thị ta thấy:  . 2
x f x  b 3   b    2 3  2 x f
x  c 4
  c  3 4 x  0 x  0  Giải 1     
(có 3 nghiệm phân biệt). f  xx x1   0 x x  2 a
Giải 2  f x  . 2 x a a
Vẽ đồ thị hàm số y
lên cùng hệ tọa độ Oxy . Ta thấy đồ thị hàm số y  cắt đồ thị hàm 2 x 2 x
số y f x tại 2 nghiệm phân biệt.
Tương tự với 3 và 4 đều có 2 nghiệm phân biệt.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 51
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Vậy có phương trình f  2
x f x  2 có 9 nghiệm phân biệt.
Chọn đáp án D.
Câu 51: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt
của phương trình f  5
x f x  2  0 là A. 8 . B. 5 . C. 6 . D. 4 . Lời giải: f  5
x f x  2  0  f  5
x f x  2  * 5
x f x  0 1 
Dựa vào đồ thị, * 5
 x f x  a 2  1   a  0 .  5
x f x  b 3  3   b  2      x  0 x  0 1     . f  x  0 x x 3   x  2    1  1  a
Xét 2 : dễ thấy x  0 không là nghiệm. Với x  0 , 2  f x  . 5 x a
Vẽ đồ thị hàm số f x  1
  a  0 và hàm số y f x trên cùng hệ trục tọa độ suy ra 5   x
phương trình có 2 nghiệm. Tương tự xét phương trình 3 phương trình có 2 nghiệm.
Vậy phương trình đã cho có 6 nghiệm.
Chọn đáp án C.
Câu 52: Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt 2
của phương trình f x  2 f x  3  0 là
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 52
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. 8 . B. 6 . C. 9 . D. 12 . Lời giải: 2
f x  2 2
f x  3  0  f x  2 f x  3 *
x  22 f x  0 
x  22 f x   2 a 0
Ta có: f x  2 f x  3    .
x  22 f x  b  0  
x  22 f x  c  0    2 x 2 2
Xét phương trình: x  2 f x  0  
mà f x  0 có hai nghiệm  x  2 . f x  0 f  x   0 có ba nghiệm. 2
Xét phương trình: x  2 f x  a  0 a Do x  2 2
 0 ; x  2 không là nghiệm của phương trình  f x    x  2 0 2 a 2  a
Xét gx   gx  2   x  2 x  23 Bảng biến thiên: a
Từ bảng biến thiên với f x  0  f x   có 2 nghiệm. x  2 2 2 2
Tương tự: x  2 f x  b và x  2 f x  c b,c  0 mỗi phương trình cũng có hai nghiệm. 2
Vậy số nghiệm của phương trình f x  2 f x  3 là 9 nghiệm.
Chọn đáp án C.
Câu 53: Cho hàm số y f x có đồ thị như hình vẽ sau:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 53
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Số nghiệm thực của phương trình f f x   f x  0 là A. 20 . B. 24 . C. 10 . D. 4 . Lời giải:
Đặt f x  t  0 . Khi đó phương trình trở thành: f t  t ,1 .
Từ đồ thị hàm số ta có:
t a ,0  a  1 
t b ,a b  1
Phương trình 1 có 4 nghiệm 
t c ,1  c   2
t d,2   d
Khi đó các phương trình f x  a , f x  b , f x  c mỗi phương trình có 6 nghiệm phân biệt
không trùng nhau. Phương trình f x  d có 2 nghiệm phân biệt không trùng với nghiệm của 3 phương trình trên.
Vậy phương trình đã cho có 20 nghiệm phân biệt.
Chọn đáp án A. DẠNG 2: BÀI TOÁN THAM SỐ
Câu 54: Cho hàm số y f x xác định trên  \ 
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f x  m có ba nghiệm thực phân biệt.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 54
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. 1; 2   . B.  1  ;2 . C.  1  ;2 . D. ; 2 . Lời giải:
Dựa vào bảng biến thiên đã cho, phương trình f x  m có ba nghiệm phân biệt khi và chỉ
khi 1  m  2 hay m 1
 ;2 vì lúc đó, đường thẳng y m cắt đồ thị hàm số y f x tại ba điểm phân biệt.
Chọn đáp án B. Câu 55: Cho hàm số 4 2
y  x  2x có đồ thị như hình bên dưới:
Tìm tất cả các giá trị thực của tham số m để phương trình 4 2
x  2x m có bốn nghiệm thực phân biệt A. m  0 . B. 0  m  1 . C. 0  m  1 . D. m  1. Lời giải:
Số nghiệm thực của phương trình 4 2
x  2x m chính là số giao điểm của đồ thị hàm số 4 2
y  x  2x và đường thẳng y m . Dựa vào đồ thị suy ra 4 2
x  2x m có bốn nghiệm thực
phân biệt khi 0  m  1.
Chọn đáp án B.
Câu 56: Cho hàm số y f (x) có bảng biến thiên như sau:
Tập tất cả các giá trị của tham số m để phương trình f (x)  m có ba nghiệm phân biệt là A. (4; ) . B. (; 2) . C. [-2;4] . D. (2; 4) . Lời giải:
+) Số nghiệm của phương trình f (x)  m bằng số giao điểm của đồ thị hàm số y f (x) và
đường thẳng y  . m
+) Dựa vào bảng biến thiên của hàm số y f (x) suy ra f (x)  m có 3 nghiệm phân biệt  m2;4.
Chọn đáp án D.
Câu 57: Tìm tất cả các giá trị của tham số m để phương trình 3 2
x  3x  2  m có ba nghiệm phân biệt.
A. m2;  . B. m; 2   . C. m 2  ;2 . D. m  2  ;2   . Lời giải: Xét hàm số 3 2
y x  3x  2 , 2
y  3x  6x . Lập bảng biến thiên:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 55
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Số nghiệm của phương trình 3 2
x  3x  2  m* bằng số giao điểm của đồ thị hàm số 3 2
y x  3x  2 và đường thẳng y m .
Dựa vào bảng biến thiên suy ra PT (*) có 3 nghiệm phân biệt khi 2  m  2 .
Chọn đáp án C.
Câu 58: Tìm m để đồ thị hàm số 4 2 2
y x  2mx m  1 cắt trục hoành tại 4 điểm phân biệt. m  1  A. m  1 . B. 1  m  1 . C. m  1 . D.  . m   1 Lời giải:
Xét phương trình: 4 2 2
x  2mx m  1  0 * Đặt 2
x tt  0 . Khi đó phương trình (*) trở thành 2 2
t  2mt m  1  0 * * Để đồ thị hàm số 4 2 2
y x  2mx m  1 cắt trục hoành tại 4 điểm phân biệt
 Phương trình (*) có 4 nghiệm phân biệt  phương trình (**) có hai nghiệm phân biệt   0 1   0 m  0    dương  S
  0  2m  0
 m  1  m  1 .    P  0  2 m  1   0 m  1  
Chọn đáp án A. Câu 59: Cho hàm số 4 2
y x  2x  3 có đồ thị hàm số như hình bên dưới. Với giá trị nào của tham số m phương trình 4 2
x  2x  3  2m  4 có hai nghiệm phân biệt? m  0 m  0 1 1 A.   1  . B. 0  m  . C. 1 . D. m  . m     2 m 2  2  2 Lời giải:
Số nghiệm của phương trình 4 2
x  2x  3  2m  4 bằng số giao điểm của đường thẳng
y  2m  4 và đồ thị hàm số 4 2
y x  2x  3 .
Dựa vào đồ thị ta có phương trình 4 2
x  2x  3  2m  4 có hai nghiệm phân biệt khi và chỉ khi m  0 2m  4  4    1 . 2m  4  3 m   2
Chọn đáp án A.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 56
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 60: Hàm số   4 2
f x ax bx c a, b, c   có bảng biến thiên
Có bao nhiêu số nguyên m để phương trình f x  3m có đúng 8 nghiệm phân biệt? A. Vô số. B. 1. C. 4. D. 2. Lời giải:
+) Lấy đối xứng phần đồ đồ thị phía dưới Ox của hàm số y f x qua trục Ox .
+) Bỏ phần đồ thị y f x phía dưới Ox .
Khi đó ta có đồ thị hàm số y f x .
Số nghiệm của phương trình f x  3m là số giao điểm của 2 đồ thị y f x và y m .
Dựa vào bảng biến thiên, ta thấy đồ thị y f x cắt đường thẳng y m tại 8 điểm phân biệt
khi và chỉ khi 0  m  2 . Vì m  nên m  1 .
Chọn đáp án B.
Câu 61: Cho hàm số y f x xác định trên \ 
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
Tất cả giá trị của tham số thực m sao cho đồ thị của hàm số y f x  m cắt trục Ox tại ba điểm phân biệt là A.  2  ;1 . B.  1  ;2 . C. 1; 2   . D.  2  ;1. Lời giải:
Xét phương trình hoành độ giao điểm: f x  m  0  f x  m * .
Số giao điểm giữa đường thẳng y  m và đồ thị y f x cũng chính là số nghiệm của phương trình * .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 57
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Dựa vào bảng biến thiên ta thấy đường thẳng y  m cắt đồ thị y f x tại ba điểm phân biệt
khi và chỉ khi 1  m  2 hay 2  m  1 . Vậy 2  m  1 .
Chọn đáp án D.
Câu 62: Cho hàm số y f (x) xác định, liên tục trên
và có bảng biến thiên như sau:
Tìm tất cả các giá trị thực của m để phương trình f (x)  1  m có đúng hai nghiệm.
A. m  0, m  1 . B. 2   m  1  .
C. m  1, m  2 .
D. m  1, m  2 . Lời giải: m  1  1  m  2 
Ta có f (x)  1  m f (x)  1  . m  
Để phương trình có hai nghiệm thì  . m  1  0 m  1   
Chọn đáp án D.
Câu 63: Đường cong trong hình vẽ là đồ thị của hàm số 4 2
y x  2x  2 . Tìm tất cả các giá trị thực của
tham số m để phương trình 4 2
x  2x m có 4 nghiệm phân biệt. A. m  2 . B. 1  m  0 . C. m  3 .
D. 3  m  2 . Lời giải:
Phương trình đã cho tương đương 4 2
x  2x  2  m  2 1 .
Số nghiệm của phương trình 1 chính là số giao điểm của đường thẳng d : y m  2 (song
song hoặc trùng với trục hoành) và đồ thị hàm số 4 2
(C) : y x  2x  2 .
Do đó 1 có 4 nghiệm phân biệt khi d cắt C tại 4 điểm phân biệt.
Dựa vào đồ thị suy ra 3  m  2  2  1  m  0 .
Chọn đáp án B.
Câu 64: Cho hàm số y f x xác định trên  \ 
1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 58
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Số giá trị nguyên của tham số m để phương trình f x  m có 3 nghiệm phân biệt là A. 1 . B. 0 . C. 3 . D. 2 . Lời giải:
Ta có số nghiệm của phương trình f x  m bằng số giao điểm của đồ thị hàm số y f x và
đường thẳng y m .
Do đó, dựa vào bảng biến thiên ta thấy, phương trình f x  m có ba nghiệm phân biệt khi và
chỉ khi 0  m  3 . Kết hợp điều kiện m  suy ra m 1;  2 .
Vậy có 2 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Chọn đáp án D.
Câu 65: Cho hàm số y f x có bảng biến thiên như sau:
Tập hợp tất cả các giá trị thực của tham số m để phương trình f x  m  0 có hai nghiệm phân biệt là A.  ; 2 . B. 1  ;2  . C. 1; 2 . D. 2;   . Lời giải:
f x  m  0  f x  m
Phương trình f x  m có hai nghiệm phân biệt  đồ thị hàm số y  m cắt đồ thị hàm số
y f x tại hai điểm phân biệt  2  m  1  1  m  2 . Vậy m 1; 2  .
Chọn đáp án B. Câu 66: Cho hàm số 3
y x  3x  2 có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị thực của tham số m để phương trình 3
x  3x  2  2m  0 có ba nghiệm thực phân biệt. A. 0  m  4 . B. 0  m  2 . C. 0  m  4 . D. 0  m  2 . Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 59
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Số nghiệm của phương trình 3
x  3x  2  2m  0 là số giao điểm của đồ thị 3
y x  3x  2 và
đường thẳng y  2m .
Nhìn vào đồ thị suy ra phương trình có 3 nghiệm phân biệt  0  2m  4  0  m  2 .
Chọn đáp án B.
Câu 67: Cho hàm số f x 3 2
x  3x . Tính tổng tất cả các giá trị nguyên của m để đồ thị hàm số
g x  f x   m cắt trục hoành tại 4 điểm phân biệt. A. 3. B. 10. C. 4. D. 6. Lời giải:
Xét hàm số f x 3 2
x  3x . Ta có đồ thị hàm số y f x như sau:
Như ta đã biết: để vẽ đồ thị hàm số y f x  từ đồ thị y f x ta thực hiện:
Bước 1: Giữ nguyên phần đồ thị y f x gồm các điểm bên phải và các điểm nằm trên trục
Oy ; bỏ phần đồ thị bên trái trục Oy .Ta được phần đồ thị P 1
Bước 2: Lấy đối xứng phần đồ thị P qua trục Oy ta được phần đồ thị P 1 2
Khi đó: Đồ thị y f x  bao gồm đồ thị P và P . 1 2
Từ đó ta có đồ thị hàm số y f x  3 2
x  3 x như sau:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 60
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Để đồ thị hàm số gx  f x   m cắt trục hoành tại 4 điểm phân biệt thì phương trình gx  0
có 4 nghiệm phân biệt. Do đó phương trình f x   m có 4 nghiệm phân biệt hay đường
thẳng y  m cắt đồ thị hàm số y f x  3 2
x  3 x tại 4 điểm phân biệt.
Dựa vào đồ thị hàm số y f x  suy ra bài toán thỏa mãn khi và chỉ khi
4  m  0  0  m  4 . Kết hợp yêu cầu đề bài m , do đó m1;2;  3 .
Chọn đáp án D.
Câu 68: Cho hàm số y f x có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để phương trình f  3
x  3x  m có 6 nghiệm phân biệt thuộc đoạn [  1; 2]? A. 3 . B. 2 . C. 6 . D. 7 . Lời giải: Đặt 3
t x  3x , với x [  1; 2] ta có bảng biến thiên
Với t (  2; 2] thì có 2 nghiêm x [  1; 2]
Để phương trình có 6 nghiệm thì phương trình f t  m có 3 nghiệm t (  2; 2]
Dựa vao đồ thị ta có m  0; m  1 .
Chọn đáp án B. 1
Câu 69: Tìm tất cả các giá trị của tham số m để phương trình 3 2
cos x  3cos x  5 cos x  3  2m  0 có 3
đúng bốn nghiệm thuộc đoạn 0 ; 2 .   3 1 1 3 1 3 3 1 A.   m   . B.  m  . C.  m  . D.   m   . 2 3 3 2 3 2 2 3 Lời giải:
Đặt cos x t  0 1 Phương trình: 3 2
cos x  3cos x  5 cos x  3  2m  0 có đúng bốn nghiệm thuộc đoạn 0 ; 2    3  1 3 2
t  3t  5t  3  2m  0 có 1 nghiệm t 0;1 3
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 61
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1 3 2
t  3t  5t  3  2
m có 1 nghiệm t 0;1 3 1 t  1
Xét hàm số f t 3 2
t  3t  5t  3 với t 0;1. Ta có f t 2
t  6t  5  0   3 t   5 Bảng biến thiên: x 0 1 5 y' + 2 y 3 3 2 3 1 Vậy 3   2
m     m  . 3 2 3
Chọn đáp án C.
Câu 70: Cho đồ thị của hàm số 3 2
y x  6x  9x  2 như hình vẽ. y 2 3 O 1 x 2 Khi đó phương trình 3 2
x  6x  9x  2  m ( m là tham số) có 6 nghiệm phân biệt khi và chỉ khi. A. 2  m  2 . B. 0  m  2 . C. 0  m  2 . D. 2  m  2 . Lời giải:
+) Đồ thị hàm số 3 2
y x  6x  9x  2 có được bằng cách biến đổi đồ thị C hàm số 3 2
y x  6x  9x  2 :
- Giữ nguyên phần đồ thị C nằm trên trục hoành.
- Lấy đối xứng phần đồ thị của C phần dưới trục hoành qua trục hoành.
- Xóa phần đồ thị còn lại của C phía dưới trục hoành. y
yx = x3 6∙x2 + 9∙x 2 2
y = m x 1
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 62
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
+) Số nghiệm của phương trình 3 2
x  6x  9x  2  m là số giao điểm của đồ thị hàm số 3 2
y x  6x  9x  2 và đồ thị hàm số y m . Để phương trình có 6 nghiệm phân biệt thì điều
kiện cần và đủ là 0  m  2 .
Chọn đáp án B.
Câu 71: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. y y = f(x) -4 O x Có bao nhiêu giá trị nguyên của tham số m để phương trình
 3sin x  cosx 1  f    f  2
m  4m  4 1 có nghiệm?
2cos x  sin x   4  A. 3 . B. 4 . C. 5 . D. Vô số. Lời giải:
3sin x cosx  1 Đặt t   2t  
1 cos x  t  3sinx  1 4t * .
2 cos x  sinx  4 2 2 2 9
Phương trình * có nghiệm  2t  1  t  3  4t   1    t  1 . 11 Suy ra 0  t  1.
Từ đồ thị y f x ta có
* y f x đồng biến trên 0;    2 * 2
m  4m  4  m  2  0;    . * t  0;   
 3sin x  cosx 1  Nên f    f  2
m  4m  4  f t   f  2
m  4m  4 2
t m  4m  4 Phương
2cos x  sin x   4 
trình 1 có nghiệm  2
0  m  4m  4  1 2
m  4m  4  1  3  m  1 .
Do m  m 3  ; 2  ;  1 .
Chọn đáp án A.
Câu 72: Cho hàm số y f x liên tục trên có đồ thị như hình vẽ.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 63
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Có bao nhiêu giá trị nguyên của n để phương trình f  2
16 cos x  6 sin 2x  8  f nn  1 có nghiệm x  ? A. 10 . B. 4 . C. 8 . D. 6 . Lời giải:
Dựa vào đồ thị hàm số ta thấy hàm số y f x đồng biến trên . Do đó: f  2 x
x    f nn   2 16 cos 6 sin 2 8
1  16 cos x  6 sin 2x  8  nn  1 1  cos 2x  16.
 6sin2x  8  nn  1  8cos2x  6sin2x nn  1 2 2 2
Phương trình có nghiệm x  2 2 2  
n n   2 8 6
1  n n  1  100
nn  2 1  1  0
n n  10  0     2 1 41 1 41           . n  n   n n 10 0 n 2 1  10
n n 10  0 2 2
Vì n nên n 3  ; 2; 1;0;1;  2 .
Chọn đáp án D.
Câu 73: Cho hàm số y f x có đồ thị như hình vẽ. 1  x
Có bao nhiêu số nguyên m để phương trình f  1  x   
m có nghiệm thuộc đoạn 2 ; 2   ? 3  2  A. 11 . B. 9 . C. 8 . D. 10 . Lời giải: x Đặt t   1 , khi 2
  x  2 thì 0  t  2 . 2 1
Phương trình đã cho trở thành
f t  2t  2  m f t  6t  6  3m . 3
Xét hàm số gt  f t  6t  6 trên đoạn 0; 2   .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 64
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Ta có gt  f t  6 . Từ đồ thị hàm số y f x suy ra hàm số f t đồng biến trên khoảng
0;2 nên ft  0, t
 0;2  gt  0, t
 0;2 và g0  1
 0 ; g2  12 .
Bảng biến thiên của hàm số g t trên đoạn 0; 2  
Phương trình đã cho có nghiệm thuộc đoạn 2 ; 2 
 khi và chỉ khi phương trình gt  3m có 10
nghiệm thuộc đoạn 0 ; 2   hay 10
  3m 12    m  4 . 3
Mặt khác m nguyên nên m 3  ; 2; 1;0;1;2;3; 
4 . Vậy có 8 giá trị m thoả mãn bài toán.
Chọn đáp án C.
Câu 74: Cho hàm số y f x có bảng biến thiên dưới đây:
Để phương trình 3 f 2x  1  m  2 có 3 nghiệm phân biệt thuộc 0;1 
 thì giá trị của tham số m
thuộc khoảng nào dưới đây? A. ; 3 . B. 1;6 . C. 6;  . D.  3;  1 . Lời giải:
Đặt t  2x 1. Ta thấy t là hàm đồng biến theo x và x 0;  1  t  1  ;  1 . m  2
Do đó phương trình 3 f 2x  
1  m  2 có 3 nghiệm phân biệt thuộc 0;  1  f (t)  có 3 3
nghiệm phân biệt thuộc 1;  1 . m  2
Dựa vào bảng biến thiên suy ra 1  m  5. 3
Chọn đáp án B.
Câu 75: Cho hàm số f (x) liên tục trên
và có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để phương trình f  2  x x  2 3 4 6 9
 1 m  0 có nghiệm là
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 65
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. 6 . B. 4 . C. 5 . D. 7 . Lời giải: Đặt t   x x     x  2 2 3 4 6 9 3 4 1 3
1  t 1; 3   .  
Dựa vào đồ thị ta có khi t   1  ;3 
 thì f t 1  5;     .  2 
Khi đó phương trình f  2  x x  2 3 4 6 9
 1 m  0 có nghiệm khi và chỉ khi phương trình 1 1 f t 2  1
  m có nghiệm thuộc 1; 3   2 2  5   1
  m      m  4  2   m  2 . 2 2
Kết hợp điều kiện m  m 2  ; 1; 0; 1;  2 .
Chọn đáp án C.
Câu 76: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. Tập hợp các giá trị thực của
tham số m để phương trình f  2 4  x  
1  m có nghiệm là A. 2; 0.   B. 4; 2  .   C. 4; 0.   D. 1;1.   Lời giải: x Đặt 2
t  4  x  1 với x   2  ;2    t' 
; t'  0  x  0 2 4  x
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 66
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Khi đó ta đi tìm m để phương trình f t  m có nghiệm trên 1;1  
Dựa vào đồ thị trên 1;1 
 , để phương trình có nghiệm  4  m  0.
Chọn đáp án C.
Câu 77: Cho hàm số bậc ba    3 2 y
f x ax bx cx d có đồ thị như hình bên dưới.
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
f x  m  5 f x  4m  4  0 có 7 nghiệm phân biệt? A. 1. B. 2. C. 3. D. 4. Lời giải:
Từ đồ thị hàm số y f x , vẽ được đồ thị hàm số y f x như sau:
f x  4 1 Ta có 2
f x  m  5 f x  4m  4  0  
f x  m  1 2 
Từ đồ thị hàm số y f x suy ra phương trình (1) có 3 nghiệm phân biệt.
Vậy để phương trình đã cho có 7 nghiệm phân biệt thì (2) có 4 nghiệm phân biệt và khác với
các nghiệm của (1)  0  m  1  4  1  m  3 . Do đó có 3 giá trị nguyên của m .
Chọn đáp án C. x  1
Câu 78: Tìm tất cả các giá trị thực của tham số m để đường thẳng (d) : y  x m cắt đồ thị (C) : y  1  x
tại 2 điểm phân biệt A, B sao cho AB  2 6.
A. m  2; m  2 .
B. m  4; m  4 . C. m  2 . D. m  4 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 67
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải: x  1 Xét phương trình:
m x x  1  (m x)(1  x) . 1  x 2
x  1  m mx x x 2
x  (m  2)x  1 m  0(1) .
Để đường thẳng (d) cắt đồ thị (C) tại 2 điểm phân biệt A, B . 2          m 4m 4 4( 1 ) m 0
(1) có 2 nghiệm phân biệt khác 1   1   
(m  2)  1  m  0 2 m  8  0  
luôn đúng với mọi m  .  2   0 2 2
Gọi Ax m x Bx m x   AB  x x x x  2 ; ; ; ;
AB AB  2. x x . A A B B B A A BB A
x x m  2
x , x là nghiệm của (1). Nên theo hệ thức viét ta có A BA B x .x  1   m A B Ta có: AB
 x x 2 2 24 2.  24 x x x x      B A 2 2 4 24 B A A B   .   2
x x 2  4x x  12  m  2  4m  1  12 2
m  4  0  m  2 . B A A B
Chọn đáp án A.
Câu 79: Có bao nhiêu giá trị nguyên của tham số m để đường thẳng y  x m cắt đồ thị hàm số x  2 y
tại hai điểm phân biệt A , B sao cho OA OB  4? x  1 A. 2. B. 1. C. 0. D. 3. Lời giải: x  2 x  1 Ta có:
 x m   2 x  1
x mx m  2  0   1 x  2
Đường thẳng y  x m cắt đồ thị hàm số y
tại hai điểm phân biệt A , B x  1
 phương trình (1) có hai nghiệm phân biệt khác 1  1   0  
 thỏa mãn với mọi số thực . m 2
m  4m  8  0 x  2
Với mọi số thực m đường thẳng y  x m cắt đồ thị hàm số y
tại hai điểm phân biệt x  1
Ax ; x m , Bx ;  x  m , trong đó x ,x là hai nghiệm phân biệt của (1). 2 2  1 1  1 2 2 Ta có: 2
OA x  x m  2 2 x mx  2
m  2m  2 2 2
m m  2m  4 . 1 1 1 1 Tương tự ta được: 2
OB m  2m  4 . m  0 Do đó: 2
OA OB  4  m  2m  0  
. Vậy có 2 giá trị thỏa mãn yêu cầu đề bài. m   2
Chọn đáp án A. 2x
Câu 80: Tìm giá trị thực của tham số m để đường thẳng d : y x m  2 cắt đồ thị hàm số y  Cx  1
tại hai điểm phân biệt A và B sao cho độ dài AB ngắn nhất. A. m  3. B. m  3. C. m  1. D. m  1.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 68
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải:
Tập xác định: D   \  1 . 2x
Xét phương trình: x m  2  x  1 2  (
g x)  x  m  1 x m  2  0 1 . x  1
Để d cắt C tại hai điểm phân biệt A và B thì (1) có hai nghiệm phân biệt x  1 2
m m   m   2 2 1 4
2  m  2m  9   0      g    m . 1  2    0
Gọi x , x là hai nghiệm của 1 thì Ax ; x m  2 , Ax ; x m  2 . 2 2  1 1  1 2 2 2 2 2 Khi đó 2 AB 2x x 2  x x 4x x       2  m 1 4 m 2  2  m 1 8         16. 1 2   1 2 1 2            
Vậy AB ngắn nhất khi m  1 .
Chọn đáp án C.
Câu 81: Cho hàm số f x 3 2
x  3x mx  1. Gọi S là tổng tất cả giá trị của tham số m để đồ thị hàm số
y f x cắt đường thẳng y  1 tại ba điểm phân biệt A0; 
1 , B, C sao cho các tiếp tuyến của
đồ thị hàm số y f x tại B, C vuông góc với nhau. Gía trị của S bằng 9 9 9 11 A. . B. . C. . D. . 2 5 4 5 Lời giải: x  0 Xét phương trình: 3 2
x  3x mx  1  1  x 2
x  6x m  0   2
x  6x m   0  *
Để đồ thị hàm số y f x cắt đồ thị hàm số y  1 tại ba điểm phân biệt A0; 
1 , Bx ; y , 1 1  m  0 m  0 
C x ; y thì phương trình * có hai nghiệm phân biệt khác 0     . 2 2  9    9  4m  0 m   4
x x  3  Theo hệ thức Viet, ta có 1 2  .
x .x m 1 2
Để tiếp tuyến của đồ thị hàm số y f x tại B, C vuông góc với nhau thì
f x . f x   1    2
3x  6x m. 2
3x  6x m  1  1 2 1 1 2 2  2 2
 9x x  18x x x x   3m 2 2
x x   6mx x  2
 36x x m  1  0 1 2 1 2 1 2 1 2 1 2 1 2  9  65 m    2       8 9 65 9 65 9 4m 9m 1 0  S    .   8 8 4 9 65 m   8
Chọn đáp án C.
Câu 82: Có bao nhiêu giá trị nguyên của tham số m  2  018;2019 
 để đồ thị hàm số 3
y x  3mx  3 và
đường thẳng y  3x  1 có duy nhất một điểm chung? A. 1 . B. 2019 . C. 4038 . D. 2018 . Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 69
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 3 x  3x  2 Xét phương trình: 3
x  3mx  3  3x  1 3
x  3x  2  3mx  3m  (1). x x  3x  2 2 2 2x  2
Xét hàm f x 3 2 
x  3  ; f x 3  2x  
; f x  0  x  1 . x x 2 2 x x Bảng biến thiên:
Yêu cầu bài toán  m  0 . Mà m  và m  2  018;2019 
 nên có 2018 giá trị thỏa mãn.
Chọn đáp án D.
Câu 83: Có bao nhiêu giá trị thực của tham số m để phương trình x  1x  2x m  0 có 3 nghiệm
phân biệt lập thành cấp số nhân tăng? A. 4 . B. 3 . C. 2 . D. 1 . Lời giải: x  1 
Ta có: x  1x  2x m  0  x  2  x m
Phương trình có 3 nghiệm phân biệt lập thành cấp số nhân tăng khi và chỉ khi m  2  1; 2;2  2 1.2   m
m   2  1; 2;2  l 2 1.  m  2   .Vậy có 3 giá trị m  4   1; 2; 4 m thỏa mãn.  2 2.m  1   1 1 m   ;1;2  2 2
Chọn đáp án B.
Câu 84: Gọi S là tập tất cả các giá trị thực của tham số m để phương trình 3 2
2x  3x  2m  1 có đúng
hai nghiệm phân biệt. Tổng các phần tử của S bằng 1 3 5 1 A.  . B.  . C.  . D. . 2 2 2 2 Lời giải: Xét hàm số: 3 2
y  2x  3x 2
y  6x  6x y  0  x  0  x  1 . Bảng biến thiên: C 3 2
:y  2x  3x
Số nghiệm của phương trình đã cho bằng số giao điểm của hai đồ thị: 
d :y  2m  1
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 70
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia m  1  2m  1  1   1 
Phương trình đã cho có hai nghiệm phân biệt     1  S   1;   . 2m  1  0 m     2   2
Chọn đáp án B. x  4
Câu 85: Giá trị k thỏa mãn đường thẳng d : y kx k cắt đồ thị H : y 
tại 2 điểm phân biệt A 2x  2
và B cùng cách đều đường thẳng y  0 . Khi đó k thuộc khoảng A. 2;  1 . B. 1; 2 . C.  1  ;0 . D 0;1 . Lời giải: x  4 Xét phương trình:
kx k x  1 2
 2kx x  2k  4  0 x  1 2x  2
Đường thẳng d cắt H tại 2 điểm phân biệt A , B khi và chỉ khi phương trình có 2 nghiệm  2  3   2 2 x (  1
 )  2k(2k  4)  0
4k  8k  1  0  phân biệt khác 1 2      
2k 1 2k  4  0 3  0  2  3 x   2
Gọi x , x là 2 nghiệm phương trình ta có Ax ; kx k và Bx ; kx k vì A , B cùng cách B BA AA B
đều đường thẳng y  0 nên kx k  (
kx k)  x x  2. A B A B 1 1 1 Mà x x   2    k     . A B  1;0 2k 2k 4
Chọn đáp án C. x
Câu 86: Cho hàm số y
C và đường thẳng d : y  x m . Gọi S là tập hợp các số thực m để x  1
đường thẳng d cắt đồ thị C tại hai điểm phân biệt A,B sao cho tam giác OAB (O là gốc tọa
độ) có bán kính đường tròn ngoại tiếp bằng 2 2 . Tổng các phần tử của S bằng A. 8. B. 4 . C. 1 . D. 2 . Lời giải: 2 x
x mx m  0 (*) Xét phương trình:
 x m   . x  1 x  1
Để đường thẳng d cắt đồ thị C tại hai điểm phân biệt A,B thì phương trình * phải có hai 2
  m  4m  0 m  4
nghiệm phân biệt khác 1 nên ta có    1    0 m  0.
Gọi x , x là hai nghiệm của phương trình * , ta có x x m . 1 2 1 2
Do đó Ax ; x m A x ; x , Bx ; x m B x ; x 2 2   2 1 1 1   1 2 m
+) OA OB x x  x x 2 2 2 2
 2x x m  2m. +) h d O d O  ,  . 1 2 1 2 1 2 2 1 O . A O . B ABm  6 Ta có SA . B h   2 . R h O . A OB 2
m  2m  4 m   OAB 2 O 4 O R m  2.  
Vậy tổng các phần tử của tập S bằng 4 .
Chọn đáp án B.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 71
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 87: Cho hàm số 4
y x   m   2 3
2 x  3m có đồ thị là (C ) . Tìm m để đường thẳng d : y  1 cắt đồ m
thị (C ) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2. m 1 1
A.   m  1 và m  0
B.   m  1 và m  0 3 2 1 1 1 1 C.   m
và m  0 D.   m  và m  0 2 2 3 2 Lời giải:
Xét phương trình: 4
x   m   2 3 2 x  3m  1  4
x   m   2 3
2 x  3m  1  0 t  1 Đặt 2
t x , t  0 , phương trình trở thành 2
t  3m  2t  3m  1  0 2   t  3m   1
Đường thẳng d : y  1 cắt đồ thị (C ) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2 khi và m
chỉ khi phương trình 2 có hai nghiệm dương phân biệt t , t thỏa mãn 0  t t  4 1 2 1 2 m  0 3m  1  1      . 1 0  3m  1  4    m  1  3
Chọn đáp án A.
Câu 88: Cho hai hàm số 2
y x x  1 và 3 2
y x  2x mx  3 . Giá trị của tham số m để đồ thị của hai
hàm số có 3 giao điểm phân biệt và 3 giao điểm đó nằm trên đường tròn bán kính bằng 3
thuộc vào khoảng nào dưới đây? A. ;  4 . B. 4;  2 . C. 0;   . D.  2  ;0. Lời giải:
Giả sử m là số thực thỏa mãn bài toán. Xét phương trình: 2 3 2 3 2
x x  1  x  2x mx  3  x x  m  1x  2  0 1.
Gọi M x ; y là một trong 3 giao điểm. 0 0  2 2 4 3 2
y x x 1
y x  2x x  2x  1 2 0 0 0 0 0 0 0 0   Ta có:    . 3 2 x x   m 1 3 2 x  2  0
x x m  1 x  2  0 3 0 0 0  0 0   0  
Từ 2 và 3 suy ra 2
y  x  1 3 2 x x  
m1x  2   m  1 2
x  m  1x  3  m  1 2
x m  1 x  3 . 0 0 0 0 0 0 0 0   0 Hay 2 2 2
y x  mx m  1 x  3  m y x  1  m  1 x  3 . 0 0 0   0  0 0    0 Rút gọn ta được 2 2
x y x my m  3  0
4 . Đây là phương trình đường tròn khi 0 0 0 0   2 2  1   m     m  3      0 * .  2   2  2 2  1   m
Với điều kiện * thì M x ; y thuộc đường tròn có bán kính R     m      3 . 0 0   2   2  2 m  1 m  2  3 3 Theo đề bài 2 R  3 
m  3  9  m  4m  23  0   . 4 m  2   3 3 Thử lại.
Với m  2  3 3 thì phương trình 1 có 1 nghiệm. Do đó, m  2  3 3 không thỏa mãn.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 72
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Với m  2  3 3 thì phương trình 1 có 3 nghiệm và cũng thỏa mãn * .
Vậy giá trị m cần tìm là m  2  3 3  4  ;  2 .
Chọn đáp án B.
Câu 89: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá
trị thực của tham số m để phương trình f sin x  m có nghiệm thuộc khoảng 0;  là A. 1; 3  . B.  1  ;1 . C.  1  ;3 . D.  1  ;1  . Lời giải:
Đặt t  sin x . Với x 0;  thì t 0;1 .
Do đó phương trình f sin x  m có nghiệm thuộc khoảng 0;  khi và chỉ khi phương trình
f t  m có nghiệm thuộc nửa khoảng 0;1 .
Quan sát đồ thị ta suy ra điều kiện của tham số m là m  1  ;1  .
Chọn đáp án D.
Câu 90: Cho hàm số y f x liên tục trên và có bảng biến thiên như hình vẽ sau:     
Tập hợp các giá trị m để phương trình f cos 2x  2m  1  0 có nghiệm thuộc khoảng  ;   3 4  là  1  1  1 1  2   2 1  A. 0; .   B. 0; .  C.  ; .  D.  ; .  2   2   4 2   4 4    Lời giải:       1 
Đặt cos 2x t,x ;  t     ;1 .  3 4   2   1 
Yêu cầu đề bài tương đương với phương trình f t  2m  1 có nghiệm t    ;1 .  2  1
Từ bảng biến thiên suy ra yêu cầu  1  2m  1  2  0  m  . 2
Chọn đáp án A.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 73
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 91: Cho hàm số y f (x) xác định, liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của m để phương trình f  2 2.
3  4 6x  9x   m  3 có nghiệm. A. 13 . B. 12 . C. 8 . D. 10 . Lời giải:  2  Với x  0;   , ta có 2 2
0  6x  9x  1  (1  3x)  1 2  0  4
 6x  9x  4   3  2
 3  3  4 6x  9x  1
 . Dựa vào đồ thị đã cho suy ra f  2
3  4 6x  9x  5  ;1   . m  3 Khi đó phương trình f  2 2.
3  4 6x  9x   m  3 có nghiệm  5  
 1  7  m  5 . 2
Do m  nên m 7
 ;  6;  5;  4;  3;  2;  1; 0; 1; 2; 3; 4; 
5 , có 13 giá trị của m thỏa đề.
Chọn đáp án A.
Câu 92: Cho hàm số y f x xác định trên và có đồ thị như hình bên. Có bao nhiêu giá trị nguyên
của tham số m để phương trình: f   4 4
4 sin x  cos x  m  có nghiệm. A. 2 . B. 4 . C. 3 . D. 5 . Lời giải:
Đặt t   4 4 x x 2 4 sin cos
 4  2sin 2x t  2; 4   .
Do đó phương trình f   4 4
4 sin x  cos x  m
có nghiệm  phương trình f t  m có nghiệm trên đoạn 2; 4   .
Dựa vào đồ thị đã cho ta thấy: phương trình f t  m có nghiệm t với t  2; 4 
  1  m  5 .
Vậy m1; 2; 3; 4;  5 .
Chọn đáp án D.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 74
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 93: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
tham số m để phương trình f f sin x  m có nghiệm thuộc khoảng 0;  . A. 1 . B. 2 . C. 3 . D. 4 . Lời giải:
Đặt t f sin x , do x0;   sin x0;1  t   1  ;1   .
Do đó phương trình f f sin x  m có nghiệm thuộc khoảng 0;  khi và chỉ khi phương
trình f t  m có nghiệm thuộc nửa khoảng  1  ;1  .
Quan sát đồ thị đã cho: yêu cầu bài toán  m 1  ;3 .
Chọn đáp án D.
Câu 94: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá
trị nguyên của tham số m để phương trình f sin x  3sin x m có nghiệm thuộc khoảng
0;  . Tổng các phần tử của S bằng A. 8  . B. 10 . C. 6  . D. 5  . Lời giải:
Đặt t  sin x , do x 0;   sin x0;1  t   0;1 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 75
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Gọi  là đường thẳng qua điểm 1;  1 và song song với đường thẳng y  3x có phương trình 1
y  3x  4 .
Gọi  là đường thẳng qua điểm 0;1 và song song với đường thẳng y  3x có phương trình 2
y  3x  1 .
Do đó phương trình f sin x  3sin x m có nghiệm thuộc khoảng 0;  khi và chỉ khi phương
trình f t  3t m có nghiệm thuộc nửa khoảng 0;1  4  m  1 .
Chọn đáp án B.
Câu 95: Cho hàm số y f x có đồ thị như hình vẽ dưới đây:
Tìm số giá trị nguyên của m để phương trình f  2
x  2x  m có đúng 4 nghiệm thực phân biệt  3 7  thuộc đoạn  ;   .  2 2  A. 1 . B. 4 . C. 2 . D. 3 . Lời giải:  3 7  Đặt 2
t x  2x , x   ;    2 2  Bảng biến thiên:  21
Dựa vào bảng biến thiên  t  1;    . Ta có: f  2
x  2x  m 1  f t  m 2 .  4   21  3 7 
Ta thấy, với mỗi giá trị t  1;  
 ta tìm được hai giá trị của x  ;   .  4   2 2   3 7 
Do đó, phương trình 1 có 4 nghiệm thực phân biệt thuộc  ;    2 2     21
Phương trình 2 có hai nghiệm thực phân biệt thuộc 1;     4 
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 76
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
 Đường thẳng y m cắt đồ thị hàm số y f t tại hai điểm phân biệt có hoành độ thuộc  21 1;    .  4 
Dựa vào đồ thị ta thấy có hai giá trị nguyên của m thỏa yêu cầu là m  3 và m  5 .
Chọn đáp án C.
Câu 96: Cho hàm số y f x có đồ thị như hình vẽ dưới đây:
Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình f sin x  m có đúng hai
nghiệm thuộc đoạn 0;    ? A. 4 . B. 7 . C. 5 . D. 6 . Lời giải:
Đặt t  sin x , x  0;  
 thì t  0;1 
 . Để phương trình f sin x  m có đúng hai nghiệm x  0;  
 thì phương trình f t  m có đúng một nghiệm t  0;1 
. Dựa vào đồ thị ta có m  7  ; 2  
 , do m nguyên nên m 7  ; 6  ; 5;  4  ;   3 . Vậy có 5 giá trị.
Chọn đáp án C.
Câu 97: Cho hàm số f x là đa thức và có đồ thị như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số m để phương trình  sinx f   f  2 4
m  8m  17 có nghiệm? A. 3. B. 4. C. 5. D. 6. Lời giải:    sin x 1 4  ; 4 , x     Ta có:   4  .
m  8m17  m 42 2  1  1, m   
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 77
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Để ý rằng trên 0;  , f x đồng biến nên f  sinx   f  2 m m   sinx 2 4 8 17  4
m  8m  17 (*)  
Phương trình (*) có nghiệm 2 1
m  8m  17 
; 4  m5;4;   3. 4 
Chọn đáp án A.
Câu 98: Cho hàm số y f x liên tục trên có đồ thị như hình vẽ bên dưới.  3 7 
Tìm m để phương trình f  2
x  2x   m có đúng 6 nghiệm thực phân biệt thuộc đoạn   ;  ?  2 2 
A. 2  m  3 hoặc f 4  m  5 .
B. 2  m  3 hoặc f 4  m  5 .
C. 2  m  3 hoặc f 4  m  5 .
D. 2  m  3 hoặc f 4  m  5 . Lời giải:  3 7  Đặt t  2
x  2x , với x    ;  .  2 2   3 7 
Ta thấy hàm số ux  2
x  2x liên tục trên đoạn   ;  và 
u  2x  2 ; 
u x  0  x  1 .  2 2  Bảng biến thiên:
Nhận xétrằng với t  0 hoặc  t  21 1
thì phương trình t  2
x  2x có 2 nghiệm phân biệt; 4
với t  1 thì phương trình t  2
x  2x có 3 nghiệm phân biệt; với mỗi t 0;1 thì phương trình t  2
x  2x có 4 nghiệm phân biệt.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 78
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia  21 Với t  2
x  2x phương trình f  2
x  2x   m thành f t  
m, t0;    4    21
Dựa vào đồ thị f ta biện luận số nghiệm của phương trình f t  
m, t0; trong các   4   trường hợp sau TH1: m  2
f t  2  t  1. Khi đó phương trình f  2
x  2x   m có 3 nghiệm phân biệt. TH2: 2  m  3 f t
t a0;  1  m  
. Khi đó phương trình f  2
x  2x   m có 6 nghiệm phân biệt. t b  1;3 TH3: m  3 f t t 0  m  
. Khi đó phương trình f  2
x  2x   m có 4 nghiệm phân biệt. t b  1;3
TH4: 3  m f 4
f t  m t a1; 4 . Khi đó phương trình f  2
x  2x   m có 2 nghiệm phân biệt.
TH5: m f 4 f t t  4  m  
. Khi đó phương trình f  2
x  2x   m có 4 nghiệm phân biệt. t b  1;4
TH6: f 4  m  5
f t  m có 3 nghiệm phân biệt thuộc 1; 5 . Khi đó phương trình f  2
x  2x   m có 6 nghiệm phân biệt. TH7: m  5
f t  m có 2 nghiệm phân biệt thuộc 1; 5 . Khi đó phương trình f  2
x  2x   m có 4 nghiệm phân biệt.  21
TH8: 5  m f    4   21 
f t  m có 1 nghiệm thuộc 1;
 . Khi đó phương trình f  2
x  2x   m có 2 nghiệm phân  4  biệt.  3 7 
Vậy phương trình f  2
x  2x   m có đúng 6 nghiệm thực phân biệt thuộc đoạn   ;  khi  2 2 
và chỉ khi 2  m  3 hoặc f 4  m  5 .
Chọn đáp án A.
Câu 99: Tìm tất cả các giá trị thực của tham số m để đường thẳng y mx m  1 cắt đồ thị của hàm số 3 2
y x  3x x  2 tại ba điểm A , B , C phân biệt sao cho AB BC.  5 
A. m (; 0) [4; ). B. m  . C. m  ;   .
D. m (2; ).  4  Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 79
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Ta có C 3 2
: y x  3x x  2 và d : y mx m  1. Xét phương trình: 3 2 3 2
x  3x x  2  mx m  1  x  3x  1  mx  1  m  0    x   x 1  1 2
x  2x m   1  0   2
x  2x m  1   0   1
Đồ thị C cắt đường thẳng d tại ba điểm A , B , C phân biệt  phương trình 1 có hai 1    m  1  0 m  2 
nghiệm phân biệt khác 1 1        g    m 2 * 1  0 m  2   
Cách 1: Đường thẳng d cắt đồ thị C tại ba điểm phân biệt sao cho AB BC  điểm B chính
là điểm uốn của đồ thị C .
Ta có y  6x  6 , y  0  x  1 , y  1  điểm uốn B1; 
1 d , m  2 . Vậy với m 2;
   thì yêu cầu bài toán được thỏa mãn.
Chú ý. Hàm số bậc ba 3 2
y ax bx cx d a  0 có hoành độ điểm uốn là nghiệm của phương
trình y  0 và điểm uốn chính là tâm đối xứng của đồ thị hàm bậc ba.  
x  1  2  m x    m A
Cách 2: Với m  2 , phương trình   1 2 1   . Ta gán x  1 , với cách gán  B x  1  2   m
x 1 2  mC
như vậy, rõ ràng x x x x , m
  2 . Suy ra AB BC với mọi m  2 . B A C B
Chọn đáp án D.
Câu 100: Tìm tất cả các giá trị thực của tham số m để đường thẳng y  mx cắt đồ thị của hàm số 3 2
y x  3x m  2 tại ba điểm phân biệt A, B, C sao cho AB BC .
A. m; 3 . B. m; 1   .
C. m;  .
D. m1;  . Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số 3 2
y x  3x m  2 C và đường thẳng  x  1
y  mx d là: 3 2
x  3x m  2  mx  x   2
1 x  2x m  2  0   2
x  2x m  2   0 (*)
Để đường thẳng y  mx cắt đồ thị của hàm số 3 2
y x  3x m  2 tại ba điểm phân biệt A, B,C    m 3
(*) có ba nghiệm phân biệt khác 1    m  3 . m   3
Đường thẳng d cắt đồ thị C tại ba điểm A,B,C phân biệt sao cho AB BC thì điểm B
chính là điểm uốn của đồ thị C . Ta có : 2
y  3x  6x y  6x  6 , y  0  x  1 . y đổi dấu khi x đi qua x  1 . Điểm uốn của
đồ thị C là B1;  m . Mặt khác điểm B1;  m thuộc đường thẳng dy  mx với mọi m .
Vậy với m  3 thì yêu cầu bài toán thỏa mãn.
Chọn đáp án A.
Câu 101: Cho hàm số   4 3 2
f x mx nx px qx r , (với m,n, p,q,r
). Hàm số y f x có đồ thị như hình vẽ bên dưới:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 80
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Tập nghiệm của phương trình f x  r có số phần tử là A. 4 . B. 3 . C. 1 . D. 2 . Lời giải:
Ta có f x 3 2
 4mx  3nx  2px q 1 5
Dựa vào đồ thị y f x ta thấy phương trình f x  0 có ba nghiệm đơn là 1  , , 3 . 4
Do đó f x  mx  14x  5x  3 và m  0 . Hay f x 3 2
 4mx  13mx  2mx  15m 2 . 13
Từ 1 và 2 suy ra n  
m , p  m và q  15m . 3  13 
Khi đó phương trình f x  r  4 3 2
mx nx px qx  0  4 3 2 m x
x x  15x    0  3   4 3 2
3x  13x  3x  45x  0  xx  x  2 3 5 3  0  5
x  0  x    x  3 ( nghiệm kép). 3  5 
Vậy tập nghiệm của phương trình f x  r là S   ;0; 3 .  3 
Chọn đáp án B.
Câu 102: Cho hàm số   4 3 2
f x ax bx cx dx m , (với a,b,c,d,m
). Hàm số y f x có đồ thị như hình vẽ bên dưới:
Tập nghiệm của phương trình f x  m có số phần tử là A. 1 . B. 2 . C. 3 . D. 4 . Lời giải:
Cách 1: Ta có f x 3 2
 4ax  3bx  2cx d 1 .
Dựa vào đồ thị ta có f x  ax  14x  5x  3 3 2
 4ax  13ax  2ax  15a 2 và a  0 . 13
Từ 1 và 2 suy ra b
a , c a
 và d  15a . 3  13 
Khi đó: f x  m  4 3 2
ax bx cx dx  0  4 3 2 a x
x x  15x    0  3 
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 81
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x  0    4 3 2  5 5
3x  13x  3x  45x  0  x     
. Vậy tập nghiệm của phương trình là S ; 0; 3 . 3 3  x  3  
Cách 2: Từ đồ thị ta có a  0 .   x  0 4 3 2
f x m ax bx cx dx m m   . 3 2
ax bx cx d   0  2 5 Ta có f x 3 2 '
 4ax  3bx  2cx d có 3 nghiệm x  3; x   ; x  1. 1 2 3 4  3b  13 3b
x x x        13 1 2 3  4a   4 4ab a   3 2c  1 2c
Áp dụng định lý Viet ta có: x x x x x x    
 c  a . 1 2 2 3 1 3 4a  2 4a    d  15  a d 15 dx x x      1 2 3    4a  4 4ax  3   13  Thế vào   2 ta có: 3 2 a x
x x  15  0    5 .  3   x   3 5 
Vậy tập nghiệm của phương trình là S   ;0; 3   . 3 
Chọn đáp án C.
__________________________HẾT__________________________
Huế, ngày 16 tháng 7 năm 2023
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 0935.785.115 82