































Preview text:
ÔN TẬP NHỮNG KIẾN THỨC CẦN NHỚ
ĐỂ VẬN DỤNG GIẢI TOÁN Vấn đề 1
CÔNG THỨC TÍNH ĐẠO HÀM x ' x
u ' '. u e e e u e x 1
x u 1 ' . ' . u .u ' x x u u 1 u '
a ' a .lna a ' u '.a .lna x ' u ' 2 x 2 u
u.v' u '.v v '.u ' ' 1 1 1 u ' ' 2 2 x x u u u u '.v v 'u 2 v v
sin x' cos x
sinu' u '.cosu 1 u ' ln x ' lnu'
(cos x)' sin x (cos x)' u '.sinu x u 1 u ' 1 u ' tan x ' tanu' ln x ' ln u ' 2 2 cos x cos u x u 1 u ' 1 u '
cotx ' cotu' log x u a ' loga ' 2 2 sin x sin u x lna u lna Vấn đề 2
CÔNG THỨC LƯỢNG GIÁC
Hê ̣ thức lươ ̣ng cơ bản
Công thức nhân đôi – nhân ba – ha ̣ bâ ̣c 2 2
sin 2x 2 sin x.cos x
sin x cos x 1 tan x. cotx 1 2 2 2 2 sin x x
cos 2x cos x sin x 2 cos x 1 1 2 sin x tan x cos cotx x x cos x sin x 2 1 cos 2 sin x ; 2 1 cos 2 cos x 2 2 2 1 1 1 tan x 2 1 cot x 3
sin 3x 3 sin x 4 sin x c (3sin – 4sı̉n) os2x 2 sin x 3
cos 3x 4 cos x 3 cos x (4cổ – 3 cô)
Công thức cô ̣ng cung
Công thức biến đổi tổng thành tı́ch a b a b
sina b sina.cosb cosa.sinb
cosa cosb 2 cos .cos 2 2
cosa b cosa.cosb sina.sinb a b a b
cosa cosb 2 sin .sin 2 2 a b tana tanb tan
1tana.tanb a b a b
sina sinb 2 sin .cos 2 2 a b tana tanb tan
1 tana.tanb a b a b
sina sinb 2 cos .sin 2 2
Công thức biến đổi tổng thành tı́ch
Công thức tı́nh sin ,
cos theo t tan 2 1 2t cosa.cosb cos
a b cosa b si n 2 2 1 t 1 2 1 t sina.cosb sin
a b sina b
Đă ̣t t tan c os 2 2 2 1 t 1 2t sina.sinb cos
a b cosa b tan 2 2 1 t
Mô ̣t số công thức khác
Mô ̣t số công thức khác 4 4 1 2 3 1cos 4x
cos x sin x 1 sin 2x 2 4
sin x cos x 2 sin x 2 cos x 4 4 6 6 3 2 5 3 cos 4x
cos x sin x 1 sin 2x 4 8
sin x cos x 2 sin x 2 cos x 2 4 4
tan x cotx sin2x
cotx tan x 2 cot2x Vấn đề 3
PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
1. Phương trình lượng giác cơ bản: si
nx 0 x k
u v k2
a. Phương trı̀nh: sin u sin v Đă ̣c biê ̣t: si
n x 1 x k2 u
v k2 2 si
n x 1 x k2 2 c
osx 0 x k u
v k2 2
b. Phương trı̀nh: cos u cos v Đă ̣c biê ̣t: c
os x 1 x k2 u v l2 c
osx 1 x k2
tan u tan v u v k
tanx 0 x k c. Phương trı̀nh: Đă ̣c biê ̣t: Ðk : , u v k
tanx 1 x k 2 4
cotu cotv u v k c
otx 0 x k d. Phương trı̀nh: 2 Ðk : , u v Đă ̣c biê ̣t: k c
otx 1 x k 4
2. Phương trı̀nh lượng giáac cổô điểên da ̣ng: a sin x b cos x c 1
Điều kiê ̣n có nghiê ̣m: 2 2 2
a b c . a b c Chia hai vế cho 2 2
a b , ta được: 1 sin x cos x 2 2 2 2 2 2 a b a b a b a b Đă ̣t sin , cos
0, 2 . Phương trı̀nh trở thành: 2 2 2 2 a b a b c c sin .
sin x cos . cos x
cos(x ) cos 2 2 2 2 a b a b
x k2 (k ) 2 2
3. Phương trı̀nh lượng giáac đẳăng cấp bâ ̣c hai da ̣ng: a sin x b sin x cos x c cos x d 2
Kiểm tra xem cos x 0 có phải là nghiê ̣m hay không ? Nếu có thı̀ nhâ ̣n nghiê ̣m này. 2
Khi cos x 0 , chia hai vế phương trı̀nh
2 cho cos x , ta được: 2 2 a.tan x .
b tan x c d(1 tan x)
Đă ̣t t tan x , đưa về phương trı̀nh bâ ̣c hai theo t : 2
(a d)t .
b t c d 0 t x
3. Phương trı̀nh đối xứ
ưng dạng: a sin x cosx b sin x cosx c 0 3
Đă ̣t t cos x sin x 2.cosx ; t 2 . 4 2 1 2
t 1 2 sin x.cos x sin x.cos x (t 1) 2
Thay vào phương trı̀nh
3 , ta được phương trı̀nh bâ ̣c hai theo t t x
4. Phương trı̀nh đối xứ
ưng dạng: a sin x cosx b sin x cosx c 0 4 1
Đă ̣t t cos x sin x 2. cosx 2
; ÐK : 0 t 2 sin x.cos x (t 1) 4 2
Giải tương tự như da ̣ng trên. Khi tı̀mx cần lưu ý phương trı̀nh chứa dấu tri ̣ tuyê ̣t đối. Vấn đề 4
PHƯƠNG TRÌNH ĐẠI SỐ 2
1. Phương trı̀nh bâ ̣c hai: ax bx c 0 1
a/ Giảai phương trı̀nh bậc hai
Nếu b là số lẻ
Nếu b là số chẳn 2
Tı́nh b 4ac 2
Tı́nh ' b ' ac với ' b b 2 Nếu ' 0
Phương trı̀nh vô nghiê ̣m.
Nếu 0 Phương trı̀nh vô nghiê ̣m. Nếu ' 0
Phương trı̀nh có nghiê ̣m
Nếu 0 Phương trı̀nh có nghiê ̣m b b ' kép: x . kép: x . 2a a Nếu ' 0
Phương trı̀nh có hai nghiê ̣m
Nếu 0 Phương trı̀nh có hai b b ' ' x x 1 1 2a a phân biê ̣t:
nghiê ̣m phân biê ̣t: b b ' ' x x 2 2 2a a
b/ Đi ̣nh lı́ Viéet
Nếu phương trı̀nh
1 có hai nghiê ̣m phân biê ̣t x ,x 1 2 thı̀: b
Tổng hai nghiê ̣m: S x x 1 2 a 2 ' c x x 1 2
Tı́ch hai nghiê ̣m: P x .x a a 1 2 a
c/ Dấu cáac nghiệm củua phương trı̀nh a 0
Phương trı̀nh có hai nghiê ̣m phân biê ̣t 0
Phương trı̀nh có hai nghiê ̣m trái dấu a.c 0 0
Phương trı̀nh có hai nghiê ̣m phân biê ̣t cùng dấu P 0 0
Phương trı̀nh có hai nghiê ̣m âm phân biê ̣t P 0 S 0 0
Phương trı̀nh có hai nghiê ̣m dương phân biê ̣t P 0 S 0 2
d/ So sáanh hai nghiệm củua phương trı̀nh bậc hai g(x) ax bx c 0 vớơi 1 số β bất kı̀ 0 0
x x a .g 0
x x a.g 0 x x a.g 0 1 2 1 2 2 1 S S 2 2 3 2
2. Phương trı̀nh bậc 3: ax b ' x c ' x d ' 0 2 x 2
(x )ax bx c 0 2 a
x bx c 0 3 Đă ̣ 2 2
t g(x) ax bx c
, b 4ac 0 Phương trı̀nh
2 có 3 nghiê ̣m phân biê ̣t
3 có 2 nghiê ̣m phân biê ̣t x g () 0 Phương trı̀nh
2 có 2 nghiê ̣m phân biê ̣t
3 có nghiê ̣m kép x hoă ̣c 3 có hai nghiê ̣m 0
g( ) 0
phân biê ̣t trong đó có 1 nghiê ̣m x 0
g( ) 0 0 Phương trı̀nh
2 có 1 nghiê ̣m
3 vô nghiê ̣m hoă ̣c
3 có nghiê ̣m kép x g ( ) 0 0 4 2
3. Phương trı̀nh bâ ̣c bốôn trù
ung phương : ax bx c 0 4 Đă ̣ 2 2 t t x
. ÐK : t 0 . Phương trı̀nh 4 at bt c 0 5 0
Phương trı̀nh 4 có 4 nghiê ̣m phân biê ̣t
5 có 2 nghiê ̣m dương phân biê ̣t P 0 S 0 c 0
Phương trı̀nh 4 có 3 nghiê ̣m phân biê ̣t
5 có 1 nghiê ̣m t 0 và 1 nghiê ̣m t 0 b 0 a
Phương trı̀nh 4 có 2 nghiê ̣m phân biê ̣t
5 có 2 nghiê ̣m trái dấu hoă ̣c 5 có nghiê ̣m kép ac 0 dương 0 S 0 B 0 A 0 hay B 0
4. Phương trı̀nh chứ
ưa căn thứưc : + A B + A B 2 A B A B B 0
5. Phương trı̀nh chứ
ưa dấâu giáa tri ̣ tuyê ̣t đốôi: + A B A B + A B A B B 0 A 0 B 0 6. Bấ
ât phương trı̀nh chứưa căn thứưc:
+ A B
A B A 0 B + 0 2 A B 2 A B A B 7. Bấ
ât phương trı̀nh chứưa dấâu giáa tri ̣ tuyê ̣t đốôi: + A B B A B
+ A B A B Vấn đề 5 HÌNH HỌC PHẲNG
Trong mă ̣t phẳng Decac Oxy cho:
o Bố n điểm: Ax ,y B x ,y C x ,y M x ,y A A ,
B B , C C và o o
o Đường thẳng : ax by c 0 . 2 2 2 2
o Đường tròn C : (x a) y b R hay
C : x y 2ax 2by c 0 m m có tâm là
I a,b 2 2
và bán kı́nh là R a b c . 2 2
Véctơ AB x x ; y y AB x x y y B A B A
Đô ̣ dài đoa ̣n thẳng B A B A
(khoảng cách giữa hai điểm A, B) x x x x
Để ba điểm Ax ,y B x ,y C x ,y A A ;
B B và C C thẳng hàng B A C A . y y y y B A C A
ax bx c
Khoảng cách từ điểm M x ,y đến đường thẳng : ax by c 0 là: d M, o o o o 2 2 a b
Để A và B đối xứng nhau qua đường thẳng là đường thẳng trung trực của đoa ̣n thẳng AB. 1 1
Diê ̣n tı́ch ΔABC: S
AB.AC.sin A
AB .AC AB AC A BC . 2 2 2 2 2 abc
p p ap bp c 1 1 1 a.h . b h . c h pr 2 a 2 b 2 c 4R Trong đó: ,
R r, p lần lượt là bán kı́nh đường tròn ngoa ̣i tiếp, bán kı́nh đường tròn nội tiếp và nửa chu vi.
Để A và B nằm về 2 phía (khác phía) so với đường thẳng ax by c.ax by c 0 A A B B .
Để A và B nằm về cùng phı́a so với đường thẳng ax by c.ax by c 0 A A B B .
Để A và B cùng nằm trong đường tròn hay cùng nằm ngoài đường tròn P .P
0 x y ax by c x y ax by c Cm B Cm 2 2 2 2 A A A A 2 2 2 2 0 A/( ) /( ) B B B B .
Để A và B nằm về hai phı́a khác nhau đối với đường tròn (1 điểm phı́a trong, một điểm phı́a ngoài) P .P
0 x y ax by c x y ax by c Cm B Cm 2 2 2 2 A A A A 2 2 2 2 0 A/( ) /( ) B B B B CHƯƠNG I
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ BÀI 1
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ Cơ sở lý thuyết 1. Định nghĩa:
+ Hàm số y f (x) đồng biến trên K x , x K
x x f (x ) f (x ) 1 2 và 1 2 1 2 .
+ Hàm số y f (x) nghịch biến trên K x , x K
x x f (x ) f (x ) 1 2 và 1 2 1 2 .
2. Điều kiện cần: Giả sử y f (x) có đạo hàm trên khoảng I.
+ Nếu y f (x) đồng biến trên khoảng I thì f '(x) 0, x I .
+ Nếu y f (x) nghịch biến trên khoảng I thì f '(x) 0, x I .
3. Điều kiện đủ: Giả sử y f (x) có đạo hàm trên khoảng I.
+ Nếu y ' f '(x) 0 , x I [ f '(x) 0 tại 1 số hữu hạn điểm] thì y f (x) đồng biến trên I.
+ Nếu y ' f '(x) 0 , x I [ f '(x) 0 tại 1 số hữu hạn điểm] thì y f (x) nghịch biến trên I.
+ Nếu y ' f '(x) 0 , thì y f (x) không đổi trên I.
Chú ý: Nếu khoảng I được thay bởi đoạn hoặc nửa khoảng thì y f (x) phải liên tục trên đó. DẠNG 1
XÉT TÍNH ĐƠN ĐIỆU (tìm khoảng tăng - giảm) CỦA HÀM SỐ y = f (x)
1. Phương pháp giải
+ Bước 1: Tìm tập xác định của hàm số. Thường gặp các trường hợp sau: P(x) - y
TXÐ: Q(x) 0 Q(x)
- y Q(x) TXÐ: Q(x) 0 P(x) - y
TXÐ: Q(x) 0 Q(x)
+ Bước 2: Tìm các điểm tại đó y ' f '(x) 0 hoặc y ' f '(x) không xác định, nghĩa là: tìm đạo hàm
y ' f '(x) . Cho y ' f '(x) 0 tìm nghiệm x với i 1; 2; 3...n. i
+ Bước 3: Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên để xét dấu y ' f '(x) .
+ Bước 4: Dựa vào bảng biến thiên, kết luận các khoảng đồng biến và nghịch biến của hàm số.
- f '(x) y ' 0 Hàm số đồng biến (tăng) trên khoảng……và……
- f '(x) y ' 0 Hàm số nghịch biến (giảm) trên khoảng…và……
2. Một số lưu ý khi giải toán
+ Lưu ý 1: Đối với hàm phân thức hữu tỷ thì dấu “=” không xảy ra. + Lưu ý 2: ax b
• Đối với hàm dạng: y
thì hàm số luôn đồng biến (hoặc nghịch biến) trên TXĐ, nghĩa là luôn cx d
tìm được y ' 0 (hoặc y ' 0 ) trên TXĐ. 2
ax bx c
• Đối với hàm dạng: y
luôn có ít nhất hai khoảng đơn điệu.
a ' x b ' 4 3 2
• Đối với hàm dạng: y ax bx cx dx e luôn có ít nhất một khoảng đồng biến và một khoảng nghịch biến.
• Cả ba hàm số trên không thể luôn đơn điệu trên .
+ Lưu ý 3: Bảng xét dấu một số hàm thường gă ̣p
a) Nhị thức bậc nhất: y f (x) ax b ,a 0 b x −∞ +∞ a
ax b trái dấu với a 0 cùng dấu với a 2
b) Tam thức bậc hai : y f (x) ax bx c ,a 0
• Nếu 0 , ta có bảng xét dấu: x −∞ +∞
f (x) cùng dấu với a
• Nếu 0 , ta có bảng xét dấu: b x −∞ +∞ 2a
f (x) cùng dấu với a 0 cùng dấu với a
• Nếu 0 , go ̣i x ,x f x 1
2 là hai nghiê ̣m của tam thức ( )
0 , ta có bảng xét dấu:
x −∞ x x +∞ 1 2
f (x) cùng dấu với a 0 trái dấu với a 0 cùng dấu với a
c) Đối với hàm mà có y ' f '(x) 0 có nhiều nghiệm, ta xét dấu theo nguyên tắc: (phương pha ́ p chung)
• Thay 1 điểm lân cận x x f x x o gần
bên ô phải của bảng xét dấu vào '( ) . [Thay số sao cho dễ tìm n o f '(x) ].
• Xét dấu theo nguyên tắc: Dấu của f '(x) đổi dấu khi đi qua nghiệm đơn và không đổi dấu khi qua nghiệm kép.
+ Lưu ý 4: Xem la ̣i 1 số cách giải phương trình lượng giác thường gặp và ta có thể đưa hàm số lượng giác về
dạng đa thức trong 1 số trường hợp.
+ Lưu ý 5: Cách tính đạo hàm hàm số dạng hữu tı̉ (phân thức). a b c d ax b ad cb y y '
. Cách nhớ: Tı́ch đường chéo chı́nh trừ tı́ch đường chéo phu ̣. cx d cx d2 cx d2 a b a c b c 2
Cách nhớ: (Anh ba ̣n ăn cháo hai lần bỏ cha ̣y) x 2 x 2 a ' b ' a ' c ' b ' c '
ax bx c
b 'a a 'b 2
x 2c 'a a 'cx c 'b b 'c y y ' 2
a 'x b 'x c ' 2
a 'x b 'x c 2 ' 2
a 'x b 'x c 2 '
Bài 1. Tìm các khoảng đơn điệu của các hàm số: 4 2 4 2 4 a/ y x 4x 3 .
b/ y x 6x 8x 1 .
c/ y x 4x 6 . 3 2 3 2 2 d/ y x
6x 9x 4 .
e/ y x 3x 3x 2 . f/ y x 2x . 2x 1 3x 1 3 2x g/ y . h/ y . i/ y . x 1 1 x x 7
Bài 2. Tìm các khoảng đơn điệu của các hàm số: 2 x 2x 1 2 x 8x 9 x 2 a/ y . b/ y . c/ y . x 2 x 5 2 x x 3 2 3 2
d/ y x 2 4 3 6x 1 .
e/ y x 1 2 x 3x 3 . f/ y x 2x .
Bài 3. Tìm các khoảng đơn điệu của các hàm số: 2 2 2
a/ y x 5x 6 . b/ y x
1 2x 5x 7 . c/ y 4x x . 2 2 3 2 2x x 3 d/ y
x 2x 3 .
e/ y x 7x 7x 15 . f/ y . 3x 2
Bài 4. Tìm các khoảng đơn điê ̣u của các hàm số sau: a/ y x sin x , x 0; .
b/ y 2 sin x cos 2x , x 0; . 2 3 c/ y sin x cos x , 0; .
d/ y sin x cos 2x sin x 2 . 4 3 e/ 2
y sin x cos x 1 , x 0;
y 2 sin x sin x , x 0; . f/ 2 3
Bài 5. Chứng minh rằng: 3
a/ Hàm số y x x cos x 4 đồng biến trên .
b/ Hàm số y 2 sin x tan x 3x đồng biến trên nửa khoảng 0; . 2 DẠNG 2
Tìm điều kiện của tham số để hàm số y = f (x) đồng biến hoặc nghịch biến I. Cơ sở lý thuyết
Cho hàm số y f x,m với m là tham số, có tập xác định D.
• Hàm số y f x,m đồng biến trên D y ' 0 x D ⇒ Tham số m
• Hàm số y f x,m nghịch biến trên D y ' 0 , x D
• Hàm số y f x,m đồng biến trên y ' f '(x,m) 0, x miny ' 0 x
• Hàm số y f x,m nghịch biến trên y ' f '(x,m) 0, x max y ' 0 x
• Hàm số đồng biến trên thì nó phải xác định trên .
II. Phương pháp giải 2
Dạng 1: Nếu y ' f '(x,m) ax bx c thì: a 0
• Để hàm số y f x,m đồng biến (tăng) trên y ' f '(x,m) 0; x 0 a 0
• Để hàm số y f x,m nghi ̣ch biến (giảm) trên y ' f '(x,m) 0; x 0
Chú ý: Đối với hàm phân số hữu tỉ thì dấu “=” không xảy ra.
Dạng 2: Nếu y ' ax b ; x ; thì: y '( ) 0
• Để hàm số y f x,m đồng biến trên ;
y ' 0 ; x ; y '() 0 y '( ) 0
• Để hàm số y f x,m nghi ̣ch biến trên ;
y ' 0 ; x ; y '() 0 2
Dạng 3: Nếu y ' f '(x) ax bx c hoặc y ' f '(x) là một hàm bất kỳ nào khác, mà ta cần
y ' f '(x) 0 hay y ' f '(x) 0 trên khoảng a,b hoặc đoạn a,b (hoặc trên nửa đoạn hay nửa khoảng
nào đó). Thì ta làm theo các bước sau:
• Bước 1: Tìm miền xác định của y ' f '(x) .
• Bước 2: Độc lập (tách) m (hay biểu thức chứa m ) ra khỏi biến x và chuyển m về một vế. Đặt vế còn lại
là g(x) . Lưu ý khi chuyển vế thành phân thức thì phải để ý điều kiện xác đi ̣nh của biểu thức để khi xét dấu g '(x)
ta đưa vào bảng xét dấu g '(x).
• Bước 3: Tính g '(x). Cho g '(x) 0 và tìm nghiệm.
• Bước 4: Lập bảng biến thiên của g '(x).
• Bước 5: Kết luận: “Lớn hơn số lớn – Bé hơn số bé”. Nghĩa là:
+ khi ta đặt m g x thì dựa vào bảng biến thiên ta sẽ lấy giá trị m số lớn nhất trong bảng biến thiên
+ khi ta đặt m g x thì dựa vào bảng biến thiên ta sẽ lấy giá trị m số nhỏ nhất trong bảng biến thiên 3 2
Dạng 4: Tìm m để hàm số y ax bx cx d có độ dài khoảng đồng biến (nghịch biến) l . Ta giải như sau:
• Bước 1: Tính y ' f '(x) . a 0
• Bước 2: Tìm điều kiện để hàm số có khoảng đồng biến và nghịch biến: 1 . 0 2 2
• Bước 3: Biến đổi x x l thành x x 4x .x l 2 . 1 2 1 2 1 2
• Bước 4: Sử dụng định lý Viét đưa (2) thành phương trình theo m .
• Bước 5: Giải phương trình, so với điều kiện (1) để chọn nghiệm.
III. Một số lưu ý khi giải toán
• Lưu ý 1: Cần sử dụng thành tha ̣o đi ̣nh lı́ Viét và so sánh nghiê ̣m của phương trı̀nh bâ ̣c hai với số β.
• Lưu ý 2: Ta có thể dùng dạng toán loại 3 để giải bài toán tìm tham số m của một bất phương trình hoặc tìm
điều kiện để phương trình có nghiệm, vô nghiệm hoặc 1, 2, …n nghiệm, …
Bài 1. Tìm tham số m để hàm số: 3 2
a/ y x 3x 3(m 2)x 3m 1 đồng biến trên . 3 2
b/ y x 2m
1 x 2 mx 2 đồng biến trên . 3 2
c/ y x m
3 x 2mx 2 đồng biến trên tâ ̣p xác đi ̣nh của nó. 3 2 2 2 d/ y x
3x 3m
1 x 3m 1 luôn giảm. 1 3 2 e/ y
3 mx m
3 x m
2 x 3 luôn tăng trên . 3 f/ y 2 m 3
x m 2 1 1 1 x 3x 5 3
luôn đồ ng biến trên . Đáp số 5 : a/ m 1 b/ 1 m c/ m 6 3 3;6 3 3 4 3 d/ m 0 e/ m 1 f/ m ; 1 2 ; 2
Bài 2. Tìm tham số m để hàm số: mx 3 2m a/ y
luôn nghi ̣ch biến trên mỗi tâ ̣p xác đi ̣nh của nó. x m mx 2 b/ y
đồ ng biến trên từng khoảng xác đi ̣nh của nó. x m 1 2mx 1 c/ y
nghi ̣ch biến trên từng khoảng xác đi ̣nh của nó. x m 2 2
x m 2x 3m 1 d/ y
nghịch biến trên từng khoảng xác đi ̣nh của nó. x 1 Đáp số 1 1 1
: a/ 3 m 1 b/ 1 m 2 c/ m d/ m 2 2 2
Bài 3. Tìm tham số m để hàm số: 3 2
a/ y x 2mx m
1 x 1 đồng biến trên đoạn 0;2 . 3 2
b/ y x 3x m
1 x 4m nghi ̣ch biến trên khoảng 1; 1 . 3 2
c/ y x 3x mx 4 đồ ng biến trên khoảng 0; . 1 3 2 d/ y
x mx 2m
1 x m 2 nghi ̣ch biến trên khoảng 2;0. 3 mx 4 e/ y
nghi ̣ch biến trên khoảng ;1 . x m 2 mx 6x 2 f/ y
nghi ̣ch biến trên nửa khoảng 1; x 2 .
g/ y x m cos x đồ ng biến trên . Đáp số 1 : a/ m 1 b/ m 10 c/ m 0 d/ m 2 3 14 e/ 2 m f/ 2 m 1 g/ m h/ 1 m 1 2 5
Bài 4. Tìm tham số m để hàm số: 3 2 2 2
a/ y x m
1 x 2m 3m
2 x 2m m đồng biến trên nửa khoảng 2; . 2 b/ 3 2 2 2 y = x + (m + ).
1 x + (m + 4m + ).
3 x − m đồ ng biến trên nửa khoảng 1; 3 . 1 c/ 3 y = x − (m + ). 1 2 x + .( m m + ).
2 x + 7 đồ ng biến trên đoạn 4; 9 3 . d/ 3 2
y = x − mx − (2 2
m − 7m + 7).x + ( 2 m − ).( 1 2m − )
3 đồ ng biến trên nửa khoảng 2; .
Bài 5. Tìm giá trị thực m để hàm số: 3 2
a/ y x 3x mx m giảm trên đoạn có độ dài bằng 1. 3 2 b/ y x
x 2 mx 1 tăng trên đoa ̣n có độ dài bằng 2. Đáp số: 9 14 a/ m . b/ m . 4 3 DẠNG 3
Ứng dụng tính đơn điệu chứng minh bất đẳng thức 1. Phương pháp giải
• Bước 1: Chuyển bất đẳng thức về dạng f (x) 0 hay , ,
. Xét hàm số y f (x) trên tập xác định
do đề bài chỉ định hoặc miềm xác định của bài toán mà ta phải tı̀m.
• Bước 2: Xét dấu y ' f '(x) . Suy ra hàm số đồng biến (hay nghịch biến).
• Bước 3: Dựa vào định nghĩa đồng biến (hay nghịch biến) để kết luận. Tức là:
+ Hàm số y f (x) đồng biến trên K x , x K
x x f (x ) f (x ) 1 2 và 1 2 1 2 .
+ Hàm số y f (x) nghịch biến trên K x , x K
x x f (x ) f (x ) 1 2 và 1 2 1 2 .
2. Một số lưu ý khi giải toán
• Lưu ý 1: Trong trường hợp ta chưa xét được dấu của f '(x) thì ta đặt h(x) f '(x) và quay lại tiếp tục xét
dấu h '(x) … cho đến khi nào xét dấu được thì thôi.
• Lưu ý 2: Nếu bất đẳng thức có hai biến thì ta đưa bất đẳng thức về dạng f (a) f (b). Xét tính đơn điệu của
hàm số f (x)trong khoảnga,b.
Bài 1. Chứng minh rằng
a/ sin x x, x 0,
tan x x, x 0; b/ 2 2 3 x
c/ tan x sin x, x 0; sin x x x 0; 2 d/ , 3! 2 3 x
e/ tan x 2 sin x 3x, x 0; tan x x x 0; 2 f/ , 3 2
Bài 2. Chứng minh rằng 2 1 3 5 x x a.
sin x tan x x, x 0; sin x x x 0 3 3 2 b. , 6 120 1 1 c. 2 sin x x
, x 0; 2 d. x sin 1
, x 0; 2 x 6x 1 1 4 2 1 x 1 e. 1 , x 0; 1 x
1 x 1 x, x 0 2 2 2 sin x x 2 f. 2 8 2 1 4x g. 2 x 3
, x 1; h. 28/ 2 sin x
x , x 0; x 2 2 DẠNG 4
Ứng dụng tính đơn điệu để giải phương trình – bất phương trình có chứa tham số m
Bài toán 1. Tı̀m m để phương trı̀nh f x; m 0 có nghiê ̣m trên D ?
• Bước 1. Độc lâ ̣p (tách) m ra khỏi biến số x và đưa về da ̣ng f x Am.
• Bước 2. Lâ ̣p bảng biến thiên của hàm số f x trên D.
• Bước 3. Dựa vào bảng biến thiên xác đi ̣nh giá tri ̣ của tham số m để đường thẳng y Am nằm ngang cắt
đồ thi ̣ hàm số y f x.
• Bước 4. Kết luâ ̣n những giá tri ̣ cần tı̀m của m để phương trı̀nh f x Am có nghiê ̣m trên D. Lưu ý:
+ Nếu hàm số y f x có GTLN và GTNN trên D thı̀ giá tri ̣ m cần tı̀m là những m thỏa mãn:
min f x Am max f x . D D
+ Nếu bài toán yêu cầu tı̀m tı̀m tham số để phương trı̀nh có k nghiê ̣m phân biê ̣t, ta chı̉ cần dựa vào bảng
biến thiên để xác đi ̣nh sao cho đường thẳng y Am nằm ngang cắt đồ thi ̣ hàm số y f x ta ̣i k điểm phân biê ̣t.
Bài toán 2. Tı̀m m để bất phương trı̀nh f x; m 0 hoă ̣c f x; m 0 có nghiê ̣m trên D ?
• Bước 1. Độc lâ ̣p (tách) m ra khỏi biến số x và đưa về da ̣ng f x Am hoă ̣c f x Am.
• Bước 2. Lâ ̣p bảng biến thiên của hàm số f x trên D.
• Bước 3. Dựa vào bảng biến thiên xác đi ̣nh giá tri ̣ của tham số m để bất phương trı̀nh có nghiê ̣m:
+ Với bất phương trı̀nh f x Am đó là những m sao cho tồn ta ̣i phần đồ thi ̣nằm trên đường
thẳng y A m, tức là Am max f x khi max f x . D D
+ Với bất phương trı̀nh f x Am đó là những m sao cho tồn ta ̣i phần đồ thi ̣ nằm dưới đường
thẳng y A m, tức là Am min f x khi min f x . D D
Bài toán 3. Tı̀m tham số m để bất phương trı̀nh f x Am hoă ̣c f x Am nghiê ̣m đúng x D ?
+ Bất phương trı̀nh f x Am nghiê ̣m đúng x D min f x Am . D
+ Bất phương trı̀nh f x Am nghiê ̣m đúng x D max f x Am . D Lưu ý:
+ Các bài toán liên quan hê ̣ phương trı̀nh, hê ̣ bất phương trı̀nh ta cần biến đổi chuyển về các
phương trı̀nh và bất phương trı̀nh.
+ Khi đổi biến, cần quan tâm đến điều kiê ̣n của biến mới. LOẠI 1
Ứng dụng tính đơn điệu để giải phương trình có chứa tham số m
Bài 1. Tìm tham số thựcm để phương trình: 2
a/ x 3x 1 m có nghiệm thực. 2
b/ m x 2 x m có đúng 3 nghiê ̣m thực phân biê ̣t. 2 2
c/ x 4x 5 x 4x m có nghiê ̣m thực trong đoa ̣n 2; 3 . Đáp số 3 1 : a/ m . b/ 2 m 2 . c/ m 1 2 6
Bài 2. Tìm tham số thực m để phương trình: a/ 2
x + mx + 2 = 2x +1 có hai nghiệm phân biệt. b/ 2 x + 9 − x =
−x + 9x + m có nghiệm. c/ 4 2
3 x −1 + m x +1 = 2 x −1 có nghiệm. d/ 6 − x +
x + 3 = mx có nghiệm. m ≤ 1 − Đáp số: 9 9 1 a/ m ≥ b/ − ≤ m ≤ 10 c/ 1 − < m ≤ d/ 1 2 4 3 m ≥ 2
Bài 3. Tìm tham số thực m để phương trình: a/ 3 + x +
6 − x − (3 + x)(6 − x) = m có nghiệm. b/ x 2 + x + 1 −
x 2 − x + 1 = m có nghiệm. LOẠI 2
Ứng dụng tính đơn điệu để giải bất phương trình có chứa tham số
Bài 1. Tìm m để bất phương trình 4x − 2 + 2 4 − x < m có nghiệm.
Đáp số: m > 14 .
Bài 2. Tìm tham số m để bất phương trình sau có nghiệm: mx −
x − 3 ≤ m + 1 Đáp số: 3 + 1 m ≤ 4
Bài 3. Tìm m để bất phương trình ( + x)( − x) 2 4 6
≤ x − 2x + m (1) nghiệm đúng với mọi x ∈[ 4; − 6]
Đáp số: m ≥ 6 .
Bài 4. Tìm m để bất phương trình 2
m 2x + 9 < x + m có nghiệm với mọi x . Đáp số: 3 m < − . 4 BÀI 2
CỰC TRỊ CỦA HÀM SỐ Cơ sở lý thuyết
1. Khái niệm cực trị của hàm số: Giả sử hàm số y f (x)xác định trên tập
D D vàx D o + x y f x a,b x a,b
f (x) f x ,
o là điểm cực đại của hàm số
( ) nếu D và o sao cho o
x a;b\ x . Khi đó: f x được gọi là giá trị cực đại của y f(x) o o + x y f x a,b x a,b f x f x
o là điểm cực tiểu của hàm số
( ) nếu D và o sao cho , o
x a;b\ x . Khi đó: f x y f x
o được gọi là giá trị cực tiểu của ( ) o + Nếu x y f x
x ; f (x )
o là điểm cực trị của hàm số ( ) thì điểm o
o được gọi là điểm cực trị của đồ thị hàm
số y f (x).
2. Điều kiện cần để hàm số có cực trị (Đi ̣nh lý Ferman).
Nếu hàm số y f (x) có đạo hàm tại x và đạt cực trị tại điểm đó thì f 'x . Nghĩa là hàm số o 0 o
y f (x) chỉ có thể đạt cực trị tại những điểm mà tại đó đạo hàm bằng 0 hoặc không có đạo hàm.
3. Điều kiện đủ để hàm số có cực trị
a. Định lý 1: Giả sử hàm số y f (x) liên tục trên khoảng a;b x và có đạo hàm a,b \ xo o
+ Nếu f '(x) đổi dấu từ âm sang dương khi x đi qua x
y f x đạt cực tiểu tại x o thì ( ) o .
+ Nếu f '(x) đổi dấu từ dương sang âm khi x đi qua x
y f x đạt cực đại tại x o thì ( ) o . x a xo b f '(x) – 0 + f(a) f(b)
y f (x) cực tiểu f(xo) x a xo b f '(x) + 0 – f(xo)
y f (x) cực đa ̣i f(a) f(b)
b. Định lý 2: Giả sử hàm số y f (x)có đạo hàm trên a; b x f ' x 0 f ' x 0 o ; o và o
+ Nếu f ' x 0 y f x x o thì
( ) đạt cực đại tại o .
+ Nếu f ' x 0 y f x x o thì
( ) đạt cực tiểu tại o . DẠNG 1
TÌM CỰC TRỊ CỦA HÀM SỐ
1. Phương pháp giải
Qui tắc 1: Dùng định lý 1
• Bước 1: Tìm miền xác định. Tính y ' f '(x) .
• Bước 2: Tìm các điểm x i 1,2,..,n y f x y f x i tại đó ' '( ) 0 hoă ̣c ' '( ) không xác đi ̣nh.
• Bước 3: Xét dấu f '(x) , từ đó suy ra điểm cực tri ̣ dựa vào đi ̣nh lý 1.
Qui tắc 2: Dùng định lý 2
• Bước 1: Tìm miền xác định. Tính y ' f '(x) .
• Bước 2: Tìm các điểm x i 1,2,..,n y f x y f x i tại đó ' '( ) 0 hoă ̣c ' '( ) không xác đi ̣nh.
• Bước 3: Xét dấu f ' (x) và f ' (x ) i
- Nếu f ' (x ) 0 x i
thì hàm số đạt cực đại tại i .
- Nếu f ' (x ) 0 x i
thì hàm số đạt cực tiểu tại i .
2. Một số lưu ý khi giải toán
Có 2 qui tắc tı̀m cực tri ̣ dựa vào đi ̣nh lı́ 1 (qui tắc 1) và đi ̣nh lı́ 2 (qui tắc 2):
• Nếu viê ̣c xét dấu của đa ̣o hàm bâ ̣c nhất dễ dàng, thı̀ nên dùng qui tắc 1.
• Nếu viê ̣c xét dấu ấy khó khăn (vı́ dụ như trong bài toán mà hàm số đã cho có da ̣ng lượng giác, hoă ̣c bài
toán có chứa tham số), thı̀ nên dùng qui tắc 2.
Nếu y ' không đổi dấu khi đi qua nghiệm (nghiê ̣m kép) thì hàm số không có cực trị.
Đối với hàm bậc 3 thì y ' 0 có 2 nghiệm phân biệt là điều kiện cần và đủ để hàm có cực trị.
Không cần xét hàm số y f (x) có hay không có đa ̣o hàm ta ̣i điểm x xo nhưng không thể bỏ qua điều
kiê ̣n “hàm số liên tục tại điểm xo ”.
y '(x ) 0 o
Hàm số đa ̣t cực tri ̣ ta ̣i x o y ' (x ) 0 o
Đối với hàm số căn thức ta không xét dấu được như bậc 1, bậc 2 thì chọn điểm để xét dấu.
Bài 1. Tìm cực tri ̣ của các hàm số sau: 3 2 3 2 2 3 5 2
a/ y x 3x 3x 5
b/ y x 3x 9x 4
c/ y x x 2x 3 2 4 3 2 4 2 4 2 d/ y
x 6x 9x 1 e/ y x
6x 8x 1
f/ y x 2x 3 3
Đáp số:a/ Hàm số không có cực trị. b/ y
y 3 31; y y . CT 1 1 CÐ 1 11 c/ y y ; y y
d/ hàm số không có cực tri ̣. CÐ 2 2 3 CT 2 4 e/ y
y 2 25 ; Hàm số không có cực tiểu. f/ y y ; y y y . CT 1 1 4 CÐ 0 3 C D
Bài 2. Tìm cực tri ̣ của các hàm số sau: 3 2x 3x 1 2 x 2x 1 2 x 8x 9 a/ y b/ y c/ y d/ y x 1 1 x x 2 x 5
Đáp số: a/ Hàm số không có cực tri ̣.
b/ Hàm số không có cực tri ̣. c/ y y 1 0 ; y y .
d/ Hàm số không có cực tri ̣. CT 5 12 CÐ
Bài 3. Tìm cực tri ̣ của các hàm số: 3 2 2 2 a/ y x 3x
b/ y x 4 x
c/ y 2x x 3 2
d/ y 2x 1 2x 8
e/ y x x 2
f/ y x 3 x Đáp số: a/ y
y 2 2 ; y y . b/ y y ; y y . CÐ 2 2 CT 2 2 CT 0 0 CÐ
c/ Hàm số không có cực đa ̣i. d/ y
y 2 2 3 2 1.Hàm số không có điểm cực đại. CT e/ y y 1 1; y y . f/ y y ; y y CT 1 2 CÐ 0 0 CT 0 0 CÐ
Bài 4. Tìm cực tri ̣ của các hàm số:
a/ y sin 2x x
b/ y 2 sin 2x 3
c/ y 3 2 cos x cos 2x
d/ y cos x sin x trên 0; 2 Đáp số: 1 1 a/ y
y k
k. y y
k k . CÐ 6 2 6 CT 6 2 6 b/ y
y k 1 . y y k . CT 2 1 5 CÐ 4 4 2 2 9 c/ y y k2 y
y k 2 1 cosk CÐ . 3 . CT 2 1
d/ Hàm số đa ̣t cực đa ̣i ta ̣i x ;y 4 12 với sin . 3 3 DẠNG 2
TÌM THAM SỐ m ĐỂ HÀM SỐ CÓ CỰC TRỊ TẠI x 0
Bài toán 1: Cho hàm số y f (x,m) . Tìm tham số m để hàm số đạt cực trị tại điểm x x . 0 Phương pháp giải + Tìm tập xác định
+ Tính y ' f '(x,m)
+ Để hàm số đa ̣t cực trị ta ̣i x x thì: f '(x ,m) 0 m . 0 0
Bài toán 2: Cho hàm số y f (x,m) . Tìm tham số m để hàm số đạt cực đại tại điểm x x . 0 Phương pháp giải + Tìm tập xác định
+ Tính y ' f '(x,m);y ' f ' (x,m) f '
x ,m 0 0
+ Để hàm số đa ̣t cực đại ta ̣i x x thì: m 0 f '
x ,m 0 0
Bài toán 3: Cho hàm số y f (x,m) . Tìm tham số m để hàm số đạt cực tiểu tại điểm x x . 0 Phương pháp giải + Tìm tập xác định
+ Tính y ' f '(x,m);y ' f ' (x,m) f '
x ,m 0 0
+ Để hàm số đa ̣t cực tiểu ta ̣i x x thì: m 0 f '
x ,m 0 0
Bài 1. Tìm tham số để hàm số: 3 2 2
a/ y x 3mx 3m
1 x m đa ̣t cực đa ̣i ta ̣i x 2 . 2 3 2
b/ y m 5mx 6mx 6x 6 đa ̣t cực tiểu ta ̣i x 1 . 3 2
c/ y x 2x mx 1 đa ̣t cực tiểu ta ̣i x 1 3 2
d/ y mx 3x 12x 2 đa ̣t cực đa ̣i ta ̣i điểm x 2 . 2 x mx 1 e/ y
đa ̣t cực đa ̣i ta ̣i x 2 . x m
Đáp số a/ m 3 b/ m 2 c/ m 1 d/ m 2 e/ m 3
Bài 2. Tìm tham số m để hàm số: 1 3 2 2 a/ y
x mx m m
1 x 1 đa ̣t cực tri ̣ ta ̣i x 1 . Khi đó hàm số đa ̣t cực đa ̣i hay cực tiểu. 3
Tı̀m cực tri ̣ tương ứng. 3 2 b/ y x
mx 4 để hàm số nhâ ̣n điểm M 2;0 làm điểm cực đa ̣i. 2
c/ y 2m
3 sin x 2m sin 2x 3m 1 đa ̣t cực tiểu ta ̣i x . 3
Đáp số a/ m 2 b/ m 3 c/ m 1
Bài 3. Tìm tham số a,b để hàm số: 4 x a/ 2 y
ax b có cực tri ̣ ta ̣i x 1 và giá tri ̣ cực tri ̣ tương ứng của hàm số bằng 2. 4 5 2 3 2 5 b/ y
a x 2ax 9x b có giá tri ̣ cực tri ̣ là những số dương và x là điểm cực đa ̣i. 3 o 9 Đáp số 1 9 9 128 9 140
:a/ a ;b b/ a ; b hoă ̣c a ; b 2 4 25 27 5 27
Bài 4. Tìm giá tri ̣ của tham số để hàm số : 3 2
a/ y x mx m
1 x 1 có cực tri ̣ ta ̣i x 2 . Khi đó hàm số đa ̣t cực đa ̣i hay cực tiểu ? Tı́nh giá
tri ̣ cực tri ̣ tương ứng. 3 2
b/ y 2x 4 2mx m
5 x 4 có cực tri ̣ khi x 0 . Khi đó hàm số đa ̣t cực đa ̣i hay cực tiểu.
Tı́nh giá tri ̣ cực tri ̣ tương ứng. 2 x 2mx 2 c/ y
có điểm cực tri ̣ khi x 2 . Khi đó hàm số đa ̣t giá tri ̣ cực tiểu hay cực đa ̣i. Tı́nh giá x 1
tri ̣ cực tri ̣ tương ứng. d/ 3 2 2
y x mx m x 5 x . Khi đo
́, nó là điểm cực đa ̣i hay cực tiểu, tı́nh giá 3 đa ̣t cực tri ̣ ta ̣i 1
tri ̣ cực tri ̣ còn la ̣i (nếu có).
Bài 5. Tìm giá tri ̣ của tham số a;b để hàm số : 1 4 2 a/ y
x 2a bx a b đa ̣t giá tri ̣ cực đa ̣i bằng 2 ta ̣i x 1 . 4 4 2 b/ y x
a 3bx 3a b đa ̣t giá tri ̣ cực tiểu bằng 1 ta ̣i x 0 3 4 2 c/ y
x 3a 2bx a 2b có giá tri ̣cực tri ̣ bằng 0 khi x 0 . Khi đó hàm số đa ̣t cực tiểu hay 4 cực đa ̣i. 2
ax bx ab d/ y
đạt cực trị tại x 0 và x 4 . bx a 2
ax 2x b e/ y
đạt cực đại bằng 5 tại x 1 . 2 x 1 2
x ax b d/ y
để hàm số đạt cực trị bằng –6 tại x 1. x 1
Bài 6. Tìm giá tri ̣ của tham số a; ;
b c để hàm số : 3 2
a/ y x ax bx c đa ̣t cực tri ̣ bằng 0 ta ̣i điểm x 2 và đồ thi ̣ hàm số đi qua điểm A0, 1 . 3 2
b/ y x ax bx c đa ̣t cực tiểu ta ̣i điểm A1,3 và đồ thi ̣hàm số cắt tru ̣c tung ta ̣i điểm có tung đô ̣ bằng 2. 4 2
c/ y ax bx c để đồ thị đi qua gốc tọa độ O và đạt cực trị bằng 9 tại x 3 .
Bài 7. Tìm giá tri ̣ của tham số a; ; b ;
c d để hàm số : 3 2
a/ y ax bx cx d đa ̣t cực tiểu ta ̣i điểm x 0, f
0 0 và đa ̣t cực đa ̣i ta ̣i x 1 , có giá tri ̣cực đa ̣i bằng 1. 3 2
b/ y ax bx cx d đạt cực tiểu bằng 0 tại x 0 và đạt cực đại bằng 4 tại 1 x . 27 3 DẠNG 3
BIỆN LUẬN HOÀNH ĐỘ CỰC TRỊ CỦA HÀM SỐ
Hàm số y f (x) có n cực tri ̣⇔ y’ = 0 có n nghiê ̣m phân biê ̣t.
Mô ̣t số lưu ý khi giải toán
• Lưu ý 1: Hoành độ cực trị thường là nghiệm của phương trình bậc 2. Do đó, ta cần phải nắm vững kiến
thức về phương trình bậc 2 như: Định lý Viét, so sánh nghiệm phương trình bậc 2 với 1 số β bất kỳ, các điều kiện
có nghiệm của phương trình, … đồ ng thời, nó liên quan đến mô ̣t số tı́nh chất của hı̀nh ho ̣c phẳng. 2 3 2
ax bx c
• Lưu ý 2: Hàm số bâ ̣c ba y ax bx cx d và hàm hữu tı̉ y
có cực đa ̣i và cực dx e a 0
tiểu (2 cực tri ̣) y ' 0 có hai nghiê ̣m phân biê ̣t 0 ax b 2 •
ax bx c
Lưu ý 3: Để A và B thuộc hai nhánh của đồ thị dạng y hoặc y thì 2 điểm A cx d ex d
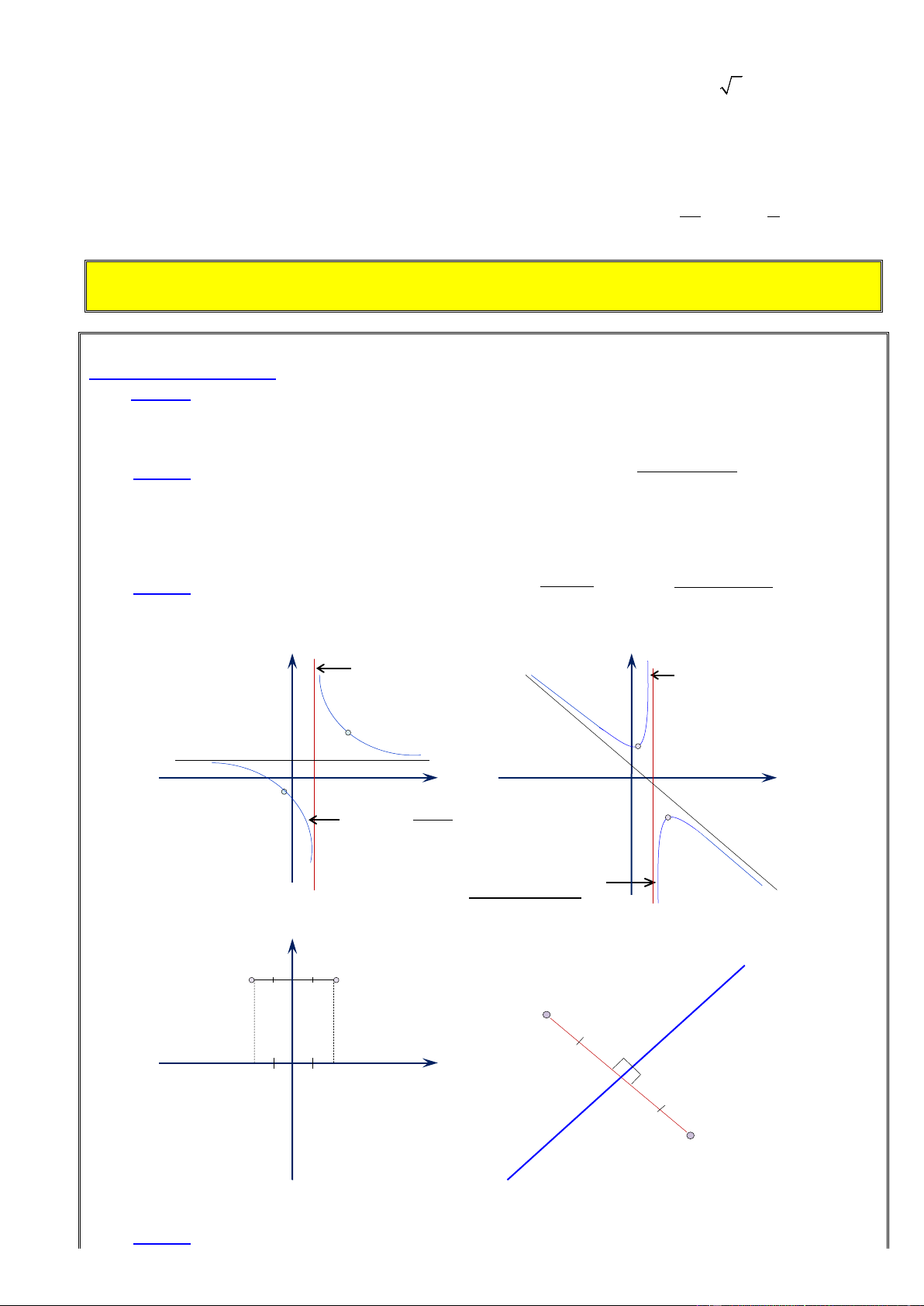
và B phải nằm về hai phía so với đường tiệm cận đứng tương ứng của đồ thị. y y
TCĐ: x = – d/c
TCĐ: x = – d/e
TCN: y = – a/c A A O x x – d/c O B ax b (C): y cx d B 2
ax bx c (C): y ex d y d A B A I x x1 O x2 B 4 3 2
• Lưu ý 4: Cực trị của hàm bâ ̣c bốn : y ax bx cx d x 0 3 2
+ Ta có: y ' 4ax 3bx 2cx y ' 0 2
4ax 3bx 2c 0 g x 2 0 2
+ Hàm số có 3 cực trị khi và chỉ khi (2) có hai nghiệm phân biệt khác 0 g 0 0
Khi đó: Hàm số có 2 cực tiểu, 1 cực đại khi a 0 .
Hàm số có 2 cực đại, 1 cực tiểu khi a 0 .
+ Hàm số có 1 cực trị khi và chỉ khi (2) có nghiệm kép hoặc vô nghiệm hoặc có 1 nghiệm 0 x 0 g 0 0
Khi đó: Hàm chỉ có cực tiểu khi a 0 (nghı̃a là có cực tiểu mà không có cực đa ̣i).
Hàm số chỉ có cực đại khi a 0 (nghı̃a là có cực đa ̣i mà không có cực tiểu). Loại 1
Tìm giá trị tham số m để hàm số n cực trị , hoặc không có cực trị Hàm bâ ̣c 3 3 2
y ax bx cx d a 0 3 2
Hàm bâ ̣c 3: y ax bx cx d a 0 *
Phương pháp giải: 2 2
- Ta có: y ' 3ax 2bx c y ' 0 3ax 2bx c 0 1 a 0
+ Hàm số
* có 2 cực trị ⇔
1 có hai nghiệm phân biệt 0 1 a 0
+ Hàm số
* không có cực trị ⇔
1 có nghiệm kép hoặc vô nghiệm 0 1
Bài 1. Tìm giá trị tham số m để hàm số có cực trị 3 2 3 2
a/ y x 3mx (m 2)x 3m 4 b/ y x m 1 x 3x m 3
c/ y m 3 2
2 x 3x mx 5 d/ 3 y
x 3 m 2 x 2x 1 3 1 3 2 3 2 e/ y
x mx (2m 3)x 1
f/ y 4 mx 2m 8x x 3 3
Bài 2. Tìm giá trị tham số m để hàm số có 2 cực trị 3 2 3 2
a/ y x m
2 x m 2 x 3
b/ y 2x (m 2)x (6 3m)x m 1 3 2 2 3 2
c/ y x 3(m 1)x (2m 3m 2)x m m
1 d/ y 1 mx m
2 x m 1 x m 2 3 2 m 3 e/ y x
3 mx 9 3mx 2m f/ 3 y
x 3 m 2 x 2x 1 3
Bài 3. Tìm giá trị tham số m để hàm số không có cực trị 3 2 3 2
a/ y x 3mx 3mx 3m 4
b/ y x m
1 x 3x 2 3 2 3 2
c/ y 4 mx 2m 8x x 3
d/ y x 2m
1 x 3x 2
Bài 4. Chứng minh rằ ng hàm số: 1 3 2 a/ y
x mx x m 1 luôn có cực đa ̣i và cực tiểu với mọi giá tri ̣ m . 3 3 2
b/ y 2x 32m
1 x 6m m
1 x 1 luôn đa ̣t cực tri ̣ ta ̣i x ,x 1
2 với mo ̣i giá tri ̣ m và biểu thức x x 2
1 không phu ̣ thuô ̣c vào m .
Hàm bâ ̣c 4 trùng phương 4 2
y ax bx c a 0 4 2
Hàm bâ ̣c 4 trùng phương : y ax bx c a 0 *
Phương pháp giải: x 0 3 2
• Ta có: y ' 4ax 2bx x 4ax 2b y ' 0 2
4ax 2b 0 g x 1 g 0 0
• Hàm số
* có 3 cực trị ⇔
1 có hai nghiệm phân biệt khác 0 0 1
Khi đó: Hàm số có 2 cực tiểu, 1 cực đại khi a 0 .
Hàm số có 2 cực đại, 1 cực tiểu khi a 0 .
• Hàm số có 1 cực trị khi và chỉ khi
1 có nghiệm kép hoặc vô nghiệm hoặc có 1 nghiệm x 0 0 0 a .b 0 1 g 0 0 g 0 0 b 0
Khi đó: Hàm số chỉ có cực tiểu khi a 0 (nghı̃a là có cực tiểu mà không có cực đa ̣i).
Hàm số chỉ có cực đại khi a 0 (nghı̃a là có cực đa ̣i mà không có cực tiểu).
Chú ý: Hàm bâ ̣c 4 trùng phương:
• Luôn có ít nhất 1 cực trị.
• Nếu có 3 cực trị thì 3 cực trị này luôn tạo thành 1 tam giác cân tại đỉnh thuộc trục oy.
Bài 1. Tìm giá trị tham số m để hàm số có cực trị 4 2 4 2
a/ y x 2m 4x 2m 5
b/ y x 2m 1 x 1 4 2 2 4 2 2
c/ y x m 4x 3
d/ y mx m 9 x 10
Bài 2. Tìm giá trị tham số m để hàm số có 1 cực trị 4 2 4 2
a/ y x 2m 1 x 1
b/ y mx (m 1)x 1 2m 4 2 1 4 1 2 2
c/ y x mx 4x m d/ y
x m
1 x m m 4 2
Bài 3. Tìm giá trị tham số m để hàm số có 3 cực trị 4 3 2 4 2
a/ y 2x 8mx 8m 1 x
b/ y x m 1 x 2 4 2
c/ y x 2mx 2m 1
d/ y m 4 2
2 x 2mx m 1
Bài 4. Chứng minh rằng hàm số luôn có cực đại và cực tiểu m D 2 3 2 1 3 2 2
a/ y x mx m 3 x 4m
b/ y x 2m
1 x m m 3 x 1 3 3 3 2 3 2 2 3
c/ y x m
2 x m 2 x 3
d/ y x 3mx 3m 1 x m Hàm phân thức 2
ax bx c
y f (x) dx e 2
ax bx c
Hàm phân thức: y f (x) * dx e
Phương pháp giải: 2 ad.x 2 .
ae x bc dc dx e 0 •
Ta có: y ' f '(x)
f '(x) 0 2 2 ad .x 2 .
ae x bc dc 0 g x dx e 1 e e g 0 •
Hàm số
* có 2 cực trị ⇔
1 có hai nghiệm phân biệt khác x d d 0 1 ad 0 •
Hàm số
* không có cực trị ⇔
1 có nghiệm kép hoặc vô nghiệm 0 1
Bài 1. Tìm giá trị tham số m để hàm số có cực trị 2 2
x x m 1 2
mx m 2 x 1 a/ y b/ y x 1 x 2 2
x m 1 x m 2 2 x mx 2 c/ y d/ y x 1 mx 1
Bài 2. Tìm giá trị tham số m để hàm số có 2 cực trị 2
x m 2
1 x m 4m 2 2
x x m a/ y b/ y x 1 x 1 2 x mx 2 2 x 2 m 1 x m c/ y d/ y x 1 x 1
Bài 3. Tìm giá trị tham số m để hàm số không có cực trị 2 x 2mx 3 2 x mx 5 2
x m 2
1 x m 4m 2 a/ y b/ y c/ y x m x 3 x 1
Bài 4. Chứng minh rằng hàm số luôn có cực đại và cực tiểu m D 2
x m m 3 1 x m 1 2 x m 2 m 4 1 x m 1 a/ y b/ y x m x m 2 2
x x m 1 2
x mx m 2 c/ y d/ y x 1 x m 1 Loại 2
Tìm giá trị tham số m để hàm số có n cực trị thỏa điều kiện cho trước
(sử dụng định lí Viét) Hàm bâ ̣c 3 3 2
y ax bx cx d a 0
Cách viết phương trı̀nh đường thẳng nối hai điểm cực tri ̣của hàm bâ ̣c ba: 3 2 y
f x ax bx cx d
• Bước 1: Tìm điều kiện để có cực trị là: y ' 0 có 2 nghiệm phân biệt.
Khi đó, giả sử x ,y x ,y 1 1 , 2
2 là các điểm cực tri ̣
• Bước 2: Chia f (x) cho f '(x) ta được: f (x) Q(x).f '(x) Ax B
y f x Q(x).f '(x ) Ax B 1 1 • 1 1
Bước 3: Vì x ,y x ,y 1 1 , 2
2 là các điểm cực tri ̣ nên: y
f x Q(x).f '(x ) Ax B 2 2 2 2
f '(x ) 0
y f x Ax B 1 1 1 1 Mặt khác: f '(x ) 0 y
f x Ax B 2 2 2 2
⇒ Các điểm x ,y x ,y 1 1 , 2
2 nằ m trên đường thẳng y Ax
B là đường thẳng nối hai điểm cực tri ̣
của hàm số bậc ba 3 2 y
f x ax bx cx d .
Bài 1. Hãy viết phương trình đường thẳng đi qua 2 điểm cực trị của hàm số sau 3 2 3 2
a/ y x 3x 6x 8
b/ y 2x 3x 12x 10
Bài 2. Tìm tham số m để hàm số sau đây có 2 cực trị. Hãy viết phương trình đường thẳng đi qua 2 điểm cực trị của hàm số sau: 3 2 2 3
a/ y x 3mx 3(m 1)x m 3 2 2
b/ y x 3m
1 x (2m 3m 2)x m m 1 3 2 2 2
Bài 3. Cho hàm số: y x 2m
1 x m 4m
1 x 2m
1 . Tı̀m m để hàm số đa ̣t cực tri ̣ ta ̣i 1 1 1
hai điểm x ,x x x 1 2 sao cho: 1 2 . x x 2 1 2
Đáp số: m 1 hoặc m 5 1 3 2 1
Bài 4. Cho hàm số: y mx m
1 x 3m
2 x . Tı̀m m để đồ thi ̣ hàm số có 2 điểm cực tri ̣ 3 3 x ;x , đồ x 2x 1 1 2
ng thời hai điểm cực tri ̣ này thỏa: 1 2 . Đáp số: 2 m hoặc m 2 3 1 3 2
Bài 5. Cho hàm số: y
x mx 2m
1 x 2 . Tı̀m m để đồ thi ̣ của hàm số có hai cực tri ̣ đều dương. 3 m 1 Đáp số: 1 m 2 3 2 2 2
Bài 6. Tìm m để đồ thi ̣ của hàm số y x 3m
1 x 3m 7m
1 x m 1 có điểm cực tiểu
ta ̣i mô ̣t điểm có hoành đô ̣ nhỏ hơn 1.
Đáp số: m 1 3 2
Bài 7. Tìm m để đồ thi ̣hàm số y x 3x 2 C có điểm cực đa ̣i và điểm cực tiểu của đồ thi ̣ C nằm
về hai phı́a khác nhau của mô ̣t đường tròn (phı́a trong đường tròn và phı́a ngoài đường tròn): C 2 2 2
: x y 2mx 4my 5m 1 0 . m Đáp số: 3 m 1 5
Bài 8. Tìm m để đồ thi ̣ hàm số C 3 2
: y 2x mx 12x 13 có cực đa ̣i và cực tiểu, đồng thời các điểm m
này cách đều tru ̣c tungOy .
Đáp số: m 0 3 2 2
Bài 9. Tìm m để đồ thi ̣ hàm số y x 3x m x m có cực đa ̣i và cực tiểu, đồng thời các điểm cực đa ̣i và
cực tiểu đố i xứng nhau qua đường thẳng : x 2y 5 0 .
Đáp số: m 0 3 2 2
Bài 10. Tìm tham số m để hàm số y x 2m
1 x m 3m 2x 4 có hai điểm cực đa ̣i và cực
tiểu nằm về hai phı́a so với tru ̣c tung.
Đáp số: 1 m 2 1 Bài 11. Cho hàm số 3 2
y x mx x 1 m . Tìm m để hàm số có cực đại và cực tiểu, đồng thời khoảng 3
cách giữa hai điểm ấy là ngắn nhất.
Đáp số: m 0
Bài 12. Tìm giá tri ̣ của tham số m để hàm số: 3 2
a/ y x 3mx 7x 3 có đường thẳng đi qua các điểm cực đại, cực tiểu vuông góc với đường thẳng
y 3x 7 . 3 2 2
b/ y x 3x m x m có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng 1 5 y x . 2 2 3 2
c/ y x 3m
1 x 6(m 2)x 1 có đường thẳng đi qua hai điểm cực trị song song với đường
thẳng y 4x 1 . 3 2
d/ y x 3m
1 x 6(m 2)x có các điểm cực đại và cực tiểu của đồ thị nằm trên đường thẳng y 4x .
Bài 13. Tìm tham số m để hàm số thỏa yêu cầu của bài toán. 3 2 2
a/ Cho hàm số y x 3mx m
1 x 1. Tìm m để hàm số có 2 cực trị thỏa: 2x x 2 2 x x 1 2 1 2 . 3 2
b/ Cho hàm số y 2x 3.2m
1 x 6m(m 1)x 1 . Tìm m để hàm số luôn đạt cực trị tại x ;x 1 2
với x x không phụ thuộc vào m. 2 1 1 3 2 1 c/ Cho hàm số y
mx m
1 x 3m
2 x . Tìm tham số m để hàm số có 2 cực trị thỏa: 3 3 x 2x 1 1 2 . 1 d/ Cho hàm số 3 2
y mx mx mx 1 . Tìm m để hàm số có 2 cực trị thỏa: x x 8 . 3 1 2 2
e/ Cho hàm số y (x m)x 3x m
1 . Tìm m để hàm số có cực đại và cực tiểu thỏa: x .x 1 CÐ CT . 3 2
f/ Cho hàm số y x 31 mx 9x m . Tìm m để hàm số có 2 cực trị, đồng thời hai hoành độ cực
trị thỏa mãn: x x 2 1 2 .
Bài 14. Tìm tham số m để hàm số thỏa yêu cầu của bài toán. 1 3 1 2
a/ Cho hàm số y mx 3m
1 x 2m m
1 x . Tìm m để hàm số có 2 cực tri ̣ thỏa: 3 2 2 x x 3 1 2 . 1 3 2 2 m
b/ Cho hàm số y mx mx m 1 x
. Tìm m để hàm số có 2 cực trị thỏa: 3 3 2
x x . x 5 12 1 1 2 . c/ Cho hàm số 3 2 2
y 2x 9mx 12m x 1. Tìm m để hàm số có 2 cực trị, đồng thời 2 hoành độ cực trị thỏa: 2 x x CÐ CT .
Bài 15. Tìm tham số m để hàm số thỏa yêu cầu của bài toán m a/ Cho hàm số 3 2 y
.x (m 1)x (m 2)x 5 . Tìm m để hàm số có 2 cực trị, đồng thời 2 điểm 3
cực trị này nằm về hai phía so với trục hoành Ox . m 1 b/ Cho hàm số 3 2 y
x mx 3m 1 . Tìm m để hàm số có cực đại và cực tiểu, đồng thời hai 3
điểm này nằm về hai phía so với trục tung Oy . c/ Cho hàm số 3 2
y x 2x mx 1 . Tìm m để hàm số có hai điểm cực trị, đồng thời 2 điểm cực trị này
nằm hai bên (khác phía nhau) so với đường thẳng x 3 .
Bài 16. Tìm tham số m để hàm số thỏa yêu cầu của bài toán 3 2 2 2
a/ Cho hàm số y x 3m
1 x 3m 7m
1 x m 1 . Tìm m để hàm số có điểm cực tiểu
tại một điểm có hoành độ nhỏ hơn 1. 3 2
b/ Cho hàm số y mx 3mx m
1 x 4 . Tìm m để hàm số có điểm cực tiểu tại một điểm có hoành độ âm.
Bài 17. Tìm tham số m để hàm số thỏa yêu cầu của bài toán. a/ Cho hàm số 3 2
y x mx x 5m 1. Tìm m để hàm số có cực trị và khoảng cách giữa 2 điểm cực trị bé hơn 2 . 2 2 900m b/ Cho hàm số 3 2 y x
mx 4 . Tìm m để hàm số có 2 cực trị là A và B thỏa: AB . 729 1 c/ Cho hàm số 3 2
y x mx x 1 m . Tìm m để hàm số có cực đại và cực tiểu, đồng thời khoảng 3
cách giữa hai điểm ấy là ngắn nhất.
Bài 18. Tìm tham số m để hàm số thỏa yêu cầu của bài toán. 1 3 2
a/ Cho hàm số y x 3m
1 x 4x 2 . Tìm m để hàm số có hai điểm cực trị là A, B sao cho 3
diện tích tam giác MAB bằng 1 với M(0;1). 1 3 2
b/ Cho hàm số y x x m
1 x m . Tìm m để hàm số có hai điểm cực trị A, B sao cho tam giác 3
ABO vuông cân với O là gốc tọa độ. 2 3m c/ Cho hàm số 3 2 y x
x . Tìm m để hàm số có cực đại A, cực tiểu B và tạo với C(–2; 3) thành tam 2 giác ABC đều. d/ Cho hàm số 3 2 3
y x 3mx 4m . Tìm m để hàm số có cực đại và cực tiểu đối xứng nhau qua đường phân giác thứ nhất.
Hàm bâ ̣c 4 trùng phương 4 2
y ax bx c a 0
• Luôn có ít nhất 1 cực trị.
• Nếu có 3 cực trị thì 3 cực trị này luôn tạo thành 1 tam giác cân tại đỉnh thuộc trục oy. Bài 1. Cho hàm số 4 2
y 3x mx 2 . Tìm tham số m để hàm số có cực đại tại A(0;–2) và đạt cực tiểu tại hai điểm 2
B; C sao cho: x x 6 m m C B .
Đáp số: m 1 4 2 2
Bài 2. Cho hàm số y x 2m x 1. Tı̀m tham số m để hàm số có 3 cực tri ̣, đồng thời 3 điểm cực tri ̣ này là
3 đı̉nh của mô ̣t tam giác vuông cân.
Đáp số: m 1 4 4
Bài 3. Cho hàm số y x 2mx 2m m . Tı̀m tham số m để hàm số có 3 cực tri ̣, đồng thời 3 điểm cực tri ̣
này lâ ̣p thành mô ̣t tam giác đều. Đáp số 3 : m 3 4 2
Bài 4. Cho hàm số y x 2mx m 1. Tı̀m tham số m để hàm số có 3 cực tri ̣, đồng thời các điểm cực tri ̣
A,B,C của đồ thi ̣ ta ̣o thành mô ̣t tam giác có bán kı́nh đường tròn ngoa ̣i tiếp bằng 1. m 1 Đáp số: 5 1 m 2
Bài 5. Tìm tham số m để hàm số thỏa yêu cầu của bài toán. a/ Cho hàm số 4 2
y 3x mx 2 . Tìm m để hàm số có cực đại tại A(0; –2) và đạt cực tiểu tại hai điểm B; 2 C sao cho: x .x
2m 8m 10 B C . b/ Cho hàm số 4 2
y x 4mx 1. Tìm m để hàm số có cực đại tại A(0;1) và đạt cực tiểu tại hai điểm B; C 2 sao cho: x x 22m m C B .
Bài 6. Tìm tham số m để hàm số thỏa yêu cầu của bài toán. a/ Cho hàm số 4 2
y x mx 3 . Tìm m để hàm số có 3 cực trị và 3 điểm này lập thành 1 tam giác đều. b/ Cho hàm số 4 2
y x mx 4 m . Tìm m để hàm số có 3 điểm cực trị là A, B, C và tam giác ABC
nhận gốc tọa độ O làm trọng tâm. c/ Cho hàm số 4 2 2
y x 2m x 1. Tìm m để hàm số có cực trị là A, B, C sao cho tam giác ABC có diện tích bằng 4. d/ Cho hàm số 4 2
y x 2mx m 1. Tìm m để hàm số có 3 cực trị, đồng thời các điểm cực trị A, B, C
của đồ thị tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1. BÀI 3
GIÁ TRỊ LỚN NHẤT (GTLN) VÀ GIÁ TRỊ NHỎ NHẤT (GTNN) CỦA HÀM SỐ
1. Định nghĩa: Giả sử hàm số y f x xác đi ̣nh trên miền D với D .
f x M, x D f x ,
m x D
M max f x
m min f x và
x D : f x M
x D : f x m D o o D o o
2. Tı́nh chất: ma x f
x f b [a,b ]
a. Tı́nh chất 1: Nếu hàm số y f x đồng biến trên a ,b thı̀ : min f
x f a [a,b ] ma x f
x f a [a,b ]
b. Tı́nh chất 2: Nếu hàm số y f x nghi ̣ch biến trên a ,b thı̀ : min f
x f b [a,b ] DẠNG 1
TÌM GIÁ TRỊ LỚN NHẤT (GTLN) VÀ GIÁ TRỊ NHỎ NHẤT (GTNN) CỦA HÀM SỐ
DỰA VÀO ĐỊNH NGHĨA VÀ TÍNH CHẤT 1. Phương pháp giải
Phương pháp 1: Dùng bảng biến thiên để tı̀m max – min. Phương pháp này thường dùng cho bài toán tı̀m
GTLN và GTNN trên mô ̣t khoảng a,b hoặc nửa đoạn a
,b,a,b .
• Bước 1: Tính f 'x.
• Bước 2: Xét dấu f 'xvà lập bảng biến thiên.
• Bước 3: Dựa vào bảng biến thiên để kết luận.
Phương pháp 2: Thường dùng khi tìm max – min của hàm số liên tục trên một đoạn a,b .
• Bước 1: Tính f 'x.
• Bước 2: Giải f 'x 0 tìm được các nghiệmx i 1,n trên đoạn a,b i (nếu có).
• Bước 3: Tính f a, f b, f x , f x ,..., f x . 1 2 n
• Bước 4: So sánh các giá trị vừa tính được và kết luận m
ax f x maxf a,f b,f x ,f x ,...,f x 1 2 n [a,b ] . m
in f x minf a, f b, f x , f x ,..., f x 1 2 n [a,b ]
Chú ý: Có thể dùng bảng biến thiên để tı̀m max – min của hàm số trên một đoạn a ,b .
2. Một số lưu ý khi giải toán
• Lưu ý 1: Phương trình f 'x 0 có thể là phương trình mũ, logarit, đại số, lượng giác, … Do đó đó, cần
nắm vững kiến thức về cách giải phương trình các loại.
a sin x b cos x c
• Lưu ý 2: Đối với hàm lượng giác dạng: 1 1 1 y .
a sin x b cos x c 2 2 2 2 Đă x 2t 1 t
̣t t tan sin x ; cos x . 2 2 2 1 t 1 t
at bt c Thay vào
, ta được hàm hữu tı̉ đa ̣i số da ̣ng: f t 2 2
a 't b 't c '
• Lưu ý 3: Khi bài toán yêu cầu tìm max – min nhưng không nói trên tập nào thì ta hiểu tı̀m max – min trên
tập xác định D của hàm số.
• Lưu ý 4: Để tìm tham số ,
m n của hàm số f (x, , m n) với x f x m n có là biến số sao cho ( , , ) max f (x, ,
m n) a và min f (x, ,
m n) b . Ta làm như sau:
+ Bước 1: Hàm số đã cho xác định và liên tục trên D mà đề cho hoặc ta tìm. f(x, , m n) a
- Hàm số có giá trị lớn nhất bằng a khi và chỉ khi
x D : f (x , ,
m n) a có nghiêm x 0 o o A B
- Giải tìm điều kiện và kết hợp đánh giá hai vế của một đẳng thức:
A B (1). A B f(x, , m n) b
+ Bước 2: Hàm số có giá trị nhỏ nhất bằng b khi và chỉ khi .
x D : f (x , ,
m n) b có nghiêm x 0 o o
Tương tự ta được phương trình (2). 1
+ Bước 3: Giải hệ phương trình ,
m n cần tìm. 2
• Lưu ý 5: Ta có thể tı̀m GTLN và GTNN của hàm số bằng cách dùng miền giá tri ̣ (đk có nghiê ̣m)
Đặt vấn đề: Tìm max – min của hàm số y f (x) trên một miền D cho trước ?
• Bước 1: Gọi y
f x trên D, thì hệ phương trình (ẩn
o là một giá trị tùy ý của ( ) x) sau có nghiệm:
f x y o x D
• Bước 2: Tùy theo điều kiện của hệ trên mà ta có các điều kiện tương ứng. Thông thường điều
kiện ấy (sau khi biến đổi) có dạng: m y M 3 y f x nên từ 3 o
. Vì o là một giá trị bất kỳ của ( ) ta suy ra mi
n f(x) m được: D ma
x f (x) M D Loại 1
TÌM GTLN VÀ GTNN CỦA HÀM SỐ TRÊN KHOẢNG
Bài 1. Tìm giá tri ̣ lớn nhất và giá tri ̣ nhỏ nhất (nếu có) của các hàm số sau: 4 x 1 a/ y x , x 0. b/ y . x 2 x x 1 1 2 x 1 9x c/ y x ,x 0;2 y , x 0 . x . d/ 2 8x 1 Đáp số:
a/ min f x 4 khi x 2 0; 1 1 b/ max y
khi x 0 và min y khi x 2 . x 3 x 3
c/ min f x 0 khi x 1 . 0;2 2 2 1 1 3 2 1 f/ min g(x) khi x ; max f (x) khi x . 0; 3 0; 6 2 2 2 4 6 2 3
Bài 2. Tìm GTLN và GTNN của các hàm số sau 2 2 3 4 x x 1
a/ y 1 8x x .
b/ y 4x 3x . c/ y . 2 x x 1 x 2 2x 10x 3 2 x 1 d/ y . e/ y . f/ y . 2 4 x 2 3x 2x 1 4 2 x x 1
Bài 3. Tìm GTLN và GTNN của các hàm số sau 1 2 2 a/ y x ,x 0 . b/ y x ,x 0 .
c/ y x 3 x x x 2 x 2 2 d/ y x 2 e/ y f/ y
x 2x 3 x 200 Loại 2
TÌM GTLN VÀ GTNN CỦA HÀM SỐ TRÊN ĐOẠN
Bài 1. Tìm giá tri ̣ lớn nhất và giá tri ̣ nhỏ nhất của các hàm số sau:
a/ y f x 3 2
3x x 7x 1 trên đoa ̣n 0;2
b/ y f x 4 2
2x 4x 3 trên đoa ̣n 0;2
c/ y x x 3 6 2 4 1 trên đoa ̣n 1;1 . d/ 9 y
f x x trên đoa ̣n 2;4 x . x x
e/ y f x 2 trên đoa ̣n 5; 3 y f x trên đoa ̣n 0;2 x 2 . f/ 3 1 x 3 . Đáp số: ma x f x khi 1 x 0 ma x f x 5 x 1 ma
x y 4 khi x 0 khi 0;2 0;2 1;1 a/ b/ c/ mi n f
x 9 khi x 2 mi n f
x 13 khi x 2 4 2 mi
ny khi x 0;2 9 3 0;2 1;1 f x 11 max khi x 2 max f
x 8 khi x 4 1 ma
xy f 0= khi x 0 2 5;3 0;2 3 d/ 2;4 e/ f/ mi n f mi n f
x 9 khi x 3 mi
ny f 2 5 x 2
x 6 khi x 3 = khi 0;2 2;4 5;3
Bài 2. Tìm giá tri ̣ lớn nhất và giá tri ̣ nhỏ nhất của các hàm số sau: 3 2
a/ y f x 2
x 3x 2 trên đoa ̣n 10;10 .
b/ y x 3x 1 trên đoa ̣n 2;1 . mi n f
x f 1 f 2 0 max f x 19 Đáp số 10;10 2;1 : a/ b/ m ax f
x f 10 132 min g x 0 2;1 10;10
Bài 3. Tìm giá tri ̣ lớn nhất và giá tri ̣ nhỏ nhất của các hàm số sau: 2 2 a/ y
x 2x 5 trên 1;3 .
b/ y x 1 3x 6x 9 trên 1; 3 . 2 2
c/ y x 2 x trên 2; 2
y x 1 2 2x 2x 4 . d/ trên 1;2 . x 1
e/ y x 2
6 x 4 trên 0;3 . f/ y trên 1;2 2 . x 1 Đáp số: m
ax f x 2 2
khi x 1;x 2 ma x f x 6 x 2 khi 1;3 1;3 a/ b/ mi n f
x 2 khi x 1 mi n f
x 0 khi x 1 1;3 1;3 ma x f
x 2 khi x 1 3 6 3 1 6 m ax f x 2. x 2; 2 khi 2 2 2 c/ d/ 1;2 mi n f
x 2 khi x 2 mi n f
x 0 khi x 1 2; 2 1;2
max y 3 13 khi x 3 ma
x f x 2 khi x 1 0;3 1;2 e/ f/ mi
ny 12 khi x 0 mi n f x 0 x 1 khi 0;3 1;2
Bài 4. Tìm giá tri ̣ lớn nhất và giá tri ̣ nhỏ nhất của các hàm số sau: 2 2 a/ y 4 x b/ y x 4 x c/ y
2 x 4 x 2 2
d/ y 3x 10 x
e/ y x 2 2 4 x f/ y 3 2x x Đáp số: ma x f
x 0 khi x 2 ma
x f x 2 2 x 2 khi 2;2 2;2 a/ b/ mi n f
x 2 khi x 0 mi n f x 2 x 2 khi 2;2 2;2 ma
x f x 2 3 max y 10 x 3 khi x 1 khi 2;4 10; 10 c/ d/ m
in f x 6 khi x 2; x 4 miny 3 10 x 10 khi 2;4 10; 10 ma xy 3 3 khi x 1
max y 2 khi x 1 2;2 1;3 e/ f/ mi
ny 0 khi x 2 m
iny 0 khi x 1, x 3 2;2 1;3
Bài 5. Tìm GTLN và GTNN của các hàm số sau 2 2 a/ y x 4x 3 trên 0;3 .
b/ y x 3x 2 trên 10;10 . Loại 3
TÌM GTLN VÀ GTNN CỦA HÀM SỐ LƯỢNG GIÁC
Bài 1. Tìm giá tri ̣ lớn nhất và giá tri ̣ nhỏ nhất của các hàm số sau:
a/ y sin 2x x trên đoa ̣n ; . b/ y
2 cos 2x 4 sin x trên đoa ̣n 0; . 2 2 2 4 3 1 1 c/ y 2 sin x sin x
trên 0; y trên 0; 3 d) sin x cos x 2 Đáp số: a/ max y khi x
và miny khi x . 2 2 2 2 ; ; 2 2 2 2
b/ max y 2 2 khi x
và miny 2 khi x 0 . 4 0; 0; 2 2 f x 2 2 3 max khi x , x c/ 0, 3 4 4 m in f
x 0 khi x 0, x 0,
Bài 2. Tìm giá tri ̣ lớn nhất và giá tri ̣ nhỏ nhất của các hàm số sau: 2 2
a/ y 2 sin x 2 sin x 1 .
b/ y cos 2x sin x cos x 4 . 4 2
c/ y cos x sin x 2 .
d/ y sin x 3 sin 2x sin x 1
cos x 2 sin x 3 e/ y f/ y . 2
sin x sin x 1
2 cos x sin x 4 1 g/ y . h/ y
1 sin x 1 cos x sin x cos x Đáp số:
max f t maxy 3 khi t sinx 1 x k2 1,1 D 2 a/ x
k2 , k . f t 3 1 y khi 6 min min
t sin x 1,1 D 2 2 7 x k2 6 f x 81 1 1 1 max
khi t sin 2x x arcsin k 16 4 2 4 b/ ,k . f x 7 min
khi t sin 2x 1 x k 2 4 2 m axy khi 1
t 1; t 0 c/ 5 1 mi
ny khi t 4 2 2 2 c osx x arccos 5 5 3 3 d/ max y khi 3 5 5 s inx x arccos 3 3 ma
x f x max f t khi 1
t sin x 0 x k , k t 1;1 e/ m in f
x min f t 0 khi t sinx 1 x k2 , k 2 t 1;1
max f(t) 2 khi t 2 1 mi ny ma x f x 4 2 2 f/ 2 4 g/ 4 8 h/ mi
n f(t) khi t min f x maxy 1 1 11 3 BÀI 4
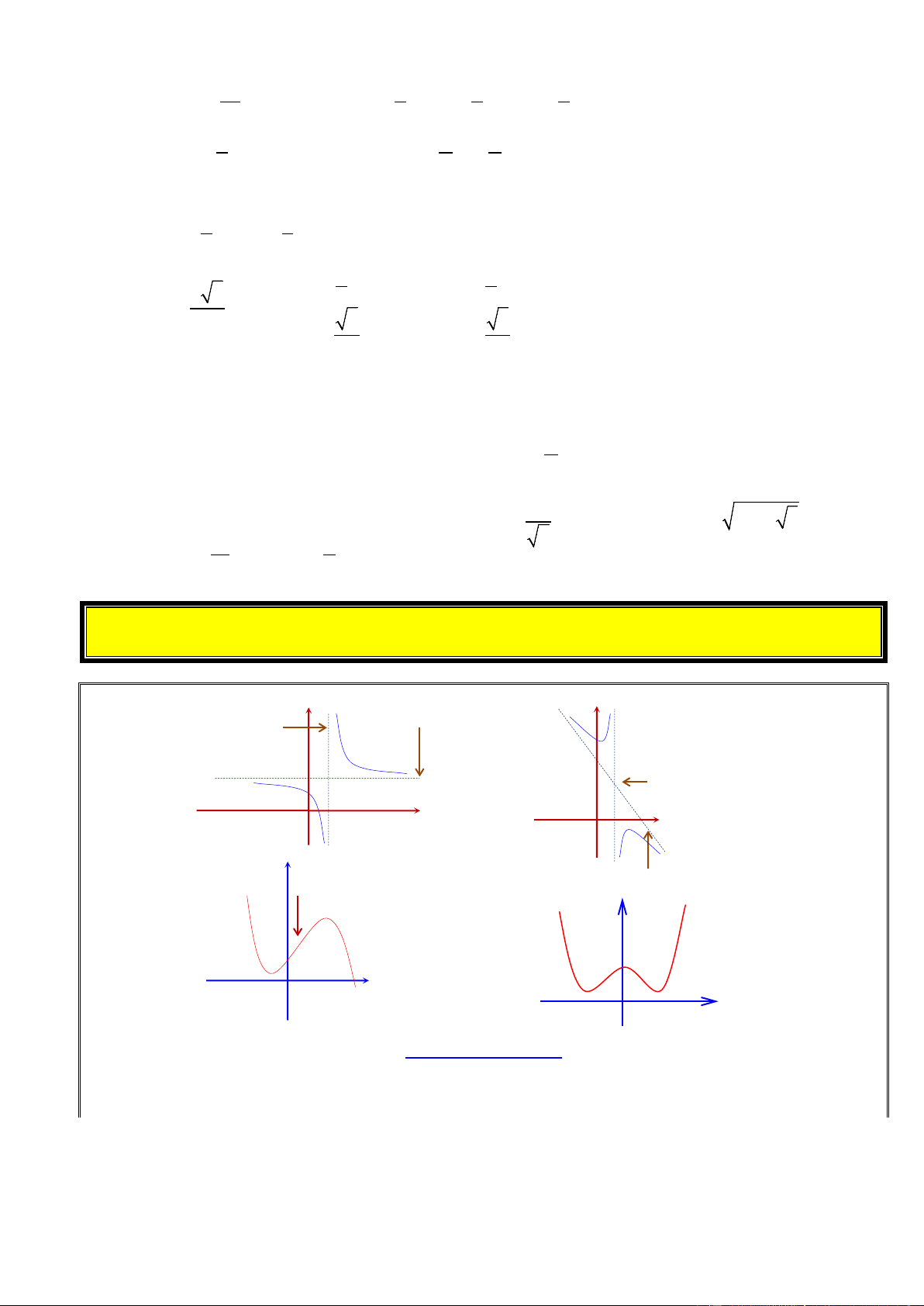
TIỆM CẬN VÀ ĐIỂM UỐN CỦA ĐỒ THỊ HÀM SỐ y y Tiê ̣m câ ̣n đứng Tiê ̣m câ ̣n ngang • I Tâm đối xứng I O x x O y Tiê ̣m câ ̣n xiên Điểm uốn y • U x O x O CƠ SỞ LÝ THUYẾT
I . Tiê ̣m câ ̣n của đồ thi ̣hàm số 1. Đi ̣nh nghı̃a
a. Đường thẳng x x đượ y f x o
c go ̣i là đường tiê ̣m câ ̣n đứng của đồ thi ̣ hàm số
( ) nếu ı́t nhất một
1 lim f (x)
xxo
2 lim f (x) x x o
trong các điều kiê ̣n sau được thỏa mãn:
TCÐ: x x o
3 lim f (x) x x o
4 lim f(x) x x o
b. Đường thẳng y y y f x
o đươ ̣c go ̣i là đường tiê ̣m câ ̣n ngang của đồ thi ̣ hàm số ( ) nếu ı́t nhất 1
1 lim f(x) yo x
trong các điều kiê ̣n sau đây được thỏa mãn:
TCN : y yo
2 lim f (x) yo x
c. Đường thẳng y ax ; b a
0 được go ̣i là đường tiê ̣m câ ̣n xiên của đồ thi ̣ hàm số y f(x) nếu
ı́t nhất một trong các điều kiê ̣n sau đây được thỏa mãn:
1 lim f(x)ax b 0 x
TCX : y ax b
2 lim f(x)ax b 0 x 2. Lưu ý P(x)
• Trường hợp y f(x)
là hàm số phân thức hữu tỷ. Q(x)
+ Nếu Q(x) 0 có nghiê ̣m x x x x
0 thı̀ đồ thi ̣ có tiê ̣m câ ̣n đứng
o ( o là điểm ta ̣i đó hàm số không
xác đi ̣nh ⇒ x xo là tiê ̣m câ ̣n đứng).
+ Nếu bâ ̣c P(x
) bâ ̣c Q(x
) thı̀ đồ thi ̣ có tiê ̣m câ ̣n ngang.
+ Nếu bâ ̣c P(x
) bâ ̣c Q(x
) 1thı̀ đồ thi ̣ có tiê ̣m câ ̣n xiên. P(x) Q (x) 0
+ Số tiê ̣m câ ̣n đứng của hàm số phân thức y
là số nghiê ̣m của hê ̣ Q(x) P (x) 0
+ Đồ thi ̣ có tiê ̣m câ ̣n ngang thı̀ không có tiê ̣m câ ̣n xiên và ngược la ̣i.
• Để xác đi ̣nh các hê ̣ số a,b trong phương trı̀nh của đường tiê ̣m câ ̣n xiên, ta có thể áp dụng các công f (x) a lim
; b lim f (x) ax x x x thức:
. Nếu a 0 thı̀ TCX trở thành TCĐ. f (x) a lim
; b lim f (x) ax x x x 2
ax bx c
• Thông thường đối với hàm da ̣ng: y
thı̀ ta tı̀m câ ̣n xiên bằng cách chia đa thức, lấy dx e
phần nguyên là tiê ̣m câ ̣n xiên do lim (phần dư) = 0. x
• Hàm số bâ ̣c ba và bâ ̣c bốn không có các đường tiê ̣m câ ̣n. 2
• Hàm số y ax bx c; (a 0)
+ Nếu: a 0 đồ thi ̣hàm số không có các đường tiê ̣m câ ̣n. b
+ Nếu: a 0 đồ thi ̣ hàm số có tiê ̣m câ ̣n xiên y a x khi x 2a và b y a x khi x 2a . 2
• Đồ thi ̣ hàm số y mx n p ax bx c; (a 0) có tiê ̣m câ ̣n là đường thẳng b
y mx n p a x . 2a
II – Điểm uốn của đồ thi ̣hàm số
1. Đi ̣nh nghı ̃a: Điểm I x ; f x
được go ̣i là điểm uốn của đồ thi ̣ hàm số y f(x) nếu tồn ta ̣i một khoảng 0 0
a,b chứa điểm x a,x x ,b
o sao cho trên mô ̣t trong hai khoảng o và o
tiếp tuyến của đồ thi ̣ ta ̣i điểm U nằm về
phı́a trên đồ thi ̣ còn trên điểm kia tiếp tuyến nằm phı́a dưới đồ thi ̣. 2. Tı́nh chất
• Nếu hàm số y f(x) có đa ̣o hàm cấp hai trên một khoảng chứa điểm x ; f ' x 0 f x o o và ' ( ) đổi
dấu khi x đi qua x
I x ; f x là một điểm uốn của đồ thi ̣ hàm số. 0 0 o thı̀ 3 2
• Đồ thi ̣ hàm số bâ ̣c ba y f(x) ax bx cx d; a
0 luôn có một điểm uốn và đó là tâm
đối xứng của đồ thi ̣. DẠNG 1
TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
Bài 1. Tìm các tiê ̣m câ ̣n của các hàm số sau 2x 5 x 10x 3 7 a/ y b/ y c/ y d/ y 1 x 1 2 x 1 2x x
Bài 2. Tìm các tiê ̣m câ ̣n của các hàm số sau 2 x 4x 1 2 x x 6 2 7x 4x 5 a/ y b/ y c/ y 2x 1 x 1 2 3x 3 x 2 3 x 3 2 2x x d/ y e/ y f/ y 2 x 2x 2 x 1 2 x 1
Bài 3. Tìm các tiê ̣m câ ̣n của các hàm số sau 2 x 1 2 a/ y x 3 b/ y c/ y x x 3 x 1 2 2 x x x 3 d/ y x e/ y f/ y x x 1 x 1 4x 2 1 2 x 5x 1 g/ y h/ y i/ y 2 x 9 2 x 4x 1 x 2
Bài 4. Tìm giá tri ̣ của tham số m để đồ thi ̣ của các hàm số sau có đúng hai tiê ̣m câ ̣n đứng 3 2 x 2 a/ y b/ y 2
4x 22m 2 3 x m 1 2
3x 2m 1 x 4 x 3 x 3 c/ y d/ y 2
x x m 2 2
x 2m 2 2 x m 1
Bài 5. Tìm m để đồ thi ̣ hàm số sau có tiê ̣m câ ̣n xiên 2
x 3m 2 x 2m 1 2
mx 2m 1 x m 3 a/ y b/ y x 5 x 2
Bài 6. Tính diê ̣n tı́ch của tam giác ta ̣o bởi tiê ̣m câ ̣n xiên của đồ thi ̣ các hàm số sau chắn trên hai tru ̣c to ̣a đô ̣ Oxy 2 3x x 1 2
3x x 4 2 x x 7 a/ y b/ y c/ y x 1 x 2 x 3
Bài 7. Tìm m để tiê ̣m câ ̣n xiên của đồ thi ̣ các hàm số sau ta ̣o với các tru ̣c to ̣a đô ̣ mô ̣t tam giác có diê ̣n tı́ch S đã
được chı̉ ra 2x mx 1 2
x 2m 1 x 2x 3 a/ y ;S 8 b/ y ;S 8 x 1 x 1
Bài 8. Chứng minh rằ ng: Tı́ch các khoảng cách từ mô ̣t điểm bất kỳ trên đồ thi ̣ của các hàm số đến hai tiê ̣m câ ̣n
bằng mô ̣t hằng số . 2 x x 1 2 2x 5x 4 2 x x 7 a) y b) y c) y x 1 x 3 x 3 mx 1
Bài 9. Định m để hàm số có tiê ̣m câ ̣n đứng đi qua A1; 2 với y 2x m 2
mx mx m 1
Bài 10. Tìm m để hàm số y
có cực tri ̣ và khoảng cách từ điểm cực tiểu của đồ thi ̣ hàm số x 1
đã cho đến đường tiê ̣m câ ̣n xiên của nó bằng 1 2 . 2
x m 2
2 x m 4m 3
Bài 11. Cho hàm số y
. Tı̀m m để khoảng cách từ gốc to ̣a đô ̣ O đến tiê ̣m câ ̣n mx 1
xiên hoă ̣c ngang là nhỏ nhất ? m 2
1 x m 1 x 2m 3
Bài 12. Cho hàm số y C , m . x 2 m m
a/ Tı̀m m để góc giữa hai tiê ̣m câ ̣n của đồ thi ̣ Cm bằng 450.
b/ Tı̀m m để đồ thi ̣ Cm có tiê ̣m câ ̣n xiên cắt hai tru ̣c to ̣a đô ̣ ta ̣i A, B sao cho ΔAOB có diê ̣n tı́ch bằng 4 ? DẠNG 2
ĐIỂM UỐN CỦA ĐỒ THỊ HÀM SỐ
Bài 1. Tìm điểm uố n của đồ thi ̣ các hàm số sau 3 2 3 2
a/ y x 6x 3x 2
b/ y x 3x 9x 9 4 2 4 2
c/ y x 6x 3 d/ x y 2x 3 4
Bài 2. Tìm giá tri ̣ của tham số ,
m n để đồ thi ̣ của hàm số sau có điểm uốn I được chı̉ ra 3 2 3 2 a/ x y
m x m 8 1 3 x ; I 1;3 3 3
b/ y x 3x 3mx 3m 4; I 1;2 3 2
c/ y mx nx 1; I 1, 4 d/ 3 2
y x mx nx I 2 2; , 3 3 BÀI 5
KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ
Các bước khảo sát sự biến thiên và vẽ đồ thi ̣hàm số.
• Bước 1: Tı̀m tâ ̣p xác đi ̣nh của hàm số.
• Bước 2: Xét sự biến thiên của hàm số. + Tı́nh y '
+ Tı̀m các điểm ta ̣i đó đa ̣o hàm y ' 0 hoă ̣c không xác đi ̣nh.
+ Tı̀m các giới ha ̣n ⇒ tiê ̣m câ ̣n (nếu có).
+ Lâ ̣p bảng biến thiên, ghi rõ dấu của đa ̣o hàm, chiều biến thiên, cực tri ̣ của hàm số.
• Bước 3: Vẽ đồ thi ̣ hàm số
+ Tı̀m điểm uốn của đồ thi ̣ (đối với hàm số bâ ̣c ba và hàm số trùng phương). - Tı́nh y '
- Tı̀m các điểm ta ̣i đó y ' 0 và xét dấu y '
+ Vẽ các đường tiê ̣m câ ̣n (nếu có) của đồ thi ̣.
+ Xác đi ̣nh mô ̣t số điểm đă ̣c biê ̣t của đồ thi ̣ như: giao điểm của đồ thi ̣ với tru ̣c to ̣a đô ̣ (trong trường hợp đồ
thi ̣ không cắt các tru ̣c to ̣a đô ̣ hoă ̣c tı̀m to ̣a đô ̣ giao điểm ấy phức ta ̣p thı̀ có thể bỏ qua). Ngoài ra, ta tı̀m thêm mô ̣t số
điểm thuô ̣c đồ thi ̣ nhằm vẽ hı̀nh chı́nh xác hơn.
+ Nhâ ̣n xét về đồ thi ̣: Chı̉ ra tru ̣c đối xứng, tâm đối xứng (nếu có) của đồ thi.̣
Bài 1. Khảo sát và vẽ đồ thi ̣ của các hàm số bâ ̣c ba sau đây: 3 2 3 3 2 a/ y x 3x 2
b/ y 2 3x x
c/ y x 3x 3x 5 3 2 3 3 d/ x y x x 1 3
e/ y x x 1
f/ y 2x x 2 2 3 2
g/ y x 1 4 x
h/ y x 2 3 x i/ y x
3x 4x 2
Bài 2. Khảo sát và vẽ đồ thi ̣ của các hàm số bâ ̣c bốn sau đây: 4 2 4 2 1 4 2
a/ y x 2x 1
b/ y 2x 4x 5 c/ y x 2x 1 2 4 2 2 2 2 2 d/ y x x 2
e/ y x 1 x 1
f/ y 2 x x 2
Bài 3. Khảo sát và vẽ đồ thi ̣ của các hàm số nhất biến sau đây: x 1 2x 1 2x 1 2x a/ y b/ y c/ y d/ y x 2 x 1 x 1 x 1
Bài 4. Khảo sát và vẽ đồ thi ̣ của các hàm số hữu tı̉ sau đây: 2 x x 1 2 x x 2 2 x x 2 1 a/ y b/ y c/ y d/ y x 1 x 1 x 1 x 1 x 1 BÀI 6
CÁC BÀI TOÁN LIÊN QUAN ĐẾN ĐỒ THỊ CỦA HÀM SỐ BÀI TOÁN 1
TIẾP TUYẾN CỦA ĐỒ THỊ
Dạng 1: Viết phương trı̀nh tiếp tuyến của đường cong C : y f x tại điểm M x ,y : o o
Phương pháp:
• Bước 1: Phương trı̀nh tiếp tuyến có da ̣ng Pttt : y k . x x y
vớik f ' x . tt o tt o o
• Bước 2: Tı́nh y ' f 'x k f ' x . tt o
• Bước 3: Thay x ,y ,k vào
Phương trı̀nh tiếp tuyến cần tı̀m. o o tt
Dạng 2: Viết phương trı̀nh tiếp tuyến của đường cong C : y f x , biết tiếp tuyến đi qua điểm
M x ;y cho trước: M M
Phương pháp: Cách 1:
• Bước 1: Gọi N x ;y là tọa độ tiếp điểm của tiếp tuyến với đồ thị C 0 0
Pttt cần tı̀m đi qua điểm M x ;y
có da ̣ng: y k x x y tt M M M M • Bước 2:
+ Tı́nh y ' f 'x k f ' x . tt 0 k f ' x tt 1 0
+ Vì tiếp tuyến tiếp xúc với đồ thị C tạiN x ;y nên: 0 0 f
x f ' x x x y 2 0 0 0 M M • Bước 3:
+ Giải phương trı̀nh 2tìm x , sau đó thay vào phương trı̀nh 1 tìm được k 0 tt + Thay k vào
* ta được Pttt cần tı̀m tt Cách 2:
• Bước 1:: Gọi Pttt có da ̣ng Pttt : y ax m 1 y y C tt
• Bước 2: Áp dụng điều kiê ̣n tiếp xúc: a y ' y C 'tt
• Bước 3: Do Pttt đi qua M nên ta thay tọa độ M vào 1 m
Dạng 3: Viết phương trı̀nh tiếp tuyến của đường cong C : y f x , biết tiếp tuyến có hệ số góc k cho tt
trước: Phương pháp:
• Bước 1: Gọi N x ;y là tọa độ tiếp điểm của tiếp tuyến với đồ thị C 0 0
Pttt cần tı̀m tại điểm N x ;y có da ̣ng: y k x x y tt 0 0 0 0
• Bước 2: Tı́nh y ' f 'x k f 'x 1 . tt 0 • Bước 3:
+ Giải phương trı̀nh
1 tìm x , sau đó thay vào đồ thị C tìm được y . 0 0
+ Thay x , y vào
* ta được Pttt cần tı̀m. 0 0
Lưu ý: Viết Pttt là tı̀m ba thành phần x ,y ,k . Một số cách tı̀m hê ̣ số góc k thường gă ̣p: o o tt tt
• Nếu Pttt // : y ax b k k a f ' x x y . tt o o o 1 1
• Nếu Pttt : y ax b k
f ' x x y . tt o o o k a
• Nếu M x ,y C Oy x 0 y f ' x . o o o o o
• Nếu M x ,y C Ox y 0 x f ' x . o o o o o
• Nếu Pttt ta ̣o với chiều dương Ox một góc thı̀ k f 'x tan x y tt o o o k a
• Nếu Pttt ta ̣o với : y ax b một góc thı̀ tt
tan x y . 1 k .a o o tt
Bài 1. Viết phương trı̀nh tiếp tuyến của C ta ̣i điểm được chı̉ ra: a/ C 3 2
: y 3x x 7 1 ta ̣i điểmA0; 1 . b/ C 4 2
: y x 2x 1 ta ̣i điểm B 1;0. x c/ C 3 4 : y
ta ̣i điểm C 1;7. d/ C 2
: y x 1
ta ̣i điểm D 0; 3 . 2x 1 2x 1
Bài 2. Viết phương trı̀nh tiếp tuyến của C ta ̣i điểm được chı̉ ra: 3 x 2 a/ C : y
ta ̣i điểm A có tung đô ̣ bằng 4 . x 1 x b/ C 1 : y
ta ̣i các giao điểm của C với tru ̣c hoành, tru ̣c tung. x 2 c/ C 3
: y x 3x 1 ta ̣i điểm uốn của đồ thi ̣ C . 1 9 d/ C 4 2
: y x 2x
ta ̣i các giao điểm của C với tru ̣c hoành. 4 4 x x e/ C 2 3 3 : y
ta ̣i điểm B có hoàn đô ̣ là 4 . x 2 f/ C 2
: y 2x 2x 1 ta ̣i các giao điểm của C với trục hoành, trục tung.
Bài 3. Viết phương trı̀nh tiếp tuyến của C , biết rằng có hê ̣ số góck được chı̉ ra: 3 2 2x 1
a/ C : y 2x 2x 5 ; k 12
b/ C : y ; k 3 x 2 2 x 3x 4
c/ C : y ; k 1 d/ C 2
: y x 4x 3 ; k 2 x 1
Bài 4. Viết phương trı̀nh tiếp tuyến của C , biết rằng song song với đường thẳng d cho trước: 3 x 2
a/ C : y
2x 3x
1 & d : y 3x 2 . 3 2x 1 3
b/ C : y
& d : y x 2 . x 2 4 1 4 2 3
c/ C : y x 3x
& d : 4x y 2015 0 . 2 2 2 x 2x 3
d/ C : y
& d : 2x y 2016 0 . 4x 6
Bài 5. Viết phương trı̀nh tiếp tuyến của C , biết rằng vuông góc với đường thẳngd cho trước: 3 x 2
a/ C : y
2x 3x
1 & d : x 8y 999 0 . 3 2x 1
b/ C : y
& đường thẳng d là đường phân giác góc phần tư thứ nhất của hệ trục Oxy. x 2 2 x 3
c/ C : y
& d : y 3x 2015 . x 1 2 x x 1
d/ C : y
& d : y x 2 . x 2
Bài 6. Viết phương trı̀nh tiếp tuyến củaC ta ̣i các giao điểm củaC với các đường được chı̉ ra: 3 2
a/ C : y 2x 3x 9x 4
& d : y 7x 4 . 3 2 2
b/ C : y 2x 3x 9x 4
& d : y x 8x 3 . 3 2 3 2
c/ C : y 2x 3x 9x 4 &
C ' : y x 4x 6x 7 .
Bài 7. Viết phương trı̀nh tiếp tuyến của C , biết đi qua điểm được chı̉ ra: 3 3
a/ C : y x 3x 2 ; A2;4
b/ C : y x 3x 1 ; B 1;6 2 2 1 3 3
c/ C : y 2 x ; C 0;4 d/ C 4 2
: y x 3x ; D 0; 2 2 2 x 2 3x 4
e/ C : y ; E 6;5
f/ C : y ; F 2;3 x 2 x 1 2 x 3x 3 2 x x 2
g/ C : y ; G 1;0
h/ C : y ; H 2;2 x 2 x 1
Bài 8. Viết phương trı̀nh tiếp tuyến của C , biết ta ̣o với chiều dương tru ̣c hoành Ox mô ̣t góc : 3 x 3 2 o x 2 o
a/ C : y
2x x 4 ; 60 .
b/ C : y
2x x 4 ; 75 . 3 3 3x 2 o
c/ C : y ; 45 x 1
Bài 9. Viết phương trı̀nh tiếp tuyến của C , biết ta ̣o với đường thẳng d mô ̣t góc : 3 x 2 o
a/ C : y
2x x 4 & d : y 3x 7 ; 45 . 3 3 x 2 1 o
b/ C : y
2x x 4 & d : y x 3 ; 30 . 3 2 4x 3 o
c/ C : y
& d : y 3x ; 45 . x 1 3x 7 o
d/ C : y
& d : x y 0 ; 60 . 5 2x 2 x x 3 o
e/ C : y & d : y x 1 ; 60 . x 2
Bài 10. Tính diê ̣n tı́ch tam giác chắn hai tru ̣c to ̣a đô ̣ bởi tiếp tuyến của đồ thi ̣ C ta ̣i điểm được chı̉ ra: x a/ C 5 11 : y
ta ̣i điểm A có hoành đô ̣ là x 2 . 2x 3 A b/ C 2
: y x 27x 26 ta ̣i điểm B có x 2 . B
Bài 11. Tìm m để tiếp tuyến của đồ thi ̣ C ta ̣i điểm được chı̉ ra chắn hai tru ̣c to ̣a đô ̣ mô ̣t tam giác có diê ̣n tı́ch S cho trước: x m 1 a/ C 2 : y ta ̣i điểm A
x và S . x 1 có 2 A 2 x m 9 b/ C 3 : y ta ̣i điểm B
x và S . x 2 có 1 B 2 3
c/ C : x 1 m x
1 ta ̣i điểm C có x 0 và S 8 . C BÀI TOÁN 2
BIỆN LUẬN SỐ NGHIỆM CỦA PHƯƠNG TRÌNH BẰNG ĐỒ THỊ CỦA HÀM SỐ 3 2
Bài 1. Cho hàm số y x 3x 1 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 3 2
b/ Dùng đồ thi ̣, biê ̣n luâ ̣n số nghiê ̣m của phương trı̀nh: x 3x m 0 . 3
Bài 2. Cho hàm số y x
3x C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 3 2m
b/ Với giá tri ̣nào của m thı̀ phương trı̀nh: x 3x 0 co 2
́ 3 nghiê ̣m thực phân biê ̣t. m 1 3
Bài 3. Cho hàm số y x 3x 1 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 3 2
b/ Dựa vào đồ thi ̣ C , biê ̣n luâ ̣n số nghiê ̣m của phương trı̀nh: x 3x m 2m 2 0 1 3 3 2
Bài 4. Cho hàm số y x x 5 4 2
a/ Khảo sát và vẽ đồ thi ̣ (C) của hàm số đã cho. 3 2
b/ Tı̀m m để phương trı̀nh x 6x m 0 có 3 nghiê ̣m thực phân biê ̣t. 3 2
Bài 5. Cho hàm số y x 3x 2 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 3
b/ Sử du ̣ng đồ thi ̣, biê ̣n luâ ̣n theo tham số m số nghiê ̣m của phương trı̀nh: (x 1) 3 m 3x 0 . 4 2
Bài 6. Cho hàm số y x 8x 10 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số (C). 4
b/ Dựa vào (C), biê ̣n luâ ̣n theo m số nghiê ̣m của phương trı̀nh: x 8x m 0 .
c/ Viết phương trı̀nh đường thẳng đi qua hai điểm cực tiểu của (C). 1 3 2 9
Bài 7. Cho hàm số y
x x 3x 3 2
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ (C) của hàm số. 3 2
b/ Tı̀m k để phương trı̀nh 2x 6x 18x k 0 có 3 nghiê ̣m phân biê ̣t. 1
c/ Viết phương trı̀nh tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng y x 2 . 5 1 3 2 2
Bài 8. Cho hàm số y
x x C 3 3
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 3 2
b/ Dựa vào C , biê ̣n luâ ̣n theo m số nghiê ̣m của phương trı̀nh: x 3x m 0 .
c/ Viết phương trı̀nh tiếp tuyến của C , biết tiếp tuyến có hê ̣ số góc bằng 3. 1 3 2
Bài 9. Cho hàm số y x 2x 3x 1 C 3
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 3 2
b/ Dựa vào C , biê ̣n luâ ̣n theo m số nghiê ̣m của phương trı̀nh: x 6x 9x m 0 .
c/ Viết phương trı̀nh tiếp tuyến của C ta ̣i giao điểm của C với tru ̣c tung. 3 2 x x 7
Bài 10. Cho hàm số y
2x C 3 2 3
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 3 2
b/ Tı̀m m để phương trı̀nh: 2x 3x 12x m 0 có đúng mô ̣t nghiê ̣m.
c/ Viết phương trı̀nh tiếp tuyến của C , biết tiếp tuyến song song với đường thẳng : 4x y 1 0 3 2
Bài 11. Cho hàm số y f (x) 2x 9x 12x 4 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 3 2
b/ Tı̀m m để phương trı̀nh 2x 9x 12x m có đúng mô ̣t nghiê ̣m dương.
c/ Viết phương trı̀nh tiếp tuyến của C ta ̣i điểm là nghiê ̣m của phương trı̀nh f ' (x) 0 . 3
Bài 12. Cho hàm số y 2x 6x 1 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . m
b/ Dựa vào C , biê ̣n luâ ̣n theo m số giao điểm của C và đường thẳng d : y . 2
c/ Viết phương trı̀nh tiếp tuyến của C ta ̣i điểm có hoành đô ̣ bằng 3 . 3 2
Bài 13. Cho hàm số y 2x 3x 1 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 3 2
b/ Tı̀m m để phương trı̀nh 2x 3x m 0 có ba nghiê ̣m phân biê ̣t.
c/ Xác đi ̣nh to ̣a đô ̣ các giao điểm của C và đường thẳng y 2x 1. 4 x 2
Bài 14. Cho hàm số y 2x 1 C 2
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số (C). 4 2
b/ Dựa vào (C), biê ̣n luâ ̣n theo m số nghiê ̣m của phương trı̀nh x 4x m 0 .
c/ Viết phương trı̀nh tiếp tuyến của (C) ta ̣i điểm Aa;2 C với a 0 . 1 4 2 9
Bài 15. Cho hàm số y x 2x C 4 4
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số (C). 4 2
b/ Dựa vào C , tı̀m m để phương trı̀nh x 8x m 0 có bốn nghiê ̣m thực phân biê ̣t.
c/ Viết phương trı̀nh tiếp tuyến của C ta ̣i giao điểm của C và tru ̣c hoành. 4 2
Bài 16. Cho hàm số y x x 2 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 4 2
b/ Tı̀m m để phương trı̀nh x x m 0 có hai nghiê ̣m thực phân biê ̣t.
c/ Viết phương trı̀nh tiếp tuyến của C , biết tiếp tuyến vuông góc với đường thẳng x 6y 1 0 . 4 2
Bài 17. Cho hàm số y 2x 4x C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 4 2
b/ Tı̀m m để phương trı̀nh x 2x m 0 có ba nghiê ̣m phân biê ̣t.
c/ Viết phương trı̀nh tiếp tuyến của C ta ̣i giao điểm của C với tru ̣c hoành, biết giao điểm đó có hoành đô ̣ là mô ̣t số âm. 4 x 2
Bài 18. Cho hàm số y 2x 1 C 4
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 4 2
b/ Dựa vào C , tı̀m m để phương trı̀nh x 8x m 0 vô nghiê ̣m.
c/ Viết phương trı̀nh tiếp tuyến của C ta ̣i điểm có hoành đô ̣ x 2 . 4 2
Bài 19. Cho hàm số y x 4x 1 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 4 2
b/ Tı̀m m để phương trı̀nh x 4x m 0 có 4 nghiê ̣m thực phân biê ̣t.
c/ Xác đi ̣nh to ̣a đô ̣ các giao điểm của C và đường thẳng y 1. Viết phương trı̀nh tiếp tuyến của C ta ̣i các giao điểm đó. 3x 2
Bài 20. Cho hàm số y C 2x 1
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C . 3x 2
b/ Biê ̣n luâ ̣n theo m số nghiê ̣m của phương trı̀nh m 1 . 2x 1
c/ Viết phương trı̀nh tiếp tuyến của C ta ̣i giao điểm của C với tru ̣c hoành.
d/ Tı̀m các điểm trên C cách đều hai tru ̣c to ̣a đô ̣. BÀI TOÁN 3
GIAO ĐIỂM CỦA HAI ĐỒ THỊ
Cho C : y f (x), C
: y g(x) 1 2
• Phương trı̀nh hoành độ giao điểm của C C
f (x) g(x) ( ) 1 và 2 là • Để C C
1 cắ t 2 ta ̣i n điểm phân biê ̣t phương trı̀nh hoành đô ̣ giao điểm [phương trı̀nh( ) ] có n nghiê ̣m phân biê ̣t.
Lưu ý 1: Nếu mô ̣t trong hai đồ thi ̣ trên có da ̣ng hữu tı̉ và có TXĐ D \ . Khi đó, để C C
1 cắ t 2 ta ̣i
n điểm phân biê ̣t phương trı̀nh hoành độ giao điểm [phương trı̀nh( )
] có n nghiê ̣m phân biê ̣t . 3 2
Lưu ý 2: Đi ̣nh lı́ Viét đối với phương trı̀nh bâ ̣c ba: ax bx cx d 0,a 0 3 2
Nếu phương trı̀nh bâ ̣c ba da ̣ng ax bx cx d 0,a
0 có ba nghiê ̣m phân biê ̣t x ,x ,x 1 2 3 thı̀: b
x x x 1 2 3 a c x
x x x x x
x x x x x x 2 2 2 2
2 x x x x x x 1 2 2 3 3 1 1 2 3 1 2 3 1 2 2 3 3 1 a d x x x 1 2 3 a
Lưu ý 3: Xem lại phần Ôn tập phương trình đại số Lưu ý 4: 3 2
Tı̀m tham số để đồ thi ̣hàm số bâ ̣c ba da ̣ng y f x ax bx cx d C cắt tru ̣c hoành Ox
ta ̣i n điểm phân biê ̣t. (Phương pháp cực tri ̣). 3 2
Lúc đó, phương trı̀nh hoành đô ̣ giao điểm: ax bx cx d 0 y f có 2 cực tri ̣. x
• Để C cắt Ox ta ̣i 3 điểm phân biê ̣t
có 3 nghiê ̣m phân biê ̣t y .y 0 CÐ CT y f
x có 2 cực tri ̣.
• Để C cắt Ox ta ̣i 2 điểm phân biê ̣t
có 2 nghiê ̣m phân biê ̣t y .y 0 CÐ CT
(lúc này đồ thi ̣ C tiếp xúc với tru ̣c hoành Ox ) y f không có cực tri ̣. x
• Để C cắt Ox ta ̣i 1 điểm duy nhất
chı̉ có 1 nghiê ̣m y f x co ́ 2 cực tri ̣. y .y 0 CÐ CT
• Để C cắt Ox ta ̣i 3 điểm phân biê ̣t có hoành độ dương
có 3 nghiê ̣m dương phân biê ̣t: y f x có 2 cực tri ̣. y .y 0 CÐ CT x 0,x 0 CÐ CT
a.f 0 0 hay a.d 0
• Để C cắt Ox ta ̣i 3 điểm phân biê ̣t có hoành độ âm
có 3 nghiê ̣m âm phân biê ̣t: y f x có 2 cực tri ̣. y .y 0 CÐ CT x 0,x 0 CÐ CT
a.f 0 0 hay a.d 0
Ho ̣c sinh tự vẽ hı̀nh. 4 2
Lưu ý 5: Tı̀m tham số để đồ thi ̣ hàm số bâ ̣c bốn trùng phương y ax bx c C cắt tru ̣c hoành Ox ta ̣i
4 điểm phân biê ̣t lâ ̣p thành cấp số cô ̣ng (cách đều nhau) ? 4 2
Phương trı̀nh hoành độ giao điểm: ax bx c 0 1 2 2
• Đă ̣t t x 0 . Lúc đó:
1 at bt c 0 2
• Để C cắt trục hoành Ox tại 4 điểm phân biê ̣t
1 có 4 nghiê ̣m phân biê ̣t 2có hai nghiê ̣m 0
phân biê ̣t dương 0 t t S 0 tham số 3 1 2 P 0
• Gọi t ,t là hai nghiê ̣m phân biê ̣t của 2. Lúc đó, 4 nghiê ̣m phân biê ̣t của
1 là: t , t , t , t 1 2 2 1 1 2
(nên sắp xếp theo thứ tự từ bé đến lớn).
• Do 4 nghiê ̣m này lâ ̣p thành cấp số cộng (hay cách đều) t t 2 t 9t t . Kết hợp 1 2 1 1 2
đi ̣nh lı́ Viét, ta tı̀m được tham số. So với 3 giá tri ̣ tham số thỏa yêu cầu bài toán. HÀM SỐ BẬC 3 3 2 y
f x ax bx cx d 3
Bài 1. Cho hàm số y x 3x 2 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C .
b/ Go ̣i d là đường thẳng đi qua điểm A3,20 và có hê ̣ số góc m . Tı̀m m để đường thẳng d cắt C ta ̣i ba điểm phân biê ̣t. 15 ĐS: m và m 24 4 3 2
Bài 2. Cho hàm số y x 6x 9x 1 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C .
b/ Go ̣i d là đường thẳng đi qua điểm A2,
1 và có hê ̣ số góc m . Tı̀m tham số m để đường thẳng d cắt đồ thi ̣
C ta ̣i ba điểm phân biê ̣t. ĐS: m 3
Bài 3. Cho hàm số 3 2
y x 3x 4 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C .
b/ Chứng minh rằng mo ̣i đường thẳng đi qua điểm I 1,2 với hê ̣ số góc k k 3 đều cắt đồ thi ̣ hàm số
C ta ̣i ba điểm phân biê ̣t I, A, B, đồng thời I là trung điểm của đoa ̣n thẳng AB. 3 2
Bài 4. Cho hàm số y x 2x 1 mx m 1
(Trı́ch đề thi ĐH khối A – 2010)
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C .
b/ Tı̀m m để đồ thi ̣ hàm số
1 cắt tru ̣c hoành ta ̣i 3 điểm phân biê ̣t có hoành độ x ,x ,x 1 2
3 thỏa mãn điều kiê ̣n 2 2 2
x x x 4 1 2 3 . 1
ĐS: m 1 m 0 4 1 2 Bài 5. Cho C
y x mx x m C m 3 2 :
. Tı̀m m để m cắt tru ̣c hoành ta ̣i ba điểm phân biê ̣t có 3 3 2 2 2
hoành đô ̣ x ,x ,x
x x x 15 1 2
3 và thỏa mãn điều kiê ̣n: 1 2 3 ĐS: m 1 3 2
Bài 6. Cho hàm số y x 2mx 3m
1 x 2 có đồ thi ̣ là C , điểm M 3,
1 , đường thẳng d có m
phương trı̀nh x y 2 0. Tı̀m các giá tri ̣ của m để đường thẳng d cắt C tại 3 điểm A0,2, , B C sao cho m
tam giác MBC có diện tích bằng 2 6
ĐS: m 2 m 5 3 2
Bài 7. Tìm m để đồ thị hàm số y x 3x m 2x 2m cắt trục hoành tại 3 điểm phân biệt có hoành độ âm. 1 ĐS: 0 m 4
Bài 8. Tìm m để đồ thị hàm số 3
y x m 2 x 2 1
2m 3m
2 x 2m 2m 1 cắt trục hoành tại
3 điểm phân biệt trong đó có hai điểm có hoành độ âm. 1 1
ĐS: 0 m m 2 3 3 2
Bài 9. Cho hàm số: y x 3x C
a/ Khảo sát và vẽ đồ thi ̣ hàm số.
b/ Go ̣i d là đường thẳng qua A1;2 và có hê ̣ số góc là m . Biê ̣n luâ ̣n theo m vi ̣ trı́ tương đối giữa đường
thẳng d và đồ thi ̣C . 3 2 2
Bài 10. Cho hàm số : y x 3(m 1)x 2(m 4m 1)x 4m(m 1) (C ) . Đi ̣nh giá tri ̣ của m để m
hàm số cắtOx ta ̣i 3 điểm phân biê ̣t có hoành đô ̣ đều lớn hơn 1. 3 2 2 3
Bài 11. Cho hàm số : y x 3mx 3(m 1)x m 1
a/ Khảo sát và vẽ đồ thi ̣ hàm số khi m 1.
b/ Tı̀m m để cắtOx ta ̣i 3 điểm phân biê ̣t. 3 2
Bài 12. Cho hàm số : y x 3x 2
a/ Khảo sát và vẽ đồ thi ̣ hàm số.
b/ Đi ̣nh m để y m(x 1) 2 cắt đồ thi ̣ ta ̣i 3 điểm A, B, C sao cho BC = 2 2 với A1;2 m 1 3 2
Bài 13. Cho hàm số : y
x mx (3m 2)x (C ) 3 m
a/ Khảo sát khi m 2 .
b/ Tı̀m m để đồ thi ̣ (C ) cắtOx ta ̣i 3 điểm phân biê ̣t. m 3 x
Bài 14. Cho hàm số : y
3x C và đường thẳng d : y m(x 3) 3
a/ Khảo sát và vẽ đồ thi ̣ hàm số C .
b/ Tı̀m m để C và d có 3 giao điểm A, B, C với A cố đi ̣nh và OA OC , BC 42 3 2
Bài 15. Cho hàm số : y x 3x 2mx 4 4m (C ) m
a/ Khảo sát khi m 1.
b/ Tı̀mm để (C )cắtOx ta ̣i 3 điểm phân biê ̣t có hoành đô ̣ đều lớn hơn 2 . m
c/ Tı̀mm để (C )cắtOx ta ̣i 3 điểm phân biê ̣t có hoành đô ̣ cách đều nhau. m
d/ Tı̀mm để (C ) cắt y mx 2 ta ̣i 3 điểm cách đều nhau. m
Bài 16. Tìm tham số m để đồ thi ̣ của các hàm số 3 2
a/ y x 3mx 6mx 8 cắt tru ̣c hoành ta ̣i 3 điểm phân biê ̣t có hoành đô ̣ lâ ̣p thành cấp số cô ̣ng. 3 2
b/ y x 3x 9x
1 ; y 4x m cắt nhau ta ̣i 3 điểm A, B, C với B là trung điểm của BC. 4 2 2
c/ y x 2m 4x m cắt tru ̣c hoành ta ̣i 4 điểm phân biê ̣t có hoành đô ̣ lâ ̣p thành cấp số cô ̣ng. 3 2
d/ y x m
1 x m
1 x 2m 1 cắt trục hoành ta ̣i 3 điểm phân biê ̣t có hoành độ lâ ̣p thành cấp số nhân. 3 2
e/ y 3x 2m
1 x 9mx 192 cắt trục hoành ta ̣i 3 điểm phân biê ̣t lâ ̣p thành cấp số nhân.
Bài 17. Tìm tham số m để các phương trı̀nh sau chı̉ có đúng 1 nghiê ̣m: 3 2 3 2
a/ 2x 3m
1 x 6mx 2 0
b/ x 3x 31 mx 1 3m 0 3 2 3 2
c/ 2x 3mx 6m
1 x 3m 12 0 d/ x 6x 3m 4x 4m 8 0 3 2 3
e/ 2x 3m
1 x 6m 2x 2 m 0
f/ x 3mx 2m 0
Bài 18. Tìm tham số m để các phương trı̀nh sau chı̉ có 2 nghiê ̣m: 3 2 2 3
a/ x m
1 x 2m 3m 2x 2m2m 1 0
b/ x 3mx 2m 0 3 2 3 2
c/ x 2m
1 x 3m
1 x m 1 0
d/ x 3x 31 mx 1 3m 0
Bài 19. Tìm tham số m để phương trı̀nh sau có 3 nghiê ̣m phân biê ̣t: 3 2 2 2 3 2
a/ x 3mx 3m
1 x m 1 0
b/ x 6x 3m 4x 4x 8 0 3 2 1 3
c/ 2x 3m
1 x 6m
1 x 2 m 0 d/
x x m 0 3
Bài 20. Tìm tham số m để các phương trı̀nh sau có 3 nghiê ̣m dương phân biê ̣t 3 2 2 2 3 2
a/ 2x 3mx 3m
1 x m 1 0
b/ x 6x 3m 4x 4m 8 0 1 3 5 2 7 3 2 c/
x x 4x m 0
x mx 2m 1 x m 2 0 3 2 6 d/
Bài 21. Tìm tham số m để các phương trı̀nh sau có 3 nghiê ̣m âm phân biê ̣t: 3 2 3 2 2 2
a/ 2x 3m
1 x 6m 2x 2 m 0
b/ x 3mx 3m
1 x m 1 0 3 2 3 2
c/ x 3x 9x m 0
d/ x x 18mx 2m 0
HÀM SỐ TRÙNG PHƯƠNG 4 2 y
f x ax bx c 4 2
Bài 1. Cho hàm số y x 3m 2x 3m có đồ thị là C m
a/ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m 1 .
b/ Tìm m để đường thẳng y 1 cắt C
tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2. m 1
ĐS: m 1,m 0 3 4 2 2
Bài 2. Cho đồ thị hàm số y x 2 m 2x m 5m 5 1
a/ Khảo sát và vẽ đồ thị hàm số C khi m 1
b/ Tìm tham số m để đồ thị hàm số
1 cắt trục hoành tại 4 điểm phân biệt. 5 5 ĐS: 1 m 2 4 2
Bài 3. Cho đồ thị hàm số y x m 1 x 3 1
a/ Khảo sát sự biến thiên và vẽ đồ thị hàm số 1 khi m 1
b/ Tìm tham số m để đường thẳng y 4 cắt đồ thị hàm số
1 tại 4 điểm phân biệt. 4 2
Bài 4. Cho hàm số: y x
2mx 2m 1 (C ) m
a/ Khảo sát và vẽ đồ thi ̣ hàm số C khi m 5 .
b/ Đi ̣nh m để hàm số (C ) có 3 cực tri ̣. m
c/ Đi ̣nh m để (C ) cắt trục hoành ta ̣i 4 điểm phân biê ̣t. m 4 2
Bài 5. Cho hàm số: y x 2(m 1)x 2m (C ) m
a/ Khảo sát và vẽ đồ thi ̣ hàm số (C ) khi m 2 .
b/ Đi ̣nh m để (C ) cắt trục hoành ta ̣i 4 điểm phân biê ̣t. m
c/ Đi ̣nh m để (C ) cắt đường thẳngy 2ta ̣i 4 điểm phân biê ̣t. m 4 2
Bài 6. Cho hàm số: y 2mx x 1 4m (C ) m 1
a/ Khảo sát và vẽ đồ thi ̣ hàm số (C ) khi m . 2
b/ Đi ̣nh m để hàm số (C ) có 3 cực tri ̣. m
c/ Đi ̣nh m để (C ) cắt đường thẳng y 3 ta ̣i 4 điểm phân biê ̣t. m 4 2
Bài 7. Cho hàm số: y x 2(m 1)x 4 (C ) m
a/ Khảo sát và vẽ đồ thi ̣ hàm số C khi m 0 .
b/ Đi ̣nhm để (C ) cắt Ox ta ̣i 4 điểm phân biê ̣t mà có hoành độ lâ ̣p thành cấp số cộng (4 điểm cách đều). m
c/ Đi ̣nhm để (C ) cắt Ox ta ̣i 4 điểm phân biê ̣t mà có hoành độ đều lớn hơn 2. m 4 2
Bài 8. Cho hàm số: y x
2mx 2m 1 (C ) m
a/ Khảo sát và vẽ đồ thi ̣ hàm số C khi m 1
b/ Biê ̣n luâ ̣n theo m số cực tri ̣ của hàm số.
c/ Đi ̣nh m để (C ) cắtOx ta ̣i 4 điểm phân biê ̣t mà có hoành độ lâ ̣p thành cấp số cộng. m 4 2
Bài 9. Cho hàm số: y x 10mx 9m (C ) m
a/ Khảo sát khi m 1.
b/ Tı̀m m để (C ) cắt Ox m
ta ̣i 4 điểm phân biê ̣t có hoành đô ̣ cách đều nhau. 4 2
Bài 10. Cho hàm số : y x 2mx 2m 1 (C ) m
a/ Khảo sát khi và vẽ đồ thi ̣ hàm số khi m 1.
b/ Tı̀m m để (C ) có 3 điểm cực tri ̣ lâ ̣p thành tam giác vuông cân. m
c/ Tı̀m m để (C ) cắt Ox m
ta ̣i 4 điểm cách đều nhau.
HÀM SỐ NHẤT BIẾN
ax b y f x cx d x
Bài 1. Cho hàm số y C x 1
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C .
b/ Tı̀m m để đường thẳng d : y x
m cắt đồ thi ̣ C ta ̣i hai điểm phân biê ̣t.
ĐS: b / m ,
0 4, 3 2x
Bài 2. Cho hàm số y C x 1
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C .
b/ Tı̀m m sao cho trên đồ thi ̣C có hai điểm Ax ,y ,B x ,y A A B
B khác nhau và thỏa điều kiê ̣n m
x y 2 A A m
x y 2 B B ĐS: m ,
6 2 5 6 2 5, \ 0 x 2
Bài 3. Cho hàm số y C x 1
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C .
b/ Go ̣i d là đường thẳng đi qua điểm M 1, 3 và có hê ̣ số góc m . Tı̀m m để d cắt C ta ̣i hai điểm phân biê ̣t. x
Bài 4. Tìm m để đường thẳng y mx 3 cắt C 2 1 : y
ta ̣i hai điểm phân biê ̣t A, B sao cho tam giác x 1 ABC vuông ta ̣i O.
ĐS: m 3 5 2x 1
Bài 5. Cho hàm số y
có đồ thi ̣ C . Go ̣i là đường thẳng đi qua điểm I 2, 0 và có hê ̣ số góc m . x 1
Tı̀m tham số m để cắt C ta ̣i 2 điểm phân biê ̣t A, B sao cho I là trung điểm của đoa ̣n thẳng AB. 2 ĐS: m 3 1 x
Bài 6. Chứng minh rằng đường thẳng d : y x m luôn cắt đồ thi ̣ hàm số C 3 : y ta ̣i hai điểm 2 x 2
phân biê ̣t A, B. Tı̀m tham số m để AB ngắn nhất. ĐS: AB 10 khi m 2 min 2x 1
Bài 7. Cho hàm số y C x 1
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C .
b/ Tı̀m tham số m để đường thẳng y 2x m cắt đồ thi ̣ C ta ̣i hai điểm phân biê ̣t A, B sao cho tam
giác OAB có diê ̣n tı́ch bằng 3 (với O là gốc to ̣a đô ̣). ĐS: m 2 2x 2
Bài 8. Cho hàm số: y C x 1
a/ Khảo sát và vẽ đồ thi ̣ hàm số C .
b/ Go ̣i d là đường thẳng qua A2;2 có hê ̣ số góc là k . Đi ̣nh k để d cắt C ta ̣i 2 điểm phân biê ̣t. 1 x
Bài 9. Cho hàm số: y C 2x
a/ Khảo sát và vẽ đồ thi ̣ hàm số C . 1 1
b/ Tı̀m m để đường thẳng d : y m x C
cắ t ta ̣i 2 điểm phân biê ̣t. 2 2 2
Bài 10. Cho hàm số : y 1 C x 1
a/ Khảo sát và vẽ đồ thi ̣ hàm số C .
b/ Tı̀m m để đường thẳng d : y x m cắt C ta ̣i 2 điểm phân biê ̣t. 3
Bài 11. Cho hàm số : y 2 C x 1
a/ Khảo sát và vẽ đồ thi ̣ hàm số C . x
b/ CMR đường thẳng d : y m luôn cắt C ta ̣i 2 điểm phân biê ̣t. 2 3 2
Bài 12. Cho hàm số : y x
3x 9x 2 C
a/ Khảo sát sự biến thiên và vẽ đồ thi ̣ hàm số C .
b/ Go ̣i A là điểm trên C có x 2 và d là đường thẳng qua A có hê ̣ số góc k . Tı̀mk để (d) cắt C ta ̣i 3 A điểm phân biê ̣t. 3 x 2
Bài 13. Cho hàm số : y
x 4 C 3
a/ Khảo sát và vẽ đồ thi ̣ hàm số C .
b/ Đi ̣nh m để d : mx y 4 3m 0 cắt C ta ̣i 3 điểm phân biê ̣t. 3
Bài 14. Cho hàm số : y x
mx 1 m (C ) m
a/ Khảo sát và vẽ đồ thi ̣ hàm số C khi m 3 .
b/ Đi ̣nh m để (C ) cắt trục hoành ta ̣i 3 điểm phân biê ̣t. m 3 2
Bài 15. Cho hàm số : y 2x 3x mx m 2
a/ Khảo sát và vẽ đồ thi ̣ hàm số (C ) khi m 1.
b/ Đi ̣nh m để (C ) cắt trục hoành ta ̣i 3 điểm phân biê ̣t. m 3 2
Bài 16. Cho hàm số : y x m 4x 4x m C
a/ Khảo sát và vẽ đồ thi ̣ hàm số C khi m 0 .
b/ Đi ̣nh k để C cắt đường thẳng y kx ta ̣i 3 điểm phân biê ̣t. x 3
Bài 17. Cho hàm số : y x 1
a/ Khảo sát và vẽ đồ thi ̣ hàm số.
b/ CMR y 2x m luôn cắtC ta ̣i 2 điểm phân biê ̣t M và N.
c/ Tı̀m m để MN min x 2
Bài 18. Cho hàm số : y C x 2
a/ CMR d : y x m luôn cắ tC ta ̣i 2 điểm P và Q thuô ̣c 2 nhánh khác nhau của đồ thi ̣.
b/ Tı̀mm để O
PQ vuông ta ̣i O.
c/ Tı̀mm để PQ min
d/ Tı̀mm để PQ 14
HÀM SỐ HỮU TỈ BẬC 2 2
ax bx c y f x dx e 2 x 1
Bài 1. Tìm các giá tri ̣ của tham số m để đường thẳng y x
m cắt đồ thi ̣ hàm số y ta ̣i hai điểm x
phân biê ̣t A, B sao cho AB = 4. ĐS: m 2 6 2 x 3x 3
Bài 2. Tìm m để đường thẳng d : y m cắt C : y
ta ̣i hai điểm A, B sao cho AB = 1. 2x 1 1 5 ĐS: m 2 2
mx x m
Bài 3. Tìm tham số m để đồ thi ̣hàm số C y m :
cắ t tru ̣c hoành ta ̣i hai điểm phân biê ̣t và hai x 1
điểm đó có hoành độ dương. 1 ĐS: m 0 2 2 x x 1
Bài 4. Tìm tham số m để đường thẳng y 2x m cắt đồ thi ̣ hàm số y
ta ̣i hai điểm phân biê ̣t x
A, B sao cho trung điểm của đoa ̣n thẳng AB thuộc trục tung. ĐS: m 1
Bài 5. Chứng minh rằ ng đường thẳng d : y 3x m luôn cắt đồ thi ̣ hàm số C 4
: y x ta ̣i hai điểm x
phân biê ̣t A, B. Go ̣i I là trung điểm của đoa ̣n thẳng AB, tı̀m tham số m để I nằm trên đường thẳng
d ' : y 2x 3 . ĐS: m 4 2 x mx 1
Bài 6. Cho hàm số: y (C ) x 1 m
a/ Khảo sát khi m 2 .
b/ Tı̀m m để (d) : y m cắt (C ) ta ̣i 2 điểm A, B sao cho OA OB . m c/ Tı̀m m để ( )
: y 2x 1 cắt (C )ta ̣i 2 điểm thuô ̣c 2 nhánh khác nhau của đồ thi ̣. m d/ Tı̀m m để ( )
: y 2x 1 cắt (C )ta ̣i 2 điểm thuô ̣c cùng một nhánh của đồ thi ̣. m BÀI TOÁN 4
CÁC BÀI TOÁN KHÁC LIÊN QUAN ĐẾN TIẾP TUYẾN CỦA ĐỒ THỊ
Tı̀m điều kiê ̣n để hai đường tiếp xúc nhau
a) Điều kiê ̣n cần và đủ để hai đường C : y f x vàC : y g x tiếp xúc nhau là hê ̣ phương trı̀nh 2 1 f
x g x
có nghiê ̣m. Nghiê ̣m của hê ̣
là hoành độ của tiếp điểm của hai đường đó. f '
x g 'x
b) Nếu C : y px q vàC : y ax bx c thı̀ C tiếp xúc với C phương trı̀nh 2 1 2 2 1 2
ax bx c px q có nghiê ̣m kép.
Bài 1. Tìm điều kiê ̣n của tham số m để hai đườngC vàC tiếp xúc nhau: 2 1 3 2
a/ C : y x 3 m x mx 2 & C : tru ̣c hoành. 1 2 3 2
b/ C : y x 2x m 1 x m & C : tru ̣c hoành. 1 2 3
c/ C : y x m x 1 1 &
C : y x 1. 1 2 3 2
d/ C : y x 2x 2x 1 &
C : y x m . 1 2
Bài 2. Tìm điều kiê ̣n của tham số m để hai đườngC vàC tiếp xúc nhau: 2 1 4 2 2
a/ C : y x 2x 1 &
C : y 2mx m 1 2 4 2 2
b/ C : y x x 1 &
C : y x m 1 2 1 4 2 9 2
c/ C : y x 2x &
C : y x m 1 2 4 4 2 2 2
d/ C : y x 1 x 1 &
C : y 2x m 1 2 2
2m 1 x m e/ C : y &
C : y x 1 2 x 1 2 x x 1 2 f/ C : y &
C : y x m 1 2 x 1
Lâ ̣p phương trı̀nh tiếp tuyến chung của hai đồ thi ̣C : y f x vàC : y g x 2 1
a/ Go ̣i : y ax b là tiếp tuyến chung của C vàC với u là hoành đô ̣ tiếp điểm của vàC , v là 1 2 1
hoành đô ̣ tiếp điểm của vàC . 2 f
u au b 1 f '
u a 2
+ tiếp xúc với C và C khi và chı̉ khi hê ̣ có nghiê ̣m. 2 1 g
v av b 3 g '
v a 4
+ Từ 2và4 f 'u g 'v u h v 5
+ Thế a từ 2vào
1 b u 6
+ Thế 2,5,6vào3 v a u b . Từ đó viết được phương trı̀nh .
b/ Nếu C và C tiếp xúc nhau ta ̣i điểm có hoành đô ̣ x thı̀ mô ̣t tiếp chung của C và C cũng là tiếp 2 1 2 1 o
tuyến củaC và C ta ̣i điểm đó. 2 1
Bài 3. Hãy viết phương trı̀nh tiếp tuyến chung của hai đồ thi ̣ 2 2
a/ C : y x 5x 6 &
C : y x 5x 11 1 2 2 2
b/ C : y x 5x 6 &
C : y x x 14 1 2 2 3
c/ C : y x 5x 6 &
C : y x 3x 10 1 2
BÀI TẬP TỔNG HỢP CHƯƠNG 1
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ mx 1
Bài 1. Cho hàm số: y 2x m
a/ Chứng minh rằng m , hàm số luôn luôn đồng biến trên mỗi khoảng xác đi ̣nh của nó.
b/ Đi ̣nhm để đường tiê ̣m câ ̣n đứng của đồ thi ̣ đi qua điểm A1; 2
c/ Đi ̣nhm để đường tiê ̣m câ ̣n ngang của đồ thi ̣ có phương trı̀nh y 5
d/ Khảo sát và vẽ đồ thi ̣ C khi m 2
e/ Viết PTTT củaC ta ̣i M trên C có x 2 M
f/ Viết PTTT của C ta ̣i giao điểm của C với tru ̣c hoành 1
g/ Viết PTTT của C có hê ̣ số góc bằng 6
h/ Viết PTTT của C , biết tiếp tuyến song song d : y 6x 1
i/ Viết PTTT của C , biết tiếp tuyến vuông góc : x 24y 7 0
j/ Viết PTTT của C , biết tiếp tuyến đi qua điểm B 1;3
m 1x 2m 1
Bài 2. Cho hàm số: y x 1
a/ Đi ̣nhm để hàm số để hàm số luôn nghi ̣ch biến trên mỗi khoảng xác đi ̣nh.
b/ Đi ̣nhm để đường tiê ̣m câ ̣n ngang của đồ thi ̣ đi qua A 3;6
c/ Đi ̣nhm để đồ thi ̣ cắt trục tung ta ̣i điểm có tung độ bằng 4.
d/ Khảo sát và vẽ đồ thi ̣C của hàm số khi m 0
e/ Viết PTTT củaC ta ̣i B trên C có tung đô ̣ là 2.
f/ Viết PTTT củaC ta ̣i giao điểm của C với tru ̣c tung. 1
g/ Viết PTTT củaC có hê ̣ số góc bằng 2
h/ Viết PTTT của C và song song với đường thẳng: d : y 2x 3
i/ Viết PTTT của C và vuông góc với đường thẳng: : x 8y 1 0
j/ Viết PTTT của C , biết tiếp tuyến đi qua điểm C 2;0 x 2
Bài 3. Cho hàm số: y x m 1
a/ Tı̀mm để hàm số luôn đồng biến trên mỗi khoảng xác đi ̣nh.
b/ Tı̀mm để đường tiê ̣m câ ̣n đứng của đồ thi ̣ là x 5 .
c/ Tı̀mm để đồ thi ̣ cắt tru ̣c hoành ta ̣i điểm có hoành đô ̣ bằng 3 .
d/ Khảo sát và vẽ đồ thi ̣ C khi m 2 .
e/ Viết PTTT của C ta ̣i A trên C có tung đô ̣ là 3.
f/ Viết PTTT của C ta ̣i giao điểm của C với tru ̣c tung. 1
g/ Viết PTTT của C có hê ̣ số góc bằng 3
h/ Viết PTTT của C và song song với đường thẳng d : y 3x
i/ Viết PTTT của C và vuông góc với đường thẳng : x 9y 4 0
j/ Viết PTTT của C , biết tiếp tuyến đi qua B 3; 1 3 2
Bài 4. Cho hàm số: y x ax bx 1
a/ Tı̀m a và b để đồ thi ̣hàm số qua 2 điểm A1,2 và B 2, 1
b/ Khảo sát và vẽ đồ thi ̣ C với a 1 và b 1 .
c/ Viết PTTT của C ta ̣i điểm M trên C có hoành đô ̣ là 1 .
d/ Viết PTTT củaC ta ̣i giao điểm của C với tru ̣c tung.
e/ Viết PTTT của C có hê ̣ số góc bằng 1 .
f/ Viết PTTT của C và song song với đường thẳng d : y 4x 7
g/ Viết PTTT của C và vuông góc với đường thẳng : x 20y 0
h/ Viết PTTT của C , biết tiếp tuyến đi qua C 2,2 3 2
Bài 5. Cho hàm số: y x m 3x m 1 C m
a/ Đi ̣nh m để hàm số có điểm cực đa ̣i là x 1. b/ Đi ̣nh m để (C
m) cắ t tru ̣c hoành ta ̣i điểm có hoành đô ̣ bằ ng 2 .
c/ Đi ̣nh m để (Cm) cắt tru ̣c tung ta ̣i điểm có tung đô ̣ bằng 3.
d/ Khảo sát và vẽ đồ thi ̣ hàm số C với m 0 .
e/ Viết PTTT của C ta ̣i điểmA trên C có tung đô ̣ bằng 1.
f/ Viết PTTT của C ta ̣i giao điểm của C với tru ̣c tung.
g/ Viết PTTT của C có hê ̣ số góc bằng 0.
h/ Viết PTTT của C và tiếp tuyến song song với đường thẳng d : y 9x 8
i/ Viết PTTT của C và tiếp tuyến vuông góc với đường thẳng : x 3y 2 0
j/ Viết PTTT của C , biết tiếp tuyến đi qua C 4,5 1 3 2
Bài 6. Cho hàm số: y x m
1 x (m 1)x 4 C m 3
a/ Đi ̣nh m để hàm số có điểm cực tiểu là x 3 .
b/ Đi ̣nh m để C
cắt tru ̣c hoành ta ̣i điểm có hoành đô ̣ bằng 1. m
c/ Chứng minh rằng hàm số luôn có 2 cực tri ̣.
d/ Khảo sát và vẽ đồ thi ̣ C khi m 0 .
e/ Viết PTTT của C ta ̣i giao điểm của C với tru ̣c tung.
f/ Viết PTTT củaC ta ̣i A trênC có hoành đô ̣ bằng 3 .
g/ Viết PTTT củaC có hê ̣ số góc bằng 3.
h/ Viết PTTT củaC và tiếp tuyến song song với đường thẳng d : y 5x 2
i/ Viết PTTT của C và tiếp tuyến vuông góc với đường thẳng : x 12y 1 0
j/ Viết PTTT của C , biết tiếp tuyến đi qua điểm C 2,5 1 4 2 1
Bài 7. Cho hàm số: y x m 2x m (C ) 2 2 m
a/ Tı̀m m để hàm số có 3 điểm cực tri ̣.
b/ Tı̀mm để hàm số có điểm cực tri ̣ làx 1, ta ̣i đó là điểm cực đa ̣i hay điểm cực tiều? Tı̀m giá tri ̣ cực tri ̣ tương ứng ?
c/ Tı̀m m để (C ) cắt tru ̣c hoành ta ̣i 4 điểm phân biê ̣t. m
d/ Khảo sát và vẽ đồ thi ̣ C khi m 1.
e/ Viết PTTT của C ta ̣i M trên C có hoành đô ̣ là 1 .
f/ Viết PTTT củaC ta ̣i điểm có hoành đô ̣ là nghiê ̣m của phương trı̀nh f ' (x) 0
g/ Viết PTTT của C và song song với đường thẳng d : y 4x 10
h/ Viết PTTT của C và vuông góc với đường thẳng : x 4y 0
i/ Viết PTTT của C , biết tiếp tuyến đi qua A1,2 4 2
Bài 8. Cho hàm số: y x
2mx 2m 1 (C ) m
a/ Tı̀m m để hàm số có 3 cực tri ̣.
b/ Tı̀m m để hàm số có điểm cực đa ̣i là x 1 .
c/ Tı̀m m để (C ) cắt tru ̣c hoành ta ̣i 4 điểm phân biê ̣t. m
d/ Khảo sát và vẽ đồ thi ̣ C khi m 1.
e/ Viết PTTT của C ta ̣i giao điểm của C với tru ̣c hoành.
f/ Viết PTTT của C ta ̣i điểm có hoành đô ̣ là nghiê ̣m của phương trı̀nh f ' (x) 44 4 2
Bài 9. Cho hàm số: y x ax b 3
a/ Tı̀m a và b để hàm số có giá tri ̣ cực tri ̣ bằng khi x 1 . 2
b/ Tı̀m a và b sao cho y
1 0 và y ' 1 8 1
c/ Khảo sát và vẽ đồ thi ̣ (C) khi a và b 1 2
d/ Viết PTTT của C ta ̣i điểm có tung đô ̣ bằng 1
e/ Viết PTTT của C ta ̣i điểm có hoành đô ̣ là nghiê ̣m của phương trı̀nh f ' x 2
f/ Viết PTTT của C và song song với đường thẳng d : y 3x 2 3 2
Bài 10. Cho hàm số : y x
3x 9x 2
a/ Khảo sát và vẽ đồ thi ̣ hàm số C .
b/ Giải bất phương trı̀nh: f 'x 1 0
c/ Viết PTTT của C ta ̣i điểm có hoành đô ̣ x f x o biết ' ( ) 6 o
d/ Viết PTTT của C và có hê ̣ số góc k 9 . 3 2
e/ Dựa vào C biê ̣n luâ ̣n số nghiê ̣m của phương trı̀nh: x 3x 9x 2 m 0
f/ Viết phương trı̀nh đường thẳng đi qua 2 điểm cực đa ̣i và cực tiểu của đồ thi ̣ hàm số. 3 2
Bài 11. Cho hàm số : y x 3x 1
a/ Khảo sát và vẽ đồ thi ̣ hàm số C 3 2
b/ Dùng đồ thi ̣ biê ̣n luâ ̣n số nghiê ̣m của phương trı̀nh: 2x 6x 2m 0
c/ Đi ̣nh k để d : y k x 2 5 cắt đồ thi ̣ ta ̣i 3 điểm phân biê ̣t.
d/ Viết PTTT của C ta ̣i điểm có hoành đô ̣ thỏa: y 'x 9
e/ Viết phương trı̀nh đường thẳng đi qua điểm cực đa ̣i và điểm cực tiểu. 1 3 2
Bài 12. Cho hàm số : y x m
1 x m 3x 4 (C ) 3 m
a/ Tı̀m m để hàm số đồng biến trên tâ ̣p xác đi ̣nh.
b/ Khảo sát và vẽ C với m 0 . 3 2
c/ Dựa vào đồ thi ̣ biê ̣n luâ ̣n số nghiê ̣m của phương trı̀nh: 2x 6x 18x 24 3k 0
d/ Viết phương trı̀nh đường thẳng đi qua điểm cực đa ̣i và điểm cực tiểu.
e/ Viết PTTT của C ta ̣i điểm có hoành đô ̣ thỏa: y ' (x) 4
f/ Tı̀m a để (d) : y a x 313 cắt C ta ̣i 3 điểm phân biê ̣t. 1 4 2
Bài 13. Cho hàm số : y
x ax b 2 7
a/ Tı̀m a và b để hàm số có cực tiểu bằng khi x 3 2
b/ Khảo sát và vẽ C khi a 3 và a 3 . 4 2
c/ Dựa vào đồ thi ̣ biê ̣n luâ ̣n số nghiê ̣m của phương trı̀nh: x 6x 2 m
d/ Viết PTTT của C ta ̣i điểm có hoành đô ̣ thỏa: y ' x 18 o 1 4 2 9
Bài 14. Cho hàm số : y x 2x 4 4
a/ Khảo sát và vẽ đồ thi ̣ của hàm số.
b/ Viết PTTT của C ta ̣i các giao điểm của C với tru ̣c hoành. 2
c/ Đi ̣nh m để C cắt Parabol (P) : y 2x ta ̣i 4 điểm phân biê ̣t.
d/ Viết PTTT củaC ta ̣i điểm có hoành đô ̣ là nghiê ̣m của phương trı̀nh: y ' (x) 8 4 2
e/ Biê ̣n luâ ̣n theo k số nghiê ̣m của phương trı̀nh: x 8x 9 4k 0 4 2
Bài 15. Cho hàm số : y x 2m 1 x 2m 1 (C ) m
a/ Đi ̣nh m để hàm số cắt tru ̣c hoành ta ̣i 4 điểm phân biê ̣t.
b/ Đi ̣nh m để hàm số có 3 cực tri ̣.
c/ Đi ̣nh m để hàm số có cực đa ̣i khi x 1 .
d/ Khảo sát và vẽ C khi m 1.
e/ Viết PTTT của C ta ̣i các giao điểm của C với đường thẳng y 3 biết hoành đô ̣ của nó là số âm.
f/ Dùng đồ thi ̣ biê ̣n luâ ̣n số nghiê ̣m của phương trı̀nh: 4 2
x 4x m 0
Document Outline
- ÔN TẬP NHỮNG KIẾN THỨC CẦN NHỚ
- ĐỂ VẬN DỤNG GIẢI TOÁN
- Vấn đề 1
- CÔNG THỨC TÍNH ĐẠO HÀM
- Vấn đề 2
- CÔNG THỨC LƯỢNG GIÁC
- Vấn đề 3
- PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
- Vấn đề 4
- PHƯƠNG TRÌNH ĐẠI SỐ
- Vấn đề 5
- HÌNH HỌC PHẲNG
- CHƯƠNG I
- ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
- BÀI 1
- TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
- DẠNG 1
- XÉT TÍNH ĐƠN ĐIỆU (tìm khoảng tăng - giảm) CỦA HÀM SỐ
- DẠNG 2
- Tìm điều kiện của tham số để hàm số đồng biến hoặc nghịch biến
- DẠNG 3
- Ứng dụng tính đơn điệu chứng minh bất đẳng thức
- DẠNG 4
- Ứng dụng tính đơn điệu để giải phương trình – bất phương trình có chứa tham số
- LOẠI 1
- Ứng dụng tính đơn điệu để giải phương trình có chứa tham số
- LOẠI 2
- Ứng dụng tính đơn điệu để giải bất phương trình có chứa tham số
- BÀI 2
- CỰC TRỊ CỦA HÀM SỐ
- DẠNG 1
- TÌM CỰC TRỊ CỦA HÀM SỐ
- DẠNG 2
- TÌM THAM SỐ ĐỂ HÀM SỐ CÓ CỰC TRỊ TẠI
- DẠNG 3
- BIỆN LUẬN HOÀNH ĐỘ CỰC TRỊ CỦA HÀM SỐ
- Loại 1
- Tìm giá trị tham số để hàm số cực trị , hoặc không có cực trị
- Hàm bậc 3
- Hàm bậc 4 trùng phương
- Hàm phân thức
- Loại 2
- Tìm giá trị tham số để hàm số có cực trị thỏa điều kiện cho trước
- (sử dụng định lí Viét)
- Hàm bậc 3
- Hàm bậc 4 trùng phương
- ( Luôn có ít nhất 1 cực trị.
- ( Nếu có 3 cực trị thì 3 cực trị này luôn tạo thành 1 tam giác cân tại đỉnh thuộc trục oy.
- BÀI 3
- GIÁ TRỊ LỚN NHẤT (GTLN) VÀ GIÁ TRỊ NHỎ NHẤT (GTNN) CỦA HÀM SỐ
- DẠNG 1
- TÌM GIÁ TRỊ LỚN NHẤT (GTLN) VÀ GIÁ TRỊ NHỎ NHẤT (GTNN) CỦA HÀM SỐ
- DỰA VÀO ĐỊNH NGHĨA VÀ TÍNH CHẤT
- Loại 1
- TÌM GTLN VÀ GTNN CỦA HÀM SỐ TRÊN KHOẢNG
- Loại 2
- TÌM GTLN VÀ GTNN CỦA HÀM SỐ TRÊN ĐOẠN
- Loại 3
- TÌM GTLN VÀ GTNN CỦA HÀM SỐ LƯỢNG GIÁC
- BÀI 4
- TIỆM CẬN VÀ ĐIỂM UỐN CỦA ĐỒ THỊ HÀM SỐ
- DẠNG 1
- TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
- DẠNG 2
- ĐIỂM UỐN CỦA ĐỒ THỊ HÀM SỐ
- BÀI 5
- KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ
- BÀI 6
- CÁC BÀI TOÁN LIÊN QUAN ĐẾN ĐỒ THỊ CỦA HÀM SỐ
- BÀI TOÁN 1
- TIẾP TUYẾN CỦA ĐỒ THỊ
- BÀI TOÁN 2
- BIỆN LUẬN SỐ NGHIỆM CỦA PHƯƠNG TRÌNH BẰNG ĐỒ THỊ CỦA HÀM SỐ
- BÀI TOÁN 3
- GIAO ĐIỂM CỦA HAI ĐỒ THỊ
- HÀM SỐ BẬC 3
- HÀM SỐ TRÙNG PHƯƠNG
- HÀM SỐ NHẤT BIẾN
- HÀM SỐ HỮU TỈ BẬC 2
- BÀI TOÁN 4
- CÁC BÀI TOÁN KHÁC LIÊN QUAN ĐẾN TIẾP TUYẾN CỦA ĐỒ THỊ
- BÀI TẬP TỔNG HỢP CHƯƠNG 1
- ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ