Chuyên đề nhắc lại và bổ sung các khái niệm về hàm số

Tài liệu gồm 18 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề nhắc lại và bổ sung các khái niệm về hàm số. Mời bạn đọc đón xem.

66 33 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Hàm số bậc nhất

Môn: Toán 9

Thông tin:

18 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊN ĐỀ NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ
A. KIẾN THỨC CẦN NHỚ
1. Khái niệm hàm số
Nếu đại lượng y phụ thuộc vào đại lượng x thay đổi sao cho với mỗi giá trị của x, ta luôn xác định được
chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x( x gọi là biến số). Ta viết: y = f(x), y =
g(x),...
Ví dụ: Ta có y = 2x + 3 là một hàm số của y theo biến x.
Lưu ý: Khi x thay đổi mà y luôn nhận giá trị không đổi thì hàm số y = f(x) gọi là hàm h
ằng.
2.Giá trị của hàm số, điều kiện xác định của hàm số
-Giá trị của hàm số f(x) tại điểm x
0
kí hiệu là y
0
= f(x
0
).
-Điều kiện xác định của hàm số y = f(x) là tất cả các giá trị của x sao cho biểu thức f(x) có nghĩa.
3. Đồ thị của hàm số
- Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm M(x;y) trong mặt phẳng tọa độ Oxy sao cho x, y
thỏa mãn hệ thức y = f(x).
- Điểm M(x
0
; y
0
) thuộc đồ thị hàm số y = f(x) <=> y
0
=f(x
0
)
4. Hàm số đồng biến và hàm số nghịch biến
Cho hàm số y = f(x) xác định với mọi giá trị x thuộc R.
-Nếu giá trị của biến x tăng lên mà giá trị y = f(x) tương ứng cũng tăng lên thì hàm số y = f(x) được gọi
là đồng biến trên R
-Nếu giá trị của biến x tăng lên mà giá trị y = f(x) tương ứng lại giảm đi thì hàm số y = f(x)được gọi là
nghịch biến trên R.
Nói cách khác, với x
1
, x
2
bất kì thuộc R:
+ Nếu x
1
< x
2
mà f(x
1
) < f(x
2
) thì hàm số y = f(x) đồng biến
+ Nếu x
1
< x
2
mà f(x
1
) > f(x
2
) thì hàm số y = f(x) nghịch biến.
Trong quá trình giải toán ta có thể sử dụng kiến thức sau đây để xét tính đồng biến hoặc nghịch biến của
hàm số trên R:
Cho x
1
, x
2
bất kì thuộc R và . Đặt khi đó:
12
xx
21
21
f(x ) f(x )
T
xx
2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
+ Nếu T > 0 thì hàm số đã cho đồng biến trên R
+ Nếu T < 0 thì hàm số đã cho nghịch biến trên R.
3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
B. CÁC DẠNG BÀI CƠ BẢN VÀ NÂNG CAO
Dạng 1. Tính giá trị của hàm số tại một điểm
Phương pháp giải: Để tính giá trị của hàm số y = f(x) tại x
0
, ta thay x = x
0
vào y = f(x) được y
0
= f(x
0
)
Bài 1. Cho hàm số
() 4 1yfx x
.Tính
(0),f
1
(),
2
f

2,f
()fa
Dạng 2.Biểu diễn tọa độ của một điểm trên mặt phẳng tọa độ Oxy
Phương pháp giải: Để biểu diễn tọa độ của điểm M(x
0
; y
0
) trên hệ trục tọa độ Oxy, ta làm như sau:
1.Vẽ đường thẳng song song với trục Oy tại điểm có hoành độ x = x
0
2. Vẽ đường thẳng song song với trục Ox tại điểm có tung độ y = y
0
3. Giao điểm của hai đường thẳng trên chính là điểm M(x
0
; y
0
)
Bài 2. Cho hàm số
2
() 2 3 2yfxxx
a) Tính
(0),f (2 1)f
b) Tìm các giá trị của x sao cho
() 7fx
Bài 3. Trong các bảng sau ghi các giá trị tương ứng của
x
và
y
. Bảng nào xác định
y
là hàm số của
x
? Vì sao?
x
1 2 4 5 7 8
y
3 5 9 11 15 17
Bài 4. Cho hàm số

2
() 3
3
yfx x
a) Tính giá trị tương ứng của
y
theo các giá trị của
x
rồi điền vào bảng:
x
– 2 –1,5 – 1 –0,5 0 0,5 1 1,5 2
2
3
5
yx
b) Hàm số đã cho là hàm đồng biến hay nghịch biến ? Vì sao ?
Bài 5. Sự tương quan giữa
x
và
y
theo bảng sau xác định một hàm số nào ?
x
2 3 0 -2 -3
y
4 6 0 -4 -6
Dạng 3: Xét sự đồng biến và nghịch biến của hàm số.
x
3 4 3 5 8
y
6 8 4 8 16
4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Phương pháp giải: ta thực hiện một trong các cách sau:
Cách 1: Với mọi x
1
, x
2
thuộc R, giả sử x
1
< x
2
-Nếu hiệu H = f(x
1
) - f(x
2
) < 0 thì hàm số đồng biến.
-Nếu hiệu H = f(x
1
) - f(x
2
) > 0 thì hàm số nghịch biến.
Cách 2: Với mọi x
1
, x
2
thuộc R và . Xét tỉ số
-Nếu T > 0 thì hàm số đồng biến
-Nếu T < 0 thì hàm số nghịch biến
Bài 6. Xét chiều biến thiên của hàm số
() 3yfx x
trong
.
Bài 7. Chứng minh hàm số
25yx
đồng biến trên
.
Bài 8. Chứng minh hàm số
1
2
3
yx
nghịch biến trên
Bài 9. Chứng tỏ rằng hàm số
2
() 4 9fx x
đồng biến trong khoảng

0;5
Bài 10. Cho hàm số
2
365yx x
với
x
. Chứng minh rằng hàm số đồng biến khi
1x 
, hàm số
nghịch biến khi
1x
.
Bài 11. Chứng minh rằng hàm số
2
34
1
xx
y
x

đồng biến trong khoảng

2; 3
.
Bài 12. Tìm hàm số
()fx
, biết
2
(1) 2fx x x
.
Dạng 4:Nâng cao và phát triển tư duy
Bài 13. Cho các số thực không âm
,,xyz
thỏa mãn
1xyz
. Tìm giá trị lớn nhất của biểu thức
2P xy yz zx xyz
.
12
xx
21
21
f(x ) f(x )
T
xx
5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
HƯỚNG DẪN
Bài 1. Cho hàm số
() 4 1yfx x
.Tính
(0),f
1
(),
2
f

2,f
()fa
.
Lời giải
(0) 4.0 1 1f 
.
 

 
 
11
4. 1 3
22
f
.

2421f 
.
() 4 1fa a
.
Bài 2. Cho hàm số
2
() 2 3 2yfxxx
a) Tính
(0),f (2 1)f
b) Tìm các giá trị của x sao cho
() 7fx
Bài 3. Trong các bảng sau ghi các giá trị tương ứng của
x
và
y
.Bảng nào xác định
y
là hàm số của
x
? Vì sao ?
x
1 2 4 5 7 8
y
3 5 9 11 15 17
a) b)
Lời giải
Bảng
)a
xác định
y
là hàm số của biến số
x
vì mỗi giá trị của
x
ta xác định được một giá trị tương
ứng của
y
Bảng
)b
không xác định
y
là hàm số của biến số
x
vì mỗi giá trị của
x
không phải khi nào ta xác
cũng định được một giá trị tương ứng của
y
. Cụ thể khi
3,x
y
lấy giá trị là
6
và
4
Bài 4.
a) Cho hàm số

2
() 3
3
yfx x
x
3 4 3 5 8
y
6 8 4 8 16
6.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
x
– 2 –1,5 – 1 –0,5 0 0,5 1 1,5 2
2
3
5
yx
11
5
12
5
13
5
14
5
3
16
5
17
5
18
5
19
5
b) Hàm số đồng biến. Vì


12 1 2
x x fx fx
Bài 5. Sự tương quan giữa
x
và
y
theo bảng sau xác định một hàm số nào ?
x
2 3 0 -2 -3
y
4 6 0 -4 -6
Lời giải
Tỉ số giữa
y
và
x
của bảng là :
4646
2
23 2 3



Vậy theo bảng là xác định được một hàm số
2yx
Bài 6. Cho hàm số
2
() 2 3 2yfxxx
a) Tính
(0),f (2 1)f
b) Tìm các giá trị của
x
sao cho
() 7fx
Lời giải
a)
(0) 2f
2
(2 1) 2(2 1) 3(2 1) 2f 
42423215 2
b)
2
() 7 2 3 2 7fx x x
2 ( 1) 5( 1) 0
(1)(25)0
xx x
xx


10x 
hoặc 2x + 5 = 0
1
x

hoặc
2,5x 
Vậy
1
x
hoặc
2,5x 
thì
() 7fx
Bài 7. Xét chiều biến thiên của hàm số
() 3yfx x
trong
:
7.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Lời giải
Cho
12 1 2
;:xx Rx x
ta có
121212
() ( ) 3 3 3( )fx fx x x x x
Vì
12 1 2
;:xx Rx x
nên
12 1 2
33 ()()x x fx fx
Vậy
() 3yfx x
đồng biến trong
Bài 8. Chứng minh hàm số
25yx
đồng biến trên
.
Lời giải
Đặt

25yfx x
TXĐ:
25x
xác định với mọi
x
Với mọi
12
,xx
bất kì và
12
xx
. Xét

121 2 1 2 12
252525252 0fx fx x x x x x x
(do
12 12
0xx xx
)

12
fx fx
Vậy hàm số

25yfx x
đồng biến. (đpcm)
Bài 9. Chứng minh hàm số
1
2
3
yx
nghịch biến trên
Lời giải
Đặt

1
2
3
ygx x
TXĐ:
1
2
3
x
xác định với mọi
x
Với mọi
12
,xx
bất kì và
12
xx
. Xét
 
12 1 2 1 2 12
11111
5555 0
33333
gx gx x x x x x x




(do

12 12 12
1
00
3
xx xx xx
)

12
gx gx
Vậy hàm số

1
2
3
ygx x
nghịch biến. (đpcm)
Bài 10. Chứng tỏ rằng hàm số
2
() 4 9fx x
đồng biến trong khoảng

0;5
8.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Lời giải
Trong khoảng

0;5
ta lấy hai giá trị tùy ý của
x
sao cho
12
xx
, ta có :

22
12 1 2
() () 4 9 4 9fx fx x x
22 22
12 12 1212
44 4( )4( )( )xx xx xxxx
Vì
12
xx
nên
12
0xx
. Mặt khác trong khoảng

0;5
nên
12
0xx
do đó
1212
4( )( )xxxx
< 0,
12
() () 0fx fx
hay
12
() ()fx fx
.
Vậy hàm số
2
() 4 9fx x
đồng biến trong khoảng

0;5
.(đpcm)
Bài 11. Cho hàm số
2
365yx x
với
x
. Chứng minh rằng hàm số đồng biến khi
1x 
, hàm số
nghịch biến khi
1x 
.
Lời giải
22
3653(1)2yx x x
Với mọi
12
,xx
bất kì và
12
xx
. Ta có
12
0xx
22
12 1 2
() () 3( 1) 2 3( 1) 2fx fx x x



22
121212
3( 1) 3( 1) 3( )( 2)xxxxxx



+ Khi
1x 
thì
12 12 1 2 1 2
2203()(2)0xx xx x xx x
hay
12
() ()fx fx
, hàm số đồng biến.
+ Khi
1x 
thì
12 12 1 21 2
2203()(2)0xx xx x xx x
hay
12
() ()fx fx
, hàm số nghịch biến.
Bài 12. Chứng minh rằng hàm số
2
34
1
xx
y
x

đồng biến trong khoảng

2; 3
.
Lời giải
Trong khoảng

2; 3
cho
x
hai giá trị tùy ý
12
23xx
, ta có
12
0xx
.
22
11 2 2
12
12
343 4
11
xx xx
yy
xx



11 2 2
12
( 1)(3 4) ( 1)(3 4)
11
xx x x
xx



9.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
=
12
3( )xx
Vì
12
23xx
nên
12
0xx
do đó
12
3( ) 0xx
hay
12
yy
.Vậy hàm số
2
34
1
xx
y
x

đồng biến trong khoảng

2; 3
.
Bài 13. Tìm hàm số
()fx
, biết
2
(1) 2fx x x
.
Lời giải
Đặt
11xtxt 
Do đó
22
() ( 1) ( 1) 2 3 4ft t t t t 
Thay t bởi x ta có
2
() 3 4fx x x
.
Bài 14. Cho các số thực không âm
,,xyz
thõa mãn
1xyz
. Tìm giá trị lớn nhất của biểu thức
2P xy yz zx xyz
.
Lời giải
Giả sử
1
min( , , )
33
xyz
zxyzz


. Ta có

22
1
0
44
xy z
xy


.
(1 2 ) ( ) (1 2 ) (1 )Pxyzxyzxyzzz
, nếu ta xem
z
là tham số ,
x
và
y
là ẩn số thì
( ) (1 2 ) (1 )fxy xy z z
là hàm số của
xy
với
2
(1 )
0
4
z
xy

.
Do
12 0z
hàm số
( ) (1 2 ) (1 )fxy xy z z
luôn đồng biến.
Suy ra

2
232
32
1
(1 ) 2 1 7 1 1 1
( ) (1 2 ) (1 2 )
44 42724108
z
zzz
fxy f z z z z z









2
71 1 1 1
()()
27 2 3 6 27
zz
. Dấu
ʺʺ
xảy ra khi
1
3
xyz
.
10.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
C.TỰ LUYỆN
Bài 1. Cho hàm số
1
()
1
x
fx
x
. Tính

423f
Bài 2. Cho hàm số

2
31 23yfx x mx x
. Tìm
m
để

13ff
Bài 3. Cho hàm số
11
()
11
xx
fx
xx


.Chứng minh rằng
() ()fx fx
.
Bài 4. Tìm điều kiện xác định của các hàm số sau:
a)
2
2
x
y
x
b)
42
1
23
y
xx

c)
32
1
2x
y
x
d)
31
2
x
y
x
e)
3
5
3
x
yx
x

f)
22yx x
Bài 5. Chứng tỏ rằng hàm số
2
() 3yfx x
nghịch biến trong khoảng

0Kx x
Bài 6. Chứng tỏ rằng hàm số
3
()yfx x
luôn luôn đồng biến trên
.
Bài 7. Xét tính đồng biến, nghịch biến của hàm số
2yx
trên khoảng

2Kx x
Bài 8. Xét tính đồng biến, nghịch biến của hàm số
4yx
trên khoảng

4Kx x
Bài 9. Tìm giá trị nhỏ nhất của hàm số:
a)
2
43yx x
b)
2
421yx x
c)
42
25yx x
Bài 10. Tìm giá trị lớn nhất của hàm số:
b)
2
63yx x
b)
2
963yxx
c)
42
45yx x
Bài 11. Tìm giá trị lớn nhất của hàm số:
a)
2
2
614
612
xx
y
xx


b)


2
0
2019
x
yx
x

Bài 12. Tìm giá trị nhỏ nhất của hàm số:
a)
2
2
1
21
xx
y
xx


b)


41 4
0
xx
yx
x


11.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
HƯỚNG DẪN
Bài 1. Ta có:


332
4231 311 32 323
423
33
311 3
4231
f




Bài 2. Ta có
  
2
1311 1 213 5fm m

2
3331 32.339 3fmm
Do đó

1
13 59382
4
ffmmmm
Bài 3. Ta có
1111 11
() ()
1111 11
xxxx xx
fx fx
xxxx xx






Bài 4. a.
2x
b.
1x 
c.
2, 0xx
d.
1, 2xx
e.
5, 9xx
f.
22x
Bài 5. Cho
12 1 2
,;xx Kx x
. Xét



2222
212 1 212121
33fx fx x x x x x x x x  
Do
12 1 2 2 1 1 2
,; 0; 0xx Kx x x x x x

2121 2 1
0x x x x fx fx
Do đó hàm số nghịch biến trên
K
Bài 6. Cho
12 1 2
,;xx x x
. Xét



2
33 2 2 2
1
2 1 21 212121 21 2 1
3
0
24
x
fx fx x x x x x xx x x x x x








Do đó hàm số luôn đồng biến trên
Bài 7. Cho
12 1 2
,;xx Kx x
. Xét

21
212 1
21
22 0
22
xx
fx fx x x
xx


Do đó hàm số đồng biến trên
K
Bài 8. Cho
12 1 2
,;xx Kx x
. Xét

12
21 2 1
21
44 0
44
xx
fx fx x x
xx


Do đó hàm số nghịch biến trên
K
Bài 9. a. Ta có

2
2
43 2 77,yx x x x
. Suy ra
min
7y 
đặt được khi
2x
b. Ta có
2
2
155
4212 ,
244
yx x x x




. Suy ra
min
5
4
y 
đặt được khi
1
4
x
c. Ta có

2
42 2
25 144,yx x x x
. Suy ra
min
4y
đặt được khi
1x 
Bài 10. a. Ta có

2
2
63 3 66,yx x x x 
. Suy ra
max
6y
đặt được khi
3x
b. Ta có

2
2
9633122,yxx x x  
. Suy ra
max
2y 
đặt được khi
1
3
x
12.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
c. Ta có

2
42 2
45 211,yx x x x  
.

2
2
33x 
Suy ra
max
1y 
đặt được khi
2x 
Bài 11. a. Ta có

22
22 2 2
614 6122 2 2
11
612 612 612
33
xx xx
y
xx xx xx
x
 
 
  

Do
 


22
22
22 25
30 333 1
33
33 33
xx
xx

 
Vậy
max
5
3
y
đặt được khi
3x
b. Ta có

2
2019
x
y
x
Áp dụng bất đẳng thức Cauchy ta được:


2
2
1
2019 2 2019 2019 8076
8076 8076
2019
xx
xxxx
x
x

Vậy
max
1
8076
y
đặt được khi
2019x
Bài 12. a. Ta có



2
2
2
22 2
111
1111133
1
11244
21
11
xx
xx
y
xx
xx
xx









Vậy
min
3
4
y
đặt được khi
1x
b. Ta có

2
41 4
4174 4 4 4
417 4 1724. 1725
xx
xx
yxxx
xx xxx






Vậy
min
25y
đặt được khi
1x
13.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
D. TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Cho hàm số
()yfx=
xác định trên
D
. Với
12
,;xx DÎ
12
xx<
, khẳng định nào sau đây đúng?
A.
12
() ()fx fx<
thì hàm số đồng biến trên
D
. B.
12
() ()fx fx<
thì hàm số nghịch biến trên
D
.
C.
12
() ()fx fx>
thì hàm số đồng biến trên
D
. D.
12
() ()fx fx=
thì hàm số đồng biến trên
D
.
Câu 2. Cho hàm số
()
yfx
=
xác định trên
D
. Với
12
,;xx DÎ
12
xx>
, khẳng định nào sau đây đúng?
A.
12
() ()fx fx<
thì hàm số đồng biến trên
D
. B.
12
() ()fx fx>
thì hàm số nghịch biến trên
D
.
C.
12
() ()fx fx>
thì hàm số đồng biến trên
D
. D.
12
() ()fx fx=
thì hàm số đồng biến trên
D
.
Câu 3. Cho hàm số
3
() xfx x=+
. Tính
(2)f
A.
4
. B.
6
. C.
8
. D.
10
.
Câu 4. Cho hàm số
3
(2)3fxxx
-=-
. Tính
2. (3)f
A.
16
. B.
8
. C.
32
. D.
64
.
Câu 5. Cho hàm số
2
(1)23xfxx
+=+
. Tính
(3) 2 (2)ff-
A.
34
. B.
17
. C.
20
. D. 0 .
Câu 6. Cho hai hàm số
4
() 6fx x=
và
3
() 7
2
x
hx =- . So sánh
(1)f
-
và
2
3
h
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
A.
2
(1)
3
fh
æö
÷
ç
÷
-=
ç
÷
ç
÷
ç
èø
. B.
2
(1)
3
fh
æö
÷
ç
÷
->
ç
÷
ç
÷
ç
èø
. C.
2
(1)
3
fh
æö
÷
ç
÷
-<
ç
÷
ç
÷
ç
èø
. D. Không đủ điều kiện so sánh.
Câu 7. Cho hai hàm số
3
() 2fx x=-
và
() 10 3hx x=-
. So sánh
(2)f -
và
(1)h -
A.
(2) (1)fh
-<-
. B.
(2) (1)fh
-£-
. C.
(2) (1)fh
-=-
. D.
(2) (1)fh
->-
.
Câu 8. Cho hai hàm số
2
() 2fx x=-
và
() 3 5gx x=+
. Giá trị nào của
a
để
1
() ()
2
fa ga=
A. 0a = . B.
1
a
=
. C.
2
a
=
. D. Không tồn tại.
Câu 9. Cho hai hàm số
2
()fx x=
và
() 5 4gx x=-
. Có bao nhiêu giá trị của
a
để
() ()fa ga=
A. 0 . B.
1
. C.
2
. D.
3
.
Câu 10. Cho hàm số
() 3 2fx x=-
có đồ thị
()C
. Điểm nào sau đây thuộc đồ thị hàm số
()C
.
A.
(0;1)M
. B.
(2; 3)N
. C.
(2; 8)P --
. D.
(2;0)Q -
.
Câu 11. Cho hai hàm số
() 5,5fx x=
có đồ thị
()C
. Điểm nào sau đây thuộc đồ thị hàm số
()C
A.
(0;1)M
. B.
(2;11)N
. C.
(2;11)P -
. D.
(2;12)P -
.
Câu 12. Cho hàm số
() 3fx x=
có đồ thị
()C
và các điểm
(1;1); (0;0); ( 1; 3); (3;9); ( 2;6)MO P Q A-- -
.
Có bao nhiêu điểm trong các điểm trên thuộc đồ thị hàm số
()C
14.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 13. Đường thẳng nào sau đây đi qua điểm
(1; 4)M
?
A.
230xy+-=
. B. 50y -=. C.
40xy-=
. D.
5310xy+-=
.
Câu 14. Đường thẳng nào sau đây đi qua điểm
(1; 1)N
?
A.
230xy+-=
. B.
30y -=
. C.
420xy+=
. D.
5310xy+-=
.
Câu 15. Hàm số
14yx=-
là hàm số?
A. Đồng biến. B. Hàm hằng. C. Nghịch biến. D. Đồng biến với
0x >
.
Câu 16. Hàm số
516yx=-
là hàm số?
A. Đồng biến. B. Hàm hằng. C. Nghịch biến. D. Nghịch biến với
0
x
>
.
Câu 17. Cho hàm số
5
21
2
m
yxm
-
=--. Tìm
m
để hàm số nhận giá trị 5- khi
2x =
A. 5m = . B.
3
m
=
. C.
2
m
=
. D.
3
m
=-
.
Câu 18. Cho hàm số
32ymx m=-+
. Tìm
m
để đồ thị hàm số đi qua điểm
(2; 3)A -
A.
3
m
=
. B.
4
m
=
. C. 5m = . D.
6
m
=
.
Câu 19. Cho hàm số
(2 3 ) 6ymx=- -
. Tìm
m
để đồ thị hàm số đi qua điểm
(3;6)A -
A.
3
m
=
. B.
4
m
=
. C.
9
m
=
. D.
2
m
=
.
Câu 20. Cho hàm số
1
()
23
x
fx
x
+
=
+
. Tính
2
()fa
với
0a <
.
A.
2
1
()
32
a
fa
a
+
=
+
. B.
2
21
()
32
a
fa
a
+
=
-
. C.
2
21
()
32
a
fa
a
-
=
+
. D.
2
1
()
32
a
fa
a
-
=
-
.
Câu 21. Cho hàm số
22
()
4
x
fx
x
-
=
+
. Tính
2
(4 )fa
với
0a ³
.
A.
2
21
(4 )
2
a
fa
a
-
=
+
. B.
2
21
(4 )
2
a
fa
a
+
=
-
. C.
2
2
(4 )
21
a
fa
a
-
=
+
. D.
2
21
(4 )
2
a
fa
a
+
=
+
.
Câu 22. Cho hàm số
()
332443yx= + --
. Tìm
x
để
3y =
A.
23x =+
. B.
3x =
. C.
32x =+
. D.
32x =-
.
Câu 23. Cho hàm số
()
322 21yx=+ - -
. Tìm
x
để
0y =
A.
1x =
. B.
21x =+
. C.
2x =
. D.
21x =-
.
15.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
HƯỚNG DẪN
Câu 1. Đáp án A.
Cho hàm số
()yfx=
xác định trên tập
D
. Khi đó :
- Hàm số đồng biến trên
12 1 2 1 2
,: ()()D x x D x x fx fx" <Î <
- Hàm số nghịch biến trên
12 1 2 1 2
,: ()()D x x D x x fx fx" <Î >
Câu 2. Đáp án C.
Cho hàm số
()yfx=
xác định trên tập
D
. Khi đó :
- Hàm số đồng biến trên
12 1 2 1 2
,: ()()D x x D x x fx fx"Î>>
- Hàm số nghịch biến trên
12 1 2 1 2
,: ()()D x x D x x fx fx"Î>>
Câu 3. Đáp án D.
Thay
2
x
=
vào hàm số ta được
3
(2) 2 2 10f =+=
Câu 4. Đáp án C.
Thay
3x =
vào hàm số ta được
3
(3) 3 3.3 2 16f =- -=
2. (3) 2.16 32f==
.
Câu 5. Đáp án D.
Thay
3
x
=
vào hàm số ta được
2
(3) 3.3 2.3 1 34f =++=
Thay
2x =
vào hàm số ta được
2
(2) 3.2 2.2 1 17f =++=
Suy ra
(3) 2 (2) 34 2.17 0ff-=-=
.
Câu 6. Đáp án A.
Thay
1
x
=-
vào hàm số
4
() 6fx x=
ta được
4
(1) 6.(1) 6f -= - =
Thay
2
3
x = vào hàm số
3
() 7
2
x
hx =- ta được
2
3.
2
3
76
32
h
æö
÷
ç
÷
=- =
ç
÷
ç
÷
ç
èø
Nên
2
(1)
3
fh
æö
÷
ç
÷
-=
ç
÷
ç
÷
ç
èø
.
Câu 7. Đáp án D.
Thay
2
x
=-
vào hàm số
3
() 2fx x=-
, ta được
3
(2) 2.(2) 16f -=-- =
Thay
1
x
=-
vào hàm số
() 10 3hx x=-
, ta được
(1) 10 3(1) 13h -= --=
Nên
(2) (1)fh->-
.
Câu 8. Đáp án D.
16.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Thay
xa=
vào hai hàm số đã cho ta được
2
;() 2 () 3 5fa a ga a=- = +
Khi
đó
222
11
()() .(2)35 35 350
22
fa ga a a a a a a= - = +- = + + +=
2
311
0
24
a
æö
÷
ç
÷
+ + =
ç
÷
ç
÷
ç
èø
(vô lý vì
2
31111
0;
244
aa"
æö
÷
ç
÷
++³>
ç
÷
ç
÷
ç
èø
)
Vậy không có giá trị của
a
thỏa mãn yêu cầu đề bài.
Câu 9. Đáp án C.
Thay vào hai hàm số đã cho ta
2
()fa a=
() 5 4ga a=-
Khi đó
22
5() 4 5 4 0()fa ga a a a a==--+=
1
140)( )
4
(
a
aa
a
é
=
ê
- -=
ê
=
ê
ë
Vậy có hai giá trị của
a
thỏa mãn yêu cầu đề bài.
Câu 10. Đáp án C.
Lần lượt thay tọa độ các điểm
,,,MNPQ
vào hàm số
() 3 2fx x=-
ta được
+) Với
(0;1)M
, thay
0; 1xy==
ta được
13.02 1 2=-=-
(Vô lý) nên
()MCÏ
+) Với
(2; 3)N
, thay
2; 3xy==
ta được
33.22 34=-=
(Vô lý) nên
()NCÏ
.
+) Với
(2; 8)P --
, thay
2; 8xy=- =-
ta được
83.(2)2 8 8-= - - -=-
(luôn đúng)
nên
()PCÎ
.
+) Với
(2;0)Q -
, thay
2; 0xy=- =
ta được
03.(2)2 0 8=--=-
(Vô lý) nên
()QCÏ
.
Câu 11. Đáp án B.
Lần lượt thay tọa độ các điểm
,,,MNPQ
vào hàm số
() 5,5fx x=
ta được
+) Với
(0;1)M
, thay
0; 1xy==
ta được
15,5.0 10==
(Vô lý) nên
()MCÏ
+) Với
(2;11)N
, thay
2; 11xy==
ta được
2.5, 5 11 11 11==
(luôn đúng) nên
()NCÎ
+) Với
(2;11)P -
, thay
2; 11xy=- =
ta được
11 5,5.( 2) 11 11=-=-
(Vô lý) nên
()PCÏ
+) Với
(2;12)P -
, thay
2; 12xy=- =
ta được
12 5,5.( 2) 12 11=-=-
(Vô lý) nên
()QCÏ
.
Câu 12. Đáp án B.
Lần lượt thay tọa độ các điểm
,,,;MOPQA
vào hàm số
() 3fx x=
ta được
+) Với
(1; 1)M
, thay
1; 1xy==
ta được
13.1 13==
(vô lý) nên
()MCÏ
.
+) Với
(0; 0)O
, thay 0; 0xy== ta được
03.0 00==
(luôn đúng) nên
()OCÎ
.
+) Với
(1; 3)P --
, thay
1; 3xy=- =-
ta được
33.(1) 3 3-= - -=-
(luôn đúng) nên
()PCÎ
.
+) Với
(3;9)Q
, thay
3; 9xy==
ta được
93.3 99==
(luôn đúng) nên
()QCÎ
.
+) Với
(2;6)A -
, thay
2; 6xy=- =
ta được
6(2).3 6 6=- =-
(vô lý) nên
()ACÏ
.
17.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy có ba điểm thuộc đồ thị
()C
trong số các điểm đã cho.
Câu 13. Đáp án C.
+) Thay
1; 4xy==
vào
230xy+-=
ta được
2.14330+-= ¹
+) Thay
1; 4xy==
vào 50y -= ta được
45 1 0-=-¹
+) Thay
1; 4xy==
vào
40xy-=
ta được
4.1 4 0-=
+) Thay
1; 4xy==
vào
5310xy+-=
ta được
5.1 3.4 1 16 0+-=¹
Vậy đường thẳng
:4 0dxy-=
đi qua
(1; 4)M
.
Câu 14. Đáp án A.
+) Thay
1; 1xy==
vào
230xy+-=
ta được
2.1 1 3 0+- =
nên điểm
N
thuộc đường
thẳng
230xy+-=
+) Thay
1; 1xy==
vào
30y -=
ta được
13 2 0-=-¹
+) Thay
1; 1xy==
vào
420xy+=
ta được
4.1 2.1 6 0+=¹
+) Thay
1; 1xy==
vào
5310xy+-=
ta được
5.1 3.1 1 7 0+-=¹
Vậy đường thẳng
:2 3 0dxy+-=
đi qua
(1; 1)N
Câu 15. Đáp án C.
TXĐ:
D =
Giả sử
12
xx<
và
12
,xx DÎ
Ta có
1122
() 1 4;() 1 4fx x fx x=- =-
Xét hiệu
12 1 2
() () 1 4 (1 4)Hfx fx x x=-=---
1221
14 14 4( )0xxxx=- -+ = - >
(vì
12
xx<
).
Vậy
14yx=-
là hàm số nghịch biến.
Câu 16. Đáp án A.
TXĐ:
D
=
Giả sử
12
xx<
và
12
,xxÎ
.
Ta có
11 22
() 5 16;() 5 16fx x fx x=- =-
Xét hiệu
121 2
() () 5 16 (5 16)Hfx fx x x=-=---
12 12
5165165( )0xx xx=--+= -<
(vì
12
xx<
).
Vậy
516yx=-
là hàm số đồng biến.
Câu 17. Đáp án B.
Thay
2; 5xy==-
vào
5
21
2
m
yxm
-
=--
18.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
ta được
5
5.221345393.
2
m
mm mm
-
-= - -- + =-- =- =
Câu 18. Đáp án C.
Thay
2; 3xy==-
vào
32ymx m=-+
ta được
.2 3 2 3 5 5mm m m- + =- - =- =
.
Câu 19. Đáp án D.
Thay
3; 6xy=- =
vào
(2 3 ) 6ymx=- -
ta được
6(23).(3)6 9 18 2mmm=- -- = =
Câu 20. Đáp án D.
Thay
2
xa=
vào
1
()
23
x
fx
x
+
=
+
, ta được
2
2
2
1
111
()
2332
23
23
a
aaa
fa
aa
a
a
+
+-+-
====
-+ -
+
+
(vì
0aaa< =-
)
Câu 21. Đáp án A.
Thay
2
4xa=
vào
22
()
4
x
fx
x
-
=
+
ta được
2
2
2
24 2
(4 )
44
a
fa
a
-
=
+
22 2
4221
24 2
24
a
aa
aa
a
-
--
===
++
+
(vì
02 2aaa³ =
)
Câu 22. Đáp án C.
Ta có
()
3324433yx= + -- =
()
32 743x+=+
()()
2
32 32x+=+
32x= +
Vậy
32x =+
Câu 23. Đáp án D.
() ()
= + - -= + = +0322 210322 21yx x
()
()
+
+ = += = = -
+
+
2
2
21 1
21 21 21
21
21
xx x x
.
---------- TOÁN HỌC SƠ ĐỒ ---------
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


CHUYÊN ĐỀ NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ
A. KIẾN THỨC CẦN NHỚ
1. Khái niệm hàm số
Nếu đại lượng y phụ thuộc vào đại lượng x thay đổi sao cho với mỗi giá trị của x, ta luôn xác định được
chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x( x gọi là biến số). Ta viết: y = f(x), y = g(x),...
Ví dụ: Ta có y = 2x + 3 là một hàm số của y theo biến x.
Lưu ý: Khi x thay đổi mà y luôn nhận giá trị không đổi thì hàm số y = f(x) gọi là hàm hằng.
2.Giá trị của hàm số, điều kiện xác định của hàm số
-Giá trị của hàm số f(x) tại điểm x0 kí hiệu là y0= f(x0).
-Điều kiện xác định của hàm số y = f(x) là tất cả các giá trị của x sao cho biểu thức f(x) có nghĩa.
3. Đồ thị của hàm số
- Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm M(x;y) trong mặt phẳng tọa độ Oxy sao cho x, y
thỏa mãn hệ thức y = f(x).
- Điểm M(x0; y0) thuộc đồ thị hàm số y = f(x) <=> y0=f(x0)
4. Hàm số đồng biến và hàm số nghịch biến
Cho hàm số y = f(x) xác định với mọi giá trị x thuộc R.
-Nếu giá trị của biến x tăng lên mà giá trị y = f(x) tương ứng cũng tăng lên thì hàm số y = f(x) được gọi
là đồng biến trên R
-Nếu giá trị của biến x tăng lên mà giá trị y = f(x) tương ứng lại giảm đi thì hàm số y = f(x)được gọi là
nghịch biến trên R.
Nói cách khác, với x1, x2 bất kì thuộc R:
+ Nếu x1< x2 mà f(x1) < f(x2) thì hàm số y = f(x) đồng biến
+ Nếu x1< x2 mà f(x1) > f(x2) thì hàm số y = f(x) nghịch biến.
Trong quá trình giải toán ta có thể sử dụng kiến thức sau đây để xét tính đồng biến hoặc nghịch biến của hàm số trên R: f(x )  f(x ) Cho x 2 1
1, x2 bất kì thuộc R và x  x . Đặt T  khi đó: 1 2 x  x 2 1
1. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
+ Nếu T > 0 thì hàm số đã cho đồng biến trên R
+ Nếu T < 0 thì hàm số đã cho nghịch biến trên R.
2. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
B. CÁC DẠNG BÀI CƠ BẢN VÀ NÂNG CAO
Dạng 1. Tính giá trị của hàm số tại một điểm
Phương pháp giải: Để tính giá trị của hàm số y = f(x) tại x0, ta thay x = x0 vào y = f(x) được y0 = f(x0) 1 Bài 1.
Cho hàm số y f (x)  4x 1 .Tính f (0), f ( ), f  2, f (a) 2
Dạng 2.Biểu diễn tọa độ của một điểm trên mặt phẳng tọa độ Oxy
Phương pháp giải: Để biểu diễn tọa độ của điểm M(x0; y0) trên hệ trục tọa độ Oxy, ta làm như sau:
1.Vẽ đường thẳng song song với trục Oy tại điểm có hoành độ x = x0
2. Vẽ đường thẳng song song với trục Ox tại điểm có tung độ y = y0
3. Giao điểm của hai đường thẳng trên chính là điểm M(x0; y0) Bài 2. Cho hàm số 2
y f (x)  2x  3x  2
a) Tính f (0), f ( 2 1)
b) Tìm các giá trị của x sao cho f (x)  7 Bài 3.
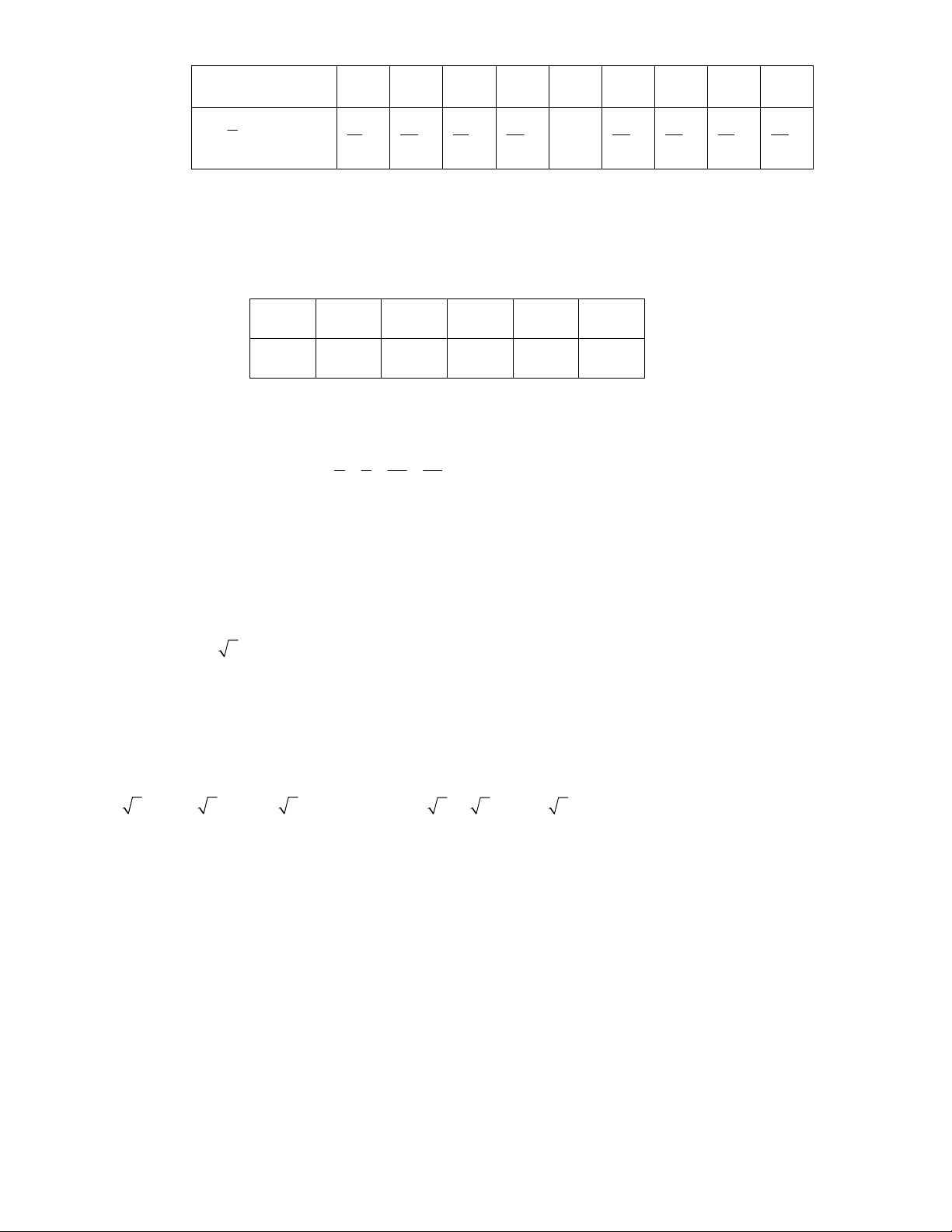
Trong các bảng sau ghi các giá trị tương ứng của x và y . Bảng nào xác định y là hàm số của x ? Vì sao? x 1 2 4 5 7 8 x 3 4 3 5 8 y y 3 5 9 11 15 17 6 8 4 8 16
Bài 4. Cho hàm số y f x  2 ( ) x  3 3
a) Tính giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng: x – 2 –1,5 – 1 –0,5 0 0,5 1 1,5 2 2 y x  3 5
b) Hàm số đã cho là hàm đồng biến hay nghịch biến ? Vì sao ?
Bài 5. Sự tương quan giữa x và y theo bảng sau xác định một hàm số nào ? x 2 3 0 -2 -3 y 4 6 0 -4 -6
Dạng 3: Xét sự đồng biến và nghịch biến của hàm số.
3. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Phương pháp giải: ta thực hiện một trong các cách sau:
Cách 1: Với mọi x1, x2 thuộc R, giả sử x1 < x2
-Nếu hiệu H = f(x1) - f(x2) < 0 thì hàm số đồng biến.
-Nếu hiệu H = f(x1) - f(x2) > 0 thì hàm số nghịch biến.
Cách 2: Với mọi x f (x ) f (x )
1, x2 thuộc R và x  x . Xét tỉ số 2 1 T  1 2 x  x 2 1
-Nếu T > 0 thì hàm số đồng biến
-Nếu T < 0 thì hàm số nghịch biến
Bài 6. Xét chiều biến thiên của hàm số y f (x)  3x trong  .
Bài 7. Chứng minh hàm số y  2x  5 đồng biến trên  . 1
Bài 8. Chứng minh hàm số y   x  2 nghịch biến trên  3
Bài 9. Chứng tỏ rằng hàm số 2
f (x)  4x  9 đồng biến trong khoảng 0;5 Bài 10. Cho hàm số 2
y  3x  6x  5 với x   . Chứng minh rằng hàm số đồng biến khi x  1, hàm số
nghịch biến khi x  1. 2  
Bài 11. Chứng minh rằng hàm số 3x x 4 y
đồng biến trong khoảng  2; 3 . x 1
Bài 12. Tìm hàm số f (x) , biết 2
f (x 1)  x x  2 .
Dạng 4:Nâng cao và phát triển tư duy
Bài 13. Cho các số thực không âm x, y, z thỏa mãn x y z 1. Tìm giá trị lớn nhất của biểu thức
P xy yz zx  2xyz .
4. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com HƯỚNG DẪN 1
Bài 1. Cho hàm số y f (x)  4x 1 .Tính f (0), f ( ), f  2, f (a) . 2 Lời giải
f (0)  4.0 1  1  .  1   1  f  4.  1       3 .  2   2 
f  2  4 2 1.
f (a)  4a 1 . Bài 2. Cho hàm số 2
y f (x)  2x  3x  2
a) Tính f (0), f ( 2 1)
b) Tìm các giá trị của x sao cho f (x)  7
Bài 3. Trong các bảng sau ghi các giá trị tương ứng của x và y .Bảng nào xác định y là hàm số của x ? Vì sao ? x 1 2 4 5 7 8 x 3 4 3 5 8 y 3 5 9 11 15 17 y 6 8 4 8 16 a) b) Lời giải
Bảng a) xác định y là hàm số của biến số x vì mỗi giá trị của x ta xác định được một giá trị tương ứng của y
Bảng b) không xác định y là hàm số của biến số x vì mỗi giá trị của x không phải khi nào ta xác
cũng định được một giá trị tương ứng của y . Cụ thể khi x  3, y lấy giá trị là 6 và 4 Bài 4.
a) Cho hàm số y f x  2 ( ) x  3 3
5. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x – 2 –1,5 – 1 –0,5 0 0,5 1 1,5 2 2 y x  3 11 5 12 13 14 3 16 17 18 19 5 5 5 5 5 5 5 5
b) Hàm số đồng biến. Vì x x f x   f x 1 2 1  2
Bài 5. Sự tương quan giữa x và y theo bảng sau xác định một hàm số nào ? x 2 3 0 -2 -3 y 4 6 0 -4 -6 Lời giải 4 6 4  6 
Tỉ số giữa y và x của bảng là :     2 2 3 2  3 
Vậy theo bảng là xác định được một hàm số y  2x Bài 6. Cho hàm số 2
y f (x)  2x  3x  2
a) Tính f (0), f ( 2 1)
b) Tìm các giá trị của x sao cho f (x)  7 Lời giải a) f (0)  2 2
f ( 2 1)  2( 2 1)  3( 2 1)  2  4  2  4 2  3 2 1  5  2 b) 2
f (x)  7  2x  3x  2  7
 2x(x 1)  5(x 1)  0
 (x 1)(2x  5)  0
x 1  0 hoặc 2x + 5 = 0
x  1 hoặc x  2,  5
Vậy x  1 hoặc x  2,
 5 thì f (x)  7
Bài 7. Xét chiều biến thiên của hàm số y f (x)  3x trong  :
6. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Lời giải
Cho x ; x R : x x ta có f (x )  f (x )  3x  3x  3(x x ) 1 2 1 2 1 2 1 2 1 2
Vì x ; x R : x x nên 3x  3x f (x )  f (x ) 1 2 1 2 1 2 1 2
Vậy y f (x)  3x đồng biến trong 
Bài 8. Chứng minh hàm số y  2x  5 đồng biến trên  . Lời giải
Đặt y f x  2x  5
TXĐ: 2x  5 xác định với mọi x
Với mọi x , x 
x x . Xét f x f x  2x  5  2x  5  2x  5  2x  5  2 x x  0 1   2   1   2  1 2  1 2  1 2 bất kì và 1 2
(do x x x x  0 ) 1 2 1 2
f x f x 1   2
Vậy hàm số y f x  2x  5 đồng biến. (đpcm) 1
Bài 9. Chứng minh hàm số y   x  2 nghịch biến trên  3 Lời giải
Đặt y g x 1
  x  2 3 1
TXĐ:  x  2 xác định với mọi x 3
Với mọi x , x  x x . Xét 1 2 bất kì và 1 2     g  1 1 1 1 1
x g x   x  5   x  5   x  5  x  5   x x  0 1   2  1   2  1 2  1 2  3   3  3 3 3 1
(do x x x x  0   x x  0 ) 1 2 1 2  1 2 3
g x g x 1   2 
Vậy hàm số y g x 1
  x  2 nghịch biến. (đpcm) 3
Bài 10. Chứng tỏ rằng hàm số 2
f (x)  4x  9 đồng biến trong khoảng 0;5
7. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Lời giải
Trong khoảng 0;5 ta lấy hai giá trị tùy ý của x sao cho x x , ta có : 1 2
f (x )  f (x )   2 4x  9   2 4x  9 1 2 1 2  2 2 2 2
 4x  4x  4(x x )  4(x x )(x x ) 1 2 1 2 1 2 1 2
Vì x x nên x x  0 . Mặt khác trong khoảng 0;5 nên x x  0 do đó 1 2 1 2 1 2
4(x x )(x x ) < 0,  f (x )  f (x )  0 hay f (x )  f (x ) . 1 2 1 2 1 2 1 2 Vậy hàm số 2
f (x)  4x  9 đồng biến trong khoảng 0; 5  .(đpcm) Bài 11. Cho hàm số 2
y  3x  6x  5 với x   . Chứng minh rằng hàm số đồng biến khi x  1 , hàm số
nghịch biến khi x  1 . Lời giải 2 2
y  3x  6x  5  3(x 1)  2
Với mọi x , x 
x x . Ta có x x  0 1 2 bất kì và 1 2 1 2 2 2
f (x )  f (x )  3(x 1)  2  3(x 1)  2 1 2 1 2     2 2
 3(x 1)   3(x 1)   3(x x )(x x  2) 1 2 1 2 1 2    
+ Khi x  1thì x x  2  x x  2  0  3(x x )(x x  2)  0 1 2 1 2 1 2 1 2
hay f (x )  f (x ) , hàm số đồng biến. 1 2
+ Khi x  1 thì x x  2  x x  2  0  3(x x )(x x  2)  0 1 2 1 2 1 2 1 2
hay f (x )  f (x ) , hàm số nghịch biến. 1 2 2  
Bài 12. Chứng minh rằng hàm số 3x x 4 y
đồng biến trong khoảng  2; 3 . x 1 Lời giải
Trong khoảng  2; 3 cho x hai giá trị tùy ý 2  x x  3 , ta có x x  0 . 1 2 1 2 2 2
3x x  4 3x x  4 1 1 2 2 y y   1 2 x 1 x 1 1 2
(x 1)(3x  4) (x 1)(3x  4) 1 1 2 2   x 1 x 1 1 2
8. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com = 3(x x ) 1 2
Vì 2  x x  3 nên x x  0 do đó   1 2 1 2 3(x x ) 0 1 2 2   hay 3x x 4
y y .Vậy hàm số y
đồng biến trong khoảng  2; 3 . 1 2 x 1
Bài 13. Tìm hàm số f (x) , biết 2
f (x 1)  x x  2 . Lời giải
Đặt x 1  t x t 1 Do đó 2 2
f (t)  (t 1)  (t 1)  2  t  3t  4
Thay t bởi x ta có 2
f (x)  x  3x  4 .
Bài 14. Cho các số thực không âm x, y, z thõa mãn x y z 1. Tìm giá trị lớn nhất của biểu thức
P xy yz zx  2xyz . Lời giải 2 2
x y z 1
x y 1 z
Giả sử z  min(x, y, z)  z
 . Ta có 0  xy   . 3 3 4 4
P xy(1 2z)  (x y)z xy(1 2z)  z(1 z) , nếu ta xem z là tham số , x và y là ẩn số thì 2 (1 z)
f (xy)  xy(1 2z)  (1 z) là hàm số của xy với 0  xy  . 4
Do 1 2z  0  hàm số f (xy)  xy(1 2z)  (1 z) luôn đồng biến. Suy ra  1 z2  2 3 2 (1 z) 2  z z 1 7  1 3 1 2 1 
f (xy)  f    (1 2z)
z(1 2z)    z z     4  4 4 27  2 4 108    7 1 1 2 1 1   1
(z  ) (z  ) 
. Dấu ʺ  ʺ xảy ra khi x y z  . 27 2 3 6 27 3
9. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com C.TỰ LUYỆN Bài 1. Cho hàm số x 1 f (x) 
. Tính f 4  2 3 x 1
Bài 2. Cho hàm số y f x 2
 3 x 1  mx  2x  3 . Tìm m để f   1  f 3    Bài 3. Cho hàm số x 1 x 1 f (x) 
.Chứng minh rằng f (x)   f (x) .
x 1  x 1
Bài 4. Tìm điều kiện xác định của các hàm số sau:  a) x 2 1 1 y  b) y  c) y x  2 4 2 x  2x  3 3 2 x  2x   d) 3 x 1 x y  e) 3
y x  5 
f) y x  2  2  x x  2 x  3
Bài 5. Chứng tỏ rằng hàm số 2
y f (x)  x  3 nghịch biến trong khoảng K  x x   0
Bài 6. Chứng tỏ rằng hàm số 3
y f (x)  x luôn luôn đồng biến trên  .
Bài 7. Xét tính đồng biến, nghịch biến của hàm số y x  2 trên khoảng K  x x    2
Bài 8. Xét tính đồng biến, nghịch biến của hàm số y  4  x trên khoảng K  x x   4
Bài 9. Tìm giá trị nhỏ nhất của hàm số: a) 2
y x  4x  3 b) 2
y  4x  2x 1 c) 4 2
y x  2x  5
Bài 10. Tìm giá trị lớn nhất của hàm số: b) 2
y  x  6x  3 b) 2
y  9x  6x  3 c) 4 2
y  x  4x  5
Bài 11. Tìm giá trị lớn nhất của hàm số: 2   x a) x 6x 14 y  b) y  x  0 2 x  6x 12 x  20192
Bài 12. Tìm giá trị nhỏ nhất của hàm số: 2   4x   1  x  4 a) x x 1 y  b) y  x  0 2 x  2x 1 x
10. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com HƯỚNG DẪN 3 3  2 4  2 3 1 3 11 3  2 3  2 3
Bài 1. Ta có: f 4  2 3        4  2 3 1 3 11 3 3 3
Bài 2. Ta có f   
   m 2 1 3 1 1 1  2  1  3  m  5 f   2 3  3 3 1  3 m
 2.3  3  9m  3
Do đó f    f   1 1
3  m  5  9m  3  8m  2  m  4              Bài 3. Ta có x 1 x 1 x 1 x 1 x 1 x 1 f (x)       f (x)  
x 1  x 1
x 1  x 1
x 1  x 1 
Bài 4. a. x  2 b. x  1  c. x  2,  x  0
d. x 1, x  2
e. x  5, x  9 f. 2  x  2 Bài 5. Cho 2 2 2 2 1 x , 2 x K; 1 x  2 x . Xét f  2
x   f  1 x   2
x  3   1x  3  2 x  1 x   2 x  1 x  2 x  1 x  Do 1 x , 2 x K; 1 x  2 x  2 x  1 x  0; 1 x  2 x  0   2 x  1 x  2 x  1
x   0  f  2
x   f  1 x
Do đó hàm số nghịch biến trên K Bài 6. Cho 1 x , 2 x   ; 1 x  2 x . Xét 2     f x 3 2
x   f  1 x  3 3  2 x  1 x   2 x  1 x  2 2 2 x  1 x 2 x  1 x    2 x  1 x  1 2  2 x    1 x   0  2  4   
Do đó hàm số luôn đồng biến trên   Bài 7. Cho x x 1 x , 2 x K; 1 x  2
x . Xét f x   f x  2 1 2 1  2 x  2  1 x  2   0 2 x  2  1 x  2
Do đó hàm số đồng biến trên K Bài 8. Cho x x 1 x , 2 x K; 1 x  2
x . Xét f x   f x  1 2 2 1  4  2 x  4  1 x   0 4  2 x  4  1 x
Do đó hàm số nghịch biến trên K Bài 9. a. Ta có 2
y x  4x  3   x  22  7  7,x . Suy ra ymin  7 đặt được khi x  2 2 5 1 b. Ta có 2  1  5 5
y  4x  2x 1  2x     , x    . Suy ra y
  đặt được khi x   2  4 4 min 4 4
c. Ta có y x x   x  2 4 2 2 2 5 1  4  4, x
 . Suy ra ymin  4 đặt được khi x  1 Bài 10. a. Ta có 2
y  x  6x  3    x  32  6  6,x . Suy ra ymax  6 đặt được khi x  3 1 b. Ta có 2
y  9x  6x  3   3x  2
1  2  2,x . Suy ra ymax  2 đặt được khi x  3
11. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2
c. Ta có y  x x   x  2 4 2 2 4 5 2 1  1  , x  . Suy ra y
  đặt được khi x   2  max 1 x  32  3 2 2 x  6x 14
x  6x 12  2 2 2
Bài 11. a. Ta có y   1 1 2 2 2 x  6x 12 x  6x 12 x  6x 12 x 32  3 2 2 2 5
Do x  32  0  x  32  3  3   1  x  2  3 x  2  3 3 3 3 3 5 Vậy max y
 đặt được khi x  3 3 x b. Ta có y  x  2 2019
Áp dụng bất đẳng thức Cauchy ta được: x   x   x  2 x x 1 2019 2 2019 2019  8076x    x  2 8076x 8076 2019 1 Vậy ymax 
đặt được khi x  2019 8076 2 x x 1 x  2 1   x   2 1 1 Bài 12. a. Ta có 1 1  1 1  3 3 y   1      2   x  2x 1 x  2 x 1 1
x  2  x 1 2  4 4 1 3 Vậy mi
y n  đặt được khi x 1 4
x  x   2 4 1 4   b. Ta có 4x 17x 4 4  4  4 y  
 4x 17   4x  17  2 4 . x 17  25   x x x x x
Vậy ymin  25 đặt được khi x 1
12. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
D. TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Cho hàm số y = f (x) xác định trên D . Với x ,x Î D; x < x , khẳng định nào sau đây đúng? 1 2 1 2 A.
f (x ) < f (x ) thì hàm số đồng biến trên D . B. f (x ) < f (x ) thì hàm số nghịch biến trên D . 1 2 1 2
C. f (x ) > f (x ) thì hàm số đồng biến trên D .
D. f (x ) = f (x ) thì hàm số đồng biến trên D . 1 2 1 2
Câu 2. Cho hàm số y = f (x) xác định trên D . Với x ,x Î D; x > x , khẳng định nào sau đây đúng? 1 2 1 2
A. f (x ) < f (x ) thì hàm số đồng biến trên D .
B. f (x ) > f (x ) thì hàm số nghịch biến trên D . 1 2 1 2
C. f (x ) > f (x ) thì hàm số đồng biến trên D .
D. f (x ) = f (x ) thì hàm số đồng biến trên D . 1 2 1 2 Câu 3. Cho hàm số 3
f (x) = x + x . Tính f (2) A. 4 . B. 6 . C. 8 . D. 10 . Câu 4. Cho hàm số 3
f (x) = x - 3x - 2 . Tính 2.f (3) A. 16 . B. 8 . C. 32 . D. 64 . Câu 5. Cho hàm số 2
f (x) = 3x + 2x + 1 . Tính f (3) - 2f (2) A. 34 . B. 17 . C. 20 . D. 0 . 3x æ2ö
Câu 6. Cho hai hàm số 4
f (x) = 6x và h(x) = 7 -
. So sánh f (-1) và h ç ÷ ç ÷ 2 çè3÷÷ø æ2ö æ2ö æ2ö A. f ( 1 - ) = h ç ÷ ç ÷ ç ÷ ç ÷ ç
. B. f (-1) > h ç ÷.
C. f (-1) < h ç ÷.
D. Không đủ điều kiện so sánh. çè3÷÷ø çè3÷÷ø çè3÷÷ø
Câu 7. Cho hai hàm số 3
f (x) = -2x và h(x) = 10 - 3x . So sánh f (-2) và h(-1)
A. f (-2) < h(-1) . B. f (-2) £ h(-1) .
C. f (-2) = h(-1) . D. f (-2) > h(-1) . 1
Câu 8. Cho hai hàm số 2
f (x) = -2x và g(x) = 3x + 5 . Giá trị nào của a để f (a) = g(a) 2 A. a = 0 .
B. a = 1. C. a = 2 . D. Không tồn tại.
Câu 9. Cho hai hàm số 2
f (x) = x và g(x) = 5x - 4 . Có bao nhiêu giá trị của a để f (a) = g(a) A. 0 . B. 1 . C. 2 . D. 3 .
Câu 10. Cho hàm số f (x) = 3x - 2 có đồ thị (C ) . Điểm nào sau đây thuộc đồ thị hàm số (C ) . A. M (0;1) . B. N(2; 3). C. P(-2;-8) . D. Q(-2; 0).
Câu 11. Cho hai hàm số f (x) = 5, 5x có đồ thị (C ) . Điểm nào sau đây thuộc đồ thị hàm số (C ) A. M (0;1) . B. N (2;11) . C. P(-2;11). D. P(-2;12) .
Câu 12. Cho hàm số f (x) = 3x có đồ thị (C ) và các điểm M(1;1);O(0; 0);P(-1;-3);Q(3;9); ( A -2;6).
Có bao nhiêu điểm trong các điểm trên thuộc đồ thị hàm số (C )
13. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com A. 4 . B. 3 . C. 2 . D. 1 .
Câu 13. Đường thẳng nào sau đây đi qua điểm M(1; 4) ?
A. 2x + y - 3 = 0 . B. y - 5 = 0 .
C. 4x - y = 0 .
D. 5x + 3y - 1 = 0 .
Câu 14. Đường thẳng nào sau đây đi qua điểm N (1;1) ?
A. 2x + y - 3 = 0 . B. y - 3 = 0 .
C. 4x + 2y = 0 .
D. 5x + 3y - 1 = 0 .
Câu 15. Hàm số y = 1 - 4x là hàm số? A. Đồng biến. B. Hàm hằng. C. Nghịch biến.
D. Đồng biến với x > 0 .
Câu 16. Hàm số y = 5x - 16 là hàm số? A. Đồng biến. B. Hàm hằng. C. Nghịch biến.
D. Nghịch biến với x > 0 . 5 - m
Câu 17. Cho hàm số y =
x - 2m - 1 . Tìm m để hàm số nhận giá trị -5 khi x = 2 2 A. m = 5 . B. m = 3 . C. m = 2 . D. m = -3 .
Câu 18. Cho hàm số y = mx - 3m + 2 . Tìm m để đồ thị hàm số đi qua điểm (2 A ;-3) A. m = 3 . B. m = 4 . C. m = 5 . D. m = 6 .
Câu 19. Cho hàm số y = (2 - 3m)x - 6 . Tìm m để đồ thị hàm số đi qua điểm ( A -3;6) A. m = 3 . B. m = 4 . C. m = 9 . D. m = 2 . x + 1
Câu 20. Cho hàm số f (x) = . Tính 2
f (a ) với a < 0 . 2 x + 3 a + 1 2a + 1 2a - 1 1 - a A. 2 f (a ) = . B. 2 f (a ) = . C. 2 f (a ) = . D. 2 f (a ) = . 3 + 2a 3 - 2a 3 + 2a 3 - 2a 2 x - 2
Câu 21. Cho hàm số f (x) = . Tính 2
f (4a ) với a ³ 0 . x + 4 2a - 1 2a + 1 a - 2 2a + 1 A. 2 f (4a ) = . B. 2 f (4a ) = . C. 2 f (4a ) = . D. 2 f (4a ) = . a + 2 a - 2 2a + 1 a + 2
Câu 22. Cho hàm số y = 3  ( 3 + 2)x - 4 - 4 3 . Tìm x để y = 3 A. x = 2 + 3 . B. x = 3 . C. x = 3 + 2 . D. x = 3 - 2 .
Câu 23. Cho hàm số y = (3 + 2 2)x - 2 -1. Tìm x để y = 0
A. x = 1 . B. x = 2 + 1 . C. x = 2 . D. x = 2 - 1.
14. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com HƯỚNG DẪN Câu 1. Đáp án A.
Cho hàm số y = f (x) xác định trên tập D . Khi đó :
- Hàm số đồng biến trên D "x ,x Î D : x < x f (x ) < f (x ) 1 2 1 2 1 2
- Hàm số nghịch biến trênD "x ,x Î D : x < x f (x ) > f (x ) 1 2 1 2 1 2 Câu 2. Đáp án C.
Cho hàm số y = f (x) xác định trên tập D . Khi đó :
- Hàm số đồng biến trên D "x ,x Î D : x > x f (x ) > f (x ) 1 2 1 2 1 2
- Hàm số nghịch biến trên D "x ,x Î D : x > x f (x ) > f (x ) 1 2 1 2 1 2 Câu 3. Đáp án D.
Thay x = 2 vào hàm số ta được 3 f (2) = 2 + 2 = 10 Câu 4. Đáp án C.
Thay x = 3 vào hàm số ta được 3
f (3) = 3 - 3.3 - 2 = 16
 2.f (3) = 2.16 = 32 . Câu 5. Đáp án D.
Thay x = 3 vào hàm số ta được 2
f (3) = 3.3 + 2.3 + 1 = 34
Thay x = 2 vào hàm số ta được 2
f (2) = 3.2 + 2.2 + 1 = 17
Suy ra f (3) - 2f (2) = 34 - 2.17 = 0 . Câu 6. Đáp án A.
Thay x = -1 vào hàm số 4
f (x) = 6x ta được 4 f (-1) = 6.(-1) = 6 2 2 3x 3. æ2ö
Thay x = vào hàm số h(x) = 7 - ta được ç ÷ 3 h ç ÷ = 7 - = 6 3 2 çè3÷÷ø 2 æ2ö Nên f ( 1 - ) = h ç ÷ ç ÷ ç . çè3÷÷ø Câu 7. Đáp án D.
Thay x = -2 vào hàm số 3
f (x) = -2x , ta được 3 f (-2) = -2.(-2) = 16
Thay x = -1 vào hàm số h(x) = 10 - 3x , ta được h(-1) = 10 - 3(-1) = 13
Nên f (-2) > h(-1) . Câu 8. Đáp án D.
15. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Thay x = a vào hai hàm số đã cho ta được 2
f (a) = -2a ;g(a) = 3a + 5 Khi 2 1 1 æ 3ö ç ÷ 11 đó 2 2 2
f (a) = g(a)  .(-2a ) = 3a + 5  a
- = 3a + 5  a + 3a + 5 = 0  a ç + ÷ + = 0 2 2 çè 2÷÷ø 4 2 æ 3ö ç ÷ 11 11 (vô lý vì a ç + ÷ + ³ > 0;"a ç ) çè 2÷÷ø 4 4
Vậy không có giá trị của a thỏa mãn yêu cầu đề bài. Câu 9. Đáp án C.
Thay vào hai hàm số đã cho ta 2
f (a) = a g(a) = 5a - 4 a é = 1 Khi đó 2 2
f (a) = g(a)  a = 5a - 4  a - 5a + 4 = 0 (a 1)(a 4) 0 ê  - - =  a ê = 4 êë
Vậy có hai giá trị của a thỏa mãn yêu cầu đề bài. Câu 10. Đáp án C.
Lần lượt thay tọa độ các điểm M,N,P,Q vào hàm số f (x) = 3x - 2 ta được
+) Với M(0;1) , thay x = 0;y = 1 ta được 1 = 3.0 - 2  1 = 2
- (Vô lý) nên M Ï (C )
+) Với N(2; 3), thay x = 2;y = 3 ta được 3 = 3.2 - 2  3 = 4 (Vô lý) nên N Ï (C ) .
+) Với P(-2;-8) , thay x = -2;y = -8 ta được -8 = 3.(-2) - 2  -8 = -8 (luôn đúng)
nên P Î (C ) .
+) Với Q(-2; 0) , thay x = -2;y = 0 ta được 0 = 3.(-2) - 2  0 = -8 (Vô lý) nên Q Ï (C ). Câu 11. Đáp án B.
Lần lượt thay tọa độ các điểm M,N,P,Q vào hàm số f (x) = 5, 5x ta được
+) Với M(0;1) , thay x = 0;y = 1 ta được 1 = 5, 5.0  1 = 0 (Vô lý) nên M Ï (C )
+) Với N (2;11) , thay x = 2;y = 11 ta được 2.5, 5 = 11  11 = 11 (luôn đúng) nên N Î (C )
+) Với P(-2;11) , thay x = -2;y = 11 ta được 11 = 5, 5.(-2)  11 = -11 (Vô lý) nên P Ï (C )
+) Với P(-2;12) , thay x = -2;y = 12 ta được 12 = 5, 5.(-2)  12 = -11 (Vô lý) nên Q Ï (C ). Câu 12. Đáp án B.
Lần lượt thay tọa độ các điểm M,O,P,Q;A vào hàm số f (x) = 3x ta được
+) Với M(1;1) , thay x = 1;y = 1 ta được 1 = 3.1  1 = 3 (vô lý) nên M Ï (C ) .
+) Với O(0; 0) , thay x = 0;y = 0 ta được 0 = 3.0  0 = 0 (luôn đúng) nên O Î (C ) .
+) Với P(-1;-3) , thay x = -1;y = -3 ta được -3 = 3.(-1)  -3 = -3 (luôn đúng) nên P Î (C ) .
+) Với Q(3;9), thay x = 3;y = 9 ta được 9 = 3.3  9 = 9 (luôn đúng) nên Q Î (C ) . +) Với (
A -2;6) , thay x = -2;y = 6 ta được 6 = (-2).3  6 = -6 (vô lý) nên A Ï (C ) .
16. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Vậy có ba điểm thuộc đồ thị (C ) trong số các điểm đã cho. Câu 13. Đáp án C.
+) Thay x = 1;y = 4 vào 2x + y - 3 = 0 ta được 2.1 + 4 - 3 = 3 ¹ 0
+) Thay x = 1;y = 4 vào y - 5 = 0 ta được 4 - 5 = -1 ¹ 0
+) Thay x = 1;y = 4 vào 4x - y = 0 ta được 4.1 - 4 = 0
+) Thay x = 1;y = 4 vào 5x + 3y - 1 = 0 ta được 5.1 + 3.4 - 1 = 16 ¹ 0
Vậy đường thẳng d : 4x - y = 0 đi qua M(1; 4) . Câu 14. Đáp án A.
+) Thay x = 1;y = 1 vào 2x + y - 3 = 0 ta được 2.1 + 1 - 3 = 0 nên điểm N thuộc đường
thẳng 2x + y - 3 = 0
+) Thay x = 1;y = 1 vào y - 3 = 0 ta được 1 - 3 = -2 ¹ 0
+) Thay x = 1;y = 1 vào 4x + 2y = 0 ta được 4.1 + 2.1 = 6 ¹ 0
+) Thay x = 1;y = 1 vào 5x + 3y - 1 = 0 ta được 5.1 + 3.1 - 1 = 7 ¹ 0
Vậy đường thẳng d : 2x + y - 3 = 0 đi qua N (1;1) Câu 15. Đáp án C. TXĐ: D = 
Giả sử x < x và x ,x Î D 1 2 1 2
Ta có f (x ) = 1 - 4x ; f (x ) = 1 - 4x 1 1 2 2
Xét hiệu H = f (x ) - f (x ) = 1 - 4x - (1 - 4x ) = 1 - 4x - 1 + 4x = 4(x - x ) > 0 (vì x < x ). 1 2 1 2 1 2 2 1 1 2
Vậy y = 1 - 4x là hàm số nghịch biến. Câu 16. Đáp án A. TXĐ: D = 
Giả sử x < x và x ,x Î  . 1 2 1 2
Ta có f (x ) = 5x - 16; f (x ) = 5x - 16 1 1 2 2
Xét hiệu H = f (x ) - f (x ) = 5x - 16 - (5x - 16) = 5x - 16 - 5x + 16 = 5(x - x ) < 0 (vì 1 2 1 2 1 2 1 2 x < x ). 1 2
Vậy y = 5x - 16 là hàm số đồng biến. Câu 17. Đáp án B. 5 - m
Thay x = 2;y = -5 vào y = x - 2m - 1 2
17. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 5 - m ta được -5 =
.2 - 2m - 1  -3m + 4 = -5  -3m = -9  m = 3. 2 Câu 18. Đáp án C.
Thay x = 2;y = -3 vào y = mx - 3m + 2 ta được .2 m - 3m + 2 = 3 -  m - = 5 -  m = 5 . Câu 19. Đáp án D.
Thay x = -3;y = 6 vào y = (2 - 3m)x - 6 ta được 6 = (2 - 3m).(-3) - 6  9m = 18  m = 2 Câu 20. Đáp án D. x + 1 Thay 2
x = a vào f (x) = , ta được 2 x + 3 2 a + 1 a + 1 a - + 1 1 - a 2 f (a ) = = = =
(vì a < 0  a = a - ) 2 2 a + 3 2 a + 3 2 - a + 3 3 - 2a Câu 21. Đáp án A. 2 x - 2 2 2 4a - 2 Thay 2
x = 4a vào f (x) = ta được 2 f (4a ) = x + 4 2 4a + 4 2 2a - 2 4a - 2 2a - 1 = = =
(vì a ³ 0  2a = 2a ) 2a + 4 2a + 4 a + 2 Câu 22. Đáp án C.
Ta có y = 3  ( 3 + )
2 x - 4 - 4 3 = 3  ( 3 + ) 2 x = 7 + 4 3  ( + )x = ( + )2 3 2 3 2  x = 3 + 2 Vậy x = 3 + 2 Câu 23. Đáp án D.
y = 0  (3 + 2 2)x - 2 -1 = 0  (3 + 2 2)x = 2 + 1 ( 2 )2 2 + 1 1 
+ 1 x = 2 + 1  x =  x =  x = 2 - 1. ( )2 2 + + 1 2 1
---------- TOÁN HỌC SƠ ĐỒ ---------
18. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com