Chuyên đề rút gọn biểu thức chứa căn thức bậc hai

Tài liệu gồm 44 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề rút gọn biểu thức chứa căn thức bậc hai. Mời bạn đọc đón xem.

101 51 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba

Môn: Toán 9

Thông tin:

44 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊN ĐỀ RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
A. KIẾN THỨC TRỌNG TÂM
Ví dụ minh họa 1: Rút gọn các biểu thức sau
a)
b)
Lời giải
a) Với ta có:
b)
Ví dụ minh họa 2: Cho biểu thức
a) Tìm điều kiện xác định và rút gọn P.
b) Tìm a để .
c) Tính giá trị của P khi
d) Tìm a để P là một số nguyên.

110
0, 4
4
22
xx x
Axx
x
xx




13 4 3 7 4 3 8 20 2 43 24 3B 
0, 4xx
21210
28
2
44
xx x x x
x
A
xx
 



13 4 3 7 4 3 8 20 2 43 24 3B 
 
22 2
23 1 2 3 820 2 4 33
 
22
33 4 820 24 33 33 4 828 63
 
22
33 4 8 33 1 43 243 833 1 35
2
1: 1
12
aa a a
P
aa







5P
322a 
Để rút gọn biểu thức chứa căn bậc hai ta thường thực hiện các bước sau:
- Bước 1: Tìm điều kiện xác định của biểu thức (nếu đề chưa cho điều kiện). Chú ý điều kiện căn
thức, điều kiện mẫu, và điều kiện phần chia.
- Bước 2: Phân tích mẫu thành nhân tử, kết hợp phân tích tử bằng các phép biến đổi đơn giản.
- Bước 3: Bỏ ngoặc, thu gọn các biểu thức một cách hợp lý. Kết hợp điều kiện bài toán để kết
luận.
2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
e) Tìm a để .
Lời giải
a) Điều kiện:
Rút gọn:
b) Với
(thỏa điều kiện).
Vậy với thì .
c) Khi , thay vào biểu thức P đã được rút gọn, ta có:
d) Ta có:
Để P là một số nguyên thì phải là một số nguyên, suy ra phải là ước nguyên của 2.
Do đó:
Vậy với thì P đạt giá trị nguyên.
1P
0
0
1
10
a
a
a
a


2
1: 1
12
aa a a
P
aa







 
12
1
1: 1
121
aa aa
a
aaa







0
1
a
a

1
55151
1
a
Paa
a
 
39
15 5 4 6
24
aa a aa
9
4
a
5P
2
322 21a 


2
2
21 1
1
1
21 1
a
P
a



211
211 22
12
211 2
211





11212 2
1
1111 1
aa a
P
aaaa a



2
1a
1a

3
12
9
2
11
4
0
11
0
1
12
Voâ nghieäm
a
a
a
a
a
a
a
a
a
a
a






0; 4;9a
3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
e) Để
. Kết hợp điều kiện suy ra:
Vậy với thì .
Ví dụ minh họa 3:
Cho biểu thức
a) Tìm điều kiện xác định và rút gọn M.
b) Tính giá trị của M, biết rằng
Lời giải
a) Điều kiện:
b) Với
B. CÁC DẠNG BÀI MINH HỌA
I. CÁC DẠNG TOÁN
Bài toán rút gọn tổng hợp thường có các bài toán phụ: tính giá trị biểu th
ức khi cho giá trị của ẩn; tìm điều
kiện của biến để biểu thức lớn hơn (nhỏ hơn) một số nào đó; tìm giá trị của biến để biểu thức có giá trị nguyên;
tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức,… Do vậy, ta phải áp dụng các phương pháp tương ứng,
thích hợp cho từng dạng toán. (Vd 2).
Dạng 1. Rút gọn biểu thức
Bài 1:
Rút gọn biểu thức: (với )
Bài 2: Rút gọn biểu thức: với
11
1110
11
aa
P
aa

 

11
2
00
11
aa
aa



10 1aa
1a 01a
01a
1P
1
x
yyyxx
M
xy

2
13 38 vàxy
0; 0xy
11
x
yyyxxxyyxxy
M
xy xy



1
11
xyxy xy xyxy
x
y
xy xy



22
38 213 3 2 21 và yx  
 
22
1 3 21 31 21 3 2M  
2
11
.
1
1
aa a
Aa
a
a






0; 1aa
11
11
aa aa
M
aa







0; 1aa
4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 3: Rút gọn biểu thức: với
Bài 4: Rút gọn biểu thức: với
Bài 5: Rút gọn biểu thức: với
Bài 6: Rút gọn biểu thức: với
Bài 7: Rút gọn biểu thức: với
Bài 8: Rút gọn biểu thức: (với )
HƯỚNG DẪN
Bài 1. Với . Ta có:
Vậy .
Bài 2. Với , ta có:
Vậy .
Bài 3.
Với :
126
:1
33 3
x
B
x
xx xx x





0x
222
2
22
xx
P
x
xx

0; 2xx
1
:
2244
aa a
Q
aaa aa





0; 4aa
24
:
22 2
xx
P
xx x






0; 4xx
11 2
.
4
44
x
x
M
x
x
xx





0; 4xx

.
ba
Nabba
aab abb






0; 0;abab
0; 1aa

2
2
2
11
11 1
..
1
11
11
aaa
aa a a
Aa a
a
aa
aa




















2
2
22
11
12 . 1 . 1
11
aa a
aa
 

1
0; 1aa

11
11 11
11 1
1
aa aa
aa aa
M
aaa
a













11 1aaa
1
M
a
0x
126
:1
33 3
x
B
x
xx xx x





 
126
:1
3
33
x
xx
xx xx






5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy khi thì .
Bài 4. Với , ta có:
Vậy .
Bài 5. Với :
Vậy,

126
:
33
3
xx
xx x
xx












236
1
:
3
3
xx
x
x
xx










13266
:
3
3
xxxx
x
xx











1
11
::
33
33
xx
xxxx
xx
xx xx

 



 
 



 

11
:1
33
xx
xx



0x
1
B
0; 2xx
222
2
22
xx
P
x
xx




22
2
22 2 2
x
x
xxx x


2
1
22
x
xx


1P
0; 4aa
1
:
2244
aa a
Q
aaa aa







2
2
2
1
:.
2221
2
2
a
aaa aa
aaaa
aa
a










 
22
21 2
..
21 2 1
aaaa
aa
aa a a



2aa

2Qaa
6.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 6. Với :
Vậy, .
Bài 7.
Với :
.
Bài 8.
Với .
0; 4xx
24
:
22 2
xx
P
xx x








22 2
4
:
2
22
xx x
x
x
xx







224 2
4
22
xxx x
x
xx








421
4
2
22
xx
x
x
xx



1
2
P
x
0; 4xx
11 2
.
4
44
x
x
M
x
x
xx







2
2
11
.
22
2
xx
x
xx
x










2
11
.2
22
2
x
xx
x








22
11 4
4
22
22
xx
x
xx
xx





0; 0;abab

.
ba
Nabba
aab abb








.
ba
ab a b
aa b ba b






7.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy biểu thức có giá trị
Dạng 2. Rút gọn biểu thức – tính giá trị của biểu thức khi cho giá trị của ẩn
Bài 1. Cho biểu thức: với
a) Rút gọn biểu thức P.
b) Tìm giá trị của P khi .
Bài 2. Cho biểu thức: với
a) Rút gọn biểu thức A.
b) Tìm x khi
Bài 3. Cho biểu thức: với .
a) Chứng minh rằng
b) Tìm các giá trị của x
để .
Bài 4. Cho biểu thức: với .
a) Rút gọn biểu thức.
b) Tính giá trị của P khi ;
Bài 5. Cho biểu thức: với .
a) Rút gọn biểu thức.
b) Tìm x để .
HƯỚNG DẪN


ba
ab a b
ab a b





ba
Nba
21 6 4
4
22
xx x x x
P
x
xx



0, 4xx
945x 
2
1142
11 1
x
A
xx x


1x 
4
2015
A
21 1
.
221
x
x
P
x
xx x





0; 1
x
x
1
x
P
x
22 5Px
33
2222
.
x
yxy
Q
x
xy y x y


x
y
743x  423y 
12 25
4
22
x
xx
P
x
xx



0; 4xx
2P
Các bước thực hiện:
- Rút gọn, chú ý điều kiện của biểu thức
- Rút gọn giá trị của biến nếu cần
- Thay vào biểu thức rút gọn
8.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 1.
a) Với , ta có:
.
Vậy với thì .
b) Ta có: thỏa mãn điều kiện xác định
.
Khi đó
Vậy với thì .
Bài 2.
a) Với
với
Vậy: với
b) Khi
(TMĐK)
0, 4xx
21 6 4
4
22
xx x x x
P
x
xx





22 1 2 6 4
22
xxx x x x x
xx



2224 264
22
xx x x x x x x x x
xx



22
22
xx x x
xx





2212
22 22
xx x x x
xx xx


 
1
2
x
x
0, 4xx
1
2
x
P
x

2
945 2 5x 
25x
94511045
25 4
252 5
P



945x  25 4P 
1x 

2222
1 1 42 1 142 1 142
11 1 1 1 1 11
xxx xxxx
A
xx x x x x xx
 




41
44 4
11 11 1
x
x
x
xxxx

 
1x 
4
1
A
x
1x 
444
1 2015
2015 1 2015
Ax
x

2016x
9.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy khi thì .
Bài 3. Cho biểu thức với .
a) Với
Ta có:
b) Ta có:
(thỏa điều kiện)
Vậy thì .
Bài 4. Với :
a)
b) Với
Suy ra:
Vậy .
Bài 5.
4
2015
A
2016x
21 1
.
221
x
x
P
x
xx x





0; 1
x
x
0; 1
x
x
21 1
.
221
x
x
P
x
xx x





 
2121
..
11
22 2
x
xxxxx
x
x
xx xx xx










1. 2
11
.
1
2
đpc
xx
xx
xx
xx
m







1
22 52 2 5
x
Px x
x

 



2225 2320xxxxx

111
20
224
xx xx




1
4
x
22 5Px
x
y

22
33
2222 22
..
xyx xyy
x
yxy xy xy
Q
x
xy y x y x xy y x y x y x y



 

2
743 2 3 2 3x 

2
423 31 31y  

2331 1
323
23 31
xy
Q
xy




323 323
3
323323



323
3
Q
10.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a) Với :
b) Với , để
(thỏa điều kiện)
Vậy với thì .
Dạng 3. Rút gọn biểu thức – tìm x để biểu thức rút gọn đạt giá trị nguyên
Bài 1. Cho biểu thức: với .
a) Rút gọn P.
b) Tìm giá trị nguyên của a để P có giá trị nguyên.
Bài 2. Cho biểu thức: với .
a) Rút gọn P.
b) Tìm giá trị nguyên của x để P
có giá trị nguyên.
0; 4xx
12 25
4
22
x
xx
P
x
xx




122 2
25
4
22
xx xx
x
x
xx



 
222425
22 22
xxx xx x
xx xx


 

32 25
22 22
xx x
xx xx


 

3225 36
22 22
xx x x x
xx xx


 

32
3
2
22
xx
x
x
xx


0; 4xx
2P
3
23 2 4 4 16
2
x
xx x x
x

16x
2P
112
:
2
aa aa a
P
a
aaaa







0; 1; 2aaa
2
2
1 1 4 1 2017
.
11 1
xxxxx
P
xx x x

 




0; 1xx
- Rút gọn biểu thức
- Lấy tử chia cho mẫu tách biểu thức thành tổng của một số nguyên và một biểu thức có tử là một
số nguyên
- Trong biểu thức mới tạo thành, ta cho mẫu là các ước nguyên của tử để suy ra x.
11.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 3. Cho biểu thức: với .
a) Rút gọn Q.
b) Tìm giá trị nguyên của x để Q có giá trị nguyên.
Bài 4. Cho biểu thức: với .
a) Rút gọn P.
b) Tìm để P có giá trị nguyên.
Bài 5. Cho biểu thức: với .
a) Rút gọn P.
b) Tìm để P có giá trị nguyên.
HƯỚNG DẪN
Bài 1. Với
a)
b) Ta có:
P nhận giá trị nguyên khi và chỉ khi: hay là ước nguyên của 8.
Kết hợp đi
ều kiện ta suy ra hoặc thì P đạt giá trị nguyên.
21 1 4
:1
11 1
xx
Q
xx x x x






0; 1xx
11
:
121
x
P
x
xx x x





0x
x
11 3
.1
33
P
aa a





0; 9aa
a
0; 1; 2aaa
112
:
2
aa aa a
P
a
aaaa









1111
2
:
2
11
aaa aaa
a
a
aa aa

 






11
22
22 2
::
222
aa aa
a
aaa
aaa
aa





22
24248
22 2
a
aa
P
aa a



24 8 8
2
22 2
a
aa a


82a
2a
21 1; 3
22 0; 4
24 2; 6
28 6; 10
aaa
aaa
aaa
aaa











0; 1; 2aaa
2a 6a
12.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 2. Cho biểu thức: với .
a) Với
b) Ta có:
Để P là số nguyên hay x là ước nguyên của 2017 (chú ý 2017 là số nguyên tố).
kết hợp điều kiện , suy ra: .
Vậy, với thì P đạt giá trị nguyên.
Bài 3. Cho biểu thức: với .
a) Với
Ta có:
2
2
1 1 4 1 2017
.
11 1
xxxxx
P
xx x x

 




0; 1xx
0; 1xx
2
2
1 1 4 1 2017
.
11 1
xxxxx
P
xx x x

 






22
2
2
11
4 1 2017
.
11 1
xx
xx x
xx x x








222
2
21 21 41
2017
.
1
xx xx xx
x
xx

 



2
2
1 2017
.
1
xx
xx




2017x
x
2017 2017
1
x
P
x
x

2017
x
2017
1
1
2017
x
x
x
x


0; 1xx
2017x
2017x
21 1 4
:1
11 1
xx
Q
xx x x x






0; 1xx
0; 1
x
x
21 1 4
:1
11 1
xx
Q
xx x x x







3
3
21 1 4
:1
11
1
xx
xxx
x












21 1 1 4
:
1
1111
xxxxxx
xx
xxx xxx









 


13.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Biểu thức rút gọn là: .
b) Tìm giá trị nguyên của x để Q có giá trị nguyên
Để Q có giá trị nguyên thì hay là ước nguyên của 3.
Suy ra: (thỏa điều kiện)
Vậy với thì Q đạt giá trị nguyên.
Bài 4. Cho biểu thức: với .
a) Với , ta có:
b) Tìm để P có giá trị nguyên.
Để P có giá trị nguyên thì phải là số nguyên.

21 1 3
:
1
11
xxx x
xx
xxx












3
:
1
11
xx x
xx
xxx












1
1
.
33
11
xx
x
xx
xx
xxx




3
x
Q
x
33 3
1
33 3
xx
Q
xx x




33x
3x
33 6
36
31 4 16
4
31 2
0
33 0
xx
x
xxx
x
xx
x
xx












0; 4;16; 36x
11
:
121
x
P
x
xx x x





0x
0x
11
:
121
x
P
x
xx x x







2
11
:
1
1
1
x
x
xx
x






2
11 1
11
.
1
xxx
x
x
x
xxx
xx







x
11
1
x
P
x
x

14.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Do đó x là ước nguyên của 1. Suy ra:
Vậy với thì P đạt giá trị nguyên.
Bài 5. Cho biểu thức: với .
a) Với , ta có:
b) Tìm để P có giá trị nguyên.
Để đạt giá trị nguyên thì phải là ước nguyên của 2.
Suy ra: (không thỏa mãn điều kiện).
Vậy với không có giá trị thỏa mãn để P đạt giá trị nguyên.
Dạng 4. Rút gọn biểu thức – tìm x để biểu thức thỏa bằng hoặ
c lớn hơn (nhỏ hơn) một số cho trước
Bài 1. Cho biểu thức:
a) Tìm điều kiện và rút gọn biểu thức.
b) Tìm các giá trị của x để .
Bài 2. Cho biểu thức:

1
1
thoûa ñieàu kieän
loaïi
x
x

1
x
11 3
.1
33
P
aa a





0; 9aa
0; 9aa
11 3
.1
33
P
aa a






33 3
.
33
aa a
a
aa







232
.
3
33
aa
aa
aa






a
2
3
P
a
3a
32 1
31 2
31 4
32 5
aa
aa
aa
aa











a
11
:
1
11
x
A
x
x
x






0A
11
1.
1
P
x
xx





- Rút gọn
- Cho biểu thức rút gọn thỏa điều kiện ta được phương trình hoặc bất phương trình, chú ý điều
kiện của ẩn trong bài toán.
15.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a) Tìm điều kiện và rút gọn biểu thức.
b) Tìm các giá trị của x để .
Bài 3. Cho biểu thức: (với )
a) Rút gọn biểu thức P.
b) Tìm các giá trị của x để .
Bài 4. Cho biểu thức: (với )
a) Rút gọn biểu thức P.
b) Tìm các giá trị của a để
Bài 5. Cho biểu thức: (với )
a) Rút gọn biểu thức M.
b) Tìm các giá trị của x
để
HƯỚNG DẪN
Bài 1. Cho biểu thức:
a) Điều kiện: . Khi đó:
Biểu thức rút gọn là:
b) Để .
Kết hợp điều kiện, suy ra: .
2
. 5 2 6. 1 2005 2 3Pxx
11
:
121
x
P
xx x x x





0; 1
x
x
1
2
P
1
:
1
1
aaa
P
a
aaa






0; 1aa
0P
112
:
1
11
x
M
x
xxx x









0, 1
x
x
0M
11
:
1
11
x
A
x
x
x






0
1
x
x

11 1 1
::
11
11 1
11
xxx
A
xx
x
xx
xx












 
11 1 1
:.
1
1
11 11
x
xx
x
xx xx


 
1
1
x
1
1
A
x
1
001011
1
A
xxx
x
  
00 1
A
x
16.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 2. Cho biểu thức:
a) Điều kiện: .
Khi đó:
b)
(thỏa mãn điều kiện).
Bài 3.
a) Với :
.
b) Với thì
(thỏa điều kiện). Vậy với thì .
Bài 4.
a) Với :
11
1.
1
P
x
xx





0
1
x
x

11 111
1. .
11
1
x
P
xxx x
xx












2
11
.
1
1
1
x
x
xx
x

2
. 5 2 6. 1 2005 2 3Pxx


22
2
1
3 2 1 2005 2 3
1
xx
x

3 2 2005 2 3x
3 2 2005 2 3x 
2005x
0; 1
x
x
11
:
121
x
P
xx x x x






2
1
1
.
11
x
x
x
xx xx







2
111
11
.
.
1
xxx
x
x
x
xxx
xx



0; 1
x
x

11
21 22
2
x
x
xx x
x

2x 2x
1
2
P
0; 1aa

1
:
1
111
aa a
P
a
aa a a






17.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
b) Với thì .
Vậy với , x > 2 thì .
Bài 5. Cho biểu thức:
a) Điều kiện: . Khi đó:
b) Để mà nên
Do đó:
Vậy thì .
Dạng 5. Rút gọn biểu thức – tìm x để biểu thức đạt giá trị lớn nhất (gtln), giá trị nhỏ nhất (gtnn)
11
:
11 1
a
aa a







1
.1 1
1
a
aa
a





0; 1aa
0; 1
010 01
1
aa
P
aa
a

  
01a 0P
112
:
1
11
x
M
x
xxx x









0, 1
x
x
112
:
1
11
x
M
x
xxx x










.1 1 2
:
1 1 11 11
xx x
xx xx x x x x







112
:
111
xx
xx x x








11
1
:
111
xx
x
xx x x







11 1
:.1
1
xx
x
xx x


1
x
x
1
00
x
M
x

0, 1
x
x
0x
0101
M
xx
1
x
0M
18.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 1. Cho các biểu thức sau:
a) Tìm giá trị nhỏ nhất của M.
b) Tìm giá trị lớn nhất của N.
Bài 2. Cho biểu thức:
với
a) Rút gọn biểu thức.
b) Tìm x để Q đạt giá trị nhỏ nhất.
Bài 3. Cho biểu thức:
với
a) Rút gọn biểu thức.
b) Tìm giá trị lớn nhất P.
Bài 4. Cho hai biểu thức:
và với
a) Tính giá trị c
ủa biểu thức P khi .
b) Rút gọn biểu thức Q.
c) Tìm giá trị của x để biểu thức đạt giá trị nhỏ nhất.
Bài 5. Cho biểu thức:
1
M
xx 12Nxx
122 12
:
1
111
x
Q
x
xxxxx x









0; 1
x
x
15 11 3 2 2 3
231 3
xxx
P
xx x x



0; 1
x
x
3
2
x
P
x
15 2
4
2
xx
Q
x
x


0; 4xx
9x
P
Q
21
:
11
x
A
x
xx x






- Rút gọn
- Biến đổi biểu thức (BT) về dạng:
+ Số không âm + hằng số
GTNN.
VD: . Khi đó GTNN của biểu thức bằng m xảy ra khi và chỉ khi .
+ Hằng số - số không âm
GTLN.
VD: . Khi đó GTLN của biểu thức bằng M xảy ra khi và chỉ khi .
+ Sử dụng bất đẳng thức Cô-si: Cho hai số dương a và b, ta có:
. Dấu “=” xảy ra khi và chỉ khi .
+
2
A
mm
0A
2
M
AM
0A
2ab ab
ab
A
BAB
19.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a) Tìm điều kiện xác định. Rút gọn A.
b) Tìm giá trị nhỏ nhất của A.
HƯỚNG DẪN
Bài 1. Cho các biểu thức sau:
a) Điều kiện:
Suy ra, (thỏa điều kiện)
Vậy .
b) Điều kiện: .
Suy ra,
(thỏa điều kiện)
Vậy .
Bài 2. Cho biểu thức:
a) Với
1
M
xx 12Nxx
0x
2
15 1 5 5
1
44 2 4 4
Mx x x x x

 


2
min
min
15 5 1 1
0
24 4 2 4
Mx x x








min
51
44
Mx
1
x
15
12 1 1
44
Nxx x x
15
11
44
xx




2
155
1
244
x




2
max
max
15 5
1
24 4
Nx








1115
10 1 1
2244
xxxx
max
55
44
Mx
122 12
:
1
111
x
Q
x
xxxxx x









0; 1
x
x
122 12
:
1
111
x
Q
x
xxxxx x











 
21
112
:
11
11 11
x
xx
xx xx





 

20.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy .
b)
Vì
Vậy,
Bài 3. Cho biểu thức:
a) Với


2
21
112
:
1
11
11
x
x
x
xx
xx















2
12 12
:
11
1
xx
xx
x


 












22
11 1 1
:.1
1
11
11
x
xx x
x
x
xx
xx




1
1
x
P
x
112 2
1
11 1
xx
P
x
xx




min
min
min max
22
11
11
Px
xx





0; 1 0 1 1xx x x
min
min
2
111011
01
xxxP
min
10Px
15 11 3 2 2 3
231 3
xxx
P
xx x x



0; 1
x
x
15 11 3 2 2 3
231 3
xxx
P
xx x x




15 11 3 2 2 3
13
31
xxx
xx
xx





15 11 3 2 3 2 3 1
31
xxxxx
xx




15 11 3 9 2 6 2 2 3 3
31
xxxx xxx
xx



15 11 3 9 2 6 2 2 3 3
31
xxxxxxx
xx


21.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy
b) .
Vì
Vậy, .
Bài 4. Cho biểu thức: và với
a) Với . Ta có:
b) Với , ta có:
c) Tìm giá trị của x để biểu thức đạt giá trị nhỏ nhất:
Áp dụng bất đẳng thức Cosi cho hai số không âm và , ta có:
Dấu bằng xảy ra khi (thỏa điều kiện)
Vậy giá trị nhỏ nhất của là .


15 2
57 2 5 2
3
31 31
xx
xx x
x
xx xx



 
52
3
x
P
x

5317
52 17
5
33 3
x
x
P
xx x




max
max
17
3
P
x




min
max
min
0
0; 1 3 0
17
0
3
x
xx P x x x
x

max
17
0
3
Px
3
2
x
P
x
15 2
4
2
xx
Q
x
x


0; 4xx
9x
39312
12
32
292
x
P
x



0; 4xx
1. 2 5 2
15 2
44
2
xx x
xx
Q
xx
x





2
3252 2
44
2
22
xx
x
xxxx x
xx
x
xx




P
Q
33Px
x
Q
x
x

x
3
x

33
2. 23
P
xx
Q
xx




3
3
xx
x

P
Q
min
23 3
P
x
Q




22.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 5. Cho biểu thức:
a) Điều kiện: .
b) với thì .
Áp dụng bất đẳng thức Cosi cho hai số dương , suy ra:
(thỏa điều kiện)
Vậy .
Dạng 6.Nâng cao phát triển tư duy
Bài 1. Cho biểu thức
42
2
11
:; 715
x
PQxx
xx x x x x


(với
0, 1xx
)
a) Rút gọn
P
b) Với giá trị nào của
x
thì
4QP
đạt giá trị nhỏ nhất
Bài 2. Cho biểu thức:
2
22 2
:
1
21
21
xx
P
x
xx
xx











với
0; 1xx
a) Rút gọn
P
b) Tìm các giá trị của
x
để
0P
c) Tính giá trị của
P
khi 743x 
d) Tìm giá trị lớn nhất của
P
và giá trị tương ứng của
x
21
:
11
x
A
x
xx x






0
1
x
x

21 2 1
::
111 1
1
xx
A
x
xx x x x
xx



 







2
2
12
.
1
1
x
xx
A
x
xx


22x
Ax
x
x

0
1
x
x
2
0; 0
x
x

2
0; 0
x
x


22 2
2. 22
x
Ax x
xx x




min
2
22 2
Axx
x

min
22 2Ax
23.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 3. Cho
2
44 44
816
xx x x x
A
xx


với
4x
a) Rút gọn
A
.Tìm
x
để
A
đạt giá trị nhỏ nhất.
b) Tìm các giá trị nguyên của
x
để
A
có giá trị nguyên.
Bài 4. Cho biểu thức:
22
2 1 1 2020
..
31
21 21
11
33
M
x
xx













a) Rút gọn M;
b) Tìm giá trị lớn nhất của M.
Bài 5. Cho biểu thức
211
:
aab
P
ab b ab a b a a b









với 0, 0, .abab
a) Chứng minh rằng
.Pab
b) Tính giá trị biểu thức
P
khi
35a 
và
0, 5.b
c)Tìm giá trị lớn nhất của
P
nếu
22
48.ab
HƯỚNG DẪN
Bài 1.Cho biểu thức
42
2
11
:; 715
x
PQxx
xx x x x x


(với
0, 1
xx

)
a) Rút gọn
P
b) Với giá trị nào của
x
thì
4
QP
đạt giá trị nhỏ nhất
Hướng dẫn
a)

3
2
11 1
:.1
1
xx
Pxx
xx x x x x
xx x






1
.1 11
1
x
Pxxxxx
xx x


b)

42
471541QPx x x
24.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com


2
2
42 2 2
816 441 4 21xx xx x x
41
QP

Dấu
""
xảy ra khi:
2x
. Vậy giá trị nhỏ nhất
4QP
là
1
Bài 2. Cho biểu thức:
2
22 2
:
1
21
21
xx
P
x
xx
xx










với
0; 1xx
a) Rút gọn
P
b) Tìm các giá trị của
x
để
0P
c) Tính giá trị của
P
khi
743x 
d) Tìm giá trị lớn nhất của
P
và giá trị tương ứng của
x
Hướng dẫn
a) Với
0; 1xx
, ta có:



2
2
1
22
.
2
11
1
x
xx
P
xx
x













2
22
21 21
1
.
2
11 11
xx xx
x
P
xx xx






 



2
2
1
22 22
.
2
11
x
xxx xxx
P
xx









22
2
11
2
.
2
11
xx
x
P
xx



1Pxx
Vậy

1Pxx
b) Ta có
0P
25.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
 
00
0
10 10
1
10 1
xx
x
xx xx
x
xx








Kết hợp với điều kiện đề bài, ta được
01x
Vậy với
01x
thì
0P
c) Với

2
7 4 3 3 2.2. 3 4 3 2x   thì

22
32 32 1P





32 321P 

321 3P 
33223P 
33 5P 
Vậy với
743x  thì 33 5P 
d) Ta có

2
11
1
24
Pxx xx x

 


Nhận thấy:
222
11111
00
22244
xxx
 

 
 
Dấu
""
xảy ra khi và chỉ khi:
111
0
224
xxx
(thỏa mãn)
Vậy với
1
4
x
thì
P
đạt giá trị lớn nhất là
1
4
Bài 3. Cho
2
44 44
816
xx x x x
A
xx


với
4x
a) Rút gọn
A
.Tìm
x
để
A
đạt giá trị nhỏ nhất.
b) Tìm các giá trị nguyên của
x
để
A
có giá trị nguyên.
Hướng dẫn
26.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a) Điều kiện để biểu thức
A
xác định là
4x
.



22
2
42 42
42 42
4
4
xx x
xx x
A
x
x

 

 



42 42
4
xx x
x
 
+ Nếu
48x
thì
420x 
nên

422 4
416
4
444
xx x
x
A
xxx



Do
48x
nên
044 8xA
.
+ Nếu
8x
thì 420x  nên

42 42
242 8
24 2168
44
44
xx x
xx x
Ax
xx
xx
 



(Theo bất đẳng thức
Cô si). Dấu bằng xảy ra khi và chỉ khi
8
24 44 8
4
xxx
x
 
.
Vậy GTNN của
A
bằng
8
khi
8x
.
b) Xét
48x
thì
16
4
4
A
x

, ta thấy
AZ
khi và chỉ khi
16
4
4
Zx
x

là ước số nguyên
dương của
16
. Hay

41;2;4;8;16 5;6;8;12;20xx
đối chiếu điều kiện suy ra
x5
hoặc
6x
.
+ Xét
8x
ta có:
2
4
x
A
x
, đặt
2
4
4
2
xm
xm
m


khi đó ta có:

2
24
8
2
m
Am
mm
 suy
ra

2; 4;8 8;20; 68mx
.
Tóm lại để
A
nhận giá trị nguyên thì

5; 6;8; 20; 68x
.
Bài 4. Cho biểu thức:
22
2 1 1 2020
..
31
21 21
11
33
M
x
xx













a) Rút gọn M;
b) Tìm giá trị lớn nhất của M.
Hướng dẫn
27.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a) Ta có:

22
2 3 3 2020
..
31
32 1 32 1
M
x
xx




 


2 3 3 2020
..
31
34 4 134 4 1
M
x
xx xx



 

2 3 3 2020
..
31
44 444 4
M
x
xx xx



 

2 3 1 1 2020
.. .
34 1
11
M
x
xx xx



 


2
1 1 1 2020
..
21
1
xx xx
M
x
xx


2
1 2 2 2020
..
211
x
M
xx x

2
2020
1
M
xx

. TXĐ:
0x
.
b) Ta có:
2
11xx
. Vì
0x
nên
2
2020 2020
2020
11
M
xx


.
Vậy giá trị lớn nhất của M là 2020 khi
0x
.
Bài 5. Cho biểu thức
211
:
aab
P
ab b ab a b a a b









với 0, 0, .abab
a) Chứng minh rằng
.Pab
b) Tính giá trị biểu thức
P
khi
35a 
và
0, 5.b
c)Tìm giá trị lớn nhất của
P
nếu
22
48.ab
Hướng dẫn
a) Ta có:
28.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com



2
211
:.
..
aabb
aab ab
P
ab b ab a a b
bab aba abab











Hay


2
2
.
ab a b
Pab
ab a b

b) Khi
2
1 3 5 625 51 51
35, .
2242 2
abab Pab






c) Theo bất đẳng thức
AM GM
ta có:
22 22
42.44 48 2.a b a b ab ab ab
Vậy
2,P
dấu đẳng thức xảy ra khi và chỉ khi
22
4 4 2, 1.ab ab
Vậy GTLN của
P
là
2.
29.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
II.TRẮC NGHIỆM RÈN PHẢN XẠ
Bài 4- Rút gọn biểu thức chứa căn
Câu 1. Giá trị của biểu thức
()
2
45 625---
là:
A.
525-
. B.
4
. C.
225+
. D.
1
.
Câu 2. Giá trị của biểu thức
()
2
25 7210+--
là:
A
22
. B.
0
. C.
2
. D.
25
.
Câu 3. Giá trị của biểu thức
32 50 3 8 18+--
là:
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 4. . Giá trị của biểu thức
125 4 45 3 20 80-+-
là:
A.
5
. B.
55-
. C.
10 5
. D.
55
.
Câu 5. Rút gọn biểu thức
4
52 25
4
a
aaa
a
+--
với
0a >
ta được
A.
a
. B.
4 a
. C.
2 a
. D.
a-
.
Câu 6. Rút gọn biểu thức
132 3
38 . 2
425 2
3
aa
aa
a
+- -
với
0a >
ta được:
A.
47
10
a . B.
21
5
a . C.
47
2
10
a . D.
47
2
5
a .
Câu 7. Giá trị của biểu thức
()
527210+-
là:
A.
4
. B. 5 . C.
2
. D.
3
.
Câu 8. Giá trị của biểu thức
()
51625-+
là:
A.
6
. B.
4
. C.
2
. D.
3
.
Câu 9. Rút gọn biểu thức
32 5
2
16 2
29 36aaa a
a
a
-+ +
với
0a >
ta được
A.
14
aaa
+
. B.
14
aaa
-
. C.
14 2
aaa
+
. D.
20 2
aaa
-
.
Câu 10. Rút gọn biểu thức
13 4 1
2 200 :
22 2 5 8
a
aa
æö
÷
ç
÷
ç
-+
÷
ç
÷
ç
÷
ç
èø
ta được
A.
66 2
a
. B.
52 2
a
. C.
54
a
. D.
54 2
a
.
Câu 11. Đẳng thức nào dưới đây là đúng?
30.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
24
22 2
2
ab ab
a
baabb
-
=
-+
. B.
24
22 2
2
ab ab
a
baabb
-
=
-+
.
C.
24
22 2
2
ab ab
ab
baabb
-
=
-+
. D.
24
22 2
2
ab ab
ab
baabb
-
=-
-+
.
Câu 12. Với đẳng thức nào dưới đây là đúng?
A.
2
ab ba a b
a
ab a b
+-
+=
+
. B.
ab ba a b
a
ab a b
+-
+=
+
.
C.
2
ab ba a b
ab a b
+-
+=
+
. D.
2
ab ba a b
b
ab a b
+-
+=
+
.
Câu 13. Chọn khẳng định đúng?
A.
2 3 6 216 3
.
32
82 6
aa
æö
æö
÷
---
ç
÷
ç
÷
ç
÷
-=
ç
÷
ç÷
ç
÷
÷
ç
ç
÷
ç
èø
-
èø
. B.
23 6 216 3
.
32
82 6
aa
æö
æö
÷
--
ç
÷
ç
÷
ç
÷
-=
ç
÷
ç÷
ç
÷
÷
ç
ç
÷
ç
èø
-
èø
.
C.
2 3 6 216
.
32
82 6
aa
æö
æö
÷
---
ç
÷
ç
÷
ç
÷
-=
ç
÷
ç÷
ç
÷
÷
ç
ç
÷
ç
èø
-
èø
. D.
2 3 6 216
.
32
82 6
aa
æö
æö
÷
--
ç
÷
ç
÷
ç
÷
-=
ç
÷
ç÷
ç
÷
÷
ç
ç
÷
ç
èø
-
èø
.
Câu 14. Chọn khẳng định đúng?
A.
()
14 7 15 5 1
:2
12 13
75
a
a
æö
÷
--
ç
÷
ç
+=
÷
ç
÷
ç
÷
ç
--
-
èø
. B.
()
14 7 15 5 1 2
:
12 13
75
a
a
æö
÷
--
ç
÷
ç
+=
÷
ç
÷
ç
÷
ç
--
-
èø
.
C.
()
14 7 15 5 1
:2
12 13
75
a
a
æö
÷
--
ç
÷
ç
+=-
÷
ç
÷
ç
÷
ç
--
-
èø
.D.
()
14 7 15 5 1
:
2
12 13
75
a
a
æö
÷
--
ç
÷
ç
+=-
÷
ç
÷
ç
÷
ç
--
-
èø
.
Câu 15. Cho biểu thức
2.
1
x
P
x
=
+
. Giá trị của
P
khi
9x =
là
A.
9
2
. B.
9
4
. C.
9
. D.
18
.
Câu 16. Cho biểu thức
1
x
P
x
=
-
0; 1.xx³¹
Giá trị của
P
khi
4x =
là:
A.
4
. B.
2
. C.
2-
. D.
2
3
.
Câu 17. Cho biểu thức
1
x
P
x
=
+
. Giá trị của
P
khi
2
23
x =
-
là
A.
4
. B.
2
. C.
3
. D.
1
.
31.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 18. Cho biểu thức
1
.
2
x
P
x
+
=
-
Giá trị của
P
khi
322
x
=+
là:
A.
432+
. B.
432-
. C.
3
. D.
32
.
Câu 19. Cho biểu thức
22xx
P
x
++
=
với
0.x >
So sánh
P
với
4
A.
4P >
. B.
4P <
. C.
4P =
. D. 4P £ .
Câu 20. Cho biểu thức
3
2
x
B
x
+
=
+
với
0.x ³
So sánh
A
với
1
A
1B >
. B.
1B <
. C.
1B =
. D. 1B £ .
Câu 21. Cho biểu thức
31
1
x
x
P
-
+
=
với
0.x ³
Tìm
x
biết
Px
=
.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 22. Cho biểu thức
1
2
x
A
x
+
=
-
với
0; 4.xx³¹
Tìm các giá trị của biết
1
2
x
A
-
=
A. 0; 5xx==. B. 0x = . C.
0; 25xx==
. D.
5; 1xx==
.
Câu 23. Cho
2
1
P
x
=
+
Có bao nhiêu giá trị
x Î
để
?P Î
A.
1
. B.
2
. C. 0 . D.
4
.
Câu 24. Cho
13
27 ;
31 3
A =-+
-
55 5 35
52 513 5
B
+
=+-
+-+
Chọn câu đúng
A.
0BA>>
. B.
0AB<<
. C.
0AB<<
. D.
0BA<<
.
Câu 25. Cho
21
2
x
A
x
-
=
+
với
0x ³
Có bao nhiêu giá trị của
x
để
A
có giá trị nguyên
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 26. Cho biểu thức
12 25
4
22
xxx
A
x
xx
++
=++
-
-+
với
0; 4xx³¹
Rút gọn biểu thức
A
ta được:
32.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
3
2
x
A
x
=
+
. B.
2
x
A
x
=
+
. C.
2
2
x
A
x
=
+
. D.
3
2
A
x
=
+
.
Câu 27. Cho biểu thức
12 25
4
22
xxx
A
x
xx
++
=++
-
-+
với
0; 4xx³¹
Tìm
x
để
2A =
A.
12
. B.
4
. C.
16
. D.
25
.
Câu 28. Cho biểu thức
()
2
1
22
.
12
21
x
xx
B
x
xx
æö
-
÷
-+
ç
÷
ç
=-
÷
ç
÷
ç
-
÷
ç
++
èø
với
0; 1xx³¹
Rút gọn biểu thức
B
ta được:
A.
Bx x
=-
. B.
Bxx
=-
. C.
Bxx
=+
. D.
2
Bx x
=+
.
Câu 29. Cho biểu thức
2
22(1)
.
12
21
xx x
B
x
xx
æö
÷
-+-
ç
÷
ç
=-
÷
ç
÷
ç
-
÷
ç
++
èø
với
0; 1xx³¹
Tìm
x
để
0B >
.
A.
1x >
. B.
2x <
. C.
01x<<
. D. 1x £ .
Câu 30. Cho biểu thức
()
2
1
22
.
12
21
x
xx
B
x
xx
æö
-
÷
-+
ç
÷
ç
=-
÷
ç
÷
ç
-
÷
ç
++
èø
với
0; 1xx³¹
Tìm giá trị lớn nhất của
B
.
A.
1
. B.
2
. C.
3
. D.
1
4
.
Câu 31. Cho biểu thức
48 12
:
4
22
xxx
P
x
xxxx
æöæö
÷÷
-
çç
÷÷
çç
=+ -
÷÷
çç
÷÷
çç
-
÷÷
çç
+-
èøèø
với
0; 4; 9xxx³¹¹
. Rút gọn biểu
thức
P
ta được
A.
4
3
x
P
x
=
-
. B.
4
3
x
P
x
=
+
. C.
3
x
P
x
=
-
. D.
4
3
x
P
x
-
=
-
.
Câu 32. Cho biểu thức
48 12
:
4
22
xxx
P
x
xxxx
æöæö
÷÷
-
çç
÷÷
çç
=+ -
÷÷
çç
÷÷
çç
-
÷÷
çç
+-
èøèø
với
0; 4; 9xxx³¹¹
. Tìm
x
để
1
P
=-
A.
9
16
x = . B.
9
;1
16
xx==-. C.
3
;1
4
xx==-. D.
3
4
x = .
33.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 33. Cho biểu thức
48 12
:
4
22
xxx
P
x
xxxx
æöæö
÷÷
-
çç
÷÷
çç
=+ -
÷÷
çç
÷÷
çç
-
÷÷
çç
+-
èøèø
với
0; 4; 9xxx³¹¹
.
A.
5
18
m = . B.
5
18
m >- . C.
5
18
m < . D.
5
18
m > .
Câu 34. Cho biểu thức
29 321
56 23
xxx
C
xx x x
-++
=--
-+ - -
với
0; 4; 9xxx³¹¹
. Rút gọn biểu
thức trên ta được:
A.
1
3
x
C
x
-
=
-
. B.
1
3
x
C
x
-
=
+
. C.
1
3
x
C
x
-
=
+
. D.
1
3
x
C
x
+
=
+
.
Câu 35. Cho biểu thức
29 321
56 23
xxx
C
xx x x
-++
=--
-+ - -
với
0; 4; 9xxx³¹¹
. Tìm
x
để
1C <
A. 09x£<. B.
09;4xx£< ¹
. C.
49x<<
. D.
04x<<
.
Câu 36. Cho biểu thức
21
:
11
x
C
xxxx
æö
÷
ç
÷
ç
=+
÷
ç
÷
ç
÷
ç
-- -
èø
với
0; 1xx>¹
Rút gọn biểu thức
C
ta được
A.
2x
C
x
-
=
. B.
2x
C
x
+
=
. C.
2x
C
x
+
=
. D.
2
x
C
x
=
+
.
Câu 37. Cho biểu thức
21
:
11
x
C
xxxx
æö
÷
ç
÷
ç
=+
÷
ç
÷
ç
÷
ç
-- -
èø
với
0; 1xx>¹
Tìm giá trị nhỏ nhất của
C
.
A.
1
C
=
. B.
2
C
=
. C.
2
C
=
. D.
22
C
=
.
Câu 38. Cho biểu thức
3
21 1 4
:1
11
1
xx
P
xxx
x
æö
æö
++
÷
÷
ç
ç
÷
÷
ç
=- -
ç
÷
÷
ç
ç
÷
÷
ç
÷
ç
èø
èø
-++
-
Rút gọn
P
.
A.
3
x
P
x
=
-
. B.
3
x
P
x
=
+
. C.
3
3
x
P
x
+
=
-
. D.
3
x
P
x
-
=
-
.
Câu 39. Cho biểu thức
3
21 1 4
:1
11
1
xx
P
xxx
x
æö
æö
++
÷
÷
ç
ç
÷
÷
ç
=- -
ç
÷
÷
ç
ç
÷
÷
ç
÷
ç
èø
èø
-++
-
Tìm các giá trị nguyên của
x
để
P
nhận giá trị nguyên dương.
34.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
1; 36xx==
. B.
1; 36xx==
. C.
4; 6xx==
. D.
16; 36xx==
.
HƯỚNG DẪN
Bài 4- Rút gọn biểu thức chứa căn
Câu 1. Đáp án A.
()
2
45 625---
() ()()
222
45 5251 45 51=- -- +=- - -
45 51=---
4551525=- - +=-
Câu 2. Đáp án A.
()
2
25 7210+--
()
2
25 525.22=+-- +
()()
22
25 52=+--
25 52=+--
255222=+-+=
.
Câu 3. Đáp án B.
32 50 3 8 18+--
16.2 25.2 3 4.2 9.2=+-- 42 52 62 32 0=+--=
..
Câu 4. Đáp án B.
125 4 45 3 20 80-+-
25.5 4 9.5 3 4.5 16.5 5 5 4.3 5 3.2 5 4 5=-+-=-+-
55 125 65 45 55.=- +-=-
Câu 5. Đáp án D.
4
52 25
4
a
aaa
a
+--
4
52. 5
4
aa
aaa
a
=+ - -
525
aa a a
=+--
a
=-
.
Câu 6. Đáp án C.
132 3
38 . 2
425 2
3
aa
aa
a
+- -
1 16.2 3
34.2 . 2
4
25 3 2
aa
aa
a
=+ - -
142 3.2
3.2 2 . . 2
45 2
3
aa a
aa
a
=+ - -
11
62 2 2 2
52
aaaa=+ - -
11 47
2.6 1 2
52 10
aa
æö
÷
ç
÷
=+--=
ç
÷
ç
÷
ç
èø
Câu 7. Đáp án D.
()
527210+-
() ()()
=+ - +=+ -
2
52525.22 52 52
() ()()
=+ -=+ -=-=5252 5252523
.
35.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 8. Đáp án B.
Ta có
() () ()()
2
51625 51525.11 51 51- + =- + +=- +
()()
51 51 514=- +=-=
.
Câu 9. Đáp án A.
Với
0a >
ta có
32 5
2
16 2
29 36aaa a
a
a
-+ +
22 4
2
16 2
29. .36.
a
aaaa aa
a
a
=- + +
2
2
2
23 4 .6aaaaa aa
a
=- + +
23 4 12 14
aaaaa a aaa
=- + + = +
.
Câu 10. Đáp án D.
Ta có
13 4 1
2 200 :
22 2 5 8
a
aa
æö
÷
ç
÷
ç
-+
÷
ç
÷
ç
÷
ç
èø
13 4
.2.100.2..8
22 5
2
a
aa
æö
÷
ç
÷
ç
=- +
÷
ç
÷
ç
÷
ç
èø
32 2.
4. 12 2. .10. 2. 4. 12 2. 64 2.
52
2
aa
aa aa=- + = - +
2 2 12 2 64 2 54 2
aa a a
=- + =
Câu 11. Đáp án B.
Ta có
----
====
-
-+
-
-
22
24 24
22 2 2 2 2
2
() ()
...
()
2
()
ab ab
ab ab ab ab ab ab
a
ab
baabb b b b
ab
ab
Câu 12. Đáp án A.
Ta có
() ()
22
.. ..
ab
ab ba a b a a b b b a
ab ab ab ab
-
+- +
+= +
++
()()()
2.
abab abab
abab a
ab a b
+-+
=+ =++-=
+
Câu 13. Đáp án B.
Ta có
2 3 6 216 2 3 2. 3 36.6
..
33
82 6 4.22 6
aa
æöæ ö
æö æö
÷÷
--- -
çç
÷÷
çç
÷÷
çç
÷÷
-= -
çç
÷÷
ç÷ç ÷
çç
÷÷
÷÷
çç
çç
÷÷
çç
èø èø
--
èøè ø
36.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
() ()
()
32 2 6 2 1
66
.26.
3
22 2 6 6
221
6363
26. .
222
66
aa
aaa
éùéù
--
êúêú
æö æö
÷÷
çç
êúêú
÷÷
=--=--
çç
÷÷
çç
êúêú
÷÷
çç
èø èø
-
-
êúêú
ëûëû
æöæö
æö æö
÷÷
--
çç
÷÷
çç
÷÷
çç
÷÷
=- =- =
çç
÷÷
ç÷ç÷
çç
÷÷
÷÷
çç
çç
÷÷
çç
èø èø
èøèø
Câu 14. Đáp án C.
Ta có
()
14 7 15 5 1
:
12 13
75a
æö
÷
--
ç
÷
ç
+
÷
ç
÷
ç
÷
ç
--
-
èø
()
7.27 5.35
.7 5
12 13
a
æö
÷
--
ç
÷
ç
=+ -
÷
ç
÷
ç
÷
ç
--
èø
()()
()
71 2 5 3 1
.7 5
12 31
a
æö
÷
ç
-- -
÷
ç
÷
ç
÷
=- -
ç
÷
ç
÷
ç
÷
--
ç
÷
èø
()
()
621
26.
6
221
a
éù
-
êú
æö
÷
ç
êú
÷
=--
ç
÷
ç
êú
÷
ç
èø
-
êú
ëû
()()()()
75.75 .7575 2.aa a=- - - =- + - =-
Câu 15. Đáp án A.
Ta có
2.9 18 18 9
.
31 4 2
91
P ====
+
+
Câu 16. Đáp án B.
Thay
4x =
(thỏa điều kiện) vào
P
ta được
42
2
21
41
P ===
-
-
.
Câu 17. Đáp án B.
Ta có
()
()()
()
2
22 3
2423
423 31
43
23
2323
x
+
+
== = =+=+
-
-
-+
()
2
31 31
x
= +=+
Khi đó ta có
()
23 2
423 423
2
311 32 32
P
+
++
====
++ + +
Câu 18. Đáp án A.
Ta có
() ()
22
322 21 21 21
xx
=+ = + = + = +
Thay
21
x
=+
vào biểu thức
P
ta được
37.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
()()
()()
22 21
211 22
432
212 21
21 21
P
++
++ +
=== =+
+- -
-+
.
Câu 19. Đáp án A.
Ta xét:
22 224 22
44
xx xx xxx
P
xxx
++ ++- -+
-= -= =
()()
2
211 11
xx x
xx
-++ -+
==
Vì
()
2
1110, 0xx"-+³> >
và
0, 0xx">>
nên
40 4PP-> >
với
0x >
Câu 20. Đáp án A.
Cách 1: Ta có
()
21
3211
1
2222 2
x
xx
B
xxxx x
++
++
== =+=+
++++ +
Vì
00220xxx³ ³ +³>
suy ra
11
01 1
22xx
>+ >
++
hay
1B >
Cách 2: ta xét hiệu
3321
11
222
xxx
B
xxx
++--
-= -= =
+++
Vì
10>
và
0, 0 2 2 0xx x"³³+³>
nên
1
0
2x
>
+
Hay
10 1.BB-> >
Câu 21. Đáp án A.
Với
0x ³
ta có
Px
=
()
()
()
2
1
31 31
111
31 210
10 1 1
xx
xx
x
xxx
xxxxx
xxxTM
+
--
==
+++
-=+-+=
-===
.
Câu 22. Đáp án C.
38.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Với
0; 4xx³¹
ta có:
111
22
2
xxx
A
x
-+-
==
-
()()()
2 1 2 122 32xxx xxx+=- -+=-+
()
()
(
00
50 50
25
5
)
xxtm
xx xx
xtm
x
é
é
==
ê
ê
- = - =
ê
ê
=
ê
=
ê
ë
ë
Vậy giá trị cần tìm là
0; 25xx==
Câu 23. Đáp án B.
Ta có
2
1
P
x
=
+
thì
()()
() { }
2 1 1 2 1; 1; 2; 2xx+ +Î = - -
Mà
10
x
+>
với
0x ³
nên
{}
11;2x +Î
+)
11 0
xx
+= =
+)
12 1
xx
+= =
Vậy có hai giá trị của
x
thỏa mãn điều kiện.
Câu 24. Đáp án C.
Ta có:
13
27
31 3
A =-+
-
()()
31 3.3
9.3
3
31 31
+
=-+
-+
31 3143 133
33 3
222
++--
=-+= =
và
55 5 35
52 513 5
B
+
=+-
+-+
()()
()()
()
()()
()
()()
5552 551 3535
52 52 51 51 3 53 5
+- + -
=+-
+- -+ +-
35 5 5 5 95 15
14 4
-+ -
=+-
12 5 20 5 5 9 5 15
5
4
-++ - +
==
Ta thấy
133
0( 1 3 3 0)
2
Ado
-
=<-<
và
50
B
=>
nên
0AB<<
Câu 25. Đáp án A.
39.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Ta có:
() ()
2452 2
21 5 5
2
22 222
xx
x
A
xx xxx
+- +
-
== = -=-
++ +++
Ta có
5
00220 0
2
xx x
x
³ ³ +³> >
+
suy ra
5
22
2x
-<
+
hay
2(1)A <
Lại có
55
22
2
2
x
x
+³ £
+
suy ra
55 1
22 (2)
22
2
A
x
-³-³-
+
Từ (1) và (2) ta có:
1
2
2
A-£ < mà
{}
0;1AAÎÎ
+ Với
()
21
1121239
2
x
Axxxxtm
x
-
= = -= + = =
+
Vậy với
1
;9
4
xx==
thì
A
đạt giá trị nguyên. Hay có 2 giá trị của
x
thỏa mãn đề bài.
Câu 26. Đáp án A.
Ta có
12 25
4
22
xxx
A
x
xx
++
=++
-
-+
()()()
()() ()()
122 2
25
22 22
xx xx
x
xx xx
+++ -
+
=-
-+ -+
()()
322425
22
xx xx x
xx
+++---
=
-+
()()
36
22
xx
xx
-
=
-+
()
()()
32
3
2
22
xx
x
x
xx
-
==
+
+-
Vậy
3
2
x
A
x
=
+
với
0; 4xx³¹
Câu 27. Đáp án C.
Với
0; 4xx³¹
ta có
3
2
x
A
x
=
+
Xét
()
()
3
22322416
2
x
AxxxxTM
x
= = = + ==
+
Vậy
16
x
=
.
Câu 28. Đáp án B.
40.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Ta có
2
22(1)
.
12
21
xx x
B
x
xx
æö
÷
-+-
ç
÷
ç
=-
÷
ç
÷
ç
-
÷
ç
++
èø
()()
()
2
2
22(1)
.
2
11
1
xxx
xx
x
æö
÷
ç
÷
ç
÷
-+-
ç
÷
ç
÷
=-
ç
÷
ç
÷
ç
÷
-+
+
÷
ç
÷
ç
èø
()()
()()
()()
()()
()()
22
22
21 21 1 1
.
2
11 11
xx xx x x
xx xx
æö
÷
ç
÷
-+ +- - +
ç
÷
ç
÷
ç
÷
=-
ç
÷
ç
÷
ç
÷
-+ -+
÷
ç
÷
ç
èø
()()
()()
22
2
1. 1
22
.
2
11
xx
xx xx
xx
-+
----+
=
-+
()
21
2
xx
xx
--
==-
Vậy
Bxx=-
Câu 29. Đáp án C.
Theo câu trước ta có
Bxx=-
Xét
()
0010Bxxxx> -> - >
Với
0, 1xx³¹
ta
có
0x ³
nên
1
10 1
10
0
)
0
(
0
x
xx
xx
x
xx
ìì
ì
ïï
ï
<
-> <
ïï
ï
ïï
->
ííí
ïïï
¹
¹¹
ïïï
î
ïï
îî
Kết hợp điều kiện ta có
01x<<
Câu 30. Đáp án D.
Ta có
Bxx=-
với
0; 1xx³¹
Khi đó
()
2
1111
4442
Bxx xx xx x
æöæö
÷÷
çç
÷÷
=-=-- =--+=- -
çç
÷÷
çç
÷÷
çç
èøèø
Nhận thấy
2
111
424
x
æö
÷
ç
÷
--£
ç
÷
ç
÷
ç
èø
với
0; 1xx³¹
Dấu “=” xảy ra khi
()
111
0
224
xxxTM-= = =
Vậy giá trị lớn nhất của
B
là
1
4
khi và chỉ khi
1
4
x =
Câu 31. Đáp án A.
Điều kiện
0, 4, 9xxx>¹¹
48 12
:
4
22
xxx
P
x
xxxx
æöæö
÷÷
-
çç
÷÷
çç
=+ -
÷÷
çç
÷÷
çç
-
÷÷
çç
+-
èøèø
()()()
48 12
:
2
22 2
xx x
xx
xxxx
æö
÷
ç
÷
ç
-
÷
ç
÷
=+ -
ç
÷
ç
÷
ç
÷
æö
÷
ç
÷
ç
÷
ç
÷
ç
÷
ç
÷
ç
÷
ç
÷
èø
+
-+ -
ç
÷
èø
41.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
()
()()
()
()
42 8 12 2
:
22 2
xxxx x
xx xx
-+ -- -
=
-+ -
()()
()
2
84
.
3
22
xx
xx
x
xx
-
+
=
-
-+
()
()()
()
42 2
4
.
33
22
xxxx
x
xx
xx
+-
==
--
-+
Vậy
4
3
x
P
x
=
-
với
0, 4, 9xxx>¹¹
Câu 32. Đáp án A.
Với điều kiện:
0, 4, 9xxx>¹¹
. Ta có:
1
P
=-
4
14 304 4 3 30
3
x
xx x x x
x
=-+-=+--=
-
()()41310xx x+-+=
1
14 3 0
39
4
()
()( )
()
16
xktm
xx
xxtm
é
=-
ê
ê
+ -=
ê
==
ê
ë
Với
9
16
x = thì
1.P =-
Câu 33. Đáp án D.
() ()
4
9: 3 1 3 . 1
3
1
.4 1
4
x
xmxPx mx x
x
x
mx x m
x
" > - >+ - >+
-
+
>+>
Ta có: với mọi giá trị
9x >
thì
19110x +>+=
44.936x >=
Vậy
10 5
36 18
m >=
Câu 34. Đáp án C.
Ta có
()()()()
56 236 23 2 3 2xx xx x xx x x x-+=--+= -- -=- -
nên
29 321
56 23
xxx
C
xx x x
-++
=--
-+ - -
()()
29 321
23
23
xxx
xx
xx
-++
=-+
--
--
()()()()
()()
29 3 321 2
23
xxx xx
xx
-- + - + + -
=
--
()()
29 9232
23
xx xx
xx
--++ - -
=
--
42.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
()()()()
()()
()()
()()
()()
-+ - + -
-- - +- +
== = ==
-
-- -- -- --
22 12
22 2 1
3
23 23 23 23
xx x x x
xx x x x x
x
xx xx xx xx
Vậy
1
3
x
C
x
+
=
-
với
0; 4; 9xxx³¹¹
Câu 35. Đáp án B.
Theo câu trước ta có
1
3
x
C
x
+
=
-
với
0; 4; 9xxx³¹¹
Để
1C <
1134
100
3333
xxx
xxx x
++-
<-<<
----
Mà
40>
nên
30 3 9xxx-< < <
Kết hợp điều kiện
0; 4; 9xxx³¹¹
suy ra
09;4xx£< ¹
.
Câu 36. Đáp án B.
ta có
21
:
11
x
C
xxxx
æö
÷
ç
÷
ç
=+
÷
ç
÷
ç
÷
ç
-- -
èø
()
()
()
()
æö
÷
ç
÷
ç
++
÷
ç
÷
= + -= -=
ç
÷
ç
÷
ç
÷
-
--
ç
÷
èø
222
.1 .1
1
11
xxx
xx
xx
xx xx
Vậy
2x
C
x
+
=
với
0; 1xx>¹
Câu 37. Đáp án D.
Theo câu trước ta có:
2x
C
x
+
=
với
0; 1xx>¹
Xét
22 2xx
Cx
xxx x
+
==+=+
Với
0, 1xx>¹
, áp dụng bất đẳng thức Cô-si cho hai số dương
x
và
2
x
ta được:
22
2.
2
22
22
xx
xx
x
x
C
+³
+³
³
43.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Dấu “=” xảy ra khi
2
2( )xxtm
x
==
Vậy giá trị nhỏ nhất của
C
là
22 2.x=
Câu 38. Đáp án A.
ĐKXĐ:
0
1
x
x
ì
ï
³
ï
í
ï
¹
ï
î
3
21 1 4
:1
11
1
xx
P
xxx
x
æö
æö
++
÷
÷
ç
ç
÷
÷
ç
=- -
ç
÷
÷
ç
ç
÷
÷
ç
÷
ç
èø
èø
-++
-
()()
21 1
1
11
x
x
xxx
æö
÷
ç
÷
ç
+
÷
ç
÷
=-
ç
÷
ç
÷
ç
÷
-
-++
ç
÷
èø
14
:
1
xx x
xx
æö
÷
++--
ç
÷
ç
÷
ç
÷
ç
÷
ç
++
èø
()()
21 1 3
:
1
11
xxx x
xx
xxx
+- - - -
=
++
-++
()()
(
1
.9)
3
11
xx xx
x
x
xxx
-++
=¹
-
-++
()
()()
1
.
3
13
xx
x
x
xx
-
==
-
--
Vậy
3
x
P
x
=
-
với
0; 1 ; 9xxx³¹¹
Câu 39. Đáp án D.
ĐKXĐ:
0
1
9
x
x
x
ì
ï
³
ï
ï
ï
¹
í
ï
ï
¹
ï
ï
î
Ta có:
33 3
1.
33 3
xx
P
xx x
-+
== =+
-- -
Để
P
nhận giá trị là số nguyên dương thì
3
3
03
10
3
Z
PZ
x
P
x
ì
ï
ï
Î
ï
ì
ï
Îï
ï
ï
-
íí
ïï
>
ïï
î
+>
ï
ï
-
ï
î
3
3
3
3
3
33
1
0
3
3
Z
Z
x
x
x
x
x
ì
ì
ï
ï
ï
ï
Î
Î
ï
ï
ï
ï
ï
-
ïï
-

íí
ïï
+-
ïï
>-
>
ïï
ïï
-
ïï
-
î
ï
î
()
ì
ï
-Î
ï
ï
ï
ï
í
ï
>
ï
ï
ï
-
ï
î
0
()(331
2
3
)
()
xU
x
x
.
44.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
()
-Î}13() {1;3x
31 4 16
36(
3
)
3
)
6
(xxxtm
xtm
xx
éé
é
-= = =
êê
ê

êê
ê
=
êê
-= =
ê
ë
ëë
Nhận thấy với
16; 36xx==
vẫn thỏa mãn (2).
Nên
16x =
hoặc
36x =
thì P nguyên dương.
------------------------- Toán Học Sơ Đồ -------------------------
| 1/44
| | Tải xuống

Có thể bạn quan tâm:

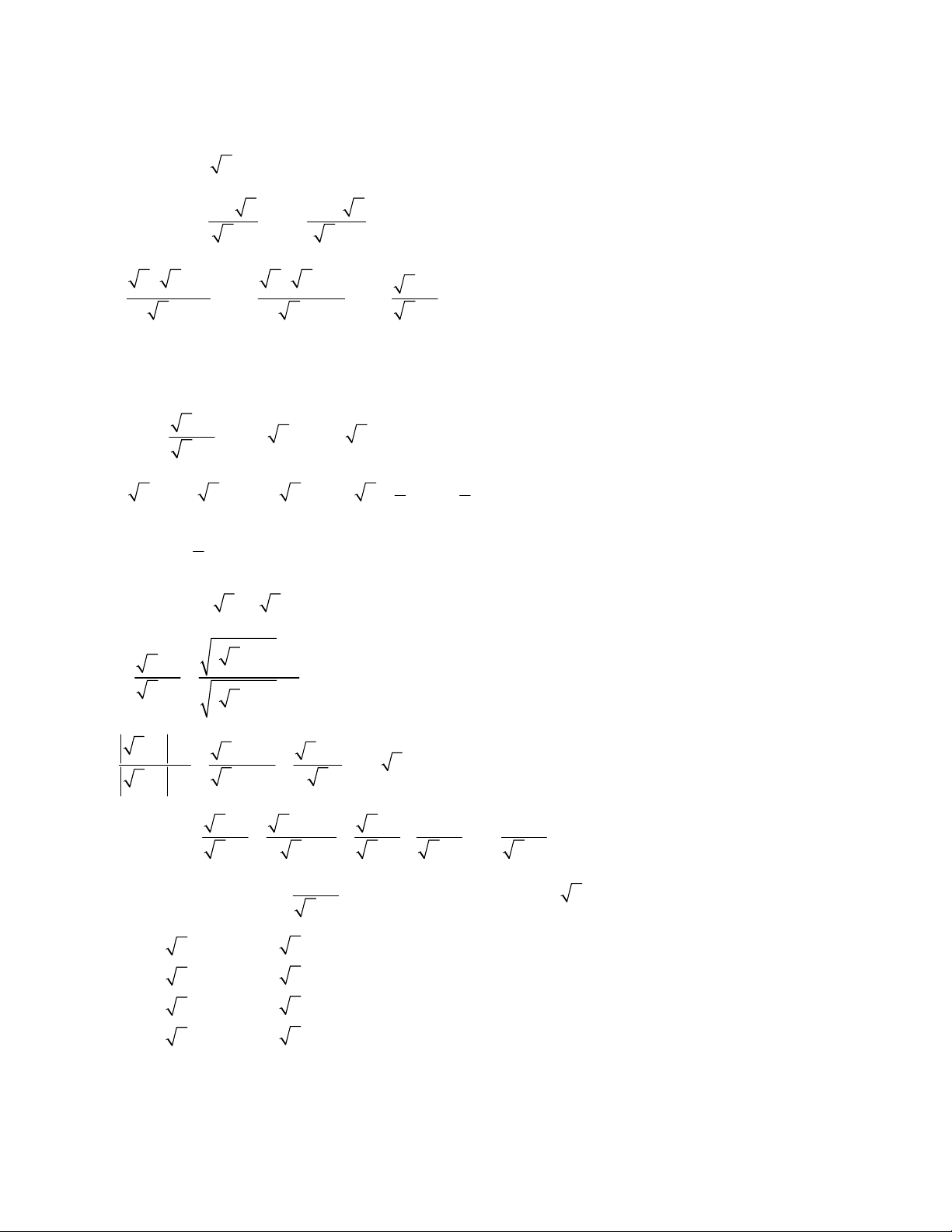
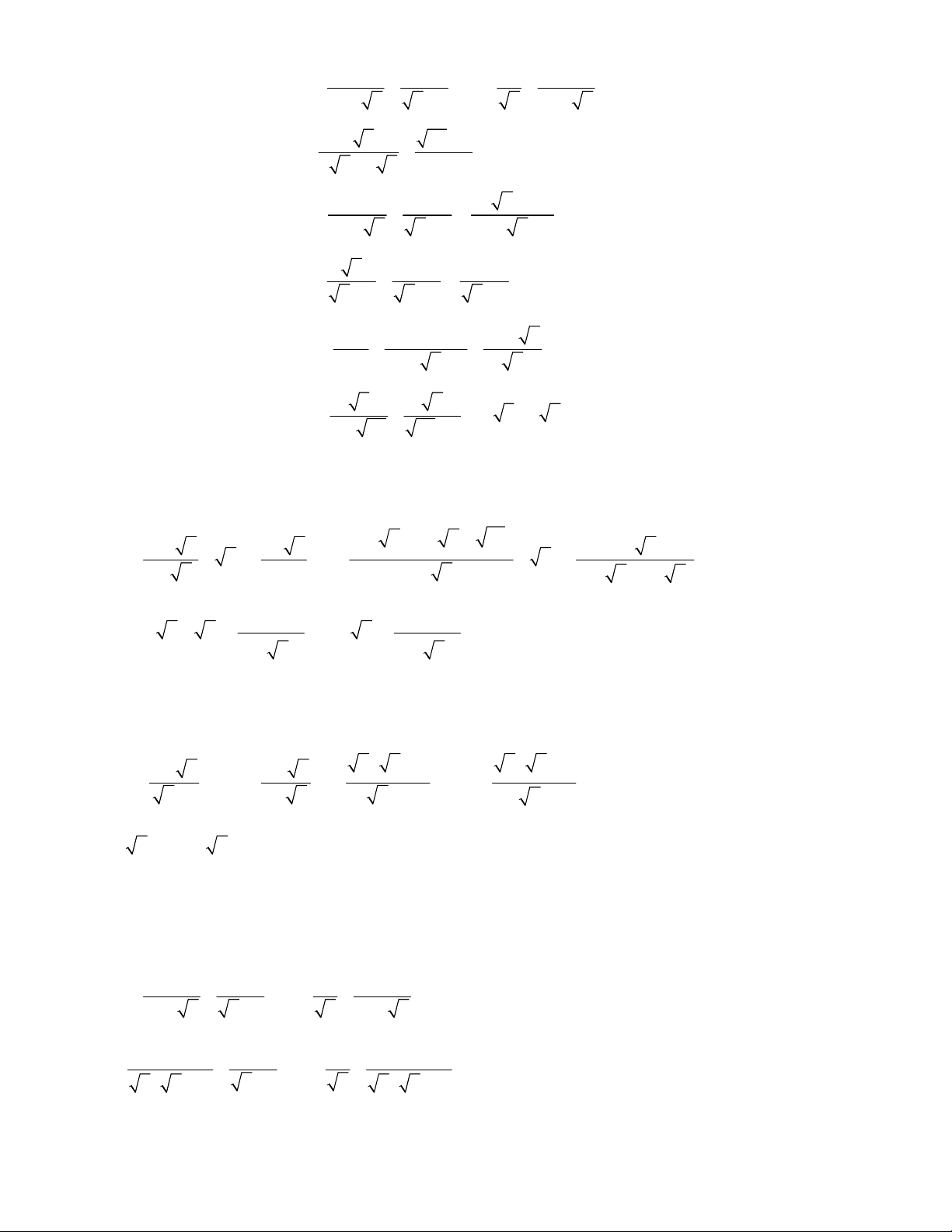
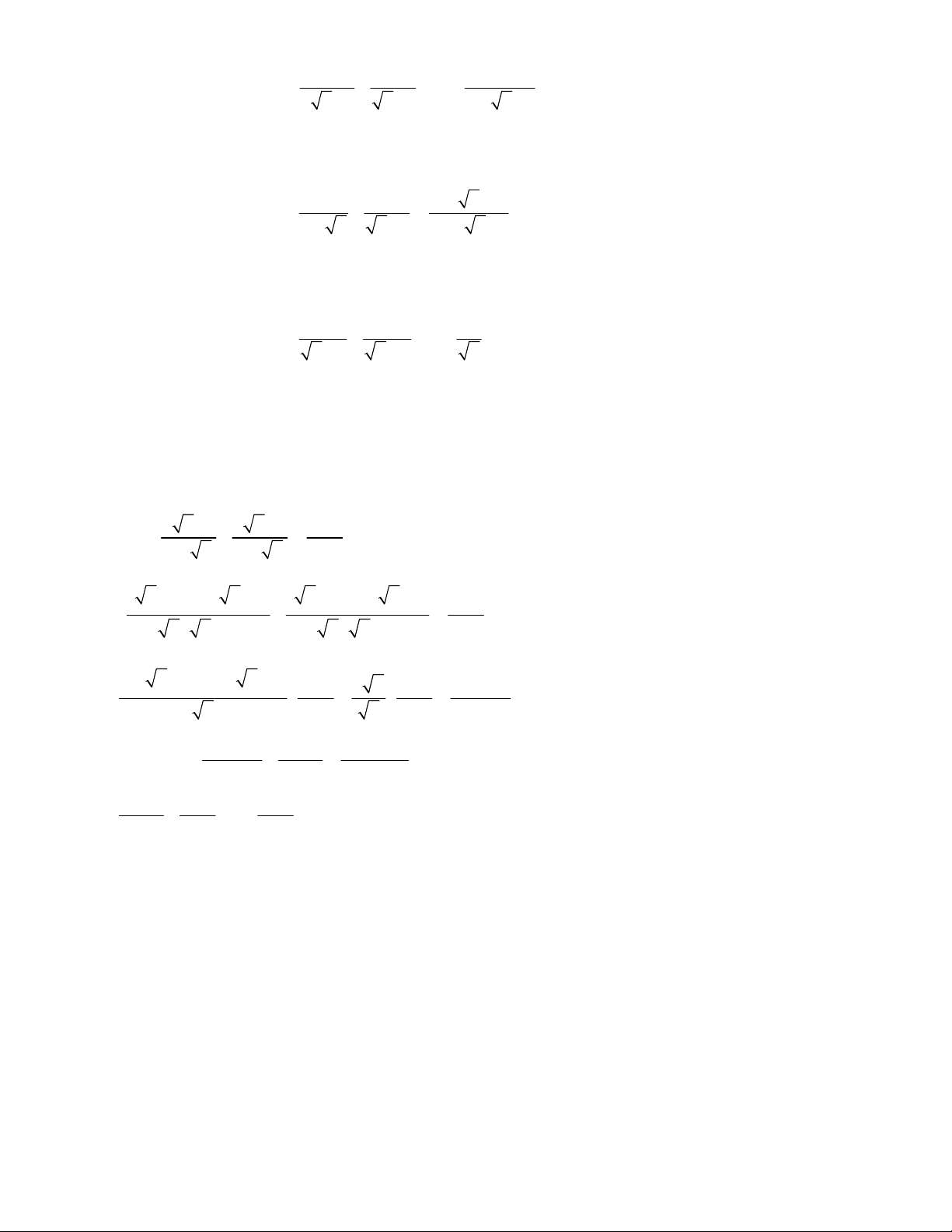
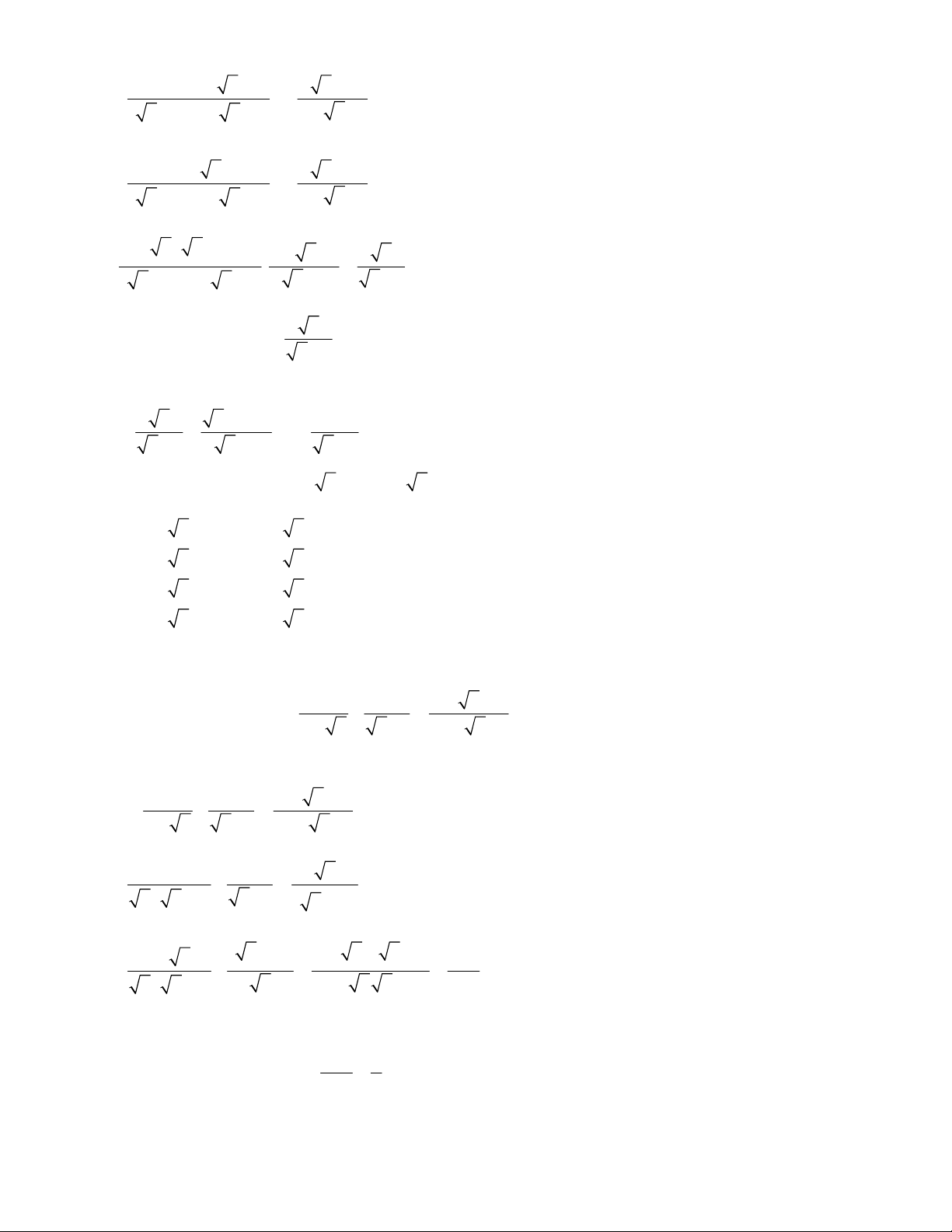
Preview text:


CHUYÊN ĐỀ RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
A. KIẾN THỨC TRỌNG TÂM
Để rút gọn biểu thức chứa căn bậc hai ta thường thực hiện các bước sau:
- Bước 1: Tìm điều kiện xác định của biểu thức (nếu đề chưa cho điều kiện). Chú ý điều kiện căn
thức, điều kiện mẫu, và điều kiện phần chia.
- Bước 2: Phân tích mẫu thành nhân tử, kết hợp phân tích tử bằng các phép biến đổi đơn giản.
- Bước 3: Bỏ ngoặc, thu gọn các biểu thức một cách hợp lý. Kết hợp điều kiện bài toán để kết luận.
Ví dụ minh họa 1: Rút gọn các biểu thức sau x x 1 x 10 a) A   
x  0, x  4 x  2 x  2 x  4 b)
B  13 4 37  4 3 8 20  2 43 24 3 Lời giải
a) Với  x  0, x  4 ta có:
x x  2   x  
1  x  2  x 10 2x 8 A    2 x  4 x  4 b)
B  13 4 37  4 3 8 20  2 43 24 3    2   2     2 2 3 1 2 3 8 20 2 4 3 3    2        2 3 3 4 8 20 2 4 3 3 3 3 4  8 28  6 3    2    2 3 3 4
8 3 3 1  43  24 3  83 3   1  35  a a
  a  2 a
Ví dụ minh họa 2: Cho biểu thức P   1 : 1
a 1   a 2        a)
Tìm điều kiện xác định và rút gọn P. b) Tìm a để . P  5 c)
Tính giá trị của P khi a  3  2 2 d)
Tìm a để P là một số nguyên.
1. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com e) Tìm a để . P  1 Lời giải a  0  a  0 a) Điều kiện:     a 1  0 a  1  a a
  a  2 a  Rút gọn: P   1 : 1
a 1   a 2       
a a  1   a a 2  a 1   1 :  1   a 1   a  2  a 1     a  0 b) Với  a  1 a 1 P  5 
 5  a 1  5 a   1 a 1 3 9
a 1  5 a  5  4 a  6  a   a  (thỏa điều kiện). 2 4 9 Vậy với a  thì . P  5 4 c) Khi a      2 3 2 2
2 1 , thay vào biểu thức P đã được rút gọn, ta có: a   2  2 1 1 1 P   a 1  2  2 1 1 2 1 1 2 11 2  2     1 2 2 1 1 2 11 2 a 1 a 1 2 a 1 2 2 d) Ta có: P     1 a 1 a 1 a 1 a 1 a 1 2
Để P là một số nguyên thì
phải là một số nguyên, suy ra a 1 phải là ước nguyên của 2. a 1  a 1  2  a  3   a  9  a 1 1  a  2 Do đó:      a  4 a 1  1  a 0     a  0     a 1  2  a  1   Voâ nghieäm Vậy với a  0;4;  9 thì
P đạt giá trị nguyên.
2. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com a 1 a 1 e) Để P  1   1  1  0 a 1 a 1
a 1  a   1 2   0   0 a 1 a 1
a 1  0  a  1
a 1. Kết hợp điều kiện suy ra: 0  a 1 Vậy với 0  a 1 thì P  1. Ví dụ minh họa 3:
x y y y x x Cho biểu thức M  1 xy a)
Tìm điều kiện xác định và rút gọn M. b)
Tính giá trị của M, biết rằng x    2 1
3 và y  3  8 Lời giải a) Điều kiện: x  0; y  0
x y y y x x
x y y x x y M   1 xy 1 xy
xy x y    x y   x y  xy   1    x y 1 xy 1 xy 2 2 b) Với
x  1 3 và y  3 8  3 2 2   2   1
M    2    2 1 3
2 1  3 1  2   1  3  2
B. CÁC DẠNG BÀI MINH HỌA I. CÁC DẠNG TOÁN
Bài toán rút gọn tổng hợp thường có các bài toán phụ: tính giá trị biểu thức khi cho giá trị của ẩn; tìm điều
kiện của biến để biểu thức lớn hơn (nhỏ hơn) một số nào đó; tìm giá trị của biến để biểu thức có giá trị nguyên;
tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức,… Do vậy, ta phải áp dụng các phương pháp tương ứng,
thích hợp cho từng dạng toán. (Vd 2).
Dạng 1. Rút gọn biểu thức 2 1 a a  1 a
Bài 1: Rút gọn biểu thức: A    a .  (với )
a  0; a  1  1 a   1 a        a a  a a
Bài 2: Rút gọn biểu thức: M   11 
với a  0; a  1
a 1  1 a      
3. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x 1   2 6 
Bài 3: Rút gọn biểu thức: B   : 1  với x  0      x  3 x x  3   x x  3 x x 2 2x  2
Bài 4: Rút gọn biểu thức: P  
với x  0; x  2 2 x x 2 x  2  a aa 1
Bài 5: Rút gọn biểu thức: Q   :
với a  0; a  4    a  2 a
a  2  a  4 a  4  x 2  x  4
Bài 6: Rút gọn biểu thức: P     :
với x  0; x  4 x 2 x 2    x  2    1 1  x  2 x
Bài 7: Rút gọn biểu thức: M   .
với x  0; x  4   x 4  
x  4 x  4  xb a
Bài 8: Rút gọn biểu thức: N    . 
 a b b a  (với )
a  0;b  0; a b a ab ab b   HƯỚNG DẪN
Bài 1. Với a  0; a  1. Ta có: 2         1 a 1      1 1 a a a a a  2 2  1 a A a .  a .       1 a   1 a   1 a         
  1 a 1 a   2 1 1
 1 2 a a .  1 a . 1 2  2   1 a 1 a2 Vậy . A  1
Bài 2. Với a  0; a  1, ta có:       a a   1  a a   a a a a 1 M  11   11       
a 1  1 a   a 1         a  1    a  
1 1 a  1 a Vậy .
M 1 a Bài 3. Với : x  0  x 1   2 6  B   : 1       x  3 x x  3   x x  3 x      x 1 2 6   :1       x
x 3 x 3  x x    x 3
4. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com    x 1  x  2 6   :       x 3 x  3   x   x   x 3         x
x 2 x 3 6 1 :      x 3    x   x 3   
x 1  x  3 x  2 x  6  6 :       x 3    x   x 3           x x x x x x   1 1 1   :       :  x 3    x
x 3  x 3   x   x 3 x 1 x 1  : 1 x  3 x  3
Vậy khi x  0 thì B  1 .
Bài 4. Với x  0; x  2 , ta có: x 2 2x  2 P   2 x x 2 x  2 2 xx  2 2   
2 x  2  x   x  2 x  2 x 2    1 2  x x  2 Vậy . P  1 Bài 5. Với :
a  0; a  4  a aa 1 Q   :    a  2 a
a  2  a  4 a  4   a a a   a a   a  2 1 2     :    .  a
a 2 a 2    a  22 a  2 a  2 a 1  
a  2 a  a  a a a   2 2 1 2  .  . a  2 a 1 a  2 a 1
a a  2 Vậy,
Q a a  2
5. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Bài 6. Với :
x  0; x  4  x 2  x  4 P     :  x 2 x 2    x  2  
x x 22 x 2 x4    :  
x 2 x 2  x 2   
x  2 x  2 x  4 x  2     
  x  2 x  2  x  4  x  4 x  2 1   
x 2 x 2 x4 x  2 1 Vậy, . P x 2 Bài 7. Với :
x  0; x  4  1 1  x  2 x M   .   x 4  
x  4 x  4  x   x    x 2 1 1    .
  x 2 x 2      x  22  x     1 1    . x  2 2    
  x  2 x  2   x 2 
x 2 x 2 1 1  4     . x  2 x  2
x 2 x 2 x4 Bài 8. Với .
a  0;b  0;a b  b aN    . 
 a b b a a ab ab b     b a     . ab a b
a a bba b       
6. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com   b a    ab a b
ab a b        b a
Vậy biểu thức có giá trị N b a
Dạng 2. Rút gọn biểu thức – tính giá trị của biểu thức khi cho giá trị của ẩn
Các bước thực hiện:
- Rút gọn, chú ý điều kiện của biểu thức
- Rút gọn giá trị của biến nếu cần
- Thay vào biểu thức rút gọn x x
2 x 1 x  6 x  4
Bài 1. Cho biểu thức: P    với x  0, x  4 x  2 x  2 x  4
a) Rút gọn biểu thức P.
b) Tìm giá trị của P khi x  9  4 5 . 1 1 4x  2
Bài 2. Cho biểu thức: A    với x  1  2 x 1 x 1 x 1
a) Rút gọn biểu thức A. 4
b) Tìm x khi A 2015  x  2 1  x 1
Bài 3. Cho biểu thức: P  . với .   x  0; x  1  x  2 x x  2  x 1 x 1 a) Chứng minh rằng P x
b) Tìm các giá trị của x để 2P  2 x  5 . 3 3 x y x y
Bài 4. Cho biểu thức: Q  . với . x y 2 2 2 2
x xy y x y a) Rút gọn biểu thức.
b) Tính giá trị của P khi x  7  4 3 ; y  4  2 3 x 1 2 x 2  5 x
Bài 5. Cho biểu thức: P    với . x  0; x  4 x  2 x  2 4  x a) Rút gọn biểu thức.
b) Tìm x để P  2 . HƯỚNG DẪN
7. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Bài 1.
a) Với x  0, x  4 , ta có: x x
2 x 1 x  6 x  4 P    x  2 x  2 x  4
xx x 22 x  1 x 2 x6 x 4 
x 2 x 2
x x  2x x  2 x  2x  4 x x  2  x  6 x  4 
x 2 x 2
x x  2x x  2 
x 2 x 2
x x  2  x  2 x   1  x  2  
x 2 x 2  x 2 x 2 x 1  . x  2 x  Vậy với x  0, x  1 4 thì . P x 2 b) Ta có: x      2 9 4 5 2
5 thỏa mãn điều kiện xác định  x  2  5 . 9  4 5 1 10  4 5 Khi đó P    2 5  4 2  5  2 5 Vậy với x  9  4 5 thì P  2 5  4 . Bài 2. a) Với x  1  1 1 4x  2 x 1 x 1 4x  2
x 1 x 1 4x  2 A        2 2 2 2 x 1 x 1 x 1 x 1 x 1 x 1
x  1x  1 4x  4 4 x   1 4    với  x  1  x   1  x   1 x   1  x   1 x 1 4 Vậy: A  với x  1  x 1 4 4 4 b) Khi A     x 1  2015 2015 x 1 2015  x  2016 (TMĐK)
8. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 4 Vậy khi A  thì x  2016 . 2015  x  2 1  x 1
Bài 3. Cho biểu thức P  . với .
x  0; x  1    x  2 x x  2  x 1 a) Với x  0; x  1  x  2 1  x 1 Ta có: P  .    x  2 x x  2  x 1     x  2 x x 1 x  2  x x 1  .      .  x
x 2 xx 2 x 1  x  
x 2 x 1 
  x  1. x  2 x 1 x 1    .  đpcm x   x 2    x 1 x   x 1
b) Ta có: 2P  2 x  5  2   2 x  5  x   
 2 x  2  2x  5 x  2x  3 x  2  0     x   1 1 1 2 x
 0  x   x    (thỏa điều kiện)  2  2 4 1 Vậy x  thì
2P  2 x  5 . 4 Bài 4. Với : x y x y x y
x y 2 2 3 3
x xy y x y x y a) Q  .  .  2 2 2 2 2 2
x xy y x y
x xy y
x yx yx y b) Với x      2 7 4 3 2 3  2  3 y      2 4 2 3 3 1  3 1 x y 2  3  3 1 1 Suy ra: Q    x y
2 3 3 1 32 3 3  2 3 3  2 3  
32 332 3 3 3  2 3 Vậy . Q  3 Bài 5.
9. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com a) Với :
x  0; x  4 x 1 2 x 2  5 x P    x  2 x  2 4  x
x  1 x 22 xx 2 25 x  
x 2 x 2 x  4
x  2 x x  2  2x  4 x 2  5 x  
x 2 x 2
x 2 x 2 3x x  2 2  5 x  
x 2 x 2  x 2 x 2
3x x  2  2  5 x 3x  6 x  
x 2 x 2  x 2 x 2
3 x x  2 3 x  
x 2 x 2 x 2 b) Với ,
x  0; x  4 để P  2 3 x
 2  3 x  2 x  4  x  4  x 16 (thỏa điều kiện) x  2 Vậy với x 16 thì P  2 .
Dạng 3. Rút gọn biểu thức – tìm x để biểu thức rút gọn đạt giá trị nguyên - Rút gọn biểu thức
- Lấy tử chia cho mẫu tách biểu thức thành tổng của một số nguyên và một biểu thức có tử là một số nguyên
- Trong biểu thức mới tạo thành, ta cho mẫu là các ước nguyên của tử để suy ra x.
a a 1 a a 1 a  2
Bài 1. Cho biểu thức: P     : với . 
a  0;a 1;a  2 a a
a a a  2   a) Rút gọn P.
b) Tìm giá trị nguyên của a để P có giá trị nguyên. 2
x 1 x 1 x  4x 1 x  2017
Bài 2. Cho biểu thức: P     .  với .
x  0; x  1 2
x 1 x 1 x 1  x a) Rút gọn P.
b) Tìm giá trị nguyên của x để P có giá trị nguyên.
10. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com  2x 1 1   x  4 
Bài 3. Cho biểu thức: Q   : 1 với .    
x  0;x  1  x x 1 x 1  x x 1 a) Rút gọn Q.
b) Tìm giá trị nguyên của x để Q có giá trị nguyên.  1 1  x
Bài 4. Cho biểu thức: P   : với . x  0    x x
x 1 x  2 x 1 a) Rút gọn P.
b) Tìm x   để P có giá trị nguyên.  1 1   3 
Bài 5. Cho biểu thức: P   . 1 với .    
a  0;a  9  a  3 a  3   a  a) Rút gọn P.
b) Tìm a  để P có giá trị nguyên. HƯỚNG DẪN Bài 1. Với
a  0;a 1;a  2
a a 1 a a 1 a  2 a) P     :
a a a a a  2  
 a  1a a  1  a  1a a  1 a  2     :  a a   1 a a   1  a2 
a a 1 a a  
1 a  2 2 a a  2 2a  2  :  :  a a  2 a a  2 a  2
2a  2 2a  4 2a  4 8 b) Ta có: P    a  2 a  2 a  2 2a  4 8 8    2  a  2 a  2 a  2
P nhận giá trị nguyên khi và chỉ khi: 8a  2 hay a  2 là ước nguyên của 8. a  2  1  a  1  ;a  3  a 2 2     a  0; a  4      a  2  4 
a  2;a  6    a  2  8 
a  6;a  1  0
Kết hợp điều kiện a  0; a  1; a  2 ta suy ra a  2 hoặc a  6 thì
P đạt giá trị nguyên.
11. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2
x 1 x 1 x  4x 1 x  2017
Bài 2. Cho biểu thức: P     .  với .
x  0; x  1 2
x 1 x 1 x 1  x a) Với
x  0; x  1 2
x 1 x 1 x  4x 1 x  2017 P     .  2
x 1 x 1 x 1  x  x  2 1   x  2 2 1
x  4x 1 x  2017    .  x   1  x   2 1 x 1  x  
  2x  2x   1   2 x  2x   2
1  x  4x 1 x  2017   . 2  x 1  x   2
x 1 x  2017  .   2  x 1 x x  2017  x x  2017 2017 b) Ta có: P   1 x x
 Để P là số nguyên  2017 x hay
x là ước nguyên của 2017 (chú ý 2017 là số nguyên tố). x  2017 x 1  
kết hợp điều kiện x  0; x  1 , suy ra: x  2017 . x  1   x  2  017 Vậy, với x  2017 thì
P đạt giá trị nguyên.  2x 1 1   x  4 
Bài 3. Cho biểu thức: Q   : 1 với .    
x  0;x  1  x x 1 x 1  x x 1 a) Với x  0; x  1  2x 1 1   x  4  Ta có: Q   : 1      x x 1 x 1  x x 1    2x 1 1   x  4    : 1     x 3 3 x 1    x x 1 1     2x 1 x x 1
x x 1 x  4      :  
  x  1xx  1  x  1xx  1  xx 1     
12. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com  
2x 1 x x 1  x  3     :  
  x  1xx  1  xx 1       x xx  3     :  
  x  1xx  1  xx 1     x x   1 x x 1 x  . 
x  1xx  1 x 3 x  3 x
Biểu thức rút gọn là: Q  . x  3
b) Tìm giá trị nguyên của x để Q có giá trị nguyên x x  3  3 3 Q   1 x  3 x  3 x  3
Để Q có giá trị nguyên thì 3 x 3 hay x  3 là ước nguyên của 3.  x  3  3  x  6 x  36    x 3 1  x 4     x  16 Suy ra:    (thỏa điều kiện)   x  3  1  x  2 x  4            x  0 x 3 3 x 0 Vậy với x  0;4;16;3  6 thì
Q đạt giá trị nguyên.  1 1  x
Bài 4. Cho biểu thức: P   : với . x  0    x x
x 1 x  2 x 1
a) Với x  0 , ta có:  1 1  x P   :    x x
x 1 x  2 x 1   1 1 x     :
x x  1 x 1  x    2 1    x  2 1
1 x x x   1 1 1 x    .    x   x 1  x x x x
b) Tìm x   để P có giá trị nguyên. 1 x 1
Để P có giá trị nguyên thì P
 1 phải là số nguyên. x x
13. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
x 1thoûa ñieàu kieän
Do đó x là ước nguyên của 1. Suy ra:  x  1   loaïi Vậy với x  1 thì
P đạt giá trị nguyên.  1 1   3 
Bài 5. Cho biểu thức: P   . 1 với .    
a  0;a  9  a  3 a  3   a
a) Với a  0; a  9 , ta có:  1 1   3  P   . 1      a  3 a  3   a
a  3  a  3  a  3   . 
a 3 a 3  a      2 aa 3  2  .  
a 3 a 3  a a 3  
b) Tìm a  để P có giá trị nguyên. 2 Để P
đạt giá trị nguyên thì a  3 phải là ước nguyên của 2. a  3  a  3  2  a  1     a  3  1  a  2  Suy ra: 
(không thỏa mãn điều kiện).   a  3  1 a  4       a  3  2  a  5 
Vậy với không có giá trị
a  thỏa mãn để P đạt giá trị nguyên.
Dạng 4. Rút gọn biểu thức – tìm x để biểu thức thỏa bằng hoặc lớn hơn (nhỏ hơn) một số cho trước - Rút gọn
- Cho biểu thức rút gọn thỏa điều kiện ta được phương trình hoặc bất phương trình, chú ý điều
kiện của ẩn trong bài toán.  1 x  1
Bài 1. Cho biểu thức: A     :
x 1 x 1  x 1  
a) Tìm điều kiện và rút gọn biểu thức.
b) Tìm các giá trị của x để . A  0  1  1
Bài 2. Cho biểu thức: P  1 .   
x 1 x x
14. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
a) Tìm điều kiện và rút gọn biểu thức.
b) Tìm các giá trị của x để P   x  2 . 5 2 6 .
1  x  2005  2  3 .  1 1  x
Bài 3. Cho biểu thức: P   : (với )   x  0; x  1  x x
x 1 x  2 x 1
a) Rút gọn biểu thức P. 1
b) Tìm các giá trị của x để P  . 2  a a a 1
Bài 4. Cho biểu thức: P     : (với )  a  0; a  1
a 1 a a a 1  
a) Rút gọn biểu thức P.
b) Tìm các giá trị của a để P  0 x 1   1 2 
Bài 5. Cho biểu thức: M     :  (với )     x  0, x  1
x 1 x x
  x 1 x 1
a) Rút gọn biểu thức M.
b) Tìm các giá trị của x để M  0 HƯỚNG DẪN  1 x  1
Bài 1. Cho biểu thức: A     :
x 1 x 1  x 1   x  0 a) Điều kiện: .  Khi đó: x  1    1 x  1 x 1 x 1 A   :       :
x 1 x 1 x 1      x   1  x   1 x 1 x 1  x 1 x 1 1 x 1  :  .
x  1 x  1 x 1  x  1 x  1 1 1  x 1 1
Biểu thức rút gọn là: A x 1 1 b) Để . A  0 
 0  x 1  0  x 1  x 1 x 1
Kết hợp điều kiện, suy ra: A  0  0  x 1.
15. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com  1  1
Bài 2. Cho biểu thức: P  1 .   
x 1 x xx  0 a) Điều kiện: .  x  1  1  1  x 11 1 Khi đó: P  1 .     .  x 1 x xx 1     
x x   1 x 1 1  .  x 1 x x   1  x  2 1 b) P   x  2 . 5 2 6.
1  x  2005  2  3 1  3  2
x 1  x  2005  2  3 2  2  2  x  1
 3  2  x  2005  2  3
 3  2  x  2005  2  3
x  2005 (thỏa mãn điều kiện). Bài 3. a) Với :
x  0; x  1  1 1  x P   :    x x
x 1 x  2 x 1    x x  2 1 1     .  x
x 1 xx 1   x   x  2 1
x  1 x x   1 1 x 1  .   . x x   1 x x. x x x 1 1 b) Với
x  0; x  1 thì   2x  
1  x  2x  2  x x 2
x  2 (thỏa điều kiện). Vậy với x  1 2 thì P  . 2 Bài 4. a) Với : a  0; a  1   a a a 1 P     :  a 1 a a   1   a   1  a    1
16. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com a 1  1     :  a 1 a 1   a 1    a 1   .    a   1  a 1 a 1  
a  0;a  1  b) Với
a  0; a  1 thì
P  0  a 1  0    0  a  1.  a 1
Vậy với 0  a  1, x > 2 thì P  0 .  x 1   1 2 
Bài 5. Cho biểu thức: M     :     
x 1 x x
  x 1 x 1 a) Điều kiện: .
x  0, x  1 Khi đó:  x 1   1 2  M     :     
x 1 x x
  x 1 x 1     x. x 1 x 1 2   :    
x x 1 x x 1  x 1 x 1  x 1 x 1               x 1 x 1 2   :  
x x 1  x 1 x 1       
  x  1 x  1   x 1   :   x x  1
   x 1 x 1        x 1 1 x 1  :  . x   1 x x 1 x x 1  x x 1 b) Để M  0 
 0 mà x  0, x  1 nên x  0 x Do đó:
M  0  x 1  0  x 1 Vậy x  1 thì M  0 .
Dạng 5. Rút gọn biểu thức – tìm x để biểu thức đạt giá trị lớn nhất (gtln), giá trị nhỏ nhất (gtnn)
17. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com - Rút gọn
- Biến đổi biểu thức (BT) về dạng:
+ Số không âm + hằng số GTNN. VD: . 2
A m m Khi
đó GTNN của biểu thức bằng m xảy ra khi và chỉ khi A  0 .
+ Hằng số - số không âm GTLN. VD: . 2
M A M Khi
đó GTLN của biểu thức bằng M xảy ra khi và chỉ khi A  0 .
+ Sử dụng bất đẳng thức Cô-si: Cho hai số dương a và b, ta có:
a b  2 ab . Dấu “=” xảy ra khi và chỉ khi a b . +
A B A B
Bài 1. Cho các biểu thức sau:
M x x 1 N  x x 1  2
a) Tìm giá trị nhỏ nhất của M.
b) Tìm giá trị lớn nhất của N.
Bài 2. Cho biểu thức:  1 2 x  2   1 2  Q     :  với     x  0; x  1
x 1 x x x x 1 
  x 1 x 1 a) Rút gọn biểu thức.
b) Tìm x để Q đạt giá trị nhỏ nhất.
Bài 3. Cho biểu thức: 15 x 11
3 x  2 2 x  3 P    với x  0; x  1 x  2 x  3 1 x x  3 a) Rút gọn biểu thức.
b) Tìm giá trị lớn nhất P.
Bài 4. Cho hai biểu thức: x  3 x 1 5 x  2 P  và Q   với x  0; x  4 x  2 x  2 x  4
a) Tính giá trị của biểu thức P khi x  9 .
b) Rút gọn biểu thức Q. P
c) Tìm giá trị của x để biểu thức
đạt giá trị nhỏ nhất. Qx 2  1
Bài 5. Cho biểu thức: A     :  x 1 x x    x 1  
18. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
a) Tìm điều kiện xác định. Rút gọn A.
b) Tìm giá trị nhỏ nhất của A. HƯỚNG DẪN
Bài 1. Cho các biểu thức sau:
M x x 1 N  x x 1  2 a) Điều kiện: x  0 2 1 5  1  5 5
M x x 1  x x    x       4 4  2  4 4 2  1 5    5 1 1 Suy ra, M   x     
   x   0  x  min (thỏa điều kiện)  2  4   4 2 4 min 5 1 Vậy . M    x  min 4 4 b) Điều kiện: . x 1 1 5
N  x x 1  2  x 1 x 1   4 4  1  5
  x 1 x 1      4  4 2  1  5 5   x 1       2  4 4 2  1 5    5 Suy ra, N   x 1       max   2  4   4 max 1 1 1 5
x 1   0  x 1   x 1   x  (thỏa điều kiện) 2 2 4 4 5 5 Vậy . M   x  max 4 4  1 2 x  2   1 2 
Bài 2. Cho biểu thức: Q     :     
x 1 x x x x 1 
  x 1 x 1 a) Với x  0; x  1  1 2 x  2   1 2  Q     :     
x 1 x x x x 1 
  x 1 x 1  2 x   1    1 1 2   :    
x 1 x  1 x  1  x 1  x  1 x     1
19. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com  2   x  1    1  x 1 2 :      x 1    x   1  x  2 1      x   1  x   1       x 1 2  x 1 2 :       x  2 1      x 1 x 1    x 1 x 1 x 1 x 1  :  . x 1  2 2  
x  1  x  1 x  1  x   x 1 1 x 1 Vậy . P x 1 x 1 x 1 2 2 b) P    1 x 1 x 1 x 1  2   2  P  1   x 1 min       min  x 1  x 1 min max Vì
x  0; x  1  x  0  x 1  1   x   2 1
x 1 1  x  0  P  1  1  min min 0 1 Vậy, P  1   x  0 min 15 x 11
3 x  2 2 x  3
Bài 3. Cho biểu thức: P    x  2 x  3 1 x x  3 a) Với x  0; x  1 15 x 11
3 x  2 2 x  3 P    x  2 x  3 1 x x  3 15 x 11
3 x  2 2 x  3   
x 3 x  1 x 1 x  3
15 x 11 3 x  2 x  3 2 x  3 x   1 
x 3 x  1
15 x 11 3x 9 x  2 x  6 2x  2 x  3 x 3 
x 3 x  1
15 x 11 3x  9 x  2 x  6  2x  2 x  3 x  3 
x 3 x  1
20. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x x
x  1 5 x 2 5 7 2  5 x 2   
x 3 x  1  x 3 x  1 x  3 5  x  2 Vậy P x  3 5  x    x 317 5 2 17 b) . P    5   x  3 x  3 x  3  17  P  max    x  3 max  x  0  Vì
x  0; x  1  17 Px  3  xx  0 max   min min  0   x  3 17 Vậy, . P   x  0 max 3 x  3 x 1 5 x  2
Bài 4. Cho biểu thức: P  và Q   với x  0; x  4 x  2 x  2 x  4 x  3 9  3 12
a) Với x  9 . Ta có: P    12 x  2 9  2 3  2
b) Với x  0; x  4 , ta có: x x
x  1. x 25 x 2 1 5 2 Q    x  2 x  4 x  4 x x x   x x xx 2 3 2 5 2 2  x     x  4 x  4
x 2 x 2 x 2 P P x  3 3
c) Tìm giá trị của x để biểu thức
đạt giá trị nhỏ nhất:   x Q Q x x 3
Áp dụng bất đẳng thức Cosi cho hai số không âm x và , ta có: x P 3    x    x 3 2 .  2 3 Q   xx  3
Dấu bằng xảy ra khi x
x  3 (thỏa điều kiện) x PP
Vậy giá trị nhỏ nhất của là  2 3  x  3   . QQ min
21. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x 2  1
Bài 5. Cho biểu thức: A     :  x 1 x x    x 1   x  0 a) Điều kiện: .  x  1    x 2  1 x 2 1 A   :       :
x 1 x x x 1  x 1   x
x  1 x 1 
x2 2 x 1 x2 A  .  x x   1 1 x x  2 2 x  0 2 b) A   x  với  thì x  0;  0 . x xx  1 x 2
Áp dụng bất đẳng thức Cosi cho hai số dương x  0;  0 , suy ra: x x  2 2   A   x    x 2 2 .  2 2   x xx  2
A  2 2  x
x  2 (thỏa điều kiện) min x Vậy . A  2 2  x  2 min
Dạng 6.Nâng cao phát triển tư duy x  1 1
Bài 1. Cho biểu thức 4 2 P  :
;Q x  7x 15 (với x  0, x  1 ) 2
x x x x x x a) Rút gọn P
b) Với giá trị nào của x thì Q  4P đạt giá trị nhỏ nhất  x  2 x  2   2 
Bài 2. Cho biểu thức: P     :   
với x  0; x  1 2  x 1 
x  2 x  1  x  2x 1 a) Rút gọn P
b) Tìm các giá trị của x để P  0
c) Tính giá trị của P khi x  7  4 3
d) Tìm giá trị lớn nhất của P và giá trị tương ứng của x
22. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
x x  4 x  4  x  4 x  4 
Bài 3. Cho A  với x  4 2 x  8x 16
a) Rút gọn A .Tìm x để A đạt giá trị nhỏ nhất.
b) Tìm các giá trị nguyên của x để A có giá trị nguyên.     2  1 1  2020
Bài 4. Cho biểu thức: M  .  .  2 2 3         x 1 2 x 1 2 x 1  1   1    3 3        a) Rút gọn M;
b) Tìm giá trị lớn nhất của M.  a
2 a b   1 1 
Bài 5. Cho biểu thức P     :    
với a  0,b  0,a  . b ab b ab a       b a a b
a) Chứng minh rằng P ab.
b) Tính giá trị biểu thức P khi a  3 5 và b  0,5.
c)Tìm giá trị lớn nhất của P nếu 2 2 a  4b  8. HƯỚNG DẪN x  1 1
Bài 1.Cho biểu thức 4 2 P  :
;Q x  7x 15 (với x  0, x  1 ) 2
x x x x x x a) Rút gọn P
b) Với giá trị nào của x thì Q  4P đạt giá trị nhỏ nhất Hướng dẫn x 1 1 x 1 a) 3 P  :  . x x 1 2
x x x x x x
x x x     1 x 1 P      
x x x  . x x  1 x x 1 x 1 1 b) 4 2
Q  4P x  7x 15  4 x   1
23. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
 x x    x x     x  2  x  2 4 2 2 2 8 16 4 4 1 4 2 1
Q  4P  1
Dấu "  " xảy ra khi: x  2 . Vậy giá trị nhỏ nhất Q  4P là 1  x  2 x  2   2 
Bài 2. Cho biểu thức: P     :   
với x  0; x  1 2  x 1 
x  2 x  1  x  2x 1 a) Rút gọn P
b) Tìm các giá trị của x để P  0
c) Tính giá trị của P khi x  7  4 3
d) Tìm giá trị lớn nhất của P và giá trị tương ứng của x Hướng dẫn
a) Với x  0; x  1, ta có:    x  2
x  2   x  2 1 P       x   1  x   1  x    . 2 2 1 
  x 2 x 1  x 2 x 1      x    2 1 P      
x   x   . 2
x   x   2 2 1 1 1 1   
x  2 x x  2  x x  2 x  2   x  2 1 P     
x   x    . 2 2 1 1    x  2 1  x x   2 1 2 P  
x   x   . 2 2 1 1
P   x x   1
Vậy P   x x   1 b) Ta có P  0
24. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com        
  x x     x x   x 0 x 0 x 0 1 0 1  0        x 1  0  x  1 x  1
Kết hợp với điều kiện đề bài, ta được 0  x  1
Vậy với 0  x  1 thì P  0 c) Với x         2 7 4 3 3 2.2. 3 4 3 2 thì   P     2    2 3 2 3 2 1  
P   3  2  3  2   1
P   3  21 3
P  3  3  2  2 3 P  3 3  5
Vậy với x  7  4 3 thì P  3 3  5  
d) Ta có P   x x   2 1 1
1  x x   x      2  4 2 2 2  1   1   1  1 1 Nhận thấy: x   0   x   0   x           2   2   2  4 4
Dấu "  " xảy ra khi và chỉ khi: 1 1 1 x
 0  x   x  (thỏa mãn) 2 2 4 1 1
Vậy với x  thì P đạt giá trị lớn nhất là 4 4
x x  4 x  4  x  4 x  4 
Bài 3. Cho A  với x  4 2 x  8x 16
a) Rút gọn A .Tìm x để A đạt giá trị nhỏ nhất.
b) Tìm các giá trị nguyên của x để A có giá trị nguyên. Hướng dẫn
25. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
a) Điều kiện để biểu thức A xác định là x  4 .  
x   x  4  22   x  4  22  x
x x  4  2  x  4  2   
x42  x42 A    x  2 x  4 4 x  4
x x  4  2  2  x  4 4x 16
+ Nếu 4  x  8 thì x  4  2  0 nên A    4  x  4 x  4 x  4
Do 4  x  8 nên 0  x  4  4  A  8 .
+ Nếu x  8 thì x  4  2  0 nên
x x  4  2  x  4  2 2x x  4 2x 8 A     2 x  4 
 2 16  8 (Theo bất đẳng thức x  4 x  4 x  4 x  4 8
Cô si). Dấu bằng xảy ra khi và chỉ khi 2 x  4 
x  4  4  x  8 . x  4
Vậy GTNN của A bằng 8 khi x  8 . 16 16
b) Xét 4  x  8 thì A  4 
, ta thấy AZ khi và chỉ khi
Z x  4 là ước số nguyên x  4 x  4
dương của 16 . Hay x  41;2;4;8;1 
6  x  5;6;8;12;2 
0 đối chiếu điều kiện suy ra x  5 hoặc x  6 . 2x 2 x m  4  2 2 m  4 8
+ Xét x  8 ta có: A
, đặt x  4  m   khi đó ta có: A   2m  suy x  4 m  2 m m ra m2;4; 
8  x 8;20;6  8 .
Tóm lại để A nhận giá trị nguyên thì x 5;6;8;20;6  8 .     2  1 1  2020
Bài 4. Cho biểu thức: M  .  .  2 2 3         x 1 2 x 1 2 x 1  1   1    3 3        a) Rút gọn M;
b) Tìm giá trị lớn nhất của M. Hướng dẫn
26. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com   2  3 3  2020 a) Ta có: M  .  3      x   . 2   x   2 x1 3 2 1 3 2 1  2  3 3  2020 M  .  . 3  
3  4x  4 x 1 3  4x  4 x 1 x 1 2  3 3  2020 M  .  . 3  
4x  4 x  4 4x  4 x  4 x 1 2 3  1 1  2020 M  . .  . 3 4  
x x 1 x x 1 x 1
1 x x 1 x x 1 2020 M  . . 2 x  2 1  x x 1 1 2x  2 2020 M  . . 2
2 x x 1 x 1 2020 M  . TXĐ: x  0 . 2 x x 1 b) Ta có: 2
x x 1  1. Vì x  0 2020 2020 nên M    2020 . 2 x x 1 1
Vậy giá trị lớn nhất của M là 2020 khi x  0 .  a
2 a b   1 1 
Bài 5. Cho biểu thức P     :    
với a  0,b  0,a  . b ab b ab a       b a a b
a) Chứng minh rằng P ab.
b) Tính giá trị biểu thức P khi a  3 5 và b  0,5.
c)Tìm giá trị lớn nhất của P nếu 2 2 a  4b  8. Hướng dẫn a) Ta có:
27. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com   a       2 2 1 1
a bb a a b ab P        b 
ababa : ab b ab aab   ab . . . a b
aba b2 Hay P  
ab a bab. 2 2 1 3 5 6 2 5  5 1    5 1
b) Khi a  3 5,b   ab    
  P ab  . 2 2 4  2  2  
c) Theo bất đẳng thức AM GM ta có: 2 2 2 2
a  4b  2 a .4b  4ab  4ab  8  ab  2. Vậy P  2,
dấu đẳng thức xảy ra khi và chỉ khi 2 2
a  4b  4  a  2,b  1.
Vậy GTLN của P là 2.
28. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
II.TRẮC NGHIỆM RÈN PHẢN XẠ
Bài 4- Rút gọn biểu thức chứa căn
Câu 1. Giá trị của biểu thức ( - )2 4 5 - 6 - 2 5 là: A. 5 - 2 5 . B. 4 . C. 2 + 2 5 . D. 1 .
Câu 2. Giá trị của biểu thức ( + )2 2 5 - 7 - 2 10 là: A 2 2 . B. 0 . C. 2 . D. 2 5 .
Câu 3. Giá trị của biểu thức 32 + 50 - 3 8 - 18 là: A. 1 . B. 0 . C. 2 . D. 3 .
Câu 4. . Giá trị của biểu thức 125 - 4 45 + 3 20 - 80 là: A. 5 . B. -5 5 .
C. 10 5 . D. 5 5 . a 4
Câu 5. Rút gọn biểu thức 5 a + 2 - a
- 25a với a > 0 ta được 4 a
A. a . B. 4 a . C. 2 a . D. - a . 1 32a a 3
Câu 6. Rút gọn biểu thức 3 8a + - .
- 2a với a > 0 4 25 3 2a ta được: 47 21 47 47 A. a . B. a . C. 2a . D. 2a . 10 5 10 5
Câu 7. Giá trị của biểu thức ( 5 + 2) 7 - 2 10 là: A. 4 . B. 5 . C. 2 . D. 3 .
Câu 8. Giá trị của biểu thức ( 5 - ) 1 6 + 2 5 là: A. 6 . B. 4 . C. 2 . D. 3 . 16 2
Câu 9. Rút gọn biểu thức 3 2 5
2 a - 9a + a +
36a với a > 0 ta được 2 a a
A. 14 a + a a .
B. 14 a - a a . C. 14 a + 2a a .
D. 20 a - 2a a . æç1 a 3 4 ö÷ 1
Câu 10. Rút gọn biểu thức ç - 2a + 200a ÷ ç ÷ : ta được ç2 2 2 5 ÷÷ 8 è ø A. 66 2a . B. 52 2a .
C. 54 a . D. 54 2a .
Câu 11. Đẳng thức nào dưới đây là đúng?
29. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2 4 a -b a b 2 4 a -b a b A. = a . B. = a . 2 2 2 b
a - 2ab + b 2 2 2 b
a - 2ab + b 2 4 a -b a b 2 4 a -b a b C. = ab . D. = a -b . 2 2 2 b
a - 2ab + b 2 2 2 b
a - 2ab + b
Câu 12. Với đẳng thức nào dưới đây là đúng? a b + b a a -b a b + b a a -b A. + = 2 a . B. + = a . ab a + b ab a + b a b + b a a -b a b + b a a -b C. + = 2 . D. + = 2 b . ab a + b ab a + b
Câu 13. Chọn khẳng định đúng? æç2 3 - 6 216 ö æ a ö ÷ - æ ö æ ö ç ÷ ç ÷ 3 - a ç2 3 - 6 216 ÷ a - ç ÷ ç ÷ 3a A. - ç ÷.ç ÷ = . B. - ç ÷.ç ÷ = . ç ÷ ç ÷ ç ÷ ç ÷ çè 8 - 2 3 ÷ ç ø è 6 ÷ø 2 çè 8 - 2 3 ÷ ç ø è 6 ÷ø 2 æç2 3 - 6 216 ö æ a ö ÷ - æ ö æ ö ç ÷ ç ÷ a - ç2 3 - 6 216 ÷ a - ç ÷ ç ÷ a C. - ç ÷.ç ÷ = . D. - ç ÷.ç ÷ = . ç ÷ ç ÷ ç ÷ ç ÷ çè 8 - 2 3 ÷ ç ø è 6 ÷ø 2 çè 8 - 2 3 ÷ ç ø è 6 ÷ø 2
Câu 14. Chọn khẳng định đúng? æç 14 - 7 15 - 5 ö÷ 1 æç 14 - 7 15 - 5 ö÷ 1 2 A. ç ÷ + ç ÷ : = . B. ç ÷ + ç ÷ : = . ç ÷ ç ç ÷ è - - ÷ø a ( - ) 2a 1 2 1 3 7 5 çè 1 - 2 1 - 3 ÷ø ( 7 - 5) a a æç 14 - 7 15 - 5 ö÷ 1 æç 14 - 7 15 - 5 ö÷ 1 a C. ç ÷ + ç ÷ : = - .D. ç ÷ + ç ÷ : = - . ç ÷ ç ç ÷ è - - ÷ø a ( - ) 2a 1 2 1 3 7 5 çè 1 - 2 1 - 3 ÷ø a ( 7 - 5) 2 2.x
Câu 15. Cho biểu thức P =
. Giá trị của P khi x = 9 là x + 1 9 9 A. . B. . C. 9 . D. 18 . 2 4 x
Câu 16. Cho biểu thức P =
x ³ 0;x ¹ 1. Giá trị của P khi x = 4 là: x - 1 2 A. 4 . B. 2 . C. -2 . D. . 3 x 2
Câu 17. Cho biểu thức P =
. Giá trị của P khi x = là x + 1 2 - 3 A. 4 . B.2 . C. 3 . D. 1 .
30. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x + 1
Câu 18. Cho biểu thức P = . x - 2
Giá trị của P khi x = 3 + 2 2 là: A. 4 + 3 2 . B. 4 - 3 2 . C. 3 . D. 3 2 . x + 2 x + 2
Câu 19. Cho biểu thức P =
với x > 0. So sánh P với 4 x A. P > 4 . B. P < 4 . C. P = 4 . D. P £ 4 . x + 3
Câu 20. Cho biểu thức B =
với x ³ 0. So sánh A với 1 x + 2
A B > 1 . B. B < 1 . C. B = 1 . D.B £ 1 . 3 x - 1
Câu 21. Cho biểu thức P =
với x ³ 0. Tìm x biết P = x . x + 1 A. 1 . B. 2 . C. 3 . D. 4 . x + 1
Câu 22. Cho biểu thức A =
với x ³ 0;x ¹ 4. Tìm các giá trị của biết x - 2 x - 1 A = 2
A. x = 0;x = 5 .
B. x = 0 . C. x = 0;x = 25 .
D. x = 5;x = 1 . 2 Câu 23. Cho P = x + 1
Có bao nhiêu giá trị x Î để P Î ? A. 1 . B. 2 . C. 0 . D. 4 . 1 3 5 + 5 5 3 5 Câu 24. Cho A = - 27 + ; B = + - 3 - 1 3 5 + 2 5 - 1 3 + 5 Chọn câu đúng
A. B > A > 0 .
B. A < B < 0 . C. A < 0 < B .
D. B < 0 < A . 2 x - 1 Câu 25. Cho A =
với x ³ 0 Có bao nhiêu giá trị của x để A có giá trị nguyên x + 2 A. 2 . B. 1 . C. 0 . D. 3 . x + 1 2 x 2 + 5 x
Câu 26. Cho biểu thức A = + +
với x ³ 0;x ¹ 4 x - x + 4 2 2 - x
Rút gọn biểu thức A ta được:
31. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 3 x x 2 x 3 A. A = . B. A = . C. A = . D. A = . x + 2 x + 2 x + 2 x + 2 x + 1 2 x 2 + 5 x
Câu 27. Cho biểu thức A = + +
với x ³ 0;x ¹ 4 x - 2 x + 2 4 - x
Tìm x đểA = 2 A. 12 . B. 4 . C. 16 . D. 25 . æ ö ç - + ÷ ( - x x x )2 1 2 2
Câu 28. Cho biểu thức B = ç ÷ - ç ÷.
với x ³ 0;x ¹ 1 ç x - 1 ÷ è + + ÷ 2 x 2 x 1ø
Rút gọn biểu thức B ta được:
A. B = x - x .
B. B = x - x .
C. B = x + x .
D. B = x + 2 x . æ ö 2 ç x - 2 x + 2 ÷ (1 - x)
Câu 29. Cho biểu thức B = ç ÷ - ç ÷.
với x ³ 0;x ¹ 1 ç x -1 ÷ è x + 2 x + 1÷ 2 ø
Tìm x để B > 0 .
A. x > 1. B. x < 2 . C. 0 < x < 1 . D. x £ 1. æ ö ç - + ÷ ( - x x x )2 1 2 2
Câu 30. Cho biểu thức B = ç ÷ - ç ÷.
với x ³ 0;x ¹ 1 ç x - 1 ÷ è x + 2 x + 1÷ 2 ø
Tìm giá trị lớn nhất của B . 1 A. 1 . B. 2 . C. 3 . D. . 4 æç 4 x 8x ö æç x - 1 2 ö ÷ ÷ P = ç ÷ + ç ÷ : ç ÷ - ç ÷ ç ÷ çè + 4 - ÷ ç ÷ 2 x x ø çèx - 2 x x ÷
Câu 31. Cho biểu thức
ø với x ³ 0;x ¹ 4;x ¹ 9. Rút gọn biểu thức P ta được 4x 4x x -4x A. P = . B. P = . C. P = . D. P = . x - 3 x + 3 x - 3 x - 3 æç 4 x 8x ö æç x - 1 2 ö ÷ ÷
Câu 32. Cho biểu thức P = ç ÷ + ç ÷ : ç ÷ -
với x ³ 0;x ¹ 4;x ¹ 9 . Tìm x để ç ÷ ç ÷ çè + 4 - ÷ ç ÷ 2 x x ø çèx - 2 x x ÷ø P = -1 9 9 3 3 A. x = . B. x = ;x = 1 - .
C. x = ;x = -1 . D. x = . 16 16 4 4
32. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com æç 4 x 8x ö æç x - 1 2 ö ÷ ÷ P = ç ÷ + ç ÷ : ç ÷ - ç ÷ ç ÷ çè + - ÷ ç ÷ 2 x 4
x ø çèx - 2 x x ÷
Câu 33. Cho biểu thức
ø với x ³ 0;x ¹ 4;x ¹ 9. 5 5 5 5 A. m = . B. m > - . C. m < . D. m > . 18 18 18 18 2 x - 9 x + 3 2 x + 1
Câu 34. Cho biểu thức C = - -
với x ³ 0;x ¹ 4;x ¹ 9 . Rút gọn biểu x - 5 x + 6 x - 2 3 - x thức trên ta được: x - 1 x - 1 x - 1 x + 1 A. C = . B. C = . C. C = . D. C = . x - 3 x + 3 x + 3 x + 3 2 x - 9 x + 3 2 x + 1
Câu 35. Cho biểu thức C = - -
với x ³ 0;x ¹ 4;x ¹ 9 . Tìm x để C < 1 x - 5 x + 6 x - 2 3 - x
A. 0 £ x < 9 .
B. 0 £ x < 9;x ¹ 4 .
C. 4 < x < 9 .
D. 0 < x < 4 . æç x 2 ö÷ 1
Câu 36. Cho biểu thức C = ç ÷ + ç ÷ :
với x > 0;x ¹ 1 ç ÷
çè x -1 x - x ÷ø x - 1
Rút gọn biểu thức C ta được x - 2 x + 2 x + 2 x A. C = . B. C = . C. C = . D. C = . x x x x + 2 æç x 2 ö÷ 1
Câu 37. Cho biểu thức C = ç ÷ + ç ÷ :
với x > 0;x ¹ 1 ç ÷
çè x -1 x - x ÷ø x - 1
Tìm giá trị nhỏ nhất của C . A. C = 1 . B. C = 2 . C. C = 2 . D. C = 2 2 . æç 2x 1 1 ö æ ÷ x 4 ö + +
Câu 38. Cho biểu thức P = ç - ÷ ç ÷ : 1 ç ÷ ç - ÷ ç ÷ ç ÷ 3 è x - 1 x - 1÷ ç ø è x + x + 1÷ø Rút gọn P . x x 3 + x - x A. P = . B. P = . C. P = . D. P = . x - 3 x + 3 x - 3 x - 3 æç 2x 1 1 ö æ ÷ x 4 ö + +
Câu 39. Cho biểu thức P = ç - ÷ ç ÷ : 1 ç ÷ ç - ÷ ç ÷ ç ÷ 3 è x - 1 x - 1÷ ç ø è x + x + 1÷ø
Tìm các giá trị nguyên của x để P nhận giá trị nguyên dương.
33. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
A. x = 1;x = 36 .
B. x = 1;x = 36 .
C. x = 4;x = 6 .
D. x = 16;x = 36 . HƯỚNG DẪN
Bài 4- Rút gọn biểu thức chứa căn Câu 1. Đáp án A. ( 2 2 2 - )2 4
5 - 6 - 2 5 = (4 - 5) - 5 - 2 5 + 1 = (4 - 5) - ( 5 - ) 1
= 4 - 5 - 5 - 1 = 4 - 5 - 5 + 1 = 5 - 2 5 Câu 2. Đáp án A. ( + )2 2 5 - 7 - 2 10 = ( + )2 2 5 - 5 - 2 5. 2 + 2 = ( + )2 - ( - )2 2 5 5
2 = 2 + 5 - 5 - 2 = 2 + 5 - 5 + 2 = 2 2 . Câu 3. Đáp án B.
32 + 50 - 3 8 - 18 = 16.2 + 25.2 - 3 4.2 - 9.2 = 4 2 + 5 2 - 6 2 - 3 2 = 0 .. Câu 4. Đáp án B.
125 - 4 45 + 3 20 - 80 = 25.5 - 4 9.5 + 3 4.5 - 16.5 = 5 5 - 4.3 5 + 3.2 5 - 4 5
= 5 5 - 12 5 + 6 5 - 4 5 = -5 5. Câu 5. Đáp án D. a 4 a 4a 5 a + 2 - a
- 25a = 5 a + 2. - a - 5 a 4 a 4 a
= 5 a + a - 2 a - 5 a = - a . Câu 6. Đáp án C. 1 32a a 3 1 16.2a a 3 3 8a + - . - 2a = 3 4.2a + - . - 2a 4 25 3 2a 4 25 3 2a 1 4 2a a 3. 2a 1 1 = 3.2 2a + . - . - 2a = 6 2a + 2a - 2a - 2a 4 5 3 2a 5 2 æ 1 1 ö ç ÷ 47 = 2a. 6 ç + - - 1÷ = 2a ç çè 5 2 ÷÷ø 10 Câu 7. Đáp án D. ( 2
5 + 2) 7 - 2 10 = ( 5 + 2) 5 - 2 5. 2 + 2 = ( 5 + 2) ( 5 - 2)
= ( 5 + 2) 5 - 2 = ( 5 + 2)( 5 - 2) = 5 - 2 = 3 .
34. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Câu 8. Đáp án B. Ta có ( - ) + = ( - ) + + = ( - ) ( + )2 5 1 6 2 5 5 1 5 2 5.1 1 5 1 5 1 = ( 5 - ) 1 ( 5 + ) 1 = 5 - 1 = 4 . Câu 9. Đáp án A. 16 2 Với a > 0 ta có 3 2 5
2 a - 9a + a + 36a 2 a a 16a 2 2 2 4
= 2 a - 9a .a + a + . 36a .a 2 a a 2 2
= 2 a - 3a a + 4a a + .6a
a = 2 a - 3a a + 4a a + 12 a = 14 a + a a . 2 a Câu 10. Đáp án D. æç1 a 3 4 ö÷ 1 æç1 a 3 4 ö÷ Ta có ç - 2a + 200a ÷ ç ÷ : = ç . - 2. a + 100. 2. a ÷ ç ÷.8 ç2 2 2 5 ÷÷ 8 ç ÷ è ø ç2 è 2 2 5 ÷ø a 32 2. a = 4. - 12 2. a + .10. 2. a = 4.
- 12 2. a + 64 2. a 5 2 2
= 2 2a - 12 2a + 64 2a = 54 2a Câu 11. Đáp án B. - - ( - 2 ) a b ( - 2 2 4 2 4 ) a b a b a b a b a b a b a b Ta có = . = . = . = a 2 2 b a - 2ab + 2 2 b b (a - 2 b) b a - 2 2 b b (a -b) Câu 12. Đáp án A. ( )2 - + - + ( )2 . . . . a b a b b a a b a a b b b a Ta có + = + ab a + b ab a + b
ab ( a + b) ( a - b)( a + b) = +
= a + b + a - b = 2 a. ab a + b Câu 13. Đáp án B. æç2 3 - 6 216 ö æ a ö æ - ç ÷ ç ÷ ç2 3 - 2. 3 36.6 ö æ a ö ÷ ÷ - Ta có - ç ÷.ç ÷ = ç ÷ - ç ÷ ç ÷ ç ÷.ç ÷ ç ÷ çè - ÷ ç ÷ ç ÷ ç ÷ 8 2 3 ø è 6 ø çè 4.2 - 2 3 ÷ ç ø è 6 ÷ø
35. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com é ù é ù ê 3 (2 - 2) ú æ ö ê 6 a = ê - ú ç ÷ ( 2 - )1 6 6 ú æ a ö . - ç ÷ = ê - ú ç ÷ - ç ÷ ê ú ç ÷ ç ÷ ê ú ç ÷ ê 2 2 - 2 è ú 6 ø ê 2( 2 - ) 2 6 . 3 1 çè ú 6 ÷ø ë û ë û æç 6 ö æ a ö æ - = ç ÷ ç ÷ ç 3 6 ö æ a ö ÷ ÷ - - ç ÷ ç ÷ = ç ÷ ç ÷ 3a 2 6 . - ç ÷ ç ÷ ç ÷.ç ÷ = ç ÷ ç ÷ ç ÷ ç ÷ 2 è ø è ø ç 2 ÷ ç ÷ è ø è ø 2 6 6 Câu 14. Đáp án C. æç 14 - 7 15 - 5 ö÷ 1 Ta có ç ÷ + ç ÷ : ç ÷ çè 1 - 2 1 - 3 ÷ø a ( 7 - 5) æç 7. 2 - 7 5. 3 - 5 ö÷ = ç ÷ + ç ÷.a ç ÷ ( 7 - 5) çè 1- 2 1 - 3 ÷ø æ ö ç- é ù 7 ç (1- 2) 5( 3 - )1÷÷ ê 6 ( 2 - ) 1 ú æ ö ç ÷ a = = ê - ú ç ÷ ç - ÷.a ÷ - ç ÷ ç 2 6 . ÷ ( 7 - 5) ê ú ç ÷ ç 1 - 2 3 - 1 ÷ ç ÷ ç ÷ ê 2( 2 - ) 1 è ú 6 ø è ø ë û
= (- 7 - 5).a ( 7 - 5) = a
- .( 7 + 5)( 7 - 5) = -2a. Câu 15. Đáp án A. 2.9 18 18 9 Ta có P = = = = . + 3 + 1 4 2 9 1 Câu 16. Đáp án B. 4 2
Thay x = 4 (thỏa điều kiện) vào P ta được P = = = 2 . - 2 - 1 4 1 Câu 17. Đáp án B. 2(2 + 3 2 ) 4 + 2 3 Ta có x = = = = + = + 2 - 3 (2- 3)(2 + 3) 4 2 3 ( 3 )21 4 - 3  x = ( + )2 3 1 = 3 + 1 2( 3 + + + )2 4 2 3 4 2 3 Khi đó ta có P = = = = 2 3 + 1 + 1 3 + 2 3 + 2 Câu 18. Đáp án A. x = + = ( + )2  x = ( + )2 3 2 2 2 1 2 1 = 2 + 1 Ta có
Thay x = 2 + 1 vào biểu thức P ta được
36. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com ( 2 + )2( 2 + + + + )1 2 1 1 2 2 P = = = . + - - ( - )( + ) = 4 +3 2 2 1 2 2 1 2 1 2 1 Câu 19. Đáp án A. x + 2 x + 2
x + 2 x + 2 - 4 x x - 2 x + 2 Ta xét: P - 4 = - 4 = = x x x
(x - x + )+ ( x - )2 2 1 1 1 + 1 = = x x Vì ( x - )2
1 + 1 ³ 1 > 0,"x > 0 và x > 0,"x > 0
nên P - 4 > 0  P > 4 với x > 0 Câu 20. Đáp án A. + ( x x + ) 2 + 1 3 x + 2 1 1 Cách 1: Ta có B = = = + = 1 + x + 2 x + 2 x + 2 x + 2 x + 2
Vì x ³ 0  x ³ 0  x + 2 ³ 2 > 0 suy ra 1 1 > 0  1 + > 1 hay B > 1 x + 2 x + 2
Cách 2: ta xét hiệu x + 3 x + 3 - x - 2 1 B - 1 = - 1 = = x + 2 x + 2 x + 2
x ³ 0,"x ³ 0  x + 2 ³ 2 > 0 1 Vì 1 > 0 và nên > 0 x + 2
Hay B - 1 > 0  B > 1. Câu 21. Đáp án A.
Với x ³ 0 ta có P = x x ( x x x + - - )1 3 1 3 1  = x  = x + 1 x + 1 x + 1
 3 x - 1 = x + x x - 2 x + 1 = 0  ( x - )2
1 = 0  x = 1  x = ( 1 TM ) . Câu 22. Đáp án C.
37. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x - 1 x + 1 x - 1 A =  =
Với x ³ 0;x ¹ 4 ta có: 2 - 2 x 2  2( x + ) 1 = ( x - ) 2 ( x - )
1  2 x + 2 = x - 3 x + 2 é x 0 x é = = ( 0 tm) ê x 5 x 0 x ( x ) 5 0 ê  - =  - =  ê  ê ê x = 5 x = ( 25 tm) ê ë ë
Vậy giá trị cần tìm là x = 0;x = 25 Câu 23. Đáp án B. 2 2( x + ) 1  ( x + ) 1 Î ( ) 2 = {1;-1;2;- } 2 Ta có P = thì Mà x + 1 > 0 x + 1
với x ³ 0 nên x + 1 Î {1; } 2
+) x + 1 = 1  x = 0
+) x + 1 = 2  x = 1
Vậy có hai giá trị của x thỏa mãn điều kiện. Câu 24. Đáp án C. 1 3 A = - 27 + Ta có: 3 - 1 3 3 + 1 3. 3 3 + 1 3 + 1 - 4 3 1 - 3 3 = ( - + = - 3 3 + 3 = = 3 - ) 1 ( 3 + ) 9.3 1 3 2 2 2 5 + 5 5 3 5 và B = + - 5 + 2 5 - 1 3 + 5 (5+ 5)( 5 - )2 5 ( 5 + ) 1 3 5 (3 - 5) 3 5 - 5 5 + 5 9 5 - 15 = ( + - = + - 5 + ) 2 ( 5 - ) 2 ( 5 - )1( 5 + )1 (3+ 5)(3- 5) 1 4 4 12 5 - 20 + 5 + 5 - 9 5 + 15 = = 5 4 1 - 3 3 A =
< 0(do1 - 3 3 < 0) Ta thấy 2
và B = 5 > 0 nên A < 0 < B Câu 25. Đáp án A.
38. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com (2 x + 4)-5 2( x x + - )2 2 1 5 5 Ta có:A = = = - = 2 - x + 2 x + 2 x + 2 x + 2 x + 2 5
Ta có x ³ 0  x ³ 0  x + 2 ³ 2 > 0  > 0 suy ra x + 2 5 2 - < 2 hay A < 2(1) x + 2 5 5 5 5 1
Lại có x + 2 ³ 2  £ suy ra 2 - ³ 2 -  A ³ - (2) + 2 x 2 + 2 2 x 2 1
Từ (1) và (2) ta có: - £ A < 2 mà A Î   A Î {0; } 1 2 2 x - 1 + Với A = 1 
= 1  2 x - 1 = x + 2  x = 3  x = 9(tm) x + 2 1 x = ;x = 9 Vậy với 4
thì A đạt giá trị nguyên. Hay có 2 giá trị của x thỏa mãn đề bài. Câu 26. Đáp án A. x + 1 2 x 2 + 5 x Ta có A = + + - + 4 2 2 - x x x
( x + )1( x + )2+2 x ( x - )2 2 + 5 x = ( - x - ) 2 ( x + ) 2 ( x - )2( x + )2 3 x ( x - )
x + 3 x + 2 + 2x - 4 x - 2 - 5 x 3x - 6 x 2 3 x = ( = = = x - ) 2 ( x + ) 2
( x - )2( x + )2 ( x + )2( x - )2 x +2 3 x Vậy A =
với x ³ 0;x ¹ 4 x + 2 Câu 27. Đáp án C. 3 x A =
Với x ³ 0;x ¹ 4 ta có x + 2 3 x Xét A = 2 
= 2  3 x = 2( x + )
2  x = 4  x = 16 (TM ) x + 2 Vậyx = 16 . Câu 28. Đáp án B.
39. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com æ ö æ ö ç ÷ 2 ç x - 2 x + 2 ÷ (1 - x) ç ÷ 2 ç x - 2 x + 2 ÷ (x - 1) Ta có B = ç ÷ - = ç ÷ ç ÷. - ÷. ç ç ç x - 1 ÷ ÷ è x + 2 x + 1÷ 2 ø ç
çç( x - )( x + ) è ( ÷ ç x + )2 2 1 1 1 ÷÷÷ø æççç( ö x - ) 2 ( x + ) 1
( x + )2( x - )1÷÷÷ ( x - )21( x + )21 = ç ÷ - ÷. ç ççè( ÷ ç ÷ ç x
)( x )2 ( x )( x )2 2 1 1 1 1 ÷ - + - + ÷÷ø ( x - )21.( x -2 x ( x - ) x x x x + - - - - + )21 2 2 1 = . = = x - x ( 2 x - )( x + )2 2 1 1
Vậy B = x - x Câu 29. Đáp án C.
B > 0  x - x > 0  x (1- x ) > 0
Theo câu trước ta có B = x - x Xét
Với x ³ 0,x ¹ 1 ta 1 ìïï - x > 0 ìï ï ï x < 1 x ìï < 1
có x ³ 0 nên x 1 ( - x ) > 0 ï ï  í  í  í x ï ¹ 0 x ï ¹ 0 x ï ¹ 0 ï ï ï ïî ïî î
Kết hợp điều kiện ta có 0 < x < 1 Câu 30. Đáp án D.
Ta có B = x - x với x ³ 0;x ¹ 1 æ ö æ ö
Khi đó B = x - x = -(x - x ) 2 1 1 ç ÷ 1 1 = - x ç - x ç + ÷ = - ç x ÷ - ÷ 4 çè 4÷÷ø 4 çè 2÷÷ø 2 1 æ 1ö ç ÷ 1 - ç x - ÷ £ 4 çè 2÷÷ø 4 Nhận thấy
với x ³ 0;x ¹ 1 1 1 1 x - = 0  x =  x = (TM ) Dấu “=” xảy ra khi 2 2 4 1 1 x =
Vậy giá trị lớn nhất củaB là 4 khi và chỉ khi 4 Câu 31. Đáp án A.
Điều kiện x > 0,x ¹ 4,x ¹ 9 æ æ ö ç ÷ æ ö ç ÷ ç 4 x 8x ö æç x - 1 2 ö ÷ ÷ ç 4 x 8x ÷ ç ÷ ç x - 1 2 ÷ P = ç ÷ + ç ÷ ç ÷ : ç ÷ - = ç + ÷ : ç - ÷ ç ÷ ç ÷ ÷ ÷ çè + - ÷ ç ÷ 2 x 4
x ø çèx - 2 x x ÷ø ç2 + x ( ç
2 - x )(2 + x )÷ ç ÷ x ( x - ç ÷ è ø )2 x ÷ ç ÷ ç ÷ è ø
40. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
4 x (2 - x ) + 8x x - 1 - 2( x - ) 2 x ( x x x - + )2 8 4 = ( = . - x )( + x ) : 2 2 x ( x - ) 2
(2- x)(2+ x) 3- x 4 x (2 + x ) x (2 - x ) 4x = ( = 2 - x )(2 + x ). x - 3 x - 3 4x Vậy P =
với x > 0,x ¹ 4,x ¹ 9 x - 3 Câu 32. Đáp án A.
Với điều kiện: x > 0,x ¹ 4,x ¹ 9 . Ta có: P = -1 4x
= -1  4x + x - 3 = 0  4x + 4 x - 3 x - 3 = 0 x - 3  4 x ( x + ) 1 - ( 3 x + ) 1 = 0 é x = -1(ktm) ê  ( x + 1) 4 ( x - 3) = 0  êê 3 9 x =  x = (tm) ê ë 4 16 9 Với x = thì P = -1. 16 Câu 33. Đáp án D. " >
m ( x - )P > x +  m( x - ) 4x x 9 : 3 1 3 . > x + 1 x - 3 x + 1
m.4x > x + 1  m > 4x
Ta có: với mọi giá trị x > 9 thì x + 1 > 9 + 1 = 10 4x > 4.9 = 36 10 5 Vậy m > = 36 18 Câu 34. Đáp án C.
Ta có x - 5 x + 6 = x - 2 x - 3 x + 6 = x ( x - 2)- 3( x - )
2 = ( x - 3)( x - ) 2 2 x - 9 x + 3 2 x + 1 2 x - 9 x + 3 2 x + 1 nên C = - - = - + x - 5 x + 6 x - 2 3 - x
( x - )2( x - )3 x -2 x - 3
2 x - 9 - ( x + ) 3 ( x - ) 3 + (2 x + ) 1 ( x - ) 2
2 x - 9 - x + 9 + 2x - 3 x - 2 = ( = x - ) 2 ( x - ) 3 ( x - )2( x - )3
41. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com x x x x x x
( x - )2+( x - )2 ( x + )1( x - - - - + - )2 2 2 2 x + 1
= ( x - )2( x - ) = 3
( x - )2( x - ) = 3
( x - )2( x - ) = 3
( x - )2( x - ) = 3 x - 3 x + 1 Vậy C =
với x ³ 0;x ¹ 4;x ¹ 9 x - 3 Câu 35. Đáp án B. x + 1 C = Theo câu trước ta có
x - 3 với x ³ 0;x ¹ 4;x ¹ 9 x + 1 x + 1 x - 3 4 Để C < 1  < 1  - < 0  < 0 x - 3 x - 3 x - 3 x - 3
Mà 4 > 0 nên x - 3 < 0  x < 3  x < 9
Kết hợp điều kiện x ³ 0;x ¹ 4;x ¹ 9 suy ra 0 £ x < 9;x ¹ 4 . Câu 36. Đáp án B. æç x 2 ö÷ 1 ta có C = ç ÷ + ç ÷ : ç ÷
çè x -1 x - x ÷ø x - 1 æ ö ç ÷ ç x 2 ÷ ç ÷ x + 2 x + 2 = ç + . x 1 . x 1 ç x - 1 x ( x - )÷÷ ç ÷ ( - ) = 1 ÷ x ( x - ç ÷ x è ø ) ( - )= 1 x + 2 Vậy C =
với x > 0;x ¹ 1 x Câu 37. Đáp án D. x + 2 C = Theo câu trước ta có:
x với x > 0;x ¹ 1 x + 2 x 2 2 C = = + = x + Xét x x x x 2
Với x > 0,x ¹ 1 , áp dụng bất đẳng thức Cô-si cho hai số dương x và x ta được: 2 2 x + ³ 2 x . x x 2  x + ³ 2 2 xC ³ 2 2
42. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2 x =  x = 2(tm) Dấu “=” xảy ra khi x
Vậy giá trị nhỏ nhất của C là 2 2  x = 2. Câu 38. Đáp án A. x ìï ³ 0 ĐKXĐ: ïí x ï ¹ 1 ïî æç 2x 1 1 ö æ ÷ x 4 ö + + P = ç - ÷ ç ÷ : 1 ç ÷ ç - ÷ ç ÷ ç ÷ 3 è x - 1 x - 1÷ ç ø è x + x + 1÷ø æ ö ç ÷ ç 2x + 1 1 ÷ æ ö ç
÷ çx + x + 1 - x - 4÷ = ç ç ÷ ( - ÷÷ ç : ç ÷ ç ÷ x - ) 1 (x + x + ç )1 x -1÷ ç ÷÷ çè x + x + 1 ÷ è ø ø
2x + 1 - x - x - 1 x - 3 x - x x + x + 1 = ( = . x ¹ 9) x - ) 1 (x + x + ) : 1 x + x + 1
( x - )1(x + x + ) ( 1 x - 3 x ( x - ) 1 x = ( = x - ) 1 ( x - ) . 3 x - 3 x Vậy P =
với x ³ 0;x ¹ 1;x ¹ 9 x - 3 Câu 39. Đáp án D. x ìï ³ 0 ïï ĐKXĐ: x ïí ¹ 1 ïxïï ¹ 9 ïî x x - 3 + 3 3 Ta có: P = = = 1 + . x - 3 x - 3 x - 3
Để P nhận giá trị là số nguyên dương thì ìï 3 ì ì ï ï 3 ï 3 ï ï ì ï Î Z ï Î Z ï Î Z P ï Î Z ï ï ï ï ï x - 3 ï x - ï x - í  í 3 3  í  í P ï > 0 ï 3 ï ï ï î 3 + - 1 ï 3 x 3 ï + > 0 ïï 1 ï > - ï ï > 0 ïî x - 3 ïïî x 3 ï - ïî x - 3 (ìïï x - ï )3ÎU( )3(1) ï  í . ï x ï > ï 0 2 ( ) ïïî x - 3
43. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1
( )  ( x - 3) Î {1; } 3 é x 3 1 é x 4 x é - = = = 16(tm) ê ê ê  ê  ê  ê ê x - 3 = 3 ê x = 6 x = 36(tm) ê ë ë ë
Nhận thấy với x = 16;x = 36 vẫn thỏa mãn (2).
Nên x = 16 hoặc x = 36 thì P nguyên dương.
------------------------- Toán Học Sơ Đồ -------------------------
44. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com