Chuyên đề Tích phân – Thầy Trần Đình Cư – TP Huế Toán 12

Chuyên đề Tích phân – Thầy Trần Đình Cư – TP Huế Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

59 30 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

110 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
CHUYÊN Đ
Ề LUYỆN THI
TÍCH PHÂN
Dùng cho h
ọc sinh lớp 12
-Ôn thi Đ
ại học và Cao
đ
ẳng
HUEÁ, 01/2013
Don't try to fix the students, fix ourselves first. The good teacher makes the poor
student good and the good student superior. When our students fail, we, as teachers,
too, have failed.
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
1
M
ỤC LỤC
Trang
A. NGUYÊN HÀM..................................................................................................................... 3
B. TÍCH PHÂN .......................................................................................................................... 4
C. PHÂN LO
ẠI VÀ
PHƯƠNG PHÁP TÍNH TÍCH PHÂN: ................................................... 6
V
ẤN ĐỀ 1: PHÉP THAY BIẾN
( )
n
t f x
........................................................................... 6
V
ẤN ĐÊ 2: TÍCH PHÂN BẰNG PHƯƠNG PHÁP LƯỢNG
GIÁC HÓA ....................... 11
D
ẠNG 1:
2 2
a x
............................................................................................................. 11
D
ẠNG 2:
2 2
x a
............................................................................................................. 14
D
ẠNG 3:
2 2
x a
............................................................................................................. 14
D
ẠNG 4:
hoaëc
a x a x
a x a x
......................................................................................... 18
V
ẤN ĐỀ 3: TÍCH PHÂN LƯỢNG GI
ÁC........................................................................... 19
D
ạng 1: Biến đổi lượng giác về tích phân cơ bản
............................................................ 19
D
ạng 2: Tích phân dạng
.................................................................. 23
D
ạng 3: Tích phân dạng
2 2
sin sin cos cos
dx
a x b x x c x
............................................... 24
D
ạng 4: Tích phân dạng
1 2
(sin )cos ; (cos )sinI f x xdx I f x xdx
............................ 25
1.Tích phân có d
ạng
sin .cos
m n
x xdx
.......................................................................... 26
2.Tích phân dạng
1 1
sin os
; ; ,
os sin
m m
n n
x c x
I dx I dx m n
c x x
.................................. 27
D
ạ
ng 5: Tích phân ch
ứa
tan ;cos ; cot ;sinx x dx x x dx
............................................ 28
D
ạng 6: Đổi biến bất kì
..................................................................................................... 29
V
ẤN ĐỀ 4: TÍCH PHÂN CÓ CHỨA GIÁ TRỊ TUYỆT ĐỐI
.......................................... 39
V
ẤN
ĐỀ 5: TÍCH PHÂN HÀM HỮU TỈ
............................................................................ 42
V
ẤN ĐỀ 6: TÍCH PHÂN MỘT SỐ HÀM ĐẶC BIỆT
....................................................... 50
V
ẤN
ĐỀ 7: TÍCH PHÂN TỪNG PHẦN
............................................................................. 58
V
ẤN ĐỀ 8: ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG
..................... 69
V
ẤN ĐỀ 9: TÍNH THỂ TÍCH
V
ẬT THỂ TRÒN XOAY
.................................................. 77
M
ỘT SỐ BÀI TẬP CẦN LÀM TRƯỚC KHI THI
................................................................ 83
D. PH
Ụ LỤC
............................................................................................................................. 95
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
2
PHƯƠNG PHÁP Đ
ẶT ẨN PHỤ KHÔNG LÀM THAY ĐỔI CẬN TÍCH PHÂN
.................. 95
SAI L
ẦM THƯỜNG GẶP TRONG TÍNH TÍCH PHÂN
..................................................... 100
Đ
Ề THI ĐẠI HỌ
C T
Ừ 2009
-2012 ..................................................................................... 107
TÀI LI
ỆU THAM KHẢO
.................................................................................................. 109
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
3
A. NGUYÊN HÀM
1. Khái ni
ệm nguyên hàm
Cho hàm s
ố
f xác đ
ịnh trên K. Hàm số
F đgl nguyên hàm c
ủa
f trên K n
ếu:
'( ) ( )F x f x
, x K
N
ếu
F(x) là m
ột nguyên hàm của
f(x) trên K thì h
ọ nguyên hàm
c
ủa
f(x) trên K là:
( ) ( )f x dx F x C
, C R.
M
ọi hàm số
f(x) liên t
ục trên K đều có nguyên hàm trên K.
2. Tính ch
ất
'( ) ( )f x dx f x C
( ) ( ) ( ) ( )f x g x dx f x dx g x dx
( ) ( ) ( 0)kf x dx k f x dx k
3. Nguyên hàm c
ủa một số hàm số thường gặp
4. Phương pháp tính nguyên hàm
a) Phương pháp đ
ổi biến số
0dx C
dx x C
1
, ( 1)
1
x
x dx C
1
lndx x C
x
x x
e dx e C
(0 1)
ln
x
x
a
a dx C a
a
cos sinxdx x C
sin cosxdx x C
2
1
tan
cos
dx x C
x
2
1
cot
sin
dx x C
x
1
cos( ) sin( ) ( 0)ax b dx ax b C a
a
1
sin( ) cos( ) ( 0)ax b dx ax b C a
a
1
, ( 0)
ax b ax b
e dx e C a
a
1 1
lndx ax b C
ax b a
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
4
N
ếu
( ) ( )f u du F u C
và
( )u u x
có đ
ạo hàm liên tục thì:
( ) . '( ) ( )f u x u x dx F u x C
b) Phương pháp tính nguyên hàm từng phần
N
ếu
u, v là hai hàm s
ố có đạo hàm liên tục trên K thì:
udv uv vdu
B. TÍCH PHÂN
1. Khái ni
ệm tích phân
Cho hàm s
ố
f liên t
ục trên K và
a, b K. N
ếu
F là m
ột nguyên hàm của
f trên K thì:
F(b) – F(a) đgl tích phân c
ủa
f t
ừ
a đ
ến
b và kí hi
ệu là
( )
b
a
f x dx
.
( ) ( ) ( )
b
a
f x dx F b F a
Đ
ối với biến số lấy tích ph
ân, ta có th
ể chọn bất kì một chữ khác thay cho
x, t
ức là:
( ) ( ) ( ) ... ( ) ( )
b b b
a a a
f x dx f t dt f u du F b F a
Ý ngh
ĩa hình học
: N
ếu hàm số
y = f(x) liên t
ục và không âm trên đoạn [a; b] thì diện tích
S c
ủa
hình thang cong gi
ới hạn bởi đồ thị của
y = f(x), tr
ục Ox và hai đườn
g th
ẳng
x = a, x = b là:
( )
b
a
S f x dx
2. Tính ch
ất của tích phân
0
0
( ) 0f x dx
( ) ( )
b a
a b
f x dx f x dx
( ) ( )
b b
a a
kf x dx k f x dx
(k: const)
( ) ( ) ( ) ( )
b b b
a a a
f x g x dx f x dx g x dx
( ) ( ) ( )
b c b
a a c
f x dx f x dx f x dx
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
5
N
ếu
f(x)
0 trên [a; b] thì
( ) 0
b
a
f x dx
N
ếu
f(x)
g(x) trên [a; b] thì
( ) ( )
b b
a a
f x dx g x dx
3. Phương pháp tính tích phân
a) Phương pháp đ
ổi biến số
( )
( )
( ) . '( ) ( )
u b
b
a u a
f u x u x dx f u du
trong đó: u = u(x) có đ
ạo hàm liên tục trên
K, y = f(u) liên t
ục và hàm hợp
f[u(x)] xác đ
ịnh trên
K, a, b K.
b) Phương pháp tích phân t
ừng phần
N
ếu
u, v là hai hàm s
ố có
đ
ạo hàm liên tục trên
K, a, b
K thì:
b b
b
a
a a
udv uv vdu
Chú ý:
C
ần xem lại các phương pháp tìm nguyên hàm.
Trong phương pháp tích phân t
ừng phần, ta cần chọn sao cho
b
a
vdu
d
ễ tính hơn
b
a
udv
.
Trong ph
ần sau sẽ trình bày kỉ thuật lựa chọn
u
và
dv
.
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
6
C. PHÂN LO
ẠI VÀ PH
ƯƠNG PHÁP TÍNH TÍCH PHÂ
N:
V
ẤN ĐỀ 1: PHÉP THAY BIẾN
( )
n
t f x
Phương pháp: Khi hàm dư
ới dấu tích phân có chứa biểu thức có dạ
ng
( )
n
f x
. Lúc đó trong
nhi
ều tr
ường hợp ( chứ không phải mọi trường hợp), ta có thể đổi biến bằng cách
- Bư
ớc 1: Đặt
1
( ) ( ) '( )
n n
n
t f x t f x nt dt f x dx
- Bư
ớc 2: Ghi nhớ “Đổi biến thì phải đổi cân”
BÀI T
ẬP MẪU: Tính các tích phân sau
Bài 1: Tính
1
3 2
0
1I x x dx
Giải:
Đ
ặt t =
2
1 x
t
2
= 1 – x
2
xdx = -tdt
Đ
ổi cận:
x
0
1
t
1
0
Khi đó:
1
3 2
0
1I x x dx
=
1
2
0
1 . .t t tdt
=
1
2 4
0
t t dt
=
3 5
1
3 5
0
t t
=
2
.
15
Bài 2: Tính
1
3
3 4
0
1I x x dx
Gi
ải:
Đ
ặt t =
3
4 3 4 3 2
3
1 1
4
x t x x dx t dt
Đ
ổi cận:
x
0
1
t
1
0
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
7
Khi đó:
1 1
3
3 4 3 4
0 0
1
3 3 3
1 .
4 16 16
0
I x x dx t dt t
Bài 3: Tính
1
1 ln
e
x
I dx
x
Gi
ải:
Đ
ặt
2
1 ln 1 ln 2
dx
t x t x tdt
x
Đ
ổi cận:
x
1
e
t
1
2
Khi đó:
2 2
3
2
1 1 1
2 2 2 1
1 ln
2
.2 2 2 .
3 3
1
e
x t
I dx t tdt t dt
x
Bài 4: Tính
2
3
1
1
dx
I
x x
Gi
ải:
Ta có:
2 2
2
3 3 3
1 1
1 1
dx x dx
x x x x
Đ
ặt
3 2 3 2 2
2
1 1 2 3
3
tdt
t x t x tdt x dx x dx
Đ
ổi cận:
x
1
2
t
2
3
Khi đó:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
8
2 2 3 3
2
2
3 3 3
1 1
2 2
2
2 1 1 1
3 3 1 1
1
1 1
3 3
1 1 1 1 1 2 1
ln 1 ln 1 ln ln ln
3 3 1 3 2
2 2
2 1
1 2 1 1 1
ln ln
3 3
2 2 1
2 1
dx x dx dt
I dt
t t
t
x x x x
t
t t
t
Bài 5: Tính
4
2
7
9
dx
I
x x
Gi
ải:
Đ
ặt
2 2 2
2 2
9 9 0 ;
9
dx tdt tdt
t x t x t tdt xdx
x
x t
Đổi cận:
x
7
4
t
4
5
Khi đó:
5
2
4
5
1 3 1 7
ln ln
6 3 6 4
9
4
dt t
t
t
BÀI T
ẬP ÁP DỤNG: Tính các tích phân sau
7
3
3
2
0
ln3
3
0
ln5
ln2
141
1) :
20
1
2) : 1 2
1
20
3) :
3
10 1
x
x
x
x x
x
dx ÑS
x
e
dx ÑS
e
e
dx ÑS
e e
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
9
4
7
3
4
4
0
8
3
2
1
3 3 3
4) : ln
8 4 2
1 1
1 1 1
5) : ln ln
2 3
1
11
6) ( 2004) : 4ln2
3
1 1
x
dx ÑS
x
dx ÑS
x x
x
dx A ÑS
x
3
2
3
3
1
3
2
ln . 2 ln 3
7) ( 2004). : 3 3 2 2
8
: 2 ln
e
x x
dx Khoái B ÑS
x
HD Ñaët t x
2
3
1 2
2
0
8) . . :
1
x
x
e dx ÑS e e
x
2 3
2
2
5
(KhoáiA-2003)
1 5
9) . . 4 : ln
4 3
4
dx
Ñaët t x ÑS
x x
3
2
1
ln 76
10) .(Döï bò khoái D-2005) ln 1. :
15
ln 1
e
x
dx Ñaët t x ÑS
x x
2
1 2
1
ln 2 2 2
11) ln . : :
3 3
1 ln
e
x
x dx HD I I I ÑS e
x x
2
1
1 62
12) . 1. : 30ln2
10 3
x x
dx t x DS
x
.
1 1
2 3
0 0
13) sin
1
x
x x dx dx
x
Hư
ớng dẫn
:
1 1
2 3
0 0
sin
1
x
I x x dx dx
x
Ta tính I
1
=
1
2 3
0
sinx x dx
đ
ặt t = x
3
ta tính đư
ợc I
1
= -1/3(cos1 - sin1)
Ta tính I
2
=
1
0
1
x
dx
x
đ
ặt t =
x
ta tính đư
ợc I
2
=
1
2
0
1
2 (1 ) 2(1 ) 2
4 2
1
dt
t
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
10
ĐS :-1/3(cos1 - 1)+
2
2
5
2
ln( 1 1)
14)
1 1
x
dx
x x
Hư
ớng dẫn
:Đ
ặt
1 1t x
. Đáp s
ố:
2 2
ln 3 ln 2
6
2
15)
2 1 4 1
dx
x x
Hư
ớng
d
ẫn
:Đặt
2
4 1 4 1 2 4t x t x tdt dx
.
6 5 5 5 5
2 2 2
2 3 3 3 3
1
2 1
1
2 1 4 1
1 1
1
2
dx tdt tdt dt dt
I
t
t
x x
t t
t
3 1
ln
2 12
BÀI T
ẬP BỔ SUNG
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
11
VẤN ĐÊ 2: TÍCH PHÂN B
ẰNG PH
ƯƠNG PHÁP LƯỢNG GIÁC HÓA
D
ẤU HIỆU
CÁCH Đ
ẶT
2 2
a x
sin vôùi / 2 / 2
cos vôùi 0
x a t t
x a t t
2 2
x a
vôùi t ; \{0}
sin 2 2
vôùi t 0; \
cos 2
a
x
t
a
x
t
2 2
x a
tan vôùi / 2 / 2
cos vôùi 0<
x a t t
x a t t
hoaëc
a x a x
a x a x
cos2Ñaët x a t
x a b x
2
sin , 0;
2
x a b a t t
D
ẠNG 1:
2 2
a x
BÀI T
ẬP MẪU: Tính các tích phân sau
Bài 1: Tính
2 2 2
0
a
I x a x dx
Giải:
Đặt x = asint,
;
2 2
t
.
dx = acostdt
Đổi cận:
x
0
a
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
12
t
0
2
Khi đó:
2 2 2
0
a
I x a x dx
=
2
2 2 2 2
0
sin 1 sin .a t a t acostdt
=
2
4 2 2
0
sina tcos tdt
=
4
2
2
0
sin 2
4
a
tdt
=
4
2
0
1 4
8
a
cos t dt
=
4
1
sin4
2
8 4
0
a
t t
=
4
16
a
Bài 2: Tính
1
2
2
2
2
1 x
I dx
x
Gi
ải:
Đ
ặt x = cost,
;
2 2
t
.
dx = - sint dt
Đ
ổi cận:
x
2
2
4
t
1
0
Khi đó:
1
2
2
2
2
1 x
I dx
x
=
0
2
2
4
1 os .c t sint
dt
cos t
=
4
2
0
sin .sint t
dt
cos t
=
2
4
2
0
sin t
dt
cos t
=
4
2
0
1
1 dt
cos t
=
tan
4
0
t t
=
1
4
. (vì
0;
4
t
nên sint
0 sin sint t
)
Bài 3: Tính
1
2 2
0
1I x x dx
Gi
ải:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
13
Đ
ặt x = sint,
;
2 2
t
.
dx = costdt
Đ
ổi cận:
x
0
1
t
0
2
Khi đó:
1
2 2
0
1I x x dx
=
2
2 2
0
sin 1 sin .t t costdt
=
2
2 2
0
1
sin
4
tcos tdt
=
2
2
0
1
sin 2
4
tdt
=
=
2
0
1
1 4
8
cos t dt
=
1 1
sin4
2
8 4
0
t t
=
16
Tính các tích phân sau:
3
2
1
3
2
3
2
3 2
2
2
2
2
2
0
8
2
0
1) 4 ; : 2sin :
3
1 3 3
2) ; : 3cos :
27
9
1
3) ; : sin :
8 4
1
4) 16 ; : 4sin
x dx HD Ñaët x t ÑS
dx HD Ñaët x t ÑS
x
x
dx HD Ñaët x t ÑS
x
x dx HD Ñaët x t
1
2
2
0
5) 1 : sinx dx HD Ñaët x t
5
2
2
1
1
6) ; : 1 3sin
9 1
dx HD Ñaët x t
x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
14
1
2
1
2
1 1
2
2
1 1
2 2
7) . :
16
1
: 1 2 1 . : 2 1 sin
2
x x dx ÑS
HD x x dx x dx Ñaët x t
D
ẠNG
2:
2 2
x a
Tính các tích phân sau:
3
6
2
2
2
3
2
2
2
2
2
2
0
5
2
2
1
1 3
1) ; : :
sin 36
9
1 1
2) ; : :
sin 6
1
1
3) ; :
cos
1
1 1
4) ; :
cos
1
dx HD Ñaët x ÑS
t
x x
dx HD Ñaët x ÑS
t
x x
x
dx HD Ñaët x
t
x
dx HD Ñaët x
t
x x
D
ẠNG 3:
2 2
x a
BÀI TẬP MẪU:
Bài 1: Tính
0
2
1
1
2 4
I dx
x x
Gi
ải:
Ta có:
0 0
2 2
2
1 1
1 1
2 4
1 3
dx dx
x x
x
Đ
ặt
1 3tanx t
v
ới
2
; . 3 1 tan
2 2
t dx t dt
Đổi cận:
x
-1
0
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
15
t
0
6
Khi đó:
0
6
2
1 0
1 3 3 3
.
6
3 3 18
2 4
0
I dx dt t
x x
Bài 2: Tính
1
3
8
0
1
x
I dx
x
Gi
ải:
Ta có:
1 1
3 3
8 2
4
0 0
1
1
x x
dx dx
x
x
Đ
ặt
4
tanx t
v
ới
3 2
1
; . 1 tan
2 2 4
t x dx t dt
Đ
ổi cận:
x
0
0
t
0
4
Khi đó:
1 1
3 3 2
4 4
8 2 2
4
0 0 0 0
1 1 tan 1 1
.
4
4 4 4 16
1 1 tan
1
0
x x t
I dx dx dt dt t
x t
x
Bài 3: Tính
2
2
0
1 sin
cosx
I dx
x
Gi
ải:
Đ
ặt
sin tanx t
v
ới
2
; 1 tan
2 2
t cosxdx t dt
Đ
ổi cận:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
16
x
0
2
t
0
4
Khi đó:
2
2 4 4
2 2
0 0 0
1 tan
4
1 sin 1 tan
cosx t
I dx dt dt
x t
BÀI T
ẬP ÁP DỤNG:
4
2
0
3
2
0
1
2
0
3
3
2
3
3
3
2
2
2
3
2
1
1) ; : 2tan :
8
4
1
2) ; : 3tan
9
3) 1 ; : tan
1 3 1
4) ; : tan :
2
1
9 2 3 1
5) ; : 2 3tan :
2
dx HD Ñaët x t ÑS
x
dx HD Ñaët x t
x
x x dx HD Ñaët x t
dx HD Ñaët x t ÑS
x
x
dx HD Ñaët x t ÑS
x
1
3
2
3
2
0
3
2 2
1
1
2
2
0
6) ; : tan 1
1
1
7) ; : 3tan
3
1 2
8) :
8
1
x
dx HD Ñaët x t hoaëc u x
x
dx HD Ñaët x t
x x
dx ÑS
x
3
2
2
1
1 3 2 2 3
9) . tan . : ln 2 3 2 1
3
x
dx Ñaët x t ÑS
x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
17
1
4 2
0
1
2
0
3
10) . :
8
1
1
:Bieán ñoåi tích phaân ñaõ cho veà daïng:
2
1
x
dx ÑS
x x
du
HD
u u
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
18
D
ẠNG 4:
hoaëc
a x a x
a x a x
Tính tích phân sau:
5
0
2
1 0
1 5
1) : cos2 2) : 5cos2
1 5
x x
HD x t HD x t
x x
D
ẠNG 5:
x a b x
Tính tích phân sau:
3
2
2
5
4
1 3
1 2 . 1 sin . :
8 12 8
x x Ñaët x t ÑS
BÀI T
ẬP BỔ SUNG
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
19
VẤN Đ
Ề
3: TÍCH PHÂN LƯ
ỢNG GIÁC
D
ạng 1: Biến đổi lượng giác về tích phân cơ bản
Ví d
ụ 1:
Tính
4
4
0
1
I dx
cos x
Gi
ải:
Đ
ặt t = tanx ;
2
1
dt dx
cos x
Đ
ổi cận:
x
0
4
t
0
1
Khi đó:
1
3
4 4
2 2
4 2
0 0 0
1
1 1 4
1 tan 1 .
3 3
0
t
I dx x dx t dt t
cos x cos x
Ví d
ụ 2:
Tính
12
0
tan4I xdx
Gi
ải:
Ta có:
12 12
0 0
sin4
tan4
4
x
xdx dx
cos x
Đặt t = cos4x ;
4s 4 sin4
4
dt
dt in xdx xdx
Đ
ổi cận:
x
0
12
t
1
1
2
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
20
Khi đó:
1
1
12 12 2
1
0 0 1
2
1
sin4 1 1 1 1
tan4 ln ln2.
1
4 4 4 4 4
2
x dt dt
I xdx dx t
cos x t t
Ví dụ 3: Tính
2
5
0
I cos xdx
Giải:
Ta có:
2 2 2
2
5 4 2
0 0 0
1 sincos xdx cos xcoxdx x coxdx
Đ
ặt t = sinx ;
dt cosxdx
Đ
ổi cận:
x
0
2
t
0
1
Khi đó:
3 5
2 2 2 2
2 2
5 2 2 2 4
0 0 0 0
1
2 8
1 sin 1 1 2 .
3 5 15
0
t t
I cos xdx x coxdx t dt t t dt t
Ví d
ụ 4:
Tính
4
3
0
tanI xdx
Gi
ải:
Đ
ặt t = tanx ;
2 2
2
1 tan 1
1
dt
dt x dx t dt dx
t
Đ
ổi cận:
x
0
4
t
0
1
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
21
Khi đó:
2
1 1 1 1 1
3 2
4
3
2 2 2 2
0 0 0 0 0 0
2
1
1
1 2 1
tan
2 2 2
1 1 1 1
0
1
1 1 1 1 1
ln 1 ln2 1 ln2 .
2 2 2 2 2
0
d t
t t t t
I xdx dt t dt tdt dt
t t t t
t
Ví dụ 5: Tính
2
3
6
I cos xdx
Gi
ải:
2 2 2 2
3 2 2 2
6 6 6 6
3
. 1 sin 1 sin sin
sin 1 1 1 5
2
sin 1
3 3 2 24 24
6
I cos xdx cos x cosxdx x cosxdx x d x
x
x
Ví dụ 7: Tính
4
4 4
0
sin4
sin
x
I dx
x cos x
Gi
ải:
4 4 4 4
4 4 4 4 2 2
2
0 0 0 0
4
2 2
2
0
sin4 2sin2 2 2sin2 2 2sin2 2
1
sin sin 1 2sin
1 sin 2
2
1 1 1 1
1 sin 2 ln 1 sin 2 ln ln2
4
1
2 2 2
1 sin 2
0
2
x xcos x xcos x xcos x
I dx dx dx dx
x cos x x cos x xcos x
x
d x x
x
Ví d
ụ 8:
Tính
3
2
4
1 sin
cos x
I dx
x
Gi
ải:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
22
2
3 2
2 2 2 2
4 4 4 4
2 2 2
4 4 4
1 sin
1 sin
1 sin 1 sin 1 sin
1 1 3 2 2
2
sin s 2 sin sin2
2 4 4
4
x
cos x cos x
I dx cosxdx cosxdx x cosxdx
x x x
cosx cosx x dx cosxdx in xdx x x
Ví d
ụ 9:
Tính
2
3
0
sinI xdx
Gi
ải:
3
2 2 2
3 2 2
0 0 0
1 2
sin sin sin 1 1
2
3 3 3
0
cos x
I xdx x xdx cos x d cosx cosx
Ví d
ụ 10:
Tính
2
0
1
dx
I
cosx
Gi
ải:
2 2 2
2 2
0 0 0
2
tan 1
2
1 2
2
0
2 2
x
d
dx dx x
I
x x
cosx
cos cos
Ví d
ụ 11:
Tính
2
4
1 sin2
dx
I
x
Gi
ải:
2 2 2 2
2 2
2
4 4 4 4
1
1 sin2 2
sin
2
4
4
1 1
2
tan
2 4 2
4
dx dx dx dx
I
x
x cosx
cos x
cos x
x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
23
Ví d
ụ 12:
Tính
2
3
sin
dx
I
x
Gi
ải:
Ta có:
2 2 2
2 2
3 3 3
sin sin
sin
sin 1 s
dx xdx xdx
x
x co x
Đ
ặt
sint cosx dt xdx
Đ
ổi cận:
x
3
2
t
1
2
0
Khi đó:
1 1
0
2 2
2 2
1
0 0
2
1 1
2 2
0 0
1 1 1
2 1 1
1 1
1
1 1 1 1 1 3
ln 1 ln 1 ln ln
2
2 1 2 1 2 2 2 2
0
dt dt
I dt
t t
t t
dt dt
t t
t t
1 1 1
ln ln3
2 3 2
D
ạng 2:
Tích phân d
ạng
Cách gi
ải:
Đ
ặt
tan
2
x
t
, đưa v
ề tích phân hữu tỉ
Ví d
ụ 1:
Tính tích phân
2
0
2cos sin 2
dx
x x
ĐS:
3
ln
2
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
24
Ví d
ụ 2
: Tính tích phân
2
0
3cos 2sin 2
dx
x x
ĐS:
1 5
ln
3 2
Ví d
ụ 3
: Tính tích phân
4
2
0
2cos 3sin2 2
dx
x x
ĐS:
1 4
ln
2 3
Ví d
ụ 4
: Tính tích phân
4
0
sin2 2
dx
x
ĐS:
3
18
Ví d
ụ 5
: Tính tích phân
4
0
1 2sin
2 cos
x
dx
x
ĐS:
2 3
2ln2
9
D
ạng 3
: Tích phân d
ạng
2 2
sin sin cos cos
dx
a x b x x c x
Cách gi
ải:
Cách 1: Đ
ặt
2
osc x
ở mẫu làm thừa số chung sau đó đ
ặt
tant x
Cách 2: h
ạ bậc
đưa v
ề dạng 2
Ví d
ụ 1:
Tính
3
6
sin sin
6
dx
I
x x
Gi
ải:
3 3 3
2
6 6 6
2
3sin sin
3 1
sin sin
sin sin
6
2 2
dx dx dx
I
x xcosx
x x
x x cosx
3 3 3
2 2
6 6 6
3
6
2 tan tan
2
2 3
s 3 tan tan tan 3 tan 1 3 tan 3 tan 1
1 1
2 3 tan
3 tan 3tan 1
d x d x
dx
co x x x x x x x
d x
x x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
25
3 3
6 6
3 tan 1
tan
3 3
2 2 2 ln tan 2 ln 3tan 1
tan
3 tan 1
6 6
1 3
2 ln 3 ln 2 ln4 ln2 2ln3 2ln2 ln
2
3
d x
d x
x x
x
x
Ví d
ụ 2
: Tính tích phân
4
2 2
0
sin 4 os
dx
x c x
ĐS:
1 1
ln
4 3
Ví d
ụ 3
: Tính tích phân
4
2 2
0
sin 4sin cos 3cos
dx
x x x x
ĐS:
1 3
ln
2 2
D
ạng 4:
Tích phân d
ạng
1 2
(sin )cos ; (cos )sinI f x xdx I f x xdx
A. Cách gi
ải:
Đối với
1
I
đặt
sint x
Đ
ối với
2
I
đ
ặt
ost c x
Ví dụ 1: Tính
2
5
0
sinI xcoxdx
Gi
ải:
Đặt t = sinx ;
dt cosxdx
Đ
ổi cận:
X
0
2
T
0
1
Khi đó:
1
2
5 5
0 0
1
sin
6
I xcoxdx t dt
.
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
26
Ví d
ụ 2:
Tính
2
2
0
sin 1I xcosx cosx dx
Giải:
Ta có:
2 2
2
2
0 0
2
2 3
0
sin 1 sin 1 2
2 .sin
I xcosx cosx dx xcosx cosx cos x dx
cosx cos x cos x xdx
Đ
ặt
sint cosx dt xdx
Đ
ổi cận:
x
0
2
t
1
0
Khi đó:
0 1
2 3 4
2 3 2 3
1 0
1
2 17
2 2
2 3 4 12
0
t t t
I t t t dt t t t dt
B. Các trư
ờng hợp đặt biệt:
1. Tích phân có d
ạng
sin .cos
m n
x xdx
v
ới
,m n
N
ếu m lẻ hoặc n lẻ thì đặt
t
hàm có ch
ứa mũ chẵn
Nếu m và n đều chẵn thì hạ bậc
Ví d
ụ 1:
Tính
2
3 3
0
sinI xcos xdx
Giải:
Đ
ặt t = sinx ;
dt cosxdx
Đ
ổi cận:
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
27
x
0
2
t
0
1
Khi đó:
1 1
4 6
2 2
3 3 3 2 3 2 3 5
0 0 0 0
1
1
sin sin 1 sin 1 .
4 6 12
0
t t
I xcos xdx x x cosxdx t t dt t t dt
Ví d
ụ 2:
Tính tích phân
2
2 3
0
sin cosx xdx
ĐS:
2
15
Ví d
ụ 3
: Tính tích phân
2
4 3
0
sin cosx xdx
ĐS:
2
35
Ví d
ụ 4
: Tính tích phân
2
2 4
0
sin cosx xdx
ĐS:
32
2. Tích phân dạng
1 1
sin os
; ; ,
os sin
m m
n n
x c x
I dx I dx m n
c x x
N
ếu m lẻ thì
1
2
cos ñoái vôùi I
sin ñoái vôùi I
ñaët t x
ñaët t x
N
ếu m và n đều chẵn và
o
m n
thì
đưa về tan và cot
o
m n
thì
đổi hàm ở tử
theo m
ẫu sau đó tách tích phân và hạ bậc
Nếu m chẵn và n lẻ thì dùng tích phân từng phần
Ví d
ụ 1:
Tính
3
2
2
6
s
cos x
I dx
in x
Gi
ải:
Đ
ặt t = sinx ;
dt cosxdx
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
28
Đ
ổi cận:
X
6
2
T
1
2
1
Khi đó:
1 1
3 2 2
2 2
2 2 2 2
1 1
6 6 2 2
1
(1 s ) 1 1 1 1
1 .
1
2
s s
2
cos x in x t
I dx cosxdx dt dt t
t
in x in x t t
Ví d
ụ 2
: Tính
3
3
2
0
sin
os
x
I dx
c x
ĐS:
1
2
Ví d
ụ 3
: Tính
3
3
5
0
sin
os
x
I dx
c x
ĐS:
9
4
Ví d
ụ 4
: Tính
2
4
4
0
sin
os
x
I dx
c x
ĐS:
1
3
Ví d
ụ 5
: Tính
2
3
3
0
sin
os
x
I dx
c x
. Hư
ớng dẫn:
3
sin
sin ,
cos
x
u x dv dx
x
ĐS:
1
3 ln 3 2
2
D
ạng 5: Tích phân chứa
tan ;cos ; cot ;sinx x dx x x dx
Cách gi
ải:
Đ
ổi về sin và cos
Đ
ặt t bằng
m
ột
hàm
ở mẫu
Ví dụ 1: Tính tích phân
3
0
tanx
1 cos
dx
x
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
29
Hư
ớng dẫn:
3 3
0 0
tanx sinx
1 cos
cos 1 cos
dx dx
x
x x
. Đ
ặt
cost x
ĐS:
3
ln
2
Ví d
ụ 2
: Tính tích phân
4
4
0
tanx
1 4cos
dx
x
Hư
ớng dẫn:
3
4 4
4
4 4
0 0
tanx sinx. os
1 4cos
os 1 4cos
c x
dx dx
x
c x x
. Đ
ặt
4
1 4cost x
ĐS:
1 8
ln
4 5
Ví dụ 3: Tính tích phân
3
4
sinx
os3
dx
c x
Hư
ớng dẫn:
3 3
2
4 4
sinx sinx
os3
osx 4cos 3
dx dx
c x
c x
ĐS:
1
ln2
6
D
ạng
6: Đ
ổi biến bất kì
Ví d
ụ 1
: Tính
2
2
sin
0
sin2
x
I e xdx
Gi
ải:
Đ
ặt t = sin
2
x ;
s 2dt in xdx
Đ
ổi cận:
x
0
2
t
0
1
Khi đó:
2
1
2
sin
0 0
1
sin2 1.
0
x t t
I e xdx e dt e e
Ví d
ụ 2:
Tính
2
2
0
sin2
1
x
I dx
cos x
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
30
Gi
ải:
Đặt t = 1 + cos
2
x ;
s 2 s 2dt in xdx in xdx dt
Đ
ổi cận:
X
0
2
T
2
1
Khi đó:
1 2
2
2
0 2 1
2
sin2
ln ln2.
1
1
x dt dt
I dx t
t t
cos x
Ví d
ụ 3:
Tính
2
4
sin
sin
x cosx
I dx
x cosx
Gi
ải:
2 2
4 4
sin
sin
2
ln sin ln 2
sin sin
4
d x cosx
x cosx
I dx x cosx
x cosx x cosx
Ví d
ụ 4:
Tính
4
2
0
sin4
1
x
I dx
cos x
Giải: Ta có:
4 4
2 2
0 0
sin4 2sin2 2
1 1
x xcos x
dx dx
cos x cos x
Đ
ặt
2
1 2sin sin2t cos x dt xcosxdx xdx
2 2
1 2 2 1 2 1 1 2 3cos x t cos x cos x t t
Đ
ổi cận:
x
0
4
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
31
t
2
3
2
Khi đó:
3 3
2
2 2
3
2 2
2
2
2 2 3
6 6
4 4 4 6ln
3
2
3 3 4
4 2 6 ln2 ln 2 6ln
2 2 3
t dt
I dt dt t t
t t t
Cách 2: S
ử dụng công thức hạ bậc, mẫu xuất hiện
3 os2c x
, đ
ặt
3 os2t c x
Ví d
ụ 5:
Tính
4
3
0
s2
sin 2
co x
I dx
x cosx
Gi
ải:
Ta có:
4 4
3 3
0 0
sin sin
s2
sin 2 sin 2
cosx x cosx x
co x
dx dx
x cosx x cosx
Đ
ặt
sin 2 sint cosx x dt cosx x dx
Đ
ổi cận:
x
0
4
t
2
2 2
Khi đó:
2 2 2 2
3 2 3 2
0 0
2
1 2 1 1 1 1 1 1
2 2
3 9
0
2 2 6 4 2
1 2 2 2 2 1 2 2 1 4 2 4 9 4 2 5
9 9 9
6 4 2
2 3 2 2 2 2 1 18 2 1 18 2 1
t
I dt dt
t
t t t t
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
32
Ví d
ụ 6:
Tính
4
0
s2
sin 2
co x
I dx
x cosx
Giải:
Ta có:
4 4
0 0
sin sin
s2
sin 2 sin 2
cosx x cosx x
co x
dx dx
x cosx x cosx
Đ
ặt
sin 2 sint cosx x dt cosx x dx
Đ
ổi cận:
x
0
4
t
2
2 2
Khi đó:
2 2 2 2
0 0
2
2
2 2
1 2ln 2 2 2ln 2 2 3 2ln3
0
3
2 1 2 ln3 ln 2 2 2 1 2ln
2 2
t
I dt dt t t
t t
Ví d
ụ 7
: Tính
2
3
2
0
sin2 1 sinI x x dx
Gi
ải:
Đ
ặt
2
1 sin 2sin sin2t x dt xcosxdx xdx
Đ
ổi cận:
x
0
2
t
1
2
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
33
Khi đó:
2
4
2
3
2 3
0 1
2
1 15
sin2 1 sin 4
4 4 4
1
t
I x x dx t dt
Ví d
ụ
8: Tính
4
0
1 tan
dx
I
x
Gi
ải:
Đặt
2
2 2 2
1
tan 1 tan
1 tan 1
dt dt
t x dt dx x dx dx
cos x x t
Đ
ổi cận:
x
0
4
t
0
1
Khi đó:
1 2 3
1 1
2 2
2 2
0 0
1 1 1
1 1 1 1 1
2 1 2 2
2 1
1 1
1 1 2 1
0 0 0
J J J
dt t dt tdt dt
I dt
t
t
t t
t t t
Tính:
1
1
0
1
1 1 ln2
ln 1
2 1 2 2
0
dt
J t
t
Tính:
2
1 1
2
2
2 2
0 0
1
1
1 1 1 ln2
ln 1
2 4 4 4
1 1
0
d t
tdt
J t
t t
Tính:
1
4
3
2
0 0
1 1
2 2 8
1
dt
J du
t
(v
ới t = tanu)
V
ậy
ln2 ln2 ln2
2 4 8 8 4
I
Ví d
ụ
9: Tính
4
2
12
1
sin
I dx
x cosx
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
34
Gi
ải:
4 4
2
2
12 12
1 1 1 1 3
4
cot
2 2 4 2
sin
sin
4
12
I dx dx x
x cosx
x
BÀI T
ẬP ÁP DỤNG:
Tính tích phân sau:
3
2
6
3
2
6
2
4
0
2
2
0
3 6 3
cos
1) : sin , :ln
sin 5sin 6
5 4 3
cos
:
sin 7sin 12
1 2sin 1
2) ( 2003) : ln2
1 sin2 2
sin2 4
3) ( 2006) : ln
3
4 cos
sin
4
. (
4
sin2 2 1 sin cos
x
dx HD Ñaët t x ÑS
x x
x
BTTT dx
x x
x
dx Khoái B ÑS
x
x
dx TN ÑS
x
x
dx K
x x x
4
0
2008)
4 3 2
: sin cos . :
4
hoái B
HD Ñaët t x x ÑS
4
6
0
tan 10 3 1
5) . ( 2008) : tan . : ln 2 3
cos2 27 2
x
dx Khoái A HD Ñaëtt x ÑS
x
2
2
2 2
0
sin2 2
6) (KhoáiA-2006). : 1 3sin x. :
3
cos 4sin
x
dx HD Ñaët t ÑS
x x
2
0
sin2 sin 34
7) (KhoáiA-2005). : 1 3cos . :
27
1 3cos
x x
dx HD Ñaët t x ÑS
x
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
35
2
0
sin2 .cos
8) (Khoái -2005). : 1 cos . : 2ln2 1
1 cos
x x
dx B HD Ñaët t x ÑS
x
2
3 2
0
2 2
3 2 5 2
0 0
9) os 1 os (Khoái A-2009). :
4
: os 1 os cos cos
c x c xdx ÑS
HD c x c xd x x dx
2
sin
0
10) cos cos . (Khoái D-2004). : 1
4
x
e x xdx ÑS e
3
2
2 2
4
sin2
11) . : 1 cos . : 5 3
cos 1 cos
xdx
HD Ñaët t x ÑS
x x
2
6 6
2
0 0
tan( )
tan 1 1 3
4
11) . . tan . :
os2x 2
(tanx+1)
x
x
dx HD I dx t x DS
c
/4
2
/4
sin
12.
1
x
dx
x x
Hư
ớng d
ẫn:
/4 /4 /4
2
1 2
2
/4 /4 /4
sin
1 sin sin
1
x
I dx x xdx x xdx I I
x x
Áp d
ụng hàm lẻ, đặt
x=-t thì
1
0I
, tích phân t
ừng phần
2
I
đư
ợc kết quả.
2
4 4
0
13) cos2 sin cosx x x dx
.
Hư
ớng dẫn:
2 2
2 2
0 0
1 1 1
cos2 1 sin 2 1 sin 2 sin2 0
2 2 2
I x x dx x d x
4
2
0
sin4 3
14) . : 2 6ln
4
2 sin
x
dx DS
x
.
www.VNMATH.com
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
36
Hư
ớng dẫn:
I =
4
0
4sin2 .cos2
3 cos2
x x
dx
x
. Đ
ặt: t = 3 + cos2x
dt = -2sin2xdx.
2
0
3sinx cos
15)
sinx cos 2
x
dx
x
.
Hư
ớng dẫn:
2
0
sinx cos 2 2 cos sinx 2
sinx cos 2
x x
I dx
x
2 2 2
0 0 0
cos sin
2 2 ... 2tan
2 8
sin cos 2
sin cos 2
x x
dx
dx dx
x x
x x
2
3 3
0 0
2
3 2
0
2
3 2
0
sin
16) sin .tan . :
cos
17) sin cos . : sin
: cos sin .
x
I x xdx HD I dx
x
x xdx HD Ñaët t x
BTTT x xdx
BÀI T
ẬP BỔ SUNG
Bài 1: Tính
3
2
0
sinx x
I dx
cos x
Gi
ải:
Ta có:
1 2
1 1 1
2 2 2
0 0 0
sin sin
I I
x x xdx x
I dx dx
cos x cos x cos x
Tính
3
1
2
0
xdx
I
cos x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
37
Đ
ặt
2
1
tan
u x
du dx
v x
dv dx
cos x
Áp d
ụng công thức tính tích phân từng phần ta được:
3 3 3 3
1
2
0 0 0 0
3 sin 3 3
tan tan ln
3 3
3 3 3
0 0
3 1
ln
3 2
d cosx
xdx x
I x x xdx dx cosx
cosx cosx
cos x
Tính
3 3
2
2 2
0 0
sin 1
2 1 1
3
0
d cosx
x
I dx
cosx
cos x cos x
V
ậy
3
ln2 1
3
I
Bài 2: Tính
2
2 2 2 2
0
sin
sin
xcosx
I dx
a cos x b x
Gi
ải:
Ta có:
2 2 2
2 2 2 2
2 2 2 2 2 2 2 2
0 0 0
sin sin sin
sin
1 sin sin sin
xcosx xcosx xcosx
I dx dx dx
a cos x b x
a x b x b a x a
Đ
ặt
2 2
2 2 2 2 2 2 2 2 2
2 2
2 2 sin
sin sin
sin
tdt b a xcosxdx
t b a x a t b a x a
tdt
xcosxdx
b a
Đ
ổi cận:
x
0
2
t
|a|
|b|
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
38
Khi đó:
2 2 2 2
2 2
1 1
.
b
a
b
b a
tdt
I t
a b
b a
a
t b a
b a
Bài 3: Tính
1
0
sinI xdx
Đặt
2t x dx td
Đ
ổi cận:
x
0
1
t
0
1
Khi đó:
1
0
2 sinI t tdt
Đ
ặt
sin
u t du dt
dv tdt v cosx
Áp d
ụng công thức tính tích phân từng phần ta được:
1
0
1 1 1
2 2 2 2 sin 2 sin1 1
0 0 0
I tcost costdt tcost t cos
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
39
VẤN Đ
Ề
4: TÍCH PHÂN CÓ CH
ỨA GIÁ TRỊ TUYỆT
Đ
ỐI
Phương pháp: Gi
ả sử ta cần tính tích phân sau:
( )
b
a
f x dx
Bư
ớc 1:
Tính nghi
ệm của phương trình
( ) 0f x
Bư
ớc 2:
Xét d
ấu
( )f x
trên đo
ạn
,a b
Bư
ớc 3:
D
ựa vào bảng xét dấu để bỏ dấu giá trị tuyệt đối và tính tích phân.
Chú ý: N
ếu phương trình
( ) 0f x
có d
ạng không mẫu mực thì ta dùng đạo hàm để xét dấu
( )f x
.
Ví d
ụ 1:
Tính tích phân sau:
2
0
1 .x x dx
ĐS: 1
Ví d
ụ 2:
Tính tích phân sau:
2
0
3 1
2
1
x
I x dx
x
ĐS:
1 8ln2 4ln3
Hư
ớng dẫn:
2
2
0
2 3
1
x x
I dx
x
Ví d
ụ 3:
Tính tích phân sau:
2
0
sinI x x dx
Hư
ớng dẫn:
2
2
0
Xeùt haøm soá ( ) sinx , 0
2
'( ) cos 1 0, 0; ( ) (0) 0 sinx 0, 0;
2 2
sinx 1
8
f x x x
f x x x f x f x x
I x dx
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
40
BÀI T
ẬP ÁP DỤNG:
Bài 1. Tính tích phân sau:
1
1
1 .
x
e dx
Hư
ớng dẫn:
1 0 1
1 1 0
1
1 1 1 . : 2
2
x x x
e dx e dx e dx ÑS e
Bài 2. Tính các tích phân sau:
5 1 4
2
4 2
3 1 1
1 3 3
3 2
1 0 0
) 2 2 ; ) ; ) 6 9
12
) 4 ; ) 2 4 ; ) 2
:
1 8 5 1 24 3 8
)8; ) ln ; ) ; )2 5 3 ; )4 ; )
14 45 3 ln2 15
x
x
a x x dx b dx c x x
x x
d x dx e dx f x x xdx
Ñaùp soá
a b c d e f
Bài 3. Tính các tích phân sau:
2
2
0 0 0
2
) sinx ; ) 2 2cos2 ) 1 sin2 ; ) 1 sinx
: )2; )4; )2 2; )4 2
a dx b xdx c xdx d dx
Ñaùp soá a b c d
Bài 4. Tính các tích phân sau:
1
1 0
1
) 2 2 : ; ) 1 sin2 : 2 2
ln2
x x
a dx ÑS b xdx ÑS
Bài 5. Tính tích phân:
2
2
0
I x x dx
( Kh
ối D
– 2004 )
Bài 6. Tính tích phân:
2
2
1 1
2
) log ) ln
e
e
a x dx b x dx
Bài 7. Tính tích phân
4
0
tan 2sin 3I x x x dx
Hư
ớng dẫn:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
41
2
2
2
Xeùt haøm ( ) tan 2sin 3 , vôùi 0 x
4
cos 1 2cos 1
'( ) 0, 0;
4
cos
( ) taêng treân 0; ( ) (0) 0
4
1 3
ln2 2 2
2 32
f x x x x
x x
f x
x
f x f x f
I
BÀI T
ẬP BỔ SUNG:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
42
V
ẤN
ĐỀ 5: TÍCH PHÂN HÀM HỮU TỈ
( )
, 0
Ta caàn phaûi chuù yù coâng th
A.Daïng1
öùc
:
ln
P x
I dx a
ax b
k k
dx ax b C
ax b a
Bài t
ập áp dụng: Tính các tích phân sau
3 4 4
2 3
1 2 3
2 2 2
1 5
) ; ) ; )
1 1 2 3
x x x
a I dx b I dx c I dx
x x x
2
( )
, 0B.Daïng2:
P x
I dx a
ax bx c
2
röôøng hôïp 1: ( ) coù hai nghieäm phaân bieätT f x ax bx c
BÀI T
ẬP ÁP DỤNG: Tính các tích phân sau
Bài 1. Tính tích phân sau:
1 4 4
1 2 3
2 2 2
0 3 3
3 1
) ; ) ; )
4 7 8 3 2
x
a I dx b I dx c I dx
x x x x x
Bài 2. Tính các tích phân sau:
5
3
2
3
3 2
x
dx
x x
Phương pháp:
- Khi b
ậc
đa thức
( ) 2P x
ta s
ử dụng ph
ương pháo hệ số bất địn
h
- Khi b
ậc đa thức
( ) 2P x
ta s
ử dụng phép chia đa thức để đưa tử số về đa thức có bậc <2
2
2
röôøng hôïp 2: ( ) coù nghieäm keùpT f x ax bx c x
Ta c
ần l
ưu ý công thức sau:
2
'( ) 1
( )
( )
u x
dx C
u x
u x
BÀI T
ẬP ÁP DỤNG:
Bài 1. Tính các tích phân sau:
1 2
2 2
0 1
1 4
) ; )
4 4 4 4 1
x
a dx b dx
x x x x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
43
Hư
ớng dẫn câu b)
2 1t x
Bài 2. Tính các tích phân sau:
1 1
2 3
2 2
0 0
3
) ; )
4 4 2 1
x x
a dx b dx
x x x x
Phương pháp: Đ
ể tránh phức tạp khi biến đổi ta thường đặt
t x
Trong hai câu trên, ta th
ấy bậc tử cao hơn bậc mẫu
nên ta có th
ể chia đa thức, sau đó đưa về
trương h
ợp trên.
2
röôøng hôïp 3: ( ) voâ nghieämT f x ax bx c
Ta c
ần lưu ý cách tính nguyên hàm
2 2
1
dx
x a
b
ằng cách đặt
tanx a t
BÀI T
ẬP ÁP DỤNG: Tính các nguyên hàm sau
2 1
2 2
0 0
1 1
4 2 3
2
0 0
3
1) ; : ; 2) ; :
2 6
2 2 1
1 3 8 3 4
3) ; : ; 4) ; :
2 4 6 27 9
4 3
1
dx dx
ÑS ÑS
x x x x
dx dx
ÑS ÑS
x x
x x
3 2
( )
.Da ,ïng: 0
P x
dx a
ax cx
C
bx d
1. Ña thöùc daïng :
3 2
( )f x ax bx cx d
coù moät nghieäm boäi ba
Ta caàn chuù yù coâng thöùc sau:
1
1 1 1
, chuù yù: , 0
1
m
n n n
dx C x x
x n x x
Ví duï: Tính caùc tích phaân sau
1
3 2
0
6 12 8
dx
x x x
Baøi taäp aùp duïng
Baøi 1. Tính caùc tích phaân sau:
4 5
3
3 3
2 3
) ; Höôùng daãn: Ñaët 1 )
1 1
x x
a dx t x b dx
x x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
44
Baøi 2. Tính caùc tích phaân sau:
4 1
2 4
3 3
2 0
4
) ; )
1 1
x x
a dx b dx
x x
2. Ña thöùc daïng :
3 2
( )f x ax bx cx d
coù hai nghieäm
Baøi toaùn môû ñaàu: Tính tích phaân
3
2
2
1
1 1
dx
x x
Höôùng daãn: Ñaët
3 4 4
2 2 3
2 3 3
1
2 3; 3 4
Luùc ñoù:
2 2
1 1
x t dx dt
x t x t
dx dt dt
t t t t
x x
Duøng phöông phaùp heä soá baát ñònh
2
3 2 2
1
1 2 2
2
2
At B C
A C t A B t B
t
t t t
Baøi taäp aùp duïng:
Baøi 1. Tính caùc tích phaân sau:
4 3
2
2 2
3 2
2 1
) ; )
2
1 2
x x
a dx b dx
x x
x x
Höôùng daãn:
2
2 2
)
2
1 2 1
x Ax B C
b
x
x x x
Baøi 2. Tính tích phaân sau
7
3
3 2
3
1
2
x
dx
x x x
3. Ña thöùc daïng :
3 2
( )f x ax bx cx d
coù ba nghieäm phaân bieät
Baøi toaùn môû ñaàu: Tính tích phaân
3
2
2
1
1
dx
x x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
45
Höôùng daãn:
2
1
1 1
1
A B C
x x x
x x
Baøi taäp aùp duïng:
Baøi 1. Tính caùc tích phaân sau:
6 5 5
2 3
2 2 2
3 3 3
1
) ; ) ; )
4 2 1 2 1
x x x
a dx b dx c dx
x x x x x x
Baøi 2. Tính tích phaân
5
3
2
3
2 1 4 4 5
x
dx
x x x
Höôùng daãn: Ñaët
2 1t x
3. Ña thöùc daïng :
3 2
( )f x ax bx cx d
coù moät nghieäm (khaùc boäi ba):
Cách gi
ải:
Bư
ớc 1:
Phân tích
3 2 2
ax bx cx d x Ax Bx C
Bư
ớc 2:
Đ
ồng nhất thức
1 1 1
2 2
( )
a b x c
P x
x
ax bx c Ax Bx C
Ví d
ụ 1:
Tính tích phân
3
2
3 2
0
2 8 10
3 3
x x
dx
x x x
Hư
ớng dẫn:
3 3
2
3 2 2
0 0
2 8 10 5 3 5 3 5
5ln 1 3 ln2
1 2
3 3 3
4 3
x x x
dx dx
x
x x x x
Ví d
ụ 2:
Tính tích phân
2
2
3 2
1
4 9 8
4 6 4
x x
dx
x x x
Hư
ớng dẫn:
2 2
2
3 2 2
1 1
4 9 8 3 1 4 1
3ln ln2
2 3 2
4 6 4 2 2
x x x
dx dx
x
x x x x x
Ví dụ 3: Tính tích phaân
0
3
1
1
1
I dx
x
Höôùng daãn:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
46
Cách 1:
0 0 1
3 2
2
1 1 1
1 1
1
1 1
1 1
A B
I dx dx dx
x
x x x
x x x
Cách 2: Ñaët
1x t
.
Luùc ñoù:
0 1 1 1
2 2
3
2 2 2
1 2 2 2
1 1 1 1 1
2 2 2
2 2 2 2 2
1 1 3 3 3
3
1
3 3 3 3 3 3
1 1 3 1 1 1 3 3
....
3 3 2 2
3 3 3 3
3 3
2 4
dt t t t t
I dx dt dt
x
t t t t t t t t t
t t dt
dt dt dt dt
t t
t t t t
t
Baøi taäp aùp duïng: Tính tích phân sau
1
3
0
1
3
3 2
0
3 3
:ln2
3
1
2 5 3
; :ln2
4
1
dx ÑS
x
x x
dx ÑS
x x x
D. Daïng
m
n
ax b
dx
cx d
, vaø moät soá kó thuaät nguyeân haøm
Caùch giaûi: Ñaët
t cx d
Ví duï 1: Tính tích phaân
3
1
2
0
2 1
1
x
dx
x
ÑS:
75
54ln2
2
Ví duï 2: Tính tích phaân
1
3
3
4
0
3 6
3 1
x
dx
x
ÑS:
805 8
ln2
8 3
1. Kó thuaät bieán ñoåi töû soá chöùa nghieäm cuûa maãu soá
Ví duï 1:
5 5
2 2
2 2
2 2
1
. Höôùngdaãn:
1 1
dx x x
I dx
x x x x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
47
Ví duï 2:
3 5
3 3
3 3
2 2
1
. Höôùngdaãn:
1 1
dx x x
I dx
x x x x
Ví duï 3:
2 2 2
4 4
5
4 4
1 1 1
1 1 1
. Höôùngdaãn:
5 5
5 5
1 1
dx dx x x
I I dx
x x
x x x x
Ví duï 4:
4 4
3 3 3
7 3
3 4 3 4
1 1 1
10
1
. Höôùngdaãn:
10
10
10 10
x x
dx dx
I I dx
x x
x x x x
2. Kó thuaät ñaët aån phuï vôùi tích phaân coù daïng
1
m
n
dx
x x
Caùch giaûi:
Böôùc 1: Nhaân töû soá vaø maãu soá cho
1n
x
Böôùc 2: Ñaët
n
t ax b
Ví duï 1: Tính tích phaân
2
2
1
1
dx
x x
. Höôùng daãn:
2 2
2 2 2
1 1
1 1
dx xdx
x x x x
. Ñaët
2
1t x
Ví duï 2: Tính tích phaân
2
4
1
4
dx
x x
. Höôùng daãn:
2 2 2
2
4
3 3 3
1 1 1
4
4 1 4 1
dx dx x dx
x x
x x x x
3. Kó thuaät bieán ñoåi töû soá coù chöùa ñaïo haøm maãu soá
Ví duï 1: Tính tích phaân sau:
3
4
2
1
x
dx
x
.
2
Höôùng daãn: Ñaët t x
Ví duï 2: Tính tích phaân sau:
2
2
4
1
1
.
1
x
K dx
x
2 2
2
2
2
2
1 1
2
1
1
1 1
Höôùng daãn:
1
1
2
x
K dx d x
x
x
x
x
x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
48
4. Kó thuaät tính tích phaân coù daïng
2
2 2
1 2
Ax C
Ax B x C Ax B x C
Caùch giaûi:
Böôùc 1: Chia caû töû caû maãu cho
2
x
Böôùc 2: Ñaët
C
t Ax
x
C
t Ax
x
ñöa veà tích phaân höõu tæ
Ví duï 1: Tính tích phaân:
2
2
2 2
1
1
1 2 1
x
dx
x x x x
ÑS:
1 12
ln
3 7
Ví duï 2: Tính tích phaân:
2 6
2
2
4
1
1
1
x
dx
x
ÑS:
1 35
ln
2 36
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
49
Ví duï 3:
2
2
4 2
2
2
2
1
1
1 1 1
. Höôùng daãn:
1
1
1
2
x
x
K dx K dx d x
x
x
x
x
x
x
Ví duï 4:
3 2
2
6 2 3
1
. Höôùng daãn: ( )
2
1 ( ) 1
x x
K dx K d x
x x
BÀI T
ẬP BỔ SUNG:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
50
VẤN Đ
Ề
6: TÍCH PHÂN M
ỘT SỐ HÀM
ĐẶC BIỆT
PHƯƠNG PHÁP:
D
ựa vào việc đán
h giá c
ận của tích phân và tính chất của hàm số dưới dấu tích phân ta có thể lựa
ch
ọn phép đặt ẩn phụ
. Ta thư
ờng gặp một số tính chất sau:
Tính ch
ất 1:
N
ếu hàm số
( )f x
liên t
ục và hàm lẻ trên
;a a
thì
( ) 0
a
a
f x dx
V
ậy, với tính chất trên ta thường lựa chọn cách đặt
x t
Ví d
ụ:
Tính tích phân
1
2
1
2
1
cos ln
1
x
I x dx
x
Tính ch
ất
2: N
ếu hàm số
( )f x
liên t
ục và hàm chẵn trên
;a a
thì
( ) 0
a
a
f x dx
Tương t
ự ta thường lựa chọn cách đặt
x t
Ví d
ụ:
Tính tích phân
1
4
2
1
sin
1
x x
I dx
x
Tính ch
ất
3: N
ếu hàm số
( )f x
liên t
ục trên
0;1
thì :
2 2
0 0
(sin ) (cos )f x dx f x dx
V
ới dạng này ta th
ường lựa chọn cách đặt
2
x t
. V
ới cách
đặt này ta dễ dàng
ch
ứng minh
đư
ợc
2
0
sin
,
4
sin cos
n
n n
x
dx n
x x
Ví d
ụ1:
Tính
2
0
sin
sin
x
I dx
x cosx
Gi
ải:
Đ
ặt
2
x t dx dt
Đ
ổi cận:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
51
x
0
2
t
2
0
Khi đó:
0
2 2
0 0
2
sin
2
s s
s sint s sin
sin
2 2
t
co t co x
I dt dt dx
co t co x x
t cos t
V
ậy
2 2
0 0
sin
2
2
2 4
sin
0
x cosx
I I I dx dx x I
x cosx
Ví d
ụ 2:
Tính
3
2
3 3
0
sin
sin
x
I dx
x cos x
Giải:
Đ
ặt
2
x t dx dt
Đ
ổi cận:
x
0
2
t
2
0
Khi đó:
3
0
3 3
2 2
3 3 3 3
3 3
0 0
2
sin
2
s s
s sin s sin
sin s
2 2
t
co t co x
I dt dt dx
co t t co x x
t co t
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
52
V
ậy
3 3
2 2
3 3
0 0
sin
2
2
2 4
sin
0
x cos x
I I I dx dx x I
x cos x
Ví d
ụ 3:
Tính
6
2
6 6
0
sin
sin
x
I dx
x cos x
Gi
ải:
Đ
ặt
2
x t dx dt
Đ
ổi cận:
x
0
2
t
2
0
Khi đó:
6
0
6 6
2 2
6 6 6 6
6 6
0 0
2
sin
2
s s
s sin s sin
sin s
2 2
t
co t co x
I dt dt dx
co t t co x x
t co t
V
ậy
6 6
2 2
6 6
0 0
sin
2
2
2 4
sin
0
x cos x
I I I dx dx x I
x cos x
Tính ch
ất
4: N
ếu
0,a
hàm s
ố
( )f x
là hàm s
ố ch
ẵn, liên tục trên
thì v
ới mọi số thực
, ta
có :
0
( )
( )
1
a a
x
a
f x
dx f x dx
a
.
Với dạng này ta thường lựa chọn cách đặt
x t
Ví d
ụ
1: Tính tích phân c
ủa hàm số sau:
1
4
1
1 2
x
x
dx
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
53
Ví d
ụ 2:
Tính tích phân:
6
4
4
1
x
tan x
I dx
e
Gi
ải:
Đ
ặt
x t dx dt
Đ
ổi cận:
x
4
4
t
4
4
Khi đó:
6 6 6 6 6
4 4 4 4 4
4 4 4 4 4
1 1 1 1 1
t t x
x t t t x
tan x tan t e tan t e tan t e tan x
I dx dt dt dt dx
e e e e e
Ta có:
6 6
4 4 4
6
4 4 4
4
4 2 2 2 2
4
1 1
1 1 1 1
x
x x
tan x e tan x
I I dx dx tan xdx
e e
tan x tan x tan x tan x tan x dx
5 3
4
4
26
5 3 15 2
|
tan x tan x
tanx x
Tính ch
ất
5: N
ếu hàm số
( )f x
liên t
ục trên
0;1
thì :
0 0
(sin ) (sin )
2
a
xf x dx f x dx
.
V
ới dạng này ta thường lựa chọn cách đặt
x t
Ví d
ụ:
Tính tích phân sau:
2
0
sin
1 cos
x x
dx
x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
54
Tính ch
ất
6: N
ếu hàm số
( )f x
liên t
ục trên
;a b
thì :
( ) ( )
2
b b
a a
f x dx f a b x dx
.
V
ới dạng này ta thường lựa chọn cách đặt
t a b x
Ví d
ụ :
Tính
2
0
1 sinx
ln
1+cosx
I dx
Gi
ải:
Đ
ặt
2
x t dx dt
Đ
ổi cận:
x
0
2
t
2
0
Khi đó:
0
2 2
0 0
2
1 sin
2
1 st 1 sx
ln ln ln
1+sint 1+sinx
1+cos
2
t
co co
I dt dt dx
t
V
ậy
2 2 2
0 0 0
2
0
1 1 s 1 1 s
2 ln ln ln . ln1
1 sinx 1 sx 1 sinx 1 sx
0 0 0
cosx inx cosx inx
I I I dx dx dx
co co
dx I
Ví d
ụ 2:
Tính
2
3
0
4sin
sin
x
I dx
x cosx
Gi
ải:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
55
Đ
ặt
2
x t dx dt
Đ
ổi cận:
x
0
2
t
2
0
Khi đó:
0
2 2
3 3 3
0 0
2
4sin
2
4 s 4 s
s sin s sin
sin s
2 2
t
co t co x
I dt dt dx
co t t co x x
t co t
2 2 2
3 3 2
0 0 0
2
2
0
4sin 4 s 4
2
sin sin sin
4
2tan 2 2 4 2
2
4
0
2
4
x co x
I I I dx dx dx
x cosx x cosx x cosx
dx x I
cos x
Tính ch
ất 7:
N
ếu
( )f x
liên t
ục trên
0;2 , 0a
thì
0 0
( ) ( ) (2 )
a a
f x dx f x f a x dx
V
ới tính chất trên ta thường đặt
2t a x
Ví d
ụ:
Tính tích phân
3
0
sin sin2 sin3x x xdx
Tính chất 8: N
ếu
( )f x
là hàm tu
ần hoàn chu kỳ T, xác định và liên tục trên
,
thì
( ) ( )
a T a T
a a
f x dx f x dx
V
ới tính chất trên ta thường đặt
t x T
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
56
Ví d
ụ:
Tính tích phân
2013
0
1 os2c xdx
BÀI T
ẬP ÁP DỤNG:
1
2004
-1
4
2
4 4
0
2
0 0
2
3
2
0 0
1) sin . . : 0
cos
2) . : . :
2 4
cos sin
sin4 sin
3) : . 4) : .
1 sin
4 4cos
sin
5) : . 6) cos : 2
4 cos
7)
x xdx Ñaët x t ÑS
x
dx HD Ñaët x t ÑS
x x
x x x
dx HD Ñaët x t dx HD Ñaët x t
x
x
x x
dx HD Ñaët x t x xdx HD Ñaët x t
x
2 4
0 0
1 sin
ln : . 8) ln 1 tan : .
1 cos 2 4
x
dx HD Ñaët x t x dx HD Ñaët x t
x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
57
BÀI T
ẬP BỔ SUNG
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
58
VẤN Đ
Ề
7: TÍCH PHÂN TỪNG PHẦN
D
ạng 1:
sin( )
( ). os( ). Trong ñoù ( ) laø ña thöùc baäc n
n n
x
x
P x c x P x
e
sin( )
Ñaët ( ) vaø cos( )
n
x
x
u P x dv x
e
Chú ý: Ch
ỉ số
(n) cho ta s
ố lần tích tích phân dạng này
D
ạng 2:
( ). ln( ).
n
P x x
Ñaët ln( ) vaø ( )
n
u x dv P x
Dạng 3:
os( ) hoaëc sin( )
b b
x b x b
a a
e c mx n dx e mx n dx
V
ới dạng này ta có thể chọn:
, os( ) hoaëc sin( )
os( ) hoaëc u sin( ) ,
x b
x b
u e dv c mx n dv mx n
u c mx n mx n dv e
Ghi nh
ớ :
Nh
ất
lô nhì đa tam lư
ợng
t
ứ
m
ũ
BÀI T
ẬP ÁP DỤNG
TÍCH PHÂN T
ỪNG PHẦN CƠ BẢN
Bài 1: Tính
1
2
0
x
I xe dx
Đ
ặt
2
2
1
2
x
x
du dx
u x
dv e dx
v e
Áp d
ụng công thức tính tích phân từng phần:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
59
1 1 1
2 2 2 2 2 2 2 2 2
0 0 0
2
1 1
1 1 1 1 1 1 1 1
2 1
2 2 2 4 2 4 2 4
0 0
1
4
x x x x x
I xe dx xe e dx e e d x e e e e
e
Bài 2: Tính
1
2
0
x
I x e dx
Đ
ặt
2
2
x
x
du xdx
u x
v e
dv e dx
Áp d
ụng công
th
ức tính tích phân từng phần:
1 1 1
2 2
0 0 0
1
2 2
0
x x x x
I x e dx x e xe dx e xe dx
Ti
ếp tục tính:
1
0
x
J xe dx
Đặt
x x
u x du dx
dv e dx v e
Áp d
ụng công thức tính tích phân từng phần:
1 1
0 0
1
1
0
x x x
J xe dx xe xe dx
V
ậy
2I e
Bài 3: Tính
1
3
0
3 1
x
I x e dx
Đ
ặt
3
3
3
3 1
1
3
x
x
du dx
u x
v e
dv e dx
Áp d
ụng công thức tính tích phân từng phần:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
60
1 1
3 3 3
0 0
1
3 3 3 3 3
3
0
1
1
3 1 3 1
3
0
1 1 1
1 1 1 1 2 5
3 1 3 1
3 3 3 3 3
0 0 0
x x x
x x x x x
I x e dx x e e dx
x e e d e x e e
e
Bài 4: Tính
1
4 1 ln
e
I x xdx
Đ
ặt
2
ln
4 1
2
dx
u x
du
x
dv x dx
v x x
Áp d
ụng công thức tính tích phân từng phần:
2 2 2 2
1 1
4 1 ln 2 ln 2 1 2 2
1 1
e e
e e
I x xdx x x x x dx e e x x e
Bài 5: Tính
2
0
cos
x
I e xdx
Đ
ặt
os sin
x x
u c x du xdx
dv e dx v e
Áp d
ụng công thức tính tích phân từng phần
1
2 2
0 0
cos sin
2
0
x x x
I
I e xdx e cosx e xdx
Tính
2
1
0
sin
x
I e xdx
Đ
ặt
sin
x x
u x du cosxdx
dv e dx v e
Áp dụng công thức tính tích phân từng phần
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
61
2 2
1
0 0
sin sin s sin
2 2
0 0
x x x x
I e xdx e x e co xdx e x I
Suy ra:
2
2
0
1 1
cos sin
2 2
2 2
0 0
x x x
e
I e xdx e cosx e x
BÀI T
ẬP CHUYỂN VỀ TÍCH PHÂN TỪNG PHẦN CƠ BẢN
Bài 1: Tính
2
2
0
sinI x xdx
Ta có:
2 2 2 2
2
0 0 0 0
1 2 1
sin 2
2 2
cos x
I x xdx x dx xdx xcos xdx
2 2
2
0
2
2 8
0
x
xdx
Tính
2
0
2xcos xdx
Đ
ặt
1
2
sin2
2
du dx
u x
dv cos xdx
v x
Áp d
ụng công thức tính tích phân từng phần:
2 2
0 0
1 1 2 1
2 sin2 sin2 0
2 2
2 2 4 2
0 0
cos x
xcos xdx x x xdx
V
ậy
2
2
2
0
4
sin
16
I x xdx
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
62
Bài 2: Tính
2
sin
0
sin2
x
I e xdx
Giải:
Ta có:
2 2
sin sin
0 0
sin2 2 sin
x x
I e xdx e xcosxdx
Đ
ặt
sint x dt cosxdx
Đ
ổi cận:
x
0
2
t
0
1
Khi đó:
1
2
sin
0 0
2 sin 2
x t
I e xcosxdx te dt
Đ
ặt
t t
u t du dt
dv e dt v e
Áp d
ụng công thức tính tích phân từng phần:
1 1
0 0
1 1 1
1
0 0 0
t t t t t
te dt te e dt te e
V
ậy I = 2
Bài 3: Tính
1
2
0
ln 1I x x dx
Đặt
2
1 2t x dt xdx
Đ
ổi cận:
x
0
1
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
63
t
1
2
Khi đó:
1 2
2
0 1
1
ln 1 ln
2
I x x dx tdt
Đ
ặt
ln
dx
u t
du
t
dv dt
v t
Áp d
ụng công thức tính tích phân từng phần:
2 2
1 1
2
ln ln 2ln2 1
1
tdt t t dt
V
ậy
1
2
0
1
ln 1 ln2
2
I x x dx
M
ỘT SỐ BÀI
T
ẬP DẠNG KHÁC CỦA TÍCH PHÂN TỪNG PHẦN
Bài 1: Tính
3
2
0
x
I dx
cos x
Đ
ặt
2
tan
co
u x
du dx
dx
v x
dv
s x
Áp d
ụng công thức tính tích phân từng phần:
3 3 3
4
2
0 0 0 0
3 sin 3
tan tan
3
3 3
0
3 3
ln ln2
3
3 3
0
d cosx
x x
I dx x x xdx dx
cosx cosx
cos x
cosx
Bài 2: Tính
2
6
ln sinI cosx x dx
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
64
Đặt
ln sin
sin
os
sin
cosx
u x
du dx
x
dv c dx
v x
Áp d
ụng công thức tính tích phân từng phần:
2 2
6 6
2 2 2
ln sin sin ln sin sin ln sin sin
6 6 6
1 1
ln 1
2 2
I cosx x dx x x cosxdx x x x
Bài 3: Tính
3
2
4
sin
xdx
I
x
Đ
ặt
2
cot
sin
u x
du dx
dx
v x
dv
x
Áp d
ụng công thức tính tích phân từng phần
3 3
2
4 4
9 4 3
1 1 3
3 3
cot cot . ln sin ln
3 36 2 2
sin
3
4 4
xdx
I x x xdx x
x
Bài 4: Tính
2
0
1 sin
.
1 osx
x
x
I e dx
c
Ta có:
2
1
2 2 2 2 2
2
0 0 0 0 0
1 sin sin 1 sin
. . .
1 osx 1 osx 1 osx 2 1 osx
cos
2
x x
x x x
I
I
x e dx x e dx x
I e dx e dx e dx
x
c c c c

Tính:
2
1
2
0
1
2
cos
2
x
e dx
I
x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
65
Đ
ặt
2
tan
2
2
x
x
u e
du e dx
dx
dv
x
v
x
cos
Áp d
ụng công thức tính tích phân từng phần
2 2 2
2
1
2
0 0 0
1
tan tan . tan .
2
2 2 2 2
cos
0
2
x
x x x
e dx x x x
I e e dx e e dx
x
Tính:
2 2 2
2
2
0 0 0
2sin co
sin
2 2
. . tan .
1 osx 2
2
2
x x x
x x
s
x x
I e dx e dx e dx
x
c
cos
V
ậy
2
I e
BÀI T
ẬP ÁP DỤNG:
Bài 1. Tính các tích phân sau:
1
4
3
1 0
3 1
) ln ; : ) ; :1
16
e
x
e
a x xdx ÑS b xe dx ÑS
Bài 2. Tính các tích phân sau:
2 2 2
2 3
0 0 0
) cos ; ) sin ; ) cos ;a x xdx b x xdx c x xdx
Hư
ớng dẫn và đáp số:
Trong bài 2,
ở các câu sau
đều sử dụng kết quả của câu trước.
3
) 1 ; )2 1 ; ) 3 6
2 2 8
a b c
Bài 3. Tính các tích phân sau:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
66
1
2
0
2
2
1
) ln 1 ; :ln 2 1 2 1
ln(1 ) 3
) ; : ln3 3ln2
2
a x x dx ÑS
x
b dx ÑS
x
Hư
ớng dẫn:
2
2
ln 1
ln 1
a)Ñaët ; )Ñaët
1
u x
u x x
b
dv dx
dv dx
x
Bài 4. Tính các tích phân sau:
2
1
2
3
1 0
3 2
1
4 1 3 1
) ln ; : 2 1 ) ln ; : ln3
9 1 8 2
ln 1 3
) ; :
4
4
e
e
x
a x xdx ÑS e b x dx ÑS
x
x
c dx ÑS
x e
Hư
ớng dẫn:
1 1
2 2
0 0
ln
1
a)Ñaët ; ) ln ln 1 ln 1
1
u x
x
b x dx x x x x dx
x
dv xdx
Bài 5. Tính các tích phân sau:
3
4
4
2
0
2
ln tan
3
) sinxln tan ; Höôùng daãn: : ln 3 ln tan
2 8
sin
ln cos
ln(cos ) 2
) ; Höôùng daãn: :ln 1
1
2 4
os
cos
u x
a x dx ÑS
dv xdx
u x
x
b dx ÑS
c x
dv dx
x
4
2
0
2
) ; : ln
4 2
os
x
c dx ÑS
c x
Bài 6. Tính các tích phân sau:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
67
0 2
2
2
8 1
0 1
2
3 0
63 1
) ln 1 ; :6 ln3 ) ln ; :
2 4 4
ln 1 1
) ; :4ln2 2 ) ln 1 ; : ln2
2
1
e
a x x dx ÑS b x xdx ÑS
x
c dx ÑS d x x dx ÑS
x
Hư
ớng dẫn:
2
, ) Ñaët 1 sau ñoù ñöa veà tính tích phaân töøng phaàn
ln
)
a c t x
u x
b Ñaët
dv xdx
Bài 7. Tính các tích phân sau:
3
2 2
2 2
1
2
1
2
2 2
0
ln ln3 1 9
) ; Höôùng daãn: ln , . : ln
20 2 5
1 1
ln 1
) ; HD: Ñaët ln 1 , . : 2 ln 2 1 1
1 1
x x x
a dx Ñaët u x dv dx ÑS
x x
x x x
x
c dx u x x dx ÑS
x x
Bài
8. Tính các tích phân sau:
2 2
2 2 2 2
0 0
2 4
2
2
0 0
3 2 1
) cos3 ; : ) sin : 1
13 8
3
) sin3 ; : )
10
cos
x x
x
e
a e xdx ÑS b e xdx ÑS e
e x
c e xdx ÑS d dx
x
Bài 9. Tính các tích phân sau:
4
2
0
4
3
3
6
sin
) . Höôùng daãn: taùch thaønh toång hai tích phaân thaønh phaàn
cos
sin
) .
sin
cos
cos
x x
a I dx
x
u x
x x
b I Ñaët
x
x
dv dx
x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
68
BÀI T
ẬP BỔ SUNG
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
69
VẤN Đ
Ề
8: ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG
D
ạng toán 1:
Tính đi
ện
tích hình ph
ẳng giới hạn bởi
( ): ( ), ( ) lieân tuïc treân ;
0(truïc hoaønh)
C y f x f x a b
y
x a
y b
đư
ợc tí
nh b
ởi công thức
( )
b
a
S f x dx
Phương pháp:
Ta c
ần phải tìm đầy đủ 4 đường như trên
Vì c
ần phải bỏ dấu trị tuyệt
đối nên ta có hai cách giải sau:
Cách 1: Phương pháp đ
ồ thị:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
70
Chú ý: N
ếu bài toán yêu cầu:
Tính đi
ện tích Hình phẳng giới
h
ạn bởi đò thị hàm số x=f(y)( liên
t
ục trên
đoạn [a,b]), trục tung và hai đường thẳng y=a,y=b.
Khi đó công th
ức tính diện tích là:
( )
b
a
S f y dy
BÀI T
ẬP ÁP DỤNG:
Bài 1.
a) Tính di
ện tích hình phẳng giới hạn bởi
2
( ): 4C y x
trục hoành và 2
đường thẳng
1; 1x x
.
b) Tính di
ện tích hình phẳng giới hạn bởi
2
( ): 4C y x
,
0y
và 2 đư
ờng thẳng
1, 3x x
.
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
71
Đáp s
ố:
22
) ; ) 4
3
a b
Bài 2. Tính di
ện tích h
ình ph
ẳng giới hạn bởi:
a) y=cosx+1, tr
ục hoành và hai đườn thẳn
g
0x
và
2
3
x
b)
3
1y x
, tr
ục hoà
nh, tr
ục tung và
đư
ờng thẳng
2x
Đáp s
ố:
3 2 7
) ; )
2 3 2
a b
Bài 3. Tính di
ện tích hình phẳng giới hạn bởi:
a) Đ
ồ thị hàm số
2
3 2y x x
và tr
ục hoành
b) Đ
ồ thị hàm số
3 2
2 2y x x x
và tr
ục hoành
Đáp s
ố:
1 37
) ; )
6 12
a b
Bài 4. Tính di
ện tích hình phẳn
g gi
ới hạn bởi đồ thị hàm số
1
x
y e
, tr
ục
hoành và hai đư
ờng
th
ẳng
ln3x
,
ln8x
Đáp s
ố:
3
)2 ln
2
a
Bài 5. Tính di
ện tích tam giác cong giới hạn bởi các đường
1x
;
x e
;
0y
;
ln
2 2
x
y
ĐS:
ln2
1
2 4
Bài 6. Tính di
ện tích hình phẳng giới hạn bởi đồ thị hàm số
2 2
2
ln ( 1)
1
x x
y
x
, tr
ục tung, trục
hoành và đư
ờng thẳng
1x e
Bài 7.
a) Tính diện tích hình phẳng giới hạn bởi đường cong
2
1y x x
, trục
Ox
và
1x
. ĐS:
1
2 2 1
3
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
72
b) Tính di
ện tích hình phẳng giới hạn bởi đường cong
1 ln x
y
x
, tr
ục
Ox
và
1x
,
x e
. ĐS:
2
2 2 1
3
Bài 8. Tính di
ện tích hình phẳng giới hạn bởi:
a)
2
2
, 0, 1, 2. : 2
x
y xe y x x ÑS e
e
b)
2 2
1
ln , 0, 1, . : 1
4
y x x y x x e ÑS e
Bài 9. Tính di
ện tích hình phẳng giới hạn bởi:
) ln( 1), 0, 0, 1
) ln( 1) truïc tung vaø hai ñöôøng thaúng -1 vaø 1
a y x y x x
b y x y y
Đáp s
ố:
)2ln2 1a
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
73
D
ạng
toán 2: Tính di
ện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), y=g(x) ( liên tục trên
đo
ạn [a;b]), 2 đường thẳng x=a, x=b.
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
74
Chú ý: N
ếu bài toán yêu cầu:
Tính đi
ện tích Hình phẳng giới hạn bởi đồ thị hàm số x=f(y),
x=g(y)( liên t
ục trên đoạn [a,b]), và hai đường thẳng y=a,y=b.
Khi đó công th
ức tính diện tích là:
( ) ( )
b
a
S f y g y dy
BÀI T
ẬP ÁP DỤNG:
Bài 1. Tính di
ện tích
hình ph
ẳng giới hạn bởi
3 2
1 2
( ): 3 ;( ): 4C y x x C y x
hai đư
ờng thẳng
x=-1;x=2. ĐS:
55
12
Bài 2.
a) Tính di
ện tích hình phẳng giới hạn bởi
2
1 2
( ): 4 ;( ): 2C y x C y x
b) Tính di
ện tích hình phẳng giới hạn bởi
1 2
( ): ln ;( ): lnC y x C y x
và x=e
ĐS:
27
) ; )2
6
a b
Bài 3. Tính di
ện tích hình phẳng giới hạn bởi các đường
c) Tính di
ện tích hình phẳng giới hạn bởi
2 2
1 2
( ): 2 ;( ): 4C y x x C y x x
d) Tính di
ện tích hình phẳng giới hạn bởi
1 2
( ): ( 1) ;( ): (1 )
x
C y e x C y e x
ĐS:
) 9; ) 1
2
e
a b
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
75
Bài 4. Cho hàm s
ố
2
2
1
x
y
x
. Tìm b sao cho di
ện tích hình phẳng giới hạn bởi (C) và các đường
th
ẳng y=1, x=0, x=b bằng
4
. ĐS:
1b
Bài 5. Tính di
ện tích hình phẳng giới hạn bởi các đư
ờng
y = 0; y =
2
(1 )
1
x x
x
.
Bài 6. Tính di
ện tích giới hạn bởi các đường:
2
( ): 0;( ): 2 0D x y C x x y
ĐS:
9
2
Bài 7. Tính di
ện tích hình phẳng giới hạn bởi các đường:
2
( ) : ;( ); sin 0D y x C y x x x
. ĐS:
2
Bài 8. Tính d
ện tích hình phẳng giới hạn bởi các đường
2
4 3y x x
và
3y x
Bài 9. Tính di
ện tích hình phẳng giới hạn bởi Parabon( P ):
2
4y x x
và đư
ờng thẳng
:d y x
Bài 10. Tính diện tích hình phẳng giới hạn bởi các đường:
2
4
4
x
y
và
2
4 2
x
y
Bài 11. Tính di
ện tích hình phẳng giới hạn bởi:
2
2
2
2
4
) 1 , , 0, 3. :
3
1
2 1
) ; 1 hai ñöôøng thaúng 0 vaø :
2 8 4
1
x
a y x x y x x ÑS
x
y
b x x y x x ÑS
y
Bài 10. Tính di
ện tich hình phẳng giới hạn bở
i
2
1 vaø y= 1y x x
Bài 11. Tính di
ện tich hình phẳng giới hạn bởi
2
4 3 vaø 1y x x y x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
76
BÀI T
ẬP BỔ SUNG
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
77
V
ẤN ĐỀ 9:
ỨNG DỤNG TÍCH PHÂN TÍNH TH
Ể TÍCH VẬT THỂ TRÒN XOAY
D
ạng toán 1
: Tính th
ể tích vật thể tròn xoay sinh bởi miền (D) giới hạn bởi y=f(x), x=a,x=b,
tr
ục hoành (y=0) quay
quanh tr
ục Ox
Phương pháp: Áp d
ụng công thức
2
( )
b
a
V f x dx
Chú ý:
Nếu đề toán yêu cầu : Tính thể tích vật thể tròn xoay sinh bởi miền (D) giới hạn bởi
x=f(y), y=a,y=b, tr
ục trục tung (x=0) quay quanh trục Oy
thì ta áp d
ụng công thức
2
( )
b
a
V f y dy
.
Trong m
ột số tr
ường hợp chúng ta cần tìm cận a, b thông qua việc thiết lập điều kiện
không âm cho hàm s
ố f(x) (hoặc f(y))
BÀI T
ẬP ÁP DỤNG:
Bài 1. Tính th
ể tích khối tròn xoay tạo thành khi :
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
78
a) Quay quanh tr
ục hoành một hình phẳng giới hạn bởi đồ thị hàm số
x
y e
, tr
ục hoành và
hai đư
ờng thẳng
0; 3x x
b) Quay quanh tr
ục tung một hình phẳng giới
h
ạn bởi đồ thị hàm số
2
3 , 0, 1y x x y
,
tr
ục hoành và hai đường thẳng
0; 3x x
ĐS:
6
) 1 ; )2
2
a e b
Bài 2. Tính th
ể tích khối tròn xoay tạo thành khi quay hình H quanh trục Ox, với
4 4
6 6
) 0; 1 os sin ; ;
2
) 0; os sin ; 0;
2
a H y y c x x x x
b H y y c x x x x
Hướng dẫn và đáp số:
Khi tính tích phân chú ý bi
ến đổi
4 4 2 2 6 6 2 2
sin os 1 2sin cos ; sin os 1 3sin cos ;x c x x x x c x x x
ĐS:
2
2
7 5
) ; )
8 16
a b
Bài 3. Tính th
ể tích khối tròn xoay tạo thành khi quay hình H quanh trục Ox, với
5
2
3
81
) 0; 3 ( 0); 0 . :
10
(5 3)
) 0; ln ; 1; :
27
a
a H y y ax x a y ÑS
e
b H y y x x x x e ÑS V
Bài 4. Tính th
ể tích khối tròn xoay
t
ạo thành khi quay quanh trục hoành một hình phẳng giới hạn
b
ởi
đ
ồ thị hàm số
sin , 0, 0,y x y x x
, tr
ục hoành và hai
đư
ờng thẳng
0; 3x x
ĐS:
2
2
Bài 5. Tính th
ể tích khối tròn xoay tạo thành khi quay quan
h tr
ục hoành một hình phẳng giới hạn
b
ởi đồ thị hàm số
a)
2
ln , 0, 2 : 2 ln2 1y x y x ÑS
.
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
79
b)
2
, 0, 1 : 1
4
x
y xe y x ÑS e
D
ạng toán 2 :
Tính th
ể tích vật thể tròn xoay sinh bởi miền (D) giới hạn bởi y=f(x), y=g(x),
x=a,x=b(a<b),f(x) và g(x) cùng d
ấu,
quayquanh tr
ụ
c Ox
Chú thích:
Phương pháp: Áp d
ụng công thức
2 2
( ) ( ) (3)
b
a
V f x g x dx
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
80
Chú ý: N
ếu đề toán yêu cầu
: Tính th
ể tích vật thể tròn xoay sinh bởi miền (D) giới hạn bởi
x=f(y),x=g(y), y=a,y=b, tr
ục tung (x=0) quay quanh trục Oy
thì ta áp d
ụng
công th
ức
2 2
( ) ( )
b
a
V f y g y dy
.
BÀI T
ẬP ÁP DỤNG:
Bài 1. Tính th
ể tích của
kh
ối tròn xoay khi quay hình phẳng xác định bởi
2 2
2
2
1
3
2
162
) , 3 . :
5
4
) ; 5 :9
56
) 2 , 1, quay quanh truïc Ox. :
15
) 2 , , quay quanh truïc Ox, :
5
480
) 2 1 , 0, 3, quay quanh truïc Oy. :
7
f) 1, 0 vaø hai tieáp tuye
a y x y x ÑS
b y y x ÑS
x
c y x y ÑS
d y x x y x ÑS
e y x x y ÑS
y x x
2
2
án vôùi 1 taïi ñieåm (1;2), quanh truïc Ox
8
:
15
1
g)y=lnx,y=0,x=e, quanh truïc Oy. :
2
y x
ÑS
e
ÑS
Bài 2. Tính th
ể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định
b
ởi
2 2
3 3
) , 0 vaø tieáp tuyeán vôùi ñöôøng y=x taïi ñieåm coù hoaønh ñoä x=1, quay quanh
truïc Oy
1
) 1, 0, 2 , quanh truïc Ox
a y x x
b y y y x
x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
81
2
c)y= 2 , 0 vaø x=3, quanh:
*Truïc Ox
*Truïc
x x y
Oy
2
1 1
3
1
0
3
1 3
2 2 2
0 0
HöôùngDaãnvaø ÑaùpSoá:
2 1
) . Phöông trình tieáp tuyeán laø y=
36 3 3
3 1
2 2 36
5
) 2ln2
3
18 59
)
5 6
59
: 1 1 1 1 9 1 1
6
x y
y
a x
V y dy y dy
b
c V vaVø
HD V y y dy y dy
Bài 3. Cho hình ph
ẳng (H) giới hạn bởi các đường :
; 0 ; 2.x y x y x
Tính th
ể tích khối tròn xoay tạo thành khi cho hình (H) quay quanh trục Oy.
Hư
ớng dẫn và đáp số:
Phương tr
ình
đ
ịnh tung độ giao điểm :
2
2 0
2
5 4 0
2
1
1
4 ( )
y
y y
y y
y
y
y
y l
Đư
ờng thẳng y = 2
– x c
ắt trục tung tại y = 2
Th
ể tích khối tròn xoay cần tìm : V = V
1
+ V
2
Trong đó V
1
=
2
1
2
0
( )
2
y
y dy
1
0
=
2
(đvtt)
V
2
3
2
2 2
2 2
1 1
1
( 2)
(2 ) ( 2) ( 2)
3
y
y dy y d y
=
3
(đvtt)
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
82
V =
5
( )
6
vtt
BÀI T
ẬP BỔ SUNG
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
83
M
ỘT SỐ BÀI TẬP CẦN LÀM TR
ƯỚC KHI THI
Bài 1. Tính tích phân:
1
5
2
0
1
x
dx
x
.
ĐS:
1 1
ln2
2 4
Bài 2. Tính các tích phân sau:
3
2
1
3
1
. ( 2009). : 2 ln 1
1
1
: Theâm löôïng vaø bôùt löôïng
1
x
x x
x
dx
Khoái D ÑS e e
e
e e dx
HD
e
Bài 3. Tính các tích phân sau:
2
1
ln 3 1
.(KhoáiB-2010) : ln . : ln
2 3
2 ln
e
x
dx HD Ñaët t x ÑS
x x
Bài 4. Tính các tích phân sau:
ln5
2
ln3
1 3
.(KhoáiB-2006) : . : ln
2
2 3
x
x x
dx HD Ñaët t e ÑS
e e
Bài 5. Tính
2
2
2
1
4
. : 2sin . : 3
3
x
I dx HD x t ÑS
x
Bài 6. Tính tích phân sau :
2
2
3
1
1 4
2
. :Chiacaû töû vaø maãu cho x . : ln
5
x
I dx HD ÑS
x x
Bài 7. Tính tích phân:
1
2
1
1 1
dx
x x
.
Hư
ớng dẫn:
1 1
2 2
2
2
1 1
1 1 1 1
... 1
2
1 1
x x x x
I dx dx
x
x x
Bài 8. Tính tích phân: I =
4
0
tan .ln(cos ) 2
. : cos . : 2 1 ln2
cos 2
x x
dx HD t x DS
x
.
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
84
Bài 9: Tính tích phân:
2
1
ln
ln
1 ln
e
x
I x dx
x x
Gi
ải:
2
1
ln
ln
1 ln
e
x
I x dx
x x
2
1 2
1 1
ln
ln
1 ln
e e
x
dx xdx I I
x x
Tính
1
1
ln
1 ln
e
x
I dx
x x
Đ
ặt
2
1 ln 1 2
dx
t x t lnx tdt
x
Đ
ổi cận:
x
1
e
t
1
2
Khi đó:
2
2 2
3
2
1
1 1 1
1
ln 4 2 2
2
2 2 1 2 1
3 3 3
1
1 ln
e
t tdt
x t
I dx t dt
t
x x
Tính
2
2
1
ln
e
I xdx
Đ
ặt
2
2lnx
du dx
u ln x
x
dv dx
v x
Áp d
ụng công thức tính tích phân từng phần
3 3
2 2
2
1 1 1
2
1
e e e
I I
e
I ln xdx xln x lnxdx e lnxdx
Tính
3
1
e
I lnxdx
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
85
Đặt
dx
u lnx
du
x
dv dx
v x
Áp d
ụng công thức tính tích phân từng ph
ần
3
1 1
1 1
1 1
e e
e e
I lnxdx xlnx dx e x e e
Suy ra:
2
2 3
1
2 2
e
I ln xdx e I e
V
ậy
1 2
4 2 2 2 2 2
2
3 3 3 3
I I I e e
Bài 10. Tính tích phân:
1
3 1 2
0
2
. : 3 1. :
3
x
e dx HD t x DS e
Bài 11: Tính tích phân:
3ln2
2
3
0
2
x
dx
I
e
Giải:
Ta có:
3ln2 3ln2
3
2 2
3
0 0
3 3
2
2
x
x x
x
dx e dx
I
e
e e
Đ
ặt
3 3 3
1
3
3
x x x
t e dt e dx dt e dx
Đ
ổi cận:
x
0
3ln2
t
1
2
Khi đó:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
86
3ln2 3ln2 2 2
3
2 2 3 2
3
0 0 1 1
3 3
1 1 1
3 3
4
4 2
2 2 2
2
2
x
x x
x
dx e dx dt
I
t
t
t t t
e
e e
2
1 1 1 1 1 1 1 1
3 2 3 2 4 3
4 4 4 4 8 4 6
2 2
1
ln t ln t ln ln ln
t
3 3 1
4 2 8
ln
Bài 12: Tính tích phân:
3
0
3
3 1 3
x
I dx
x x
Gi
ải:
Đ
ặt
2
1 1 2t x t x tdt dx
Đ
ổi cậ
n:
x
0
3
t
1
2
Khi đó:
3 2 2 2 2
2 3
2 2
0 1 1 1 1
3 4 2 8
2 2 6 6
1
3 2 3 2
3 1 3
x t t dt
I dx tdt dt t dt
t
t t t t
x x
2
2 2
3
6 6 1 6 3
2
1 1
t t ln t ln
Bài 13: Tính tích phân:
2
3
0
3 2cos
sin
sinx x
I dx
x cosx
Gi
ải:
Đ
ặt
2
x t dx dt
Đ
ổi cận:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
87
x
0
2
t
2
0
Khi đó:
0
2 2
3 3 3
0 0
2
3 2cos 3cos 2sin 3cos 2sin
sin s sin s s
sinx x t t x x
I dx dt dx
x cosx co t t co x inx
Suy ra: 2I = I + I =
2
3
0
3 2cos
sin
sinx x
dx
x cosx
+
2
3
0
3cos 2sin
s s
x x
dt
co x inx
=
2
2
0
s s
dx
co x inx
2
2
0
2
4
dx
cos x
2
2
0
4
1
2
4
d x
cos x
1
2
2 4
0
tan x
1. Vậy I =
1
2
.
Bài 14: Tính tích phân:
4
2
0
1
1 1 2
x
I dx
x
Gi
ải:
Đ
ặt
1 1 2 1
1 2
dx
t x dt dx t dt
x
và
2
2
2
t t
x
Đổi cận:
x
0
4
t
2
4
Khi đó:
2
4 4 4
3 2
2 2 2
0 2 2
2 2 1
1 1 1 3 4 2
2 2
1 1 2
t t t
x t t t
I dx dt dt
t t
x
4
2
2
1 4 2
3
2
t dt
t
t
2
4
1 2
3 4
2 2
2
t
t ln t
t
2ln2-
1
4
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
88
Bài 15: Tính tích phân:
1
2 3
0
s
1
x
I x inx dx
x
Gi
ải:
1
2 3
0
s
1
x
I x inx dx
x
1 1
2 3
1 2
0 0
s
1
x
x inx dx dx I I
x
Tính
1
2 3
1
0
sI x inx dx
Đ
ặt
3 2 2
3
3
dt
t x dt x dx x dx
Đ
ổi cận:
x
0
1
t
0
1
Khi đó:
1 1
2 3
1
0 0
1
s int
3
I x inx dx s dt
1
1 1
1 1
3 3
0
cost cos
Tính
1
2
0
1
x
I dx
x
Đặt
2
2t x t x tdt dx
Đ
ổi cận:
x
0
1
t
0
1
Khi đó:
1 1 1 1 1 1
2
2 3
2 2 2 2
0 0 0 0 0 0
1
1
2 2 1 2 2 2 2 2 2
1
1 1 1 1
0
x t dt dt
I dx dt dt dt t I
x
t t t t
Tính
1
3
2
0
1
dt
I
t
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
89
Đ
ặt
2 2
1 1t tanu dt tan u du u du
Đ
ổi cận:
x
0
1
t
0
4
Khi đó:
1
4
3
2
0 0
1
dt
I du
t
4
4
0
u
Suy ra:
2 3
2 2 2
2
I I
V
ậy:
1 7 1
1 1 2 1
3 2 3 3 2
I cos cos
Bài 16: Tính tích phân:
6
0
4
2
tan x
I dx
cos x
Gi
ải:
2
6 6
2
2
0 0
4
1
2
1
tan x
tan x
I dx dx
cos x
tan x
Đ
ặt
2
2
1
dx
t tanx dt tan x dx
cos x
Đ
ổi cận:
x
0
6
t
0
1
3
Khi đó:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
90
1 1
3 3
2
6 6
2 2 2
0 0 0 0
1
4
1 1
2
1 1 1
tan x
d t
tan x
I dx dx dx
cos x
tanx t t
1
1 1 3
3
1 2
0
t
Bài 17: Tính tích phân:
1
2
1
1 1
dx
I
x x
Gi
ả
i:
Đ
ặt
2
2 2 2 2 2
2
1 1 1
1 1 2 1 1
2 2
t
t x x t x x t tx x x x dx dt
t
t
Đ
ổi cận:
x
-1
1
t
2 1
2 1
Khi đó:
1 2 1 2 1 2 1 2 1
2 2
2
2
1
2 1 2 1 2 1 2 1
1 1 1 1
1 1
2 2
1 1 1
1 2 1 2 1 2
1
1 1
dx dt dt
t t
I dt dt
t t t
t t
x x
2 1 2 1
2
2 1 2 1
1 1 1 1 1
2 1 2 1
dt
dt
t t t
t
2 1 2 1
1 1 1
1 1 1
2 2
2 1 2 1
ln t ln t ln t
t
Bài 18: Tính tích phân:
Gi
ải:
4 4 4
1 2
2 2
4 4 4
sin
sin
1 1
sinx xdx
I dx xdx I I
x x x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
91
Tính
4
1
2
4
sin
1
xdx
I
x
Đ
ặt
x t dx dt
Đ
ổi cận:
x
4
4
t
4
4
Khi đó:
4 4 4
1
2 2 2
4 4 4
sin sin sin
1 1 1
xdx tdt xdx
I
x t x
Suy ra
1 1 1 1
2 0 0I I I I
Tính
4
2
4
sinI x xdx
Đ
ặt
u x du dx
dv sinxdx v cosx
Áp d
ụng công thức tính tích phân từng phần
4 4
2
4 2
2 2
4 4
sin s s s 2
4 4
4 4
I x xdx xco x co xdx inx
Suy ra:
1 2
2
2
4
I I I
Bài 19: Tính tích phân:
2
2
0
3 2
dx
I
cos x cosx
Gi
ải:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
92
2 2 2
1 2
2
0 0 0
1 2
3 2
dx dx dx
I I I
cosx cosx
cos x cosx
Tính
2 2
2
1
0
2
0 0
1
1
1 2 2
2
|
dx dx x
I tan
x
cosx
cos
Tính
2
2 2
2
2
0 0
1
2
2
3
2
x
tan
dx
I dx
x
cosx
tan
Đặt
2 2
3
3 1 1
2 2 2
x x
tan tant tan dx tan t dt
Đ
ổi cận:
x
0
2
t
0
6
Khi đó:
2
6
2 2
6
2
0
2
0 0 0
1
2 2
2
2
3 3 3 3
3
2
|
x
tan
dx
I dx dt t
x
cosx
tan
V
ậy:
1 2
1
3 3
I I I
Bài 20: Tính tích phân:
2
3
0
2
2
sin x
I dx
cosx
Giải:
Đ
ặt
2t cosx dt sinxdx
Đ
ổi cận:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
93
x
0
2
t
3
2
Khi đó:
2 3 3 3
2 2
3 3 3 3 2 3
0 0 3 2 2 2
2 2 2 1 1
2 2 2 2 2
2 2
sin x sinxcosx t t
I dx dx dt dt dt dt
t t t t
cosx cosx
Bài 21: Tính tích phân:
2
2
3
0
sin
sin x
I e xcos xdx
Gi
ải:
Đ
ặt
2
2t sin x dt cosxsinxdx
Đ
ổi cận:
x
0
2
t
0
1
Khi đó:
2 2
1 1 1
2 2
3 2
0 0 0 0 0
1 1 1
sin sin 1
2 2 2
sin x sin x t t t
I e xcos xdx e cos x xcosxdx e t dt e dt te dt
1
1
1
0
0
1 1 1 1 1
2 2 2 2 2
|
t t
e te dt e I
Tính
1
1
0
t
I te dt
Đ
ặt
t t
u t du dt
dv e dt v e
Áp d
ụng công thức tính tích phân từng phần
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
94
1 1
1 1
1
0 0
0 0
1 1
| |
t t t t
I te dt te e dt e e e e
V
ậy:
1
1 1 1 1
1
2 2 2 2
I e I e
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
95
D. PH
Ụ LỤC
PHƯƠNG PHÁP Đ
ẶT ẨN PHỤ KHÔNG LÀM THAY ĐỔI CẬN TÍCH PHÂN
Bài toán m
ở
đầu
: Tính tích phân I=
5
3
3 2
3
3 2x x dx
Khi g
ặp bài toán này, chắc chắn rằng tất cả các bạn
đều nghĩ cách khai triển biểu thức dưới dấu
tích phân đ
ể đưa về các tích
phân cơ b
ản để tính. Đó là một cách suy nghĩ thường hay gặp phải.
Nhưng b
ạn hãy thử làm xem sao, và hãy thử thay (x
3
-3x
2
+2)
3
b
ằng (x
3
-3x
2
+3)
7
, (x
3
-3x
2
+3)
9
....
r
ồi tính nhé!. Sau đó mời các bạn nghiên cứu lời giải sau:
L
ời giải:
Đ
ặt x=2
-t
3: 5
5: 3
dx dt
x t
x t
3 5 5
3 3 3
3 2 3 2 3 2
5 3 3
5
3
3 2
3
(2 ) 3(2 ) 2 3 2 3 2
3 2 2 0 0
I t t dt t t dt t t dt
x x dx I I I
Khi đ
ọc xong lời giải trên chắc chắn các bạn sẽ đặt câu hỏi :
T
ại sao lại đặt ẩn phụ như vậy?
Đ
ể
tìm câu tr
ả lời xin mời các bạn nghiên cứu tiếp bài toán
t
ổng quát
sau:
Bài toán t
ổng quát
: Cho f(x) là hàm l
ẻ,
liên t
ục trên [
-a; a].
Ch
ứng minh rằng
( ) 0
a
a
f x dx
Đây là m
ột bài tập khá quen thuộc với các bạn khi học tích phân và nhiều bạn đã biết cách giải.
Xong các b
ạn hãy xem kỹ lời giải sa
u đ
ể “ phát hiện” ra vấn
đ
ề.
L
ời giải: Đặt x=
-t
:
:
dx dt
x a t a
x a t a
( ) ( ) ( )
a a a
a a a
I f x dx f t dt f t dt
. Do f(x) là hàm l
ẻ nên f(
-x)=-f(x) do đó
( ) ( ) ( ) 2 0 0
a a a
a a a
I f t dt f t dt f x dx I I I
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
96
Qua 2 bài toán trên, đi
ểm chung của cách đặt ẩn phụ là gì?
Câu tr
ả lời là :
Đ
ặt ẩn phụ nh
ưng không làm thay đ
ổi cận của tích phân.
Cách đặt tổng quát khi gặp tích phân
( )
b
a
f x dx
mà không thay đ
ổi cận là
đ
ặt x=a+b
-t.
Bài toán m
ở
đầu
còn có cách gi
ải khác khá hay
để dẫn tới một “ suy nghĩ” mới như sau:
Đ
ặt x=1
-t
3: 4
5: 4
dx dt
x t
x t
4 4
3 3
3 2 3
4 4
(1 ) 3(1 ) 2 3I t t dt t t dt
.
S
ử dụng kết quả chứng minh của bài toán 2 ta được I=0 ( do f(t)=
-t
3
+3t là hàm s
ố lẻ).
Vậy “ suy nghĩ” mới ở đây là gì? Việc đặt ẩn phụ như vậy ta đã dẫn đến tích phân có cận “đối
x
ứng” . Trong trường hợp tổng quát để dẫn đến cận “ đối xứng” khi gặp
tích phân
( )
b
a
f x dx
các
b
ạn hãy
đặt
2
a b
x t
Bây gi
ờ chúng ta cùng vận dụng suy nghĩ đó để giải một số bài toán sau:
Bài toán 3: Tính tích phân
6 6
4
4
sin cos
6 1
x
x x
I dx
( Đ
ề thi đại học năm 2000).
L
ời giải:
Đ
ặt x=
-t
:
4 4
:
4 4
dx dt
x t
x t
( cách đ
ặt này đã không làm thay đổi cận của tích phân) .
Khi đó
6 6 6 6 6 6
4 4 4
4 4 4
sin ( ) cos ( ) sin cos sin cos
6 . 6 .
6 1 6 1 6 1
t x
t t x
t t t t x x
I dt dt dx
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
97
6 6 6 6
4 4 4
6 6
4 4 4
sin cos sin cos
2 6 . sin cos
6 1 6 1
x
x x
x x x x
I dx dx x x dx
4 4 4 4
2 2 2 2
4 4 4 4
3 3 5 3
1 3 in cos 1 in 2 1 in 2 4
4 4 8 8
s x x dx s x dx s x dx cos x dx
5 3 5
4
sin4
8 32 16
-
4
x
x
.
Chú ý: Bài toán 3 có dạng tổng quát sau: Nếu f(x) là hàm số liên tục, chẵn thì
( ) ( ) 1
( )
2
1 1
b b b
x
x x
b b b
f x f x
I dx a dx I f x dx
a a
.
Bài toán 4: Tính tích phân I =
2
0
sin
cos 4
x x
dx
x
Thông thường khi gặp tích phân trên, hầu hết các bạn đều nghĩ đến phương pháp tính tích phân
t
ừng phần. Xong các bạn hãy thử làm nh
ư t
h
ế và so sánh với lời giải sau:
Lời giải :
Đặt
0 :
: 0
dx dt
x t x t
x t
Khi đó
0
2 2 2 2
0 0 0
( )sin( ) ( )sin sin sin
cos ( ) 4 cos 4 cos 4 cos 4
t t t t t t t
I dt dt dt dt
t t t t
2 2 2
0 0 0
sin sin sin
cos 4 cos 4 cos 4
x x x x
dx dx dx I
x x x
2 2
0 0
sin sin
2
2
cos 4 cos 4
x x
I dx I dx
x x
Đ
ặt
0 : 1
: 1
sinxdx dt
cosx t x t
x t
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
98
1 1
2
1 1
1
2
ln
2 2 ( 2)( 2) 8 2
4
1
dt dt t
I
t t t
t
ln3
4
Chú ý: Bài toán 4 có th
ể tổng quát như sau:
Cho hàm s
ố f(x) liên tục và thoả mãn: f(a+b
-x) = f(x) .
Khi đó
( ) ( )
2
b b
a a
a b
xf x dx f x dx
( đ
ể chứng minh kết quả trên các bạn hãy đặt x= a+b
-t ).
Bài toán 5: Tính tích phân I =
2
1
1 1
xdx
x
( Đ
ề thi khối A n
ăm 2004)
V
ới bài toán trên, cách
đặt như thế nào để không thay đổi cận của tích phân.
L
ời giải:
Đ
ặt
1x t 1
Khi đó
2 2
2( 1)
hay x= 1 1: 1
2 : 2
dx t dt
x t
x t
x -1 = (t -1) (t -1)
( cách đ
ặt này
đ
ảm bảo cận không đổi !)
2
2 2 2
3 2
2
1 1 1
( 1) ( 1) 1
3 4 1 1
2 . 2 . 2 3 4 .
t t
t t t
dt dt t t dt
t t t
3 2
2
2 3 4 ln | |
3 2
1
t t
t t
5
2ln2
3
.
Chú ý: Bài toán 5 có th
ể tổng quát dạng
( )
b
a
p x
dx
mx n c
v
ới p(x) là đa thức chứa biến x; m,n,c
là các h
ằng số . Ta có thể đặt
t mx n c
ho
ặc
t mx n
đ
ều gi
ải
được.
Bài toán 6: Tính tích phân
3
2
0
sin
I
sin cos
x
dx
x x
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
99
L
ời giải:
Đ
ặt
0 :
2 2
: 0
2
dx dt
x t x t
x t
3
0
3 3
2 2
0 0
2
sin
2
s s
I
sin cos sin cos
sin cos
2 2
t
co t co x
dt dt dx J
t t x x
t t
3 3 3 3
2 2 2 2
0 0 0 0
sin s sin s
I+J (1 sin .cos )
sin cos sin cos sin cos
x co x x co x
dx dx dx x x dx
x x x x x x
2
0
1 1 1
(1 sin2 ) s2
2
2 4 2 2
0
x dx x co x
. V
ậy
1
1
4
2
I J
I
I J
Chú ý: Bài toán 6 có thể tổng quát thành các dạng sau:
n
m
2
n n
m m
0
sin sin
;
sin cos
sin cos
b
k
a
mx ax
dx
mx mx
ax ax
Qua 6 bài toán trên, tác gi
ả muốn các bạn học sinh có thêm một cách nhìn mới để tiếp cận với
phương pháp đ
ặt ẩn phụ trong tính tích phân. Rất mong nhận
được sự quan tâm trao đổi.
Cu
ối cùng mời các bạn
v
ận dụng vào một số bài tập sau:
Tính các tích phân:
1
1
0
4 3
3 1 2
x
I dx
x
1
2
3
2
1
lg 1I x x dx
1
2
3
1
3
I lg x 1000
2
x dx
2
2
4
2
cos .ln 1I x x x dx
2004
5
3 2
5
2000
6 16I x x dx
2
5
2 1
x 4 7 3
6
1
I e 6 16
n
x
x x dx
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
100
4
7
4
sin .sin2 .cos3
2 1
x
x x x
I dx
1
8
2
1
( 1)( 1)
x
dx
I
e x
2
9
2
sin .sin2 .cos5
1
x
x x x
I dx
e
3
10
6
( cot )I x tgx gx dx
11
2
0
sin
cos 1
x x
I dx
x
2
12
0
sin
sin cos
x
I dx
x x
2
13
0
cos sinI x x dx
2
14
3
0
4sin
sin cos
x
I dx
x x
SAI L
ẦM THƯỜNG GẶP TRONG TÍNH TÍCH
PHÂN
Trong đ
ề thi tốt nghiệp THPT, Đại học
, Cao đ
ẳng, THCN của hàng năm bài toán tích phân hầu
như không th
ể thiếu, bài toán về tích phân là một trong những bài toán khó vì nó cần đến sự áp
d
ụng l
inh ho
ạt của định nghĩa, các tính chất , các phương pháp tính của tích phân.
Chuyên đ
ề này hy vọng sẽ góp phần giúp các em học sinh hiểu sâu hơn và tránh được những sai
l
ầm th
ư
ờng mắc phải khi giải bài toán về tích phân.
- Đưa ra hệ thống lí thuyết, hệ thống các phương pháp giải.
- Bài t
ập ứng với từng dạng toán, và chỉ ra những lỗi thường mắc phải của học sinh.
Bài t
ập 1:
Tính tích phân sau I =
2
2
2
( 1)
dx
x
Gi
ải:
Hàm s
ố y =
2
1
( 1)x
không xác đ
ịnh tại x=
-1
2;2
suy ra hàm s
ố không liên tục trên
2;2
do đó tích phân trên không t
ồn tại.
Chuù yù: Nhiều học sinh thường mắc sai lầm như sau:
I =
2
2
2
( 1)
dx
x
=
2
2
2
( 1)
( 1)
d x
x
=-
1
1x
2
2
=-
1
3
-1 = -
4
3
Nguyên nhân sai l
ầm :
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
101
Hàm s
ố y =
2
1
( 1)x
không xác đ
ịnh tại x=
-1
2;2
suy ra hàm s
ố không liên tục trên
2;2
nên không s
ử dụng được công thức newtơn
– leibnitz như cách gi
ải trên.
Chú ý đối với học sinh:
Khi tính
( )
b
a
f x dx
c
ần chú ý xem hàm số y=f(x) có liên tục trên
;a b
không? n
ếu có thì áp
d
ụng phương pháp đã
h
ọc để tính tích phân đã cho còn nếu không thì kết luận ngay tích phân này
không t
ồn tại.
Bài 2 :Tính tích phân: I =
0
1 sin
dx
x
Gi
ải:
I =
0
1 sin
dx
x
=
0
2
0 0
2 4
2 4
1 cos cos
2 2 4
x
d
dx x
tg
x
x
= tg
2
4 4
tg
Sai l
ầm thư
ờng gặp: Đ
ặt t = tan
2
x
thì dx =
2
2
1
dt
t
;
1
1 sin x
=
2
2
1
(1 )
t
t
1 sin
dx
x
=
2
2
(1 )
dt
t
=
2
2( 1)t
d(t+1) =
2
1t
+ c
I =
0
1 sin
dx
x
=
2
tan 1
2
x
0
=
2
tan 1
2
-
2
tan0 1
do tan
2
không xác đ
ịnh nên tích phân trên không tồn tại
Nguyên nhân sai l
ầm:
Đ
ặt t = tan
2
x
x
0;
t
ại x =
thì tan
2
x
không có ngh
ĩa.
Chú ý đ
ối với học
sinh:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
102
Đ
ối với phương pháp đổi biến số khi đặt t = u(x) thì u(x) phải là một hàm số liên tục và có đạo
hàm liên t
ục trên
;a b
.
M
ột số bài tập tương tự:
Tính các tích phân sau
1/
0
sin
dx
x
2/
0
1 cos
dx
x
Bài 3: Tính I =
4
2
0
6 9x x
dx
Sai l
ầm thường gặp:
I =
4
2
0
6 9x x
dx =
2
4 4
2
4
0
0 0
3
1 9
3 3 3 4
2 2 2
x
x dx x d x
Nguyên nhân sai l
ầm:
Phép bi
ến đổi
2
3 3x x
v
ới x
0;4
là không tương đương.
L
ờ
i gi
ải đúng:
I =
4
2
0
6 9x x
dx
=
4 4 3 4
2
0 0 0 3
3 3 3 3 3 3 3x dx x d x x d x x d x
= -
2 2
3 4
0 3
3 3
9 1
5
2 2 2 2
x x
Chú ý đ
ối với học sinh
:
2
2
, 1,
n
n
f x f x n n N
I =
2
2
b
n
n
a
f x
b
a
f x dx
ta ph
ải xét dấu hàm số f
(x) trên
;a b
r
ồi dùng tính chất tích phân
tách I thành t
ổng các phân không chứa dấu giá trị tuyệt đối.
M
ột số bài tập tương tự:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
103
1/ I =
0
1 sin2x
dx ; 2/ I =
3
3 2
0
2x x x
dx
3/ I =
2
2
2
1
2
1
2x
x
dx 4/ I =
3
2 2
6
cot 2tg x g x
dx
Bài 4: Tính I =
0
2
1
2 2
dx
x x
Sai l
ầm thường gặp:
I =
0
0
1
2
1
1
arctan 1 arctan1 arctan0
4
1 1
d x
x
x
Nguyên nhân sai l
ầm :
Đáp s
ố của bài toán thì không sai. Nhưng
söû duïng coâng thöùc treân khoâng coù trong baûng nguyeân
haøm
L
ời giải đúng:
Đ
ặt x+1 = tant
2
1 tandx t dt
v
ới x=
-1 thì t = 0
v
ới x = 0 thì t =
4
Khi đó I =
2
4 4
4
0
0 0
1 tan
4
tan 1
t dt
dt t
t
Chú ý đối với học sinh:
Khi g
ặp tích phân dạng
2
1
1
b
a
dx
x
ta dùng phương pháp đổi biến số đặt t = tanx hoặc t = cotx
2
1
1
b
a
dx
x
thì
đặt x = sint hoặc x = cost
M
ột số bài tập tương tự
:
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
104
1/ I =
8
2
4
16x
dx
x
2/ I =
1
3
2
0
2 2 3
1
x x
dx
x
3/ I =
1
3
3
8
0
1
x dx
x
Bài 5: Tính :I =
1
3
4
2
0
1
x
dx
x
Suy lu
ận sai lầm:
Đ
ặt x= sint , dx = costdt
3 3
2
sin
cos
1
x t
dx dt
t
x
Đ
ổi cận: với x = 0 thì t = 0
v
ới x=
1
4
thì t = ?
Nguyên nhân sai l
ầm:
Khi g
ặp tích phân của hàm số có chứa
2
1 x
thì th
ường đặt x = sint nhưng đối với tích phân
này s
ẽ gặp khó khăn khi đổi cận cụ thể với x =
1
4
không tìm
được chính xác t = ?
L
ời giải đúng:
Đ
ặt t =
2
1 x
dt =
2
1
x
dx tdt xdx
x
Đ
ổi cận: với x = 0 thì t = 1; với x =
1
4
thì t =
15
4
I =
1
3
4
2
0
1
x
dx
x
=
15 15
2
15
3
4 4
2
4
1
1 1
1
15 15 15 2 33 15 2
1
3 4 192 3 192 3
t tdt
t
t dt t
t
Chú ý đ
ối với học sinh:
Khi g
ặp tích phân của hàm số có chứa
2
1 x
thì th
ường đặt x = sint
ho
ặc gặp tích phân của hàm số có chứa 1+x
2
thì
đặt x = tant nhưng cần chú ý đến cận của tích
phân đó n
ếu cận là giá trị lượng giác của góc đặc biệt thì mới làm được theo phương pháp này
còn nếu không thì phải nghĩ đến phương pháp khác.
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
105
M
ột số bài tập t
ương tự:
1/ tính I =
7
3
2
0
1
x
dx
x
2/tính I =
2
2
1
1
dx
x x
Bài 6: Tính I =
1
2
4
1
1
1
x
dx
x
Sai l
ầm th
ường
gaëp : I =
1 1
2
2
2
2
1 1
2
1
1
1
1
1
1
2
x
x
dx
x
x
x
x
Đ
ặt t = x+
2
1 1
1dt dx
x
x
Đ
ổi cận với x =
-1 thì t = -2 ; v
ới x=1 thì t=2;
I =
2
2
2
2
dt
t
=
2
2
1 1
( )
2 2
dt
t t
=(ln
2t
-ln
2t
)
2 2
2 2
2
ln
2
t
t
= ln
2 2 2 2 2 2
ln 2ln
2 2 2 2 2 2
Nguyên nhân sai l
ầm
:
2
2
4
2
2
1
1
1
1
1
x
x
x
x
x
là sai vì trong
1;1
ch
ứa x = 0 nên không thể chia cả
tử cả mẫu cho x = 0 được. Nhưng từ sai lầm này nếu các bạn thấy rằng x=0 không thuộc thuộc
t
ập xác
đ
ịnh thì cách làm như trên thật tuyệ
t v
ời.
L
ời giải đúng:
Xét hàm s
ố F(x) =
2
2
1 2 1
ln
2 2 2 1
x x
x x
( áp d
ụng phương pháp hệ số bất định )
F
’
(x) =
2 2
4
2
1 2 1 1
(ln )
1
2 2 2 1
x x x
x
x x
Do đó I =
1
2
4
1
1
1
x
dx
x
=
1
1
1
ln
2
2 2
2 2
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
106
Chú ý đ
ối với học sinh:
Khi tính tích phân c
ần chia cả tử cả mẫu của hàm số cho x cần để ý rằng
trong đo
ạn lấy tích phân phải không chứa điểm x = 0 .
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
107
Đ
Ề THI
ĐẠI HỌC TỪ 2009
-2012
NĂM 2012: Tính các tích phân sau
Bài 1. ĐH Kh
ối A
– 2012: I =
3
2
1
1 ln 1x
dx
x
. ĐS:
2 2
ln2 ln3
3 3
Bài 2. ĐH Kh
ối B
– 2012:
1
3
4 2
0
3 2
x
dx
x x
ĐS:
3
ln3 ln2
2
Bài 3. ĐH Kh
ối D
– 2012:
4
0
1 sin2I x x dx
ĐS:
2
1
32 4
Bài 4. CD Kh
ối A,B,D
-2012:
3
0
1
x
I dx
x
ĐS:
8
3
NĂM 2011: Tính các tích phân sau
Bài 1. ĐH Kh
ối A
– 2011: I =
4
0
sin ( 1)cos
sin cos
x x x x
dx
x x x
. ĐS:
2 2
ln( )
4 8 2
Bài 2. ĐH Kh
ối B
– 2011:
3
2
0
1 sin
os
x x
dx
c x
ĐS:
2 1 2 3
3 ln
3 2
2 3
Bài 3. ĐH Kh
ối D
– 2011:
4
0
4 1
2 1 2
x
I dx
x
ĐS:
34 3
10ln
3 5
Bài 4. CD Kh
ối A,B,D
-2011:
2
1
2 1
1
x
I dx
x x
ĐS:
ln3
NĂM 2010: Tính các tích phân sau
Bài 1. ĐH Kh
ối A
– 2010
1
2 2
0
2
1 2
x x
x
x e x e
I dx
e
ĐS:
1 1 1 2
ln
3 2 3
e
I
Bài 2. ĐH Kh
ối B
– 2010
2
1
ln
(2 ln )
e
x
I dx
x x
ĐS:
1 3
ln
3 2
I
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
108
Bài 3. ĐH Kh
ối D
– 2010
1
3
2 ln
e
I x xdx
x
ĐS:
2
2
2
e
I
Bài 4. CD Kh
ối A,B,D
-2010
1
0
2 1
1
x
I dx
x
ĐS:
2
2
2
e
I
NĂM 2009: Tính các tích phân sau
Bài 1. ĐH Kh
ối A
– 2009
2
3 2
0
(cos 1)cosI x xdx
ĐS:
8
15 4
I
Bài 2. ĐH Kh
ối B
– 2009
3
2
1
3 ln
( 1)
x
I dx
x
ĐS:
1 27
3 ln
4 16
I
Bài 3. ĐH Kh
ối D
– 2009
3
1
1
x
dx
I
e
ĐS:
2
ln 1 2e e
Bài 4. CD Kh
ối A,B,D
-2009
1
-2
0
x x
I e x e dx
ĐS:
1
2
e
LUY
ỆN THI ĐẠI HỌC
CH
ẤT LƯỢNG CAO
CHUYÊN Đ
Ề: TÍCH PH
ÂN
Gv: Ths.Tr
ần Đình Cư.
SĐT: 01234332133, 0978421673. TP HU
Ế
109
TÀI LI
ỆU THAM KHẢO
1. Đ
ậu Thế Cấp, Huỳnh Công Thái (2008),
Các k
ĩ thuật và ph
ương pháp tính tích phân
2. Ph
ạm Kim Chung (2008),
Bài gi
ảng tích phân
3. Tr
ần Đình Cư (2011),
Bài gi
ảng l
uy
ện thi cấp tốc chuyên đề tích phân.
4. Phan Huy Kh
ải (2008),
Nguyên hàm- Tích phân và
ứng dụng
5. Tr
ần Sĩ Tùng (2010),
Tuy
ển tập các bài toán tích phân
6. Toán hoc và tu
ổi trẻ
| 1/110
| | Tải xuống

Có thể bạn quan tâm:

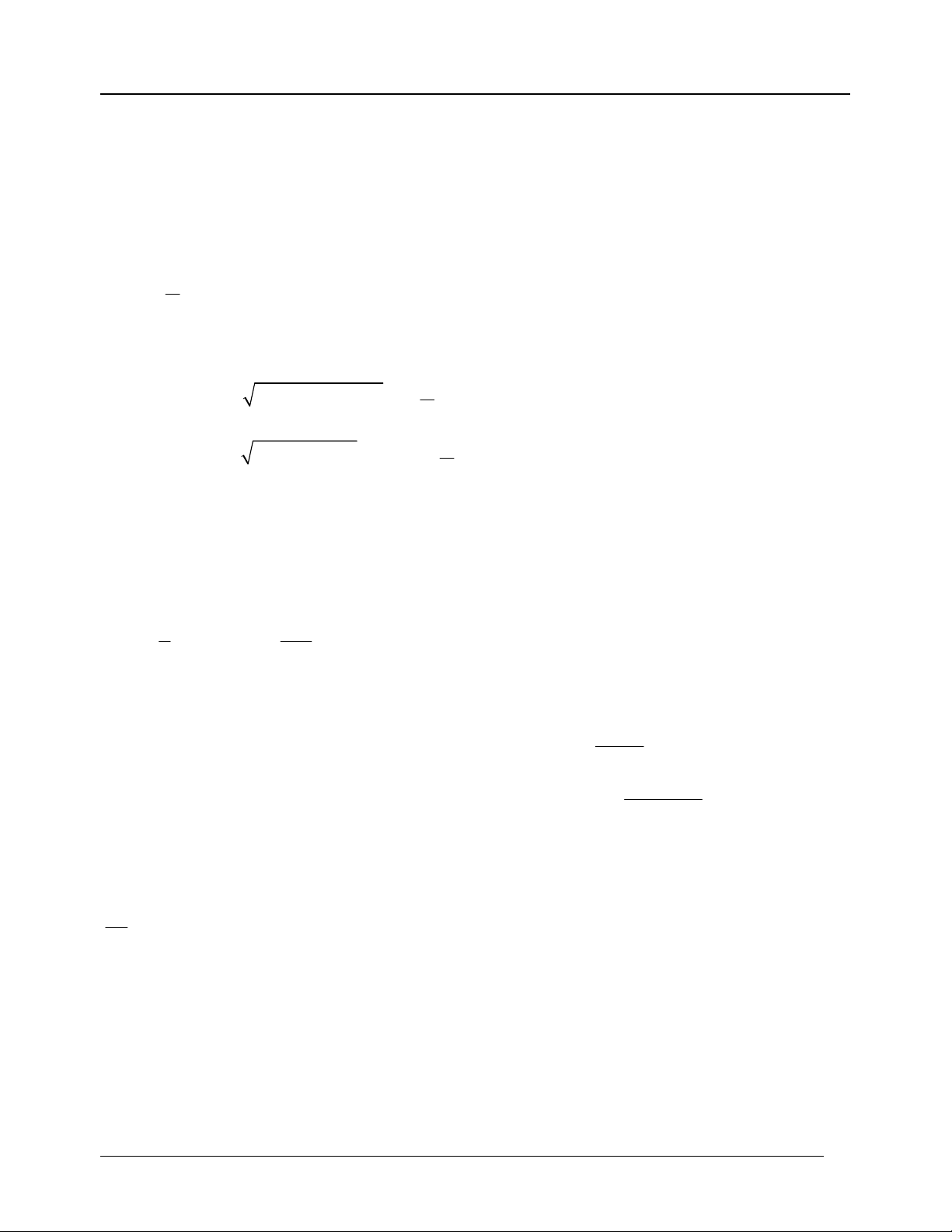
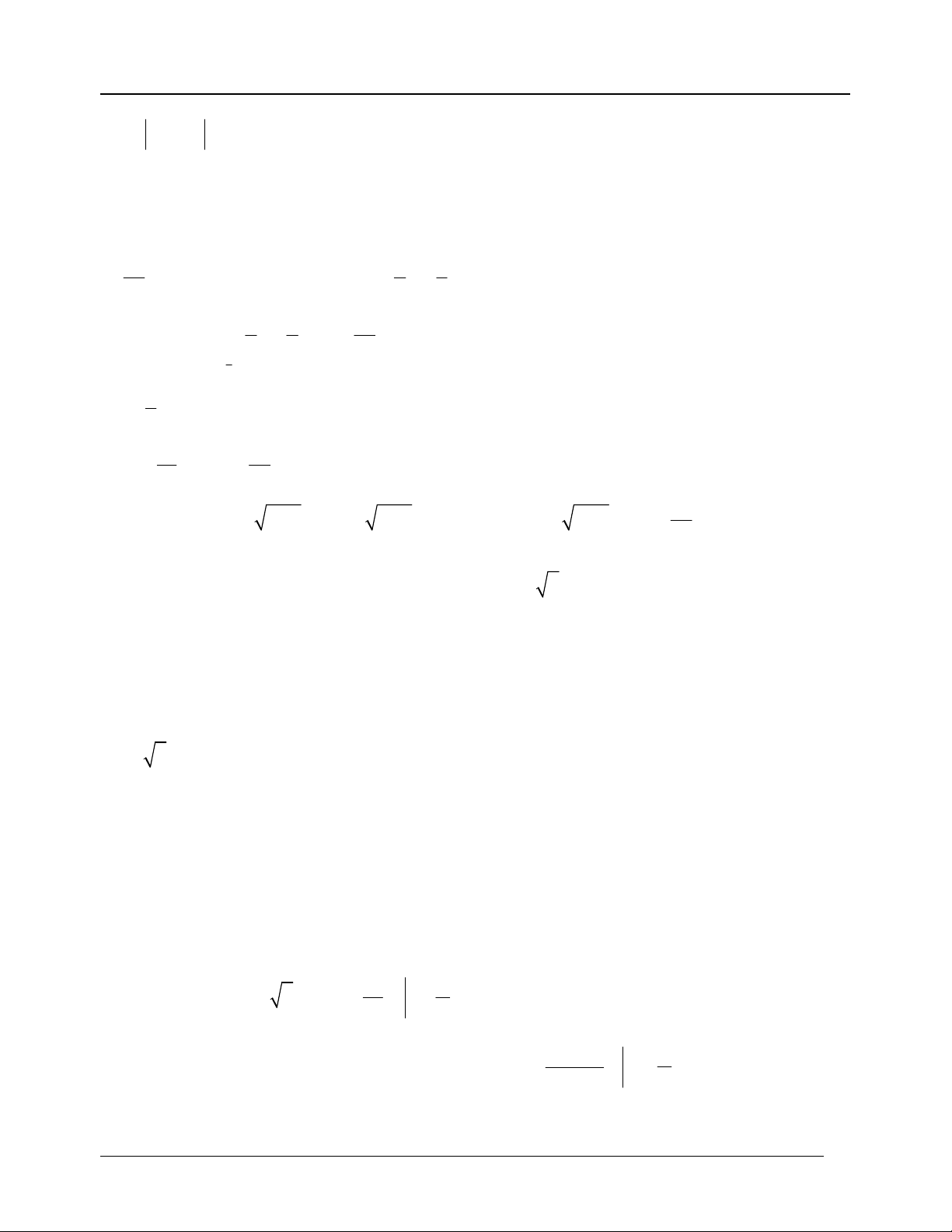
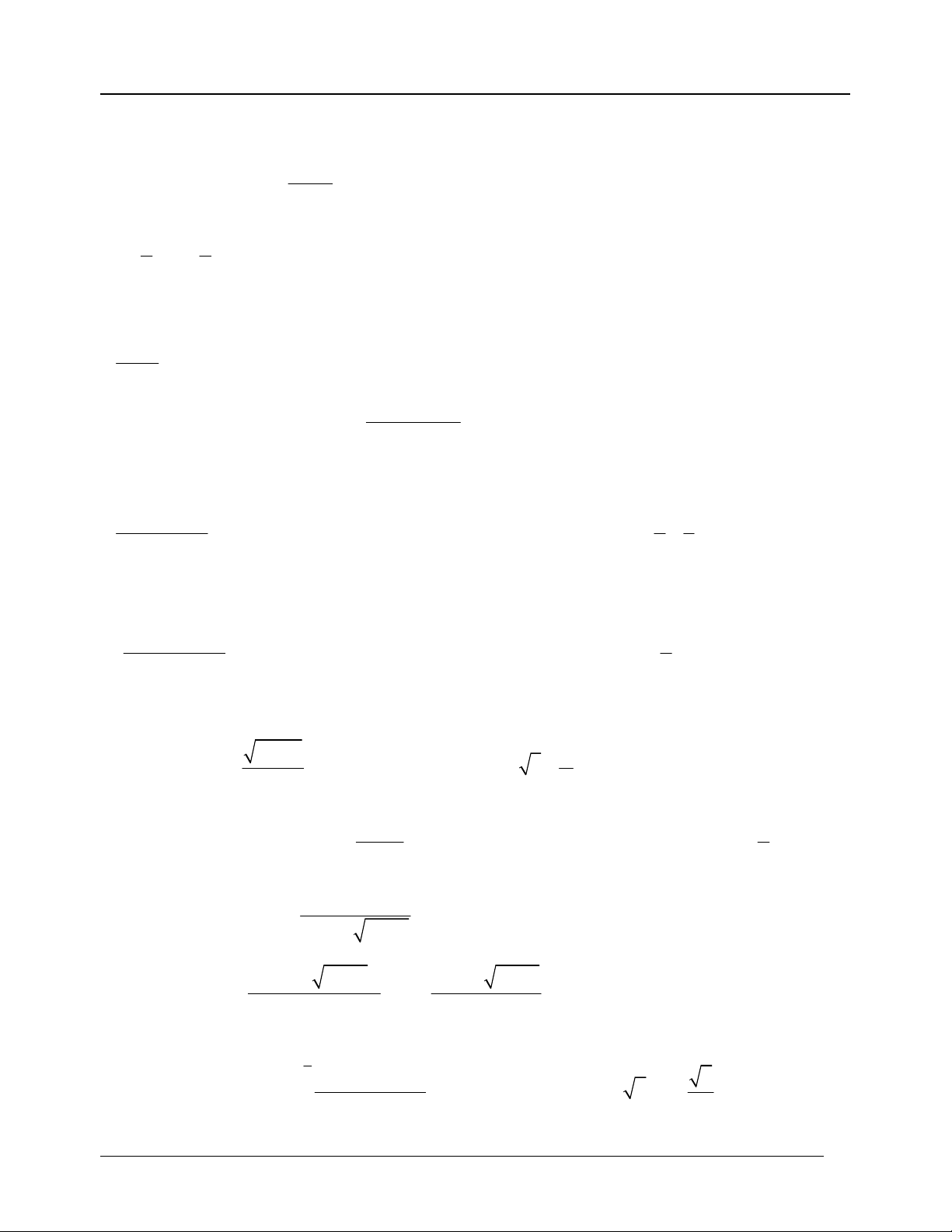
Preview text:

CHUYÊN ĐỀ LUYỆN THI TÍCH PHÂN
Dùng cho học sinh lớp 12-Ôn thi Đại học và Cao đẳng
Don't try to fix the students, fix ourselves first. The good teacher makes the poor
student good and the good student superior. When our students fail, we, as teachers, too, have failed. HUEÁ, 01/2013
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN MỤC LỤC Trang
A. NGUYÊN HÀM. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
B. TÍCH PHÂN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
C. PHÂN LOẠI VÀ PHƯƠNG PHÁP TÍNH TÍCH PHÂN: . . . . . . . . . . . . . . . . . . . . . . . . . . 6
VẤN ĐỀ 1: PHÉP THAY BIẾN n
t f (x) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6
VẤN ĐÊ 2: TÍCH PHÂN BẰNG PHƯƠNG PHÁP LƯỢNG GIÁC HÓA . . . . . . . . . . . . 11 DẠNG 1: 2 2
a x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 DẠNG 2: 2 2
x a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 DẠNG 3: 2 2
x a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 a x a x DẠNG 4: hoaëc
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 a x a x
VẤN ĐỀ 3: TÍCH PHÂN LƯỢNG GI ÁC. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Dạng 1: Biến đổi lượng giác về tích phân cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 dx
Dạng 2: Tích phân dạng
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
asin x b cos x c dx
Dạng 3: Tích phân dạng
. . . . . . . . . . . . . . . . . . . . . . . . 24 2 2
asin x bsin x cos x c cos x
Dạng 4: Tích phân dạng I f (sin x)cos xdx; I f (cos x)sin xdx 1  2  . . . . . . . . . . . . . . 25
1.Tích phân có dạng sinm .cosn x xdx
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 sinm x cosmx
2.Tích phân dạng I dx; I dx; m,n     1  n 1 
 . . . . . . . . . . . . . . . . . 27 cos x sinn x
Dạng 5: Tích phân chứa tan x;cos xdx; cot x;sin xdx  
. . . . . . . . . . . . . . . . . . . . . . 28
Dạng 6: Đổi biến bất kì . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
VẤN ĐỀ 4: TÍCH PHÂN CÓ CHỨA GIÁ TRỊ TUYỆT ĐỐI . . . . . . . . . . . . . . . . . . . . . 39
VẤN ĐỀ 5: TÍCH PHÂN HÀM HỮU TỈ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
VẤN ĐỀ 6: TÍCH PHÂN MỘT SỐ HÀM ĐẶC BIỆT . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
VẤN ĐỀ 7: TÍCH PHÂN TỪNG PHẦN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
VẤN ĐỀ 8: ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG. . . . . . . . . . . 69
VẤN ĐỀ 9: TÍNH THỂ TÍCH VẬT THỂ TRÒN XOAY . . . . . . . . . . . . . . . . . . . . . . . . . 77
MỘT SỐ BÀI TẬP CẦN LÀM TRƯỚC KHI THI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
D. PHỤ LỤC. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95 1
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
PHƯƠNG PHÁP ĐẶT ẨN PHỤ KHÔNG LÀM THAYĐỔI CẬN TÍCH PHÂN. . . . . . . . . 95
SAI LẦM THƯỜNG GẶP TRONG TÍNH TÍCH PHÂN . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
ĐỀ THI ĐẠI HỌ C TỪ 2009-2012 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
TÀI LIỆU THAM KHẢO. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109 2
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN A. NGUYÊN HÀM
1. Khái niệm nguyên hàm
 Cho hàm số f xác định trên K. Hàm số F đgl nguyên hàm của f trên K nếu:
F '(x)  f (x) , x  K
 Nếu F(x) là một nguyên hàm của f(x) trên K thì họ nguyên hàm của f(x) trên K là:
f (x)dx F(x)  C  , C  R.
 Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K. 2. Tính chất
f '(x)dx f (x)  C
  f (x)  g(x)dx f (x)dx g(x)dx   
kf (x)dx k f (x)dx (k  0)  
3. Nguyên hàm của một số hàm số thường gặp  0dx Cxx a a dx
C (0  a  1) 
dx x C  ln a
 cos xdx  sin x C1  xx dx
C, ( 1)  1
 sin xdx   cos x C  1 1 
dx  ln x C  
dx  tan x C x  2 cos xx x
e dx e C  1 
dx   cot x C  2 sin x   1 cos(ax axb 1
b)dx  sin(ax b)  C (a  0)  axb e dx eC, (a  0) aa  1 1 1 
dx  ln ax b C
sin(ax b)dx   cos(ax b)  C (a  0)  ax b a a
4. Phương pháp tính nguyên hàm
a) Phương pháp đổi biến số 3
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Nếu f (u)du F(u)  C
và u u(x) có đạo hàm liên tục thì:
f u(x).u'(x)dx Fu(x)  C
b) Phương pháp tính nguyên hàm từng phần
Nếu u, v là hai hàm số có đạo hàm liên tục trên K thì: udv uv vdu   B. TÍCH PHÂN
1. Khái niệm tích phân
 Cho hàm số f liên tục trên K và a, b K. Nếu F là một nguyên hàm của f trên K thì: b
F(b) – F(a) đgl tích phân của f từ a đến b và kí hiệu là f (x)dx  . a
b f(x)dx F(b)F(a) a
 Đối với biến số lấy tích phân, ta có thể chọn bất kì một chữ khác thay cho x, tức là: b b b
f (x)dx f (t)dt f (u)du  ...  F(b)  F(a)    a a a
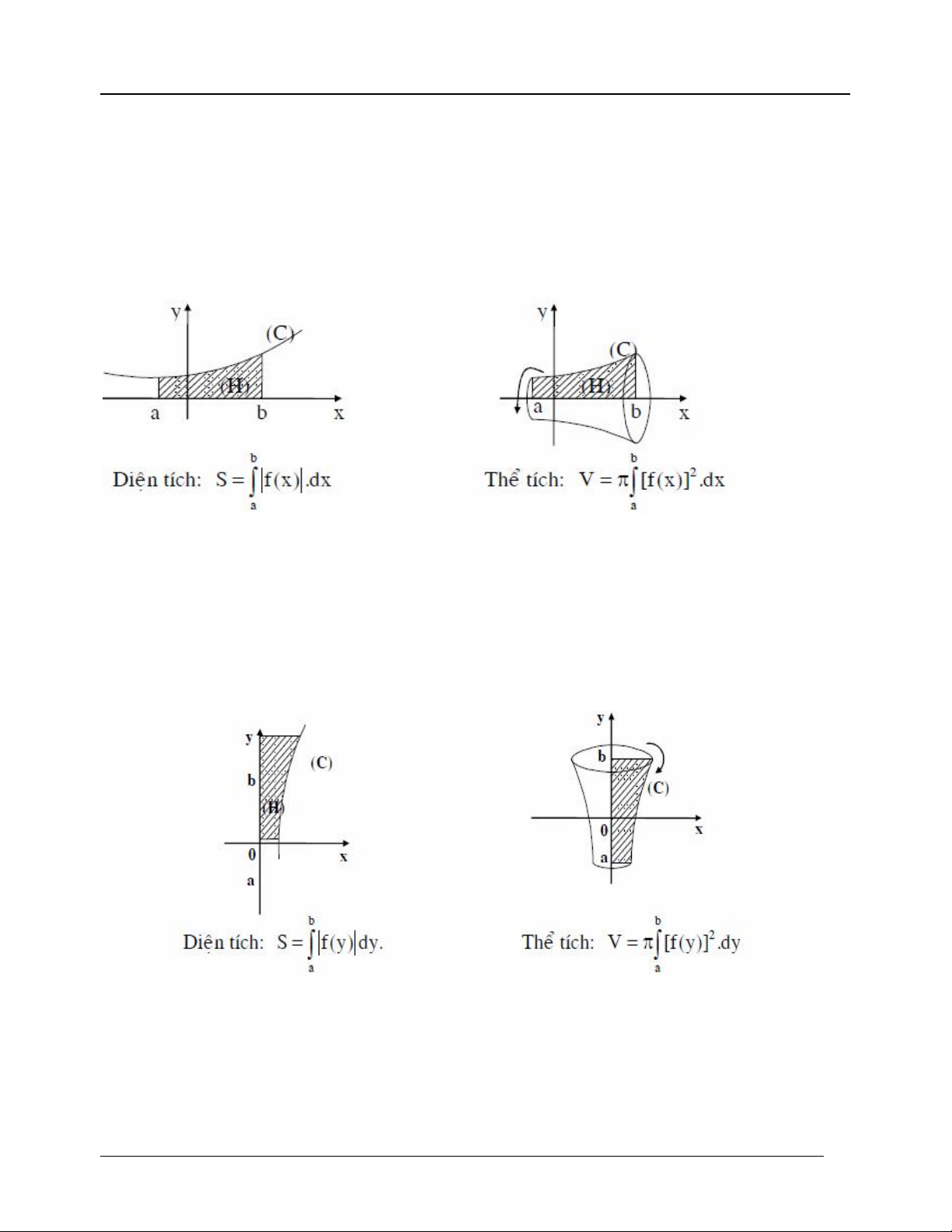
Ý nghĩa hình học: Nếu hàm số y = f(x) liên tục và không âm trên đoạn [a; b] thì diện tích S của
hình thang cong giới hạn bởi đồ thị của y = f(x), trục Ox và hai đườn g thẳng x = a, x = b là: b
S f (x)dxa
2. Tính chất của tích phân 0 b a
f (x)dx  0 
f (x)dx   f (x)dx   0 a b b b
kf (x)dx k f (x)dx   (k: const) a a b b b b c b
  f (x)  (
g x)dx f (x)dx  ( g x)dx   
f (x)dx f (x)dx f (x)dx    a a a a a c 4
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN b
 Nếu f(x)  0 trên [a; b] thì f (x)dx  0 a b b
 Nếu f(x)  g(x) trên [a; b] thì f (x)dx g(x)dx   a a
3. Phương pháp tính tích phân
a) Phương pháp đổi biến số b f u b u(x) ( )
.u'(x)dx f (u)du   a u(a)
trong đó: u = u(x) có đạo hàm liên tục trên K, y = f(u) liên tục và hàm hợp f[u(x)] xác định trên
K, a, b K.
b) Phương pháp tích phân từng phần
Nếu u, v là hai hàm số có đạo hàm liên tục trên K, a, b  K thì: b b b
udv uv vdu   a a a Chú ý:
Cần xem lại các phương pháp tìm nguyên hàm. b b
 Trong phương pháp tích phân từng phần, ta cần chọn sao cho vdu  dễ tính hơn udv  . a a
Trong phần sau sẽ trình bày kỉ thuật lựa chọn u và dv . 5
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
C. PHÂN LOẠI VÀ PHƯƠNG PHÁP TÍNH TÍCH PHÂN:
VẤN ĐỀ 1: PHÉP THAY BIẾN n
t f (x)
Phương pháp: Khi hàm dưới dấu tích phân có chứa biểu thức có dạng n f (x) . Lúc đó trong
nhiều trường hợp ( chứ không phải mọi trường hợp), ta có thể đổi biến bằng cách - Bước 1: Đặt n n n 1 t f (x) t f (x) nt     
dt f '(x)dx
- Bước 2: Ghi nhớ “Đổi biến thì phải đổi cân”
BÀI TẬP MẪU: Tính các tích phân sau 1 Bài 1: Tính 3 2
I x 1 x dx 0 Giải: Đặt t = 2
1 x  t2 = 1 – x2  xdx = -tdt Đổi cận: x 0 1 t 1 0 1 1 1 3 5  t t  1 2 Khi đó: 3 2
I x 1 x dx  =  2
1 t .t.tdt =  2 4
t t dt =   = . 3 5    0 15 0 0 0 1 Bài 2: Tính 3 3 4
I x 1 x dx 0 Giải: 3 Đặt t = 3 4 3 4 3 2
1 x t  1 x x dx   t dt 4 Đổi cận: x 0 1 t 1 0 6
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 1 3 3 1 3 Khi đó: 3 3 4 3 4
I x 1 x dx t dt t  .  4  16 0 16 0 0 e 1 ln x
Bài 3: Tính I dxx 1 Giải: Đặt 2
 1 ln   1 ln  2 dx t x t x tdt x Đổi cận: x 1 e t 1 2 e 2 2 3 2 2 2 1 1 ln x 2 t 2   Khi đó: I
dx t.2tdt 2 t dt 2  .  x   3 1 3 1 1 1 2 dx
Bài 4: Tính I   3 1 x 1  x Giải: 2 2 2 dx x dx Ta có:    3 3 3 1 x 1  x 1 x 1 x tdt Đặt 3 2 3 2 2 2
t  1 x t  1 x  2tdt  3x dx x dx  3 Đổi cận: x 1 2 t 2 3 Khi đó: 7
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 2 2 3 3 dx x dx 2 dt 1  1 1  I      dt     2    3 3 3 x x xx 3 1 1
t 1 3  t 1 t 1 1 1 2 2  1       
t   t   3 1 t 1 3 1 1 2 1 ln 1 ln 1   ln    ln  ln  3 2 3 t 1   2 3  2 2 1   1 2 1 1 1  ln     ln 3 3 2 2 1  2  21 4 dx
Bài 5: Tính I   2 7 x x  9 Giải: dx tdt tdt  Đặt 2 2 2
t x  9  t x  9t  0  tdt xdx;   2 2 x x t  9 Đổi cận: x 7 4 t 4 5 5 dt 1 t  3 5 1 7 Khi đó:  ln  ln
 2t 9 6 t3 4 6 4 4
BÀI TẬP ÁP DỤNG: Tính các tích phân sau 7 3 x 141 1) dx ÑS :  3 2  x 20 0 1 ln3 x 2) e dx ÑS :1 2   xe 3 0 1 ln 5 x e 20 3) dx ÑS :  x xe e  3 ln 2 10  1 8
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 4 7 3 x 3 3 3 4) dx ÑS :  ln  4 4   x 8 4 2 0 1 1 8  1 1 1 5) dx ÑS : ln  ln  x 1x 2 3 3 2 x 11 6) dx (A  2004) ÑS :  4ln2 1 x1 3 1 e 3 2 ln x. 2  ln x 3 7)
dx (Khoái B  2004). ÑS :   3 3 3 3  2 2  x 8 1 3 2
HD :Ñaët t  2  ln x 3 2 x 1  x 2 8) e . dx.
ÑS : e e  2 0 x 1 2 3 dx 2 (KhoáiA-2003) 1 5 9) .
. Ñaët t x  4 ÑS : ln  2 x x  4 3 5 4 3 e 2 ln x 76 10)
dx.(Döï bò khoái D-2005)
Ñaët t  ln x 1. ÑS :  x lnx1 15 1 e  ln x  2 2 2 2 11)
 ln x dx. HD : I I I ÑS :e   1 2  x 1 ln x 3 3 1  2 x x 1 62 12) dx. t x 1. DS :  30ln2  . x 10 3 1 1 1 2 3 13) sin x x x dx dx  1 x 0 0 1 1 x Hướng dẫn : 2 3
I x sin x dx dx  1 x 0 0 1 Ta tính I 2 3 1 = x sin x dx
đặt t = x3 ta tính được I1 = -1/3(cos1 - sin1) 0 1 x 1 1 Ta tính I2 = dx
đặt t = x ta tính được I 2 (1
)dt  2(1 )  2  1   x 2 = 2 1 t 4 2 0 0 9
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
ĐS :-1/3(cos1 - 1)+2  2 5 ln( x 1 1) 14) dx
2 x1 x1
Hướng dẫn :Đặt t x 1 1 . Đáp số: 2 2 ln 3  ln 2 6 15) dx
22x1 4x1 Hướng dẫn :Đặt 2
t  4x 1  t  4x 1 2tdt  4dx . 6 5 5 5 5 dx 1 tdt tdt dt dt I          2    3 1 ln
2x 1 4x 1 2 t 1
t  2 t 1 1 t 2 12 t    2 2 3 3 3 3 1 1 2 BÀI TẬP BỔ SUNG 10
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
VẤN ĐÊ 2: TÍCH PHÂN BẰNG PHƯƠNG PHÁP LƯỢNG GIÁC HÓA CÁCH ĐẶT DẤU HIỆU
x a sint vôùi / 2  t / 2 2 2 a x
x a cost vôùi 0  t   a   x  vôùi t   ;\ {0} sint  2 2     2 2 x aa   x
vôùi t  0;  \  cost      2 
x a tant vôùi / 2  t / 2 2 2 x a
x a cost vôùi 0< t
a x hoaëc ax
Ñaët x acos2t a x a x  
x ab x
x a  b a 2 sin t,t  0;  2    DẠNG 1: 2 2 a x
BÀI TẬP MẪU: Tính các tích phân sau a Bài 1: Tính 2 2 2
I x a x dx 0 Giải: Đặt x = asint, t   ;  .  dx = acostdt 2 2    Đổi cận: x 0 a 11
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN t 0 2 a 2 Khi đó: 2 2 2
I x a x dx  = 2 2 2 a sin t a   2
1 sin t.acostdt 0 0 2 4 2 a 4 2 a 4 a  1  4  a = 4 2 2 a sin tcos tdt  = 2 sin 2tdt 1 cos4t dt = t  sin 4t   2 = 4  =   8 8  4 16 0 0 0  0 1 2 1 x
Bài 2: Tính I dx  2 x 2 2 Giải: Đặt x = cost, t   ;  .  dx = - sint dt 2 2    Đổi cận: x 2 2 4 t 1 0 1 2 1 x 0 2
1 cos t.sint 4 sin t .sin t 4 2 sin t Khi đó: I dx  =  dt dt dt 2 x  = 2 cos t  = 2  = cos t 2 cos t 2 0 0 2 4 4  1   1 dt 
= tant t 4 = 1 . (vì t  0; nên sint  0  sint  sint ) 2    cos t  4  4 0  0  1 Bài 3: Tính 2 2
I x 1 x dx 0 Giải: 12
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN Đặt x = sint, t   ;  .  dx = costdt 2 2    Đổi cận: x 0 1 t 0 2 1 2 2 1 2 1 Khi đó: 2 2
I x 1 x dx  = 2 2
sin t 1 sin t.costdt  = 2 2 sin tcos tdt 2 sin 2tdt 4  = 4  = 0 0 0 0 2 1 1  1 
= 1cos4tdt= t  sin4t   2 = 8 8  4 16 0  0
Tính các tích phân sau: 3 2 1) 4  x dx ;
HD : Ñaët x  2sint ÑS :  3 1 3 2 1 3  3 2) dx ;
HD : Ñaët x  3cost ÑS :   9 x 3 2 27 3 2 2 2 2 2 x 1 3) dx ;
HD : Ñaët x  sint ÑS :   2  x 8 4 0 1 8 2 4) 16  x dx;
HD :Ñaët x  4sint 0 1 2 2 5) 1 x dx
HD :Ñaët x  sint 0 5 2 1 6) dx ;
HD : Ñaët x 1  3sint  9x 2 1 1 13
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 2 7) x x dx. ÑS :   16 1 2 1 1 1 HD : x x dx  1   2x  2 2 1 dx.
Ñaët : 2x 1  sint 2 1 1 2 2 DẠNG 2: 2 2 x a
Tính các tích phân sau: 6 1 3 1) dx ;
HD : Ñaët x ÑS :  2  sint x x 36 3 2 9 2 3 1 1 2) dx ;
HD : Ñaët x ÑS :  2  sint x x 6 2 1 2 2 2 x 1 3) dx ;
HD : Ñaët x   2x  cost 0 1 5 2 1 1 4) dx ;
HD : Ñaët x   2 x x  cost 1 1 DẠNG 3: 2 2 x a BÀI TẬP MẪU: 0 1
Bài 1: Tính I dx  2x 2x4 1  Giải: 0 0 1 1 Ta có: dx dx  2  x  2x  4    x   1   32 2 1 1   
Đặt x 1  3 tant với t    dx     2 ; .
3 1 tan tdt  2 2  Đổi cận: x -1 0 14
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN t 0 6 0 6 1 3 3 3 Khi đó: I dx dt t   6  . 2 x  2x  4 3 3 18 1  0 0 1 3 x
Bài 2: Tính I dx  8 1 x 0 Giải: 1 3 1 3 x x Ta có: dx dx  8  1 x 1 x 2 4 0 0     1 Đặt 4
x  tant với 3 t   ; .  x dx     2 1 tan tdt  2 2  4 Đổi cận: x 0 0 t 0 4 1 3 1 3 4 2 4 x x 1 1 tan t 1 1 Khi đó: I dx dx dt dt t     4  . 8 1 x 1 x 2 2 4 4 1 tan t 4 4 16 0 0 0 0 0 2 cosx
Bài 3: Tính I dx  2 1 sin x 0 Giải: 
Đặt sin x  tant với t    cosxdx     2 ; 1 tan tdt  2 2  Đổi cận: 15
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN x 0 2 t 0 4 2 4 2 4 cosx 1 tan t Khi đó: I dx dt dt   2  2  1 sin x 1 tan t 4 0 0 0 BÀI TẬP ÁP DỤNG: 4 1 1) dx ;
HD : Ñaët x  2tant ÑS :  2 4  x 8 0 3 1 2) dx ;
HD : Ñaët x  3tant  2x 9 0 1 2 3) x 1 x dx ;
HD : Ñaët x tant 0 3 1 3 1 4) dx ;
HD : Ñaët x tant ÑS :   1 x 3 2 2 3 3 3 2 2 9  2x 3 1 5) dx ;
HD : Ñaët 2x 3tant ÑS :  2 x 2 3 2 1 3 x 2 6) dx ;
HD : Ñaët x tant hoaëc u x 1  x  3 2 0 1 3 1 7) dx ;
HD : Ñaët x  3 tant  2 2 1 x x  3 1 1  2 8) dx ÑS :  x  2 2 8 0 1 3 2 1 x 3 2  2 3 9) dx.
Ñaët x  tant. ÑS : ln 2  3 2 1   2    x 3 1 16
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 x 3 10) dx. ÑS :  4 2 x x 1 8 0 1 1
:Bieán ñoåi tích phaân ñaõ cho veà daïng: du HD  2 2 u u 1 0 17
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN a x a x DẠNG 4: hoaëc a x a x Tính tích phân sau: 5 0 2 1 x 5 1) :  cos2 2)  x HD x t
HD : x  5cos2t  1   x 5  x 1  0
DẠNG 5: x ab x 3 2 1  3 
Tính tích phân sau:  x  12  x 2 .
Ñaët x  1 sin t. ÑS :    8 12 8  5   4 BÀI TẬP BỔ SUNG 18
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
VẤN ĐỀ 3: TÍCH PHÂN LƯỢNG GIÁC
Dạng 1: Biến đổi lượng giác về tích phân cơ bản 4 1
Ví dụ 1: Tính I dx  4 cos x 0 Giải: 1
Đặt t = tanx ;  dt dx 2 cos x Đổi cận: x 0 4 t 0 1 4 4 1 3 1 1  t  1 4 Khi đó: I dx    2 1 tan xdx   2
1 t dt  t    . 4 2  cos x cos x 3   0 3 0 0 0 12
Ví dụ 2: Tính I  tan 4xdx 0 Giải: 12 12 sin 4x Ta có: tan 4xdx dx   cos4x 0 0 dt
Đặt t = cos4x ;  dt  4sin4xdx  sin 4xdx   4 Đổi cận: x 0 12 t 1 1 2 19
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 1 12 12 2 1 sin 4x 1 dt 1 dt 1 1
Khi đó: I  tan 4xdx dx     ln t     1  ln2. cos4x 4 t 4 t 4 4 0 0 1 1 2 2 2 Ví dụ 3: Tính 5 I cos xdx 0 Giải: 2 2 2 2 Ta có: 5 4
cos xdx cos xcoxdx     2
1 sin xcoxdx 0 0 0
Đặt t = sinx ;  dt cosxdx Đổi cận: x 0 2 t 0 1 Khi đó: 2 2  
I cos xdx     x 2
coxdx   t  2 2 2 2t t 1 5 2 2 dt   2 4  t t  3 5 8 1 sin 1 1 2 dt  t     . 3 5   0 15 0 0 0 0 4 Ví dụ 4: Tính 3 I  tan xdx 0 Giải: dt
Đặt t = tanx ;  dt   2
1 tan xdx   2
1 t dt dx  2t 1 Đổi cận: x 0 4 t 0 1 20
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN Khi đó: 4 3 2 t t 1 2t t 1 d t    1 3 1  2 1 1 1 1 1 
I  tan xdx dt t dt tdt dt      2  2    2  2 t 1  t 1 2 t 1 2 0 2 t 1 0 0 0 0 0 0 1 1    1 2 t   1 1 1 ln 1
  ln2  1 ln2. 2 2 0 2 2 2 2 Ví dụ 5: Tính 3 I cos xdx 6 Giải: 2 2 2
I cos xdx cos x.cosxdx    1sin x 2 3 2 2 cosxdx   2
1 sin xd sin x 6 6 6 6 3  sin x  2 1 1 1 5  sin x    1    3 3 2 24 24   6 4 sin 4x
Ví dụ 7: Tính I dx  4 4 sin x cos x 0 Giải: 4 4 4 4 sin 4x 2sin2xcos2x 2sin2xcos2x 2sin2xcos2x I dx dx dx dx   4 4  4 4  2 2  sin x cos x sin x cos x 1 2sin xcos x 1 2 0 0 0 0 1 sin 2x 2 4 1   1 2  1 2 1 
d 1 sin 2x   ln 1 sin 2x    4   ln  ln2 1 2  2  2 2 0 1 sin 2x 0 2 2 3 cos x
Ví dụ 8: Tính I dx 1sinx 4 Giải: 21
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 2 2  2 3 2 1 sin x cos x cos x  2 I dx cosxdx cosxdx    
1sinxcosxdx  1 sin x 1 sin x 1 sin x 4 4 4 4 2    
cosx cosx sin x 2 2 1 1 2 3  2 2
dx cosxdx
sin2xdx  sin x  sin2x   2   4    4 4 4 4 4 2 Ví dụ 9: Tính 3 I  sin xdx 0 Giải: 2 2 2   3 2 I xdx x xdx      2
cos xd cosx 3 cos x 1 2 sin sin sin 1  cosx   2  1  3 3 3 0 0 0   0 2 dx
Ví dụ 10: Tính I  1cosx 0 x d    2 2 2 dx dx  2  x Giải: I     tan    2  1 1 cosx 2 x 2 x 2 0 0 0 2cos cos 0 2 2 2 dx
Ví dụ 11: Tính I  1sin2x 4 Giải: 2 2 2 2 dx dx dx 1 dx I     1     sin2x      x cosx2 2 2 sin 2 cos x  4 4 4  2cos x    4   4  4     1   2 1  tan x   2  4    2 4 22
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 dx
Ví dụ 12: Tính I   sinx 3 Giải: 2 2 2 dx sin xdx sin xdx Ta có:     2  2 sin x sin x 1 cos x 3 3 3
 Đặt t cosx dt  sin xdx Đổi cận: x 3 2 1 t 0 2 Khi đó: 1 1 0 2 2 dt dt 1  1 1  I     dt  2  2  1 t 1 t
2 1 t 1 t    1 0 0  2 1 1 1 2 2 1 dt 1 dt 1          
t   t   1 1 3 ln 1 ln 1 2   ln  ln 2 t 1 2 t 1 2 2  2 2    0 0 0  1 1 1   ln  ln3 2 3 2 dx
Dạng 2: Tích phân dạng asinx bcosx c x
Cách giải: Đặt t  tan , đưa về tích phân hữu tỉ 2 2 dx 3
Ví dụ 1: Tính tích phân  ĐS: ln
2cos x  sin x  2 2 0 23
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 dx 1 5
Ví dụ 2: Tính tích phân  ĐS: ln
3cos x  2sin x  2 3 2 0 4 dx 1 4
Ví dụ 3: Tính tích phân  ĐS: ln 2
2cos x  3sin2x  2 2 3 0 4 dx 3
Ví dụ 4: Tính tích phân  ĐS: sin2x  2 18 0 4 1 2sin x 23
Ví dụ 5: Tính tích phân dxĐS:  2ln2 2  cos x 9 0 dx
Dạng 3: Tích phân dạng  2 2
asin x bsin x cos x c cos x Cách giải: Cách 1: Đặt 2
cos x ở mẫu làm thừa số chung sau đó đặt t  tan x
Cách 2: hạ bậc đưa về dạng 2 3 dx
Ví dụ 1:Tính I   
sin x sin x  6  6    Giải: 3 3 3 dx dx 2dx I            sin sin     x xcosx x x sin x 2 3 1 3 sin sin  sin x cosx 6 6  6  6   2 2    3 3 2dx 2d tan x 3 d tan x         2 3 2 cos x 2
3 tan x  tan xtan x 3tan x  1
 3 tan x 3 tan x   1 6 6 6 3  1 1   2 3  d  tan x   3 tan x 3 tan x 1 6 24
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 3 d tan x
3 d  3 tan x   1       x  3   x x  3 2 2 2 ln tan 2 ln 3 tan 1 tan  3 tan x 1 6 6 6 6  1          3   2 ln 3 ln
2 ln 4 ln2  2ln3  2ln2  ln   3   2  4 dx 1 1
Ví dụ 2: Tính tích phân  ĐS: ln 2 2
sin x  4cos x 4 3 0 4 dx 1 3
Ví dụ 3: Tính tích phân  ĐS: ln 2 2
sin x  4sin x cos x  3cos x 2 2 0
Dạng 4: Tích phân dạng I f (sin x)cos xdx; I f (cos x)sin xdx 1  2  A. Cách giải:
Đối với I đặt t  sin x 1
Đối với I đặt t cosx 2 2 Ví dụ 1: Tính 5 I  sin xcoxdx 0 Giải:
Đặt t = sinx ;  dt cosxdx Đổi cận: X 0 2 T 0 1 2 1 1 Khi đó: 5 5
I  sin xcoxdx t dt    . 6 0 0 25
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2
Ví dụ 2: Tính I  sin xcosx
1cosx2 dx 0 Giải: Ta có: 2 I  sin xcosx  1cosx 2
2 dx  sin xcosx   2
1 2cosx cos xdx 0 0 2   2 3
cosx  2cos x cos x.sin xdx 0
 Đặt t cosx dt  sin xdx Đổi cận: x 0 2 t 1 0 0 1 2 3 4  t 2t t  1 17
Khi đó: I   2 3
t  2t t dt  2 3
t  2t t dt      2 3 4   0 12 1 0
B. Các trường hợp đặt biệt:
1. Tích phân có dạng sinm .cosn x xdx
với m,n   
Nếu m lẻ hoặc n lẻ thì đặt t hàm có chứa mũ chẵn
Nếu m và n đều chẵn thì hạ bậc 2 Ví dụ 1: Tính 3 3
I  sin xcos xdx 0 Giải:
Đặt t = sinx ;  dt cosxdx Đổi cận: 26
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN x 0 2 t 0 1 Khi đó: 2 2  t t  1 3 3 3 I xcos xdx x    2  x 1 3 cosxdx t   2  t  1 dt   3 5 t t  4 6 1 sin sin 1 sin 1
dt      . 4 6   0 12 0 0 0 0 2 2
Ví dụ 2: Tính tích phân 2 3 sin x cos xdxĐS: 15 0 2 2
Ví dụ 3: Tính tích phân 4 3 sin x cos xdxĐS: 35 0 2
Ví dụ 4: Tính tích phân 2 4 sin x cos xdxĐS: 32 0 sinm x cosmx
2. Tích phân dạng I dx; I dx; m,n     1  n 1   cos x sinn x
ñaët t  cos x ñoái vôùi I  Nếu m lẻ thì 1 
ñaët t  sin x ñoái vôùi I  2
 Nếu m và n đều chẵn và
o m n thì đưa về tan và cot
o m n thì đổi hàm ở tử theo mẫu sau đó tách tích phân và hạ bậc
 Nếu m chẵn và n lẻ thì dùng tích phân từng phần 2 3 cos x
Ví dụ 1: Tính I dx  2 s in x 6 Giải:
Đặt t = sinx ;  dt cosxdx 27
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN Đổi cận: X 6 2 1 T 1 2 Khi đó: 1 2 3 2 2 1 2 1 cos x (1 sin x) 1 t  1   1  1 I dx cosxdx dt
1 dt    t        1  . 2 2 2 2 s in x sin x tt   t  2 1 1 2 6 6 2 2 3 3 sin x 1
Ví dụ 2: Tính I dxĐS: 2 cos x 2 0 3 3 sin x 9
Ví dụ 3: Tính I dxĐS: 5 cos x 4 0 4 2 sin x 1
Ví dụ 4: Tính I dxĐS: 4 cos x 3 0 3 2 sin x sin x 1
Ví dụ 5: Tính I dx
. Hướng dẫn: u  sin x, dv dx
ĐS: 3  ln 3  2 3 cos x 3 cos x 2 0
Dạng 5: Tích phân chứa tan x;cos xdx; cot x;sin xdx   Cách giải:  Đổi về sin và cos
 Đặt t bằng một hàm ở mẫu 3 t anx
Ví dụ 1: Tính tích phân dx 1cosx 0 28
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 3 3 t anx sinx 3 Hướng dẫn: dx dxt x ĐS: ln 1  . Đặt cos  cos x cos x 1 cos x 2 0 0   4 t anx
Ví dụ 2: Tính tích phân dx  4 1 4cos x 0 4 4 3 t anx sinx.cos x 1 8 Hướng dẫn: dx dxt   x ĐS: ln 4  . Đặt 4 1 4cos 4 1 4cos x cos x  4 4 5 0 0 1 4cos x 3 sinx
Ví dụ 3: Tính tích phân dxcos3x 4 3 3 sinx sinx 1 Hướng dẫn: dx dx   ln2 cos3x  ĐS: 6  cosx  2 4cos x  3 4 4
Dạng 6: Đổi biến bất kì 2 Ví dụ 1: Tính 2 sin x I e sin2xdx 0 Giải:
Đặt t = sin2x ;  dt  sin2xdx Đổi cận: x 0 2 t 0 1 2 1 x t t 1 Khi đó: 2 sin I e
sin2xdx e dt ee 1.   0 0 0 2 sin2x
Ví dụ 2: Tính I dx  2 1 cos x 0 29
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN Giải:
Đặt t = 1 + cos2x ;  dt  sin2xdx  sin2xdx  dt Đổi cận: X 0 2 T 2 1 2 1 2 sin2x dt dt 2 Khi đó: I dx     ln t  ln2.  2     1 cos x t t 1 0 2 1
2  sin x cosx
Ví dụ 3: Tính I dx sinx cosx   4 Giải: 2 2
 sin x cosx
d sin x cosxI dx        x cosx  2 ln sin  ln 2
 sin x cosx  sin x cosx 4 4 4 4 sin 4x
Ví dụ 4: Tính I dx  2 1 cos x 0 4 4 sin 4x 2sin2xcos2x Giải: Ta có: dx dx  2  2 1 cos x 1 cos x 0 0  Đặt 2
t  1 cos x dt  2sin xcosxdx  sin2xdx  2 2
cos x t 1 cos2x  2cos x 1  2t   1 1  2t  3 Đổi cận: x 0 4 30
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 3 t 2 2 Khi đó: 3 2 2  2t  3 3 2 2 dt  6   6  I   4  dt  4  dt      
4t6ln t  23  tt   t 2 2 3  2 2  3   3  4  4 2   6 ln2  ln  2  6ln  2   2      3
Cách 2: Sử dụng công thức hạ bậc, mẫu xuất hiện 3  cos2x , đặt t  3  cos2x 4 cos2x
Ví dụ 5: Tính I dx
 sinxcosx23 0 Giải: 4 4 cos2x
cosx sinxcosx sinx Ta có: dx dx   
sin x cosx  23
sinx cosx 23 0 0
 Đặt t cosx  sin x  2  dt  cosx  sin xdx Đổi cận: x 0 4 t 2 2  2 Khi đó: 2 2 t  2 2 2  1 2   1 1  2  2 1 1 1 1 I dt   dt           3   2 3   2 tt t   t t  0 2  2 6  4 2 3 9 0 0 1 2  2 2 2 1 2 2 1 4 2  4  9 4 2  5         6  4 2
9 9 232 2 9 2 2  1 18 2  1 18 2  1 31
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 4 co x Ví dụ 6: s2 Tính I dx
 sinx cosx 2 0 Giải: 4 4 cos2x
cosx sinxcosx sinx Ta có: dx dx  sinx   cosx  2
sin x cosx  2 0 0
 Đặt t cosx  sin x  2  dt  cosx  sin xdx Đổi cận: x 0 4 t 2 2  2 Khi đó: 2 2 t  2 2 2  2  I dt   dt     
tt  2 2 1 2ln
 2  2  2ln2  23 2ln3  tt 0 0  0     3 2 1 2 ln3 ln 2 2        2 1 2ln  2  2 2 3
Ví dụ 7: Tính I  sin2x   2 1 sin xdx 0 Giải:  Đặt 2
t  1 sin x dt  2sin xcosxdx  sin2xdx Đổi cận: x 0 2 t 1 2 32
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 3 t 2 1 15
Khi đó: I  sin2x  2 1 sin x 2 4 3 dx t dt   4     4 1 4 4 0 1 4 dx
Ví dụ 8: Tính I  1tanx 0 Giải: 1 dt dt
 Đặt t  tan x dt dx   2
1 tan x dx dx   2  2 2 cos x
1 tan x 1 t Đổi cận: x 0 4 t 0 1 1 1   1 1 1 dt 1 t 1 1 dt 1 tdt 1 dt I     dt         2 2 2 2 Khi đó: 1 t 1 t 2 1 t 2 1 t
2 1 t 2 t 1 2 t 1 0    0      0 0 0  
    1 J J2 J3 1 1 dt 1 1 ln2  Tính: J   ln t 1  1 2  t 1 2 0 2 0 1 1 d  2 1 1 t tdt   1 1 1 ln2  Tính: 2 J    ln t 1  2  2  2 2 t 1 4 t 1 4 0 4 0 0 1 4 1 dt 1  Tính: J   du  3  2 2  (với t = tanu) t 1 2 8 0 0 ln2 ln2 ln2 Vậy I        2 4 8 8 4 4 1
Ví dụ 9: Tính I dx   sinx cosx2 12 33
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN Giải: 4 4 1 1 1 1   4 3 I dx
dx   cot x              x cosx2 2 2 4 2 sin 2  sin x   12 12  4    12
BÀI TẬP ÁP DỤNG: Tính tích phân sau: 3 3 x 6 3 cos  1) dx
HD :Ñaët t  sin x, ÑS :ln  2   sin x 5sin x 6 54  3 6 3 cos : x BTTT dx  2   sin x 7sin x 12 6 4 2 1 2sin x 1 2)
dx (Khoái B  2003) ÑS : ln2  1sin2x 2 0 2 sin2x 4 3) dx (TN  2006) ÑS : ln  2 4  cos x 3 0 sin x    4   4  4  dx Khoái B  2008)  sin2x 2 0
1sinx  cosx . ( 4  3 2
HD :Ñaët t  sin x  cos x. ÑS : 4 6 4 tan x 10 3 1 5)
dx. (Khoái A  2008)
HD :Ñaët t  tan x. ÑS :  ln  2 3 cos2x 27 2 0 2 sin2x 2 2 6) dx (KhoáiA-2006).
HD :Ñaët t  1 3sin x. ÑS :  2 2 x x 3 0 cos 4sin
2 sin2x  sin x 34 7) dx (KhoáiA-2005).
HD :Ñaët t  1 3cos x. ÑS :  13cosx 27 0 34
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ www.VNMATH.com
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 sin2x.cos 8)
x dx (KhoáiB-2005).
HD :Ñaët t  1 cos x. ÑS : 2ln2 1  1cosx 0 2 9) 3 cos x  2
1 cos xdx (Khoái A-2009). ÑS :  4 0 2
HD :cos x   2 3 2
1 cos xd   5 2
cos x  cos xdx 0 0 2 10)  sinx e
cos xcosxdx. (Khoái D-2004).
ÑS : e 1     4 0 3 sin2xdx 2 11)
. HD :Ñaët t  1 cos x. ÑS : 5  3  2 2
cos x 1  cos x 4 6 tan(x  ) 6 2 tan x 1 1 3 4 11) dx. HD I  
dx. t  tan x. DS :   2 cos2x (t anx+1) 2 0 0 /4 sin 12. x dx  2 /4 1 x x /4 /4 /4 sin x Hướng dẫn: 2 I dx
1 x sin xdx
x sin xdx I I    1 2 2 /4 1 x x/4 /4
Áp dụng hàm lẻ, đặt x=-t thì I  0 , tích phân từng phần I được kết quả. 1 2 2 13) cos2x   4 4
sin x  cos xdx . 0 2 2  1  1  1  Hướng dẫn: 2 2
I  cos2x 1 sin 2x dx  1 sin 2x d      sin2x  0  2  2  2 0 0  4 sin 4x 3 14) dx. DS : 2  6ln  . 2 2  sin x 4 0 35
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 4 x x Hướng dẫn: 4sin2 .cos2 I = dx
. Đặt: t = 3 + cos2x  dt = -2sin2xdx. 3  cos2x 0 2 3sinx  cos 15) x dx  . 0 s inx  cos x  2
2 sinx  cos x  2   2cos x  sinx  2
Hướng dẫn: I dx 0 sinxcosx 2 2 2
cosx sinx 2   2  2 dx dx dx  ...   2tan   
sin x  cos x  2
sin x  cos x  2 2 8 0 0   0 3 3 2 sin 16)  sin .tan . : x I x xdx HD I dx   cosx 0 0 2 3 2
17) sin x cos xdx. HD :Ñaët t  sin x 0 2 3 2
BTTT : cos xsin xdx. 0 BÀI TẬP BỔ SUNG 3 x  sin x
Bài 1: Tính I dx  2 cos x 0 Giải: 1 1 1 x  sin x xdx sin x Ta có: I dx   dx  2  2  2 cos x cos x cos x 0 0 0     1 I I2 3 xdx  Tính I  1  2 cos x 0 36
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂNu x  du dx Đặt  1   dv dx  v  tan x 2  cos x
Áp dụng công thức tính tích phân từng phần ta được: 3 3 3 3 xdx 3 sin x 3
d cosx3 I   x tan x  3  tan xdx   dx     ln cosx 1    3 2   cos x 3 cosx 3 cosx 3 0 0 0 0 0 0 3 1   ln 3 2 3 3 sin xd cosx 1  Tính I dx     3  2 1  1 2 2 2 cos x cos x cosx 0 0 0 3 Vậy I    ln2 1 3 2 sin xcosx
Bài 2: Tính I dx  2 2 2 2 0
a cos x b sin x Giải: Ta có: 2 2 2 sin xcosx sin xcosx sin xcosx I dx dx dx    2 2 2 2 2
a cos x b sin x a  2 1 sin x 2 2  b sin x  2 2 b a  2 2 0 0 0 sin x a 2tdt  2 2 2
b a sin xcosxdx  Đặt t  2 2 b a  2 2 2 sin x a t  2 2 b a  2 2 sin x a          sin tdt xcosxdx  2 2  b a Đổi cận: x 0 2 t |a| |b| 37
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN b tdt 1 b b a 1 Khi đó: I   t  
t b a b a a a b a  . 2 2  2 2 2 2 b a 1
Bài 3: Tính I  sin xdx 0
 Đặt t x dx  2td Đổi cận: x 0 1 t 0 1 Khi đó: 1
I  2 tsintdt 0 u tdu dt Đặt   dv sintdt   v  cosx
Áp dụng công thức tính tích phân từng phần ta được:
I   tcost 1 1  costdt   
tcost1   t1 2 2 2 2 sin  2sin1 cos  1 0 0 0 0 38
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
VẤN ĐỀ 4: TÍCH PHÂN CÓ CHỨA GIÁ TRỊ TUYỆT ĐỐI b
Phương pháp: Giả sử ta cần tính tích phân sau: f (x)dxa
Bước 1: Tính nghiệm của phương trình f (x)  0
Bước 2: Xét dấu f (x) trên đoạn a,b  
Bước 3: Dựa vào bảng xét dấu để bỏ dấu giá trị tuyệt đối và tính tích phân.
Chú ý: Nếu phương trình f (x)  0 có dạng không mẫu mực thì ta dùng đạo hàm để xét dấu f (x) . 2
Ví dụ 1: Tính tích phân sau: x x 1dx.  ĐS: 1 0 2 3x 1
Ví dụ 2: Tính tích phân sau: I   x  2dx  ĐS: 1 8ln2  4ln3 x 1 0 2 2 x  2x  3
Hướng dẫn: I dxx 1 0 2
Ví dụ 3: Tính tích phân sau: I  sin x x dx 0 Hướng dẫn:
Xeùt haøm soá f (x)  sinx  x, 0  x   2    
f '(x)  cos x 1  0, x
  0;f (x)  f (0)  0  sinx  x  0,x  0;  2   2      2
I  x sinx 2 dx   1 8 0 39
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN BÀI TẬP ÁP DỤNG: 1
Bài 1. Tính tích phân sau: x e 1dx. 1 1 0 1 x x x 1 Hướng dẫn:
e 1dx e 1dx e 1dx. ÑS : e   2    2 1  1  0
Bài 2. Tính các tích phân sau: 5 x
a)  x  2  x 2  1 4 2 dx ; b) dx ; c) x  6x  9  4 2  x x 12 3  1  1 1 3 3 x 3 2 d) 4  x dx ; e) 2  4dx ; f )
x  2x xdx    1  0 0 Ñaùpsoá : 1 8 5 a b c d    1 24 3  8 )8; ) ln ; ) ; )2 5 3 ; e)4  ; f ) 14 45 3 ln2 15
Bài 3. Tính các tích phân sau: 2 2
a) sinx dx ; b) 2  2cos2xdx c) 1 sin2xdx; d) 1 sinxdx     0 0 0  2
Ñaùpsoá : a)2; b)4; c)2 2; d)4 2
Bài 4. Tính các tích phân sau: 1 xx 1
a) 2  2 dx ÑS : ; b) 1 sin2xdx ÑS : 2 2  ln2  1  0
Bài 5. Tính tích phân: 2 2 I x x dx  ( Khối D – 2004 ) 0 2 e
Bài 6. Tính tích phân: a) log x dx b) ln x dx  2  1 1 2 e 4
Bài 7. Tính tích phân I  tan x  2sin x  3x dx 0 Hướng dẫn: 40
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Xeùt haøm f (x)  tan x  2sin x  3x, vôùi 0  x  4 cosx  2 1 2cos x   1   f '(x)   0, 0; 2 cos x  4     
f (x) taêng treân 0;f (x)  f (0)  0  4    2 1 3 I  ln2  2  2  2 32 BÀI TẬP BỔ SUNG: 41
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
VẤN ĐỀ 5: TÍCH PHÂN HÀM HỮU TỈ  P(x) A.Daïng1:I dx,a  0  ax b
Ta caàn phaûi chuù yù coâng thöùc k k
dx  ln ax b Cax b a
Bài tập áp dụng: Tính các tích phân sau 3 4 2 4 3 x 1 x  5 )  ; )  ; ) x a I dx b I dx c I dx 1  2  3 x  1 x 1 2x  3 2 2 2 ( ) B.Daïng2: P x I dx,a  0  2
ax bx c 2  rö
T ôøng hôïp 1: f (x)  ax bx c coù hai nghieäm phaân bieät
BÀI TẬP ÁP DỤNG: Tính các tích phân sau
Bài 1. Tính tích phân sau: 1 4 4 3 1 )  ; )  ; ) x a I dx b I dx c I dx 1  2 2  2 3  2 x  4 x  7x  8 x  3x  2 0 3 3 5 3 x
Bài 2. Tính các tích phân sau: dx  2x 3x2 3 Phương pháp:
- Khi bậc đa thức P(x)  2 ta sử dụng phương pháo hệ số bất địn h
- Khi bậc đa thức P(x)  2 ta sử dụng phép chia đa thức để đưa tử số về đa thức có bậc <2 T
f x ax bx c  x 2 2 röôøng hôïp 2: ( ) coù nghieäm keùp u'(x) 1
Ta cần lưu ý công thức sau: dx    C  2u(x) u(x) BÀI TẬP ÁP DỤNG:
Bài 1. Tính các tích phân sau: 1 2 1 4 ) ; ) x a dx b dx  2  2 x  4x  4 4x  4x 1 0 1 42
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Hướng dẫn câu b) t  2x 1
Bài 2. Tính các tích phân sau: 1 2 1 3 x  3 ) ; ) x a dx b dx  2  2 x  4x  4 x  2x 1 0 0
Phương pháp: Để tránh phức tạp khi biến đổi ta thường đặt t  x
Trong hai câu trên, ta thấy bậc tử cao hơn bậc mẫu nên ta có thể chia đa thức, sau đó đưa về trương hợp trên. 2  rö
T ôøng hôïp 3: f (x)  ax bx cvoâ nghieäm 1
Ta cần lưu ý cách tính nguyên hàm dx
bằng cách đặt x atant 2 2 x a
BÀI TẬP ÁP DỤNG: Tính các nguyên hàm sau 2 1 dx dx 3 1) ; ÑS : ; 2) ; ÑS :  2  2 x  2x  2 2 x x 1 6 0 0 1 1 dx 1  3dx 8 34 3) ; ÑS :   ; 4) ; ÑS :   4 2  x  4x  3 2  4 6   
x x  3 2 27 9 0 0 1 P(x) C.Daïng: dx,a  0  3 2
ax bx cx d 1. Ña thöùc daïng : 3 2
f (x)  ax bx cx d coù moät nghieäm boäi ba
Ta caàn chuù yù coâng thöùc sau: 1 1 1 m dx    Cx x   nxn  , chuù yù: , 0 n 1 1  n x x 1
Ví duï: Tính caùc tích phaân sau dx  3 2
x  6x 12x  8 0 Baøi taäp aùp duïng
Baøi 1. Tính caùc tích phaân sau: 4 5 3 ) x
; Höôùng daãn: Ñaët  1 ) x a dx t x b dx    x  3 1 x  3 2 3 1 43
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Baøi 2. Tính caùc tích phaân sau: 4 2 1 4 x  4 ) ; ) x a dx b dx    x  3 1 x  3 2 0 1 2. Ña thöùc daïng : 3 2
f (x)  ax bx cx d coù hai nghieäm 3
Baøi toaùn môû ñaàu: Tính tích phaân 1 dx
 x 1x 2 2 1 Höôùng daãn: Ñaët
x 1  t dx dt
x  2  t  3; x  3  t  4 3 4 4 Luùc ñoù: dx dt dt       x 1x 2 2 1 t t  2 3 t    2t 2 3 3
Duøng phöông phaùp heä soá baát ñònh 1 At B C  
 1  A C 2t  2A B t  2B 3 2 2   t  2t t t  2
Baøi taäp aùp duïng:
Baøi 1. Tính caùc tích phaân sau: 4 3 2 2x 1 ) ; ) x a dx b dx  2  x x  2 x  2 3 2 1 x  2 2 Höôùng daãn: ) x Ax B C b  
x  2x   x  2 x 2 1 2 1 7 3
Baøi 2. Tính tích phaân sau x 1 dx  3 2
x  2x x 3 3. Ña thöùc daïng : 3 2
f (x)  ax bx cx d coù ba nghieäm phaân bieät 3
Baøi toaùn môû ñaàu: Tính tích phaân 1   dx 2 2 x   1 x 44
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN Höôùng daãn: 1 A B C     2 x   1 x x x 1 x 1
Baøi taäp aùp duïng:
Baøi 1. Tính caùc tích phaân sau: 6 5 2 5 3 x 1 ) x x a    x dx; b) dx; c) dx 2 x  4
x 2 2x  1 x 2 2 3 3 3 x   1 5 3
Baøi 2. Tính tích phaân x   x  dx 2 3 2
1 4x  4x  5
Höôùng daãn: Ñaët t  2x 1 3. Ña thöùc daïng : 3 2
f (x)  ax bx cx d coù moät nghieäm (khaùc boäi ba): Cách giải:
Bước 1: Phân tích 3 2  
    2 ax bx cx d x
Ax Bx CP(x) a b x c
Bước 2: Đồng nhất thức 1 1 1   2 2
ax bx c x  Ax Bx C 3 2 2x  8x 10
Ví dụ 1: Tính tích phân dx  3 2
x x  3x  3 0 3 2 3 2x  8x 10  5 3x  5  3 5 Hướng dẫn: dx  
dx  5ln 1 3  ln2   3 2   2   
x x  3x  3
x 1 x  3  2 0 0 4 3 2 2 4x  9x  8
Ví dụ 2: Tính tích phân dx  3 2
x  4x  6x  4 1 2 2 2 4x  9x  8  3 x 1  4 1 Hướng dẫn: dx   dx  3ln  ln2  3 2  2
x  4x  6x  4
x 2 x  2x  2    3 2 1 1 0 1
Ví dụ 3: Tính tích phaân I dx  3x 1 1  Höôùng daãn: 45
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 0 0 1 C 1 1  A Bách 1: I dx dx   dx  3   x 1             x 1 2x x 1 x 1 x x 1 1 1  2 1  
Cách 2: Ñaët x 1  t . Luùc ñoù: 0 1   1 2 1  2 1 dt 1 t  3t  3 t  3tI dx    dt dt  3    x 1           t  2 t 3t 3 3  t
 2t 3t 3  t 2 1 2 2 2 t 3t 3      1  1  1  1  1 1  1 t  3  1  1 1 t  3 3  dtdt dt    dt dt       .... 2    2  2 3  t t 3t 3   3 t 2 t 3t 3 2      2  2   2  2  2   3  3  t     2   4     
Baøi taäp aùp duïng: Tính tích phân sau 1 3 3 dx ÑS :ln2   3x 1 3 0 1 3 x  2x  5 3 dx; ÑS :ln2   3 2
x x x 1 4 0
ax bm D. Daïng dx
, vaø moät soá kó thuaät nguyeân haøm
cx dn
Caùch giaûi: Ñaët t cx d 2x  3 1 1
Ví duï 1: Tính tích phaân dxÑS: 75 54ln2  x  2 2 0 1 1 36x3 3
Ví duï 2: Tính tích phaân dxÑS: 805 8  ln2 3x  4 8 3 0 1
1. Kó thuaät bieán ñoåi töû soá chöùa nghieäm cuûa maãu soá 5 5 2 2 Ví duï 1: dx x x 1 I    
x   . Höôùngdaãn: dx 2 1 xx   2 1 x 2 2 46
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 3 5 3 3 Ví duï 2: dx x x 1 I    
x   . Höôùngdaãn: dx 3 1 xx   3 1 x 2 2 2 2 2 4 4 Ví duï 3: dx 1 dx 1 x 1  . Höôùngdaãn:  x I I   dx  5   5x  5x
5 x 4x  1 5 x 4 1 1 1 x   1 4 x dx dx   4 3 3 3 x 10 1 
Ví duï 4: I  . Höôùngdaãn:I   dx  7 3   3 x 10x x  4 x 10 3 10 x  4 1 1 1 x 10 1
2. Kó thuaät ñaët aån phuï vôùi tích phaân coù daïng dx
xx m n Caùch giaûi:
Böôùc 1: Nhaân töû soá vaø maãu soá cho n 1 x   Böôùc 2: Ñaët n
t ax b 2 2 2
Ví duï 1: Tính tích phaân dx. Höôùng daãn: dx xdx    . Ñaët 2 t x 1 x  2 x  2 x   2 1 x  2 1 1 x   1 x   1 1 2 2 2 2 2
Ví duï 2: Tính tích phaân dx. Höôùng daãn: dx dx x dx   4 4x     x 4 4x x x  3 4x   3 1 x  3 1 1 1 4x   1 1
3. Kó thuaät bieán ñoåi töû soá coù chöùa ñaïo haøm maãu soá 3
Ví duï 1: Tính tích phaân sau: x dx. 2
Höôùng daãn: Ñaët t x 4 x 1 2 2 2 x
Ví duï 2: Tính tích phaân sau: 1 K dx.  4x 1 1 1 2 1  2 2 x 1  1  Höôùng daãn: K dx d x    2   2 1    x 1 1 1 x   2 x x      22  x  47
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN  2 Ax C
4. Kó thuaät tính tích phaân coù daïng   2
Ax B x C 2
Ax B x C 1 2  Caùch giaûi:
Böôùc 1: Chia caû töû caû maãu cho 2 xC t Ax    Böôùc 2: Ñaët x
ñöa veà tích phaân höõu tæC t Ax   x  2 2 x   1
Ví duï 1: Tính tích phaân:   dx ÑS: 1 12 ln 2 x x   1  2 3 7 1 x  2x   1 2 6  2 2 x   1
Ví duï 2: Tính tích phaân: dxÑS: 1 35 ln 4 x 1 2 36 1 48
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN Ví duï 3: 1 2 1 2 x 1 x 1  1  K
dx. Höôùng daãn: K dx d x   4   2 x 1    2 1  1   x x   2 x x      22  x  3 2 Ví duï 4: x 1 x 2 K
dx. Höôùng daãn: K d(x )  6  2 3 x 1 2 (x ) 1 BÀI TẬP BỔ SUNG: 49
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
VẤN ĐỀ 6: TÍCH PHÂN MỘT SỐ HÀM ĐẶC BIỆT PHƯƠNG PHÁP:
Dựa vào việc đánh giá cận của tích phân và tính chất của hàm số dưới dấu tích phân ta có thể lựa
chọn phép đặt ẩn phụ. Ta thường gặp một số tính chất sau: a
Tính chất 1: Nếu hàm số f (x) liên tục và hàm lẻ trên  ; a a   thì
f (x)dx  0 a
Vậy, với tính chất trên ta thường lựa chọn cách đặt x  t 1 2  1 x
Ví dụ: Tính tích phân I  cos x ln dx    1 x   1  2 a
Tính chất 2: Nếu hàm số f (x) liên tục và hàm chẵn trên  ; a a   thì
f (x)dx  0 a
Tương tự ta thường lựa chọn cách đặt x  t 1 4 x  sin x
Ví dụ: Tính tích phân I dx  2x 1 1  2 2
Tính chất 3: Nếu hàm số f (x) liên tục trên 0;1 
 thì : f (sin x)dx f (cos x)dx   0 0
Với dạng này ta thường lựa chọn cách đặt x   t . Với cách đặt này ta dễ dàng chứng minh 2 2 n sin x được dx  , n    n sin n x  cos x 4 0 2 sin x
Ví dụ1: Tính I dx
0 sinx cosx Giải:
Đặt x   t dx  dt 2 Đổi cận: 50
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN x 0 2 t 0 2 Khi đó:
sin t 0   2 2  2  cost cos x I   dt dt dx       0 cost  sint 0
cos x  sin x sin  t cost 2  2   2      2 2 sin x cosx
Vậy I I  2I
dx dx x   2   I  sin x cosx 2 4 0 0 0 2 3 x Ví dụ 2: sin Tính I dx  3 3 sin x cos x 0 Giải:
Đặt x   t dx  dt 2 Đổi cận: x 0 2 t 0 2 Khi đó: 3
sin  t 0   2 3 2 3  2  cos t cos x I   dt dt dx   3 3  3 3       3 3
cos t sin t
cos x sin x 0 0 sin  t cos  t 2  2   2      51
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 3 3 2 sin x cos x
Vậy I I  2I
dx dx x   2   I  3 3 sin x cos x 2 4 0 0 0 2 6 sin x
Ví dụ 3: Tính I dx  6 6 sin x cos x 0 Giải:
Đặt x   t dx  dt 2 Đổi cận: x 0 2 t 0 2 Khi đó: 6
sin  t 0   2 6 2 6  2  cos t cos x I   dt dt dx   6 6  6 6       6 6
cos t sin t
cos x sin x 0 0 sin  t cos  t 2  2   2      2 6 6 2 sin x cos x
Vậy I I  2I
dx dx x   2   I  6 6 sin x cos x 2 4 0 0 0
Tính chất 4: Nếu a  0, hàm số f (x) là hàm số chẵn, liên tục trên  thì với mọi số thực , ta a f (x) a có :
dx f (x)dxx  . a 1 a 0
Với dạng này ta thường lựa chọn cách đặt x  t 1 4 x
Ví dụ 1: Tính tích phân của hàm số sau: dx  12x 1  52
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 4 6 tan x
Ví dụ 2: Tính tích phân: I dxxe 1  4 Giải:
Đặt x  t dx  dt Đổi cận: x  4 4 t  4 4   4 6 4 6 4 t 6 4 t 6 4 x 6 tan x tan t e tan t e tan t e tan x Khi đó: I dx   dt   dt dt dxx     e       1 t e 1 t e 1 t e 1 x e 1    4 4 4 4 4 Ta có: 4 6 4 x 6 4 tan x e tan x 6 I I dx
dx tan xdx   x   e   1 x e 1    4 4 4 4 4  tan x    2 tan x   2 1  tan x  2 tan x   2
1  tan x 11 dx  4 5 3 tan x tan x  26 4   
tanx x   5 3 |  15 2   4 a
Tính chất 5: Nếu hàm số f (x) liên tục trên 0;1 
 thì : xf (sin x)dx
f (sin x)dx  2  . 0 0
Với dạng này ta thường lựa chọn cách đặt x t x sin x
Ví dụ: Tính tích phân sau: dx  2 1 cos x 0 53
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN b b
Tính chất 6: Nếu hàm số f (x) liên tục trên  ; a b 
 thì : f (x)dx
f (a b x)dx  2  . a a
Với dạng này ta thường lựa chọn cách đặt t a b x 2 1 sinx
Ví dụ : Tính I  ln dx  1+cosx 0 Giải:
Đặt x   t dx  dt 2 Đổi cận: x 0 2 t 0 2 Khi đó:
1 sin t 0   2 2  2  1 cost 1 cosx I   ln dt  ln dt  ln dx      1+sint 1+sinx 0 0 1+cos  t 2  2    Vậy 2 2 2  1 cosx 1 sinx   1 cosx 1 s    2  ln  ln  ln . inx I I I dx dx      ln 1dx  1 sinx 1 cosx   1 sinx 1 cosx 0 0  0 2
 0dx  0  I  0 0 2 4sin x
Ví dụ 2: Tính I dx
 sinxcosx3 0 Giải: 54
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Đặt x   t dx  dt 2 Đổi cận: x 0 2 t 0 2 Khi đó:
4sin t 0   2 2  2  4cost 4cos x I   dt dt dx  3  3  3     
0 co s t  sin t
0 co s x  sin x     2 sin  t cos  t    2     2   2 2 2 4sin x 4cos x 4
I I  2I dx dx dx    
sin x cosx3
sinx cosx3
sinx cosx2 0 0 0 2 4   
dx  2tan x    
 2  2  2  4  I  2    4 0 2 2cos x   0  4   
Tính chất 7: Nếu f (x) liên tục trên 0;2,a  0   thì a a
f (x)dx   f (x)  f (2a x) dx     0 0
Với tính chất trên ta thường đặt t  2a x 3
Ví dụ: Tính tích phân sin xsin2xsin3xdx 0
Tính chất 8: Nếu f (x) là hàm tuần hoàn chu kỳ T, xác định và liên tục trên , thì aT aT
f (x)dx f (x)dx   a a
Với tính chất trên ta thường đặt t x T 55
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2013
Ví dụ: Tính tích phân 1 cos2xdx 0 BÀI TẬP ÁP DỤNG: 1 2004 1) x
sin xdx. Ñaët x  t. ÑS : 0 -1 2 4 cos 2) x dx. HD :Ñaët x    t. ÑS :  4 4 cos x  sin x 2 4 0 sin4x x sin 3) :   . 4) x dx HD Ñaët x t dx
HD :Ñaët x t.   2 1 sin x 4  4cos x 0 0 2 x sin x 3 5)
dx HD :Ñaët x t. 6) x cos xdx
HD :Ñaët x  2t  2  4  cos x 0 0 2 4    7) 1 sin ln
x dx HD :Ñaët x    t. 8) ln   
 1 tanxdx HD :Ñaët x    t. 1 cos x  2 4 0 0 56
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN BÀI TẬP BỔ SUNG 57
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
VẤN ĐỀ 7: TÍCH PHÂN TỪNG PHẦN b b b
udv uv vduaa a
sin( x )
Dạng 1: P (x).cos( x ). Trong ñoù P (x) laø ña thöùc baäc n nn xe
sin( x )
Ñaët u P (x) vaø dv  
 cos( x ) nxe
Chú ý: Chỉ số (n) cho ta số lần tích tích phân dạng này
Dạng 2: P (x).ln( x ). u  x dv P x n  Ñaët ln( ) vaø ( ) n b b Dạng 3:  xb e
cos(mx n)dx hoaëc xb e
sin(mx n)dx   a a
Với dạng này ta có thể chọn:  xbu e
,dv cos(mx n) hoaëc dv  sin(mx n)  
u cos(mx n) 
hoaëc u  sin(mx n),  xb dv e
Ghi nhớ : Nhất lô nhì đa tam lượng tứ mũ
BÀI TẬP ÁP DỤNG TÍCH PHÂN TỪNG PHẦN CƠ BẢN 1 Bài 1: Tính 2x I xe dx 0 du dx u x Đặt     2x 1 2x
dv e dx v e  2
Áp dụng công thức tính tích phân từng phần: 58
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 1 1 x 1 x 1 1 x 1 1 x 1 1 x 1 2 2 2 2 2
I xe dx xee dx e e d     x 2 2 1 2 1 2  e e
e   2e   1 2 0 2 2 4 2 4 0 2 4 0 0 0 2 e 1  4 1 Bài 2: Tính 2 x I x e dx 0 2 u x
du  2xdx Đặt    x x
dv e dx v e
Áp dụng công thức tính tích phân từng phần: 1 1 1 x x 1 2 2    2 x   2 x I x e dx x e xe dx e xe dx    0 0 0 0 1 Tiếp tục tính: x J xe dx 0 u x du dx Đặt    x x
dv e dx v e
Áp dụng công thức tính tích phân từng phần: 1 1 x x 1 x
J xe dx xexe dx  1   0 0 0
Vậy I e  2 1
Bài 3: Tính  3    3 1  x I x e dx 0 du  3   3 1 dx u x Đặt     3  x 1 3x
dv e dx v   e  3
Áp dụng công thức tính tích phân từng phần: 59
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1
I   x    x 1 3
1 e dx   3x   1  x 1 3 3 3 1  x ee dx 3  0 0 0 1    x   1  x 1 1  xx 1  x 1 1  x 1 3 3 ee d   3
e     x   3 3 2 5 3 1 3 1 ee   3 3 0 3 3 0 3 0 3 e 0 e
Bài 4: Tính I  4x   1lnxdx 1    ln  dx u xdu  Đặt       x dv 4x   1dx  2
v  2x x
Áp dụng công thức tính tích phân từng phần: e   e e e I 4x   1 ln xdx   2
2x xln x  2x   2
1 dx  2e e   2 x x 2  e  2 1 1 1 1 2 Bài 5: Tính x
I e cos xdx 0
u cosx
du  sin xdx Đặt    x x
dv e dx v e
Áp dụng công thức tính tích phân từng phần 2 2 x I e cos x xdx e cosx  2 xe sin xdx  0 0 0  1 I 2 Tính x
I e sin xdx 1 0
u  sin x
du cosxdx Đặt    x x
dv e dx v e
Áp dụng công thức tính tích phân từng phần 60
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 2 x  sin x  sin  2 x  s x I e xdx e x e co xdx e  sin xI 1  2 0 0 0 0  2 2 x 1  x xe 1
Suy ra: I e cos xdx e cosx
2  e sin x 2  2   2 0  0 0   
BÀI TẬP CHUYỂN VỀ TÍCH PHÂN TỪNG PHẦN CƠ BẢN 2 Bài 1: Tính 2
I x sin xdx 0   2 2 2 2 1 cos2x 1 Ta có: 2 I x sin xdx x dx
xdx xcos2xdx       2 2     0 0 0 0     2 2 2 x xdx  2   2 8 0 0 2
 Tính xcos2xdx 0 du dxu x Đặt     1
dv cos2xdx v  sin2x  2
Áp dụng công thức tính tích phân từng phần: 2 2 1 1 cos2x 1
xcos2xdx x sin2x 2  sin2xdx  0   2    2 2 4 2 0 0 0 0 2 2  4 Vậy 2
I x sin xdx   16 0 61
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 Bài 2: Tính sin x I e sin2xdx 0 Giải: 2 2 Ta có: sin x sin  sin2  2 x I e xdx e sin xcosxdx   0 0
Đặt t  sin x dt cosxdx Đổi cận: x 0 2 t 0 1 Khi đó: 2 1 sin  2 x sin  2 t I e xcosxdx te dt   0 0 u t du dt Đặt    t t
dv e dt v e
Áp dụng công thức tính tích phân từng phần: 1 1 t t 1 t t 1 t 1
te dt te e dt te e  1   0 0 0 0 0 Vậy I = 2 1
Bài 3: Tính I x ln 2 x   1dx 0 Đặt 2
t x 1 dt  2xdx Đổi cận: x 0 1 62
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN t 1 2 Khi đó: 1 I x  x   2 2 1 ln 1 dx  lntdt 2  0 1   ln  dx u tdu  Đặt    tdv dt v t
Áp dụng công thức tính tích phân từng phần: 2 2 2
lntdt t lnt dt  2ln2 1   1 1 1 1 1
Vậy I x ln 2 x   1 dx  ln2   2 0
MỘT SỐ BÀI TẬP DẠNG KHÁC CỦA TÍCH PHÂN TỪNG PHẦN 3 x
Bài 1: Tính I dx  2 cos x 0 u x  du dx Đặt  dx   dv   v  tan x 2  cos x
Áp dụng công thức tính tích phân từng phần: 3 4 3 3 x 3 sin x 3 d cosxI
dx x tan x  3  tan xdx   dx   2    cos x 3 cosx 3 cosx 0 0 0 0 0 3 3   ln cosx 3   ln2 3 3 0 2
Bài 2: Tính I cosx ln  sinxdx 6 63
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN   lnsin   cosx u xdu dx Đặt    sin x
dv cosdx
v  sin x
Áp dụng công thức tính tích phân từng phần:   2 I cosx
xdx x x 2
2  cosxdx x   x 2 2 ln sin sin ln sin sin ln sin  sin x 6 6 6 6 6 1  1   ln 1 2  2    3 xdx
Bài 3: Tính I   2 sin x 4 u x  du dx Đặt  dx   dv  
v   cot x 2  sin x
Áp dụng công thức tính tích phân từng phần   3 3 xdx 3 3 94 3 1  1 3 I   x cot x  cot xdx   .  ln sin x   ln  2 sin x 3 3 36 2 2 4 4 4 4 2 1 sin x
Bài 4: Tính I  . x e dx 1cosx 0 2 2 x 2 2 x 2 1 sin x x e dx sin x x 1 e dx sin x Ta có: I  .e dx   .e dx   . x e dx 1      cosx 1 cosx 1 cosx 2 2 x 1 o c sx 0 0 0 0 0 cos 2  I2  1 I 2 1 x e dx Tính: I  1 2  2 x 0 cos 2 64
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN xu e x   du e dx Đặt  dx  dv     x   tan x v 2 cos  2  2
Áp dụng công thức tính tích phân từng phần 2 x 2 2 1 e dx x x x x x 2 I   e tan 
2  tan .e dx e  tan . x e dx 1 2   2 x 2 2 2 0 0 0 cos 0 2 x x 2 2 2 sin cos 2 sin x x Tính: x 2 2 I  .e dx  . x e dx  tan . x e dx 2 1    cosx 2 x 2 0 0 0 2cos 2 Vậy 2 I e BÀI TẬP ÁP DỤNG:
Bài 1. Tính các tích phân sau: e 4 1 3 3e 1
a) x ln xdx ; ÑS : b) x xe dx ; ÑS :1  16  1 0
Bài 2. Tính các tích phân sau: 2 2 2 2 3
a) x cos xdx ;
b) x sin xdx ;
c) x cos xdx ;    0 0 0
Hướng dẫn và đáp số:
Trong bài 2, ở các câu sau đều sử dụng kết quả của câu trước. 3   a) 1 ; b)2 1 ;
c) 3 6 2  2    8
Bài 3. Tính các tích phân sau: 65
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 a) ln   2
x  1 x dx ;
ÑS :ln 2  1 2 1 0 2 ln(1 x) 3 b) dx ; ÑS : ln3  3ln2  2 x 2 1 Hướng dẫn:  u   2 x   x
u  lnx   1 ln 1 a)Ñaët ; b)Ñaët    1   dv dx dv dx 2  x
Bài 4. Tính các tích phân sau: 1 2 e 4 a x xdx ÑS   e   2 3 1 x 3 1 ) ln ; : 2 1 b) x ln dx ; ÑS : ln3  9  1 x 8 2 1 0 e ln x 1 3 c) dx ; ÑS :   3 2 x 4 4e 1 Hướng dẫn: 1 1 2 2 u  ln x 1 a)Ñaët  ; ) ln  x b x dx  x ln 
 1 x xln1 xdx  dv xdx 1 x   0 0
Bài 5. Tính các tích phân sau: 3     a   xu lntan x 3
) sinx ln tan dx ; Höôùng daãn: 
ÑS : ln 3 ln tan  
dv  sin xdx 2  8  4
u  ln cos x 4   ln(cos x)  2 b) dx; Höôùng daãn:   ÑS :ln 1  2 1 cos xdv dx 2 4 0 2  cos x 4 x 2 c) dx ; ÑS :  ln  2 cos x 4 2 0
Bài 6. Tính các tích phân sau: 66
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 0 a x    x 2 2 63 2 e 1 ) ln 1 dx ; ÑS :6  ln3
b) x ln xdx ; ÑS :  2  4 4 8  1 0 1 ln 1 x c dx ÑSd x    2x   1 ) ; :4ln2 2 ) ln
1 dx ; ÑS :  ln2  1 x 2 3 0 Hướng dẫn:
a,c) Ñaët t  1 x sau ñoù ñöa veà tính tích phaân töøng phaàn 2 u  ln x
b)Ñaët dv xdx
Bài 7. Tính các tích phân sau: 3 x ln x x ln3 1 9 a) dx ;
Höôùng daãn: Ñaët u  ln x,dv dx. ÑS :  ln  x  21 x  2 2 2 20 2 5 1 1 Bài x ln 2 1 x  1 x  ) ; HD: Ñaët  ln   2  1 , x c dx u x x
dx. ÑS : 2 ln 2 1 1 2  2   0 1 x 1 x
8. Tính các tích phân sau: 2 2 2x 3  e  2 2x 2 1
a) e cos3xdx ; ÑS :
b) e sin xdx ÑS :    2e  1 13 8 0 0 2 2 4 x 3 ) sin3 ; :   e ) x c e xdx ÑS d dx   2 10 cos x 0 0
Bài 9. Tính các tích phân sau:
4 x  sin xa)I dx.
Höôùng daãn: taùch thaønh toång hai tích phaân thaønh phaàn  2 cos x 0 u x 4 x sin ) x b I . Ñaët    3  sin  cos x x dv dx  3  cos x 6 67
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN BÀI TẬP BỔ SUNG 68
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
VẤN ĐỀ 8: ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG Dạng toán 1: Tính điện tích hình phẳng giới hạn bởi (
C) : y f (x), f (x) lieân tuïc treân  ; a b   
y  0(truïc hoaønh) b
được tính bởi công thức S f (x)dx  x a a  y b Phương pháp:
 Ta cần phải tìm đầy đủ 4 đường như trên
 Vì cần phải bỏ dấu trị tuyệt đối nên ta có hai cách giải sau:
Cách 1: Phương pháp đồ thị: 69
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Chú ý: Nếu bài toán yêu cầu: Tính điện tích Hình phẳng giới hạn bởi đò thị hàm số x=f(y)( liên
tục trên đoạn [a,b]), trục tung và hai đường thẳng y=a,y=b. b
Khi đó công thức tính diện tích là: S f (y)dya BÀI TẬP ÁP DỤNG: Bài 1.
a) Tính diện tích hình phẳng giới hạn bởi 2
(C) : y  4  x trục hoành và 2 đường thẳng x  1  ; x  1.
b) Tính diện tích hình phẳng giới hạn bởi 2
(C) : y  4  x , y  0 và 2 đường thẳng
x  1, x  3. 70
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN Đáp số: 22 a) ; b) 4 3
Bài 2. Tính diện tích hình phẳng giới hạn bởi: 2
a) y=cosx+1, trục hoành và hai đườn thẳn g x  0 và x  3 b) 3
y x 1, trục hoành, trục tung và đường thẳng x  2 Đáp số: 3 2 7 a)  ; b) 2 3 2
Bài 3. Tính diện tích hình phẳng giới hạn bởi: a) Đồ thị hàm số 2
y  x  3x  2 và trục hoành b) Đồ thị hàm số 3 2
y x  2x x  2 và trục hoành Đáp số: 1 37 a) ; b) 6 12
Bài 4. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y e 1, trục hoành và hai đường
thẳng x  ln3, x  ln8 3
Đáp số: a)2  ln 2
Bài 5. Tính diện tích tam giác cong giới hạn bởi các đường x x ln ln2
 1; x e ; y  0 ; y ĐS: 1    2 2 2 4 2 2 x ln (x 1)
Bài 6. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y  , trục tung, trục 2 x 1
hoành và đường thẳng x e 1 Bài 7.
a) Tính diện tích hình phẳng giới hạn bởi đường cong 2
y x 1 x , trục Ox và x  1. ĐS: 1 2 2  1 3 71
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 ln x
b) Tính diện tích hình phẳng giới hạn bởi đường cong y
, trục Ox và x  1, x x 2
e . ĐS: 2 2  1 3
Bài 8. Tính diện tích hình phẳng giới hạn bởi: a) x 2 2
y xe ,y  0, x  1, x  2. ÑS :e   2 e 1 b) 2
y x ln x,y  0, x  1, x e.
ÑS :  2e   1 4
Bài 9. Tính diện tích hình phẳng giới hạn bởi:
a)y  ln(x 1),y  0, x  0, x  1
b)y  ln(x 1) truïc tung vaø hai ñöôøng thaúng y  -1 vaø y  1
Đáp số: a)2ln2 1 72
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Dạng toán 2: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), y=g(x) ( liên tục trên
đoạn [a;b]), 2 đường thẳng x=a, x=b. 73
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Chú ý: Nếu bài toán yêu cầu: Tính điện tích Hình phẳng giới hạn bởi đồ thị hàm số x=f(y),
x=g(y)( liên tục trên đoạn [a,b]), và hai đường thẳng y=a,y=b. b
Khi đó công thức tính diện tích là: S f (y)  g(y)dya BÀI TẬP ÁP DỤNG:
Bài 1. Tính diện tích hình phẳng giới hạn bởi 3 2
(C ) :y x  3x ;(C ) : y  4x hai đường thẳng 1 2 55 x=-1;x=2. ĐS: 12 Bài 2.
a) Tính diện tích hình phẳng giới hạn bởi 2
(C ) :y  4  x ;(C ) : y  x  2 1 2
b) Tính diện tích hình phẳng giới hạn bởi (C ) :y  ln x ;(C ) : y  ln x và x=e 1 2 27 ĐS: a) ; b)2 6
Bài 3. Tính diện tích hình phẳng giới hạn bởi các đường
c) Tính diện tích hình phẳng giới hạn bởi 2 2
(C ) :y x  2x ;(C ) : y  x  4x 1 2
d) Tính diện tích hình phẳng giới hạn bởi ( ) :  ( 1) ;( ) :  (1 x C y e x C ye )x 1 2 e
ĐS: a) 9; b) 1 2 74
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 x
Bài 4. Cho hàm số y
. Tìm b sao cho diện tích hình phẳng giới hạn bởi (C) và các đường 2 x 1 thẳng y=1, x=0, x=b bằng
. ĐS: b  1 4
Bài 5. Tính diện tích hình phẳng giới hạn bởi các đường x(1 x) y = 0; y = . 2 x 1
Bài 6. Tính diện tích giới hạn bởi các đường: 2
(D) : x y  0;(C) : x  2x y  0 9 ĐS: 2 Bài 7. Tính diện tích hình phẳng giới hạn bởi các đường: 2
(D) : y x;(C);y  sin x x 0  x . ĐS: 2
Bài 8. Tính dện tích hình phẳng giới hạn bởi các đường 2
y x  4x  3 và y x  3
Bài 9. Tính diện tích hình phẳng giới hạn bởi Parabon( P ): 2
y  x  4x và đường thẳng
d : y x
Bài 10. Tính diện tích hình phẳng giới hạn bởi các đường: 2 2 x 4 x y   và y  4 4 2
Bài 11. Tính diện tích hình phẳng giới hạn bởi: 2 x 4
a)y x 1 x ,y
, x  0, x  3. ÑS : 2  x 3 1 y 2 2 1 b)x
;x  1 y hai ñöôøng thaúng x  0 vaø x ÑS :  2  y 2 8 4 1
Bài 10. Tính diện tich hình phẳng giới hạn bởi 2
y x 1 vaø y= x 1
Bài 11. Tính diện tich hình phẳng giới hạn bởi 2
y x  4x  3 vaø y x 1 75
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN BÀI TẬP BỔ SUNG 76
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
VẤN ĐỀ 9: ỨNG DỤNG TÍCH PHÂN TÍNH THỂ TÍCH VẬT THỂ TRÒN XOAY
Dạng toán 1 : Tính thể tích vật thể tròn xoay sinh bởi miền (D) giới hạn bởi y=f(x), x=a,x=b,
trục hoành (y=0) quay quanh trục Ox b
Phương pháp: Áp dụng công thức 2
V  f (x)dxa Chú ý:
 Nếu đề toán yêu cầu : Tính thể tích vật thể tròn xoay sinh bởi miền (D) giới hạn bởi
x=f(y), y=a,y=b, trục trục tung (x=0) quay quanh trục Oy b
thì ta áp dụng công thức 2
V  f (y)dy. a
 Trong một số trường hợp chúng ta cần tìm cận a, b thông qua việc thiết lập điều kiện
không âm cho hàm số f(x) (hoặc f(y)) BÀI TẬP ÁP DỤNG:
Bài 1. Tính thể tích khối tròn xoay tạo thành khi : 77
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
a) Quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số x
y e , trục hoành và
hai đường thẳng x  0; x  3
b) Quay quanh trục tung một hình phẳng giới hạn bởi đồ thị hàm số 2
y  3  x , x  0,y  1,
trục hoành và hai đường thẳng x  0; x  3 ĐS: a  6 ) e   1 ; b)2 2
Bài 2. Tính thể tích khối tròn xoay tạo thành khi quay hình H quanh trục Ox, với  4 4 
a)H  y  0;y  1 cos x  sin x;x   ; x 2     6 6 
b)H  y  0;y cos x  sin x;x  0;x   2  
Hướng dẫn và đáp số: Khi tính tích phân chú ý biến đổi 4 4 2 2 6 6 2 2
sin x cos x  1 2sin x cos x; sin x  o
c s x  1 3sin x cos x; 2 7 5 ĐS: 2 a) ; b) 8 16
Bài 3. Tính thể tích khối tròn xoay tạo thành khi quay hình H quanh trục Ox, với         5 2 81 ) 0; 3 ( 0); 0 . : a a H y y ax x a y ÑS 10
b H  y y x x x x   3 (5e  3) ) 0; ln ; 1; e ÑS :V  27
Bài 4. Tính thể tích khối tròn xoay tạo thành khi quay quanh trục hoành một hình phẳng giới hạn
bởi đồ thị hàm số y  sin x,y  0,x  0,x , trục hoành và hai đường thẳng x  0; x  3 ĐS: 2 2
Bài 5. Tính thể tích khối tròn xoay tạo thành khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số
a) y x y x ÑS    2 ln , 0, 2 : 2 ln2 1 . 78
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN b) x
y xe y x ÑS  2 , 0, 1 : e   1 4
Dạng toán 2 : Tính thể tích vật thể tròn xoay sinh bởi miền (D) giới hạn bởi y=f(x), y=g(x), x=a,x=b(aChú thích: b
Phương pháp: Áp dụng công thức 2 2
V  f (x)  g (x) dx (3) a 79
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Chú ý: Nếu đề toán yêu cầu : Tính thể tích vật thể tròn xoay sinh bởi miền (D) giới hạn bởi
x=f(y),x=g(y), y=a,y=b, trục tung (x=0) quay quanh trục Oy b
thì ta áp dụng công thức 2 2
V  f (y)  g (y) dy. a BÀI TẬP ÁP DỤNG:
Bài 1. Tính thể tích của khối tròn xoay khi quay hình phẳng xác định bởi 2 2 162
a)y x ,y  3x . ÑS : 5 4
b)y  ;y  x  5 ÑS :9 x 2 56
c)y  2  x ,y  1, quay quanh truïc Ox. ÑS : 15 2
d)y  2x x ,y x, quay quanh truïc Ox, ÑS : 5
e)y  2x  1 480 3
1 , x  0,y  3, quay quanh truïc Oy. ÑS : 7 2
f)y x 1, x  0 vaø hai tieáp tuye 2
án vôùi y x 1 taïi ñieåm (1;2), quanh truïc Ox 8 ÑS : 15 2 e 1
g)y=lnx,y=0,x=e, quanh truïc Oy. ÑS : 2
Bài 2. Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định 2 2 3 3
a)y x , x  0 vaø tieáp tuyeán vôùi ñöôøng y=x taïi ñieåm coù hoaønh ñoä x=1, quay quanh bởi truïc Oy 1
b)y  1,y  0,y  2x, quanh truïc Ox x 80
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2
c)y= 2x x ,y  0 vaø x=3, quanh: *Truïc Ox *TruïcOy
HöôùngDaãn vaø ÑaùpSoá: 2 1 a)
. Phöông trình tieáp tuyeán laø y= x  36 3 3 2 1 1 3  3 1  V y dy y dy     2 2   36 0 1 3  5  b)  2ln2  3    18 59 c)V  vaVø x 5 y 6 1    HD V y y         dy      y dy   y     3 2 2   2 59 : 1 1 1 1 9 1 1       6 0 0
Bài 3. Cho hình phẳng (H) giới hạn bởi các đường : x y ; x  0 ; y   x  2.
Tính thể tích khối tròn xoay tạo thành khi cho hình (H) quay quanh trục Oy.
Hướng dẫn và đáp số:
Phương trình định tung độ giao điểm : 2  y  0
y  2  y   2
y  5y  4  0 y  2   y  1  y  1 
y  4 (l)
Đường thẳng y = 2 – x cắt trục tung tại y = 2
Thể tích khối tròn xoay cần tìm : V = V1 + V2 2 y 1 Trong đó V 1 2 1 =
( y) dy  = (đvtt) 0 2 0 2 3 2 (y 2) V 2 2 2 2 2
(2 y) dy  (y 2) d(y 2)          = (đvtt) 1 1 3 1 3 81
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 5 V = (vtt) 6 BÀI TẬP BỔ SUNG 82
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
MỘT SỐ BÀI TẬP CẦN LÀM TRƯỚC KHI THI 1 5 x
Bài 1. Tính tích phân: dx. 2 x 1 0 1 1 ĐS: ln2  2 4
Bài 2. Tính các tích phân sau: 3
dx . (KhoáiD 2009). ÑS : 2
  ln e e   x  2 1 e 1 1 3 1 x x
: Theâm löôïng vaø bôùt löôïng  e e dx HDx e 1 1
Bài 3. Tính các tích phân sau: e ln x 3 1 dx.(KhoáiB-2010)
HD : Ñaët t  ln x. ÑS : ln 
x2lnx2 2 3 1
Bài 4. Tính các tích phân sau: ln 5 1 x 3 dx.(KhoáiB-2006)
HD : Ñaët t e . ÑS : ln  2x e  2 x e  3 2 ln3 2 2 4  x
Bài 5. Tính I
dx. HD :x  2sint. ÑS : 3   2 x 3 1 2 2 1 x 2 4
Bài 6. Tính tích phân sau : I
dx. HD :Chiacaû töû vaø maãu cho x . ÑS : ln  3 x x 5 1 1 dx
Bài 7. Tính tích phân:  . 2 1  1  x  1 x 1 2 1 2
1 x  1 x
1 x  1 x
Hướng dẫn: I dx dx .  ..  1  
 1 x2   2 2x 1 1 x  1 
4 tan x.ln(cos x) 2
Bài 8. Tính tích phân: I =
dx.HD :t  cos x. DS : 2 1 ln2  . cos x 2 0 83
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN e  ln x
Bài 9: Tính tích phân: 2 I    ln x dx
1  x 1  ln xGiải: e  ln xe e 2 I ln x    ln x dx 2 
dx  ln xdx I I   1 2
1  x 1  ln x  1 x 1  ln x 1 e ln x Tính I dx 1 1 x 1lnx Đặt 2  1 ln   1  2 dx t x t lnx tdt x Đổi cận: x 1 e t 1 2 e  2 2 t   2 3 1 ln tdt xt  2 4 2 2 Khi đó: I dx  2  2  
  2t 1 dt  2 1   1  x 1 ln x t 3   1 3 3 1 1 1 e Tính 2 I  ln xdx 2 1  2 2lnx u ln xdu dx Đặt    x dv dx v x
Áp dụng công thức tính tích phân từng phần e e e e 2 2
I ln xdx xln x lnxdx e  2 lnxdx 2    1 1 1 1   I3 I3 e
Tính I lnxdx 3 1 84
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂNdxu lnxdu  Đặt    xdv dx v x
Áp dụng công thức tính tích phân từng phần e e e e
I lnxdx xlnx dx e x e e 1  1 3     1 1 1 1 e Suy ra: 2
I ln xdx e  2I e  2 2  3 1 4 2 2 2 2 2
Vậy I I I  
e  2  e   1 2 3 3 3 3 1 x 2
Bài 10. Tính tích phân: 3 1 2 e
dx. HD :t  3x 1. DS : e  3 0 3ln 2 dx
Bài 11: Tính tích phân: I    xe  2 3 0 2 Giải: x 3ln 2 3ln 2 3 dx e dx Ta có: I      x e 22 2 3 x x 0 0    3 3 e e  2     x 1 x x Đặt 3 3 3
t e dt e dx  3dt e dx 3 Đổi cận: x 0 3ln2 t 1 2 Khi đó: 85
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN x 3ln 2 3ln 2 2 2   3 dx e dx dt 1 1 1 I                   e   3 3 2 2 x x x   3 4t 4t t t 2 2  2  t 2 2 2 3 0 0 1 1 3 3 e e 2         1 1 1  2  1 1 1  1 1 
 3 ln t ln t  2 
   ln ln    ln   2  t 2 3 2 4 3 4 4  1 4 4 8     4 6   3  3  1  ln  4  2    8 3 x  3
Bài 12: Tính tích phân: I dx
03 x1 x3 Giải: Đặt 2
t x 1  t x 1 2tdt dx Đổi cận: x 0 3 t 1 2 Khi đó: 3 2 2 2 3 2 x  3 t  4 2t  8   2   2  6  6 dt I dx tdt dt t dt   2  2   2
3 x 1  x  3 3t t  2 3t t  2 t 1 0 1 1 1 1   2 2 2 t t 3 6
 6ln t 1  6ln  3 1 1 2
2 3sinx  2cos x
Bài 13: Tính tích phân: I dx
 sinxcosx3 0 Giải:
Đặt x   t dx  dt 2 Đổi cận: 86
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN x 0 2 t 0 2 2 0 2 3sinx  2cos x 3cost  2sint
3cos x  2sin x Khi đó: I dx   dt dx    
sin x cosx3
cost  sin t3
cosx sinx3 0 0 2
2 3sinx  2cos x
2 3cos x  2sin x 2 dx Suy ra: 2I = I + I = dx  + dt   = 
sin x cosx3 3 2 0
0 cos x  sinx
0 cos x  sinx d x    2 dx 2 1   4    1       1 tan x    2  1. Vậy I = .   2   2  4 2 0 2 2cos x    0 2 cos x  0 4       4  4 x 1
Bài 14: Tính tích phân: I    dx 1 1 2x 2 0 Giải: dx 2 t 2t
Đặt t  1 1 2x dt
dx  t   1 dt và x   1 2x 2 Đổi cận: x 0 4 t 2 4  2 4
4 t  2t  2t x    4 3 2 1 1 1
1 t  3t  4t  2 Khi đó: I    dx dt dt   1 1 2x 2 2 2 2 t 2 t 0 2 2 4 1  4 2  2 1  t 2  4 1  t  3   dt  
  3t  4ln t    2ln2- 2 2  t t  2 2 t   2 4 2  87
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1  x
Bài 15: Tính tích phân: 2 3
I   x sinx  dx   0 1 x   Giải: 1   1 1 2 3 x   s x I x inx  dx  2 3 
x sinx dx
dx I I 1 x    1 2 1 x 0   0 0 1 Tính 2 3
I x sinx dx 1 0 dt Đặt 3 2 2
t x dt  3x dx x dx  3 Đổi cận: x 0 1 t 0 1 1 1 1 1 1 1 Khi đó: 2 3
I x sinx dx
sintdt cost   co 1 s 1 1  3    3 0 3 0 0 1 x Tính I dx 2 1 x 0 Đặt 2
t x t x  2tdt dx Đổi cận: x 0 1 t 0 1 Khi đó: 1 1 2 1 1 1 1 x t  1  dt 1   2  2 1  2  2  2  2 dt I dx dt dt dt t  2  2I 2   2  2    2  2 3 1 x 1 tt 1 t 1 0 t 1 0 0 0 0 0 0 1 dt Tính I  3  2t 1 0 88
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Đặt t tanu dt   2
tan udu   2 1 1 u du  Đổi cận: x 0 1 t 0 4 1 4 dt Khi đó: I   du u  3  2  4 t 1 4 0 0 0
Suy ra: I  2  2I  2  2 3 2 1 7 1
Vậy: I   co 1 s  
1  2    co 1 s  3 2 3 3 2
 tanx    6   4 
Bài 16: Tính tích phân: I   dxcos2x 0 Giải:
 tanx   6   6 2  4  tan x 1 I dx   dxcos2x  tan x 2 2 0 0 1 dx
Đặt t tanx dt    2 tan x 1 dx 2  cos x Đổi cận: x 0 6 t 0 1 3 Khi đó: 89
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 1 tan x  1 6   6 2 3 3  4  tan x 1 1 d t   1 I 1 1 3  dx   dx   dx      cos2x     3 tanx  2 1 t  2 1
t  2 t 1 2 0 0 0 0 1 0 1 dx
Bài 17: Tính tích phân: I   2 1  1  x  1 x Giải: 2 t 1 1  1  Đặt 2 2 2 2 2
t x  1 x t x  1 x t  2tx x  1 x x   dx  1 dt  2 2t 2 t    Đổi cận: x -1 1 t 2 1 2 1 Khi đó: 1  1  1  1 1 1    1 2 1   2  2 1   2  2 1  2 1 dx 2  t  1 2  t  1 dt 1  dt I   dt dt                x x 1 t 2 1 t 2 1 t 2 1 1     1 t 2 2 t 1 2 1 2 1 2 1 2 1 2 1  2 1 1 dt 1   1 1 1  1  1  1        dt   2 1 2 1   ln 1 t
ln t ln 1 t  1 2 2 1 t 2    t t t 1   2  2  t 2 1  2 1   2 1  2 1 4 sinx
Bài 18: Tính tích phân: I dx  2 1 x x  4 Giải: 4 4 4 sinx sin xdx I dx
 sin xdx I I    1 2 2 2 1 x x 1 x    4 4 4 90
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 4 sin xdx Tính I  1  2 1 x  4
Đặt x  t dx  dt Đổi cận: x  4 4 t  4 4  4 4 4 sin xdx sintdt sin xdx Khi đó: I     1    2 2 2 1 x 1 t 1 x   4 4 4
Suy ra 2I I I  0  I  0 1 1 1 1 4
Tính I x sin xdx 2 4 u xdu dx Đặt   dv sinxdx   v  cosx
Áp dụng công thức tính tích phân từng phần 4 4 4 2 4 2
I x sin xdx  xcos x
cos xdx    sinx    2 2   4 4     4 2 4 4 2 Suy ra: I I I      2 1 2 4 2 dx
Bài 19: Tính tích phân: I   2
cos x  3cosx  2 0 Giải: 91
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 2 2 2 dx dx dx I     I I  2   1 2
cos x  3cosx  2 1 cosx 2  cosx 0 0 0 2 2 dx 1 dx x  Tính 2 I    tan  1 1    cosx x |0 1 2 2 2 0 0 cos 2 2 x 2 2 1  tan dx Tính 2 I   dx 2  2   cosx 2 x 0 0 3  tan 2 xx  3 Đặt 2
tan  3tant  1 tan dx     2 1 tan tdt 2  2  2 Đổi cận: x 0 2 t 0 6 2 x 2 2 1  tan 6 dx 2 2 Khi đó: 2 6 I   dx dt t  2     cosx x |0 2 2 0 0 3 0 3 3 3 3  tan 2
Vậy: I I I  1 1 2 3 3 2 sin2x
Bài 20: Tính tích phân: I dx  2cosx3 0 Giải:
Đặt t  2  cosx dt  sinxdx Đổi cận: 92
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN x 0 2 t 3 2 Khi đó: 2 2 2 3 3 3 sin2x sinxcosx t  2 t  2  1 1  I dx  2 dx  2 dt 2 dt 2      dt  2 dt     2  cosx3 2cosx3 3 3  2 3 t t t t  0 0 3 2  2 2   1  1  3 1  2    2  t |2 t  18 2
Bài 21: Tính tích phân: 2 sin x 3 I e sin xcos xdx 0 Giải: Đặt 2
t sin x dt  2cosxsinxdx Đổi cận: x 0 2 t 0 1 2 2 1 1 1 sin x sin x 1 t 1 t 1 Khi đó: 2 2 3 2  sin  sin     1  t I e xcos xdx e cos x xcosxdx e t dt e dt te dt 2 2  2  0 0 0 0 0 1 1 1 t 1 t 1 1 1
e |  te dt e  I  0 1 2 2 2 2 2 0 1 Tính t I te dt 1 0 u t du dt Đặt    t t
dv e dt v e
Áp dụng công thức tính tích phân từng phần 93
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 1 1 1 t t t t
I te dt te e dt e e e e 1  1 1  |  | 0 0 0 0 1 1 1 1
Vậy: I e   I e 1 1 2 2 2 2 94
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN D. PHỤ LỤC
PHƯƠNG PHÁP ĐẶT ẨN PHỤ KHÔNG LÀM THAY ĐỔI CẬN TÍCH PHÂN 5 3
Bài toán mở đầu : Tính tích phân I=   3 2
x  3x  2 dx 3 
Khi gặp bài toán này, chắc chắn rằng tất cả các bạn đều nghĩ cách khai triển biểu thức dưới dấu
tích phân để đưa về các tích phân cơ bản để tính. Đó là một cách suy nghĩ thường hay gặp phải.
Nhưng bạn hãy thử làm xem sao, và hãy thử thay (x3-3x2+2)3 bằng (x3-3x2+3)7 , (x3-3x2+3)9 ....
rồi tính nhé!. Sau đó mời các bạn nghiên cứu lời giải sau: dx  dt
Lời giải: Đặt x=2-t 
 x  3: t  5
x  5: t  3  3 
I    (2  t) 3(2  t)  2 5
dt   t  3t  2 5 3
3 dt  t 3t 23 3 2 3 2 3 2 dt 5 3  3  5
   x 3x  23 3 2
dx  I  2I  0  I  0 3 
Khi đọc xong lời giải trên chắc chắn các bạn sẽ đặt câu hỏi : Tại sao lại đặt ẩn phụ như vậy? Để
tìm câu trả lời xin mời các bạn nghiên cứu tiếp bài toán tổng quát sau:
Bài toán tổng quát: Cho f(x) là hàm lẻ, liên tục trên [-a; a]. a Chứng minh rằng
f (x)dx  0 a
Đây là một bài tập khá quen thuộc với các bạn khi học tích phân và nhiều bạn đã biết cách giải.
Xong các bạn hãy xem kỹ lời giải sau để “ phát hiện” ra vấn đề. dx  dt Lời giải: Đặt x= -t 
 x  a : t a
x a : t  aaa a
I f (x)dx   f (t)dt f (t)dt   
. Do f(x) là hàm lẻ nên f(-x)=-f(x) do đó a aa a a a
I f (t)dt   f (t)dt   f (x)dx  I  2I  0  I  0    aaa 95
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Qua 2 bài toán trên, điểm chung của cách đặt ẩn phụ là gì?
Câu trả lời là : Đặt ẩn phụ nhưng không làm thay đổi cận của tích phân. b
Cách đặt tổng quát khi gặp tích phân f (x)dx
mà không thay đổi cận là đặt x=a+b-t. a
Bài toán mở đầu còn có cách giải khác khá hay để dẫn tới một “ suy nghĩ” mới như sau:dx  dt 4  4 3 3 Đặt x=1-t 
 x  3 : t  4  I     3 2
(1 t)  3(1 t)  2 dt    3
t  3tdt .
x  5: t  4 4 4  
Sử dụng kết quả chứng minh của bài toán 2 ta được I=0 ( do f(t)= -t3+3t là hàm số lẻ).
Vậy “ suy nghĩ” mới ở đây là gì? Việc đặt ẩn phụ như vậy ta đã dẫn đến tích phân có cận “đối b
xứng” . Trong trường hợp tổng quát để dẫn đến cận “ đối xứng” khi gặp tích phân f (x)dx  các a a b bạn hãy đặt x   t 2
Bây giờ chúng ta cùng vận dụng suy nghĩ đó để giải một số bài toán sau: 4 6 6 sin x  cos x
Bài toán 3: Tính tích phân I dx
( Đề thi đại học năm 2000).  6x 1  4 Lời giải:  dx  dt  
Đặt x=-t  x   : t  ( cách đặt này đã không làm thay đổi cận của tích phân) . 4 4  x   : t    4 4  4 6 6 4 6 6 4 6 6
sin (t)  cos (t)
t sin t  cos t
x sin x  cos x Khi đó I   dt  6 . dt  6 . dx        6 t 1 6t 1 6x 1   4 4 4 96
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 4 6 6 4 6 6 4
x sin x  cos x sin x  cos  2  6 . x I dx dx x x dxxx   6 6 sin cos    6 1 6 1    4 4 4 4          s x x 4 4 4 2 2 3 2 3 2 5 3 1 3 in cos dx
1 sin 2x dx
1 sin 2x dx   cos4x dx      4     4     8 8       4 4 4 4  5x 3  4 5   sin 4x   . 8 32    16 - 4
Chú ý: Bài toán 3 có dạng tổng quát sau: Nếu f(x) là hàm số liên tục, chẵn thì b f (x) b f (x) 1 b x I dx a dx I f (x)dxx   . a 1 x a 1 2 bbb x sin x
Bài toán 4: Tính tích phân I = dx  2 cos x  4 0
Thông thường khi gặp tích phân trên, hầu hết các bạn đều nghĩ đến phương pháp tính tích phân
từng phần. Xong các bạn hãy thử làm như thế và so sánh với lời giải sau: dx  dt
Lời giải : Đặt x  t
   x  0 : t
x : t  0 
0 (t)sin(t)
(t)sint sint tsint Khi đó I   dt dt dt dt  2  2  2  2
cos (t)  4 cos t  4 cos t  4 cos t  4 0 0 0 sin x x sin x sin x dx dx dx I  2  2  2 cos x  4 cos x  4 cos x  4 0 0 0 sin x sin  2 x I dx I dx  2  2 cos x  4 2 cos x  4 0 0
sinxdx  dt Đặt cosx t
  x  0 : t  1
x : t  1   97
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1  1 dt dt t  2 1 I     ln    2 2  ln3
t  4 2 (t  2)(t  2) 8 t  2 1  4 1 1 
Chú ý: Bài toán 4 có thể tổng quát như sau:
Cho hàm số f(x) liên tục và thoả mãn: f(a+b-x) = f(x) . b b a b
Khi đó xf (x)dx f (x)dx  2  a a
( để chứng minh kết quả trên các bạn hãy đặt x= a+b-t ). 2 xdx
Bài toán 5: Tính tích phân I = 
( Đề thi khối A năm 2004) 1 1  x 1
Với bài toán trên, cách đặt như thế nào để không thay đổi cận của tích phân.
Lời giải: Đặt t  1 x 1
dx  2(t 1)dt Khi đó 2 2 x -1 = (t -1) hay x=(t -1) 1 
  x  1: t  1
( cách đặt này đảm bảo cận không đổi !)
x  2 : t  2  2 2      2 3 2 2 (t 1) (t 1) 1  
t  3t  4t 1  2 1  2 .dt  2
.dt  2 t  3t  4  .dttt  t  1 1 1  3 2  t t  2 5
 2  3  4t  ln | t |   2ln2 . 3 2    1 3 b p x
Chú ý: Bài toán 5 có thể tổng quát dạng ( ) dx
với p(x) là đa thức chứa biến x; m,n,c a
mx n c
là các hằng số . Ta có thể đặt t mx n c hoặc t mx n đều giải được. 2 3 sin x
Bài toán 6: Tính tích phân I  dx  sinx cosx 0 98
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN  dx  dt  
Lời giải: Đặt x   t  x  0 : t  2 2  x   : t  0  2 3
sin  t 0   2 3 2 3  2  cos t cos I x   dt dt dx J        sint  cost sin x  cos x 0 0 sin  t  cos  t 2  2   2      2 3 2 3 2 3 3 2 sin x cos x sin x cos  I+J xdx dx
dx  (1 sin x.cos x)dx  sinx     cos x sin x  cos x sin x  cos x 0 0 0 0 I J 2 1  1  1 
 (1 sin2x)dx x cos2x    2   . Vậy 1 
  I  2 1  4  2 2 I J  4 0 0  2
Chú ý: Bài toán 6 có thể tổng quát thành các dạng sau: b k 2 n m sin mx sin ; ax dx   n m n m sin mx  cosmx a 0
sin ax  cos ax
Qua 6 bài toán trên, tác giả muốn các bạn học sinh có thêm một cách nhìn mới để tiếp cận với
phương pháp đặt ẩn phụ trong tính tích phân. Rất mong nhận được sự quan tâm trao đổi.
Cuối cùng mời các bạn vận dụng vào một số bài tập sau: Tính các tích phân: 1 4x  3 1 I dx 2
I  3 lg x 1  x dx 1  2    0 3x 1  2 1  1  2     2 3 I lg x 1000  x dx I  cos x.ln   2
x x 1 dx 4  3   2 1    2 2004 5 I 2 1 
  x 6x 165 3 2 dx 2 x 4 7 I  e   3 6 16 n x x x dx 6  5 2  000 1  99
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
4 sin x.sin2x.cos3x 1 I dx dx I  7    8 x 2 (e 1)(x 1) 2x 1 1   4
2 sin x.sin2x.cos5x 3 I dx
I x(tgx  cot gx)dx 9  xe  10 1  2 6 x sin x 2 I sin xdx I dx 11  2 cos x  1 12 0 0 sin x  cos x 2 2 x I 4sin 
cos x  sin x dx I dx 13   14  3 0
0 sin x  cos x
SAI LẦM THƯỜNG GẶP TRONG TÍNH TÍCH PHÂN
Trong đề thi tốt nghiệp THPT, Đại học , Cao đẳng, THCN của hàng năm bài toán tích phân hầu
như không thể thiếu, bài toán về tích phân là một trong những bài toán khó vì nó cần đến sự áp
dụng linh hoạt của định nghĩa, các tính chất , các phương pháp tính của tích phân.
Chuyên đề này hy vọng sẽ góp phần giúp các em học sinh hiểu sâu hơn và tránh được những sai
lầm thường mắc phải khi giải bài toán về tích phân.
- Đưa ra hệ thống lí thuyết, hệ thống các phương pháp giải.
- Bài tập ứng với từng dạng toán, và chỉ ra những lỗi thường mắc phải của học sinh. 2 dx
Bài tập 1: Tính tích phân sau I =  2 (x 1) 2  Giải: 1 Hàm số y =
không xác định tại x= -1  2  ;2   2 (x 1) 
 suy ra hàm số không liên tục trên 2;2  
do đó tích phân trên không tồn tại.
Chuù yù: Nhiều học sinh thường mắc sai lầm như sau: 2 dx 2 d(x 1) 1 1 4 I =  = 2 =- -1 = - 2  =- (x 1) 2 (x 1) x 1 2 3 3 2  2 
Nguyên nhân sai lầm : 100
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 Hàm số y =
không xác định tại x= -1  2  ;2   2 (x 1) 
 suy ra hàm số không liên tục trên 2;2  
nên không sử dụng được công thức newtơn – leibnitz như cách giải trên.
Chú ý đối với học sinh: b Khi tính f (x)dx
cần chú ý xem hàm số y=f(x) có liên tục trên  ; a b   không? nếu có thì áp a
dụng phương pháp đã học để tính tích phân đã cho còn nếu không thì kết luận ngay tích phân này không tồn tại. dx
Bài 2 :Tính tích phân: I = 1sinx 0 Giải:x d   dx dx   2 4   x    I =  =   tg   tg  1   = tg 2  sin x   0    x      2 4 4  4 0 0 0 2 1 cos x cos       2   2 4      x 2dt 1 2 1 t
Sai lầm thư ờng gặp: Đặt t = tan thì dx = ; = 2 2
1 t 1 sin x 2 (1 t) dx 2dt 2   = t   + c 1  = 2 2( 1)  sin x 2 (1  d(t+1) =  t) t 1 dx 2  2  2  I =  = = - 1 sin x x 0 tan 0 1 0 tan 1 tan 1 2 2
do tan không xác định nên tích phân trên không tồn tại 2
Nguyên nhân sai lầm: x x
Đặt t = tan x 0; không có nghĩa. 2 
 tại x = thì tan 2
Chú ý đối với học sinh: 101
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Đối với phương pháp đổi biến số khi đặt t = u(x) thì u(x) phải là một hàm số liên tục và có đạo hàm liên tục trên  ; a b   .
Một số bài tập tương tự: Tính các tích phân sau  dx dx 1/  2/ sin x 1cosx 0 0 4 Bài 3: Tính I = 2 x  6x  9  dx 0
Sai lầm thường gặp: 4 x  3 1 9 I = 2 x  6x  9 
dx =  x 3 dx  x 3dx 3  2 4 4 2 4     4 0 2 2 2 0 0 0
Nguyên nhân sai lầm:
Phép biến đổi x  2
3  x  3 với x  0;4 
 là không tương đương. Lời giải đúng: 4 I = 2 x  6x  9  dx 0 4 4 3 4
=  x 32dx x 3d  x 3  
 x 3dx 3 x 3dx 3 0 0 0 3 x 32 x  3 3  2 9 1 = - 4     5 0 3 2 2 2 2 2n
Chú ý đối với học sinh: 2n f x  f x ,n 1,nN b n b I =
n f x2 2  
f xdx
ta phải xét dấu hàm số f(x) trên  ; a b 
 rồi dùng tính chất tích phân a a
tách I thành tổng các phân không chứa dấu giá trị tuyệt đối.
Một số bài tập tương tự: 102
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 3 1/ I = 1 sin2x  dx ; 2/ I = 3 2
x  2x x  dx 0 0 2  1  3 3/ I = 2 x   2   dx 4/ I = 2 2
tg x  cot g x  2 2  dx  x  1  2 6 0 dx
Bài 4: Tính I =  2x 2x 2 1 
Sai lầm thường gặp: 0 d x   1 I =  arctan x 1  arctan1 arctan 0   2   0 4 1   x   1 1 1
Nguyên nhân sai lầm :
Đáp số của bài toán thì không sai. Nhưng söû duïng coâng thöùc treân khoâng coù trong baûng nguyeân haøm Lời giải đúng:
Đặt x+1 = tant  dx   2 1 tan tdt với x=-1 thì t = 0 với x = 0 thì t = 4 2
4 1 tan tdt 4 Khi đó I = 4  dt t    0 tan t 1 4 0 0
Chú ý đối với học sinh:
Khi gặp tích phân dạng b 1  dx
ta dùng phương pháp đổi biến số đặt t = tanx hoặc t = cotx 2 1 x a b 1  dx
thì đặt x = sint hoặc x = cost 2 a 1 x
Một số bài tập tương tự: 103
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN 1 8 2 x 16 1 3 2x  2x  3 3 3 x dx 1/ I = dx  2/ I = dx x  3/ I = 2 x  1 8 4 0 0 1 x 1 4 3 x Bài 5: Tính :I = dx  2 0 1 x
Suy luận sai lầm: Đặt x= sint , dx = costdt 3 3 x sin t dx dt   2 1 x cost
Đổi cận: với x = 0 thì t = 0 1 với x= thì t = ? 4
Nguyên nhân sai lầm:
Khi gặp tích phân của hàm số có chứa 2
1 x thì thường đặt x = sint nhưng đối với tích phân
này sẽ gặp khó khăn khi đổi cận cụ thể với x = 1 không tìm được chính xác t = ? 4 Lời giải đúng: x Đặt t = 2 1 x  dt =
dx tdt xdx 2 1 x 15
Đổi cận: với x = 0 thì t = 1; với x = 1 thì t = 4 4 1 4 3 x I = dx  2 0 1 x 15 4 1 t  15 2 tdt 4 3 15  t   15 15 15  2 33 15 2 =     2 1 t  4
dt  t          1 t 3  4 192  3 192 3 1 1    
Chú ý đối với học sinh: Khi gặp tích phân của hàm số có chứa 2
1 x thì thường đặt x = sint
hoặc gặp tích phân của hàm số có chứa 1+x2 thì đặt x = tant nhưng cần chú ý đến cận của tích
phân đó nếu cận là giá trị lượng giác của góc đặc biệt thì mới làm được theo phương pháp này
còn nếu không thì phải nghĩ đến phương pháp khác. 104
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Một số bài tập tương tự: 7 3 x 2 dx 1/ tính I = dx  2/tính I =  2 2 0 1 x 1 x x 1 1 2 x 1 Bài 6: Tính I = dx  4 1 x 1  1  1  1 1 1 1  2  2 xx
Sai lầm thường gaëp : I =   dx   2 1 2 1  1   1 x   2 x   2 xx    1  1 
Đặt t = x+  dt  1 dx  2 x x   
Đổi cận với x = -1 thì t = -2 ; với x=1 thì t=2; 2 dt 2 1 1 t  2 I =  = (  )dt t  -ln t  2 ) 2 2  ln 2  =(ln 2 t  2 2  2  2  2  t  2 t  2 t  2 2  2 2  2 2  2 = ln  ln  2ln 2  2 2  2 2  2 1 2 1 2 x 1
Nguyên nhân sai lầm: x  là sai vì trong  1  ;1 4 1 x 1 
 chứa x = 0 nên không thể chia cả 2  x 2 x
tử cả mẫu cho x = 0 được. Nhưng từ sai lầm này nếu các bạn thấy rằng x=0 không thuộc thuộc
tập xác định thì cách làm như trên thật tuyệ t vời. Lời giải đúng: 2 1 x x 2 1 Xét hàm số F(x) = ln
( áp dụng phương pháp hệ số bất định ) 2 2 2 x x 2 1 2 2 1 x x 2 1 x 1 F’(x) = (ln )  2 4 2 2 x x 2 1 x 1 1 2 x 1 2 1 x x 2 1 1 2  2 Do đó I = dx  = ln 1  ln 4 1 x 2 1  1  2 2 x x 2 1 2 2  2 105
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
Chú ý đối với học sinh: Khi tính tích phân cần chia cả tử cả mẫu của hàm số cho x cần để ý rằng
trong đoạn lấy tích phân phải không chứa điểm x = 0 . 106
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN
ĐỀ THI ĐẠI HỌC TỪ 2009 -2012
NĂM 2012: Tính các tích phân sau 3 1 lnx   1 2 2
Bài 1. ĐH Khối A – 2012: I = dx. ĐS:  ln2  ln3 2 x 3 3 1 1 3 x 3
Bài 2. ĐH Khối B – 2012: dxĐS: ln3  ln2 4 2 x  3x  2 2 0 4 2 1
Bài 3. ĐH Khối D – 2012: I x
 1sin2xdx ĐS:  32 4 0 3 x 8
Bài 4. CD Khối A,B,D-2012: I dxĐS: 3 0 x 1
NĂM 2011: Tính các tích phân sau
4 x sin x  (x 1)cos x 2 2
Bài 1. ĐH Khối A – 2011: I = dx. ĐS:  ln(  )
x sin x  cos x 4 8 2 0 3 1 x sin x 21 2  3
Bài 2. ĐH Khối B – 2011: dxĐS: 3   ln 2 cos x 3 2 0 2  3 4 4x 1 34 3
Bài 3. ĐH Khối D – 2011: I dxĐS: 10ln 3 5 0 2x 1  2 2 2x 1
Bài 4. CD Khối A,B,D-2011: I dxĐS: ln3 x x 1 1  
NĂM 2010: Tính các tích phân sau 1 2 x 2 x e  2 x x e 1 1 1 2e
Bài 1. ĐH Khối A – 2010 I dx
ĐS: I   ln 1 2 x e 3 2 3 0 e ln x 1 3
Bài 2. ĐH Khối B – 2010 I dx
ĐS: I    ln 2 x(2  ln x) 3 2 1 107
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN e  3  2 e 2
Bài 3. ĐH Khối D – 2010 I  2x  ln xdx  ĐS: I    x  2 1  1 2x 1 2 e 2
Bài 4. CD Khối A,B,D-2010 I dxĐS: I   x 1 2 0
NĂM 2009: Tính các tích phân sau 2 8
Bài 1. ĐH Khối A – 2009 3 2
I  (cos x 1)cos xdxĐS: I   15 4 0 3 3  ln x 1  27 
Bài 2. ĐH Khối B – 2009 I dxĐS: I  3  ln 2 (x 1) 4  16  1  3 dx
Bài 3. ĐH Khối D – 2009 I   ĐS:  2
ln e e   1  2 x e 1 1 1 1
Bài 4. CD Khối A,B,D-2009   -2x    x I e
x e dx ĐS: 2  e 0 108
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
LUYỆN THI ĐẠI HỌC CHẤT LƯỢNG CAO
CHUYÊN ĐỀ: TÍCH PHÂN TÀI LIỆU THAM KHẢO
1. Đậu Thế Cấp, Huỳnh Công Thái (2008), Các kĩ thuật và phương pháp tính tích phân
2. Phạm Kim Chung (2008), Bài giảng tích phân
3. Trần Đình Cư (2011), Bài giảng luyện thi cấp tốc chuyên đề tích phân.
4. Phan Huy Khải (2008), Nguyên hàm- Tích phân và ứng dụng
5. Trần Sĩ Tùng (2010), Tuyển tập các bài toán tích phân
6. Toán hoc và tuổi trẻ 109
Gv: Ths.Trần Đình Cư. SĐT: 01234332133, 0978421673. TP HUẾ
Document Outline

  • www.VNMATH.com