Chuyên đề tiếp tuyến và sự tiếp xúc của đồ thị hàm số – Lê Bá Bảo Toán 12

Tài liệu gồm 62 trang, được biên soạn bởi thầy giáo Lê Bá Bảo (giáo viên Toán trường THPT Đặng Huy Trứ, tỉnh Thừa Thiên Huế), tóm tắt lý thuyết và hướng dẫn giải các dạng toán chuyên đề tiếp tuyến và sự tiếp xúc của đồ thị hàm số trong chương trình Giải tích 12 chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

62 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
G
G
i
i
á
á
o
o
v
v
i
i
ê
ê
n
n
:
:
L
L
Ê
Ê
B
B
Á
Á
B
B
Ả
Ả
O
O
_
_
T
T
r
r
ư
ư
ờ
ờ
n
n
g
g
T
T
H
H
P
P
T
T
Đ
Đ
ặ
ặ
n
n
g
g
H
H
u
u
y
y
T
T
r
r
ứ
ứ
,
,
H
H
u
u
ế
ế
S
S
Đ
Đ
T
T
:
:
0
0
9
9
3
3
5
5
.
.
7
7
8
8
5
5
.
.
1
1
1
1
5
5
Đ
Đ
ă
ă
n
n
g
g
k
k
í
í
h
h
ọ
ọ
c
c
t
t
h
h
e
e
o
o
đ
đ
ị
ị
a
a
c
c
h
h
ỉ
ỉ
:
:
1
1
1
1
6
6
/
/
0
0
4
4
N
N
g
g
u
u
y
y
ễ
ễ
n
n
L
L
ộ
ộ
T
T
r
r
ạ
ạ
c
c
h
h
,
,
T
T
P
P
H
H
u
u
ế
ế
H
H
o
o
ặ
ặ
c
c
T
T
r
r
u
u
n
n
g
g
t
t
â
â
m
m
K
K
m
m
1
1
0
0
H
H
ư
ư
ơ
ơ
n
n
g
g
T
T
r
r
à
à
KH¶O S¸T HµM Sè
TIÕP TUYÕN Vµ Sù TIÕP XóC
Cè lªn c¸c em nhÐ!
HuÕ, th¸ng 9/2020
Phiªn b¶n 2020
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 1
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
Chuyên đề: KH¶O S¸T HµM Sè
I- LÝ THUYẾT
Cho hàm số
y f x
, có đồ thị (C).
1. Tiếp tuyến của đồ thị (C) tại điểm
0 0 0
; ( )M x y C
:
/
0 0 0
y y f x x x
(*)
Lưu ý: + Điểm
0 0 0
; ( )M x y C
được gọi là tiếp điểm.
+ Đường thẳng bất kỳ đi qua
0 0 0
;M x y
có hệ số góc
k
,
có phương trình:
00
y y k x x
+ Như vậy, hệ số góc của tiếp tuyến của (C) tại
0 0 0
; ( )M x y C
có hệ số góc
/
0
k f x
. Hay hoành độ tiếp điểm là nghiệm của phương trình:
/
k f x
. Rõ ràng,
tiếp tuyến của (C) hoàn toàn xác định nếu biết hệ số góc của tiếp tuyến hoặc hoành độ tiếp điểm.
Nhắc: Cho hai đường thẳng
1 1 1
: y k x m
và
2 2 2
: y k x m
.
Lúc đó:
1 2 1 2
kk
và
12
mm
1 2 1 2
.1kk
2. Điều kiện tiếp xúc: Cho hai hàm số
(C),y f x
và
(C'),y g x
.
(C) và (C’) tiếp xúc nhau khi chỉ khi hệ phương trình
//
f x g x
f x g x
có nghiệm.
Đặc biệt: Đường thẳng
y kx m
là tiếp tuyến với
(C) : y f x
khi chỉ khi hệ sau có nghiệm:
/
()
()
f x kx m
f x k
II- MỘT SỐ DẠNG TOÁN THƯỜNG GẶP
Dạng 1: VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN TẠI TIẾP ĐIỂM
Câu 1: (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Gọi
d
là tiếp tuyến tại điểm cực đại của
đồ thị hàm số
3
32y x x
. Khẳng định nào sau đây đúng?
A.
d
có hệ số góc âm. B.
d
có hệ số góc dương.
C.
d
song song với đường thẳng
4y 
. D.
d
song song với trục
Ox
.
Lời giải:
Ta có đồ thị hàm số
3
32y x x
nhận điểm
1;0A
làm điểm cực đại. Mà
10y

.
Suy ra phương trình đường thẳng
d
:
0y
. Do đó
d
song song với đường thẳng
4y 
.
x
y
O
(C)
M
O
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 2
Câu 2: (THPT Tây Thụy Anh - Thái Bình - Lần 2 - 2018 - BTN) Tiếp tuyến tại điểm cực tiểu của đồ
thị hàm số
32
1
2 3 5
3
y x x x
A. Có hệ số góc dương. B. Song song với trục hoành.
C. Có hệ số góc bằng
1
. D. Song song với đường thẳng
1x
.
Lời giải:
Ta có
2
43y x x
,
1
0
3
x
y
x

. Điểm cực tiểu của đồ thị hàm số là
3; 5A
.
Suy ra tiếp tuyến của đồ thị hàm số tại điểm cực tiểu có phương trình là
5y 
.
Câu 3: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Hệ số góc của tiếp tuyến
tại
1;0A
của đồ thị hàm số
32
32y x x
là
A.
1
. B.
1
. C.
3
. D.
0
.
Lời giải:
Đặt
32
32f x x x
. Ta có
2
36f x x x

.
Hệ số góc của tiếp tuyến tại
1;0A
của đồ thị hàm số
đã cho là:
2
1 3.1 6.1 3f
.
Câu 4: (CỤM 8 TRƯỜNG CHUYÊN LẦN 1) Cho hàm số
3
21y x x
có đồ thị
C
. Tính hệ số góc
k
của tiếp tuyến với
C
tại điểm có hoành độ bằng
1
.
A.
25k
. B.
5k 
. C.
10k
. D.
1k
.
Lời giải:
Ta có :
2
32yx

. Hệ số góc của tiếp tuyến tại điểm có hoành độ bằng
1
là
11ky

.
Câu 5: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019) Cho hàm số
4
1yx
có đồ thị
là
()C
. Tiếp tuyến của đồ thị
()C
tại điểm với hoành độ bằng 0 có hệ số góc là
A.
0
. B.
1
. C.
4
. D.
1
.
Lời giải:
+) Ta có
43
14y x y x
+) Tiếp tuyến của đồ thị
()C
tại điểm với hoành độ bằng 0 có hệ số góc là
(0) 0ky

Câu 6: (CHUYÊN QUỐC HỌC HUẾ NĂM 2018-2019 LẦN 1) Tìm hệ số góc của tiếp tuyến của đồ thị
hàm số
34
2
x
y
x
tại điểm có tung độ
7
3
y 
.
A.
9
5
. B.
5
9
. C.
5
9
. D.
10
.
Lời giải:
7 3 4 7
1
3 2 3
x
yx
x
. Ta có:
2
5
2
y
x
. Vậy hệ số góc cần tìm là
5
1
9
y

.
Câu 7: (TRƯỜNG THPT NGUYỄN ĐỨC CẢNH LẦN 03) Cho hàm số
2
24y x x
có đồ thị
C
. Phương trình tiếp tuyến của
C
tại điểm có hoành độ
0x
là
A.
43yx
. B.
1
2
2
yx
. C.
1
2
2
yx
. D.
1
2
2
yx
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 3
Ta có
2
1
24
x
y
xx

;
1
0
2
y

;
02y
.
Suy ra phương trình tiếp tuyến tại điểm có hoành độ
0x
là
1
0 0 2 2
2
y y x y x
.
Câu 8: (CHUYÊN QUỐC HỌC HUẾ LẦN 3 2018-2019) Viết phương trình tiếp tuyến của đồ thị hàm
số
1
2
x
y
x
tại điểm
1;0M
.
A.
11
33
yx
. B.
1
1
3
yx
. C.
1yx
. D.
11
99
yx
.
Lời giải:
TXĐ:
\2D
. Ta có
1
1
3
f
.
Phương trình tiếp tuyến của đồ thị tại điểm
1;0M
là:
1 1 1
10
3 3 3
y x y x
.
Câu 9: (GKI CS2 LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 01) Cho hàm số
32
1
21
3
y x x x
có đồ thị là
C
. Phương trình tiếp tuyến của
C
tại điểm
1
1;
3
M



là
A.
32yx
. B.
32yx
. C.
2
3
yx
. D.
2
3
yx
Lời giải:
Ta có:
2
2 2; 1 1.

y x x y
Phương trình tiếp tuyến của
C
tại điểm
1
1;
3
M



là:
1 1 2
1 1 1
3 3 3
y y x x x
Câu 10: (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
3
3y x x
có đồ
thị
C
.Hệ số góc
k
của tiếp tuyến với đồ thị
C
tại điểm có tung độ bằng
4
là
A.
0.k
B.
2.k
C.
6.k
D.
9.k
Lời giải:
Ta có hoành độ tiếp điểm của tiếp tuyến là nghiệm của phương trình
3
3 4 1 x x x
Ta có
2
' 3 3 yx
Hệ số góc của tiếp tuyến là
' 1 6ky
.
Câu 11: (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Cho đồ thị
H
:
24
3
x
y
x
.
Viết phương trình tiếp tuyến của đồ thị
H
tại giao điểm của
H
và
Ox
.
A.
2.yx
B.
2 4. yx
C.
2 4. yx
D.
2 4.yx
Lời giải:
24
0 2 2;0
3
x
y y x M
x
nên giao điểm của
H
và
Ox
là
2;0M
.
2
2
3
3
yx
x
nên hệ số góc tiếp tuyến là
22y
.
Vậy phương trình tiếp tuyến của đồ thị
H
tại giao điểm của
H
và
Ox
là
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 4
2 2 0 2 4y x x
.
Câu 12: (THPT NGUYỄN HUỆ - HÀ NỘI 18-19) Cho hàm số
3
1y x x
có đồ thị
C
. Phương
trình tiếp tuyến của
C
tại giao điểm của
C
với trục tung là
A.
21yx
. B.
1yx
. C.
22yx
. D.
1yx
.
Lời giải:
Gọi M là giao điểm của
C
và trục tung. Khi đó
0; 1M
.
Ta có
2
31yx

. Phương trình tiếp tuyến của
C
tại M là
. 0 . 0 1 1
M M M
y y x x x y y x x

.
Câu 13: (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Phương trình tiếp tuyến
của đường cong
32
32y x x
tại điểm có hoành độ
0
1x
là
A.
97yx
. B.
97yx
. C.
97yx
. D.
97yx
.
Lời giải:
Xét hàm số
3 2 2
( ) 3 2 '( ) 3 6 '(1) 9.y f x x x f x x x f
Ta có
0 0 0
1 2 1;2x y M
.
Phương trình tiếp tuyến tại điểm
0
1;2M
có dạng:
0 0 0
'( ) 2 9 1 9 7y y f x x x y x y x
.
Câu 14: (THPT YÊN PHONG 1 BẮC NINH NĂM HỌC 2018-2019 LẦN 2) Tiếp tuyến với đồ thị hàm
số
42
1
23
4
y x x
tại điểm cực tiểu của đồ thị cắt đồ thị ở
,AB
khác tiếp điểm. Tính độ dài
đoạn thẳng
AB
.
A.
2
. B.
2
. C.
22
. D.
42
.
Lời giải:
Ta có:
3
0
4 ; 0
2
x
y x x y
x


.
BBT:
Từ BBT suy ra điểm cực tiểu của đồ thị hàm số là
0;3M
.
Tiếp tuyến của đồ thị tại điểm cực tiểu là đường thẳng
3y
.
Phương trình hoành độ giao điểm của đồ thị và tiếp tuyến là:
4 2 4 2
0
11
2 3 3 2 0
44
22
x
x x x x
x

2 2;3 ;B 2 2;3 4 2A AB
.
Câu 15: (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Tìm
m
để mọi tiếp tuyến của đồ thị
hàm số
32
2 3 1y x mx m x
đều có hệ số góc dương.
A.
0m
. B.
1m
. C.
1m
. D.
m 
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 5
Lời giải:
Hệ số góc tiếp tuyến của đồ thị hàm số
32
2 3 1y x mx m x
là
2
3 2 2 3y x mx m
Vì hệ số góc dương với mọi
x
nên ta có
2
22
30
3 2 2 3 0 6 9 0 3 0
0
a
y x mx m m m m m


.
Câu 16: Cho hàm số
21
1
x
y
x
có đồ thị
C
. Tiếp tuyến với đồ thị
C
tại
2;5M
cắt hai đường tiệm
cận tại
E
và
.F
Khi đó độ dài
EF
bằng
A.
10
. B.
2 10
. C.
13
. D.
2 13
.
Lời giải:
Tiệm cận đứng của đồ thị
C
là:
1x
.
Tiệm cận ngang của đồ thị
C
là:
1y
.
Ta có
2
3
1
y
x
.
Tiếp tuyến với
C
tại
2;5M
là:
2 2 5y y x
2
3
25
21
yx
3 11yx
.
Gọi
E
là giao điểm của tiếp tuyến với tiệm cận đứng suy ra
1;8E
.
Gọi
F
là giao điểm của tiếp tuyến với tiệm cận ngang suy ra
3;2F
.
Vậy
22
3 1 2 8 40 2 10EF
.
Câu 17: (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho hàm số
4 2cos2y x x
có đồ thị là
C
. Hoành độ của các điểm trên
C
mà tại đó tiếp tuyến của
C
song song
hoặc trùng với trục hoành là
A.
4
x k k
. B.
2
x k k
. C.
x k k

. D.
2x k k

.
Lời giải:
Ta có
4 4sin2yx

.
Khi đó, hoành độ của các điểm trên
C
mà tại đó tiếp tuyến của
C
song song hoặc trùng
với trục hoành là nghiệm của phương trình:
0 4 4sin 2 0yx
sin2 1 2 2
24
x x k x k k


.
Câu 18: (THPT Lương Thế Vinh Đồng Nai lần 2 – 2019) Đường thẳng nào sau đây là tiếp tuyến của
đồ thị hàm số
3
32y x x
?
A.
9 12yx
. B.
9 14yx
. C.
9 13yx
. D.
9 11yx
.
Lời giải:
3
32y x x
2
33yx
.
Gọi
d
là tiếp tuyến của đồ thị hàm số tại điểm
00
;M x y
.
Hệ số góc tiếp tuyến bằng
2
00
9 3 3 9f x x
0 0 1
0 0 2
2 0 : 9 18
2 4 : 9 14
x y d y x
x y d y x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 6
Vậy đường thẳng
9 14yx
là tiếp tuyến của đồ thị hàm số
3
32y x x
.
Câu 19: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Trên đồ thị
1
:
2
x
Cy
x
có bao nhiêu điểm
M
mà tiếp tuyến với
C
tại
M
song song với đường thẳng
:1d x y
A.
4
. B.
1
. C.
2
. D.
0
.
Lời giải:
Xét hàm số
1
:.
2
x
Cy
x
TXĐ:
2
1
\ 2 , ' 0
2
Dy
x
.
Để tiếp tuyến với
C
tại
M
song song với đường thẳng
:1d y x
suy ra
2
1
'1
2
y VN
x

. Vậy không có tiếp tuyến thỏa mãn.
Câu 20: (THPT NĂM 2018-2019 LẦN 04) Tìm điểm
M
có hoành độ âm trên đồ thị
3
12
:
33
C y x x
sao cho tiếp tuyến tại
M
vuông góc với đường thẳng
12
33
yx
.
A.
2 ; 4M 
. B.
4
1;
3
M



. C.
4
2;
3
M



. D.
2; 0M
.
Lời giải:
Giả sử
3
12
;
33
M a a a




,
0a
;
2
1yx

2
1y a a
Tiếp tuyến tại
M
vuông góc với đường thẳng
12
33
yx
nên ta có:
3ya
2
13a
2
2
a
a

.
Vì
M
có hoành độ âm nên ta chọn
2a 
. Suy ra
2;0M
.
Câu 21: (THPT MAI ANH TUẤN-THANH HÓA-2019) Cho hàm số
32
3 9 1y x x x
có đồ thị
C
. Hệ số góc lớn nhất của tiếp tuyến với đồ thị
C
là
A.
1
. B.
6
. C.
12
. D.
9
.
Lời giải:
Ta có
2
' 3 6 9; y x x
2
' 3 1 12 12yx
Vậy hệ số góc lớn nhất của tiếp tuyến với đồ thị
C
là
12
.
Câu 22: Cho hàm số
3
2
2
42
3
x
y x x
, gọi đồ thị của hàm số là
C
. Viết phương trình tiếp tuyến
của
C
có hệ số góc lớn nhất.
A.
9 25
2 12
yx
. B.
25
5
12
yx
. C.
9 25
4 12
yx
. D.
75
2 12
yx
.
Lời giải:
Gọi
d
là tiếp tuyến cần tìm phương trình và
0
x
là hoành độ tiếp điểm của
d
với
C
thì
hệ số góc của
d
:
2
2
0 0 0 0
9 1 9
'( ) 2 2 4
2 2 2
k y x x x x



;
0
91
22
kx
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 7
Vậy
9
max
2
k
đạt được khi và chỉ khi
0
1
2
x
.
Suy ra phương trình tiếp tuyến
d
:
9 1 1 9 25
2 2 2 2 12
y x y x
.
Câu 23: (THPT Lương Thế Vinh - Hà Nội - Lần 1 - 2017 - 2018) Cho hàm số
32
3 6 5y x x x
. Tiếp
tuyến của đồ thị hàm số có hệ số góc nhỏ nhất có phương trình là
A.
39yx
. B.
33yx
. C.
3 12yx
. D.
36yx
.
Lời giải:
Ta có:
2
3 6 6y x x
2
3 1 3 3x
. Dấu
""
xảy ra khi
1x
9y
.
Do đó, tiếp tuyến của đồ thị có hệ số góc nhỏ nhất bằng 3 và là tiếp tuyến tại điểm
1;9M
.
Phương trình tiếp tuyến là:
3 1 9yx
36yx
.
Câu 24: (THPT Chuyên Hùng Vương - Phú Thọ - Lần 1 - 2018) Tiếp tuyến của đồ thị hàm số
43
21
x
y
x
cùng với 2 tiệm cận tạo thành một tam giác có diện tích bằng:
A.
6
. B.
7
. C.
5
. D.
4
.
Lời giải:
Ta có:
2
10
.
21
y
x
Gọi
00
;M x y
là điểm nằm trên đồ thị hàm số ,
0
1
2
x 
.
Phương trình tiếp tuyến tại
M
:
0 0 0
()y f x x x y
0
0
2
0
0
43
10
21
21
x
y x x
x
x
Tiệm cận đứng:
1
2
x 
, tiệm cận ngang:
2y
Gọi
A
là giao điểm của tiếp tuyến với tiệm cận đứng
1
2
A
x
00
0
2
00
0
4 3 4 8
10 1
2 2 1 2 1
21
A
xx
yx
xx
x





. Vậy
0
0
48
1
;
2 2 1
x
A
x



Gọi
B
là giao điểm của tiếp tuyến với tiệm cận
ngang
2
B
y
0
0
2
0
0
43
10
2
21
21
B
x
xx
x
x
0
1
2
2
B
xx
. Vậy
0
41
;2
2
x
B



Giao điểm 2 tiệm cận là
1
;2
2
I



Ta có:
00
10 10
0;
2 1 2 1
IA IA
xx



;
00
2 1;0 2 1IB x IB x
Tam giác
IAB
vuông tại
I
nên
0
0
1 1 10
. . 2 1 5
2 2 2 1
IAB
S IAIB x
x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 8
Câu 25: (SỞ GD&ĐT QUẢNG NINH NĂM 2018-2019 LẦN 01) Cho hàm số
2
2
x
y
x
, có đồ thị
(C)
và điểm
00
(x ;y ) (C)M
(với
0
0x
). Biết rằng khoảng cách từ
( 2;2)I
đến tiếp tuyến của
(C)
tại M là lớn nhất, mệnh đề nào sau đây đúng?
A.
00
20xy
. B.
00
24xy
. C.
00
22xy
. D.
00
22xy
.
Lời giải:
Tập xác định
\ 2 .D
2
4
(x 2)
y
,
0
0
0
2
(x ; )
2
x
M
x
Phương trình tiếp tuyến tại M là
22
0
0 0 0
2
00
2
4
(x x ) 4 ( 2) 2 0
( 2) 2
x
y x x y x
xx

Khoảng cách từ I đến tiếp tuyến là
22
00
0
2 4 2 4
00
4( 2) ( 2) .2 2
8 16
4 (x 2) 4 (x 2)
xx
x
d


Áp dụng bất đẳng thức cosi ta có
00
2 4 2
00
8 16 8 2
22
4 ( 2) 8( 2)
xx
xx

Dấu bằng xảy ra khi
2
0
( 2) 4x 
0
0
0
4
x
x

. Vì
0
0x
nên
0
4x 
0
4y
00
24xy
.
Câu 26: (THPT Lương Thế Vinh - Hà Nội - Lần 1 - 2018) Cho hàm số
1
23
x
y
x
. Gọi
I
là giao điểm
của hai tiệm cận của đồ thị hàm số. Khoảng cách từ
I
đến tiếp tuyến của đồ thị hàm số đã cho
đạt giá trị lớn nhất bằng
A.
1
2
d
. B.
1d
. C.
2d
. D.
5d
.
Lời giải:
Tọa độ giao điểm
31
;
22
I



.
Gọi tọa độ tiếp điểm là
0
0
0
1
;
23
x
x
x



. Khi đó phương trình tiếp tuyến
với đồ thị hàm số tại
điểm
0
0
0
1
;
23
x
x
x



là:
2
2
0
0 0 0 0
2
0
0
1
1
2 3 2 4 3 0
23
23
x
y x x x x y x x
x
x
.
Khi đó:
2
2
0 0 0
00
4 4 2
0 0 0
31
2 3 2 4 3
2 3 2 3
1
22
,
2
1 2 3 1 2 3 2 2 3
x x x
xx
dI
x x x
Dấu
""
xảy ra khi và chỉ khi
2
00
0
00
2 3 1 2
2 3 1
2 3 1 1
xx
x
xx



.
Vậy
1
max ,
2
dI
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 9
Câu 27: [THPT TRẦN QUỐC TUẤN - Lần 1- 2018] Cho hàm số
3
32y x x
có đồ thị
C
. Đường
thẳng
:2d y x
cắt đồ thị
C
tại ba điểm
A
,
B
,
0;2C
. Gọi
12
,kk
lần lượt là hệ số góc của
tiếp tuyến của
C
tại
A
và
B
. Tính
12
.kk
.
A.
9
. B.
27
. C.
81
. D.
81
.
Lời giải:
Ta có:
2
33yx
Xét phương trình hoành độ giao điểm của đường thẳng
d
và đồ thị
C
là :
33
0
3 2 2 4 0
2
x
x x x x x
x

Vậy đường thẳng
d
cắt đồ thị
C
tại ba điểm phân biệt:
2;2A
,
2;4B
và
0;2C
.
Gọi
12
,kk
lần lượt là hệ số góc của tiếp tuyến của
C
tại
A
và
B
, ta có:
1
29ky
,
2
29ky

. Vậy
12
81kk
.
Câu 28: (SGD Bà Rịa - Vũng Tàu - Lần 1 - 2018 ) Cho hàm số
21
22
x
y
x
có đồ thị
C
. Gọi
00
;M x y
(với
0
1x
) là điểm thuộc
C
, biết tiếp tuyến của
C
tại
M
cắt tiệm cận đứng và tiệm cận
ngang lần lượt tại
A
và
B
sao cho
8
OIB OIA
SS

(trong đó
O
là gốc tọa độ,
I
là giao điểm hai
tiệm cận). Tính giá trị của
00
4.S x y
A.
8S
. B.
17
4
S
. C.
23
4
S
. D.
2S
.
Lời giải:
Ta có
2
2
22
y
x
, TCĐ:
1
1 xd
, TCN:
2
1 yd
,
1;1I
.
Phương trình tiếp tuyến
tại điểm
00
;M x y
có dạng
0
0
2
0
0
21
2
22
22
x
y x x
x
x
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 10
1
Ad
0
0
1;
1
x
A
x



,
2
Bd
0
2 1;1Bx
.
0
2 2;0IB x
,
0
1
0;
1
IA
x


.
8
OIB OIA
SS

11
.1. 8. .1.
22
IB IA
8IB IA
0
0
1
2 2 8
1
x
x
2
0
14x
0
3x
(do
0
1x
)
0
5
4
y
00
4S x y
5
3 4. 8
4
.
Câu 29: (THI THỬ THPTQG VTV7 NĂM 2018-2019) Đồ thị hàm số
21
2
x
y
x
có bao nhiêu cặp tiếp
tuyến vuông góc với nhau?
A.
1
. B. Vô số. C.
0
. D.
2
.
Lời giải:
TXĐ:
\2D
. Ta có:
2
2 1 5
2
2
x
yy
x
x
.
Tiếp tuyến
1
d
của đồ thị hàm số tại
11
;M x y
có dạng:
1 1 1
y y x x x y
.
Tiếp tuyến
2
d
của đồ thị hàm số tại
22
;N x y
có dạng:
2 2 2
y y x x x y
.
22
1 2 1 2 1 2
22
12
55
. 1 1 2 . 2 25
22
d d y x y x x x
xx


(vô lý).
Vậy không có cặp tiếp tuyến nào của đồ thị vuông góc với nhau.
Câu 30: (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Cho hàm số
, , , , ; 0, 0
ax b
y f x a b c d c d
cx d
có đồ thị
.C
Đồ thị của hàm số
y f x
như
hình vẽ dưới đây. Biết
C
cắt trục tung tại điểm có tung độ bằng
2.
Viết phương trình tiếp
tuyến của
C
tại giao điểm của
C
với
trục hoành.
A.
3 2 0.xy
B.
3 2 0.xy
C.
3 2 0.xy
D.
3 2 0.xy
Lời giải:
Đồ thị hàm số
y f x
đi qua
0; 2
suy ra
2bd
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 11
Ta có
2
ad bc
y
cx d
. Đồ thị hàm số
y
có tiệm cận đứng
1x 
nên
cd
, đi qua
0;3
nên
2
3
ad bc
d
hay
ad
. Do đó
2
23
1
1
x
yy
x
x
.
Phương trình tiếp tuyến tại
2;0
là
1
2 3 2 0
3
y x x y
.
Câu 31: (THPT Can Lộc - Hà Tĩnh - Lần 1 - 2017 - 2018) Cho hàm số
y f x
xác định và có đạo hàm
trên thỏa mãn
23
2 1 1f x f x x
. Viết phương trình tiếp tuyến của đồ thị hàm
số
y f x
tại điểm có hoành độ bằng
1
.
A.
16
77
yx
. B.
18
77
yx
. C.
15
77
yx
. D.
16
77
yx
.
Lời giải:
Từ
23
2 1 1f x f x x
(*), cho
0x
ta có
23
1 1 0ff
10
11
f
f

Đạo hàm hai vế của (*) ta được
2
4. 2 1 . 2 1 3 1 . 1 1f x f x f x f x



.
Cho
0x
ta được
2
4 1 . 1 3. 1 . 1 1f f f f




1 . 1 . 4 3 1 1f f f


(**).
Nếu
10f
thì (**) vô lý, do đó
11f 
, khi đó (**) trở thành
1 . 4 3 1f
1
1
7
f
Phương trình tiếp tuyến
1
11
7
yx
18
77
yx
.
Câu 32: (THPT Chuyên Hà Tĩnh - Lần 1 - 2018 - BTN) Cho hàm số
y f x
có đạo hàm liên tục trên
, thỏa mãn
2
2 2 1 2 12f x f x x
. Phương trình tiếp tuyến của đồ thị hàm số
y f x
tại điểm có hoành độ bằng
1
là:
A.
22yx
B.
46yx
C.
26yx
D.
42yx
Lời giải:
Từ
2
2 2 1 2 12f x f x x
(*), cho
0x
và
1
2
x
ta được
2 0 1 0
0 2 1 3
ff
ff


12f
Lấy đạo hàm hai vế của (*) ta được
4 2 2 1 2 24f x f x x

, cho
0x
và
1
2
x
ta được
4 0 2 1 0
4 1 2 0 12
ff
ff




14f

.
Phương trình tiếp tuyến của đồ thị hàm số
y f x
tại điểm
1x
là
1 1 1y f x f
4 1 2yx
42yx
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 12
Câu 33: (HSG BẮC NINH NĂM 2018-2019) Có bao nhiêu giá trị của tham số thực
m
để đồ thị hàm số
2
2x mx m
y
xm

cắt trục
Ox
tại hai điểm phân biệt và các tiếp tuyến của đồ thị tại hai điểm
đó vuông góc với nhau.
A.
5
. B.
2
. C.
0
. D.
1
.
Lời giải:
22
23
3
x mx m m m
y x m
x m x m

2
2
3
1
mm
y
xm
.
Xét phương trình hoành độ giao điểm của đồ thị hàm số đã cho với trục
Ox
.
2
2
0
x mx m
xm

2
2 0 * f x x mx m x m
.
Để đồ thị hàm số đã cho cắt trục
Ox
tại hai điểm phân biệt và các tiếp tuyến tại hai điểm đó
vuông góc với nhau thì phương trình (*) phải có hai nghiệm phân biệt
12
;xx
khác
m
và
12
.1y x y x


.
2
2
22
12
22
12
0
30
33
. 1 1 1
mm
f m m m
m m m m
y x y x
x m x m



1
0
0
1
3
0
5
m
m
m
m
m
m


5m
.
Câu 34: (TOÁN HỌC TUỔI TRẺ - LẦN 5 - 2019) Cho hàm số bậc bốn
y f x
xác định và liên tục
trên , hàm số
2
23g x x
và đường thẳng
d
có đồ thị như hình vẽ. Biết
A
là điểm chung
của đồ thị
fx
và
gx
,
1
A
x
. Điểm
B
thuộc đồ thị
gx
,
9
4
B
x 
và
d
là tiếp tuyến của
đồ thị hàm số
y f x
. Giá trị
A
fx
bằng
A.
1
. B.
3
2
. C.
5
2
. D.
2
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 13
Vì các điểm
A
,
B
thuộc đồ thị hàm số
(x)g
nên ta có
11A;
,
9 57
48
B;



13 65
48
AB ;


. Do
d
đi qua hai điểm
A
và
B
nên ta chọn vectơ pháp tuyến là
65 26
d
n;
.
Phương trình đường thẳng d là:
53
65 1 26 1 0 65 26 39 0
22
x y x y y x
Mà
d
là tiếp tuyến của đồ thị hàm số
y f x
nên
5
2
A
fx

.
Câu 35: (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Cho hàm
số
32
1 2 1 y x m x x m
có đồ thị
C
(
m
là tham số thực). Gọi
12
,mm
là các giá trị của
m
để đường thẳng
:1 d y x m
cắt
C
tại ba điểm phân biệt
,,A B C
sao cho tổng hệ số
góc của các tiếp tuyến với
C
tại
,,A B C
bằng
19
. Khi đó
12
mm
bằng
A.
4
. B.
2
.
C.
0
. D.
2
.
Lời giải:
Phương trình hoành độ giao điểm của
d
và
C
:
*0
1
0101
2
223
mmxx
x
mmxxxmxxmxy
Để
d
và
C
cắt nhau tại ba điểm phân biệt thì
*
phải có hai nghiệm phân biệt khác
1
, tức

;
2
1
2
1
;04;
021
0
m
m
. Khi đó
d
và
C
cắt nhau tại ba điểm phân biệt
1;,1;,2;1
2211
mxxCmxxBmA
với
21
;xx
là nghiệm của phương trình
*
Hệ số góc tiếp tuyến của
C
tại
A
là:
my 221
. Hệ số góc tiếp tuyến của
C
tại
B
là:
1123
1
2
11
xmxxy
.
Hệ số góc tiếp tuyến của
C
tại
C
là:
1123
2
2
22
xmxxy
.
Theo giả thiết, ta có:
22
1 2 1 2
3 2 1 4 2 19x x m x x m
.
2
1 2 1 2 1 2
3 6 2 1 4 2 19 **x x x x m x x m
mxx
mxx
21
21
thay vào
**
, ta được
2
3 6 2 1 4 2 19m m m m m
.
1
2
12
2
3
2 15 0 2
5
m
m m m m
m
Câu 36: Cho hàm số
2
1
x
y
x
đồ thị
C
. Gọi
d
là khoảng cách từ giao điểm hai tiệm cận của đồ thị
C
đến một tiếp tuyến của
C
. Giá trị lớn nhất của
d
có thể đạt được là
A.
33
. B.
3
. C.
2
. D.
22
.
Lời giải:
Tiệm cận đứng
1
d
:
10x 
, tiệm cận ngang
2
d
:
10y 
tâm đối xứng là
1;1I
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 14
Phương trình tiếp tuyến tại điểm
2
;
1
a
M a C
a



là:
2
12
1
1
a
y x a
a
a

d
.
Khi đó
2
2
4 4 2
12
2
1
1
1
22
1
,2
1 1 1 2
1 1 1
1 1 1
a
a
a
a
a
d I d
a
a a a

.
Câu 37: (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Gọi
A
là điểm có hoành độ bằng
1
thuộc
đồ thị
C
của hàm số
42
2y x mx m
(
m
là tham số thực). Ta luôn tìm được
a
m
b
với
a
b
là phân số tối giản để tiếp tuyến với đồ thị
C
tại
A
cắt đường tròn
22
: 2 3 0x y y
tạo thành một dây cung có độ dài nhỏ nhất. Khi đó, tổng
ab
bằng:
A.
12
. B.
3
. C.
29
. D.
10
.
Lời giải:
Đường tròn
2
2
: 1 4xy
có tâm
0;1I
,
2R
.
Ta có
1;1Am
;
3
44y x mx
1 4 4ym
suy ra
: 4 4 1 1y m x m
.
Dễ thấy luôn đi qua điểm cố định
3
;0
4
F
và điểm
F
nằm trong đường tròn
.
d
R
N
M
I
F
Giả sử cắt
tại
M
,
N
, ta có:
2 2 2
2 ; 2 4 ;MN R d I d I
.
Do đó
MN
nhỏ nhất
;dI
lớn nhất
;d I IF
IF
.
Khi đó đường thẳng có một véc-tơ chỉ phương
3
;1
4
u IF
;
1; 4 4um
nên:
.0un
3
1. 4 4 0
4
m
13
16
m
suy ra
13a
,
16b
. Vậy
13 16 29ab
.
Câu 38: (THPT NGÔ QUYỀN HÀ NỘI NĂM 2018 - 2019 LẦN 01) Cho hàm đa thức bậc bốn
y f x
có đồ thị
C
. Hàm số
y f x
có đồ thị như hình vẽ dưới đây. Gọi đường thẳng
là tiếp tuyến của đồ thị
C
tại điểm có hoành độ bằng
1
. Hỏi
và
C
có bao nhiêu điểm
chung?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 15
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải:
Ta có tiếp tuyến
của
C
tại
1x
là
1 1 1y f x f
.
Dựa vào đồ thị của hàm số
fx
, ta có
10f
.
Vậy
:1yf
.
Gọi
1
a
,
2
a
là hai nghiệm còn lại của
fx
. Dựa vào đồ thị hàm số ta có bảng biến thiên:
Dựa vào bảng biến thiên ta có
:1yf
và
C
có ba điểm chung.
Câu 39: (THPT KINH MÔN II HẢI DƯƠNG NĂM 2018-2019 LẦN 03) Cho hàm số
1
1
x
yC
x
.
Điểm
M
thuộc
C
có hoành độ lớn hơn
1
, tiếp tuyến của
C
tại
M
cắt hai tiệm cận của
C
lần lượt tại
A
,
B
. Diện tích nhỏ nhất của tam giác
OAB
bằng
A.
4 2 2
. B.
4
. C.
42
. D.
42
.
Lời giải:
Tập xác định:
\1D
. Ta có:
2
2
1
y
x

,
1x
.
Đồ thị hàm số có đường tiệm cận ngang
1y
và đường tiệm cận đứng
1x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 16
Giả sử
;1
M
M m y C m
12
1
11
M
m
y
mm

;
2
2
1
ym
m

.
Phương trình tiếp tuyến
là:
2
22
1
1
1
y x m
m
m
2
2
2 1 2 1 0x m y m m
.
Gọi
A
là giao điểm của
và đường tiệm cận ngang. Tọa độ điểm
A
là nghiệm của hệ
phương trình:
2
1
22
21
1
1
1
y
xm
y x m
m
m
2 1;1Am
.
Gọi
B
là giao điểm của
và đường tiệm cận đứng. Tọa độ điểm
B
là nghiệm của hệ phương
trình:
2
1
34
22
1
1
11
1
1
x
m
y
y x m
mm
m
m

4
1;1
1
B
m




.
Suy ra:
2
2 2 4
2
4 16 2
2 2 4 1 1 4
11
1
AB m m m
mm
m




.
2
4
21
;
41
mm
dO
m


2
4
4
21
1 1 2
; . . . 1 4
2 2 1
41
OAB
mm
S d O AB m
m
m

2
2
21
21
11
mm
mm
mm



(vì
1m
)
22
3 4 1
11
mm
mm

.
Áp dụng bất đẳng thức Cô-si cho hai số
1m
và
2
1m
:
2
1 2 2
1
m
m
2
4 1 4 2 2
1
m
m
.
Vậy diện tích nhỏ nhất của tam giác
OAB
bằng
4 2 2
khi
2
1
12
1
1
m
m
m
m

.
Câu 40: (THPT QUỲNH LƯU– 2018-2019– LẦN 1) Cho hàm số
1
21
x
y
x

(C),
( )y x m d
. Với mọi
m
đường thẳng
()d
luôn cắt đồ thị (C) tại hai hai điểm phân biệt A và B. Gọi k1, k2 lần lượt là
hệ số góc của các tiếp tuyến với (C) tại A và B. Giá trị nhỏ nhất của
2020 2020
12
T k k
bằng
A.
1
. B.
2
. C.
1
2
. D.
2
3
.
Lời giải:
+ Phương trình hoành độ giao điểm:
2
2 2 1 0
1
1
21
2
x mx m
x
xm
x
x

(*)
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 17
+ Phương trình (*) có:
2
' 2( 1) 0,m m m
nên (d) luôn cắt ( C ) tại 2 điểm phân biệt A,B.
Gọi
,ab
là các hoành độ giao điểm
1
2
ab




. Khi đó ta có:
1
2
a b m
m
ab

.
+ Khi đó:
2020 2020
12
4040 4040 2020
1 1 2
(2 1) (2 1) [(2 1)(2 1)]
T k k
a b a b
2020 2020
22
2
4 2( ) 1 2( 1) 2 1
ab a b m m
+ Nhận xét: Giá trị nhỏ nhất bằng 2 khi:
2020 2020
(2 1) (2 1)
1 1.
1
2
ab
a b m m
ab

Câu 41: (SỞ GD&ĐT KIÊN GIANG NĂM 2018-2019) Cho hàm số
32
3 3 5y x x x
có đồ thị
C
.
Tìm tất cả những giá trị nguyên của
2019;2019k 
để trên đồ thị
C
có ít nhất một điểm
mà tiếp tuyến tại đó vuông góc với đường thẳng
:3d y k x
.
A.
2021
. B.
2017
. C.
2022
. D.
2016
.
Lời giải:
TXĐ :
D
. Ta có :
2
' 3 6 3y x x
.
TH1 :
3k
. Khi đó
:0dy
không tồn tại tiếp tuyến vuông góc với
d
.
TH2 :
3k
.
Ta có :
2
00
3 3 6 3 1k x x
2
00
1
3 6 3 0 *
3
xx
k
Theo yêu cầu bài toán , phương trình
*
có nghiệm
3
' 0 0 3
3
k
k
Vậy
2019; 2018;...;0;1;2k
Có
2022
giá trị nguyên của
k
thỏa đề bài.
Câu 42: (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Gọi
,MN
là hai điểm di động trên
đồ thị
C
của hàm số
32
34y x x x
sao cho tiếp tuyến của
C
tại
M
và
N
luôn song
song với nhau. Hỏi khi
,MN
thay đổi, đường thẳng
MN
luôn đi qua nào trong các điểm dưới
đây?
A. Điểm
1; 5N 
B. Điểm
1; 5M
C. Điểm
1;5Q
D. Điểm
1;5P
Lời giải:
Vì tiếp tuyến của đồ thị hàm bậc ba tại
2
điểm
,MN
thuộc đồ thị hàm số song song với nhau
nên đường thẳng
MN
phải đi qua điểm uốn của
C
.
Ta có
2
3 6 1; 6 6y x x y x
Cho
0 6 6 0 1y x x

. Điểm uốn
1;5Q
.
Câu 43: Cho hàm số
2
1
x
y
x
đồ thị
C
. Gọi
d
là khoảng cách từ giao điểm hai tiệm cận của đồ thị
C
đến một tiếp tuyến của
C
. Giá trị lớn nhất của
d
có thể đạt được là
A.
33
. B.
3
. C.
2
. D.
22
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 18
Lời giải:
Tiệm cận đứng
1
d
:
10x 
, tiệm cận ngang
2
d
:
10y 
tâm đối xứng là
1;1I
.
Phương trình tiếp tuyến tại điểm
2
;
1
a
M a C
a



là:
2
12
1
1
a
y x a
a
a

d
.
Khi đó
2
2
4 4 2
12
2
1
1
1
22
1
,2
1 1 1 2
1 1 1
1 1 1
a
a
a
a
a
d I d
a
a a a

.
Câu 44: (MĐ 101 BGD&ĐT NĂM 2017-2018) Cho hàm số
42
17
42
y x x
có đồ thị
C
. Có bao nhiêu
điểm
A
thuộc
C
sao cho tiếp tuyến của
C
tại
A
cắt
C
tại hai điểm phân biệt
1 1 2 2
; ; ;M x y N x y
khác
A
thỏa mãn
1 2 1 2
6( )y y x x
.
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải:
Ta có
42
17
;
42
A C A t t t



;
3
7y x x

3
7.
y t t t
Phương trình tiếp tuyến của
C
tại
A
là
3 4 2
17
7
42
y t t x t t t
3 4 2
37
7
42
y t t x t t
Phương trình hoành độ giao điểm:
4 2 3 4 2
1 7 3 7
7
4 2 4 2
x x t t x t t
4 2 3 4 2
14 4 7 3 14 0x x t t x t t
2
22
2 3 14 0x t x tx t
22
2 3 14 0 1
xt
x tx t
Tiếp tuyến cắt đồ thị
C
tại hai điểm phân biệt
1 1 2 2
; ; ;M x y N x y
khác
A
khi phương trình
1
có hai nghiệm phân biệt khác
t
22
2 2 2
77
3 14 0
21
2 3 14 0
3
t
tt
t
t t t





2
Khi đó:
12
2
12
2
3 14
x x t
x x t

và
3 4 2
11
3 4 2
22
37
7
42
37
7
42
y t t x t t
y t t x t t
3
1 2 1 2
7y y t t x x
Ta có
1 2 1 2
6( )y y x x
3
1 2 1 2
76t t x x x x
3
7 6 0tt
2
1 6 0t t t
2
1
10
2
60
3
tn
t
tn
tt
tl


(do
2
)
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 19
Với
1t 
ta có
13
1;
4
A




Với
2t 
ta có
2; 10A 
có hai điểm thỏa yêu cầu bài toán.
Câu 45: Cho hàm số
3
2018y x x
có đồ thị là
C
.
1
M
là điểm trên
C
có hoành độ
1
2x
. Tiếp
tuyến của
C
tại
1
M
cắt
C
tại điểm
2
M
khác
1
M
, tiếp tuyến của
C
tại
2
M
cắt
C
tại
điểm
3
M
khác
2
M
,….., tiếp tuyến của
C
tại
1n
M
cắt
C
tại điểm
n
M
khác
1n
M
4;5;....n
, gọi
;
nn
xy
là tọa độ của điểm
n
M
. Tìm
n
để
2019
2018 2 0
nn
xy
.
A.
685.n
B.
679.n
C.
675.n
D.
673.n
Lời giải:
Ta có:
32
2018 3 2018y x x y x
Giả sử:
k
MC
, với
3
1,2,...... ; 2018
k k k k
k M x x x
Phương trình tiếp tuyến của
C
tại
k
M
là
23
: 3 2018 2018
k k k k k
y x x x x x
Gọi
1k
M
là giao điểm của
k
với
C
Phương trình hoành độ giao điểm của
k
với
C
:
3 2 3
2018 3 2018 2018
k k k k
x x x x x x x
3 3 2
2018 3 2018 0
k k k k
x x x x x x x
2
22
2 0 2 0
k k k k k
x x x x x x x x x x
2
k
k
xx
xx

Suy ra
3
1
2 ; 8 2018.2
k k k k
M x x x
,
1,2,....k
Hay
1
2
kk
xx

, với
1,2,....k
*
1
2,
nn
x x n
n
x
là một cấp số nhân với
1
2x
và công bội
2q 
.
1
*
2. 2 ,
n
n
xn
3 3 1
8. 2 2018.2. 2
nn
n
y

Mà
2019
2018 2 0
nn
xy
nên
1 3 3 1
2019
2018.2. 2 8. 2 2018.2. 2 2 0
n n n
33
3 2019
3 3 2
1 .2 2 673
3 2019
n
n
n
n
n
.
Câu 46: (THPT Kinh Môn – Hải Dương 2019) Xét đồ thị
C
của hàm số
3
3y x ax b
với
a
,
b
là
các số thực. Gọi
M
,
N
là hai điểm phân biệt thuộc
C
sao cho tiếp tuyến với
C
tại hai
điểm đó có hệ số góc bằng
3
. Biết khoảng cách từ gốc tọa độ tới đường thẳng
MN
bằng
1
. Khi
đó giá trị lớn nhất của
22
ab
bằng
A.
0
. B.
3
2
. C.
2
. D.
2
3
.
Lời giải:
Giả sử
11
;M x y
,
22
;N x y
. Ta có
2
33y x a

. Từ giả thiết ta có
1
2
3
3
yx
yx
2
1
2
2
1
1
xa
xa


.
Mặt khác
3
1 1 1
3y x ax b
2
1 1 1
2x x a ax b
nên
11
21y a x b
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 20
Tương tự
22
21y a x b
.
Suy ra phương trình đường thẳng
MN
là
2 1 0a x y b
.
Giả thiết có
,1d O MN
2
1
2 1 1
b
a

22
4 4 2b a a
.
Vậy
2 2 2
3 4 2a b a a
2
2 2 2
3
3 3 3
a



.
Giá trị lớn nhất của
22
ab
bằng
2
3
đạt được khi và chỉ khi
2
3
a
,
10
3
b 
. Vậy:
673.n
Câu 47: (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Cho hàm số
32
39y x x x
có đồ thị
C
. Gọi
, , ,A B C D
là bốn điểm trên đồ thị
C
với hoành độ lần lượt là
, , ,a b c d
sao cho tứ giác
ABCD
là một hình thoi đồng thời hai tiếp tuyến tại
A
và
C
song song với nhau và đường thẳng
AC
tạo với hai trục tọa độ tam giác cân. Tính tích
abcd
.
A.
60
. B.
120
. C.
144
. D.
180
.
Lời giải:
Đặt
; , ; , ; , ;A a y a B b y b C c y c D d y d
.
Theo giả thiết
22
3 6 9 3 6 9 2y a y c a a c c a c

(vì
ac
).
Do đường thẳng
AC
cắt hai trục tọa độ tạo thành tam giác cân nên hệ số góc của đường thẳng
AC:
1k 
.
TH1:
3 2 3 2
3 9 3 9
1 1 1 10
y c y a
c c c a a a
k ac
c a c a

.
Do
ABCD
là hình thoi nên ta có
2
12
1
1
BD
b d a c
b a c d
AB DC
bd
y d y b
y
AC BD
db



.
Do đó
120abcd
.
TH2:
1k 
. Lập luận tương tự ta thu được
120abcd
.
Dạng 2: VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN ĐI QUA MỘT ĐIỂM CHO TRƯỚC
Câu 48: Có bao nhiêu tiếp tuyến của đồ thị
23
2
x
y
x
đi qua giao điểm của hai đường tiệm cận?
A.
1
. B. Không có. C. Vô số. D.
2
.
Lời giải:
Đồ thị hàm số nhận đường thẳng
2
d
x
c
làm tiệm cận đứng.
Đồ thị hàm số nhận đường thẳng
2
a
y
c

làm tiệm cận ngang.
Vậy
2;2I
là giao điểm của hai đường tiệm cận.
TXĐ:
\ 2 .D
2
7
'
( 2)
y
x
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 21
Gọi tiếp tuyến tại
00
;M x y
của đồ thị hàm số
23
2
x
y
x
có dạng:
0 0 0
: ' .( )y y x x x y
hay
0
0
2
00
23
7
: .( )
( 2) 2
x
y x x
xx

Vì
đi qua
0
0
2
00
23
7
2;2 .( 2 )
( 2 2
2
)
x
Ix
xx

00
0
2
0 0 0 0
2 3 2 3
77
.( 2)
( 2) 2 ( 2) 2
22
xx
x
x x x x


0
0
2 10
412 0
2
x
x
, phương trình vô nghiệm.
Vậy không tồn tại tiếp tuyến nào của đồ thị hàm số
23
2
x
y
x
mà đi qua giao điểm của hai
tiệm cận.
Câu 49: [SGD SOC TRANG_2018] Từ điểm
1; 9M 
có thể vẽ được bao nhiêu tiếp tuyến tới đồ thị
hàm số
32
4 6 1y x x
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải:
Lấy điểm
32
0 0 0
;4 6 1A x x x
thuộc đồ thị hàm số, tiếp tuyến tại A có phương trình
2 3 2
0 0 0 0 0
12 12 4 6 1y x x x x x x
.
Để tiếp tuyến qua
M
thì
2 3 2
0 0 0 0 0
9 12 12 1 4 6 1x x x x x
32
0 0 0
8 6 12 10 0x x x
Phương trình có hai nghiệm
0
1x 
và
0
5
4
x
. Nên qua M có thể kẻ được hai tiếp tuyến tới đồ
thị hàm số.
Câu 50: Cho hàm số
3
2
2
42
3
x
y x x
, gọi đồ thị của hàm số là
C
. Viết phương trình tiếp tuyến
của
C
đi qua điểm
2;9A
.
A.
2yx
. B.
85yx
. C.
25yx
. D.
8 25yx
.
Lời giải:
Phương trình đường thẳng
d
đi qua điểm
2;9A
có hệ số góc
k
là
( 2) 9y k x
.
d
tiếp xúc với
C
tại điểm có hoành độ
0
x
khi hệ
3
2
0
0 0 0
2
00
2
4 2 ( 2) 9 (1)
3
2 2 4 (2)
x
x x k x
x x k
có
nghiệm
0
x
.
Thay
2
vào
1
ta được:
3
22
0
0 0 0 0 0
2
4 2 ( 2 2 4)( 2) 9
3
x
x x x x x
32
0 0 0 0
4 15 12 9 0 3x x x x
.
Thay
0
3x
vào
2
ta được
8k 
.
Vậy phương trình tiếp tuyến
d
là
8 25yx
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 22
Câu 51: Cho hàm số
2
1
1
xx
y
x

có đồ thị
C
. Viết phương trình tiếp tuyến của
C
xuất phát từ
( 1;3)M
.
A.
31yx
;
3yx
. B.
13y
;
3yx
. C.
3y
;
31yx
. D.
3y
;
3yx
.
Lời giải:
Ta có
2
2
2
( 1)
xx
y
x
. Gọi
00
( ; )M x y
là tọa độ tiếp điểm của tiếp tuyến
d
với
C
22
0 0 0 0
0
2
00
21
: ( )
( 1) 1
x x x x
d y x x
xx

Cách 1:
22
0 0 0 0
0
2
00
21
3 ( 1 )
( 1) 1
x x x x
M d x
xx

2 2 2
0 0 0 0 0 0 0
3( 1) ( 2 )( 1) ( 1)( 1)x x x x x x x
2
0 0 0 0
1
2 5 2 0 2,
2
x x x x
Với
0
2x 
Phương trình tiếp tuyến
3y
.
Với
0
1
2
x 
Phương trình tiếp tuyến
3yx
.
Cách 2: Gọi d là đường thẳng đi qua
( 1;3)M
, có hệ số góc
k
, khi đó phương trình
d
có
dạng:
( 1) 3y k x
.
d
tiếp xúc đồ thị
C
tại điểm có hoành độ
0
x
khi hệ phương trình sau có nghiệm
0
x
:
2
00
0
0
2
00
2
0
1
( 1) 3 (1)
1
2
(2)
( 1)
xx
kx
x
xx
k
x

Thế
2
vào
1
ta được:
22
0 0 0 0
0
2
00
12
( 1) 3
1 ( 1)
x x x x
x
xx

2
0 0 0 0
1
2 5 2 0 2,
2
x x x x
.
Với
0
20xk
Phương trình tiếp tuyến
3y
.
Với
0
1
3
2
xk
Phương trình tiếp tuyến
3yx
.
Câu 52: (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Cho hàm số
32
32 y x x
có đồ thị
C
và điểm
;2Mm
. Gọi
S
là tập hợp tất cả các giá trị thực của
m
để qua
M
kẻ đúng hai tiếp
tuyến đến
C
. Tổng tất cả các phần tử của
S
bằng
A.
8
3
. B.
3
. C.
2
3
. D.
2
.
Lời giải:
2
36
y x x
Phương trình tiếp tuyến tại
00
;A x y
có dạng
2 3 2
0 0 0 0 0
3 6 3 2 y x x x x x x
Tiếp tuyến qua
;2Mm
, ta có:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 23
2 3 2
0 0 0 0 0
2 3 6 3 2 x x m x x x
32
00
2 3 1 6 4 0
o
x x m x m
2
0 0 0
2 2 3 1 2 0 1 x x m x
0
2
00
20
2 3 1 2 0 2

x
x m x
Qua
M
kẻ đúng hai tiếp tuyến đến
C
khi phương trình
1
có đúng hai nghiệm phân biệt
phương trình
2
có nghiệm kép khác
2
hoặc phương trình
2
có hai nghiệm phân biệt
trong đó có một nghiệm bằng
2
.
Trường hợp 1. Phương trình
2
có nghiệm kép khác
2
0
31
2
4

m
5
3
1
3

m
m
m
5
3
1

m
m
.
Trường hợp 2. Phương trình
2
có hai nghiệm phân biệt trong đó có một nghiệm bằng
2
0
2.4 2 3 1 2 0

m
5
1 hoaëc
3
2
mm
m
2m
. Vậy
5
;2; 1
3




S
.
Câu 53: Cho hàm số
2
1

x
y
x
có đồ thị (C ) và điểm
;1Aa
. Biết
m
a
n
( với mọi
, m n N
và
m
n
tối
giản ) là giá trị để có đúng một tiếp tuyến của(C ) đi qua
.A
Khi đó giá trị
mn
là
A.
2
. B.
7
. C.
5
. D.
3
.
Lời giải:
TXĐ:
\1D
.
2
1
'
1

y
x
Tiếp tuyến tại tiếp điểm có hoành độ
00
1xx
của (C ) có phương trình.
0
0
2
0
0
2
1
1
1

x
y x x
x
x
Đường thẳng
đi qua
;1Aa
2
00
0
0
2
0
0
0
2 6 3 0 *
2
1
1
1
1
x x a
x
ax
x
x
x
Có duy nhất 1 tiếp tuyến qua A
*pt
có duy nhất 1 nghiệm khác 1
2
'0
3 2 0
3
5
10
2
2.1 6.1 3 0




a
m
a m n
a
n
a
.
Câu 54: (THPT NGÔ QUYỀN HÀ NỘI NĂM 2018 - 2019 LẦN 01) Cho hàm số
3
1
x
y
x
có đồ thị là
C
, điểm
M
thay đổi thuộc đường thẳng
: 1 2d y x
sao cho qua
M
có hai tiếp tuyến của
C
với hai tiếp điểm tương ứng là
A
,
B
. Biết rằng đường thẳng
AB
luôn đi qua điểm cố
định là
H
. Độ dài đoạn
OH
là
A.
34
. B.
10
. C.
29
. D.
58
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 24
Gọi
;1 2M m m d
. Gọi
là đường thẳng đi qua
M
có hệ số góc là
k
, khi đó phương trình
đường thẳng
: 1 2y k x m m
.
Để
là tiếp tuyến của đồ thị
C
thì hệ phương trình
2
3
12
1
4
1
x
k x m m
x
k
x

có nghiệm.
Thay
2
4
1
k
x

vào phương trình
3
12
1
x
k x m m
x
ta được
2
2 2 2 0mx m x m
*
.
Qua
M
kẻ được hai tiếp tuyến với
C
khi và chỉ khi phương trình
2
2 2 2 0g x mx m x m
có hai nghiệm phân biệt
1x
2
0
0
2 2 0
1
1 4 2 2 0
am
m
m m m
m
g m m m


.
Gọi
;
AA
A x y
,
;
BB
B x y
là hai tiếp điểm, với
A
x
,
B
x
là hai nghiệm của phương trình
*
.
Theo địnhlý Vi-et ta có
22
2
AB
AB
m
xx
m
m
xx
m


.
Gọi
I
là trung điểm của đoạn thẳng
AB
thì
23
;
1
mm
I
mm




.
Mặt khác
2
;
1
BA
BA
m x x
AB x x
m



một vectơ pháp tuyến của đường thẳng
AB
là
2 ;1n m m
.
Phương trình đường thẳng đi qua hai điểm
AB
có một vectơ pháp tuyến
2 ;1n m m
và đi
qua điểm
23
;
1
mm
I
mm




là
2 1 7 0mx m y m
.
Gọi
;
HH
H x y
là điểm cố định mà đường thẳng
AB
đi qua.
Khi đó,
2 1 7 0 2 1 7 0
H H H H H
mx m y m m x y y
với mọi
0m
và
1m
.
Suy ra
2 1 0 3
3; 7
7 0 7
H H H
HH
x y x
H
yy



. Vậy
22
3 7 58OH
.
Câu 55: Cho hàm số
3
1
x
y
x
có đồ thị là
C
, điểm
M
thay đổi thuộc đường thẳng
: 1 2d y x
sao
cho qua
M
có hai tiếp tuyến của
C
với hai tiếp điểm tương ứng là
A
,
B
. Khoảng cách từ
O
đến đường thẳng
AB
lớn nhất bằng
A.
34
. B.
10
. C.
58
. D.
29
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 25
Lời giải:
Kế thừa lời giải trên, ta có đường thẳng
: 2 1 7 0AB mx m y m
luôn đi qua điểm cố
định
3; 7H 
.
Gọi
K
là hình chiếu vuông góc của
O
trên
AB
. Ta có
58OK OH
. Đẳng thức xảy ra khi
và chỉ khi
KH
, tức là
OH AB
hay
3
7.2 3 1 0
17
m m m
(thỏa điều kiện
0m
và
1m
). Vậy khoảng cách từ
O
đến đường thẳng
AB
lớn nhất bằng
58
.
Câu 56: (THPT SƠN TÂY HÀ NỘI NĂM 2018-2019 LẦN 01) Cho hàm số
3
1yx
có đồ thị
()C
.
Trên đường thẳng
:1d y x
tìm được hai điểm
1 1 1
;M x y
,
2 2 2
;M x y
mà từ mỗi điểm đó
kẻ được đúng hai tiếp tuyến đến
C
. Tính giá trị biểu thức
22
1 2 1 2
31
53
S y y y y
A.
113
15
. B.
41
15
. C.
14
15
. D.
59
15
.
Lời giải:
Giả sử
:1M d y x
, ta gọi
;1M a a
. Đường thẳng
đi qua
;1M a a
có hệ số góc
k
có phương trình là:
( ) 1y k x a a
.
Đường thẳng
tiếp xúc với
C
khi và chỉ khi hệ phương trình sau có nghiệm:
3
2
1 ( ) 1
3
x k x a a
xk
32
2
( ) 2 3 0 *
3
g x x ax a
xk
.
Từ
M
kẻ được đúng hai tiếp tuyến đến
C
khi và chỉ khi phương trình
(*)
có hai nghiệm
phân biệt
hàm số
32
( ) 2 3y g x x ax a
có hai điểm cực trị
1
x
,
2
x
thỏa mãn
1
0gx
hoặc
2
0gx
2
( ) 6 6 0g x x ax
có hai nghiệm phân biệt
1
x
,
2
x
và
1
0gx
hoặc
2
0gx
.
Xét
2
0
' 0 6 6 0
x
g x x ax
xa
.
Ta có:
3
0
0
1
0
(0) 0
1
( ) 0
0
a
a
a
a
g
a
ga
aa





. Suy ra:
1
1;0M
và
2
1;2M
.
Vậy:
2 2 2
1 2 1 2
3 1 3 1 41
0 2 0.2
5 3 5 3 15
S y y y y
.
Câu 57: (THPT NINH BÌNH BẠC LIÊU NĂM 2018-2019 LẦN 04) Cho đồ thị
32
:3C y x x
. Có bao
nhiêu số nguyên
10;10b
để có đúng một tiếp tuyến của
C
đi qua điểm
0; ?Bb
A. 2. B. 9. C. 17. D. 16.
Lời giải:
Gọi
32
0 0 0 0
;3M x x x
là tiếp điểm.
Tiếp tuyến
của
()C
tại
0
M
có dạng
2 3 2
0 0 0 0 0
3 6 3y x x x x x x
qua
2 3 2 3 2
0 0 0 0 0 0 0
(0; ) 3 6 0 3 2 3 (*)B b b x x x x x b x x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 26
Có đúng một tiếp tuyến của
C
đi qua điểm
0; (*)Bb
có đúng 1 nghiệm
0
x
.
Đặt
32
23g x x x
;
2
g 6 6x x x

;
0
0
1
x
gx
x

.
Ta có bảng biến thiên của hàm
()gx
Dựa vào bảng biến thiên suy ra phương trình
*
có đúng 1 nghiệm
00
11
bb
bb




.
Vì
b
nguyên và
10;10b
, suy ra
9; 8;...; 1;2;3;....;9b
, có 17 giá trị của
b
.
Câu 58: Cho hàm số

2
1
x
y
x
có đồ thị
()C
và điểm
( ;1)Aa
. Gọi
S
là tập hợp tất cả các giá trị thực
của tham số
a
để có đúng một tiếp tuyến của
()C
đi qua
A
. Tổng tất cả các giá trị các phần tử
của
S
là
A.
1
. B.
3
2
. C.
5
2
. D.
1
2
.
Lời giải:
ĐK:
1x
;
2
1
'
( 1)
y
x
Đường thẳng
d
qua
A
có hệ số góc
k
là
( ) 1y k x a
d
tiếp xúc với
()C

2
2
( ) 1 1
1
1
2
( 1)
x
k x a
x
k
x
có nghiệm.
Thế
2
vào
1
ta có :
22
2
12
( ) 1 2 1 3 2, 1
1
( 1)
x
x a x a x x x x x
x
x
2
2 6 3 0 3x x a
Để đồ thị hàm số có một tiếp tuyến qua
A
thì hệ là số nghiệm của hệ phương trình trên có
nghiệm duy nhất
phương trình
3
có nghiệm duy nhất khác
1
2
' 9 2 6 0
3
1 6 3 0
2 6 3 0 (3)
2
' 9 2 6 0
1
2 6 3 0
a
a
a
x x a
a
a
a
Cách 2: TXĐ :
\1D
;
2
1
1
y
x
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 27
Giả sử tiếp tuyến đi qua
;1Aa
là tiếp tuyến tại điểm có hoành độ
0
xx
, khi đó phương trình
tiếp tuyến có dạng :
0
0
2
0
0
2
1
1
1
x
y x x d
x
x

Vì
Ad
nên thay tọa độ điểm A vào phương trình đường thẳng
d
ta có :
2
00
0
0
2
0
0
0
2 6 3 0 1
2
1
1
1
1
1

x x a
x
ax
x
x
x
Để chỉ có một tiếp tuyến duy nhất đi qua
A
thì phương trình
1
có nghiệm duy nhất khác
1
9 2 6 0
3
1 6 3 0
2
9 2 6 0
1
2 6 3 0
a
a
a
a
a
a

Dạng 3: VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN KHI BIẾT HỆ SỐ GÓC CỦA TIẾP TUYẾN
Câu 59: (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
có đồ thị như
hình vẽ
Đồ thị hàm số đã cho có bao nhiêu tiếp tuyến vuông góc với trục
Oy
?
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải:
Từ đồ thị ta có hai tiếp tuyến vuông góc với trục
Oy
là
1; 2yy
.
Câu 60: (THPT Thăng Long – Hà Nội – Lần 1 – 2018) Có bao nhiêu điểm thuộc đồ thị hàm số
21
1
x
y
x
thỏa mãn tiếp tuyến với đồ thị có hệ số góc bằng
2018
?
A.
1
. B.
0
. C. Vô số. D.
2
.
Lời giải:
Tập xác định
\1D
.
2
1
0, 1
1
yx
x
.
Hệ số góc tiếp tuyến tại điểm
0
x
trên đồ thị bằng
0
2018yx
2
1
2018
1x

vô nghiệm.
Vậy không có tiếp tuyến nào của đồ thị hàm số có hệ số góc bằng
2018
.
Câu 61: (THPT LƯƠNG TÀI - BẮC NINH - LẦN 2 - 2017 - 2018 - BTN) Biết tiếp tuyến của đồ thị hàm
số
42
2y ax bx
tại điểm
1; 1A
vuông góc với đường thẳng
2 3 0xy
. Tính
22
ab
.
A.
22
10ab
. B.
22
13ab
. C.
22
2ab
. D.
22
5ab
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 28
Lời giải:
Ta có
32
4 2 2 2y ax bx x ax b
.
Đường thẳng
2 3 0xy
có hệ số góc
1
2
k
.
Suy ra
12f
2 2 2 2 1a b a b
.
1; 1A
thuộc đồ thị hàm số nên
2 1 1a b a b
Ta có hệ phương trình:
22
2 1 2
5
13
a b a
ab
a b b



.
Câu 62: (GKI NHÂN CHÍNH HÀ NỘI NĂM 2018-2019 LẦN 01) Cho hàm số
32
1
32
3
y x x
có đồ
thị là
C
. Viết phương trình tiếp tuyến với đồ thị
C
biết tiếp tuyến có hệ số góc
9k 
A.
16 9 3yx
. B.
93yx
. C.
16 9 3yx
. D.
16 9 3yx
.
Lời giải:
Ta có:
2
6y x x

.
Gọi
00
; M x y
là tiếp điểm của tiếp tuyến với
C
.
Ta có hệ số góc của tiếp tuyến là:
0
9yx

2
00
69xx
2
00
6 9 0xx
0
3x
.
Với
0
3x 
3; 16M
.
Suy ra phương trình tiếp tuyến với đồ thị
C
tại
3; 16M
có dạng:
16 9 3yx
.
Câu 63: (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Tiếp tuyến của đồ thị
1
:
1
x
Cy
x
tại điểm có tung độ bằng
1
song song với đường thẳng
A.
: 2 1d y x
. B.
:1d y x
. C.
:1d y x
. D.
: 2 2d y x
.
Lời giải:
Ta có:
2
2
1
y
x
. Gọi
0
;1A x C
thì
0
0
0
1
10
1
x
x
x
.
Tiếp tuyến của
C
tại điểm
A
có phương trình:
0 0 0 2 1y y x y x
.
Suy ra tiếp tuyến song song với
: 2 2d y x
.
Câu 64: (THPT Hồng Bàng - Hải Phòng - Lần 1 - 2018) Cho đường cong
32
: 2 3 4C y x x x
và
đường thẳng
:3 4 0d x y
. Phương trình nào dưới đây là phương trình của đường thẳng
tiếp xúc với
C
và song song với
d
?
A.
268
3
27
yx
. B.
34yx
. C.
81 27 32 0xy
. D.
81 27 140 0xy
.
Lời giải:
Tiếp tuyến song song với
d
nên hệ số góc của tiếp tuyến là
3k
, mà
0
k y x
.
Suy ra
0
2
00
0
0
3 4 3 3
4
3
x
xx
x

. Do đó ta có hai điểm
0;4M
,
4 32
;
3 27
N



.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 29
Tại
0;4M
, ta có tiếp tuyến là:
34yx
trùng với
d
nên không thỏa.
Tại
4 32
;
3 27
N



ta có tiếp tuyến là
4 32
3
3 27
yx



81 27 140 0xy
.
Câu 65: (THPT Phan Đăng Lưu - Huế - Lần I -2018) Tìm phương trình tiếp tuyến của đồ thị hàm số
2
1
x
y
x
, biết tiếp tuyến vuông góc với đường thẳng
1
5
3
yx
và tiếp điểm có hoành độ
dương.
A.
3 10yx
. B.
32yx
. C.
36yx
. D.
32yx
.
Lời giải:
Gọi
0
x
là hoành độ tiếp điểm
0
0x
.
Vì tiếp tuyến vuông góc với đường thẳng
1
5
3
yx
nên ta có:
0
3yx

2
0
3
3
1x
2
0
11x
2
00
20xx
0
0
0
2
x
x
(loaïi)
0
2x
0
4y
.
Vậy phương trình tiếp tuyến cần tìm là:
3 2 4yx
3 10x
.
Câu 66: (THPT Hải An - Hải Phòng - Lần 1 - 2017 - 2018) Tìm số tiếp tuyến song song với trục hoành
của đồ thị hàm số
42
2 10y x x
.
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải:
3
0
0 4 4 0
1
x
y x x
x

.
Hàm số đã cho là hàm bậc 4 trùng phương có hệ số
0a
nên có 3 điểm cực trị (1 cực đại, 2
cực tiểu) tuy nhiên, tiếp tuyến song song với trục hoành tại 2 điểm cực tiểu là trùng nhau nên
có
2
tiếp tuyến thoả mãn yêu cầu bài toán.
Câu 67: (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 02) Có bao nhiêu tiếp tuyến của đồ thị
hàm số
3
32 y x x
song song với đường thẳng
9 14 0 xy
?
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải:
Gọi
C
là đồ thị của hàm số
3
32y x x
.
Tập xác định:
D
.
Đạo hàm:
2
33
yx
. Gọi
: 9 14 0 : 9 14 d x y d y x
.
Gọi
là tiếp tuyến cần tìm.
// : 9 14d y x
Phương trình
có dạng
9 , 14 y x m m
.
tiếp xúc
C
3
2
3 2 9
*
3 3 9

x x x m
x
có nghiệm
3
3 2 9
2 14
*
2
2 18
2


x x x m
x m l
x
x m n
x
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 30
Suy ra phương trình tiếp tuyến cần tìm là
: 9 18 yx
.
Câu 68: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Cho hàm số
2
xb
y
ax
,
2ab 
. Biết rằng
a
,
b
là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm
1; 2A
song song với
đường thẳng
:3 4 0d x y
. Khi đó giá trị của
3ab
bằng
A.
2
. B.
4
. C.
1
. D.
5
.
Lời giải:
Ta có:
2
2
2
ab
y
ax

.
Do
1; 2A
thuộc đồ thị hàm số nên
1
2 3 2
2
b
ba
a
.
Do tiếp tuyến tại
1; 2A
song song với
:3 4 0d x y
nên
13y

2
2
3
2
ab
a

Thay
32ba
ta được:
2
3 2 2 3 2a a a
2
5 15 10 0aa
1
2
a
a
.
+) Với
21ab
(loại, do
2ab 
)
+) Với
11ab
. Phương trình tiếp tuyến tại
1;2A
là
3 1 2yx
song song với
d
.
Vậy
1a
,
1b
, suy ra
32ab
.
Câu 69: (CHUYÊN VINH LẦN 3-2018) Cho đồ thị
1
:
2
x
Cy
x
và
12
,dd
là hai tiếp tuyến của
C
song song với nhau. Khoảng cách lớn nhất giữa
1
d
và
2
d
là
A.
3
. B.
23
. C.
2
. D.
22
.
Lời giải:
Do
1
:
2
x
Cy
x
,
2
1
0
2
y x x
x
.
12
,dd
là hai tiếp tuyến của
C
song song với nhau lần lượt có các hoành độ tiếp điểm là
1 2 1 2
, ,x x x x
nên ta có
12
= y x y x

22
12
11
22xx

12
12
12
xx
xx
xx

.
Gọi
11
11
11
11
; ; ;
22
xx
M x N x
xx

.
PTTT
1
d
tại
1
1
1
1
;
2
x
Mx
x



:
1
1
2
11
1
1
22
x
y x x
xx
1
1
2
11
1
1
0
22
x
x x y
xx
.
Khi đó
1 2 1
,;d d N d
dd
1
2
1
42
11
2
4
11
14
4
x
x
xx

.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 31
Áp dụng BĐT Cô-Si ta có
22
11
22
11
11
4 2 4 . 4xx
xx
12
;
2
1
2
1
44
2
2
1
4
dd
d
x
x
.
Dạng 4: HAI ĐỒ THỊ TIẾP XÚC
Câu 70: [Sở GD&ĐT Bình Phước-2017] Đồ thị của hàm số
32
f x x ax bx c
tiếp xúc với trục
hoành tại gốc tọa độ và cắt đường thẳng
1x
tại điểm có tung độ bằng
3
khi.
A.
2, 0a b c
. B.
2, 2, 0abc
. C.
0, 2a b c
. D.
0, 2a c b
.
Lời giải:
32
()f x x ax bx c
có đồ thị là
C
.
Vì
C
tiếp xúc với
Ox
tại gốc tọa độ nên ta có:
32
( ) 0 0
()
( ) 0 0
f x c
f x x ax
f x b





.
Theo giả thiết
C
cắt đường thẳng
1x
tại điểm có tung độ bằng
3
suy ra.
(1) 3 1 3 2f a a
.
Câu 71: Tìm tất cả các giá trị của tham số
m
sao cho tiệm cận ngang của đồ thị hàm số
2
1
mx
y
xm

tiếp xúc với parabol
2
7yx
.
A.
7m
. B.
7m
. C.
4m
. D.
m
.
Lời giải:
Đồ thị hàm số có tiệm cận ngang khi
1
1 2 0
2
m
mm
m

.
Khi đó đồ thị hàm số có tiệm cận ngang là
ym
.
tiếp xúc với parabol
2
77y x m
.
Câu 72: (Chuyên Thái Bình-Thái Bình-L4-2018) Họ parabol
2
: 2 3 2
m
P y mx m x m
0m
luôn tiếp xúc với đường thẳng
d
cố định khi
m
thay đổi. Đường thẳng
d
đó đi qua điểm nào
dưới đây?
A.
0; 2 .
B.
0;2 .
C.
1;8 .
D.
1; 8 .
Lời giải:
Gọi
00
;H x y
là điểm cố định mà
m
P
luôn đi qua.
Khi đó ta có:
2
0 0 0
2 3 2y mx m x m
2
0 0 0 0
2 1 6 2 0m x x x y
,
0m
.
2
00
00
2 1 0
6 2 0
xx
xy
.
Do
2
00
2 1 0xx
có nghiệm kép nên
m
P
luôn tiếp xúc với đường thẳng
: 6 2d y x
.
Ta thấy
0; 2 d
.
III- BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 73: Viết tất cả các phương trình tiếp tuyến của đồ thị
32
: 2 1,C y x x
biết tiếp tuyến song song
với đường thẳng
1.yx
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 32
A.
1; 1.y x y x
B.
31
; 1.
27
y x y x
C.
31
.
27
yx
D.
3; 1.y x y x
Câu 74: Viết phương trình tiếp tuyến của
3
:2C y x x
tại điểm
1; 1 .M
A.
2 3.yx
B.
2.yx
C.
1.yx
D.
.yx
Câu 75: Viết phương trình tiếp tuyến của đồ thị
32
: 2 1C y x x
tại điểm
1;0 .A
A.
1.yx
B.
1.yx
C.
.yx
D.
2 2.yx
Câu 76: Viết phương trình tiếp tuyến của đồ thị
32
: 2 1C y x x
tại giao điểm của
C
và
.Oy
A.
1.y 
B.
2.y
C.
1.y
D.
2 1.yx
Câu 77: Viết tất cả các phương trình tiếp tuyến của đồ thị
32
: 2 1,C y x x
biết tiếp tuyến song song
với đường thẳng
2.yx
A.
1; 1.y x y x
B.
31
; 1.
27
y x y x
C.
11
; 1.
27
y x y x
D.
3; 1.y x y x
Câu 78: Viết tất cả các phương trình tiếp tuyến của đồ thị
32
: 2 1,C y x x
biết tiếp tuyến song song
với đường thẳng
1.yx
A.
1; 1.y x y x
B.
31
; 1.
27
y x y x
C.
31
.
27
yx
D.
3; 1.y x y x
Câu 79: Có bao nhiêu tiếp tuyến của đồ thị
32
: 2 1,C y x x
biết tiếp tuyến song song với đường
thẳng
1?yx
A.
1.
B.
2.
C.
3.
D.
4.
Câu 80: Viết tất cả các phương trình tiếp tuyến của đồ thị
32
: 2 1,C y x x
biết tiếp tuyến vuông góc
với đường thẳng
7 0.xy
A.
365
7 5; 7 .
27
y x y x
B.
14
7 5; 7 .
27
y x y x
C.
365
7 5; 7 .
27
y x y x
D.
365
7 5; 7 .
27
y x y x
Câu 81: Viết phương trình tiếp tuyến của đồ thị
32
: 3 2C y x x
tại điểm
1; 2 .A 
A.
1.yx
B.
9 7.yx
C.
9.yx
D.
2.yx
Câu 82: Viết phương trình tiếp tuyến của đồ thị
32
: 3 2C y x x
tại giao điểm của
C
và
.Oy
A.
1.y 
B.
2.y
C.
4.y
D.
2 1.yx
Câu 83: Viết tất cả các phương trình tiếp tuyến của đồ thị
32
: 3 2C y x x
, biết tiếp tuyến song song
với đường thẳng
9 2.yx
A.
9 7; 9 25.y x y x
B.
9 7; 9 25.y x y x
C.
9 7; 9 25.y x y x
D.
9 ; 9 25.y x y x
Câu 84: Viết tất cả các phương trình tiếp tuyến của đồ thị
32
: 3 2C y x x
biết tiếp tuyến song song
với đường thẳng
9 7.yx
A.
9 25.yx
B.
9 7; 9 25.y x y x
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 33
C.
9 7; 9 25.y x y x
D.
9 ; 9 25.y x y x
Câu 85: Có bao nhiêu tiếp tuyến của đồ thị
32
: 3 2,C y x x
biết tiếp tuyến song song với đường
thẳng
9 7?yx
A.
1.
B.
2.
C.
3.
D.
4.
Câu 86: Viết tất cả các phương trình tiếp tuyến của đồ thị
32
: 3 2,C y x x
biết tiếp tuyến vuông
góc với đường thẳng
3 0.xy
A.
3 3.yx
B.
3 1.yx
C.
3 3.yx
D.
3 2.yx
Câu 87: Viết phương trình tiếp tuyến của đồ thị
21
:
2
x
Cy
x
song song với đường thẳng
: 3 2 0.xy
A.
3 4.yx
B.
3 2.yx
C.
3 14.yx
D.
3 4.yx
Câu 88: Viết tất cả các phương trình tiếp tuyến của đồ thị
3
: 3 2C y x x
có hệ số góc bằng 9 .
A.
9 18; 9 22.y x y x
B.
9 14; 9 18.y x y x
C.
9 18; 9 22.y x y x
D.
9 14; 9 18.y x y x
Câu 89: Viết phương trình tiếp tuyến của đồ thị
2
:
1
x
Cy
x
tại điểm
1
3; .
2
A



A.
1
1.
2
yx
B.
11
.
44
yx
C.
1
.
6
yx
D.
.yx
Câu 90: Viết phương trình tiếp tuyến của đồ thị
2
:
1
x
Cy
x
tại giao điểm của
C
và
.Ox
A.
1.yx
B.
2.yx
C.
1.yx
D.
2.yx
Câu 91: Viết phương trình tiếp tuyến của đồ thị
2
:
1
x
Cy
x
tại giao điểm của
C
và
.Oy
A.
1.yx
B.
2.yx
C.
1.yx
D.
2.yx
Câu 92: Viết phương trình tiếp tuyến của đồ thị
2
:,
1
x
Cy
x
biết tiếp tuyến song song với đường
thẳng
0.xy
A.
2; .y x y x
B.
2; 2.y x y x
C.
1; 2.y x y x
D.
2; 4.y x y x
Câu 93: Viết phương trình tiếp tuyến của đồ thị
2
:,
1
x
Cy
x
biết tiếp tuyến song song với đường
thẳng
2 0.xy
A.
2; .y x y x
B.
2; 2.y x y x
C.
1; 2.y x y x
D.
2.yx
Câu 94: Có bao nhiêu tiếp tuyến của đồ thị
2
:,
1
x
Cy
x
biết tiếp tuyến song song với đường thẳng
2 0?xy
A.
1.
B.
2.
C.
3.
D.
4.
Câu 95: Viết phương trình tiếp tuyến của đồ thị
32
: 3 1C y x x x
tại điểm có hoành độ
0
x
thỏa
mãn
0
3.yx

A.
15
.
44
yx
B.
5
1.
4
yx
C.
21yx
D.
5
1.
4
yx
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 34
Câu 96: Biết tiếp tuyến của đồ thị
32
: 3 1C y x x x
tại điểm có hoành độ
0
3
2
x
cắt trục
,Ox Oy
lần lượt tại
,,AB
tính diện tích
S
của tam giác
.OAB
A.
1
.
5
S
B.
2
.
5
S
C.
4.S
D.
4
.
5
S
Câu 97: Viết phương trình tiếp tuyến của đồ thị
42
: 2 1C y x x
tại điểm có hoành độ
0
x
thỏa mãn
0
16 0.yx


A.
8 4.yx
B.
8 4; 8 4.y x y x
C.
8 4; 8 4.y x y x
D.
8 4; 8 .y x y x
Câu 98: Tìm hệ số góc nhỏ nhất
min
k
của tiếp tuyến với đồ thị
32
11
: 2 .
33
C y x x
A.
min
4.k 
B.
min
4.k
C.
min
0.k
D.
min
2.k 
Câu 99: Viết phương trình tiếp tuyến với đồ thị
32
11
: 2 ,
33
C y x x
biết tiếp tuyến có hệ số góc nhỏ
nhất.
A.
43yx
B.
4 3.yx
C.
2 3.yx
D.
2 3.yx
Câu 100: Tìm hệ số góc lớn nhất
max
k
của tiếp tuyến với đồ thị
32
12
: 2 .
33
C y x x
A.
max
4.k 
B.
max
4.k
C.
max
6.k
D.
max
2.k 
Câu 101: Viết phương trình tiếp tuyến với đồ thị
32
12
: 2 ,
33
C y x x
biết tiếp tuyến có hệ số góc lớn
nhất.
A.
4 3.yx
B.
4 3.yx
C.
4 2.yx
D.
2 3.yx
Câu 102: Trong các đường thẳng có phương trình được cho dưới đây, đường thẳng nào là tiếp tuyến
của đồ thị
3
: 3 1?C y x x
A.
3 3.yx
B.
3 1.yx
C.
3.yx
D.
3 3.yx
Câu 103: Trong các đường thẳng có phương trình được cho dưới đây, đường thẳng nào là tiếp tuyến
của đồ thị
32
: 2 1?C y x x
A.
3.yx
B.
1.yx
C.
2.yx
D.
.yx
Câu 104: Biết các tiếp tuyến có hệ số góc bằng
1
của đồ thị
32
: 2 1C y x x
tiếp xúc với
C
tại các
điểm
,.AB
Tính độ dài đoạn thẳng
.AB
A.
1447
.
24
B.
1447
.
3
C.
1447
.
27
D.
1447
.
9
Câu 105: Tiếp tuyến của đồ thị
3
: 4 3 1C y x x
đi qua điểm
1;2A
có phương trình là
A.
9 7; 2.y x y x
B.
9 11; 2.y x y x
C.
9 11; 2.y x y
D.
9 7; 2.y x y
Câu 106: Tiếp tuyến của đồ thị
21
:
1
x
Cy
x
qua điểm
1;4A
có phương trình là
A.
1 13
.
33
yx
B.
11
.
33
yx
C.
1
4.
3
yx
D.
5.yx
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 35
Câu 107: Cho hàm số
32
31y x x x
có đồ thị
C
. Tiếp tuyến của
C
tại điểm thuộc đồ thị
C
có
hoành độ dương và là nghiệm của phương trình
. 11 0y x y
có phương trình là
A.
3.yx
B.
4 2.yx
C.
2.yx
D.
4 3.yx
Câu 108: Cho hàm số
32
3y x x
có đồ thị
C
. Gọi
M
là điểm thuộc đồ thị
C
có hoành độ bằng 1.
Với giá trị nào của tham số
m
thì tiếp tuyến của
C
tại
M
song song với đường thẳng
2
: 4 2 1?d y m x m
A.
1.m
B.
1.m 
C.
2.m
D.
2.m 
Câu 109: Cho hàm số
42
2 1 2y x m x m
có đồ thị
C
. Gọi
A
là điểm thuộc đồ thị hàm số có
hoành độ bằng 1. Với giá trị nào của tham số
m
thì tiếp tuyến với đồ thị
C
tại
A
vuông góc
với đường thẳng
: 4 1 0?xy
A.
1.m
B.
1.m 
C.
2.m
D.
2.m 
Câu 110: Cho hàm số
32
2 3 5y x x
có đồ thị
C
. Gọi
:d y kx m
là tiếp tuyến của
C
tại điểm có
hệ số góc tiếp tuyến nhỏ nhất. Tỉ số
2:T m k
có giá trị bằng
A.
7.T 
B.
5.T 
C.
5.T
D.
7.T
Câu 111: Cho hàm số
y f x
có đồ thị
C
và điểm
0 0 0
;M x f x
thuộc
C
. Phương trình tiếp tuyến
của
C
tại
0
M
là:
A.
00
y f x x x

. B.
0 0 0
y f x x x y
. C.
00
y y f x x

. D.
0 0 0
y y f x x x
.
Câu 112: Cho hàm số
y f x
có đạo hàm trong khoảng
;ab
, đồ thị là đường cong
C
. Để đường
thẳng
: y ax b
là tiếp tuyến của
C
tại điểm
0 0 0
;M x f x
, điều kiện cần và đủ là
A.
/
0
a f x
. B.
/
00
ax b f x
. C.
/
0
00
a f x
ax b f x

. D.
/
0
/
00
a f x
ax b f x

.
Câu 113: Phương trình tiếp tuyến của đường cong
3
: 2 3C y x x
tại điểm
1;2M
là
A.
22yx
. B.
31yx
. C.
1yx
. D.
2yx
.
Câu 114: Tiếp tuyến của đường cong
:C y x x
tại điểm
1;1M
có phương trình
A.
31
.
22
yx
B.
31
.
22
yx
C.
31
.
22
yx
D.
3
.
22
x
y 
Câu 115: Tiếp tuyến với đồ thị hàm số
4
1
y
x
tại điểm với hoành độ
1x 
có phương trình
A.
3yx
. B.
2yx
. C.
1yx
. D.
2yx
.
Câu 116: Cho hàm số
2
5yx
có đồ thị
C
. Phương trình tiếp tuyến của
C
tại
M
có tung độ
0
1y 
, với hoành độ
0
0x
là kết quả nào sau đây?
A.
2 6 6 1yx
. B.
2 6 6 1yx
. C.
2 6 6 1yx
. D.
2 6 6 1yx
.
Câu 117: Cho hàm số
2
54y x x
có đồ thị
C
. Tiếp tuyến của
C
tại các giao điểm của
C
với
trục
Ox
, có phương trình:
A.
33yx
hoặc
3 12yx
. B.
33yx
hoặc
3 12yx
.
C.
23yx
hoặc
23yx
. D.
23yx
hoặc
23yx
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 36
Câu 118: Tiếp tuyến của đồ thị hàm số
21
1
x
y
x
tại điểm có hoành độ bằng
2
, có hệ số góc bằng
A.
1
. B.
3
. C. 3. D. 5.
Câu 119: Cho đường cong
3
:C y x
. Tiếp tuyến của
C
có hệ số góc
12k
, có phương trình:
A.
12 16yx
. B.
12 8yx
. C.
12 2yx
. D.
12 4yx
.
Câu 120: Cho hàm số
2
23y x x
có đồ thị
C
. Tại điểm
00
;M x y C
, tiếp tuyến có hệ số góc
bằng
2
thì
00
xy
bằng
A. 2. B. 3. C. 4. D. 5.
Câu 121: Gọi
C
là đồ thị của hàm số
3
2
2 3 1
3
x
y x x
. Có hai tiếp tuyến của
C
cùng có hệ số
góc bằng
3
4
. Đó là các tiếp tuyến
A.
3 29
4 24
yx
hoặc
3
3
4
yx
. B.
3 37
4 12
yx
hoặc
3
3
4
yx
.
C.
3 37
4 12
yx
hoặc
3 13
44
yx
. D.
3 29
4 24
yx
hoặc
3
3
4
yx
.
Câu 122: Cho hàm số
32
2 3 4 5y x x x
có đồ thị là
C
. Trong số các tiếp tuyến của
C
, có một tiếp
tuyến có hệ số góc nhỏ nhất. Hệ số góc của tiếp tuyến này bằng
A.
3,5
. B.
5,5
. C.
7,5
. D.
9,5
.
Câu 123: Cho hàm số
32
69y x x x
có đồ thị
C
. Tiếp tuyến của
C
song song với đường thẳng
:9d y x
có phương trình
A.
9 40yx
. B.
9 40yx
. C.
9 32yx
. D.
9 32yx
.
Câu 124: Gọi
C
là đồ thị của hàm số
4
y x x
. Tiếp tuyến của
C
vuông góc với đường thẳng
: 5 0d x y
có phương trình là
A.
53yx
. B.
35yx
. C.
23yx
. D.
4yx
.
Câu 125: Cho hàm số
32
31y x x
có đồ thị là
C
. Gọi
là tiếp tuyến của
C
tại điểm
1;5A
và
B
là giao điểm thứ hai của
với
C
. Diện tích tam giác
OAB
bằng
A. 5. B. 6. C. 12. D.
6 82
.
Câu 126: Cho hàm số
32
4 6 1y x x
có đồ thị
C
. Tiếp tuyến của
C
đi qua điểm
1; 9M 
có
phương trình
A.
24 15yx
. B.
15 21
.
44
yx
C.
24 15yx
hoặc
15 21
.
44
yx
D.
24 33yx
.
Câu 127: Cho hàm số
42
3y x x
có đồ thị là
C
. Các tiếp tuyến không song song với trục hoành kẻ từ
gốc tọa độ
0;0O
đến
C
là
A.
2yx
hoặc
2yx
. B.
yx
hoặc
yx
.
C.
4
3
yx
hoặc
4
3
yx
. D.
3yx
hoặc
3yx
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 37
Câu 128: Cho hàm số
2
1
4
x
yx
có đồ thị
C
. Từ điểm
2; 1M
có thể kẻ đến
C
hai tiếp tuyến
phân biệt. Hai tiếp tuyến này có phương trình
A.
1yx
hoặc
3yx
. B.
3yx
hoặc
1yx
.
C.
3yx
hoặc
1yx
. D.
1yx
hoặc
3yx
.
Câu 129: Cho hàm số
21
1
x
y
x
có đồ thị
C
. Gọi
d
là tiếp tuyến của
C
, biết
d
đi qua điểm
4; 1A
.
Gọi
M
là tiếp điểm của
d
và
C
, tọa độ điểm
M
là
A.
2;5 , 0; 1MM
. B.
2;5 , 2;1MM
. C.
0; 1 , 2;1MM
. D.
3
1; , 2;1
2
MM




.
Câu 130: Cho hàm số
2
1
x
y
x
có đồ thị
C
. Trong tất cả các tiếp tuyến của
C
, tiếp tuyến thỏa mãn
khoảng cách từ giao điểm của hai tiệm cận đến nó là lớn nhất, có phương trình
A.
2yx
hoặc
2yx
. B.
2yx
hoặc
1yx
.
C.
2yx
hoặc
2yx
. D.
1yx
hoặc
1yx
.
Câu 131: Từ điểm
2
;0
3
A



kẻ đến đồ thị hàm số
3
52
63
m
y x mx
hai tiếp tuyến vuông góc nhau thì
tập tất cả các giá trị của
m
bằng
A.
1
2
m
hoặc
2m
. B.
1
2
m 
hoặc
2m 
.
C.
1
2
m
hoặc
2m 
. D.
1
2
m 
hoặc
2m
.
Câu 132: Cho hàm số
2
1
x
y
x
có đồ thị
C
. Tiếp tuyến của
C
tại điểm có hoành độ bằng
2
đi qua
0;Ma
thì
a
bằng
A.
10.a
B.
9.a
C.
3.a
D.
1.a
Câu 133: Cho hàm số
4 2 2
2 2 1y x m x m
có đồ thị
C
. Tất cả các giá trị của tham số
m
để tiếp tuyến
của
C
tại giao điểm của
C
và đường thẳng
:1dx
song song với đường thẳng
: 12 4yx
là
A.
0m
. B.
1m
. C.
2m 
. D.
3m
.
Câu 134: Cho hàm số
3
2y x x
có đồ thị
C
. Để đường thẳng
:4d y x m
tiếp xúc với
C
thì tập
tất cả các giá trị của
m
là
A.
0m
và
4m
. B.
1m
và
2m
.
C.
3m
. D. Không có giá trị của
m
.
Câu 135: Cho hàm số
42
3 5 4y x m x
có đồ thị là
m
C
. Để
m
C
tiếp xúc với đường thẳng
63yx
tại điểm có hoành độ bằng
1
thì giá trị thích hợp của
m
là
A.
1m 
. B.
2m 
. C.
2m
. D. Không có giá trị
m
.
Câu 136: Cho hàm số
2
3
ax
y
bx
có đồ thị là
C
. Tại điểm
2; 4M 
thuộc
C
, tiếp tuyến của
C
song song với đường thẳng
:7 5 0d x y
. Khi đó biểu thức liên hệ giữa
a
và
b
là
A.
2 0.ba
B.
2 0.ab
C.
3 0.ba
D.
3 0.ab
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 38
Câu 137: Cho hàm số
2
xb
y
ax
có đồ thị là
C
. Biết rằng
a
và
b
là các giá trị thỏa mãn tiếp tuyến của
C
tại điểm
1; 2M
song song với đường thẳng
: 3 4 0d x y
. Khi đó giá trị của
ab
bằng
A.
2
. B.
1
. C.
1
. D.
0
.
Câu 138: Cho hàm số
23
ax b
y
x
có đồ thị là
C
. Nếu
C
đi qua
1;1A
và tại điểm
B
trên
C
có
hoành độ bằng
2
, tiếp tuyến của
C
có hệ số góc
5k
thì các giá trị của
a
và
b
là
A.
2; 3ab
. B.
3; 2ab
. C.
2; 3ab
. D.
3; 2ab
.
Câu 139: Cho hàm số
1
ax b
y
x
có đồ thị là
C
. Nếu
C
đi qua
3;1A
và tiếp xúc với đường thẳng
: 2 4d y x
, thì các cặp số
;ab
theo thứ tự là
A.
2;4
hoặc
10;28
. B.
2; 4
hoặc
10; 28
.
C.
2;4
hoặc
10;28
. D.
2; 4
hoặc
10; 28
.
Câu 140: Cho hàm số
2
2
ax bx
y
x
có đồ thị là
C
. Để
C
qua điểm
5
1;
2
A



và tiếp tuyến của
C
tại
gốc tọa độ có hệ số góc bằng
3
thì mối liên hệ giữa
a
và
b
là
A.
4 1.ab
B.
4 1.ab
C.
4 0.ab
D.
4 0.ab
Câu 141: Cho hàm số
42
1 14
33
y x x
có đồ thị
C
. Có bao nhiêu điểm
A
thộc
C
sao cho tiếp tuyến
của
C
tại
A
cắt đồ thị
C
tại hai điểm phân biệt
11
;M x y
,
22
;N x y
(
M
,
N
khác
A
) sao
cho
2 1 2 1
8y y x x
.
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 142: Cho hàm số
2
1
x
y
x

có đồ thị
C
và điểm
;1Aa
. Gọi
S
là tập hợp tất cả các giá trị thực của
a
để có đúng một tiếp tuyến từ
C
đi qua
A
. Tổng tất cả giá trị của phần tử
S
bằng
A.
1
. B.
3
2
. C.
5
2
. D.
1
2
.
IV – ĐỀ TỔNG ÔN TẬP
§Ò Sè 1
Câu 1: Cho hàm số
1
1
x
y
x
. Phương trình tiếp tuyến của đồ thị hàm số tại điểm
1;0M
là
A.
13
.
22
yx
B.
11
.
22
yx
C.
11
.
22
yx
D.
11
.
42
yx
Câu 2: Cho hàm số
3
3y x x
có đồ thị
C
.Hệ số góc
k
của tiếp tuyến với đồ thị
C
tại điểm có
tung độ bằng
4
là
A.
0.k
B.
2.k 
C.
6.k
D.
9.k
Câu 3: Cho hàm số
32
1
21
3
y x x x
có đồ thị là
C
. Phương trình tiếp tuyến của
C
tại điểm
1
1;
3
M



là
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 39
A.
3 2.yx
B.
3 2.yx
C.
2
.
3
yx
D.
2
.
3
yx
Câu 4: Phương trình tiếp tuyến của đồ thị
24
:
3
x
Hy
x
tại giao điểm của
H
và
Ox
là
A.
2.yx
B.
2 4.yx
C.
2 4.yx
D.
2 4.yx
Câu 5: Cho hàm số
2
24y x x
có đồ thị
C
. Phương trình tiếp tuyến của
C
tại điểm có hoành
độ
0x
là
A.
43yx
. B.
1
2
2
yx
. C.
1
2
2
yx
. D.
1
2
2
yx
.
Câu 6: Cho hàm số
3
1y x x
có đồ thị
C
. Phương trình tiếp tuyến của
C
tại giao điểm của
C
với trục tung là
A.
21yx
. B.
1yx
. C.
22yx
. D.
1yx
.
Câu 7: Có bao nhiêu tiếp tuyến của đồ thị hàm số
3
32y x x
song song với đường thẳng
9 14 0xy
?
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 8: Đường thẳng nào sau đây là tiếp tuyến của đồ thị hàm số
3
32y x x
?
A.
9 12yx
. B.
9 14yx
. C.
9 13yx
. D.
9 11yx
.
Câu 9: Cho hàm số
32
1
32
3
y x x
có đồ thị là
C
. Phương trình tiếp tuyến với đồ thị
C
biết tiếp
tuyến có hệ số góc
9k 
là
A.
16 9 3yx
. B.
93yx
. C.
16 9 3yx
. D.
16 9 3yx
.
Câu 10: Cho hàm số
y f x
có đồ thị như hình vẽ
Đồ thị hàm số đã cho có bao nhiêu tiếp tuyến vuông góc với trục
Oy
?
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 11: Cho hàm số
32
3 9 1y x x x
có đồ thị
C
. Hệ số góc lớn nhất của tiếp tuyến với đồ thị
C
bằng
A.
1
B.
6
C.
12
D.
9
Câu 12: Tiếp tuyến với đồ thị hàm số
42
1
23
4
y x x
tại điểm cực tiểu của đồ thị cắt đồ thị ở
,AB
khác tiếp điểm. Độ dài đoạn thẳng
AB
bằng
A.
2
. B.
2
. C.
22
. D.
42
.
Câu 13: Cho hàm số
4 2cos2y x x
có đồ thị là
C
. Hoành độ của các điểm trên
C
mà tại đó tiếp
tuyến của
C
song song hoặc trùng với trục hoành là
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 40
A.
4
x k k
. B.
2
x k k
. C.
x k k

. D.
2x k k

.
Câu 14: Cho hàm số
, , , , ; 0, 0
ax b
y f x a b c d c d
cx d
có đồ thị
.C
Đồ thị của hàm số
y f x
như hình vẽ dưới đây. Biết
C
cắt trục tung tại điểm có tung độ bằng
2.
Phương trình tiếp tuyến của
C
tại giao điểm của
C
với trục hoành là
A.
3 2 0.xy
B.
3 2 0.xy
C.
3 2 0.xy
D.
3 2 0.xy
Câu 15: Cho hàm số
1
1
x
yC
x
. Điểm
M
thuộc
C
có hoành độ lớn hơn
1
, tiếp tuyến của
C
tại
M
cắt hai tiệm cận của
C
lần lượt tại
A
,
B
. Diện tích nhỏ nhất của tam giác
OAB
bằng
A.
4 2 2
. B.
4
. C.
42
. D.
42
.
Câu 16: Cho hàm số
1
21
x
y
x

(C),
()y x m d
. Với mọi
m
đường thẳng
()d
luôn cắt đồ thị (C) tại hai
hai điểm phân biệt A và B. Gọi k1, k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A và B.
Giá trị nhỏ nhất của
2020 2020
12
T k k
bằng
A.
1
. B.
2
. C.
1
2
. D.
2
3
.
Câu 17: Cho hàm số
2
1
x
y
x
đồ thị
C
. Gọi
d
là khoảng cách từ giao điểm hai tiệm cận của đồ thị
C
đến một tiếp tuyến của
C
. Giá trị lớn nhất của
d
có thể đạt được là
A.
33
. B.
3
. C.
2
. D.
22
.
Câu 18: Cho hàm số
3
1yx
có đồ thị
()C
. Trên đường thẳng
:1d y x
tìm được hai điểm
1 1 1
;M x y
,
2 2 2
;M x y
mà từ mỗi điểm đó kẻ được đúng hai tiếp tuyến đến
C
. Giá trị biểu
thức
22
1 2 1 2
31
53
S y y y y
bằng
A.
113
15
. B.
41
15
. C.
14
15
. D.
59
15
.
Câu 19: Cho hàm đa thức bậc bốn
y f x
có đồ thị
C
. Hàm số
y f x
có đồ thị như hình vẽ dưới
đây. Gọi đường thẳng
là tiếp tuyến của đồ thị
C
tại điểm có hoành độ bằng
1
. Hỏi
và
C
có bao nhiêu điểm chung?
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 41
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 20: Phương trình tiếp tuyến của đồ thị hàm số
y f x
thỏa mãn
23
1 2 1f x x f x
tại điểm
có hoành độ
1x
là
A.
16
77
yx
. B.
16
77
yx
. C.
16
77
yx
. D.
16
77
yx
.
HẾT
§Ò Sè 2
Câu 1: Tọa độ điểm
M
có hoành độ âm trên đồ thị
3
12
:
33
C y x x
sao cho tiếp tuyến tại
M
vuông góc với đường thẳng
12
33
yx
là
A.
2 ; 4M 
. B.
4
1;
3
M



. C.
4
2;
3
M



. D.
2 ; 0M
.
Câu 2: Hệ số góc của tiếp tuyến của đồ thị hàm số
34
2
x
y
x
tại điểm có tung độ
7
,
3
y 
bằng
A.
9
.
5
B.
5
.
9
C.
5
.
9
D.
10.
Câu 3: Tập hợp tất cả các giá trị của tham số
m
để mọi tiếp tuyến của đồ thị hàm số
32
2 3 1y x mx m x
đều có hệ số góc dương là
A.
\ 0 .
B.
1; .
C.
\ 1 .
D.
.
Câu 4: Hỏi trên đồ thị
1
:
2
x
Cy
x
có bao nhiêu điểm
M
mà tiếp tuyến với
C
tại
M
song song với
đường thẳng
: 1?d x y
A.
4
. B.
1
. C.
2
. D.
0
.
Câu 5: Gọi
d
là tiếp tuyến tại điểm cực đại của đồ thị hàm số
3
32y x x
. Khẳng định nào sau đây
đúng?
A.
d
có hệ số góc âm. B.
d
có hệ số góc dương.
C.
d
song song với đường thẳng
4y 
. D.
d
song song với trục
Ox
.
Câu 6: Gọi
,MN
là hai điểm di động trên đồ thị
C
của hàm số
32
34y x x x
sao cho tiếp
tuyến của
C
tại
M
và
N
luôn song song với nhau. Hỏi khi
,MN
thay đổi, đường thẳng
MN
luôn đi qua nào trong các điểm có tọa độ dưới đây?
A.
1; 5 .
B.
1; 5 .
C.
1;5 .Q
D.
1;5 .P
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 42
Câu 7: Hỏi trên đồ thị hàm số
21
2
x
y
x
có bao nhiêu cặp tiếp tuyến vuông góc với nhau?
A.
1
. B. Vô số. C.
0
. D.
2
.
Câu 8: Cho hàm số
2
xb
y
ax
,
2ab 
. Biết rằng
a
,
b
là các giá trị thỏa mãn tiếp tuyến của đồ thị
hàm số tại điểm
1; 2A
song song với đường thẳng
: 3 4 0d x y
. Khi đó, giá trị
3ab
bằng
A.
2
. B.
4
. C.
1
. D.
5
.
Câu 9: Cho hàm số
1
()
2
x
yC
x
và
: 2 1d y x m
(
m
là tham số thực). Gọi
1
k
,
2
k
là hệ số góc của
tiếp tuyến của
C
tại giao điểm của
d
và
C
. Giá trị
12
.kk
bằng
A.
1
4
. B.
2
. C.
3
. D.
4
.
Câu 10: Cho hàm số
32
3 3 5y x x x
có đồ thị
C
. Có bao nhiêu giá trị nguyên của
k
trên
2019;2019


để trên đồ thị
C
có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường
thẳng
: 3 ?d y k x
A.
2021
. B.
2017
. C.
2022
. D.
2016
.
Câu 11: Có bao nhiêu giá trị của tham số thực
m
để đồ thị hàm số
2
2x mx m
y
xm

cắt trục
Ox
tại hai
điểm phân biệt và các tiếp tuyến của đồ thị tại hai điểm đó vuông góc với nhau?
A.
5
B.
2
C.
0
D.
1
Câu 12: Cho hàm số
32
32y x x
có đồ thị
C
và điểm
;2Mm
. Gọi
S
là tập hợp tất cả các giá trị
thực của
m
để qua
M
kẻ đúng hai tiếp tuyến đến
C
. Tổng tất cả các phần tử của
S
bằng
A.
8
.
3
B.
3.
C.
2
.
3
D.
2.
Câu 13: Cho hàm số
2
2
x
y
x
, có đồ thị
(C)
và điểm
00
;M x y C
(với
0
0x
). Biết rằng khoảng cách
từ
2;2I
đến tiếp tuyến của
(C)
tại M là lớn nhất, đẳng thức nào sau đây đúng?
A.
00
20xy
. B.
00
24xy
. C.
00
22xy
. D.
00
22xy
.
Câu 14: Gọi
: , ,d y ax b a b
là tiếp tuyến của đồ thị hàm số
2
.
23
x
y
x
Biết
d
cắt trục hoành và
trục tung lần lượt tại hai điểm
,AB
sao cho
OAB
cân tại
O
. Khi đó,
ab
bằng
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 15: Cho hàm số
32
13
2
22
y x x C
. Xét hai điểm
;
A
Aay
và
;
B
B b y
phân biệt của đồ thị
C
mà tiếp tuyến tại
A
và
B
song song. Biết rằng đường thẳng
AB
đi qua
5;3D
. Phương trình
của đường thẳng
AB
là
A.
20xy
. B.
80xy
. C.
3 4 0xy
. D.
2 1 0xy
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 43
Câu 16: Cho hàm số
32
1 2 1y x m x x m
có đồ thị
C
(
m
là tham số thực). Gọi
12
,mm
là các giá
trị của
m
để đường thẳng
:1d y x m
cắt
C
tại ba điểm phân biệt
,,A B C
sao cho tổng hệ
số góc của các tiếp tuyến với
C
tại
,,A B C
bằng
19
. Khi đó
12
mm
bằng
A.
4
. B.
2
.
C.
0
. D.
2
.
Câu 17: Gọi
S
là tập hợp tất cả các giá trị tham số
m
để đồ thị hàm số
3 2 2 3
( ) 3 3 2f x x mx mx m m
tiếp xúc với trục hoành. Tổng các phần tử của
S
bằng
A.
0
. B.
1
. C.
2
3
. D.
4
3
.
Câu 18: Cho hàm số bậc bốn
y f x
xác định và liên tục trên , hàm số
2
23g x x
và đường
thẳng
d
có đồ thị như hình vẽ dưới đây.
Biết
A
là điểm chung của đồ thị
fx
và
gx
,
1
A
x
. Điểm
B
thuộc đồ thị
gx
,
9
4
B
x 
và
d
là tiếp tuyến của đồ thị hàm số
y f x
. Giá trị
A
fx
bằng
A.
1
. B.
3
2
. C.
5
2
. D.
2
.
Câu 19: Gọi
A
là điểm có hoành độ bằng
1
thuộc đồ thị
C
của hàm số
42
2y x mx m
(
m
là tham
số thực). Ta luôn tìm được
a
m
b
với
a
b
là phân số tối giản để tiếp tuyến
với đồ thị
C
tại
A
cắt đường tròn
22
: 2 3 0x y y
tạo thành một dây cung có độ dài nhỏ nhất. Khi đó,
tổng
ab
bằng
A.
12
. B.
3
. C.
29
. D.
10
.
Câu 20: Cho hàm số
42
1
3
4
y x x
có đồ thị
()C
. Có bao nhiêu điểm
A
thuộc
()C
sao cho tiếp tyến của
()C
tại
A
cắt
()C
tại hai điểm phân biệt
11
;M x y
,
22
;N x y
(,MN
khác
A
) thỏa mãn
1 2 1 2
5y y x x
A.
1
. B.
2
. C.
0
. D.
3
.
HẾT
§Ò Sè 1
B¶NG §¸P ¸N TR¾C NGHIÖM §Ò 1
Câu
1
2
3
4
5
6
7
8
9
10
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 44
Đáp án
B
C
C
B
C
B
B
B
D
C
Câu
11
12
13
14
15
16
17
18
19
20
Đáp án
C
D
A
D
A
B
C
B
B
A
LêI GI¶I CHI TIÕT
Câu 1: Cho hàm số
1
1
x
y
x
. Phương trình tiếp tuyến của đồ thị hàm số tại điểm
1;0M
là
A.
13
22
yx
B.
11
22
yx
C.
11
22
yx
D.
11
42
yx
Lời giải:
Ta có
2
21
1
2
1
yy
x

Phương trình tiếp tuyến của đồ thị hàm số tại điểm
1;0M
là
1
10
2
yx
11
.
22
yx
Chọn đáp án B.
Câu 2: Cho hàm số
3
3y x x
có đồ thị
C
.Hệ số góc
k
của tiếp tuyến với đồ thị
C
tại điểm có
tung độ bằng
4
là
A.
0k
B.
2k 
C.
6k
D.
9k
Lời giải:
Ta có hoành độ tiếp điểm của tiếp tuyến là nghiệm của phương trình
3
3 4 1x x x
Ta có
2
' 3 3.yx
Hệ số góc của tiếp tuyến là
' 1 6ky
.
Chọn đáp án C.
Câu 3: Cho hàm số
32
1
21
3
y x x x
có đồ thị là
C
. Phương trình tiếp tuyến của
C
tại điểm
1
1;
3
M



là
A.
32yx
. B.
32yx
. C.
2
3
yx
. D.
2
3
yx
Lời giải:
Ta có:
2
2 2 1 1 2 2 1y x x y

Phương trình tiếp tuyến của
C
tại điểm
1
1;
3
M



là:
12
1 1 .
33
y y x y x
Chọn đáp án C.
Câu 4: Phương trình tiếp tuyến của đồ thị
24
:
3
x
Hy
x
tại giao điểm của
H
và
Ox
là
A.
2.yx
B.
2 4.yx
C.
2 4.yx
D.
2 4.yx
Lời giải:
24
0 2 2;0
3
x
y y x M
x
nên giao điểm của
H
và
Ox
là
2;0M
.
2
2
3
3
yx
x
nên hệ số góc tiếp tuyến là
22y

.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 45
Vậy phương trình tiếp tuyến của đồ thị
H
tại giao điểm của
H
và
Ox
là
2 2 0 2 4y x x
.
Chọn đáp án B.
Câu 5: Cho hàm số
2
24y x x
có đồ thị
C
. Phương trình tiếp tuyến của
C
tại điểm có hoành
độ
0x
là
A.
43yx
. B.
1
2
2
yx
. C.
1
2
2
yx
. D.
1
2
2
yx
.
Lời giải:
Ta có
2
1
24
x
y
xx

;
1
0
2
y

;
02y
.
Suy ra phương trình tiếp tuyến tại điểm có hoành độ
0x
là
1
0 0 2 2
2
y y x y x
.
Chọn đáp án C.
Câu 6: Cho hàm số
3
1y x x
có đồ thị
C
. Phương trình tiếp tuyến của
C
tại giao điểm của
C
với trục tung là
A.
21yx
. B.
1yx
. C.
22yx
. D.
1yx
.
Lời giải:
Gọi M là giao điểm của
C
và trục tung. Khi đó
0; 1M
.
Ta có
2
31yx

.
Phương trình tiếp tuyến của
C
tại M là:
. 0 . 0 1 1
M M M
y y x x x y y x x

.
Chọn đáp án B.
Câu 7: Có bao nhiêu tiếp tuyến của đồ thị hàm số
3
32y x x
song song với đường thẳng
9 14 0xy
?
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải:
Gọi
C
là đồ thị của hàm số
3
32y x x
. Tập xác định:
D
.
Đạo hàm:
2
33yx

. Gọi
: 9 14 0 : 9 14d x y d y x
. Gọi
là tiếp tuyến cần tìm.
// : 9 14d y x
Phương trình
có dạng
9 , 14y x m m
.
tiếp xúc
C
3
2
3 2 9
*
3 3 9
x x x m
x

có nghiệm
3
3 2 9
2 14
*
2
2 18
2
x x x m
x m l
x
x m n
x


Suy ra phương trình tiếp tuyến cần tìm là
: 9 18yx
.
Vậy có
1
tiếp tuyến thỏa yêu cầu bài toán.
Chọn đáp án B.
Câu 8: Đường thẳng nào sau đây là tiếp tuyến của đồ thị hàm số
3
32y x x
?
A.
9 12yx
. B.
9 14yx
. C.
9 13yx
. D.
9 11yx
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 46
Lời giải:
3
32y x x
2
33yx
.
Gọi
d
là tiếp tuyến của đồ thị hàm số tại điểm
00
;M x y
.
Hệ số góc tiếp tuyến bằng
2
00
9 3 3 9f x x
0 0 1
0 0 2
2 0 : 9 18
2 4 : 9 14
x y d y x
x y d y x
.
Vậy đường thẳng
9 14yx
là tiếp tuyến của đồ thị hàm số
3
32y x x
.
Chọn đáp án B.
Câu 9: Cho hàm số
32
1
32
3
y x x
có đồ thị là
C
. Phương trình tiếp tuyến với đồ thị
C
biết tiếp
tuyến có hệ số góc
9k 
là
A.
16 9 3yx
. B.
93yx
. C.
16 9 3yx
. D.
16 9 3yx
.
Lời giải:
Ta có:
2
6y x x

.
Gọi
00
;M x y
là tiếp điểm của tiếp tuyến với
C
.
Ta có hệ số góc của tiếp tuyến là
0
9yx

2
00
69xx
2
00
6 9 0xx
0
3x
.
Với
0
3x 
3; 16M
.
Suy ra phương trình tiếp tuyến với đồ thị
C
tại
3; 16M
có dạng:
16 9 3yx
.
Chọn đáp án D.
Câu 10: Cho hàm số
y f x
có đồ thị như hình vẽ
Đồ thị hàm số đã cho có bao nhiêu tiếp tuyến vuông góc với trục
?Oy
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải:
Từ đồ thị ta có hai tiếp tuyến vuông góc với trục
Oy
là
;12yy
.
Chọn đáp án C.
Câu 11: Cho hàm số
32
3 9 1y x x x
có đồ thị
C
. Hệ số góc lớn nhất của tiếp tuyến với đồ thị
C
bằng
A.
1
B.
6
C.
12
D.
9
Lời giải:
Ta có
2
' 3 6 9y x x
;
2
' 3 1 12 12yx
Vậy hệ số góc lớn nhất của tiếp tuyến với đồ thị
C
là
12
.
Chọn đáp án C.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 47
Câu 12: Tiếp tuyến với đồ thị hàm số
42
1
23
4
y x x
tại điểm cực tiểu của đồ thị cắt đồ thị ở
,AB
khác tiếp điểm. Độ dài đoạn thẳng
AB
bằng
A.
2
. B.
2
. C.
22
. D.
42
.
Lời giải:
Ta có:
3
0
4 ; 0
2
x
y x x y
x


.
BBT:
Từ BBT suy ra điểm cực tiểu của đồ thị hàm số là
0;3M
.
Tiếp tuyến của đồ thị tại điểm cực tiểu là đường thẳng
3y
.
Phương trình hoành độ giao điểm của đồ thị và tiếp tuyến là:
4 2 4 2
0
11
2 3 3 2 0
44
22
x
x x x x
x

2 2;3 ;B 2 2;3 4 2A AB
.
Chọn đáp án D.
Câu 13: Cho hàm số
4 2cos2y x x
có đồ thị là
C
. Hoành độ của các điểm trên
C
mà tại đó tiếp
tuyến của
C
song song hoặc trùng với trục hoành là
A.
4
x k k
. B.
2
x k k
. C.
x k k

. D.
2x k k

.
Lời giải:
Ta có
4 4sin 2yx

.
Khi đó, hoành độ của các điểm trên
C
mà tại đó tiếp tuyến của
C
song song hoặc trùng
với trục hoành là nghiệm của phương trình:
0 4 4sin2 0yx
sin2 1 2 2
24
x x k x k k


.
Chọn đáp án A.
Câu 14: Cho hàm số
, , , , ; 0, 0
ax b
y f x a b c d c d
cx d
có đồ thị
.C
Đồ thị của hàm số
y f x
như hình vẽ dưới đây. Biết
C
cắt trục tung tại điểm có tung độ bằng
2.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 48
Phương trình tiếp tuyến của
C
tại giao điểm của
C
với trục hoành là
A.
3 2 0.xy
B.
3 2 0.xy
C.
3 2 0.xy
D.
3 2 0.xy
Lời giải:
Đồ thị hàm số
y f x
đi qua
0; 2
suy ra
2bd
.
Ta có
2
ad bc
y
cx d
. Đồ thị hàm số
y
có tiệm cận đứng
1x 
nên
cd
, đi qua
0;3
nên
2
3
ad bc
d
hay
ad
. Do đó
2
23
1
1
x
yy
x
x
.
Phương trình tiếp tuyến tại
2;0
là
1
2 3 2 0
3
y x x y
.
Chọn đáp án D.
Câu 15: Cho hàm số
1
1
x
yC
x
. Điểm
M
thuộc
C
có hoành độ lớn hơn
1
, tiếp tuyến của
C
tại
M
cắt hai tiệm cận của
C
lần lượt tại
A
,
B
. Diện tích nhỏ nhất của tam giác
OAB
bằng
A.
4 2 2
. B.
4
. C.
42
. D.
42
.
Lời giải:
Tập xác định:
\1D
.
Ta có:
2
2
1
y
x

,
1x
.
Đồ thị hàm số có đường tiệm cận ngang
1y
và đường tiệm cận đứng
1x
.
Giả sử
;1
M
M m y C m
12
1
11
M
m
y
mm

;
2
2
1
ym
m

.
Phương trình tiếp tuyến
là:
2
22
1
1
1
y x m
m
m
2
2
2 1 2 1 0x m y m m
.
Gọi
A
là giao điểm của
và đường tiệm cận ngang. Tọa độ điểm
A
là nghiệm của hệ
phương trình:
2
1
22
21
1
1
1
y
xm
y x m
m
m
2 1;1Am
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 49
Gọi
B
là giao điểm của
và đường tiệm cận đứng. Tọa độ điểm
B
là nghiệm của hệ phương
trình:
2
1
34
22
1
1
11
1
1
x
m
y
y x m
mm
m
m

4
1;1
1
B
m




.
Suy ra:
2
2 2 4
2
4 16 2
2 2 4 1 1 4
1
1
1
AB m m m
m
m
m



.
2
4
21
;
41
mm
dO
m


2
4
4
21
1 1 2
; . . . 1 4
22
1
41
OAB
mm
S d O AB m
m
m

2
2
21
21
1
1
mm
mm
m
m


(vì
1m
)
22
3 4 1
11
mm
mm

.
Áp dụng bất đẳng thức Cô-si cho hai số
1m
và
2
1m
:
2
1 2 2
1
m
m
2
4 1 4 2 2
1
m
m
.
Vậy diện tích nhỏ nhất của tam giác
OAB
bằng
4 2 2
khi
2
1
12
1
1
m
m
m
m

.
Chọn đáp án A.
Câu 16: Cho hàm số
1
21
x
y
x

(C),
()y x m d
. Với mọi
m
đường thẳng
()d
luôn cắt đồ thị (C) tại hai
hai điểm phân biệt A và B. Gọi k1, k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A và B.
Giá trị nhỏ nhất của
2020 2020
12
T k k
bằng
A.
1
. B.
2
. C.
1
2
. D.
2
3
.
Lời giải:
+ Phương trình hoành độ giao điểm:
2
2 2 1 0
1
1
21
2
x mx m
x
xm
x
x

(*)
+ Phương trình (*) có:
2
' 2( 1) 0,m m m
nên (d) luôn cắt ( C ) tại 2 điểm phân biệt A,B.
Gọi
,ab
là các hoành độ giao điểm
1
2
ab




. Khi đó ta có:
1
2
a b m
m
ab

.
+ Khi đó:
[]
2020 2020
12
4040 4040 2020
1 1 2
(2 1) (2 1) (2 1)(2 1)
T k k
a b a b
2020 2020
22
2
4 2( ) 1 2( 1) 2 1ab a b m m
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 50
+ Nhận xét: Giá trị nhỏ nhất bằng 2 khi:
2020 2020
(2 1) (2 1)
1 1.
1
2
ab
a b m m
ab

Chọn đáp án B.
Câu 17: Cho hàm số
2
1
x
y
x
đồ thị
C
. Gọi
d
là khoảng cách từ giao điểm hai tiệm cận của đồ thị
C
đến một tiếp tuyến của
C
. Giá trị lớn nhất của
d
có thể đạt được là
A.
33
. B.
3
. C.
2
. D.
22
.
Lời giải:
Tiệm cận đứng
1
d
:
10x 
, tiệm cận ngang
2
d
:
10y 
tâm đối xứng là
1;1I
.
Phương trình tiếp tuyến tại điểm
2
;
1
a
M a C
a



là:
2
12
1
1
a
y x a
a
a

d
.
Khi đó
2
2
4 4 2
12
2
1
1
1
1
22
,2
1 1 1 2
1 1 1
1 1 1
a
a
a
a
a
d I d
a
a a a

.
Chọn đáp án C.
Câu 18: Cho hàm số
3
1yx
có đồ thị
()C
. Trên đường thẳng
:1d y x
tìm được hai điểm
1 1 1
;M x y
,
2 2 2
;M x y
mà từ mỗi điểm đó kẻ được đúng hai tiếp tuyến đến
C
. Giá trị biểu
thức
22
1 2 1 2
31
53
S y y y y
bằng
A.
113
15
. B.
41
15
. C.
14
15
. D.
59
15
.
Lời giải:
Giả sử
:1M d y x
, ta gọi
;1M a a
. Đường thẳng
đi qua
;1M a a
có hệ số góc
k
có
phương trình là:
( ) 1y k x a a
.
Đường thẳng
tiếp xúc với
C
khi và chỉ khi hệ phương trình sau có nghiệm:
3
2
1 ( ) 1
3
x k x a a
xk
32
2
( ) 2 3 0 *
3
g x x ax a
xk
.
Từ
M
kẻ được đúng hai tiếp tuyến đến
C
khi và chỉ khi phương trình
(*)
có hai nghiệm
phân biệt
hàm số
32
( ) 2 3y g x x ax a
có hai điểm cực trị
1
x
,
2
x
thỏa mãn
1
0gx
hoặc
2
0gx
2
( ) 6 6 0g x x ax
có hai nghiệm phân biệt
1
x
,
2
x
và
1
0gx
hoặc
2
0gx
.
Xét
2
0
' 0 6 6 0
x
g x x ax
xa
.
Ta có:
3
0
0
1
0
(0) 0
1
( ) 0
0
a
a
a
a
g
a
ga
aa





.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 51
Suy ra:
1
1;0M
và
2
1;2M
. Vậy:
2 2 2
1 2 1 2
3 1 3 1 41
0 2 0.2
5 3 5 3 15
S y y y y
.
Chọn đáp án B.
Câu 19: Cho hàm đa thức bậc bốn
y f x
có đồ thị
C
. Hàm số
y f x
có đồ thị như hình vẽ dưới
đây. Gọi đường thẳng
là tiếp tuyến của đồ thị
C
tại điểm có hoành độ bằng
1
. Hỏi
và
C
có bao nhiêu điểm chung?
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Ta có tiếp tuyến
của
C
tại
1x
là
1 1 1y f x f
.
Dựa vào đồ thị của hàm số
fx
, ta có
10f
. Vậy
:1yf
.
Gọi
1
a
,
2
a
là hai nghiệm còn lại của
fx
. Dựa vào đồ thị hàm số ta có bảng biến thiên:
Dựa vào bảng biến thiên ta có
:1yf
và
C
có ba điểm chung.
Chọn đáp án B.
Câu 20: Phương trình tiếp tuyến của đồ thị hàm số
y f x
thỏa mãn
23
1 2 1f x x f x
tại điểm
có hoành độ
1x
là
A.
16
77
yx
. B.
16
77
yx
. C.
16
77
yx
. D.
16
77
yx
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 52
Lời giải:
Ta có:
23
1 2 1f x x f x
(*)
.
Đạo hàm hai vế (*)
ta được
:
2
4. 1 2 . 1 2 1 3 1 1f x f x f x f x

(**)
Khi
0x
từ
(*) và (**) ta có hệ
23
2
4 1 . 1 1
11
3 1 . 1
ff
f f f f


10
11
1
1
7
fl
f tm
f
Phương trình tiếp tuyến của đồ thị hàm số
y f x
tại điểm có hoành độ
1x
là:
1 1 1y f x f
hay
16
77
yx
.
Chọn đáp án A.
§Ò Sè 02
B¶NG §¸P ¸N TR¾C NGHIÖM §Ò 02
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
D
C
D
D
C
C
C
A
D
C
Câu
11
12
13
14
15
16
17
18
19
20
Đáp án
D
A
B
D
D
D
C
C
C
B
LêI GI¶I CHI TIÕT
Câu 1: Tọa độ điểm
M
có hoành độ âm trên đồ thị
3
12
:
33
C y x x
sao cho tiếp tuyến tại
M
vuông góc với đường thẳng
12
33
yx
là
A.
2 ; 4M 
. B.
4
1;
3
M



. C.
4
2;
3
M



. D.
2 ; 0M
.
Lời giải:
Ta có:
2
1yx

2
1y a a
. Giả sử
3
12
;
33
M a a a




,
0a
Tiếp tuyến tại
M
vuông góc với đường thẳng
12
33
yx
nên ta có:
3ya
2
13a
2
2
a
a

.
Vì
M
có hoành độ âm nên ta chọn
2a 
. Suy ra
2;0M
.
Chọn đáp án D.
Câu 2: Hệ số góc của tiếp tuyến của đồ thị hàm số
34
2
x
y
x
tại điểm có tung độ
7
,
3
y 
bằng
A.
9
.
5
B.
5
.
9
C.
5
.
9
D.
10.
Lời giải:
Ta có:
7 3 4 7
1
3 2 3
x
yx
x
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 53
Ta có:
2
5
2
y
x
. Vậy hệ số góc cần tìm là
5
1
9
ky
.
Chọn đáp án C.
Câu 3: Tập hợp tất cả các giá trị của tham số
m
để mọi tiếp tuyến của đồ thị hàm số
32
2 3 1y x mx m x
đều có hệ số góc dương là
A.
\ 0 .
B.
1; .
C.
\ 1 .
D.
.
Lời giải:
Vì hệ số góc dương với mọi
x
nên ta xét:
2
22
30
3 2 2 3 0 6 9 0 3 0
0
a
y x mx m m m m m


.
Chọn đáp án D.
Câu 4: Hỏi trên đồ thị
1
:
2
x
Cy
x
có bao nhiêu điểm
M
mà tiếp tuyến với
C
tại
M
song song với
đường thẳng
: 1?d x y
A.
4
. B.
1
. C.
2
. D.
0
.
Lời giải:
TXĐ:
2
1
\ 2 , ' 0
2
Dy
x
.
Để tiếp tuyến với
C
tại
M
song song với đường thẳng
:1d y x
suy ra
2
1
'1
2
y VN
x

.
Vậy không có tiếp tuyến thỏa mãn.
Chọn đáp án D.
Câu 5: Gọi
d
là tiếp tuyến tại điểm cực đại của đồ thị hàm số
3
32y x x
. Khẳng định nào sau đây
đúng?
A.
d
có hệ số góc âm. B.
d
có hệ số góc dương.
C.
d
song song với đường thẳng
4y 
. D.
d
song song với trục
Ox
.
Lời giải:
Ta có đồ thị hàm số
3
32y x x
nhận điểm
1;0A
làm điểm cực đại.
Mà
10y

.
Suy ra phương trình đường thẳng
d
:
0y
.
Do đó
d
song song với đường thẳng
4y 
.
Chọn đáp án C.
Câu 6: Gọi
,MN
là hai điểm di động trên đồ thị
C
của hàm số
32
34y x x x
sao cho tiếp
tuyến của
C
tại
M
và
N
luôn song song với nhau. Hỏi khi
,MN
thay đổi, đường thẳng
MN
luôn đi qua nào trong các điểm có tọa độ dưới đây?
A.
1; 5 .
B.
1; 5 .
C.
1;5 .Q
D.
1;5 .P
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 54
Vì tiếp tuyến của đồ thị hàm bậc ba tại
2
điểm
,MN
thuộc đồ thị hàm số song song với nhau
nên đường thẳng
MN
phải đi qua điểm uốn của
C
.
Ta có
2
3 6 1; 6 6y x x y x
Cho
0 6 6 0 1y x x

. Điểm uốn
1;5 .Q
Chọn đáp án C.
Câu 7: Hỏi trên đồ thị hàm số
21
2
x
y
x
có bao nhiêu cặp tiếp tuyến vuông góc với nhau?
A.
1
. B. Vô số. C.
0
. D.
2
.
Lời giải:
TXĐ:
\2D
. Ta có:
2
2 1 5
2
2
x
yy
x
x
.
Tiếp tuyến
1
d
của đồ thị hàm số tại
11
;M x y
có dạng:
1 1 1
y y x x x y
.
Tiếp tuyến
2
d
của đồ thị hàm số tại
22
;N x y
có dạng:
2 2 2
y y x x x y
.
22
1 2 1 2 1 2
22
12
55
. 1 1 2 . 2 25
22
d d y x y x x x
xx


(vô lý).
Vậy không có cặp tiếp tuyến nào của đồ thị vuông góc với nhau.
Chọn đáp án C.
Câu 8: Cho hàm số
2
xb
y
ax
,
2ab 
. Biết rằng
a
,
b
là các giá trị thỏa mãn tiếp tuyến của đồ thị
hàm số tại điểm
1; 2A
song song với đường thẳng
: 3 4 0d x y
. Khi đó, giá trị
3ab
bằng
A.
2
. B.
4
. C.
1
. D.
5
.
Lời giải:
Có
2
2
2
ab
y
ax

. Do
1; 2A
thuộc đồ thị hàm số nên
1
2 3 2
2
b
ba
a
.
Do tiếp tuyến tại
1; 2A
song song với
: 3 4 0d x y
nên
13y

2
2
3
2
ab
a

Thay
32ba
ta được phương trình
2
3 2 2 3 2a a a
2
5 15 10 0aa
1
2
a
a
.
+) Với
21ab
(loại, do
2ab 
)
+) Với
11ab
. Phương trình tiếp tuyến tại
1;2A
là
3 1 2yx
song song với
d
.
Vậy
1a
,
1b
, suy ra
32ab
.
Chọn đáp án A.
Câu 9: Cho hàm số
1
()
2
x
yC
x
và
: 2 1d y x m
(
m
là tham số thực). Gọi
1
k
,
2
k
là hệ số góc của
tiếp tuyến của
C
tại giao điểm của
d
và
C
. Giá trị
12
.kk
bằng
A.
1
4
. B.
2
. C.
3
. D.
4
.
Lời giải:
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 55
Xét phương trình hoành độ giao điểm
1
2 1 (1)
2
x
xm
x
.
Phương trình
(1)
có hai nghiệm phân biệt
2
( ) 2 ( 6) 2 3 0
2
f x x m x m
x

có hai nghiệm
phân biệt
2
( 2) 0
4 12 0
f
m
mm

.
Gọi
12
,xx
là hai nghiệm của phương trình
(1)
, khi đó
12
12
6
2
32
.
2
m
xx
m
xx

.
Hệ số góc của tiếp tuyến của
C
tại giao điểm của
d
và
C
là
1
2
1
2
2
2
1
2
1
2
k
x
k
x
.
Ta có
12
2 2 2 2
1 2 1 2 1 2
1 1 1 1
. . 4
2 2 . 2( ) 4 3 2 6
2. 4
22
kk
x x x x x x m m




.
Chọn đáp án D.
Câu 10: Cho hàm số
32
3 3 5y x x x
có đồ thị
C
. Có bao nhiêu giá trị nguyên của
k
trên
2019;2019


để trên đồ thị
C
có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường
thẳng
: 3 ?d y k x
A.
2021
. B.
2017
. C.
2022
. D.
2016
.
Lời giải:
Ta có :
2
' 3 6 3y x x
.
TH1 :
3k
. Khi đó
:0dy
không tồn tại tiếp tuyến vuông góc với
d
.
TH2 :
3k
.
Ta có :
2
00
3 3 6 3 1k x x
2
00
1
3 6 3 0 *
3
xx
k
Theo yêu cầu bài toán , phương trình
*
có nghiệm
3
' 0 0 3
3
k
k
Vậy
2019; 2018;...;0;1;2k
Có
2022
giá trị nguyên của
k
thỏa đề bài.
Chọn đáp án C.
Câu 11: Có bao nhiêu giá trị của tham số thực
m
để đồ thị hàm số
2
2x mx m
y
xm

cắt trục
Ox
tại hai
điểm phân biệt và các tiếp tuyến của đồ thị tại hai điểm đó vuông góc với nhau?
A.
5
B.
2
C.
0
D.
1
Lời giải:
22
23
3
x mx m m m
y x m
x m x m

2
2
3
1
mm
y
xm
.
Xét phương trình hoành độ giao điểm của đồ thị hàm số đã cho với trục
Ox
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 56
2
2
0
x mx m
xm

2
2 0 *f x x mx m x m
.
Để đồ thị hàm số đã cho cắt trục
Ox
tại hai điểm phân biệt và các tiếp tuyến tại hai điểm đó
vuông góc với nhau thì phương trình (*) phải có hai nghiệm phân biệt
12
;xx
khác
m
và
12
.1y x y x


.
2
2
22
12
22
12
0
30
33
. 1 1 1
mm
f m m m
m m m m
y x y x
x m x m



1
0
0
1
3
0
5
m
m
m
m
m
m

5m
.
Chọn đáp án D.
Câu 12: Cho hàm số
32
32y x x
có đồ thị
C
và điểm
;2Mm
. Gọi
S
là tập hợp tất cả các giá trị
thực của
m
để qua
M
kẻ đúng hai tiếp tuyến đến
C
. Tổng tất cả các phần tử của
S
bằng
A.
8
.
3
B.
3.
C.
2
.
3
D.
2.
Lời giải:
Ta có:
2
36y x x

Phương trình tiếp tuyến tại
00
;A x y
có dạng
2 3 2
0 0 0 0 0
3 6 3 2y x x x x x x
Tiếp tuyến qua
;2Mm
, ta có:
2 3 2
0 0 0 0 0
2 3 6 3 2x x m x x x
32
00
2 3 1 6 4 0
o
x x m x m
2
0 0 0
2 2 3 1 2 0 1x x m x
0
2
00
20
2 3 1 2 0 2
x
x m x

Qua
M
kẻ đúng hai tiếp tuyến đến
C
khi phương trình
1
có đúng hai nghiệm phân biệt
phương trình
2
có nghiệm kép khác
2
hoặc phương trình
2
có hai nghiệm phân biệt
trong đó có một nghiệm bằng
2
.
Trường hợp 1: Phương trình
2
có nghiệm kép khác
2
.
0
31
2
4
m

5
3
1
3
m
m
m

5
3
1
m
m

.
Trường hợp 2: Phương trình
2
có hai nghiệm phân biệt trong đó có một nghiệm bằng
2
.
0
2.4 2 3 1 2 0m

hoÆc
5
1
3
2
mm
m
2m
.
Vậy
5
;2; 1
3
S




.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 57
Chọn đáp án A.
Câu 13: Cho hàm số
2
2
x
y
x
, có đồ thị
(C)
và điểm
00
;M x y C
(với
0
0x
). Biết rằng khoảng cách
từ
2;2I
đến tiếp tuyến của
(C)
tại M là lớn nhất, đẳng thức nào sau đây đúng?
A.
00
20xy
. B.
00
24xy
. C.
00
22xy
. D.
00
22xy
.
Lời giải:
Tập xác định
\ 2 .D
2
4
( 2)
y
x
,
0
0
0
2
;
2
x
Mx
x



Phương trình tiếp tuyến tại M là
2
2
0
0 0 0
2
0
0
2
4
4 2 2 0
2
( 2)
x
y x x x x y x
x
x
Khoảng cách từ I đến tiếp tuyến là
2
2
00
0
44
22
00
4( 2) 2 .2 2
8 16
4 2 4 2
xx
x
d
xx


Áp dụng bất đẳng thức Cauchy, ta có
00
42
2
00
8 16 8 2
22
4 2 8 2
xx
xx

Dấu bằng xảy ra khi
2
0
( 2) 4x 
0
0
0
4
x
x

. Vì
0
0x
nên
0
4x 
0
4y
00
2 4.xy
Chọn đáp án B.
Câu 14: Gọi
: , ,d y ax b a b
là tiếp tuyến của đồ thị hàm số
2
.
23
x
y
x
Biết
d
cắt trục hoành và
trục tung lần lượt tại hai điểm
,AB
sao cho
OAB
cân tại
O
. Khi đó,
ab
bằng
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải:
TXĐ:
3
\
2
D



. Ta có:
2
1
0,
23
y x D
x
.
Mặt khác,
OAB
cân tại
O
hệ số góc của tiếp tuyến là
1
.
Gọi tọa độ tiếp điểm
00
;xy
, với
0
3
2
x 
. Ta có:
00
2
0
1
1 2 1
23
y x x
x
.
+) Với
00
11xy
. Phương trình tiếp tuyến là:
yx
loại vì
A B O
.
+) Với
00
20xy
. Phương trình tiếp tuyến là:
2yx
thỏa mãn.
Vậy
: 2 1; 2 3d y x a b a b
.
Chọn đáp án D.
Câu 15: Cho hàm số
32
13
2
22
y x x C
. Xét hai điểm
;
A
Aay
và
;
B
B b y
phân biệt của đồ thị
C
mà tiếp tuyến tại
A
và
B
song song. Biết rằng đường thẳng
AB
đi qua
5;3D
. Phương trình
của đường thẳng
AB
là
A.
20xy
. B.
80xy
. C.
3 4 0xy
. D.
2 1 0xy
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 58
Lời giải:
Gọi
32
13
;2
22
A a a a




và
32
13
;2
22
B b b b




với
ab
là hai điểm phân biệt thuộc đồ thị
C
mà tiếp tuyến tại
A
và
B
song song với nhau.
Ta có
22
33
33
22
f a f b a a b b

22
2a b a b
2ab
.
Gọi
3 3 2 2
13
;2
2 4 4
ab
I a b a b



là trung điểm của đoạn
AB
.
Với
2ab
ta có
3 4 2
86
1; 2
44
ab
ab
I





hay
1;1I
.
Lại có
3 3 2 2
13
;
22
AB b a b a b a


cùng phương với
22
2; 3u a b ab a b
.
Hay
2; 2u ab
. Nên đường thẳng
AB
có một véc tơ pháp tuyến là
2 ;2n ab
.
Suy ra phương trình đường thẳng
AB
là
2 1 2 1 0ab x y
.
Do đường thẳng
AB
đi qua
5;3D
nên
4 2 4 0ab
4 12 0 3ab ab
.
Thay
3ab 
vào phương trình
AB
ta được:
2 1 0xy
.
Cách khác: Đồ thị hàm số
32
13
2
22
y x x C
có điểm uốn là
1;1I
.
Do đó đường thẳng
AB
đi qua
5;3D
và
1;1I
có phương trình là
2 1 0xy
.
Chọn đáp án D.
Câu 16: Cho hàm số
32
1 2 1y x m x x m
có đồ thị
C
(
m
là tham số thực). Gọi
12
,mm
là các giá
trị của
m
để đường thẳng
:1d y x m
cắt
C
tại ba điểm phân biệt
,,A B C
sao cho tổng hệ
số góc của các tiếp tuyến với
C
tại
,,A B C
bằng
19
. Khi đó
12
mm
bằng
A.
4
. B.
2
.
C.
0
. D.
2
.
Lời giải:
Phương trình hoành độ giao điểm của
d
và
C
:
3 2 2
2
1
1 0 1 0
0*
x
y x m x x m x x mx m
x mx m
Để
d
và
C
cắt nhau tại ba điểm phân biệt thì
*
phải có hai nghiệm phân biệt khác
1
, tức
0
11
; 4 0; ;
1 2 0
22
m
m

 

. Khi đó
d
và
C
cắt nhau tại ba điểm phân biệt
1 1 2 2
1; 2 , ; 1 , ; 1A m B x x m C x x m
với
12
;xx
là nghiệm của phương trình
*
Hệ số góc tiếp tuyến của
C
tại
A
là:
1 2 2ym

. Hệ số góc tiếp tuyến của
C
tại
B
là:
2
1 1 1
3 2 1 1y x x m x
.
Hệ số góc tiếp tuyến của
C
tại
C
là:
2
2 2 2
3 2 1 1y x x m x
.
Theo giả thiết, ta có:
22
1 2 1 2
3 2 1 4 2 19x x m x x m
.
2
1 2 1 2 1 2
3 6 2 1 4 2 19 * *x x x x m x x m
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 59
12
12
x x m
x x m


thay vào
**
, ta được
2
3 6 2 1 4 2 19m m m m m
.
2
1
12
2
3
2 15 0 2.
5
m
m m m m
m

Chọn đáp án D.
Câu 17: Gọi
S
là tập hợp tất cả các giá trị tham số
m
để đồ thị hàm số
3 2 2 3
( ) 3 3 2f x x mx mx m m
tiếp xúc với trục hoành. Tổng các phần tử của
S
bằng
A.
0
. B.
1
. C.
2
3
. D.
4
3
.
Lời giải:
Ta có :
2
3 6 3y x mx m
;
66y x m


Cách 1:
TH1 :
y
có nghiệm kép và tâm đối xứng của đồ thị hàm số thuộc trục hoành
2
32
0
0
0
1
1
0
4 4 0
m
mm
m
m
m
ym
mm



.
TH2 : Đồ thị hàm số
y f x
có 2 cực trị và
CÐ CT
.0yy
2
2 2 2 2
0
2 2 2 2 0
mm
m m m m m m m m m m

2
2
2
0
1
2
3
2
mm
m
m m m
m m m


.
Vậy
1
0 ; 1;
3
m




, nên
12
01
33
S
.
Cách 2:
Đồ thị hàm số
y f x
tiếp xúc trục hoành
3 2 2 3
2
3 3 2 0 1
3 6 3 0 2
x mx mx m m
x mx m
có nghiệm.
2
2
21
x
m
x

. Thế vào
1
:
4 3 4 6
3
23
3 3 2
0
2 1 2 1
2 1 2 1
x x x x
x
xx
xx


.
3 3 2
0
1
2
1
6 14 10 2 0
1
3
x
x
x
x x x x
x
. Thay vào
1
, ta được
1
0 ; 1;
3
m




.
Chọn đáp án C.
Câu 18: Cho hàm số bậc bốn
y f x
xác định và liên tục trên , hàm số
2
23g x x
và đường
thẳng
d
có đồ thị như hình vẽ dưới đây.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 60
Biết
A
là điểm chung của đồ thị
fx
và
gx
,
1
A
x
. Điểm
B
thuộc đồ thị
gx
,
9
4
B
x 
và
d
là tiếp tuyến của đồ thị hàm số
y f x
. Giá trị
A
fx
bằng
A.
1
. B.
3
2
. C.
5
2
. D.
2
.
Lời giải:
Vì các điểm
A
,
B
thuộc đồ thị hàm số
(x)g
nên ta có
1; 1A
,
9 57
;
48
B



13 65
;
48
AB


.
Do
d
đi qua hai điểm
A
và
B
nên ta chọn vectơ pháp tuyến là
65;26
d
n
.
Phương trình đường thẳng d là:
53
65 1 26 1 0 65 26 39 0
22
x y x y y x
Mà
d
là tiếp tuyến của đồ thị hàm số
y f x
nên
5
2
A
fx

.
Chọn đáp án C.
Câu 19: Gọi
A
là điểm có hoành độ bằng
1
thuộc đồ thị
C
của hàm số
42
2y x mx m
(
m
là tham
số thực). Ta luôn tìm được
a
m
b
với
a
b
là phân số tối giản để tiếp tuyến
với đồ thị
C
tại
A
cắt đường tròn
22
: 2 3 0x y y
tạo thành một dây cung có độ dài nhỏ nhất. Khi đó,
tổng
ab
bằng
A.
12
. B.
3
. C.
29
. D.
10
.
Lời giải:
Đường tròn
2
2
: 1 4xy
có tâm
0;1I
,
2R
.
Ta có
1;1Am
;
3
44y x mx

1 4 4ym

suy ra
: 4 4 1 1y m x m
.
Dễ thấy
luôn đi qua điểm cố định
3
;0
4
F



và điểm
F
nằm trong đường tròn
.
d
R
N
M
I
F
Giả sử
cắt
tại
M
,
N
, ta có:
2 2 2
2 ; 2 4 ;MN R d I d I
.
Do đó
MN
nhỏ nhất
;dI
lớn nhất
;d I IF
IF
.
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 61
Khi đó đường thẳng
có một véc-tơ chỉ phương
3
;1
4
u IF


;
1; 4 4um
nên:
.0un
3
1. 4 4 0
4
m
13
16
m
suy ra
13a
,
16b
. Vậy
13 16 29ab
.
Chọn đáp án C.
Câu 20: Cho hàm số
42
1
3
4
y x x
có đồ thị
()C
. Có bao nhiêu điểm
A
thuộc
()C
sao cho tiếp tyến của
()C
tại
A
cắt
()C
tại hai điểm phân biệt
11
;M x y
,
22
;N x y
(,MN
khác
A
) thỏa mãn
1 2 1 2
5y y x x
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải:
Ta có:
3
' 6 .y x x
Gọi
42
0 0 0
1
;3
4
A x x x



là tọa độ tiếp điểm của tiếp tuyến tại A. Phương trình
tiếp tuyến tại A là đường thẳng (d) có phương trình:
3 4 2
0 0 0 0 0
1
63
4
y x x x x x x
Phương trình hoành độ giao điểm của (d) và (C) là:
3 4 2 4 2
0 0 0 0 0
11
6 3 3
44
x x x x x x x x
2
22
0 0 0
2 3 12 0x x x x x x
0
2
00
0
2 3 12 0 (2)
xx
x x x x

(d) cắt (C) tại hai điểm phân biệt khác A khi và chỉ chi phương trình (2) có hai nghiệm phân
biệt khác
0
x
0
0
2
(3)
66
x
x

Khi đó, phương trình (2) có hai nghiệm phân biệt
12
,xx
và (d) cắt (C) tại hai điểm phân
biệt
11
( ; )M x y
,
22
( ; )N x y
trong đó:
3 4 2
1 0 0 1 0 0 0
3
1 2 0 0 1 2
3 4 2
2 0 0 2 0 0 0
1
63
4
6
1
63
4
y x x x x x x
y y x x x x
y x x x x x x
Từ giả thiết ta suy ra:
3
0 0 1 2 1 2
( 6 )( ) 5( )x x x x x x
3
00
65xx
(Vì
12
xx
)
0
0
0
1
1 21
2
1 21
2
x
x
x




Kết hợp với điều kiện (3) có hai giá trị
0
x
thỏa mãn yêu cầu bài toán là
1 21
1; .
2
xx

Chọn đáp án B.
_____________HẾT_____________
Huế, ngày 07 tháng 9 năm 2020
| 1/62
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


Giáo viên: LÊ BÁ BẢO_ Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115
Đăng kí học theo địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Hoặc Trung tâm Km 10 Hương Trà KH¶O S¸T HµM Sè
TIÕP TUYÕN Vµ Sù TIÕP XóC Phiªn b¶n 2020 Cè lªn c¸c em nhÐ! HuÕ, th¸ng 9/2020
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
Chuyên đề: KH¶O S¸T HµM Sè
Chủ đề 7: TIÕP TUYÕN – Sù TIÕP XóC
Môn: TOÁN 12 _GIẢI TÍCH I- LÝ THUYẾT Cho hàm số y
f x , có đồ thị (C). y (C)
1. Tiếp tuyến của đồ thị (C) tại điểm M x ;y (C ): 0 0 0 / MO y y f x x x 0 0 0 (*)
Lưu ý: + Điểm M x ;y
(C ) được gọi là tiếp điểm. 0 0 0 O x
+ Đường thẳng bất kỳ đi qua M
x ;y có hệ số góc k , 0 0 0 có phương trình: y y k x x 0 0
+ Như vậy, hệ số góc của tiếp tuyến của (C) tại M x ;y (C ) 0 0 0 / / có hệ số góc k
f x . Hay hoành độ tiếp điểm là nghiệm của phương trình: k f x . Rõ ràng, 0
tiếp tuyến của (C) hoàn toàn xác định nếu biết hệ số góc của tiếp tuyến hoặc hoành độ tiếp điểm.
Nhắc: Cho hai đường thẳng : y k x m và : y k x m . 1 1 1 2 2 2 Lúc đó: k k và m m k .k 1 1 2 1 2 1 2 1 2 1 2
2. Điều kiện tiếp xúc: Cho hai hàm số y f x , (C) và y g x , (C') . f x g x
(C) và (C’) tiếp xúc nhau khi chỉ khi hệ phương trình có nghiệm. / / f x g x
Đặc biệt: Đường thẳng y kx
m là tiếp tuyến với (C) : y
f x khi chỉ khi hệ sau có nghiệm: f (x) kx m / f (x) k
II- MỘT SỐ DẠNG TOÁN THƯỜNG GẶP Dạng 1:
VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN TẠI TIẾP ĐIỂM Câu 1:
(SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Gọi d là tiếp tuyến tại điểm cực đại của đồ thị hàm số 3
y x  3x  2 . Khẳng định nào sau đây đúng?
A. d có hệ số góc âm.
B. d có hệ số góc dương.
C. d song song với đường thẳng y  4 .
D. d song song với trục Ox . Lời giải:
Ta có đồ thị hàm số 3
y x  3x  2 nhận điểm A1;0 làm điểm cực đại. Mà y  1  0 .
Suy ra phương trình đường thẳng d : y  0 . Do đó d song song với đường thẳng y  4 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 1
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 2:
(THPT Tây Thụy Anh - Thái Bình - Lần 2 - 2018 - BTN) Tiếp tuyến tại điểm cực tiểu của đồ 1 thị hàm số 3 2 y
x  2x  3x  5 3
A. Có hệ số góc dương.
B. Song song với trục hoành.
C. Có hệ số góc bằng 1.
D. Song song với đường thẳng x  1. Lời giải: x 1 Ta có 2
y  x  4x  3, y  0  
. Điểm cực tiểu của đồ thị hàm số là A3; 5 . x  3
Suy ra tiếp tuyến của đồ thị hàm số tại điểm cực tiểu có phương trình là y  5 . Câu 3:
(CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Hệ số góc của tiếp tuyến
tại A1;0 của đồ thị hàm số 3 2
y x  3x  2 là A. 1. B. 1  . C. 3  . D. 0 . Lời giải:
Đặt f x 3 2
x  3x  2 . Ta có f x 2  3x  6x .
Hệ số góc của tiếp tuyến tại A1;0 của đồ thị hàm số    
đã cho là: f   2 1 3.1 6.1 3 . Câu 4:
(CỤM 8 TRƯỜNG CHUYÊN LẦN 1) Cho hàm số 3
y x  2x 1 có đồ thị C  . Tính hệ số góc
k của tiếp tuyến với C  tại điểm có hoành độ bằng 1. A. k  25 . B. k  5 . C. k  10 . D. k  1 . Lời giải: Ta có : 2
y  3x  2 . Hệ số góc của tiếp tuyến tại điểm có hoành độ bằng 1 là k y  1  1 . Câu 5:
(CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019) Cho hàm số 4
y x 1 có đồ thị
là (C) . Tiếp tuyến của đồ thị (C) tại điểm với hoành độ bằng 0 có hệ số góc là A. 0 . B. 1  . C. 4 . D. 1. Lời giải: +) Ta có 4 3
y x 1  y  4x
+) Tiếp tuyến của đồ thị (C) tại điểm với hoành độ bằng 0 có hệ số góc là k y (  0)  0 Câu 6:
(CHUYÊN QUỐC HỌC HUẾ NĂM 2018-2019 LẦN 1) Tìm hệ số góc của tiếp tuyến của đồ thị 3  4x 7 hàm số y y   . x  tại điểm có tung độ 2 3 9 5 5 A. . B.  . C. . D. 10 . 5 9 9 Lời giải: 7 3  4x 7 5 y       x  1 y 
. Vậy hệ số góc cần tìm là y  5 1  . 3 x  . Ta có: 2 3 x  22 9 Câu 7:
(TRƯỜNG THPT NGUYỄN ĐỨC CẢNH LẦN 03) Cho hàm số 2 y
x  2x  4 có đồ thị
C. Phương trình tiếp tuyến của C tại điểm có hoành độ x  0 là 1 1 1
A. y  4x  3 . B. y x  2 .
C. y   x  2 .
D. y   x  2 . 2 2 2 Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 2
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x 1 Ta có y  ; y  1 0   ; y 0  2 . 2 x  2x  4 2
Suy ra phương trình tiếp tuyến tại điểm có hoành độ x  0 là
y y  x   1 0 0  2  y   x  2 . 2 Câu 8:
(CHUYÊN QUỐC HỌC HUẾ LẦN 3 2018-2019) Viết phương trình tiếp tuyến của đồ thị hàm x  1 số y M 1;0 . x  tại điểm   2 1 1 1 1 1 A. y x  . B. y x  1.
C. y x  1 . D. y x  . 3 3 3 9 9 Lời giải: TXĐ: D  \   2 . Ta có f   1 1  . 3 1 1 1
Phương trình tiếp tuyến của đồ thị tại điểm M 1;0 là: y   x   1  0  y x  . 3 3 3 Câu 9:
(GKI CS2 LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 01) Cho hàm số 1  1  3 2 y
x x  2x 1 có đồ thị là C  . Phương trình tiếp tuyến của C  tại điểm M 1;   là 3  3  2 2
A. y  3x  2 . B. y  3  x  2 . C. y x  .
D. y  x  3 3 Lời giải: Ta có: 2
y  x  2x  2; y  1  1.  1 
Phương trình tiếp tuyến của C  tại điểm M 1; 
 là: y y  x   1 1 2 1 1 
x 1  x   3  3 3 3
Câu 10: (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số 3
y x  3x có đồ
thị C  .Hệ số góc k của tiếp tuyến với đồ thị C  tại điểm có tung độ bằng 4 là A. k  0. B. k  2. C. k  6. D. k  9. Lời giải:
Ta có hoành độ tiếp điểm của tiếp tuyến là nghiệm của phương trình 3
x  3x  4  x  1 Ta có 2
y '  3x  3  Hệ số góc của tiếp tuyến là k y '  1  6 . 2x  4
Câu 11: (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Cho đồ thị  H  : y  . x  3
Viết phương trình tiếp tuyến của đồ thị  H  tại giao điểm của  H  và Ox . A. y  2 . x
B. y  2x  4.
C. y  2x  4.
D. y  2x  4. Lời giải: 2x  4 y
y  0  x  2  M 2;0 nên giao điểm của H  và Ox là M 2;0 . x  3 2 y      x
nên hệ số góc tiếp tuyến là y2 2 . x  3 3 2
Vậy phương trình tiếp tuyến của đồ thị  H  tại giao điểm của  H  và Ox là
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 3
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
y  2 x  2  0  2x  4 .
Câu 12: (THPT NGUYỄN HUỆ - HÀ NỘI 18-19) Cho hàm số 3
y x x 1 có đồ thị C  . Phương
trình tiếp tuyến của C  tại giao điểm của C  với trục tung là
A. y  2x 1.
B. y  x 1.
C. y  2x  2 .
D. y  x 1. Lời giải:
Gọi M là giao điểm của C M 0; 1  và trục tung. Khi đó  . Ta có 2
y  3x 1. Phương trình tiếp tuyến của C  tại M là
y y x . x x   y y0. x  0 1  x 1. M M M
Câu 13: (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Phương trình tiếp tuyến của đường cong 3 2
y x  3x  2 tại điểm có hoành độ x  1 là 0
A. y  9x  7 . B. y  9  x  7 . C. y  9  x  7 .
D. y  9x  7 . Lời giải: Xét hàm số 3 2 2
y f (x)  x  3x  2  f '(x)  3x  6x f '(1)  9.
Ta có x  1  y  2  M 1; 2 . 0 0 0  
Phương trình tiếp tuyến tại điểm M 1; 2 có dạng: 0  
y y f '(x ) x x
y  2  9 x 1  y  9x  7 . 0 0  0   
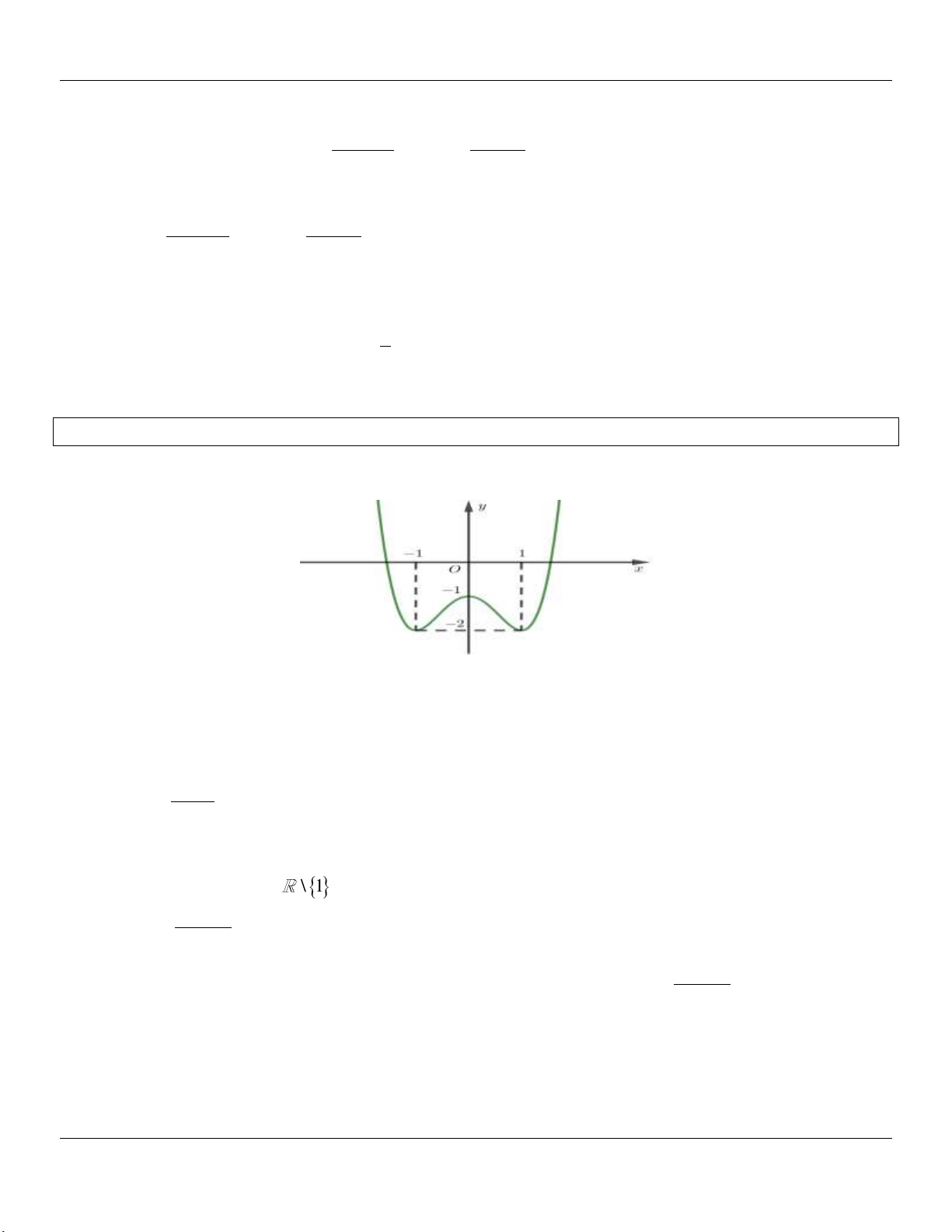
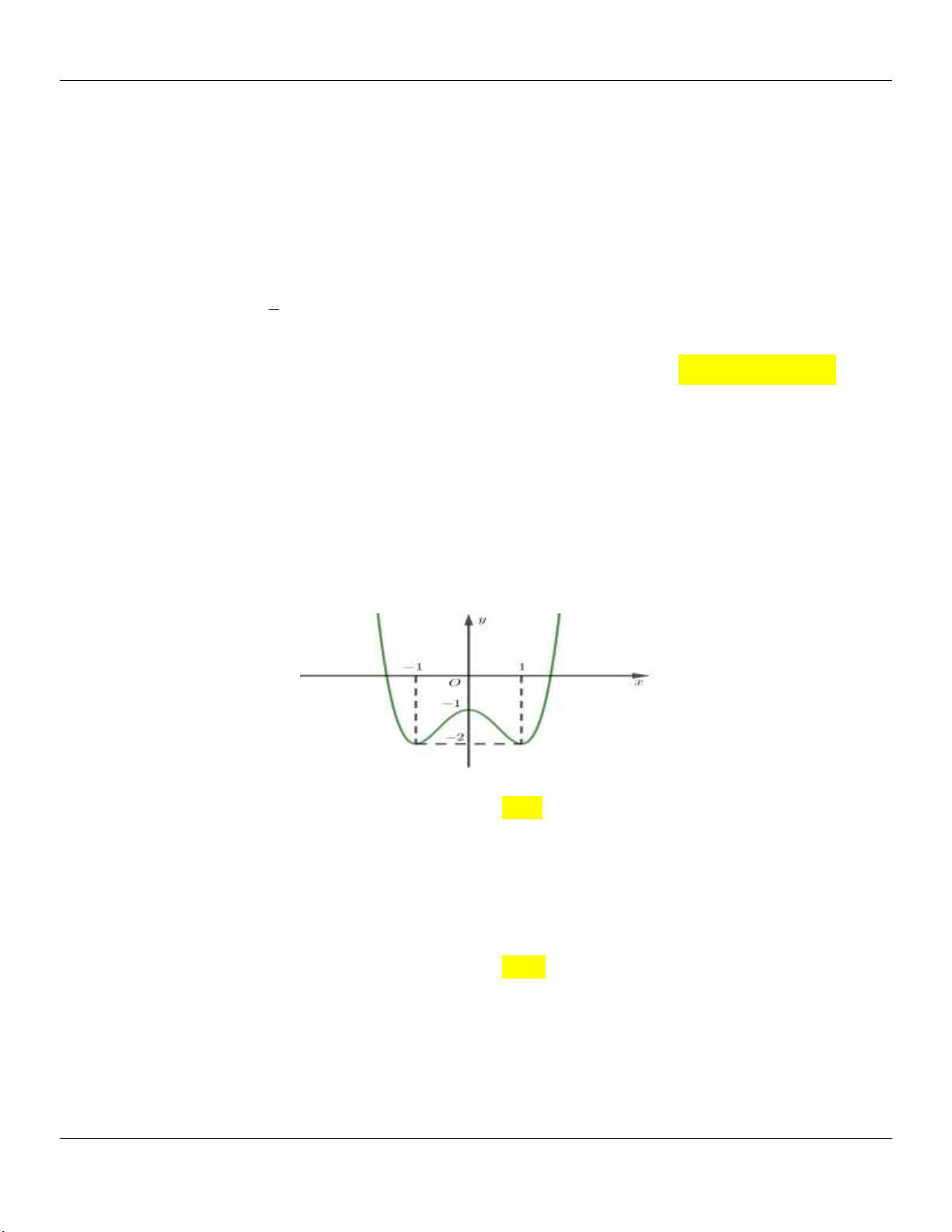
Câu 14: (THPT YÊN PHONG 1 BẮC NINH NĂM HỌC 2018-2019 LẦN 2) Tiếp tuyến với đồ thị hàm 1 số 4 2 y  
x  2x  3 tại điểm cực tiểu của đồ thị cắt đồ thị ở ,
A B khác tiếp điểm. Tính độ dài 4 đoạn thẳng AB . A. 2 . B. 2 . C. 2 2 . D. 4 2 . Lời giải: x  0 Ta có: 3
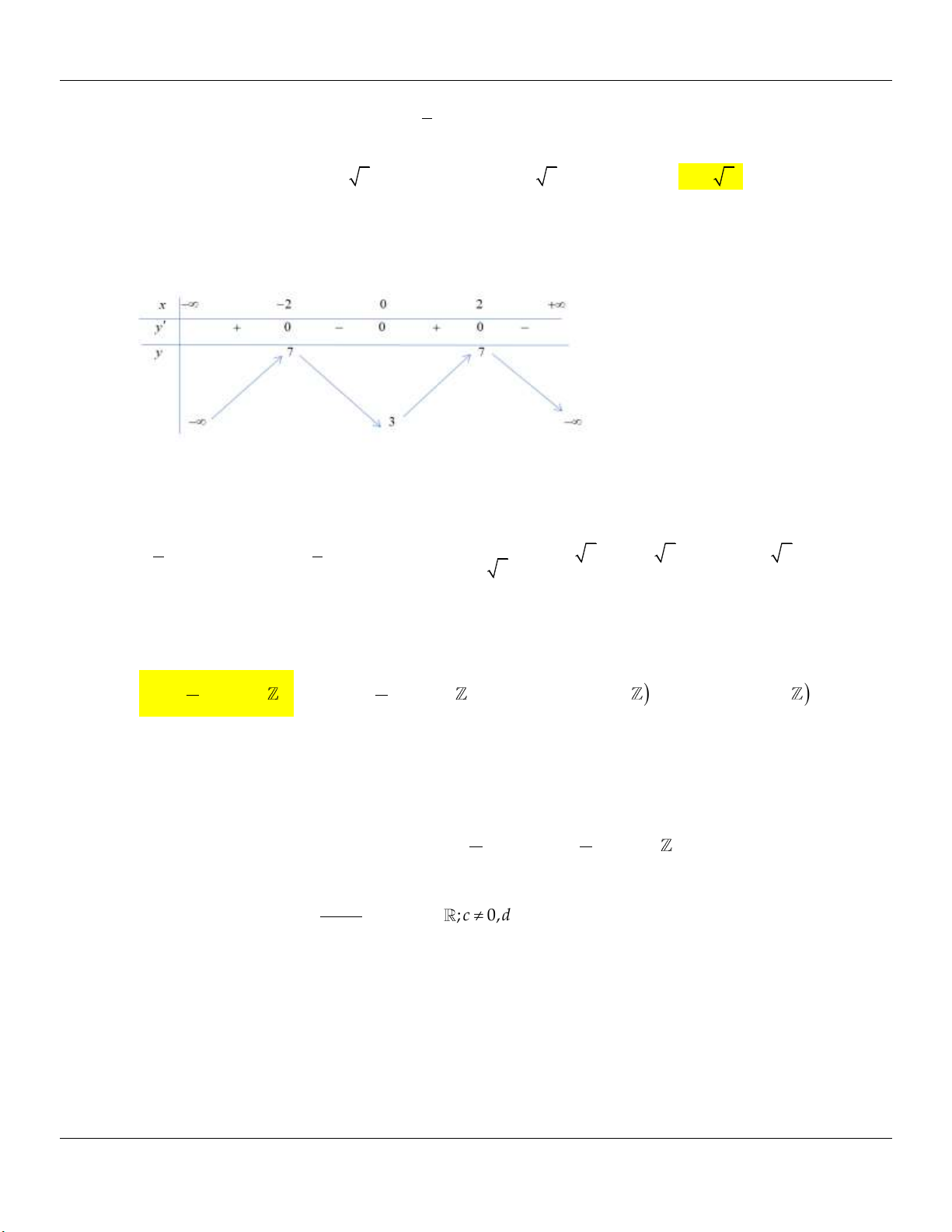
y  x  4 ; x y  0   . x  2  BBT:
Từ BBT suy ra điểm cực tiểu của đồ thị hàm số là M 0;3 .
Tiếp tuyến của đồ thị tại điểm cực tiểu là đường thẳng y  3 .
Phương trình hoành độ giao điểm của đồ thị và tiếp tuyến là: x  0 1 1 4 2 4 2
x  2x  3  3   x  2x  0    A 2
 2;3;B2 2;3  AB  4 2 . 4 4 x  2  2
Câu 15: (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Tìm m để mọi tiếp tuyến của đồ thị hàm số 3 2
y x mx  2m  
3 x  1 đều có hệ số góc dương. A. m  0 . B. m  1 . C. m  1 . D. m  .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 4
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải:
Hệ số góc tiếp tuyến của đồ thị hàm số 3 2
y x mx  2m   3 x  1 là 2
y  3x  2mx  2m  3
Vì hệ số góc dương với mọi x nên ta có a  3  0
y  3x  2mx  2m  3  0  
m  6m  9  0  m  2 2 2 3  0  m .   0 2x 1
Câu 16: Cho hàm số y
có đồ thị C  . Tiếp tuyến với đồ thị C  tại M 2;5 cắt hai đường tiệm x 1
cận tại E và F. Khi đó độ dài EF bằng A. 10 . B. 2 10 . C. 13 . D. 2 13 . Lời giải:
Tiệm cận đứng của đồ thị C  là: x  1 .
Tiệm cận ngang của đồ thị C  là: y  1. 3  Ta có y   . x  2 1 3 
Tiếp tuyến với C  tại M 2;5 là: y y2 x  2  5  y
x  2       y 3x 11. 2   5 2 1
Gọi E là giao điểm của tiếp tuyến với tiệm cận đứng suy ra E 1;8 .
Gọi F là giao điểm của tiếp tuyến với tiệm cận ngang suy ra F 3; 2 .
Vậy EF    2    2 3 1 2 8  40  2 10 .
Câu 17: (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho hàm số y  4x  2cos 2x
có đồ thị là C  . Hoành độ của các điểm trên C  mà tại đó tiếp tuyến của C  song song
hoặc trùng với trục hoành là   A. x
k k  . B. x   k k  . C. x    k k  . D. x k2 k   . 4 2 Lời giải:
Ta có y  4  4sin 2x .
Khi đó, hoành độ của các điểm trên C  mà tại đó tiếp tuyến của C  song song hoặc trùng
với trục hoành là nghiệm của phương trình:  
y  0  4  4sin 2x  0  sin 2x  1  2x
k2  x   k k   . 2 4
Câu 18: (THPT Lương Thế Vinh Đồng Nai lần 2 – 2019) Đường thẳng nào sau đây là tiếp tuyến của đồ thị hàm số 3
y x  3x  2 ?
A. y  9x 12 .
B. y  9x 14 .
C. y  9x 13 .
D. y  9x 11 . Lời giải: 3
y x  3x  2 2
y  3x  3.
Gọi d là tiếp tuyến của đồ thị hàm số tại điểm M x ; y . 0 0  x  2
  y  0  d : y  9x 18
Hệ số góc tiếp tuyến bằng 9  f  x  2  3x  3  9 0 0 1  . 0 0
x  2  y  4  d : y  9x14  0 0 2
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 5
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Vậy đường thẳng y  9x 14 là tiếp tuyến của đồ thị hàm số 3
y x  3x  2 . x
Câu 19: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Trên đồ thị C  1 : y  có bao nhiêu điểm x  2
M mà tiếp tuyến với C  tại M song song với đường thẳng d : x y  1 A. 4 . B. 1. C. 2 . D. 0 . Lời giải: x  1  Xét hàm số C  1 : y  . TXĐ: D  \   2 , y '   0 . x  2 x  22
Để tiếp tuyến với C  tại M song song với đường thẳng d : y x 1 suy ra 1  y ' 
1 VN . Vậy không có tiếp tuyến thỏa mãn. 2   x  2
Câu 20: (THPT NĂM 2018-2019 LẦN 04) Tìm điểm M có hoành độ âm trên đồ thị  1 2 C  1 2 3 : y x x
sao cho tiếp tuyến tại M vuông góc với đường thẳng y   x  . 3 3 3 3  4   4  A. M  2  ;  4 . B. M 1;    . C. M 2 ;   . D. M  2  ; 0 .  3   3  Lời giải:  1 2  Giả sử 3 M a ; a a    , a  0 ; 2
y  x 1  ya 2  a 1  3 3  1 2
Tiếp tuyến tại M vuông góc với đường thẳng y   x  nên ta có: 3 3 a  2
ya  3 2
a 1  3   . a  2 
Vì M có hoành độ âm nên ta chọn a  2 . Suy ra M  2  ;0 .
Câu 21: (THPT MAI ANH TUẤN-THANH HÓA-2019) Cho hàm số 3 2
y  x  3x  9x 1 có đồ thị
C. Hệ số góc lớn nhất của tiếp tuyến với đồ thị C là A. 1. B. 6 . C. 12 . D. 9 . Lời giải: Ta có 2 y '  3
x  6x  9; y   x  2 ' 3 1 12  12
Vậy hệ số góc lớn nhất của tiếp tuyến với đồ thị C  là 12 . 3 2x Câu 22: Cho hàm số 2 y  
x  4x  2, gọi đồ thị của hàm số là C . Viết phương trình tiếp tuyến 3
của C  có hệ số góc lớn nhất. 9 25 25 9 25 7 5 A. y x  . B. y  5x  . C. y x  . D. y x  . 2 12 12 4 12 2 12 Lời giải:
Gọi d  là tiếp tuyến cần tìm phương trình và x là hoành độ tiếp điểm của d  với C  thì 0 2 9  1  9 9 1
hệ số góc của d  : 2
k y '(x )  2
x  2x  4   x
 ; k   x  . 0 0 0  0  2  2  2 0 2 2
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 6
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 9 1 Vậy max k
đạt được khi và chỉ khi x  . 2 0 2 9  1   1  9 25
Suy ra phương trình tiếp tuyến d  : y x   yx      . 2  2   2  2 12
Câu 23: (THPT Lương Thế Vinh - Hà Nội - Lần 1 - 2017 - 2018) Cho hàm số 3 2
y x  3x  6x  5 . Tiếp
tuyến của đồ thị hàm số có hệ số góc nhỏ nhất có phương trình là
A. y  3x  9 .
B. y  3x  3 .
C. y  3x 12 .
D. y  3x  6 . Lời giải: Ta có: 2
y  3x  6x  6   x  2 3 1
 3  3 . Dấu "  " xảy ra khi x  1  y  9 .
Do đó, tiếp tuyến của đồ thị có hệ số góc nhỏ nhất bằng 3 và là tiếp tuyến tại điểm M 1;9 .
Phương trình tiếp tuyến là: y  3 x  
1  9  y  3x  6 .
Câu 24: (THPT Chuyên Hùng Vương - Phú Thọ - Lần 1 - 2018) Tiếp tuyến của đồ thị hàm số 4x  3 y
cùng với 2 tiệm cận tạo thành một tam giác có diện tích bằng: 2x 1 A. 6 . B. 7 . C. 5 . D. 4 . Lời giải: 10 Ta có: y   2x   . 2 1 1
Gọi M x ; y là điểm nằm trên đồ thị hàm số , x   . 0 0  0 2 10 4x  3
Phương trình tiếp tuyến tại M : y f (
x ) x x y y x x  2  0  0 0  0  0 2x   1 2x 1 0 0 1
Tiệm cận đứng: x   , tiệm cận ngang: y  2 2
Gọi A là giao điểm của tiếp tuyến với tiệm cận đứng 1         10 1 4x 3 4x 8 1 4x 8 x   0 0  y    x   . Vậy 0 A  ;  A   2 A 2x  2 0 1  2
 2x 1 2x 1 2 2x 1 0 0   0 0
Gọi B là giao điểm của tiếp tuyến với tiệm cận 10 4x  3 1  4x 1 
ngang  y  2  2  x x
x  2x  . Vậy 0 B ; 2   2  B 0  0 BB 0 2x   1 2x 1 2  2  0 0  1 
Giao điểm 2 tiệm cận là I  ; 2    2   10  10
Ta có: IA   0;   IA
; IB  2x 1;0  IB  2x 1 0  2x 1 2x 1  0 0  0 1 1 10
Tam giác IAB vuông tại I nên SI . A IB  . 2x 1  5 IAB 0 2 2 2x  . 1 0
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 7
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2x
Câu 25: (SỞ GD&ĐT QUẢNG NINH NĂM 2018-2019 LẦN 01) Cho hàm số y x  , có đồ thị (C) 2
và điểm M (x ; y )  (C) (với x  0 ). Biết rằng khoảng cách từ I (2; 2) đến tiếp tuyến của (C) 0 0 0
tại M là lớn nhất, mệnh đề nào sau đây đúng?
A. 2x y  0 .
B. 2x y  4 .
C. 2x y  2 .
D. 2x y  2 . 0 0 0 0 0 0 0 0 Lời giải: 4 2x
Tập xác định D  \   2 . y  M (x ; ) 2 (x , 0 2) 0 x  2 0 4 2x
Phương trình tiếp tuyến tại M là 0 2 2 y  (x x ) 
 4x  (x  2) y  2x  0 2 0 0 0 (x  2) x  2 0 0 2 2
4(2)  (x  2) .2  2x   0 0 8x 16
Khoảng cách từ I đến tiếp tuyến là 0 d   2 4 2 4 4  (x  2) 4  (x  2) 0 0 8  x 16 8 x  2
Áp dụng bất đẳng thức cosi ta có 0 0   2 2 2 4 2 4  (x  2) 8(x  2) 0 0 x  0 Dấu bằng xảy ra khi 2 (x  2)  4 0 
. Vì x  0 nên x  4  y  4  2x y  4  . 0 x  4   0 0 0 0 0 0 x 1
Câu 26: (THPT Lương Thế Vinh - Hà Nội - Lần 1 - 2018) Cho hàm số y
. Gọi I là giao điểm 2x  3
của hai tiệm cận của đồ thị hàm số. Khoảng cách từ I đến tiếp tuyến của đồ thị hàm số đã cho
đạt giá trị lớn nhất bằng 1 A. d  . B. d  1 . C. d  2 . D. d  5 . 2 Lời giải:  3 1 
Tọa độ giao điểm I  ;   .  2 2   x 1 
Gọi tọa độ tiếp điểm là 0  x ;
 . Khi đó phương trình tiếp tuyến  với đồ thị hàm số tại 0 2x  3  0   x 1  điểm 0  x ;  là: 0 2x  3  0  1 x 1 y   x x
x  2x  3 y  2x  4x  3  0 . 2   0 0  0 2 2 2x 3 0 0 2x  3 0 0 3 1  2x 32 2
 2x  4x  3 0 0 0 2 2 2  x  3 2x  3 1
Khi đó: d I,  0 0       x  4   x  4  x  2 2 1 2 3 1 2 3 2 2 3 0 0 0 2x  3 1 x  2
Dấu "  " xảy ra khi và chỉ khi 2x  32 0 0 1   . 0   2x  3  1  x  1  0  0 Vậy d I  1 max ,  . 2
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 8
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 27: [THPT TRẦN QUỐC TUẤN - Lần 1- 2018] Cho hàm số 3
y x  3x  2 có đồ thị C  . Đường
thẳng d : y x  2 cắt đồ thị C  tại ba điểm A , B , C 0; 2 . Gọi k , k lần lượt là hệ số góc của 1 2
tiếp tuyến của C  tại A và B . Tính k .k . 1 2 A. 9 . B. 27 . C. 81. D. 81. Lời giải: Ta có: 2 y  3x  3
Xét phương trình hoành độ giao điểm của đường thẳng d và đồ thị C  là : x  0 3 3
x  3x  2  x  2  x  4x  0   x  2 
Vậy đường thẳng d cắt đồ thị C  tại ba điểm phân biệt: A2; 2 , B 2; 4 và C 0; 2 .
Gọi k , k lần lượt là hệ số góc của tiếp tuyến của C  tại A và B , ta có: 1 2 k y 2
  9 , k y 2  9 . Vậy k k  81. 2   1   1 2 2x  1
Câu 28: (SGD Bà Rịa - Vũng Tàu - Lần 1 - 2018 ) Cho hàm số y
có đồ thị C  . Gọi M x ; y 0 0  2x  2
(với x  1) là điểm thuộc C  , biết tiếp tuyến của C  tại M cắt tiệm cận đứng và tiệm cận 0
ngang lần lượt tại A và B sao cho S  8S
(trong đó O là gốc tọa độ, I là giao điểm hai OIB OIA
tiệm cận). Tính giá trị của S x  4 y . 0 0 17 23 A. S  8 . B. S  . C. S  . D. S  2 . 4 4 Lời giải: 2  Ta có y    
, TCĐ: x 1 d , TCN: y 1 d , I 1;  1 . 2  1  2x  22 2  2x 1
Phương trình tiếp tuyến  tại điểm M x ; y có dạng y x x  2  0  0 0 0  2x 2 2x  2 0 0
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 9
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x   1  A    d 0  A1;
 , B    d B 2x 1;1 . IB  2x  2;0 , IA  0;  . 0  0  1 x 1  2 x 1 0   0  1 S  1 1 8S
 .1.IB  8. .1.IA IB  8IA  2x  2  8
 x 1  4  x  3 0 2 OIB OIA 2 2 0 x 1 0 0 5
(do x  1)  y   S x  5 4 y  3  4.  8 . 0 0 4 0 0 4 2x 1
Câu 29: (THI THỬ THPTQG VTV7 NĂM 2018-2019) Đồ thị hàm số y  có bao nhiêu cặp tiếp x  2
tuyến vuông góc với nhau? A. 1. B. Vô số. C. 0 . D. 2 . Lời giải: 2x 1 5 TXĐ: D  \   2 . Ta có: y   y  . x  2 x  22
Tiếp tuyến d của đồ thị hàm số tại M x ; y có dạng: y y x
x x y . 1   1  1 1  1  1
Tiếp tuyến d của đồ thị hàm số tại N x ; y có dạng: y y x x xy . 2   2  2 2  2  2
d d y x y x  5 5 .  1     1
  x  2 . x  2  2  5 (vô lý). 2 2  1 2  2 2 1 2 1 2 x  2 x  2 1   2 
Vậy không có cặp tiếp tuyến nào của đồ thị vuông góc với nhau.
Câu 30: (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Cho hàm số
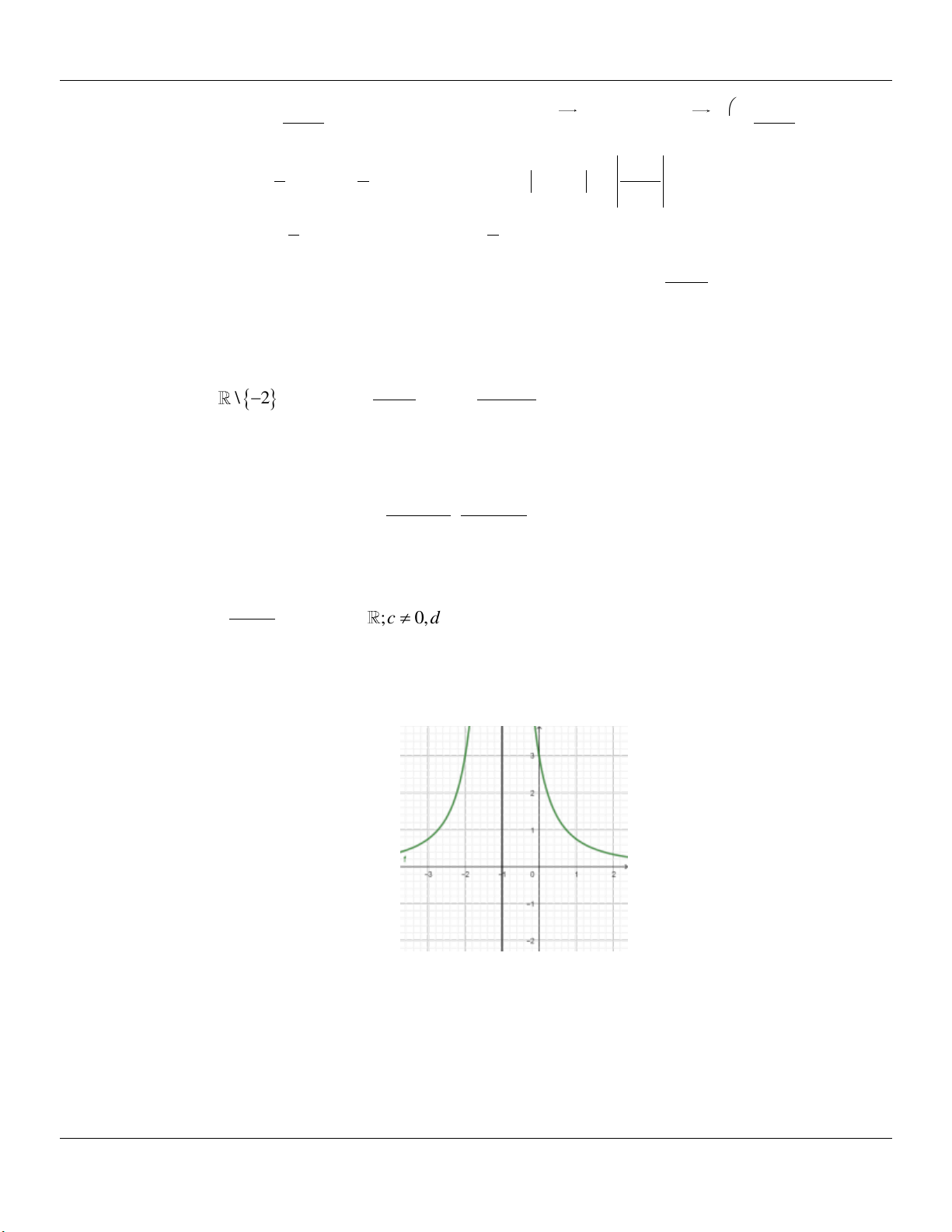
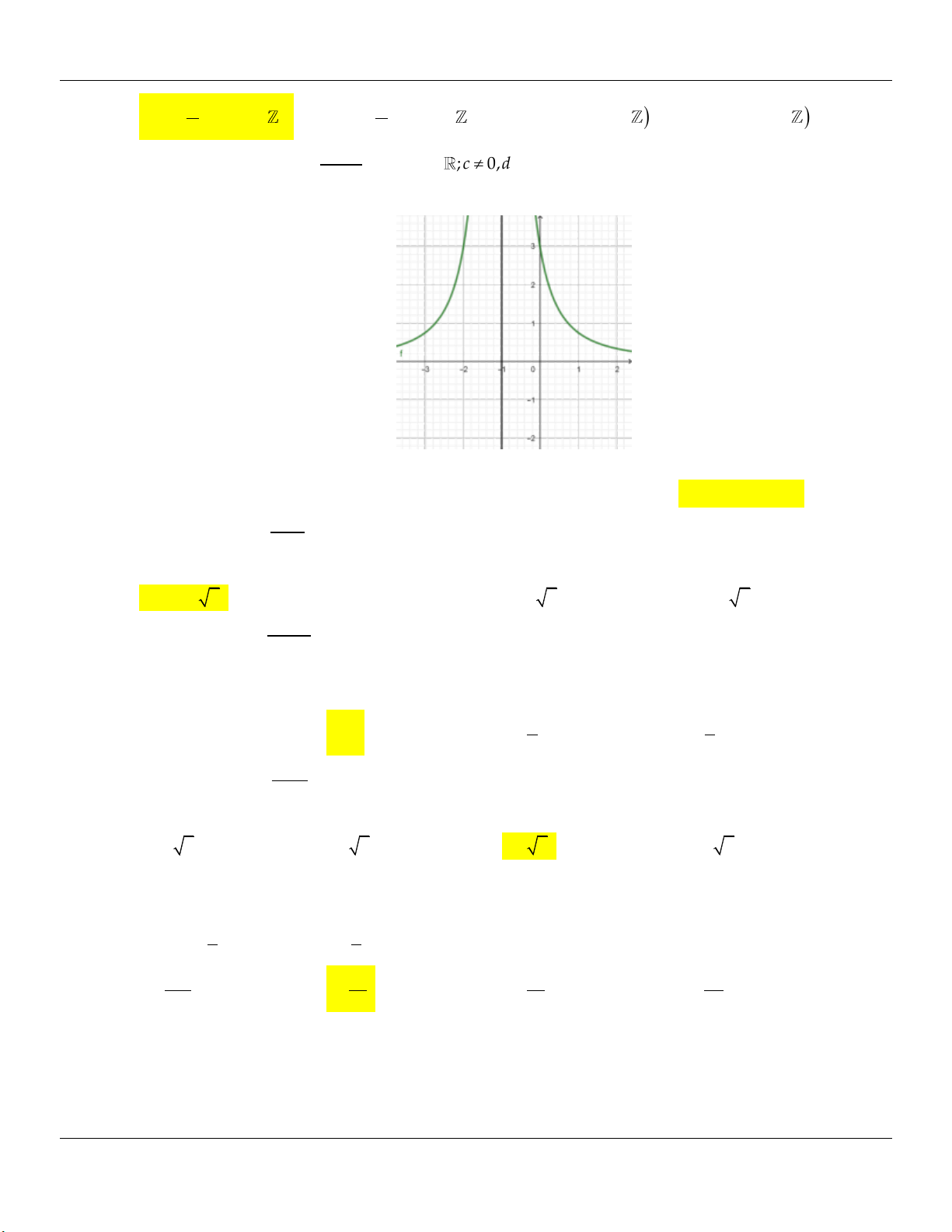
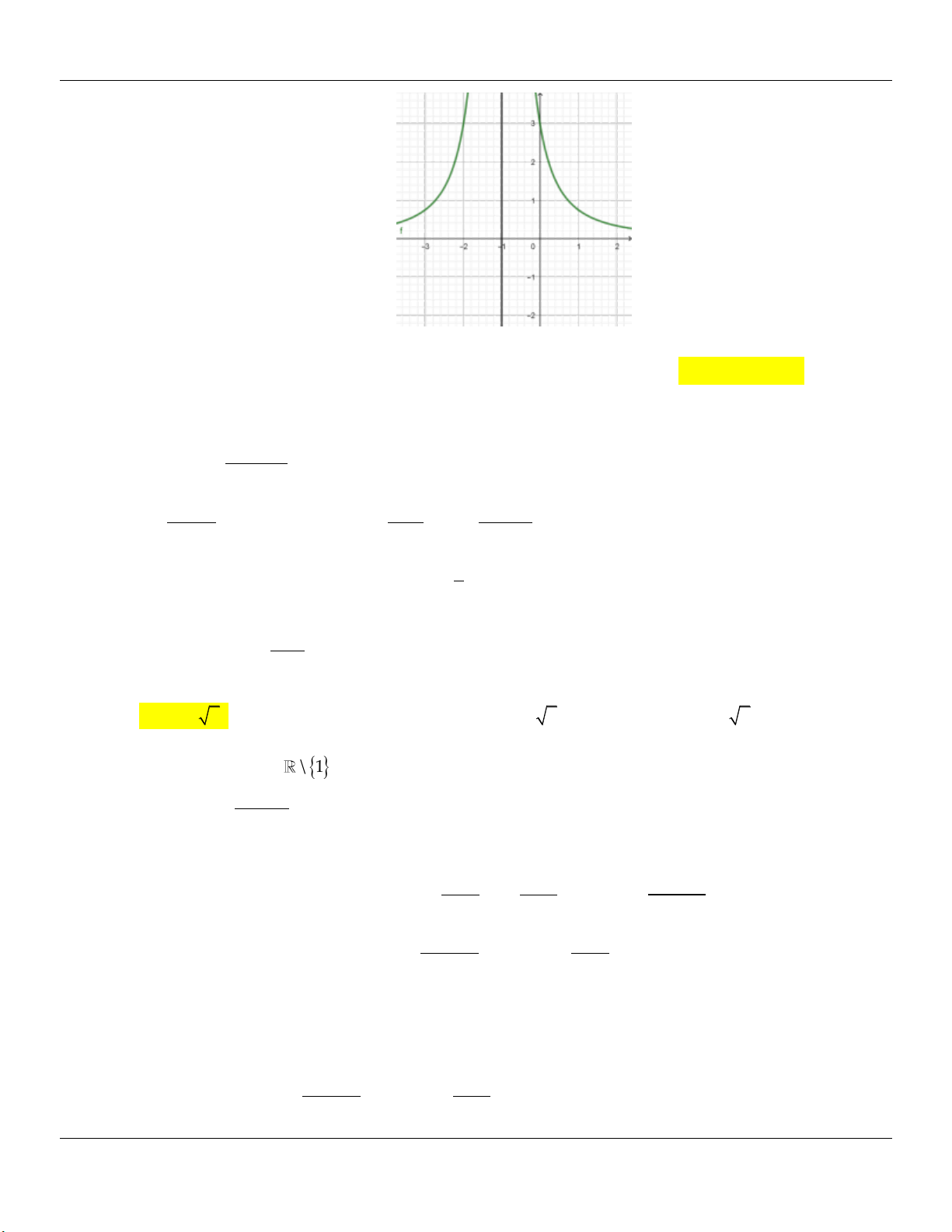
   ax b y f x  ,a, ,
b c, d  ;c  0, d  0 có đồ thị C . Đồ thị của hàm số y f  x như cx d
hình vẽ dưới đây. Biết C  cắt trục tung tại điểm có tung độ bằng 2. Viết phương trình tiếp
tuyến của C  tại giao điểm của C  với trục hoành.
A. x  3y  2  0.
B. x  3y  2  0.
C. x  3y  2  0.
D. x  3y  2  0. Lời giải:
Đồ thị hàm số y f x đi qua 0; 2 suy ra b  2d .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 10
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia ad bc Ta có y   
. Đồ thị hàm số y có tiệm cận đứng x  1 nên c
d , đi qua 0;3 nên cx d 2 ad bc x  2 3 3 
hay a d . Do đó y   y  . 2 d x 1 x  2 1 1
Phương trình tiếp tuyến tại 2;0 là y   x  2  3x y  2  0 . 3
Câu 31: (THPT Can Lộc - Hà Tĩnh - Lần 1 - 2017 - 2018) Cho hàm số y f x xác định và có đạo hàm 2 3 trên thỏa mãn  f  2x   1    f
 1 x  x
. Viết phương trình tiếp tuyến của đồ thị hàm
số y f x tại điểm có hoành độ bằng 1. 1 6 1 8 1 5 1 6 A. y x  .
B. y   x  . C. y x  .
D. y   x  . 7 7 7 7 7 7 7 7 Lời giải: f   1  0 2 3 2 3 Từ  f  2x   1    f
 1 x  x
(*), cho x  0 ta có  f    1    f     1   0     f    1  1 2
Đạo hàm hai vế của (*) ta được 4. f 2x  
1 . f  2x   1  3 f
 1 x . f   1 x 1. 2
Cho x  0 ta được 4 f   1 . f   1  3. f    1  . f  
 1 1  f  1.f  1.43f   1 1  (**). Nếu f  
1  0 thì (**) vô lý, do đó f   1  1
 , khi đó (**) trở thành  f   1 .4  
3  1  f   1 1   7 1 1 8
Phương trình tiếp tuyến y    x   1 1  y   x  . 7 7 7
Câu 32: (THPT Chuyên Hà Tĩnh - Lần 1 - 2018 - BTN) Cho hàm số y f x có đạo hàm liên tục trên
, thỏa mãn f x  f   x 2 2 2 1 2
12x . Phương trình tiếp tuyến của đồ thị hàm số y f x
tại điểm có hoành độ bằng 1 là:
A. y  2x  2
B. y  4x  6
C. y  2x  6
D. y  4x  2 Lời giải: 1 2 f
0  f  1  0
Từ f x  f   x 2 2 2 1 2
12x (*), cho x  0 và x  ta được   f   1  2 2  f
 0  2 f   1  3 1
Lấy đạo hàm hai vế của (*) ta được 4 f 2x  2 f 1 2x  24x , cho x  0 và x  ta được 2 4 f  
0  2 f  1  0   f   1  4 . 4 f  
 1  2 f 0 12
Phương trình tiếp tuyến của đồ thị hàm số y f x tại điểm x  1 là
y f   1  x   1  f  
1  y  4  x  
1  2  y  4x  2 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 11
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 33: (HSG BẮC NINH NĂM 2018-2019) Có bao nhiêu giá trị của tham số thực m để đồ thị hàm số 2
x  2mx m y
cắt trục Ox tại hai điểm phân biệt và các tiếp tuyến của đồ thị tại hai điểm x m đó vuông góc với nhau. A. 5 . B. 2 . C. 0 . D. 1. Lời giải: 2 2
x  2mx m 3m m 2 3m m y   x  3m   y 1 . x m x mx m2
Xét phương trình hoành độ giao điểm của đồ thị hàm số đã cho với trục Ox . 2
x  2mx m  0  f x 2
x  2mx m  0 * x  m . x m
Để đồ thị hàm số đã cho cắt trục Ox tại hai điểm phân biệt và các tiếp tuyến tại hai điểm đó
vuông góc với nhau thì phương trình (*) phải có hai nghiệm phân biệt x ; x khác m  và 1 2
y x .yx  1  . 1   2    m 1   m  0 2
  m m  0     m 0    f m 2
 3m m  0   1  m  5 .  m        3        y x  2 2 3m m 3m m y x .  1 1   1   1 2   m 0 x m2    x m2      1 2   m  5
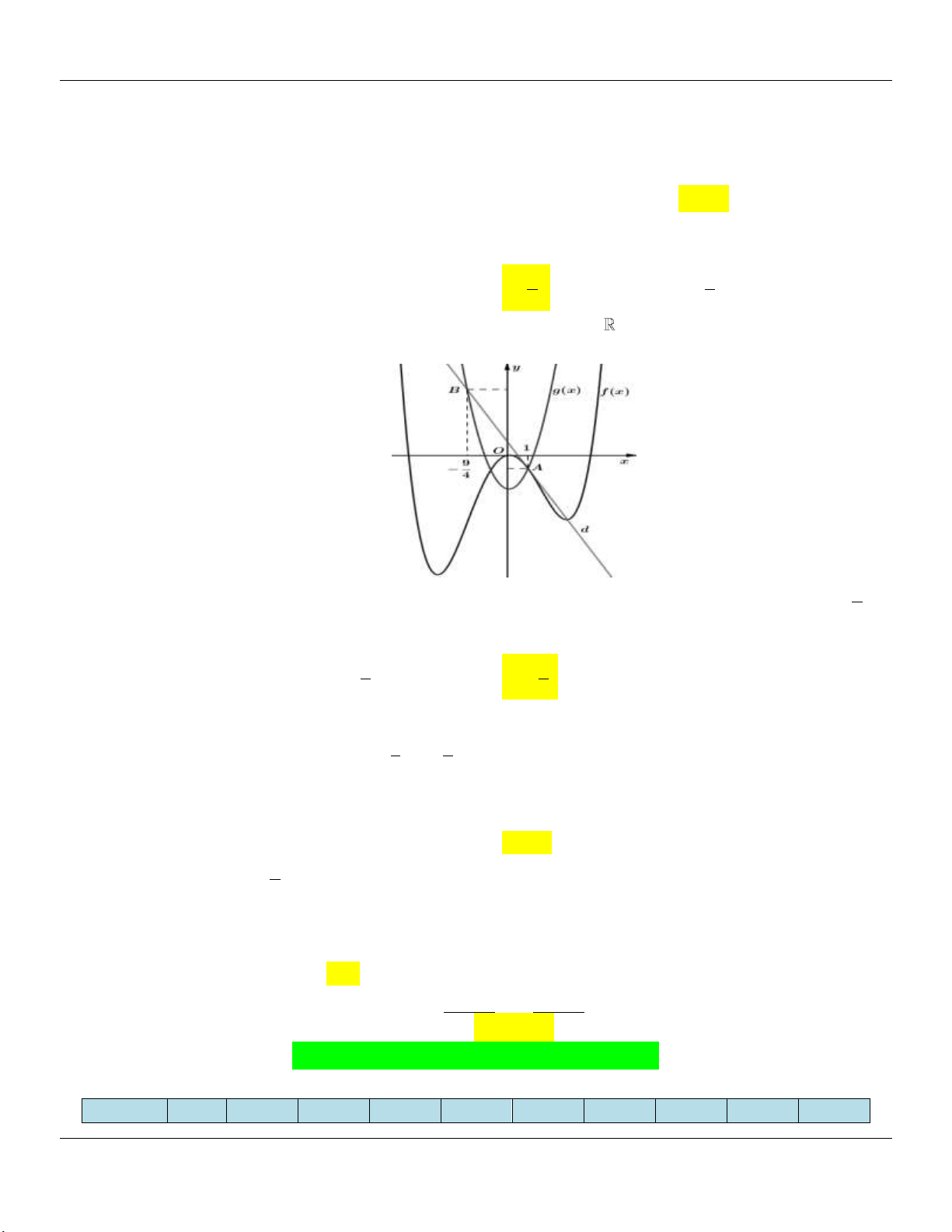
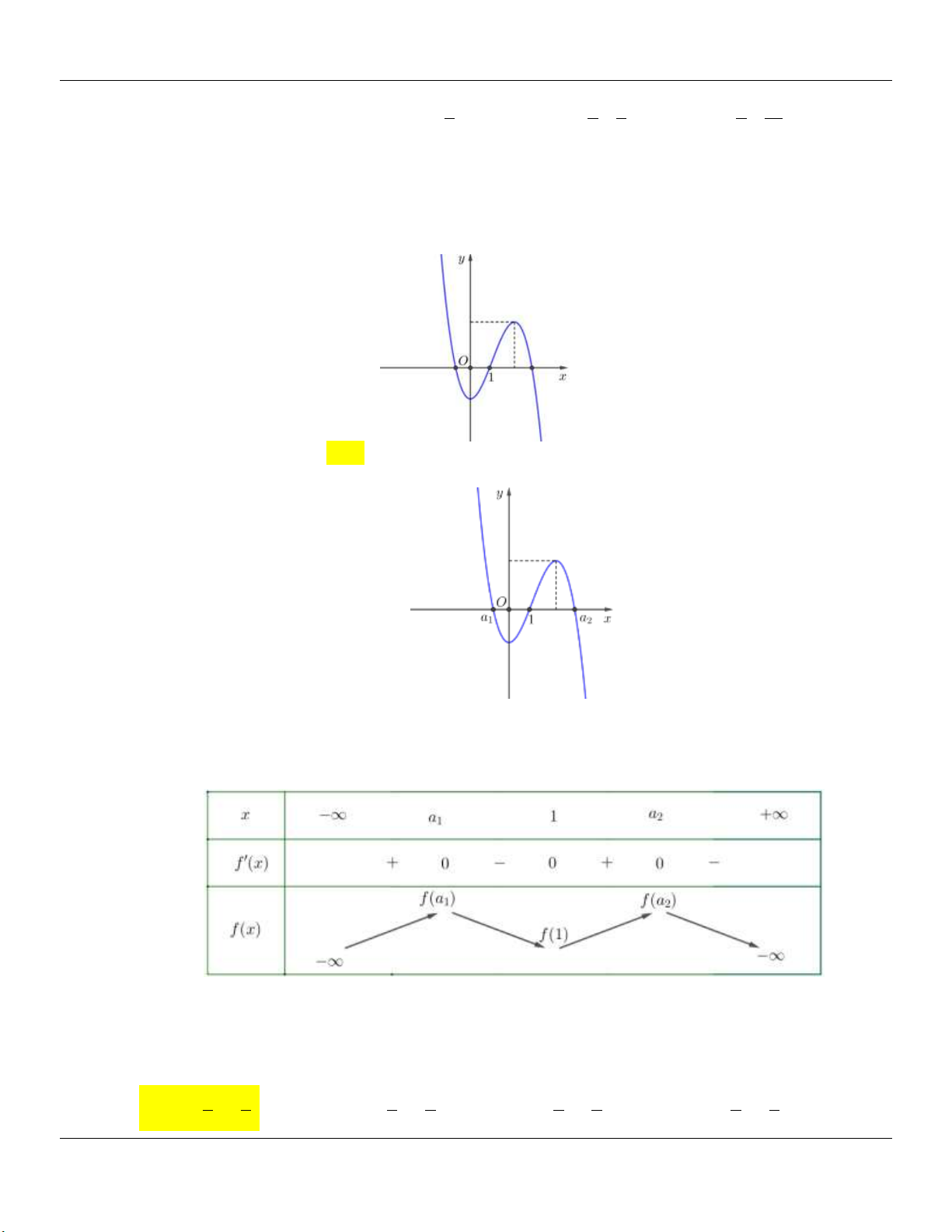
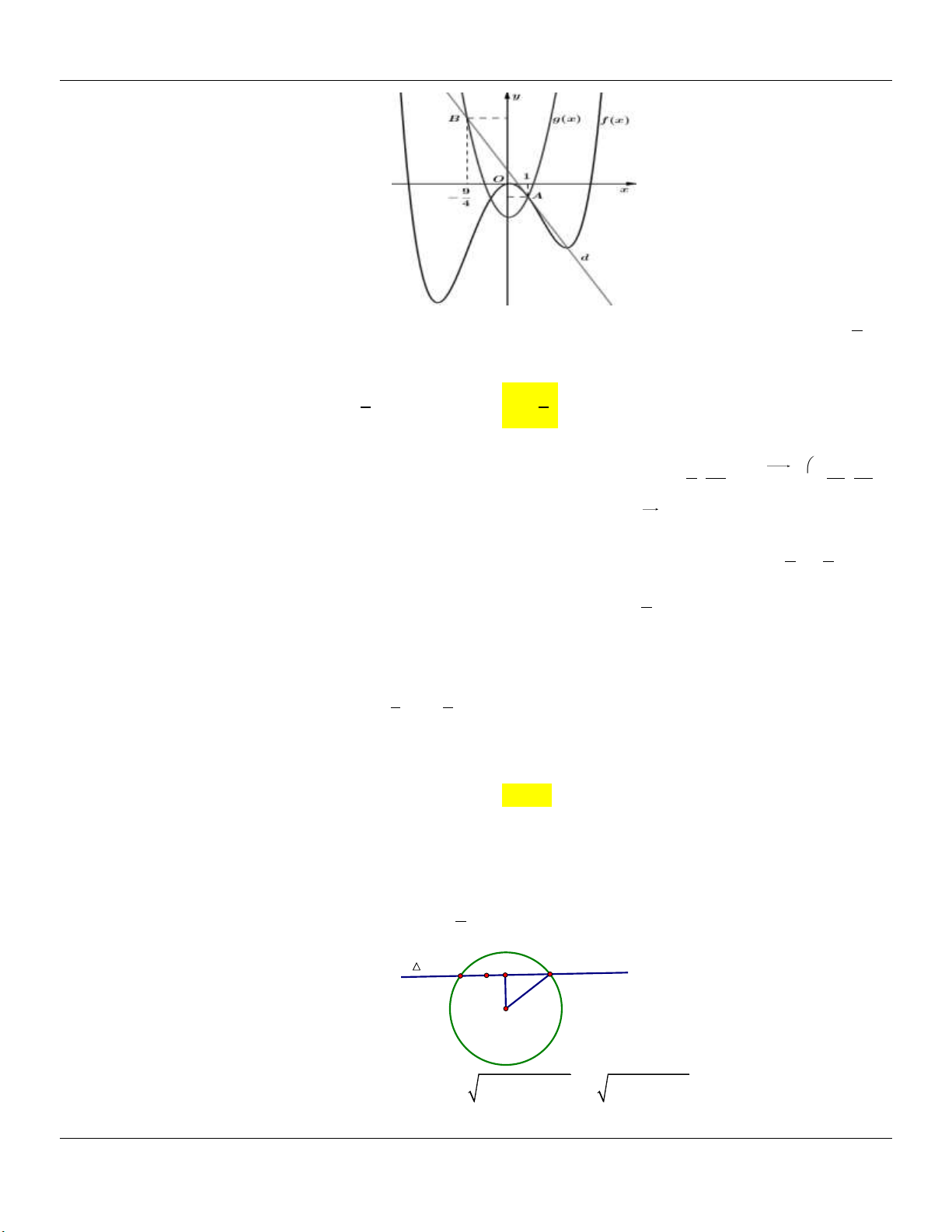
Câu 34: (TOÁN HỌC TUỔI TRẺ - LẦN 5 - 2019) Cho hàm số bậc bốn y f x xác định và liên tục trên
, hàm số g x 2
 2x  3 và đường thẳng d có đồ thị như hình vẽ. Biết A là điểm chung 9
của đồ thị f x và g x , x  1. Điểm B thuộc đồ thị g x , x   và d là tiếp tuyến của A B 4
đồ thị hàm số y f x . Giá trị f  x bằng A 3 5 A. 1  . B.  . C.  . D. 2 . 2 2 Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 12
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia  9 57 
Vì các điểm A , B thuộc đồ thị hàm số g(x) nên ta có A1;  1 , B ;    4 8   13 65   AB   ;
 . Do d đi qua hai điểm A và B nên ta chọn vectơ pháp tuyến là  4 8 
n  65;26 . d
Phương trình đường thẳng d là:
x    y   5 3 65 1 26
1  0  65x  26 y  39  0  y   x  2 2
Mà d là tiếp tuyến của đồ thị hàm số y f x nên f  x   . A  5 2 Câu 35: (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Cho hàm số 3
y x  m   2
1 x x  2m  1 có đồ thị C  ( m là tham số thực). Gọi m , m là các giá trị của 1 2
m để đường thẳng d : y x m  1 cắt C  tại ba điểm phân biệt ,
A B, C sao cho tổng hệ số
góc của các tiếp tuyến với C  tại ,
A B, C bằng 19 . Khi đó m m bằng 1 2 A. 4 . B. 2 . C. 0 . D. 2 . Lời giải:
Phương trình hoành độ giao điểm của d và C: x  1 y  3
x  m   1 2
x x m  0  x   1  2
x mx m  0    2
x mx m  0   *
Để d và C cắt nhau tại ba điểm phân biệt thì  
* phải có hai nghiệm phân biệt khác 1, tức   0 1 1 
m     ; 4       ; 0     ;
 . Khi đó d và C cắt nhau tại ba điểm phân biệt 1 2m  0  2   2   A ;
1 m  2, Bx ; x m C x x m
với x ; x là nghiệm của phương trình   * 1 1 1,  ;2 2 1 1 2
Hệ số góc tiếp tuyến của C tại A là: y   
1  2  2m . Hệ số góc tiếp tuyến của C  tại B là: y
x x m x  . 1  3 2 1  2 1 1 1
Hệ số góc tiếp tuyến của C tại C là: y
x x m x  . 2  3 2 2  2 1 1 2 Theo giả thiết, ta có: 2 2 3 x x 2 m 1 x x 4 2m 19 . 1 2 1 2 2 3 x x 6x x 2 m 1 x x 4 2m 19 ** 1 2 1 2 1 2 x x   m  1 2 thay vào *  * , ta được 2 3m 6m 2 m 1 m 4 2m 19 . x x  m 1 2 m 3 2 1 m 2m 15 0 m m 2 1 2 m 5 2 x  2
Câu 36: Cho hàm số y
C . Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị
x  đồ thị   1
C đến một tiếp tuyến của C. Giá trị lớn nhất của d có thể đạt được là A. 3 3 . B. 3 . C. 2 . D. 2 2 . Lời giải:
Tiệm cận đứng d : x 1  0 , tiệm cận ngang d : y 1  0  tâm đối xứng là I 1;  1 . 1 2
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 13
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia a  2  1  a  2
Phương trình tiếp tuyến tại điểm M ; a  
 C là: y x a  d  . 2    a 1  a  1 a 1 1  a  2    2 1 a 2   a  1 a 1 a 1 2 2
Khi đó d I, d       2 . 1 1 1 2 1 1 a 1  4 4  2 a  1 a  1 a  2 1
Câu 37: (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Gọi A là điểm có hoành độ bằng 1 thuộc a a
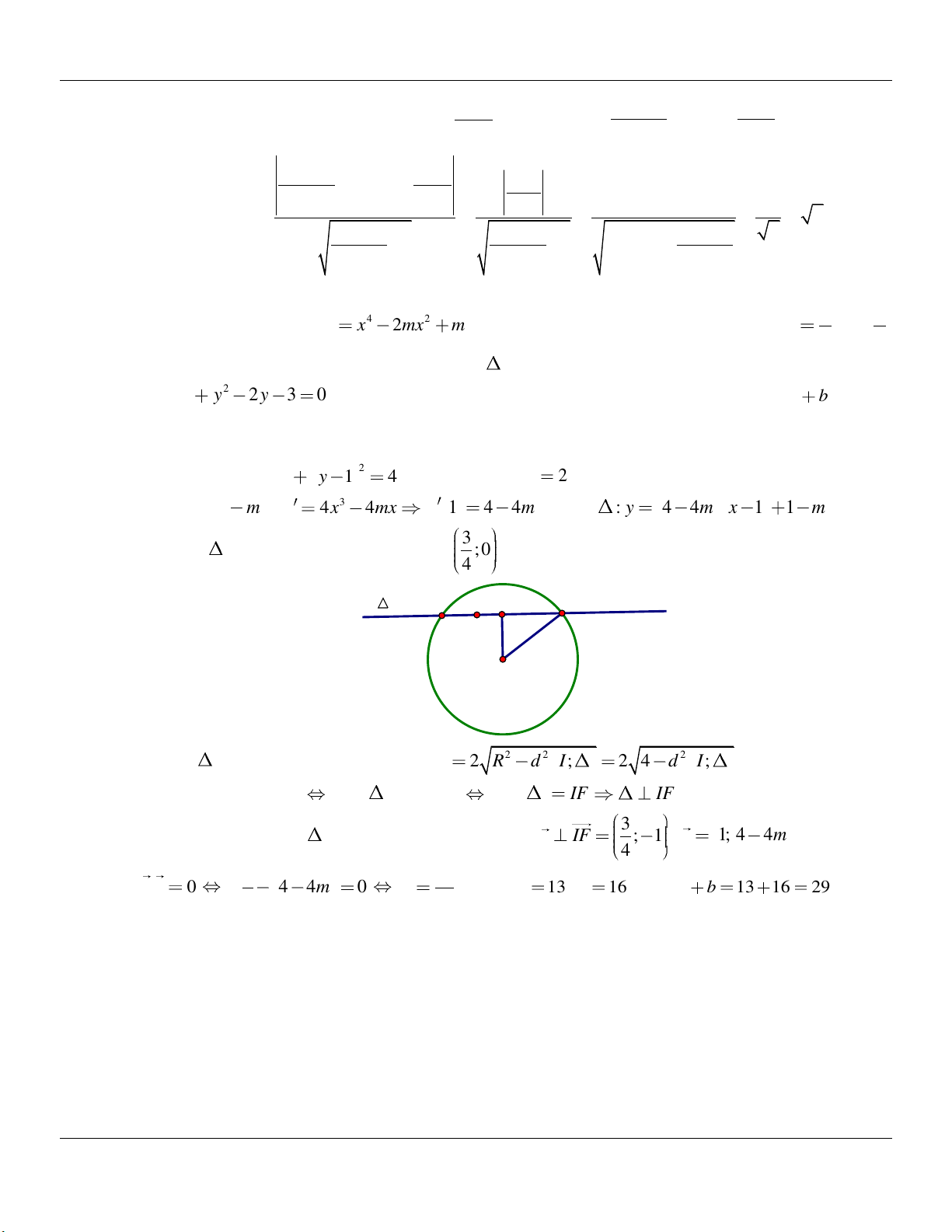
đồ thị C của hàm số 4 2 y x 2mx
m ( m là tham số thực). Ta luôn tìm được m với b b
là phân số tối giản để tiếp tuyến với đồ thị
C tại A cắt đường tròn 2 2  : x y 2 y 3
0 tạo thành một dây cung có độ dài nhỏ nhất. Khi đó, tổng a b bằng: A. 12 . B. 3 . C. 29 . D. 10 . Lời giải: 2 Đường tròn 2  : x y 1
4 có tâm I 0;1 , R 2 .
Ta có A 1;1 m ; 3 y 4x 4mx y 1 4 4m suy ra : y 4 4m x 1 1 m . 3 Dễ thấy
luôn đi qua điểm cố định F
; 0 và điểm F nằm trong đường tròn  . 4 M N F d R I Giả sử
cắt  tại M , N , ta có: 2 2 2 MN 2 R d I; 2 4 d I; .
Do đó MN nhỏ nhất d I ; lớn nhất d I; IF IF . 3 Khi đó đường thẳng
có một véc-tơ chỉ phương u IF ; 1 ; u 1; 4 4m nên: 4 3 13 u.n 0 1. 4 4m 0 m suy ra a 13 , b 16 . Vậy a b 13 16 29 . 4 16
Câu 38: (THPT NGÔ QUYỀN HÀ NỘI NĂM 2018 - 2019 LẦN 01) Cho hàm đa thức bậc bốn
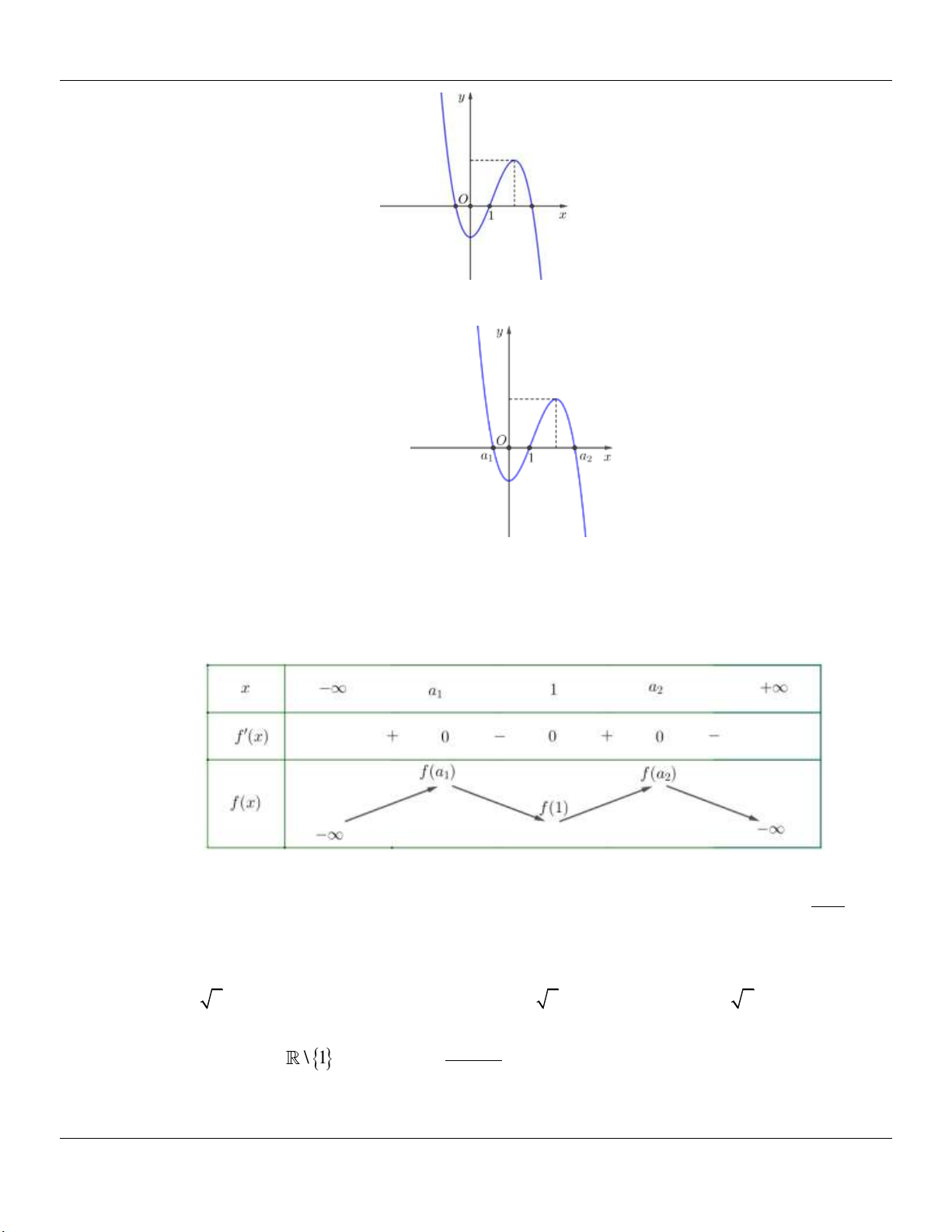
y f x có đồ thị C  . Hàm số y f  x có đồ thị như hình vẽ dưới đây. Gọi đường thẳng
 là tiếp tuyến của đồ thị C tại điểm có hoành độ bằng 1. Hỏi  và C có bao nhiêu điểm chung?
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 14
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. 2 . B. 3 . C. 1. D. 4 . Lời giải:
Ta có tiếp tuyến  của C  tại x  1 là y f   1  x   1  f   1 .
Dựa vào đồ thị của hàm số f  x , ta có f   1  0 .
Vậy  : y f   1 .
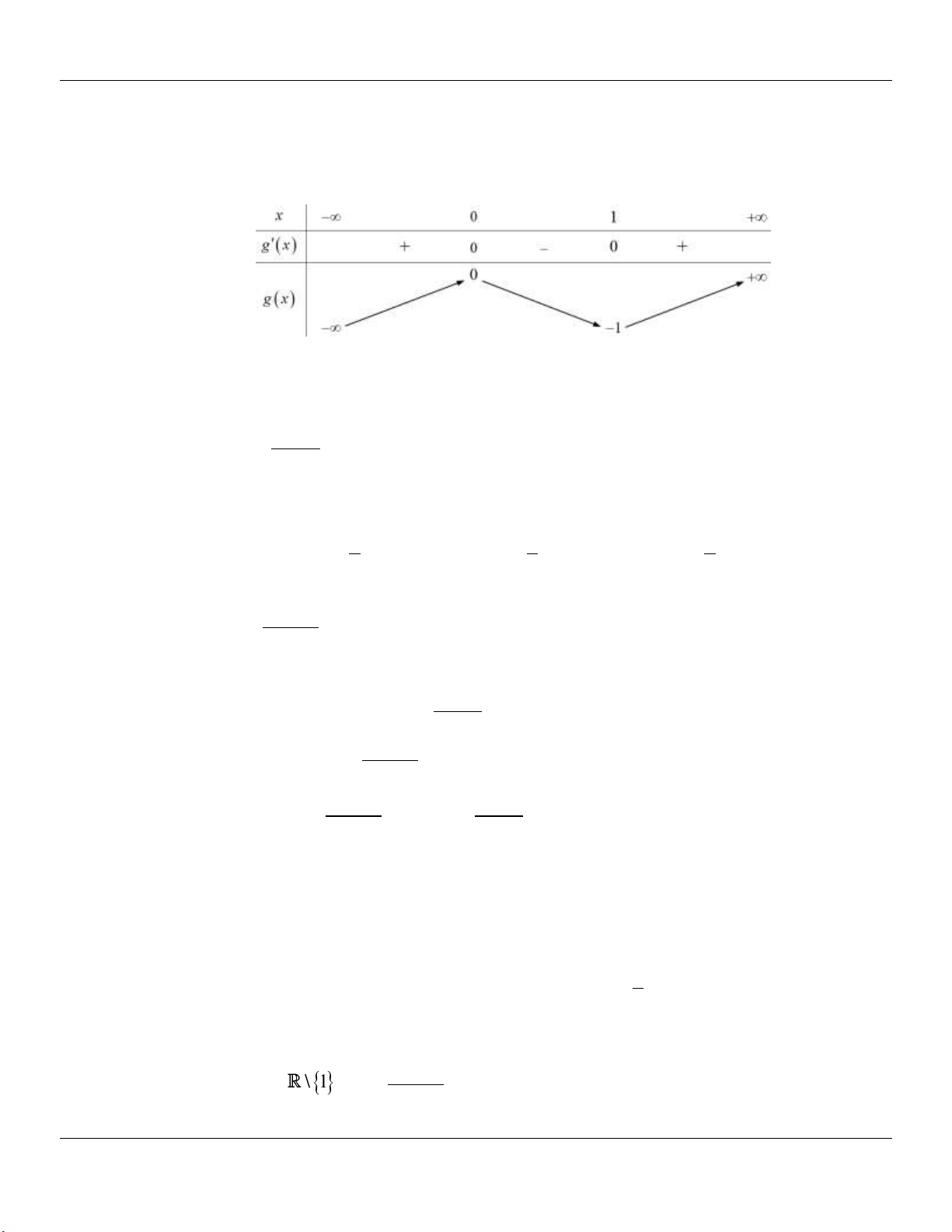
Gọi a , a là hai nghiệm còn lại của f  x . Dựa vào đồ thị hàm số ta có bảng biến thiên: 1 2
Dựa vào bảng biến thiên ta có  : y f  
1 và C  có ba điểm chung. x 1
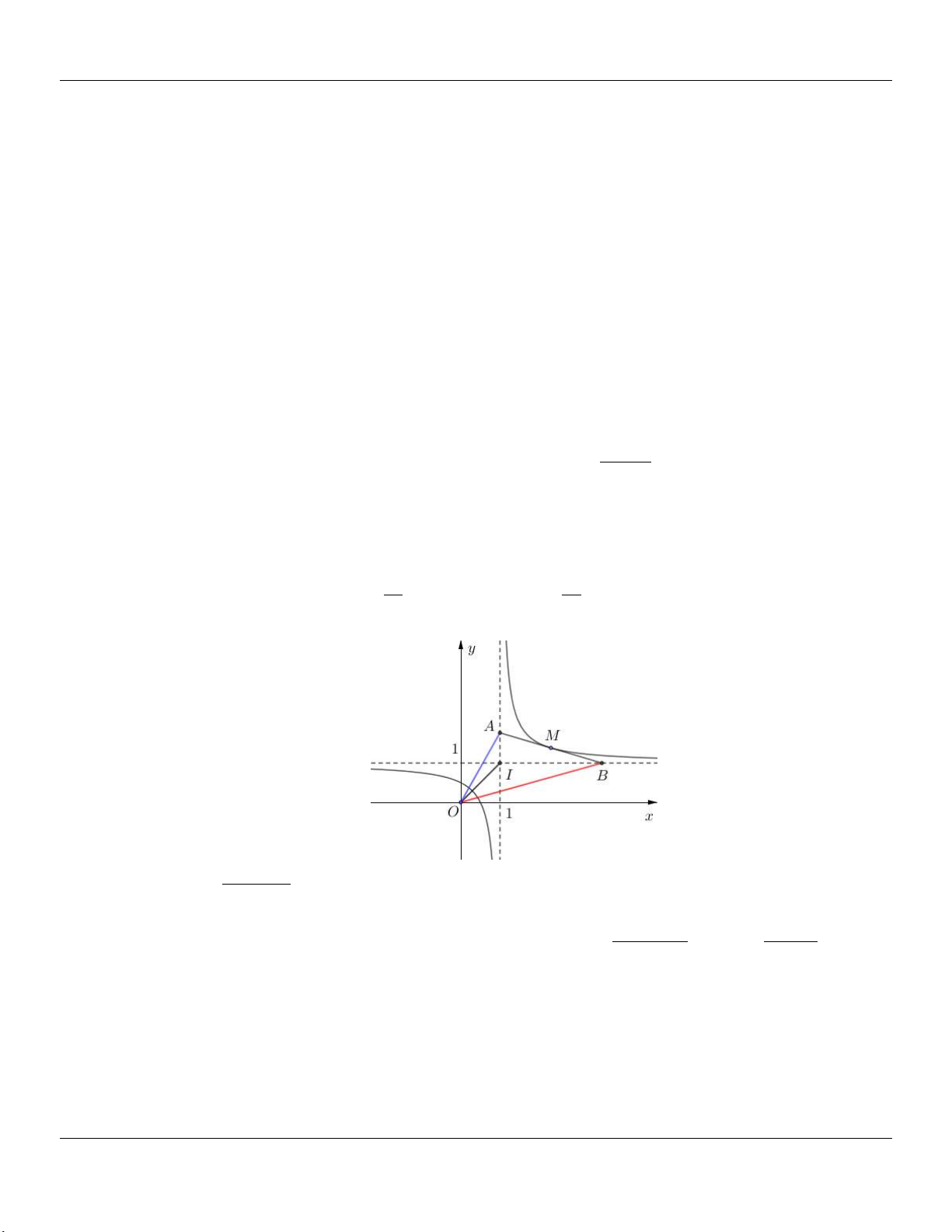
Câu 39: (THPT KINH MÔN II HẢI DƯƠNG NĂM 2018-2019 LẦN 03) Cho hàm số y  Cx  . 1
Điểm M thuộc C  có hoành độ lớn hơn1 , tiếp tuyến của C  tại M cắt hai tiệm cận của C
lần lượt tại A , B . Diện tích nhỏ nhất của tam giác OAB bằng A. 4  2 2 . B. 4 . C. 4 2 . D. 4  2 . Lời giải: 2
Tập xác định: D  \  
1 . Ta có: y      , x 1 . x  2 1
Đồ thị hàm số có đường tiệm cận ngang y  1 và đường tiệm cận đứng x  1 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 15
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia m 1 2 2
Giả sử M m; y  C  m   1 y  1
; ym   . M M m 1 m 1 m  2 1 2 2
Phương trình tiếp tuyến  là: y   x m 1 2   m  1 m 1
x  m  2 2 2 1
y m  2m 1  0 .
Gọi A là giao điểm của  và đường tiệm cận ngang. Tọa độ điểm A là nghiệm của hệ y 1  phương trình:  2 2
x  2m 1  A2m 1;  1 . y   x m 1 2    m    1 m 1
Gọi B là giao điểm của  và đường tiệm cận đứng. Tọa độ điểm B là nghiệm của hệ phương x 1  m  3 4  4  trình:  2 2  y  1  B 1;1   . y   x m 1     2     m 1 m    m 1 m 1 1 m 1 2 2  4  2 16 2 4
Suy ra: AB  2  2m   4   m   1   m 1  4 . 2    m 1 m   1 m 1 2    2 m  2m 1 1 1 2 4 d O  m 2m 1 ;   S
d O AB m   OAB  ; . . .   1 4 4  4  m  4 1 2 2
 m   m 1 4 1 2 2 m  2m 1 m  2m 1   2 2
(vì m  1)  m  3   4  m 1 . m 1 m 1 m 1 m 1 2
Áp dụng bất đẳng thức Cô-si cho hai số m 1 và : m   2 1   2 2 m 1 m  1   m   2 4 1   4  2 2 . m 1  2 m 1 
Vậy diện tích nhỏ nhất của tam giác OAB bằng 4  2 2 khi 
m 1  m  1 2 . m 1 x 1
Câu 40: (THPT QUỲNH LƯU– 2018-2019– LẦN 1) Cho hàm số y
(C), y x m (d ) . Với mọi 2x 1
m đường thẳng (d ) luôn cắt đồ thị (C) tại hai hai điểm phân biệt A và B. Gọi k1, k2 lần lượt là
hệ số góc của các tiếp tuyến với (C) tại A và B. Giá trị nhỏ nhất của 2020 2020 T kk bằng 1 2 1 2 A. 1. B. 2 . C. . D. . 2 3 Lời giải: 2
2x  2mx m 1  0 x 1 
+ Phương trình hoành độ giao điểm:
x m   1 (*) 2x 1 x   2
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 16
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia + Phương trình (*) có: 2
 '  m  2(m 1)  0, m
 nên (d) luôn cắt ( C ) tại 2 điểm phân biệt A,B.
a b  m  1  
Gọi a, b là các hoành độ giao điểm a b    . Khi đó ta có:   .  m 1 2  ab    2 1 1 2 + Khi đó: 2020 2020 T kk    1 2 4040 4040 2020 (2a 1) (2b 1)
[(2a 1)(2b 1)] 2 2    
4ab  2(a b)   2 2020 1  2
 (m 1)  2m  2020 1 2020 2020 (2a 1)  (2b 1) 
+ Nhận xét: Giá trị nhỏ nhất bằng 2 khi: 
a b  1  m m  1. 1  a b   2
Câu 41: (SỞ GD&ĐT KIÊN GIANG NĂM 2018-2019) Cho hàm số 3 2
y x  3x  3x  5 có đồ thị C  .
Tìm tất cả những giá trị nguyên của k  20
 19;2019 để trên đồ thị C có ít nhất một điểm
mà tiếp tuyến tại đó vuông góc với đường thẳng d  : y  k  3 x . A. 2021 . B. 2017 . C. 2022 . D. 2016 . Lời giải: TXĐ : D  . Ta có : 2
y '  3x  6x  3 .
TH1 : k  3 . Khi đó d  : y  0  không tồn tại tiếp tuyến vuông góc với d  . TH2 : k  3 . 1
Ta có : k  3 2
3x  6x  3  1  2
 3x  6x  3  0 * 0 0   0 0  k  3 3 
Theo yêu cầu bài toán , phương trình * có nghiệm   '  0   0  k  3 k  3
Vậy k 2019; 2018 
;...;0;1; 2  Có 2022 giá trị nguyên của k thỏa đề bài.
Câu 42: (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Gọi M , N là hai điểm di động trên
đồ thị C  của hàm số 3 2
y  x  3x x  4 sao cho tiếp tuyến của C  tại M và N luôn song
song với nhau. Hỏi khi M , N thay đổi, đường thẳng MN luôn đi qua nào trong các điểm dưới đây? A. Điểm N  1  ; 5   B. Điểm M 1; 5   C. Điểm Q 1;5
D. Điểm P 1;5 Lời giải:
Vì tiếp tuyến của đồ thị hàm bậc ba tại 2 điểm M , N thuộc đồ thị hàm số song song với nhau
nên đường thẳng MN phải đi qua điểm uốn của C  . Ta có 2 y  3
x  6x 1; y  6x  6
Cho y  0  6x  6  0  x  1. Điểm uốn Q 1;5 . x  2
Câu 43: Cho hàm số y
C . Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị
x  đồ thị   1
C đến một tiếp tuyến của C. Giá trị lớn nhất của d có thể đạt được là A. 3 3 . B. 3 . C. 2 . D. 2 2 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 17
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải:
Tiệm cận đứng d : x 1  0 , tiệm cận ngang d : y 1  0  tâm đối xứng là I 1;  1 . 1 2  a  2  1  a  2
Phương trình tiếp tuyến tại điểm M ; a  
 C là: y x a  d  . 2    a 1  a  1 a 1 1  a  2    2 1 a 2   a  1 a 1 a 1 2 2
Khi đó d I, d       2 . 1 1 1 2 1 1 a 1  4 4  2 a  1 a  1 a  2 1 1 7
Câu 44: (MĐ 101 BGD&ĐT NĂM 2017-2018) Cho hàm số 4 2 y x
x có đồ thị C  . Có bao nhiêu 4 2
điểm A thuộc C  sao cho tiếp tuyến của C  tại A cắt C  tại hai điểm phân biệt
M x ; y ; N x ; y khác A thỏa mãn y y  6(x x ) . 1 1   2 2  1 2 1 2 A. 1. B. 2 . C. 0 . D. 3 . Lời giải:  1 7 
Ta có A  C  4 2
A t; t t   ; 3
y  x  7x yt  3  t  7t.  4 2 
Phương trình tiếp tuyến của C  tại A là 3 7 y   1 7 3
t  7t  x t  4 2
t t y   3t  7t 4 2 x t t 4 2 4 2
Phương trình hoành độ giao điểm: 1 7 3 7 4 2 x x   3 t  7t  4 2 x t t 4 2
x x   3t t 4 2 14 4 7
x  3t 14t  0 4 2 4 2 x t
 x t2  2 2
x  2tx  3t 14  0   2 2
x  2tx  3t 14  0    1
Tiếp tuyến cắt đồ thị C  tại hai điểm phân biệt M x ; y ; N x ; y khác A khi phương trình 1 1   2 2   
1 có hai nghiệm phân biệt khác t    2 t
   2t   7 t 7 3 14  0      21 2 2 2 2 t
  2t  3t 14  0 t     3  3 7 3 4 2 
y t  7t x t t  1   x x  2  t 1 1 2  4 2 Khi đó:  và 
y y   3 t  7t x x 1 2  1 2  2 x x  3t 14  3 7 1 2
y   3t  7t 4 2 x t t 2 2  4 2
Ta có y y  6(x x )   3
t  7t  x x  6 x x 1 2   1 2  1 2 1 2 t  1  n t 1  0  3
t  7t  6  0  t   2
1 t t  6  0  
 t  2 n (do 2 ) 2
t t  6  0 t  3  l
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 18
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia  13 
Với t  1 ta có A 1  ;    4 
Với t  2 ta có A 2  ; 10  
 có hai điểm thỏa yêu cầu bài toán. Câu 45: Cho hàm số 3
y x  2018x có đồ thị là C  . M là điểm trên C  có hoành độ x  2 . Tiếp 1 1
tuyến của C  tại M cắt C  tại điểm M khác M , tiếp tuyến của C  tại M cắt C  tại 1 2 1 2
điểm M khác M ,….., tiếp tuyến của C  tại M
C tại điểm M khác M 3 2 n 1  cắt   n n 1 
n  4;5;.... , gọi x ; y là tọa độ của điểm M . Tìm n để 2019
2018x y  2  0 . n n n n n A. n  685. B. n  679. C. n  675. D. n  673. Lời giải: Ta có: 3 2
y x  2018x y  3x  2018
Giả sử: M C , với k   M  3 1, 2,......
x ; x  2018x k k k k k  
Phương trình tiếp tuyến của C  tại M là  y x x xx x k  2k  k  3 : 3 2018 2018 k k k Gọi M  với Ck 1  là giao điểm của k
Phương trình hoành độ giao điểm của  với C  : k 3 x x   2 x
xx  3 2018 3 2018  x  2018x 3 3  x x x x x x x k
  k   k  2 2018 3  2018 k   0 k k k k     x x x x x x x x x x x x kk     k k      k 2 2 2 2 0   2 k   0 x  2  xk Suy ra M      3 2x ; 8x 2018.2x , k  1, 2,.... k 1 k k k  Hay x  2
x , với k 1,2,.... k 1  k *  x  2  x , n  
  x là một cấp số nhân với x  2 và công bội q  2 . n n 1  n 1   3n3 n 1  x   n    y  8.    n  2 2018.2. 2 n  n 1 * 2. 2 , n 1  3n3 n 1  Mà 2019
2018x y  2  0 nên         2019 2018.2. 2 8. 2 2018.2. 2  2  0 n n   3n   3 3n 3 2 3n 2019   1 .2  2    n  673 . 3  n  2019
Câu 46: (THPT Kinh Môn – Hải Dương 2019) Xét đồ thị C  của hàm số 3
y x  3ax b với a , b là
các số thực. Gọi M , N là hai điểm phân biệt thuộc C  sao cho tiếp tuyến với C  tại hai
điểm đó có hệ số góc bằng 3 . Biết khoảng cách từ gốc tọa độ tới đường thẳng MN bằng 1. Khi
đó giá trị lớn nhất của 2 2
a b bằng 3 2  A. 0 . B. . C. 2 . D. . 2 3 Lời giải:
 yx  3 2    1  x a 1
Giả sử M x ; y , N x ; y . Ta có 2
y  3x  3a . Từ giả thiết ta có   1  . 2 2  1 1  y   x  3 2 x a  1 2   2 Mặt khác 3
y x  3ax b x  2
x a  2ax b nên y  2a 1 x b . 1   1 1  1 1 1 1 1
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 19
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Tương tự y  2a 1 x b . 2   2
Suy ra phương trình đường thẳng MN là 2a  
1 x y b  0 . b
Giả thiết có d O, MN   1   1  2 2
b  4a  4a  2 . 2a  2 1 1 2  2  2 2  Vậy 2 2 2
a b  3a  4a  2  3  a      .  3  3 3 2  2  10
Giá trị lớn nhất của 2 2 a b bằng
đạt được khi và chỉ khi a  , b   . Vậy: n  673. 3 3 3
Câu 47: (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Cho hàm số 3 2
y  x  3x  9x có đồ thị C  . Gọi ,
A B, C, D là bốn điểm trên đồ thị C  với hoành độ lần lượt là a,b, c, d sao cho tứ giác ABCD
là một hình thoi đồng thời hai tiếp tuyến tại A và C song song với nhau và đường thẳng AC
tạo với hai trục tọa độ tam giác cân. Tính tích abcd . A. 60 . B. 120 . C. 144 . D. 180 . Lời giải: Đặt A ;
a y a, B ;
b y b, C ;
c yc , Dd; yd .
Theo giả thiết ya  yc 2 2  3
a  6a  9  3
c  6c  9  a c  2 (vì a c ).
Do đường thẳng AC cắt hai trục tọa độ tạo thành tam giác cân nên hệ số góc của đường thẳng AC: k  1 .
y c  y a 3 2 3 2
c  3c  9c a  3a  9a TH1: k  1  1  1  ac  1  0 c a c  . a b
  d a c  2 AB DC b
  a c d
Do ABCD là hình thoi nên ta có   
  yd   yb  bd  12  . AC BD y  1     BD 1  d b Do đó abcd  120 .
TH2: k  1 . Lập luận tương tự ta thu được abcd  120 .
Dạng 2:
VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN ĐI QUA MỘT ĐIỂM CHO TRƯỚC 2x  3
Câu 48: Có bao nhiêu tiếp tuyến của đồ thị y
đi qua giao điểm của hai đường tiệm cận? x  2 A. 1. B. Không có. C. Vô số. D. 2 . Lời giải: d
Đồ thị hàm số nhận đường thẳng x    2
 làm tiệm cận đứng. c a
Đồ thị hàm số nhận đường thẳng y
 2 làm tiệm cận ngang. c
Vậy I 2; 2 là giao điểm của hai đường tiệm cận. 7 TXĐ: D  \   2 . y '  2 (x  2)
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 20
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2x  3
Gọi tiếp tuyến tại M x ; y của đồ thị hàm số y  có dạng: 0 0  x  2  7 2x  3
: y y ' x .(x x )  y hay 0  : y  .(x x )  0  0 0 2 0 (x  2) x  2 0 0 7 2x  3 Vì  đi qua I  2  ;2 0  2  .( 2   x )  2 0 (x  2) x  2 0 0 7  2x  3 7  2x  3 0 0  2  .(x  2)   2   2 0 (x  2) x  2 (x  2) x  2 0 0 0 0 2x 10 0  2   4  1
 0 , phương trình vô nghiệm. x  2 0 2x  3
Vậy không tồn tại tiếp tuyến nào của đồ thị hàm số y
mà đi qua giao điểm của hai x  2 tiệm cận.
Câu 49: [SGD SOC TRANG_2018] Từ điểm M  1  ; 9
  có thể vẽ được bao nhiêu tiếp tuyến tới đồ thị hàm số 3 2
y  4x  6x 1 A. 1. B. 0 . C. 3 . D. 2 . Lời giải:
Lấy điểm A 3 2
x ; 4x  6x 1 thuộc đồ thị hàm số, tiếp tuyến tại A có phương trình 0 0 0  y   2
12x 12x  x x  3 2
 4x  6x 1. 0 0 0 0 0
Để tiếp tuyến qua M thì 9    2
12x 12x  1   x  3 2
 4x  6x 1 3 2  8
x  6x 12x 10  0 0 0 0 0 0 0 0 0 5
Phương trình có hai nghiệm x  1 và x
. Nên qua M có thể kẻ được hai tiếp tuyến tới đồ 0 0 4 thị hàm số. 3 2x Câu 50: Cho hàm số 2 y  
x  4x  2, gọi đồ thị của hàm số là C . Viết phương trình tiếp tuyến 3
của C  đi qua điểm A2;9 .
A. y  x  2 . B. y  8  x  5 .
C. y x  25 .
D. y  8x  25 . Lời giải:
Phương trình đường thẳng d  đi qua điểm A2;9 có hệ số góc k là y k(x  2)  9 . 3  2x0 2  
x  4x  2  k(x  2)  9 (1)
d  tiếp xúc với C  tại điểm có hoành độ x khi hệ 0 0 0  3 có 0  2 2
x  2x  4  k (2)  0 0 nghiệm x . 0 3 2x Thay 2 vào   1 ta được: 0 2 2 
x  4x  2  ( 2
x  2x  4)(x  2)  9 0 0 0 0 0 3 3 2
 4x 15x 12x  9  0  x  3 . 0 0 0 0
Thay x  3 vào 2 ta được k  8. 0
Vậy phương trình tiếp tuyến d  là y  8x  25 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 21
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2 x x 1
Câu 51: Cho hàm số y
có đồ thị C  . Viết phương trình tiếp tuyến của C  xuất phát từ x 1 M (1;3) .
A. y  3x 1 ; y  3x . B. y  13 ; y  3x .
C. y  3 ; y  3
x 1. D. y  3 ; y  3x . Lời giải: 2 x  2x Ta có y 
M (x ; y ) là tọa độ tiếp điểm của tiếp tuyến d với C  2 (x  . Gọi 1) 0 0 2 2 x  2x x x 1 0 0 0 0 d : y  (x x )  2 0 (x 1) x 1 0 0 2 2 x  2x x x 1 Cách 1: 0 0 0 0
M d  3  ( 1   x )  2 0 (x 1) x 1 0 0 1 2 2 2
 3(x 1)  (x  2x )(x 1)  (x 1)(x x 1) 2
 2x  5x  2  0  x  2, x  0 0 0 0 0 0 0 0 0 0 0 2
 Với x  2  Phương trình tiếp tuyến y  3 . 0  1 Với x
 Phương trình tiếp tuyến y  3x . 0 2
Cách 2: Gọi d là đường thẳng đi qua M (1;3) , có hệ số góc k , khi đó phương trình d có dạng:
y k (x 1)  3 .
d tiếp xúc đồ thị C  tại điểm có hoành độ x khi hệ phương trình sau có nghiệm x : 0 0 2  x x 1 0 0
k(x 1)  3 (1)  0  x 1 0  2 x   2x 0 0  k (2) 2 (x 1)  0 2 2 x x 1 x  2x 1 Thế 2 vào   1 ta được: 0 0 0 0  (x 1)  3 2
 2x  5x  2  0  x  2, x  . 2 0 x 1 (x 1) 0 0 0 0 2 0 0
 Với x  2  k  0  Phương trình tiếp tuyến y  3 . 0 1
 Với x   k  3
  Phương trình tiếp tuyến y  3x . 0 2
Câu 52: (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Cho hàm số 3 2
y x  3x  2 có đồ thị C  và điểm M  ; m 2
  . Gọi S là tập hợp tất cả các giá trị thực của m để qua M kẻ đúng hai tiếp
tuyến đến C  . Tổng tất cả các phần tử của S bằng 8 2 A. . B. 3 . C. . D. 2 . 3 3 Lời giải: 2
y  3x  6x
Phương trình tiếp tuyến tại Ax ; y có dạng y   2 3x  6x x x
x  3x  2 0 0   0  3 2 0 0  0 0
Tiếp tuyến qua M  ; m 2   , ta có:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 22
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2    2
3x  6x m x  3 2
x  3x  2 3 2  2
x  3x 1 m  6x m  4  0 0 0   0 0 0 0 0 ox  2  0   0 x  2 2 2
x  3m 1 x  2  0 1   0 0   0    2 2
x  3m 1 x  2  0 2  0   0  
Qua M kẻ đúng hai tiếp tuyến đến C  khi phương trình  
1 có đúng hai nghiệm phân biệt
 phương trình 2 có nghiệm kép khác 2 hoặc phương trình 2 có hai nghiệm phân biệt
trong đó có một nghiệm bằng 2 .
Trường hợp 1. Phương trình 2 có nghiệm kép khác 2  5   0 m     5 m    3   3m 1     .  3 2  m  1    4 m    1 m  3
Trường hợp 2. Phương trình 2 có hai nghiệm phân biệt trong đó có một nghiệm bằng 2    5 0  m   m   1 hoaëc 5    
3  m  2 . Vậy S   ; 2; 1  .  2  .4  2  3m  1  2  0  3  m  2 x  2 m
Câu 53: Cho hàm số y
có đồ thị (C ) và điểm Aa  ;1 . Biết  m a
( với mọi m, n N và tối x 1 n n
giản ) là giá trị để có đúng một tiếp tuyến của(C ) đi qua A. Khi đó giá trị m n là A. 2 . B. 7 . C. 5 . D. 3 . Lời giải: 1 TXĐ: D  \   1 . y '    x  2 1
Tiếp tuyến tại tiếp điểm có hoành độ x x  1 của (C ) có phương trình. 0  0  1 x  2 y   x x   2   0 0    x   1 x 1 0 0 2 1 x  2
2x  6x a  3  0 *
Đường thẳng  đi qua Aa  ;1 0 0 0  1   a x    2  0     x 1 x 1 x   0  0 0
Có duy nhất 1 tiếp tuyến qua A  pt * có duy nhất 1 nghiệm khác 1  '  0 3   2a  0 3  m     a  
m n  5 . 2
2.1  6.1 a  3  0 a 1  0 2 n x  3
Câu 54: (THPT NGÔ QUYỀN HÀ NỘI NĂM 2018 - 2019 LẦN 01) Cho hàm số y  có đồ thị là x 1
C, điểm M thay đổi thuộc đường thẳng d : y 1 2x sao cho qua M có hai tiếp tuyến của
C với hai tiếp điểm tương ứng là A , B . Biết rằng đường thẳng AB luôn đi qua điểm cố
định là H . Độ dài đoạn OH là A. 34 . B. 10 . C. 29 . D. 58 . Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 23
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Gọi M  ;1
m  2m  d . Gọi  là đường thẳng đi qua M có hệ số góc là k , khi đó phương trình
đường thẳng  : y k x m 1 2m .
x  3  kxm12m  x 1
Để  là tiếp tuyến của đồ thị C  thì hệ phương trình  có nghiệm. 4  
 x   k 2 1 4 x  3 Thay k        vào phương trình
k x m 1 2m ta được x  2 1 x 1 2
mx  22  mx m  2  0 * . Qua
M kẻ được hai tiếp tuyến với
C khi và chỉ khi phương trình g x 2
mx  22  mx m  2  0 có hai nghiệm phân biệt x  1 a m  0       
m2  mm   m 0 2 2  0   .    g    m 1
1  m  4  2m m  2  0
Gọi Ax ; y , Bx ; y là hai tiếp điểm, với x , x là hai nghiệm của phương trình * . B B A A A B  2m  2 x x   A B  Theo địnhlý Vi-et ta có m  . m  2 x x   A B  m
m  2 m  3 
Gọi I là trung điểm của đoạn thẳng AB thì I ;   .  m m 1  
2mx x B A
Mặt khác AB   x x ;
  một vectơ pháp tuyến của đường thẳng AB là B A m 1   n  2 ; m 1 m .
Phương trình đường thẳng đi qua hai điểm AB có một vectơ pháp tuyến n  2 ;
m 1 m và đi
m  2 m  3  qua điểm I ; 
 là 2mx  1 my  7  m  0 .  m m 1 
Gọi H x ; y
là điểm cố định mà đường thẳng AB đi qua. H H
Khi đó, 2mx  1 my m  7  0  m2x y  
1  y  7  0 với mọi m  0 và m  1. H H H H H
2x y 1  0 x  3  2 2 Suy ra H H H     H  3  ; 7
  . Vậy OH   3     7    58 . y  7  0 y  7   HH x  3
Câu 55: Cho hàm số y
có đồ thị là C  , điểm M thay đổi thuộc đường thẳng d : y  1 2x sao x 1
cho qua M có hai tiếp tuyến của C  với hai tiếp điểm tương ứng là A , B . Khoảng cách từ
O đến đường thẳng AB lớn nhất bằng A. 34 . B. 10 . C. 58 . D. 29 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 24
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải:
Kế thừa lời giải trên, ta có đường thẳng AB : 2mx  1 my m  7  0 luôn đi qua điểm cố định H  3  ; 7 .
Gọi K là hình chiếu vuông góc của O trên AB . Ta có OK OH  58 . Đẳng thức xảy ra khi
và chỉ khi K H , tức là OH AB hay
m    m 3 7.2 3 1  0  m
(thỏa điều kiện m  0 và 17
m  1). Vậy khoảng cách từ O đến đường thẳng AB lớn nhất bằng 58 .
Câu 56: (THPT SƠN TÂY HÀ NỘI NĂM 2018-2019 LẦN 01) Cho hàm số 3
y x 1 có đồ thị (C) .
Trên đường thẳng d : y x 1 tìm được hai điểm M x ; y , M x ; y mà từ mỗi điểm đó 2  2 2  1  1 1  3 1
kẻ được đúng hai tiếp tuyến đến C  . Tính giá trị biểu thức S   2 2
y y y y  1 2 1 2  5 3 113 41 14 59 A. . B. . C. . D. . 15 15 15 15 Lời giải:
Giả sử M d : y x 1, ta gọi M a; a  
1 . Đường thẳng  đi qua M a; a  
1 có hệ số góc k
có phương trình là: y k(x a)  a 1.
Đường thẳng  tiếp xúc với C  khi và chỉ khi hệ phương trình sau có nghiệm: 3  3 2
x 1  k(x a)  a 1
g(x)  2x 3ax a  0 *    . 2 3  x k 2 3  x k
Từ M kẻ được đúng hai tiếp tuyến đến C  khi và chỉ khi phương trình (*) có hai nghiệm phân biệt  hàm số 3 2
y g(x)  2x  3ax a có hai điểm cực trị x , x thỏa mãn g x  0 1  1 2
hoặc g x  0 2
g (x)  6x  6ax  0 có hai nghiệm phân biệt x , x và g x  0 hoặc 1  2  1 2 g x  0 . 2  x  0 Xét g ' x 2
 0  6x  6ax  0   . x aa  0 a  0   a  1 
Ta có: g(0)  0  a  0   . Suy ra: M 1;  0 và M 1;2 . 2   1     a 1 3 g(a)  0
a a  0 3 1 3 1 41 Vậy: S   2 2
y y y y     2 0  2  0.2   . 1 2 1 2  5 3 5 3 15
Câu 57: (THPT NINH BÌNH BẠC LIÊU NĂM 2018-2019 LẦN 04) Cho đồ thị C  3 2
: y x  3x . Có bao
nhiêu số nguyên b   10
 ;10 để có đúng một tiếp tuyến của C đi qua điểm B0;b? A. 2. B. 9. C. 17. D. 16. Lời giải: Gọi M  3 2
x ; x  3x là tiếp điểm. 0 0 0 0 
Tiếp tuyến  của (C) tại M có dạng y   2 3x  6x x xx  3x 0 0   0  3 2 0 0 0
 qua B(0;b)  b   2
3x  6x 0  x  3 2 3 2
x  3x b
  2x  3x (*) . 0 0 0 0 0 0 0
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 25
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Có đúng một tiếp tuyến của C  đi qua điểm B 0;b  (*) có đúng 1 nghiệm x . 0 x
Đặt g x 3 2
 2x  3x ; x 2 g
 6x  6x ; gx 0  0   . x 1
Ta có bảng biến thiên của hàm g(x)  b   0 b  0
Dựa vào bảng biến thiên suy ra phương trình * có đúng 1 nghiệm     .  b   1  b 1
Vì b nguyên và b   10
 ;10 , suy ra b 9
 ;8;...;1;2;3;....; 
9 , có 17 giá trị của b . x  2
Câu 58: Cho hàm số y
có đồ thị (C) và điểm (
A a;1) . Gọi S là tập hợp tất cả các giá trị thực x  1
của tham số a để có đúng một tiếp tuyến của (C) đi qua A . Tổng tất cả các giá trị các phần tử của S là 3 5 1 A. 1 . B. . C. . D. . 2 2 2 Lời giải: 1
ĐK: x  1 ; y '  (x  2 1)
Đường thẳng d qua A có hệ số góc k là y k(x a)  1  x
k(x a)  1  2  1  x  1
d tiếp xúc với (C)    có nghiệm. k  1 2 2    (x  1) 1 x  2 Thế 2 vào   1 ta có :
(x a)  1 
 x a  2
x  2x  1   2
x  3x  2, x  1 (x  2 1) x  1  2
2x  6x a  3  0 3
Để đồ thị hàm số có một tiếp tuyến qua A thì hệ là số nghiệm của hệ phương trình trên có
nghiệm duy nhất  phương trình 3 có nghiệm duy nhất khác 1
'  9  2a  6  0     a   3 1 6 3 0 a 2   
 2x  6x a  3  0 (3)   
'  9  2a  6   2  0 a    1
 2  6  a  3   0 1 
Cách 2: TXĐ : D  \   1 ; y   x  2 1
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 26
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Giả sử tiếp tuyến đi qua Aa
;1 là tiếp tuyến tại điểm có hoành độ x x , khi đó phương trình 0 1  x  2
tiếp tuyến có dạng : y x xd 2   0 0   x   1 x 1 0 0
Vì A d nên thay tọa độ điểm A vào phương trình đường thẳng d ta có : 2 1 x  2
2x  6x  3 a  0 1 1  a x    2  0  0 0   0 x 1 x 1 x  1  0  0 0
Để chỉ có một tiếp tuyến duy nhất đi qua A thì phương trình  
1 có nghiệm duy nhất khác 1
  9  2a  6  0   3 1
  6  a  3  0 a     2 
  9  2a  6  0   a  1
2  6  a  3  0 Dạng 3:
VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN KHI BIẾT HỆ SỐ GÓC CỦA TIẾP TUYẾN
Câu 59: (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số y f x có đồ thị như hình vẽ
Đồ thị hàm số đã cho có bao nhiêu tiếp tuyến vuông góc với trục Oy ? A. 3 . B. 0 . C. 2 . D. 1. Lời giải:
Từ đồ thị ta có hai tiếp tuyến vuông góc với trục Oy là y  1; y  2 .
Câu 60: (THPT Thăng Long – Hà Nội – Lần 1 – 2018) Có bao nhiêu điểm thuộc đồ thị hàm số 2x 1
y x  thỏa mãn tiếp tuyến với đồ thị có hệ số góc bằng 2018 ? 1 A. 1. B. 0 . C. Vô số. D. 2 . Lời giải:
Tập xác định D  \   1 . 1  y      . x   0, x 1 2 1 1 
Hệ số góc tiếp tuyến tại điểm x    
0 trên đồ thị bằng y  0 x  2018  vô nghiệm. x   2018 2 1
Vậy không có tiếp tuyến nào của đồ thị hàm số có hệ số góc bằng 2018 .
Câu 61: (THPT LƯƠNG TÀI - BẮC NINH - LẦN 2 - 2017 - 2018 - BTN) Biết tiếp tuyến của đồ thị hàm số 4 2
y ax bx  2 tại điểm A1; 
1 vuông góc với đường thẳng x  2 y  3  0 . Tính 2 2 a b . A. 2 2
a b  10 . B. 2 2
a b  13 . C. 2 2
a b  2 . D. 2 2
a b  5 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 27
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải: Ta có 3
y  ax bx x  2 4 2 2 2ax b . 1
Đường thẳng x  2 y  3  0 có hệ số góc k  . 2 Suy ra f  
1  2   22a b  2
  2a b  1 . A1; 
1 thuộc đồ thị hàm số nên a b  2  1  a b  1 2a b 1 a  2 Ta có hệ phương trình: 2 2    a b  5  . a b  1  b    3 1
Câu 62: (GKI NHÂN CHÍNH HÀ NỘI NĂM 2018-2019 LẦN 01) Cho hàm số 3 2 y
x  3x  2 có đồ 3
thị là C  . Viết phương trình tiếp tuyến với đồ thị C  biết tiếp tuyến có hệ số góc k  9 A. y 16  9
 x  3. B. y  9x  3 . C. y 16  9
 x 3 . D. y 16  9  x  3 . Lời giải: Ta có: 2
y  x  6x .
Gọi M x ; y là tiếp điểm của tiếp tuyến với C  . 0 0 
Ta có hệ số góc của tiếp tuyến là: y x  9  2
x  6x  9  2
x  6x  9  0  x  3  . 0  0 0 0 0 0
Với x  3  M  3  ; 16 . 0
Suy ra phương trình tiếp tuyến với đồ thị C  tại M  3
 ; 16 có dạng: y 16  9  x  3 .
Câu 63: (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Tiếp tuyến của đồ thị   1 x C : y
tại điểm có tung độ bằng 1 song song với đường thẳng x 1
A. d  : y  2x 1.
B. d  : y  x 1.
C. d  : y x 1 .
D. d  : y  2  x  2 . Lời giải: 2  1 x Ta có: y      
. Gọi Ax ;1 C thì 0 1 x 0 . 0    0 x  2 1 x 1 0
Tiếp tuyến của C  tại điểm A có phương trình: y y0 x  0  y 0  2  x 1.
Suy ra tiếp tuyến song song với d  : y  2  x  2 .
Câu 64: (THPT Hồng Bàng - Hải Phòng - Lần 1 - 2018) Cho đường cong C  3 2
: y x  2x  3x  4 và
đường thẳng d : 3x y  4  0 . Phương trình nào dưới đây là phương trình của đường thẳng
tiếp xúc với C  và song song với d ? 268 A. y  3x  .
B. y  3x  4 .
C. 81x  27 y  32  0 . D. 81x  27 y 140  0 . 27 Lời giải:
Tiếp tuyến song song với d nên hệ số góc của tiếp tuyến là k  3 , mà k y x . 0  x  0 0  4 32  Suy ra 2 
3x  4x  3  3 
. Do đó ta có hai điểm M 0; 4 , N  ; . 0 0 4    x    3 27  0  3
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 28
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Tại M 0; 4 , ta có tiếp tuyến là: y  3x  4 trùng với d nên không thỏa.  4 32   4  32 Tại N  ; 
 ta có tiếp tuyến là y  3 x    
 81x  27 y 140  0 .  3 27   3  27
Câu 65: (THPT Phan Đăng Lưu - Huế - Lần I -2018) Tìm phương trình tiếp tuyến của đồ thị hàm số x  2 1 y
, biết tiếp tuyến vuông góc với đường thẳng y
x  5 và tiếp điểm có hoành độ x 1 3 dương.
A. y  3x 10 . B. y  3  x  2 . C. y  3  x  6 . D. y  3  x  2 . Lời giải:
Gọi x là hoành độ tiếp điểm  x  0 . 0  0 1
Vì tiếp tuyến vuông góc với đường thẳng y
x  5 nên ta có: y x  3  0  3 3  x  0 (loaïi) 
   x 1 1 2
x  2x  0 0 
x  2  y  4 . 0 2  0 0  0 0 x   3 2 1 x  2  0 0
Vậy phương trình tiếp tuyến cần tìm là: y  3
 x  2  4  3x 10 .
Câu 66: (THPT Hải An - Hải Phòng - Lần 1 - 2017 - 2018) Tìm số tiếp tuyến song song với trục hoành của đồ thị hàm số 4 2
y x  2x 10 . A. 3 . B. 0 . C. 2 . D. 1. Lời giải: x  0 3
y  0  4x  4x  0   . x  1 
Hàm số đã cho là hàm bậc 4 trùng phương có hệ số a  0 nên có 3 điểm cực trị (1 cực đại, 2
cực tiểu) tuy nhiên, tiếp tuyến song song với trục hoành tại 2 điểm cực tiểu là trùng nhau nên
có 2 tiếp tuyến thoả mãn yêu cầu bài toán.
Câu 67: (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 02) Có bao nhiêu tiếp tuyến của đồ thị hàm số 3
y x  3x  2 song song với đường thẳng 9x y  14  0 ? A. 0 . B. 1 . C. 3 . D. 2 . Lời giải:
Gọi C  là đồ thị của hàm số 3
y x  3x  2 .
Tập xác định: D  . Đạo hàm: 2
y  3x  3 . Gọi d : 9x y  14  0  d : y  9x  14 .
Gọi  là tiếp tuyến cần tìm.
 // d : y  9x 14  Phương trình  có dạng y  9x m, m  1  4 . 3
x x   x   3 2 9 m
tiếp xúc C      * có nghiệm 2 3x  3  9 3
x  3x  2  9x m
x  2  m  14   l   *  x  2    x  2   m  18  n x  2 
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 29
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Suy ra phương trình tiếp tuyến cần tìm là  : y  9x  18 . x b
Câu 68: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Cho hàm số y  , ab  2   . Biết rằng ax  2
a , b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A1; 2 song song với
đường thẳng d : 3x y  4  0 . Khi đó giá trị của a  3b bằng A. 2  . B. 4 . C. 1  . D. 5 . Lời giải: ab  2 Ta có: y   . ax  22 1 b
Do A1; 2 thuộc đồ thị hàm số nên  2
  b  3 2a . a  2 ab  2
Do tiếp tuyến tại A1; 2 song song với d : 3x y  4  0 nên y  1  3      a  2 3 2 a 1
Thay b  3  2a ta được: a   a    a  2 3 2 2 3 2 2
 5a 15a 10  0   . a  2
+) Với a  2  b  1 (loại, do ab  2 )
+) Với a  1  b  1. Phương trình tiếp tuyến tại A1; 2 là y  3  x  
1  2 song song với d .
Vậy a  1 , b  1, suy ra a  3b  2 . x
Câu 69: (CHUYÊN VINH LẦN 3-2018) Cho đồ thị C  1 : y
và d , d là hai tiếp tuyến của C  2x 1 2
song song với nhau. Khoảng cách lớn nhất giữa d và d là 1 2 A. 3 . B. 2 3 . C. 2 . D. 2 2 . Lời giải: x  1 Do C  1 : y
, y x  x   0 . 2x 2 2x
d , d là hai tiếp tuyến của C  song song với nhau lần lượt có các hoành độ tiếp điểm là 1 2 1 1 x x
x , x x x , nên ta có y x = yx    1 2
x  x . 1   2 1 2  1 2   2 2 2x 2x 1 2 x  x  1 2 1 2  x 1  x 1 Gọi 1 1 M x ;
; N  x ;  . 1 1 2x 2x  1   1   x 1  1 x 1 1 x 1 PTTT d tại 1 M x ;  : y x x  
x x y   0 . 2  1  1 2  1  1 1 1 2x  2x 2x 2x 2x 1  1 1 1 1 2 x 4 Khi đó dd  1  . d , d N ;d 1 2   1  1 1 2 1 4x  4 1 2 4x x 1 1
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 30
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1 1 4 4 Áp dụng BĐT Cô-Si ta có 2 2 4x   2 4x .  4  d    2 . 1 2 1 2 d ; d 1 2  x x 1 2 1 1 2 4x  1 2 x1 Dạng 4:
HAI ĐỒ THỊ TIẾP XÚC
Câu 70: [Sở GD&ĐT Bình Phước-2017] Đồ thị của hàm số   3 2
f x x ax bx c tiếp xúc với trục
hoành tại gốc tọa độ và cắt đường thẳng x  1 tại điểm có tung độ bằng 3 khi.
A. a  2,b c  0 .
B. a  2,b  2, c  0 . C. a b  0, c  2 .
D. a c  0,b  2 . Lời giải: 3 2
f (x)  x ax bx c có đồ thị là C  .  f (x)  0 c   0
Vì C  tiếp xúc với Ox tại gốc tọa độ nên ta có: 3 2   
f (x)  x ax .
f (x)  0 b   0
Theo giả thiết C  cắt đường thẳng x  1 tại điểm có tung độ bằng 3 suy ra.
f (1)  3  1 a  3  a  2 . mx  2
Câu 71: Tìm tất cả các giá trị của tham số m sao cho tiệm cận ngang của đồ thị hàm số y x m 1 tiếp xúc với parabol 2 y x  7 . A. m  7 . B. m  7 . C. m  4 . D. m  . Lời giải: m  
Đồ thị hàm số có tiệm cận ngang khi m  m 1 1  2  0   . m  2
Khi đó đồ thị hàm số có tiệm cận ngang là y m  .
 tiếp xúc với parabol 2
y x  7  m  7 .
Câu 72: (Chuyên Thái Bình-Thái Bình-L4-2018) Họ parabol  P y mx m x mm  0 m  2 :   2 3   2
luôn tiếp xúc với đường thẳng d cố định khi m thay đổi. Đường thẳng d đó đi qua điểm nào dưới đây? A. 0; 2. B. 0; 2. C. 1;8. D. 1; 8  . Lời giải:
Gọi H x ; y là điểm cố định mà  P luôn đi qua. m  0 0  Khi đó ta có: 2
y mx  2 m  3 x m  2  m  2
x  2x  1  6x y  2  0 , m  0 . 0 0  0 0   0 0 0 2
x  2x 1  0 0 0   .
6x y  2  0  0 0 Do 2
x  2x  1  0 có nghiệm kép nên  P luôn tiếp xúc với đường thẳng d : y  6x  2 . m  0 0 Ta thấy 0; 2    d .
III- BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 73: Viết tất cả các phương trình tiếp tuyến của đồ thị C 3 2
: y x  2x  1, biết tiếp tuyến song song
với đường thẳng y  x  1.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 31
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 31 31
A. y x  1; y  x  1. B. y  x
; y  x  1. C. y  x  .
D. y  x  3; y  x  1. 27 27
Câu 74: Viết phương trình tiếp tuyến của C 3
: y x  2x tại điểm M 1;   1 .
A. y  2x  3.
B. y x  2.
C. y x  1. D. y   . x
Câu 75: Viết phương trình tiếp tuyến của đồ thị C 3 2
: y x  2x  1 tại điểm A1;0.
A. y x  1.
B. y  x  1. C. y   . x
D. y  2x  2.
Câu 76: Viết phương trình tiếp tuyến của đồ thị C 3 2
: y x  2x  1 tại giao điểm của C và Oy. A. y  1. B. y  2. C. y  1.
D. y  2x  1.
Câu 77: Viết tất cả các phương trình tiếp tuyến của đồ thị C 3 2
: y x  2x  1, biết tiếp tuyến song song
với đường thẳng y  x  2. 31
A. y x  1; y  x  1.
B. y  x
; y  x  1. 27 11
C. y  x
; y  x  1.
D. y  x  3; y  x  1. 27
Câu 78: Viết tất cả các phương trình tiếp tuyến của đồ thị C 3 2
: y x  2x  1, biết tiếp tuyến song song
với đường thẳng y  x  1. 31 31
A. y x  1; y  x  1. B. y  x
; y  x  1. C. y  x  .
D. y  x  3; y  x  1. 27 27
Câu 79: Có bao nhiêu tiếp tuyến của đồ thị C 3 2
: y x  2x  1, biết tiếp tuyến song song với đường
thẳng y  x  1? A. 1. B. 2. C. 3. D. 4.
Câu 80: Viết tất cả các phương trình tiếp tuyến của đồ thị C 3 2
: y x  2x  1, biết tiếp tuyến vuông góc
với đường thẳng x  7y  0. 365 14
A. y  7x  5; y  7x  .
B. y  7x  5; y  7x  . 27 27 365 365
C. y  7x  5; y  7x  .
D. y  7x  5; y  7x  . 27 27
Câu 81: Viết phương trình tiếp tuyến của đồ thị C 3 2
: y x  3x  2 tại điểm A 1  ; 2  .
A. y x  1.
B. y  9x  7. C. y  9 . x D. y  2 . x
Câu 82: Viết phương trình tiếp tuyến của đồ thị C 3 2
: y x  3x  2 tại giao điểm của C và Oy. A. y  1. B. y  2. C. y  4.
D. y  2x  1.
Câu 83: Viết tất cả các phương trình tiếp tuyến của đồ thị C 3 2
: y x  3x  2 , biết tiếp tuyến song song
với đường thẳng y  9x  2.
A. y  9x  7; y  9x  25.
B. y  9x  7; y  9x  25.
C. y  9x  7; y  9x  25.
D. y  9x; y  9x  25.
Câu 84: Viết tất cả các phương trình tiếp tuyến của đồ thị C 3 2
: y x  3x  2 biết tiếp tuyến song song
với đường thẳng y  9x  7.
A. y  9x  25.
B. y  9x  7; y  9x  25.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 32
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
C. y  9x  7; y  9x  25.
D. y  9x; y  9x  25.
Câu 85: Có bao nhiêu tiếp tuyến của đồ thị C 3 2
: y x  3x  2, biết tiếp tuyến song song với đường
thẳng y  9x  7 ? A. 1. B. 2. C. 3. D. 4.
Câu 86: Viết tất cả các phương trình tiếp tuyến của đồ thị C 3 2
: y x  3x  2, biết tiếp tuyến vuông
góc với đường thẳng x  3y  0. A. y  3  x  3. B. y  3  x  1. C. y  3  x  3. D. y  3  x  2. x
Câu 87: Viết phương trình tiếp tuyến của đồ thị C 2 1 : y
song song với đường thẳng x  2
 : 3x y  2  0.
A. y  3x  4.
B. y  3x  2.
C. y  3x  14.
D. y  3x  4.
Câu 88: Viết tất cả các phương trình tiếp tuyến của đồ thị C 3
: y x  3x  2 có hệ số góc bằng 9 .
A. y  9x  18; y  9x  22.
B. y  9x  14; y  9x  18.
C. y  9x  18; y  9x  22.
D. y  9x  14; y  9x  18. x   1 
Câu 89: Viết phương trình tiếp tuyến của đồ thị C 2 : y
tại điểm A 3; . x  1  2  1 1 1 1
A. y x  1.
B. y x  . C. y  . x D. y  . x 2 4 4 6 x
Câu 90: Viết phương trình tiếp tuyến của đồ thị C 2 : y
tại giao điểm của C và . Ox x  1
A. y x  1.
B. y x  2.
C. y x  1.
D. y x  2. x
Câu 91: Viết phương trình tiếp tuyến của đồ thị C 2 : y
tại giao điểm của C và Oy. x  1
A. y x  1.
B. y x  2.
C. y x  1.
D. y x  2. x
Câu 92: Viết phương trình tiếp tuyến của đồ thị C 2 : y
, biết tiếp tuyến song song với đường x  1
thẳng x y  0.
A. y x  2; y  . x
B. y x  2; y x  2. C. y x  1; y x  2. D. y x  2; y x  4. x
Câu 93: Viết phương trình tiếp tuyến của đồ thị C 2 : y
, biết tiếp tuyến song song với đường x  1
thẳng x y  2  0.
A. y x  2; y  . x
B. y x  2; y x  2. C. y x  1; y x  2. D. y x  2. x
Câu 94: Có bao nhiêu tiếp tuyến của đồ thị C 2 : y
, biết tiếp tuyến song song với đường thẳng x  1
x y  2  0? A. 1. B. 2. C. 3. D. 4.
Câu 95: Viết phương trình tiếp tuyến của đồ thị C 3 2
: y x  3x x  1 tại điểm có hoành độ x thỏa 0
mãn y x  3. 0  1 5 5 5
A. y   x  .
B. y   x  1. C. y  2  x  1
D. y   x  1. 4 4 4 4
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 33
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 3
Câu 96: Biết tiếp tuyến của đồ thị C 3 2
: y x  3x x  1 tại điểm có hoành độ x
cắt trục Ox, Oy 0 2
lần lượt tại A, B, tính diện tích S của tam giác OA . B 1 2 4 A. S  . B. S  . C. S  4. D. S  . 5 5 5
Câu 97: Viết phương trình tiếp tuyến của đồ thị C 4 2
: y x  2x  1 tại điểm có hoành độ x thỏa mãn 0
y x  16  0. 0 
A. y  8x  4.
B. y  8x  4; y  8x  4.
C. y  8x  4; y  8  x  4.
D. y  8x  4; y  8 . x 1 1
Câu 98: Tìm hệ số góc nhỏ nhất k
của tiếp tuyến với đồ thị C 3 2
: y x  2x  . min 3 3 A. k  4. B. k  4. C. k  0. D. k  2. min min min min 1 1
Câu 99: Viết phương trình tiếp tuyến với đồ thị C 3 2
: y x  2x  , biết tiếp tuyến có hệ số góc nhỏ 3 3 nhất. A. y  4  x  3
B. y  4x  3.
C. y  2x  3.
D. y  2x  3. 1 2
Câu 100: Tìm hệ số góc lớn nhất k
của tiếp tuyến với đồ thị C 3 2
: y   x  2x  . max 3 3 A. k  4. B. k  4. C. k  6. D. k  2. max max max max 1 2
Câu 101: Viết phương trình tiếp tuyến với đồ thị C 3 2
: y   x  2x  , biết tiếp tuyến có hệ số góc lớn 3 3 nhất. A. y  4  x  3.
B. y  4x  3.
C. y  4x  2.
D. y  2x  3.
Câu 102: Trong các đường thẳng có phương trình được cho dưới đây, đường thẳng nào là tiếp tuyến
của đồ thị C 3
: y x  3x  1? A. y  3  x  3. B. y  3  x  1. C. y  3 . x D. y  3  x  3.
Câu 103: Trong các đường thẳng có phương trình được cho dưới đây, đường thẳng nào là tiếp tuyến
của đồ thị C 3 2
: y x  2x  1?
A. y  x  3.
B. y  x  1.
C. y  x  2. D. y   . x
Câu 104: Biết các tiếp tuyến có hệ số góc bằng 1
 của đồ thị C 3 2
: y x  2x  1 tiếp xúc với C tại các điểm A, .
B Tính độ dài đoạn thẳng . AB 1447 1447 1447 1447 A. . B. . C. . D. . 24 3 27 9
Câu 105: Tiếp tuyến của đồ thị C 3 : y  4
x  3x  1 đi qua điểm A1;2 có phương trình là
A. y  9x  7; y  x  2. B. y  9
x  11; y  x  2. C. y  9
x  11; y  2. D. y  9
x  7; y  2. x
Câu 106: Tiếp tuyến của đồ thị C 2 1 : y
qua điểm A1; 4 có phương trình là x  1 1 13 1 1 1 A. y x  .
B. y x  .
C. y x  4.
D. y x  5. 3 3 3 3 3
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 34
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Câu 107: Cho hàm số 3 2
y x  3x x  1 có đồ thị C . Tiếp tuyến của C tại điểm thuộc đồ thị C có
hoành độ dương và là nghiệm của phương trình y  .
x y  11  0 có phương trình là
A. y  x  3.
B. y  4x  2.
C. y  x  2. D. y  4  x  3.
Câu 108: Cho hàm số 3 2
y x  3x có đồ thị C . Gọi M là điểm thuộc đồ thị C có hoành độ bằng 1.
Với giá trị nào của tham số m thì tiếp tuyến của C tại M song song với đường thẳng d y   2 :
m  4x  2m  1? A. m  1. B. m  1. C. m  2. D. m  2.
Câu 109: Cho hàm số 4
y x  m   2 2
1 x m  2 có đồ thị C . Gọi A là điểm thuộc đồ thị hàm số có
hoành độ bằng 1. Với giá trị nào của tham số m thì tiếp tuyến với đồ thị C tại A vuông góc
với đường thẳng  : x  4y  1  0? A. m  1. B. m  1. C. m  2. D. m  2.
Câu 110: Cho hàm số 3 2
y  2x  3x  5 có đồ thị C . Gọi d : y kx m là tiếp tuyến của C tại điểm có
hệ số góc tiếp tuyến nhỏ nhất. Tỉ số T  2m : k có giá trị bằng A. T  7. B. T  5. C. T  5. D. T  7.
Câu 111: Cho hàm số y f x có đồ thị C và điểm M x ; f x
thuộc C . Phương trình tiếp tuyến 0  0  0
của C tại M là: 0
A. y f x x x
. B. y f x
x x y . C. y y f x x . D. y y f x x x . 0  0 0  0  0 0   0  0   0  0
Câu 112: Cho hàm số y f x có đạo hàm trong khoảng a;b , đồ thị là đường cong C . Để đường
thẳng  : y ax b là tiếp tuyến của C tại điểm M x ; f x
, điều kiện cần và đủ là 0  0  0 / a   f x / a   f x0  0  A. /
a f x . B. /
ax b f x . C.  . D.  . 0  0 0  ax b   f x /  ax b   f x  0  0 0  0
Câu 113: Phương trình tiếp tuyến của đường cong C 3
: y x  2x  3 tại điểm M 1; 2 là
A. y  2x  2 .
B. y  3x  1 .
C. y x  1.
D. y  2  x .
Câu 114: Tiếp tuyến của đường cong C : y x x tại điểm M 1;1 có phương trình 3 1 3 1 3 1 x 3
A. y x  .
B. y   x  .
C. y x  . D. y   . 2 2 2 2 2 2 2 2 4
Câu 115: Tiếp tuyến với đồ thị hàm số y
tại điểm với hoành độ x  1 có phương trình x  1
A. y  x  3 .
B. y  x  2 .
C. y x  1 .
D. y x  2 .
Câu 116: Cho hàm số 2
y  x  5 có đồ thị C . Phương trình tiếp tuyến của C tại M có tung độ
y  1 , với hoành độ x  0 là kết quả nào sau đây? 0 0
A. y  2 6 x  6  1 . B. y  2
 6 x  6 1. C. y  2 6 x  6  1. D. y  2 6 x  6 1 .
Câu 117: Cho hàm số 2
y x  5x  4 có đồ thị C . Tiếp tuyến của C tại các giao điểm của C với
trục Ox , có phương trình:
A. y  3x  3 hoặc y  3  x  12 .
B. y  3x  3 hoặc y  3  x  12 .
C. y  2x  3 hoặc y  2  x  3 .
D. y  2x  3 hoặc y  2  x  3 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 35
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2x  1
Câu 118: Tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ bằng 2 , có hệ số góc bằng x  1 A. 1  . B. 3  . C. 3. D. 5.
Câu 119: Cho đường cong C 3
: y x . Tiếp tuyến của C có hệ số góc k  12 , có phương trình:
A. y  12x  16 .
B. y  12x  8 .
C. y  12x  2 .
D. y  12x  4 .
Câu 120: Cho hàm số 2
y x  2x  3 có đồ thị C . Tại điểm M x ; y C , tiếp tuyến có hệ số góc 0 0   
bằng 2 thì x y bằng 0 0 A. 2. B. 3. C. 4. D. 5. 3 x
Câu 121: Gọi C là đồ thị của hàm số 2 y  
 2x  3x  1. Có hai tiếp tuyến của C cùng có hệ số 3 3
góc bằng . Đó là các tiếp tuyến 4 3 29 3 3 37 3 A. y x
hoặc y x  3 . B. y x
hoặc y x  3 . 4 24 4 4 12 4 3 37 3 13 3 29 3 C. y x
hoặc y x  . D. y x
hoặc y x  3 . 4 12 4 4 4 24 4
Câu 122: Cho hàm số 3 2
y  2x  3x  4x  5 có đồ thị là C . Trong số các tiếp tuyến của C , có một tiếp
tuyến có hệ số góc nhỏ nhất. Hệ số góc của tiếp tuyến này bằng A. 3,5 . B. 5,5 . C. 7,5 . D. 9,5 .
Câu 123: Cho hàm số 3 2
y x  6x  9x có đồ thị C . Tiếp tuyến của C song song với đường thẳng
d : y  9x có phương trình
A. y  9x  40 .
B. y  9x  40 .
C. y  9x  32 .
D. y  9x  32 .
Câu 124: Gọi C là đồ thị của hàm số 4
y x x . Tiếp tuyến của C vuông góc với đường thẳng
d : x  5y  0 có phương trình là
A. y  5x  3 .
B. y  3x  5 .
C. y  2x  3 .
D. y x  4 .
Câu 125: Cho hàm số 3 2
y x  3x  1 có đồ thị là C . Gọi  là tiếp tuyến của C tại điểm A1; 5 và B
là giao điểm thứ hai của  với C . Diện tích tam giác OAB bằng A. 5. B. 6. C. 12. D. 6 82 .
Câu 126: Cho hàm số 3 2
y  4x  6x  1 có đồ thị C . Tiếp tuyến của C đi qua điểm M  1  ; 9   có phương trình 15 21
A. y  24x  15 . B. y x  . 4 4 15 21
C. y  24x  15 hoặc y x  .
D. y  24x  33 . 4 4
Câu 127: Cho hàm số 4 2
y x  3x có đồ thị là C . Các tiếp tuyến không song song với trục hoành kẻ từ
gốc tọa độ O0;0 đến C là
A. y  2x hoặc y  2x .
B. y x hoặc y  x . 4 4
C. y x hoặc y   x .
D. y  3x hoặc y  3x . 3 3
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 36
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2 x
Câu 128: Cho hàm số y
x  1 có đồ thị C . Từ điểm M 2;1 có thể kẻ đến C hai tiếp tuyến 4
phân biệt. Hai tiếp tuyến này có phương trình
A. y  x  1 hoặc y x  3 .
B. y  x  3 hoặc y x  1.
C. y  x  3 hoặc y x  1 .
D. y  x  1 hoặc y x  3 . 2x  1
Câu 129: Cho hàm số y
có đồ thị C . Gọi d là tiếp tuyến của C , biết d đi qua điểm A4; 1   . x  1
Gọi M là tiếp điểm của d và C , tọa độ điểm M là  3 
A. M 2; 5 , M 0; 1
 . B. M2;5, M 2  ;1 . C. M0; 1  , M 2  ;1. D. M 1  ; , M  2    ;1 .  2  x  2
Câu 130: Cho hàm số y
có đồ thị C . Trong tất cả các tiếp tuyến của C , tiếp tuyến thỏa mãn x  1
khoảng cách từ giao điểm của hai tiệm cận đến nó là lớn nhất, có phương trình
A. y  x  2 hoặc y  x  2 .
B. y  x  2 hoặc y  x  1 .
C. y x  2 hoặc y x  2 .
D. y  x  1 hoặc y  x  1 .  2  5 2m
Câu 131: Từ điểm A ;0 kẻ đến đồ thị hàm số 3
y x mx
hai tiếp tuyến vuông góc nhau thì  3  6 3
tập tất cả các giá trị của m bằng 1 1 A. m  hoặc m  2 .
B. m   hoặc m  2 . 2 2 1 1 C. m  hoặc m  2 .
D. m   hoặc m  2 . 2 2 x  2
Câu 132: Cho hàm số y
có đồ thị C . Tiếp tuyến của C tại điểm có hoành độ bằng 2 đi qua x  1
M 0; a thì a bằng A. a  10. B. a  9. C. a  3. D. a  1.
Câu 133: Cho hàm số 4 2 2
y x  2m x  2m  1 có đồ thị C . Tất cả các giá trị của tham số m để tiếp tuyến
của C tại giao điểm của C và đường thẳng d : x  1 song song với đường thẳng
 : y  12x  4 là A. m  0 . B. m  1 . C. m  2 . D. m  3 .
Câu 134: Cho hàm số 3
y x x  2 có đồ thị C . Để đường thẳng d : y  4x m tiếp xúc với C thì tập
tất cả các giá trị của m là
A. m  0 và m  4 .
B. m  1 và m  2 . C. m  3 .
D. Không có giá trị của m .
Câu 135: Cho hàm số 4
y x   m   2 3
5 x  4 có đồ thị là C . Để C
tiếp xúc với đường thẳng m m y  6
x  3 tại điểm có hoành độ bằng 1
 thì giá trị thích hợp của m là A. m  1 . B. m  2 . C. m  2 .
D. Không có giá trị m . ax  2
Câu 136: Cho hàm số y
có đồ thị là C . Tại điểm M  2  ; 4
  thuộc C , tiếp tuyến của Cbx  3
song song với đường thẳng d : 7x y  5  0 . Khi đó biểu thức liên hệ giữa a và b là
A. b  2a  0.
B. a  2b  0.
C. b  3a  0.
D. a  3b  0.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 37
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x b
Câu 137: Cho hàm số y
có đồ thị là C . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của ax  2
C tại điểm M1;2 song song với đường thẳng d :3x y  4  0 . Khi đó giá trị của a b bằng A. 2 . B. 1 . C. 1  . D. 0 . ax b
Câu 138: Cho hàm số y
có đồ thị là C . Nếu C đi qua A1;1 và tại điểm B trên C có 2x  3 hoành độ bằng 2
 , tiếp tuyến của C có hệ số góc k  5 thì các giá trị của a và b là
A. a  2;b  3 .
B. a  3; b  2 .
C. a  2; b  3 .
D. a  3; b  2  . ax b
Câu 139: Cho hàm số y
có đồ thị là C . Nếu C đi qua A3;1 và tiếp xúc với đường thẳng x  1
d : y  2x  4 , thì các cặp số a;b theo thứ tự là
A. 2; 4 hoặc 10; 28 . B. 2; 4
  hoặc 10;28 . C.  2
 ;4 hoặc 10;28 . D. 2; 4   hoặc  1  0; 2  8 . 2 ax bx  5 
Câu 140: Cho hàm số y
có đồ thị là C . Để C qua điểm A 1;  
 và tiếp tuyến của C tại x  2  2 
gốc tọa độ có hệ số góc bằng 3
 thì mối liên hệ giữa a và b là
A. 4a b  1.
B. a  4b  1.
C. 4a b  0.
D. a  4b  0. 1 14
Câu 141: Cho hàm số 4 2 y x
x có đồ thị C . Có bao nhiêu điểm A thộc C sao cho tiếp tuyến 3 3
của C tại A cắt đồ thị C tại hai điểm phân biệt M x ; y , N x ; y ( M , N khác A ) sao 2 2  1 1 
cho y y  8 x x . 2 1  2 1 A. 2 . B. 1 . C. 3 . D. 0 . x  2
Câu 142: Cho hàm số y
có đồ thị C và điểm Aa;1 . Gọi S là tập hợp tất cả các giá trị thực của a x  1
để có đúng một tiếp tuyến từ C đi qua A . Tổng tất cả giá trị của phần tử S bằng 3 5 1 A. 1 . B. . C. . D. . 2 2 2
IV – ĐỀ TỔNG ÔN TẬP §Ò Sè 1 x  1
Câu 1: Cho hàm số y
. Phương trình tiếp tuyến của đồ thị hàm số tại điểm M 1;0 là x  1 1 3 1 1 1 1 1 1
A. y x  .
B. y x  .
C. y x  .
D. y x  . 2 2 2 2 2 2 4 2 Câu 2: Cho hàm số 3
y x  3x có đồ thị C .Hệ số góc k của tiếp tuyến với đồ thị C tại điểm có tung độ bằng 4 là A. k  0. B. k  2. C. k  6. D. k  9. 1 Câu 3: Cho hàm số 3 2
y x x  2x  1 có đồ thị là C . Phương trình tiếp tuyến của C tại điểm 3  1  M 1;  là  3 
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 38
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2 2
A. y  3x  2. B. y  3  x  2.
C. y x  .
D. y  x  . 3 3 x
Câu 4: Phương trình tiếp tuyến của đồ thị H 2 4 : y
tại giao điểm của H và Ox là x  3 A. y  2 . x
B. y  2x  4. C. y  2  x  4.
D. y  2x  4. Câu 5: Cho hàm số 2
y x  2x  4 có đồ thị C . Phương trình tiếp tuyến của C tại điểm có hoành độ x  0 là 1 1 1
A. y  4x  3 .
B. y x  2 .
C. y   x  2 .
D. y   x  2 . 2 2 2 Câu 6: Cho hàm số 3
y x x  1 có đồ thị C . Phương trình tiếp tuyến của C tại giao điểm của C với trục tung là
A. y  2x  1 .
B. y  x  1 .
C. y  2x  2 .
D. y  x  1 .
Câu 7: Có bao nhiêu tiếp tuyến của đồ thị hàm số 3
y x  3x  2 song song với đường thẳng
9x y  14  0 ? A. 0 . B. 1 . C. 3 . D. 2 .
Câu 8: Đường thẳng nào sau đây là tiếp tuyến của đồ thị hàm số 3
y x  3x  2 ?
A. y  9x  12 .
B. y  9x  14 .
C. y  9x  13 .
D. y  9x  11 . 1 Câu 9: Cho hàm số 3 2
y x  3x  2 có đồ thị là C . Phương trình tiếp tuyến với đồ thị C biết tiếp 3
tuyến có hệ số góc k  9 là A. y  16  9
 x  3 . B. y  9  x  3 . C. y  16  9
 x  3 . D. y 16  9  x  3 .
Câu 10: Cho hàm số y f x có đồ thị như hình vẽ
Đồ thị hàm số đã cho có bao nhiêu tiếp tuyến vuông góc với trục Oy ? A. 3 . B. 0 . C. 2 . D. 1 . Câu 11: Cho hàm số 3 2
y  x  3x  9x  1 có đồ thị C . Hệ số góc lớn nhất của tiếp tuyến với đồ thị C bằng A. 1 B. 6 C. 12 D. 9 1
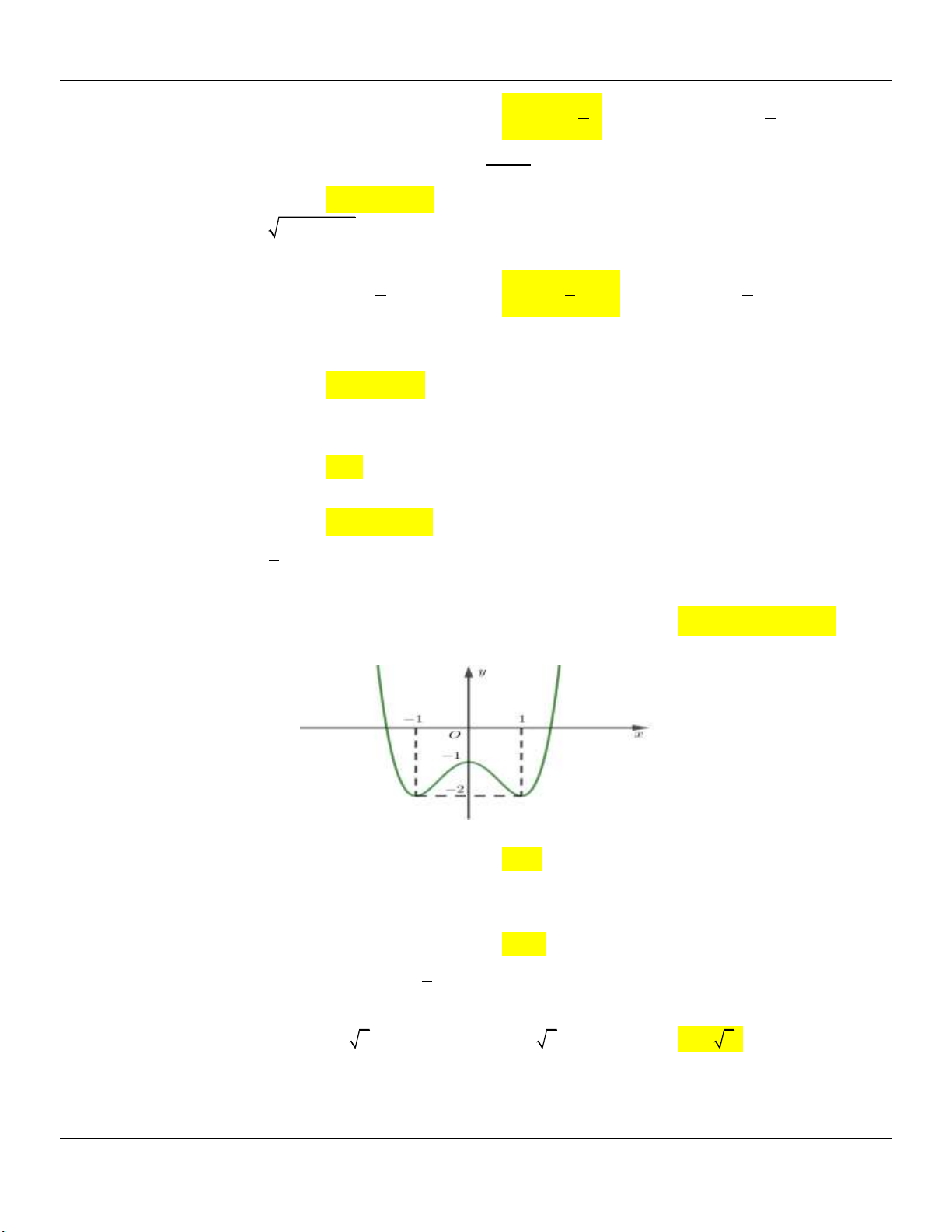
Câu 12: Tiếp tuyến với đồ thị hàm số 4 2
y   x  2x  3 tại điểm cực tiểu của đồ thị cắt đồ thị ở A, B 4
khác tiếp điểm. Độ dài đoạn thẳng AB bằng A. 2 . B. 2 . C. 2 2 . D. 4 2 .
Câu 13: Cho hàm số y  4x  2cos 2x có đồ thị là C . Hoành độ của các điểm trên C mà tại đó tiếp
tuyến của C song song hoặc trùng với trục hoành là
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 39
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia   A. x
k k  . B. x
k k  . C. x    k k  . D. x k2 k  . 4 2 ax b
Câu 14: Cho hàm số y f x 
,a,b,c,d ;c  0,d  0 có đồ thị C. Đồ thị của hàm số y f xcx d
như hình vẽ dưới đây. Biết C cắt trục tung tại điểm có tung độ bằng 2.
Phương trình tiếp tuyến của C tại giao điểm của C với trục hoành là
A. x  3y  2  0.
B. x  3y  2  0.
C. x  3y  2  0.
D. x  3y  2  0. x  1
Câu 15: Cho hàm số y
C . Điểm M thuộc C có hoành độ lớn hơn1 , tiếp tuyến của C tại x  1
M cắt hai tiệm cận của C lần lượt tại A , B . Diện tích nhỏ nhất của tam giác OAB bằng A. 4  2 2 . B. 4 . C. 4 2 . D. 4  2 . x  1
Câu 16: Cho hàm số y
(C), y x m (d) . Với mọi m đường thẳng (d) luôn cắt đồ thị (C) tại hai 2x  1
hai điểm phân biệt A và B. Gọi k1, k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A và B.
Giá trị nhỏ nhất của 2020 2020 T kk bằng 1 2 1 2 A. 1 . B. 2 . C. . D. . 2 3 x  2
Câu 17: Cho hàm số y
đồ thị C . Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị x  1
C đến một tiếp tuyến của C . Giá trị lớn nhất của d có thể đạt được là A. 3 3 . B. 3 . C. 2 . D. 2 2 . Câu 18: Cho hàm số 3
y x  1 có đồ thị (C) . Trên đường thẳng d : y x  1 tìm được hai điểm
M x ; y , M x ; y mà từ mỗi điểm đó kẻ được đúng hai tiếp tuyến đến C . Giá trị biểu 2  2 2  1  1 1  3 1 thức S   2 2
y y y y  bằng 1 2 1 2  5 3 113 41 14 59 A. . B. . C. . D. . 15 15 15 15
Câu 19: Cho hàm đa thức bậc bốn y f x có đồ thị C . Hàm số y f x có đồ thị như hình vẽ dưới
đây. Gọi đường thẳng  là tiếp tuyến của đồ thị C tại điểm có hoành độ bằng 1 . Hỏi  và
C có bao nhiêu điểm chung?
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 40
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia A. 2 . B. 3 . C. 1 . D. 4 .
Câu 20: Phương trình tiếp tuyến của đồ thị hàm số y f x thỏa mãn 2 f   x 3 1 2
x f 1 x tại điểm
có hoành độ x  1 là 1 6 1 6 1 6 1 6
A. y   x  .
B. y   x  . C. y x  . D. y x  . 7 7 7 7 7 7 7 7 HẾT §Ò Sè 2 1 2
Câu 1: Tọa độ điểm M có hoành độ âm trên đồ thị C 3
: y x x  sao cho tiếp tuyến tại M 3 3 1 2
vuông góc với đường thẳng y   x  là 3 3  4   4  A. M  2  ;  4 . B. M 1   ;  . C. M  2 ;  . D. M  2  ; 0 .  3   3  3  4x 7
Câu 2: Hệ số góc của tiếp tuyến của đồ thị hàm số y
tại điểm có tung độ y   , bằng x  2 3 9 5 5 A. . B.  . C. . D. 10. 5 9 9
Câu 3: Tập hợp tất cả các giá trị của tham số m để mọi tiếp tuyến của đồ thị hàm số 3 2
y x mx  2m  3 x  1 đều có hệ số góc dương là A.  \  0 . B. 1; . C.  \  1 . D.  . x
Câu 4: Hỏi trên đồ thị C 1 : y
có bao nhiêu điểm M mà tiếp tuyến với C tại M song song với x  2
đường thẳng d : x y  1? A. 4 . B. 1 . C. 2 . D. 0 .
Câu 5: Gọi d là tiếp tuyến tại điểm cực đại của đồ thị hàm số 3
y x  3x  2 . Khẳng định nào sau đây đúng?
A. d có hệ số góc âm.
B. d có hệ số góc dương.
C. d song song với đường thẳng y  4 .
D. d song song với trục Ox .
Câu 6: Gọi M, N là hai điểm di động trên đồ thị C của hàm số 3 2
y  x  3x x  4 sao cho tiếp
tuyến của C tại M và N luôn song song với nhau. Hỏi khi M,N thay đổi, đường thẳng
MN luôn đi qua nào trong các điểm có tọa độ dưới đây? A. 1; 5. B. 1; 5. C. Q1; 5. D. P 1; 5.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 41
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2x  1
Câu 7: Hỏi trên đồ thị hàm số y
có bao nhiêu cặp tiếp tuyến vuông góc với nhau? x  2 A. 1 . B. Vô số. C. 0 . D. 2 . x b
Câu 8: Cho hàm số y
, ab  2 . Biết rằng a , b là các giá trị thỏa mãn tiếp tuyến của đồ thị ax  2
hàm số tại điểm A1; 2 song song với đường thẳng d : 3x y  4  0 . Khi đó, giá trị a  3b bằng A. 2  . B. 4 . C. 1  . D. 5 . x  1
Câu 9: Cho hàm số y
(C) và d : y  2
x m  1 ( m là tham số thực). Gọi k , k là hệ số góc của x  2 1 2
tiếp tuyến của C tại giao điểm của d và C . Giá trị k .k bằng 1 2 1 A. . B. 2 . C. 3 . D. 4 . 4 Câu 10: Cho hàm số 3 2
y x  3x  3x  5 có đồ thị C . Có bao nhiêu giá trị nguyên của k trên  201  9; 2019 
 để trên đồ thị C có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường
thẳng d : y  k  3x? A. 2021 . B. 2017 . C. 2022 . D. 2016 . 2
x  2mx m
Câu 11: Có bao nhiêu giá trị của tham số thực m để đồ thị hàm số y
cắt trục Ox tại hai x m
điểm phân biệt và các tiếp tuyến của đồ thị tại hai điểm đó vuông góc với nhau? A. 5 B. 2 C. 0 D. 1 Câu 12: Cho hàm số 3 2
y x  3x  2 có đồ thị C và điểm M  ; m 2
  . Gọi S là tập hợp tất cả các giá trị
thực của m để qua M kẻ đúng hai tiếp tuyến đến C . Tổng tất cả các phần tử của S bằng 8 2 A. . B. 3. C. . D. 2. 3 3 2x
Câu 13: Cho hàm số y
, có đồ thị (C) và điểm M x ; y C (với x  0 ). Biết rằng khoảng cách 0 0    x  2 0
từ I 2; 2 đến tiếp tuyến của (C) tại M là lớn nhất, đẳng thức nào sau đây đúng?
A. 2x y  0 .
B. 2x y  4 .
C. 2x y  2 .
D. 2x y  2 . 0 0 0 0 0 0 0 0 x  2
Câu 14: Gọi d :y ax b, a, b  là tiếp tuyến của đồ thị hàm số y
. Biết d cắt trục hoành và 2x  3
trục tung lần lượt tại hai điểm A, B sao cho OAB cân tại O . Khi đó, a b bằng A. 1  . B. 0 . C. 2 . D. 3  . 1 3 Câu 15: Cho hàm số 3 2 y
x x  2 C . Xét hai điểm Aa; y và Bb; y phân biệt của đồ thị CB A  2 2
mà tiếp tuyến tại A và B song song. Biết rằng đường thẳng AB đi qua D5; 3 . Phương trình
của đường thẳng AB là
A. x y  2  0 .
B. x y  8  0 .
C. x  3y  4  0 .
D. x  2y  1  0 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 42
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Câu 16: Cho hàm số 3
y x  m   2
1 x x  2m  1 có đồ thị C ( m là tham số thực). Gọi m ,m là các giá 1 2
trị của m để đường thẳng d : y x m  1 cắt C tại ba điểm phân biệt A,B,C sao cho tổng hệ
số góc của các tiếp tuyến với C tại A,B,C bằng 19 . Khi đó m m bằng 1 2 A. 4  . B. 2 . C. 0 . D. 2  .
Câu 17: Gọi S là tập hợp tất cả các giá trị tham số m để đồ thị hàm số 3 2 2 3
f (x)  x  3mx  3mx m  2m
tiếp xúc với trục hoành. Tổng các phần tử của S bằng 2 4 A. 0 . B. 1 . C. . D. . 3 3
Câu 18: Cho hàm số bậc bốn y f x xác định và liên tục trên
, hàm số g x 2
 2x  3 và đường
thẳng d có đồ thị như hình vẽ dưới đây. 9
Biết A là điểm chung của đồ thị f x và gx , x  1 . Điểm B thuộc đồ thị gx , x   và A B 4
d là tiếp tuyến của đồ thị hàm số y f x . Giá trị f x bằng A  3 5 A. 1  . B.  . C.  . D. 2  . 2 2
Câu 19: Gọi A là điểm có hoành độ bằng 1 thuộc đồ thị C của hàm số 4 2
y x  2mx m ( m là tham a a
số thực). Ta luôn tìm được m  với là phân số tối giản để tiếp tuyến  với đồ thị C tại b b
A cắt đường tròn   2 2
: x y  2y  3  0 tạo thành một dây cung có độ dài nhỏ nhất. Khi đó,
tổng a b bằng A. 12 . B. 3 . C. 29 . D. 10 . 1 Câu 20: Cho hàm số 4 2
y x  3x có đồ thị (C) . Có bao nhiêu điểm A thuộc (C) sao cho tiếp tyến của 4
(C) tại A cắt (C) tại hai điểm phân biệt M x ; y , N x ; y (M,N khác A ) thỏa mãn 2 2  1 1 
y y  5 x x 1 2  1 2 A. 1 . B. 2 . C. 0 . D. 3 . HẾT §Ò Sè 1
B¶NG §¸P ¸N TR¾C NGHIÖM §Ò 1 Câu 1 2 3 4 5 6 7 8 9 10
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 43
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Đáp án B C C B C B B B D C Câu 11 12 13 14 15 16 17 18 19 20 Đáp án C D A D A B C B B A LêI GI¶I CHI TIÕT x  1
Câu 1: Cho hàm số y
. Phương trình tiếp tuyến của đồ thị hàm số tại điểm M 1;0 là x  1 1 3 1 1 1 1 1 1 A. y x  B. y x  C. y x  D. y x  2 2 2 2 2 2 4 2 Lời giải: 2 1 Ta có y   y 1  2   x   2 1 1
Phương trình tiếp tuyến của đồ thị hàm số tại điểm M 1;0 là y  x  1  1 1 0  y x  . 2 2 2
Chọn đáp án B. Câu 2: Cho hàm số 3
y x  3x có đồ thị C .Hệ số góc k của tiếp tuyến với đồ thị C tại điểm có tung độ bằng 4 là A. k  0 B. k  2 C. k  6 D. k  9 Lời giải:
Ta có hoành độ tiếp điểm của tiếp tuyến là nghiệm của phương trình 3
x  3x  4  x  1 Ta có 2
y'  3x  3. Hệ số góc của tiếp tuyến là k y'1  6 .
Chọn đáp án C. 1 Câu 3: Cho hàm số 3 2
y x x  2x  1 có đồ thị là C . Phương trình tiếp tuyến của C tại điểm 3  1  M 1;  là  3  2 2
A. y  3x  2 . B. y  3  x  2 .
C. y x  .
D. y  x  3 3 Lời giải: Ta có: 2
y  x  2x  2  y1  1  2  2  1  1  1 2
Phương trình tiếp tuyến của C tại điểm M 1;  là: y   y  1 x  
1  y x  .  3  3 3
Chọn đáp án C. x
Câu 4: Phương trình tiếp tuyến của đồ thị H 2 4 : y
tại giao điểm của H và Ox là x  3 A. y  2 . x
B. y  2x  4. C. y  2  x  4.
D. y  2x  4. Lời giải: 2x  4 y
y  0  x  2  M2;0 nên giao điểm của H và Ox là M2;0 . x  3 2  y       x
nên hệ số góc tiếp tuyến là y2 2 . x  3 3 2
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 44
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Vậy phương trình tiếp tuyến của đồ thị H tại giao điểm của H và Ox là y  2
 x  2  0  2  x  4 .
Chọn đáp án B. Câu 5: Cho hàm số 2
y x  2x  4 có đồ thị C . Phương trình tiếp tuyến của C tại điểm có hoành độ x  0 là 1 1 1
A. y  4x  3 .
B. y x  2 .
C. y   x  2 .
D. y   x  2 . 2 2 2 Lời giải: x  1 Ta có y  ; y  1
0   ; y 0  2 . 2 x  2x  4 2
Suy ra phương trình tiếp tuyến tại điểm có hoành độ x  0 là y y x   1 0
0  2  y   x  2 . 2
Chọn đáp án C. Câu 6: Cho hàm số 3
y x x  1 có đồ thị C . Phương trình tiếp tuyến của C tại giao điểm của C với trục tung là
A. y  2x  1 .
B. y  x  1 .
C. y  2x  2 .
D. y  x  1 . Lời giải:
Gọi M là giao điểm của C 
và trục tung. Khi đó M 0; 1 . Ta có 2
y  3x  1 .
Phương trình tiếp tuyến của C tại M là: y yx .x x   y y0.x  0  1  x  1 . M M M
Chọn đáp án B.
Câu 7: Có bao nhiêu tiếp tuyến của đồ thị hàm số 3
y x  3x  2 song song với đường thẳng
9x y  14  0 ? A. 0 . B. 1 . C. 3 . D. 2 . Lời giải:
Gọi C là đồ thị của hàm số 3
y x  3x  2 . Tập xác định: D  . Đạo hàm: 2
y  3x  3 . Gọi d : 9x y  14  0  d : y  9x  14 . Gọi  là tiếp tuyến cần tìm.
 // d : y  9x  14  Phương trình  có dạng y  9x m, m  14   . 3       x 3x 2 9x m
tiếp xúc C   * có nghiệm 2 3x  3  9 3
x  3x  2  9x m   
x   m   l * 2 14   x  2    x  2   m  18  nx  2  
Suy ra phương trình tiếp tuyến cần tìm là  : y  9x  18 .
Vậy có 1 tiếp tuyến thỏa yêu cầu bài toán.
Chọn đáp án B.
Câu 8: Đường thẳng nào sau đây là tiếp tuyến của đồ thị hàm số 3
y x  3x  2 ?
A. y  9x  12 .
B. y  9x  14 .
C. y  9x  13 .
D. y  9x  11 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 45
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải: 3
y x  3x  2 2
y  3x  3 .
Gọi d là tiếp tuyến của đồ thị hàm số tại điểm M x ; y . 0 0  x  2
  y  0  d : y  9x  18
Hệ số góc tiếp tuyến bằng 9  f x  2  3x  3  9 0 0 1   . 0 0
x  2  y  4  d : y  9x  14  0 0 2
Vậy đường thẳng y  9x  14 là tiếp tuyến của đồ thị hàm số 3
y x  3x  2 .
Chọn đáp án B. 1 Câu 9: Cho hàm số 3 2
y x  3x  2 có đồ thị là C . Phương trình tiếp tuyến với đồ thị C biết tiếp 3
tuyến có hệ số góc k  9 là A. y  16  9
 x  3 . B. y  9  x  3 . C. y  16  9
 x  3 . D. y 16  9  x  3 . Lời giải: Ta có: 2
y  x  6x .
Gọi M x ; y là tiếp điểm của tiếp tuyến với C . 0 0 
Ta có hệ số góc của tiếp tuyến là yx  9  2
x  6x  9 2
x  6x  9  0  x  3  . 0  0 0 0 0 0
Với x  3  M  3  ; 16 . 0
Suy ra phương trình tiếp tuyến với đồ thị C tại M  3
 ; 16 có dạng: y 16  9  x  3 .
Chọn đáp án D.
Câu 10: Cho hàm số y f x có đồ thị như hình vẽ
Đồ thị hàm số đã cho có bao nhiêu tiếp tuyến vuông góc với trục Oy ? A. 3 . B. 0 . C. 2 . D. 1 . Lời giải:
Từ đồ thị ta có hai tiếp tuyến vuông góc với trục Oy là y   ; 1 y  2 .
Chọn đáp án C. Câu 11: Cho hàm số 3 2
y  x  3x  9x  1 có đồ thị C . Hệ số góc lớn nhất của tiếp tuyến với đồ thị C bằng A. 1 B. 6 C. 12 D. 9 Lời giải: Ta có 2 y'  3
x  6x  9 ; y   x  2 ' 3 1  12  12
Vậy hệ số góc lớn nhất của tiếp tuyến với đồ thị C là 12 .
Chọn đáp án C.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 46
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 1
Câu 12: Tiếp tuyến với đồ thị hàm số 4 2
y   x  2x  3 tại điểm cực tiểu của đồ thị cắt đồ thị ở A, B 4
khác tiếp điểm. Độ dài đoạn thẳng AB bằng A. 2 . B. 2 . C. 2 2 . D. 4 2 . Lời giải: x  0 Ta có: 3
y  x  4x; y  0   . x  2   BBT:
Từ BBT suy ra điểm cực tiểu của đồ thị hàm số là M 0; 3 .
Tiếp tuyến của đồ thị tại điểm cực tiểu là đường thẳng y  3 .
Phương trình hoành độ giao điểm của đồ thị và tiếp tuyến là: 1 1 x  0 4 2 4 2
x  2x  3  3   x  2x  0    A 2
 2;3;B2 2;3  AB  4 2 . 4 4 x  2  2
Chọn đáp án D.
Câu 13: Cho hàm số y  4x  2cos 2x có đồ thị là C . Hoành độ của các điểm trên C mà tại đó tiếp
tuyến của C song song hoặc trùng với trục hoành là   A. x
k k  . B. x
k k  . C. x    k k  . D. x k2 k  . 4 2 Lời giải:
Ta có y  4  4 sin 2x .
Khi đó, hoành độ của các điểm trên C mà tại đó tiếp tuyến của C song song hoặc trùng
với trục hoành là nghiệm của phương trình:  
y  0  4  4 sin 2x  0  sin 2x  1  2x
k2  x   k k  . 2 4
Chọn đáp án A. ax b
Câu 14: Cho hàm số y f x 
,a,b,c,d ;c  0,d  0 có đồ thị C. Đồ thị của hàm số y f xcx d
như hình vẽ dưới đây. Biết C cắt trục tung tại điểm có tung độ bằng 2.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 47
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Phương trình tiếp tuyến của C tại giao điểm của C với trục hoành là
A. x  3y  2  0.
B. x  3y  2  0.
C. x  3y  2  0.
D. x  3y  2  0. Lời giải:
Đồ thị hàm số y f x đi qua 0; 2 suy ra b  2d . ad bc Ta có y   
. Đồ thị hàm số y có tiệm cận đứng x  1nên c d , đi qua 0; 3 nên cx d2 ad bc x  2 3 3 
hay a d . Do đó y   y  . 2 d x  1 x  2 1 1
Phương trình tiếp tuyến tại 2;0 là y  x  2  3x y  2  0 . 3
Chọn đáp án D. x  1
Câu 15: Cho hàm số y
C . Điểm M thuộc C có hoành độ lớn hơn1 , tiếp tuyến của C tại x  1
M cắt hai tiệm cận của C lần lượt tại A , B . Diện tích nhỏ nhất của tam giác OAB bằng A. 4  2 2 . B. 4 . C. 4 2 . D. 4  2 . Lời giải:
Tập xác định: D   \  1 . 2
Ta có: y      , x 1 . x  2 1
Đồ thị hàm số có đường tiệm cận ngang y  1 và đường tiệm cận đứng x  1 . m  1 2 2
Giả sử M m; y C m  1 y   1
; ym   . MM m  1 m  1 m 2 1 2 2
Phương trình tiếp tuyến  là: y  
x m  1  2   m m   1 1
x  m  2 2 2
1 y m  2m  1  0 .
Gọi A là giao điểm của  và đường tiệm cận ngang. Tọa độ điểm A là nghiệm của hệ y  1  phương trình:  2 2
x  2m  1  A 2m  1;1 y  
x m  1    . 2     m m   1 1
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 48
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Gọi B là giao điểm của  và đường tiệm cận đứng. Tọa độ điểm B là nghiệm của hệ phương x  1  m  3 4  4  trình:  2 2  y   1   . y  
x m  1    B1;1    2    m 1   m m 1 m 1 m   1 1 2 2  4  2 16 2 4
Suy ra: AB  2  2m   4m  1   m  1    4 . 2    m  1  m   m  1 1 2    2
m  2m  1 1 1 2 4 dO  m 2m 1 ;   S
d O AB m   OAB  ; . . .  1 4 4  4  m  14 2 2
 m   m 1 4 1 2    2 m 2m 1 m  2m  1   (vì m  1 ) m  1 m  1 2 2  m  3   4  m  1 . m  1 m  1 2
Áp dụng bất đẳng thức Cô-si cho hai số m  1 và : m   2 1   2 2 m  1 m  1   m   2 4 1   4  2 2 . m  1  2 m  1 
Vậy diện tích nhỏ nhất của tam giác OAB bằng 4  2 2 khi 
m  1  m  1  2 . m   1
Chọn đáp án A.x  1
Câu 16: Cho hàm số y
(C), y x m (d) . Với mọi m đường thẳng (d) luôn cắt đồ thị (C) tại hai 2x  1
hai điểm phân biệt A và B. Gọi k1, k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A và B.
Giá trị nhỏ nhất của 2020 2020 T kk bằng 1 2 1 2 A. 1 . B. 2 . C. . D. . 2 3 Lời giải: 2
2x  2mx m  1  0 x  1 
+ Phương trình hoành độ giao điểm:
x m   1 (*) 2x  1  x   2 + Phương trình (*) có: 2
'  m  2(m  1)  0, m
 nên (d) luôn cắt ( C ) tại 2 điểm phân biệt A,B.      a b m 1  
Gọi a, b là các hoành độ giao điểm a b    . Khi đó ta có:  m  1 .  2  ab    2 1 1 2 + Khi đó: 2020 2020 T kk    1 2 4040 4040 (2a  1) (2b  1)
[(2a  1)(2b  1)]2020 2 2    2 2020 2020
4ab  2(a  ) b  1  2
 (m  1)  2m  1    
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 49
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2020 2020 (  2a 1)  (2b  1) 
+ Nhận xét: Giá trị nhỏ nhất bằng 2 khi: 
a b  1  m m  1. 1 a b   2
Chọn đáp án B. x  2
Câu 17: Cho hàm số y
đồ thị C . Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị x  1
C đến một tiếp tuyến của C . Giá trị lớn nhất của d có thể đạt được là A. 3 3 . B. 3 . C. 2 . D. 2 2 . Lời giải:
Tiệm cận đứng d : x  1  0 , tiệm cận ngang d : y  1  0  tâm đối xứng là I 1;1 . 1 2  a  2  1  a  2
Phương trình tiếp tuyến tại điểm M a;  
 C là: y x a  d . 2    a  1  a a   1 1 1  a  2 1   a  2 2   a  1 a 1 a  1 2 2
Khi đó dI,d        2 . 1 1 1 2  1  1 a  1  4 4  2 a 1 a 1 a 12
Chọn đáp án C. Câu 18: Cho hàm số 3
y x  1 có đồ thị (C) . Trên đường thẳng d : y x  1 tìm được hai điểm
M x ; y , M x ; y mà từ mỗi điểm đó kẻ được đúng hai tiếp tuyến đến C . Giá trị biểu 2  2 2  1  1 1  3 1 thức S   2 2
y y y y  bằng 1 2 1 2  5 3 113 41 14 59 A. . B. . C. . D. . 15 15 15 15 Lời giải:
Giả sử M d : y x  1 , ta gọi M a; a  1 . Đường thẳng  đi qua M a; a  1 có hệ số góc k có
phương trình là: y k(x a)  a  1 .
Đường thẳng  tiếp xúc với C khi và chỉ khi hệ phương trình sau có nghiệm: 3
x  1  k(x a)  a  1 3 2  (
g x)  2x  3ax a  0 *    . 2 3x k 2 3x k
Từ M kẻ được đúng hai tiếp tuyến đến C khi và chỉ khi phương trình (*) có hai nghiệm phân biệt  hàm số 3 2 y  (
g x)  2x  3ax a có hai điểm cực trị x , x thỏa mãn g x  0 hoặc 1  1 2 g x  0 2
g (x)  6x  6ax  0 có hai nghiệm phân biệt x , x và gx  0 hoặc gx  0 . 2  1  2  1 2 x  0 Xét g'x 2
 0  6x  6ax  0   . x   aa  0 a  0   a  1  Ta có:  (
g 0)  0  a  0   .   a  1 3 ( g a)  0 a a    0
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 50
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 3 1 3 1 41 Suy ra: M 1
 ;0 và M 1;2 . Vậy: S   2 2
y y y y     2 0  2  0.2   . 1 2 1 2  2   1   5 3 5 3 15
Chọn đáp án B.
Câu 19: Cho hàm đa thức bậc bốn y f x có đồ thị C . Hàm số y f x có đồ thị như hình vẽ dưới
đây. Gọi đường thẳng  là tiếp tuyến của đồ thị C tại điểm có hoành độ bằng 1 . Hỏi  và
C có bao nhiêu điểm chung? A. 2 . B. 3 . C. 1 . D. 4 . Lời giải
Ta có tiếp tuyến  của C tại x  1 là y f 1x  1  f 1 .
Dựa vào đồ thị của hàm số f x , ta có f 1  0 . Vậy  : y f 1 .
Gọi a , a là hai nghiệm còn lại của f x . Dựa vào đồ thị hàm số ta có bảng biến thiên: 1 2
Dựa vào bảng biến thiên ta có  : y f 1 và C có ba điểm chung.
Chọn đáp án B.
Câu 20: Phương trình tiếp tuyến của đồ thị hàm số y f x thỏa mãn 2 f   x 3 1 2
x f 1 x tại điểm
có hoành độ x  1 là 1 6 1 6 1 6 1 6
A. y   x  .
B. y   x  . C. y x  . D. y x  . 7 7 7 7 7 7 7 7
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 51
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải: Ta có: 2 f   x 3 1 2
x f 1 x(*). 2 Đạo hàm hai vế (*)
4. f 1  2x. f 1  2x  1  3 f 1  xf 1  x ta được: (**)
 f 1  0l  2    f 1 3   f 1  f   1  1  tm
Khi x  0 từ (*) và (**) ta có hệ   f    f  2 4 1 .
1  1  3 f 1. f 1   f   1 1    7
Phương trình tiếp tuyến của đồ thị hàm số y f x tại điểm có hoành độ x  1 là: 1 6
y f 1x  1  f 1 hay y   x  . 7 7
Chọn đáp án A. §Ò Sè 02
B¶NG §¸P ¸N TR¾C NGHIÖM §Ò 02 Câu 1 2 3 4 5 6 7 8 9 10 Đáp án D C D D C C C A D C Câu 11 12 13 14 15 16 17 18 19 20 Đáp án D A B D D D C C C B LêI GI¶I CHI TIÕT 1 2
Câu 1: Tọa độ điểm M có hoành độ âm trên đồ thị C 3
: y x x  sao cho tiếp tuyến tại M 3 3 1 2
vuông góc với đường thẳng y   x  là 3 3  4   4  A. M  2  ;  4 . B. M 1   ;  . C. M  2 ;  . D. M  2  ; 0 .  3   3  Lời giải:  1 2  Ta có: 2
y  x  1  ya 2
a  1. Giả sử 3
M a ; a a    , a  0  3 3  1 2
Tiếp tuyến tại M vuông góc với đường thẳng y   x  nên ta có: 3 3 a  2
ya  3 2
a  1  3   . a  2  
Vì M có hoành độ âm nên ta chọn a  2 . Suy ra M  2  ;0 .
Chọn đáp án D. 3  4x 7
Câu 2: Hệ số góc của tiếp tuyến của đồ thị hàm số y
tại điểm có tung độ y   , bằng x  2 3 9 5 5 A. . B.  . C. . D. 10. 5 9 9 Lời giải: 7 3  4x 7 Ta có: y       x  1  . 3 x  2 3
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 52
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 5 Ta có: y     
. Vậy hệ số góc cần tìm là k y  5 1 . x  22 9
Chọn đáp án C.
Câu 3: Tập hợp tất cả các giá trị của tham số m để mọi tiếp tuyến của đồ thị hàm số 3 2
y x mx  2m  3 x  1 đều có hệ số góc dương là A.  \  0 . B. 1; . C.  \  1 . D.  . Lời giải:
Vì hệ số góc dương với mọi x nên ta xét: a  3  0
y  3x  2mx  2m  3  0  
m  6m  9  0  m  32 2 2  0  m .    0
Chọn đáp án D. x
Câu 4: Hỏi trên đồ thị C 1 : y
có bao nhiêu điểm M mà tiếp tuyến với C tại M song song với x  2
đường thẳng d : x y  1? A. 4 . B. 1 . C. 2 . D. 0 . Lời giải: 1  TXĐ: D   \  2 , y'    . x  2 0 2
Để tiếp tuyến với C tại M song song với đường thẳng d : y x  1 suy ra 1  y'   1 VN . 2   x 2
Vậy không có tiếp tuyến thỏa mãn.
Chọn đáp án D.
Câu 5: Gọi d là tiếp tuyến tại điểm cực đại của đồ thị hàm số 3
y x  3x  2 . Khẳng định nào sau đây đúng?
A. d có hệ số góc âm.
B. d có hệ số góc dương.
C. d song song với đường thẳng y  4 .
D. d song song với trục Ox . Lời giải:
Ta có đồ thị hàm số 3
y x  3x  2 nhận điểm A1;0 làm điểm cực đại. Mà y 1    0 .
Suy ra phương trình đường thẳng d : y  0 .
Do đó d song song với đường thẳng y  4 .
Chọn đáp án C.
Câu 6: Gọi M, N là hai điểm di động trên đồ thị C của hàm số 3 2
y  x  3x x  4 sao cho tiếp
tuyến của C tại M và N luôn song song với nhau. Hỏi khi M,N thay đổi, đường thẳng
MN luôn đi qua nào trong các điểm có tọa độ dưới đây? A. 1; 5. B. 1; 5. C. Q1; 5. D. P 1; 5. Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 53
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Vì tiếp tuyến của đồ thị hàm bậc ba tại 2 điểm M, N thuộc đồ thị hàm số song song với nhau
nên đường thẳng MN phải đi qua điểm uốn của C . Ta có 2 y  3
x  6x  1; y  6  x  6 Cho y  0  6
x  6  0  x  1. Điểm uốn Q1;5.
Chọn đáp án C. 2x  1
Câu 7: Hỏi trên đồ thị hàm số y
có bao nhiêu cặp tiếp tuyến vuông góc với nhau? x  2 A. 1 . B. Vô số. C. 0 . D. 2 . Lời giải: 2x  1 5 TXĐ: D   \   2 . Ta có: y   y  . x  2 x  22
Tiếp tuyến d của đồ thị hàm số tại M x ; y có dạng: y yx
x x y . 1   1  1 1  1  1
Tiếp tuyến d của đồ thị hàm số tại N x ; y có dạng: y yx
x x y . 2   2  2 2  2  2
d d yx yx  5 5 .  1     1
  x  2 . x  2  2  5 (vô lý). 2 2  1 2  2 2 1 2 1 2 x  2 x  2 1   2 
Vậy không có cặp tiếp tuyến nào của đồ thị vuông góc với nhau.
Chọn đáp án C. x b
Câu 8: Cho hàm số y
, ab  2 . Biết rằng a , b là các giá trị thỏa mãn tiếp tuyến của đồ thị ax  2
hàm số tại điểm A1; 2 song song với đường thẳng d : 3x y  4  0 . Khi đó, giá trị a  3b bằng A. 2  . B. 4 . C. 1  . D. 5 . Lời giải: ab  2 1  b Có y        
. Do A1; 2 thuộc đồ thị hàm số nên 2 b 3 2a . ax  22 a  2 ab  2
Do tiếp tuyến tại A1; 2 song song với d : 3x y  4  0 nên y1  3      a  2 3 2 a
Thay b  3  2a ta được phương trình a  a    a  2 3 2 2 3 2 2
 5a  15a  10  1 0   . a   2
+) Với a  2  b  1 (loại, do ab  2 )
+) Với a  1  b  1 . Phương trình tiếp tuyến tại A1; 2 là y  3
 x  1  2 song song với d .
Vậy a  1 , b  1 , suy ra a  3b  2 .
Chọn đáp án A. x  1
Câu 9: Cho hàm số y
(C) và d : y  2
x m  1 ( m là tham số thực). Gọi k , k là hệ số góc của x  2 1 2
tiếp tuyến của C tại giao điểm của d và C . Giá trị k .k bằng 1 2 1 A. . B. 2 . C. 3 . D. 4 . 4 Lời giải:
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 54
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia x  1
Xét phương trình hoành độ giao điểm 2
x m  1  (1) . x  2 2
 f(x)  2x (m  6)x  2m  3  0
Phương trình (1) có hai nghiệm phân biệt   có hai nghiệm  x  2   f ( 2  )  0 phân biệt    m . 2
  m  4m  12   0  m  6 x x   1 2 
Gọi x , x là hai nghiệm của phương trình (1) , khi đó 2  . 1 2 3  2mx .x  1 2  2  1 k   1  x  2 1 2
Hệ số góc của tiếp tuyến của C tại giao điểm của d và C là  . 1 k  2   x  22 2 1 1 1 1 Ta có k .k  .    4 . 1 2
x  22 x  22 2 2
x .x  2(x x )  4 3  2m m  6  1 2  1 2 1 2   2.  4    2 2 
Chọn đáp án D. Câu 10: Cho hàm số 3 2
y x  3x  3x  5 có đồ thị C . Có bao nhiêu giá trị nguyên của k trên  201  9; 2019 
 để trên đồ thị C có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường
thẳng d : y  k  3x? A. 2021 . B. 2017 . C. 2022 . D. 2016 . Lời giải: Ta có : 2
y'  3x  6x  3 .
TH1 : k  3 . Khi đó d : y  0  không tồn tại tiếp tuyến vuông góc với d . TH2 : k  3 . 1
Ta có : k  3 2
3x  6x  3  1  2
 3x  6x  3   0 * 0 0   0 0  k  3 3 
Theo yêu cầu bài toán , phương trình * có nghiệm  '  0   0  k  3 k  3
Vậy k 2019; 2
 018;...;0;1;2  Có 2022 giá trị nguyên của k thỏa đề bài.
Chọn đáp án C. 2
x  2mx m
Câu 11: Có bao nhiêu giá trị của tham số thực m để đồ thị hàm số y
cắt trục Ox tại hai x m
điểm phân biệt và các tiếp tuyến của đồ thị tại hai điểm đó vuông góc với nhau? A. 5 B. 2 C. 0 D. 1 Lời giải: 2 2
x  2mx m 3m m 2 3m m y   x  3m   y  1 . x m x mx m2
Xét phương trình hoành độ giao điểm của đồ thị hàm số đã cho với trục Ox .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 55
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 2
x  2mx m  0  f x 2
x  2mx m  0 * x  m . x m
Để đồ thị hàm số đã cho cắt trục Ox tại hai điểm phân biệt và các tiếp tuyến tại hai điểm đó
vuông góc với nhau thì phương trình (*) phải có hai nghiệm phân biệt x ; x khác m  và 1 2
yx .yx  1  . 1   2  m  1     m 0 2
  m m  0     m 0 
  f m 2
 3m m  0   1  m  5 .  m       3        yx  2 2 3m m 3m m y x .  1  1   1    1 2  m 0  
x m2  x m2     1 2  m   5
Chọn đáp án D. Câu 12: Cho hàm số 3 2
y x  3x  2 có đồ thị C và điểm M  ; m 2
  . Gọi S là tập hợp tất cả các giá trị
thực của m để qua M kẻ đúng hai tiếp tuyến đến C . Tổng tất cả các phần tử của S bằng 8 2 A. . B. 3. C. . D. 2. 3 3 Lời giải: Ta có: 2
y  3x  6x
Phương trình tiếp tuyến tại Ax ; y có dạng y   2 3x  6x
x x x  3x  2 0 0   0  3 2 0 0  0 0
Tiếp tuyến qua M  ; m 2   , ta có: 2    2
3x  6x m x  3 2
x  3x  2 0 0 0 0 0 3 2  2
x  3x 1 m  6x m  4  0  x  2 2 2
x  3m  1 x  2  0 1 0 0   0    0 0   ox  2  0 0   2 2
x  3m  1 x  2   0 2  0   0  
Qua M kẻ đúng hai tiếp tuyến đến C khi phương trình 1 có đúng hai nghiệm phân biệt
 phương trình 2 có nghiệm kép khác 2 hoặc phương trình 2 có hai nghiệm phân biệt
trong đó có một nghiệm bằng 2 .
Trường hợp 1: Phương trình 2 có nghiệm kép khác 2 .    5 0  m     5    3 m     3m  1   .  3  2  m  1   4     m 1 m   3
Trường hợp 2: Phương trình 2 có hai nghiệm phân biệt trong đó có một nghiệm bằng 2 .     0 5      m h 1 oÆc m    3  m  2 . 2  .4  2  3m12   0 m   2 5  Vậy S   ; 2; 1   . 3 
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 56
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
Chọn đáp án A. 2x
Câu 13: Cho hàm số y
, có đồ thị (C) và điểm M x ; y C (với x  0 ). Biết rằng khoảng cách 0 0    x  2 0
từ I 2; 2 đến tiếp tuyến của (C) tại M là lớn nhất, đẳng thức nào sau đây đúng?
A. 2x y  0 .
B. 2x y  4 .
C. 2x y  2 .
D. 2x y  2 . 0 0 0 0 0 0 0 0 Lời giải:
Tập xác định D   \   2 . 4  2xy  , 0 M x ;  2 (x  2) 0 x  2  0  4 2x
Phương trình tiếp tuyến tại M là y x x
 4x x  2 y  2x  0 2   0 0  0 2 2 0 (x  2) x  2 0 0
Khoảng cách từ I đến tiếp tuyến là 4( 2
 )  x  22 2 .2  2x 0 0 8  x  16 0 d   4  x  24 4  x  24 2 2 0 0 8  x  16 8 x  2
Áp dụng bất đẳng thức Cauchy, ta có 0 0   2 2 4  x  24 8x  22 2 0 0 x  0 Dấu bằng xảy ra khi 2 (x  2)  4 0  
. Vì x  0 nên x  4  y  4  2x y  4. 0 x  4   0 0 0 0 0 0
Chọn đáp án B. x  2
Câu 14: Gọi d :y ax b, a, b  là tiếp tuyến của đồ thị hàm số y
. Biết d cắt trục hoành và 2x  3
trục tung lần lượt tại hai điểm A, B sao cho OAB cân tại O . Khi đó, a b bằng A. 1  . B. 0 . C. 2 . D. 3  . Lời giải:  3 1 
TXĐ: D  \  . Ta có: y   0, x   D .  2  2x 32
Mặt khác, OAB cân tại O  hệ số góc của tiếp tuyến là 1  . 3 1 
Gọi tọa độ tiếp điểm x ; y , với x   . Ta có: y   1   x  2   x  1  . 0 0  0 2 2x  3 0 2 0 0
+) Với x  1  y  1 . Phương trình tiếp tuyến là: y  x loại vì A B O . 0 0 +) Với x  2
  y  0 . Phương trình tiếp tuyến là: y  x  2 thỏa mãn. 0 0
Vậy d :y  x  2  a  1; b  2  a b  3 .
Chọn đáp án D. 1 3 Câu 15: Cho hàm số 3 2 y
x x  2 C . Xét hai điểm Aa; y và Bb; y phân biệt của đồ thị CB A  2 2
mà tiếp tuyến tại A và B song song. Biết rằng đường thẳng AB đi qua D5; 3 . Phương trình
của đường thẳng AB là
A. x y  2  0 .
B. x y  8  0 .
C. x  3y  4  0 .
D. x  2y  1  0 .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 57
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia Lời giải:  1 3   1 3  Gọi 3 2
A a; a a   2  và 3 2
B b; b b  
2  với a b là hai điểm phân biệt thuộc đồ thị C  2 2   2 2 
mà tiếp tuyến tại A và B song song với nhau. 3 3
Ta có f a  f b 2 2
a  3a b  3b 2 2
a b  2a b  a b  2 . 2 2  a b 1 3  Gọi I ;  3 3
a b    2 2 a b   
2  là trung điểm của đoạn AB .  2 4 4 
 8  6ab 34  2ab 
Với a b  2 ta có I 1;   2  hay I 1;1 . 4 4     1 3 
Lại có AB b a;  3 3
b a    2 2 b  
a  cùng phương với u  2 2
2 ; a b ab  3a b .  2 2 
Hay u2;  2  ab . Nên đường thẳng AB có một véc tơ pháp tuyến là n2  ab; 2 .
Suy ra phương trình đường thẳng AB là 2  abx  1  2y  1  0 .
Do đường thẳng AB đi qua D5; 3 nên 42  ab  4  0  4ab  12  0  ab  3 .
Thay ab  3 vào phương trình AB ta được: x  2y  1  0 . 1 3
Cách khác: Đồ thị hàm số 3 2 y
x x  2 C có điểm uốn là I 1;1 . 2 2
Do đó đường thẳng AB đi qua D5; 3 và I 1;1 có phương trình là x  2y  1  0 .
Chọn đáp án D. Câu 16: Cho hàm số 3
y x  m   2
1 x x  2m  1 có đồ thị C ( m là tham số thực). Gọi m ,m là các giá 1 2
trị của m để đường thẳng d : y x m  1 cắt C tại ba điểm phân biệt A,B,C sao cho tổng hệ
số góc của các tiếp tuyến với C tại A,B,C bằng 19 . Khi đó m m bằng 1 2 A. 4  . B. 2 . C. 0 . D. 2  . Lời giải:
Phương trình hoành độ giao điểm của d và C : x  1 3
y x  m   2
1 x x m  0  x   1  2
x mx m  0   2
x mx m   0  *
Để d và C cắt nhau tại ba điểm phân biệt thì * phải có hai nghiệm phân biệt khác 1 , tức   0     
m   1 1 ; 4  0; 
  ; . Khi đó d và C cắt nhau tại ba điểm phân biệt 1   2m  0  2   2 
A1; m  2 ,Bx ; x m  1 ,C x ; x m  1 với x ; x là nghiệm của phương trình * 1 1   2 2  1 2
Hệ số góc tiếp tuyến của C tại A là: y1  2  2m . Hệ số góc tiếp tuyến của C tại B là: yx  2
 3x  2 m  1 x  1. 1 1   1
Hệ số góc tiếp tuyến của C tại C là: yx  2
 3x  2 m  1 x  1. 2 2   2
Theo giả thiết, ta có: 3 2 2 x x
 2 m  1 x x  4  2m  19 . 1 2    1 2
 3x x 2  6x x  2 m  1 x x  4  2m  19 * * 1 2 1 2   1 2  
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 58
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia
x x m 1 2 
thay vào * * , ta được 2
3m  6m  2m  
1 m  4  2m  19 .
x x  m 1 2 m  3 2 1
m  2m  15  0  
m m  2  . 1 2 m  5   2
Chọn đáp án D.
Câu 17: Gọi S là tập hợp tất cả các giá trị tham số m để đồ thị hàm số 3 2 2 3
f (x)  x  3mx  3mx m  2m
tiếp xúc với trục hoành. Tổng các phần tử của S bằng 2 4 A. 0 . B. 1 . C. . D. . 3 3 Lời giải: Ta có : 2
y  3x  6mx  3m ; y  6x  6m Cách 1:
TH1 : y có nghiệm kép và tâm đối xứng của đồ thị hàm số thuộc trục hoành m  0 2
m m  0  m  0         . y  mm 1   0  m  1 3 2 4  m  4m   0
TH2 : Đồ thị hàm số y f x có 2 cực trị và y .y  0 CÐ CT 2 m m  0 2 m m  0     1    2
m m  2m m   . 2   2 m m     2
2m m m 2 2 m m  2
2m m m   0 3  2 
 m m  2  m  1  1 2
Vậy m 0 ; 1 ;   , nên S  0  1   .  3  3 3 Cách 2: 3 2 2 3
x  3mx  3mx m  2m   0 1
Đồ thị hàm số y f x tiếp xúc trục hoành   có nghiệm. 2
3x  6mx  3m   0  2 x 4 3 4 6 3x 3x x 2x   2 2  m  . Thế vào 1 : 3 x      0 . 2x  1 2x  1
2x  1 2x  2 1 2x 3 1   1 x  0 x      1  2
 x  1 . Thay vào1 , ta được m0 ; 1;  . 3   3 x    3 2 6
x  14x  10x  2  0  1 x   3
Chọn đáp án C.
Câu 18: Cho hàm số bậc bốn y f x xác định và liên tục trên
, hàm số g x 2
 2x  3 và đường
thẳng d có đồ thị như hình vẽ dưới đây.
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 59
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia 9
Biết A là điểm chung của đồ thị f x và gx , x  1 . Điểm B thuộc đồ thị gx , x   và A B 4
d là tiếp tuyến của đồ thị hàm số y f x . Giá trị f x bằng A  3 5 A. 1  . B.  . C.  . D. 2  . 2 2 Lời giải:  9 57   13 65 
Vì các điểm A , B thuộc đồ thị hàm số g(x) nên ta có A1;  1 , B   ;   AB    ;  .  4 8   4 8 
Do d đi qua hai điểm A và B nên ta chọn vectơ pháp tuyến là n  65; 26 . d
Phương trình đường thẳng d là:
x   y   5 3 65 1 26
1  0  65x  26y  39  0  y   x  2 2
Mà d là tiếp tuyến của đồ thị hàm số y f x nên f x   . A  5 2
Chọn đáp án C.
Câu 19: Gọi A là điểm có hoành độ bằng 1 thuộc đồ thị C của hàm số 4 2
y x  2mx m ( m là tham a a
số thực). Ta luôn tìm được m  với là phân số tối giản để tiếp tuyến  với đồ thị C tại b b
A cắt đường tròn   2 2
: x y  2y  3  0 tạo thành một dây cung có độ dài nhỏ nhất. Khi đó,
tổng a b bằng A. 12 . B. 3 . C. 29 . D. 10 . Lời giải:
Đường tròn   x  y  2 2 :
1  4 có tâm I 0;1 , R  2 .
Ta có A1;1  m ; 3
y  4x  4mx y1  4  4m suy ra  : y  4  4mx  1  1  m .  3 
Dễ thấy  luôn đi qua điểm cố định F  ;0 và điểm F nằm trong đường tròn   .  4  M N F d R I
Giả sử  cắt   tại M , N , ta có: 2 2 MN
R d I  2 2 ;
 2 4  d I; .
Do đó MN nhỏ nhất  dI;  lớn nhất  dI;   IF    IF .
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 60
Chuyên đề KHẢO SÁT HÀM SỐ Luyện thi THPT Quốc gia  3 
Khi đó đường thẳng  có một véc-tơ chỉ phương u IF  ;  
1 ; u  1; 4  4m nên:  4  3 .
u n  0  1.  4  4m  0  13 m
suy ra a  13 , b  16 . Vậy a b  13  16  29 . 4 16
Chọn đáp án C. 1 Câu 20: Cho hàm số 4 2
y x  3x có đồ thị (C) . Có bao nhiêu điểm A thuộc (C) sao cho tiếp tyến của 4
(C) tại A cắt (C) tại hai điểm phân biệt M x ; y , N x ; y (M,N khác A ) thỏa mãn 2 2  1 1 
y y  5 x x 1 2  1 2 A. 1 . B. 2 . C. 0 . D. 3 . Lời giải:  1  Ta có: 3 y'  x  6 . x Gọi 4 2 A x ; x  
3x  là tọa độ tiếp điểm của tiếp tuyến tại A. Phương trình 0 0 0  4  1
tiếp tuyến tại A là đường thẳng (d) có phương trình: y   3
x  6x x x  4 2  x  3x 0 0 0 0 0 4
Phương trình hoành độ giao điểm của (d) và (C) là:  3 2
x  6x x x  1 4 2 1 4 2
x  3x x  3x  x x   2 2
x  2x x  3x  12  0 0 0 0  0 0 0 0 0 4 4 x x  0 0   2
x  2x x  3x  12  0 (2)  0 0
(d) cắt (C) tại hai điểm phân biệt khác A khi và chỉ chi phương trình (2) có hai nghiệm phân x   2 biệt khác x 0   (3) 0  6  x  6  0
Khi đó, phương trình (2) có hai nghiệm phân biệt x , x và (d) cắt (C) tại hai điểm phân 1 2
biệt M(x ; y ) , N(x ; y ) trong đó: 1 1 2 2 y  
 3x 6x x x  1 4 2  x  3x 1 0 0 1 0 0 0  4 
y y   3 x  6x x x 1 2 0 0   1 2 
y   3x 6x x x  1 4 2  x  3x 2 0 0 2 0 0 0  4
Từ giả thiết ta suy ra: 3
(x  6x )(x x )  5(x x ) 3
x  6x  5 (Vì x x ) 0 0 1 2 1 2 0 0 1 2  x  1  0   1   21  x  0  2   1   21 x  0  2 1   21
Kết hợp với điều kiện (3) có hai giá trị x thỏa mãn yêu cầu bài toán là x  1  ; x  . 0 2
Chọn đáp án B.
_____________HẾT_____________
Huế, ngày 07 tháng 9 năm 2020
Lớp Toán thầy LÊ BÁ BẢO TP Huế -Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm BDKT Km10 Hương Trà 61