Chuyên đề tìm GTLN, GTNN của biểu thức Toán 8

Sưu tầm chuyên đề tìm GTLN, GTNN của biểu thức TOÁN 8. Tài liệu được biên soạn dưới dạng file PDF gồm 27 trang với hai phần: các kiến thức thường sử dụng và dạng toán kèm cách giải giúp bạn củng cố kiến thức, ôn tập và có đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!

82 41 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 8

Môn: Toán 8

Thông tin:

26 trang 9 tháng trước

Tác giả:

Profile Hoàng Ngân
Trang 1
CHUYÊN ĐỀ : TÌM GTLN, GTNN CỦA BIỂU THỨC
A. Các kiến thức thường sử dụng là:
+ Bất đẳng thức Côsi: “Cho hai số không âm a, b; ta có bất đẳng thức:
2
ab
ab
+
;
Dấu “=” xảy ra khi và chỉ khi a = b”.
+ Bất đẳng thức:
( )
( )( )
2
2 2 2 2
ac bd a b c d+ + +
(BĐT: Bunhiacopxki);
Dấu “=” xảy ra khi và chỉ khi
ab
cd
=
.
+
a b a b+ +
; Dấu “=” xảy ra khi và chỉ khi ab
0.
+ Sử dụng “bình phương” để tìm giá trị lớn nhất, giá trị nhỏ nhất.
Nếu
2
()y a f x=+
thì min y = a khi f(x) = 0.
Nếu
2
()y a f x=−
thì max y = a khi f(x) = 0.
+ Phương pháp “tìm miền giá trị” (cách 2 ví dụ 1 dạng 2).
B. CÁC DẠNG TOÁN VÀ CÁCH GIẢI
• Dạng 1: CÁC BÀI TOÁN MÀ BIỂU THỨC CHO LÀ MỘT ĐA THỨC
Bài toán 1: Tìm GTNN của các biểu thức:
a)
2
4 4 11A x x= + +
b) B = (x-1)(x+2)(x+3)(x+6)
c)
Giải:
a)
( )
2
22
4 4 11 4 4 1 10 2 1 10 10A x x x x x= + + = + + + = + +
Min A = 10 khi
1
2
x =−
.
b) B = (x-1)(x+2)(x+3)(x+6) = (x-1)(x+6)(x+2)(x+3)
= (x
2
+ 5x – 6)(x
2
+ 5x + 6) = (x
2
+ 5x)
2
– 36
-36
Min B = -36 khi x = 0 hoặc x = -5.
c)
= (x
2
– 2x + 1) + (y
2
– 4y + 4) + 2 = (x – 1)
2
+ (y – 2)
2
+ 2
2
Min C = 2 khi x = 1; y = 2.
Bài toán 2: Tìm GTLN của các biểu thức:
Trang 2
a) A = 5 – 8x – x
2
b) B = 5 – x
2
+ 2x – 4y
2
– 4y
Giải:
a) A = 5 – 8x – x
2
= -(x
2
+ 8x + 16) + 21 = -(x + 4)
2
+ 21
21
Max A = 21 khi x = -4.
b) B = 5 – x
2
+ 2x – 4y
2
– 4y
= -(x
2
– 2x + 1) – (4y
2
+ 4y + 1) + 7
= -(x – 1)
2
– (2y + 1)
2
+ 7
7
Max B = 7 khi x = 1,
1
2
y =−
.
Bài toán 3: Tìm GTNN của:
a)
1 2 3 4M x x x x= − + − + − + −
b)
( )
2
2 1 3 2 1 2N x x= − − − +
Giải:
a)
1 2 3 4M x x x x= − + − + − + −
Ta có:
1 4 1 4 1 4 3x x x x x x− + − = − + − − + − =
Dấu “=” xảy ra khi và chỉ khi (x – 1)(4 – x)
0 hay
14x
2 3 2 3 2 3 1x x x x x x− + − = − + − − + − =
Dấu “=” xảy ra khi và chỉ khi (x – 2)(3 – x)
0 hay
23x
Vậy Min M = 3 + 1 = 4 khi
23x
.
b)
( )
2
2
2 1 3 2 1 2 2 1 3 2 1 2N x x x x= − − − + = − − − +
Đặt
21tx=−
thì t
0
Do đó N = t
2
– 3t + 2 =
2
3
2
1
()
4
t −−
1
4
N −
.
Dấu “=” xảy ra khi và chỉ khi
33
0
22
tt− = =
Do đó
1
4
N =−
khi
35
21
33
24
21
31
22
21
24
xx
tx
xx

− = =

= − =


− = − = −


Vậy min
15
44
Nx= − =
hay
1
4
x =−
.
Bài toán 4: Cho x + y = 1. Tìm GTNN của biểu thức M = x
3
+ y
3
.
Trang 3
Giải:
M = x
3
+ y
3
= (x + y)(x
2
– xy + y
2
) = x
2
- xy + y
2
2
2 2 2 2
22
1
()
2 2 2 2 2
22
x y x y x y
xy x y

= + + − + = + + −


22
1
()
2
M x y +
Ngoài ra: x + y = 1
x
2
+ y
2
+ 2xy = 1
2(x
2
+ y
2
) – (x – y)
2
= 1
=> 2(x
2
+ y
2
) ≥ 1
Do đó
22
1
2
xy+
và
22
11
22
x y x y+ = = =
Ta có:
22
1
()
2
M x y+
và
22
1 1 1 1
( ) .
2 2 2 4
x y M+ =
Do đó
1
4
M
và dấu “=” xảy ra
1
2
xy = =
Vậy GTNN của
11
42
M x y= = =
Bài toán 5: Cho hai số x, y thỏa mãn điều kiện:
(x
2
– y
2
+ 1)
2
+ 4x
2
y
2
– x
2
– y
2
= 0.
Tìm GTLN và GTNN của biểu thức x
2
+ y
2
.
Giải:
(x
2
– y
2
+ 1)
2
+ 4x
2
y
2
– x
2
– y
2
= 0
[(x
2
+ 1) – y
2
]
2
+ 4x
2
y
2
– x
2
– y
2
= 0
x
4
+ 2x
2
+ 1 + y
4
– 2y
2
(x
2
+ 1) + 4x
2
y
2
– x
2
– y
2
= 0
x
4
+ y
4
+ 2x
2
y
2
+ x
2
– 3y
2
+ 1 = 0
x
4
+ y
4
+ 2x
2
y
2
- 3x
2
– 3y
2
+ 1 = -4x
2
(x
2
+y
2
)
2
-3(x
2
+y
2
)+1=-4x
2
Đặt t = x
2
+ y
2
. Ta có: t
2
– 3t + 1 = -4x
2
Suy ra: t
2
– 3t + 1 ≤ 0
Trang 4
2
2
3 9 5
2. . 0
2 4 4
3 5 3 5
2 4 2 2
5 3 5
2 2 2
3 5 3 5
22
tt
tt
t
t
− + −

− −


− −
−+
Vì t = x
2
+ y
2
nên :
GTLN của x
2
+ y
2
=
35
2
+
GTNN của x
2
+ y
2
=
35
2
−
Bài toán 6: Cho 0 ≤ a, b, c ≤ 1. Tìm GTLN và GTNN của biểu thức:
P = a + b + c – ab – bc – ca.
Giải:
Ta có: P = a + b + c – ab – bc – ca
= (a – ab) + (b - bc) + (c – ca)
= a(1 – b) + b(1 – c) + c(1 – a) 0 (vì
0 , , 1abc
)
Dấu “=” có thể xảy ra chẳng hạn: a = b = c = 0
Vậy GTNN của P = 0
Theo giả thiết ta có: 1 – a
0; 1 – b
0; 1 – c
0;
(1-a)(1-b)(1-c) = 1 + ab + bc + ca – a – b – c – abc
0
P = a + b + c – ab – bc – ac
11abc −
Dấu “=” có thể xảy ra chẳng hạn: a = 1; b = 0; c tùy ý
0;1
Vậy GTLN của P = 1.
Bài toán 7: Cho hai số thực x, y thỏa mãn điều kiện: x
2
+ y
2
= 1.
Tìm GTLN và GTNN của x + y.
Giải:
Ta có: (x + y)
2
+ (x – y)
2
(x + y)
2
2(x
2
+ y
2
)
(x + y)
2
Mà x
2
+ y
2
= 1
(x + y)
2
2
Trang 5
2 2 2x y x y + − +
- Xét
2xy+
Dấu “=” xảy ra
2
2
2
xy
xy
xy
=
= =
+=
- Xét
2xy+ −
Dấu “=” xảy ra
2
2
2
xy
xy
xy
=
−
= =
+ = −
Vậy x + y đạt GTNN là
2−
2
2
xy
−
= =
.
Bài toán 8: Cho các số thực dương thỏa mãn điều kiện: x
2
+ y
2
+ z
2
27.
Tìm GTLN và GTNN của biểu thức: x + y + z + xy + yz + zx.
Giải:
Ta có: (x – y)
2
+ (x – z)
2
+ (y – z)
2
0
2x
2
+ 2y
2
+ 2z
2
- 2xy - 2yz - 2zx
0
(x + y + z)
2
= x
2
+ y
2
+ z
2
+2(xy + yz + zx)
3(x
2
+ y
2
+ z
2
)
81
x + y + z
9 (1)
Mà xy + yz + zx
x
2
+ y
2
+ z
2
27 (2)
Từ (1) và (2) => x + y + z + xy + yz + zx
36.
Vậy max P = 36 khi x = y = z = 3.
Đặt A = x + y + z và B = x
2
+ y
2
+ z
2
22
( 1) 1 1
2 2 2 2
A B A B B
PA
− + + +
= + = − −
Vì B
27
1
2
B +
−
-14
P
-14
Vậy min P = -14 khi
2 2 2
1
27
x y z
x y z
+ + = −
+ + =
Hay
13; 13; 1x y z= − = = −
.
Bài toán 9:
Giả sử x, y là các số dương thỏa mãn đẳng thức: x + y =
10
. Tìm giá trị của x và y
để biểu thức: P = (x
4
+ 1)(y
4
+ 1) đạt GTNN. Tìm GTNN ấy.
Giải:
Ta có: P = (x
4
+ 1)(y
4
+ 1) = (x
4
+ y
4
) + (xy)
4
+ 1
Đặt t = xy thì:
Trang 6
x
2
+ y
2
= (x + y)
2
– 2xy = 10 – 2t
x
4
+ y
4
= (x
2
+ y
2
)
2
– 2x
2
y
2
= (10 – 2t)
2
– 2t
2
= 2t
2
– 40t + 100
Do đó: P = 2t
2
– 40t + 100 + t
4
+ 1 = t
4
+ 2t
2
– 40t + 101
= (t
4
– 8t
2
+ 16) + 10(t
2
– 4t + 4) + 45 = (t
2
– 4)
2
+ 10(t – 2)
2
+ 45
45P
và dấu “=” xảy ra
x + y =
10
và xy = 2.
Vậy GTNN của P = 45
x + y =
10
và xy = 2.
Bài toán 10:
Cho x + y = 2. Tìm GTNN của biểu thức: A = x
2
+ y
2
.
Giải:
Ta có: x + y = 2
y = 2 – x
Do đó: A = x
2
+ y
2
= x
2
+ (2 – x)
2
= x
2
+ 4 – 4x + x
2
= 2x
2
– 4x + 4
= 2( x
2
– 2x) + 4
= 2(x – 1)
2
+ 2
2
Vậy GTNN của A là 2 tại x = y = 1.
• Dạng 2: CÁC BÀI TOÁN MÀ BIỂU THỨC CHO LÀ MỘT PHÂN THỨC
Bài toán 1:
Tìm GTLN và GTNN của:
2
43
1
x
y
x
+
=
+
.
Giải:
* Cách 1:
2
22
4 3 ax 4 3
11
x x a
ya
xx
+ − + + −
= = +
++
Ta cần tìm a để
2
ax 4 3xa− + + −
là bình phương của nhị thức.
Ta phải có:
1
' 4 (3 ) 0
4
a
aa
a
=−
= + − =
=
- Với a = -1 ta có:
22
22
4 3 x 4 4 ( 2)
11
1 1 1
x x x
y
x x x
+ + + +
= = − + = − +
+ + +
1.y −
Dấu “=” xảy ra khi x = -2.
Trang 7
Vậy GTNN của y = -1 khi x = -2.
- Với a = 4 ta có:
22
22
4 3 -4x 4 1 (2 1)
4 4 4
1 1 1
x x x
y
x x x
+ + − −
= = + = −
+ + +
Dấu “=” xảy ra khi x =
1
2
.
Vậy GTLN của y = 4 khi x =
1
2
.
* Cách 2:
Vì x
2
+ 1
0 nên:
2
2
43
yx 4 3 0
1
x
y x y
x
+
= − + − =
+
(1)
y là một giá trị của hàm số
(1) có nghiệm
- Nếu y = 0 thì (1)
3
4
x = −
- Nếu y
0 thì (1) có nghiệm
' 4 ( 3) 0yy = − −
( 1)( 4) 0yy + −
10
40
y
y
+
−
hoặc
10
40
y
y
+
−
14y −
Vậy GTNN của y = -1 khi x = -2.
Vậy GTLN của y = 4 khi x =
1
2
.
Bài toán 2: Tìm GTLN và GTNN của:
2
2
1
1
xx
A
xx
−+
=
++
.
Giải:
Biểu thức A nhận giá trị a khi và chỉ khi phương trình ẩn x sau đây có nghiệm:
2
2
1
1
xx
a
xx
−+
=
++
(1)
Do x
2
+ x + 1 = x
2
+ 2.
1
2
.x +
2
1 3 1 3
0
4 4 2 4
x

+ = + +


Nên (1)
ax
2
+ ax + a = x
2
– x + 1
(a – 1)x
2
+ (a + 1)x + (a – 1) = 0 (2)
• Trường hợp 1: Nếu a = 1 thì (2) có nghiệm x = 0.
• Trường hợp 2: Nếu a
1 thì để (2) có nghiệm, điều kiện cần và đủ là
0
, tức
là:
2
( 1) 4( 1)( 1) 0 ( 1 2 2)( 1 2 2) 0
1
(3 1)( 3) 0 3( 1)
3
a a a a a a a
a a a a
+ − − − + + − + − +
− −
Trang 8
Với
1
3
a =
hoặc a = 3 thì nghiệm của (2) là
( 1) 1
2( 1) 2(1 )
aa
x
aa
− + +
==
−−
Với
1
3
a =
thì x = 1
Với a = 3 thì x = -1
Kết luận: gộp cả 2 trường hợp 1 và 2, ta có:
GTNN của
1
3
A =
khi và chỉ khi x = 1
GTLN của A = 3 khi và chỉ khi x = -1
Bài toán 3:
a) Cho a, b là các số dương thỏa mãn ab = 1. Tìm GTNN của biểu thức:
22
4
( 1)( )A a b a b
ab
= + + + +
+
.
b) Cho m, n là các số nguyên thỏa
1 1 1
23mn
+=
. Tìm GTLN của B = mn.
Giải:
a) Theo bất đẳng thức Côsi cho hai số dương a
2
và b
2
2 2 2 2
2 2 2a b a b ab+ = =
(vì ab = 1)
22
4 4 4
( 1)( ) 2( 1) 2 ( ) ( )A a b a b a b a b a b
a b a b a b
= + + + + + + + = + + + + +
+ + +
Cũng theo bất đẳng thức côsi cho hai số dương a + b và
4
ab+
.
Ta có: (a + b) +
44
2 ( ). 4ab
a b a b
+ =
++
Mặt khác:
22a b ab+ =
Suy ra:
4
2 ( ) ( ) 2 4 2 8A a b a b
ab
+ + + + + + + =
+
Với a = b = 1 thì A = 8
Vậy GTNN của A là 8 khi a = b = 1.
b) Vì
1 1 1
23mn
+=
nên trong hai số m, n phải có ít nhất một số dương. Nếu có một trong
hai số là âm thì B < 0. Vì ta tìm GTLN của B = mn nên ta chỉ xét trường hợp cả hai số
m, n cùng dương.
Ta có:
1 1 1
3(2 ) 2 (2 3)( 3) 9
23
m n mn m n
mn
+ = + = − − =
Vì m, n
N
*
nên n – 3
-2 và 2m – 3
-1.
Trang 9
Ta có: 9 =1.9 = 3.3 = 9.1; Do đó xảy ra:
+
2 3 1 2
3 9 12
mm
nn
− = =


− = =

và B = mn = 2.12 = 24
+
2 3 1 3
3 3 6
mm
nn
− = =


− = =

và B = mn = 3.6 = 18
+
2 3 9 6
3 1 4
mm
nn
− = =


− = =

và B = mn = 6.4 = 24
Vậy GTLN của B = 24 khi
2
12
m
n
=
=
hay
6
4
m
n
=
=
Bài toán 4: Giả sử x và y là hai số thỏa mãn x > y và xy = 1. Tìm GTNN của biểu
thức:
22
xy
A
xy
+
=
−
.
Giải:
Ta có thể viết:
2 2 2 2 2
2 2 ( ) 2x y x xy y xy x y xy
A
x y x y x y
+ − + + − +
= = =
− − −
Do x > y và xy = 1 nên:
2
( ) 2 2 2
22
x y xy x y x y
A x y
x y x y x y
− + − −
= = − + = + +
− − −
Vì x > y
x – y > 0 nên áp dụng bất đẳng thức côsi với 2 số không âm, ta có:
2
2. .
22
x y x y
A
xy
−−
+
−
Dấu “=” xảy ra
2
2
( ) 4 ( ) 2
2
xy
x y x y
xy
−
= − = − =
−
(Do x – y > 0)
Từ đó:
2
23
2
A + =
Vậy GTNN của A là 3
2
1
xy
xy
−=
=
12
12
x
y
=+
= − +
hay
12
12
x
y
=−
= − −
Thỏa điều kiện xy = 1
Bài toán 5: Tìm GTLN của hàm số:
2
1
1
y
xx
=
++
.
Giải:
Ta có thể viết:
2
2
11
1
13
24
y
xx
x
==
++

++


Vì
2
1 3 3
2 4 4
x

+ +


. Do đó ta có:
4
3
y
. Dấu “=” xảy ra
1
2
x = −
.
Vậy: GTLN của
4
3
y =
tại
1
2
x
−
=
Trang 10
Bài toán 6: Cho t > 0. Tìm GTNN của biểu thức:
1
()
4
f t t
t
=+
.
Giải:
Ta có thể viết:
2 2 2
1 4 1 (2 1) 4 (2 1)
( ) 1
4 4 4 4
t t t t
f t t
t t t t
+ − + −
= + = = = +
Vì t > 0 nên ta có:
( ) 1ft
Dấu “=” xảy ra
1
2 1 0
2
tt − = =
Vậy f(t) đạt GTNN là 1 tại
1
2
t =
.
Bài toán 7: Tìm GTNN của biểu thức:
2
2
1
()
1
t
gt
t
−
=
+
.
Giải:
Ta có thể viết:
2
22
12
( ) 1
11
t
gt
tt
−
= = −
++
g(t) đạt GTNN khi biểu thức
2
2
1t +
đạt GTLN. Nghĩa là t
2
+ 1 đạt GTNN
Ta có: t
2
+ 1
1
min (t
2
+ 1) = 1 tại t = 0
min g(t) = 1 – 2 = -1
Vậy GTNN của g(x) là -1 tại t = 0.
Bài toán 8: Cho x, y, z là các số dương thỏa mãn điều kiện: xyz = 1. Tìm GTNN của
biểu thức:
3 3 3
111
( ) ( ) ( )
E
x y z y z x z x y
= + +
+ + +
.
Giải:
Đặt
1 1 1 1
; ; 1a b c abc
x y z xyz
= = = = =
Do đó:
11
( ). ( )a b x y a b xy x y c a b
xy
+ = + + = + + = +
Tương tự: y + z = a(b + c)
z + x = b(c + a)
3 3 3
2 2 2
3 3 3
1 1 1 1 1 1
. . .
( ) ( ) ( )
1 1 1
. . .
( ) ( ) ( )
E
x y z y z x z x y
a b c
abc
a b c b c a c a b b c c a a b
= + +
+ + +
= + + = + +
+ + + + + +
Ta có:
3
2
a b c
b c c a a b
+ +
+ + +
(1)
Thật vậy: Đặt b + c = x; c + a = y; a + b = z
Trang 11
2
;;
2 2 2
x y z
abc
y z x z x y x y z
abc
++
+ + =
+ − + − + −
= = =
Khi đó,
2 2 2
a b c y z x z x y x y z
VT
b c c a a b x y z
+ − + − + −
= + + = + +
+ + +
1 1 1 3 3 3
111
2 2 2 2 2 2
y x z x z y
x y x z y z

= + + + + + − + + − =


Nhân hai vế (1) với a + b + c > 0. Ta có:
( ) ( ) ( ) 3
()
2
a a b c b a b c c a b c
abc
b c c a a b
+ + + + + +
+ + + +
+ + +
2 2 2
3
3 3 3
2 2 2 2
a b c a b c abc
E
b c c a a b
++
+ + =
+ + +
GTNN của E là
3
2
khi a = b = c = 1.
Bài toán 9: Cho x, y là các số thực thỏa mãn: 4x
2
+ y
2
= 1 (*).
Tìm GTLN, GTNN của biểu thức:
23
22
xy
a
xy
+
=
++
.
Giải:
Từ
23
22
xy
a
xy
+
=
++
a(2x+y+z) = 2x+3y
2ax + ay + 2a – 2x +3y = 0
2(a – 1)x + (a – 3)y = -2a (1)
Áp dụng bất đẳng thức Bunhiacopxki cho hai bộ số (2x; y) và (a – 1; a – 3)
Ta có: 4a
2
= [2x(a-1)+y(a-3)]
2
≤ (4x
2
+y
2
).[(a-1)
2
+(a-3)
2
]
=>
2 2 2
4 ( 1) ( 3)a a a= − + −
(vì 4x
2
+y
2
= 1)
Do đó ta có:
2 2 2 2 2
4 ( 1) ( 3) 2 1 6 9a a a a a a a − + − = − + + − +
22
2 8 10 0 4 5 0a a a a + − + −
50
( 1)( 5) 0
10
a
aa
a
+
− +
−
(Vì a + 5 > a – 1)
15a
* Thay a = 1 vào (1) ta được: -2y = -2
y = 1
Thay y = 1 vào (*) ta có: x = 0
(x; y) = (0;1)
* Thay a = -5 vào (1) ta được: 2(-5 – 1)x + (-5 – 3)y = -2(-5)
65
12 8 10 6 4 5
4
x
x y x y y
−−
− − = + = − =
Trang 12
Thay vào (*) ta được:
2
2
65
41
4
x
x
−−

+=


2
34
100 60 9 0
10 5
x x x y + + = = − = −
34
( ; ) ;
10 5
xy
−−

=


Vậy GTLN của a là 1 khi x = 0; y = 1.
GTNN của a là -5 khi
34
;
10 5
xy= − = −
.
Bài toán 10:
Giả sử x, y là hai số dương thỏa mãn điều kiện: x + y = 1.
Hãy tìm gái trị nhỏ nhất cảu biểu thức:
M =
2
2
11
xy
xy


+ + +




Giải:
Ta có: M =
2
2
11
xy
xy


+ + +




=
22
22
11
22xy
xy
+ + + + +
= 4 + x
2
+ y
2
+
( )
22
22
2 2 2 2
1
41
xy
xy
x y x y

+
= + + +


Vì x, y > 0 nên ta có thể viết:
( )
2
02x y x y xy− = +
Mà x + y = 1 nên 1
22
11
2 2 16xy
xy
xy
= =
(1)
Dấu “=” xảy ra khi và chỉ khi
1
2
xy==
Ngoài ra ta cũng có:
2 2 2 2 2 2 2
( ) 0 2 2( ) 2x y x y xy x y xy x y− + + + +
2 2 2 2 2
2( ) ( ) 2( ) 1x y x y x y + + +
(vì x + y = 1)
22
1
2
xy +
(2)
Dấu “=” xảy ra khi và chỉ khi
1
2
xy==
Từ (1) và (2) cho ta:
22
22
1 1 25
4 ( )(1 ) 4 (1 16)
22
M x y
xy
= + + + + + =
Trang 13
Do đó:
25
2
M
Dấu “=” xảy ra khi và chỉ khi đồng thời ở (1) và (2) cùng xảy ra dấu “=” nghĩa là khi
1
2
xy==
Vậy GTNN của
25
2
M =
khi và chỉ khi
1
2
xy==
.
* Dạng 3: CÁC BÀI TOÁN MÀ BIỂU THỨC CHO CÓ CHỨA CĂN THỨC.
Bài toán 1: Tìm GTLN của hàm số:
24y x x= − + −
.
Giải:
* Cách 1:
Điều kiện:
20
2 4(*)
40
x
x
x
−
−
Áp dụng bất đẳng thức Bunhiacopxki: (ac + bd)
2
(a
2
+ b
2
)(c
2
+ d
2
)
Dấu “=” xảy ra khi và chỉ khi
ab
cd
=
.
Chọn
2; 1; 4 ; 1a x c b x d= − = = − =
với
24x
Ta có:
( ) ( ) ( )
( )
( ) ( )
2 2 2
2 2 2
2
2
2 4 2 4 . 1 1
2 4 .2
42
y x x x x
y x x
yy

= − + − − + − +


− + −


Vì y > 0 nên ta có:
02y
Dấu “=” xảy ra
2 4 2 4 3x x x x x − = − − = − =
(Thỏa mãn (*))
Vậy GTLN của y là 2 tại x = 3.
* Cách 2:
Ta có:
24y x x= − + −
Điều kiện:
20
24
40
x
x
x
−
−
Vì y > 0 nên y đạt GTLN khi và chỉ khi y
2
đạt GTLN.
Ta có:
22
2 4 2 ( 2)(4 ) 2 2 ( 2)(4 )y x x x x y x x= − + − + − − = + − −
Do
20
24
40
x
x
x
−
−
nên áp dụng bất đẳng thức côsi cho hai số không âm
cho ta:
2 ( 2)(4 ) ( 2) (4 ) 2x x x x− − − + − =
Trang 14
Do đó
2
2 2 4y + =
Dấu “=” xảy ra
2 4 3x x x − = − =
(thỏa mãn điều kiện).
Vậy GTLN của hàm số y là 2 tại x = 3.
Bài toán 2: Tìm GTLN, GTNN của hàm số:
3 1 4 5 (1 5)y x x x= − + −
.
Giải:
a) GTLN:
Áp dụng bất đẳng thức Bunhiacopxki cho hai bộ số:
(3; 4) và (
( 1; 5 )xx−−
ta có:
( ) ( )
22
2 2 2 2
(3. 1 4. 5 ) (3 4 ). 1 5 100y x x x x

= − + − + − + − =


<=>
2
100y
=> y
10
Dấu “=” xảy ra <=
15
34
xx−−
−
hay
15
9 16
xx−−
=
=> x =
61
25
(thỏa mãn điều kiện)
Vậy GTLN của y là10 khi x =
61
25
* b) Gía trị nhỏ nhất:
Ta có: y =
3 1 4 5 3 1 3 5 5x x x x x− + − = − + − + −
=
( )
3 1 5 5x x x− + − + −
Đặt: A =
15xx− + −
thì t
2
= 4 + 2
( )( )
15xx−−
4
=> A
2
và dấu “=” xảy ra khi x = 1 hoặc x = 5
Vậy y
3 . 2 + 0 = 6
Dấu “=” xảy ra khi x = 5
Do đó GTNN của y là 6 khi x = 5
Bài toán 3: GTNN của y là 6 khi x = 5
Tìm GTNN của biểu thức: M =
( )
2
2
1994 ( 1995)xx− + +
Giải:
M =
( )
2
2
1994 ( 1995)xx− + +
=
1994 1995xx− + +
Áp dụng bất đẳng thức:
a b a b+ +
ta có:
Trang 15
M =
1994 1995 1994 1995x x x x− + + = − + +
=> M
1994 1995 1xx − + − =
Dấu “=” xảy ra khi và chỉ khi (x – 1994) . (1995 – x)
0
<=> 1994
1995x
Vậy GTNN của M = 1 1994
1995x
Bài toán 4:
Tìm GTNN của B = 3a + 4
2
1 a−
với -1
1a
Giải:
B = 3a + 4
( )
2
2
3 16
1 5 5 1
5 25
a a a− = + −
Và áp dụng bất đẳng thức Cô si với hai số không âm cho ta
( )
( )
2
2
2
2
3
16
1
3 16
5
25
5 5 1 5 5
5 25 2 2
a
a
aa

+−


+ − +
=> B
22
9 25 41 25
55
2 25
aa

+ + −
=


=> Do đó B
5
và dấu “=” xảy ra khi và chỉ khi.
2
3
5
16
1
25
a
a
=
=−
<=> a =
3
5
Vậy GTNN của B = 5 <=> a =
3
5
Bài toán 5:
Tìm GTNN của biểu thức:
A =
2
3
2 2 7xx+ − +
Giải:
Điều kiện:
( )
22
2 7 0 2 1 8 0x x x x− + = − − + +
<=> -(x-1)
2
+ 8
0
( )
2
18x= −
2 2 1 2 2x= − −
1 2 2 2 2 1x= − +
Với điều kiện này ta viết:
Trang 16
( )
2
22
2 7 1 8 8 2 7 8 2 2x x x x x− + = − − + = − + =
=> 2 +
( )
2
2 7 2 2 2 2 2 1xx− + + = +
Do đó:
( )
2
1 1 2 1
2
2 2 1
2 2 7xx
−
=
+
+ − +
Vậy A
21
3
2
−

và dấu “=” xảy ra <=> x -1 = 0
<=> x = 1 (thỏa mãn điều kiện)
Vậy GTNN của A =
( )
3
2 1 1
2
x− = =
Bài toán 6:
Tìm GTNN của biểu thức: A =
2
53
1
x
x
−
−
Giải:
Điều kiện: 1 – x
2
> 0 <=> x
2
< 1 <=> - 1 < x < 1
=> A > 0 => GTNN của A A
2
đạt GTNN.
Ta có: A
2
=
( )
(
)
( )
22
2
2
22
2
5 3 3 5
25 30 9
16 16
11
1
xx
xx
xx
x
−−
−+
= = +
−−
−
Vậy GTNN của A = 4 khi
3
5
x =
Bài toán 7: Cho x > 0 ; y = 0 thỏa mãn x + y
1
Tìm GTNN của biểu thức: A =
2
1xx−
Giải:
Điều kiện: 1 – x
2
0 1 1x = −
Áp dụng bất đẳng thức Cô si hai số: x
2
0
và 1 – x
2
0
Ta có: x
2
+ 1 – x
2
( )
2 2 2
2 1 1 2 1x x x x − = −
<=> 1
1
2
2
AA =
Vậy GTLN của A =
1
2
khi x =
2
2
hay x =
2
2
−
Bài toán 8:
Tìm GTLN của biểu thức: y =
1996 1998xx− + −
Trang 17
Giải:
Biểu thức có nghĩa khi 1996
1998x
Vì y
0
với mọi x thỏa mãn điều kiện 1996
1998x
Áp dụng bất đẳng thức Cô si ta có:
2
( )( )
1996 1998 ( 1996) (1998 ) 2x x x x− − − + − =
Dấu “=” xảy ra khi và chỉ khi x – 1996 = 1998 – x
<=> x = 1997
Do đó y
2
42y =
Vậy GTLN của y là 2 khi x = 1997
Bài toán 9:
Cho
01x
. Tìm GTLN của biểu thức y = x +
( )
21 x−
Giải:
Ta có:
( )
21y x x= + −
= x + 2
( )
1
1
2
x−
Vì 0
1x
nên 1 – x
0
Áp dụng bất đẳng thức Cô si đối với 2 số:
1
2
và (1 – x) cho ta:
( ) ( )
1 1 3
2 1 1
2 2 2
y x x x x= + − + + − =
Dấu “=” xảy ra <=>
11
1
22
xx= − = =
Vậy GTLN của y là
3
2
tại x =
1
2
Bài toán 10:
Cho M =
3 4 1 15 8 1a a a a+ − − + + − −
Tìm TGNN của M
Giải:
M =
3 4 1 15 8 1a a a a+ − − + + − −
=
1 4 1 4 1 8 1 16a a a a− − − + + − − − +
=
( ) ( )
22
1 2 1 4aa− − + − −
Điều kiện để M xác định là a – 1
01a =
Ta có:
1 2 1 4M a a= − − + − −
Đặt x =
1a −
điều kiện x
0
Trang 18
Do đó: M =
24xx− + −
Ta xét ba trường hợp sau:
1) Khi x
2
thì
( )
2 2 2x x x− = − − = −
Và
( )
4 4 4x x x− = − − = −
=> M = 2 – x + 4 – x = 6 – 2x
6 2.2 2 − =
Vậy x < 2 thì M
2
2) Khi x
4
thì
22xx− = −
và x-4 =x-4
=> M =
2 4 2 6 2 4 6 2x x x− + − = − − =
Vậy x > 4 thì M
2
3) Khi 2 < x < 4 thì
22xx− = −
và
44xx− = −
=> M = x – 2 + 4 – x = 2 (không phụ thuộc vào x)
Trong trường hợp này thì: 2
14a −
<=> 4
1 16a −
<=> 5
17a
Cả ba trường hợp cho ta kết luận:
GTNN của M = 2 tương ứng với:
5 17a
C. CÁC BÀI TẬP TỰ LUYỆN:
Bài 1:
Tìm GTNN của biểu thức: A = (2x – 3)
2
– 7 với x
1−
hoặc x
3
.
Gợi ý:
- Xét 2 trường hợp: x ≥ 3 và x ≤ -1
- Kết luận: Min A = 2 <=> x = 3
Chú ý: Mặc dù A = (2x – 3)
2
– 7
7−
. Xảy ra đẳng thức khi và chỉ khi x =
3
2
nhưng
giá trị không thỏa mãn x
1−
, không thỏa mãn x
3
. Do đó không thể kết luận được
GTNN của A bằng – 7.
Bài 2:
Gọi x
1
; x
2
là các nghiệm của phương trình:
x
2
– (2m – 1) x + (m – 2) = 0
Trang 19
Tìm các giá trị của m để
22
12
xx+
có giá trị nhỏ nhất
Gợi ý:
= 4(m - 1 )
2
+ 5 > 0. Phương trình đã cho có nghiệm với mọi m theo hệ thức Vi-ét,
ta có:
2 2 2 2 2
1 2 1 2 1 2
( ) 2 (2 1) 2( 2) 4 6 5x x x x x x m m m m+ = + − = − − − = − +
=
2
3 11 11
2
2 4 4
m

− +


=> Min (
( )
22
12
11
4
xx+=
với m =
3
4
Bài toán 3:
Cho x, y là hai số thỏa mãn: x + 2y = 3. Tìm GTNN của E = x
2
+ 2y
2
Gợi ý:
Rút x theo y và thế vào E
Bài toán 4:
Tìm GTLN và GTNN của biểu thức: A = x
2
+ y
2
Biết rằng x và y là các số thực thỏa mãn: x
2
+ y
2
– xy = 4
Gợi ý:
Từ x
2
+ y
2
– xy = 4 <=> 2x
2
+ 2y
2
– 2xy = 8
<=> A + (x – y)
2
= 8
<=> Max A = 8 khi x = y
Mặt khác: 2x
2
+ 2y
2
= 8 + 2xy
<=> 3A = 8 + (x + y)
2
8
=> A
8
3
=
min A =
8
3
khi x = - y
Bài toán 5:
Cho x, y thỏa mãn: x
2
+ 4y
2
= 25.
Tìm GTLN và GTNN của biểu thức: M = x + 2y.
Giải:
Áp dụng bất đẳng thức: Bunhiacôpxki
(x +2y)
2
22
( 4 )xy+
(1
2
+ 1
2
) = 50
<=>
2 50 50 50x y M+ = −
Trang 20
Vậy Max M =
50
khi x =
55
;
2 2 2
y =
Min M = -5
2
khi x = -
5
2
; y = -
5
22
Bài tóan 6:
Cho x, y là hai số dương thỏa mãn điều kiện: xy = 1. Tìm GTLN của biểu thức:
A =
4 2 2 4
xy
x y x y
+
++
Gợi ý:
Từ (x
2
– y)
2
4 2 2
02x y x y = +
=>
4 2 2
1
22
xx
x y x y
=
+
Tương tự:
42
1
2
y
yx
+
=> A
1
=> Max A = 1 khi
2
2
1
1
xy
y x x y
xy
=
= = = =
=
Bài tóan 7:
Tìm GTNN của biểu thức:
A =
( ) ( )
2 1 1 2 1 1x x x x+ + + + + − +
Gợi ý:
B =
1 1 1 1xx+ + + − + =
Min B = 2 khi - 1
0x
Bài toán 8: Tìm GTNN của biểu thức:
B = (x – a )
2
+ (x – b)
2
+ (x – c)
2
với a, b, c cho trước.
Gợi ý:
Biểu diễn B =
( )
( )
2
2
2 2 2
3.
33
abc
abc
x a b c
++
++

− + + + −


=> GTNN của B = (a
2
+ b
2
+ c
2
) -
( )
2
3
abc++
Bài toán 9: Tìm GTNN của biểu thức:
P = x
2
– 2xy + 6y
2
– 12x +
3y + 45
Gợi ý:
Biểu diễn P = (x – 6 – y)
2
+ 5(y – 1)
2
+ 4
Trang 21
Vậy Min P = 4 khi y = 1 ; x = 7
Bài toán 10: Tìm GTLN của biểu thức:
E = – x
2
+ 2xy – 4y
2
+ 2x + 10y – 3
Gợi ý:
Biểu diễn E = 10 – (x – y – 1)
2
– 3 (y – 2)
2
=> GTLN của E = 10 y = 2 ; x = 3
Bài toán 11: Tìm GTLN của biểu thức: P =
2 4 5x y z+ +
Biết x, y, z là các biến thỏa mãn : x
2
+ y
2
+ z
2
= 169
Gợi ý: Áp dụng bất đẳng thức Bunhiacôpxki
Max P = 65 khi
=
=
=
==
5
513
5
52
5
26
5
42
z
y
x
z
y
x
Bài toán 12:
Tìm GTNN của biểu thức sau:
a) A =
2
1
2
x
x
+
+
b) B =
2
8
32x
−
+
c) C =
2
2
1
1
x
x
−
+
Gợi ý:
a) Áp dụng bất đẳng thức Cô si cho ta:
A = (x + 2) +
5
4 2 5 4
2x
− −
+
b) B =
2
8
4
32x
−
−
+
(vì
2
11
)
3 2 2x
+
c) C =
2
2
2
11
1
x
x
− + − =
+
Min C = - 1 khi x = 0
Bài toán 13:
Tìm GTNN của biểu thức A =
2
2
2 2000
;( 0)
xx
x
x
−+
Gợi ý:
A =
2 2 2 2
22
2000 2 2000 2000 ( 2000) 1999
2000 2000
x x x x
xx
− + − +
=
Với x
0
Với mọi x
Với mọi x
Trang 22
=
2
2
( 2000) 1999 1999
2000 2000 2000
x
x
−
+
Vậy Min A =
1999
2000
Khi x = 2000
Bài toán 14:
Tìm GTNN của biểu thức:
P =
4 3 2
2
4 16 56 80 356
25
x x x x
xx
+ + + +
++
Gợi ý:
Biểu diễn P = 4
2
2
256
( 2 5) 64
25
xx
xx
+ + +
++
(áp dụng BĐT Côsi)
=> Min P = 64 khi x = 1 hoặc x = -3
Bài toán 15:
Tìm GTNN của A =
2
44xx
x
++
với x > 0
B =
2
1
x
x −
với x > 1
C =
2
2
2
1
xx
xx
++
++
D =
1
(1 ) 1x
x

++


với x > 0
E =
5
1
x
xx
+
−
với 0 < x < 1
F =
2
21
x
x
+
−
với x > 1
Gợi ý:
A = x+
44
4 2 4 8x
xx
+ + =
(vì x > 0)
=> Min A = 8 khi x = 2
B =
2
1 1 1
2 ( 1) 2 2 4
11
x
x
xx
−+
= + − + + =
−−
(vì x > 1)
=> Min B = 4 <=> x = 2
C =
22
22
( 1) 1 2 1
2
11
x x x x
x x x x
+ + + + +
=
+ + + +
D = (1 + x)
11
1 2 .2. 4x
x
x

+ =


(vì x > 0)
E =
( ) ( )
5 1 5 1
5 5 5
5 2 5 2 5 5
1 1 1
xx
x x x x x
x x x x x x
−−
−+
+ = + + + = +
− − −
Trang 23
F =
1 1 2 1 2 1 1 2 1
2
2 1 2 1 2 2 1 2
x x x
x x x
− + − −
+ = + + +
− − −
=
13
2
22
+=
=> Min F =
3
2
khi x = 3.
Bài 16: Tìm GTLN và GTNN của biểu thức:
P =
2
22
86x xy
xy
+
+
Gợi ý:
P = 9 -
2
22
( 3 )
11
yx
xy
+
− −
+
P = 9 -
2
22
( 3 )
9
xy
xy
−
+
Bài 17: Cho x, y là hai số dương thỏa mãn: x + y = 10
Tìm GTNN của biểu thức S =
11
xy
+
Gợi ý: S =
yx
11
+
=
10
(10 )
xy
xy x x
+
=
−
S có GTNN <=> x(10-x) có GTLN <=> x = 5.
=> GTNN của S =
2
5
khi x = y = 5.
Bài 18: Tìm GTNN của biểu thức:
E =
22
11x x x x+ + + − +
Gợi ý:
Ta có E > 0 với mọi x
Xét E
2
= 2 (x
2
+ 1 +
42
1) 4xx+ +
=> Min E = 2 khi x = 0
Bài 19: Cho a và b là hai số thỏa mãn: a
3
; a + b
5
Tìm GTNN của biểu thức S = a
2
+ b
2
Gợi ý:
a+ b
5 2 2 10 3 2 13a b a b = + = +
(vì a
3)
=> 13
2
( )
( )
2
22
3 2 13a b a b + +
=> Min S = 13
Bài 20:
Cho phương trình: x
2
- 2mx – 3m
2
+ 4m – 2 = 0
Trang 24
Tìm m để cho
12
xx−
đạt GTNN.
Gợi ý:
'2
(2 1) 1 0m = − + =
phương trình luôn có 2 nghiệm phân biệt x
1
; x
2
. Theo
định lý vi-ét ta có:
12
2
12
2
. 3 4 2
x x m
x x m m
+=
= − + −
Do đó
( )
2
12
4 2 4 4 2x x m− = − + =
m
R
GTNN của
12
xx−
là 2 khi m =
1
2
Bài 21:
Tìm giá trị nhỏ nhất của:
y =
1 2 ... 1998x x x− + − + + −
Gợi ý:
y =
( ) ( )
1 1 1998 2 1997x x x x− + − + − + −
+ …+
( )
998 999xx− + −
Ta có:
1 1998xx− + −
nhỏ nhất bằng 1997 khi x
1;1998
2 1997xx− + −
nhỏ nhất bằng 1995 khi x
2;1997
998 1999xx− + −
nhỏ nhất bằng 1 khi x
999;1000
Vậy y đạt GTNN bằng 1 + 3 + …+ 1997
Số các số hạng của 1 + 3 + … + 1997 là (1997 – 1) : 2 + 1 = 999
Vậy Min y = 999
2
khi 999
1000x
Bài 22:
Cho biểu thức: M = x
2
+ y
2
+ 2z
2
+ t
2
Với x, y, z, t là các số nguyên không âm , tìm gia strị nhỏ nhất của M và các giá trị
tương ứng của x, y, z, t. Biết rằng:
2 2 2
2 2 2
21
3 4 101
x y t
x y z
− + =
+ + =
Gợi ý:
Theo giả thiết: x
2
– y
2
+ t
2
= 21
x
2
+ 3y
2
+ 4z
2
= 101
=> 2x
2
+ 2y
2
+ 4z
2
+ t
2
= 122
(1)
(2)
Trang 25
=> 2M = 122 + t
2
Do đó 2M
122 61M =
Vậy Min M = 61 khi t = 0
Từ (1) => x > y
00x y x y = + −
Do đó: (x + y )(x – y) = 21.1 = 7.3
Từ (2) => 3y
2
2
101 33 0 5yy = =
Ta chọn x = 5 ; y = 2 => z = 4
Vậy Min M = 61 tại x = 5 ; y = 2 ; z = 4; t = 0
Bài 23:
Cho phương trình: x
4
+ 2x
2
+2ax – (a – 1)
2
= 0 (1)
Tìm giá trị của a để nghiệm của phương trình đó:
a) Đạt GTNN.
b) Đạt gía trị lớn nhất.
Gợi ý:
Gọi m là nghiệm của phương trình (1) thì:
m
4
+ 2m
2
+ 2am + a
2
+ 2a + 1 = 0 (2)
Viết (2) dưới dạng phương trình bậc hai ẩn a.
a
2
+ 2 (m + 1) a + (m
4
+ 2m
2
+ 1) = 0
Để tồn tại a thì
'
0
Giải điều kiện này được m
4
- m
2
0
<=> m(m – 1)
0 0 1m =
Vậy nghịêm của phương trình đạt GTNN là 0 với a = -1
Vậy nghịêm của phương trình đạt GTLN là 1 với a = -2
Bài 24: Tìm GTNN, GTLN của t =
2
2
22
1
xx
x
++
+
Gợi ý: Vì x
2
+ 1 > 0 với mọi x
Đặt a =
2
2
22
1
xx
x
++
+
=> (a – 1) x
2
– 2 x +a – 2 = 0 (1)
a là một giá trị của hàm số <=> (1) có nghiệm.
- Nếu a = 1 thì (1) <=> x =
1
2
−
- Nếu a
1 thì (1) có nghiệm <=>
'
0
Trang 26
Min A =
35
2
−
với x =
1 5 3+ 5
; ax A =
22
M
−−
với x =
51
2
−
Bài 25:
Tìm GTNN, GTLN của A =
22
22
x xy y
x xy y
−+
++
Gợi ý: Viết A dưới dạng sau với y
0
(
2
2
2
2
1
1
1
1
xx
yy
aa
A
aa
xx
yy

−+

−+

==
++

++


(đặt
x
a
y
=
)
Giải tương tự bài 24 được:
1
3
3
A
Còn với y = 0 thì A = 1
Do đó: Min A =
1
3
với x = y ; max A = 3 với x = - y
Bài 26: Cho a + b = 1. Tìm GTNN của biểu thức:
Q = a
3
+ b
3
+ ab
Gợi ý:
Với Q dưới dạng Q = (a + b)
( )
2
3a b ab ab

+ − +

= 1 – 2ab = 1 – 2a (1 – a)
=> Q = 2a
2
– 2a + 1
1
2
Do đó: Min Q =
1
2
khi a = b =
1
2
| 1/26
| | Tải xuống

Có thể bạn quan tâm:

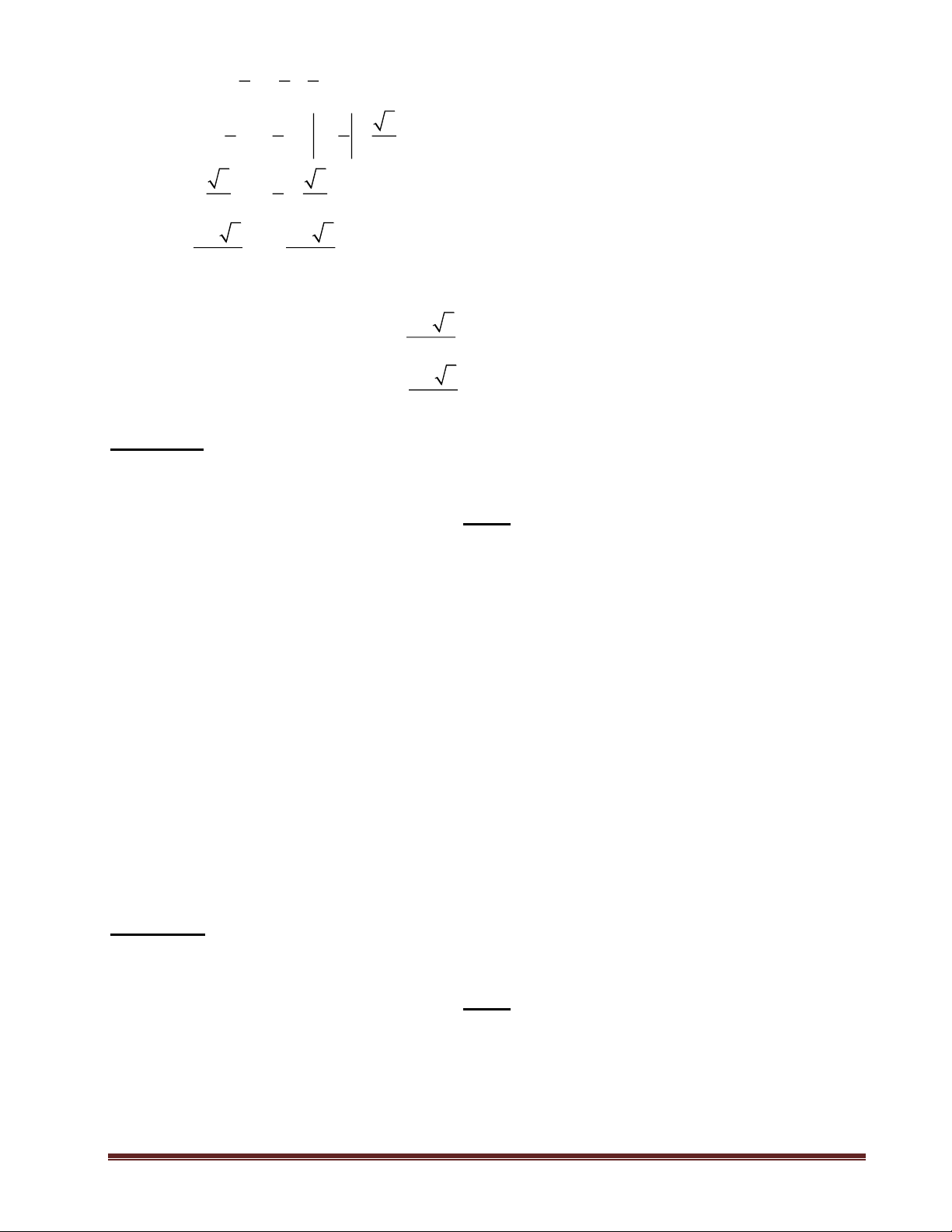
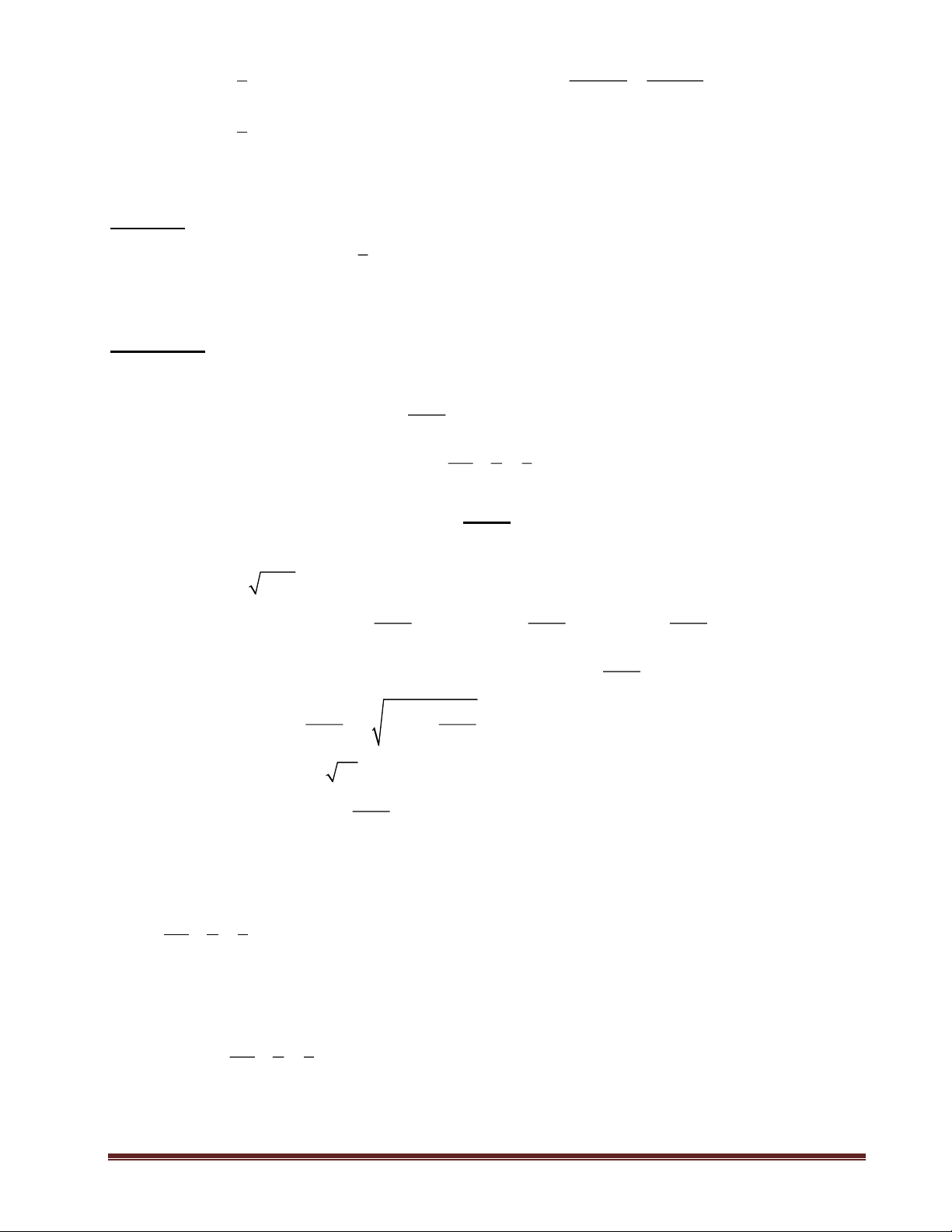
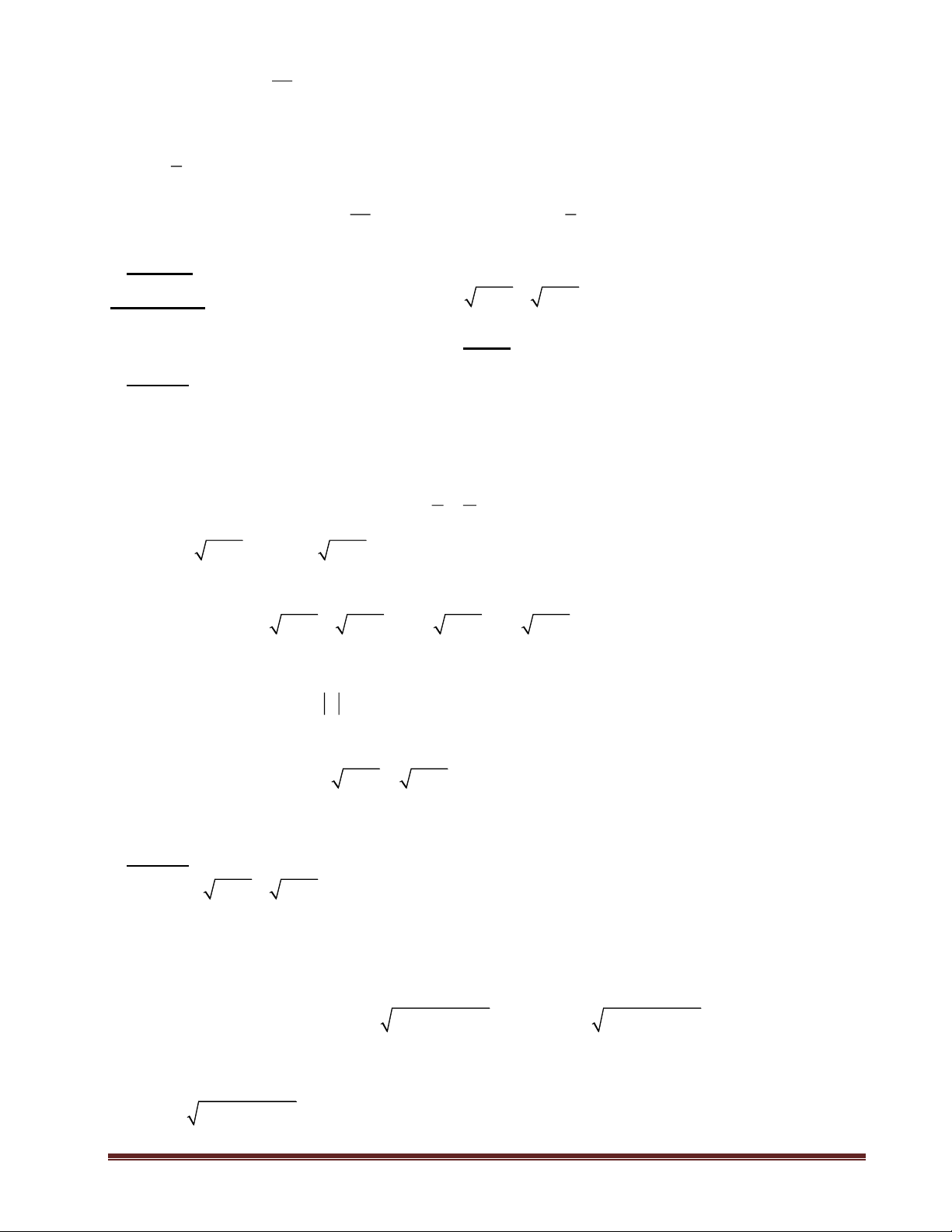
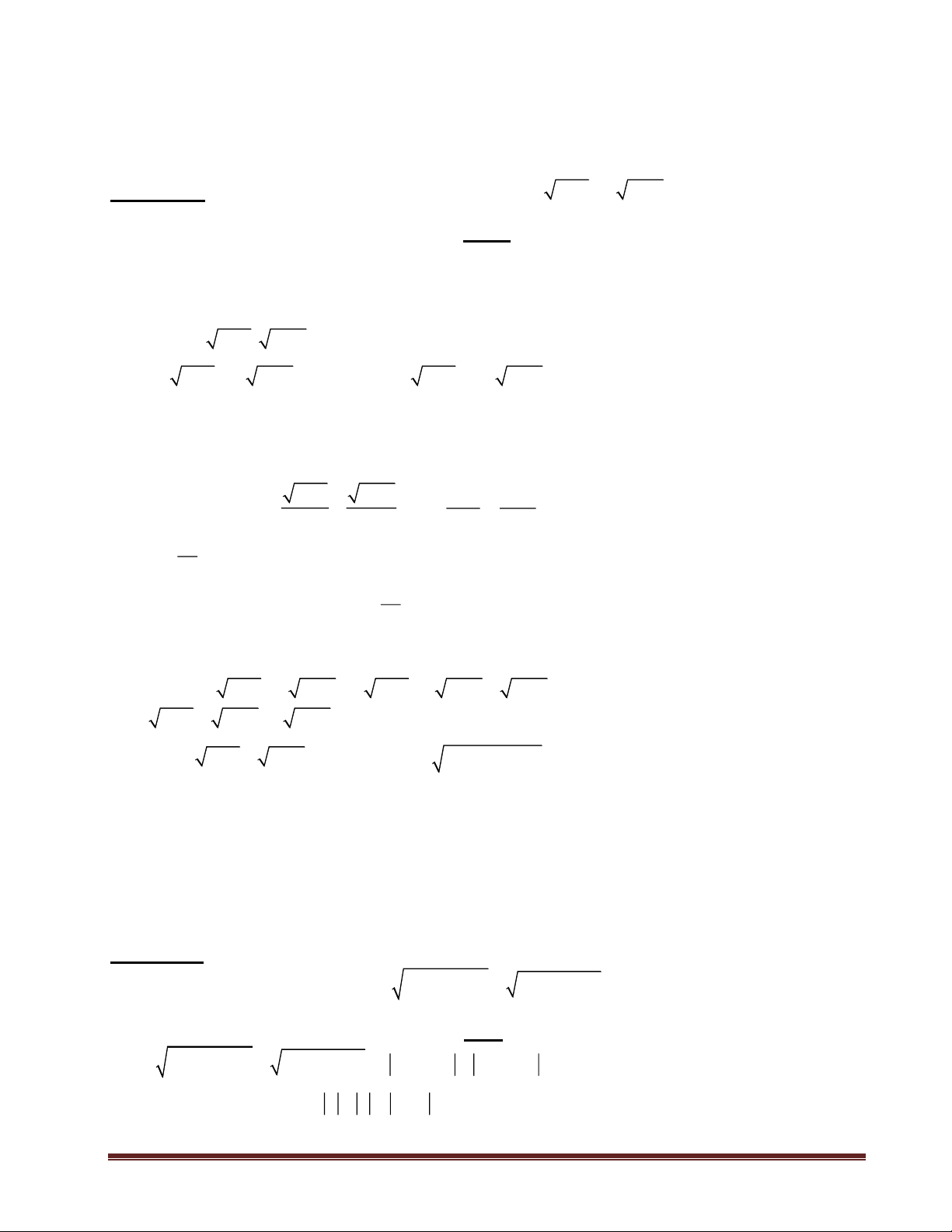
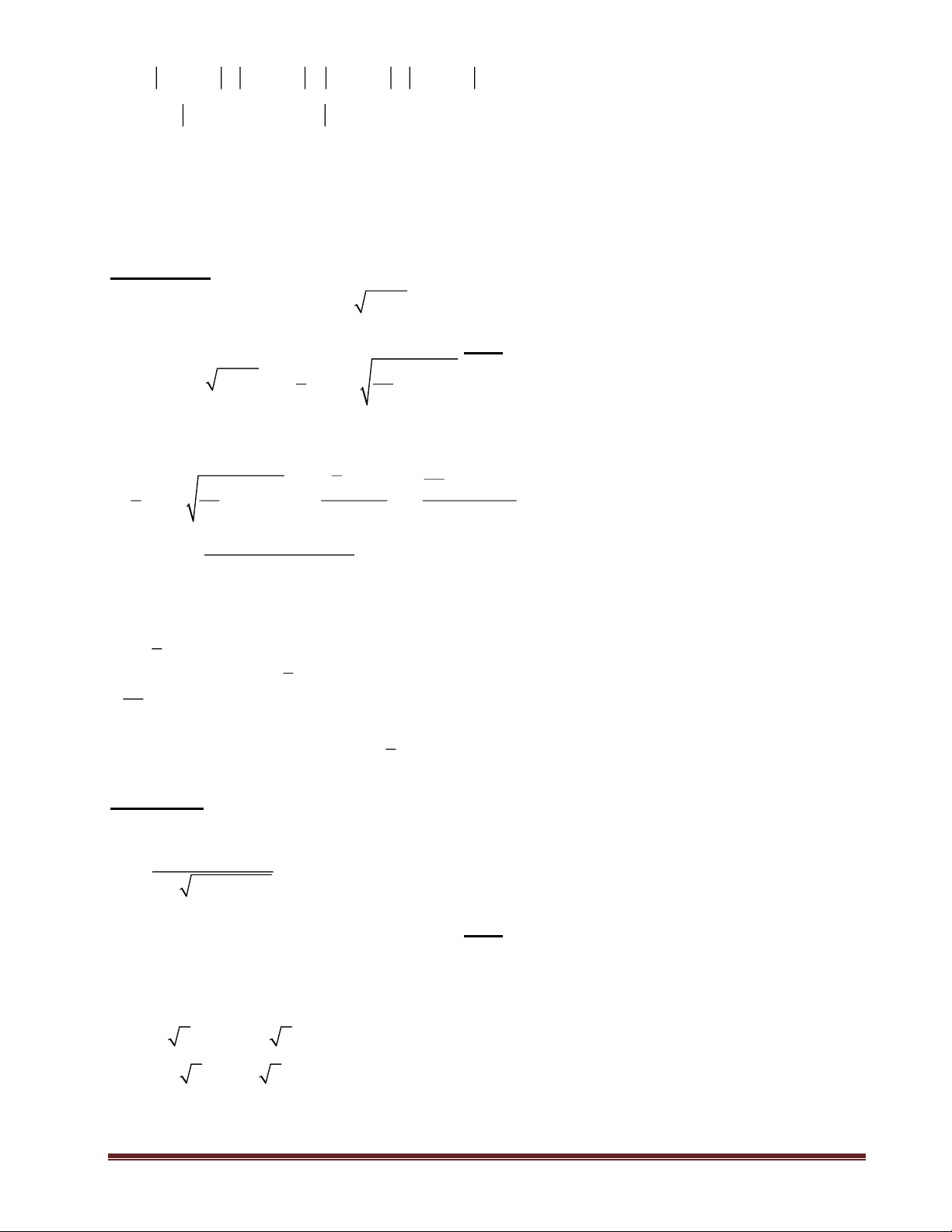
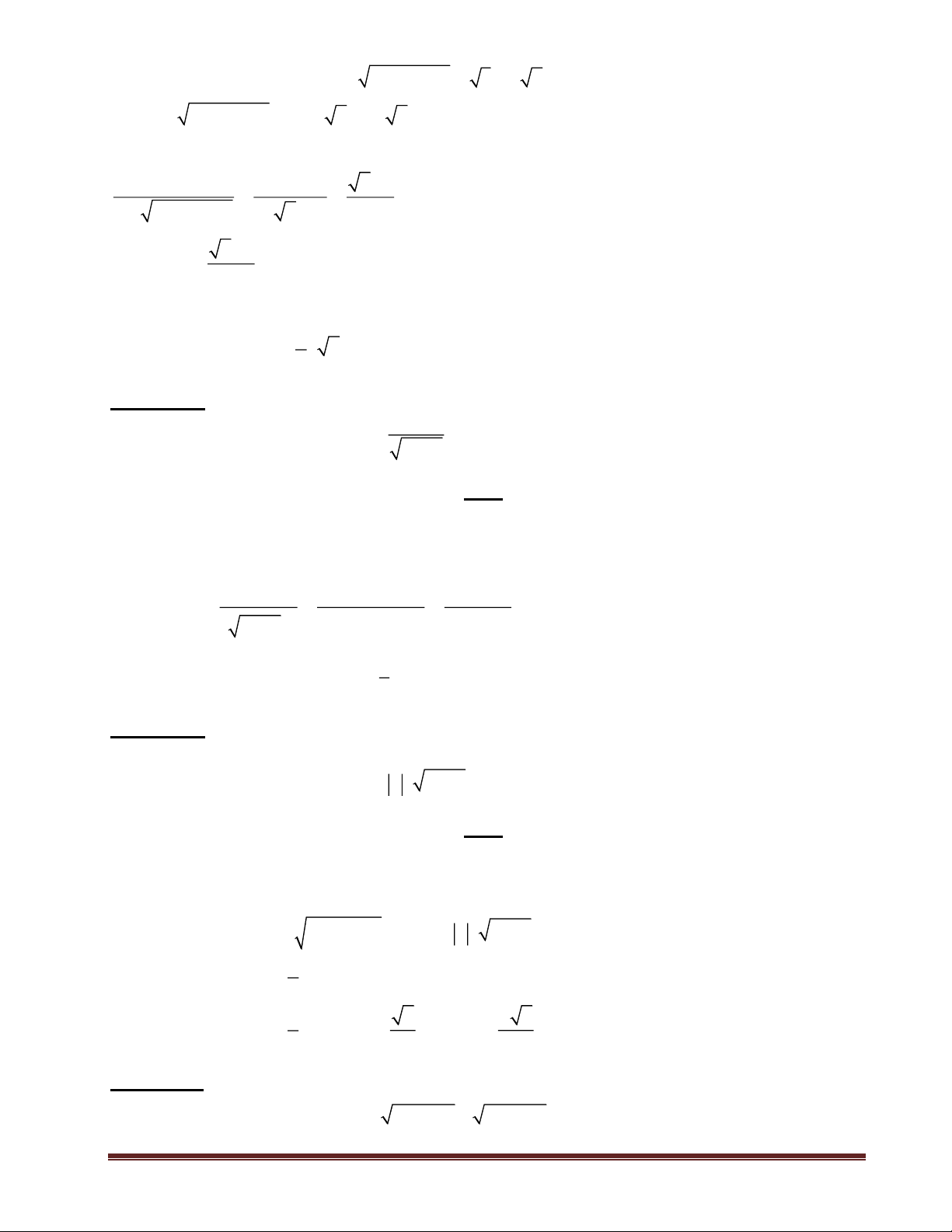
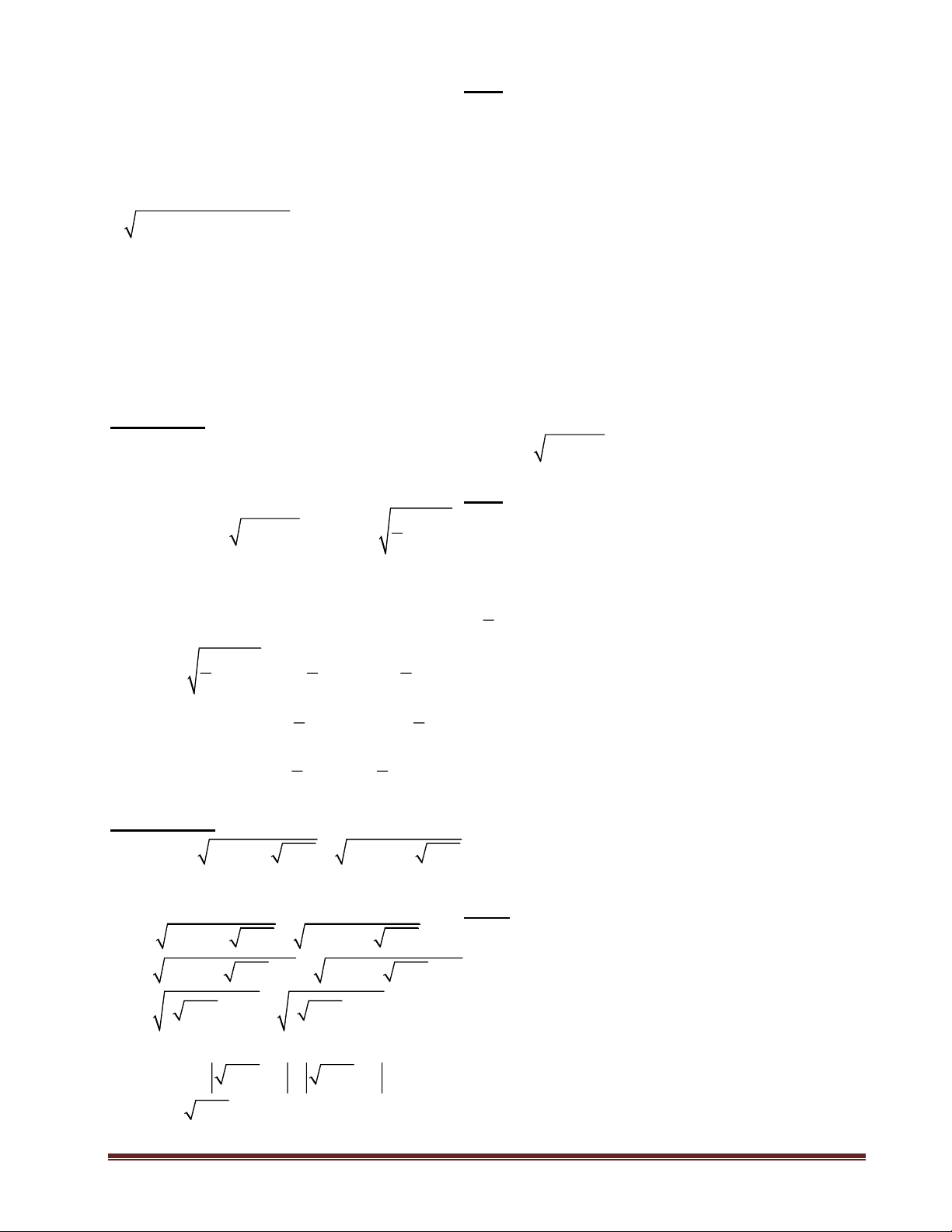
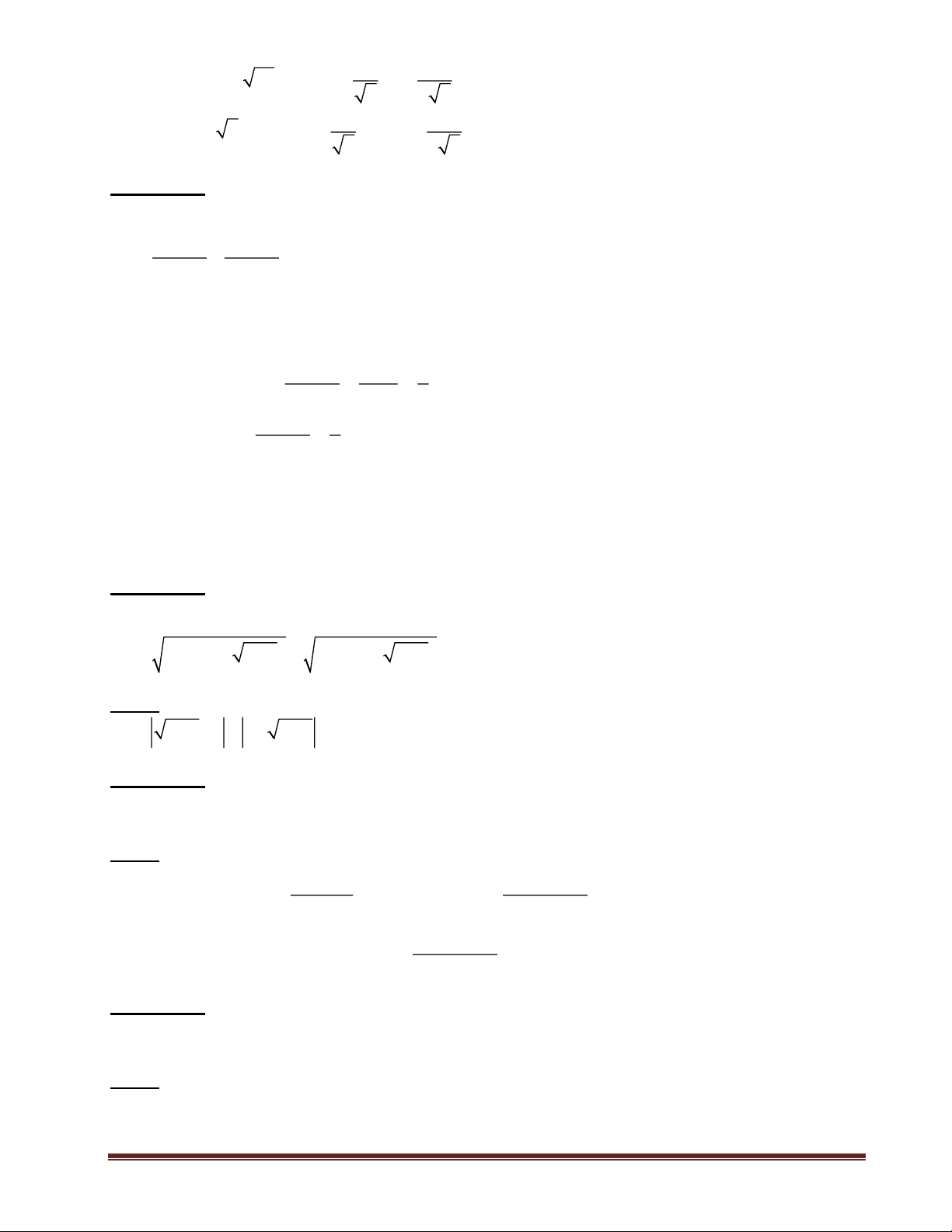
Preview text:

CHUYÊN ĐỀ : TÌM GTLN, GTNN CỦA BIỂU THỨC
A. Các kiến thức thường sử dụng là:
+ Bất đẳng thức Côsi: “Cho hai số không âm a, b; ta có bất đẳng thức:
a + b ab ; 2
Dấu “=” xảy ra khi và chỉ khi a = b”.
+ Bất đẳng thức: ( + )2  ( 2 2 + )( 2 2 ac bd a b
c + d ) (BĐT: Bunhiacopxki);
Dấu “=” xảy ra khi và chỉ khi a b = . c d
+ a + b a + b ; Dấu “=” xảy ra khi và chỉ khi ab  0.
+ Sử dụng “bình phương” để tìm giá trị lớn nhất, giá trị nhỏ nhất.
Nếu y = a + f x 2
( ) thì min y = a khi f(x) = 0.
Nếu y = a − f x 2
( ) thì max y = a khi f(x) = 0.
+ Phương pháp “tìm miền giá trị” (cách 2 ví dụ 1 dạng 2).
B. CÁC DẠNG TOÁN VÀ CÁCH GIẢI
• Dạng 1: CÁC BÀI TOÁN MÀ BIỂU THỨC CHO LÀ MỘT ĐA THỨC
Bài toán 1: Tìm GTNN của các biểu thức: a) 2
A = 4x + 4x +11 b) B = (x-1)(x+2)(x+3)(x+6) c) 2 2
C = x − 2x + y − 4 y + 7 Giải:
a) A = x + x + = x + x + + = ( x + )2 2 2 4 4 11 4 4 1 10 2 1 +10  10  1
Min A = 10 khi x = − . 2
b) B = (x-1)(x+2)(x+3)(x+6) = (x-1)(x+6)(x+2)(x+3)
= (x2 + 5x – 6)(x2 + 5x + 6) = (x2 + 5x)2 – 36  -36
 Min B = -36 khi x = 0 hoặc x = -5. c) 2 2
C = x − 2x + y − 4 y + 7
= (x2 – 2x + 1) + (y2 – 4y + 4) + 2 = (x – 1)2 + (y – 2)2 + 2  2
 Min C = 2 khi x = 1; y = 2.
Bài toán 2: Tìm GTLN của các biểu thức: Trang 1 a) A = 5 – 8x – x2
b) B = 5 – x2 + 2x – 4y2 – 4y Giải:
a) A = 5 – 8x – x2 = -(x2 + 8x + 16) + 21 = -(x + 4)2 + 21  21  Max A = 21 khi x = -4.
b) B = 5 – x2 + 2x – 4y2 – 4y
= -(x2 – 2x + 1) – (4y2 + 4y + 1) + 7
= -(x – 1)2 – (2y + 1)2 + 7  7  1
Max B = 7 khi x = 1, y = − . 2
Bài toán 3: Tìm GTNN của:
a) M = x −1 + x − 2 + x − 3 + x − 4
b) N = ( x − )2 2 1 − 3 2x −1 + 2 Giải:
a) M = x −1 + x − 2 + x − 3 + x − 4 Ta có:
x −1 + x − 4 = x −1 + 4 − x x −1+ 4 − x = 3
Dấu “=” xảy ra khi và chỉ khi (x – 1)(4 – x)  0 hay 1 x  4
x − 2 + x − 3 = x − 2 + 3 − x x − 2 + 3 − x = 1
Dấu “=” xảy ra khi và chỉ khi (x – 2)(3 – x)  0 hay 2  x  3
Vậy Min M = 3 + 1 = 4 khi 2  x  3.
b) N = (2x − )2 2
1 − 3 2x −1 + 2 = 2x −1 − 3 2x −1 + 2
Đặt t = 2x −1 thì t  0 Do đó N = t2 1 1 – 3t + 2 = 3 2 (t − ) −  N  − . 2 4 4
Dấu “=” xảy ra khi và chỉ khi 3 3 t − = 0  t = 2 2  3  5 2x −1 = x =   Do đó 1 3 3 2 4 N = − khi t =  2x −1 =     4 2 2 3 1   2x −1 = − x = −  2  4 Vậy min 1 5 1 N = −
x = hay x = − . 4 4 4
Bài toán 4: Cho x + y = 1. Tìm GTNN của biểu thức M = x3 + y3. Trang 2 Giải:
M = x3 + y3 = (x + y)(x2 – xy + y2) = x2 - xy + y2 2 2 2 2 2 x y x y 1  x y  2 2 = + + − xy + = (x + y ) + −   2 2 2 2 2  2 2  1 2 2
M  (x + y ) 2
Ngoài ra: x + y = 1  x2 + y2 + 2xy = 1  2(x2 + y2) – (x – y)2 = 1 => 2(x2 + y2) ≥ 1 Do đó 1 1 1 2 2 x + y  và 2 2 x + y =  x = y = 2 2 2 1 1 1 1 1 Ta có: 2 2 M  (x + y ) và 2 2 (x + y )   M  . = 2 2 2 2 4 Do đó 1 M  và dấu “=” xảy ra 1  x = y = 4 2 Vậy GTNN của 1 1 M =  x = y = 4 2
Bài toán 5: Cho hai số x, y thỏa mãn điều kiện:
(x2 – y2 + 1)2 + 4x2y2 – x2 – y2 = 0.
Tìm GTLN và GTNN của biểu thức x2 + y2. Giải:
(x2 – y2 + 1)2 + 4x2y2 – x2 – y2 = 0
 [(x2 + 1) – y2]2 + 4x2y2 – x2 – y2 = 0
 x4 + 2x2 + 1 + y4 – 2y2(x2 + 1) + 4x2y2 – x2 – y2 = 0
 x4 + y4 + 2x2y2 + x2 – 3y2 + 1 = 0
 x4 + y4 + 2x2y2 - 3x2 – 3y2 + 1 = -4x2  (x2+y2)2-3(x2+y2)+1=-4x2
Đặt t = x2 + y2. Ta có: t2 – 3t + 1 = -4x2 Suy ra: t2 – 3t + 1 ≤ 0 Trang 3 3 9 5 2
t − 2. .t + −  0 2 4 4 2  3  5 3 5  t −   t −     2  4 2 2 5 3 5  −  t −  2 2 2 3 − 5 3 + 5   t  2 2 Vì t = x2 + y2 nên : 3 + 5 GTLN của x2 + y2 = 2 3 − 5 GTNN của x2 + y2 = 2
Bài toán 6: Cho 0 ≤ a, b, c ≤ 1. Tìm GTLN và GTNN của biểu thức:
P = a + b + c – ab – bc – ca. Giải:
Ta có: P = a + b + c – ab – bc – ca
= (a – ab) + (b - bc) + (c – ca)
= a(1 – b) + b(1 – c) + c(1 – a) 0 (vì 0  a, , b c  1)
Dấu “=” có thể xảy ra chẳng hạn: a = b = c = 0 Vậy GTNN của P = 0
Theo giả thiết ta có: 1 – a  0; 1 – b  0; 1 – c  0;
 (1-a)(1-b)(1-c) = 1 + ab + bc + ca – a – b – c – abc  0
 P = a + b + c – ab – bc – ac 1− abc 1
Dấu “=” có thể xảy ra chẳng hạn: a = 1; b = 0; c tùy ý 0;  1 Vậy GTLN của P = 1.
Bài toán 7: Cho hai số thực x, y thỏa mãn điều kiện: x2 + y2 = 1.
Tìm GTLN và GTNN của x + y. Giải:
Ta có: (x + y)2 + (x – y)2  (x + y)2  2(x2 + y2)  (x + y)2
Mà x2 + y2 = 1  (x + y)2  2 Trang 4
x + y  2  − 2  x + y  2
- Xét x + y  2 x = y  Dấu “=” xảy ra 2    x = y = x + y = 2 2
- Xét x + y  − 2 x = y  − Dấu “=” xảy ra 2    x = y =
x + y = − 2 2 − 2
Vậy x + y đạt GTNN là − 2  x = y = . 2
Bài toán 8: Cho các số thực dương thỏa mãn điều kiện: x2 + y2 + z2  27.
Tìm GTLN và GTNN của biểu thức: x + y + z + xy + yz + zx. Giải:
Ta có: (x – y)2 + (x – z)2 + (y – z)2  0  2x2 + 2y2 + 2z2 - 2xy - 2yz - 2zx  0
 (x + y + z)2 = x2 + y2 + z2 +2(xy + yz + zx)  3(x2 + y2 + z2)  81  x + y + z  9 (1)
Mà xy + yz + zx  x2 + y2 + z2  27 (2)
Từ (1) và (2) => x + y + z + xy + yz + zx  36.
Vậy max P = 36 khi x = y = z = 3.
Đặt A = x + y + z và B = x2 + y2 + z2 2 2 A − B ( A +1) B +1 B +1  P = A + = −  − 2 2 2 2 B +1 Vì B  27  −  -14  P  -14 2  + + = − Vậy min P = x y z 1 -14 khi  2 2 2
x + y + z = 27
Hay x = − 13; y = 13; z = 1 − . Bài toán 9:
Giả sử x, y là các số dương thỏa mãn đẳng thức: x + y = 10 . Tìm giá trị của x và y
để biểu thức: P = (x4 + 1)(y4 + 1) đạt GTNN. Tìm GTNN ấy. Giải:
Ta có: P = (x4 + 1)(y4 + 1) = (x4 + y4) + (xy)4 + 1 Đặt t = xy thì: Trang 5
x2 + y2 = (x + y)2 – 2xy = 10 – 2t
x4 + y4 = (x2 + y2)2 – 2x2y2 = (10 – 2t)2 – 2t2 = 2t2 – 40t + 100
Do đó: P = 2t2 – 40t + 100 + t4 + 1 = t4 + 2t2 – 40t + 101
= (t4 – 8t2 + 16) + 10(t2 – 4t + 4) + 45 = (t2 – 4)2 + 10(t – 2)2 + 45
P  45 và dấu “=” xảy ra  x + y = 10 và xy = 2.
Vậy GTNN của P = 45  x + y = 10 và xy = 2. Bài toán 10:
Cho x + y = 2. Tìm GTNN của biểu thức: A = x2 + y2. Giải:
Ta có: x + y = 2  y = 2 – x
Do đó: A = x2 + y2 = x2 + (2 – x)2 = x2 + 4 – 4x + x2 = 2x2 – 4x + 4 = 2( x2 – 2x) + 4 = 2(x – 1)2 + 2  2
Vậy GTNN của A là 2 tại x = y = 1.
• Dạng 2: CÁC BÀI TOÁN MÀ BIỂU THỨC CHO LÀ MỘT PHÂN THỨC Bài toán 1: Tìm GTLN và GTNN của: 4x + 3 y = . 2 x +1 Giải: * Cách 1: 2 4x + 3
−ax + 4x + 3 − a y = = a + 2 2 x +1 x +1 Ta cần tìm a để 2
−ax + 4x + 3− a là bình phương của nhị thức.  = − Ta phải có: a 1
 ' = 4 + a(3− a) = 0   a = 4 - Với a = -1 ta có: 2 2 4x + 3 x + 4x + 4 (x + 2) y = = 1 − + = −1+ 2 2 x +1 x +1 x +1  y  1.
− Dấu “=” xảy ra khi x = -2. Trang 6
Vậy GTNN của y = -1 khi x = -2. - Với a = 4 ta có: 2 2 4x + 3 -4x + 4x −1 (2x −1) y = = 4 + = 4 −  4 2 2 x +1 x +1 x +1
Dấu “=” xảy ra khi x = 1 . 2
Vậy GTLN của y = 4 khi x = 1 . 2 * Cách 2: 4x + 3 Vì x2 + 1  0 nên: 2 y =
 yx − 4x + y − 3 = 0 (1) 2 x +1
y là một giá trị của hàm số  (1) có nghiệm - Nếu y = 0 thì (1) 3  x = − 4
- Nếu y  0 thì (1) có nghiệm   ' = 4 − y( y − 3)  0  ( y +1)( y − 4)  0 y +1 0  +   y  hoặc 1 0  y − 4  0 y − 4  0  1 −  y  4
Vậy GTNN của y = -1 khi x = -2.
Vậy GTLN của y = 4 khi x = 1 . 2 2 x − x +1
Bài toán 2: Tìm GTLN và GTNN của: A = . 2 x + x +1 Giải:
Biểu thức A nhận giá trị a khi và chỉ khi phương trình ẩn x sau đây có nghiệm: 2 x − x +1 a = (1) 2 x + x +1 2 1 1 3  1  3 Do x2 + x + 1 = x2 + 2. .x + + = x + +  0   2 4 4  2  4
Nên (1)  ax2 + ax + a = x2 – x + 1  (a – 1)x2 + (a + 1)x + (a – 1) = 0 (2)
• Trường hợp 1: Nếu a = 1 thì (2) có nghiệm x = 0.
• Trường hợp 2: Nếu a  1 thì để (2) có nghiệm, điều kiện cần và đủ là   0, tức là: 2
(a +1) − 4(a −1)(a −1)  0  (a +1+ 2a − 2)(a +1− 2a + 2)  0 1
 (3a −1)(a − 3)  0   a  3(a  1) 3 Trang 7 Với 1 − a + a + a =
hoặc a = 3 thì nghiệm của (2) là ( 1) 1 x = = 3 2(a −1) 2(1− a) Với 1 a = thì x = 1 3 Với a = 3 thì x = -1
Kết luận: gộp cả 2 trường hợp 1 và 2, ta có: GTNN của 1 A = khi và chỉ khi x = 1 3
GTLN của A = 3 khi và chỉ khi x = -1 Bài toán 3:
a) Cho a, b là các số dương thỏa mãn ab = 1. Tìm GTNN của biểu thức: 4 2 2
A = (a + b +1)(a + b ) + . a + b
b) Cho m, n là các số nguyên thỏa 1 1 1 + = . Tìm GTLN của B = mn. 2m n 3 Giải:
a) Theo bất đẳng thức Côsi cho hai số dương a2 và b2 2 2 2 2
a + b  2 a b = 2ab = 2 (vì ab = 1) 4 4 4 2 2
A = (a + b +1)(a + b ) +
 2(a + b +1) + = 2 + (a + b + ) + (a + b) a + b a + b a + b
Cũng theo bất đẳng thức côsi cho hai số dương a + b và 4 . a + b 4 4 Ta có: (a + b) +  2 (a + b). = 4 a + b a + b
Mặt khác: a + b  2 ab = 2 4
Suy ra: A  2 + (a + b +
) + (a + b)  2 + 4 + 2 = 8 a + b Với a = b = 1 thì A = 8
Vậy GTNN của A là 8 khi a = b = 1. 1 1 1 b) Vì
+ = nên trong hai số m, n phải có ít nhất một số dương. Nếu có một trong 2m n 3
hai số là âm thì B < 0. Vì ta tìm GTLN của B = mn nên ta chỉ xét trường hợp cả hai số m, n cùng dương. 1 1 1 Ta có:
+ =  3(2m + n) = 2mn  (2m − 3)(n − 3) = 9 2m n 3
Vì m, n  N* nên n – 3  -2 và 2m – 3  -1. Trang 8
Ta có: 9 =1.9 = 3.3 = 9.1; Do đó xảy ra: 2m − 3 =1 m = 2 +    và B = mn = 2.12 = 24 n − 3 = 9 n =12 2m − 3 =1 m = 3 +    và B = mn = 3.6 = 18 n − 3 = 3 n = 6 2m − 3 = 9 m = 6 +    và B = mn = 6.4 = 24 n − 3 =1 n = 4 m = m = 6 Vậy GTLN của B = 24 khi 2  hay  n =12 n = 4
Bài toán 4: Giả sử x và y là hai số thỏa mãn x > y và xy = 1. Tìm GTNN của biểu 2 2 thức: x + y A = . x − y Giải: 2 2 2 2 2 Ta có thể viết: x + y
x − 2xy + y + 2xy
(x − y) + 2xy A = = = x − y x − y x − y 2
(x − y) + 2xy 2 x − y 2 x − y
Do x > y và xy = 1 nên: A = = x − y + = + + x − y x − y 2 x − y 2
Vì x > y  x – y > 0 nên áp dụng bất đẳng thức côsi với 2 số không âm, ta có: x − y 2 x − y A  2. . + 2 x − y 2 Dấu “=” xảy ra x − y 2 2  =
 (x − y) = 4  (x − y) = 2 (Do x – y > 0) 2 x − y Từ đó: 2 A  2 + = 3 2  − = Vậy GTNN của A là 3 x y 2   xy =1 x =1+ 2  = −  x 1 2  hay  Thỏa điều kiện xy = 1 y = 1 − + 2 y = −1− 2 1
Bài toán 5: Tìm GTLN của hàm số: y = . 2 x + x +1 Giải: Ta có thể viết: 1 1 y = = 2 2 x + x +1  1  3 x + +    2  4 2  1  3 3 Vì x + +    . Do đó ta có: 4 y  . Dấu “=” xảy ra 1  x = − .  2  4 4 3 2 Vậy: GTLN của 4 − y = tại 1 x = 3 2 Trang 9
Bài toán 6: Cho t > 0. Tìm GTNN của biểu thức: 1
f (t) = t + . 4t Giải: 2 2 2 Ta có thể viết: 1 4t +1 (2t −1) + 4t (2t −1)
f (t) = t + = = = +1 4t 4t 4t 4t
Vì t > 0 nên ta có: f (t)  1 Dấu “=” xảy ra 1
 2t −1 = 0  t = 2
Vậy f(t) đạt GTNN là 1 tại 1 t = . 2 2 t −1
Bài toán 7: Tìm GTNN của biểu thức: g(t) = . 2 t +1 Giải: 2 Ta có thể viết: t −1 2 g(t) = =1− 2 2 t +1 t +1
g(t) đạt GTNN khi biểu thức 2 đạt GTLN. Nghĩa là t2 + 1 đạt GTNN 2 t +1
Ta có: t2 + 1  1  min (t2 + 1) = 1 tại t = 0  min g(t) = 1 – 2 = -1
Vậy GTNN của g(x) là -1 tại t = 0.
Bài toán 8: Cho x, y, z là các số dương thỏa mãn điều kiện: xyz = 1. Tìm GTNN của biểu thức: 1 1 1 E = + + . 3 3 3
x ( y + z) y (z + x) z (x + y) Giải: Đặt 1 1 1 1 a = ;b = ; c =  abc = =1 x y z xyz Do đó: 1 1
+ = a + b x + y = (a + b).xy x + y = c(a + b) x y
Tương tự: y + z = a(b + c) z + x = b(c + a) 1 1 1 1 1 1  E = . + . + . 3 3 3 x ( y + z) y (z + x) z (x + y) 2 2 2 1 1 1 a b c 3 3 3 = a . + b . + c . = + + a(b + c) b(c + a) c(a + b) b + c c + a a + b a b c 3 Ta có: + +  (1) b + c c + a a + b 2
Thật vậy: Đặt b + c = x; c + a = y; a + b = z Trang 10 x + y + z
a + b + c = 2
y + z − x
z + x − y
x + y − za = ;b = ; c = 2 2 2 Khi đó, a b c
y + z − x
z + x − y
x + y − z VT = + + = + + b + c c + a a + b 2x 2 y 2z 1  y x  1  z x  1  z y  3 3 3 = + + + + + − 1+1+1− =       2  x y  2  x z  2  y z  2 2 2
Nhân hai vế (1) với a + b + c > 0. Ta có:
a(a + b + c)
b(a + b + c)
c(a + b + c) 3 + +
 (a + b + c) b + c c + a a + b 2 2 2 2 3 a b c a + b + c 3 abc 3 3  + +   =  E b + c c + a a + b 2 2 2 2
 GTNN của E là 3 khi a = b = c = 1. 2
Bài toán 9: Cho x, y là các số thực thỏa mãn: 4x2 + y2 = 1 (*).
Tìm GTLN, GTNN của biểu thức: 2x + 3y a = . 2x + y + 2 Giải: Từ 2x + 3y a =  a(2x+y+z) = 2x+3y 2x + y + 2
 2ax + ay + 2a – 2x +3y = 0
 2(a – 1)x + (a – 3)y = -2a (1)
Áp dụng bất đẳng thức Bunhiacopxki cho hai bộ số (2x; y) và (a – 1; a – 3)
Ta có: 4a2 = [2x(a-1)+y(a-3)]2 ≤ (4x2+y2).[(a-1)2+(a-3)2] => 2 2 2
4a = (a −1) + (a − 3) (vì 4x2+y2 = 1) Do đó ta có: 2 2 2 2 2
4a  (a −1) + (a − 3) = a − 2a +1+ a − 6a + 9 2 2
 2a + 8a −10  0  a + 4a − 5  0 a + 5  0
 (a −1)(a + 5)  0  
(Vì a + 5 > a – 1) 1 a  5 a −1 0
* Thay a = 1 vào (1) ta được: -2y = -2  y = 1
Thay y = 1 vào (*) ta có: x = 0  (x; y) = (0;1)
* Thay a = -5 vào (1) ta được: 2(-5 – 1)x + (-5 – 3)y = -2(-5) 6 − x − 5  1
− 2x −8y =10  6x + 4y = 5 −  y = 4 Trang 11 2 Thay vào (*) ta được:  6 − x − 5  2 4x + =1    4  3 4  −3 −4  2
 100x + 60x + 9 = 0  x = −  y = −  ( ; x y) = ;   10 5  10 5 
Vậy GTLN của a là 1 khi x = 0; y = 1. 3 4
GTNN của a là -5 khi x = − ; y = − . 10 5 Bài toán 10:
Giả sử x, y là hai số dương thỏa mãn điều kiện: x + y = 1.
Hãy tìm gái trị nhỏ nhất cảu biểu thức: 2 2  1   1  M = x + + y +      x   y Giải: 2 2  1   1  Ta có: M = x + + y +      x   y  1 1 = 2 2 x + + 2 + y + + 2 2 2 x y 2 2 x + y  1  = 4 + x2 + y2 + = 4 + ( 2 2 x + y 1+   2 2 ) 2 2 x yx y
Vì x, y > 0 nên ta có thể viết:
( x − y)2 0= x+ y  2 xy 1 1
Mà x + y = 1 nên 1  2 xy =  2 = 16 (1) 2 2 xy x y
Dấu “=” xảy ra khi và chỉ khi 1 x = y = 2 Ngoài ra ta cũng có: 2 2 2 2 2 2 2
(x − y)  0  x + y  2xy  2(x + y )  2xy + x + y 2 2 2 2 2
 2(x + y )  (x + y)  2(x + y )  1 (vì x + y = 1) 1 2 2
x + y  (2) 2
Dấu “=” xảy ra khi và chỉ khi 1 x = y = 2 Từ (1) và (2) cho ta: 1 1 25 2 2
M = 4 + (x + y )(1+ )  4 + (1+16) = 2 2 x y 2 2 Trang 12 Do đó: 25 M  2
Dấu “=” xảy ra khi và chỉ khi đồng thời ở (1) và (2) cùng xảy ra dấu “=” nghĩa là khi 1 x = y = 2 Vậy GTNN của 25 M = khi và chỉ khi 1 x = y = . 2 2
* Dạng 3: CÁC BÀI TOÁN MÀ BIỂU THỨC CHO CÓ CHỨA CĂN THỨC.
Bài toán 1: Tìm GTLN của hàm số: y = x − 2 + 4 − x . Giải: * Cách 1:  −  Điều kiện: x 2 0   2  x  4(*) 4 − x  0
Áp dụng bất đẳng thức Bunhiacopxki: (ac + bd)2  (a2 + b2)(c2 + d2)
Dấu “=” xảy ra khi và chỉ khi a b = . c d
Chọn a = x − 2;c =1;b = 4 − x;d =1 với 2  x  4 Ta có:  
y = ( x − 2 + 4 − x )2  ( x − 2)2 + ( 4 − x )2 2 .( 2 2 1 +1 )   2
y  (x − 2) +(4− x).2  2
y  4  y  2
Vì y > 0 nên ta có: 0  y  2
Dấu “=” xảy ra  x − 2 = 4 − x x − 2 = 4 − x x = 3 (Thỏa mãn (*))
Vậy GTLN của y là 2 tại x = 3. * Cách 2:
Ta có: y = x − 2 + 4 − x  −  Điều kiện: x 2 0   2  x  4 4 − x  0
Vì y > 0 nên y đạt GTLN khi và chỉ khi y2 đạt GTLN. Ta có: 2 2
y = x − 2 + 4 − x + 2 (x − 2)(4 − x)  y = 2 + 2 (x − 2)(4 − x) x − 2  0
Do 2  x  4  
nên áp dụng bất đẳng thức côsi cho hai số không âm 4 − x  0
cho ta: 2 (x − 2)(4 − x)  (x − 2) + (4 − ) x = 2 Trang 13 Do đó 2 y  2 + 2 = 4
Dấu “=” xảy ra  x − 2 = 4− x x = 3 (thỏa mãn điều kiện).
Vậy GTLN của hàm số y là 2 tại x = 3.
Bài toán 2: Tìm GTLN, GTNN của hàm số: y = 3 x −1 + 4 5 − x(1 x  5) . Giải: a) GTLN:
Áp dụng bất đẳng thức Bunhiacopxki cho hai bộ số:
(3; 4) và ( ( x −1; 5 − x) ta có:   y = x − + − x  + ( x − )2 + ( − x )2 2 2 2 2 (3. 1 4. 5 ) (3 4 ). 1 5 =100   <=> 2 y  100 => y  10
Dấu “=” xảy ra <= x −1 5 − x − − − x 1 5 x hay = 3 4 9 16 61 => x = (thỏa mãn điều kiện) 25
Vậy GTLN của y là10 khi x = 61 25 * b) Gía trị nhỏ nhất:
Ta có: y = 3 x −1 + 4 5 − x = 3 x −1 + 3 5 − x + 5 − x
= 3( x −1+ 5− x ) + 5− x
Đặt: A = x −1 + 5 − x thì t2 = 4 + 2 (x − ) 1 (5 − x)  4
=> A  2 và dấu “=” xảy ra khi x = 1 hoặc x = 5 Vậy y  3 . 2 + 0 = 6
Dấu “=” xảy ra khi x = 5
Do đó GTNN của y là 6 khi x = 5
Bài toán 3: GTNN của y là 6 khi x = 5
Tìm GTNN của biểu thức: M = (x − )2 2 1994 + (x +1995) Giải: M = ( x − )2 2 1994
+ (x +1995) = x −1994 + x +1995
Áp dụng bất đẳng thức: a + b a + b ta có: Trang 14
M = x −1994 + x +1995 = x −1994 + 1995 + x
=> M  x −1994 +1995 − x =1
Dấu “=” xảy ra khi và chỉ khi (x – 1994) . (1995 – x)  0
<=> 1994  x 1995
Vậy GTNN của M = 1  1994  x 1995 Bài toán 4: Tìm GTNN của B = 3a + 4 2
1− a với -1  a  1 Giải: 3 16
B = 3a + 4 1− a = 5  a + 5 (1− a)2 2 5 25
Và áp dụng bất đẳng thức Cô si với hai số không âm cho ta 2  3  2 16  a   + (1− a)2 3 16     a + ( − a)2 5 25 5 5 1  5 + 5 5 25 2 2 2 2
 9 + 25a + 41− 25a  => B  5  = 5  2  25 
=> Do đó B 5 và dấu “=” xảy ra khi và chỉ khi.  3 a =  5 3  <=> a = 16 2  = 5 1− a 25
Vậy GTNN của B = 5 <=> a = 3 5 Bài toán 5:
Tìm GTNN của biểu thức: 3 A = 2 2 + 2x − x + 7 Giải: Điều kiện: 2 x − x +  = −( 2 2 7 0 x − 2x + ) 1 + 8  0
<=> -(x-1)2 + 8  0 = ( x − )2 1  8 = 2
− 2  x −1 2 2
=1− 2 2  x  2 2 +1
Với điều kiện này ta viết: Trang 15 x − x + = −(x − )2 2 2 2 7 1 + 8  8 =
2x − x + 7  8 = 2 2 => 2 + 2
2x − x + 7  2 + 2 2 = 2( 2 + ) 1 Do đó: 1 1 2 −1  = 2 2 + 2x − x + 7 2 ( 2 + ) 1 2 Vậy A 2 −1  3
và dấu “=” xảy ra <=> x -1 = 0 2
<=> x = 1 (thỏa mãn điều kiện)
Vậy GTNN của A = 3 ( 2 − )1 = x =1 2 Bài toán 6:
Tìm GTNN của biểu thức: A = 5 − 3x 2 1− x Giải:
Điều kiện: 1 – x2 > 0 <=> x2 < 1 <=> - 1 < x < 1
=> A > 0 => GTNN của A  A2 đạt GTNN.
(5−3x)2 25−30x +9x (3−5x)2 2 Ta có: A2 = ( = = +  − − − x ) 16 16 2 2 2 2 1 x 1 x 1 Vậy GTNN của A = 4 khi 3 x = 5
Bài toán 7: Cho x > 0 ; y = 0 thỏa mãn x + y  1
Tìm GTNN của biểu thức: A = 2 x  1− x Giải:
Điều kiện: 1 – x2  0 = 1 −  x 1
Áp dụng bất đẳng thức Cô si hai số: x2  0 và 1 – x2  0 Ta có: x2 + 1 – x2 2  x ( 2 − x ) 2 2 1
=1 2 x  1− x 1
<=> 1  2 A = A  2 Vậy GTLN của A = 1 2 − 2 khi x =  hay x = 2 2 2 Bài toán 8:
Tìm GTLN của biểu thức: y = x −1996 + 1998 − x Trang 16 Giải:
Biểu thức có nghĩa khi 1996  x 1998
Vì y  0 với mọi x thỏa mãn điều kiện 1996  x 1998
Áp dụng bất đẳng thức Cô si ta có:
2 ( x −1996)(1998 − x)  (x −1996) + (1998 − x) = 2
Dấu “=” xảy ra khi và chỉ khi x – 1996 = 1998 – x <=> x = 1997
Do đó y2  4 = y  2
Vậy GTLN của y là 2 khi x = 1997 Bài toán 9:
Cho 0  x 1. Tìm GTLN của biểu thức y = x + 2(1− x) Giải: 1
Ta có: y = x + 2(1− x) = x + 2  (1− x) 2
Vì 0  x 1 nên 1 – x  0
Áp dụng bất đẳng thức Cô si đối với 2 số: 1 và (1 – x) cho ta: 2 1 y = x +  ( − x) 1
x + + ( − x) 3 2 1 1 = 2 2 2
Dấu “=” xảy ra <=> 1 1
=1− x = x = 2 2
Vậy GTLN của y là 3 tại x = 1 2 2 Bài toán 10:
Cho M = a + 3 − 4 a −1 + a +15 − 8 a −1 Tìm TGNN của M Giải:
M = a + 3 − 4 a −1 + a +15 − 8 a −1
= a −1− 4 a −1 + 4 + a −1− 8 a −1 +16 2 2
= ( a −1 − 2) + ( a −1 − 4)
Điều kiện để M xác định là a – 1  0 = a 1 Ta có: M = a −1 − 2 + a −1 − 4
Đặt x = a −1 điều kiện x  0 Trang 17
Do đó: M = x − 2 + x − 4
Ta xét ba trường hợp sau:
1) Khi x  2 thì x − 2 = −( x − 2) = 2 − x
Và x − 4 = −( x − 4) = 4 − x
=> M = 2 – x + 4 – x = 6 – 2x  6 − 2.2 = 2 Vậy x < 2 thì M  2
2) Khi x  4 thì x − 2 = x − 2 và x-4 =x-4
=> M = x − 2 + x − 4 = 2x − 6  2 4 − 6 = 2 Vậy x > 4 thì M  2
3) Khi 2 < x < 4 thì x − 2 = x − 2 và x − 4 = 4 − x
=> M = x – 2 + 4 – x = 2 (không phụ thuộc vào x)
Trong trường hợp này thì: 2  a −1  4
<=> 4  a −116
<=> 5  a 17
Cả ba trường hợp cho ta kết luận:
GTNN của M = 2 tương ứng với: 5  a 17
C. CÁC BÀI TẬP TỰ LUYỆN: Bài 1:
Tìm GTNN của biểu thức: A = (2x – 3)2 – 7 với x  −1 hoặc x  3. Gợi ý:
- Xét 2 trường hợp: x ≥ 3 và x ≤ -1
- Kết luận: Min A = 2 <=> x = 3
Chú ý: Mặc dù A = (2x – 3)2 – 7  7
− . Xảy ra đẳng thức khi và chỉ khi x = 3 nhưng 2
giá trị không thỏa mãn x  −1 , không thỏa mãn x  3. Do đó không thể kết luận được GTNN của A bằng – 7. Bài 2:
Gọi x1; x2 là các nghiệm của phương trình:
x2 – (2m – 1) x + (m – 2) = 0 Trang 18
Tìm các giá trị của m để 2 2
x + x có giá trị nhỏ nhất 1 2 Gợi ý:
 = 4(m - 1 )2 + 5 > 0. Phương trình đã cho có nghiệm với mọi m theo hệ thức Vi-ét, ta có: 2 2 2 2 2
x + x = (x + x ) − 2x x = (2m −1) − 2(m − 2) = 4m − 6m + 5 1 2 1 2 1 2 2  3  11 11 = 2m − +     2  4 4 11 => Min ( ( 2 2 x + x = với m = 3 1 2 ) 4 4 Bài toán 3:
Cho x, y là hai số thỏa mãn: x + 2y = 3. Tìm GTNN của E = x2 + 2y2 Gợi ý:
Rút x theo y và thế vào E Bài toán 4:
Tìm GTLN và GTNN của biểu thức: A = x2 + y2
Biết rằng x và y là các số thực thỏa mãn: x2 + y2 – xy = 4 Gợi ý:
Từ x2 + y2 – xy = 4 <=> 2x2 + 2y2 – 2xy = 8 <=> A + (x – y)2 = 8 <=> Max A = 8 khi x = y
Mặt khác: 2x2 + 2y2 = 8 + 2xy
<=> 3A = 8 + (x + y)2  8 8 8
=> A  = min A = khi x = - y 3 3 Bài toán 5:
Cho x, y thỏa mãn: x2 + 4y2 = 25.
Tìm GTLN và GTNN của biểu thức: M = x + 2y. Giải:
Áp dụng bất đẳng thức: Bunhiacôpxki (x +2y)2 2 2
 (x + 4y ) (12 + 12) = 50
<=> x + 2y  50 = − 50  M  50 Trang 19 Vậy Max M = 5 5 50 khi x = ; y = 2 2 2 5 5 Min M = -5 2 khi x = - ; y = - 2 2 2 Bài tóan 6:
Cho x, y là hai số dương thỏa mãn điều kiện: xy = 1. Tìm GTLN của biểu thức: x y A = + 4 2 2 4 x + y x + y Gợi ý: Từ (x2 – y)2 4 2 2
 0 = x + y  2x y x x 1 =>  = 4 2 2 x + y 2x y 2 Tương tự: y 1  4 2 y + x 2 2 x = y
=> A  1 => Max A = 1 khi 2
y = x = x = y =1 xy =1  Bài tóan 7:
Tìm GTNN của biểu thức:
A = x + 2(1+ x +1) + x + 2(1− x +1) Gợi ý:
B = x +1 +1 + 1− x +1 = Min B = 2 khi - 1  x  0
Bài toán 8: Tìm GTNN của biểu thức:
B = (x – a )2 + (x – b)2 + (x – c)2 với a, b, c cho trước. Gợi ý: 2  + +  + + Biểu diễn B = a b c x − + ( a b c 2 2 2 3.
a + b + c ) ( )2 −    3  3
(a +b + c)2
=> GTNN của B = (a2 + b2 + c2) - 3
Bài toán 9: Tìm GTNN của biểu thức:
P = x2 – 2xy + 6y2 – 12x + 3y + 45 Gợi ý:
Biểu diễn P = (x – 6 – y)2 + 5(y – 1)2 + 4 Trang 20
Vậy Min P = 4 khi y = 1 ; x = 7
Bài toán 10: Tìm GTLN của biểu thức:
E = – x2 + 2xy – 4y2 + 2x + 10y – 3 Gợi ý:
Biểu diễn E = 10 – (x – y – 1)2 – 3 (y – 2)2
=> GTLN của E = 10  y = 2 ; x = 3
Bài toán 11: Tìm GTLN của biểu thức: P = 2x + 4y + 5  z
Biết x, y, z là các biến thỏa mãn : x2 + y2 + z2 = 169
Gợi ý: Áp dụng bất đẳng thức Bunhiacôpxki   x = 265  y  
Max P = 65 khi x = = z y 2 4  = 525  5    13 5  z = 5  Bài toán 12:
Tìm GTNN của biểu thức sau: 2 x +1 a) A = Với x  0 x + 2 8 − b) B = Với mọi x 2 3x + 2 2 x −1 c) C = Với mọi x 2 x +1 Gợi ý:
a) Áp dụng bất đẳng thức Cô si cho ta: 5 A = (x + 2) + − 4  2 5 − 4 x + 2 8 − 1 1 b) B =  4 − (vì  ) 2 3x + 2 2 3x + 2 2 2 2x c) C = 1 − +
 −1 = Min C = - 1 khi x = 0 2 x +1 Bài toán 13: 2
Tìm GTNN của biểu thức A = x − 2x + 2000 ;(x  0) 2 x Gợi ý: 2 2 2 2
2000x − 2  2000x + 2000
(x − 2000) +1999x A = = 2 2 2000x 2000x Trang 21 2 (x − 2000) 1999 1999 = +  2 2000x 2000 2000
Vậy Min A = 1999 Khi x = 2000 2000 Bài toán 14:
Tìm GTNN của biểu thức: 4 3 2
4x +16x + 56x + 80x + 356 P = 2 x + 2x + 5 Gợi ý: Biểu diễn P = 4 256 2 (
x + 2x + 5) +
 64 (áp dụng BĐT Côsi) 2 x + 2x + 5
=> Min P = 64 khi x = 1 hoặc x = -3 Bài toán 15: 2
Tìm GTNN của A = x + 4x + 4 với x > 0 x 2 x B = với x > 1 x −1 2 x + x + 2 C = 2 x + x +1  1  D = (1+ x) 1+   với x > 0  x x 5 E = + với 0 < x < 1 1− x x x 2 F = + với x > 1 2 x −1 Gợi ý: 4 4
A = x+ + 4  2 x  + 4 = 8 (vì x > 0) x x => Min A = 8 khi x = 2 2 x −1+1 1 B = = 2 + (x −1) +  2 + 2 = 4 (vì x > 1) x −1 x −1
=> Min B = 4 <=> x = 2 2 2 (x + x +1) +1 2  x + x +1 C =  = 2 2 2 x + x +1 x + x +1  1  1 D = (1 + x) 1+  2 x.2. = 4   (vì x > 0)  x x x 5 − 5x + 5x x 5(1− x) x 5(1− x) E = + = + + 5  2  + 5 = 2 5 + 5 1− x x 1− x x 1− x x Trang 22 x −1+1 2 x −1 2 1 x −1 2 1 F = + = + +  2  + 2 x −1 2 x −1 2 2 x −1 2 1 3 3
= + 2 = => Min F = khi x = 3. 2 2 2
Bài 16: Tìm GTLN và GTNN của biểu thức: 2 8x + 6xy P = 2 2 x + y Gợi ý: 2 ( y + 3x) P = 9 - −1 1 − 2 2 x + y 2 (x − 3y) P = 9 -  9 2 2 x + y
Bài 17: Cho x, y là hai số dương thỏa mãn: x + y = 10
Tìm GTNN của biểu thức S = 1 1 + x y x + y 10 Gợi ý: S = 1 1 + = = x y xy x(10 − x)
S có GTNN <=> x(10-x) có GTLN <=> x = 5.
=> GTNN của S = 2 khi x = y = 5. 5
Bài 18: Tìm GTNN của biểu thức: E = 2 2
x + x +1 + x − x +1 Gợi ý:
Ta có E > 0 với mọi x Xét E2 = 2 (x2 + 1 + 4 2 x + x +1)  4 => Min E = 2 khi x = 0
Bài 19: Cho a và b là hai số thỏa mãn: a  3 ; a + b  5
Tìm GTNN của biểu thức S = a2 + b2 Gợi ý:
a+ b  5 = 2a + 2b 10 = 3a + 2b 13 (vì a  3)
=> 132  ( a + b)2  ( 2 2 3 2 13 a + b ) => Min S = 13 Bài 20:
Cho phương trình: x2 - 2mx – 3m2 + 4m – 2 = 0 Trang 23
Tìm m để cho x − x đạt GTNN. 1 2 Gợi ý: ' 2
 = (2m −1) +1  0 = phương trình luôn có 2 nghiệm phân biệt x1; x2. Theo định lý vi-ét ta có:
x + x = 2m 1 2  2 x .x = 3 − m + 4m − 2  1 2
Do đó x − x = (4m − 2)2 + 4  4 = 2 m R 1 2 1
GTNN của x − x là 2 khi m = 1 2 2 Bài 21:
Tìm giá trị nhỏ nhất của:
y = x −1 + x − 2 +...+ x −1998 Gợi ý:
y = ( 1x −1 + x −1998 ) + ( x − 2 + x −1997 ) + …+ ( x − 998 + x − 999 )
Ta có: x −1 + x −1998 nhỏ nhất bằng 1997 khi x 1;199  8
x − 2 + x −1997 nhỏ nhất bằng 1995 khi x 2;1997
x − 998 + x −1999 nhỏ nhất bằng 1 khi x 999;1000
Vậy y đạt GTNN bằng 1 + 3 + …+ 1997
Số các số hạng của 1 + 3 + … + 1997 là (1997 – 1) : 2 + 1 = 999
Vậy Min y = 9992 khi 999  x 1000 Bài 22:
Cho biểu thức: M = x2 + y2 + 2z2 + t2
Với x, y, z, t là các số nguyên không âm , tìm gia strị nhỏ nhất của M và các giá trị
tương ứng của x, y, z, t. Biết rằng: 2 2 2
x − y +t = 21 (1)  2 2 2
x + 3y + 4z =101 (2) Gợi ý: Theo giả thiết: x2 – y2 + t2 = 21 x2 + 3y2 + 4z2 = 101
=> 2x2 + 2y2 + 4z2 + t2 = 122 Trang 24 => 2M = 122 + t2
Do đó 2M 122 = M  61 Vậy Min M = 61 khi t = 0
Từ (1) => x > y  0 = x + y x − y  0
Do đó: (x + y )(x – y) = 21.1 = 7.3 Từ (2) => 3y2 2
 101 = y  33 = 0  y  5
Ta chọn x = 5 ; y = 2 => z = 4
Vậy Min M = 61 tại x = 5 ; y = 2 ; z = 4; t = 0 Bài 23:
Cho phương trình: x4 + 2x2 +2ax – (a – 1)2 = 0 (1)
Tìm giá trị của a để nghiệm của phương trình đó: a) Đạt GTNN.
b) Đạt gía trị lớn nhất. Gợi ý:
Gọi m là nghiệm của phương trình (1) thì:
m4 + 2m2 + 2am + a2 + 2a + 1 = 0 (2)
Viết (2) dưới dạng phương trình bậc hai ẩn a.
a2 + 2 (m + 1) a + (m4 + 2m2 + 1) = 0 Để tồn tại a thì '   0
Giải điều kiện này được m4 - m2  0 <=> m(m – 1)  0 = 0  m 1
Vậy nghịêm của phương trình đạt GTNN là 0 với a = -1
Vậy nghịêm của phương trình đạt GTLN là 1 với a = -2 2 x + 2x + 2
Bài 24: Tìm GTNN, GTLN của t = 2 x +1
Gợi ý: Vì x2 + 1 > 0 với mọi x 2
Đặt a = x + 2x + 2 => (a – 1) x2 – 2 x +a – 2 = 0 (1) 2 x +1
a là một giá trị của hàm số <=> (1) có nghiệm. −
- Nếu a = 1 thì (1) <=> x = 1 2
- Nếu a  1 thì (1) có nghiệm <=> '   0 Trang 25 3 − 5 − − − Min A = với x = 1 5 3+ 5 ; Max A = với x = 5 1 2 2 2 2 Bài 25: 2 2
x − xy + y Tìm GTNN, GTLN của A = 2 2
x + xy + y
Gợi ý: Viết A dưới dạng sau với y  0 2  x x − +1   2  y y a − a +1 ( A = =
(đặt x = a ) 2 2   a + a +1 x x y + +1    y y
Giải tương tự bài 24 được: 1  A  3 3 Còn với y = 0 thì A = 1
Do đó: Min A = 1 với x = y ; max A = 3 với x = - y 3
Bài 26: Cho a + b = 1. Tìm GTNN của biểu thức: Q = a3 + b3 + ab Gợi ý:
Với Q dưới dạng Q = (a + b) (a + b)2 −3ab + ab  
= 1 – 2ab = 1 – 2a (1 – a) 1 => Q = 2a2 – 2a + 1  2 Do đó: Min Q = 1 1 khi a = b = 2 2 Trang 26