Chuyên đề trắc nghiệm phương pháp đổi biến số tính tích phân Toán 12
Tài liệu gồm 23 trang, trình bày lý thuyết trọng tâm, các dạng toán trọng tâm kèm phương pháp giải và bài tập trắc nghiệm tự luyện chuyên đề phương pháp đổi biến số tính tích phân, có đáp án và lời giải chi tiết; hỗ trợ học sinh lớp 12 trong quá trình học tập chương trình Toán 12 phần Giải tích chương 3.
Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu
Môn: Toán 12 3.9 K tài liệu
Tác giả:
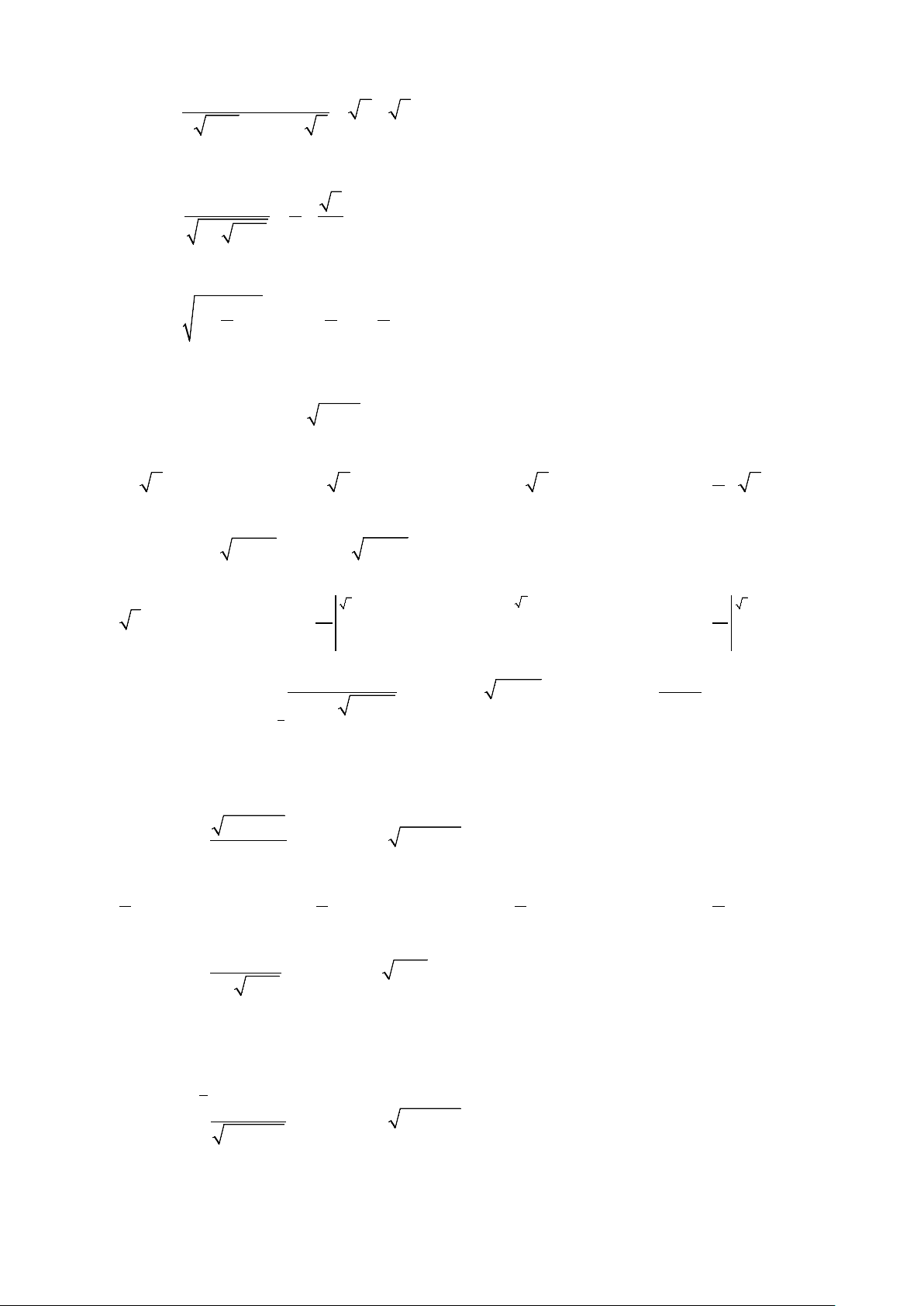
Preview text:
CHỦ ĐỀ 8: PHƯƠNG PHÁP ĐỔI BIẾN SỐ TÍNH TÍCH PHÂN
1) Định lí: Cho hàm số f (x) liên tục trên đoạn [ ;
a b]. Giả sử hàm số x = ϕ (t) có đạo hàm liên tục trên
đoạn [α;β ] sao cho ϕ (α ) = ;
a ϕ (β ) = b và a ≤ ϕ (t) ≤ b với mọi t ∈[α;β ]. b β Khi đó f
∫ (x)dx = f
∫ (φ(t))ϕ '(t)dt. a α
Chú ý: Trong nhiều trường hợp ta còn sử dụng phép biến đổi biến số ở dạng sau: b
Cho hàm số f ( x) liên tục trên đoạn [a;b]. Để tính f ( x)dx ∫
, đôi khi ta chọn hàm số u = u (x) làm a
biến số mới, trong đó trên đoạn [ ;
a b],u(x) có đạo hàm liên tục và u(x)∈[α;β ].
Giả sử có thể viết f ( x) = g (u ( x))u '( x), x ∈[ ;
a b], với g (u) liên tục trên đoạn[α;β ]. b u(b) Khi đó, ta có f
∫ (x)dx = g ∫ (u)du. a u(a)
2) Các dạng toán trọng tâm
Dạng 1: Đổi biến số với các hàm vô tỉ quen thuộc
Trong biểu thức của f ( x) dx có chứa căn thì đặt căn đó bằng t.
Trong biểu thức của f ( x) dx có chứa biểu thức lũy thừa bậc cao thì đặt biểu thức đó bằng t.
Trong biểu thức của f ( x) dx có chứa hàm mũ với biểu thức trên mũ là một hàm số thì đặt biểu thức trên mũ bằng t.
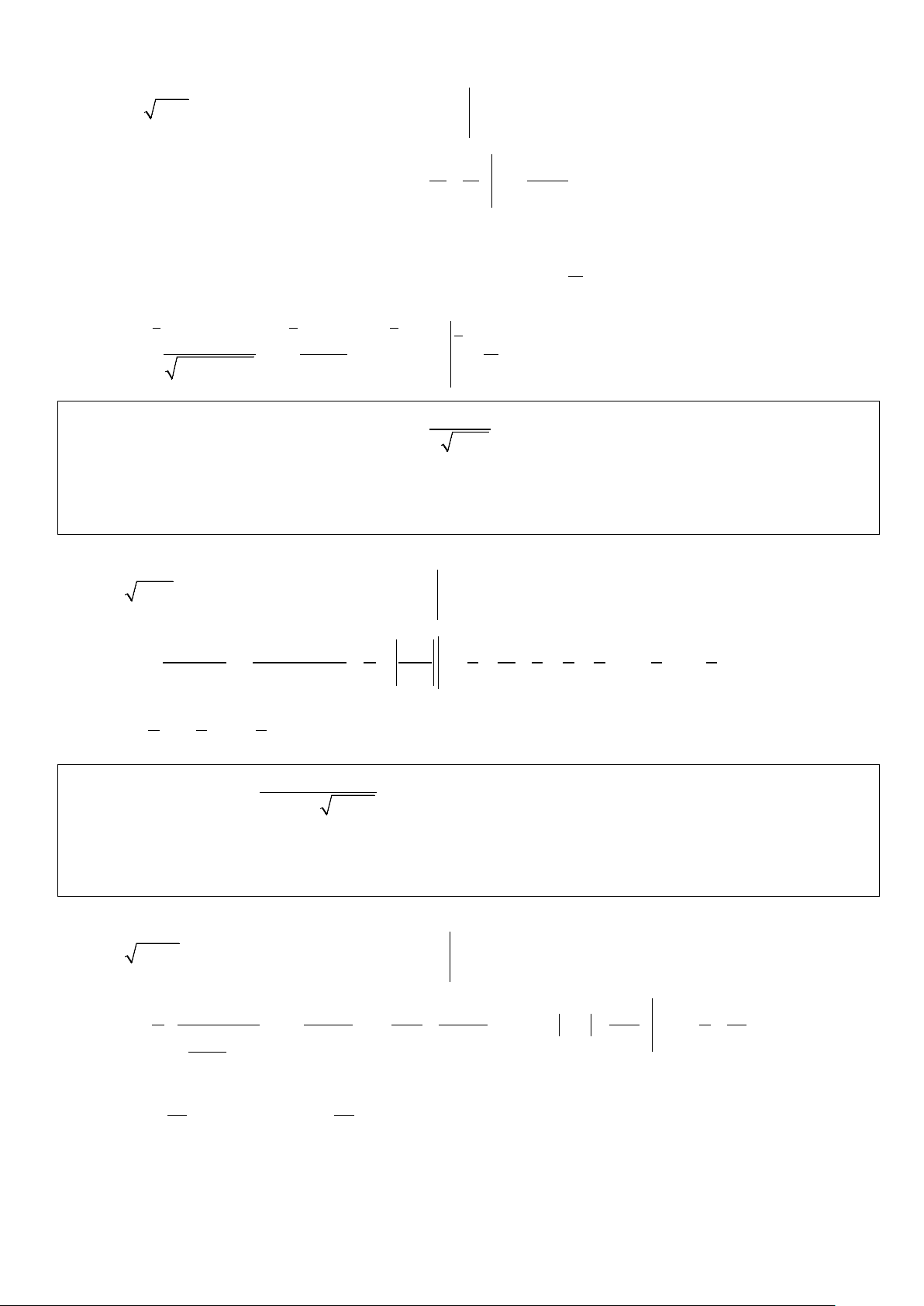
Ví dụ 1: Tính các tích phân sau bằng phương pháp đổi biến số: 4 ln3 9 1 a) dx I = . ∫ b) dx I = . ∫ c) 3 I = . x 1− x . dx ∫ d) 2 I = . dx ∫ + + x 2 0 3 2x 1 0 e +1 1 0 4 − x Lời giải
Chú ý: Đổi biến nhớ phải đổi cận.
x = 0 ⇒ t =1 a) Đặt 2
t = 2x −1 ⇔ t = 2x +1 ⇔ dx = tdt. Đổi cận .
x = 4 ⇒ t = 3 3 3 3 Khi đó t 3 I dt = = − dt = ∫ ∫ (t − t + ) 2 1 3ln 3
= 3− 3.ln 6 −1+ 3.ln 4 = 2 + 3.ln . 3+ t t + 3 3 1 1 1 b) Đặt x 2 x x 2 = +1 ⇔ = +1 ⇔ 2 t t e t e
tdt = e dx ⇔ dx = dt. 2 t −1 2 2
Đổi cận x = 0 ⇒ t = 2 dt t −1 , khi đó I = 2 = ln = − ln 3 3− 2 2 . ∫ 2 ( )
x = ln 3 ⇒ t = 2 t −1 t +1 2 2 x =1⇒ t = 0 c) Đặt 3 3 2
t = 1− x ⇔ t =1− x ⇔ 3t dt = − . dx Đổi cận x = 9 ⇒ t = 2 − 2 − 2 − 7 4 2 −
Khi đó I ∫ ( 3t)t( 2t)dt ∫ ( 6 3 t t ) t t 468 1 3 dt 3 − = − − = − = − = . 7 4 7 0 0 0
x = 0 ⇒ t = 0
d) Đặt x = 2sin t ⇒ dx = 2costdt (t ∈[0;π ]). Đổi cận π . x =1⇒ t = 6 π π π π 6 6 6 π Khi đó 4cost 4cost 3 I = dt =
dt =2 dt =2t = . ∫ ∫ ∫ 2 4 − 4sin t 2cost 3 0 0 0 0 55
Ví dụ 2: [Đề thi THPT Quốc gia 2018] Cho dx
= a ln 2 + bln 5 + c ln11 ∫
với a,b,c là các số hữu tỷ. + 16 x x 9
Mệnh đề nào dưới đây là đúng.
A. a − b = − .c
B. a + b = .c
C. a + b = 3 .c
D. a −b = 3 − . c Lời giải x =16 ⇒ t = 5 Đặt 2
t = x + 9 ⇒ t = x + 9 ⇒ 2tdt = . dx Đổi cận x = 55 ⇒ t = 8 8 8 8 Khi đó 2tdt 2dt 2 t − 3 1 5 1 1 2 1 1 I = = = ln
= ln − ln = ln 2 + ln 5 − ln11 ∫ ∫ t − 9 t t − 3 t + 3 6 t + 3 3 11 3 4 3 3 3 5 ( 2 ) 5 ( )( ) 5 Do đó 2 1 1
a = ;b = ;c = − ⇒ a − b = − . c Chọn A. 3 3 3 6 Ví dụ 3: Cho dx I =
= a ln 3+ bln 2 + c ∫
với a,b,c là các số hữu tỷ, tính tổng + + + 2 2x 1 4x 1
A = a + 4b +12 . c A. A = 2. − B. A = 4. − C. A = 4. D. A = 2. Lời giải x = 6 ⇒ t = 5 Đặt 2
t = 4x +1 ⇒ t = 4x +1⇒ tdt = 2 . dx Đổi cận x = 2 ⇒ t = 3 5 5 5 5 Khi đó 1 tdt tdt 1 1 1 3 1 I = dt = = − ∫ ∫ ∫
dt =ln t +1 + = ln − 2 2 2 2 t +1 (t+1) t +1 (t+1) t +1 2 12 3 3 3 3 + t 2 1 1 ln 3 ln 2 a 1;b 1;c − = − − ⇒ = = − = 12 12
Do đó A = a + 4b +12c =1− 4 −1 = 4. − Chọn B.
Dạng 2: Tích phân đổi biến số với hàm ẩn b b b Chú ý tính chất: f
∫ (x)dx = f
∫ (t)dt = f
∫ (u)du (tích phân không phụ thuộc vào biến). a a a 6
Ví dụ 1: Cho hàm số f (x) liên tục trên thỏa mãn f ∫ (x)dx =12. 0 2
Tính tích phân I = f ∫ (3x) . dx 0 A. I = 6. B. I = 36. C. I = 2. D. I = 4. Lời giải 2 2 6 6 Ta có: I = f ∫ ( x) 1 dx = f
∫ ( x)d ( x) t=3x 1 → f ∫ (t) 1 dt = f ∫ (x) 12 3 3 3 dx = = 4. Chọn D. 3 3 3 3 0 0 0 0 3 2
Ví dụ 2: Cho hàm số f (x) liên tục trên [ 1; − +∞) và f
∫ ( x+1)dx = 8. Tính I = .xf ∫ (x)dx 0 1 A. I = 2. B. I = 8. C. I = 4. D. I =16. Lời giải
x = 0 ⇒ t =1 Đặt 2
t = x +1 ⇒ t = x +1⇒ 2tdt = dx và đổi cận .
x = 3 ⇒ t = 2 3 2 2 2 Khi đó I = f
∫ ( x+1)dx = 2 t.f
∫ (t)dt = 8⇒ t.f
∫ (t)dt = 4 ⇒ .xf
∫ (x)dx = 4. Chọn C. 0 1 1 1
9 f ( x )dx 1 3 Ví dụ 3: Cho = a ∫ và f
∫ (2x)dx = b. Tính tích phân I = f
∫ (x)dx theo a và b. 4 x 0 0 A. a I = + 2 . b B. I a b = 2a + . b
C. I = 2(a + b). D. I + = . 2 2 Lời giải 9 f ( x ) 9 3 3 dx Ta có: = 2 ( ) ( ) t= x → 2 ( ) = ⇒ 2 ( ) a f x d x f t dt a f t dt = ∫ ∫ ∫ ∫ x 2 4 4 2 2 3 Do đó 2 ∫ ( ) a f x dx = . 2 2 1 1 2 2 Lại có: f ∫ ( x) 1 dx = f
∫ ( x)d ( x) u=2x 1 → f
∫ (u)d (u) 1 2 2 2 = f
∫ (x)dx = b 2 2 2 0 0 0 0 2 3 2 3
Do đó ∫ ( ) = 2 ⇒ ∫ ( ) = ∫ ( ) + ∫ ( ) = 2 a f x dx b f x dx f x dx f x dx b + . Chọn A. 2 0 0 0 2 π 6 ln 2
Ví dụ 4: Cho hàm số f (x) liên tục trên thỏa mãn f
∫ (sin3x).cos3xdx =1 và x. ∫ ( x e f e )dx = 3. 0 0 2
Tính tích phân I = f ∫ (x) . dx 0 A. I = 4. B. I = 5. C. I = 2. D. I = 6. Lời giải π π 6 6 1 1 Ta có: f ( x) 1 xdx = f ∫ ( x) d (
x) t=sin3x 1 → f ∫ (t) 1 sin 3 .cos3 sin 3 . sin 3 .dt = f ∫ (x).dx 1 = ∫ 3 3 3 0 0 0 0 1
⇒ f (x).dx 3 = ∫ 0 ln 2 ln 2 2 2 Lại có: x . ∫
( x) = ∫ ( x) ( x e f e dx f e d e ) x u=e → f
∫ (u)du = f ∫ (x)dx = 3 0 0 1 1 2 1 2 Do đó I = f
∫ (x)dx = f
∫ (x)dx+ f
∫ (x)dx = 3+3 = 6. Chọn D. 0 0 1 π 2 16 f x 2 ( )
Ví dụ 5: Cho hàm số f (x) liên tục trên thỏa mãn cot xf ∫ (sin x)dx = dx =1. ∫ π x 1 4 1 f (4x) Tính tích phân I = . dx ∫ 1 x 8 A. I = 3. B. 3 I = . C. I = 2. D. 5 I = . 2 2 Lời giải π π 2 = ∫ ( ) 2 2 cos cot sin x A xf x dx = f ∫ ( 2 sin x)dx π π sin x 4 4 1 f (t) 1 f (x) Đặt 2
t = sin x ⇒ dt = 2sin x cos xdx, đổi cận suy ra A = dt =1⇒ dx = 2. ∫ ∫ 1 2t 1 x 2 2 16 f ( x ) 4 = f u f u f x u x ( ) 4 ( ) 4 ( ) Mặt khác 1 B = dx =1 → 2udu ⇒ B = 2 du =1⇒ dx = ∫ ∫ 2 x u ∫ u ∫ x 2 1 1 1 1 1 f (4x) 4 = f v dv f v f x v x ( ) 4 ( ) 4 4 ( ) Xét 5 I = dx → I = . = dv =
dx = A + B = . ∫ x ∫ v ∫ ∫ Chọn D. 1 1 4 1 v 1 x 2 8 2 2 2 4
Ví dụ 6: Cho các khẳng định sau: π 1 1 π 2 (1). sin ∫ (1 x
− x)dx = sin x . dx ∫
(2). sin dx = sin x . dx ∫ 2 ∫ 0 0 0 0 π 1 4 2 2 (3). f ∫ (x) 1 dx = f
∫ (sin2x)cos2x .
dx (4). f (x)dx =2 .x f ( 2 x + ∫ ∫ )1 . dx 2 0 0 1 1
Số khẳng định đúng là: A. 1. B. 2. C. 3. D. 4. Lời giải 1 1 0 1 1 Ta có sin ∫ (1− ) =− sin
∫ (1− ) (1− ) t 1=−x x dx x d x
→ − sin tdt = sin tdt = sin x . dx ∫ ∫ ∫ 0 0 1 0 0 π π π π 2 2 sin x =2 sin x x dx
d =2 sin udu =2 sin x . dx ∫ 2 ∫ 2 2 ∫ ∫ 0 0 0 0 π π 4 4 1 1 1 f ∫ ( x) 1 xdx = f ∫ ( x)d ( x) 1 = f ∫ (v) 1 sin 2 cos 2 sin 2 sin 2 dv = f ∫ (x) . dx 2 4 4 4 0 0 0 0 2 2 .x f ∫ (x + ) 2 1 dx = f
∫ (x + )1d (x + ) 5 5 2 2 2 1 = f
∫ (z)dz = f ∫ (x) . dx 1 1 1 1
Số khẳng định đúng là 2. Chọn B. π 4 1 2 x f (x)
Ví dụ 7: Cho hàm số f (x) liên tục trên thỏa mãn f
∫ (tan x).dx = a và dx = . b ∫ 2 x +1 0 0 1
Tính tích phân I = f
∫ (x)dx theo a và b. 0 A. I a = a − . b
B. I = a + . b C. I = .
D. I = a + b −1. b Lời giải x = 0 ⇒ t = 0 Đặt 1
x = tan t ⇒ dx = dt. Đổi cận 2 π cos t x =1⇒ t = 4 π π π 1 2 x f (x) 4 2
tan t. f (tant) 4 4 Khi đó 1 2 dx = .
dt = tan t. f ∫ ∫ ∫ (tant) 2
dt = tan .x f tan x dx b = 2 2 2 ∫ ( ) x +1 tan t +1 cos t 0 0 0 0 π π π 4 4 4 Suy ra f ∫ (tan x) 2 dx + tan .x f ∫ (tan x)dx =∫( 2
1+ tan x). f (tan x)dx 0 0 0 π π 4 f (tan x) 4 1 1 dx =
= f tan x d tan x = f u du = f x . dx ∫ 2 ∫ ( ) ( ) ∫ ( ) ∫ ( ) cos x 0 0 0 0 1 Do đó I = f
∫ (x)dx = a + .b Chọn A. 0
Dạng 3: Tích phân đổi biến số với hàm số chẵn, hàm số lẻ
Bài toán tổng quát: Giả sử hàm số f (x) liên tục trên đoạn [− ;
a a]. Chứng minh rằng: a a a) f
∫ (x)dx = 2 f
∫ (x)dx nếu f (x) là hàm số chẵn. −a 0 a b) f
∫ (x)dx = 0 nếu f (x) là hàm số lẻ. −a Lời giải
a) Hàm số f (x) là hàm chẵn thì f (−x) = f (x) 0 0 0 0 a Ta có: f
∫ (x)dx = − f
∫ (−x)d (−x) t=−x → − f
∫ (t)dt = − f
∫ (x)dx = f ∫ (x) . dx −a −a a a 0 a 0 a a Do đó f
∫ (x)dx = f
∫ (x)dx+ f
∫ (x)dx = 2 f ∫ (x) . dx −a −a 0 0
b) Hàm số f (x) là hàm lẻ thì f (−x) = − f (x) a a a −a a Ta có: f
∫ (x)dx = − f
∫ (−x)dx = f
∫ (−x)d (−x) t=−x → f
∫ (t)dt = − f
∫ (x)dx −a −a −a a a a a Do đó 2 f
∫ (x)dx =0 ⇔ f ∫ (x)dx = 0. −a −a
Ví dụ 1: Cho hàm số f (x) liên tục trên thỏa mãn f (x) + f (−x) = 2 + 2cos2x, x ∀ ∈ . 3π 2 Tính I = f ∫ (x) . dx 3 − π 2 A. I = 6. − B. I = 0. C. I = 2. − D. I = 6. Lời giải
Lấy tích phân 2 vế của f (x) + f (−x) = cos 2x cận từ 3π 3π − → ta có: 2 2 3π 3π 3π 3π 2 2 2 2 f
∫ (x)dx+ f ∫ (−x)dx = 2 + 2cos 2xdx = 2 cos x dx =12 ∫ ∫
(Sử dụng máy tính Casio). 3 − π 3 − π 3 − π 3 − π 2 2 2 2 3π 3π x = − ⇒ t =
Đặt t = x ⇒ dt = −dx và đổi cận 2 2 . 3π 3π x = ⇒ t = − 2 2 3π 3π 3π 3π 2 2 2 2 Khi đó f
∫ (−x)dx = − f
∫ (t)dt = f
∫ (t)dt = f ∫ (x) . dx 3 − π 3 − π 3π 3π − − 2 2 2 2 3π 3π 2 2 Suy ra f
∫ (x)dx+ f
∫ (−x)dx = 2I =12 ⇒ I = 6. 3 − π 3 − π 2 2
Cách 2: Vì 2 + 2cos 2x = 2 + 2cos( 2
− x) ta có thể chọn ( ) 2 2cos 2x f x + = . 2 3π 2
Sau đó sử dụng Casio để bấm 2 + 2cos 2x I = . dx ∫ Chọn D. 3 − π 2 2
Ví dụ 2: Cho hàm số y = f (x) xác định và liên tục trên , thỏa mãn π 6
f (x) + f (−x) = cos 2x, x ∀ ∈ . Khi đó I = f
∫ (x)dx bằng: −π 6 A. 2. B. 2. − C. 1 . D. 3 . 2 4 Lời giải
Lấy tích phân 2 vế của f (x) + f (−x) = cos 2x , x ∀ ∈ π π
cận từ − → ta có: 6 6 π π π π π 6 6 6 6 6 f
∫ (x)dx+ f ∫ (−x) 1 dx = xdx = xd ∫ ∫ ( x) 1 3 cos 2 cos 2 2 = sin 2x = . −π −π −π 2 −π 2 −π 2 6 6 6 6 6 π π x = − ,t π π π π − = 6 6 6 6 Đặt 6 6
t = −x ⇒ dt = −dx ⇒ ⇒ f
∫ (−x)dx = − f
∫ (t)dt = f
∫ (t)dt = f ∫ (x) . dx π π x = ,t −π π −π −π = − 6 6 6 6 6 6 π π π π 6 6 6 6 Suy ra f
∫ (x)dx+ f ∫ (−x)dx = f ∫ (x) 3 dx = ⇒ f ∫ (x) 3 2 dx = . Chọn D. −π −π −π 2 −π 4 6 6 6 6 π 6
Cách 2: Vì cos 2x = cos( 2
− x) ta chọn f (x) cos 2x cos 2x 3 = ⇒ dx = . 2 ∫ −π 2 4 6
Ví dụ 3: Cho hàm số y= f (x) liên tục trên đoạn [0; ]
1 thỏa mãn f (x) + 2 f (1− x) = 3x, x ∀ ∈ . 1
Tính tích phân I = f ∫ (x) . dx 0 A. 3 I = . B. I =1. C. 1 I = . D. I = 2. 2 2 Lời giải 1 1 1 1
Cách 1: Ta có f (x) + f ( − x) = x ⇒ f
∫ (x)dx+ f ∫ ( − x) 3 2 3 2 1 3 2 1
dx = 3 xdx = x = . ∫ 2 2 0 0 0 0 1 0 1 1 x = 0,t =1
Đặt t =1− x ⇒ dt = −dx ⇒ ⇒ f
∫ (1− x)dx = − f
∫ (t)dt = f
∫ (t)dt = f ∫ (x) . dx x = 1,t = 0 0 1 0 0 1 1 1 1 Suy ra f
∫ (x)dx+ f
∫ ( − x)dx = f ∫ (x) 3 dx = ⇒ f ∫ (x) 1 1 2 1 3
dx = ⇔ I = . Chọn C. 2 2 2 0 0 0 0
Cách 2: Ta có f (x) + 2 f (1− x) = 3x ⇒ f (1− x) + 2 f (x) = 3(1− x) = 3−3 .x
f (x) + 2 f (1− x) = 3x (1) Khi đó lấy 2.(2) −( ) 1 , ta được f
( − x) + f ( x) = − x (2), 1 2 3 3
3 f (x) = 2(3−3x) −3x ⇔ f (x) = 2 −3 .x 1 1 2 1 Vậy I = f
∫ (x)dx = ∫( − x) 3x 1
2 3 dx = 2x − = . Chọn C. 2 2 0 0 0
Ví dụ 4: Cho hàm số f (x) liên tục trên và thỏa mãn f (x) + f (−x) 2 = x , x ∀ ∈ . 1 Tính I = f ∫ (x) . dx 1 − A. 2 I = . B. I =1. C. I = 2. D. 1 I = . 3 3 Lời giải 1 1 1 1 1
Ta có f (x) + f (−x) 2 = x ⇒ f
∫ (x)+ f (−x) 2 dx = x dx ⇔ f ∫
∫ (x)dx+ f ∫ (−x) 2 dx = x . dx ∫ 1 − 1 − 1 − 1 − 1 − 1 1 − 1 1 x = 1, − t =1
Đặt t = −x ⇒ dt = −dx ⇒ ⇒ f
∫ (−x)dx = − f
∫ (t)dt = f
∫ (t)dt = f ∫ (x) . dx x = 1,t = 1 − 1 − 1 1 − 1 − 1 1 1 1 3 1 1 Suy ra f
∫ (x)dx+ f ∫ (x) 2 dx = x dx ⇔ f ∫ ∫ (x) x 2 dx = = ⇒ f ∫ (x) 1 2
dx = . Chọn D. − − − − 3 − 3 − 3 1 1 1 1 1 1
Ví dụ 5: Cho hàm số f (x) liên tục trên và số thực a dương. Biết rằng với mọi x∈[0;a] thì f (x) > 0 a
và f (x). f (a − x) =1. Tính dx I = . ∫ 1+ f x 0 ( ) A. a I = . B. I a = 2 . a C. I = . a D. I = − . 2 2 Lời giải 1
f (a − x)
Ta có: f (x). f (a − x) =1⇔ (1+ f (x)) f (a − x) =1+ f (a − x) ⇔ =
1+ f (x) 1+ f (a − x) a a dx
f (a − x)
Lấy tích phân 2 vế ta có: I = = dx ∫1 ∫ + f x 1+ f a − x 0 ( ) 0 ( )
a 1+ f (a − x) 0 f (t) a a a f t Đặt t dt
= a − x ⇒ dt = −dx khi đó dx = −dt = dt = dt − ∫ f a ∫ ∫ ∫ ∫ − x 1+ f t 1+ f t 1+ f t 0 ( ) a ( ) ( ) ( ) 0 ( ) 0 0 ( ) a dx = a − . ∫ Khi đó a
I = a − I ⇔ I = . Chọn A. a + f x 2 0 ( ) a a
Cách 2: Vì f (x). f (a − x) =1 ta có thể chọn ( ) =1⇒ ( − ) =1 dx x a f x f a x ⇒ I = = = . ∫ 2 2 2 0 0
BÀI TẬP TỰ LUYỆN 6 2 Câu 1: Cho f
∫ (x)dx =12. Tính I = f ∫ (3x) . dx 0 0 A. I = 6. B. I = 36. C. I = 2. D. I = 4. 10 2
Câu 2: Cho f (x)dx = 8. − ∫ Tính I = f ∫ (5x) . dx 5 1 A. 4 I = . B. 8 I = − . C. 8 I = . D. 4 I = − . 5 5 5 5 10 5 Câu 3: Cho f
∫ (x)dx =10. Tính I = f ∫ (2x) . dx 4 2 A. I =10. B. I = 5. C. I = 2. D. I = 4. 6 2
Câu 4: (Đề thi THPT Quốc gia năm 2017) Cho f
∫ (x)dx =12. Tính tích phân I = f ∫ (3x) . dx 0 0 A. I = 6. B. I = 36. C. I = 2. D. I = 4. 4 2 Câu 5: Cho f
∫ (x)dx =16. Tính tích phân I = f ∫ (2x) . dx 0 0 A. I = 32. B. I = 8. C. I =16. D. I = 4. π 1 6
Câu 6: Cho tích phân f
∫ (x)dx = 9. Tính tích phân I = f
∫ (sin3x).cos3xd .x 0 0 A. I = 5. B. I = 9. C. I = 3. D. I = 2. 10 3 Câu 7: Cho f
∫ (x)dx =18. Tính I = f (3x+ ∫ ) 1 . dx 4 1 A. I =18. B. I = 6. C. I = 9. D. I =15. 4 1 Câu 8: Cho f
∫ (x)dx = 2. Tính tích phân I = f ∫ (4x) . dx 0 0 A. I = 8. B. 1 I = . C. I = 4. D. I = 2. 2 2017 1
Câu 9: Cho hàm số f (x) thỏa mãn f
∫ (x)dx =1. Tính tích phân I = f ∫ (2017x) . dx 0 0 1 1 A. f
∫ (2017x)dx = 2017. B. f
∫ (2017x)dx = 0. 0 0 1 1 C. f
∫ (2017x)dx =1. D. f ∫ ( x) 1 2017 dx = . 2017 0 0 π 1 4
Câu 10: Cho f (x) là hàm số liên tục trên và f
∫ (x)dx = 2017. Tính I = f
∫ (sin2x)cos2xd .x 0 0 A. 2 I = . B. 2017 I = . C. I = 2017. D. 2017 I = − . 2017 2 2 2 1
Câu 11: Cho tích phân f
∫ (x)dx = .a Hãy tính tích phân I = .xf ( 2x + ∫ )1dx theo a. 1 0 A. I = 2 . a B. I = 4 . a C. a I = . D. a I = . 2 4 e f (ln x)
Câu 12: Cho hàm số y = f (x) liên tục trên và thỏa mãn dx = .e ∫
Mệnh đề nào đúng? x 1 1 1 e e A. f ∫ (x)dx =1. B. f
∫ (x)dx = .e C. f ∫ (x)dx =1. D. f
∫ (x)dx = .e 0 0 0 0 x 2 3x
Câu 13: Biết F (x) là một nguyên hàm của hàm số e y =
trên (0;+∞). Tính e dx. x ∫ x 1
A. I = 3F (2) − F ( ) 1 .
B. I = F (6) − F (3) F (6) − F (3) C. I = .
D. I = 3F (6) − F (3). 3 4
Câu 14: Cho hàm số f (x) liên tục trên và f
∫ (x)dx = 2. Mệnh đề nào sau đây sai? 2 − 2 3 A. f ∫ (2x)dx =1. B. f
∫ (x+ )1dx = 2. 1 − 3 − 2 6 C. f ∫ (2x)dx = 2. D. 1 f
∫ (x−2)dx =1. 2 1 − 0 2
Câu 15: Cho f (x) có đạo hàm trên đoạn [1;2], f (2) = 2 và f (4) = 2018. Tính I = f ' ∫ (2x) . dx 1 A. I = 1008. − B. I = 2018. C. I =1008. D. I = 2018. − 3 8
Câu 16: Biết f
∫ (3x− )1dx = 20 . Hãy tính tích phân I = f ∫ (x) . dx 1 2 A. I = 20. B. I = 40. C. I =10. D. I = 60. 27 3
Câu 17: Biết f
∫ (x)dx = 81. Tính I = f ∫ (9x) . dx 0 0 A. I = 3. B. I = 81. C. I = 27. D. I = 9. π 9 f ( x ) 2
Câu 18: Cho f (x) liên tục trên thỏa mãn dx = 4 ∫ và f
∫ (sin x).cos xdx = 2. 1 x 0 3
Tính tích phân I = f ∫ (x) . dx 0 A. I = 2. B. I = 6. C. I = 4. D. I =10. 2
Câu 19: Cho hàm số f (x) có đạo hàm liên tục trên khoảng [1;2] thỏa mãn f '
∫ (x)dx =10 và 1
2 f '(x)dx = ln2. ∫
Biết rằng hàm số f (x) > 0, x
∀ ∈[1;2]. Tính f (2). f x 1 ( ) A. f (2) = 10. − B. f (2) = 20. C. f (2) =10. D. f (2) = 20. − 3 2
Câu 20: Cho hàm số f (x) liên tục trên khoảng [ 1; − +∞) và f
∫ ( x+1)dx = 4. Tính xf (x)d .x ∫ 0 1 A. I = 8. B. I = 4. C. I =16. D. I = 2. π 1 4
Câu 21: Biết xf
∫ (x)dx = 4. Tính f
∫ (cos2x).sin4xd .x 0 0 A. I = 2. B. I = 6. C. I = 8. D. I = 4. π 1 2
Câu 22: Biết xf ∫ (x) 1 dx = . Tính sin 2 . x f ∫ (sin x) . dx 1 2 π 2 6 A. π I = 2. B. I = . C. 1 I = . D. I =1. 3 2 2 4
Câu 23: Biết f
∫ ( 2x)xdx =1. Tính f (x) . dx ∫ 0 0 A. I = 2. B. I = 4. C. 1 I = . D. I =1. 2 2 1
Câu 24: Biết f
∫ (x)dx = 3. Tính f ∫ ( 2x ) . dx 0 1 − A. I = 3. B. I = 6. C. 3 I = . D. I = 0. 2 2 3
Câu 25: Cho f (x) là hàm số liên tục trên thỏa mãn f (x)dx = 5 − ∫ và f
∫ (2x)dx =10.Tính giá trị của 0 1 2 I = f ∫ (3x) . dx 0 A. I = 8. B. I = 5. C. 3 I = . D. I = 6. 5 5 2
Câu 26: Biết f
∫ (x)dx =15. Tính f ∫ (5−3x)+7 . dx 1 − 0 A. I =15. B. I = 37. C. I = 27. D. I =19. 2 4
Câu 27: Biết f (x)dx = 3. − ∫ Tính x f ∫ . dx 2 1 2 A. I = 6. − B. 3 I = − . C. I = 1. − D. I = 5. 2 π 4 1 2 x f (x)
Câu 28: Cho f (x) liên tục trên và các tích phân f
∫ (tan x)dx = 4 và dx = 2. ∫ Tính tích phân 2 x +1 0 0 1 I = f ∫ (x) . dx 0 A. I = 6. B. I = 2. C. I = 3. D. I =1. 2 Câu 29: Biết 2 −1 a x dx = − + c ∫
với a,b,c là các số nguyên dương. Tính 2 3
a + b + c . b 1 A. 37. B. 11. C. 45. D. 27. 1 Câu 30: Biết 6 − 3 b xdx = a − ∫
với a,b là các số nguyên dương. Tính 2 a − . b − 3 1 A. 31. B. 18. C. 12. D. 24. 1 Câu 31: Biết dx 1 b = a − ∫ với a,b +
∈ . Tính tổng a + . b x +1 + x 3 3 0 A. 28. B. 30. C. 32. D. 36. 2 Câu 32: Biết dx
a − b + c = ∫
với a,b,c +
∈ . Tính a + b + .c x +1 − x −1 3 1 A. 36. B. 42. C. 27. D. 54. 2 Câu 33: Biết dx = a b − a ∫
với a,b,c là các số nguyên dương. Tính giá trị của biểu thức + − + 1 ( x )1 x x x 1 P = b − . a A. P = 5. − B. P = 1. − C. P = 5. D. P =1. 2
Câu 34: Cho a,b,c là các số nguyên dương thỏa mãn dx
= a − b − c ∫ . Tính + + + 1 ( x )1 x x x 1
P = a + b + . c A. P = 24. B. P =12. C. P =18. D. P = 46. 6 Câu 35: Biết dx
= a − b − c ∫
với a,b,c +
∈ . Tính P = a − . bc − + − 5 x x 1 (x ) 1 x A. P =16. B. P = 19. − C. P =19. D. P = 16. − 0 Câu 36: Biết dx a b = − ∫
với a,b nguyên dương. Tính 2
T = a − 2b +1. − + + 3 3 1 1 1 x A. T =1. B. T = 4. C. T = 2. − D. T = 5. 4 Câu 37: Biết 1 + = 2 = 2 a x dx + ∫
với a là phân số tối giản. Tính tổng a + . b x b b 1 A. 14. B. 3. C. 17. D. 20. 2
Câu 38: Tính tích phân 2
I = 2x x −1dx ∫ bằng cách đặt 2
u = x −1, mệnh đề nào dưới đây đúng? 1 3 2 3 2
A. I = 2 u . du ∫ B. I = u . du ∫ C. I = udu. ∫ D. 1 I = u . du 2 ∫ 1 1 0 1 2 Câu 39: Cho 2
I = x 4 − x dx ∫ và 2
t = 4 − x . Khẳng định nào sau đây sai? 1 2 3 3 3 3 A. I = 3. B. t I = . C. 2 I = t dt. t I = . 2 ∫ D. 3 0 0 0 3 3
Câu 40: Cho tích phân dx I = ∫
và đặt t = 2x + 3, ta được m I = dt ∫ với , m n là những số 2 + 1 ( x + ) 1 2x + 3 t n 2 2
nguyên. Tính T = 3m + . n A. T = 7. B. T = 2. C. T = 4. D. T = 5. e Câu 41: Cho 1+ 3ln x I = dx ∫
và đặt t = 1+ 3ln x . Khẳng định nào sau đây đúng? x 1 e 2 2 e A. 2 2 I = t dt. 2 I = tdt. 2 2 I = t dt. 2 I = tdt. 3 ∫ B. 3 ∫ C. 3 ∫ D. 3 ∫ 1 1 1 1 3 Câu 42: Cho x I = dx ∫
và đặt t = x +1 . Khẳng định nào sau đây đúng? + + 0 1 x 1 2 2 2 2
A. I = ∫( 2t +t)dt. B. I = ∫( 2
2t + 2t)dt.
C. I = ∫( 2t −t)dt. D. I = ∫( 2
2t − 2t)dt. 1 1 1 1 π 2 Câu 43: Cho sin 2x I = dx ∫
và đặt t = 1+ cos x . Khẳng định nào sau đây đúng? + 0 1 cos x 1 3 1 3 2 2 A. 4t − 4t I − + = dt. ∫ B. 4t 4t I = dt. 2
I = 4 t −1 dt. D. I = 4 ∫ ( 2 1− t )dt. t ∫ C. ∫ ( ) t 2 2 1 1 π 2 Câu 44: Cho 2 sin x 3 I = e sin xcos xdx ∫ và đặt 2
t = sin x . Khẳng định nào sau đây đúng? 0 1 1 1 1 A. 1 t t I = 1 e dt + te dt ∫ ∫ . B. t t
I = e dt − te dt ∫ ∫ . 2 2 0 0 0 0 1 1 1 1 C. = 2 t t I e dt + te dt ∫ ∫ . D. = 2 t t I
e dt − te dt ∫ ∫ . 0 0 0 0 1 Câu 45: Cho 3 I = 1− xdx ∫ và đặt 3
t = 1− x . Khẳng định nào sau đây đúng? 0 1 1 1 1
A. I = 3 tdt. ∫ B. 3 I = t dt. ∫ C. 2 I = 3 t dt. ∫ D. 3 I = 3 t dt. ∫ 0 0 0 0 π 4
Câu 46: Cho I = (2sin x − ∫ )4 2
1 sin 4xdx và đặt t = cos 2x . Khẳng định nào đúng? 0 1 2 1 2 1 2 A. 1 4 I = t dt. 1 3 I = t dt. 5 I = t dt. 4 I = t dt. 2 ∫ B. 2 ∫ C. ∫ D. ∫ 0 0 0 0 2 Câu 47: Cho 2
I = 2x x −1dx ∫ và đặt 2
u = x −1. Tìm khẳng định sai? 1 2 3 3 A. I = u . du ∫ B. 2 I = 27. C. I = udu. 2 I = u u . 3 ∫ D. 3 1 0 0 e Câu 48: Cho ln x I = dx ∫ và đặt 2
t = 3ln x +1 . Khẳng định nào đúng? 2 1 x 3ln x +1 2 4 2 e e A. 1 I − = dt. 1 1 I = dt. 2 I = tdt. 1 t 1 I = dt. 3 ∫ B. 2 ∫ C. t 3 ∫ D. 4 ∫ t 1 1 1 1
Câu 49: Cho I = x ∫ ( − x )10 2 1 dx và đặt 2
u =1− x . Khẳng định nào sau đây đúng? A. 10 I = 2 − u du. ∫ B. 10 I = 2u du. ∫ C. 1 10 I = u . du 1 I = − u . du 2 ∫ D. 10 2 ∫ ln m x
Câu 50: Tìm tham số m thỏa mãn e dx I = = ln 2. ∫ x e + 2 0 A. 1 m = . B. m = 2. C. m = 4.
D. m = 0,m = 4. 2 ln 6 Câu 51: Biết dx = 3ln a − ln b ∫
với a,b là các số nguyên dương. Tìm P = . ab x e + 2 x x− − 3 ln3 A. P =10. B. P = 10. − C. P =15. D. P = 20. 5 Câu 52: Biết dx
= a ln 3− bln 5 ∫ với a,b∈ . Tính 2 2
a + ab + 3b . + 1 x 3x 1 A. 4. B. 5. C. 1. D. 0. 4 Câu 53: Biết 1 2
dx = a + bln ∫ với a,b∈ .
Mệnh đề nào dưới đây là đúng? 3+ 2x +1 3 0
A. a + b = 3.
B. a − b = 3.
C. a − b = 5.
D. a + b = 5. 1 Câu 54: Biết dx 1 = + ln + e a b ∫
với a,b là các số hữu tỉ. Tính 3 3
S = a + b . x e +1 2 0 A. S = 2. B. S = 2. − C. S = 0. D. S =1. e Câu 55: Biết ln x
dx = ln a + b ∫ với a,b∈ .
Khẳng định nào sau đây đúng? x(ln x + 2)2 1 A. 2a + 3b = 3 B. 1 − b =1 C. 2 2 4a + 9b =11 D. 2ab = 1 a
LỜI GIẢI BÀI TẬP TỰ LUYỆN 2 2 6
Câu 1: I = f ∫ ( x) 1 dx = f
∫ ( x)d ( x) 1 = f ∫ (x) 1 3 3 3
dx = .12 = 4. Chọn D. 3 3 3 0 0 0 2 2 10
Câu 2: I = f ∫ ( x) 1 dx = f
∫ ( x)d ( x) 1 = f ∫ (x) 1 dx = (− ) 8 5 5 5 . 8 = − . Chọn B. 5 5 5 5 1 1 5 5 5 10
Câu 3: I = f ∫ ( x) 1 dx = f
∫ ( x)d ( x) 1 = f ∫ (x) 1 2 2 2
dx = .10 = 5. Chọn B. 2 2 2 2 2 4 2 2 6
Câu 4: I = f ∫ ( x) 1 dx = f
∫ ( x)d ( x) 1 = f ∫ (x) 1 3 3 3
dx = .12 = 4. Chọn D. 3 3 3 0 0 0 2 2 4
Câu 5: I = f ∫ ( x) 1 dx = f
∫ ( x)d ( x) 1 = f ∫ (x) 1 2 2 2
dx = .16 = 8. Chọn B. 2 2 2 0 0 0 π π 6 6 1
Câu 6: I = f ∫ ( x) 1 xdx = f ∫ ( x)d ( x) 1 = f ∫ (x) 1 sin 3 cos3 sin 3 sin 3
dx = .9 = 3. Chọn C. 3 3 3 0 0 0 3 3 10
Câu 7: I = f ∫ ( x+ ) 1 dx = f
∫ ( x+ )d ( x+ ) 1 = f ∫ (x) 1 3 1 3 1 3 1
dx = .18 = 6. Chọn B. 3 3 3 1 1 4 1 1 4
Câu 8: I = f ∫ ( x) 1 dx = f
∫ ( x)d ( x) 1 = f ∫ (x) 1 1 4 4 4
dx = .2 = . Chọn B. 4 4 4 2 0 0 0 1 1 2017
Câu 9: I = f ∫ ( x) 1 dx = f ∫ ( x)d ( x) 1 = f ∫ (x) 1 2017 2017 2017 dx = . Chọn D. 2017 2017 2017 0 0 0 π π 4 4 1
Câu 10: I = f ∫ ( x) 1 xdx = f ∫ ( x)d ( x) 1 = f ∫ (x) 2017 sin 2 cos 2 sin 2 sin 2 dx = . Chọn B. 2 2 2 0 0 0 1 1 2 Câu 11: = ∫ ( 2 + ) 1 = ∫ ( 2 + ) ( 2 + ) 1 . 1 1 1 = ∫ ( ) a I x f x dx f x d x
f x dx = . Chọn C. 2 2 2 0 0 0 e f (ln x) e 1 Câu 12:
dx = e ⇔ f ∫
∫ (ln x)d (ln x) = e ⇔ f
∫ (x)dx = .e Chọn B. x 1 1 0 2 3x 2 3x e dx
e d (3x) 6 x 6 Câu 13: e dx = = = F ∫ ∫ ∫
(x) = F (6)− F (3). Chọn B. x 3x x 1 1 3 3 2 2 4
Câu 14: I = f ∫ ( x) 1 dx = f
∫ ( x)d ( x) 1 = f ∫ (x) 1 2 2 2
dx = .2 =1 nên đáp án C sai. Chọn C. − 2 − 2 − 2 1 1 2 2 2 2 1 1 f 4 − f 2
Câu 15: I = f '
∫ (2x)dx = f '
∫ (2x)d (2x) = f (2x) ( ) ( ) = = 1008. Chọn C. 2 2 2 1 1 1 3 3 8 Câu 16: f ∫ ( x− ) 1 3 1 dx = 20 ⇔ f
∫ (3x− )1d (3x− )1 = 20 ⇔ f
∫ (x)dx = 60. Chọn D. 3 1 1 2 3 3 27
Câu 17: I = f ∫ ( x) 1 dx = f
∫ ( x)d ( x) 1 = f ∫ (x) 1 9 9 9
dx = .81 = 9. Chọn D. 9 9 9 0 0 0 9 f ( x ) 9 f ( x ) 9 3 Câu 18: dx = 4 ⇔ 2 dx = 4 ⇔ f ∫ ∫
∫ ( x)d ( x) = 2 ⇔ f ∫ (x)dx = 2 1 x 1 2 x 1 1 π π 2 2 1 Ta có f
∫ (sin x).cos xdx = 2 ⇔ f
∫ (sin x)d (sin x) = 2 ⇔ f ∫ (x)dx = 2 0 0 0 3 1 3 Ta có I = f
∫ (x)dx = f
∫ (x)dx+ f
∫ (x)dx = 2+ 2 = 4. Chọn C. 0 0 1 2 2 Câu 19: f '
∫ (x)dx =10 ⇔ f (x) =10 ⇔ f (2)− f ( )1 =10 1 1 2 f '(x)
2 d ( f (x)) 2 f 2 f (2) Ta có dx = ln 2 ⇔
dx = ln 2 ⇔ ln f x = ln 2 ⇔ ln = ln 2 ⇔ = 2 ∫ f x ∫ f x f 1 f 1 1 ( ) 1 ( ) ( ) ( ) 1 ( ) ( )
Từ đó suy ra f (2) = 20, f ( ) 1 =10. Chọn B. Câu 20: Đặt 2
t = x +1 ⇔ t = x + 2 ⇔ 2tdt = .
dx Với x = 0 ⇒ t =1, x = 3 ⇒ t = 2 3 2 2
Ta có f x +1dx = 4 ⇔ f ∫
∫ (t).2tdt = 4 ⇔ xf
∫ (x)dx = 2. Chọn D. 0 0 0 π π 4 4
Câu 21: I = 2sin 2 .xcos 2 .x f ∫
(cos2x)dx = − cos2 .xf ∫
(cos2x)d (cos2x) 0 0 0 1 = − tf
∫ (t)dt = xf
∫ (x)dx = 4. Chọn D. 1 0 π π 2 2 1
Câu 22: I = 2sin .xcos .x f ∫
(sin x)dx = 2 sin .xf ∫
(sin x)d (sin x) = 2 t.f
∫ (t)dt =1. Chọn D. π π 1 6 6 2 2 4 Câu 23: Ta có 1 = f
∫ ( 2x)d ( 2x) 1 = f ∫ (t) 1 1
dt = I ⇒ I = 2. Chọn A. 2 2 2 0 0 0 1 0 1
Câu 24: I = f
∫ ( 2x )dx+ f
∫ ( 2x )dx = f ∫ ( 2
− x)dx + f ∫ (2x)dx 1 − 0 1 − 0 0 2 2 2 = f ∫ (t) t d − + f
∫ (u) u 1 d = f ∫ (x) 1 dx + f ∫ (x)dx = 3. Chọn A. 2 2 2 2 2 0 0 0 6 6 6
Câu 25: Ta có = f
∫ (t) t 1 10 d = f
∫ (x)dx ⇒ f ∫ (x)dx = 20. 2 2 2 2 2 6 6 2 6 Lại có I = f ∫ (u) u 1 d = f ∫ (x) 1 dx = f
∫ (x)dx+ f
∫ (x)dx = 5. Chọn B. 3 3 3 0 0 0 2 2 2 1 − 5
Câu 26: I = f
∫ ( − x)dx+ dx = f ∫
∫ (t) 5−t 1 5 3 7 d + 7.2 = f ∫ (x)dx+14 = 19. Chọn D. 3 3 0 0 5 1 − 2 2
Câu 27: I = f (t)d (2t) = 2 f (x)dx = 6. − ∫ ∫ Chọn A. 1 1 π 1 1 4 f x f tan t
Câu 28: Ta có 2 = f ∫ (x) ( ) ( ) dx − dx = I − d tan t ∫ 2 ∫ 2 ( ) x +1 tan t +1 0 0 0 π π 4 f (tan t) 4 1 = I − .
dt = I − f tan x dx ⇒ I = 6. ∫ Chọn A. 2 2 ∫ ( ) tan t +1 cos t 0 0 3 2 3 3 3 + Câu 29: t 1 t 3 3 −1 I = td ∫ = t.tdt = = . ∫ Chọn A. 2 3 3 1 1 1 3 2 3 3 3 − Câu 30: 6 t 2t 2t 54 − 6 3 18 − 2 3 I = td ∫ = t. dt = = = . ∫ Chọn D. 3 3 9 9 3 3 3 3 1 2 1
Câu 31: I = ∫( x +1− x)dx = td
∫ ( 2t − )1− ud ∫ ( 2u) 0 1 0 2 1 3 2 3 1 2t 2u 2
= t tdt − u udu = − = ∫ ∫ ( − ) 2 4 2 −4 .2 .2 2 2 1 − = . Chọn D. 3 3 3 3 3 1 0 1 0 2 3 1 Câu 32: x +1 + x −1 1 I = dx = td ( 2t − ) 1 1 + ud ( 2 u − ∫ ∫ ∫ )1 2 2 2 1 2 0 3 1 3 3 3 1 1 1 t u 3 3 2 2 1 t.2tdt u.2udu − = + = + = + . 2 ∫ 2 ∫ Chọn A. 3 3 3 3 2 0 2 0 2 Câu 33: Ta có dx I = . ∫ 1 x(x + ) 1 ( x +1− x)
Lại có: x(x + ) + x ( x + − x) 1 1 1 = 1⇒ = x +1 + x x +1 − x 2 2 2 2 x +1 + x 1 1 dx d (x + ) 1 ⇒ I = dx = − ∫ ∫ dx = 2 + ∫ ∫ + + + 1 x(x ) 1 1 x x 1 1 2 x 1 2 x 1
= (2 x + 2 x +1) 2 = 2 3 − 2 ⇒ a = 2;b = 3⇒ P = b − a =1. Chọn D. 1 2 Câu 34: Ta có dx I = . ∫ 1 x(x + ) 1 ( x +1+ x)
Lại có: ( x(x + ) + x)( x + − x) 1 1 1 = 1⇒ = x +1 − x x +1 + x 2 2 2 2 x +1 − x 1 1 dx d (x + ) 1 ⇒ I = dx = − ∫ ∫ dx = 2 − ∫ ∫ + + + 1 x(x ) 1 1 x x 1 1 2 x 1 2 x 1
= (2 x − 2 x +1) 2 = 4 2 − 2 3 − 2 = 32 − 12 − 2 ⇒ a = 32;b =12;c = 2 1
Vậy a + b + c = 46. Chọn D. 6 Câu 35: Ta có dx I = . ∫ 5 x(x − ) 1 ( x + x −1)
Lại có: ( x + x − )( x − x − ) 1 1 1 =1⇒ = x − x −1 x + x −1 6 6 6 6 x − x −1 1 1 dx d (x + ) 1 ⇒ I = dx = − ∫ ∫ dx = 2 − ∫ ∫ − − − 5 x(x ) 1 5 x 1 x 5 2 x 1 5 2 x
= (2 x −1− 2 x) 6 = 2 5 − 2 6 − 4+ 2 5 = 80 − 24 − 4 ⇒ a = 80;b = 24;c = 4 5
Vậy a − bc = 16. − Chọn D. x = 1 − ⇒ t = 0 Câu 36: Đặt 2
t = 1+ x ⇒ t =1+ x ⇒ 2tdt = . dx Đổi cận x = 0 ⇒ t =1 1 1 1 Khi đó 2tdt 1 4 I = = ∫ ∫ t + − dt = (t + )3 8 − 32 2 1 1 − 4 t +1 = 1+ t t +1 3 3 0 0 0 Do đó 2
a = 8;b = 32 ⇒ T = 8 = 32.2 +1 =1. Chọn A. 4 4 2 4 4 Câu 37: Ta có 1 1 1 2 3 x 2dx ∫ ∫ x dx ∫ x dx x 2 x + + = + = + = + x x x 3 1 1 1 1 20 14 = = 2 + = 2 a
+ ⇒ a + b =17. Chọn C. 3 3 b Câu 38: Đặt 2
u = x −1⇒ du = 2x . dx 3
Đổi cận x =1⇒ u = 0; x = 2 ⇒ u = 3. Khi đó I = udu. ∫ Chọn C. 0 Câu 39: Đặt 2 2 2 t = ⇒ =
= 4 − x ⇒ t = 4 − x ⇒ tdt = −x .
dx Đổi cận x 1 t 3 x = 2 ⇒ t = 0 0 3 3 3 Khi đó = ∫ (− ) 2 t I t tdt = t dt = = 3. ∫
Khẳng định sai là B. Chọn B. 3 3 0 0 1 x = ⇒ t = 2 Câu 40: Đặt 2
t = 2x + 3 ⇒ t = 2x + 3 ⇒ 2tdt = 2dx ⇔ tdt = . dx Đổi cận 2 x = 3 ⇒ t = 3 3 3 tdt 2dt m = 2 Khi đó I = = = ⇒ ∫ ∫
⇒ T = 3m + n = 5. Chọn D. 2 2 t − 3 t −1 n = 1 − 2 1 + 1t 2 x =1⇒ t =1 Câu 41: Đặt 2 3 = 1+ 3ln ⇒ =1+ 3ln ⇒ 2 dx t x t x tdt = . Đổi cận x
x = e ⇒ t = 2 2 2 Khi đó 2 2 2
I = t. tdt = t dt. ∫ 3 3 ∫ Chọn C. 1 1 x = 0 ⇒ t =1 Câu 42: Đặt 2
t = x +1 ⇒ t = x +1⇒ 2tdt = . dx Đổi cận x = 3 ⇒ t = 2 2 2 2 2 Khi đó t −1 I = 2tdt = ∫
∫(t − )1.2tdt = ∫( 2
2t − 2t)dt. Chọn D. 1+ t 1 1 1 x = 0 ⇒ t = 2 Câu 43: Đặt 2
t = 1− cos x ⇒ t =1− cos x ⇒ 2tdt = −sin x . dx Đổi cận π x = ⇒ t =1 2 π 2 1 2sin xcos xdx 2( 2t − ) 1 .( 2 − tdt) 2 Ta có I = = = 4 ∫ ∫
∫ ( 2t − )1dt. Chọn C. + x t 0 1 cos 2 1 x = 0 ⇒ t = 0 Câu 44: Đặt 2
t = sin x ⇒ dt = 2sin x cos x . dx Đổi cận π x = ⇒ t =1 2 π 2 e 1 1 Khi đó 2 sin x 2 t I = e x x xdx = e ∫ ∫ ( 2 − t ) dt 1 .sin cos .cos . 1 t t
= e dt − te dt ∫ ∫ . Chọn B. 2 2 0 1 0 0 Câu 45: Đặt 3 3 2 2
t = 1− x ⇒ t =1− x ⇔ 3t dt = −dx ⇔ dx = 3
− t dt. Với x = 0 ⇒ t =1, x =1⇒ t = 0 0 1 Ta có I = t. ∫ ( 2 3 − t dt) 3 = 3 t dt. ∫ Chọn D. 1 0 Câu 46: Đặt π
t = cos 2x ⇔ dt = 2 − sin 2x .
dx Với x = 0 ⇒ t =1, x = ⇒ t = 0 4 π π 4 4
Khi đó I = ∫(2sin x − ) 1 4 2 4 5 1 sin 4xdx = cos 2 .2
x cos 2xsin 2xdx = t dt. ∫ ∫ Chọn C. 0 0 0 Câu 47: Đặt 2
u = x −1 ⇔ du = 2x .
dx Với x =1⇒ u = 0, x = 2 ⇒ u = 3 2 3 3 Ta có 2 2 2 I = x −1.2xdx = udu = u u = 27. ∫ ∫
Do đó đáp án A sai. Chọn A. 3 3 1 0 0 Câu 48: Đặt 2 2 2 6ln = 3ln +1 ⇒ = 3ln +1 ⇔ 2 x t x t x tdt = .
dx Với x =1⇒ t =1, x = e ⇒ t = 2 x e 2 2 Ta có ln x tdt 1 1 I = dx = = dt. ∫ ∫ ∫ Chọn A. 2 x 3ln x +1 3 t 3 1 1 1 Câu 49: Đặt 2
u =1− x ⇔ du = 2 − x .
dx Ta có I = x ∫ (1− x )10 2 1 10 dx = − u du. 2 ∫ Chọn D. ln m x ln m e dx d ( x e + 2) ln m Câu 50: Ta có ∫ ∫ ( x m e m + = = + = + − = x x ) ( ) 2 ln 2 ln 2 ln 3 ln e + 2 e + 2 3 0 0 0 ln m x Mà e dx m + 2 m + 2 = ln 2 ⇒ ln = ln 2 ⇔ = ln 2 ⇔ m = 4. ∫ Chọn C. x e + 2 3 3 0 ln 6 ln 6 ln 6 dx e dx d ( x x e ) x ln 6 Câu 51: Ta có e − 2 = = = ln = ∫ x − x ∫ 2 e ∫ + 2e − 3 x e + 2 − 3 x x e e −1 x e − 2 x e −1 ln3 ln3 ln3 ( )( ) ln3 4 1
= ln − ln = 3ln 2 − ln 5. Do đó suy ra a = 2,b = 5 ⇒ P = ab =10. Chọn A. 5 2 2tdt = 3dx Câu 52: Đặt 2 2
t = 3x +1 ⇒ t = 3x +1 ⇔
t −1 . Với x =1⇒ t = 2, x = 5 ⇒ t = 4 x = 3 2tdt 5 4 4 4 Ta có dx 3 2tdt t −1 3 1 I = = = = ln = ln − ln = 2ln 3− ln 5 ∫ ∫ 2 ∫ 2 x 3x +1 t −1 t −1 t +1 5 3 1 2 2 2 t 3 Do đó suy ra 2 2 a = 2,b = 1
− ⇒ a + ab + 3b = 5. Chọn B. Câu 53: Đặt 2
t = 2x +1 ⇒ t = 2x +1 ⇔ 2tdt = 2dx ⇔ dx = tdt. Với x = 0 ⇒ t =1, x = 4 ⇒ t = 3 4 3 3 3 Ta có 1 tdt 3 dx dt = = − = ∫ ∫ ∫ ( − t + ) 2 1 t 3ln 3 = 2 + 3ln 3+ 2x +1 3+ t 3+ t 3 0 1 1 1
Do đó suy ra a = 2,b = 3 ⇒ a + b = 5. Chọn D. 1 1 1 dx e dx d ( x x e ) x 1 Câu 54: e e 1 2e 1 = = = ln = ln − ln = ln = 1− ln + e ∫ xe ∫ ∫ +1 x x e e +1 x x e e +1 x e +1 e +1 2 e +1 2 0 0 ( ) 0 ( ) 0 Do đó suy ra 3 3 a =1,b = 1
− ⇒ S = a + b = 0. Chọn C. e ln e x ln (ln ) e xd x Câu 55: Ta có 1 2 dx = = − d ln x ∫ 2 ∫ 2 ∫ 2 ( ) x ln x + 2 ln x + 2 ln x + 2 1 ( ) 1 ( ) 1 (ln x + 2) 2 e 3 2 1 3 3 1 1 = ln ln x + 2 +
= ln + −1 = − + ln ⇒ a = ,b = − ⇒ − b = 1. Chọn B. ln x + 2 2 3 3 2 2 3 a 1
Document Outline
- ITMTTL~1
- IIBITP~1
- IIILIG~1