22 trang 49 lượt tải

Chuyên đề trắc nghiệm phương pháp đổi biến tìm nguyên hàm Toán 12

98

Chuyên đề trắc nghiệm phương pháp đổi biến tìm nguyên hàm Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 năm trước
Danh sách Quiz
/22
CHỦ ĐỀ 3: PHƯƠNG PHÁP ĐỔI BIẾN TÌM NGUYÊN HÀM
DẠNG 1. ĐỔI BIẾN SỐ HÀM SỐ VÔ TỈ (Đặt t = hàm theo biến x)
Mẫu 1: Đổi biến hàm số vô tỷ đơn giản
Nguyên hàm
( )
f x dx
∫
trong đó
( ) ( )
n
f x gx=
ta đặt
( ) ( )
n
n
t gx t gx= ⇒=
( )
1n
nt dt g x dx
−
′
⇒=
. Khi đó
( ) ( )
.f x dx h t dt=
∫∫
Mẫu 2: Nguyên hàm dạng
( )
.
x
f a dx
∫
Ta đặt
( )
( )
.
ln
.ln .ln
xx x
f t dt
dt
t a dt a adx dx f a dx
ta ta
=⇒= ⇒= ⇒ =
∫∫
.
Mẫu 3: Nguyên hàm dạng
( )
ln
.
f x dx
x
∫
Ta đặt
Khi đó
(
)
( )
ln
.
f x dx
f t dt
x
=
∫∫
Chú ý: Nếu nguyên hàm Mẫu 2 và Mẫu 3 có chứa căn thức, ta nên đặt t bằng căn thức.
Ví dụ với nguyên hàm
2
ln .
ln 1
x dx
I
xx
=
+
∫
ta nên đặt
2 22
ln 1 ln 1.t xt x= +⇒ = +
11
2 2ln . ln . .tdt x dx tdt x dx
xx
⇒ = ⇒=
Khi đó
2
ln 1
tdt
I dt t C x C
t
= = =+ = ++
∫∫
.
Ví dụ 1: Tìm các nguyên hàm sau:
a)
32
4.
I x x dx= +
∫
b)
( )
3
2
4.I x x dx= +
∫
c)
( )
.
1
dx
I
xx
=
+
∫
d)
3
1
.
9
I dx
xx
=
+
∫
Lời giải
a) Đặt
2 22
4 4 2d 2 .t x t x t t xdx tdt xdx= +⇒ = +⇒ = ⇔ =
Khi đó
( ) ( )
22 2 4 2
4 4. 4I x x xdx t t tdt t t dt= +=− =−
∫ ∫∫
( ) ( )
53
22
53
44 4
4
.
53 5 3
xx
tt
CC
++
= − += − +
b) Đặt
2 22
4 42 2 .t x t x tdt xdx tdt xdx= +⇒ = +⇒ = ⇔ =
Khi đó
( )
( )
5
2
5
3
2 34
4
4. .
55
x
t
I x x dx t tdt t dt C C
+
= + = = = += +
∫ ∫∫
c) Đặt
2
2t x t x tdt dx= ⇒=⇒ =
Khi đó
( )
( )
( )
( )
2
21
2 2 11
2.
11 1
1
t t dt
tdt dt
I dt
tt tt t t
tt
+−

= = = = −

++ +
+

∫ ∫∫ ∫
2ln 2 ln 1 2ln 2ln .
1
1
tx
t tC C C
t
x
= − ++= += +
+
+
d) Đặt
3 23 2
9 92 3
t x t x tdt x dx
= +⇒ = +⇒ =
Ta có:
( )
2
2
3 33
13 2
3 9.
93 9
x tdt
I dx dx
tt
xx x x
= = =
−
++
∫∫ ∫
( )( )
( ) ( )
( )( )
2
33
2 2 1 11 1
3 3 339 33 9 3 3
9
t t dt
dt dt
tt tt t t
t
+−−



= = = = −

−+ −+ − +
−

∫∫ ∫ ∫
3
3
1 3 1 93
ln ln .
93 9
93
tx
CC
t
x
− +−
= += +
+
++
Ví dụ 2: Tìm các nguyên hàm sau:
a)
21
.
1
x
x
e
I dx
e
+
=
+
∫
b)
2
ln 1
.
ln
x
I dx
xx
+
=
∫
c)
ln . 2ln 1
.
xx
I dx
x
+
=
∫
d)
ln
.
. ln 2
x
I dx
xx
=
+
∫
Lời giải
a) Đặt
xx
t e dt e dx dt tdx=⇒= ⇒=
Khi đó
( )
( )
( )
( )
( )
2
22
22
21 21
ln ln
1
xx
dt t
t dt t dt
I t tC e e C
tt
tt tt
+
++
= = = = ++ = + +
+
++
∫∫∫
( )
( )
ln ln 1 ln 1 .
xx x
eeCxeC= + ++=+ ++
Cách 2:
21 1
1
11 1 1

+ ++
= = = += +

++ + +

∫ ∫ ∫ ∫∫
x xx x x
xx x x
e e e e e dx
I dx dx dx dx
ee e e
(
)
( )
1
ln 1 .
1
x
x
x
de
x e xC
e
+
= += + ++
+
∫
b) Đặt
ln
dx
t x dt
x
= ⇒=
Khi đó
2 22
1 1 ln
ln ln ln .
22
t tx
I dt t dt t C x C
tt
+

= = + = + += + +


∫∫
c) Đặt
2
2
2ln 1 2ln 1 2 .
dx dx
t x t x tdt tdt
xx
= +⇒ = +⇒ = ⇔ =
Khi đó:
(
)
2 53
42
11
2 2 10 6
t tt
I tdt t t dt C
−
= = − = −+
∫∫
( )
( )
53
2ln 1 2ln 1
.
10 6
xx
tC
++
⇒= − +
d) Đặt
2
ln 2 ln 2 2
dx
t x t x tdt
x
= +⇒ = +⇒ =
Khi đó
( )
( )
3
23
2
2 ln 2
22
.2 2 2 4 4 ln 2 .
33
x
tt
I tdt t dt t C x C
t
+
−
= = − = − + = − ++
∫∫
Ví dụ 3: Tìm nguyên hàm của các hàm số sau:
a)
1
41
xdx
I
x
=
+
∫
b)
32
2
2I x x dx= +
∫
c)
2
3
1
x dx
I
x
=
−
∫
Lời giải
a) Đặt
(
)
2
22
2
1
1
24
.
1
42
41 41 1
8
41
4
t tdt
tdt dx
xdx
t x t x I t dt
tt
t
x
x
−
=
= + ⇔ = + → → = = = −
−
=
+
∫∫ ∫
(
)
3
3
41
11
41 .
83 8 3
x
t
tC x C

+


= −+= − ++




b) Đặt
( )
2 2 2 22 3 2 2
2 2 2 2 2 . 2.
t x t x x t xdx tdt x dx x xdx t tdt= + ⇔ = + → = − ⇔ = → = = −
(
)
( )
( )
(
)
53
22
53
2 3 2 42
2
22 2
2. . 2 2 2.
53 5 3
xx
tt
I x x dx t t tdt t t dt C C
++
= + = − = − = − += − +
∫ ∫∫
c) Đặt
( )
( )
2
2
2
22
2
3
22
2
1
1 11 2
1
1
dx tdt
t tdt
x dx
t xt xx t I
t
xt
x
= −
−
= − ⇔ = − ⇔ = − → → = = −
= −
−
∫∫
( ) ( )
( )
( )
53
53
2
2 42
1 21
2
21 2 2 1 2 2 1
53 5 3
xx
tt
t dt t t dt t C x C

−−


=− − =− − + =− − ++=− − + − +




∫∫
( )
( )
( )
53
22
53
23 2
3
22 2
2. . 2 2. .
53 5 3
xx
tt
I x x dx t t tdt C C
−+
= + = − = − += − +
∫∫
Ví dụ 4: Tìm nguyên hàm của các hàm số sau:
a)
4
1x
I dx
x
+
=
∫
b)
5
1 13
dx
I
x
=
++
∫
Lời giải
a) Đặt
( )( )
2
2
4
2
2
2
22
11 2
11
1
1
tdt dx
t dt
t x t x I dt
tt
t
xt
=

= +⇔ = +⇔ ⇔ = = +


−+
−
= −

∫∫
4
1 11
2 2 1 ln
1
11
tx
It C x C
t
x
− +−
= + + = ++ +
+
++
b) Đặt
( )
2
2
5
23
22 1
13 13 1
1
31 3 1
3
tdt dx
tdt
t x t x I dt
t
tt
x
=

= + ⇒=+ ⇔ ⇒= = −
−

++
=

∫∫
(
)
( )
5
22
ln 1 1 3 ln 1 3 1
33
I tt C x x
= − ++= +− ++
Ví dụ 5: Tìm nguyên hàm của các hàm số sau:
a)
2
6
11
x
x
e dx
I
e
=
+−
∫
b)
( )
7
2
1
dx
I
xx
=
+
∫
Lời giải
a) Đặt
( )
( )
2
22
6
2
21
2
2
1 1 22
11
1
x
xx
x
t t dt
tdt e dx
t e t e I t t dt
tt
et
+
=

= −⇔ = − ⇔ ⇒ = = −+ −

++
= +

∫∫
( )
(
)
3
32
1
1
2 2 2ln 1 2 2 1 2ln 1 1
32 3 2
x
x
xx
e
tt e
tt C e e C

−

−

= − + − + + = − − −− −+ +





b) Đặt
(
)
7
2
2
2
22 2
1
1
1
tdt dx
tdt
tx I C C
t
tx
x
tt
=
−−
= ⇒ ⇒ = = += +
+
=
+
+
∫
Ví dụ 6: Tìm nguyên hàm
1.I x x dx= +
∫
A.
( )(
)
2
13 2 1 .
3
Ix x xC
= + + ++
B.
( )( )
2 13 2 1
.
15
xxx
IC
+−+
= +
C.
( )
2
21 1
.
15
xx
IC
++
= +
D.
( )(
)
3 13 2 1
.
5
xxx
IC
+−+
= +
Lời giải
Đặt
2
1 12t x t x tdt dx= +⇒ = +⇒ =
Ta có:
( ) ( )
( )
53 3
2 42 2
22 2
1 .2 2 2 3 5
5 3 15
tt t
I t t tdt t t dt C t= − = − = − += −
∫∫
( )
( )
2 13 2 1
.
15
xxx
C
+++
= +
Chọn B.
Ví dụ 7: Tìm nguyên hàm
2
.
2
x
I dx
x
=
−
∫
A.
(
)
4
4 2.
3
Ix xC
= + −+
B.
( )
2
2 2.
3
Ix xC
= + −+
C.
( )
2
4 2.
3
Ix xC
= + −+
D.
( )
4
2 2.
3
Ix xC= + −+
Lời giải
Đặt
2
t 2 22x t x tdt dx= −⇒ =−⇒ =
Khi đó
( )
( ) ( )
2
3
22
22
44
.2 4 8 8 6
33
t
t
I tdt t dt t C t t C
t
+
= = + = ++= ++
∫∫
( )
4
24.
3
xx C= − ++
Chọn A.
Ví dụ 8: Tìm nguyên hàm
.
23 2
dx
I
xx
=
++ +
∫
A.
( )
ln 2 3 .Ix C= ++ +
B.
( )
2ln 2 3 .Ix C= ++ +
C.
(
)
2ln 2 3 .Ix x C
=+ ++ +
D.
22
ln .
3
23
x
IC
x
+
= +
++
Lời giải
Đặt
2
2 22t x t x tdt dx= +⇒ =+⇒ =
Khi đó
( )
2
22
2ln 3 2ln 2 3 .
3
3
tdt dt
I tC x C
t
tt
= = = ++ = ++ +
+
+
∫∫
Chọn B.
Ví dụ 9: Tìm nguyên hàm
.
11
xdx
I
x
=
++
∫
A.
(
)
3
2
1.
3
I x xC= + −+
B.
( )
3
2
1 21 .
3
I x xC= + − −+
C.
( )
3
3
1 1.
2
I x xC= + − −+
D.
( )
3
1
1 1.
3
I x xC= + − −+
Lời giải
Đặt
2
1 12
t x t x tdt dx= +⇒ = +⇒ =
Khi đó
( )
( )
( )
2
3
22
1 .2
2
1 .2 2 2
13
t tdt
t
I t tdt t t dt t C
t
−
= = − = − = −+
+
∫ ∫∫
( )
(
)
33
22
11 1 .
33
xxCxxC
= + −−+ = + −+
Chọn A.
Ví dụ 10: Tìm nguyên hàm
1
x
dx
I
e
=
+
∫
A.
ln .
1
x
x
e
IC
e
= +
+
B.
1
ln .
x
x
e
IC
e
+
= +
C.
2
ln .
1
x
x
e
IC
e
= +
+
D.
2ln .
1
x
x
e
IC
e
= +
+
Lời giải
Đặt
xx
dt
t e dt e dx tdx dx
t
=⇒= = ⇒=
Khi đó
( )
( )
1 11
ln
11 1 1
dt t t t
I dt dt C
tt tt t t t

+−

= = =−=+



++ + +


∫∫ ∫
ln ln .
11
xx
xx
ee
CC
ee
= += +
++
Chọn A.
Ví dụ 11: Giả sử
(
)
Fx
là một nguyên hàm của hàm số
( )
2
.
21
x
xx
e
fx
ee
=
++
Biết rằng
( )
0 0,F =
tìm
( )
Fx
A.
( )
11
.
2
1
x
Fx
e
= −
+
B.
( )
( )
ln 1 ln 2.
x
Fx e
= +−
C.
( )
11
.
2
1
x
Fx
e
−
= +
+
D.
(
)
( )
ln 1 ln 2.
x
Fx e
=− +−
Lời giải
Ta có:
( )
2
21
x
xx
e dx
Fx
ee
=
++
∫
. Đặt
xx
t e dt e dx=⇒=
Khi đó
( )
( )
22 2
1
1
1
2 1 21
1
x
xx
dt
e dx dt
C
t
e e tt
t
+
−
= = = +
+
+ + ++
+
∫ ∫∫
Do đó
( )
1
,
1
x
Fx C
e
−
= +
+
do
( )
11
00 0
22
F CC
−
=⇒ +=⇔=
Suy ra
( )
11
.
2
1
x
Fx
e
−
= +
+
Chọn C.
Ví dụ 12: Giả sử
( )
Fx
là một nguyên hàm của hàm số
( )
2
1.
xx
fx e e= +
. Biết rằng
( )
0 0,F =
tìm
( )
Fx
A.
( )
( ) ( )
2 1 13 2 4 2
.
15
x xx
e ee
Fx
+ + −−
=
B.
( )
( )
2
2 1 1 82
.
15
xx
ee
Fx
+ +−
=
C.
( )
( )
( )
2 1 1 5 2 28 2
.
15
x xx
e ee
Fx
+ + +−
=
D.
( )
( ) ( )
2 1 13 2 4 2
.
15
x xx
e ee
Fx
− + + −+
=
Lời giải
Ta có:
2
1.
xx
I e e dx= +
∫
Đặt
2
1 12
xx x
t e t e tdt e dx= +⇒ = +⇒ =
Khi đó
( )
(
)
( )
32
53
2 42
23 5
22
1 .2 2 2
5 3 15
tt
tt
I t t tdt t t dt C C
−
= − = − = − += +
∫∫
( )
( ) (
)
2 1 13 2
15
x xx
e ee
Fx C
+ +−
⇒= +
Lại có:
( )
2.2 2 4 2
00
15 15
F CC
−
= +=⇒=
Vậy
( )
( ) ( )
2 1 13 2 4 2
.
15
x xx
e ee
Fx
+ + −−
=
Chọn A.
Ví dụ 13: Tìm nguyên hàm của hàm số
( )
( )
2
ln
2 ln
x
fx
xx
=
+
A.
1
2ln ln 2 .
ln 2
xC
x
−
− ++
+
B.
2
ln ln 2 .
ln 2
xC
x
++ +
+
C.
2
ln 2 .
ln 2
xC
x
++ +
+
D.
1
2ln ln 2 .
ln 2
xC
x
+ ++
+
Lời giải
Đặt
1
lnt x dt dx
x
= ⇒=
Khi đó
( ) ( ) ( ) ( )
22 2 2
ln 2 2 1 2
2
2 ln 2 2 2
xdx tdt t
dt dt
t
xxt t t

+−
= = = −

+
+ ++ +


∫ ∫∫ ∫
22
ln 2 ln ln 2 .
2 ln 2
t Cx C
tx
= ++ += ++ +
++
Chọn B.
DẠNG 2. ĐỔI BIẾN SỐ HÀM VÔ TỈ (Đặt x = hàm theo biến t)
Mẫu 1: Nếu
( )
fx
có chứa
22
ax−
ta đặt
sin ;
22
x a tt
ππ


= ∈−




2 22
cos
sin cos
dx a tdt
aa ta t
=
⇒
−=
Mẫu 2: Dạng
22
xa+
thì đổi biến số
tan , ;
22
xa t t
ππ


= ∈−




2
22 2 22
cos
tan
cos
adt
dx
t
a
ax aa t
t
=
⇒
+= + =
Mẫu 3: Dạng
22
xa
−
thì ta đặt
sin
a
x
t
=
(hoặc
cos
a
x
t
=
).
2
2 2 22
cos
sin
cot
a tdt
dx
t
xa a t
−
=
⇒
−=
Mẫu 4: Dạng
22
dx
xa+
∫
thì ta đặt
tan .xa t=
Mẫu 5: Nếu
( )
fx
có chứa
ax
ax
+
−
thì đặt
( )
2
2
cos 2 2 .sin 2
cos 2
1 cos 2 cos
1 cos 2
sin
dx d a t a tdt
xa t
ax t t
ax t
t
= = −
= →
++
= =
−−
Một số kết quả quan trọng cần lưu ý khi giải trắc nghiệm:
( )
22
1
arctan 0
dx x
Ca
aa
xa
= +≠
+
∫
22
1
ln
2
dx x a
C
a xa
xa
+
= +
−
−
∫
( )
2
2
ln 0
dx
x x aCa
xa
= + ++ ≠
+
∫
( )
22
arcsin 0
dx x
Ca
a
ax
= +>
−
∫
Ví dụ 1: Tìm nguyên hàm của các hàm số sau:
a)
( )
1
2
;2
4
dx
Ia
x
= =
−
∫
b)
( )
2
2
1 ;1I x dx a=−=
∫
c)
( )
2
3
2
;1
1
x dx
Ia
x
= =
−
∫
d)
( )
22
4
9 ;3I x x dx a=−=
∫
Lời giải
a) Đặt
(
)
1
2
22
2sin 2cos
2cos
2sin
2cos
4
4 4 4sin 2cos
dx d t tdt
dx tdt
x t I dt t C
t
x
x tt
= =
= ⇒ → = = = = +
−
−=− =
∫∫∫
Từ phép đặt
1
2sin arcsin arcsin
22
xx
x tt I C
 
= ⇔ = → = +
 
 
b) Đặt
( )
22
sin cos
sin
1 1 sin cos
dx d t tdt
xt
x tt
= =
= ⇒
−=− =
Khi đó
2
2
1 cos 2 1 1 1
1 cos .cos cos 2 sin 2 .
2 2 2 24
tt
I x dx t tdt dt dt tdt t C
+
=−= = = + =+ +
∫ ∫ ∫ ∫∫
Từ
22
2
cos 1 sin 1
sin sin 2 2sin .cos 2 1
arcsin
t tx
x t t ttx x
tx
=−=−
= ⇒ → = = −
=
2
2
arcsin 1
1
22
x
I x xC → = + − +
c) Đặt
( )
22
sin cos
sin
1 1 sin cos
dx d t tdt
xt
x tt
= =
= →
−=− =
Khi đó,
22
2
3
2
sin .cos 1 cos 2 1 1
sin sin 2
cos 2 2 4
1
x dx t tdt t
I tdt dt t t C
t
x
−
= = = = =−+
−
∫ ∫ ∫∫
Từ
22
2
cos 1 sin 1
sin sin 2 2sin .cos 2 1
arcsin
t tx
x t t ttx x
tx
=−=−
= ⇒ → = = −
=
2
3
arcsin 1
1
22
x
I x xC → = − − +
d) Đặt
(
)
22
3sin 3cos
3sin
9 9 9sin 3cos
dx d t tdt
xt
x tt
= =
= →
−=− =
2 2 2 22 2
4
81 81 1 cos4
9 9sin .3cos 81 sin .cos sin 2
4 42
t
I x x dx t tdt t tdt tdt dt
−
= −= = = =
∫ ∫ ∫ ∫∫
81 1 1 81 1
cos 4 sin 4
42 2 42 8
t
dt tdt t C

= − =−+



∫∫
Từ
2
2
2
cos 1 sin 1
2
9
3sin sin 2 1
39
arcsin
3
x
tt
xx
xt t
x
t
=−=−
= ⇒ → = −

=


Mà
2
2 22
2
2 22
cos2 1 2sin 1 2 1 sin 4 2sin 2 .cos 2 2. 1 . 1
3 9 39 9
x x xx x
t t t tt


= − = − = − → = = − −




Từ đó ta được
22
4
arcsin
81 2
3
1 .1 .
4 2 69 9
x
xx x
IC







= −− − +





Ví dụ 2: Tìm nguyên hàm của các hàm số sau:
a)
( )
1
2
;1
1
dx
Ia
x
= =
+
∫
b)
2
2
25I x x dx= ++
∫
c)
( )
2
3
2
;2
4
x dx
Ia
x
= =
+
∫
Lời giải
a) Đặt
( )
( )
( )
2
2
2
1
2
22
1 tan
tan 1 tan
tan
cos
1 tan
1 1 tan
dt
t dt
dx d t t dt
x x I dt t C
t
t
xt
+
= = = +
= → → = = = +
+
+=+
∫∫
Từ giả thiết đặt
1
tan arctan arctan .x t t x I xC= ⇔ = → = +
b) Ta có
( ) ( )
2
1
22
2
25 1 4 1 4
tx
I x x dx x d x I t dt
= +
= + + = + + + → = +
∫∫ ∫
Đặt
( )
2
2
2
2
22
2
2 tan
2 cos
cos
2 tan
2
2
cos
cos
.cos
4 4 4 tan
cos
cos
du
dt d u
du du udu
u
tu I
u
u
u
tu
u
u
= =
= → → = = =
+= + =
∫ ∫∫
( )
( ) ( )
( )( )
( )
( )
( )
2
sin 1 sin 1 sin sin sin
1 1 1 1 1 sin
sin ln .
2 1 sin 1 sin 2 1 sin 2 1 sin 2 1 sin
1 sin
du u u du du
u
du C
uu u u u
u
+ +−
+
== =+= +
+− − + −
−
∫ ∫ ∫∫
Từ phép đặt
22
22
2 22
14
2 tan tan 1 sin 1 cos 1
24
cos 4 4
tt t
t uu u u
u tt
= ⇔ = → = + → = − = − =
++
Từ đó ta được
22
2
22
1
11
1 1 sin 1 1
4 25
ln ln ln .
1
2 1 sin 2 2
11
4 25
tx
u
t xx
IC C C
tx
u
t xx
+
++
+
+ ++
= += += +
+
−
−−
+ ++
c) Đặt
( )
( )
2
2
22
2
2 tan 2 1 tan
cos
2 tan
4 4 tan 4
dt
dx d t t dt
t
xt
xt
= = = +
= →
+= +
( )
22
2
22
3
3
2
4 tan .2 1 tan
sin
4 tan 1 tan 4
cos
2 1 tan
t t dt
t
I t tdt dt
t
t
+
⇒= = + =
+
∫ ∫∫
( )
( )
2
2
42
2
sin . sin
sin .cos
44
cos
1 sin
td t
t tdt
t
t
= =
−
∫∫
Đặt
( )
( )
(
)
( )( )
2
2
2
3
2
2
11
1
sin 4 4 4
1 21 1
1
uu
uu
u t I du du du
u uu
u

+ −−

= → = = =


− +−

−

∫ ∫∫
( ) ( )
( )( )
2
22
11 2
1 1 11
11
du du du
du
u u uu
uu

=− =+−

− + −+

−+
∫ ∫∫∫
( )
( )
( )
( )
( )( )
( )( )
22
1 1 11
11
11
d u d u u u du
uu
uu
− + −+
=−+ −
−+
−+
∫∫∫
11 11 11
11 11 11 1 1
du du
du
uu uu uu u u

=−−− + =−−− −

−+ +− −+ + −

∫ ∫∫
11 11 1
ln 1 ln 1 ln
1 1 11 1
u
uu C C
u u u uu
−
=−−−++−+=−+ +
− + −+ +
3
1 1 1 1 1 sin 1
ln ln .
1 1 1 sin sin 1 sin 1
ut
IC C
u u u tt t t
−−
→ = − + + = − + +
−+ + − + +
Lại có
22
22 2
2 22
14
2 tan tan 1 tan 1 cos sin
24
cos 4 4
xx x
xtt t t t
t xx
= ⇔ = → = + = + ⇔ = → =
++
2
3
2
22 2
1
11
4
sin ln .
4
11 1
44 4
x
x
x
tI C
xx x
x
xx x
−
+
⇔ = → = − + +
+
−+ +
++ +
Ví dụ 3: Tìm nguyên hàm của các hàm số sau:
a)
1
2
.
1
dx
I
x
=
−
∫
b)
2
22
.
4
dx
I
xx
=
−
∫
c)
3
2
.
22
dx
I
xx
=
−−
∫
Lời giải
a) Đặt
2
2
2
2
2
1 cos
cos
sin
sin
1
sin
sin
1
1 cot
11
sin
tdt
tdt
dx d
dx
t
t
t
x
t
xt
x
t
−

−
= =

=


=⇒⇔


−=
−= −
( )
1
2 22
2
cos
cos sin
sin .cot sin 1 cos
1
dt
dx tdt tdt
I
tt t t
x
−
⇒= = =− =
−
−
∫ ∫ ∫∫
( )
(
)( )
( )
( )
( ) ( )
( )
cos 1 cos 1 cos
1 1 1 cos
cos ln .
1 cos 1 cos 2 1 cos 1 cos 2 1 cos
dt t t
t
dt C
tt t t t
− ++
+
= = = +
− + − ++ −
∫∫
Từ phép đặt
2
2
22
1
2
2
1
1
1 1 11
cos 1 sin 1 cos ln .
sin 2
1
1
x
x
x
x tt t I C
tx
x
x
x
−
+
−
= ⇒ =− =− ⇔ = ⇒= +
−
−
b) Đặt
2
2
2 22
2
2
2
2 2cos
2cos
sin
sin
2
sin
8cot
sin
4
4 2cos 4
44
sin
sin
tdt
tdt
dx d
dx
t
t
t
x
t
t
x t xx
x
t
t
−

−
= =
=



= → ← →


−= ⇒ −=
−= −
Khi đó,
2
22
2
2
2cos 1 1
sin cos .
8cot
44
4
sin .
sin
dx tdt
I tdt t C
t
xx
t
t
−
= = =−=+
−
∫∫ ∫
Từ
22
22
2
2
2 4 44
cos 1 sin 1 cos .
sin 4
xx
x tt t I C
t xx
x
−−
= → = − = − ⇔ = → = +
c)
( )
( )
(
)
1
33
2 2 22
2
1
.
22 3
13
3
tx
dx
dx dt dt
II
xx t
x
t
= −
−
= = → = =
−− −
−−
−
∫ ∫ ∫∫
Đặt
2
2
2
2
2
3 3 cos
3 cos
sin
sin
3
sin
sin
3
3 3 cot
33
sin
udu
dt d
udu
dt
u
u
t
u
u
tu
t
u

−
= =
−


=

= → ← →


−=
−= −
( )
( )
( )( )
3
22
2
2
cos cos
3 cos sin
1 cos 1 cos
sin 1 cos
sin . 3 cot
3
du du
dt udu udu
I
uu
uu
uu
t
−
→ = = = − = =
−+
−
−
∫∫ ∫∫ ∫
( ) ( )
( )( )
( )
1 cos 1 cos
1 1 1 cos
cos ln .
2 1 cos 1 cos 2 1 cos
uu
u
du C
uu u
− ++
+
= = +
−+ −
∫
22
2
2
3
2
22
3 22
11
3 3 31 1
1
cos 1 cos ln ln .
sin 2 2
3 22
11
1
t xx
t
tx
t u tI C C
ut
t
t xx
tx
− −−
++
−
−
= ⇒ =− ⇔ = ⇒ = += +
− −−
−−
−
Ví dụ 4: Cho nguyên hàm
22
1.
I x x dx= −
∫
Bằng cách đặt
sin ;
22
x tt
ππ


= ∈−




mệnh đề nào sau đây
là đúng?
A.
( )
1 cos 4 .I t dt= −
∫
B.
( )
1 cos 4 .I t dt
= +
∫
C.
sin 4
.
8 32
tt
IC=−+
D.
sin 4
.
8 32
tt
IC=++
Lời giải
Ta có:
22
cos
sin ;
22
1 1 sin cos cos
dx tdt
x tt
x ttt
ππ
=


= ∈− ⇒


−=− = =


Khi đó
( )
22 2
1 1 sin 4
sin .cos sin 2 1 cos 4 .
4 8 8 32
tt
I t tdt tdt t dt I C
= = = − ⇒=− +
∫ ∫∫
Chọn C.
Ví dụ 5: Cho nguyên hàm
2
9.I x dx= −
∫
Bằng cách đặt
3
,
cos
x
t
=
với
0; .
2
t
π

∈


Mệnh đề nào dưới
đây là đúng?
A.
2
3
sin
9.
cos
t
I dt
t
= −
∫
B.
2
3
sin
9.
cos
t
I dt
t
=
∫
C.
2
4
sin
9.
cos
t
I dt
t
= −
∫
D.
2
4
sin
9.
cos
t
I dt
t
=
∫
Lời giải
Ta có
(
)
2 22
9 3 19
9 3 1. . sin
cos
cos cos cos
I d t dt
t
t tt
−

=− = −−


∫∫
22
22 3
sin sin sin
9. 9.
cos cos cos
tt t
dt dt
tt
= =
∫∫
Chọn B.
Ví dụ 6: Tính nguyên hàm
2
.
4
dx
I
x
=
−
∫
A.
arcsin .
2
x
IC= +
B.
.I xC= +
C.
arccos .
2
x
IC= +
D.
arcsin .I xC= +
Lời giải
Đặt
22
2cos
2sin ;
22
4 4 sin 2 cos 2cos
dx tdt
x tt
x ttt
ππ
=


= ∈− ⇒


−=− = =


Khi đó
2cos
arcsin .
2cos 2
tdt x
I dt t C C
t
= = =+= +
∫∫
Chọn A.
Tổng quát:
( )
22
arcsin 0
dx x
Ca
a
ax
= +>
−
∫
Ví dụ 7: Tính nguyên hàm
2
.
1
dx
I
xx
=
−−
∫
A.
1
arcsin .
5
x
IC
+
= +
B.
21
arcsin .
25
x
IC
+
= +
C.
( )
arcsin 2 1 .I xC= ++
D.
21
arcsin .
5
x
IC
+
= +
Lời giải
Ta có:
222
1
2
1
51 51
42 42
dx
dx dx
I
xx
xx

+


= = =
−−
 
−+ −+
 
 
∫∫ ∫
1
21
2
arcsin arcsin .
55
2
x
x
CC
+
+
= += +
Chọn D.
Ví dụ 8: Tính nguyên hàm
(
)
2
5
2
1
x dx
I
x
=
−
∫
bằng cách đặt
sin ;
22
x tt
ππ


= ∈−




ta được:
A.
2
2 tan .
I tC= +
B.
3
tan
.
3
t
IC= +
C.
2
tan
.
2
t
IC
= +
D.
5
tan
.
5
t
IC= +
Lời giải
Đặt
22
cos
sin ; .
22
1 1 sin cos cos
dx tdt
x tt
x ttt
ππ
=


= ∈− ⇒


−=− = =


Khi đó:
( )
22 3
2
5 22
sin .cos sin 1 tan
. tan tan .
3
cos cos cos
t tdt t t
I dt td t C
t tt
= = = = +
∫∫ ∫
Chọn B.
Ví dụ 9: Tính nguyên hàm
1
1
x
I dx
x
+
=
−
∫
bằng cách đặt
cos 2 0;
2
x tt
π


= ∈




ta được:
A.
2
4 cos .I tdt= −
∫
B.
2
2 cos .I tdt= −
∫
C.
2
4 sin .I tdt= −
∫
D.
3
cos
4.
sin
t
I dt
t
= −
∫
Lời giải
Đặt
cos 2 2sin 2 4sin cos .
x t dx tdt t tdt= ⇒=− =−
Mặt khác
22
22
1 cos 2 2cos cos cos cos
1 cos2 sin sin
2sin sin
t t ttt
t tt
tt
+
= = = =
−
Khi đó
( )
2
cos
. 4sin cos 4 cos .
sin
t
I t t dt tdt
t
=−=−
∫∫
Chọn A.
Ví dụ 10: Tính nguyên hàm
2
1x
I dx
x
−
=
∫
bằng cách đặt
1
0;
cos 2
xt
t
π


= ∈




ta được.
A.
3
tan .I xdx=
∫
B.
2
tan .I xdx=
∫
C.
3
cot .I xdx=
∫
D.
2
cot .I xdx=
∫
Lời giải
Đặt
(
)
22
cos
1 sin
0;
cos 2
cos cos
t
t
x t dx dt dt
t
tt
π
′
−


= ∈ ⇒= =




Lại có:
2
2
1
1 tan tan tan
cos
ttt
t
−= = =
Do đó
2
2
tan sin
. tan .
1
cos
cos
tt
I dt tdt
t
t
= =
∫∫
Chọn B.
BÀI TẬP TỰ LUYỆN
Câu 1: Xét
( )
5
34
43.I x x dx
= −
∫
Bằng cách đặt
4
4 3,ux= −
hỏi khẳng định nào đúng?
A.
5
1
.
4
I u du=
∫
B.
5
1
.
21
I u du=
∫
C.
5
1
.
16
I u du=
∫
D.
5
.I u du=
∫
Câu 2: Cho
( )
10
2
1.I x x dx= −
∫
Đặt
2
1,ux= −
hỏi khẳng định nào đúng?
A.
10
2I u du=
∫
B.
10
2I u du= −
∫
C.
10
1
2
I u du= −
∫
D.
10
1
2
I u du=
∫
Câu 3: Xét
,
41
x
I dx
x
=
+
∫
bằng cách đặt
4 1,tx= +
mệnh đề nào sau đúng?
A.
3
1
.
83
t
I tC

= ++


B.
3
1
.
43
t
I tC

= −+


C.
3
1
.
83
t
I tC

= −+


D.
3
1
.
43
t
I tC

= ++


Câu 4: Tìm nguyên hàm của hàm số
( )
2
1.
fx x x
= +
A.
22
1
1.
2
x xC++
B.
(
)
3
22
1
1.
3
x xC
++
C.
(
)
3
2
1
1.
3
xC++
D.
22
1
1.
3
x xC++
Câu 5: Tìm nguyên hàm của hàm số
( )
5
cos .sinfx x x=
A.
6
1
cos
6
xC−+
B.
6
1
sin
6
xC
−+
C.
6
1
cos
6
xC+
D.
4
1
cos
4
xC−+
Câu 6: Tìm một nguyên hàm
( )
Fx
của hàm số
( )
( )
4
2
21f x xx= +
thỏa mãn
( )
1 6.F =
A.
( )
( )
5
22
1
2
55
xx
Fx
+
= −
B.
( )
( )
5
2
1
2
55
x
Fx
+
= −
C.
( )
( )
5
22
1
2
55
xx
Fx
+
= +
D.
(
)
( )
4
2
1
2
55
x
Fx
+
= −
Câu 7: Tìm một nguyên hàm
( )
Fx
của hàm số
( )
( )
9
2
1f x xx= +
thỏa mãn
( )
21
0.
20
F =
A.
( )
( )
10
2
1
11
20
Fx x=− ++
B.
( )
( )
10
2
1
11
20
Fx x= ++
C.
( )
( )
10
2
2 11Fx x
= +−
D.
( )
( )
10
2
12Fx x
=++
Câu 8: Tìm nguyên hàm của hàm số
( ) ( )
5
3.fx x x= −
A.
( )
6
31
3
62
x
xC
−

− −+


B.
( )
6
31
3
72
x
xC
−

− ++


C.
( )
6
31
3
72
x
xC
−

− −+


D.
( )
6
31
3
72
x
xC
−

+ −+


Câu 9: Biết
( )
Fx
là một nguyên hàm của
( )
2
ln
ln 1
x
fx x
x
= +
thỏa
( )
1
1.
3
F =
Tính
( )
2
.Fe


A.
(
)
2
8
.
3
Fe
=


B.
( )
2
8
.
9
Fe =


C.
( )
2
1
.
3
Fe =


D.
(
)
2
1
.
9
Fe
=


Câu 10: Gọi
( )
Fx
là một nguyên hàm của hàm số
(
)
2
8
x
fx
x
=
−
thỏa
( )
2 0.
F =
Tìm tổng các nghiệm
phương trình
(
)
.
Fx x
=
A.
13+
B. 2. C. 1. D.
13−
Câu 11: Tìm một nguyên hàm
(
)
Fx
của hàm số
( )
2
2
.
1
x
fx
xx
=
+−
A.
( )
( )
32 2
22
11
33
Fx x x x=−− −
B.
( )
(
)
32 2
22
11
33
Fx x x x=+− −
C.
( )
( )
32 2
22
11
33
Fx x x x=−+ −
D.
(
)
( )
32 2
22
11
33
Fx x x x=++ −
Câu 12: Hàm số
(
)
2
ln ln 1xx
fx
x
+
=
có 1 nguyên hàm
( )
Fx
là thỏa
( )
1
1.
3
F
=
Tìm
( )
2
.Fe
A.
(
)
2
1
.
3
Fe=
B.
(
)
2
8
.
3
Fe
=
C.
(
)
2
8
.
9
Fe
=
D.
(
)
2
1
.
9
Fe
=
Câu 13: Tìm một nguyên hàm
( )
Fx
của hàm số
( )
3
x
x
e
fx
e
=
+
thỏa
( )
0 27.
F
=
A.
( )
2 33
x
Fx e= +−
B.
( )
33
x
Fx e= +−
C.
( )
2 33
x
Fx e
= ++
D.
( )
33
x
Fx e
= ++
Câu 14: Hàm số
(
)
3
2
2
x
fx
xx
=
−
có một nguyên hàm là
( )
Fx
thỏa
( )
1
1.
3
F −=
Tính
( )
1.F
A.
( )
12F =
B.
( )
1
1
3
F =
C.
( )
5
1
3
F
= −
D.
( )
3
1
5
F = −
Câu 15: Tìm một nguyên hàm
( )
Fx
của hàm số
( )
2
x
fx
x
=
−
thỏa mãn
( )
2
3.
3
F =
A.
( ) ( )
3
2
2 4 2 4.
3
Fx x x= − − −+
B.
( ) ( )
3
1
2 4 2 4.
3
Fx x x
= − + −+
C.
(
) ( )
3
2
2 4 2 4.
3
Fx x x
= − + −−
D.
(
) ( )
3
2
2 2 2 4.
3
Fx x x= − + −−
Câu 16: Hàm số
( )
1
1
fx
x
=
+
có một nguyên hàm là
( )
Fx
thỏa
( )
0 2 ln 2.F =
Tính
( )
1.F
A.
( )
1 2 ln 2.F = −
B.
( )
1 2 ln 2.F =
C.
( )
1 2.
F =
D.
( )
1 0.F =
Câu 17: Tìm một nguyên hàm
( )
Fx
của hàm số
(
)
1
2 14
fx
x
=
−+
thỏa
( )
1 2 4 ln 5.F = −
A.
( )
2114ln214xx++− ++
B.
( )
2114ln214
xx
−+− −+
C.
( )
7
211 ln214
2
xx−−− −+
D.
( )
7
2 1 1 ln 2 1 4
2
xx−−+ ++
Câu 18: Hàm số
(
)
2
3
1
x
fx
x
=
+
có một nguyên hàm là
( )
Fx
thỏa
(
)
2
0.
3
F
=
Tính
( )
1.F
A.
( )
32
1.
2
F =
B.
( )
3
1.
2
F =
C.
( )
22
1.
3
F =
D.
( )
2
1.
3
F =
Câu 19: Tìm nguyên hàm của hàm số
( )
2
12
cos .fx
x
x
=
A.
12
sin
2
C
x
−+
B.
12
cos
2
C
x
−+
C.
12
sin
2
C
x
+
D.
12
cos
2
C
x
+
Câu 20: Cho
(
)
Fx
là một nguyên hàm của hàm số
( )
1
3
x
fx
e
=
+
thỏa mãn
( )
1
0 ln 4.
3
F = −
Tìm tập
nghiệm S của phương trình
( )
( )
3 ln 3 2.
x
Fx e+ +=
A.
{ }
2S =
B.
{ }
2; 2S = −
C.
{ }
1; 2S =
D.
{ }
2;1S = −
Câu 21: Giả sử
(
)
(
)
( )
2017
11
1,
ab
xx
x x dx C
ab
−−
− =−+
∫
với a, b là các số nguyên dương. Tính
2.ab−
A.
2 2017
ab
−=
B.
2 2018
ab−=
C.
2 2019
ab−=
D.
2 2020
ab−=
Câu 22: Tìm nguyên hàm của hàm số
(
)
2
.
1
x
x
e
fx
e
=
+
A.
( )
ln 1
xx
ee C− ++
B.
( )
ln 1
xx
ee C+ ++
C.
( )
ln 1
x
eC++
D.
2xx
e eC
−+
Câu 23: Tìm nguyên hàm của hàm số
( )
1
.
1
fx
x
=
+
A.
( )
2 2 ln 1x xC− ++
B.
(
)
2 2 ln 1x xC
+ ++
C.
( )
ln 1 xC++
D.
( )
2 2 ln 1
xC+ ++
Câu 24: Tìm nguyên hàm của hàm số
( )
2
.
1
x
fx
x
+
=
+
A.
( )
3
41
4
x xC+ ++
B.
( )
2
41
3
x xC+ ++
C.
( )
21 1
x
C
xx
+
++
D.
1
1
1
xC
x
++ +
+
Câu 25: Tìm nguyên hàm của hàm số
( )
21
.
1
x
fx
x
−
=
−
A.
1
21
1
xC
x
− −+ +
−
B.
( )
2
2 11
3
x xC
+ −+
C.
( )
2
2 11
3
x xC− + −+
D.
( )
2
2 11
3
x xC− − −+
LỜI GIẢI CHI TIẾT
Câu 1: Đặt
4 33
1
4 3 16
16
u x du x dx x dx du
= −⇔ = ⇔ =
Khi đó
55
11
.
16 16
I u du u du= =
∫∫
Chọn C.
Câu 2: Đặt
2
1
12 .
2
u x du xdx xdx du=−⇔ =− ⇔ =−
Khi đó
10
1
.
2
I u du= −
∫
Chọn C.
Câu 3: Đặt
2
41 41 4 2
2
t
t x t x dx tdt dx dt= +⇔ = +⇔ = ⇔ =
Khi đó
2
23
1
11
4
..
2 8 83
t
tt t
I dt dt t C
t
−

−
= = = −+


∫∫
Chọn C.
Câu 4:
( )
( )
(
)
3
2 22 2
11
1 11 1 .
23
f x dx x x dx x d x x C
= + = + += + +
∫∫ ∫
Chọn C.
Câu 5:
( ) ( )
55 6
1
cos .sin cos cos cos .
6
f x dx x xdx xd x x C= =− =−+
∫∫ ∫
Chọn A.
Câu 6:
(
)
( )
( )
(
)
( )
5
2
4
2 22
1
21 1 1 .
5
x
f x dx x x dx x d x C
+
= + = + += +
∫∫ ∫
Suy ra
( )
( )
5
2
1
5
x
Fx C
+
= +
mà
( )
2
16 .
5
FC
= → = −
Vậy
( )
( )
5
2
1
2
.
55
x
Fx
+
= −
Chọn B.
Câu 7:
( ) (
)
( ) ( ) ( )
( )
10
2
99
2 22
1
1
1 11 .
2 20
x
F x f x dx x x dx x d x C
+
= = + = + += +
∫∫ ∫
Mà
( )
21
0 1.
20
FC= → =
Vậy
( )
(
)
10
2
1
1 1.
20
Fx x= ++
Chọn B.
Câu 8:
( )
( ) ( ) ( ) (
) ( )
5 565
3 3 3.3 3 3.3 .fxxxxxxx= − =−−− − =−− + −
Khi đó
( ) ( ) ( )
( ) ( )
76
65
33
3 3. 3 .
72
xx
f x dx x x dx C
−−

= −− + − = − +

∫∫
Chọn C.
Câu 9:
2 22
ln ln
ln 1 ln 1 2 2. .
xx
t x t x tdt dx dx tdt
xx
= +⇔ = +⇔ = ⇔ =
Khi đó
( )
(
)
3
2
3
2
ln 1
33
x
t
f x dx t dt C C
+
= = += +
∫∫
mà
(
)
1
1 0.
3
FC=⇒=
Vậy
( )
(
)
( )
3
2
ln 1
22
.
33
x
Fx Fe
+
= → =
Chọn B.
Câu 10: Đặt
22 2
88dx dt xt xx tt= − ⇔=−⇔ =−
Khi đó
( )
2
8
x
t
f x d dt dt t C x C
t
−
= =− =−+ =− − +
∫ ∫∫
Mà
( )
2 0 2.FC= → =
Vậy
( )
2
2 8 1 3.Fx x x x x=⇔− − =⇔=−
Chọn D.
Câu 11: Ta có
(
)
(
)
22 2
2
1
1 11 1
1
xx xx xx
xx
+− −−=⇔ =−−
+−
Khi đó
( )
(
)
( )
(
)
2 2 2 32 2
22
2 12 2 1 1 1 .
33
xx xfx x x xx fxd x x x C
= − − = − −⇒ = − − −+
∫
Chọn A.
Câu 12: Đặt
2 22
ln ln
ln 1 ln 1 2 2. .
xx
d x xd
t x t x tt d d tt
xx
= +⇔ = +⇔ = ⇔ =
Khi đó
( )
(
)
3
2
3
2
ln 1
33
x
x
t
f x d t dt C C
+
= = += +
∫∫
mà
( )
1
1 0.
3
FC=⇒=
Vậy
( )
(
)
( )
3
2
ln 1
22
.
33
x
Fx Fe
+
= → =
Chọn C.
Câu 13: Đặt
2
3 32xd
x xx
t e t e ed t t= +⇔ = +⇔ =
Khi đó
(
)
2
22 23
x
x
t
f x d dt dt t C e C
t
= = = + = ++
∫ ∫∫
Mà
( )
0 3 3 3.FC= → =
Vậy
( )
2 3 3.
x
Fx e= ++
Chọn C.
Câu 14: Đặt
22 2
22d dxt x t x tt x
= − ⇔=−⇔ =−
Khi đó
( )
(
)
(
)
22
2
2
2
2
2
x dx
xt
f x d x t dt t dt
t
x
−
= = −= −
−
∫∫ ∫ ∫
(
)
3
3
22
1
2 2 22
33
t
tC x x C= −+= − − − +
mà
( )
1
1 2.
3
FC− = → =
Vậy
( )
1
1.
3
F =
Chọn B.
Câu 15: Đặt
2
2 22xdt x t x d tt= −⇔ =−⇔ =
Khi đó
( )
(
)
( )
2
3
23
2 22
.2 2 4 4 2 4 2
33
xd
t
f x d t t t dt t t C x x C
t
+
= = + = + + = − + −+
∫∫ ∫
Mà
(
)
2
3 4.
3
FC= → =
Vậy
( )
( )
3
2
2 4 2 4.
3
Fx x x= − + −+
Chọn B.
Câu 16: Đặt
2
2xdt x x t d tt= ⇔= ⇔ =
Khi đó
( )
22
2 2 2 ln 1 2 2 ln 1 .
11
x
t
f x d dt dt t t C x x C
tt

= = − = − ++ = − ++

++

∫ ∫∫
Mà
( )
0 2 ln 2 2 ln 2.
FC= → =
Vậy
( )
1 2 2 ln 2 2 ln 2 2.
F =−+=
Chọn C.
Câu 17: Đặt
2
21 21x x xdt t d tt= −⇔ = −⇔ =
Khi đó
( )
4
1 4 ln 4 2 1 4 ln 2 1 4 .
44
x xx
t
f x d dt dt t t C C
tt

= = − =− + + = −− −+ +

++

∫ ∫∫
Mà
(
)
1 2 4 ln 5 1.
FC= − → =
Vậy
( )
2114ln214.
xx
Fx= −+− −+
Chọn B.
Câu 18: Đặt
3 23 2
2
11
3
x
t
txtxxddt
= +⇔ = +⇔ =
Khi đó
(
)
3
2 22 2
: 1.
3 33 3
t
f x dx tdt dt t C x C= = = + = ++
∫ ∫∫
Mà
( )
2
0 0.
3
FC= → =
Vậy
( )
22
1.
3
F =
Chọn C.
Câu 19: Ta có
( )
2
1 2 1 22 12
cos . cos sin .
22
f x dx dx d C
x xx x
x

= =− =−+


∫∫ ∫
Chọn A.
Câu 20: Đặt
.
xx
dt
t e dt e dx dx
t
=⇔= ⇔=
Khi đó
(
)
( )
11
ln ln .
33 3 3
3
x
x
dt t e
f x dx C C
tt t
e
= = += +
++
+
∫∫
Mà
( )
1
0 0.
3
FC= − → =
Do đó
( )
( )
3 ln ln 3 .
xx
Fx e e=−+
Vậy
( )
( )
3 ln 3 2 ln 2 2.
xx
Fx e e x+ + =⇔ =⇔=
Chọn A.
Câu 21: Ta có
(
) ( )( )
( ) ( ) ( )
2017 2017 2018 2017
1 1 11 1 1 1x x dx x x dx x x d x

−=−−−−=−−− −

∫∫ ∫
( ) ( )
2019 2018
11
2019
.
2018
2019 2018
xx
a
C
b
−−
=
= − + →
=
Vậy
2 2020.
ab
−=
Chọn D.
Câu 22: Ta có
( )
( ) ( )
2
ln 1 .
11
x
xx
x
xx x
xx
ee
fxdddeeeC
ee
= = = − ++
++
∫∫∫
Chọn A.
Câu 23: Đặt
2
2xdt x x t d tt
= ⇔= ⇔ =
Khi đó
( )
22
2 2 2 ln 1 2 2 ln 1 .
11
x
t
f x d dt dt t t C x x C
tt

= = − = − ++ = − ++

++

∫ ∫∫
Chọn A.
Câu 24: Đặt
2
1 12xdt x t x d tt
= +⇔ = +⇔ =
Khi đó
( )
( )
2
23
12
.2 2 2 2 .
3
xd
t
f x d t t t dt t t C
t
+
= = + = ++
∫∫ ∫
Chọn B.
Câu 25: Đặt
22
1 11 2xdt xt xx t d tt= −⇔ =−⇔=− ⇔ =−
Khi đó
( )
( )
( )
(
)
( )
2
2
21 1
2
.2 22 4 1 2 11 .
3
x
t
f x d t dt t t dt x x C
t
−−
= − =− − + =− + −+
∫∫ ∫
Chọn C.

Tài liệu khác của Toán 12

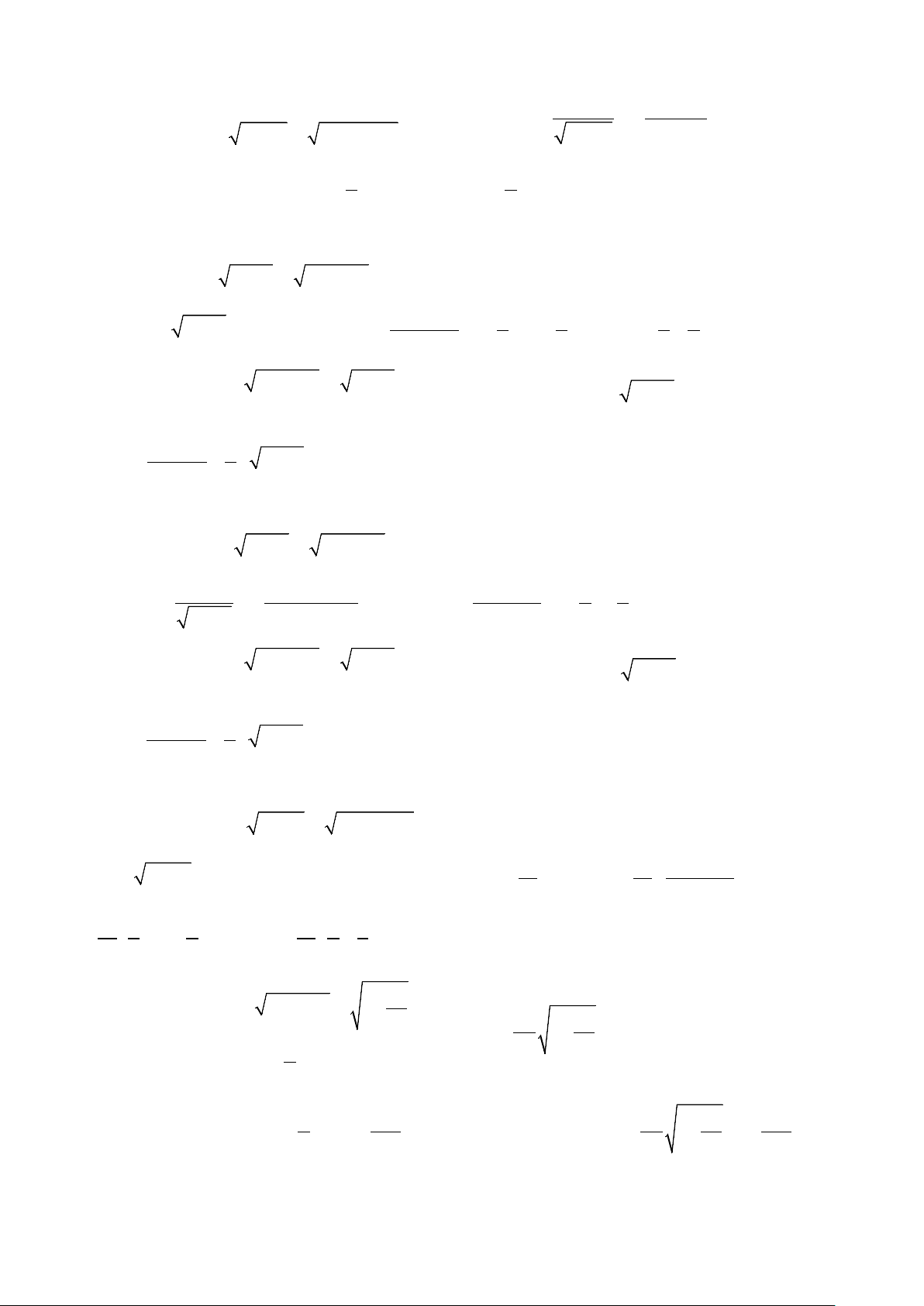
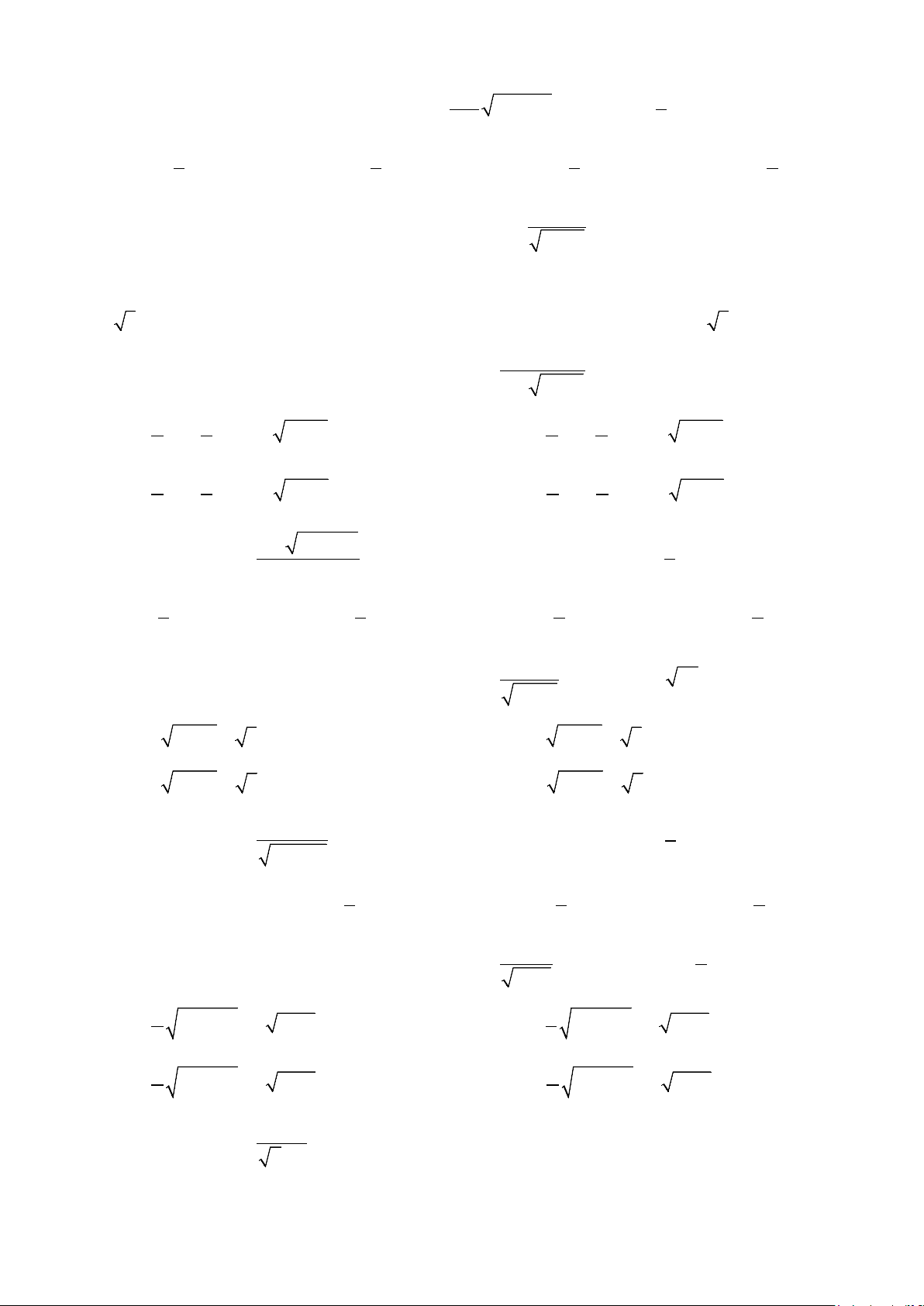
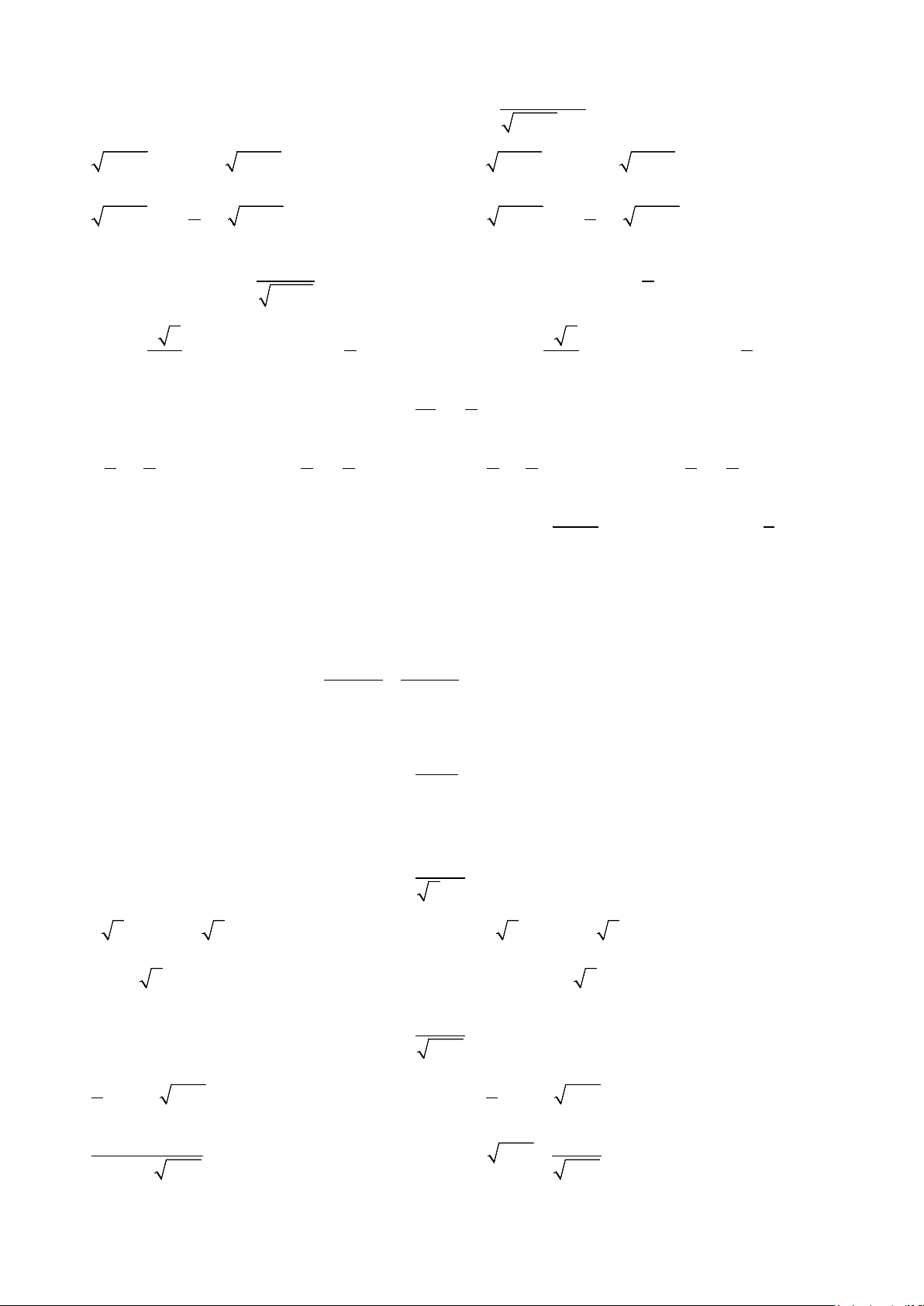
Preview text:

CHỦ ĐỀ 3: PHƯƠNG PHÁP ĐỔI BIẾN TÌM NGUYÊN HÀM
DẠNG 1. ĐỔI BIẾN SỐ HÀM SỐ VÔ TỈ (Đặt t = hàm theo biến x)
Mẫu 1: Đổi biến hàm số vô tỷ đơn giản
Nguyên hàm f (x)dx ∫ trong đó ( ) n
f x = g (x) ta đặt = ( ) n n t
g x ⇒ t = g (x) n 1
⇒ nt − dt = g′(x)dx . Khi đó f
∫ (x)dx = h ∫ (t)dt.
Mẫu 2: Nguyên hàm dạng ( x f a ) . dx ∫ dt f t dt Ta đặt x x
t = a ⇒ dt = a adx ⇒ dx = ⇒ f ∫ ( xa ) ( ). ln dx = t.ln a ∫ . t.ln a
f (ln x)dx
Mẫu 3: Nguyên hàm dạng . ∫ x
f (ln x)dx Ta đặt 1
t = ln x ⇒ dt = . dx Khi đó = f ∫ ∫ (t)dt. x x
Chú ý: Nếu nguyên hàm Mẫu 2 và Mẫu 3 có chứa căn thức, ta nên đặt t bằng căn thức. Ví dụ với nguyên hàm ln .xdx I = ∫ ta nên đặt 2 2 2
t = ln x +1 ⇒ t = ln x +1. 2 x ln x +1 1 1 ⇒ 2tdt = 2ln .
x dx ⇒ tdt = ln . x . dx Khi đó tdt 2 I =
= dt = t + C = ln x +1 + C x x ∫ t ∫ .
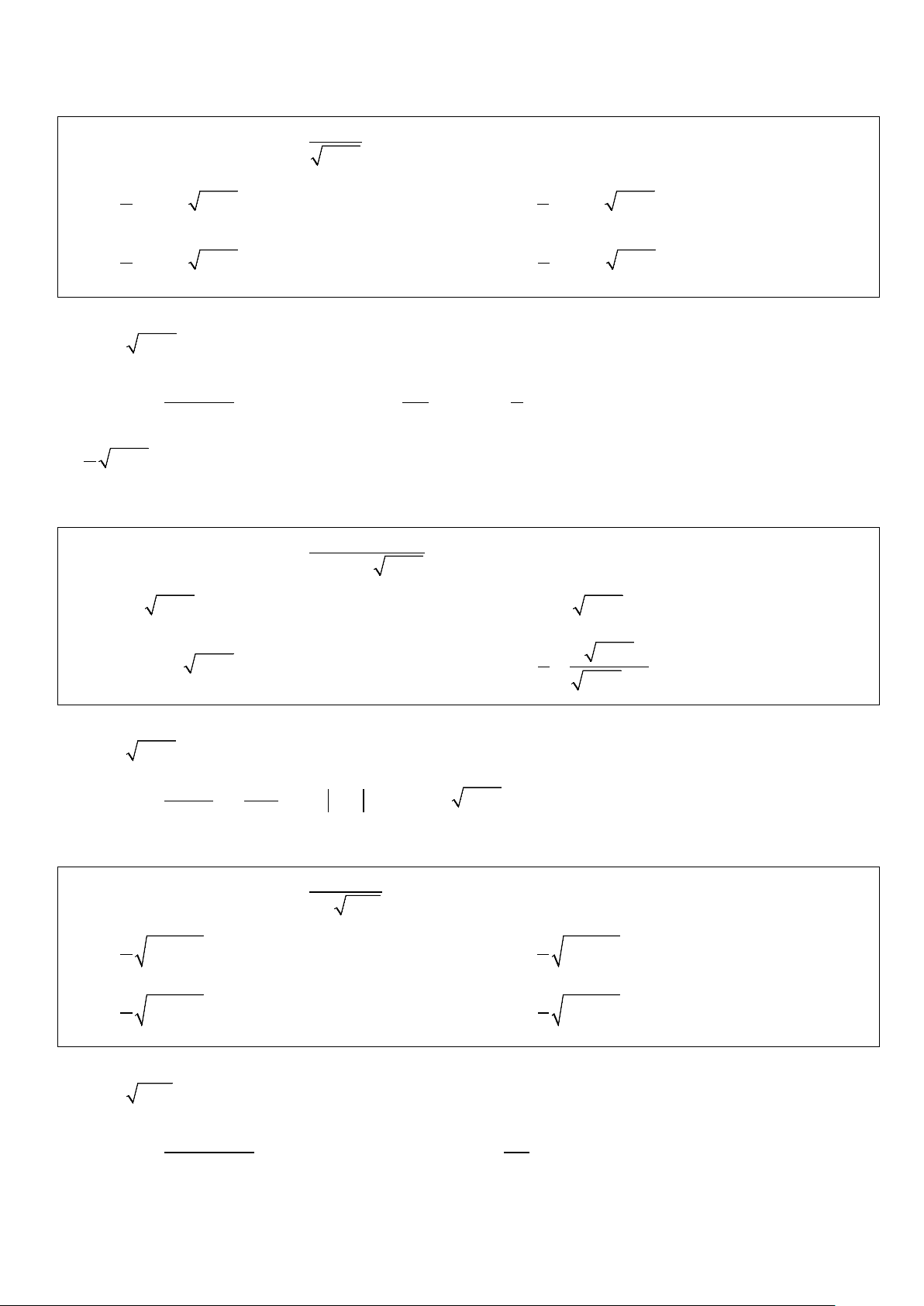
Ví dụ 1: Tìm các nguyên hàm sau: a) 3 2 I = x x + 4 . dx ∫
b) I = x (x + ∫ )3 2 4 . dx c) dx I 1 = ∫ d) I = . dx ∫ x( + x). 1 3 x x + 9 Lời giải a) Đặt 2 2 2
t = x + 4 ⇒ t = x + 4 ⇒ 2tdt = 2xdx ⇔ tdt = x . dx Khi đó 2 2
I = x x + xdx = ∫
∫( 2t − )t tdt = ∫( 4 2 4 4 .
t − 4t )dt 4 (x + )5 (x t t + )3 2 2 5 3 4 4 4 = − + C = − + C. 5 3 5 3 b) Đặt 2 2 2
t = x + 4 ⇒ t = x + 4 ⇒ 2tdt = 2xdx ⇔ tdt = x . dx x + 4 Khi đó I = x ∫ (x + 4) t ( )5 2 5 3 2 3 4
dx = t .tdt = t dt = + C = + C. ∫ ∫ 5 5 c) Đặt 2
t = x ⇒ t = x ⇒ 2tdt = dx 2tdt 2dt
2(t +1− t)dt Khi đó 1 1 I 2  = = = = − ∫ ∫ ∫ ∫  dt. 2 t (1+ t) t (t + ) 1 t (t + ) 1  t t +1
= 2ln − 2ln +1 + = 2ln t + = 2ln x t t C C + C. t +1 x +1 d) Đặt 3 2 3 2
t = x + 9 ⇒ t = x + 9 ⇒ 2tdt = 3x dx 2 Ta có: 1 3x 2tdt I = dx = dx = ∫ ∫ ∫ 3 3 3 x x + 9 3x x + 9 3( 2t − 9).t 2 dt 2 dt
1 (t + 3) − (t − 3) dt  1  1 1  = = = = − ∫ 2 3 t ∫ ∫ ∫
− 9 3 (t 3)(t 3) 9 (t 3)(t 3)
9  t 3 t 3  − + − + − +  3 1 t − 3 1 x + 9 − 3 = ln + C = ln + C. 3 9 t + 3 9 x + 9 + 3
Ví dụ 2: Tìm các nguyên hàm sau: x 2 a) 2e +1 I + = . dx ∫ b) ln x 1 I = . dx x ∫ e +1 x ln x c) ln .x 2ln x +1 I = . dx ∫ d) ln x I = . dx x ∫ .x ln x + 2 Lời giải a) Đặt x x
t = e ⇒ dt = e dx ⇒ dt = tdx (2t + )1dt (2t + )1dt
d ( 2t + t) Khi đó 2 I = = =
= ln t + t + C = ln ∫ ∫ ∫ ( 2x x
e + e + C 2 2 ) t (t + ) 1 t + t t + t
= ln x + ln ( x + ) 1 + = + ln ( x e e C x e + ) 1 + C. x e + x e + x e +  x ex Cách 2: 2 1 1 = = = ∫ e dx I dx dx dx dx x ∫ x ∫ +1 x  = + ∫ x ∫ e +1 e +1  e +1  e +1 d ( x e + ) 1 = + x = ln ∫
( xe + + x +C x )1 . e +1 b) Đặt = ln dx t x ⇒ dt = x 2 2 2 Khi đó t +1  1 t ln = = + = + ln x I dt t dt t + C = + ln ln x + ∫ ∫  C. tt  2 2 c) Đặt 2 2 = 2ln +1 ⇒ = 2ln +1 ⇒ 2 dx dx t x t x tdt = ⇔ tdt = . x x 2 5 3 Khi đó: t −1 1 = = ∫ ∫( 4 2 − ) t t I tdt t t dt = − + C 2 2 10 6 ( x + )5 ( x + )3 2ln 1 2ln 1 ⇒ t = − + C. 10 6 d) Đặt 2 = ln + 2 ⇒ = ln + 2 ⇒ 2 dx t x t x tdt = x t − 2 2t 2 ln x + 2 Khi đó I = .2tdt = 2 ∫ ∫(t − 2) ( )3 2 3 2 dt = − 4t + C =
− 4 ln x + 2 + C. t 3 3
Ví dụ 3: Tìm nguyên hàm của các hàm số sau: 2 a) xdx I =
I = x x + 2dx x dx I = 1 ∫ b) 3 2 ∫ c) ∫ 4x +1 2 3 1− x Lời giải 2 t −1 2 = 4 .tdt tdt dx a) Đặt 2  xdx 4 2 1
t = 4x +1 ⇔ t = 4x +1 →  t − t  → I = = = ∫ ∫ ∫( 2 2 t −1 dt 1 ) x = 4x +1 t 8  4 1  t  1  ( x )3 3 4 1  +  t C  4x 1 = − + = − + + C. 8 3 8  3      b) Đặt 2 2 2 2 2 3 2
t = x + ⇔ t = x + 
→ x = t − ⇔ xdx = tdt 
→ x dx = x xdx = ( 2 2 2 2 2 2 . t − 2).tdt 5 3 2 2 5 3 x + 2 2 x + 2 2 3 = + 2. = . ∫ ∫ ( 2 − 2) = ∫( 4 2 − 2 t = − 2.t I x x dx t t tdt t t dt + C = − + C 2 ) ( ) ( ) 5 3 5 3 dx = 2 − tdt x dx 1−  t tdt 2 2 ( )2 2 2
c) Đặt t = 1− x ⇔ t = 1− x ⇔ x = 1− t  →   → I = = 2 − ∫ ∫ 2 x =  ( 2 1− t )2 3 1− x t  5 3  t tx x  − − 2∫( 2 1 2 1 2 1 t ) dt 2∫( 4 2 t 2t ) 5 3 2 ( ) ( ) 1 dt 2 t C 2 1 x  = − − = − − + = − − + + = − − + − + C 5 3  5 3      5 3 2 2 x − 2 2 x + 2 2 3 = + 2. = . ∫ ∫ ( 2 − 2 t = − 2.t I x x dx t t tdt + C = − + C. 3 ) 5 3 ( ) ( ) 5 3 5 3
Ví dụ 4: Tìm nguyên hàm của các hàm số sau: a) x +1 I = dx dx I = 4 ∫ b) x 5 ∫ 1+ 1+ 3x Lời giải 2 2tdt = dx   a) Đặt 2 2t dt 2
t = x +1 ⇔ t = x +1 ⇔  ⇔ I = = ∫ ∫2 +  dt 2 4 2 x = t −1 t −1   (t ) 1 (t ) 1  − +  t −1 x +1 −1 I = 2t +
+ C = 2 x +1 + ln + C 4 t +1 x +1 +1 2tdt = 3dx b) Đặt 2  2tdt 2  1  2
t = 1+ 3x ⇒ t = 1+ 3x ⇔  t −1 ⇒ I = = ∫ ∫1−  dt 5 x = 3(1+ t) 3  t +1  3 2 2 I =
t − ln t +1 + C =
1+ 3x − ln 1+ 3x +1 5 ( ) ( ) 3 3
Ví dụ 5: Tìm nguyên hàm của các hàm số sau: 2x a) e dx I = dx I = 6 ∫ b) ∫ 1 x + e −1 7 x ( + x)2 1 Lời giải x 2
2tdt = e dx 2t t +1 dt a) Đặt x 2 t e t ( xe ) ( )  2 2 1 1  I 2 ∫ ∫t t 2  = − ⇔ = − ⇔ ⇒ = = − + −  dt 6 x 2 e = t +1 1+ tt +1   ( x et t −   )3 3 2 1 x e −1 2
2t 2ln t 1  C 2 2 x e 1 2ln  ( xe 1 )1 = − + − + + = − − − − − + + C 3 2 3 2        2tdt = dx b) Đặt 2tdt 2 − 2 t xI C − = ⇒ ⇒ = = + = + C ∫ 2 7 t  = x
t (1+ t)2 1+ t 1+ x
Ví dụ 6: Tìm nguyên hàm I = x x +1 . dx ∫ 2(x + )
1 (3x − 2) x +1 A. 2 I = (x + )
1 (3x + 2) x +1 + C. B. I = + C. 3 15 (x + )2 2 1 x +1 3(x + )
1 (3x − 2) x +1 C. I = + C. D. I = + C. 15 5 Lời giải Đặt 2
t = x +1 ⇒ t = x +1 ⇒ 2tdt = dx 5 3 3 Ta có: = ∫( 2 − ) = ∫( 4 2 − ) 2t 2t 2 1 .2 2 2 t I t t tdt t t dt = − + C = ( 2 3t − 5) 5 3 15 2(x + ) 1 (3x + 2) x +1 = + C. Chọn B. 15
Ví dụ 7: Tìm nguyên hàm 2x I = . dx ∫ x − 2 A. 4
I = (x + 4) x − 2 + C. B. 2
I = (x + 2) x − 2 + C. 3 3 C. 2
I = (x + 4) x − 2 + C. D. 4
I = (x + 2) x − 2 + C. 3 3 Lời giải Đặt 2
t = x − 2 ⇒ t = x − 2 ⇒ 2tdt = dx 2( 2t + 2) 3 Khi đó I = tdt = ∫ ∫( 2t + ) 4t 4 .2 4 8 dt =
+ 8t + C = t ( 2t + 6) + C t 3 3 4 =
x − 2 (x + 4) + C. Chọn A. 3
Ví dụ 8: Tìm nguyên hàm dx I = . ∫ x + 2 + 3 x + 2
A. I = ln ( x + 2 + 3) + C.
B. I = 2ln ( x + 2 + 3) + C. C. I +
= x + 2ln ( x + 2 + 3) + C. D. 2 x 2 I = ln + C. 3 x + 2 + 3 Lời giải Đặt 2
t = x + 2 ⇒ t = x + 2 ⇒ 2tdt = dx Khi đó 2tdt 2dt I = =
= 2ln t + 3 + C = 2ln x + 2 + 3 + C. ∫ Chọn B. 2 ∫ ( ) t + 3t t + 3
Ví dụ 9: Tìm nguyên hàm xdx I = . ∫ 1+ x +1 A. 2 I = (x + )3 1 − x + C. B. 2 I = (x + )3
1 − 2x −1+ C. 3 3 C. 3 I = (x + )3
1 − x −1+ C. D. 1 I = (x + )3
1 − x −1+ C. 2 3 Lời giải Đặt 2
t = x +1 ⇒ t = x +1 ⇒ 2tdt = dx ( 2t − ) 3 1 .2tdt Khi đó I = = ∫
∫(t − )1.2tdt = ∫( 2 2t − 2t) 2t 2 dt = − t + C 1+ t 3 2 = (x + )3 2
1 − x −1+ C = (x + )3
1 − x + C. Chọn A. 3 3
Ví dụ 10: Tìm nguyên hàm dx I = ∫ x e +1 x x A. + = ln e I + C. B. e 1 I = ln + C. x e +1 x e 2x x C. = ln e I + C. D. = 2ln e I + C. x e +1 x e +1 Lời giải Đặt x x dt
t = e ⇒ dt = e dx = tdx ⇒ dx = t  + −  Khi đó dt t 1 t 1 1  t I = ∫ ( ∫ ∫ + ) =   = − = +  t  (t + ) dt    dt ln C t t 1 1   t t +1 t +1 x x = ln e + = ln e C + C. Chọn A. x e +1 x e +1 x
Ví dụ 11: Giả sử F (x) là một nguyên hàm của hàm số ( ) e f x = . 2x e + 2 x e +1
Biết rằng F (0) = 0, tìm F (x) A. F (x) 1 1 = − . B. ( ) = ln( x F x e + ) 1 − ln 2. x e +1 2 C. F (x) 1 − 1 = + .
D. ( ) = −ln( x F x e + ) 1 − ln 2. x e +1 2 Lời giải x Ta có: ( ) e dx F x = ∫ . Đặt x x
t = e ⇒ dt = e dx 2x e + 2 x e +1 x e dx dt d (t + ) 1 Khi đó 1 − = = = + C ∫ 2x x ∫ 2 ∫ e + 2e +1 t + 2t +1 (t + )2 1 t +1 Do đó F (x) 1 − − = + C, do F ( ) 1 1 0 = 0 ⇒ + C = 0 ⇔ C = x e +1 2 2 Suy ra F (x) 1 − 1 = + . Chọn C. x e +1 2
Ví dụ 12: Giả sử F (x) là một nguyên hàm của hàm số ( ) x 2 = +1. x f x e
e . Biết rằng F (0) = 0, tìm F (x) 2( x + ) 1 x +1(3 x e e e − 2) − 4 2 ( x + )2 2 1 x e e +1 − 8 2
A. F (x) = .
B. F (x) = . 15 15 2( x + ) 1 x +1(5 x e e e + 2) − 28 2 2 − ( x + ) 1 x +1(3 x e e e − 2) + 4 2
C. F (x) = .
D. F (x) = . 15 15 Lời giải Ta có: x 2 = +1. x I e e dx ∫ Đặt x 2 = +1 x ⇒ = +1 ⇒ 2 x t e t e tdt = e dx 3 2 5 3 2t 2t 2t 3t − 5 Khi đó I = t
∫ ( 2t − )1.2tdt = ∫( 4 2 2t − 2t ) ( ) dt = − + C = + C 5 3 15 2( x + ) 1 x +1(3 x e e e − 2) ⇒ F (x) = + C 15 Lại có: F ( ) 2.2 2 4 2 0 C 0 C − = + = ⇒ = 15 15 2( x + ) 1 x +1(3 x e e e − 2) − 4 2 Vậy F (x) = . Chọn A. 15
Ví dụ 13: Tìm nguyên hàm của hàm số ( ) ln x f x = x(2 + ln x)2 A. 1 −
− 2ln ln x + 2 + C. B. 2 ln ln x + 2 + + C. ln x + 2 ln x + 2 C. 2 ln x + 2 + + C. D. 1
+ 2ln ln x + 2 + C. ln x + 2 ln x + 2 Lời giải Đặt 1
t = ln x ⇒ dt = dx x   Khi đó ln xdx tdt t + 2 − 2 1 2 = = dt =  −  dt ∫ ∫ ∫ ∫ x(2 + ln x)2 (t + 2)2 (t + 2)2
t + 2 (t + 2)2    2 2 = ln t + 2 +
+ C = ln ln x + 2 + + C. Chọn B. t + 2 ln x + 2
DẠNG 2. ĐỔI BIẾN SỐ HÀM VÔ TỈ (Đặt x = hàm theo biến t)   π π  
Mẫu 1: Nếu f ( x) có chứa 2 2
a − x ta đặt x = asin t t ∈ −  ;    2 2    
dx = a costdt  ⇒  2 2 2
a − a sin t = a cost    π π   Mẫu 2: Dạng 2 2
x + a thì đổi biến số x = a tan t, t ∈ −  ;  2 2     adt dx =  2  cos t ⇒  a  2 2 2 2 2
a + x = a + a tan t =  cost a aMẫu 3: Dạng 2 2
x − a thì ta đặt x = (hoặc x = ). sin t cost  −a costdt dx =  2 ⇒  sin t  2 2 2 2
x − a = a cot t dxMẫu 4: Dạng ∫
thì ta đặt x = a tan t. 2 2 x + a
dx = d (a cos 2t) = 2 − . a sin 2tdt + 
Mẫu 5: Nếu f ( x) có chứa a x thì đặt x = a cos 2t  → 2 a − xa + x 1+ cos 2t cos t  = = 2  a − x 1− cos 2t sin t
 Một số kết quả quan trọng cần lưu ý khi giải trắc nghiệm: dx 1 x  = arctan + C ∫ (a ≠ 0) 2 2 x + a a a dx 1 x + a  = ln + C ∫ 2 2 x − a 2a x − a dx  2
= ln x + x + a + C ∫ (a ≠ 0) 2 x + a dx x  = arcsin + C ∫ (a > 0) 2 2 a − x a
Ví dụ 1: Tìm nguyên hàm của các hàm số sau: a) dx I = ; a = 2 b) 2 I =
1− x dx; a = 1 2 ∫ ( ) 1 ∫ ( ) 2 4 − x 2 c) x dx I = ; a = 1 d) 2 2
I = x 9 − x ; dx a = 3 4 ∫ ( ) 3 ∫ ( ) 2 1− x Lời giảidx = d
(2sint) = 2costdt a) Đặt dx 2cos = 2sin tdt x t ⇒   → I = =
= dt = t + C 1 ∫ ∫ ∫ 2 2 2
 4 − x = 4 − 4sin t = 2cost 4 − x 2cost Từ phép đặt 2sin arcsin  x  arcsin  x x t t I  = ⇔ =  → = +     C 1  2   2  dx = d  (sint) = costdt
b) Đặt x = sin t ⇒  2 2
 1− x = 1− sin t = cost Khi đó 2 1+ cos 2t 1 1 t 1 I =
1− x dx = cost.costdt = dt = dt +
cos 2tdt = + sin 2t + C. 2 ∫ ∫ ∫ 2 2 ∫ 2 ∫ 2 4  2 2 Từ
cost = 1− sin t = 1− x 2
x = sin t ⇒  
→sin 2t = 2sin t.cost = 2x 1− x t  = arcsin x arcsin x 1 2  → I =
+ x 1− x + C 2 2 2 dx = d  (sint) = costdt
c) Đặt x = sin t  →  2 2
 1− x = 1− sin t = cost 2 2 Khi đó, x dx sin t.costdt 2 1− cos 2t 1 1 I = = = sin tdt =
dt = t − sin 2t + C 3 ∫ ∫ ∫ ∫ 2 1− x cost 2 2 4  2 2 Từ
cost = 1− sin t = 1− x 2
x = sin t ⇒  
→sin 2t = 2sin t.cost = 2x 1− x t  = arcsin x arcsin x 1 2  → I =
− x 1− x + C 3 2 2 dx = d
(3sint) = 3costdt
d) Đặt x = 3sin t  →  2 2
 9 − x = 9 − 9sin t = 3cost 2 2 2 2 2 81 2 81 1− cos 4 = 9 − = 9sin .3cos = 81 sin .cos = sin 2 t I x x dx t tdt t tdt tdt = dt 4 ∫ ∫ ∫ 4 ∫ 4 ∫ 2 81 1 1  81 t 1 dt cos 4tdt sin 4t  = − = − +  ∫ ∫    C 4 2 2  4  2 8   2 2 cos = 1− sin = 1 x t t − 2 Từ  9 2 = 3sin ⇒   →sin 2 x = 1 x x t t −   x  3 9 t = arcsin   3     2 2 2 2     Mà 2 x 2x 2x x 2 cos 2 = 1− 2sin = 1− 2 =   1−  →sin 4 = 2sin 2 .cos 2 = 2. 1− .1 x t t t t t −  3  9 3 9  9   arcsin  x     2 2      Từ đó ta được 81 3 x x 2 =  − 1− .1 x I −   + C. 4 4  2 6 9  9     
Ví dụ 2: Tìm nguyên hàm của các hàm số sau: 2 a) dx I = ; a = 1 b) 2 I =
x + 2x + 5dx x dx I = ; a = 2 1 ∫ ( ) 2 ∫ x ∫ c) 3 ( ) +1 2 2 x + 4 Lời giải
dx = d (tan t) dt = = ( 2 1+ tan t dt 1+ tan t dt 2 ) ( 2 )
a) Đặt x = tan x  → cos t  → I =
= dt = t + C 1 ∫ 2 ∫  2 2 1+ tan 1  + = 1+ tan t x t
Từ giả thiết đặt x = tan t ⇔ t = arctan x 
→ I = arctan x + C. 1 b) Ta có 2 I =
x + 2x + 5dx = ∫ ∫ (x + )2
1 + 4d (x + ) t=x 1+ 2 1 → I = t + 4dt 2 ∫  = ( ) 2 2 tan du dt d u =  2 Đặt  cos u 2du du cos t = 2 tan udu u  →   → I = = = 2 ∫ ∫ ∫ 2 2 2  2 2 2 cosu cos
4 + t = 4 + 4 tan u = .cos u u  cosu cosu
d (sin u) 1 (1+ sinu) + (1− sinu) 1 d sin u 1 d sin u 1 1+ sin u = = d u = + = + C ∫1 ∫ ∫ ∫
− sin u 2 (1+ sin u)(1− sin u) (sin ) ( ) ( ) ln . 2
2 1− sin u 2 1+ sin u 2 1− sin u 2 2 Từ phép đặt t 1 t 2 2 4 = 2 tan ⇔ tan =  → = 1+  →sin = 1− cos = 1 t t u u u u − = 2 2 2 2 cos u 4 4 + t 4 + t t x +1 1+ 1+ 2 2 Từ đó ta được 1 1+ sin u 1 4 + t 1 x + 2x + 5 I = ln + C = ln + C = ln + C. 2 2 1− sin u 2 t 2 x +1 1− 1− 2 2 4 + t x + 2x + 5  = ( ) 2 2 tan dt dx d t = = 2( 2 1+  tan t dt 2 )
c) Đặt x = 2 tan t  →  cos t  2 2
x + 4 = 4 tan t + 4 2 4 tan t.2( 2 1+ tan t) 2 dt 2 2 sin ⇒ = = 4 tan 1+ tan = 4 t I t tdt dt 3 ∫ ∫ ∫ 3 2 2 1+ tan t cos t 2 2 sin t.costdt
sin t.d (sin t) = 4 = 4 ∫ 4 cos ∫ t (1−sin t)2 2 2 uu
1 (1+ u) − (1− u) 2 2 
Đặt u = sin t  → I = 4 du = 4 ∫ ∫  du = 4∫   du 3 ( − )2 2 1− u  2  (1+ u)(1 1 − u u )  2  1 1  du du 2du = − ∫  du = + −  ∫ ∫ ∫
1− u 1+ u  (1− u)2 (1+ u)2 (1− u)(1+ u) d (1− u) d (1+ u)
(1− u)(1+ u)du = − + − ∫ ( ∫ ∫ 1− u)2 (1+ u)2 (1− u)(1+ u) 1 1  1 1  1 1 du du = − − − + ∫  du = − − − − 1 ∫ ∫ − u 1+ u
1+ u 1− u  1− u 1+ u 1+ u 1− u 1 1 1 1 u −1 = − −
− ln 1+ u + ln u −1 + C = − + ln + C 1− u 1+ u u −1 1+ u u +1 1 1 u −1 1 1 sin t −1  → I = − + ln + C = − + ln + C. 3 u −1 1+ u u +1
sin t − t sin t +1 sin t +1 2 2 Lại có x 1 2 x 2 4 2 = 2 tan ⇔ tan =  → = 1+ tan = 1+ ⇔ cos =  →sin x x t t t t t = 2 2 2 2 cos t 4 4 + x 4 + x x −1 2 x 1 1 4 ⇔ sin =  → = − + ln + x t I + C. 3 2 4 x + −1 x +1 x x +1 2 2 2 4 + x 4 + x 4 + x
Ví dụ 3: Tìm nguyên hàm của các hàm số sau: a) dx I = . dx I = . dx I = . 1 ∫ b) ∫ c) ∫ 2 x −1 2 2 2 x x − 4 3 2 x − 2x − 2 Lời giải   1  −costdtdx = d =    − costdt 2 1   sin t  sin tdx = a) Đặt 2 x = ⇒  ⇔  sin t sin t  2 1  2 x −1 = −1
x −1 = cot t  2  sin t dx − costdt sin tdt d (cost) ⇒ I = = = − = 1 ∫ ∫ 2 ∫ 2 ∫ 2 2 x −1 sin t.cot t sin t 1− cos t d (cost)
1 (1− cost) + (1+ cost) 1 1+ cost = ∫ ( = = + ∫ − t)( + t) ( − t) + ( +
t) d (cost) ln C. 1 cos 1 cos 2 1 cos 1 cos 2 1− cost 2 x −1 2 1+ Từ phép đặt 1 2 2 1 x −1 1 = ⇒ cos = 1− sin = 1− ⇔ cos = ⇒ = ln x x t t t I + C. 2 1 2 sin t x x 2 x −1 1− x   2  2 − costdt  2 − costdtdx = d =   2 dx =  2 2   sin t  sin t b) Đặt  sin t x =  →  ← → sin t   4  2 2 2 8cot t 2 x − 4 = − 4
x − 4 = 2cost ⇒ x x − 4 = 2  2 sin t   sin t Khi đó, dx 2 − costdt 1 1 I = = = −
sin tdt = cost + C. 2 ∫ ∫ ∫ 2 2 − 2 8cot 4 t x x 4 4 sin t. 2 sin t 2 2 Từ 2 2 2 4 x − 4 x − 4 x = 
→cos t = 1− sin t = 1− ⇔ cost =  → I = + C. 2 2 sin t x x 4x dx d (x − ) 1 c) t=x 1 − dt dt I = =  → I = = . 3 ∫ ∫ ∫ ∫ x − 2x − 2 (x − ) 3 2 2 2 1 − 3 t − 3 t − ( 3)2 2   3  − 3 cosududt = d   =  − 3 cosudu   2 3  sin u   sin udt = Đặt 2 t =  →  ← →  sin u sin u  3  2 2  t − 3 = − 3
t − 3 = 3 cot u 2  sin u dt − 3 cosudu sin udu d (cosu) d (cosu)  → I = = = − = = 3 ∫ ∫ ∫ ∫ ∫ 2 2 2 2 t − 3 sin . u 3 cot u sin u 1− cos u
(1− cosu)(1+ cosu)
1 (1− cosu) + (1+ cosu) 1 1+ cosu = ∫ ( = + − u)( +
u) d (cosu) ln C. 2 1 cos 1 cos 2 1− cosu 2 2 t − 3 x − 2x − 2 2 1+ 1 3 + 2 3 t − 3 1 t 1 x −1 t = ⇒ cos u = 1− ⇔ cost = ⇒ I = ln + C = ln + C. 2 3 2 2 sin u t t 2 t − 3 2 x − 2x − 2 1− 1− t x −1
Ví dụ 4: Cho nguyên hàm 2 2   π π I   = x 1− x . dx ∫
Bằng cách đặt x = sin t t ∈ −  ;  mệnh đề nào sau đây   2 2     là đúng?
A. I = ∫(1− cos4t)dt.
B. I = ∫(1+ cos4t)dt. C. t sin 4t I = − + C. D. t sin 4t I = + + C. 8 32 8 32 Lời giải  π π     dx = costdt
Ta có: x = sin t t ∈ − ;  ⇒     2 2   2 2  
 1− x = 1− sin t = cost = cost  Khi đó 2 2 1 2 1 = = = ∫ ∫ ∫( − ) t sin 4 sin .cos sin 2 1 cos 4 t I t tdt tdt t dt ⇒ I = − + C. Chọn C. 4 8 8 32
Ví dụ 5: Cho nguyên hàm 2  π I = x − 9 . dx ∫ Bằng cách đặt 3 x = , với t 0;  ∈ 
. Mệnh đề nào dưới cost  2  đây là đúng? 2 2 2 2 A. sin = 9 t I − dt. ∫ B. sin = 9 t I dt. sin = 9 t I − dt. sin = 9 t I dt. 3 cos ∫ C. ∫ D. ∫ t 3 cos t 4 cos t 4 cos t Lời giải Ta có 9  3  1 9 I = − 9d = 3 −1. − . ∫ ∫ (−   sin t)dt 2 2 2 cos t  cost  cos t cos t 2 2 sin t sin t sin = 9 . = 9 t dt dt. ∫ 2 2 ∫ Chọn B. 3 cos t cos t cos
Ví dụ 6: Tính nguyên hàm dx I = . ∫ 2 4 − x A. = arcsin x I + C.
B. I = x + C. C. = arccos x I + C.
D. I = arcsin x + C. 2 2 Lời giải  π π    dx = 2costdt
Đặt x = 2sin t t ∈ −  ;  ⇒   2 2   2 2 
 4 − x = 4 − sin t = 2 cost = 2cost  Khi đó 2costdt = = = + = arcsin x I dt t C + C. ∫ 2cost ∫ Chọn A. 2 Tổng quát: dx = arcsin x + C ∫ (a > 0) 2 2 a − x a
Ví dụ 7: Tính nguyên hàm dx I = . ∫ 2 1− x − x A. x +1 I + = arcsin + C. B. 2x 1 I = arcsin + C. 5 2 5 C. I + = arcsin (2x + ) 1 + C. D. 2x 1 I = arcsin + C. 5 Lời giải  1 d x  +   Ta có: dx dx  2 I  = = = ∫ ∫ ∫ 2 2 2 1− x − x 5  1  5  1  x  x − + − + 4 2 4 2      1 x + 2 2x +1 = arcsin + C = arcsin + C. Chọn D. 5 5 2 2
Ví dụ 8: Tính nguyên hàm x dx   π π I  = ∫
bằng cách đặt x = sin t t ∈ −  ; ta được: (  − x )5 2 1   2 2  3 2 5 A. 2
I = 2 tan t + C. B. tan t I = + C. C. tan t I = + C. D. tan t I = + C. 3 2 5 Lời giải  π π    dx = costdt
Đặt x = sin t t ∈ −  ;  ⇒   . 2 2   2 2 
 1− x = 1− sin t = cost = cost  2 2 3 Khi đó: sin t.costdt sin t 1 2 = = = ∫ ∫ ∫ ( ) tan . tan tan t I dt td t = + C. Chọn B. 5 2 2 cos t cos t cos t 3
Ví dụ 9: Tính nguyên hàm 1+ x   π I  = dx ∫
bằng cách đặt x = cos 2t t ∈0; ta được: 1− x  2    3 A. 2 I = 4 − cos tdt. ∫ B. 2 I = 2 − cos tdt. ∫ C. 2 I = 4 − sin tdt. ∫ D. cos = 4 t I − dt. ∫ sin t Lời giải
Đặt x = cos 2t ⇒ dx = 2 − sin 2tdt = 4
− sin t costdt. 2 2 Mặt khác 1+ cos 2t 2cos t cos t cost cost = = = = 2 2 1− cos 2t 2sin t sin t sin t sin t Khi đó cost I = . ∫ ( 4 − sin t cost) 2 dt = 4 − cos tdt. sin t ∫ Chọn A. 2 Ví dụ 10:   π Tính nguyên hàm x −1 I  = dx ∫ bằng cách đặt 1 x = t ∈ 0; ta được. x cost  2    A. 3 I = tan xd . x ∫ B. 2 I = tan xd . x ∫ C. 3 I = cot xd . x ∫ D. 2 I = cot xd . x ∫ Lời giải 1   π  (cost)′ − Đặt sin = ∈  0; t x t ⇒  dx = dt =   dt 2 2 cost   2  cos t cos t Lại có: 1 2
−1 = tan t = tan t = tan t 2 cos t Do đó tan t sin t 2 I = . dt = tan tdt. ∫ 2 1 cos ∫ Chọn B. t cost
BÀI TẬP TỰ LUYỆN
Câu 1: Xét I = x ( x − ∫ )5 3 4 4
3 dx. Bằng cách đặt 4
u = 4x − 3, hỏi khẳng định nào đúng? A. 1 5 I = u . du 1 I = u du. 1 I = u du. I = u du 4 ∫ B. 5 21 ∫ C. 5 16 ∫ D. 5 . ∫
Câu 2: Cho I = x ∫ ( − x )10 2 1 . dx Đặt 2
u =1− x , hỏi khẳng định nào đúng? A. 10 I = 2u du ∫ B. 10 I = − 2u du ∫ C. 1 10 I = − u du 1 I = u du 2 ∫ D. 10 2 ∫ Câu 3: Xét x I = dx, ∫
bằng cách đặt t = 4x +1, mệnh đề nào sau đúng? 4x +1 3   3   3   3   A. 1 t I = 1 t 1 t 1 t
 + t  + C.
B. I =  −t  + C.
C. I =  −t  + C.
D. I =  + t  + C. 8  3  4  3  8  3  4  3 
Câu 4: Tìm nguyên hàm của hàm số f (x) 2 = x 1+ x . A. 1 2 2
x 1+ x + C.
B. 1 (x 1+ x )3 2 2 + C. C. 1 ( 1+ x )3 2 + C. D. 1 2 2
x 1+ x + C. 2 3 3 3
Câu 5: Tìm nguyên hàm của hàm số f (x) 5 = cos . x sin x A. 1 6 − cos x + C B. 1 6 − sin x + C C. 1 6 cos x + C D. 1 4 − cos x + C 6 6 6 4
Câu 6: Tìm một nguyên hàm F (x) của hàm số f (x) = x(x + )4 2 2 1 thỏa mãn F ( ) 1 = 6. x (x + )5 2 2 1 (x + )5 2 1 A. F (x) 2 = − B. F (x) 2 = − 5 5 5 5 x (x + )5 2 2 1 (x + )4 2 1 C. F (x) 2 = + D. F (x) 2 = − 5 5 5 5
Câu 7: Tìm một nguyên hàm F (x) của hàm số f (x) = x(x + )9 2 1 thỏa mãn F ( ) 21 0 = . 20 A. F (x) 1 = − (x + )10 2 1 +1
B. F (x) 1 = (x + )10 2 1 +1 20 20
C. F (x) = (x + )10 2 2 1 −1
D. F (x) = (x + )10 2 1 + 2
Câu 8: Tìm nguyên hàm của hàm số f (x) = x( − x)5 3 . A. ( x)6  3− x 1 3   − − − + x    C B. ( − x)6 3 1 3 + +   C  6 2   7 2  C. ( x)6  3− x 1 3   − − − + x    C D. ( + x)6 3 1 3 − +   C  7 2   7 2 
Câu 9: Biết F (x) là một nguyên hàm của f (x) ln x 2 =
ln x +1 thỏa F ( ) 1 1 = . Tính F  (e) 2  . x 3  A.F  (e) 2 8  = .  B.F  (e) 2 8  = . F e  = F e  = 3  C.  ( ) 2 1. 9  D.  ( ) 2 1. 3  9
Câu 10: Gọi F (x) là một nguyên hàm của hàm số ( ) x f x =
thỏa F (2) = 0. Tìm tổng các nghiệm 2 8 − x
phương trình F (x) = .x A. 1+ 3 B. 2. C. 1. D. 1− 3
Câu 11: Tìm một nguyên hàm F (x) của hàm số ( ) 2x f x = . 2 x + x −1
A. F (x) 2 3 2 = x − ( 2 x − ) 2 1 x −1
B. F (x) 2 3 2 = x + ( 2 x − ) 2 1 x −1 3 3 3 3
C. F (x) 2 3 2 = x − ( 2 x + ) 2 1 x −1
D. F (x) 2 3 2 = x + ( 2 x + ) 2 1 x −1 3 3 3 3 2
Câu 12: Hàm số f (x) ln x ln x +1 =
có 1 nguyên hàm F (x) là thỏa F ( ) 1 1 = . Tìm 2 F (e). x 3 A. 2 F (e) 1 = . B. 2 F (e) 8 = . C. 2 F (e) 8 = . D. 2 F (e) 1 = . 3 3 9 9 x
Câu 13: Tìm một nguyên hàm F (x) của hàm số ( ) e f x = thỏa F (0) = 27. x e + 3 A. ( ) = 2 x F x e + 3 − 3 B. ( ) x
F x = e + 3 − 3 C. ( ) = 2 x F x e + 3 + 3 D. ( ) x F x = e + 3 + 3 3 Câu 14: Hàm số ( ) x f x =
có một nguyên hàm là F (x) thỏa F (− ) 1 1 = . Tính F ( ) 1 . 2 2x − x 3 A. F ( ) 1 = 2 B. F ( ) 1 1 = C. F ( ) 5 1 = − D. F ( ) 3 1 = − 3 3 5
Câu 15: Tìm một nguyên hàm F (x) của hàm số ( ) x f x = thỏa mãn F ( ) 2 3 = . x − 2 3
A. F (x) 2 =
(x − 2)3 − 4 x − 2 + 4.
B. F (x) 1 =
(x − 2)3 + 4 x − 2 + 4. 3 3
C. F (x) 2 =
(x − 2)3 + 4 x − 2 − 4.
D. F (x) 2 =
(x − 2)3 + 2 x − 2 − 4. 3 3
Câu 16: Hàm số f (x) 1 =
có một nguyên hàm là F (x) thỏa F (0) = 2ln 2.Tính F ( ) 1 . x +1 A. F ( ) 1 = 2 − ln 2. B. F ( ) 1 = 2ln 2. C. F ( ) 1 = 2. D. F ( ) 1 = 0.
Câu 17: Tìm một nguyên hàm F (x) của hàm số f (x) 1 = thỏa F ( ) 1 = 2 − 4ln 5. 2x −1 + 4
A. 2x +1 +1− 4ln ( 2x +1 + 4)
B. 2x −1 +1− 4ln ( 2x −1 + 4) C. 7
2x −1 −1− ln ( 2x −1 + 4) D. 7
2x −1 −1+ ln ( 2x +1 + 4) 2 2 2 Câu 18: Hàm số ( ) x f x =
có một nguyên hàm là F (x) thỏa F ( ) 2 0 = .Tính F ( ) 1 . 3 x +1 3 A. F ( ) 3 2 1 = . B. F ( ) 3 1 = . C. F ( ) 2 2 1 = . D. F ( ) 2 1 = . 2 2 3 3
Câu 19: Tìm nguyên hàm của hàm số f (x) 1 2 = cos . 2 x x A. 1 2 − sin + C B. 1 2 − cos + C C. 1 2 sin + C D. 1 2 cos + C 2 x 2 x 2 x 2 x
Câu 20: Cho F (x) là một nguyên hàm của hàm số f (x) 1 = thỏa mãn F ( ) 1 0 = − ln 4. Tìm tập x e + 3 3
nghiệm S của phương trình 3 ( ) + ln( x F x e + 3) = 2. A. S = { } 2 B. S = { 2; − } 2 C. S = {1; } 2 D. S = { 2; − } 1 1 a − 1 b x − x
Câu 21: Giả sử x ∫ (1− x)2017 ( ) ( ) dx = −
+ C, với a, b là các số nguyên dương. Tính 2a − . b a b
A. 2a − b = 2017
B. 2a − b = 2018
C. 2a − b = 2019
D. 2a − b = 2020 2x
Câu 22: Tìm nguyên hàm của hàm số ( ) e f x = . x e +1
A. x − ln ( x e e + ) 1 + C
B. x + ln ( x e e + ) 1 + C C. ln ( xe + ) 1 + C D. 2x x
e − e + C
Câu 23: Tìm nguyên hàm của hàm số f (x) 1 = . x +1
A. 2 x − 2ln (1+ x) + C
B. 2 x + 2ln (1+ x) + C
C. ln (1+ x) + C
D. 2 + 2ln (1+ x) + C
Câu 24: Tìm nguyên hàm của hàm số f (x) x + 2 = . x +1
A. 3 (x + 4) x +1 + C
B. 2 (x + 4) x +1 + C 4 3 C. x + C D. 1 x +1 + + C 2(x + ) 1 x +1 x +1
Câu 25: Tìm nguyên hàm của hàm số f (x) 2x −1 = . 1− x A. 1 2 − 1− x + + C B. 2 (2x + ) 1 1− x + C 1− x 3 C. 2 − (2x + ) 1 1− x + C D. 2 − (2x − ) 1 1− x + C 3 3
LỜI GIẢI CHI TIẾT Câu 1: Đặt 4 3 3 1
u = 4x − 3 ⇔ du = 16x dx ⇔ x dx = du 16 Khi đó 1 5 1 5 I = u du = u du. ∫16 16 ∫ Chọn C. Câu 2: Đặt 2 1
u = 1− x ⇔ du = 2
− xdx ⇔ xdx = − . du Khi đó 1 10 I = − u du. 2 2 ∫ Chọn C. Câu 3: Đặt 2 = 4 +1 ⇔ = 4 +1 ⇔ 4 = 2 t t x t x dx
tdt ⇔ dx = dt 2 2 t −1 2 3 −   Khi đó 4 t t 1 1 = . t I dt = dt = ∫ ∫
 − t  + C. Chọn C. t 2 8 8  3  Câu 4: f ∫ (x) 1
dx = x + x dx = + x d ∫ ∫ ( + x ) 1 1 1 1 = ( 1+ x )3 2 2 2 2 + C. Chọn C. 2 3 Câu 5: f ∫ (x) 5 5 dx = cos .
x sin xdx = − cos xd ∫ ∫ (cos x) 1 6
= − cos x + C. Chọn A. 6 x +1 Câu 6: f
∫ (x)dx = 2x
∫ (x + )1 dx = ∫(x + )1d (x + ) ( )5 2 4 2 2 2 1 = + C. 5 (x + )5 2 1 (x + )5 2 1 Suy ra F (x) = + C mà F ( ) 2 1 = 6 
→C = − . Vậy F (x) 2 = − . Chọn B. 5 5 5 5 1 x +1
Câu 7: F (x) = f
∫ (x)dx = x
∫ (x + )1 dx = ∫(x + )1 d (x + ) ( )10 2 9 9 2 2 2 1 = + C. 2 20 Mà F ( ) 21 0 = 
→C = 1. Vậy F (x) 1 = (x + )10 2 1 +1. Chọn B. 20 20
Câu 8: f (x) = x( − x)5 = −( − x − ) ( − x)5 = −( − x)6 + ( − x)5 3 3 3 . 3 3 3. 3 . 7 6 3 − x 3 − x Khi đó f
∫ (x)dx = −
∫ (3− x)6 + 3.(3− x)5 ( ) ( )  dx = − + C.   Chọn C. 7 2 Câu 9: 2 2 2 ln x ln = ln +1 ⇔ = ln +1 ⇔ 2 = 2. x t x t x tdt dx ⇔ dx = tdt. x x ln x +1 2 t ( )3 2 3 Khi đó f
∫ (x)dx = t dt = + C = + C ∫ mà F ( ) 1 1 = ⇒ C = 0. 3 3 3 ( x+ )3 2 ln 1 Vậy F (x) =  → F (e) 2 2 = . Chọn B. 3 3 Câu 10: Đặt 2 2 2
t = 8 − x ⇔ t = 8 − x ⇔ xdx = t − dt Khi đó f ∫ (x) t − 2 d x =
dt = − dt = t
− + C = − 8 − x + C ∫ t ∫ Mà F (2) = 0 
→C = 2. Vậy F (x) 2
= x ⇔ 2 − 8 − x = x ⇔ x = 1− 3. Chọn D. Câu 11: Ta có ( 2 x + x −1)( 2 x − x −1) 1 2 = 1 ⇔ = x − x −1 2 x + x −1
Khi đó f (x) = x ( 2 x − x − ) 2 2
= x − x x − ⇒ f ∫ (x) 2 3 2 2 1 2 2 1 d x = x − ( 2 x − ) 2
1 x −1 + C. Chọn A. 3 3 Câu 12: Đặt 2 2 2 ln x ln
t = ln x +1 ⇔ t = ln x +1 ⇔ 2t t = 2. x d d x ⇔ d x = tdt. x x ln x +1 2 t ( )3 2 3 Khi đó f
∫ (x)dx = t dt = + C = + C ∫ mà F ( ) 1 1 = ⇒ C = 0. 3 3 3 ( x+ )3 2 ln 1 Vậy F (x) =  → F (e) 2 2 = . Chọn C. 3 3 Câu 13: Đặt x 2 = + 3 x ⇔ = + 3 x t e t e
⇔ e d x = 2tdt Khi đó ∫ ( ) 2t f x d x =
dt = 2 dt = 2t + C = 2 x e + 3 + C ∫ t ∫ Mà F (0) = 3 3 
→C = 3. Vậy ( ) = 2 x F x
e + 3 + 3. Chọn C. Câu 14: Đặt 2 2 2
t = 2 − x ⇔ t = 2 − x ⇔ tdt = −xdx 2 2 Khi đó ∫ ( ) x 2 − t f x d x = xdx = ∫ ∫ ( t
− )dt = ∫( 2t − 2)dt 2 2 − x t 3 t 1 =
− 2t + C = ( 2 − x )3 2 2
− 2 2 − x + C mà F (− ) 1 1 = 
→C = 2. Vậy F ( ) 1 1 = .Chọn B. 3 3 3 3 Câu 15: Đặt 2
t = x − 2 ⇔ t = x − 2 ⇔ d x = 2tdt 2 Khi đó f ∫ (x) t + 2 d x = tdt = ∫ ∫( t + ) 2 2 .2 2
4 dt = t + 4t + C = ( 2 − x)3 2 3
+ 4 2 − x + C t 3 3 Mà F ( ) 2 3 = 
→C = 4. Vậy F (x) = ( − x)3 2 2
+ 4 2 − x + 4. Chọn B. 3 3 Câu 16: Đặt 2
t = x ⇔ x = t ⇔ d x = 2tdt Khi đó f ∫ (x) 2t  2 dx = dt = 2 −
dt = 2t − 2ln t +1 + C = 2 x − 2ln x +1 + ∫ ∫  C. t +1  t +1
Mà F (0) = 2ln 2 
→C = 2ln 2. Vậy F ( )
1 = 2 − 2ln 2 + 2ln 2 = 2. Chọn C. Câu 17: Đặt 2
t = 2x −1 ⇔ t = 2x −1 ⇔ d x = tdt Khi đó f ∫ (x) t  4 dx = dt = 1−
dt = t − 4ln t + 4 + C = 2x −1 − 4ln 2x −1 + 4 + ∫ ∫  C. t + 4  t + 4  Mà F ( ) 1 = 2 − 4ln 5 
→C = 1. Vậy F (x) = 2x −1 +1− 4ln 2x −1 + 4 . Chọn B. Câu 18: Đặt 3 2 3 2 2 = +1 ⇔ = +1 t t x t x ⇔ x d x = dt 3 Khi đó f ∫ (x) 2t 2 2 2 3 dx = : tdt =
dt = t + C = x +1 + C. ∫ 3 ∫ 3 3 3 Mà F ( ) 2 0 = 
→C = 0. Vậy F ( ) 2 2 1 = . Chọn C. 3 3
Câu 19: Ta có f ∫ (x) 1 2 1 2  2  1 2 dx =
cos dx = − . cos d = − sin + ∫ ∫   C. Chọn A. 2 x x 2 x x  2 x Câu 20: Đặt x x dt
t = e ⇔ dt = e dx ⇔ dx = . t x Khi đó ∫ ( ) dt 1 t 1 e f x dx = = + = + ∫ t (t + ) ln C ln C. 3 3 t + 3 3 x e + 3 Mà F ( ) 1 0 = − 
→C = 0. Do đó 3 ( ) = ln x − ln ( x F x e e + 3). 3
Vậy 3 ( ) + ln( x + 3) = 2 ⇔ ln x F x e
e = 2 ⇔ x = 2. Chọn A.
Câu 21: Ta có x
∫ ( − x)2017 dx = −∫( − x − )( − x)2017 dx = 
∫ ( − x)2018 −( − x)2017 1 1 1 1 1 1  d (1− x)  
( − x)2019 ( − x)2018 1 1 a = 2019 = − + C  → 
. Vậy 2a − b = 2020. Chọn D. 2019 2018 b  = 2018 2x x Câu 22: Ta có ∫ ( ) e e f x d x = d x = d ∫ ∫ ( xe ) x = e − ln ( x
e + + C Chọn A. x x )1 . e +1 e +1 Câu 23: Đặt 2
t = x ⇔ x = t ⇔ d x = 2tdt Khi đó f ∫ (x) 2t  2 dx = dt = 2 −
dt = 2t − 2ln t +1 + C = 2 x − 2ln x +1 + ∫ ∫  C. Chọn A. t +1  t +1 Câu 24: Đặt 2
t = x +1 ⇔ t = x +1 ⇔ d x = 2tdt 2 Khi đó f ∫ (x) t +1 d x = .2tdt = ∫ ∫( 2 2t + 2) 2 3
dt = t + 2t + C. Chọn B. t 3 Câu 25: Đặt 2 2
t = 1− x ⇔ t = 1− x ⇔ x = 1− t ⇔ d x = 2 − tdt 2 2 1− t −1 Khi đó f ∫ (x) ( ) d x = ∫
(− t)dt = − ∫( 2t − t + ) 2 . 2 2 2
4 1 dt = − (2x + )
1 1− x + C. Chọn C. t 3
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1

Tài liệu liên quan: