Chuyên đề trắc nghiệm ứng dụng tích phân tính diện tích Toán 12

Chuyên đề trắc nghiệm ứng dụng tích phân tính diện tích Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Môn:

Toán 12 3.8 K tài liệu

Thông tin:
45 trang 1 năm trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chuyên đề trắc nghiệm ứng dụng tích phân tính diện tích Toán 12

Chuyên đề trắc nghiệm ứng dụng tích phân tính diện tích Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

89 45 lượt tải Tải xuống

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn: Toán 12 3.8 K tài liệu

Thông tin:

45 trang 1 năm trước

Tác giả:

Profile Mai Nguyệt
CHỦ ĐỀ 12: ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH
A. LÝ THUYẾT
1) Công thức tính diện tích của hình phẳng giới hạn bởi hai đồ thị hàm số
Cho hai đồ thị của hai hàm số
( ) ( )
,= =y f x y gx
liên tục trên đoạn
[
]
;ab
và hai đường thẳng
( )
;= = <x ax ba b
. Khi đó hình phẳng giới
hạn bởi bốn đường
( ) ( )
,= =y f x y gx
và hai đường thẳng
;= =x ax b
có diện tích S được tính theo công thức:
(
)
( )
= −
∫
b
a
S f x g x dx
.
Đặc biệt: Trong trường hợp
(
)
gx
là trục hoành (
( )
0=gx
) ta được công thức tính diện tích của hình
phẳng giới hạn bởi đồ thị hàm số
( )
=y fx
, trục hoành và hai đường thẳng
là:
()
b
a
S f x dx=
∫
(1).
Để tính diện tích S ta phải tính tích phân (1), muốn vậy ta phải phá dấu giá trị tuyệt đối:
Nếu
( )
[ ]
0, ;≥ ∀∈f x x ab
thì
( ) (
)
= =
∫∫
bb
aa
S f x dx f x dx
.
Nếu
( )
[ ]
0, ;
≤ ∀∈f x x ab
thì
( ) ( )
(
)
= = −
∫∫
bb
aa
S f x dx f x dx
.
Muốn xét dấu của biểu thức
( )
fx
ta thường có một số cách làm như sau:
Cách 1: Sử dụng bảng xét dấu cho
( )
fx
với ghi nhớ qua nghiệm bội lẻ
( )
fx
đổi dấu, qua nghiệm
bội chẵn
( )
fx
không đổi dấu.
Cách 2: Dựa vào đồ thị của hàm số
( )
=y fx
trên đoạn
[ ]
;ab
để suy ra dấu của
( )
fx
trên đoạn đó:
- Nếu trên đoạn
[
]
;
ab
đồ thị hàm số
( )
=y fx
nằm phía trên trục hoành thì
( )
[ ]
0, ;≥ ∀∈f x x ab
.
- Nếu trên đoạn
[ ]
;ab
đồ thị hàm số
( )
=y fx
nằm phía dưới trục hoành thì
( )
[ ]
0, ;≤ ∀∈f x x ab
.
Cách 3: Nếu
( )
fx
không đổi dấu trên
[ ]
;ab
thì ta có:
( ) ( )
= =
∫∫
bb
aa
S f x dx f x dx
.
Cách 4: Sử dụng máy tính CASIO, tuy nhiên xu hướng ra đề thi THPT Quốc gia sẽ hạn chế CASIO
nên cần chú ý cách giải tổng quát và hiểu rõ bản chất!
Chú ý:
- Khi tính diện tích của hình phẳng giới hạn bởi hai đồ thị hàm số ta có:
( )
( )
(
)
=−=
∫∫
bb
aa
S f x g x dx h x dx
ta làm hoàn toàn tương tự như trên.
- Nếu đề bài không cho các đường thẳng giới hạn
;= =x ax b
ta giải phương trình
( )
(
)
=f x gx
(hoặc
(
)
0=
fx
trong trường hợp
( )
gx
là trục hoành) để tìm cận của tích phân.
2) Ứng dụng tính diện tích hình tròn và hình Elip
a) Tính diện tích hình tròn
Trong hệ tọa độ Oxy cho đường tròn có phương trình:
( )
222
0
+= >x y rr
. Khi đó hình tròn đó có diện
tích là:
2
= πSr
.
2 2 2 22
+ = ⇔=± −xyr y rx
Ta có
Với
0≥y
, ta có:
22
= −y rx
có đồ thị là nửa đường tròn phía trên trục hoành.
Bằng cách đặt
sin=xr t
ta có diện tích
2
22 22
1
0
2
2
−
π
= −= −=
∫∫
rr
r
r
S r x dx r x dx
.
Do đó
2
1
2= = πSS r
.
b) Tính diện tích hình Elip
Trong hệ tọa độ Oxy cho elip có phương trình:
22
22
1, 0+ = <<
xy
ba
ab
.
Chứng minh tương tự ta có diện tích của elip là:
= πS ab
(đvdt).
II. VÍ DỤ MINH HỌA
Ví dụ 1:
Tính diện tích hình phẳng trên được giới hạn bởi đồ thị hàm số
2
22
=−+ −
yx x
, trục hoành và
các đường thẳng
0, 3= =xx
.
Lời giải
Diện tích S của hình phẳng trên là
3
2
0
22=−+ −
∫
S x x dx
.
Ta có:
[ ]
2
2 2 0, 0;3− + − ≤ ∀∈xx x
.
(
)
3
33
3
22 2
00
0
22 22 2 6
3

=−+ − = − + = − + =


∫∫
x
S x x dx x x dx x x
(đvdt).
Ví dụ 2: Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số
( )
2
1
−−
= =
−
x
y fx
x
, trục hoành và các
đường thẳng
1, 0=−=xx
.
Lời giải
Gọi S là diện tích của hình phẳng trên, ta có:
0
1
2
1
−
−−
=
−
∫
x
S dx
x
Ta có:
[ ]
2
0, 1; 0
1
−−
≥ ∀∈−
−
x
x
x
Do đó:
( )
00 0 0
11 1 1
13
22 3
1
11 1 1
−− − −
− −−
−− −−

= = = = −−

−− − −

∫∫ ∫ ∫
x
xx
S dx dx dx dx
xx x x
(
)
0
1
3ln 1 3ln 2 1
−
=−− − = −xx
(đvdt).
Ví dụ 3: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
2
1, 1= −+ =+yx x yx
là
A.
4
3
−
B.
4
3
C. 1 D.
2
3
Lời giải
Phương trình hoành độ giao điểm 2 đồ thị là:
22
0
1 1 20
2
=
−+= +⇔ − = ⇔
=
x
xx x x x
x
Diện tích cần tìm là:
( )
2 22
2 22
0 00
11 2 2S x x x dx x x dx x x dx= −+−− = − = −
∫ ∫∫
2
3
2
0
4
33

=−=


x
x
. Chọn B.
Ví dụ 4: Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị của hàm số
= +
x
ye x
và các đường thẳng
1 0, ln 5− += =
xy x
.
A.
5 ln 4= −S
B.
4 ln 5= −
S
C.
4 ln 5= +S
D.
5 ln 4= +S
Lời giải
Ta có:
10 1
− += ⇔ = +xy yx
.
Phương trình hoành độ giao điểm của hai đồ thị là:
1 10+ = +⇔ =⇔ =
xx
e xx e x
Diện tích hình phẳng cần tìm là:
( ) ( )
ln 5 ln 5
ln 5
0
00
1 1 4 ln 5= −= − =− =−
∫∫
x xx
S e dx e dx e x
. Chọn B.
Ví dụ 5: Tính diện tích hình phẳng giới hạn bởi các đường
32
11 6; 6 ; 0; 2=+−= ==y x x y xx x
.
Lời giải
Đặt
( )
(
)
3 23 2
11 6 6 6 11 6
=+−−=−+−fxx x xxx x
( )
1; 2
0
3( )
= =
= ⇔
=
xx
fx
x loai
. Gọi S là diện tích phần giới hạn bởi các đường ta có:
Bảng xét dấu:
Khi đó
( ) ( )
12
32 32
01
6 11 6 6 11 6=− −+− + −+−
∫∫
S x x x dx x x x dx
12
42 42
33
01
11 11 5
26 26
42 42 2

=−−+ − + −+ − =


xx xx
xx xx
(đvdt).
Ghi nhớ: Nếu phương trình
( )
0=fx
có k nghiệm phân biệt
12
; ...
k
xx x
thuộc
( )
;ab
thì trên mỗi khoảng
( ) ( ) ( )
1 12
; , ; ,... ;
k
ax x x x b
biểu thức
( )
fx
có dấu không đổi.
Khi đó để tính tích phân
(
)
=
∫
b
a
S f x dx
ta có thể tính như sau:
( ) ( ) ( ) ( )
12
1
...= = + ++
∫∫∫ ∫
k
xx
bb
a ax x
S f x dx f x dx f x dx f x dx
.
Áp dụng với bài trên ta có:
( )
( )
12
32 32
01
6 11 6 6 11 6= −+− + −+−
∫∫
S x x x dx x x x dx
.
Ví dụ 6: Tính diện tích hình phẳng giới hạn bởi các đường:
2
2 0; 0
− += +=y yx xy
.
Lời giải
Phương trình tung độ giao điểm là:
2
0
2
3
=
− =−⇔
=
y
yy y
y
.
Gọi S là diện tích hình phẳng giới hạn với các đường đã cho ta có:
x
0
1
2
( )
hx
−
0 + 0
( )
( )
3
3 33
32
2 22
0 00
0
39
2 33
32 2

= − −− = − = − + = − + =


∫ ∫∫
yy
S y y y dy y y dy y y dy
(đvdt).
Nhận xét: Đối với bài toán này việc tính theo dx gặp khá nhiều khó khăn, do đó ta nên tính diện tích hình
phẳng theo dy bằng cách coi x là hàm của biến y, diện tích hình phẳng giới hạn bởi các đường cong
( )
=x gy
,
( )
=x hy
(g và h là hai hàm liên tục trên đoạn
[ ]
;cd
) và hai đường thẳng
,= =y cy d
là:
( )
( )
= −
∫
d
c
S g y h y dy
.
Ví dụ 7: Cho đồ thị hàm số
( )
=
y fx
trên đoạn
[ ]
2; 2−
như hình vẽ ở bên
và có diện tích
12 3
22 76
,
15 15
= = =SS S
. Tính tích phân
( )
2
2−
=
∫
I f x dx
.
A.
32
15
=I
B.
8=
I
C.
18
5
=I
D.
32
15
= −I
Lời giải
Ta có
( )
2
312
2
76 22 32
2.
15 15 15
−
= =−− = − =
∫
I f x dx S S S
. Chọn A.
Ví dụ 8: Cho hàm số
( )
fx
liên tục trên ℝ. Đồ thị hàm số
( )
′
=y fx
được cho như hình bên. Diện tích các hình phẳng
( ) ( )
,KH
lần lượt là
5
12
và
8
3
. Biết
( )
19
1
12
−=f
, tính
( )
2f
.
A.
( )
11
2
6
=f
B.
C.
( )
23=f
D.
( )
20=f
Lời giải
Ta có:
( ) ( ) ( ) ( ) ( )
0
1
55
0 1 0 12
12 12
−
′
= = − −= ⇒ = + −=
∫
K f x dx f f f f
.
Lại có:
( )
( ) ( ) ( )
( )
22
00
8 82
0 2 (2) 0
3 33
H f x dx f x dx f f f f
−
′′
= =− = − =⇒ = −=
∫∫
. Chọn B.
Ví dụ 9: Cho
(
)
H
là hình phẳng giới hạn bởi hai parabol
2
=
yx
và
2
= −yx
đường tròn có phương trình
22
2+=xy
(phần tô đậm trong
hình vẽ). Tính diện tích S của hình
( )
H
A.
2
3
=π+S
B.
2
2
3
= π−S
C.
2
3
=π−S
D.
2
2
3
= π+S
Lời giải
Xét phần tô đậm nằm phía trên trục Ox, nửa đường tròn phía trên Ox có phương trình
2
2= −yx
.
Giải phương trình hoành độ giao điểm:
2 2 42 2
2 20 1 1= − ⇔ + −=⇔ =⇔=±x x xx x x
Diện tích phần không tô đậm phía trên trục hoành là:
(
)
1
22
1
2
−
= −−
∫
S x x dx
( )
1
1
3
44
2 sin
2 22
1
1
44
22
2 2 2sin 2 sin 2cos
3 33
ππ
=
−π −π
−
−
= − − → − − = −
∫∫ ∫
xt
x
x dx td t tdt
( )
4
4
4
4
2 sin 2 2 1
1 cos 2
3 2 3 23
π
π
π
−π
−
π

= + −= + −=+


∫
t
t dt t
Diện tích nửa đường tròn là
2
2
π
′
= = π
R
S
.
Khi đó
( )
( )
12
22
23 3
π

′
= − = π− − =π−


H
S SS
. Chọn C.
Ví dụ 10: Cho hình thang cong
( )
H
giới hạn bởi các đường
, 0, 0= = =
x
y ey x
và
ln 4=x
. Đường thẳng
(
)
0 ln 4
= <<xk k
chia
( )
H
thành hai phần có diện tích là
1
S
và
2
S
như hình vẽ
bên. Tìm k để
12
2=
SS
.
A.
2
ln 4
3
=k
B.
ln 2=k
C.
8
ln
3
=k
D.
ln 3=k
Lời giải
Do
ln 4
ln 4 ln 4
1 21
0
00
22 2 2
22
33 3 3
= ⇒= = = = =
∫∫
x xx
S S S S e dx e dx e
.
Do đó
1
0
1 2 3 ln 3= = −= ⇔ = ⇔ =
∫
k
xk k
S e dx e e k
. Chọn D.
Ví dụ 11: Cho hình thang
( )
H
giới hạn bởi các đường
11
, ,2
2
= = =
yxx
x
và trục hoành. Đường thẳng
1
2
2

= <<


xk k
chia
( )
H
thành hai phần có
diện tích là
1
S
và
2
S
như hình vẽ dưới đây. Tìm tất cả giá trị thực của k để
12
3
=SS
A.
2=k
B.
1=k
C.
7
5
=k
D.
3=k
Lời giải
Gọi S là diện tích hình
( )
2
1
2
1
2 ln 2⇒= =
∫
H S dx
x
.
Lại có
2
2
1 1 ln 2 ln 2
ln 2 ln ln ln 2 2
42 2
= = − = = ⇒ = = ⇒=
∫
k
S dx k S k k
x
. Chọn A.
Ví dụ 12: [Đề tham khảo Bộ giáo dục và Đào tjao 2018] Cho
( )
H
là hình phẳng giới hạn bởi parabol
2
3=yx
, cung tròn có phương
trình
2
4= −yx
(với
02≤≤x
) và trục hoành (phần tô đậm trong
hình vẽ). Diện tích của
( )
H
bằng:
A.
43
12
π+
B.
43
6
π−
C.
4 23 3
6
π+ −
D.
53 2
3
−π
Lời giải
Phương trình hoành độ giao điểm là:
22
42
02
34 1
34
≤≤
= − ⇒ ⇔=
= −
x
xx x
xx
.
Dựa vào hình vẽ ta có:
1
12
3
22
11
01
0
3
34 3
33
= + − = += +
∫∫
x
S x dx x dx I I
.
Với
2
2
1
1
4= −
∫
I x dx
, sử dụng CASIO hoặc đặt
2sin 2 cos= ⇒=x t dx tdt
Đổi cận
( ) ( )
2
22
2
1
66
6
1
6
4 4sin .2 cos 2 1 cos 2 2 sin 2
2
2
π
ππ
ππ
π
π
=⇒=
⇒= − = + = −
π
= ⇒=
∫∫
xt
I t tdt t dt t t
xt
( )
1
1
4 33
6
⇒ = π−I
. Do đó
43
6
π−
=
S
. Chọn B.
Ví dụ 13: Tính diện tích S của phần hình phẳng giới hạn bởi đường
Parabol đi qua gốc tọa độ và hai đoạn thẳng AC và BC như hình vẽ bên:
A.
25
6
=
S
B.
20
3
=S
C.
10
3
=S
D.
9=S
Lời giải
Gọi
1
S
là diện tích hình phẳng giới hạn bởi các đường
2
, 2, 0, 2= =+==yxyx x x
.
(
)
2
2
2 32 3
2
1
0
0
2 2 10
2 2 2.2
2 3 2 33

⇒ = +− = + − = + − =


∫
xx
S x x dx x
.
Khi đó diện tích hình phẳng phần gạch chéo là
1
20
2.
3
= =
SS
. Chọn B.
Ví dụ 14: Ông An có một mảnh vườn hình elip có độ dài trục lớn
bằng 16m và có độ dài trục bé bằng 10m. Ông muốn trồng hoa trên
một dải đất rộng 8m và nhận trục bé của elip làm trục đối xứng (như
hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng/1
2
m
.
Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền
được làm tròn đến hàng nghìn).
A. 7.862.000 đồng B. 7.653.000 đồng
C. 7.128.000 đồng D. 7.826.000 đồng
Lời giải
Chọn hệ trục như hình vẽ với
2 16; 2 10
= =ab
Suy ra
8; 5= =ab
.
Khi đó phương trình elip là:
22
1
64 25
+=
xy
.
Xét đường cong nằm phía trên trục Ox có phương trình là
2
25 1
64
= −
x
y
.
Ta có:
4
2
4
51
64
−
= −
∫
x
S dx
. Đặt
sin ;
8 22
ππ

= ∈−




x
tt
suy ra
1
cos
8
=tdt dx
.
Đổi cận
1
4 sin
26
1
4 sin
26
−π
=−⇒ = ⇒=−
π
= ⇒ = ⇒=
x tt
x tt
. Do đó
66
22
66
5 1 sin .8cos 40 cos
ππ
ππ
−−
=−=
∫∫
S t tdt tdt
( )
6
6
6
6
sin 2 20
20 1 cos 2 5 10 3
23
π
π
−π
π
−
π

=+=+ =+


∫
t
t dt t
.
Vậy diện tích trồng hoa là
( )
2
40
2 20 3
3
π
= = +
T
SS m
.
Do đó số tiền ông An cần để trồng hoa là:
.100.000 7.653.000= ≈
T
TS
. Chọn B.
Ví dụ 15: Một viên gạch hoa hình vuông có cạnh 40cm. Người thiết kế đã sử
dụng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn
cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi cánh hoa của viên
gạch bằng
A.
2
800
3
cm
B.
2
400
3
cm
C.
2
250cm
D.
2
800cm
Lời giải
Chọn hệ trục tọa độ như hình vẽ:
Với
( )
20; 20A
, xét hình phẳng ở góc phần tư thứ nhất.
Hai parabol có phương lần lượt là:
2
=y ax
và
2
=x ay
Do parabol qua điểm
( )
2
20 1
20; 20
20 20
⇒= =Aa
2
20
20
=
⇒
=
x
y
yx
Diện tích phần tô đậm ở góc phần tư thứ nhất là:
20
20
23
3
0
0
2 400
20 20
20 3 60 3

= − = −=


∫
xx
S x dx x
. Chọn B.
Ví dụ 16: Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng
chân đế 12m. Người ta căng hai sợi dây trang trí AB, CD nằm ngang đồng
thời chia hình giới hạn bởi parabol và mặt đất thành ba phần có diện tích
bằng nhau (xem hình vẽ bên). Tỉ số
AB
CD
bằng:
A.
3
1
2
B.
3
1 22+
C.
1
2
D.
4
5
Lời giải
Chọn hệ trục tọa độ như hình vẽ
Parabol có dạng
2
=y ax
, do
( )
P
đi qua điểm
( )
1
6;18
2
⇒=a
.
Diện tích thiết diện của cổng trào là:
6
2
0
6
18 144
2
−

=−=


∫
x
S dx
.
Để diện tích 3 phần bằng nhau thì diện tích mỗi phần là
0
48
3
=
S
.
Gọi
22
;; ;
22



bd
Bb Dd
khi đó
=
AB b
CD d
Ta có:
22 2 3
3
0
0
24 24 72
22 2 6

− =⇔ − =⇒=


∫
b
b
b x bx x
dx b
Tương tự ta có
22
3
3
0
1
48 144
22
2

− =⇒= ⇒ =


∫
d
d x AB
dx d
CD
. Chọn
A.
Ví dụ 17: [Đề Sở GD&DT Thanh Hóa] Một công ty quảng
cáo X muốn làm một bức tranh trang trí hình MNEIF ở chính
giữa một tường hình chữ nhật ABCD có chiều cao BD = 6m,
chiều dài CD = 12m (hình vẽ bên). Cho biết MNEF là hình
chữ nhật có MN = 4m, cung EIF có hình dạng là một phần
của cung parabol có đỉnh I là trung điểm của cạnh AB và đi
qua hai điểm C, D. Kinh phí làm bức tranh là 900.000
đồng/
2
m
. Hỏi công ty X cần bao nhiêu tiền để làm bức tranh
đó?
A. 20.400.000 đồng B. 20.600.000 đồng
C. 20.800.000 đồng D. 21.200.00 đồng
Lời giải
Gọi O là trung điểm của MN và trùng với gốc tọa độ
( ) ( )
2; 0 , 2; 0⇒−MN
.
Phương trình parabol đỉnh
(
)
0; 6
I
và đi qua hai điểm
(
) (
)
6; 0 , 6; 0−
CD
là
(
)
2
1
:6
6
= −
Py x
.
Diện tích bức tranh là diện tích giới hạn bởi hàm số
(
)
2
6
6
= = −
x
y fx
và
2, 2=−=xx
.
Khi đó
( )
2
22
22 3
2
22
2
208
6 66
6 6 18 9
−−
−

=−=− =− =


∫∫
xx x
S dx dx x m
.
Số tiền công ty X cần dùng để làm bức tranh là
208
900.000 20.800.000
9
=×=T
đồng. Chọn C.
Ví dụ 18: [Đề Chuyên Đại học Vinh 2017] Trong công viên Toán
học có những mảnh đất hình dáng khác nhau. Mỗi mảnh được
trồng một loài hoa và nó được tạo thành bởi một trong những
đường cong đẹp trong toán học. Ở đó có một mảnh đất mang tên
Bernoulli, nó được tạo thành từ đường Lemniscate có phương trình
trong hệ tọa độ Oxy là
(
)
22 2
16 25= −
yx x
như hình vẽ bên.
Tính diện tích S của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ trục tọa độ Oxy tương ứng với chiều
dài 1 mét.
A.
( )
2
125
6
=Sm
B.
( )
2
125
4
=
Sm
C.
( )
2
250
3
=Sm
D.
(
)
2
125
3
=Sm
Lời giải
Hoành độ giao điểm của đồ thị với trục hoành là
0; 5; 5= =−=
xx x
.
Dễ thấy diện tích mảnh đất Bernoulli bao gồm diện tích 4 mảnh đất nhỏ bằng nhau.
Xét diện tích s của mảnh đất nhỏ trong góc phần tư thứ nhất ta có:
[ ]
( )
5
22 2
0
1 125 125 125
4 25 ; 0;5 25 4.
4 12 12 3
= − ∈ ⇒= − = ⇒ = =
∫
yxxx sxxdx S m
. Chọn D.
Ví dụ 19: [Đề Chuyên Đại học Vinh 2017] Ông B có một khu vườn giới
hạn bởi đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ Oxy
như hình vẽ bên thì parabol có phương trình
2
=yx
và đường thẳng là
25=y
. Ông B dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi
đường thẳng đi qua O và điểm M trên parabol để trồng hoa. Hãy giúp ông B
xác định điểm M bằng cách tính độ dài OM để diện tích mảnh vườn nhỏ
bằng
9
2
.
A.
25=OM
B.
3 10=OM
C.
15=OM
D.
10=OM
Lời giải
Giả sử
( )
2
;
M aa
, suy ra phương trình
: =
OM y ax
.
Diện tích khu vườn là
( )
23 3
2
0
0
9
3
23 62

= − = − = =⇔=


∫
a
a
xx a
S ax x dx a a
.
Khi đó
24
9 81 3 10= += +=OM a a
. Chọn B.
Ví dụ 20: Trong đợt hội trại “Khi tôi 18” được tổ chức tại THPT X,
Đoàn trường có thực hiện một dự án ảnh trưng bày trên một pano có
dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi
ảnh dự thi và dán lên khu vực hình chữ nhật ABCD, phần còn lại sẽ được
trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là 100.000 đồng cho
một
2
m
bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano
sẽ là bao nhiêu? (làm tròn đến hàng nghìn)
A. 615.000 đồng B. 450.000 đồng
C. 451.00 đồng D. 616.000 đồng
Lời giải
Gọi S là diện tích hình phẳng giới hạn bởi parabol có phương trình
2
4= −yx
và trục hoành.
Suy ra
( )
2
22
2
32
4
3
−
=−=
∫
S x dx m
.
Gọi điểm
( )
;0 , 0>Ca a
, suy ra
( )
( ) ( )
22
;0
;4 , ;4
−
− −−
Da
BaaAaa
.
Gọi
1
S
là diện tích ABCD, suy ra
( )
22
1
. 24= = −S AB BC a a m
.
Gọi
2
S
là diện tích có hoa văn, suy ra
2 12
;= −
S S SS
nhỏ nhất khi và
chỉ khi
1
S
lớn nhất.
Xét hàm số
( )
2
2 (4 a ), a (0; 4)fa a=−∈
Ta có
( ) ( )
2
2
86 0
3
′′
=− ⇒ =⇔=fa a fa a
.
Xét bảng biến thiên hàm số
(
)
fa
với
( )
0; 4∈a
.
Ta có
( )
( ) ( )
2
1
0;4
2 32 3 32 3
max max
99
3

==⇒=


fa f S m
.
Suy ra
(
)
2
2
32 32 3
min 4, 51
39
=−≈
Sm
. Suy ra số tiền ít nhất cần là 451.000 đồng. Chọn C.
Ví dụ 21: Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình
vuông cạnh 10(cm) bằng cách khoét bỏ đi bốn phần bằng nhau có hình
dạng parabol như hình bên. Biết rằng
( )
5
=AB cm
đồng thời
( )
4=OH cm
. Tính diện tích bề mặt hoa văn đó?
A.
(
)
2
140
3
cm
B.
(
)
2
160
3
cm
C.
( )
2
40
3
cm
D.
(
)
2
50 cm
Lời giải
Dựa vào đề bài ta tính được
Parabol có PT
( )
2
16
:4
25
=−+Py x
.
Gọi
1
S
là diện tích hình phẳng trong hình bên
Suy ra
( )
5
2
23
1
5
2
16 40
4
25 3
−

=−+=


∫
S x dx cm
.
Gọi S là diện tích hoa văn cần tính
Suy ra
( )
23
1
140
10 4
3
=−=S S cm
. Chọn A.
Ví dụ 22: Sân trường có một bồn hoa hình tròn có tâm O. Một nhóm học
sinh lớp 12 được giao thiết kế bồn hoa, nhóm này định chia bồn hoa thành
bốn phần, bởi hai đường parabol có cùng đỉnh O và đối xứng nhau qua O.
Hai đường parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một
hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích
12
,SS
dùng để
trồng hoa, phần diện tích
34
,SS
dùng để trồng cỏ (Diện tích làm tròn đến
chữ số thập phân thứ hai).
Biết kinh phí để trồng hoa là 150.000 đồng/
2
1m
, kinh phí để trồng cỏ là 100.000 đồng/
2
1m
. Hỏi nhà trường
cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn).
A. 6.060.000 đồng B. 5.790.000 đồng
C. 3.270.000 đồng D. 3.000.000 đồng
Lời giải
Chọn hệ trục tọa độ như hình vẽ
( ) ( ) ( )
0; 0 ; 2; 2 ; 2; 2−OA B
Khi đó phương trình parabol phía trên có dạng là:
( )
2
: =P y ax
trong đó
( )
(
)
1
2; 2
2
∈ ⇒=
B Pa
.
Suy ra
( )
2
:
2
=
x
Py
.
Phương trình cung tròn nằm phía trên trục Ox là
22 22 2
8= −= −=−y R x OA x x
Khi đó
2
2
2
1
2
8
2
−

= −−


∫
x
S x dx
.
Diện tích hình tròn là
22
8=π=π =πS R OA
Ta có
( )
21
150.2 100. 2= +−T S SS
Bấm máy ta được
( )
11
150.2 100. 2 3.270= + −≈T S SS
nghìn đồng. Chọn C.
Ví dụ 23: [Đề thi THPT Quốc gia năm 2018] Cho hai hàm số
( )
32
1
2
= + +−f x ax bx cx
và
( )
2
1= ++g x dx ex
( )
,,, ,∈abcde
. Biết rằng
đồ thị của hàm số
( )
=y fx
và
( )
=y gx
cắt nhau tại 3 điểm có hoành độ lần
lượt là
3; 1;1−−
(tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã
cho có diện tích bằng:
A.
9
2
B. 8
C. 4 D. 5
Lời giải
Ta có phương trình hoành độ giao điểm của hai hàm số là:
( ) ( )
32 2 3 2
13
10
22
+ + −= + +⇔ + − +− −=ax bx cx dx ex ax b d x c e x
Vì phương trình có các nghiệm
3; 1;1−−
nên:
( ) ( ) (
)
( )
( )
32
3
311
2
+ − + − −= + + −ax b d x c e x a x x x
( )
( )
( )
3 2 32
3
33
2
⇔ + − + − − = + −−ax b d x c e x a x x x
Đồng nhất hệ số ta được:
1
2
3
3
2
3
1
3
2
2
=
−=
−=−⇔ − =


−

= −
−=
a
bd a
ce a bd
a
ce
(thực ra chỉ cần tìm được
1
2
=a
)
Suy ra diện tích hình phẳng cần tìm là:
1
32
3
1
3 34
2
−
= + −− =
∫
S x x x dx
. Chọn C.
Ví dụ 24: [Đề thi THPT Quốc gia năm 2018] Cho hai hàm số
( )
32
2= + +−
f x ax bx cx
và
( )
2
2= ++
g x dx ex
( )
,,, ,∈
abcde
. Biết
rằng đồ thị của hàm số
(
)
=y fx
và
( )
=y gx
cắt nhau tại 3 điểm có
hoành độ lần lượt là
2; 1; 1−−
(tham khảo hình vẽ). Hình phẳng giới hạn
bởi hai đồ thị đã cho có diện tích bằng:
A.
37
6
B.
13
2
C.
9
2
D.
37
12
Lời giải
Ta có phương trình hoành độ giao điểm của hai hàm số là:
( ) ( )
32 2 3 2
2 2 40+ + −= + +⇔ + − + − −=ax bx cx dx ex ax b d x c e x
Vì phương trình có các nghiệm
2; 1; 1−−
nên:
( )
( ) ( )( )( )
32
4 211+ − + − −= + + −ax b d x c e x a x x x
Đồng nhất hệ số ta được:
2=
a
Suy ra diện tích hình phẳng cần tìm:
( )( )(
)
1
3
37
2 211
6
−
= + +− =
∫
S x x x dx
. Chọn A.
Ví dụ 25: Cho hàm số
(
)
=y fx
có đồ thị
(
)
′
=
y fx
cắt trục Ox tại ba điểm
có hoành độ thỏa mãn
<<
abc
như hình vẽ. Mệnh đề nào dưới đây là
đúng?
A.
( ) ( ) ( )
>>fc fa fb
B.
( ) ( ) ( )
>>
fc fb fa
C.
( ) ( ) ( )
>>fa fb fc
D.
( ) ( ) ( )
>>fb fa fc
Lời giải
Ta có
(
) {
}
0 ;;
′
=⇔=
f x x abc
. Dựa vào BBT, ta thấy
( ) ( ) ( )
{ }
;fb fa fc<
.
Lại có
(
)
( )
(
)
( )
( )
(
)
12
bc
bc
ab
ab
S f x dx S f x dx f x f x f a f c
′′
= < = ⇔− < ⇔ <
∫∫
.
Vậy
(
) (
) (
)
>>
fc fa fb
. Chọn A.
Ví dụ 26: Cho hàm số
( )
fx
có đạo hàm trên ℝ, đồ thị hàm số
( )
′
=y fx
như trong hình vẽ. Hỏi phương trình
( )
0=fx
có tất cả bao nhiêu nghiệm
biết
( )
0>fa
?
A. 3 B. 2
C. 1 D. 0
Lời giải
Ta có
( )
{ }
0 ;;
′
=⇔=f x x abc
. Dựa vào BBT, ta thấy
( ) ( ) (
)
{ }
;>fb fa fc
.
Lại có
( )
( )
(
) (
)
(
)
( )
12
bc
bc
ab
ab
S f x dx S f x dx f x f x f a f c
′′
= > = ⇔ >− ⇔ <
∫∫
.
Do đó
( )
( ) ( )
0
>>>fb fc fa
. Vậy phương trình
( )
0=fx
vô nghiệm. Chọn D.
Ví dụ 27: (Đề thi THPT Quốc gia 2017 – Mã đề 102) Cho
( )
=y fx
có đồ thị
của
( )
′
=y fx
như hình vẽ. Đặt
(
) ( ) ( )
2
21= −+gx f x x
. Mệnh đề nào đúng?
A.
( ) ( ) ( )
3 31> −>gg g
B.
( ) ( ) (
)
331−> >g gg
C.
( ) ( ) ( )
1 33> −>gg g
D.
( ) ( ) ( )
13 3> >−gg g
Lời giải
Ta có
( ) ( )
( )
2 21
′′
= −+gx f x x
;
( ) ( )
01
′′
=⇔=+gx f x x
.
Nhận thấy nghiệm của
( )
0
′
=gx
chính là nghiệm của
( )
1
′
= +fx x
, cũng là hoành độ giao điểm của hai
đồ thị hàm số
( )
′
=y fx
và đường thẳng
{ }
1 3; 1; 3= + → = −yx x
.
Vẽ đường thẳng
1= +
yx
và chia đồ thị thành 2 phần diện tích hình phẳng.
Khi đó
(
)
( ) ( ) ( ) ( ) (
) (
)
11
1
33
2 2 1 1 30 1 3
−−
′′
= − + = = − − >⇒ > −


∫∫
S f x x dx g x dx g g g g
Và
( ) ( ) (
) (
) (
)
( ) ( )
33
2
11
2 2 1 1 30 1 3
′′
= +− =− = − >⇒ >


∫∫
S x f x dx g x dx g g g g
Lại có
( ) ( ) ( ) ( ) ( ) (
)
12 1 2
22 1 3 1 3 3 3> ⇔ > ⇔ − −> − ⇔ > −SS SSgg gg g g
.
Vậy
( ) ( ) ( )
13 3> >−gg g
. Chọn D.
Ví dụ 28: (Đề thi THPT Quốc gia 2017 – Mã đề 103) Cho
( )
=y fx
có đồ thị của
( )
′
=y fx
như hình vẽ. Đặt
( ) ( )
2
2= +gx f x x
. Mệnh đề nào đúng?
A.
( ) ( ) ( )
3 31> −>gg g
B.
( ) ( ) ( )
331−> >g gg
C.
(
) (
)
( )
1 33> −>gg g
D.
( ) ( ) ( )
13 3> >−
gg g
Lời giải
Ta có
( )
(
)
( )
(
)
2 2; 0
gx f x x gx f x x
′′ ′ ′
= + =⇔=−
.
Nhận thấy nghiệm của
( )
0
′
=gx
chính là nghiệm của
cũng là hoành độ giao điểm của hai đồ
thị hàm số
( )
′
=y fx
và đường thẳng
{ }
3; 1; 3= − → = −
yx x
.
Vẽ đường thẳng
= −yx
và chia đồ thị thành 2 phần diện tích hình phẳng.
Khi đó
( ) ( ) ( ) ( ) ( ) ( )
11
1
33
2 2 3 10 3 1
−−
′′
= −− =− = − − > ⇒ − >


∫∫
S x f x dx g x dx g g g g
Và
( ) ( ) ( ) ( ) ( ) ( )
33
2
11
2 2 ( x) 3 1 0 3 1S f x dx g x dx g g g g
′′
= −− = = − > ⇒ >


∫∫
.
Lại có
( ) ( ) ( ) ( ) ( ) ( )
12 1 2
22 31 31 3 3>⇔ > ⇔−− > − ⇔−>SS SSg ggg g g
.
Vậy
( ) ( ) ( )
331−> >g gg
. Chọn B.
C. BÀI TẬP TỰ LUYỆN
Câu 1: Cho hàm số
(
)
=y fx
liên tục trên
[ ]
;
ab
. Diện tích hình phẳng S giới hạn bởi đường cong
( )
=y fx
, trục hoành, các đường thẳng
được xác định bằng công thức nào?
A.
( )
= −
∫
b
a
S f x dx
B.
( )
=
∫
a
b
S f x dx
C.
( )
=
∫
b
a
S f x dx
D.
( )
=
∫
b
a
S f x dx
Câu 2: Công thức tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số
( )
1
=
y fx
,
(
)
2
=
y fx
và
các đường thẳng
( )
,
= = <
x ax ba b
là công thức nào sau đây?
A.
( ) ( )
12
= −
∫
b
a
S f x f x dx
B.
( ) (
)
21
= −
∫
b
a
S f x f x dx
C.
( )
( )
12
= −


∫
b
a
S f x f x dx
D.
(
)
( )
12
= +
∫
b
a
S f x f x dx
Câu 3: Gọi S là diện tích hình phẳng giới hạn bởi các đường
2
,2= = −y xy x
và
0
=y
. Mệnh đề nào sau
đây là đúng?
A.
( )
12
2
01
2
= +−
∫∫
S x dx x dx
B.
( )
2
2
0
2= +−
∫
S x x dx
C.
1
2
0
1
2
= +
∫
S x dx
D.
( )
1
2
0
2= −−
∫
S x x dx
Câu 4: Diện tích hình phẳng S giới hạn bởi các đồ thị hàm số
3
,2
=−=
y x xy x
và các đường
1, 1=−=
xx
được xác định bởi công thức nào sau đây?
A.
( )
1
3
1
3
−
= −
∫
S x x dx
B.
( )
1
3
1
3
−
= −
∫
S x x dx
C.
( ) (
)
01
33
10
33
−
=− +−
∫∫
S x x dx x x dx
D.
( ) ( )
01
33
10
33
−
= − +−
∫∫
S x x dx x x dx
Câu 5: Diện tích hình phẳng S giới hạn bởi các đồ thị của hai hàm số
2, 4= = −
y xy x
và trục hoành Ox
được tính bởi công thức nào dưới đây?
A.
( )
44
00
24
= +−
∫∫
S xdx x dx
B.
( )
24
02
24= +−
∫∫
S xdx x dx
C.
( )
4
0
24= −+
∫
S x x dx
D.
( )
2
0
42= −−
∫
S x x dx
Câu 6: Diện tích hình phẳng S giới hạn bởi các đường
2
, 0, 0=−==y x xy x
và
2=x
được tính bởi công
thức nào sau đây?
A.
( )
2
2
0
= −
∫
S x x dx
B.
( ) ( )
21
22
10
= −− −
∫∫
S xx xxdx
C.
(
)
( )
12
22
01
= −+ −
∫∫
S xx xxdx
D.
( )
2
2
0
= −
∫
S x x dx
Câu 7: Diện tích hình phẳng S giới hạn bởi đồ thị của hai hàm số
2
=yx
và
2
2
= −yx
được xác định bởi
công thức nào sau đây?
A.
( )
1
2
1
1
−
= −
∫
S x dx
B.
(
)
1
2
0
41= −
∫
S x dx
C.
( )
1
2
1
1
−
= −
∫
S x dx
D.
(
)
1
2
0
21
= −
∫
S x dx
Câu 8: Hình phẳng giới hạn bởi các đường
2
1, 2, 0, 2=−= = =−x xyyxx
có diện tích S được tính theo
công thức nào dưới đây?
A.
( )
2
2
1
2
−
= −
∫
S x x dx
B.
( ) ( )
02
22
10
22
−
= − −−
∫∫
S x x dx x x dx
C.
( ) ( )
02
22
10
22
−
= − +−
∫∫
S x x dx x x dx
D.
2
2
1
2
−
= −
∫
S x x dx
Câu 9: Tìm công thức tính diện tích S của hình phẳng
( )
H
giới
hạn bởi các đồ thị hàm số
( ) ( )
,= =y f x y gx
và hai đường
thẳng
như hình vẽ dưới đây.
A.
( ) (
)
( ) (
)
=− +−


∫∫
cb
ac
S f x g x dx g x f x dx
B.
( ) (
) ( )
( )
=− +−


∫∫
cb
ac
S g x f x dx f x g x dx
C.
( ) ( )
= −


∫
b
a
S g x f x dx
D.
( ) ( )
= −


∫
b
a
S f x g x dx
Câu 10: Cho đồ thị hàm số
(
)
=y fx
. Diện tích hình
phẳng S (phần tô đậm trong hình) được xác định bằng
công thức nào?
A.
( ) ( )
02
20−
= −
∫∫
S f x dx f x dx
B.
( ) ( )
02
20−
= +
∫∫
S f x dx f x dx
C.
(
)
(
)
02
20
−
= +
∫∫
S f x dx f x dx
D.
( )
(
)
02
20
−
= +
∫∫
S f x dx f x dx
Câu 11: Công thức nào sau đây dùng để tính diện tích hình
phẳng S phần gạch của hình vẽ.
A.
(
)
(
)
= −
∫∫
bb
aa
S g x dx f x dx
B.
( ) ( )
= −
∫∫
bb
aa
S f x dx g x dx
C.
( ) ( )
= −
∫∫
bb
aa
S g x dx f x dx
D.
( ) ( )
= +
∫∫
bb
aa
S g x dx f x dx
Câu 12: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm
số
( )
=y fx
, trục hoành, đường thẳng
,= =
x ax b
(như
hình
bên dưới). Hỏi cách tính S nào dưới đây đúng?
A.
( ) (
)
= +
∫∫
cb
ac
S f x dx f x dx
B.
( ) (
)
= +
∫∫
cb
ac
S f x dx f x dx
C.
( )
( )
=−+
∫∫
cb
ac
S f x dx f x dx
D.
( )
=
∫
b
a
S f x dx
Câu 13: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
42
2= −yx x
và trục hoành như hình vẽ. Tìm khẳng định sai?
A.
( )
2
2−
=
∫
S f x dx
B.
( )
2
0
2=
∫
S f x dx
C.
( )
2
0
2= −
∫
S f x dx
D.
( )
( )
02
22−−
=−−
∫∫
S f x dx f x dx
( )
=y fx
Câu 14: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
và trục hoành (như hình vẽ). Công thức nào dùng để tính diện tích S?
A.
( )
2
2
−
=
∫
S f x dx
B.
(
) (
)
12
21−
= +
∫∫
S f x dx f x dx
C.
( ) ( )
12
21−
= −
∫∫
S f x dx f x dx
D.
( )
( )
02
20
−
= +
∫∫
S f x dx f x dx
Câu 15: Cho hàm số
( )
=y fx
liên tục trên đoạn
[
]
;ab
. Gọi
D là
hình phẳng giới hạn bởi đồ thị
( ) ( )
: =C y fx
, trục hoành, hai
đường
thẳng
,
= =x ax b
(như hình vẽ bên dưới). Giả sử
D
S
là diện
tích của
hình phẳng D. Chọn công thức đúng trong các phương án A, B, C, D dưới đây?
A.
( ) ( )
0
0
= +
∫∫
b
D
a
S f x dx f x dx
B.
(
) ( )
0
0
=−+
∫∫
b
D
a
S f x dx f x dx
C.
( )
( )
0
0
= −
∫∫
b
D
a
S f x dx f x dx
D.
( ) ( )
0
0
=−−
∫∫
b
D
a
S f x dx f x dx
Câu 16: Cho đồ thị hàm số
( )
=y fx
. Diện tích hình
phẳng (phần gạch chéo) trong hình được tính theo công thức:
A.
( )
4
2−
=
∫
S f x dx
B.
( ) (
) ( )
0 04
22 2−
= ++
∫∫∫
S f x dx f x dx f x dx
C.
( ) ( )
04
20−
= +
∫∫
S f x dx f x dx
D.
( )
(
)
( )
0 24
20 2
−
= ++
∫∫∫
S f x dx f x dx f x dx
Câu 17: Gọi S là diện tích hình phẳng giới hạn bởi các đường
( )
=y fx
, trục hoành (phần gạch sọc trong
hình vẽ). Đặt
( )
( )
12
31
,
−
= =
∫∫
a f x dx b f x dx
. Mệnh đề
nào đúng?
A.
+ab
B.
−ab
C.
−ba
D.
−−
ba
Câu 18: Gọi S là diện tích hình phẳng
( )
H
được giới hạn
bởi các đường
( )
=y fx
, trục hoành và hai đường thẳng
1, 2=−=xx
(như hình vẽ). Đặt
( ) ( )
02
10
,
−
= =
∫∫
a f x dx b f x dx
. Mệnh đề nào dưới đây
đúng?
A.
=−−S ab
B.
= −S ab
C.
= +S ba
D.
= −S ba
Câu 19: Tìm công thức tính diện tích hình phẳng giới hạn bởi phần gạch sọc trong hình vẽ.
A.
( ) ( )
34
2
11
3 0, 5 1 log 0,5 2= +−+ −−
∫∫
xx
S x dx x dx
B.
( ) ( )
34
2
11
3 0, 5 1 log 0, 5 2= +++ −−
∫∫
xx
S x dx x dx
C.
( )
( )
14
2
01
3 0, 5 1 log 0,5 2= +−− −−
∫∫
xx
S x dx x dx
D.
( )
( )
14
2
01
3 0, 5 1 log 0, 5 2= +−+ −−
∫∫
xx
S x dx x dx
Câu 20: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
( )
=x gy
, trục tung và hai đường thẳng
,= =y ay b
như hình
vẽ bên.
Khẳng định nào sau đây đúng?
A.
( )
=
∫
b
a
S g y dx
B.
( )
=
∫
a
b
S g y dy
C.
(
)
=
∫
b
a
S g y dy
D.
(
)
=
∫
b
a
S g y dx
Câu 21: Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ
thị hàm số
( ) ( )
,= =x f y x gy
và hai đường thẳng
,= =y ay b
như hình vẽ bên. Khẳng định nào sau đây đúng?
A.
(
) (
) ( ) ( )
=− +−


∫∫
cb
ac
S g y f y dx f y g y dx
B.
( ) ( )
+


∫
b
a
S g y f y dy
C.
( )
( )
( )
( )
=− +−


∫∫
cb
ac
S g y f y dy f y g y dy
D.
(
) ( )
= −


∫
b
a
S g y f y dy
Câu 22: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị
hàm số
(
)
=
y fx
, trục hoành, đường thẳng
(như hình bên). Biết
( )
3= −
∫
b
a
f x dx
và
( )
5=
∫
c
b
f x dx
. Tìm S.
A.
3=S
B.
5=S
C.
8
=S
D.
2=S
Câu 23: Cho hai hàm số
(
)
=fx x
và
( )
6= −gx x
có đồ thị như
hình vẽ. Gọi S là diện tích hình phẳng (phần gạch chéo) trong hình.
Công thức nào sau đây sai?
A.
( ) ( )
46
04
= +
∫∫
S f x dx g x dx
B.
( ) ( )
6
0
= −
∫
S f x g x dx
C.
2
2
0
6= −+
∫
S y y y dy
D.
(
)
2
2
0
6
= −−
∫
S y y dy
Câu 24: Tính diện tích hình phẳng S giới hạn bởi các đồ thị của các đường
2
41=−+yx x
,
( )
3= ≤−y mm
và
0, 3= =
xx
.
A.
36= +Sm
B.
63= −Sm
C.
36= −Sm
D.
36=−−Sm
Câu 25: Tính diện tích hình phẳng S giới hạn bởi các đồ thị của các đường
2
10
3
= −y xx
và
1
21
−≤
=
−>
x khi x
y
x khi x
.
A.
13=S
B.
15
2
=S
C.
13
2
=S
D.
7=S
Câu 26: (Đề thi minh họa – Bộ GD&ĐT 2017) Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số
3
= −yx x
và đồ thị hàm số
2
= −y xx
.
A.
37
12
=
S
B.
9
4
=S
C.
81
12
=
S
D.
13=
S
Câu 27: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
3
3= −yx x
và đồ thị hàm số
=yx
.
A.
3=S
B.
4=S
C.
6=S
D.
8=S
Câu 28: Tính diện tích S của hình phẳng giới hạn bởi đường cong
2
1= +−yx x
và đường thẳng
21= +yx
.
A.
9
2
=S
B.
4=S
C.
11
2
=S
D.
3=S
Câu 29: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
2
=yx
và
=yx
.
A.
1
6
= −S
B.
2
3
=S
C.
1=
S
D.
1
6
=S
Câu 30: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
2
2= +yx x
và các đường thẳng
0, 1, 1= =−=yx x
.
A.
2
3
=S
B.
2=S
C.
4
3
=S
D.
8
3
=S
Câu 31: Tính diện tích S của hình phẳng giới hạn bởi
2
53=−+yx x
và
2
2 21=− +−y xx
.
A.
1
54
=S
B.
833
54
=S
C.
263
162
=S
D.
35
54
=S
Câu 32: Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số
2
5
= −+yx x
và
32
25=− + ++y xxx
.
A.
1
=S
B.
2
=S
C.
3=S
D.
4
=
S
Câu 33: Tính diện tích hình phẳng S giới hạn bởi đồ thị của hai hàm số
2
2=
yx
và
42
2= −yx x
trong miền
0>x
.
A.
64
15
=
S
B.
32
25
=S
C.
32
15
=
S
D.
15
32
=
S
Câu 34: Tính diện tích S của hình phẳng giới hạn bởi đồ thị
( )
1= +ye x
và
( )
1= +
x
y ex
.
A.
1
2
= −
e
S
B.
1
=S
C.
3
2
=S
D.
21= −
Se
Câu 35: Tính diện tích S của hình phẳng
( )
H
giới hạn bởi các đường
,6
= = −
y xy x
và trục hoành.
A.
20
3
=S
B.
25
3
=S
C.
16
3
=S
D.
22
3
=
S
Câu 36: Tính diện tích S của hình phẳng giới hạn bởi các đường
ln=yxx
, trục hoành và đường thẳng
=xe
.
A.
2
1= −
Se
B.
2
1
4
+
=
e
S
C.
2
1
2
−
=
e
S
D.
2
1
4
−
=
e
S
Câu 37: Tính diện tích S của hình phẳng giới hạn bởi các đường
( )
2
1, 1=−=−
x
y x ey x
.
A.
8
3
= +Se
B.
2
3
= +Se
C.
2
3
= −Se
D.
8
3
= −Se
Câu 38: Biết rằng hình thang cong
( )
H
giới hạn bởi các đường
2 , 0, , 3
=−===y xy x kx
với
2<k
và có
diện tích bằng
k
S
. Xác định giá trị của k để
16=
k
S
.
A.
2 15= +k
B.
2 31
= +
k
C.
2 15= −k
D.
2 31
= −k
Câu 39: Cho hình phẳng
( )
H
giới hạn bởi các đường
( )
ln , 0, 1= = = >y xy x k k
. Tìm k để diện tích hình
phẳng
( )
H
bằng 1.
A.
2=k
B.
=ke
C.
3
=ke
D.
2
=ke
Câu 40: Cho hai hàm số
( )
=
y fx
và
( )
=y gx
liên tục trên đoạn
[ ]
;ab
với
<ab
. Kí hiệu
1
S
là diện tích
hình phẳng giới hạn bởi các đường
( ) ( )
2 ,2 ,= = =y f x y gx x a
và
=xb
;
2
S
là diện tích hình phẳng giới
hạn bởi các đường
( ) ( )
2, 2,= −= −=y f x y gx x a
và
=xb
. Chọn khẳng định đúng?
A.
12
=SS
B.
12
2=SS
C.
12
22= −SS
D.
12
22= +SS
Câu 41: Trong mặt phẳng tọa độ, cho hình chữ nhật
( )
H
có một cạnh nằm trên trục hoành và có hai đỉnh
trên một đường chéo là
( )
1; 0−A
và
(
)
;
Ca a
với
0>
a
. Biết
rằng đồ thị hàm số
=yx
chia hình
( )
H
thành hai phần có diện
tích bằng nhau, tìm a.
A.
9=a
B.
4=a
C.
1
2
=
a
D.
3=a
Câu 42: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị
( )
21
:
1
−
=
+
x
Cy
x
, tiệm cận ngang của đồ thị
( )
C
, trục tung và
đường thẳng
(
)
0= >x aa
. Tìm a để
3ln 5=
S
.
A.
5=a
B.
4=a
C.
3
=a
D.
2=
a
Câu 43: Tính diện tích hình phẳng trong phần tô đậm của hình
vẽ bên.
A.
8
3
B.
11
3
C.
7
3
D.
10
3
Câu 44: Tìm công thức tính diện tích S của hình phẳng
( )
H
giới hạn bởi các đồ thị hàm số
( )
=y fx
,
( )
=y gx
và hai đường thẳng
như hình vẽ bên cạnh. Biết rằng
( ) ( )
[ ]
,;≥ ∀∈f x g x x ab
và
( )
( )
[ ]
,;≤ ∀∈f x g x x cd
.
A.
( ) ( ) ( ) ( )
=− +−


∫∫
cb
ac
S g x f x dx f x g x dx
B.
( ) ( ) ( ) ( )
=− +−


∫∫
cb
ac
S f x g x dx g x f x dx
C.
( ) ( )
= −


∫
b
a
S g x f x dx
D.
( ) ( )
= −


∫
b
a
S f x g x dx
Câu 45: Diện tích phần gạch chéo trong hình vẽ bằng bao nhiêu?
A.27ln2
B. 27ln3
C. 28ln3
D. 29ln3
Câu 46: Diện tích hình phẳng tô đậm trong hình vẽ bằng bao nhiêu?
A.
3
2
B.
3
4
C.
1
6
D.
1
2
Câu 47: Biết diện tích phần gạch chéo của hình vẽ bên bằng
++
b
ae c
e
với a, b, c là các số nguyên. Tính
=++P abc
.
A.
1
3
=P
B.
0
=P
C.
1
2
= −P
D.
1
5
=P
Câu 48: Cho đồ thị
( )
=y fx
như hình vẽ. Diện tích S của hình phẳng (phần gạch chéo) được xác định bởi
công thức nào?
A.
( )
2
2−
=
∫
S f x dx
B.
(
) ( )
12
21−
= +
∫∫
S f x dx f x dx
C.
( )
( )
22
11
−
= +
∫∫
S f x dx f x dx
D.
( ) ( )
12
21−
= −
∫∫
S f x dx f x dx
Câu 49: Tính diện tích hình phẳng giới hạn bởi parabol như hình vẽ
và trục hoành Ox.
A.
4
3
B.
17
2
C. 9 D.
1
9
Câu 50: Tính diện tích hình phẳng giới hạn bởi parabol như hình vẽ và đường thẳng
3
=y
.
A.
3
4
=
S
B.
4
3
=S
C.
14
3
=
S
D.
6
=S
Câu 51: Tính diện tích hình phẳng giới hạn bởi
( )
=y fx
có đồ thị như hình vẽ và Ox, Oy. Biết rằng đồ thị
hàm số
( )
=y fx
đi qua hai điểm
( )
1
0;1 , ; 0
2

−


AB
.
A.
1 ln 2−
B.
1
1 ln
2
−
C.
1
2 ln
2
−
D.
11
ln
22
−
Câu 52: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
2
2= −yx
, đường thẳng
=
yx
và trục
hoành.
A.
= π
S
B.
3
4
π
=
S
C.
2
π
=S
D.
4
π
=
S
Câu 53: Cho S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
2= −y xx
và trục hoành. Tìm số nguyên lớn nhất không vượt quá S.
A. 0 B. 1 C. 2 D. 3
Câu 54: Tính diện tích S của hình phẳng
(
)
H
giới hạn bởi hai đồ thị
của hai hàm số
3, 4= = −
x
yyx
và trục tung.
A.
92
2 ln 3
= +S
B.
93
2 ln 3
= +S
C.
73
2 ln 3
= −
S
D.
72
2 ln 3
= −S
Câu 55: Diện tích hình phẳng giới hạn bởi đường cong
( )
20= >y ax a
, trục hoành và đường thẳng
=
xa
bằng
2
ka
. Tính
giá trị của tham số k.
A.
7
3
=k
B.
4
3
=k
C.
12
5
=k
D.
6
5
=k
Câu 56: Tính diện tích hình phẳng S giới hạn bởi các đồ thị của các đường
2
21=−+yx x
,
1= +yx
,
0=x
,
=xm
với
( )
0;3∈m
.
A.
32
3
32
= −
mm
S
B.
23
3
23
= −
mm
S
C.
32
2
32
=−+
mm
Sm
D.
32
2
32
=−−
mm
Sm
Câu 57: Biết diện tích hình phẳng S giới hạn bởi các đồ thị của các đường
2
21=−+yx x
,
1
= −yx
và
0,= =x xm
với
0<
m
bằng
5
6
. Tìm giá trị của tham số m.
A.
3= −m
B.
2
= −
m
C.
1= −
m
D.
4= −m
Câu 58: Cho hàm số
4 22
1
22
2
=−+
y x mx
. Tìm các giá trị của tham số m
sao
cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng
cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình
phẳng có diện tích bằng
64
15
.
A.
∈∅m
B.
{
}
1
∈±m
C.
2
;1
2


∈±



m
D.
1
;1
2

∈± ±


m
Câu 59: Tính diện tích S của phần hình phẳng gạch sọc (như hình vẽ bên dưới) giới hạn bởi đồ thị của hàm
số bậc ba
32
= + ++y ax bx cx d
và trục hoành.
A.
31
5
π
=S
B.
27
4
=
S
C.
19
3
=
S
D.
31
5
=S
Câu 60: Gọi S là diện tích hình phẳng giới hạn bởi các đường
( )
22
2 ,2 0= = >
my x mx y m
. Tìm giá trị của m
để
3=S
.
A.
3
2
=m
B.
2
=m
C.
3=
m
D.
1
2
=m
Câu 61: Cho hình thang cong
( )
H
giới hạn bởi các đường
=
x
ye
,
0, 0, ln 4= = =yxx
. Đường thẳng
( )
0 ln 4= <<xk k
chia
( )
H
thành hai phần có diện tích là
1
S
và
2
S
như hình vẽ bên. Tìm k để
12
48+=SS
.
A.
2
ln 4
3
=
k
B.
ln 2=k
C.
8
ln
3
=k
D.
2
ln
3
=k
Câu 62: Cho hình thang cong
( )
H
giới hạn bởi các đường
11
, ,2
2
= = =yxx
x
và
trục hoành. Đường thẳng
1
,2
2

= <<


xk k
chia
( )
H
thành hai phần có diện tích
là
1
S
và
2
S
như hình vẽ dưới đây. Tìm tất cả các giá trị thực của k để
12
3=SS
.
A.
2
=
k
B.
1=
k
C.
7
5
=
k
D.
3
=
k
Câu 63: Cho hình thang cong
( )
H
giới hạn bởi các đường
=
x
ye
;
0; 0= =yx
và
ln 4=x
. Đường thẳng
( )
0 ln 4= <<xk k
chia
( )
H
thành hai
phần có diện tích là
12
,SS
và như hình vẽ bên dưới. Tìm k để
12
2=SS
.
A.
8
ln
3
=k
B.
2
ln 4
3
=k
C.
ln 3=k
D.
ln 2=k
Câu 64: Cho hình thang cong
( )
H
giới hạn bởi các đường
; 0; 1; l n 6= = = =
x
y ey x x
. Đường thẳng
(
)
1 ln 6= <<xk k
chia
( )
H
thành hai phần có diện tích
1
S
và
2
S
như hình vẽ bên. Tìm k để
22
12
= +PS S
đạt giá trị nhỏ nhất.
A.
6
2
−+
=
e
k
B.
6
2
+
=
e
k
C.
6
ln
2
+
= −
e
k
D.
6
ln
2
+
=
e
k
Câu 65: Cho hình thang cong
( )
H
giới hạn bởi các đường
; 0; 1; l n 6
= = = =
x
y ey x x
. Đường thẳng
( )
1 ln 6= <<xk k
chia
( )
H
thành hai
phần có diện tích là
1
S
và
2
S
như hình vẽ bên. Tìm k để
12
2<−SS
.
A.
4
1
2
+
<<
e
k
B.
4
2
+
<
e
k
C.
4
ln
2
+
<
e
k
D.
4
1 ln
2
+
<<
e
k
Câu 66: Cho hình thang cong
( )
H
giới hạn bởi các đường
; 0; 0; ln 4= = = =
x
y ey x x
. Đường thẳng
( )
0 ln 4= <<xk k
chia
( )
H
thành hai phần có diện tích là
1
S
và
2
S
như hình vẽ bên. Gọi X là tập hợp
tất cả các giá trị k để
. Tính tổng các phần tử của tập hợp X.
A. ln5 B. ln6
C. ln12 D.
5
ln
2
Câu 67: Gọi
( )
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
44=−+yx x
,
trục tung và trục hoành. Xác định k để đường thẳng d đi qua điểm
( )
0; 4A
có hệ số góc k chia
( )
H
thành
hai phần có diện tích bằng nhau (như hình vẽ bên).
A.
4= −k
B.
8= −
k
C.
6= −k
D.
2
= −k
Câu 68: Cho hình thang cong
( )
H
giới hạn bởi các đường
, 0, 0, 1
= = = =
x
y ey x x
. Đường thẳng
( )
01= <<xk k
chia
( )
H
thành
hai phần có diện tích là
1
S
và
2
S
như hình vẽ bên. Tìm
k
để
12
>SS
.
A.
1
2
+
>
e
k
B.
1
ln 1
2
+
<<
e
k
C.
1
0 ln
2
+
<<
e
k
D.
1
ln
2
+
>
e
k
Câu 69: Cho hàm số
( )
=y fx
liên tục trên ℝ và hàm số
( )
( )
2
= =y g x xf x
có
đồ thị trên đoạn
[ ]
0; 2
như hình vẽ. Biết diện tích miền tô màu là
5
2
=S
. Tính
( )
4
1
=
∫
I f x dx
.
A.
5
4
=I
B.
5
2
=I
C.
5=I
D.
11
2
=I
Câu 70: Một sân chơi dành riêng cho trẻ em hình chữ nhật có chiều dài 50m và chiều rộng 30m, người ta
làm một con đường trong sân (như hình vẽ). Biết viền ngoài và viền trong của con đường là hai đường elip
và chiều rộng của mặt đường là 2m. Kinh phí để làm mỗi
2
m
làm đường 500.000 đồng. Tính tổng số tiền
làm con đường đó (số tiền làm tròn đến hàng nghìn).
A. 119.000.000 đồng B. 152.000.000 đồng C. 119.320.000 đồng
Câu 71: Người ta trồng hoa và phần đất được gạch sọc được giới hạn bởi
cạnh AB, CD, đường trung bình MN của mảnh đất hình chữ nhật ABCD và
một đường cong hình sin (như hình vẽ). Biết
( )
2= πAB m
và
( )
2=
AD m
.
Tính diện tích phần còn lại.
A.
41
π−
B.
( )
41
π−
C.
42
2
π−
D.
43
2
π−
Câu 72: Ông An muốn là cửa rào sắt có hình dạng kích
thước như hình vẽ bên, biết đường cong phía trên là một
parabol. Giá
2
1
m
của rào sắt là 700.000 đồng. Hỏi ông An
phải trả bao nhiêu tiền để làm cửa sắt (làm tròn đến hàng phần nghìn).
A. 6.520.000 đồng B. 6.320.000 đồng
C. 6.417.000 đồng D. 6.620.000 đồng
Trục hoành và hai đường thẳng
55
;
22
xx
−
= =
Câu 73: Một khuôn viên dạng nửa hình tròn có đường kính bằng
45
m. Trên đó người ta thiết kế hai phần
để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa đường tròn và hai đầu mút
của cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau
một khoảng bằng 4m. Phần còn lại của khuôn viên (phần không
tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như
hình vẽ và kinh phí để trồng cỏ Nhật Bản là 100.000 đồng/
2
m
.
Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản? (làm tròn đến hàng
nghìn)
A. 3.895.000 đồng B. 1.948.000 đồng C.
2.388.000 đồng D. 1.194.000 đồng
Câu 74: (Đề thi THPT Quốc gia 2017 – Mã đề 101) Cho
(
)
=y fx
có
đồ thị của
( )
′
=y fx
như hình vẽ. Đặt
( ) ( )
2
2= −hx f x x
. Mệnh đề nào
đúng?
A.
( ) ( ) ( )
4 22= −>hh h
B.
( ) ( ) ( )
4 22= −<hh h
C.
( ) ( ) ( )
24 2> >−hhh
D.
(
)
(
)
( )
2 24> −>
hh h
Câu 75: (Đề thi THPT Quốc gia 2017 – Mã đề 104) Cho
( )
=y fx
có đồ thị của
( )
′
=y fx
như hình vẽ.
Đặt
( ) ( ) ( )
2
21
= ++
gx f x x
. Mệnh đề nào đúng?
A.
( ) ( ) ( )
13 3< <−gg g
B.
( ) ( ) ( )
1 33< −<gg g
C.
( ) ( ) ( )
3 31= −<gg g
D.
(
) (
) (
)
3 31= −>
gg g
Câu 76: Cho
( )
=y fx
có đồ thị của
( )
′
=y fx
như hình vẽ. Đặt
( ) ( )
cos= +gx f x x
. Mệnh đề nào dưới đây đúng?
A.
( ) ( )
0
2
π

< π<


ggg
B.
( ) (
)
0
2
π

< <π


g gg
C.
( ) (
)
0
2
π

< π<


g gg
D.
( ) (
)
0
2
π

π> >


ggg
D. LỜI GIẢI CHI TIẾT
Câu 1: Ta có
( )
=
∫
b
a
S f x dx
. Chọn D.
Câu 2: Ta có
(
)
(
)
12
= −
∫
b
a
S f x f x dx
. Chọn A.
Câu 3: Phương trình hoành độ giao điểm
2
1
2
2
=
=−⇔
= −
x
xx
x
.
Dựa vào đồ thị hàm số ta có
( )
12 1
22
01 0
1
2
2
= +− =+
∫∫ ∫
S x dx x dx x dx
. Chọn C.
Câu 4: Phương trình hoành độ giao điểm
( )
33
2
0
2 30
3
=
−= ⇔ − =⇔
=
x
xxxx x
xl
Do đó
( ) ( )
01
33
10
33
−
=− +−
∫∫
S x x dx x x dx
. Chọn C.
Câu 5: Phương trình hoành độ giao điểm
24 2=−⇔=x xx
.
Dựa vào đồ thị hàm số ta có
( )
24
02
24= +−
∫∫
S xdx x dx
. Chọn B.
Câu 6: Phương trình hoành độ giao điểm
2
0
0
1
=
−=⇔
=
x
xx
x
.
Dựa vào đồ thị hàm số ta có
(
) (
)
21
22
10
= −− −
∫∫
S xx xxdx
. Chọn B.
Câu 7: Phương trình hoành độ giao điểm
22
1
2
1
=
=−⇔
= −
x
xx
x
.
Ta có
( )
( )
1 11
22 2 2
1 10
2 21 41
−−
= −− = − = −
∫ ∫∫
S x x dx x dx x dx
. Chọn B.
Câu 8: Phương trình hoành độ giao điểm
2
0
20
2
=
−=⇔
=
x
xx
x
.
Dựa vào đồ thị hàm số ta có
( ) ( )
02
22
10
22
−
= − −−
∫∫
S x x dx x x dx
. Chọn B.
Câu 9: Dựa vào đồ thị hàm số ta có
( ) ( ) ( ) ( )
=− +−


∫∫
cb
ac
S f x g x dx g x f x dx
. Chọn A.
Câu 10: Dựa vào đồ thị hàm số ta có
( ) ( )
02
20−
= −
∫∫
S f x dx f x dx
. Chọn A.
Câu 11: Dựa vào đồ thị hàm số ta có
( )
(
)
= −
∫∫
bb
aa
S f x dx g x dx
. Chọn B.
Câu 12: Dựa vào đồ thị hàm số ta có
( ) ( )
=−+
∫∫
cb
ac
S f x dx f x dx
. Chọn C.
Câu 13: Ta có diện tích 2 bên trục tung bằng nhau nên
(
)
2
0
2
=
∫
S f x dx
. Chọn B.
Câu 14: Dựa vào đồ thị hàm số ta có
( )
( )
12
21−
= −
∫∫
S f x dx f x dx
. Chọn C.
Câu 15: Dựa vào đồ thị hàm số ta có
( ) ( )
0
0
=−+
∫∫
b
D
a
S f x dx f x dx
. Chọn B.
Câu 16: Dựa vào đồ thị hàm số ta có
( ) ( ) ( )
0 04
22 2
−
= ++
∫∫∫
S f x dx f x dx f x dx
. Chọn B.
Câu 17: Dựa vào đồ thị hàm số ta có
(
)
(
)
12
31
−
= −=−
∫∫
S f x dx f x dx a b
. Chọn B.
Câu 18: Dựa vào đồ thị hàm số ta có
( ) ( )
02
10−
=−+=−
∫∫
S f x dx f x dx b a
. Chọn D.
Câu 19: Dựa vào đồ thị hàm số ta có
( ) (
)
14
2
01
3 0,5 1 log 0,5 2= +−+ −−
∫∫
xx
S x dx x dx
. Chọn D.
Câu 20: Dựa vào đồ thị hàm số ta có
( )
=
∫
b
a
S g y dy
. Chọn C.
Câu 21: Dựa vào đồ thị hàm số ta có
( ) ( ) ( ) (
)
=− +−


∫∫
cb
ac
S g y f y dy f y g y dy
. Chọn C.
Câu 22: Ta có
( )
( )
( )
( ) (
)
3 58= + =− + =−− + =
∫ ∫ ∫∫
b c bc
a b ab
S f x dx f x dx f x dx f x dx
. Chọn C.
Câu 23: Ta có
( ) ( ) ( ) ( )
4 6 46
0 4 04
=+=+
∫ ∫ ∫∫
S f x dx f x dx f x dx g x dx
. Chọn B.
Câu 24:
( )
3
2
3
2 22
0
41 41 4 4 2 0
−≥
= −+− →−+−≥−+=− ≥
∫
m
Sxx mdx xx mxx x
( )
( )
3
3
3
22
0
0
41 2 1 3 6
3

⇒ = − +− = − + − =− −


∫
x
S x x m dx x m x m
. Chọn D.
Câu 25: Xét PT:
1
22
1
0
0
10 13
13
33
3
=

− =−⇔ ⇒ = −

=

∫
x
xx x S xx dx
x
.
Lại có
3
22
2
1
3
10 7
22
2
33
3
=

− =−⇔ ⇒ = + −

= −

∫
x
xx x S xx dx
x
13
23 23
12
01
13 7 13
2
2 3 63 2

⇒= + = − + − =


xx xx
S S S x+
. Chọn C.
Câu 26: Xét PT:
1
3 2 32
2
0
12
2
−
=
−=− ⇔ = ⇒ = + −
= −
∫
x
x x x x x S x x x dx
x
( ) ( )
01 0 1
32 32 32 32
20 2 0
22 2 2
−−
= +− + +− = +− +− +−
∫∫∫ ∫
x x x dx x x x dx x x x dx x x x dx
01
43 43
22
20
8 5 37
4 3 4 3 3 12 12
−

= +− − +− =+=


xx xx
xx
. Chọn A.
Câu 27: Xét PT:
2 02
3 3 33
2 20
0
3 4 44
2
−−
=
− =⇔ ⇒= − = − + −
= ±
∫∫∫
x
x x x S x x dx x x dx x x dx
x
( ) ( )
02
02
44
3 3 22
20
20
4 4 22 8
44
−
−

=− +− =− +− =


∫∫
xx
x x dx x x dx x x
. Chọn D.
Câu 28: Xét PT:
2
1
12 1
2
= −
+ −= +⇔
=
x
xx x
x
( )
2
22
32
22
11
1
9
22 2
32 2
−−
−

⇒ = −− =− −− =− − − =


∫∫
xx
S x x dx x x dx x
. Chọn A.
Câu 29: Xét PT:
( )
1
11
23
2 22
00
0
0
1
1
23 6
=

=⇔ ⇒= − = − = − =

=

∫∫
x
xx
x x S x x dx x x dx
x
. Chọn D.
Câu 30: Ta có
1 01
2 22
1 10
2 22
−−
= + = + ++
∫∫∫
S x x dx x x dx x x dx
( ) ( )
01
01
33
2 2 22
10
10
2
22
3 33
−
−

=−+ + + =− + + + =


∫∫
xx
x x dx x x dx x x
. Chọn A.
Câu 31: Xét PT:
2 22
1
5 3 2 2 1 3 7 40
4
3
=
− + =− + −⇔ − + = ⇔
=
x
xx xx xx
x
( )
44
4
2
33
3
2 23
11
1
71
3 74 3 74 4
2 54

⇒= −+ =− −+ =− − + =


∫∫
x
S x x dx x x dx x x
. Chọn A.
Câu 32: Xét PT:
2 32 3
0
52 52 20
1
=
−+=− + ++⇔ − =⇔
= ±
x
xx xxx x x
x
1 01
3 33
1 10
22 22 22
−−
⇒= − = − + −
∫∫∫
S x x dx x x dx x x dx
(
) ( )
01
01
44
3 3 22
10
10
22 22 1
22
−
−

= − +− − = − − − =


∫∫
xx
x x dx x x dx x x
. Chọn A.
Câu 33: Xét PT:
( )
22
42 2 42 42
00
0
22 4 4
2
=
− = ⇔ ⇒= − = −
=±−
∫∫
x
xx x Sxx xxdx
x
( )
2
2
53
42
0
0
4 64 64
4
5 3 15 15

→ − = − = − ⇒ =


∫
xx
x x dx S
. Chọn A.
Câu 34: Xét PT:
( )
( )
0
11
1
=
+ =+ ⇔= ⇔
=
xx
x
e x e x ex xe
x
(
)
( )
1
11
2
00
0
1
22

⇒= − = − = + − =−


∫∫
x x xx
ex e
S x e e dx x e e dx e xe
. Chọn A.
Câu 35: Xét PT:
(
)
44
00
64 6 6
=−⇔=⇒=+− =−+−
∫∫
x x x S x x dx x x dx
4
23
0
22
6
3
23
2


=−− − =



xx
x
. Chọn D.
Câu 36: Xét PT:
1
0 01
0
ln 0 ln ln ln
1
=
=⇔ ⇒= = +
=
∫∫∫
ee
x
xx S xxdx xxdx xxdx
x
( )
1
2
22 2 2
01
1 1 11 1
ln ln ln ln ln . ln
2 22 2 4
= − + → = = − = − +
∫∫ ∫ ∫ ∫
e
x
x xdx x xdx x xdx xd x x x x dx x x C
x
1
2 22
22
01
11 1
ln ln
24244

+
⇒=− − + − =


e
x xe
S xx xx
. Chọn B.
Câu 37: Xét PT:
(
) ( )
( )
1
22
0
1
1
11 1 1
0
1
=
=
− = −⇔ ⇔ ⇒ = − − −
=
= +
∫
xx
x
x
x
xex S xex dx
x
ex
( )
( )
1
1
3
2
0
0
8
11
33

= − − − = −−− + =−


∫
x xxx
x
x e x dx xeee x e
. Chọn D.
Câu 38: Xét PT:
( ) ( )
32 3
2
20 2 2 2 2−=⇔=⇒ = − = − + −
∫∫ ∫
kk
x x S x dx x dx x dx
23
22 2
2
5
2 2 2 16 2 31
22 2 2

= − + − =− − = ⇒=−


k
xx k
x xk k
. Chọn D.
Câu 39: Xét PT:
( )
1
11
ln 0 1 ln ln ln=⇔=⇒= = −
∫∫
kk
k
x x S x dx x x xd x
( )
ln 1 1= − −=⇒=kk k ke
. Chọn B.
Câu 40:
( )
( )
( ) ( )
( ) ( )
12 1
1
2 2 ; 2 ( 2)
2
bb b
aa a
S f x g x dx S f x g x dx f x g x dx S
= − = −− − = − =
∫∫ ∫
. Chọn B.
Câu 41: Diện tích hình phẳng giới hạn bởi các đường
, 0, 0,= = = =y xy x x a
là
33
0
0
22
33
′
= = =
∫
a
a
S xdx x a
.
Lại có
( )
( )
( )
( )
3
1 21
1 13
2 32
′
=+⇒= ⇔ =+⇒=
HH
SaaSS a aaa
. Chọn D.
Câu 42:
1
00
21 3
2 3ln 1 3ln 1 3ln 5 4
11
−
= − = = + = += ⇒=
++
∫∫
aa
a
x
S dx dx x a a
xx
. Chọn B.
Câu 43:
( )
44
02
10
2
3
= −− =
∫∫
S xdx x dx
. Chọn D.
Câu 44:
( ) (
)
( ) ( )
( ) (
) ( )
( )
=− +− = − + −


∫∫∫ ∫
cb c b
ac a c
S f x g x dx f x g x dx f x g x dx g x f x dx
. Chọn B.
Câu 45: Phương trình hoành độ giao điểm của
( )
fx
và
( )
hx
là
2
27
3= ⇔=xx
x
.
Phương trình hoành độ giao điểm của
( )
gx
và
( )
hx
là
2
27
9
27
= ⇔=
x
x
x
.
Khi đó, diện tích cần tìm là
( ) ( )
( ) ( )
39
03
27 ln 3= − +− =
∫∫
S f x g x dx h x g x dx
. Chọn B.
Câu 46: Diện tích cần tìm là
22
22
00
11
.1.1
4 42 6
∆
= −= − =
∫∫
xx
S dx S dx
. Chọn C.
Câu 47: Phương trình hoành độ giao điểm của
( )
C
và d là
1
ln 1
=
= ⇔
=
x
x
e
xe
.
Diện tích cần tìm là
( ) ( ) ( ) ( )
1
1
1
1
1
1
1
1 ln 1 ln 1 1 ln ln= + + − =− + −+ − − −
∫∫
e
e
e
e
S x dx x dx e x x x x x x
e
1
12 1
11 2
2
= =
= − + − − = + − →
= −
ab
ee
c
ee e
. Vậy
112 0= + + =+− =
P abc
. Chọn B.
Câu 48:
( )
(
)
( )
(
)
1 2 12
2 1 21−−
= + =−+
∫ ∫ ∫∫
S f x dx f x dx f x dx f x dx
. Chọn C.
Câu 49: Vì parabol đi qua 3 điểm
( ) ( ) ( ) ( )
2
0; 0 , 2; 0 , 1;1; : 2 → = − +A B I Py x x
Do đó, diện tích hình phẳng cần tính là
( )
22
2
00
4
2
3
= =−=
∫∫
S f x dx x x dx
. Chọn A.
Câu 50: Vì parabol đi qua điểm
( )
0;3A
, đỉnh
( ) ( )
2
1; 2 : 2 3
→ = − +I Pyx x
Phương trình hoành độ giao điểm của
( )
P
và d là
2
0
2 33
2
=
− +=⇔
=
x
xx
x
.
Do đó, diện tích cần tính là
( ) ( )
22
2
00
4
2
3
= − =−=
∫∫
S f x g x dx x x dx
. Chọn A.
Câu 51: Gọi phương trình đồ thị hàm số là
+
=
+
ax b
y
cx d
.
Vì đồ thị đi qua
( )
1
0;1 , ; 0
2

−


AB
và có hai đường tiệm cận là
1; 2=−=
xy
.
Suy ra
21
1
+
=
+
x
y
x
. Do đó, diện tích cần tìm là
0
1
2
21
1 ln 2
1
−
+
= = −
+
∫
x
S dx
x
. Chọn A.
Câu 52: Phương trình hoành độ giao điểm của đồ thị hàm số
2
2= −yx
và đường thẳng
=yx
là:
2
22
0
21
2
≥
− =⇔ ⇔=
−=
x
xx x
xx
Ta có:
12 2
22
01 1
1
22
2
=+−=+−
∫∫ ∫
S xdx x dx x dx
Xét
2
2
1
2 −
∫
x dx
, ta đặt
2 sin=xt
( )
2
22
2 sin
2 22
1
44
2 2 2sin 2 sin 2cos
ππ
=
ππ
= − → − =
∫∫ ∫
xt
I x dx td t tdt
( )
2
2
4
4
sin 2 1
1 cos 2
2 42 4
π
π
π
π
ππ

= + = + =−⇒=


∫
t
t dt t S
.
Cách 2: Diện tích cần tìm là hình quạt có góc ở đỉnh bằng
2
45 1
45 . . .2
360 8 4
°π
°⇒ = π = π =
°
SR
. Chọn D.
Câu 53: Phương trình hoành độ giao điểm là
2
0
20
2
=
−=⇔
=
x
xx
x
Diện tích hình phẳng cần tìm là:
( )
2
22
3
2 22
00
0
4
22
33

=−=− =−=


∫∫
x
S x x dx x x dx x
.
Vậy số nguyên lớn nhất không vượt quá S là 1. Chọn B.
Câu 54: Phương trình hoành độ giao điểm của 2 đồ thị là:
( )
34 3 4=−⇔ = +=
xx
x fx x
Do
( ) ( )
3 ln 3 1 0
′
= + > ∀∈
x
fx x
và
( )
14
=
f
nên
( ) ( )
11= ⇔=fx f x
.
Diện tích cần tìm là:
( )
1
11
2
00
0
3 72
3 4 43 4
ln 3 2 2 ln 3

= +− = − − = − − = −


∫∫
x
xx
x
S x dx x dx x
. Chọn D.
Câu 55: Phương trình hoành độ giao điểm
( )
2 0 0; 0 0= > ≥ ⇔=ax a x x
Diện tích cần tìm là:
2
32
0
0
24 4
2 2.
33 3
= = = ⇒=
∫
a
S axdx a x a k
. Chọn B.
Câu 56: Ta có:
( )
22
21 1 3− +− + = −xx x xx
Khi đó
( )
( )
23 2 3
0;3
22
00
0
33
33
23 2 3
∈
= − → − = − = −
∫∫
m
mm
m
xx mm
S x x dx x x dx
. Chọn B.
Câu 57: Diện tích cần tìm là:
( )
( )
0 00
0
2 22
2 21
<
= − + − − = − → = −
∫ ∫∫
m
m mm
S x x x dx x x dx S x x dx
0
32 2 3
5
1
32 2 36

= − = − =⇔=−


m
xx mm
m
. Chọn C.
Câu 58: Ta có:
(
)
32 22
22
0
24 2 2 0
2
=
′
=−= −=⇔
=
x
y x mx x x m
xm
Hàm số có 3 điểm cực trị khi
0≠
m
Do
1
0
2
= >⇒a
điểm cực đại của đồ thị hàm số là
( )
0; 2
Phương trình đường thẳng cùng phương với trục hoành qua điểm cực đại là
:2=dy
Phương trình hoành độ giao điểm
2
4 22
22
00
1
2 22
2
2
4
= =
− +=⇔ ⇔
= ±
=
xx
x mx
xm
xm
Giả sử
0>m
do tính chất đối xứng nên
2
2
5 23
4 22
0
0
14
22
2 53


= − + =−+




∫
m
m
x mx
S x m x dx
55 5
32 32 64 64
1
5 3 15 15
=− + = = ⇔=
mm m
m
Tương tự
01<⇒ =−
mm
. Vậy
{ }
1∈±m
. Chọn B.
Câu 59: Dựa vào đồ thị suy ra
( )
(
)
2
21=+−y ax x
Do đồ thị hàm số đi qua điểm
( )
0; 2 2 2 1⇒= ⇒=aa
Khi đó
( )( )
1
2
2
27
21
4
−
=+− =
∫
S x x dx
. Chọn B.
Câu 60: Tọa độ giao điểm của 2 đồ thị là nghiệm của hệ
(
)
2
4
33
2
2
0
2 80
2
2
4
2
=
=
⇒=⇔−=⇔
=
=
x
x
y
x
mx x x m
m
xm
m
y mx
Khi đó
2
2
23
3
0
0
2
2 2.
23 6

= −= −


∫
m
m
xx
S mx dx m x
mm
22 2
84 4 3
3
33 3 2
= − = =⇔=
mm m
m
. Chọn A.
Câu 61: Ta có
ln 4
12
0
3+= =
∫
x
S S e dx
Lại có:
12 1
0
0
55 8
4 8 1 ln
33 3
+ = ⇒ = = ⇔ = = −⇒ =
∫
k
k
x xk
S S S e dx e e k
. Chọn C.
Câu 62: Ta có
2
2
1
12
2
1
2
1
ln ln 4 2ln 2+= = = =
∫
S S dx x
x
Do
1
121 1
3
3 2ln 2 ln 2
32
= ⇒+ = ⇒=
S
SSS S
Mặt khác
1
1
2
1
2
13
ln ln 2 ln 2 ln 8 2 8 2
2
= = = = = ⇒ = ⇔=
∫
k
k
S dx x k k k
x
. Chọn A.
Câu 63: Do
ln 4
ln 4 ln 4
1 21
0
00
22 2 2
22
33 3 3
= ⇒= = = = =
∫∫
x xx
S S S S e dx e dx e
Do đó
1
0
1 2 3 ln 3= = −= ⇔ = ⇔ =
∫
k
xx k
S e dx e e k
. Chọn C.
Câu 64: Ta có
ln 6
12
1
6+= =−
∫
x
S S e dx e
Do
( ) ( ) ( )
22
22
1 11 1
6 2 26 6= +−− = − − +−P S e S S eS e
Khi đó
( )
min 1
26
6
2 2.2 2
−
−−
⇔= = =
e
be
PS
a
Lại có:
1
1
6 66
ln
22 2
−+ +
= = −= ⇒ = ⇒ =
∫
k
xk k
ee e
S e dx e e e k
. Chọn D.
Câu 65: Ta có
ln 6
12
1
6
+= =−
∫
x
S S e dx e
Do
12 1 1 1
26 2 2
2
< −⇒ <−− −⇔ <−
e
S S S eS S
Lại có:
1
1
44
2 1 ln
22 2
++
= = −< − ⇔ < ⇒< <
∫
k
xk k
ee e
S e dx e e e k
. Chọn D.
Câu 66: Ta có
ln 4
12
0
3+= =
∫
x
S S e dx
Do
22
12
22
12
12
12
12
2; 1
5
5
1; 2
3
= =
+=
+ = ⇒ →
= =
+=
SS
SS
SS
SS
SS
Lại có:
1
0
1 2 ln 3
1
ln 2
11
−= =
= = −⇒ ⇔ ⇒
=
−=
∫
k
k
xk
k
ek
S e dx e
k
e
tổng các phần tử của tập hợp X là
ln 3 ln 2 ln 6+=
.
Chọn B.
Câu 67: Đồ thị hàm số
2
44=−+yx x
cắt trục hoành tại điểm
( )
2; 0
Diện tích phần gạch chéo là
( )
( )
2
3
2
2
0
0
2
8
2
33
−
=−= =
∫
x
S x dx
Đường thẳng d đi qua điểm
( )
0; 4A
có hệ số góc k suy ra
:4= +d y kx
Đường thẳng d cắt Ox tại điểm
(
)
4
;0 0
−

<


Ck
k
(Do C có hoành độ dương).
Theo giả thiết bài toán ta có:
1 4 14 4
. . .4 6
2 23 2 3
−
= =⇔ =⇒=
S
OC OA k
k
. Chọn C.
Câu 68: Ta có
1
12
0
1+= =−
∫
x
S S e dx e
Do đó
12 1 1 1
1
1
2
−
>⇔>−−⇔>
e
SS Se S S
Lại có:
1
0
11 1
1 ln
22 2
−+ +
= = −> ⇔ > ⇔ >
∫
k
xk k
ee e
S e dx e e k
Kết hợp
1
0 1 ln 1
2
+
<<⇒ <<
e
kk
. Chọn B.
Câu 69: Ta có
( )
2
1
5
2
=
∫
g x dx
suy ra
( )
2
2
1
5
2
=
∫
xf x dx
. Đặt
2
=
tx
ta có:
2=dt xdx
Đổi cận suy ra
( )
(
)
( )
24 4
2
11 1
15
55
22
= = ⇒ =⇒=
∫∫ ∫
xf x dx f t dt f t dt I
. Chọn C.
Câu 70: Đường elip phía ngoài có phương trình
22
22
1
25 15
+=
xy
và có diện tích
1
25.15= πS
Đường elip phía trong có phương trình
22
22
1
23 13
+=
xy
và có diện tích
2
23.13S
= π
Diện tích mặt đường là
12
= −SSS
Do đó kinh phí để làm đường là:
( )
12
.500,000 119.320.000=−=T SS
đồng. Chọn C.
Câu 71: Gọi O là trung điểm của MN. Chọn hệ trục tọa độ Oxy có trục Ox // BC, Oy // AB.
Khi đó đồ thị có dạng
sin=y A bx
.
Do
2 max 1 1=⇒ =⇒=
AD y A
Do hàm số tuần hoàn với chu kì
2 1 sinπ⇒ = ⇒ =b yx
.
Diện tích phần đất trồng hoa là:
0
0
2 sin 2cos 4
π
π
= =−=
∫
S xdx x
Diện tích phần đất còn lại là:
( )
2 .2 4 4 1π − = π−
. Chọn B.
Câu 72: Chọn hệ trục tọa độ như hình vẽ.
Trong đó
( )
53 53
;; ;;C0;2
22 22

−


AB
Giả sử đường cong phía trên là một Parabol có dạng
2
= ++y ax bx c
với
,,∈
abc
. Do Parabol đi qua các
điểm
( )
53 53
;; ;;0;2
22 22

−


A BC
nên ta có hệ phương trình:
25 5 3
2
42 2
25
25 5 3
0
42 2
2
2
−
− +=
=
+ += ⇔ = ⇒


=
=

a bc
a
a bc b
c
c
phương trình parabol là:
2
2
2
25
−
= +yx
Diện tích S của cửa rào sắt là diện tích phần hình phẳng giới hạn bởi đồ thị hàm số
2
2
2
25
−
= +yx
, trục hoành
và hai đường thẳng
55
;
22
−
= =xx
.
Ta có:
5
5
3
2
2
2
5
5
2
2
2 2 55
2 .2
25 25 3 6
−
−

−

= +=− + =




∫
x
S x dx x
.
Vậy ông An phải trả số tiền để làm cái cửa sắt là
700000. 6417000= =TS
đồng. Chọn C.
Câu 73: Ta có
21
= −SS S
Trong đó
1
S
là diện tích hình phẳng giới hạn bởi các đường
22
20 , , 2, 2= − = =−=
y x y xx x
được tô màu
trong hình bên,
2
S
là diện tích nửa hình tròn có bán kính bằng
25
.
( )
(
)
2
2
22
2
1
2 5 20
2
−
⇒=π − − −
∫
S x x dx
Suy ra
( )
2
19,476≈⇒Sm
Chi phí sẽ bằng
100.000 1.948.000=S
đồng. Chọn B.
Câu 74: Ta có
( ) ( ) ( ) ( )
2 2; 0
′′ ′ ′
= − =⇔=hx f x xhx f x x
.
Nhận thấy nghiệm của
( )
0
′
=hx
chính là nghiệm của
( )
′
=fx x
cũng là hoành độ giao điểm của hai đồ thị
hàm số
(
)
′
=y fx
và đường thẳng
{ }
2; 2; 4= − → = −yx x
.
Vẽ đường thẳng
=
yx
và chia đồ thị thành 2 phần diện tích hình phẳng.
Khi đó
( ) ( ) ( ) ( ) ( ) ( )
22
1
22
2 2 2 20 2 2
−−
′′
= − = = − − >⇒ > −


∫∫
S f x x dx h x dx h h h h
.
Và
( ) ( )
( ) ( ) ( ) ( )
44
2
22
2 2 2 40 2 4
′′
= − =− = − >⇒ >


∫∫
S x f x dx g x dx h h h h
Lại có
( ) ( )
( ) ( ) ( ) (
)
12 1 2
22 2 2 2 4 4 2>⇔>⇔−−>−⇔>−SS SShh hh h h
.
Vậy
( ) (
) ( )
24 2> >−hhh
. Chọn C.
Câu 75: Ta có
( ) ( ) ( ) ( ) ( )
2 2 1; 0 1
′′ ′ ′
= + + = ⇔ =−−
gx f x x gx f x x
.
Nhận thấy nghiệm của
(
)
0
′
=
gx
chính là nghiệm của
( )
1
′
=−−fx x
cũng là hoành độ giao điểm của hai đồ thị hàm số
( )
′
=y fx
và đường thẳng
{
}
1 3; 1; 3= − − → = −yx x
.
Vẽ đường thẳng
= −yx
và chia đồ thị thành 2 phần diện tích hình phẳng.
Khi đó
( )
( ) ( ) ( ) ( ) ( ) ( )
11
1
33
2 2 1 3 10 3 1
−−
′′
= − + − =− = −− >⇒ − >


∫∫
S x f x dx g x dx g g g g
Và
( ) ( )
(
) (
) (
) ( ) ( )
33
2
11
2 2 1 3 10 3 1S f x x dx g x dx g g g g
′′
= −− − = = − > ⇒ >


∫∫
Lại có
( ) ( ) ( ) ( ) ( ) ( )
12 1 2
22 31 31 3 3>⇔ > ⇔−− > − ⇔−>SS SSg ggg g g
.
Vậy
( ) ( ) ( )
331−> >g gg
. Chọn A.
Câu 76: Ta có
( ) ( ) ( ) ( )
sin ; 0 sin
′′ ′ ′
=− =⇔=gx f x xgx f x x
Nhận thấy nghiệm của
(
)
0
′
=gx
chính là nghiệm của
( )
sin
′
=fx x
cũng là hoành độ giao điểm của hai đồ
thị hàm số
( )
′
=y fx
và đường thẳng
sin 0; ;
2
π

= → = π


yx x
.
Vẽ đường thẳng
sin=
yx
và chia đồ thị thành 2 phần diện tích hình phẳng.
Khi đó
( )
(
)
(
)
( )
22
1
00
sin 0 0 0
22
ππ
ππ
 
′′
= − =− = − >⇒ >

 

 
∫∫
S x f x dx g x dx g g g g
.
Và
( )
( ) ( ) ( )
2
22
sin 0
22
ππ
ππ
ππ
 
′′
= − = = π− > ⇒ π>

 

 
∫∫
S f x x dx g x dx g g g g
.
Lại có
( ) ( )
( ) (
)
12
00
22
ππ
 
>⇔ − >π− ⇔ >π
 
 
SS g g g g g g
.
Vậy
( ) ( )
0
2
π

< π<


g gg
. Chọn B.
| 1/45

Tài liệu khác của Toán 12

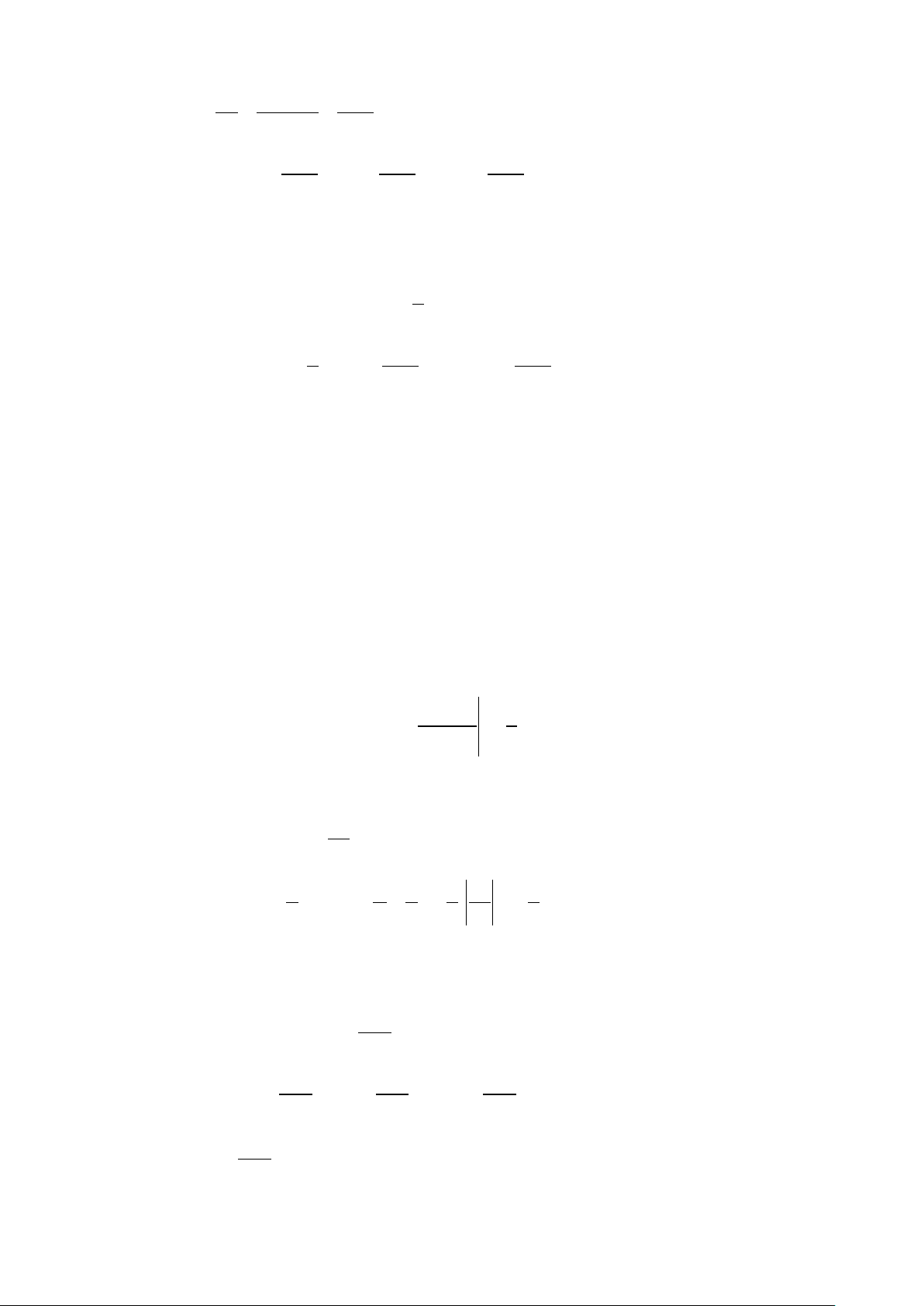
Preview text:

CHỦ ĐỀ 12: ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH A. LÝ THUYẾT
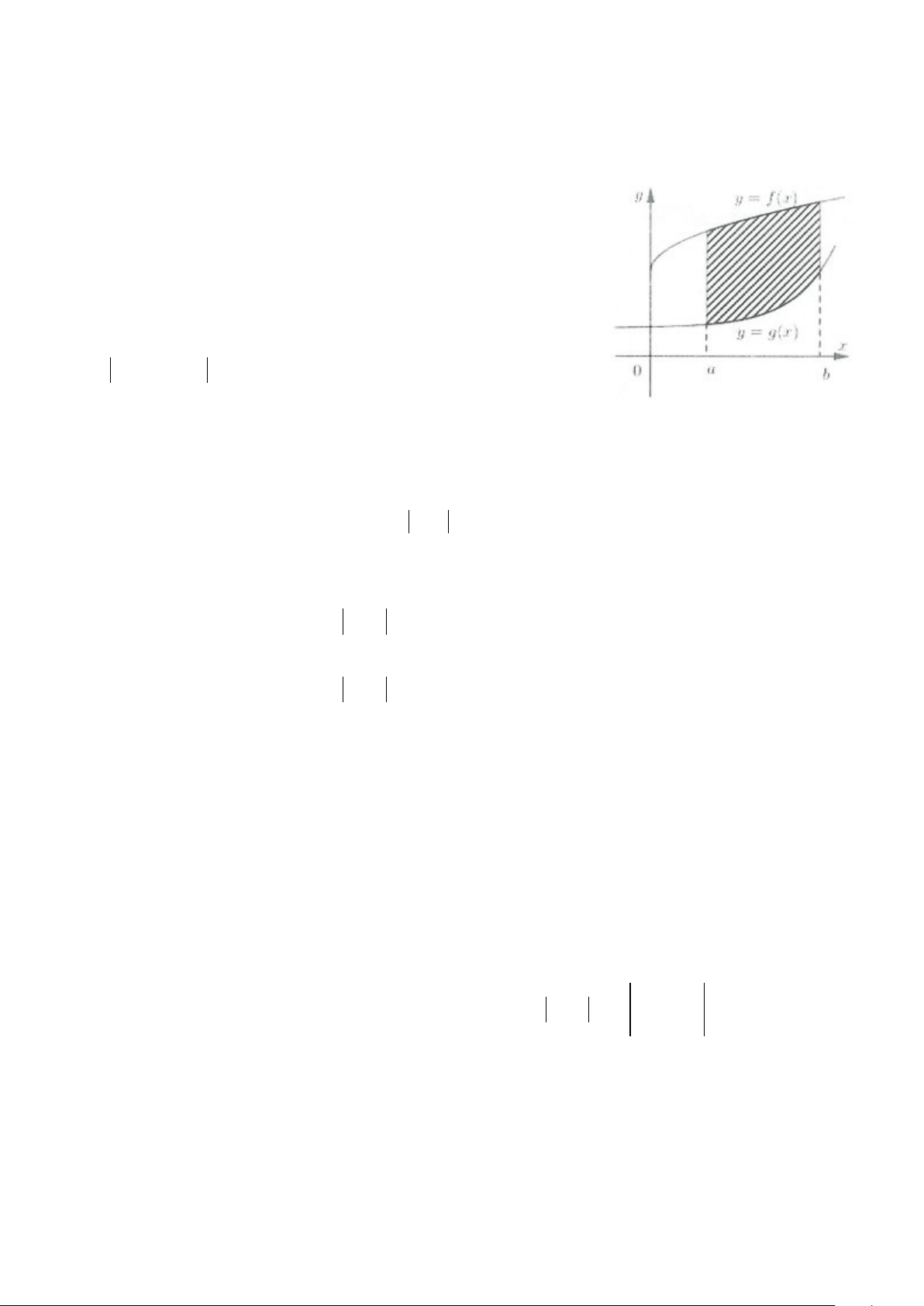
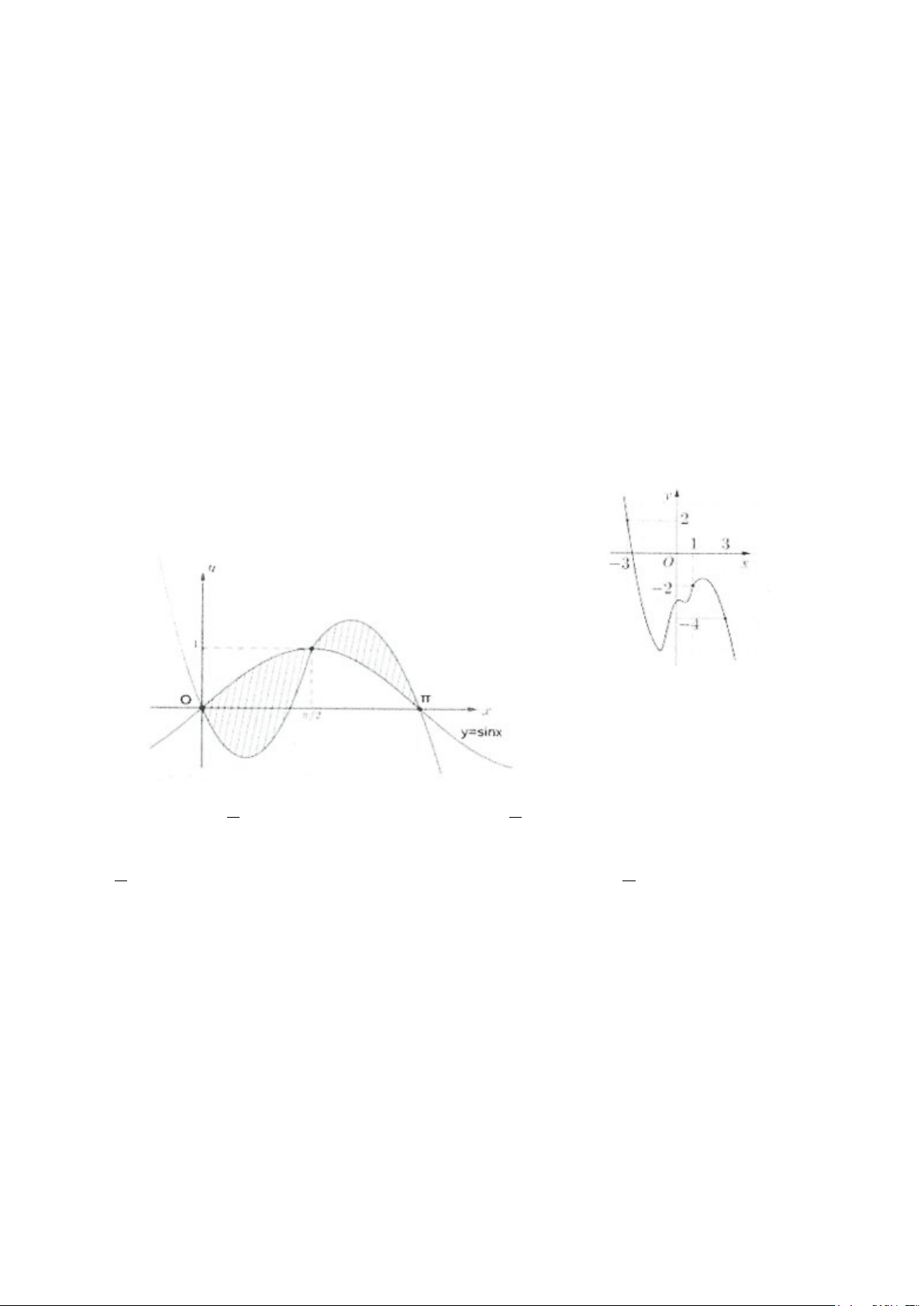
1) Công thức tính diện tích của hình phẳng giới hạn bởi hai đồ thị hàm số
Cho hai đồ thị của hai hàm số y = f (x), y = g (x) liên tục trên đoạn
[ ;ab] và hai đường thẳng x = ;ax = b(a < b). Khi đó hình phẳng giới
hạn bởi bốn đường y = f (x), y = g (x) và hai đường thẳng x = ;
a x = b có diện tích S được tính theo công thức: b
S = f (x) − ∫
g (x) dx . a
Đặc biệt: Trong trường hợp g (x) là trục hoành ( g (x) = 0 ) ta được công thức tính diện tích của hình
phẳng giới hạn bởi đồ thị hàm số y = f (x) , trục hoành và hai đường thẳng x = a, x = b là: b
S = f (x) dx ∫ (1). a
Để tính diện tích S ta phải tính tích phân (1), muốn vậy ta phải phá dấu giá trị tuyệt đối: b b
 Nếu f ( x) ≥ 0,∀x ∈[ ;
a b] thì S = f (x) dx = ∫
∫ f (x)dx . a a b b
 Nếu f ( x) ≤ 0,∀x ∈[ ;
a b] thì S = f (x) dx = (− ∫
∫ f (x))dx . a a
Muốn xét dấu của biểu thức f (x) ta thường có một số cách làm như sau:
Cách 1: Sử dụng bảng xét dấu cho f ( x) với ghi nhớ qua nghiệm bội lẻ f ( x) đổi dấu, qua nghiệm
bội chẵn f (x) không đổi dấu.
Cách 2: Dựa vào đồ thị của hàm số y = f ( x) trên đoạn [a;b] để suy ra dấu của f ( x) trên đoạn đó: - Nếu trên đoạn [ ;
a b] đồ thị hàm số y = f (x) nằm phía trên trục hoành thì f (x) ≥ 0,∀x∈[ ; a b]. - Nếu trên đoạn [ ;
a b] đồ thị hàm số y = f (x) nằm phía dưới trục hoành thì f (x) ≤ 0,∀x∈[ ; a b]. b b
Cách 3: Nếu f ( x) không đổi dấu trên [ ;
a b] thì ta có: S = f (x) dx = ∫
∫ f (x)dx . a a
Cách 4: Sử dụng máy tính CASIO, tuy nhiên xu hướng ra đề thi THPT Quốc gia sẽ hạn chế CASIO
nên cần chú ý cách giải tổng quát và hiểu rõ bản chất! Chú ý:
- Khi tính diện tích của hình phẳng giới hạn bởi hai đồ thị hàm số ta có: b b
S = f (x) − g (x) dx = ∫
∫ h(x) dx ta làm hoàn toàn tương tự như trên. a a
- Nếu đề bài không cho các đường thẳng giới hạn x = ;
a x = b ta giải phương trình f (x) = g (x) (hoặc
f (x) = 0 trong trường hợp g (x) là trục hoành) để tìm cận của tích phân.
2) Ứng dụng tính diện tích hình tròn và hình Elip
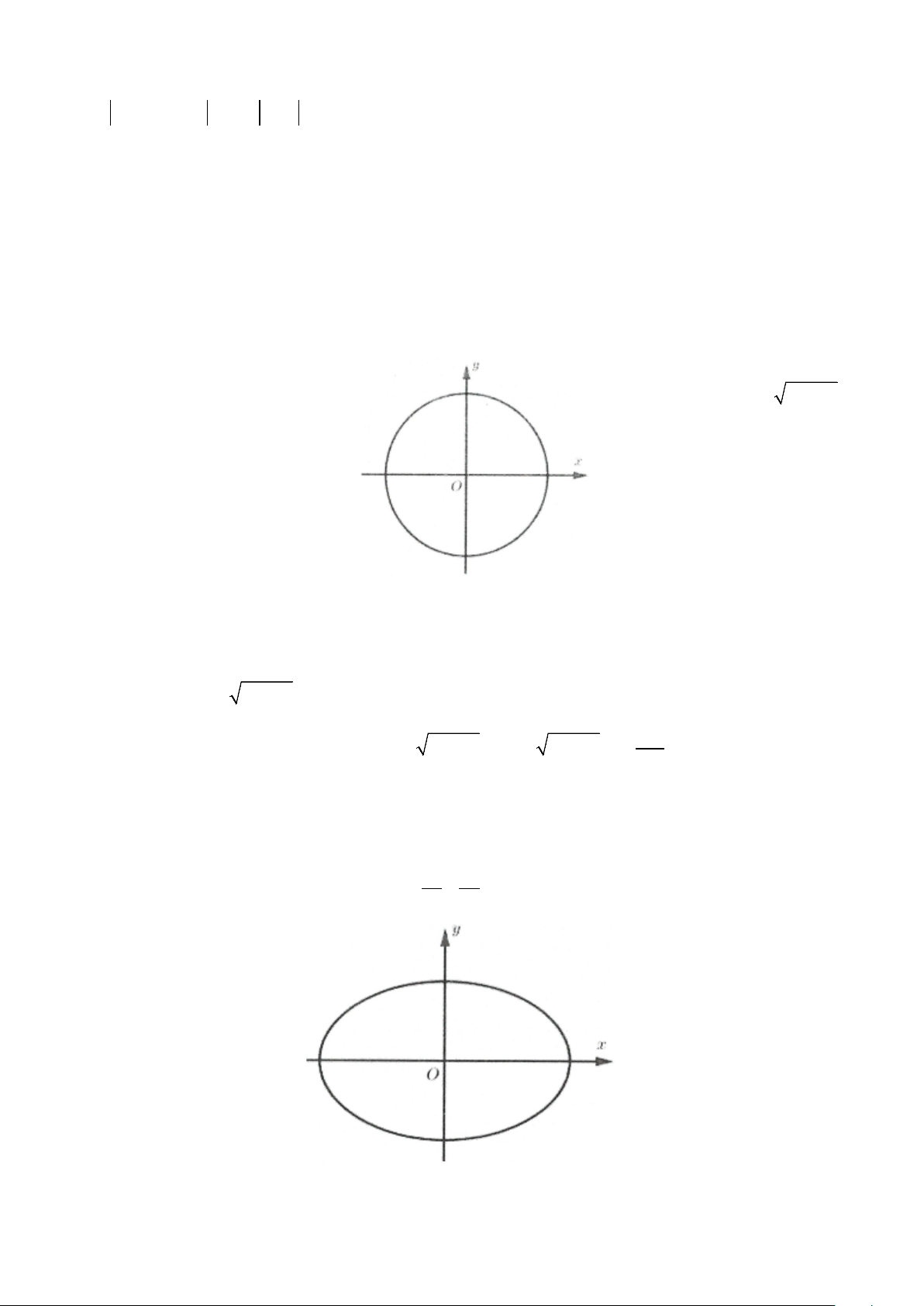
a) Tính diện tích hình tròn
Trong hệ tọa độ Oxy cho đường tròn có phương trình: 2 2 2
x + y = r (r > 0) . Khi đó hình tròn đó có diện tích là: 2 S = πr . 2 2 2 2 2 Ta có
x + y = r ⇔ y = ± r − x Với y ≥ 0, ta có: 2 2
y = r − x có đồ thị là nửa đường tròn phía trên trục hoành. r r 2 Bằng cách đặt π
x = r sin t ta có diện tích 2 2 2 2 = − = 2 − = r S r x dx r x dx . 1 ∫ ∫ − 2 r 0 Do đó 2
S = 2S = πr . 1
b) Tính diện tích hình Elip 2 2
Trong hệ tọa độ Oxy cho elip có phương trình: x + y =1,0 < b < a . 2 2 a b
Chứng minh tương tự ta có diện tích của elip là: S = πab (đvdt). II. VÍ DỤ MINH HỌA
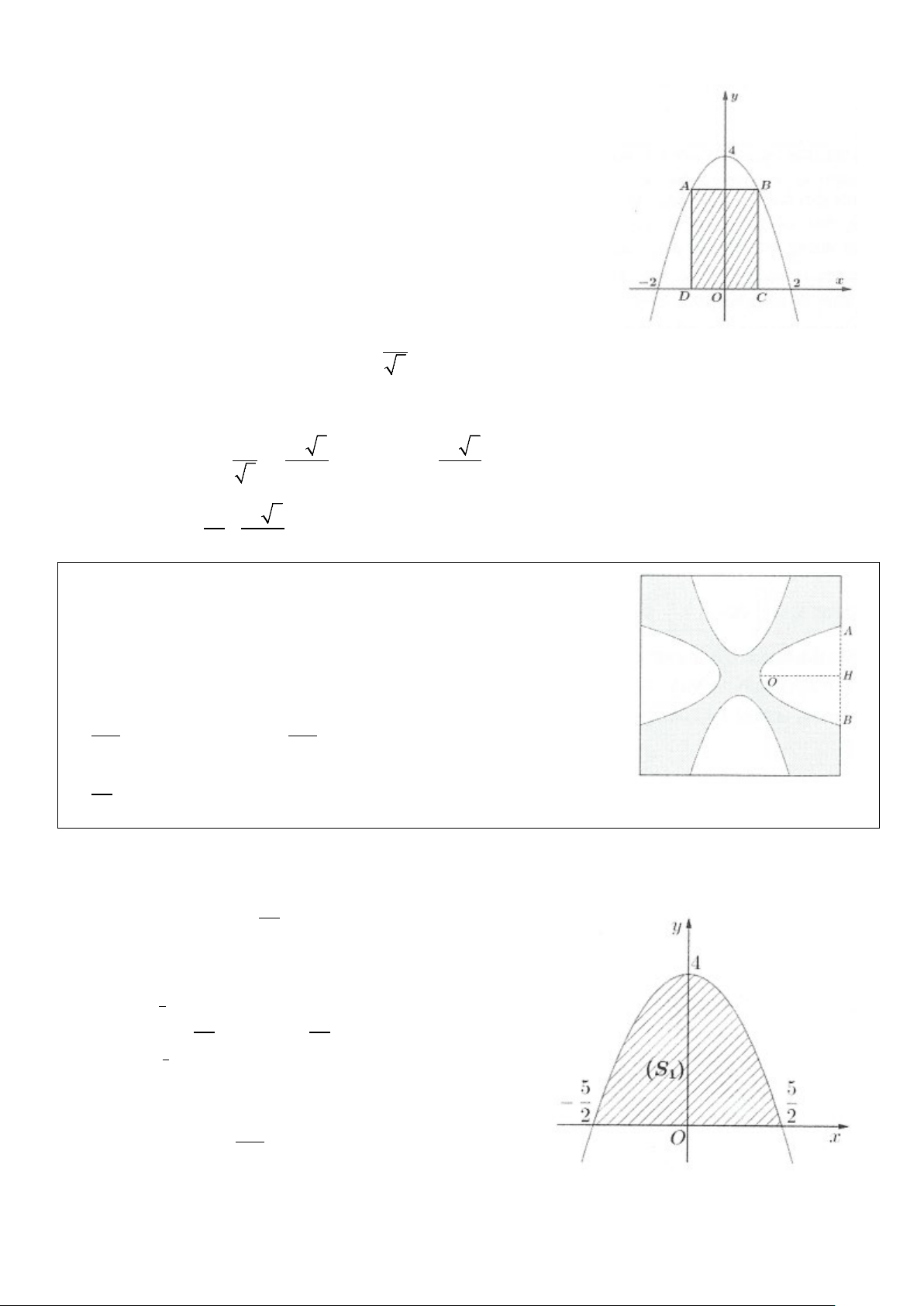
Ví dụ 1: Tính diện tích hình phẳng trên được giới hạn bởi đồ thị hàm số 2
y = −x + 2x − 2, trục hoành và
các đường thẳng x = 0, x = 3. Lời giải 3
Diện tích S của hình phẳng trên là 2
S = −x + 2x − 2 ∫ dx . 0 Ta có: 2
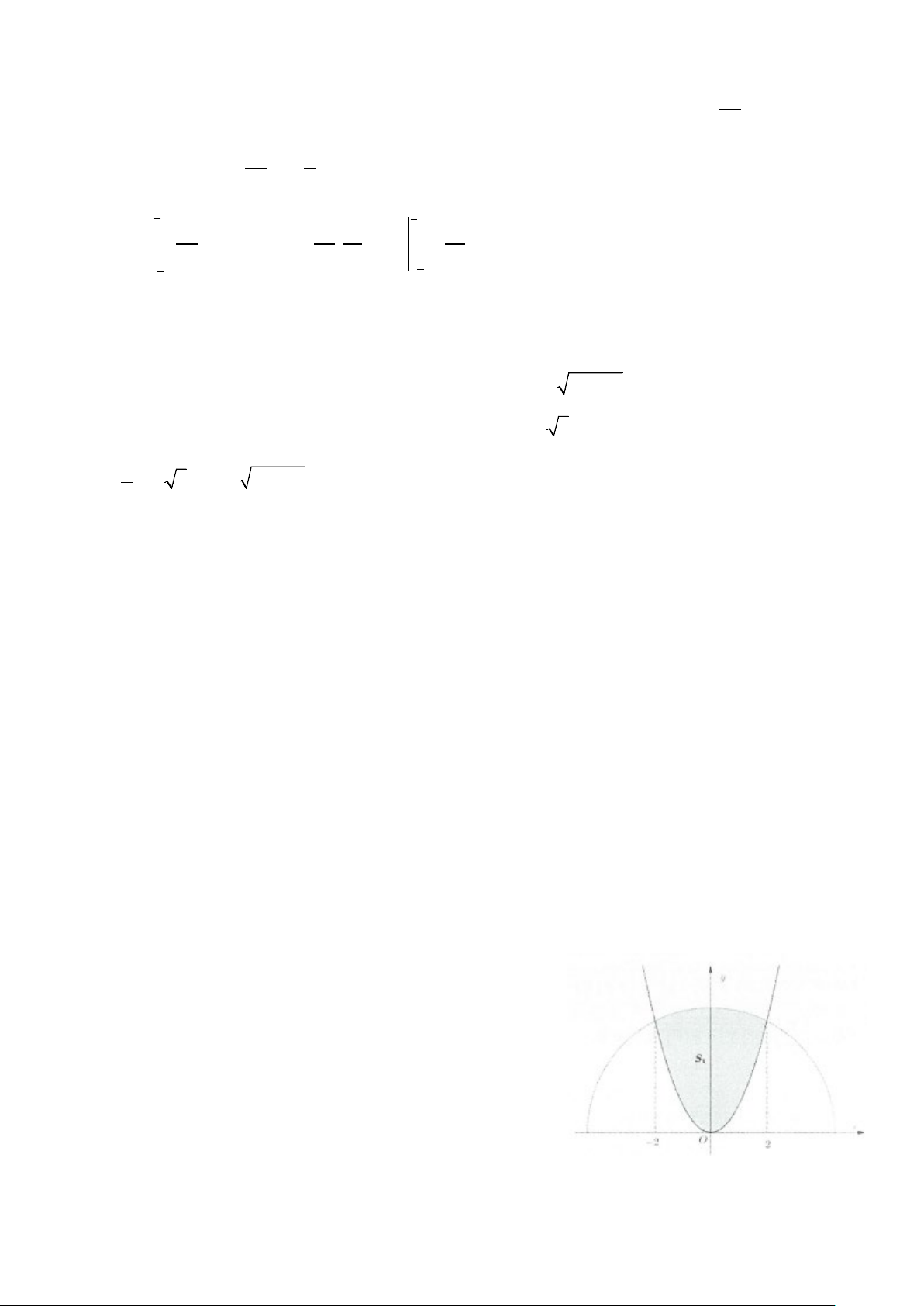
−x + 2x − 2 ≤ 0,∀x ∈[0; ] 3 . 3 3 3  x
S = −x + 2x − 2 dx = ∫ ∫(x −2x+ 2) 3 2 2 2
dx =  − x + 2x = 6 (đvdt).  3 0 0  0
Ví dụ 2: Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số y = f (x) −x − 2 = , trục hoành và các x −1
đường thẳng x = 1, − x = 0 . Lời giải 0
Gọi S là diện tích của hình phẳng trên, ta có: − − 2 = ∫ x S dx x − − 1 1
Ta có: −x − 2 ≥ 0,∀x∈[ 1; − 0] x −1 0 0 0 −x − 2  −x − 2  −(x − ) 0 1 − 3 Do đó:  3 S dx dx dx 1  = = = = − − ∫ ∫   ∫ ∫   dx x −  x −  x −  x − − 1 − 1 − 1 − 1 1 1 1 1 
= (−x −3ln x −1) 0 = 3ln 2 −1 (đvdt). 1 −
Ví dụ 3: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 2
y = x − x +1, y = x +1 là A. 4 − B. 4 C. 1 D. 2 3 3 3 Lời giảix = 0
Phương trình hoành độ giao điểm 2 đồ thị là: 2 2
x − x +1 = x +1 ⇔ x − 2x = 0 ⇔  x = 2 2 2 2 Diện tích cần tìm là: 2 2
S = x − x +1− x −1 dx = x − 2x dx = ∫ ∫ ∫( 2
2x − x )dx 0 0 0 2 3  x  2 4
=  x −  = . Chọn B.  3  3 0
Ví dụ 4: Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số = x
y e + x và các đường thẳng
x − y +1 = 0, x = ln 5 .
A. S = 5 − ln 4
B. S = 4 − ln 5 C. S = 4 + ln 5 D. S = 5 + ln 4 Lời giải
Ta có: x − y +1 = 0 ⇔ y = x +1.
Phương trình hoành độ giao điểm của hai đồ thị là: x + = +1 ⇔ x e x x e =1 ⇔ x = 0 ln5 ln5
Diện tích hình phẳng cần tìm là: = x −1 = ∫
∫ ( x − )1 = ( x S e dx e dx
e − x) ln5 = 4 − ln5. Chọn B. 0 0 0
Ví dụ 5: Tính diện tích hình phẳng giới hạn bởi các đường 3 2
y = x +11x − 6; y = 6x ; x = 0; x = 2 . Lời giải
Đặt f (x) = ( 3 x + x − ) 2 3 2
11 6 − 6x = x − 6x +11x − 6 f (x) x =1; x = 2 = 0 ⇔ 
. Gọi S là diện tích phần giới hạn bởi các đường ta có: x = 3 (loai) Bảng xét dấu: x 0 1 2 h(x) − 0 + 0 1 2 Khi đó S = −∫( 3 2
x − 6x +11x − 6)dx + ∫( 3 2
x − 6x +11x − 6)dx 0 1 1 2 4 2 4 2  x x   x x  3 11 3 11 5 = − − 2x +
− 6x +  − 2x + − 6x = (đvdt).  4 2   4 2  2 0 1
Ghi nhớ: Nếu phương trình f (x) = 0 có k nghiệm phân biệt x ; x ...x thuộc ( ;
a b) thì trên mỗi khoảng 1 2 k
( ;ax , x ;x ,... x b biểu thức f (x) có dấu không đổi. k ; 1 ) ( 1 2 ) ( ) b
Khi đó để tính tích phân S = ∫ f (x) dx ta có thể tính như sau: a b x x b S = f (x) 1
dx = f (x) 2
dx + f (x)dx +...+ ∫ ∫ ∫
∫ f (x)dx . a a 1 x k x 1 2
Áp dụng với bài trên ta có: S = ∫( 3 2
x − 6x +11x − 6)dx + ∫( 3 2
x − 6x +11x − 6)dx . 0 1
Ví dụ 6: Tính diện tích hình phẳng giới hạn bởi các đường: 2
y − 2y + x = 0; x + y = 0 . Lời giảiy = 0
Phương trình tung độ giao điểm là: 2
2y − y = −y ⇔  .  y = 3
Gọi S là diện tích hình phẳng giới hạn với các đường đã cho ta có: 3 3 3 3 3 2  y y  2 S = y − y − ∫ (−y) 2 dy = y − y dy = ∫ ∫( 2 − y + y) 3 9 2 3 3 dy = − +  = (đvdt).  3 2  2 0 0 0 0
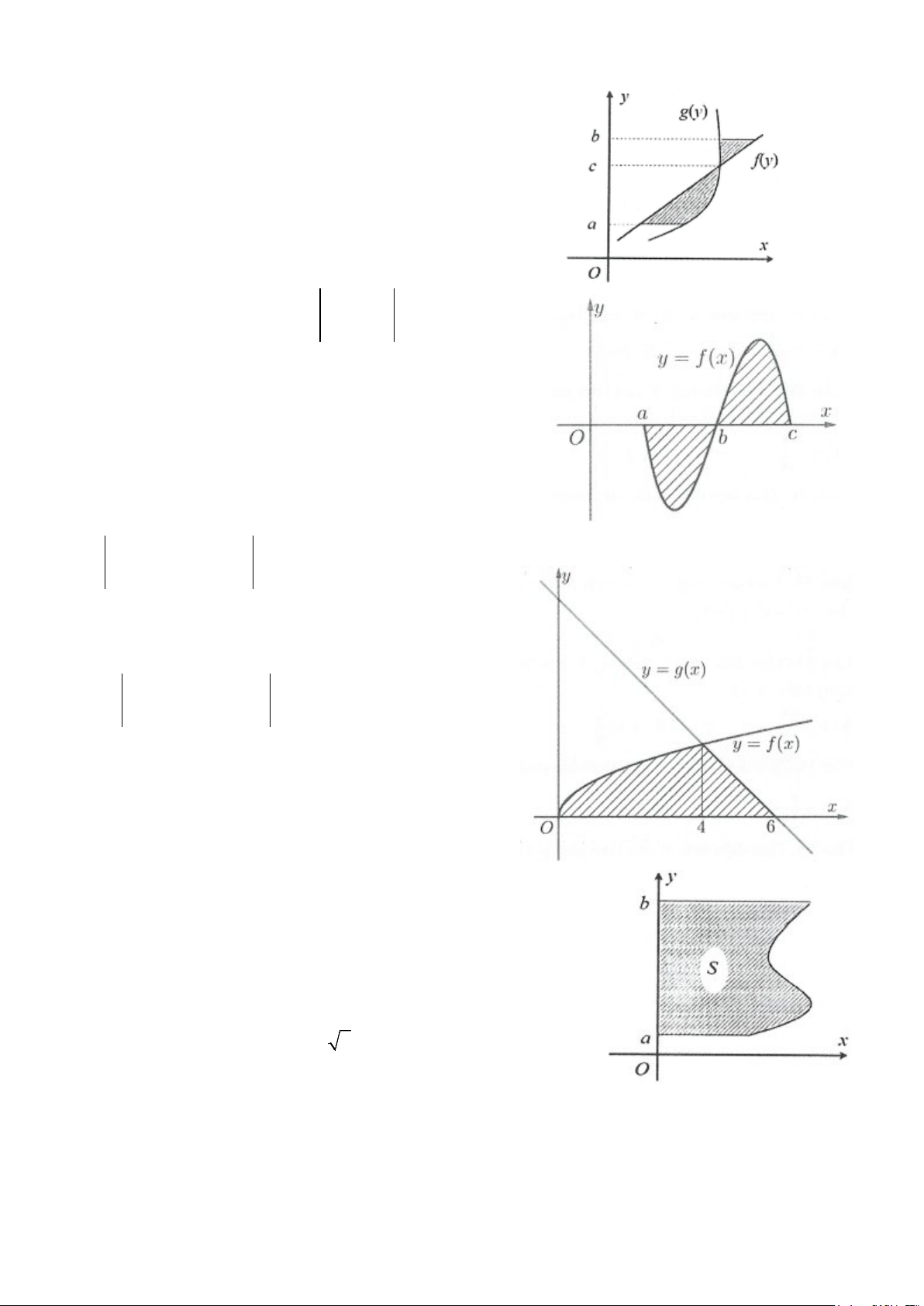
Nhận xét: Đối với bài toán này việc tính theo dx gặp khá nhiều khó khăn, do đó ta nên tính diện tích hình
phẳng theo dy bằng cách coi x là hàm của biến y, diện tích hình phẳng giới hạn bởi các đường cong
x = g ( y) , x = h( y) (g và h là hai hàm liên tục trên đoạn [ ;
c d]) và hai đường thẳng y = c, y = d là: d
S = g ( y) − ∫
h( y) dy . c
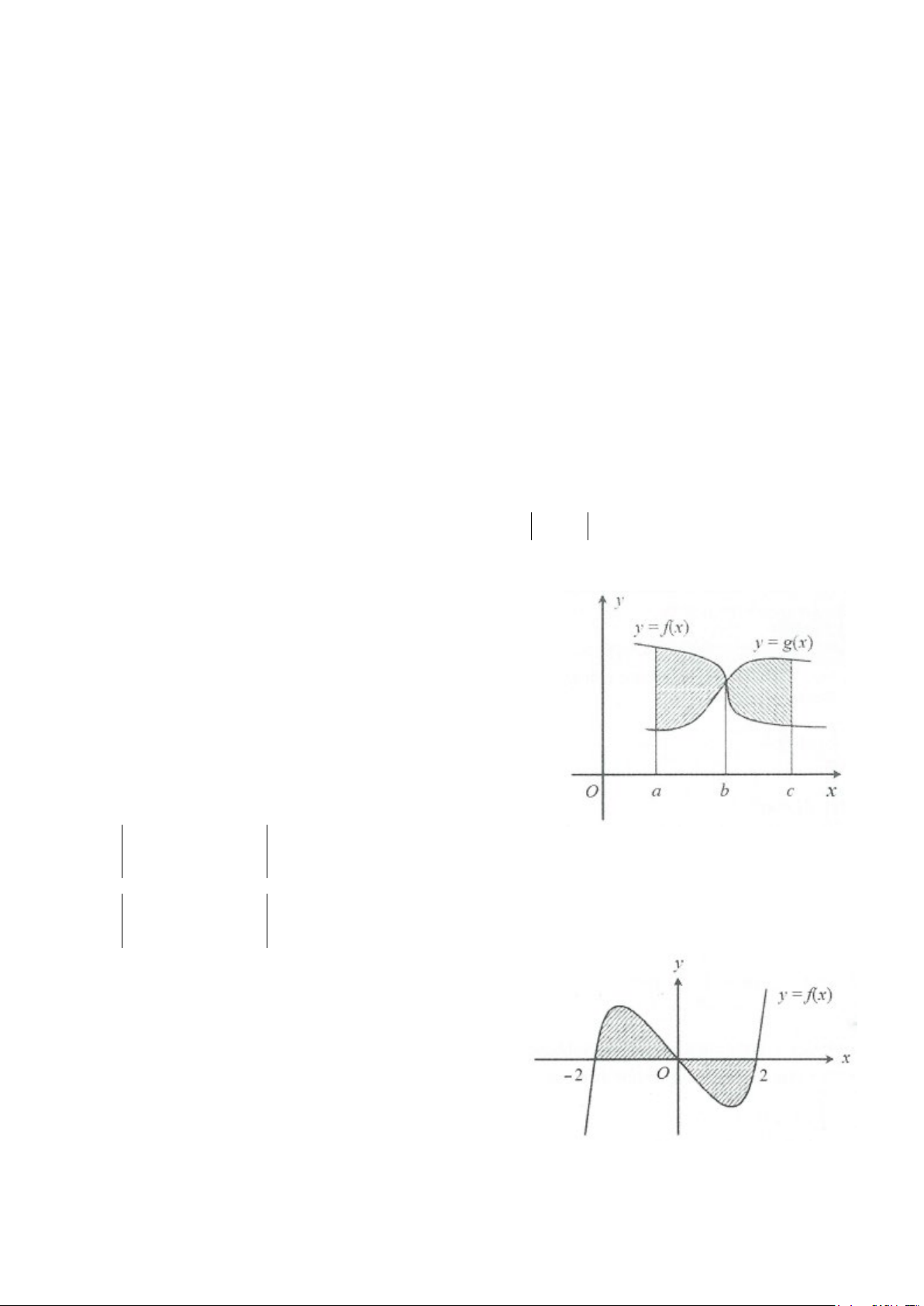
Ví dụ 7: Cho đồ thị hàm số y = f (x) trên đoạn [ 2;
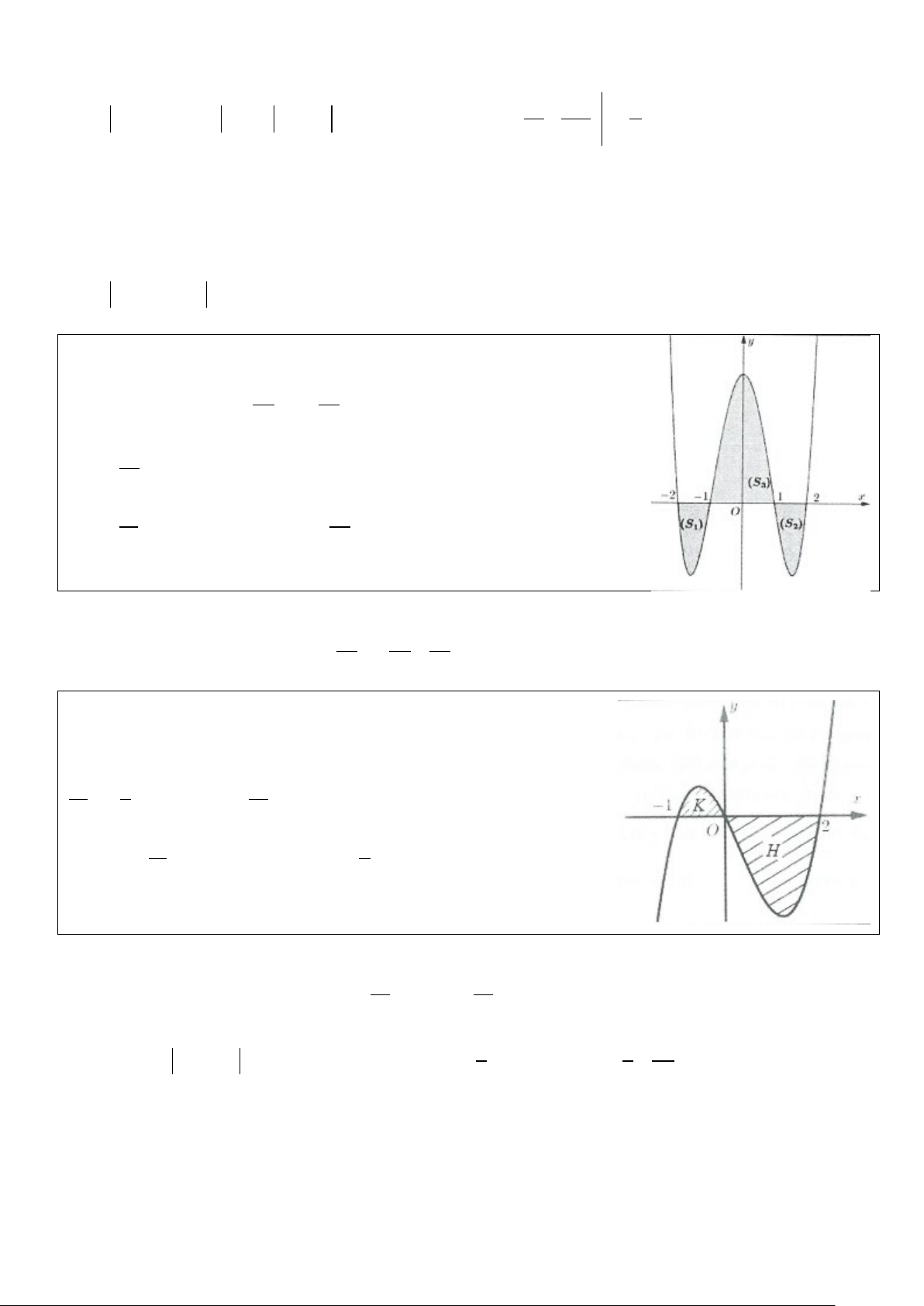
− 2] như hình vẽ ở bên 2 và có diện tích 22 76 S = S = , S =
. Tính tích phân I = ∫ f (x)dx . 1 2 3 15 15 2 − A. 32 I = B. I = 8 15 C. 18 I = D. 32 I = − 5 15 Lời giải 2
Ta có I = f (x) 76 22 32
dx = S − S − S = − 2. = ∫ . Chọn A. 3 1 2 − 15 15 15 2
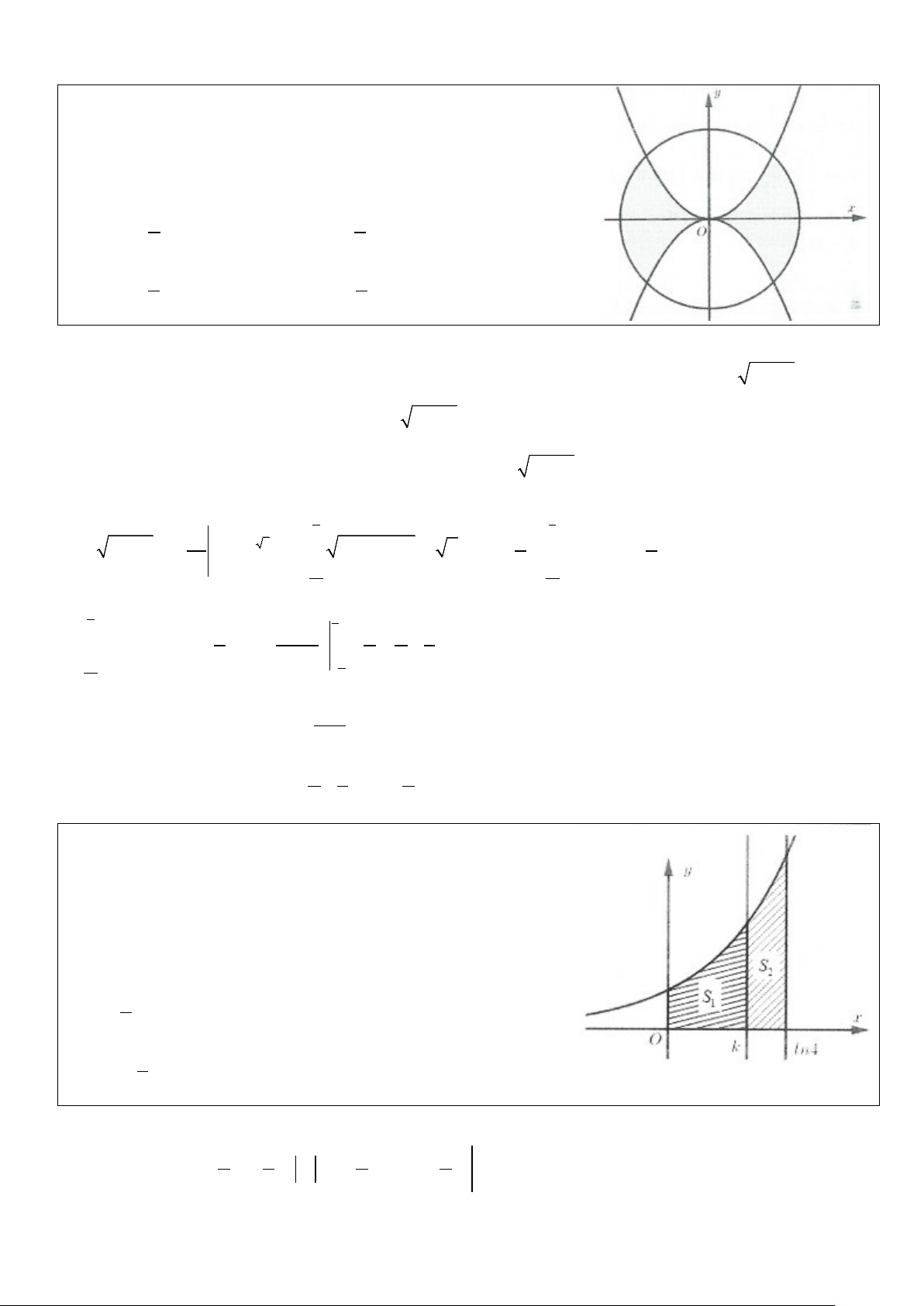
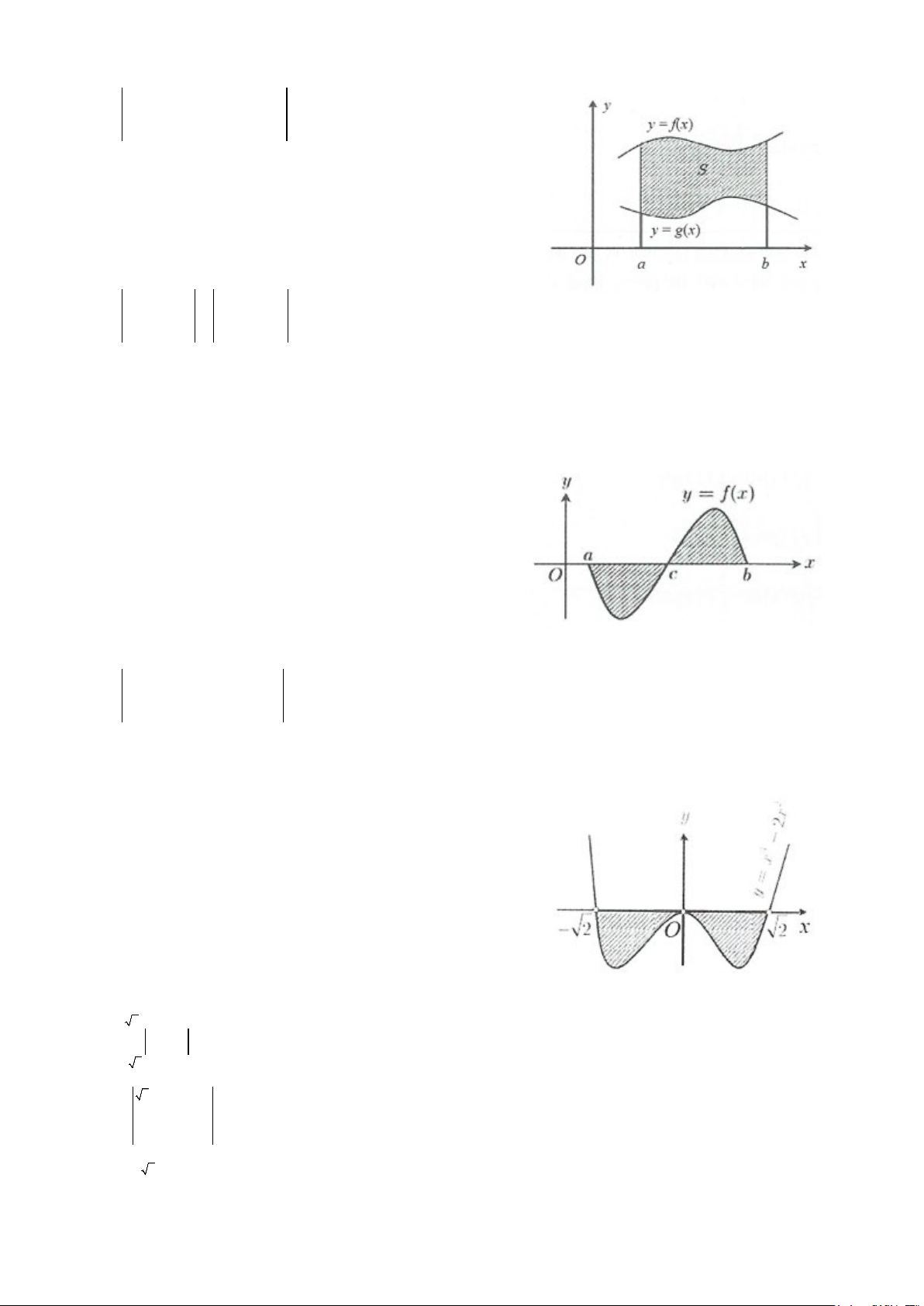
Ví dụ 8: Cho hàm số f (x) liên tục trên ℝ. Đồ thị hàm số y = f ′(x)
được cho như hình bên. Diện tích các hình phẳng (K ),(H ) lần lượt là
5 và 8 . Biết f (− ) 19 1 = , tính f (2) . 12 3 12 A. f ( ) 11 2 = B. f ( ) 2 2 = − 6 3 C. f (2) = 3 D. f (2) = 0 Lời giải 0
Ta có: K = f ′
∫ (x)dx = f ( )− f (− ) 5 = ⇒ f ( ) 5 0 1 0 = + f (− ) 1 = 2 . − 12 12 1 2 2
Lại có: H = f (x)dx = − f (x)dx = f ( ) − f ( ) 8 = ⇒ f = f ( ) 8 2 0 2 (2) 0 − ′ ′ − = ∫ ∫ . Chọn B. 3 3 3 0 0
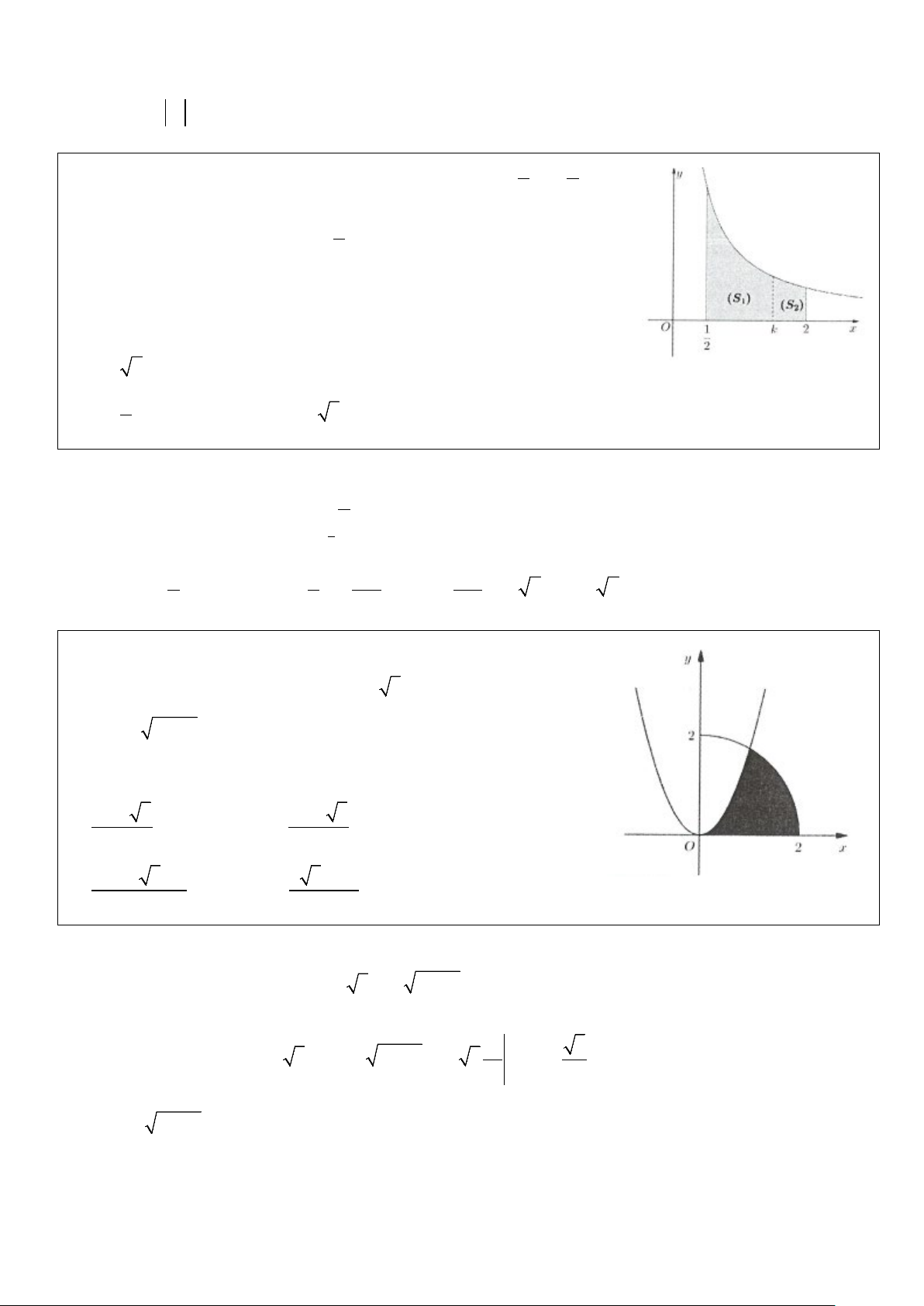
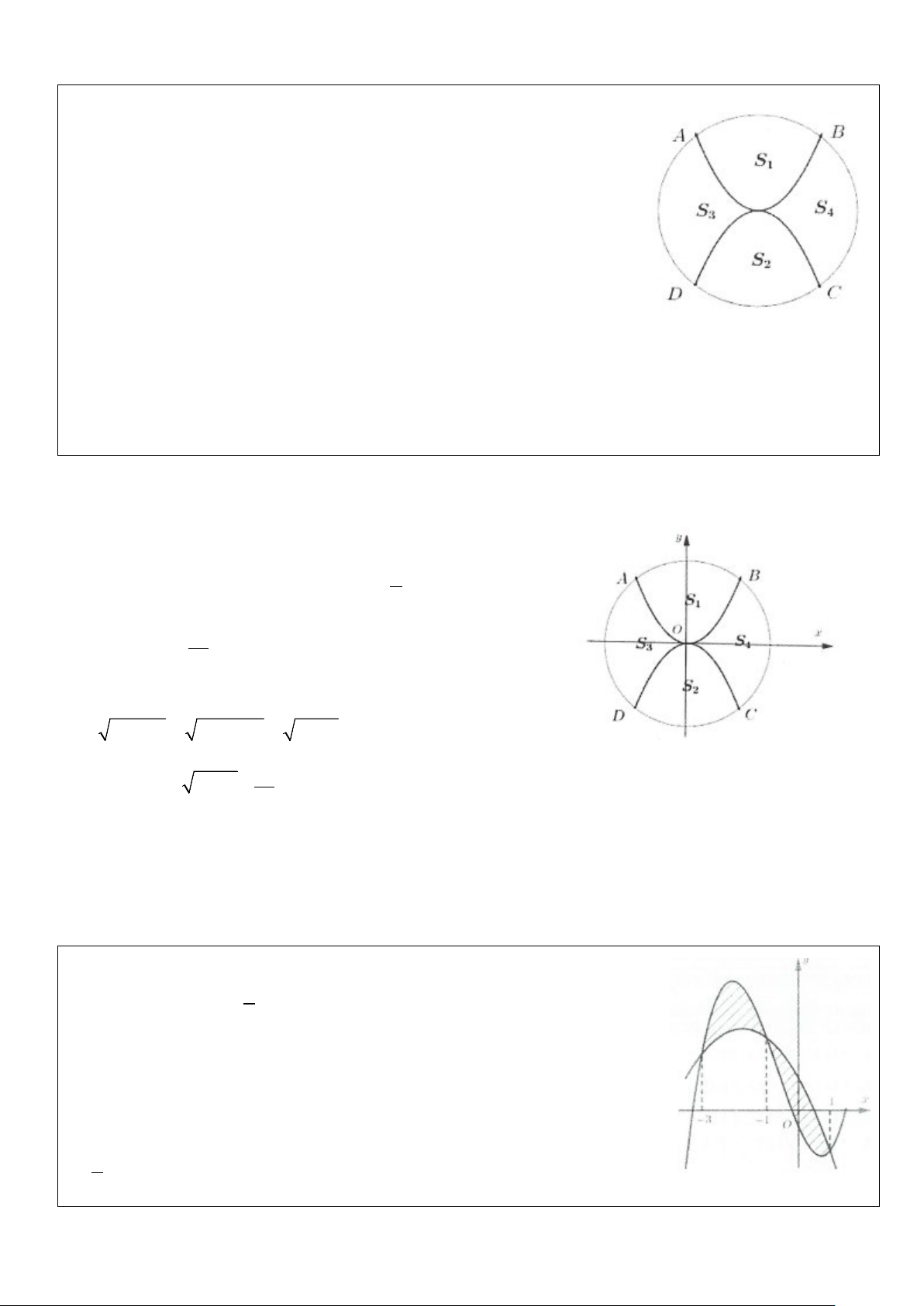
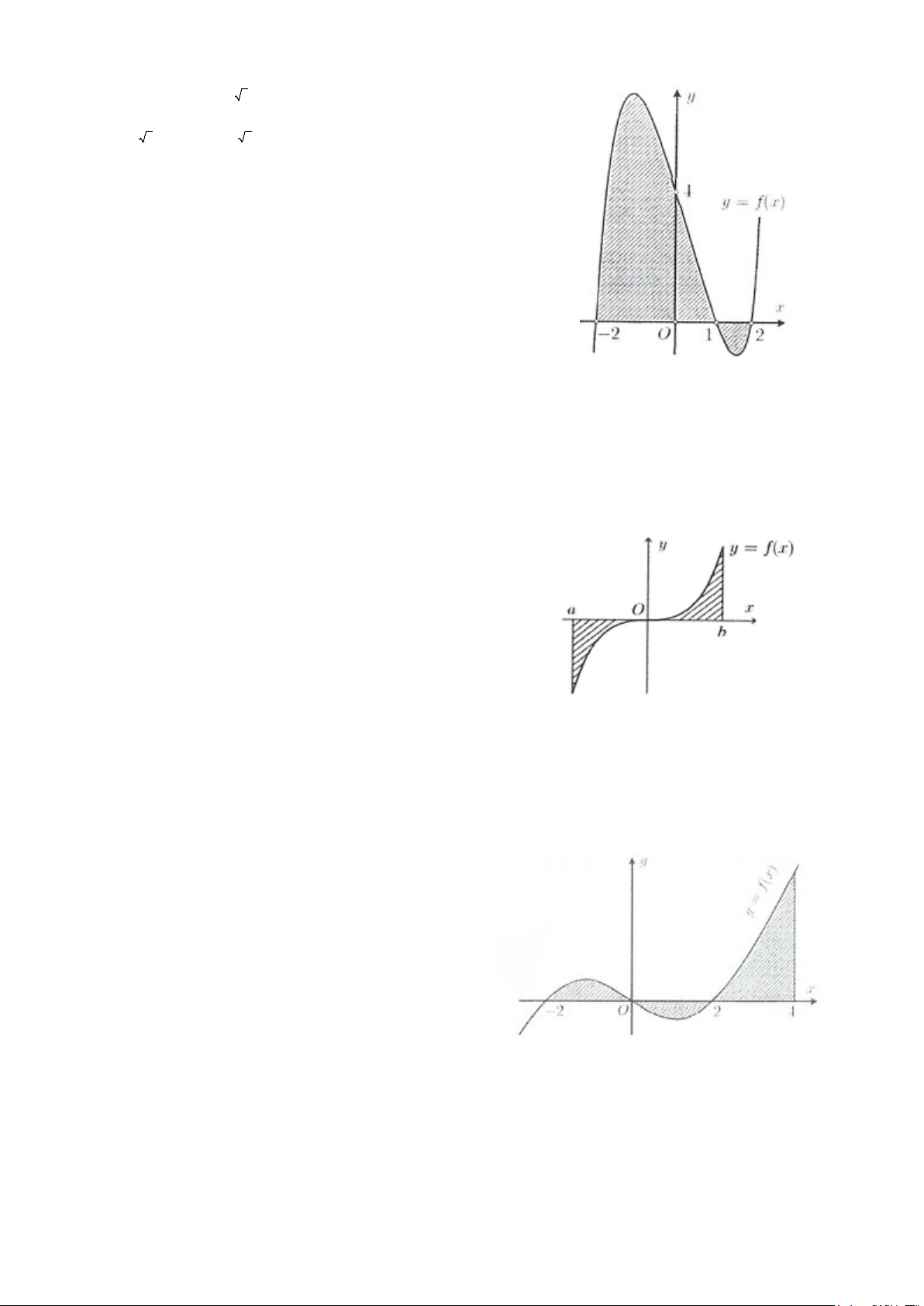
Ví dụ 9: Cho (H ) là hình phẳng giới hạn bởi hai parabol 2 y = x và 2
y = −x đường tròn có phương trình 2 2
x + y = 2 (phần tô đậm trong
hình vẽ). Tính diện tích S của hình (H ) A. 2 S = π + B. 2 S = 2π − 3 3 C. 2 S = π − D. 2 S = 2π + 3 3 Lời giải
Xét phần tô đậm nằm phía trên trục Ox, nửa đường tròn phía trên Ox có phương trình 2 y = 2 − x .
Giải phương trình hoành độ giao điểm: 2 2 4 2 2
x = 2 − x ⇔ x + x − 2 = 0 ⇔ x =1 ⇔ x = 1 ± 1
Diện tích phần không tô đậm phía trên trục hoành là: S = ( 2 2 2 − x − ∫ x )dx 1 − π π 1 1 3 4 2 x x= t 2 = − x dx −  → − td ( t) 4 2 sin 2 2 2 2 2 2sin
2 sin − = 2cos tdt − ∫ ∫ ∫ − 3 − −π 3 −π 3 1 1 4 4 π π 4 = ∫ ( + t) 4 2  sin 2t  2 π 1
1 cos 2 dt − = t + − = + 3  2  π −π  − 3 2 3 4 4 2
Diện tích nửa đường tròn là π ′ = R S = π . 2
Khi đó S = 2 S S . Chọn C. H ( ′− )  π 1  2 ( ) = 2 π − − = π −  2 3    3
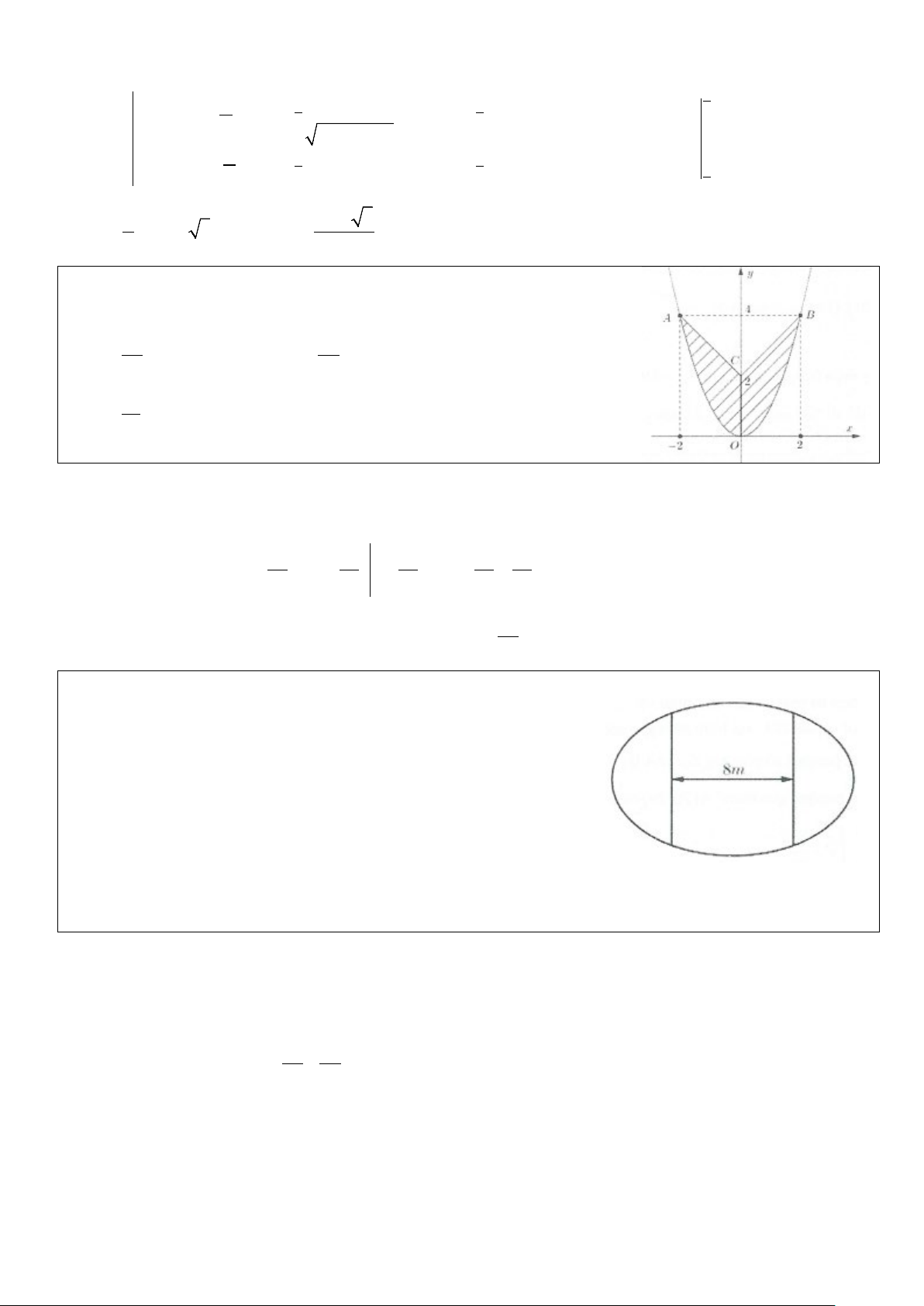
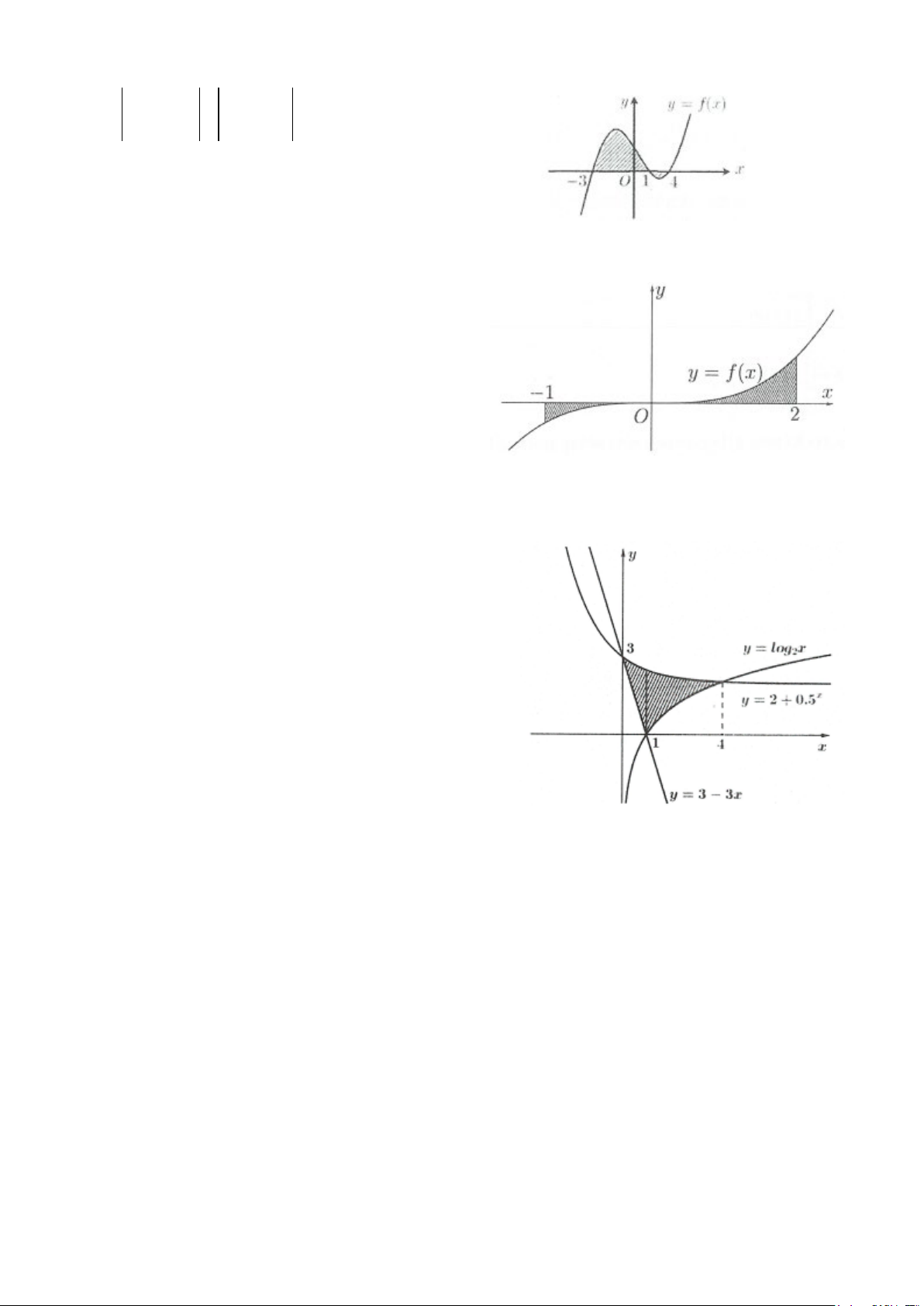
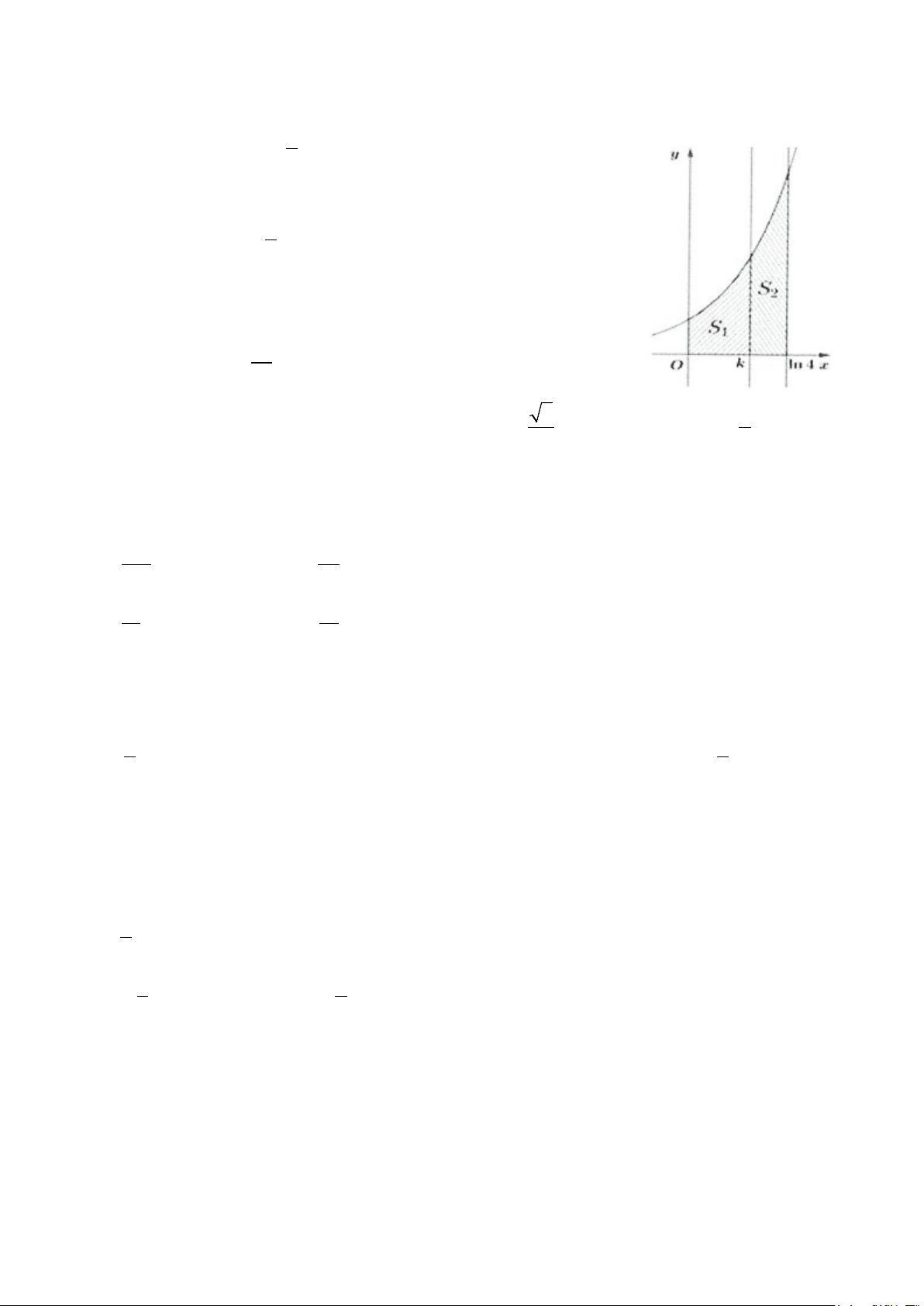
Ví dụ 10: Cho hình thang cong (H ) giới hạn bởi các đường = x
y e , y = 0, x = 0 và x = ln 4 . Đường thẳng x = k (0 < k < ln 4)
chia (H ) thành hai phần có diện tích là S và S như hình vẽ 1 2
bên. Tìm k để S = 2S . 1 2 A. 2 k = ln 4 B. k = ln 2 3 C. 8 k = ln D. k = ln 3 3 Lời giải ln 4 ln 4 ln 4 Do 2 2 x 2 x 2 = 2 ⇒ = = = = x S S S S e dx e dx e = 2 . 1 2 1 3 3 ∫ 3 ∫ 3 0 0 0 k Do đó = x
= k −1 = 2 ⇔ k S e dx e
e = 3 ⇔ k = ln 3. Chọn D. 1 ∫0
Ví dụ 11: Cho hình thang (H ) giới hạn bởi các đường 1 1
y = , x = , x = 2 x 2
và trục hoành. Đường thẳng  1 x k k 2 = < < 
chia (H ) thành hai phần có 2   
diện tích là S và S như hình vẽ dưới đây. Tìm tất cả giá trị thực của k để 1 2 S = 3S 1 2 A. k = 2 B. k =1 C. 7 k = D. k = 3 5 Lời giải 2
Gọi S là diện tích hình (H ) 1 ⇒ S = dx = 2ln 2 ∫ . 1 x 2 2 Lại có 1 1 ln 2 ln 2 S =
dx = ln 2 − ln k = S = ⇒ ln k =
= ln 2 ⇒ k = 2 . Chọn A. 2 ∫ x 4 2 2 k
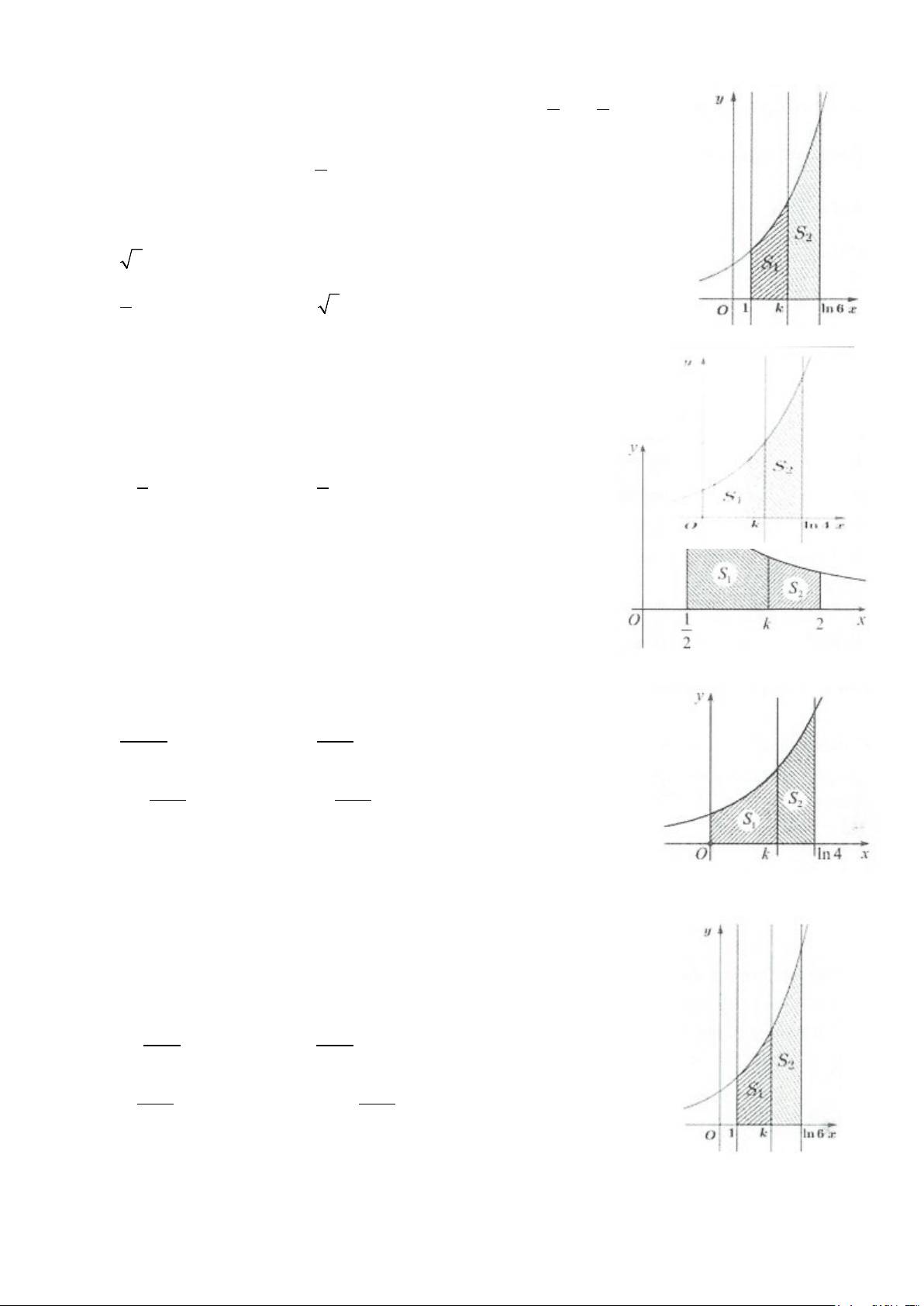
Ví dụ 12: [Đề tham khảo Bộ giáo dục và Đào tjao 2018] Cho (H )
là hình phẳng giới hạn bởi parabol 2
y = 3x , cung tròn có phương trình 2
y = 4 − x (với 0 ≤ x ≤ 2) và trục hoành (phần tô đậm trong
hình vẽ). Diện tích của (H ) bằng: A. 4π + 3 B. 4π − 3 12 6 C. 4π + 2 3 − 3 D. 5 3 − 2π 6 3 Lời giải 0 ≤ x ≤ 2
Phương trình hoành độ giao điểm là: 2 2
3x = 4 − x ⇒  ⇔ x =1. 4 2 3  x = 4 − x 1 1 2 3 Dựa vào hình vẽ ta có: 2 2 3 = 3 + 4 − = 3 + = + ∫ ∫ x S x dx x dx I I . 1 1 3 3 0 1 0 2 Với 2 I =
4 − x dx , sử dụng CASIO hoặc đặt x = 2sin t ⇒ dx = 2costdt 1 ∫1 π π π π 2 x =1⇒ t = 2 2 Đổi cận 6 2 ⇒ I =
4 − 4sin t.2costdt = 2 1+ cos 2t dt = 2t − sin 2t 1 ∫ ∫ ( ) ( ) x = 2 π π π ⇒ t = 6 6 2 π 6 1 π − ⇒ I = 4π − 3 3 . Do đó 4 3 S = . Chọn B. 1 ( ) 6 6
Ví dụ 13: Tính diện tích S của phần hình phẳng giới hạn bởi đường
Parabol đi qua gốc tọa độ và hai đoạn thẳng AC và BC như hình vẽ bên: A. 25 S = B. 20 S = 6 3 C. 10 S = D. S = 9 3 Lời giải
Gọi S là diện tích hình phẳng giới hạn bởi các đường 2
y = x , y = x + 2, x = 0, x = 2 . 1 2 2
⇒ S = ∫(x + − x ) 2 3 2 3  x x  2 2 2 10 2
dx =  + 2x −  = + 2.2 − = . 1  2 3  2 3 3 0 0
Khi đó diện tích hình phẳng phần gạch chéo là 20 S = 2.S = . Chọn B. 1 3
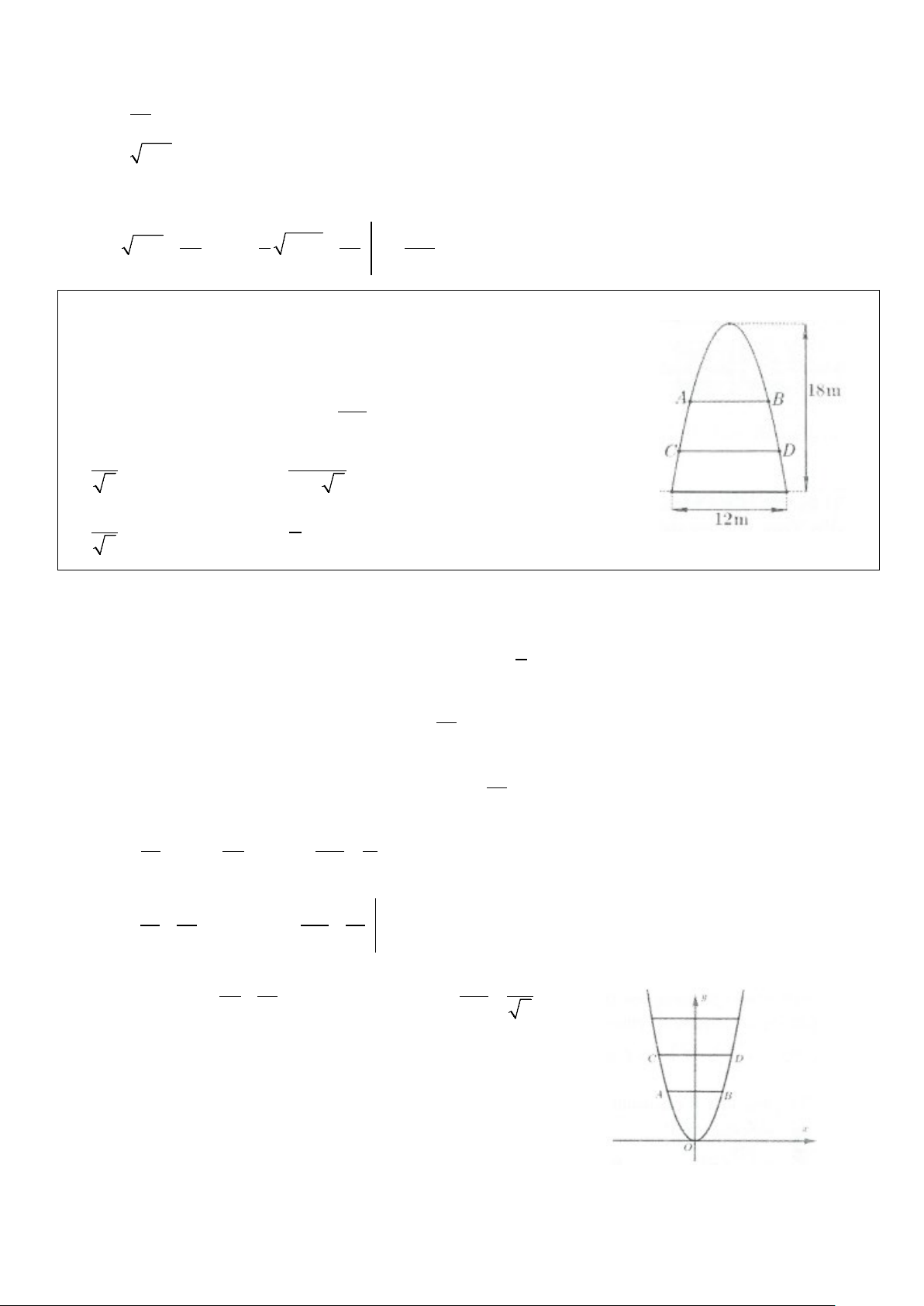
Ví dụ 14: Ông An có một mảnh vườn hình elip có độ dài trục lớn
bằng 16m và có độ dài trục bé bằng 10m. Ông muốn trồng hoa trên
một dải đất rộng 8m và nhận trục bé của elip làm trục đối xứng (như
hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng/1 2 m .
Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền
được làm tròn đến hàng nghìn). A. 7.862.000 đồng B. 7.653.000 đồng C. 7.128.000 đồng D. 7.826.000 đồng Lời giải
Chọn hệ trục như hình vẽ với 2a =16;2b =10
Suy ra a = 8;b = 5 . 2 2
Khi đó phương trình elip là: x + y =1. 64 25 2
Xét đường cong nằm phía trên trục Ox có phương trình là = 25 1− x y . 64 4 2 Ta có: x   π π  = 5 1− ∫ x S
dx . Đặt sin t = t ∈ −  ; suy ra 1 costdt = dx . 8    2 2   8 − 64 4   1 x 4 sin − π = − ⇒ t = ⇒ t = − Đổi cận 2 6 . Do đó 1 x 4 sin π = ⇒ t = ⇒ t = 2 6 π π 6 6 2 2 S = 5
1− sin t.8costdt = 40 cos ∫ ∫ tdt π π − − 6 6 π π 6 = ∫ ( + t) 6  sin 2t  20 20 1 cos 2 dt = 5 π t + = +   10 3 .  2 −π π  3 − 6 6
Vậy diện tích trồng hoa là 40 S 2 π = S = + m . T 20 3 ( 2 ) 3
Do đó số tiền ông An cần để trồng hoa là:
T = S .100.000 ≈ . Chọn B. T 7.653.000
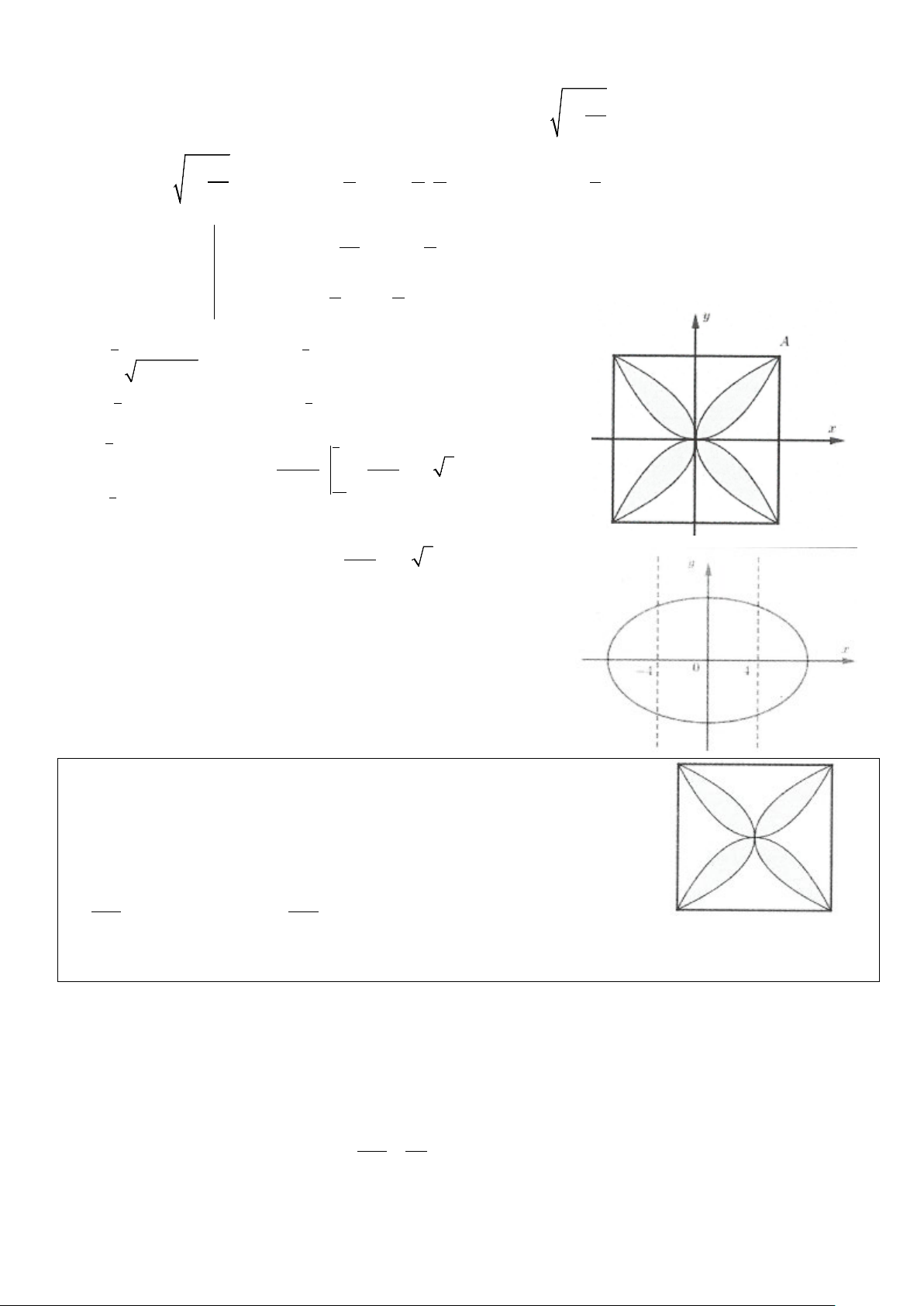
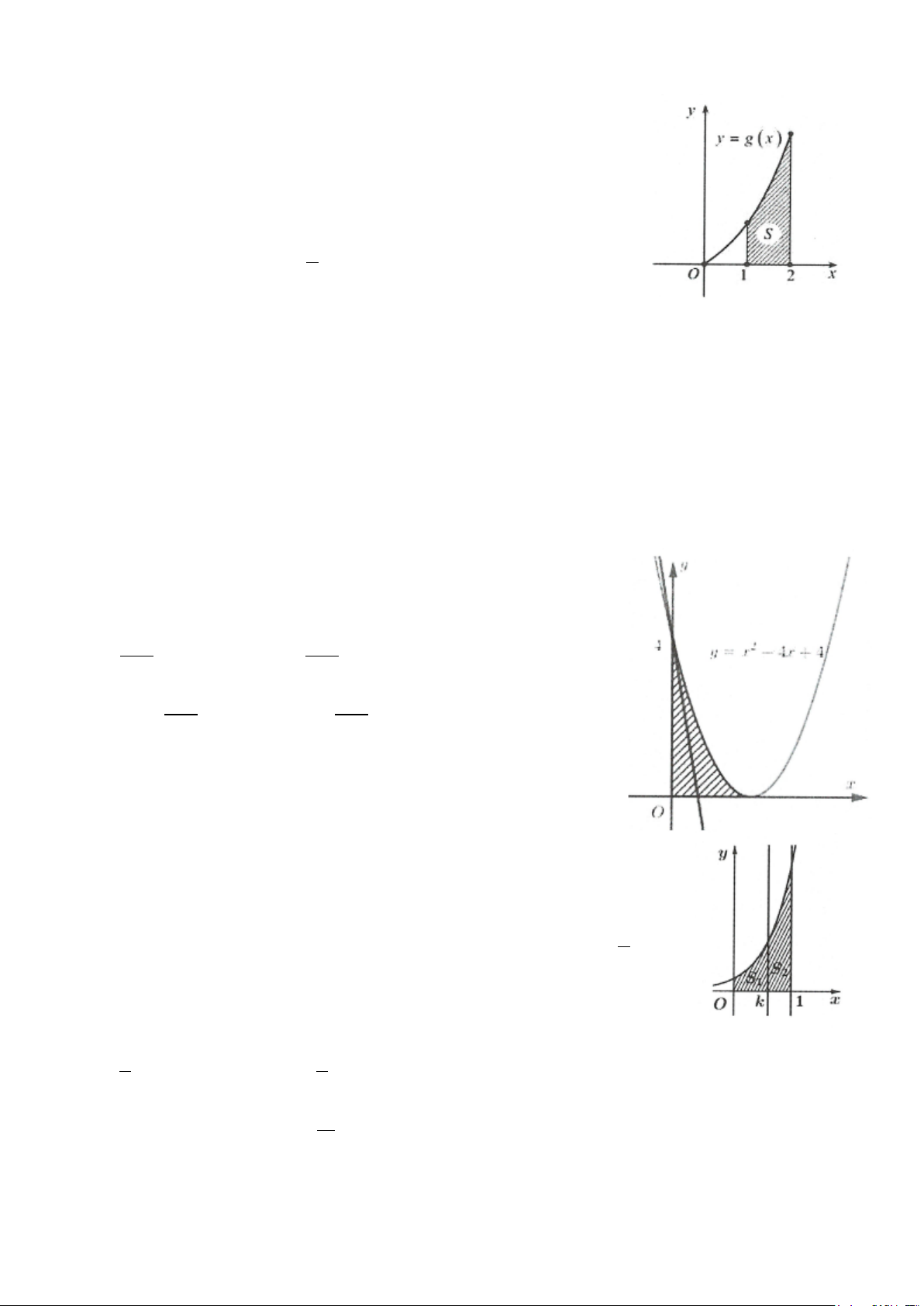
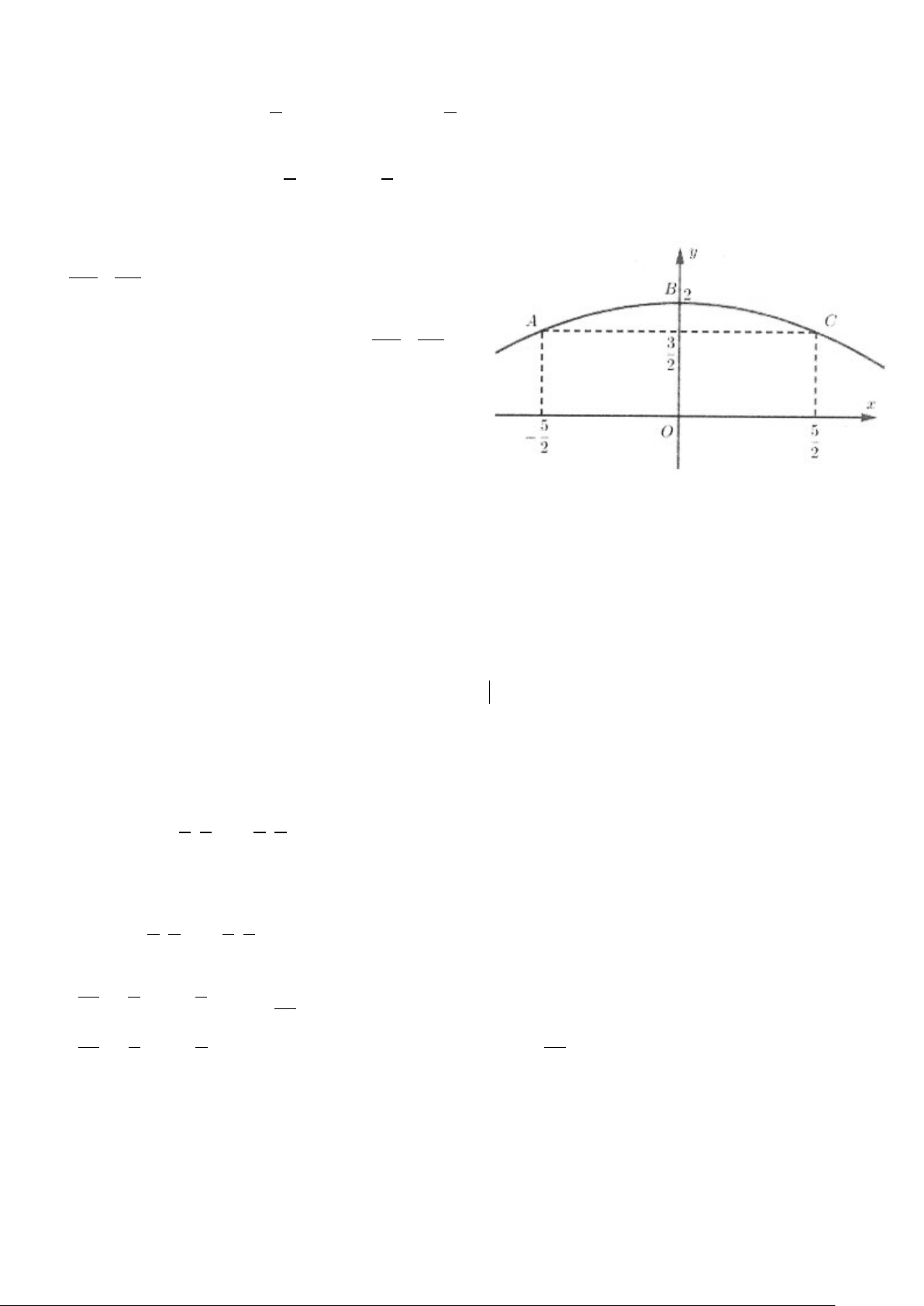
Ví dụ 15: Một viên gạch hoa hình vuông có cạnh 40cm. Người thiết kế đã sử
dụng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn
cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng A. 800 2 cm B. 400 2 cm 3 3 C. 2 250cm D. 2 800cm Lời giải
Chọn hệ trục tọa độ như hình vẽ:
Với A(20;20) , xét hình phẳng ở góc phần tư thứ nhất.
Hai parabol có phương lần lượt là: 2 y = ax và 2 x = ay
Do parabol qua điểm A( ) 20 1 20;20 ⇒ a = = 2 20 20 2  xy = ⇒  20  y = 20x
Diện tích phần tô đậm ở góc phần tư thứ nhất là: 20 20 2 3    2  3 400 = ∫ x x S  20x −  dx =  20x −  = . Chọn B.  20   3 60  3 0 0
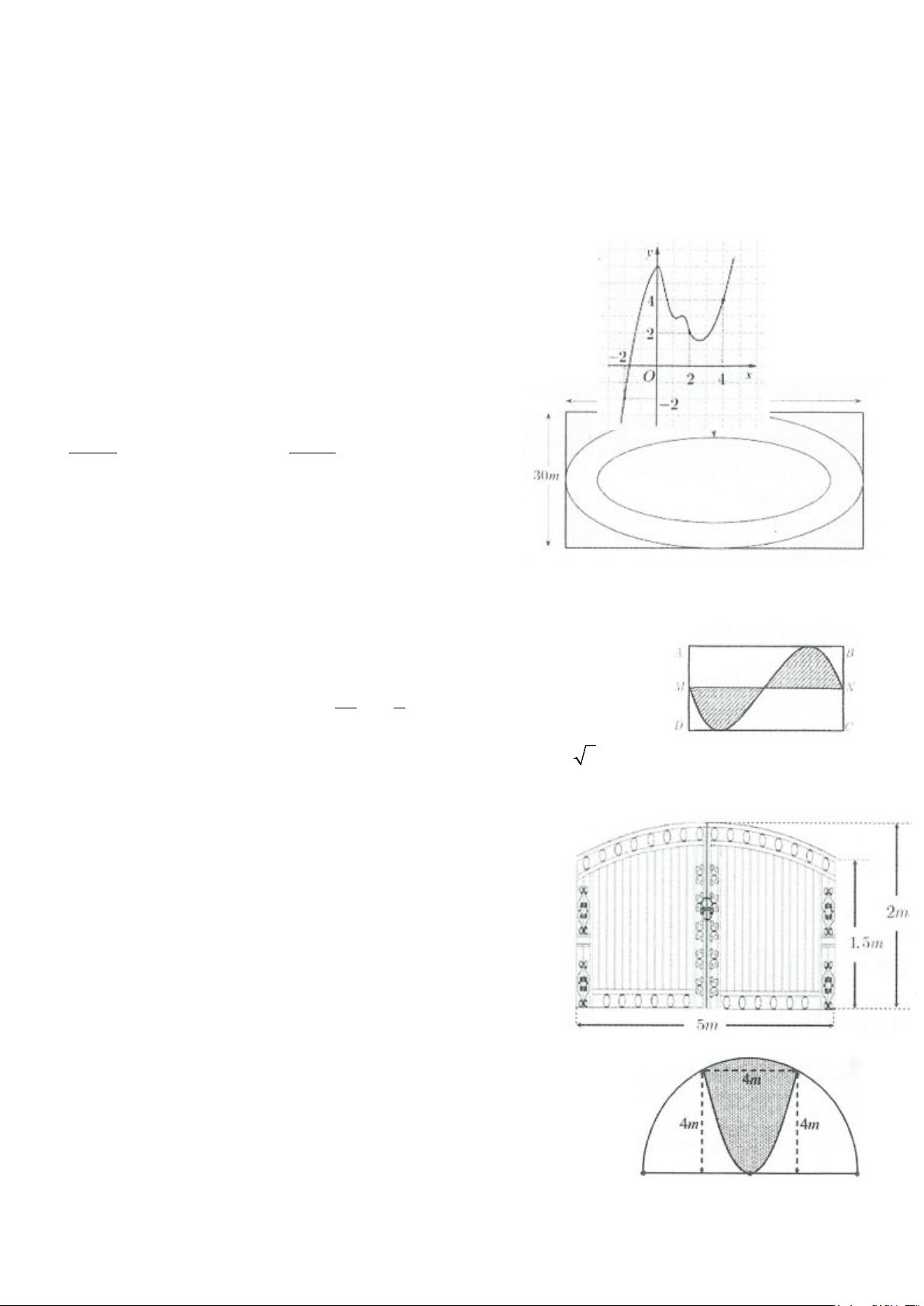
Ví dụ 16: Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng
chân đế 12m. Người ta căng hai sợi dây trang trí AB, CD nằm ngang đồng
thời chia hình giới hạn bởi parabol và mặt đất thành ba phần có diện tích
bằng nhau (xem hình vẽ bên). Tỉ số AB bằng: CD A. 1 B. 3 3 2 1+ 2 2 C. 1 D. 4 2 5 Lời giải
Chọn hệ trục tọa độ như hình vẽ Parabol có dạng 2
y = ax , do (P) đi qua điểm ( ) 1 6;18 ⇒ a = . 2 6 2  
Diện tích thiết diện của cổng trào là: = ∫ x S 18 −  dx = 144 . 0 −  2 6 
Để diện tích 3 phần bằng nhau thì diện tích mỗi phần là S0 = 48 . 3 2 2
b   d  Gọi B AB b  ; b ; Dd; khi đó = 2 2      CD d 2 2 2 3  b x   b x x b b Ta có: 3
∫ − dx = 24 ⇔  −  = 24 ⇒ b = 72  2 2   2 6 0  0 d 2 2  d x  Tương tự ta có 3 AB 1
∫ − dx = 48⇒ d =144 ⇒ = . Chọn 3  2 2 CD 0  2 A.
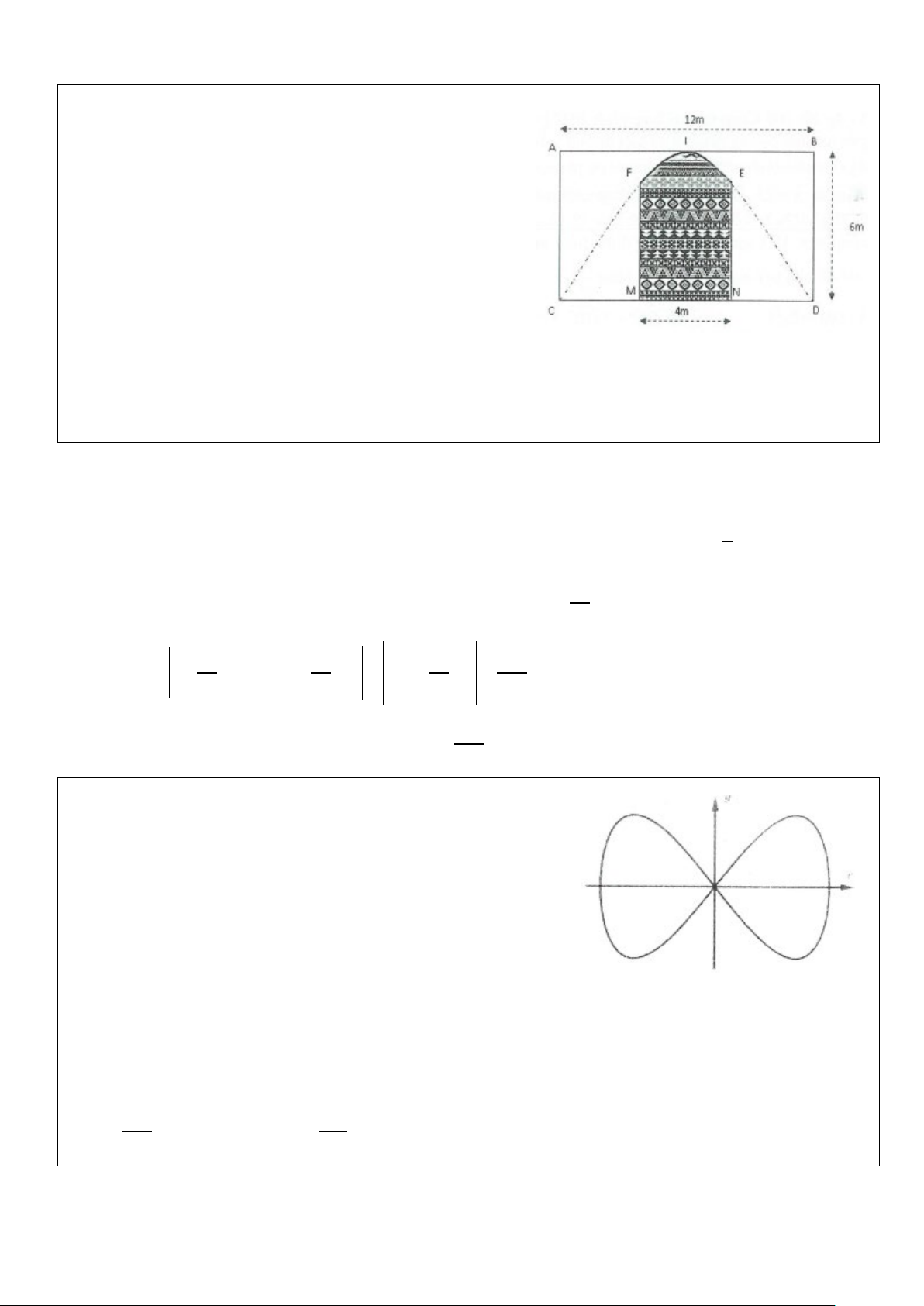
Ví dụ 17: [Đề Sở GD&DT Thanh Hóa] Một công ty quảng
cáo X muốn làm một bức tranh trang trí hình MNEIF ở chính
giữa một tường hình chữ nhật ABCD có chiều cao BD = 6m,
chiều dài CD = 12m (hình vẽ bên). Cho biết MNEF là hình
chữ nhật có MN = 4m, cung EIF có hình dạng là một phần
của cung parabol có đỉnh I là trung điểm của cạnh AB và đi
qua hai điểm C, D. Kinh phí làm bức tranh là 900.000 đồng/ 2
m . Hỏi công ty X cần bao nhiêu tiền để làm bức tranh đó? A. 20.400.000 đồng B. 20.600.000 đồng C. 20.800.000 đồng D. 21.200.00 đồng Lời giải
Gọi O là trung điểm của MN và trùng với gốc tọa độ ⇒ M ( 2; − 0), N (2;0) .
Phương trình parabol đỉnh I (0;6) và đi qua hai điểm C ( 6;
− 0), D(6;0) là (P) 1 2 : y = 6 − x . 6 2
Diện tích bức tranh là diện tích giới hạn bởi hàm số = ( ) = 6 − x y f x và x = 2, − x = 2 . 6 2 2 2 2 2 3 xx   x  Khi đó 208 S = 6 − dx = ∫
∫ 6− dx = 6x−  = ( 2 m ) . − 6 −  6   18  9 2 2 2 −
Số tiền công ty X cần dùng để làm bức tranh là 208 T =
×900.000 = 20.800.000 đồng. Chọn C. 9
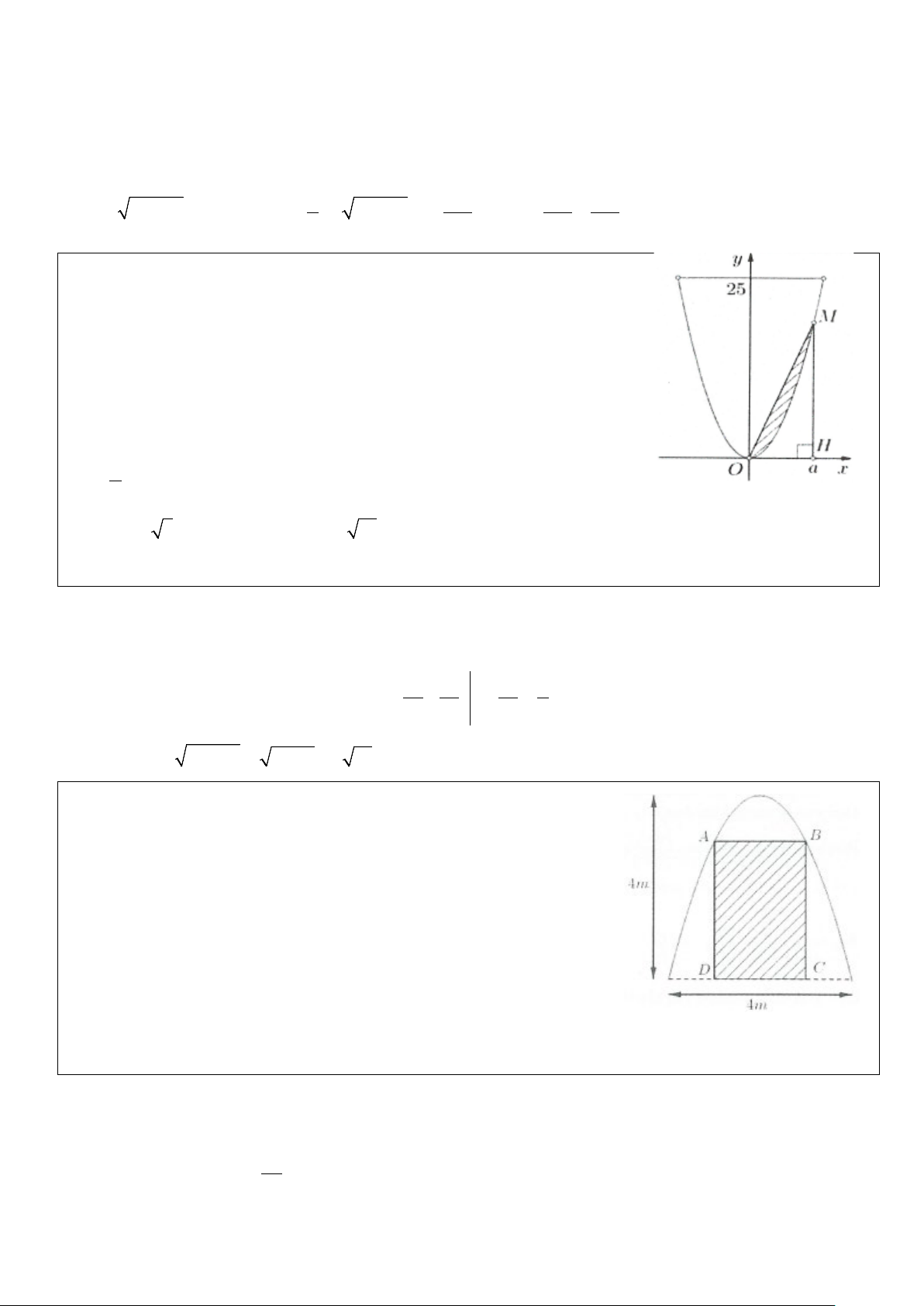
Ví dụ 18: [Đề Chuyên Đại học Vinh 2017] Trong công viên Toán
học có những mảnh đất hình dáng khác nhau. Mỗi mảnh được
trồng một loài hoa và nó được tạo thành bởi một trong những
đường cong đẹp trong toán học. Ở đó có một mảnh đất mang tên
Bernoulli, nó được tạo thành từ đường Lemniscate có phương trình
trong hệ tọa độ Oxy là 2 2 y = x ( 2 16
25 − x ) như hình vẽ bên.
Tính diện tích S của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ trục tọa độ Oxy tương ứng với chiều dài 1 mét. A. 125 S = ( 2 m ) B. 125 S = ( 2 m ) 6 4 C. 250 S = ( 2 m ) D. 125 S = ( 2 m ) 3 3 Lời giải
Hoành độ giao điểm của đồ thị với trục hoành là x = 0; x = 5; − x = 5 .
Dễ thấy diện tích mảnh đất Bernoulli bao gồm diện tích 4 mảnh đất nhỏ bằng nhau.
Xét diện tích s của mảnh đất nhỏ trong góc phần tư thứ nhất ta có: 5 2 y = x − x x ∈[ ] 1 2 125 125 125 4 25 ; 0;5 ⇒ s = x 25 − x dx = ⇒ S = 4. = ∫ ( 2 m ). Chọn D. 4 12 12 3 0
Ví dụ 19: [Đề Chuyên Đại học Vinh 2017] Ông B có một khu vườn giới
hạn bởi đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ Oxy
như hình vẽ bên thì parabol có phương trình 2
y = x và đường thẳng là
y = 25. Ông B dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi
đường thẳng đi qua O và điểm M trên parabol để trồng hoa. Hãy giúp ông B
xác định điểm M bằng cách tính độ dài OM để diện tích mảnh vườn nhỏ bằng 9 . 2 A. OM = 2 5 B. OM = 3 10 C. OM =15 D. OM =10 Lời giải Giả sử M ( 2
a;a ) , suy ra phương trình OM : y = ax.  x x a a
Diện tích khu vườn là S = ∫(ax − x ) 2 3 3 2 a 9
dx = a −  = = ⇔ a = 3 .  2 3  6 2 0 0 Khi đó 2 4
OM = a + a = 9 + 81 = 3 10 . Chọn B.
Ví dụ 20: Trong đợt hội trại “Khi tôi 18” được tổ chức tại THPT X,
Đoàn trường có thực hiện một dự án ảnh trưng bày trên một pano có
dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi
ảnh dự thi và dán lên khu vực hình chữ nhật ABCD, phần còn lại sẽ được
trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là 100.000 đồng cho một 2
m bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano
sẽ là bao nhiêu? (làm tròn đến hàng nghìn) A. 615.000 đồng B. 450.000 đồng C. 451.00 đồng D. 616.000 đồng Lời giải
Gọi S là diện tích hình phẳng giới hạn bởi parabol có phương trình 2
y = 4 − x và trục hoành. 2 Suy ra S = ( 2 4 − x ) 32 2 dx = ∫ m . − 3 2 D(− ;0 a )
Gọi điểm C (a;0),a > 0 , suy ra  . B( 2
a;4 − a ), A( 2 −a;4 −  a )
Gọi S là diện tích ABCD, suy ra S = A .
B BC = 2a 4 − a m . 1 ( 2 ) 2 1
Gọi S là diện tích có hoa văn, suy ra S = S − S ;S nhỏ nhất khi và 2 2 1 2
chỉ khi S lớn nhất. 1
Xét hàm số f (a) 2
= 2a(4 − a ),a ∈(0;4) Ta có f ′(a) 2
= − a ⇒ f ′(a) 2 8 6 = 0 ⇔ a = . 3
Xét bảng biến thiên hàm số f (a) với a ∈(0;4) . Ta có f (a)  2  32 3 32 3 max = f = ⇒ S max =   m . 1 ( ) 2 (0;4)  3  9 9 Suy ra S (min) 32 32 3 2 = −
≈ 4,51m . Suy ra số tiền ít nhất cần là 451.000 đồng. Chọn C. 2 3 9
Ví dụ 21: Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình
vuông cạnh 10(cm) bằng cách khoét bỏ đi bốn phần bằng nhau có hình
dạng parabol như hình bên. Biết rằng AB = 5(cm) đồng thời
OH = 4(cm) . Tính diện tích bề mặt hoa văn đó? A. 140 ( 2 cm ) B. 160 ( 2 cm ) 3 3 C. 40 ( 2 cm ) D. ( 2 50 cm ) 3 Lời giải
Dựa vào đề bài ta tính được Parabol có PT (P) 16 2 : y = − x + 4. 25
Gọi S là diện tích hình phẳng trong hình bên 1 5 2 Suy ra  16 2  40 S = − x + 4 dx = ∫   ( 3 cm . 1 ) 5  25  3 − 2
Gọi S là diện tích hoa văn cần tính Suy ra 2 140 S =10 − 4S = ( 3 cm . Chọn A. 1 ) 3
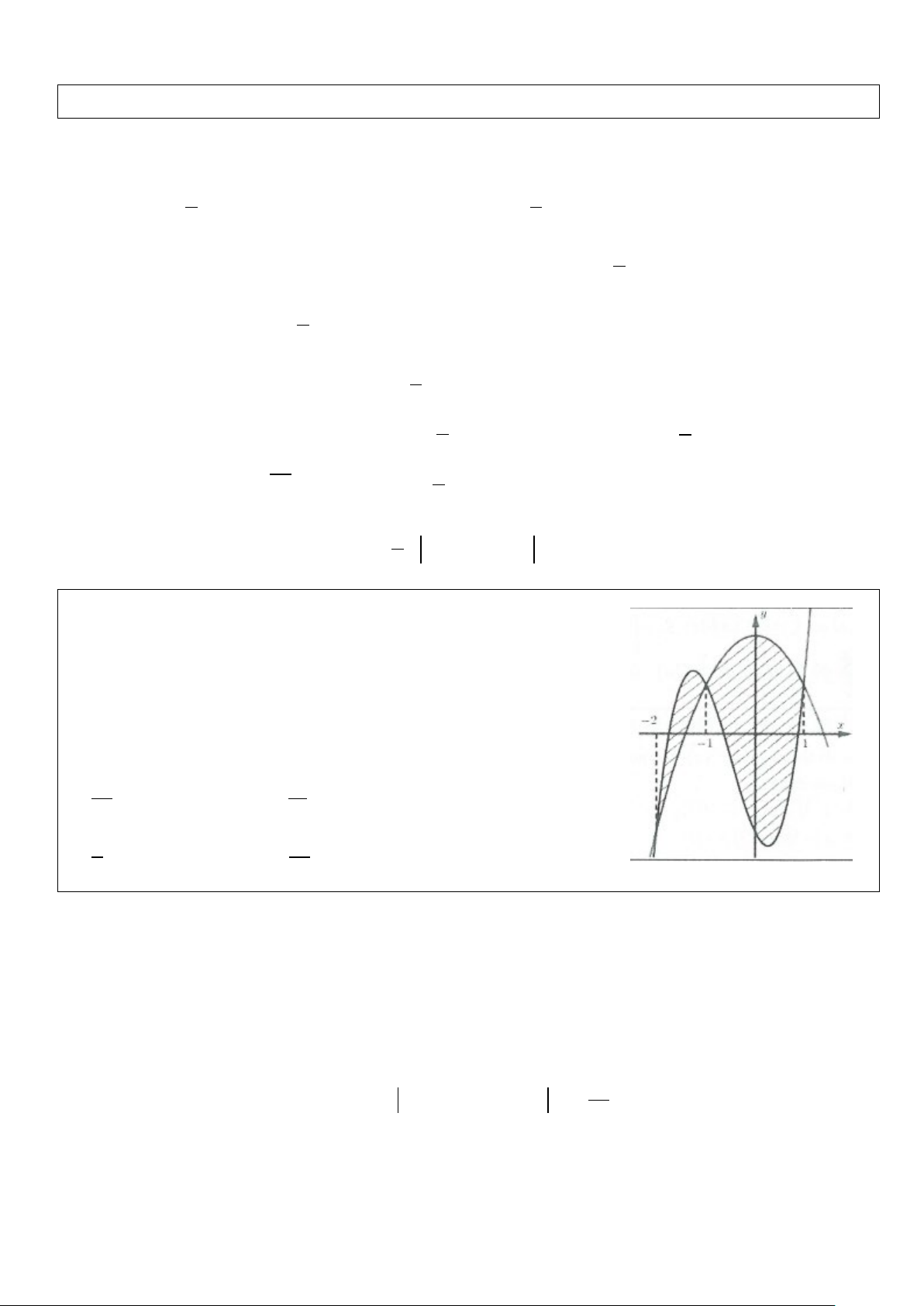
Ví dụ 22: Sân trường có một bồn hoa hình tròn có tâm O. Một nhóm học
sinh lớp 12 được giao thiết kế bồn hoa, nhóm này định chia bồn hoa thành
bốn phần, bởi hai đường parabol có cùng đỉnh O và đối xứng nhau qua O.
Hai đường parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một
hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích S , S dùng để 1 2
trồng hoa, phần diện tích S , S dùng để trồng cỏ (Diện tích làm tròn đến 3 4
chữ số thập phân thứ hai).
Biết kinh phí để trồng hoa là 150.000 đồng/ 2
1m , kinh phí để trồng cỏ là 100.000 đồng/ 2
1m . Hỏi nhà trường
cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn). A. 6.060.000 đồng B. 5.790.000 đồng C. 3.270.000 đồng D. 3.000.000 đồng Lời giải
Chọn hệ trục tọa độ như hình vẽ O(0;0); A( 2; − 2); B(2;2)
Khi đó phương trình parabol phía trên có dạng là: (P) 2
: y = ax trong đó B( )∈(P) 1 2;2 ⇒ a = . 2 2 Suy ra ( ) : = x P y . 2
Phương trình cung tròn nằm phía trên trục Ox là 2 2 2 2 2
y = R − x = OA − x = 8 − x 2 2   Khi đó 2 = ∫ x S  8 − x − dx . 1  −  2 2  Diện tích hình tròn là 2 2
S = πR = πOA = 8π
Ta có T =150.2S +100. S − 2S 2 ( 1 )
Bấm máy ta được T =150.2S +100. S − 2S ≈ 3.270 nghìn đồng. Chọn C. 1 ( 1 )
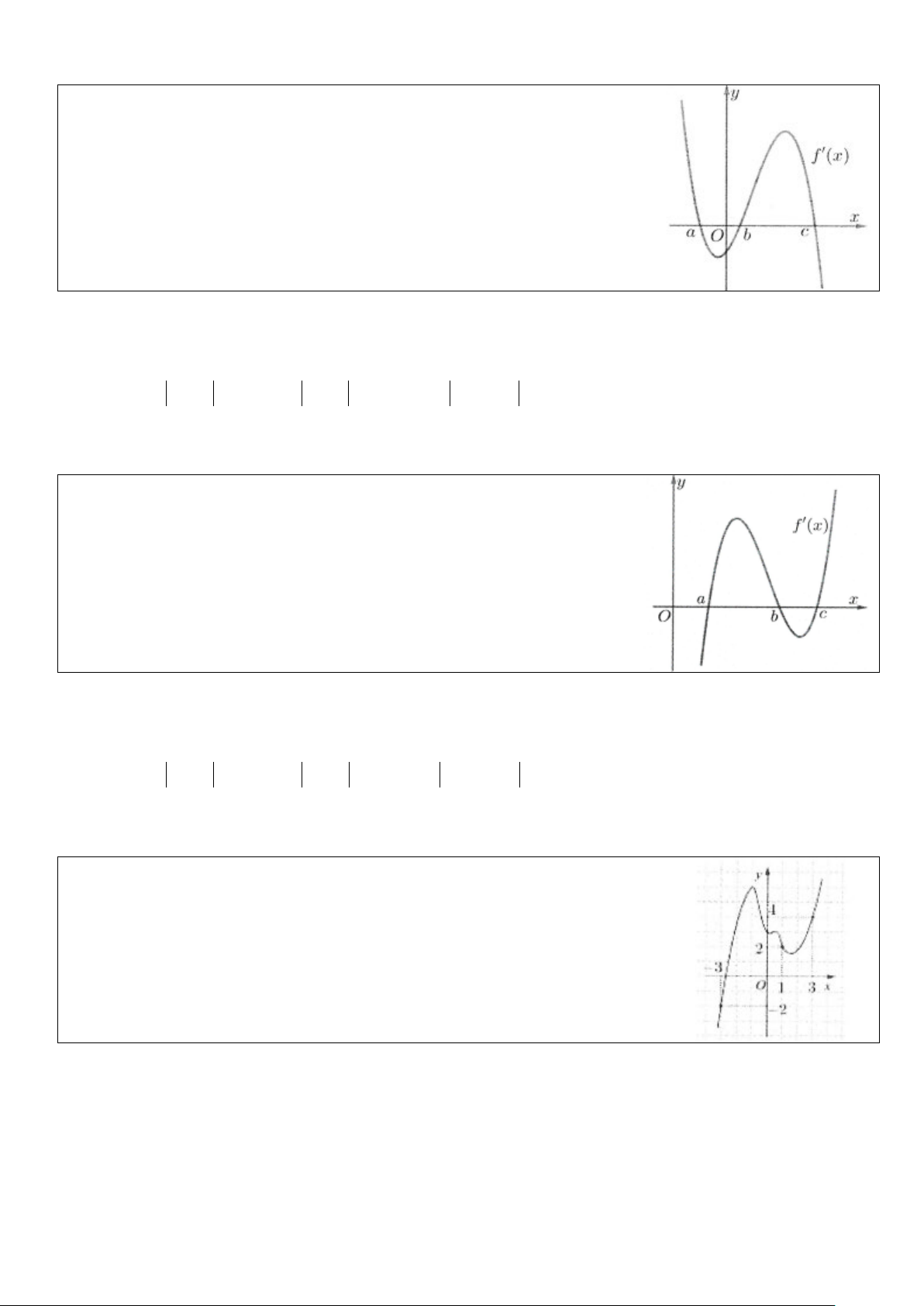
Ví dụ 23: [Đề thi THPT Quốc gia năm 2018] Cho hai hàm số f (x) 3 2 1
= ax + bx + cx − và g (x) 2
= dx + ex +1 (a,b,c,d,e∈ ) . Biết rằng 2
đồ thị của hàm số y = f (x) và y = g (x) cắt nhau tại 3 điểm có hoành độ lần lượt là 3 − ; 1;
− 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng: A. 9 B. 8 2 C. 4 D. 5 Lời giải
Ta có phương trình hoành độ giao điểm của hai hàm số là: 3 2 1 2 3
ax + bx + cx − = dx + ex + ⇔ ax + (b − d ) 2
x + (c − e) 3 1 x − = 0 2 2
Vì phương trình có các nghiệm 3 − ; 1; − 1 nên: 3
ax + (b − d ) 2
x + (c − e) 3
x − = a(x + 3)(x + ) 1 (x − ) 1 2 3
⇔ ax + (b − d ) 2
x + (c − e) 3 x − = a( 3 2
x + 3x − x − 3) 2  1  a =   2
b − d = 3a  
Đồng nhất hệ số ta được:  3
c − e = −a ⇔ b − d = (thực ra chỉ cần tìm được 1 a = ) 2  2 3  −  = 3 − a  1  2 c − e =  2 1
Suy ra diện tích hình phẳng cần tìm là: 1 3 2 S =
x + 3x − x − 3 dx = 4 . Chọn C. 2 ∫3−
Ví dụ 24: [Đề thi THPT Quốc gia năm 2018] Cho hai hàm số f (x) 3 2
= ax + bx + cx − 2 và g (x) 2
= dx + ex + 2 (a,b,c,d,e∈ ) . Biết
rằng đồ thị của hàm số y = f (x) và y = g (x) cắt nhau tại 3 điểm có
hoành độ lần lượt là 2 − ; 1;
− 1 (tham khảo hình vẽ). Hình phẳng giới hạn
bởi hai đồ thị đã cho có diện tích bằng: A. 37 B. 13 6 2 C. 9 D. 37 2 12 Lời giải
Ta có phương trình hoành độ giao điểm của hai hàm số là: 3 2 2 3
ax + bx + cx − = dx + ex + ⇔ ax + (b − d ) 2 2 2
x + (c − e) x − 4 = 0
Vì phương trình có các nghiệm 2 − ; 1; − 1 nên: 3
ax + (b − d ) 2
x + (c − e) x − 4 = a(x + 2)(x + ) 1 (x − ) 1
Đồng nhất hệ số ta được: a = 2 1
Suy ra diện tích hình phẳng cần tìm: S =
(x + )(x + )(x − ) 37 2 2 1 1 dx = ∫ . Chọn A. − 6 3
Ví dụ 25: Cho hàm số y = f (x) có đồ thị y = f ′(x) cắt trục Ox tại ba điểm
có hoành độ thỏa mãn a < b < c như hình vẽ. Mệnh đề nào dưới đây là đúng?
A. f (c) > f (a) > f (b) B. f (c) > f (b) > f (a)
C. f (a) > f (b) > f (c) D. f (b) > f (a) > f (c) Lời giải
Ta có f ′(x) = 0 ⇔ x = { ; a ; b }
c . Dựa vào BBT, ta thấy f (b) < { f (a); f (c)} . b c Lại có b c
S = f ′ x dx < S = f ′ x dx ⇔ − f x < f x ⇔ f a < f c . 1 ∫ ( ) 2 ∫ ( ) ( ) ( ) ( ) ( ) a b a b
Vậy f (c) > f (a) > f (b) . Chọn A.
Ví dụ 26: Cho hàm số f (x) có đạo hàm trên ℝ, đồ thị hàm số y = f ′(x)
như trong hình vẽ. Hỏi phương trình f (x) = 0 có tất cả bao nhiêu nghiệm
biết f (a) > 0 ? A. 3 B. 2 C. 1 D. 0 Lời giải
Ta có f ′(x) = 0 ⇔ x = { ; a ; b }
c . Dựa vào BBT, ta thấy f (b) > { f (a); f (c)}. b c Lại có b c
S = f ′ x dx > S = f ′ x dx ⇔ f x > − f x ⇔ f a < f c . 1 ∫ ( ) 2 ∫ ( ) ( ) ( ) ( ) ( ) a b a b
Do đó f (b) > f (c) > f (a) > 0 . Vậy phương trình f (x) = 0 vô nghiệm. Chọn D.
Ví dụ 27: (Đề thi THPT Quốc gia 2017 – Mã đề 102) Cho y = f (x) có đồ thị
của y = f ′(x) như hình vẽ. Đặt g (x) = f (x) −(x + )2 2 1 . Mệnh đề nào đúng?
A. g (3) > g ( 3 − ) > g ( ) 1 B. g ( 3
− ) > g (3) > g ( ) 1 C. g ( ) 1 > g ( 3
− ) > g (3) D. g ( )
1 > g (3) > g ( 3 − ) Lời giải
Ta có g′(x) = 2 f ′(x) − 2(x + )
1 ; g′(x) = 0 ⇔ f ′(x) = x +1.
Nhận thấy nghiệm của g′(x) = 0 chính là nghiệm của f ′(x) = x +1, cũng là hoành độ giao điểm của hai
đồ thị hàm số y = f ′(x) và đường thẳng y = x +1 → x = { 3 − ;1; } 3 .
Vẽ đường thẳng y = x +1 và chia đồ thị thành 2 phần diện tích hình phẳng. 1 1
Khi đó 2S = 2  f ′ x − x +1  dx = g′ x dx = g 1 − g 3
− > 0 ⇒ g 1 > g 3 − 1 ∫  ( ) ( ) ∫ ( ) ( ) ( ) ( ) ( ) 3 − 3 − 3 3
Và 2S = 2  x +1 − f ′ x dx = − g′ x dx = g 1 − g 3 > 0 ⇒ g 1 > g 3 2 ∫( ) ( ) ∫ ( ) ( ) ( ) ( ) ( ) 1 1
Lại có S > S ⇔ 2S > 2S ⇔ g 1 − g 3
− > g 1 − g 3 ⇔ g 3 > g 3 − . 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) Vậy g ( )
1 > g (3) > g ( 3 − ). Chọn D.
Ví dụ 28: (Đề thi THPT Quốc gia 2017 – Mã đề 103) Cho y = f (x) có đồ thị của
y = f ′(x) như hình vẽ. Đặt g (x) = f (x) 2 2
+ x . Mệnh đề nào đúng?
A. g (3) > g ( 3 − ) > g ( ) 1 B. g ( 3
− ) > g (3) > g ( ) 1 C. g ( ) 1 > g ( 3
− ) > g (3) D. g ( )
1 > g (3) > g ( 3 − ) Lời giải
Ta có g′(x) = 2 f ′(x) + 2x ; g′(x) = 0 ⇔ f ′(x) = −x.
Nhận thấy nghiệm của g′(x) = 0 chính là nghiệm của f ′(x) = −x cũng là hoành độ giao điểm của hai đồ
thị hàm số y = f ′(x) và đường thẳng y = −x  → x = { 3 − ;1; } 3 .
Vẽ đường thẳng y = −x và chia đồ thị thành 2 phần diện tích hình phẳng. 1 1
Khi đó 2S = 2 −x − f ′ x dx = − g′ x dx = g 3
− − g 1 > 0 ⇒ g 3 − > g 1 1 ∫  ( ) ∫ ( ) ( ) ( ) ( ) ( ) 3 − 3 − 3 3
Và 2S = 2  f ′ x − (− x) dx = g′ x dx = g 3 − g 1 > 0 ⇒ g 3 > g 1 . 2 ∫ ( )  ∫ ( ) ( ) ( ) ( ) ( ) 1 1
Lại có S > S ⇔ 2S > 2S ⇔ g 3
− − g 1 > g 3 − g 1 ⇔ g 3 − > g 3 . 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) Vậy g ( 3
− ) > g (3) > g ( ) 1 . Chọn B. C. BÀI TẬP TỰ LUYỆN
Câu 1: Cho hàm số y = f (x) liên tục trên [a;b]. Diện tích hình phẳng S giới hạn bởi đường cong
y = f (x) , trục hoành, các đường thẳng x = a, x = b được xác định bằng công thức nào? b a b b
A. S = −∫ f (x)dx
B. S = ∫ f (x)dx
C. S = ∫ f (x)dx
D. S = ∫ f (x) dx a b a a
Câu 2: Công thức tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số y = f x , y = f x và 2 ( ) 1 ( )
các đường thẳng x = a, x = b(a < b) là công thức nào sau đây? b b
A. S = f x − ∫ f x dx
B. S = f x − ∫ f x dx 2 ( ) 1 ( ) 1 ( ) 2 ( ) a a b b
C. S =  f x − f x  ∫ dx
D. S = f x + ∫ f x dx 1 ( ) 2 ( ) 1 ( ) 2 ( ) a a
Câu 3: Gọi S là diện tích hình phẳng giới hạn bởi các đường 2
y = x , y = 2 − x và y = 0. Mệnh đề nào sau đây là đúng? 1 2 2 A. 2 S = x dx + ∫ ∫(x−2)dx
B. S = ∫( 2x + x −2)dx 0 1 0 1 1 C. 1 2 S = + x dx D. 2 S = x − (2 − ∫ x) dx 2 ∫0 0
Câu 4: Diện tích hình phẳng S giới hạn bởi các đồ thị hàm số 3
y = x − x, y = 2x và các đường x = 1, − x =1
được xác định bởi công thức nào sau đây? 1 1 A. S = ( 3 3x − ∫ x )dx B. S = ( 3 3x − ∫ x )dx 1 − 1 − 0 1 0 1 C. S = ( 3
x − 3x)dx + ( 3 3x − ∫ ∫ x )dx D. S = ∫ ( 3
3x − x )dx + ∫( 3x −3x)dx 1 − 0 1 − 0
Câu 5: Diện tích hình phẳng S giới hạn bởi các đồ thị của hai hàm số y = 2x, y = 4 − x và trục hoành Ox
được tính bởi công thức nào dưới đây? 4 4 2 4 A. S = 2xdx + (4 − ∫ ∫ x)dx B. S = 2xdx + (4 − ∫ ∫ x)dx 0 0 0 2 4 2
C. S = ( 2x − 4+ ∫ x)dx
D. S = ∫(4− x − 2x)dx 0 0
Câu 6: Diện tích hình phẳng S giới hạn bởi các đường 2
y = x − x, y = 0, x = 0 và x = 2 được tính bởi công thức nào sau đây? 2 2 1 A. S = ( 2 x − ∫ x )dx B. S = ( 2 x − x) − ( 2 x − ∫ ∫ x)dx 0 1 0 1 2 2 C. S = ( 2 x − x) + ( 2 x − ∫ ∫ x)dx D. S = ( 2 x − ∫ x)dx 0 1 0
Câu 7: Diện tích hình phẳng S giới hạn bởi đồ thị của hai hàm số 2 y = x và 2
y = 2 − x được xác định bởi công thức nào sau đây? 1 1 1 1 A. S = ( 2 x − ∫ )1dx B. S = 4 ( 2 1− ∫ x )dx C. S = ( 2 1− ∫ x )dx D. S = 2 ( 2 x − ∫ )1dx 1 − 0 1 − 0
Câu 8: Hình phẳng giới hạn bởi các đường 2 x = 1
− , x = 2, y = 0, y = x − 2x có diện tích S được tính theo
công thức nào dưới đây? 2 0 2
A. S = ∫ ( 2x −2x)dx
B. S = ∫ ( 2x −2x)dx − ∫( 2x −2x)dx 1 − 1 − 0 0 2 2
C. S = ∫ ( 2x −2x)dx + ∫( 2x −2x)dx D. 2 S = x − 2 ∫ x dx 1 − 0 1 −
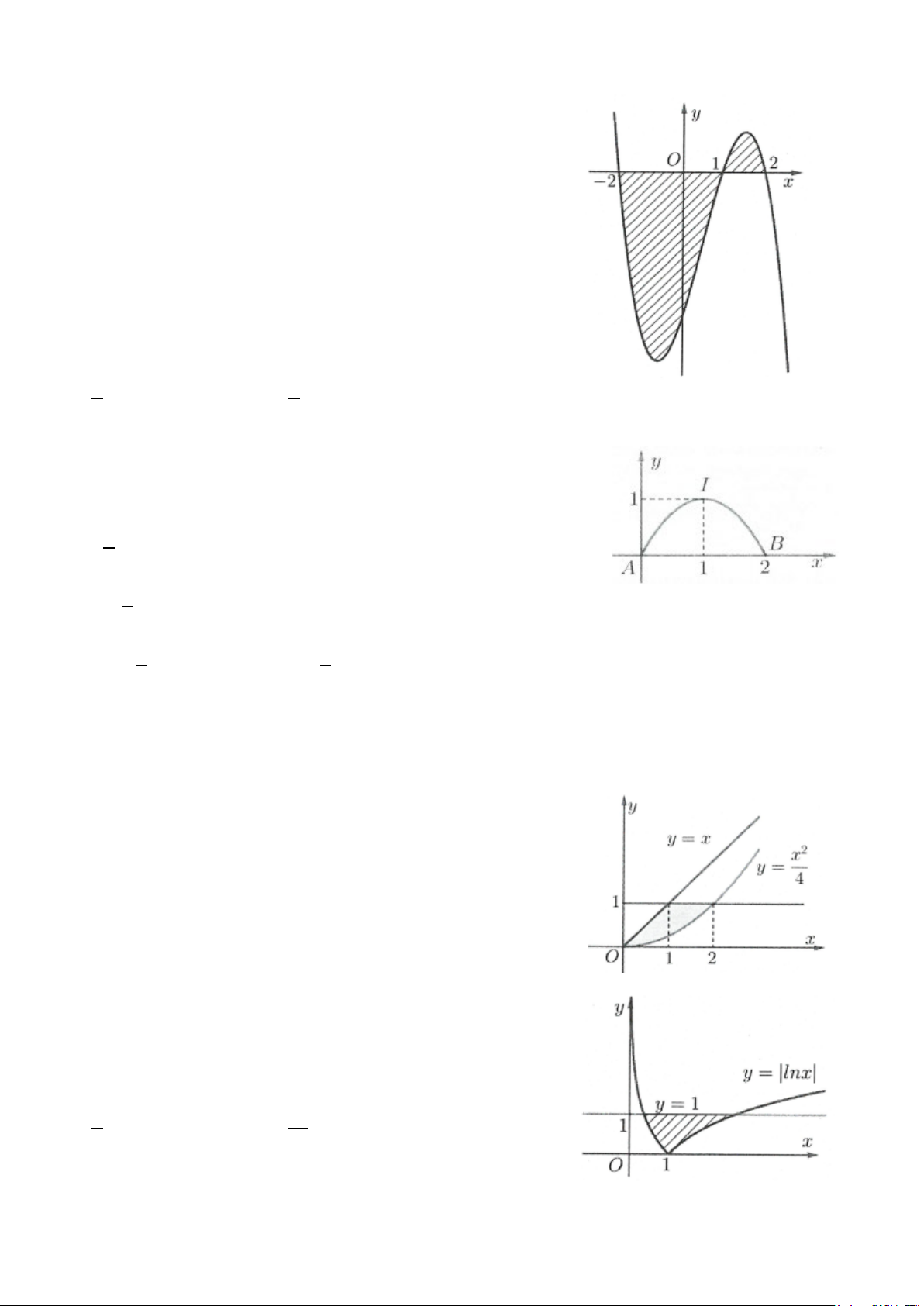
Câu 9: Tìm công thức tính diện tích S của hình phẳng (H ) giới
hạn bởi các đồ thị hàm số y = f (x), y = g (x) và hai đường
thẳng x = a, x = b như hình vẽ dưới đây. c b A. S = 
∫ f (x)− g(x)dx+ 
∫ g(x)− f (x)     dx a c c b B. S = 
∫ g(x)− f (x)dx+ 
∫ f (x)− g(x)     dx a c b C. S = 
∫ g(x)− f (x)   dx a b D. S = 
∫ f (x)− g(x)   dx a
Câu 10: Cho đồ thị hàm số y = f (x) . Diện tích hình
phẳng S (phần tô đậm trong hình) được xác định bằng công thức nào? 0 2
A. S = f (x)dx − ∫
∫ f (x)dx 2 − 0 0 2
B. S = f (x)dx + ∫
∫ f (x)dx 2 − 0 0 2
C. S = f (x)dx + ∫
∫ f (x)dx 2 − 0 0 2
D. S = f (x)dx + ∫
∫ f (x)dx 2 − 0
Câu 11: Công thức nào sau đây dùng để tính diện tích hình
phẳng S phần gạch của hình vẽ. b b
A. S = g (x)dx − ∫
∫ f (x)dx a a b b
B. S = f (x)dx − ∫
∫ g(x)dx a a b b
C. S = g (x)dx − ∫
∫ f (x)dx a a b b
D. S = g (x)dx + ∫
∫ f (x)dx a a
Câu 12: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm
số y = f (x) , trục hoành, đường thẳng x = a, x = b (như hình
bên dưới). Hỏi cách tính S nào dưới đây đúng? c b
A. S = f (x)dx + ∫
∫ f (x)dx a c c b
B. S = f (x)dx + ∫
∫ f (x)dx a c c b
C. S = − f (x)dx + ∫
∫ f (x)dx a c b
D. S = ∫ f (x)dx a
Câu 13: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 4 2
y = x − 2x và trục hoành như hình vẽ. Tìm khẳng định sai? 2
A. S = ∫ f (x) dx − 2 2
B. S = 2 ∫ f (x)dx 0 2 C. S = 2
− ∫ f (x)dx 0 0 2 D. S = −
f (x)dx − ∫
∫ f (x)dx − 2 − 2
Câu 14: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y = f (x)
và trục hoành (như hình vẽ). Công thức nào dùng để tính diện tích S? 2
A. S = ∫ f (x)dx 2 − 1 2
B. S = f (x)dx + ∫
∫ f (x)dx 2 − 1 1 2
C. S = f (x)dx − ∫
∫ f (x)dx 2 − 1 0 2
D. S = f (x)dx + ∫
∫ f (x)dx 2 − 0
Câu 15: Cho hàm số y = f (x) liên tục trên đoạn [a;b]. Gọi D là
hình phẳng giới hạn bởi đồ thị (C) : y = f (x) , trục hoành, hai đường
thẳng x = a, x = b (như hình vẽ bên dưới). Giả sử S là diện tích của D
hình phẳng D. Chọn công thức đúng trong các phương án A, B, C, D dưới đây? 0 b
A. S = f x dx f x dx D ( ) + ∫ ∫ ( ) a 0 0 b
B. S = − f x dx f x dx D ( ) + ∫ ∫ ( ) a 0 0 b
C. S = f x dx f x dx D ( ) − ∫ ∫ ( ) a 0 0 b
D. S = − f x dx f x dx D ( ) − ∫ ∫ ( ) a 0
Câu 16: Cho đồ thị hàm số y = f (x) . Diện tích hình
phẳng (phần gạch chéo) trong hình được tính theo công thức: 4
A. S = ∫ f (x)dx 2 − 0 0 4
B. S = f (x)dx + f (x)dx + ∫ ∫
∫ f (x)dx 2 − 2 2 0 4
C. S = f (x)dx + ∫
∫ f (x)dx 2 − 0 0 2 4
D. S = f (x)dx + f (x)dx + ∫ ∫
∫ f (x)dx 2 − 0 2
Câu 17: Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f (x) , trục hoành (phần gạch sọc trong 1 2
hình vẽ). Đặt a = f (x)dx,b = ∫
∫ f (x)dx. Mệnh đề 3 − 1 nào đúng? A. a + b
B. a − b
C. b − a
D. −b − a
Câu 18: Gọi S là diện tích hình phẳng (H ) được giới hạn
bởi các đường y = f (x) , trục hoành và hai đường thẳng x = 1, − x = 2 (như hình vẽ). Đặt 0 2
a = f (x)dx,b = ∫
∫ f (x)dx . Mệnh đề nào dưới đây 1 − 0 đúng?
A. S = −a − b
B. S = a − b
C. S = b + a
D. S = b − a
Câu 19: Tìm công thức tính diện tích hình phẳng giới hạn bởi phần gạch sọc trong hình vẽ. 3 4
A. = ∫(3 +0,5x − )1 + ∫(log −0,5x S x dx x − 2 dx 2 ) 1 1 3 4
B. = ∫(3 +0,5x + )1 + ∫(log −0,5x S x dx x − 2 dx 2 ) 1 1 1 4
C. = ∫(3 +0,5x − )1 − ∫(log −0,5x S x dx x − 2 dx 2 ) 0 1 1 4
D. = ∫(3 +0,5x − )1 + ∫(log −0,5x S x dx x − 2 dx 2 ) 0 1
Câu 20: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
x = g ( y) , trục tung và hai đường thẳng y = a, y = b như hình vẽ bên.
Khẳng định nào sau đây đúng? b a
A. S = ∫ g( y)dx
B. S = ∫ g( y)dy a b b b
C. S = ∫ g( y)dy
D. S = ∫ g( y)dx a a
Câu 21: Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ
thị hàm số x = f ( y), x = g ( y) và hai đường thẳng
y = a, y = b như hình vẽ bên. Khẳng định nào sau đây đúng? c b A. S = 
∫ g(y)− f (y)dx+ 
∫ f (y)− g(y)     dx a c b B. S
∫ g(y)+ f (y)   dy a c b C. S = 
∫ g(y)− f (y)dy + 
∫ f (y)− g(y)     dy a c b D. S = 
∫ g(y)− f (y)   dy a
Câu 22: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị
hàm số y = f (x) , trục hoành, đường thẳng x = a, x = b b c
(như hình bên). Biết f (x)dx = 3 − ∫
và ∫ f (x)dx = 5. Tìm S. a b A. S = 3 B. S = 5 C. S = 8 D. S = 2
Câu 23: Cho hai hàm số f (x) = x và g (x) = 6 − x có đồ thị như
hình vẽ. Gọi S là diện tích hình phẳng (phần gạch chéo) trong hình.
Công thức nào sau đây sai? 4 6
A. S = f (x)dx + ∫
∫ g(x)dx 0 4 6
B. S = f (x) − ∫
g (x) dx 0 2 C. 2
S = y − 6y + ∫ y dy 0 2 D. S = ( 2 6 − y − ∫ y )dy 0
Câu 24: Tính diện tích hình phẳng S giới hạn bởi các đồ thị của các đường 2
y = x − 4x +1, y = m(m ≤ 3 − )
và x = 0, x = 3.
A. S = 3m + 6
B. S = 6 − 3m
C. S = 3m − 6 D. S = 3 − m − 6
Câu 25: Tính diện tích hình phẳng S giới hạn bởi các đồ thị của các đường 10 2 y = x − x và 3 −x khi x ≤1 y =  .
x − 2 khi x > 1 A. S =13 B. 15 S = C. 13 S = D. S = 7 2 2
Câu 26: (Đề thi minh họa – Bộ GD&ĐT 2017) Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số 3
y = x − x và đồ thị hàm số 2
y = x − x . A. 37 S = B. 9 S = C. 81 S = D. S =13 12 4 12
Câu 27: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 3
y = x − 3x và đồ thị hàm số y = x . A. S = 3 B. S = 4 C. S = 6 D. S = 8
Câu 28: Tính diện tích S của hình phẳng giới hạn bởi đường cong 2
y = x + x −1 và đường thẳng y = 2x +1. A. 9 S = B. S = 4 C. 11 S = D. S = 3 2 2
Câu 29: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y = x và y = x . A. 1 S = − B. 2 S = C. S =1 D. 1 S = 6 3 6
Câu 30: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y = x + 2x và các đường thẳng y = 0, x = 1, − x =1. A. 2 S = B. S = 2 C. 4 S = D. 8 S = 3 3 3
Câu 31: Tính diện tích S của hình phẳng giới hạn bởi 2
y = x − 5x + 3 và 2 y = 2
− x + 2x −1. A. 1 S = B. 833 S = C. 263 S = D. 35 S = 54 54 162 54
Câu 32: Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số 2
y = x − x + 5 và 3 2 y = 2
− x + x + x + 5. A. S =1 B. S = 2 C. S = 3 D. S = 4
Câu 33: Tính diện tích hình phẳng S giới hạn bởi đồ thị của hai hàm số 2 y = 2x và 4 2
y = x − 2x trong miền x > 0 . A. 64 S = B. 32 S = C. 32 S = D. 15 S = 15 25 15 32
Câu 34: Tính diện tích S của hình phẳng giới hạn bởi đồ thị y = (e + ) 1 x và = (1+ x y e ) x . A. = e S −1 B. S =1 C. 3 S =
D. S = 2e −1 2 2
Câu 35: Tính diện tích S của hình phẳng (H ) giới hạn bởi các đường y = x, y = 6 − x và trục hoành. A. 20 S = B. 25 S = C. 16 S = D. 22 S = 3 3 3 3
Câu 36: Tính diện tích S của hình phẳng giới hạn bởi các đường y = xln x , trục hoành và đường thẳng x = e . 2 2 2 A. 2 + − − S = e −1 B. 1 = e S C. 1 = e S D. 1 = e S 4 2 4
Câu 37: Tính diện tích S của hình phẳng giới hạn bởi các đường y = (x − ) x 2
1 e , y = x −1. A. 8 S = e + B. 2 S = e + C. 2 S = e − D. 8 S = e − 3 3 3 3
Câu 38: Biết rằng hình thang cong (H ) giới hạn bởi các đường y = 2 − x, y = 0, x = k, x = 3 với k < 2 và có
diện tích bằng S . Xác định giá trị của k để S = . k 16 k A. k = 2 + 15 B. k = 2 + 31 C. k = 2 − 15 D. k = 2 − 31
Câu 39: Cho hình phẳng (H ) giới hạn bởi các đường y = ln x, y = 0, x = k (k > )
1 . Tìm k để diện tích hình phẳng (H ) bằng 1. A. k = 2 B. k = e C. 3 k = e D. 2 k = e
Câu 40: Cho hai hàm số y = f (x) và y = g (x) liên tục trên đoạn [ ;
a b] với a < b . Kí hiệu S là diện tích 1
hình phẳng giới hạn bởi các đường y = 2 f (x), y = 2g (x), x = a và x = b ; S là diện tích hình phẳng giới 2
hạn bởi các đường y = f (x) − 2, y = g (x) − 2, x = a và x = b . Chọn khẳng định đúng?
A. S = S
B. S = 2S
C. S = 2S − 2
D. S = 2S + 2 1 2 1 2 1 2 1 2
Câu 41: Trong mặt phẳng tọa độ, cho hình chữ nhật (H ) có một cạnh nằm trên trục hoành và có hai đỉnh
trên một đường chéo là A( 1;
− 0) và C ( ;a a ) với a > 0 . Biết
rằng đồ thị hàm số y = x chia hình (H ) thành hai phần có diện
tích bằng nhau, tìm a. A. a = 9 B. a = 4 C. 1 a = D. a = 3 2
Câu 42: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) 2x −1 : y =
, tiệm cận ngang của đồ thị (C), trục tung và x +1
đường thẳng x = a(a > 0) . Tìm a để S = 3ln 5. A. a = 5 B. a = 4 C. a = 3 D. a = 2
Câu 43: Tính diện tích hình phẳng trong phần tô đậm của hình vẽ bên. A. 8 B. 11 3 3 C. 7 D. 10 3 3
Câu 44: Tìm công thức tính diện tích S của hình phẳng (H ) giới hạn bởi các đồ thị hàm số y = f (x) ,
y = g (x) và hai đường thẳng x = a, x = b như hình vẽ bên cạnh. Biết rằng f (x) ≥ g (x),∀x∈[ ; a b] và
f (x) ≤ g (x),∀x∈[ ; c d] . c b A. S = 
∫ g(x)− f (x)dx+ 
∫ f (x)− g(x)     dx a c c b B. S = 
∫ f (x)− g(x)dx+ 
∫ g(x)− f (x)     dx a c b C. S = 
∫ g(x)− f (x)   dx a b D. S = 
∫ f (x)− g(x)   dx a
Câu 45: Diện tích phần gạch chéo trong hình vẽ bằng bao nhiêu? A.27ln2 B. 27ln3 C. 28ln3 D. 29ln3
Câu 46: Diện tích hình phẳng tô đậm trong hình vẽ bằng bao nhiêu? A. 3 B. 3 2 4 C. 1 D. 1 6 2
Câu 47: Biết diện tích phần gạch chéo của hình vẽ bên bằng + b ae
+ c với a, b, c là các số nguyên. Tính P = a + b + c . e A. 1 P = B. P = 0 3 C. 1 P = − D. 1 P = 2 5
Câu 48: Cho đồ thị y = f (x) như hình vẽ. Diện tích S của hình phẳng (phần gạch chéo) được xác định bởi công thức nào? 2
A. S = ∫ f (x)dx 2 − 1 2
B. S = f (x)dx + ∫
∫ f (x)dx 2 − 1 2 − 2
C. S = f (x)dx + ∫
∫ f (x)dx 1 1 1 2
D. S = f (x)dx − ∫
∫ f (x)dx 2 − 1
Câu 49: Tính diện tích hình phẳng giới hạn bởi parabol như hình vẽ và trục hoành Ox. A. 4 B. 17 3 2 C. 9 D. 1 9
Câu 50: Tính diện tích hình phẳng giới hạn bởi parabol như hình vẽ và đường thẳng y = 3. A. 3 S = B. 4 S = 4 3 C. 14 S = D. S = 6 3
Câu 51: Tính diện tích hình phẳng giới hạn bởi y = f (x) có đồ thị như hình vẽ và Ox, Oy. Biết rằng đồ thị
hàm số y = f (x) đi qua hai điểm A( )  1 0;1 , B ;0 −  . 2    A. 1− ln 2 B. 1 1− ln 2 C. 1 2 − ln D. 1 1 − ln 2 2 2
Câu 52: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y = 2 − x , đường thẳng y = x và trục hoành. A. π π π S = π B. 3 S = C. S = D. S = 4 2 4
Câu 53: Cho S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = 2x − x và trục hoành. Tìm số nguyên lớn nhất không vượt quá S. A. 0 B. 1 C. 2 D. 3
Câu 54: Tính diện tích S của hình phẳng (H ) giới hạn bởi hai đồ thị
của hai hàm số = 3x y
, y = 4 − x và trục tung. A. 9 2 S = + B. 9 3 S = + C. 7 3 S = − D. 7 2 S = − 2 ln 3 2 ln 3 2 ln 3 2 ln 3
Câu 55: Diện tích hình phẳng giới hạn bởi đường cong
y = 2 ax (a > 0), trục hoành và đường thẳng x = a bằng 2 ka . Tính
giá trị của tham số k. A. 7 k = B. 4 k = C. 12 k = D. 6 k = 3 3 5 5
Câu 56: Tính diện tích hình phẳng S giới hạn bởi các đồ thị của các đường 2
y = x − 2x +1, y = x +1, x = 0 ,
x = m với m∈(0;3) . 3 2 2 3 3 2 3 2 A. m 3 = − m S B. 3 = m − m S
C. = m − m S + 2m
D. = m − m S − 2m 3 2 2 3 3 2 3 2
Câu 57: Biết diện tích hình phẳng S giới hạn bởi các đồ thị của các đường 2
y = x − 2x +1, y =1− x và
x = 0, x = m với m < 0 bằng 5 . Tìm giá trị của tham số m. 6 A. m = 3 − B. m = 2 − C. m = 1 − D. m = 4 − Câu 58: Cho hàm số 1 4 2 2
y = x − 2m x + 2 . Tìm các giá trị của tham số m sao 2
cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng
cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình
phẳng có diện tích bằng 64 . 15   A. m∈∅ B. m∈{± } 1 C. 2 m    ; 1 ∈ ± D. 1 m∈± ; 1 ± 2      2 
Câu 59: Tính diện tích S của phần hình phẳng gạch sọc (như hình vẽ bên dưới) giới hạn bởi đồ thị của hàm số bậc ba 3 2
y = ax + bx + cx + d và trục hoành. A. 31π S = B. 27 S = 5 4 C. 19 S = D. 31 S = 3 5
Câu 60: Gọi S là diện tích hình phẳng giới hạn bởi các đường 2 2
2my = x ,2mx = y (m > 0) . Tìm giá trị của m để S = 3. A. 3 m = B. m = 2 C. m = 3 D. 1 m = 2 2
Câu 61: Cho hình thang cong (H ) giới hạn bởi các đường = x
y e , y = 0, x = 0, x = ln 4. Đường thẳng
x = k (0 < k < ln 4) chia (H ) thành hai phần có diện tích là S và S như hình vẽ bên. Tìm k để 1 2 4S + S = 8. 1 2 A. 2 k = ln 4 B. k = ln 2 3 C. 8 k = ln D. 2 k = ln 3 3
Câu 62: Cho hình thang cong (H ) giới hạn bởi các đường 1 1
y = , x = , x = 2 và x 2
trục hoành. Đường thẳng  1 x k, k 2 = < < 
chia (H ) thành hai phần có diện tích 2   
là S và S như hình vẽ dưới đây. Tìm tất cả các giá trị thực của k để S = 3S . 1 2 1 2 A. k = 2 B. k =1 C. 7 k = D. k = 3 5
Câu 63: Cho hình thang cong (H ) giới hạn bởi các đường = x y e ;
y = 0; x = 0 và x = ln 4 . Đường thẳng x = k (0 < k < ln 4) chia (H ) thành hai
phần có diện tích là S , S và như hình vẽ bên dưới. Tìm k để S = 2S . 1 2 1 2 A. 8 k = ln B. 2 k = ln 4 3 3 C. k = ln 3 D. k = ln 2
Câu 64: Cho hình thang cong (H ) giới hạn bởi các đường = x
y e ; y = 0; x =1; x = ln 6 . Đường thẳng x = k (1< k < ln 6) chia (H )
thành hai phần có diện tích S và S như hình vẽ bên. Tìm k để 1 2 2 2
P = S + S đạt giá trị nhỏ nhất. 1 2 A. − + 6 + = e k B. 6 = e k 2 2 C. e + 6 k e + = − ln D. 6 k = ln 2 2
Câu 65: Cho hình thang cong (H ) giới hạn bởi các đường = x
y e ; y = 0; x =1; x = ln 6 . Đường thẳng x = k (1< k < ln 6) chia (H ) thành hai
phần có diện tích là S và S như hình vẽ bên. Tìm k để S < S − 2 . 1 2 1 2 A. + 4 1 + < < e k B. 4 < e k 2 2 C. e + 4 k e + < ln D. 4 1< k < ln 2 2
Câu 66: Cho hình thang cong (H ) giới hạn bởi các đường = x
y e ; y = 0; x = 0; x = ln 4 . Đường thẳng x = k (0 < k < ln 4) chia (H )
thành hai phần có diện tích là S và S như hình vẽ bên. Gọi X là tập hợp 1 2
tất cả các giá trị k để 2 2
S + S = 5 . Tính tổng các phần tử của tập hợp X. 1 2 A. ln5 B. ln6 C. ln12 D. 5 ln 2
Câu 67: Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 4x + 4 ,
trục tung và trục hoành. Xác định k để đường thẳng d đi qua điểm A(0;4) có hệ số góc k chia (H ) thành
hai phần có diện tích bằng nhau (như hình vẽ bên). A. k = 4 − B. k = 8 − C. k = 6 − D. k = 2 −
Câu 68: Cho hình thang cong (H ) giới hạn bởi các đường = x
y e , y = 0, x = 0, x =1. Đường thẳng x = k (0 < k < ) 1 chia (H ) thành
hai phần có diện tích là S và S như hình vẽ bên. Tìm k để S > S . 1 2 1 2 A. +1 e + > e k B. 1 ln < k <1 2 2 C. e +1 0 e + < k < ln D. 1 k > ln 2 2
Câu 69: Cho hàm số y = f (x) liên tục trên ℝ và hàm số y g (x) xf ( 2 = = x ) có
đồ thị trên đoạn [0;2] như hình vẽ. Biết diện tích miền tô màu là 5 S = . Tính 2 4
I = ∫ f (x)dx . 1 A. 5 I = B. 5 I = 4 2 C. I = 5 D. 11 I = 2
Câu 70: Một sân chơi dành riêng cho trẻ em hình chữ nhật có chiều dài 50m và chiều rộng 30m, người ta
làm một con đường trong sân (như hình vẽ). Biết viền ngoài và viền trong của con đường là hai đường elip
và chiều rộng của mặt đường là 2m. Kinh phí để làm mỗi 2
m làm đường 500.000 đồng. Tính tổng số tiền
làm con đường đó (số tiền làm tròn đến hàng nghìn). A. 119.000.000 đồng B. 152.000.000 đồng C. 119.320.000 đồng
Câu 71: Người ta trồng hoa và phần đất được gạch sọc được giới hạn bởi
cạnh AB, CD, đường trung bình MN của mảnh đất hình chữ nhật ABCD và
một đường cong hình sin (như hình vẽ). Biết AB = 2π(m) và AD = 2(m).
Tính diện tích phần còn lại. A. 4π −1 B. 4(π − ) 1 C. 4π − 2 D. 4π − 3 2 2
Câu 72: Ông An muốn là cửa rào sắt có hình dạng kích
thước như hình vẽ bên, biết đường cong phía trên là một parabol. Giá 2
1m của rào sắt là 700.000 đồng. Hỏi ông An
phải trả bao nhiêu tiền để làm cửa sắt (làm tròn đến hàng phần nghìn). A. 6.520.000 đồng B. 6.320.000 đồng C. 6.417.000 đồng D. 6.620.000 đồng
Trục hoành và hai đường thẳng 5 − 5 x = ; x = 2 2
Câu 73: Một khuôn viên dạng nửa hình tròn có đường kính bằng 4 5 m. Trên đó người ta thiết kế hai phần
để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa đường tròn và hai đầu mút
của cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau
một khoảng bằng 4m. Phần còn lại của khuôn viên (phần không
tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như
hình vẽ và kinh phí để trồng cỏ Nhật Bản là 100.000 đồng/ 2 m .
Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản? (làm tròn đến hàng nghìn) A. 3.895.000 đồng B. 1.948.000 đồng C. 2.388.000 đồng D. 1.194.000 đồng
Câu 74: (Đề thi THPT Quốc gia 2017 – Mã đề 101) Cho y = f (x) có
đồ thị của y = f ′(x) như hình vẽ. Đặt h(x) = f (x) 2 2
− x . Mệnh đề nào đúng?
A. h(4) = h( 2 − ) > h(2)
B. h(4) = h( 2 − ) < h(2)
C. h(2) > h(4) > h( 2 − )
D. h(2) > h( 2 − ) > h(4)
Câu 75: (Đề thi THPT Quốc gia 2017 – Mã đề 104) Cho y = f (x) có đồ thị của y = f ′(x) như hình vẽ.
Đặt g (x) = f (x) + (x + )2 2 1 . Mệnh đề nào đúng? A. g ( )
1 < g (3) < g ( 3 − ) B. g ( ) 1 < g ( 3 − ) < g (3)
C. g (3) = g ( 3 − ) < g ( ) 1
D. g (3) = g ( 3 − ) > g ( ) 1
Câu 76: Cho y = f (x) có đồ thị của y = f ′(x) như hình vẽ. Đặt
g (x) = f (x) + cos x . Mệnh đề nào dưới đây đúng?
A. g (0) g ( )  π   π < π < g   B. g
< g (0) < g (π   ) 2     2  C.  π  g  π < g (π) <    g (0)
D. g (π) > g (0) > g    2   2 
D. LỜI GIẢI CHI TIẾT b
Câu 1: Ta có S = ∫ f (x) dx. Chọn D. a b
Câu 2: Ta có S = f x − ∫
f x dx . Chọn A. 1 ( ) 2 ( ) ax =1
Câu 3: Phương trình hoành độ giao điểm 2
x = 2 − x ⇔  . x = 2 − 1 2 1
Dựa vào đồ thị hàm số ta có 2
S = x dx + (2 − x) 1 2 dx = + ∫ ∫
x dx . Chọn C. 2 ∫ 0 1 0 x = 0
Câu 4: Phương trình hoành độ giao điểm 3 3
x − x = 2x ⇔ x − 3x = 0 ⇔  2 x = 3  (l) 0 1 Do đó S = ( 3
x − 3x)dx + ( 3 3x − ∫ ∫
x )dx . Chọn C. 1 − 0
Câu 5: Phương trình hoành độ giao điểm 2x = 4 − x ⇔ x = 2. 2 4
Dựa vào đồ thị hàm số ta có S = 2xdx + (4 − ∫ ∫
x)dx . Chọn B. 0 2 x = 0
Câu 6: Phương trình hoành độ giao điểm 2
x − x = 0 ⇔  . x = 1 2 1
Dựa vào đồ thị hàm số ta có S = ( 2 x − x) − ( 2 x − ∫ ∫
x)dx . Chọn B. 1 0 x =1
Câu 7: Phương trình hoành độ giao điểm 2 2
x = 2 − x ⇔  . x = 1 − 1 1 1 Ta có 2 S = x − ( 2 2 − x ) 2
dx = 2 1− x dx = 4 ( 2 1− ∫ ∫
∫ x )dx . Chọn B. 1 − 1 − 0 x = 0
Câu 8: Phương trình hoành độ giao điểm 2
x − 2x = 0 ⇔  . x = 2 0 2
Dựa vào đồ thị hàm số ta có S = ∫ ( 2x −2x)dx − ∫( 2x −2x)dx . Chọn B. 1 − 0 c b
Câu 9: Dựa vào đồ thị hàm số ta có S = 
∫ f (x)− g(x)dx+ 
∫ g(x)− f (x)   
dx . Chọn A. a c 0 2
Câu 10: Dựa vào đồ thị hàm số ta có S = f (x)dx − ∫
∫ f (x)dx . Chọn A. 2 − 0 b b
Câu 11: Dựa vào đồ thị hàm số ta có S = f (x)dx − ∫
∫ g(x)dx . Chọn B. a a c b
Câu 12: Dựa vào đồ thị hàm số ta có S = − f (x)dx + ∫
∫ f (x)dx . Chọn C. a c 2
Câu 13: Ta có diện tích 2 bên trục tung bằng nhau nên S = 2 ∫ f (x)dx . Chọn B. 0 1 2
Câu 14: Dựa vào đồ thị hàm số ta có S = f (x)dx − ∫
∫ f (x)dx . Chọn C. 2 − 1 0 b
Câu 15: Dựa vào đồ thị hàm số ta có S = − f x dx
f x dx . Chọn B. D ( ) + ∫ ∫ ( ) a 0 0 0 4
Câu 16: Dựa vào đồ thị hàm số ta có S = f (x)dx + f (x)dx + ∫ ∫
∫ f (x)dx . Chọn B. 2 − 2 2 1 2
Câu 17: Dựa vào đồ thị hàm số ta có S = f (x)dx − f (x)dx = a − ∫ ∫ b . Chọn B. 3 − 1 0 2
Câu 18: Dựa vào đồ thị hàm số ta có S = − f (x)dx + f (x)dx = b − ∫ ∫ a . Chọn D. 1 − 0 1 4
Câu 19: Dựa vào đồ thị hàm số ta có = ∫(3 +0,5x − )1 + ∫(log −0,5x S x dx x
− 2 dx . Chọn D. 2 ) 0 1 b
Câu 20: Dựa vào đồ thị hàm số ta có S = ∫ g( y)dy . Chọn C. a c b
Câu 21: Dựa vào đồ thị hàm số ta có S = 
∫ g(y)− f (y)dy + 
∫ f (y)− g(y)   
dy . Chọn C. a c b c b c
Câu 22: Ta có S = ∫ f (x)dx + ∫ f (x) dx = −∫ f (x)dx + ∫ f (x)dx = −( 3
− ) + 5 = 8 . Chọn C. a b a b 4 6 4 6
Câu 23: Ta có S = f (x) dx + f (x) dx = f (x)dx + ∫ ∫ ∫
∫ g(x)dx. Chọn B. 0 4 0 4 3 Câu 24: 2 − ≥3 2 2 = − 4 +1−  → − 4 +1− ≥ − 4 + 4 = ∫ m S x x m dx x x m x x (x − 2)2 ≥ 0 0 3 3 S ∫(  x  ⇒ =
x − 4x +1− m) 3 2 2
dx =  − 2x + (1− m) x = 3
− m − 6 . Chọn D.  3 0  0 x = 0 1 Câu 25: Xét PT: 10 2 13 2  
x − x = −x ⇔ 13 ⇒ S = x − x dx . 1 3 ∫ x  3   = 0   3 x = 3 3 Lại có 10 2  7 2 x x x 2   − = − ⇔
2 ⇒ S = ∫2 + x − x dx 2 3 x  3   = − 1   3 1 3 2 3 2 3 13x x   7x x  13
⇒ S = S + S =  −  +  2x+ −  = . Chọn C. 1 2  2 3   6 3  2 0 1 x = 0 1 Câu 26: Xét PT: 3 2  3 2
x − x = x − x ⇔ x =1 ⇒ S = x + x − 2  ∫ x dx 2 x = 2 − −  0 1 0
= x + x − 2x dx + x + x − 2x dx = ∫ ∫
∫ (x + x −2x) 1 3 2 3 2 3 2 dx + − ∫ ( 3 2
x + x − 2x)dx 2 − 0 2 − 0 0 1 4 3 4 3  x x   x x  2 2 8 5 37
=  + − x  − + − x  = + = . Chọn A.  4 3   4 3  3 12 12 2 − 0 2 0 2 x = 0 Câu 27: Xét PT: 3 3 3 3
x − 3x = x ⇔
⇒ S = x − 4x dx = x − 4x dx + x −  4 ∫ ∫ ∫ x dx x = 2 ± 2 − 2 − 0 0 2 0∫(  x   x  = x − 4x) 2
dx + ∫(4x − x ) 4 4 3 3 2 2
dx =  − 2x  + 2x −  = 8. Chọn D. −  4   4 2 0 2  − 0 x = 1 − Câu 28: Xét PT: 2
x + x −1 = 2x +1 ⇔  x = 2 2 2 2
⇒ S = x − x − dx = − ∫
∫ (x − x− ) 3 2  x x  2 2 9 2
2 dx = − − − 2x = . Chọn A. − −  3 2  2 1 1 1 − 1 1 1 2 3 x = 0  x x Câu 29: Xét PT: 2 2 x = x ⇔
⇒ S = x − x dx =  ∫ ∫( 2 x − x ) 1
dx =  −  = . Chọn D. x = 1  2 3  6 0 0 0 1 0 1 Câu 30: Ta có 2 2 2
S = x + 2x dx = x + 2x dx + x + 2 ∫ ∫ ∫ x dx 1 − 1 − 0 0 1 0 = − ∫ (x + x) 1
dx + ∫(x + x) 3 3  x   x  2 2 2 2 2 2
2 dx = − + x  +  + x  = . Chọn A. −  3   3  3 1 0 1 − 0 x =1 Câu 31: Xét PT: 2 2 2 x 5x 3 2x 2x 1 3x 7x 4 0  − + = − + − ⇔ − + = ⇔ 4 x =  3 4 4 4 3 3 ⇒ S =
x − x + dx = − ∫ ∫ ( x − x+ ) 2 3  x  2 2 3 7 1 3 7 4 3 7
4 dx = − x − + 4x = . Chọn A.  2  54 1 1 1 x = 0 Câu 32: Xét PT: 2 3 2 3 x − x + 5 = 2
− x + x + x + 5 ⇔ 2x − 2x = 0 ⇔  x = 1 ± 1 0 1 3 3 3
⇒ S = 2x − 2x dx = 2x − 2x dx + 2x − 2 ∫ ∫ ∫ x dx 1 − 1 − 0 0 1 0∫(  x   x  = 2x − 2x) 1 dx + − ∫ (2x −2x) 4 4 3 3 2 2
dx =  − x  − − x  =1. Chọn A. −  2   2 1 0 1  − 0 2 2 x = 0 Câu 33: Xét PT: 4 2 2 4 2
x − 2x = 2x ⇔
⇒ S = x − 4x = ∫ ∫( 4 2 x −  4x )dx x = ± − 2 0 0 2 2 
→ ∫(x − x ) 5 3  x x  4 2 4 64 64 4 dx =  −  = − ⇒ S = . Chọn A.  5 3  15 15 0 0 x =
Câu 34: Xét PT: (e + ) x = ( + xe ) 0 1 1
x ⇔ ex = x xe ⇔  x = 1 1
1∫ ( x ) 1∫ ( x) 2  ex  ⇒ = − = − = e S x e e dx x e e dx  + x e − x
xe  = −1. Chọn A.  2  2 0 0 0 4 4
Câu 35: Xét PT: x = 6 − x ⇔ x = 4 ⇒ S = x + x − 6 dx = − ∫
∫ (x+ x −6)dx 0 0 4   2 3  x x  22 = − − − 6x = . Chọn D. 2 3 3    2  0 e 1  = 0 e x
Câu 36: Xét PT: xln x = 0 ⇔
⇒ S = x ln x dx = x ln x dx +  x ln ∫ ∫ ∫ x dx x = 1 0 0 1 1 e 1 = − ln + ln  → ln = ln ∫ ( ) 2 2 1 2 1 2 1 1 2 = ln − . = ln − x x xdx x xdx x xdx xd x x x x dx x x + ∫ ∫ ∫ C 2 2 2 ∫ x 2 4 0 1 1 2 2 e 2  1 x   x  2 1 2 e +1
⇒ S = − x ln x −  +  x ln x −  = . Chọn B.  2 4   2 4  4 0 1 1 x =1 x =1
Câu 37: Xét PT: (x − ) x 2
1 e = x −1 ⇔  ⇔ ⇒ S = x e x dx x
∫ ( − )1 x −( 2 − )1 e = x +1 x = 0 0 1 1 3
= ∫(x − ) xe −(   2 x − ) x x x x 8 1
1 dx =  xe − e − e − + x = e − . Chọn D.  3  3 0 0 3 2 3
Câu 38: Xét PT: 2 − x = 0 ⇔ x = 2 ⇒ S = 2 − x dx = ∫
∫(2− x)dx+ ∫(x−2)dx k k 2 2 3 2 2 2  x   x  5  k
= 2x −  +  − 2x = −2k −  =16 ⇒ k = 2 − 31. Chọn D.  2   2  2  2 2  k k k
Câu 39: Xét PT: ln = 0 ⇔ =1⇒ = ln = ln k x x S x dx x x − ∫ ∫ xd (ln x) 1 1 1
= k ln k − (k − )
1 =1⇒ k = e . Chọn B. b b b Câu 40: 1
S = 2 f x − 2g x ;
dx S = f x − 2 − (g x − 2) dx = f x − g x dx = S . Chọn B. 1 ∫ ( ) ( ) 2 ∫ ( ) ( ) ∫ ( ) ( ) 1 2 a a a
Câu 41: Diện tích hình phẳng giới hạn bởi các đường y = x, y = 0, x = 0, x = a là a 2 a 3 2 3 S′ = xdx = x = ∫ a . 3 3 0 0 Lại có S = a a S S a a a a . Chọn D. H ( + ) 1 2 3 1 1 ⇒ ′ = ⇔ = H ( + ) ( ) ( ) 1 ⇒ = 3 2 3 2 a a Câu 42: 2x −1 3 S = − 2 dx =
dx = 3ln x +1 a = 3ln a +1 = 3ln 5 ⇒ a = 4 ∫ ∫ . Chọn B. 1 x +1 x +1 0 0 4 4 Câu 43: S = xdx − (x − ) 10 2 dx = ∫ ∫ . Chọn D. 3 0 2 c b c b
Câu 44: S = ∫ f (x)− g(x) dx + ∫ f (x)− g(x) dx = 
∫ f (x)− g(x)dx+ 
∫ g(x)− f (x)   
dx . Chọn B. a c a c
Câu 45: Phương trình hoành độ giao điểm của f (x) và h(x) là 2 27 x = ⇔ x = 3 . x 2
Phương trình hoành độ giao điểm của g (x) và h(x) là 27 = x ⇔ x = 9 . x 27 3 9
Khi đó, diện tích cần tìm là S = ∫ f (x)− g(x) dx + ∫ h(x)− g(x) dx = 27ln3. Chọn B. 0 3 2 2 2 2
Câu 46: Diện tích cần tìm là x x 1 1 S = dx − S = dx − = ∫ . Chọn C. ∆ .1.1 4 ∫ 4 2 6 0 0  1 x =
Câu 47: Phương trình hoành độ giao điểm của (C) và d là ln x 1  = ⇔ .  ex = e 1 e 1
Diện tích cần tìm là S = ( + x)dx + ( − x) 1 1 ln
1 ln dx =1− + e −1+ (xln x − x) −(xln x − ∫ ∫ x) e 1 e 1 1 1 e e 1 2 1 a = b = 1
= e − + −1−1 = e + − 2  → 
. Vậy P = a + b + c =1+1− 2 = 0. Chọn B. e e ec = 2 − 1 2 1 2
Câu 48: S = f (x) dx + f (x) dx = − f (x)dx + ∫ ∫ ∫
∫ f (x)dx. Chọn C. 2 − 1 2 − 1
Câu 49: Vì parabol đi qua 3 điểm A(
) B( ) I ( ) →(P) 2 0;0 , 2;0 , 1;1;
: y = −x + 2x 2 2
Do đó, diện tích hình phẳng cần tính là S = f (x) 2 4
dx = 2x − x dx = ∫ ∫ . Chọn A. 3 0 0
Câu 50: Vì parabol đi qua điểm A(0;3) , đỉnh I ( )  →(P) 2 1;2
: y = x − 2x + 3 x = 0
Phương trình hoành độ giao điểm của (P) và d là 2
x − 2x + 3 = 3 ⇔  . x = 2 2 2
Do đó, diện tích cần tính là S = f (x) − g (x) 2 4
dx = x − 2x dx = ∫ ∫ . Chọn A. 3 0 0
Câu 51: Gọi phương trình đồ thị hàm số là ax + = b y . cx + d
Vì đồ thị đi qua A( )  1 0;1 , B ;0 − 
và có hai đường tiệm cận là 2    x = 1; − y = 2 . Suy ra 2x +1 y =
. Do đó, diện tích cần tìm là x +1 0 2 +1 = = 1− ln 2 ∫ x S dx . Chọn A. x + 1 1 − 2
Câu 52: Phương trình hoành độ giao điểm của đồ thị hàm số 2
y = 2 − x và đường thẳng y = x là: x ≥ 0 2
2 − x = x ⇔  ⇔ x =1 2 2 2 − x = x 1 2 2 Ta có: 2 1 2 S = xdx + 2 − x dx = + 2 − ∫ ∫ x dx 2 ∫ 0 1 1 2 Xét 2 2 − ∫
x dx , ta đặt x = 2 sin t 1 π π 2 2 2 x= t 2 I = 2 − x dx  → 2 − 2sin ∫ ∫ td ( 2 sint) 2 2 sin 2 = 2cos ∫ tdt 1 π π 4 4 π π 2 = ∫( + t) 2  sin 2t  π 1 1 cos 2 π dt = t + = − ⇒ S =  .  2  π π  4 2 4 4 4
Cách 2: Diện tích cần tìm là hình quạt có góc ở đỉnh bằng 45° 2 1 45 S . R . .2 π ° ⇒ = π = π = . Chọn D. 360° 8 4 x = 0
Câu 53: Phương trình hoành độ giao điểm là 2
2x − x = 0 ⇔  x = 2 2 2 2 3  x
Diện tích hình phẳng cần tìm là: 2 S = x − x dx = ∫ ∫( 2 x − x ) 2 4 2 2
dx =  x −  = .  3  3 0 0 0
Vậy số nguyên lớn nhất không vượt quá S là 1. Chọn B.
Câu 54: Phương trình hoành độ giao điểm của 2 đồ thị là: 3x = 4 − ⇔ ( ) = 3x x f x + x = 4 Do ′( ) = 3x f x
ln 3+1 > 0(∀x∈ ) và f ( )
1 = 4 nên f (x) = f ( ) 1 ⇔ x =1. 1 1 1 x 2  x
Diện tích cần tìm là: S =
x + x − dx = ∫
∫( − x − x) 3 7 2 3 4 4 3 dx = 4x − −  = − . Chọn D.  ln 3 2  2 ln 3 0 0 0
Câu 55: Phương trình hoành độ giao điểm 2 ax = 0(a > 0; x ≥ 0) ⇔ x = 0 2 a Diện tích cần tìm là: 2 3 4 2 4
S = 2 axdx = 2 a.
x = a ⇒ k = ∫ . Chọn B. 3 3 3 0 0 Câu 56: Ta có: 2
x − x + − (x + ) 2 2 1 1 = x − 3x m m m Khi đó 2 m ( ∈ ) = − → ( 2 − ) 2 3 2 3 0;3 3x x 3 3 3 = − = m − ∫ ∫ m S x x dx x x dx . Chọn B. 2 3 2 3 0 0 0 0 0 0
Câu 57: Diện tích cần tìm là: 2 S x x ( x) 2 m 0 dx x x dx S ( 2 2 2 1 < = − + − − = −  → = x − ∫ ∫ ∫ x)dx m m m 0 3 2 2 3  x x m m 5 =  −  = − = ⇔ m = 1 − . Chọn C.  3 2  2 3 6 mx = 0 Câu 58: Ta có: 3 2
y′ = 2x − 4m x = 2x( 2 2
x − 2m ) = 0 ⇔  2 2 x = 2m
Hàm số có 3 điểm cực trị khi m ≠ 0 Do 1
a = > 0 ⇒ điểm cực đại của đồ thị hàm số là (0;2) 2
Phương trình đường thẳng cùng phương với trục hoành qua điểm cực đại là d : y = 2 2 1 x = 0 x = 0
Phương trình hoành độ giao điểm 4 2 2
x − 2m x + 2 = 2 ⇔  ⇔ 2 2 2 x = 4  mx = 2 ± m 2 2 5 2 3 m m    x m x
Giả sử m > 0 do tính chất đối xứng nên 1 4 2 2 4 S = 2 − x + ∫  2m x dx =   − +  2   5 3  0  0 5 5 5 32m 32m 64m 64 = − + = = ⇔ m =1 5 3 15 15
Tương tự m < 0 ⇒ m = 1 − . Vậy m∈{± } 1 . Chọn B.
Câu 59: Dựa vào đồ thị suy ra y = a(x + )(x − )2 2 1
Do đồ thị hàm số đi qua điểm (0;2) ⇒ 2 = 2a ⇒ a =1 1
Khi đó S = (x + )(x − )2 27 2 1 dx = ∫ . Chọn B. − 4 2
Câu 60: Tọa độ giao điểm của 2 đồ thị là nghiệm của hệ 2  x 4 y = xx =  2m ⇒ = 2mx ⇔ x( 0 3 3 x −8m = 0 ⇔ 2 ) 4   mx = 2m 2 y = 2mx 2 2 2 3  x   x m m Khi đó 2 3
S = ∫  2mx − dx =  2m. x −  2m   3 6  m 0  0 2 2 2 8m 4m 4m 3 = − =
= 3 ⇔ m = . Chọn A. 3 3 3 2 ln 4 Câu 61: Ta có + = = 3 1 2 ∫ x S S e dx 0 k Lại có: 5 5 k x x k 8
4S + S = 8 ⇒ S = = e dx ⇔ = e = e −1⇒ k = ln . Chọn C. 1 2 1 ∫ 0 3 3 3 0 2 Câu 62: Ta có 1 2 S + S =
dx = ln x = ln 4 = 2ln 2 1 2 1 ∫1 x 2 2 Do S 3 1
S = 3S ⇒ S + = 2ln 2 ⇒ S = ln 2 1 2 1 1 3 2 k Mặt khác 1 k 3 S =
dx = ln x = ln 2k = ln 2 = ln 8 ⇒ 2k = 8 ⇔ k = 2 . Chọn A. 1 1 ∫1 x 2 2 2 ln 4 ln 4 ln 4 Câu 63: Do 2 2 x 2 x 2 = 2 ⇒ = = = = x S S S S e dx e dx e = 2 1 2 1 3 3 ∫ 3 ∫ 3 0 0 0 k Do đó = x
= x −1 = 2 ⇔ k S e dx e
e = 3 ⇔ k = ln 3 . Chọn C. 1 ∫0 ln 6 Câu 64: Ta có + = = 6 − 1 2 ∫ x S S e dx e 1 Do 2
P = S + (6 − e − S )2 2
= 2S − 2 6 − e S + 6 − e 1 1 1 ( ) 1 ( )2 −b 2(6 − e) Khi đó 6 − ⇔ = = = e P S min 1 2a 2.2 2 k Lại có: x k 6 − e k e + 6 e + 6
S = e dx = e − e = ⇒ e = ⇒ k = ln . Chọn D. 1 ∫ 2 2 2 1 ln 6 Câu 65: Ta có + = = 6 − 1 2 ∫ x S S e dx e 1
Do < − 2 ⇒ < 6 − − − 2 ⇔ < 2 − e S S S e S S 1 2 1 1 1 2 k Lại có: x k e k e + 4 e + 4
S = e dx = e − e < 2 − ⇔ e < ⇒ 1< k < ln . Chọn D. 1 ∫ 2 2 2 1 ln 4 Câu 66: Ta có + = = 3 1 2 ∫ x S S e dx 0 2 2 S + S = 5 S = 2; S =1 Do 2 2 1 2 1 2
S + S = 5 ⇒   → 1 2 S + S =  3 S =  1;S = 2 1 2 1 2 kk e −1 = 2 k = ln 3 Lại có: S = x e dx = k e −1⇒ ∫  ⇔
⇒ tổng các phần tử của tập hợp X là ln 3+ ln 2 = ln 6 . 1  k e −1 =1  k = ln 2 0 Chọn B.
Câu 67: Đồ thị hàm số 2
y = x − 4x + 4 cắt trục hoành tại điểm (2;0) − 2
Diện tích phần gạch chéo là = ( − ) ( ) 2 3 2 2 8 2 = = ∫ x S x dx 3 3 0 0
Đường thẳng d đi qua điểm A(0;4) có hệ số góc k suy ra d : y = kx + 4
Đường thẳng d cắt Ox tại điểm  4 − C ;0(k <  
0) (Do C có hoành độ dương).  k
Theo giả thiết bài toán ta có: 1 S 4 1 4 − 4 OC.OA = = ⇔ .
.4 = ⇒ k = 6. Chọn C. 2 2 3 2 k 3 1 Câu 68: Ta có + = = −1 1 2 ∫ x S S e dx e 0 Do đó −1 > ⇔ > −1− ⇔ > e S S S e S S 1 2 1 1 1 2 k Lại có: x k e −1 k e +1 e +1
S = e dx = e −1 > ⇔ e > ⇔ k > ln 1 ∫ 2 2 2 0 Kết hợp e +1 0 < k <1⇒ ln
< k <1. Chọn B. 2 2 2 Câu 69: Ta có ( ) 5 =
∫ g x dx suy ra ∫ xf ( 2x) 5 dx = . Đặt 2
t = x ta có: dt = 2xdx 2 2 1 1 2 4 4
Đổi cận suy ra ∫ xf ( 2x) 1
dx = ∫ f (t) 5
dt = ⇒ ∫ f (t)dt = 5 ⇒ I = 5 . Chọn C. 2 2 1 1 1
Câu 70: Đường elip phía ngoài có phương trình 2 2
x + y =1 và có diện tích S = π25.15 2 2 25 15 1 2 2
Đường elip phía trong có phương trình x + y =1 2 2 23 13
và có diện tích S = π23.13 2
Diện tích mặt đường là S = S − S 1 2
Do đó kinh phí để làm đường là:
T = (S − S .500,000 =119.320.000 đồng. Chọn C. 1 2 )
Câu 71: Gọi O là trung điểm của MN. Chọn hệ trục tọa độ Oxy có trục Ox // BC, Oy // AB.
Khi đó đồ thị có dạng y = Asin bx .
Do AD = 2 ⇒ max y =1⇒ A =1
Do hàm số tuần hoàn với chu kì 2π ⇒ b =1⇒ y = sin x . π
Diện tích phần đất trồng hoa là: S 2 sin xdx 2cos π = = − x = 4 ∫ 0 0
Diện tích phần đất còn lại là: 2 .2 π − 4 = 4(π − ) 1 . Chọn B.
Câu 72: Chọn hệ trục tọa độ như hình vẽ. Trong đó  5 3   5 3 A ; ; B ;  −    ;C(0;2)  2 2   2 2 
Giả sử đường cong phía trên là một Parabol có dạng 2
y = ax + bx + c với a,b,c ∈  . Do Parabol đi qua các điểm  5 3   5 3 A ; ; B ;  −   
;C (0;2) nên ta có hệ phương trình:  2 2   2 2  25 5 3
a − b + c =  2 −  4 2 2 a =   25 25 5 3  2 − 
a + b + c = ⇔ b = 0 ⇒ phương trình parabol là: 2 y = x + 2 4 2 2   25 c = 2 c = 2    
Diện tích S của cửa rào sắt là diện tích phần hình phẳng giới hạn bởi đồ thị hàm số 2 − 2 y = x + 2 , trục hoành 25 và hai đường thẳng 5 − 5 x = ; x = . 2 2 5 5 2 3 2  −    Ta có: 2 2 2 55 = x + ∫ x S  2 dx =   − . + 2x = . 5  25   25 3  5 6 − − 2 2
Vậy ông An phải trả số tiền để làm cái cửa sắt là T = 700000.S = 6417000 đồng. Chọn C.
Câu 73: Ta có S = S − S 2 1
Trong đó S là diện tích hình phẳng giới hạn bởi các đường 2 2
y = 20 − x , y = x , x = 2,
− x = 2 được tô màu 1
trong hình bên, S là diện tích nửa hình tròn có bán kính bằng 2 5 . 2 1 ⇒ S = π(2 5) 2 2 − ( 2 2 20 − x − ∫ x )dx 2 2 − Suy ra S ≈ ( 2
19,476 m ) ⇒ Chi phí sẽ bằng
100.000S =1.948.000 đồng. Chọn B.
Câu 74: Ta có h′(x) = 2 f ′(x) − 2 ;
x h′(x) = 0 ⇔ f ′(x) = x .
Nhận thấy nghiệm của ′
h (x) = 0 chính là nghiệm của f ′(x) = x cũng là hoành độ giao điểm của hai đồ thị
hàm số y = f ′(x) và đường thẳng y = −x  → x = { 2; − 2; } 4 .
Vẽ đường thẳng y = x và chia đồ thị thành 2 phần diện tích hình phẳng. 2 2
Khi đó 2S = 2  f ′ x − xdx = ′
h x dx = h 2 − h 2
− > 0 ⇒ h 2 > h 2 − . 1 ∫  ( )  ∫ ( ) ( ) ( ) ( ) ( ) 2 − 2 − 4 4
Và 2S = 2 x − f ′ x dx = − g′ x dx = h 2 − h 4 > 0 ⇒ h 2 > h 4 2 ∫ ( ) ∫ ( ) ( ) ( ) ( ) ( ) 2 2 Lại có
S > S ⇔ 2S > 2S ⇔ h 2 − h 2
− > h 2 − h 4 ⇔ h 4 > h 2 − 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) .
Vậy h(2) > h(4) > h( 2 − ) . Chọn C. Câu 75: Ta có
g′(x) = 2 f ′(x) + 2(x + )
1 ; g′(x) = 0 ⇔ f ′(x) = −x −1.
Nhận thấy nghiệm của g′(x) = 0 chính là nghiệm của
f ′(x) = −x −1 cũng là hoành độ giao điểm của hai đồ thị hàm số y = f ′(x) và đường thẳng
y = −x −1 → x = { 3 − ;1; } 3 .
Vẽ đường thẳng y = −x và chia đồ thị thành 2 phần diện tích hình phẳng. 1 1
Khi đó 2S = 2 − x +1 − f ′ x dx = − g′ x dx = g 3
− − g 1 > 0 ⇒ g 3 − > g 1 1 ∫  ( ) ( ) ∫ ( ) ( ) ( ) ( ) ( ) 3 − 3 − 3 3
Và 2S = 2  f ′ x − −x −1  dx = g′ x dx = g 3 − g 1 > 0 ⇒ g 3 > g 1 2 ∫ ( ) ( ) ∫ ( ) ( ) ( ) ( ) ( ) 1 1
Lại có S > S ⇔ 2S > 2S ⇔ g 3
− − g 1 > g 3 − g 1 ⇔ g 3 − > g 3 . 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) Vậy g ( 3
− ) > g (3) > g ( ) 1 . Chọn A.
Câu 76: Ta có g′(x) = f ′(x) −sin ;
x g′(x) = 0 ⇔ f ′(x) = sin x
Nhận thấy nghiệm của g′(x) = 0 chính là nghiệm của f ′(x) = sin x cũng là hoành độ giao điểm của hai đồ thị hàm số y  π
= f ′(x) và đường thẳng y sin x x 0; ;  =  → = π . 2   
Vẽ đường thẳng y = sin x và chia đồ thị thành 2 phần diện tích hình phẳng. π π 2 2
Khi đó S = sin x − f x dx = − g x dx = g 0  π  − g > ∫  ∫   0 ⇒ g 0  π  ′ ′ > g . 1 ( ) ( ) ( ) ( )  2    2  0 0  π π
Và S =  f x − sin  π 
xdx = g x dx = g π − g > ∫  ∫   0  π  ′ ′ ⇒ g π > g . 2 ( ) ( ) ( ) ( )   π π  2   2  2 2 Lại có S S g 0  π   π  > ⇔ − g > g π − g ⇔     g 0 > g π . 1 2 ( ) ( ) ( ) ( )  2   2  Vậy  π  g < g (π) <  
g (0). Chọn B.  2 
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1