Chuyên đề trắc nghiệm ứng dụng tích phân tính thể tích Toán 12

Tài liệu gồm 33 trang, trình bày lý thuyết trọng tâm, các dạng toán trọng tâm kèm phương pháp giải và bài tập trắc nghiệm tự luyện chuyên đề ứng dụng tích phân tính thể tích, có đáp án và lời giải chi tiết; hỗ trợ học sinh lớp 12 trong quá trình học tập chương trình Toán 12 phần Giải tích chương 3.

67 34 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

33 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
CHỦ ĐỀ 13: ỨNG DỤNG TÍCH PHÂN TÍNH THỂ TÍCH
1) Tính thể tích vật thể
Cắt một vật thể
( )
H
bởi hai mặt phẳng
( )
P
và
( )
Q
vuông góc với trục
Ox
lần lượt tại
( )
;.x a x b a b= =
Một mặt phẳng tuỳ ý vuông góc với
Ox
tại điểm
x
(
) cắt
( )
H
theo thiết
diện là
( )
Sx
(hình vẽ). Giả sử
( )
Sx
liên tục trên đoạn
;.ab
Khi đó thể tích
V
của vật thể
( )
H
giới hạn bởi hai mặt phẳng
( )
P
và
( )
Q
được tính bởi công thức:
( )
.
b
a
V S x dx=
2) Tính thể tích vật tròn xoay sinh bởi diện tích S quay quanh trục Ox
Giả sử một hình thang cong giới hạn bởi đồ thị hàm số
( )
y f x=
, trục
Ox
và hai đường thẳng
xa=
và
( )
x b a b=
quay quanh trục
Ox
tạo thành một khối
tròn xoay (hình vẽ). Khi đó ta có thể tích vật thể là:
( )
=
b
a
dxxSV
Mặt khác tại điểm
x
ta có
( )
Sx
là một hình tròn có
bán kính
( )
R f x=
( ) ( )
22
S x R f x

= =
. Vậy
( )
2
.
b
Ox
a
V f x dx
=
Trong trường hợp
( )
Sx
giới hạn bởi hai đồ thị hàm số
( )
y f x=
và
( )
y g x=
ta được khối tròn xoay có thể
tích là:
( ) ( )
22
.
b
Ox
a
V f x g x dx
=−
Chú ý: Khi bài toán không cho hai đường thẳng giới hạn
xa=
và
xb=
thì ta giải phương trình
( ) ( )
f x g x=
để tìm cận của tích phân, trong đó
xa=
là nghiệm nhỏ nhất và
xb=
là nghiệm lớn nhất
của phương trình.
3) Tính thể tích vật tròn xoay sinh bởi diện tích S quay quanh trục Oy
Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi
đồ thị hàm số
( )
y f x=
trục
Oy
và hai đường thẳng
( ) ( )
;.y f a y f b==
- Bước 1: Biến đổi
( )
y f x=
về dạng
( )
1
.x f y=
- Bước 2: Khi đó
( )
( )
( )
2
1
.
fb
Oy
fa
V f y dy
=
Tương tự: Trong trường hợp
Oy
V
sinh ra bởi diện tích hình phẳng
của hai đồ thị hàm số
( ) ( )
;y f x y g x==
và hai đường thẳng
;y m y n==
ta có
( ) ( )
22
11
.
n
Oy
m
V f y g y dy
=−
Chú ý: Khi quay diện tích hình phẳng
S
quanh trục
Ox
ta được khối tròn xoay có thể tích
Ox
V
. Khi quay
quanh trục
Oy
ta được khối tròn xoay có thể tích
.
Oy
V
Hầu như
Ox
V
không bằng
Oy
V
. Chúng chỉ bằng nhau trong một số trường hợp đặc biệt.
4) Ứng dụng tính thể tích khối cầu, khối chỏm cầu và một số hình đặc biệt
a) Thể tích của khối cầu
Trong hệ tọa độ Oxy cho nửa đường tròn có phương trình:
( )
222
: ryxP =+
với
0; 0ry
(hình vẽ). Quay nửa hình tròn đó
quanh trục hoành ta được một mặt cầu có bán kính
.r
Thể tích của mặt cầu này là:
( )
3
4
3
Vrđvtt
=
.
Thật vậy: Ta có
22222
xryryx −==+
Với
0y
ta có:
22
xry −=
có đồ thị là nửa đường tròn phía
trên trục hoành.
Khi đó thể tích khối cầu
(
)
( )
3
2
2 2 2 2 2
0
0
22
3
r
rr
r
x
V r x dx r x dx r x
−

= − = − = −



( )
33
3
4
2
33
rr
r đvtt

= − =


b) Thể tích khối chỏm cầu
Khi quay hình phẳng tô đậm quanh trục
Ox
ta được khối 3 chỏm
cầu bán kính
r
và chiều cao
.h
Khi đó:
(
)
( )
2
2 2 2 2
rr
C
r h r h
V r x dx r x dx

−−
= − = −

2
32
.
33
r
rh
r x h
x h r

−


= − = −




c) Thể tích khối nêm (xem hình vẽ)
Đặt
22
; ; tan
tan
h
NP R x
OP x h MN MPN
R
MN NP

=−
= = = =
=
( )
R
R
V S x dx
−
=
trong đó
( )
( )
22
11
. . .
22
h
S x MN NP R x
R
= = −
( )
3 2 3
2 2 3
1 1 2 2 2 tan
. . 2
2 2 3 3 3
R
R
h h R R h R
V R x dx R
RR
−

= − = − = =


5) Hệ thống Ví dụ minh họa
Ví dụ 1: Cho hình phẳng
( )
H
giới hạn bởi các đường
2
; 0; 2y x y x= = =
. Tính thể tích
V
của khối tròn
xoay thu được khi quay
( )
H
quanh trục
.Ox
A.
8
.
3
V =
B.
32
.
5
V =
C.
8
.
3
V
=
D.
32
.
5
V
=
Lời giải:
Thể tích cần tính là
2
2
5
4
0
0
32
..
55
x
V x dx

= = =
Chọn D.
Ví dụ 2: Cho hình phẳng
D
giới hạn bởi đường cong
1
2
+= xy
, trục hoành và các đường thẳng
0, 1.xx==
Khối tròn xoay tạo thành khi quay
D
quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.
4
.
3
V
=
B.
2.V
=
C.
4
.
3
V =
D.
2.V =
Lời giải:
Thể tích cần tính bằng
(
)
1
2
2
0
4
1.
3
V x dx
= + =
Chọn A.
Ví dụ 3: Cho hình phẳng
D
giới hạn bởi đường cong
xy cos2+=
, trục hoành và các đường thẳng
0;
2
xx
==
. Khối tròn xoay tạo thành khi quay
D
quanh trục hoành có thể tích
V
bằng:
A.
( )
1.V

=+
B.
1.V
=−
C.
1.V
=+
D.
( )
1.V

=−
Lời giải:
Thể tích cần tính bằng
( )
( ) ( ) ( )
22
2
2
0
00
2 cos 2 cos 2 1 .V x dx x dx x sinx

= + = + = + = +

Chọn A.
Ví dụ 4: Cho
( )
H
là hình phẳng giới hạn bởi đường cong
( )
xxyC 4:
2
+−=
và đường thẳng
:.d y x=
Tính thể tích
V
của vật thể tròn xoay do hình phẳng
( )
H
quay xung quanh trục hoành.
A.
81
.
10
V
=
B.
81
.
5
V
=
C.
108
.
5
V
=
D.
108
.
10
V
=
Lời giải:
Phương trình hoành độ giao điểm là:
=
=
=+−=+−
3
0
034
22
x
x
xxxxx
Thể tích cần tìm là:
( )
3
2
22
0
108
4.
5
V x x x dx
= − − =
Chọn C.
Ví dụ 5: Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường
( )
3
ln 1 ; 0; 1y x x y x= + = =
khi xoay quanh trục
.Ox
A.
2ln2 1
.
33
V

=−


B.
ln2 1
.
33
V

=−


C.
2
2ln2 1
.
33
V

=−


D.
2
ln2 1
.
33
V

=−


Lời giải:
Phương trình hoành độ giao điểm là:
( )
001ln
3
==+ xxx
Gọi
V
là thể tích khối tròn xoay cần tìm ta có:
( )
1
23
0
ln 1V x x dx
=+
Đặt
( )
( )
2
1
3
1
3
3
32
3
2
0
0
3
ln 1
1
1
ln 1
3
1
3
x
du
ux
x
x
V x x dx
x
dv x dx
v
=

=+
+

+

= + −


+
=


=
( )
2ln2 1
.
33
đvtt

=−


Chọn A.
Ví dụ 6: Thể tích
V
của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
( )
0, ln 1 ; 1y y x x x= = + =
xung quanh trục
Ox
là
A.
5
.
6
V
=
B.
( )
12ln2 5 .
6
V
=−
C.
5
.
18
V
=
D.
( )
12ln2 5 .
18
V
=−
Lời giải:
Phương trình hoành độ giao điểm của
( )
C
và
Ox
là
( )
001ln ==+ xxx
Thể tích khối tròn xoay cần tính là
( )
1
2
0
ln 1x x dx
+
. Đặt
( )
+
=
+
=
=
+=
3
1
1
1ln
32
x
dv
x
dx
du
dxxdv
xu
Ta có:
( ) ( )
( )
( )
1
11
3
22
00
0
11
ln 1 ln 1 1 12ln2 5
3 18
x
x x dx x x x dx
+
+ = + − − + = −

Do đó
( )
52ln12
18
−=
V
. Chọn D.
Ví dụ 7: Tính thể tích hình khối do hình phẳng giới hạn bởi các đường
2
5; 3x y x y= + = −
quay quanh
.Oy
A.
153
.
3
V
=
B.
9
.
2
V
=
C.
81
.
10
V
=
D.
153
.
5
V
=
Lời giải:
Tung độ giao điểm là:
=
−=
−=+−
2
1
35
2
y
y
yy
( )
( )
2
2
2
2
1
153
53
5
CASIO
V y y dy V

−
= − + − − ⎯⎯⎯→ =
Vậy
5
153
=V
(đvtt). Chọn D.
Ví dụ 8: Gọi
( )
H
là hình phẳng giới hạn bởi
( ) ( )
: 2 , :
x
C y d y x a= = − +
và trục
.Oy
Biết rằng
( )
C
và
( )
d
cắt nhau tại một điểm duy nhất có hoành độ bằng 1. Tính thể tích
V
của khối tròn xoay sinh bởi
( )
H
khi nó quay quanh trục
.Ox
A.
19 3
.
3 ln4
V

=−


B.
19 3
.
3 ln4
V

=+


C.
35 3
.
3 ln4
V

=−


D.
35 3
.
3 ln 4
V

=+


Lời giải:
Theo đề bài ta có
3:)(312 +−==+−= xydaa
.
Gọi
1
V
là thể tích khối tròn xoay thu được khi quay hình phẳng
( )
1
S
được giới hạn bởi các đường
( ) ( )
, , ,C d Oy Ox
như hình bên quanh
trục
Ox
( )
( )
13
2
2
1
01
23
x
V dx x dx

= + −

1
83
.
3 ln4
V

= −


Gọi
2
V
là thể tích khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi các đường
( )
,d Ox
như hình bên quanh trục hoành,
Suy ra
( )
3
2
2
0
3 9 .V x dx

= − =
Khi đó
21
19 3
.
3 ln4
V V V

= − = −


Chọn A.
Ví dụ 9: Để tạo ra những chiếc chậu hoa hình quả lê, người ta dùng
một chiếc khuôn là đường cong có phương trình trong hệ trục tọa độ là
( ) ( )
3
0.y x k x k= −
Biết rằng mỗi đơn vị trong hệ trục tọa độ
Oxy
tương ứng với chiều dài 1 dm. Hãy xác định
k
để thể tích chậu hoa là
12,15
dm
3
.
A. k = 2. B. k = 4. C. k = 3. D.
4
243=k
.
Lời giải:
Ta có:
( )
−= xkxy
32
đồ thị cắt trục
Ox
tại điểm
( )
0; .k
Thể tích của chậu hoa là:
( )
4 5 5 5
3
0
0
12,15
4 5 4 5
k
k
x x k k
V x k x dx k
= − = − = − =
3243
5
== kk
. Chọn C.
Ví dụ 10: Cho hình thang cong
( )
H
giới hạn bởi các
đường
1
; 0; 1; 5y y x x
x
= = = =
. Đường
thẳng
xk=
với
51 k
chia
( )
H
thành hai phần là
( )
1
S
và
( )
2
S
quay quanh trục
Ox
ta thu được hai khối
tròn xoay có thể tích lần lượt là
1
V
và
2
.V
Xác đinh
k
để
12
2.VV=
A.
5
.
3
k =
B.
15
.
7
k =
C.
ln5.k =
D.
3
25.k =
Lời giải:
Ta có
( )
( ) ( )
( ) ( )
2
11
2
2
5
2
1
1
1 15
2.
57
1
k
k
dx
F k F
x
V
dx
F x k
x x V F F k
dx
x


−

= − = = = = =
−



Chọn B.
Ví dụ 11: Cho hình thang cong
( )
H
giới hạn bởi các đường
; 0; 1; 7y x y x x= = = =
. Đường
thẳng
xk=
với
71 k
chia
( )
H
thành hai phần là
( )
1
S
và
( )
2
S
quay quanh trục
Ox
ta thu được hai khối tròn xoay có
thể tích lần lượt là
1
V
và
2
.V
Xác đinh
k
để
12
2.VV=
A.
33.k =
B.
33.k =
C.
33
.
2
k =
D.
3
33.k =
Lời giải:
Ta có
( )
( )
( )
( ) ( )
( ) ( )
( ) ( )
2
2
11
7
2
2
1
1 49
22
2 7 2 2
k
k
x dx
F k F
V
x
x F x F k F k
V F F k
x dx
−

= = = = = − = −

−

( )
33
33.
2
F k k = =
Chọn B.
Ví dụ 12: [Đề Tham khảo Bộ Giáo dục và Đào tạo 2017] Tính thể
V
của phần vật thể giới hạn bởi hai
mặt phẳng
1x =
và
3,x =
biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
Ox
tại điểm có
hoành độ
( )
13xx
thì được một thiết diện là một hình chữ nhật có độ dài hai cạnh là
3x
và
23
2
−x
?
A.
32 2 15.V =+
B.
124
.
3
V
=
C.
124
.
3
V =
D.
( )
32 2 15 .V
=+
Lời giải:
Ta có:
( ) ( )
( )
3 3 3
2 2 2 2
1 1 1
1
3 3 2 3 3 2 3 2 3 2
2
HCN
S x S x x V S x dx x x dx x d x= = − = = − = − −
( )
3
3
2
1
1 124
3 2 .
33
x= − =
Chọn C.
Ví dụ 13: Tính thể tích của vật thể nằm giữa hai mặt phẳng
0x =
và
1,x =
biết thiết diện của vật thể cắt
bởi mặt phẳng
( )
P
vuông góc với trục
Ox
tại điểm có hoành độ
( )
01xx
là một hình chữ nhật có độ
dài hai cạnh là
x
và
( )
1ln
2
+x
.
A.
ln2 1.−
B.
( )
1
ln2 1 .
2
−
C.
1
ln 2 .
2
−
D.
1
ln2 1.
2
−
Lời giải:
Do thiết diện là hình chữ nhật nên diện tích thiết diện là:
( )
( )
1ln
2
+= xxxS
Ta có thể tích cần tính là
( )
1
2
0
ln 1V x x dx=+
( ) ( ) ( ) ( ) ( ) ( )
( )
11
1
2 2 2 2 2 2
0
00
1 1 1
ln 1 1 1 ln 1 1 ln 1
2 2 2
V x d x x x x d x= + + = + + − + +

1
0
11
ln2 2 ln2 .
22
xdx− = −
Chọn C.
Ví dụ 14: Tính thể tích của vật thể nằm giữa hai mặt phẳng
0x =
và
,x
=
biết thiết điện của vật thể cắt
bởi mặt phẳng
( )
P
vuông góc với trục
Ox
tại điểm có hoành độ
( )
0xx

là một tam giác đều có cạnh
bằng
xsin2
.
A.
8 3.V =
B.
2 3.V
=
C.
2 3.V =
D.
3.V =
Lời giải:
Diện tích thiết diện là
( )
( )
2
2 sin . 3
3sin
4
x
S x x==
Ta có thể tích cần tính là
0
0
3sin 3cos 2 3.V xdx x
= = − =
Chọn C.
Ví dụ 15: [Đề Chuyên Đại học Vinh 2017] Gọi
V
là thể tích khối
tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
; 0; 4y x y x= = =
quanh trục
.Ox
Đường thẳng
( )
04x a a=
cắt đồ thị hàm số
xy =
tại
M
(hình vẽ bên). Gọi
1
V
là thể tích
khối tròn xoay tạo thành khi quay tam giác
OMH
quanh trục
.Ox
Biết rằng
1
2VV =
. Khi đó
A.
2 2.a =
B.
5
.
2
a =
C.
2.a =
D.
3.a =
Lời giải:
Ta có
4
1
0
8 4 .V xdx V
= = =
Gọi
N
là giao điểm của đường thẳng
xa=
và trục hoành. Khi đó
1
V
là thể tích tạo được khi xoay hai tam giác
OMN
và
MNH
quanh trục
Ox
với
N
là hình chiếu của
M
trên
.OH
Ta có
( )
( )
( )
22
1
1 1 4
4 4 3.
3 3 3
V a a a a a a
= + − = = =
Chọn D.
Ví dụ 16: Có một vật thể là hình tròn xoay có dạng giống như một
cái ly như hình vẽ dưới đây: Người ta đo được đường kính của
miệng ly là
4 cm
và chiều cao là
6.cm
Biết rằng thiết diện của
chiếc ly cắt bởi mặt phẳng qua trục đối xứng là một parabol. Tính
thể tích
( )
3
V cm
của vật thể đã cho?
A.
72
.
5
V
=
B.
12.V =
C.
12 .V
=
D.
72
.
5
V =
Lời giải:
Chọn hệ trục tọa độ như hình suy ra phương trình Parabol là:
2
2
3 12 2 12
.
23
xy
yx
−+
= =
Thể tích của vật là thể tích khối tròn xoay khi quay hình
( )
H
giới hạn
bởi các đường
2 12
, 0, 6; 0
3
y
x x y y
+
= = = − =
quanh trục tung.
Khi đó
0
0
2
6
6
2 12 1
4 12 .
33
y
V dy y y
−
−
+

= = + =


Chọn C.
Ví dụ 17: Một chiếc đồng hồ cát như hình vẽ, gồm hai phần đối xứng nhau qua mặt
nằm ngang và đặt trong một hình trụ. Thiết diện thẳng đứng qua trục của nó là hai
parabol chung đỉnh và đối xứng nhau qua mặt nằm ngang. Ban đầu lượng cát dồn
hết ở phần trên của đồng hồ thì chiều cao h của mực cát bằng
4
3
chiều cao của bên
đó (xem hình). Cát chảy từ trên xuống dưới với lưu lượng không đổi 2,90 cm
3
/
phút. Khi chiều cao của cát còn 4 cm thì bề mặt trên cùng của cát tạo thành một
đường tròn chu vi 8
cm (xem hình). Biết sau 30 phút thì cát chảy hết xuống phần
bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài là bao nhiêu cm? (Kết
quả làm tròn đến hàng đơn vị)
A. 8 cm.
B. 12 cm.
C. 9 cm.
D. 10 cm.
Lời giải:
Gọi (α) là mặt phẳng song song với đáy của hình trụ và cắt đồng hồ cát.
Khi đó mặt cắt là một hình tròn có bán kính là
x
nên diện tích hình tròn là
22
xRS
t
==
.
Chọn hệ trục tọa độ
Oxy
như hình vẽ, gọi phương trình của parabol
( )
P
là
cbxaxy ++=
2
.
Vì
( )
P
đi qua điểm
( ) ( ) ( )
0;0 , 4;4 , 4; 4O A B −
Nên phương trình
( )
:P
2
2
4 4 .
4
x
y x y S y
= = =
→ Thể tích cát ban đầu là
0
h
t
V S dy=
vì mặt cắt vuông góc
với
.Oy
Suy ra
( )
0
4
h
V y dy
=
mà thể tích khối cát
3
2,9.30 87 .
c
V cm==
( )
22
0
0
87
4 87 2 87 2 87 .
2
h
h
y dy y h h
= = = =
Vậy chiều cao của khối trụ bên ngoài là
4 4 87
2. . 2. . 9,92
3 3 2
h cm
=
. Chọn D.
Ví dụ 18: Một chậu nước hình bán cầu băng nhôm có bán kính
10 ,R cm=
đặt trong một khung hình hộp
chữ nhật (Hình 1). Trong chậu có chứa sẵn một khối nước hình chỏm cầu có chiều cao
4.h cm=
Người ta
bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi (Hình 2). Bán
kính của viên bi gần bằng:
A. 9,63. B. 2,09. C. 1,72. D. 4,01.
Lời giải:
Gọi
x
là bán kính viên bi hình cầu. Điều kiện:
501020 xx
Chú ý: Công thức thể tích chỏm cầu:
2
.
3
h
V h R

=−


Thể tích khối nước hình chỏm cầu khi chưa thả viên bi vào:
3
416
3
4
1016
3
2
1
=
−=
−=
h
RhV
Khi thả viên bi vào thì khối chỏm cầu gồm khối nước và viên bi có thể tích là:
( )
( )
3
2304
3
2
2
2
2
2
xxx
RxV
−
=
−=
Ta có phương trình:
( )
323
12
44162304
3
4
xxxxVV
=−−=−
32
9,626 5 ( )
3 30 104 0 2,0940 5 .
1,72 ( )
x lo
x x x
x lo

− + =
=−
¹i
¹i
Chọn B.
Ví dụ 19: Từ một khối gỗ hình trụ có đường kính 6 dm, bác
nông dân dùng cưa để cắt theo mặt cắt đi qua một điểm trên
đường sinh cách đáy 1 dm và đi qua đường kính của đáy
(như hình vẽ) để được một "khối nêm”. Giúp bác nông dân
tính thể tích của "khối nêm” đó ?
A.
3
0,06 .m
B.
3
0,006 .m
C.
3
0,018 .m
D.
3
0,006 .m
Lời giải:
Chọn hệ trục tọa độ như hình vẽ. Khi đó khúc gỗ bé có đáy là nửa
hình tròn có phương trình:
( )
2
9 3;3y x x= − −
Một mặt phẳng cắt vuông góc với trục
Ox
tại điểm có hoành độ
, 3;3xx−
cắt khúc gỗ bé theo thiết diện có diện tích là
( )
Sx
(xem hình).
Dễ thấy
NP y=
và
tan9tan
2
xNPMN −==
( )
( )
tan9
2
1
.
2
1
2
xPNMNxS −==
trong đó
3
1
tan =
Khi đó thể tích khúc gỗ bé là :
( )
( )
33
23
33
1
9 tan 0,006 .
2
V S x x dx m
−−
= = − =

Chọn D.
Ví dụ 20: [Đề thi chuyên Đại học Vinh 2017] Bạn A có
một cốc thủy tinh hình trụ, đường kính trong lòng đáy cốc
là 6 cm, chiều cao trong lòng cốc là 10 cm đang đựng một
lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước
chạm miệng cốc thì ở đáy mực nước trùng với đường kính
đáy. Tính thể tích lượng nước trong cốc.
A.
3
15 .cm
B.
3
60 .cm
C.
3
60 .cm
D.
3
70 .cm
Lời giải:
Áp dụng công thức thể tích nêm có bán kính đấy
3,R =
chiều cao
10h =
ta có:
2 3 2
3
2 2 .tan 2.3 .10
60 .
3 3 3
R h R
V cm
= = = =
Chọn C.
BÀI TẬP TỰ LUYỆN
Câu 1: Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
ba;
. Gọi
D
là hình phẳng giới hạn bởi đồ thị hàm số
(
)
,
y fx
=
trục hoành và hai đường thẳng
( )
,.x ax ba b= = <
Thể tích khối tròn xoay tạo thành khi quay
D
quanh trục hoành được tính theo công thức.
A.
(
)
2
.
b
a
V f x dx
π
=
∫
B.
( )
2
2.
b
a
V f x dx
π
=
∫
C.
( )
22
.
b
a
V f x dx
π
=
∫
D.
( )
2
.
b
a
V f x dx
π
=
∫
Câu 2: Viết công thức tính thể tích
V
của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi
đồ thị hàm số
( )
,y fx=
trục
Ox
và hai đường thẳng
(
)
,,x ax ba b= = <
xung quanh trục
.Ox
A.
( )
2
.
b
a
V f x dx
π
=
∫
B.
( )
2
.
b
a
V f x dx=
∫
C.
( )
.
b
a
V f x dx
π
=
∫
D.
( )
.
b
a
V f x dx=
∫
Câu 3: Cho
( )
H
là miền hình phẳng giới hạn bởi các đường
( )
,
x ax ba b= = <
và đồ thị của hai hàm
số
( ) ( )
,y f x y gx= =
. Gọi
V
là thể tích của vật thể tròn xoay khi quay
(
)
H
quanh
.
Ox
Mệnh đề nào dưới
đây là đúng?
A.
( ) ( )
22
.
b
a
V f x g x dx
π
= −
∫
B.
( ) ( )
2
.
b
a
V f x g x dx
π
= −
∫
C.
( ) (
)
22
.
b
a
V f x g x dx
= −
∫
D.
( ) (
)
2
.
b
a
V f x g x dx= −
∫
Câu 4: Cho hình
(
)
D
giới hạn bởi các đường
( )
, 0, , .y fx y x x e
π
= = = =
Quay
(
)
D
quanh trục
Ox
ta
được khối tròn xoay có thể tích
.V
Khi đó
V
được xác định bằng công thức nào sau đây?
A.
( )
.
e
V f x dx
π
π
=
∫
B.
( )
2
.
e
V f x dx
π
π
=
∫
C.
( )
2
.
e
V f x dx
π
π
=
∫
D.
(
)
.
e
V f x dx
π
=
∫
Câu 5: Thể tích
V
của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol
( )
2
:
xyP =
và đường thẳng
:dy x=
quay xung quanh
Ox
được xác định bởi công thức nào?
A.
( )
1
2
2
0
.
V x x dx
π
= −
∫
B.
11
24
00
.V x dx x dx
ππ
= +
∫∫
C.
11
24
00
.V x dx x dx
ππ
= −
∫∫
D.
( )
1
2
2
0
.
V x x dx
π
= −
∫
Câu 6: Thể tích
V
của khối tròn xoay khi cho hình phẳng
( )
H
giới hạn bởi đồ thị của parabol
( )
2
:Pyx=
và đường thẳng
xyd 2: =
quay xung quanh trục
Ox
được xác định bằng công thức nào sau đây?
A.
22
24
00
4.
V x dx x dx
ππ
= −
∫∫
B.
( )
2
2
2
0
2.
V x x dx
π
= −
∫
C.
22
24
00
4.
V x dx x dx
ππ
= +
∫∫
D.
( )
2
2
2
0
2.V x x dx
π
= −
∫
Câu 7: Cho hình phẳng
( )
H
giới hạn bởi các đường
2
xy =
và
xy =
. Khối tròn xoay tạo ra khi
( )
H
quay quanh
Ox
có thể tích
V
được xác định bằng công thức nào?
A.
( )
1
4
0
.V x x dx
π
= −
∫
B.
(
)
1
2
0
.V x x dx
π
= −
∫
C.
( )
1
2
0
.V x x dx
π
= −
∫
D.
( )
1
4
0
.V x x dx
π
= −
∫
Câu 8: Thể tích
V
của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
2
yx=
và
2
2
+−= xxy
quanh trục
Ox
được xác định bằng công thức nào sau đây?
A.
(
)
2
2
2
1
32 .
V x x dx
π
= −+
∫
B.
( )
2
2
22
1
24 .
V x x x dx
π

= −+ −


∫
B.
( )
2
2
22
1
4 32 .V x x x dx
π

= − −+


∫
D.
( )
2
2
22
1
32 4 .V x x x dx
π

= −+ +


∫
Câu 9: Hình phẳng
( )
H
giới hạn bởi đường parabol
( )
1:
2
+= xyP
, trục tung và tiếp tuyến với
( )
P
tại
điểm
( )
1; 2M
khi quay quanh trục
.Ox
Công thức nào sau đây sử dụng để tính thể tích
V
của hình
( )
H
?
A.
( )
1
2
2
0
1.
V x dx
π
= +
∫
B.
( )
1
2
22
0
14 .V x x dx
π

= +−


∫
C.
( )
1
2
0
2.V x dx
π
=
∫
D.
(
)
1
2
2
0
21 .V x x dx
π
= −+
∫
Câu 10: Tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng
1
x =
và
3,x
=
biết rằng khi cắt vật
thể bởi mặt phẳng tùy ý vuông góc với trục
Ox
tại điểm có hoành độ
( )
13xx≤≤
thì được thiết diện là một
hình chữ nhật có hai cạnh là
3x
và
2
3 2.x −
A.
32 2 15.V = +
B.
124
.
3
V
π
=
C.
124
.
3
V =
D.
( )
32 5 .
V
π
= +
Câu 11: Tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng
0x =
và
3,
x
=
có thiết diện bị cắt bởi
mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
( )
03
xx≤≤
là một hình chữ nhật có hai kích thước
bằng
x
và
2
29 .x−
A.
3.V =
B.
18.
V
=
C.
20.V =
D.
22.V =
Câu 12: Tính thể tích
V
của phẩn vật thể giới hạn bởi hai mặt phẳng
0x =
và
2,x =
có thiết diện bị cắt bởi
mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
( )
02xx≤≤
là một hình chữ nhật có hai kích thước
bằng
x
và
2
24 .
x−
A.
8
.
3
V
=
B.
16
.
3
V
=
C.
16.V
=
D.
3
.
16
V =
Câu 13: Tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng
0
x =
và
1,
x =
có thiết diện bị cắt bởi
mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
( )
01xx
≤≤
là một tam giác đều có cạnh bằng
.x
A.
3
.
3
V =
B.
12
.
5
V =
C.
1.
V =
D.
12
.
5
V
π
=
Câu 14: Tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng
0x =
và
,x
π
=
biết rằng thiết diện
của vật thể bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
( )
0xx
π
≤≤
thì được thiết
diện là một hình chữ nhật có hai cạnh là
x
và
2 sin .x
A.
8 3.V =
B.
3 3.V =
C.
2 3.V =
D.
3.V
=
Câu 15: Tính thể tích
V
của vật thể nằm giữa hai mặt phẳng
0, ;
2
xx
π
= =
biết rằng thiết diện của vật thể cắt
bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
0
2
xx
π

≤≤


là tam giác đều có cạnh là
2 cos sin .xx+
A.
3.V =
B.
2 3.V =
C.
2 3.V
π
=
D.
3
.
2
V
π
=
Câu 16: Tính thể tích
V
của khối tròn xoay trong không gian
,Oxyz
giới hạn bởi hai mặt phẳng
0,xx
π
= =
và có thiết diện cắt bởi mặt phẳng vuông góc với
Ox
tại điểm
( )
;0;0x
bất kỳ là đường tròn bán kính
xsin
.
A.
2.V =
B.
.V
π
=
C.
4.V
π
=
D.
2.V
π
=
Câu 17: Tính thể tích
V
của vật thể nằm giữa hai mặt phẳng
0x =
và
2,x =
biết rằng thiết diện của vật thể
bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
( )
02xx≤≤
là một nửa hình tròn đường
kính
2
5x
.
A.
85.V
π
=
B.
2 5.V =
C.
4.V
π
=
D.
45.V
π
=
Câu 18: Tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng
1x =
và
4x =
biết rằng khi cắt vật thể
bởi mặt phẳng tùy ý vuông góc với trục
Ox
tại điểm có hoành độ
( )
14xx≤≤
thì được thiết diện là một
hình lục giác đều có độ dài cạnh là
2.x
A.
63 3 .V
π
=
B.
126 3.V =
C.
63 3.
V =
D.
126 3 .V
π
=
Câu 19: Cho hình phẳng giới hạn bởi các đường
3 , , 0, 1
y xy xx x
= = = =
quay xung quanh trục
.Ox
Tính
thể tích
V
của khối tròn xoay tạo thành.
A.
8
.
3
V
π
=
B.
4
.
3
V
π
=
C.
2
.
3
V
π
=
D.
.V
π
=
Câu 20: Hình
(
)
H
giới hạn bởi
2
4 4, 0, 0, 1yx x y x x
=−+ = = =
quay xung quanh trục
.
Ox
Tính thể tích
V
của khối tròn xoay tạo thành.
A.
8
.
3
V
π
=
B.
4
.
3
V
π
=
C.
2
.
3
V
π
=
D.
31
.
5
V
π
=
Câu 21: Tính thể tích
V
của vật thể tròn xoay sinh bởi khi quay hình phẳng giới hạn bởi đồ thị hàm số
xxy 2
2
−=
, trục hoành, đường thẳng
0
x =
và đường thẳng
1x =
quay quanh trục hoành.
A.
2
.
3
V
π
=
B.
8
.
15
V
π
=
C.
16
.
15
V
π
=
D.
4
.
3
V
π
=
Câu 22: Cho hình phẳng giới hạn bởi đường cong
sin ,
yx=
trục hoành và hai đường thẳng
0x =
và
π
=x
.
Tính thể tích
V
của khối tròn xoay thu được khi quay hình này xung quanh trục
.Ox
A.
2
.
2
V
π
=
B.
2
.
VR
π
=
C.
2
.
3
V
π
=
D.
2.V
π
=
Câu 23: Gọi
( )
H
là hình phẳng giới hạn bởi
, 0, 0, 1
x
y ey x x= = = =
. Tính thể tích
V
của vật thể tròn
xoay được sinh ra khi ta quay hình
( )
H
quanh trục
.Ox
A.
( )
1.Ve
π
= −
B.
(
)
3.Ve
π
= +
C.
.
Ve
π
=
D.
1.
Ve= +
Câu 24: Tính thể tích
V
của vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
31
, 0, 1, 0
x
ye x x y
+
= = = =
quay quanh
.Ox
A.
2
.Ve
π
=
B.
.
Ve
π
=
C.
( )
2
.V ee
π
= +
D.
( )
2
.V ee
π
= −
Câu 25: Tính thể tích của vật thể tròn xoay được sinh ra khi hình phẳng giới hạn bởi các đường
31
, 0, 1, 0
x
ye x x y
+
= = = =
quay quanh
.Ox
A.
( )
42
3.
6
ee
π
−
B.
3
1
.
3
ee
π

−


C.
( )
3
1
.
3
ee
π
+
D.
( )
3
.ee
π
−
Câu 26: Cho hình phẳng
( )
H
giới hạn bởi các đường
1−=
xy
, trục
hoành và
4.x =
Tính thể tích
V
của khối tròn xoay tạo thành khi quay
hình phẳng
( )
H
quanh trục
.
Ox
A.
7
.
6
V
π
=
B.
2
7
.
6
V
π
=
C.
7
.
6
V =
D.
5
.
3
V
π
=
Câu 27: (Sở GD & ĐT Tp Hồ Chí Minh 2017) Trong không gian với
hệ tọa độ
,Oxyz
cho vật thể
( )
H
giới hạn bởi hai mặt phẳng có phương trình
xa=
và
( )
.
x ba b
= <
Gọi
( )
Sx
là diện tích thiết diện của
( )
H
bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
với
bxa
≤
≤
. Giả sử hàm số
( )
y Sx=
liên tục trên
[ ]
;.ab
Thể tích
V
của vật thể
( )
H
được xác định bởi
công thức nào?
A.
(
)
.
b
a
V S x dx=
∫
B.
( )
2
.
b
a
V S x dx=


∫
C.
( )
.
b
a
V S x dx
π
=
∫
D.
( )
2
.
b
a
V S x dx
π
=


∫
Câu 28: Cho hình phẳng
( )
D
giới hạn bởi các đồ thị hàm số
2
x
ey =
trục
Ox
và hai đường thẳng
0, 1.xx= =
Viết công thức tính thể tích
V
của khối tròn xoay khi quay hình
( )
D
quay quanh trục
.Ox
A.
1
2
0
.
x
V e dx
π
=
∫
B.
1
0
.
x
V e dx
π
=
∫
C.
2
1
2
0
.
x
V e dx

=


∫
D.
1
2
0
.
x
e dx
π
∫
Câu 29: Cho hai hàm số
( )
1
y fx=
và
( )
2
y fx
= liên tục trên đoạn
[ ]
ba;
và có đồ thị như hình vẽ bên. Gọi
S
là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng
,.x ax b= =
Thể tích
V
của vật thể tròn
xoay tạo thành khi quay
S
quanh trục
Ox
được tính
bởi công thức nào sau đây?
A.
( ) (
)
2
12
.
b
a
V f x f x dx
π
= −


∫
B.
( ) ( )
22
12
.
b
a
V f x f x dx

= −

∫
C.
( ) ( )
12
.
b
a
V f x f x dx
π
= −


∫
D.
(
) ( )
22
12
.
b
a
V f x f x dx
π

= −

∫
Câu 30: Nêu công thức tính thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình
vẽ) xung quanh trục hoành
.Ox
A.
( )
12
2
01
2.V x dx x dx
ππ
= −+
∫∫
B.
( )
2
0
2.
V x dx
π
= −
∫
C.
12
01
2.V xdx xdx
ππ
= −−
∫∫
D.
( )
12
2
01
2.V x dx x dx
ππ
= +−
∫∫
Câu 31: Nêu công thức tính thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc
của hình vẽ) xung quanh trục hoành
.Ox
A.
( )
44
02
2.V xdx x dx
π

= +−


∫∫
B.
( )
44
2
02
2.V xdx x dx
π

= −−


∫∫
C.
( )
24
2
02
2.V xdx x dx
π

= +−


∫∫
D.
( )
24
02
2.V xdx x dx
π

= −−


∫∫
Câu 32: Tính thể tích
V
của vật thể tròn xoay thu được khi quay
hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành
.Ox
A.
15
.
ln 4
V
π
=
B.
8
.
ln 2
V
π
=
C.
15
.
ln 2
V
π
=
D.
17
.
ln 4
V
π
=
Câu 33: Tính thể tích
V
của vật thể tròn xoay thu được khi quay hình
phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành
.
Ox
A.
4 ln 4 3.V
π
= −
B.
( )
4 ln 2 3 .V
π
= −
C.
4 ln 2 3 .V
ππ
= −
D.
( )
4 ln 4 3 .V
π
= −
Câu 34: Cho hình phẳng
( )
H
giới hạn bởi các đường
ln , 0, 1,y xy x x k= = = =
với
1k >
như hình vẽ. Gọi
k
V
là thể tích
khối tròn xoay thu được khi quay hình
(
)
H
quanh trục
.
Ox
Biết rằng
π
=
k
V
, hãy chọn khẳng định đúng?
A.
3 4.k
<<
B.
1 2.k<<
C.
2 3.k<<
D.
4 5.k<<
Câu 35: Tính thể tích
V
của vật thể tròn xoay thu được khi quay hình
phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành
.Ox
A.
2.V
π
=
B.
.Ve
π
=
C.
( )
1.Ve
π
= +
D.
.V
π
=
Câu 36: Tính thể tích
V
của vật thể tròn xoay thu được khi quay
hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành
.Ox
A.
35
.
3
V
π
=
B.
31
.
3
V
π
=
C.
32
.
3
V
π
=
D.
34
.
3
V
π
=
Câu 37: Tính thể tích
V
của vật thể tròn xoay thu được khi quay hình
phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành
.Ox
A.
24 .
π
B.
27 .
π
C.
25 .
π
D.
26 .
π
Câu 38: Tính thể tích
V
của vật thể tròn xoay thu được khi quay hình
phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành
.Ox
A.
81
.
10
V
π
=
B.
81
.
5
V
π
=
C.
108
.
5
V
π
=
D.
50 .
V
π
=
Câu 39: Tính thể tích
V
của vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ)
xung quanh trục hoành
.
Ox
A.
12
.
5
V
π
=
B.
53
.
15
V
π
=
C.
153
.
5
V
π
=
D.
31
.
13
V
π
=
Câu 40: Tính thể tích
V
của vật thể tròn xoay thu được khi
quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh
trục hoành
.Ox
A.
27
.
2
V
π
=
B.
9
.
2
V
π
=
C.
11
.
3
V
π
=
D.
55
.
6
V
π
=
Câu 41: Tính thể tích
V
của vật thể tròn xoay thu được khi quay
hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành
.Ox
A.
125
.
3
V
π
=
B.
25
.
3
V
π
=
C.
157
.
3
V
π
=
D.
13
.
2
V
π
=
Câu 42: Tính thể tích
V
của vật thể tròn xoay thu được khi
quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục
hoành
.Ox
A.
55
.
6
V
π
=
B.
24
.
3
V
π
=
C.
25
.
3
V
π
=
D.
125
.
9
V
π
=
Câu 43: Tính thể tích V của vật thể tròn xoay thu được khi quay hình phẳng (phân gạch sọc của hình vẽ)
xung quanh trục hoành
.Ox
A.
11 .V
π
=
B.
31
.
3
V
π
=
C.
32
.
3
V
π
=
D.
34
.
3
V
π
=
Câu 44: Biết
2
ln
4
4
15
π
π
+=V
là thể tích của vật thể tròn xoay thu được khi quay hình phẳng (phần gạch
sọc của hình vẽ) xung quanh trục hoành
.Ox
Tìm
,k
biết
1.
k
>
A.
4
.
3
e
k =
B.
2
.
2
e
k =
C.
3
ln 2.
2
k =
D.
4.k
=
Câu 45: Ký hiệu
(
)
H
là hình phẳng giới hạn bởi các đường
( )
2
2
1 , 0, 2
xx
y xe y x
−
=−==
. Tính thể tích
V
của khối tròn xoay thu được khi quay hình
( )
H
xung quanh
.
Ox
A.
( )
23
.
2
e
V
e
π
−
=
B.
( )
3
.
2
e
V
e
π
−
=
C.
( )
21
.
2
e
V
e
π
−
=
D.
( )
1
.
2
e
V
e
π
−
=
Câu 46: Tính thể tích
V
của vật thể tròn xoay sinh ra khi cho hình phẳng giới hạn bởi đồ thị hàm số
x
xy
ln=
, trục hoành và đường thẳng
xe=
quay quanh
.Ox
A.
3
21
.
9
e
V
π
+
=
B.
3
21
.
9
e
V
π
−
=
C.
3
21
.
3
e
V
π
+
=
D.
3
21
.
3
e
V
π
−
=
Câu 47: Gọi
V
là thể tích của khối tròn xoay sinh ra khi cho hình
( )
H
giới hạn bởi
1
1, 0
yy
x
=+=
,
1, ( 1)x x kk= = >
quay xung quanh
.Ox
Tìm
k
để
15
ln16 .
4
V
π

= +


A.
4.k =
B.
4.ke=
C.
2
.ke=
D.
8.k =
Câu 48: Cho hình
( )
H
giới hạn bởi các đường
x
xy ln
=
,
trục hoành và đường thẳng
.xe=
Tính thể tích khối tròn
xoay tạo thành khi quay
( )
H
quanh trục
.
Ox
A.
( )
3
52
.
25
e
π
−
B.
( )
3
52
.
27
e
π
−
C.
( )
3
52
.
25
e
π
+
D.
( )
3
52
.
27
e
π
+
Câu 49: Cho hình phẳng giới hạn bởi các đường
ln , 0,y x xy x e= = =
quay xung quanh trục
.
Ox
Thể tích
khối tròn xoay tạo thành bằng bao nhiêu ?
A.
3
41
.
9
e
π
+
B.
3
41
.
9
e
π
−
C.
3
21
.
9
e
π
+
D.
3
21
.
9
e
π
−
Câu 50: Cho hình phẳng giới hạn bởi các đường
32
6 9, 0y x x xy=−+ =
quay xung quanh trục
.Ox
Thể tích
của khối tròn xoay tạo thành bằng
A.
729
.
35
π
B.
27
.
4
π
C.
256608
.
35
π
D.
776
.
5
π
Câu 51: Cho hình phẳng giới hạn bởi các đường
22
2, 4y xy x= =
quay xung quanh trục
.Ox
Thế tích của
khối tròn xoay tạo thành bằng
A.
88
.
5
π
B.
9
.
70
π
C.
4
.
3
π
D.
6
.
5
π
Câu 52: Gọi
( )
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
4 x
x
y
−
=
, trục
Ox
và đường thẳng
1.x =
Tính thể tích
V
của khối tròn xoay thu được khi quay hình
( )
H
xung quanh trục
.Ox
A.
4
ln .
3
V
π
=
B.
14
ln .
23
V =
C.
4
ln .
23
V
π
=
D.
3
ln .
24
V
π
=
Câu 53: Cho hình phẳng giới hạn bởi các đường
cos 4 , , 0,
8
y x Ox x x
π
= = =
quay xung quanh trục
.Ox
Thể
tích của khối tròn xoay tạo thành bằng
A.
2
.
2
π
B.
2
.
16
π
C.
.
4
π
D.
1
.
16
π
π
+



Câu 54: Cho hình phẳng giới hạn bởi các đường
1−=
xy
, trục
Ox
và đường thẳng
3x =
quay xung
quanh trục
.Ox
Thể tích của khối tròn xoay tạo thành bằng
A.
3
.
2
π
B.
3.
π
C.
2.
π
D.
.
π
Câu 55: Cho hình phẳng giới hạn bởi các đường
3
1, 0, 0, 1yx y x x=+= = =
quay xung quanh trục
.Ox
Thể tích của khối tròn xoay tạo thành bằng
A.
79
.
63
π
B.
23
.
14
π
C.
5
.
4
π
D.
9.
π
Câu 56: Cho hình phẳng giới hạn bởi các đường
( )
2
, 0, 0y ax y bx a b
= = ≠≠
quay xung quanh trục
.Ox
Thể tích của khối tròn xoay tạo thành bằng
A.
3
3
11
.
35
b
a
π

−


B.
5
3
.
5
b
a
π
C.
5
3
.
3
b
a
π
D.
5
3
11
.
35
b
a
π

−


Câu 57: Cho hình phẳng giới hạn bởi các đường
22
1
4,
3
y xy x
=−=
quay xung quanh trục
.Ox
Thể tích của khối tròn xoay tạo thành bằng
A.
24 3
.
5
π
B.
28 3
.
5
π
C.
28 2
.
5
π
D.
24 2
.
5
π
Câu 58: Cho hình phẳng giới hạn bởi các đường
3 , , 0, 1y xy xx x= = = =
quay xung quanh trục
.
Ox
Thể
tích của khối tròn xoay tạo thành bằng
A.
8
.
3
π
B.
4
.
3
π
C.
2
.
3
π
D.
.
π
LỜI GIẢI CHI TIẾT
Câu 1: Thể tích khối tròn xoay cần tính là
( )
2
.
b
a
V f x dx
π
=
∫
Chọn A.
Câu 2: Thể tích khối tròn xoay cần tính là
( )
2
.
b
a
V f x dx
π
=
∫
Chọn A.
Câu 3: Thể tích khối tròn xoay cần tính là
( ) (
)
22
.
b
a
V f x g x dx
π
= −
∫
Chọn A.
Câu 4: Thể tích khối tròn xoay cần tính là
( )
2
.
e
V f x dx
π
π
=
∫
Chọn C.
Câu 5: Phương trình hoành độ giao điểm của
( )
P
và
d
là
2
0
.
1
x
xx
x
=
= ⇔
=
Dựa vào hình vẽ, thể tích khối tròn xoay cần tính là
11
24
00
.
V x dx x dx
ππ
= −
∫∫
Chọn C.
Câu 6: Phương trình hoành độ giao điểm của
( )
P
và
d
là
2
0
2.
2
x
xx
x
=
= ⇔
=
Do
( )
2;0,2
2
∈∀> xxx
nên thể tích khối tròn xoay cần tính là
11
24
00
4.V x dx x dx
ππ
= −
∫∫
Chọn A.
Câu 7: Phương trình hoành độ giao điểm của
( )
P
và
( )
C
là
2
0
.
1
x
xx
x
=
= ⇔
=
Vậy thể tích của khối tròn xoay cần tính là
( )
( )
( )
11
2
2
24
00
.V x x dx x x dx
ππ
=−=−
∫∫
Chọn D.
Câu 8: Phương trình hoành độ giao điểm của
( )
P
và
d
là
2
1
22 .
2
x
xx x
x
=
−+= ⇔
=
Vậy thể tích của khối tròn xoay cần tính là
( )
2
2
22
1
4 32 .V x x x dx
π

= − −+


∫
Chọn C.
Câu 9: Ta có
( )
2
' 1 '1 2yx y= + → =
nên phương trình tiếp tuyến của
( )
P
là
2.yx=
Phương trình hoành độ giao điểm của
( )
P
và
d
là
2
1 2 1.x xx+= ⇔ =
Vậy thể tích khối tròn xoay cần tính là
( )
1
2
22
0
14 .
V x x dx
π

= +−


∫
Chọn B.
Câu 10: Diện tích hình chữ nhật
ABCD
là
( )
2
3 3 2.Sx x x= −
Do đó, thể tích cần tính là
( )
33
2
11
124
33 2 .
3
V S x dx x x dx= = −=
∫∫
Chọn C.
Câu 11: Diện tích hình chữ nhật
ABCD
là
( )
2
29 .
Sx x x
= −
Do đó, thể tích cần tính là
( )
33
2
00
2 9 18.V S x dx x x dx
= = −=
∫∫
Chọn B.
Câu 12: Diện tích hình chữ nhật
ABCD
là
( )
2
24 .Sx x x= −
Do đó, thể tích cần tính là
( )
22
2
00
16
24 .
3
V S x dx x x dx
= = −=
∫∫
Chọn B.
Câu 13: Diện tích tam giác đều cạnh
x
là
(
)
2
3
.
4
x
Sx=
Do đó, thể tích cần tính là
( )
13
2
00
33
.
43
x
V S x dx dx= = =
∫∫
Chọn A.
Câu 14: Diện tích hình chữ nhật
ABCD
là
( )
x
xx
S
sin2
=
.
Do đó, thể tích cần tính là
( )
00
2 sin 2 3.V S x dx x xdx
ππ
= = =
∫∫
Chọn C.
Câu 15: Diện tích tam giác đều cạnh
x
là
( )
( )
( )
2
2 sin cos . 3
3 sin cos .
4
xx
Sx x x
+
= = +
Do đó, thể tích cần tính là
(
)
( )
22
00
3 sin cos 2 3.V S x dx x x dx
ππ
= = +=
∫∫
Chọn B.
Câu 16: Diện tích đường tròn bán kính
xsin
là
(
)
( )
2
. sin sin .Sx x x
ππ
= =
Do đó, thể tích cần tính là
( )
00
.sin 2 .V S x dx xdx
ππ
ππ
= = =
∫∫
Chọn D.
Câu 17: Bán kính đường tròn
2
5
2
2
xd
R ==
⇒
Diện tích nửa đường tròn bán kính
R
là
( )
4
5
.
8
x
Sx
π
=
Do đó, thể tích cần tính là
( )
22
4
00
5
. 4.
8
x
V S x dx dx
ππ
= = =
∫∫
Chọn C.
Câu 18: Diện tích tam giác đều cạnh
2x
là
(
)
3
4
32
2
2
x
x
S
=
=
∆
Suy ra diện tích lục giác đều cạnh
2x
là
(
)
2
6 63 .Sx S x
∆
=×=
Do đó, thể tích cần tính là
( )
44
2
11
6 3 126 3.
V S x dx x dx= = =
∫∫
Chọn B.
Câu 19: Dựa vào hình vẽ, thể tích cần tính là
( )
11
2
2
00
8
3.
3
V x dx x dx
π
ππ
= −=
∫∫
Chọn A.
Câu 20:
( )
1
2
2
0
31
44 .
5
V xx
π
π
= −+ =
∫
Chọn D.
Câu 21:
(
) ( )
11
2
2 432
00
8
2 44 .
15
V x x dx x x x dx
π
ππ
= − = −+ =
∫∫
Chọn B.
Câu 22:
( )
2
2
00
1 cos 2
sin .
22
x
V x dx dx
ππ
π
ππ
−
= = =
∫∫
Chọn A.
Câu 23:
(
)
(
)
11
2
00
1.
xx
V e dx e dx e
π ππ
= = = −
∫∫
Chọn A.
Câu 24:
2
22
1
2
22
11
.
x
x
V x e dx xe dx e
π ππ

= = =


∫∫
Chọn A.
Câu 25:
( )
( )
11
2
31 231 4 2
00
3.
6
xx
V e dx e dx e e
π
ππ
++
= = = −
∫∫
Chọn A.
Câu 26: Phương trình hoành độ giao điểm của
( )
C
và
Ox
là
101 =⇔=− xx
.
Do đó, thể tích khối tròn xoay cần tính là
(
)
(
)
44
2
11
7
1 21 .
6
V x dx x x dx
π
ππ
= − = −+=
∫∫
Chọn A.
Câu 27: Công thức thể tích vật thể
( )
H
là:
( )
.
b
a
V S x dx=
∫
Chọn A.
Câu 28:
2
11
2
00
.
x
x
V e dx e dx
ππ

= =


∫∫
Chọn B.
Câu 29: Dựa vào hình vẽ ta có:
( ) ( )
0
2
1
>> xfxf
với mọi
[
]
( )
( )
[ ]
22
12
; ;.x ab f x f x x ab
∈ ⇒ > ∀∈
Thể tích khối tròn xoay tạo thành khi quay
S
quanh trục là:
(
) (
)
( ) ( )
22
22 22
12 12
..
bb
aa
V f x f x dx f x f x dx
ππ

=−=−

∫∫
Chọn D.
Câu 30:
( )
( )
12 12
2
22
01 01
2 2.V x dx x dx x dx x dx
ππ ππ

= + − = +−


∫∫ ∫∫
Chọn D.
Câu 31:
( )
(
) ( )
4 4 44
2
22
0 2 02
2 2.
V x dx x dx xdx x dx
π π ππ
= −− = −−
∫ ∫ ∫∫
Chọn B.
Câu 32:
( )
2
22
2
00
0
4 15
24 .
ln 4 ln 4
x
xx
V dx dx
π
π ππ
= = = =
∫∫
Chọn A.
Câu 33:
( )
44
2
11
ln ln .V x dx xdx
ππ
= =
∫∫
Lại có:
( )
44 4
4
1
11 1
ln ln ln 4 ln 4 4 ln 4 3.xdx x x xd x dx= − = −= −
∫∫ ∫
Do đó
( )
4 ln 4 3 .V
π
= −
Chọn D.
Câu 34:
( )
2
11
ln ln
kk
V x dx xdx
ππ
= =
∫∫
Lại có:
( ) ( )
1
11 1
ln ln ln ln ln 1
kk k
k
xdx x x xd x k k dx k k k= − = − = −−
∫∫ ∫
Do đó
( )
ekkkkkkkV
k
=⇒=
→=−⇔=+−⇔=
>
1ln01ln11ln
1
π
. Chọn C.
Câu 35: Thể tích
V
của vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung
quanh trục hoành
Ox
là:
22 2
01 1
1 ln ln
ee e
V dx xdx e xdx
ππ π

=−=−


∫∫ ∫
Sử dụng máy tính CASIO ta được:
π
2=V
. Chọn A.
Câu 36: Ta có:
2
0
40 .
4
x
xx
x
=
−=⇔
=
Thể tích
V
của vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục
hoành
Ox
là:
(
)
(
)
4
44
3
2
2 22
00
0
32
4 42 .
33
x
V x x dx x x dx x
π
π ππ

= − = − = −=


∫∫
Chọn C.
Câu 37: Giải phương trình hoành độ giao điểm:
=
=
⇔
−=
≥
⇔−=
3
0
6
0
6
22
2
x
x
xxx
x
xxx
Thể tích
V
của vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục
hoành
Ox
là:
(
)
( )
3
36 6
3
2
22 2
03 3
0
66
3
x
V x dx x x dx x x dx
π
ππ π
= + − =+−
∫∫ ∫
6
3
2
3
9 3 27 .
3
x
x
ππ π

=+ −=


Chọn B.
Câu 38: Phương trình hoành độ giao điểm của 2 đồ thị là:
=
=
⇔=−⇔
−=
3
0
03
4
22
x
x
xxx
xx
Khi đó thể tích khối tròn xoay tạo thành là:
( ) ( )
33
2
2 2 43 2
00
108
4 8 15 .
5
CASIO
V x x x dx x x x dx V
π
ππ

= − − = − + → =


∫∫
Chọn C.
Câu 39: Phương trình hoành độ giao điểm của 2 đồ thị là:
=
−=
⇔=−−⇔−=−
2
1
0253
22
x
x
xxxx
Khi đó thể tích khối tròn xoay tạo thành là:
( )
( )
2
2
2
2
1
53V x x dx
π
−

= − −−


∫
( )
2
42
1
153
11 6 16 .
5
CASIO
x x x dx V
π
π
−
= − + + → =
∫
Chọn C.
Câu 40: Lấy đối xứng đường thẳng
2+−= xy
qua trục
Ox
ta được đường thẳng
2
+=
x
y
.
Giải phương trình
−=
−
=
⇔
+=+
1
2
22
x
x
x
x
. Thể tích khối tròn xoay tạo thành là
( )
( )
11
2
2
21
55
22 .
6
CASIO
V x dx x dx V
π
ππ
−
−−
= + + + = → =
∫∫
Chọn C.
Câu 41: Lấy đối xứng đường thẳng
x
y 2
−=
qua trục
Ox
ta được đường thẳng
xy 2=
.
Giải
0
2.
4
x
xx
x
=
= ⇔
=
Thể tích khối tròn xoay tạo thành là
( )
45
2
2
04
157
2.
3
CASIO
V x dx x dx V
π
ππ
= + = → =
∫∫
Chọn C.
Câu 42: Lấy đối xứng đường thẳng
1yx
= −
qua trục
Ox
ta được đường thẳng
1yx= −
Giải phương trình
=
=
⇔−=−
2
1
11
x
x
xx
Thể tích khối tròn xoay tạo thành là
( )
( )
24
2
2
12
55
11 .
6
CASIO
V x dx x dx V
π
ππ
= − + − → =
∫∫
Chọn A.
Câu 43: Xét phương trình
22
44
24 2
2 16 8 9 14 0
xx
xx x
x xx x x
≤≤

+=−⇔ ⇔ ⇔=

+=−+ −+=

Thể tích khối tròn xoay tạo thành là:
( ) ( )
24
2
22
2 4.V x dx x dx
ππ
−
= ++ −
∫∫
24
23
2
22
32
2 16 4 .
2 33
xx
x xx
π
ππ
−

= + + −+ =


Chọn C.
Câu 44: Thể tích khối tròn xoay tạo thành là:
22
11
11
1
kk
x
V dx
xx
ππ
+
 
= = +
 
 
∫∫
2
1
1
21 1 1
1 2 ln 1 2 ln 1
k
k
V dx x x k k
xx x k
ππ π

= + + = + − = + −+ +−


∫
Do
4ln2
1
2ln4
4
15
2ln4
4
15
=⇔+
−=+⇒+= kk
k
kV
π
π
. Chọn D.
Câu 45: Phương trình hoành độ giao điểm của
( )
C
và
Ox
là
( )
2
2
1 0 1.
xx
xe x
−
− =⇔=
Khi đó,
( )
( )
( )
22 2
22
2
2 22 2
1
11
1
1 2. .
2 22
xx xx xx
e
V xedx edx x e
e
π
ππ
π
−− −
−
= − = −= =
∫∫
Chọn D.
Câu 46: Phương trình hoành độ giao điểm của
( )
C
và
Ox
là
ln 0 ln 0 1.xx x x=⇔ =⇔=
Khi đó, thể tích cần tính là
( )
1
3
2
0
21
ln
9
e
V x x dx
ππ
+
= =
∫
(bấm máy). Chọn A.
Câu 47: Thể tích khối tròn xoay là
2
1
1
11
1 2 ln
k
k
V dx x x
xx
ππ

= + = −+


∫
1 15 1 15
2 ln ln16 2ln ln16 4.
44
kk kk k
kk
ππ

= −+ = + →−+ = + ⇒=


Chọn A.
Câu 48: Phương trình hoành độ giao điểm của
( )
C
và
Ox
là
.ln 0 ln 0 1.xx x x=⇔ =⇔=
Khi đó, thể tích cần tính là
( )
( )
3
1
2
0
52
.ln
27
e
V x x dx
π
π
−
= =
∫
(bấm máy). Chọn B.
Câu 49: Phương trình hoành độ giao điểm của
( )
C
và
Ox
là
ln 0 ln 0 1.xx x x
=⇔ =⇔=
Khi đó, thể tích cần tính là
( )
1
3
2
0
21
ln
9
e
V x x dx
ππ
+
= =
∫
(bấm máy). Chọn C.
Câu 50: Phương trình hoành độ giao điểm của
(
)
C
và
Ox
là
32
0
6 90 .
3
x
xxx
x
=
− +=⇔
=
Khi đó, thể tích cần tính là
( )
3
2
32
0
729
69 .
35
V x x x dx
π
π
= −+ =
∫
Chọn A.
Câu 51: Ta có
2
4 4 2.
yxyxyx= ⇔= ⇔=
Phương trình hoành độ giao điểm của
( )
1
C
và
( )
2
C
là
2
0
2.
1
x
xx
x
=
= ⇔
=
Khi đó, thể tích cần tính là
( )
( )
1
2
2
2
0
6
22 .
5
V x x dx
π
π
=−=
∫
Chọn D.
Câu 52: Phương trình hoành độ giao điểm của
( )
C
và
Ox
là
2
0 0.
4
x
x
x
=⇔=
−
Khi đó,
2
1
2
0
4
ln
4 23
x
V dx
x
π
π

= =


−

∫
(bấm máy). Chọn C.
Câu 53:
( )
2
88
8
2
00
0
1 cos8 sin 8
cos 4 .
2 2 16 16
x xx
V x dx dx
ππ
π
π
πππ
+

= = =+=


∫∫
Chọn B.
Câu 54: Phương trình hoành độ giao điểm của
( )
C
và
Ox
là
1 0 1.xx−= ⇔ =
Khi đó,
(
)
( )
3
33
2
2
11
1
1 1 2.
2
x
V x dx x dx x
π ππ π

= − = − = −=


∫∫
Chọn C.
Câu 55:
( ) ( )
1
11
74
2
3 63
00
0
23
1 21 .
7 2 14
xx
V x dx x x dx x
π
ππ π

= + = + + = ++ =


∫∫
Chọn B.
Câu 56: Phương trình hoành độ giao điểm của
( )
C
và
d
là
2
0
.
x
ax bx
b
x
a
=
= ⇔
=
Khi đó, thể tích khối tròn xoay cần tính là
5
24 22
3
0
11
.
35
b
a
b
V a x b x dx
a
ππ

= −=−


∫
Chọn D.
Câu 57: Phương trình hoành độ giao điểm của
( )
C
và
( )
P
là
22
3
1
4.
3
3
x
xx
x
= −
−= ⇔
=
Do đó, thể tích khối tròn xoay cần tính là
(
)
2
3
2
2
2
3
28 3
4.
35
x
V x dx
π
π
−

= −− =


∫
Chọn B.
Câu 58: Thể tích khối tròn xoay cần tính là
( )
11
2
2
00
8
3.
3
V x dx x dx
π ππ
= −=
∫∫
Chọn A.
| 1/33
| | Tải xuống

Có thể bạn quan tâm:

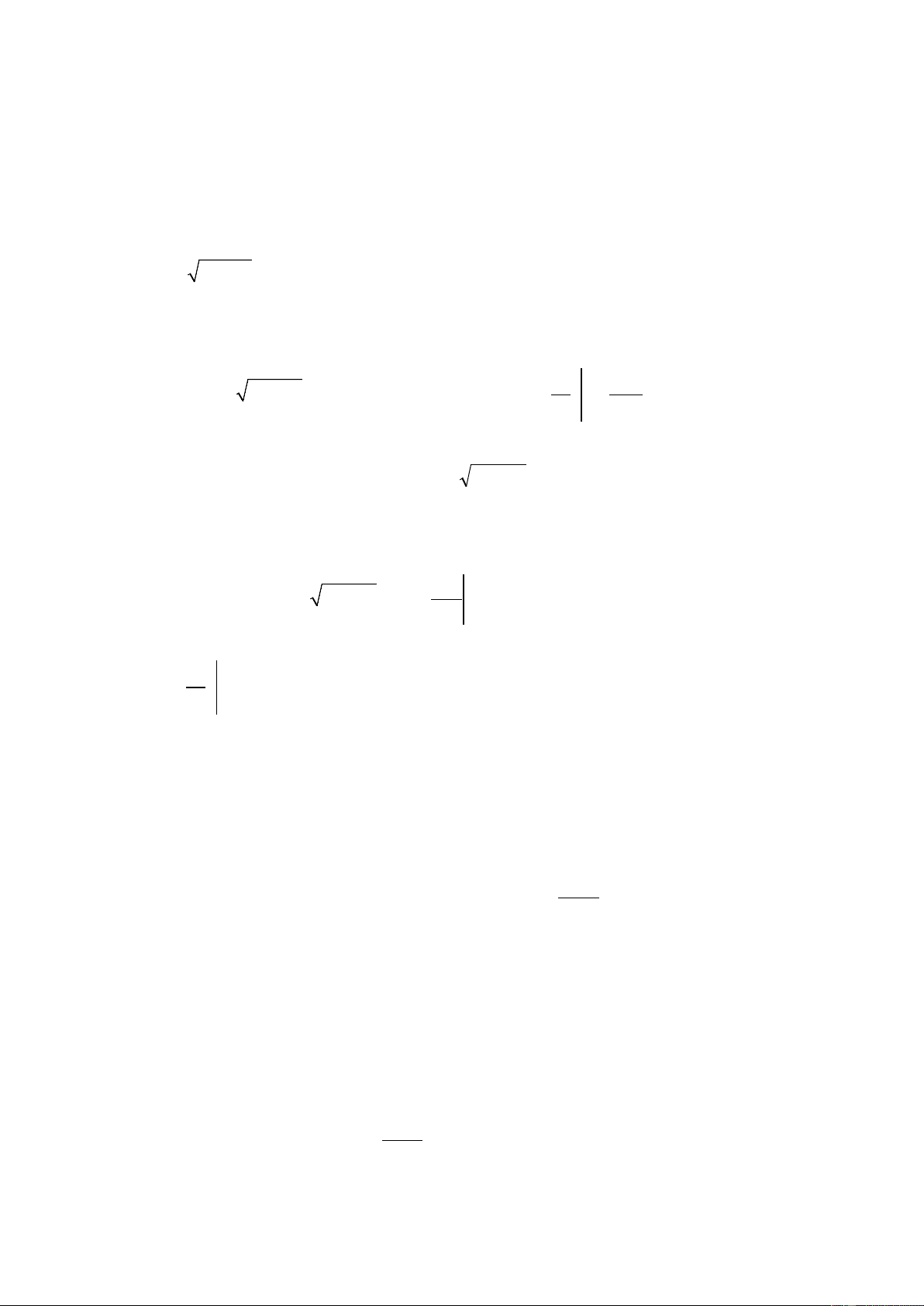
Preview text:

CHỦ ĐỀ 13: ỨNG DỤNG TÍCH PHÂN TÍNH THỂ TÍCH
1) Tính thể tích vật thể
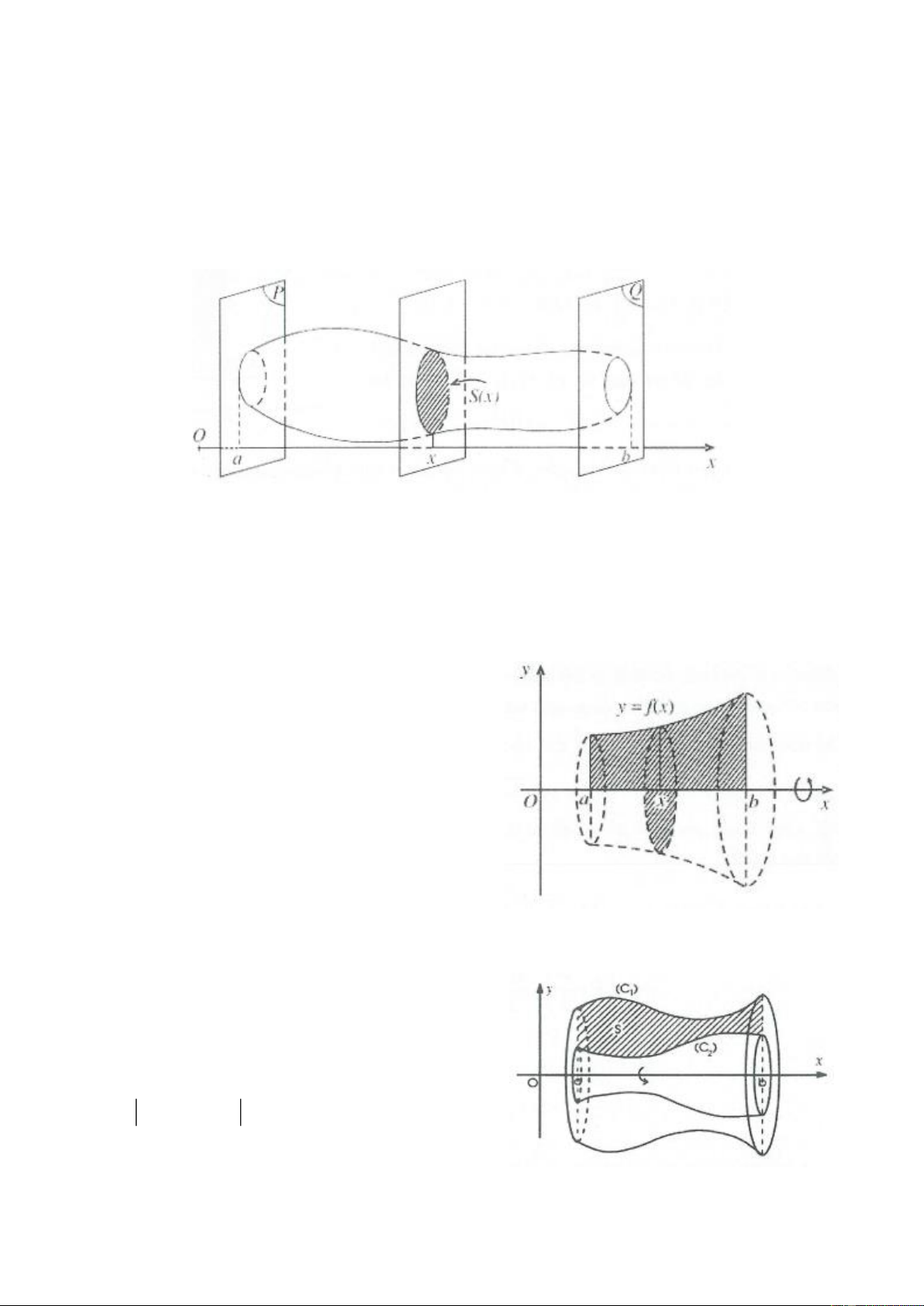
Cắt một vật thể (H ) bởi hai mặt phẳng ( P) và (Q) vuông góc với trục Ox lần lượt tại x = ;
a x = b (a b). Một mặt phẳng tuỳ ý vuông góc với Ox tại điểm x ( a x b ) cắt (H ) theo thiết
diện là S ( x) (hình vẽ). Giả sử S ( x) liên tục trên đoạn  ; a b.
Khi đó thể tích V của vật thể (H ) giới hạn bởi hai mặt phẳng (P) và (Q) được tính bởi công thức: b V = S
 (x)d .x a
2) Tính thể tích vật tròn xoay sinh bởi diện tích S quay quanh trục Ox
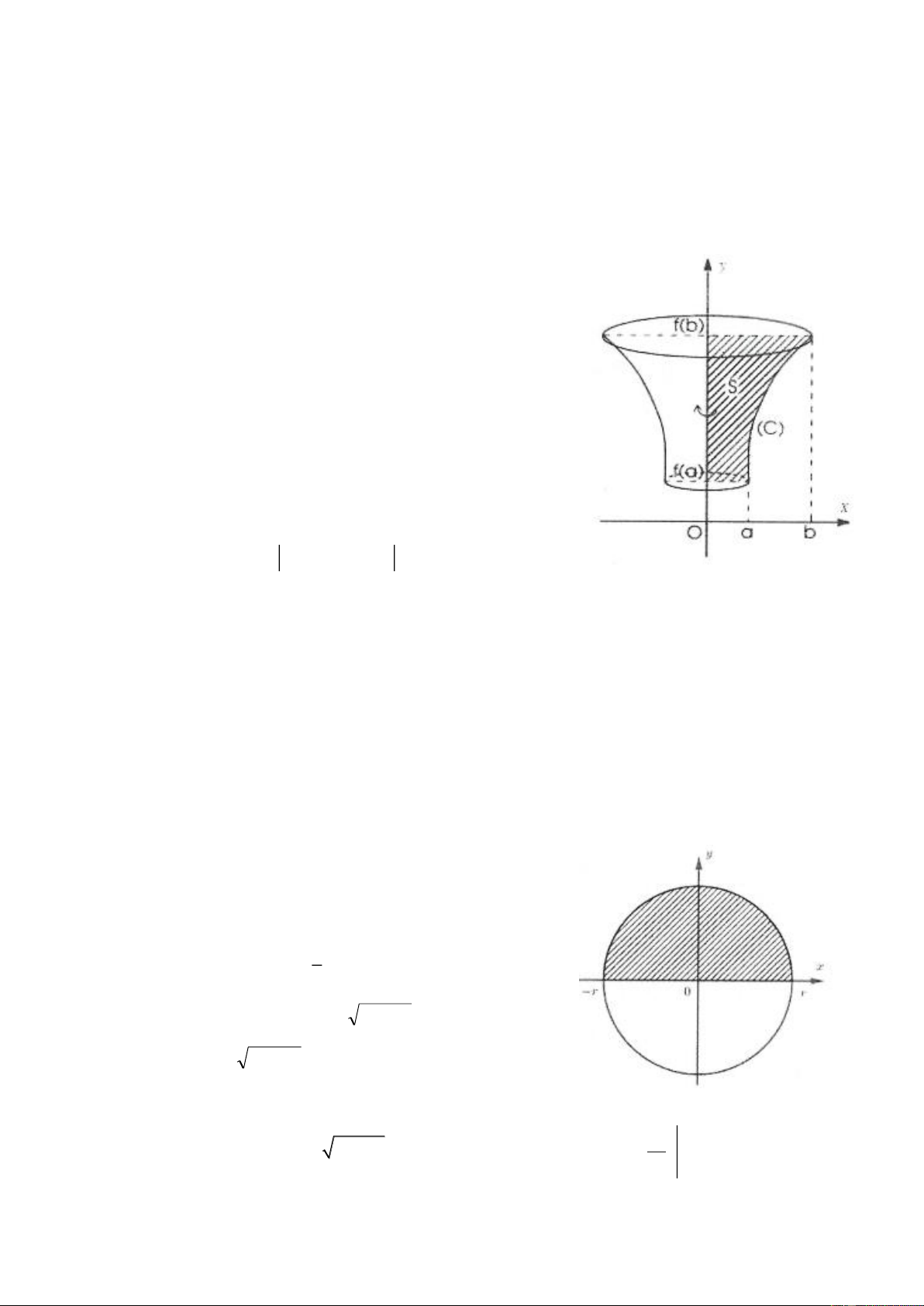
Giả sử một hình thang cong giới hạn bởi đồ thị hàm số
y = f ( x) , trục Ox và hai đường thẳng x = a và
x = b (a b) quay quanh trục Ox tạo thành một khối
tròn xoay (hình vẽ). Khi đó ta có thể tích vật thể là:
V = b S(x)  dx a
Mặt khác tại điểm x ta có S ( x) là một hình tròn có
bán kính R = f ( x)  ( ) b 2 2
S x =  R =  f (x) . Vậy 2 V =  f x dxOx ( ) . a
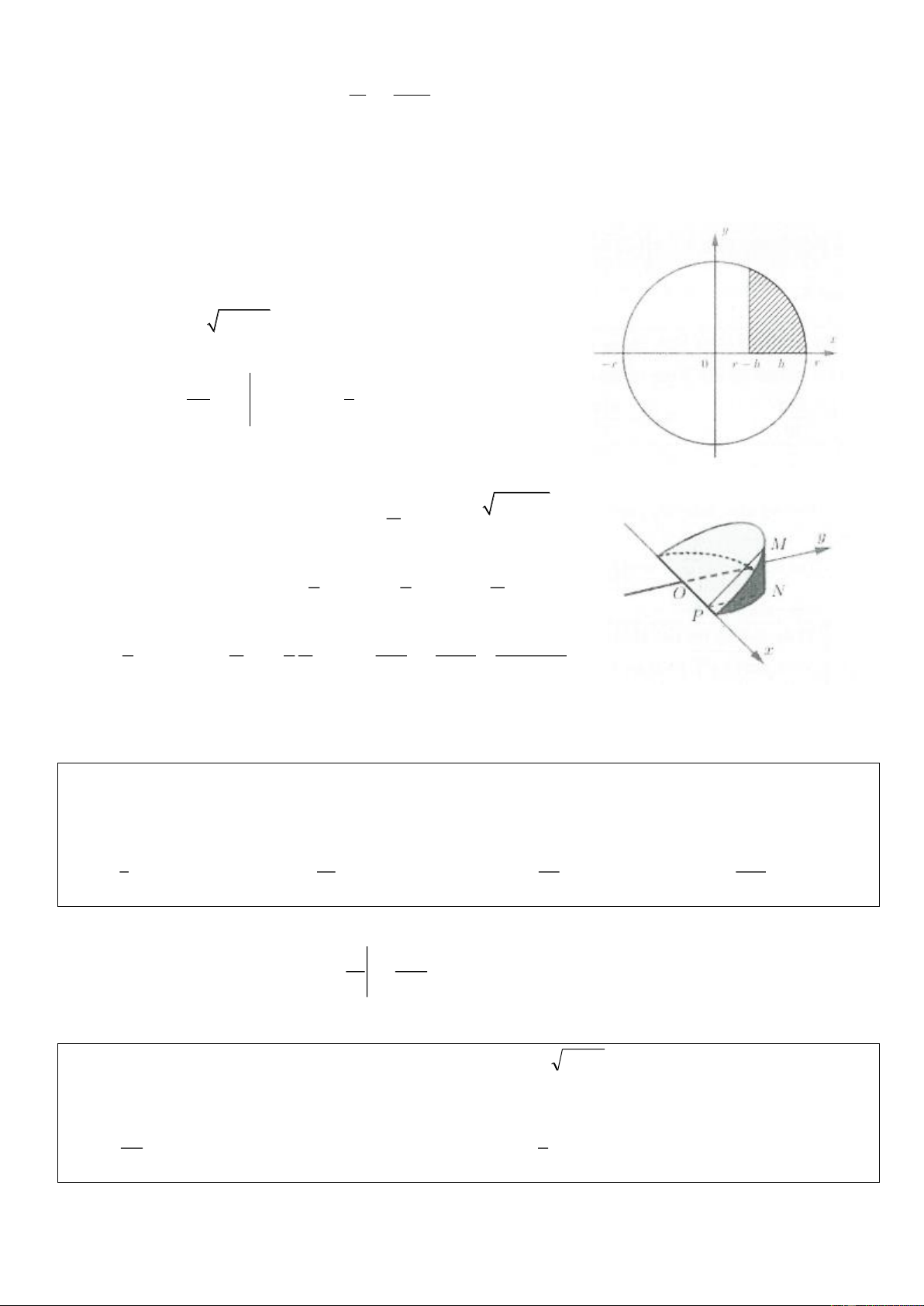
Trong trường hợp S ( x) giới hạn bởi hai đồ thị hàm số
y = f ( x) và y = g ( x) ta được khối tròn xoay có thể tích là: b 2 V =  f x − g x dxOx ( ) 2 ( ) . a
Chú ý: Khi bài toán không cho hai đường thẳng giới hạn x = a và x = b thì ta giải phương trình
f ( x) = g ( x) để tìm cận của tích phân, trong đó x = a là nghiệm nhỏ nhất và x = b là nghiệm lớn nhất của phương trình.
3) Tính thể tích vật tròn xoay sinh bởi diện tích S quay quanh trục Oy
Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi
đồ thị hàm số y = f (x) trục Oy và hai đường thẳng
y = f (a); y = f (b).
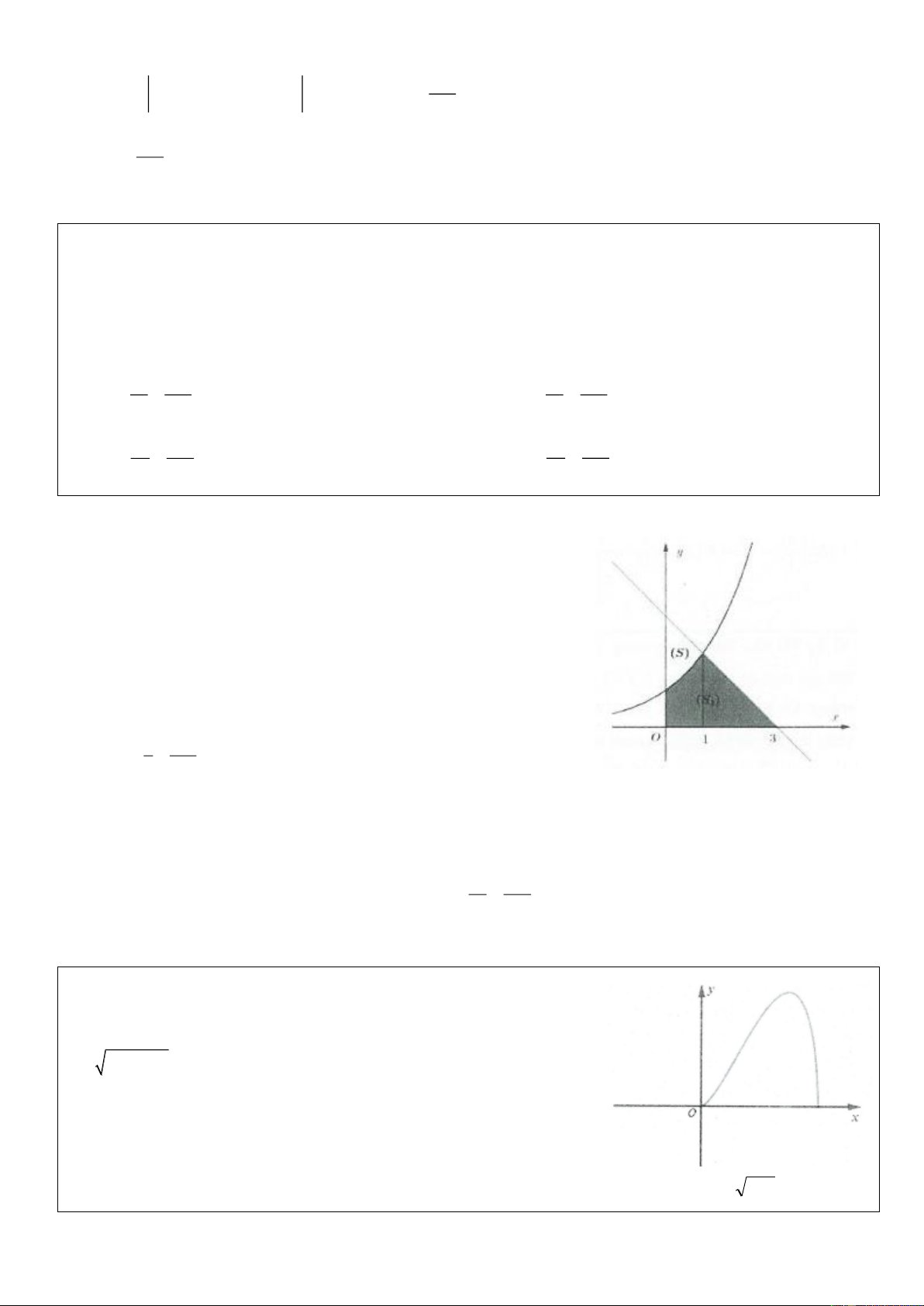
- Bước 1: Biến đổi y = f ( x) về dạng x = f y . 1 ( ) f (b) - Bước 2: Khi đó 2 V =  f y d . yOy 1 ( ) f (a)
Tương tự: Trong trường hợp V sinh ra bởi diện tích hình phẳng Oy
của hai đồ thị hàm số y = f ( x); y = g ( x) và hai đường thẳng n
y = m; y = n ta có 2 V =  f y − g y dyOy ( ) 2 . 1 1 ( ) m
Chú ý: Khi quay diện tích hình phẳng S quanh trục Ox ta được khối tròn xoay có thể tích V . Khi quay Ox
quanh trục Oy ta được khối tròn xoay có thể tích V . Oy
Hầu như V không bằng V . Chúng chỉ bằng nhau trong một số trường hợp đặc biệt. Ox Oy
4) Ứng dụng tính thể tích khối cầu, khối chỏm cầu và một số hình đặc biệt
a) Thể tích của khối cầu
Trong hệ tọa độ Oxy cho nửa đường tròn có phương trình: (P) 2 2 2
: x + y = r với r  0; y  0 (hình vẽ). Quay nửa hình tròn đó
quanh trục hoành ta được một mặt cầu có bán kính . r 4
Thể tích của mặt cầu này là: 3
V =  r (đvtt ). 3 Thật vậy: Ta có 2 2 2 2 2
x + y = r y =  r − x Với y  0 ta có: 2 2
y = r − x có đồ thị là nửa đường tròn phía trên trục hoành. r r r   Khi đó thể x
tích khối cầu V =   ( r − x ) dx = 2 (r − x ) 3 2 2 2 2 2 2
dx = 2  r x −   3 −  r 0 0 3 3  r  4 r 3 = 2 r −  = (đvtt)  3  3
b) Thể tích khối chỏm cầu
Khi quay hình phẳng tô đậm quanh trục Ox ta được khối 3 chỏm
cầu bán kính r và chiều cao . h r 2 r Khi đó: V =  r − x dx =  r − x dx   C ( 2 2) ( 2 2) r −h r −h r 2  r x   h  3 2 =  
− x  =h r − .    3   3  r −h
c) Thể tích khối nêm (xem hình vẽ) 2 2  = − Đặ h NP R x t OP = ;
x h = MN;  = MPN  tan =   R
MN = NP tan R 1 1 h V = S
 (x)dx trong đó S(x) = MN.NP = ( 2 2 R − x ). . − 2 2 R R 1 R   
V =  (R − x ) 3 2 3 h 1 h 2R 2R h 2R tan 2 2 3 . dx = . 2R −  = = 2 R 2 R  3  3 3 −R
5) Hệ thống Ví dụ minh họa
Ví dụ 1: Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x ; y = 0; x = 2. Tính thể tích V của khối tròn
xoay thu được khi quay (H ) quanh trục . Ox 8 32 8 32 A. V = . B. V = . C. V = . D. V = . 3 5 3 5 Lời giải: 2 2 5 x 32 Thể tích cần tính là 4
V =  x dx = . = .  Chọn D. 5 5 0 0
Ví dụ 2: Cho hình phẳng D giới hạn bởi đường cong 2 y =
x +1 , trục hoành và các đường thẳng
x = 0, x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 4 4 A. V = . B. V = 2. C. V = . D. V = 2. 3 3 Lời giải: 1 2 4
Thể tích cần tính bằng V =  ( 2 x +1) dx = . Chọn A. 3 0
Ví dụ 3: Cho hình phẳng D giới hạn bởi đường cong y = 2 + cosx , trục hoành và các đường thẳng  x = 0; x =
. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng: 2 A. V = ( + ) 1 .
B. V =  −1. C. V =  +1.
D. V = ( − ) 1 . Lời giải:   2 2  2
Thể tích cần tính bằng V =  ( 2 + cos x ) dx =  (2 + cos x)dx =  (2x + sinx) 2 = ( +   ) 1  . Chọn A. 0 0 0
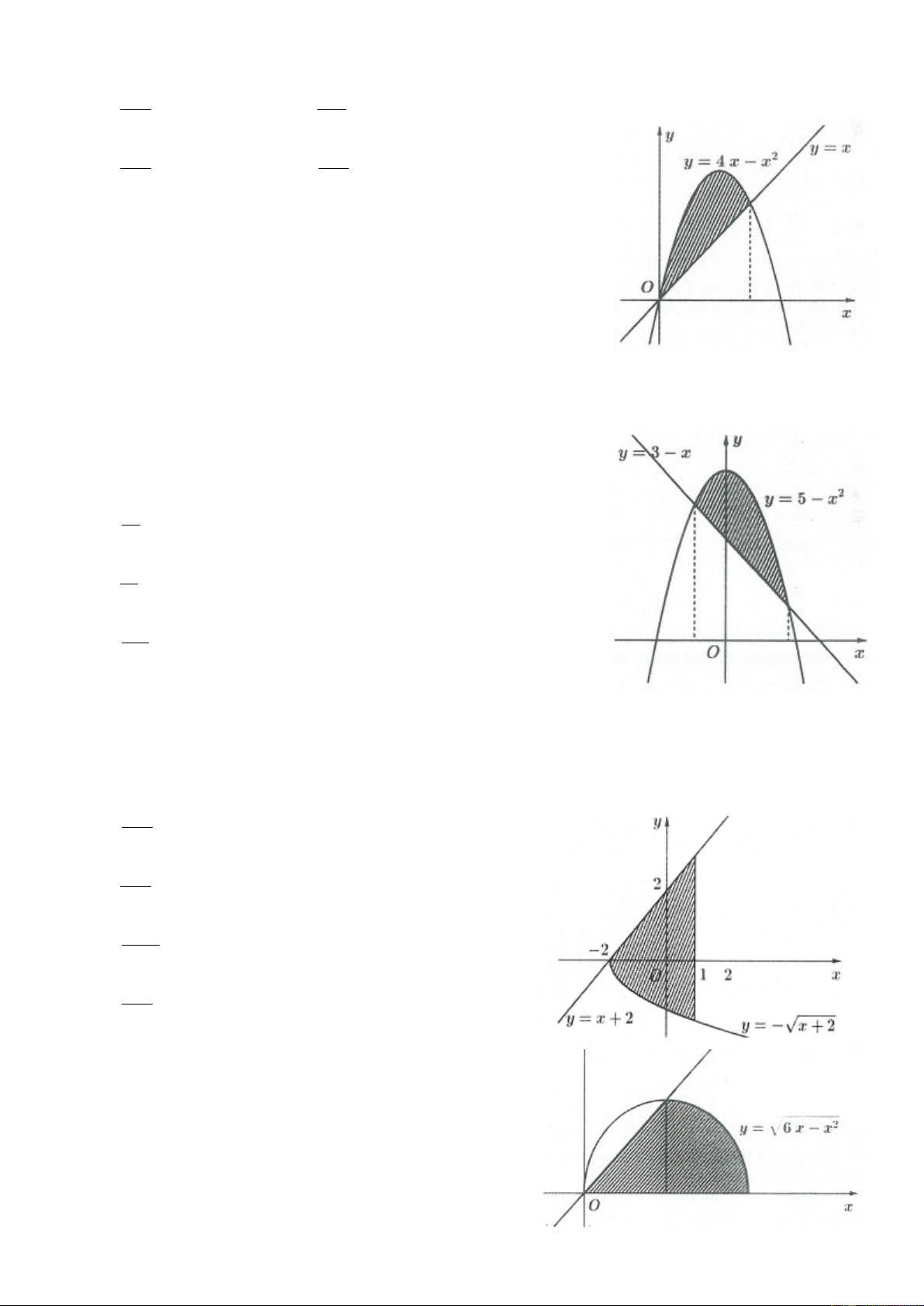
Ví dụ 4: Cho (H ) là hình phẳng giới hạn bởi đường cong (C): y = −x2 + 4x và đường thẳng d : y = . x
Tính thể tích V của vật thể tròn xoay do hình phẳng (H ) quay xung quanh trục hoành. 81 81 108 108 A. V = . B. V = . C. V = . D. V = . 10 5 5 10 Lời giải:x = 0
Phương trình hoành độ giao điểm là: − 2
x + 4x = x  − 2
x + 3x = 0   x = 3 3 2 108
Thể tích cần tìm là: V =   ( 2 4x − x ) 2 − x dx = . Chọn C. 5 0
Ví dụ 5: Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường y = x ( 3
ln 1+ x ); y = 0; x =1 khi xoay quanh trục . Ox 2ln 2 1 ln 2 1 2ln 2 1 ln 2 1 A. V    = − .   B. V    = − .   C. 2 V    = − .   D. 2 V    = − .    3 3   3 3   3 3   3 3  Lời giải:
Phương trình hoành độ giao điểm là: x ln(1 3
+ x ) = 0  x = 0 1
Gọi V là thể tích khối tròn xoay cần tìm ta có: 2 V =  x ln  ( 3 1+ x ) dx 0 2  x du = u  = ln( 3 3 1+ x ) 1   3 1 3   + + Đặ 1 x x 1 t    V =   ln ( 3 1+ x ) 2 − x dx  3 2  =  +   dv x dx x 1 3 =  0 0 v   3 2ln 2 1    = − 
 (đvtt). Chọn A.  3 3 
Ví dụ 6: Thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
y = 0, y = x ln ( x + )
1 ; x = 1 xung quanh trục Ox là 5  A. V = . B. V = (12ln2−5). 6 6 5  C. V = . D. V = (12ln2−5). 18 18 Lời giải:
Phương trình hoành độ giao điểm của (C) và Ox là x ln(x + ) 1 = 0  x = 0  = dx du 1 u = ln(x + ) 1  x +1
Thể tích khối tròn xoay cần tính là 2  x ln (x +  ) 1 dx . Đặt    dv = 2 3 x dx x +1 0  dv =  3 1 1 3 1 x +1 1 Ta có: 2 x ln  (x+ ) 1 dx = ln ( x + ) 1
− ( 2x − x+ )1dx = (12ln2−5) 3 18 0 0 0  Do đó V =
(12ln 2−5). Chọn D. 18
Ví dụ 7: Tính thể tích hình khối do hình phẳng giới hạn bởi các đường 2
x = y + 5; x = 3− y quay quanh Oy. 153 9 81 153 A. V = . B. V = . C. V = . D. V = . 3 2 10 5 Lời giải:y = −1
Tung độ giao điểm là: − 2
y + 5 = 3 − y   y = 2 2
V =   (−y +5)2 −(3− y)2 CASIO 153 2 dy ⎯⎯⎯ →V =  5 1 − 153 Vậy V =  (đvtt). Chọn D. 5
Ví dụ 8: Gọi (H ) là hình phẳng giới hạn bởi ( ) : = 2x C y
, (d ) : y = −x + a và trục Oy. Biết rằng (C ) và
(d ) cắt nhau tại một điểm duy nhất có hoành độ bằng 1. Tính thể tích V của khối tròn xoay sinh bởi (H) khi nó quay quanh trục . Ox 19 3  19 3  A. V = − .   B. V = + .    3 ln 4   3 ln 4   35 3   35 3  C. V = − .   D. V = + .    3 ln 4   3 ln 4  Lời giải: Theo đề bài ta có 2 = 1
− + a a = 3  (d) : y = −x + 3.
Gọi V là thể tích khối tròn xoay thu được khi quay hình phẳng (S 1 ) 1
được giới hạn bởi các đường (C), (d ), O ,
y Ox như hình bên quanh 1 3 2 2 trục Ox  =  2x V dx +  3 − x dx   1 ( ) ( ) 0 1 8 3 V     = − . 1    3 ln 4 
Gọi V là thể tích khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi các đường (d ), Ox 2
như hình bên quanh trục hoành, 3 2 19 3  Suy ra V =  3 − x dx = 9 . 
Khi đó V = V −V = − . Chọn A. 2 ( ) 2 1    3 ln 4  0
Ví dụ 9: Để tạo ra những chiếc chậu hoa hình quả lê, người ta dùng
một chiếc khuôn là đường cong có phương trình trong hệ trục tọa độ là 3 y =
x (k − x) (k  0). Biết rằng mỗi đơn vị trong hệ trục tọa độ Oxy
tương ứng với chiều dài 1 dm. Hãy xác định k để thể tích chậu hoa là 12,15 dm3. A. k = 2. B. k = 4. C. k = 3. D. 4 k = 243 . Lời giải:
Ta có: y2 = x3(k − x) đồ thị cắt trục Ox tại điểm (0;k ). k kx x   k k
Thể tích của chậu hoa là: V =  x  (k − x) 4 5 5 5 3 dx =   k −  =   −  =12,15  4 5   4 5  0 0 5
k = 243  k = 3 . Chọn C.
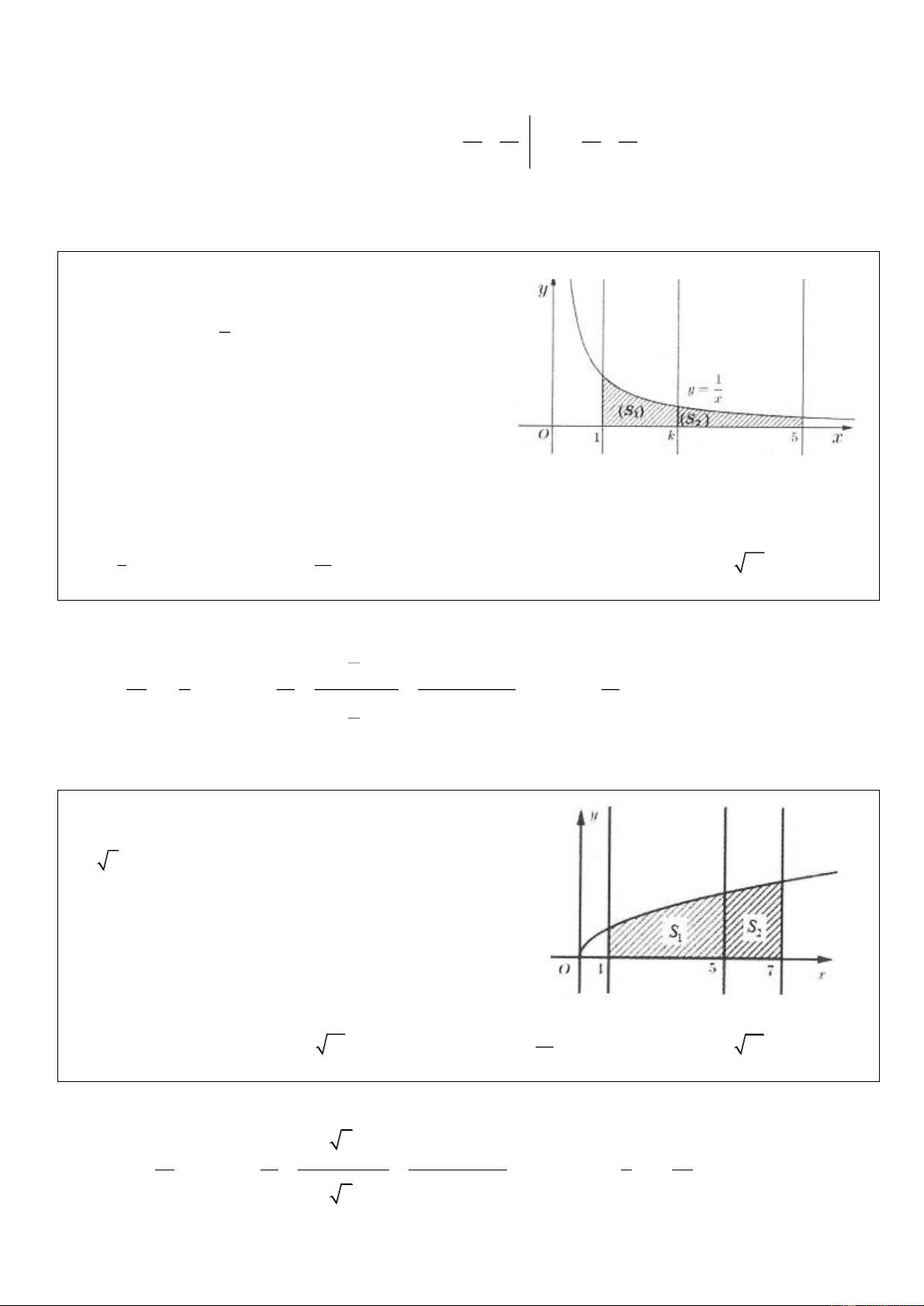
Ví dụ 10: Cho hình thang cong (H ) giới hạn bởi các đườ 1 ng y =
; y = 0; x = 1; x = 5 . Đường x
thẳng x = k với 1  k  5 chia (H ) thành hai phần là
(S và (S quay quanh trục Ox ta thu được hai khối 2 ) 1 )
tròn xoay có thể tích lần lượt là V và V . Xác đinh k để 1 2 V = 2V . 1 2 5 15 A. k = . B. k = . C. k = ln 5. D. 3 k = 25. 3 7 Lời giải: k 2  1   dx   dx 1 Vx F k − F 1 15 Ta có = − = F x  = = = 2  k = .  Chọn B. 2 ( ) ( ) ( ) 1 1 5 2 x x V  1  F 5 − F k 7 2 ( ) ( )  dx    x k
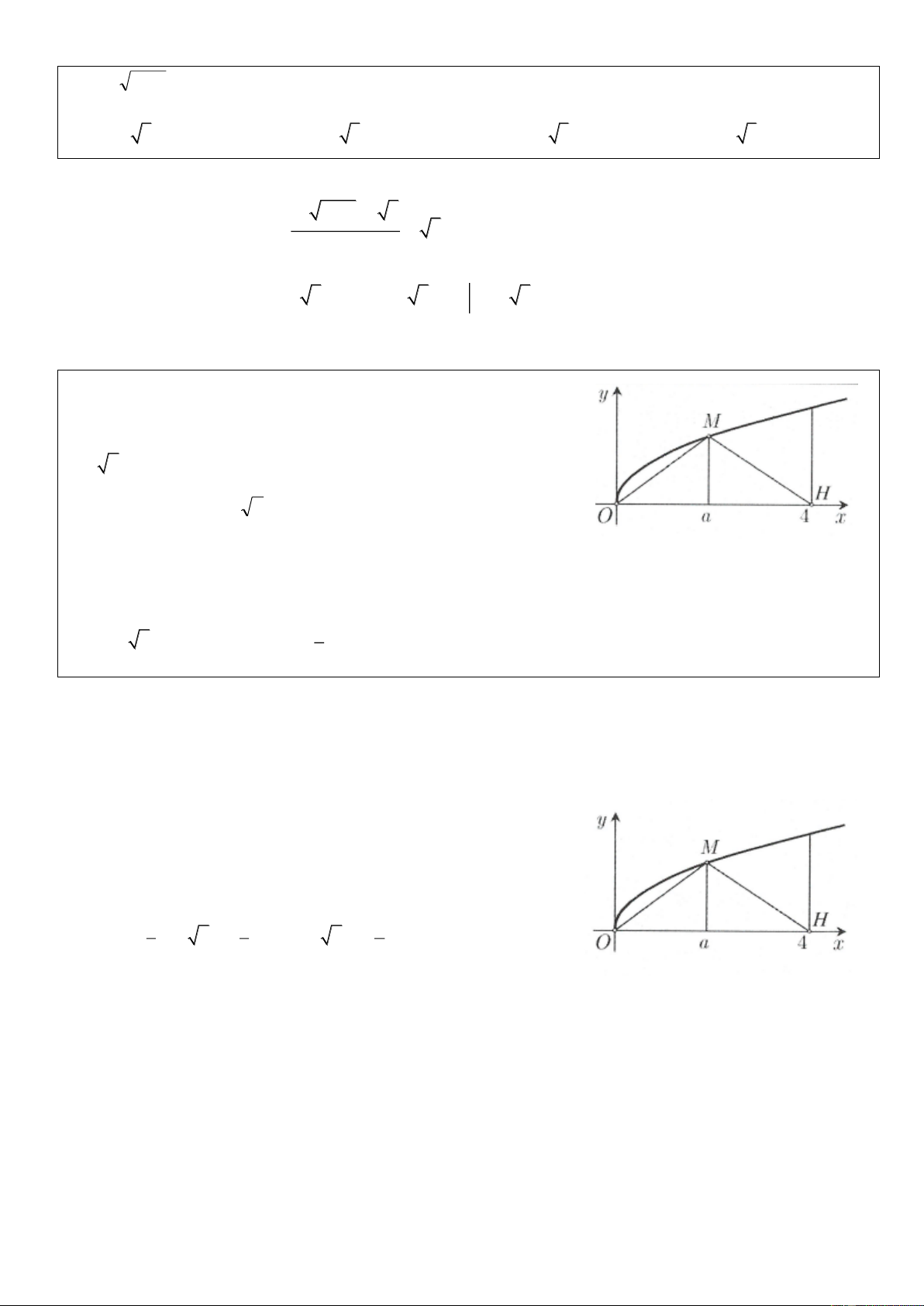
Ví dụ 11: Cho hình thang cong (H ) giới hạn bởi các đường
y = x; y = 0; x =1; x = 7. Đường
thẳng x = k với 1  k  7 chia (H ) thành hai phần là (S và 1 )
(S quay quanh trục Ox ta thu được hai khối tròn xoay có 2 )
thể tích lần lượt là V và V . Xác đinh k để V = 2V . 1 2 1 2 33 A. k = 33. B. k = 33. C. k = . D. 3 k = 33. 2 Lời giải: k  ( x)2 dx 2 x V
F (k ) − F ( ) 1 1  49  Ta có x = = F  (x) 1 1  = = = 2  F k − = 2 − F k   7 2 V −  (   x )2 F 7 F k 2 2 2 ( ) ( ) ( ) ( ) dx kF (k) 33 =
k = 33. Chọn B. 2
Ví dụ 12: [Đề Tham khảo Bộ Giáo dục và Đào tạo 2017] Tính thể V của phần vật thể giới hạn bởi hai
mặt phẳng x =1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có
hoành độ x (1 x  )
3 thì được một thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và 3 2 x − 2 ? 124 124
A. V = 32 + 2 15. B. V = . C. V = .
D. V = (32 + 2 15). 3 3 Lời giải: 3 3 3 1 Ta có: S ( x) 2 = S
= 3x 3x − 2 V = S x dx = x x − dx = x − d x −    HCN ( ) 2 2 3 3 2 3 2 ( 2 3 2) 2 1 1 1 1 124 = (3x −2) 33 2 = . Chọn C. 3 3 1
Ví dụ 13: Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 1, biết thiết diện của vật thể cắt
bởi mặt phẳng ( P) vuông góc với trục Ox tại điểm có hoành độ x (0  x  )
1 là một hình chữ nhật có độ
dài hai cạnh là x và ln( 2 x + ) 1 . 1 1 1 A. ln 2 −1. B. (ln 2 − ) 1 . C. ln 2 − . D. ln 2 −1. 2 2 2 Lời giải:
Do thiết diện là hình chữ nhật nên diện tích thiết diện là: S(x) = xln( 2 x + ) 1 1
Ta có thể tích cần tính là V = x ln ( 2 x +  )1dx 0 1 1 V = ln ( x + ) 1 d ( x + ) 1 1 = (x + )1ln(x + ) 1 1 1 2 2 2 2 1 −
( 2x + )1d (ln( 2x +   )1 0 2 2 2 0 0 1 1 1 ln 2 − 2xdx = ln 2 − .  Chọn C. 2 2 0
Ví dụ 14: Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = , biết thiết điện của vật thể cắt
bởi mặt phẳng ( P) vuông góc với trục Ox tại điểm có hoành độ x (0  x   ) là một tam giác đều có cạnh bằng 2 sin x . A. V = 8 3. B. V = 2 3. C. V = 2 3. D. V = 3. Lời giải: ( x )2 2 sin . 3
Diện tích thiết diện là S ( x) = = 3sin x 4  
Ta có thể tích cần tính là V =
3 sin xdx = − 3 cos x = 2 3.  Chọn C. 0 0
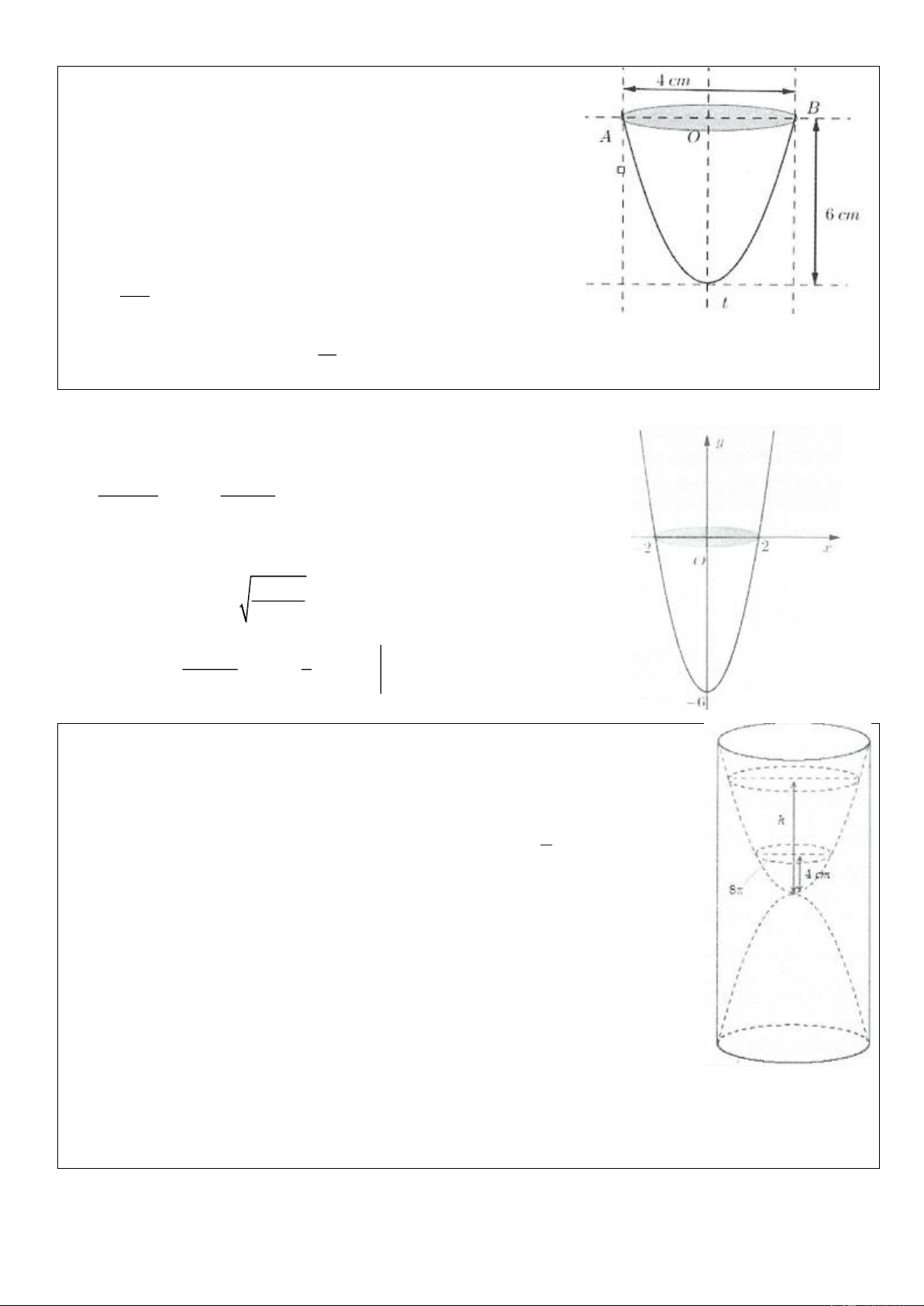
Ví dụ 15: [Đề Chuyên Đại học Vinh 2017] Gọi V là thể tích khối
tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
y = x; y = 0; x = 4 quanh trục .
Ox Đường thẳng x = a (0  a  4)
cắt đồ thị hàm số y = x tại M (hình vẽ bên). Gọi V1 là thể tích
khối tròn xoay tạo thành khi quay tam giác OMH quanh trục . Ox
Biết rằng V = 2V . Khi đó 1 5 A. a = 2 2. B. a = . C. a = 2. D. a = 3. 2 Lời giải: 4
Ta có V =  xdx = 8  V = 4 .  1 0
Gọi N là giao điểm của đường thẳng x = a và trục hoành. Khi đó
V là thể tích tạo được khi xoay hai tam giác OMN và MNH 1
quanh trục Ox với N là hình chiếu của M trên OH. 2 2 1 1 4 Ta có V =  a a +  4 − a a
= a = 4  a = 3. 1 ( ) ( )( ) 3 3 3 Chọn D.
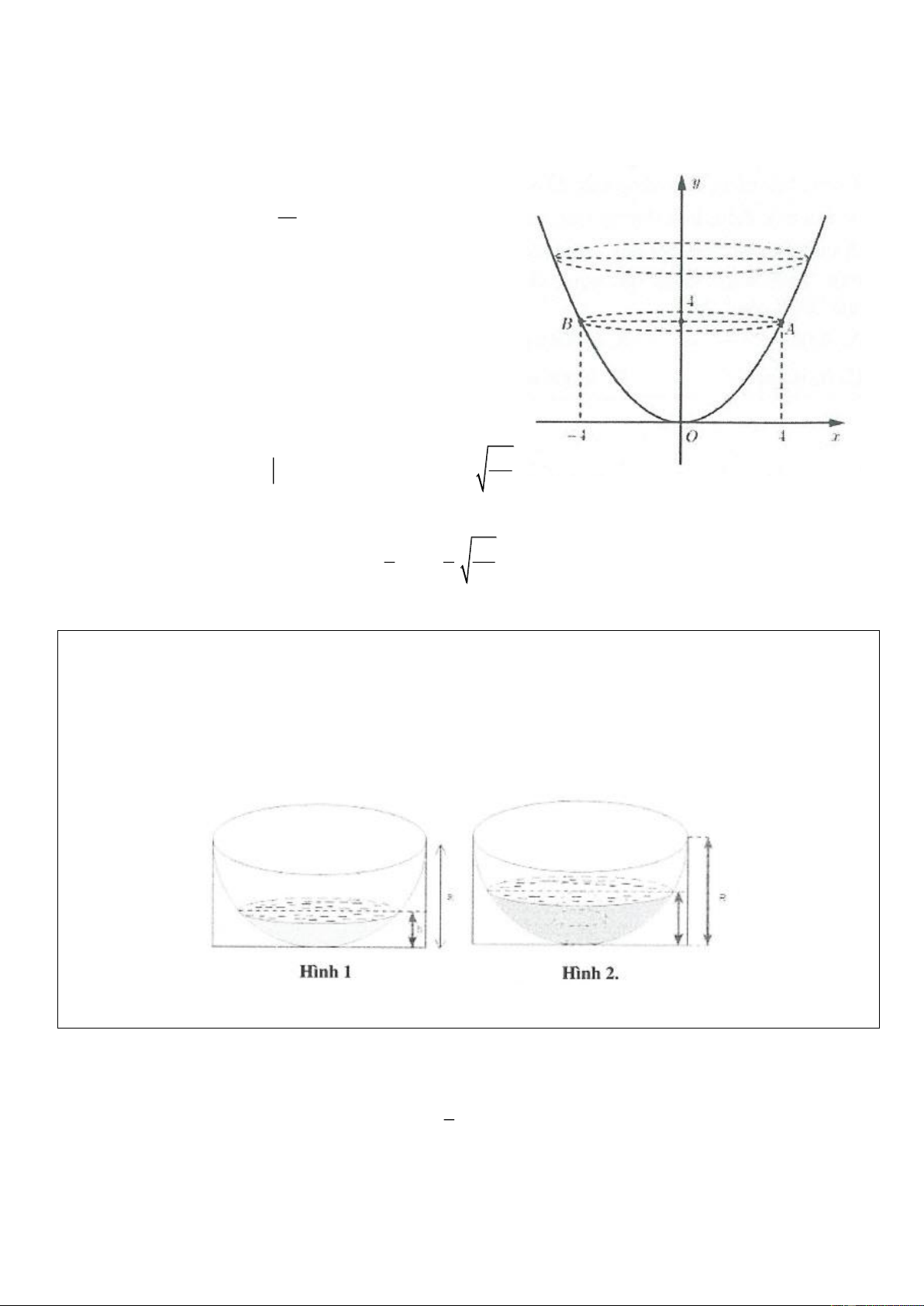
Ví dụ 16: Có một vật thể là hình tròn xoay có dạng giống như một
cái ly như hình vẽ dưới đây: Người ta đo được đường kính của
miệng ly là 4 cm và chiều cao là 6 .
cm Biết rằng thiết diện của
chiếc ly cắt bởi mặt phẳng qua trục đối xứng là một parabol. Tính thể tích ( 3
V cm ) của vật thể đã cho? 72 A. V = . B. V =12. 5 72 C. V = 12. D. V = . 5 Lời giải:
Chọn hệ trục tọa độ như hình suy ra phương trình Parabol là: 2 3x −12 2y +12 2 y =  x = . 2 3
Thể tích của vật là thể tích khối tròn xoay khi quay hình (H ) giới hạn 2 y +12
bởi các đường x = , x = 0, y = 6
− ; y = 0 quanh trục tung. 3 0 0 +   Khi đó 2y 12 1 2 V =  dy =  y + 4y =12.    Chọn C. 3  3  6 − 6 −
Ví dụ 17: Một chiếc đồng hồ cát như hình vẽ, gồm hai phần đối xứng nhau qua mặt
nằm ngang và đặt trong một hình trụ. Thiết diện thẳng đứng qua trục của nó là hai
parabol chung đỉnh và đối xứng nhau qua mặt nằm ngang. Ban đầu lượng cát dồn 3
hết ở phần trên của đồng hồ thì chiều cao h của mực cát bằng chiều cao của bên 4
đó (xem hình). Cát chảy từ trên xuống dưới với lưu lượng không đổi 2,90 cm3/
phút. Khi chiều cao của cát còn 4 cm thì bề mặt trên cùng của cát tạo thành một
đường tròn chu vi 8 cm (xem hình). Biết sau 30 phút thì cát chảy hết xuống phần
bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài là bao nhiêu cm? (Kết
quả làm tròn đến hàng đơn vị) A. 8 cm. B. 12 cm. C. 9 cm. D. 10 cm. Lời giải:
Gọi (α) là mặt phẳng song song với đáy của hình trụ và cắt đồng hồ cát.
Khi đó mặt cắt là một hình tròn có bán kính là x nên diện tích hình tròn là 2 2 S = R  = x  . t
Chọn hệ trục tọa độ Oxy như hình vẽ, gọi phương trình của parabol ( P) là y = ax2 +bx + c .
Vì ( P) đi qua điểm O(0;0), A(4;4), B(4; 4 − ) 2 Nên phương trình ( x P) : 2 y =
x = 4y S = 4 . y 4 h
→ Thể tích cát ban đầu là V = S dy  vì mặt cắt vuông góc t 0 h
với Oy. Suy ra V = (4 y)dy mà thể tích khối cát 0 3
V = 2,9.30 = 87 cm . c h  ( h 4 y) 87 2 2
dy =87  2 y
= 87  2 h = 87  h = . 0 2 0 4 4 87
Vậy chiều cao của khối trụ bên ngoài là 2. .h = 2. .
 9,92 cm . Chọn D. 3 3 2
Ví dụ 18: Một chậu nước hình bán cầu băng nhôm có bán kính R = 10 c ,
m đặt trong một khung hình hộp
chữ nhật (Hình 1). Trong chậu có chứa sẵn một khối nước hình chỏm cầu có chiều cao h = 4 c . m Người ta
bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi (Hình 2). Bán
kính của viên bi gần bằng: A. 9,63. B. 2,09. C. 1,72. D. 4,01. Lời giải:
Gọi x là bán kính viên bi hình cầu. Điều kiện: 0  2x 10  0  x  5 h
Chú ý: Công thức thể tích chỏm cầu: 2 V    = h R − .    3 
Thể tích khối nước hình chỏm cầu khi chưa thả viên bi vào: V =   h    2
h R −  =  4 416 16 10  −  =  1  3   3  3
Khi thả viên bi vào thì khối chỏm cầu gồm khối nước và viên bi có thể tích là:  x x  − x V =  x R −  = 2 ( 2 2 )2 2 4 (30 2 )  3  3 Ta có phương trình 4 : 3 2 V −V = x   4 x
 30 − 2x − 416 = 4 x  2 1 ( ) 3 3
x  9,626  5 (lo¹i)  3 2
 3x −30x +104 = 0  x  2,0940  5 .  Chọn B.x = 1 − ,72 (lo¹i) 
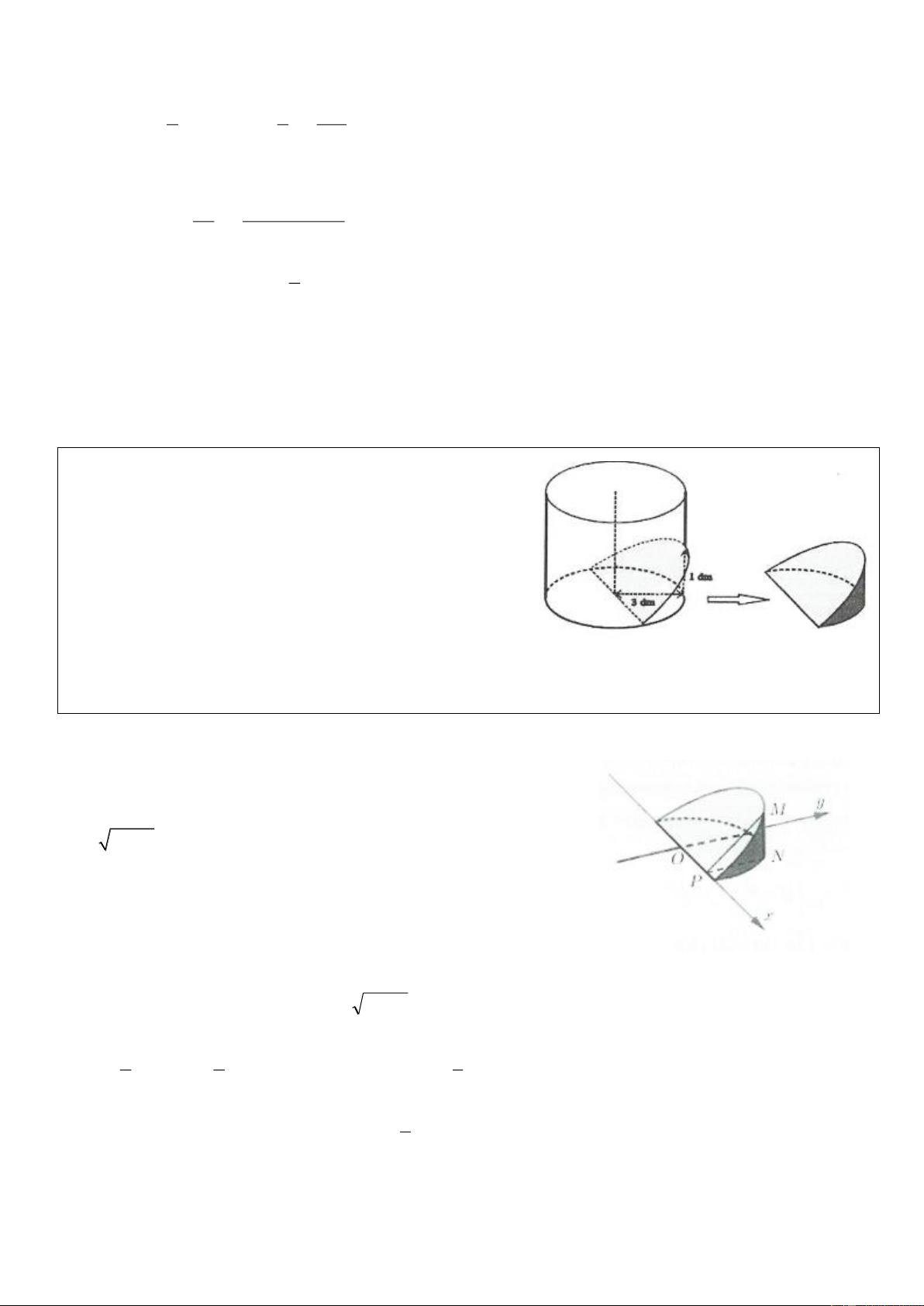
Ví dụ 19: Từ một khối gỗ hình trụ có đường kính 6 dm, bác
nông dân dùng cưa để cắt theo mặt cắt đi qua một điểm trên
đường sinh cách đáy 1 dm và đi qua đường kính của đáy
(như hình vẽ) để được một "khối nêm”. Giúp bác nông dân
tính thể tích của "khối nêm” đó ? A. 3 0,06 m . B. 3 0,006 m . C. 3 0,018 m . D. 3 0,006 m . Lời giải:
Chọn hệ trục tọa độ như hình vẽ. Khi đó khúc gỗ bé có đáy là nửa
hình tròn có phương trình: 2
y = 9 − x ( x  3 − ;  3 )
Một mặt phẳng cắt vuông góc với trục Ox tại điểm có hoành độ , x x  3 − ;  3
cắt khúc gỗ bé theo thiết diện có diện tích là S ( x) (xem hình).
Dễ thấy NP = y và MN = NP tan = 9 2 − x tan 1 S(x) 1 1 = MN.PN = (9 2
− x )tan trong đó tan = 2 2 3 3 3 Khi đó thể 1
tích khúc gỗ bé là : V = S  (x) =  ( 2 9 − x ) 3
tan dx = 0, 006 m . Chọn D. 2 3 − 3 −
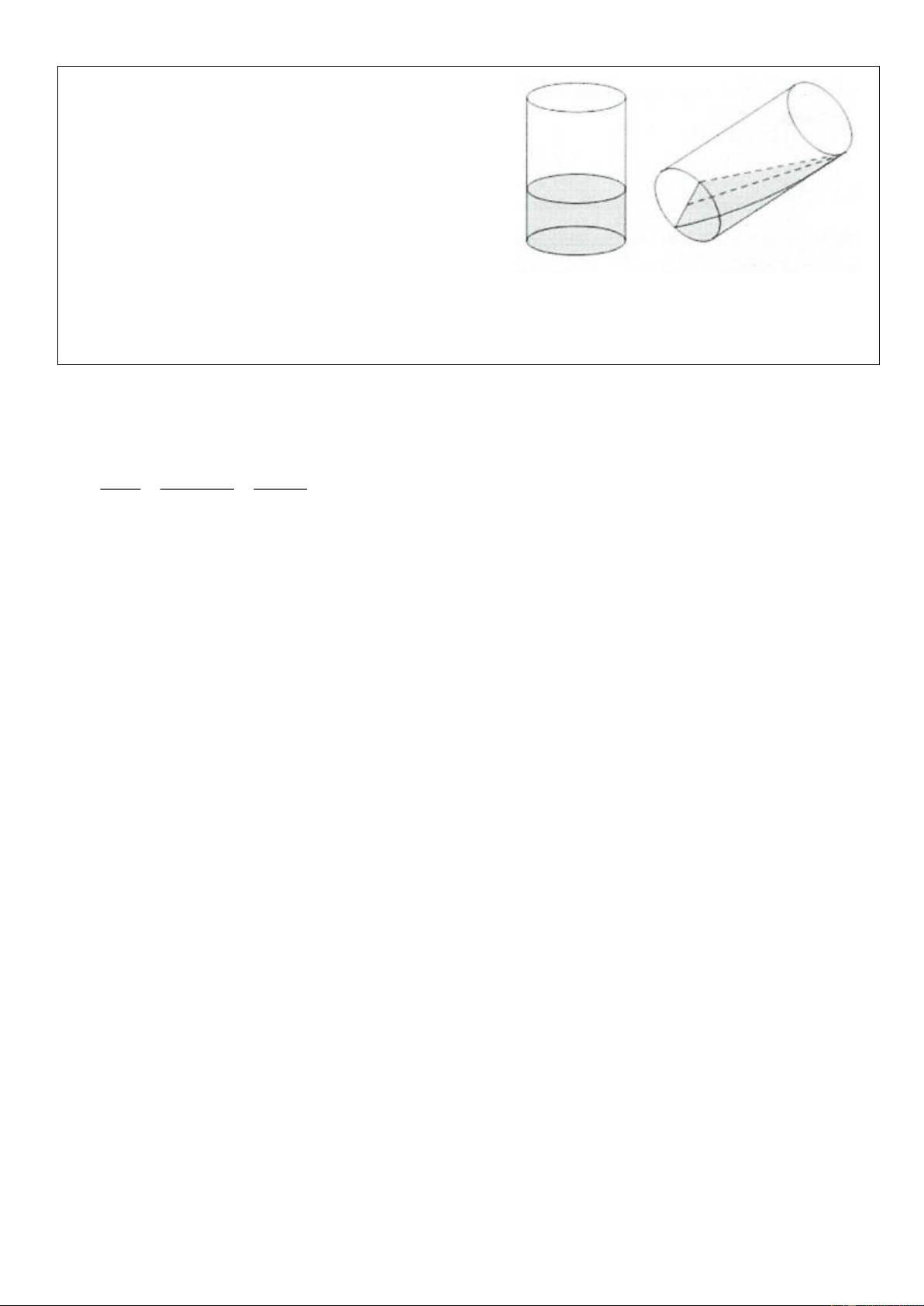
Ví dụ 20: [Đề thi chuyên Đại học Vinh 2017] Bạn A có
một cốc thủy tinh hình trụ, đường kính trong lòng đáy cốc
là 6 cm, chiều cao trong lòng cốc là 10 cm đang đựng một
lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước
chạm miệng cốc thì ở đáy mực nước trùng với đường kính
đáy. Tính thể tích lượng nước trong cốc. A. 3 15 cm . B. 3 60 cm . C. 3 60 cm . D. 3 70 cm . Lời giải:
Áp dụng công thức thể tích nêm có bán kính đấy R = 3, chiều cao h =10 ta có: 2 3 2 2R h 2R .tan 2.3 .10 3 V = = =
= 60 cm . Chọn C. 3 3 3
BÀI TẬP TỰ LUYỆN
Câu 1: Cho hàm số y = f (x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y = f (x), trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích khối tròn xoay tạo thành khi quay
D quanh trục hoành được tính theo công thức. b b A. 2 V = π f ∫ (x) . dx B. 2 V = 2π f ∫ (x) . dx a a b b C. 2 2 V = π f ∫ (x) . dx D. 2 V = π f ∫ (x) . dx a a
Câu 2: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi
đồ thị hàm số y = f (x), trục Ox và hai đường thẳng x = a, x = b (a < b), xung quanh trục . Ox b b b b A. 2 V = π f ∫ (x) . dx B. 2 V = f ∫ (x) . dx
C. V = π f ∫ (x) . dx D. V = f ∫ (x) . dx a a a a
Câu 3: Cho (H ) là miền hình phẳng giới hạn bởi các đường x = a, x = b (a < b) và đồ thị của hai hàm
số y = f (x), y = g (x) . Gọi V là thể tích của vật thể tròn xoay khi quay (H ) quanh .
Ox Mệnh đề nào dưới đây là đúng? b b A. 2 V = π f ∫ (x) 2 − g (x) . dx
B. V = π f
∫ (x)− g(x) 2 . dx a a b b C. 2 V = f ∫ (x) 2 − g (x) . dx D. V = f
∫ (x)− g(x) 2 . dx a a
Câu 4: Cho hình (D) giới hạn bởi các đường y = f (x), y = 0, x = π, x = .e Quay (D) quanh trục Ox ta
được khối tròn xoay có thể tích V. Khi đó V được xác định bằng công thức nào sau đây? π e π π
A. V = π f ∫ (x) . dx B. 2 V = π f ∫ (x) . dx C. 2 V = π f ∫ (x) . dx D. V = f ∫ (x) . dx e π e e
Câu 5: Thể tích V của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol (P) 2
: y = x và đường thẳng
d : y = x quay xung quanh Ox được xác định bởi công thức nào? 1 1 1
A. V = π ∫(x − x)2 2 . dx B. 2 4
V = π x dx +π x . dx ∫ ∫ 0 0 0 1 1 1 C. 2 4
V = π x dx −π x . dx ∫ ∫
D. V = π ∫(x − x )2 2 . dx 0 0 0
Câu 6: Thể tích V của khối tròn xoay khi cho hình phẳng (H ) giới hạn bởi đồ thị của parabol (P) 2 : y = x
và đường thẳng d : y = 2x quay xung quanh trục Ox được xác định bằng công thức nào sau đây? 2 2 2 A. 2 4
V = π 4x dx −π x . dx ∫ ∫
B. V = π ∫(x −2x)2 2 . dx 0 0 0 2 2 2 C. 2 4
V = π 4x dx +π x . dx ∫ ∫
D. V = π ∫(2x − x )2 2 . dx 0 0 0
Câu 7: Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x và y = x . Khối tròn xoay tạo ra khi (H )
quay quanh Ox có thể tích V được xác định bằng công thức nào? 1 1
A. V = π ∫( 4x − x) . dx
B. V = π ∫( 2x − x) . dx 0 0 1 1 C. V = π ∫( 2 x − x ) .
dx D. V = π ∫( 4 x − x ) . dx 0 0
Câu 8: Thể tích V của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường y = 2x và 2
y = x − x + 2
quanh trục Ox được xác định bằng công thức nào sau đây? 2 2
A. V = π ∫(x −3x + 2)2 2 . dx B.V π  ∫ (x x 2)2 2 2 4x  = − + − . dx    1 1 2 2
B. V π 4x ∫ 2 2 2   (x 3x 2)2 2 2  = − − + . dx D. V = π 
∫(x −3x+2) +4x . dx     1 1
Câu 9: Hình phẳng (H ) giới hạn bởi đường parabol (P): 2
y = x +1, trục tung và tiếp tuyến với (P) tại
điểm M (1;2) khi quay quanh trục .
Ox Công thức nào sau đây sử dụng để tính thể tích V của hình (H ) ? 1 1
A. V = π (x + ∫ )2 2 1 .
dx B. V π  ∫ (x )2 2 2 1 4x  = + − . dx    0 0 1 1
C. V = π ∫(2x)2 . dx
D. V = π (x − 2x + ∫ )2 2 1 . dx 0 0
Câu 10: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x =1 và x = 3, biết rằng khi cắt vật
thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (1≤ x ≤ 3) thì được thiết diện là một
hình chữ nhật có hai cạnh là 3x và 2 3x − 2. A. π V = 32 + 2 15. B. 124 V = . C. 124 V = .
D. V = (32+ 5)π. 3 3
Câu 11: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3, có thiết diện bị cắt bởi
mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ 3) là một hình chữ nhật có hai kích thước bằng x và 2 2 9 − x . A. V = 3. B. V =18. C. V = 20. D. V = 22.
Câu 12: Tính thể tích V của phẩn vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 2, có thiết diện bị cắt bởi
mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ 2) là một hình chữ nhật có hai kích thước bằng x và 2 2 4 − x . A. 8 V = . B. 16 V = . C. V =16. D. 3 V = . 3 3 16
Câu 13: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x =1, có thiết diện bị cắt bởi
mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ )
1 là một tam giác đều có cạnh bằng .x A. 3 π V = . B. 12 V = . C. V =1. D. 12 V = . 3 5 5
Câu 14: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = π , biết rằng thiết diện
của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ π ) thì được thiết
diện là một hình chữ nhật có hai cạnh là x và 2 sin x. A. V = 8 3. B. V = 3 3. C. V = 2 3. D. V = 3.
Câu 15: Tính thể tích π
V của vật thể nằm giữa hai mặt phẳng x = 0, x = ; biết rằng thiết diện của vật thể cắt 2
bởi mặt phẳng vuông góc với trục  π
Ox tại điểm có hoành độ x 0 x  ≤ ≤ 
là tam giác đều có cạnh là 2   
2 cos x + sin x. A. π V = 3. B. V = 2 3. C. V = 2π 3. D. 3 V = . 2
Câu 16: Tính thể tích V của khối tròn xoay trong không gian Oxyz, giới hạn bởi hai mặt phẳng x = 0, x = π
và có thiết diện cắt bởi mặt phẳng vuông góc với Ox tại điểm ( ;0
x ;0) bất kỳ là đường tròn bán kính sin x . A. V = 2. B. V = π. C. V = 4π. D. V = 2π.
Câu 17: Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = 2, biết rằng thiết diện của vật thể
bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ 2) là một nửa hình tròn đường kính 2 5x . A. V = 8 5π. B. V = 2 5. C. V = 4π. D. V = 4 5π.
Câu 18: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x =1 và x = 4 biết rằng khi cắt vật thể
bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (1≤ x ≤ 4) thì được thiết diện là một
hình lục giác đều có độ dài cạnh là 2 .x A. V = 63 3π. B. V =126 3. C. V = 63 3. D. V =126 3π.
Câu 19: Cho hình phẳng giới hạn bởi các đường y = 3x, y = x, x = 0, x =1 quay xung quanh trục . Ox Tính
thể tích V của khối tròn xoay tạo thành. A. 8π π π V = . B. 4 V = . C. 2 V = . D. V = π. 3 3 3
Câu 20: Hình (H ) giới hạn bởi 2
y = x − 4x + 4, y = 0, x = 0, x =1 quay xung quanh trục .
Ox Tính thể tích V
của khối tròn xoay tạo thành. A. 8π π π π V = . B. 4 V = . C. 2 V = . D. 31 V = . 3 3 3 5
Câu 21: Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng giới hạn bởi đồ thị hàm số
y = x2 − 2x , trục hoành, đường thẳng x = 0 và đường thẳng x =1 quay quanh trục hoành. A. 2π π π π V = . B. 8 V = . C. 16 V = . D. 4 V = . 3 15 15 3
Câu 22: Cho hình phẳng giới hạn bởi đường cong y = sin x, trục hoành và hai đường thẳng x = 0 và x = π .
Tính thể tích V của khối tròn xoay thu được khi quay hình này xung quanh trục . Ox 2 2 A. π π V = . B. 2 V = π R . C. V = . D. V = 2π. 2 3
Câu 23: Gọi (H ) là hình phẳng giới hạn bởi x
y = e , y = 0, x = 0, x =1. Tính thể tích V của vật thể tròn
xoay được sinh ra khi ta quay hình (H ) quanh trục . Ox
A. V = π (e − ) 1 .
B. V = π (e + 3).
C. V = π .e
D. V = e +1.
Câu 24: Tính thể tích V của vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường 3x 1 y e + =
, x = 0, x =1, y = 0 quay quanh . Ox A. 2 V = πe .
B. V = π .e C. V = π ( 2 e + e). D. V = π ( 2 e − e).
Câu 25: Tính thể tích của vật thể tròn xoay được sinh ra khi hình phẳng giới hạn bởi các đường 3x 1 y e + =
, x = 0, x =1, y = 0 quay quanh . Ox A. π ( 4 2 3e − e ). B. 1 3 π  e e − 1  .
C. π ( 3e +e).
D. π ( 3e − e). 6  3  3
Câu 26: Cho hình phẳng (H ) giới hạn bởi các đường y = x −1, trục
hoành và x = 4. Tính thể tích V của khối tròn xoay tạo thành khi quay
hình phẳng (H ) quanh trục . Ox 2 A. 7π π π V = . B. 7 V = . C. 7 V = . D. 5 V = . 6 6 6 3
Câu 27: (Sở GD & ĐT Tp Hồ Chí Minh 2017) Trong không gian với
hệ tọa độ Oxyz, cho vật thể (H ) giới hạn bởi hai mặt phẳng có phương trình x = a và x = b (a < b). Gọi
S (x) là diện tích thiết diện của (H ) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x
với a ≤ x ≤ b . Giả sử hàm số y = S (x) liên tục trên [a;b]. Thể tích V của vật thể (H ) được xác định bởi công thức nào? b b A. V = S ∫ (x) . dx
B. V = S ∫ (x) 2 . dxa a b b
C. V = π S ∫ (x) . dx
D. V = π S ∫ (x) 2 . dxa a x
Câu 28: Cho hình phẳng (D) giới hạn bởi các đồ thị hàm số 2
y = e trục Ox và hai đường thẳng
x = 0, x =1. Viết công thức tính thể tích V của khối tròn xoay khi quay hình (D) quay quanh trục . Ox 1 1 2 1   1 A. 2 x V = π e . dx ∫ B. x V = π e . dx ∫ C. 2x V =  e dx ∫  . D. 2x π e . dx ∫ 0 0  0  0
Câu 29: Cho hai hàm số y = f x và y = f x liên tục trên đoạn [a;b] và có đồ thị như hình vẽ bên. Gọi 2 ( ) 1 ( )
S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x = a, x = .
b Thể tích V của vật thể tròn
xoay tạo thành khi quay S quanh trục Ox được tính
bởi công thức nào sau đây? b
A. V = π  f
∫ (x)− f (x) 2 . dx B. 1 2  a b 2 V =  f ∫ (x) 2 − f x  . dx  1 2 ( ) a b b
C. V = π  f x − f x  . dx ∫ D. 2 V = π  f ∫ (x) 2 − f x  . dx  1 2 ( ) 1 ( ) 2 ( )  a a
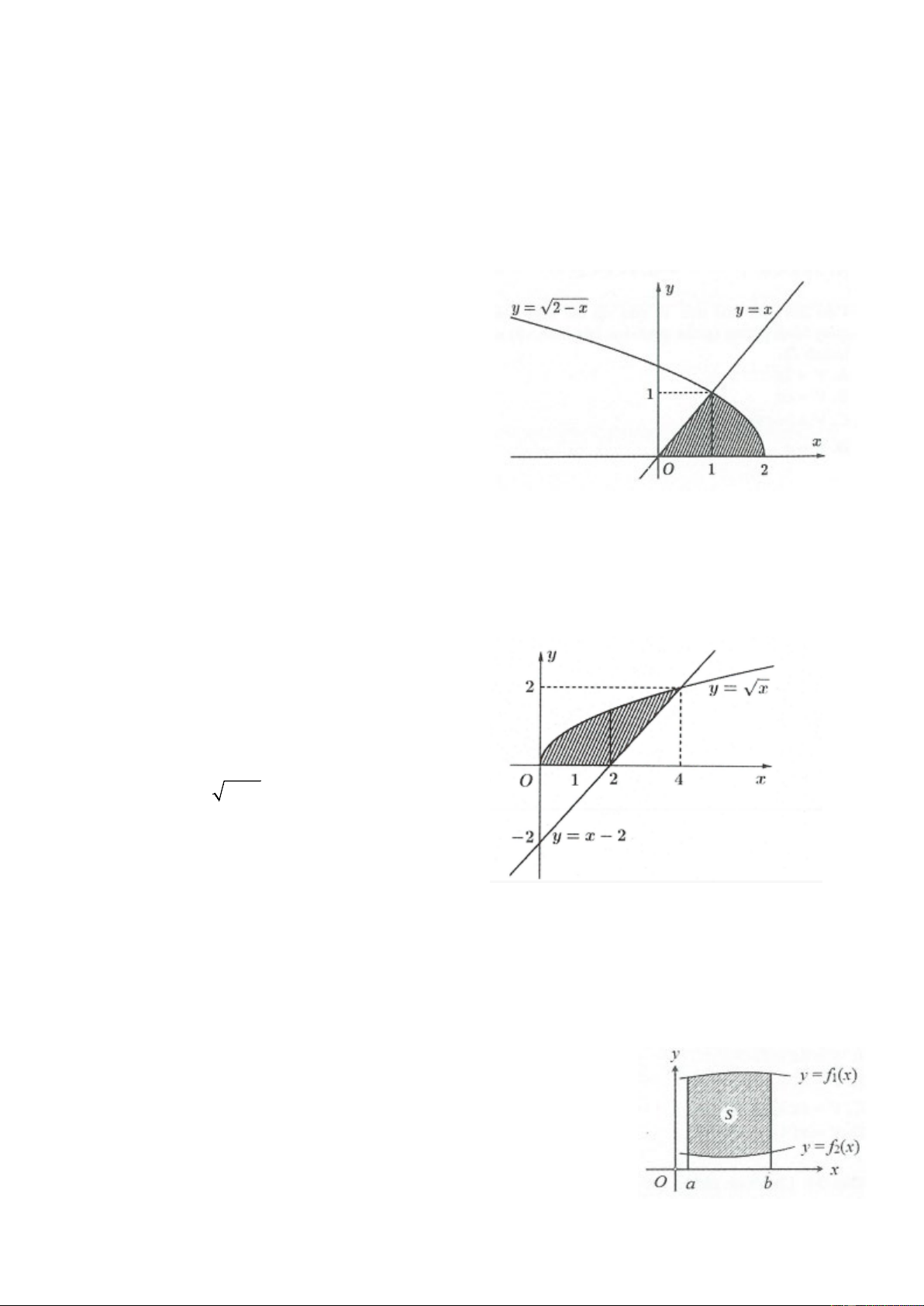
Câu 30: Nêu công thức tính thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình
vẽ) xung quanh trục hoành . Ox 1 2
A. V = π ∫(2− x) 2 dx +π x . dx ∫ 0 1 2
B. V = π ∫(2− x) . dx 0 1 2
C. V = π xdx −π 2 − x . dx ∫ ∫ 0 1 1 2 D. 2 V = π x dx +π ∫ ∫(2− x) . dx 0 1
Câu 31: Nêu công thức tính thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc
của hình vẽ) xung quanh trục hoành . Ox 4 4  
A. V = π  xdx + ∫
∫(x−2)dx. 0 2  4 4  
B. V = π  xdx − ∫
∫(x−2)2 dx. 0 2  2 4  
C. V = π  xdx + ∫
∫(x−2)2 dx. 0 2  2 4  
D. V = π  xdx − ∫
∫(x−2)dx. 0 2 
Câu 32: Tính thể tích V của vật thể tròn xoay thu được khi quay
hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành . Ox A. 15π π V = . B. 8 V = . ln 4 ln 2 C. 15π π V = . D. 17 V = . ln 2 ln 4
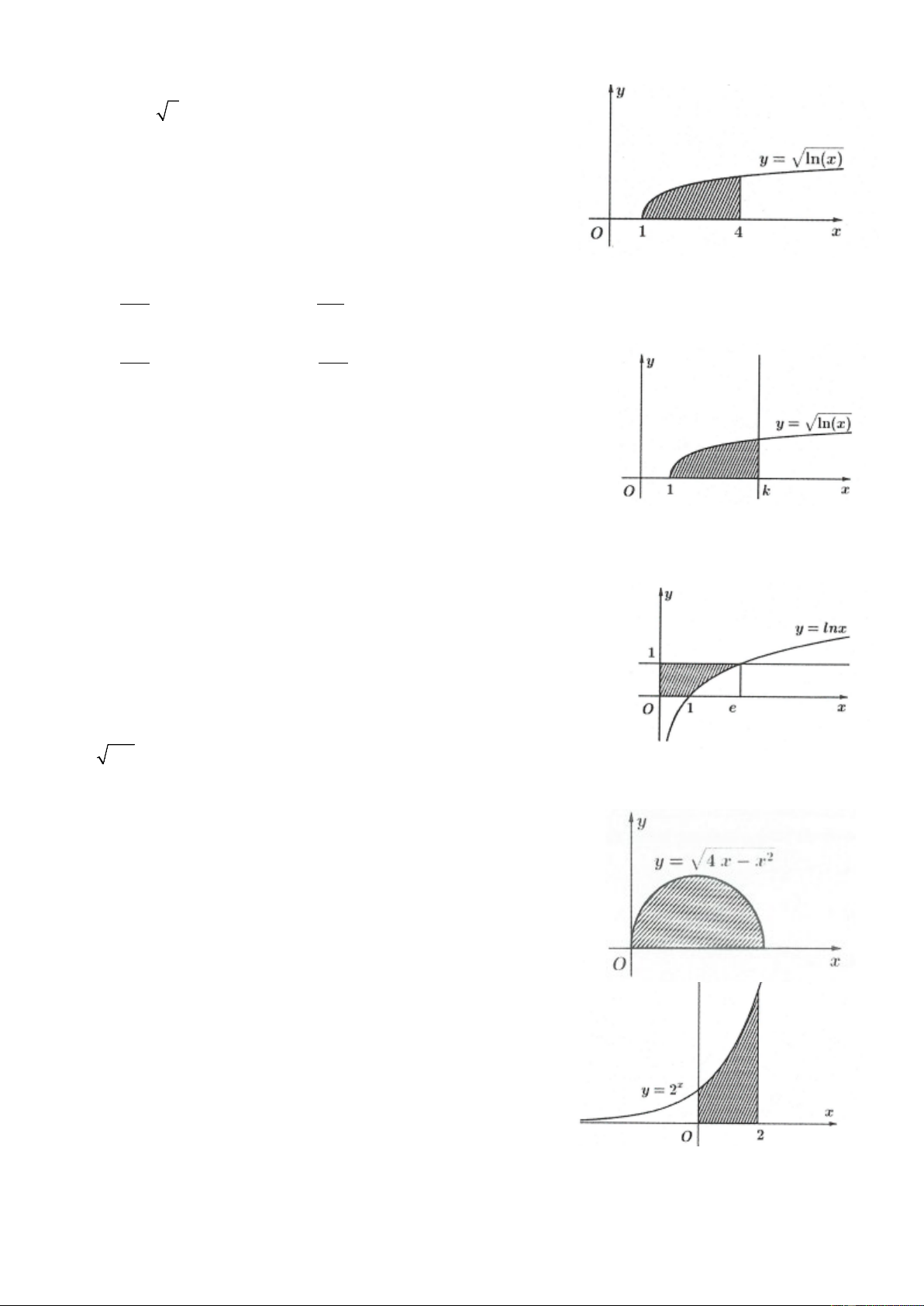
Câu 33: Tính thể tích V của vật thể tròn xoay thu được khi quay hình
phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành . Ox
A. V = 4π ln 4 −3.
B. V = π (4ln 2 −3).
C. V = 4π ln 2 −3π.
D. V = π (4ln 4 −3).
Câu 34: Cho hình phẳng (H ) giới hạn bởi các đường
y = ln x, y = 0, x =1, x = k với k >1 như hình vẽ. Gọi V là thể tích k
khối tròn xoay thu được khi quay hình (H ) quanh trục . Ox Biết rằng
V = π , hãy chọn khẳng định đúng? k
A. 3 < k < 4.
B. 1< k < 2.
C. 2 < k < 3.
D. 4 < k < 5.
Câu 35: Tính thể tích V của vật thể tròn xoay thu được khi quay hình
phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành . Ox A. V = 2π.
B. V = eπ.
C. V = (e + ) 1 π. D. V = π.
Câu 36: Tính thể tích V của vật thể tròn xoay thu được khi quay
hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành . Ox A. 35π π V = . B. 31 V = . 3 3 C. 32π π V = . D. 34 V = . 3 3
Câu 37: Tính thể tích V của vật thể tròn xoay thu được khi quay hình
phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành . Ox A. 24π. B. 27π. C. 25π. D. 26π.
Câu 38: Tính thể tích V của vật thể tròn xoay thu được khi quay hình
phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành . Ox A. 81 V = π. 10 B. 81 V = π. 5 C. 108 V = π. 5 D. V = 50π.
Câu 39: Tính thể tích V của vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành . Ox A. 12π V = . 5 B. 53π V = . 15 C. 153π V = . 5 D. 31π V = . 13
Câu 40: Tính thể tích V của vật thể tròn xoay thu được khi
quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành . Ox A. 27π V = . 2 B. 9π V = . 2 C. 11π V = . 3 D. 55π V = . 6
Câu 41: Tính thể tích V của vật thể tròn xoay thu được khi quay
hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành . Ox A. 125π V = . 3 B. 25π V = . 3 C. 157π V = . 3 D. 13π V = . 2
Câu 42: Tính thể tích V của vật thể tròn xoay thu được khi
quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục hoành . Ox A. 55π V = . 6 B. 24π V = . 3 C. 25π V = . 3 D. 125π V = . 9
Câu 43: Tính thể tích V của vật thể tròn xoay thu được khi quay hình phẳng (phân gạch sọc của hình vẽ) xung quanh trục hoành . Ox A. V =11π. B. 31π V = . 3 C. 32π V = . 3 D. 34π V = . 3 Câu 44: Biết 15π V =
+ 4π ln 2 là thể tích của vật thể tròn xoay thu được khi quay hình phẳng (phần gạch 4
sọc của hình vẽ) xung quanh trục hoành .
Ox Tìm k, biết k >1. 2 A. 4e k = . B. e k = . 3 2 C. 3 k = ln 2. D. k = 4. 2
Câu 45: Ký hiệu (H ) là hình phẳng giới hạn bởi các đường = ( − ) 2x−2 1 x y x e
, y = 0, x = 2 . Tính thể tích
V của khối tròn xoay thu được khi quay hình (H ) xung quanh . Ox π (2e −3) π (e −3) π (2e − ) 1 π (e − ) 1 A. V = . B. V = . C. V = . D. V = . 2e 2e 2e 2e
Câu 46: Tính thể tích V của vật thể tròn xoay sinh ra khi cho hình phẳng giới hạn bởi đồ thị hàm số
y = x ln x , trục hoành và đường thẳng x = e quay quanh . Ox 3 3 3 3 A. 2e +1 V − + − = π. B. 2e 1 V = π. C. 2e 1 V = π. D. 2e 1 V = π. 9 9 3 3
Câu 47: Gọi V là thể tích của khối tròn xoay sinh ra khi cho hình (H ) giới hạn bởi 1 y = +1, y = 0, x
x =1, x = k (k >1) quay xung quanh .
Ox Tìm k để 15 V π  ln16 = +  .  4  A. k = 4.
B. k = 4 .e C. 2 k = e . D. k = 8.
Câu 48: Cho hình (H ) giới hạn bởi các đường y = xln x ,
trục hoành và đường thẳng x = .e Tính thể tích khối tròn
xoay tạo thành khi quay (H ) quanh trục . Ox π ( 3 5e − 2) π ( 3 5e − 2) π ( 3 5e + 2) π ( 3 5e + 2) A. . B. . C. . D. . 25 27 25 27
Câu 49: Cho hình phẳng giới hạn bởi các đường y = x ln x, y = 0, x = e quay xung quanh trục . Ox Thể tích
khối tròn xoay tạo thành bằng bao nhiêu ? 3 3 3 3 A. 4e +1π. B. 4e −1π. C. 2e +1π. D. 2e −1π. 9 9 9 9
Câu 50: Cho hình phẳng giới hạn bởi các đường 3 2
y = x − 6x + 9x, y = 0 quay xung quanh trục . Ox Thể tích
của khối tròn xoay tạo thành bằng A. 729π π π π . B. 27 . C. 256608 . D. 776 . 35 4 35 5
Câu 51: Cho hình phẳng giới hạn bởi các đường 2 2
y = 2x , y = 4x quay xung quanh trục . Ox Thế tích của
khối tròn xoay tạo thành bằng A. 88π π π π . B. 9 . C. 4 . D. 6 . 5 70 3 5
Câu 52: Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số x y =
, trục Ox và đường thẳng x =1. 2 4 − x
Tính thể tích V của khối tròn xoay thu được khi quay hình (H ) xung quanh trục . Ox A. 4 π π V = π ln . B. 1 4 V = ln . C. 4 V = ln . D. 3 V = ln . 3 2 3 2 3 2 4
Câu 53: Cho hình phẳng giới hạn bởi các đường π
y = cos 4x, Ox, x = 0, x = quay xung quanh trục . Ox Thể 8
tích của khối tròn xoay tạo thành bằng 2 2 A. π π π  π . B. . C. . D. +1π   . 2 16 4  16 
Câu 54: Cho hình phẳng giới hạn bởi các đường y = x −1 , trục Ox và đường thẳng x = 3 quay xung quanh trục .
Ox Thể tích của khối tròn xoay tạo thành bằng A. 3π. B. 3π. C. 2π. D. π. 2
Câu 55: Cho hình phẳng giới hạn bởi các đường 3
y = x +1, y = 0, x = 0, x =1 quay xung quanh trục . Ox
Thể tích của khối tròn xoay tạo thành bằng A. 79π π π . B. 23 . C. 5 . D. 9π. 63 14 4
Câu 56: Cho hình phẳng giới hạn bởi các đường 2
y = ax , y = bx (a ≠ 0, b ≠ 0) quay xung quanh trục . Ox
Thể tích của khối tròn xoay tạo thành bằng 3 5 5 5 A. b  1 1  − π b b b  1 1    . B. π. C. π. D. − π   . 3 a  3 5  3 5a 3 3a 3 a  3 5 
Câu 57: Cho hình phẳng giới hạn bởi các đường 2 1 2
y = 4 − x , y = x quay xung quanh trục . Ox 3
Thể tích của khối tròn xoay tạo thành bằng A. 24π 3 π π π . B. 28 3 . C. 28 2 . D. 24 2 . 5 5 5 5
Câu 58: Cho hình phẳng giới hạn bởi các đường y = 3x, y = x, x = 0, x =1 quay xung quanh trục . Ox Thể
tích của khối tròn xoay tạo thành bằng A. 8π. B. 4 π. C. 2 π. D. π. 3 3 3
LỜI GIẢI CHI TIẾT b
Câu 1: Thể tích khối tròn xoay cần tính là 2 V = π f ∫ (x) . dx Chọn A. a b
Câu 2: Thể tích khối tròn xoay cần tính là 2 V = π f ∫ (x) . dx Chọn A. a b
Câu 3: Thể tích khối tròn xoay cần tính là 2 V = π f ∫ (x) 2 − g (x) . dx Chọn A. a π
Câu 4: Thể tích khối tròn xoay cần tính là 2 V = π f ∫ (x) . dx Chọn C. ex = 0
Câu 5: Phương trình hoành độ giao điểm của (P) và d là 2 x = x ⇔  . x =1 1 1
Dựa vào hình vẽ, thể tích khối tròn xoay cần tính là 2 4
V = π x dx −π x . dx ∫ ∫ Chọn C. 0 0 x = 0
Câu 6: Phương trình hoành độ giao điểm của (P) và d là 2 x = 2x ⇔  . x = 2 1 1 Do 2 2
x > x ,∀x ∈( ;
0 2) nên thể tích khối tròn xoay cần tính là 2 4
V = π 4x dx −π x . dx ∫ ∫ Chọn A. 0 0 x = 0
Câu 7: Phương trình hoành độ giao điểm của (P) và (C) là 2 x = x ⇔  . x =1 1 1
Vậy thể tích của khối tròn xoay cần tính là V = π ∫ (x )2 2
− ( x)2 dx = π ∫( 4 x − x ) . dx Chọn D. 0 0 x =1
Câu 8: Phương trình hoành độ giao điểm của (P) và d là 2
x − x + 2 = 2x ⇔  . x = 2 2
Vậy thể tích của khối tròn xoay cần tính là V π 4x ∫ (x 3x 2)2 2 2  = − − + . dx Chọn C.   1 Câu 9: Ta có 2 y ' = x +1 → y '( )
1 = 2 nên phương trình tiếp tuyến của (P) là y = 2 .x
Phương trình hoành độ giao điểm của (P) và d là 2
x +1 = 2x ⇔ x =1. 1
Vậy thể tích khối tròn xoay cần tính là V π  ∫ (x )2 2 2 1 4x  = + − . dxChọn B.   0
Câu 10: Diện tích hình chữ nhật ABCD là S (x) 2 = 3x 3x − 2. 3 3
Do đó, thể tích cần tính là V = S ∫ (x) 2 124
dx = 3x 3x − 2 dx = . ∫ Chọn C. 3 1 1
Câu 11: Diện tích hình chữ nhật ABCD là S (x) 2 = 2x 9 − x . 3 3
Do đó, thể tích cần tính là V = S ∫ (x) 2
dx = 2x 9 − x dx =18. ∫ Chọn B. 0 0
Câu 12: Diện tích hình chữ nhật ABCD là S (x) 2 = 2x 4 − x . 2 2
Do đó, thể tích cần tính là V = S ∫ (x) 2 16
dx = 2x 4 − x dx = . ∫ Chọn B. 3 0 0 2
Câu 13: Diện tích tam giác đều cạnh x là S (x) x 3 = . 4 1 3 2
Do đó, thể tích cần tính là V = S ∫ (x) x 3 3 dx = dx = . ∫ Chọn A. 4 3 0 0
Câu 14: Diện tích hình chữ nhật ABCD là S(x) = 2x sin x . π π
Do đó, thể tích cần tính là V = S
∫ (x)dx = 2x sin xdx = 2 3. ∫ Chọn C. 0 0 ( x + x )2 2 sin cos . 3
Câu 15: Diện tích tam giác đều cạnh x là S (x) =
= 3 (sin x + cos x). 4 π π 2 2
Do đó, thể tích cần tính là V = S ∫ (x)dx = 3
∫ (sin x+cos x)dx = 2 3. Chọn B. 0 0
Câu 16: Diện tích đường tròn bán kính sin x là S (x) = π ( x )2 . sin = π sin . x π π
Do đó, thể tích cần tính là V = S
∫ (x)dx = π.sin xdx = 2π. ∫ Chọn D. 0 0 2
Câu 17: Bán kính đường tròn d x 5 R = = 2 2 4 π
⇒ Diện tích nửa đường tròn bán kính R là ( ) 5 x S x = . 8 2 2 4
Do đó, thể tích cần tính là = ∫ ( ) 5 = π. x V S x dx dx = 4π. ∫ Chọn C. 8 0 0 (2x)2
Câu 18: Diện tích tam giác đều cạnh 2x là 3 2 S = = ∆ x 3 4
Suy ra diện tích lục giác đều cạnh 2x là S (x) 2 = 6× S = ∆ 6 3x . 4 4
Do đó, thể tích cần tính là V = S ∫ (x) 2
dx = 6 3x dx =126 3. ∫ Chọn B. 1 1 1 1 Câu 19: π
Dựa vào hình vẽ, thể tích cần tính là V = π ∫( x)2 2 8 3 dx −π x dx = . ∫ Chọn A. 3 0 0 1 Câu 20: π
V = π ∫(x − x + )2 2 31 4 4 = . Chọn D. 5 0 1 1 Câu 21: π
V = π ∫(x − x)2 2 dx = π ∫( 4 3 2
x − x + x ) 8 2 4 4 dx = . Chọn B. 15 0 0 π π 2 Câu 22: π π ∫( )2 1 cos 2 sin x V x dx π − = = dx = . ∫ Chọn A. 2 2 0 0 1 1 2
Câu 23: = π ( x ) x V e
dx = π e dx = π (e − ∫ ∫ ) 1 . Chọn A. 0 0 2 2 1 x 2   Câu 24: 2 2 x 2
V = π ∫ x e dx =π xe dx =πe . ∫ Chọn A. 1   1 1 1 2 Câu 25: + + π
V = π ∫( 3x 1 e ) 2 3x 1 dx = π e dx = ∫ ( 4 2
3e − e ). Chọn A. 6 0 0
Câu 26: Phương trình hoành độ giao điểm của (C) và Ox là x −1= 0 ⇔ x =1. 4 4
Do đó, thể tích khối tròn xoay cần tính là π
V = π ∫( x − )2 dx =π ∫(x − x + ) 7 1 2 1 dx = . Chọn A. 6 1 1 b
Câu 27: Công thức thể tích vật thể (H ) là: V = S ∫ (x) . dx Chọn A. a 2 1 x 1   Câu 28: 2 x
V = π ∫e dx π = e . dx ∫ Chọn B. 0   0
Câu 29: Dựa vào hình vẽ ta có: f x > f x > với mọi x∈[ ; a b] 2 ⇒ f (x) 2 > f x x ∀ ∈ a;b . 1 2 ( ) [ ] 1( ) 2 ( ) 0
Thể tích khối tròn xoay tạo thành khi quay S quanh trục là: b b V = π f
∫ (x)− f (x) 2 . dx = π  f
∫ (x)− f (x) 2 2 2 2 2  . dx Chọn D. 1 2  1 2  a a 1 2 1 2
Câu 30: V = π x dx +π  ∫ ∫( 2− x)2 2  2 dx = π x dx +π ∫ ∫(2− x) . dx Chọn D.   0 1 0 1 4 4 4 4
Câu 31: V = π ∫( x)2 dx −π ∫(x −2)2 dx =π xdx −π ∫ ∫(x−2)2 . dx Chọn B. 0 2 0 2 2 2 2 x Câu 32: π
V = π ∫( x )2 x 4 15 2
dx = π 4 dx = π = . ∫ Chọn A. ln 4 ln 4 0 0 0 4 4
Câu 33: V = π ∫( ln x)2 dx =π ln x . dx ∫ 1 1 4 4 4 Lại có: 4
ln xdx = xln x − xd ∫
∫ (ln x) =4ln4− dx = 4ln4−3. ∫ 1 1 1 1
Do đó V = π (4ln 4 −3). Chọn D. k k
Câu 34: V = π ∫( ln x)2 dx =π ln xdx ∫ 1 1 k k k Lại có: ln = ln k
xdx x x − xd (ln x) = k ln k − dx = k ln k − (k − ∫ ∫ ∫ )1 1 1 1 1
Do đó V = ⇔ k ln k − k +1 =1 ⇔ k(ln k − ) k 1 = 0   > → 1 π
ln k =1⇒ k = e . Chọn C.
Câu 35: Thể tích V của vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung e e e  
quanh trục hoành Ox là: 2 2 2
V = π 1 dx −π ln xdx = π ∫ ∫ e − ln xdx ∫  0 1  1 
Sử dụng máy tính CASIO ta được: V = π 2 . Chọn A.x = 0 Câu 36: Ta có: 2
4x − x = 0 ⇔  . x = 4
Thể tích V của vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục 4 4 4 2 3   hoành π
Ox là: V = π ∫( 2
x − x ) dx =π ∫( 2 x − x ) 2 x 32 4 4
dx =π 2x −  = . Chọn C.  3  3 0 0 0 x ≥ 0 x = 0
Câu 37: Giải phương trình hoành độ giao điểm: x = 6x − 2 x ⇔  ⇔ 2 2 
x = 6x − xx = 3
Thể tích V của vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục 3 3 6 2 3 6 π hoành Ox là: 2 = π + π ∫ ∫( 2 6 − ) x V x dx x x dx = + π ∫( 2
6x − x )dx 3 0 3 0 3 6 3   2 = 9π +π 3 x
x −  = 27π. Chọn B.  3  3 x = 0 Câu 38:
Phương trình hoành độ giao điểm của 2 đồ thị là: x = 4x − 2 x ⇔ 2
x − 3x = 0 ⇔  x = 3
Khi đó thể tích khối tròn xoay tạo thành là: 3 π V π  ∫ ( x x ) 3 2 2 2 x  = − − dx = π ∫( 4 3 2
x − x + x ) CASIO 108 4 8 15
dx →V = .  Chọn C.   5 0 0 x = −1
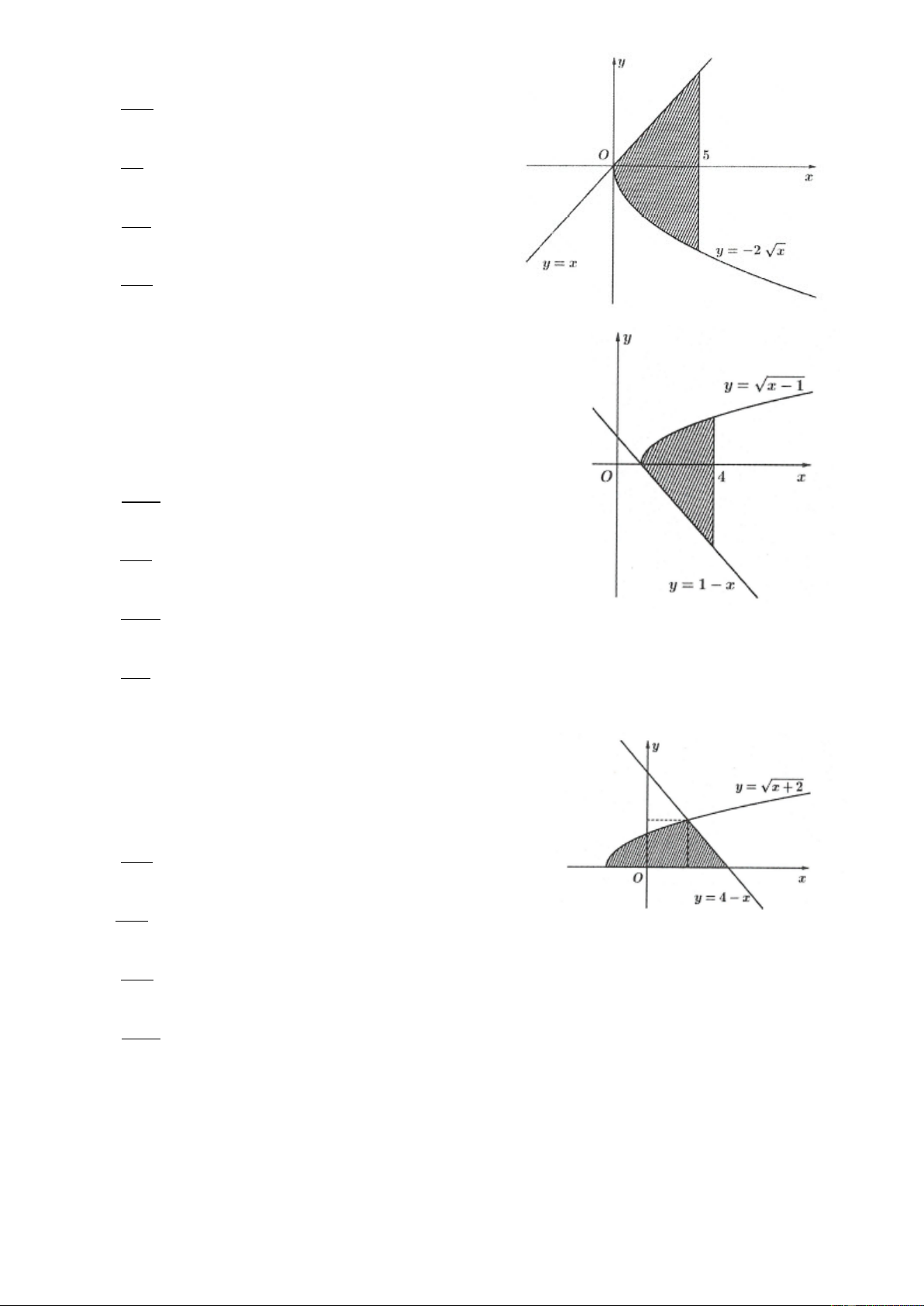
Câu 39: Phương trình hoành độ giao điểm của 2 đồ thị là: 3− x = 5 − 2 x ⇔ 2
x − x − 2 = 0 ⇔  x = 2 2
Khi đó thể tích khối tròn xoay tạo thành là: V π  ∫ ( 2 5 x )2 (3 x)2 = − − − dx   1 − 2 = ∫ ( 4 2 π π
x − x + x + ) CASIO 153 11
6 16 dx →V = . Chọn C. − 5 1
Câu 40: Lấy đối xứng đường thẳng y = − x + 2 qua trục Ox ta được đường thẳng y = x + 2 . x = −2
Giải phương trình x + 2 = x + 2 ⇔ 
. Thể tích khối tròn xoay tạo thành là x = −1 1 − π
V = π ∫ ( x + ) 1
2 dx +π ∫(x+ )2 CASIO 55 2
2 dx = →V = . Chọn C. − − 6 2 1
Câu 41: Lấy đối xứng đường thẳng y = 2 −
x qua trục Ox ta được đường thẳng y = 2 x . x = 0
Giải 2 x = x ⇔ 
. Thể tích khối tròn xoay tạo thành là x = 4 4 π V = π ∫( x) 5 2 2 CASIO 157 2
dx +π x dx = →V = . ∫ Chọn C. 3 0 4
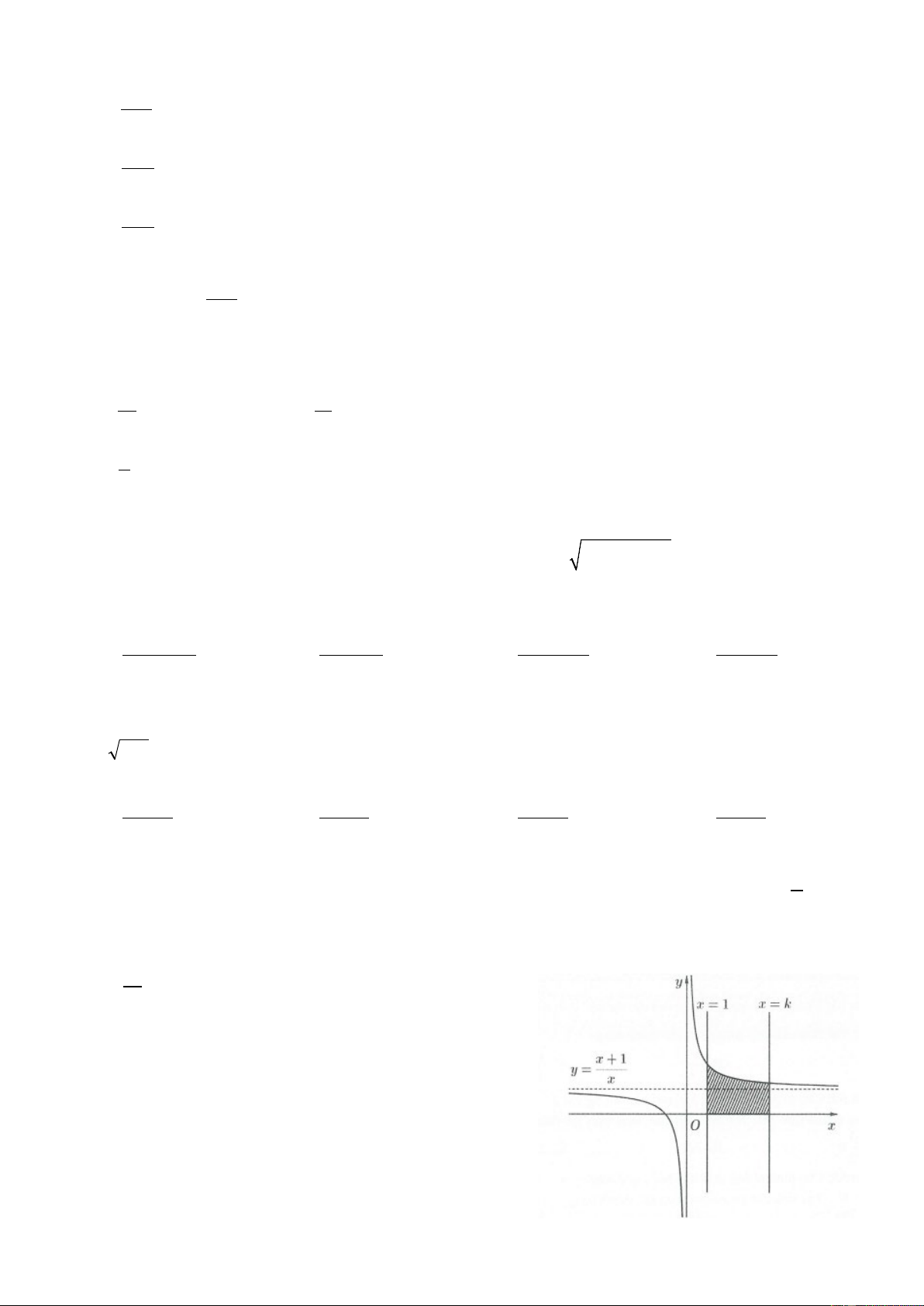
Câu 42: Lấy đối xứng đường thẳng y =1− x qua trục Ox ta được đường thẳng y = x −1 x =1
Giải phương trình x −1 = x −1 ⇔  x = 2 2 4
Thể tích khối tròn xoay tạo thành là π
V = π ∫( x − )2 dx +π ∫( − x)2 CASIO 55 1 1
dx →V = . Chọn A. 6 1 2 x ≤ 4  x ≤ 4
Câu 43: Xét phương trình x + 2 = 4 − x ⇔  ⇔  ⇔ x = 2 2 2
x + 2 =16 −8x + x
x − 9x +14 = 0 2 4
Thể tích khối tròn xoay tạo thành là: V = π ∫ (x + 2)dx +π ∫(4− x)2 . dx 2 − 2 2 4 2 3  x    2 x 32π
= π  + 2x +π 16x − 4x +  = . Chọn C.  2   3  3 2 − 2 k 2 k 2
Câu 44: Thể tích khối tròn xoay tạo thành là:  x +1  1 V π ∫  dx π ∫1  = = +   x   x  1 1   2 1   1 k k   1 V π 1 ∫
dx π  x 2ln x π   k 1 2ln k 1  = + + = + − = + − + + −  2  x x   x   k  1 1  Do 15π 15 1 V = + 4π ln 2 ⇒
+ 4ln 2 = k − + 2ln k ⇔ k = 4. Chọn D. 4 4 k
Câu 45: Phương trình hoành độ giao điểm của (C) và Ox là ( − ) 2x−2 1 x x e = 0 ⇔ x =1. 2 2 2 − − π − π π − e x x x x x x 1
Khi đó, V = π ∫(x − ) 2 2 2 2 1 e dx = e d ∫ ( 2x −2x) 2 2 ( ) = .e = . Chọn D. 2 2 1 2e 1 1
Câu 46: Phương trình hoành độ giao điểm của (C) và Ox là x ln x = 0 ⇔ ln x = 0 ⇔ x =1. 1 3
Khi đó, thể tích cần tính là V = π ∫(x x)2 2e +1 ln dx =
π (bấm máy). Chọn A. 9 0 2 k k
Câu 47: Thể tích khối tròn xoay là  1   1 V π 1 ∫  dx π  x 2ln x  = + = − +   x   x  1  1  1  15  1 15
= π k − + 2ln k = π + ln16 
→k − + 2ln k = + ln16 ⇒ k =     4. Chọn A.k   4  k 4
Câu 48: Phương trình hoành độ giao điểm của (C) và Ox là .xln x = 0 ⇔ ln x = 0 ⇔ x =1. 1 π 5e − 2 2 ( 3 )
Khi đó, thể tích cần tính là V = π ( .xln x) dx = ∫
(bấm máy). Chọn B. 27 0
Câu 49: Phương trình hoành độ giao điểm của (C) và Ox là x ln x = 0 ⇔ ln x = 0 ⇔ x =1. 1 3
Khi đó, thể tích cần tính là V = π ∫(x x)2 2e +1 ln dx =
π (bấm máy). Chọn C. 9 0 x = 0
Câu 50: Phương trình hoành độ giao điểm của (C) và Ox là 3 2
x − 6x + 9x = 0 ⇔  . x = 3 3 π
Khi đó, thể tích cần tính là V = π ∫(x − x + x)2 3 2 729 6 9 dx = . Chọn A. 35 0 Câu 51: Ta có 2
y = 4x ⇔ y = 4x ⇔ y = 2 x. x = 0
Phương trình hoành độ giao điểm của (C và (C là 2 2x = x ⇔  . 2 ) 1 ) x =1 1 π
Khi đó, thể tích cần tính là V = π ∫ ( x )2 2 − ( x)2 6 2 2 dx = . Chọn D. 5 0
Câu 52: Phương trình hoành độ giao điểm của (C) và Ox là
x = 0 ⇔ x = 0. 2 4 − x 2 1   Khi đó, x π 4 V = π ∫  dx = ln 
(bấm máy). Chọn C. 2 4 x  − 2 3 0   π π π 8 8 2 8 Câu 53: = ∫( )2 1+ cos8xx sin 8  π π cos 4 x V x dx = π dx =π + = ∫   . Chọn B. 2  2 16  16 0 0 0
Câu 54: Phương trình hoành độ giao điểm của (C) và Ox là x −1 = 0 ⇔ x =1. 3 3 3 2  
Khi đó, = π ∫( −1)2 =π ∫( − )1 x V x dx x
dx =π  − x = 2π. Chọn C.  2 1 1  1 1 1 1 7 4   Câu 55: π
V = π ∫(x + )2 3 dx = π ∫( 6 3 x + x + ) x x 23 1 2
1 dx = π  + + x = . Chọn B.  7 2  14 0 0 0 x = 0
Câu 56: Phương trình hoành độ giao điểm của (C) và d là 2 ax bx  = ⇔ b . x =  a b a 5
Khi đó, thể tích khối tròn xoay cần tính là 2 4 2 2 b  1 1 V π a x b x dx  = − = − π ∫   . Chọn D. 3 a  3 5 0  1 x = − 3
Câu 57: Phương trình hoành độ giao điểm của (C) và (P) là 2 2
4 − x = x ⇔  . 3 x = 3 2   π
Do đó, thể tích khối tròn xoay cần tính là V = π ∫ ( 2 − x ) 2 3 2 x 28 3 4 −   dx = . Chọn B.  3  5 − 3 1 1
Câu 58: Thể tích khối tròn xoay cần tính là V = π ∫( x)2 2 8 3
dx −π x dx = π. ∫ Chọn A. 3 0 0
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1