TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI I. TÓM TẮT LÝ THUYẾT
 Định lý: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc
tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng. A ABC,A'B'C ' GT AB BC  , B   B ' A 'B' B 'C ' A' KL ABC ∽ A 'B'C ' B C B' C'
II. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Chứng minh hai tam giác đồng dạng Phương pháp giải:
Bước 1: Xét hai tam giác, chọn ra hai góc bằng nhau và chứng minh (nếu cần);
Bước 2: Lập tỉ số các cạnh tạo nên mỗi góc đó, rồi chứng minh chúng bằng nhau;
Bước 3: Từ đó, chứng minh hai tam giác đồng dạng. 1. Cho 
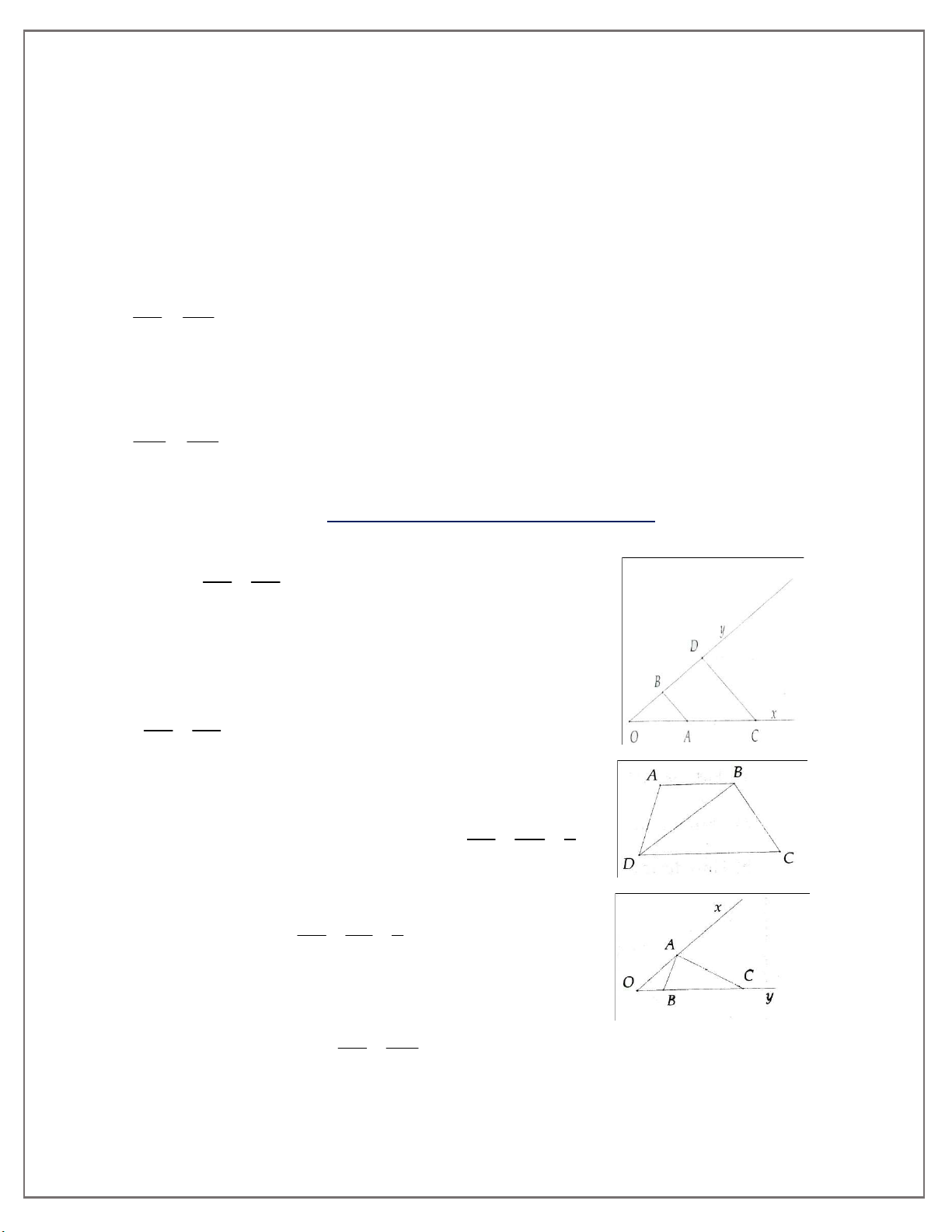
xOy , trên Ox lấy các điểm A và C, trên Oy lấy các điểm B và D. Chứng minh rằng
AOB ∽ COD nếu biết một trong các trường hợp sau: OA OB a)  ; b) OA.OD  OB.OC. OC OD 2. Cho 
xoy , trên Ox lấy các điểm A và C, trên Oy lấy các điểm B và D. Chứng minh rằng
AOD ∽ BOC nếu OA  4cm,OC  15cm,OB  6cm và OD  10cm.
3. Cho hình thang ABCD AB  CD , biết AB  9cm,BD  12cm,DC 16cm. Chứng minh ABD ∽ BDC. 4. Cho 
xoy , trên Ox lấy điểm A sao cho OA  4cm, trên Oy lấy các điểm B và C sao cho
OB  2cm,OC  8cm. Chứng minh rằng AOB ∽ COA.
Dạng 2. Sử dụng các trường hợp đồng dạng thứ hai để tính độ dài các cạnh hoặc chứng minh các góc bằng nhau
Phương pháp giải: Sử dụng trường hợp đồng dạng thứ hai (nếu cần) để chứng minh hai tam
giác đồng dạng, từ đó suy ra các cặp góc tương ứng bằng nhau hoặc cặp cạnh tương ứng còn lại bằng nhau.
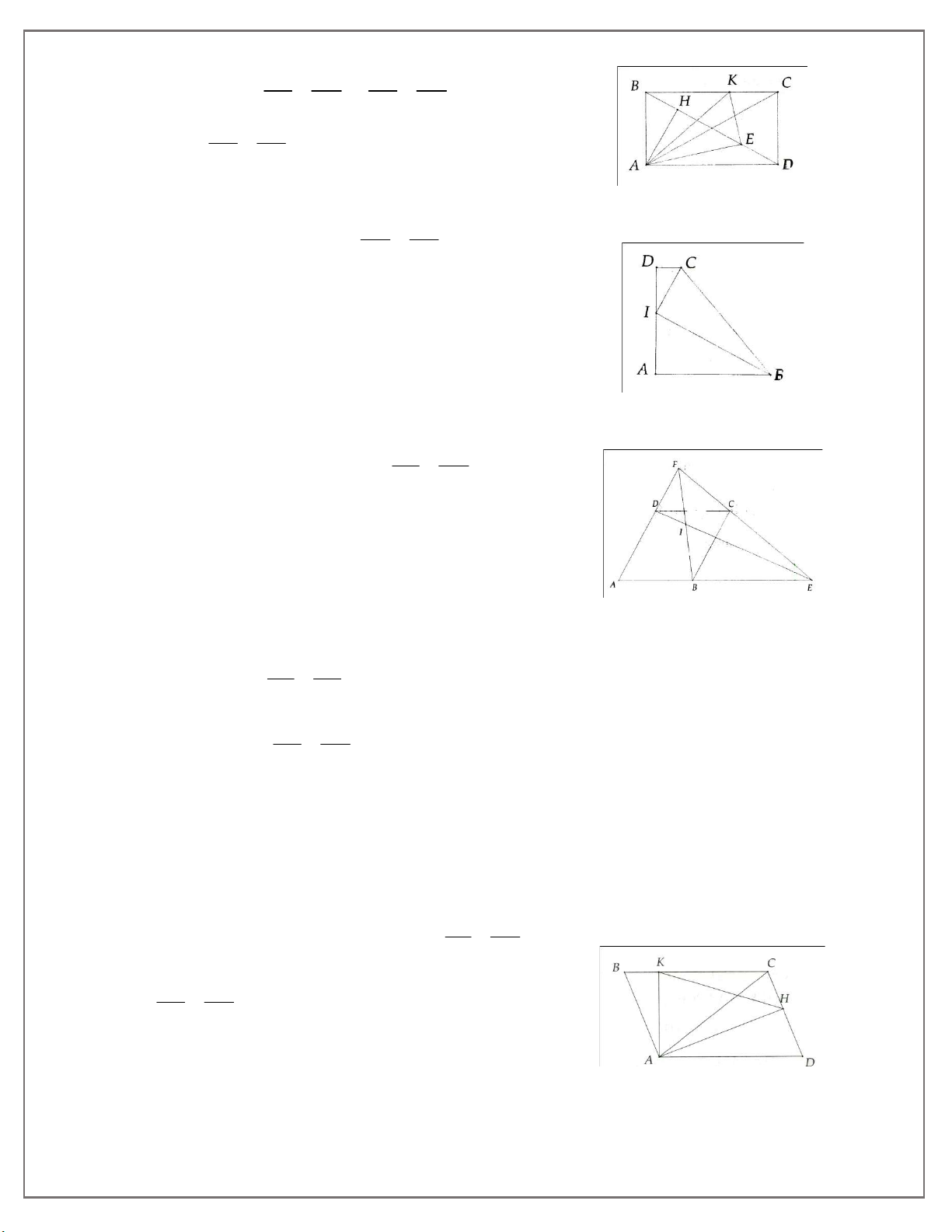
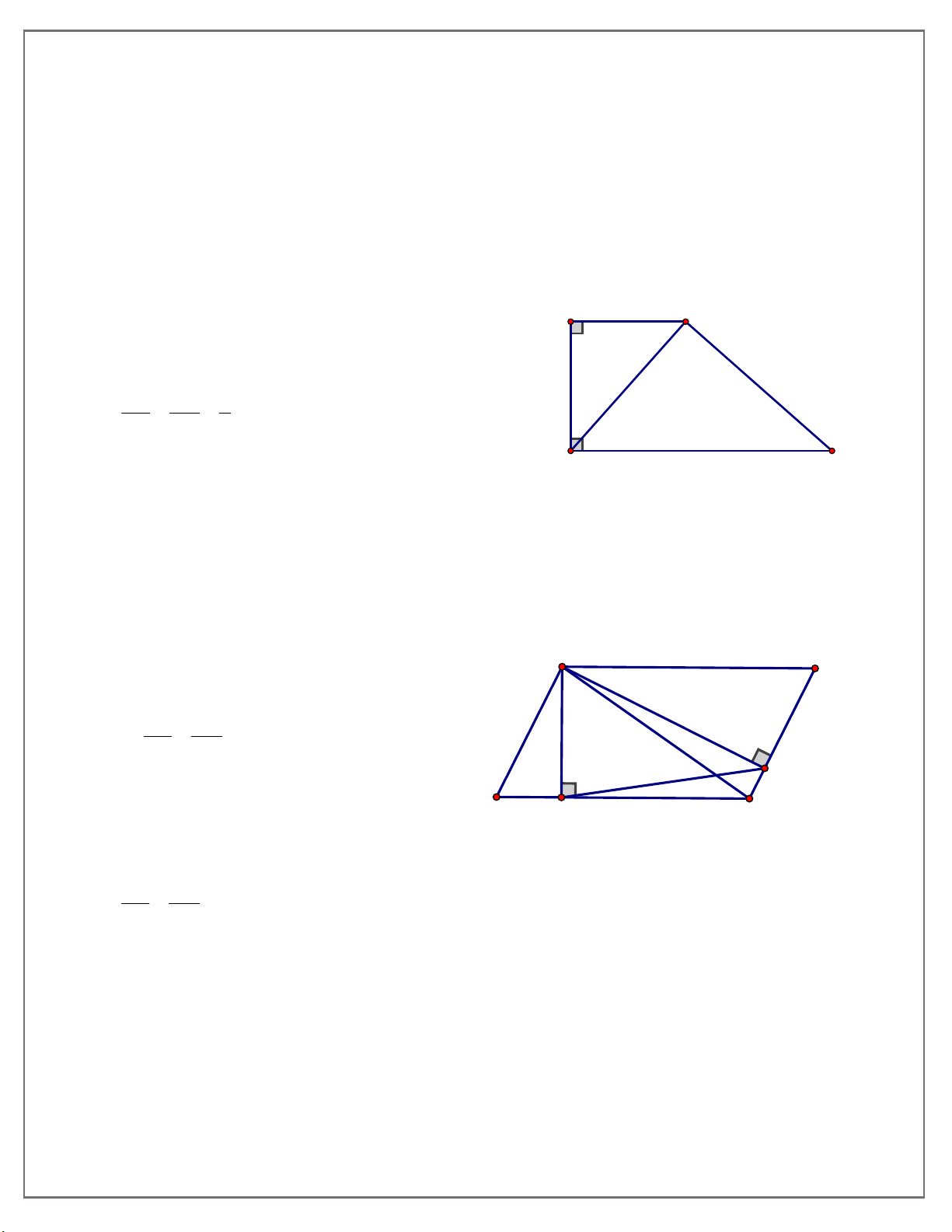
5. Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Lấy điểm E
trên DH và điểm K trên BC sao cho DE CK  . Chứng minh: DH CB
1. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com a) A  DE ∽ A  CK; b) A  EK ∽ ADC; c)  0 AEK  90 .
6. Cho hình thang ABCD biết    0
A D  90 . Trên cạnh AD lấy điểm I sao cho AB.DC  AI.DI. Chứng minh: a) A  BI ∽ D  IC; b)  0 BIC  90 . 7. Cho hình thoi ABCD,  0
A  60 . Qua C kẻ đường thẳng d bất kì cắt các tia đối của các tia
BA, DA theo thứ tự tại E và F. Gọi I là giao điểm của BF và ED. Chứng minh: a) EB AD  ; b) E  BD ∽ B  DF; BA DF c)  0 BID  120 .
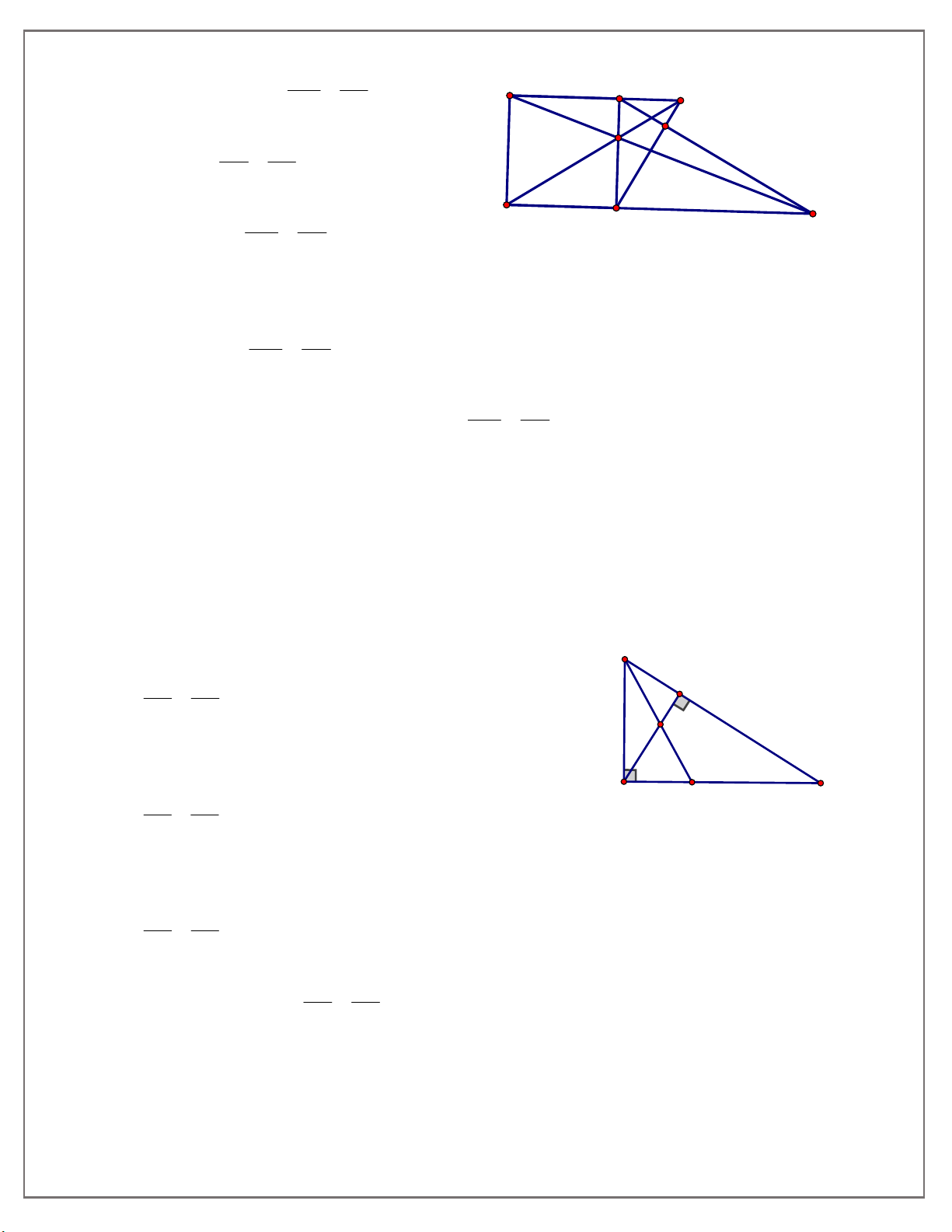
8. Cho hình bình hành ABCD,  0
A  90 . Kẻ AH  CD tại H, AK  BC tại K. Chứng minh: a) AH DA  ; b)  AKH   ACH. AK DC
HƯỚNG DẪN GIẢI CÁC DẠNG BÀI 1A. a) Có OA OB  nên ta chứng minh được OC OD A  OB  C  OD ( . c g.c) b) Có OA.OD = OB.OC OA OB    ĐPCM. OC CO 2. Chứng minh được A  OD  B  OC ( . c g.c)
3. Ta chứng minh được  AB BD 3 ABD   BDC và   . BD DC 4 Từ đó suy ra A  BD  B  DC ( . c g.c)
4. Chứng minh được OA OB 1   OC OA 2 và  AOB   COA nên ta có A  OB  C  OA ( . c g.c)
5. a) Ta chứng minh được DE DH  (1) CK CB
2. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com DA HD DA HD HDA  ADB     (2) Từ (1) và (2) DB AD AC BC suy ra DE DA  mà  ADE   ACK nên ta có CK AC A  DE  A  CK (c  g  c) .
b) Từ phần a) ta suy ra được AE AD  . AK AC Chứng minh được  EAK   CAD nên ta có A  EK  A  DC ( . c g.c) c) Có AEK  A  DC   AEK   0 ADC  90 6.
a) Theo đề bài ta chỉ ta được AB DI  từ đó suy ra AI DC A  BI  D  IC (c  g  c) b) Chứng minh được  AIB   DCI mà  DIC   0 DCI    0 90 BIC  90 7. a) Có BE CE BC / / AD   ; BA CF Lại có EC AD DC / / AB   FC DF Suy ra ĐPCM.
b) Do ABCD là hình thoi có  0 A  60 nên: AB = BD = DC = CA = AD Ta có  EB AD EBD   0 BDF  120 và theo câu a)  BA DF hay EB BD 
 EBD  BDF ( .cg.c) BD DF c) Từ phần b) ta có:  BED  
DBF từ đó chứng minh được
BDI  EDB mêm suy ra  BID   0 EBD  120 8.
3. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
a) Chứng minh AHD  AKB và AB = CD suy ra ĐPCM. b) Từ phần a ta có AH AK  và chứng minh được BC BA  HAK   ABC . Từ đó ta có K  AH  A  BC; Mà A  BC  C  DA nên suy ra K  AH  C  DA từ đó chứng minh được  AKH   ACH
PHIẾU BÀI TỰ LUYỆN SỐ 1
Bài 1: Cho hình thang ABCD AB//CD , biết AB  9cm,BD  12cm,DC  16cm. Chứng minh ABD” BDC. Bài 2: Cho 
xOy , phân giác Ot. Trên Ox lấy các điểm A và C ' sao cho
OA  4cm,OC '  9cm , trên Oy lấy các điểm A ' và C sao cho OA'  12cm,OC  3cm, trên
tia Ot lấy các điểm B và B ' sao cho OB  6cm,OB '  18cm. Chứng minh: a) O  AB AB AC BC ” O  A'B '; b)   . A'B ' A'C ' B 'C '
Bài 3: Cho  ABC có AB  8cm , AC  16cm ,. Gọi D và E là hai điểm lần lượ t trên các
cạnh AB, AC sao cho BD  2cm , CE  13cm . Chứng minh : a) AEB ” ADC b)  AED   ABC c) AE.AC  A . B AD
Bài 4: Chứng minh rằng nếu  A’B’C’ đồng dạng với  ABC theo tỉ số k thì tỉ số hai
đường trung tuyến tương ứng cũng bằng k.
Bài 5: Cho tam giác ABC có AB  9cm,AC  12cm,BC  7cm. Chứng minh   B  2C.
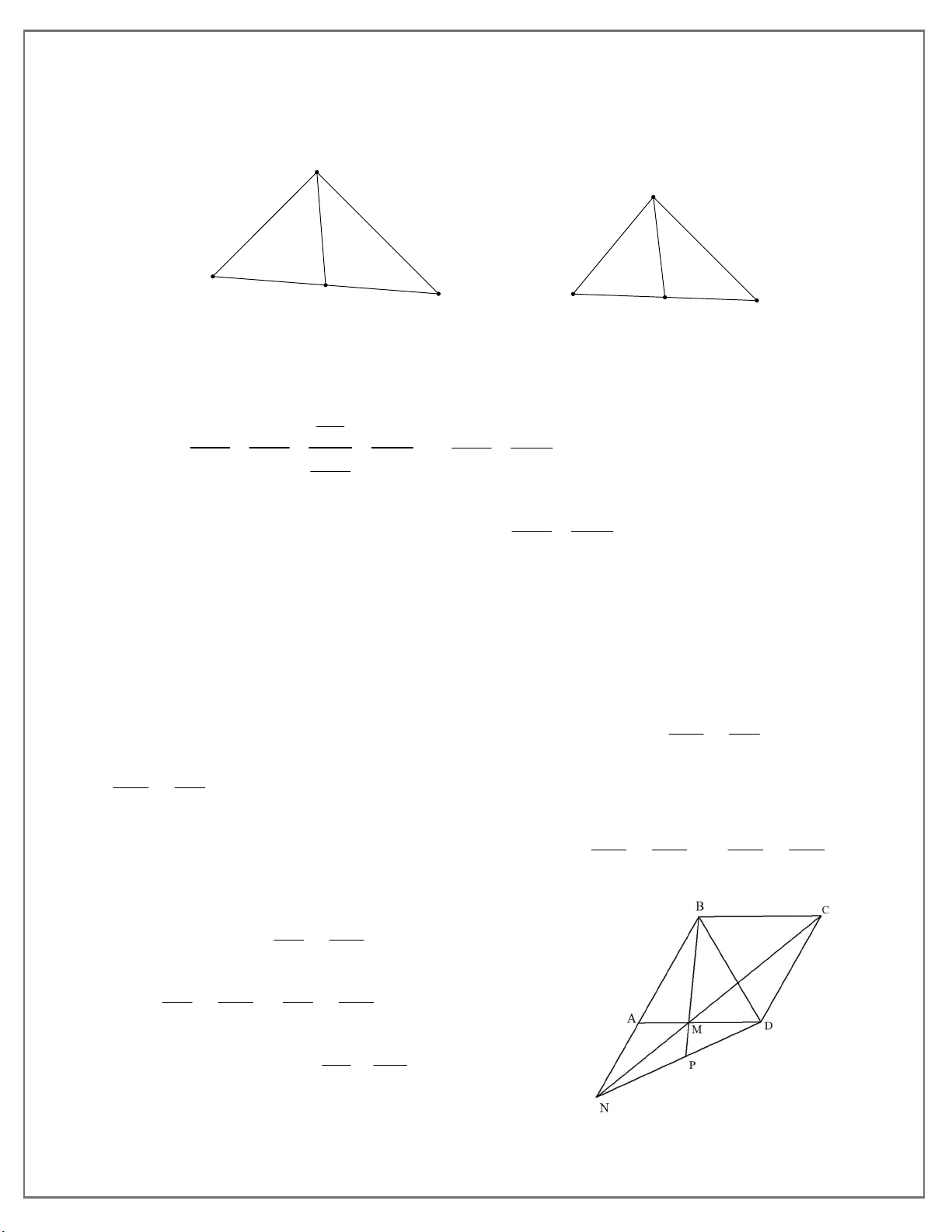
Bài 6: Cho hình thoi ABCD có  0
A  60 . Gọi M là một cạnh thuộc cạnh AD. Đường thẳng
CM cắt đường thẳng AB tại N. a) Chứng minh 2 AB  DM.BN ;
b) BM cắt DN tại P. Tính góc  BPD .
Bài 7*: Cho tam giác ABC có AB  2cm ; AC  3cm ; BC  4cm . Chứng minh rằng:    BAC  ABC  2.ACB .
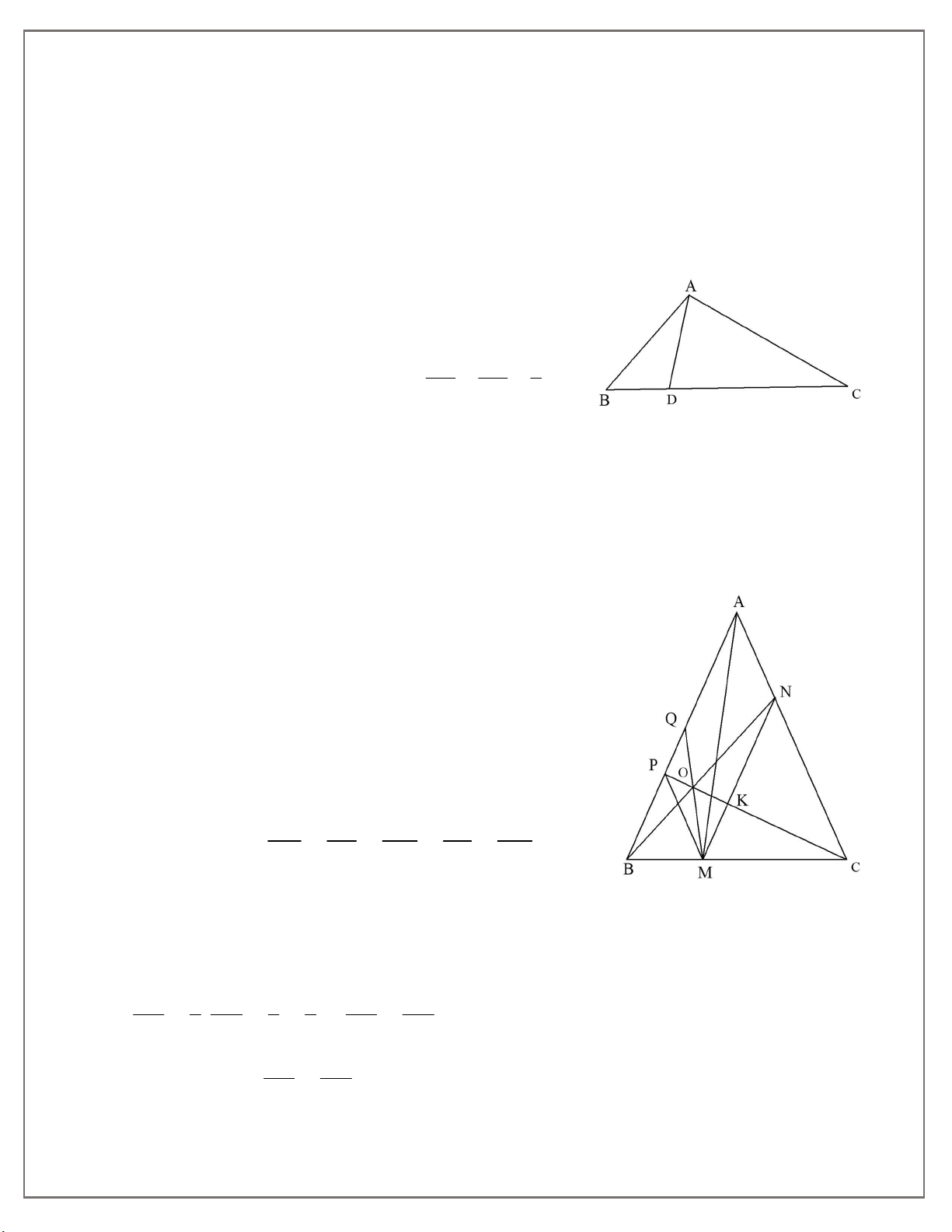
Bài 8*: Cho ABC cân tại A. Lấy M tùy ý thuộc BC, kẻ MN song song với AB (với N ∈
AC), kẻ MP song song với AC ( với P ∈ AB). Gọi O là giao điểm của BN và CP. Chứng minh rằng   OMP  AMN .
4. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Bài 9: Cho ABC, biết AB = 3cm, AC = 6cm, BC = 4cm. Trên AB lấy điểm E sao cho AE =
2cm, trên AC lấy điểm D sao cho AD = 1cm. a) Chứng minh: AD AE  . AB AC b) Chứng minh: A  DE” A  BC
c) Tính độ dài đoạn DE.
Bài 10: Cho ABC, biết AB = 3cm, AC = 6cm, BC = 6cm. Trên AB lấy điểm E sao cho AE =
2cm, trên AC lấy điểm D sao cho AD = 1cm. a) Chứng minh: AD AE  . AB AC b) Chứng minh: A  DE” A  BC
c) Tính độ dài đoạn DE.
Bài 11: Cho ABC, biết AB = 7,5cm, AC = 9cm, BC = 12cm. Trên AB, AC theo thứ tự lấy
điểm M và N sao cho AN = 3cm, AM = 2,5cm. a) Chứng minh: A  MN” ABC
b) Tính độ dài đoạn MN.
HƯỚNG DẪN LỜI GIẢI SỐ 1
Bài 1: Ta chứng minh được   ABD  BDC và AB BD 3   . BD DC 4 A B Từ đó suy ra A  BD ” B  DC( .cgc) Bài 2: a) Chứng minh được OAB C ” OAB   ( . c g.c) D b) Chứng minh được AB AC BC 1    A'B ' A'C ' B 'C ' 3 Bài 3:
a) Xét tam giác AEB và tam giác ADC có AB 8 1   ; AE 3 1    AB AE  AC 16 2 AD 6 2 AC AD
Mặt khác lai có góc A chung  AEB ” ADC (c-g-c)
b) Chứng minh tương tự câu a) ta có AED” A  BC   AED   ABC (hai góc tương ứng) c) Theo câu b) ta có  AE AD AED ”  ABC    AE.AC  A . B AD AB AC Bài 4:
5. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com A A' B D C B' D' C'
HD: a) ABC ” A 'B'C' có AD và A'D ' lần lượt là trung tuyến xuất phát từ đỉnh A và A’
xuống cạnh BC và B’C’ của hai tam giác đó. BC Ta có AB BC 2 BD AB BD k     .  Có B   B ' . A' B ' B 'C ' B 'C ' B ' D ' A' B ' B ' D ' 2 Vậy ABD AB AD
” A'B 'D ' (c-g-c) Từ đó suy ra k   A' B ' A' D '
Bài 5: Trên tia đối của tia BA lấy điểm E sao cho BE  BC  7cm . Chứng minh được ABC ” ACE( . c g.c) suy ra   BCA  E Từ đó ta có     
ABC  BCE  E  2E  2BCA
Bài 6: a) Ta có AM//BC ( do AD // BC) suy ra NA NB N  AM” N  BC   hay AM BC NA NB  (1) (vì BC = AB). AM AB
Ta có NA // DC ( do AB // DC) suy ra NA CD N  AM” C  DM   hay NA AB  (2) AM DM AM DM (vì CD  AB ). Từ (1) và (2) suy ra NA AB  hay 2 AB  DM.BN AB DM . b) Từ NB AB NB BD    AB DM BD DM
Xét  BND và  DBM có NB BD  và BD DM   0 NBD  BDM  60 .
6. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Suy ra BND” DBM  .cg.c       0
 MBD  BND  MBD  MBN  BND  MBN  60 Mà   
BPD  BND  MBN nên   0 BPD 60 . Bài 7*:
Trên đoạn thẳng BC lấy điểm D sao cho BD  1cm
 CD  BC  BD  3 cm  CD  AC nên ACD cân tại C, do vậy   DAC  ADC (1) BD AB 1 ABD và CBA có  ABD chung và   . BA CB 2 Suy ra A  BD ” C  BA (c.g.c)    BAD  BCA (2) Từ (1) và (2) ta có :        
BAC  BAD  DAC  ACB  ADC  ACB  ABC  BAD Do đó    BAC  ABC  2.ACB . Bài 8*:
Giả sử MB  MC . Gọi Q là giao điểm MO và AB ; K là giao điểm CP và MN.
Vì MNAP là hình bình hành nên   QPM  ANM (1)
Vì ∆ABC cân tại A nên suy ra PBM cân tại P và NCM cân tại N.
Do đó PB  PM  AN và NC  NM  AP kết hợp với MN//AP , suy ra PQ PQ KM PB NA     (2) PM PB KN PA NM
Từ (1) và (2) suy ra QPM ” ANM (c.g.c)    QMP  AMN hay  
OMP  AMN . Điều phải chứng minh. Bài 9: a) AD 1 AE 2 1  ; AD AE     AB 3 AC 6 3 AB AC AB AC   b) ABC,ADE :   AD AE  A  BC ~ A  DE    B  AC  DAE 
7. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com c) AB BC 1 4 A  BC ” A  DE    3  DE  BC  (cm) AD DE 3 3 Bài 10: a) AD 1 AE 2 1 AD AE  ;     AB 3 AC 6 3 AB AC AB AC   b) AD AE  A  BC ” ADE  (c.g.c)   B  AC  DAE  c) AB BC 1 A  BC ” A  DE    3  DE  BC  2(cm) AD DE 3 Bài 11: a) AM 2,5 1 AN 3 1 AM AN   ;     AB 7,5 3 AC 9 3 AB AC  AB AC    AM AN  A  BC ” A  MN (c.g.c)  BAC   MAN b) AB BC 1 A  BC ” A  MN    3  MN  BC  4(cm) AM MN 3 PHIẾU TỰ LUYỆN SỐ 2 Bài 1: Cho A  BC có AB  1
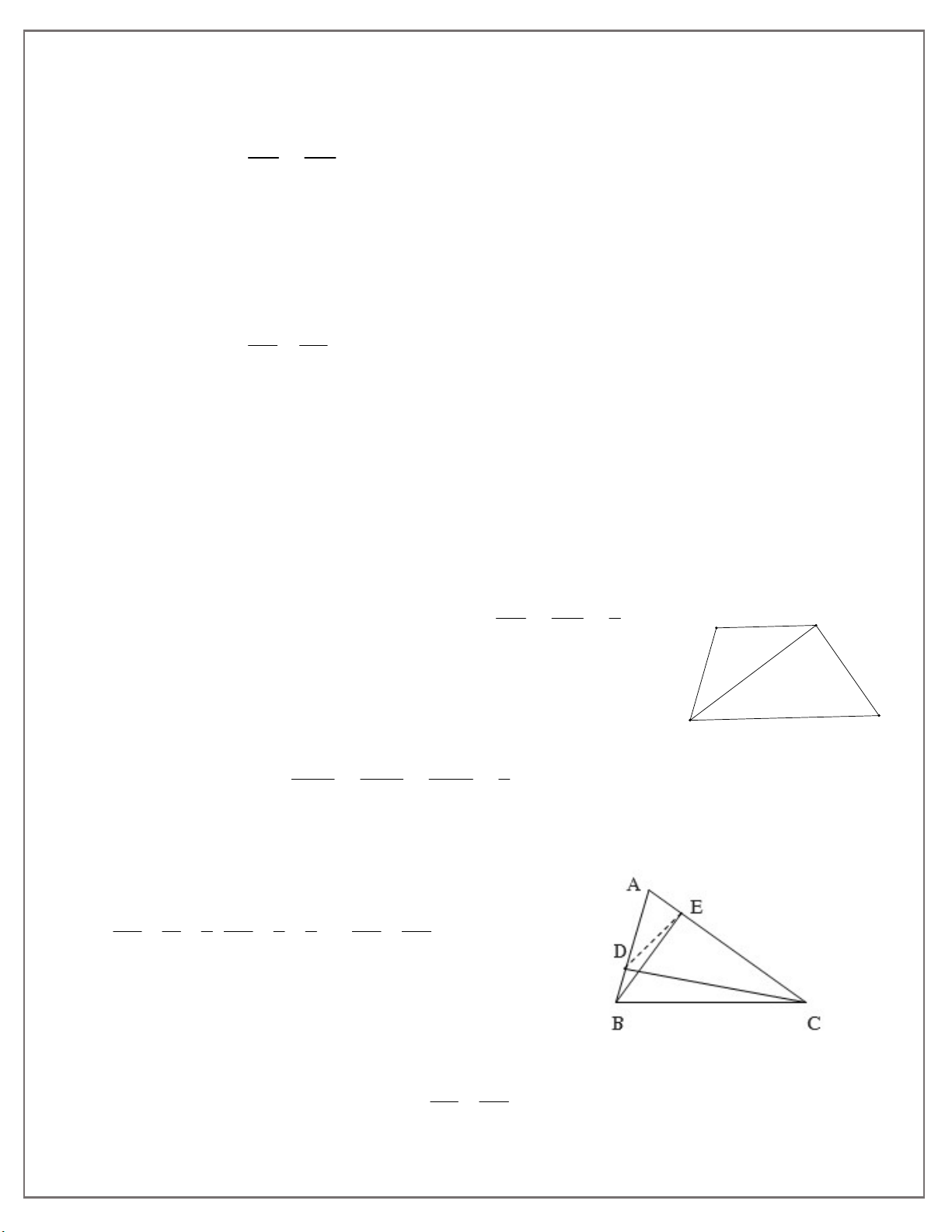
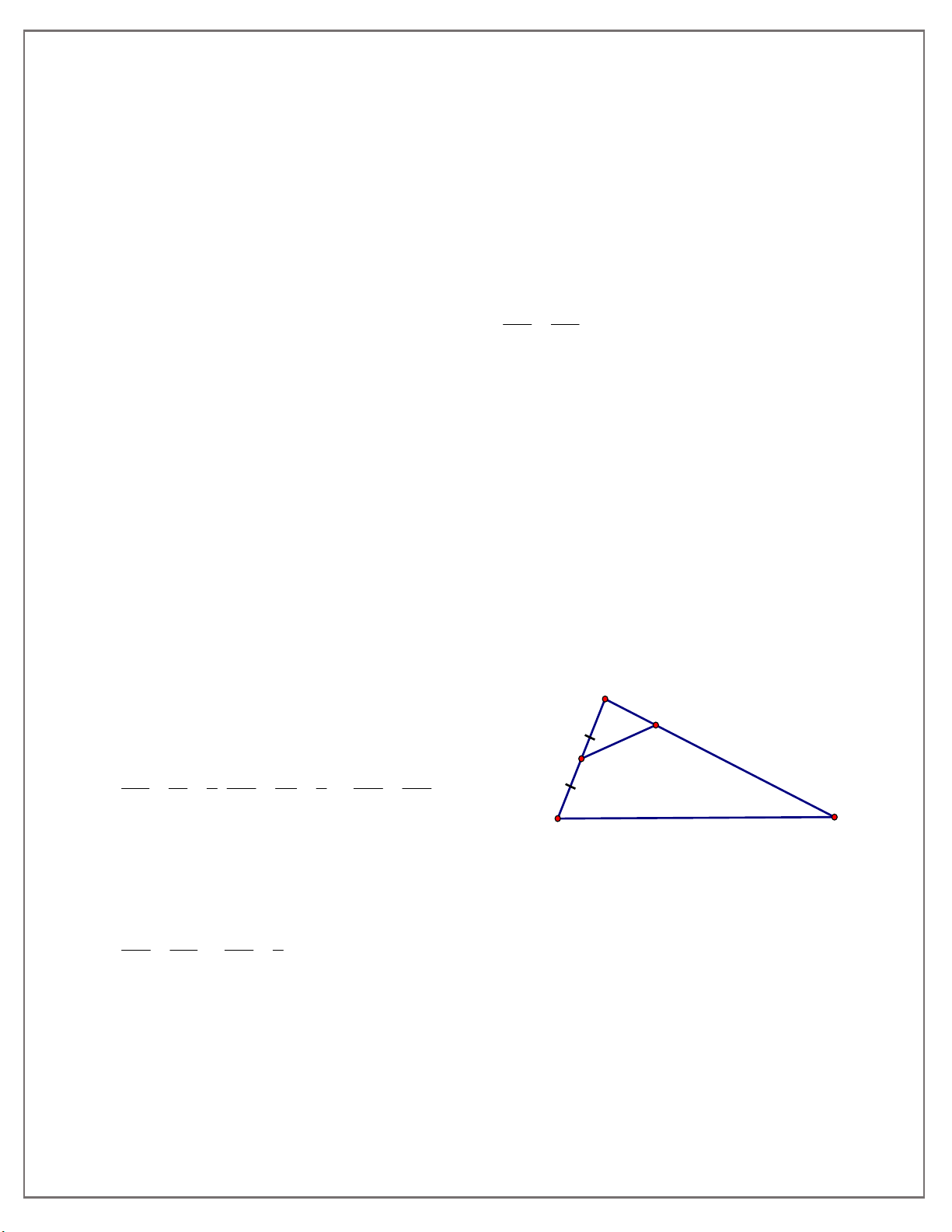
8cm, AC  27cm, BC  30cm . Gọi D là trung điểm của AB, E
thuộc cạnh AC sao cho AE  6c . m a) Chứng minh rằng: AED S A  BC b) Tính độ dài DE .
Bài 2: Hình thang ABCD  AB / / CD có AB  2c , m BD  4c ,
m CD  8cm . Chứng minh rằng A   DBC .
Bài 3: Cho hình thoi ABCD có góc  0
A  60 . Qua C kẻ đường thẳng d cắt tia đối của các tia B , A DA
theo thứ tự ở E, F . Chứng minh rằng: EB AD a)  BA DF b) EBD S BDF
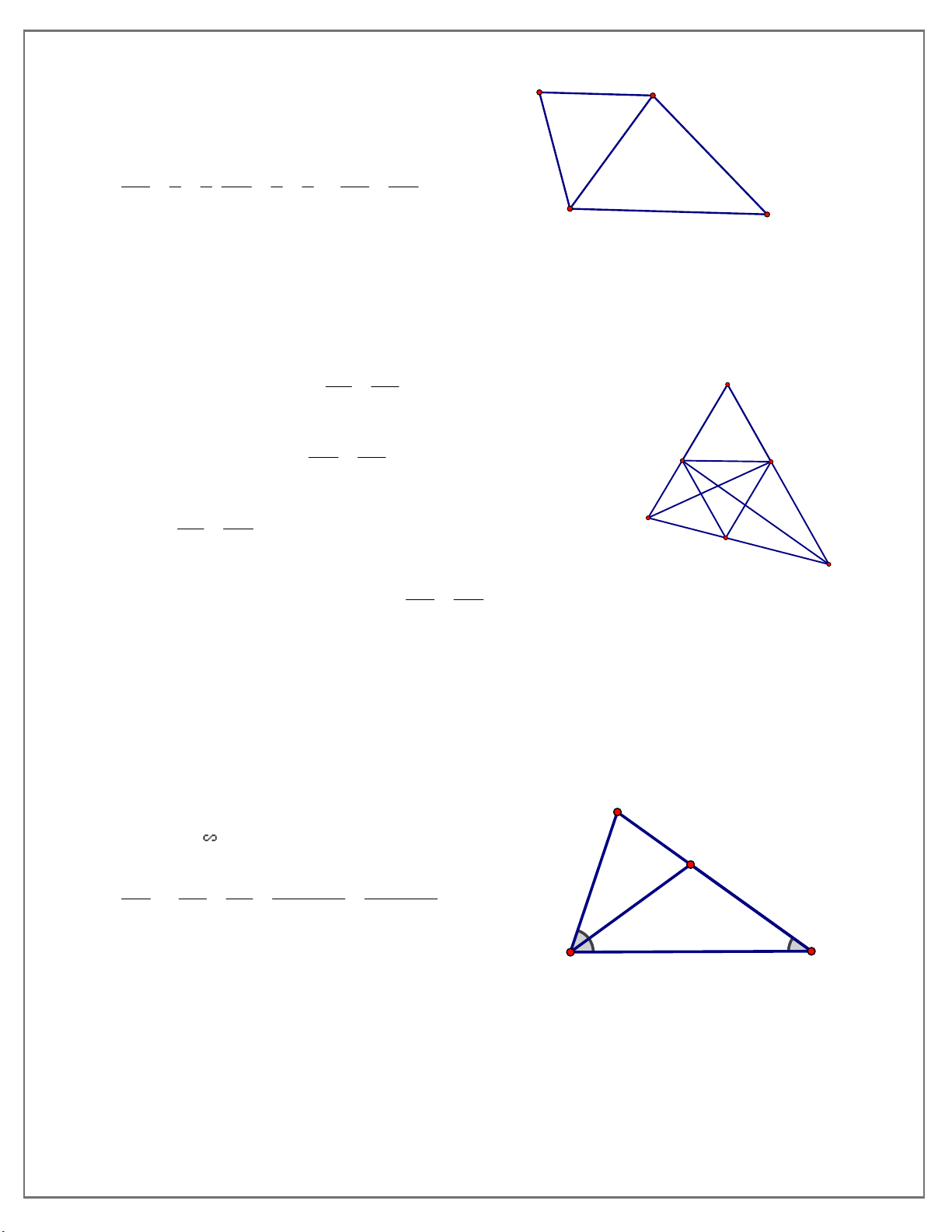
Bài 4: Cho  ABC có B  2 C , AB  8 cm, BC  1 0 c . m a) Tính AC
b) Nếu ba cạnh của tam giác trên là ba số tự nhiên liên tiếp thì mỗi cạnh là bao nhiêu?
Bài 5: Cho hình thang ABCD( AB / /CD) , A   0
D  90 ; AB  2;CD  4,5; BD  3 . Chứng minh rằng BC  BD
8. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
Bài 6: Cho hình bình hành ABCD . Kẻ AH  CD, AK  BC . Chứng minh rằng KAH S A  BC
Bài 7: Cho hình vuông ABCD . Trên cạnh BC lấy điểm E . Tia AE cắt đường thẳng CD tại M , tia
DE cắt đường thẳng AB tại N . Chứng minh rằng a) N  BC S B  CM b) BM  CN Bài 8: Cho A
 BC vuông tại A có BE là đường phân giác của A  BC ( E  AC ). Kẻ FD EA
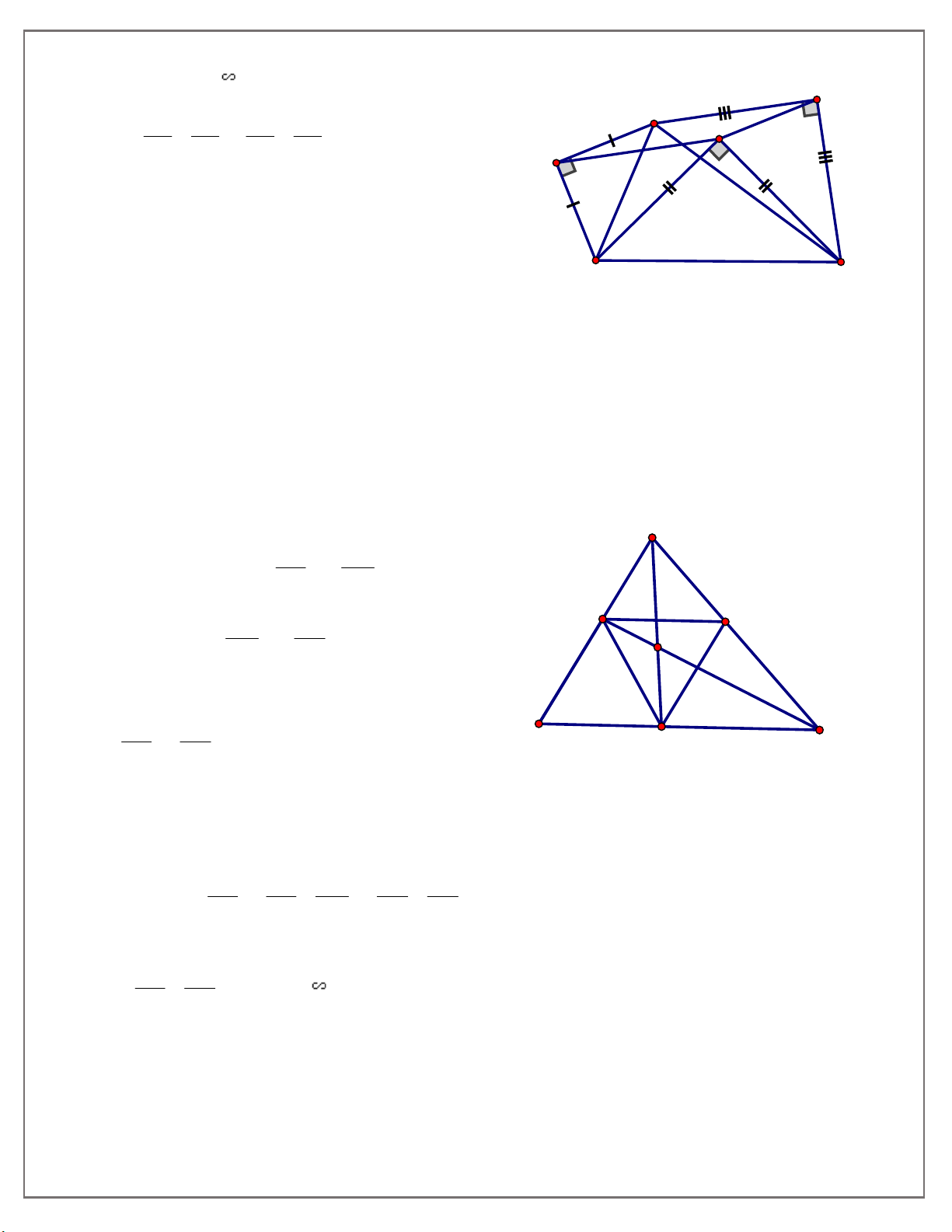
AD  BC(D  BC), AD cắt BE tại F. Chứng minh  FA EC Bài 9: Cho A
 BC nhọn, lấy các cạnh AB, AC và BC dựng các tam giác vuông cân
ABD, ACE, BCF, hai tam giác đầu dựng ra phía ngoài A
 BC , còn tam giác thứ 3 dựng trong
cùng một nửa mặt phẳng bờ BC với A
 BC . Chứng minh rằng tứ giác AEFD là hình bình hành.
Bài 10: Cho hình thoi ABCD cạnh a có  0
A = 60 , một đường thẳng bất kỳ qua C cắt tia đối của các tia B , A DA tại M , N
a) Chứng minh rằng tích BM. DN có giá trị không đổi
b) Gọi K là giao điểm của BN và DM . Tính số đo của góc BKD
LỜI GIẢI PHIẾU TỰ LUYỆN SỐ 2 Bài 1:
a) Xét  AED và  ABC ta có: A  E A chung D AE 6 1 AD 9 1 AD AD   ;     AB 18 3 AC 27 3 AB AC B C Hay AED S A  BC (c - g - c) b) Vì AED S A  BC nên ta có: DE AE DE 1     DE  10cm CB AB 30 3 Bài 2:
9. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com Xét ABD và B  DC ta có: A B  ABD   BDC ( 2 góc so le trong) AB 2 1 BD 4 1 AB BD   ;     BD 4 2 DC 8 2 BD DC D C Vậy ABD S B  DC (c - g - c)  A   DBC Bài 3: EB EC A a) Do BC / / AF nên ta có:  BA CF AD EC Mà CD / / AE nên ta có:  D DF CF B EB AD Do đó:  F BA DF C E EB BD
b) Vì AB  BD  AD theo a ta có:  BD DF Mà  EBD   BDF = 1200 Do đó EBD S BDF (c - g - c) Bài 4:
Vẽ tia phân giác BE của  ABC A
  ABE  ACB (c – g - c) E AB AE BE AE + BE AC =    AC AB CB AB + CB AB + CB 2
 AC = AB(AB + CB) = 8(8 + 10) = 144 B C  AC = 12 cm
b) Gọi AC = b, AB = a, BC = c
Thì từ câu a ta có b2 = a(a + c) (1). Vì b > a nên có thể b = a + 1 hoặc b = a + 2
+ Nếu b = a + 1 thì (a + 1)2= a2 + ac  2a + 1 = ac  a(c – 2) = 1
10. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com
 a = 1; b = 2; c = 3 (loại)
+ Nếu b = a + 2 thì a(c – 4) = 4
- Với a = 1 thì c = 8 (loại)
- Với a = 2 thì c = 6 (loại)
- Với a = 4 thì c = 6 ; b = 5 Vậy a = 4; b = 5; c = 6 Bài 5: Xét BAD và D  BC có A B  ABD   BDC (2 góc so le trong) AB BD 2   BD DC 3  BAD S D  BC (c - g - c) D C  A   0 DBC  90  BC  BD Bài 6: Ta có : S  AH.DC  AK.BC ABCD A B  AH.AB  AK.BC AB AK   BC AH K Xét A  BC và KAH có D H C  B   KAH (cùng phụ với  BAK ) AB AK  (chứng minh trên) BC AH  A  BC S KAH (c- g - c) Bài 7:
11. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com AB EB a) Ta có AB / /CM   (1) A B CM EC N O BN EB BN / /CD   (2) E CD EC AB BN D C M Từ (1) và (2)   (3) CM CD
Mặt khác AB  BC  CD nên từ (3) suy ra BC BN  CM CB BC BN Xét N  BC và B  CM có:  NBC   0 BCM  90 ;  CM CB  N  BC S B  CM (c – g - c)
b) Gọi O là giao điểm của BM và CN . Xét O  CM có  OMC   MCO   BCN   0 MCO  90  0 MOC  90  BM  CN Bài 8:
Ta có: BF là đường phân giác của BAD B FD BD D   (1) FA AB F
BE là đường phân giác của B  AC A C EA AB E   (2) EC BC Mặt khác DBA S A  BC (c – g - c) DB AB   (3) AB BC FD EA Từ (1), (2) và (3) suy ra  FA EC Bài 9:
12. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com Ta có BAD B
 CF (Hai tam giác vuông cân) E A BD BA BD BF     F BF BC BA BC D Mặt khác  DBF   0 ABC  45    B 1  1  B  DF S B  AC (c - g - c) B C   BDF   BAC
Chứng minh tương tự ta có BDF S B  AC   FEC   BAC Ta có  DAE   0 ADF     BAC  0     BDF  0 90 90 180  AE / /DF
Chứng minh tương tự ta được AD // EF. Vậy tứ giác AEFD là hình bình hành. Bài 10:
a) Gọi độ dài cạnh của hình thoi ABCD là a M MB CM Ta có BC / / AN   (1) 1 BA CN B C CM AD CD / / AM   (2) 1 K CN DN Từ (1) và (2) suy ra MB AD 2 =  MB.DN = BA.AD = a.a = a A N D BA DN
 BM. DN có giá trị không đổi. b)  MBD và  BDN có   0 MBD = BDN =120 MB MB CM AD BD Mặt khác =  =  ( Do ABCD BD BA CN DN DN là hình thoi có  0 A = 60 nên AB  BC  CD  DA ) MB BD  
  MBD  BDN (c - g - c) BD DN Suy ra  M 1 = 1 B .
Mặt khác  MBD và  BDN có  BDM =  BDK và  M 1 = 1 B nên   0 BKD = MBD = 120 .
========== TOÁN HỌC SƠ ĐỒ ==========
13. TOÁN HỌC SƠ ĐỒ - THCS.TOANMATH.com