Chuyên đề tự luận nguyên hàm, tích phân và ứng dụng – Nguyễn Chiến Toán 12

Chuyên đề tự luận nguyên hàm, tích phân và ứng dụng – Nguyễn Chiến Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

67 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 1
NGUYÊN HÀM - TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
I. NGUYÊN HÀM
1. Nguyên hàm
Định nghĩa: Cho hàm số
fx
xác định trên
K
(
K
là khoảng, đoạn hay nửa khoảng). Hàm số
Fx
được gọi là nguyên hàm của hàm số
fx
trên
K
nếu
'F x f x
với mọi
xK
.
Kí hiệu:
xf x d F x C
.
Định lí:
1) Nếu
Fx
là một nguyên hàm của
trên
K
thì với mỗi hằng số
C
, hàm số
G x F x C
cũng là một nguyên hàm của
fx
trên
K
.
2) Nếu
Fx
là một nguyên hàm của hàm số
trên
K
thì mọi nguyên hàm của
fx
trên
K
đều có dạng
F x C
, với
C
là một hằng số.
Do đó
,F x C C
là họ tất cả các nguyên hàm của
fx
trên
K
.
2. Tính chất của nguyên hàm
xf x d f x
và
'xf x d f x C
;
dx dxd f x f x
Nếu F(x) có đạo hàm thì:
( ) ( )d F x F x C
xxkf x d k f x d

với
k
là hằng số khác
0
.
x x xf x g x d f x d g x d


Công thức đổi biến số: Cho
y f u
và
.u g x
Nếu
( ) ( )f x dx F x C
thì
( ) '( ) ( )f g x g x dx f u du

()F u C
3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số
fx
liên tục trên
K
đều có nguyên hàm trên
K
.
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 2
BẢNG NGUYÊN HÀM CÁC HÀM SỐ THƢỜNG GẶP
1.
0dx C
2.
dx x C
3.
1
1
1
1
x dx x C

16.
1
1
dx , 1
1
ax b
ax b c
a
4.
2
11
dx C
xx
17.
2
1 1 1
.dx C
a ax b
ax b
5.
1
lndx x C
x

18.
1
ln
dx
ax b C
ax b a
6.
xx
e dx e C
19.
1
ax b ax b
e dx e C
a


7.
ln
x
x
a
a dx C
a

20.
1
ln
kx b
kx b
a
a dx C
ka

8.
cos sinxdx x C
21.
1
cos sinax b dx ax b C
a
9.
sin cosxdx x C
22.
1
sin cosax b dx ax b C
a
10.
tan . ln |cos |x dx x C
23.
1
tan ln cosax b dx ax b C
a
11.
cot . ln |sin |x dx x C
24.
1
cot ln sinax b dx ax b C
a
12.
2
1
tan
cos
dx x C
x

25.
2
11
tan
cos
dx ax b C
ax b a
13.
2
1
cot
sin
dx x C
x
26.
2
11
cot
sin
dx ax b C
ax b a
14.
2
1 tan tanx dx x C
27.
2
1
1 tan tanax b dx ax b C
a
15.
2
1 cot cotx dx x C
28.
2
1
1 cot cotax b dx ax b C
a
BẢNG NGUYÊN HÀM MỞ RỘNG
22
1
arctan
dx x
C
a x a a

22
arcsin arcsin
xx
dx x a x C
aa
22
1
ln
2
dx a x
C
a x a a x


22
arccos arccos
xx
dx x a x C
aa
22
22
ln
dx
x x a C
xa
22
arctan arctan ln
2
x x a
dx x a x C
aa
22
arcsin
dx x
C
a
ax

22
arccot arccot ln
2
x x a
dx x a x C
aa
22
1
arccos
dx x
C
aa
x x a

1
ln tan
sin 2
dx ax b
C
ax b a

22
22
1
ln
dx a x a
C
ax
x x a

1
ln tan
sin 2
dx ax b
C
ax b a

ln ln
b
ax b dx x ax b x c
a



22
cos sin
cos
ax
ax
e a bx b bx
e bxdx C
ab

2 2 2
22
dx arcsin
22
x a x a x
a x C
a
22
sin cos
sin
ax
ax
e a bx b bx
e bxdx C
ab

Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 3
CÁC PHƢƠNG PHÁP TÍNH NGUYÊN HÀM
1. PHƢƠNG PHÁP ĐỔI BIẾN
a. Đổi biến dạng 1:
Nếu
( ) ( )f x F x C
và với
u t
là hàm số có đạo hàm thì :
( ) ( )f u du F u C
PHƢƠNG PHÁP CHUNG
Bước 1: Chọn
xt
, trong đó
t
là hàm số mà ta chọn thích hợp .
Bước 2: Lấy vi phân hai vế :
'dx t dt
Bước 3: Biến đổi :
( ) 'f x dx f t t dt g t dt




Bước 4: Khi đó tính :
( ) ( ) ( )f x dx g t dt G t C

.
* Các dấu hiệu đổi biến thƣờng gặp :
Dấu hiệu
Cách chọn
22
ax
Đặt
sinx a t
; với
;.
22
t





hoặc
cosx a t
;
với
0; .t
22
xa
Đặt
a
.
tsin
x
; với
; \ 0
22
t





hoặc
cos
a
x
t
với
0; \ .
2
t



22
ax
Đặt
tanx a t
; với
;.
22
t





hoặc
cotx a t
với
0; .t
.
ax
ax
hoặc
.
ax
ax
Đặt
cos2x a t
x a b x
Đặt
2
()– sinx a b a t
22
1
ax
Đặt
tanx a t
; với
;.
22
t





b. Đổi biến dạng 2:
Nếu hàm số
fx
liên tục thì đặt
xt
. Trong đó
t
cùng với đạo hàm của nó (
' t
là
những hàm số liên tục) thì ta được :
( ) ' ( ) ( )f x dx f t t dt g t dt G t C



.
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 4
PHƢƠNG PHÁP CHUNG.
Bước 1: Chọn
tx
. Với
x
là hàm số mà ta chọn thích hợp.
Bước 2: Tính vi phân hai vế :
'dt t dt
.
Bước 3: Biểu thị :
( ) ' ( )f x dx f t t dt g t dt




.
Bước 4: Khi đó :
( ) ( ) ( )I f x dx g t dt G t C

* Các dấu hiệu đổi biến thƣờng gặp :
Dấu hiệu
Cách chọn
Hàm số mẫu số có
t
là mẫu số
Hàm số :
;f x x
tx
Hàm
.sinx+b.cosx
.sinx+d.cosx+e
a
fx
c
x
tan ; os 0
22
x
tc




Hàm
1
fx
x a x b

Với :
0xa
và
0xb
.
Đặt :
t x a x b
Với
0xa
và
0xb
.
Đặt :
t x a x b
2. NGUYÊN HÀM TỪNG PHẦN
Nếu u(x) , v(x) là hai hàm số có đạo hàm liên tục trên K:
( ). '( ) ( ). ( ) ( ). '( )u x v x dx u x v x v x u x dx

Hay
udv uv vdu

( với
’ , ’du u x dx dv v x dx
)
PHƢƠNG PHÁP CHUNG
Bước 1: Ta biến đổi tích phân ban đầu về dạng :
12
( ) ( ). ( )I f x dx f x f x dx

Bước 2: Đặt :
1
1
2
2
' ( )
()
()
()
du f x dx
u f x
v f x dx
dv f x

Bước 3: Khi đó:
. . .u dv u v v du

Dạng I:
sin
( ) cos .
x
x
I P x x dx
e


Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 5
Đặt
()
sin
cos .
x
u P x
x
dv x dx
e



'. '( )
cos
sin
x
u du P x dx
x
vx
e



Vậy
cos
( ) sin
x
x
I P x x
e





-
cos
sin . '( )
x
x
x P x dx
e





Dạng II:
( ).lnI P x xdx
Đặt
ln
()
ux
dv P x dx
1
( ) ( )
du dx
x
v P x dx Q x

Vậy
.
1
( ).QI ln dx xQx x
x
Dạng III
sin
cos
x
x
I e dx
x

Đặt
sin
.
cos
x
ue
x
dv dx
x

cos
sin
x
du e dx
x
v
x


Vậy
cos
sin
x
x
Ie
x


-
cos
sin
x
x
e dx
x


.
Bằng phương pháp tương tự tính được
cos
sin
x
x
e dx
x


sau đó thay vào
I
ra kết quả.
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 6
TÍCH PHÂN
1. CÔNG THỨC TÍNH TÍCH PHÂN
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a
.
* Nhận xét: Tích phân của hàm số
f
từ a đến b có thể kí hiệu bởi
()
b
a
f x dx
hay
()
b
a
f t dt
. Tích phân đó
chỉ phụ thuộc vào
f
và các cận a, b mà không phụ thuộc vào cách ghi biến số.
2. TÍNH CHẤT CỦA TÍCH PHÂN
Giả sử cho hai hàm số
()fx
và
g( )x
liên tục trên K . a,b,c là ba số bất kỳ thuộc K. Khi đó ta có :
1.
( ) 0
a
a
f x dx
2.
( ) ( )
ba
ab
f x dx f x dx

.
3.
( ) ( ) ( )
b c b
a a c
f x dx f x dx f x dx
4.
( ) ( ) ( ) ( )
b b b
a a a
f x g x dx f x dx g x dx
.
5.
( ) . ( )
bb
aa
kf x dx k f x dx

.
6. Nếu
( ) 0, ;f x x a b
thì :
( ) 0 ;
b
a
f x dx x a b
7. Nếu
; : ( ) ( ) ( ) ( )
bb
aa
x a b f x g x f x dx g x dx

.
8. Nếu
;x a b
Nếu
()M f x N
thì
()
b
a
M b a f x dx N b a
.
PHƢƠNG PHÁP TÍNH TÍCH PHÂN
I. ĐỔI BIẾN
a. Phƣơng pháp đổi biến số dạng 1.
Định lí . Nếu 1) Hàm
()x u t
có đạo hàm liên tục trên
;

.
2) Hàm hợp
( ( ))f u t
được xác định trên
;

.
3)
( ) , ( )u a u b


.
Khi đó:
'
( ) ( ( )) ( )
b
a
I f x dx f u t u t dt


.
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 7
PHƢƠNG PHÁP CHUNG
Bước 1: Đặt
x u t
Bước 2: Tính vi phân hai vế :
( ) '( )x u t dx u t dt
Đổi cận:
x b t
x a t


Bước 3: Chuyển tích phân đã cho sang tích phân theo biến t
Vậy:
( ) ( ) '( ) ( )
b
a
I f x dx f u t u t dt g t dt


( ) ( ) ( )G t G G

b. Phương pháp đổi biến dạng 2
Định lí: Nếu hàm số
()u u x
đơn điệu và có đạo hàm liên tục trên đoạn
;ab
sao cho
( ) ( ) '( ) ( )f x dx g u x u x dx g u du
thì:
()
()
( ) ( )
ub
b
a u a
I f x dx g u du

.
PHƢƠNG PHÁP CHUNG
Bƣớc 1: Đặt
'
( ) ( )u u x du u x dx
Bƣớc 2: Đổi cận :
()
()
x b u u b
x a u u a


Bƣớc 3: Chuyển tích phân đã cho sang tích phân theo u
Vậy:
()
()
( ) ( ) . '( ) ( )
ub
bb
a a u a
I f x dx g u x u x dx g u du
II. TÍCH PHÂN TỪNG PHẦN
Định lí . Nếu u(x) và v(x) là các hàm số có đạo hàm liên tục trên
;ab
thì:
''
( ) ( ) ( ) ( ) ( ) ( )
bb
aa
b
u x v x dx u x v x v x u x dx
a


Hay
b
a
udv
b
uv
a
b
a
vdu
PHƢƠNG PHÁP CHUNG
Bƣớc 1: Viết
()f x dx
dưới dạng
'
udv uv dx
bằng cách chọn một phần thích hợp của
()fx
làm
()ux
và phần còn lại
'( )dv v x dx
Bƣớc 2: Tính
'du u dx
và
v dv
'( )v x dx
Bƣớc 3: Tính
'( )
b
a
vu x dx
và
b
uv
a
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 8
Cách đặt
u
và
dv
trong phƣơng pháp tích phân từng phần.
Đặt u theo thứ tự ưu tiên:
Lốc-đa-mũ-lượng
()
b
x
a
P x e dx
( )ln
b
a
P x xdx
( )cos
b
a
P x xdx
cos
b
x
a
e xdx
u
P(x)
lnx
P(x)
x
e
dv
x
e dx
P(x)dx
cosxdx
cosxdx
Chú ý: Nên chọn
u
là phần của
()fx
mà khi lấy đạo hàm thì đơn giản, chọn
'
dv v dx
là phần của
()f x dx
là vi phân một hàm số đã biết hoặc có nguyên hàm dễ tìm.
TÍCH PHÂN CÁC HÀM SỐ SƠ CẤP CƠ BẢN
1. Tích phân hàm hữu tỉ
Dạng 1:
11
ln
dx adx
I ax b
ax b a ax b a




( với
0a
)
Chú ý: Nếu
1
11
( ) . .( )
( ) (1 )
kk
k
dx
I ax b adx ax b
ax b a a k




Dạng 2:
2
0
dx
Ia
ax bx c


(
2
0ax bx c
với mọi
;x

)
Xét
2
4b ac
.
+ Nếu
0
:
12
;
22
bb
xx
aa

2
1 2 1 2 1 2
1 1 1 1 1
( )( ) ( )ax bx c a x x x x a x x x x x x



thì :
1
12
1 2 1 2 1 2 1 2 2
1 1 1 1 1
ln ln ln
( ) ( ) ( )
xx
I dx x x x x
a x x x x x x a x x a x x x x






+ Nếu
0
:
0
22
0
11
( ) 2
b
x
ax bx c a x x a




thì
22
00
11
( ) ( )
dx dx
I
ax bx c a x x a x x



+ Nếu
0
thì
2
2
2
2
24
dx dx
I
ax bx c
b
ax
aa

















Đặt
2
22
1
tan 1 tan
2 4 2
b
x t dx t dt
a a a
 
Dạng 3:
2
,0
mx n
I dx a
ax bx c


.
(trong đó
2
()
mx n
fx
ax bx c

liên tục trên đoạn
;

)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 9
+) Bằng phương pháp đồng nhất hệ số, ta tìm
A
và
B
sao cho:
2
2 2 2
( )'mx n A ax bx c B
ax bx c ax bx c ax bx c

22
(2 )A ax b B
ax bx c ax bx c

+) Ta có
2 2 2
(2 )mx n A ax b B
I dx dx dx
ax bx c ax bx c ax bx c

. Tích phân
2
2
(2 )
ln
A ax b
dx A ax bx c
ax bx c

Tích phân
2
dx
ax bx c

thuộc dạng 2.
Tính tích phân
()
()
b
a
Px
I dx
Qx
với P(x) và Q(x) là đa thức của x.
Nếu bậc của
()Px
lớn hơn hoặc bằng bậc của
()Qx
thì dùng phép chia đa thức.
Nếu bậc của
()Px
nhỏ hơn bậc của
()Qx
thì xét các trường hợp:
+ Khi
()Qx
chỉ có nghiệm đơn
12
, ,...,
n
thì đặt
12
12
()
...
()
n
n
A
AA
Px
Q x x x x
.
+ Khi
()Qx
có nghiệm đơn và vô nghiệm
22
( ) , 4 0Q x x x px q p q
thì đặt
2
()
.
()
P x A Bx C
Q x x x px q

+ Khi
()Qx
có nghiệm bội
2
( ) ( )( )Q x x x

với

thì đặt:
2
()
()
A
P x B C
Q x x x
x


.
23
( ) ( ) ( )Q x x x

với

thì đặt:
2 3 2 3 2
()
( ) ( ) ( ) ( ) ( ) ( )
P x A B C D E
x x x x x x x
.
2. Tích phân hàm vô tỉ
( , ( ))
b
a
R x f x dx
trong đó
( , ( ))R x f x
có dạng:
+)
,
ax
Rx
ax




. Đặt
cos2x a t
,
0;
2
t



+)
22
,R x a x
. Đặt
sinx a t
hoặc
cosx a t
+)
,
n
ax b
Rx
cx d




. Đặt
n
ax b
t
cx d
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 10
+)
2
1
, ( )
()
R x f x
ax b x x
Với
2
' k axx bx
. Đặt
2
t x x
hoặc
1
t
ax b
+)
22
,R x a x
. Đặt
tanx a t
,
;
22
t





+)
22
,R x x a
. Đặt
cos
a
x
x
,
0; \
2
t



+)
12
; ;...;
i
n
nn
R x x x
Gọi
12
; ; ...;
i
k BSCNN n n n
. Đặt
k
xt
a. Tích phân dạng :
2
1
0
ax
I dx a
bx c


Từ :
2
2
2
2
f(x)=ax
24
2
b
xu
b
a
bx c a x du dx
aa
K
a








Khi đó ta có :
* Nếu
2 2 2 2
0, 0 ( ) ( ) .a f x a u k f x a u k
(1)
* Nếu :
2
0
0 ( )
( ) .
2
2
a
b
f x a x
b
f x a x a u
a
a



(2)
* Nếu :
0
.
+ Với
0a
:
1 2 1 2
( ) ( ) .f x a x x x x f x a x x x x
(3)
+ Với
0a
:
1 2 1 2
( ) ( ) .f x a x x x x f x a x x x x
(4)
Căn cứ vào phân tích trên , ta có một số cách giải sau :
Phƣơng pháp :
* Trường hợp :
2 2 2 2
0, 0 ( ) ( ) .a f x a u k f x a u k
Khi đó đặt :
2
ax .bx c t a x
2
2
2
01
2
;
2
2
2
,
.
2
tc
x dx tdt
ba
ba
bx c t ax
x t t x t t
tc
t a x t a
ba





* Trường hợp :
2
0
0 ( )
( ) .
2
2
a
b
f x a x
b
f x a x a u
a
a



Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 11
Khi đó :
1
ln : 0
22
1 1 1
1
ln : 0
22
22
bb
xx
aa
a
I dx dx
bb
a
bb
a x x
xx
aa
aa
a










* Trường hợp :
0, 0a
- Đặt :
1
2
12
2
ax
x x t
bx c a x x x x
x x t
* Trường hợp :
0, 0a
- Đặt :
1
2
12
2
ax
x x t
bx c a x x x x
x x t
b. Tích phân dạng :
2
0
ax
mx n
I dx a
bx c


Phƣơng pháp :
+Bước 1: Phân tích
2
2 2 2
. ax
( ) 1
ax ax ax
Ad bx c
mx n B
fx
bx c bx c bx c

+Bước 2: Quy đồng mẫu số , sau đó đồng nhất hệ số hai tử số để suy ra hệ hai ẩn số A,B
+Bước 3: Giải hệ tìm A,B thay vào (1)
+Bước4 : Tính
2
2
1
2 ax
ax
I A bx c B dx
bx c

(2)
Trong đó
2
1
0
ax
dx a
bx c

đã biết cách tính ở trên.
c. Tích phân dạng :
2
1
0
ax
I dx a
mx n bx c

Phƣơng pháp :
+Bước 1: Phân tích :
2
2
11
ax
ax
n
mx n bx c
m x bx c
m



. (1)
+Bước 2: Đặt :
2
2
11
1
1 1 1
ax
n
y t dy dx
x t m x t
n
x
ym
x t bx c a t b t c
y y y




+Bước 3: Thay tất cả vào (1) thì
I
có dạng :
'
2
'
dy
I
Ly My N


.
Tích phân này chúng ta đã biết cách tính .
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 12
d. Tích phân dạng :
;;
m
x
I R x y dx R x dx
x










( Trong đó :
;R x y
là hàm số hữu tỷ đối với hai biến số
,xy
và
, , ,
là các hằng số đã biết )
Phương pháp :
+Bước 1: Đặt :
m
x
t
x


(1)
+Bước 2: Tính
x
theo
t
bằng cách nâng lũy thừa bậc
m
hai vế của (1) ta có dạng
xt
+Bước 3: Tính vi phân hai vế :
'dx t dt
và đổi cận
+Bước 4: Tính :
'
'
; ; '
m
x
R x dx R t t t dt
x










3. Tích phân hàm lƣợng giác
Một số công thức lƣợng giác
a. Công thức cộng:
cos cos .cos sin .sin()a b a b a b
sin sin .cos sin .() cosa b a b b a
tan tan
()
1 tan .ta
t
n
an
ab
b
b
a
a
b. Công thức nhân:
2
2 2 2 2
2
cos 2 cos – sin 2cos –1
1
1– 2sin
tan
1 tan
a a a a a
a
a
2
sin2 2sin .cos
2tan
1 tan
a
aa
a
a

;
2
2tan
tan2
1 tan
a
a
a
3
cos3 4cos 3cos

;
3
sin3 3sin 4sin

c. Công thức hạ bậc:
2
1 cos2
sin
2
a
a
;
2
1 cos2
cos
2
a
a
;
2
1 cos2
tan
1 cos2
a
a
a
3
3sin sin3
sin
4

;
3
cos3 3cos
cos
4

d. Công thức tính theo t :
tan
2
a
t
2
2
sin
1
t
a
t
2
2
1
cos
1
t
a
t
2
2
tan
1
t
a
t
e.Công thức biến đổi tích thành tổng:
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 13
1
cos .cos cos( ) cos( )
2
1
sin .sin cos( ) cos( )
2
1
sin .cos sin( ) sin( )
2
f. Công thức biến đổi tổng thành tích:
Một số dạng tích phân lƣợng giác
Nếu gặp
sin .cos
b
a
I f x xdx
. Đặt
sintx
.
Nếu gặp dạng
cos .sin
b
a
I f x xdx
. Đặt
costx
.
Nếu gặp dạng
2
tan
cos
b
a
dx
I f x
x
. Đặt
tantx
.
Nếu gặp dạng
2
cot
sin
b
a
dx
I f x
x
. Đặt
cottx
.
I. Dạng 1:
nn
12
= sinx dx ; cosx dxII

2. Phƣơng pháp
2.1. Nếu
n
chẵn thì sử dụng công thức hạ bậc
2.2. Nếu
3n
thì sử dụng công thức hạ bậc hoặc biến đổi theo 2.3.
2.3. Nếu 3 n lẻ (
21np
) thì thực hiện biến đổi:
n 2p+1 2
2
1
= sin dx = sin dx sin sin 1 cos cos
p
p
I x x x xdx x d x
0 1 2 2 2
cos ... 1 cos ... 1 cos cos
kp
kp
kp
p p p p
C C x C x C x d x


2 1 2 1
0 1 3
1 1 1
cos cos ... cos ... cos
3 2 1 2 1
kp
kp
kp
p p p p
C x C x C x C x C
kp






n 2p+1 2
2
2
= cos dx = cos dx cos cos 1 sin sin
p
p
I x x x xdx x d x
cos cos 2cos .cos
22
cos cos 2sin .sin
22
sin sin 2sin .cos
22
sin sin 2cos .sin
22
sin( )
tan tan
cos cos
sin( )
tan tan
cos cos



















Hệ quả:
cos sin 2 cos 2 sin
44
cos sin 2cos 2 sin
44


Công thức thƣờng dùng:
44
66
3 cos4
cos sin
4
5 3cos4
cos sin
8




Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 14
0 1 2 2 2
2 1 2 1
0 1 3
sin ... 1 sin ... 1 sin sin
11
1
sin sin ... sin ... sin
3 2 1 2 1
kp
kp
kp
p p p p
kp
kp
kp
p p p p
C C x C x C x d x
C x C x C x C x C
kp








II. Dạng 2:
mn
J = sin cos x x dx
Với
*), (mn
1. Phƣơng pháp:
1.1. Trường hợp 1:
,mn
là các số nguyên
a. Nếu
m
chẵn,
n
chẵn thì sử dụng công thức hạ bậc, biến đổi tích thành tổng.
b. Nếu m chẵn, n lẻ thì biến đổi:
m 2p+1 2
2
= sin cos sin cos cos sin 1 sin sin
p
m p m
I x x dx x x xdx x x d x
0 1 2 2 2
1 3 2 1 2 1
01
sin sin ... 1 sin ... 1 sin sin
sin sin sin sin
... 1 ... 1
1 3 2 1 2 1
kp
kp
m
kp
p p p p
m m k m p m
kp
kp
p p p p
x C C x C x C x d x
x x x x
C C C C C
m m k m p m





c. Nếu m chẵn,
n lẻ (n 2p 1) thì biến đổi:
2p+1 n 2
2
sin cos cos sin sin cos 1 cos cos
p
n p n
I x x dx x x xdx x x d x
0 1 2 2 2
1 3 2 1 2 1
01
cos cos ... 1 cos ... 1 cos cos
cos cos cos cos
... 1 ... 1
1 3 2 1 2 1
kp
nk
p
kp
p p p p
n n k n p n
kp
kp
p p p p
x C C x C x C x d x
x x x x
C C C C C
n n k n p n





d. Nếu
,mn
lẻ thì sử dụng biến đổi 1.2 hoặc 1.3 cho số mũ lẻ bé hơn.
1.2. Nếu
,mn
là các số hữu tỉ thì biến đổi và đặt
u sinx
11
22
22
sin cos sin cos cos 1
nm
m
m n m
B x xdx x x xdx u u du

(*)
• Tích phân (*) tính được 1 trong 3 số
11
;;
2 2 2
m n m k
nguyên
III. Dạng 3:
nn
12
= tan ; = t .co ( )I x d nx I x dx

•
2
2
1 tan tan tan
cos
dx
x dx d x x C
x
•
2
2
1 cot cot cot
sin
dx
x dx d x x C
x
•
cos
sin
tan ln cos
cos cos
dx
x
xdx dx x C
xx
•
sin
cos
cot ln sin
sin sin
dx
x
xdx dx x C
xx
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 15
ỨNG DỤNG TÍCH PHÂN
1. Diện tích hình phẳng
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số
()y f x
liên tục trên đoạn
;ab
, trục hoành và
hai đường thẳng
xa
,
xb
được xác định:
()
b
a
S f x dx
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số
()y f x
,
()y g x
liên tục trên đoạn
;ab
và
hai đường thẳng
xa
,
xb
được xác định:
( ) ( )
b
a
S f x g x dx
Trên
;ab
hàm số
()fx
không đổi dấu thì:
( ) ( )
bb
aa
f x dx f x dx

Nắm vững cách tính tích phân của hàm số chứa giá trị tuyệt đối
Diện tích của hình phẳng giới hạn bởi các đường
()x g y
,
()x h y
và hai đường thẳng
yc
,
yd
được xác định:
( ) ( )
d
c
S g y h y dy
2. Thể tích vật thể và thể tích khối tròn xoay
a) Thể tích vật thể:
Gọi
B
là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục
Ox
tại các điểm a và b;
()Sx
là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm
x
,
()a x b
. Giả sử
()Sx
là hàm số liên tục trên đoạn
;ab
.
b) Thể tích khối tròn xoay:
b
a
S x dxV ()
x
O
a
b
()
S(x)
x
11
22
( ): ( )
( ): ( )
()
C y f x
C y f x
H
xa
xb
1
()C
2
()C

b
a
S f x f x dx
12
( ) ( )
a
1
c
y
O
b
x
2
c
()
()
y f x
y0
H
xa
xb
a
1
c
2
c
()y f x
y
O
x
3
c
b
b
a
S f x dx()
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 16
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
()y f x
, trục
hoành và hai đường thẳng
xa
,
xb
quanh trục
Ox
:
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
()x g y
, trục
hoành và hai đường thẳng
yc
,
yd
quanh trục
Oy
:
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới
hạn bởi các đường
()y f x
,
()y g x
và hai đường thẳng
xa
,
xb
quanh trục
Ox
:
22
( ) ( )
b
a
V f x g x dx

.
( ): ( )
( ):
C y f x
Ox y 0
xa
xb
2
()
b
x
a
V f x dx
a
()y f x
y
O
b
x
c
y
O
d
x
( ): ( )
( ):
C x g y
Oy x 0
yc
yd
2
()
d
y
c
V g y dy
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 17
BÀI TẬP TÌM NGUYÊN HÀM BẰNG CÁCH DÙNG BẢNG NGUYÊN HÀM
VÀ CÁC PHÉP BIẾN ĐỔI SƠ CẤP
1.
dxx )37(
16.
23
2
xx
dx
2.
dx
x
xx
3
2
5
17.
dx
x
x
2
)2(
3.
dxx
x
)2
3
(
18.
dx
x
x
cos1
sin4
3
4.
2
21
21
xx
dx
x

19.
dx
x
x
2
3
5.
dx
x
xx
2
4
335
20.
45
3
2
xx
xdx
6.
dx
x
x
2
22
)2(
21.
dx
2
cotx) -(tanx
7.
dxx
xx
3
31
22.
dx
x
x
e
12
3
8.
dxxx 232
3
2
23.
21
11
x
dx
xx

9.
dx
x
x
3
4
24.
dx
x 32
e
10.
2
3
3x x x
dx
x

25.
dx
x
x
x
2
cos
e
4e
11.
xdx2sin
26.
dx
x 13
2
12.
xdxx 3cos.2sin
27.
dx
x
x
sin1
cos
3
13.
dxx )12sin(
28.
3
cos sinx xdx
14.
dx
x
2
sin2
2
29.
xdx
2
tan
15.
5
)23( x
dx
30.
dx
x
x
4
e
13
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 18
BÀI TẬP TÌM NGUYÊN HÀM BẰNG PHƢƠNG PHÁP ĐỔI BIẾN
1.
dxx
10
)23(
21.
dx
x
x
3
2
25
3
2.
dxx
35
22.
dx
x
e
x
3.
xdxx .1
2
23.
2014
2
x
xdx
4.
35x
dx
24.
5
)23( x
dx
5.
dxxx
243
)5(
25.
xdxx
72
)12(
6.
dxxx .1
26.
xdxxcossin
2014
7.
dxex
x 1
2
.
27.
dx
x
x
5
cos
sin
8.
dx
x
x
3
ln
28.
gxdxcot
9.
dxxx .1
32
29.
x
tgxdx
2
cos
10.
dxxx .1
23
30.
tgxdx
11.
xdxx
23
sincos
31.
2
2
1 x
dxx
12.
2
)1( xx
dx
32.
5
2x
e
dx
13.
1
x
e
dx
33.
dxxx .1
22
14.
1
2
xx
dx
34.
1
( ln )
x
x
xe
dx
x e x
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 19
15.
3
2
x
x
e
dxe
35.
x
dx
sin
16.
dxx .1
2
36.
x
dx
cos
17.
2
4 x
dx
37.
1
tanx
dx
18.
2
1 x
dx
38.
1
cotx
dx
19.
dx
x
e
tgx
2
cos
39.
(sinx+cos )
sinx cos
x dx
x
20.
xdxe
x
sin
cos4
40.
3
sin xdx
BÀI TẬP TÌM NGUYÊN HÀM BẰNG PHƢƠNG PHÁP
NGUYÊN HÀM TỪNG PHẦN
1.
xdxx sin.
21.
dxxx
ln
2.
xdxxcos
22.
xdxln
3.
dxxx
sin)1(
23.
dxx
2
ln
4.
xdxx 2sin
24.
dxxx
ln
2
5.
xdxx 2cos
25.
dxxsin
6.
dxex
x
.
26.
x
xdxln
7.
xdxxln
27.
dx
x
x
2
)1ln(
8.
dxxx
cos
2
28.
dxxx )1ln(
2
9.
xdxx sin)5(
2
29.
xdx
x
2
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 20
10.
dxxx
2
sin
30.
dxx )1ln(
2
11.
dxex
x
2
3
31.
dxxx
ln)32(
12.
xdxx 2cos
2
32.
dx
x
xxx
1
1ln.
2
2
13.
xdxxx cos)32(
2
33.
dxexx
x
2
tantan1
14.
xdxe
x
cos.
34.
dxx
lncos
15.
dx
x
x
2
cos
35.
dxxx )1ln(2
16.
xdxx
2
tan
36.
dx
x
x
x
1
1
ln.
17.
dxex
x
)32(
37.
dxxx
2ln
2
18.
dxex
x
2
38.
dxxx
)cos1ln(.cos
19.
dxe
x
39.
dxxe
x
cos
2
20.
dxxe
x
sin
40.
dx
x
x
2
cos
)ln(cos
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 21
CÁC PHƢƠNG PHÁP TÍNH TÍCH PHÂN
1. TÍNH TÍCH PHÂN BẰNG CÁCH SỬ DỤNG CÁC NGUYÊN HÀM CƠ BẢN VÀ
CÁC TÍNH CHẤT CỦA TÍCH PHÂN
Ví dụ 1: Tính tích phân I=
2
3
1
( 2 1)x x dx
Giải:
I =
2
3
1
( 2 1)x x dx
=
4
22
1
13
1 2 2 1 1 2
4 4 4
x
xx






Ví dụ 2: Tính tích phân I=
1
31
1
3
x
e dx
Giải:
I=
1
31
1
3
x
e dx
=
31
1 4 0
1
3
1
()
33
x
e
ee




Ví dụ 3: Tính tích phân
2
4
sin
.
sin
x cosx
I dx
x cosx



Giải:
22
44
sin
sin
2
ln sin ln 2
sin sin
4
d x cosx
x cosx
I dx x cosx
x cosx x cosx








Ví dụ 4: Tính tích phân
2
0
.
1
dx
I
cosx
Giải:
2 2 2
22
0 0 0
2
tan 1
2
12
2
0
22
x
d
dx dx x
I
xx
cosx
cos cos



Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 22
TÍNH TÍCH PHÂN BẰNG CÁC PHÉP BIẾN ĐỔI SƠ CẤP
1. I =
1
0
2
)12( dxxx
16. I =
1
0
12
dxe
x
2. I =
1
1
3
)
5
2
27( dxxx
17. I =
1
0
()
x
e x dx
3. I =
1
2
0
( 1)
x
e x dx
18. I =
2
0
13cos2
3sin
dx
x
x
4. I =
2
1
3
23
22
dx
x
xxx
19. I =
2
4
0
sin xdx
5. I =
1
3
0
()x x x dx
20. I =
4
0
44
)cos(sin
dxxx
6. I =
2
32
-1
x -2x - x 2 dx
21. I =
2
0
66
)cos(sin
dxxx
7. I =
dx
xx
2
1
32
4
31
22. I =
dxxx
3
6
2
cottan
8. I=
e
dx
x
xxxx
1
3
125
23. I =
3
4
2
0
sin x
dx
cos x
9. I =
dx
x
x
8
2
3
2
3
2
43
24. I =
dx
x
2
4
4
sin
1
10. I =
dx
x
xxx
e
2
1
3
3
7112
25. I =
dx
x
0
6
cos
1
11. I =
2
1
( 1)( 1)x x x dx
26. I =
dxxxnsix )cos(2cos
44
0
12. I =
1
sin xdx
27. I =
4
3
4
2sin
dxx
13. I =
4
0
cos
xdx
28. I =
3
4
2
2sin
4
dx
x
14. I =
4
0
tan
xdx
29. I =
3
4
2
cot2tan
dxxx
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 23
15. I =
4
0
cot
xdx
30. I =
2
0
1 cosx
dx
1 cosx
LUYỆN TẬP DÙNG VI PHÂN 1
1/
1
2
2
.
11 5
dx
I
x
6. I =
xdxxcox 2cos
2
0
2
2. I =
x
1
x
0
e
dx
e1
7. I =
dxx
3
sin
2
1
2
3.
1
3 4 3
0
(1 )I x x dx
8. I =
dxx
2
0
5
sin
4.
22
3
3
1
35I x dx
9. I =
2
23
0
sin2x(1 sin x) dx
5. I =
dxxx
2015
3
0
2
)2()1(
10. I =
e
1
sin(lnx)
dx
x
LUYỆN TẬP DÙNG VI PHÂN 2
1.
2
3
6
.I cos xdx
6.
4
0
1
21
I dx
x
2. I=
dx
x
e
x
4
0
2
2tan
cos
7. I =
2
2
sin x
4
e sin2xdx
3. I=
dxxx
20152
3
1
)2(
8. I =
2
4
0
1 2sin x
dx
1 sin2x
4.
1
32
0
2I x x dx
9. I =
3
0
sinx.ln(cosx)dx
5. I =
1
2
0
x
dx
4x
10. I =
4
2
0
tgx dx
x
.
cos
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 24
2. PHƢƠNG PHÁP ĐỔI BIẾN SỐ
a. Phƣơng pháp đổi biến số dạng 1.
Định lí . Nếu 1) Hàm
()x u t
có đạo hàm liên tục trên đoạn
;

,
2) Hàm hợp
( ( ))f u t
được xác định trên
;

,
3)
( ) , ( )u a u b


,
thì
'
( ) ( ( )) ( )
b
a
I f x dx f u t u t dt


.
PHƢƠNG PHÁP CHUNG
Bƣớc 1: Đặt x = u(t)
Bƣớc 2: Tính vi phân hai vế:
dttudxtux )(')(
Đổi cận:
t
t
ax
bx
Bƣớc 3: Chuyển tích phân đã cho sang tích phân theo biến t
Vậy:
dttgdttutufdxxfI
b
a
)()(')()(
)()()(
GGtG
* Các dấu hiệu đổi biến thƣờng gặp :
Dấu hiệu
Cách chọn
22
ax
Đặt x = |a| sint; với
;.
22
t





hoặc x = |a| cost; với
0; .t
22
xa
Đặt x =
a
.
sint
; với
; \ 0 .
22
t





hoặc x =
.
a
cost
; với
0; \ .
2
t



22
ax
Đặt x = |a|tant; với
;.
22
t





hoặc x = |a|cost; với
0; .t
.
ax
ax
hoặc
.
ax
ax
Đặt x = acos2t
x a b x
Đặt x = a + (b – a)sin
2
t
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 25
22
1
ax
Đặt x = atant; với
;.
22
t





Ví dụ 1:
1
2
0
1 x dx
Giải:
Đặt x=sint với :
;
22
t





.
dx=costdt
Đổi cận:
x
0
1
t
0
2
Do đó : f(x)dx=
2 2 2
1
1 1 sin ostdt=cos 1 os2t
2
x dx tc tdt c dt
Vậy :
1
2
00
1 os2t
1 1 1 1 1
( ) sin2
2
2 2 2 2 2 2 4
0
c dt
f x dx t t


Ví dụ 2: Tính
1
22
0
.1I x x dx
Giải:
Đặt x = sint
,;
22
t





.
dx = costdt
Đổi cận:
x
0
1
t
0
2
Khi đó:
1
22
0
.1I x x dx
2
22
0
sin 1 sin .t t costdt

2
22
0
1
sin
4
tcos tdt
2
2
0
1
sin 2
4
tdt
2
0
1
14
8
cos t dt

11
sin4
2
84
0
tt




16
Ví dụ 3: Tính
1
3
8
0
.
1
x
I dx
x
Giải:
Ta có:
11
33
2
8
4
00
.
1
1
xx
dx dx
x
x

Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 26
Đặt
4
tanxt
với
32
1
; . 1 tan .
2 2 4
t x dx t dt




Đổi cận:
x
0
0
t
0
4
Khi đó:
11
3 3 2
44
2
82
4
0 0 0 0
1 1 tan 1 1
..
4
1 4 1 tan 4 4 16
1
0
x x t
I dx dx dt dt t
xt
x


Ví dụ 4: Tính
15
2
2
42
1
1
.
1
x
I dx
xx

Giải:
Ta có:
1 5 1 5 1 5
2
2 2 2
2
2
2
42
2
1 1 1
2
1
1
1
1
1
.
1
1
1
1
1
x
x
x
dx dx dx
xx
x
x
x
x










Đặt
2
11
1.t x dt dx
xx



Đổi cận:
x
1
15
2
t
0
1
Khi đó:
1
2
0
.
1
dt
I
t
Đặt
2
tan 1 tan .t u dt u du
Đổi cận:
x
0
1
t
0
4
Vậy
1
2
44
22
0 0 0
1 tan
..
4
1 1 tan 4
0
dt u
I du du u
tu


Ví dụ 5: Tính
dx
x
x
2
0
2
sin1
cos
Giải:
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 27
Đặt sinx = tant với
2
; 1 tan .
22
t cosxdx t dt




Đổi cận:
x
0
2
t
0
4
Khi đó:
2
2 4 4
22
0 0 0
1 tan
.
1 sin 1 tan 4
cosx t
I dx dt dt
xt

b. Phương pháp đổi biến dạng 2
Định lí: Nếu hàm số
()u u x
đơn điệu và có đạo hàm liên tục trên đoạn
ba;
sao cho
duugdxxuxugdxxf )()(')()(
thì:
)(
)(
)()(
bu
au
b
a
duugdxxfI
.
PHƢƠNG PHÁP CHUNG
Bƣớc 1: Đặt
dxxuduxuu )()(
'
Bƣớc 2: Đổi cận :
)(
)(
auu
buu
ax
bx
Bƣớc 3: Chuyển tích phân đã cho sang tích phân theo biến u
Vậy:
)(
)(
)()('.)()(
bu
au
b
a
b
a
duugdxxuxugdxxfI
Ví dụ 1: Tính
ln2
2
2
0
3
.
32
xx
xx
ee
I dx
ee

Giải:
Đặt
x
et
dxedt
x
Đổi cận:
x
0
ln2
t
1
2
Khi đó:
ln2 ln2 2 2
2
2 2 2
0 0 1 1
22
11
3 3 3 2 1
3 2 3 2 3 2 1 2
22
1 1 3 4 9 4 27
2 2ln 1 ln 2 2 ln3 ln2 ln4 ln3 2ln ln ln ln ln
11
1 2 2 3 4 3 16
x x x
x
x x x x
e e e t
I dx e dx dt dt
e e e e t t t t
dt dt t t
tt





Ví dụ 2: Tính
1
0
ln 2
.
2
x
I dx
x
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 28
Giải:
Đặt
ln 2 .
2
dx
t x dt
x
Đổi cận:
x
1
1
t
ln2
0
Khi đó:
1 0 ln2
22
0 ln2 0
ln2
ln 2
ln 2
..
0
2 2 2
x
t
I dx tdt tdt
x
BÀI TẬP TÍCH PHÂN ĐỔI BIẾN DẠNG 1
Luyện tập 1
1. I =
1
2
2
0
1
12
dx
x
KQ:
4
2
6.
1
0
1
1
dx
x
x
I
KQ:
2
2
2. I =
2
2
1
1
32
dx
xx
KQ:
6
7.
dx
x
x
I
2/1
0
2
2
1
KQ:
11
2 4 2
I




3.
a
dxxaxI
0
222
KQ:
16
4
a
8.
dx
x
x
I
0
1
1
1
KQ:
4
1
4.
1
2
2
2
2
1
.
x
I dx
x
KQ:
4
1
9.
dx
xx
I
6
23
2
9
1
KQ:
36
5.
1
42
0
.
1
x
I dx
xx

KQ:
18
3
10.
dx
xx
I
1
0
2
1
1
KQ:
9
3
Luyện tập 2
1. I =
2
3
2
2
1xx
dx
KQ:
12
11.
dxxI
3
1
2
4
KQ:
3
2.
x
I dx
x
2
0
2
2
KQ:
2
12.
3
1
2
54xx
dx
I
KQ:
2
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 29
3.
dxxxI
2
1
22
4
KQ:
4
3
3
2
13.
x x dx
1
2
2
0
1 2 1
KQ:
8
13
12
4. I=
1
2
1
3
2
41
dx
xx
KQ:
3
8
14.
dx
xa
xa
I
a
0
KQ:
4
1
a
5. I=
4
4
24
2
5tan2tancos
sin
xxx
xdx
KQ:
8
3
3
2
ln2
15.
0
2
1
1
.
24
I dx
xx

KQ:
18
3
6.
dx
x
x
I
3
1
2
2
39
KQ:
223
22
ln
2
3
632
16.
dx
x
x
I
1
0
2
3
4
KQ:
33
3
2
7.
dxxxI
1
0
2
1
KQ:
3
122
17.
dx
xx
dx
I
0
1
2
22
KQ: 0
8.
dxxI
1
2
1
2
1
KQ:
8
3
3
18.
dxxxxI
2
0
2
2
KQ:
3
2
9.
2
0
22
a
xa
dx
I
0a
KQ:
6
19/
dx
xx
x
I
3
4
2
cos1cos
tan
KQ:
22
10.
a
xa
dx
I
0
22
0a
KQ:
a4
20.
1
3
2
0
1.I x dx
KQ:
16
3
BÀI TẬP TÍCH PHÂN ĐỔI BIẾN DẠNG 2
Luyện tập 1
1.
1
32
0
.1I x x dx
KQ:
15
2
6.
1
1 ln
.
e
x
I dx
x
KQ:
122
3
2
2.
3
2
0
21
1
xx
I dx
x

KQ:
5
54
7.
1
3
2
0
.
1
x
I dx
xx

KQ:
15
1
15
22
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 30
3.
1
1
.
1 ln
e
I dx
xx
KQ:-ln2
8.
1
15 8
0
. 1 3 . .I x x dx
KQ:
270
29
4.
2
3
1
.
1
dx
I
xx
KQ:
12ln
3
2
9.
4
2
7
.
9
dx
I
xx
KQ:
4
7
ln
6
1
5.
1
4
34
0
1.I x x dx
KQ:
20
31
10. I =
3
0
3
3. 1 3
x
dx
xx
KQ:
2
3
ln63
Luyện tập 2
1.
3
6
0
tan
cos2
x
I dx
x
KQ:
3
2
ln
2
1
6
1
11.
x
I dx
xx
2
3
0
cos2
(cos sin 3)

KQ:
32
1
2.
ln3
2
ln2
12
x
xx
e dx
I
ee
KQ: 2ln3 - 1
12.
I x x dx
1
5 3 6
0
(1 )
KQ:
168
1
3.
dx
I
xx
3
24
4
sin .cos
KQ:
3
438
13.
x dx
I
x
2
3
3
2
0
4
KQ:
3
24
5
8
2
3
4. I =
dx
xx
3
4
35
4
sin .cos
KQ:
134
8
14.
x
I dx
x
6
0
sin
cos2
KQ:
1 3 2 2
ln
2 2 5 2 6
5.
xdx
I
xx
4
2
0
tan
cos 1 cos
KQ:
23
15.
x
I dx
xx
5
2
1
1
31
KQ:
5
9
ln
27
100
6.
I dx
xx
4
3
4
1
1
( 1)
KQ:
2
3
ln
4
1
16.
5
2
ln( 1 1)
11

x
I dx
xx
KQ:
2ln3ln
22
7.
x
I dx
x
4
0
21
1 2 1

KQ:
2ln22
17.
x
dx
I
e
3ln2
2
3
0
2
KQ:
8
1
2
3
ln
4
3
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 31
8. I
4
0
2
211
1
dx
x
x
KQ:
4
1
2ln2
18.
I x x xdx
2
6
35
1
2 1 cos .sin .cos
KQ:
91
12
9.
xx
I dx
x
4
0
cos sin
3 sin2
KQ:
12
19.
x dx
I
x
1
2
6
0
4
KQ:
18
10.
xx
xx
ee
I dx
ee
ln3
32
0
2
4 3 1

KQ:
3
5ln8
20.
x
I dx
x
4
2
0
1
1 1 2

KQ:
1
2ln2
4
3. TÍCH PHÂN TỪNG PHẦN
Định lí . Nếu u(x) và v(x) là các hàm số có đạo hàm liên tục trên
;ab
thì:
''
( ) ( ) ( ) ( ) ( ) ( )
bb
aa
b
u x v x dx u x v x v x u x dx
a


Hay
b
a
udv
a
b
uv
b
a
vdu
PHƢƠNG PHÁP CHUNG
Bƣớc 1: Viết f(x)dx dưới dạng
'
udv uvdx
bằng cách chọn một phần thích hợp của f(x) làm u(x)
và phần còn lại
dxxvdv )('
Bƣớc 2: Tính
dxudu '
và
dvv
dxxv )('
Bƣớc 3: Tính
b
a
dxxvu )('
và
a
b
uv
*Cách đặt u và dv trong phƣơng pháp tích phân từng phần.
Đặt u theo thứ tự ưu
tiên:
Lốc-đa-mũ-lượng
()
b
x
a
P x e dx
( )ln
b
a
P x xdx
( )cos
b
a
P x xdx
cos
b
x
a
e xdx
u
P(x)
lnx
P(x)
x
e
dv
x
e dx
P(x)dx
cosxdx
cosxdx
Chú ý: Nên chọn u là phần của f(x) mà khi lấy đạo hàm thì đơn giản, chọn
'
dv v dx
là phần của f(x)dx là vi
phân một hàm số đã biết hoặc có nguyên hàm dễ tìm.
Có ba dạng tích phân thƣờng đƣợc áp dụng tích phân từng phần:
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 32
Dạng 1
sin
()
ax
ax
f x cosax dx
e





Đặt
( ) '( )
sin sin
cos
ax ax
u f x du f x dx
ax ax
dv ax dx v cosax dx
ee









Dạng 2:
( )ln( )f x ax dx
Đặt
ln( )
()
()
dx
du
u ax
x
dv f x dx
v f x dx

Dạng 3:
dx
bx
bx
e
ax
cos
sin
Đặt
1
cos
sin
ax
ax
du ae dx
ue
dv bxdx
v bx
b

Hoặc
1
sin
cos
ax
ax
du ae dx
ue
dv bxdx
v bx
b


Trong trường hợp này, ta phải tính tích phân từng phần hai lần sau đó trở thành tích phân ban đầu. Từ đó
suy ra kết quả tích phân cần tính.
Ví dụ 1: Tính
1
2
0
.
x
I xe dx
Giải
Đặt
2
2
.
1
2
x
x
du dx
ux
ve
dv e dx

Áp dụng công thức tính tích phân từng phần:
1 1 1
2
2 2 2 2 2 2 2 2 2
0 0 0
11
1 1 1 1 1 1 1 1 1
21
00
2 2 2 4 2 4 2 4 4
x x x x x
e
I xe dx xe e dx e e d x e e e e
Ví dụ
2: Tính
2
2
0
os3xdx
x
ec
Giải:
Đặt: u = e
2x
, du= 2e
2x
dx
dv = cos3xdx, v =
sin3x
3
2
2
2x 2x
1
0
0
sin3x 2 2
sin3x dx=
3 3 3 3
e
I e e I



Tính
1
I
Đặt
2x 2x
' 2eu e u
-cos3x
sin3x, v'=
3
v
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 33
22
2
2x 2x 2x
1
0
00
os3x 2
sin3x dx os3x dx
33





c
I e e e c
1
3
I
Do đó:
2 1 2 4
3 3 3 3 9 9
3e 2
13
ee
I I I
I




Ví dụ 3: Tính
2
sin
0
sin2 .
x
I e xdx
Giải:
22
sin sin
00
sin2 2 sin
xx
I e xdx e xcosxdx



Đặt t = sinx
dt = cosxdx
Đổi cận:
x
0
2
t
0
1
Khi đó:
1
2
sin
00
2 sin 2
xt
I e xcosxdx te dt


Đặt:
tt
u t du dt
dv e dt v e





Áp dụng công thức tính tích phân từng phần:
11
00
1 1 1
1
0 0 0
t t t t t
te dt te e dt te e

Vậy I = 2
Ví dụ 4 : Tính
2
6
ln sin .I cosx x dx
Đặt:
ln sin
.
sin
os
sin
cosx
ux
du dx
x
dv c dx
vx


Áp dụng công thức tính tích phân từng phần:
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 34
22
66
1
2 2 2
ln sin sin ln sin in ln sin sin ln 2 1
2
6 6 6
I cosx x dx x x cosxdx x x x



Ví dụ 5: Tính
1
4 1 ln .
e
I x xdx
Đặt:
2
ln
41
2
dx
ux
du
x
dv x dx
v x x




Áp dụng công thức tính tích phân từng phần:
2 2 2 2
11
4 1 ln 2 ln 2 1 2 2
11
ee
ee
I x xdx x x x x dx e e x x e

BÀI TẬP TÍCH PHÂN TỪNG PHẦN
1.
1
3
0
3 1 .
x
I x e dx

KQ:
3
5
3
2
e
16.
1
2
0
ln 1 .I x x dx
KQ:
2
1
2ln
2.
2
0
cos .
x
I e xdx
KQ:
2
1
2
e
17.
xx
I dx
x
4
3
0
sin
cos
KQ:
4
2
3.
ln3
2
1
2
x
I x x e dx
KQ:
e 123ln83ln
2
18.
dxxeI
x
2
0
sin
2sin
KQ: 2
4.
2
3
2
1
ln( 1)x
I dx
x
. KQ:
5
2ln2 ln5
8
19.
x
I = dx
x
2
2
1
ln( 1)
KQ:
3ln
2
3
2ln3
5.
2
0
2
sin
xdxxI
KQ:
16
4
2
20.
3
2
4
.
sin
xdx
I
x
KQ:
2
3
ln
2
1
36
)349(
6.
3
2
3
x sin x
I dx.
cos x
KQ:
32
32
ln
3
4
21. I =
2
2
0
2 1 osx c xdx
KQ:
8
82
2
7.
I x dx
3
2
2
1
KQ:
2ln
4
1
12ln
2
25
22. I =
2
2
2
0
2
x
xe
dx
x
KQ: 1
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 35
8.
2
0
1 sin
..
1 osx
x
x
I e dx
c
KQ:
2
e
23.
dxxxI
3
2
2
ln
KQ: 2-3ln3
9.
I x x dx
2
0
sin ln(1 sin )

KQ:
1
2
24.
dxxeI
x
2
0
2
3cos
KQ:
13
23
e
10.
x
I dx
x
8
3
ln
1
KQ:
43ln62ln20
25.
2
1
1
2
1
( 1 )
x
x
I x e dx
x
KQ:
2
5
2
3
e
11.
1
2
0
2
x
I x e dx
KQ:
4
35
2
e
26.
dxxxI
4
0
2
cos
KQ:
2
8
2
12. I =
4
2
0
4 3 sin 2x x xdx

KQ:
8
48
2
27.
dxxI
e
1
3
ln
KQ: 6-2e
13.
dxexI
x
1
0
3
2
KQ:
2
1
28.
dxxexI
x
0
1
3
2
1
KQ:
28
9
14.
dxxxI
e
1
23
ln
KQ:
32
15
4
e
29.
dxxxI
3
4
2
tan
KQ:
2ln31
24
2
15.
1
0
22
1ln dxxxI
KQ:
69
4
2ln
3
1
30.
e
x
I x dx
xx
2
1
ln
ln
1 ln




KQ:
3
2123 e
\
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 36
BÀI TẬP TÍCH PHÂN HÀM HỮU TỈ
1.
1
0
2
65xx
dx
I
KQ:
3
4
ln
16.
dx
x
xx
I
1
0
2
3
1
1
KQ:
32
1
2.
2
1
0
49
56
x
I dx
xx

KQ:
2
3ln ln2
3
17.
x
I dx
x
2
2001
2 1002
1
.
(1 )
KQ:
1001
2.2002
1
3.
x
I dx
x
3
2
3
4
0
1
KQ:
12
32ln
4
1
18.
x
I dx
x
2
2
4
1
1
1
KQ:
12
12
ln
22
1
4.
x
I dx
xx
2
2
2
1
7 12

KQ:
1 25ln2 16ln3
19.
dx
xx
x
I
1
0
2
65
114
KQ
:
2ln
2
1
5.
dx
x
x
I
1
0
3
2
)1(
KQ:
2ln
8
3
20.
dx
xx
x
I
4
3
2
44
96
KQ:
2ln3
2
3
6.
1
0
2
23 xx
dx
I
KQ:
9
8
ln
3
2
21.
x
I dx
x
99
1
101
0
71
21
KQ:
900
12
100
7.
dx
x
xx
I
3
2
3
2
)1(
1
KQ:
2ln
8
15
22.
dx
x
x
I
2
0
2
4
12
KQ:
4ln2
2

8.
3
1
3
xx
dx
I
KQ:
2
3
ln
2
1
23.
dx
xx
x
I
3
1
24
2
1
1
9.
x
I dx
x
1
7
25
0
(1 )
KQ:
7
2
1
24.
3
1
26
)1(xx
dx
I
KQ:
117 41 3
135 12
10.
2
0
2
22xx
dx
I
KQ:
2
25.
3
2
1
(2 1)
25
x dx
I
xx

KQ:
2ln
8
3
11.
1
0
3
1
1
dx
x
xx
I
KQ:
2ln
6
11
26.
4
3
1
4
)1(xx
dx
I
KQ:
2
3
ln
4
1
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 37
12.
x
I dx
x
1
4
6
0
1
1
KQ:
12
27.
1
0
1
1
dx
x
x
I
KQ:
11
4ln2
3
13.
dx
x
x
I
1
0
2
4
1
2
KQ:
3
2
4
28.
dx
xx
x
I
2
1
25
5
)1(
1
KQ:
165
31
33ln2ln6
5
1
14.
dx
I
xx
2
53
1
KQ:
8
3
5ln
2
1
2ln
2
3
29.
1
0
22
)1(x
dx
I
KQ:
84
1
15.
dx
I
xx
3
62
1
(1 )
KQ:
117 41 3
135 12
30.
0
1
2
23
23
9962
dx
xx
xxx
I
KQ
:
13ln192ln33
BÀI TẬP TÍCH PHÂN LƢỢNG GIÁC 1
1.
4
4
0
1
.I dx
cos x
KQ:
3
4
16. I =
2
33
0
( cosx sinx)dx
KQ: 0
2.
2
33
0
sin .I xcos xdx
KQ:
12
1
17.
2
22
0
3sin 4cos
3sin 4cos
xx
I dx
xx
KQ:
3ln
6
3
3.
2
2
0
sin2
.
1
x
I dx
cos x
KQ: ln2
18.
x
I dx
x
6
0
tan( )
4
cos2
KQ:
2
31
4.
2
3
0
sin .I xdx
KQ:
3
2
19.
I =
2
22
0
os cos 2c x xdx
KQ:
8
5. I =
3
2
2
0
sinxcos
1 os
x
dx
cx
KQ:
2
2ln1
20. I =
2
3
0
4sin
sinx+cosx
xdx
KQ: 2
6.
2
2 2 2 2
0
sin
.
sin
xcosx
I dx
a cos x b x
KQ:
ba
1
21. I =
3
6
1
sinxsin x+
6
dx



KQ:
2
3
ln2
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 38
7.
I =
2
10 10 4 4
0
sin os sin cosx c x x x dx

KQ:
64
15
22.
dx
xx
x
I
6
0
22
cossin2
2sin
KQ:
4
5
ln
8.
2
2
0
sin 1 .I xcosx cosx dx

KQ:
12
17
23. I =
2
34
0
sin cosx xdx
KQ:
35
2
9.
4
2
12
1
.
sin
I dx
x cosx
KQ:
2
3
24. I =
11
0
sin xdx
KQ:
21
118
10.
4
44
0
sin4
.
sin
x
I
x cos x
KQ: ln2
25.
dx
x
x
I
2
0
2cos7
cos
KQ:
26
11. I =
2
0
2 sinx+cosx
dx
KQ:
2arctan
2
2
arctan2
26.
dx
x
x
I
3/
0
3
cos2
sin
KQ:
6
5
ln3
2
5
I
12. I =
6
2
4
4
os
sin
cx
dx
x
KQ:
12
23
8
5
27.
/2
cosx
0
e sin2xdx
KQ: 2(e - 2)
13. I =
2
2
0
sin2
4 os
x
dx
cx
KQ:
4
3
ln
28.
2
2
0
os3xdx
x
ec
KQ:
32
13
e

14.
4
0
.
1 tan
dx
I
x
KQ:
4
2ln
8
29.
4
2
0
sin
cos
xx
I dx
x
KQ:
22
22
ln
2
1
4
2
15.
4
2
0
sin4
.
1
x
I dx
cos x
KQ:
3
4
ln62
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 39
BÀI TẬP TÍCH PHÂN LƢỢNG GIÁC 2
1.
4
3
0
tan .I xdx
KQ:
2ln1
2
1
11.
x
I dx
xx
4
2
6
tan
cos 1 cos
KQ:
3
73
2.
3
4
42
cos.sin
xx
dx
I
KQ:
3
438
12.
3
22
6
tg x cotg x 2dx

KQ: ln2
3.
x
I dx
x
2
2
6
sin
sin3
. KQ:
32ln
4
1
13.
x
I dx
xx
4
44
0
sin4
sin cos
KQ:
22
4.
xx
I dx
x
4
2
0
cos2
1 sin2
KQ:
164
2
14.
4
66
0
sin4
os sin
x
dx
c x x
KQ:
2ln
3
4
5.
x
I dx
xx
4
66
0
sin4
sin cos
KQ:
3
2
15.
x
I dx
xx
2
3
0
sin
sin 3 cos
KQ:
3
6
6.
xx
I dx
x
2
4
2
3
sin 1 cos
cos
KQ
13
12
7
16.
dx
xx
x
I
3
6
2
6sin5sin
cos
KQ:
345
363
ln
7.
dxxxI .
2
1
sin.sin
2
6
2
KQ:
31
2 4 2



17.
dxxeI
x
1
0
2
)(sin
KQ:
142
1
e
I
8.
x
x
I e dx
x
2
0
1 sin
.
1 cos



KQ:
2
e
18.
dx
x
xx
I
2
0
2
3
cos1
cos.sin
KQ:
2ln1
2
1
9.
dx
x
x
I
2
2
4
sin
4
sin
KQ: 0
19.
2
0
3
5sin
xdxeI
x
KQ:
2
3
.
20
1
e
10.
4
0
1
1 sin 2
dx
x
KQ: 1
20.
dx
xx
x
I
6
0
2
sinsin56
cos
KQ:
9
10
ln
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 40
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI
1.
2
1
xx
0
(2x 1)e dx
(ĐH Dược_81 )
2. Với
x 0;
4



xác định a,b sao cho
1 acosx bcosx
cosx 1 sinx 1 sinx


3. Tính
/4
3
0
dx dx
IJ
cosx
cos x

(ĐH BK TH_82)
4.
/2
0
sinx cosx 1
dx
sinx 2cosx 3


(Bộ Đề)
5.
1
3
0
(3x 1)dx
(x 3)
(Bộ Đề)
6.
1
3
0
xdx
(x 1)
(Bộ Đề)
7.
1
2
4
0
x1
dx
x1
(Bộ Đề)
8.
2x 2
0
e sin xdx
(Bộ Đề)
9.
/2
0
cosxdx
2 cos2x
(Bộ Đề)
10.
1
2
1
dx
x 2xcos 1
,(0< < )

(Bộ Đề)
11.
2a
22
a
x a dx ,(a>0)
(Bộ Đề)
12.
/2
3
0
4sin xdx
1 cosx
(Bộ Đề)
13.
a
22
0
x a dx
(Bộ Đề)
14.
2
0
1 sinxdx
(Bộ Đề)
15.
3 /8
22
/8
dx
sin xcos x
(Bộ Đề)
16.
2
1
dx
x 1 x 1
(Bộ Đề)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 41
17. Gpt
x
2
0
(u x )du sinx
(Bộ Đề)
18.
b
2
1
xln xdx
(BK_94)
19.
/2
2
0
xcos xdx
(BK_94)
20.
2
2
2/ 3
dx
x x 1
(BK_95)
21.
0
cosx sinxdx
(BK_98)
22. Cho hàm số:
f(x) sinx.sin2x.cos5x
a. Tìm họ nguyên hàm của g(x).
b. Tính tích phân:
2
x
2
f(x)
I dx
e1

(BK_99)
23.
ln2
2x
x
0
e
dx
e1
(BK_00)
24.
1
2
0
x1
dx
x1
(XD_96)
25.
/4
0
cosx 2sinx
dx
4cosx 3sinx
(XD_98)
26.
1
3
0
3dx
1x
(XD_00)
27.
1
42
0
dx
x 4x 3
(ĐH Mỏ_95)
28.
/3
22
/6
tg x cotg x 2dx

(ĐH Mỏ_00)
29.
/3
/6
dx
sinxsin(x /6)

(ĐH Mỏ_00)
30.
66
/4
x
/4
sin x cos x
dx
61

(ĐH Mỏ_01)
31.
2
2
1
ln(x 1)
dx
x
(ĐH Hàng Hải_00)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 42
32.
/2
3
sinxdx
sinx cosx
(ĐH GT VT_95)
33.
3
52
0
x . 1 x dx
(ĐH GT VT_96A)
34.
1/9
3x
25
0
x1
5 dx
4x 1
sin (2x 1)




(ĐH GT VT_97)
35.
7/3
3
0
x1
dx
3x 1
x
2
4
2
(10 sin x)dx

(ĐH GT VT_98)
36.
13
10
x
I dx x.arctgxdx
5 4x


(ĐH GT VT_99)
37.
/2
2
/2
x cosx
dx
4 sin x

(ĐH GT VT_00)
38.
/2
3
0
5cosx 4sin x
dx
(cosx sin x)
(ĐH GT VT_01)
39.
/2
4
44
0
cos x
dx
cos x sin x
(ĐH GTVT HCM_99)
40.
/3
2
6
/4
sin x
dx
cos x
(ĐH GTVT HCM_00)
41.
2
2
2
2
x1
dx
x x 1
(HV BCVT_97)
42.
/2
3
2
0
sinxcos x
dx
1 cos x
(HV BCVT_98)
43.
1
4
x
1
x
dx
12
(HV BCVT_99)
44.
2
0
xsinxcos xdx
(HV NH_98)
45.
/2
22
0
I cos xcos 2xdx
/2
22
0
J sin xcos 2xdx
(HV NH HCM_98)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 43
46.
/3
2
0
x sinx
dx
cos x
1
3
2
0
x
dx
x x 1
(HV NH HCM_00)
14
2
2
00
sin4x
xln(x 1)dx dx
1 cos x

47.
2
0
1 sinxdx
(ĐH NThương_94)
48.
11
2
22
00
dx x 3x 2
dx
x3
(x 3x 2)



(ĐH NThương_99)
49.
/4
3
0
cos2x
dx
sinx cosx 2

(ĐH NThương_00A)
50.
1
32
2
0
x 2x 10x 1
dx
x 2x 9

(ĐH NThương_00)
1
2
2
0
x 3x 10
dx
x 2x 9


51.
/4
66
0
sin4x
dx
sin x cos x
(ĐH NThương_01A)
52.
2
5
2
2
I ln(x 1 x ) dx



(ĐH KT_95)
53.
1
5 3 6
0
x (1 x ) dx
(ĐH KT_97)
54.
/4
42
0
dx
I dx
cos x x 1
1
5
0
x
J=

(ĐH TM_95)
55.
1
0
x 1 xdx
(ĐH TM_96)
56.
7 ln2
9x
x
3
2
00
x 1 e
I dx dx
1e
1x
J=

(ĐH TM_97)
57.
ln2
x
0
dx
e5
(ĐH TM_98A)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 44
58.
4
2
1
dx
x (1 x)
(ĐH TM_99)
59.
/2
3
0
4sinx
dx
(sinx cosx)
(ĐH TM_00)
60.
11
0
sin xdx
(HV QHQT_96)
61.
/4
24
0
sin xcos xdx
(ĐH NN_96)
62.
e
2
1/2
lnx
dx
(1 x)
(ĐH NN_97)
63.
/4
2
0
cos xcos4xdx
(ĐH NN_98)
64.
7/3
3
0
x1
dx
3x 1
(ĐH NN_99)
65.
1
22
0
(1 x x ) dx
(ĐH NN_01D)
66.
/2
x2
0
e cos xdx
(ĐH Thuỷ Lợi_96)
67.
0
1 cos2xdx
(ĐH Thuỷ Lợi_97)
68.
32
2
4 2 5
11
x 1 dx
I dx
x x 1 x(x 1)
J=

(ĐH Thuỷ Lợi_99)
69.
/4
0
ln 1 tgx dx
(ĐH Thuỷ Lợi_01A)
70.
/2
22
0
3sinx 4cosx
dx
3sin x 4cos x
(ĐH Thuỷ Lợi_00)
3
32
0
x 2x xdx
71.
/4
0
sinx.cosx
dx
sin2x cos2x
(ĐH Văn Hóa_01D)
72.
/2
2 2 2 2
0
sinxcosx
dx a,b 0
a cos x b sin x
;
(HV TCKT_95)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 45
73.
2 / 2
2
2
0
x
dx
1x
(HV TCKT_97)
74.
/4
2
0
x(2cos x 1)dx
(HV TCKT_98)
75.
/3
2
/4
cosx sinx 1
dx dx
3 sin2x
x1
1
4
0
x


(HV TCKT_99)
/2
43
00
sinx 7cosx 6
dx xcos xsin xdx
4sinx 3cosx 5




76.
1
42
0
x
dx
x x 1
(HV TCKT_00)
77.
/2
2
0
(x 1)sinxdx
(ĐH Mở_97)
78.
/2
3
0
4sin x
dx
1 cosx
(ĐH Y HN_95)
79.
11
2
2x x
1/2 0
dx
1 x dx
ee

(ĐH Y HN_98)
80.
4 /3
dx
x
sin
2
(ĐH Y HN_99)
81.
/3 2
2
4
2
/4 1
x
tg xdx dx
x 7x 12


(ĐH Y HN_00)
82.
3
2
2
x 1dx
(ĐH Y HN_01B)
83.
1
2
0
x 1dx
(ĐH Y TB_97B)
84.
/4
2
0
dx
2 cos x
(ĐH Y TB_00)
85.
1
23
0
(1 x ) dx
(ĐH Y HP_00)
86.
2
/2
x
/2
x sin x
I dx
12

(ĐH Dược_96 )
87.
/2
x
0
1 sinx
e dx
1 cosx
(ĐH Dược_00)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 46
88.
10
2
1
x lg xdx
(ĐH Dược_01A)
89.
x
ln3 2
2
x
00
dx
x.e dx
e1

(HV QY_97)
90.
32
3
24
22
dx sinx
dx
x x 1 4 5x


(HV QY_98)
91.
1/ 2
0
dx
1 cosx
(HV QY_99)
92.
/2
2
/2
cosxln(x 1 x )dx


(HV KT Mật Mã_99)
1 /3
4
64
0 /6
x 1 dx
dx
x 1 sin xcosx

93.
1
2
0
xtg xdx
(HV KT Mật Mã_00)
94.
1
2
0
xdx
(x 1)
(HV KTQS_95)
95.
/4
3
4
0
4sin x
dx
1 cos x
(HV KTQS_96)
96.
/2
3
3
/3
sin x sinx
cotgxdx
sin x
(HV KTQS_97)
97.
1
2
1
dx
1 x 1 x
(HV KTQS_98)
98.
/2
0
cosxln(1 cosx)dx
(HV KTQS_99)
1/ 3
22
0
dx
(2x 1) x 1
99.
2
b
2
2
0
ax
dx
ax
(a, b là số thực dương cho trước) (HV KTQS_01A)
100.
a
2 2 2
0
x x a dx a 0 ,
(ĐH AN_96)
101.
2
0
xsin xdx
2 cos x
(ĐH AN_97)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 47
102.
/2 4
33
4
00
dx
(cos x sin x)dx
cos x

(ĐH AN_98)
1
2x 2
0
xe dx x sinxdx
0

103.
4
2
7
dx
x x 9
(ĐH AN_99)
104.
22
22
00
3sin xdx x x 1dx

(ĐH TD TT_00)
105.
2
2
1
(xlnx) dx
(PV BC TT_98)
106.
3
e
2
1
ln 2 ln x
dx
x
(PV BC TT_98)
107.
/4
2
0
1 sin2x
dx
cos x
(PV BC TT_00)
108.
1
3
0
3dx
1x
(ĐH Luật _00)
109.
1
2 2x
0
(1 x) e dx
(ĐH CĐ_98)
110.
2 /2 /2
2
x
0 0 0
dx dx
(2x 1)cos xdx
1 sin2x
e1

(ĐH CĐ_99)
111.
12
2x 2
01
dx ln(x 1)
dx
e 3 x

(ĐH CĐ_00)
112.
/2 1
x2
2x
/6 0
1 sin2x cos2x (1 e )
dx dx
sinx cosx
1e

(ĐH NN I_97)
113.
/2 /2
2x
00
cosxdx
e sin3xdx
1 cosx


(ĐH NN I_98B)
114.
1
19
0
x(1 x) dx
(ĐH NN I_99B)
115.
2 /4
2
3
10
dx
xtg xdx
x(x 1)

(ĐH NN I_00)
116.
6
/2
4
/4
cos x
dx
sin x
(ĐH NN I_01A)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 48
117.
2
1
ln(1 x)dx
(ĐH Lâm Nghiệp_97)
118.
1
4
2
1
x sinx
dx
x1
(ĐH Lâm Nghiệp_98)
119.
/2
0
dx
2 sinx cosx

(ĐH Lâm Nghiệp_00)
120.
1
2
0
x .sinxdx
(ĐH SP HN I_99D)
121.
a
2 2 2
0
x a x dx (a 0) 
(ĐH SP HN I_00)
122.
1
32
0
x 1 x dx
(ĐH SP HN I_01B)
123.
2
2
1
xdx
x2
(ĐH THợp_93)
124.
3
0
xsin xdx
(ĐH THợp_94)
/2
0
dx
sinx cosx
125.
1
0
dx
1x
(ĐH QG_96)
126.
/2 1
3
2
00
sin xdx dx
x 1 x
1 cos x


(ĐH QG_97A, B, D)
11
2
22
00
x dx xdx
4 x 4 x


127.
1 1 /4
3
32
x2
0 0 0
dx sin x
x 1 x dx dx
e 1 cos x
(ĐH QG_98)
128. Tính
22
/ 6 / 6
00
sin x cos x
I dx; J dx
sinx 3 cosx sinx 3 cosx




.
Từ đó suy ra:
5 / 3
3 / 2
cos2x
dx
cosx 3 sin x
(ĐH QG HCM_01A)
129.
/4 /4
x
00
2cosxdx
5e sin2xdx
3 2sinx


(ĐH SP II _97)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 49
130. Cho f(x) liên tục trên R :
f(x) f( x) 2 2cos2x x R
. Tính
3 /2
3 /2
f(x)dx

(ĐH SP II _98A)
131.
/2
10 10 4 4
0
(sin x sin x cos xsin x)dx

(ĐH SP II _00)
132.
30
2
2
11
3x 2 dx
dx
x 4 x 2
x1

(CĐ SP HN_00)
133.
1 /4
22
00
(sinx 2cosx)
x 1 x dx dx
3sinx cosx

(CĐ SP HN_00)
134.
22
0
sin xcos xdx
(CĐ SP MGTW_00 )
135.
/2 4
01
1 sinx dx
ln( )dx
1 cosx
x(1 x)

(CĐ SP KT_00)
136.
11
2
2
x
11
1x
1 x arcsinxdx dx
12


(CĐ PCCC_00)
137.
2
1
x x 2
1
(e sinx e x )dx
(ĐH TN_00)
138.
3
3
2
0
t
dt
t 2t 1
(ĐH SP Vinh_98)
139.
11
2
2
4
1/2 0
1x
dx x 1dx
1x

(ĐH SP Vinh_99)
140.
1
2
2
0
(x x)dx
x1
(ĐH HĐ_99)
141.
/4
3
00
dx
sin xcos3xdx
1 tgx


(ĐH HĐ_00)
142.
2
2
1
lnx
dx
x
(ĐH Huế_98)
143.
/2
6
66
0
sin x
dx
sin x cos x
(ĐH Huế_00)
144.
2
7
dx
2 x 1
(ĐH ĐN_97)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 50
145.
/2
2
00
cosx cosxdx
dx
1 sinx
1 cos x


(ĐH ĐN_98)
146.
/4 2
4
00
dx
xlnxdx
cos x

(ĐH ĐN_99)
147.
/2 /2
/4 0
sinx cosx sinxdx
dx
sinx cosx 1 2cosx



(ĐH ĐN_00)
148.
1
2
2
0
x x arctgx
dx
1x

(ĐH Tnguyên_00)
149.
21
2 10
3
00
x1
dx (1 3x)(1 2x 3x ) dx
3x 2

(ĐH Quy Nhơn)
150.
2
ee
1 1 1
2 lnx lnx
dx sin xdx dx
2x x
(ĐH Đà Lạt)
151.
23
2
23
00
x1
x x 1dx dx
x1

(ĐH Cần Thơ)
/2 /2 /4
33
44
0 0 0
cos x sin x sin4x
dx dx dx
sinx cosx sinx cosx
sin x cos x

2
e 1 1
3x
2
1 0 0
lnxdx x
x e dx dx
1x
x(ln x 1)
152.
/2 /2
2 3 2
00
sin2x(1 sin x) dx sinxcosx(1 cosx) dx



2
/2 3
53
2
x1
00
x 2x
(x 1)sinxdx dx

(ĐH Thuỷ sản NT)
153.
/2 /2
2
2
00
sinxdx
dx xcos xdx
cos x 3


(ĐH BK HCM)
/2 1
4
3
00
xdx
cos 2xdx
(2x 1)

154.
1
2
00
xsinx
dx x 1 xdx
9 4cos x

(ĐH Y Dược HCM)
155.
2
x
-
sin xdx
1 sinxdx
13


(ĐH Ngoại thương)
e1
2 3 2
10
xln xdx x 1 x dx

Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 51
156.
2
00
xsinxdx
arctg(cosx)dx
1 cos x


(ĐH SP HCM)
/3 1
4
2
0 0 0
sinxdx 4x 11
dx cos xdx
sinx cosx
x 5x 6


157.
1
x
3
x
0 0 0
e
dx xsinxdx x sinxdx
1e

(ĐH QG HCM)
1/2 /2
4
24
00
x sin2xdx
dx
x 1 1 sin x


/2 1 /4
4
4
0 0 0
sin2x xdx
dx sin xdx
2x 1
1 cos x

/2 1
2 3 x 2
00
sin xcos xdx e sin ( x)dx

158.
11
x 2x
2
00
1
e dx (x 1)e dx
1x





(ĐHDL NN Tin Học)
21
x
00
x 1dx e dx

159.
1 5 1
x2
2 20
x
0 4 0
(1 e )
1 x dx x(x 4) dx dx
e

(DL)
e ln2
2 2x x
2x x
10
1 ln x e 3e
dx dx
x
e 3e 2



160.
3
1
2
0
x
dx
x1
(Dự bị_02)
161.
x
ln2
3
x
0
e
dx
e1
(Dự bị_02)
162.
0
2x
3
1
x e x 1 dx

(Dự bị_02)
163.
/2
6
35
0
1 cos x.sin x.cos xdx
(Dự bị_02)
164.
23
2
5
dx
x x 4
(Đề chung_03A )
165.
/4
0
xdx
1 cos2x
(Dự bị_03)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 52
166.
1
32
0
x 1 x dx
(Dự bị_03)
167.
2
/4
0
1 2sin x
dx
1 sin2x
(Đề chung_03B)
168.
2x
ln5
x
ln2
e
dx
e1
(Dự bị_03)
169. Cho hàm số:
x
3
a
f(x) bxe
(x 1)

, tìm a, b biết rằng:
f '(0) 22
và
1
0
f(x)dx 5
. (Dự bị_03)
170.
2
2
0
x x dx
(Đề chung_03D)
171.
2
1
3x
0
x e dx
(Dự bị_03)
172.
2
e
1
x1
ln xdx
x
(Dự bị_03)
173.
2
1
x
dx
1 x 1
(Đề chung_04A)
174.
e
1
1 3ln x.ln x
dx
x
(Đề chung_04B)
175.
3
2
2
ln x x dx
(Đề chung_04D)
176.
/2
0
sin2x sin x
dx
1 3cosx
(Đề chung_05A)
177.
/2
0
sin2x.cosx
dx
1 cosx
(Đề chung_05B)
178.
/2
sin x
0
e cosx cosxdx
(Đề chung_05D)
179.
7
3
0
x2
dx
x1
(Dự bị_05)
180.
/2
2
0
sin xtgxdx
(Dự bị_05)
181.
/2
cosx
0
e sin2xdx
(Dự bị_04)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 53
182.
42
2
2
0
x x 1
dx
x4

(Dự bị_05)
183.
/4
sin x
0
tgx e cosx dx
(Dự bị_05)
184.
e
2
1
x ln xdx
(Dự bị_05)
185.
/2
22
0
sin2x
dx
cos x 4sin x
(Dự bị_05)
186.
6
2
dx
2x 1 4x 1
(Dự bị_06)
187.
1
2x
0
x 2 e dx
(Đề chung_06D)
188.
/2
0
(x 1)sin2xdx
(Dự bị_06)
189.
2
1
x 2 ln xdx
(Dự bị_06)
190.
ln5
xx
ln3
dx
dx
e 2e 3

(Dự bị_06)
191.
10
5
dx
x 2 x 1
(Dự bị_06)
192.
e
1
3 2 ln x
dx
x 1 2ln x
(Dự bị_06)
193.
53
3
2
0
x 2x
dx
x1
(CĐ SP_04A)
194.
3
3
x 2 x 2
(CĐ GTVT_04)
195.
4
2
5
0
x
dx
x1
(CĐ KTKT_04A)
196.
3
3
1
dx
xx
(Dự bị_04)
197.
ln8
x 2x
ln3
e 1.e dx
(Dự bị_04)
198.
2
0
x.sin xdx
(Dự bị_05)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 54
199.
1
0
x 1 xdx
(Dự bị_04)
200.
3
e
2
1
ln x
dx
x ln x 1
(Dự bị_05)
201.
/2
2
0
(2x 1)cos xdx
(Dự bị_05)
THI ĐH 2005 -2008
Bài 1. ĐH, CĐ Khối A – 2005
2
0
cos31
sin2sin
dx
x
xx
I
KQ:
34
27
Bài 2. ĐH, CĐ Khối B – 2005
dx
x
xx
I
2
0
cos1
cos2sin
KQ:
2ln2 1
Bài 3. ĐH, CĐ Khối D – 2005
2
0
sin
coscos
xdxxeI
x
KQ:
e1
4

Bài 4. Tham khảo 2005
dx
x
x
I
7
0
3
1
2
KQ:
141
10
23,1
Bài 5. Tham khảo 2005
3
0
2
sin
xtgxdxI
KQ:
3
ln2
8
Bài 6. Tham khảo 2005
4
0
sin
cos.
dxxetgxI
x
KQ:
1
2
ln 2 e 1
Bài 7. Tham khảo 2005
e
xdxxI
1
2
ln
KQ:
3
21
e
99
Bài 8. CĐ Khối A, B – 2005
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 55
dxxxI
1
0
23
3.
KQ:
6 3 8
5
Bài 9. CĐ Xây Dựng Số 3 – 2005
3
1
313
3
dx
xx
x
I
KQ:
6ln3 8
Bài 10. CĐ GTVT – 2005
dxxxI
1
0
25
1
KQ:
8
105
Bài 11. CĐ Kinh Tế Kỹ Thuật I – 2005
2
0
3
5sin
xdxeI
x
KQ:
3
2
3.e 5
34
Bài 12. CĐ Tài Chính Kế Toán IV – 2005
dxxxI
5
3
0
3
.1
KQ:
848
105
Bài 13. CĐ Truyền Hình Khối A – 2005
4
0
2
2sin1
sin21
dx
x
x
I
KQ:
1
ln2
2
Bài 14. CĐSP Tp.HCM – 2005
0
1
2
42xx
dx
I
KQ:
3
18
Bài 15. CĐ KT-KT Cần Thơ – 2005
e
dx
x
x
I
1
2
ln
KQ:
2
1
e
Bài 16. CĐSP Vĩnh Long – 2005
dx
x
x
I
3
7
0
3
13
1
KQ:
46
15
Bài 17. CĐ Bến Tre – 2005
2
0
1sin
3cos
dx
x
x
I
KQ:
2 3ln2
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 56
Bài 18. CĐSP Sóc Trăng Khối A – 2005
3
0
2
2
2
0
22
cos2sin
sin
2
cos.cos2sin
sin
xx
xdxx
J
x
xx
xdx
I
KQ:
I ln2
3
J
34

Bài 19. CĐ Cộng Đồng Vĩnh Long – 2005
e
xdxxI
1
ln
KQ:
2
e1
4
Bài 20. CĐ Công Nghiệp Hà Nội – 2005
dxxxI sin
4
0
2
KQ:
2
4
2
Bài 21. CĐSP Hà Nội – 2005
dx
x
xxx
I
2
0
2
23
4
942
KQ:
6
8
Bài 22. CĐ Tài Chính – 2005
1
0
3
1x
xdx
I
KQ:
1
8
Bài 23. CĐSP Vĩnh Phúc – 2005
e
xx
dx
I
1
2
ln1
KQ:
6
Bài 24. CĐSP Hà Nội – 2005
2
0
20042004
2004
cossin
sin
dx
xx
x
I
KQ:
4
Bài 25. CĐSP KonTum – 2005
2
0
3
cos1
sin4
dx
x
x
I
KQ: 2
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 57
NĂM 2006
Bài 1. ĐH, CĐ Khối A – 2006
2
22
0
sin2x
I dx
cos x 4sin x
KQ:
2
3
Bài 2. Tham khảo 2006
6
2
dx
I
2x 1 4x 1
KQ:
31
ln
2 12
Bài 3. ĐH, CĐ Khối D – 2006
1
2x
0
I x 2 e dx
KQ:
2
5 3e
2
Bài 4. Tham khảo 2006
2
0
I x 1 sin2xdx

KQ:
1
4
Bài 5. Tham khảo 2006
2
1
I x 2 lnxdx
KQ:
5
ln4
4
Bài 6. ĐH, CĐ Khối B – 2006
ln5
xx
ln3
dx
I
e 2e 3

KQ:
3
ln
2
Bài 7. Tham khảo 2006
10
5
dx
I
x 2 x 1

KQ:
2ln2 1
Bài 8. Tham khảo 2006
e
1
3 2lnx
I dx
x 1 2lnx
KQ:
10 11
2
33
Bài 9. CĐ KTKT Công Nghiệp II – 2006
1
2
0
I xln 1 x dx
KQ:
1
ln2
2
(Đổi biến
2
t 1 x
, từng phần)
Bài 10. CĐ Cơ Khí – Luyện Kim – 2006
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 58
2
2
1
ln 1 x
I dx
x
KQ:
3
3ln2 ln3
2
Bài 11. CĐ Nông Lâm – 2006
1
2
0
I x x 1dx
KQ:
2 2 1
3
Bài 12. ĐH Hải Phòng – 2006
1
2
0
x
I dx
1x
KQ:
1
ln2
2
Bài 13. CĐ Y Tế – 2006
2
4
sinx cosx
I dx
1 sin2x
KQ:
ln 2
Bài 14. CĐ Tài Chính Kế Toán – 2006
3
2
0
I xln x 5 dx
KQ:
1
14ln14 5ln5 9
2

Bài 15. CĐ Sƣ Phạm Hải Dƣơng – 2006
2
3
0
cos2x
I dx
sinx cosx 3

KQ:
1
32
Bài 16. Hệ CĐ – ĐH Hùng Vƣơng – 2006
4
0
I x 1 cosxdx

KQ:
2
1
8
Bài 17. CĐ KTKT Đông Du – 2006
4
0
cos2x
I dx
1 2sin2x
KQ:
1
ln3
4
Bài 18. CĐ Sƣ Phạm Quảng Bình – 2006
ln2
2x
x
0
e
I dx
e2
KQ:
8
23
3
Bài 19. CĐ Sƣ Phạm Quảng Ngãi – 2006
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 59
3
2
0
4sin x
I dx
1 cosx
KQ: 2
Bài 20. CĐ Sƣ Phạm Trà Vinh – 2006
4
2
0
x
I dx
cos x
KQ:
2
ln
42
Bài 21. CĐ Bán Công – Công Nghệ - Tp.HCM – 2006
3
1
x3
I dx
3 x 1 x 3
KQ:
6ln3 8
Bài 22. CĐ Sƣ Phạm Tiền Giang – 2006
9
3
1
I x. 1 x dx
KQ:
468
7
Bài 23. CĐ Bến Tre – 2006
e
3
1
x1
I lnxdx
x



KQ:
3
2e 11
9 18
Bài 24.
1
23
0
I x 2 x dx
KQ:
2
3 3 2 2
9
Bài 25.
2
0
2
cos12
xdxxI
KQ:
2
1
1
2 4 2





Bài 26.
1
0
3
2
1 dxxexI
x
KQ:
2
e1
4 14
Bài 27. CĐ KT-KT Công Nghiệp I – 2006
2
0
sin3x
I dx
2cos3x 1
KQ: Không tồn tại
Bài 28. CĐ KT-KT Công Nghiệp II – 2006
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 60
1
2
0
I xln 1 x dx
KQ:
1
ln2
2
Bài 29. CĐ Xây dựng số 2 – 2006
2
1
x x 1
I dx
x5
KQ:
32
10ln3
3
Bài 30. CĐ Xây dựng số 3 – 2006
1
3
0
I x cos x sinxdx
KQ:
5
4
Bài 31. CĐ GTVT III – 2006
2
0
cosx
I dx
5 2sinx
KQ:
15
ln
23
2
0
J 2x 7 ln x 1 dx
KQ:
24ln3 14
Bài 32. CĐ Kinh tế đối ngoại – 2006
4
8
0
I 1 tg x dx

KQ:
76
105
Bài 33. CĐSP Hƣng Yên - Khối A– 2006
4
2
3
4x 3
I dx
x 3x 2

KQ:
18ln2 7ln3
Bài 34. CĐSP Hƣng Yên - Khối B– 2006
3
6
0
sin3x sin 3x
I dx
1 cos3x
KQ:
11
ln2
63

Bài 35. CĐSP Hƣng Yên - Khối D
1
, M– 2006
e
3
2
1
lnx 2 ln x
I dx
x
KQ:
32
3
3 3 2 2
8
Bài 36. CĐ Bán công Hoa Sen – Khối A – 2006
4
44
0
I cos x sin x dx

KQ:
1
2
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 61
Bài 37. CĐ Bán công Hoa Sen – Khối D – 2006
4
0
cos2 x
I dx
1 2sin2x
KQ:
1
ln3
4
Bài 38. CĐSP Trung Ƣơng – 2006
2
0
I sinxsin2xdx
KQ:
2
3
Bài 39. CĐSP Hà Nam – Khối A – 2006
1
2
0
x
I dx
x3
KQ :
41
ln
34
Bài 40. CĐSP Hà Nam – Khối M – 2006
2
2
1
I x cosxdx
KQ:
2
2
4
Bài 41. CĐSP Hà Nam – Khối A (DB) – 2006
e
2
1
dx
I
x 1 ln x
KQ:
4
Bài 42. CĐKT Y Tế I – 2006
2
4
sinx cosx
I dx
1 sin2x
KQ:
ln 2
Bài 43. CĐ Tài Chính Hải Quan – 2006
3
4
ln tgx
I dx
sin2x
KQ:
2
1
ln 3
16
Bài 44. CĐ Kĩ thuật Cao Thắng – 2006
2
3
2
0
I sin2x 1 sin x dx

KQ:
15
4
Bài 45. CĐKT Tp.HCM Khóa II - 2006
e
0
lnx
I dx
x
KQ:
4 2 e
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 62
Bài 46. CĐCN Thực phẩm Tp.HCM – 2006
1
2
0
1
I dx
x 2x 2

KQ:
4
Bài 47. CĐ Điện lực Tp.HCM – 2006
7
3
3
0
x2
I dx
3x 1
KQ:
46
15
Bài 48. CĐ Kinh tế công nghệ Tp.HCM Khối A– 2006
4
2
0
x
I dx
cos x
KQ:
2
ln
42
Bài 49. CĐ Kinh tế công nghệ Tp.HCM Khối D
1
– 2006
2
1
I 4x 1 lnxdx
KQ:
6ln2 2
Bài 50. CĐSP Hà Nội Khối D
1
– 2006
3
6
dx
I
sinx.sin x
3



KQ:
2
ln2
3
.
NĂM 2007
Bài 1. ĐH, CĐ khối A – 2007
Tính diện tích hình phẳng giới hạn bởi các đƣờng:
x
y e 1 x, y 1 e x
.
KQ:
1
2
e
Bài 2. ĐH, CĐ khối B – 2007
Cho hình phẳng H giới hạn bởi các đƣờng
y xlnx
,
y 0, y e
. Tính thể tích của khối tròn xoay
tạo thành khi quay hình H quanh trục Ox.
KQ:
3
5e 2
27
Bài 3. ĐH, CĐ khối D – 2007
Tính tích phân
e
32
1
I x ln xdx
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 63
KQ:
4
5e 1
32
Bài 4. Tham khảo khối A – 2007
4
0
2x 1
dx
1 2x 1

KQ:
2 ln2
Bài 5. Tham khảo khối B – 2007
Tính diện tích hình phẳng giới hạn bởi các đƣờng
2
1
0 à
1

xx
y v y
x
. KQ:
1
ln2 1
42

Bài 6. Tham khảo khối B – 2007
Tính diện tích hình phẳng giới hạn bởi các đƣờng
22
à2 y x v y x
. KQ:
1
23
Bài 7. Tham khảo khối D – 2007
1
2
0
x x 1
dx
x4
KQ:
3
1 ln2 ln3
2

Bài 8. Tham khảo khối D – 2007
2
2
0
x cosxdx
KQ:
2
2
4
Bài 9. CĐSPTW – 2007
Tính diện tích hình phẳng giới hạn bởi các đƣờng có phƣơng trình
2
y x 2
;
y x; x 1; x 0
.
KQ:
7
6
Bài 10. CĐ GTVT – 2007
3
2
0
4cos x
dx
1 sin x
KQ: 2
Bài 11. CĐDL Công nghệ thông tin Tp.HCM – 2007
7
3
0
x2
dx
x1
KQ:
231
10
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 64
Bài 12. CĐ Khối A – 2007
2007
1
2
1
3
11
1 dx
xx



KQ:
2008 2008
32
2008
Bài 13. CĐ Cơ khí luyện kim – 2007
e
2
1
x ln x dx
KQ:
3
1
5e 2
27
Bài 14. CĐSP Vĩnh Phúc – 2007
4
2
1
x sin x dx
KQ:
32
1
384 32 4


Bài 15. CĐ Khối B – 2007
Tính diện tích hình phẳng giới hạn bởi các đƣờng
,
2
y x cos x
,
x0
,
x 
.
KQ:
2
Bài 16. CĐ Khối D – 2007
0
2
x 1 dx
KQ: 1
Bài 17. CĐ Dệt may thời trang Tp.HCM – 2007
3
22
1
dx
x x 1
KQ:
3
1
3 12

Bài 18. CĐ Hàng hải – 2007
3
3
2
1
x x 1dx
KQ:
14 3
5
Bài 19. CĐ Kinh tế kĩ thuật Thái Bình – 2007
0
2x
1
x e x 1 dx

KQ:
2
3 31
e
4 60
Bài 20. CĐ Công nghiệp Phúc Yên – 2007
1
x
0
xe dx
KQ: 1
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 65
NĂM 2008
Bài 1) Tính I =
4
0
6
tan
cos
x
dx
x
- ĐH, CĐ Khối A – 2008 KQ:
1 10
ln 2 3
2
93

Bài 2) Tính I =
4
0
sin
4
sin2 2 1 sin cos
x dx
x x x



- ĐH, CĐ Khối B – 2008 KQ:
4 3 2
4
Bài 3) Tính I =
2
3
1
ln x
dx
x
- ĐH, CĐ Khối D – 2008 KQ:
3 2ln2
16
Bài 4) Tính I =
3
3
2
22
xdx
x
- Dự bị 1 - khối A-2008 KQ:
3
3 12
5 36
45



Bài 5) Tính
/2
0
sin2
3 4sin os2
xdx
I
x c x

- Dự bị 2 - khối A-2008 KQ:
1
ln2
2

Bài 6) Tính
2
0
( 1)
41
x dx
I
x
- Dự bị 1 - khối B-2008
Bài 7) Tính
1
3
2
0
4
x dx
I
x
- Dự bị 2 - khối B-2008
Bài 8) Tính
1
2
2
0
.
4
x
x
I x e dx
x




- Dự bị 1 - khối D-2008
Bài 9) CĐ Khối A, B, D – 2008. Tính diện tích hình phẳng giới hạn bởi parabol
2
:4P y x x
và đƣờng thẳng
:d y x
. KQ:
9
2
(đvdt)
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 66
NĂM 2009
Bài 1) Tính I =
2
32
0
(cos 1)cosx xdx
- ĐHKA-2009 KQ:
45
8
Bài 2) Tính I =
3
1
2
1
ln3
dx
x
x
- ĐHKB-2009 KQ:
)
16
27
ln3(
4
1
Bài 3) Tính I =
3
1
1
1
dx
e
x
- ĐHKD-2009 KQ: ln(e
2
+e+1) – 2
NĂM 2010
Bài 1) Tính I =
1
22
0
2
12
xx
x
x e x e
dx
e

- ĐHKA-2010 KQ:
1 1 1 2
ln
3 2 3
e



Bài 2) Tính I =
2
1
ln
(2 ln )
e
xdx
xx
- ĐHKB-2010 KQ:
13
ln
32

Bài 3) Tính I =
1
3
2 ln
e
I x xdx
x




- ĐHKD-2010 KQ:
2
1
2
e
NĂM 2011
Bài 1) Tính I =
4
0
sin ( 1)cos
sin cos
x x x x
dx
x x x

- ĐHKA-2011 KQ:
2
ln 1
4 2 4









Bài 2) Tính I =
3
2
0
1 sin
os
xx
dx
cx
- ĐHKB-2011 KQ:
2
3 ln(2 3)
3
Bài 3) Tính I =
4
0
41
2 1 2
x
dx
x

- ĐHKD-2011 KQ:
34 3
10ln
35
NĂM 2012
Bài 1) Tính tích phân
3
2
1
1 ln( 1)x
I dx
x

- KA-2012 KQ:
22
ln2 ln3
33

Bài 2) Tính tích phân
1
3
42
0
.
32
x
I dx
xx

- ĐHKB-2012 KQ:
1
2ln3 3ln2
2
Nguyên hàm và tích phân
Nguyễn Chiến chienmath43@gmail.com
Nguyễn Chiến: 0973.514.674 67
Bài 3) Tính tích phân
/4
0
I x(1 sin2x)dx

- ĐHKD-2012 KQ:
2
1
32 4
NĂM 2013
Bài 1) Tính tích phân
2
2
2
1
1
ln
x
I xdx
x
- ĐHKA-2013 KQ:
53
ln2
22
Bài 2) Tính tích phân
1
2
0
2I x x dx
- ĐHKB-2013 KQ:
2 2 1
3
Bài 3) Tính tích phân
1
2
2
0
( 1)
1
x
I dx
x
- ĐHKD-2013 KQ:
1 ln2
NĂM 2014
Bài 1) Tính diện tích hình phẳng giới hạn bởi đƣờng cong
2
y x x 3
và
đƣờng thẳng
y 2x 1
- ĐHKA-2014 KQ:
1
6
Bài 2) Tính tích phân
2
2
2
1
31
xx
dx
xx
- ĐHKB-2014 KQ:
1 ln3
Bài 3) Tính tích phân I =
4
0
(x 1)sin2xdx
.- ĐHKD-2014 KQ:
3
4
NĂM 2015
Bài 1) THPTQG 2015 Tính tích phân
x
x 3 e d
1
0
I = ( - ) x
KQ:
43e
Bài 2) Dự bị THPTQG 2015 Tính tích phân
3
0
1
x
I dx
x
KQ:
8
3
NĂM 2016
THPTQG 2016 Tính tích phân
3
2
0
3 16I x x x dx
KQ:
88
| 1/67
| | Tải xuống

Có thể bạn quan tâm:

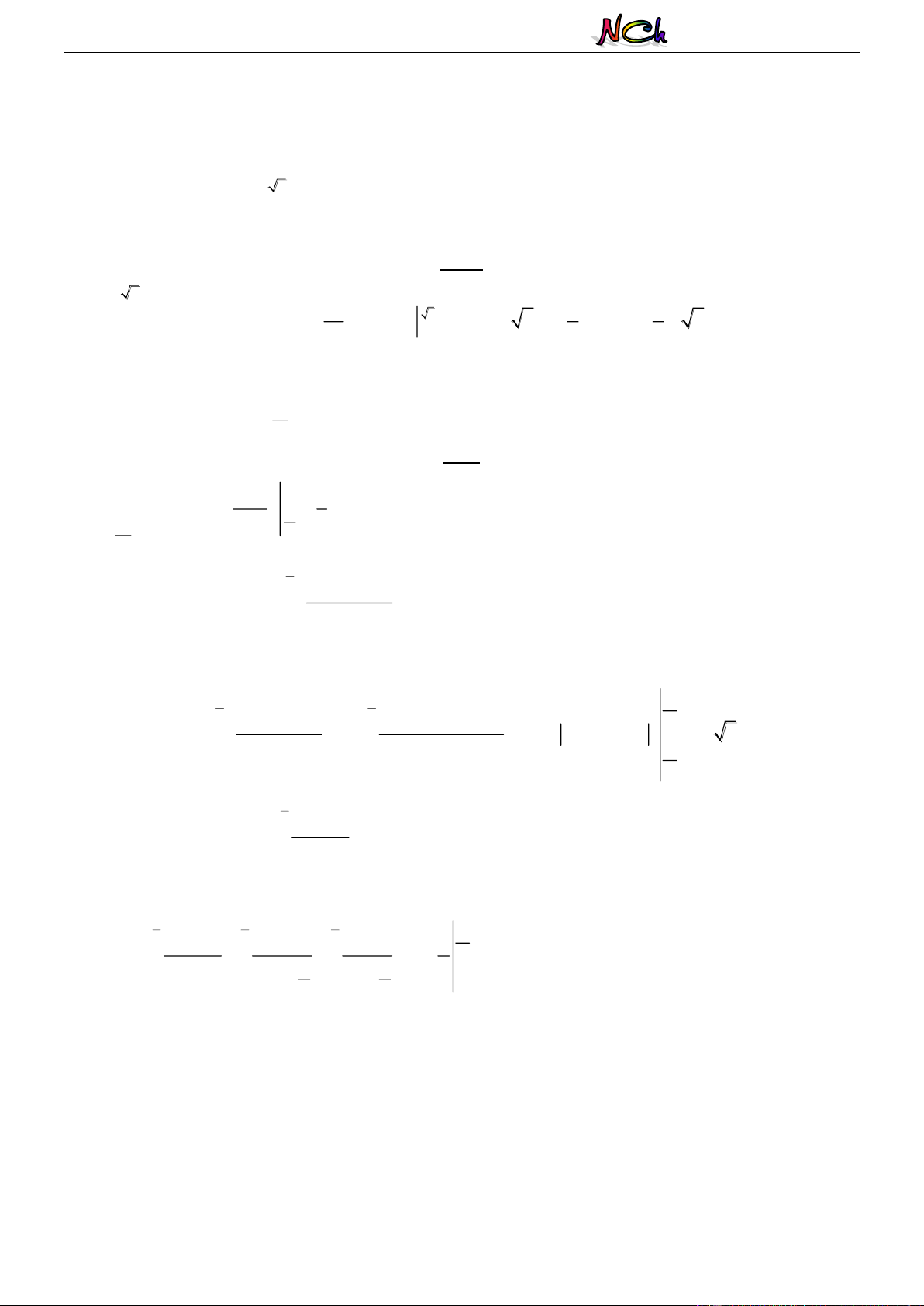
Preview text:

Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
NGUYÊN HÀM - TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN I. NGUYÊN HÀM 1. Nguyên hàm
Định nghĩa: Cho hàm số f x xác định trên K ( K là khoảng, đoạn hay nửa khoảng). Hàm số F x
được gọi là nguyên hàm của hàm số f x trên K nếu F 'x  f x với mọi xK . Kí hiệu: f  x x
d F x  C . Định lí:
1) Nếu F x là một nguyên hàm của f x trên K thì với mỗi hằng số C , hàm số
G x  F x  C cũng là một nguyên hàm của f x trên K .
2) Nếu F x là một nguyên hàm của hàm số f x trên K thì mọi nguyên hàm của f x trên
K đều có dạng F x  C , với C là một hằng số.
Do đó F x  C,C  là họ tất cả các nguyên hàm của f x trên K .
2. Tính chất của nguyên hàm    f  x x
d   f x và f '  x x
d f x  C ; d f
 xdx  f xdx
 Nếu F(x) có đạo hàm thì: d
 F(x)  F(x)C kf  x x d k f  x x
d với k là hằng số khác 0 .   f
 x gx x d f   x x d g  x x d
Công thức đổi biến số: Cho y f u và u g x.
Nếu f (x)dx F(x)  C  thì f
 g(x)g'(x)dx f (u)du
F(u)  C
3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f x liên tục trên K đều có nguyên hàm trên K .
Nguyễn Chiến: 0973.514.674 1
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
BẢNG NGUYÊN HÀM CÁC HÀM SỐ THƢỜNG GẶP 1. 0dx C
2. dx x C    1    3. 1 x dx xC      1  ax b         1 16. ax b   1 1 dx c , 1  a  1 1 1 1 1 1 4. dx    C  17. dx   .  C  2 x xax b2 a ax b 1 dx 1 5.
dx  ln x C  18.
 ln ax b Cx ax b a 6. x x
e dx e Caxb 1  19. ax b e dx eCa x aa kx b 1 kx b 7. x a dx   C  20. a dx   C  ln a k ln a
8. cos xdx  sin x C  1 21. cos
 axbdx  sinaxbC a
9. sin xdx   co s x C  1 22. sin
 axbdx   cosaxbC a 10. tan .
x dx   ln | cos x | C   1 23. tan
 axbdx   ln cosaxb C a 11. cot .
x dx  ln | sin x | C   1 24. cot
 axbdx  ln sinaxb C a 1 1 1 12.
dx  tan x C  25. dx
tan ax b C  2 cos x 2
cos ax b   a 1 1 1 13.
dx   cot x C  26. dx  
cot ax b C  2 sin x 2
sin ax b   a 14.  2
1 tan xdx  tan x C 1 27.  2
1 tan ax bdx  tan ax b  C a 15.  2
1 cot xdx  cot x C 1 28.  2
1 cot ax bdx   cot ax b  C a
BẢNG NGUYÊN HÀM MỞ RỘNG dx 1 xx x arctan  C  2 2 arcsin dx x arcsin
a x C  2 2 a x a a a a dx 1 a xx x ln  C  2 2 arccos dx x arccos
a x C  2 2 a x 2a a x a a dxx x a ln  2 2
x x a   Cdx x    2 2 arctan arctan
ln a x   C 2 2 x a a a 2 dx xx x a arcsin  Cdx x    2 2 arc cot arc cot
ln a x   C 2 2  a a x a a 2 dx 1 x   dx 1 ax b arccos  C   ln tan  C  2 2  a a x x a
sin ax ba 2 2 2 dx 1
a x a    dx 1 ax b ln  C    C
sin ax b ln tan 2 2  a x a 2 x x ab ax e a bx b bx ax  cos sin  ln
 axbdx  x lnaxb xc    e cos bx dx Ca  2 2 a b 2 2 2 ax x a x a x e a bx b bx ax  sin cos  2 2 a x dx   arcsin  Ce sin bx dx   C  2 2 a 2 2 a b
Nguyễn Chiến: 0973.514.674 2
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
CÁC PHƢƠNG PHÁP TÍNH NGUYÊN HÀM
1. PHƢƠNG PHÁP ĐỔI BIẾN
a. Đổi biến dạng 1: Nếu
f (x)  F(x)  C
và với u   t  là hàm số có đạo hàm thì : f (u)du F(u)  CPHƢƠNG PHÁP CHUNG
 Bước 1: Chọn x   t , trong đó  t là hàm số mà ta chọn thích hợp .
 Bước 2: Lấy vi phân hai vế : dx   'tdt
 Bước 3: Biến đổi : f (x)dx f   t '
 tdt g tdt
 Bước 4: Khi đó tính : f (x)dx g(t)dt G(t)  C   .
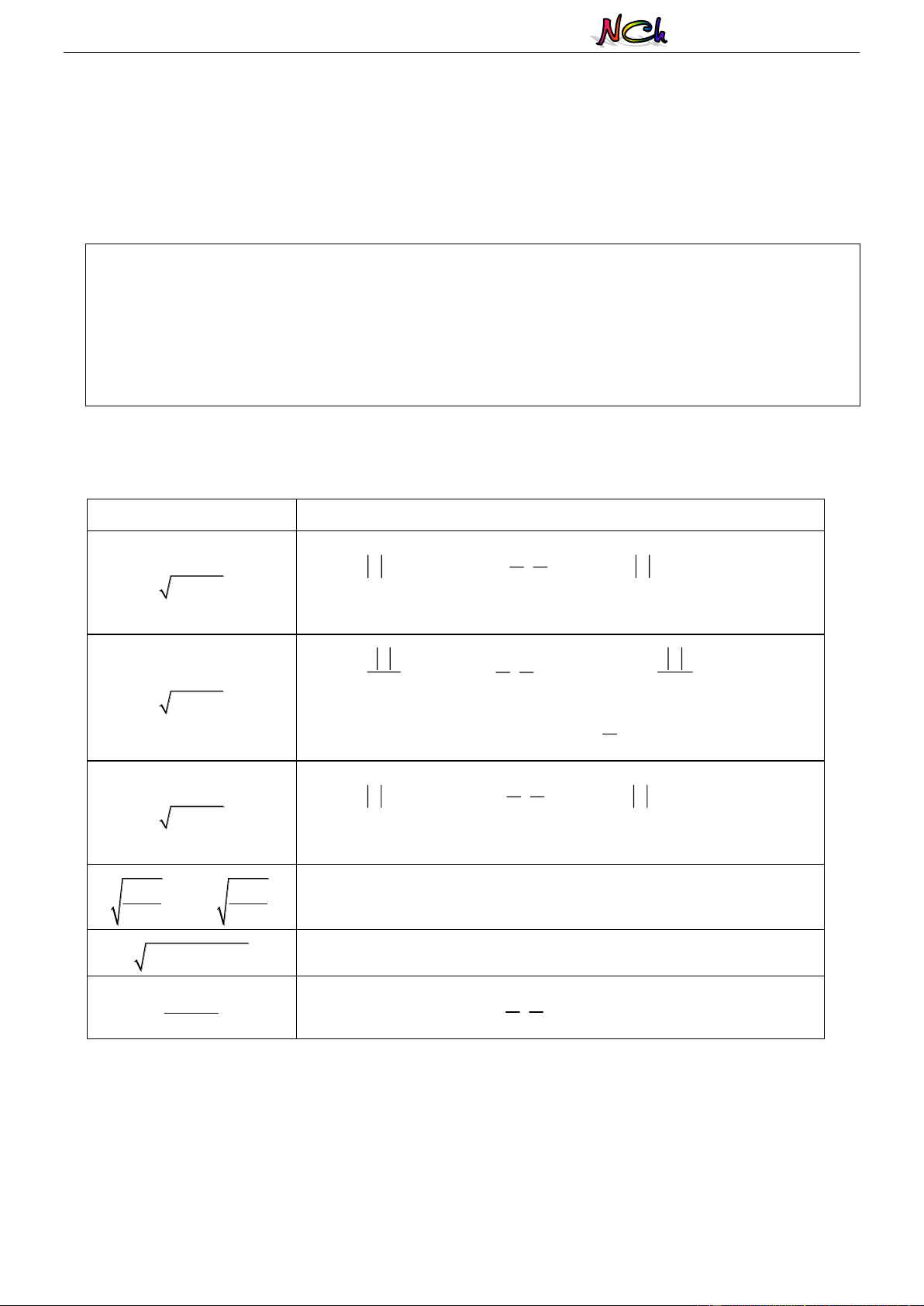
* Các dấu hiệu đổi biến thƣờng gặp : Dấu hiệu Cách chọn    
Đặt x a sin t ; với t   ; . 
 hoặc x a cost ; 2 2  2 2  a x
với t 0; . a     a Đặt x  . ; với t   ; \   0   hoặc x  sin t  2 2  cos t 2 2 x a  
với t 0;  \  .  2     
Đặt x a tan t ; với t   ; . 
 hoặc x a cot t 2 2  2 2  a x
với t 0; . a x a x . hoặc .
Đặt x a cos 2t a x a x
x abx Đặt 2
x a  (b – a)sin t 1    
Đặt x a tan t ; với t   ; .   2 2 a x  2 2 
b. Đổi biến dạng 2:
Nếu hàm số f x liên tục thì đặt x   t  . Trong đó  t  cùng với đạo hàm của nó ( 't  là
những hàm số liên tục) thì ta được :
f (x)dx f      t'
 tdt g(t)dt G(t)  C  .
Nguyễn Chiến: 0973.514.674 3
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com PHƢƠNG PHÁP CHUNG.
 Bước 1: Chọn t   x . Với  x là hàm số mà ta chọn thích hợp.
 Bước 2: Tính vi phân hai vế : dt   'tdt .
 Bước 3: Biểu thị : f (x)dx f   t '
 tdt g(t)dt .
 Bước 4: Khi đó : I f (x)dx g(t)dt G(t)  C  
* Các dấu hiệu đổi biến thƣờng gặp : Dấu hiệu Cách chọn Hàm số mẫu số có t là mẫu số Hàm số : f  ; x  x
t    xa x  x  Hàm f x .s inx+b.cosx  t  tan ; o c s  0   . c s inx+d.cosx+e 2  2  1
Với : x a  0 và x b  0 .
Hàm f x  
x a x b
 Đặt : t x a x b
Với x a  0 và x b  0 . Đặt : t
x a  x b
2. NGUYÊN HÀM TỪNG PHẦN
Nếu u(x) , v(x) là hai hàm số có đạo hàm liên tục trên K:
u(x).v '(x)dx u(x).v(x)  v(x).u '(x)dx  
Hay udv uv vdu
 ( với du  ’uxd ,x dv  ’vxdx ) PHƢƠNG PHÁP CHUNG
 Bước 1: Ta biến đổi tích phân ban đầu về dạng : I
f (x)dx
f (x). f (x)dx   1 2  
du f ' (x) ( ) dx u f x  1  Bước 2: Đặt : 1   
dv f (x) v f (x)dx  2  2    Bước 3: Khi đó: . u dv  . u v  . v du   sin  x   
Dạng I: I P(x) 
cos x.dx   x e  
Nguyễn Chiến: 0973.514.674 4
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com u   P(x) u
 '.du P '(x)dx    si  n x    cos x Đặt        dv   cos x.dx v  sin   x        x e    x e    cos x cos x    
Vậy I P(x) sin  x - sin
 x .P'(x)dx     xexe
Dạng II: I P(x).ln xdx u   ln x  1  du dx  Đặ 1 t   x  Vậy I ln .
x Q x  Q(x). dx    x
dv P(x)dx
v P(x)dx Q(x)   s  in x Dạng III x I e   dx cos x   x u   e   x du e dx   Đặt  sin  x    cos xdv    .dx v     cos x    sin x    cos x cos x Vậy x I e   - x  edx . sin x   sin x   cos x
Bằng phương pháp tương tự tính được x  e
dx sau đó thay vào I ra kết quả. sin x  
Nguyễn Chiến: 0973.514.674 5
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com TÍCH PHÂN
1. CÔNG THỨC TÍNH TÍCH PHÂN b b
f (x)dx F (x)  F (b)  F (a)  . a a b b
* Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi f (x)dx  hay f (t)dt  . Tích phân đó a a
chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
2. TÍNH CHẤT CỦA TÍCH PHÂN
Giả sử cho hai hàm số f (x) và g(x) liên tục trên K . a,b,c là ba số bất kỳ thuộc K. Khi đó ta có : a
1. f (x)dx  0  a b a
2. f (x)dx   f (x)dx   . a b b c b
3. f (x)dx
f (x)dx f (x)dx    a a c b b b
4.  f (x)  g(x)dx f (x)dx g(x)dx   . a a a b b
5. kf (x)dx k. f (x)dx   . a a b
6. Nếu f (x)  0, x   ;
a b thì : f (x)dx  0 x     ;aba b b 7. Nếu x   ;
a b: f (x)  g(x)  f (x)dx g(x)dx   . a a b 8. Nếu x   ;
a b Nếu M f (x)  N thì M b a  f (x)dx N  b a. a
PHƢƠNG PHÁP TÍNH TÍCH PHÂN I. ĐỔI BIẾN
a. Phƣơng pháp đổi biến số dạng 1.
Định lí . Nếu 1) Hàm x u(t) có đạo hàm liên tục trên ;  .
2) Hàm hợp f (u(t)) được xác định trên ;  . 3) u()  ,
a u( )  b . b  Khi đó: ' I
f (x)dx
f (u(t))u (t)dt   . a
Nguyễn Chiến: 0973.514.674 6
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com PHƢƠNG PHÁP CHUNG
Bước 1: Đặt x u t
Bước 2: Tính vi phân hai vế : x u(t)  dx u '(t)dt x b t   Đổi cận:  x a t  
Bước 3: Chuyển tích phân đã cho sang tích phân theo biến t b    Vậy: I
f (x)dx f
 u(t)u'(t)dt g(t)dt
G(t)  G( )  G()  a  
b. Phương pháp đổi biến dạng 2
Định lí: Nếu hàm số u u(x) đơn điệu và có đạo hàm liên tục trên đoạn  ; a b sao cho
f (x)dx g u(x)u '(x)dx g(u)du thì: b u (b) I
f (x)dx g(u)du   . a u (a) PHƢƠNG PHÁP CHUNGBƣớc 1: Đặt '
u u(x)  du u ( ) x dx    x b u u(b)
Bƣớc 2: Đổi cận :  x a
u u(a)
Bƣớc 3: Chuyển tích phân đã cho sang tích phân theo u b b u (b) Vậy: I
f (x)dx g
 u(x).u'(x)dx g(u)dua a u (a)
II. TÍCH PHÂN TỪNG PHẦN
Định lí . Nếu u(x) và v(x) là các hàm số có đạo hàm liên tục trên  ; a b thì: b b b b b ' u x v x dx   u x v x  ' ( ) ( ) ( ) ( )
v(x)u (x)dx  Hay udvbuv vdua a a a a a PHƢƠNG PHÁP CHUNG
Bƣớc 1: Viết f (x)dx dưới dạng '
udv uv dx bằng cách chọn một phần thích hợp của
f (x) làm u(x) và phần còn lại dv v '(x)dx
Bƣớc 2: Tính du u 'dx và v dv
  v'(x)dxbb
Bƣớc 3: Tính vu '(x)dx  và uv a a
Nguyễn Chiến: 0973.514.674 7
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
Cách đặt u và dv trong phƣơng pháp tích phân từng phần.
Đặt u theo thứ tự ưu tiên: b b b b P(x) x e dx
P(x) ln xdx
P(x) cos xdxx e cos xdx
Lốc-đa-mũ-lượng a a a a u P(x) lnx P(x) x e dv x e dx P(x)dx cosxdx cosxdx
Chú ý: Nên chọn u là phần của f (x) mà khi lấy đạo hàm thì đơn giản, chọn '
dv v dx là phần của
f (x)dx là vi phân một hàm số đã biết hoặc có nguyên hàm dễ tìm.
TÍCH PHÂN CÁC HÀM SỐ SƠ CẤP CƠ BẢN
1. Tích phân hàm hữu tỉ    dx 1 adx 1 Dạng 1: I    ln ax b  
( với a  0 ) ax b a ax b a      dx 1 k 1    Chú ý: Nếu k 1 I  
(ax b) .adx  .(ax b)   
(ax b)k a a(1 k)    dx Dạng 2: I a  0  ( 2
ax bx c  0 với mọi x ;   ) 2  
ax bx c  Xét 2
  b  4ac . b    b   
+ Nếu   0 : x  ; x  1 2 2a 2a 1 1 1  1 1       thì : 2
ax bx c
a(x x )(x x )
a(x x ) x x x x   1 2 1 2 1 2  1  1 1  1  1 x x1  I    dx
ln x x  ln x x   ln  1 2 
a(x x ) x x x x
a(x x ) 
a(x x ) x x    1 2  1 2 1 2 1 2 2   1 1  b   dx 1 dx 1  + Nếu   0 :  x    thì I       2 2 0 
ax bx c
a(x x )  2a  2 2
ax bx c
a (x x )
a(x x ) 0   0 0   dx dx
+ Nếu   0 thì I     2 2 2
ax bx c      b     a x        2  2a  4a        Đặ b 1 t x   tan t dx   2 1 tan t dt 2 2  2a 4a 2 amx n Dạng 3: I dx,  a  0 . 2
ax bx c   (trong đó mx n f (x) 
liên tục trên đoạn ;  ) 2
ax bx c
Nguyễn Chiến: 0973.514.674 8
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
+) Bằng phương pháp đồng nhất hệ số, ta tìm A và B sao cho: 2 mx n (
A ax bx c) ' B ( A 2ax  ) b B     2 2 2
ax bx c
ax bx c
ax bx c 2 2
ax bx c
ax bx c    mx n (
A 2ax b) B +) Ta có I dx dx dx    2 2 2
ax bx c
ax bx c
ax bx c     (
A 2ax b)  . Tích phân 2
dx Aln ax bx c  2
ax bx c    dx Tích phân  thuộc dạng 2. 2
ax bx cb P(x)
Tính tích phân I dx
với P(x) và Q(x) là đa thức của x. Q(x) a
 Nếu bậc của P(x) lớn hơn hoặc bằng bậc của Q(x) thì dùng phép chia đa thức.
 Nếu bậc của P(x) nhỏ hơn bậc của Q(x) thì xét các trường hợp:
+ Khi Q(x) chỉ có nghiệm đơn  , ,..., thì đặt 1 2 n P(x) A A A 1 2   ... n  . Q(x) x  x  x  1 2 n
+ Khi Q(x) có nghiệm đơn và vô nghiệm Q x   x   2
x px q 2 ( )
,   p  4q  0 thì đặt P(x) A Bx C   . 2 Q(x) x 
x px q
+ Khi Q(x) có nghiệm bội 2 (
Q x)  (x )(x   ) với    thì đặt: P(x) A B C    . Q(x) x  x   x   2 2 3 (
Q x)  (x ) (x   ) với    thì đặt: P(x) A B C D E      . 2 3 2 3 2
(x  ) (x   ) (x  ) (x  ) (x   ) (x   ) x  
2. Tích phân hàm vô tỉ b
R(x, f (x))dx  trong đó R( ,
x f (x)) có dạng: aa x     +) R x,  
 . Đặt x acos 2t , t  0;   a x    2  +) R  2 2 , x
a x . Đặt x a sint hoặc x a cost ax b ax b
+) R x, n    . Đặt n t cx d   cx d
Nguyễn Chiến: 0973.514.674 9
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 1 +) R  , x f (x)  2
(ax b)  x   x   1 Với  2
x   x  '  k ax b . Đặt 2
t   x   x   hoặc t ax b     +) R  2 2 , x
a x . Đặt x a tant , t   ;    2 2  a   +) R  2 2 , x
x a . Đặt x
, t 0;  \   cos x  2  +) R n n n 1 2 x;
x;...; i x Gọi k BSCNN n ; n ; ...; n . Đặt  k x t 1 2 i   1
a. Tích phân dạng : I dx  a  0 2  ax  bx cb x   u 2      b  2a Từ : 2
f(x)=ax  bx c a x         du dx 2  2a  4a       K  2a Khi đó ta có : * Nếu  
a   f x a  2 2 u k  2 2 0, 0 ( )
f (x)  a. u k (1) a  0 2  b  
* Nếu :   0  f (x)  a x      b (2)  2a
f (x)  a x   a. u  2a * Nếu :   0 .
+ Với a  0 : f (x)  a x x x x
f (x)  a. x x x x (3) 1   2   1   2 
+ Với a  0 : f (x)  a x x x x f ( ) x  a. x x x x (4) 1  2   1  2 
Căn cứ vào phân tích trên , ta có một số cách giải sau :  Phƣơng pháp :
* Trường hợp :   a   f x a 2 2 u k  2 2 0, 0 ( )
f (x)  a. u k Khi đó đặt : 2
ax  bx c t a.x 2  t c 2 x  ; dx tdt  2     b  2 bx c t 2 a ax  b2 a              2 x t t , x t t  0 1  t c
t a.x t a   b  2 aa  0 2    * Trườ b
ng hợp :   0  f (x)  a x      b  2a
f (x)  a x   a. u  2a
Nguyễn Chiến: 0973.514.674 10
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com  1  b   b  ln x  : x   0     1 1 1 a  2a   2a Khi đó :  I dx dx    b      a b  1 b b a x x   ln x  : x   0 2a 2a    a  2a   2a
* Trường hợp :   0, a  0 x x t 1  - Đặt : 2
ax  bx c a x x x x   1   2 
x x t 2 
* Trường hợp :   0, a  0 x x t 1  - Đặt : 2
ax  bx c a x x x x   1
 2  x x t 2   mx n
b. Tích phân dạng : I dx  a  0 2  ax  bx cPhƣơng pháp : . A d   2 ax  bx c mx n+Bướ B
c 1: Phân tích f (x)      1 2 2 2 ax  bx c ax  bx c ax  bx c
+Bước 2: Quy đồng mẫu số , sau đó đồng nhất hệ số hai tử số để suy ra hệ hai ẩn số A,B
+Bước 3: Giải hệ tìm A,B thay vào (1)   +Bướ 1
c4 : Tính I  2A 2
ax  bx c   B dx  (2) 2   ax  bx c  Trong đó 1 dx
a  0 đã biết cách tính ở trên. 2  ax  bx c  1
c. Tích phân dạng : I dx  a  0
 mx n 2 ax  bx cPhƣơng pháp : +Bướ 1 1 c 1: Phân tích :   . (1) mx n 2    n  2 ax bx c m x  ax  bx c    m   1  n  1 y t   dy   dx    x t   m x t +Bướ 1 n c 2: Đặt :  x    2 y m  1  1   1  2 x
t  ax  bx c at bt c      y   y   y   ' +Bướ dy
c 3: Thay tất cả vào (1) thì I có dạng : I    . 2    ' Ly My N
Tích phân này chúng ta đã biết cách tính .
Nguyễn Chiến: 0973.514.674 11
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com     x   
d. Tích phân dạng : I R
  ;x ydx R   ;xmdx    x       ( Trong đó : R ;
x y là hàm số hữu tỷ đối với hai biến số ,
x y và ,  , , là các hằng số đã biết )
Phương pháp :    +Bướ x
c 1: Đặt : t m  (1) x  
+Bước 2: Tính x theo t bằng cách nâng lũy thừa bậc m hai vế của (1) ta có dạng x   t
+Bước 3: Tính vi phân hai vế : dx   'tdt và đổi cận   '      +Bướ x c 4: Tính : R   ;xmdx R
 t;t'tdt    x       '
3. Tích phân hàm lƣợng giác
Một số công thức lƣợng giác
a. Công thức cộng: cos(a  ) b  cos . a cos b sin . a sin b tan a  tan b sin(a  ) b  sin . a cosb  sin . b cos a t ( an a b)  1 tan . a tan b b. Công thức nhân: 2  a 2 2 2 2
cos 2a  cos a – sin a  2cos a –1 1 1– 2sin tan a  2 1 tan a 2 tan a 2 tan a sin 2a  2sin . a cos a  ; tan 2a  2 1 tan a 2 1 tan a 3
cos3  4cos   3cos ; 3
sin 3  3sin  4sin 
c. Công thức hạ bậc: 1 cos 2a 1 cos 2a 1 cos 2a 2 sin a  ; 2 cos a  ; 2 tan a  2 2 1 cos 2a 3sin sin 3 cos 3 3cos 3 sin    ; 3 cos    4 4 a
d. Công thức tính theo t : t  tan 2 2t 2 1 t 2t sin a  cos a  tan a  2 1 t 2 1 t 2 1 t
e.Công thức biến đổi tích thành tổng:
Nguyễn Chiến: 0973.514.674 12
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 1 cos.cos  
cos(  ) cos(  ) 2 1 sin.sin  
cos(  ) cos(  ) 2 1 sin.cos  
sin(  )sin(  ) 2
f. Công thức biến đổi tổng thành tích:       Hệ quả: cos  cos   2 cos .cos 2 2            
cos  sin  2 cos    2 sin       cos  cos   2  sin .sin  4   4  2 2            
cos  sin  2 cos     2 sin       sin   sin   2 sin .cos  4   4  2 2      
Công thức thƣờng dùng: sin   sin   2 cos .sin   2 2 3 cos 4 4 4 cos   sin   sin(   ) 4 tan   tan     cos cos  5 3cos 4 6 6 cos   sin   sin(   ) 8
tan   tan   cos cos
Một số dạng tích phân lƣợng giác b
 Nếu gặp I f
 sin x.cosxdx . Đặt t sin x. a b
 Nếu gặp dạng I f
 cosx.sin xdx. Đặt t  cosx. a bdx
Nếu gặp dạng I f  tan x
. Đặt t  tan x . 2 cos x a bdx
Nếu gặp dạng I f  cot x
. Đặt t  cot x . 2 sin x a n n
I. Dạng 1: I = sinx dx ; I cosx dx   1 2 2. Phƣơng pháp
2.1. Nếu n chẵn thì sử dụng công thức hạ bậc
2.2. Nếu n  3 thì sử dụng công thức hạ bậc hoặc biến đổi theo 2.3.
2.3. Nếu 3  n lẻ ( n  2 p 1) thì thực hiện biến đổi: p p
I = sin xn dx = sin x2p+1 dx  sin x2 sin xdx   2 1 cos x d cos x 1    k p  0 1 2    C C x    k C
2 x    p k p C  2 cos ... 1 cos ... 1 cos xd cos x  p p p pk p  1   1   2k 1    k    C x C x   C x 1 p cos cos ... cos ... pC cos x2 1 0 1 3   C p  3 p 2k 1 p 2 p 1 pp p
I = cos xn dx = cos x2p+1 dx  cos x2 cos xdx   2 1 sin x d sin x 2   
Nguyễn Chiến: 0973.514.674 13
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com k p  0 1 2 k p
C C sin x ...   1 k C   2
sin x ...   1 p C x d x p p p p  2 sin  sin   k p 1   1   k p
 C sin x C sin x ... kC sin x2 1   1 ... pC x   C p p p p sin 2 1 0 1 3  3 2k 1 2 p 1  II. Dạng 2: m n J = sin x cos x dx  Với ( , m n  *) 1. Phƣơng pháp:
1.1. Trường hợp 1: ,
m n là các số nguyên
a. Nếu m chẵn, n chẵn thì sử dụng công thức hạ bậc, biến đổi tích thành tổng.
b. Nếu m chẵn, n lẻ thì biến đổi: I
 xm  x2p+1dx   x  x2 xdx   x  p m p m 2 = sin cos sin cos cos sin
1 sin xd sin x  k p m k p    sin x 0 1 2
C C sin x  ...    1 k C   2
sin x ...   1 p C x d x p p p p  2 sin  sin     mmk  m p m c. Nếu m chẵn, sin x 1 sin x 3  k sin x2 1 p x k p sin 2 1 0 1 CC ...   1 C ...   1 C   C pm 1 p m  3 p 2k 1 pm
2 p 1 m
n lẻ (n 2p 1) thì biến đổi: I   x2p+1 
xn dx   x  x2 xdx   x  p n p n 2 sin cos cos sin sin cos
1 cos xd cos x  k p n k p     cos x 0 1 2
C C cos x  ...    1 k C    2
cos x ...   1 p C x d x p p p p  2 cos  cos     nnk  n p n d. Nếu cos x 1 cos x 3  k cos x2 1 p x k p  cos 2 1 0 1   CC ...   1 C ...   1 C   C pn 1 p n  3 p 2k 1 pn
2 p 1 n  ,
m n lẻ thì sử dụng biến đổi 1.2 hoặc 1.3 cho số mũ lẻ bé hơn. 1.2. Nếu ,
m n là các số hữu tỉ thì biến đổi và đặt u sinx       m m n  n 1 m B x xdx x x xdx u
  u m 1 2 2 2 2 sin cos sin cos cos 1 du (*)   
• Tích phân (*) tính đượ
m 1 n 1 m k c  1 trong 3 số ; ; nguyên 2 2 2 n n
III. Dạng 3: I = tan x dx ; I = c t o x dx (n  . )   1   2   •  dx 2
1 tan xdx   d
 tan x  tan xC 2 cos x •  dx 2
1 cot xdx     d
 cot x  cot xC 2 sin x sin x d cos x • tan xdx dx  
 ln cos x C    cos x cos x cos x d sin x • cot xdx dx
 ln sin x C    sin x sin x
Nguyễn Chiến: 0973.514.674 14
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
ỨNG DỤNG TÍCH PHÂN
1. Diện tích hình phẳng
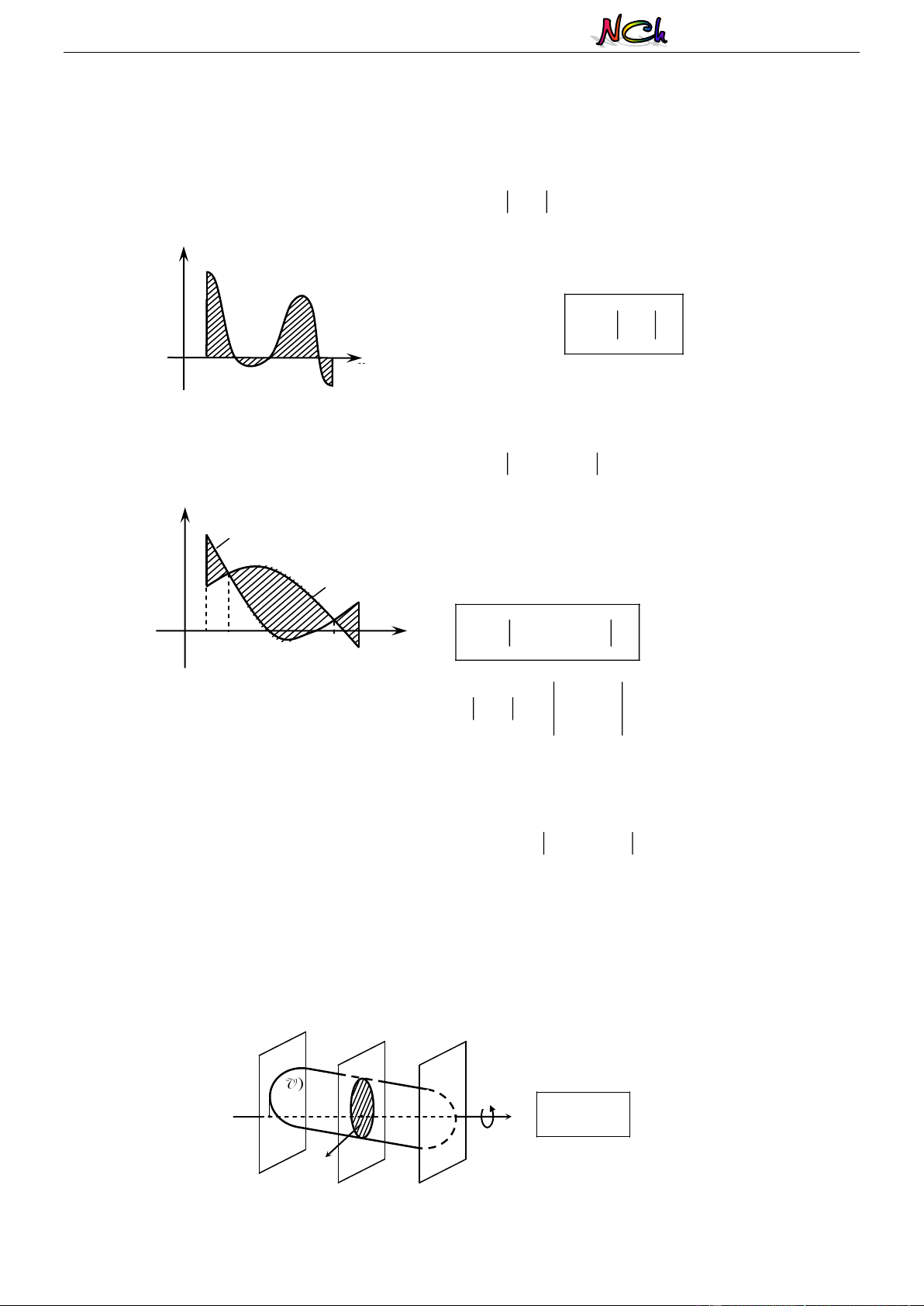
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f (x) liên tục trên đoạn  ;
a b , trục hoành và b
hai đường thẳng x a , x b được xác định: S f (x) dxa y yf (x)
y f (x)  by 0 (H) S   f x ( ) dxx   a a O a c c c b x 1 2 3  x b
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f (x) , y g(x) liên tục trên đoạn  ; a b và b
hai đường thẳng x a , x b được xác định: S
f (x)  g(x) dxa y
(C ) : y f (x) (C ) 1  1 1
(C ) : y f (x) (H) 2 2 x a (C ) 2 x b b S f x ( )  a c O c 1 b x 2  f x ( ) dx 1 2 a b b  Trên  ;
a b hàm số f (x) không đổi dấu thì:
f (x) dx f (x)dx   a a
 Nắm vững cách tính tích phân của hàm số chứa giá trị tuyệt đối
 Diện tích của hình phẳng giới hạn bởi các đường x g(y) , d x  (
h y) và hai đường thẳng y c , y d được xác định: S
g( y)  h( y) dyc
2. Thể tích vật thể và thể tích khối tròn xoay a) Thể tích vật thể:
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b;
S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x , (a x  )
b . Giả sử S(x) là hàm số liên tục trên đoạn  ; a b . ( ) b x V a bS x( dx ) O x a S(x)
b) Thể tích khối tròn xoay:
Nguyễn Chiến: 0973.514.674 15
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
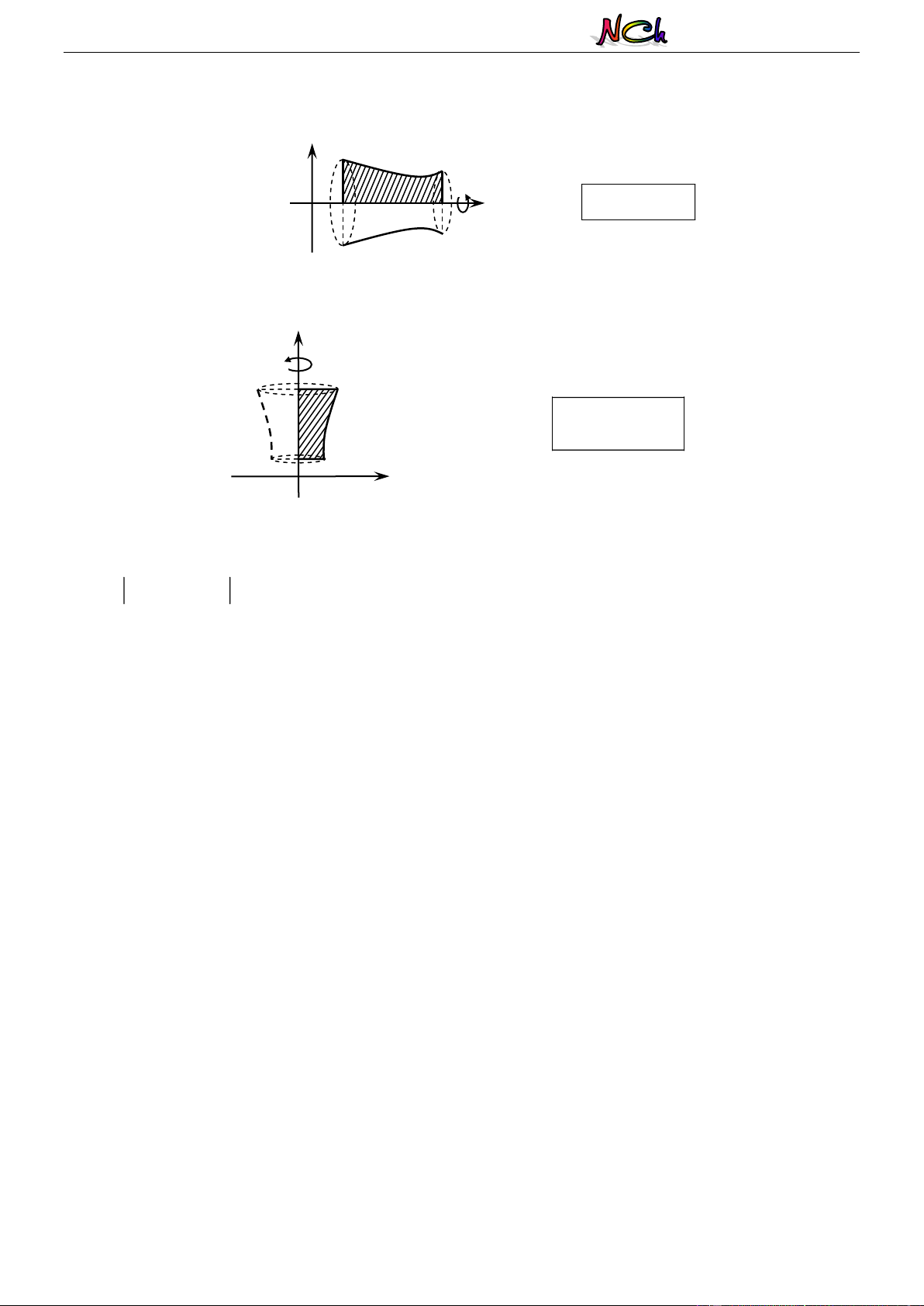
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y f (x) , trục
hoành và hai đường thẳng x a , x b quanh trục Ox : y
y f (x) (
C) : y f (x) ( 
Ox) : y 0 bV   f x dx ax( )2 O b x x   a a  x b
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x g( y) , trục
hoành và hai đường thẳng y c , y d quanh trục Oy : y d (
C) : x g(y) ( 
Oy) : x 0 dV   g y dyy( )2 y   c c c y d x O
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới
hạn bởi các đường y f (x) , y g(x) và hai đường thẳng x a , x b quanh trục Ox : b 2 2 V  
f (x)  g (x) dx  . a
Nguyễn Chiến: 0973.514.674 16
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
BÀI TẬP TÌM NGUYÊN HÀM BẰNG CÁCH DÙNG BẢNG NGUYÊN HÀM
VÀ CÁC PHÉP BIẾN ĐỔI SƠ CẤP 1.  (7x  ) 3 dx dx 16.  2 x  3x  2 5  x x x 2.   dx 17.  dx 2 3 (x x2 ) 2 3 4sin3 x
3.  (  2x)dx 18.  dx x 1 cos x 2 x  2x 1 x3 4. dx 19.  dx 2x 1 x  2 5x4  3x 3 3xdx 5.   dx 20.  2 x2 x  5x  4 (x2 2 ) 2 21.  2 (tanx c - otx) dx 6.   dx x2 x 7.  1 3     xdx 2 3 1  22.   dx x 3 xx e
8.  2 x  33 x2  2dx 2x 1 23.     dx
x 1  x   1 x 4 2 x 3 9.   dx 24.   e dx 3 x 2 3
3x x x  x e  10. dxx 25.  e 4  2 dx x  cos x  11. sin 2xdx 26.  3x1 2 dx
12. sin 2x.cos3xdx cos3 x 27.  dx 1 sin x 13. sin(2x  ) 1 dx 28. 3 cos x sin xdx  2 2 x tan xdx 14.  2sin dx 29. 2 dx 3x e 1 15. 30.  dx 3 (  5 2x) x 4
Nguyễn Chiến: 0973.514.674 17
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
BÀI TẬP TÌM NGUYÊN HÀM BẰNG PHƢƠNG PHÁP ĐỔI BIẾN 1.  3 ( x  10 ) 2 dx 3x2 21.  dx 5  2x3 2. 5 xdx  3 e x 22.  dx x 3. x2 . 1 xdx   xdx 23.  2 x  2014 dx dx 4.  24.  5x  3 3 (  5 2x) 5. (x3  4 ) 5 x2dx 25. (2x2  7 ) 1 xdx 6. x x dx . 1  
26. sin2014 xcos xdx 2 7.  x x e 1 . dx sin x 27.  dx 5 cos x 3 ln x 28.  cot gxdx 8. dxx 9. x2 x3 dx . 1   tgxdx 29.  2 cos x 10. x3 x2 dx . 1   30. tgxdx 11.  3 cos x 2 sin xdx 2 x dx 31.  1  2 x dx dx 12.  32.  x 1 (  2 x ) 2 x e  5 dx 2 2 13. 
33.  x 1  x dx . x e  1 dx x xe 1 14.  34. dx  2 x x x  1  x(e ln x)
Nguyễn Chiến: 0973.514.674 18
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 2 x e dx dx 15.  35.  x e  sin x 3
16.  1 x2 dx . dx 36.  cos x dx 1 17.  37. dx  4  2 tanx x dx 1 18.  38. dx   2 1 x cotx etgx (s inx+ cos x)dx 19.  dx 39.  2  cos x s inx cos x
20. e4cosx sin xdx 40. 3 sin xdx
BÀI TẬP TÌM NGUYÊN HÀM BẰNG PHƢƠNG PHÁP
NGUYÊN HÀM TỪNG PHẦN
1.  x.sin xdx 21. x dx x  ln
2.  xcos xdx 22.  ln xdx 3. (x ) 1 dx x   sin 23. dx x  2 ln
4.  xsin 2xdx 24. x2 dx x  ln
5.  xcos 2xdx 25. sin x dx 6.  x ex . dx ln xdx 26.  x 7.  xln xdx ln 1 ( x) 27.   dx x2 8. x2 dx x  cos 28.  xln 1 (  x2 )dx 9. (x2  ) 5 sin xdx 29.  x 2 xdx
Nguyễn Chiến: 0973.514.674 19
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 10. x dx x  2 sin 30. ln(x2  ) 1 dx 11.   x e x2 3 dx 31. (2x ) 3 dx x   ln
x.lnx x2 1
12.  x2 cos 2xdx 32. dxx2  1
13. (x2  2x  ) 3 cos xdx
33. 1 tan x  2 tan xexdx
14. ex.cos xdx 34. cos xdx  ln x 15.  dx 35.  2xln 1 (  x)dx 2 cos x 16.  x 2 tan xdx 1  x 36. x.ln dx  1  x 17. (2x e xdx   )3 37. x2 ln dx x  2 18. x e x dx  2 38. cos x.ln 1 ( cos x dx   ) 2 19.  e x dx 39. e x dx x  cos 20. e x dx x  sin ln(cos x) 40. dx  2 cos x
Nguyễn Chiến: 0973.514.674 20
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
CÁC PHƢƠNG PHÁP TÍNH TÍCH PHÂN
1. TÍNH TÍCH PHÂN BẰNG CÁCH SỬ DỤNG CÁC NGUYÊN HÀM CƠ BẢN VÀ
CÁC TÍNH CHẤT CỦA TÍCH PHÂN 2 3
Ví dụ 1: Tính tích phân I=
(x  2x 1)dx  1 Giải: 2 4 3  x   1  3 I =
(x  2x 1)dx  = 2 2 
x x  1 2 2  11   2 1      4   4  4 1 1 3 x 1 
Ví dụ 2: Tính tích phân I= e dx  1  3 Giải: 1 3x 1  3 x 1   e  1 I= e dx  = 1 4 0    (e e ) 1  1   3  3 3 3 
2  sin x cosx
Ví dụ 3: Tính tích phân I d . x      sin x cosx  4 Giải:    2 2
 sin x cosx
d sin x cosxI dx        x cosx  2 ln sin  ln 2       sin x cosx  sin x cosx 4 4 4  2 dx
Ví dụ 4: Tính tích phân I  .  1 cosx 0 Giải:     x d    2 2 2 dx dx  2  x I     tan 2  1    1 cosx x x 2 2 2 0 0 0 2cos cos 0 2 2
Nguyễn Chiến: 0973.514.674 21
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
TÍNH TÍCH PHÂN BẰNG CÁC PHÉP BIẾN ĐỔI SƠ CẤP 1 1 2 2 1
1. I = (2x x  ) 1 dx 16. I =   e x dx 0 0 1 1 2 x 2. I =  3
(7x  2x  )dx
17. I = (e x)dx  5 1 0 1  3. I = x 2
(e x 1)dx 2 sin 3x 18. I =  dx 0 2cos 3x  1 0 2 3  x  2 x  2x 2 4. I =   dx 2 3 4 x 19. I =  sin x dx 1 0 1  5. I = 3
(x x x )dx 4 20. I =  4 (sin x  4
cos x)dx 0 0 2  6. I = 3 2
 x - 2x - x  2 dx 2 21. I =  6 (sin x  6
cos x)dx -1 0 2   1 3  7. I =    4 dx   3 2 3 tan x x2 cot dx   1  x x  22. I =  6 e
5x3  x x  2x 1 8. I=   dx 3 4 sin x x 23. I =  dx 1 2 0 cos x  8  2  9. I = 3  4x dx  2 1 3 2    2  3 x  24. I = dx 4  sin x 4 e2  2 x 11  7x 3 x 1 10. I = dx   25. I = dx  3x 6 1 cos x 0 2 
11. I = ( x 1)(x x 1)dx  4 4 26. I = cos 2x( n si
x  cos x)dx  1 0  3 12. I = sin xdx 4 27. I =  sin 2x dx 1  4   4 3 4 13. I = cos xdx 28. I =  dx 2  sin 2x 0 4   4 3 2 14. I =  tan xdx
29. I = tan x 2cot x   dx  0 4
Nguyễn Chiến: 0973.514.674 22
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com   4 2  15. I = cot xdx 1 cos x 30. I =  dx 0 1 cos x 0
LUYỆN TẬP DÙNG VI PHÂN 1 1  dx 1/ I   2 2  11 5x . 2
6. I = cox x cos 2xdx  2 0 1 x  e 2  2. I =  dx 2   x 
7. I = sin  x  dx  0 e 1 1  3  1  3. 3 4 3
I x (1 x ) dx  2 8. I = 5 sin dx x  0 0 22  3 2 4. 3 I  3x  5dx  9. I = 2 3  sin 2x(1 sin x) dx 1 0 3 e sin(ln x) 2 2015 5. I = (x  ) 1 (2 x) dx   10. I =  dx x 0 1
LUYỆN TẬP DÙNG VI PHÂN 2  4 1 2 6. I dx 1. 3 I cos xd . x 2x 1 0  6   4 etan x2 2 2 7. I = sin x  e sin 2x dx 2. I= dx  2 cos x  0 4 3  3. I= x(2 x2 ) dx 2015   2 4 1 2sin x 8. I =  dx 1 1  sin 2x 0 1  4. 3 2 I x 2  x dx 3 9. I = 0  sin x.ln(cosx)dx 0 1  x 4 5. I =  dx tgx dx 2  10. I =  . 2 0 4 x cos x 0
Nguyễn Chiến: 0973.514.674 23
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
2. PHƢƠNG PHÁP ĐỔI BIẾN SỐ
a. Phƣơng pháp đổi biến số dạng 1.
Định lí . Nếu 1) Hàm x u(t) có đạo hàm liên tục trên đoạn ;  ,
2) Hàm hợp f (u(t)) được xác định trên ;   , 3) u( )  ,
a u( )  b , b  thì ' I
f (x)dx
f (u(t))u (t)dt   . aPHƢƠNG PHÁP CHUNG
Bƣớc 1: Đặt x = u(t)
Bƣớc 2: Tính vi phân hai vế: x u t
( )  dx u' t ( )dt x b t   Đổi cận:  x a t  
Bƣớc 3: Chuyển tích phân đã cho sang tích phân theo biến t b    Vậy: I f (x dx )
f u t()   u' t
( )dt   g t()dt G(t)  G() G()  a  
* Các dấu hiệu đổi biến thƣờng gặp : Dấu hiệu Cách chọn    
Đặt x = |a| sint; với t   ; .   2 2  2 2  a x
hoặc x = |a| cost; với t 0; . a     Đặt x = .; với t   ; \   0 .   sint  2 2  2 2 x a a   hoặc x =
. ; với t 0;  \  . cost  2     
Đặt x = |a|tant; với t   ; .   2 2  2 2  a x
hoặc x = |a|cost; với t 0; . a x a x . hoặc . Đặt x = acos2t a x a x
xabx Đặt x = a + (b – a)sin2t
Nguyễn Chiến: 0973.514.674 24
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 1    
Đặt x = atant; với t   ; .   2 2 a x  2 2  1 Ví dụ 1: 2 1 x dx  0 Giải:    
Đặt x=sint với : t   ;   .  dx=costdt  2 2  Đổi cận: x 0 1  t 0 2 1 Do đó : f(x)dx= 2 2 2
1 x dx  1 sin t o
c stdt=cos tdt  1 o c s2t  dt 2   1 2 1 o c s2t  dt 1  1  1   1   1 Vậy :
f (x)dx   t  sin 2t 2          2 2  2  2  2 2  4 0 0 0 1 Ví dụ 2: Tính 2 2 .I x 1 x dx  0 Giải:    
Đặt x = sint ,t   ;   .  dx = costdt  2 2  Đổi cận: x 0 1  t 0 2    1 2 2 1 2 1 Khi đó: 2 2 .I x 1 x dx  2 2
 sin t 1 sin t.costdt  2 2  sin tcos tdt  2  sin 2tdt  4 4 0 0 0 0   2 1    1  1 
1 cos4t dt t  sin 4t   2  8 8  4  16 0 0 1 3 x
Ví dụ 3: Tính I d . x  8 1 x 0 Giải: 1 3 1 3 x x Ta có: dx d . x   8 1 x 1  4 0 0 x 2
Nguyễn Chiến: 0973.514.674 25
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com    4  1
Đặt x  tant với 3 t   ; .  x dx     2
1 tan t dt.  2 2  4 Đổi cận: x 0 0  t 0 4    1 3 1 3 4 2 4 x x 1 1 tan t 1 1  Khi đó: I dx dx dt dt t 4  ..     8 1 x 1  x 2 2 4 4 1 tan t 4 4 16 0 0 0 0 0 1 5 2 2 x 1
Ví dụ 4: Tính I d . x  4 2 x x 1 1 Giải: 1 5 1 5 1 5 1  1  1 1   2 2 2 2 2 2 x 1 xx  Ta có: dx dx d . x    4 2 2 x x 1 1 2  1  1 1 1 x 1   2 x 1 x    x  1  1 
Đặt t x   dt  1 d . x   2 xx  Đổi cận: 1  5 x 1 2 t 0 1 1 dt Khi đó: I  .  2 1 t 0 Đặt t u dt   2 tan
1 tan ud . u Đổi cận: x 0 1  t 0 4    1 4 2 4 dt 1 tan u  Vậy I  
du du u 4  ..    2 2 1 t 1 tan u 4 0 0 0 0  2 cos x Ví dụ 5: Tính dx  1  2 sin x 0 Giải:
Nguyễn Chiến: 0973.514.674 26
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com    
Đặt sinx = tant với t    cosxdx     2 ;
1 tan t dt.  2 2  Đổi cận:  x 0 2  t 0 4    2 4 2 4 cosx 1 tan t  Khi đó: I dx dt dt  .    2 2 1 sin x 1 tan t 4 0 0 0
b. Phương pháp đổi biến dạng 2
Định lí: Nếu hàm số u u(x)đơn điệu và có đạo hàm liên tục trên đoạn a;b sao cho b u (b)
f (x)dx gu(x)u'(x)dx g u
( )du thì: I   f (x)dx   g(u)du . a u (a) PHƢƠNG PHÁP CHUNG Bƣớ '
c 1: Đặt u u(x)  du u (x)dx x b
u u(b)
Bƣớc 2: Đổi cận :  x a
u u(a)
Bƣớc 3: Chuyển tích phân đã cho sang tích phân theo biến u b b u(b) Vậy: I
f (x)dx gu(x)  
.u'(x)dx   g(u)du a a u(a) ln 2 2 x e  3 x e
Ví dụ 1: Tính I d . x  2 x e  3 x e  2 0 Giải: Đặt x
t e dt exdx Đổi cận: x 0 ln2 t 1 2 Khi đó: ln 2 2 x x ln 2 x 2 2 e  3e e  3 t    x 3 2 1 I dx e dx dt   dt       2 x x 2 x x 2 e  3e  2 e  3e  2 t  3t  2
t 1 t  2  0 0 1 1 2 2 1 1 2 2  dt dt t   t          3 4 9 4 27 2 2 ln 1 ln 2 2 ln 3 ln 2 ln 4 ln 3  2 ln ln  ln ln  ln t 1 t  2 1 1 2 3 4 3 16 1 1 1 ln 2  x
Ví dụ 2: Tính I d . x  2  x 0
Nguyễn Chiến: 0973.514.674 27
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com Giải: dx
Đặt t  ln 2  x  dt  . 2  x Đổi cận: x 1 1 t ln2 0 1 ln 2  x 0 ln 2 2 2 t ln 2 ln 2 Khi đó: I dx   tdt tdt   ..    2  x 2 0 2 0 ln 2 0
BÀI TẬP TÍCH PHÂN ĐỔI BIẾN DẠNG 1 Luyện tập 1 1 1 1   2 x 1  2 6. I   dx KQ: 2  1. I = dx  KQ: 1  x 2 2  4 0 0 1 2x 2 1  1/ 2 x2 1   1  2. I = dx  KQ: 7. I dx  KQ: I     2   6 2 2  4 2  1 3 2x x 0 1  x a 4 a  0 1  x
3. I   x2 a2  x2dx KQ: 8. I dx  KQ:1 16 1  x 4 0 1 1 2 6 1 x  1  4. I d . x  KQ:1 9. I dx KQ: 2 x 4 2 9 36 3 2 x x  2 2 1 x  3 1 1  3 5. I d . x  KQ: 10. I dx KQ: 4 2 x x 1 18 x2  x 1 9 0 0 Luyện tập 2 2 dx  3 1. I =  KQ: 11. I   x2 4 dx  KQ:   3 2 12 2 x x 1  1 3 2 2  x 3 dx  2. I dx    I   KQ: x 2  2 KQ: 12. 2 x  4x  5 2 1 0
Nguyễn Chiến: 0973.514.674 28
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 2 2 3 1 3. I x2 4 x2 dx   KQ:  2   3 4
1 2x 1 x2 dx 3 1  1 13.  KQ: 12 8 0 1 2 8 0 a x    4. I= dx  KQ: 14. I dx  KQ: a1   2 3  1 x 4x 1 a x  4  a 3  0 1  3 4 2 sin xdx 2 3 15. I d . x  KQ: 5. I=  KQ: 2  ln  2 x  2x  4 18 4 2
cos x tan x  2 tan x  1    5 3 8 4 3 1 3 9 x2 3 3 2  2 x 2 6. I dx    KQ: 2 3  6  ln 16. I dx  KQ:  3 3 x2 2 32 2 2 3 0 4  x 1 1 2 2 1 0 dx 7. I x x2 dx  1 KQ: 17. I dx  KQ: 0 3 2 1  2  0  x x 2 1  2 3 2 2 8. I   x2 1 dx  KQ: 
18. I x 2x x dx   KQ: 3 8 3  1 0 2 a  2 3 dx  tan x 9. I   a  0 KQ: 19/ I dx  KQ: 2  2 2 2 6  cos x 1 2 cos x 0 a x 4 a 1 dx  3 2 3 10. I   a  0 KQ:
20. I   1 x d . x KQ: a2  x2 4a 16 0 0
BÀI TẬP TÍCH PHÂN ĐỔI BIẾN DẠNG 2 Luyện tập 1 1 2 e 1 ln x 2 1. 3 2 .I x 1 x dx  KQ: 2 2   6. I d . x  KQ: 1 15 x 3 0 1 3 2 2x x 1 1 3 54 x 2 2 1 2. I dx  KQ: 7. I d . x  KQ:  x 1 5 2   15 15 x x 1 0 0
Nguyễn Chiến: 0973.514.674 29
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com e 1 1 29 3. I d . x  KQ:-ln2 8. 15 8
I x . 1 3x .d . x  KQ: x 1 ln x 270 1   0 2 dx 4 2  dx 1 7 ln 2   4. I  .  KQ: 1 9. I  .  KQ: ln 3  3 2  6 4 1 x 1 x 7 x x 9 1 3 4 31 x  3 3 5. 3 I x  4 x   1 d .x KQ: 10. I = dx  KQ:  3  6ln 20
3. x 1  x  3 2 0 0 Luyện tập 2   6 3 tan 1 1 2 2 1.   x I dx KQ:   ln cos2x I dx 1  cos 2x 6 2 3 11.  3 KQ: 0
0 (cos x  sin x  3) 32 ln 3 2 x e dx 1 2. I   KQ: 2ln3 - 1 5 3 6 1
12. I x (1  x ) dx  KQ: x x    ln 2 e 1 e 2 168 0  2 x d 3 x 3 3  8 3  dx 8 3  4 13. I   KQ:    4 2  3. I   KQ: 3 2 2 0 4  x 2  5   sin x 4 .cos x 3 4   3 dx  6 sin x 1 3  2 2 4 8 3   4. I =  KQ: 1 I dx ln 4 14.  KQ: 3  sin x 5 .cos x cos2x 0 2 2 5  2 6 4  5 x2 1 4 100 9 tan xdx 15. I dx  KQ: ln 5. I   KQ: 3  2 1 x 3x  1 27 5 cos x 2 0 1 cos x 4 3 1 5   1 3 ln( 1 1)  2 2  6. I dx  KQ:  x I dx KQ: ln 3 ln 2 ln 16. x 1 x 1 1 x(x4  1) 4 2 2 4 2x 1 3ln2 dx 3 3 1 7. I dx  KQ: 2  2ln 2 17. I    2 KQ: ln 0 1 2x 1 0 3 x 4 2 8 e  2
Nguyễn Chiến: 0973.514.674 30
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 4 x  1 1 2 6 8. I   dx KQ: 2 ln 2  3 5  2 1 cos .sin .cos 12 2 18. I x x xdx  KQ: 4 0 1  1  2x  1 91  1 x2dx
4 cos x  sin x  19. I   KQ: 9. I dx  KQ:  x6 0 4 18 0 3  sin2x 12 ln3 3x 2x e 2  e 4 8  ln 5 x 1 1 10. I dx KQ: 20. I dx  KQ: 2 ln 2  x x 2 4 0 e e 4  3 1 3 0 1 1 2x
3. TÍCH PHÂN TỪNG PHẦN
Định lí . Nếu u(x) và v(x) là các hàm số có đạo hàm liên tục trên  ; a b thì: b b b '
u x v x dx  u x v x  ' ( ) ( ) ( ) ( )
v(x)u (x)dx   a a a b b b
Hay udv uv   vdu a a a PHƢƠNG PHÁP CHUNG  '
Bƣớc 1: Viết f(x)dx dưới dạng udv uv dx bằng cách chọn một phần thích hợp của f(x) làm u(x)
và phần còn lại dv v'(x)dx
Bƣớc 2: Tính du u'dx v   và
dv v'(x)dx b b
Bƣớc 3: Tính vu'(x)dx và uv a a
*Cách đặt u và dv trong phƣơng pháp tích phân từng phần. Đặt u theo thứ tự ưu b b b b tiên: P(x) x e dx
P(x)ln xdxx
P(x) cos xdxe cos xdx
Lốc-đa-mũ-lượng a a a a u P(x) lnx P(x) x e dv x e dx P(x)dx cosxdx cosxdx '
Chú ý: Nên chọn u là phần của f(x) mà khi lấy đạo hàm thì đơn giản, chọn dv v dx là phần của f(x)dx là vi
phân một hàm số đã biết hoặc có nguyên hàm dễ tìm.
Có ba dạng tích phân thƣờng đƣợc áp dụng tích phân từng phần:
Nguyễn Chiến: 0973.514.674 31
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com u   f (x)
du f '(x)dx sin ax       sin ax   sin ax
Dạng 1 f (x) cosax dx    Đặt           dv cos ax dx v cosax dx      ax    e    ax ax  e   e          dx   ln( ) du u ax  
Dạng 2: f (x) ln(ax)dx Đặt   x     dv f (x)dx
v f (x)dx    sinbx
Dạng 3: eax dx  cosbxaxdu ae dx ax ax u   e  du ae dx ax Đặt    Hoặc u   e  1   
dv  cosbxdx v  sin bx  1      dv sin bxdx v cos bxbb
Trong trường hợp này, ta phải tính tích phân từng phần hai lần sau đó trở thành tích phân ban đầu. Từ đó
suy ra kết quả tích phân cần tính. 1 Ví dụ 1: Tính 2 x I xe d . x  0 Giải du dx u   x  Đặt    1 . 2 x 2 xdv e dx v e  2
Áp dụng công thức tính tích phân từng phần: 1 1 1 e x 1 1 x 1 x 1 1 x I xe dx xee dx e e d 2x 1 1 1 x 1 1  e e
e  e   2 1 2 2 2 2 2 2 2 2 2 1     2 0 2 2 4 2 4 0 2 4 4 0 0 0 Ví dụ  2 2: Tính 2 x e o c s3xdx  0 Giải: Đặ t: u = e2x, du= 2e2xdx sin 3x dv = cos3xdx, v = 3   2  2  sin 3x  2 e 2 2x 2x I ee sin 3x dx=   I    1  3  3 3 3 0 0 Tính I Đặt 2x 2x u eu '  2e 1 -cos3x v  sin 3x, v'= 3
Nguyễn Chiến: 0973.514.674 32
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com    2 2 2  c  1 os3x 2 2 x 2 x 2 x I e sin 3x dx  ee o c s3x dx     I 1    3  3 3 0 0 0 Do đó:   e 2  1  e 2 4 I     I     I   3 3  3  3 9 9  3e  2  I   13  2
Ví dụ 3: Tính sin x I e sin 2xd . x  0 Giải:   2 2 sin x sin  sin 2  2 x I e xdx e sin xcosxdx   0 0
Đặt t = sinx dt = cosxdx Đổi cận:  x 0 2 t 0 1 Khi đó:  2 1 sin  2 x sin  2 t I e xcosxdx te dt   0 0 Đặt: u   t du dt    t t dv e dt v   e
Áp dụng công thức tính tích phân từng phần: 1 1 1 1 1 t t t t t te dt tee dt tee 1   0 0 0 0 0 Vậy I = 2  2
Ví dụ 4 : Tính I cosx ln 
sin xd .x  6  cosx u
  lnsin x du dx Đặt:    sin x . dv  os c dx
v  sin x
Áp dụng công thức tính tích phân từng phần:
Nguyễn Chiến: 0973.514.674 33
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com      2
I cosx ln sin xdx  sin x ln sin x 2
2  cosxdx  in xlnsin x 2 2 1  sin x  ln 2     1      2 6 6 6 6 6 e
Ví dụ 5: Tính I  4x   1ln xd .x 1 Đặt:  dxu  ln x  du         x dv 4x   1 dx 2
v  2x x
Áp dụng công thức tính tích phân từng phần: e e   e e I 4x   1 ln xdx   2
2x xln x  2x   2
1 dx  2e e   2 x x  2  e  2 1 1 1 1
BÀI TẬP TÍCH PHÂN TỪNG PHẦN 1 1  2 5 1 1.  3    3 1 x I x e d . x KQ:  16. I x ln  2 x  
1d .x KQ: ln2 3 3 e 2 0 0    2 2 e  1 4   2. x
I e cos xd . x  KQ: x sin x I dx 2 2 17.  3 KQ: 0 0 cos x 4 ln3  2
I    2x 2xx 3.
e dx KQ: ln2 3  8ln3 12  e 18. I esinx sin 2 dx x  KQ: 2 1 0 2 2 ln(x  1) 5 2 ln(x 1) 3 4. I dx  . KQ: 2 ln 2  ln 5 I = dx 3ln 2  ln 3 3 19.  KQ: x 8 1 x2 2 1   2 2   4 3 xdx  9 (  4 3) 1 3 5. I   2 x sin xdx KQ: 20. I  .  KQ:  ln 16 2  sin x 36 2 2 0 4   3 2 x sin x 2     4 2  3 2 8 6. I dx.  KQ:  2 ln
21. I = 2x    1 o c s xdx KQ: 2  cos x 3 2  3 8 0 3 3 2 2 x 2 5 2 1 x e 7. I x d 1 x  KQ:  ln 2   1  ln 2 22. I = dx  KQ: 1 2 2 4 x  2 0   2
Nguyễn Chiến: 0973.514.674 34
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com  3 2  2 1 sin x
23. I  lnx xdx KQ: 2-3ln3 8. I  . x e d . x  KQ: 2 e 2 1 o c sx 0   2  2   3e  2
24. I e2x cos 3 dx x  KQ: 9. I
sin x ln(1 sin x d ) x  KQ: 1 13 2 0 0 8 ln x 2 1 5 1  3 10. I dx  KQ: 20ln 2  6ln 3  4 25.  ( 1 )  x x I x e dx KQ: 2 e 3 x  1 x 2 1 2 1 2 5  3 2 e  2 11.   2 2x I x e dx KQ: 4   8 26. I x cos xdx  KQ: 0 4 2 0  e 4 3 2    8  4 27. I ln dx x  KQ: 6-2e 12. I =   2
x  4x  3sin 2xdx KQ: 1 8 0 1 1 0  9 13. I x3 2 ex dx  KQ: 28. I x
 e2x  3 x 1dx KQ: 0 2 1 28  e 5 4 e  1 2  14. I x3 2 ln dx x  KQ: 3   1 3 29. 2 KQ:  ln 2 32 I x tan dx x  1 24  4 1 1 4  e  ln x  3e   2 1 2  I   2 x ln 2 x   2 15. 1 dx KQ: ln 2   30. I  
 ln x dx KQ: 3 9 6
1  x 1 ln x 0  3 \
Nguyễn Chiến: 0973.514.674 35
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
BÀI TẬP TÍCH PHÂN HÀM HỮU TỈ 1 dx 1 4 x3  x 1 1  1. I   KQ: ln 16. I dx  KQ:  2 x  5x  6 3 x2 1 2 3 0 0 1 2 4x  9 2001 2 x 1 2. I dx  KQ: 3ln  ln 2 17. I d . x  2 x  5x  6 3 2 1002 KQ: 1001 0 1 (1 x ) 2 . 2002 3 2 1 x2 1 2 1 3 x2 18. I dx  ln 1  4 KQ: ln2  3 3. I dx  KQ:  1 1 x 2 2 2  1 x4 0 1 4 12 2 x2 1 4x  11 1 4. I dx  KQ: 1 25ln2 16ln3 19. I dx  KQ: ln 2 x2 x2  5x  6 2 1  7x 12 0 1 x2 4 3 6x  9 3 5. I dx  KQ:   ln 2 20. I dx  KQ:   3ln 2 (x  3 ) 1 8 x2  4x  4 2 0 3 1 dx 1 99 2 8 7x   1 6. I     ln 2100  1 2 KQ: 21. I dxx 3 x 2 3 9 101 KQ: 0      0 2x   1 900 3 x2  x 1 2 15 2x 1  7. I dx  KQ:     ln 2 22. I dx  KQ: 4 ln 2 (x  3 ) 1 8 x2  4 2 2 0 3 dx 3 1 3 x2 1 8. I   KQ: ln 23. I dx  3 x x 4 2 2 2 x x 1 1 1 1 x7 3 1 dx 117  41 3  9. I dxI   KQ: 24.  KQ: 7 6 2 x (x  0 (1 x2 5 ) 2 ) 1 135 12 1 2 dx  3 (2x 1)dx  10. I   KQ: 3 I    2 25. KQ: ln x  2x  2 2 2   2 0 x 2x 5 8 1 1 3 4 x x 1 11 3 dx 1 3 11. I   dx KQ:  ln 2 26. I   KQ: ln x 1 6 4 x(x  ) 1 4 2 0 1
Nguyễn Chiến: 0973.514.674 36
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 1 x4 1  1 1  x 11 12. I dx  KQ: I dx KQ:  4ln2 27. 1 3 0 x6  1 12 x 0 1 2  x4  2 2 1  x5 1 31 13. I dx  KQ:  28. I dx  KQ: 6ln2  ln  33  1  x2 4 3 x(x5  2 ) 1 5 165 0 1 2 dx  1 3 1 3 dx 1  14. I   KQ: ln 2  ln 5  29. I   KQ:  x5  x3 2 (x  2 ) 1 4 8 1 2 2 8 0 3 dx 117  41 3  0 3 2x  2 6x  9x I  9 15. I   KQ: 
dx KQ 33ln 2 19ln3 135 12 30.  2 : 1 x  3x  2 1 x6(1 x2) 1
BÀI TẬP TÍCH PHÂN LƢỢNG GIÁC 1   4 1 4 16. I = 2 KQ: 0 1. I d . x  KQ: 3 3  ( cos x  sin x)dx 4 cos x 0 0 3   2  1 2 3sin  4 cos 3 2. 3 3
I  sin xcos xd . x  KQ: 17.   x x I dx KQ:  ln 3 2 2
3sin x  4 cos x 6 0 12 0    2 sin 2x 6 tan(x  ) 1 3 3. I d . x  KQ: ln2 18. I 4  dx 2  KQ: 1 cos x cos2x 2 0 0   2 2 2  4. 3 I  sin xd . x  KQ: 19. I = 2 2 o
c s x cos 2xdx  KQ: 0 3 0 8   2 3 s inxcos x 1 ln 2 2 4sin xdx 5. I = dx  KQ: 20. I =  KQ: 2 2 1 o c s x s inx+cosx 0  3 0 2   2 sin xcosx 1 3 1 3 6. I d . x  KQ: 21. I = dx  KQ: 2 ln 2 2 2 2  a     0 a cos x b sin x b  sinxsin x+   2 6  6 
Nguyễn Chiến: 0973.514.674 37
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com   2 15 6 sin 2x 5 7. I =  10 10 4 4 sin x  o
c s x  sin x cos xdx KQ: 22. I dx KQ: ln 2 2sin x  2 cos x 0 64 0 4   2 2 2 17 2
8. I  sin xcosx
1 cosxd .x KQ: 23. I = 3 4 sin x cos xdx  KQ: 0 12 0 35   118 4 1 3 24. I = 11 sin xdx  KQ: 9. I   KQ: 0 21   dx
sin x cosx . 2  2 12   4 sin 4x 2 cos x  10. I  .  KQ: ln2 25. I dx  KQ: 4 4 sin x cos x 7  0 cos 2x 6 2 0   / 3 3 sin x 5 5 2 dx   I   2  26. I dx  KQ: 3ln 11. I =  KQ: 2 arctan  arctan 2 2  cos x 2 6 2  s inx+cosx   2 0 0     / 2 2 6 os c x 5 23 cos x 12. I = e sin 2xdx  KQ: 2(e - 2) dx  KQ:  27. 4  sin x 8 12 0 4   2 sin 2x 3 2  3  e  2 13. I = dx  KQ: ln 28. 2 x e o c s3xdx  KQ: 2 4  o c s x 4 13 0 0   4 dx  ln 2 4   14. sin 2 1 2 2 I  .  KQ:  29.   x x I dx KQ:  ln 1 tan x 8 4 2  0 cos x 4 2 2 2 0  4 sin 4x 4 15. I d . x  KQ: 2  6ln 2 1 cos x 3 0
Nguyễn Chiến: 0973.514.674 38
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
BÀI TẬP TÍCH PHÂN LƢỢNG GIÁC 2   4 1 4 1. 3 I  tan xd . x  KQ: 1 ln2 tan x I dx 3  7 2 11.  KQ: 0  cos x 2 1 cos x 3 6   3 dx 8 3  4 3 2. I   KQ: 12. 2 2    KQ: ln2 2 4 tg x cot g x 2dx sin . x cos  x 3  4 6   2 2 sin x 1 4 sin 4x ln2  3 3. I dx  . KQ: I dx sin3x 13. KQ: 2  2  4 4 sin x 4 0  cos x 6   4 x cos2x 4 2  sin 4x 4 4. I dx   dx  KQ: ln 2  KQ: 14. 6 6 1 sin2x2  0 4 16 o
c s x sin x 3 0   4 sin 4x 2 2 sin x 3 5. I dx  KQ: 15. I dx  KQ: 6 sin x 6 3 0  cos x 3 0 sin x 6  3 cos x   4 sin x 2 1 cos x 3 36 3 7 cos x 6. I dx  KQ   16. I dx  KQ: ln 2 3 1 2 54 3  sin 5sin   cos x 12 x x 6  3 6  1  e   1 2 3   1  17. I ex 2 sin ( xdx  ) KQ: I  2 1
7. I  sin x. sin x dx .   KQ:    2 4   2 4 2    1 0  2 6   2  1 sin x   2 3 x sin x.cos x  1 8. I e . dx   KQ: 2 e 18. I dx  KQ: 1 ln2 2 1 cos x   1  cos x 2 0  0      sin 2 3 2   x  1 4  x 19. I   3 e sin 5xdx KQ: 2 .e 9. I dx   KQ: 0 20    0  sin  x 2  4    4 1 6 cos x 10 10. dx  KQ: 1 20. I dx  KQ: ln 1 sin 2x 6  5sin x  2 sin x 0 9 0
Nguyễn Chiến: 0973.514.674 39
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI 1 2  1. x x (2x 1)e dx  (ĐH Dược_81 ) 0   1 a cos x bcos x 2. Với x  0;   xác định a,b sao cho    4  cos x 1 sin x 1  sin x / 4 dx dx 3. Tính I  J   (ĐH BK TH_82) 3 cos x 0 cos x / 2 sin x  cosx 1 4. dx  (Bộ Đề) sin x  2cos x  3 0 1 (3x 1)dx 5.  (Bộ Đề) 3  0 (x 3) 1 xdx 6.  (Bộ Đề) 3  0 (x 1) 1 2 x 1 7. dx  (Bộ Đề) 4  0 x 1  8. 2x 2 e sin xdx  (Bộ Đề) 0 / 2 cos xdx 9.  (Bộ Đề) 2  cos 2x 0 1 dx 10. ,(0< <  )   (Bộ Đề) 2    1 x 2x cos 1  2a 11. 2 2 x  a dx ,(a>0)  (Bộ Đề) a / 2 3 4sin xdx 12.  (Bộ Đề) 1  cos x 0 a 13. 2 2 x  a dx  (Bộ Đề) 0 2 14. 1  sin xdx  (Bộ Đề) 0 3 / 8 dx 15.  (Bộ Đề) 2 2 /8 sin x cos x 2 dx 16.  (Bộ Đề) x 1  x 1 1
Nguyễn Chiến: 0973.514.674 40
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com x 17. Gpt 2 (u  x )du  sin x  (Bộ Đề) 0 b 18. 2 x ln xdx  (BK_94) 1 / 2 19. 2 x cos xdx  (BK_94) 0 2 dx 20.  (BK_95) 2 2 / 3 x x 1  21. cos x sin xdx  (BK_98) 0
22. Cho hàm số: f(x)  sin x.sin2x.cos5x
a. Tìm họ nguyên hàm của g(x).  2 f(x) b. Tính tích phân: I  dx  (BK_99) x  e  1 2 ln 2 2x e 23. dx  (BK_00) x 0 e  1 1 2 x 1 24. dx  (XD_96) x  1 0 / 4 cosx  2sin x 25. dx  (XD_98) 4cos x  3sin x 0 1 3dx 26.  (XD_00) 3  0 1 x 1 dx 27.  (ĐH Mỏ_95) 4 2   0 x 4x 3 / 3 28. 2 2 tg x  cot g x  2dx  (ĐH Mỏ_00) / 6 / 3 dx 29.  (ĐH Mỏ_00) sin x sin(x   / 6) / 6  / 4 6 6 sin x  cos x 30. dx  (ĐH Mỏ_01) x  6  1 / 4 2 ln(x 1) 31. dx  (ĐH Hàng Hải_00) 2 1 x
Nguyễn Chiến: 0973.514.674 41
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com / 2 sin xdx 32.  (ĐH GT VT_95) sin x  cos x 3 3 33. 5 2 x . 1  x dx  (ĐH GT VT_96A) 0 1/ 9 x 1  34. 3x  5   dx (ĐH GT VT_97) 2 5  sin (2x 1) 4x 1 0  7 / 3 x  1 35. dx  3 3x 1 0 x 2 4 (10  sin x  )dx  (ĐH GT VT_98) 2  1 3 x 36. I  dx  x.arctgxdx   (ĐH GT VT_99) 5  4x 1  0 / 2 x  cosx 37. dx  (ĐH GT VT_00) 2   / 2 4 sin x / 2 5cosx  4sinx 38. dx  (ĐH GT VT_01) 3 (cosx  sin x) 0 / 2 4 cos x 39. dx  (ĐH GTVT HCM_99) 4 4  0 cos x sin x / 3 2 sin x 40. dx  (ĐH GTVT HCM_00) 6 / 4 cos x  2 2 x  1 41. dx  (HV BCVT_97) 2 2  x x 1 / 2 3 sin x cos x 42. dx  (HV BCVT_98) 2  0 1 cos x 1 4 x 43. dx  (HV BCVT_99) x 11 2    44. 2 x sin x cos xdx  (HV NH_98) 0 / 2 45. 2 2 I  cos x cos 2xdx  0 / 2 2 2 J  sin x cos 2xdx  (HV NH HCM_98) 0
Nguyễn Chiến: 0973.514.674 42
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com / 3 x  sin x 46. dx  2 0 cos x 1 3 x dx  (HV NH HCM_00) 2 0 x  x 1 1 4 sin 4x 2 x ln(x 1)dx dx   2  0 01 cos x 2 47. 1  sin xdx  (ĐH NThương_94) 0 1 1 2 dx x  3x  2 48. dx   (ĐH NThương_99) 2 2 (x  3x  2) x  3 0 0 / 4 cos2x 49.   (ĐH NThương_00A) sin x  cos x  2 dx 3 0 1 3 2 x  2x 10x 1 50. dx  (ĐH NThương_00) 2   0 x 2x 9 1 2 x  3x 10 dx  2   0 x 2x 9  / 4 sin 4x 51. dx  (ĐH NThương_01A) 6 6 sin x  cos x 0 2 5   52. 2 I  ln(x  1  x ) dx    (ĐH KT_95) 2  1 53. 5 3 6 x (1  x ) dx  (ĐH KT_97) 0 / 4 dx 1 5 x 54. I  J = dx   (ĐH TM_95) 4 2  0 cos x x 1 0 1 55. x 1  xdx  (ĐH TM_96) 0 7 9 ln 2 x x 1  e 56. I  dx J = dx   (ĐH TM_97) x 3 2   0 0 1 e 1 x ln 2 dx 57.  (ĐH TM_98A) x e  5 0
Nguyễn Chiến: 0973.514.674 43
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 4 dx 58.  (ĐH TM_99) 2  1 x (1 x) / 2 4sin x 59. dx  (ĐH TM_00) 3  0 (sin x cos x)  60. 11 sin xdx  (HV QHQT_96) 0 / 4 61. 2 4 sin x cos xdx  (ĐH NN_96) 0 e ln x 62. dx  (ĐH NN_97) 2  1/ 2 (1 x) / 4 63. 2 cos x cos 4xdx  (ĐH NN_98) 0 7 / 3 x  1 64. dx  (ĐH NN_99) 3 3x 1 0 1 65. 2 2 (1  x  x ) dx  (ĐH NN_01D) 0 / 2 66. x 2 e cos xdx  (ĐH Thuỷ Lợi_96) 0  67. 1  cos 2xdx  (ĐH Thuỷ Lợi_97) 0 3 2 2 x 1 dx 68. I  dx J =   (ĐH Thuỷ Lợi_99) 4 2 5    1 x x 1 1 x(x 1) / 4 69. ln  1 tgxdx (ĐH Thuỷ Lợi_01A) 0 / 2 3sin x  4cosx 70. dx  (ĐH Thuỷ Lợi_00) 2 2  0 3sin x 4cos x 3 3 2 x  2x  xdx  0 / 4 sin x.cosx 71. dx  (ĐH Văn Hóa_01D) sin 2x  cos2x 0 / 2 sin x cos x 72. dx ;a, b  0  (HV TCKT_95) 2 2 2 2 0 a cos x  b sin x
Nguyễn Chiến: 0973.514.674 44
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 2 / 2 2 x 73. dx  (HV TCKT_97) 2 0 1  x / 4 74. 2 x(2cos x 1)dx  (HV TCKT_98) 0 / 3 cosx  sinx 1 4 x 1 75. dx dx   (HV TCKT_99) 2 3  sin 2x   / 4 x 1 0 / 2  sin x  7cos x  6 4 3 dx x cos x sin xdx   4sin x  3cos x  5 0 0 1 x 76. dx  (HV TCKT_00) 4 2   0 x x 1 / 2 77. 2 (x 1)sin xdx  (ĐH Mở_97) 0 / 2 3 4sin x 78. dx  (ĐH Y HN_95) 1  cos x 0 1 1 dx 79. 2 1  x dx   (ĐH Y HN_98) 2x x  1  / 2 0 e e 4 / 3 dx 80.  (ĐH Y HN_99) x  sin 2 /3 2 2 x 81. 4 tg xdx dx   (ĐH Y HN_00) 2    / 4 1 x 7x 12 3 82. 2 x  1dx  (ĐH Y HN_01B) 2 1 83. 2 x  1dx  (ĐH Y TB_97B) 0 / 4 dx 84.  (ĐH Y TB_00) 2  0 2 cos x 1 85. 2 3 (1  x ) dx  (ĐH Y HP_00) 0 / 2 2 x sin x  86. I  dx  (ĐH Dược_96 ) x   / 2 1 2 / 2 1 sin x 87. x e dx  (ĐH Dược_00) 1  cos x 0
Nguyễn Chiến: 0973.514.674 45
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 10 88. 2 x lg xdx  (ĐH Dược_01A) 1 x ln 3 2 dx  89. 2 x.e dx   (HV QY_97) x 0 e 1 0 3 2 dx sin x 90. dx   (HV QY_98) 2 3 4 2 x x 1 2  4  5x 1/ 2 dx 91.  (HV QY_99) 1  cos x 0/2 92. 2 cos x ln(x  1  x )dx  (HV KT Mật Mã_99) / 2 1 4 /3 x 1 dx dx   6 4  0 x 1 / 6 sin x cos x 1 93. 2 xtg xdx  (HV KT Mật Mã_00) 0 1 xdx 94.  (HV KTQS_95) 2  0 (x 1) / 4 3 4sin x 95. dx  (HV KTQS_96) 4  0 1 cos x / 2 3 sin x  sin x 96. cot gxdx  (HV KTQS_97) 3 / 3 sin x 1 dx 97.  (HV KTQS_98) 2 1  1 x  1 x / 2 98. cos x ln(1  cos x)dx  (HV KTQS_99) 0 1/ 3 dx  2 2 0 (2x 1) x 1 b 2 a  x 99.  
(a, b là số thực dương cho trước) (HV KTQS_01A) a  x  dx 2 2 0 a 100. 2 2 2 x x  a dx a ,  0  (ĐH AN_96) 0  xsin xdx 101.  (ĐH AN_97) 2  0 2 cos x
Nguyễn Chiến: 0973.514.674 46
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com / 2 4 dx 102. 3 3 (cos x  sin x)dx   (ĐH AN_98) 4 0 0 cos x 1  2x 2 xe dx x sin xdx   0 0 4 dx 103.  (ĐH AN_99) 2 7 x x  9  2 2 104. 2 2 3sin xdx x x 1dx   (ĐH TD TT_00) 0 0 2 105. 2 (x ln x) dx  (PV BC TT_98) 1 e 3 2 ln 2  ln x 106. dx  (PV BC TT_98) x 1 / 41 sin2x 107. dx  (PV BC TT_00) 2 0 cos x 1 3dx 108.  (ĐH Luật _00) 3  0 1 x 1 109. 2 2x (1  x) e dx  (ĐH CĐ_98) 0 2 / 2 / 2 dx dx 110. 2 (2x 1)cos xdx    (ĐH CĐ_99) x 1 sin 2x 0 e 1 0 0 1 2 dx ln(x 1) 111. dx   (ĐH CĐ_00) 2x 2  0 e 3 1 x / 2 1 x 2 1 sin 2x  cos 2x (1 e ) 112. dx dx   (ĐH NN I_97) 2x sin x  cos x   / 6 0 1 e / 2 / 2 cos xdx 113. 2x e sin 3xdx   (ĐH NN I_98B) 1 cos x 0 0 1 114. 19 x(1  x) dx  (ĐH NN I_99B) 0 2 / 4 dx 115. 2 xtg xdx   (ĐH NN I_00) 3  1 x(x 1) 0  / 2 6 cos x 116. dx  (ĐH NN I_01A) 4  sin x / 4
Nguyễn Chiến: 0973.514.674 47
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 2 117. ln(1  x)dx  (ĐH Lâm Nghiệp_97) 1 1 4 x  sin x 118. dx  (ĐH Lâm Nghiệp_98) 2  1 x 1  / 2 dx 119.  (ĐH Lâm Nghiệp_00) 2  sin x  cos x 0 1 120. 2 x .sin xdx  (ĐH SP HN I_99D) 0 a 121. 2 2 2 x a  x dx (a  0)  (ĐH SP HN I_00) 0 1 122. 3 2 x 1  x dx  (ĐH SP HN I_01B) 0 2 xdx 123.  (ĐH THợp_93) 2 1 x 2    124. 3 x sin xdx  (ĐH THợp_94) 0 / 2 dx  sin x  cos x 0 1 dx 125.  (ĐH QG_96) 1  x 0 / 2 3 1 sin xdx dx 126.   (ĐH QG_97A, B, D) 2 1  cos x x 1  x 0 0 1 2 1 x dx xdx   2 2   0 4 x 0 4 x 1 1 / 4 3 dx sin x 127. 3 2 x 1 x dx dx    (ĐH QG_98) x 2  0 e 1 0 0 cos x / 6 2 / 6 2 sin x cos x 128. Tính I  dx; J  dx   .   0 sin x 3 cosx 0 sin x 3 cosx 5 / 3 cos2x Từ đó suy ra: dx  (ĐH QG HCM_01A) 3  / 2 cos x 3 sin x / 4 / 4 2cosxdx 129. x 5e sin 2xdx   (ĐH SP II _97) 3  2sin x 0 0
Nguyễn Chiến: 0973.514.674 48
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
130. Cho f(x) liên tục trên R : f (x)  f (x)  2  2cos 2x x  R . Tính 3 / 2 f (x)dx  (ĐH SP II _98A) 3  / 2 / 2 131. 10 10 4 4 (sin x  sin x  cos x sin x)dx  (ĐH SP II _00) 0 3 2 0 3x  2 dx 132. dx   (CĐ SP HN_00) 2 x 1 x  4  x  2 1 1  1 / 4 (sinx  2cosx) 133. 2 2 x 1  x dx dx   (CĐ SP HN_00) 3sin x  cos x 0 0  134. 2 2 sin x cos xdx  (CĐ SP MGTW_00 ) 0 / 2 4 1  sin x dx 135. ln( )dx   (CĐ SP KT_00) 1 cos x x(1 x ) 0 1 1 1 2 1 x 136. 2 1  x arcsin xdx dx   (CĐ PCCC_00) x  1  1 1 2  1 2 137. x x 2 (e sin x  e x )dx  (ĐH TN_00) 1  3 3 t 138. dt  (ĐH SP Vinh_98) 2   0 t 2t 1 1 2 1 1  x 139. 2 dx x 1dx   (ĐH SP Vinh_99) 4  1/ 21 x 0 1 2 (x  x)dx 140.  (ĐH HĐ_99) 2 0 x  1  / 4 dx 141. 3 sin x cos3xdx   (ĐH HĐ_00) 1  tgx 0 0 2 ln x 142. dx  (ĐH Huế_98) 2 1 x / 2 6 sin x 143. dx  (ĐH Huế_00) 6 6  0 sin x cos x 2 dx 144.  (ĐH ĐN_97) 2  x  1 7
Nguyễn Chiến: 0973.514.674 49
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com / 2  cos x cos xdx 145. dx   (ĐH ĐN_98) 2 1  sin x 0 1  cos x 0 / 4 2 dx 146. x ln xdx   (ĐH ĐN_99) 4 0 cos x 0 / 2 / 2 sin x  cos x sin xdx 147. dx   (ĐH ĐN_00) sin x  cos x 1  2cos x / 4 0 1 2 x  x  arctgx 148. dx  (ĐH Tnguyên_00) 2  0 1 x 2 1 x 1 149. 2 10
dx (1  3x)(1  2x  3x ) dx   (ĐH Quy Nhơn) 3 3x  2 0 0 2 e  e 2  ln x ln x 150. dx sin xdx dx    (ĐH Đà Lạt) 2x x 1 1 1 2 3 2 x 1 151. 2 3 x x 1dx dx   (ĐH Cần Thơ) x 1 0 0 / 2 3 / 2 3 / 4 cos x sin x sin 4x dx dx dx    4 4 sin x  cos x sin x  cos x  0 0 0 sin x cos x e 1 1 2 ln xdx x 3 x x e dx dx    2 x(ln x 1) 1 x 1 0 0 / 2 / 2 152. 2 3 2 sin 2x(1  sin x) dx sin x cos x(1  cos x) dx   0 0 / 2 3 5 3  2 x 2x (x 1)sin xdx dx   (ĐH Thuỷ sản NT) 2 x 1  0 0 / 2 / 2 sin xdx 153. 2 dx x cos xdx   (ĐH BK HCM) 2  0 cos x 3 0 / 2 1 4 xdx cos 2xdx   3  0 0 (2x 1)  1 x sin x 154. dx x 1  xdx   (ĐH Y Dược HCM) 2  0 9 4cos x 0  2  sin xdx 155. 1 sin xdx   (ĐH Ngoại thương) x 1 3  - e 1 2 3 2 x ln xdx x 1  x dx   1 0
Nguyễn Chiến: 0973.514.674 50
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com   x sin xdx 156. arctg(cos x)dx   (ĐH SP HCM) 2  0 1 cos x 0 /3 1  sin xdx 4x 11 4 dx cos xdx    2 sin x  cos x   0 0 x 5x 6 0 1 x   e 157. 3 dx x sin xdx x sin xdx     (ĐH QG HCM) x  01 e 0 0 1/ 2 4 / 2 x sin 2xdx dx   2 4   0 x 1 0 1 sin x / 2 1 / 4 sin 2x xdx 4 dx sin xdx    4 1  cos x 2x 1 0 0 0 / 2 1 2 3 x 2 sin x cos xdx e sin ( x  )dx   0 0 1 1  1  158. x 2x  e dx (x 1)e dx   (ĐHDL NN Tin Học) 2     0 1 x 0 2 1 x x 1 dx e dx   0 0 1 5 1 x 2 (1 e ) 159. 2 20 1 x dx x(x  4) dx dx    (DL) x 0 4 0 e e 2 ln 2 2x x 1 ln x e  3e dx dx   2x x x   1 0 e 3e 2 1 3 x 160. dx  (Dự bị_02) 2 x  1 0 ln 2 x e 161. dx  (Dự bị_02) e 13 x 0 0 162. x   2x 3 e  x 1dx (Dự bị_02) 1   / 2 163. 6 3 5 1  cos x.sin x.cos xdx  (Dự bị_02) 0 2 3 dx 164.  (Đề chung_03A ) 2  5 x x 4  / 4 xdx 165.  (Dự bị_03) 1  cos2x 0
Nguyễn Chiến: 0973.514.674 51
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 1 166. 3 2 x 1  x dx  (Dự bị_03) 0  / 4 2 1  2sin x 167. dx  (Đề chung_03B) 1  sin 2x 0 ln 5 2x e 168. dx  (Dự bị_03) x ln 2 e  1 a 169. Cho hàm số: x f(x) 
 bxe , tìm a, b biết rằng: 3 (x  1) 1 f '(0)  2  2 và f(x)dx  5  . (Dự bị_03) 0 2 170. 2 x  x dx  (Đề chung_03D) 0 1 2 171. 3 x x e dx  (Dự bị_03) 0 e 2 x  1 172. ln xdx  (Dự bị_03) x 1 2 x 173. dx  (Đề chung_04A)   1 1 x 1 e 1  3ln x.ln x 174. dx  (Đề chung_04B) x 1 3 175. ln   2 x  xdx (Đề chung_04D) 2 / 2 sin2x  sinx 176. dx  (Đề chung_05A)  0 1 3cosx / 2 sin2x.cosx 177. dx  (Đề chung_05B) 1  cos x 0 / 2 178.   sinx e  cosxcosxdx (Đề chung_05D) 0 7 x  2 179. dx  (Dự bị_05) 3  0 x 1  / 2 180. 2 sin xtgxdx  (Dự bị_05) 0 / 2 181. cos x e sin 2xdx  (Dự bị_04) 0
Nguyễn Chiến: 0973.514.674 52
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 2 4 2 x  x  1 182. dx  (Dự bị_05) 2 x  4 0 / 4 183.   sin x tgx  e cosxdx (Dự bị_05) 0 e 184. 2 x ln xdx  (Dự bị_05) 1 / 2 sin 2x 185. dx  (Dự bị_05) 2 2 0 cos x  4sin x 6 dx 186.  (Dự bị_06)    2 2x 1 4x 1 1 187. x  2 2x e dx (Đề chung_06D) 0 / 2 188. (x  1)sin 2xdx  (Dự bị_06) 0 2 189. x  2lnxdx (Dự bị_06) 1 ln 5 dx 190. dx  (Dự bị_06) x x e  2e  3 ln 3 10 dx 191.  (Dự bị_06)   5 x 2 x 1 e 3  2 ln x 192. dx  (Dự bị_06)  1 x 1 2 ln x 3 5 3 x  2x 193. dx  (CĐ SP_04A) 2 0 x  1 3
194.   x  2  x  2  (CĐ GTVT_04) 3  2 4 x 195. dx  (CĐ KTKT_04A) 5 0 x  1 3 dx 196.  (Dự bị_04) 3 x  x 1 ln 8 197. x 2x e  1.e dx  (Dự bị_04) ln 3 2  198. x.sin xdx  (Dự bị_05) 0
Nguyễn Chiến: 0973.514.674 53
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 1 199. x 1  xdx  (Dự bị_04) 0 3 e 2 ln x 200. dx  (Dự bị_05) x ln x  1 1 / 2 201. 2 (2x  1)cos xdx  (Dự bị_05) 0 THI ĐH 2005 -2008
Bài 1. ĐH, CĐ Khối A – 2005  2 sin 2x  sin x 34 I   dx KQ: 1  3cos x 27 0
Bài 2. ĐH, CĐ Khối B – 2005  2 sin 2x cos x I  dx  KQ: 2 ln 2 1 1  cos x 0
Bài 3. ĐH, CĐ Khối D – 2005  2 I    sin e x  cos x cos xdx KQ: e  1 4 0
Bài 4. Tham khảo 2005 7 x  2 141 I  dx  KQ: 3 x 1 10 23,1 0
Bài 5. Tham khảo 2005  3 3 I   2 sin xtgxdx KQ: ln 2  8 0
Bài 6. Tham khảo 2005  4 1 I  tgx  sin e x.cos x dx KQ: 2 ln 2 e 1 0
Bài 7. Tham khảo 2005 e 2 3 1 I  x2 ln xdx KQ: e  9 9 1
Bài 8. CĐ Khối A, B – 2005
Nguyễn Chiến: 0973.514.674 54
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 1 6 3  8 I  x3. x2 dx   3 KQ: 5 0
Bài 9. CĐ Xây Dựng Số 3 – 2005 3 x  3 I   dx
KQ: 6 ln 3  8 3 x  1  x   3 1
Bài 10. CĐ GTVT – 2005 1 8 I  x5 1 x2 dx   KQ: 105 0
Bài 11. CĐ Kinh Tế Kỹ Thuật I – 2005  3 2 2 x 3.e  5 I   3e sin5xdx KQ: 34 0
Bài 12. CĐ Tài Chính Kế Toán IV – 2005 3 848 I  x3 x5 . 1 dx   KQ: 105 0
Bài 13. CĐ Truyền Hình Khối A – 2005  4 1 2 2 sin x 1 I   dx KQ: ln 2 1  sin 2x 2 0
Bài 14. CĐSP Tp.HCM – 2005 0 dx 3 I   KQ: 2 x  2x  18  4 1
Bài 15. CĐ KT-KT Cần Thơ – 2005 e ln x 2 I   dx 1 x KQ: 2 e 1
Bài 16. CĐSP Vĩnh Long – 2005 7 3 x 1 46 I  dx  KQ: 3 x 3  1 15 0
Bài 17. CĐ Bến Tre – 2005  2 cos 3x I   dx
KQ: 2  3ln 2 sin x  1 0
Nguyễn Chiến: 0973.514.674 55
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
Bài 18. CĐSP Sóc Trăng Khối A – 2005  2 xdx I   sin x I  ln2 0 2 sin x  2 2 cos . x cos 2 KQ:  3  J   3 4 3 2 x xdx J   sin 2 sin 2x cos x 0
Bài 19. CĐ Cộng Đồng Vĩnh Long – 2005 e 2 e 1 I  xln xdx KQ: 4 1
Bài 20. CĐ Công Nghiệp Hà Nội – 2005 2  4 2  I  x sin xdx  KQ:  4 2 0
Bài 21. CĐSP Hà Nội – 2005 2 x3  2x2  4x  9  I  dx   x KQ: 6 2  4 8 0
Bài 22. CĐ Tài Chính – 2005 1 xdx 1 I   KQ: 3 x 1 8 0   
Bài 23. CĐSP Vĩnh Phúc – 2005 e dx  I   KQ: 2 6 1 x 1  ln x
Bài 24. CĐSP Hà Nội – 2005  2 2004 sin x  I   dx KQ: 2004 sin x  2004 cos x 4 0
Bài 25. CĐSP KonTum – 2005  2 3 4sin x I   dx KQ: 2 1  cos x 0
Nguyễn Chiến: 0973.514.674 56
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com NĂM 2006
Bài 1. ĐH, CĐ Khối A – 2006  2 sin2x 2 I  dx  KQ: 2 2 3 0 cos x  4sin x
Bài 2. Tham khảo 2006 6 dx 3 1 I   KQ: ln  2x 1 4x 1 2 12 2
Bài 3. ĐH, CĐ Khối D – 2006 1 2 5  3e 2x
I  x2e dx KQ: 2 0
Bài 4. Tham khảo 2006  2  I  x    1 sin2x dx KQ: 1 4 0
Bài 5. Tham khảo 2006 2 5
I  x2lnxdx KQ:  ln 4 4 1
Bài 6. ĐH, CĐ Khối B – 2006 ln5 dx 3 I   ln x x e KQ:  2e  3 2 ln3
Bài 7. Tham khảo 2006 10 dx I   KQ: 2 ln 2 1 x  2 x 1 5
Bài 8. Tham khảo 2006 e 3 2ln x 10 11 I  dx  KQ: 2  x 1 2ln x 3 3 1
Bài 9. CĐ KTKT Công Nghiệp II – 2006 1 2 1 I  x ln  1x dx KQ: ln 2  2 0 (Đổ 2
i biến t  1 x , từng phần)
Bài 10. CĐ Cơ Khí – Luyện Kim – 2006
Nguyễn Chiến: 0973.514.674 57
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 2 ln1 x 3 I  dx  3ln2  ln3 2 x KQ: 2 1
Bài 11. CĐ Nông Lâm – 2006 1 2 2 2 1 I  x x 1dx  KQ: 3 0
Bài 12. ĐH Hải Phòng – 2006 1 x 1 I  dx  ln 2 2 1 KQ:  x 2 0
Bài 13. CĐ Y Tế – 2006  2 sin x  cosx I  dx  KQ: ln 2  1 sin2x 4
Bài 14. CĐ Tài Chính Kế Toán – 2006 3 1 2 I  x ln
 x 5dx KQ: 14ln145ln59 2 0
Bài 15. CĐ Sƣ Phạm Hải Dƣơng – 2006  2 cos2x 1 I  dx   KQ: sin x  cosx  33 32 0
Bài 16. Hệ CĐ – ĐH Hùng Vƣơng – 2006  4  2 I  x    1 cosx dx KQ: 1 8 0
Bài 17. CĐ KTKT Đông Du – 2006  4 cos2x 1 I  dx  ln3 1 2sin2x KQ: 4 0
Bài 18. CĐ Sƣ Phạm Quảng Bình – 2006 ln2 2x e 8 I  dx  KQ: 2 3  x 3 0 e  2
Bài 19. CĐ Sƣ Phạm Quảng Ngãi – 2006
Nguyễn Chiến: 0973.514.674 58
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com  2 3 4sin x I  dx 1 KQ: 2  cosx 0
Bài 20. CĐ Sƣ Phạm Trà Vinh – 2006  4 x I  2  dx   ln 2 cos x KQ: 4 2 0
Bài 21. CĐ Bán Công – Công Nghệ - Tp.HCM – 2006 3 x  3 I  dx 
KQ: 6 ln 3  8     3 x 1 x 3 1
Bài 22. CĐ Sƣ Phạm Tiền Giang – 2006 9 468 3 I  x. 1 x dx  KQ:  7 1
Bài 23. CĐ Bến Tre – 2006 e 3  x 1 3 2e 11 I   ln x dx  x KQ: 9 18 1   Bài 24. 1 2 3 2 I  x 2  x dx  KQ: 3 3 2 2 9 0 Bài 25.  2 2 1   I  2x    2 1 cos xdx KQ:   1 2 4 2    0 Bài 26. 1 2 I e 1  x 2 e x  3 x 1 dx KQ:  4 14 0
Bài 27. CĐ KT-KT Công Nghiệp I – 2006  2 sin3x I  dx  2cos3x1 KQ: Không tồn tại 0
Bài 28. CĐ KT-KT Công Nghiệp II – 2006
Nguyễn Chiến: 0973.514.674 59
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 1 2 1 I  xln  1x dx KQ: ln 2  2 0
Bài 29. CĐ Xây dựng số 2 – 2006 2 x x 1 32 I  dx  10ln3 x  5 KQ: 3 1
Bài 30. CĐ Xây dựng số 3 – 2006 1 3 5
I  xcos xsinxdx KQ: 4 0
Bài 31. CĐ GTVT III – 2006  2 cosx 1 5 I  dx  ln 5 2sinx KQ: 2 3 0 2 J  2x  7lnx  
1dx KQ: 24ln314 0
Bài 32. CĐ Kinh tế đối ngoại – 2006  4 I   8 1 tg x 76 dx KQ: 105 0
Bài 33. CĐSP Hƣng Yên - Khối A– 2006 4 4x  3 I  dx   2 x 3x  2
KQ: 18ln 2 7ln3 3
Bài 34. CĐSP Hƣng Yên - Khối B– 2006  6 3 sin3x sin 3x 1 1 I  dx    ln2 1 cos3x KQ: 6 3 0
Bài 35. CĐSP Hƣng Yên - Khối D1 , M– 2006 e 3 2 ln x 2  ln x 3 3 2 I  dx  3 3 2 2 x KQ:   8 1
Bài 36. CĐ Bán công Hoa Sen – Khối A – 2006  4 I   4 4 cos x sin x 1 dx KQ: 2 0
Nguyễn Chiến: 0973.514.674 60
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
Bài 37. CĐ Bán công Hoa Sen – Khối D – 2006  4 cos2x I  dx  1 ln3 1 2sin2x KQ: 4 0
Bài 38. CĐSP Trung Ƣơng – 2006  2 I 2  sin xsin2xdx  KQ: 3 0
Bài 39. CĐSP Hà Nam – Khối A – 2006 1 x 4 1 I  dx   ln  x KQ :  32 3 4 0
Bài 40. CĐSP Hà Nam – Khối M – 2006  2 2 2  I  x cosxdx  KQ:  2 4 1
Bài 41. CĐSP Hà Nam – Khối A (DB) – 2006 e dx  I   x 2 1 ln x KQ: 4 1 
Bài 42. CĐKT Y Tế I – 2006  2 sin x  cosx I  dx  KQ: ln 2  1 sin2x 4
Bài 43. CĐ Tài Chính Hải Quan – 2006  3 lntgx 1 2 I  dx  KQ: ln 3 16  sin 2x 4
Bài 44. CĐ Kĩ thuật Cao Thắng – 2006  2 3 2 15 I  sin2x 
1sin x dx KQ: 4 0
Bài 45. CĐKT Tp.HCM Khóa II - 2006 e lnx I  dx   x KQ: 4 2 e 0
Nguyễn Chiến: 0973.514.674 61
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
Bài 46. CĐCN Thực phẩm Tp.HCM – 2006 1 1  I  dx  KQ: 2 x  2x  2 4 0
Bài 47. CĐ Điện lực Tp.HCM – 2006 7 3 x  2 46 I  dx  KQ: 3 3x 1 15 0
Bài 48. CĐ Kinh tế công nghệ Tp.HCM Khối A– 2006  4 x  2 I  dx  KQ:  ln 2 cos x 4 2 0
Bài 49. CĐ Kinh tế công nghệ Tp.HCM Khối D1 – 2006 2 I  4x   1lnxdx
KQ: 6 ln 2  2 1
Bài 50. CĐSP Hà Nội Khối D1 – 2006  3 dx I   2 ln2    KQ: .  sin x.sin x  3 6  3    NĂM 2007
Bài 1. ĐH, CĐ khối A – 2007 x
Tính diện tích hình phẳng giới hạn bởi các đƣờng: y  e  
1 x, y  1 e x . e KQ: 1 2
Bài 2. ĐH, CĐ khối B – 2007
Cho hình phẳng H giới hạn bởi các đƣờng y  x ln x , y  0, y  e . Tính thể tích của khối tròn xoay
tạo thành khi quay hình H quanh trục Ox.   3 5e  2 KQ: 27
Bài 3. ĐH, CĐ khối D – 2007 e Tính tích phân 3 2 I  x ln xdx  1
Nguyễn Chiến: 0973.514.674 62
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 4 5e 1 KQ: 32
Bài 4. Tham khảo khối A – 2007 4 2x 1 dx  KQ: 2  ln2 1 2x 1 0
Bài 5. Tham khảo khối B – 2007 x 1 x
Tính diện tích hình phẳng giới hạn bởi các đƣờng y  0 à v y . KQ: 2 x 1  1  ln2  1 4 2
Bài 6. Tham khảo khối B – 2007
Tính diện tích hình phẳng giới hạn bởi các đƣờng 2 2 y x à
v y  2  x . KQ:  1  2 3
Bài 7. Tham khảo khối D – 2007 1 xx   1 3 dx  1 ln2  ln3 2 x KQ:  4 2 0
Bài 8. Tham khảo khối D – 2007  2 2  2 x cosxdx  KQ:  2 4 0
Bài 9. CĐSPTW – 2007
Tính diện tích hình phẳng giới hạn bởi các đƣờng có phƣơng trình 2 y  x  2 ; y  x; x  1  ; x  0 . 7 KQ: 6
Bài 10. CĐ GTVT – 2007 2 3 4cos x dx  1 KQ: 2  sin x 0
Bài 11. CĐDL Công nghệ thông tin Tp.HCM – 2007 7 x  2 231 dx  KQ: 3 x  1 10 0
Nguyễn Chiến: 0973.514.674 63
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com
Bài 12. CĐ Khối A – 2007 1 2007 1  1 2008 2008 3  2 1 dx  2x  KQ:  x  2008 1  3
Bài 13. CĐ Cơ khí luyện kim – 2007 e 2 1 3 xlnx dx  KQ: 5e  2 27 1
Bài 14. CĐSP Vĩnh Phúc – 2007  4 3 2 2   1 xsinx dx KQ:   384 32 4 1
Bài 15. CĐ Khối B – 2007 2
Tính diện tích hình phẳng giới hạn bởi các đƣờng y  x , y  x  cos x , x  0 , x   . KQ: 2
Bài 16. CĐ Khối D – 2007 0 x  1 dx  KQ: 1 2 
Bài 17. CĐ Dệt may thời trang Tp.HCM – 2007 3 dx 3  KQ: 1  2 x  2 x  1 3 12 1 
Bài 18. CĐ Hàng hải – 2007 3 3 2 14 3 x x  1dx  KQ: 5 1
Bài 19. CĐ Kinh tế kĩ thuật Thái Bình – 2007 0 2x 3 2 31 x e  x   1dx KQ: e  4 60 1 
Bài 20. CĐ Công nghiệp Phúc Yên – 2007 1 x xe dx  KQ: 1 0
Nguyễn Chiến: 0973.514.674 64
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com NĂM 2008  6 4 tan x 1 10 Bài 1) Tính I = dx
- ĐH, CĐ Khối A – 2008
KQ: ln 2  3  cos x 2 9 3 0     sin x dx   4  4  4  3 2 Bài 2) Tính I =
- ĐH, CĐ Khối B – 2008 KQ:
sin 2x  2 1 sin x  cos x 4 0   2 ln x 3  2 ln 2 Bài 3) Tính I = dx
- ĐH, CĐ Khối D – 2008 KQ: 3 x 16 1 3 xdx 3  12  Bài 4) Tính I =
- Dự bị 1 - khối A-2008 KQ: 3  5 36   3 2x  2 4  5  2  /2 sin 2xdx 1
Bài 5) Tính I  
- Dự bị 2 - khối A-2008
KQ:   ln 2 3  4sin x  o c s2x 2 0 2 (x 1)dx
Bài 6) Tính I  
- Dự bị 1 - khối B-2008 4x 1 0 1 3 x dx
Bài 7) Tính I  
- Dự bị 2 - khối B-2008 2  0 4 x 1  xBài 8) Tính 2 I   . x x e
dx - Dự bị 1 - khối D-2008 2   0 4 x
Bài 9) CĐ Khối A, B, D – 2008. Tính diện tích hình phẳng giới hạn bởi parabol  9 P 2
: y  x  4x và đƣờng thẳng d : y x . KQ: (đvdt) 2
Nguyễn Chiến: 0973.514.674 65
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com NĂM 2009  2 8  Bài 1) Tính I = 3 2
(cos x 1) cos xdx - ĐHKA-2009 KQ:  5 4 0 3 3  ln x 1 27 Bài 2) Tính I =
dx - ĐHKB-2009 KQ: 3 (  ln ) 2 x 1 4 16 1    3 1 Bài 3) Tính I =
dx - ĐHKD-2009 KQ: ln(e2+e+1) – 2 ex 1 1 NĂM 2010 1 2 x 2 x e  2 x x e 1 1 1 2e Bài 1) Tính I = dx - ĐHKA-2010 KQ:  ln   1 2 x e 3 2  3  0 e ln xdx 1 3 Bài 2) Tính I =  - ĐHKB-2010 KQ:   ln 2 x(2  ln x) 3 2 1 e  3  2 e
Bài 3) Tính I = I  2x  ln xdx   - ĐHKD-2010 KQ: 1 x  2 1 NĂM 2011
4 x sin x  (x 1) cos x   2    Bài 1) Tính I = dx - ĐHKA-2011 KQ:  ln  1   
x sin x  cos x  4 2   4  0   3 1 x sin x 2 Bài 2) Tính I = dx  - ĐHKB-2011 KQ: 3   ln(2  3) 2 os c x 3 0 4 34 3 4x 1  Bài 3) Tính I = dx - ĐHKD-2011 KQ: 10 ln 2x 1  2 3 5 0 NĂM 2012 3  1 ln(x 1) 2 2
Bài 1) Tính tích phân I dx- KA-2012 KQ:  ln 2  ln 3 2 x 3 3 1 1 3 1 x 2ln33ln2
Bài 2) Tính tích phân I d . x - ĐHKB-2012 KQ: 4 2 x  3x  2 2 0
Nguyễn Chiến: 0973.514.674 66
Nguyên hàm và tích phân Nguyễn Chiến
chienmath43@gmail.com 2   1 / 4 
Bài 3) Tính tích phân I  x(1 sin 2x)dx  - ĐHKD-2012 KQ: 32 4 0 NĂM 2013 2 2 x 1 5 3
Bài 1) Tính tích phân I  ln xdx - ĐHKA-2013 KQ: ln 2  2 x 2 2 1 1 2 2 1
Bài 2) Tính tích phân 2
I x 2  x dx - ĐHKB-2013 KQ: 3 0 1 2 (x 1)
Bài 3) Tính tích phân I dx  - ĐHKD-2013 KQ: 1 ln 2 2 x 1 0 NĂM 2014
Bài 1) Tính diện tích hình phẳng giới hạn bởi đƣờng cong 2
y  x  x  3 và đƣờ 1
ng thẳng y  2x 1- ĐHKA-2014 KQ: 6 2 2  3 1
Bài 2) Tính tích phân x x dx - ĐHKB-2014 KQ: 1 ln3 2 x x 1  4 3
Bài 3) Tính tích phân I = (x 1) sin 2xdx  .- ĐHKD-2014 KQ: 4 0 NĂM 2015 1
Bài 1) THPTQG 2015 Tính tích phân x I = ( x - 3 e ) d x
KQ: 4  3e 0 3 x 8
Bài 2) Dự bị THPTQG 2015 Tính tích phân I dx KQ: x 1 3 0 NĂM 2016 3
THPTQG 2016 Tính tích phân I  3x   2 x
x 16 dx KQ: 88 0
Nguyễn Chiến: 0973.514.674 67