Cực trị của hàm số – Lê Văn Đoàn Toán 12

Cực trị của hàm số – Lê Văn Đoàn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

17 9 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 63 -

§ 2. CÖÏC TRÒ CUÛA HAØM SOÁ



A. KIẾN THỨC CƠ BẢN

Khái niệm cực đại, cực tiểu

Cho hàm số

( )y f x

xác định, liên tục trên

( ; ),a b

(có thể

là

,

b là

)

và

( ; ) :

x a b





 Nếu tồn tại số

0h 

sao cho

( ) ( )

f x f x





với mọi

( ; )

x x h x h

  

 

và

x x





thì ta

nói hàm số

( )f x

đạt cực đại tại điểm .x



 Nếu tồn tại số

0h 

sao cho ( ) ( )f x f x



với mọi ( ; )x x h x h  

 

và x x



thì ta

nói hàm số

( )f x

đạt cực tiểu tại điểm .x



Các định lí

1. Định lí 1 (điều kiện cần)

Nếu hàm số ( )y f x có đạo hàm trên khoảng

( ; )a b

và đạt cực đại (hoặc cực tiểu) tại



thì ( ) 0.f x







2. Định lí 2 (điều kiện đủ)

Giả sử ( )y f x liên tục trên khoảng ( ; )K x h x h  

 

và có đạo hàm trên K hoặc

trên

\ { },K x



với

0.h 

Khi đó:

 Nếu ( ) 0f x



 trên khoảng

( ; )

x h x



 

và ( ) 0f x



 trên khoảng

( ; )

x x h



 

thì



là

một điểm cực đại của hàm số

( ).f x

 Nếu ( ) 0f x



 trên khoảng ( ; )x h x

 

và ( ) 0f x



 trên khoảng ( ; )x x h

 

thì x



là

một điểm cực tiểu của hàm số

( ).f x

x h





x h





x h





x h





( )

f x







( )

f x







( )

f x

( )

f x

Điểm

cực đại

Điểm

cực tiểu

Điểm

cực tiểu

Tiếp tuyến

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 64 -

Nói cách khác

 Nếu ( )f x



đổi dấu từ âm sang dương khi

đi qua điểm x



(theo chiều tăng) thì hàm số

( )y f x

đạt cực tiểu tại điểm .x



 Nếu ( )f x



đổi dấu từ dương sang âm khi

đi qua điểm



(theo chiều tăng) thì hàm số

( )y f x

đạt cực đại tại điểm .x



2. Định lí 3

Giả sử

( )y f x

có đạo hàm cấp 2 trong khoảng ( ; ),x h x h 

 

với

0.h 

Khi đó:

 Nếu

( ) 0, ( ) 0

y x y x

 

 

 

thì



là điểm cực tiểu.

 Nếu ( ) 0, ( ) 0

o o

y x y x

 

  thì x



là điểm cực đại.

Chú ý. Một hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số

bằng 0, hoặc tại đó hàm số không có đạo hàm, chẳng hạn hàm số

y x



B. CÁC DẠNG TOÁN THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI

Daïng toaùn 1: Tìm ñieåm cöïc ñaïi, cöïc tieåu, giaù trò cöïc ñaïi, giaù trò cöïc tieåu



 Bài toán: Tìm các điểm cực đại, cực tiểu (nếu có) của hàm số

( ).y f x

 Phương pháp:



Bước 1. Tìm tập xác định D của hàm số.



Bước 2. Tính đạo hàm ( ).y f x

 

 Tìm các điểm

, ( 1,2, 3,..., )

x i n



mà tại đó đạo hàm

bằng 0 hoặc không xác định.



Bước 3. Sắp xếp các điểm

x theo thứ tự tăng dần và lập bảng biến thiên.



Bước 4. Từ bảng biến thiên, suy ra các điểm cực trị (dựa vào nội dung định lý 2).

BÀI TẬP VẬN DỤNG

1. Cho hàm số ( )y f x có bảng biến thiên:

 Hàm số đạt cực tiểu tại: 1.x  

 Hàm số đạt cực đại tại: 2.x 

 Giá trị CĐ (cực đại) của hàm số:

y 

CĐ

 Giá trị CT (cực tiểu) của hàm số:

y  

 Điểm cực đại của đồ thị hàm số:

(2;1).

 Điểm cực tiểu đồ thị hàm số:

( 1; 3).

N  

2. Cho hàm số ( )y f x có bảng biến thiên:

 Hàm số đạt cực tiểu tại: ...............................

 Hàm số đạt cực đại tại: ...............................

 Giá trị CĐ (cực đại) của hàm số: ................

 Giá trị CT (cực tiểu) của hàm số: ...............

 Điểm cực đại của đồ thị hàm số: ................

 Điểm cực tiểu của đồ thị hàm số: ...............

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 65 -

3. Cho hàm số ( )y f x có bảng biến thiên:

 1 0 1























 Hàm số đạt cực tiểu tại: ...............................

 Hàm số đạt cực đại tại: ...............................

 Giá trị CĐ (cực đại) của hàm số: ................

 Giá trị CT (cực tiểu) của hàm số: ...............

 Điểm cực đại của đồ thị hàm số: ................

 Điểm cực tiểu của đồ thị hàm số: ..............

4. Cho hàm số ( )y f x có bảng biến thiên:

 1 0 1







0   0



4







 Hàm số đạt cực tiểu tại: ...............................

 Hàm số đạt cực đại tại: ...............................

 Giá trị CĐ (cực đại) của hàm số: ................

 Giá trị CT (cực tiểu) của hàm số: ................

 Điểm cực đại của đồ thị hàm số: ................

 Điểm cực tiểu của đồ thị hàm số: ...............

5. Cho hàm số ( )y f x có đồ thị:

 Hàm số đạt cực tiểu tại: ...............................

 Hàm số đạt cực đại tại: ...............................

 Giá trị CĐ (cực đại) của hàm số: ................

 Giá trị CT (cực tiểu) của hàm số: ...............

 Điểm cực đại của đồ thị hàm số: ................

 Điểm cực tiểu của đồ thị hàm số: ..............

6. Cho hàm số ( )y f x có đồ thị:

 Hàm số đạt cực tiểu tại: ...............................

 Hàm số đạt cực đại tại: ...............................

 Giá trị CĐ (cực đại) của hàm số: ................

 Giá trị CT (cực tiểu) của hàm số: ................

 Điểm cực đại của đồ thị hàm số: ................

 Điểm cực tiểu của đồ thị hàm số: ...............

7. Cho hàm số ( )y f x có đồ thị:

 Hàm số đạt cực tiểu tại: ...............................

 Hàm số đạt cực đại tại: ...............................

 Giá trị CĐ (cực đại) của hàm số: ................

8. Cho hàm số ( )y f x có đồ thị:

 Hàm số đạt cực tiểu tại: ...............................

 Hàm số đạt cực đại tại: ...............................

 Giá trị CĐ (cực đại) của hàm số: ................



SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 66 -

8. Giá trị cực đại của hàm số

3 1

y x x

  

bằng

A. 3. B. 1.

C. 1. D. 4.

Lời giải. Tập xác định . D

1 1

3 3, 0

1 3

x y

y x y

x y



   



 

    



   





Giới hạn:

lim



 

và

lim .



 



1 1







0  0









Giá trị cực đại 3.y 

CĐ

Chọn A.

9. Giá trị cực đại hàm số

12 1

y x x

  

bằng

17.

B. 2.

C. 45. D. 15.

......................................................................

10. Điểm cực đại của đồ thị hàm số:

3 2

3 1y x x    là

A. 0.x  B. ( 2; 19).M  

C. (0;1).N D. 2.x  

.......................................................................

11. Điểm cực tiểu của đồ thị hàm số:

4 2

2 5y x x    là

A. ( 1;6).A  B. 0.x 

C. 5. D. (0;5).B

......................................................................

12. Điểm cực đại của đồ thị hàm số:

4 2

4 3y x x   là

A. (0; 1). B. (0;3).

( 2; 1).



( 2; 1).

 

.......................................................................

13. Giá trị của tiểu của đồ thị hàm số

4 2

2 2y x x    bằng

A. 2. B. (0;2).

C. (1;3). D. 3.

......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 67 -

14. Cho hàm số

x x

 

 



Điểm cực tiểu

của hàm số đã cho là

 



( 2; 3).

 

.......................................................................

15. Gọi

M n

lần lượt là giá trị cực đại, giá

trị cực tiểu của hàm số

3 3

x x

 

 



Giá trị của

M n



bằng

.......................................................................

16. Tìm giá trị cực đại

(nếu có) của hàm số

3 2 .

y x x

  



CĐ



CĐ



CĐ

y 

CĐ

.......................................................................

17. Tìm cực đại của hàm số

1 .

y x x

 



 



.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 68 -

BÀI TẬP VỀ NHÀ 1

Câu 1. (Đề thi THPT QG năm 2019 – Mã đề 104) Cho hàm số ( )f x có bảng biến thiên:

Hàm số đã cho đạt cực tiểu tại

A. 2.x   B. 1.x  C. 3.x  D. 2.x 

Câu 2. (Sở GD & ĐT Tp. HCM năm 2018) Cho hàm số

( )y f x

có đồ thị như hình vẽ. Mệnh

đề nào đúng ?

A. Hàm số có giá trị cực tiểu bằng 2.

B. Hàm số có giá trị lớn nhất bằng 2.

C. Hàm số đạt cực đại tại 0x  và cực tiểu tại 2.x 

D. Hàm số có ba điểm cực trị.

Câu 3. (THPT Chuyên Vĩnh Phúc 2018) Hàm số

2 1







có bao nhiêu điểm cực trị ?

A. 1. B. 0.

C. 2. D. 3.

Câu 4. (Sở GD & ĐT Bạc Liêu 2019) Điểm cực tiểu của hàm số

3 2

3 9 2y x x x    là

A. 11.x  B. 3.x 

7.x 

D. 1.x  

Câu 5. (THPT Thăng Long – Hà Nội 2018) Cho hàm số

4 2

2 1.y x x    Điểm cực tiểu

của hàm số là

A. 1.x  B. (0; 1).

C. 1.x   D. 0.x 

Câu 6. (THPT Nhân Chính Hà Nội 2019) Cho hàm số

20.y x x   Mệnh đề nào sai ?

A. Hàm số nghịch biến trên khoảng ( ; 4). 

B. Hàm số đạt cực đại tại 5.x 

C. Hàm số đồng biến trên khoảng (5; ).

D. Hàm số không có cực trị.

Câu 7. (Sở GD & ĐT Tp. HCM – Cụm 5 năm 2017) Khoảng cách giữa hai điểm cực trị của

đồ thị hàm số

2 1

x x

 





bằng

4 5.

B. 4.

C. 8.

5 2.

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 69 -

18. Cho hàm số ( )y f x xác định và liên tục

trên , có

3 2

( ) ( 2) ( 9).f x x x x



  

Hàm

số ( )y f x đạt cực tiểu tại điểm

0.x 

B. 2.x 

C. 9.x  D. 1.x 

Lời giải. Tập xác định: . D

Ta có:

3 2

( ) ( 2) ( 9) 0f x x x x



   

( 2) 0 2.

9 0 9

x x







    



  





Bảng xét dấu ( )f x



(mỗi ô thử 1 điểm):



2 9



( )

f x









( )

f x

Hàm số đã cho ( )y f x đạt cực tiểu tại

điểm 9.x 

Chọn đáp án C.

19. Cho hàm số ( )y f x xác định và liên tục

trên , có ( ) ( 1)(3 ).f x x x



   Hàm

số ( )y f x đạt cực đại tại điểm

A. 1.x  B. 2.x 

C. 3.x  D. 0.x 

.......................................................................

20. Cho hàm ( )f x có

2 3

( ) ( 1)( 2)

f x x x x



  

.x  

Điểm cực tiểu của hàm số ( )f x là

A. 2.x   B. 0.x 

C. 1.x  D. 3.x  

.......................................................................

21. Cho hàm số ( )y f x và có đạo hàm

2 3

( ) ( 1) ( 2) (2 3), .f x x x x x



    

Số

điểm cực trị của hàm số ( )y f x là

A. 3. B. 2. C. 0. D. 1.

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 70 -

22. Cho hàm số

( )f x

xác định, liên tục trên  và có đồ thị hàm số



 ( )y f x là đường cong

như hình vẽ. Hỏi mệnh đề nào đúng ?

A. Hàm số

( )y f x

đạt cực đại tại điểm 4/3.x  

B. Hàm số

( )y f x

đạt cực tiểu tại điểm

0.x 

C. Hàm số

( )y f x

đạt cực tiểu tại điểm 2.x  

D. Hàm số

( )y f x

đạt cực đại tại điểm 4/3.x 

Lời giải tham khảo

Đồ thị hàm số ( )y f x



 cắt trục : 0Ox y  tại

2, 0 ( ) 0 .

x x f x



 





     









Bảng xét dấu:

 2 0 2



( )f x



 0



0  0



( )

f x

Từ bảng biến thiên, suy ra hàm số ( )y f x đạt cực tiểu tại 2.x   Chọn đáp án C.

23. Cho hàm số

( )f x

xác định, liên tục trên  và có đồ thị hàm số



 ( )y f x là đường cong

như hình vẽ. Hỏi mệnh đề nào đúng ?

A. Hàm số

( )y f x

đạt cực tiểu tại điểm 1.x  

B. Hàm số

( )y f x

đạt cực tiểu tại điểm

0.x 

C. Hàm số

( )y f x

đạt cực đại tại điểm 2.x  

D. Hàm số

( )y f x

đạt cực đại tại điểm 2.x 

..................................................................................................................................................................

2.1. Cho hàm số

( )f x

có đồ thị ( )f x



của nó trên khoảng K như hình vẽ. Khi đó trên

hàm số

( )y f x

có bao nhiêu điểm cực trị ?

A. 1.

B. 4.

C. 3.

D. 2.

..................................................................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 71 -

24. Đồ thị hàm số ( )y f x



 có đồ thị như hình vẽ dưới đây. Hàm số

( ) 3 2019

y f x x  

có mấy điểm cực trị ?

A. 1.

B. 2.

C. 3.

D. 4.

........................................................................................

25. Cho hàm số ( )f x xác định trên  và có đồ thị ( )f x



như hình vẽ bên dưới. Hàm số

( ) ( )g x f x x  đạt cực đại tại

A. 1.x  

B. 0.x 

C. 1.x 

D. 2.x 

........................................................................................

26. Cho hàm số ( )y f x xác định và liên tục trên , có đồ thị của hàm đạo hàm

( )

y f x





như hình vẽ. Xác định giá cực tiểu của hàm số ( ) ( ) .g x f x x 

A. (1) 1.f 

B. 1.x 

C. (0).f

D. (2) 2.f 

........................................................................................

27. Cho hàm số ( )f x có đồ thị ( )y f x



 như hình. Hỏi hàm

( ) ( ) 2

g x f x x x    

đạt cực đại tại

A. 1.x  

B. 0.x 

C. 1.x 

D. 2.x 

........................................................................................

28. Cho hàm số

( )y f x

có đạo hàm, liên tục trên



và có đồ thị

( )y f x





như hình vẽ. Xét

hàm số

2 4 2

( ) 3 ( 2) 3 .

g x f x x x    Hàm số

( )g x

đạt cực đại tại điểm

A. 1.x  

B. 1.x 

C. 0.x 

D. 2.x 

........................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 72 -







y f x





BÀI TẬP VỀ NHÀ 2

Câu 8. (THPT Lê Quý Đôn – Đà Nẵng 2019) Cho hàm số ( )y f x liên tục trên , có đạo

hàm

2 3 4

( ) (1 ) (3 ) ( 2) .f x x x x x



    Điểm cực tiểu của hàm số ( )y f x là

A. 2.x 

B. 3.x 

C. 1.x 

D. 0.x 

Câu 9. (THPT Chuyên Lê Thánh Tông – Quảng Nam 2019) Cho hàm số ( )y f x liên tục

trên  và có đạo hàm

2018 2019

( ) ( 2)( 1) ( 2) .f x x x x



    Khẳng định nào đúng ?

A. Hàm số ( )y f x đạt cực đại tại điểm 1x  và đạt cực tiểu tại các điểm 2.x  

B. Hàm số ( )y f x đồng biến trên mỗi khoảng (1;2) và (2; ).

C. Hàm số ( )y f x có ba điểm cực trị.

D. Hàm số ( )y f x nghịch biến trên khoảng ( 2;2).

Câu 10. (THPT HOA LƯ A – Hà Nội năm 2018) Cho hàm số ( )y f x có đạo hàm trên  và

đồ thị hàm số ( )y f x



 trên  như hình vẽ. Mệnh đề nào đúng ?

A. Hàm số ( )y f x có 1 điểm cực đại và 1 điểm cực tiểu.

B. Hàm số ( )y f x có 2 điểm cực đại và 2 điểm cực tiểu.

C. Hàm số ( )y f x có 1 điểm cực đại và 2 điểm cực tiểu.

D. Hàm số ( )y f x có 2 điểm cực đại và 1 điểm cực tiểu.

Câu 11. (Sở GD & ĐT Hâu Giang 2018) Cho hàm số ( )y f x xác định và liên tục trên  và

hàm số ( )y f x



 có đồ thị như hình vẽ dưới đây. Khẳng định nào đúng ?

A. ( )f x đạt cực đại tại 1.x 

B. ( )f x đạt cực đại tại 0.x 

C. ( )f x đạt cực đại tại 1.x  

D. ( )f x đạt cực đại tại 2.x  

Câu 12. (THPT Chuyên Lương Văn Chánh – Phúc Yên 2018) Cho hàm số ( )y f x có đạo

hàm liên tục trên

.

Đồ thị hàm số ( )y f x



 như hình vẽ. Số điểm cực trị của hàm

số ( ) 5y f x x  là

A. 2.

B. 3.

C. 4.

D. 1.

Câu 13. (THPT Mộ Đức – Quãng Ngãi năm 2018) Cho hàm số ( )y f x có đạo hàm trên

.

Biết hàm số ( )y f x



 có đồ thị như hình vẽ. Khẳng định nào sau đây đúng về cực trị

của hàm số ( ) ( ) .g x f x x 

A. Hàm số có một điểm cực đại và một điểm cực tiểu.

B. Hàm số không có điểm cực đại và một điểm cực tiểu.

C. Hàm số có một điểm cực đại và một điểm cực tiểu.

D. Hàm số có hai điểm cực đại và một điểm cực tiểu.

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 73 -

29. Cho hàm số

 ( )y f x

có đồ thị như hình vẽ. Đồ thị hàm số ( )y f x có mấy cực trị ?

D. 5.

Từ đồ thị hàm số ( ).y f x Hãy nên cách vẽ đồ thị hàm

số ( ) .y f x

 .....................................................................................

30. Cho hàm số  ( )y f x có đồ thị như hình vẽ bên dưới. Hỏi đồ thị hàm số  ( )y f x có bao

nhiêu điểm cực trị ?

A. 2.

B. 3.

C. 4.

D. 5.

........................................................................................

31. Biết đồ thị hàm số

3 2

3 .y x x  có dạng như hình vẽ. Hỏi đồ thị hàm số

3 2

y x x

 

có bao nhiêu điểm cực trị ?

A. 2.

B. 3.

C. 4.

D. 5.

........................................................................................

32. (Đề thi THPT Quốc Gia năm 2017 – Mã đề 102 câu 42) Cho hàm số ( )y f x có bảng biến

thiên như sau:

Đồ thị hàm số ( )y f x có bao nhiêu điểm cực trị ?

A. 2.

B. 3.

C. 4.

D. 5.

...............................................................................................................................................

33. Cho hàm số   

4 2

y x ax b với , a b là hai số thực dương. Hỏi đồ thị hàm số đã cho có

bao nhiêu điểm cực trị ?

A. 3.

B. 7.

C. 6.

D. 5.

..........................................................................................................................................

.........................................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 74 -

34. Cho hàm số

 ( )y f x

có đồ thị như hình vẽ. Đồ thị hàm số ( )y f x có mấy cực trị ?

A. 2.

B. 3.

C. 4.

D. 5.

Từ đồ thị hàm số ( ).y f x Hãy nên cách vẽ đồ thị hàm

số ( ).y f x

 .....................................................................................

35. Cho hàm số

3 2

3 3 1y x x x     có đồ thị như hình. Đồ thị

3 3 1

y x x x

    

có bao nhiêu điểm cực trị ?

A. 1.

B. 2.

C. 3.

D. 4.

........................................................................................

36. Cho hàm số

5 2

3 2 2y x x x    có đồ thị bên. Đồ thị

3 2 2y x x x    có bao

nhiêu điểm cực trị ?

A. 5.

B. 2.

C. 3.

D. 4.

........................................................................................

37. (THPT Chuyên Đại Học Vinh 2019) Cho hàm số ( )y f x có bảng biến thiên như sau:

Đồ thị hàm số ( )y f x có bao nhiêu điểm cực trị ?

A. 2.

B. 3.

C. 4.

D. 1.

...............................................................................................................................................

38. Cho hàm số ( )y f x có đạo hàm

4 5 3

( ) ( 1) ( 2) ( 3) , .f x x x x x



       Số điểm cực

trị của hàm số

 

y f x là

A. 2.

B. 3.

C. 5.

D. 1.

...............................................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 75 -



BÀI TẬP VỀ NHÀ 3

Câu 14. (THPT Hoa Lư A – Ninh Bình năm 2018) Cho hàm số ( )y f x liên tục trên  và có

đồ thị như hình vẽ. Hỏi đồ thị hàm số ( )y f x có tất cả bao nhiêu điểm cực trị ?

A. 5.

B. 3.

C. 2.

D. 4.

Câu 15. (Sở GD & ĐT Đồng Tháp 2019) Cho đồ thị hàm số

4 2

( )

f x ax bx c

  

như hình

vẽ. Hàm số

4 2

y ax bx c   có bao nhiêu cực trị ?

A. 3.

B. 5.

C. 6.

Câu 16. (Sở GD & ĐT Trà Vinh 2019) Cho hàm số

3 2

( )f x ax bx cx d   

có bảng biến

thiên bên dưới. Hàm số ( )y f x có mấy cực trị ?

A. 5.

B. 3.

C. 2.

D. 4.

Câu 17. (Sở GD & ĐT Bình Dương 2018) Cho hàm số

3 2

6 9y x x x   có bảng biến thiên

dưới. Hàm số

6 9y x x x   có mấy cực trị ?

A. 3.

B. 5.

C. 6.

Câu 18. (Sở GD & ĐT Phú Thọ năm 2017) Cho bảng biến thiên của hàm số

3y x x 

bên

dưới. Hàm số

3y x x  có mấy điểm cực trị ?

A. 5.

B. 3.

C. 2.

D. 4.

Câu 19. (Sở GD & ĐT Đồng Nai năm 2018) Cho đồ thị hàm số

( 2)( 1)y x x   như hình

vẽ. Đồ thị hàm số

2 ( 1)y x x   có mấy điểm cực trị ?

A. 5.

B. 3.

C. 2.

D. 1.

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 76 -

39. Gọi , A B lần lượt là hai điểm cực tiểu của

đồ thị hàm số

4 2

2 3y x x  

và C là

điểm cực đại. Tính độ dài AB và diện tích

tam giác OAB với O là gốc tọa độ. Tìm tọa

độ trọng tâm G của tam giác .ABC

Lời giải. Tập xác định . D

Có

0 3

4 4 0 .

1 2

x y

y x x

x y



  





   



   







1 0 1





 0  0  0 

 3



Hai điểm cực tiểu của đồ thị hàm số là

( 1;2),A  (1;2)B và điểm cực đại là

(0;3).

2 2

( ) ( ) 2.

B A B A

AB x x y y    

 Tính diện tích OAB với (0;0) :O

( 1;2)

1.2 1.2 2.

(1;2)

OAB







 



    













 Tọa độ trọng tâm G của tam giác

ABC

7 3

3 3

A B C

x x x

y y y





 



 



 











 











 

 

 



 





Cần nhớ:

( ; ).

B A B A

AB x x y y  





2 2

( ) ( ) .

B A B A

AB x x y y    

 I là trung điểm

A B

x x

y y





























 G là trọng tâm

A B C

x x x

ABC

y y y





 







 





 











Diện tích tam giác :ABC

Tính

( ; )

ABC

AB a b

S ad bc

AC c d











  













40. Gọi , A B lần lượt là hai điểm cực đại của

đồ thị hàm số

4 2

8 2y x x   

và

là điểm cực tiểu. Tính độ dài AB và diện

tích tam giác OAB với O là gốc tọa độ.

Tìm tọa độ trọng tâm G của .ABC

......................................................................

41. Gọi , A B lần lượt là điểm cực đại và

điểm cực tiểu của đồ thị hàm số

3 2

3 4.y x x  

Tìm tọa độ trọng tâm

G và diện tích của .OAB Tính

......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 77 -

42. Biết

(0;2)

và

(2; 2)



là các điểm cực trị

của đồ thị hàm số

3 2

y ax bx cx d

   

Tính giá trị của hàm số tại

 

Lời giải. Ta có:

3 2 .

y ax bx c



  



Do điểm

(0;2)

là cực trị

3 2

(0) 0

(0;2)

M y ax bx cx d

















    

























(1)



Do điểm

(2; 2)



là cực trị

3 2

(2) 0

( 2;2)

N y ax bx cx d

















     





12 4 0

8 4 2 2

a b c

a b c d





  









    





(2)

Từ

(1), (2) 1; 3; 0; 2.

a b c d

     

Do đó:

3 2

3 2 ( 2) 18.

y x x y

      

Cần nhớ:

Nếu

( ; )

M x y

 

là cực trị của đồ thị hàm số

( )

y f x



( ) 0

( ; ) ( )

y x

M x y y f x











 





 







 

Nếu là điểm cực đại, bổ sung

( ) 0.

y x





Nếu là điểm cực tiểu, bổ sung

( ) 0.

y x





43. Đồ thị hàm số

3 2

2 1

y x bx cx

   

có

(1; 6)



là một điểm cực trị. Tìm tọa độ

điểm cực trị còn lại của đồ thị hàm số đó.

.......................................................................

44. Biết

1; , (2;3)

A B

 

















 

là các điểm cực trị của đồ thị

3 2

y ax bx cx d

   

Tìm

(3).

............................................................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 78 -

BÀI TẬP VỀ NHÀ 4

Câu 20. (THPT Chuyên Vĩnh Phúc năm 2018) Gọi

là hai điểm cực trị của đồ thị hàm số

1 2

3 3

y x x

    

Tọa độ trung điểm của

là

0; .

 



















 

1 2

; .

3 3

 



















 

(0;1).

(1;0).

Câu 21. (THPT Hậu Lộc 2 – Thanh Hóa 2018) Cho hàm số

3 2

y x x

  

có đồ thị là

( ).

Gọi

A B

là các điểm cực trị của

( ).

Độ dài đoạn thẳng

bằng

2 5.

5 2.

Câu 22. (THPT Quãng Xương – Thanh Hóa 2018) Đồ thị hàm số

3 2

y x x

  

có hai điểm

cực trị

Diện tích tam giác

OAB

với

(0;0)

là gốc tọa độ bằng

Câu 23. (THPT Hoa Lư A – Ninh Bình năm 2018) Gọi

và

là các điểm cực tiểu của đồ thị

hàm số

4 2

2 1.

y x x

  

Diện tích của tam giác

OAB

(

là gốc tọa độ) bằng

Câu 24. (THPT Thạch Thành – Thanh Hóa 2018) Đồ thị hàm số

4 2

y x ax b

  

có điểm cực

tiểu là

( 1;4).



Giá trị của

a b



bằng



Câu 25. (THPT Kim Liên – Hà Nội 2018) Cho hàm số

3 2

y x x ax b

   

có đồ thị

( ).

Biết đồ thị

( )

có điểm cực trị là

(1;3).

Giá trị của

a b



bằng

Câu 26. (Sở GD & GD Thanh Hóa năm 2018) Đồ thị hàm số

3 2

y x ax bx c

   

đi qua

điểm

(1;0)

và có điểm cực trị

( 2;0).



Giá trị của biểu thức

2 2 2

a b c

 

bằng

25.



14.

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 79 -

Daïng toaùn 2. Tìm tham soá m ñeå haøm soá ñaït cöïc trò taïi ñieåm x = x

cho tröôùc.

Phöông trình ñöôøng thaúng noái hai ñieåm cöïc trò



 Bài toán. Tìm tham số để hàm số ( )y f x đạt cực trị tại điểm

?x x



 Phương pháp:



Bước 1. Tìm tập xác định D. Tính đạo hàm .y





Bước 2. Dựa vào nội dung định lí 1:

Nếu hàm số ( )y f x có đạo hàm trên khoảng

( ; )a b

và đạt cực đại (hoặc cực

tiểu) tại



thì

( ) 0.f x









Bước 3. Với

vừa tìm, thế vào hàm số và thử lại (dựa vào định lí 2 và 3).

 Lưu ý:

 Đối với hàm số bậc ba nên thử lại bằng nội dung định lý 3 (phù hợp trắc nghiệm).

Giả sử

( )y f x

có đạo hàm cấp 2 trong khoảng ( ; ).a b

Nếu

( ) 0, ( ) 0y x y x

 

 

 

thì



là điểm cực tiểu.

Nếu

( ) 0, ( ) 0

o o

y x y x

 

 

thì



là điểm cực đại.

 Đối với các hàm khác chẳng hạn như bậc bốn trùng phương (thiếu ),b hoặc hàm

phân thức,… nên thử lại bằng định lí 2 (tính y



và xét dấu, lập bảng biến thiên).

1. Cho hàm

3 2 2

( 4) 3.

y x mx m x    

Tìm

để hàm số đạt cực đại tại

x 

A. 1.m  B. 5.m 

C. {1;5}.m  D.

3.m 

Lời giải. Có

2 2

2 4

2 2

y x mx m

y x m







   









 





Vì 3x  là cực đại

(3) 0

























6 5 0

6 2 0

m m















  







   

 





 

 

 





 





Cần nhớ: Hàm

3 2

y ax bx cx d   



x x



là cực đại

( ) 0

y x





























x x



là cực tiểu

( ) 0

y x



























2. Cho hàm

2 2

( 1) .

y mx m m x

    

Tìm

để hàm số đạt cực đại tại

x 

A. 2.m  B. 3.m 

C. 1.m   D. 0.m 

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 80 -

3. Cho

3 2 2

( 4) 3.

y x mx m x    

Tìm

để hàm số đạt cực tiểu tại 3.x 

A. 1.m   B. 5.m 

C. 1.m  D.

7.m  

.......................................................................

4. Cho hàm số

4 2 2

2( 1) .

y x m x m   

Tìm điều kiện của tham số m để hàm số

đạt cực tiểu tại điểm 0.x 

1.m  

B. 1.m  

C. 1.m   D.

\( 1;1).

m  

4 4( 1) 0 .

y x m x

x m









    



 





1 0 1.m m    

Khi đó:

 0





 0 

HS đạt cực tiểu tại 0x  nên nhận

m  

1 0 1m m    

và có bảng xét dấu:

.............................................................................

1 0 1m m    

và có bảng xét dấu

.............................................................................

5. Hàm số

4 2

2 1y x mx   

đạt cực tiểu

tại điểm 0x  khi

0.m 

B. 1 0.m  

1.m  

D. 0.m 

.......................................................................

6. Hàm số

4 2 4

2 2 5

y x mx m m    

đạt cực tiểu tại điểm 1x   khi

A. 1.m   B. 1.m  

C. 1.m  D. 1.m 

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 81 -

7. Cho hàm số

3 2

3 9 1.y x x x   

Viết

phương trình đường thẳng nối hai điểm

cực trị của đồ thị hàm số đã cho.

A. 8 2.y x  B. 8 2.y x  

C. 8 2.y x  D. 3 1 0.x y  

Lời giải 1. Phương trình đường thẳng nối hai

điểm cực trị của đồ thị hàm số bậc ba là đường

thẳng y x   với x  là phần dư bậc

nhất trong phép chia

cho .y



Chia đa thức:

3 2 2

3 2

3 9 1 3 6 9

1 1

2 3

3 3

6 1

2 3

8 2

x x x x x

x x x x

x x

    

  

  

  

 

Phương trình đường thẳng nối hai điểm

cực trị là 8 2.y x   Chọn đáp án B.

Cách 2. Sử dụng casio bấm MODE 2 và

100

CALC x i

y y

y i y x

   



 

     



8. Biết đồ thị hàm số

3 1y x x  

có hai

điểm cực trị , .A B Khi đó phương trình

đường thẳng AB là

A. 2.y x   B. 2.y x 

C. 2 1.y x   D. 2 1.y x 

.......................................................................

9. Cho hàm số

3 2

3 2.y x x  

Đường

thẳng đi qua hai điểm cực trị của đồ thị

hàm số đã cho có phương trình là

A. 4.y x  B. 2 2.y x 

C. 1.y x   D. 2 2.y x  

.......................................................................

10. Cho hàm số

3 2

3 1.y x x   

Viết

phương trình đường thẳng nối hai điểm

cực trị của đồ thị hàm số đã cho.

A. 7 0.y   B. 2 1.y x 

C. 2 1.y x  D. 7 1.y x 

.......................................................................



SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 82 -

11. Tìm

để đường thẳng nối điểm cực đại

với điểm cực tiểu của đồ thị hàm số

  

y x x m

đi qua điểm

(3; 1).



.......................................................................

12. Tìm

để đường thẳng nối điểm cực đại

với điểm cực tiểu của đồ thị hàm số

3 2

y x x mx

   

qua

(0;1).

.......................................................................

13. Tìm giá trị của tham số

để đường thẳng

: (2 1) 3

d y m x m

   

vuông góc với

đường thẳng đi qua hai điểm cực trị của đồ

thị hàm số

3 2

3 1.

y x x

  

Lời giải.

Sử dụng casio, tìm được đường thẳng nối

hai điểm cực trị là

: 2 1.

d y x



  

Vì

1 2

. 1

d d a a



   

(2 1).( 2) 1

    

  

Cần nhớ: Cho hai đường thẳng

và

có

dạng

1 1 1

d y a x b

 

và

2 2 2

d y a x b

 

thì

1 2

a a

d d

b b





















 và

1 2 1 2

d d a a

   

14. Tìm

để đường thẳng

: 2

d y x

 

vuông góc với đường thẳng đi qua hai

điểm cực trị của đồ thị hàm số

3 2

2 3( 1) 6 .

y x m x mx

   

.......................................................................

15. Tìm giá trị thực của tham số

sao cho

đường thẳng đi qua hai điểm cực trị của đồ

thị hàm số

3 2

y x x mx

   

song

song với đường thẳng

: 4 3.

d y x

  

.......................................................................

16. Tìm giá trị thực của tham số

để đư

ờng

ẳng đi qua hai điểm cực trị của đồ thị

hàm số

3 2

y x x mx

   

vuông góc

với đường thẳng

: 4 3 0.

d x y

  

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 83 -

BÀI TẬP VỀ NHÀ 5

Câu 27. (Đề thi THPT Quốc Gia năm 2017 – Mã đề 102 câu 32) Tìm giá trị thực của tham số

để hàm số

3 2 2

( 4) 3

y x mx m x

    

đạt cực đại tại



 



 

Câu 28. (THPT Ngô Sĩ Liên – Bắc Giang năm 2018) Biết rằng hàm số

3 2

2 3

y x x mx

   

đạt cực tiểu tại



Giá trị của

bằng

Câu 29. (THPT Chuyên Lê Quý Đôn Đà Nẵng năm 2018) Tìm tham số thực

để hàm số

3 2 2

3 3( 1)

y x mx m x

   

đạt cực đại tại điểm







Câu 30. (THPT Kiến An – Hải Phòng năm 2018) Tìm tất cả các giá trị thực của tham số

để

hàm số

3 2 2

( 6) 1

y mx x m x

    

đạt cực tiểu tại



 



Câu 31. (THPT Việt Trì – Phú Thọ 2018) Hàm số

3 2 2

3( 1) 3( 1) .

y x m x m x

    

Hàm số

đạt cực trị tại điểm có hoành độ



khi



0, 4.

m m

 



0, 1.

m m

 

Câu 32. (THPT Chuyên Biên Hòa – Hà Nam 2018) Hàm số

3 2

2 4 2019

y x ax bx

   

đạt

cực trị tại

 

Khi đó hiệu

a b



bằng





 

Câu 33. (Sở GD & ĐT Hà Nội 2018) Tìm tất cả các giá trị thực của tham số

để hàm số

4 2

y x mx

 

đạt cực tiểu tại











Câu 34. (THPT Quảng Xương I – Thanh Hóa 2017) Tìm tất cả các giá trị của tham số

để

hàm số

( 1)

y m x

 

đạt cực đại tại







C. Không có



SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 84 -

Câu 35. (THPT Ngô Sĩ Liên – Bắc Giang năm 2018) Phương trình đưdờng thẳng đi qua hai

điểm cực trị của đồ thị hàm số

3 2

3 5 1

y x x x

   

là

16 8

3 3

y x

   

16 8

3 3

y x

  

1 8

3 3

y x

   

1 8

3 3

y x

  

Câu 36. (THPT Trần Phú – Tp. Hồ Chí Minh năm 2017) Tìm giá trị thực của tham số

sao

cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

3 2

y x x mx

   

song song với đường thẳng

: 4 3 0.

d x y

  



Câu 37. (THPT Lương Văn Chánh Phú Yên 2018) Biết đường thẳng

: (3 1) 3

d y m x

  

vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

3 2

3 1.

y x x

  

Giá trị của

bằng



 



 

Câu 38. (Tạp Chí Toán Học & Tuổi Trẻ năm 2018) Cho hàm số

3 2

3 4.

y x x

   

Biết có hai

giá trị

1 2

m m

của tham số

để đường thẳng đi qua hai điểm cực trị của đồ thị hàm

số tiếp xúc với đường tròn

2 2

( ) : ( ) ( 1) 5.

C x m y m

    

Tổng

1 2

m m



bằng

10.



Câu 39. (Toán Học Bắc Trung Nam) Đồ thị hàm số

3 5

x x

 





có hai điểm cực trị

A B

nằm trên đường thẳng

có phương trình

: .

d y ax b

 

Giá trị của

a b



bằng



Câu 40. (THPT Chuyên KHTN Hà Nội năm 2017) Cho hàm số

2 1

mx x m

  

 



Tìm

tham số

để đường thẳng nối hai điểm cực trị của đồ thị hàm số này vuông góc với

đường phân giác của góc phần tư thứ nhất trong mặt phẳng tọa độ.

  



 

 

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 85 -

Daïng toaùn 3. Bieän luaän hoaønh ñoä cöïc trò (Vaän duïng & vaän duïng cao)



 Cần nhớ:

......................................................................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 86 -

1. Cho hàm số

3 2 2

3 3 .

y x mx mx m

   

Tìm

để hàm số có

điểm cực trị ?

Lời giải. Tập xác định





Hàm số đã cho có

điểm cực trị



3 6 3 0

y x mx m



   

có hai nghiệm

phân biệt.

3 0 ( )

( ) 36 0

m m





 







    























 Cần nhớ. Hàm số có

cực trị



 

có

nghiệm phân biệt. PT

ax bx c

  

có hai nghiệm phân biệt















 





2. Cho hàm

3 2

(1 ) 3 3 5.

y m x x x

    

Tìm

để hàm số có

điểm cực trị ?

.......................................................................

3. Cho

3 2

(2 1) (2 ) 1.

y x m x m x

      

Tìm

để hàm số có

điểm cực trị ?

.......................................................................

4. Cho

3 2

2 ( 2) (6 3 ) 1.

y x m x m x

     

Tìm

để hàm số có

điểm cực trị ?

.......................................................................

5. Cho hàm số

3 2 2

4 .

y x mx x m

   

Tìm

để hàm số không có cực trị ?

Lời giải. Tập xác định





Hàm số không có cực trị

2 4 0

y x mx



    

vô nghiệm hoặc

có nghiệm kép

)1 0 (

(2 ) 16





 









   





4 16 0 2 2.

m m

      

6. Cho

3 2

(3 2) 1.

y x mx m x

     

Tìm

để hàm số không có cực trị ?

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 87 -

7. Cho

3 2

( 1) ( 1) .

y m x m x x

    

Tìm

để hàm số có

điểm cực trị, đồng thời

điểm cực đại nằm bên trái điểm cực tiểu.

Lời giải. Tập xác định





Hàm số có

điểm cực trị, đồng thời điểm

cực đại nằm bên trái điểm cực tiểu

3( 1) 2( 1) 1 0

y m x m x



      

có

nghiệm phân biệt thỏa mãn



1 0

[2( 1)] 12( 1) 0

a m

m m





  









     





4 20 16 0

m m















  





1 4.

1 4









   





 





 Cần nhớ:

















 























 





И

8. Cho hàm số

3 2

3 3 1.

y mx mx x

   

Tìm

để hàm số có

điểm cực trị và

điểm cực đại nằm bên trái điểm cực tiểu.

.......................................................................

9. Cho hàm

3 2

( 2) 3 5.

y m x x mx

    

Tìm

để hàm số có

điểm cực trị và

điểm cực tiểu nằm bên trái điểm cực đại.

.......................................................................

10. Cho

3 2

( 6) 1.

y m x mx x

    

Tìm

để hàm số có

điểm cực trị và điểm

cực đại nằm bên trái điểm cực tiểu.

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 88 -

11. Cho

3 2

( 1) 7.

y mx m x mx

    

Tìm

để hàm số có

điểm cực trị và điểm cực

tiểu nằm bên trái điểm cực đại.

.......................................................................

12. Cho

3 2

( 1) ( 1) 1.

y m x m x x

     

Tìm

để hàm số có

điểm cực trị v

điểm cực tiểu nằm bên trái điểm cực đại.

......................................................................

.......................................................................

13. Cho hàm số

4 2

 ( 1) 4.

y x m x

   

Tìm

để hàm số có ba điểm cực trị ?

Lời giải. Ta có:

2( 1) .

x m x









Xét

0 .











 

 









H/số có

cực trị



 

có

nghiệm

phân biệt

 

 

  

 Cần nhớ:

M :























W :











































 





















 

14. Cho hàm số

4 2

( 2) 1.

x x

 





Tìm

để hàm số có ba điểm cực trị ?

.......................................................................

15. Cho hàm số

4 2

2( 1) 2.

y mx m x

   

Tìm

để hàm số có

điểm cực tiểu và

điểm cực đại ?

.......................................................................

16. Cho hàm số

4 2 2

( 9) 1.

y mx m x

   

Tìm

để hàm số có

điểm cực đại và

điểm cực tiểu ?

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 89 -

BÀI TẬP VỀ NHÀ 6

Câu 41. (THPT Chuyên Hạ Long – Quảng Ninh năm 2018) Tìm tất cả các giá trị thực của tham

số

để hàm số

3 2

3 ( 1) 2

y x x m x

    

có hai điểm cực trị.







 

Câu 42. (THPT Hồng Quang – Hải Dương năm 2018) Tìm tất cả tham số thực của

để hàm

số

3 2

1 1

( 2) 2

3 3

y m x x mx

    

có cực đại, cực tiểu.

( 3; 2) ( 2;1).

    

( 3;1).

 

( ; 3) (1; ).

    

( 2;1).

 

Câu 43. (THPT Chuyên Lê Hồng Phong – Nam Định năm 2018) Tìm tham số

để hàm số

3 2

( 2) 2018

y x mx m x    

không có cực trị.

 

hoặc



1 2.

  

Câu 44. (THPT Nguyễn Thị Minh Khai – Tp. Hồ Chí Minh năm 2017) Có bao nhiêu giá trị

nguyên của tham số thực

để hàm số

3 2

( 2) 3 5

y m x x mx

    

có điểm cực

đại nằm bên trái điểm cực tiểu.

C. Vô số. D.

Câu 45. (THPT Chuyên Nguyễn Thượng Hiền – Tp. Hồ Chí Minh năm 2017) Cho hàm số

3 2

( 1) 7.

y mx m x mx

    

Tìm tất cả các giá trị thực của tham số

sao cho

đồ thị hàm số đã cho có điểm cực tiểu nằm bên trái điểm cực đại.





và



  

 

hoặc



Câu 46. (Sở GD & ĐT Vĩnh Phúc năm 2018) Tìm tất cả các giá trị của tham số

để hàm số

4 2

3 2

y x mx

  

có ba điểm cực trị.









Câu 47. (Sở GD & ĐT Kiên Giang năm 2018) Tìm điều kiện của tham số thực

để hàm số

4 2

2( 1) 3

y x m x

   

có ba cực trị.



 



Câu 48. (THPT Ngô Quyền – Hải Phòng năm 2017) Có bao nhiêu số nguyên của

để hàm

số

4 2 2

2( 5) 4

y mx m x

   

có đúng

điểm cực tiểu và

điểm cực đại ?

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 90 -

17. Cho hàm số

3 2 2

4 (1 ) 1.

y x x m x

    

Tìm

để đồ thị hàm số đã cho có

điểm

cực trị nằm hai bên so với trục tung

Lời giải. Để đồ thị hàm số có

điểm cực

trị nằm về hai bên so với trục tung

2 2

3 8 1 0

y x x m



     

có nghiệm

phân biệt trái dấu

. 0 3.(1 ) 0

a c m

    

  

hoặc



Cần nhớ: Hàm số

3 2

y ax bx cx d

   

có hai điểm cực trị nằm hai bên trục tung

. 0.

Oy a c

 

18. Cho

3 2 2

( 3 ) 4.

y x x m m x

     

Tìm

để để đồ thị hàm số đã cho có

điểm cực trị nằm hai bên so

.......................................................................

19. Cho

3 2 2

(3 1) ( 6) .

y x m x m m x

     

Tìm

để để đồ thị hàm số đã cho có

điểm cực trị nằm về hai phía trục tung

.......................................................................

20. Cho

3 2 2

(2 1) ( 1) .

y mx m x m x

    

Tìm

để để đồ thị hàm số đã cho có

điểm cực trị nằm về 2 bên trục tung.

.......................................................................

21. Cho

3 2 2

( 1) ( 4 3) .

y x m x m m x

     

Tìm

để đồ thị hàm số có hai điểm cực trị

nằm bên phải trục tung.

.......................................................................

22. Cho hàm số

3 2

( 2) .

y x mx m x

   

Tìm

để đồ thị hàm s

ố có hai điểm cực

trị nằm bên trái trục tung.

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 91 -

23. Cho hàm số

3 2 2

3 2 .y x x m m    Tìm

để hàm số có giá trị cực đại bằng 3.

Lời giải. Tập xác định . D

Ta có:

3 6 0y x x



  

0 2

2 2 4

x y m m



   







    







0 2







0  0



2m m





2 4

m m

 

2y m m  

CĐ

3 2 1m m m      hoặc

m 

24. Cho hàm

3 2 2

3 4 .y x x m m   

Tìm

để hàm số có giá trị đại bằng 9.

.......................................................................

25. Tìm ,m biết giá trị cực tiểu của hàm số

3 1y x x m    thỏa

2 9 0.

y  

.......................................................................

26. Tìm ,m biết giá trị cực tiểu của hàm s

ố

3 2 2

3 2y x x m m    bằng 4.

.......................................................................

27. Tìm

để hàm số

3 2

3 2y x x m   có

giá trị cực tiểu và giá trị cực đại trái dấu ?

Lời giải. Ta có:

3 6 0y x x



  

0 2

2 2 4

x y m



  







   





CĐ

Vì giá trị cực tiểu và giá trị cực đại trái dấu

nên

. 0y y 

CĐ

2 .(2 4) 0m m  

4 8 0 0 2.m m m     

Cần nhớ:

Giá trị cực đai, giá trị cực tiểu của hàm số

trái dấu

. 0.y y 

CĐ

28. Tìm

để hàm số

3 1y x x m   

có

giá trị cực tiểu và giá trị cực đại trái dấu ?

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 92 -

29. Tìm

để đồ thị hàm số

3 2

y x x m

  

có

cực trị nằm hai bên trục hoành

Cách giải 1. Ta có:

3 6 0

y x x



  

2 4

x y m



  







   





CĐ

Để đồ thị hàm số có hai cực trị nằm hai bên

trục

. 0

y y

 

CĐ

( 4) 0

m m

  

0 4.

  

Cách giải 2.

Để hàm số có hai cực trị nằm hai bên trục



đồ thị hàm số

3 2

y x x m

  

cắt

tại

điểm phân biệt



phương

trình hoành độ giao điểm với trục

3 2

3 0

x x m

  



3 2

3 ( )

m x x g x

    

có

nghiệm phân biệt



đường thẳng

nằm ngang

y m



cắt

2 3

( ) 3

g x x x

 

tại

điểm

g m g

  

Ta có:

( ) 3 6 0

g x x x



   

0 0

0 4.

2 4

x g



  



   



  





CĐ

30. Cho hàm

3 2

2 (1 2 ) 3 .

y x m x mx m

    

Tìm tham số

để đồ thị hàm số đ

ã cho

có hai điểm cực trị nằm hai bên trục

Lời giải. Để hàm số có hai điểm cực trị

nằm hai bên



đồ thị hàm số

3 2

2 (1 2 ) 3

y x m x mx m

    

cắt trụ

( 0)

Ox y



tại

điểm phân biệt



3 2

2 (1 2 ) 3 0

x m x mx m

    

có ba nghiệm phân biệt.

(Sử dụng casio, giải phương trình bậc

cho

100,



được nghiệm đẹp

0,5).





(2 1)( ) 0

x x mx m

   

có ba

nghiệm phân biệt

 

và

( ) 0 :

g x x mx m

   

có

hai nghiệm phân biệt khác



4 0

1 1 1

2 2 4

m m

g m





   



 













  



 









 





0 4

m m





  









 





Nhận xét. Để tìm tham số

để đồ thị hàm số bậc ba

3 2

y ax bx cx d

   

có hai điểm

cực trị nằm hai bên so với trục hoành

(giá trị cực đại và giá trị cực tiểu trái dấu), có các

phương pháp:

Phương pháp 1. Nếu





tìm được

nghiệm

x x













thì YCBT

. 0 .

y y m

  

CĐ

Phương pháp 2. Đồ thị cắt trục

tại

điểm phân biệt

 

có

nghiệm phân biệt

(sử dụng được khi





không nghiệm đẹp và



có nghiệm đẹp).

Phương pháp 3. Sử dụng khi





hoặc



không tìm được nghiệm đẹp.



Tìm điều kiện để hàm số có

cực trị

( 0





có

nghiệm phân biệt).



Gọi

1 2

x x

là

nghiệm của phương trình





Viết phương trình đường thẳng nối hai điểm cực trị

1 1

2 2

( )

y x x

y x

y x x

 





 



  





 





là

giá trị cực đại và giá trị cực tiểu.



Yêu cầu bài toán

CT 1 2 1 2

. 0 ( ). ( ) 0 ( ).( ) 0,

y y y x y x x x

   

       

CĐ

sau đó sử

dụng định lí Viét với

1 2

x x

là

nghiệm của

0 .

y m



 

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 93 -

31. Cho hàm số

3 2

6 1.

y x x m

    

Tìm

để đồ thị hàm số có hai điểm cực trị nằm

hai bên trục hoành

.......................................................................

32. Cho hàm số

3 2

3 .

y x mx m

  

Tìm

để đồ thị hàm số có hai điểm cực trị n

ằm

hai bên trục hoành

.......................................................................

33. Cho hàm

3 2

( 2) 3 2 .

y x m x mx m

    

Tìm tham số

để đồ thị hàm số đã cho có

hai điểm cực trị nằm hai bên trục

.......................................................................

34. Cho hàm số

3 2

3 2.

y x x mx m

    

Tìm

để đồ thị hàm số có hai điểm cự

trị nằm hai bên trục hoành

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 94 -

BÀI TẬP VỀ NHÀ 7

Câu 49. (THPT Kinh Môn – Hải Dương năm 2018) Có bao nhiêu giá trị nguyên của tham số

để hàm số

3 2 2

( 3) 2( 1) ( 4) 1

y m x m m x m x

       

có hai điểm cực trị

nằm về hai phía của trục

Câu 50. (Tạp chí Toán Học & Tuổi Trẻ số 484) Có bao nhiêu giá trị nguyên của

để hàm số

3 2

( ) 2 6 1

f x x x m

   

có các giá trị cực trị trái dấu ?

Câu 51. (THPT Tân Bình – Tp. Hồ Chí Minh 2019) Cho hàm số

3 2

18 2 1

y x x x m

    

có hai điểm cực trị

1 1 2 2

( ; ), ( ; )

x y x y

thỏa

1 2

x x



Tìm

để

1 2

4 10.

y y

 

11.

 

  

12.

 

Câu 52. (Tạp chí Toán Học & Tuổi Trẻ số 484) Tìm điều kiện của tham số

để hàm số

3 2 2

( 1) ( 4 3) 3

y x m x m m x

      

có các điểm cực trị của đồ thị hàm số

nằm bên phải của trục tung.

5 1.

   

5 3.

   

3 1.

   

 

hoặc

 

Câu 53. (THPT Chuyên Quốc Học Huế năm 2019) Có mấy giá trị nguyên của

( 20;18)

 

để đồ thị hàm số

3 2

3 3

( ) ( 1) 3

2 2

f x x m x mx    

nằm về cùng phía

19.

20.

18.

Câu 54. (THPT Nguyễn Khuyến – Tp. HCM 2018) Tìm tham số thực

để đồ thị hàm số

3 2

2 (1 )

y x x m x m

    

có hai điểm cực trị nằm về hai phía đối với trục hoành.

  



  

  

Câu 55. (THPT Chuyên Hoàng Văn Thụ – Hòa Bình năm 2018) Tìm tham số

để hàm số

3 2

3( 1) 12 3

y x m x mx m

    

có hai điểm cực trị

1 2

x x

thỏa mãn

1 2

3 .

x x

 





 

 

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 95 -

35. Cho hàm số

3 2

y x mx x m

    

Tìm tham số

để hàm số có

điểm cực

trị

và

thỏa mãn

2 2

1 2

x x

 

Lời giải. Ta có

2 1.

y x mx



  

Hàm số có

điểm cực trị

và

thỏa

2 2

1 2

x x

 



 

có

nghiệm

1 2

x x

thỏa

2 2

1 2

x x

 

2 2

1 2

x x









  





 





1 2 1 2

4 4 0 : ( )

( ) 2 2

x x x x





 









  





2 2

S P

  

với

1 2

S x x m

P x x





    







   





4 2 2 0.

m m

    

 Cần nhớ:

2 2 2

1 2

2 ,

x x S P

  

2 2

1 2

0 4 ,...

x x l S P l

     

36. Cho hàm số

3 2

y x mx x

  

Tìm

tham số

để hàm số có

điểm cực trị

và

thỏa mãn

2 2

1 2 1 2

x x x x

  

.......................................................................

37. Cho hàm số

3 2

y x mx x m

    

Tìm tham số

để hàm số có

điểm cực

trị

và

thỏa

2 2

1 2 1 2

4 2.

x x x x

  

.......................................................................

38. Cho hàm số

3 2

y x x mx m

   

Tìm tham số

để hàm số có

cực trị

và

thỏa mãn

1 2

3 0.

x x

 

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 96 -

39. Cho hàm số

3 2

3 .

y x x m

  

Tìm

để

đồ thị hàm số có

điểm cực trị

A B

sao

cho

OAB



vuông tại

với

(0;0).

Lời giải.

Ta có:

3 6 0

y x x



  

0 (0; )

2 4 (2; 4)

x y m A m

x y m B m



   







     





Suy ra

(0; )

(2; 4)

OA m

OB m













 







(ĐK:

0).



Vì

OAB



vuông tại

nên

OA OB



 

. 0 0.2 ( 4) 0

OAOB m m

     

 

0 (L)

4 (N)

















vì

0 (0;0) .

m A O

  

Vậy



là giá trị cần tìm.

 Sai lầm thường gặp của học sinh là quên điều

kiện



như trên.

40. Cho hàm số

3 1.

y x mx

   

Tìm

để đồ thị hàm số có

điểm cực trị

A B

sao cho

OAB



vuông tại

với

(0;0).

.......................................................................

41. Cho hàm số

3 2

3 8 .

y x mx m

  

Tìm

để đồ thị hàm số có

điểm cực trị

A B

sao cho

OAB



vuông tại

với

(0;0).

.......................................................................

42. Cho hàm số

3 2 3

3 4 .

y x mx m

  

Tìm

để đồ thị hàm số có

điểm cực trị

A B

thỏa mãn

20.



.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 97 -

43. Cho hàm số

4 2 2

2 2.

y x m x

  

Tìm

để đồ thị hàm số có

điểm cực trị

(0;2),

B C

thỏa mãn



Lời giải. Ta có:

3 2

4 4 .

y x m x



 

2 2

0 4 .( ) 0

y x x m

x m









    









Đồ thị hàm số có 3 điểm cực trị

0 0.

m m

   

Khi đó:

4 4

0 2 (0;2)

2 ( ;2 )

x y A

x m y m B m m

x m y m C m m



   



     



       





Theo đề



2 2

( ) ( ) 2

C B C B

x x y y

    

2 2

( 2 ) 0 2

   

4 4 1.

m m

    

So điều kiện, suy ra

 

thỏa bài toán.

44. Cho hàm số

4 2

2 1.

y x mx

  

Tìm

để đồ thị hàm số có

điểm cực trị

(0;1),

B C

thỏa mãn



.......................................................................

45. Cho hàm số

3 2 3

3 4 .

y x mx m

  

Tìm

để đồ thị hàm số có hai điểm cực trị là

và

sao cho điện tích

OAB



bằng

.......................................................................

46. Cho hàm số

4 2 2

2 2 4 .

y x mx m m

   

Tìm

để đồ thị hàm số có ba điểm cực tr

ị

tạo thành tam giác có diện tích bằng

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 98 -

47. Cho hàm

4 2

(3 1) 2 2.

y x m x m

    

Tìm

để đồ thị hàm số có ba điểm cực trị

tạo thành một tam giác có trọng tâm là

.......................................................................

48. Cho hàm số

4 2

4 3 2.

y x mx m

   

Tìm

để đồ thị hàm số có

đi

ểm cực trị

tạo thành tam giác có trọng tâm

 



















 

.......................................................................

49. Cho hàm số

4 2

2 1.

y x mx

  

Tìm

để

đồ thị hàm số có ba điểm cực trị tạo thành

một tam giác vuông cân.

Cần nhớ: Đồ thị hàm số

4 2

y ax bx c

  

có ba cực trị

, ,

A Oy B C



thì luôn tạo

thành tam giác cân tại

Khi đó ta luôn có

cos .

b a







Áp dụng:

Hàm số có ba cực trị

 

1.2 0 0.

m m

   

Đồ thị hàm số có ba điểm cực trị tạo thành

tam giác vuông cân

90 .

  

(2 ) 8.1

cos 90 0

(2 ) 8.1



   



8 8 0

  

1 1

m m

     

(thỏa

0).



50. Cho hàm số

4 2

6 4) 1 .

(

y x m x m



   

Tìm

để đồ thị hàm số có ba điểm cực trị

tạo thành tam giác vuông cân.

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 99 -

51. Cho hàm số

4 2

2 2 .

y x mx m

  

Tìm

để đồ thị hàm số có ba điểm cực trị tạo

thành tam giác đều.

.......................................................................

52. Cho hàm số

4 2 3

2 .

y x mx m

  

Tìm

để đồ thị hàm số có ba điểm cực trị tạ

thành tam giác có một góc bằng

30 .



.......................................................................

53. Cho hàm số

4 2 2

2 9 2 .

y x mx m

   

Tìm

để đồ thị hàm số có ba điểm cực trị

nằm trên các trục tọa độ.

Lời giải.

Ta có:

4 4 0

y x mx

x m









   



 





0 9 2

x y m

x m y m



    



     



   





(0;2 9)

( ; 9)

A m Oy

B m m

C m m





 



  











Vì điểm

A Oy



nên để ba điểm cực trị

nằm trên các trục tọa độ thì

B C Ox



B C

y y

  

9 0 3.

m m

     

Nhận xét: Để ba điểm cực trị của hàm số

bậc bốn trùng phương nằm trên các trục

tọa độ thì



CĐ

(hoặc

0).



54. Cho hàm số

4 2

2 4.

y x mx

   

Tìm

để đồ thị hàm số có ba điểm cực trị nằ

trên các trục tọa độ.

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 100 -

55. Cho

3 2 2

( 1) .

y x mx m x

   

Gọi

là

tập hợp các giá trị của tham số

để đồ thị

hàm số có hai điểm cực trị là

và

sao

cho

A B

nằm khác phía và cách đều

đường thẳng

: 5 9.

d y x

 

Tích các phần

tử của

bằng

.......................................................................

56. Biết rằng đường thẳng

d y x m

 

ắt

đồ thị hàm số

3 2

y x x

 

ại ba điểm

phân bi

ệt sao cho có một giao điểm cách

đều hai giao điểm còn lại. Tìm

.......................................................................

57. Cho hàm số

3 2

3 1

y x x m

   

có đồ thị

( ).

Biết đồ thị

( )

cắt trục hoành tại ba

điểm phân biệt lập có hoành độ lập thành

cấp số cộng.

.......................................................................

58. Hỏi có tất cả bao nhiêu giá trị của

ể đồ

thị hàm số

3 2

y x mx x m

   

ắt trục

hoành t

ại ba điểm phân biệt, đồng thời

phần diện tích phía trên

và di

ện tích

phía dưới

giới hạn bởi đồ thị và tr

ục

bằng nhau.

.......................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 101 -

BÀI TẬP VỀ NHÀ 8

Câu 56. (THPT Chuyên Hùng Vương – Phú Thọ 2018) Biết



là giá trị của tham số

để

hàm số

3 2

3 1

y x x mx

   

có hai điểm cực trị

1 2

x x

sao cho

2 2

1 2 1 2

13.

x x x x

  

Mệnh đề nào dưới đây đúng ?

( 1;7).

 



(7;10).





( 15; 7).

  



( 7; 1).

  



Câu 57. (THPT Chuyên Vĩnh Phúc năn 2018) Với giá trị nào của tham số

thì đồ thị hàm số

3 2

2 3( 1) 6( 2) 1

y x m x m x

     

có cực đại, cực tiểu thỏa mãn

x x

 

CĐ



 

Câu 58. (THPT Thăng Long – Hà Nội 2018) Biết hàm số

3 2

( 1) (2 1)

y x m x m x

    

có

hai điểm cực trị

1 2

, .

x x

Giá trị nhỏ nhất của biểu thức

2 2

1 2 1 2

10( )

T x x x x

   

bằng

78.

18.



22.



Câu 59. (THPT Thanh Miện – Hải Dương năm học 2018) Biết rằng đồ thị hàm số

3 2

1 1

( ) 2

3 2

f x x mx x

   

có giá trị tuyệt đối của hoành độ hai điểm cực trị là độ

dài hai cạnh của tam giác vuông có cạnh huyền là

Hỏi có mấy giá trị của

Câu 60. (THPT Chuyên Hạ Long – Quảng Ninh năm 2019) Tìm tất cả giá trị thực của tham số

để đồ thị hàm số

3 2

y x mx

  

có hai điểm cực trị

và

sao cho các điểm

A B

và

(1; 2)



thẳng hàng.



 



 

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 102 -

Câu 61. (THPT Chuyên Hùng Vương – Gia Lai năm 2018) Gọi

A B

là hai điểm cực trị của

đồ thị hàm số

3 2

( ) 3

f x x x m

  

với

là tham số thực khác

Tìm tham số

để

trọng tâm tam giác

OAB

thuộc đường thẳng

3 3 8 0.

x y

  



Câu 62. (THPT Chuyên Trần Phú – Hải Phòng năm 2018) Gọi

1 2

m m

là các giá trị của tham

số

để đồ thị hàm số

3 2

2 3 1

y x x m

   

có hai điểm cực trị là

B C

sao cho

tam giác

OBC

có diện tích bằng

với

là gốc tọa độ. Tích số

1 2

m m

bằng

15.



12.

20.



Câu 63. (THP Chuyên Lê Hồng Phong – Nam Định 2018) Tìm tham số

đề đồ thị hàm số

4 2

2 1

y x mx

  

có ba điểm cực trị

(0;1), ,

A B C

thỏa mãn

4 ?



 

Câu 64. (HKI – THPT Nguyễn Thượng Hiền – Tp. Hồ Chí Minh năm 2019) Có bao nhiêu số

thực

để đồ thị hàm số

3 2

y x x m

  

có hai điểm cực trị

và

sao cho tam

giác

OAB

vuông tại

Câu 65. (HKI – THPT Trần Phú – Tp. Hồ Chí Minh năm 2019) Gọi

là tập các số thực

để đồ thị hàm số

3 2

6 2

y x m x m

  

có hai điểm cực trị

và

sao cho

2 34.



Tính tích các phần tử của



Câu 66. (Đề minh họa – Bộ GD & ĐT năm 2017) Cho

3 2 2

( 1) .

y x mx m x

   

Gọi

là

tập hợp các giá trị của tham số

để đồ thị hàm số có hai điểm cực trị là

và

sao

cho

A B

nằm khác phía và cách đều đường thẳng

: 5 9.

d y x

 

Tích các phần tử

của

bằng

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 103 -

27.



Câu 67. (Tạp Chí Toán Học & Tuổi Trẻ số 485) Tìm

để đồ thị của hàm số

4 2

y x kx k

  

có ba điểm cực trị tạo thành một tam giác nhận điểm

 

















 

làm trọng tâm ?

;1 .

 

 



 

 

 

1; .

 

 

 

 

 

 

;1 .

 

 



 

 

 

1; .

 

 

 

 

 

 

Câu 68. (TT Diệu Hiền – Cần Thơ năm 2018) Cho hàm số

4 2

2( 1)

y x m x m

   

có đồ thị

( ).

Tìm tham số

sao cho

( )

có ba điểm cực trị

, ,

A B C

thỏa mãn

OA BC



trong đó

là gốc tọa độ,

là điểm cực trị thuộc trục tung.



hoặc



2 2 2.

 

3 3 3.

 

5 5 5.

 

Câu 69. (THPT Chuyên Bắc Ninh năm 2018) Tìm tất cả các giá trị thực của tham số

sao cho

đồ thị của hàm số

4 2 2

2( 1)

y x m x m

   

có ba điểm cực trị tạo thành một tam giác

vuông cân.



1, 0.

m m

  



0, 1.

m m

 

Câu 70. (THPT Chuyên Vĩnh Phúc năm 2018) Cho hàm số

4 2 4

2 2 .

y x mx m m

   

Tìm

tham số

để các điểm cực trị của đồ thị hàm số lập thành một tam giác đều.

2 2.



Câu 71. (THPT Hậu Lộc 2-Thanh Hóa-lần 1-năm 2017-2018) Tìm giá trị của

để đồ thị hàm

số

4 2

2 2

y x mx

  

có ba điểm cực trị tạo thành một tam giác có diện tích bằng



3 3.



SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 104 -

Câu 72. (THPT Chuyên Vĩnh Phúc năm 2018) Tìm tham số thực

để đồ thị của hàm số

4 2

y x mx

 

có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn



0 1.

 

0 4.

 



Câu 73. (THPT Lương Văn Chánh – Phú Yên năm 2018) Gọi

là tập hợp tất cả các giá trị

thực của tham số

để đồ thị

( )

của hàm số

4 2 2 4

2 5

y x m x m

   

có ba điểm

cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ

tạo thành một tứ giác nội

tiếp. Tìm số phần tử của

Câu 74. (THPT Cổ Loa – Hà Nội năm 2018) Gọi

là tập hợp tất cả các giá trị thực của tham

số

để đồ thị hàm số

4 2

2 2

y x mx  

có ba điểm cực trị, đồng thời ba điểm

cực trị này cùng với gốc tọa độ

tạo thành bốn đỉnh của một tứ giác nội tiếp được.

Tổng tất cả các phần tử của

bằng

2 2 3.



2 2 3.

 



Câu 75. (THPT Hồng Bàng – Hải Phòng 2018) Cho hàm số

4 2

2( 4) 5

y x m x m

    

có

đồ thị

( ).

Tìm

để

( )

có ba điểm cực trị tạo thành một tam giác nhận gốc tọa

độ

làm trọng tâm.



hoặc

 



 

Câu 76. (Sở GD & ĐT Vĩnh Phúc năm 2018) Tìm tất cả các giá trị của tham số

để đồ thị

hàm số

4 2 2

2 2

y x m x m

  

có ba điểm cực trị

, ,

A B C

sao cho

, , ,

O A B C

là bốn

đỉnh của một hình thoi (với

là gốc tọa độ).

 



SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 105 -

Daïng toaùn 4: Cöïc trò cuûa haøm hôïp vaø haøm soá trò tuyeät ñoái (vaän duïng cao)



1. Cho hàm số

( )

y f x



có bảng biến thiên như sau:



0 2



( )

f x





0  0



Hỏi trên khoảng

( 5, 5)

thì hàm số

( ) ( )g x f x đạt cực đại tại điểm nào sau đây ?

2.x 

2.x  

C. 0.x 

D. 2.x 

Thử điểm:

2 ( 2; 5)x  

thì

(2) 4. (4) 0.

g f

 

 

( ) 2 . ( ),g x x f x

 



( ) 0 .

( ) 0

g x

f x















 





  





  





5

2

( )

g x



 0



0  0



( )

g x

Suy ra hàm số

( )g x

đạt cực đại tại 0.x  Chọn đáp án C.

2. Cho hàm

( )y f x

có bảng biến thiên. Hàm số

( ) ( 2)g x f x  đạt cực đại tại điểm nào ?



1 2



( )

f x



 0  0



A. 2.x  

B. 1.x  

C. 0.x 

D. 2.x 

........................................................................................................................

3. Cho hàm số

( )y f x

có bảng biến thiên. Hàm số

( ) ( 5)g x f x  có mấy điểm cực trị ?



4 1 2



( )

f x



 0



0  0



A. 3.

B. 5.

D. 6.

........................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 106 -

4. (Đề thi THPT QG năm 2019 – Câu 46 Mã đề 101) Cho hàm số

( ),

f x

bảng biến thiên của

hàm số

( )f x



như sau:

Số điểm cực trị của hàm số

( 2 )y f x x  là

A. 9. B. 3. C.

D. 5.

...................................................................................................................................................................

5. (Đề thi THPT QG năm 2019 – Câu 48 Mã đề 103) Cho hàm số

( ),

f x

bảng biến thiên của

hàm số

( )f x



như sau:

Số điểm cực trị của hàm số

( 2 )y f x x  là

A. 9. B. 3. C.

D. 5.

...................................................................................................................................................................

6. (Đề thi THPT QG năm 2019 – Câu 50 Mã đề 104) Cho hàm số

( ),

f x

bảng biến thiên của

hàm số

( )f x



như sau:

Số điểm cực trị của hàm số

(4 4 )y f x x  là

A. 9. B. 3. C.

D. 5.

...................................................................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 107 -

7. Cho hàm số

( )

y f x



có đạo hàm liên tục trên  và bảng biến thiên

Hàm số

4 2 6 4 2

( ) 15 ( 4 6) 10 15 60g x f x x x x x       đạt cực tiểu tại

0.x 



Chọn

mệnh đề đúng ?

; 2

 







   











 



 







   











 



; 1

 







   











 



( 1;0).x  



Ta có:

3 4 2 5 3

( ) 15.( 4 8 ). ( 4 6) 60 60 120g x x x f x x x x x

 

        

3 4 2 2

60( 2 ) ( 4 6) 1 .x x f x x x

 



       

 

 

Đặt

4 2 2 2

4 6 ( 2) 2 2t x x x          và có

( ) 0, 2f t t



   

(nhìn bảng).

4 2

( 4 6) 0f x x



    

4 2 2

( 4 6) 1 0, .f x x x x



         



2



60( 2 )x x 



0  0



0 

4 2 2

( 4 6) 1

f x x x



    



( )g x



 0



0  0



( )g x



(0)g

( 2)g 

( 2)g

Suy ra hàm số đạt cực tiểu tại điểm

2 2 ; 1

x x

 







        











 



Chọn đáp án C.

8. Cho hàm số

( )

y f x



có đạo hàm liên tục trên  và bảng biến thiên như sau:

Hàm số

4 2 6 2

( ) 15 ( 2 3) 10 30g x f x x x x     có bao nhiêu điểm cực trị ?

A. 2. B. 3. C.

D. 5.

...................................................................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 108 -

9. Cho hàm số

( )

y f x



có đạo hàm liên tục trên  và bảng biến thiên như sau:

Hàm số

4 2 6 2

( ) 15 ( 2 2) 10 30g x f x x x x      có bao nhiêu điểm cực trị ?

A. 2. B. 3. C.

D. 5.

...................................................................................................................................................................

10. Cho hàm số

( )

y f x



có đạo hàm liên tục trên  và bảng biến thiên như sau:

Hàm số

4 2 6 2

2 ( 4 5) 12y f x x x x      có bao nhiêu điểm cực trị ?

A. 2. B. 3. C.

D. 5.

...................................................................................................................................................................

11. Cho hàm số

3 2

( ) ( 3 1)g x f x x   có bảng biến thiên như sau:

Hàm số

( )y f x

có mấy điểm cực trị ?

A. 0. B. 1. C. 2. D. 3.

...................................................................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 109 -

12. Cho hàm số

( )y f x

xác định trên  và hàm số

( )y f x





có đồ thị như hình vẽ. Tìm số

điểm cực trị của hàm số

( 3).y f x 

A. 2.

B. 3.

C. 4.

D. 5.

................................................................................................

13. Cho hàm số

( )y f x

xác định trên  và hàm số

( )y f x





có đồ thị như hình vẽ. Hàm

số

(1 )y f x  đạt cực đại tại

A. 1.x  

2.x  

C. 3.x 

D. 0.x 

................................................................................................

14. Cho hàm

( )f x

có đồ thị

( )f x



có đồ thị như hình. Hàm số

(1 2 )y f x

 

có mấy cực trị ?

A. 4.

C. 3.

D. 9.

................................................................................................

15. Cho hàm số

( )f x

có đồ thị

( )f x



có đồ thị như hình. Hàm số

( )y f x có mấy cực trị ?

A. 5.

C. 3.

D. 9.

................................................................................................

16. Cho hàm

( )f x

có đồ thị

( )f x



có đồ thị như hình. Hàm số

( 2)y f x  có mấy cực trị ?

A. 5.

C. 3.

D. 9.

................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 110 -

Câu 1. Cho hàm số

( )y f x

có đạo hàm, liên tục trên  và có đồ thị

( )y f x





như hình vẽ.

Xét hàm số

2 4 2

( ) 3 ( 2) 3 .

g x f x x x   

Hàm số

( )g x

đạt cực đại tại điểm

A. 0.x 

B. 1.x 

C. 1.x  

3.x 

Lời giải tham khảo

Ta có:

2 3 2 2

( ) 6 . ( 2) 6 6 6 ( 2) ( 2) 1g x x f x x x x f x x

 

  

        

 

 

2 2

( ) 0 2 1 1

( 2) ( 2) 1

2 1 ( ) 3

g x x x

f x x

x K x















        





    







    





(xem hình vẽ)

Bảng biến thiên:

Từ bảng biến thiên, suy ra hàm số

( )g x

đạt cực đại tại 0.x  Chọn đáp án A.

Câu 2. Cho hàm số

( )y f x

có đạo hàm và liên tục trên  và có đồ thị

( )y f x





như hình.

Xét hàm số

2 4

( ) 3 ( 2 ) ( 1) .

g x f x x x   

Hàm số

( )g x

đạt cực đại tại điểm

A. 1.x  

B. 1.x 

C. 3.x 

D. 2.x 

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 111 -

Câu 3. Cho hàm số

( )y f x

có đạo hàm trên  và có đồ thị

( )y f x





như hình vẽ. Xét hàm

số

2 4 2

( ) ( 1) 2 3 .

g x f x x x    

Tìm khẳng định đúng ?

A. Hàm số

( )g x

có 2 điểm cực đại và 3 điểm cực tiểu.

B. Hàm số

( )g x

có 3 điểm cực đại và 2 điểm cực tiểu.

C. Hàm số

( )g x

có 2 điểm cực đại và 2 điểm cực tiểu.

D. Hàm số

( )g x

có 1 điểm cực đại và 1 điểm cực tiểu.

Câu 4. Cho hàm số

( )y f x

có đạo hàm và liên tục trên  và có đồ thị

( )y f x





như hình

vẽ. Xét

2 3 2

( ) ( 2 ) 2 2 .

g x f x x x x     Hàm số

( )g x

có mấy điểm cực tiểu ?

A. 0.

B. 1.

C. 2.

D. 3.

Câu 5. Cho hàm số

( )y f x

có đạo hàm và liên tục trên  và có đồ thị

( )y f x





như hình

vẽ. Xét hàm

4 2

( ) ( 2)

2 2

x x

g x f x     Hàm số

( )g x

có bao nhiêu điểm cực tiểu ?

A. 4.

B. 1.

C. 2.

D. 3.

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 112 -

 Hàm số





y f x

 có

2 1



với

là số cực trị dương của hàm số

( ).

y f x



 Hàm số

( )

y f x



có

a b



cực trị với

là số cực trị của hàm số

( )

y f x



và

là số nghiệm

đơn của phương trình

( ) 0

f x



(số giao điểm cắt của đồ thị

( )

y f x



và trục

1. Cho hàm số

3 2

( ) (2 1) (2 ) 2.

f x x m x m x

     

Tìm

để đồ thị hàm số





y f x



có

điểm cực trị.

 

 

  

   

Lời giải. Hàm số





y f x

 có

điểm cực trị

2 1 5 2

a a

    

( ) 3 2(2 1) 2 0

f x x m x m



      

có

nghiệm dương phân biệt

0 4(2 1) 12(2 ) 0

0 2 1 0

0 2 0

m m

S m

P m

 

 

     

 

    

 

 

  

 

 

4 5 0

m m





  









 





m m





   



   





 





Chọn đáp án A.

2. Tìm số nguyên bé nhất của

để hàm số

2 5 3

y x mx x

   

có

điểm cực trị.



.............................................................................................................................

3. Có mấy giá trị nguyên của

để hàm

5 (3 1)

y x x m x m

    

có

điểm cực trị.

.............................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 113 -

4. Có mấy giá trị nguyên của tham số

để hàm số

3 2

y x x m

   có

điểm cực trị.

31.

17.

D. Vô số.

Đặt

3 2

( ) 6 .

f x x x m

  

Để hàm

( )

y f x



có

cực trị

a b

  

với



là số cực trị của

( )

y f x



và



là số nghiệm đơn của

phương trình

( ) 0.

f x



Xét

3 2 3 2

( ) 0 6 0 6 ( )

f x x x m m x x g x

         

có:

( ) 3 12 0 0

g x x x x



     

hoặc



Để phương trình

( ) 0

f x



có

nghiệm

0 32

 

và do





nên:

{1;2;3;...;31}



có

(31 1) 1 31.

  

Chọn đáp án B.

5. Có mấy giá trị nguyên của

để hàm số

4 3 2

3 4 12

y x x x m

    có

điểm cực trị ?

.............................................................................................................................

6. Tính tổng các giá trị của

để đồ thị hàm số

3 2

y x x m

   có

điểm cực trị ?

10.

.............................................................................................................................

7. Có mấy giá trị nguyên

]

10 1

[

; 0

 

để hàm số

3 2

3 (3 2) 2

y mx mx m x m

     

có

điểm cực trị ?

10.

11.

.............................................................................................................................

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 114 -

BÀI TẬP VỀ NHÀ 9

Câu 77. Hàm số

( )y f x

có đúng ba điểm cực trị là

2, 1, 0. 

Hàm số

( ) ( 2 )g x f x x 

có bao nhiêu điểm cực trị ?

A. 6.

B. 5.

C. 3.

D. 4.

Câu 78. Cho hàm số

( )y f x

xác định, liên tục trên  và có đúng hai điểm cực trị

1,x  

1,x 

đồng thời có đồ thị như hình vẽ dưới. Hàm số

02) ( 2021)(g x f x x   có

bao nhiêu điểm cực trị ?

A. 4.

B. 3.

C. 1.

D. 2.

Câu 79. Cho đồ thị hàm số

3 2

( )f x ax bx cx d    như hình vẽ bên dưới. Tìm số điểm cực

trị của đồ thị hàm số

( ) ( 3 ).g x f x x 

A. 5.

B. 6.

C. 4.

D. 3.

Câu 80. Cho hàm số

( )y f x

có đồ thị hàm

( )f x ax bx c



   như hình bên dưới. Hỏi hàm

số

( ) ( )g x f x x  có bao nhiêu cực trị ?

A. 0.

B. 1.

C. 2.

D. 3.

Câu 81. Cho hàm số

( )y f x

có đồ thị của hàm số

( )

f x



như hình bên dưới. Hàm số

( ) ( )g x f x có bao nhiêu điểm cực trị ?

A. 4.

B. 3.

C. 5.

D. 2.

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 115 -

Câu 82. Cho hàm số bậc bốn

( ).y f x

Hàm số

( )y f x





có đồ thị như hình vẽ bên. Số điểm

cực đại của hàm số

( 2 2)y f x x   là

A. 1.

B. 2.

C. 4.

D. 3.

Câu 83. Cho hàm số

( )y f x

liên tục trên . Biết hàm số

( )y f x





có bảng xét dấu sau

Số điểm cực tiểu của hàm số

( ) (6 )g x f x  là

A. 5.

B. 7.

C. 3.

D. 4.

Câu 84. Cho hàm số

( )y f x

liên tục trên . Biết hàm số

( )y f x





có bảng xét dấu sau

Hàm số

( ) ( 2 4)g x f x x   có bao nhiêu điểm cực tiểu ?

A. 1.

B. 3.

C. 2.

D. 4.

Câu 85. Cho hàm số

( )y f x

liên tục trên . Biết hàm số

( )y f x





có bảng xét dấu:

Số điểm cực trị của hàm số

( ) ( 1)g x f x x   là

A. 0.

B. 1.

C. 3.

D. 2.

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 116 -

Câu 86. Cho hàm số

( )y f x

có đạo hàm trên  và có bảng biến thiên của

( )y f x





như sau:

Hàm số

( ) ( 4 2)g x f x x   có bao nhiêu điểm cực trị ?

B. 8.

C. 9.

D. 10.

Câu 87. Cho hàm số

( )y f x

có đạo hàm trên  và có bảng biến thiên của

( ).

y f x





Hàm

số

( )

g x f

 





















 

có mấy điểm cực trị ?

A. 4.

B. 5.

C. 6.

D. 8.

Câu 88. Cho hàm số

( )y f x

có đạo hàm trên  và có đồ thị hàm số

( )

f x



như hình vẽ. Hàm

số

( ) 2 ( )g x f x x  đạt cực đại tại điểm

A. 1.x  

B. 0.x 

C. 1.x 

D. 2.x 

Câu 89. Cho hàm số

( )y f x

liên tục trên  và có đồ thị hàm số

( )f x



như hình bên dưới.

Hàm số

3 2

( ) ( ) 2

g x f x x x x    

đạt cực đại tại điểm

A. 1.x 

B. 1.x  

C. 0.x 

D. 2.x 

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 117 -

Câu 90. Cho hàm số

( )y f x

liên tục trên  và có đồ thị hàm số

( )f x



như hình bên dưới.

Hàm số

4 2 6 2

( ) 15 ( 2 ) 10 30 20g x f x x x x      có bao nhiêu điểm cực trị ?

A. 0.

B. 3.

C. 2.

D. 5.

Câu 91. Cho hàm số

( )f x



như hình vẽ. Hàm số

2 6 4 2

( ) ( )

g x f x x x x   

đạt cực tiểu tại

bao nhiêu điểm ?

A. 3.

B. 2.

C. 0.

D. 1.

Câu 92. Cho hàm số

( )y f x

có đạo hàm

( ) ( 1)( 4)f x x x



   với mọi .x   Hàm số

( ) (3 )g x f x  có bao nhiêu điểm cực đại ?

A. 0.

B. 1.

C. 2.

D. 3.

Câu 93. Cho hàm

( )f x

có đạo hàm

( ) 2 , .f x x x x



     Hàm số

( ) 1 4

g x f x x

 







  











 

có mấy điểm cực trị ?

A. 0.

B. 1.

C. 2.

D. 3.

Câu 94. Cho hàm số

( )y f x

có đạo hàm

( ) 2 , .f x x x x



     Hàm số

( 8 )y f x x 

có bao nhiêu điểm cực trị ?

A. 6.

B. 3.

C. 5.

D. 2.

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 118 -

Câu 95. Tổng tất cả các giá trị nguyên của tham số

để hàm số

4 3 2

3 4 12 2

y x x x m

   

có

điểm cực trị bằng

Câu 96. Giá trị nguyên dương nhỏ nhất của tham số

để hàm số

3 2

5 2 1

y x x x m

    

có

điểm cực trị bằng

Câu 97. Cho hàm số

3 2

( 3) ( 4) 3 2

y m x mx m x m

      

với

là tham số thực. Giá

trị nguyên nhỏ nhất của

để hàm số đã cho có

điểm cực trị bằng



Câu 98. Cho hàm số

4 2

2( 1) 2 3

y x m x m

    

với

là tham số thực. Số giá trị nguyên

không âm của

để hàm số đã cho có

điểm cực trị là

Câu 99. Tìm tham số

để hàm số

( 6) 2020

y x mx m x    

có

điểm cực trị ?

 

 



SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 119 -

Câu 100. Cho hàm số

3 2

( ) (2 1) (2 ) 2.f x x m x m x      Tìm tham số

để đồ thị hàm số

 

y f x có 5 điểm cực trị.

m 

m 

C. 1 2.m  

D. 2.m 

Câu 101. Cho hàm số

( )y f x

có đồ thị đạo hàm

( )f x



như hình vẽ. Có bao nhiêu giá trị

nguyên của tham số

thuộc khoảng ( 12;12) sao cho hàm số ( ) 12y f x mx  

có đúng một điểm cực trị ?

A. 5.

B. 18.

C. 20.

D. 12.

Câu 102. Cho hàm số

( )f x

có đạo hàm trên . Đồ thị hàm số

( )y f x





như hình vẽ. Tìm

để hàm số ( )y f x mx  có ba điểm cực trị ?

A. 0 4.m 

B. 0 4.m 

C. 4.m 

0.m 

Câu 103. Cho hàm số

( )f x

có đạo hàm

3 2

( ) 2 , .f x x x x



      Có tất cả bao nhiêu giá trị

nguyên dương của tham số

để hàm số ( ) ( ) 3g x f x mx   có 3 điểm cực trị.

A. 1.

B. 2.

C. 3.

D. 4.

Câu 104. Cho hàm số

( )f x

có đạo hàm

2 2

( ) ( 3)( 1), .f x x x x



      Có bao nhiêu giá trị

nguyên dương của tham số

để hàm số ( )y f x mx  có 4 điểm cực trị ?

A. 0.

B. 1.

C. 2.

D. 3.

SỞ GD & ĐT TP. HỒ CHÍ MINH ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12

TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN Môn: Toán, Năm học: 2019 – 2020

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 120 -



Câu 105. Cho hàm số

( )

f x

có

( ) ( 1)( 2 1), .

f x x x x mx x



     



Hỏi có mấy số nguyên

không vượt quá

2018

sao cho hàm số

( ) ( )

g x f x



có

điểm cực trị ?

2019.

2016.

2017.

2018.

Câu 106. Cho hàm số

( )

f x

có đạo hàm

2 2

( ) ( )( 4 3), .

f x x x x x x



     



Tính tổng tất cả

các giá trị nguyên của tham số

để hàm số

( ) ( )

g x f x m

 

có

điểm cực trị.

Câu 107. Cho hàm số

( )

f x

có đồ thị hàm số

( )

y f x





được cho như hình vẽ bên. Hàm số

( ) ( ) (0)

g x f x x f

  

có nhiều nhất bao nhiêu điểm cực trị trong khoảng

( 2;3).



Bấm Tải xuống để xem toàn bộ.

| 1/58

| | Tải xuống

Preview text:

SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
§ 2. CÖÏC TRÒ CUÛA HAØM SOÁ 
A. KIẾN THỨC CƠ BẢN
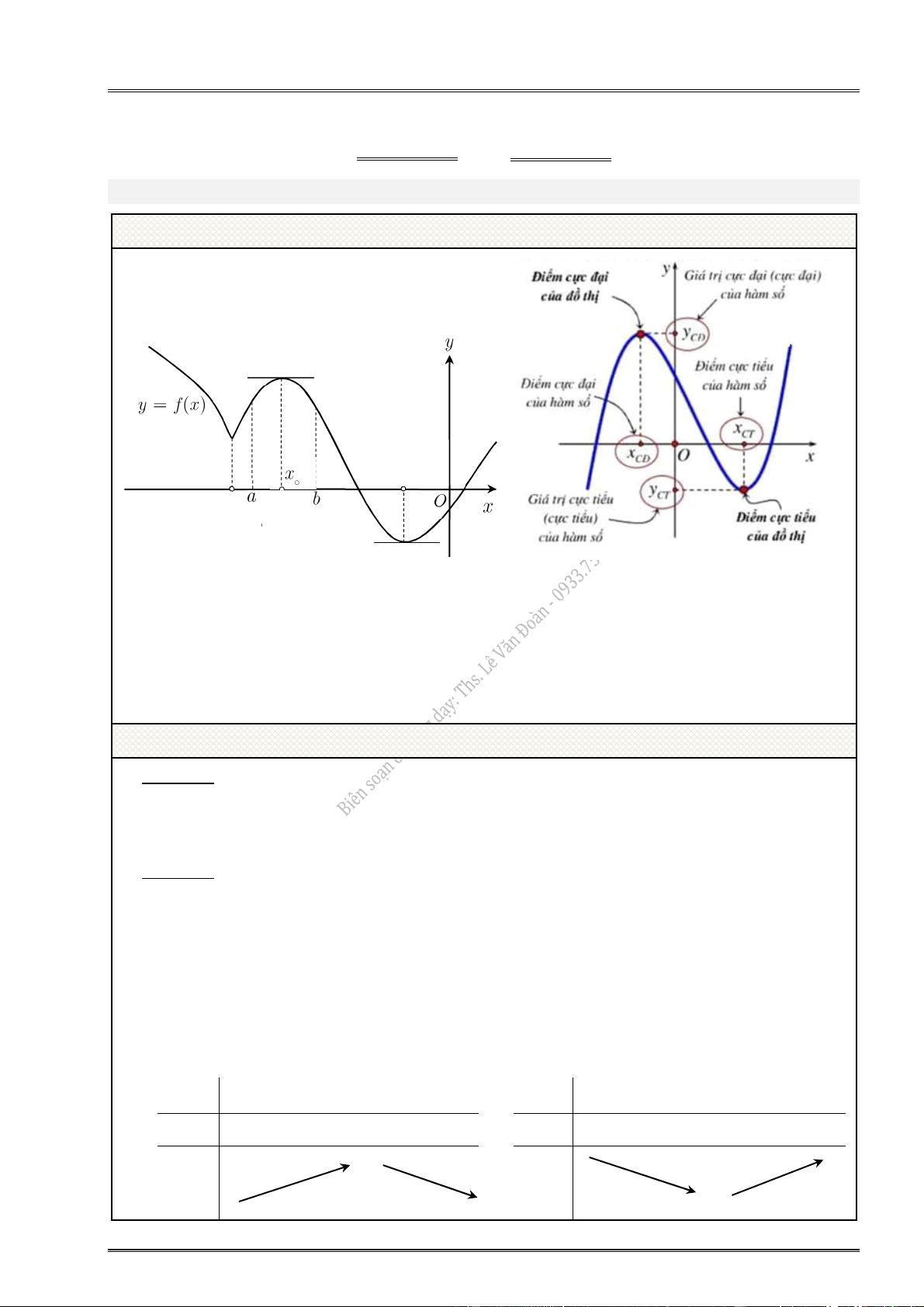
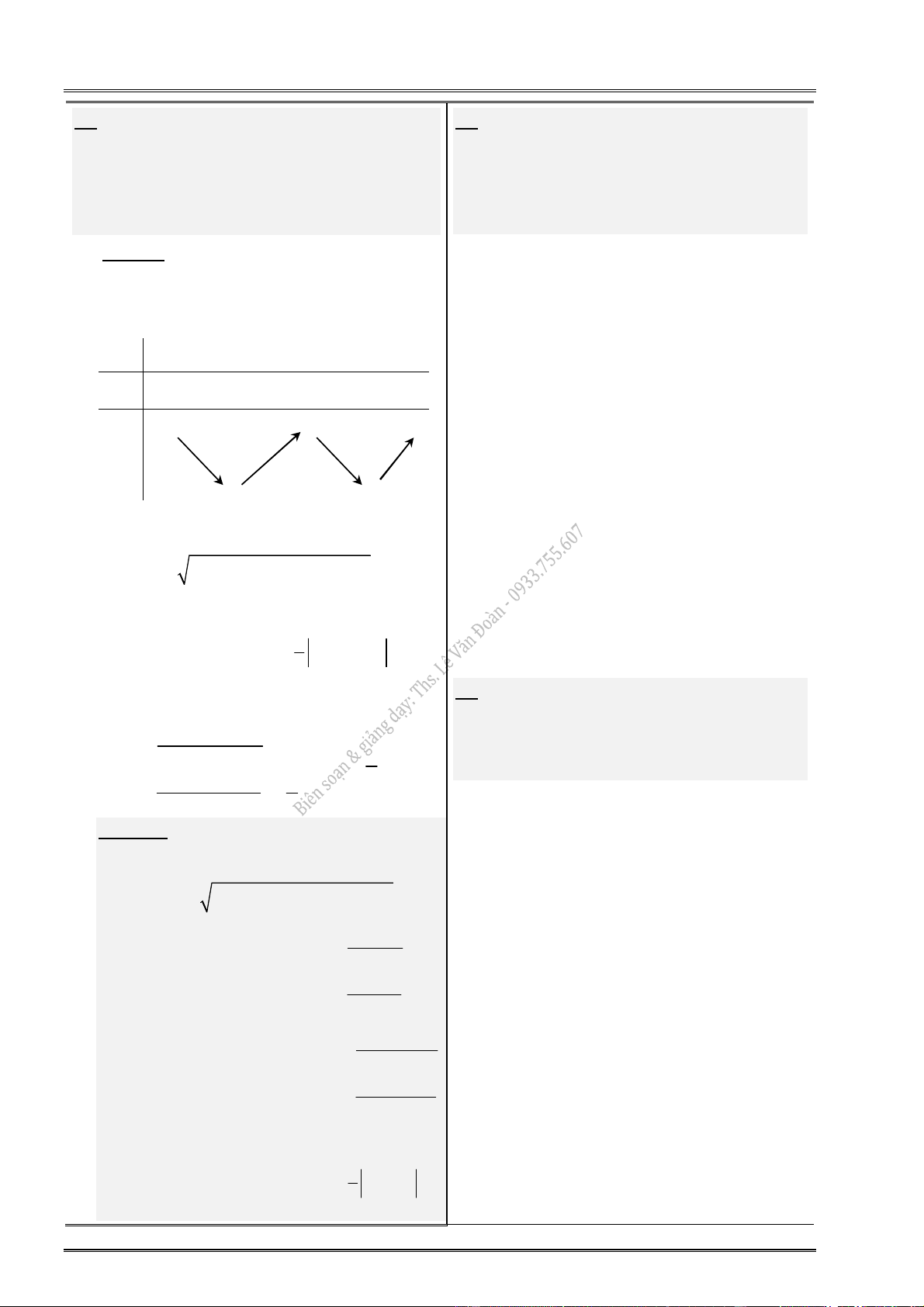
Khái niệm cực đại, cực tiểu Tiếp tuyến Điểm cực tiểu Điểm Điểm cực tiểu cực đại
Cho hàm số y  f (x ) xác định, liên tục trên (a;b), (có thể a là , b là  )
 và x  (a;b) : 
 Nếu tồn tại số h  0 sao cho f (x)  f (x ) với mọi x  (x  h; x  h) và x  x thì ta    
nói hàm số f (x ) đạt cực đại tại điểm x . 
 Nếu tồn tại số h  0 sao cho f (x)  f (x ) với mọi x  (x  h; x  h) và x  x thì ta    
nói hàm số f (x ) đạt cực tiểu tại điểm x .  Các định lí
1. Định lí 1 (điều kiện cần)
Nếu hàm số y  f (x ) có đạo hàm trên khoảng (a;b) và đạt cực đại (hoặc cực tiểu) tại x  thì f (  x )  0. 
2. Định lí 2 (điều kiện đủ)
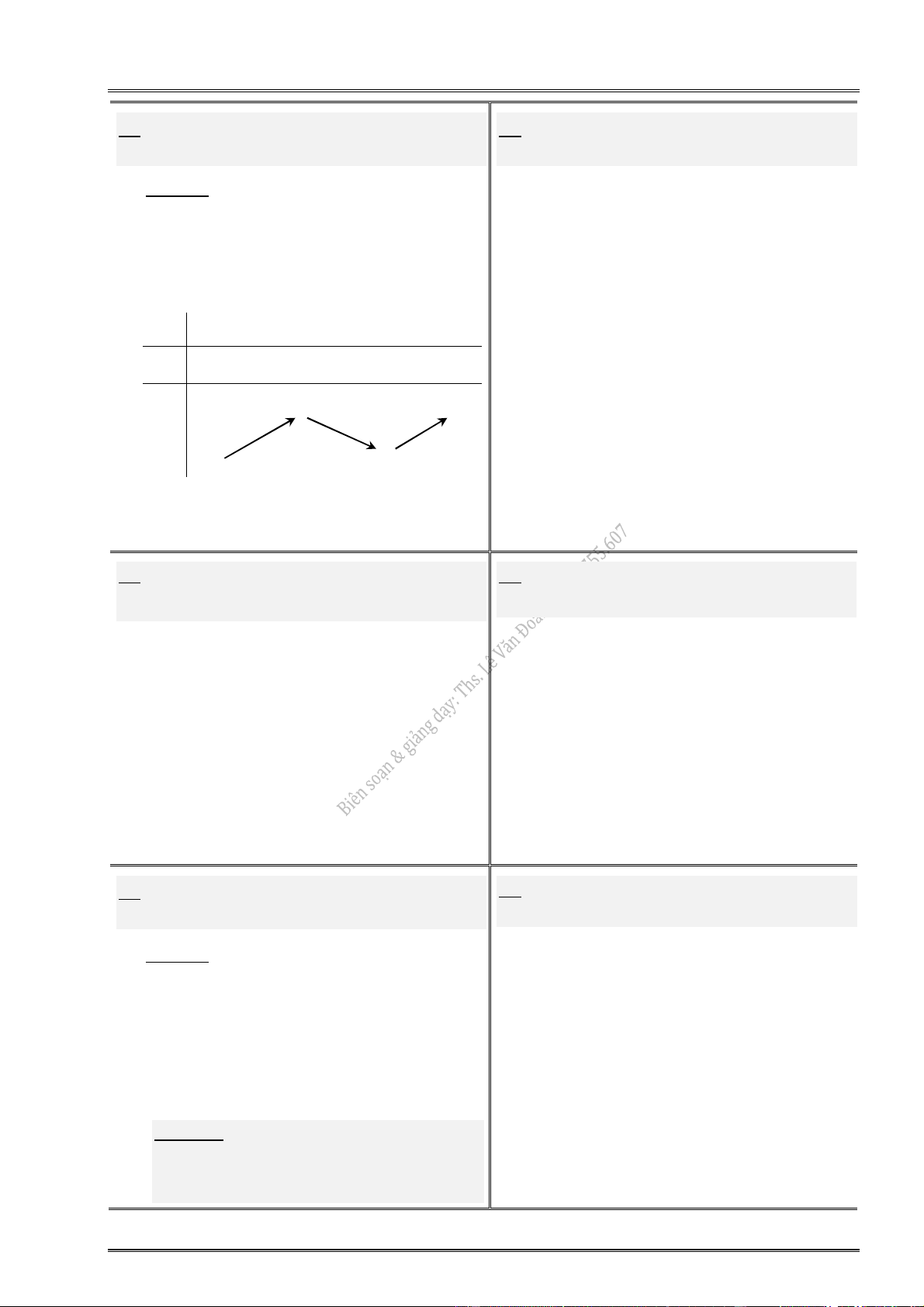
Giả sử y  f (x ) liên tục trên khoảng K  (x  h; x  h) và có đạo hàm trên K hoặc  
trên K \ {x }, với h  0. Khi đó:   Nếu f (
 x)  0 trên khoảng (x h; x ) và f (x)  0 trên khoảng (x ; x  h) thì x là     
một điểm cực đại của hàm số f (x).  Nếu f (
 x)  0 trên khoảng (x h; x ) và f (x)  0 trên khoảng (x ; x  h) thì x là     
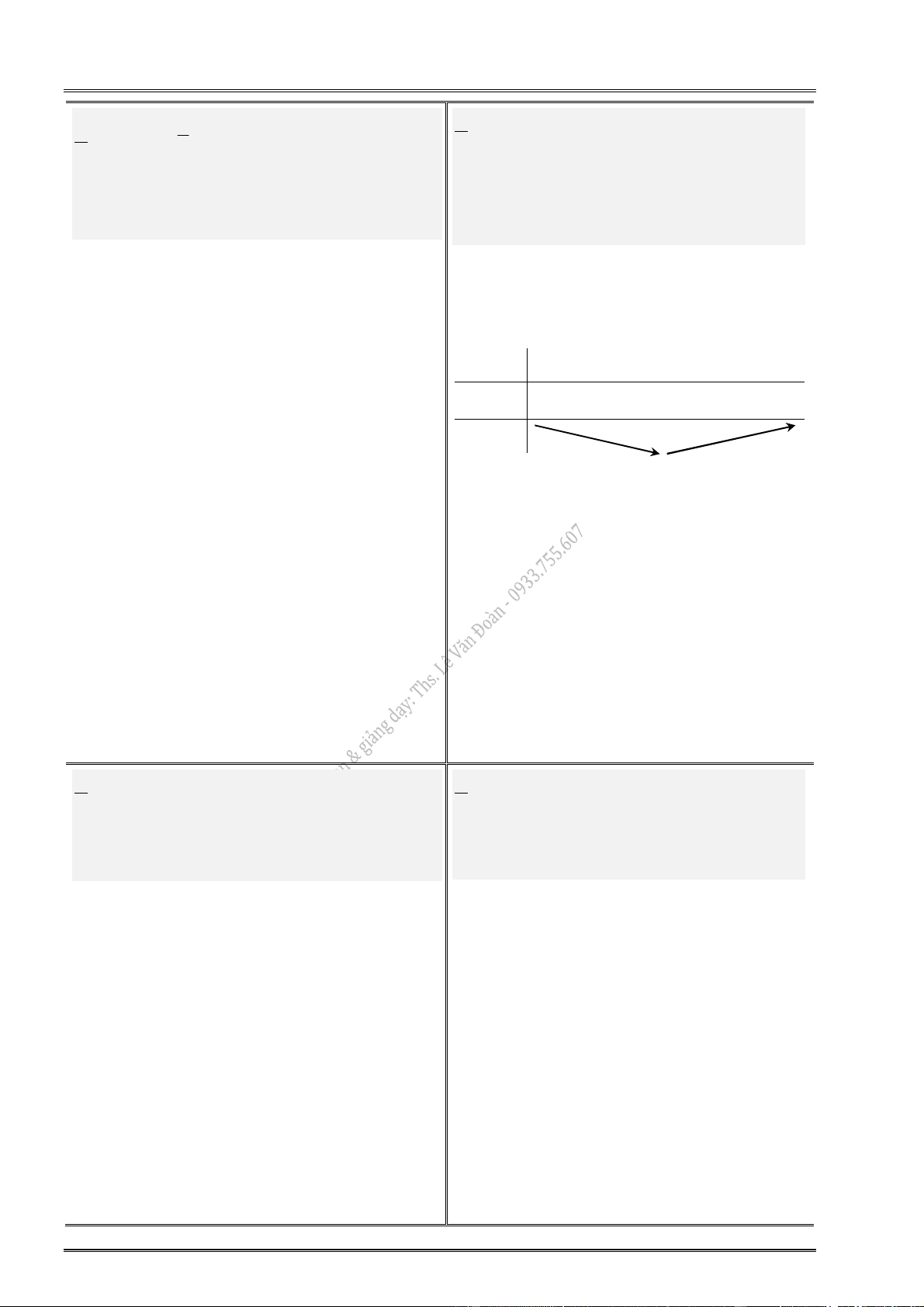
một điểm cực tiểu của hàm số f (x). x
x  h x x  h x
 x x  h    x h    f (  x)  0  f (  x)  0  y f (x ) CĐ f (x ) y CT
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 63 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
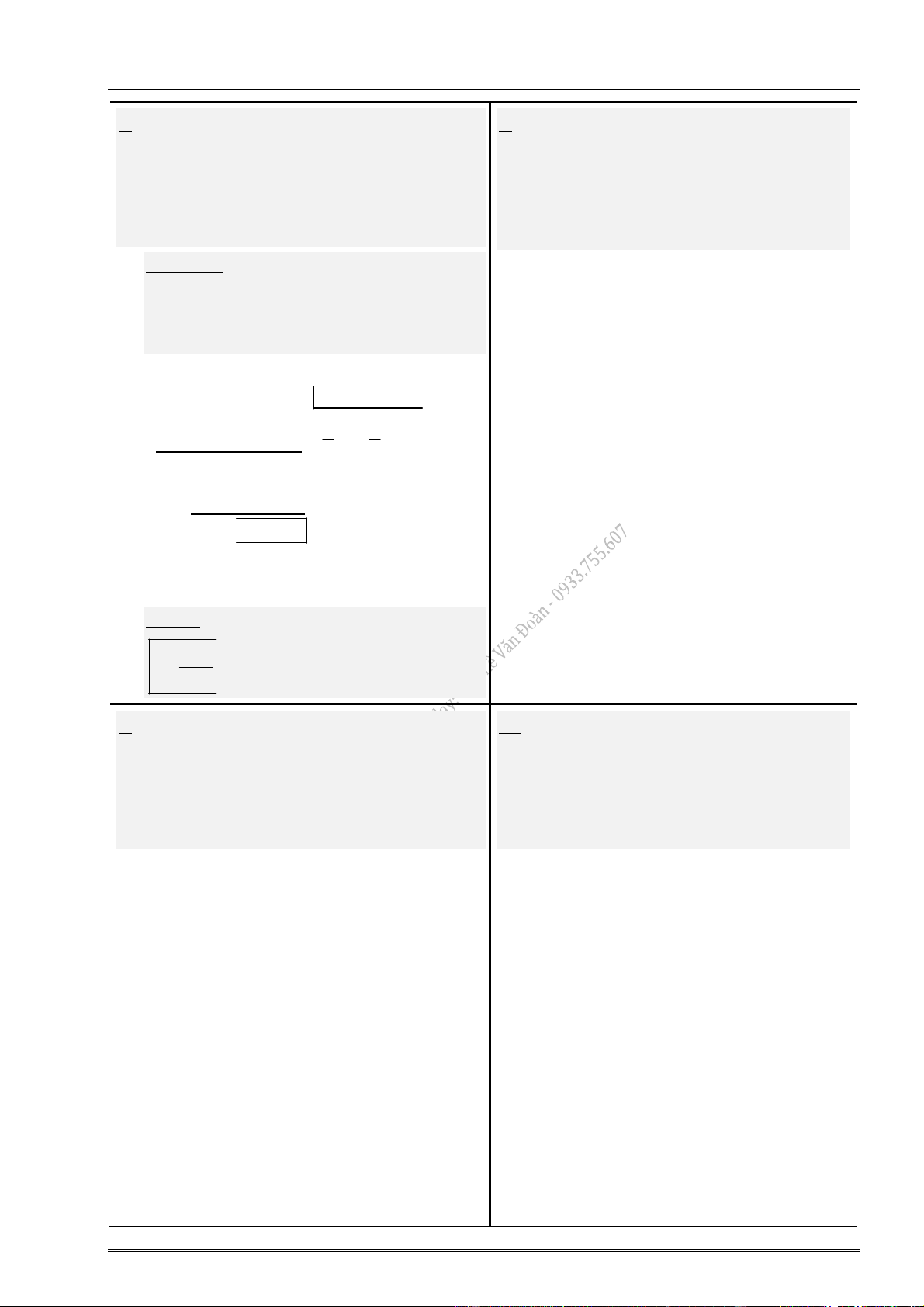
Môn: Toán, Năm học: 2019 – 2020 Nói cách khác:  Nếu f (
 x) đổi dấu từ âm sang dương khi x đi qua điểm x (theo chiều tăng) thì hàm số 
y  f (x ) đạt cực tiểu tại điểm x .   Nếu f (
 x) đổi dấu từ dương sang âm khi x đi qua điểm x (theo chiều tăng) thì hàm số 
y  f (x ) đạt cực đại tại điểm x .  2. Định lí 3
Giả sử y  f (x ) có đạo hàm cấp 2 trong khoảng (x  h; x  h), với h  0. Khi đó:    Nếu y (
 x )  0, y (x )  0 thì x là điểm cực tiểu.     Nếu y (
 x )  0, y (x )  0 thì x là điểm cực đại. o o 
Chú ý. Một hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số
bằng 0, hoặc tại đó hàm số không có đạo hàm, chẳng hạn hàm số y  x .
B. CÁC DẠNG TOÁN THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI
Daïng toaùn 1: Tìm ñieåm cöïc ñaïi, cöïc tieåu, giaù trò cöïc ñaïi, giaù trò cöïc tieåu 
 Bài toán: Tìm các điểm cực đại, cực tiểu (nếu có) của hàm số y  f (x).  Phương pháp:
 Bước 1. Tìm tập xác định D của hàm số.
 Bước 2. Tính đạo hàm y  f (x). Tìm các điểm x , (i  1,2,3,...,n) mà tại đó đạo hàm i
bằng 0 hoặc không xác định.
 Bước 3. Sắp xếp các điểm x theo thứ tự tăng dần và lập bảng biến thiên. i
 Bước 4. Từ bảng biến thiên, suy ra các điểm cực trị (dựa vào nội dung định lý 2).
BÀI TẬP VẬN DỤNG
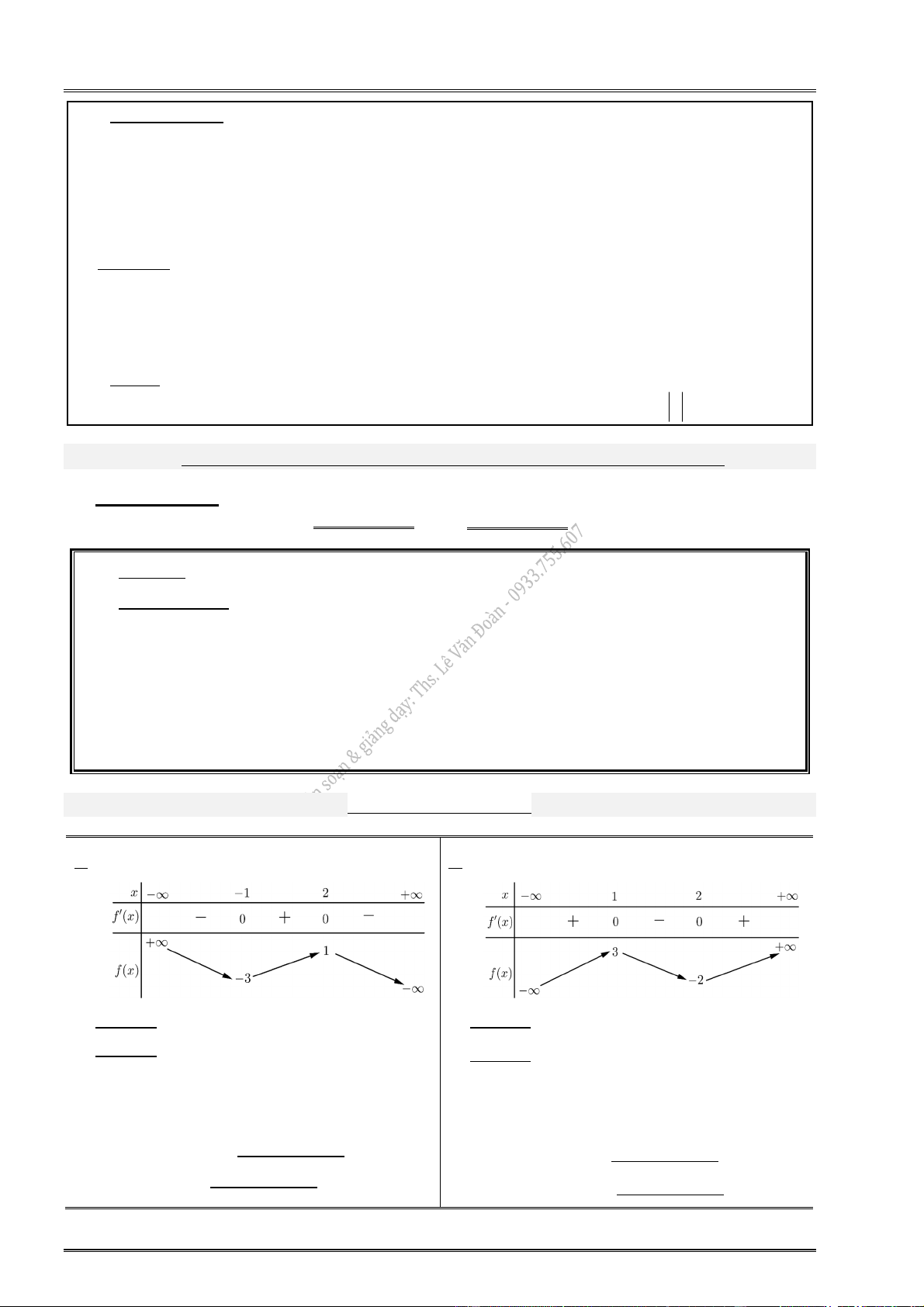
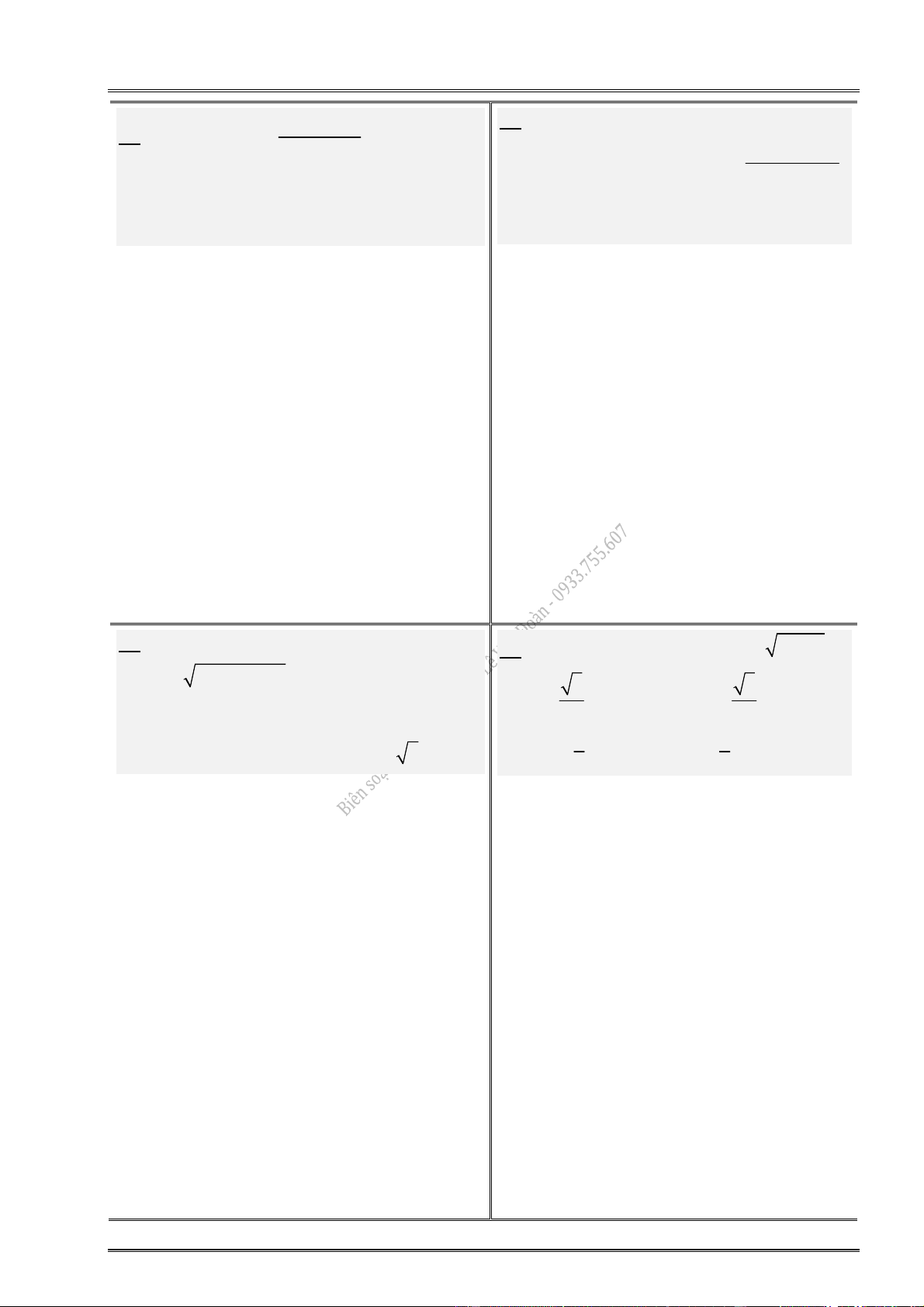
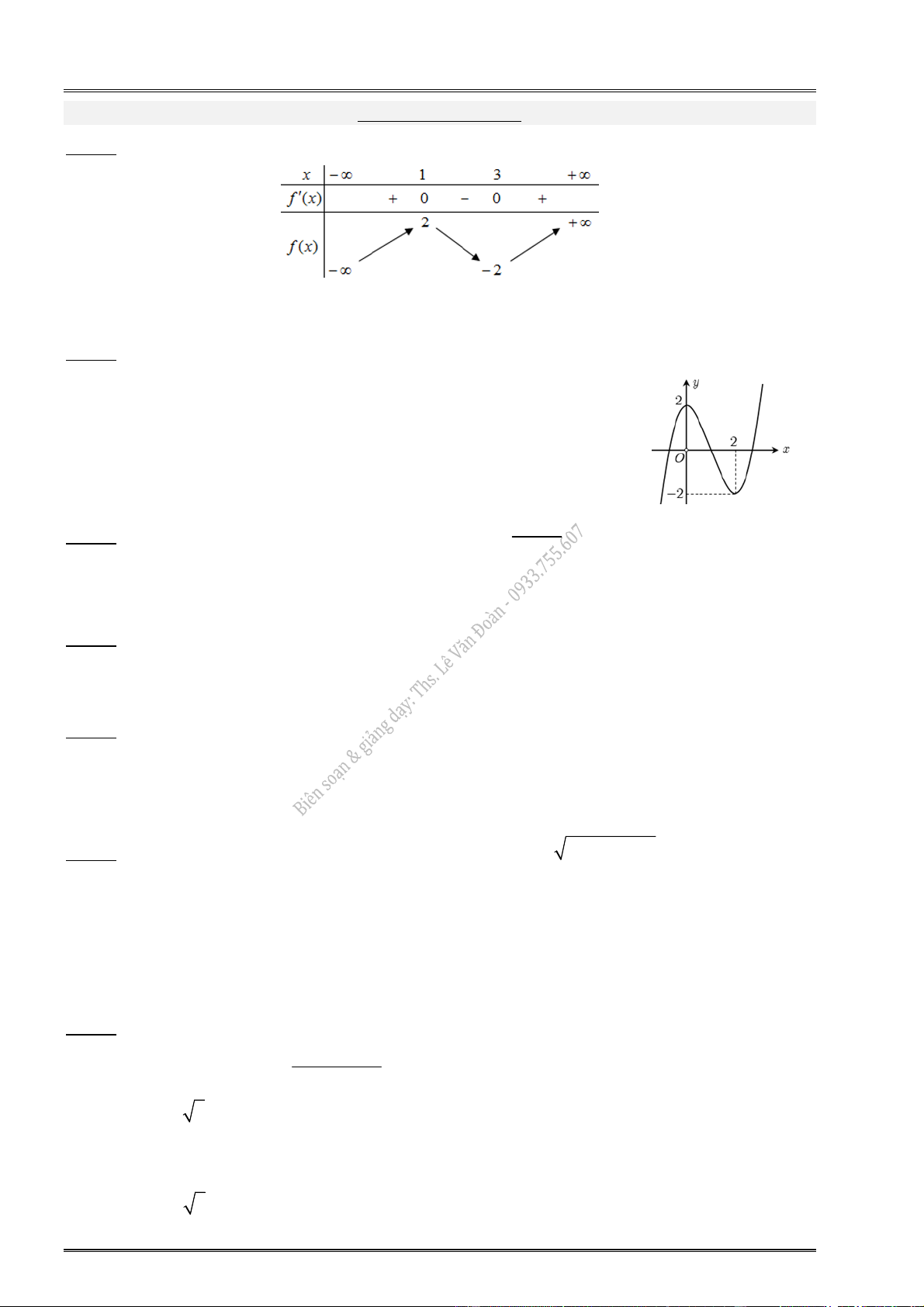
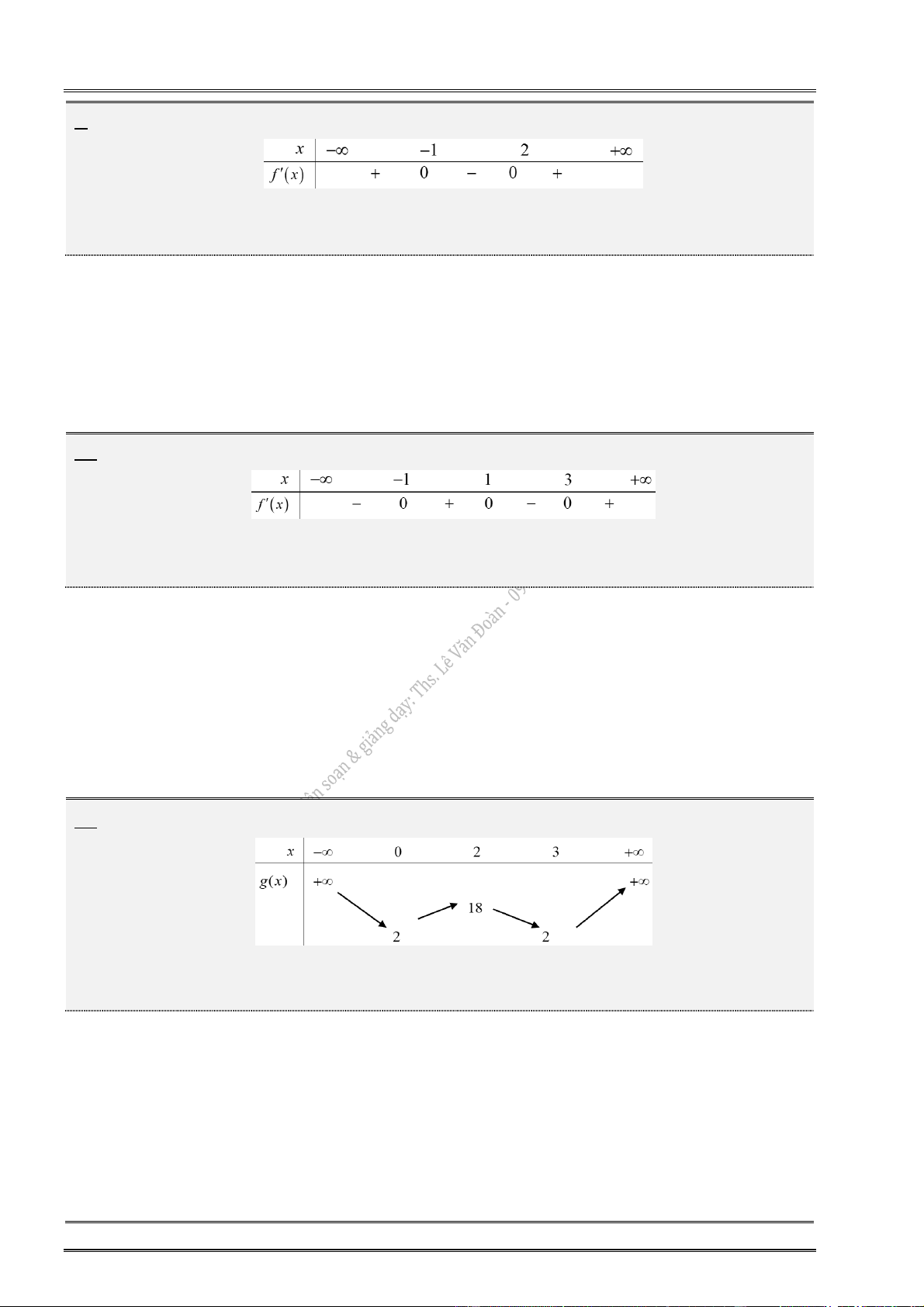
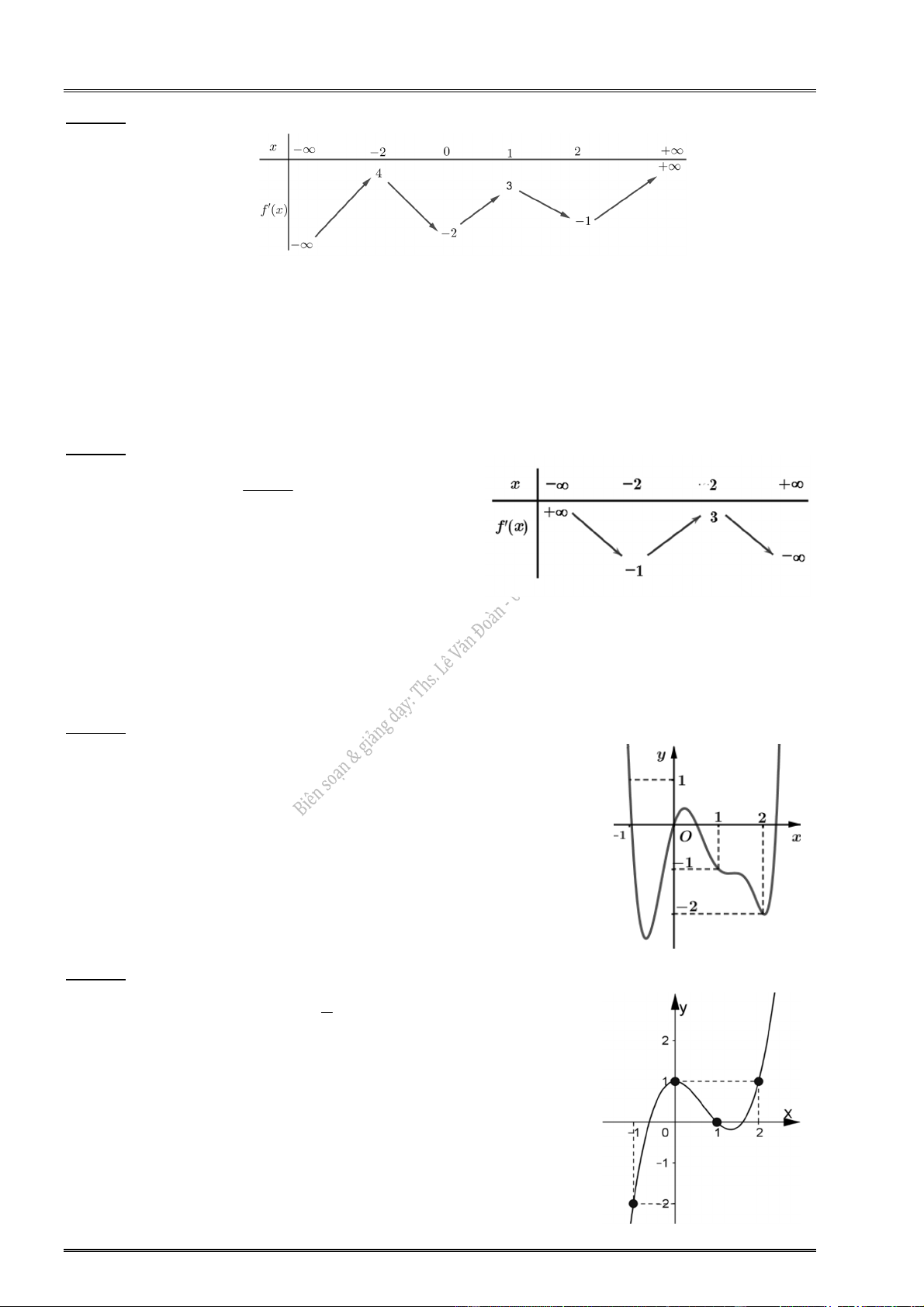
1. Cho hàm số y  f (x) có bảng biến thiên: 2. Cho hàm số y  f (x) có bảng biến thiên:
 Hàm số đạt cực tiểu tại: x  1.
 Hàm số đạt cực tiểu tại: ...............................
 Hàm số đạt cực đại tại: x  2.
 Hàm số đạt cực đại tại: ...............................
 Giá trị CĐ (cực đại) của hàm số: y  1. CĐ
 Giá trị CĐ (cực đại) của hàm số: ................
 Giá trị CT (cực tiểu) của hàm số: y  3. CT
 Giá trị CT (cực tiểu) của hàm số: ...............
 Điểm cực đại của đồ thị hàm số: M(2;1).
 Điểm cực đại của đồ thị hàm số: ................
 Điểm cực tiểu đồ thị hàm số: N( 1  ; 3  ).
 Điểm cực tiểu của đồ thị hàm số: ...............
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 64 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
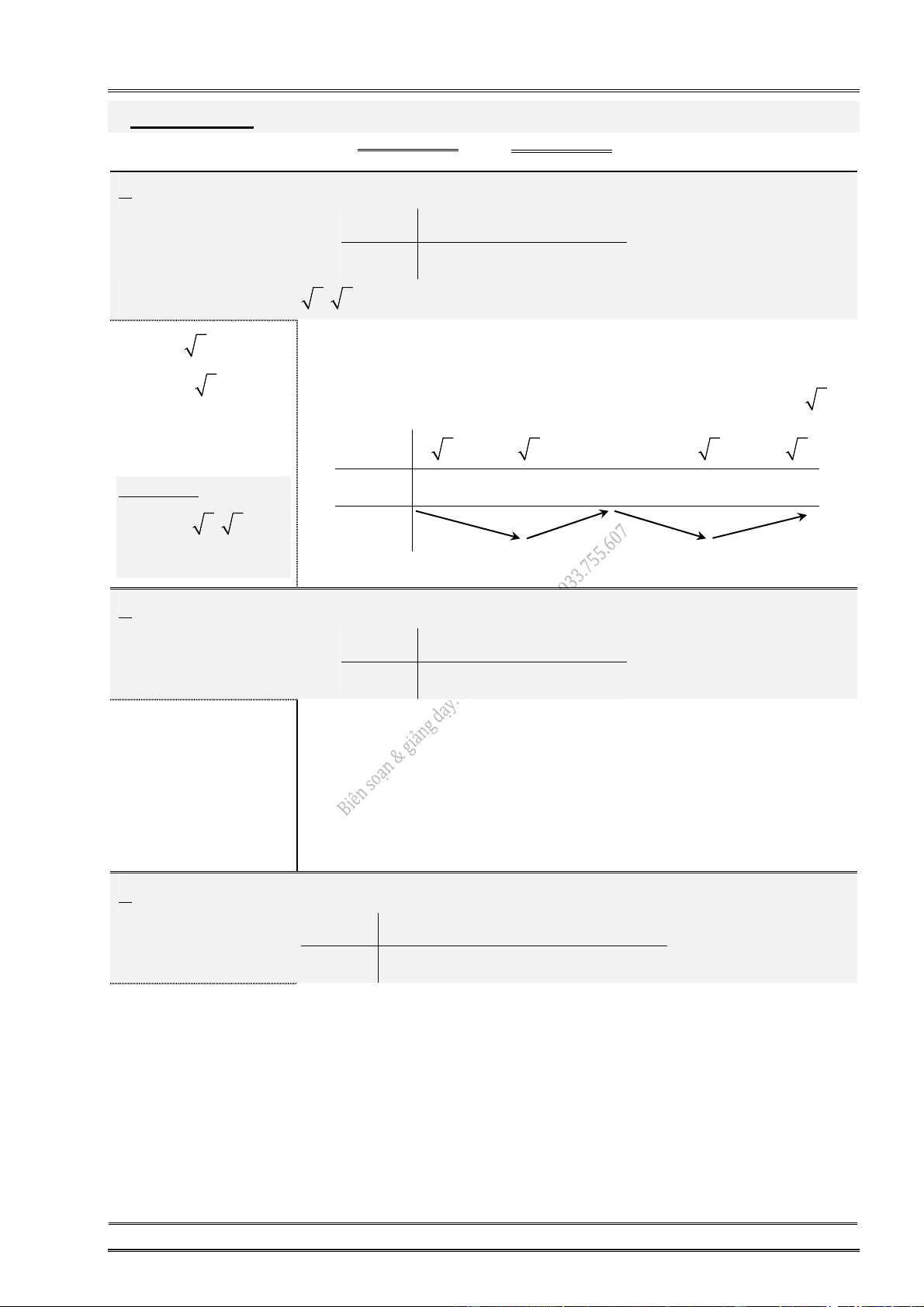
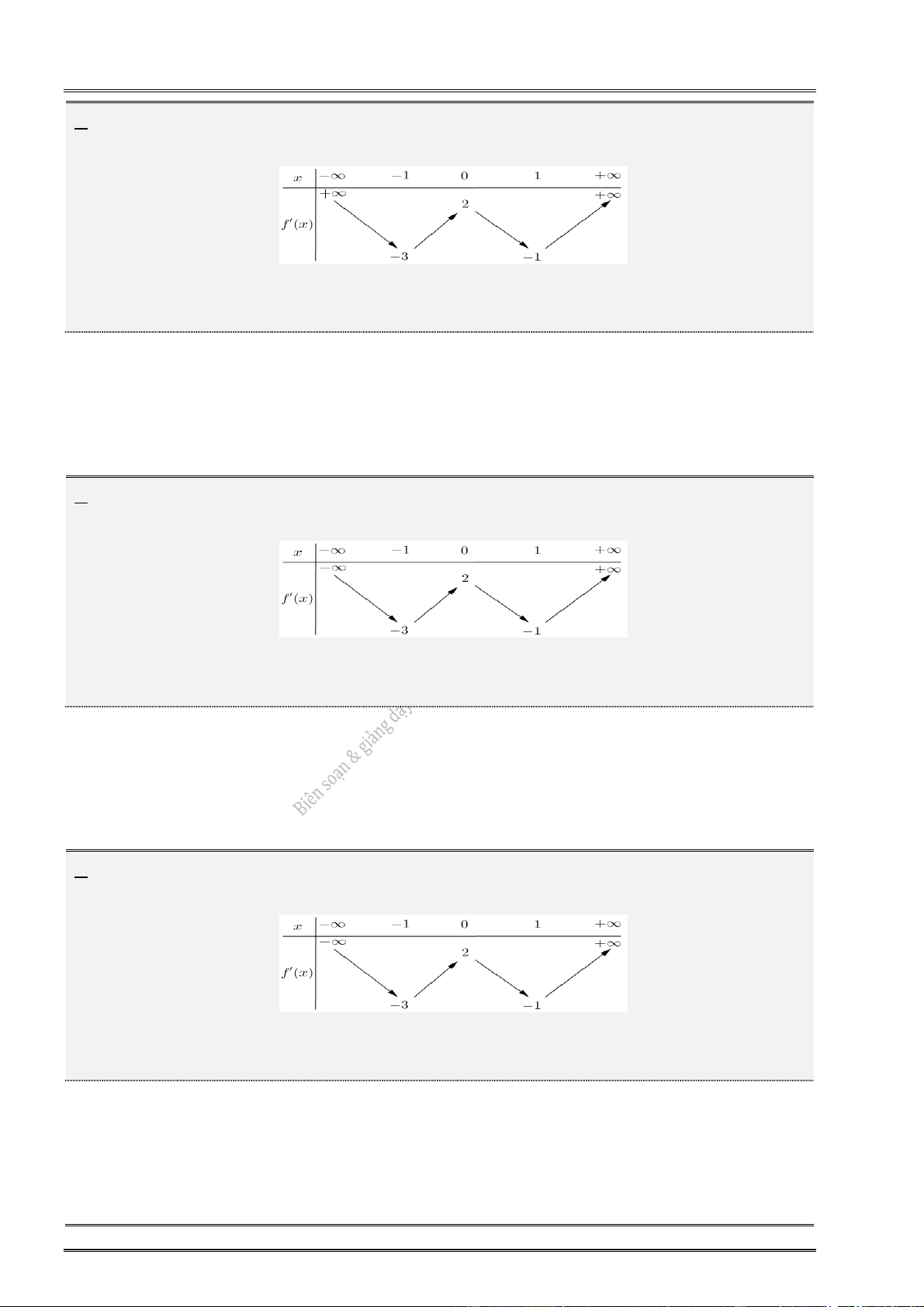
3. Cho hàm số y  f (x) có bảng biến thiên: 4. Cho hàm số y  f (x) có bảng biến thiên: x  1 0 1  x  1 0 1  y    0   y  0   0  1   4   y y  1    4
 Hàm số đạt cực tiểu tại: ...............................  Hàm số đạt cực tiểu tại: ...............................
 Hàm số đạt cực đại tại: ...............................  Hàm số đạt cực đại tại: ...............................
 Giá trị CĐ (cực đại) của hàm số: ................  Giá trị CĐ (cực đại) của hàm số: ................
 Giá trị CT (cực tiểu) của hàm số: ...............  Giá trị CT (cực tiểu) của hàm số: ................
 Điểm cực đại của đồ thị hàm số: ................  Điểm cực đại của đồ thị hàm số: ................
 Điểm cực tiểu của đồ thị hàm số: ..............  Điểm cực tiểu của đồ thị hàm số: ...............
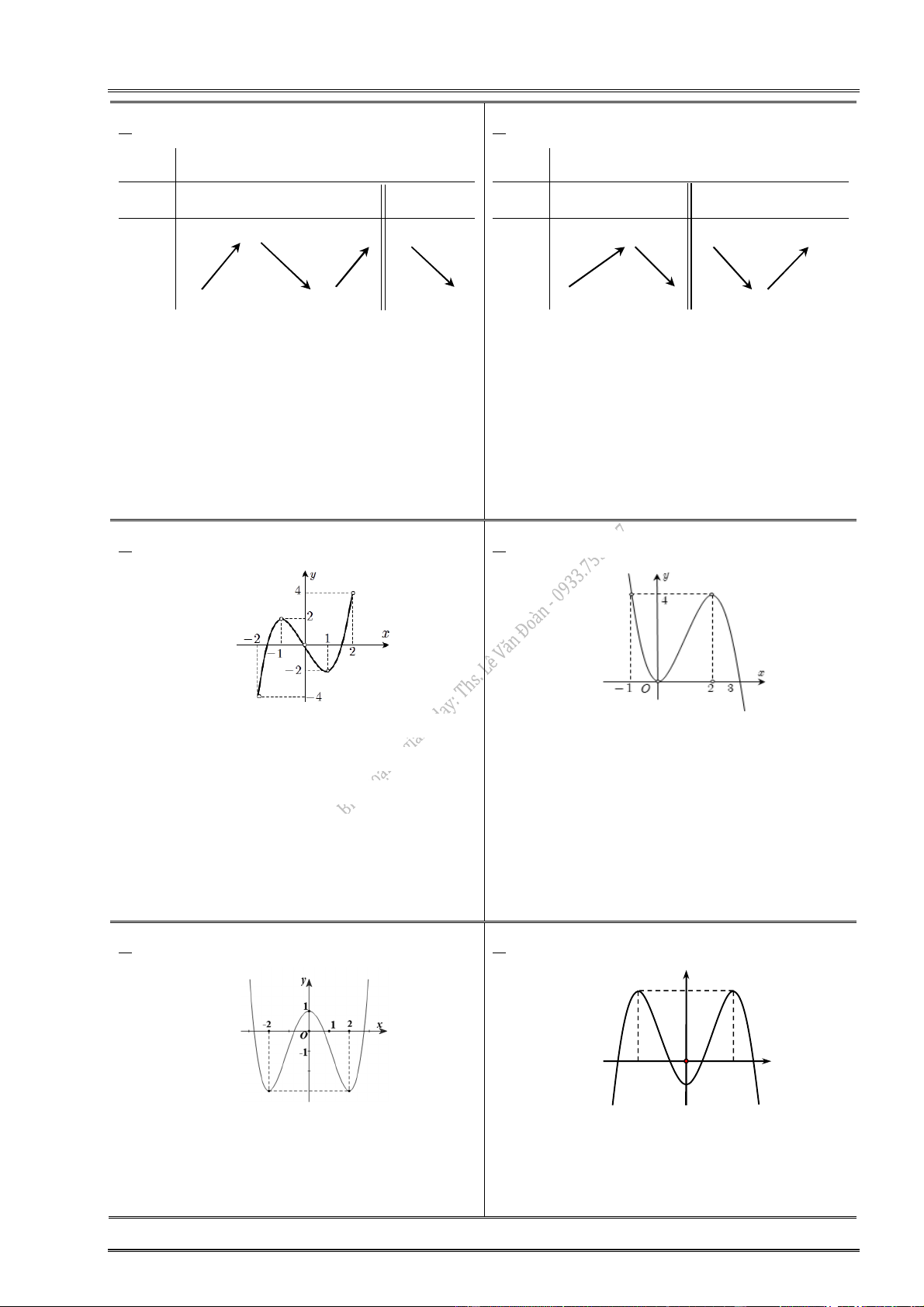
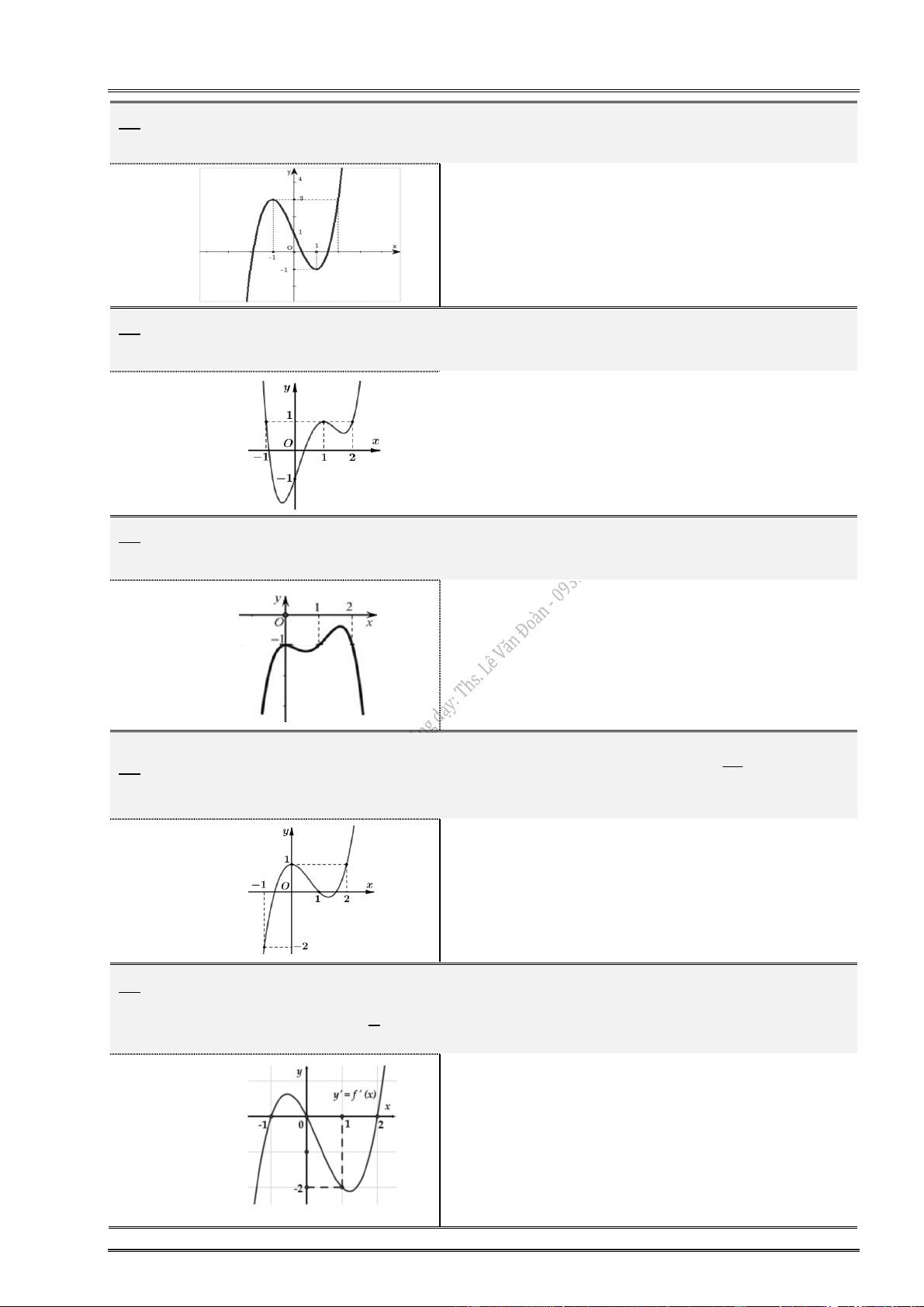
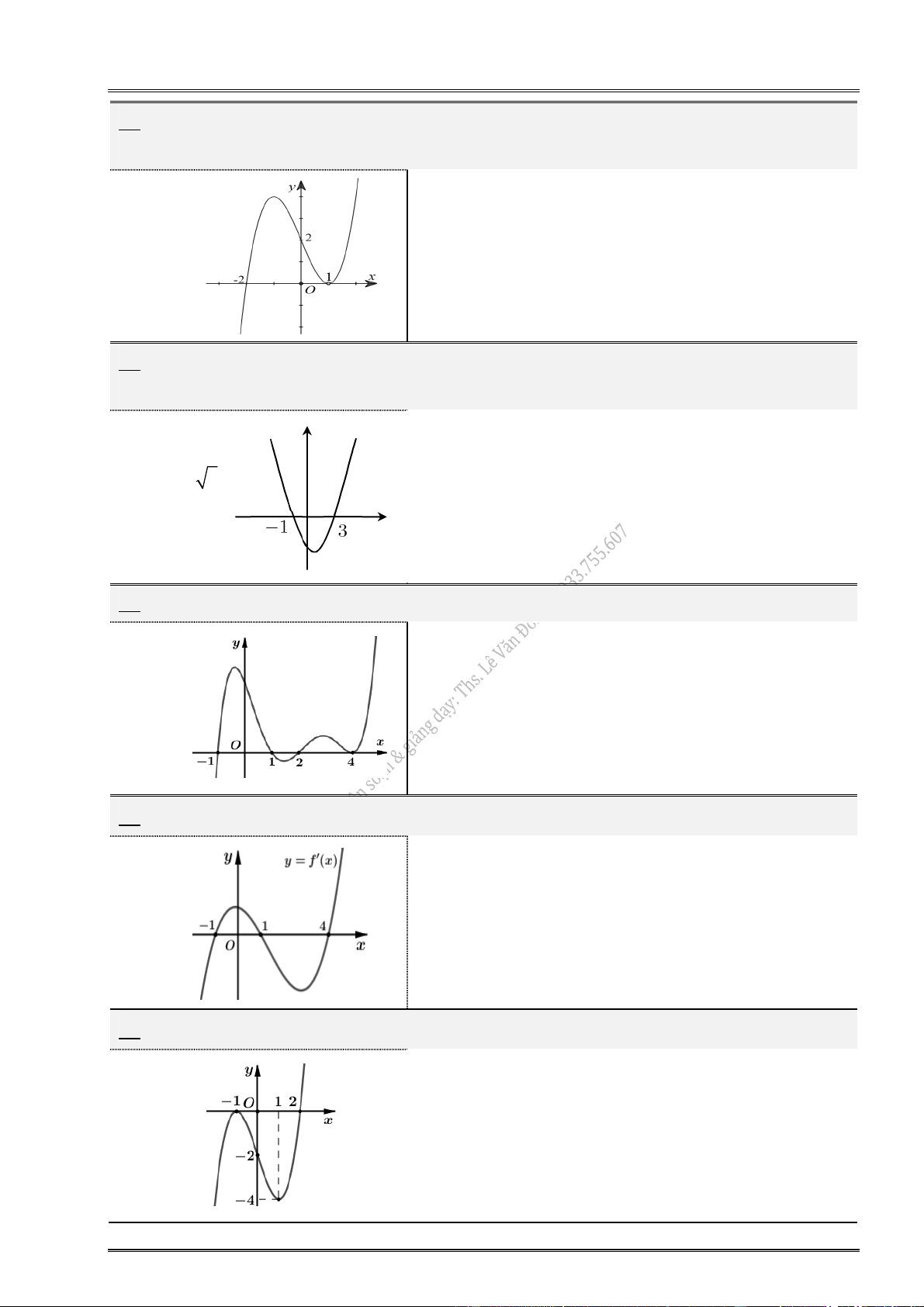
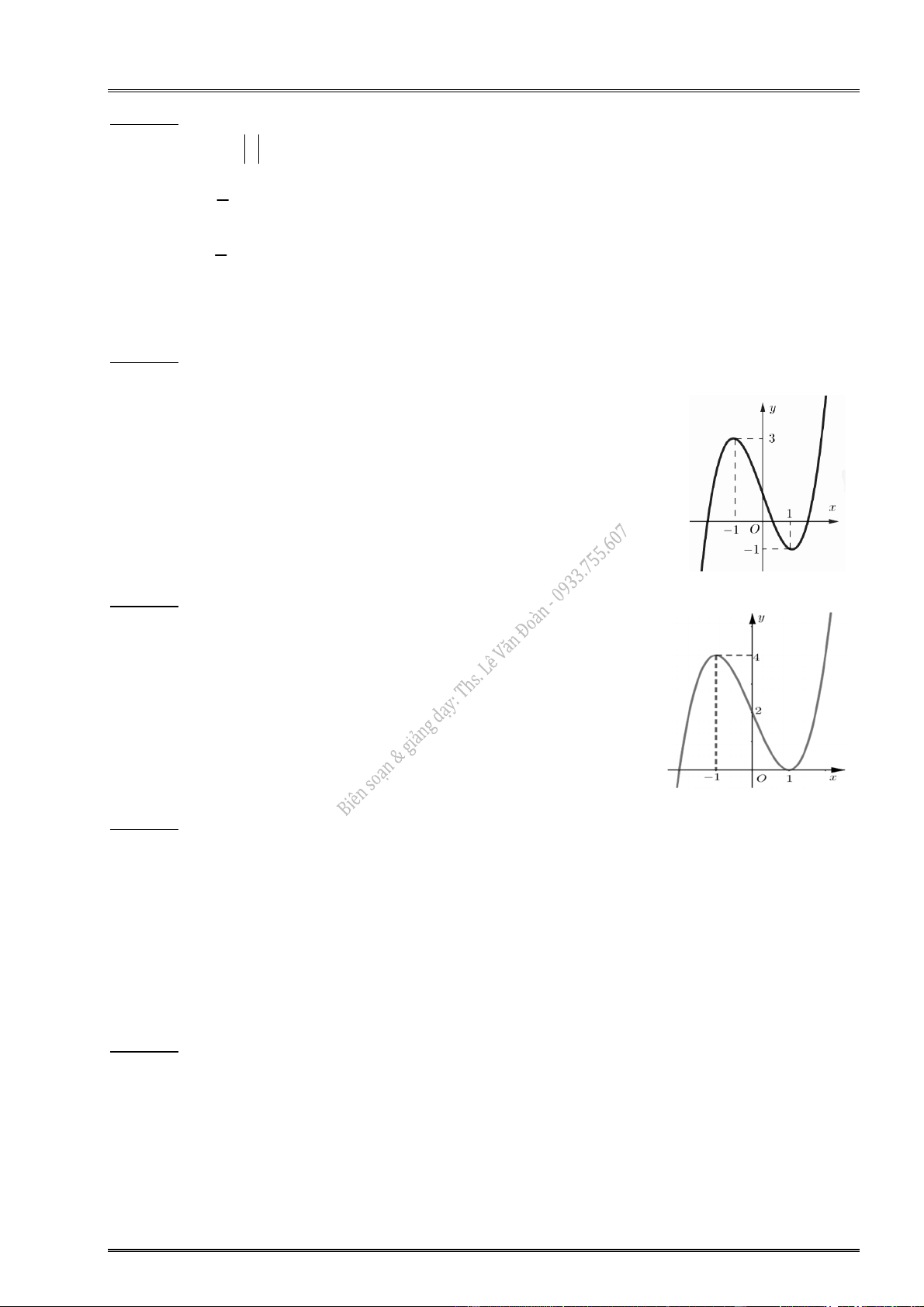
5. Cho hàm số y  f (x) có đồ thị:
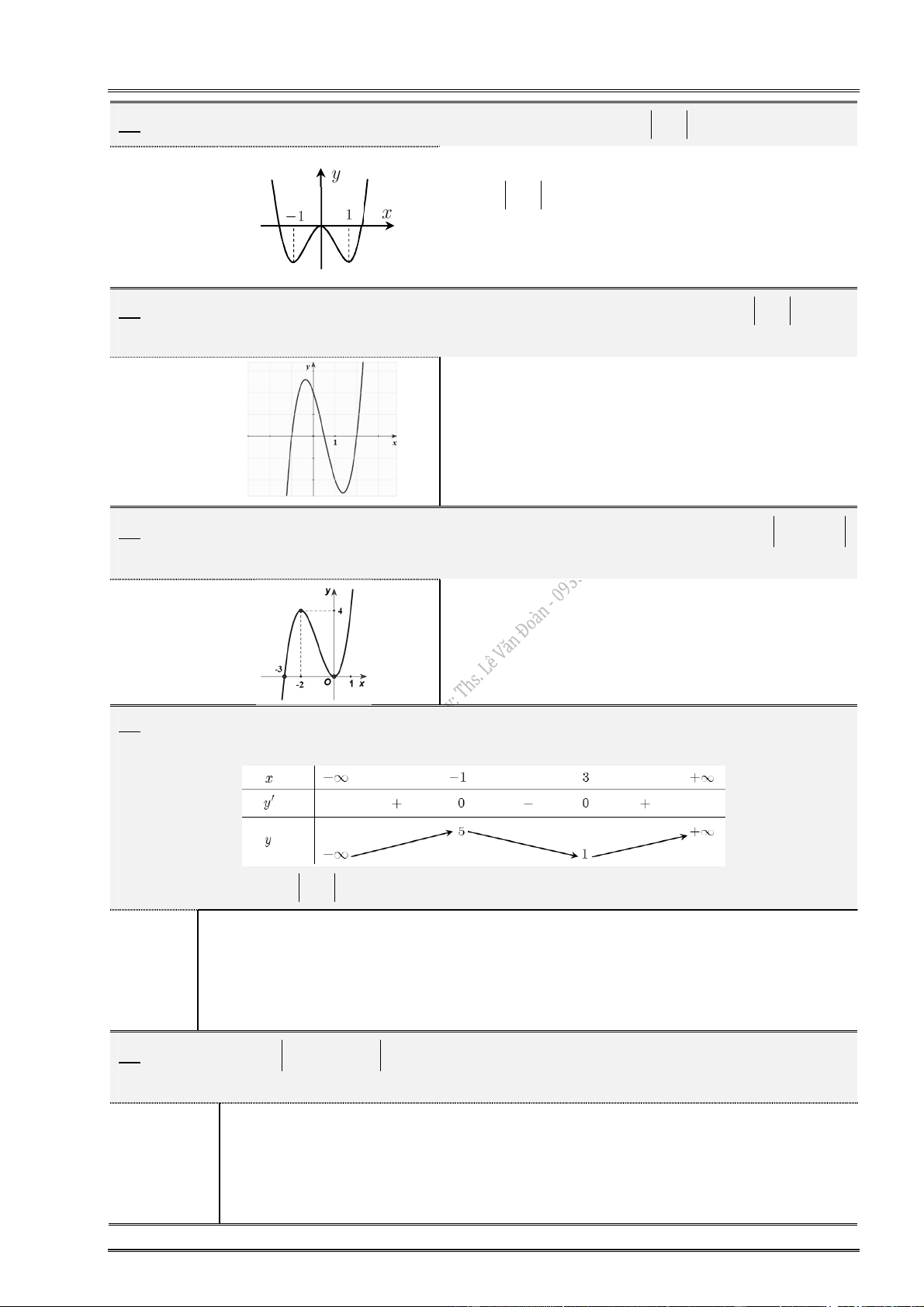
6. Cho hàm số y  f (x) có đồ thị:
 Hàm số đạt cực tiểu tại: ...............................  Hàm số đạt cực tiểu tại: ...............................
 Hàm số đạt cực đại tại: ...............................  Hàm số đạt cực đại tại: ...............................
 Giá trị CĐ (cực đại) của hàm số: ................  Giá trị CĐ (cực đại) của hàm số: ................
 Giá trị CT (cực tiểu) của hàm số: ...............  Giá trị CT (cực tiểu) của hàm số: ................
 Điểm cực đại của đồ thị hàm số: ................  Điểm cực đại của đồ thị hàm số: ................
 Điểm cực tiểu của đồ thị hàm số: ..............  Điểm cực tiểu của đồ thị hàm số: ...............
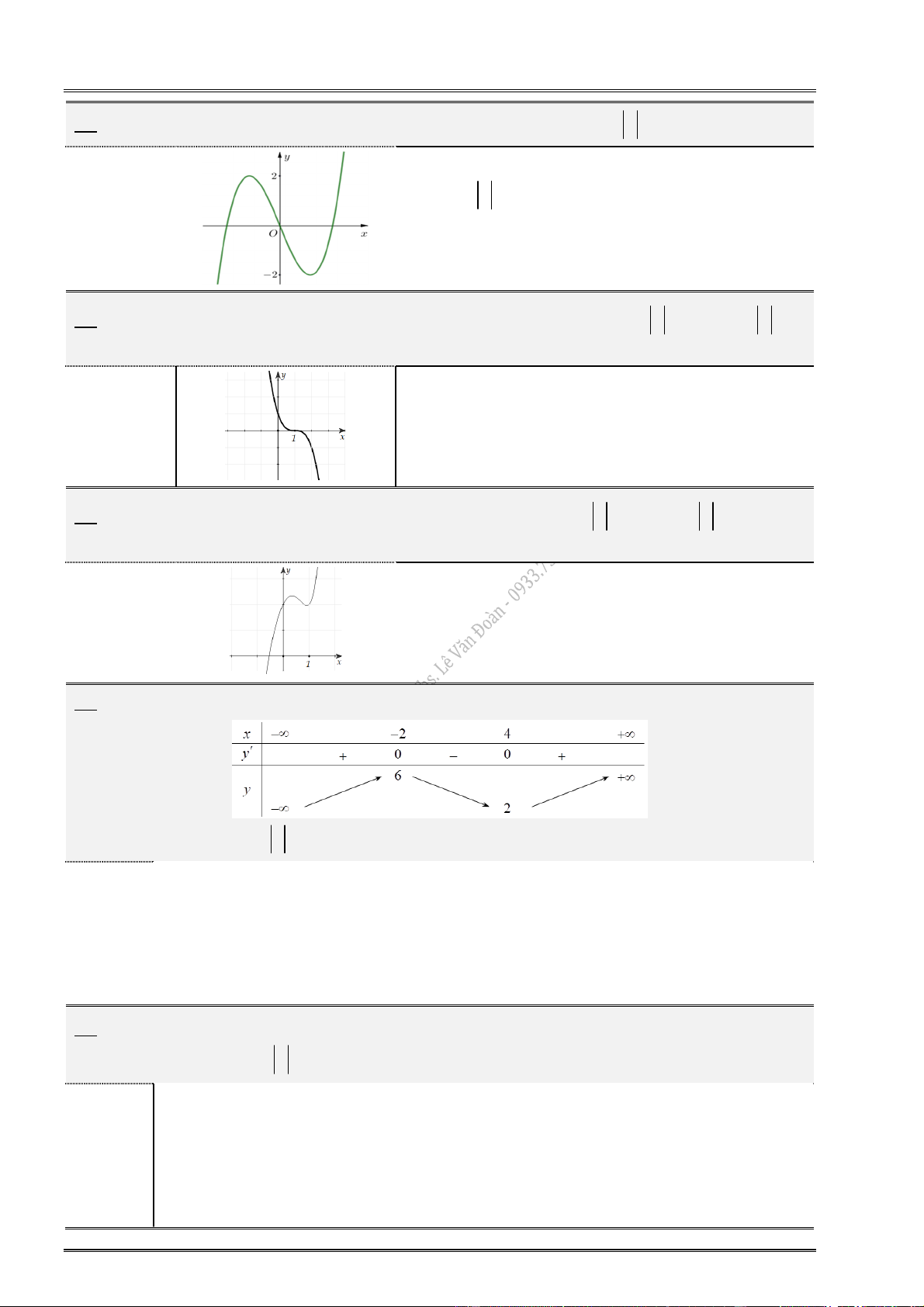
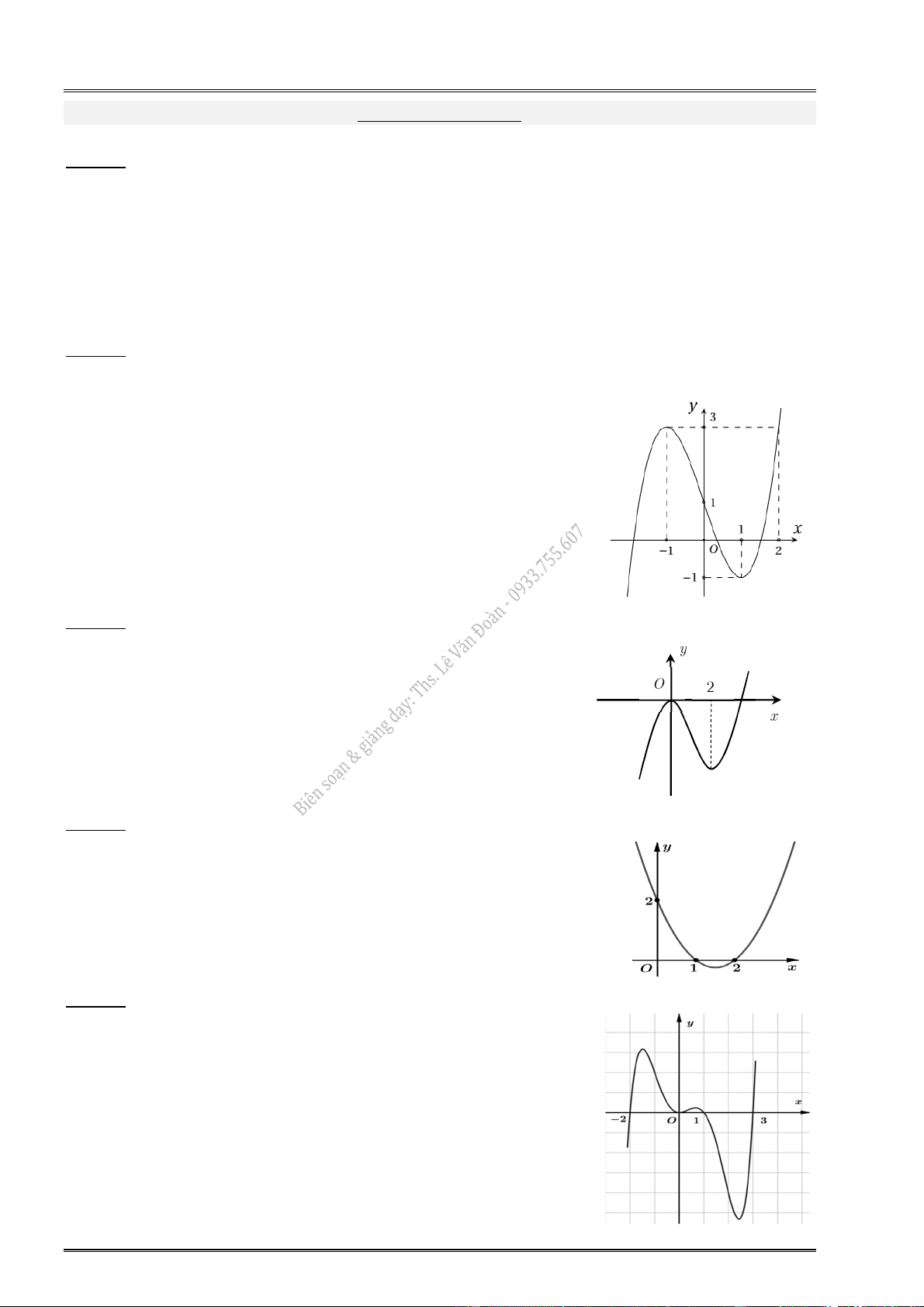
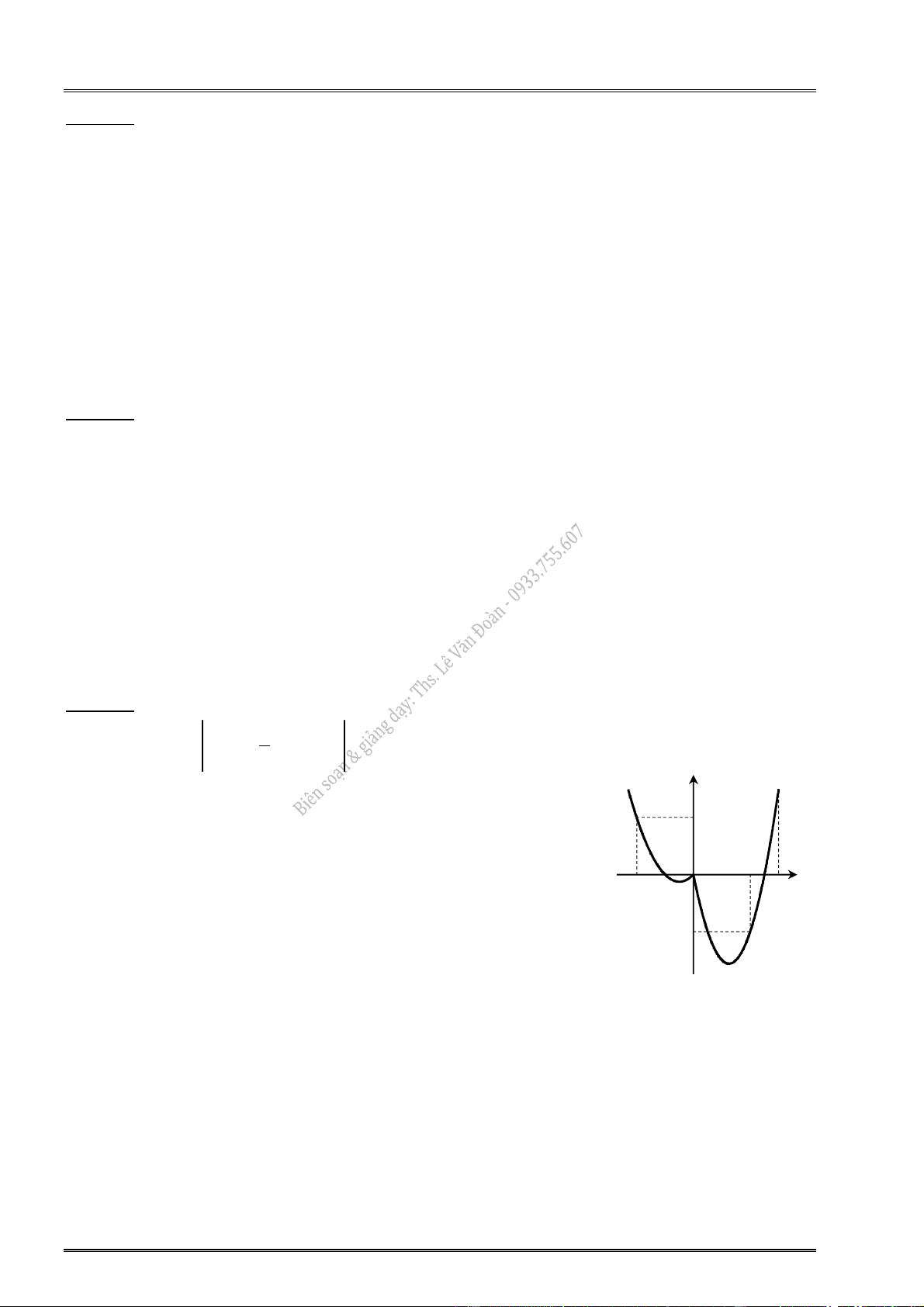
7. Cho hàm số y  f (x) có đồ thị:
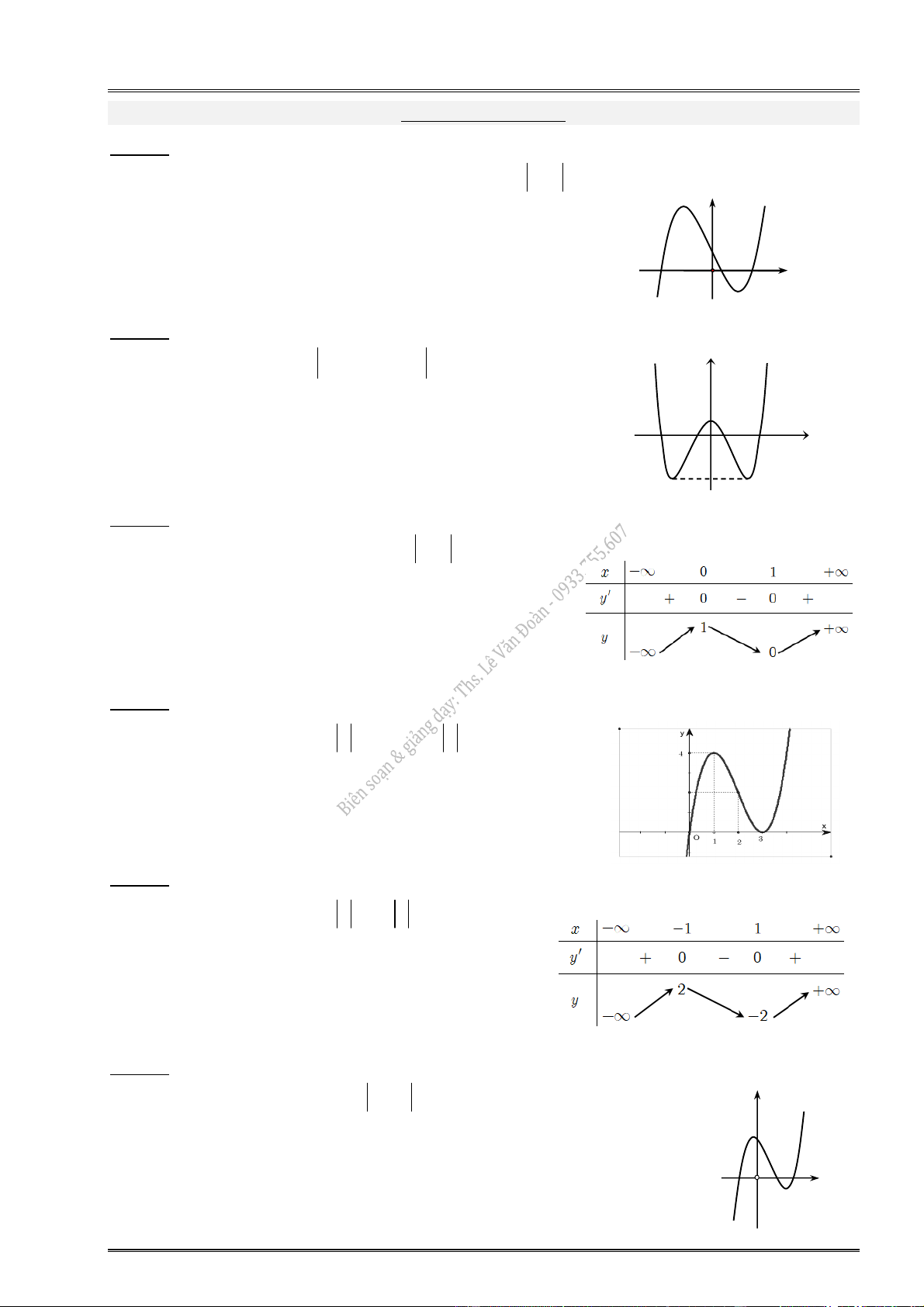
8. Cho hàm số y  f (x) có đồ thị: y 3 O x 2  2 1 
 Hàm số đạt cực tiểu tại: ...............................  Hàm số đạt cực tiểu tại: ...............................
 Hàm số đạt cực đại tại: ...............................  Hàm số đạt cực đại tại: ...............................
 Giá trị CĐ (cực đại) của hàm số: ................  Giá trị CĐ (cực đại) của hàm số: ................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 65 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
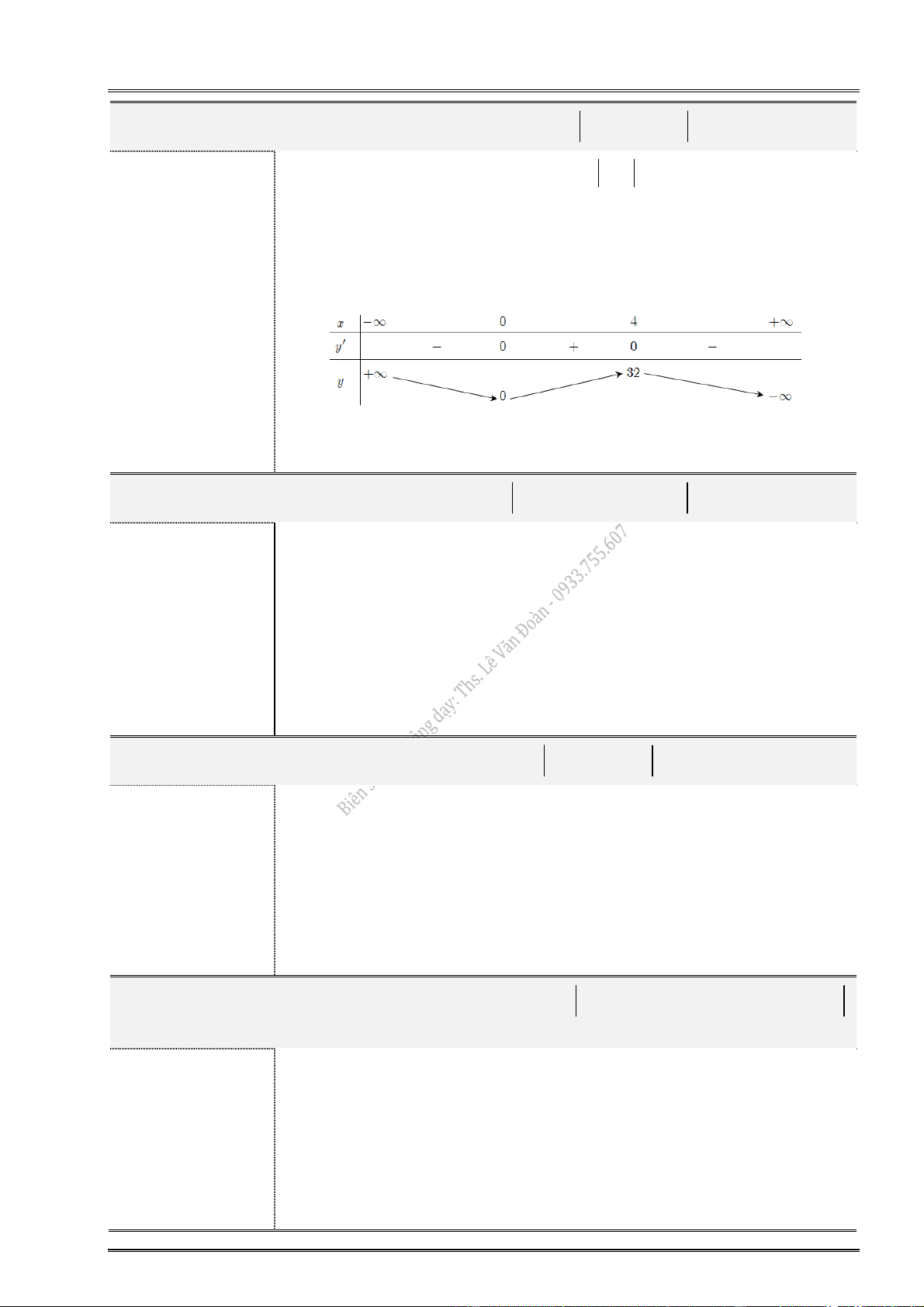
8. Giá trị cực đại của hàm số 3
y  x  3x  1 9. Giá trị cực đại hàm số 3
y  x  12x  1 bằng bằng A. 3. B. 1. A. 17. B. 2. C. 1. D. 4. C. 45. D. 15.
Lời giải. Tập xác định D  . 
......................................................................
x  1  y  1 2
y  3x  3, y  0     
...................................................................... 
x  1  y  3 
......................................................................
Giới hạn: lim y   và lim y   .  x x
...................................................................... x  1 1 
...................................................................... y  0  0 
...................................................................... 3 
...................................................................... y
......................................................................  1
......................................................................
Giá trị cực đại y  3. Chọn A.
...................................................................... CĐ
10. Điểm cực đại của đồ thị hàm số:
11. Điểm cực tiểu của đồ thị hàm số: 3 2 y  x   3x  1 là 4 2 y  x   2x  5 là
A. x  0. B. M( 2  ; 1  9). A. ( A 1  ;6).
B. x  0.
C. N (0;1).
D. x  2. C. 5.
D. B(0; 5).
.......................................................................
......................................................................
.......................................................................
......................................................................
.......................................................................
......................................................................
.......................................................................
......................................................................
.......................................................................
......................................................................
.......................................................................
......................................................................
12. Điểm cực đại của đồ thị hàm số:
13. Giá trị của tiểu của đồ thị hàm số 4 2
y  x  4x  3 là 4 2 y  x
  2x  2 bằng A. (0; 1  ). B. (0; 3). A. 2. B. (0;2). C. ( 2; 1  ). D. ( 2; 1  ). C. (1; 3). D. 3.
.......................................................................
......................................................................
.......................................................................
......................................................................
.......................................................................
......................................................................
.......................................................................
......................................................................
.......................................................................
......................................................................
.......................................................................
......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 66 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 2 x  x  1
15. Gọi M, n lần lượt là giá trị cực đại, giá
14. Cho hàm số y   Điểm cực tiểu x  1 2 x  3x  3
trị cực tiểu của hàm số y   của hàm số đã cho là x  2
A. x  1.
B. x  2. Giá trị của 2
M  2n bằng
C. x  0. D. ( 2  ; 3  ). A. 6. B. 7. C. 8. D. 9.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
16. Tìm giá trị cực đại y (nếu có) của hàm số y  x  x CĐ
17. Tìm cực đại của hàm số 2 1 . 2
y  3  2x  x . 2 2 A.  B.   A. y  0. B. y  2. 2 2 CĐ CĐ 1 1    C. y  3. D. y  3. C. D. CĐ CĐ 2 2
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 67 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 BÀI TẬP VỀ NHÀ 1 Câu 1.
(Đề thi THPT QG năm 2019 – Mã đề 104) Cho hàm số f (x) có bảng biến thiên:
Hàm số đã cho đạt cực tiểu tại A. x  2. B. x  1. C. x  3. D. x  2. Câu 2.
(Sở GD & ĐT Tp. HCM năm 2018) Cho hàm số y  f (x) có đồ thị như hình vẽ. Mệnh đề nào đúng ?
A. Hàm số có giá trị cực tiểu bằng 2.
B. Hàm số có giá trị lớn nhất bằng 2.
C. Hàm số đạt cực đại tại x  0 và cực tiểu tại x  2.
D. Hàm số có ba điểm cực trị. x  1 Câu 3.
(THPT Chuyên Vĩnh Phúc 2018) Hàm số y 
có bao nhiêu điểm cực trị ? 2x  1 A. 1. B. 0. C. 2. D. 3. Câu 4.
(Sở GD & ĐT Bạc Liêu 2019) Điểm cực tiểu của hàm số 3 2
y  x  3x  9x  2 là
A. x  11. B. x  3.
C. x  7. D. x  1. Câu 5.
(THPT Thăng Long – Hà Nội 2018) Cho hàm số 4 2 y  x
  2x  1. Điểm cực tiểu của hàm số là A. x  1. B. (0; 1  ). C. x  1. D. x  0. Câu 6.
(THPT Nhân Chính Hà Nội 2019) Cho hàm số 2
y  x  x  20. Mệnh đề nào sai ?
A. Hàm số nghịch biến trên khoảng ( ;  4  ).
B. Hàm số đạt cực đại tại x  5.
C. Hàm số đồng biến trên khoảng (5; )  .
D. Hàm số không có cực trị. Câu 7.
(Sở GD & ĐT Tp. HCM – Cụm 5 năm 2017) Khoảng cách giữa hai điểm cực trị của 2 x  2x  1
đồ thị hàm số y  bằng x  1 A. 4 5. B. 4. C. 8. D. 5 2.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 68 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
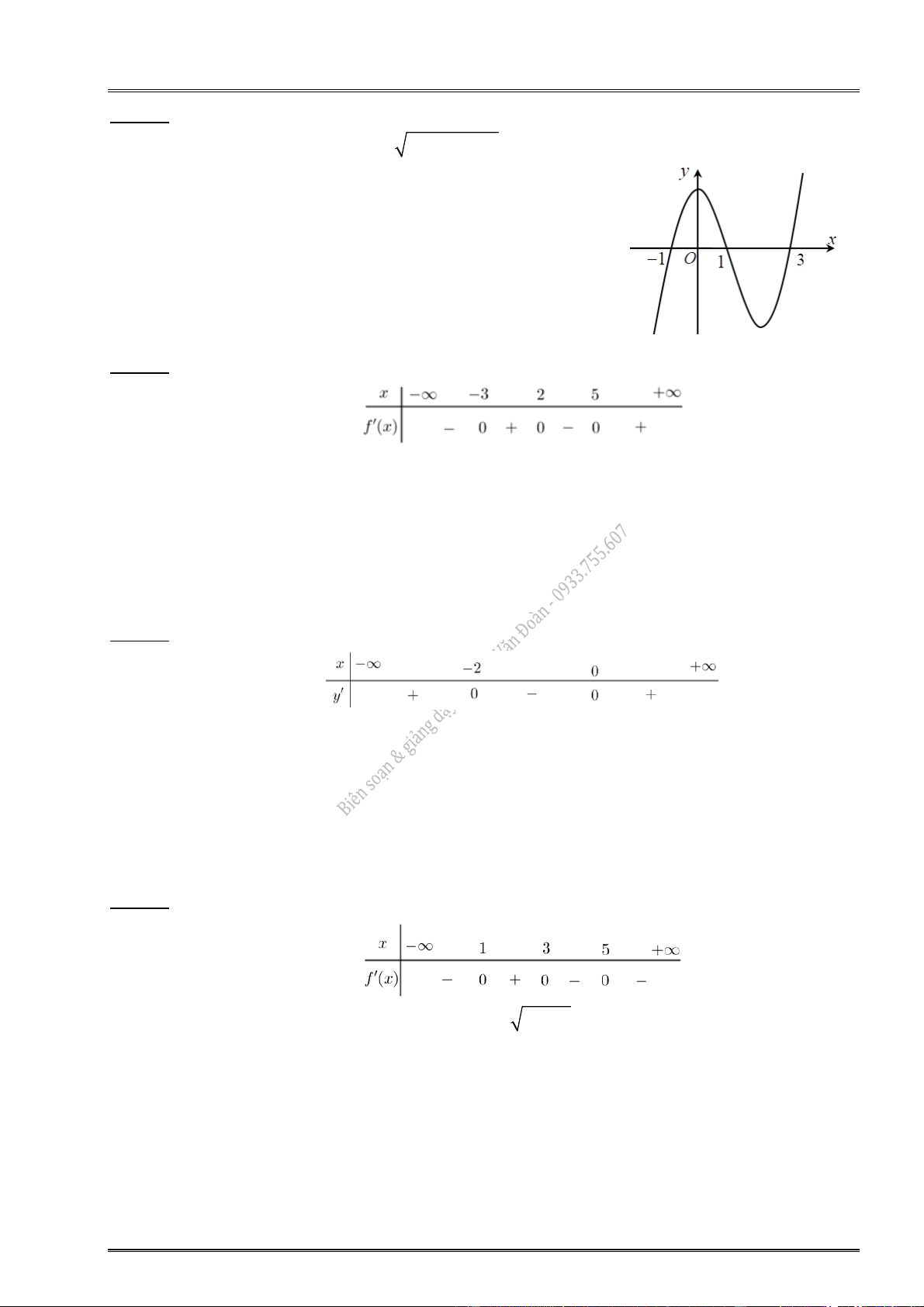
18. Cho hàm số y  f (x ) xác định và liên tục 19. Cho hàm số y  f (x ) xác định và liên tục trên ,  có 3 2 f (
 x)  x (x  2) (x  9). Hàm trên ,  có f (
 x)  (x  1)(3  x). Hàm
số y  f (x ) đạt cực tiểu tại điểm
số y  f (x ) đạt cực đại tại điểm
A. x  0.
B. x  2.
A. x  1.
B. x  2.
C. x  9.
D. x  1.
C. x  3.
D. x  0.
Lời giải. Tập xác định: D  . 
....................................................................... Ta có: 3 2 f (
 x)  x (x  2) (x  9)  0
.......................................................................  3 x 0   x  0  
.......................................................................  2 (x 2) 0      x  2 .  
.......................................................................  x 9 0    x  9  
....................................................................... Bảng xét dấu f (
 x) (mỗi ô thử 1 điểm):
....................................................................... x  0 2 9 
....................................................................... f (  x)  0  0  0 
....................................................................... f (x)
.......................................................................
Hàm số đã cho y  f (x) đạt cực tiểu tại
....................................................................... điểm x  9.
....................................................................... Chọn đáp án C.
.......................................................................
20. Cho hàm f (x) có 2 3 f (
 x)  x (x  1)(x  2) 21. Cho hàm số y  f(x) và có đạo hàm
x  . Điểm cực tiểu của hàm số f (x) là 2 3 f (
 x)  (x  1) (x  2) (2x  3), x. Số
A. x  2.
B. x  0.
điểm cực trị của hàm số y  f (x) là
C. x  1. D. x  3. A. 3. B. 2. C. 0. D. 1.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 69 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
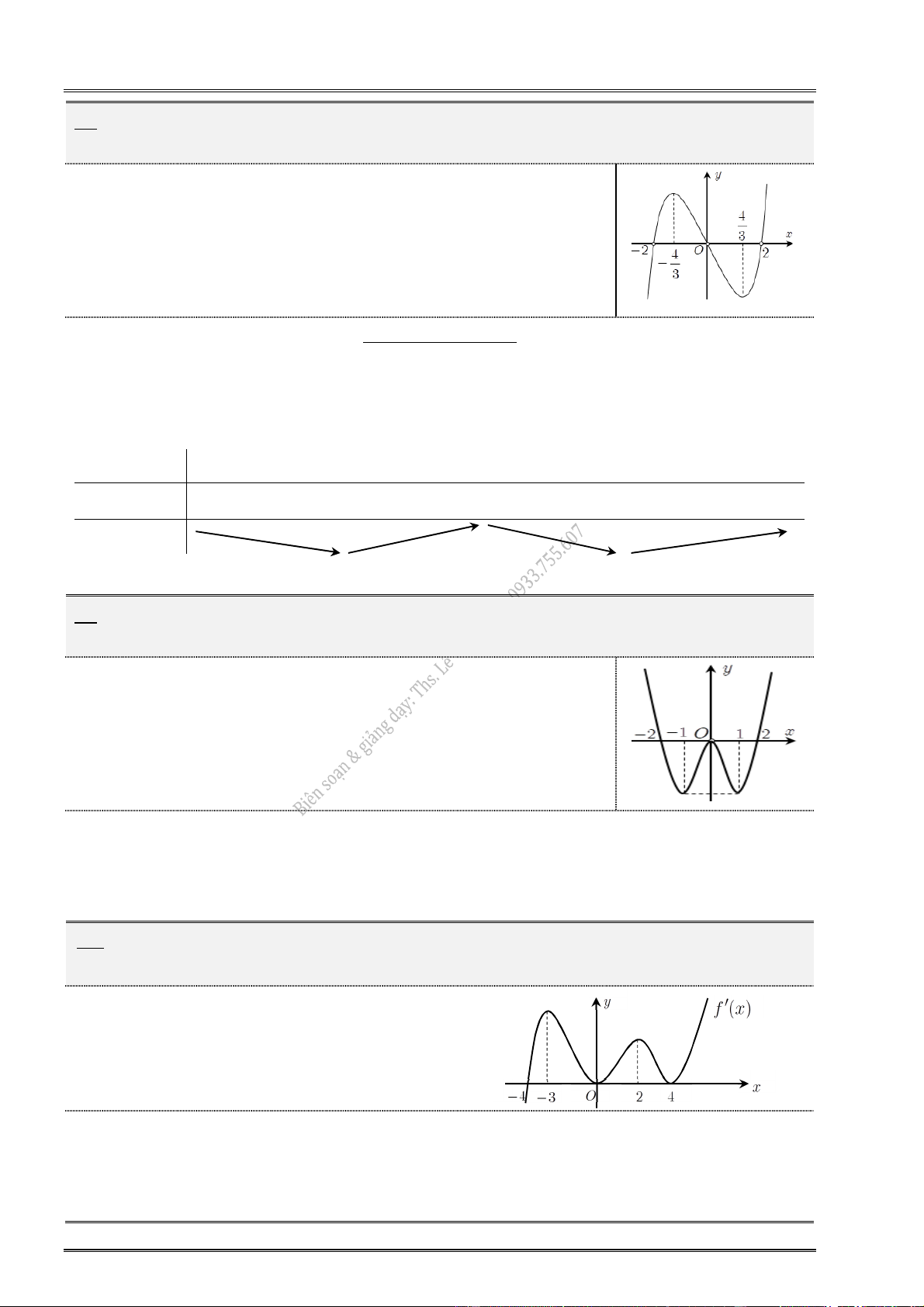
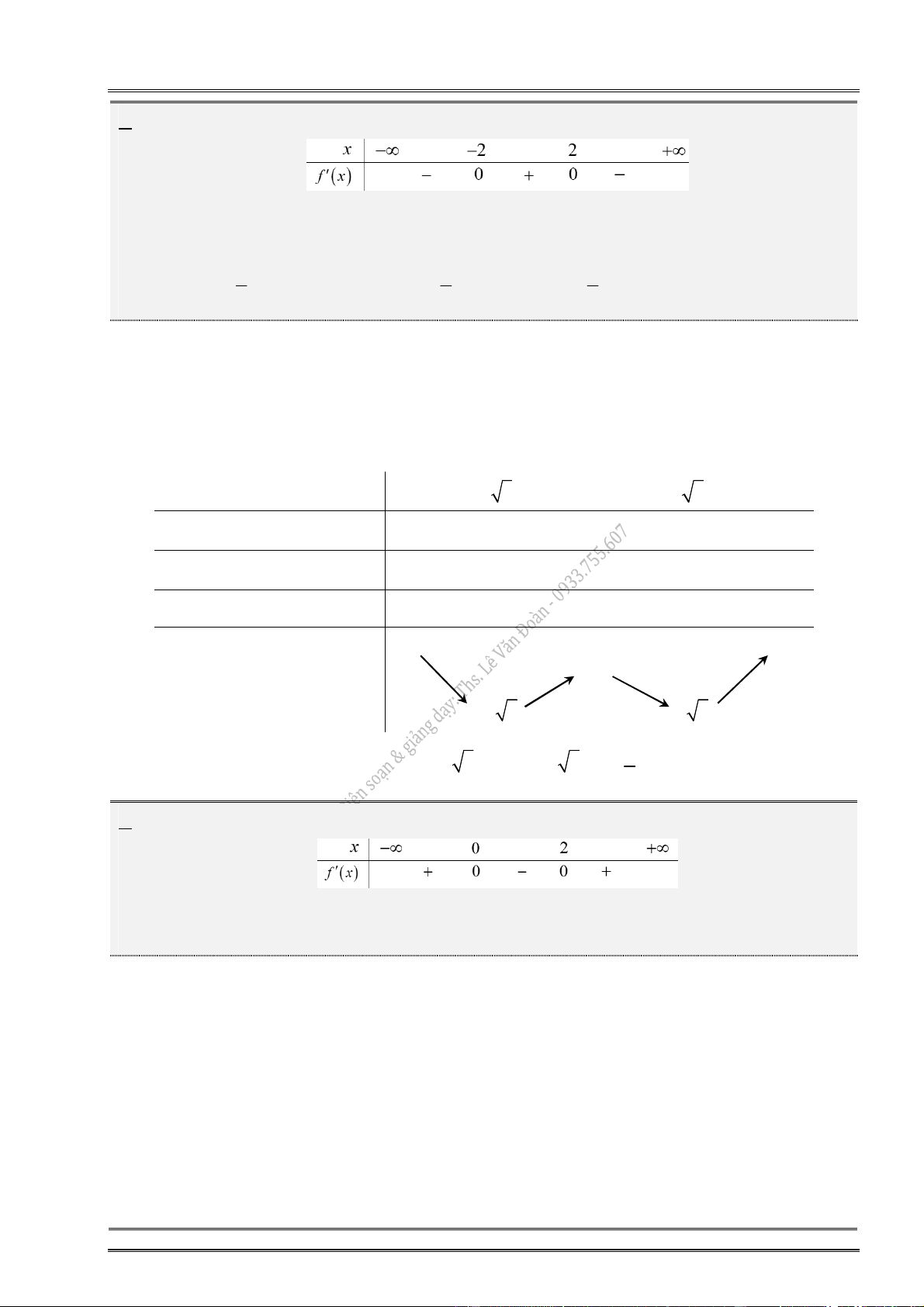
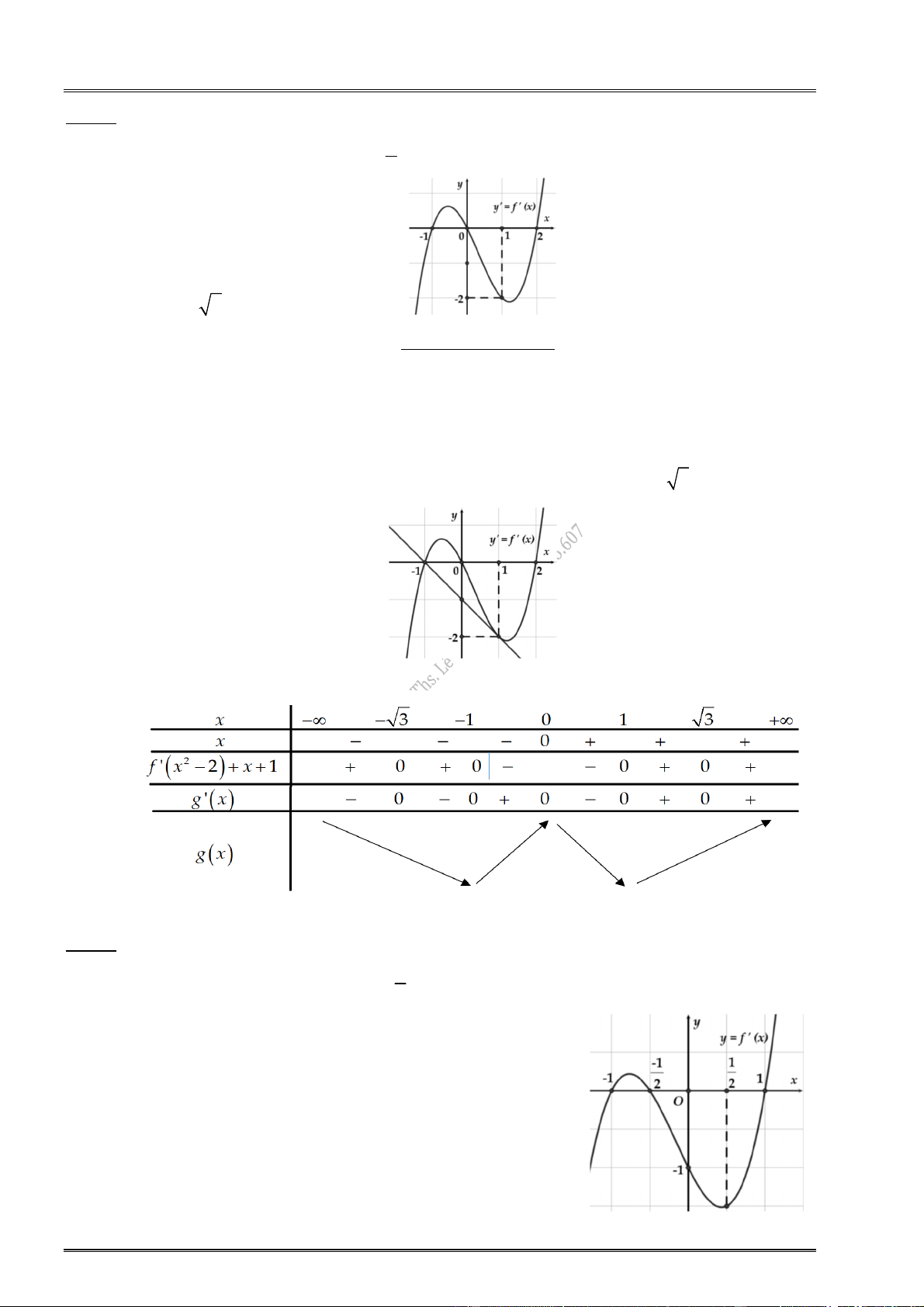
22. Cho hàm số f (x) xác định, liên tục trên  và có đồ thị hàm số y  f (x) là đường cong
như hình vẽ. Hỏi mệnh đề nào đúng ?
A. Hàm số y  f (x) đạt cực đại tại điểm x  4  /3.
B. Hàm số y  f (x) đạt cực tiểu tại điểm x  0.
C. Hàm số y  f (x) đạt cực tiểu tại điểm x  2.
D. Hàm số y  f (x) đạt cực đại tại điểm x  4/3.
Lời giải tham khảo x  2 
Đồ thị hàm số y  f (
 x) cắt trục Ox : y  0 tại x  2, x  0  f (x)  0  .  x  0  Bảng xét dấu: x  2 0 2  f (  x)  0  0  0  f (x)
Từ bảng biến thiên, suy ra hàm số y  f (x) đạt cực tiểu tại x  2. Chọn đáp án C.
23. Cho hàm số f (x) xác định, liên tục trên  và có đồ thị hàm số y  f (x) là đường cong
như hình vẽ. Hỏi mệnh đề nào đúng ?
A. Hàm số y  f (x) đạt cực tiểu tại điểm x  1.
B. Hàm số y  f (x) đạt cực tiểu tại điểm x  0.
C. Hàm số y  f (x) đạt cực đại tại điểm x  2.
D. Hàm số y  f (x) đạt cực đại tại điểm x  2.
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 2.1.
Cho hàm số f (x) có đồ thị f (
 x) của nó trên khoảng K như hình vẽ. Khi đó trên K,
hàm số y  f (x) có bao nhiêu điểm cực trị ? A. 1. B. 4. C. 3. D. 2.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 70 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
24. Đồ thị hàm số y  f (
 x) có đồ thị như hình vẽ dưới đây. Hàm số y  f (x)  3x  2019
có mấy điểm cực trị ? A. 1.
........................................................................................ B. 2.
........................................................................................ C. 3.
........................................................................................ D. 4.
........................................................................................
25. Cho hàm số f (x) xác định trên  và có đồ thị f (
 x) như hình vẽ bên dưới. Hàm số
g(x)  f (x)  x đạt cực đại tại A. x  1  .
........................................................................................
B. x  0.
........................................................................................
C. x  1.
........................................................................................
D. x  2.
........................................................................................
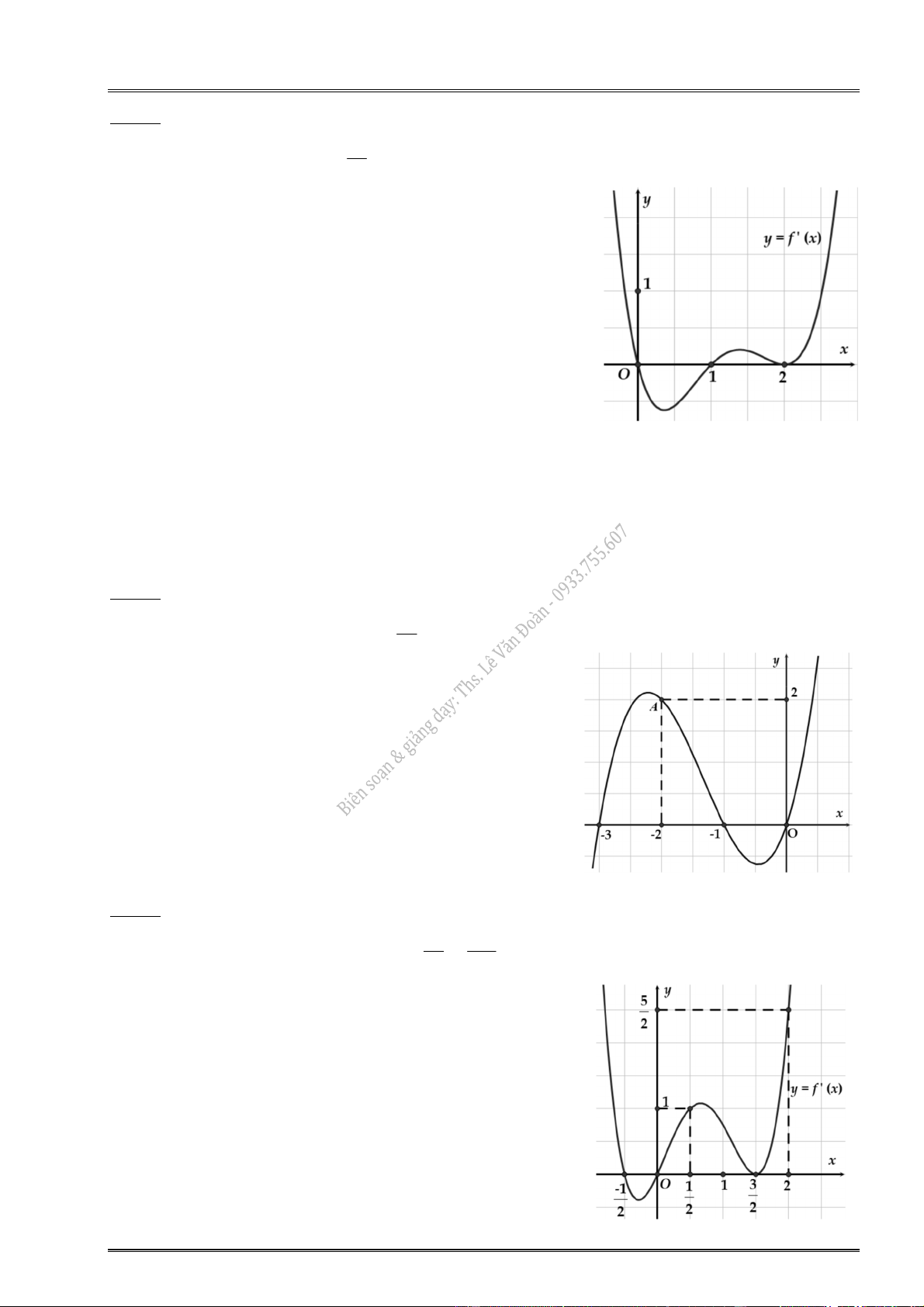
26. Cho hàm số y  f (x) xác định và liên tục trên ,
 có đồ thị của hàm đạo hàm y  f (x)
như hình vẽ. Xác định giá cực tiểu của hàm số g(x)  f (x)  x.
A. f (1)  1.
........................................................................................
B. x  1.
........................................................................................
C. f (0).
........................................................................................
D. f (2)  2.
........................................................................................ 3 x
27. Cho hàm số f (x) có đồ thị y  f (
 x) như hình. Hỏi hàm 2
g(x)  f (x) 
 x  x  2 3 đạt cực đại tại A. x  1  .
........................................................................................
B. x  0.
........................................................................................
C. x  1.
........................................................................................
D. x  2.
........................................................................................
28. Cho hàm số y  f (x) có đạo hàm, liên tục trên  và có đồ thị y  f (
 x) như hình vẽ. Xét 3 hàm số 2 4 2
g(x)  3f (x  2)  x  3x . Hàm số g(x) đạt cực đại tại điểm 2 A. x  1  .
........................................................................................
B. x  1.
........................................................................................
........................................................................................
C. x  0.
........................................................................................
D. x  2.
........................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 71 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 BÀI TẬP VỀ NHÀ 2 Câu 8.
(THPT Lê Quý Đôn – Đà Nẵng 2019) Cho hàm số y  f (x) liên tục trên ,  có đạo hàm 2 3 4 f (
 x)  x(1  x) (3  x) (x  2) . Điểm cực tiểu của hàm số y  f(x) là A. x  2. B. x  3. C. x  1. D. x  0. Câu 9.
(THPT Chuyên Lê Thánh Tông – Quảng Nam 2019) Cho hàm số y  f (x) liên tục trên  và có đạo hàm 2018 2019 f (
 x)  (x  2)(x  1) (x  2) . Khẳng định nào đúng ?
A. Hàm số y  f (x) đạt cực đại tại điểm x  1 và đạt cực tiểu tại các điểm x  2  .
B. Hàm số y  f (x) đồng biến trên mỗi khoảng (1;2) và (2; )  .
C. Hàm số y  f (x) có ba điểm cực trị.
D. Hàm số y  f (x) nghịch biến trên khoảng ( 2  ;2).
Câu 10. (THPT HOA LƯ A – Hà Nội năm 2018) Cho hàm số y  f (x) có đạo hàm trên  và
y  f  x y đồ thị hàm số
( ) trên  như hình vẽ. Mệnh đề nào đúng ?
A. Hàm số y  f (x) có 1 điểm cực đại và 1 điểm cực tiểu.
B. Hàm số y  f (x) có 2 điểm cực đại và 2 điểm cực tiểu. O x
C. Hàm số y  f (x) có 1 điểm cực đại và 2 điểm cực tiểu.
D. Hàm số y  f (x) có 2 điểm cực đại và 1 điểm cực tiểu.
Câu 11. (Sở GD & ĐT Hâu Giang 2018) Cho hàm số y  f (x) xác định và liên tục trên  và
hàm số y  f (
 x) có đồ thị như hình vẽ dưới đây. Khẳng định nào đúng ? y
A. f (x) đạt cực đại tại x  1.
y  f   x 
B. f (x) đạt cực đại tại x  0. 2 O 2 x
C. f (x) đạt cực đại tại x  1  .
D. f (x) đạt cực đại tại x  2  .
Câu 12. (THPT Chuyên Lương Văn Chánh – Phúc Yên 2018) Cho hàm số y  f (x) có đạo hàm liên tục trên .
 Đồ thị hàm số y  f (
 x) như hình vẽ. Số điểm cực trị của hàm
số y  f (x)  5x là A. 2. B. 3. C. 4. D. 1.
Câu 13. (THPT Mộ Đức – Quãng Ngãi năm 2018) Cho hàm số y  f (x) có đạo hàm trên . 
Biết hàm số y  f (
 x) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng về cực trị
của hàm số g(x)  f (x)  x.
A. Hàm số có một điểm cực đại và một điểm cực tiểu.
B. Hàm số không có điểm cực đại và một điểm cực tiểu.
C. Hàm số có một điểm cực đại và một điểm cực tiểu.
D. Hàm số có hai điểm cực đại và một điểm cực tiểu.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 72 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
29. Cho hàm số y  f (x) có đồ thị như hình vẽ. Đồ thị hàm số y  f (x) có mấy cực trị ? A. 2.
Từ đồ thị hàm số y  f (x). Hãy nên cách vẽ đồ thị hàm B. 3.
số y  f (x ) . C. 4.
 ..................................................................................... D. 5.
 .....................................................................................
30. Cho hàm số y  f (x) có đồ thị như hình vẽ bên dưới. Hỏi đồ thị hàm số y  f (x ) có bao nhiêu điểm cực trị ? A. 2.
........................................................................................ B. 3.
........................................................................................
........................................................................................ C. 4.
........................................................................................ D. 5.
........................................................................................
31. Biết đồ thị hàm số 3 2
y  x  3x . có dạng như hình vẽ. Hỏi đồ thị hàm số 3 2
y  x  3x
có bao nhiêu điểm cực trị ? A. 2.
........................................................................................ B. 3.
........................................................................................ C. 4.
........................................................................................ D. 5.
........................................................................................
32. (Đề thi THPT Quốc Gia năm 2017 – Mã đề 102 câu 42) Cho hàm số y  f (x) có bảng biến thiên như sau:
Đồ thị hàm số y  f (x) có bao nhiêu điểm cực trị ? A. 2.
............................................................................................................................................... B. 3.
............................................................................................................................................... C. 4.
............................................................................................................................................... D. 5.
............................................................................................................................................... 33. Cho hàm số  4  2 y x ax b với ,
a b là hai số thực dương. Hỏi đồ thị hàm số đã cho có
bao nhiêu điểm cực trị ? A. 3.
.......................................................................................................................................... B. 7.
......................................................................................................................................... C. 6.
......................................................................................................................................... D. 5.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 73 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
34. Cho hàm số y  f (x) có đồ thị như hình vẽ. Đồ thị hàm số y  f ( x ) có mấy cực trị ? A. 2.
Từ đồ thị hàm số y  f (x). Hãy nên cách vẽ đồ thị hàm y  f x B. 3. số ( ). C. 4.
 .....................................................................................  D. 5.
..................................................................................... 3 35. Cho hàm số 3 2 y  x
  3x  3x  1 có đồ thị như hình. Đồ thị 2
y   x  3x  3 x  1
có bao nhiêu điểm cực trị ? A. 1.
........................................................................................ B. 2.
........................................................................................ C. 3.
........................................................................................ D. 4. 5 36. Cho hàm số 5 2
y  x  3x  2x  2 có đồ thị bên. Đồ thị 2
y  x  3x  2 x  2 có bao nhiêu điểm cực trị ? A. 5.
........................................................................................ B. 2.
........................................................................................ C. 3.
........................................................................................ D. 4.
37. (THPT Chuyên Đại Học Vinh 2019) Cho hàm số y  f (x) có bảng biến thiên như sau:
Đồ thị hàm số y  f ( x ) có bao nhiêu điểm cực trị ? A. 2.
............................................................................................................................................... B. 3.
............................................................................................................................................... C. 4.
............................................................................................................................................... D. 1.
...............................................................................................................................................
38. Cho hàm số y  f (x) có đạo hàm 4 5 3 f (
 x)  (x  1) (x  2) (x  3) , x  .  Số điểm cực
trị của hàm số y  f  x  là A. 2.
............................................................................................................................................... B. 3.
............................................................................................................................................... C. 5.
............................................................................................................................................... D. 1.
...............................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 74 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 BÀI TẬP VỀ NHÀ 3
Câu 14. (THPT Hoa Lư A – Ninh Bình năm 2018) Cho hàm số y  f (x) liên tục trên  và có
đồ thị như hình vẽ. Hỏi đồ thị hàm số y  f (x) có tất cả bao nhiêu điểm cực trị ? y A. 5. B. 3. C. 2. O x D. 4.
Câu 15. (Sở GD & ĐT Đồng Tháp 2019) Cho đồ thị hàm số 4 2
f (x)  ax bx  c như hình vẽ. Hàm số 4 2
y  ax  bx  c có bao nhiêu cực trị ? y A. 3. 1 B. 5. O x C. 6.  3 D. 7.
Câu 16. (Sở GD & ĐT Trà Vinh 2019) Cho hàm số 3 2
f (x)  ax bx  cx  d có bảng biến
thiên bên dưới. Hàm số y  f (x) có mấy cực trị ? A. 5. B. 3. C. 2. D. 4.
Câu 17. (Sở GD & ĐT Bình Dương 2018) Cho hàm số 3 2
y  x  6x  9x có bảng biến thiên 3 dưới. Hàm số 2
y  x  6x  9 x có mấy cực trị ? A. 3. B. 5. C. 6. D. 7.
Câu 18. (Sở GD & ĐT Phú Thọ năm 2017) Cho bảng biến thiên của hàm số 3
y  x  3x bên 3
dưới. Hàm số y  x  3 x có mấy điểm cực trị ? A. 5. B. 3. C. 2. D. 4.
Câu 19. (Sở GD & ĐT Đồng Nai năm 2018) Cho đồ thị hàm số 2
y  (x  2)(x  1) như hình vẽ. Đồ thị hàm số 2
y  x  2 (x  1) có mấy điểm cực trị ? y A. 5. B. 3. C. 2. O x D. 1.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 75 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 39. Gọi ,
A B lần lượt là hai điểm cực tiểu của 40. Gọi ,
A B lần lượt là hai điểm cực đại của đồ thị hàm số 4 2
y  x  2x  3 và C là đồ thị hàm số 4 2 y  x 
 8x  2 và C
điểm cực đại. Tính độ dài AB và diện tích
là điểm cực tiểu. Tính độ dài AB và diện
tam giác OAB với O là gốc tọa độ. Tìm tọa
tích tam giác OAB với O là gốc tọa độ.
độ trọng tâm G của tam giác ABC.
Tìm tọa độ trọng tâm G của A  BC.
Lời giải. Tập xác định D  . 
...................................................................... x   0  y  3 
...................................................................... Có 3
y  4x  4x  0  . x   1   y  2 
...................................................................... x  1  0 1 
...................................................................... y  0  0  0 
......................................................................  3 
...................................................................... y
...................................................................... 2 2
......................................................................
Hai điểm cực tiểu của đồ thị hàm số là
...................................................................... ( A 1
 ;2), B(1;2) và điểm cực đại là C(0;3).
...................................................................... 2 2
 AB  (x  x )  (y  y )  2. B A B A 
...................................................................... Tính diện tích O  AB với ( O 0;0) :  O 
......................................................................  A  ( 1  ;2) 1   S  1  .21.2  2. O 
......................................................................  B  (1;2) O  AB 2  41. Gọi ,
A B lần lượt là điểm cực đại và
 Tọa độ trọng tâm G của tam giác ABC : 
điểm cực tiểu của đồ thị hàm số
x  x  x  A B C x    0 3 2
y  x  3x  4. Tìm tọa độ trọng tâm G  7  3 
 G 0;  
y  y  y G O  AB AB 7  3 và diện tích của . Tính .  A B C y    G  3 3
...................................................................... Cần nhớ: 
......................................................................
 AB  (x  x ;y  y ). B A B A
...................................................................... 2 2
 AB  (x  x )  (y  y ) . B A B A
......................................................................  x x  A B x  
......................................................................  I   I là trung điểm 2 AB  .  y y
......................................................................  A B y   I  2
......................................................................  x x  x  
...................................................................... A B C x    G   G là trọng tâm 3 A  BC 
...................................................................... y y  y   A B C y   G  3
......................................................................
 Diện tích tam giác A  BC :
......................................................................  A
 B ( ;a ) b 1 
...................................................................... Tính  S  ad b  c . A
 C ( ;cd) A  BC 2 
......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 76 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
42. Biết M(0;2) và N(2; 2
 ) là các điểm cực trị 43. Đồ thị hàm số 3 2
y  2x  bx  cx  1 có của đồ thị hàm số 3 2
y  ax  bx  cx  d. M(1; 6
 ) là một điểm cực trị. Tìm tọa độ
Tính giá trị của hàm số tại x  2  .
điểm cực trị còn lại của đồ thị hàm số đó. Lời giải. Ta có: 2
y   3ax  2bx  c.
.......................................................................
 Do điểm M(0;2) là cực trị
....................................................................... y  (0)  0   
....................................................................... 3 2 M
 (0;2)  y  ax  bx  cx  d 
....................................................................... c   0 
.......................................................................   (1) d   2 
.......................................................................  Do điểm N(2; 2  ) là cực trị
....................................................................... y  (2)  0 
.......................................................................   3 2 N
 (2;2)  y  ax bx  cx  d 
....................................................................... 12
 a  4b  c  0 
.......................................................................   (2)
8a  4b  2c  d  2 
.......................................................................
Từ (1), (2)  a  1;b  3
 ;c  0;d  2.
....................................................................... Do đó: 3 2
y  x  3x  2  y(2)  18.
....................................................................... Cần nhớ:
.......................................................................
Nếu M (x ;y ) là cực trị của đồ thị hàm số  
....................................................................... y  (x )  0
y  f (x) 
.......................................................................     M
 (x ;y )  y  f (x)   
.......................................................................
Nếu là điểm cực đại, bổ sung y  (  x )  0. o
.......................................................................
Nếu là điểm cực tiểu, bổ sung y  (  x )  0. o
.......................................................................  7   44. Biết A 1  ; , B(2;3) 
y  ax  bx  cx  d y 
là các điểm cực trị của đồ thị 3 2 . Tìm (3).  2
............................................................................................................................................................
............................................................................................................................................................
............................................................................................................................................................
............................................................................................................................................................
............................................................................................................................................................
............................................................................................................................................................
............................................................................................................................................................
............................................................................................................................................................
............................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 77 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 BÀI TẬP VỀ NHÀ 4
Câu 20. (THPT Chuyên Vĩnh Phúc năm 2018) Gọi ,
A B là hai điểm cực trị của đồ thị hàm số 1 2 3
y   x  x   Tọa độ trung điểm của AB là 3 3  2    1 2   A. 0; .    ; .  B.  3  3 3 C. (0;1). D. (1;0).
Câu 21. (THPT Hậu Lộc 2 – Thanh Hóa 2018) Cho hàm số 3 2
y  x  3x  2 có đồ thị là (C ). Gọi ,
A B là các điểm cực trị của (C ). Độ dài đoạn thẳng AB bằng A. 2 5. B. 5. C. 4. D. 5 2.
Câu 22. (THPT Quãng Xương – Thanh Hóa 2018) Đồ thị hàm số 3
y  x  3x  2 có hai điểm cực trị ,
A B. Diện tích tam giác OAB với (
O 0;0) là gốc tọa độ bằng 1 A. 2. B. . 2 C. 1. D. 3.
Câu 23. (THPT Hoa Lư A – Ninh Bình năm 2018) Gọi A và B là các điểm cực tiểu của đồ thị hàm số 4 2
y  x  2x  1. Diện tích của tam giác OAB (O là gốc tọa độ) bằng A. 2. B. 4. C. 1. D. 3.
Câu 24. (THPT Thạch Thành – Thanh Hóa 2018) Đồ thị hàm số 4 2
y  x  ax  b có điểm cực
tiểu là M(1; 4). Giá trị của 2a  b bằng A. 1  . B. 1. C. 0. D. 2.
Câu 25. (THPT Kim Liên – Hà Nội 2018) Cho hàm số 3 2
y  x  2x  ax  b có đồ thị (C ).
Biết đồ thị (C ) có điểm cực trị là (
A 1; 3). Giá trị của 4a b bằng A. 3. B. 2. C. 4. D. 1.
Câu 26. (Sở GD & GD Thanh Hóa năm 2018) Đồ thị hàm số 3 2
y  x  ax  bx  c đi qua điểm (
A 1;0) và có điểm cực trị M(2;0). Giá trị của biểu thức 2 2 2
a b  c bằng A. 25. B. 1  . C. 7. D. 14.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 78 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Daïng toaùn 2. Tìm tham soá m ñeå haøm soá ñaït cöïc trò taïi ñieåm x = xo cho tröôùc.
Phöông trình ñöôøng thaúng noái hai ñieåm cöïc trò 
 Bài toán. Tìm tham số để hàm số y  f (x) đạt cực trị tại điểm x  x ?   Phương pháp:
 Bước 1. Tìm tập xác định D. Tính đạo hàm y .
 Bước 2. Dựa vào nội dung định lí 1:
Nếu hàm số y  f (x) có đạo hàm trên khoảng (a;b) và đạt cực đại (hoặc cực
tiểu) tại x thì f (  x )  0.  
 Bước 3. Với m vừa tìm, thế vào hàm số và thử lại (dựa vào định lí 2 và 3).  Lưu ý:
 Đối với hàm số bậc ba nên thử lại bằng nội dung định lý 3 (phù hợp trắc nghiệm).
Giả sử y  f (x ) có đạo hàm cấp 2 trong khoảng ( ; a b). Nếu y (
 x )  0, y (x )  0 thì x là điểm cực tiểu.    Nếu y (
 x )  0, y (x )  0 thì x là điểm cực đại. o o 
 Đối với các hàm khác chẳng hạn như bậc bốn trùng phương (thiếu b), hoặc hàm
phân thức,… nên thử lại bằng định lí 2 (tính y và xét dấu, lập bảng biến thiên). 1 3 x 1. Cho hàm 3 2 2
y  x  mx  (m  4)x  3. 2. Cho hàm 2 2 y 
 mx  (m  m  1)x. 3 3
Tìm m để hàm số đạt cực đại tại x  3.
Tìm m để hàm số đạt cực đại tại x  1.
A. m  1.
B. m  5.
A. m  2.
B. m  3.
C. m  {1;5}.
D. m  3. C. m  1  .
D. m  0.  2 2 y
   x  2mx  m  4 
....................................................................... Lời giải. Có  . y
   2x  2m 
....................................................................... y  (3)  0 
.......................................................................
Vì x  3 là cực đại   y   (3)  0 
.......................................................................  m    1  2
....................................................................... m  6m  5  0       m   5  m  5. 6  2m  0 
.......................................................................  m   3 
....................................................................... Cần nhớ: Hàm 3 2
y  ax  bx  cx  d
....................................................................... y  (x )  0  
.......................................................................
x  x là cực đại    .  y   (x )  0  
....................................................................... y  (x )  0
.......................................................................  
x  x là cực tiểu    .  y   (x )  0  
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 79 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 1 4. Cho hàm số 4 2 2
y  x  2(m  1)x  m . 3. Cho 3 2 2
y  x  mx  (m  4)x  3. Tìm 3
Tìm điều kiện của tham số m để hàm số
m để hàm số đạt cực tiểu tại x  3.
đạt cực tiểu tại điểm x  0. A. m  1  .
B. m  5.
A. m  1. B. m  1  .
C. m  1.
D. m  7. C. m  1  . D. m  \  ( 1  ;1).
....................................................................... x  0 3 y 4x 4(m 1)x 0        . 
....................................................................... 2 x  m  1 
.......................................................................
 m  1  0  m  1. Khi đó:
....................................................................... x  0 
....................................................................... y  0 
....................................................................... y
.......................................................................
HS đạt cực tiểu tại x  0 nên nhận m  1  .
.......................................................................
 m  1  0  m  1 và có bảng xét dấu:
.......................................................................
.............................................................................
.......................................................................
.............................................................................
.......................................................................
.............................................................................
.......................................................................
 m  1  0  m  1 và có bảng xét dấu
.......................................................................
.............................................................................
.......................................................................
.............................................................................
.......................................................................
............................................................................. 5. Hàm số 4 2 y  x 
 2mx  1 đạt cực tiểu 6. Hàm số 4 2 4
y  x  2mx  m  2m  5
tại điểm x  0 khi
đạt cực tiểu tại điểm x  1 khi
A. m  0. B. 1
  m  0. A. m  1  . B. m  1  .
C. m  1.
D. m  0.
C. m  1.
D. m  1.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 80 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 7. Cho hàm số 3 2
y  x  3x  9x  1. Viết 8. Biết đồ thị hàm số 3
y  x  3x  1 có hai
phương trình đường thẳng nối hai điểm điểm cực trị ,
A B. Khi đó phương trình
cực trị của đồ thị hàm số đã cho.
đường thẳng AB là
A. y  8x  2. B. y  8  x  2.
A. y  x   2.
B. y  x  2.
C. y  8x  2.
D. x  3y  1  0. C. y  2
 x  1. D. y  2x 1.
Lời giải 1. Phương trình đường thẳng nối hai
.......................................................................
điểm cực trị của đồ thị hàm số bậc ba là đường thẳng y  x
   với x
   là phần dư bậc
.......................................................................
nhất trong phép chia y cho y .
....................................................................... Chia đa thức:
....................................................................... 3 2 2
x  3x  9x  1 3x  6x  9
.......................................................................  1 1 3 2
x  2x  3x x 
....................................................................... 3 3 2
 x  6x  1
.......................................................................  2
 x  2x  3
....................................................................... 8x  2
.......................................................................
Phương trình đường thẳng nối hai điểm
....................................................................... cực trị là y  8
 x  2. Chọn đáp án B.
.......................................................................
Cách 2. Sử dụng casio bấm MODE 2 và
....................................................................... y .y CALC x  i y 
  i
 y  x   .  m  100 3y
....................................................................... 9. Cho hàm số 3 2
y  x  3x  2. Đường 10. Cho hàm số 3 2 y  x
  3x  1. Viết
thẳng đi qua hai điểm cực trị của đồ thị
phương trình đường thẳng nối hai điểm
hàm số đã cho có phương trình là
cực trị của đồ thị hàm số đã cho.
A. y  x  4.
B. y  2x  2.
A. y  7  0.
B. y  2x  1.
C. y  x   1. D. y  2  x  2.
C. y  2x  1.
D. y  7x  1.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 81 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
11. Tìm m để đường thẳng nối điểm cực đại 12. Tìm m để đường thẳng nối điểm cực đại
với điểm cực tiểu của đồ thị hàm số
với điểm cực tiểu của đồ thị hàm số  3 y
x  x  m M  3 2
y  x  3x  mx  2 M đi qua điểm (3; 1). qua (0;1).
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
13. Tìm giá trị của tham số m để đường thẳng 14. Tìm m để đường thẳng d : y  x  2
d : y  (2m 1)x  3  m vuông góc với
vuông góc với đường thẳng đi qua hai
đường thẳng đi qua hai điểm cực trị của đồ
điểm cực trị của đồ thị hàm số thị hàm số 3 2
y  x  3x  1. 3 2
y  2x  3(m  1)x  6mx. Lời giải.
.......................................................................
Sử dụng casio, tìm được đường thẳng nối
.......................................................................
hai điểm cực trị là d : y  2  x  1.
.......................................................................
Vì d  d   a .a  1 1 2
....................................................................... 3  (2m 1).( 2
 )  1  m   4
.......................................................................
Cần nhớ: Cho hai đường thẳng d và d có
....................................................................... 1 2
dạng d : y  a x  b và d : y  a x  b thì
....................................................................... 1 1 1 2 2 2 a   a 
....................................................................... 1 2 d  d  
và d  d  a a  1. 1 2 b   b  1 2 1 2 1 2 
.......................................................................
15. Tìm giá trị thực của tham số m sao cho 16. Tìm giá trị thực của tham số m để đường
đường thẳng đi qua hai điểm cực trị của đồ
thẳng đi qua hai điểm cực trị của đồ thị thị hàm số 3 2
y  x  3x  mx  2 song hàm số 3 2
y  x  3x  mx  2 vuông góc
song với đường thẳng d : y  4  x  3.
với đường thẳng d : 4x  y  3  0.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 82 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 BÀI TẬP VỀ NHÀ 5
Câu 27. (Đề thi THPT Quốc Gia năm 2017 – Mã đề 102 câu 32) Tìm giá trị thực của tham số m 1 để hàm số 3 2 2 y 
x  mx  (m  4)x  3 đạt cực đại tại x  3. 3
A. m  1. B. m  1  .
C. m  5.
D. m  7.
Câu 28. (THPT Ngô Sĩ Liên – Bắc Giang năm 2018) Biết rằng hàm số 3 2
y  x  2x  mx  3
đạt cực tiểu tại x  1. Giá trị của m bằng A. 4. B. 3. C. 2. D. 1.
Câu 29. (THPT Chuyên Lê Quý Đôn Đà Nẵng năm 2018) Tìm tham số thực m để hàm số 3 2 2
y  x  3mx  3(m  1)x đạt cực đại tại điểm x  1. o
A. m  0, m  2. B. m  2. C. m  0.
D. m  0, m  2.
Câu 30. (THPT Kiến An – Hải Phòng năm 2018) Tìm tất cả các giá trị thực của tham số m để hàm số 3 2 2
y  mx  x  (m  6)x  1 đạt cực tiểu tại x  1. A. m  1. B. m  4  . C. m  2  . D. m  2.
Câu 31. (THPT Việt Trì – Phú Thọ 2018) Hàm số 3 2 2
y  x  3(m  1)x  3(m  1) x. Hàm số
đạt cực trị tại điểm có hoành độ x  1 khi A. m  1.
B. m  0, m  4. C. m  4.
D. m  0, m  1.
Câu 32. (THPT Chuyên Biên Hòa – Hà Nam 2018) Hàm số 3 2
y  x  2ax  4bx  2019 đạt cực trị tại x  1
 . Khi đó hiệu a b bằng 4 A. 1  . B.  3 3 3 C.  D.   4 4
Câu 33. (Sở GD & ĐT Hà Nội 2018) Tìm tất cả các giá trị thực của tham số m để hàm số 4 2
y  x  mx đạt cực tiểu tại x  0. A. m  0. B. m  0. C. m  0. D. m  0.
Câu 34. (THPT Quảng Xương I – Thanh Hóa 2017) Tìm tất cả các giá trị của tham số m để 1 hàm số 4
y  (m  1)x đạt cực đại tại x  0. 4 A. m  1. B. m  1. C. Không có . m
D. m  1.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 83 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 35. (THPT Ngô Sĩ Liên – Bắc Giang năm 2018) Phương trình đưdờng thẳng đi qua hai
điểm cực trị của đồ thị hàm số 3 2
y  x  3x  5x  1 là 16 8 16 8 A. y  
x   B. y  x   3 3 3 3 1 8 1 8
C. y   x 
 D. y  x   3 3 3 3
Câu 36. (THPT Trần Phú – Tp. Hồ Chí Minh năm 2017) Tìm giá trị thực của tham số m sao
cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y  x  3x  mx  2
song song với đường thẳng d : 4x  y  3  0.
A. m  1.
B. m  2.
C. m  3.
D. m  4.
Câu 37. (THPT Lương Văn Chánh Phú Yên 2018) Biết đường thẳng d : y  (3m  1)x  3
vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y  x  3x  1. Giá trị của m bằng 1 1 A.  B.   6 3 1 1 C.  D.   3 6
Câu 38. (Tạp Chí Toán Học & Tuổi Trẻ năm 2018) Cho hàm số 3 2 y  x
  3x  4. Biết có hai
giá trị m , m của tham số m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm 1 2
số tiếp xúc với đường tròn 2 2
(C ) : (x  m)  (y  m  1)  5. Tổng m  m bằng 1 2 A. 0. B. 10. C. 6. D. 6  . 2 3x  x  5
Câu 39. (Toán Học Bắc Trung Nam) Đồ thị hàm số y  có hai điểm cực trị , A B x  2
nằm trên đường thẳng d có phương trình d : y  ax  .
b Giá trị của a  b bằng A. 1  . B. 1. C. 3. D. 5. 2
mx  2x  m  1
Câu 40. (THPT Chuyên KHTN Hà Nội năm 2017) Cho hàm số y   Tìm 2x  1
tham số m để đường thẳng nối hai điểm cực trị của đồ thị hàm số này vuông góc với
đường phân giác của góc phần tư thứ nhất trong mặt phẳng tọa độ. 1
A. m    2
B. m  1. C. m  1  . 1 D. m   2
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 84 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Daïng toaùn 3. Bieän luaän hoaønh ñoä cöïc trò (Vaän duïng & vaän duïng cao)   Cần nhớ:
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 85 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 1. Cho hàm số 3 2 2
y  x  3mx  3mx  m . 2. Cho hàm 3 2
y  (1  m)x  3x  3x  5.
Tìm m để hàm số có 2 điểm cực trị ?
Tìm m để hàm số có 2 điểm cực trị ?
Lời giải. Tập xác định D  .
.......................................................................
Hàm số đã cho có 2 điểm cực trị 
....................................................................... 2
y  3x  6mx  3m  0 có hai nghiệm
....................................................................... phân biệt.
....................................................................... a   3  0 L ( )    Đ m  0     . 2  ( 6m) 36m 0  
.......................................................................       m 1  
.......................................................................
 Cần nhớ. Hàm số có n cực trị  y  0 có n
....................................................................... nghiệm phân biệt. PT 2
ax  bx  c  0 a   0 
.......................................................................
có hai nghiệm phân biệt   .   0  3. Cho 3 2 y  x
  (2m  1)x  (2  m)x  1. 4. Cho 3 2
y  2x (m  2)x  (6  3m)x  1.
Tìm m để hàm số có 2 điểm cực trị ?
Tìm m để hàm số có 2 điểm cực trị ?
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
....................................................................... 1 1 5. Cho hàm số 3 2 2 y 
x  mx  4x  m . 6. Cho 3 2
y   x  mx  (3m  2)x  1. 3 3
Tìm m để hàm số không có cực trị ?
Tìm m để hàm số không có cực trị ?
Lời giải. Tập xác định D  .
.......................................................................
Hàm số không có cực trị
....................................................................... 2
 y  x  2mx  4  0 vô nghiệm hoặc
....................................................................... có nghiệm kép
....................................................................... a   1  0 L ( )  Đ
.......................................................................   2 
  (2m)  16  0 
....................................................................... 2
 4m 16  0  2   m  2.
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 86 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 7. Cho 3 2
y  (m  1)x  (m  1)x  x. Tìm 8. Cho hàm số 3 2
y  mx  3mx  3x  1.
m để hàm số có 2 điểm cực trị, đồng thời
Tìm m để hàm số có 2 điểm cực trị và
điểm cực đại nằm bên trái điểm cực tiểu.
điểm cực đại nằm bên trái điểm cực tiểu.
Lời giải. Tập xác định D  .
.......................................................................
Hàm số có 2 điểm cực trị, đồng thời điểm
.......................................................................
cực đại nằm bên trái điểm cực tiểu
....................................................................... 2
 y  3(m  1)x  2(m  1)x  1  0 có
.......................................................................
2 nghiệm phân biệt thỏa mãn a  0
....................................................................... a   m 1  0   
....................................................................... 2 
  [2(m  1)]  12(m  1)  0 
....................................................................... m   1 
.......................................................................   2 
4m  20m  16  0 
....................................................................... m   1
.......................................................................     1  m  4. 1   m  4 
....................................................................... 
.......................................................................  Cần nhớ:
....................................................................... a   0   a   0   N :    И :     0
.......................................................................    0 y   y 
....................................................................... 9. Cho hàm 3 2
y  (m  2)x  3x  mx  5. 10. Cho 3 2
y  (m  6)x  mx  x  1. Tìm
Tìm m để hàm số có 2 điểm cực trị và
m để hàm số có 2 điểm cực trị và điểm
điểm cực tiểu nằm bên trái điểm cực đại.
cực đại nằm bên trái điểm cực tiểu.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 87 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 1 1 11. Cho 3 2 y 
mx  (m  1)x  mx  7. Tìm 12. Cho 3 2
y  (m  1)x  (m  1)x  x  1. 3 3
m để hàm số có 2 điểm cực trị và điểm cực
Tìm m để hàm số có 2 điểm cực trị và
tiểu nằm bên trái điểm cực đại.
điểm cực tiểu nằm bên trái điểm cực đại.
.......................................................................
......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
....................................................................... 13. Cho hàm số 4 2
y  x  (m  1)x  4. Tìm 14. Cho hàm số 4 2
y  mx  (m  2)x  1.
m để hàm số có ba điểm cực trị ?
Tìm m để hàm số có ba điểm cực trị ? Lời giải. Ta có: 3
y  4x  2(m  1)x.
....................................................................... x  0 
....................................................................... Xét y  0   . m   1 2 x 
.......................................................................  2
.......................................................................
H/số có 3 cực trị  y  0 có 3 nghiệm
....................................................................... m   1 phân biệt   0  m  1. 2
.......................................................................  Cần nhớ:
....................................................................... a   0   a   0 
.......................................................................  M :    W :   b   0     b 0 
....................................................................... a  b  0   a  b  0    :     :  
....................................................................... a   0     a 0 
....................................................................... 15. Cho hàm số 4 2
y  mx  2(m  1)x  2. 16. Cho hàm số 4 2 2
y  mx  (m  9)x  1.
Tìm m để hàm số có 2 điểm cực tiểu và 1
Tìm m để hàm số có 2 điểm cực đại và 1 điểm cực đại ? điểm cực tiểu ?
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 88 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 BÀI TẬP VỀ NHÀ 6
Câu 41. (THPT Chuyên Hạ Long – Quảng Ninh năm 2018) Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y  x  3x  (m  1)x  2 có hai điểm cực trị. A. m  2. B. m  2. C. m  2. D. m  4.
Câu 42. (THPT Hồng Quang – Hải Dương năm 2018) Tìm tất cả tham số thực của m để hàm 1 1 số 3 2
y  (m  2)x  x  mx  2 có cực đại, cực tiểu. 3 3 A. m  ( 3  ; 2  )  ( 2  ;1). B. m  ( 3  ;1). C. m  ( ;  3  ) (1; )  . D. m  ( 2  ;1).
Câu 43. (THPT Chuyên Lê Hồng Phong – Nam Định năm 2018) Tìm tham số m để hàm số 1 3 2 y 
x  mx  (m  2)x  2018 không có cực trị. 3 A. m  1.
B. m  1 hoặc m  2. C. m  2.
D. 1  m  2.
Câu 44. (THPT Nguyễn Thị Minh Khai – Tp. Hồ Chí Minh năm 2017) Có bao nhiêu giá trị
nguyên của tham số thực m để hàm số 3 2
y  (m  2)x  3x  mx  5 có điểm cực
đại nằm bên trái điểm cực tiểu. A. 2. B. 3. C. Vô số. D. 0.
Câu 45. (THPT Chuyên Nguyễn Thượng Hiền – Tp. Hồ Chí Minh năm 2017) Cho hàm số 1 3 2
y  mx  (m  1)x  mx  7. Tìm tất cả các giá trị thực của tham số m sao cho 3
đồ thị hàm số đã cho có điểm cực tiểu nằm bên trái điểm cực đại. A. m  0.
B. m  5 và m  0. 1 1
C.   m  0.
D. m   hoặc m  0. 2 2
Câu 46. (Sở GD & ĐT Vĩnh Phúc năm 2018) Tìm tất cả các giá trị của tham số m để hàm số 4 2
y  x  3mx  2 có ba điểm cực trị. A. m  0. B. m  0. C. m  0. D. m  0.
Câu 47. (Sở GD & ĐT Kiên Giang năm 2018) Tìm điều kiện của tham số thực m để hàm số 4 2
y  x  2(m  1)x  3 có ba cực trị. A. m  0. B. m  1. C. m  1. D. m  0.
Câu 48. (THPT Ngô Quyền – Hải Phòng năm 2017) Có bao nhiêu số nguyên của m để hàm số 4 2 2
y  mx  2(m  5)x  4 có đúng 2 điểm cực tiểu và 1 điểm cực đại ? A. 2. B. 4. C. 5. D. 3.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 89 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 17. Cho hàm số 3 2 2
y  x  4x  (1  m )x  1. 18. Cho 3 2 2 y  x
  x  (m  3m)x  4.
Tìm m để đồ thị hàm số đã cho có 2 điểm
Tìm m để để đồ thị hàm số đã cho có 2
cực trị nằm hai bên so với trục tung Oy.
điểm cực trị nằm hai bên so Oy.
Lời giải. Để đồ thị hàm số có 2 điểm cực
.......................................................................
trị nằm về hai bên so với trục tung Oy
....................................................................... 2 2
 y  3x  8x  1  m  0 có nghiệm
....................................................................... phân biệt trái dấu 2
 a.c  0  3.(1  m )  0
.......................................................................  m  1 
....................................................................... hoặc m  1.
....................................................................... Cần nhớ: Hàm số 3 2
y  ax  bx  cx  d
có hai điểm cực trị nằm hai bên trục tung
.......................................................................
Oy  a.c  0.
....................................................................... 19. Cho 3 2 2
y  x  (3m  1)x  (m  m  6)x. 20. Cho 3 2 2
y  mx (2m 1)x (m 1) . x
Tìm m để để đồ thị hàm số đã cho có 2
Tìm m để để đồ thị hàm số đã cho có 2
điểm cực trị nằm về hai phía trục tung Oy.
điểm cực trị nằm về 2 bên trục tung.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
....................................................................... 2 1 21. Cho 3 2 2
y  x  (m  1)x  (m  4m  3)x. 22. Cho hàm số 3 2 y 
x  mx  (m  2)x. 3 3
Tìm m để đồ thị hàm số có hai điểm cực trị
Tìm m để đồ thị hàm số có hai điểm cực
nằm bên phải trục tung.
trị nằm bên trái trục tung.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 90 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 23. Cho hàm số 3 2 2
y  x  3x  m  2m. Tìm 24. Cho hàm 3 2 2
y  x  3x  m  4m. Tìm
m để hàm số có giá trị cực đại bằng 3.
m để hàm số có giá trị đại bằng 9.
Lời giải. Tập xác định D  . 
....................................................................... Ta có: 2
y  3x  6x  0
.......................................................................  2
x  0  y  m  2m 
.......................................................................  .  2
x  2  y  m  2m  4 
....................................................................... x
.......................................................................  0 2  y
.......................................................................  0  0 
....................................................................... 2 m  2m  y
.......................................................................  2 m  2m  4
....................................................................... 2
 y  m  2m
....................................................................... CĐ 2
 3  m  2m  m  1 
....................................................................... hoặc m  3. 25. Tìm ,
m biết giá trị cực tiểu của hàm số 26. Tìm ,
m biết giá trị cực tiểu của hàm số 3
y  x  3x  1  m thỏa 2y  9  0. 3 2 2
y  x  3x  m  2m bằng 4  . CT
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
27. Tìm m để hàm số 3 2
y  x  3x  2m có 28. Tìm m để hàm số 3
y  x  3x  1  m có
giá trị cực tiểu và giá trị cực đại trái dấu ?
giá trị cực tiểu và giá trị cực đại trái dấu ? Lời giải. Ta có: 2
y  3x  6x  0
.......................................................................
x  0  y  2m 
.......................................................................  CĐ .  x  2  y  2m  4  CT 
.......................................................................
Vì giá trị cực tiểu và giá trị cực đại trái dấu
....................................................................... nên y .y
 0  2m.(2m  4)  0 CĐ CT
....................................................................... 2
 4m  8m  0  0  m  2.
....................................................................... Cần nhớ:
.......................................................................
Giá trị cực đai, giá trị cực tiểu của hàm số
trái dấu  y .y  0.
....................................................................... CĐ CT
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 91 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
29. Tìm m để đồ thị hàm số 3 2
y  x  3x  m 30. Cho hàm 3 2
y  2x  (1  2m)x  3mx  m.
có 2 cực trị nằm hai bên trục hoành Ox.
Tìm tham số m để đồ thị hàm số đã cho
có hai điểm cực trị nằm hai bên trục Ox.
Cách giải 1. Ta có: 2
y  3x  6x  0
Lời giải. Để hàm số có hai điểm cực trị
x  0  y  m   CĐ .
nằm hai bên Ox  đồ thị hàm số  x  2  y  m  4  CT  3 2
y  2x  (1  2m)x  3mx  m cắt trục
Để đồ thị hàm số có hai cực trị nằm hai bên
Ox (y  0) tại 3 điểm phân biệt
trục Ox  y .y  0 CĐ CT  PT 3 2
2x  (1  2m)x  3mx  m  0  ( m m  4)  0 có ba nghiệm phân biệt.  0  m  4.
(Sử dụng casio, giải phương trình bậc 3,
cho m  100, được nghiệm đẹp x  0, 5). Cách giải 2.
 PT (2x 1)(x mx  ) m  0 có ba
Để hàm số có hai cực trị nằm hai bên trục nghiệm phân biệt
Ox  đồ thị hàm số 3 2
y  x  3x  m 1
cắt Ox tại 3 điểm phân biệt  phương  x  và 2
g(x )  x  mx  m  0 : có 2
trình hoành độ giao điểm với trục Ox : 1 3 2 x 3x m  0  3 2  m  x   3x  ( g x)
hai nghiệm phân biệt khác  2
có 3 nghiệm phân biệt  đường thẳng  2
  m  4m  0
nằm ngang y  m cắt 2 3
g(x )  3x  x tại      3 1    1 1 điểm  g  m  g .   CT g  m   0 CĐ    2 2 4  Ta có: 2 g (
 x)  3x  6x  0 m
  0  m  4    x  0  g  0    . CT 1   0  m  4.  m    x  2  g  4     2 CĐ
Nhận xét. Để tìm tham số m để đồ thị hàm số bậc ba 3 2
y  ax  bx  cx  d có hai điểm
cực trị nằm hai bên so với trục hoành Ox (giá trị cực đại và giá trị cực tiểu trái dấu), có các phương pháp: x  x 
Phương pháp 1. Nếu y  0 tìm được 2 nghiệm 1 
thì YCBT  y .y  0  m. x  x  CĐ CT 2 
Phương pháp 2. Đồ thị cắt trục Ox tại 3 điểm phân biệt  y  0 có 3 nghiệm phân biệt
(sử dụng được khi y  0 không nghiệm đẹp và y  0 có nghiệm đẹp).
Phương pháp 3. Sử dụng khi y  0 hoặc y  0 không tìm được nghiệm đẹp.
 Tìm điều kiện để hàm số có 2 cực trị (y  0 có 2 nghiệm phân biệt).
 Gọi x , x là 2 nghiệm của phương trình y  0 1 2 y
 (x )  x    
Viết phương trình đường thẳng nối hai điểm cực trị 1 1 y  x
     là y  (x )  x     2 2 
giá trị cực đại và giá trị cực tiểu.
 Yêu cầu bài toán  y .y
 0  y(x ).y(x )  0  ( x
  ).( x
  )  0, sau đó sử CĐ CT 1 2 1 2
dụng định lí Viét với x , x là 2 nghiệm của y  0  . m 1 2
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 92 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 31. Cho hàm số 3 2 y  x 
 6x  m  1. Tìm 32. Cho hàm số 3 2
y  x  3mx  m. Tìm m
m để đồ thị hàm số có hai điểm cực trị nằm
để đồ thị hàm số có hai điểm cực trị nằm
hai bên trục hoành Ox.
hai bên trục hoành Ox.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
....................................................................... 33. Cho hàm 3 2
y  x  (m  2)x  3mx  2m. 34. Cho hàm số 3 2
y  x  3x  mx  m  2.
Tìm tham số m để đồ thị hàm số đã cho có
Tìm m để đồ thị hàm số có hai điểm cực
hai điểm cực trị nằm hai bên trục Ox.
trị nằm hai bên trục hoành Ox.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 93 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 BÀI TẬP VỀ NHÀ 7
Câu 49. (THPT Kinh Môn – Hải Dương năm 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 3 2 2
y  (m  3)x  2(m  m  1)x  (m  4)x  1 có hai điểm cực trị
nằm về hai phía của trục O . y A. 4. B. 5. C. 6. D. 7.
Câu 50. (Tạp chí Toán Học & Tuổi Trẻ số 484) Có bao nhiêu giá trị nguyên của m để hàm số 3 2
f (x)  2x  6x  m  1 có các giá trị cực trị trái dấu ? A. 2. B. 9. C. 3. D. 7. 3
Câu 51. (THPT Tân Bình – Tp. Hồ Chí Minh 2019) Cho hàm số 3 2
y  x  x  18x  2m  1 2
có hai điểm cực trị (x ;y ), (x ;y ) thỏa x  x . Tìm m để y  4y  10. 1 1 2 2 1 2 1 2 23
A. m  11. B. m    2 21 C. m   
D. m  12. 2
Câu 52. (Tạp chí Toán Học & Tuổi Trẻ số 484) Tìm điều kiện của tham số m để hàm số 2 3 2 2 y 
x  (m  1)x  (m  4m  3)x  3 có các điểm cực trị của đồ thị hàm số 3
nằm bên phải của trục tung.
A. 5  m  1.
B. 5  m  3.
C. 3  m  1.
D. m  5 hoặc m  1.
Câu 53. (THPT Chuyên Quốc Học Huế năm 2019) Có mấy giá trị nguyên của m  ( 2  0;18) 3 3m để đồ thị hàm số 3 2
f (x)  x  (m  1)x  3mx 
nằm về cùng phía Ox. 2 2 A. 1. B. 19. C. 20. D. 18.
Câu 54. (THPT Nguyễn Khuyến – Tp. HCM 2018) Tìm tham số thực m để đồ thị hàm số 3 2
y  x  2x  (1  m)x  m có hai điểm cực trị nằm về hai phía đối với trục hoành. 1 A.   m  0. B. m  0. 4 1 1 C.   m  0.
D. m    4 4
Câu 55. (THPT Chuyên Hoàng Văn Thụ – Hòa Bình năm 2018) Tìm tham số m để hàm số 3 2
y  x  3(m  1)x  12mx  3m có hai điểm cực trị x , x thỏa mãn x  3  x . 1 2 1 2 A. m  1. B. m  1. 3 3 C. m   D. m   2 2
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 94 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 1 1 35. Cho hàm số 3 2
y  x  mx  x  m  1. 36. Cho hàm số 3 2
y  x  mx  x. Tìm 3 3
Tìm tham số m để hàm số có 2 điểm cực
tham số m để hàm số có 2 điểm cực trị x1
trị x và x thỏa mãn 2 2 x  x  2. 2 2 1 2 1 2
và x thỏa mãn x  x  x x  7. 2 1 2 1 2 Lời giải. Ta có 2
y   x  2mx  1.
.......................................................................
Hàm số có 2 điểm cực trị x và x thỏa 1 2
....................................................................... 2 2
x  x  2  y  0 có 2 nghiệm x , x 1 2 1 2
....................................................................... thỏa 2 2 x  x  2 1 2
....................................................................... a   0   2
.......................................................................  4  m  4  0 : L ( ) Đ      0    2  (
 x  x )  2x x  2
....................................................................... 2 2 x   x  2  1 2 1 2   1 2 
....................................................................... 2
 S  2P  2
.......................................................................  b S
  x  x    2m
....................................................................... 1 2  với a  c
....................................................................... P
  x x   1 1 2  a
....................................................................... 2
 4m  2  2  m  0.
.......................................................................  2 2 2
Cần nhớ: x  x  S  2 , P 1 2
....................................................................... 2 2
x  x  l  0  S  4P  l ,... 1 2
....................................................................... 1 1 37. Cho hàm số 3 2
y  x  mx  x  m  1. 38. Cho hàm số 3 2 y 
x  x  mx  m. 3 3
Tìm tham số m để hàm số có 2 điểm cực
Tìm tham số m để hàm số có 2 cực trị x 1
trị x và x thỏa 2 2
x  x  4x x  2. 1 2 1 2 1 2
và x thỏa mãn x  3x  0. 2 1 2
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 95 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 39. Cho hàm số 3 2
y  x  3x  m. Tìm m để 40. Cho hàm số 3 y  x
  3mx  1. Tìm m
đồ thị hàm số có 2 điểm cực trị , A B sao
để đồ thị hàm số có 2 điểm cực trị , A B cho O
 AB vuông tại O với ( O 0;0). sao cho O
 AB vuông tại O với ( O 0;0). Lời giải.
....................................................................... Ta có: 2
y  3x  6x  0
.......................................................................
x  0  y  m  ( A 0;m) 
.......................................................................  . 
x  2  y  m  4  B(2;m  4) 
.......................................................................  O
 A  (0;m)
.......................................................................  Suy ra  (ĐK: m  0). O
 B  (2;m  4)
.......................................................................   
....................................................................... Vì O
 AB vuông tại O nên OA  OB  
.......................................................................  O .
AOB  0  0.2  m(m  4)  0
....................................................................... m   0 (L)   vì m  0  ( A 0;0)  . O
....................................................................... m   4 (N) 
.......................................................................
Vậy m  4 là giá trị cần tìm.
.......................................................................
 Sai lầm thường gặp của học sinh là quên điều
kiện m  0 như trên.
....................................................................... 41. Cho hàm số 3 2
y  x  3mx  8m. Tìm m 42. Cho hàm số 3 2 3
y  x  3mx  4m . Tìm
để đồ thị hàm số có 2 điểm cực trị , A B
m để đồ thị hàm số có 2 điểm cực trị sao cho O
 AB vuông tại O với ( O 0;0). ,
A B thỏa mãn AB  20.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 96 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 43. Cho hàm số 4 2 2
y  x  2m x  2. Tìm m 44. Cho hàm số 4 2
y  x  2mx  1. Tìm m
để đồ thị hàm số có 3 điểm cực trị ( A 0;2),
để đồ thị hàm số có 3 điểm cực trị ( A 0;1), ,
B C thỏa mãn BC  2. ,
B C thỏa mãn BC  4. Lời giải. Ta có: 3 2
y   4x  4m x.
....................................................................... x  0
....................................................................... 2 2 y 0 4x.(x m ) 0         2 2 x  m 
.......................................................................
Đồ thị hàm số có 3 điểm cực trị
....................................................................... 2
 m  0  m  0. Khi đó:
.......................................................................
x  0  y  2  ( A 0;2) 
.......................................................................  4 4
x  m  y  2  m  B(m;2  m )
.......................................................................  4 4 x  m
  y  2  m  C( m  ;2  m ) 
....................................................................... Theo đề BC  2
....................................................................... 2 2
 (x  x )  (y  y )  2
....................................................................... C B C B 2 2  ( 2  m)  0  2
.......................................................................
....................................................................... 2
 4m  4  m  1  .
.......................................................................
So điều kiện, suy ra m  1 thỏa bài toán. 45. Cho hàm số 3 2 3
y  x  3mx  4m . Tìm m 46. Cho hàm số 4 2 2
y  x  2mx  2m  4m.
để đồ thị hàm số có hai điểm cực trị là A
Tìm m để đồ thị hàm số có ba điểm cực trị
và B sao cho điện tích O  AB bằng 4.
tạo thành tam giác có diện tích bằng 1.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 97 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 1 48. Cho hàm số 4 2
y  x  4mx  3m  2. 47. Cho hàm 4 2
y  x  (3m  1)x  2m  2. 4
Tìm m để đồ thị hàm số có 3 điểm cực trị
Tìm m để đồ thị hàm số có ba điểm cực trị  5     
tạo thành một tam giác có trọng tâm là O.
tạo thành tam giác có trọng tâm G 0;  3
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
....................................................................... 49. Cho hàm số 4 2
y  x  2mx  1. Tìm m để 50. Cho hàm số 4 2 y  x  6
( m  4)x  1  m.
đồ thị hàm số có ba điểm cực trị tạo thành
Tìm m để đồ thị hàm số có ba điểm cực trị một tam giác vuông cân.
tạo thành tam giác vuông cân.
Cần nhớ: Đồ thị hàm số 4 2
y  ax  bx  c
.......................................................................
có ba cực trị A O , y ,
B C thì luôn tạo
....................................................................... thành tam giác cân tại .
A Khi đó ta luôn có
....................................................................... 3
b  8a  cosA.
....................................................................... 3 b  8a
....................................................................... Áp dụng:
.......................................................................
Hàm số có ba cực trị  ab  0
.......................................................................
 1.2m  0  m  0.
.......................................................................
Đồ thị hàm số có ba điểm cực trị tạo thành
tam giác vuông cân  A  90 . 
....................................................................... 3 (2m)  8.1
.......................................................................   cos 90  0 3 (2m)  8.1
....................................................................... 3  8m  8  0
.......................................................................
....................................................................... 3  m  1   m  1  (thỏa m  0).
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 98 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 51. Cho hàm số 4 2
y  x  2mx  2m. Tìm m 52. Cho hàm số 4 2 3
y  x  2mx  m . Tìm m
để đồ thị hàm số có ba điểm cực trị tạo
để đồ thị hàm số có ba điểm cực trị tạo thành tam giác đều.
thành tam giác có một góc bằng 30.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
....................................................................... 53. Cho hàm số 4 2 2
y  x  2mx  9  2m . 54. Cho hàm số 4 2 y  x
  2mx  4. Tìm m
Tìm m để đồ thị hàm số có ba điểm cực trị
để đồ thị hàm số có ba điểm cực trị nằm
nằm trên các trục tọa độ.
trên các trục tọa độ. Lời giải.
....................................................................... x  0 
....................................................................... Ta có: 3
y  4x  4mx  0   2 x  m  0 
.......................................................................  2
.......................................................................
x  0  y  9  2m   2
 x   m  y  m  9
.......................................................................  2
x  m  y  m  9
....................................................................... 
.......................................................................  2  (
A 0;2m  9)  Oy 
.......................................................................  2  B
 ( m;m  9)  
....................................................................... 2 C  ( m;m  9) 
.......................................................................
Vì điểm A Oy nên để ba điểm cực trị
.......................................................................
nằm trên các trục tọa độ thì ,
B C Ox
.......................................................................
 y  y  0 B C
....................................................................... 2
 m  9  0  m  3  .
.......................................................................
Nhận xét: Để ba điểm cực trị của hàm số
.......................................................................
bậc bốn trùng phương nằm trên các trục
....................................................................... tọa độ thì y  0 (hoặc y  0). CĐ CT
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 99 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 1
56. Biết rằng đường thẳng d : y  x m cắt 55. Cho 3 2 2
y  x  mx  (m  1)x. Gọi S là 3 đồ thị hàm số 3 2
y  x  3x tại ba điểm
tập hợp các giá trị của tham số m để đồ thị
phân biệt sao cho có một giao điểm cách
hàm số có hai điểm cực trị là A và B sao
đều hai giao điểm còn lại. Tìm . m cho ,
A B nằm khác phía và cách đều
.......................................................................
đường thẳng d : y  5x  9. Tích các phần tử của S bằng
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
....................................................................... 57. Cho hàm số 3 2
y  x  3x  m  1 có đồ thị 58. Hỏi có tất cả bao nhiêu giá trị của m để đồ
(C). Biết đồ thị (C) cắt trục hoành tại ba thị hàm số 3 2
y  x  mx  x  m cắt trục
điểm phân biệt lập có hoành độ lập thành
hoành tại ba điểm phân biệt, đồng thời cấp số cộng.
phần diện tích phía trên Ox và diện tích
phía dưới Ox, giới hạn bởi đồ thị và trục
....................................................................... Ox bằng nhau.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 100 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 BÀI TẬP VỀ NHÀ 8
Câu 56. (THPT Chuyên Hùng Vương – Phú Thọ 2018) Biết m là giá trị của tham số m để  hàm số 3 2
y  x  3x  mx  1 có hai điểm cực trị x , x sao cho 2 2
x  x  x x  13. 1 2 1 2 1 2
Mệnh đề nào dưới đây đúng ?
A. m  (1;7). 
B. m  (7;10). 
C. m  (15;7). 
D. m  (7;1). 
Câu 57. (THPT Chuyên Vĩnh Phúc năn 2018) Với giá trị nào của tham số m thì đồ thị hàm số 3 2
y  2x  3(m  1)x  6(m  2)x  1 có cực đại, cực tiểu thỏa mãn x  x  2. CĐ CT A. m  1. B. m  2. C. m  1  . D. m  2  . 1
Câu 58. (THPT Thăng Long – Hà Nội 2018) Biết hàm số 3 2 y 
x  (m  1)x  (2m  1)x có 3
hai điểm cực trị x , x . Giá trị nhỏ nhất của biểu thức 2 2
T  x  x  10(x  x ) bằng 1 2 1 2 1 2 A. 78. B. 1. C. 18. D. 22.
Câu 59. (THPT Thanh Miện – Hải Dương năm học 2018) Biết rằng đồ thị hàm số 1 1 3 2 f (x) 
x  mx  x  2 có giá trị tuyệt đối của hoành độ hai điểm cực trị là độ 3 2
dài hai cạnh của tam giác vuông có cạnh huyền là 7. Hỏi có mấy giá trị của m ? A. 3. B. 1. C. 0. D. 2.
Câu 60. (THPT Chuyên Hạ Long – Quảng Ninh năm 2019) Tìm tất cả giá trị thực của tham số
m để đồ thị hàm số 3 2
y  x  3mx  2 có hai điểm cực trị A và B sao cho các điểm ,
A B và M(1; 2  ) thẳng hàng. A. m  2. B. m   2. C. m  2. D. m   2.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 101 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 61. (THPT Chuyên Hùng Vương – Gia Lai năm 2018) Gọi ,
A B là hai điểm cực trị của đồ thị hàm số 3 2
f (x)  x  3x  m với m là tham số thực khác 0. Tìm tham số m để
trọng tâm tam giác OAB thuộc đường thẳng 3x  3y  8  0. A. m  5. B. m  2. C. m  6. D. m  4.
Câu 62. (THPT Chuyên Trần Phú – Hải Phòng năm 2018) Gọi m , m là các giá trị của tham 1 2
số m để đồ thị hàm số 3 2
y  2x  3x  m  1 có hai điểm cực trị là , B C sao cho
tam giác OBC có diện tích bằng 2, với O là gốc tọa độ. Tích số m m bằng 1 2 A. 15. B. 12. C. 6. D. 20.
Câu 63. (THP Chuyên Lê Hồng Phong – Nam Định 2018) Tìm tham số m đề đồ thị hàm số 4 2
y  x  2mx  1 có ba điểm cực trị ( A 0;1), ,
B C thỏa mãn BC  4 ? A. m  2. B. m  4. C. m  4  . D. m   2.
Câu 64. (HKI – THPT Nguyễn Thượng Hiền – Tp. Hồ Chí Minh năm 2019) Có bao nhiêu số
thực m để đồ thị hàm số 3 2
y  x  3x  m có hai điểm cực trị A và B sao cho tam
giác OAB vuông tại O. A. 2. B. 1. C. 3. D. 0.
Câu 65. (HKI – THPT Trần Phú – Tp. Hồ Chí Minh năm 2019) Gọi S là tập các số thực m để đồ thị hàm số 3 2
y  x  6m x  2m có hai điểm cực trị A và B sao cho
AB  2 34. Tính tích các phần tử của S. A. 1. B. 4. C. 1. D. 2. 1
Câu 66. (Đề minh họa – Bộ GD & ĐT năm 2017) Cho 3 2 2 y 
x  mx  (m  1)x. Gọi S là 3
tập hợp các giá trị của tham số m để đồ thị hàm số có hai điểm cực trị là A và B sao cho ,
A B nằm khác phía và cách đều đường thẳng d : y  5x  9. Tích các phần tử của S bằng
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 102 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 A. 27. B. 27. C. 9. D. 9.
Câu 67. (Tạp Chí Toán Học & Tuổi Trẻ số 485) Tìm k để đồ thị của hàm số 4 2
y  x  2kx  k  1  
có ba điểm cực trị tạo thành một tam giác nhận điểm G 0;   làm trọng tâm ?  3 1     1  
A. k   ;1. k    1; .  B. 3     2   1     1  
C. k   ;1. k    1; .  D. 2     3  
Câu 68. (TT Diệu Hiền – Cần Thơ năm 2018) Cho hàm số 4 2
y  x  2(m  1)x  m có đồ thị
(C). Tìm tham số m sao cho (C) có ba điểm cực trị , A ,
B C thỏa mãn OA  BC,
trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung.
A. m  0 hoặc m  2.
B. m  2  2 2.
C. m  3  3 3.
D. m  5  5 5.
Câu 69. (THPT Chuyên Bắc Ninh năm 2018) Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 4 2 2
y  x  2(m  1)x  m có ba điểm cực trị tạo thành một tam giác vuông cân. A. m  0. B. m  1  , m  0. C. m  1.
D. m  0, m  1.
Câu 70. (THPT Chuyên Vĩnh Phúc năm 2018) Cho hàm số 4 2 4
y  x  2mx  m  2m. Tìm
tham số m để các điểm cực trị của đồ thị hàm số lập thành một tam giác đều. A. m  2 2. B. 3 m  3. C. 3 m  4. D. m  1.
Câu 71. (THPT Hậu Lộc 2-Thanh Hóa-lần 1-năm 2017-2018) Tìm giá trị của m để đồ thị hàm số 4 2
y  x  2mx  2 có ba điểm cực trị tạo thành một tam giác có diện tích bằng 1. A. 3 m  3. B. m  3. C. m  3 3. D. m  1.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 103 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 72. (THPT Chuyên Vĩnh Phúc năm 2018) Tìm tham số thực m để đồ thị của hàm số 4 2
y  x  2mx có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1. A. m  1.
B. 0  m  1. C. 3 0  m  4. D. m  0.
Câu 73. (THPT Lương Văn Chánh – Phú Yên năm 2018) Gọi S là tập hợp tất cả các giá trị
thực của tham số m để đồ thị (C) của hàm số 4 2 2 4
y  x  2m x  m  5 có ba điểm
cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ O tạo thành một tứ giác nội
tiếp. Tìm số phần tử của S. A. 1. B. 0. C. 2. D. 3.
Câu 74. (THPT Cổ Loa – Hà Nội năm 2018) Gọi S là tập hợp tất cả các giá trị thực của tham 3m
số m để đồ thị hàm số 4 2
y  2x  2mx 
có ba điểm cực trị, đồng thời ba điểm 2
cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được.
Tổng tất cả các phần tử của S bằng A. 2  2 3. B. 2  2 3. C. 1  . D. 0.
Câu 75. (THPT Hồng Bàng – Hải Phòng 2018) Cho hàm số 4 2
y  x  2(m  4)x  m  5 có
đồ thị (C ). Tìm m để (C ) có ba điểm cực trị tạo thành một tam giác nhận gốc tọa m m
độ O làm trọng tâm. 17
A. m  1 hoặc m   2 B. m  1. C. m  4. 17 D. m   2
Câu 76. (Sở GD & ĐT Vĩnh Phúc năm 2018) Tìm tất cả các giá trị của tham số m để đồ thị hàm số 4 2 2
y  x  2m x  2m có ba điểm cực trị , A , B C sao cho , O , A , B C là bốn
đỉnh của một hình thoi (với O là gốc tọa độ). A. m  1  . B. m  1. C. m  2. D. m  3.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 104 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Daïng toaùn 4: Cöïc trò cuûa haøm hôïp vaø haøm soá trò tuyeät ñoái (vaän duïng cao) 
1. Cho hàm số y  f (x) có bảng biến thiên như sau: x  0 2  f (  x)  0  0 
Hỏi trên khoảng ( 5, 5) thì hàm số 2
g(x)  f (x ) đạt cực đại tại điểm nào sau đây ? x  0
A. x  2.  2  g (
 x)  2x.f (x ),   2 g (  x)  0   x  0 x  0 .  
B. x   2. 2 f (  x )  0    2  x  2   x   2   
C. x  0. x
D. x  2.  5  2 0 2 5 Thử điểm: g (  x)  0  0  0 
x  2  ( 2; 5) thì g(x) g (
 2)  4.f (4)  0.
Suy ra hàm số g(x) đạt cực đại tại x  0. Chọn đáp án C.
2. Cho hàmy  f (x) có bảng biến thiên. Hàm số 2
g(x)  f (x  2) đạt cực đại tại điểm nào ? x  1 2  f (  x)  0  0 
A. x  2.
........................................................................................................................
B. x  1.
........................................................................................................................
........................................................................................................................
C. x  0.
........................................................................................................................
D. x  2.
........................................................................................................................
3. Cho hàm số y  f (x) có bảng biến thiên. Hàm số 2
g(x)  f (x  5) có mấy điểm cực trị ? x  4 1 2  f (
 x)  0  0  0 
........................................................................................................................ A. 3.
........................................................................................................................ B. 5.
........................................................................................................................
........................................................................................................................ C. 7.
........................................................................................................................ D. 6.
........................................................................................................................
........................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 105 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
4. (Đề thi THPT QG năm 2019 – Câu 46 Mã đề 101) Cho hàm số f (x), bảng biến thiên của hàm số f (  x) như sau:
Số điểm cực trị của hàm số 2
y  f (x  2x) là A. 9. B. 3. C. 7. D. 5.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
5. (Đề thi THPT QG năm 2019 – Câu 48 Mã đề 103) Cho hàm số f (x), bảng biến thiên của hàm số f (  x) như sau:
Số điểm cực trị của hàm số 2
y  f (x  2x) là A. 9. B. 3. C. 7. D. 5.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
6. (Đề thi THPT QG năm 2019 – Câu 50 Mã đề 104) Cho hàm số f (x), bảng biến thiên của hàm số f (  x) như sau:
Số điểm cực trị của hàm số 2
y  f (4x  4x) là A. 9. B. 3. C. 7. D. 5.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 106 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
7. Cho hàm số y  f (x) có đạo hàm liên tục trên  và bảng biến thiên Hàm số 4 2 6 4 2
g(x)  15f ( x 
 4x  6)  10x  15x  60x đạt cực tiểu tại x  0. Chọn  mệnh đề đúng ?  5     3    3    A. x    ;2  B. x    2;  C. x   
;1  D. x  ( 1  ;0).   2    2   2   Ta có: 3 4 2 5 3 g (
 x)  15.(4x  8x).f ( x
  4x  6)  60x  60x  120x 3 4 2 2       60( x 2x) f ( x
  4x  6) x 1 .   Đặt 4 2 2 2 t  x   4x  6  (
 x  2)  2  2 và có f (t)  0, t   2  (nhìn bảng). 4 2  f (  x   4x  6)  0 4 2 2  f (  x 
 4x  6)  x  1  0, x  .  x   2 0 2  3 60( x   2x)  0  0  0  4 2 2 f (  x
  4x  6)  x  1  |  |  |  g (  x)  0  0  0    g(x) g(0) g( 2) g( 2)  3   
Suy ra hàm số đạt cực tiểu tại điểm x   2  x   2   
;1 Chọn đáp án C.   2 
8. Cho hàm số y  f (x) có đạo hàm liên tục trên  và bảng biến thiên như sau: Hàm số 4 2 6 2
g(x)  15f (x  2x  3)  10x  30x có bao nhiêu điểm cực trị ? A. 2. B. 3. C. 7. D. 5.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 107 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
9. Cho hàm số y  f (x) có đạo hàm liên tục trên  và bảng biến thiên như sau: Hàm số 4 2 6 2
g(x)  15f ( x 
 2x  2)  10x  30x có bao nhiêu điểm cực trị ? A. 2. B. 3. C. 7. D. 5.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
10. Cho hàm số y  f (x) có đạo hàm liên tục trên  và bảng biến thiên như sau: Hàm số 4 2 6 2
y  2f ( x 
 4x  5)  x  12x có bao nhiêu điểm cực trị ? A. 2. B. 3. C. 7. D. 5.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
................................................................................................................................................................... 11. Cho hàm số 3 2
g(x)  f (x  3x  1) có bảng biến thiên như sau:
Hàm số y  f (x) có mấy điểm cực trị ? A. 0. B. 1. C. 2. D. 3.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 108 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
12. Cho hàm số y  f (x) xác định trên  và hàm số y  f (
 x) có đồ thị như hình vẽ. Tìm số
điểm cực trị của hàm số 2
y  f (x  3). A. 2.
................................................................................................ B. 3.
................................................................................................
................................................................................................ C. 4.
................................................................................................ D. 5.
................................................................................................
13. Cho hàm số y  f (x) xác định trên  và hàm số y  f (
 x) có đồ thị như hình vẽ. Hàm số 2
y  f (1  x ) đạt cực đại tại
A. x  1.
................................................................................................
................................................................................................
B. x   2.
................................................................................................
C. x  3.
................................................................................................
D. x  0.
................................................................................................
14. Cho hàm f (x) có đồ thị f (
 x) có đồ thị như hình. Hàm số y  f(12x) có mấy cực trị ? A. 4.
................................................................................................ B. 7.
................................................................................................
................................................................................................ C. 3.
................................................................................................ D. 9.
................................................................................................
15. Cho hàm số f (x) có đồ thị f (
 x) có đồ thị như hình. Hàm số 2
y  f (x ) có mấy cực trị ? A. 5.
................................................................................................ B. 7.
................................................................................................
................................................................................................ C. 3.
................................................................................................ D. 9.
................................................................................................
16. Cho hàm f (x) có đồ thị f (
 x) có đồ thị như hình. Hàm số 2
y  f (x  2) có mấy cực trị ? A. 5.
................................................................................................ B. 7.
................................................................................................
................................................................................................ C. 3.
................................................................................................ D. 9.
................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 109 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 1. Cho hàm số y  f(x) có đạo hàm, liên tục trên  và có đồ thị y  f (
 x) như hình vẽ. 3 Xét hàm số 2 4 2
g(x)  3f (x  2)  x  3x . Hàm số (
g x) đạt cực đại tại điểm 2
A. x  0.
B. x  1.
C. x  1. D. x  3.
Lời giải tham khảo 2 3 2 2           Ta có: g (x) 6x.f (x 2) 6x 6x
6x f (x  2)  (x  2)  1    x  0 x  0   2 g (  x)  0 
 x  2  1  x  1  2 2 (xem hình vẽ) f (  x  2)  (  x  2)  1   2
x  2  1 (K)  x   3  Bảng biến thiên:
Từ bảng biến thiên, suy ra hàm số g(x) đạt cực đại tại x  0. Chọn đáp án A.
Câu 2. Cho hàm số y  f(x) có đạo hàm và liên tục trên  và có đồ thị y  f (  x) như hình. 3 Xét hàm số 2 4
g(x)  3f (x  2x)  (x  1) . Hàm số (
g x) đạt cực đại tại điểm 2
A. x  1.
B. x  1.
C. x  3.
D. x  2.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 110 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 3. Cho hàm số y  f(x) có đạo hàm trên  và có đồ thị y  f (
 x) như hình vẽ. Xét hàm 6 x số 2 4 2
g(x)  f(x 1) 
 2x  3x . Tìm khẳng định đúng ? 3 A. Hàm số (
g x) có 2 điểm cực đại và 3 điểm cực tiểu. B. Hàm số (
g x) có 3 điểm cực đại và 2 điểm cực tiểu. C. Hàm số (
g x) có 2 điểm cực đại và 2 điểm cực tiểu. D. Hàm số (
g x) có 1 điểm cực đại và 1 điểm cực tiểu.
Câu 4. Cho hàm số y  f (x) có đạo hàm và liên tục trên  và có đồ thị y  f (  x) như hình 4 x vẽ. Xét 2 3 2
g(x)  f (x  2x) 
 2x  2x . Hàm số (
g x) có mấy điểm cực tiểu ? 2 A. 0. B. 1. C. 2. D. 3.
Câu 5. Cho hàm số y  f (x) có đạo hàm và liên tục trên  và có đồ thị y  f (  x) như hình 4 2 x 3x vẽ. Xét hàm 2
g(x)  f (x  2)  
 Hàm số g(x) có bao nhiêu điểm cực tiểu ? 2 2 A. 4. B. 1. C. 2. D. 3.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 111 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
 Hàm số y  f  x  có 2a  1 với a là số cực trị dương của hàm số y  f(x).
 Hàm số y  f (x) có a  b cực trị với a là số cực trị của hàm số y  f (x) và b là số nghiệm
đơn của phương trình f (x)  0 (số giao điểm cắt của đồ thị y  f (x) và trục Ox). 1. Cho hàm số 3 2
f (x)  x  (2m  1)x  (2  m)x  2. Tìm m để đồ thị hàm số y  f  x  có 5 điểm cực trị. 5
Lời giải. Hàm số y  f  x  có 5 điểm cực trị  2a  1  5  a  2 A.  m  2. 4 2  f (
 x)  3x  2(2m  1)x  2  m  0 có 2 nghiệm dương phân biệt 5   2    B.  m  2. 0
4(2m  1)  12(2  m)  0    2 4
 m  m  5  0 4    S    0 2      m  1  0     1    m  2 5 P  0 2     m  0 2 C.   m  2.   4  5 m
  1  m  5  5  4
D. 2  m     
 m  2. Chọn đáp án A. 4 1 4   m  2 2 3
2. Tìm số nguyên bé nhất của m để hàm số 2
y  x  2mx  5 x  3 có 5 điểm cực trị.
............................................................................................................................. A. 2  .
............................................................................................................................. B. 2.
.............................................................................................................................
............................................................................................................................. C. 5.
............................................................................................................................. D. 0.
.............................................................................................................................
............................................................................................................................. 3
3. Có mấy giá trị nguyên của m để hàm 2
y  x  5x  (3m  1) x  m có 5 điểm cực trị.
............................................................................................................................. A. 3.
.............................................................................................................................
............................................................................................................................. B. 5.
.............................................................................................................................
............................................................................................................................. C. 7.
.............................................................................................................................
............................................................................................................................. D. 9.
.............................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 112 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
4. Có mấy giá trị nguyên của tham số m để hàm số 3 2
y  x  6x  m có 5 điểm cực trị. Đặt 3 2
f (x)  x  6x  m. Để hàm y  f (x) có 5 cực trị  a  b  5, a  y  f x b  A. 1. với 2 là số cực trị của ( ) và
3 là số nghiệm đơn của
phương trình f (x)  0. Xét 3 2 3 2
f (x)  0  x  6x  m  0  m  x
  6x  g(x) có: B. 31. 2 g (
 x)  3x  12x  0  x  0 hoặc x  4. C. 17. D. Vô số.
Để phương trình f (x)  0 có 3 nghiệm 0  m  32 và do m   nên:
m  {1;2; 3;...; 31} có (31  1)  1  31. Chọn đáp án B.
5. Có mấy giá trị nguyên của m để hàm số 4 3 2
y  3x  4x 12x  m có 7 điểm cực trị ?
............................................................................................................................. A. 3.
............................................................................................................................. B. 4.
............................................................................................................................. C. 5.
.............................................................................................................................
............................................................................................................................. D. 6.
.............................................................................................................................
6. Tính tổng các giá trị của m để đồ thị hàm số 3 2
y  x  3x  m có 5 điểm cực trị ? A. 3.
.............................................................................................................................
............................................................................................................................. B. 5.
............................................................................................................................. C. 6.
............................................................................................................................. D. 10.
.............................................................................................................................
7. Có mấy giá trị nguyên m  [ 1  0;1 ] 0 để hàm số 3 2
y  mx  3mx  (3m  2)x  2  m có 5 điểm cực trị ? A. 7.
.............................................................................................................................
............................................................................................................................. B. 9.
............................................................................................................................. C. 10.
............................................................................................................................. D. 11.
.............................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 113 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020 BÀI TẬP VỀ NHÀ 9
Câu 77. Hàm số y  f (x) có đúng ba điểm cực trị là 2  , 1, 0. Hàm số 2
g(x)  f (x  2x)
có bao nhiêu điểm cực trị ? A. 6. B. 5. C. 3. D. 4.
Câu 78. Cho hàm số y  f (x) xác định, liên tục trên  và có đúng hai điểm cực trị x  1,
x  1, đồng thời có đồ thị như hình vẽ dưới. Hàm số 2
g(x)  f (x  2x  1)  2020 có
bao nhiêu điểm cực trị ? A. 4. B. 3. C. 1. D. 2.
Câu 79. Cho đồ thị hàm số 3 2
f (x)  ax  bx  cx  d như hình vẽ bên dưới. Tìm số điểm cực
trị của đồ thị hàm số 3
g(x)  f (x  3x). A. 5. B. 6. C. 4. D. 3.
Câu 80. Cho hàm số y  f (x)
f  x  ax  bx  c có đồ thị hàm 2 ( )
như hình bên dưới. Hỏi hàm số 2
g(x)  f (x  x ) có bao nhiêu cực trị ? A. 0. B. 1. C. 2. D. 3.
Câu 81. Cho hàm số y  f (x) có đồ thị của hàm số f (
 x) như hình bên dưới. Hàm số 2
g(x)  f (x ) có bao nhiêu điểm cực trị ? A. 4. B. 3. C. 5. D. 2.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 114 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 82. Cho hàm số bậc bốn y  f (x). Hàm số y  f (
 x) có đồ thị như hình vẽ bên. Số điểm cực đại của hàm số 2
y  f ( x  2x  2) là A. 1. B. 2. C. 4. D. 3.
Câu 83. Cho hàm số y  f (x) liên tục trên .
 Biết hàm số y  f (
 x) có bảng xét dấu sau
Số điểm cực tiểu của hàm số 2
g(x)  f (6  x ) là A. 5. B. 7. C. 3. D. 4.
Câu 84. Cho hàm số y  f (x) liên tục trên .
 Biết hàm số y  f (
 x) có bảng xét dấu sau Hàm số 2
g(x)  f (x  2x  4) có bao nhiêu điểm cực tiểu ? A. 1. B. 3. C. 2. D. 4.
Câu 85. Cho hàm số y  f (x) liên tục trên .
 Biết hàm số y  f (
 x) có bảng xét dấu:
Số điểm cực trị của hàm số 2
g(x)  f (x  x  1) là A. 0. B. 1. C. 3. D. 2.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 115 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 86. Cho hàm số y  f (x) có đạo hàm trên  và có bảng biến thiên củay  f (
 x) như sau: Hàm số 2
g(x)  f (x  4x  2) có bao nhiêu điểm cực trị ? A. 7. B. 8. C. 9. D. 10.
Câu 87. Cho hàm số y  f (x) có đạo hàm trên  và có bảng biến thiên của y  f (  x). Hàm  2 x 1   
số g(x)  f   
 có mấy điểm cực trị ?  x  A. 4. B. 5. C. 6. D. 8.
Câu 88. Cho hàm số y  f (x) có đạo hàm trên  và có đồ thị hàm số f (
 x) như hình vẽ. Hàm số 2
g(x)  2f (x)  x đạt cực đại tại điểm A. x  1. B. x  0. C. x  1. D. x  2.
Câu 89. Cho hàm số y  f (x) liên tục trên  và có đồ thị hàm số f (
 x) như hình bên dưới. 1 Hàm số 3 2
g(x)  f (x)  x  x  x  2 đạt cực đại tại điểm 3 A. x  1. B. x  1. C. x  0.
D. x  2.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 116 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 90. Cho hàm số y  f (x) liên tục trên  và có đồ thị hàm số f (
 x) như hình bên dưới. Hàm số 4 2 6 2
g(x)  15f ( x
  2x )  10x  30x  20 có bao nhiêu điểm cực trị ? A. 0. B. 3. C. 2. D. 5. 1
Câu 91. Cho hàm số f (
 x) như hình vẽ. Hàm số 2 6 4 2
g(x)  f (x )  x  x  x đạt cực tiểu tại 3 bao nhiêu điểm ? A. 3. B. 2. C. 0. D. 1.
Câu 92. Cho hàm số y  f (x) có đạo hàm 2 f (
 x) (x 1)(x  4) với mọi x  .  Hàm số
g(x)  f (3  x) có bao nhiêu điểm cực đại ? A. 0. B. 1. C. 2. D. 3.  1   
Câu 93. Cho hàm f (x) có đạo hàm 2 f (
 x)  x  2x, x  .
 Hàm số g(x)  f 1
  x  4x   2 
có mấy điểm cực trị ? A. 0. B. 1. C. 2. D. 3.
Câu 94. Cho hàm số y  f (x) có đạo hàm 2 f (
 x)  x  2x, x  .  Hàm số 2
y  f (x  8x)
có bao nhiêu điểm cực trị ? A. 6. B. 3. C. 5. D. 2.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 117 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 95. Tổng tất cả các giá trị nguyên của tham số m để hàm số 4 3 2
y  3x  4x 12x  2m
có 7 điểm cực trị bằng A. 3. B. 2. C. 6. D. 4.
Câu 96. Giá trị nguyên dương nhỏ nhất của tham số m để hàm số 3 2
y  x  x  5x  2m  1
có 3 điểm cực trị bằng A. 2. B. 4. C. 5. D. 7. 1 Câu 97. Cho hàm số 3 2 y 
(m  3)x  mx  (m  4)x  3m  2 với m là tham số thực. Giá 3
trị nguyên nhỏ nhất của m để hàm số đã cho có 1 điểm cực trị bằng A. 5. B. 3  . C. 0. D. 2. Câu 98. Cho hàm số 4 2
y  x  2(m  1)x  2m  3 với m là tham số thực. Số giá trị nguyên
không âm của m để hàm số đã cho có 3 điểm cực trị là A. 3. B. 4. C. 5. D. 6. 1 3
Câu 99. Tìm tham số m để hàm số 2 y 
x  mx  (m  6) x  2020 có 5 điểm cực trị ? 3 A. m  2  . B. m  6  . C. m  0. D. m  3.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 118 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 100. Cho hàm số 3 2
f (x)  x  (2m  1)x  (2  m)x  2. Tìm tham số m để đồ thị hàm số
y  f  x  có 5 điểm cực trị. 5 A.  m  2. 4 5 B.  m  2. 4 C. 1
  m  2. D. m  2.
Câu 101. Cho hàm số y  f (x) có đồ thị đạo hàm f (
 x) như hình vẽ. Có bao nhiêu giá trị
nguyên của tham số m thuộc khoảng ( 1
 2;12) sao cho hàm số y  f(x)  mx  12
có đúng một điểm cực trị ? A. 5. B. 18. C. 20. D. 12.
Câu 102. Cho hàm số f (x) có đạo hàm trên .
 Đồ thị hàm số y  f (
 x) như hình vẽ. Tìm m
để hàm số y  f (x)  mx có ba điểm cực trị ?
A. 0  m  4.
B. 0  m  4. C. m  4. D. m  0.
Câu 103. Cho hàm số f (x) có đạo hàm 3 2 f (  x)  x
  2x , x  .
 Có tất cả bao nhiêu giá trị
nguyên dương của tham số m để hàm số g(x)  f (x)  mx  3 có 3 điểm cực trị. A. 1. B. 2. C. 3. D. 4.
Câu 104. Cho hàm số f (x) có đạo hàm 2 2 f (
 x)  (x  3)(x  1), x  .  Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số y  f (x)  mx có 4 điểm cực trị ? A. 0. B. 1. C. 2. D. 3.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 119 -
SỞ GD & ĐT TP. HỒ CHÍ MINH
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 12
TRUNG TÂM TÂN VƯƠNG – 594/9 HƯƠNG LỘ 2 – BÌNH TÂN
Môn: Toán, Năm học: 2019 – 2020
Câu 105. Cho hàm số f (x) có 2 f (
 x)  x(x  1)(x  2mx  1), x  .
 Hỏi có mấy số nguyên
m không vượt quá 2018 sao cho hàm số 2
g(x)  f (x ) có 7 điểm cực trị ? A. 2019. B. 2016. C. 2017. D. 2018.
Câu 106. Cho hàm số f (x) có đạo hàm 2 2 f (
 x)  (x  x)(x  4x  3), x  .  Tính tổng tất cả
các giá trị nguyên của tham số m để hàm số 2
g(x)  f (x  m) có 3 điểm cực trị. A. 0. B. 6. C. 3. D. 2.
Câu 107. Cho hàm số f (x) có đồ thị hàm số y  f (
 x) được cho như hình vẽ bên. Hàm số 1 2
g(x)  f (x)  x  f (0) có nhiều nhất bao nhiêu điểm cực trị trong khoảng (2;3). 2 y A. 6. 2 O 2 x B. 2. 2 3 C. 5. 2 D. 3.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 120 -

Cực trị của hàm số – Lê Văn Đoàn Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số