11 trang 5 lượt tải

Đạo Hàm Cấp 1 - Bài Tập Tuần 4 | Giải tích hàm | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội

10

Cá hồi bơi ngược dòng để vượt quãng đường 300km. Vận tốc dòng chảy là 6km/h. Giả sử năng lượng tiêu hao của cá khi bơi trên dòng nước đứng yên trong t giờ là 3 E( v) cv t( Ju)n, trong đó c là hằng số, v là vận tốc bơi của cá khi nước đứng yên. Tốc độ tiêu hao năng lượng ( đơn vị: J – km/h) của cá theo vận tốc v khi v 12 km/ là bao nhiêu? Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
.

Môn: Giải tích hàm 10 tài liệu

Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 0.9 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 tuần trước
Tải xuống Chia sẻ Báo cáo
Danh sách Quiz
Tải xuống
/11
Bài 1: Tính đạo hàm cấp 1
1.
3
(x) ln , (2 1),
1 cos
x
e
f x n n
2.
sinx
(x) 2 1f x
3. Tính f’(1) của hàm
2
( ) ( 1) 3 1f x x x x
4.
3 2
15
17 3
1. 2
( )
2
x x
f x
x
5. Tính
' '
(1) (3)f f
biết
2
( ) 4 3f x x x
6. Cho
2
1
x
f x
x
. Tính f’(3)
8. Cho
( 1) arcsin
1
x
y x x
x
. Tính f’(1) 7. Cho
2
1
1f x x
x
.Tính f’(1)
9. Cho hàm
( ) ( 1)( 2)...( 100f x x x x x
. Tính f’(0)
10.
2
3
2
4
4
1. 2
2 1 . 1
x x
y
x x
. Tính f’(0)
Bài 2: Tính đạo hàm hàm ngược:
1. Cho
( ) arctan( ) 2f x x
Tính
1
'(2)f
2. Cho
2
( ) ln( ) 2 3f x e x x
Tính
1
'(5)f
3. Cho
( ) arctan
x
f x e x
. Tính
1
'(1)f
4. Cho
( ) ln(ln )f x x
Tính
1
'(x)f
t ại 1
5. Cho
3
( ) 1 arctanf x x
. Tính
1
'(x)f
t ại 1
6. Cho
2
( )
x x
f x e e
Tính
1
'(x)f
t ại 2
Bài 3: o hàm hàm hTính đạ ợp:
1. Cho
1
. arctan 1y x g
x
-1), bi t g(0) = 2, Tính y’( ế g’(0) = 1
2. Cho
( ) . 2sin( 3) , g(0) 2, '(0)
x
f x e g x g
. Tính f’(3)
3. Cho
( ) ln( (e 1))
x
f x f
Tính f’(x)
4. Cho
2
cos
( ) ( 2). , '(1) 3, f(1) 2
x
g x x f f
x
. Tính g (0). ’
CuuDuongThanCong.com https://fb.com/tailieudientucntt
5. Cho
2 3 2
( ) . 1 , (0) 2, '(0)
x
g x e f x f f
. Tính g’(- 1)
6. Cho
( )
ln 1
f x
y e
. Tính y’
7. Cho
2
1
x
f x
x
. Tính f’(3)
8. Cho
2
1
1f x x
x
. Tính f’(1)
Bài 3: o hàm hàm tham s Tính đạ ố
1.
arctan
( )
ln(1 t)
x t t
y x
y
. Tính y’(0)
2.
3
2
ln 2 1
( )
sinh( 2)
x t
y x
y t t
- . Tính y’( 1)
3. Viết phương tình tiếp tuy ng cong tham s ến đườ ố
2
2
( ) 3 4
t
x t e t
y t t t
t i t=0 ạ
4. Tìm h sệ ố góc ti p tuyế ến k c ng cong tham sủa đườ ố
3
2
( ) sinh( 1) 2
( ) 6 3
x t t
y t t t
Bài 4: Tìm các tham s sao cho: ố
1.
2
4 , 2
( )
sinh( 2) 2 ,
ax x x
f x
x bx x
để hàm s liên t c và kh vi tố ụ ả ại x = -2
2.
, 1
( )
, 1
x
x x
f x
ax b x
có đạo hàm tại x = -1
3.
2
( ). , 0
1, 0
bx
x a e x
y
ax bx x
có các ti p tuy n trái và ph i x = 0 trùng nhauế ế ải tạ
4.
2
, 0
( )
ln(1 )
, 0
ax bx c x
y f x
x x
x
x
vi t i x = 0khả ạ
Bài 5: ng d Ứ ụng
1. (C) có phương trình
( ).
x
m
y mx n e
, biết
(0,1) ( )M C
. Tìm m, n để tiếp tuyến tại
M(0,1) song song v i y = 2x+1 ớ
CuuDuongThanCong.com https://fb.com/tailieudientucntt
2. Phương trình chuyển độ ất điểm đượng của ch c cho bởi
5
1 2
sin
5 8
t
s t
( t tính
bằng giây (s), s tính theo mét (m)). T c a ch m t i giây th 2 là bao ốc độ ủ ất điể ạ ứ
nhiêu?
3. Cá h ng 300km. V n t c dòng ch y là ồi bơi ngược dòng để vượt quãng đườ ậ ố ả
6km/h. Gi s ng tiêu hao c ng yên trong ả ử năng lượ ủa cá khi bơi trên dòng nước đứ
t giờ là
3
( ) ( )E v cv t Jun
, trong đó c là hằ ốc bơi của cá khi nướng số, v là vận t c
đứ ậ ống yên. T : J ốc độ tiêu hao năng lượng ( đơn vị – km/h) của cá theo v n t c v
khi
12 /v km
là bao nhiêu? HD:
300
6
t
v
.
4. Cho c cho bcung (C) đượ ởi phương trình:
2
3
,1 3
x t
t
y t
. Tìm M trên (C) sao
cho ti p tuy n t i M song song v i AB, A(1,1), B(9,27) ế ế ạ ớ
Bài 6:
1. Cho
2
1
(x) x.arccos x
2
f
. Tính df(0)
2. Cho hàm số
sinx
y
x
. Tính
2
2
d y
dx
3. Cho hàm
2
1
( ) (tan ) ln cos
2
f x x x
. Tính
2
16
df
4. Cho hàm số
( ) sinh
1
x
f x
x
. Tìm vi phân c a f khi x gi m tủ ả ừ 0 xu -0,001 ống
5. Cho hàm số
2
ln(10 )
( )
x
f x
x
. Tìm vi phân của f khi x tăng từ n 3,001 3 đế
6. Cho
2
2
( ) ln(1 x 2 x ), sinh
4
t
y f x x
. Tính dy theo dt t ại t = 2
Bài 7:
1. Tìm tham số a, b để
( )
b
f x ax
khi
0x
, biết
3
( ) 1 3 cos ln(1f x x x
2. Tìm a để
2
2 1
( ) 1
a
x
f x e
x x
khi
x 
3. Tìm
,a b
sao cho
1
lim
x b
x
x
e
x a
4. Tìm a để
( 2)
2
2
sin( 2)
lim
4
a
x
x
x
e
x
5. Tìm a, b để
2
1
( ) cosh 1 sinh
2
b
f x x x ax
khi
0x
CuuDuongThanCong.com https://fb.com/tailieudientucntt
6. Tìm
a
để
2
0
ax-ln(1+x) 1
lim
2
x
x
7. Tìm a,b để
2
1
( ) arcsin( ). ln ( 1)
x b
f x e e x a x
khi
1
x
8. Tìm a,b để
1
( ) 5 cos 5sin
b
f x x x x ax
khi
0x
9. Tìm
để
( ) 1
x
f x e x
là VCB b c 2 khi ậ
0x
Bài 8:
1. Tìm h sệ ố
4
x
trong khai tri n Maclaurint cể ủa
( ) ln(cosxf x
2. Tìm h sệ ố
4
x
trong khai tri n Maclaurint cể ủa
2
2
( )
x x
f x e
3. Khai tri n Taylor cể ủa hàm
1
( )
2 3
f x
x
tại
0
2x
n b đế ậc 2
4. Khai tri n Maclaurint cể ủa hàm
2
( ) cos .sinxf x x
n c p 4 đế ấ
5. Tìm h sệ ố
3
x
trong khai tri n Maclaurint ể
2
ln(3 )
( )
1 arctan(2
x
f x
x
6. Khai tri n Taylor hàm ể
2
1
( ) .ln
x
f x e x
n b c 2 tđế ậ ại
0
2x
7. Tìm h sệ ố
3
x
trong khai tri n Maclaurint ể
2
( ) (1 3 )arctan( 1
x
f x x e
8. Khai tri n Maclaurint cùa hàm ể
100
40
(1 )
(1 2 )
x
y
x
n đế
2
x
9. Khai tri n Maclaurint hàm ể
( )
1
x
x
f x
e
n c p 4 đế ấ
Bài 9:
1. Cho hàm số
3
3
( ) 1 sinf x x
. Tính
(5)
(0)f
2. Cho hàm số
2
2
( )
1
x x
f x
x x
. Tính
(4)
(0)f
3. Cho hàm số
4
( ) ( 1)ln(1 )f x x x
. Tính
(10)
(0)f
Bài 10: Tìm gi n bới hạ ằng các phướng pháp đã học:
1.
0
1 1
lim
arcsin
x
x x
2.
1
1
lim
ln
x
x
x
x x
3.
2
lim .ln arctan
x
x x
4.
2
4
0
cos 1
2
lim
x
x
x
x
5.
0
arctan arcsin
lim
tan sinx
x
x x
x
6.
arctan
3
0
ln(1 ) 1
lim
2 4
x
x
e x
x
7.
1
3
2
0
cosh 2 x 1 3
lim
ln(1 tan ) arcsin
2
x
x x
x
x x
8.
2
0
arcsin
lim
1 tan
x
x
x xe
x x x
9.
1
lim tan
2 1
x
x
x
x
10.
1
1
lim
x
x
x
x
e
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Bài toán thực tế
Câu 1 : V i m i lo i v i có kh c chi u ngang) c s n xuớ ỗ ạ ả ổ ( kích thướ ề ố định, chi phí để ả ất
x mét (m) là C = f(x), đơn vị ồng (đ) là đ
Hãy cho bi cết đơn vị ủa
'( )f x
.
Về ặ m t thực tế
'(9000)f
có ý nghĩa gì ?
'(2000) 20f
u gì ? nói lên điề
Câu 2 : M t thùng hình tr c. Thùng b ng c ra ộ ụ chứa 1000l nướ ị thủ ở đáy và thoát nướ
ngoài . Th c còn lể tích nướ ại sau t giây đượ ởi phương trình :c cho b
( ) 1000(1 ),0 6
60
t
V t t
a) Tìm t c thoát ra ngoài theo th i gian t. ố ộc đ nướ ờ
b) Tạ ậi các th nh vời điểm 0, 10, 20, 30, 40, 50, 60, xác đị n t c thoát và ốc dòng nướ
lượng nước còn lại.
Câu 3 : Phân bón có th i s ng cây tr ng. M t nghiên c Kenya ể làm thay đổ ản lượ ồ ộ ứu ở
trên ngô cho bi t sế ản lượ ột địa phương cụng của ngô ( tại m thể) theo số kg phân bón
(x) đượ ễn dước biểu di i dạng
( )y f x
, trong đó f tính theo kilogam.
a) Nêu ý nghĩa
(5) 11500f
và
'(5) 350f
b) Ướ ịc tính s ng ngô theo các giá trản lượ đã cho ở câu trên nếu sử dụng 5,2 kg phân
bón.
Câu 4 : V ng thái là ới 1 mol khí lý tưởng , phương trình trạ
8.31PV T
trong đó P (
kPascal), V (lit) , T ( Kenvin). T i th i m nhiạ ờ điể ệt độ đạt được
0
300 K
và th tích khí ể
đạt 100L, Vân t t là ốc tăng nhiệ
0,1 /K s
và v n t tích là ậ ốc tăng thể
0, 2 /L s
, tính t ốc độ
thay đổi của áp suất P.
Câu 5 : Chi phí ( đô la ) khi sả ất x đơn vị nào đó là n xu hàng hóa cụ thể
2
( ) 5000 10 0.05C x x
.
a) Hãy tìm t n thiên trung bình c a C theo x khi m n xu i ố ộc đ biế ủ ức sả ất thay đổ
I, từ x = 100 đến x =105.
II, từ n x =101 x = 100 đế
b, Hãy tìm t n thiên t c th i c ng v i x khi x = 100. u này ốc độ biế ứ ờ ủa C tương ứ ớ ( Điề
đư ọợc g i là chi phí biên.)
Câu 6 : Chi phí s n xu t x ao-ả ấ xơ vàng từ ới là C = f(x) đô la . một mỏ vàng m
CuuDuongThanCong.com https://fb.com/tailieudientucntt
a) Ý nghĩa của đạo hàm
'(x)f
là gì ?. Đơn vị tính của nó là gì ?
b)
'(800) 17f
có nghĩa là gì?
c) Bạn nghĩ các giá trị của
'(x)f
s m trong th i gian ng n ? Trong thẽ tăng hay giả ờ ắ ời
gian dài thì sao ? Gi i thích. ả
Câu 7 : S ng vi khu n sau t gi trong m t thí nghi m có ki m soát là n =f(t). ố lượ ẩ ờ ộ ệ ể
a) Ý nghĩa của đạo hàm
'(5)f
là gì ? tính c a nó là gì ? Đơn vị ủ
b) Giả ạ ẩ sử không giới h n không gian và ch ng cho vi khuất dinh dưỡ n. Bạn nghĩ cái
nào lớn hơn
'(5) , '(10f f
. N u ngu n cung ng ch ng b i h n thì ế ồ ứ ất dinh dưỡ ị giớ ạ
điều đó có ảnh hưởng điến kết qu c n ko?. Gi i thích. ả ủa bạ ả
Câu 8 : S ng ( tính b ng pound) c c bi c bán b i m t công ty ố lượ ằ ủa cà fe xay đặ ệt đượ ở ộ
cà phê v ound là Q = f (p). ới giá p đô la/p
a) Ý nghĩa của đạo hàm
'(8)f
là gì? đơn vị tính của nó là gì?
b) f(8) là dương hay âm ? giải thích.
Câu 9 : Lượ hòa tan trong nướ ệt độ ủa nướng oxy có thể c tùy thuộc vào nhi c c.(
Vì v y s ô nhi m nhi ng ô-xy c cho ậ ự ễ ệt ảnh hưởng đến hàm lượ ủa nước) . Đồ thị
thấ ếy làm th hòa tan o-nào độ xy S bi n thiên ế
Câu 10 : Hãy tìm nh ng cong ững điểm trên đườ
4 2
6 4y x x
mà t p tuyại đó tiế ến
nằm ngang.
Câu 11: Phương trình chuyển động của một hạt là
3 2
( ) 2 5 3 4s t t t t
, trong đó s
đư ố ủợc tính b c tính b ng giây. Hãy tìm gia tằng centimet và t đượ ằ c c a hạt như một
hàm s theo th i gian. Gia t c sau 2 s là bao nhiêu? ố ờ ố
Câu 12 : Phương trình chuyển động của một hạt là
3
( ) 3s t t
, trong đó s được tính
bằng m và t được tính bằng giây. Hãy tìm :
a) Vận tốc và gia tốc như các hàm theo t
b) Gia tốc sau 2 s và ,
c) Gia t c khi v n t c b ng 0. ố ậ ố ằ
Câu 13 : ng c t là : Phương trình chuyển độ ủa một hạ
4 3 2
( ) 2s t t t t
Trong đó s đượ ằng mét và t được tính b c tính bằng giây.
a) Hãy tìm v n t c và gia tậ ố ốc như các hàm số theo t.
b) Tìm gia tốc sau 1 giây.
c) Vẽ đồ ị ị ậ th hàm v trí, v n tốc, gia tốc trên cùng một màn hình hi n th . ể ị
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Câu 14 : Đị ột lượng khí đượnh luật Boyle phát biểu rằng khi m c nén tại áp suất không
đổ ủi, thì áp suất P c a khí tỷ ủ l ngh ch vệ ị ới thể tích V c a khí.
a) Giả ằ ấ ế sử r ng áp su t c ng khí chiủa lượ m 0,106
3
m
tại
0
25 C
là 50 kPa. Hãy viết
V như một hàm số theo P.
b) Hãy tính
/dV dP
khi P = 50kPa. Ý nghĩa của đạo hàm là gì? Đơn vị tính của
nó là gì?
Câu 15 : Tìm phương trình các tiế ủa đườp tuyến c ng cong
1
1
x
y
x
mà nó song song
với đường thẳng x – 2y = 2.
Câu 16 : M t nhà máy s n xu t các súc v i v i chi u r ng c ng q v i này ( ộ ả ấ ả ớ ề ộ ố định. Lượ ả
theo yard) đượ ột hàm theo giá bán p ( đơn vị là đôla / yard), vì vậc bán là m y chúng ta
có th ể viết q = f(p) . Lúc đó tổng thu nhập với giá bán p là
( ) . (R p p f
.
a) Có ý nghĩa gì khi phát biểu rằng f(20) = 10,000 và
'(20) 350f
.
b) Giả sử có các thông s ố như câu a, tìm R’ (20) và giải thích cho đáp án của bạn.
Câu 17 : M t v t có tr c kéo lê d c theo m t ph ng b i m t l c tác ộ ậ ọng lượng W đượ ọ ặ ẳ ở ộ ự
độ ậ ế ạng dọc theo sợi dây thừng nối với v t. N u dây thừng t o một góc
v i m t ph ng, ớ ặ ẳ
lúc đó độ lớn của lực là
W
sin cos
F
Trong đó
là h ng s s ma sát. ằ ố được gọi là hệ ố
a) Tìm t n thiên c a F theo ố ộc đ biế ủ
.
b) bi Khi nào t ốc độ ế ằn thiên b ng 0?
c) Nếu W = 50 lb và
0.6
, hãy v c theo ẽ đồ thị ủa F như là hàm số
và s ử
dụng nó để xác định giá trị của
sao cho
/ 0dF d
. Giá trị đó có phù hợp
với kết qu cả ủa bạn trong câu b không?
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Câu 18: N u f và g là các hàm s c c bi u di i, ế ố mà đồ thị ủa chúng đượ ể ễn bên dướ
cho
( ) ( ( )), ( ) ( ( )), w( ) ( (u x f g x v x g f x and x g
Tìm m hàm, n u nó ỗi đạo ế
t n t u nó không t n t i, gi i thích t i sao. ồ ại. Nế ồ ạ ả ạ
a)
'(1)u
b)
v'(1)
c)
w '(1)
Câu 19: N u f là hàm s c c bi u di i, cho ế ố mà đồ thị ủa nó đượ ể ễn bên dướ
2
( ) ( ( )) ( ) (h x f f x and g x f
. S d c tính giá tr c a mử ụng đồ thị f để ướ ị ủ ỗi đạo
hàm.
a)
'(2)h
b)
g'(2)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Câu 20 : S d ch chuy n c a m t h t trên m t dây rung c cho bự ị ể ủ ộ ạ ộ đượ ởi phương trình
( ) 10 sin(10
4
s t t
trong đó s đượ ằng centimet và t được tính b c tính bằng giây.
Tìm v n t t sau t giây. ậ ốc c a hủ ạ
Câu : N ng c a v c cho là 21 ếu phương trình chuyển độ ủ ật đượ
( ) cos( ts t A
,
người ta nói r ng hằ ạt đó có chuyển động điều hòa đơn.
(a) Tìm v n t i gian t. ậ ốc c a hủ ạt tại thờ
(b) Vận t c bố ằng 0 khi nào?
Câu 22 : Ngôi sao bi n quang ki là ngôi sao mà ánh sáng c a nó ế ểu Thiên Vương ủ
luôn phiên tăng và giảm. Ngôi sao dễ dàng nhìn th y nh t ki là ngôi sao Delta ấ ấ ểu đó
Cephei, có kho ng th i gian gi a nhả ờ ữ ững l sáng c i là 5,4 ngày. ần độ ủa nó đạt cực đạ
Độ sáng trung bình c sáng của ngôi sao nào là 4,0 và độ ủa nó biến đổi
0,35
. Khi
xem xét các d u này sáng c a Delta Cephei t i thữ liệ , độ ủ ạ ời gian t, trong đó t được
tính theo ngày, đã được mô ph ng qua hàm s ỏ ố
2
( ) 4 0.35sin(
5.4
t
B t
a) Tìm t n thiên c sáng sau t ngày. ố ộc đ biế ủ ộa đ
b) Tìm tố ộc đ tăng ( có 2 chữ số thập phân) sau một ngày.
Câu 23 : Chúng ta có công th dài chi u sáng ban ngày theo gi ức tính độ ế ờ ở
Philadelphia vào ngày th ứ t của năm :
2
( ) 12 2.8sin( ( 80)
365
L t t
Sử d ng công th so sánh sụ ức này để ố lượng gi chi nào ờ ếu sáng ban ngày tăng như thế
ở Philadelphia vào ngày 21 tháng 3 và ngày 21 tháng 5.
Câu 24 : M t h t chuy ng d c theo m ng th ng v d ch chuy n s(t), vộ ạ ển độ ọ ột đườ ẳ ới độ ị ể ận
t c v(t) và gia t c a(t). Ch ng minh : ố ố ứ
( ) ( ).
dv
a t v t
ds
Giải thích sự khác nhau giữa ý nghĩa đạo hàm của
/ /dv dt and dv d
Câu 25 t qu bóng d báo th i ti t. T i th m t : Không khí đang được bơm vào mộ ả ự ờ ế ạ ời điể
bất kì, thể tích của quả bóng là V(t) và bán kính c a nó là r(t). ủ
a) Đạo hàm của dV/dt và dV/dr bi u th u gì? ể ị cho điề
b) Biểu di i d ng dr/dt. ễn dV/dt dướ ạ
VI PHÂN
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Câu 26 : C nh c a m t hình l c là 30 cm v i sai s cho phép cạ ủ ộ ập phương đo đượ ớ ố ủa
phép đo là 0.1 cm. Sử ụng vi phân để dĩ tối đa, sai số tương đố d ước tính sai số khả i
và sai s theo t l tính (a) th tích c a hình l n tích ố ỉ ệ phần trăm để ể ủ ập phương và (b) diệ
bề mặt của hình l ập phương.
Câu 27 : Bán kính của một đĩa hình tròn được tính là 24 cm với sai s t ố ối đa là 0.2 cm.
a) Sử d c tính sai s t a di ụng vi phân để ướ ố ối đa củ ện tích cái đĩa.
b) Sai số i là bao nhiêu ? Sai s theo t l tương đố ố ỉ ệ phần trăm là bao nhiêu?
Câu 28 : Chu vi c t hình của mộ ầu đo đượ dĩ là 0.5 cm.c là 84 cm và sai số khả
a) Sự d c tính sai s t a di n tích b m t. Sai sụng vi phân để ướ ố ối đa củ ệ ề ặ ố tương đối
là bao nhiêu?
b) Sự d c tính sai sụng vi phân để ướ ố t a di n tích b m t. Sai sối đa củ ệ ề ặ ố tương đối
là bao nhiêu?
c) Sự d c tính sai s t a th tích. Sai s i là bao ụng vi phân để ướ ố ối đa củ ể ố tương đố
nhiêu?
Câu 29: Sử d t l p dày 0.05 cm lên ụng vi phân để ước tính lượng sơn dùng để sơn mộ ớ
m t mái vòm hình bán cộ ầu có đường kính 50m.
Câu 30 : a) S d tìm công th c tính th tích x p x cử ụng vi phân để ứ ể ấ ỉ ủ ộ ỏa m t cái v hình
trụ có chi u cao h, bán dày ề kính trong r, độ
r
.
b)Sai s n tri n bao nhiêu khi s dố tiế ể ử ụng công thứ ừc t câu a.
Câu 31 M t c nh c: ộ ạ ủa hình tam giác vuông dài 20 cm và góc đối đỉnh đo được là 30
độ ố, với sai s khả . dĩ là 0.1 độ
a) Sử d c tính tính chi u dài c nh huy ụng vi phân để ướ sai số để ề ủa cạ ền.
b) Sai số theo tỉ l ệ phần trăm là bao nhiêu?
Câu 32: N u m n tr n tr nh lu t Ôm phát ế ột dòng điện I đi qua một cái điệ ở có điệ ở R, Đị ậ
biểu r sằng độ ụt áp là V = IR. N i mếu V không đổi và R được đo vớ ột sai số nào đó,
s d ng t r ng sai s i khi tính I x p x b ng ( v l n ) ử ụng vi phân để chứ ỏ ằ ố tương đố ấ ỉ ằ ề độ ớ
với sai số tương đối của R.
Câu 33 : Khi máu ch y vào m ng F ( th tích máu trên m ả ạch máu, thông lượ ể ỗi đơn vị
thời gian ch y qua mả ột điểm được cho) được cho bởi công thức:
4
.F k R
Trong đó k là hằng số, R là bán kính m ch máu. ạ
Chứng minh r i c a F g i c a R ằng độ biến thiên tương đố ủ ấp độ biến thiên tương đố ủ
kho ng 4 lả ần. Bán kính tăng 5% ảnh hưởng như thế nào đến lưu lượ ng máu.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Max -Min
Câu 1 : Kính vi n v d ng ngày ễ ọng Hubble được tàu không gian Discovery đưa vào sử ụ
24/04/1990. Mô hình v n t c c a tàu trong s m nh này, t lúc r i b phóng t = 0 cho ậ ố ủ ứ ệ ừ ờ ệ
đế ẩn khi được tên lửa đ y nhanh kh i b t i th c cho b i ỏ ệ ạ ời điểm t = 126 giây, đượ ở
3 2
( ) 0.001302 0.09029 23.61 3.0v t t t t
( đv là feet/giây)
Hãy s d c tính các giá tr c i và c c ti u tuy i gia tử ụng mô hình này để ướ ị ực đạ ự ể ệt đố ốc
c a tàu gi a lúc củ ữ ất cánh và lúc phóng đi hoàn toàn.
Câu 2 : Tìm các điểm tới hạn của hàm s ố
2
3 2 2
4 3 2
3/4 1/4
2
4
2 2
5
1 1
, ( ) 4 , ( ) 2 4
3 2
, ( ) 2 3 36 , ( ) 1
, ( ) 1
1
, ( ) , ( ) 2
1
, ( ) ( 4) , ( ) 2cos sin
a f x x x k g t t
b f x x x x l g x x
c g t t t t
y
d g y e h t t t
y y
f f x x x h f
Câu 3 : Giữa
0
0 C
và
0
30 C
, th tích V (cm kh i) c c cho ể ố ủa 1 kg nước ở nhiệt độ T đượ
gần đúng bởi công thức sau :
2 3
999.87 0.06426 0.0085043 0.000067V T T
Tìm nhi mà t c có mệt độ ại đó nướ ật độ l n nh ớ ất.
Câu 4 : Mô hình giá trung bình (USD) m ng tr ng tột pound đườ ắ ừ năm 1993 đến năm
2003 được cho bởi hàm số sau :
2 3 4 5
( ) 0.4074 0.04458 0.03629 0.008956 0.0009037 0.00003S t t t t t
Trong đó t được tính theo năm kể tháng 8 năm 1993.Ướ ời điểm khi đườ từ c tính th ng
có giá r t nh t trong quãng th i gian t - 2003 ẻ nhất và đắ ấ ờ ừ năm 1993
CuuDuongThanCong.com https://fb.com/tailieudientucntt

Tài liệu khác của Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội

Preview text:

Bài 1: Tính đạo hàm cấp 1 x e 1. 3 f (x)  ln ,x   (2n 1),n  f  x  1 2.  sinx (x) 2 1 cosx 3 2 15 3. Tính f’(1) của hàm   2 (f ) x  ( x x 1)  3  x 1  x 1. x 2 4. f ( ) x  17 3 x  2  x  5. Tính ' ' f  biết 2 (f )x  x 4  x 3   . Tính f’(3)  (1) f (3) 6. Cho 2 f   x  x 1 x  1
8. Cho y  x ( x1) arcsin . Tính f’(1) 7. Cho 2 f  x 1   x.Tính f’(1) x 1  x 9. Cho hàm (f )x (x  1 x )(  x2)  ...( x10  0. Tính f’(0) 2 3   10. x 1. x 2 y  . Tính f’(0) 2x 2 4 4 1 . x  1
Bài 2: Tính đạo hàm hàm ngược: 1. Cho ( f ) x arc  tan( )x 2   Tính  1 f   '(2) 2. Cho 2 (f )x ln  ( e ) x 2 x 3  Tính  1 f   '(5) 3. Cho 1 ( ) x f x e a
 rctanx . Tính  f  '(1) 4. Cho (f )x ln  (ln )x Tính  1 f   '(x) tại 1 5. Cho f x   x 3 ( ) 1 ar  ctan. Tính  1 f   '(x) tại 1 6. Cho 2 1 ( ) x x f x e 
e Tính  f   '(x) tại 2
Bài 3: Tính đạo hàm hàm hợp:    1. Cho 1 y  .x agrctan 1 
 Tính y’(-1), biết g(0) = 2, g’(0) = 1    x 2. Cho ( ) x f x . e  2 g sin( x 3) , g(0) 2
 , g'(0) . Tính f’(3) 3. Cho ( )  ln( (ex f x f 1)) Tính f’(x)   4. Cho cos 2 x g( )x  ( x  2). f , f'(1) 3, f(1)    2. Tính g’(0).  x1  CuuDuongThanCong.com
https://fb.com/tailieudientucntt 5. Cho 2x  3 g x  e  2 ( ) . f x  
1 , f (0)  2, f '(0) . Tính g’(-1) 6. Cho y   f (x) ln e  1. Tính y’   7. Cho x 2 f    x . Tính f’(3)  x1   8. Cho 1 2 f  x 1   x. Tính f’(1)  x
Bài 3: Tính đạo hàm hàm tham số x  tarctant 1. ( y ) x   . Tính y’(0)  y ln(1 t) x   ln 3t 2   1 2. ( y ) x   . Tính y’(-1) 2 y sinh(t  t 2) x  t  
3. Viết phương tình tiếp tuyến đường cong tham số  t e 2 t tại t=0 2  ( y t) t  3t 4 3    
4. Tìm hệ số góc tiếp tuyến k của đường cong tham s  ố( x t) sinh(t 1) 2 2  ( y t) 6t  3t
Bài 4: Tìm các tham số sao cho: 2 a  x  4 , x x  2 1. f ( ) x  
để hàm số liên tục và khả vi tại x = -2 sinh(x 2) 2bx , x    x x , x   1 2. f ( ) x   có đạo hàm tại x = -1  ax ,b x 1  (  ). bx x a e , x 0 3. y  
có các tiếp tuyến trái và phải tại x = 0 trùng nhau 2 ax  bx1, x 0 2 ax  bx ,c x 0 
4. y  f ( )x   ln(1 x ) x khả vi tại x = 0 ,x   0  x
Bài 5: Ứng dụn g 1. (C) có phương trình x ( ). m y mx n e , biết ( M0,1) (  )
C. Tìm m, n để tiếp tuyến tại
M(0,1) song song với y = 2x+1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 
2. Phương trình chuyển động của chất điểm được cho bởi 1 5 2 t s  t  sin ( t tính 5  8
bằng giây (s), s tính theo mét (m)). Tốc độ của chất điểm tại giây thứ 2 là bao nhiêu?
3. Cá hồi bơi ngược dòng để vượt quãng đường 300km. Vận tốc dòng chảy là
6km/h. Giả sử năng lượng tiêu hao của cá khi bơi trên dòng nước đứng yên trong t giờ là 3 ( E ) v c v (t J )
un, trong đó c là hằng số, v là vận tốc bơi của cá khi nước
đứng yên. Tốc độ tiêu hao năng lượng ( đơn vị: J – km/h) của cá theo vận tốc v khi v 12  k / m là bao nhiêu? HD:t 300  v . 6 2  
4. Cho cung (C) được cho bởi phương trình: x t 
,1 t 3. Tìm M trên (C) sao 3  y  t
cho tiếp tuyến tại M song song với AB, A(1,1), B(9,27) Bài 6:   1. Cho 1 2 f (x)  x.arccos x  . Tính df(0)  2 2 2. Cho hàm số sinx d y y  . Tính x 2 dx 2   3. Cho hàm 1 2 f ( )x  (tan ) x ln  cos x. Tính df   2 16  4. Cho hàm số  x  f ( x ) sinh
 . Tìm vi phân của f khi x giảm từ 0 xuống -0,001  x 1 2  5. Cho hàm số ln(10 x ) f ( ) x 
. Tìm vi phân của f khi x tăng từ 3 đến 3,001 x  6. Cho t 2 2
y  f ( )x  ln(1 x 2 x ), x sinh . Tính dy theo dt tại t = 2 4 Bài 7:
1. Tìm tham số a, b để ( ) b f x ax khi x 0 , biết 3 (f )x 1  3 x co  s x ln  (1  2   2. Tìm a để  a x 2 1 f ( ) x  e  1   khi x   x  x xb    3. Tìm , a b  x 1 sao cho lim    e x  x a    a 4. Tìm a để sin(x 2)  ( x 2) lim       e  2 x 2  x  4  5. Tìm a, b để 1 2 ( ) c  osh 1   sinh b f x x x ax khi x 0 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 6. Tìm a  để ax-ln(1+x) 1 lim  2  0 x x 2 7. Tìm a,b để 2 x b 1
f ( x ) arcsin(e  e ). lnx a( x 1) khi x 1  8. Tìm a,b để 1 ( ) 5 cos 5sin b f x x x x ax    khi x 0 9. Tìm   để ( ) x f x  e 1   x là VCB bậc 2 khi x 0 Bài 8: 1. Tìm hệ số 4
x trong khai triển Maclaurint của (f ) x l  n(cosx 2. Tìm hệ số 4
x trong khai triển Maclaurint của 2 2 ( ) x x f x e  
3. Khai triển Taylor của hàm 1 f ( ) x  tại x 2 đến bậc 2 0 2 3x
4. Khai triển Maclaurint của hàm 2 (f )x co  s . x sinx đến cấp 4 2 5. Tìm hệ số  3 ln(3 x )
x trong khai triển Maclaurint f( ) x  1 arctan(2x 6. Khai triển Taylor hàm 2 x 1 f( ) x e  
.ln x đến bậc 2 tại x 2 0 7. Tìm hệ số 3
x trong khai triển Maclaurint 2 ( ) (1  3  )arctan(x f x x e  1 100 
8. Khai triển Maclaurint cùa hàm (1 x ) y  đến 2 x 40 (1 2x )
9. Khai triển Maclaurint hàm x f ( ) x  đến cấp 4 x e 1 Bài 9: 1. Cho hàm số 3 3 (f )x  1 s  in x. Tính (5) f (0) 2 2. Cho hàm số 1 x x f ( ) x  . Tính (4) f (0) 2 1 x x 3. Cho hàm số 4 (f )x ( x 1)  ln(1  )x. Tính (10) f (0)
Bài 10: Tìm giới hạn bằng các phướng pháp đã học:   x     1. 1 1 x 1 2 lim    2.li m lim  x .ln arctanx x 0 x arcsinx
x1 lnx x 3. x    2 x cosx  1 arctanx  arcsinx arctanx e ln(1  ) x  1 4. 2 lim 5. lim 6. lim  4 x 0 x x 0 tanx  sinx x 0 3 2 4 x  cosh 2 x   1 x 13 3  x x  7. arcsinx xe lim 8.l im  2 x 0 x   x 0 2   ln(1 tanx ) arcsinx x 1 x tanx 2 1 1 1 x   x   x  1 x x 9. lim tan  1li0. m   x  2x 1 x   e    CuuDuongThanCong.com
https://fb.com/tailieudientucntt Bài toán thực tế
Câu 1 : Với mỗi loại vải có khổ ( kích thước chiều ngang) cố định, chi phí để sản xuất
x mét (m) là C = f(x), đơn vị là ồ đ ng (đ)
 Hãy cho biết đơn vị của f'( ) x .
 Về mặt thực tế f'(9000) có ý nghĩa gì ? 
'(f2000)  20 nói lên điều gì ?
Câu 2 : Một thùng hình trụ chứa 1000l nước. Thùng bị thủng ở đáy và thoát nước ra
ngoài . Thể tích nước còn lại sau t giây được cho bởi phương trình : t V( )t 1000(1 ),0 t  6 60 a) Tìm tốc ộ
đ nước thoát ra ngoài theo thời gian t.
b) Tại các thời điểm 0, 10, 20, 30, 40, 50, 60, xác định vận tốc dòng nước thoát và lượng nước còn lại.
Câu 3 : Phân bón có thể làm thay đổi sản lượng cây trồng. Một nghiên cứu ở Kenya
trên ngô cho biết sản lượng của ngô ( tại một địa phương cụ thể) theo số kg phân bón
(x) được biểu diễn dưới dạng y f ( )x , trong đó f tính theo kilogam. a) Nêu ý nghĩa (f5) 1  1500 và '(f5) 350
b) Ước tính sản lượng ngô theo các giá trị đã cho ở câu trên nếu sử dụng 5,2 kg phân bón.
Câu 4 : Với 1 mol khí lý tưởng , phương trình trạng thái là PV 8 .31 T trong đó P (
kPascal), V (lit) , T ( Kenvin). Tại thời điểm nhiệt độ đạt được 0 300 K và thể tích khí
đạt 100L, Vân tốc tăng nhiệt là 0,1 K / s và vận tốc tăng thể tích là 0, 2L / s, tính tốc độ
thay đổi của áp suất P.
Câu 5 : Chi phí ( đô la ) khi sản xuất x đơn vị hàng hóa cụ thể nào đó là 2 (C )x 50  00 10  x 0.  05 . a) Hãy tìm tốc ộ
đ biến thiên trung bình của C theo x khi mức sản xuất thay đổi
I, từ x = 100 đến x =105.
II, từ x = 100 đến x =101
b, Hãy tìm tốc độ biến thiên tức thời của C tương ứng với x khi x = 100. ( Điều này được ọ g i là chi phí biên.)
Câu 6 : Chi phí sản xuất x ao-xơ vàng từ một mỏ vàng mới là C = f(x) đô la . CuuDuongThanCong.com
https://fb.com/tailieudientucntt
a) Ý nghĩa của đạo hàm f '(x) là gì ?. Đơn vị tính của nó là gì ?
b) '(f800) 17 có nghĩa là gì?
c) Bạn nghĩ các giá trị của f '(x) sẽ tăng hay giảm trong thời gian ngắn ? Trong thời
gian dài thì sao ? Giải thích.
Câu 7 : Số lượng vi khuẩn sau t giờ trong một thí nghiệm có kiểm soát là n =f(t).
a) Ý nghĩa của đạo hàm f '(5) là gì ? Đơn vị tính của nó là gì ?
b) Giả sử không giới hạn không gian và chất dinh dưỡng cho vi khuẩn. Bạn nghĩ cái
nào lớn hơn '(f5) , f '(10. Nếu nguồn cung ứng chất dinh dưỡng bị giới hạn thì
điều đó có ảnh hưởng điến kết quả của bạn ko?. Giải thích.
Câu 8 : Số lượng ( tính bằng pound) của cà fe xay đặc biệt được bán bởi một công ty
cà phê với giá p đô la/ o p und là Q = f (p).
a) Ý nghĩa của đạo hàm f '(8) là gì? đơn vị tính của nó là gì?
b) f(8) là dương hay âm ? giải thích.
Câu 9 : Lượng oxy có thể hòa tan trong nước tùy thuộc vào nhiệt độ của nước.(
Vì vậy sự ô nhiễm nhiệt ảnh hưởng đến hàm lượng ô-xy của nước) . Đồ thị cho
thấy làm thế nào độ hòa tan o-xy S biến thiên
Câu 10 : Hãy tìm những điểm trên đường congy 4 2  x 6  x 4
 mà tại đó tiếp tuyến nằm ngang.
Câu 11: Phương trình chuyển động của một hạt là 3 2 (s )t 2  t 5  t 3  t 4 , trong đó s
được tính bằng centimet và t được tính bằng giây. Hãy tìm gia tốc của hạt như một
hàm số theo thời gian. Gia tốc sau 2 s là bao nhiêu?
Câu 12 : Phương trình chuyển động của một hạt là 3 (s )t  t 3
 , trong đó s được tính
bằng m và t được tính bằng giây. Hãy tìm :
a) Vận tốc và gia tốc như các hàm theo t b) Gia tốc sau 2 s và ,
c) Gia tốc khi vận tốc bằng 0.
Câu 13 : Phương trình chuyển động của một hạt là :s 4 3 2 ( )t  t 2  t  t 
Trong đó s được tính bằng mét và t được tính bằng giây.
a) Hãy tìm vận tốc và gia tốc như các hàm số theo t.
b) Tìm gia tốc sau 1 giây. c) Vẽ đồ t ị h hàm vị trí, ậ
v n tốc, gia tốc trên cùng một màn hình hiển thị. CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 14 : Định luật Boyle phát biểu rằng khi một lượng khí được nén tại áp suất không
đổi, thì áp suất P của khí tỷ lệ nghịch với thể tích V của khí.
a) Giả sử rằng áp suất của lượng khí chiếm 0,1063 m tại 0 25 C là 50 kPa. Hãy viết
V như một hàm số theo P.
b) Hãy tính dV / dP khi P = 50kPa. Ý nghĩa của đạo hàm là gì? Đơn vị tính của nó là gì?
Câu 15 : Tìm phương trình các tiếp tuyến của đường cong x 1 y  x mà nó song song 1
với đường thẳng x – 2y = 2.
Câu 16 : Một nhà máy sản xuất các súc vải với chiều rộng cố định. Lượng q vải này (
theo yard) được bán là một hàm theo giá bán p ( đơn vị là đôla / yard), vì vậy chúng ta
có thể viết q = f(p) . Lúc đó tổng thu nhập với giá bán p là (R )p .p  (f .
a) Có ý nghĩa gì khi phát biểu rằng f(20) = 10,000 và '(f20)  3  50.
b) Giả sử có các thông số như câu a, tìm R’ (20) và giải thích cho đáp án của bạn.
Câu 17 : Một vật có trọng lượng W được kéo lê dọc theo mặt phẳng bởi một lực tác
động dọc theo sợi dây thừng nối với vật. Nếu dây thừng tạo một gó cv ới mặt phẳng,
lúc đó độ lớn của lực là W  F   sin  cos 
Trong đó  là hằng số được gọi là hệ số ma sát. a) Tìm tốc ộ đ biến thiên của F theo  .
b) Khi nào tốc độ biến thiên bằng 0?
c) Nếu W = 50 lb và   0.6, hãy vẽ đồ thị của F như là hàm số theo  và sử
dụng nó để xác định giá trị của  sao cho dF / d  0. Giá trị đó có phù hợp
với kết quả của bạn trong câu b không? CuuDuongThanCong.com
https://fb.com/tailieudientucntt
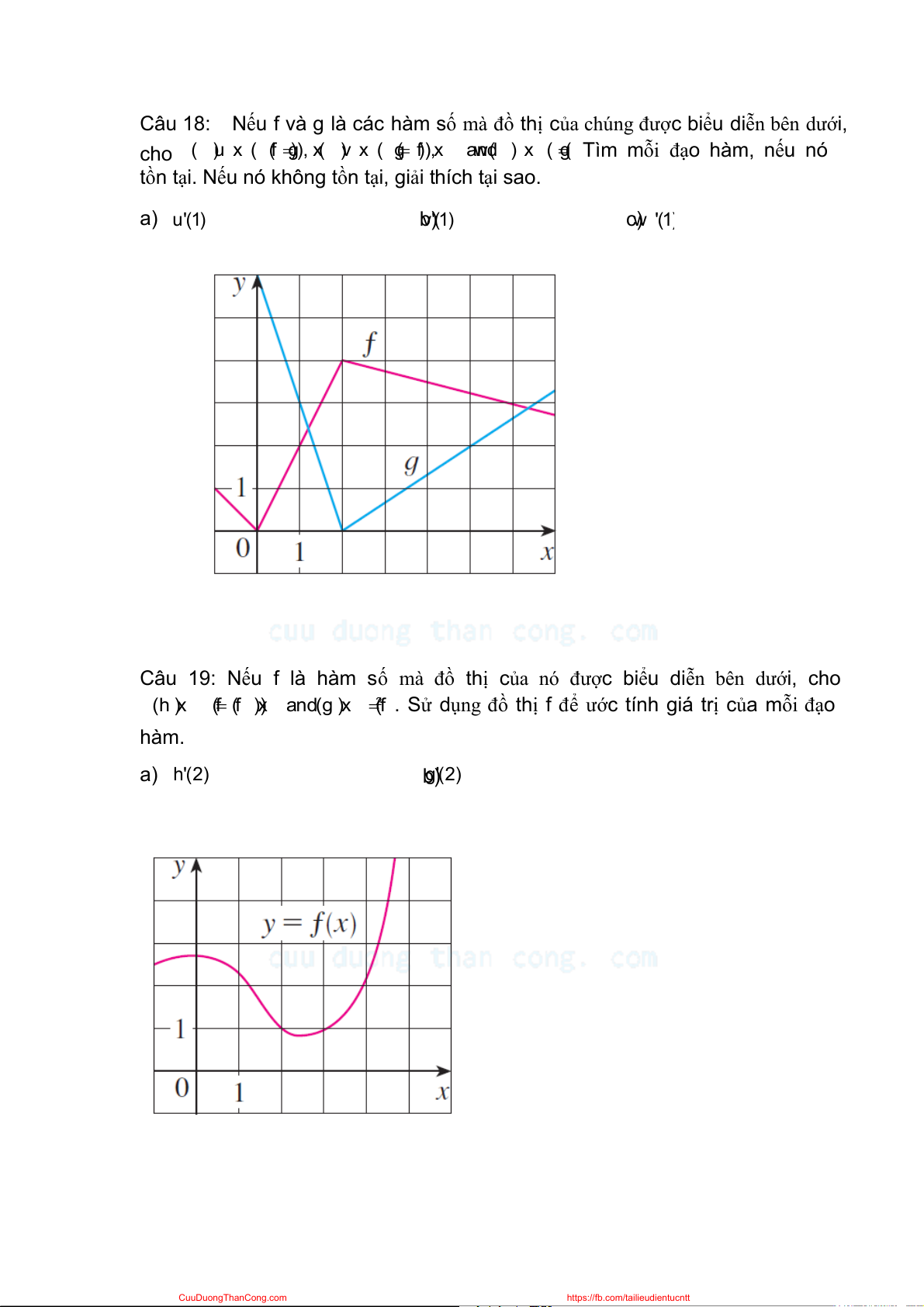
Câu 18: Nếu f và g là các hàm số mà đồ thị của chúng được biểu diễn bên dưới, cho ( )u x ( (f )  ) g , ( x )v x ( (g )f),x w an(d ) x ( ( g
 Tìm mỗi đạo hàm, nếu nó
tồn tại. Nếu nó không tồn tại, giải thích tại sao. a) u'(1) b) v'(1) c) w '(1)
Câu 19: Nếu f là hàm số mà đồ thị của nó được biểu diễn bên dưới, cho 2 (h )x (f (f ))x an ( d g )x (
f . Sử dụng đồ thị f để ước tính giá trị của mỗi đạo hàm. a) ' h (2) b) g'(2) CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 20 : Sự dịch chuyển của một hạt trên một dây rung được cho bởi phương trình 1 ( s t) 10 sin(10
 t trong đó s được tính bằng centimet và t được tính bằng giây. 4
Tìm vận tốc của hạt sau t giây.
Câu 21 : Nếu phương trình chuyển động của vật được cho là (s )t co A s(  t  ,
người ta nói rằng hạt đó có chuyển động điều hòa đơn.
(a) Tìm vận tốc của hạt tại thời gian t.
(b) Vận tốc bằng 0 khi nào?
Câu 22 : Ngôi sao biến quang kiểu Thiên Vương là ngôi sao mà ánh sáng của nó
luôn phiên tăng và giảm. Ngôi sao dễ dàng nhìn thấy nhất kiểu đó là ngôi sao Delta
Cephei, có khoảng thời gian giữa những lần độ sáng của nó đạt cực đại là 5,4 ngày.
Độ sáng trung bình của ngôi sao nào là 4,0 và độ sáng của nó biến đổ  i 0 ,35. Khi
xem xét các dữ liệu này, độ sáng của Delta Cephei tại thời gian t, trong đó t được
tính theo ngày, đã được mô phỏng qua hàm số 2 t ( B t ) 4 0.35sin( 5.4 a) Tìm tốc ộ đ biến thiên của ộ đ sáng sau t ngày. b) Tìm tốc ộ
đ tăng ( có 2 chữ số thập phân) sau một ngày.
Câu 23 : Chúng ta có công thức tính độ dài chiếu sáng ban ngày theo giờ ở 
Philadelphia vào ngày thứ t của năm L: 2 ( t ) 12 2.8sin( (t 80) 365
Sử dụng công thức này để so sánh số lượng giờ chiếu sáng ban ngày tăng như thế nào
ở Philadelphia vào ngày 21 tháng 3 và ngày 21 tháng 5.
Câu 24 : Một hạt chuyển động dọc theo một đường thẳng với độ dịch chuyển s(t), vận
tốc v(t) và gia tốc a(t). Chứng minh : dv a( t) ( v t). ds
Giải thích sự khác nhau giữa ý nghĩa đạo hàm của dv / dt and / dv d
Câu 25 : Không khí đang được bơm vào một quả bóng dự báo thời tiết. Tại thời điểm t
bất kì, thể tích của quả bóng là V(t) và bán kính của nó là r(t).
a) Đạo hàm của dV/dt và dV/dr biểu thị cho điều gì?
b) Biểu diễn dV/dt dưới dạng dr/dt. VI PHÂN CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 26 : Cạnh của một hình lập phương đo được là 30 cm với sai số cho phép của
phép đo là 0.1 cm. Sử dụng vi phân để ước tính sai số khả dĩ tối đa, sai số tương đối
và sai số theo tỉ lệ phần trăm để tính (a) thể tích của hình lập phương và (b) diện tích
bề mặt của hình lập phương.
Câu 27 : Bán kính của một đĩa hình tròn được tính là 24 cm với sai số tối đa là 0.2 cm.
a) Sử dụng vi phân để ước tính sai số tối đa của diện tích cái đĩa.
b) Sai số tương đối là bao nhiêu ? Sai số theo tỉ lệ phần trăm là bao nhiêu?
Câu 28 : Chu vi của một hình cầu đo được là 84 cm và sai số khả dĩ là 0.5 cm.
a) Sự dụng vi phân để ước tính sai số tối đa của diện tích bề mặt. Sai số tương đối là bao nhiêu?
b) Sự dụng vi phân để ước tính sai số tối đa của diện tích bề mặt. Sai số tương đối là bao nhiêu?
c) Sự dụng vi phân để ước tính sai số tối đa của thể tích. Sai số tương đối là bao nhiêu?
Câu 29: Sử dụng vi phân để ước tính lượng sơn dùng để sơn một lớp dày 0.05 cm lên
một mái vòm hình bán cầu có đường kính 50m.
Câu 30 : a) Sử dụng vi phân để tìm công thức tính thể tích xấp xỉ của một cái vỏ hình
trụ có chiều cao h, bán kính trong r, độ dày  r.
b)Sai số tiến triển bao nhiêu khi sử dụng công thức ừ t câu a.
Câu 31 : Một cạnh của hình tam giác vuông dài 20 cm và góc đối đỉnh đo được là 30 độ, với sai ố s khả dĩ là 0.1 độ.
a) Sử dụng vi phân để ước tính sai số để tính chiều dài của cạnh huyền .
b) Sai số theo tỉ lệ phần trăm là bao nhiêu?
Câu 32: Nếu một dòng điện I đi qua một cái điện trở có điện trở R, Định luật Ôm phát
biểu rằng độ sụt áp là V = IR. Nếu V không đổi và R được đo với một sai số nào đó,
sử dụng vi phân để chứng tỏ rằng sai số tương đối khi tính I xấp xỉ bằng ( về độ lớn )
với sai số tương đối của R.
Câu 33 : Khi máu chảy vào mạch máu, thông lượng F ( thể tích máu trên mỗi đơn vị
thời gian chảy qua một điểm được cho) được cho bởi công thức: 4 F  . k R
Trong đó k là hằng số, R là bán kính mạch máu.
Chứng minh rằng độ biến thiên tương đối của F gấp độ biến thiên tương đối của R
khoảng 4 lần. Bán kính tăng 5% ảnh hưởng như thế nào đến lưu lượng máu. CuuDuongThanCong.com
https://fb.com/tailieudientucntt Max -Min
Câu 1 : Kính viễn vọng Hubble được tàu không gian Discovery đưa vào sử dụng ngày
24/04/1990. Mô hình vận tốc của tàu trong sứ mệnh này, từ lúc rời bệ phóng t = 0 cho
đến khi được tên lửa ẩ
đ y nhanh khỏi bệ tại thời điểm t = 126 giây, được cho bởi 3 2 ( )v 0t.00  1302 t0.0  9029 t 23  .61 t 3 .0 ( đv là feet/giây )
Hãy sử dụng mô hình này để ước tính các giá trị cực đại và cực tiểu tuyệt đối gia tốc
của tàu giữa lúc cất cánh và lúc phóng đi hoàn toàn.
Câu 2 : Tìm các điểm tới hạn của hàm số 1 1 2 a, f (x)  4 x x , k ( g )t 2t 4 3 2 3 2 2 , b f (x ) 2x  3x  36x l , g( ) x 1  x 4 3 2 , c g( t) t  t  t  1 y  1 3/4 1/4 d, ( g ) y  , e ( h )t t  2 t 2 y  y 1 4 2 2 5 f , f (x ) x (x 4) h, f (  ) 2cos   sin Câu 3 : Giữa 0 0 C và 0
30 C, thể tích V (cm khối) của 1 kg nước ở nhiệt độ T được cho
gần đúng bởi công thức sau : 2 3 99 V 9.8  7 0.06  426 0 T .0 085043 T 0.0  00067
Tìm nhiệt độ mà tại đó nước có mật độ lớn nhất .
Câu 4 : Mô hình giá trung bình (USD) một pound đường trắng từ năm 1993 đến năm
2003 được cho bởi hàm số sau : 2 3 4 5 ( ) 0. S 40 t 74  0.0445  8 0.03 t 6  29 0.t00 8956 0 t .00  09037 t 0.0  0003
Trong đó t được tính theo năm kể từ tháng 8 năm 1993.Ước tính thời điểm khi đường
có giá rẻ nhất và đắt nhất trong quãng thời gian từ năm 1993- 2003 CuuDuongThanCong.com
https://fb.com/tailieudientucntt

Tài liệu liên quan: