Đề chọn học sinh giỏi tỉnh Toán 11 năm 2024 – 2025 sở GD&ĐT Hà Tĩnh

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 11 THPT HÀ TĨNH
NĂM HỌC 2024 – 2025
ĐỀ THI CHÍNH THỨC Môn thi: TOÁN
(Đề thi có 02 trang, gồm 05 câu)
Thời gian làm bài: 150 phút
Câu 1. (4,0 điểm)
a) Giải phương trình (1+ tan x tan 2x)sin 4x + cos4x −1= 0.
b) Cho một tam giác có ba ô tròn ở các đỉnh và ba ô tròn ở trung
điểm của các cạnh (xem hình vẽ bên).
Viết ngẫu nhiên sáu chữ số 1, 2, 3, 4, 5, 6 vào sáu ô tròn đó sao
cho mỗi ô chỉ viết đúng một chữ số và chữ số ở các ô là đôi một
khác nhau. Tính xác suất để tổng ba số trong các ô ở đỉnh và tổng
ba số trong các ô còn lại là hai số tự nhiên liên tiếp. Câu 2. (4,0 điểm) 2 a) Cho ba số thực  
a,b,c∈(1;+∞) thỏa mãn 2 2 c 2 log b + c   + c = b . a logb .logb 9loga log a  b 
Tính giá trị của biểu thức P = log b + log c . 2 a b
b) Trong hội trường, xét một dãy gồm 25 chiếc ghế được xếp thành Nguồn âm O
hàng dọc và cách đều nhau, tức là khoảng cách giữa hai ghế liên tiếp
bất kì bằng nhau. Một nguồn phát âm thanh được đặt tại điểm O
thẳng hàng với dãy ghế và nằm ngoài dãy ghế (xem hình vẽ bên). Ghế đầu tiên
Biết rằng mức cường độ âm tại điểm M cách O một khoảng R (mét) Ghế thứ 9
được kí hiệu là L và tính theo công thức c L = (đơn vị: Ben), M log M 2 R
với c là một hằng số dương. Xem mỗi ghế như một điểm, người ta đo
được mức cường độ âm tại ghế đầu tiên là 4 (Ben) và tại ghế cuối
cùng là 2 (Ben). Hỏi mức cường độ âm tại ghế thứ 9 bằng bao nhiêu? Ghế cuối cùng Câu 3. (6,0 điểm)
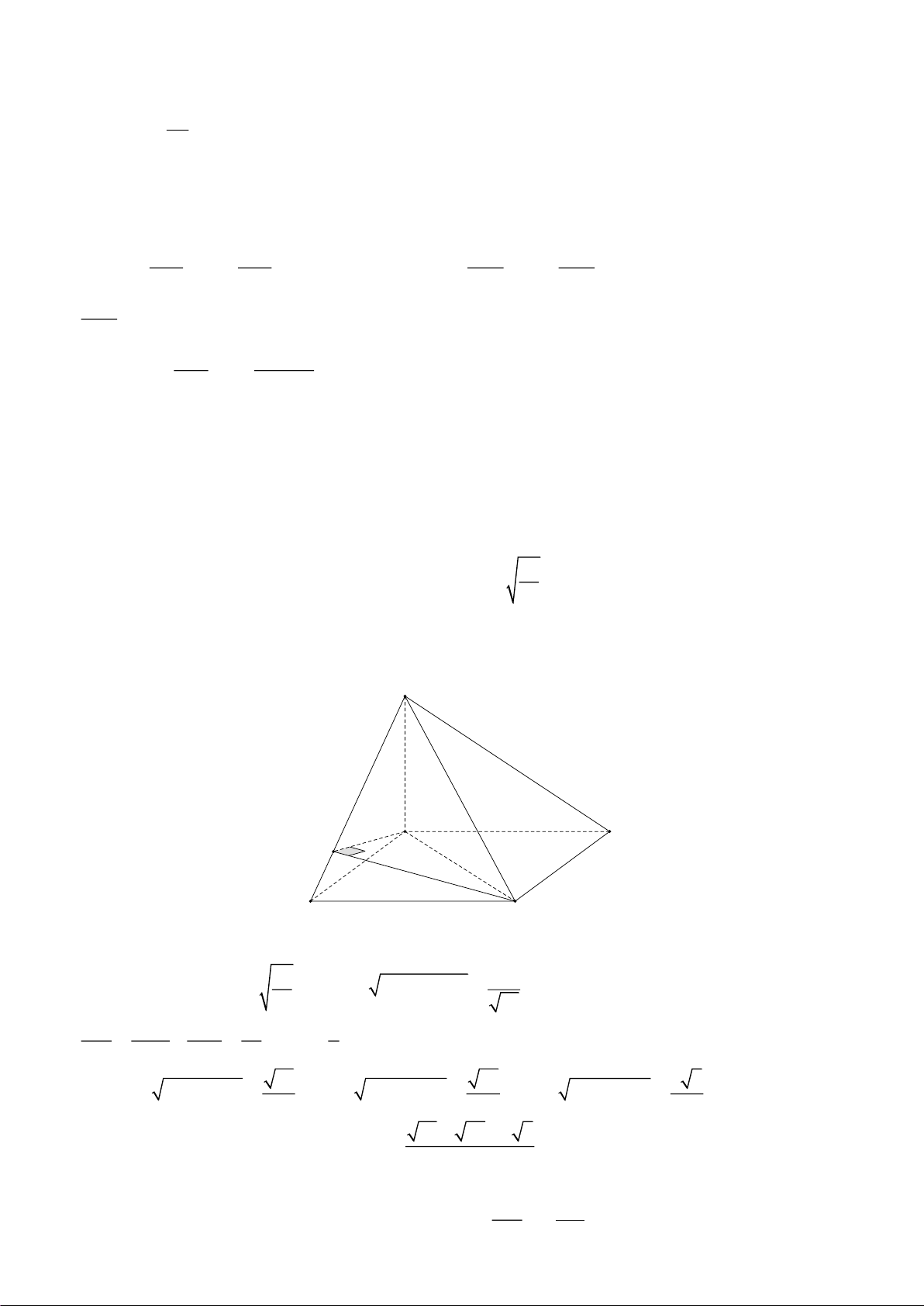
a) Trên bãi cỏ bằng phẳng có một cây xanh thân
thẳng đứng. Để có bóng mát và thuận tiện cho việc
cắm trại, một nhóm bạn đã đóng ba cái móc trên mặt
đất vào các vị trí B, C, D sao cho ABCD là một hình
chữ nhật trong đó điểm A được coi là trùng với gốc
cây và AB = 3 (mét), AD = 4 (mét). Trên thân cây cố
định một điểm gọi là S , căng ba sợi dây không giãn
thành các đoạn thẳng SB, SC, SD làm khung trại, phủ
vải bạt xung quanh tạo thành lều trại là hình chóp tứ
giác S.ABCD (xem hình vẽ bên).
Biết rằng đường thẳng AC tạo với mặt phẳng (SBC) một góc bằng α thỏa mãn 52 cosα =
. Hỏi nhóm bạn đó phải sử dụng tất cả bao nhiêu mét dây để làm khung của 61
chiếc lều trại nói trên? (không tính phần dây dùng để buộc vào thân cây và móc). Trang 1/2
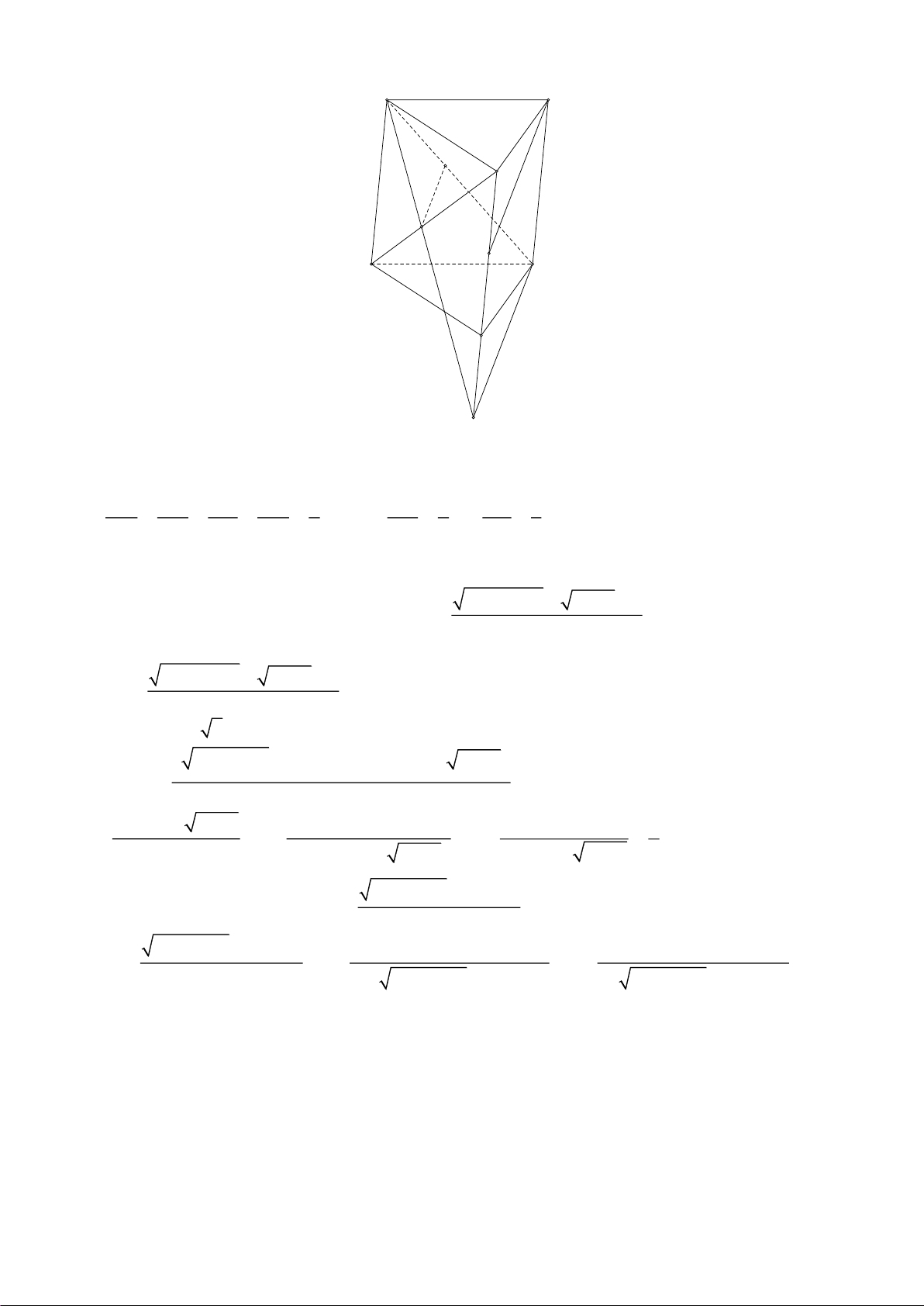
b) Cho lăng trụ tam giác ABC.A′B C
′ ′ có M là trung điểm BB′. Các điểm E, F lần lượt
nằm trên các đường thẳng AB ,′ CA′ sao cho EF //C M
′ . Tính các tỉ số AE và CF . AB′ CA′ Câu 4. (4,0 điểm) 2
a) Tìm tất cả các số thực a, b để tồn tại giới hạn
x + ax + b − 6x +1 lim + x và giới 2 x→0 x hạn này là hữu hạn.
b) Xét một tam giác đều ABC có cạnh bằng 1. Ta xây dựng quá trình tạo hình có dạng bông tuyết như sau:
Đầu tiên, chia mỗi cạnh của tam giác ABC thành ba đoạn thẳng bằng nhau. Trên mỗi
đoạn thẳng ở giữa, dựng một tam giác đều nằm ngoài tam giác ABC rồi xóa đáy của nó, ta được hình (H . 1 )
Sau đó, chia mỗi cạnh của (H thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng 1 )
ở giữa, dựng một tam giác đều nằm ngoài (H rồi xóa đáy của nó, ta được hình (H . 2 ) 1 )
Cứ tiếp tục quá trình như trên ta được dãy các hình (H , H , H , ..., H . n ,... 1 ) ( 2 ) ( 3 ) ( )
(tham khảo hình vẽ dưới đây).
Tính chu vi và diện tích của hình (H . 4 )
Câu 5. (2,0 điểm) u  =1, u = 2 1 2
Cho dãy số (u xác định bởi  2 n )  u + n+ 3 1 * u = ∀ ∈  + n n ,  . 2  un   Tính 1 1 1 lim  + + ...+  . n→+∞  u u u u u u 1 2 2 3 n n 1 + 
---------------------------HẾT----------------------------
- Thí sinh không được sử dụng tài liệu;
- Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ………………………………….………………… Số báo danh: ............................................... Trang 2/2
NHÓM CHINH PHỤC ĐỀ HỌC SINH GIỎI Câu 1.
a) Giải phương trình 1 tan x tan 2xsin 4x  cos 4x 1  0 . Hướng dẫn cos x  0
Điều kiện xác định  . cos 2x  0    Phương trình
cos x cos 2x sin x sin 2x 
sin 4x  cos 4x 1  0    cos x cos 2x  cos x    sin 2x 0
.sin 4x  cos 4x 1  0 2
 2sin 2x  2sin 2x  0 
 x  k k   . cos x cos 2x sin 2x 1
b) Cho một tam giác có ba ô tròn ở các đỉnh và ba ô tròn ở trung điểm của các cạnh (xem hình vẽ). Viết
ngẫu nhiên sáu chữ số 1, 2, 3, 4, 5, 6 vào sáu ô tròn đó sao cho mỗi ô chỉ viết đúng một chữ số và chữ số ở
các ô là đôi một khác nhau. Tính xác suất để tổng ba số trong các ô ở đỉnh và tổng ba số trong các ô còn lại
là hai số tự nhiên liên tiếp. Hướng dẫn n   720 .
Gọi a, b, c và x, y, z lần lượt là các số điền vào ba ô tròn ở đỉnh và ba ô tròn ở trung điểm của ba cạnh.
Ta có a  b  c  x  y  z  1 2  3  4  5  6  21 .
Trường hợp 1: a  b  c  x  y  z 1  a  b  c  11
Có tất cả 3 bộ a;b; 
c thỏa mãn là 1; 4;  6 ; 2;3;  6 ; 2; 4;  5 . Mỗi bộ 1; 4;  6 ;2;3;  6 ;2; 4; 
5 có 3! cách điền các số a, b, c .
Tương ứng có 3! cách điền các số x, y, z .
Suy ra trường hợp này có 3.3!.3!  108 (cách).
Trường hợp 2: x  y  z  11.
Tương tự trường hợp 1, có 108 cách. 108 108 3
Vậy xác suất là P   . 720 10 Câu 2. 2  c 
a) Cho ba số thực a, ,
b c  1;  thỏa mãn 2 2 2 log b  log . c log 
  9log c  log b . a b b a a  b 
Tính giá trị của biểu thức P  log b  log c . 2 b a Hướng dẫn
Đặt x  log b và y  log c . Vì a,b, c  1 nên x, y  0 . a b Ta được 2
4x  y 2 y   1  9xy  4x 2 2
 4x  9xy  2y  4x  y  0     
x  y x  y   4x y 0 (L) 4 2 1  0 
 x  2y 1  .
x  2y 1  0 1 1 1
Vậy P  log b  log c 
log b  log c  x  2 y  . 2 b a b   a 2 2 2
b) Trong hội trường, xét một dãy gồm 25 chiếc ghế được xếp thành hàng dọc và cách đều nhau, tức là
khoảng cách giữa hai ghế liên tiếp bất kì bằng nhau. Một nguồn phát ra âm thanh đặt tại điểm O thẳng hàng
với dãy ghế và nằm ngoài dãy ghế
NHÓM CHINH PHỤC ĐỀ HỌC SINH GIỎI
Biết rằng mức cường độ âm tại điểm M cách O một khoảng R (mét) được kí hiệu là L và tính theo công M c thức L  log
(đơn vị: Ben), với c là một hằng số dương. Xem mỗi ghế như một điểm, người ta đo M 2 R
được mức cường độ âm tại ghế đầu tiên và ghế cuối cùng lần lượt là 4 (Ben) và 2 (Ben). Hỏi mức cường độ
âm tại ghế thứ 9 bằng bao nhiêu? Hướng dẫn Gọi ,
A B, C lần lượt là ghế đầu tiên, ghế thứ 9 và ghế cuối cùng  AC  3AB . c c c c Có 4 L  log  4  10 . Tương tự 2 L  log  2  10 . A 2 2 OA OA C 2 2 OC OC 2 OA 
100  OC 10.OA  OB  4.OA. 2 OC 4 2 Do đó c 10 .OA L  log  log  4 1 log 2 (Ben). B 2 2   OB 16.OA Câu 3.
a) Trên một bãi cỏ bằng phẳng có cây xanh thân thẳng đứng, để có bóng mát và thuận tiện cho việc cắm trại
một nhóm bạn đã đóng ba cái móc trên mặt đất vào các vị trí B, C, D sao cho ABCD là một hình chữ nhật
trong đó điểm A được coi là trùng với gốc cây và AB  3 (mét), AD  4 (mét). Trên thân cây cố định một
điểm gọi là S , căng ba sợi dây không giãn thành các đoạn thẳng SB, SC, SD làm khung trại, phủ vải bạt
xung quanh tạo thành lều trại là hình chóp tứ giác S.ABCD (xem hình vẽ). Biết rằng đường thẳng AC tạo 52
với mặt phẳng  SBC  một góc bằng  thỏa mãn cos 
. Hỏi nhóm bạn đó phải sử dụng tổng bao 61
nhiêu mét dây để dựng chiếc lều trên? (không tính phần dây dùng để buộc vào thân cây và móc) Hướng dẫn S A D H B C
Gọi H là hình chiếu của A trên SB thì AH   SBC     ACH 52 15
Có CH  AC.cos ACH  5 2 2
 AH  AC  CH  61 61 1 1 1 4 5      SA  . 2 2 2 SA AH AB 25 2 61 89 5 5 Suy ra 2 2 SB  SA  AB  , 2 2 SD  SA  AD  , 2 2 SC  SA  AC  . 2 2 2 61  89  5 5
Vậy tổng số mét dây mà nhóm bạn sử dụng là . 2
b) Cho lăng trụ tam giác ABC.AB C
  có M là trung điểm BB . Các điểm E, F lần lượt nằm trên các đườ AE CF ng thẳng AB ,
 CA sao cho EF // C M
 . Tính các tỉ số AB và CA . Hướng dẫn
NHÓM CHINH PHỤC ĐỀ HỌC SINH GIỎI A' C' F B' E M A C B D
Gọi D là điểm đối xứng với M qua B thì C M  // CD .
Gọi E  AD  AB . Kẻ EF // CD ( F  AC ) thì EF // C M  . A F  A E  AE AA 2 AE CF 3 Ta có     . Do đó 2   FC ED EB B D  3 AB và 5 CA . 5 Câu 4. 2
x  ax  b  6x 1  x
a) Tìm tất cả các số thực a, b để tồn tại giới hạn lim
và giới hạn này là hữu hạn. 2 x0 x Hướng dẫn 2      Đặ x ax b 6x 1 x t L  lim . 2 x0 x
Vì L hữu hạn nên b 1  0  b  1. 2
 x  ax 1 2x  1  3x  1 6x 1     Khi đó L  lim . 2 x0 x 3x   1  6x 1 3x  2 1  6x   1 9 9 Có lim  lim  lim  . 2 x0 x0 2 x
x 3x   1  6x 1    x 0 3x   1  6x 1 2 2
x  ax 1  2x   1
Do đó L hữu hạn khi và chỉ khi I  lim hữu hạn. 2 x0 x
x  ax 1  2x   1
x  ax 1 2x  2 2 2 1 3
 x  a  4 Có I  lim  lim  lim . 2 x0 x0 2 2 x  x  x ax 1 2x  1      x 0 2
x  x  ax 1  2x     1  
Vì I hữu hạn nên a  4 .
Vậy a  4, b 1 .
b) Xét một tam giác đều ABC có cạnh bằng 1. Ta xây dựng quá trình tạo hình có dạng bông tuyết như sau:
Chia mỗi cạnh của tam giác ABC thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một
tam giác đều nằm ngoài tam giác ABC rồi xóa đáy của nó, ta được hình H . 1 
Chia mỗi cạnh của  H thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một tam giác 1 
đều nằm ngoài H rồi xóa đáy của nó, ta được hình H . 2  1
Cứ tiếp tục như thế để tạo nên các hình  H , H , ... . 3   4 
NHÓM CHINH PHỤC ĐỀ HỌC SINH GIỎI
Tính chu vi và diện tích của hình  H . 4  Hướng dẫn
Với mỗi số tự nhiên n , gọi a , d , P , S lần lượt là số cạnh, độ dài mỗi cạnh, chu vi, diện tích của hình n n n n H . n 
Vì mỗi cạnh ở hình  H
tạo ra 4 cạnh cho hình  H
nên a  3.4n . n 1   n  n 1 1
Mỗi cạnh của hình  H có độ dài bằng
độ dài cạnh của hình  H nên d  . n  n 1   3 n 3n n   Do đó chu vi củ 4 256 a hình  H
là P  a .d  3. . Suy ra P  . n  n n n    3  4 27 1
Trên mỗi cạnh của hình  H
được đặt thêm một tam giác đều có cạnh bằng d để tạo thành hình  H , n 1   n  3 n 2 n 3  1  3  4 
có a tam giác như thế nên S  S  a . . d  S  S  . . n n 1  n n      4  3 n  n 1 n 12  9   n k 1 n  3  4 
S  S   S  S   n 0  k k 1     k 1  12 k 9 1 n 3 3  4     S  S  1      n 0 20   9    n 3 3 3  4     862 3 S   1
     . Suy ra S  . n 4 20   9  4   2187 u  1, u  2 1 2 
Câu 5. Cho dãy số u xác định bởi 2   n  u 3 n 1  * u  , n   .  n2 u  n  1 1 1  Tính lim   ...  . n u u u u u u  1 2 2 3 n n 1   Hướng dẫn 1 1 1 Dễ thấy * u  0, n   . Đặt S   ... . n n u u u u u u 1 2 2 3 n n 1  2 u  3 2 u u u  3 Ta có n 1  2 u 
 u u  u  3 n2 n n 1    n2 n2 n n 1  u u u u u n n 1  n2 n 1  n2 u u 3 u u 3 n n 1     n n 1  *    , n   . (*) u u u u u u u u n 1  n2 n 1  n2 n 1  n2 n 1  n2 n n     Do đó 1 1 1 u u 1 1 u u 2 1 u k 1  k S        1 n        . n . n u u  u u   u u u u 3 u u 3 3 u k 3 1 2 2 k k 1 k 2  k k 1   1 2  2 n 1   n 1  u u 3  u  Mặt khác từ (*) ta có n n 1  *    0, n   . Do đó dãy n 
 là dãy giảm, bị chặn dưới bởi 0 u u u u u n 1  n2 n 1  n2  n 1 
nên có giới hạn hữu hạn.   Đặ u u u u 1 1 t lim n  L , vì dãy n 
 là dãy giảm nên n 1   , n  , suy ra L  . u u u u 2 2 n 1   n 1  n 1  2
Mặt khác, từ giả thiết ta có 2 * u u  u  3, n   . n2 n n 1  Do đó 2 2 u u  u
 u u  u  u u  u  u u  u k  k 2 k  k 1   k 1  k 1   k 2 k k 1  k 1  k 1  k
NHÓM CHINH PHỤC ĐỀ HỌC SINH GIỎI u  u u  u k 2 k k 1  k 1  *   , k   . u u k 1  k u  u u  u u  u u  u
Lần lượt cho k  1, 2,..., n ta được n2 n n 1  n 1  n n2 3 1    ...   4 . u u u u n 1  n n 1  2 1 1
Chuyển qua giới hạn ta được
 L  4  L  2  3 . Mà L  nên L  2  3 . L 2 2 1 3 Vậy lim S     . n  2 3 n 3 3 3 u  u
Từ đẳng thức n2
n  4 chuyển qua giới hạn tìm được L  2  3 . un 1 
Mà L  2 nên L  2  3 . 1 3 Vậy lim S     . n  2 3 2 n 3 3
Xem thêm: ĐỀ THI HSG TOÁN 11
https://toanmath.com/de-thi-hsg-toan-11
Document Outline

• 1.CHÍNH THỨC-ĐỀ-HSG Lớp 11 năm học 2024 - 2025
• Nhóm chinh phục đề HSG-Giải đề HSG 11 tỉnh Hà Tĩnh
• HSG 11