Đề chọn học sinh giỏi tỉnh Toán 11 năm 2024 – 2025 sở GD&ĐT Tuyên Quang

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 11 THPT TUYÊN QUANG
NĂM HỌC 2024 – 2025 Môn thi: TOÁN ĐỀ THI CHÍNH THỨC
Thời gian: 180 phút (không kể thời gian giao đề)
(Đề này có 01 trang)
Câu 1 (4,0 điểm). Giải các phương trình và bất phương trình sau: x x x a) 2x  5  4x  8  x 1. b)           4 3 1 3 3 1 2 . 2 1 2
Câu 2 (3,0 điểm). Cho dãy số u xác định bởi: u  và 2 u  u  , n     . n  1 2 n 1  3 n 3 Chứng minh rằng:
a) u  1 với mọi * n   ; n
b) Dãy số u có giới hạn hữu hạn và tính giới hạn đó. n 
Câu 3 (5,0 điểm). Cho tam giác nhọn ABC có CA  CB và nội tiếp trong đường tròn (O). 
Gọi R là điểm chính giữa cung nhỏ AB; T và S lần lượt là trung điểm của C , A C . B Đường trung
trực của các cạnh C ,
A CB lần lượt cắt CR tại Q và . P
1. Chứng minh rằng:
a) QT.CP  PS.C ; Q
b) Hai điểm P và Q đối xứng nhau qua đường trung trực của đoạn thẳng CR.
2. So sánh diện tích hai tam giác RTQ và RPS.
Câu 4 (3,0 điểm). Cho đa giác đều (H ) có 30 đỉnh nội tiếp trong đường tròn (O).
a) Có bao nhiêu đường chéo của đa giác (H ) không phải là đường kính của (O) ?
b) Tính số tam giác tù có ba đỉnh là ba đỉnh của đa giác (H ).
Câu 5 (3,0 điểm). Giả sử x ; x ;...; x
là một hoán vị của tập A  1976;1977;...; 205  3 . 1 2 78
a) Tìm dư khi chia a  x x ...x cho 79. 1 2 78
b) Chứng minh rằng tồn tại m, n 1; 2;...; 7 
8 , m  n thỏa mãn: mx  nx chia hết cho 79. m n
Câu 6 (2,0 điểm). Cho đa thức P(x) có hệ số hữu tỉ, bậc 5 và P  3
1  3   25. Chứng minh
rằng tồn tại một tam thức bậc hai Q(x) có hệ số hữu tỉ thỏa mãn
P(1)  25.P(0)  25.P(1)  25 132.Q(1).Q(0).Q(1)  0. -----Hết-----
Ghi chú: Thí sinh không được sử dụng tài liệu và máy tính cầm tay trong khi làm bài.
Họ và tên thí sinh:………………………………………………..SBD:…………… HƯỚNG DẪN CHẤM
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 11, NĂM HỌC 2024-2025
Môn: Toán (Đề thi chính thức) -----
Câu 1 (4,0 điểm). Giải các phương trình và bất phương trình sau: x x x a) 2x  5  4x  8  x 1. b)           4 3 1 3 3 1 2 . Hướng dẫn chấm Điểm
a) Điều kiện xác định: x  1 (*). Với điều kiện (*), ta có 0,5 PT  2x  5  x 1  4x  8 (1).
Bình phương hai vế của (1) ta được 0,5 2
(1)  3x  4  2 (2x  5)(x 1)  4x  8  2 2x  3x  5  x  4 (2). Vì x  1 nên
  x  x     x  2 2 2 (2) 4 2 3 5 4
 7x  4x  36  0 (3). 0,5 18
Giải (3) ta được hai nghiệm x  
(loại) và x  2 (thỏa mãn). 7 0,5
Vậy phương trình có nghiệm duy nhất x  2. x x  3 1   3 1 b) Ta có BPT     3   4. 0,5 2 2     x  3 1 3 Đặt t  
 , t  0 ta được t   4 (*). 0,5 2   t Giải (*): 2
(*)  t  4t  3  0  1  t  3. 0,5 x  3 1
Suy ra BPT  1  
  3  0  x  log 3. 3 1 2    2 0,5
Vậy nghiệm của bất phương trình là 0  x  log 3. 3 1  2 2 1 2
Câu 2 (3,0 điểm). Cho dãy số u xác định bởi: u  và 2 u  u  , n     . n  1 2 n 1  3 n 3 Chứng minh rằng:
a) u  1 với mọi * n   ; n
b) Dãy số u có giới hạn hữu hạn và tính giới hạn đó. n  Hướng dẫn chấm Điểm
a) Chứng minh: u  1 (*) với mọi * n   . n 0,25
Với n  1 thì (*) là đúng.
Giả sử (*) đúng với n  k, k  1. Khi đó u  1. Hiển nhiên u  0. Do đó 2 u  1. k k k 0,5 2 1 2 Suy ra 2 u  u   1  u  1. 0,5 k 1  k k 1 3 3 
Vậy (*) đúng với n  k 1. Theo Nguyên lí quy nạp thì (*) đúng. 0,25 1 2 1 1 b) Ta có 2 u  u  u   u  u  u   u  u  0,5 n n n n  2 3 2 1 2 . 1 n n   n  n  3 3 3 3
Theo a) thì u  1. Suy ra u  
1 u  2  0  u  u , n      u tăng (1). 0,5 n n n 1  n  n  n
Từ (*) và (1) suy ra dãy u có giới hạn hữu hạn, lim u  a  1 thỏa mãn n  n n 1 2 0,5 2 a  a 
 a  1  lim u  1. 3 3 n n
Câu 3 (5,0 điểm). Cho tam giác nhọn ABC có CA  CB và nội tiếp trong đường tròn (O). 
Gọi R là điểm chính giữa cung nhỏ AB; T và S lần lượt là trung điểm của C , A C . B Đường
trung trực của các cạnh C ,
A CB lần lượt cắt CR tại Q và . P
1. Chứng minh rằng:
a) QT.CP  PS.C ; Q
b) Hai điểm P và Q đối xứng nhau qua đường trung trực của đoạn thẳng C . R
2. So sánh diện tích hai tam giác RTQ và RPS. Hướng dẫn chấm Điểm
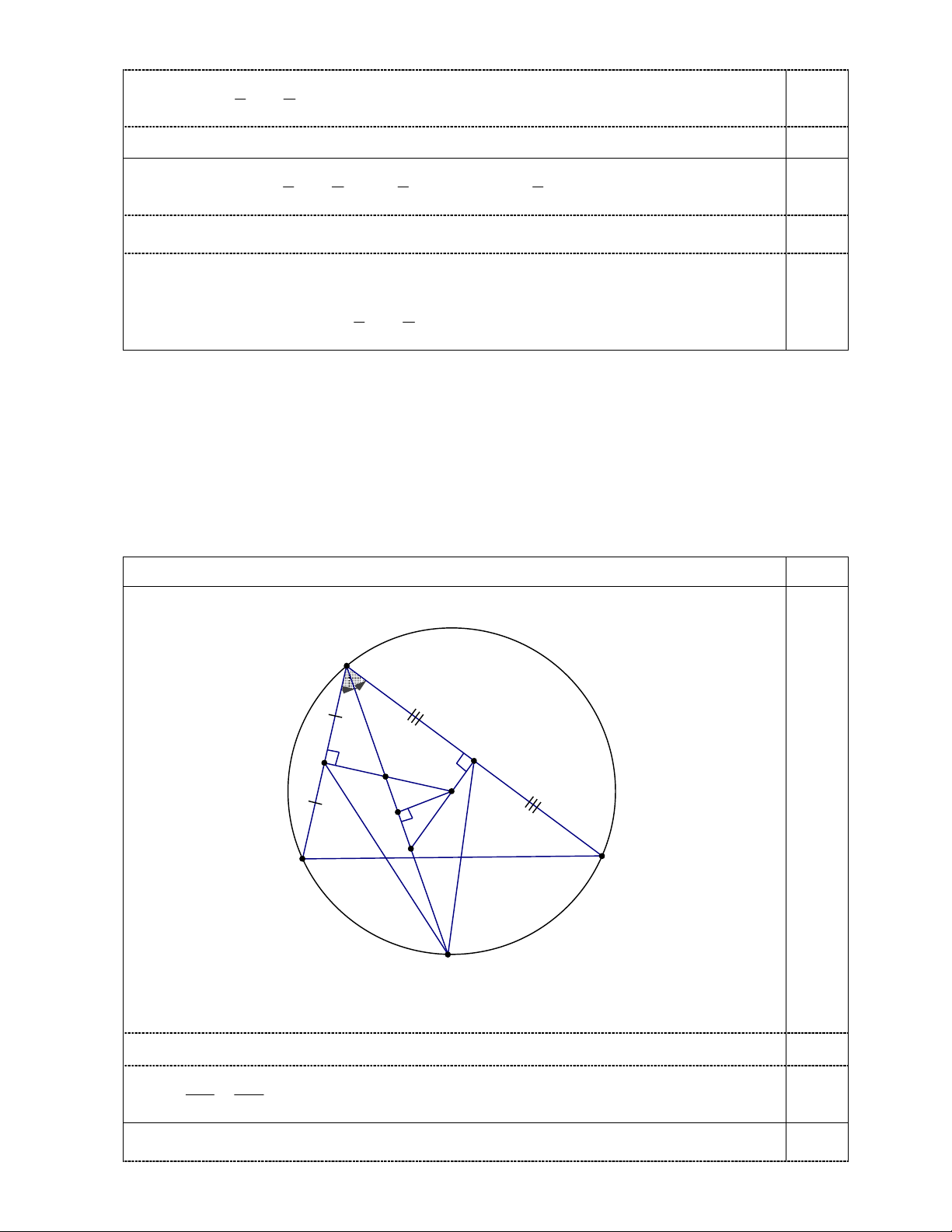
1a) Xét thế hình của bài toán như sau: C S T Q O 0,5 H P A B R
Vì R là điểm chính giữa cung nhỏ  AB nên   TCQ  PCS.
Suy ra hai tam giác vuông QTC và PSC đồng dạng. 0,5 QT QC Do đó 
 QT.PC  PS.C . Q 0,5 PS PC 1b) Theo a) thì   Q  TC  PS 
C  TQC  CPS (1). 0,5 3 (1) Mặt khác   
PQO  TQC  QPO (2). 0,5
Từ (2) suy ra tam giác OPQ cân đỉnh .
O Suy ra P, Q đối xứng nhau qua đường cao 0,5
OH của tam giác OP . Q
Vì CR là một dây cung của đường tròn (O) nên OH là trung trực của C . R Do đó 0,5
P, Q đối xứng nhau qua đường trung trực của đoạn thẳng C . R 2. Từ (1) suy ra  
TQR  SPR (3). 0,25 1  .QT.Q . R sin TQR (3) SRTQ QT .QR Do đó 2   (4). 0,5 S 1 PS PR RPS  . .PS.P . R sin SPR 2
Theo b) thì PR  CQ, RQ  CP (5). 0,25 SRTQ QT .CP Từ (4) và (5) suy ra  (6). 0,25 S PS.CQ RPS S
Từ a) và (6) suy ra RTQ  1  S  S
. Vậy hai tam giác RTQ và RPS có diện RTQ RPS S 0,25 RPS tích bằng nhau.
Câu 4 (3,0 điểm). Cho đa giác đều (H ) có 30 đỉnh nội tiếp trong đường tròn (O).
a) Có bao nhiêu đường chéo của đa giác (H ) không phải là đường kính của (O) ?
b) Tính số tam giác tù có ba đỉnh là ba đỉnh của đa giác (H ). Hướng dẫn chấm Điểm a) Có 2
C đoạn thẳng có hai điểm đầu mút là đỉnh của đa giác (H ). 0,5 30
Trong các đoạn thẳng trên, có 30 đoạn thẳng là cạnh của đa giác (H ). Suy ra số đường 0,5 chéo của (H ) là 2 C  30. 30
Trong các đường chéo của (H ), có 15 đường chéo là đường kính của (O) (các đường 0,5
chéo A A , A A ,..., A A ). 1 16 2 17 15 30 Suy ra có 2
C  30 15  390 đường chéo của đa giác (H ) không phải là đường kính 30 0,5 của (O).
b) Giả sử (H )  A A ...A . Xét các tam giác tù A A A (i  j) có đỉnh góc tù là A . 1 2 30 1 i j 1 0,25 Khi đó  i 2; 3;...;1 
4 vì nếu i  15 thì 0 A  90 . 1
Với mỗi i  2, 3,..., 14 thì có 15  i cách chọn điểm A (chọn trong các đỉnh j 0,5 A , A
,..., A ). Suy ra có 13  12  ... 1  91 tam giác tù có đỉnh góc tù là A . 16i 17i 30 1
Tương tự, có 91 tam giác tù có đỉnh góc tù là A , với k  2, 3,..., 30. Do đó số tam k 0,25
giác tù được tạo thành từ các đỉnh của (H ) là 30.91  2730 (tam giác).
Câu 5 (3,0 điểm). Giả sử x ; x ;...; x
là một hoán vị của tập A  1976;1977;...; 205  3 . 1 2 78
a) Tìm dư khi chia a  x x ...x cho 79. 1 2 78 4
b) Chứng minh rằng tồn tại m, n 1; 2;...; 7 
8 , m  n thỏa mãn: mx  nx chia hết cho 79. m n Hướng dẫn chấm Điểm
a) Ta thấy A  79.25 1; 79.25  2;...; 79.25  77; 79.25  7  8 . 0,5 Suy ra a 
k  1.2.3...78 (mod 79).  0,5 k A 
Vì 79 là một số nguyên tố nên theo Định lí Wilson thì a  1.2.3...78  1 (mod 79). 0,5
Do đó dư khi chia a cho 79 là 78.
b) Giả sử không tồn tại m, n 1; 2;...; 7 
8 , m  n thỏa mãn: mx  nx chia hết cho m n
79 (1). Vì x và i đều không chia hết cho 79 nên ix cũng không chia hết cho 79 với 0,5 i i
mọi i  1, 2,..., 78 (2).
Từ (1) và (2) suy ra kx
là một hệ thặng dư thu gọn modun 79. k  0,25 k 1  , 78
Theo Định lí Wilson thì  ix   1.2.3...78  1 (mod 79) (1). i 0,25 i 1  , 78
Mặt khác  ix   78!.
x  (1)(1)  1 (mod 79) i  (2). i 0,25 i 1  , 78 i 1  , 78
Từ (1) và (2) suy ra 1  1
 (mod 79), điều này là vô lí. Do đó điều giả sử là sai. 0,25
Vậy tồn tại m, n 1; 2;...; 7 
8 , m  n thỏa mãn mx  nx chia hết cho 79. m n
Câu 6 (2,0 điểm). Cho đa thức P(x) có hệ số hữu tỉ, bậc 5 và P  3
1 3  25. Chứng minh
rằng tồn tại một tam thức bậc hai Q(x) có hệ số hữu tỉ thỏa mãn
P(1)  25. P(0)  25. P(1)  25 132.Q(1).Q(0).Q(1)  0. Hướng dẫn chấm Điểm Đặt 3
  1 3. Khi đó 3
 1  3    3 3 2 1
 3    3  3  4  0. 0,25
Theo định lí Bézout, tồn tại đa thức Q(x)  [
 x] và ba số a, b, c   sao cho
P x  Q x  3 2
x  x  x   2 ( ) ( ) 3 3
4  ax  bx  c, x   .  0,25 Suy ra 2
a  b  c  P  3 1  3  2
 25  a  b  c  25  0.
Nếu a  0 thì thì tồn tại R(x)  [
 x], deg R(x)  1 và hai số d, e  sao cho 3 2
x  x  x    2 3 3 4
ax  bx  c  25 R(x)  dx  , e x   .  0,25 Suy ra 3
d  e  0  d 3  d  e  0  d  e  0.
Vì deg R(x)  1 và R(x)  [
 x] nên R(x) có nghiệm hữu tỉ   . Suy ra đa thức 0,25 3 2
x  3x  3x  4 cũng có nghiệm  . 3 3 Mặt khác 3 2
x  x  x 
  x     3    3 x    2 3 3 3 3 4 1 3 1 3
(x 1)  3(x 1)  9  0,25
chỉ có nghiệm thực duy nhất là . Điều này là vô lí. Vậy a  0. 5 25  c
Nếu b  0 thì    ,
 vô lí. Vậy b  0  c  25. Hay b 0,25
P x  Q x  3 2 ( )
( ) x  3x  3x  4  25, x   .  (*). P( 1  )  1  1Q(1)  25  Thay x  1
 ; 0; 1 vào (*) ta được: P(0)  4  Q(0)  25 . 0,25
P(1)  3Q(1)  25 
Suy ra  P(1)  25. P(0)  25. P(1)  25 132.Q(1).Q(0).Q(1)  0. 0,25 -----Hết-----
Ghi chú: Nếu thí sinh làm bài theo cách khác (với kiến thức trong chương trình THPT hoặc
THPT chuyên) thì vẫn cho điểm theo các phần đúng tương ứng.
Document Outline

• Đề thi chính thức (c)
• HDC đề thi chính thức (c)