Đề chọn học sinh giỏi Toán 11 năm 2024 – 2025 sở GD&ĐT Quảng Bình
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề thi chọn học sinh giỏi môn Toán 11 năm học 2024 – 2025 và chọn đội dự tuyển dự thi chọn học sinh giỏi Quốc gia môn Toán năm học 2025 – 2026 sở Giáo dục và Đào tạo tỉnh Quảng Bình. Kỳ thi được diễn ra vào ngày 31 tháng 03 năm 2025. Đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm.
Chủ đề: Đề HSG Toán 11 151 tài liệu
Môn: Toán 11 3.6 K tài liệu
Tác giả:
Preview text:
SỞ GD&ĐT QUẢNG BÌNH
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2024-2025
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG ĐỀ CHÍNH THỨC
QUỐC GIA NĂM HỌC 2025-2026
Khóa ngày 31 tháng 3 năm 2025 Môn thi: TOÁN HỌC BÀI THI THỨ NHẤT Thời gian: 1 SỐ BÁO DANH:……………
80 phút (không kể thời gian giao đề)
Đề gồm có 01 trang và 04 câu
Câu 1 (2,5 điểm):
a) Giải phương trình sin 2x cos 2x 5sin x 3cos x 4 0.
b) Bác Bình vay của Ngân hàng Chính sách xã hội với số tiền 360 triệu đồng để xây nhà. Sau
mỗi tháng, bác Bình phải trả lãi cho Ngân hàng với lãi suất 0, 4% /tháng và cứ sau 6 tháng thì bác
Bình phải trả 36 triệu đồng tiền gốc cho Ngân hàng. Cứ như vậy, sau 60 tháng thì bác Bình đã trả
hết tiền cho Ngân hàng. Tìm tổng số tiền lãi mà bác Bình phải trả.
Câu 2 (2,5 điểm):
a) Cho 2024 số thực a , a ,..., a
thỏa mãn a , a ,..., a
0;2025 . Chứng minh phương 1 2 2024 1 2 2024 trình 2024 2 2 2 x
2025(a a ... a
)x a a ... a 1 0 luôn có nghiệm. 1 2 2024 1 2 2024 f (x) 1 3 f (x)
f (x) 7 3
b) Cho f (x) là một đa thức thỏa mãn lim 2. lim . x 1 x Tính 1 3 x 1 x x 2
Câu 3 (1,5 điểm):
a) Biển số xe ôtô của tỉnh Quảng Bình có dạng 73A ab .
c de (trong đó: 73A là mã số cố định
của tỉnh Quảng Bình; a, ,
b c, d ,e là các chữ số không đồng thời bằng 0 ). Một biển số xe ôtô được
gọi là biển số “đẹp” nếu thỏa mãn a b c d .
e Bác An chọn ngẫu nhiên một biển số xe ôtô của
tỉnh Quảng Bình. Tính xác suất để bác An chọn được biển số “đẹp”.
b) Sắp xếp 3 bạn nam B , B , B và 5 bạn nữ vào 8 cái ghế được xếp theo hàng ngang (mỗi 1 2 3
bạn ngồi một cái ghế). Hỏi có bao nhiêu cách sắp xếp thỏa mãn tất cả các điều kiện sau: B , B , B 1 2 3
ngồi theo thứ tự đó từ trái qua phải; giữa B và B có ít nhất 1 bạn nữ; giữa B và B có nhiều nhất 1 2 2 3 2 bạn nữ.
Câu 4 (3,5 điểm): Cho hình lăng trụ ABC.A B C
và điểm M di động trên cạnh AB thỏa mãn
AM x 0 x 1. Mặt phẳng đi qua M song song với các đường thẳng AC , A B và cắt AB
các cạnh AA , AC , C B
, BC tương ứng tại các điểm N, P, Q, K.
a) Chứng minh giao điểm của MN và QK luôn nằm trên một đường thẳng cố định. Nêu cách
dựng các điểm N, P, Q, K. 2
b) Tính tỉ số QB x . QC khi 3
c) Trong trường hợp ABC.A B C
là hình lăng trụ đều có tất cả các cạnh bằng 1, tìm giá trị lớn
nhất của diện tích ngũ giác MNPQK.
-------------HẾT -------------
SỞ GD&ĐT QUẢNG BÌNH
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2024-2025
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG ĐỀ CHÍNH THỨC
QUỐC GIA NĂM HỌC 2025-2026
Khóa ngày 31 tháng 3 năm 2025 Môn thi: TOÁN HỌC BÀI THI THỨ HAI
SỐ BÁO DANH:……………
Thời gian: 180 phút (không kể thời gian giao đề)
Đề gồm có 01 trang và 05 câu
Câu 1 (2,0 điểm):
x y z
y z x
z x y 3
a) Tìm tất cả các bộ ba số thực ,
x y, z thỏa mãn 2 2 2 3 3 3 2025 2025 2025 . 2025
b) Cho đa thức bậc hai 2
f x x bx c với b, c là hai số nguyên. Chứng minh luôn tồn tại
số nguyên a thỏa mãn f a f 2024. f 2025. u 5
Câu 2 (2,0 điểm): Cho dãy số u xác định bởi 1 . n 2025 2024 * u u 3u u , n n 1 n n n
a) Chứng minh lim u . n n 1
b) Với mỗi số nguyên dương n, đặt v Tính lim v . n . 2024 n u 1 2024 u 1 ... 2024 u 1 n 1 2 n
Câu 3 (3,5 điểm): Cho tam giác nhọn ABC AB AC nội tiếp đường tròn O. Hai đường cao
BE, CF E AC, F AB cắt nhau tại H. Gọi M , N, P, Q tương ứng là trung điểm của các đoạn thẳng BC, ,
CA AB, AH . Tia MH cắt O tại . L
a) Chứng minh AL, BC, EF đồng quy tại một điểm T.
b) Gọi K là giao điểm của NP và EF. Chứng minh AK vuông góc với OH.
c) Đường thẳng đi qua A song song với BC cắt OQ tại .
D Chứng minh giao điểm ( khác M )
của hai đường tròn ngoại tiếp hai tam giác MNP và MLT nằm trên đường thẳng DM.
Câu 4 (1,5 điểm): Cho n-giác đều A A ...A n , n 3. Mỗi một đỉnh của n-giác đều A A ...A 1 2 n 1 2 n
được tô bởi một màu trong m màu cho trước m ,m 3 sao cho hai đỉnh kề nhau được tô bởi hai
màu khác nhau. Tìm số cách tô màu có thể thực hiện được trong các trường hợp sau:
a) Khi n 4, m 5.
b) Khi n 2024, m 2025.
Câu 5 (1,0 điểm): Tìm tất cả các cặp số nguyên dương ; m n thỏa mãn 2
m 2 chia hết cho . m n 2.
-------------HẾT -------------
SỞ GD&ĐT QUẢNG BÌNH
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2024-2025
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG HƯỚNG DẪN CHẤM
QUỐC GIA NĂM HỌC 2025-2026
Khóa ngày 31 tháng 3 năm 2025 Môn thi: TOÁN HỌC BÀI THI THỨ NHẤT
Đáp án này gồm có 07 trang YÊU CẦU CHUNG
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu cầu phải
lập luận lôgic chặt chẽ, đầy đủ, chi tiết và rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với những bước
giải sau có liên quan.
* Ở câu 4 nếu học sinh không vẽ hình ở phần nào thì cho điểm 0 ở phần đó.
* Điểm thành phần của mỗi câu được chia đến 0,25 điểm.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tuỳ theo mức điểm của từng câu.
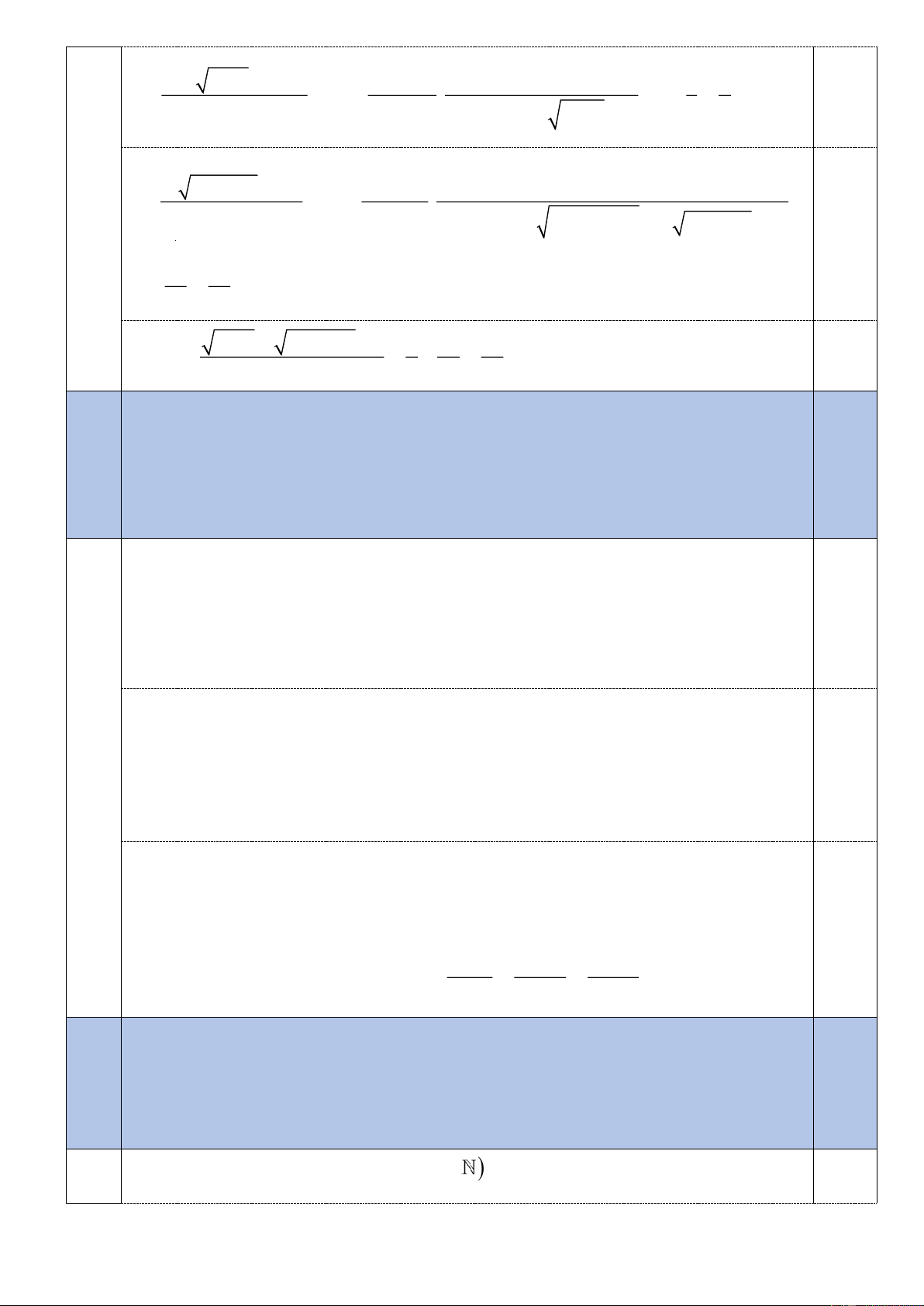
* Điểm của toàn bài là tổng điểm (không làm tròn số) của điểm tất cả các câu. Câu Nội dung Điểm Giải phương trình 1a
sin 2x cos 2x 5sin x 3cos x 4 0 * 1,25 Ta có: x 2 * sin 2 2sin x
1 5sin x 3cos x 4 0 0,25 x x 2 2sin .cos
2sin x 5sin x 3 3cos x 0 0,25 cos .
x 2sin x 3 2sin x 3sin x 1 0 0,25
2sin x 3cos x sin x 1 0 3 sin x VN 2sin x 3 0 2 0,25
cos x sin x 1 0 2 cos x 1 4 2 2 x k2
Giải (1) ta có: cos x cos x cos 2 , k . 4 2 4 4 x k2 0,25
Vậy phương trình có hai họ nghiệm là x
k2 ; x k2 với k . 2
Bác Bình vay của Ngân hàng Chính sách xã hội với số tiền 360 triệu đồng để xây
nhà. Sau mỗi tháng, bác Bình phải trả lãi cho Ngân hàng với lãi suất 0, 4% /tháng 1b
và cứ sau 6 tháng thì bác Bình phải trả 36 triệu đồng tiền gốc cho Ngân hàng. Cứ 1,25
như vậy, sau 60 tháng thì bác Bình đã trả hết tiền cho Ngân hàng. Tìm tổng số tiền
lãi mà bác Bình phải trả. 1
Gọi S là số tiền lãi sau 6 tháng lần thứ n n 1;10 . n 0,25
Sau 6 tháng lần thứ 1 số tiền lãi là S 6.0, 4%.360 . 1
Sau 6 tháng lần thứ 2 số tiền lãi là S 6.0, 4%. 360 36 . 2 0,25
Sau 6 tháng lần thứ 3 số tiền lãi là S 6.0, 4%. 360 36.2 . 3 … 0,25
Sau 6 tháng lần thứ 10 số tiền lãi là S 6.0, 4%. 360 36.9 . 10 Tổng số tiền lãi là 0,25
S S S ... S 6.0, 4% 1
0.360 36 1 2 ... 9 1 2 10 . 1188 S 47,52 (triệu đồng). 25 0,25
Vậy tổng số tiền lãi mà bác Bình phải trả là 47,52 (triệu đồng).
Cho 2024 số thực a , a ,..., a
thỏa mãn a , a ,..., a 0;2025 . Chứng minh 1 2 2024 1 2 2024 2a phương trình 2024 2 2 2 x
2025(a a ... a
)x a a ... a
1 0 luôn có 1,25 1 2 2024 1 2 2024 nghiệm. Xét f x 2024 2 2 2 x
2025(a a ... a
)x a a ... a 1 là hàm số liên 1 2 2024 1 2 2024 0,25 tục trên . Ta có f
1 a a 2025 a a 2025 ... a a 2025 0 . 1 1 2 2 2024 2024 0,25
Dấu " " xảy ra khi a a ... a 0 . 1 2 2024 f
1 a a 2025 a a 2025 ... a a 2025 0 . 1 1 2 2 2024 2024 0,25
Dấu " " xảy ra khi a a ... a 0 . 1 2 2024
TH1: Nếu a a ... a
0 thì * có hai nghiệm x 1; x 1 . 1 2 2024 0,25
TH2: Nếu tồn tại a 0,i 1; 2024 thì f 1 . f
1 0 . Do đó (*) có ít nhất một i
nghiệm thuộc khoảng 1 ; 1 . 0,25 Vậy (*) luôn có nghiệm. f (x) 1 3 f (x)
f (x) 7 3 2b
Cho f (x) là một đa thức thỏa mãn lim 2. lim . 1,25 x 1 x Tính 1 3 x 1 x x 2 f (x) 1 Vì lim 2 lim f x 1 0 f 1 1. 0,25 x 1 x nên 1 x 1 3 3 f (x)
f (x) 7 3 f (x) 1
f (x) 7 2 Ta có . 3 0,25 x x 2 x 1 2
x x 2 x 1 2 x x 2 2 f (x) 1 f x 1 1 1 1 lim lim . 2. . 0,25 x 1 x 1 2 x x 2 x 1 x 1
2x x2
f x 8 4 1
3 f (x) 7 2
f x 1 1 lim
x x 1 lim . 2 1 x x 2 x 1 x 1
x x 2
f(x)72 2 3 3
2. f (x) 7 4 0,25 1 1 2. . 48 24 3 f (x)
f (x) 7 3 Vậy 1 1 7 lim . 0,25 3 x 1 x x 2 4 24 24
Biển số xe ôtô của tỉnh Quảng Bình có dạng 73A ab .
c de (trong đó: 73A là mã số
cố định của tỉnh Quảng Bình; a, ,
b c, d ,e là các chữ số không đồng thời bằng 0 ). 3a
Một biển số xe ôtô được gọi là biển số “đẹp” nếu thỏa mãn a b c d e . Bác 0,75
An chọn ngẫu nhiên một biển số xe ôtô của tỉnh Quảng Bình. Tính xác suất để bác
An chọn được biển số “đẹp”.
Số phần tử của không gian mẫu là: n 5 10 1 99999 .
Gọi A là biến cố: “bác An chọn được biển số xe “đẹp”. 0,25
Ta có 0 a b c d e 9 . Đặt b b 1, c c 2, d d 3,e e 4 . 1 1 1 1
Lúc đó 0 a b c d e 13. 1 1 1 1
Ta thấy, mỗi cách lấy một bộ ; a ; b ; c d;
e thỏa mãn 0 a b c d e 9 tương
ứng với mỗi cách lấy một bộ ;
a b ;c ; d ;e thỏa mãn 0 a b c d e 13 . 1 1 1 1 1 1 1 1 0,25
Số cách lấy một bộ ;
a b ;c ; d ;e thỏa mãn 0 a b c d e 13 là 1 1 1 1 1 1 1 1 5 C 2002 . 14 Vì a, ,
b c, d ,e là các chữ số không đồng thời bằng 0 nên số biển số xe ôtô “đẹp”
của tỉnh Quảng Bình là 2002 1 2001.
Số phần tử thuận lợi cho biến cố A là n A 2001. 0,25 n A
Vậy xác suất của biến cố 2001 667
A là P A . n 99999 33333
Sắp xếp 3 bạn nam B , B , B và 5 bạn nữ vào 8 cái ghế được xếp theo hàng 1 2 3
ngang (mỗi bạn ngồi một cái ghế). Tìm số cách sắp xếp thỏa mãn tất cả các điều 3b kiện sau: 0,75
B , B , B ngồi theo thứ tự đó từ trái qua phải; giữa B và B có ít nhất 1 1 2 3 1 2
bạn nữ; giữa B và B có nhiều nhất 2 bạn nữ. 2 3 Gọi
x là số bạn nữ ngồi bên trái B x . 1 0,25 3
y là số bạn nữ ngồi giữa B và B * y . 1 2
z là số bạn nữ ngồi giữa B và B z , z 2 . 2 3
t là số bạn nữ ngồi bên phải B t . Đặt y y 1. 3 1
x y z t 4 1
Từ giả thiết ta có z 2 *
x, y ,z,t 1
Sử dụng kết quả của bài toán “số nghiệm nguyên không âm của phương trình
x x ... x m với * , n m là n 1 C
” ta có các trường hợp sau: 1 2 n mn 1
TH1: z 0 thì số nghiệm của (*) bằng 2 C . 6 0,25
TH2: z 1 thì số nghiệm của (*) bằng 2 C . 5
TH3: z 2 thì số nghiệm của (*) bằng 2 C . 4
Do đó, số cách sắp xếp thỏa mãn bài toán là 2 2 2
C C C .5! 31.5! 3720 . 6 5 4 0,25
Cho hình lăng trụ ABC.A B C
và điểm M di động trên cạnh AB thỏa mãn
AM x 0 x 1. Mặt phẳng đi qua M song song với các đường thẳng AB AC , A B
và cắt các cạnh AA , AC , C B
, BC tương ứng tại các điểm N, P, Q, K.
a) Chứng minh giao điểm của MN và QK luôn nằm trên một đường thẳng cố 4 3,5
định. Nêu cách dựng các điểm N, P, Q, K. 2
b) Tính tỉ số QB x . QC khi 3
c) Trong trường hợp ABC.A B C
là hình lăng trụ đều có tất cả các cạnh bằng 1,
tìm giá trị lớn nhất của diện tích ngũ giác MNPQK.
Chứng minh giao điểm của MN và QK luôn nằm trên một đường thẳng cố định. 4a 1,5
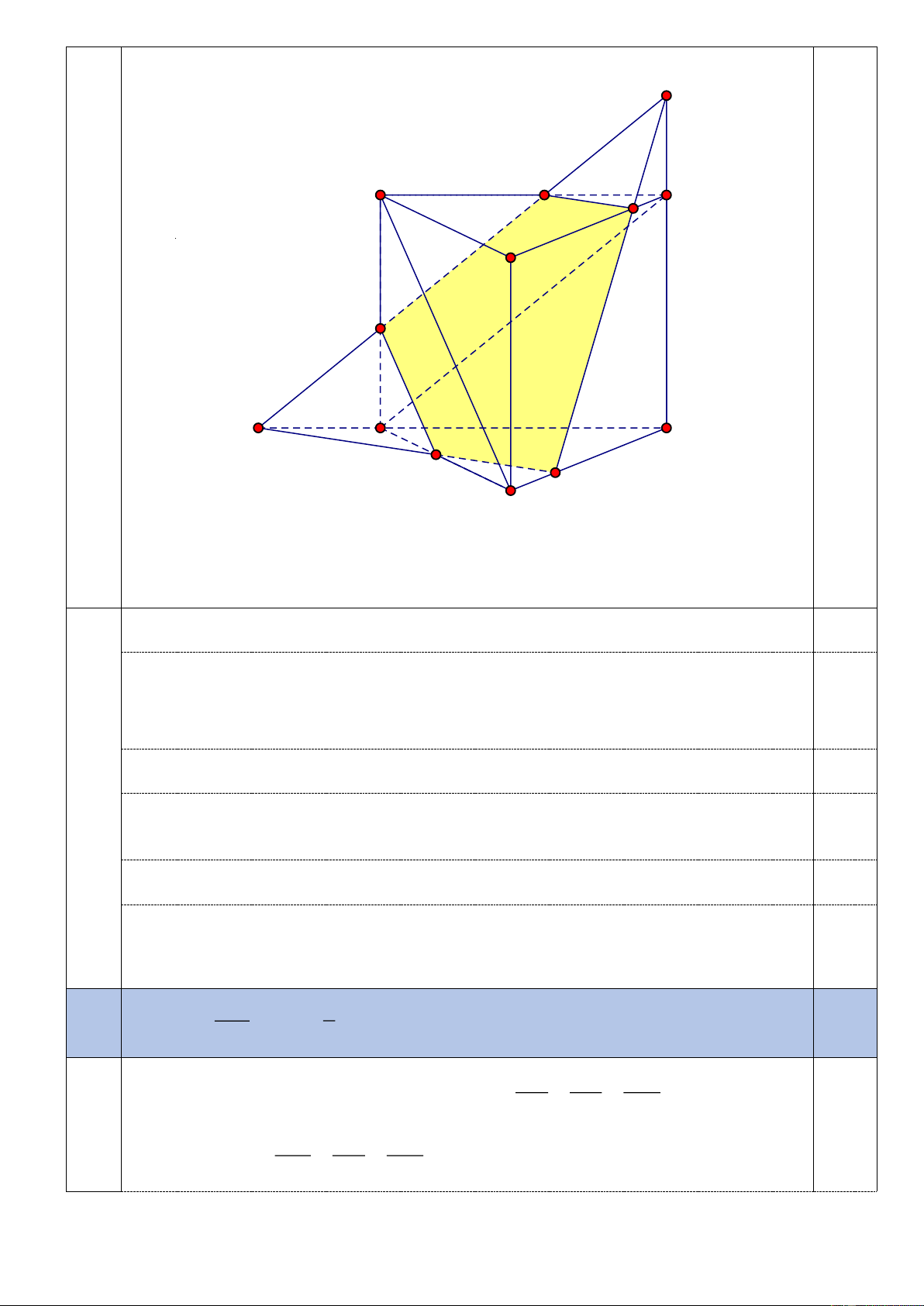
Nêu một cách dựng các điểm N, P, Q, K. 4 J A M B K C 4a N A' I B' P Q C'
Chú ý: Nếu học sinh vẽ các đoạn thẳng A N , A P
, A I, BM (theo hình biễu diễn
trên) bằng nét liền vẫn chấp nhận được.
Ta có MN ABB A
; QK BCC B
; BB ABB A BCC B . 0,25
Mà MN và BB luôn cắt nhau. Nên theo định lý ba giao tuyến thì MN ,QK , BB
đồng quy. Do đó giao điểm của MN và QK luôn nằm trên đường thẳng BB cố 0,25 định (đpcm)
Trong mặt phẳng ABB A
, kẻ MN || A B
, N AA . 0,25
Gọi I, J tương ứng là giao điểm của đường thẳng MN với các đường thẳng A B 0,25 và BB .
Trong mặt phẳng ACC A
, kẻ NP || AC ,P A C . 0,25
Trong mặt phẳng A B C
, Q là giao điểm của IP với B C . 0,25
Trong mặt phẳng BCC B
, K là giao điểm của JQ với BC . 2 4b Tính tỉ số QB x . 1,0 QC khi 3 Trong mặt phẳng NA MA x ABB A
, có MN || A B nên NA MB 1 ; x 0,25 AM NA x
có IA || AM nên IA NA 1 . x 5 IB
IA AB AB 1 AM 2 x Suy ra 1 1 . 1 0,25 IA IA IA x IA 1 x
Trong mặt phẳng ACC A
, có NP || AC nên PC NA x x 0,25 PC PA 2 PA NA 1 x 1 x
Trong mặt phẳng A B C , kẻ B K
|| AC , K IP I A' B' P Q K C' 0,25 QB KB
1 xKB 1 xIB 2 x Ta có 3 QC PC xPA xIA . x Vậy khi 2 QB x thì 2 3 QC .
Chú ý: Nếu học sinh sử dụng trực tiếp định lý Menelaus trong mặt phẳng để tìm tỉ số QB
QC vẫn cho điểm tối đa của phần này (nếu đúng).
Trong trường hợp ABC.A B C
là hình lăng trụ đều có tất cả các cạnh bằng 1, tìm 4c
giá trị lớn nhất của diện tích ngũ giác 1,0 MNPQK .
Theo (1) ta có IB 2 x.A B 2 x . 2 x 2 x
Theo (3) ta có QB .B C . 2 2 Trong mặt phẳng JB MB 1 x ABB A , có
JB 2 x.BB 2 x JB IB 2 . x
Xét tam giác IJB vuông tại B ta có: 2 2 IJ
IB JB 2 x 2 . 0,25 Tương tự, ta có 5 2 2 JQ
JB QB 2 x. . 2
Áp dụng định lý cosin cho tam giác IQB ta có 3 2 2 IQ
IB QB 2IB .QB .cos IB Q 2 x. . 2 Ta thấy, 2 2 2
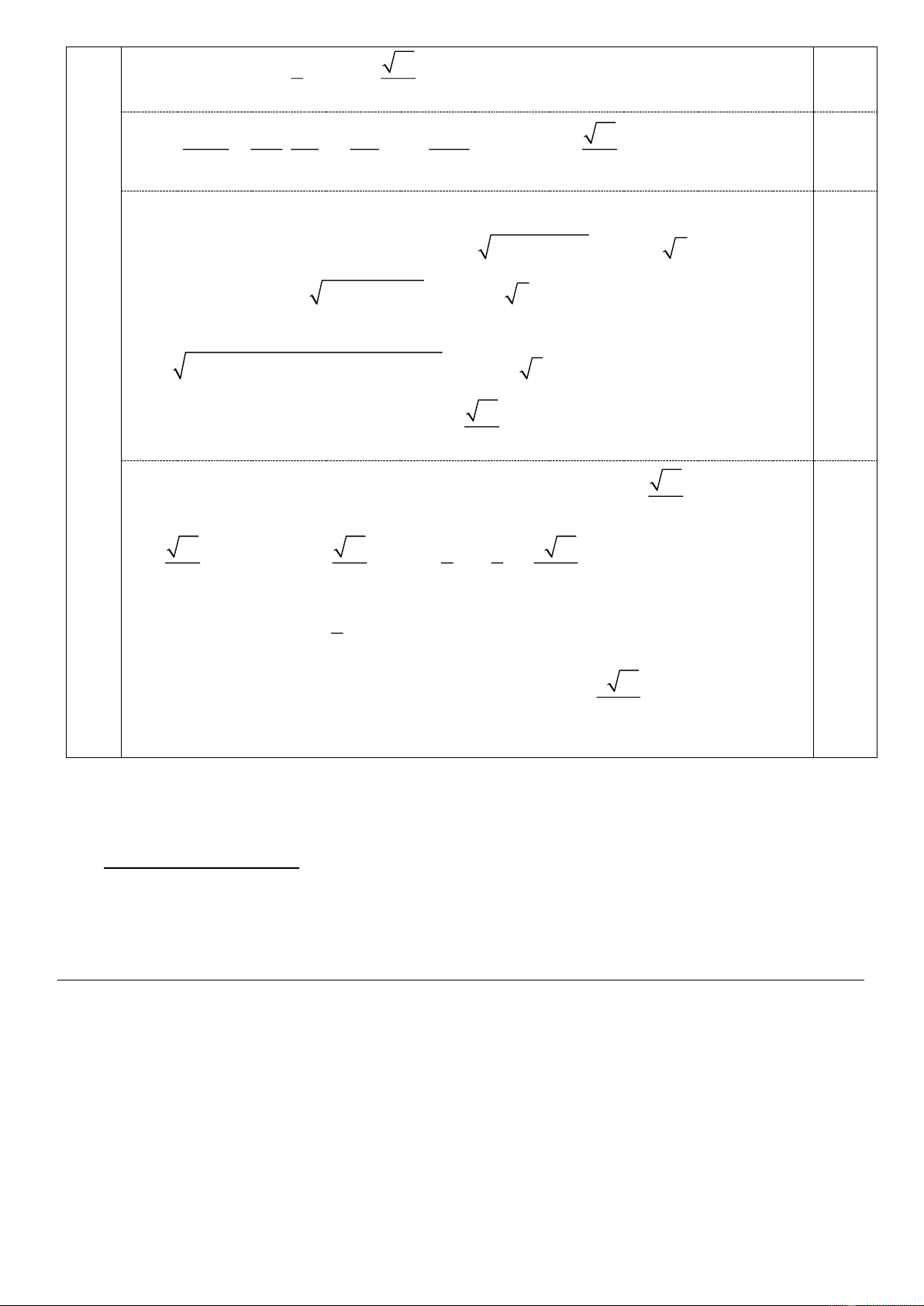
IJ IQ JQ nên tam giác IJQ vuông tại Q . Do đó, diện tích tam 6 1 15 giác IJQ là S .I . Q JQ x . I JQ 2 2 2 8 2 2 S JM JK JB 1 x 15 2 Ta có JMK . S . x . 0,25 JMK 1 S JI JQ JB 2 x 8 I JQ
Vì AM x nên A N
1 x, A I 1 x, A P 1 x .
Xét tam giác INA vuông tại A ta có 2 2 IN A I A N 1 x 2 . Tương tự, ta có 2 2 NP A N A P 2 x. 2 .
Áp dụng định lý cosin cho tam giác IPA ta có 0,25 2 2 IP A I A P
2A I.A . P cos IA P
1 x. 3 . Do đó, diện tích 15
tam giác INP là S x I NP 1 2 4 Diện tích hình ngũ giác 15
MNPQK là S S S S x x . I JQ JMK I NP 2 1 2 2 8 15 S
1 2x2x 2 15 1 3 3 15 2 2 x . 8 8 2 2 16 0,25 Dấu " " xảy ra khi 1 x . 2
Vậy giá trị lớn nhất của diện tích ngũ giác MNPQK bằng 3 15 khi M là trung 16 điểm của AB.
-------------HẾT -----------
SỞ GD&ĐT QUẢNG BÌNH
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2024-2025
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG HƯỚNG DẪN CHẤM
QUỐC GIA NĂM HỌC 2025-2026
Khóa ngày 31 tháng 3 năm 2025 Môn thi: TOÁN HỌC BÀI THI THỨ HAI
Đáp án này gồm có 07 trang YÊU CẦU CHUNG
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu cầu phải
lập luận lôgic chặt chẽ, đầy đủ, chi tiết và rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với những bước
giải sau có liên quan.
* Ở câu 3 nếu học sinh không vẽ hình hoặc vẽ hình sai ở ý nào thì cho điểm 0 đối với ý đó.
* Điểm thành phần của mỗi câu được chia đến 0,25 điểm. Đối với những phần được chia
đến 0,5 điểm thì tổ giám khảo thống nhất để chia đến 0,25 điểm. 7
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tuỳ theo mức điểm của từng câu.
* Điểm của toàn bài là tổng điểm (không làm tròn số) của điểm tất cả các câu. Câu Nội dung Điểm
Tìm tất cả các bộ ba số thực x, y, z thỏa mãn 1a 2 2 2 1,0
x y z
y z x
z x y 3 3 3 3 2025 2025 2025 (*) 2025
Áp dụng bất đẳng thức Cauchy ta có 0,25 2 2 2 2 2 2 x 3 yz
y 3zx
z 3x y 3 2 2025 2025 2025
3. 2025x y z x y z (1) Mặt khác, ta có
x y z x y z x 2 y 2 z 2 2 2 2 2 1 1 1 3 3 (2) 0,25
Dấu " " khi x y z 1. 2 2 2
x y z 2 x y z 1
Vì 2025 1 nên từ (2) suy ra: 3 2025 2025 (3) 3 2025 0,25
x y z
y z x
z x y 3 Từ (1) và (3 2 2 2 ) suy ra 3 3 3 2025 2025 2025 (4) 2025 Từ (4) suy ra:
* x y z 1. 0,25
Vậy x y z 1 thỏa mãn bài toán.
Cho đa thức bậc hai 2
f x x bx c với b, c là hai số nguyên. Chứng minh 1b 1,0
luôn tồn tại số nguyên a thỏa mãn f a f 2024. f 2025 . Với mỗi 2 x
ta có: f x. f x
1 f xx 1
bx 1 c 0,25
f x 2
x 2x 1 bx b c f x f x 2x b 1 0,25 2
f x 2xf x bf x f x 2
f x xf x 2 2
x bf x bx c 2 f x x
b f x x c f f x x. 0,25
Do đó f f x x f x. f x 1 , x (*)
Thay x 2024 vào (*) ta được f f 2024 2024 f 2024. f 2025 . Vì ,
b c, 2024 là ba số nguyên nên a f 2024 2024 là một số nguyên. 0,25
Vậy tồn tại số nguyên a f 2024 2024 thỏa mãn
f a f 2024. f 2025 (đpcm) 8 u 5
Cho dãy số u xác định bởi 1 . n 2025 2024 * u u 3u u , n n 1 n n n
a) Chứng minh lim u . n n 2 2,0 1
b) Với mỗi số nguyên dương n, đặt v n . 2024 u 1 2024 u 1 ... 2024 u 1 1 2 n Tính lim v . n n 2a
Chứng minh lim u . n 1,25 n
Ta chứng minh bằng quy nạp: * u 3, n * n
Với n 1 ta có u 5 3. Do đó, (*) đúng. 0,25 1
Giả sử (*) đúng với n k 1 hay u 3, k 1. k
Ta cần chứng minh: (*) đúng với n k 1 hay u 3 1 k 1 Thật vậy, ta có: 2025 2024 2025 2024 u u 3u
u u 3 u 3u u 3 k 1 k k k k 1 k k k u 3 2024 u 1 u 3 0 u 3 k 1 k k k 1 0,25 (vì 2024 u 3;u 1 0, k
1). Do đó (1) đúng. k k *
Vậy theo nguyên lý quy nạp u 3, n * n Ta cũng có : 2025 2024 * 2024 u u 3u u , n
u u u u n n n n n n n 3 n * 0, n 1 1 0,25 *
u u , n
. Do đó, dãy số u là dãy số tăng. n n 1 n
Giả sử lim u L L u 5 . Lấy giới hạn hai vế công thức truy hồi ta được: n 1 n L 0 0,25 2025 2024 L L 3L L (vô lý) L 3
Vậy lim u (đpcm) n 0,25 n
Với mỗi số nguyên dương 1 n, đặt v n . 2024 u 1 2024 u 1 ... 2024 u 1 1 2 n 2b 0,75 Tính lim v . n n Ta có: 2025 2024 * u 3 u 3u u 3, n n 1 n n n 0,25
u 3 2024 u u n n 1 3 n * , n 1 9 1 u 3 n * , n 2024 u 1 u . 3 n n 1 u 3 u 3 u 3 u 3 u 3 2 Do đó 1 2 n 1 n 1 v . ... . n u 3 u 3 u 3 u
3 u 3 u , * n . 0,25 3 2 3 n n 1 n 1 n 1 2 Vậy lim v lim 0 n n n u . 0,25 3 n 1
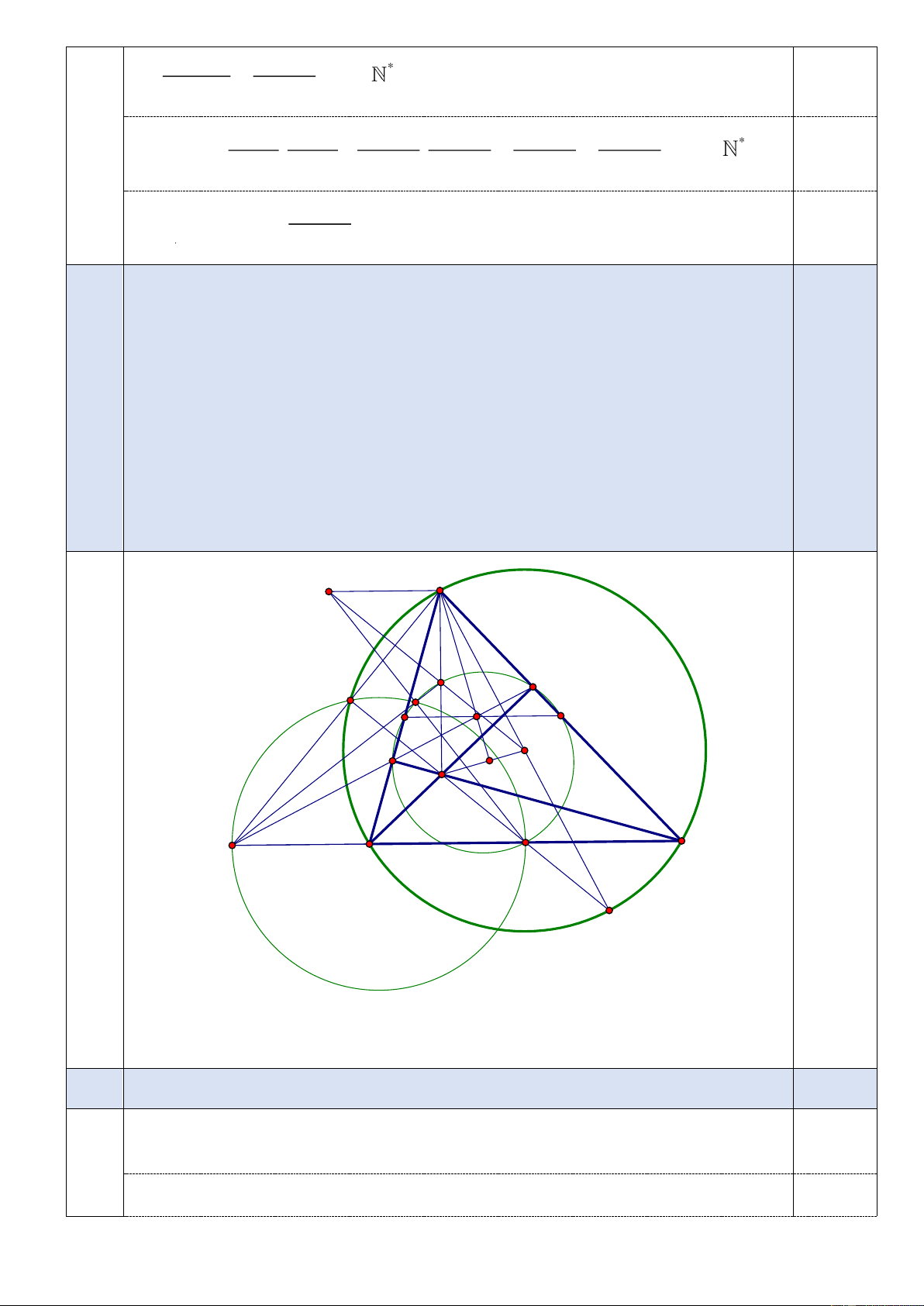
Cho tam giác nhọn ABC AB AC nội tiếp đường tròn O. Hai đường cao
BE, CF E AC, F AB cắt nhau tại H. Gọi M , N, P, Q tương ứng là
trung điểm của các đoạn thẳng BC, ,
CA AB, AH . Tia MH cắt O tại . L
a) Chứng minh AL, BC, EF đồng quy tại một điểm T. 3 3,5
b) Gọi K là giao điểm của NP và EF. Chứng minh AK vuông góc với OH.
c) Đường thẳng đi qua A song song với BC cắt OQ tại . D Chứng minh giao
điểm ( khác M ) của hai đường tròn ngoại tiếp hai tam giác MNP và MLT nằm
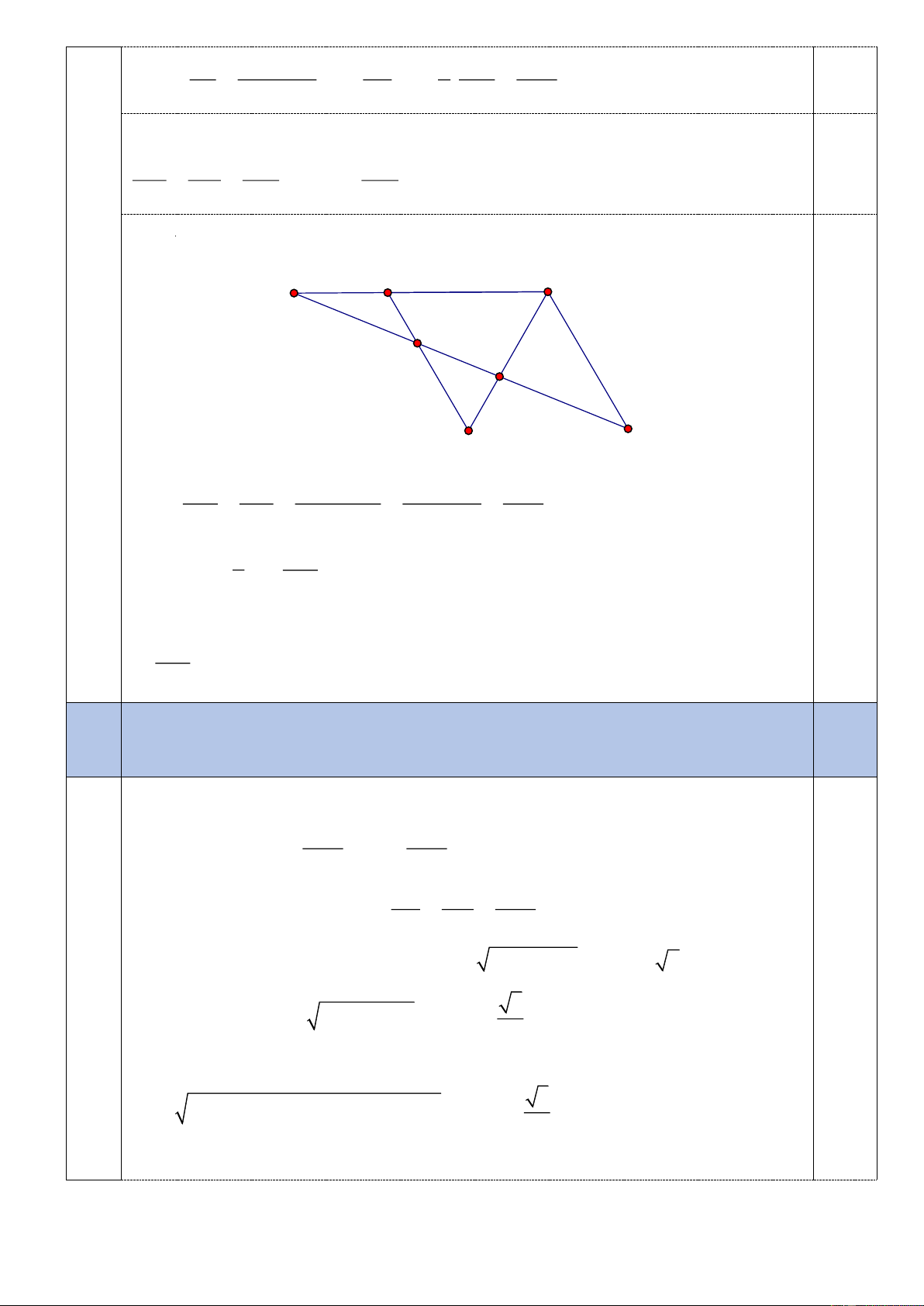
trên đường thẳng DM. D A Q E X L K N P O F H T B M C A'
Quy ước: Trong bài toán này ký hiệu XY , XYZ tương ứng là ký hiệu của
đường tròn đường kính XY và đường tròn ngoại tiếp tam giác XYZ . 3a
Chứng minh AL, BC, EF đồng quy tại một điểm T. 1,25
Gọi A là giao điểm của AO với O . 0,5
Vì BHCA là hình bình hành nên H , M , A thẳng hàng.
Do đó: L, H , M , A thẳng hàng nên ALA 90 ALH 90 L AH 1 0,25 10
AL là trục đẳng phương của hai đường tròn O và AH .
BC là trục đẳng phương của hai đường tròn BC và O . 0,25
EF là trục đẳng phương của hai đường tròn AH và BC . Suy ra A ,
L BC, EF đồng quy tại tâm đẳng phương T của ba đường tròn O , 0,25
BC và AH (đpcm) 3b
Gọi K là giao điểm của NP và EF. Chứng minh AK vuông góc với OH. 1,25
Vì E, F, N, P cùng nằm trên đường tròn Euler MNP của tam giác ABC nên 0,25
KE.KF KN.KP (2)
Vì AEH AFH 90 nên E, F AH , do đó P K . E KF (3) K / AH 0,25
Vì ANO APO 90 nên N, P AO , do đó P KN.KP (4). K / AO
Từ (2), (3), (4) suy ra P P
, do đó AK là trục đẳng phương của hai K / AH K / AO 0,25
đường tròn AH và AO (5)
Gọi Q là trung điểm của AO thì Q là tâm đường tròn AO. 0,25
Vì QQ là đường trung bình của tam giác AHO nên QQ || OH (6)
Từ (5) suy ra AK QQ (7) 0,25
Từ (6), (7) suy ra AK OH (đpcm)
Đường thẳng đi qua A song song với BC cắt OQ tại . D Chứng minh giao 3c
điểm (khác M ) của hai đường tròn ngoại tiếp hai tam giác MNP và MLT nằm 1,0
trên đường thẳng DM.
Gọi X (khác M ) là giao điểm của DM với MLT .
+ Chứng minh T , X ,Q thẳng hàng: 0,25
Vì X MLT và (1) suy ra MXT MLT MLA 90 (8)
Vì AD || BC nên ADX XMT ALX (vì MXLT nội tiếp) X ADL (9)
Vì O,Q tương ứng là tâm của O và AH nên OQ là đường trung trực của 0,25
đoạn thẳng AL . Do đó DLQ DAQ 90 nên L ADQ (10)
Từ (9), (10) suy ra: X ADQ DXQ 180 DAQ 90 DXQ 90 (11) 0,25
Từ (8) và (11) suy ra T , X ,Q thẳng hàng (12)
+ Chứng minh X MNP :
Từ (9), (12) suy ra TE.TF T . ATL T . Q TX mà
E, F,Q MNP
X MNP 0,25
Vậy giao điểm (khác M ) của hai đường tròn ngoại tiếp hai tam giác MNP và
MLT nằm trên đường thẳng DM (đpcm) 4
Cho n-giác đều A A ...A n , n 3. Mỗi một đỉnh của n-giác đều A A ...A 1 2 n 1 2 n 1,5 11
được tô bởi một màu trong m màu cho trước m ,m 3 sao cho hai đỉnh kề
nhau được tô bởi hai màu khác nhau. Tìm số cách tô màu có thể thực hiện được
trong các trường hợp sau:
a) Khi n 4, m 5 .
b) Khi n 2024, m 2025 . 4a
Khi n 4, m 5 . 0,5
Không mất tính tổng quát giả sử ta tô màu theo thứ tự các đỉnh A , A , A , A . 1 2 3 4
Đỉnh A có 5 cách tô màu. 1
Đỉnh A có 4 cách tô màu. 2
TH1: đỉnh A được tô màu cùng màu với đỉnh A . Lúc đó, có 1 cách tô màu 0,25 3 1
đỉnh A và có 4 cách tô màu đỉnh A . 3 4
Trong trường hợp này, có tất cả 5.4.1.4 80 cách tô màu.
TH2: đỉnh A được tô màu khác màu với đỉnh A . Lúc đó, có 3 cách tô màu 3 1
đỉnh A và có 3 cách tô màu đỉnh A . 3 4 0,25
Trong trường hợp này, có tất cả 5.4.3.3 180 cách tô màu.
Vậy có 260 cách tô màu khi n 4,m 5. 4b
Khi n 2024, m 2025 . 1,0
Gọi S là số cách tô màu n-giác đều A A ...A thỏa mãn bài toán. n 1 2 n
Ta giải bài toán trong trường hợp tổng quát với ,
m n bất kỳ thỏa mãn ,
m n ; m 3; n 3 . 0,25
TH1: đỉnh A và đỉnh A A 1 n 1
được tô bởi hai màu khác nhau. Lúc đó, đỉnh n
được tô màu khác với màu của hai đỉnh trên nên đỉnh A có tất cả m 2 cách tô n
màu. Trong trường hợp này, ta có số cách tô màu là m 2 S . n 1
TH2: đỉnh A và đỉnh A A được tô 1 n 1
được tô bởi cùng một màu. Lúc đó, đỉnh n
màu khác với màu trên nên đỉnh A có tất cả m 1 cách tô màu. Trong trường n hợp này 0,25
, ta có số cách tô màu là m 1 S . n2
Như vậy, ta có công thức truy hồi S m 2S m 1 S , n 5. n n 1 n2
Khi n 3: đỉnh A có m cách tô màu, đỉnh A có m 1 cách tô màu, đỉnh A 1 2 3
có m 2 cách tô màu. Do đó S m m 1 m 2 . 3
Khi n 4 và theo câu a) ta có:
S m m 1 1 m 1 m m 1 m 2 m 2 mm 2
1 m 3m 3 . 4 0,25
S m(m 1)(m 2) 3
Do đó, ta có dãy số S xác định bởi S mm 1 2 m 3m 3 . 4 n S
m 2S m 1 S , n 5 n n 1 n2 12
Từ hệ thức truy hồi trên, ta có S m m n m n n n 1 1 1 , 3; 3.
Thay n 2024, m 2025 , ta được 0,25 S 2025 2024 2024 1 2025 1 2024 2024. 2024
Vậy khi n 2024,m 2025 ta có 2024 2024 2024 cách tô màu.
Tìm tất cả các cặp số nguyên dương ; m n thỏa mãn 2 m 2 chia hết cho 5 1,0 . m n 2. TH1: m 1 2 m 2 1 1 Khi đó . Vì n 0 nên
không thể là số nguyên. 0,25 . m n 2 n 2 n 2
Trường hợp m 1 không thỏa mãn. TH2: m 2 Giả sử ;
m n là cặp số nguyên dương thỏa mãn bài toán. Ta có: 0,25 2 m 2 .
m n 2 n 2 m 2 .
m n 2 m .
m n 2 2m n . m n 2
2m n .
m n 2 2m n k . m n 2 với * k (1)
TH 2.1: k 1
Từ (1) ta có: 2m n .
m n 2 m 2n 2 2 (2)
Vì m 2 nên m 2 0 n 2 0. m m 2 1 m 4 m 3 0,25 Do đó: 2 2 2 hoặc hoặc . n 2 1 n 2 2 n 3 n 4 m 4 Thử lại, ta thấy thỏa mãn bài toán. n 3
TH 2.2: k 2
Từ (1) ta có: 2m n k . m n 2 2 .
m n 2 m n . m n 2 m 1 n 1 1 0 (3) 0,25
Vì m 2, n 1 nên (3) không xảy ra. Vậy có một bộ ;
m n 4; 3 thỏa mãn bài toán.
-------- HẾT -------- 13