Đề chọn HSG Toán 11 năm 2024 – 2025 trường THPT Đức Hợp – Hưng Yên

TRƯỜNG THPT ĐỨC HỢP
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2024-2025 TỔ TOÁN TIN Môn thi: TOÁN
Đề gồm có 01 trang Câu 1 (2,0 điểm): a)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 2 cos x +1 − 3. π b) + α − α
Rút gọn biểu thức A = 1 sin 1 sin +
, cho biết 0 < α < . 1− sinα 1+ sinα 2
Câu 2 (2,0 điểm): Giải các phương trình sau: a) 2
2cos x − 3sin x = 0. 1 b) log (x − )2
1 + log x +1 = log 5 − x . 2 2 ( ) 2 ( ) 2 Câu 3 (2,0 điểm): f (x) +1
( 2x + x) f (x)+ 2
a) Cho hàm số f (x) thỏa mãn lim = 16. Tính lim . x 1 → x −1 x 1 → x −1
b) Học sinh Nam tới Hội chợ Xuân 2025 và tham gia trò chơi ném bóng, mỗi lần ném người chơi
phải đặt cược một số tiền sau đó mới được chơi. Lần chơi đầu tiên Nam đặt 20 000 đồng, mỗi lần chơi tiếp
theo tiền đặt gấp đôi lần tiền đặt cược trước. Nam chơi thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi Nam
thắng hay thua bao nhiêu tiền? Câu 4 (1,0 điểm):
Cho hàm số y = f (x) liên tục trên  và 𝑎𝑎, 𝑏𝑏 là các số thực bất kì. Xét hàm số
g(x) = f (a) + f (b) − 2 f (x) . Chứng minh rằng phương trình g(x) = 0 luôn có nghiệm thực Câu 5 (1,0 điểm):
Cho các số thực x, y thỏa mãn các điều kiện 5𝑥𝑥 − 𝑦𝑦 , 2𝑥𝑥 − 3𝑦𝑦 , 𝑥𝑥 + 2𝑦𝑦 theo thứ tự lập thành cấp số
cộng, và các số (𝑦𝑦 + 1)2 , 𝑥𝑥𝑦𝑦 + 1 , (𝑥𝑥 − 1)2 theo thứ tự lập thành cấp số nhân. Tìm 𝑥𝑥, 𝑦𝑦 . Câu 6 (2,0 điểm):
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SA = SB = SC , đường cao SO của hình chóp
S.ABC có độ dài bằng 2a .
a) Chứng minh rằng SA ⊥ BC
b) M là điểm thuộc đường cao AH của tam giác ABC (M khác A và H ). Mặt phẳng (P) đi qua M và
vuông góc với AH cắt hình chóp theo thiết diện. Tìm vị trí của M để diện tích thiết diện lớn nhất. --------Hết---------
Lưu ý: Giám thị không giải thích gì thêm. Học sinh không được sử dụng tài liệu.
TRƯỜNG THPT ĐỨC HỢP
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2024-2025 TỔ TOÁN TIN Môn thi: TOÁN HƯỚNG DẪN CHẤM
Đáp án này gồm có 06 trang Câu Nội dung Điểm Câu 1 (2,0 điểm):
1a a) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 2 cosx +1−3. 1,0 1
− ≤ cos x ≤1⇒ 0 ≤ cos x +1≤ 2 ⇒ 0 ≤ cos x +1 ≤ 2 0,50 ≤ + ≤ ⇒ − ≤ + − ≤ − 0 2 cos x 1 2 2
3 2 cos x 1 3 2 2 3 0,25
GTNN bằng -3 khi cos x = 1
− ⇔ x = π + k2π ,k ∈ 0,25
GTLN bằng 2 2 − 3 khi cos x =1 ⇔ x = k2π ,k ∈ + α − α π
1b b) Rút gọn biểu thức A = 1 sin 1 sin +
, cho biết 0 < α < . 1− sinα 1+ sinα 2 1,0 2  + α − α  + α − α Khi đó 2 1 sin 1 sin 1 sin 1 sin 4 4 A =  +  = + + 2 =   = 0,50 2 1− sinα 1+ sinα 1− sinα 1+ sinα 1− sin α cos α   2 π
Vì 0 < α < nên cosα > 0 do đó 2 A = 2 cosα 0,50 .
Câu 2 (2,0 điểm): Giải các phương trình sau: 2a a) 2
2cos x − 3sin x = 0 . 1,0 Ta có: 2 x − x = ⇔ ( 2 − x) 2 2cos 3sin 0 2 1 sin
− 3sin x = 0 ⇔ 2sin x + 3sin x − 2 = 0 0,5 sin x = 2( − VN) 2
2sin x 3sin x 2 0  + − = ⇔ 1  0,25 sin x =  2  π x = + k2π 1 π  6 sin x = = sin ⇔  ,k ∈ 2 6  5π x = + k2π  0,25  6 π 5π
Vậy phương trình có 2 họ nghiệm là x = + k2π , x =
+ k2π ,k ∈ 6 6 1
2b b) log (x − )2
1 + log x +1 = log 5 − x . 1,0 2 2 ( ) 2 ( ) 2 Đk: 1 − < x < 5; 1 x ≠ . 0,25 1 Ta có log (x − )2
1 + log x +1 = log 5 − x 2 2 ( ) 2 ( ) 2
⇔ log x −1 + log x +1 = log 5 − x 2 2 ( ) 2 ( )
⇔ log x −1 x +1 = log 5 − x ⇔ x −1 x +1 = 5 − x 0,25 2 ( ) 2 ( ) ( ) x >1 x <1 0,25 ⇔ ( hoặc   x −  ) 1 (x + ) 1 = 5 − x (  −x + 
)1(x + )1 = 5− x x > 1 x < 1 ⇔  hoặc  ⇔ x = 2 thỏa mãn. 2
x + x − 6 = 0 2
x − x + 4 = 0
Vậy phương trình có nghiệm duy nhất x = 2 . 0,25 Câu 3 (2,0 điểm): 3a f (x) +1
( 2x + x) f (x)+ 2 1,0
a) Cho hàm số f (x) thỏa mãn lim = 16. Tính lim . x 1 → x −1 x 1 → x −1 2 2
(x + x) f (x) + 2
(x + x)( f (x) + ) 2
1 − x − x + 2 lim = lim x 1 → − x 1 x 1 → x −1 0,25 2
(x + x)( f (x) + ) 2 1 x + x − 2 = lim − lim x 1 → − x 1 x 1 → x −1 2
(x + x)( f (x) + ) 1 * 2 f (x) +1 lim = lim(x + x).lim = 2.16 = 32 0,25 x 1 → − x 1 → x 1 x 1 → x −1 2 * x + x − 2 (x −1)(x + 2) lim = lim
= lim(x + 2) = 3 0,25 x 1 → − x 1 → − x 1 x 1 x 1 → 2 Vậy
(x + x) f (x) + 2 lim = 32 − 3 = 29 0,25 x 1 → x −1
b) Học sinh Nam tới Hội chợ Xuân 2025 và tham gia trò chơi ném bóng, mỗi lần
ném người chơi phải đặt cược một số tiền sau đó mới được chơi. Lần chơi đầu tiên
3b Nam đặt 20 000 đồng, mỗi lần chơi tiếp theo tiền đặt gấp đôi lần tiền đặt cược trước. 1,0
Nam chơi thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi Nam thắng hay thua bao nhiêu tiền?
Số tiền Nam đặt trong mỗi lần là cấp số nhân có 𝑢𝑢1 = 20 000 và công bội 𝑞𝑞 = 2.
Nam thua trong 9 lần đầu tiên nên tổng số tiền thua là: 0,5
𝑆𝑆9 = 𝑢𝑢1 + 𝑢𝑢2 + ⋯ + 𝑢𝑢9 = 𝑢𝑢1�1 − 𝑝𝑝9� = 10220000 đồng 1 − 𝑝𝑝
Số tiền mà Nam thắng trong lần thứ 10 là: 𝑢𝑢10 = 𝑢𝑢1𝑞𝑞9 = 10240000 đồng
Ta có: 𝑢𝑢10 − 𝑆𝑆9 = 20 000 > 0 nên Nam thắng 20 000 đồng 0,5
Câu 4 (1,0 điểm): Cho hàm số y = f (x) liên tục trên . Xét hàm số 4
g(x) = f (a) + f (b) − 2 f (x) . Chứng minh rằng phương trình g(x) = 0 luôn có 1,00 nghiệm.
Đặt g(x) = f (a) + f (b) − 2 f (x) khi đó g(x) cũng là hàm số liên tục trên đoạn [ ; a b]. Ta có :
g(a) = f (a) + f (b) − 2 f (a) = f (b) − f (a) và 0,25
g(b) = f (a) + f (b) − 2 f (b) = f (a) − f (b) . Do đó : 2
g(a).g(b) = [
− f (b) − f (a)] . x = a
Nếu f (a) = f (b) thì  thỏa mãn bài toán. 0,25 x = b
Nếu f (a) ≠ f (b) thì 2
g(a).g(b) = [
− f (b) − f (a)] < 0 0,25
nên phương trình g(x) = 0 có ít nhất 1 nghiệm thuộc khoảng ( ; a b).
Vậy phương trình g(x) = 0 luôn có nghiệm. 0,25
Câu 5 (1,0 điểm): Cho các số thực x, y thỏa mãn các điều kiện 𝟓𝟓𝒙𝒙 − 𝒚𝒚 , 𝟐𝟐𝒙𝒙 − 𝟑𝟑𝒚𝒚 , 𝒙𝒙 + 5
𝟐𝟐𝒚𝒚 theo thứ tự lập thành cấp số cộng, và các số (𝒚𝒚 + 𝟏𝟏)𝟐𝟐 , 𝒙𝒙𝒚𝒚 + 𝟏𝟏 , (𝒙𝒙 − 𝟏𝟏)𝟐𝟐 theo thứ 1,0
tự lập thành cấp số nhân. Tìm 𝒙𝒙, 𝒚𝒚 .
5𝑥𝑥 − 𝑦𝑦 , 2𝑥𝑥 − 3𝑦𝑦 , 𝑥𝑥 + 2𝑦𝑦 theo thứ tự lập thành cấp số cộng nên
2(2x −3y) = (x + 2y) + (5x − y) ⇔ 2x + 7y = 0 (1) 0,25
(𝑦𝑦 + 1)2 , 𝑥𝑥𝑦𝑦 + 1 , (𝑥𝑥 − 1)2 theo thứ tự lập thành cấp số nhân nên (
xy +1 = ( y + ) 1 (x − ) 1 (2)
xy + )2 = ( y + )2 (x − )2 1 1 1 ⇔  0,25 xy +1 = − 
( y + )1(x − )1(3)
Giải hệ gồm (1) và (2) ta được nghiệm (x y) 14 4 ; ;  = −  0,25 9 9   
Giải hệ gồm (1) và (3) ta được nghiệm ( ;
x y) = (0;0) và (x y)  9 9 ; ;  = −  0,25 4 14   
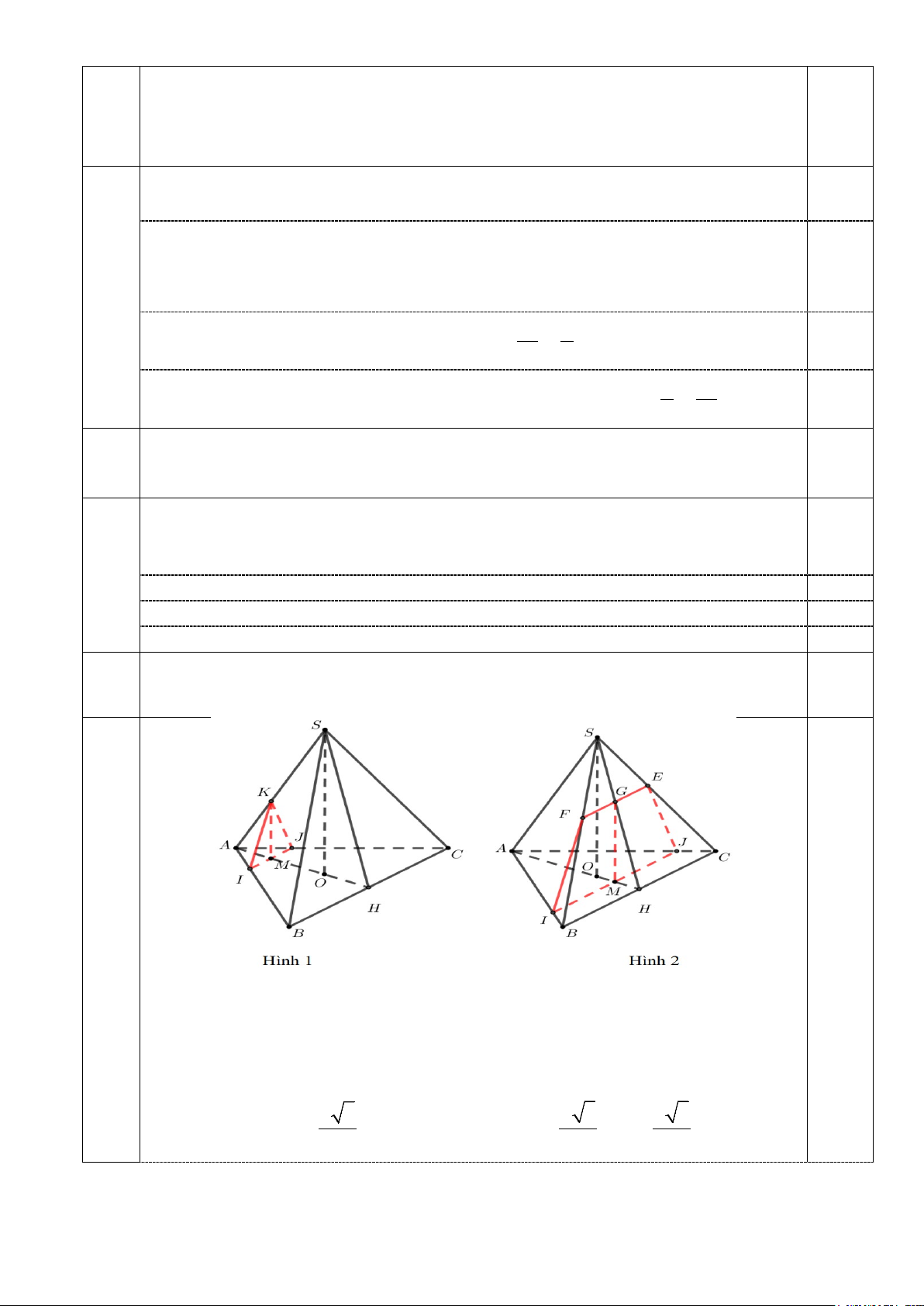
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SA = SB = SC , đường cao
6a SO của hình chóp S.ABC có độ dài bằng 2a . 1,0
a) Chứng minh rằng SA ⊥ BC
Từ 𝑆𝑆𝑆𝑆 = 𝑆𝑆𝑆𝑆 = 𝑆𝑆𝑆𝑆 → 𝑂𝑂𝑆𝑆 = 𝑂𝑂𝑆𝑆 = 𝑂𝑂𝑆𝑆 → 𝑂𝑂 là tâm đường tròn ngoại
tiếp tam giác 𝑆𝑆𝑆𝑆𝑆𝑆 => 𝑂𝑂 cũng là trực tâm tam giác 𝑆𝑆𝑆𝑆𝑆𝑆 → 𝑂𝑂𝑆𝑆 vuông 0,25 góc 𝑆𝑆𝑆𝑆 (1)
Mà SO vuông góc với (ACB) nên SO vuông góc với BC (2) 0,25
Từ (1) và (2) suy ra BC vuông góc với (OSA) 0,25 Vậy BC vuông góc với SA 0,25
b) M là điểm thuộc đường cao AH của tam giác ABC (M khác A và H ). Mặt
6b phẳng (P) đi qua M và vuông góc với AH cắt hình chóp theo thiết diện. Tìm vị trí 1,0
của M để diện tích thiết diện lớn nhất.
Vì (P) đi qua M và vuông góc với AH nên (P) song song hoặc chứa AH
. Do đó: Giao tuyến (P) với (SAH) song song hoặc trùng với AH => Gọi giao tuyến là
GM. Theo định lí giao tuyến thì (P), (SCB), (ABC) đôi một cắt nhau nên giao tuyến EF (qua G) // BC // IJ (qua M)
Chú ý: Vẽ đúng hình cả hai trường hợp thiết diện là tam giác và tính đúng cho 0,5
điểm, hình thang cân và tính đúng cho 0,5 điểm  a 3  a a
Đặt 𝑆𝑆𝐴𝐴 = 𝑥𝑥, x ∈0; , SO = 3 3
SO = 2a;OH = ;OA = 2  0,5   6 3 TH1. Nếu a 3 0 < x ≤
thì thiết diện là tam giác KIJ. Thiết diện có diện 3 tích lớn nhất, khi 2 a 3
AM = AO = AH = hay a 3 x = 3 3 2 TH2. Nếu a 3 a 3 < x <
thì thiết diện là hình thang IJEF. 3 2 Ta có: IJ AM x 2x 3 = = ⇒ IJ = BC AH a 3 3 2 0,25 a 3 x EF SG OM − 3 = = =
⇒ EF = 2(x 3 − a) BC SH OH a 3 6 a 3 − x EF GM MH 2 = = =
⇒ GM = 2(3a − 2x 3) BC SO OH a 3 6
Khi đó, diện tích thiết diện IJEF là = ( + ) = ( − )( − ) 2 1 1 3 4 3 3 6 4 3 a S IJ EF GM x a a x ≤ (BĐT Cô-si). 0,25 2 3 4 2
Vậy diện tích thiết diện lớn nhất là 3a khi 3a 3 x = 4 8 2
Kết hợp các trương hợp, diện tích thiết diện lớn nhất là 3a khi 3a 3 x = 4 8 ------Hết-------
Xem thêm: ĐỀ THI HSG TOÁN 11
https://toanmath.com/de-thi-hsg-toan-11
Document Outline

• ĐỀ XUẤT HSG TOÁN 11 CẤP TRƯỜNG NĂM HỌC 2024-2025
• HSG 11