Đề cuối học kỳ 2 Toán 11 năm 2022 – 2023 trường THPT Quang Trung – TP HCM

Gới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra cuối học kỳ 2 môn Toán 11 năm học 2022 – 2023 trường THPT Quang Trung, thành phố Hồ Chí Minh; đề thi có đáp án và hướng dẫn chấm điểm.

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 11

Môn: Toán 11

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
TRƯỜNG THPT QUANG TRUNG
KIỂM TRA CUỐI KỲ – HỌC KỲ II
NĂM HỌC: 2022 – 2023
MÔN: TOÁN – KHỐI 11
Thời gian: 90 phút
Bài 1: (1,5 điểm) Tính các giới hạn sau:
a.
32
2
3
5 3 27
lim
3 30
x
xxx
xx
→
− −+
+−
b.
2
2
2 53
lim
7 10
x
x
xx
→
+−
−+
c.
(
)
2
lim 4 16 1 2
x
xx x
→+∞
+ −−
Bài 2: (1,5 điểm)
a. Xét tính liên tục của hàm số
( )
2
42
3 85
1
32
2 11 1
xx
khi x
fx
x
x x khi x
−+
>
=
+−
+− ≤
tại
0
1x =
b. Tìm
a
để hàm số
(
)
x
f
sau liên tục tại
0
2x = −
Bài 3: (1,5 điểm) Tìm đạo hàm các hàm số sau:
a.
432
3 4 7 2022yx x x x=− + −+
b.
2
32
54
x
y
xx
−
=
−+
c.
( )
2
31 37yx xx= − +−
Bài 4: (2,25 điểm)
a. Cho hàm số
42
65yx x=−+
có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại điểm có
hoành độ
2
0
=x
.
b. Cho hàm số
32
3 14 1yx x x=+−+
có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp
tuyến đó song song với đường thẳng
: 10 27
dy x= −
.
c. Cho hàm số
31
2
x
y
x
+
=
−
có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đó
vuông góc với đường thẳng
1
:9
7
dy x
= −
.
Bài 5: (3,25 điểm)
Cho hình chóp S.ABCD, có đáy ABCD là hình chữ nhật,
,3AB a AD a= =
,
( )
,SA ABCD⊥
3SA a=
.
a. Chứng minh rằng
( )
BC SAB⊥
.
b. Chứng minh rằng
( ) ( )
SAD SCD⊥
.
c. Tính góc giữa đường thẳng SB và mặt phẳng (ABCD).
d. Tính góc giữa hai mặt phẳng (SCD) và (ABCD).
e. Tính góc giữa đường thẳng SC và mặt phẳng (SAD).
------HẾT------
TRƯỜNG THPT QUANG TRUNG
1
ĐÁP ÁN TOÁN KHỐI 11 –HK 2 – 2022-2023
Bài 1: Tính các giới hạn sau:
a.
32
2
3
5 3 27
lim
3 30
x
xxx
xx
→
− −+
+−
( )
( )
( )( )
2
3
3 29
lim
3 3 10
x
x xx
xx
→
− −−
=
−+
(0.25đ)
2
3
29
lim
3 10
x
xx
x
→
−−
=
+
=
6
19
(0.25đ)
b.
2
2
2 53
lim
7 10
x
x
xx
→
+−
−+
( )( )
( )
2
2 59
lim
2 5 2 53
x
x
xx x
→
+−
=
− − ++
(0.25đ)
( )
( )
2
2
lim
5 2 53
x
xx
→
=
− ++
=
1
9
−
(0.25đ)
c.
(
)
2
lim 4 16 1 2
x
xx x
→+∞
+ −−
22
2
4 16 1 4
lim
16 1
42
x
xx x
xx
xx
→+∞
+ −−
=
+−+
(0.25đ)
2
1
16
lim
16 1
42
x
x
xx
→+∞
−
=
+−+
= 4 (0.25đ)
Bài 2:
a. Xét tính liên tục của hàm số
(
)
(
)
( )
2
42
3 85
1
32
2 11 1
xx
x
fx
x
xx x
−+
>
=
+−
+− ≤
tại
0
1x =
•
( ) ( )
1
1 8 lim
x
f fx
−
→
=−=
(0.25đ)
•
(
)
2
11
3 85
lim lim
32
xx
xx
fx
x
++
→→
−+
=
+−
( )( )
( )
1
13 5 3 2
lim
34
x
xx x
x
+
→
− − ++
=
+−
( )
( )
1
lim 3 5 3 2 8
x
xx
+
→
= − ++ =−
(0.25đ)
Do
(
)
(
)
(
)
11
1 lim lim 8
xx
f fx fx
−+
→→
= = = −
Vậy: hàm số liên tục tại
0
1
x =
(0.25đ)
b. Tìm a để hàm số liên tục tại
0
2x = −
( )
( )
( )
32
2
2 5 10
2
32
11 2
xx x
x
fx
xx
ax x
−−+
≠−
=
++
−=−
•
( )
2 2 11fa−=−−
•
32
2
2
2 5 10
lim
32
x
xx x
xx
→−
−−+
++
(0.25đ)
( )
( )
( )( )
2
2
22 5 5
lim
21
x
x xx
xx
→−
− −+
=
++
2
2
2 55
lim 23
1
x
xx
x
→−
−+
= = −
+
ycbt
( ) ( )
2
2 lim
x
f fx
→−
⇔ −=
(0.25đ)
6a⇔=
(0.25đ)
Bài 3: Đạo hàm của các hàm số sau:
a.
43 2
3 4 7 2022yx x x x=− + −+
TRƯỜNG THPT QUANG TRUNG
2
⇒
( ) ( ) ( )
( ) ( )
// /
//
/4 3 2
3 4 7 2022yx x x x=− + −+
(0.25đ)
/ 32
4 9 87y xxx
= − +−
(0.25đ)
b.
2
32
54
x
y
xx
−
=
−+
( )
( )
( )
( )
( )
/
/
22
/
2
2
32 54 32 54
54
x xx x xx
y
xx
− −+− − −+
=
−+
(0.25đ)
( )
2
2
2
3 42
54
xx
xx
− ++
=
−+
(0.25đ)
c.
( )
2
31 37
yx xx= − +−
( )
( )
(
)
/
/
'2 2
31 3731 37y x xx x xx= − +−+ − +−
( )
2
2
23
3 37 31
2 37
x
xx x
xx
+
= + −+ −
+−
(0.25đ)
=
2
2
12x 25x 45
2 x 3x 7


(0.25đ)
Bài 4:
a) Cho hàm số
( )
42
65yx x C=−+
.
00
x 2y 3 
(0.25đ)
/3
4 12
yx x= −
( )
/
28ky= =
(0.25đ
Pttt:
8 19yx= −
(0.25đ)
b) Cho hàm số
( )
32
3 14 1yx x x C=+−+
.
/2
y 3x 6x 14 
d
d : y 10x 27 k 10 
Gọi
là tiếp tuyến tại điểm
00
M x ;y
Ta có:
// d
d
2
00
k k 10
3x 6x 24 0


0
0
x2
x4

(0.25đ)
Với
00
x 2, y 7,k 10 
Pttt
: y 10x 27
( loại ) (0.25đ)
Với
00
x 4, y 41,k 10
Pttt
: y 10x 81
( nhận) (0.25đ)
c) Cho hàm số
3x 1
yC
x2
/
2
7
y
x2
d
11
d:y x 9 k
77

Gọi
/
là tiếp tuyến tại điểm
00
M x ;y
Ta có:
/
d
/
/
d
2
0
k .k 1
k7
7
7
x2



0
0
x3
x1
(0.25đ)
Với
00
x 3, y 10, k 7 
Pttt
: y 7x 31
(0.25đ)
Với
00
x 1, y 4, k 7  
TRƯỜNG THPT QUANG TRUNG
3
Pttt
: y 7x 3
(0.25đ)
Bài 5: Cho hình chóp S.ABCD có
( )
SA ABCD⊥
,
đáy hình chữ nhật,
,3AB a AD a= =
,
3
SA a
=
.
a. Chứng minh:
( )
BC SAB⊥
Ta có:
( )
( )
( )
:
BC SA SA ABCD
BC AB
SAB SA AB A
⊥⊥
⊥
∩=
(0.25đ)
Vậy:
( )
BC SAB⊥
(0.25đ)
b. Chứng minh:
( ) ( )
SCD SAD⊥
Ta có:
( )
( )
( )
:
CD SA SA ABCD
CD AD
SAD SA AD A
⊥⊥
⊥
∩=
Nên
( )
CD SAD⊥
(0.25đ)
Mà
( )
CD SCD⊂
Vậy:
( ) ( )
SCD SAD⊥
(0.25đ)
c. Tính góc giữa SB và
( )
ABCD
.
•
( )
SB ABCD B=
•
( )
SA ABCD⊥
tại A.
Suy ra AB là hình chiếu vuông góc của SB lên
( )
ABCD
Nên góc giữa SB và
( )
ABCD
là góc
SBA
∧
(trong tam giác vuông SAB) (0.25đ)
Xét
SAB∆
vuông tại A có
0
tan 3 60SBA SBA
∧∧
=⇒=
(0.5đ)
d. Tính góc giữa
( )
SCD
và
( )
ABCD
.
Ta có:
( ) ( )
( )
( )
:
:
SCD ABCD CD
ABCD AD CD D
SCD SD CD D
=
⊥=
⊥=
Suy ra góc giữa
(
)
SCD
và
( )
ABCD
cũng là
góc giữa AD và SD, đó là góc
SDA
∧
(trong tam
giác vuông SCD) (0.25đ)
Xét
SOA∆
vuông tại O:
0
tan 1 45SDA SDA
∧∧
=⇒=
(0.5đ)
e. Tính góc giữa SC và (SAD).
•
( )
SC SAD S=
•
( )
CD SAD D⊥=
Suy ra SD là hình chiếu vuông góc của SC lên
( )
SAD
.
Nên góc giữa SC và
( )
SAD
cũng là góc giữa
SC và SD, đó là góc
CSD
∧
(trong tam giác
vuông SCD) (0.25đ)
Xét
SCD∆
vuông tại D có
tan 6 arctan 6CSD CSD
∧∧
=⇒=
(0.5đ)
…HẾT…
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT QUANG TRUNG
KIỂM TRA CUỐI KỲ – HỌC KỲ II
NĂM HỌC: 2022 – 2023
MÔN: TOÁN – KHỐI 11 Thời gian: 90 phút
Bài 1: (1,5 điểm) Tính các giới hạn sau: 3 2 a.
x − 5x − 3x + 27 lim b. 2x + 5 − 3 lim c. + − − →+∞ ( 2 lim
4x 16x 1 2x x ) 2 x→3 3x + x − 30 2
x→2 x − 7x +10 Bài 2: (1,5 điểm) 2 3x −8x + 5  khi x >1 a.
Xét tính liên tục của hàm số f (x) =  x + 3 − 2 tại x =1 0  4 2 x + 2x −11 khi x ≤1
b. Tìm a để hàm số f(x) sau liên tục tại x = 2− 0 3 2
2x − x − 5x +10  ≠ − f (x) khi x 2 2 =  x + 3x + 2 ax −11 khi x = 2 −
Bài 3: (1,5 điểm) Tìm đạo hàm các hàm số sau: a. 4 3 2
y = x − 3x + 4x − 7x + 2022 b. 3x − 2 y =
c. y = ( x − ) 2
3 1 x + 3x − 7 2 x − 5x + 4 Bài 4: (2,25 điểm) a. Cho hàm số 4 2
y = x − 6x + 5 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x = . 0 2 b. Cho hàm số 3 2
y = x + 3x −14x +1 có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp
tuyến đó song song với đường thẳng d : y =10x − 27 . c. Cho hàm số 3x +1 y =
có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đó x − 2
vuông góc với đường thẳng 1
d : y = x − 9 . 7 Bài 5: (3,25 điểm)
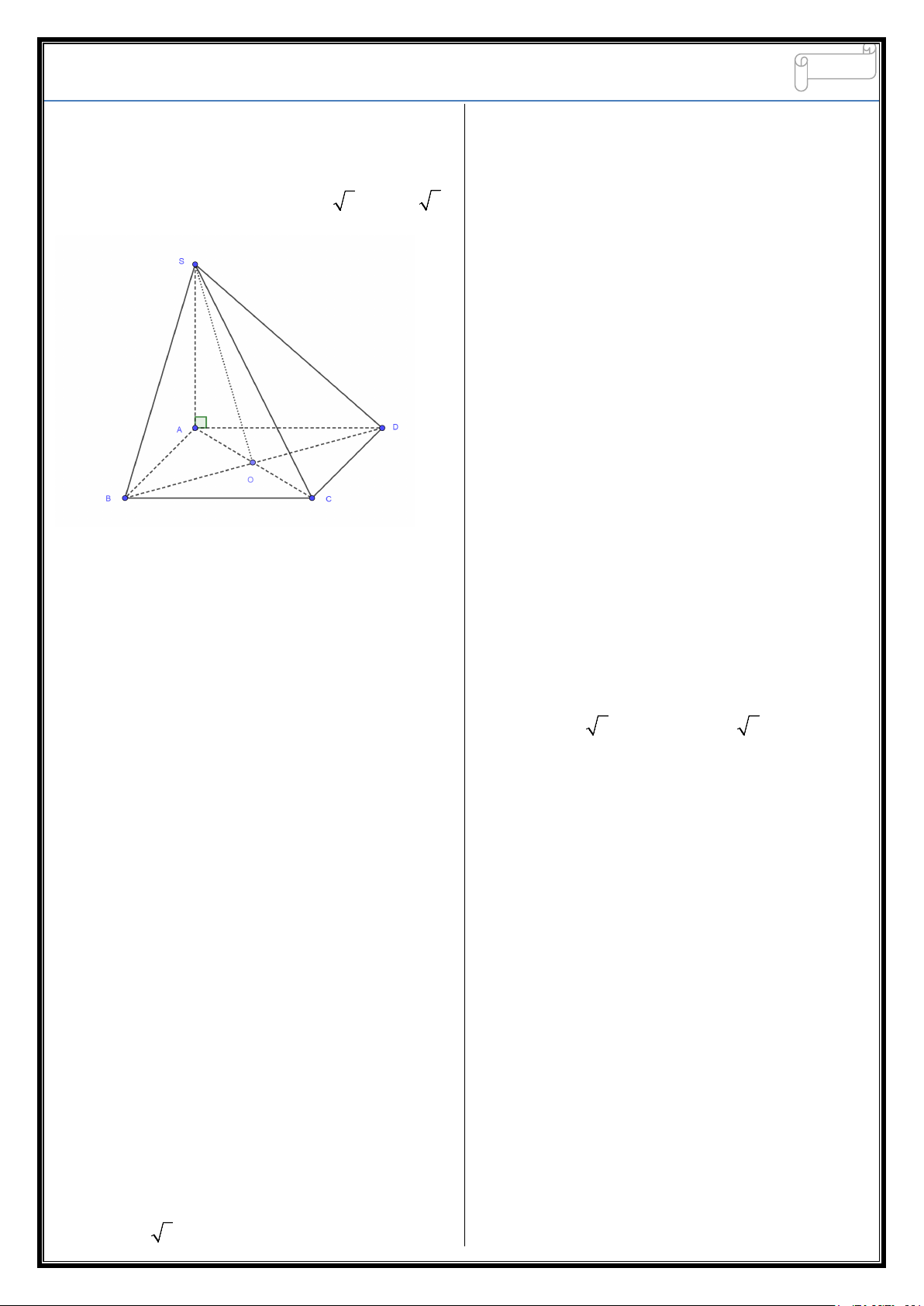
Cho hình chóp S.ABCD, có đáy ABCD là hình chữ nhật, AB = a, AD = a 3 , SA ⊥ ( ABCD), SA = a 3 .
a. Chứng minh rằng BC ⊥ (SAB) .
b. Chứng minh rằng (SAD) ⊥ (SCD) .
c. Tính góc giữa đường thẳng SB và mặt phẳng (ABCD).
d. Tính góc giữa hai mặt phẳng (SCD) và (ABCD).
e. Tính góc giữa đường thẳng SC và mặt phẳng (SAD). ------HẾT------
TRƯỜNG THPT QUANG TRUNG 1
ĐÁP ÁN TOÁN KHỐI 11 –HK 2 – 2022-2023 Bài 2:
Bài 1: Tính các giới hạn sau:
a. Xét tính liên tục của hàm số 3 2 2 3x −8x + 5 a.
x − 5x − 3x + 27 lim (x >  ) 1 2 x→3 3x + x − 30
f (x) =  x + 3 − 2 tại x =1 0  4 2
x + 2x −11(x ≤  ) 1
(x −3)( 2x −2x −9) = lim (0.25đ) x→3 (x −3)(3x +10) • f ( ) 1 = 8 − = lim f (x) (0.25đ) x 1− → 2 x − 2x − 9 = lim 2 − + • f (x) 3x 8x 5 lim = lim x→3 3x +10 x 1+ x 1+ → → x + 3 − 2 (x − )
1 (3x −5)( x +3 + 2) = 6  (0.25đ) 19 = lim x 1+ → x + 3− 4 = lim (3x − 5) + + = − (0.25đ) + ( x 3 2) 8 b. 2x + 5 − 3 lim x 1 → 2
x→2 x − 7x +10 Do f ( )
1 = lim f (x) = lim f (x) = 8 − x 1− x 1+ → → 2x + 5 − 9 = lim (0.25đ)
x→2 (x − 2)(x − 5)( 2x +5 +3)
Vậy: hàm số liên tục tại x =1 (0.25đ) 0 2
b. Tìm a để hàm số liên tục tại x = 2 − = lim 0
x→2 (x − 5)( 2x +5 +3) 3 2
2x − x − 5x +10  ≠ − f (x) x 2 2 ( ) =  x + 3x + 2 = 1 − (0.25đ)
ax −11(x = 2 −  ) 9 • f ( 2 − ) = 2 − a −11 c. + − − →+∞ ( 2 lim
4x 16x 1 2x x ) 3 2
2x − x − 5x +10 2 2
4x +16x −1− 4 • lim (0.25đ) = lim x (0.25đ) 2 x→ 2 − x + 3x + 2 x→+∞ 16 1 x 4 + − + 2x 2 x x (x − 2)( 2 2x − 5x + 5) = lim x→ 2 − (x + 2)(x + )1 1 16 − 2 2x − 5x + 5 = lim x = lim = 2 − 3 x→+∞ 16 1 x→ 2 − x +1 4 + − + 2 2 x x ycbt ⇔ f ( 2
− ) = lim f (x) (0.25đ) x→ 2 − = 4 (0.25đ) ⇔ a = 6 (0.25đ)
Bài 3: Đạo hàm của các hàm số sau: a. 4 3 2
y = x − 3x + 4x − 7x + 2022
TRƯỜNG THPT QUANG TRUNG 2 ⇒ / y = ( 4 x )/ −( 3 x )/ + ( 2 3
4x )/ −(7x)/ + (2022)/
 Gọi  là tiếp tuyến tại điểm Mx ; y 0 0  (0.25đ) Ta có:    / /d / 3 2
y = 4x − 9x + 8x − 7 (0.25đ)  k  k  10  d 2 b. 3x − 2 y =  3x  6x 24  0 0 0 2 x − 5x + 4 x  2 ( 0 3x   − 2)/ ( 2
x − 5x + 4) −(3x − 2)( 2 x − 5x + 4 (0.25đ) x  4 / )/ y =  0 (x −5x+4)2 2
 Với x  2, y  7,k  10 (0.25đ) 0 0
Pttt: y  10x27 ( loại ) (0.25đ) 2 3 − x + 4x + 2 = ( (0.25đ) x − 5x + 4)2 2
 Với x  4, y  41,k  10 0 0
c. y = ( x − ) 2
3 1 x + 3x − 7
Pttt: y  10x 81( nhận) (0.25đ) 3x 1 ' y = ( x − ) 2
x + x − + ( x − )( 2 3 1 3 7 3 1 x + 3x − 7 )/ /
c) Cho hàm số y    C x2 7 2 2x + 3
= 3 x + 3x − 7 + (3x − ) 1  / y  2 2 x + 3x − 7 x22 (0.25đ) 1 1 2
 d : y  x9  k  d = 12x  25x45 (0.25đ) 7 7 2 2 x  3x7  Gọi /
 là tiếp tuyến tại điểm Mx ; y 0 0  Bài 4: Ta có:  /  d
a) Cho hàm số 4 2
y = x − 6x + 5(C) .  k .k  1  x  2  y  3 (0.25đ) /  d 0 0  k  7 /  7  / 3
y = 4x −12x   7 x 22 0  / k = y (2) = 8 (0.25đ x  3 0   (0.25đ)
Pttt: y = 8x −19 (0.25đ) x  1  0
b) Cho hàm số 3 2
y = x + 3x −14x +1(C) .
 Với x  3, y  10,k  7 0 0  / 2 y  3x 6x14 Pttt: y  7x  31 (0.25đ)
 d : y  10x27  k  10
 Với x  1, y  4,k  7 d 0 0
TRƯỜNG THPT QUANG TRUNG 3 Pttt: y  7x  3 (0.25đ)
d. Tính góc giữa (SCD) và ( ABCD) . (
SCD) ( ABCD) = CD
Bài 5: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) ,  Ta có: (
ABCD) : AD ⊥ CD = D
đáy hình chữ nhật, AB = a, AD = a 3 , SA = a 3 . (  SCD
): SD ⊥ CD = D
Suy ra góc giữa (SCD) và ( ABCD) cũng là ∧
góc giữa AD và SD, đó là góc SDA (trong tam giác vuông SCD) (0.25đ) Xét S
∆ OA vuông tại O: ∧ ∧ 0
tan SDA =1⇒ SDA = 45 (0.5đ)
e. Tính góc giữa SC và (SAD).
• SC  (SAD) = S
• CD ⊥ (SAD) = D
Suy ra SD là hình chiếu vuông góc của SC lên
a. Chứng minh: BC ⊥ (SAB) (SAD).
BC ⊥ SA(SA ⊥ ( ABCD))
Nên góc giữa SC và(SAD)cũng là góc giữa  ∧
Ta có: BC ⊥ AB (0.25đ)
SC và SD, đó là góc CSD (trong tam giác (  SAB vuông SCD) (0.25đ)
): SA∩ AB = A  Xét SC
∆ D vuông tại D có
Vậy: BC ⊥ (SAB) (0.25đ) ∧ ∧
tan CSD = 6 ⇒ CSD = arctan 6 (0.5đ)
b. Chứng minh: (SCD) ⊥ (SAD) …HẾT… C
D ⊥ SA(SA ⊥ ( ABCD))  Ta có: C   D ⊥ AD (  SAD
): SA∩ AD = A
Nên CD ⊥ (SAD) (0.25đ)
Mà CD ⊂ (SCD)
Vậy: (SCD) ⊥ (SAD) (0.25đ)
c. Tính góc giữa SB và ( ABCD) .
• SB ( ABCD) = B
• SA ⊥ ( ABCD) tại A.
Suy ra AB là hình chiếu vuông góc của SB lên ( ABCD) ∧
Nên góc giữa SB và( ABCD) là góc SBA
(trong tam giác vuông SAB) (0.25đ) Xét S
∆ AB vuông tại A có ∧ ∧ 0
tan SBA = 3 ⇒ SBA = 60 (0.5đ)
Document Outline

  • Đề HK2_ Khối 11_THPT Quang Trung_TPHCM năm 2022_2023
  • Đáp án Đề HK2_ Khối 11_THPT Quang Trung_TPHCM năm 2022_2023