Đề cương giữa kì 1 Toán 8 năm 2024 – 2025 trường THCS Lương Thế Vinh – BR VT

TRƯỜNG THCS LƯƠNG THẾ VINH TỔ TOÁN - TIN
ĐỀ CƯƠNG ÔN TẬP GIỮA KÌ I TOÁN 8
Năm học: 2024 – 2025 A. LÝ THUYẾT I. Phạm vi ôn tập
1. Chương I: từ đầu đến hết bài Phân tích đa thức thành nhân tử.
2. Chương II: hết chương.
2. Chương III: từ đầu đến hết bài hình bình hành.
II. Câu hỏi ôn tập
1. Phát biểu định nghĩa đơn thức, đa thức, đơn thức đồng dạng.
2. Phát biểu các quy tắc cộng trừ đơn thức đồng dạng, cộng trừ đa thức, nhân đơn thức
với đơn thức, đơn thức với đa thức, nhân đa thức với đa thức.
3. Phát biểu quy tắc chia đơn thức cho đơn thức, chia đa thức cho đơn thức.
4. Viết bảy hằng đẳng thức đáng nhớ.
5. Nêu các phương pháp phân tích đa thức thành nhân tử.
6. Viết công thức diện tích xung quanh, thể tích của hình chóp tam giác đều, tứ giác đều
7. Phát biểu định lí Pythagore và định lí Pythagore đảo.
8. Phát biểu định nghĩa tứ giác, hình thang.
9. Phát biểu định nghĩa, tính chất, dấu hiệu nhận biết của hình thang cân, hình bình hành. B- BÀI TẬP -
Xem lại các bài tập trong SGK, SBT. - Làm thêm các bài tập sau TRẮC NGHIỆM
Câu 1: Trong các biểu thức đại số sau, biểu thức nào là đơn thức − 3 x + y A. 2 2 + x y . B. 1 3 4 5 x y . C. . D. 3
− x y + 7x . 5 3y 4
Câu 1: Trong những đơn thức sau, đơn thức nào không phải là đơn thức thu gọn?
A. 2 . B. x C. 2 3 x y . D.
Câu 2: Hai đơn thức đồng dạng là 2 3 3 2 2 3 2 3 2 3 2 2 A. 2x y và 3x y B. −x y và 3 − x y C. 3x y và x y D. 5 − x y và 5 − y x 1
TRƯỜNG THCS LƯƠNG THẾ VINH TỔ TOÁN - TIN 2 5 2 5
Câu 2: Kết quả của phép tính 3x y − ( 5 − x y ) là 4 10 4 10 2 5 2 5 A. 15x y B. −15x y C. −2x y D. 8x y
Câu 3: Thực hiện phép tính 2 ( 3 x 3x − 2x − )
1 ta được kết quả là A. 6 3 2 3x − 2x − x B. 5 3 2 3x − 2x − x C. 5 3 3x − 2x −1 D. 6 2 2 3x − 2x − x
Câu 5: Tích của đa thức x + 2 và đa thức x + 5 là đa thức A. 2 x +10 B. 2 x + 7x +10 C. 2 x − 7x +10 D. 2 x − 3x +10
Câu 7: Khẳng định nào sau đây là đúng 2 2 2 2
A. (x − 2) = x − 2x + 4
B. (x − 2) = x − 2x − 4 2 2 2 2
C. (x − 2) = x − 4x + 4
D. (x − 2) = x − 4x − 4 Câu 8: Cho 3 + = ( + )( 2 x 125 x 5 x +
+ 25) . Chọn phương án thích hợp để điền vào chỗ trống. A. 5x B. 5x − C. 10x D. 1 − 0x
Câu 9: Tứ giác ABCD có A = 125 ,  B = 75 ,  D = 65.Số đo C là A. 125. B. 65 . C. 90 . D. 95 . 3 3
Câu 14: Biểu thức x + 64y bằng 2 2 2 2
A. (x + 4y)(x − 4xy +16y )
B. (x + 4y)(x − 4xy + 4y ) 2 2 2 2
C. (x + 4y)(x + 4xy +16y )
D. (x + 4y)(x − 8xy +16y )
Câu 15: Phân tích đa thức x (x − 3) + 4(x − 3) ta được
A. (x − 3)(x + 4)
B. (x − 3)(x − 4)
C. (x + 3)(x + 4)
D. (x + 3)(x − 4)
Câu 16: Giá trị của biểu thức (x − y)(x + y) tại x = 8 − , y = 6 là A. 100 − . B. 28 . C. 100 . D. 28 −
Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao
của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là :
A. 6 cm 3 . B. 18 cm 3 . C. 12 cm 3 . D. 9 cm 3 .
Câu 16: Cho hình chóp tam giác đều S.ABC có thể tích là 100 cm 3 ; chiều cao của hình
chóp là 3cm. Độ dài cạnh đáy của hình chóp đó là 1 1 1 1
A. . B. .
C. . D. . 3 4 5 2
Câu 16: Cho hình chóp tứ giác đều S.ABCD có cạnh AB = 8cm, chiều cao SO = 10cm.
Thể tích của hình chóp tứ giác đều S.ABCD là : 800 640 A. cm 3 . B.
cm 3 . C. 800 cm 3 . D. 640 cm 3 . 3 3 2
TRƯỜNG THCS LƯƠNG THẾ VINH TỔ TOÁN - TIN
Câu 16: Cho hình chóp S.ABCD đều có thể tích bằng 200cm 3 ,
chiều cao SO bằng 12cm. Độ dài cạnh của hình chóp tứ giác đó là :
A.12 cm. B.13 cm.
C.11 cm. D.16 cm. TỰ LUẬN PHẦN ĐẠI SỐ
Bài 1. Trong các biểu thức sau, biểu thức nào là đơn thức? 2 1 1 x y , 3 − x −1, 2 − x y , 13 − , − 5 6 − , ( )3 7 2 xy x
Bài 2. Thu gọn, chỉ ra phần hệ số và tìm bậc của các đơn thức sau 1) 2 2 5x .3xy 2) 2 x yz.(−2xy )3 3) (− x y)2 2 3 3 2 .8x yz 2  −  1 3 1 5 5 2 1 2 3 3 − x y z . x .y . x −2 y . 9 − x y 4) 2xy . x y   5) ( )3 4 5 6 5 4 6) ( ) ( )  3  9 6
Bài 3. Sắp xếp các đơn thức sau thành nhóm các đơn thức đồng dạng 3   2 1 12 − x y − xyz 100 − −3yxz −2xy.x . y − xy   8  3  8  1 − 
Bài 4. Cho đơn thức: 2 2 2 A = x y . x y   . 3  4 
a) Thu gọn đơn thức A rồi xác định hệ số và tìm bậc của đơn thức.
b) Tính giá trị của A tại x = 1 − , y =1.
Bài 5. Thực hiện phép tính: 1) xy + 5xy 2) 2 2 3xy −12xy 2 3 4 2 3 4
3) 3x y z + (−4x y z ) 4) 2 2 2
3x y + 4x y − x y 1 1 1 5) 2 2 2 5xy + xy − xy 6) 3 3 3 2x + 3x − x 2 4 3
Bài 6. Thu gọn rồi tìm bậc của các đa thức sau 1) 6 5 4 4 4 4
A = x + y + x y +1− x y 2) 2 2 2 2
B = x − 2x y + 5x + 2x y 1 3) 3 3 2 2
C = x − 5xy + 3x + xy − x + xy − x 2 3
TRƯỜNG THCS LƯƠNG THẾ VINH TỔ TOÁN - TIN
Bài 7. Thu gọn rồi tính giá trị của các đa thức sau 1 1 1 1 a) 2 2 2 2 A =
x y + xy − xy + xy − 5xy −
x y tại x = , y = 1. 3 2 3 2 1 2 1 1 b) 2 2 2 2 B = xy +
x y − xy + xy − x y + 2xy tại x = , y = 1. 2 3 3 2 c) 2 4 2 2 4 9
C = 2x y + 4xyz − 2x − 5 + 3x y − 4xyz + 3 − y tại x =1, y = 1 −
Bài 8. Thực hiện phép tính 2 2 2 2 2 2 2 2
1) ( x − 2yz + z ) − (3yz − z + 5x )
2) ( x − 2yz + z ) + (3yz − z + 5x ) 3 2 3 3 3 2 2 2 2
3) ( x + 6x + 5y ) − (2x − 5x + 7y )
4) ( x − 2xy + y ) + ( y + 2xy + x + ) 1
Bài 9. Tìm đa thức A biết 1) A − ( 4 2 2
12x −15x y + 2xy + 7) = 0 2) ( 2 2 3 x y − xy + y ) 2 3 25 13
− A =11x y − 2y 3) A − ( 2 xy − y ) 2 2 4 3
= x − 7xy + 8y 4) ( 2 2 x − xy ) 2 2 2 6 3
+ A = x + y − 2xy Bài 10. Cho 3 2 2 2 3 2 2 2
A = 5x y − 4xy − 6x y , B = 8
− xy + xy − 4x y và 3 3 3 2 2 2
C = x + 4x y − 6xy − 4xy + 5x y
a) Tính A − B − C b) Tính B + A − C c) Tính C − A − B
Bài 11. Thực hiện phép nhân:  2 1  1) 4 3 2 3x 2 − x + 5x − x +   2) 2 4 − ( 2 3 3 2 5x y 3x y − 2x y − xy)  3 3  3) (3x + 5)(2x − 7) 4) ( 5x − + 2)( 3 − x − 4) 5) ( − )( 2 x 5 −x − x + ) 1 6) ( 2 x − 2x − ) 1 (x −3)
Bài 12. Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến
a) A = x ( x + ) − x ( 2 x + x ) 3 3 2 3 + x − 2x + 3  
b) B = x ( x − ) 1 1 2 3 + 6x − x +1    2 3 
c) C = ( x − )( 2
x + x + ) + ( x − ) ( x + ) 2 1 1 2 2 2 − x (2 + x)
d) D = ( x + )( 2 x − x + ) 3 2 3 1 9 3 1 − 54x
Bài 13. Tính giá trị của biểu thức: 4
TRƯỜNG THCS LƯƠNG THẾ VINH TỔ TOÁN - TIN 1) = ( + )( 2 + + ) 2 A x 1 x 2x 4 − x (x + 3) với 10 x = − 3
2) B = 6x (2x − 7) − (3x − 5)(4x + 7) tại x = -2
3) C = (x − 3)(x + 3) − (x + 2)(x − ) 1 tại 1 x = 3  3  4) D = 4 x −1 + ( 2 12x − 3x ) : ( 3 − x) − (2x −   )1 tại x = 3  4 
Bài 14. Phân tích các đa thức thành nhân tử: 1) 2 2 5x z −15xyz + 30xz 2) 2 2 2 2
2x y − 3xy + 4x y 3) x( y + ) 1 + 8( y + ) 1 4) 2 x ( x − ) 1 + 4(1− x) 5) 2
5x − 5xy −10x +10y 6) ( x − y)2 − ( x − y)2 3 2 2 3
7) ( x − y)2 − ( x + y)2 9 4 8) 2 2
x − 4y +16x + 64 9) 3 3 a − 3a + 3b − b 10) 2 2 25 − a − 2ab − b 11) 2
4x − 25 + (2x + 7)(5 − 2x) 12) 2 2 2 2 2 2 2 2 a x − a y − b x + b y 13) 2 x − 2023x + 2022 14) 2 2 x − y +12y − 36 15) ( + )2 2 y 2 − x + 2x −1 16) 2 2 16x − y 17) 2 6x −11x + 3 18) 3 1+ 27x 19) 3 2 x + 3x −16x − 48 20) 3 2 x − x − x +1 21) 3 2 x + 2x − 2x −1
22) 4x (x − 3y) +12y(3y − x)
23) ( x − 7)( x − 5)( x − 4)( x − 2) − 72 24) ( x + )
1 ( x + 3)( x + 5)( x + 7) +15
Bài 15. Tìm x, biết: 1) 2
x(x + 2) − x = 12 2) 2 x − 4x = 0 3) 4x (x − 5) − (x − ) 1 (4x − 3) = 5
4) (3x − 4)(x − 2) = 3x (x − 9) − 3
5) (x − 5)(x − 4) − (x + ) 1 (x − 2) = 7 6) ( − )2 2x 1 − 25 = 0 7) 3x (x − ) 1 −1 + x = 0 8) ( + ) 2 2 x 3 − x − 3x = 0 9) 3 2 8x − 50x = 0
10) (4x −3) −3x (3− 4x) = 0 11) 2 2x + 7x − 4 = 0 12) ( + )( 2 − + )− ( 2 2x 1 4x 2x 1 8x x + 2) =17 5
TRƯỜNG THCS LƯƠNG THẾ VINH TỔ TOÁN - TIN 13) 3 2 x − 7x − 6 = 0
14) 4x − 25 − (2x − 5)(2x + 7) = 0
15) 2x( x − 202 ) 3 + (2023 − x) = 0 16) 2
x ( x − 5) − 4x + 20 = 0 17) 2
x − 6x + 8 = 0 18) 3 2
x + x − 2x = 0 19) ( x + )( −
) −( + )2 +( + )3 = ( − )( 2 5 4 3x 3x 2 2x 1 2x 1 4x + 2x + ) 1
Bài 16. Thực hiện phép chia a) 7 2 10x y z : ( 2 − xy) b) ( 2 2
x y + 6xy −10xy ) : (−2xy) c) ( 4 5 3 3 4 2 5 2 3
x y z − x y z + x y z ) ( 3 2 2 15 3 10 : 5x y z )
Bài 17. Chứng minh các biểu thức sau không âm với mọi x, y: 1) 2 A = x − 8x + 20 2) 2 B = 4x −12x +11 3) 2 C = x − x +1 4) 2 2 D = x + 5y + 2x + 6y + 34 5) 2 2 E = x − 2x + y + 4y + 6 6) = ( − )2 + ( + )( + ) − ( 2 F 15x 1 3 7x 3 x 1 x − 73)
Bài 18. Tìm giá trị nhỏ nhất của biểu thức: a) 2 A = x − 20x +101 b) 2
B = 2x − 3x − 5 c) 2
C = 2x − x + 2017 d) D = x ( x − 7)(x − 3)(x − 4) e) E = (x + )( 2
1 x − 4)(x + 5) + 2023 f) 2 2
F = 2x + y + 2xy − 8x + 2024
Bài 19. Tìm giá trị lớn nhất của biểu thức: a) 2 A = 4x − x + 3
b) B = 5 − (x + 6)(x + 3)(x + 2)(x − ) 1 PHẦN HÌNH HỌC Bài 1.
a) Tính thể tích của hình chóp tam giác đều, biết diện tích đáy bằng 6cm 2 và chiều cao bằng 4cm
b) Tính thể tích của hình chóp tứ giác đều, biết chiều cao bằng 10cm và cạnh đáy bằng 4cm.
c) Tính diện tích xung quanh và diện tích toàn phần của hình chóp tứ giác đều biết cạnh
đáy là 12cm, chiều cao mặt bên là 8cm. 6
TRƯỜNG THCS LƯƠNG THẾ VINH TỔ TOÁN - TIN
d) Tính chu vi đáy của hình chóp tứ giác đều biết thể tích của hình chóp là 125cm 3
,chiều cao của hình chóp là 15cm.
e) Tính diện tích xung quanh của hình chóp tam giác đều biết độ dài cạnh đáy là 10 cm,
chiều cao mặt bên là 12cm. Bài 2.
Bạn Mai cần dán giấy bóng kính màu xung quanh
một chiếc lồng đèn hình chóp tam giác đều với
kích thước như hình bên. Hỏi diện tích giấy mà Mai cần là bao nhiêu?
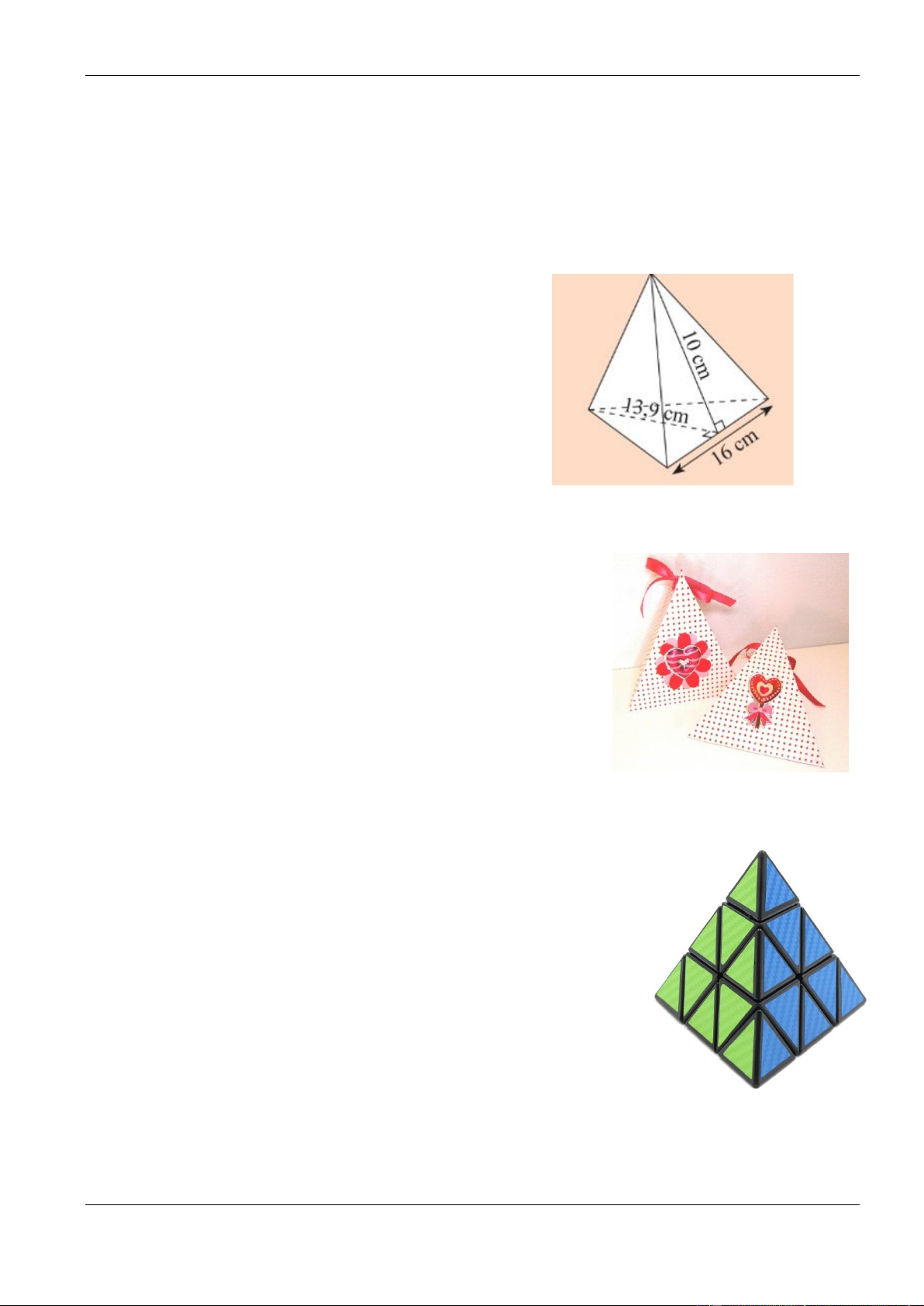
Bài 3. Hình bên là một cái hộp giấy hình chóp tam giác
đều do bạn Lan tự tay làm để đựng quà sinh nhật tặng cho
bạn thân. Biết diện tích đáy của hình chóp bằng 170cm 2 ,
chiều cao của hình chóp bằng 16cm.
Thể tích của chiếc hộp là bao nhiêu ? (làm tròn kết quả
đến hàng phần mười)
Bài 4. Một khối rubik có dạng hình chóp tam giác đều ( các
mặt khối rubic là các tam giác đều bằng nhau), có chu vi
đáy bằng 234 mm, đường cao của mặt bên hình chóp là 67,5 mm .
a/ Tính diện tích xung quanh, diện tích toàn của khối rubik đó.
b/ Biết chiều cao của khối rubik là 63,7 mm. Tính thể tích của khối rubik đó. 7
TRƯỜNG THCS LƯƠNG THẾ VINH TỔ TOÁN - TIN
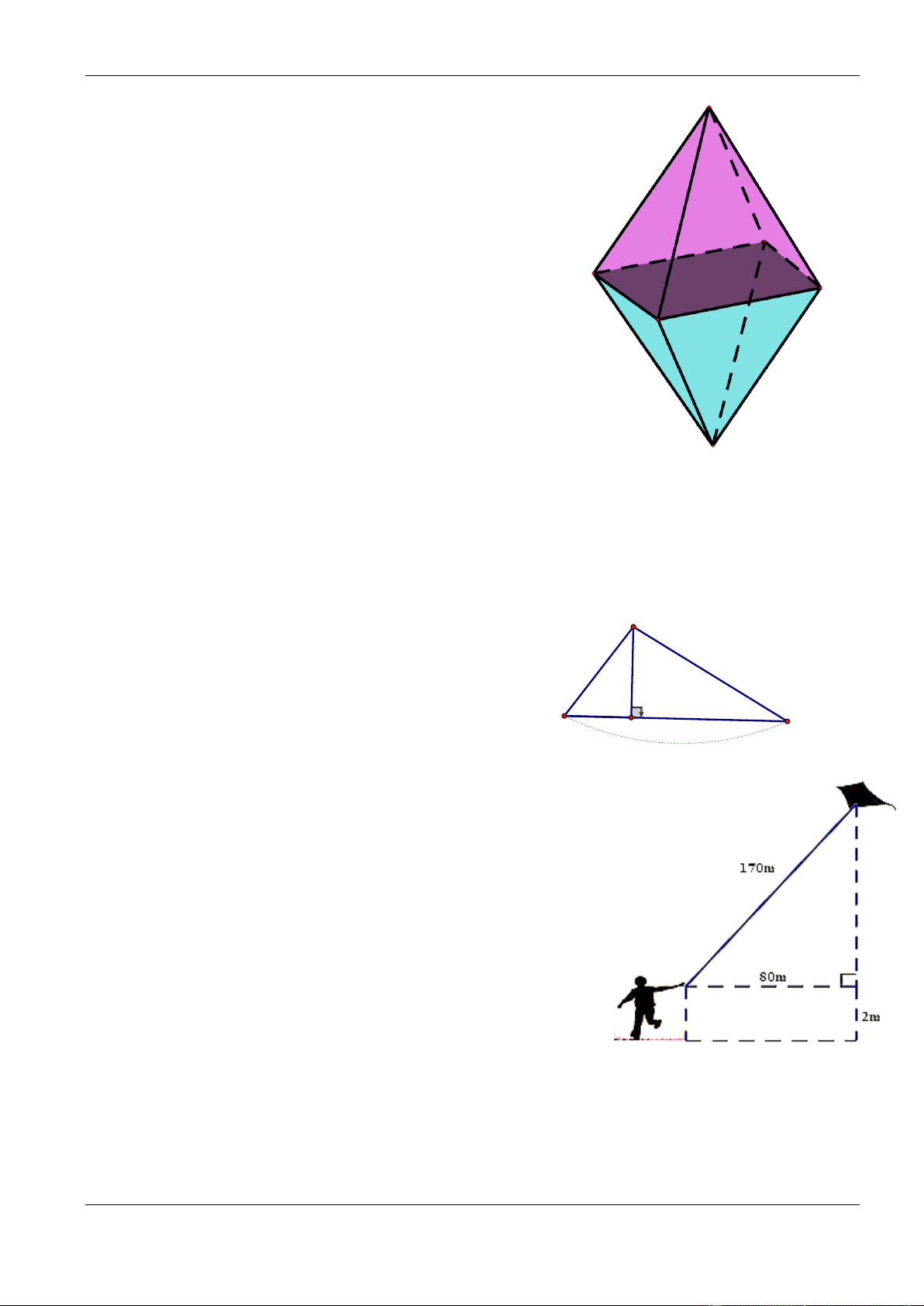
Bài 5. Bạn Hà làm một cái lòng đèn hình quả trám
(xem hình bên) là hình ghép từ hai hình chóp tứ giác
đều có cạnh đáy 20cm, cạnh bên 32cm, khoảng cách
giữa hai đỉnh của hai hình chóp là 30cm.
a/ Tính thể tích của lòng đèn.
b/ Bạn Hà muốn làm 50 cái lòng đèn hình quả trám
này cần phải chuẩn bị bao nhiêu mét thanh tre?
(mối nối giữa các que tre có độ dài không đáng kể) ?
Bài 6. Cho tam giác ABC có BC = 10cm , AB = 6cm và AC = 8cm . Tam giác ABC là tam giác gì? Vì sao?
Bài 7. Cho tam giác ABC vuông tại A biết AB = 5 cm A
và AC = 12cm. Tính độ dài cạnh BC ? 5cm ?
Bài 8. Cho  ABC, kẻ AH ⊥ BC. 3cm ?
Biết AB = 5cm ; BH = 3cm ; BC = 10cm (h-vẽ). B H C 10cm a) Biết 0
C = 30 . Tính HAC ?
b) Tính độ dài các cạnh AH, HC, AC.
Bài 9. Một bạn học sinh thả diều ngoài đồng, cho biết đoạn
dây diều từ tay bạn đến diều dài 170m và bạn đứng cách
nơi diều được thả lên theo phương thẳng đứng là 80m.
Tính độ cao của con diều so với mặt đất, biết tay bạn học
sinh cách mặt đất 2m. Hình 3 Hình 1 D
TRƯỜNG THCS LƯƠNG THẾ VINH TỔ TOÁN - TIN
Bài 10. Cho hình thang ABCD có AD∥BC hai đường chéo AC, BD cắt nhau tại O .
Biết OC = OB . Chứng minh hình thang ABCD là hình thang cân.
Bài 11. Cho hình thang ABCD như Hình 7. biết AC = BD.
a) Hình thang ABCD là hình thang gì?
b) Chứng minh ADB = DAC .
Bài 12. Cho hình thang ABCD (AB//CD) . AC cắt BD tại O. Biết OA OB . Chứng
minh rằng: ABCD là hình thang cân.
Bài 13. Tứ giác ABCD có AB//C , D AB C , D AD
BC . Chứng minh ABCD là hình thang cân.
Bài 14. Cho ΔABC , hai đường phân giác góc B , C cắt nhau tại O . Qua O kẻ đường
thẳng song song với BC , đường thẳng này cắt A ,
B AC lần lượt tại M và N .
a) Tứ giác BCOM , BCNO là các hình gì?
b) Chứng minh MN = MB + NC.
Bài 15. Cho ΔABC cân tại ,
A hai đường trung tuyến BD, CE
a) Chứng minh ΔAED là tam giác cân.
b) Chứng minh tứ giác BCDE là hình thang cân.
Bài 16. Cho hình thang cân ABCD (AB//CD) có AB = 3,BC = CD = 13 (cm). Kẻ các
đường cao AK và BH.
a) Chứng minh rằng CH = DK . b) Tính độ dài BH
Bài 17. Cho hình thang ABCD cân có AB // CD và AB < CD. Kẻ các đường cao AE, BF.
a. Chứng minh rằng: DE = CF.
b. Gọi I là giao điểm của 2 đường chéo hình thang ABCD. Chứng minh: IA = IB. 9
TRƯỜNG THCS LƯƠNG THẾ VINH TỔ TOÁN - TIN
c. Tia DA và tia CB cắt nhau tại O. Chứng minh OI vừa là trung trực của AB vừa là trung trực của DC.
Bài 18. Cho hình bình hành ABCD . Gọi O là giao điểm hai đường thẳng AC và BD .
Qua điểm O vẽ đường thẳng song song với AB cắt hai cạnh A ,
D BC lần lượt tại M,N . Trên A ,
B CD lần lượt lấy các điểm P,Q sao cho AP
CQ . Gọi I là giao điểm của AC và PQ . Chứng minh: a) Các tứ giác AM ,
NB APCQ là hình bình hành;
b) Ba điểm M,N,I thẳng hàng;
c) Ba đường thẳng AC,MN,PQ đồng quy.
Bài 19. Cho hình bình hành ABCD . Gọi O là giao điểm hai đường thẳng AC và BD .
Qua điểm O , vẽ đường thẳng a cắt hai đường thẳng A ,
D BC lần lượt tại E, F . Qua O vẽ
đường thẳng b cắt hai cạnh A ,
B CD lần lượt tại K,H . Chứng minh tứ giác EKFH là hình bình hành. 10