Đề cương giữa kì 2 Toán 11 năm 2022 – 2023 trường chuyên Bảo Lộc – Lâm Đồng

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề cương ôn tập kiểm tra giữa học kì 2 môn Toán 11 năm học 2022 – 2023 trường THPT chuyên Bảo Lộc, tỉnh Lâm Đồng.

47 24 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 11

Môn: Toán 11

Thông tin:

16 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
1
TRƯỜNG THPT CHUYÊN BẢO LỘC
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ II, MÔN TOÁN LỚP 11 CB
NĂM HỌC 2022 – 2023
A. LÝ THUYẾT:
I. ĐẠI SỐ & GỈAI TÍCH:
+ Giới hạn của dãy số, giới hạn của hàm số lượng giác, giới hạn của hàm số gồm các dạng vô định:
0
; ; 0. ;
0
+ Hàm số liên tục gồm các dạng tóan: xét tính liên tục của hàm số tại một điểm, trên một khỏang, trên R; xác định a
để hàm số liên tục.
II. HÌNH HỌC.
+ Véc tơ trong không gian
+ Quan hệ vuông góc: gồm các dạng tóan chứng minh đường thẳng vuông góc với đường thẳng
+ Góc: góc giữa đường thẳng và đường thẳng
B. BÀI TẬP
I.Phần bài tập phục vụ cho phần trắc nghiệm trong đề kiểm tra.(gồm 100 câu trắc nghiệm)
PHẦN TRẮC NGHIỆM ĐẠI SỐ VÀ GIẢI TÍCH
BÀI 1. GIỚI HẠN CỦA DÃY SỐ
DẠNG 1. DÃY SỐ DẠNG PHÂN THỨC
Câu 1. Tính
3
1
lim
3
n
L
n
.
A.
1L
. B.
0L
. C.
3L
. D.
2L
.
Câu 2.
2
2
1
lim
21
n
n
bằng
A.
0
. B.
1
2
. C.
. D.
1
2
.
Câu 3.
3
32
45
lim
37
nn
nn


bằng
A.
1
. B.
. C.
1
4
. D.
1
2
.
Câu 4. Giới hạn
53
25
8 2 1
lim
2 4 2019
nn
nn


bằng
A.
2
. B.
4
. C.

. D.
0
.
Câu 5. Giá trị của
2
2
4 3 1
lim
31
nn
B
n

bằng:
A.
4
9
. B.
4
3
. C.
0
. D.
4
.
Câu 6.
2
4 1 2
lim
23
nn
n
bằng
A.
3
2
. B. 2. C. 1. D.

.
Câu 7. Dãy số
n
u
với
2
3
3 1 3
45
n
nn
u
n

có giới hạn bằng phân số tối giản
a
b
. Tính
.ab
A.
192
. B.
68
. C.
32
. D.
128
.
DẠNG 2. DÃY SỐ CHỨA CĂN THỨC.
Câu 8.
2
lim 3 1n n n
bằng
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
2
A.
3
. B.

. C.
0
. D.
3
2
.
Câu 9. Tính giới hạn
2
lim 4n n n
.
A.
3
. B.
1
. C.
2
. D.
4
.
DẠNG 3. DÃY SỐ CHỨA LŨY THỪA.
Câu 10. Dãy số nào sau đây có giới hạn bằng
0
?
A.
4
n



. B.
1
3
n



. C.
5
3
n



. D.
5
3
n



.
Câu 11.
lim 2
n
n
bằng.
A.
2
. B.

. C.

. D.
0
.
Câu 12.
2018
lim
2019
n



bằng.
A.
0
. B.

. C.
1
2
. D.
2
.
Câu 13. Tính giới hạn
11
3.2 2.3
lim
43
nn
n

.
A.
3
2
. B.
0
. C.
6
5
. D.
6
.
Câu 14. Tính
21
lim
2.2 3
n
n
.
A. 2. B. 0. C. 1. D.
1
2
.
DẠNG 4. TỔNG CẤP SỐ NHÂN LÙI VÔ HẠN.
Câu 15. Tính tổng
của cấp số nhân lùi vô hạn có số hạng đầu
1
1u
và công bội
1
2
q 
.
A.
2S
. B.
3
2
S
. C.
1S
. D.
2
3
S
.
Câu 16. Tổng vô hạn sau đây
2
2 2 2
2 ... ...
3 3 3
n
S
có giá trị bằng
A.
. B.
3
. C.
4
. D.
2
.
Câu 17. Tổng
1 1 1
1 ...
242
n
bằng
A.
1
2
. B. 2. C. 1. D.

.
BÀI 2. GIỚI HẠN CỦA HÀM SỐ
DẠNG 1. GIỚI HẠN HỮU HẠN
Câu 1. Cho các giới hạn:
0
lim 2
xx
fx
;
0
lim 3
xx
gx
, hỏi
0
lim 3 4
xx
f x g x


bằng
A.
5
. B.
2
. C.
6
. D.
3
.
Câu 2. Cho
3
lim 2
x
fx

. Tính
3
lim 4 1
x
f x x



.
A.
5
. B.
6
. C.
11
. D.
9
.
Câu 3. Giá trị của
2
1
lim 2 3 1
x
xx

bằng
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
3
A.
2
. B.
1
. C.

. D.
0
.
Câu 4. Tính giới hạn
3
3
lim
3
x
x
L
x
A.
L
. B.
0L
. C.
L
. D.
1L
.
Câu 5. Giới hạn
2
1
23
lim
1
x
x
x

x
bằng?
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 6.
2
3
lim 4
x
x
bằng
A.
5
. B.
1
. C.
5
. D.
1
.
Câu 7.
2
2
2 1 5 3
lim
23
x
xx
x

bằng.
A.
. B.
1
7
. C.
7
. D.
3
.
DẠNG 2. GIỚI HẠN MỘT BÊN
Câu 8.Tính
3
1
lim
3
x
x
.
A.
1
6
. B.

. C.
0
. D.

.
Câu 9. Trong các mệnh đề sau, mệnh đề nào sai?
A.
0
1
lim
x
x

. B.
0
1
lim
x
x

. C.
5
0
1
lim
x
x

. D.
0
1
lim
x
x

.
Câu 10. Giới hạn
1
21
lim
1
x
x
x

bằng
A.
.
B.
.
C.
2
.
3
D.
1
.
3
Câu 11.
1
2
lim
1
x
x
x
bằng:
A.

. B.
1
2
. C.

D.
1
2
.
Câu 12.
2
1
31
lim
1
x
xx
x


bằng?
A.
1
2
. B.
1
2
. C.
3
2
D.
3
2
.
DẠNG 3. GIỚI HẠN TẠI VÔ CỰC
Câu 13. Tính giới hạn
32
lim 2 1
x
xx


A.

. B.

. C.
2
. D.
0
.
Câu 14. Chọn kết quả đúng trong các kết quả sau của
53
lim 4 3 1
x
x x x

là:
A.

. B.
0
. C.
4
. D.

.
Câu 15. Tính giới hạn
21
lim
42
x
x
x

.
A.
1
2
. B.
1
. C.
1
4
. D.
1
2
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
4
Câu 16.
1
lim
32
x
x
x

bằng:
A.
. B.
1
2
. C.
1
3
. D.
1
2
.
Câu 17. Giới hạn
2
2
32
lim
21
x
xx
x


có kết quả là
A.

B.

C.
2
D.
1
2
Câu 18. Giới hạn
33
3 4 5
2 3 1
lim
4 2 3
x
xx
x x x


bằng
A.
2
. B.
1
2
. C.
3
. D.
3
2
.
Câu 19.
2
12
lim
9
x
xx
x


bằng
A.
2
9
. B.
1
. C.
1
. D.
1
9
.
Câu 20. Tìm
2
35
lim
41
x
xx
x


.
A.
1
4
. B.
1
. C.
0
. D.
1
4
.
Câu 21. Giá trị của
2
21
lim
11
x
x
x


bằng
A.
0
. B.
2
. C.

. D.
2
.
Câu 22. Giới hạn
2
22
lim
2
x
x
x


bằng
A.

.
B. 1. C.

.
D. -1
Câu 23. Cho hàm số
34
7
4 1 2 1
32
xx
fx
x

. Tính
lim
x
fx

.
A.
2
. B.
8
. C.
4
. D.
0
.
Câu 24. Tìm tất cả các giá trị thực của tham số m thỏa mãn
2
2
75
lim 4.
2 8 1
x
m x x
xx




A.
4m 
. B.
8m 
. C.
2m
. D.
3m 
.
DẠNG 4. GIỚI HẠN VÔ ĐỊNH
Câu 25. Tính
2
3
9
lim
3
x
x
x
bằng:
A.
3
. B.
6
. C.

. D.
3
.
Câu 26. Tính giới hạn
2
2
56
lim
2
x
xx
I
x

.
A.
1I 
. B.
0I
. C.
1I
. D.
5I
.
Câu 27. Tính giới hạn
3
1
1
lim .
1
x
x
A
x
A.
.A
B.
0.A
C.
3.A
D.
.A
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
5
Câu 28. Cho giới hạn
2
2
2
32
lim
4
x
x x a
xb

trong đó
a
b
là phân số tối giản. Tính
22
.S a b
A.
20S
. B.
17S
. C.
10S
. D.
25S
.
Câu 29. Cho
3
2
1
1
lim
1
x
xa
xb
với
,ab
là các số nguyên dương và
a
b
là phân số tối giản. Tính tổng
S a b
.
A.
5
. B.
10
. C.
3
. D.
4
.
Câu 30.
1
32
lim
1
x
x
x

bằng
A.
1
4
. B.

. C.
1
2
. D.
1
.
Câu 31. Giới hạn
2
0
3 4 2
lim
x
xx
x
bằng
A.
1
2
. B.
1
2
. C.
3
4
. D.
2
3
.
Câu 32. Tìm
2
2
56
lim
4 1 3
x
xx
x


là
A.
3
.
2
B.
2
3
. C.
3
2
. D.
1
2
.
Câu 33. Tìm
2
1
21
lim
2
x
xx
xx


.
A.
5
. B.

. C.
0
. D.
1
.
Câu 34. Giới hạn:
5
3 1 4
lim
34
x
x
x


có giá trị bằng:
A.
9
4
. B.
3
. C.
18
. D.
3
8
.
Câu 35. Tính
32
2
0
82
lim
x
x
x

.
A.
1
12
. B.
1
4
. C.
. D.
1
6
.
Câu 36. Tính
2
3
26
lim
3
x
x
ab
x
(
a
,
b
nguyên). Khi đó giá trị của
P a b
bằng
A.
7
. B.
10
. C.
5
. D.
6
.
Câu 37. Giới hạn
3
1 5 1
lim
43
x
x x a
b
xx

, với
, , 0a b Z b
và
a
b
là phân số tối giản. Giá trị của
ab
là
A.
1
. B.
1
. C.
. D.
.
Câu 38. Biết
2
3
12
lim
3
x
xa
xb

(
a
b
là phân số tối giản). Tính
2018ab
.
A.
2021
. B.
2023
. C.
2024
. D.
2022
.
Câu 39. Tính
2
2
28
lim .
2 5 1
x
xx
x



TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
6
A.
3
. B.
1
2
. C.
6
. D.
8
.
Câu 40. Biết
0
3 1 1
lim
x
xa
xb

, trong đó
a
,
b
là các số nguyên dương và phân số
a
b
tối giản. Tính giá
trị biểu thức
22
P a b
.
A.
13P
. B.
0P
. C.
5P
. D.
40P
.
Câu 41. Tính
2
lim 4 2
x
x x x

.
A.
4
. B.
2
. C.
4
. D.
2
.
Câu 42. Tìm giới hạn
2
lim 4 1
x
I x x x

.
A.
2I 
. B.
4I 
. C.
1I
. D.
1I 
.
Câu 43.
lim 1 3
x
xx

bằng
A.
0
. B.
2
. C.

. D.

.
Câu 44. Tìm giới hạn
22
M lim 4 .
x
x x x x

Ta được M bằng
A.
3
.
2
B.
1
.
2
C.
3
.
2
D.
1
.
2
Câu 45. Tìm
33
lim 1 2
x
xx

.
A.
1
. B.

. C.

. D.
1
.
BÀI 3. HÀM SỐ LIÊN TỤC
DẠNG 1. CÂU HỎI LÝ THUYẾT
Câu 1. Cho hàm số
y f x
liên tục trên khoảng
;ab
. Điều kiện cần và đủ để hàm số liên tục trên
;ab
là
A.
lim
xa
f x f a
và
lim
xb
f x f b
. B.
lim
xa
f x f a
và
lim
xb
f x f b
.
C.
lim
xa
f x f a
và
lim
xb
f x f b
. D.
lim
xa
f x f a
và
lim
xb
f x f b
.
Câu 2. Cho hàm số
()y f x
liên tục trên đoạn
;ab
. Mệnh đề nào dưới đây đúng?
A. Nếu
( ). ( ) 0f a f b
thì phương trình
( ) 0fx
không có nghiệm nằm trong
;ab
.
B. Nếu
( ). ( ) 0f a f b
thì phương trình
( ) 0fx
có ít nhất một nghiệm nằm trong
;ab
.
C. Nếu
( ). ( ) 0f a f b
thì phương trình
( ) 0fx
có ít nhất một nghiệm nằm trong
;ab
.
D. Nếu phương trình
( ) 0fx
có ít nhất một nghiệm nằm trong
;ab
thì
( ). ( ) 0f a f b
.
Câu 3. Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại
1x
?
A. . B. .
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
7
C. . D. .
Câu 4. Hàm số nào sau đây liên tục tại
1x
:
A.
2
1
1
xx
x
x
f
. B.
2
2
2
1
xx
x
fx

. C.
2
1
x
f
x
x
x

. D.
1
1
f
x
x
x
.
Câu 5. Hàm số nào dưới đây gián đoạn tại điểm
0
1x 
.
A.
2
12y x x
. B.
21
1
x
y
x
. C.
1
x
y
x
. D.
2
1
1
x
y
x
.
Câu 6. Hàm số nào sau đây gián đoạn tại
2x
?
A.
34
2
x
y
x
. B.
sinyx
. C.
42
21y x x
D.
tanyx
.
Câu 7. Hàm số
1
x
y
x
gián đoạn tại điểm
0
x
bằng?
A.
0
2018x
. B.
0
1x
. C.
0
0x
D.
0
1x 
.
Câu 8. Cho hàm số
2
3
1
x
y
x
. Mệnh đề nào sau đây đúng?
A. Hàm số không liên tục tại các điểm
1x 
. B. Hàm số liên tục tại mọi
x
.
C. Hàm số liên tục tại các điểm
1x 
. D. Hàm số liên tục tại các điểm
1x
.
Câu 9. Trong các hàm số sau, hàm số nào liên tục trên
?
A.
3
y x x
. B.
cotyx
. C.
21
1
x
y
x
. D.
2
1yx
.
DẠNG 2. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM
Câu 10. Để hàm số
2
3 2 1
41
x x x
y
khi
khx a xi
liên tục tại điểm
1x 
thì giá trị của
a
là
A.
4
. B. 4. C. 1. D.
1
.
DẠNG 3. LIÊN TỤC TRÊN KHOẢNG
Câu 11. Cho hàm số
2
32
5 2 2
x x x
y
kx
khi
hi x

. Chọn mệnh đề sai trong các mệnh đề sau:
A. Hàm số liên tục tại
0
1x
.
B. Hàm số liên tục trên
.
C. Hàm số liên tục trên các khoảng
;2 , 2;
.
D. Hàm số gián đoạn tại
0
2x
.
Câu 12. Cho hàm số
3 1 1
1
x khi x
y
x m khi x
,
m
là tham số. Tìm
m
để hàm số liên tục trên
.
A.
5m
. B.
1m 
. C.
3m
. D.
3m 
.
DẠNG 4. CHỨNG MINH PHƯƠNG TRÌNH CÓ NGHIỆM
Câu 13. Cho phương trình
42
2 5 1 0 (1)x x x
. Chọn khẳng định đúng trong các khẳng định sau
A. Phương trình
1
có đúng một nghiệm trên khoảng
2;1
.
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
8
B. Phương trình
1
vô nghiệm.
C. Phương trình
1
có ít nhất hai nghiệm trên khoảng
0;2
.
D. Phương trình
1
vô nghiệm trên khoảng
1;1
.
PHẦN TRẮC NGHIỆM HÌNH HỌC
BÀI 1. VECTƠ TRONG KHÔNG GIAN
Câu 1. Trong các khẳng định sau, khẳng định nào sai?
A. Nếu giá của ba vectơ
a
,
b
,
c
cắt nhau từng đôi một thì ba vectơ đó đồng phẳng.
B. Nếu trong ba vectơ
a
,
b
,
c
có một vectơ
0
thì ba vectơ đó đồng phẳng.
C. Nếu giá của ba vectơ
a
,
b
,
c
cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng.
D. Nếu trong ba vectơ
a
,
b
,
c
có hai vectơ cùng phương thì ba vectơ đó đồng phẳng.
Câu 2. Cho hình hộp
.ABCD A B C D
. Gọi
,IJ
lần lượt là trung điểm của
AB
và
CD
. Khẳng định
nào dưới đây là đúng?
A.
AI CJ
. B.
D A IJ

. C.
BI D J
. D.
A I JC
.
Câu 3. Cho hình lập phương
. ' ' ' 'ABCD A B C D
. Mệnh đề nào sau đây sai?
A.
''AB AD AA AC
. B.
AC AB AD
.
C.
AB CD
. D.
AB CD
.
Câu 4. Cho tứ diện
ABCD
. Mệnh đề nào dưới đây là mệnh đề đúng?
A.
BC AB DA DC
. B.
AC AD BD BC
.
C.
AB AC DB DC
. D.
AB AD CD BC
.
Câu 5. Cho hình hộp
. ' ' ' 'ABCD A B C D
. Chọn đẳng thức vectơ đúng:
A.
''AC AB AB AD
. B.
''DB DA DD DC
.
C.
'AC AC AB AD
. D.
'DB DA DD DC
.
Câu 6. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Khẳng định nào sau đây đúng?
A.
SA SD SB SC
. B.
0SA SB SC SD
.
C.
SA SC SB SD
. D.
SA SB SC SD
.
Câu 7. Cho hình lăng trụ tam giác
.ABC A B C
. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
AB
?
A.
AB

. B.
AC
. C.
AC

. D.
AB
.
Câu 8. Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
. Khi đó, vectơ bằng vectơ
AB
là vectơ nào dưới đây?
A.
''DC
. B.
BA
. C.
CD
. D.
''BA
.
Câu 9. Cho hình hộp
1 1 1 1
.ABCD A BC D
. Chọn khẳng định đúng.
A.
11
,,BA BD BD
đồng phẳng. B.
11
,,BA BD BC
đồng phẳng.
C.
1 1 1
,,BA BD BC
đồng phẳng. D.
11
,,BD BD BC
đồng phẳng.
Câu 10. Cho hình hộp
.ABCD EFGH
. Gọi
I
là tâm hình bình hành
ABEF
và
K
là tâm hình bình hành
BCGF
. Trong các khẳng định sau, khẳng định nào đúng?
A.
BD
,
EK
,
GF
đồng phẳng. B.
BD
,
IK
,
GC
đồng phẳng.
C.
BD
,
AK
,
GF
đồng phẳng. D.
BD
,
IK
,
GF
đồng phẳng
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
9
BÀI 2. HAI ĐƯỜNG THẲNG VUÔNG GÓC
DẠNG 1. GÓC CỦA HAI VÉCTƠ
Câu 1. Cho hình chóp
.S ABC
có
2BC a
, các cạnh còn lại đều bằng
a
. Góc giữa hai vectơ
SB
và
AC
bằng
A.
60
. B.
120
. C.
30
. D.
90
.
Câu 2. Cho hình lập phương
.ABCD A B C D
. Tính
,c BD A C

os
A.
,0c BD A C

os
. B.
,1c BD A C

os
.
C.
1
,
2
c BD A C

os
. D.
2
,
2
c BD A C

os
.
Câu 3. Cho hình chóp
.O ABC
có ba cạnh
OA
,
OB
,
OC
đôi một vuông góc và
OA OB OC a
. Gọi
M
là trung điểm cạnh
AB
. Góc tạo bởi hai vectơ
BC
và
OM
bằng
A.
135
. B.
150
. C.
120
. D.
60
.
DẠNG 2. GÓC CỦA HAI ĐƯỜNG THẲNG
Câu 4. Cho hình lập phương
. ' ' ' '.ABCD A B C D
Tính góc giữa hai đường thẳng
AC
và
'.AB
A.
60
B.
45
C.
75
D.
90
Câu 5. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
2AB a
,
BC a
. Các cạnh bên
của hình chóp cùng bằng
2a
. Tính góc giữa hai đường thẳng
AB
và
SC
.
A.
45
. B.
30
. C.
60
. D.
arctan2
.
Câu 6. Cho hình lập phương
.ABCD A B C D
. Góc giữa hai đường thẳng
AC

và
BD
bằng.
A.
60
. B.
30
. C.
45
. D.
90
.
Câu 7. Cho tứ diện đều
ABCD
. Số đo góc giữa hai đường thẳng
AB
và
CD
là
A.
45
. B.
90
. C.
60
. D.
30
.
Câu 8. Cho tứ diện
OABC
có
;OA OB OC a
,,OA OB OC
vuông góc với nhau từng đôi một. Gọi
I
là trung điểm
BC
. Tính góc giữa hai đường thẳng
AB
và
OI
.
A.
45
. B.
30
. C.
90
. D.
60
.
Câu 9. Cho tứ diện đều
ABCD
,
M
là trung điểm của cạnh
BC
. Tính giá trị của
cos ,AB DM
.
A.
3
2
. B.
3
6
. C.
1
2
. D.
2
2
.
Câu 10. Cho hình lập phương
. ' ' ' 'ABCD A B C D
có cạnh bằng
.a
Góc giữa hai đường thẳng
'CD
và
''AC
bằng.
A.
0
30 .
B.
0
90 .
C.
0
60 .
D.
0
45 .
DẠNG 3. HAI ĐƯỜNG THẲNG VUÔNG GÓC
Câu 11. Trong không gian, cho đường thẳng
và điểm
O
. Qua
O
có bao nhiêu đường thẳng vuông góc
với đường thẳng
?
A. 3. B. vô số. C. 1. D. 2.
Câu 12. Trong các mệnh đề sau, mệnh đề nào sai
A. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
Câu 13. Trong hình hộp
.ABCD AB C D
có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh
đề nào sai?
A.
BB BD
. B.
A C BD

. C.
A B DC

. D.
BC AD

.
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
10
Câu 14. Cho hình lập phương
.ABCD A B C D
. Đường thẳng nào sau đây vuông góc với đường thẳng
BC
?
A.
AD
. B.
AC
. C.
BB
. D.
AD
.
Câu 15. Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
và
SA SC
,
SB SD
. Trong các mệnh đề
sau mệnh đề nào sai?
A.
AC SD
. B.
BD AC
. C.
BD SA
. D.
AC SA
.
II.Phần bài tập phục vụ cho phần tự luận trong đề kiểm tra.
Bài 1.Tính các giới hạn sau:
1)
2
3
: ñs ,
n
nn
lim
12
53
2
2
; 2)
13
20372
2
nn
)n)(n(
lim
n
; 3)
nn
nn
.
lim
24
453
, đs : 5;
4)
)n)(n)(n(
nn
lim
n
2312
14
2
24
; 5)
2
22
321
12
)n)(n(
)n)(n(
lim
n
; 6)
14
32
23
2
nn
n
lim
n
;
7)
4
3
: ñs ,
n
nn
lim
24
19
2
; 8)
2
2
21
13
n
nn
lim
, đs : 0; 9)
1
2
2
nn
nn
lim
;
10)
2
1
- : ñs nnnlim
2
; 11)
2
1
: ñs ,nnnlim 1
22
; 12)
3
241
22
n
nnn
lim
;
13)
nn
nn
.
lim
242
143
Bài 2.Tính các giới hạn sau:
1)
2
3
23
lim
3
x
xx
x

; 2)
2
2
2
4
lim
32
x
x
xx

; 3)
1
32
lim
1
x
x
x

;
4)
0
4
lim
93
x
x
x

; 5)
32
lim 3 5 7
x
xx


; 6)
2
lim 1
x
xx


7)
2
lim ( 2 )
x
x x x


8)
22
lim 2 3
x
x x x

; 9)
2
2
lim
23
x
x x x
x


;
10)
2
2
lim
23
x
x x x
x


; 11)
2
3
2 10
lim
33
x
xx
xx



; 12)
2
3
12
lim
3
x
x
x
.
Bài 3. Xét tính liên tục của hàm số
-1x neáu ,x
-1x neáu ,x
)x(f
2
1
23
tại x = -1
Bài 4. Xét tính liên tục của hàm số
1- x neáu 1
1- x neáu
x
xx
)x(f
1
45
3
2
trên tập xác định của nó;
Bài 5. Xét tính liên tục của hàm số sau trên TXĐ của nó,
-1x neáu ,x
-1x neáu ,x
)x(f
2
2
52
Bài 6. Xét tính liên tục của các hàm số sau trên TXĐ của nó:
a)
2
2
2
,1
1
1, 1
xx
khi x
fx
x
x x khi x

; b)
2
25
,5
5
10, 5
x
khi x
fx
x
khi x
.
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
11
Bài 7. Tìm giá trị tham số a để hàm số sau liên tục tại x=2,
2
2
2
8
3
x neáu ,ax
x neáu,
x
x
)x(f
Bài 8. a) Tìm
m
để hàm số
3
1
,1
1
2 1, 1
x
khi x
fx
x
m khi x

liên tục tại
1x
.
b) Tìm
a
để hàm số
44
, 4 0
10 , 0 4
xx
khi x
y
x
a x khi x
liên tục trên
4;4
.
Bài 9. Cho hàm số
253
2
1
3
2
x neáu,x
x neáu,
x
)x(f
a) Tìm TXĐ của hàm số; b) Tìm điểm trên TXĐ mà hàm số gián đoạn.
Bài 10. a) CMR phương trình
4 3 2
3 1 0x x x x
có nghiệm thuộc
1;1
.
b) CMR phương trình:
3
15 1 0xx
có ít nhất một nghiệm dương nhỏ hơn 1.
Bài 11. Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Chứng minh rằng AC vuông góc B’D’,
AB’ vuông góc CD’ và AD’ vuông góc CB’
Bài 12. Cho tứ diện đều ABCD cạnh bằng a. Gọi M là trung điểm của BC. Tính cosin của góc giữa hai đường thẳng
AB và DM
Bài 13. Cho tứ diện ABCD có AB = CD = a, AC = BD = b, AD = BC = c
a) Chứng minh các đọan nối trung điểm các cặp cạnh đối thì vuông góc với 2 cạnh đó
b) Tính cosin của góc giữa hai đường thẳng AC và DB
Bài 14. Cho hình chóp S.ABCD có đáy là hình bình hành với AB = a, AD = 2a, SAB là tam giác vuông cân tại A, M
là điểm trên cạnh AD (M khác A và D). Mặt phẳng
) qua M song song với mặt phẳng (SAB) cắt BC, SC, SD lần
lượt tại N, P, Q
a) Chứng minh MNPQ là hình thang vuông; b) Đặt x = AM. Tính diện tích của MNPQ theo a và x
Bài 15 :Cho töù dieän ABCD .Goïi M vaø N laàn löôït laø trung ñieåm cuûa AB vaø CD. Chöùng minh ba veùc tô

󰇍
󰇍
󰇍
󰇍
󰇍
, 
󰇍
󰇍
󰇍
󰇍
󰇍
, 
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
. ñoàng phaúng
Bài 16:Cho töù dieän ABCD .Goïi M vaø N laàn löôït laø trung ñieåm cuûa AB vaø CD .Treân caùc caïnh AD vaø BC laàn löôït
lấy P vaø Q sao cho 
󰇍
󰇍
󰇍
󰇍
󰇍
=
2
3

󰇍
󰇍
󰇍
󰇍
󰇍
, 
󰇍
󰇍
󰇍
󰇍
󰇍
=
2
3

󰇍
󰇍
󰇍
󰇍
󰇍
. Chöùng minh boán ñieåm M,N,P,Q cuøng thuoäc moät maët phaúng
Bài 17: Cho tứ diện
ABCD
. Trên các cạnh
AD
và
BC
lần lượt lấy
M
,
N
sao cho
3AM MD
,
3BN NC
.
Gọi
P
,
Q
lần lượt là trung điểm của
AD
và
BC
.Chứng minh rằng ba vectơ
MN
,
DC
,
PQ
đồng phẳng.
Bài 18: Cho tứ diện
.ABCD
Trên cạnh
AD
lấy điểm
M
sao cho
2AM MD
và trên cạnh
BC
lấy điểm
N
sao
cho
2.NB NC
Chứng minh rằng ba vectơ
,AB CD
và
MN
đồng phẳng.
Bài 19: Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC =
2a
. Tính góc giữa AB và SC.
Bài 20: Cho tứ diện
ABCD
có AB = AC = AD và
0
60BAC BAD
. Chứng minh rằng nếu M, N là lần lượt
trung điểm của AB và CD thì MM
MN AB
Bài 21:Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N, P lần lượt là trung điểm của AB, BC, C’D’. Tính góc giữa
hai đường thẳng MN và AP
ĐỀ THAM KHẢO
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
12
SỞ GIÁO DỤC & ĐÀO TẠO LÂM ĐỒNG
TRƯỜNG TRUNG HỌC PHỔ THÔNG…
Mã đề thi: 01
(Đề gồm 6 trang)
KIỂM TRA MINH HOA GIỮA HỌC KỲ II
MÔN THI: TOÁN _ 11 CB
THỜI GIAN: 90 PHÚT
(Không kể thời gian phát đề)
PHẦN TRẮC NGHIỆM (7 điểm:Gồm 35 câu, mỗi câu đúng 0,2 đ)
Câu 1: Trong các khẳng định sau, khẳng định nào đúng?
A.
. . 1 cos ,ab a b a b
B.
. . cos ,ab a b a b
C.
. . 1 sin ,ab a b a b
D.
. . sin ,ab a b a b
Câu 2: Khẳng định nào sau đây đúng?
A.
3
1
lim
3
x
x

B.
3
1
lim
3
x
x

C.
3
11
lim
33
x
x
D.
3
1
lim 0
3
x
x
Câu 3: Khẳng định nào sau đây đúng?
A.
4 2 2
2
41
lim 3
2
n n n
n

B.
4 2 2
2
41
lim 4
2
n n n
n
C.
4 2 2
2
41
lim 4
2
n n n
n

D.
4 2 2
2
41
lim 5
2
n n n
n

Câu 4: Khẳng định nào sau đây đúng?
A.
23
lim 3 3nn
B.
23
lim 3nn 
C.
23
lim 3 0nn
D.
23
lim 3nn 
Câu 5: Cho hàm số
2
3 khi 1
()
2 khi 1
xx
fx
xx


. Chọn khẳng định đúng trong các khẳng định sau.
A.
1
lim ( ) 1
x
fx
B.
1
lim ( ) 4
x
fx
C.
1
lim ( ) 2
x
fx
D.
1
lim ( ) 1
x
fx

Câu 6: Cho hình lập phương
.ABCD EFGH
. Số đo góc giữa đường thẳng AH
và EB là?A.
0
45 .
B.
0
90 .
C.
0
120 .
D.
0
60 .
Câu 7: Cho hàm số
2
12
2
2
12
x
x
fx
x
xx


. Tìm khẳng định đúng
trong các khẳng định sau:
A.
2
22
12
lim lim 1
2
xx
x
f x x
x







B.
22
lim lim 1
xx
f x x



C.
2
22
12
lim lim
2
xx
x
fx
x



D.
2
22
12
lim lim 1
2
xx
x
f x x
x







Câu 8: Khẳng định nào sau đây đúng?
A.
4
lim 4
x
x

B.
4
lim
x
x


C.
4
lim 0
x
x

D.
4
lim
x
x


Câu 9: Khẳng định nào sau đây đúng?
A.
2
2
2
lim 2 lim
2
n
n n n
n n n

B.
2
2
3
lim 2 lim
2
n
n n n
n n n

C.
2
2
3
lim 2 lim
2
n
n n n
n n n

D.
2
2
2
lim 2 lim
2
n
n n n
n n n

TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
13
Câu 10: Cho tứ diện đều
.ABCD
Số đo góc giữa hai đường thẳng
AB
và
CD
bằng:
A.
0
60 .
B.
0
45 .
C.
0
90 .
D.
0
30 .
Câu 11: Khẳng định nào sau đây sai?
A.
11
2 3 1
lim lim
1
23
xx
x
x
x


B.
11
2 3 1
lim lim
1
23
xx
x
x
x



C.
11
23
lim lim
1
23
xx
xx
x
x



D.
11
23
lim lim
1
23
xx
xx
x
x


Câu 12: Khẳng định nào sau đây đúng?
A.
3
4
44
lim 4
4
x
xx
x


B.
3
4
44
lim 4
4
x
xx
x

C.
3
4
44
lim 2
4
x
xx
x


D.
3
4
44
lim 8
4
x
xx
x


Câu 13: Cho cấp số nhân
()
n
u
với số hạng đầu
1
u
và công bội
q
với
1q
. Khi đó khẳng định nào
sau đây đúng?
A.
21
1
1 1 1 1
1
n
u
u u q u q u q
q
B.
21
1
1 1 1 1
21
n
u
u u q u q u q
q
C.
21
1
1 1 1 1
2
1
n
u
u u q u q u q
q
D.
21
1
1 1 1 1
1
n
u
u u q u q u q
q
Câu 14: Cho tứ diện đều MNPQ. Khẳng định nào sau đây đúng?
A.
0
, 90MN MQ
B.
0
, 120MN MQ
C.
0
, 60MN MQ
D.
0
, 45MN MQ
Câu 15: Cho
1q
. Khi đó, khẳng định nào sau đây đúng?
A.
lim 1
n
q
B.
lim
n
q 
C.
lim
n
q 
D.
lim 0
n
q
Câu 16: Cho hình hộp
1 1 1 1
.ABCD A B C D
. Khi đó, vectơ bằng vectơ
1
AB
là vectơ nào dưới đây?
A.
AC'
.B.
1
DC
. C.
CD
. D.
BA
.
Câu 17: Khẳng định nào sau đây đúng?
A.
2
1
2 3 3
lim
2 7 5
x
xx
x





B.
2
1
2 3 1
lim
2 7 5
x
xx
x





C.
2
1
23
lim 0
27
x
xx
x




D.
2
1
2 3 6
lim
2 7 5
x
xx
x





Câu 18: Khẳng định nào sau đây đúng?
A.
2
lim 1 4
x
x

B.
2
lim 1 2
x
x

C.
2
lim 1 3
x
x

D.
2
lim 1 1
x
x

Câu 19: Trong các khẳng định sau, khẳng định nào là khẳng định đúng?
A. Nếu hàm số
()y f x
liên tục trên khoảng
;ab
và
( ). ( ) 0f a f b
thì tồn tại ít nhất một điểm
sao cho .
B. Nếu hàm số
()y f x
liên tục trên đoạn và
( ). ( ) 0f a f b
thì tồn tại ít nhất một điểm
sao cho .
C. Nếu hàm số
()y f x
liên tục trên khoảng
;ab
và
( ). ( ) 0f a f b
thì tồn tại ít nhất một điểm
sao cho .
D. Nếu hàm số
()y f x
liên tục trên đoạn và
( ). ( ) 0f a f b
thì tồn tại ít nhất một điểm
sao cho .
;c a b
0fc
;ab
;c a b
0fc
;c a b
0fc
;ab
;c a b
0fc
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
14
y
2
1
-1 0 x
3
2
3
O
y
x
Câu 20: Cho phương trình
3
3 1 0 (1)xx
. Chọn khẳng định đúng nhất trong các khẳng định sau:
A. Phương trình (1) có ít nhất một nghiệm thuộc khoảng
0;1
.
B. Phương trình (1) có ít nhất ba nghiệm thuộc khoảng
0;1
.
C. Phương trình (1) có ít nhất bốn nghiệm thuộc khoảng
0;1
.
D. Phương trình (1) có ít nhất hai nghiệm thuộc khoảng
0;1
.
Câu 21: Khẳng định nào sau đây đúng?
A.
1
lim ,
k
k
n

B.
1
lim 1,
k
k
n

C.
1
lim 0,
k
k
n

D.
1
lim ,
k
k
n

Câu 22: Cho hàm số có đồ thị như hình dưới đây:
Quan sát đồ thị và cho biết khẳng định nào sau đây đúng ?
A.
3
lim ( ) 2
x
fx


B.
3
lim ( )
x
fx


C.
3
lim ( )
x
fx


D.
3
lim ( ) 0
x
fx

Câu 23: Khẳng định nào sau đây đúng?
A.
2
2
22
63
lim lim
42
xx
x x x
xx


B.
2
2
22
63
lim lim
42
xx
x x x
xx


C.
2
2
22
63
lim lim
42
xx
x x x
xx


D.
2
2
22
63
lim lim
42
xx
x x x
xx


Câu 24: Cho hình hộp
1 1 1 1
.ABCD A BC D
. Chọn khẳng định đúng?
A.
1 1 1 1
,,AB A D B D
đồng phẳng. B.
1 1 1
,,DB BD C A
đồng phẳng.
C.
1 1 1
,,AB AD B A
đồng phẳng. D.
1
,,AA AD AB
đồng phẳng.
Câu 25: Khẳng định nào sau đây đúng?
A.
lim 0,k
k
n

B.
lim ,k
k
n
C.
lim ,k
k
n
D.
lim 1,k
k
n

Câu 26: Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ACD. Khi đó khẳng định nào sau đây
đúng? A.
3BA BC BD GB
B.
4BA BC BD BG
C.
3BA BC BD GB
D.
3BA BC BD BG
Câu 27: Công thức nào dưới đây đúng? A.
lim(u ) lim lim
n n n n
v v u
B.
lim(u ) lim lim
n n n n
v u v
C.
lim(u ) lim .lim
n n n n
v u v
D.
lim(u ) lim lim
n n n n
v u v
Câu 28: Cho hàm số có đồ thị như hình dưới đây:
Hàm số
()y f x
gián đoạn tại điểm có hoành độ bằng bao nhiêu?
A. 2 B. 1 C.
1
D. 0
Câu 29: Khẳng định nào sau đây đúng nhất?
fx
fx
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
15
A. Có ít nhất ba điểm không đồng phẳng. B. Có ít nhất sáu điểm không đồng phẳng.
C. Có ít nhất bốn điểm không đồng phẳng. D. Có ít nhất năm điểm
không đồng phẳng.
Câu 30: Cho hình lập phương
.ABCD EFGH
. Hãy xác định góc giữa cặp
vectơ
AB

và
EG

? A.
0
90 .
B.
0
120 .
C.
0
45 .
D.
0
60 .
Câu 31: Cho hàm số
1 5 , 1
, 1
xx
fx
x m x


. Giá trị của m để hàm số liên
tục trên tập xác định là: A.
2
B.
5
C.
3
D.
4
Câu 32: Khẳng định nào dưới đây đúng?
A.
2
2
2
2
11
1
1
lim lim
31
3 3 1
3
nn
nn
nn
nn




B.
2
2
2
2
11
1
1
lim lim
33
3 3 1
1
nn
nn
nn
nn




C.
2
2
2
2
21
1
1
lim lim
13
3 3 1
3
nn
nn
nn
nn




D.
2
2
2
2
11
1
1
lim lim
31
3 3 1
3
nn
nn
nn
nn




Câu 33: Trong các khẳng định sau đây, khẳng định nào sai?
A. Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm phân biệt.
B. Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua hai đường thẳng cắt nhau.
C. Một mặt phẳng được hoàn toàn XD khi biết nó đi qua ba điểm phân biệt không thẳng hàng.
D. Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua một đường thẳng và một điểm nằm
ngoài đường thẳng đó.
Câu 34: Khẳng định nào sau đây sai?
A.
2
2
lim 2 lim
2
11
n n n
n

B.
2
2
lim 2 lim
2
11
n
n n n
n

C.
2
2
lim 2 lim
2
11
n
n n n
n

D.
2
2
lim 2 lim
2
11
n n n
n

Câu 35: Cho hàm số
2
1
()
6
fx
xx

. Hàm số liên tục trên khoảng nào sau đây?
A.
;3
B.
3; 
C.
2;3
D.
3;2
PHẦN TỰ LUẬN ( 3 điểm)
Câu 1( 1,5 điểm) : Tính giới hạn sau:
a.
2
2
31
lim
25
nn
n

b.
2
lim 2
x
x x x


Câu 2( 0,5 điểm): Cho hàm số
2
, khi 2
()
2
, khi 2
xx
x
fx
x
m x x


(
m
là tham số )
Tìm điều kiện của tham số m để hàm số liên tục trên toàn tập xác định.
Câu 3 ( 1 điểm): Cho tứ diện
A BCD
có
AC AB AD
,
CAB DAB DAC
. Gọi
là góc giữa
AC
và
BD
. Tính
cos
. Từ đó suy ra
AC BD
.
fx
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
16
----------- HẾT ----------
Ghi chú: Thí sinh không được sử dụng tài liệu. CBCT không giải thích gì thêm.
Họ và tên Thí sinh:………………………………………………….Chữ ký: ………………………………
Họ và tên CBCT1:……………………………………………… ….Chữ ký: ………………………………
Họ và tên CBCT2:……………………………………………… ….Chữ ký: ………………………………
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

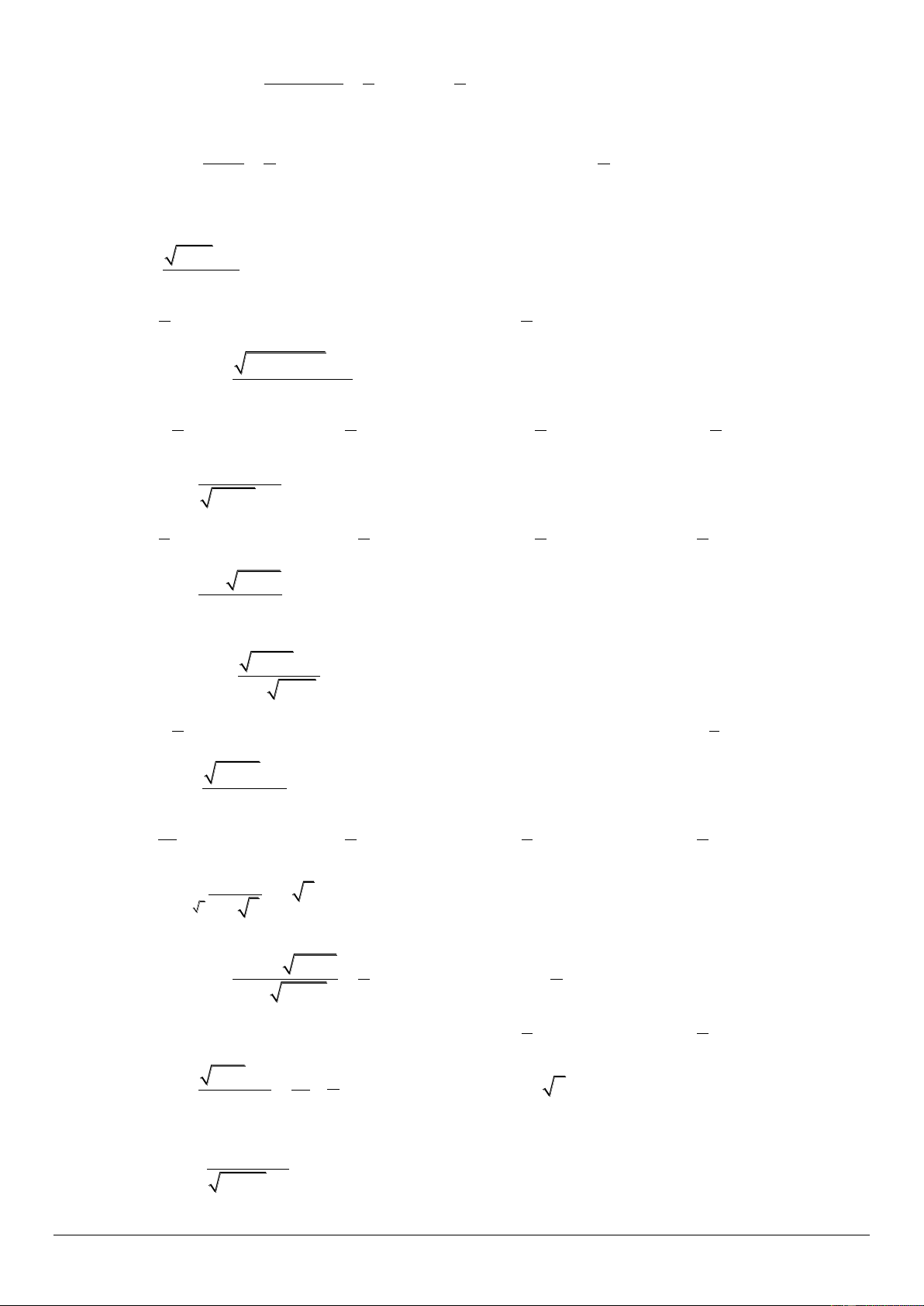
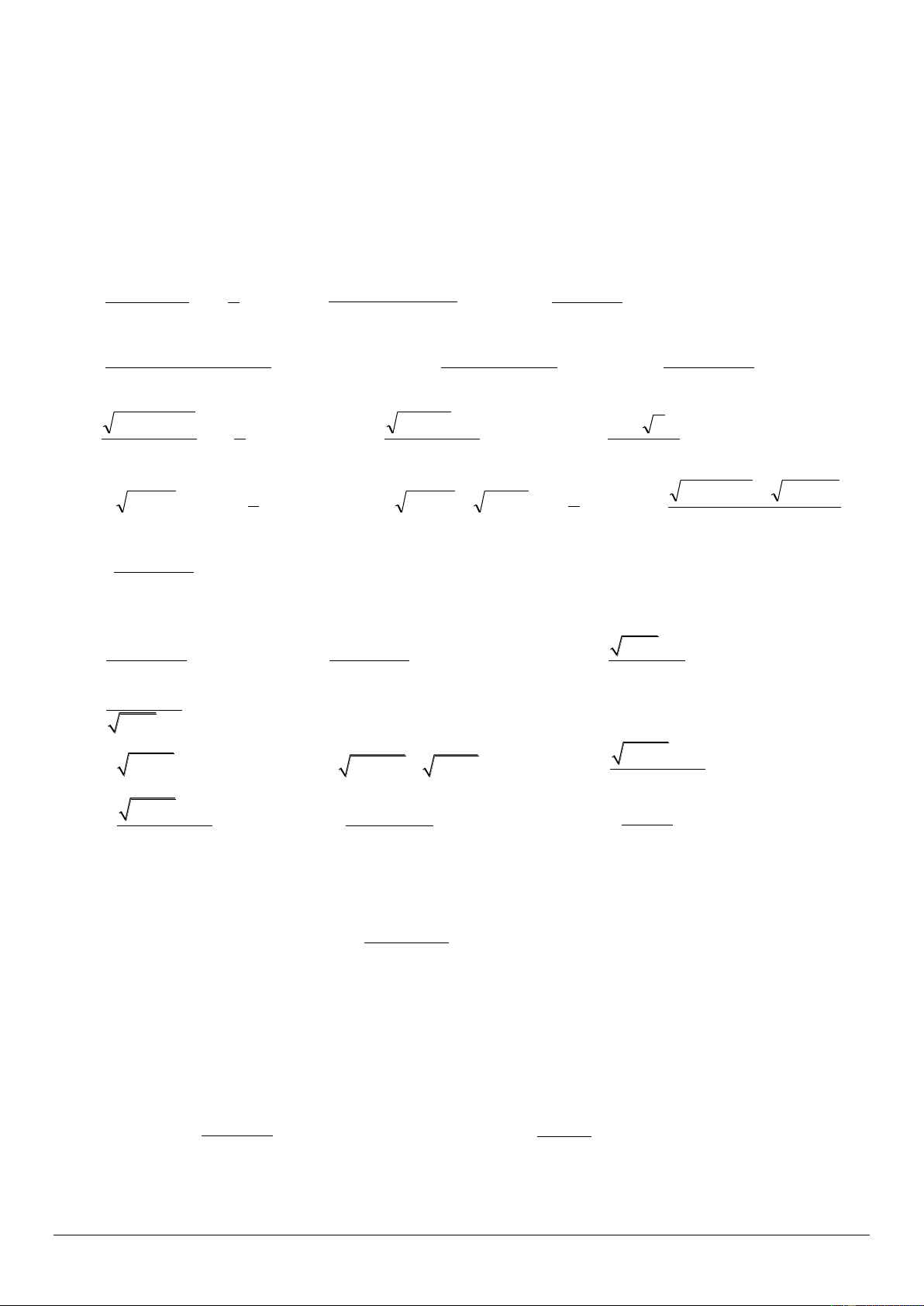
Preview text:

TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
TRƯỜNG THPT CHUYÊN BẢO LỘC
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ II, MÔN TOÁN LỚP 11 CB
NĂM HỌC 2022 – 2023 A. LÝ THUYẾT:
I. ĐẠI SỐ & GỈAI TÍCH:
+ Giới hạn của dãy số, giới hạn của hàm số lượng giác, giới hạn của hàm số gồm các dạng vô định: 0  ; ; 0. ;     0 
+ Hàm số liên tục gồm các dạng tóan: xét tính liên tục của hàm số tại một điểm, trên một khỏang, trên R; xác định a để hàm số liên tục. II. HÌNH HỌC. + Véc tơ trong không gian
+ Quan hệ vuông góc: gồm các dạng tóan chứng minh đường thẳng vuông góc với đường thẳng
+ Góc: góc giữa đường thẳng và đường thẳng B. BÀI TẬP
I.Phần bài tập phục vụ cho phần trắc nghiệm trong đề kiểm tra.(gồm 100 câu trắc nghiệm)
PHẦN TRẮC NGHIỆM ĐẠI SỐ VÀ GIẢI TÍCH
BÀI 1. GIỚI HẠN CỦA DÃY SỐ
DẠNG 1. DÃY SỐ DẠNG PHÂN THỨC n 1 Câu 1. Tính L  lim . 3 n  3 A. L  1. B. L  0 . C. L  3. D. L  2 . 2 1 n Câu 2. lim bằng 2 2n 1 1 1 1 A. 0 . B. . C. . D.  . 2 3 2 3 n  4n  5 Câu 3. lim bằng 3 2 3n n  7 1 1 1 A. 1. B. . C. . D. . 3 4 2 5 3 8n  2n 1 Câu 4. Giới hạn lim bằng 2 5
2n  4n  2019 A. 2  . B. 4 . C.  . D. 0 . 2 4n  3n 1 Câu 5.
Giá trị của B  lim  bằng: 3n  2 1 4 4 A. . B. . C. 0 . D. 4 . 9 3 2
4n 1  n  2 Câu 6. lim bằng 2n  3 3 A. . B. 2. C. 1. D.  . 2
3n  13 n2 a Câu 7.
Dãy số u với u
có giới hạn bằng phân số tối giản . Tính . a b n n 4n 53 b A. 192 . B. 68 . C. 32 . D. 128 .
DẠNG 2. DÃY SỐ CHỨA CĂN THỨC. Câu 8.  2 lim
n  3n 1  n bằng 1
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB 3 A. 3  . B.  . C. 0 . D.  . 2 Câu 9. Tính giới hạn  2
lim n n  4n . A. 3 . B. 1. C. 2 . D. 4 .
DẠNG 3. DÃY SỐ CHỨA LŨY THỪA.
Câu 10. Dãy số nào sau đây có giới hạn bằng 0 ? nn n n 4   1   5   5  A.    . B.   . C.   . D.   .    3   3   3 
Câu 11. lim 2n bằng. n A. 2 . B.  . C.  . D. 0 . n  2018  Câu 12. lim   bằng.  2019  1 A. 0 . B.  . C. . D. 2 . 2 n 1  n 1 3.2 2.3  
Câu 13. Tính giới hạn lim . 4  3n 3 6 A. . B. 0 . C. . D. 6  . 2 5 2n 1 Câu 14. Tính lim . 2.2n  3 1 A. 2. B. 0. C. 1. D. . 2
DẠNG 4. TỔNG CẤP SỐ NHÂN LÙI VÔ HẠN. 1
Câu 15. Tính tổng S của cấp số nhân lùi vô hạn có số hạng đầu u  1 và công bội q   . 1 2 3 2 A. S  2 . B. S  . C. S  1. D. S  . 2 3 2 2 2
Câu 16. Tổng vô hạn sau đây S  2   ...
... có giá trị bằng 2 3 3 3n 8 A. . B. 3 . C. 4 . D. 2 . 3 1 1 1 Câu 17. Tổng 1   ... bằng 2 4 2n 1 A. . B. 2. C. 1. D.  . 2
BÀI 2. GIỚI HẠN CỦA HÀM SỐ
DẠNG 1. GIỚI HẠN HỮU HẠN Câu 1.
Cho các giới hạn: lim f x  2 ; lim g x  3 , hỏi lim 3  f
x4gx bằng xx xx xx 0 0 0 A. 5 . B. 2 . C. 6  . D. 3 . Câu 2.
Cho lim f x  2  . Tính lim  f
 x  4x 1 . x 3  x 3  A. 5 . B. 6 . C. 11. D. 9 . Câu 3. Giá trị của lim  2
2x  3x   1 bằng x 1  2
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB A. 2 . B. 1. C.  . D. 0 . x  3 Câu 4.
Tính giới hạn L  lim x 3  x  3
A. L   . B. L  0 .
C. L   . D. L  1. 2 x  2x  3 Câu 5. Giới hạn lim bằng? x 1  x 1 A. 1. B. 0 . C. 3 . D. 2 . Câu 6. 2 lim x  4 bằng x 3 A. 5  . B. 1. C. 5 . D. 1  . 2
2 x 1  5 x  3 Câu 7. lim bằng. x 2  2x  3 1 1 A. . B. . C. 7 . D. 3 . 3 7
DẠNG 2. GIỚI HẠN MỘT BÊN 1 Câu 8.Tính lim . x3 x  3 1 A.  . B.  . C. 0 . D.  . 6 Câu 9.
Trong các mệnh đề sau, mệnh đề nào sai? 1 1 1 1 A. lim   . B. lim   . C. lim   . D. lim   .    5  x0 x x0 x x0 x x0 x 2  x 1
Câu 10. Giới hạn lim bằng x 1  x 1 2 1 A. .  B. .  C. . D. . 3 3 x  2 Câu 11. lim bằng:  x 1  x 1 1 1 A.  . B. . C.  D.  . 2 2 2 3x 1  x Câu 12. lim  x     1 x  bằng? 1 1 1 3 3 A. . B.  . C. D.  . 2 2 2 2
DẠNG 3. GIỚI HẠN TẠI VÔ CỰC
Câu 13. Tính giới hạn  3 2
lim 2x x   1 x A.   . B.  . C. 2 . D. 0 .
Câu 14. Chọn kết quả đúng trong các kết quả sau của  5 3
lim 4x  3x x   1 là: x A.  . B. 0 . C. 4 . D.  . 2x 1
Câu 15. Tính giới hạn lim
x 4x  . 2 1 1 1 A. . B. 1. C. . D. 2 4 2 3
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB 1 x Câu 16. lim bằng:
x 3x  2 1 1 1 1 A. . B. . C.  . D.  . 3 2 3 2 2 x  3x  2
Câu 17. Giới hạn lim có kết quả là 2 x 2x 1 1 A.  B.  C. 2 D. 2 3 3 2x  3x  1
Câu 18. Giới hạn lim bằng 3 4 5
x 4x  2x x  3 1 3 A. 2  . B. . C. 3  . D. . 2 2
x  1x  2 Câu 19. lim bằng 2 x x  9 2 1 A. . B. 1. C. 1  . D.  . 9 9 2 x  3x  5 Câu 20. Tìm lim . x 4x 1 1 1 A.  . B. 1. C. 0 . D. . 4 4 2x 1
Câu 21. Giá trị của lim bằng x 2 x 1 1 A. 0 . B. 2  . C.  . D. 2 . 2 x  2  2
Câu 22. Giới hạn lim bằng x x  2 A.  . B. 1. C.  . D. -1 3 4 4x 1 2x 1
Câu 23. Cho hàm số f x      
. Tính lim f x . 3  2x7 x A. 2 . B. 8 . C. 4 . D. 0 . 2 m x  7x  5
Câu 24. Tìm tất cả các giá trị thực của tham số m thỏa mãn lim  4  . 2
x  2x  8x 1 A. m  4  . B. m  8  .
C. m  2 . D. m  3  .
DẠNG 4. GIỚI HẠN VÔ ĐỊNH 2 x  9 Câu 25. Tính lim bằng: x 3  x  3 A. 3 . B. 6 . C.  . D. 3  . 2 x  5x  6
Câu 26. Tính giới hạn I  lim . x2 x  2 A. I  1  . B. I  0 . C. I  1. D. I  5 . 3 x 1
Câu 27. Tính giới hạn A  lim . x 1  x 1 A. A   .  B. A  0. C. A  3. D. A   .  4
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB 2 x  3x  2 a
Câu 28. Cho giới hạn lim
 trong đó a là phân số tối giản. Tính 2 2
S a b . 2 x2 x  4 b b A. S  20 .
B. S  17 .
C. S  10 . D. S  25 . 3 x 1 a Câu 29. Cho lim
 với a, b là các số nguyên dương và a là phân số tối giản. Tính tổng 2 x 1  x 1 b b
S a b . A. 5 . B. 10 . C. 3 . D. 4 . x  3  2 Câu 30. lim bằng x 1  x 1 1 1 A. . B.  . C. . D. 1. 4 2 2
x  3x  4  2
Câu 31. Giới hạn lim bằng x0 x 1 1 3 2 A.  . B. . C.  . D.  . 2 2 4 3 2 x  5x  6 Câu 32. Tìm lim là x2 4x 1  3 3 2 3 1 A. . B.  . C.  . D. . 2 3 2 2 x  2x 1 Câu 33. Tìm lim . 2 x 1  x x  2 A. 5  . B.  . C. 0 . D. 1. 3x 1  4
Câu 34. Giới hạn: lim có giá trị bằng: x 5  3  x  4 9 3 A.  . B. 3  . C. 18  . D.  . 4 8 3 2 8  x  2 Câu 35. Tính lim . 2 x0 x 1 1 1 1 A. . B. . C. . D. . 12 4 3 6 2 2x  6 Câu 36. Tính lim
a b ( a , b nguyên). Khi đó giá trị của P a b bằng x 3 x  3 A. 7 . B. 10 . C. 5 . D. 6 .
x 1 5x 1 a a
Câu 37. Giới hạn lim  , với ,
a b Z,b  0 và
là phân số tối giản. Giá trị của a b là x 3  x  4x  3 b b 8 1 A. 1. B. 1  . C. . D. . 9 9 x 1  2 a a Câu 38. Biết lim  (
là phân số tối giản). Tính a b  2018 . 2 x 3  x  3 b b A. 2021. B. 2023. C. 2024 . D. 2022 . 2 x  2x  8 Câu 39. Tính lim . x 2  2x  5 1 5
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB 1 A. 3  . B. . C. 6  . D. 8 . 2 3x 1 1 a a Câu 40. Biết lim
 , trong đó a , b là các số nguyên dương và phân số tối giản. Tính giá x0 x b b trị biểu thức 2 2
P a b . A. P  13 . B. P  0 . C. P  5 . D. P  40 . Câu 41. Tính    .   2 lim x 4x 2 x xA. 4  . B. 2  . C. 4 . D. 2 .
Câu 42. Tìm giới hạn I     .   2 lim x 4x 1 x xA. I  2  . B. I  4  . C. I  1. D. I  1  . Câu 43. lim    bằng   x 1 x 3 x A. 0 . B. 2 . C.  . D.  .
Câu 44. Tìm giới hạn   2 2 M lim x  4x x x Ta được M bằng  . x 3 1 3 1 A.  . B. . C. . D.  . 2 2 2 2 Câu 45. Tìm    .   3 3 lim x 1 x 2 xA. 1  . B.  . C.  . D. 1.
BÀI 3. HÀM SỐ LIÊN TỤC
DẠNG 1. CÂU HỎI LÝ THUYẾT Câu 1.
Cho hàm số y f x liên tục trên khoảng  ;
a b . Điều kiện cần và đủ để hàm số liên tục trên  ;ablà
A. lim f x  f a và lim f x  f b .
B. lim f x  f a và lim f x  f b .     xa x bxa x b
C. lim f x  f a và lim f x  f b .
D. lim f x  f a và lim f x  f b .     xa x bxa x bCâu 2.
Cho hàm số y f (x) liên tục trên đoạn  ;
a b . Mệnh đề nào dưới đây đúng?
A. Nếu f (a). f ( )
b  0 thì phương trình f (x)  0 không có nghiệm nằm trong  ; a b .
B. Nếu f (a). f ( )
b  0 thì phương trình f (x)  0 có ít nhất một nghiệm nằm trong  ; a b .
C. Nếu f (a). f ( )
b  0 thì phương trình f (x)  0 có ít nhất một nghiệm nằm trong  ; a b .
D. Nếu phương trình f (x)  0 có ít nhất một nghiệm nằm trong  ;
a b thì f (a). f ( ) b  0 . Câu 3.
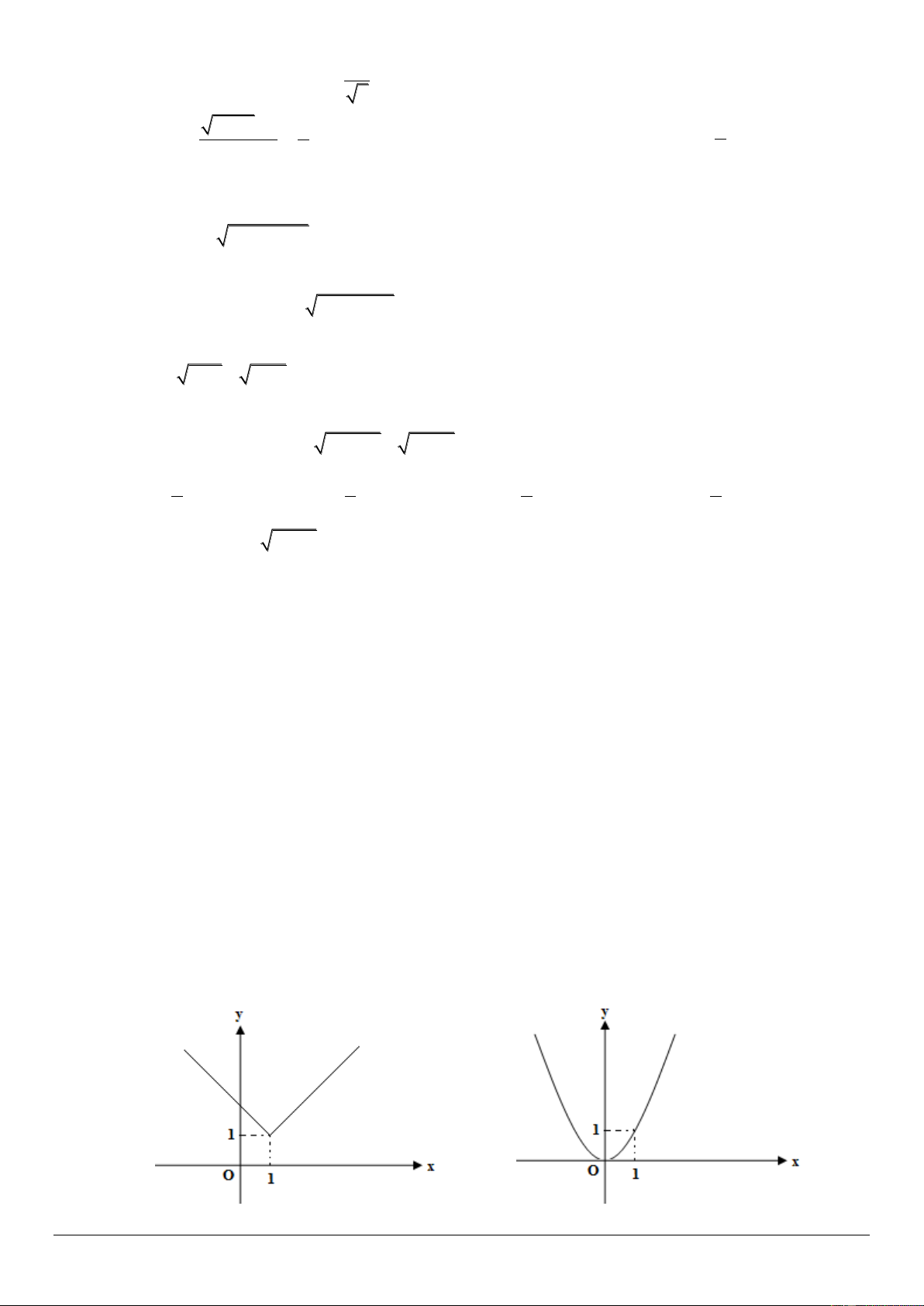
Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại x 1? A. . B. . 6
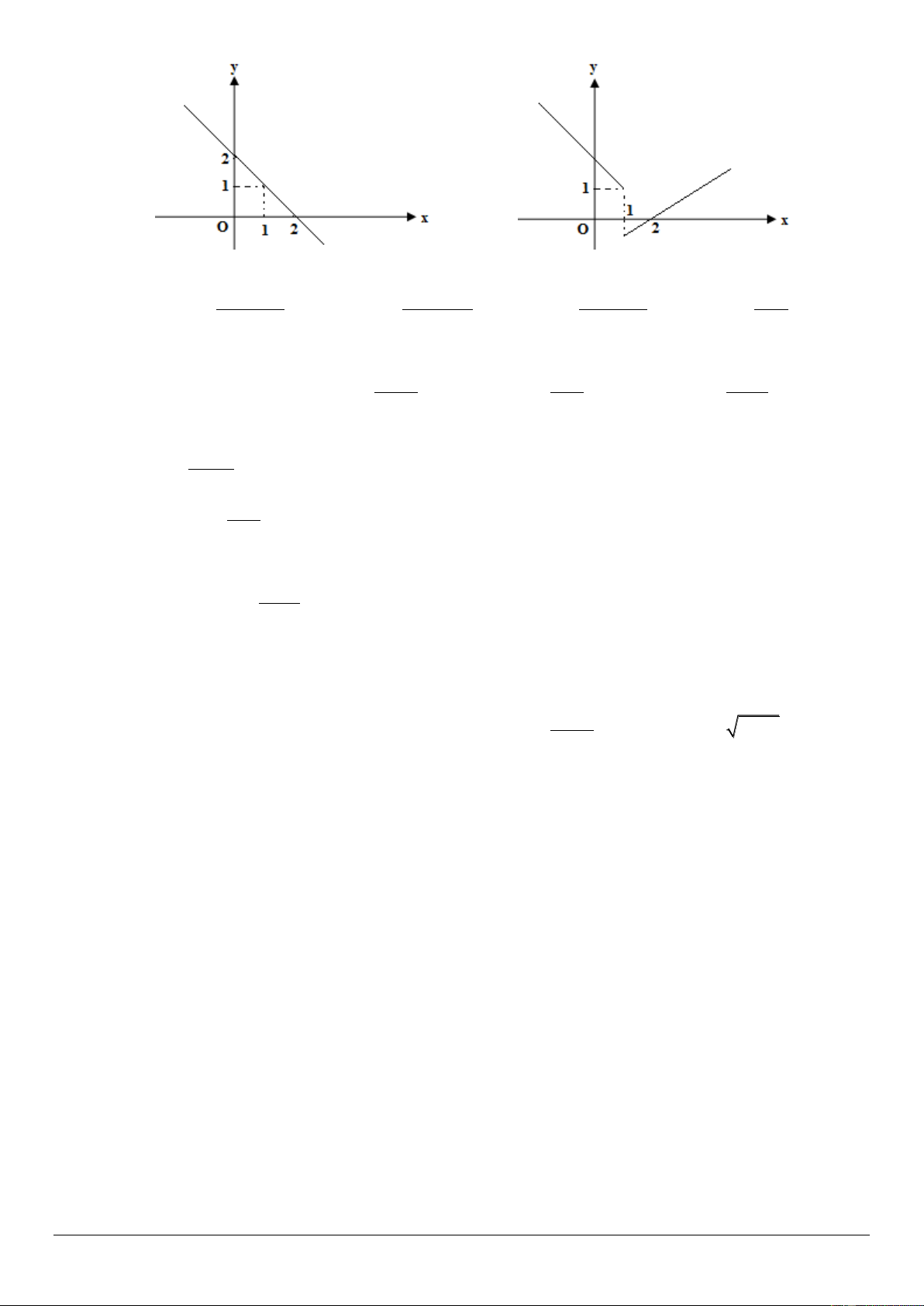
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB C. . D. . Câu 4.
Hàm số nào sau đây liên tục tại x  1 : x x x x  2 x x x
A. f x 2 1  .
B. f x 2 
. C. f x 2 1 
. D. f x 1  . x 1 2 x 1 x x 1 Câu 5.
Hàm số nào dưới đây gián đoạn tại điểm x  1  . 0 2x 1 x x 1
A. y   x   2
1 x  2 . B. y  . C. y  . D. y  . x 1 x 1 2 x 1 Câu 6.
Hàm số nào sau đây gián đoạn tại x  2 ? 3x  4 A. y  .
B. y  sin x . C. 4 2
y x  2x 1
D. y  tan x . x  2 x Câu 7. Hàm số y
gián đoạn tại điểm x bằng? x 1 0 A. x  2018 . B. x  1. C. x  0 D. x  1  . 0 0 0 0 x  3 Câu 8. Cho hàm số y
. Mệnh đề nào sau đây đúng? 2 x 1
A. Hàm số không liên tục tại các điểm x  1
 . B. Hàm số liên tục tại mọi x .
C. Hàm số liên tục tại các điểm x  1  .
D. Hàm số liên tục tại các điểm x  1 . Câu 9.
Trong các hàm số sau, hàm số nào liên tục trên  ? 2x 1 A. 3
y x x .
B. y  cot x . C. y  . D. 2 y x 1 . x 1
DẠNG 2. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM    
Câu 10. Để hàm số y   2x 3x 2 khi x 1
x   thì giá trị của a là 4x a khi x  1  liên tục tại điểm 1 A. 4  . B. 4. C. 1. D. 1  .
DẠNG 3. LIÊN TỤC TRÊN KHOẢNG   
Câu 11. Cho hàm số y   2 x x 3 khi x
2 . Chọn mệnh đề sai trong các mệnh đề sau: 5x  2 k hi x  2
A. Hàm số liên tục tại x  1. 0
B. Hàm số liên tục trên  .
C. Hàm số liên tục trên các khoảng  ;  2, 2; .
D. Hàm số gián đoạn tại x  2 . 0 x khi x  
Câu 12. Cho hàm số y  3 1 1 x m khi x  1
 , m là tham số. Tìm m để hàm số liên tục trên  . A. m  5 . B. m  1  . C. m  3 . D. m  3  .
DẠNG 4. CHỨNG MINH PHƯƠNG TRÌNH CÓ NGHIỆM
Câu 13. Cho phương trình 4 2
2x  5x x 1  0 (1) . Chọn khẳng định đúng trong các khẳng định sau
A. Phương trình  
1 có đúng một nghiệm trên khoảng  2   ;1 . 7
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
B. Phương trình   1 vô nghiệm.
C. Phương trình  
1 có ít nhất hai nghiệm trên khoảng 0; 2 .
D. Phương trình  
1 vô nghiệm trên khoảng  1   ;1 .
PHẦN TRẮC NGHIỆM HÌNH HỌC
BÀI 1. VECTƠ TRONG KHÔNG GIAN Câu 1.
Trong các khẳng định sau, khẳng định nào sai?   
A. Nếu giá của ba vectơ a , b , c cắt nhau từng đôi một thì ba vectơ đó đồng phẳng.    
B. Nếu trong ba vectơ a , b , c có một vectơ 0 thì ba vectơ đó đồng phẳng.   
C. Nếu giá của ba vectơ a , b , c cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng.   
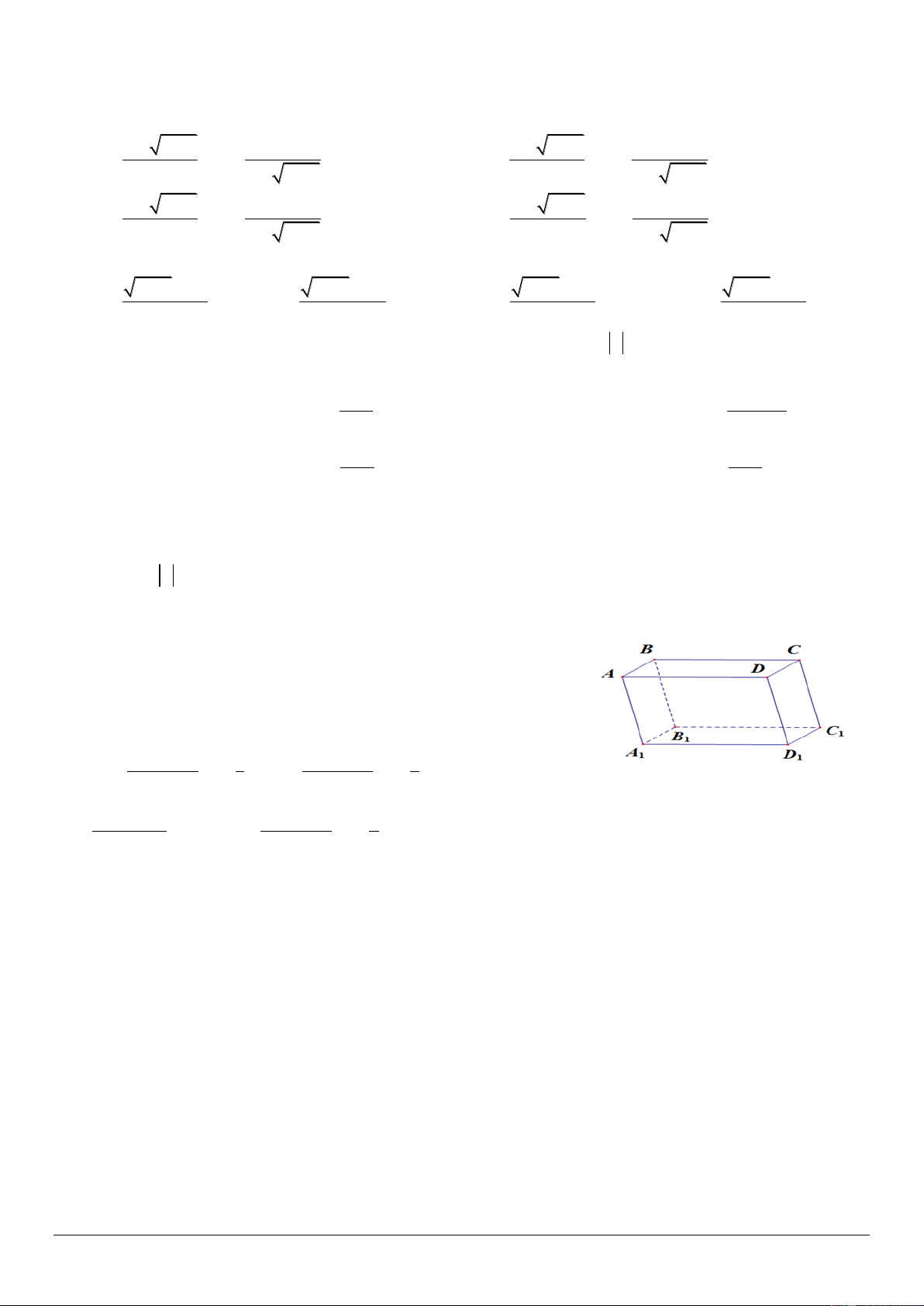
D. Nếu trong ba vectơ a , b , c có hai vectơ cùng phương thì ba vectơ đó đồng phẳng. Câu 2. Cho hình hộp ABC . D A BCD
  . Gọi I, J lần lượt là trung điểm của AB và CD . Khẳng định
nào dưới đây là đúng?        
A. AI CJ . B. D A    IJ .
C. BI D J  . D. A I   JC . Câu 3.
Cho hình lập phương ABC .
D A' B 'C ' D ' . Mệnh đề nào sau đây sai?
   
  
A. AB AD AA'  AC ' .
B. AC AB AD .    
C. AB CD .
D. AB CD . Câu 4.
Cho tứ diện ABCD . Mệnh đề nào dưới đây là mệnh đề đúng?
   
   
A. BC AB DA DC .
B. AC AD BD BC .
   
   
C. AB AC DB DC .
D. AB AD CD BC . Câu 5. Cho hình hộp ABC .
D A' B 'C ' D ' . Chọn đẳng thức vectơ đúng:
   
   
A. AC '  AB AB '  AD .
B. DB '  DA DD '  DC .
   
   
C. AC '  AC AB AD .
D. DB DA DD '  DC . Câu 6.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Khẳng định nào sau đây đúng?
   
    
A. SA SD SB SC .
B. SA SB SC SD  0 .
   
   
C. SA SC SB SD .
D. SA SB SC SD . Câu 7.
Cho hình lăng trụ tam giác AB . C A BC
 . Vectơ nào sau đây là vectơ chỉ phương của đường thẳng AB ?     A. A B   . B. A C  . C. A C   . D. A B  .  Câu 8.
Cho hình hộp chữ nhật ABC .
D A' B 'C ' D' . Khi đó, vectơ bằng vectơ AB là vectơ nào dưới đây?    
A. D 'C ' . B. BA . C. CD .
D. B ' A' . Câu 9. Cho hình hộp ABC .
D A B C D . Chọn khẳng định đúng. 1 1 1 1
  
  
A. BA , BD , BD đồng phẳng.
B. BA , BD , BC đồng phẳng. 1 1 1 1
  
  
C. BA , BD , BC đồng phẳng. D. B ,
D BD , BC đồng phẳng. 1 1 1 1 1
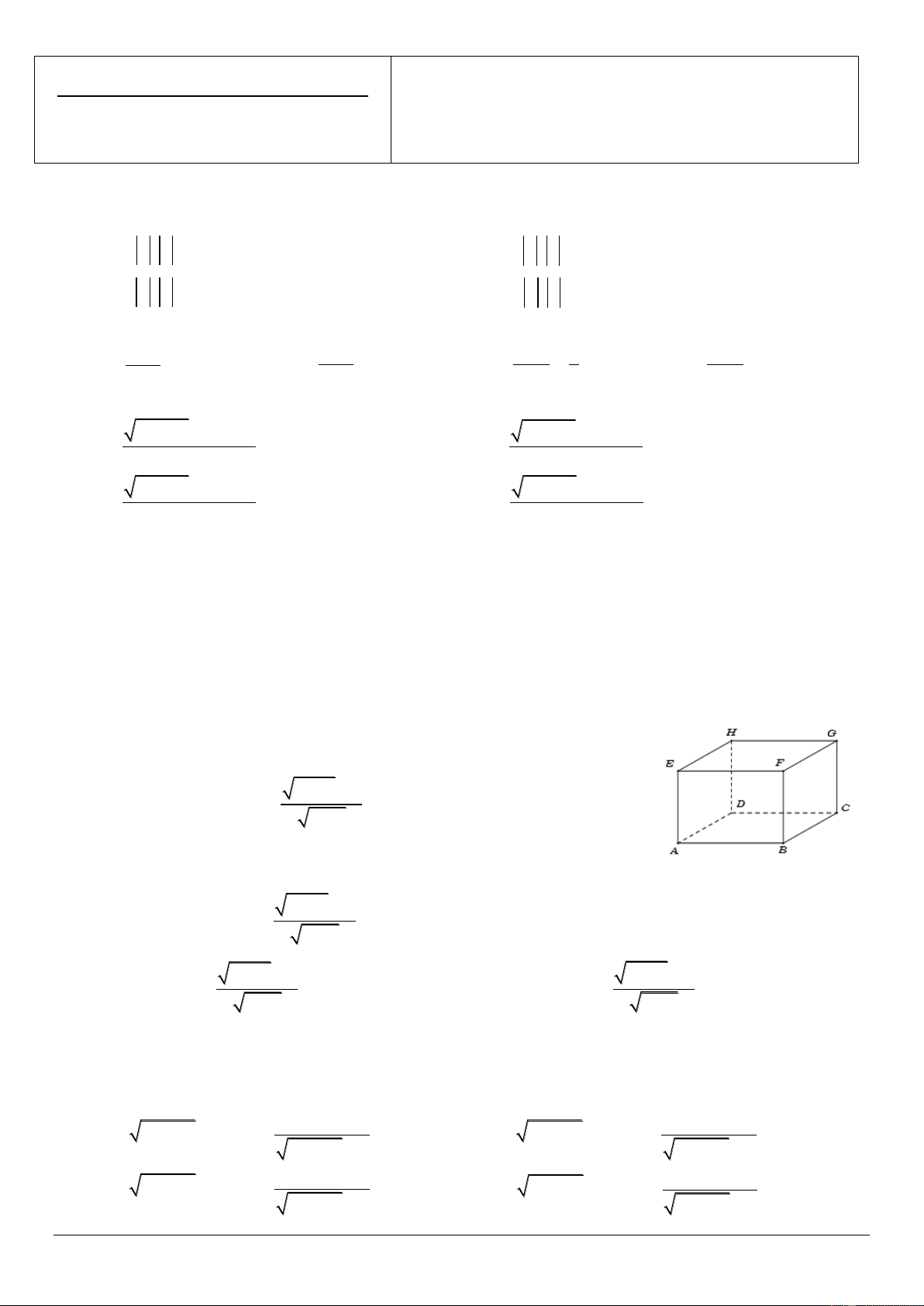
Câu 10. Cho hình hộp ABC .
D EFGH . Gọi I là tâm hình bình hành ABEF và K là tâm hình bình hành
BCGF . Trong các khẳng định sau, khẳng định nào đúng?
  
  
A. BD , EK , GF đồng phẳng.
B. BD , IK , GC đồng phẳng.
  
  
C. BD , AK , GF đồng phẳng.
D. BD , IK , GF đồng phẳng 8
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
BÀI 2. HAI ĐƯỜNG THẲNG VUÔNG GÓC
DẠNG 1. GÓC CỦA HAI VÉCTƠ  Câu 1.
Cho hình chóp S.ABC có BC a 2 , các cạnh còn lại đều bằng a . Góc giữa hai vectơ SB và  AC bằng A. 60 . B. 120 . C. 30 . D. 90 .   Câu 2.
Cho hình lập phương ABC . D A BCD
  . Tính cosB , D A C      
A. cos B , D A C    0.
B. cos B , D A C   1.    
C. cos BD A C   1 ,  .
D. cos BD A C   2 ,  . 2 2 Câu 3. Cho hình chóp .
O ABC có ba cạnh OA , OB , OC đôi một vuông góc và OA OB OC a . Gọi  
M là trung điểm cạnh AB . Góc tạo bởi hai vectơ BC và OM bằng A. 135 . B. 150 . C. 120 . D. 60 .
DẠNG 2. GÓC CỦA HAI ĐƯỜNG THẲNG Câu 4.
Cho hình lập phương ABC .
D A' B 'C ' D '. Tính góc giữa hai đường thẳng AC và A' . B A. 60 B. 45 C. 75 D. 90 Câu 5.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  2a , BC a . Các cạnh bên
của hình chóp cùng bằng a 2 . Tính góc giữa hai đường thẳng AB và SC . A. 45 . B. 30 . C. 60 . D. arctan 2 . Câu 6.
Cho hình lập phương ABC . D A BCD
  . Góc giữa hai đường thẳng A C
  và BD bằng. A. 60 . B. 30 . C. 45 . D. 90 . Câu 7.
Cho tứ diện đều ABCD . Số đo góc giữa hai đường thẳng AB và CD là A. 45 . B. 90 . C. 60 . D. 30 . Câu 8.
Cho tứ diện OABC có OA OB OC  ; a O , A O ,
B OC vuông góc với nhau từng đôi một. Gọi I
là trung điểm BC . Tính góc giữa hai đường thẳng AB và OI . A. 45 . B. 30 . C. 90 . D. 60 . Câu 9.
Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Tính giá trị của cos  A , B DM  . 3 3 1 2 A. . B. . C. . D. . 2 6 2 2
Câu 10. Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng .
a Góc giữa hai đường thẳng CD ' và A'C ' bằng. A. 0 30 . B. 0 90 . C. 0 60 . D. 0 45 .
DẠNG 3. HAI ĐƯỜNG THẲNG VUÔNG GÓC
Câu 11. Trong không gian, cho đường thẳng d và điểm O . Qua O có bao nhiêu đường thẳng vuông góc
với đường thẳng d ? A. 3. B. vô số. C. 1. D. 2.
Câu 12. Trong các mệnh đề sau, mệnh đề nào sai
A. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
Câu 13. Trong hình hộp ABC . D A BCD
  có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào sai?
A. BB  BD . B. A C    BD . C. A B   DC.
D. BC  A D  . 9
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
Câu 14. Cho hình lập phương ABC . D A BCD
  . Đường thẳng nào sau đây vuông góc với đường thẳng BC ? A. A D  . B. AC . C. BB . D. AD .
Câu 15. Cho hình chóp S.ABCD có đáy là hình thoi tâm O và SA SC , SB SD . Trong các mệnh đề
sau mệnh đề nào sai?
A. AC SD .
B. BD AC .
C. BD SA .
D. AC SA.
II.Phần bài tập phục vụ cho phần tự luận trong đề kiểm tra.
Bài 1.Tính các giới hạn sau: n n n 3 2  n  5 3 (2n  7 3 )( n  20) 3  . 5 4 1) lim : ñs , ; 2) lim ; 3) lim , đs : 5; n n 2n2  1 2 2 n n  3n 1 4  2 4n4  n2  1 2 2 (n  2)(n 1) 2 2 n  3 4) lim ; 5) lim ; 6) lim ; n (2n  )( 1 3  n)(n2  ) 2 2 n (n 1)(2n  3) 3 n n  4 2 n 1 9n2  n  1 3 2 3n  1  n 2n n 7) lim : ñs , ; 8) lim , đs : 0; 9) lim ; 4n  2 4 2 1  2n 2 n  n 1 2 2 lim n n  n   n  2 2 1 2  n  n 1 lim n  n  n  1 4 2 1 10) - : ñs : ñs , lim 2 ; 11) 2 ; 12) n  ; 3 n n 3  4  1 13) lim n n . 2 4  2
Bài 2.Tính các giới hạn sau: 2 x  2x  3 2 x  4 x  3  2 1) lim ; 2) lim ; 3) lim ; x 3  3  x 2
x2 x  3x  2 x 1  x 1 4x 4) lim ; 5)  3 2
lim 3x  5x  7 ; 6)  2
lim x x   1 x0 9  x  3 x x 2
x x  2x 7) 2
lim ( x x  2x) 8)    ; 9) lim ;   2 2 lim x 2x x 3 xx x 2x  3 2
x x  2x 2 2x x 10 2 1 2x 10) lim ; 11) lim ; 12) lim . x 2x  3 3    x 3   x x 3x 3 x 3  x 3  2 n , eáu x  -1
Bài 3. Xét tính liên tục của hàm số f(x)   tại x = -1 x2 1 n , eáu x  -1 2 x  x 5  4 n eáu  x - 1
Bài 4. Xét tính liên tục của hàm số f(x)   x3 1
trên tập xác định của nó;  n 1 eáu  x - 1 2x  5 n , eáu x  -1
Bài 5. Xét tính liên tục của hàm số sau trên TXĐ của nó, f(x)   x2  2 n , eáu x  -1
Bài 6. Xét tính liên tục của các hàm số sau trên TXĐ của nó: 2
x x  2 2   x  25 , khi x  1  
a) f x   , khi x 5  x 1 ;
b) f x  x  5 . 2
x x 1, khi x 1 1  0, khi x  5 10
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB 3 8  x ,neáu x  2
Bài 7. Tìm giá trị tham số a để hàm số sau liên tục tại x=2, f(x)   x  2 x  n , a eáu x  2 3 1   x  
Bài 8. a) Tìm m để hàm số f x , khi x 1   1 x
liên tục tại x  1 .
2m 1, khi x 1
 4  x  4  x    
b) Tìm a để hàm số , khi 4 x 0 y   4  ;4 x liên tục trên  . a 10x,
khi 0  x  4  3 ,neáu x  2
Bài 9. Cho hàm số f(x)   2 x 1 3x  5,neáu x  2
a) Tìm TXĐ của hàm số; b) Tìm điểm trên TXĐ mà hàm số gián đoạn. Bài 10. a) CMR phương trình 4 3 2
x x  3x x 1  0 có nghiệm thuộc  1   ;1 . b) CMR phương trình: 3
x 15x 1  0 có ít nhất một nghiệm dương nhỏ hơn 1.
Bài 11. Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Chứng minh rằng AC vuông góc B’D’,
AB’ vuông góc CD’ và AD’ vuông góc CB’
Bài 12. Cho tứ diện đều ABCD cạnh bằng a. Gọi M là trung điểm của BC. Tính cosin của góc giữa hai đường thẳng AB và DM
Bài 13. Cho tứ diện ABCD có AB = CD = a, AC = BD = b, AD = BC = c
a) Chứng minh các đọan nối trung điểm các cặp cạnh đối thì vuông góc với 2 cạnh đó
b) Tính cosin của góc giữa hai đường thẳng AC và DB
Bài 14. Cho hình chóp S.ABCD có đáy là hình bình hành với AB = a, AD = 2a, SAB là tam giác vuông cân tại A, M
là điểm trên cạnh AD (M khác A và D). Mặt phẳng  ) qua M song song với mặt phẳng (SAB) cắt BC, SC, SD lần lượt tại N, P, Q
a) Chứng minh MNPQ là hình thang vuông; b) Đặt x = AM. Tính diện tích của MNPQ theo a và x
Bài 15 :Cho töù dieän ABCD .Goïi M vaø N laàn löôït laø trung ñieåm cuûa AB vaø CD. Chöùng minh ba veùc tô 𝐵 𝐶 , 𝐴 𝐷 , 𝑀 𝑁 . ñoàng phaúng
Bài 16:Cho töù dieän ABCD .Goïi M vaø N laàn löôït laø trung ñieåm cuûa AB vaø CD .Treân caùc caïnh AD vaø BC laàn löôït
lấy P vaø Q sao cho 𝐴 𝑃 = 2 𝐴 𝐷 , 𝐵 𝑄 = 2 𝐵 𝐶
. Chöùng minh boán ñieåm M,N,P,Q cuøng thuoäc moät maët phaúng 3 3
Bài 17: Cho tứ diện ABCD . Trên các cạnh AD và BC lần lượt lấy M , N sao cho AM  3MD , BN  3NC .
  
Gọi P , Q lần lượt là trung điểm của AD và BC .Chứng minh rằng ba vectơ MN , DC , PQ đồng phẳng.  
Bài 18: Cho tứ diện ABC .
D Trên cạnh AD lấy điểm M sao cho AM  2MD và trên cạnh BC lấy điểm N sao      cho NB  2  N .
C Chứng minh rằng ba vectơ A ,
B CD và MN đồng phẳng.
Bài 19: Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC = a 2 . Tính góc giữa AB và SC.  
Bài 20: Cho tứ diện ABCD có AB = AC = AD và 0
BAC BAD  60 . Chứng minh rằng nếu M, N là lần lượt
trung điểm của AB và CD thì MM MN AB
Bài 21:Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N, P lần lượt là trung điểm của AB, BC, C’D’. Tính góc giữa
hai đường thẳng MN và AP ĐỀ THAM KHẢO 11
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
SỞ GIÁO DỤC & ĐÀO TẠO LÂM ĐỒNG
KIỂM TRA MINH HOA GIỮA HỌC KỲ II
TRƯỜNG TRUNG HỌC PHỔ THÔNG…
MÔN THI: TOÁN _ 11 CB Mã đề THỜI GIAN: 90 PHÚT thi: 01
(Đề gồm 6 trang)
(Không kể thời gian phát đề)
PHẦN TRẮC NGHIỆM (7 điểm:Gồm 35 câu, mỗi câu đúng 0,2 đ)
Câu 1: Trong các khẳng định sau, khẳng định nào đúng?             A. .
a b a . b 1 cosa,bB. .
a b a . b cos a,b             C. .
a b a . b 1sina,bD. .
a b a . b sin  , a b
Câu 2: Khẳng định nào sau đây đúng? 1 1 1 1 1 A. lim   lim   lim  lim  0     x 3  3  B. x x 3  3  C. x x 3  3  D. x 3 x 3  3  x
Câu 3: Khẳng định nào sau đây đúng? 4 2 2
n n  4n 1 4 2 2
n n  4n 1 A. lim  3  lim  4 2 n B. 2 2 n  2 4 2 2
n n  4n 1 4 2 2
n n  4n 1 C. lim  4  lim  5  2 n D. 2 2 n  2
Câu 4: Khẳng định nào sau đây đúng? A.  2 3
lim n  3n   3 B.  2 3
lim n  3n    C.  2 3
lim n  3n   0 D.  2 3
lim n  3n   
x  3 khi x 1
Câu 5: Cho hàm số f (x)  
. Chọn khẳng định đúng trong các khẳng định sau. 2
x  2 khi x 1
A. lim f (x)  1
B. lim f (x)  4
C. lim f (x)  2
D. lim f (x)  1      x 1  x 1  x 1  x 1 
Câu 6: Cho hình lập phương ABC .
D EFGH . Số đo góc giữa đường thẳng AH và EB là?A. 0 45 . B. 0 90 . C. 0 120 . D. 0 60 . 2  x 1  2  x  2
Câu 7: Cho hàm số f x   x  2 . Tìm khẳng định đúng  x 1 x  2
trong các khẳng định sau:  x 1 2   
A. lim f x 2  lim x 1 
B. lim f x  lim  x   1     x2 x2  x  2   x2 x2 x 1  2  x 1 2   
C. lim f x 2  lim
D. lim f x 2  lim   x 1       x2 x2 x  2 x2 x2 x  2  
Câu 8: Khẳng định nào sau đây đúng? A. 4 lim x  4 B. 4 lim x   C. 4 lim x  0 D. 4 lim x   x x x x
Câu 9: Khẳng định nào sau đây đúng? 2n 3  n A. lim  2
n  2n n  lim B. lim  2
n  2n n  lim 2
n  2n n 2
n  2n n 3n 2  n C. lim  2
n  2n n  lim D. lim  2
n  2n n  lim 2
n  2n n 2
n  2n n 12
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
Câu 10: Cho tứ diện đều ABC .
D Số đo góc giữa hai đường thẳng AB và CD bằng: A. 0 60 . B. 0 45 . C. 0 90 . D. 0 30 .
Câu 11: Khẳng định nào sau đây sai? 2  x  3 1  2  x  3 1 A. lim  lim B. lim  lim x 1  x 1 x 1  2  x  3 x 1  x 1 x 1  2  x  3 2  x  3 x 2  x  3 x C. lim  lim D. lim  lim x 1  x 1 x 1  2  x  3 x 1  x 1 x 1  2  x  3
Câu 12: Khẳng định nào sau đây đúng? 3 x  4  4x 3 x  4  4x 3 x  4  4x 3 x  4  4x A. lim  4  lim  4 lim  2  lim  8  x4 x B. 4 x4 x C. 4 x4 x D. 4 x4 x  4
Câu 13: Cho cấp số nhân (u ) với số hạng đầu u và công bội q với q  1 . Khi đó khẳng định nào n 1 sau đây đúng?  uu A. 2 n 1 1
u u q u q    u q   2 n 1 1
u u q u q    u q    1 1 1 1 1 B. q 1 1 1 1 21 q  uu n 2 C. 2 1 1
u u q u q    u q   n
u u q u q    u q   1 1 1 1 1 D. 2 1 1 q 1 1 1 1 1 q
Câu 14: Cho tứ diện đều MNPQ. Khẳng định nào sau đây đúng?
 
 
 
  A. MN MQ 0 ,
 90 B. MN MQ 0 , 120 C. MN MQ 0 ,
 60 D. MN MQ 0 ,  45
Câu 15: Cho q  1 . Khi đó, khẳng định nào sau đây đúng? A. lim n q  1 B. lim n q   C. lim n q   D. lim n q  0
Câu 16: Cho hình hộp ABC .
D A B C D . Khi đó, vectơ bằng vectơ 1 1 1 1 
A B là vectơ nào dưới đây? 1    
A. AC' .B. D C . C. CD . D. BA . 1
Câu 17: Khẳng định nào sau đây đúng? 2
x  2x 3 3 2
x  2x 3 1 A. lim     B. lim    C. x 1   2x  7  5 x 1   2x  7  5 2
x  2x 3  2
x  2x 3 6 lim    0 D. lim    x 1   2x  7  x 1   2x  7  5
Câu 18: Khẳng định nào sau đây đúng?
A. lim 1 x  4
B. lim 1 x  2
C. lim 1 x  3
D. lim 1 x  1     x2 x2 x2 x2
Câu 19: Trong các khẳng định sau, khẳng định nào là khẳng định đúng?
A. Nếu hàm số y f (x) liên tục trên khoảng  ;
a b và f (a). f ( )
b  0 thì tồn tại ít nhất một điểm c  ;
a b sao cho f c  0 .
B. Nếu hàm số y f (x) liên tục trên đoạn  ;
a b và f (a). f ( )
b  0 thì tồn tại ít nhất một điểm c  ;
a b sao cho f c  0 .
C. Nếu hàm số y f (x) liên tục trên khoảng  ;
a b và f (a). f ( )
b  0 thì tồn tại ít nhất một điểm c  ;
a b sao cho f c  0 .
D. Nếu hàm số y f (x) liên tục trên đoạn  ;
a b và f (a). f ( )
b  0 thì tồn tại ít nhất một điểm c  ;
a b sao cho f c  0 . 13
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
Câu 20: Cho phương trình 3
x  3x 1  0 (1) . Chọn khẳng định đúng nhất trong các khẳng định sau:
A. Phương trình (1) có ít nhất một nghiệm thuộc khoảng 0  ;1 .
B. Phương trình (1) có ít nhất ba nghiệm thuộc khoảng 0  ;1 .
C. Phương trình (1) có ít nhất bốn nghiệm thuộc khoảng 0  ;1 .
D. Phương trình (1) có ít nhất hai nghiệm thuộc khoảng 0  ;1 .
Câu 21: Khẳng định nào sau đây đúng? 1  1  1  1  A. lim   ,  k  B. lim
1,k  C. lim
 0,k  D. lim   ,  k  k n k n k n k n
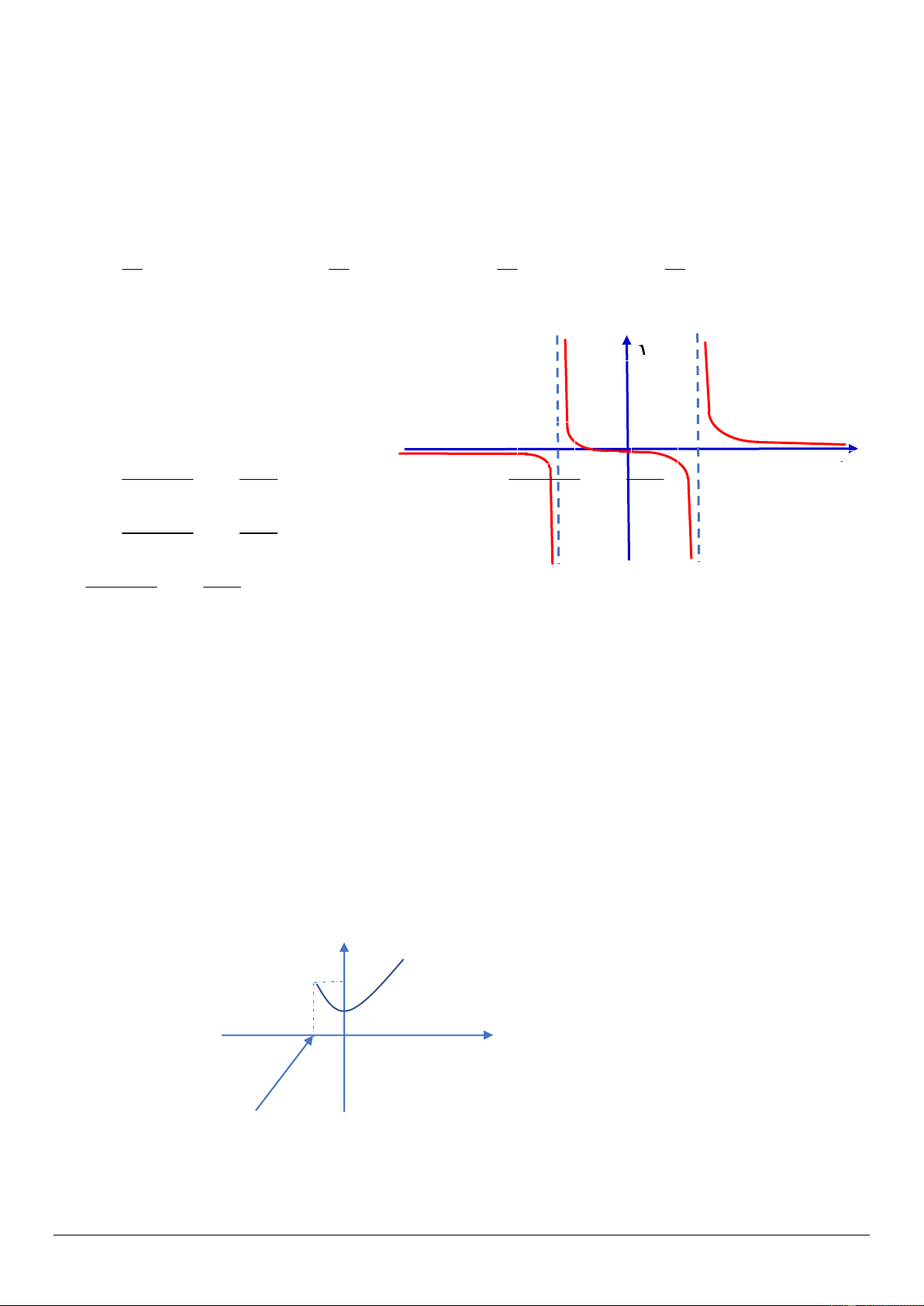
Câu 22: Cho hàm số f x có đồ thị như hình dưới đây:
Quan sát đồ thị và cho biết khẳng định nào sau đây đúng ? y
A. lim f (x)  2 
B. lim f (x)     x 3  x 3 
C. lim f (x)  
D. lim f (x)  0   x 3  x 3 
Câu 23: Khẳng định nào sau đây đúng? 3  O 2 x x  6 x  3 2 x x  6 x  3 A. lim  lim lim 2  lim 3 x 2 x2 x2 x  4 x B. 2 2 x2 x2 x  4 x  2 2 x x  6 x  3 C. lim  lim 2 x2 x2 x  4 x D. 2 2 x x  6 x  3 lim  lim 2 x2 x2 x  4 x  2
Câu 24: Cho hình hộp ABC .
D A B C D . Chọn khẳng định đúng? 1 1 1 1
  
   A. A ,
B A D , B D đồng phẳng. B. D ,
B BD ,C A đồng phẳng. 1 1 1 1 1 1 1
  
   C. A , B A ,
D B A đồng phẳng.
D. AA , A , D AB đồng phẳng. 1 1 1 1
Câu 25: Khẳng định nào sau đây đúng?     A. lim k
n  0, k  B. lim k n   ,  k  C. lim k n   ,  k  D. lim k n  1, k 
Câu 26: Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ACD. Khi đó khẳng định nào sau đây
   
   
đúng? A. BABC BD  3GB
B. BA BC BD  4BG
   
   
C. BA BC BD  3GB
D. BA BC BD  3BG
Câu 27: Công thức nào dưới đây đúng?
A. lim(u  v )  lim v  limu B. lim(u  v )  limu  lim v n n n n n n n n
C. lim(u  v )  limu .lim v
D. lim(u  v )  limu  lim v n n n n n n n n
Câu 28: Cho hàm số f x có đồ thị như hình dưới đây: y 2 1 -1 0 x
Hàm số y f (x) gián đoạn tại điểm có hoành độ bằng bao nhiêu? A. 2 B. 1 C. 1  D. 0
Câu 29: Khẳng định nào sau đây đúng nhất? 14
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
A. Có ít nhất ba điểm không đồng phẳng.
B. Có ít nhất sáu điểm không đồng phẳng.
C. Có ít nhất bốn điểm không đồng phẳng.
D. Có ít nhất năm điểm không đồng phẳng.
Câu 30: Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp  
vectơ AB và EG ? A. 0 90 . B. 0 120 . C. 0 45 . D. 0 60 .   x x
Câu 31: Cho hàm số f x 1 5 , 1  
. Giá trị của m để hàm số liên
x m , x 1
tục trên tập xác định là: A. 2 B. 5 C. 3 D. 4
Câu 32: Khẳng định nào dưới đây đúng? 1 1   1 1   2 1 1 2 n n 1 2 n n 2 n n 1 n n A. lim  lim B. lim  lim 2 3n  3n 1 3 1 2 3n  3n 1 3 3 3   1  2 n n 2 n n 2 1   1 1   2 1 1 2 n n 1 2 n n 2 n n 1 n n C. lim  lim D. lim  lim 2 3n  3n 1 1 3 2 3n  3n 1 3 1 3   3   2 n n 2 n n
Câu 33: Trong các khẳng định sau đây, khẳng định nào sai?
A. Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm phân biệt.
B. Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua hai đường thẳng cắt nhau.
C. Một mặt phẳng được hoàn toàn XD khi biết nó đi qua ba điểm phân biệt không thẳng hàng.
D. Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua một đường thẳng và một điểm nằm
ngoài đường thẳng đó.
Câu 34: Khẳng định nào sau đây sai? 2  2n A. lim  2
n n  2n   lim B. lim  2
n n  2n   lim 2 2 1 1 1 1 n n 2  n 2  C. lim  2
n n  2n   lim D. lim  2
n n  2n   lim 2 2 1 1 1 1 n n 1
Câu 35: Cho hàm số f (x)  f x 2
x x  . Hàm số
liên tục trên khoảng nào sau đây? 6 A.  ;3   B.  3;   C.  2  ;3 D.  3  ;2
PHẦN TỰ LUẬN ( 3 điểm)
Câu 1( 1,5 điểm) : Tính giới hạn sau: 2 3n n 1 a. lim 2 lim
x  2x x 2 2n  b. x  5
Câu 2( 0,5 điểm): Cho hàm số
x x  2  , khi x  2 f (x)   x  2 ( m là tham số )
mx, khi x  2
Tìm điều kiện của tham số m để hàm số liên tục trên toàn tập xác định. Câu 3 ( 1 điểm):   
Cho tứ diện ABCD có AC AB AD , CAB DAB DAC . Gọi là góc giữa AC và BD . Tính
cos . Từ đó suy ra AC BD . 15
TRƯỜNG THPT CHUYÊN BẢO LỘC ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2 MÔN TOÁN KHỐI 11 CB
----------- HẾT ----------
Ghi chú: Thí sinh không được sử dụng tài liệu. CBCT không giải thích gì thêm.
Họ và tên Thí sinh:………………………………………………….Chữ ký: ………………………………
Họ và tên CBCT1:……………………………………………… ….Chữ ký: ………………………………
Họ và tên CBCT2:……………………………………………… ….Chữ ký: ……………………………… 16