Đề cương học kì 1 Hình học 11 – Lê Văn Đoàn

Tài liệu gồm 111 trang, được biên soạn bởi nhóm Toán thầy Lê Văn Đoàn: Ths. Lê Văn Đoàn – Ths. Trương Huy Hoàng – Ths. Nguyễn Tiến Hà – Bùi Sỹ Khanh – Nguyễn Đức Nam – Đỗ Minh Tiến

41 21 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

LOREM IPSUM

DOLOR SIT

AMET

TÀI LIỆU TOÁN 11

Năm học: 2020 – 2021.

Lưu hành nội bộ.

www.facebook.com/Nhóm-

Toán-Thầy-Lê-Văn-Đoàn-

112798047209867/

0933.755.607 thầy Đoàn

0983.047.188 thầy Nam

Nhomtoanlevandoan

@gmail.com

Sở GD & ĐT Tp. Hồ Chí Minh

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 1 -

Chương 1. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG

NỘI DỤNG

 Phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm và phép quay.

 Khái niệm về phép dời hình và hai hình bằng nhau.

 Phép vị tự, tâm vị tự của hai đường tròn.

 Khái niệm về phép đồng dạng và hai hình đồng dạng.

§ 1. MỞ ĐẦU VỀ PHÉP BIẾN HÌNH



 Định nghĩa

Phép biến hình là một quy tắc để ứng với mỗi điểm

thuộc mặt phẳng, ta xác định được một

điểm duy nhất



thuộc mặt phẳng ấy. Điểm



gọi là ảnh của điểm

qua phép biến hình đó.

 Kí hiệu và thuật ngữ: Cho phép biến hình



Nếu



là ảnh của điểm

qua

thì ta viết

( ).M F M





Ta nói phép biến hình

biến điểm

thành





Nếu

là một hình nào đó thì

{ ( ), }H M M F M M H

  

  

được gọi là ảnh của

qua

Kí hiệu là

( ).H F H





 Phép dời hình:



Phép dời hình là phép biến hình không làm thay đổi khoảng cách giữa hai điểm bất kì.



Phép dời hình:



Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm

đó.



Biến đường thẳng thành đường thẳng.



Biến tia thành tia.



Biến đoạn thẳng thành đoạn thẳng bằng đoạn thẳng đã cho.



Biến tam giác thành tam giác bằng tam giác đã cho.



Biến đường tròn thành đường tròn có cùng bán kính với đường tròn ban đầu.



Biến góc thành góc bằng góc ban đầu.

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 2 -

§ 2. PHÉP TỊNH TIẾN



 Định nghĩa

Trong mặt phẳng cho véctơ



Phép biến hình biến mỗi điểm

thành điểm



sao cho

MM v









được gọi là phép tịnh tiến theo véctơ



Phép tịnh tiến theo véctơ



được kí hiệu



Như vậy:

( ) .

M T M MM v

 

  







 Tính chất: Phép tịnh tiến là phép biến hình:



Bảo toàn khoảng cách giữa hai điểm bất kì.



Biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó.



Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho.



Biến một tam giác thành một tam giác bằng tam giác đã cho.



Biến một đường tròn thành đường tròn có cùng bán kính.

 Biểu thức tọa độ của phép tịnh tiến

Trong mặt phẳng tọa độ

,Oxy

gọi

( ; )

M M

M x y

 



là ảnh của

( ; )

M M

M x y

qua phép tịnh tiến theo

( ; ).v a b



Khi đó:

( )

M M

x a x

M T M

y b y







 





  





 







BÀI TẬP TỰ LUẬN CƠ BẢN

1. Trong mặt phẳng

,Oxy

cho

(2;1),v 



điểm

(3;2).M

Tìm tọa độ điểm

sao cho

( ).

A T M



Vì

là ảnh của

qua phép tịnh tiến



2 3 5

( ) (5;3).

1 2 3

A T M A





  



  





  







( ).

M T A



Vì

là ảnh của

qua phép tịnh tiến



........................................................................................

2. Trong mặt phẳng

,Oxy

cho

( 1; 3),v  



điểm

( 1;4).M 

Tìm tọa độ

sao cho

( ).

A T M



...................................................................................

( ).

M T A



........................................................

...................................................................................

( ).

A T M



........................................................................................

( ).

M T A







...........................................................

........................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 3 -

3. Trong mặt phẳng

,Oxy

cho đường thẳng

: 2 3 12 0.d x y  

Tìm ảnh của

qua phép tịnh tiến

(4; 3).v  



Học sinh nghe giảng và bổ sung lời giải 1

Gọi

( )

d T d d d

 

 





nên



có dạng

2 3 0.x y m  

Cho

3 2 ( 3;2) : 2 3 12 0.x y M d x y         

Ta có:

...........................

( ) (.........;.........).

...........................

M T M M











 

  













(1; 1) : 2 3 0M d x y m

 

     

...........................................................................................................

Suy ra

: 2 3 5 0.d x y



  

Học sinh nghe giảng và bổ sung lời giải 2

Gọi

( ; ) : 2 3 12 0M x y d x y   

và

( ; ) ( ).

M M v

M x y T M

 







.............. ..............

( ) (.............; ..............).

.............. ..............

x x

M T M M

y y



 

 

 

 



   

 

 

 

 

 



Vì

( 4;  3) : 2 3 12 0 2( 4) 3( 3) 12 0

M M M M

M x y d x y x y

   

           

2 3 5 0 : 2 3 5 0.

M M M M

x y M d x y

   

 

        

Do đó ảnh của đường thẳng

qua phép tịnh tiến

(4; 3)v  



là

: 2 3 5 0.d x y



  

Học sinh nghe giảng và bổ sung lời giải 3

Chọn

( 3;2)M d 

và

(0;4) .N d

Vì

............................

( ; ) ( ) (........;........).

............................

M M v

M x y T M M



 











 

  













Vì

...............................

( ; ) ( ) (........;........).

...............................

N N v

N x y T N N



 











 

  













Nếu gọi

( )

d T d







thì

, M N d

 



nên



có véctơ chỉ phương là

(3;2).

u M N



 

 





Suy ra véctơ pháp tuyến của



là

(2; 3)

n  



và đi qua đi qua

(4;1)N



nên có dạng:

: 2( 4) 3( 1) 0 2 3 5 0.d x y x y



       

 Lưu ý. Học sinh sẽ làm cách của giáo viên trên lớp.

4. Trong mặt phẳng

,Oxy

cho đường thẳng

: 2 3 5 0.d x y  

Tìm ảnh của

qua phép tịnh tiến

(3;2).v 



 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 4 -

5. Trong mặt phẳng

,Oxy

cho đường thẳng

: 3 2 0.d x y  

Tìm ảnh của

qua phép tịnh tiến

( 4;2).v  



 Lời giải. .............................................................................................................................................................

.................................................................................................................................................................................

6. Trong mặt phẳng

,Oxy

cho đường thẳng

: 2 4 0.d x y  

Tìm ảnh của

qua phép tịnh tiến

v AB





với

(3;1),  ( 1;8).A B 

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

7. Trong mặt phẳng

,Oxy

cho đường thẳng

: 3 4 5 0.d x y  

Tìm ảnh của

qua phép tịnh tiến

v AB





với

(0;2),  (2;3).A B

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

8. Trong mặt phẳng

,Oxy

cho đường thẳng

: 3 2 0.d x y  

Tìm ảnh của

qua phép tịnh tiến

2v AB





với

( 2;3),  (0;2).A B

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 5 -

9. Trong mặt phẳng

,Oxy

cho đường tròn

2 2

( ) : ( 4) ( 3) 6.C x y   

Hãy tìm ảnh của đường tròn

( )C

qua phép tịnh tiến

(3;2).v 



Lời giải tham khảo

Đường tròn

( )C

có tâm

(4; 3),I 

bán kính

6.R 

Gọi

3 4 7

( ; ) ( ) (7; 1).

2 3 1

I I v

I x y T I I



 







  



 

   





   







Gọi

( ) ( ) ( )

C T C C

 

 



có tâm

(7; 1)I





và bán kính

6R R



 

có dạng:

2 2

( ) : ( 7) ( 1) 6C x y



   

là ảnh của đường tròn

( )C

đã cho.

10. Trong mặt phẳng

,Oxy

cho đường tròn

2 2

( ) : ( 2) ( 4) 16.C x y   

Hãy tìm ảnh của đường

tròn

( )C

qua phép tịnh tiến

(2; 3).v  



 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

11. Trong mặt phẳng

,Oxy

cho đường tròn

( ) : ( 1) ( 3) 25.C x y



   

Hãy tìm ảnh của đường

tròn

( )C

qua phép tịnh tiến

v AB





với

( 1;1),  (1; 2).A B 

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

12. Trong mặt phẳng

,Oxy

cho đường tròn

2 2

( ) : 4 6 8 0.C x y x y    

Hãy tìm ảnh của đường

tròn

( )C

qua phép tịnh tiến

(5; 2).v  



 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 6 -

BÀI TẬP TRẮC NGHIỆM

1. Trong mặt phẳng tọa độ

,Oxy

cho véctơ

(3; 1).u  



Phép tịnh tiến theo véctơ



biến điểm

(1; 4)M 

thành điểm

(4; 5).M





( 2; 3).M



 

(3; 4).M





(4;5).M



..............................................................................................................

2. Trong mặt phẳng tọa độ

,Oxy

nếu phép tịnh tiến biến điểm

(3;2)A

thành điểm

(2; 3)A



thì nó

biến điểm

(2;5)B

thành điểm

(5;2).B



(1;6).B



(5;5).B



(5;5).B



..............................................................................................................

3. Trong mặt phẳng tọa độ

,Oxy

cho véctơ

( 1;3).v  



Phép tịnh tiến theo véctơ



biến điểm

(3; 3)A 

thành điểm

(2; 6).A





(2; 0).A



(4; 0).A



( 2; 0).A





..............................................................................................................

4. Trong mặt phẳng tọa độ

,Oxy

cho điểm

( 4;2),M





biết



là ảnh của

qua phép tịnh tiến theo

véctơ

(1; 5).v  



Tìm tọa độ điểm

( 3;5).M 

(3;7).M

( 5;7).M 

( 5; 3).M  

..............................................................................................................

5. Trong mặt phẳng tọa độ

,Oxy

cho điểm

( 5;2)M 

và điểm

( 3;2)M





là ảnh của

qua phép tịnh

tiến theo véctơ



Tìm tọa độ véctơ



( 2; 0).v  



(0;2).v 



( 1;0).v  



(2; 0).v 



..............................................................................................................

6. Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

(0;2), ( 2;1)M N 

và véctơ

(1;2).v 



Phép tịnh tiến

theo véctơ



biến

,M N

thành hai điểm

,M N

 

tương ứng. Tính độ dài

.M N

 

5.M N

 



7.M N

 



1.M N

 



3.M N

 



..............................................................................................................

7. Trong mặt phẳng tọa độ

,Oxy

cho hình bình hành

ABCD

với

(1; 4), (8;2)A B

và giao điểm của

hai đường chéo

và

là

(3; 2).I 

Nếu

là phép tịnh tiến theo véctơ



biến đoạn thẳng

thành đoạn thẳng

thì vectơ



có tọa độ là

(3;12).

(5;3).

( 3; 2). 

(7; 5).

..............................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 7 -

8. Trong mặt phẳng tọa độ

,Oxy

cho

ABC

biết

(2;4), (5;1), ( 1; 2).A B C  

Phép tịnh tiến theo

véctơ



biến

ABC

thành

A B C

  



tương ứng các điểm. Tọa độ trọng tâm



của

A B C

  



là

( 4; 2).G



 

(4;2).G



(4; 2).G





( 4;4).G





..............................................................................................................

9. Trong mặt phẳng tọa độ

,Oxy

tìm phương trình đườn thẳng





là ảnh của đường thẳng

: 2 1 0x y   

qua phép tịnh tiến theo véctơ

(1; 1).v  



: 2 0.x y



  

: 2 3 0.x y



   

: 2 1 0.x y



   

: 2 2 0.x y



   

..............................................................................................................

10. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 5 1 0x y   

và vectơ

(4;2).v 



Khi đó

ảnh của đường thẳng



qua phép tịnh tiến theo vectơ



là

5 15 0.x y  

5 15 0.x y  

5 6 0.x y  

5 7 0.x y   

..............................................................................................................

11. Trong mặt phẳng tọa độ

,Oxy

cho

( 4;2)v  



và đường thẳng

: 2 5 0.x y



   

Hỏi





là

ảnh của đường thẳng



nào sau đây qua



: 2 5 0.x y   

: 2 9 0.x y   

: 2 15 0.x y   

: 2 11 0.x y   

..............................................................................................................

12. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

1 2

x t

y t





 









  





và đường thẳng

: 2 1 0.x y



   

Tìm tọa độ vectơ



biết

( ) .



  



(0; 1).v  



(0;2).v 



(0;1).v 



( 1;1).v  



..............................................................................................................

13. Trong mặt phẳng tọa độ

,Oxy

phép tịnh tiến theo vectơ

(4;6)u 



biến đường thẳng

có phương

trình

1 0x y  

thành

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 8 -

9 0.x y  

9 0.x y  

9 0.x y  

9 0.x y   

..............................................................................................................

14. Trong mặt phẳng tọa độ

,Oxy

nếu phép tịnh tiến biến điểm

(2; 1)A 

thành điểm

(3;0)A



thì nó

biến đường thẳng nào sau đây thành chính nó ?

1 0.x y  

100 0.x y  

2 4 0.x y  

2 1 0.x y  

..............................................................................................................

15. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

.: 3 2 5 0x ya   

Phép tịnh tiến theo vectơ

(1; 2)u  



biến đường thẳng đó thành đường thẳng



có phương trình là

3 2 4 0.x y  

3 2 0.x y 

3 2 10 0.x y  

3 2 7 0.x y  

..............................................................................................................

16. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng



có phương trình

4 3 0.x y  

Ảnh của

đường thẳng qua phép tịnh tiến

theo vectơ

(2; 1)u  



có phương trình là

4 5 0.x y  

4 10 0.x y  

4 6 0.x y  

..............................................................................................................

17. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng



có phương trình

3 4 1 0.x y  

Thực hiện

phép tịnh tiến theo phương của trục hoành về bên phải một đơn vị, đường thẳng



biến thành

đường thẳng





có phương trình là

3 4 5 0.x y  

3 4 2 0.x y  

3 4 3 0.x y  

3 4 10 0.x y  

..............................................................................................................

18. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng



có phương trình

2 3 0.x y  

Thực hiện

phép tịnh tiến theo phương của trục hoành về bên trái hai đơn vị, đường thẳng



biến thành

đường thẳng





có phương trình là

2 7 0.x y  

2 2 0.x y  

2 8 0.x y  

2 6 0.x y  

..............................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 9 -

19. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : 2 8 0.T x y x   

Phép tịnh tiến theo

vectơ

(3; 1),u  



biến đường tròn

( )T

thành đường tròn

( )T



có phương trình là

2 2

8 2 8 0.x y x y    

2 2

4 5 0.x y x y    

2 2

4 4 3 0.x y x y    

2 2

6 4 2 0.x y x y    

..............................................................................................................

20. Trong mặt phẳng tọa độ

,Oxy

tìm phương trình đường tròn

( )C



là ảnh của đường tròn

2 2

( ) : 4 2 1 0C x y x y    

qua phép tịnh tiến theo

(1; 3).v 



2 2

( ) : ( 3) ( 4) 2.C x y



   

2 2

( ) : ( 3) ( 4) 4.C x y



   

2 2

( ) : ( 3) ( 4) 4.C x y



   

2 2

( ) : ( 3) ( 4) 4.C x y



   

..............................................................................................................

21. Trong mặt phẳng tọa độ

,Oxy

cho

(3; 1)v  



và đường tròn

2 2

( ) : ( 4) 16.C x y  

Ảnh của

( )C

qua phép tịnh tiến



là

2 2

( 1) ( 1) 16.x y   

2 2

( 1) ( 1) 16.x y   

2 2

( 7) ( 1) 16.x y   

2 2

( 7) ( 1) 16.x y   

..............................................................................................................

22. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : 2 3 0.T x y x y    

Phép tịnh tiến theo

phương của trục hoành về bên phải

đơn vị, biến đường tròn

( )T

thành đường tròn

( )T



có

phương trình là

2 2

9 2 17 0.x y x y    

2 2

4 2 4 0.x y x y    

2 2

5 4 5 0.x y x y    

2 2

7 2 1 0.x y x y    

..............................................................................................................

23. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : 2 3 0.T x y x y    

Phép tịnh tiến theo

phương của trục tung về dưới

đơn vị, biến đường tròn

( )T

thành đường tròn

( )T



có phương

trình là

2 2

2 9 0.x y y   

2 2

2 6 2 0.x y x y    

2 2

4 5 0.x y x y    

2 2

2 7 0.x y x   

..............................................................................................................

ĐÁP ÁN TRẮC NGHIỆM

1.A 2.B 3.B 4.C 5.D 6.A 7.B 8.A 9.A 10.A

11.D 12.C 13.A 14.B 15.A 16.C 17.B 18.A 19.A 20.B

21.C 22.A 23.D

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 10 -

BÀI TẬP RÈN LUYỆN TỰ LUẬN

BT 1. Trong mặt phẳng tọa độ

,Oxy

cho

(3;5),  ( 1;1),  ( 1;2),A B v  



đường thẳng

và đường tròn

( )C

có phương trình:

2 2

: 2 3 0, ( ) : ( 2) ( 3) 25.d x y C x y      

a) Tìm ảnh của các điểm

, A B

 

theo thứ tự là ảnh của

, A B

qua phép tịnh tiến



b) Tìm tọa độ điểm

sao cho

là ảnh của

qua phép tịnh tiến



c) Tìm phương trình đường thẳng



đường tròn

( )C



lần lượt là ảnh của

, ( )d C

qua phép

tịnh tiến



BT 2. Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có ảnh qua phép tịnh tiến theo

(2;5)v 



là

tam giác

A B C

  

và tam giác

A B C

  

có trọng tâm là

( 3; 4),G





biết rằng

( 1;6),  (3;4).A B

Tìm

,  ,  .A B C

 

BT 3. Trong mặt phẳng tọa độ

,Oxy

cho một phép tịnh tiến biến đường tròn

( )C

thành đường tròn

( ).C



Hãy xác định phép tịnh tiến đó trong các trường hợp sau:

2 2

( ) : ( 1) ( 2) 16,C x y   

2 2

( ) : ( 10) ( 5) 16.C x y



   

2 2

( ) : 2 6 1 0,C x y x y    

2 2

( ) : 4 2 4 0.C x y x y



    

2 2

( ) : ( ) ( 2) 5,C x m y   

2 2 2

( ) : 2( 2) 6 12 0.C x y m y x m



      

BT 4. Trong mặt phẳng tọa độ

,Oxy

cho véctơ

( 2;1)v  



và hai đường thẳng

: 2 3 3 0d x y  

và

: 2 3 5 0.d x y  

a) Viết phương trình của đường thẳng



là ảnh của

qua



b) Tìm tọa độ của



có giá vuông góc với đường thẳng

để

là ảnh của

qua



BT 5. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 3 9 0.d x y  

a) Tìm phép tịnh tiến theo véctơ



có phương song song với trục

,Ox

biến

thành đường

thẳng



đi qua gốc tọa độ. Khi đó hãy viết phương trình đường thẳng



b) Tìm phép tịnh tiến theo véctơ



có giá song song với trục

,Oy

biến

thành



đi qua điểm

(1;1).A

BT 6. Trong mặt phẳng tọa độ

,Oxy

hãy xác định phép tịnh tiến theo



cùng phương với trục hoành

biến đường thẳng

: 4 4 0d x y  

thành đường thẳng



qua

(1; 3).A 

BT 7. Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng lần lượt có phương trình là

: 3 5 3 0d x y  

và

: 3 5 24 0.d x y



  

Tìm



biết

v 



và

( ) .

T d d







BT 8. Trong mặt phẳng tọa độ

,Oxy

phép tịnh tiến theo



biến điểm

(3; 1)M 

thành một điểm trên

đường thẳng

: 9 0.d x y  

Tìm tọa độ



biết rằng





BT 9. Trong mặt phẳng tọa độ

,Oxy

hãy xác định tọa độ điểm

trên trục hoành sao cho phép tịnh

tiến theo

( 2; 3)v  



biến điểm

thành điểm



nằm trên trục tung.

BT 10. Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

, d d



lần lượt có phương trình là

: 3 7 0,  : 3 13 0d x y d x y



     

và véctơ

(1; 1).u  



Tìm tọa độ của véctơ



trong phép

tịnh tiến



biến

thành



biết rằng hai véctơ



và



cùng phương.

BT 11. Trong mặt phẳng tọa độ

,Oxy

cho hai parabol

( ) : 4 7P y x x  

và

( ) : .P y x





Tìm phép

tịnh tiến biến

( )P

thành

( ).P



§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 11 -

§ 3. PHÉP ĐỐI XỨNG TRỤC (giảm tải)



 Định nghĩa



Điểm



được gọi là đối xứng với điểm

qua đường thẳng

nếu

là đường trung trực của

đoạn thẳng

.MM



Khi điểm

nằm trên

thì ta xem

đối xứng với chính nó qua đường

thẳng



Phép biến hình biến mỗi điểm

thành điểm



đối xứng với

qua đường thẳng

được

gọi là phép đối xứng qua đường thẳng

hay gọi là tắt là phép đối xứng trục.



Đường thẳng

được gọi là trục đối xứng. Kí hiệu:



Như vậy:

( )M M MM M M



   

 

d o o

với

là hình chiếu vuông góc

lên

 Biểu thức tọa độ

Trong mặt phẳng tọa độ

,Oxy

với mỗi điểm

( ; ),

M M

M x y

gọi

( ; ) ( ).

M M d

M x y M

 



 §



Nếu chọn

là trục

,Ox

thì ta có:

M M

x x

y y

















 







Nếu chọn

là trục

,Oy

thì ta có:

M M

x x

y y







 















 Tính chất

Phép đối xứng trục là một phép dời hình nên có đầy đủ tính chất của phép dời hình:



Bảo toàn khoảng cách giữa hai điểm bất kì.



Biến một đường thẳng thành đường thẳng.



Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho.



Biến một tam giác thành một tam giác bằng tam giác đã cho.



Biến một đường tròn thành một đường tròn có cùng bán kính.

 Trục đối xứng của một hình

Đường thẳng

gọi là trục đối xứng của hình

nếu phép đối xứng trục

biến

thành chính

nó, tức là

( ).

H H §

BÀI TẬP TRẮC NGHIỆM

1. Trong mặt phẳng tọa độ

,Oxy

phép đối xứng trục biến điểm

(2;1)A

thành

(2;5)A



có trục đối

xứng là

A. Đường thẳng

3.y 

B. Đường thẳng

3.x 

..............................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 12 -

C. Đường thẳng

6.y 

D. Đường thẳng

3 0.x y  

..............................................................................................................

2. Trong mặt phẳng tọa độ

,Oxy

cho

ABC

với

(2;6), ( 1;2), (6;1).A B C

Gọi

là trọng tâm của

.ABC

Phép đối xứng trục

biến điểm

thành điểm



có tọa độ là

(2; 4).

(3; 3).

; 3 .

 



















 

; 4 .

 



















 

..............................................................................................................

3. Trong mặt phẳng tọa độ

,Oxy

nếu phép đối xứng trục biến điểm

(3;1)M

thành điểm

( 1; 3)M



 

thì nó biến điểm

( 3; 4)N  

thành điểm

(3;4).N



(3; 4).N





(4; 3).N





(4; 3).N



..............................................................................................................

4. Trong mặt phẳng tọa độ

,Oxy

nếu phép đối xứng trục biến điểm

(0;1)A

thành điểm

( 1; 0)A





thì

nó biến điểm

( 5;5)B 

thành điểm

( 5; 5).B





(5;5).B



(5; 5).B





( 1;1).B





..............................................................................................................

5. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 2 0.d x y  

Ảnh của

qua phép đối xứng

trục tung có phương trình

2 0.x y  

2 0.x y  

2 0.x y  

2 2 0.x y  

..............................................................................................................

6. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : 4 5 1 0.C x y x y    

Tìm ảnh đường

tròn

( )C



của

( )C

qua phép đối xứng trục

.Oy

2 2

4 5 1 0.x y x y    

2 2

4 5 1 0.x y x y    

2 2

2 2 8 10 2 0.x y x y    

2 2

4 5 1 0.x y x y    

..............................................................................................................

7. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : 2 3 1 0.C x y x y    

Phép đối xứng qua

trục

biến đường tròn đó thành đường tròn

( )C



có phương trình

2 2

2 3 1 0.x y x y    

2 2

2 3 1 0.x y x y    

2 2

2 3 1 0.x y x y    

2 2

2 3 1 0.x y x y    

..............................................................................................................

8. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : 2 3 1 0.C x y x y    

Phép đối xứng qua

trục

biến đường tròn đó thành đường tròn

( )C



có phương trình là

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 13 -

2 2

2 3 1 0.x y x y    

2 2

2 3 1 0.x y x y    

2 2

2 3 1 0.x y x y    

2 2

2 3 1 0.x y x y    

..............................................................................................................

9. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : 2 5 0.T x y x y    

Phép đối xứng trục

biến đường tròn

( )T

thành đường tròn

( )T



có phương trình là

2 2

2 5 0.x y x y    

2 2

2 5 0.x y x y    

2 2

2 5 0.x y x y    

2 2

2 5 0.x y x y    

..............................................................................................................

10. Trong mặt phẳng tọa độ

,Oxy

cho parabol

( )P

có phương trình

2 5.y x x  

Phép đối xứng

trục

biến parabol

( )P

thành parabol

( )P



có phương trình là

2 5.y x x   

2 5.y x x  

2 5.y x x   

2 5.y x x   

..............................................................................................................

11. Trong mặt phẳng tọa độ

,Oxy

cho parabol

( )P

có phương trình

2 3.y x x  

Phép đối xứng

trục

biến parabol

( )P

thành parabol

( )P



có phương trình là

2 3.y x x  

2 3.y x x  

2 3.y x x   

4 3.y x x   

..............................................................................................................

12. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 2 1 0x y   

và điểm

(3;2).A

Trong các

điểm dưới đây, điểm nào là điểm đối xứng của

qua đường thẳng



( 1;4).M 

( 2;5).N 

(6; 3).P 

(1;6).Q

..............................................................................................................

13. Trong mặt phẳng tọa độ

,Oxy

gọi

là đường phân giác của góc phần tư thứ nhất. Phép đối xứng

trục

biến điểm

(4;3)A

thành điểm



có tọa độ là

( 4; 3). 

(4; 3).

( 4;3).

(3;4).

..............................................................................................................

14. Trong mặt phẳng tọa độ

,Oxy

gọi

là đường phân giác của góc phần tư thứ hai. Phép đối xứng

trục

biến điểm

(5; 2)P 

thành điểm



có tọa độ là

(5;2).

( 5;2).

(2; 5).

( 2;5).

..............................................................................................................

15. Trong mặt phẳng tọa độ

,Oxy

phép đối xứng qua đường thẳng

0x y 

biến đường thẳng

4 5 1 0x y  

thành đường thẳng có phương trình là

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 14 -

4 5 1 0.x y   

5 4 1 0.x y  

5 4 1 0.x y  

4 5 1 0.x y  

..............................................................................................................

16. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng



có phương trình

2 3 6 0.x y  

Đường

thẳng đối xứng của



qua trục hoành có phương trình là

2 3 6 0.x y  

2 3 6 0.x y  

4 6 0.x y  

3 2 6 0.x y  

..............................................................................................................

17. Gọi

là đường phân giác của góc phần tư thứ nhất. Ta xét đường thẳng

: 3 4 5 0.x y   

Phép đối xứng trục

biến đường thẳng



thành đường thẳng





có phương trình là

4 3 5 0.x y  

3 4 5 0.x y  

4 3 5 0.x y  

3 4 5 0.x y  

..............................................................................................................

18. Gọi

là đường phân giác của góc phần tư thứ hai. Ta xét đường thẳng

: 5 3.y x  

Phép đối

xứng trục

biến đường thẳng



thành đường thẳng





có phương trình là

5 3 0.x y  

5 3 0.x y  

5 3.y x  

5 3.y x 

..............................................................................................................

19. Trong mặt phẳng tọa độ

,Oxy

phép đối xứng qua đường thẳng

0x y 

biến đường tròn có

phương trình

2 2

2 1 0x y x   

thành đường tròn có phương trình

2 2

2 1 0.x y y   

2 2

2 1 0.x y x   

2 2

2 1 0.x y y   

2 2

2 1 0.x y x   

..............................................................................................................

20. Trong mặt phẳng tọa độ

,Oxy

gọi

là đường phân giác của góc phần tư thứ nhất. Ta xét đường

tròn

2 2

( ) : ( 2) ( 3) 9.T x y   

Phép đối xứng trục

biến đường tròn

( )T

thành đường tròn

( )T



có phương trình là

2 2

( 3) ( 2) 9.x y   

2 2

( 2) ( 3) 9.x y   

2 2

( 3) ( 2) 9.x y   

2 2

( 3) ( 2) 9.x y   

..............................................................................................................

ĐÁP ÁN TRẮC NGHIỆM

1.A 2.C 3.D 4.A 5.B 6.B 7.B 8.C 9.A 10.B

11.C 12.A 13.D 14.C 15.B 16.A 17.A 18.A 19.A 20.A

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 15 -

§ 4. PHÉP ĐỐI XỨNG TÂM (giảm tải)



 Định nghĩa

Cho điểm

Phép biến hình biến điểm

thành chính nó, biến mỗi điểm

khác

thành điểm



sao cho

là trung điểm của đoạn thẳng



được gọi là phép đối xứng tâm

nghĩa là

0.IM IM



 

  

Phép đối xứng tâm

thường được kí hiệu là

 Biểu thức tọa độ

Trong mặt phẳng tọa độ

,Oxy

cho

( ; ), ( ; )

I I M M

I x y M x y

và

( ; )

M M

M x y

 



là ảnh của

qua phép

đối xứng tâm

Khi đó:

M I M

x x x

y y y







 







 





 Tính chất: Phép đối xứng tâm



Bảo toàn khoảng cách giữa hai điểm bất kì.



Biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đã cho.



Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho.



Biến một tam giác thành một tam giác bằng tam giác đã cho.



Biến một đường tròn thành một đường tròn có cùng bán kính.

 Tâm đối xứng của một hình

Điểm

được gọi là tâm đối xứng của hình

nếu phép đối xứng tâm

biến hình

thành

chính nó. Khi đó

được gọi là hình có tâm đối xứng.

1. Trong mặt phẳng tọa độ

,Oxy

nếu phép đối xứng tâm biến điểm

(5;2)A

thành điểm

( 3;4)A





thì

nó biến điểm

(1; 1)B 

thành điểm

(1;7).B



(1;6).B



(2;5).B



(1; 5).





.................................................................................................................

2. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(2; 1)I



và

ABC

với

(1;4), ( 2;3), (7;2).A B C



Phép

đối xứng tâm

biến trọng tâm

của

ABC

thành điểm



có tọa độ là

( 2; 5).G





(2; 5).G





( 1; 4).G



 

(0; 5).





.................................................................................................................

3. Trong mặt phẳng tọa độ

,Oxy

cho phép đối xứng tâm có tâm là điểm gốc tọa độ. Khi đó nó biến

đường thẳng

3 4 13 0x y  

thành đường thẳng

3 4 13 0.x y  

3 4 13 0.x y  

3 4 13 0.x y  

3 4 13 0.x y   

.................................................................................................................

4. Trong mặt phẳng tọa độ

,Oxy

cho phép đối xứng tâm với tâm là điểm

(1; 1).I



Khi đó nó biến

đường thẳng

2 3 5 0x y  

thành đường thẳng

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 16 -

2 3 7 0.x y  

2 3 7 0.x y  

2 3 7 0.x y  

2 3 4 0.x y  

.................................................................................................................

5. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(2; 1)I 

và đường thẳng



có phương trình

2 2 0.x y  

Ảnh của



qua phép đối xứng tâm

là đường thẳng có phương trình

2 2 0.x y  

2 3 0.x y  

2 6 0.x y  

2 4 0.x y  

.................................................................................................................

6. Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng song song

và

lần lượt có phương trình

3 4 1 0x y  

và

3 4 5 0.x y  

Nếu phép đối xứng tâm biến

thành

thì tâm đối xứng

phải là điểm nào trong các điểm sau đây ?

(2; 2).I 

(2;2).I

( 2;2).I 

(2;0).I

.................................................................................................................

7. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(2; 1)I 

và đường tròn

2 2

( ) : 9.T x y 

Phép đối xứng

tâm

biến đường tròn

( )T

thành đường tròn

( )T



có phương trình là

2 2

8 4 11 0.x y x y    

2 2

4 6 5 0.x y x y    

2 2

2 4 0.x y x y   

2 2

6 2 2 0.x y x y    

.................................................................................................................

8. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : 8 10 32 0.C x y x y    

Phương trình

của đường tròn

( )C



đối xứng của

( )C

qua gốc tọa độ

có phương trình là

2 2

( 4) ( 5) 9.x y   

2 2

( 4) ( 5) 16.x y   

2 2

( 4) ( 5) 4.x y   

D. Một phương trình khác.

.................................................................................................................

9. Trong mặt phẳng tọa độ

,Oxy

cho parabol

( ) : .P y x x 

Phương trình của parabol

( )Q

đối

xứng với

( )P

qua gốc tọa độ

là

.y x x  

.y x x 

.y x x  

2 .y x x 

.................................................................................................................

BẢNG ĐÁP ÁN

1.A 2.D 3.D 4.B 5.A 6.A 7.A 8.A 9.A

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 17 -

§ 5. PHÉP QUAY



1. Ñònh nghóa



Cho điểm

và góc lượng giác

.

Phép biến hình biến

thành chính nó, biến mỗi điểm

khác

thành điểm



sao cho

OM OM





và góc lượng giác

( ; )OM OM



bằng



được gọi là phép

quay tâm

góc quay

.



Điểm

gọi là tâm quay,



gọi là góc quay.



Phép quay tâm

góc

,

kí hiệu là

( ; )



 Câu hỏi:

 Phép quay nào biến lá cờ

( )C

thành lá cờ

( ) :C



...................................................................................

 Phép quay nào biến lá cờ

( )C



thành lá cờ

( ) :C

..................................................................................

2. Tính chaát

Phép quay là phép biến hình



Bảo toàn khoảng cách giữa hai điểm bất kì.



Biến một đường thẳng thành một đường thẳng.



Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho.



Biến một tam giác thành một tam giác bằng tam giác đã cho.



Biến một đường tròn thành đường tròn có cùng bán kính.

Giả sử phép quay tâm

góc quay



biến đường thẳng

thành đường thẳng



Khi đó:



Nếu



 

thì góc giữa

và



bằng

.



Nếu



  

thì góc giữa

và



bằng

. 

3. Phöông phaùp xaùc ñònh moät aûnh qua pheùp quay

Phương pháp 1. Sử dụng định nghĩa

Trong mặt phẳng tọa độ

,Oxy

gọi

( ; )

M M

M x y

 



là ảnh của

( ; )

M M

M x y

qua phép quay tâm

( ; ),I a b

góc quay

.

Khi đó:



( ; )

(1)

( ; ) ( )

(2)

M M I

IM IM

M x y Q M

MIM



 













 













Từ

(1),

sử dụng công thức tính độ dài, sẽ tìm được phương trình thứ nhất theo

ẩn.

Từ

(2),

sử dụng định lý hàm số cos, sẽ tìm được phương trình thứ hai theo

ẩn.

Giải hệ phươngtrình này tìm được

,  ,

M M

x y

 

từ đó suy ra tọa độ điểm

( ; ).

M M

M x y

 



Phương pháp 2. Sử dụng công thức tọa độ.

( ; )

( )cos ( )sin

( ; ) ( )

( )sin ( )cos

M M M

M M I

M M M

x x a y b a

M x y Q M

y x a y b b



 



 







    





  





    





§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 18 -

BÀI TẬP TỰ LUẬN

1. Trong mặt phẳng

,Oxy

cho điểm

(2;3),A

đường thẳng

: 2 3 2 0d x y  

và đường tròn có

phương trình:

2 2

( ) : 4 4 1 0.C x y x y    

a) Tìm ảnh của điểm

(2;3)A

qua phép

( ;90 )



Học sinh nghe giảng và bổ sung cách giải 1

Gọi

( ;90 )

( ),

A Q A







với

( ; ).A a b

Suy ra:



(1)

90 (2)

OA OA

A OA

















 





Giải

(1) :

OA OA



 

...............................................................................................................................

(3)

Giải

(2) :

 

,  90 . 0

OA OA OA OA OAOA

  

      

     

................................................................

(4)

Từ

(3), (4) 

2 2

2 3 0

a b





 









 





.........................................................................................................................

Vì quay theo chiều dương nên chọn

( 3;2).A





Lời giải tham khảo 2

Vận dụng

( ; )

( )cos ( )sin

( ; ) ( )

( )sin ( )cos

M M M

M M I

M M M

x x a y b a

M x y Q M

y x a y b b



 



 







    





 





    





Khi đó:

( ;90 )

cos 90 sin 90 2.0 3.1 3

( ) ( 3;2).

sin 90 cos 90 2.1 3.0 2

A A A

x x y

A Q A A

y x y











       



 

   





      





 Nhận xét. Học sinh giải theo cách giải của giáo viên trên lớp. Về trắc nghiệm nên giải theo cách 2.

b) Viết phương trình đường thẳng



là ảnh của

qua phép

( ;90 )



Lời giải tham khảo

Vì

( ;90 )

( )

d Q d d d



 

   

phương trình

: 3 2 0.d x y m



  

Chọn

( 1;0) : 2 3 2 0.M d x y    

Khi đó

( ;90 )

1.cos 90 0.sin 90 0

( ) (0; 1).

1.sin 90 0.cos 90 1

M Q M M











     



 

   





     





(0; 1) 3.0 2.( 1) 0 2.M d M d m m

 

          

Vậy

: 3 2 2 0.d x y



  

 Nhận xét. Đối với góc quay



bất kỳ, để tìm ảnh ta cần chọn ra

điểm trên

và tìm ảnh của

điểm này.

Khi đó đường thẳng



đi qua hai điểm ảnh vừa tìm.

c) Viết phương trình đường tròn

( )C



là ảnh của

( )C

qua phép

( ;90 )



Lời giải tham khảo

Đường tròn

( )C

có tâm

(2;2)I

và bán kính

2 2

2 2 ( 1) 3.R     

Gọi

( ;90 )

( ) ( ) 3.

C Q C R R



 

   

Khi đó

( ;90 )

2 cos 90 2 sin 90 2

( ; ) ( ) ( 2;2).

2 sin 90 2 cos90 2

I I O

I x y Q I I



 









     



 

   





    





Do đó:

2 2

( ) : ( 2) ( 2) 9.C x y



   

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 19 -

2. Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

(1;0),  (0; 2).A B 

Tìm

, A B

 

lần lượt là ảnh của

, A B

qua phép quay tâm

góc quay

90 .

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

3. Trong mặt phẳng tọa độ

,Oxy

hãy tìm ảnh của đường tròn

( )C

qua phép quay tâm

góc quay



trong các trường hợp sau đây:

2 2

( ) : ( 2) ( 1) 1,C x y   

90 .  

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

2 2

( ) : 2 4 1 0,C x y x y    

90 .   

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

2 2

( ) : ( 1) 1,C x y  

60 .  

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

2 2

( ) : 4 2 0,C x y x y   

30 .   

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 20 -

4. Trong mặt phẳng tọa độ

,Oxy

hãy tìm ảnh của đường thẳng

qua phép quay tâm

góc quay



trong các trường hợp sau đây:

: 2 0,  90 .d x y     

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

: 3 11 0,  90 .d x y      

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

: 3 5 0,  60 .d x y     

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

: 2 6 0,  45 .d x y     

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 21 -

BÀI TẬP TRẮC NGHIỆM

1. Cho hai đường thẳng bất kì

và



Có bao nhiêu phép quay biến đường thẳng

thành đường

thẳng

 ?d



A. Không có phép nào. B. Có một phép duy nhất.

C. Chỉ có hai phép. D. Có vô số phép.

2. Cho hai đường thẳng song song

và



một đường thẳng

không song song với chúng. Có bao

nhiêu phép quay biến đường thẳng

thành đường thẳng



và biến đường thẳng

thành chính

nó ?

A. Không có phép nào. B. Có một phép duy nhất.

C. Chỉ có hai phép. D. Có vô số phép.

3. Cho bốn đường thẳng

,, ,a b a b

 

trong đó

,a a b b

 

 

và

cắt

Có bao nhiêu phép quay biến

các đường thẳng

và

lần lượt thành các đường thẳng



và

 ?b



A. Không có phép nào B. Có một phép duy nhất.

C. Chỉ có hai phép. D. Có vô số phép.

4. Cho hình vuông

ABCD

có tâm

Phép quay tâm

với góc quay nào dưới đây biến hình vuông

ABCD

thành chính nó ?

30 .

45 .

60 .

120 .

5. Cho tam giác

ABC

đều tâm

(

là tâm của đường tròn ngoại tiếp). Ta thực hiện phép quay

tâm

biến tam giác

ABC

thành chính nó. Một số đo của góc quay



là

45 .

60 .

90 .

120 .

6. Trong mặt phẳng với hệ tọa độ

,Oxy

ta xét phép quay

( ; ).Q O 

Trong các mệnh đề sau, mệnh đề

nào sai ?

A. Nếu

90  

thì

biến trục hoành

x Ox



thành trục tung

.y Oy



B. Nếu

270  

thì

biến trục tung

y Oy



thành trục hoành

.x Ox



C. Nếu

90   

thì

biến trục tung

y Oy



thành trục hoành

.x Ox



D. Nếu

180  

thì

biến trục hoành

x Ox



thành chính nó.

7. Trong câu này ta chỉ xét các phép quay với góc quay



thỏa điều kiện

0 180 .   

Cho hai

đường thẳng

và

cắt nhau tại điểm

Phát biểu nào sau đây là đúng ?

A. Không tồn tại phép quay nào biến đường thẳng

thành đường thẳng

B. Có duy nhất một phép quay biến đường thẳng

thành đường thằng

C. Có đúng hai phép quay biến đường thẳng

thành đường thẳng

D. Có vô số phép quay biến đường thẳng

thành đường thẳng

8. Cho hình vuông

ABCD

tâm

Ta xét các mệnh đề sau:



Phép quay

( ; 45 )Q O 

biến hình vuông

ABCD

thành chính nó.



Phép quay

( ;60 )Q O 

biến hình vuông

ABCD

thành chính nó.



Phép quay

( ;90 )Q O 

biến hình vuông

ABCD

thành chính nó.



Phép quay

( ;180 )Q O 

biến hình vuông

ABCD

thành chính nó.

Trong các mệnh đề trên:

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 22 -

A. Có duy nhất một mệnh đề đúng. B. Có hai mệnh đề đúng.

C. Có ba mệnh đề đúng. D. Tất cả bốn mệnh đề đều đúng.

9. Cho ngũ giác đều ABCDE tâm O. Ta xét các mệnh đề sau:



Phép quay

( ;72 )Q O 

biến ngũ giác đều

ABCDE

thành chính nó.



Phép quay

( ;90 )Q O 

biến ngũ giác đều

ABCDE

thành chính nó.



Phép quay

( ;144 )Q O 

biến ngũ giác đều

ABCDE

thành chính nó.



Phép quay

( ;216 )Q O 

biến ngũ giác đều

ABCDE

thành chính nó.

Trong các mệnh đề trên:

A. Có duy nhất một mệnh đề đúng. B. Có hai mệnh đề đúng.

C. Có ba mệnh đề đúng. D. Tất cả bốn mệnh đề đều đúng.

10. Chọn

giờ làm mốc, khi kim giờ chỉ một giờ đúng thì kim phút đã quay được một góc bao nhiêu

độ ?

360 .

360 . 

180 . 

720 .

11. Cho hình vuông

ABCD

tâm

(các đỉnh ghi theo chiều kim đồng hồ). Ảnh của cạnh

qua phép

quay

( ;270 )Q O 

là

.AB

.BC

.CD

.DA

12. Cho hình thoi

ABCD

có góc



60ABC  

(các đỉnh của hình thoi ghi theo chiều kim đồng hồ).

Ảnh của cạnh

qua qua phép quay

( ;60 )Q A 

là

.AB

.BC

.CD

.DA

13. Cho tam giác đều

ABC

có tâm

và các đường cao

, ,AA BB CC

  

(các đỉnh của tam giác ghi

theo chiều kim đồng hồ). Ảnh của đường cao



qua phép quay

( ;240 )Q O 

là

.AA



.BB



.CC



qua

.d BC

14. Trong mặt phẳng tọa độ

,Oxy

cho điểm

( ; ).A x y

Biểu thức tọa độ của

( ,90 )

( )

A Q A







là

x y

y x



















 





x y

y x







 

















x y

y x







 











 





x y

y x

























15. Trong mặt phẳng tọa độ

,Oxy

cho điểm

( ; ).A x y

Biểu thức tọa độ của

( , 90 )

( )

A Q A









là

x y

y x



















 





x y

y x







 

















x y

y x







 











 





x y

y x

























16. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(4;1).M

Phép quay

( ;90 )Q O 

biến điểm

thành điểm



có tọa độ là

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 23 -

(1;4).

( 1;4).

(1; 4).

( 1; 4). 

.................................................................................................................

17. Trong mặt phẳng tọa độ

,Oxy

cho phép quay tâm

biến điểm

(1;0)A

thành điểm

(0;1).A



Khi

đó nó biến điểm

(1; 1)M 

thành điểm

( 1; 1).M



 

(1;1).M



( 1;1).M





(1;0).M



.................................................................................................................

18. Trong mặt phẳng tọa độ

,Oxy

cho

ABC

với

(1;4), ( 2;2), (7; 9).A B C 

Phép quay

( ;90 )Q O 

biến trọng tâm

của

ABC

thành điểm



có tọa độ là

(1; 2).

(1;2).

(3; 1).

( 3;1).

.................................................................................................................

19. Trong mặt phẳng tọa độ

,Oxy

qua phép quay tâm

góc quay

90

biến điểm

( 3;5)M 

thành

điểm nào ?

(3;4).

( 5; 3). 

(5; 3).

( 3; 5). 

.................................................................................................................

20. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(4;1).A

Biểu thức tọa độ của điểm

( , 90 )

( )

A Q A

 





là ?

( 1;4).A 

(1; 4).A 

(4; 1).A 

( 4; 1).A  

.................................................................................................................

21. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(0; 3).A

Tìm tọa độ điểm



là ảnh của

qua phép quay

( , 45 )

 

1 3

;

2 2

 



















 

3 1

;

4 4

 



















 

3 1

;

2 2

 





















 

3 3

;

2 2

 



















 

.................................................................................................................

22. Trong mặt phẳng tọa độ

,Oxy

cho điểm

.(1;1)M

Hỏi điểm nào sau đây là ảnh của điểm

qua

phép quay tâm

,(0;0)O

góc quay

45

.)(0; 2M



.)( 2;0M



.)(0;1M



1; 1).(M 



.................................................................................................................

23. Trong mặt phẳng tọa độ

,Oxy

tìm phép quay

biến điểm

( 1;5)A 

thành điểm

(5;1)A



( , 90 )

( ) .

Q A A

 





( ,90 )

( ) .

Q A A







( ,180 )

( ) .

Q A A







( , 270 )

( ) .

Q A A

 





.................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 24 -

24. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

có phương trình

5 3 15 0.x y  

Tìm ảnh



của

qua phép quay

( ,90 )



với

là gốc tọa độ ?

5 3 6 0.x y  

3 5 15 0.x y  

5 7 0.x y  

3 5 7 0.x y   

.................................................................................................................

25. Trong mặt phẳng tọa độ

,Oxy

cho

(2;1)I

và đường thẳng

: 2 3 4 0.d x y  

Tìm ảnh của

qua

( ,45 )



5 2 3 2 0.x y    

5 3 10 2 0.x y    

5 3 2 0.x y   

5 3 11 2 0.x y    

.................................................................................................................

26. Trong mặt phẳng tọa độ

,Oxy

có hai đường thẳng

và

có phương trình lần lượt là

4 3 5 0x y  

và

7 4 0.x y  

Nếu có phép quay biến đường thẳng này thành đường thẳng

kia thì số đo của góc quay



là

45 .

60 .

90 .

120 .

.................................................................................................................

27. Trong mặt phẳng tọa độ

,Oxy

hãy viết phương trình đường tròn

( )C



là ảnh của

2 2

( ) : 2 4 4 0C x y x y    

qua phép quay

( ; 90 )





2 2

( 2) ( 1) 9.x y   

2 2

( 2) ( 1) 9.x y   

2 2

( 2) ( 1) 9.x y   

2 2

( 1) ( 2) 9.x y   

.................................................................................................................

28. Trong mặt phẳng tọa độ

Oxy

, cho đường tròn

2 2

( ) : 6 5 0.C x y x   

Tìm ảnh đường tròn

( )C



của

( )C

qua

( ,90 )



2 2

( 3) 4.x y  

2 2

6 6 0.x y y   

2 2

( 3) 4.x y  

2 2

6 5 0.x y x   

.................................................................................................................

ĐÁP ÁN TRẮC NGHIỆM

1.D 2.B 3.B 4.B 5.D 6.D 7.D 8.B 9.C 10.B

11.B 12.B 13.B 14.B 15.A 16.B 17.B 18.B 19.B 20.B

21.D 22.A 23.A 24.B 25.D 26.A 27.A 28.C

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 25 -

§ 6. PHÉP VỊ TỰ VÀ PHÉP ĐỒNG DẠNG



1. Ñònh nghóa

Cho điểm

cố định và một số thực

không đổi,

0.k 

Phép biến hình biến mỗi điểm

thành

điểm



sao cho

.OM k OM





 

được gọi là phép vị tự tâm

tỉ số

và kí hiệu là

( ; )O k

được

gọi là tâm vị tự) (hiểu khác, đây là phép zoom).

2. Tính chaát



Định lí 1. Nếu phép vị tự tâm

tỉ số

biến hai điểm

và

lần lượt thành hai điểm



và



thì

.M N k MN

 



 

và . .M N k MN

 





Định lí 2. Phép vị tự biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi

thứ tự của ba điểm đó.



Hệ quả:



Biến đường thẳng không qua tâm vị tự thành đường thẳng song song với đường thẳng đã cho.



Biến đường thẳng qua tâm vị tự thành chính nó.



Biến tia thành tia.



Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với



Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là



Biến góc bằng góc ban đầu.



Lưu ý.



Qua phép

( ; )O k

đường thẳng

biến thành chính nó khi đường thẳng

qua tâm vị tự



Nếu

 

( ; )

;1/

( ) ( ).

I k

M V M M V M

 

  

3. AÛnh cuûa ñöôøng troøn qua pheùp vò tröï



Định lí 3. Phép vị tự tỉ số

biến một đường tròn

( ; )I R

thành đường tròn có bán kính

. .R k R







Chú ý. Nếu phép vị tự tâm

tỉ số

biến đường tròn

( ; )I R

thành đường tròn

( ; )I R

 

thì

R R

k k

R R

 

   

và

. .OI k OI





 

4. Taâm vò töï cuûa hai ñöôøng troøn



Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia. Tâm

của phép vị tự này được gọi là tâm vị tự của hai đường tròn.



Nếu tỉ số vị tự

0k 

thì tâm vị tự đó gọi là tâm vị tự ngoài, nếu tỉ số vị tự

0k 

thì tâm vị tự đó

gọi là tâm vị tự trong.



Cách xác định tâm vị tự:

Nếu

là tâm vị tự ngoài, ta có:

IO IO



 



 

Nếu

là tâm vị tự trong, ta có:

IO IO



  



 

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 26 -

1. Trong mặt phẳng

,Oxy

cho đường thẳng

: 3 2 6 0.d x y  

Viết phương trình của đường thẳng



là ảnh của

qua phép vị tự tâm

(1;2)I

tỉ số vị tự

2k  

Học sinh nghe giảng và bổ sung lời giải

Gọi

( ; ) : 3 2 6 0M x y d x y   

(1)

Gọi

( ; )M x y

  

là ảnh của

qua phép vị tự tâm

tỉ số

2 :k  

1 2( 1) .........................

2 ; .

2 2( 2) ..........................

x x x

IM IM M

y y y

 



 

 

    

 









     



 









  

    

 

 

 

 

3 6

(1) 3 2 6 0 3 2 9 0

2 2

x y

   

 

 

 

 

 

 

       

 

 

 

 

 

 

   

: 3 2 9 0.M d x y

   

    

Vậy

: 3 2 9 0d x y



  

là ảnh của

thỏa bài toán.

2. Trong mặt phẳng

,Oxy

cho đường thẳng

: 2 3 0.d x y  

Viết phương trình của đường thẳng



là ảnh của

qua phép vị tự tâm

(0;0)O

tỉ số vị tự

2k 

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

3. Trong mặt phẳng

,Oxy

cho đường thẳng

: 2 0.d x y  

Viết phương trình của đường thẳng



là ảnh của

qua phép vị tự tâm

(0;0)O

tỉ số vị tự

3k  

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

4. Trong mặt phẳng

,Oxy

cho đường tròn

2 2

( ) : ( 3) ( 1) 9.C x y   

Viết phương trình của đường

tròn

( )C



là ảnh của

( )C

qua phép vị tự tâm

(1;2)I

tỉ số vị tự

2k  

Học sinh nghe giảng và bổ sung lời giải

Đường tròn

( )C

có tâm

(3; 1)I 

và bán kính

3.R 

Gọi

( ; )K x y

  

là tâm và



là bán kính của

( )C



là ảnh của

( ).C

Khi đó:

1 2( 1) ................................ ...

.........

2 2( 2) ................................ ..

' 2 ................................

x x x

IK IK

y y y

R R

 

 

 

    

 





 



 



 



 

       

  

  



 

  







 

 

 

..........

...........

















Vậy

2 2

( ) : ( 3) ( 6) 36.C x y



   

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 27 -

5. Trong mặt phẳng

,Oxy

cho đường tròn

2 2

( ) : ( 1) ( 3) 2.C x y   

Viết phương trình của đường

tròn

( )C



là ảnh của

( )C

qua phép vị tự tâm

(0;0)O

tỉ số vị tự

3k 

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

6. Trong mặt phẳng

,Oxy

cho đường tròn

2 2

( ) : ( 1) ( 2) 5.C x y   

Viết phương trình của đường

tròn

( )C



là ảnh của

( )C

qua phép vị tự tâm

(1;2)I

tỉ số vị tự

2k  

 Lời giải. ............................................................................................................................................................

.................................................................................................................................................................................

BÀI TẬP TRẮC NGHIỆM

1. Cho hình thang

ABCD

có hai cạnh đáy là

và

mà

3 .AB CD

Phép vị tự biến điểm

thành điểm

và biến điểm

thành điểm

có tỉ số là

 

  

3.k 

3.k  

.......................................................................................................

...................................................................................................... `

2. Cho tam giác

ABC

có trọng tâm

gọi

, , A B C

  

lần lượt là trung điểm các cạnh

, , .BC CA AB

Với giá trị nào của

thì phép vị tự

( ; )V G k

biến tam giác

ABC

thành tam giác

.A B C

  

2.k 

2.k  

 

  

.......................................................................................................

3. Trong mặt phẳng tọa độ

,Oxy

cho phép vị tự tâm

(3; 1)I 

có tỉ số

2.k  

Khi đó nó biến điểm

(5;4)M

thành điểm

( 1; 11).M



 

( 7;11).M





(1;9).M



(1; 9).M





.......................................................................................................

4. Trong mặt phẳng tọa độ

,Oxy

cho phép vị tự tỉ số

2k 

và biến điểm

(1; 2)A 

thành điểm

( 5;1).A





Khi đó nó biến điểm

(0;1)B

thành điểm

(0;2).B



(12; 5).B





( 7;7).B





(11;6).B



.......................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 28 -

5. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(3;2).A

Ảnh của

qua phép vị tự tâm

tỉ số

1k  

là

(3;2).

(2; 3).

( 2; 3). 

( 3; 2). 

......................................................................................................

6. Trong mặt phẳng

,Oxy

tìm ảnh



của điểm

(1; 3)A 

qua phép vị tự tâm

tỉ số

2.

(2;6).A



(1;3).A



( 2;6).A





( 2; 6).A



 

......................................................................................................

7. Tìm ảnh



của

(1;2)A

qua phép vị tự tâm

(3; 1).I 

tỉ số

2.k 

(3;4).A



(1;5).A



( 5; 1).A



 

( 1;5).A





......................................................................................................

8. Cho

( 3;2), (1;1), (2; 4).P Q R 

Gọi

, , P Q R

  

lần lượt là ảnh của

, , P Q R

qua phép vị tự tâm

tỉ số

  

Khi đó tọa độ trọng tâm của tam giác

P Q R

  

là

1 1

;

9 3

 



















 

 



















 

2 1

;

3 3

 







 











 

 



















 

......................................................................................................

9. Trong mặt phẳng tọa độ

,Oxy

cho ba điểm

(0;3), (2; 1), ( 1;5).A B C 

Phép vị tự tâm

tỉ số

biến

thành

Khi đó giá trị

là

  

1.k  

 

2.k 

......................................................................................................

10. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 2 4 0, ( 1;2).d x y I   

Tìm ảnh



của

qua phép vị tự tâm

tỉ số

2.k  

2 4 0.x y  

2 8 0.x y   

2 8 0.x y  

2 4 0.x y  

......................................................................................................

11. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 3 5 0.d x y  

Tìm ảnh



của

qua phép

vị tự tâm

tỉ số

  

3 9 0.x y   

3 10 0.x y  

9 3 15 0.x y  

9 3 10 0.x y  

......................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 29 -

12. Trong mặt phẳng tọa độ

,Oxy

cho phép vị tự tâm

(1;1)I

tỉ số

  

Khi đó nó biến đường

thẳng

5 1 0x y  

thành đường thẳng có phương trình là

15 3 10 0.x y  

15 3 23 0.x y  

15 3 23 0.x y  

5 3 8 0.x y  

.......................................................................................................

13. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 5 2 7 0.d x y  

Tìm ảnh



của

qua phép

vị tự tâm

tỉ số

2.k  

5 2 14 0.x y  

5 4 28 0.x y  

5 2 7 0.x y  

5 2 14 0.x y  

.......................................................................................................

14. Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

: 1

2 4

x y

 

và

: 2 6 0.d x y



  

Phép vị

tự

( , )

( ) .

O k

V d d





Tìm

 

  

 

  

.......................................................................................................

15. Tìm ảnh đường tròn

( )C



của đường tròn

2 2

( ) : ( 1) ( 2) 5C x y   

qua phép vị tự tâm

tỉ số

2.k  

2 2

( ) : ( 2) ( 4) 10.C x y



   

2 2

( ) : ( 2) ( 4) 10.C x y



   

2 2

( ) : ( 2) ( 4) 20.C x y



   

2 2

( ) : ( 2) ( 4) 20.C x y



   

.......................................................................................................

16. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : ( 3) ( 1) 5.C x y   

Tìm ảnh đường tròn

( )C



của đường tròn

( )C

qua phép vị tự tâm

(1;2)I

và tỉ số

2.k  

2 2

6 16 4 0.x y x y    

2 2

6 16 4 0.x y x y    

2 2

( 3) ( 8) 20.x y   

2 2

( 3) ( 8) 20.x y   

.......................................................................................................

17. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : ( 1) ( 1) 4C x y   

. Tìm ảnh

( )C



của

( )C

qua phép vị tự tâm

( 1;2)I 

tỉ số

3.k 

2 2

14 4 1 0.x y x y    

.......................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 30 -

2 2

4 7 5 0.x y x y    

2 2

( 5) ( 1) 36.x y   

2 2

( 7) ( 2) 9.x y   

......................................................................................................

18. Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

(1; 1), (2;3)A B

và đường thẳng

có phương trình

4 1.y x  

Thực hiện liên tiếp hai phép đối xứng tâm

và

(theo thứ tự), đường thẳng

biến thành đường thẳng



có phương trình là

4 5.y x 

4 17.y x  

4 12.y x 

4 4.y x  

.......................................................................................................

19. Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

( 1; 0), (1;1)A B

và đường tròn

( )T

có phương trình

2 2

4 0.x y x  

Thực hiện liên tiếp hai phép đối xứng tâm

và

(theo thứ tự), đường tròn

( )T

biến thành đường tròn

( )T



có phương trình là

2 2

4 2 4 0.x y x y    

2 2

4 4 4 0.x y x y    

2 2

6 2 1 0.x y x y    

2 2

4 8 0.x y y   

.......................................................................................................

20. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng



có phương trình

5 1 0.x y  

Thực hiện

phép tịnh tiến theo phương của trục hoành về phía trái 2 đơn vị, sau đó tiếp tục thực hiện phép

tịnh tiến theo phương của trục tung về phía trên 3 đơn vị, đường thẳng



biến thành đường

thẳng





có phương trình là

5 14 0.x y  

5 7 0.x y  

5 5 0.x y  

5 12 0.x y  

.......................................................................................................

21. Trong mặt phẳng tọa độ

O ,xy

cho đường thẳng



có phương trình

3 2.y x  

Thực hiện liên

tiếp hai phép tịnh tiến theo các vectơ

( 1;2)u  



và

(3;1),v 



đường thẳng



biến thành đường

thẳng

có phương trình là

3 1.y x  

3 5.y x  

3 9.y x  

3 15.y x  

.......................................................................................................

22. Trong mặt phẳng

,Oxy

cho điểm

(2; 4).M

Hỏi phép đồng dạng có được bằng cách thực hiện liên

tiếp phép vị tự tâm

tỉ số



và phép quay tâm

góc quay

90 

sẽ biến điểm

thành

điểm nào sau đây ?

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 31 -

(2; 1).

(2;1).

( 1;2).

(1;2).

......................................................................................................

23. Trong mặt phẳng

,Oxy

cho đường thẳng

: 2 0d x y 

thỏa mãn phép đồng dạng có được bằng

cách thực hiện liên tiếp phép vị tự tâm

tỉ số

2k  

và phép đối xứng trục

sẽ biến đường

thẳng

thành đường thẳng nào sau đây ?

2 0.x y  

2 0.x y 

4 0.x y 

2 2 0.x y  

......................................................................................................

24. Trong mặt phẳng

,Oxy

cho đường tròn

2 2

( ) : ( 2) ( 2) 4.C x y   

Hỏi phép đồng dạng có được

bằng cách thực hiện liên tiếp phép vị tự tâm

tỉ số



và phép quay tâm

góc quay

90

sẽ

biến

( )C

thành đường tròn nào sau đây ?

2 2

( 2) ( 2) 1.x y   

2 2

( 1) ( 1) 1.x y   

2 2

( 2) ( 1) 1.x y   

2 2

( 1) ( 1) 1.x y   

......................................................................................................

25. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 2 0.d x y 

Phép đồng dạng là phép thực

hiện liên tiếp qua phép vị tự tâm

(1; 2)I 

tỉ số

3k 

và phép quay tâm

góc quay

90

sẽ biến

đường thẳng

thành đường thẳng nào sau đây ?

2 6 0.x y  

2 6 0.x y  

2 6 0.x y  

2 3 0.x y  

......................................................................................................

26. Phép đồng dạng là phép thực hiện liên tiếp qua phép vị tự tâm

(4;2)I

tỉ số

3k  

và phép đối

xứng qua trục

: 2 4 0d x y  

sẽ biến

(0;1)M

thành điểm nào sau đây ?

(16;5).

(14;9).

(12;13).

(18;1).

......................................................................................................

27. Trong mặt phẳng tọa độ

Oxy

, cho đường tròn

2 2

( ) : ( 1) ( 2) 4.C x y   

Phép đồng dạng là

phép thực hiện liên tiếp qua phép vị tự tâm

tỉ số

2k  

và phép quay tâm

góc quay

180

sẽ biến đường tròn

( )C

thành đường tròn nào sau đây ?

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 32 -

2 2

4 8 2 0.x y x y    

2 2

4 8 2 0.x y x y    

2 2

( 2) ( 4) 16.x y   

2 2

( 2) ( 4) 16.x y   

.......................................................................................................

28. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : ( 1) ( 2) 9.C x y   

Phép đồng dạng là

phép thực hiện liên tiếp qua phép vị tự tâm

(1; 1)I 

tỉ số



và phép tịnh tiến theo

(3; 4)v 



sẽ biến đường tròn

( )C

thành đường tròn có phương trình là

2 2

( 4) ( 4) 9.x y   

2 2

( 4) ( 4) 1.x y   

2 2

( 4) ( 4) 1.x y   

2 2

( 1) 1.x y  

.......................................................................................................

29. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(3; 1).P 

Thực hiện liên tiếp hai phép vị tự

( ; 4)V O

và

;

V O

 



















 

điểm

biến thành điểm



có tọa độ là

(4; 6).P





(6; 2).P





( 6;2).P





(12; 4).P





.......................................................................................................

30. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 2 0d x y 

thỏa mãn phép đồng dạng có được

bằng cách thực hiện liên tiếp phép vị tự tâm

tỉ số

2k  

và phép đối xứng trục

sẽ biến

đường thẳng

thành đường thẳng nào sau đây ?

2 0.x y 

4 0.x y 

2 0.x y  

2 2 0.x y  

.......................................................................................................

BẢNG ĐÁP ÁN

1.B 2.D 3.A 4.C 5.D 6.D 7.D 8.B 9.A 10.C

11.D 12.B 13.A 14.A 15.C 16.C 17.C 18.B 19.B 20.A

21.C 22.A 23.A 24.D 25.C 26.C 27.D 28.B 29.C 30.C

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 33 -

ÔN TẬP CHƯƠNG 1

1. Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

( ) : 2 3 1 0d x y  

và

( ) : 2 0.d x y  

Có bao nhiêu phép tịnh tiến biến

thành

A. Vô số. B.

..................................................................................................................

2. Cho

( 1;5)v  



và điểm

(4;2).M



Biết



là ảnh của

qua phép tịnh tiến



Tìm

( 4;10).M 

( 3;5).M 

(3;7).M

(5; 3).M 

..................................................................................................................

3. Cho điểm

(1; 4)A



và

( 2; 3),u  



biết



là ảnh của

qua phép tịnh tiến



Tìm tọa độ điểm

(1; 4).A

( 3; 1).A  

( 1; 4).A  

(3;1).A

..................................................................................................................

4. Cho hai đường thẳng song song

và



Tìm khẳng định nào đúng ?

A. Có đúng một phép tịnh tiến biến

thành



B. Có vô số phép tịnh tiến biến

thành



C. Phép tịnh tiến theo véc tơ



có giá vuông góc với đường thẳng

biến

thành



D. Cả ba khẳng định trên đều đúng.

5. Điểm

( 2; 4)M 

là ảnh của điểm nào sau đây qua phép tịnh tiến theo véctơ

( 1;7).v  



( 1; 3).F  

( 3;11).P 

(3;1).E

(1; 3).Q

..................................................................................................................

6. Trong mặt phẳng tọa độ

,Oxy

cho

( 2; 3).v  



Tìm ảnh của điểm

(1; 1)A 

qua phép tịnh tiến theo

véctơ



( 2;1).A





( 1;2).A





(2; 1).A





( 1; 2).A



 

..................................................................................................................

7. Phép biến hình nào sau đây không là phép dời hình ?

A. Phép tịnh tiến.

B. Phép đối xứng tâm.

C. Phép đối xứng trục.

D. Phép vị tự.

..................................................................................................................

8. Cho hình bình hành

.ABCD

Ảnh của điểm

qua phép tịnh tiến theo véctơ



là

..................................................................................................................

9. Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

(2; 5).M

Phép tịnh tiến theo

(1;2)v 



biến điểm

thành điểm



Tọa độ điểm



là

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 34 -

(3;7).M



(1;3).M



(3;1).M



(4;7).M



..................................................................................................................

10. Hình nào dưới nào dưới đây không có trục đối xứng ?

A. Tam giác cân.

B. Hình thang cân.

C. Hình elip.

D. Hình bình hành.

..................................................................................................................

11. Trong mặt phẳng tọa độ

,Oxy

cho véctơ

( 3;5).v  



Tìm ảnh của điểm

(1;2)A

qua phép tịnh

tiến theo véctơ



(4; 3).A





( 2;3).A





( 4;3).A





( 2;7).A





..................................................................................................................

12. Cho

4 5 .IA IB

 

Tỉ số vị tự

của phép vị tự tâm

biến

thành

là

 

..................................................................................................................

13. Trong mặt phẳng

,Oxy

cho đường tròn

2 2

( ) : ( 1) ( 1) 4.C x y   

Phép vị tự tâm

(với

là gốc tọa độ) tỉ số

2k 

biến

( )C

thành đường tròn nào trong các đường tròn có phương trình

sau ?

2 2

( 1) ( 1) 8.x y   

2 2

( 2) ( 2) 8.x y   

2 2

( 2) ( 2) 16.x y   

2 2

( 2) ( 2) 16.x y   

..................................................................................................................

14. Trong mặt phẳng với hệ tọa độ

,Oxy

cho véctơ

(2; 1)v  



và điểm

( 3;2).M 

Tìm tọa độ ảnh



của điểm

qua phép tịnh tiến theo véctơ



(5; 3).M



(1; 1).M





( 1;1).M





(1;1).M



..................................................................................................................

15. Cho hình chữ nhật có

là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm

góc

, 0 2   

biến hình chữ nhật trên thành chính nó ?

A. Không có. B.

..................................................................................................................

16. Phép tịnh tiến biến gốc tọa độ

thành điểm

(1;2)A

sẽ biến điểm

thành điểm



có tọa độ là

(2;4).A



( 1; 2).A



 

(4;2).A



(3; 3).A



..................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 35 -

17. Trong mặt phẳng

,Oxy

cho

(2; 3), (1; 0).A B

Phép tịnh tiến theo

(4; 3)u  



biến điểm

, A B

tương ứng thành

, A B

 

khi đó, độ dài đoạn thẳng

A B

 

bằng

10.

13.

..................................................................................................................

18. Trong mặt phẳng tọa độ

Oxy

cho vectơ

(3; 1).u  



Phép tịnh tiến theo vectơ



biến điểm

(1; 4)M 

thành

(4; 5).M





(3; 4).





(2; 3).M





(4;5).



..................................................................................................................

19. Cho hình chữ nhật

.MNPQ

Phép tịnh tiến theo véctơ



biến điểm

thành điểm

A. Điểm

B. Điểm

C. Điểm

D. Điểm

..................................................................................................................

20. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(3; 1).A 

Tìm tọa độ điểm

sao cho điểm

là ảnh

của điểm

qua phép tịnh tiến theo véctơ

(2; 1).u  



( 1; 0).B 

(5; 2).

B 

(1; 2).B 

(1; 0).B

..................................................................................................................

21. Cho hình hộp

.ABCD A B C D

   

(như hình vẽ). Chọn mệnh đề đúng?

A. Phép tịnh tiến theo



biến điểm



thành điểm



B. Phép tịnh tiến theo





biến điểm



thành điểm



C. Phép tịnh tiến theo



biến điểm



thành điểm



D. Phép tịnh tiến theo





biến điểm



thành điểm



22. Trong mặt phẳng tọa độ

,Oxy

phép tịnh tiến theo vectơ

(1;2)v 



biến điểm

(4;5)M

thành điểm

nào sau đây ?

(1;6).P

(3;1).Q

(5;7).N

(4;7).R

..................................................................................................................

23. Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

(1;1)A

và

(2;3).I

Phép vị tự tâm

tỉ số

 

biến điểm

thành điểm



Tọa độ điểm



là

(0;7).A



(7;0).A



(7;4).A



(4;7).



..................................................................................................................

24. Trong mặt phẳng tọa độ

,Oxy

phép tính tiến theo véctơ



biến điểm

( ; )M x y

thành điểm

( ; )M x y

  

sao cho

2x x



 

và

4.y y



 

Tọa độ của



là

( 2; 4).

(4; 2).

( 2; 4). 

(2;4).

..................................................................................................................

25. Trong mặt phẳng

,Oxy

cho điểm

(2;1)A

và vectơ

(1;3).a 



Phép tịnh tiến theo véctơ



biến

điểm

thành điểm



Tọa độ điểm



là

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 36 -

( 1; 2).A



 

(1;2).A



(4;3).A



(3; 4).A



..................................................................................................................

26. Cho hình thoi

ABCD

tâm

Phép tịnh tiến theo véc tơ



biến điểm

thành

A. Điểm

B. Điểm

C. Điểm

D. Điểm

..................................................................................................................

27. Trong mặt phẳng tọa độ

,Oxy

phép tịnh tiến theo véc tơ

(1; 3)v 



biến điểm

(1;2)A

thành điểm

nào trong các điểm sau ?

(2; 5).M

(1; 3).P

( 3; 4).Q  

(3; 4).N

..................................................................................................................

28. Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

( 3;2).M 

Tọa độ của điểm



là ảnh của điểm

qua phép tịnh tiến theo véctơ

(2; 1)v  



là

( 1;1).

(3; 2).

(5; 3).

( 5; 3).

..................................................................................................................

29. Trong mặt phẳng với hệ tọa độ

,Oxy

phép quay tâm

(4; 3)I 

góc quay

180

biến đường thẳng

: 5 0d x y  

thành đường thẳng



có phương trình

3 0.x y  

3 0.x y  

5 0.x y  

3 0.x y  

...................................................................................................................

30. Cho đường thẳng

: 2 0.d x y  

Phép hợp thành của phép đối xứng tâm

và phép tịnh

tiến theo

(3;2)v 



biến

thành đường thẳng nào sau đây ?

4 0.x y  

3 3 2 0.x y  

2 2 0.x y  

3 0.x y  

...................................................................................................................

31. Trong mặt phẳng

,Oxy

tìm phương trình đường tròn

( )C



là ảnh của đường tròn

2 2

( ) : 1C x y 

qua phép đối xứng tâm

(1; 0).I

2 2

( 2) 1.x y  

2 2

( 2) 1.x y  

2 2

( 2) 1.x y  

2 2

( 2) 1.x y  

...................................................................................................................

32. Trong mặt phẳng

,Oxy

qua phép quay

( , 90 ), (3; 2)Q O M



  

là ảnh của điểm

( 3; 2).M  

( 3;2).M 

(2; 3).M

(2; 3).M 

...................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 37 -

33. Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 6 0.x y   

Viết phương trình

đường thẳng





là ảnh của đường thẳng



qua phép quay tâm

góc

90 .

2 6 0.x y  

2 6 0.x y  

2 6 0.x y  

2 6 0.x y  

...................................................................................................................

34. Trong mặt phẳng

,Oxy

cho đường tròn

2 2

( ) : ( 1) ( 3) 4.C x y   

Phép tịnh tiến theo vectơ

(3;2)v 



biến đường tròn

( )C

thành đường tròn có phương trình nào sau đây ?

2 2

( 2) ( 5) 4.x y   

2 2

( 4) ( 1) 4.x y   

2 2

( 1) ( 3) 4.x y   

2 2

( 2) ( 5) 4.x y   

...................................................................................................................

35. Trong mặt phẳng

,Oxy

cho điểm

( 3;6).B 

Tìm tọa độ điểm

sao cho

là ảnh của

qua

phép quay tâm

góc quay

90 . 

( 6; 3).E  

( 3; 6).E  

(6; 3).E

(6; 3).E 

...................................................................................................................

36. Trong mặt phẳng với hệ tọa độ

,Oxy

tìm tọa độ điểm



là ảnh của điểm

(2;1)M

qua phép đối

xứng tâm

(3; 2).I 

(1; 3).M





( 5;4).M





(4; 5).M





(1;5).M



...................................................................................................................

37. Trong mặt phẳng với hệ tọa độ

O ,xy

cho tam giác

ABC

có

(2; 4), (5;1), ( 1; 2).A B C  

Phép tịnh

tiến



biến tam giác

ABC

tành tam giác

.A B C

  

Tìm tọa độ trọng tâm của tam giác

.A B C

  

( 4;2).

(4;2).

(4; 2).

( 4; 2). 

...................................................................................................................

38. Trong mặt phẳng với hệ toạ độ

O ,xy

cho véctơ

( 1;2),v  



điểm

(3;5).A

Tìm tọa độ của các điểm



là ảnh của

qua phép tịnh tiến theo



(2;7).A



( 2;7).A





(7;2).A



( 2;7).A





...................................................................................................................

39. Trong mặt phẳng

,Oxy

ảnh của điểm

( 2; 3)M 

qua phép đối xứng trục

: 0x y  

là

(3;2).M



( 3; 2).M



 

(3; 2).M





( 3;2).M





...................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 38 -

40. Trong mặt phẳng tọa độ

,Oxy

cho các điểm

(3;1), ( 1; 1).I J  

Ảnh của

qua phép quay

( ; 90 )

 

là

(1;5).J



(5; 3).J





( 3;3).J





(1; 5).J





...................................................................................................................

41. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : ( 1) ( 2) 4.C x y   

Tìm ảnh của đường

tròn

( )C

qua phép vị tự tâm

tỉ số

2.

2 2

( 2) ( 4) 16.

x y   

2 2

( 2) ( 4) 16.x y   

2 2

( 2) ( 4) 16.

x y   

2 2

( 2) ( 4) 16.

x y   

...................................................................................................................

42. Cho lục giác đều

ABCDEF

tâm

như hình bên. Tam giác

EOD

là ảnh của tam giác

AOF

qua phép quay tâm

góc quay

.

Tìm

.

60 .  

60 .   

120 .  

120 .



  

...................................................................................................................

43. Trong mặt phẳng tọa độ

,Oxy

cho véctơ

(1;2).v 



Tìm ảnh của điểm

( 2; 3)A 

qua phép tịnh

tiến theo vectơ



(5; 1).A





( 1;5).





(3; 1).A





( 3;1).





...................................................................................................................

44. Trong mặt phẳng

,Oxy

cho đường thẳng

có phương trình

2 1 0.x y  

Để phép tịnh tiến

theo



biến đường thẳng

thành chính nó thì



phải là véctơ nào trong các véctơ sau đây ?

( 1;2).v  



(2;1).v 



(2; 4).v  



(2;4).v 



...................................................................................................................

45. Trong mặt phẳng

,Oxy

cho véctơ

( 3;2)v  



và đường thẳng

: 3 6 0.x y   

Viết phương

trình đường thẳng





là ảnh của đường thẳng



qua phép tịnh tiến theo



: 3 15 0.x y



   

: 3 5 0.x y



   

: 3 15 0.x y



   

: 3 15 0.x y



   

...................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 39 -

46. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(1;2).M

Phép tịnh tiến theo véctơ

( 3;4)u  



biến điểm

thành điểm



có tọa độ là

( 2;6).M





(2;5).M



(2; 6).M





(4; 2).M





...................................................................................................................

......................................................................................................

47. Trong mặt phẳng

,Oxy

cho đường thẳng

: 2 0.x y   

Hãy viết phương trình đường thẳng

là ảnh của đường thẳng



qua phép quay tâm

góc quay

90 .

: 2 0.d x y  

: 2 0.d x y  

: 2 0.d x y  

: 4 0.d x y  

...................................................................................................................

48. Trong mặt phẳng tọa độ

,Oxy

tìm phương trình đường thẳng





là ảnh của đường thẳng

: 2 1 0x y   

qua phép tịnh tiến theo véctơ

(1; 1).v  



: 2 3 0.x y



   

: 2 0.x y



  

: 2 1 0.x y



   

: 2 2 0.x y



   

...................................................................................................................

49. Trong mặt phẳng tọa độ

,Oxy

cho đường tròn

2 2

( ) : ( 2) ( 1) 9.C x y   

Gọi

( )C



là ảnh của

đường tròn

( )C

qua việc thực hiện liên tiếp phép vị tự tâm

tỉ số

 

và phép tịnh tiến

theo vectơ

(1; 3).v  



Tính bán kính



của đường tròn

( ).C



9.R





3.R





27.R





1.R





...................................................................................................................

50. Trong mặt phẳng

,Oxy

cho điểm

(2; 1).I 

Gọi

( )C

là đồ thị hàm số

sin 3 .y x

Phép vị tự tâm

(2; 1),I 

tỉ số

 

biến

( )C

thành

( ).C



Viết phương trình đường cong

( ).C



3 1

sin(6 18).

2 2

y x  

3 1

sin(6 18).

2 2

y x  

3 1

sin(6 18).

2 2

y x   

3 1

sin(6 18).

2 2

y x   

...................................................................................................................

51. Cho tam giác

ABC

có diện tích bằng

6cm .

Phép vị tự tỷ số

2k  

biến tam giác

ABC

thành

tam giác

.A B C

  

Tính diện tích tam giác

A B C

  

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 40 -

12cm .

24cm .

6cm .

3cm .

...................................................................................................................

52. Trong mặt phẳng tọa độ

,Oxy

cho điểm

(3; 4).A

Gọi



là ảnh của điểm

qua phép quay tâm

(0; 0),O

góc quay

90 .

Điểm



có tọa độ là

( 3;4).A





(4; 3).A





(3; 4).A





( 4;3).A





...................................................................................................................

53. Trong mặt phẳng

,Oxy

cho

(3;3)v 



và đường tròn

2 2

( ) : 2 4 4 0.C x y x y    

Ảnh của

( )C

qua phép tịnh tiến vectơ



là đường tròn nào ?

2 2

( 4) ( 1) 4.x y   

2 2

( 4) ( 1) 9.x y   

2 2

( 4) ( 1) 9.x y   

2 2

8 2 4.x y x y   

...................................................................................................................

54. Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: .d y x

Tìm ảnh của

qua phép quay tâm

góc quay

90 .

: 2 .d y x





: .d y x



 

: 2 .d y x



 

: .d y x





...................................................................................................................

55. Trong mặt phẳng

,Oxy

tìm phương trình đường tròn

( )C



là ảnh của đường tròn

2 2

( ) : 1C x y 

qua phép đối xứng tâm

(1; 0).I

2 2

( 2) 1.x y  

2 2

( 2) 1.x y  

2 2

( 2) 1.x y  

2 2

( 2) 1.x y  

...................................................................................................................

ĐÁP ÁN BÀI TẬP ÔN CUỐI CHƯƠNG

1.D 2.D 3.D 4.B 5.B 6.B 7.D 8.B 9.A 10.D

11.D 12.A 13.D 14.C 15.C 16.A 17.A 18.A 19.D 20.D

21.A 22.C 23.D 24.A 25.D 26.D 27.A 28.A 29.B 30.D

31.C 32.C 33.A 34.A 35.A 36.C 37.D 38.A 39.D 40.A

41.B 42.B 43.B 44.A 45.D 46.A 47.A 48.B 49.D 50.D

51.B 52.D 53.B 54.B 55.C

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 41 -

§ 1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG



1. Môû ñaàu veà hình hoïc khoâng gian

Đối tượng cơ bản:



Điểm: kí hiệu

, , , ...A B C



Đường thẳng: kí hiệu

1 2

, , , , , , ...a b c d d d



Mặt phẳng: kí hiệu

( ), ( ), ( ), ( ), ...P Q  

Quan hệ cơ bản:



Thuộc: kí hiệu

.

Ví dụ:

, ( ).A d M P 



Chứa, nằm trong: kí hiệu

.

Ví dụ:

( ), ( ).d P b  

Hình biểu diễn của một hình trong không gian:



Đường thẳng được biểu diễn bởi đường thẳng. Đoạn thẳng biểu diễn bởi đoạn thẳng.



Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi hai đường thẳng song song

(hoặc cắt nhau).



Hai đoạn thẳng song song hoặc bằng nhau được biểu diễn bởi hai đoạn thẳng song song và

bằng nhau.



Dùng nét vẽ liền ( __ ) để biểu diễn cho những đường trông thấy và dùng nét đứt đoạn (----)

để biểu diễn cho những đường bị che khuất.

2. Caùc tính chaát thöøa nhaän trong hình hoïc khoâng gian



Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt không thẳng hàng cho trước.



Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.



Nếu 1 đường thẳng có 2 điểm phân biệt thuộc một mặt phẳng

thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.



Tồn tại bốn điểm không cùng thuộc một mặt phẳng.



Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng

còn có một điểm chung khác nữa.

Từ tính chất này suy ra: Nếu hai mặt phẳng phân biệt có một

điểm chung thì chúng sẽ có một đường thẳng chung đi qua

điểm chung ấy. Đường thẳng chung là duy nhất chứa tất cả

các điểm chung của hai mặt phẳng đó. Đường thẳng chung

đó được gọi là giao tuyến của hai mặt phẳng.



Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.

3. Ñieàu kieän xaùc ñònh maët phaúng



Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.



Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng

không đi qua điểm đó. Mặt phẳng hoàn toàn có thể mở rộng ra đến vô cực.



Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.

ĐƯỜNG THẲNG VÀ MẶT PHẲNG

TRONG KHÔNG GIAN

Chöông

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 42 -

4. Hình choùp vaø hình töù dieän



Cho đa giác

1 2 3

.......

AA A A

nằm trong mặt phẳng

( )

và điểm

( ).S 

Lần lượt nối điểm

với

các đỉnh

1 2 3

, , , ...,

A A A A

ta được

tam giác

1 2 2 3 1

, , ..., .

SAA SA A SA A

Hình gồm đa giác

1 2 3

...

AA A A

và

tam giác

1 2 2 3 1

, , ...,

SAA SA A SA A

được gọi là hình chóp, kí hiệu hình chóp này

là

1 2 3

. ... .

S A A A A

Khi đó ta gọi:



là đỉnh của hình chóp.



1 2 3

...

AA A A

là mặt đáy của hình chóp.



Các tam giác

1 2 2 3 1

, , ...,

SAA SA A SA A

gọi là mặt bên.



1 2 3

, , , ...,

SA SA SA SA

được gọi là các cạnh bên.



Ta gọi hình chóp có đáy là tam giác, tứ giác, ngũ giác,..., lần lượt là hình chóp tam giác, hình chóp

tứ giác, hình chóp ngũ giác, ....



Cho bốn điểm

, , , A B C D

không đồng phẳng. Hình gồm

tam giác

, ,ABC ACD

ABD

và

BCD

gọi là hình tứ diện (hay ngắn gọn gọi là tứ diện) và kí hiệu là

.ABCD

Các điểm

, , , A B C D

là bốn đỉnh của tứ diện.



Các đoạn thẳng

, , , , , AB BC CD DA CA BD

gọi là các cạnh của tứ diện.



Hai cạnh không đi qua một đỉnh gọi là hai cạnh đối diện của tứ diện.



Các tam giác

, , , ABC ACD ABD BCD

gọi là các mặt của tứ diện.



Hình tứ diện có bốn mặt là các tam giác đều gọi là hình tứ diện đều.

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 43 -

Daïng toaùn 1: Tìm giao tuyeán cuûa hai maët phaúng

 Phương pháp giải



Tìm hai điểm chung phân biệt của hai mặt phẳng.



Đường thẳng nối hai điểm chung đó là giao tuyến của chúng.

BÀI TẬP VẬN DỤNG

1. Cho tứ diện

.SABC

Gọi

, M N

lần lượt là hai điểm trên cạnh

và

sao cho

không

song song với

.AC

Tìm giao tuyến của các cặp mặt phẳng sau:

( )SMN

và

( ).SAC

Ta có:

( ) ( )S SMN SAC 

(1)

Trong

( ),ABC

gọi

.E MN AC 

Ta có:

, ( ) ( )

E MN MN SMN E SMN

E AC AC SAC E SAC





   







   





( ) ( )E SMN SAC  

(2)

Từ

(1), (2) ( ) ( ) .SMN SAC SE  

( )SAN

và

( ).SCM

Ta có:

( ) ( )S SAN SCM 

(3)

Trong

( ),ABC

gọi

.F AN CM 

Ta có:

, ( ) ( )

( ) ( )

, ( ) ( )

F AN AN SAN F SAN

F SAN SCM

F CM CM SCM F SCM





   



  





   





(4)

Từ

(3), (4) ( ) ( ) .SAN SCM SF  

( )SMC

và

( ),ADN

với

là trung điểm của

.SB

................................................................................................................................................................................

 Cần nhớ:



Điểm thuộc đường thẳng, đường thẳng nằm trong mặt phẳng, điểm thuộc mặt phẳng.

Nghĩa là

, ( ) ( ).M d d P M P   



Với việc giải hình trong không gian là tập hợp nhiều mặt phẳng, điều kiện đầu tiên để hai đường thẳng cắt

nhau là hai đường thẳng trước hết phải đồng phẳng (cùng nằm trong một mặt phẳng). Khi gọi giao điểm

của hai đường thẳng cần kiểm tra hai đường thẳng đó đồng phẳng ở mặt phẳng nào, kiểm tra được điều đó

là đã trả lời được câu hỏi “có cắt nhau không ?”, “làm đúng không ?”

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 44 -

2. Cho tứ diện

.SABC

Gọi

, K M

lần lượt là hai điểm trên cạnh

và

sao cho

không song

song

.AC

Gọi

là trung điểm của cạnh

.BC

Tìm giao tuyến của

( )SAN

và

( ).ABM

.............................................................................................

( )SAN

và

( ).BCK

................................................................................................................................................................................

3. Cho hình chóp

. .S ABC

Trên cạnh

, SA SC

lấy

, M N

sao cho

không song song

.AC

Gọi

là trung điểm

.BC

Tìm giao tuyến của các cặp mặt phẳng:

( )MNK

và

( ).ABC

.............................................................................................

( )MNK

và

( ).SAB

................................................................................................................................................................................

4. Cho hình chóp

.S ABCD

có đáy

ABCD

là tứ giác lồi. Tìm giao tuyến của:

( )SAC

và

( ).SBD

.............................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 45 -

( )SAB

và

( ).SCD

..............................................................................

( )SAD

và

( ).SBC

.............................................................................................

5. Cho hình chóp

. ,S ABCD

trong đó mặt đáy

ABCD

có các cặp cạnh đối không song song. Gọi điểm

thuộc cạnh

.SA

Tìm giao tuyến của các cặp mặt phẳng:

( )SAC

và

( ).SBD

.............................................................................................

( )SAB

và

( ).SCD

..............................................................................

( )MBC

và

( ).SAD

.............................................................................................

6. Cho hình chóp

.S ABCD

có đáy

ABCD

là tứ giác lồi. Trên cạnh

lấy điểm

Tìm giao tuyến

của các cặp mặt phẳng sau đây:

( )SAC

và

( ).SBD

.............................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 46 -

( )SAB

và

( ).SCD

................................................................................................................................................................................

( )BCM

và

( ).SAD

................................................................................................................................................................................

( )CDM

và

( ).SAB

................................................................................................................................................................................

( )BDM

và

( ).SAC

................................................................................................................................................................................

7. Cho hình chóp

.S ABCD

có đáy là hình thang với

AB CD

và

.AB CD

Lấy điểm

nằm trên

đoạn

.BC

Tìm giao tuyến của các cặp mặt phẳng sau đây:

( )SAC

và

( ).SBD

.............................................................................................

( )SAB

và

( ).SCD

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 47 -

( )SAM

và

( ).SBD

................................................................................................................................................................................

( )SDM

và

( ).SAB

................................................................................................................................................................................

8. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Lấy điểm

trên cạnh

,SA

trung điểm

là

Tìm giao tuyến của các cặp mặt phẳng sau:

( )SAC

và

( ).SBD

.............................................................................................

( )BMN

và

( ).SAD

................................................................................................................................................................................

( )BMN

và

( ).SAC

................................................................................................................................................................................

( )MCD

và

( ).SBD

................................................................................................................................................................................

( )MCD

và

( ).SAB

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 48 -

9. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, , M N P

lần lượt là trung điểm

các cạnh

, , .BC CD SA

Tìm giao tuyến của các cặp mặt phẳng sau:

( )SAC

và

( ).SBD

.............................................................................................

( )MNP

và

( ).SAB

................................................................................................................................................................................

( )MNP

và

( ).SAD

................................................................................................................................................................................

( )MNP

và

( ).SBC

................................................................................................................................................................................

( )MNP

và

( ).SCD

................................................................................................................................................................................

10. Cho hình chóp

. .S ABC

Trên cạnh

, SA SC

lấy

, M N

sao cho

không song song

.AC

Gọi

là điểm nằm miền trong của tam giác

.ABC

Tìm giao tuyến của:

( )MNO

và

( ).ABC

.............................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 49 -

( )MNO

và

( ).SAB

................................................................................................................................................................................

( )SMO

và

( ).SBC

................................................................................................................................................................................

( )ONC

và

( ).SAB

................................................................................................................................................................................

11. Cho tứ diện

ABCD

có

nằm trên cạnh

, AB N

nằm trên cạnh

thỏa

2 ,MB MA



2 .AN ND

Gọi

là điểm thuộc miền trong của tam giác

.BCD

Tìm giao tuyến giữa:

( )CMN

và

( ).BCD

.............................................................................................

( )MNP

và

( ).SAD

................................................................................................................................................................................

( )MNP

và

( ).ABC

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 50 -

12. Cho tứ diện

.SABC

Lấy điểm

, E F

lần lượt trên đoạn

, SA SB

sao cho

không song song

với

.AB

Gọi

là trọng tâm của tam giác

.ABC

Hãy tìm giao tuyến giữa hai mặt phẳng:

( )EFG

và

( ).ABC

.............................................................................................

( )EFG

và

( ).SBC

................................................................................................................................................................................

( )EFG

và

( ).SGC

................................................................................................................................................................................

13. Cho hình chóp

.S ABCD

có đáy là tứ giác lồi. Hai điểm

, G H

lần lượt là trọng tâm của

SAB

và

.SCD

Tìm giao tuyến của các cặp mặt phẳng sau:

( )SGH

và

( ).ABCD

.............................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 51 -

( )SAC

và

( ).SGH

................................................................................................................................................................................

( )SAC

và

( ).BGH

................................................................................................................................................................................

( )SCD

và

( ).BGH

................................................................................................................................................................................

14. Cho tứ diện

.SABC

Gọi

, , D E F

lần lượt là trung điểm của

, , .AB BC SA

a) Tìm giao tuyến

của

( )SCD

và

( ).SAE

.............................................................................................

b) Tìm giao tuyến

của hai mặt phẳng

( )SCD

và

( ).BFC

................................................................................................................................................................................

c) Hỏi

và

có cắt nhau không ? Giải thích ? Nếu có, gọi giao điểm đó là

chứng minh

.IH SC

Tính tỉ số



................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 52 -

Daïng toaùn 2: Tìm giao ñieåm cuûa ñöôøng thaúng

vaø maët phaúng

( )

 Phương pháp giải

Nếu đường thẳng

cắt đường thẳng



( , d d



đồng phẳng) và

( )d 





thì giao điểm của

và

( )

chính là giao điểm

của

và



Nếu không có giao điểm như thế thì ta sẽ làm theo các bước sau:



Bước 1. Tìm mặt phẳng phụ

( )

thỏa

điều kiện:



Chứa đường thẳng



Có

điểm chung với

( ).



Càng lớn càng tốt.



Bước 2. Tìm giao tuyến

của

( )

và

( ).

 Bước 3. Trong

( ),

gọi

.I d u 

Khi đó:

, ( )

( ).

I u u

I d







 



  











 Lưu ý. Trong một số bài toán tìm giao tuyến nâng cao, ta có thể dễ dàng tìm được một điểm chung,

nhưng khó xác định điểm chung còn lại. Khi đó ta nghĩ đến việc tìm giao điểm của đường

thẳng nằm trong mặt phẳng này với mặt phẳng kia. Đó chính là điểm chung thứ hai của

hai mặt phẳng.

BÀI TẬP VẬN DỤNG

1. Cho tứ diện

SABC

có

là điểm nằm trên tia đối của tia

, SA O

là điểm thuộc miền của trong

tam giác

.ABC

Hãy tìm:

a) Giao điểm của đường thẳng

và

( ).SOA

Trong

( ),ABC

gọi

.E OA BC 

Ta có:

, ( ) ( )

E OA OA SOA E SOA

E BC





   













Suy ra:

( ).E BC SOA 

 Cần nhớ: Trước khi làm, ta cần kiểm tra xem đường

có

đồng phẳng và cắt đường thẳng nào nằm trong mặt phẳng

( )SOA

hay không ? Nếu có thì sẽ làm như trên, nếu không thì

sử dụng phương pháp mặt phụ.

b) Giao điểm của đường thẳng

và

( ).SBC



Chọn mặt phẳng phụ

( )MAE

chứa

.MO



Xét hai mặt phẳng

( )MAE

và

( ) :SBC

Ta có:

, ( ) ( )

( ) ( )

( )

S AM AM MAE S MAE

S MAE SBC

S SBC





   



  











(1)

Mặt khác:

, ( ) ( )

( ) ( )

, ( ) ( )

E AO BC MAE E MAE

E MAE SBC

E BC BC SBC E SBC





   



  





   





(2)

Từ

(1), (2) ( ) ( ) .MAE SBC SE  



Trong

( ),MAE

gọi

.F MO SE 

Khi đó

( ).

, ( )

F MO

F MO SBC

F SE SE SBC









  





 





§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 53 -

2. Cho tứ diện

SABC

có hai điểm

, M N

lần lượt thuộc hai cạnh

, SA SB

và

là điểm nằm trong

tam giác

.ABC

Hãy tìm

a) Giao điểm của đường thẳng

và

( ).SOC

....................................................................................................

b) Giao điểm của đường thẳng

và

( ).SOC

................................................................................................................................................................................

c) Giao điểm của đường thẳng

và

( ).CMN

................................................................................................................................................................................

3. Cho hình chóp

. .S ABC

Trên cạnh

lấy

sao cho

3 ,SA SM

trên cạnh

lấy điểm

sao

cho

2 .SC SN

Điểm

thuộc cạnh

.AB

Hãy tìm

a) Giao điểm của đường thẳng

và

( ).ABC

....................................................................................................

b) Giao điểm của đường thẳng

và

( ).MNP

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 54 -

4. Cho tứ diện

.ABCD

Trên

và

lần lượt lấy các điểm

, M N

sao cho

không song song

với

.CD

Gọi

là điểm thuộc miền trong của tam giác

.BCD

Hãy tìm

a) Giao điểm của đường thẳng

và

( ).BCD

....................................................................................................

b) Giao điểm của đường thẳng

và

( ).BMN

................................................................................................................................................................................

5. Cho hình chóp

.S ABCD

với

ABCD

là hình bình hành. Gọi

là điểm lấy trên cạnh

, SB N

là

điểm thuộc miền trong của tam giác

.SCD

Hãy tìm của

a) Đường thẳng

và

( ).ABCD

....................................................................................................

b) Đường thẳng

và

( ).MAN

................................................................................................................................................................................

c) Đường thẳng

và

( ).MAN

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 55 -

d) Đường thẳng

và

( ).CMN

................................................................................................................................................................................

6. Cho hình chóp

.S ABCD

có đáy hình bình hành tâm

có

là trọng tâm tam giác

.SAB

Tìm:

a) Giao tuyến của

( )SGC

và

( ).ABCD

....................................................................................................

b) Giao điểm của đường thẳng

và

( ).SGC

................................................................................................................................................................................

c) Giao điểm của đường thẳng

và

( ).GCD

................................................................................................................................................................................

d) Giao điểm của đường thẳng

và

( ).BCG

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 56 -

ÔN TẬP HÌNH PHẲNG

1) Đường trung bình

2) Trọng tâm

3) Định lý Talét

Đồng dạng (đồng hồ cát):

4) Định lý Menelaus

Cho tam giác

,ABC

các điểm

, , D E F

lần lượt nằm trên các đường thẳng

, , .BC CA AB

Khi đó:

, , D E F

thẳng hàng

FA DB EC

FB DC EA

   

Chứng minh phần thuận: Giả sử

, , D E F

thẳng hàng.

Từ

dựng

, ( ).CG AB G AC



DBF

có

DB FB

CG BF

DC CG

 

(1)



EC CG

CG AF

EA FA

 

(2)

Lấy

(1) (2),

ta được:

DB EC FB CG FA DB EC

DC EA CG FA FB DC EA

      

(đpcm).

Chứng minh phần đảo: (học sinh tự chứng minh).

là đường trung bình của tam giác

ABC

thì

.MN BC 

MN BC

Trọng tâm là giao điểm của ba đường trung tuyến.

Nếu

là trọng tâm tam giác

ABC

thì:

CG CM

AM AN MN

MN BC

AB AC BC

   



IA IB AB

AB CD

ID IC CD

   



§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 57 -

7. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, M N

lần lượt là trung điểm của

và

.CD

a) Tìm giao điểm

của

với

( ).BMN

Trong

( ),ABCD

gọi

.E BN AD



 

Ta có:

, ( ) ( )

( ).

E BN BN BMN E BMN

E AD BMN

E AD



 



   





  













Mà theo đề bài

( ) .E AD BMN E E



   

b) Tìm giao điểm

của

và

( ).BMN

Chứng minh rằng:

2 .FS FD

Cách giải 1. Sử dụng Menelaus:

Xét

SAE

có

, , M F E

thẳng hàng

1 1.2. 1 2 .

MS EA FD FD

FS FD

MA ED FS FS

       

Cách giải 2. Sử dụng dựng hình.

Dựng

, ( )DI SA I FE



Ta có:

FS SM

FMS FID

FD DI

   

mà

FS MA

SM MA

FD DI

   



Mà

là trung điểm

và

2 2 2 .

MA FS

DI MA FS FD

DI FD

     

Cách giải 3. Sử dụng trọng tâm.

Trong tam giác

,SAE

ta có

là đường trung tuyến

(1)

Vì trong tam giác

ABE

có

ND AB

và

ND AB

nên

là đường trung bình.

Suy ra

là trung điểm của

nên

là đường trung tuyến của tam giác

SAE

(2)

Mà

F SD EM F  

là trọng tâm của tam giác

2 .SAE FS FD 

 Bình luận. Tùy vào giáo viên trên lớp có hay không cho sử dụng định lý Menelaus mà ta chọn phương

pháp giải cho phù hợp. Đối với cách giải dựng hình ở cách 2 bản chất là chứng minh lại định lý

Menelaus. Nếu không cho sử dụng ta cũng nên học để biết cách dựng hình từ đâu và cách làm.

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 58 -

8. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành,

là trung điểm của

.SD

a) Tìm

( ).I BM SAC 

Chứng minh:

2 .BI IM

....................................................................................................

................................................................................................................................................................................

b) Tìm

( ).E SA BCM 

Chứng minh:

là trung điểm của

.SA

................................................................................................................................................................................

9. Cho tứ diện

.ABCD

Gọi

và

lần lượt là trung điểm của

và

.BC

Trên cạnh

lấy điểm

sao cho

2 .BK KD

a) Tìm giao điểm

của đường thẳng

và

( ).

IJK

Chứng minh:

.DE DC

....................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 59 -

b) Tìm giao điểm

của

với

( ).IJK

Chứng minh:

2FA FD

và

.FK IJ

................................................................................................................................................................................

c) Gọi

và

là hai điểm bất kì lần lượt nằm trên hai cạnh

và

.CD

Tìm giao điểm của

với

( ).IJK

................................................................................................................................................................................

10. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang, đáy lớn

và

2 .AB CD

Gọi

, , I J K

lần lượt là trung điểm của các cạnh

, , .SA AB BC

a) Tìm giao điểm của

và

( ).SBD

....................................................................................................

b) Tìm giao điểm

của

và

( ).IJK

Tính tỉ số



................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 60 -

c) Tìm giao điểm

của

và

( ).IJK

Tính tỉ số



................................................................................................................................................................................

11. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật tâm

Gọi

là trung điểm của

, SB N

là điểm thuộc đoạn

sao cho

2 .SN ND

a) Tìm giao tuyến của

( )SBD

và

( ).SAC

....................................................................................................

b) Tìm giao điểm

của đường thẳng

và mặt phẳng

( ).ABCD

Tính



................................................................................................................................................................................

c) Tìm giao điểm

của đường thẳng

và mặt phẳng

( ).AMN

Gọi

giao điểm của

và

.SO

Tính tỉ số:



................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 61 -

Daïng 3: Tìm thieát dieän cuûa hình (H) khi caét bôûi maët phaúng (P)

 Phương pháp giải

Ta tìm các đoạn giao tuyến nối tiếp nhau của mặt phẳng

( )

với các mặt của hình chóp cho đến

khi khép kín thành một đa giác phẳng. Đa giác đó là thiết diện cần tìm và các đoạn giao tuyến

chính là các cạnh của thiết diện.

1. Cho tứ diện

.ABCD

Trên các đoạn

,CA

, CB BD

cho lần lượt các điểm

, , M N P

sao cho

không song song với

.AB

Gọi

( )

là mặt phẳng xác định bởi ba điểm

, , .M N P

Dựng thiết diện

tạo bởi

( )

và tứ diện

.ABCD

Lời giải tham khảo

Ta có:

, , ( ) ( ) ( ).M N P MNP   



Ta có:

( ) ( )MNP BCD MP 

(1)



Tương tự:

( ) ( )MNP ABC MN 

(2)



Xét

( )MNP

và

( ) :ACD

Ta có:

, ( ) ( )

( ) ( ).

( )

N AC AC ACD N ACD

N ACD MNP

N MNP





   



  











Trong

( ),BCD

gọi

.E MP CD 

Ta có:

, ( ) ( )

( ) ( ).

, ( ) ( )

E MP MP MNP E MNP

E MNP ACD

E CD CD ACD E ACD





   



  





   





Suy ra

( ) ( )MNP ACD NP 

(3)



Trong

( ),ACD

gọi

.F NE AD 

Suy ra

( ) ( )MNP ACD NF 

(4)

Từ

(1),(2),(3),(4) 

thiết diện tạo bởi

( )

và tứ diện

ABCD

là tứ giác

.MNFP

 Bình luận. Bài toán thiết diện là bài toán tổng hợp của bài toán tìm giao điểm của đường thẳng với mặt

phẳng, bài toán tìm giao tuyến của mặt phẳng với mặt phẳng. Để kiểm tra xem thiết diện ta tìm đã “đúng

chưa ?”, có các cách như sau:

1. Mặt phẳng cắt đã “cắt rời” khối đa diện ban đầu thành hai khối đa diện mới chưa ?

2. Kiểm tra các đỉnh của đa giác thiết diện có nằm trên các cạnh của khối đa diện chưa ?

3. Kiểm tra các cạnh của đa giác thiết diện có nằm trên các mặt của khối đa diện chưa ?

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 62 -

2. Cho hình chóp

. .S ABC

Trên cạnh

, SA SB

lần lượt lấy

, M N

sao cho

không song song với

.AB

Gọi

là điểm thuộc miền trong tam giác

.ABC

Xác định thiết diện khi cắt hình chóp bởi

mặt phẳng

( ).MNP

....................................................................................................

................................................................................................................................................................................

3. Cho tứ diện

.SABC

Gọi

, K N

lần lượt là trung điểm

, SA BC

và

là điểm thuộc đoạn

sao cho

3 2 .SM MC

a) Tìm thiết diện của

( )KMN

với hình chóp.

.....................................................................................

................................................................................................................................................................................

b) Mặt phẳng

( )KMN

cắt

tại

Đặt

. .IA k IB

Tìm

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 63 -

4. Cho tứ diện

.ABCD

Trên

lấy điểm

Điểm

trên

thỏa

2 , BN NC P

là trung

điểm

.CD

Xác định thiết diện khi cắt bởi

( ).MNP

....................................................................................................

................................................................................................................................................................................

5. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang đáy lớn

.AD

Lấy

trên cạnh

.SB

Tìm

thiết diện cắt bởi

( ).AMD

....................................................................................................

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 64 -

6. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, , M N P

là các điểm lần lượt

trên các cạnh

, , .CB CD SA

Tìm thiết diện của hình chóp với

( ).MNP

....................................................................................................

................................................................................................................................................................................

7. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang đáy lớn

.AD

Gọi

, H K

là trung điểm của

và

, AB M

là điểm lấy trong hình thang

ABCD

sao cho đường thẳng

cắt hai đường

thẳng

, .AD CD

Tìm thiết diện của hình chóp với

( ).HKM

....................................................................................................

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 65 -

Daïng toaùn 4: Chöùng minh ba ñieåm thaúng haøng

 Phương pháp giải

Để chứng minh ba điểm

, , A B C

thẳng hàng, ta cần chứng minh ba điểm này lần lượt thuộc hai

mặt phẳng phân biệt

( )

và

( ).

Nghĩa là chúng cùng thuộc giao tuyến

của hai mặt phẳng

( )

và

( )

nên chúng thẳng hàng.

BÀI TẬP ÁP DỤNG

1. Cho tứ diện

.SABC

Trên các cạnh

, , SA SB SC

lần lượt lấy các điểm

, , M N P

sao cho

cắt

tại

, I NP

cắt

tại

và

cắt

tại

Chứng minh ba điểm

, , I J K

thẳng hàng.

Lời giải tham khảo

Gọi đường thẳng

là giao tuyến của hai mặt phẳng

( )MNP

và

( ).ABC

Ta có:

, ( ) ( )

K MP MP MNP K MNP

K MP AC K d

K AC AC ABC K ABC





   



    





   





(1)

Tương tự:

, ( ) ( )

I MN MN MNP I MNP

I MN AB I d

I AB AB ABC I ABC





   



    





   





(2)

, ( ) ( )

J NP NP MNP J MNP

J NP BC J d

J BC NP ABC J ABC





   



    





   





(3)

Từ

(1),(2),(3),

suy ra

, , I J K

cùng thuộc

d 

ba điểm

, , I J K

thẳng hàng (đpcm).



Bình luận. Cái khó của học sinh là tìm ra hai mặt phẳng

( )MNP

và

( )ABC

để tìm giao tuyến và ba điểm

, , I J K

đều thuộc giao tuyến. Để tìm ra nó, ta dựa vào kinh nghiệm sau:

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 66 -

2. Cho tứ diện

ABCD

có

là trọng tâm tam giác

.BCD

Gọi

, , M N P

lần lượt là trung điểm của

các cạnh

, , .AB BC CD

a) Xác định giao tuyến của

( )ADN

và

( ).ABP

....................................................................................................

b) Gọi

I AG MP 

và

.J CM AN 

Chứng minh

, , D I J

thẳng hàng.

................................................................................................................................................................................

3. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

hai điểm

, M N

lần lượt là trung

điểm của

, ,SB SD

điểm

thuộc

và không là trung điểm của

.SC

a) Tìm giao điểm của

với

( ).MNP

....................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 67 -

b) Tìm giao điểm của

với mặt phẳng

( ).MNP

................................................................................................................................................................................

c) Gọi

, , F G H

lần lượt là giao điểm của

và

, AB QP

và

, AC QN

và

.AD

Chứng minh ba

điểm

, , F G H

thẳng hàng.

................................................................................................................................................................................

4. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

hai điểm

, M N

lần lượt là trung

điểm của

, ,SB SD

điểm

thuộc

và không là trung điểm của

.SC

a) Tìm giao điểm của

với

( ).MNP

....................................................................................................

b) Tìm giao điểm của

với mặt phẳng

( ).MNP

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 68 -

c) Gọi

, , F G H

lần lượt là giao điểm của

và

, AB QP

và

, AC QN

và

.AD

Chứng minh ba

điểm

, , F G H

thẳng hàng.

................................................................................................................................................................................

5. Cho hình chóp

.S ABCD

có

không song song với

.BC

Lấy

thuộc

và

là giao điểm

với

.BD

a) Tìm giao điểm

của

với

( ).ADM

....................................................................................................

................................................................................................................................................................................

b) Gọi

.I AN DM 

Chứng minh

, , S I O

thẳng hàng.

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 69 -

BÀI TẬP RÈN LUYỆN GIAO TUYẾN



GIAO ĐIỂM



THẲNG HÀNG



TỈ SỐ

BT 1. Cho tứ diện

ABCD

có

là trọng tâm tam giác

.BCD

Gọi

, , M N P

lần lượt là trung điểm

của

, , .AB BC CD

a) Tìm giao tuyến của

( )ADN

và

( ).ABP

b) Gọi

I AG MP 

và

.J CM AN 

Chứng minh

, , D I J

thẳng hàng.

BT 2. Cho hình chóp

. .S ABCD

Gọi

, , E F H

lần lượt là các điểm thuộc cạnh

, , .SA SB SC

a) Tìm giao điểm

( ).K SD EFH 

b) Gọi

O AC BD 

và

.I EH FK 

Chứng minh:

, , S I O

thẳng hàng.

c) Gọi

M AD BC 

và

.N EK FH 

Chứng minh:

, , S M N

thẳng hàng.

d) Gọi

P AB CD 

và

.Q EF HK 

Chứng minh:

, , A P Q

thẳng hàng.

BT 3. Cho tứ diện

.ABCD

Gọi

, ,M N P

lần lượt là các điểm thuộc cạnh

, , AB AC BD

và

, , .MN BC I MP AD J NJ IP K     

Chứng minh:

, , C D K

thẳng hàng.

BT 4. Cho hình chóp

. .S ABCD

Gọi

và

là hai điểm trên hai cạnh

, .AD SB

a) Tìm giao tuyến của

( )SBI

và

( ).SAC

Tìm giao điểm

của

và

( ).SAC

b) Tìm giao tuyến của

( )SBD

và

( ).SAC

Tìm giao điểm

của

và

( ).SAC

c) Gọi

, .O AD BC M OJ SC   

Chứng minh rằng:

, , , A K L M

thẳng hàng.

BT 5. Cho tứ giác

ABCD

có các cạnh đối đôi một không song song và điểm

( ).S ABCD

Lấy điểm

thuộc cạnh

,AD

lấy điểm

thuộc cạnh

.SB

a) Tìm

( ).K IJ SAC 

( ).L DJ SAC 

c) Gọi

, .O AD BC M OJ SC   

Chứng minh rằng:

, , K L M

thẳng hàng.

BT 6. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

, M N

lần lượt là trung

điểm của

, .SA SC

a) Tìm giao tuyến của

( )BMN

với các mặt phẳng

( )SAB

và

( ).SBC

b) Tìm

( )I SO BMN 

và

( ).K SD BMN 

c) Tìm

( )E AD BMN 

và

( ).F CD BMN 

d) Chứng minh rằng ba điểm

, , B E F

thẳng hàng.

BT 7. Cho hình chóp

. .S ABCD

Gọi

, M N

là 2 điểm lần lượt nằm trên 2 cạnh

và

.SD

a) Tìm giao điểm

của

và

( ).SAC

b) Tìm giao điểm

của

và

( ).SAC

c) Chứng minh:

, , I J C

thẳng hàng.

d) Xác định thiết diện của mặt phẳng

( )BCN

với hình chóp.

BT 8. Cho tứ diện

ABCD

có

là trung điểm của

.AB

Lấy

, I J

lần lượt thuộc

, AC BD

sao cho

2IA IC

và

3 .JB JD

a) Tìm giao điểm

của

và

( ).IJK

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 70 -

b) Tìm giao tuyến

của

( )IJK

và

( ).BCD

c) Gọi

là giao điểm của

với

.CD

Chứng minh:

, , I O E

thẳng hàng.

d) Tính các tỉ số

và



BT 9. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang,

là đáy lớn và

2 .AD BC

Gọi

, M N

lần lượt là trung điểm của

, SB SC

và

.O AC BD 

a) Tìm giao tuyến của

( )ABN

và

( ).SCD

b) Tìm giao điểm

của

và

( ).SAB

c) Gọi

.K AN DM 

Chứng minh

, , S K O

thẳng hàng. Đặt

. .KS k KO

Tìm

BT 10. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

, M N

lần lượt là trung

điểm của

, .SA SC

Gọi

( )P

là mặt phẳng qua

, M N

và

a) Tìm giao tuyến của

( )P

với các mặt phẳng

( ), ( ), ( ), ( ).SAB SBC SAD SDC

b) Tìm

( ), ( ), ( ), ( ).I SO P K SD P E DA P F DC P       

c) Chứng tỏ rằng ba điểm:

, , E B F

thẳng hàng.

BT 11. Cho hình chóp

.S ABCD

có đáy

ABCD

là tứ giác có các cặp cạnh đối không song song nhau.

Gọi

, M E

là trung điểm

, SA AC

và

F CD

sao cho

3 .CD CF

a) Tìm giao tuyến của

( )SAB

và

( ).SCD

b) Tìm giao điểm

của

và

( ).MEF

Đặt

. .NS k ND

Tìm

c) Gọi

H SE CM 

và

.K MF NE 

Chứng minh

, , D H K

thẳng hàng.

d) Tính các tỉ số sau:

; ; ; ;

HM HS KM KN KH

HC HE KF KE KD



BT 12. Cho tứ diện

.ABCD

Trên các cạnh

, , AB AC BD

lần lượt lấy ba điểm

, , E F G

sao cho

3 , 2 , 4 .AB AE AC AF DB DG  

a) Tìm giao tuyến của hai mặt phẳng

( )EFG

và

( ).BCD

b) Tìm giao điểm

của đường thẳng

với

( ).EFG

Tính tỉ số



c) Tìm giao điểm

của đường thẳng

với

( ).EFG

Tính tỉ số



d) Chứng minh ba điểm

, , F H I

thẳng hàng.

e) Gọi

là trung điểm của

, BC AJ

cắt

tại

Tính tỉ số



§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 71 -

Daïng toaùn 5: Chöùng minh ba ñöôøng thaúng ñoàng quy

 Phương pháp giải

Để chứng minh ba đường thẳng

, , a b c

đồng quy, ta làm theo các bước sau:



Chọn mặt phẳng

( )P

chứa đường thẳng

và

Giả sử

.I a b 



Tìm mặt phẳng

( )Q

chứa

và

( )R

chứa

sao cho

( ) ( ) .Q R c I c   

Suy ra:

, , a b c

đồng quy tại

Nghĩa là:

( ), ( ),

( ) ( )

a P b P I a b

a P Q

a b c I

b P R

c Q R





   



 



   





 



 





BÀI TẬP VẬN DỤNG

1. Cho hình chóp

.S ABCD

có

không song song

.CD

Gọi

là trung điểm

và

là giao

điểm

với

.BD

a) Tìm giao điểm

của

với

( ).MAB

Chọn mặt phẳng phụ

( )SCD

chứa

.SD

Xét

( )SCD

và

( ) :MAB

Trong

( ),ABCD

gọi

.E AB CD 

Ta có:

, ( ) ( )

E AB AB ABM E ABM

E CD CD SCD E SCD





   







   





( ) ( )E ABM SCD  

(1)

Mà

( )

, ( ) ( )

M ABM

M SC SC SCD M SCD













   





( ) ( )M ABM SCD  

(2)

Từ

(1), (2) ( ) ( ) .ABM SCD EM  

Trong

( )SCD

gọi

.N SD EM 

Khi đó:

( ).

, ( )

N SD

N SD ABM

N EM EM ABM









  





 





b) Chứng minh rằng ba đường thẳng

, , SO AM BN

đồng quy.



Phân tích: Nhận thấy rằng

( ), ( )AM SAC BN SBD 

nên ta quan tâm đến

mặt này.

Xét

( )SAC

và

( )SBD

có:

( ) ( )S SAC SBD 

(3)

Ta có:

, ( ) ( )

( ) ( )

, ( ) ( )

O AC AC SAC O SAC

O SAC SBD

O BD BD SBD O SBD





   



  





   





(4)

Từ

(3), (4) ( ) ( ) .SAC SBD SO  

Mặt khác, trong

( ),ABM

gọi

.I AM BN 

( )

( ) ( ) .

( )

I AM SAC

I SAC SBD I SO

I BN SBD





 



     





 





Do đó

, , SO AM BN

đồng quy.

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 72 -

2. Cho hình chóp

.S ABCD

có đáy

ABCD

là tứ giác lồi. Lấy

trên cạnh

.SC

Gọi

là giao điểm của

và

( ).ADM

Gọi

là giao điểm

và

.BD

Chứng

minh rằng

, , SO AM DN

đồng qui.

...............................................................................................

3. Cho hình chóp

. , ( ).S ABCD AB CD

Trên cạnh

lấy

không trùng với

và

a) Tìm giao điểm

của

với

( ).ABE

...............................................................................................

b) Chứng minh ba đường thẳng

, , AB CD EF

đồng qui.

.................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 73 -

§ 2. HAI ĐƯỜNG THẲNG SONG SONG

1. Vò töông ñoái cuûa hai ñöôøng thaúng phaân bieät

Cho hai đường thẳng phân biệt

và

Định nghĩa



Hai đường thẳng gọi là đồng phẳng nếu chúng cùng nằm trong một mặt phẳng.



Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng.



Hai đường thẳng gọi là song song nếu chúng đồng phẳng và không có điểm chung.

2. Tính chaát hai ñöôøng thaúng song song



Tính chất 1. Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một

và chỉ một đường thẳng song song với đường thẳng đã cho.



Tính chất 2. (Định lý về giao tuyến của ba mặt phẳng). Nếu ba mặt phẳng phân biệt đôi một cắt

nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song

với nhau.

Hệ quả. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến

của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường

thẳng đó.



Tính chất 3. Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song

với nhau.

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 74 -

Daïng toaùn 1: Chöùng minh hai ñöôøng thaúng song song

 Phương pháp giải



Cách 1. Chứng minh hai đường thẳng

, a b

đồng phẳng, rồi dùng các định lý trong hình học

phẳng, chẳng hạn định lý đường trung bình, định lý đảo Thales,… để chỉ ra

.a b



Cách 2. Chứng minh hai đường thẳng đó cùng song song với đường thẳng thứ ba. Cụ thể,

chứng minh:

c a

a b

c b

















Cách 3. Áp dụng định lý về giao tuyến của ba mặt phẳng và hệ quả của nó.

Chẳng hạn: chứng minh:

( ), ( )

( ) ( )

b c a b c

b c a b

a a c

 

 











    











  







 

  

1. Cho tứ diện

ABCD

có

, I J

lần lượt là trọng tâm tam giác

ABC

và

.ABD

Chứng minh:

.IJ CD



Gọi

, E F

lần lượt là trung điểm của

, .BC BD

EF

là đường trung bình của tam giác

.BCD

EF CD 

(1)

Vì

là trọng tâm

ABC

  

Vì

là trọng tâm

ABD

  

Suy ra:

AI AJ

IJ EF

AE AF

   

(2)

Từ

(1), (2),

suy ra

.IJ CD

2. Cho tứ diện

.ABCD

Gọi

, , , , , M N P Q R S

lần lượt là trung điểm của

, ,AB CD

,BC

,AD

, .AC BD

Chứng minh

MNPQ

là hình bình hành. Từ đó suy ra ba đoạn thẳng

, , MN PQ RS

cắt

nhau tại trung điểm

của mỗi đoạn.

Ta có:

, , , , , M N P Q R S

lần lượt là trung điểm của các

cạnh:

, ,AB CD

,BC

,AD , .AC BD

, , , , , , , MP PN NQ QM MR RN NS SM

lần lượt là

đường trung bình của các tam giác

,ABC

,BCD

,ACD

,ABD

,ABC

,ACD

,BCD

.ABD

MP AC NQ

MPNQ

MQ BD PN





 







 

là hình bình hành.

MR BC SN

MRNS

MS AD RN





 







 

là hình bình hành.

Gọi

G MN RS 

và

.G MN PQ



 

G

là trung điểm của

và

.MN

G G



 

nên ba đoạn thẳng

, , MN PQ RS

cắt nhau tại

trung điểm của mỗi đoạn (đpcm).

B D

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 75 -

3. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

, M N

lần lượt là trung

điểm của

, .SA SD

Chứng minh:

MN AD

và

.MN BC

...................................................................................................... `

.......................................................................................................

MO SC

và

.NO SB

................................................................................................................................................................................

4. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

, M N

lần lượt là trung

điểm của

, .AB AD

Gọi

, , I J G

lần lượt là trọng tâm của các tam giác:

,SAB

, .SAD AOD

Chứng

minh rằng:

.IJ MN

...................................................................................................... `

.......................................................................................................

IJ BD

và

.GJ SO

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 76 -

5. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật tâm

Gọi

là trọng tâm tam giác

SAD

và

là điểm trên cạnh

sao cho

3 , DC DE I

là trung điểm

.AD

a) Tìm giao điểm

của

và

( ).SBC

.......................................................................................................

b) Chứng minh:

.GE SP

................................................................................................................................................................................

6. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang, cạnh đáy lớn

với

2 ,AB CD

cắt

tại

Gọi

là trọng tâm của tam giác

SBC

và

là trung điểm của

.SC

a) Tìm giao điểm đường thẳng

và

( ).ADM

.......................................................................................................

b) Chứng minh:

.GO MD

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 77 -

Daïng toaùn 2: Giao tuyeán song song

 Phương pháp giải

Để tìm giao tuyến của hai mặt phẳng

( )

và

( )

có chứa hai đường thẳng song song lần lượt nằm

trong hai mặt phẳng, ta làm như sau:

Ta có:

( ) ( )

( ), ( )

a b Ax

a b

 





 



  





 







với

.Ax a b 

BÀI TẬP VẬN DỤNG

1. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Điểm

thuộc cạnh

.SA

Điểm

, E F

lần lượt là trung điểm của

và

.BC

Tìm giao tuyến giữa các cặp mặt phẳng sau:

( )SAB

và

( ).SCD

Ta có:

( ) ( )

( ), ( )

S SAB SCD

AB CD

AB SAB CD SCD





 







 







( ) ( )SAB SCD Sx  

với

.Sx AB CD 

 Nhận xét. Có hai phương pháp tìm giao tuyến, một là tìm hai

điểm chung và nối chúng lại. Hai là giao tuyến đi

qua một điểm chung và song song với hai đường

thẳng lần lượt song song nằm trong hai mặt.

( )SBC

và

( ).SAD

................................................................................................................................................................................

( )MBC

và

( ).SAD

................................................................................................................................................................................

( )MEF

và

( ).SAC

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 78 -

2. Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

là trọng tâm của tam giác

.SAD

a) Tìm giao tuyến của

( )SAB

và

( ).SCD

.......................................................................................................

b) Tìm giao điểm của đường thẳng

và mặt phẳng

( ).GBC

................................................................................................................................................................................

3. Cho hình chóp

.S ABCD

có đáy là

ABCD

là hình thang, đáy lớn

.AB

Gọi

là trung điểm của

.SC

a) Tìm giao tuyến của

( )SAC

và

( ).SBD

.......................................................................................................

b) Tìm giao điểm của đường thẳng

và

( ).MAD

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 79 -

4. Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

là trung điểm

,SC

là trung điểm

của

,SM

là trung điểm của

và

thuộc cạnh

sao cho

3 .ND NA

a) Tìm giao tuyến của

( )SAC

và

( ).SBD

.......................................................................................................

b) Tìm giao tuyến của

( )SAD

và

( ).SBC

.......................................................................................................

c) Chứng minh:

.IJ SA

................................................................................................................................................................................

d) Chứng minh:

.NJ AB

................................................................................................................................................................................

5. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là trọng tâm của tam giác

SBC

và

là một điểm nằm trên đoạn thẳng

sao cho

3 .BE BD

a) Tìm giao tuyến của

( )SAB

và

( ).SCD

.......................................................................................................

b) Tìm giao tuyến của

( )SAC

và

( ).SBC

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 80 -

c) Tìm giao điểm của đường thẳng

và

( ).ADG

................................................................................................................................................................................

d) Chứng minh:

.GE SA

................................................................................................................................................................................

6. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang đáy lớn

,AB

3 ,AB a

2 .CD a

Gọi

là

giao điểm của

và

, BD M

là điểm trên cạnh

sao cho

5 3 .AM SA

a) Tìm giao tuyến của

( )SAD

và

( ).SBC

......................................................................................................

b) Tìm giao điểm

của đường thẳng

và

( ).MCD

Chứng minh:

.ON SD

................................................................................................................................................................................

c) Gọi

.I SO MC 

Tính tỉ số:



................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 81 -

§ 3. ĐƯỜNG THẲNG SONG SONG MẶT PHẲNG



1. Vò töông ñoái cuûa ñöôøng thaúng vôùi maët phaúng

Cho đường thẳng

và mặt phẳng

( ).P

Có ba trường hợp xảy ra:



Đường thẳng

và

( )P

có

điểm chung phân biệt

( )d P 

(hình 1)



Đường thẳng

và

( )P

có

điểm chung duy nhất

( )d P A  

(hình 2)



Đường thẳng

và

( )P

không có điểm chung nào

( )d P 

(hình 3)

Hình 1 Hình 2 Hình 3

Định nghĩa. Đường thẳng

và mặt phẳng

( )P

gọi là song song với nhau nếu chúng không có điểm

chung.

2. Caùc ñònh lí



Định lí 1. Nếu đường thẳng

không nằm trong mặt phẳng

( )

và

song song với đường thẳng



nằm trong

( )

thì

song song với

( ).



Định lí 2. Cho đường thẳng

song song với mặt phẳng

( ).

Nếu mặt phẳng

( )

chứa

và cắt

( )

theo giao tuyến

thì

song song với

Hệ quả: Nếu hai mặt phẳng phân biệt cắt nhau và cùng song song với một đường thẳng

thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.



Định lí 3. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và

song song với đường thẳng kia.

Daïng toaùn 1: Chöùng minh ñöôøng thaúng d song song maët phaúng

(P)

 Phương pháp giải

Để chứng minh đường thẳng

song song với mặt phẳng

( ),P

ta cần chứng minh đường thẳng

song song với một đường thẳng



nằm trong mặt phẳng

( ).P

Hiển nhiên đường thẳng

này

không nằm trong

( ).P

Cụ thể, để chứng minh

( ),d P

ta cần:

( ) ( ).

( )

d d

d P d P

d P











 













BÀI TẬP ÁP DỤNG

1. Cho tứ diện

.ABCD

Gọi

và

lần lượt là trọng tâm của các tam giác

ACD

và

.BCD

Chứng

minh rằng

song song với các mặt phẳng

( )ABC

và

( ).ABD

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 82 -

Gọi

là trung điểm của

.CD

Vì

và

lần lượt là trọng tâm của các tam giác

ACD

và

BCD

EM EN

EA EB

   

Áp dụng định lý Thales vào

.ABE MN AB  

Ta có:

( ) ( ).

( )

MN AB

AB ABC MN ABC

MN ABC





 













Tương tự:

( ) ( )

( )

MN AB

AB ABD MN ABD

MN ABD





 













(đpcm).

2. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, M N

lần lượt là trung điểm của

các cạnh

và

.CD

a) Chứng minh:

( )MN SBC

và

( ).MN SAD

....................................................................................................... `

........................................................................................................

b) Gọi

là trung điểm của

.SA

Chứng minh:

( )SB MNE

và

( ).SC MNE

................................................................................................................................................................................

3. Cho hình chóp

.S ABCD

có đáy

ABCD

là

hình bình hành tâm

Gọi

, M N

lần lượt

là trung điểm

, .SA SD

Chứng minh:

( )BC SAD

và

).(AD SBC

..........................................................................................

B D

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 83 -

( )MN ABCD

và

( ).MN SBC

..................................................................................

)(MO SCD

và

( ).NO SBC

..........................................................................................

4. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật tâm

Gọi

là trọng tâm tam giác

SAD

và

là điểm trên cạnh

sao cho

3 , DC DE I

là trung điểm

.AD

a) Chứng minh:

( )OI SAB

và

( ).OI SCD

........................................................................................................ `

........................................................................................................

b) Tìm giao điểm

của

và

( ).SBC

Chứng minh:

( ).GE SBC

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 84 -

5. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, , M N P

lần lượt là trung điểm

của

,AB

và

.SA

a) Chứng minh:

( )MN SAD

và

( ).SB MNP

....................................................................................................... `

........................................................................................................

b) Gọi

, G I

là trọng tâm của tam giác

ABC

và

.SBC

Chứng minh:

( ).GI SAB

................................................................................................................................................................................

6. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang đáy lớn

,AB

với

2 .AB CD

Gọi

là giao

điểm của

và

, BD I

là trung điểm của

, SA G

là trọng tâm của tam giác

SBC

và

là một

điểm trên cạnh

sao cho

3 2 .SE SD

a) Chứng minh:

( ).DI SBC

................................................................................................................................................................................

b) Chứng minh:

( ).GO SCD

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 85 -

c) Chứng minh:

( ).SB ACE

................................................................................................................................................................................

7. Cho hình chóp

.S ABCD

có đáy là hình thang

( ).AB CD

Biết

2 .AB CD

Gọi

, G H

lần lượt là

trọng tâm tam giác

SAD

và

,SBC

gọi

, E F

lần lượt là trung điểm của

, .AD BC

a) Tìm giao tuyến của

( )SAB

và

( ).SCD

.................................................................................................

b) Chứng minh rằng:

( ).GH SCD

................................................................................................................................................................................

c) Gọi

là giao điểm của

và

, DH L

là giao điểm của

và

.DF

Chứng minh ba điểm

, , S K L

thẳng hàng và tính tỉ số



................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 86 -

8. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

, M N

lần lượt là trung

điểm của

và

.CD

a) Tìm giao điểm

( ).E AD BMN 

................................................................................................

b) Tìm giao điểm

( ).F SD BMN 

Chứng minh:

2 .SF FD

................................................................................................................................................................................

c) Gọi

là trung điểm

,ME

.G AN BD 

Chứng minh:

( ).FG SAB

................................................................................................................................................................................

d) Gọi

.H MN SG 

Chứng minh:

.OH GF

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 87 -

Daïng toaùn 2: Tìm thieát dieän song song vôùi moät ñöôøng thaúng

 Phương pháp giải

Để tìm thiết diện của mặt phẳng

( )

đi qua một điểm và song song với hai đường thẳng chéo nhau

hoặc

( )

chứa một đường thẳng và song song với một đường thẳng,thường sử dụng tính chất sau:

( ) ( )

( ) ( ) ( ) ,

( )

d a

 

  







 



  













với

a d

( ).M a

1. Cho hình chóp

. ,S ABCD

đáy

ABCD

là hình thang, đáy lớn

.AB

Gọi

là giao điểm của

và

; , BD E K

lần lượt là trung điểm

, .BC SC

a) Chứng minh:

( ).EK SAB

....................................................................................................... `

........................................................................................................

b) Gọi mặt phẳng

( )P

qua

và song song với

và

.SA

Tìm thiết diện cắt của hình chóp

S ABCD

với mặt phẳng

( ).P

Lời giải tham khảo



Ta có

( ) ( )

( ) ( ) ( ) ,

( )

O P ABCD

BC ABCD ABCD P Ox

BC P





 



   









với

.Ox BC

Trong

( ),ABCD

gọi

, ( )

M Ox DC

M N P

M Ox AB





 



 





 





(1)



Ta lại có:

( ) ( )

( ) ( ) ( ) ,

( )

N P SAB

SA P SAB P Ny

SA SAB





 



  













với

.Ny SA

Trong

( ),SAB

gọi

( )T Ny SB T P   

(2)



Tương tự

( ) ( )

( ) ( ) ( ) ,

( )

T P SBC

BC P SBC P Tz

BC SBC





 



  













với

.Tz BC

Trong

( ),SBC

gọi

( )R Tz SC R P   

(3)



Từ

(1), (2), (3),

suy ra thiết diện cần tìm là tứ giác

.MNTR

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 88 -

2. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành,

là giao điểm của

và

, BD M

là

trung điểm

.SA

a) Chứng minh:

( ).OM SCD

....................................................................................................... `

........................................................................................................

b) Gọi

( )

là mặt phẳng đi qua

đồng thời song song với

và

.AD

Tìm thiết diện của mặt

phẳng

( )

với hình chóp

. .S ABCD

................................................................................................................................................................................

3. Cho tứ diện

.ABCD

Gọi

, I J

lần lượt là trung điểm của

và

, CD M

là một điểm trên đoạn

.IJ

Gọi

( )P

là mặt phẳng qua

song song với

và

.CD

a) Tìm giao tuyến của mặt phẳng

( )P

và

( ).ICD

....................................................................................................... `

........................................................................................................

b) Xác định thiết diện của tứ diện với mặt phẳng

( ).P

Thiết diện là hình gì ?

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 89 -

4. Cho hình chóp

. .S ABCD

Gọi

, M N

thuộc cạnh

, .AB CD

Gọi

( )

là mặt phẳng qua

và song

song

.SA

..................................................................

a) Tìm thiết diện của

( )

và hình chóp.

....................................................................................................... `

........................................................................................................

b) Tìm điều kiện của

, M N

để thiết diện là hình thang.

................................................................................................................................................................................

5. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

và

lần lượt là trọng

tâm của các tam giác

ABC

và

.SBC

a) Chứng minh:

( ).KJ SAB

....................................................................................................... `

........................................................................................................

b) Gọi

( )P

là mặt phẳng chứa

và song song với

.AD

Tìm thiết diện của hình chóp cắt bởi mặt

phẳng

( ).P

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 90 -

6. Cho tứ diện

.ABCD

Gọi

là điểm thuộc

sao cho

2 .MC MB

Gọi

, N P

lần lượt là trung

điểm của

và

.AD

a) Chứng minh:

( ).NP ABC

....................................................................................................... `

........................................................................................................

b) Tìm giao điểm

( )Q AC MNP 

và tính



Suy ra thiết diện của hình chóp bị cắt bởi

( ).MNP

................................................................................................................................................................................

c) Chứng minh:

( ),MG ABD

với

là trọng tâm của tam giác

.ACD

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 91 -

7. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, , M N P

lần lượt là trung điểm

của các cạnh

, , .AB AD SB

a) Chứng minh:

( ).BD MNP

....................................................................................................... `

........................................................................................................

b) Tìm giao điểm của

( )MNP

với

.BC

................................................................................................................................................................................

c) Tìm giao tuyến của hai mặt phẳng

( )MNP

và

( ).SBD

................................................................................................................................................................................

d) Tìm giao tuyến của hai mặt phẳng

( )MNP

và

( ).SBD

................................................................................................................................................................................

8. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

là trọng tâm

; SAB N

là

một điểm thuộc đoạn

sao cho:

;



là trung điểm

.AB

a) Chứng minh:

( ).OI SAD

....................................................................................................... `

........................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 92 -

b) Chứng minh:

( ).GN SDC

................................................................................................................................................................................

c) Gọi

( )

là mặt phẳng đi qua

và song song với

và

.BC

Mặt

( )

cắt

, SB SC

lần lượt tại

và

Tìm hình tính thiết diện cắt bởi mặt phẳng

( )

với hình chóp

. .S ABCD

................................................................................................................................................................................

9. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Điểm

thuộc cạnh

thỏa

3 2 .MA MS

Hai điểm

và

lần lượt là trung điểm của

và

.BC

a) Xác định giao tuyến của

( )MEF

và

( ).SAC

....................................................................................................... `

........................................................................................................

b) Xác định giao điểm

của mặt phẳng

( )MEF

với cạnh

.SD

Tính tỉ số:



................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 93 -

................................................................................................................................................................................

c) Tìm giao điểm

của

với

( ).SBD

Tính tỉ số:



................................................................................................................................................................................

d) Tìm thiết diện tạo bởi mặt phẳng

( )MEF

cắt các mặt của hình chóp

. .S ABCD

................................................................................................................................................................................

10. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang đáy lớn

.AB

Gọi

, M N

lần lượt là trung

điểm của các cạnh

và

.SD

a) Tìm giao tuyến của:

( )SAD

và

( ).SBC

................................................................................................

b) Tìm giao điểm

của

và mặt phẳng

( ).SAC

................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 94 -

c) Tìm giao điểm

của

và mặt phẳng

( ).BMN

Suy ra:

( ).IJ SAB

................................................................................................................................................................................

d) Gọi

( )

là mặt phẳng chứa đường thẳng

và song song với

.CD

Thiết diện của mặt phẳng

( )

và hình chóp

.S ABCD

là hình gì ?

................................................................................................................................................................................

BÀI TẬP ÔN TẬP: GIAO TUYẾN



GIAO ĐIỂM



SONG SONG



THIẾT DIỆN

BT 1. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

, M N

lần lượt là trung

điểm

, .SA SD

Chứng minh rằng:

( ).BC SAD

)( .AD SBC

( ).MN ABCD

( ).MN SBC

)( .MO SCD

( ).NO SBC

BT 2. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Gọi

là trọng tâm tam giác

SAD

và

là điểm trên cạnh

sao cho

3 , DC DE I

là trung điểm

.AD

a) Chứng minh:

( )OI SAB

và

( ).OI SCD

b) Tìm giao điểm

của

và

( ).SBC

Chứng minh:

( ).GE SBC

BT 3. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, M N

lần lượt là trung điểm

của

và

.CD

a) Chứng minh:

( )MN SBC

và

( ).MN SAD

b) Gọi

là điểm trên cạnh

.SA

Chứng minh:

( )SB MNP

và

( ).SC MNP

c) Gọi

, G I

là trọng tâm của tam giác

ABC

và

.SBC

Chứng minh:

( ).GI SAB

BT 4. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang đáy lớn

,AB

với

2 .AB CD

Gọi

là

giao điểm của

và

, BD I

là trung điểm của

, SA G

là trọng tâm của tam giác

SBC

và

là một điểm trên cạnh

sao cho

3 2 .SE SD

Chứng minh:

( ).DI SBC

( ).GO SCD

( ).SB ACE

BT 5. Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

Gọi

, M N

là trung điểm các cạnh

.,AB AD

Gọi

, I J

thuộc

, SM SN

sao cho

SI SJ

SM SN

  

Chứng minh:

( ).MN SBD

( ).IJ SBD

( ).SC IJO

BT 6. Cho tứ diện

ABCD

có

là trọng tâm của tam giác

ABD

và

là điểm trên cạnh

sao cho

2 .BI IC

Chứng minh rằng:

( ).IG ACD

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 95 -

BT 7. Cho tứ diện

.ABCD

Gọi

, G P

lần lượt là trọng tâm của các tam giác

ACD

và

.ABC

Chứng

minh rằng:

( )GP ABC

và

( ).GP ABD

BT 8. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành,

là giao điểm của

và

, BD M

là trung điểm

.SA

a) Chứng minh:

( ).OM SCD

b) Gọi

( )

là mặt phẳng đi qua

đồng thời song song với

và

.AD

Tìm thiết diện của

mặt phẳng

( )

với hình chóp

. .S ABCD

BT 9. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang đáy lớn

.AB

Gọi

là trung điểm

, ( )CD 

là mặt phẳng qua

đồng thời song song với

và

.BC

Tìm thiết diện của

( )

với

hình chóp

. .S ABCD

Thiết diện là hình gì ?

BT 10. Cho hình chóp

. .S ABCD

Gọi

, M N

thuộc cạnh

, .AB CD

Gọi

( )

là mặt phẳng qua

và

song song

.SA

a) Tìm thiết diện của

( )

và hình chóp.

b) Tìm điều kiện của

để thiết diện là hình thang.

BT 11. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là trung điểm của cạnh

và

( )P

là mặt phẳng qua

và song song với

.BD

a) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng

( ).P

b) Gọi

, E F

lần lượt là giao điểm của

( )P

với các cạnh

và

.SD

Tìm tỉ số diện tích của

SME

với

SBC

và tỉ số diện tích của

SMF

với

.SCD

c) Gọi

là giao điểm của

và

, CB J

là giao điểm của

và

.CD

Chứng minh

, , K A J

nằm trên đường thẳng song song với

và tìm tỉ số



BT 12. Cho tứ diện

.ABCD

Gọi

, M N

là hai điểm lần lượt nằm trên hai cạnh

và

.AD

Xác định

thiết diện của tứ diện cắt bởi mặt phẳng

( )

qua

và song song với

.CD

Xác định vị trí của

hai điểm

, M N

để thiết diện là hình bình hành.

BT 13. Cho tứ diện

.ABCD

Gọi

, I J

lần lượt là trung điểm của

và

, CD M

là một điểm trên đoạn

.IJ

Gọi

( )P

là mặt phẳng qua

song song với

và

.CD

a) Tìm giao tuyến của mặt phẳng

( )P

và

( ).ICD

b) Xác định thiết diện của tứ diện với mặt phẳng

( ).P

Thiết diện là hình gì ?

BT 14. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

và

lần lượt là trọng

tâm của các tam giác

ABC

và

.SBC

a) Chứng minh KJ // (SAB)

b) Gọi

( )P

là mặt phẳng chứa

và song song với

.AD

Tìm thiết diện của hình chóp cắt bởi

mặt phẳng

( ).P

BT 15. Cho tứ diện

.ABCD

Gọi

1 2

,G G

lần lượt là trọng tâm của các tam giác

ACD

và

.BCD

Chứng

minh rằng:

1 2

( )G G ABC

và

1 2

( ).G G ABD

BT 16. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là trọng tâm của

, SAB I

là trung điểm

,AB

lấy điểm

trong đoạn

sao cho

3 .AD AM

a) Tìm giao tuyến của hai mặt phẳng

( )SAD

và

( ).SBC

b) Đường thẳng qua

và song song

cắt

tại

Chứng minh

( ).NG SCD

c) Chứng minh:

( ).MG SCD

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 96 -

BT 17. Cho hình chóp

. ,S ABCD

đáy

ABCD

là hình thang với đáy lớn

và

2 .AD BC

Gọi

là

giao điểm của

và

, BD G

là trọng tâm của tam giác

.SCD

a) Chứng minh:

( ).OG SBC

b) Cho

là trung điểm của

.SD

Chứng minh:

( ).CM SAB

c) Gọi

là điểm trên cạnh

sao cho

2 3 .SC SI

Chứng minh:

( ).SA BDI

BT 18. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, , M N P

lần lượt là trung

điểm của các cạnh

, , .AB AD SB

a) Chứng minh:

( ).BD MNP

b) Tìm giao điểm của

( )MNP

với

.BC

c) Tìm giao tuyến của hai mặt phẳng

( )MNP

và

( ).SBD

d) Tìm thiết diện của hình chóp với

( ).MNP

BT 19. Cho tứ diện

.ABCD

Gọi

là điểm thuộc

sao cho

2 .MC MB

Gọi

, N P

lần lượt là

trung điểm của

và

.AD

a) Chứng minh:

( ).NP ABC

b) Tìm giao điểm

của

với

( )MNP

và tính



Suy ra thiết diện của hình chóp bị cắt

bởi

( ).MNP

c) Chứng minh:

( ),MG ABD

với

là trọng tâm của tam giác

.ACD

BT 20. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành.

a) Tìm giao tuyến của

( )SAC

và

( ); ( )SBD SAB

và

( ).SCD

b) Một mặt phẳng qua

và song song với

cắt

tại

, ( , ),E E S E A 

cắt

tại

, ( , ).F F S F D 

Tứ giác

BEFC

là hình gì ?

c) Gọi

thuộc đoạn

sao cho

3AD AM

và

là trọng tâm tam giác

,SAB

là trung

điểm

.AB

Đường thẳng qua

và song song

cắt

tại

Chứng minh:

( )NG SCD

và

( ).MG SCD

BT 21. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành, tâm

Gọi

, , M N P

lần lượt là

trung điểm của

, , .SA BC CD

a) Tìm giao tuyến của hai mặt phẳng

( )SAC

và

), ( )(SBD SAB

và

( ).SCD

b) Tìm giao điểm

của

và

( ).MNP

c) Chứng minh:

( ).NE SAP

BT 22. Cho tứ diện

.ABCD

Lấy điểm

trên cạnh

sao cho

2 .AM MB

Gọi

là trọng tâm

BCD

và

trung điểm của

, CD H

là điểm đối xứng của

qua

a) Chứng minh:

( ).GD MCH

b) Tìm giao điểm

của

với

( ).ACD

Tính tỉ số



BT 23. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, I K

lần lượt là trung điểm

của

, .BC CD

a) Tìm giao tuyến của

( )SIK

và

( ), ( )SAC SIK

và

( ).SBD

b) Gọi

là trung điểm của

.SB

Chứng minh:

( ).SD ACM

c) Tìm giao điểm

của

và

( ).SIK

Tính tỉ số



§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 97 -

BT 24. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

là trọng tâm

,SAB

trên

lấy điểm

sao cho

3 .AD AE

Gọi

là trung điểm

.AB

a) Chứng minh:

( ).EG SCD

b) Đường thẳng qua

song song

cắt

tại

Chứng minh:

( ).GF SCD

c) Gọi

là điểm thuộc cạnh

sao cho

2 .CI ID

Chứng minh:

( ).GO SAI

BT 25. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là trung điểm của

và

là trọng tâm tam giác

.ABC

a) Chứng minh:

( ).SB AMN

b) Tìm giao tuyến của

( )AMN

với

( ).SAB

c) Tìm giao điểm

của

với

( ).AMN

Tính tỉ số:



d) Gọi

là trung điểm của

.ID

Chứng minh:

( ).QC AMN

BT 26. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, M N

lần lượt là trung điểm

của

, .BC CD

a) Tìm giao tuyến của

( )SMD

và

( ).SAB

b) Tìm giao tuyến của

( )SMN

và

( ).SBD

c) Gọi

là điểm trên cạnh

sao cho

2 .HA HS

Tìm giao điểm

của

và

( ).SBD

Tính tỉ số:



d) Gọi

là giao điểm của

và

.DM

Chứng minh:

( ).HG SBC

BT 27. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang với

là đáy lớn và

2 .AD BC

Gọi

là giao điểm của

và

, BD G

trọng tâm của tam giác

.SCD

a) Chứng minh:

( ).OG SBC

b) Gọi

là trung điểm của cạnh

.SD

Chứng minh:

( ).CM SAB

c) Giả sử điểm

trên đoạn

sao cho

2 3 .SC SI

Chứng minh:

( ).SA BID

d) Xác định giao điểm

của

và mặt phẳng

( ).SAC

Tính tỉ số:



BT 28. Cho hình chóp

. .S ABC

Gọi

, , M P I

lần lượt là trung điểm của

, , .AB SC SB

Một mặt phẳng

( )

qua

và song song với

và cắt các cạnh

, SA BC

tại

, .N Q

a) Chứng minh:

( ).BC IMP

b) Xác định thiết diện của

( )

với hình chóp. Thiết diện này là hình gì ?

c) Tìm giao điểm của đường thẳng

và mặt phẳng

( ).SMQ

BT 29. Cho hình chóp

.S ABCD

có đáy là một hình tứ giác lồi. Gọi

, M N

là trung điểm của

và

.CD

Gọi

( )

là mặt phẳng qua

, M N

và song song với đường thẳng

.AC

a) Tìm giao tuyến của

( )

với

( ).ABCD

b) Tìm giao điểm của đường thẳng

với

( ).

c) Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng

( ).

BT 30. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang với

.AB CD

Gọi

, , M N I

lần lượt là

trung điểm của

, , .AD BC SA

a) Tìm giao tuyến của hai mặt phẳng

( )IMN

và

( ); ( )SAC IMN

và

( ).SAB

b) Tìm giao điểm của

và

( ).IMN

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 98 -

c) Tìm thiết diện của mặt phẳng

( )IDN

với hình chóp

. .S ABCD

BT 31. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

là trọng tâm

; SAB N

là một điểm thuộc đoạn

sao cho:

;



là trung điểm

.AB

a) Chứng minh:

( )OI SAD

và

.GN SD

b) Gọi

( )

là mặt phẳng đi qua

và song song với

và

.BC

Mặt phẳng

( )

cắt

, SB SC

lần lượt tại

và

Tìm hình tính thiết diện cắt bởi mặt phẳng

( )

với hình chóp

. .S ABCD

BT 32. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

, H K

lần lượt là trung

điểm các cạnh

, SA SB

và

là điểm thuộc cạnh

,CD

khác

và

).D

a) Tìm giao tuyến của:

( )KAM

và

( ), ( )SBC SBC

và

( ).SAD

b) Tìm thiết diện tạo bởi

( )HKO

với hình chóp

. .S ABCD

Thiết diện là hình gì ?

c) Gọi

là trung điểm đoạn

.HK

Tìm

( ).I OL SBC 

Chứng minh:

.SI BC

BT 33. Cho tứ diện

,ABCD

có

, M N

là trung điểm của cạnh

, AB BC

và gọi

là trọng tâm tam giác

.ACD

a) Tìm giao điểm

của

và

( ).BCD

b) Tìm

( ) ( ).d MNG BCD 

Giả sử

.d CD P 

Chứng minh:

( ).GP ABC

c) Gọi

( )

là mặt phẳng chứa

và

.AD

Tìm thiết diện của

( )

với tứ diện.

BT 34. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Điểm

thuộc cạnh

thỏa

3 2 .MA MS

Hai điểm

và

lần lượt là trung điểm của

và

.BC

a) Xác định giao tuyến của hai mặt phẳng

( )MEF

và

( ).SAC

b) Xác định giao điểm

của mặt phẳng

( )MEF

với cạnh

.SD

Tính tỉ số:



c) Tìm giao điểm

của

với

( ).SBD

Tính tỉ số:



d) Tìm thiết diện tạo bởi mặt phẳng

( )MEF

cắt các mặt của hình chóp

. .S ABCD

BT 35. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

, M N

là trung điểm

, .SA SD

a) Xác định giao điểm của

và

( ).OMD

b) Xác định thiết diện hình chóp với mặt phẳng

( )P

qua

và song song với

.SC

BT 36. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là trung điểm của

, ( )SC P

là mặt phẳng qua

và song song với

.BD

a) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng

( ).P

b) Gọi

, E F

lần lượt là giao điểm của

( )P

với các cạnh

và

.SD

Hãy tìm tỉ số diện tích của

tam giác

SME

với tam giác

SBC

và tỉ số diện tích của tam giác

SMF

và tam giác

.SCD

c) Gọi

là giao điểm của

và

, CB J

là giao điểm của

và

.CD

Chứng ba điểm

, , K A J

nằm trên một đường thẳng song song với

và tìm tỉ số



BT 37. Cho hình chóp

.S ABCD

có

là trọng tâm

.ABC

Gọi

, , , , , M N P Q R H

lần lượt là trung

điểm của

, , , , , .SA SC CB BA QN AG

a) Chứng minh rằng:

, , S R G

thẳng hàng và

2 4 .SG MH RG 

b) Gọi



là trọng tâm

.SBC

Chứng minh:

( )GG SAB





và

( ).GG SAC





§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 99 -

§ 4. HAI MẶT PHẲNG SONG SONG



1. Vò töông ñoái cuûa hai maët phaúng phaân bieät

Cho hai mặt phẳng phân biệt

( )P

và

( ).Q

Có hai trường hợp xảy ra:

Có

điểm chung

( ) ( ) .P Q a  

Không có điểm chung

( ) ( ).P Q 

Định nghĩa. Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung.

2. Caùc ñònh lí



Định lí 1. Nếu mặt phẳng

( )

chứa hai đường thẳng cắt nhau

, a b

và

, a b

cùng song song với

mặt phẳng

( )

thì

( )

song song với

( ).



Muốn chứng minh hai mặt phẳng song song, ta phải chứng minh có hai đường thẳng cắt nhau

thuộc mặt phẳng này lần lượt song song với mặt phẳng kia.



Muốn chứng minh đường thẳng

( ),a Q

ta chứng minh đường thẳng a nằm trong mặt phẳng

( ) ( ).P Q



Định lí 2. Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song

song với mặt phẳng đã cho.



Nếu đường thẳng

song song với mặt phẳng

( )

thì trong

( )

có một đường thẳng song song

với

và qua

có duy nhất một mặt phẳng song song với

( ).

Dó đó để chứng minh đường

thẳng

song song với

( )

ta phải chứng minh

thuộc mặt phẳng

( )

và có

( ) ( ) ( ).d   



Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì

song song với nhau.



Cho điểm

không nằm trên mặt phẳng

( ).

Mọi đường thẳng đi

qua

và song song với

( )

đều nằm trong mặt phẳng đi qua

và song song với

( ).



Định lí 3. Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt

phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với

nhau.



Hệ quả: Hai mặt phẳng song song chắn trên hai cát tuyến song song

những đoạn thẳng bằng nhau.



Định lí Thales: Ba mặt phẳng đôi một song song chắn trên hai cát

tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 100 -

Chöùng minh hai maët phaúng song song

 Phương pháp giải Chứng minh hai mặt phẳng song song

( ) ( ).P Q

Ta chứng minh mặt phẳng

( )P

có hai đường thẳng CẮT NHAU và lần lượt song song với mặt

phẳng

( ).Q

Cụ thể, để chứng minh

( ) ( ),P Q

ta cần chỉ ra:

( ) (1)

( ) (2)

( ) ( ).

, ( )

a Q

b Q

P Q

a b P

a b A















 







Trước hết ta cần chứng minh

(1)

và chứng minh

(2),

sau đó gộp lại như trên.

1. Cho hình chóp

.S ABCD

với đáy

ABCD

là hình thang mà

AD BC

và

2 .AD BC

Gọi

, M N

lần lượt là trung điểm của

và

.AD

Chứng minh:

( ) ( ).BMN SCD

Ta có:

, M N

lần lượt là trung điểm của

và

.AD

MN

là đường trung bình

.SAD MN SD  

Ta có:

( ) ( ).

( )

MN SD

SD SCD MN SCD

MN SCD





 













Mà có

2ND AD BC 

và

ND BC

nên suy ra

BNDC

là

hình bình hành

.BN CD 

Ta có:

( ) ( ).

( )

NB CD

CD SCD NB SCD

NB SCD





 













Khi đó:

( )

( ) ( ).

( ), ( )

MN SCD

NB SCD

BMN SCD

MN BMN NB BMN

MN NB N











 



 







 Bình luận: Bản chất bài toán là tập hợp của hai bài toán chứng minh đường song song mặt.

Học sinh cần xem lại những phần suy luận ngược, cụ thể luôn đặt câu hỏi:

( )d d d





     

Dù ®o¸n d song song víi ®êng nµo n»m trong ( ) d vµ d n»m trong tam gi¸c hay ®ång hå c¸t nµo ?

Thales.

2. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

, , M N P

lần lượt là trung

điểm

, , SA SB SD

và

, K I

là trung điểm của

, .BC OM

....................................................................

a) Chứng minh:

.( () )OMN SCD

...................................................................................................... `

.......................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 101 -

b) Chứng minh:

.( () )PMN ABCD

.................................................................................................................................................................................

c) Chứng minh:

( ).KI SCD

.................................................................................................................................................................................

3. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

, M N

lần lượt là trung

điểm của

, .SA SD

....................................................................

a) Chứng minh:

( ) ( ).OMN SBC

...................................................................................................... `

.......................................................................................................

b) Gọi

, , P Q R

lần lượt là trung điểm của

, , .AB ON SB

Chứng minh:

( ).PQ SBC

.................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 102 -

c) Chứng minh:

( ) ( ).MOR SCD

.................................................................................................................................................................................

4. Cho hai hình bình hành

ABCD

và

ABEF

có chung cạnh

và không đồng phẳng.

Gọi

, , I J K

lần lượt là trung điểm các

cạnh

, , .AB CD EF

Chứng minh:

a) Chứng minh:

.( () )ADF BCE

...........................................................................................

b) Chứng minh:

( () ).DIK JBE

.................................................................................................................................................................................

5. Cho các hình bình hành

ABCD ABEF

nằm trên hai mặt phẳng khác nhau. Trên

các đường chéo

, AC BF

lấy các điểm

, M N

sao cho

2 , 2 .MC AM NF BN

 

Qua

, M N

lần lượt kẻ các đường thẳng

song song với cạnh

,AB

cắt các cạnh

, AD AF

theo thứ tự tại

1 1

, .M N

a) Chứng minh:

.MN DE

...........................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 103 -

...........................................................................................

b) Chứng minh:

1 1

( ).M N DEF

................................................................................

c) Chứng minh:

1 1

( ) ( ).MNM N DEF

...........................................................................................

6. Cho hình chóp

.S ABCD

có đáy

ABCD

là

hình bình hành tâm

Gọi

, , , M N P E

lần lượt là trung điểm

, , ,

SA BC CD SC

và

trên cạnh

thỏa

3 .AI IS

a) Tìm giao tuyến của

( )SAD

và

( ).MOP

...........................................................................................

b) Tìm

( ),K IE ABC 

( )

H BC EIM 

và

với

. .CH k CB

................................................................................

c) Gọi

là trọng tâm

.SBC

Tìm thiết diện hình

chóp

.S ABC

bị cắt bởi

( ).IMG

...........................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 104 -

7. Cho hình chóp

.S ABC

có

là trọng tâm của tam giác

.ABC

Trên đoạn

lấy hai điểm

, M N

sao cho

.SM MN NA 

a) Chứng minh: ( ).GM SBC

....................................................................................................... `

.......................................................................................................

b) Gọi

là điểm đối xứng của

qua

Chứng minh:

( ) ( ).MCD NBG

.................................................................................................................................................................................

c) Gọi

( ).H DM SBC 

Chứng minh

là trọng tâm

.SBC

.................................................................................................................................................................................

8. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Gọi

là trung điểm của

, SC N

là điểm trên đường chéo

sao cho

3 .BD BN

a) Xác định giao tuyến của

( )SDC

và

( ).SAB

....................................................................................................... `

.......................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 105 -

b) Tìm giao điểm

của đường thẳng

và

( ).SAB

Tính tỉ số:



.................................................................................................................................................................................

c) Gọi

.K AN BC 

Chứng minh rằng:

( ).MK SBD

.................................................................................................................................................................................

d) Gọi

, .I AN DC L IM SD   

Tính tỉ số

và

IKM

IAL





.................................................................................................................................................................................

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 106 -

§ 5. BÀI TẬP ÔN CHƯƠNG 2



BT 1. (THPT Bình Hưng Hòa – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình

bình hành. Điểm

nằm trên cạnh

sao cho

2 .SM MB

Gọi

là trọng tâm của tam giác

.SCD

a) Tìm giao tuyến của hai mặt phẳng

( )SAD

và

( ).SBC

b) Chứng minh đường thẳng

song song với mặt phẳng

( ).ABCD

c) Xác định thiết diện của hình chóp

.S ABCD

cắt bởi mặt phẳng

( ),

biết rằng

( )

chứa đường

thẳng

và song song với đường thẳng

.SA

BT 2. (THPT Bình Tân – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành,

gọi

là trọng tâm của tam giác

; SAB I

là trung điểm của

.AB

a) Tìm giao tuyến của

( )SAB

và

)( ();SCD SID

và

( .)SAC

b) Tìm giao điểm

( ).M SA CDG 

c) Xác định thiết diện với hình chóp

.S ABCD

với

( ).CDG

d) Giả sử

( ).N SB CDG 

Tính tỉ số



BT 3. (THPT Lê Quý Đôn – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có

ABCD

là hình bình hành.

Gọi

, , M N P

lần lượt là trung điểm

, , ; SA BC CD G

là trọng tâm tam giác

SCD

và

.E AP BD 

a) Tìm giao điểm

của

và mặt phẳng

( ).SBD

b) Chứng minh:

( )MN SCD

và

( ).GE SAC

c) Lấy điểm

thuộc cạnh

sao cho

(0 1),

n n

  

mặt phẳng

( )P

qua

song song

, SA CD

cắt

, , SD SC BC

lần lượt tại

, , .K L R

Tìm hình tính của thiết diện được tạo bởi

( )P

với hình chóp

. .S ABCD

d) Cho



Q HR AC 

. Tính

theo

để thiết diện

HKLQ

là hình thoi.

BT 4. (THPT Nguyễn Chí Thanh – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

đáy là hình thang,

AD BC

và

2 .AD BC

Gọi

, E F

lần lượt là trung điểm của

và

.AD

a) Xác định giao tuyến của hai mặt phẳng

( )BCE

và

( ).SAD

Suy ra giao điểm

của

( )BCE

với

.SD

b) Chứng minh

( ).CI BEF

c) Tìm giao diểm

của

với

( ).SBC

Chứng minh:

( ) ( ).SBF KCD

d) Gọi

là giao điểm của

và

; ( )BF 

là một mặt phẳng đi qua

và song song

, .SA BC

Xác định thiết diện của

( )

với hình chóp

. .S ABCD

BT 5. (THPT Nguyễn Hiền – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có đáy

ABCD

là một hình

thang

,AD BC

biết

2 .AD BC

Gọi

và J lần lượt là trọng tâm các tam giác

SAD

và

.SBC

a) Tìm giao tuyến của

( )ADJ

và

( ); ( )SBC BIC

và

( ).SAD

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 107 -

b) Tìm giao điểm

,M N

của

( )ADJ

và

, ,SB SC

giao điểm

,P Q

của

( )BCI

và

, .SA SD

c) Chứng minh

, PM NQ

cùng song song

( ).ABCD

d) Cho

cắt

tại

; E CQ

cắt

tại

và

cắt

tại

Tính tỷ số



BT 6. (THPT Nguyễn Hữu Cảnh – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình

bình hành. Gọi

, E F

lần lượt là trung điểm của cạnh

và

.SC

a) Tìm giao tuyến của hai mặt phẳng

( )SDE

với

( ), ( )SBC SAB

với

( ).SCD

b) Gọi

là trọng tâm tam giác

, SAB K

là điểm trên cạnh

sao cho

2 .SK KD

Chứng

minh

song song với mặt phẳng

( ).ABCD

c) Gọi

là giao điểm của đường thẳng

và

( ).SBD

Tính tỉ số



BT 7. (THPT Nguyễn Thị Minh Khai v– Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có mặt đáy

ABCD

là hình thang, cạnh đáy lớn

2 .AD BC

Gọi

,I K

lần lượt là trung điểm

và

.SI

Trên cạnh

lấy điểm

sao cho

2 .AM MB

a) Tìm giao tuyến của 2 mặt phẳng

( )SAD

và

( .)KBC

b) Tìm giao điểm

của đường thẳng

và mặt phẳng

( .)SKM

c) Gọi

là trọng tâm

.SAD

Chứng minh rằng

( ).JK GMC

d) Chứng minh thiết diện tạo bởi

( )KBC

với hình chóp

.S ABCD

là 1 hình bình hành.

BT 8. (THPT Nguyễn Thượng Hiền – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có đáy

ABCD

là

hình bình hành tâm

Gọi

, , E I N

lần lượt là trung điểm của

, , .SA BC CD

a) Tìm giao tuyến của hai mặt phẳng

( )ECD

và

( ).SAB

Suy ra giao điểm

của đường thẳng

và mặt phẳng

( ).ECD

b) Chứng minh:

( ) ( ).OEI SCD

Tìm giao tuyến của hai mặt phẳng

( )EIN

và

( ).SCD

c) Lấy điểm

thuộc cạnh

sao cho

2 ,BH SH

gọi

là trung điểm của

,AB

là trọng

tâm của tam giác

.SBC

Chứng minh rằng:

( ).AH MNG

BT 9. (THPT Bình Hưng Hòa – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình

bình hành tâm

Gọi

, , M N P

lần lượt là trung điểm của

, , .SB BC CD

a) Tìm giao tuyến của hai mặt phẳng

( )MNP

và

( ).SBD

b) Chứng minh mặt phẳng

( )OMN

song song với mặt phẳng

( ).SCD

c) Xác định thiết diện của hình chóp

.S ABCD

cắt bởi mặt phẳng

( )P

đi qua điểm

song song

với

và

.SC

Thiết diện là hình gì ?

BT 10. (THPT Lê Trọng Tấn – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có đáy là hình bình hành.

Gọi

, I G

lần lượt là trọng tâm của tam giác

, .SAD ACD

a) Tìm giao tuyến của hai mặt phẳng

( )SAB

và

( ).SCD

b) Chứng minh rằng

song song với mặt phẳng

( ).SBC

c) Tìm giao điểm của

và mặt phẳng

( ).IBC

d) Thiết diện của hình chóp bị cắt bởi mặt phẳng

( )IBC

là hình gì ? Giải thích.

§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. §êng & mÆt trong kh«ng gian

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 108 -

BT 11. (THPT Trần Phú – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang có

đáy là

và

.CD

Biết đáy lớn

3 .AB CD

Gọi

, E F

và

lần lượt là các điểm trên các cạnh

, AB SB

và

sao cho:

2 , 2EB EA FB FS 

và

2 .IA ID

a) Chứng minh

( )EF SAD

và

) ( ).(CEF SAD

b) Chứng minh

( ).FI SCD

c) Tìm giao điểm

của

và mặt phẳng

( ).SCD

Chứng minh

.GC SD

BT 12. (THPT Tân Bình – Tp. Hồ Chí Minh) Cho hình chóp

.S ABC

có

là trọng tâm

SAB

và

trên

thỏa

SM SC



a) Tìm giao tuyến của mặt phẳng

( )ABC

và mặt phẳng

( ).BMG

b) Gọi

( )

là mặt phẳng chứa

và mp

( ) .SA 

Nêu cách vẽ thiết diện tạo bởi mặt phẳng

( )

và hình chóp

. .S ABC

Thiết diện là hình gì ?

BT 13. (THPT Tây Thạnh – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang

(đáy lớn

2 .AB AD

Gọi

là giao điểm của hai đường thẳng

và

; BC

, M N

lần

lượt là trung điểm của các cạnh

, .SA AB

a) Tìm giao tuyến của hai mặt phẳng

( )SAD

và

( ).SBC

b) Tìm giao điểm

của đường thẳng

với mặt phẳng

( ).MBC

c) Gọi

.O AC DN 

Chứng minh rằng:

,NC AD

( ).SC OMN

BT 14. (THPT Nguyễn Thượng Hiền – Tp. Hồ Chí Minh) Cho hình chóp

.S ABCD

có đáy

ABCD

là

hình bình hành tâm

Gọi

, I J

lần lượt là trung điểm của

, SA SB

và

là trọng tâm tam giác

.SCD

a) Tìm giao tuyến của

( )IOJ

và

( ),ABCD

suy ra giao điểm

của

và

( ).IOJ

b) Gọi

là trung điểm của

.CD

Chứng minh rằng

( ) ( ).IOH SBC

c) Gọi

là điểm thuộc cạnh

.BC

Mặt phẳng

( )

qua

và song song

cắt

, , AD SD SC

lần lượt tại

, , .P Q R

Xác định thiết diện tạo thành bởi mặt phẳng

( )

và hình chóp. Thiết

diện là hình gì ?

§iÖn tho¹i ghi danh: 0983.047.188 (ThÇy Nam) – 0933.755.607 (ThÇy §oµn)

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn

MỤC LỤC

Trang

Chương 1. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG

...................................................... 1

§ 1. MỞ ĐẦU VỀ PHÉP BIẾN HÌNH .......................................................................................... 1

§ 2. PHÉP TỊNH TIẾN .................................................................................................................... 2

§ 3. PHÉP ĐỐI XỨNG TRỤC ..................................................................................................... 11

§ 4. PHÉP ĐỐI XỨNG TÂM ....................................................................................................... 15

§ 5. PHÉP QUAY ........................................................................................................................... 17

§ 6. PHÉP VỊ TỰ VÀ PHÉP ĐỒNG DẠNG ............................................................................. 25

ÔN TẬP CHƯƠNG 1 ............................................................................................................ 33

Chương 2. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN

........... 41

§ 1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG ............................................... 41

Dạng toán 1. Tìm giao tuyến của hai mặt phẳng ............................................................... 43

Dạng toán 2. Tìm giao điểm của đường thẳng và mặt phẳng ......................................... 52

Dạng toán 3. Tìm thiết diện .................................................................................................. 61

Dạng toán 4. Chứng minh ba điểm thẳng hàng ................................................................ 65

Dạng toán 5. Chứng minh ba điểm đồng quy ................................................................... 71

§ 2. HAI ĐƯỜNG THẲNG SONG SONG .............................................................................. 73

Dạng toán 1. Chứng minh đường thẳng song song mặt phẳng ...................................... 74

Dạng toán 2. Giao tuyến song song ..................................................................................... 77

§ 3. ĐƯỜNG THẲNG SONG SONG MẶT PHẲNG ............................................................ 81

Dạng toán 1. Chứng minh đường thẳng song song mặt phẳng ....................................... 81

Dạng toán 2. Tìm thiết diện song song ................................................................................ 87

§ 4. HAI MẶT PHẲNG SONG SONG ..................................................................................... 99

§ 5. ÔN TẬP CHƯƠNG 2 .......................................................................................................... 106

ĐỊA CHỈ GHI DANH



TRUNG TÂM THẾ VINH – 45A LÊ THÚC HOẠCH – Q. TÂN PHÚ (ĐỐI DIỆN TRƯỜNG THPT TRẦN PHÚ).



TRUNG TÂM HOÀNG GIA – 56 PHỐ CHỢ – P. TÂN THÀNH – Q. TÂN PHÚ (SAU CHỢ TÂN PHÚ).



71/25/10 PHÚ THỌ HÒA – P. PHÚ THỌ HÒA – Q. TÂN PHÚ – TP. HỒ CHÍ MINH.

ĐIỆN THOẠI GHI DANH



0983.047.188 – Zalo (Thầy Nguyễn Đức Nam) – Face: https://www.facebook.com/marion.zack/



0933.755.607 – Zalo (Thầy Lê Văn Đoàn) – 0929.031.789 – Face: https://www.facebook.com/levan.doan.902

NHÓM TOÁN THẦY LÊ VĂN ĐOÀN

Ths. Lê Văn Đoàn – Ths. Trương Huy Hoàng – Ths. Nguyễn Tiến Hà – Thầy Bùi Sỹ Khanh – Thầy Nguyễn

Đức Nam – Thầy Đỗ Minh Tiến – Thầy Nguyễn Duy Tùng – Thầy Trần Nguyễn Vĩnh Nghi – Thầy Hoàng

Minh Thiện – Thầy Trần Quốc Tuấn.

§iÖn tho¹i ghi danh: 0983.047.188 (ThÇy Nam) – 0933.755.607 (ThÇy §oµn)

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn

THỜI KHÓA BIỂU CÁC LỚP TOÁN ĐANG HỌC

KHỐI 6 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

19’15 – 21’15 T6A T6A Giải đề

KHỐI 7 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

17’30 -19’30

T7A T7A Giải đề

KHỐI 8 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

19’15 – 21’15 T8A T8A Giải đề

KHỐI 9 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

17’30 -19’30 T9A T9B T9A T9B Giải đề

KHỐI 10 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

17’45 -19’15 T10C T10C

19’30 – 21’00 T10A1

T10A2

10HG

T10B T10A1

T10A2

10HG

T10B T10A1

T10A2

10HG

T10B

Giải đề

KHỐI 11 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

17’45 -19’15 T11A T11B1

T11B2

T11A T11B1

T11B2

T11A T11B1

T11B2

Giải đề

19’30 – 21’00 T11-C T11-C T11-C

KHỐI 12 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

17’45 -19’15

T12A1

T12A2

T12HG1

T12C T12A1

T12A2

T12HG1

T12C T12A1

T12A2

T12HG1

T12C

T12HG2

Lớp

chuyên

đề VD và

VDC

19’30 – 21’00 T12B T12B T12HG2 T12B T12HG2

Bấm Tải xuống để xem toàn bộ.

| 1/111

| | Tải xuống

Preview text:

Sở GD & ĐT Tp. Hồ Chí Minh TÀI LIỆU TOÁN 11 Năm học: 2020 – 2021. Lưu hành nội bộ. LOREM IPSUM DOLOR SIT AMET www.facebook.com/Nhóm- 0933.755.607 thầy Đoàn Nhomtoanlevandoan Toán-Thầy-Lê-Văn-Đoàn- 0983.047.188 thầy Nam @gmail.com 112798047209867/
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
Chương 1. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG NỘI DỤNG
 Phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm và phép quay.
 Khái niệm về phép dời hình và hai hình bằng nhau.
 Phép vị tự, tâm vị tự của hai đường tròn.
 Khái niệm về phép đồng dạng và hai hình đồng dạng.
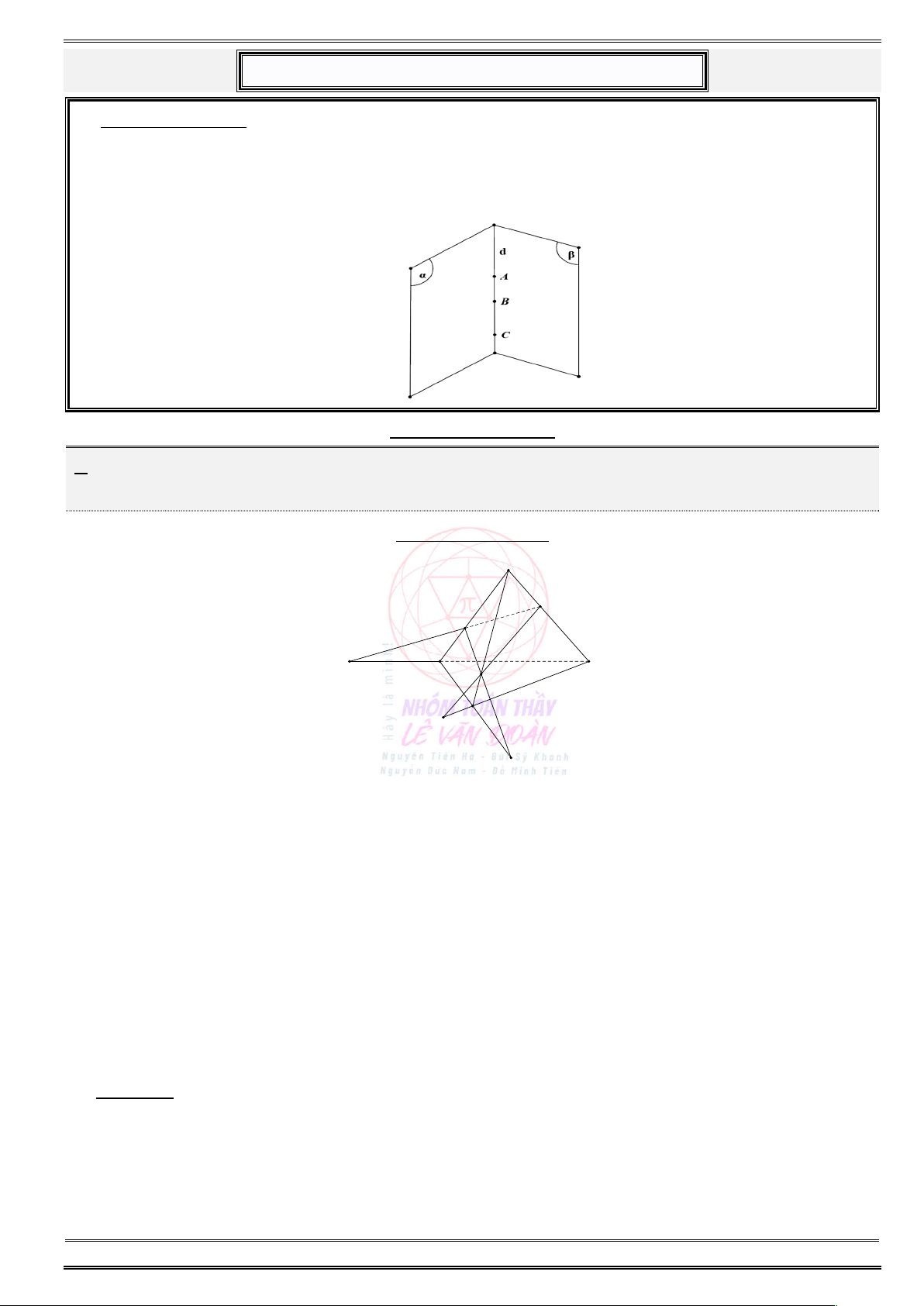
§ 1. MỞ ĐẦU VỀ PHÉP BIẾN HÌNH   Định nghĩa
Phép biến hình là một quy tắc để ứng với mỗi điểm M thuộc mặt phẳng, ta xác định được một
điểm duy nhất M  thuộc mặt phẳng ấy. Điểm M  gọi là ảnh của điểm M qua phép biến hình đó.
 Kí hiệu và thuật ngữ: Cho phép biến hình F.
 Nếu M  là ảnh của điểm M qua F thì ta viết M   F(M ). Ta nói phép biến hình F biến điểm
M thành M .
 Nếu H là một hình nào đó thì H   {M  M   F(M ), M  H} được gọi là ảnh của H qua F.
Kí hiệu là H   F(H ).  Phép dời hình:
 Phép dời hình là phép biến hình không làm thay đổi khoảng cách giữa hai điểm bất kì.  Phép dời hình:
 Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
 Biến đường thẳng thành đường thẳng.  Biến tia thành tia.
 Biến đoạn thẳng thành đoạn thẳng bằng đoạn thẳng đã cho.
 Biến tam giác thành tam giác bằng tam giác đã cho.
 Biến đường tròn thành đường tròn có cùng bán kính với đường tròn ban đầu.
 Biến góc thành góc bằng góc ban đầu.
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 1 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
§ 2. PHÉP TỊNH TIẾN   Định nghĩa 
Trong mặt phẳng cho véctơ v. Phép biến hình biến mỗi điểm M thành điểm M  sao cho    M'
MM   v được gọi là phép tịnh tiến theo véctơ v. 
Phép tịnh tiến theo véctơ v được kí hiệu T. v v  
Như vậy: M   T(M )  MM   v. M v
 Tính chất: Phép tịnh tiến là phép biến hình:
 Bảo toàn khoảng cách giữa hai điểm bất kì.
 Biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó.
 Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho.
 Biến một tam giác thành một tam giác bằng tam giác đã cho.
 Biến một đường tròn thành đường tròn có cùng bán kính.
 Biểu thức tọa độ của phép tịnh tiến
Trong mặt phẳng tọa độ O , xy gọi M (
 x ;y ) là ảnh của M(x ;y ) qua phép tịnh tiến theo M  M  M M  x   a  x 
v  (a;b). 
Khi đó: M   T(M ) M M    v y   b  y  M M 
BÀI TẬP TỰ LUẬN CƠ BẢN 
1. Trong mặt phẳng O ,
xy cho v  (2;1), điểm M(3;2). Tìm tọa độ điểm A sao cho
a) A  T(M ). b) M  T( ) A . v v  
Vì A là ảnh của M qua phép tịnh tiến v :
Vì M là ảnh của A qua phép tịnh tiến v : x   2  3  5
........................................................................................
A  T(M )  A    ( A 5; 3). v y   1  2  3  A 
........................................................................................ 
2. Trong mặt phẳng O ,
xy cho v  (1; 3), điểm M(1;4). Tìm tọa độ A sao cho
a) A  T(M ).
c) A  T (M ). v 2v
................................................................................... ........................................................................................
................................................................................... ........................................................................................
................................................................................... ........................................................................................ b) M  T( )
A . ........................................................ d) M  T ( )
A . ........................................................... v v
................................................................................... ........................................................................................
................................................................................... ........................................................................................
................................................................................... ........................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 2 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
3. Trong mặt phẳng O ,
xy cho đường thẳng d : 2x  3y  12  0. Tìm ảnh của d qua phép tịnh tiến v  (4;3).
Học sinh nghe giảng và bổ sung lời giải 1
Gọi d   T (d)  d   d nên d  có dạng 2x  3y  m  0. v Cho x  3
  y  2  M( 3
 ;2)  d : 2x  3y  12  0. x 
 ...........................  
Ta có: M   T(M ) M    M (..  .......;.........). v y 
 ...........................  M  Do M (
 1;1)  d  : 2x  3y  m  0  ...........................................................................................................
Suy ra d  : 2x  3y  5  0.
Học sinh nghe giảng và bổ sung lời giải 2
Gọi M(x;y)  d : 2x  3y  12  0 và M (
 x ;y )  T(M ). M  M  v x   .............. x   ..............   
Do M   T(M ) M    
 M(.............; ..............). v y   .............. y   ..............  M   Vì M (x  4; y
 3)  d : 2x  3y  12  0  2(x  4)  3(y  3)  12  0 M  M  M  M   2x  3y
 5  0  M   d  : 2x  3y  5  0. M  M  M  M  
Do đó ảnh của đường thẳng d qua phép tịnh tiến v  (4;3) là d  : 2x  3y  5  0.
Học sinh nghe giảng và bổ sung lời giải 3 Chọn M( 3
 ;2)  d và N(0;4)  d. x 
 ............................   Vì M (
 x ;y )  T(M ) M    M (..  ......;........). M  M  v y 
 ............................  M  x 
 ...............................   Vì N (
 x ;y )  T(N ) N    N (..  ......;........). N  N  v y 
 ...............................  N   
Nếu gọi d   T(d) thì M , N   d nên d  có véctơ chỉ phương là u  M N    (3;2). v d  
Suy ra véctơ pháp tuyến của d  là n  (2;3) và đi qua đi qua N (4  ;1) nên có dạng: d
d  : 2(x  4)  3(y  1)  0  2x  3y  5  0.
 Lưu ý. Học sinh sẽ làm cách của giáo viên trên lớp.
4. Trong mặt phẳng O ,
xy cho đường thẳng d : 2x  3y  5  0. Tìm ảnh của d qua phép tịnh tiến v  (3;2).
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 3 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
5. Trong mặt phẳng O ,
xy cho đường thẳng d : 3x  y  2  0. Tìm ảnh của d qua phép tịnh tiến v  (4;2).
 Lời giải. .............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
6. Trong mặt phẳng O ,
xy cho đường thẳng d : 2x  y  4  0. Tìm ảnh của d qua phép tịnh tiến 
v  AB với ( A 3;1), B( 1  ;8).
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
7. Trong mặt phẳng O ,
xy cho đường thẳng d : 3x  4y  5  0. Tìm ảnh của d qua phép tịnh tiến 
v  AB với ( A 0;2), B(2;3).
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
8. Trong mặt phẳng O ,
xy cho đường thẳng d : x  3y  2  0. Tìm ảnh của d qua phép tịnh tiến 
v  2AB với (
A 2;3), B(0;2).
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 4 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
9. Trong mặt phẳng O ,
xy cho đường tròn 2 2
(C ) : (x  4)  (y  3)  6. Hãy tìm ảnh của đường tròn 
(C) qua phép tịnh tiến v  (3;2).
Lời giải tham khảo
Đường tròn (C) có tâm I (4;3), bán kính R  6. x   3  4  7   Gọi I (
 x ;y )  T(I ) I    I (  7;1). I  I  v y   2  3  1  I   Gọi (C )
  T(C )  (C )
 có tâm I (7;1) và bán kính R  R  6 có dạng: v 2 2 (C )
 : (x  7)  (y  1)  6 là ảnh của đường tròn (C) đã cho.
10. Trong mặt phẳng O ,
xy cho đường tròn 2 2
(C ) : (x  2)  (y  4)  16. Hãy tìm ảnh của đường 
tròn (C) qua phép tịnh tiến v  (2;3).
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
11. Trong mặt phẳng O ,
xy cho đường tròn 2 (C ) : (x 1) (y 3)   
 25. Hãy tìm ảnh của đường  
tròn (C) qua phép tịnh tiến v  AB với ( A 1  ;1), B(1; 2  ).
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
12. Trong mặt phẳng O ,
xy cho đường tròn 2 2
(C ) : x  y  4x  6y  8  0. Hãy tìm ảnh của đường 
tròn (C) qua phép tịnh tiến v  (5;2).
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 5 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
BÀI TẬP TRẮC NGHIỆM  
1. Trong mặt phẳng tọa độ O ,
xy cho véctơ u  (3;1). Phép tịnh tiến theo véctơ u biến điểm M(1; 4  ) thành điểm A. M (  4;5). B. M (  2;3).
.............................................................................................................. C. M (  3;4). D. M (4  ;5).
..............................................................................................................
2. Trong mặt phẳng tọa độ O ,
xy nếu phép tịnh tiến biến điểm (
A 3;2) thành điểm A (  2; 3) thì nó
biến điểm B(2; 5) thành điểm
.............................................................................................................. A. B (  5;2). B. B (  1;6).
.............................................................................................................. C. B (  5;5). D. B (  5;5).
..............................................................................................................  
3. Trong mặt phẳng tọa độ O ,
xy cho véctơ v  (1;3). Phép tịnh tiến theo véctơ u biến điểm ( A 3; 3  ) thành điểm A. A (  2;6). B. A (  2;0).
.............................................................................................................. C. A (4  ;0). D. A (  2;0).
..............................................................................................................
4. Trong mặt phẳng tọa độ O ,
xy cho điểm M (
 4;2), biết M  là ảnh của M qua phép tịnh tiến theo 
véctơ v  (1;5). Tìm tọa độ điểm M .
A. M(3;5).
B. M(3; 7).
.............................................................................................................. C. M( 5  ;7).
D. M(5;3).
..............................................................................................................
5. Trong mặt phẳng tọa độ O ,
xy cho điểm M( 5
 ;2) và điểm M (3;2) là ảnh của M qua phép tịnh  
tiến theo véctơ v . Tìm tọa độ véctơ v .  
A. v  (2; 0). B. v  (0;2).
..............................................................................................................  
C. v  (1; 0).
D. v  (2; 0).
.............................................................................................................. 
6. Trong mặt phẳng tọa độ O ,
xy cho hai điểm M(0;2), N( 2
 ;1) và véctơ v  (1;2). Phép tịnh tiến 
theo véctơ v biến M, N thành hai điểm M , N  tương ứng. Tính độ dài M N  .
.............................................................................................................. A. M N
   5. B. M N
   7. .............................................................................................................. C. M N    1. D. M N    3.
..............................................................................................................
7. Trong mặt phẳng tọa độ O ,
xy cho hình bình hành ABCD với (
A 1;4), B(8;2) và giao điểm của 
hai đường chéo AC và BD là I(3; 2
 ). Nếu T là phép tịnh tiến theo véctơ u biến đoạn thẳng 
AB thành đoạn thẳng CD thì vectơ u có tọa độ là
.............................................................................................................. A. (3;12). B. (5; 3).
..............................................................................................................
C. (3;2). D. (7; 5  ).
..............................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 6 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
8. Trong mặt phẳng tọa độ O , xy cho AB  C biết (
A 2;4), B(5;1), C( 1  ; 2
 ). Phép tịnh tiến theo 
véctơ BC biến AB 
C thành AB C
  tương ứng các điểm. Tọa độ trọng tâm G  của AB C   là
.............................................................................................................. A. G (
 4;2). B. G (4  ;2).
.............................................................................................................. C. G (  4;2). D. G (  4;4).
..............................................................................................................
9. Trong mặt phẳng tọa độ O ,
xy tìm phương trình đườn thẳng  là ảnh của đường thẳng 
 : x  2y  1  0 qua phép tịnh tiến theo véctơ v  (1;1).
A.  : x  2y  0.
..............................................................................................................
B.  : x  2y  3  0.
..............................................................................................................
C.  : x  2y  1  0.
..............................................................................................................
D.  : x  2y  2  0.
.............................................................................................................. 
10. Trong mặt phẳng tọa độ O ,
xy cho đường thẳng  : x  5y 1  0 và vectơ v  (4;2). Khi đó 
ảnh của đường thẳng  qua phép tịnh tiến theo vectơ v là
A. x  5y  15  0.
..............................................................................................................
B. x  5y  15  0.
..............................................................................................................
C. x  5y  6  0.
.............................................................................................................. D. x
  5y  7  0.
.............................................................................................................. 
11. Trong mặt phẳng tọa độ O ,
xy cho v  (4;2) và đường thẳng  : 2x  y  5  0. Hỏi  là
ảnh của đường thẳng  nào sau đây qua T. v
A.  : 2x  y  5  0.
..............................................................................................................
B.  : 2x  y  9  0.
..............................................................................................................
C.  : 2x  y  15  0.
..............................................................................................................
D.  : 2x  y  11  0.
.............................................................................................................. x   1  2t 
12. Trong mặt phẳng tọa độ O ,
xy cho đường thẳng  :  và đường thẳng y   1  t  
 : x  2y  1  0. Tìm tọa độ vectơ v biết T( )    . v 
A. v  (0;1).
.............................................................................................................. 
B. v  (0;2).
.............................................................................................................. 
C. v  (0;1).
.............................................................................................................. 
D. v  (1;1).
.............................................................................................................. 
13. Trong mặt phẳng tọa độ O ,
xy phép tịnh tiến theo vectơ u  (4;6) biến đường thẳng a có phương
trình x  y  1  0 thành
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 7 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
A. x  y  9  0.
..............................................................................................................
B. x  y  9  0.
..............................................................................................................
C. x  y  9  0.
.............................................................................................................. D. x   y  9  0.
..............................................................................................................
14. Trong mặt phẳng tọa độ O ,
xy nếu phép tịnh tiến biến điểm (
A 2;1) thành điểm A (3;0) thì nó
biến đường thẳng nào sau đây thành chính nó ?
A. x  y  1  0.
..............................................................................................................
B. x  y  100  0.
..............................................................................................................
C. 2x  y  4  0.
..............................................................................................................
D. 2x  y  1  0.
..............................................................................................................
15. Trong mặt phẳng tọa độ O ,
xy cho đường thẳng a : 3x  2y  5  .
0 Phép tịnh tiến theo vectơ 
u  (1;2) biến đường thẳng đó thành đường thẳng a  có phương trình là
A. 3x  2y  4  0.
..............................................................................................................
B. 3x  2y  0.
..............................................................................................................
C. 3x  2y  10  0.
..............................................................................................................
D. 3x  2y  7  0.
..............................................................................................................
16. Trong mặt phẳng tọa độ O ,
xy cho đường thẳng  có phương trình 4x  y  3  0. Ảnh của 
đường thẳng qua phép tịnh tiến T theo vectơ u  (2;1) có phương trình là
A. 4x  y  5  0.
..............................................................................................................
B. 4x  y  10  0.
..............................................................................................................
C. 4x  y  6  0.
..............................................................................................................
D. x  4y  6  0.
..............................................................................................................
17. Trong mặt phẳng tọa độ O ,
xy cho đường thẳng  có phương trình 3x  4y  1  0. Thực hiện
phép tịnh tiến theo phương của trục hoành về bên phải một đơn vị, đường thẳng  biến thành
đường thẳng  có phương trình là
A. 3x  4y  5  0.
..............................................................................................................
B. 3x  4y  2  0.
..............................................................................................................
C. 3x  4y  3  0.
D. 3x  4y  10  0.
..............................................................................................................
18. Trong mặt phẳng tọa độ O ,
xy cho đường thẳng  có phương trình 2x  y  3  0. Thực hiện
phép tịnh tiến theo phương của trục hoành về bên trái hai đơn vị, đường thẳng  biến thành
đường thẳng  có phương trình là
A. 2x  y  7  0.
..............................................................................................................
B. 2x  y  2  0.
..............................................................................................................
C. 2x  y  8  0.
D. 2x  y  6  0.
..............................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 8 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
19. Trong mặt phẳng tọa độ O ,
xy cho đường tròn 2 2
(T ) : x  y  2x  8  0. Phép tịnh tiến theo 
vectơ u  (3;1), biến đường tròn (T ) thành đường tròn (T )  có phương trình là A. 2 2
x  y  8x  2y  8  0.
.............................................................................................................. B. 2 2
x  y  4x  y  5  0.
.............................................................................................................. C. 2 2
x  y  4x  4y  3  0.
.............................................................................................................. D. 2 2
x  y  6x  4y  2  0.
20. Trong mặt phẳng tọa độ O ,
xy tìm phương trình đường tròn (C )
 là ảnh của đường tròn  2 2
(C ) : x  y  4x  2y  1  0 qua phép tịnh tiến theo v  (1;3). A. 2 2 (C )
 : (x  3)  (y  4)  2.
.............................................................................................................. B. 2 2 (C )
 : (x  3)  (y  4)  4.
.............................................................................................................. C. 2 2 (C )
 : (x  3)  (y  4)  4.
.............................................................................................................. D. 2 2 (C )
 : (x  3)  (y  4)  4. 
21. Trong mặt phẳng tọa độ O ,
xy cho v  (3;1) và đường tròn 2 2
(C ) : (x  4)  y  16. Ảnh của
(C ) qua phép tịnh tiến T là v A. 2 2
(x  1)  (y  1)  16.
.............................................................................................................. B. 2 2
(x  1)  (y  1)  16.
.............................................................................................................. C. 2 2
(x  7)  (y  1)  16.
.............................................................................................................. D. 2 2
(x  7)  (y  1)  16.
22. Trong mặt phẳng tọa độ O ,
xy cho đường tròn 2 2
(T ) : x  y  x  2y  3  0. Phép tịnh tiến theo
phương của trục hoành về bên phải 4 đơn vị, biến đường tròn (T ) thành đường tròn (T )  có phương trình là A. 2 2
x  y  9x  2y  17  0.
.............................................................................................................. B. 2 2
x  y  4x  2y  4  0.
.............................................................................................................. C. 2 2
x  y  5x  4y  5  0.
.............................................................................................................. D. 2 2
x  y  7x  2y  1  0.
23. Trong mặt phẳng tọa độ O ,
xy cho đường tròn 2 2
(T ) : x  y  x  2y  3  0. Phép tịnh tiến theo
phương của trục tung về dưới 2 đơn vị, biến đường tròn (T ) thành đường tròn (T )  có phương trình là A. 2 2
x  y  2y  9  0.
.............................................................................................................. B. 2 2
x  y  2x  6y  2  0.
.............................................................................................................. C. 2 2
x  y  x  4y  5  0.
.............................................................................................................. D. 2 2
x  y  2x  7  0.
..............................................................................................................
ĐÁP ÁN TRẮC NGHIỆM 1.A 2.B 3.B 4.C 5.D 6.A 7.B 8.A 9.A 10.A 11.D 12.C 13.A 14.B 15.A 16.C 17.B 18.A 19.A 20.B 21.C 22.A 23.D
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 9 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
BÀI TẬP RÈN LUYỆN TỰ LUẬN 
BT 1. Trong mặt phẳng tọa độ O , xy cho (
A 3;5), B(1;1), v  (1;2), đường thẳng d và đường tròn
(C ) có phương trình: 2 2
d : x  2y  3  0, (C ) : (x  2)  (y  3)  25. 
a) Tìm ảnh của các điểm A , B  theo thứ tự là ảnh của ,
A B qua phép tịnh tiến v . 
b) Tìm tọa độ điểm C sao cho A là ảnh của C qua phép tịnh tiến v .
c) Tìm phương trình đường thẳng d , đường tròn (C )
 lần lượt là ảnh của d, (C) qua phép  tịnh tiến v . 
BT 2. Trong mặt phẳng tọa độ O ,
xy cho tam giác ABC có ảnh qua phép tịnh tiến theo v  (2;5) là
tam giác AB C
  và tam giác AB C
  có trọng tâm là G (3;4), biết rằng ( A 1  ;6), ( B 3;4). Tìm
A , B , C .
BT 3. Trong mặt phẳng tọa độ O ,
xy cho một phép tịnh tiến biến đường tròn (C ) thành đường tròn (C )
 . Hãy xác định phép tịnh tiến đó trong các trường hợp sau: a) 2 2
(C ) : (x  1)  (y  2)  16, 2 2 (C )
 : (x  10)  (y  5)  16. b) 2 2
(C ) : x  y  2x  6y  1  0, 2 2 (C )
 : x  y  4x  2y  4  0. c) 2 2
(C ) : (x  m)  (y  2)  5, 2 2 2 (C )
 : x  y  2(m  2)y  6x  12  m  0. 
BT 4. Trong mặt phẳng tọa độ O ,
xy cho véctơ v  (2;1) và hai đường thẳng d : 2x  3y  3  0 và
d : 2x  3y  5  0. 1
a) Viết phương trình của đường thẳng d  là ảnh của d qua T. v 
b) Tìm tọa độ của u có giá vuông góc với đường thẳng d để d là ảnh của d qua T. 1 u
BT 5. Trong mặt phẳng tọa độ O ,
xy cho đường thẳng d : 3x  y  9  0. 
a) Tìm phép tịnh tiến theo véctơ v có phương song song với trục Ox, biến d thành đường
thẳng d  đi qua gốc tọa độ. Khi đó hãy viết phương trình đường thẳng d . 
b) Tìm phép tịnh tiến theo véctơ u có giá song song với trục Oy, biến d thành d  đi qua điểm ( A 1;1). 
BT 6. Trong mặt phẳng tọa độ O ,
xy hãy xác định phép tịnh tiến theo v cùng phương với trục hoành
biến đường thẳng d : x  4y  4  0 thành đường thẳng d  qua ( A 1; 3  ).
BT 7. Trong mặt phẳng tọa độ O ,
xy cho hai đường thẳng lần lượt có phương trình là  
d : 3x  5y  3  0 và d  : 3x  5y  24  0. Tìm v, biết v  13 và T(d)  d . v 
BT 8. Trong mặt phẳng tọa độ O ,
xy phép tịnh tiến theo v biến điểm M(3; 1
 ) thành một điểm trên  
đường thẳng d : x  y  9  0. Tìm tọa độ v , biết rằng v  5.
BT 9. Trong mặt phẳng tọa độ O ,
xy hãy xác định tọa độ điểm M trên trục hoành sao cho phép tịnh 
tiến theo v  (2; 3) biến điểm M thành điểm M  nằm trên trục tung.
BT 10. Trong mặt phẳng tọa độ O ,
xy cho hai đường thẳng d, d lần lượt có phương trình là  
d : 3x  y  7  0, d  : 3x  y  13  0 và véctơ u  (1;1). Tìm tọa độ của véctơ v trong phép  
tịnh tiến T biến d thành d , biết rằng hai véctơ v và u cùng phương. v
BT 11. Trong mặt phẳng tọa độ O , xy cho hai parabol 2
(P) : y  x  4x  7 và 2 (P )
 : y  x . Tìm phép
tịnh tiến biến (P) thành (P )  .
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 10 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
§ 3. PHÉP ĐỐI XỨNG TRỤC (giảm tải)   Định nghĩa
 Điểm M  được gọi là đối xứng với điểm M qua đường thẳng d nếu d là đường trung trực của
đoạn thẳng MM . Khi điểm M nằm trên d thì ta xem M đối xứng với chính nó qua đường thẳng . d
 Phép biến hình biến mỗi điểm M thành điểm M  đối xứng với M qua đường thẳng d được
gọi là phép đối xứng qua đường thẳng ,
d hay gọi là tắt là phép đối xứng trục. M Mo d M'
 Đường thẳng d được gọi là trục đối xứng. Kí hiệu: § . d  
 Như vậy: M   § (M )  MM  M 
M với M là hình chiếu vuông góc M lên . d d o o o
 Biểu thức tọa độ
Trong mặt phẳng tọa độ O ,
xy với mỗi điểm M(x ;y ), gọi M (
 x ;y )  § (M). M M M  M  d x   x   
Nếu chọn d là trục Ox, thì ta có: M M   y   y   M  M  x   x    
Nếu chọn d là trục Oy, thì ta có: M M   y   y  M  M   Tính chất
Phép đối xứng trục là một phép dời hình nên có đầy đủ tính chất của phép dời hình:
 Bảo toàn khoảng cách giữa hai điểm bất kì.
 Biến một đường thẳng thành đường thẳng.
 Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho.
 Biến một tam giác thành một tam giác bằng tam giác đã cho.
 Biến một đường tròn thành một đường tròn có cùng bán kính.
 Trục đối xứng của một hình
Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng trục § biến H thành chính d
nó, tức là H  § (H ). d
BÀI TẬP TRẮC NGHIỆM
1. Trong mặt phẳng tọa độ O ,
xy phép đối xứng trục biến điểm (
A 2;1) thành A (  2;5) có trục đối xứng là
A. Đường thẳng y  3.
..............................................................................................................
B. Đường thẳng x  3.
..............................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 11 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
C. Đường thẳng y  6.
..............................................................................................................
D. Đường thẳng x  y  3  0.
2. Trong mặt phẳng tọa độ O , xy cho AB  C với ( A 2;6), B( 1
 ;2), C(6;1). Gọi G là trọng tâm của
ABC. Phép đối xứng trục § biến điểm G thành điểm G  có tọa độ là Ox A. (2; 4). B. (3; 3  ).
.............................................................................................................. 7    4   
.............................................................................................................. C.  ; 3  .   ; 4  .  D. 3  3 
..............................................................................................................
3. Trong mặt phẳng tọa độ O ,
xy nếu phép đối xứng trục biến điểm M(3;1) thành điểm M (1;3)
thì nó biến điểm N(3; 4  ) thành điểm A. N (3  ;4). B. N (3  ;4).
.............................................................................................................. C. N (4
 ;3). D. N (4  ;3).
..............................................................................................................
4. Trong mặt phẳng tọa độ O ,
xy nếu phép đối xứng trục biến điểm (
A 0;1) thành điểm A (1;0) thì nó biến điểm B( 5  ;5) thành điểm A. B (  5;5). B. B (  5;5).
.............................................................................................................. C. B (  5;5). D. B (  1;1).
..............................................................................................................
5. Trong mặt phẳng tọa độ O ,
xy cho đường thẳng d : x  y  2  0. Ảnh của d qua phép đối xứng
trục tung có phương trình
A. x  y  2  0.
..............................................................................................................
B. x  y  2  0.
..............................................................................................................
C. x  y  2  0.
..............................................................................................................
D. x  2y  2  0.
6. Trong mặt phẳng tọa độ O ,
xy cho đường tròn 2 2
(C ) : x  y  4x  5y  1  0. Tìm ảnh đường tròn (C )
 của (C ) qua phép đối xứng trục Oy. A. 2 2
x  y  4x  5y  1  0.
.............................................................................................................. B. 2 2
x  y  4x  5y  1  0.
.............................................................................................................. C. 2 2
2x  2y  8x  10y  2  0.
.............................................................................................................. D. 2 2
x  y  4x  5y  1  0.
..............................................................................................................
7. Trong mặt phẳng tọa độ O , xy cho đường tròn 2 2
(C ) : x  y  2x  3y  1  0. Phép đối xứng qua
trục Ox biến đường tròn đó thành đường tròn (C )  có phương trình A. 2 2
x  y  2x  3y  1  0.
.............................................................................................................. B. 2 2
x  y  2x  3y  1  0.
.............................................................................................................. C. 2 2
x  y  2x  3y  1  0.
.............................................................................................................. D. 2 2
x  y  2x  3y  1  0.
..............................................................................................................
8. Trong mặt phẳng tọa độ O ,
xy cho đường tròn 2 2
(C ) : x  y  2x  3y  1  0. Phép đối xứng qua
trục Oy biến đường tròn đó thành đường tròn (C )  có phương trình là
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 12 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh A. 2 2
x  y  2x  3y  1  0.
.............................................................................................................. B. 2 2
x  y  2x  3y  1  0.
.............................................................................................................. C. 2 2
x  y  2x  3y  1  0.
.............................................................................................................. D. 2 2
x  y  2x  3y  1  0.
9. Trong mặt phẳng tọa độ O ,
xy cho đường tròn 2 2
(T ) : x  y  2x  y  5  0. Phép đối xứng trục
§ biến đường tròn (T ) thành đường tròn (T )  có phương trình là Ox A. 2 2
x  y  2x  y  5  0.
.............................................................................................................. B. 2 2
x  y  2x  y  5  0.
.............................................................................................................. C. 2 2
x  y  2x  y  5  0.
.............................................................................................................. D. 2 2
x  y  x  2y  5  0.
10. Trong mặt phẳng tọa độ O ,
xy cho parabol (P) có phương trình 2
y  2x  x  5. Phép đối xứng
trục § biến parabol (P) thành parabol (P )  có phương trình là Oy A. 2
y  2x  x  5.
.............................................................................................................. B. 2
y  2x  x  5.
.............................................................................................................. C. 2
y  2x  x  5.
.............................................................................................................. D. 2
y  2x  x  5.
11. Trong mặt phẳng tọa độ O ,
xy cho parabol (P) có phương trình 2
y  x  2x  3. Phép đối xứng
trục § biến parabol (P) thành parabol (P )  có phương trình là Ox A. 2
y  x  2x  3.
.............................................................................................................. B. 2
y  x  2x  3.
.............................................................................................................. C. 2 y  x
  2x  3.
.............................................................................................................. D. 2 y  x   4x  3.
12. Trong mặt phẳng tọa độ O ,
xy cho đường thẳng  : 2x  y  1  0 và điểm ( A 3;2). Trong các
điểm dưới đây, điểm nào là điểm đối xứng của A qua đường thẳng  ?
A. M(1; 4). B. N( 2  ;5).
..............................................................................................................
C. P(6;3). D. Q(1;6).
..............................................................................................................
13. Trong mặt phẳng tọa độ O ,
xy gọi a là đường phân giác của góc phần tư thứ nhất. Phép đối xứng trục Đ biến điểm (
A 4;3) thành điểm A có tọa độ là a
A. (4;3). B. (4; 3  ).
.............................................................................................................. C. ( 4  ;3). D. (3; 4).
..............................................................................................................
14. Trong mặt phẳng tọa độ O ,
xy gọi b là đường phân giác của góc phần tư thứ hai. Phép đối xứng
trục Đ biến điểm P(5;2) thành điểm P  có tọa độ là b A. (5;2). B. ( 5  ;2).
.............................................................................................................. C. (2; 5  ). D. ( 2  ;5).
..............................................................................................................
15. Trong mặt phẳng tọa độ O ,
xy phép đối xứng qua đường thẳng x  y  0 biến đường thẳng
4x  5y  1  0 thành đường thẳng có phương trình là
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 13 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh A. 4
 x  5y  1  0.
..............................................................................................................
B. 5x  4y  1  0.
..............................................................................................................
C. 5x  4y  1  0.
D. 4x  5y  1  0.
..............................................................................................................
16. Trong mặt phẳng tọa độ O ,
xy cho đường thẳng  có phương trình 2x  3y  6  0. Đường
thẳng đối xứng của  qua trục hoành có phương trình là
A. 2x  3y  6  0.
..............................................................................................................
B. 2x  3y  6  0.
..............................................................................................................
C. 4x  y  6  0.
D. 3x  2y  6  0.
..............................................................................................................
17. Gọi a là đường phân giác của góc phần tư thứ nhất. Ta xét đường thẳng  : 3x  4y  5  0.
Phép đối xứng trục Đ biến đường thẳng  thành đường thẳng  có phương trình là a
A. 4x  3y  5  0.
..............................................................................................................
B. 3x  4y  5  0.
..............................................................................................................
C. 4x  3y  5  0.
D. 3x  4y  5  0.
..............................................................................................................
18. Gọi b là đường phân giác của góc phần tư thứ hai. Ta xét đường thẳng  : y  5x  3. Phép đối
xứng trục Đ biến đường thẳng  thành đường thẳng  có phương trình là b
A. x  5y  3  0.
..............................................................................................................
B. x  5y  3  0.
..............................................................................................................
C. y  5x  3.
D. y  5x  3.
..............................................................................................................
19. Trong mặt phẳng tọa độ O ,
xy phép đối xứng qua đường thẳng x  y  0 biến đường tròn có phương trình 2 2
x  y  2x  1  0 thành đường tròn có phương trình A. 2 2
x  y  2y  1  0.
.............................................................................................................. B. 2 2
x  y  2x  1  0.
.............................................................................................................. C. 2 2
x  y  2y  1  0.
.............................................................................................................. D. 2 2
x  y  2x  1  0.
20. Trong mặt phẳng tọa độ O ,
xy gọi a là đường phân giác của góc phần tư thứ nhất. Ta xét đường tròn 2 2
(T ) : (x  2)  (y  3)  9. Phép đối xứng trục Đ biến đường tròn (T ) thành đường tròn a (T )  có phương trình là A. 2 2
(x  3)  (y  2)  9.
.............................................................................................................. B. 2 2
(x  2)  (y  3)  9.
.............................................................................................................. C. 2 2
(x  3)  (y  2)  9.
.............................................................................................................. D. 2 2
(x  3)  (y  2)  9.
ĐÁP ÁN TRẮC NGHIỆM 1.A 2.C 3.D 4.A 5.B 6.B 7.B 8.C 9.A 10.B 11.C 12.A 13.D 14.C 15.B 16.A 17.A 18.A 19.A 20.A
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 14 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
§ 4. PHÉP ĐỐI XỨNG TÂM (giảm tải)   Định nghĩa
Cho điểm I. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác I thành điểm
M  sao cho I là trung điểm của đoạn thẳng MM  được gọi là phép đối xứng tâm I, nghĩa là   
IM  IM   0. Phép đối xứng tâm I thường được kí hiệu là § . I
 Biểu thức tọa độ
Trong mặt phẳng tọa độ O ,
xy choI(x ;y ), M(x ;y ) và M (
 x ;y ) là ảnh của M qua phép I I M M M  M  x   2x  x  
đối xứng tâm I. Khi đó: M I M  . y   2y  y  M I M 
 Tính chất: Phép đối xứng tâm
 Bảo toàn khoảng cách giữa hai điểm bất kì.
 Biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đã cho.
 Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho.
 Biến một tam giác thành một tam giác bằng tam giác đã cho.
 Biến một đường tròn thành một đường tròn có cùng bán kính.
 Tâm đối xứng của một hình
Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành
chính nó. Khi đó H được gọi là hình có tâm đối xứng.
1. Trong mặt phẳng tọa độ Ox ,
y nếu phép đối xứng tâm biến điểm (
A 5;2) thành điểm A (3;4) thì nó biến điểm ( B 1; 1  ) thành điểm A. B (  1;7). B. B (  1;6).
................................................................................................................. C. B (  2;5). D. B (  1;5).
.................................................................................................................
2. Trong mặt phẳng tọa độ Ox ,
y cho điểm I(2; 1  ) và AB  C với ( A 1;4), ( B 2  ;3), C(7;2).Phép
đối xứng tâm § biến trọng tâm G của AB 
C thành điểm G  có tọa độ là I A. G (  2;5). B. G (  2;5).
................................................................................................................. C. G (
 1;4). D. G (0;5).
.................................................................................................................
3. Trong mặt phẳng tọa độ Ox ,
y cho phép đối xứng tâm có tâm là điểm gốc tọa độ. Khi đó nó biến
đường thẳng 3x  4y  13  0 thành đường thẳng
A. 3x  4y  13  0.
.................................................................................................................
B. 3x  4y  13  0.
.................................................................................................................
C. 3x  4y  13  0.
................................................................................................................. D. 3
 x  4y  13  0.
.................................................................................................................
4. Trong mặt phẳng tọa độ Ox ,
y cho phép đối xứng tâm với tâm là điểm I(1; 1  ). Khi đó nó biến
đường thẳng 2x  3y  5  0 thành đường thẳng
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 15 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
A. 2x  3y  7  0.
.................................................................................................................
B. 2x  3y  7  0.
.................................................................................................................
C. 2x  3y  7  0.
D. 2x  3y  4  0.
.................................................................................................................
5. Trong mặt phẳng tọa độ Ox ,
y cho điểm I(2; 1
 ) và đường thẳng  có phương trình
x  2y 2  0. Ảnh của  qua phép đối xứng tâm § là đường thẳng có phương trình I
A. x  2y  2  0.
.................................................................................................................
B. x  2y  3  0.
.................................................................................................................
C. x  2y  6  0.
D. 2x  y  4  0.
.................................................................................................................
6. Trong mặt phẳng tọa độ Ox ,
y cho hai đường thẳng song song a và b lần lượt có phương trình
3x  4y 1  0 và 3x  4y  5  0. Nếu phép đối xứng tâm biến a thành b thì tâm đối xứng
phải là điểm nào trong các điểm sau đây ?
A. I (2;2).
B. I(2;2).
................................................................................................................. C. I( 2  ;2). D. I(2; 0).
.................................................................................................................
7. Trong mặt phẳng tọa độ Ox ,
y cho điểm I(2; 1  ) và đường tròn 2 2
(T ) : x  y  9. Phép đối xứng
tâm § biến đường tròn (T ) thành đường tròn (T )  có phương trình là I A. 2 2
x  y  8x  4y  11  0.
................................................................................................................. B. 2 2
x  y  4x  6y  5  0.
................................................................................................................. C. 2 2
x  y  2x  4y  0.
................................................................................................................. D. 2 2
x  y  6x  2y  2  0.
8. Trong mặt phẳng tọa độ Ox , y cho đường tròn 2 2
(C ) : x  y  8x  10y  32  0. Phương trình
của đường tròn (C )
 đối xứng của (C) qua gốc tọa độ O có phương trình là A. 2 2
(x  4)  (y  5)  9.
................................................................................................................. B. 2 2
(x  4)  (y  5)  16.
................................................................................................................. C. 2 2
(x  4)  (y  5)  4.
.................................................................................................................
D. Một phương trình khác.
9. Trong mặt phẳng tọa độ Ox , y cho parabol 2
(P) : y  x  x. Phương trình của parabol (Q) đối
xứng với (P) qua gốc tọa độ O là A. 2 y  x   x.
................................................................................................................. B. 2
y  x  x.
................................................................................................................. C. 2 y  x   x.
................................................................................................................. D. 2
y  x  2x. BẢNG ĐÁP ÁN 1.A 2.D 3.D 4.B 5.A 6.A 7.A 8.A 9.A
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 16 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh § 5. PHÉP QUAY  1. Ñònh nghóa
 Cho điểm O và góc lượng giác .
 Phép biến hình biến O thành chính nó, biến mỗi điểm M khác
O thành điểm M  sao cho OM   OM và góc lượng giác (OM;OM )
 bằng  được gọi là phép
quay tâm O góc quay . 
 Điểm O gọi là tâm quay,  gọi là góc quay.
 Phép quay tâm O góc ,
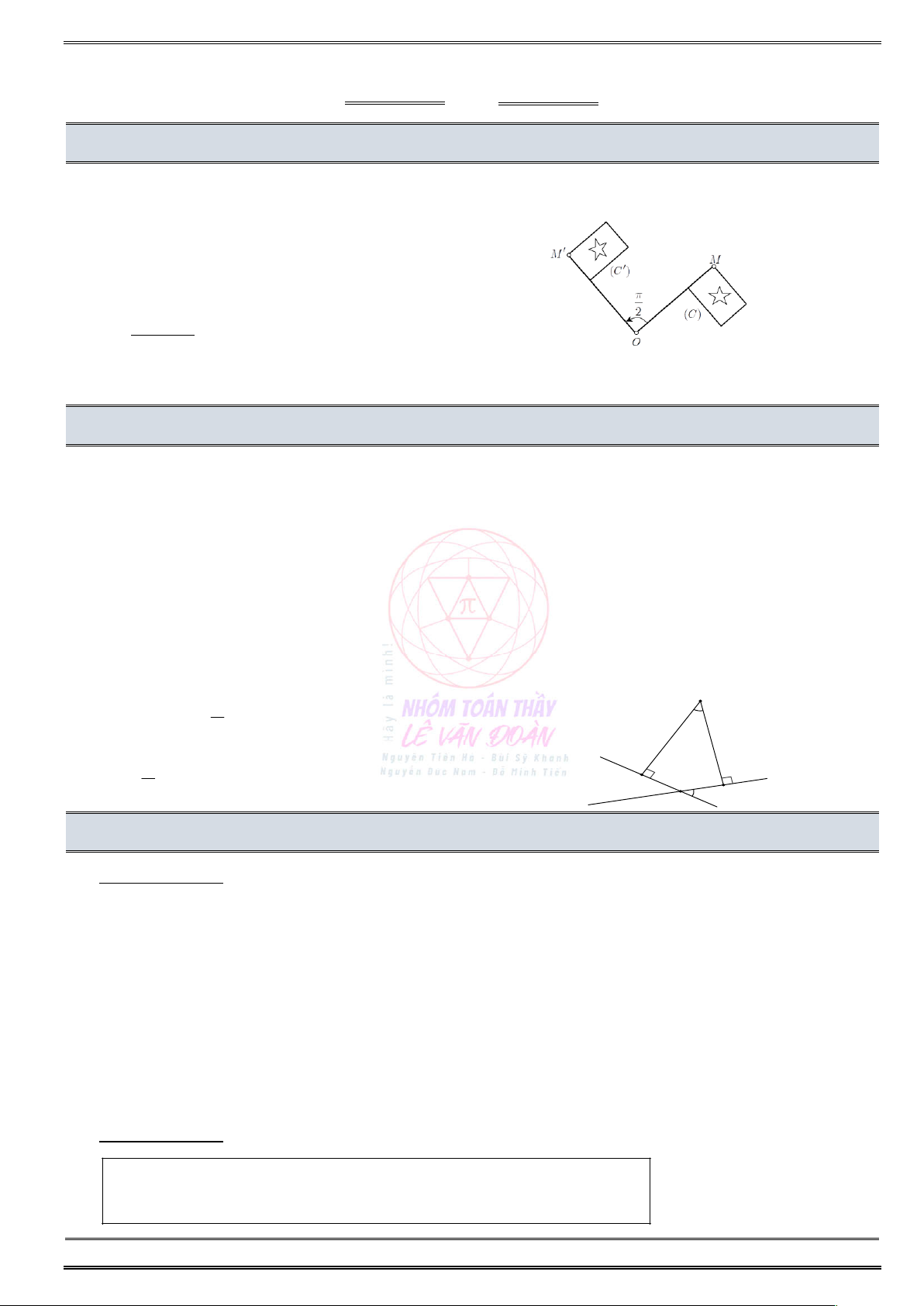
 kí hiệu là Q . (O;)  Câu hỏi:
 Phép quay nào biến lá cờ (C ) thành lá cờ (C )
 : ...................................................................................
 Phép quay nào biến lá cờ (C )
 thành lá cờ (C ) : .................................................................................. 2. Tính chaát
Phép quay là phép biến hình
 Bảo toàn khoảng cách giữa hai điểm bất kì.
 Biến một đường thẳng thành một đường thẳng.
 Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho.
 Biến một tam giác thành một tam giác bằng tam giác đã cho.
 Biến một đường tròn thành đường tròn có cùng bán kính.
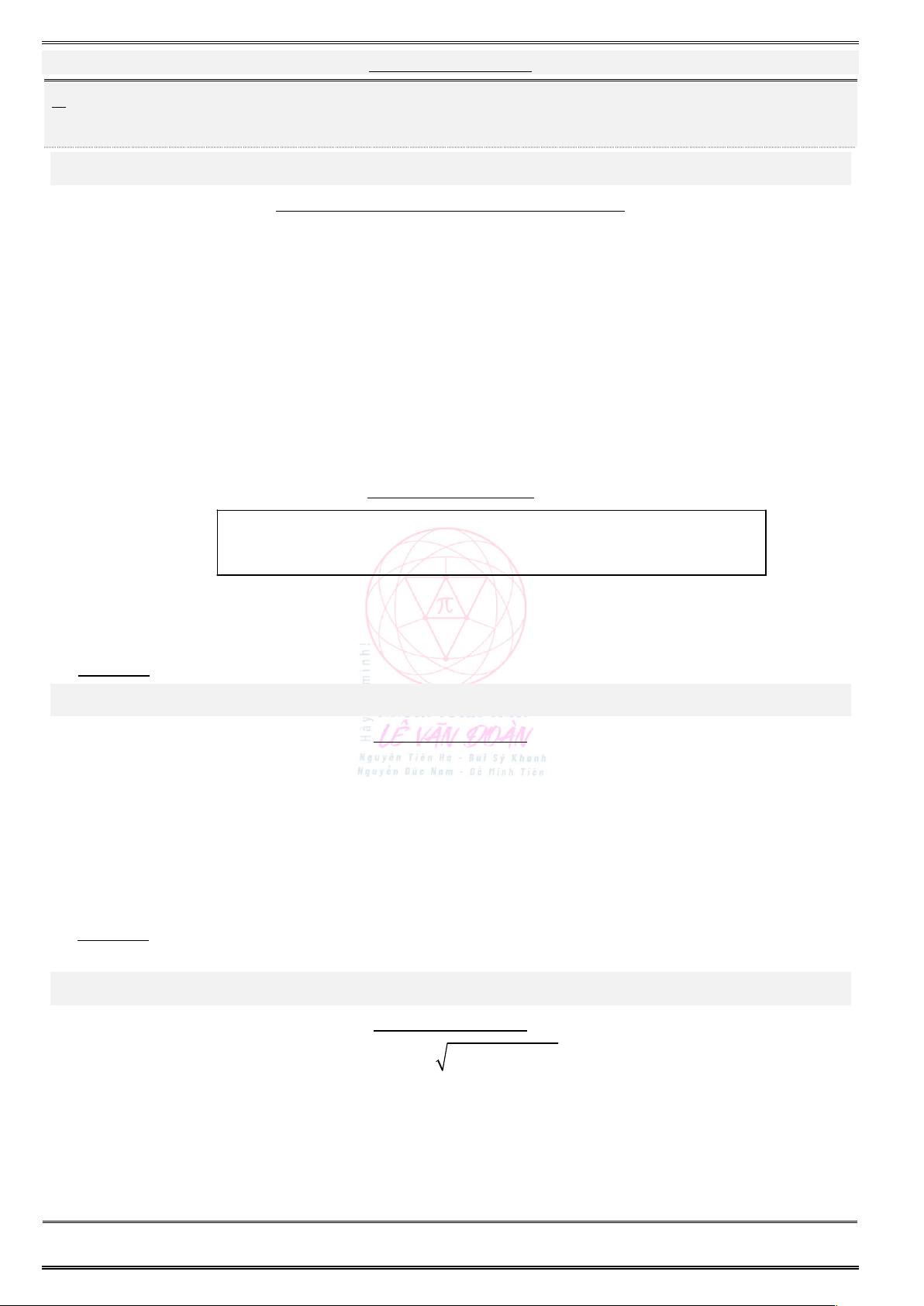
Giả sử phép quay tâm O góc quay  biến đường thẳng d thành đường thẳng d . Khi đó:  O  Nếu 0   
thì góc giữa d và d  bằng .  α 2  d  Nếu
    thì góc giữa d và d  bằng   .  2 d' α I
3. Phöông phaùp xaùc ñònh moät aûnh qua pheùp quay
Phương pháp 1. Sử dụng định nghĩa
Trong mặt phẳng tọa độ Ox , y gọi M (
 x ;y ) là ảnh của M(x ;y ) qua phép quay tâm I(a;b), M  M  M M I
 M   IM (1)  góc quay .
 Khi đó: M (x ;y )  Q (M )   M  M  (I ; )  MI 
M    (2) 
Từ (1), sử dụng công thức tính độ dài, sẽ tìm được phương trình thứ nhất theo 2 ẩn.
Từ (2), sử dụng định lý hàm số cos, sẽ tìm được phương trình thứ hai theo 2 ẩn.
Giải hệ phươngtrình này tìm được x , y , M  x y M 
M  từ đó suy ra tọa độ điểm ( ; ). M  M 
Phương pháp 2. Sử dụng công thức tọa độ. x 
 (x a)cos   (y b)sin   a M (
 x ;y )  Q (M )  M M M    M  M  (I ; ) y 
 (x a)sin   (y b)cos   b  M M M 
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 17 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh BÀI TẬP TỰ LUẬN
1. Trong mặt phẳng O , xy cho điểm (
A 2;3), đường thẳng d : 2x  3y  2  0 và đường tròn có phương trình: 2 2
(C ) : x  y  4x  4y  1  0. a) Tìm ảnh của điểm (
A 2;3) qua phép Q . (O; 90)
Học sinh nghe giảng và bổ sung cách giải 1 O
 A  OA (1)  Gọi A  Q ( ), A với (
A a;b). Suy ra:  (O; 90)  A  OA  90 (2) 
Giải (1) : OA  OA  ............................................................................................................................... (3)       Giải (2) : O ,
A OA  90  OA  OA  .
OAOA  0  ................................................................ (4)  2 2 a  b  13  Từ (3), (4)   
......................................................................................................................... 2
 a  3b  0 
Vì quay theo chiều dương nên chọn A (  3;2).
Lời giải tham khảo 2 x 
 (x a)cos   (y b)sin   a   Vận dụng M (
 x ;y )  Q (M ) M M M   M  M  (I ; ) y 
 (x a)sin   (y b)cos   b  M M M  x 
 x cos 90  y sin 90  2.0  3.1  3  
Khi đó: A  Q ( ) A A A A    A (  3;2). (O; 90) y 
 x sin 90  y cos 90  2.1  3.0  2  A A A 
 Nhận xét. Học sinh giải theo cách giải của giáo viên trên lớp. Về trắc nghiệm nên giải theo cách 2.
b) Viết phương trình đường thẳng d  là ảnh của d qua phép Q . (O; 90)
Lời giải tham khảo Vì d   Q
(d)  d   d  phương trình d  : 3x  2y  m  0. (O; 90) Chọn M( 1
 ;0)  d : 2x  3y  2  0. x 
 1.cos 90  0.sin 90  0  
Khi đó M   Q (M ) M    M (  0;1). (O; 90) y 
 1.sin 90  0.cos 90  1  M 
Do M  d  M (0
 ;1)  d   3.0  2.(1)  m  0  m  2. Vậy d : 3x  2y  2  0.
 Nhận xét. Đối với góc quay  bất kỳ, để tìm ảnh ta cần chọn ra 2 điểm trên d và tìm ảnh của 2 điểm này.
Khi đó đường thẳng d  đi qua hai điểm ảnh vừa tìm.
c) Viết phương trình đường tròn (C )
 là ảnh của (C ) qua phép Q . (O; 90)
Lời giải tham khảo
Đường tròn (C ) có tâm I(2;2) và bán kính 2 2
R  2  2  (1)  3. Gọi (C )   Q
(C )  R  R  3. (O; 90) x 
 2 cos 90  2 sin 90  2   Khi đó I (
 x ;y )  Q (I ) I    I (  2;2). I  I  (O; 90) y 
 2 sin 90  2 cos 90  2  I   Do đó: 2 2 (C )
 : (x  2)  (y  2)  9.
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 18 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
2. Trong mặt phẳng tọa độ Ox , y cho hai điểm ( A 1;0), ( B 0; 2
 ). Tìm A , B lần lượt là ảnh của , A B qua phép quay tâm , O góc quay 90.
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
3. Trong mặt phẳng tọa độ Ox ,
y hãy tìm ảnh của đường tròn (C ) qua phép quay tâm , O góc quay
 trong các trường hợp sau đây: a) 2 2
(C ) : (x  2)  (y  1)  1,   90.
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. b) 2 2
(C ) : x  y  2x  4y  1  0,   9  0.
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. c) 2 2
(C ) : x  (y  1)  1,   60.
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. d) 2 2
(C ) : x  y  4x  2y  0,   3  0.
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 19 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
4. Trong mặt phẳng tọa độ Ox ,
y hãy tìm ảnh của đường thẳng d qua phép quay tâm ,
O góc quay 
trong các trường hợp sau đây:
a) d : x  y  2  0,   90.
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
b) d : x  3y  11  0,   90  . 
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
c) d : x  3y  5  0,   60.
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
d) d : 2x  y  6  0,   45.
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 20 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
BÀI TẬP TRẮC NGHIỆM
1. Cho hai đường thẳng bất kì d và d . Có bao nhiêu phép quay biến đường thẳng d thành đường thẳng d  ?
A. Không có phép nào.
B. Có một phép duy nhất. C. Chỉ có hai phép. D. Có vô số phép.
2. Cho hai đường thẳng song song a và a , một đường thẳng c không song song với chúng. Có bao
nhiêu phép quay biến đường thẳng a thành đường thẳng a  và biến đường thẳng c thành chính nó ?
A. Không có phép nào.
B. Có một phép duy nhất.
C. Chỉ có hai phép. D. Có vô số phép.
3. Cho bốn đường thẳng a, ,
b a , b trong đó a  a , b  b và a cắt b. Có bao nhiêu phép quay biến
các đường thẳng a và b lần lượt thành các đường thẳng a  và b ?
A. Không có phép nào
B. Có một phép duy nhất.
C. Chỉ có hai phép. D. Có vô số phép.
4. Cho hình vuông ABCD có tâm .
O Phép quay tâm O với góc quay nào dưới đây biến hình vuông
ABCD thành chính nó ? A. 30 .  B. 45 .  C. 60. D. 120 . 
5. Cho tam giác ABC đều tâm O (O là tâm của đường tròn ngoại tiếp). Ta thực hiện phép quay
tâm O biến tam giác ABC thành chính nó. Một số đo của góc quay  là A. 45 .  B. 60. C. 90. D. 120 . 
6. Trong mặt phẳng với hệ tọa độ Ox ,
y ta xét phép quay Q(O; ).
 Trong các mệnh đề sau, mệnh đề nào sai ?
A. Nếu   90 thì Q biến trục hoành x O
 x thành trục tung y O  y.
B. Nếu   270 thì Q biến trục tung y Oy 
thành trục hoành x O  x.
C. Nếu   90 thì Q biến trục tung y Oy 
thành trục hoành x O  x.
D. Nếu   180 thì Q biến trục hoành x O
 x thành chính nó.
7. Trong câu này ta chỉ xét các phép quay với góc quay  thỏa điều kiện 0    180. Cho hai
đường thẳng a và b cắt nhau tại điểm .
O Phát biểu nào sau đây là đúng ?
A. Không tồn tại phép quay nào biến đường thẳng a thành đường thẳng b.
B. Có duy nhất một phép quay biến đường thẳng a thành đường thằng b.
C. Có đúng hai phép quay biến đường thẳng a thành đường thẳng b.
D. Có vô số phép quay biến đường thẳng a thành đường thẳng b.
8. Cho hình vuông ABCD tâm .
O Ta xét các mệnh đề sau:
 Phép quay Q(O;45 )
 biến hình vuông ABCD thành chính nó.
 Phép quay Q(O;60 )
 biến hình vuông ABCD thành chính nó.
 Phép quay Q(O;90 )
 biến hình vuông ABCD thành chính nó.  Phép quay ( Q O;180 )
 biến hình vuông ABCD thành chính nó.
Trong các mệnh đề trên:
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 21 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
A. Có duy nhất một mệnh đề đúng.
B. Có hai mệnh đề đúng.
C. Có ba mệnh đề đúng.
D. Tất cả bốn mệnh đề đều đúng.
9. Cho ngũ giác đều ABCDE tâm O. Ta xét các mệnh đề sau:
 Phép quay Q(O;72 )
 biến ngũ giác đều ABCDE thành chính nó.
 Phép quay Q(O;90 )
 biến ngũ giác đều ABCDE thành chính nó.  Phép quay ( Q O;144 )
 biến ngũ giác đều ABCDE thành chính nó.
 Phép quay Q(O;216 )
 biến ngũ giác đều ABCDE thành chính nó.
Trong các mệnh đề trên:
A. Có duy nhất một mệnh đề đúng.
B. Có hai mệnh đề đúng.
C. Có ba mệnh đề đúng.
D. Tất cả bốn mệnh đề đều đúng.
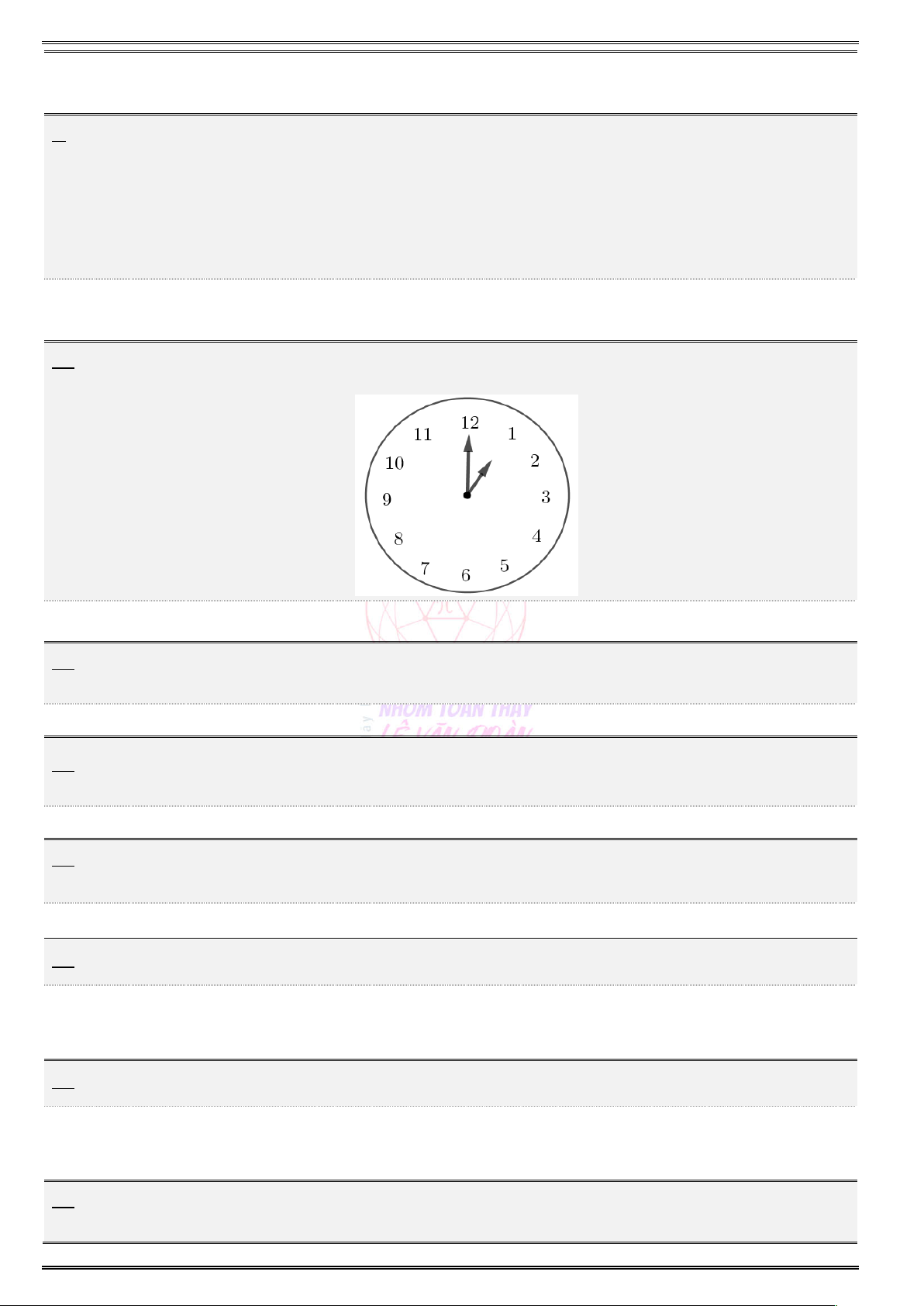
10. Chọn 12 giờ làm mốc, khi kim giờ chỉ một giờ đúng thì kim phút đã quay được một góc bao nhiêu độ ? A. 360. B. 3  60. C. 1  80. D. 720.
11. Cho hình vuông ABCD tâm O (các đỉnh ghi theo chiều kim đồng hồ). Ảnh của cạnh AB qua phép quay Q(O;270 )  là A. A . B B. BC. C. CD. D. D . A 
12. Cho hình thoi ABCD có góc ABC  60 (các đỉnh của hình thoi ghi theo chiều kim đồng hồ).
Ảnh của cạnh CD qua qua phép quay Q( ; A 60 )  là A. A . B B. BC. C. CD. D. D . A
13. Cho tam giác đều ABC có tâm O và các đường cao AA , BB , CC  (các đỉnh của tam giác ghi
theo chiều kim đồng hồ). Ảnh của đường cao AA qua phép quay Q(O;240 )  là
A. AA .
B. BB .
C. CC . D. d qua ,
O d  BC.
14. Trong mặt phẳng tọa độ Ox , y cho điểm (
A x;y). Biểu thức tọa độ của A  Q là  ( ) A (O,90 ) x    y     x    y   x    y   x    y  A.   B.   C.   D.   y    x              y x  y x  y x 
15. Trong mặt phẳng tọa độ Ox , y cho điểm (
A x;y). Biểu thức tọa độ của A  Q là  ( ) A (O,90 ) x    y     x    y   x    y   x    y  A.   B.   C.   D.   y    x              y x  y x  y x 
16. Trong mặt phẳng tọa độ Ox ,
y cho điểm M(4;1). Phép quay Q(O;90 )
 biến điểm M thành điểm
M  có tọa độ là
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 22 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh A. (1; 4). B. ( 1  ;4).
................................................................................................................. C. (1; 4  ). D. (1;4).
.................................................................................................................
17. Trong mặt phẳng tọa độ Ox ,
y cho phép quay tâm O biến điểm (
A 1;0) thành điểm A (0;1). Khi
đó nó biến điểm M(1; 1  ) thành điểm A. M (
 1;1). B. M (1;1).
................................................................................................................. C. M (  1;1). D. M (  1;0).
.................................................................................................................
18. Trong mặt phẳng tọa độ Ox , y cho AB  C với ( A 1;4), B( 2  ;2), C(7; 9
 ). Phép quay Q(O;90 ) 
biến trọng tâm G của AB 
C thành điểm G  có tọa độ là A. (1; 2  ). B. (1;2).
................................................................................................................. C. (3; 1  ). D. ( 3  ;1).
.................................................................................................................
19. Trong mặt phẳng tọa độ Ox ,
y qua phép quay tâm ,
O góc quay 90 biến điểm M( 3  ;5) thành điểm nào ? A. (3; 4).
B. (5;3).
................................................................................................................. C. (5; 3  ). D. (3;5).
.................................................................................................................
20. Trong mặt phẳng tọa độ Ox , y cho điểm (
A 4;1). Biểu thức tọa độ của điểm A  Q ( ) A là ? (O,90) A. ( A 1  ; 4). B. ( A 1; 4  ).
................................................................................................................. C. ( A 4;1). D. ( A 4  ; 1  ).
.................................................................................................................
21. Trong mặt phẳng tọa độ Ox , y cho điểm (
A 0;3). Tìm tọa độ điểm A là ảnh của A qua phép quay Q ? (O, 45  )  1 3    3 1  
................................................................................................................. A.  ;     ;   B.    2 2  4 4
.................................................................................................................  3 1      3 3    C.  ; 
.................................................................................................................    ;   D.    2 2   2 2 
.................................................................................................................
22. Trong mặt phẳng tọa độ Ox ,
y cho điểm M(1;1). Hỏi điểm nào sau đây là ảnh của điểm M qua phép quay tâm ( O 0;0 , ) góc quay 45 ? A. M (  0; 2 . ) B. M (  2;0 . )
................................................................................................................. C. M (  0; ) 1 . D. M  1 ( ;1).
.................................................................................................................
23. Trong mặt phẳng tọa độ Ox ,
y tìm phép quay Q biến điểm (
A 1;5) thành điểm A (5;1)? A. Q ( )
A  A . (O, 90  )
................................................................................................................. B. Q ( )
A  A . (O,90)
................................................................................................................. C. Q ( )
A  A . (O,180)
................................................................................................................. D. Q ( ) A  A . (O, 270  )
.................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 23 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
24. Trong mặt phẳng tọa độ Ox ,
y cho đường thẳng d có phương trình 5x  3y  15  0. Tìm ảnh d 
của d qua phép quay Q
với O là gốc tọa độ ? (O,90)
A. 5x  3y  6  0.
.................................................................................................................
B. 3x  5y  15  0.
.................................................................................................................
C. 5x  y  7  0. D. 3
 x  5y  7  0.
.................................................................................................................
25. Trong mặt phẳng tọa độ Ox ,
y cho I(2;1) và đường thẳng d : 2x  3y  4  0. Tìm ảnh của d qua Q ? (I ,45) A. x
  5y  2  3 2  0.
................................................................................................................. B. x
  5y  3  10 2  0.
.................................................................................................................
C. x  5y  3  2  0.
................................................................................................................. D. x
  5y  3  11 2  0.
26. Trong mặt phẳng tọa độ Ox ,
y có hai đường thẳng a và b có phương trình lần lượt là
4x  3y  5  0 và x  7y  4  0. Nếu có phép quay biến đường thẳng này thành đường thẳng
kia thì số đo của góc quay  là A. 45 .  B. 60.
................................................................................................................. C. 90. D. 120 . 
.................................................................................................................
27. Trong mặt phẳng tọa độ Ox ,
y hãy viết phương trình đường tròn (C )  là ảnh của 2 2
(C ) : x  y  2x  4y  4  0 qua phép quay Q . (O; 90  ) A. 2 2
(x  2)  (y  1)  9.
................................................................................................................. B. 2 2
(x  2)  (y  1)  9.
................................................................................................................. C. 2 2
(x  2)  (y  1)  9.
................................................................................................................. D. 2 2
(x  1)  (y  2)  9.
28. Trong mặt phẳng tọa độ Oxy , cho đường tròn 2 2
(C ) : x  y  6x  5  0. Tìm ảnh đường tròn (C )
 của (C ) qua Q . (O,90) A. 2 2
x  (y  3)  4.
................................................................................................................. B. 2 2
x  y  6y  6  0.
................................................................................................................. C. 2 2
x  (y  3)  4.
................................................................................................................. D. 2 2
x  y  6x  5  0.
.................................................................................................................
ĐÁP ÁN TRẮC NGHIỆM 1.D 2.B 3.B 4.B 5.D 6.D 7.D 8.B 9.C 10.B 11.B 12.B 13.B 14.B 15.A 16.B 17.B 18.B 19.B 20.B 21.D 22.A 23.A 24.B 25.D 26.A 27.A 28.C
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 24 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
§ 6. PHÉP VỊ TỰ VÀ PHÉP ĐỒNG DẠNG  1. Ñònh nghóa
Cho điểm O cố định và một số thực k không đổi, k  0. Phép biến hình biến mỗi điểm M thành  
điểm M , sao cho OM   k.OM được gọi là phép vị tự tâm O tỉ số k và kí hiệu là V (O được (O;k )
gọi là tâm vị tự) (hiểu khác, đây là phép zoom). B' M' 4 M P' A 3 P O 2 6 A' O B N' N 2. Tính chaát
 Định lí 1. Nếu phép vị tự tâm I tỉ số k biến hai điểm M và N lần lượt thành hai điểm M  và   N  thì M N
   k.MN và M N
   k.MN.
 Định lí 2. Phép vị tự biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi
thứ tự của ba điểm đó.  Hệ quả:
 Biến đường thẳng không qua tâm vị tự thành đường thẳng song song với đường thẳng đã cho.
 Biến đường thẳng qua tâm vị tự thành chính nó.  Biến tia thành tia.
 Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với k .
 Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là k .
 Biến góc bằng góc ban đầu.  Lưu ý.  Qua phép V
đường thẳng d biến thành chính nó khi đường thẳng d qua tâm vị tự O. (O;k )
 Nếu M  V
(M )  M V (M ).  (I ;k ) I;1/k
3. AÛnh cuûa ñöôøng troøn qua pheùp vò tröï
 Định lí 3. Phép vị tự tỉ số k biến một đường tròn (I;R) thành đường tròn có bán kính R  k . . R
 Chú ý. Nếu phép vị tự tâm O tỉ số k biến đường tròn (I; )
R thành đường tròn (I ;R )  thì R R   k   k  
và OI   k.OI . R R
4. Taâm vò töï cuûa hai ñöôøng troøn
 Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia. Tâm
của phép vị tự này được gọi là tâm vị tự của hai đường tròn.
 Nếu tỉ số vị tự k  0 thì tâm vị tự đó gọi là tâm vị tự ngoài, nếu tỉ số vị tự k  0 thì tâm vị tự đó
gọi là tâm vị tự trong.
 Cách xác định tâm vị tự: R'  R  R
Nếu I là tâm vị tự ngoài, ta có: IO   IO .  O R I O'  R 
Nếu I là tâm vị tự trong, ta có: IO    IO . R
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 25 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
1. Trong mặt phẳng Ox ,
y cho đường thẳng d : 3x  2y  6  0. Viết phương trình của đường thẳng
d là ảnh của d qua phép vị tự tâm I(1;2) tỉ số vị tự k  2 ?
Học sinh nghe giảng và bổ sung lời giải
Gọi M(x;y)  d : 3x  2y  6  0 (1) Gọi M (  x ;y )
 là ảnh của M qua phép vị tự tâm I tỉ số k  2 :   x
  1  2(x 1) x
  .........................    
 IM  2IM      M    ; . y
   2  2(y  2) y
  ..........................       x  3    y  6 (1)  3   2  
  6  0  3x   2y  9  0 
 M   d : 3x   2y  9  0.   2       2   
Vậy d  : 3x  2y  9  0 là ảnh của d thỏa bài toán.
2. Trong mặt phẳng Ox ,
y cho đường thẳng d : 2x  y  3  0. Viết phương trình của đường thẳng
d là ảnh của d qua phép vị tự tâm (
O 0; 0) tỉ số vị tự k  2 ?
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
3. Trong mặt phẳng Ox ,
y cho đường thẳng d : x y  2  0. Viết phương trình của đường thẳng
d là ảnh của d qua phép vị tự tâm (
O 0; 0) tỉ số vị tự k  3 ?
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
4. Trong mặt phẳng Ox , y cho đường tròn 2 2
(C ) : (x  3)  (y  1)  9. Viết phương trình của đường tròn (C )
 là ảnh của (C) qua phép vị tự tâm I(1;2) tỉ số vị tự k  2 ?
Học sinh nghe giảng và bổ sung lời giải
Đường tròn (C) có tâm I(3; 1
 ) và bán kính R  3. Gọi K (  x ;y )
 là tâm và R là bán kính của (C ) là ảnh của (C).   x
  1  2(x 1) ..
 .............................. x    ............     I
 K   2IK       Khi đó:   y
   2  2(y  2)  ..
 ..............................  y    ............ R     2 R    R  ' 2R ..   
 ..............................        R ...........  Vậy 2 2 (C )
 : (x  3)  (y  6)  36.
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 26 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
5. Trong mặt phẳng Ox , y cho đường tròn 2 2
(C ) : (x  1)  (y  3)  2. Viết phương trình của đường tròn (C )
 là ảnh của (C) qua phép vị tự tâm (
O 0; 0) tỉ số vị tự k  3 ?
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
6. Trong mặt phẳng Ox , y cho đường tròn 2 2
(C ) : (x  1)  (y  2)  5. Viết phương trình của đường tròn (C )
 là ảnh của (C) qua phép vị tự tâm I(1;2) tỉ số vị tự k  2 ?
 Lời giải. ............................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
BÀI TẬP TRẮC NGHIỆM
1. Cho hình thang ABCD có hai cạnh đáy là AB và CD mà AB  3C .
D Phép vị tự biến điểm A
thành điểm C và biến điểm B thành điểm D có tỉ số là 1 1 A. k  
B. k   
....................................................................................................... 3 3
...................................................................................................... `
C. k  3. D. k  3  .
2. Cho tam giác ABC có trọng tâm , G gọi A ,  B ,
 C  lần lượt là trung điểm các cạnh BC, C , A A . B
Với giá trị nào của k thì phép vị tự V( ;
G k) biến tam giác ABC thành tam giác AB C  .
A. k  2.
B. k  2.
....................................................................................................... 1 1 C. k  
D. k   
....................................................................................................... 2 2
3. Trong mặt phẳng tọa độ Ox ,
y cho phép vị tự tâm I(3; 1
 ) có tỉ số k  2
 . Khi đó nó biến điểm M(5;4) thành điểm A. M (  1  ; 1
 1). B. M ( 7  ;11).
....................................................................................................... C. M (  1;9). D. M (  1; 9  ).
.......................................................................................................
4. Trong mặt phẳng tọa độ Ox ,
y cho phép vị tự tỉ số k  2 và biến điểm ( A 1; 2  ) thành điểm A (  5
 ;1).Khi đó nó biến điểm ( B 0;1) thành điểm A. B (  0;2). B. B (  12; 5  ).
....................................................................................................... C. B (  7  ;7). D. B (  11;6).
.......................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 27 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
5. Trong mặt phẳng tọa độ Ox , y cho điểm (
A 3;2). Ảnh của A qua phép vị tự tâm O tỉ số k  1 là A. (3;2). B. (2; 3).
...................................................................................................... C. ( 2  ;3). D. ( 3  ;2).
......................................................................................................
6. Trong mặt phẳng Ox ,
y tìm ảnh A của điểm (
A 1;3) qua phép vị tự tâm O tỉ số 2. A. A (  2;6). B. A (  1;3).
...................................................................................................... C. A (  2  ;6). D. A (  2  ; 6  ).
......................................................................................................
7. Tìm ảnh A của (
A 1;2) qua phép vị tự tâm I(3;1). tỉ số k  2. A. A (  3;4). B. A (  1;5).
...................................................................................................... C. A (  5  ; 1  ). D. A (  1  ;5).
......................................................................................................
8. Cho P(3;2), Q(1;1), (
R 2;4). Gọi P ,  Q ,
 R lần lượt là ảnh của P, Q, R qua phép vị tự tâm O 1
tỉ số k    Khi đó tọa độ trọng tâm của tam giác P Q  R   là 3 1 1    1   A.  ;  
......................................................................................................  0;    B. 9 3  9
...................................................................................................... 2 1   2    C.  ;     ;0  D.
...................................................................................................... 3 3 9 
9. Trong mặt phẳng tọa độ Oxy, cho ba điểm (
A 0; 3),B(2;1),C(1;5). Phép vị tự tâm A tỉ số k
biến B thành C . Khi đó giá trị k là 1
A. k    B. k  1. 
...................................................................................................... 2
...................................................................................................... 1 C. k   D. k  2.
...................................................................................................... 2
10. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : 2x  y  4  0, I (1;2). Tìm ảnh d của d
qua phép vị tự tâm I tỉ số k  2.
A. 2x  y  4  0.
......................................................................................................
B. 2x  y  8  0.
......................................................................................................
C. 2x  y  8  0.
......................................................................................................
D. 2x  y  4  0.
......................................................................................................
11. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : 3x  y  5  0. Tìm ảnh d của d qua phép 2
vị tự tâm O tỉ số k    3
A. 3x  y  9  0.
......................................................................................................
B. 3x  y  10  0.
......................................................................................................
C. 9x  3y  15  0.
......................................................................................................
D. 9x  3y  10  0.
......................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 28 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh 1
12. Trong mặt phẳng tọa độ Ox ,
y cho phép vị tự tâm I(1;1) tỉ số k    Khi đó nó biến đường 3
thẳng 5x y  1  0 thành đường thẳng có phương trình là
A. 15x  3y  10  0.
.......................................................................................................
B. 15x  3y  23  0.
.......................................................................................................
C. 15x  3y  23  0.
.......................................................................................................
D. 5x  3y  8  0.
.......................................................................................................
13. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : 5x  2y  7  0. Tìm ảnh d của d qua phép
vị tự tâm O tỉ số k  2.
A. 5x  2y  14  0.
.......................................................................................................
B. 5x  4y  28  0.
.......................................................................................................
C. 5x  2y  7  0.
.......................................................................................................
D. 5x  2y  14  0.
....................................................................................................... x y
14. Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d : 
 1 và d : 2x  y  6  0. Phép vị 2 4 tự V
(d)  d . Tìm k. (O,k ) 3 2 A. k  
B. k   
....................................................................................................... 2 3
....................................................................................................... 1 1 C. k  
D. k   
....................................................................................................... 3 3
15. Tìm ảnh đường tròn (C )  của đường tròn 2 2
(C ) : (x  1)  (y  2)  5 qua phép vị tự tâm O tỉ số k  2. A. 2 2 (C )
 : (x  2)  (y  4)  10.
....................................................................................................... B. 2 2 (C )
 : (x  2)  (y  4)  10.
....................................................................................................... C. 2 2 (C )
 : (x  2)  (y  4)  20.
....................................................................................................... D. 2 2 (C )
 : (x  2)  (y  4)  20.
.......................................................................................................
16. Trong mặt phẳng tọa độ Oxy, cho đường tròn 2 2
(C ) : (x  3)  (y  1)  5. Tìm ảnh đường tròn (C )
 của đường tròn (C) qua phép vị tự tâm I(1;2) và tỉ số k  2.  A. 2 2
x  y  6x  16y  4  0.
....................................................................................................... B. 2 2
x  y  6x  16y  4  0.
....................................................................................................... C. 2 2
(x  3)  (y  8)  20.
....................................................................................................... D. 2 2
(x  3)  (y  8)  20.
.......................................................................................................
17. Trong mặt phẳng tọa độ Oxy, cho đường tròn 2 2
(C ) : (x  1)  (y  1)  4 . Tìm ảnh (C )  của (C)
qua phép vị tự tâm I (1;2) tỉ số k  3. A. 2 2
x  y  14x  4y  1  0.
.......................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 29 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh B. 2 2
x  y  4x  7y  5  0.
...................................................................................................... C. 2 2
(x  5)  (y  1)  36.
...................................................................................................... D. 2 2
(x  7)  (y  2)  9.
......................................................................................................
18. Trong mặt phẳng tọa độ Ox , y cho hai điểm (
A 1;1), B(2; 3) và đường thẳng a có phương trình
y  4x  1. Thực hiện liên tiếp hai phép đối xứng tâm § và § (theo thứ tự), đường thẳng a A B
biến thành đường thẳng a có phương trình là
A. y  4x  5.
.......................................................................................................
B. y  4x  17.
.......................................................................................................
C. y  4x 12.
....................................................................................................... D. y  4  x 4.
.......................................................................................................
19. Trong mặt phẳng tọa độ Ox , y cho hai điểm (
A 1; 0), B(1;1) và đường tròn (T ) có phương trình 2 2
x  y  4x  0. Thực hiện liên tiếp hai phép đối xứng tâm § và § (theo thứ tự), đường tròn A B
(T ) biến thành đường tròn (T )  có phương trình là A. 2 2
x  y  4x  2y  4  0.
....................................................................................................... B. 2 2
x  y  4x  4y  4  0.
....................................................................................................... C. 2 2
x  y  6x  2y  1  0.
....................................................................................................... D. 2 2
x  y  4y  8  0.
.......................................................................................................
20. Trong mặt phẳng tọa độ Ox ,
y cho đường thẳng  có phương trình 5x y 1  0. Thực hiện
phép tịnh tiến theo phương của trục hoành về phía trái 2 đơn vị, sau đó tiếp tục thực hiện phép
tịnh tiến theo phương của trục tung về phía trên 3 đơn vị, đường thẳng  biến thành đường
thẳng  có phương trình là
A. 5x y  14  0.
.......................................................................................................
B. 5x y  7  0.
.......................................................................................................
C. 5x  y  5  0.
.......................................................................................................
D. 5x  y  12  0.
.......................................................................................................
21. Trong mặt phẳng tọa độ Ox ,
y cho đường thẳng  có phương trình y  3
 x  2. Thực hiện liên  
tiếp hai phép tịnh tiến theo các vectơ u  ( 1
 ;2) vàv  (3;1), đường thẳng  biến thành đường
thẳng d có phương trình là A. y  3  x 1.
....................................................................................................... B. y  3  x 5.
....................................................................................................... C. y  3  x  9.
....................................................................................................... D. y  3  x  15.
22. Trong mặt phẳng Oxy, cho điểm M (2; 4). Hỏi phép đồng dạng có được bằng cách thực hiện liên 1
tiếp phép vị tự tâm O tỉ số k 
và phép quay tâm O góc quay 90 sẽ biến điểm M thành 2 điểm nào sau đây ?
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 30 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh A. (2;1).
...................................................................................................... B. (2;1).
...................................................................................................... C. (1;2).
...................................................................................................... D. (1; 2).
......................................................................................................
23. Trong mặt phẳng Oxy, cho đường thẳng d : 2x  y  0 thỏa mãn phép đồng dạng có được bằng
cách thực hiện liên tiếp phép vị tự tâm O tỉ số k  2 và phép đối xứng trục Oy sẽ biến đường
thẳng d thành đường thẳng nào sau đây ?
A. 2x  y  0.
......................................................................................................
B. 2x  y  0.
......................................................................................................
C. 4x  y  0.
......................................................................................................
D. 2x  y  2  0.
......................................................................................................
24. Trong mặt phẳng Oxy, cho đường tròn 2 2
(C ) : (x  2)  (y  2)  4. Hỏi phép đồng dạng có được 1
bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k 
và phép quay tâm O góc quay 90 sẽ 2
biến (C ) thành đường tròn nào sau đây ? A. 2 2
(x  2)  (y  2)  1.
...................................................................................................... B. 2 2
(x  1)  (y  1)  1.
...................................................................................................... C. 2 2
(x  2)  (y  1)  1.
...................................................................................................... D. 2 2
(x  1)  (y  1)  1.
......................................................................................................
25. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : x  2y  0. Phép đồng dạng là phép thực
hiện liên tiếp qua phép vị tự tâm I (1;2) tỉ số k  3 và phép quay tâm O góc quay 90 sẽ biến
đường thẳng d thành đường thẳng nào sau đây ?
A. 2x  y  6  0.
......................................................................................................
B. x  2y  6  0.
......................................................................................................
C. 2x  y  6  0.
......................................................................................................
D. 2x  y  3  0.
......................................................................................................
26. Phép đồng dạng là phép thực hiện liên tiếp qua phép vị tự tâm I (4;2) tỉ số k  3 và phép đối
xứng qua trục d : x  2y  4  0 sẽ biến M (0;1) thành điểm nào sau đây ? A. (16;5).
...................................................................................................... B. (14;9).
...................................................................................................... C. (12;13).
...................................................................................................... D. (18;1).
......................................................................................................
27. Trong mặt phẳng tọa độ Oxy , cho đường tròn 2 2
(C ) : (x  1)  (y  2)  4. Phép đồng dạng là
phép thực hiện liên tiếp qua phép vị tự tâm O tỉ số k  2 và phép quay tâm O góc quay 0 180
sẽ biến đường tròn (C ) thành đường tròn nào sau đây ?
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 31 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh A. 2 2
x  y  4x  8y  2  0.
....................................................................................................... B. 2 2
x  y  4x  8y  2  0.
....................................................................................................... C. 2 2
(x  2)  (y  4)  16.
....................................................................................................... D. 2 2
(x  2)  (y  4)  16.
.......................................................................................................
28. Trong mặt phẳng tọa độ Oxy, cho đường tròn 2 2
(C ) : (x  1)  (y  2)  9. Phép đồng dạng là 1 
phép thực hiện liên tiếp qua phép vị tự tâm I (1;1) tỉ số k 
và phép tịnh tiến theo v  (3; 4) 3
sẽ biến đường tròn (C ) thành đường tròn có phương trình là A. 2 2
(x  4)  (y  4)  9.
....................................................................................................... B. 2 2
(x  4)  (y  4)  1.
....................................................................................................... C. 2 2
(x  4)  (y  4)  1.
.......................................................................................................
....................................................................................................... D. 2 2
(x 1)  y  1.
29. Trong mặt phẳng tọa độ Ox ,
y cho điểm P(3;1). Thực hiện liên tiếp hai phép vị tự V (O;4) và  1 V O  ;    
điểm P biến thành điểm P  có tọa độ là  2 A. P (  4; 6  ).
....................................................................................................... B. P (  6; 2  ).
....................................................................................................... C. P (  6  ;2).
....................................................................................................... D. P (  12; 4  ).
.......................................................................................................
30. Trong mặt phẳng tọa độ Ox ,
y cho đường thẳng d : 2x  y  0 thỏa mãn phép đồng dạng có được
bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k  2 và phép đối xứng trục Oy sẽ biến
đường thẳng d thành đường thẳng nào sau đây ?
A. 2x  y  0.
.......................................................................................................
B. 4x  y  0.
....................................................................................................... C. 2
 x y  0.
.......................................................................................................
D. 2x  y  2  0.
....................................................................................................... BẢNG ĐÁP ÁN 1.B 2.D 3.A 4.C 5.D 6.D 7.D 8.B 9.A 10.C 11.D 12.B 13.A 14.A 15.C 16.C 17.C 18.B 19.B 20.A 21.C 22.A 23.A 24.D 25.C 26.C 27.D 28.B 29.C 30.C
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 32 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh ÔN TẬP CHƯƠNG 1
1. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng (d ) : 2x  3y  1  0 và 1
(d ) : x  y  2  0. Có bao nhiêu phép tịnh tiến biến d thành d . 2 1 2 A. Vô số. B. 4.
.................................................................................................................. C. 1. D. 0.
..................................................................................................................  2. Cho v  ( 1
 ;5) và điểm M (4;2). Biết M  là ảnh của M qua phép tịnh tiến T. Tìm M. v
A. M (4;10). B. M (3; 5).
..................................................................................................................
C. M (3; 7). D. M (5;3).
..................................................................................................................  
3. Cho điểm A (
 1;4) và u  (2;3), biết A là ảnh của A qua phép tịnh tiến u. Tìm tọa độ điểm . A A. ( A 1; 4). B. (
A 3;1). .................................................................................................................. C. (
A 1;4). D. ( A 3;1).
..................................................................................................................
4. Cho hai đường thẳng song song d và d .
 Tìm khẳng định nào đúng ?
A. Có đúng một phép tịnh tiến biến d thành d . 
B. Có vô số phép tịnh tiến biến d thành d .  
C. Phép tịnh tiến theo véc tơ v có giá vuông góc với đường thẳng d biến d thành d . 
D. Cả ba khẳng định trên đều đúng. 
5. Điểm M (2; 4) là ảnh của điểm nào sau đây qua phép tịnh tiến theo véctơ v  (1;7).
A. F(1;3). B. P(3;11).
..................................................................................................................
C. E(3;1). D. Q(1; 3).
.................................................................................................................. 
6. Trong mặt phẳng tọa độ Oxy, cho v  (2; 3). Tìm ảnh của điểm (
A 1;1) qua phép tịnh tiến theo  véctơ v. A. A (  2  ;1). B. A (  1;2).
.................................................................................................................. C. A (  2;1). D.
.................................................................................................................. A (  1  ; 2  ).
7. Phép biến hình nào sau đây không là phép dời hình ?
A. Phép tịnh tiến.
..................................................................................................................
B. Phép đối xứng tâm.
..................................................................................................................
C. Phép đối xứng trục. D. Phép vị tự.
.................................................................................................................. 
8. Cho hình bình hành ABCD. Ảnh của điểm D qua phép tịnh tiến theo véctơ AB là A. B. B. C.
.................................................................................................................. C. D. D. . A
.................................................................................................................. 
9. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M (2; 5). Phép tịnh tiến theo v  (1;2) biến điểm
M thành điểm M . Tọa độ điểm M  là
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 33 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh A. M (  3;7). B. M (  1;3).
.................................................................................................................. C. M (  3;1). D. M (  4;7).
..................................................................................................................
10. Hình nào dưới nào dưới đây không có trục đối xứng ? A. Tam giác cân.
.................................................................................................................. B. Hình thang cân.
.................................................................................................................. C. Hình elip. D. Hình bình hành.
.................................................................................................................. 
11. Trong mặt phẳng tọa độ Oxy, cho véctơ v  (3; 5). Tìm ảnh của điểm (
A 1;2) qua phép tịnh  tiến theo véctơ v. A. A (  4; 3  ). B. A (  2;3).
.................................................................................................................. C. A (  4;3). D. A (
 2;7). ..................................................................................................................  
12. Cho 4IA  5IB. Tỉ số vị tự k của phép vị tự tâm I , biến A thành B là 4 3 A. k   B. k  
.................................................................................................................. 5 5 5 1
.................................................................................................................. C. k   D. k   4 5
..................................................................................................................
13. Trong mặt phẳng Oxy, cho đường tròn 2 2
(C ) : (x  1)  (y  1)  4. Phép vị tự tâm O (với O
là gốc tọa độ) tỉ số k  2 biến (C ) thành đường tròn nào trong các đường tròn có phương trình sau ? A. 2 2
(x  1)  (y  1)  8.
.................................................................................................................. B. 2 2
(x  2)  (y  2)  8.
.................................................................................................................. C. 2 2
(x  2)  (y  2)  16.
.................................................................................................................. D. 2 2
(x  2)  (y  2)  16.
.................................................................................................................. 
14. Trong mặt phẳng với hệ tọa độ Oxy, cho véctơ v  (2;1) và điểm M (3;2). Tìm tọa độ ảnh 
M  của điểm M qua phép tịnh tiến theo véctơ v. A. M (  5;3). B. M (
 1;1). .................................................................................................................. C. M (
 1;1). D. M (1;1).
..................................................................................................................
15. Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc ,
 0    2
biến hình chữ nhật trên thành chính nó ? A. Không có. B. 4.
.................................................................................................................. C. 2. D. 3.
..................................................................................................................
16. Phép tịnh tiến biến gốc tọa độ O thành điểm (
A 1;2) sẽ biến điểm A thành điểm A có tọa độ là A. A (  2;4). B. A (  1  ; 2  ).
.................................................................................................................. C. A (  4;2). D. A (  3;3).
..................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 34 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh 
17. Trong mặt phẳng Oxy, cho (
A 2;3), B(1; 0). Phép tịnh tiến theo u  (4; 3  ) biến điểm , A B
tương ứng thành A ,
 B khi đó, độ dài đoạn thẳng AB bằng A. 10. B. 10.
.................................................................................................................. C. 13. D. 5.
..................................................................................................................  
18. Trong mặt phẳng tọa độ Oxy cho vectơ u  (3;1). Phép tịnh tiến theo vectơ u biến điểm M (1;4) thành A. M (
 4;5). B. M (3;4). .................................................................................................................. C. M (
 2;3). D. M (4;5).
.................................................................................................................. 
19. Cho hình chữ nhật MNPQ. Phép tịnh tiến theo véctơ MN biến điểm Q thành điểm A. Điểm Q. B. Điểm N.
.................................................................................................................. C. Điểm M. D. Điểm P.
..................................................................................................................
20. Trong mặt phẳng tọa độ Oxy, cho điểm (3
A ;1). Tìm tọa độ điểm B sao cho điểm A là ảnh 
của điểm B qua phép tịnh tiến theo véctơ u  (2; 1  ).
A. B(1; 0).
B. B(5;2).
..................................................................................................................
C. B(1;2).
D. B(1; 0).
..................................................................................................................
21. Cho hình hộp ABC . D AB C  D
  (như hình vẽ). Chọn mệnh đề đúng? 
A. Phép tịnh tiến theo DC biến điểm A thành điểm B . D' C'  B'
B. Phép tịnh tiến theo AB biến điểm A thành điểm C . A'  D
C. Phép tịnh tiến theo AC biến điểm A thành điểm D . C  A
D. Phép tịnh tiến theo AA biến điểm A thành điểm B . B 
22. Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vectơ v  (1;2) biến điểm M (4; 5) thành điểm nào sau đây ?
A. P(1; 6).
B. Q(3;1).
..................................................................................................................
C. N (5; 7). D. ( R 4;7).
..................................................................................................................
23. Trong mặt phẳng tọa độ Oxy, cho hai điểm (
A 1;1) và I(2; 3). Phép vị tự tâm I tỉ số k  2 
biến điểm A thành điểm A .
 Tọa độ điểm A là A. A (  0;7). B. A (  7;0).
.................................................................................................................. C. A (  7;4). D. A (  4;7).
.................................................................................................................. 
24. Trong mặt phẳng tọa độOxy, phép tính tiến theo véctơ v biến điểm M (x;y) thành điểm  M (  x ;y )
 sao cho x  x  2 và y  y  4. Tọa độ của v là A. (2; 4). B. (4;2).
..................................................................................................................
C. (2;4). D. (2; 4).
..................................................................................................................  
25. Trong mặt phẳng Oxy, cho điểm (
A 2;1) và vectơ a  (1;3). Phép tịnh tiến theo véctơ a biến
điểm A thành điểm A .
 Tọa độ điểm A là
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 35 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh A. A (  1  ; 2
 ). B. A (1;2).
.................................................................................................................. C. A (  4;3). D. A (  3;4).
.................................................................................................................. 
26. Cho hình thoi ABCD tâm I . Phép tịnh tiến theo véc tơ IA biến điểm C thành
A. Điểm B. B. Điểm C.
.................................................................................................................. C. Điểm D. D. Điểm I .
.................................................................................................................. 
27. Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo véc tơ v  (1; 3) biến điểm ( A 1;2) thành điểm nào trong các điểm sau ?
A. M (2; 5).
B. P(1; 3).
..................................................................................................................
C. Q(3;4). D. N (3; 4).
..................................................................................................................
28. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M (3;2). Tọa độ của điểm M  là ảnh của điểm 
M qua phép tịnh tiến theo véctơ v  (2;1) là A. (1;1). B. (3;2).
.................................................................................................................. C. (5;3). D. (5; 3).
..................................................................................................................
29. Trong mặt phẳng với hệ tọa độ Oxy, phép quay tâm I (4;3) góc quay 180 biến đường thẳng
d : x  y  5  0 thành đường thẳng d có phương trình
A. x  y  3  0.
...................................................................................................................
B. x  y  3  0.
...................................................................................................................
C. x  y  5  0.
...................................................................................................................
D. x  y  3  0.
...................................................................................................................
30. Cho đường thẳng d : x  y  2  0. Phép hợp thành của phép đối xứng tâm O và phép tịnh 
tiến theo v  (3;2) biến d thành đường thẳng nào sau đây ?
A. x  y  4  0.
...................................................................................................................
B. 3x  3y  2  0.
...................................................................................................................
C. 2x  y  2  0.
...................................................................................................................
D. x  y  3  0.
31. Trong mặt phẳng Oxy, tìm phương trình đường tròn (C )
 là ảnh của đường tròn 2 2
(C ) : x  y  1 qua phép đối xứng tâm I(1; 0). A. 2 2
(x  2)  y  1.
................................................................................................................... B. 2 2
x  (y  2)  1.
................................................................................................................... C. 2 2
(x  2)  y  1.
................................................................................................................... D. 2 2
x  (y  2)  1.
...................................................................................................................
32. Trong mặt phẳng Oxy, qua phép quay Q(O,90 ),  M (
 3;2)là ảnh của điểm
A. M (3;2). B. M (3;2). ...................................................................................................................
C. M (2; 3).
D. M (2;3). ...................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 36 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
33. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng  : x  2y  6  0. Viết phương trình đường thẳng 
 là ảnh của đường thẳng  qua phép quay tâm O góc 90.
A. 2x  y  6  0.
...................................................................................................................
B. 2x  y  6  0.
...................................................................................................................
C. 2x  y  6  0.
...................................................................................................................
D. 2x  y  6  0.
...................................................................................................................
34. Trong mặt phẳng Oxy, cho đường tròn 2 2
(C ) : (x  1)  (y  3)  4. Phép tịnh tiến theo vectơ
v  (3;2) biến đường tròn (C) thành đường tròn có phương trình nào sau đây ? A. 2 2
(x  2)  (y  5)  4.
................................................................................................................... B. 2 2
(x  4)  (y  1)  4.
................................................................................................................... C. 2 2
(x  1)  (y  3)  4.
................................................................................................................... D. 2 2
(x  2)  (y  5)  4.
...................................................................................................................
35. Trong mặt phẳng Oxy, cho điểm B(3; 6). Tìm tọa độ điểm E sao cho B là ảnh của E qua
phép quay tâm O góc quay 9  0 . 
A. E(6;3). B.
................................................................................................................... E(3;6).
...................................................................................................................
C. E(6; 3). D. E(6;3).
36. Trong mặt phẳng với hệ tọa độ Oxy, tìm tọa độ điểm M  là ảnh của điểm M (2;1) qua phép đối
xứng tâm I (3;2). A. M (  1;3).
................................................................................................................... B. M (  5;4).
................................................................................................................... C. M (  4;5).
................................................................................................................... D. M (  1;5).
...................................................................................................................
37. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có (
A 2; 4), B(5;1), C (1;2). Phép tịnh
tiến T biến tam giác ABC tành tam giác AB C
 . Tìm tọa độ trọng tâm của tam giác AB C  . BC A. (4;2). B. (4; 2).
................................................................................................................... C. (4;2). D. (4;2).
................................................................................................................... 
38. Trong mặt phẳng với hệ toạ độ Oxy, cho véctơ v  (1;2), điểm (3
A ; 5).Tìm tọa độ của các điểm 
A là ảnh của A qua phép tịnh tiến theo v. A. A (  2;7). B. A (
 2;7). ................................................................................................................... C. A (  7;2). D. A (
 2;7). ...................................................................................................................
39. Trong mặt phẳng Oxy, ảnh của điểm M (2; 3) qua phép đối xứng trục  : x  y  0 là A. M (  3;2).
................................................................................................................... B. M (  3;2).
................................................................................................................... C. M (  3;2). D. M (  3;2).
...................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 37 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh
40. Trong mặt phẳng tọa độ Oxy, cho các điểm I (3;1), J (1;1). Ảnh của J qua phép quay Q (I ; 90  ) là A. J (  1;5).
................................................................................................................... B. J (  5;3).
................................................................................................................... C. J (  3;3).
................................................................................................................... D. J (  1;5).
...................................................................................................................
41. Trong mặt phẳng tọa độ Oxy, cho đường tròn 2 2
(C ) : (x  1)  (y  2)  4. Tìm ảnh của đường
tròn (C ) qua phép vị tự tâm O tỉ số 2. A. 2 2
(x  2)  (y  4)  16.
................................................................................................................... B. 2 2
(x  2)  (y  4)  16.
................................................................................................................... C. 2 2
(x  2)  (y  4)  16.
................................................................................................................... D. 2 2
(x  2)  (y  4)  16.
...................................................................................................................
42. Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF
qua phép quay tâm O góc quay . Tìm . A B
A.   60.
...................................................................................................................
B.   60. O F
C ................................................................................................................... C.   120 . 
................................................................................................................... D.   12  0. E D 
43. Trong mặt phẳng tọa độ Oxy, cho véctơ v  (1;2). Tìm ảnh của điểm (
A 2; 3) qua phép tịnh  tiến theo vectơ v. A. A (  5;1). B. A (
 1;5). ................................................................................................................... C. A (  3;1). D. A (  3
 ;1). ...................................................................................................................
44. Trong mặt phẳng Oxy, cho đường thẳng d có phương trình 2x  y  1  0. Để phép tịnh tiến  
theo v biến đường thẳng d thành chính nó thì v phải là véctơ nào trong các véctơ sau đây ? 
A. v  (1;2).
................................................................................................................... 
B. v  (2;1). 
...................................................................................................................
C. v  (2;4). 
...................................................................................................................
D. v  (2; 4).
................................................................................................................... 
45. Trong mặt phẳng Oxy, cho véctơ v  ( 3
 ;2) và đường thẳng  : x  3y  6  0. Viết phương  trình đường thẳng 
 là ảnh của đường thẳng  qua phép tịnh tiến theo v.
A.  : 3x  y  15  0.
...................................................................................................................
B.  : 3x  y  5  0.
...................................................................................................................
C.  : x  3y  15  0.
...................................................................................................................
D.  : x  3y  15  0.
...................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 38 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh 
46. Trong mặt phẳng tọa độ Oxy, cho điểm M (1; 2). Phép tịnh tiến theo véctơ u  ( 3  ;4) biến điểm
M thành điểm M  có tọa độ là A. M (
 2;6). B. M (2;5).
................................................................................................................... C. M (  2;6). D.
...................................................................................................... M (  4;2).
47. Trong mặt phẳng Oxy, cho đường thẳng  : x  y  2  0. Hãy viết phương trình đường thẳng
d là ảnh của đường thẳng  qua phép quay tâm O, góc quay 90.
A. d : x  y  2  0.
...................................................................................................................
B. d : x  y  2  0.
...................................................................................................................
C. d : x  y  2  0.
...................................................................................................................
D. d : x  y  4  0.
...................................................................................................................
48. Trong mặt phẳng tọa độ Oxy, tìm phương trình đường thẳng 
 là ảnh của đường thẳng 
 : x  2y  1  0 qua phép tịnh tiến theo véctơ v  (1; 1  ).
A.  : x  2y  3  0.
...................................................................................................................
B.  : x  2y  0.
...................................................................................................................
C.  : x  2y  1  0.
...................................................................................................................
D.  : x  2y  2  0.
...................................................................................................................
49. Trong mặt phẳng tọa độ Oxy, cho đường tròn 2 2
(C ) : (x  2)  (y  1)  9. Gọi (C )  là ảnh của 1
đường tròn (C ) qua việc thực hiện liên tiếp phép vị tự tâm O, tỉ số k   và phép tịnh tiến 3  theo vectơ v  (1; 3
 ). Tính bán kính R của đường tròn (C ). 
A. R  9.
...................................................................................................................
B. R  3.
...................................................................................................................
C. R  27.
................................................................................................................... D. R  1.
...................................................................................................................
50. Trong mặt phẳng Oxy, cho điểm I (2;1). Gọi (C ) là đồ thị hàm số y  sin 3x. Phép vị tự tâm 1
I (2;1), tỉ số k   biến (C ) thành (C ).
 Viết phương trình đường cong (C ).  2 3 1 A. y 
 sin(6x  18).
................................................................................................................... 2 2 3 1
................................................................................................................... B. y 
 sin(6x  18). 2 2
................................................................................................................... 3 1
C. y    sin(6x  18).
................................................................................................................... 2 2
................................................................................................................... 3 1 D. y    sin(6x  18). 2 2
...................................................................................................................
51. Cho tam giác ABC có diện tích bằng 2
6cm . Phép vị tự tỷ số k  2
 biến tam giác ABC thành
tam giác AB C
 . Tính diện tích tam giác AB C   ?
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 39 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam) Ch¬ng 1. PhÐp biÕn h×nh A. 2 12cm .
................................................................................................................... B. 2 24cm .
................................................................................................................... C. 2 6cm . D. 2 3cm .
...................................................................................................................
52. Trong mặt phẳng tọa độ Oxy, cho điểm (
A 3; 4). Gọi A là ảnh của điểm A qua phép quay tâm
O(0; 0), góc quay 90. Điểm A có tọa độ là A. A (  3;4). B. A (  4; 3
 ). ................................................................................................................... C. A (  3;4). D. A (
 4;3). ................................................................................................................... 
53. Trong mặt phẳng Oxy, cho v  (3; 3) và đường tròn 2 2
(C ) : x  y  2x  4y  4  0. Ảnh của 
(C ) qua phép tịnh tiến vectơ v là đường tròn nào ? A. 2 2
(x  4)  (y  1)  4.
................................................................................................................... B. 2 2
(x  4)  (y  1)  9.
................................................................................................................... C. 2 2
(x  4)  (y  1)  9.
................................................................................................................... D. 2 2
x  y  8x  2y  4.
...................................................................................................................
54. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : y  x. Tìm ảnh của d qua phép quay tâm O, góc quay 90.
A. d  : y  2x.
...................................................................................................................
B. d  : y  x  .
................................................................................................................... C. d  : y  2  x.
D. d  : y  x.
...................................................................................................................
55. Trong mặt phẳng Oxy, tìm phương trình đường tròn (C )
 là ảnh của đường tròn 2 2
(C ) : x  y  1 qua phép đối xứng tâm I(1; 0). A. 2 2
x  (y  2)  1.
................................................................................................................... B. 2 2
(x  2)  y  1.
................................................................................................................... C. 2 2
(x  2)  y  1.
................................................................................................................... D. 2 2
x  (y  2)  1.
...................................................................................................................
ĐÁP ÁN BÀI TẬP ÔN CUỐI CHƯƠNG 1.D 2.D 3.D 4.B 5.B 6.B 7.D 8.B 9.A 10.D 11.D 12.A 13.D 14.C 15.C 16.A 17.A 18.A 19.D 20.D 21.A 22.C 23.D 24.A 25.D 26.D 27.A 28.A 29.B 30.D 31.C 32.C 33.A 34.A 35.A 36.C 37.D 38.A 39.D 40.A 41.B 42.B 43.B 44.A 45.D 46.A 47.A 48.B 49.D 50.D 51.B 52.D 53.B 54.B 55.C
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 40 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
ĐƯỜNG THẲNG VÀ MẶT PHẲNG Chöông TRONG KHÔNG GIAN II
§ 1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 
1. Môû ñaàu veà hình hoïc khoâng gian
Đối tượng cơ bản:  Điểm: kí hiệu ,
A B, C , ...
 Đường thẳng: kí hiệu a, , b ,
c d, d , d , ... 1 2
 Mặt phẳng: kí hiệu (P), (Q), (), (), ... Quan hệ cơ bản:
 Thuộc: kí hiệu  . Ví dụ: A  d, M  (P).
 Chứa, nằm trong: kí hiệu  . Ví dụ: d  (P), b  ().
Hình biểu diễn của một hình trong không gian:
 Đường thẳng được biểu diễn bởi đường thẳng. Đoạn thẳng biểu diễn bởi đoạn thẳng.
 Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi hai đường thẳng song song (hoặc cắt nhau).
 Hai đoạn thẳng song song hoặc bằng nhau được biểu diễn bởi hai đoạn thẳng song song và bằng nhau.
 Dùng nét vẽ liền ( __ ) để biểu diễn cho những đường trông thấy và dùng nét đứt đoạn (----)
để biểu diễn cho những đường bị che khuất.
2. Caùc tính chaát thöøa nhaän trong hình hoïc khoâng gian
 Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt không thẳng hàng cho trước.
 Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
 Nếu 1 đường thẳng có 2 điểm phân biệt thuộc một mặt phẳng
thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
 Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
 Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng
còn có một điểm chung khác nữa.
Từ tính chất này suy ra: Nếu hai mặt phẳng phân biệt có một
điểm chung thì chúng sẽ có một đường thẳng chung đi qua
điểm chung ấy. Đường thẳng chung là duy nhất chứa tất cả
các điểm chung của hai mặt phẳng đó. Đường thẳng chung
đó được gọi là giao tuyến của hai mặt phẳng.
 Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
3. Ñieàu kieän xaùc ñònh maët phaúng
 Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.
 Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng
không đi qua điểm đó. Mặt phẳng hoàn toàn có thể mở rộng ra đến vô cực.
 Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 41 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
4. Hình choùp vaø hình töù dieän
 Cho đa giác AA A .......A nằm trong mặt phẳng () và điểm S  (). Lần lượt nối điểm S với 1 2 3 n
các đỉnh A , A , A , ..., A ta được n tam giác SA A , SA A , ..., SA A . Hình gồm đa giác 1 2 3 n 1 2 2 3 n 1
AA A ...A và n tam giác SAA , SA A , ..., SA A được gọi là hình chóp, kí hiệu hình chóp này 1 2 3 n 1 2 2 3 n 1 S
là S.A A A ...A . Khi đó ta gọi: 1 2 3 n
 S là đỉnh của hình chóp.
 AA A ...A là mặt đáy của hình chóp. 1 2 3 n
 Các tam giác SAA , SA A , ..., SA A gọi là mặt bên. A3 1 2 2 3 n 1 A1
 SA , SA , SA , ..., SA được gọi là các cạnh bên. 1 2 3 n A2
 Ta gọi hình chóp có đáy là tam giác, tứ giác, ngũ giác,..., lần lượt là hình chóp tam giác, hình chóp
tứ giác, hình chóp ngũ giác, ....  Cho bốn điểm ,
A B, C, D không đồng phẳng. Hình gồm 4 tam giác ABC, ACD, ABD và
BCD gọi là hình tứ diện (hay ngắn gọn gọi là tứ diện) và kí hiệu là ABC . D Các điểm ,
A B, C, D là bốn đỉnh của tứ diện.
 Các đoạn thẳng AB, BC, CD, D , A C ,
A BD gọi là các cạnh của tứ diện.
 Hai cạnh không đi qua một đỉnh gọi là hai cạnh đối diện của tứ diện.
 Các tam giác ABC, ACD, ABD, BCD gọi là các mặt của tứ diện.
 Hình tứ diện có bốn mặt là các tam giác đều gọi là hình tứ diện đều.
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 42 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
Daïng toaùn 1: Tìm giao tuyeán cuûa hai maët phaúng
 Phương pháp giải
 Tìm hai điểm chung phân biệt của hai mặt phẳng.
 Đường thẳng nối hai điểm chung đó là giao tuyến của chúng.
BÀI TẬP VẬN DỤNG
1. Cho tứ diện SABC. Gọi M, N lần lượt là hai điểm trên cạnh AB và BC sao cho MN không
song song với AC. Tìm giao tuyến của các cặp mặt phẳng sau:
a) (SMN ) và (SAC ).
Ta có: S  (SMN )  (SAC ) (1)
Trong (ABC ), gọi E  MN  AC. E
  MN, MN  (SMN)  E  (SMN)  Ta có:  E
  AC, AC  (SAC )  E  (SAC ) 
 E  (SMN )  (SAC) (2)
Từ (1), (2)  (SMN )  (SAC )  SE.
b) (SAN ) và (SCM ).
Ta có: S  (SAN )  (SCM ) (3)
Trong (ABC ), gọi F  AN  CM. F
  AN, AN  (SAN)  F  (SAN)  Ta có: 
 F  (SAN )  (SCM ) (4) F
  CM, CM  (SCM )  F  (SCM ) 
Từ (3), (4)  (SAN )  (SCM )  SF.
c) (SMC ) và (ADN ), với D là trung điểm của S . B
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................  Cần nhớ:
 Điểm thuộc đường thẳng, đường thẳng nằm trong mặt phẳng, điểm thuộc mặt phẳng.
Nghĩa là M  d, d  (P)  M  (P).
 Với việc giải hình trong không gian là tập hợp nhiều mặt phẳng, điều kiện đầu tiên để hai đường thẳng cắt
nhau là hai đường thẳng trước hết phải đồng phẳng (cùng nằm trong một mặt phẳng). Khi gọi giao điểm
của hai đường thẳng cần kiểm tra hai đường thẳng đó đồng phẳng ở mặt phẳng nào, kiểm tra được điều đó
là đã trả lời được câu hỏi “có cắt nhau không ?”, “làm đúng không ?”
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 43 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
2. Cho tứ diện SABC. Gọi K, M lần lượt là hai điểm trên cạnh SA và SC sao cho KM không song
song AC. Gọi N là trung điểm của cạnh BC. Tìm giao tuyến của S
a) (SAN ) và (ABM ).
.............................................................................................
.............................................................................................
............................................................................................. A C
.............................................................................................
............................................................................................. B
b) (SAN ) và (BCK).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
3. Cho hình chóp S.ABC. Trên cạnh S ,
A SC lấy M, N sao cho MN không song song AC. Gọi K
là trung điểm BC. Tìm giao tuyến của các cặp mặt phẳng:
a) (MNK ) và (ABC ).
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
b) (MNK ) và (SAB).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
4. Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Tìm giao tuyến của: S
a) (SAC ) và (SBD).
.............................................................................................
.............................................................................................
............................................................................................. A D
............................................................................................. C
............................................................................................. B
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 44 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) (SAB) và (SCD).
c) (SAD) và (SBC ).
.............................................................................. .............................................................................................
.............................................................................. .............................................................................................
.............................................................................. .............................................................................................
.............................................................................. .............................................................................................
.............................................................................. .............................................................................................
.............................................................................. .............................................................................................
5. Cho hình chóp S.AB ,
CD trong đó mặt đáy ABCD có các cặp cạnh đối không song song. Gọi điểm
M thuộc cạnh S .
A Tìm giao tuyến của các cặp mặt phẳng:
a) (SAC ) và (SBD).
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
b) (SAB) và (SCD).
c) (MBC) và (SAD).
.............................................................................. .............................................................................................
.............................................................................. .............................................................................................
.............................................................................. .............................................................................................
.............................................................................. .............................................................................................
.............................................................................. .............................................................................................
.............................................................................. .............................................................................................
6. Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Trên cạnh SA lấy điểm M . Tìm giao tuyến
của các cặp mặt phẳng sau đây: S
a) (SAC ) và (SBD).
............................................................................................. M
.............................................................................................
.............................................................................................
............................................................................................. A D
.............................................................................................
............................................................................................. C
............................................................................................. B
.............................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 45 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) (SAB) và (SCD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) (BCM) và (SAD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) (CDM) và (SAB).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
e) (BDM ) và (SAC).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
7. Cho hình chóp S.ABCD có đáy là hình thang với AB CD và AB  CD. Lấy điểm M nằm trên
đoạn BC. Tìm giao tuyến của các cặp mặt phẳng sau đây: S
a) (SAC ) và (SBD).
.............................................................................................
.............................................................................................
............................................................................................. A
............................................................................................. D
............................................................................................. B M C
.............................................................................................
.............................................................................................
.............................................................................................
b) (SAB) và (SCD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 46 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
c) (SAM) và (SBD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) (SDM) và (SAB).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Lấy điểm M trên cạnh , SA
trung điểm CD là N. Tìm giao tuyến của các cặp mặt phẳng sau:
a) (SAC ) và (SBD). S
.............................................................................................
............................................................................................. M
............................................................................................. A
............................................................................................. D
............................................................................................. N O B C
b) (BMN ) và (SAD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) (BMN ) và (SAC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) (MCD) và (SBD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
e) (MCD) và (SAB).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 47 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm
các cạnh BC, CD, S .
A Tìm giao tuyến của các cặp mặt phẳng sau: S
a) (SAC ) và (SBD).
.............................................................................................
............................................................................................. A D
............................................................................................. B C
.............................................................................................
b) (MNP) và (SAB).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) (MNP) và (SAD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) (MNP) và (SBC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
e) (MNP) và (SCD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
10. Cho hình chóp S.ABC. Trên cạnh S ,
A SC lấy M, N sao cho MN không song song AC. Gọi
O là điểm nằm miền trong của tam giác ABC. Tìm giao tuyến của: S
a) (MNO) và (ABC ).
.............................................................................................
............................................................................................. A B
............................................................................................. O
............................................................................................. C
.............................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 48 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) (MNO) và (SAB).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) (SMO) và (SBC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) (ONC ) và (SAB).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
11. Cho tứ diện ABCD có M nằm trên cạnh ,
AB N nằm trên cạnh AD thỏa MB  2M , A AN  2N .
D Gọi P là điểm thuộc miền trong của tam giác BCD. Tìm giao tuyến giữa: A
a) (CMN ) và (BCD).
.............................................................................................
.............................................................................................
............................................................................................. B D
............................................................................................. P
............................................................................................. C
.............................................................................................
b) (MNP) và (SAD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) (MNP) và (ABC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 49 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
12. Cho tứ diện SABC. Lấy điểm E, F lần lượt trên đoạn S ,
A SB sao cho EF không song song
với AB. Gọi G là trọng tâm của tam giác ABC. Hãy tìm giao tuyến giữa hai mặt phẳng:
a) (EFG) và (ABC ).
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
b) (EFG) và (SBC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) (EFG) và (SGC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
13. Cho hình chóp S.ABCD có đáy là tứ giác lồi. Hai điểm G, H lần lượt là trọng tâm của S  AB và S  C .
D Tìm giao tuyến của các cặp mặt phẳng sau:
a) (SGH ) và (ABCD).
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
.............................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 50 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) (SAC ) và (SGH ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) (SAC ) và (BGH ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) (SCD) và (BGH ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
14. Cho tứ diện SABC. Gọi ,
D E, F lần lượt là trung điểm của ,
AB BC, S . A S
a) Tìm giao tuyến SH của (SCD) và (SAE).
............................................................................................. F
.............................................................................................
............................................................................................. A C
.............................................................................................
............................................................................................. D E
............................................................................................. B
b) Tìm giao tuyến CI của hai mặt phẳng (SCD) và (BFC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Hỏi SH và CI có cắt nhau không ? Giải thích ? Nếu có, gọi giao điểm đó là , O chứng minh OH
IH  SC. Tính tỉ số  OS
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 51 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
Daïng toaùn 2: Tìm giao ñieåm cuûa ñöôøng thaúng d vaø maët phaúng ( ) 
 Phương pháp giải
Nếu đường thẳng d cắt đường thẳng d  (d, d  đồng phẳng) và d   ( )
 thì giao điểm của d và ( )
 chính là giao điểm I của d và d .
Nếu không có giao điểm như thế thì ta sẽ làm theo các bước sau: β
 Bước 1. Tìm mặt phẳng phụ () thỏa 3 điều kiện: d
 Chứa đường thẳng d.
 Có 1 điểm chung với ( )  . u  Càng lớn càng tốt.
 Bước 2. Tìm giao tuyến u của ( )  và (). α I   , u u  ( )   
Bước 3. Trong (), gọi I  d  u. Khi đó: 
 I  d  (). I   d 
 Lưu ý. Trong một số bài toán tìm giao tuyến nâng cao, ta có thể dễ dàng tìm được một điểm chung,
nhưng khó xác định điểm chung còn lại. Khi đó ta nghĩ đến việc tìm giao điểm của đường
thẳng nằm trong mặt phẳng này với mặt phẳng kia. Đó chính là điểm chung thứ hai của hai mặt phẳng.
BÀI TẬP VẬN DỤNG
1. Cho tứ diện SABC có M là điểm nằm trên tia đối của tia S ,
A O là điểm thuộc miền của trong
tam giác ABC . Hãy tìm:
a) Giao điểm của đường thẳng BC và (SO ) A . M S
Trong (ABC ), gọi E  OA  BC . E   ,
OA OA  (SO ) A  E  ( ) SOA  Ta có:  . F E   BC 
Suy ra: E  BC  (SO ). A A C
 Cần nhớ: Trước khi làm, ta cần kiểm tra xem đường BC có
đồng phẳng và cắt đường thẳng nào nằm trong mặt phẳng O E ( )
SOA hay không ? Nếu có thì sẽ làm như trên, nếu không thì B
sử dụng phương pháp mặt phụ.
b) Giao điểm của đường thẳng MO và (SBC ).
 Chọn mặt phẳng phụ (MAE) chứa MO.
 Xét hai mặt phẳng (MAE) và (SBC) : S
  AM, AM  (MAE)  S  (MAE)  Ta có: 
 S  (MAE)  (SBC ) (1) S   (SBC )  E
  AO, BC  (MAE)  E  (MAE)  Mặt khác: 
 E  (MAE)  (SBC ) (2) E
  BC, BC  (SBC )  E  (SBC ) 
Từ (1), (2)  (MAE)  (SBC )  SE. F   MO  
Trong (MAE), gọi F  MO  SE. Khi đó 
 F  MO  (SBC ). F
  SE, SE  (SBC ) 
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 52 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
2. Cho tứ diện SABC có hai điểm M , N lần lượt thuộc hai cạnh S ,
A SB và O là điểm nằm trong
tam giác ABC . Hãy tìm S
a) Giao điểm của đường thẳng AB và (SOC ).
.................................................................................................... N M
.................................................................................................... A C
.................................................................................................... O
.................................................................................................... B
....................................................................................................
b) Giao điểm của đường thẳng MN và (SOC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Giao điểm của đường thẳng SO và (CMN ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
3. Cho hình chóp S.ABC. Trên cạnh SA lấy M sao cho SA  3SM, trên cạnh SC lấy điểm N sao
cho SC  2SN. Điểm P thuộc cạnh AB. Hãy tìm S
a) Giao điểm của đường thẳng MN và (ABC ).
....................................................................................................
.................................................................................................... A C
....................................................................................................
.................................................................................................... B
....................................................................................................
....................................................................................................
b) Giao điểm của đường thẳng BC và (MNP).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 53 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
4. Cho tứ diện ABCD. Trên AC và AD lần lượt lấy các điểm M, N sao cho MN không song song
với CD. Gọi P là điểm thuộc miền trong của tam giác BCD. Hãy tìm
a) Giao điểm của đường thẳng MN và (BCD).
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
b) Giao điểm của đường thẳng AP và (BMN ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
5. Cho hình chóp S.ABCD với ABCD là hình bình hành. Gọi M là điểm lấy trên cạnh SB, N là
điểm thuộc miền trong của tam giác SCD. Hãy tìm của S
a) Đường thẳng MN và (ABCD).
....................................................................................................
.................................................................................................... M
.................................................................................................... N
.................................................................................................... A D
.................................................................................................... O
.................................................................................................... B C
....................................................................................................
b) Đường thẳng SC và (MAN ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Đường thẳng SD và (MAN ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 54 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
d) Đường thẳng SA và (CMN ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
6. Cho hình chóp S.ABCD có đáy hình bình hành tâm O có G là trọng tâm tam giác SAB. Tìm: S
a) Giao tuyến của (SGC ) và (ABCD).
....................................................................................................
....................................................................................................
.................................................................................................... G A D
.................................................................................................... O
.................................................................................................... B C
....................................................................................................
b) Giao điểm của đường thẳng AD và (SGC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Giao điểm của đường thẳng SO và (GCD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) Giao điểm của đường thẳng SD và (BCG).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 55 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
ÔN TẬP HÌNH PHẲNG
1) Đường trung bình A
MN là đường trung bình của tam giác ABC thì M N 1  MN  BC.  MN  BC. 2 B C 2) Trọng tâm A
Trọng tâm là giao điểm của ba đường trung tuyến.
Nếu G là trọng tâm tam giác ABC thì: M G N 2 CG  CM. 3 B C 3) Định lý Talét A AM AN MN      M N MN BC AB AC BC B C
Đồng dạng (đồng hồ cát): A B IA IB AB AB CD     I ID IC CD C D
4) Định lý Menelaus
Cho tam giác ABC, các điểm ,
D E, F lần lượt nằm trên các đường thẳng BC, ,
CA AB. Khi đó: FA DB EC ,
D E, F thẳng hàng     1. FB DC EA
Chứng minh phần thuận: Giả sử ,
D E, F thẳng hàng. A
Từ C, dựng CG  ,
AB (G  AC ). F DB FB E  D
 BF có CG  BF   (1) G DC CG EC CG B D C
 CG  AF   (2) EA FA DB EC FB CG FA DB EC Lấy (1)(2), ta được:        1 (đpcm). DC EA CG FA FB DC EA
Chứng minh phần đảo: (học sinh tự chứng minh).
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 56 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
7. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của SA và CD. S M F I A E D N B C
a) Tìm giao điểm E của AD với (BMN ).
Trong (ABCD), gọi E   BN  AD. E
   BN, BN  (BMN)  E  (BMN)  Ta có: 
 E   AD  (BMN ). E    AD 
Mà theo đề bài E  AD  (BMN )  E  E .
b) Tìm giao điểm F của SD và (BMN ). Chứng minh rằng: FS  2FD.
Cách giải 1. Sử dụng Menelaus: MS EA FD FD
Xét SAE có M, F, E thẳng hàng     1  1.2.
 1  FS  2FD. MA ED FS FS
Cách giải 2. Sử dụng dựng hình.
Dựng DI  S ,
A (I  FE) FS SM FS MA
 Ta có: FMS  F  ID  
, mà SM  MA    FD DI FD DI MA FS
 Mà D là trung điểm AE và DI  MA   2 
 2  FS  2FD. DI FD
Cách giải 3. Sử dụng trọng tâm.
Trong tam giác SAE, ta có EM là đường trung tuyến (1) 1
Vì trong tam giác ABE có ND  AB và ND 
AB nên ND là đường trung bình. 2
Suy ra D là trung điểm của AE nên SD là đường trung tuyến của tam giác SAE (2)
Mà F  SD  EM  F là trọng tâm của tam giác SAE  FS  2FD.
 Bình luận. Tùy vào giáo viên trên lớp có hay không cho sử dụng định lý Menelaus mà ta chọn phương
pháp giải cho phù hợp. Đối với cách giải dựng hình ở cách 2 bản chất là chứng minh lại định lý
Menelaus. Nếu không cho sử dụng ta cũng nên học để biết cách dựng hình từ đâu và cách làm.
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 57 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của SD. S
a) Tìm I  BM  (SAC ). Chứng minh: BI  2IM.
.................................................................................................... M
....................................................................................................
.................................................................................................... A D
....................................................................................................
....................................................................................................
.................................................................................................... B C
....................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
b) Tìm E  SA  (BCM ). Chứng minh: E là trung điểm của S . A
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
9. Cho tứ diện ABCD. Gọi I và J lần lượt là trung điểm của AC và BC . Trên cạnh BD lấy điểm
K sao cho BK  2KD. A
a) Tìm giao điểm E của đường thẳng CD và (IJK ).
Chứng minh: DE  DC .
....................................................................................................
....................................................................................................
.................................................................................................... I
.................................................................................................... K
.................................................................................................... B D
.................................................................................................... J
.................................................................................................... C
....................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 58 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) Tìm giao điểm F của AD với (IJK ). Chứng minh: FA  2FD và FK  IJ .
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Gọi M và N là hai điểm bất kì lần lượt nằm trên hai cạnh AB và CD. Tìm giao điểm của MN với (IJK ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
10. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB và AB  2CD. Gọi I, J , K
lần lượt là trung điểm của các cạnh S ,
A AB, BC .
a) Tìm giao điểm của IK và (SBD). S
....................................................................................................
....................................................................................................
.................................................................................................... I
....................................................................................................
.................................................................................................... A B
.................................................................................................... J
.................................................................................................... K
.................................................................................................... D C
.................................................................................................... FS
b) Tìm giao điểm F của SD và (IJK ). Tính tỉ số  FD
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 59 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian GS
c) Tìm giao điểm G của SC và (IJK ). Tính tỉ số  GC
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
11. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O. Gọi M là trung điểm của SB, N
là điểm thuộc đoạn SD sao cho SN  2ND. S
a) Tìm giao tuyến của (SBD) và (SAC ).
....................................................................................................
.................................................................................................... N M
....................................................................................................
.................................................................................................... A D
.................................................................................................... O
.................................................................................................... B C
.................................................................................................... EN
b) Tìm giao điểm E của đường thẳng MN và mặt phẳng (ABCD). Tính  EM
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Tìm giao điểm K của đường thẳng SC và mặt phẳng (AMN ). Gọi J giao điểm của AK và SO. JK Tính tỉ số:  JA
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 60 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
Daïng 3: Tìm thieát dieän cuûa hình (H) khi caét bôûi maët phaúng (P)
 Phương pháp giải
Ta tìm các đoạn giao tuyến nối tiếp nhau của mặt phẳng () với các mặt của hình chóp cho đến
khi khép kín thành một đa giác phẳng. Đa giác đó là thiết diện cần tìm và các đoạn giao tuyến
chính là các cạnh của thiết diện.
1. Cho tứ diện ABCD. Trên các đoạn C ,
A CB, BD cho lần lượt các điểm M, N, P sao cho MN
không song song với AB. Gọi () là mặt phẳng xác định bởi ba điểm M, N, P. Dựng thiết diện
tạo bởi () và tứ diện ABCD.
Lời giải tham khảo A N F E B P D M C
Ta có: M, N , P  ()  ()  (MNP).
 Ta có: (MNP)  (BCD)  MP (1)
 Tương tự: (MNP)  (ABC)  MN (2)
 Xét (MNP) và (ACD) : N
  AC, AC  (ACD)  N  (ACD)  Ta có: 
 N  (ACD)  (MNP). N   (MNP) 
Trong (BCD), gọi E  MP  CD. E
  MP, MP  (MNP)  E  (MNP)  Ta có: 
 E  (MNP)  (ACD). E   C ,
D CD  (ACD)  E  (ACD) 
Suy ra (MNP)  (ACD)  NP (3)
 Trong (ACD), gọi F  NE  AD. Suy ra (MNP)  (ACD)  NF (4)
Từ (1),(2),(3),(4)  thiết diện tạo bởi () và tứ diện ABCD là tứ giác MNFP.
 Bình luận. Bài toán thiết diện là bài toán tổng hợp của bài toán tìm giao điểm của đường thẳng với mặt
phẳng, bài toán tìm giao tuyến của mặt phẳng với mặt phẳng. Để kiểm tra xem thiết diện ta tìm đã “đúng
chưa ?”, có các cách như sau:
1. Mặt phẳng cắt đã “cắt rời” khối đa diện ban đầu thành hai khối đa diện mới chưa ?
2. Kiểm tra các đỉnh của đa giác thiết diện có nằm trên các cạnh của khối đa diện chưa ?
3. Kiểm tra các cạnh của đa giác thiết diện có nằm trên các mặt của khối đa diện chưa ?
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 61 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
2. Cho hình chóp S.ABC . Trên cạnh S ,
A SB lần lượt lấy M, N sao cho MN không song song với
AB. Gọi P là điểm thuộc miền trong tam giác ABC . Xác định thiết diện khi cắt hình chóp bởi mặt phẳng (MNP). S
....................................................................................................
.................................................................................................... M
....................................................................................................
....................................................................................................
.................................................................................................... A C
.................................................................................................... P N
....................................................................................................
.................................................................................................... B
....................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
3. Cho tứ diện SABC . Gọi K, N lần lượt là trung điểm ,
SA BC và M là điểm thuộc đoạn SC
sao cho 3SM  2MC . S
a) Tìm thiết diện của (KMN ) với hình chóp.
..................................................................................... M
..................................................................................... K
.....................................................................................
..................................................................................... A C
.....................................................................................
..................................................................................... N
..................................................................................... B
.....................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
b) Mặt phẳng (KMN ) cắt AB tại I . Đặt IA  k. . IB Tìm k.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 62 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
4. Cho tứ diện ABCD. Trên AB lấy điểm M . Điểm N trên BC thỏa BN  2NC , P là trung
điểm CD. Xác định thiết diện khi cắt bởi (MNP). A
....................................................................................................
.................................................................................................... M
....................................................................................................
....................................................................................................
.................................................................................................... B D
....................................................................................................
.................................................................................................... P N
.................................................................................................... C
....................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
5. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AD. Lấy M trên cạnh SB. Tìm
thiết diện cắt bởi (AMD).
.................................................................................................... S
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
.................................................................................................... A D
....................................................................................................
.................................................................................................... B C
....................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 63 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N , P là các điểm lần lượt trên các cạnh C , B C , D S .
A Tìm thiết diện của hình chóp với (MNP).
.................................................................................................... S
....................................................................................................
....................................................................................................
....................................................................................................
.................................................................................................... A D
....................................................................................................
....................................................................................................
.................................................................................................... B C
....................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
7. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AD. Gọi H , K là trung điểm của
SB và AB, M là điểm lấy trong hình thang ABCD sao cho đường thẳng KM cắt hai đường
thẳng AD, CD. Tìm thiết diện của hình chóp với (HKM ).
.................................................................................................... S
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
.................................................................................................... A D
....................................................................................................
.................................................................................................... B C
....................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 64 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
Daïng toaùn 4: Chöùng minh ba ñieåm thaúng haøng
 Phương pháp giải
Để chứng minh ba điểm , A ,
B C thẳng hàng, ta cần chứng minh ba điểm này lần lượt thuộc hai mặt phẳng phân biệt ( )
 và (). Nghĩa là chúng cùng thuộc giao tuyến d của hai mặt phẳng ( ) 
và () nên chúng thẳng hàng. BÀI TẬP ÁP DỤNG
1. Cho tứ diện SABC . Trên các cạnh S ,
A SB, SC lần lượt lấy các điểm M, N, P sao cho MN cắt
AB tại I, NP cắt BC tại J và MP cắt AC tại K. Chứng minh ba điểm I, J, K thẳng hàng.
Lời giải tham khảo S P M C K A N B J I
Gọi đường thẳng d là giao tuyến của hai mặt phẳng (MNP) và (ABC ). K
  MP, MP  (MNP)  K  (MNP) 
Ta có: K  MP  AC  
 K  d (1) K
  AC, AC  (ABC )  K  (ABC )  Tương tự: I
  MN, MN  (MNP)  I  (MNP) I MN AB     
 I  d (2) I   ,
AB AB  (ABC )  I  (ABC )  J
  NP, NP  (MNP)  J  (MNP) J NP BC     
 J  d (3) J
  BC, NP  (ABC )  J  (ABC ) 
Từ (1),(2),(3), suy ra I, J, K cùng thuộc d  ba điểm I, J, K thẳng hàng (đpcm).
 Bình luận. Cái khó của học sinh là tìm ra hai mặt phẳng (MNP) và (ABC ) để tìm giao tuyến và ba điểm
I, J, K đều thuộc giao tuyến. Để tìm ra nó, ta dựa vào kinh nghiệm sau:
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 65 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
2. Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Gọi M, N , P lần lượt là trung điểm của
các cạnh AB, BC , CD. A
a) Xác định giao tuyến của (ADN ) và (ABP ).
....................................................................................................
.................................................................................................... M
....................................................................................................
.................................................................................................... B D
.................................................................................................... G
.................................................................................................... N P
.................................................................................................... C
....................................................................................................
b) Gọi I  AG  MP và J  CM  AN. Chứng minh D, I, J thẳng hàng.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm ,
O hai điểm M, N lần lượt là trung điểm của S , B S ,
D điểm P thuộc SC và không là trung điểm của SC. S
a) Tìm giao điểm của SO với (MNP).
....................................................................................................
....................................................................................................
.................................................................................................... A
.................................................................................................... D
.................................................................................................... O
.................................................................................................... B C
....................................................................................................
....................................................................................................
....................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 66 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) Tìm giao điểm của SA với mặt phẳng (MNP).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Gọi F, G, H lần lượt là giao điểm của QM và A ,
B QP và AC, QN và . AD Chứng minh ba
điểm F, G, H thẳng hàng.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm ,
O hai điểm M, N lần lượt là trung điểm của S , B S ,
D điểm P thuộc SC và không là trung điểm của SC. S
a) Tìm giao điểm của SO với (MNP).
....................................................................................................
....................................................................................................
.................................................................................................... A
.................................................................................................... D
.................................................................................................... O
.................................................................................................... B C
....................................................................................................
....................................................................................................
b) Tìm giao điểm của SA với mặt phẳng (MNP).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 67 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
c) Gọi F, G, H lần lượt là giao điểm của QM và A ,
B QP và AC, QN và . AD Chứng minh ba
điểm F, G, H thẳng hàng.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
5. Cho hình chóp S.ABCD có AD không song song với BC. Lấy M thuộc SB và O là giao điểm AC với B . D
a) Tìm giao điểm N của SC với (ADM ). S
.................................................................................................... M
....................................................................................................
.................................................................................................... A
.................................................................................................... B
....................................................................................................
.................................................................................................... O
.................................................................................................... D C
....................................................................................................
....................................................................................................
................................................................................................................................................................................
b) Gọi I  AN  DM. Chứng minh S, I, O thẳng hàng.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 68 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
BÀI TẬP RÈN LUYỆN GIAO TUYẾN  GIAO ĐIỂM  THẲNG HÀNG  TỈ SỐ BT 1.
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Gọi M, N, P lần lượt là trung điểm của ,
AB BC, CD.
a) Tìm giao tuyến của (ADN ) và (ABP).
b) Gọi I  AG  MP và J  CM  AN . Chứng minh ,
D I, J thẳng hàng. BT 2.
Cho hình chóp S.ABC .
D Gọi E, F, H lần lượt là các điểm thuộc cạnh S , A S , B SC.
a) Tìm giao điểm K  SD  (EFH ).
b) Gọi O  AC  BD và I  EH  FK. Chứng minh: S, I, O thẳng hàng.
c) Gọi M  AD  BC và N  EK  FH . Chứng minh: S, M, N thẳng hàng.
d) Gọi P  AB  CD và Q  EF  HK. Chứng minh: ,
A P, Q thẳng hàng. BT 3. Cho tứ diện ABC .
D Gọi M, N, P lần lượt là các điểm thuộc cạnh A ,
B AC, BD và
MN  BC  I, MP  AD  J, NJ  IP  K. Chứng minh: C, ,
D K thẳng hàng. BT 4.
Cho hình chóp S.ABC .
D Gọi I và J là hai điểm trên hai cạnh A , D SB.
a) Tìm giao tuyến của (SBI ) và (SAC ). Tìm giao điểm K của IJ và (SAC ).
b) Tìm giao tuyến của (SBD) và (SAC ). Tìm giao điểm L của DJ và (SAC ).
c) Gọi O  AD  BC, M  OJ  SC. Chứng minh rằng: , A K, ,
L M thẳng hàng. BT 5.
Cho tứ giác ABCD có các cạnh đối đôi một không song song và điểm S  (ABCD). Lấy điểm
I thuộc cạnh A ,
D lấy điểm J thuộc cạnh SB.
a) Tìm K  IJ  (SAC ).
b) L  DJ  (SAC ).
c) Gọi O  AD  BC, M  OJ  SC. Chứng minh rằng: K, ,
L M thẳng hàng. BT 6.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm .
O Gọi M, N lần lượt là trung điểm của S , A SC.
a) Tìm giao tuyến của (BMN ) với các mặt phẳng (SAB) và (SBC ).
b) Tìm I  SO  (BMN ) và K  SD  (BMN ).
c) Tìm E  AD  (BMN ) và F  CD  (BMN ).
d) Chứng minh rằng ba điểm ,
B E, F thẳng hàng. BT 7.
Cho hình chóp S.ABC .
D Gọi M, N là 2 điểm lần lượt nằm trên 2 cạnh BC và S . D
a) Tìm giao điểm I của BN và (SAC ).
b) Tìm giao điểm J của MN và (SAC ).
c) Chứng minh: I, J, C thẳng hàng.
d) Xác định thiết diện của mặt phẳng (BCN ) với hình chóp. BT 8.
Cho tứ diện ABCD có K là trung điểm của .
AB Lấy I, J lần lượt thuộc AC, BD sao cho
IA  2IC và JB  3JD.
a) Tìm giao điểm E của AD và (IJK ).
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 69 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) Tìm giao tuyến d của (IJK) và (BCD).
c) Gọi O là giao điểm của d với CD. Chứng minh: I, ,
O E thẳng hàng. OI OC d) Tính các tỉ số và  OE OD BT 9.
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD là đáy lớn và AD  2BC. Gọi
M, N lần lượt là trung điểm của S ,
B SC và O  AC  BD.
a) Tìm giao tuyến của (ABN ) và (SCD).
b) Tìm giao điểm P của DN và (SAB).
c) Gọi K  AN  DM. Chứng minh S, K, O thẳng hàng. Đặt KS  k.KO. Tìm k.
BT 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm .
O Gọi M, N lần lượt là trung điểm của S ,
A SC. Gọi (P) là mặt phẳng qua M, N và B.
a) Tìm giao tuyến của (P) với các mặt phẳng (SAB), (SBC ), (SAD), (SDC ).
b) Tìm I  SO  (P), K  SD  (P), E  DA  (P), F  DC  (P).
c) Chứng tỏ rằng ba điểm: E, ,
B F thẳng hàng.
BT 11. Cho hình chóp S.ABCD có đáy ABCD là tứ giác có các cặp cạnh đối không song song nhau.
Gọi M, E là trung điểm S ,
A AC và F  CD sao cho CD  3CF.
a) Tìm giao tuyến của (SAB) và (SCD).
b) Tìm giao điểm N của SD và (MEF). Đặt NS  k.N . D Tìm k.
c) Gọi H  SE  CM và K  MF  NE. Chứng minh ,
D H, K thẳng hàng. HM HS KM KN KH d) Tính các tỉ số sau: ; ; ; ;  HC HE KF KE KD
BT 12. Cho tứ diện ABC .
D Trên các cạnh A ,
B AC, BD lần lượt lấy ba điểm E, F, G sao cho
AB  3AE, AC  2AF, DB  4DG.
a) Tìm giao tuyến của hai mặt phẳng (EFG) và (BCD). HC
b) Tìm giao điểm H của đường thẳng CD với (EFG). Tính tỉ số  HD IA
c) Tìm giao điểm I của đường thẳng AD với (EFG). Tính tỉ số  ID
d) Chứng minh ba điểm F, H, I thẳng hàng. AK
e) Gọi J là trung điểm của BC, AJ cắt EF tại K. Tính tỉ số  AJ
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 70 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
Daïng toaùn 5: Chöùng minh ba ñöôøng thaúng ñoàng quy
 Phương pháp giải
Để chứng minh ba đường thẳng , a ,
b c đồng quy, ta làm theo các bước sau:
 Chọn mặt phẳng (P) chứa đường thẳng a và b. Giả sử I  a  . b
 Tìm mặt phẳng (Q) chứa a và (R) chứa b sao cho (Q)  ( )
R  c  I  . c Suy ra: , a ,
b c đồng quy tại I. a
  (P), b  (P), I  a b
a (P)(Q)  Nghĩa là: 
 a  b  c  I. b   (P)  ( ) R
c (Q)(R) 
BÀI TẬP VẬN DỤNG 1.
Cho hình chóp S.ABCD có AB không song song CD. Gọi M là trung điểm SC và O là giao
điểm AC với BD.
a) Tìm giao điểm N của SD với (MAB).
Chọn mặt phẳng phụ (SCD) chứa S . D
Xét (SCD) và (MAB) :
Trong (ABCD), gọi E  AB  CD. E   A ,
B AB  (ABM )  E  (ABM )  Ta có:  E   C ,
D CD  (SCD)  E  (SCD) 
 E  (ABM)  (SCD) (1) M   (ABM)  Mà  M 
 SC, SC  (SCD)  M  (SCD) 
 M  (ABM)  (SCD) (2)
Từ (1), (2)  (ABM )  (SCD)  EM.
Trong (SCD) gọi N  SD  EM . Khi đó: N   SD 
 N  SD  (ABM). N
  EM, EM  (ABM) 
b) Chứng minh rằng ba đường thẳng S ,
O AM, BN đồng quy.
 Phân tích: Nhận thấy rằng AM  (SAC ), BN  (SBD) nên ta quan tâm đến 2 mặt này.
Xét (SAC ) và (SBD) có: S  (SAC )  (SBD) (3) O
  AC, AC  (SAC)  O  (SAC)  Ta có: 
 O  (SAC )  (SBD) (4) O   B ,
D BD  (SBD)  O  (SBD) 
Từ (3), (4)  (SAC )  (SBD)  S .
O Mặt khác, trong (ABM), gọi I  AM  BN. I
  AM  (SAC)   
 I  (SAC )  (SBD)  I  SO. Do đó S ,
O AM, BN đồng quy. I
  BN  (SBD) 
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 71 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
2. Cho hình chóp S.ABCD có đáy ABCD ...............................................................................................
là tứ giác lồi. Lấy M trên cạnh SC . Gọi N
...............................................................................................
là giao điểm của SB và (ADM ). Gọi
O là giao điểm AC và BD. Chứng ...............................................................................................
minh rằng SO, AM, DN đồng qui.
............................................................................................... S
...............................................................................................
...............................................................................................
...............................................................................................
...............................................................................................
...............................................................................................
............................................................................................... A D
...............................................................................................
............................................................................................... B C
...............................................................................................
3. Cho hình chóp S.ABC ,
D (AB  CD). Trên cạnh SC lấy E không trùng với S và C . S
a) Tìm giao điểm F của SD với (ABE ).
...............................................................................................
...............................................................................................
...............................................................................................
............................................................................................... A D
...............................................................................................
............................................................................................... B
............................................................................................... C
...............................................................................................
b) Chứng minh ba đường thẳng AB, CD, EF đồng qui.
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 72 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
§ 2. HAI ĐƯỜNG THẲNG SONG SONG
1. Vò töông ñoái cuûa hai ñöôøng thaúng phaân bieät
Cho hai đường thẳng phân biệt a và b. Định nghĩa
 Hai đường thẳng gọi là đồng phẳng nếu chúng cùng nằm trong một mặt phẳng.
 Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng.
 Hai đường thẳng gọi là song song nếu chúng đồng phẳng và không có điểm chung.
2. Tính chaát hai ñöôøng thaúng song song
 Tính chất 1. Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một
và chỉ một đường thẳng song song với đường thẳng đã cho.
 Tính chất 2. (Định lý về giao tuyến của ba mặt phẳng). Nếu ba mặt phẳng phân biệt đôi một cắt
nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
Hệ quả. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến
của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
 Tính chất 3. Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 73 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
Daïng toaùn 1: Chöùng minh hai ñöôøng thaúng song song
 Phương pháp giải
 Cách 1. Chứng minh hai đường thẳng a, b đồng phẳng, rồi dùng các định lý trong hình học
phẳng, chẳng hạn định lý đường trung bình, định lý đảo Thales,… để chỉ ra a  b.
 Cách 2. Chứng minh hai đường thẳng đó cùng song song với đường thẳng thứ ba. Cụ thể, c   a  chứng minh:   a  . b c   b 
 Cách 3. Áp dụng định lý về giao tuyến của ba mặt phẳng và hệ quả của nó. b  c a  b c    
Chẳng hạn: chứng minh: b   ( ),
 c  ()  a  b    (  )
  ()  a a    c  
1. Cho tứ diện ABCD có I , J lần lượt là trọng tâm tam giác ABC và ABD. Chứng minh: IJ  CD.
Gọi E, F lần lượt là trung điểm của BC , BD. A
 EF là đường trung bình của tam giác BCD.
 EF CD (1) AI
Vì I là trọng tâm A  BC   J AE I AJ B D
Vì J là trọng tâm A  BD   F AF AI AJ E Suy ra:  
 IJ  EF (2) AE AF C
Từ (1), (2), suy ra IJ  CD.
2. Cho tứ diện ABCD. Gọi M, N , P, Q, ,
R S lần lượt là trung điểm của AB, CD, BC, AD,
AC, BD. Chứng minh MNPQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ, RS cắt
nhau tại trung điểm G của mỗi đoạn.
Ta có: M, N , P, Q, ,
R S lần lượt là trung điểm của các A
cạnh: AB, CD, BC, AD, AC, BD.
 MP, PN, N , Q QM, ,
MR RN, NS, SM lần lượt là
đường trung bình của các tam giác ABC, B , CD AC , D AB ,
D ABC, AC , D B , CD ABD. M Q M
 P  AC  NQ   
 MPNQ là hình bình hành. M
 Q  BD  PN  R G M
 R  BC  SN S   B 
 MRNS là hình bình hành. D M
 S  AD  RN 
Gọi G  MN  RS và G   MN  PQ. P N
 G là trung điểm của RS và MN.
 G  G  nên ba đoạn thẳng MN, P ,
Q RS cắt nhau tại C
trung điểm của mỗi đoạn (đpcm).
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 74 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của S ,
A SD. Chứng minh: S
a) MN  AD và MN  BC .
...................................................................................................... ` N
....................................................................................................... M
....................................................................................................... A
....................................................................................................... D
....................................................................................................... O B
....................................................................................................... C
b) MO  SC và NO  SB.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung
điểm của AB, AD. Gọi I, J, G lần lượt là trọng tâm của các tam giác: SA , B SA , D AOD. Chứng minh rằng: S a) IJ  MN .
...................................................................................................... `
....................................................................................................... J
....................................................................................................... I
....................................................................................................... N A D G
....................................................................................................... M O
....................................................................................................... B C
b) IJ  BD và GJ  SO.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 75 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O. Gọi G là trọng tâm tam giác
SAD và E là điểm trên cạnh DC sao cho DC  3DE, I là trung điểm AD. S
a) Tìm giao điểm P của IE và (SBC ).
.......................................................................................................
....................................................................................................... G
....................................................................................................... A I D
....................................................................................................... E
....................................................................................................... O B C
.......................................................................................................
b) Chứng minh: GE  SP.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
6. Cho hình chóp S.ABCD có đáy ABCD là hình thang, cạnh đáy lớn AB với AB  2C , D AC cắt
BD tại O. Gọi G là trọng tâm của tam giác SBC và M là trung điểm của SC. S
a) Tìm giao điểm đường thẳng SB và (ADM ).
.......................................................................................................
.......................................................................................................
....................................................................................................... A B
.......................................................................................................
....................................................................................................... D C
.......................................................................................................
.......................................................................................................
b) Chứng minh: GO  MD.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 76 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
Daïng toaùn 2: Giao tuyeán song song
 Phương pháp giải
Để tìm giao tuyến của hai mặt phẳng () và () có chứa hai đường thẳng song song lần lượt nằm
trong hai mặt phẳng, ta làm như sau: A
  ()  ()  Ta có: a   b  ( )
  ()  Ax
Ax  a  b  với . a   ( ),
 b  () 
BÀI TẬP VẬN DỤNG
1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thuộc cạnh S .
A Điểm E, F
lần lượt là trung điểm của AB và BC . Tìm giao tuyến giữa các cặp mặt phẳng sau:
a) (SAB) và (SCD). S S
  (SAB)  (SCD)  x  Ta có: A  B CD M  A
 B  (SAB), CD  (SCD) 
 (SAB)  (SCD)  Sx với Sx  AB CD. A D
 Nhận xét. Có hai phương pháp tìm giao tuyến, một là tìm hai
điểm chung và nối chúng lại. Hai là giao tuyến đi
qua một điểm chung và song song với hai đường B C
thẳng lần lượt song song nằm trong hai mặt.
b) (SBC ) và (SAD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) (MBC ) và (SAD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) (MEF ) và (SAC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 77 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
2. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi G là trọng tâm của tam giác SAD.
a) Tìm giao tuyến của (SAB) và (SCD). S
.......................................................................................................
.......................................................................................................
....................................................................................................... A
....................................................................................................... D
....................................................................................................... B C
.......................................................................................................
b) Tìm giao điểm của đường thẳng SD và mặt phẳng (GBC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
3. Cho hình chóp S.ABCD có đáy là ABCD là hình thang, đáy lớn AB. Gọi M là trung điểm của SC.
a) Tìm giao tuyến của (SAC ) và (SBD). S
.......................................................................................................
.......................................................................................................
....................................................................................................... A B
.......................................................................................................
....................................................................................................... D C
.......................................................................................................
b) Tìm giao điểm của đường thẳng SB và (MAD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 78 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
4. Cho hình chóp S.ABCD có đáy là hình bình hành tâm ,
O M là trung điểm SC, I là trung điểm
của SM, J là trung điểm của AO và N thuộc cạnh AD sao cho ND  3N . A
a) Tìm giao tuyến của (SAC ) và (SBD). S
.......................................................................................................
.......................................................................................................
.......................................................................................................
.......................................................................................................
b) Tìm giao tuyến của (SAD) và (SBC ). D C
.......................................................................................................
....................................................................................................... A B
....................................................................................................... c) Chứng minh: IJ  . SA
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) Chứng minh: NJ  AB.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm của tam giác SBC
và E là một điểm nằm trên đoạn thẳng BD sao cho 3BE  BD.
a) Tìm giao tuyến của (SAB) và (SCD). S
.......................................................................................................
....................................................................................................... G
....................................................................................................... A B
....................................................................................................... E
....................................................................................................... D C
.......................................................................................................
b) Tìm giao tuyến của (SAC ) và (SBC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 79 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
c) Tìm giao điểm của đường thẳng SB và (ADG).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................ d) Chứng minh: GE  . SA
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
6. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB, AB  3a, CD  2a. Gọi O là
giao điểm của AC và B ,
D M là điểm trên cạnh SA sao cho 5AM  3 . SA S
a) Tìm giao tuyến của (SAD) và (SBC ).
......................................................................................................
......................................................................................................
......................................................................................................
...................................................................................................... A B
......................................................................................................
...................................................................................................... D C
......................................................................................................
......................................................................................................
b) Tìm giao điểm N của đường thẳng SB và (MCD). Chứng minh: ON  SD.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................ OI
c) Gọi I  SO  MC . Tính tỉ số:  SI
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 80 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
§ 3. ĐƯỜNG THẲNG SONG SONG MẶT PHẲNG 
1. Vò töông ñoái cuûa ñöôøng thaúng vôùi maët phaúng
Cho đường thẳng d và mặt phẳng (P). Có ba trường hợp xảy ra:
 Đường thẳng d và (P ) có 2 điểm chung phân biệt  d  (P) (hình 1)
 Đường thẳng d và (P ) có 1 điểm chung duy nhất  d  (P)  A (hình 2)
 Đường thẳng d và (P ) không có điểm chung nào  d  (P) (hình 3) d d d A P P P Hình 1 Hình 2 Hình 3
Định nghĩa. Đường thẳng d và mặt phẳng (P ) gọi là song song với nhau nếu chúng không có điểm chung. 2. Caùc ñònh lí
 Định lí 1. Nếu đường thẳng d không nằm trong mặt phẳng () và d song song với đường thẳng
d  nằm trong () thì d song song với ().
 Định lí 2. Cho đường thẳng a song song với mặt phẳng (). Nếu mặt phẳng () chứa a và cắt
() theo giao tuyến b thì b song song với a.
Hệ quả: Nếu hai mặt phẳng phân biệt cắt nhau và cùng song song với một đường thẳng
thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
 Định lí 3. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và
song song với đường thẳng kia.
Daïng toaùn 1: Chöùng minh ñöôøng thaúng d song song maët phaúng (P)
 Phương pháp giải
Để chứng minh đường thẳng d song song với mặt phẳng (P), ta cần chứng minh đường thẳng d
song song với một đường thẳng d  nằm trong mặt phẳng (P). Hiển nhiên đường thẳng d này
không nằm trong (P). d  d 
Cụ thể, để chứng minh d  (P), ta cần: d
   (P)  d  (P).  d   (P)  BÀI TẬP ÁP DỤNG
1. Cho tứ diện ABC .
D Gọi M và N lần lượt là trọng tâm của các tam giác ACD và BC . D Chứng
minh rằng MN song song với các mặt phẳng (ABC ) và (ABD).
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 81 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
Gọi E là trung điểm của C . D A
Vì M và N lần lượt là trọng tâm của các tam giác ACD và EM EN 1 BCD     EA EB 3
Áp dụng định lý Thales vào A
 BE  MN  A . B M  N  AB  M Ta có: AB 
 (ABC )  MN  (ABC ).  M
 N  (ABC)  B D M  N  AB N  E  Tương tự: AB 
 (ABD)  MN  (ABD)  (đpcm). C M
 N  (ABD) 
2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của
các cạnh AB và C . D S
a) Chứng minh: MN  (SBC ) và MN  (SAD).
....................................................................................................... `
........................................................................................................
........................................................................................................ A D
........................................................................................................
........................................................................................................ B C
........................................................................................................
b) Gọi E là trung điểm của S .
A Chứng minh: SB  (MNE) và SC  (MNE).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
3. Cho hình chóp S.ABCD có đáy ABCD là a) BC  (SAD) và AD  (SBC).
hình bình hành tâm O. Gọi M, N lần lượt .......................................................................................... là trung điểm S ,
A SD. Chứng minh:
.......................................................................................... S
..........................................................................................
..........................................................................................
..........................................................................................
.......................................................................................... A D
.......................................................................................... O
.......................................................................................... B C
..........................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 82 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) MN  (ABCD) và MN  (SBC ).
c) MO  (SCD) và NO  (SBC ).
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
.................................................................................. ..........................................................................................
4. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O. Gọi G là trọng tâm tam giác
SAD và E là điểm trên cạnh DC sao cho DC  3DE, I là trung điểm A . D
a) Chứng minh: OI  (SAB) và OI  (SCD). S
........................................................................................................ `
........................................................................................................
........................................................................................................ A D
........................................................................................................
........................................................................................................ O
........................................................................................................ B C
........................................................................................................
b) Tìm giao điểm P của IE và (SBC ). Chứng minh: GE  (SBC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 83 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N , P lần lượt là trung điểm
của AB, CD và S . A
a) Chứng minh: MN  (SAD) và SB  (MNP). S
....................................................................................................... `
........................................................................................................
........................................................................................................ A D
........................................................................................................
........................................................................................................
........................................................................................................ B C
........................................................................................................
b) Gọi G, I là trọng tâm của tam giác ABC và SBC. Chứng minh: GI  (SAB).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
6. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB, với AB  2C .
D Gọi O là giao
điểm của AC và BD, I là trung điểm của S ,
A G là trọng tâm của tam giác SBC và E là một
điểm trên cạnh SD sao cho 3SE  2S . D S A B O D C
a) Chứng minh: DI  (SBC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
b) Chứng minh: GO  (SCD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 84 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
c) Chứng minh: SB  (ACE).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
7. Cho hình chóp S.ABCD có đáy là hình thang (AB  CD ). Biết AB  2C .
D Gọi G, H lần lượt là
trọng tâm tam giác SAD và SBC , gọi E, F lần lượt là trung điểm của AD, BC . S
a) Tìm giao tuyến của (SAB ) và (SCD ).
.................................................................................................
.................................................................................................
................................................................................................. H G
................................................................................................. A B
................................................................................................. E F
................................................................................................. D C
.................................................................................................
b) Chứng minh rằng: GH  (SCD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Gọi K là giao điểm của CG và DH , L là giao điểm của CE và DF. Chứng minh ba điểm SK
S, K, L thẳng hàng và tính tỉ số  SL
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 85 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm .
O Gọi M, N lần lượt là trung
điểm của SA và C . D S
a) Tìm giao điểm E  AD  (BMN ).
................................................................................................
................................................................................................ M
................................................................................................ D
................................................................................................ A
................................................................................................ N O
................................................................................................
................................................................................................ B C
b) Tìm giao điểm F  SD  (BMN). Chứng minh: SF  2F . D
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Gọi I là trung điểm ME, G  AN  B .
D Chứng minh: FG  (SAB).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) Gọi H  MN  SG. Chứng minh: OH GF.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 86 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
Daïng toaùn 2: Tìm thieát dieän song song vôùi moät ñöôøng thaúng
 Phương pháp giải
Để tìm thiết diện của mặt phẳng () đi qua một điểm và song song với hai đường thẳng chéo nhau
hoặc () chứa một đường thẳng và song song với một đường thẳng,thường sử dụng tính chất sau: M   ( )   ()
d ( )  ( )
  ()  a,  M  a  với a d ( ). d   () 
1. Cho hình chóp S.ABC ,
D đáy ABCD là hình thang, đáy lớn A .
B Gọi O là giao điểm của AC và B ;
D E, K lần lượt là trung điểm BC, SC. S
a) Chứng minh: EK  (SAB).
....................................................................................................... `
........................................................................................................ y z K
........................................................................................................ T
........................................................................................................ R N A B
........................................................................................................ E O
........................................................................................................ D C x M
........................................................................................................
b) Gọi mặt phẳng (P) qua O và song song với BC và S .
A Tìm thiết diện cắt của hình chóp S.ABCD
với mặt phẳng (P).
Lời giải tham khảo O
  (P)  (ABCD)    Ta có B  C  (ABCD)
 (ABCD)  (P)  Ox, Ox  BC  với . B  C (P)   M
  Ox  DC  Trong (ABCD), gọi 
 M, N  (P) (1) M   Ox  AB  N
  (P)  (SAB)    Ta lại có: S  A  (P)
 (SAB)  (P)  Ny, Ny  SA  với . S
 A  (SAB) 
Trong (SAB), gọi T  Ny  SB  T  (P) (2) T
  (P) (SBC)    Tương tự B  C  (P)
 (SBC )  (P)  Tz, Tz  BC  với . B
 C  (SBC) 
Trong (SBC), gọi R  Tz  SC  R  (P) (3)
 Từ (1), (2), (3), suy ra thiết diện cần tìm là tứ giác MNT . R
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 87 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, O là giao điểm của AC và BD, M là trung điểm S . A
a) Chứng minh: OM  (SCD). S
....................................................................................................... `
........................................................................................................
........................................................................................................ A D
........................................................................................................ O
........................................................................................................ B C
........................................................................................................
b) Gọi () là mặt phẳng đi qua M, đồng thời song song với SC và A .
D Tìm thiết diện của mặt
phẳng () với hình chóp S.ABC . D
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
3. Cho tứ diện ABC .
D Gọi I, J lần lượt là trung điểm của AB và CD, M là một điểm trên đoạn
IJ. Gọi (P ) là mặt phẳng qua M song song với AB và C . D A
a) Tìm giao tuyến của mặt phẳng (P ) và (ICD).
....................................................................................................... ` I
........................................................................................................
........................................................................................................
........................................................................................................ B D M
........................................................................................................ J
........................................................................................................ C
........................................................................................................
b) Xác định thiết diện của tứ diện với mặt phẳng (P). Thiết diện là hình gì ?
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 88 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
4. Cho hình chóp S.ABC .
D Gọi M, N thuộc cạnh AB, CD. Gọi () là mặt phẳng qua MN và song song S . A S
a) Tìm thiết diện của () và hình chóp.
....................................................................................................... `
........................................................................................................
........................................................................................................ A D
........................................................................................................ N
........................................................................................................ M B C
........................................................................................................
..................................................................
........................................................................................................
..................................................................
........................................................................................................
..................................................................
........................................................................................................
b) Tìm điều kiện của M, N để thiết diện là hình thang.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi K và J lần lượt là trọng
tâm của các tam giác ABC và SBC.
a) Chứng minh: KJ  (SAB).
....................................................................................................... `
........................................................................................................
........................................................................................................
........................................................................................................
........................................................................................................
........................................................................................................
........................................................................................................
b) Gọi (P ) là mặt phẳng chứa KJ và song song với A .
D Tìm thiết diện của hình chóp cắt bởi mặt phẳng (P).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 89 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
6. Cho tứ diện ABC .
D Gọi M là điểm thuộc BC sao cho MC  2M .
B Gọi N, P lần lượt là trung
điểm của BD và A . D A
a) Chứng minh: NP  (ABC).
....................................................................................................... `
........................................................................................................ P
........................................................................................................
........................................................................................................ B D N
........................................................................................................ M
........................................................................................................ C
........................................................................................................ QA
b) Tìm giao điểm Q  AC  (MNP ) và tính
 Suy ra thiết diện của hình chóp bị cắt bởi (MNP). QC
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Chứng minh: MG  (ABD), với G là trọng tâm của tam giác AC . D
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 90 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
7. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh A ,
B AD, SB. S
a) Chứng minh: BD  (MNP).
....................................................................................................... `
........................................................................................................ P
........................................................................................................ A D N
........................................................................................................ M B
........................................................................................................ C
b) Tìm giao điểm của (MNP) với BC.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Tìm giao tuyến của hai mặt phẳng (MNP) và (SBD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) Tìm giao tuyến của hai mặt phẳng (MNP) và (SBD).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm SAB; N là AN 1
một điểm thuộc đoạn AC sao cho:
 ; I là trung điểm A . B AC 3
a) Chứng minh: OI  (SAD). S
....................................................................................................... `
........................................................................................................
........................................................................................................ G
........................................................................................................ A D
........................................................................................................ N I
........................................................................................................ O B C
........................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 91 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) Chứng minh: GN  (SDC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
c) Gọi () là mặt phẳng đi qua O và song song với SA và BC. Mặt () cắt SB, SC lần lượt tại L
và K. Tìm hình tính thiết diện cắt bởi mặt phẳng () với hình chóp S.ABC . D
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thuộc cạnh SA thỏa
3MA  2MS. Hai điểm E và F lần lượt là trung điểm của AB và BC. S
a) Xác định giao tuyến của (MEF ) và (SAC ).
....................................................................................................... ` M
........................................................................................................
........................................................................................................ A D
........................................................................................................ E
........................................................................................................ B F C
........................................................................................................ KS
b) Xác định giao điểm K của mặt phẳng (MEF ) với cạnh S . D Tính tỉ số:  KD
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 92 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................ IM
c) Tìm giao điểm I của MF với (SBD). Tính tỉ số:  IF
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) Tìm thiết diện tạo bởi mặt phẳng (MEF ) cắt các mặt của hình chóp S.ABC . D
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
10. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi M , N lần lượt là trung
điểm của các cạnh AD và S . D S
a) Tìm giao tuyến của: (SAD ) và (SBC ).
................................................................................................
................................................................................................ N
................................................................................................
................................................................................................ A B
................................................................................................ M
................................................................................................ D C
................................................................................................
b) Tìm giao điểm I của BN và mặt phẳng (SAC ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 93 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
c) Tìm giao điểm J của SC và mặt phẳng (BMN ). Suy ra: IJ  (SAB ).
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
d) Gọi () là mặt phẳng chứa đường thẳng MN và song song với C .
D Thiết diện của mặt phẳng ()
và hình chóp S.ABCD là hình gì ?
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
BÀI TẬP ÔN TẬP: GIAO TUYẾN  GIAO ĐIỂM  SONG SONG  THIẾT DIỆN BT 1.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm .
O Gọi M, N lần lượt là trung điểm S , A S .
D Chứng minh rằng:
a) BC  (SAD).
b) AD  (SBC ).
c) MN  (ABCD).
d) MN  (SBC ).
e) MO  (SCD).
f) NO  (SBC ). BT 2.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Gọi G là trọng tâm tam giác SAD
và E là điểm trên cạnh DC sao cho DC  3DE, I là trung điểm A . D
a) Chứng minh: OI  (SAB) và OI  (SCD).
b) Tìm giao điểm P của IE và (SBC). Chứng minh: GE  (SBC ). BT 3.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm
của AB và C . D
a) Chứng minh: MN  (SBC ) và MN  (SAD).
b) Gọi P là điểm trên cạnh S .
A Chứng minh: SB  (MNP) và SC  (MNP).
c) Gọi G, I là trọng tâm của tam giác ABC và SBC. Chứng minh: GI  (SAB). BT 4.
Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn A ,
B với AB  2C . D Gọi O là
giao điểm của AC và B ,
D I là trung điểm của S ,
A G là trọng tâm của tam giác SBC và E
là một điểm trên cạnh SD sao cho 3SE  2S . D Chứng minh:
a) DI  (SBC).
b) GO  (SCD).
c) SB  (ACE). BT 5.
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N là trung điểm các cạnh A SI SJ , B A . D 2
Gọi I, J thuộc SM, SN sao cho    Chứng minh: SM SN 3
a) MN  (SBD).
b) IJ  (SBD).
c) SC  (IJO). BT 6.
Cho tứ diện ABCD có G là trọng tâm của tam giác ABD và I là điểm trên cạnh BC sao cho
BI  2IC. Chứng minh rằng: IG  (ACD).
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 94 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian BT 7. Cho tứ diện ABC .
D Gọi G, P lần lượt là trọng tâm của các tam giác ACD và ABC. Chứng
minh rằng: GP  (ABC) và GP  (ABD). BT 8.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, O là giao điểm của AC và B , D M là trung điểm S . A
a) Chứng minh: OM  (SCD). b) Gọi ( )
 là mặt phẳng đi qua M, đồng thời song song với SC và AD. Tìm thiết diện của mặt phẳng ( )
 với hình chóp S.ABC . D BT 9.
Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi M là trung điểm C , D ( )
 là mặt phẳng qua M, đồng thời song song với SA và BC. Tìm thiết diện của ( )  với
hình chóp S.ABC .
D Thiết diện là hình gì ?
BT 10. Cho hình chóp S.ABC .
D Gọi M, N thuộc cạnh A , B C . D Gọi ( )
 là mặt phẳng qua MN và song song S . A
a) Tìm thiết diện của ( )  và hình chóp.
b) Tìm điều kiện của MN để thiết diện là hình thang.
BT 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SC
và (P) là mặt phẳng qua AM và song song với BD.
a) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P).
b) Gọi E, F lần lượt là giao điểm của (P) với các cạnh SB và S .
D Tìm tỉ số diện tích của S  ME với S
 BC và tỉ số diện tích của S  MF với S  C . D
c) Gọi K là giao điểm của ME và C ,
B J là giao điểm của MF và C .
D Chứng minh K, , A J EF
nằm trên đường thẳng song song với EF và tìm tỉ số  KJ
BT 12. Cho tứ diện ABC .
D Gọi M, N là hai điểm lần lượt nằm trên hai cạnh BC và AD. Xác định
thiết diện của tứ diện cắt bởi mặt phẳng ( )
 qua MN và song song với C .
D Xác định vị trí của
hai điểm M, N để thiết diện là hình bình hành.
BT 13. Cho tứ diện ABC .
D Gọi I, J lần lượt là trung điểm của AB và C ,
D M là một điểm trên đoạn
IJ. Gọi (P) là mặt phẳng qua M song song với AB và C . D
a) Tìm giao tuyến của mặt phẳng (P) và (ICD).
b) Xác định thiết diện của tứ diện với mặt phẳng (P). Thiết diện là hình gì ?
BT 14. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi K và J lần lượt là trọng
tâm của các tam giác ABC và SBC. a) Chứng minh KJ // (SAB)
b) Gọi (P) là mặt phẳng chứa KJ và song song với AD. Tìm thiết diện của hình chóp cắt bởi mặt phẳng (P).
BT 15. Cho tứ diện ABC .
D Gọi G ,G lần lượt là trọng tâm của các tam giác ACD và BC . D Chứng 1 2
minh rằng: G G  (ABC ) và G G  (ABD). 1 2 1 2
BT 16. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm của S  A , B I là trung điểm A ,
B lấy điểm M trong đoạn AD sao cho AD  3AM.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Đường thẳng qua M và song song AB cắt CI tại N. Chứng minh NG  (SCD).
c) Chứng minh: MG  (SCD).
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 95 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
BT 17. Cho hình chóp S.ABC ,
D đáy ABCD là hình thang với đáy lớn AD và AD  2BC. Gọi O là
giao điểm của AC và B ,
D G là trọng tâm của tam giác SC . D
a) Chứng minh: OG  (SBC ).
b) Cho M là trung điểm của S .
D Chứng minh: CM  (SAB).
c) Gọi I là điểm trên cạnh SC sao cho 2SC  3SI. Chứng minh: SA  (BDI ).
BT 18. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung
điểm của các cạnh A , B A , D S . B
a) Chứng minh: BD  (MNP).
b) Tìm giao điểm của (MNP) với BC .
c) Tìm giao tuyến của hai mặt phẳng (MNP) và (SBD).
d) Tìm thiết diện của hình chóp với (MNP).
BT 19. Cho tứ diện ABC .
D Gọi M là điểm thuộc BC sao cho MC  2M .
B Gọi N, P lần lượt là
trung điểm của BD và AD.
a) Chứng minh: NP  (ABC ). QA
b) Tìm giao điểm Q của AC với (MNP) và tính
 Suy ra thiết diện của hình chóp bị cắt QC bởi (MNP).
c) Chứng minh: MG  (ABD), với G là trọng tâm của tam giác AC . D
BT 20. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Tìm giao tuyến của (SAC ) và (SBD); (SAB) và (SCD).
b) Một mặt phẳng qua BC và song song với AD cắt SA tại E, (E  S, E  )
A , cắt SD tại
F, (F  S, F  D). Tứ giác BEFC là hình gì ?
c) Gọi M thuộc đoạn AD sao cho AD  3AM và G là trọng tâm tam giác SA , B I là trung
điểm AB. Đường thẳng qua M và song song AB cắt CI tại N. Chứng minh:
NG  (SCD) và MG  (SCD).
BT 21. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, tâm O. Gọi M, N, P lần lượt là trung điểm của S ,
A BC, C . D
a) Tìm giao tuyến của hai mặt phẳng (SAC ) và (SBD), (SAB) và (SCD).
b) Tìm giao điểm E của SB và (MNP).
c) Chứng minh: NE  (SAP).
BT 22. Cho tứ diện ABC .
D Lấy điểm M trên cạnh AB sao cho AM  2M .
B Gọi G là trọng tâm B
 CD và I trung điểm của C ,
D H là điểm đối xứng của G qua I.
a) Chứng minh: GD  (MCH ). GK
b) Tìm giao điểm K của MG với (ACD). Tính tỉ số  GM
BT 23. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, K lần lượt là trung điểm của BC, C . D
a) Tìm giao tuyến của (SIK) và (SAC ), (SIK) và (SBD).
b) Gọi M là trung điểm của S .
B Chứng minh: SD  (ACM). MF
c) Tìm giao điểm F của DM và (SIK). Tính tỉ số  MD
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 96 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
BT 24. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm S  A , B
trên AD lấy điểm E sao cho AD  3AE. Gọi M là trung điểm AB.
a) Chứng minh: EG  (SCD).
b) Đường thẳng qua E song song AB cắt MC tại F. Chứng minh: GF  (SCD).
c) Gọi I là điểm thuộc cạnh CD sao cho CI  2I .
D Chứng minh: GO  (SAI ).
BT 25. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC và
N là trọng tâm tam giác ABC.
a) Chứng minh: SB  (AMN ).
b) Tìm giao tuyến của (AMN) với (SAB). IS
c) Tìm giao điểm I của SD với (AMN ). Tính tỉ số:  ID
d) Gọi Q là trung điểm của I .
D Chứng minh: QC  (AMN).
BT 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của BC, C . D
a) Tìm giao tuyến của (SMD) và (SAB).
b) Tìm giao tuyến của (SMN ) và (SBD).
c) Gọi H là điểm trên cạnh SA sao cho HA  2HS. Tìm giao điểm K của MH và (SBD). KH Tính tỉ số:  KM
d) Gọi G là giao điểm của BN và DM. Chứng minh: HG  (SBC ).
BT 27. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD là đáy lớn và AD  2BC. Gọi
O là giao điểm của AC và B ,
D G trọng tâm của tam giác SC . D
a) Chứng minh: OG  (SBC ).
b) Gọi M là trung điểm của cạnh S .
D Chứng minh: CM  (SAB).
c) Giả sử điểm I trên đoạn SC sao cho 2SC  3SI. Chứng minh: SA  (BID). KB
d) Xác định giao điểm K của BG và mặt phẳng (SAC ). Tính tỉ số:  KG
BT 28. Cho hình chóp S.ABC. Gọi M, ,
P I lần lượt là trung điểm của A ,
B SC, S . B Một mặt phẳng ( )
 qua MP và song song với AC và cắt các cạnh S ,
A BC tại N, Q.
a) Chứng minh: BC  (IMP).
b) Xác định thiết diện của ( )
 với hình chóp. Thiết diện này là hình gì ?
c) Tìm giao điểm của đường thẳng CN và mặt phẳng (SMQ).
BT 29. Cho hình chóp S.ABCD có đáy là một hình tứ giác lồi. Gọi M, N là trung điểm của SC và C . D Gọi ( )
 là mặt phẳng qua M, N và song song với đường thẳng AC. a) Tìm giao tuyến của ( )
 với (ABCD).
b) Tìm giao điểm của đường thẳng SB với ( )  .
c) Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng ( )  .
BT 30. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB C .
D Gọi M, N, I lần lượt là trung điểm của A ,
D BC, S . A
a) Tìm giao tuyến của hai mặt phẳng (IMN) và (SAC ); (IMN ) và (SAB).
b) Tìm giao điểm của SB và (IMN ).
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 97 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
c) Tìm thiết diện của mặt phẳng (IDN ) với hình chóp S.ABC . D
BT 31. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm S  A ; B N AN 1
là một điểm thuộc đoạn AC sao cho:
 ; I là trung điểm AB. AC 3
a) Chứng minh: OI  (SAD) và GN  S . D b) Gọi ( )
 là mặt phẳng đi qua O và song song với SA và BC. Mặt phẳng ( )  cắt S , B SC
lần lượt tại L và K. Tìm hình tính thiết diện cắt bởi mặt phẳng ( )
 với hình chóp S.ABC . D
BT 32. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi H, K lần lượt là trung điểm các cạnh S ,
A SB và M là điểm thuộc cạnh C ,
D (M khác C và D).
a) Tìm giao tuyến của: (KAM) và (SBC ), (SBC ) và (SAD).
b) Tìm thiết diện tạo bởi (HKO) với hình chóp S.ABC .
D Thiết diện là hình gì ?
c) Gọi L là trung điểm đoạn HK. Tìm I  OL  (SBC ). Chứng minh: SI  BC.
BT 33. Cho tứ diện ABC ,
D có M, N là trung điểm của cạnh A ,
B BC và gọi G là trọng tâm tam giác AC . D
a) Tìm giao điểm E của MG và (BCD).
b) Tìm d  (MNG)  (BCD). Giả sử d CD  P. Chứng minh: GP  (ABC ).
c) Gọi () là mặt phẳng chứa MN và  A .
D Tìm thiết diện của () với tứ diện.
BT 34. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thuộc cạnh SA thỏa
3MA  2MS. Hai điểm E và F lần lượt là trung điểm của AB và BC.
a) Xác định giao tuyến của hai mặt phẳng (MEF) và (SAC ). KS
b) Xác định giao điểm K của mặt phẳng (MEF) với cạnh S . D Tính tỉ số:  KD IM
c) Tìm giao điểm I của MF với (SBD). Tính tỉ số:  IF
d) Tìm thiết diện tạo bởi mặt phẳng (MEF) cắt các mặt của hình chóp S.ABC . D
BT 35. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N là trung điểm S , A S . D
a) Xác định giao điểm của NC và (OMD).
b) Xác định thiết diện hình chóp với mặt phẳng (P) qua MO và song song với SC.
BT 36. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC, (P)
là mặt phẳng qua AM và song song với BD.
a) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P).
b) Gọi E, F lần lượt là giao điểm của (P) với các cạnh SB và S .
D Hãy tìm tỉ số diện tích của
tam giác SME với tam giác SBC và tỉ số diện tích của tam giác SMF và tam giác SC . D
c) Gọi K là giao điểm của ME và C ,
B J là giao điểm của MF và C . D Chứng ba điểm K EF , ,
A J nằm trên một đường thẳng song song với EF và tìm tỉ số  KJ
BT 37. Cho hình chóp S.ABCD có G là trọng tâm A
 BC. Gọi M, N, P, , Q ,
R H lần lượt là trung điểm của S ,
A SC, C , B B ,
A QN, AG.
a) Chứng minh rằng: S, ,
R G thẳng hàng và SG  2MH  4RG.
b) Gọi G  là trọng tâm S
 BC. Chứng minh: GG  (SAB) và GG  (SAC).
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 98 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
§ 4. HAI MẶT PHẲNG SONG SONG 
1. Vò töông ñoái cuûa hai maët phaúng phaân bieät
Cho hai mặt phẳng phân biệt (P) và (Q). Có hai trường hợp xảy ra: Q P a P Q
Có 1 điểm chung  (P)  (Q)  a.
Không có điểm chung  (P)  (Q).
Định nghĩa. Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung. 2. Caùc ñònh lí
 Định lí 1. Nếu mặt phẳng () chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với
mặt phẳng () thì () song song với ().
 Muốn chứng minh hai mặt phẳng song song, ta phải chứng minh có hai đường thẳng cắt nhau
thuộc mặt phẳng này lần lượt song song với mặt phẳng kia.
 Muốn chứng minh đường thẳng a  (Q), ta chứng minh đường thẳng a nằm trong mặt phẳng (P)  (Q).
 Định lí 2. Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song
song với mặt phẳng đã cho.
 Nếu đường thẳng d song song với mặt phẳng () thì trong () có một đường thẳng song song
với d và qua d có duy nhất một mặt phẳng song song với (). Dó đó để chứng minh đường
thẳng d song song với () ta phải chứng minh d thuộc mặt phẳng () và có
()  ()  d  ().
 Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
 Cho điểm A không nằm trên mặt phẳng (). Mọi đường thẳng đi
qua A và song song với () đều nằm trong mặt phẳng đi qua A
và song song với ().
 Định lí 3. Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt
phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
 Hệ quả: Hai mặt phẳng song song chắn trên hai cát tuyến song song
những đoạn thẳng bằng nhau.
 Định lí Thales: Ba mặt phẳng đôi một song song chắn trên hai cát
tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 99 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
Chöùng minh hai maët phaúng song song
 Phương pháp giải Chứng minh hai mặt phẳng song song (P)  (Q).
Ta chứng minh mặt phẳng (P ) có hai đường thẳng CẮT NHAU và lần lượt song song với mặt phẳng (Q). a   (Q) (1)
b (Q) (2) 
Cụ thể, để chứng minh (P)  (Q), ta cần chỉ ra: 
 (P)  (Q). a  , b  (P)
a b  A 
Trước hết ta cần chứng minh (1) và chứng minh (2), sau đó gộp lại như trên.
1. Cho hình chóp S.ABCD với đáy ABCD là hình thang mà AD  BC và AD  2BC . Gọi M, N
lần lượt là trung điểm của SA và AD. Chứng minh: (BMN )  (SCD). S
Ta có: M, N lần lượt là trung điểm của SA và AD.
 MN là đường trung bình S
 AD  MN  S . D M MN   SD  Ta có: SD 
 (SCD)  MN  (SCD).  MN   (SCD) A D  N
Mà có 2ND  AD  BC và ND  BC nên suy ra BNDC là
hình bình hành  BN CD. B C M
 N  (SCD) NB  CD       NB   (SCD)  Ta có: C
 D  (SCD)  NB  (SCD). 
 (BMN )  (SCD).  Khi đó: M
 N  (BMN ), NB  (BMN ) NB   (SCD)   M
 N  NB  N 
 Bình luận: Bản chất bài toán là tập hợp của hai bài toán chứng minh đường song song mặt.
Học sinh cần xem lại những phần suy luận ngược, cụ thể luôn đặt câu hỏi: d  ( )
Dù ®o¸n d song song víi ®êng nµo n»m tro 
  ng (  )  d  d d vµ d   n»m  tro  ng ta  m gi  ¸c hay   ®ång hå  c¸t  nµo ?  Thales.
2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N , P lần lượt là trung điểm S ,
A SB, SD và K, I là trung điểm của BC, OM. S
a) Chứng minh: (OMN )  (SCD).
...................................................................................................... ` M P
....................................................................................................... N
....................................................................................................... I A D
....................................................................................................... O
....................................................................................................... B K C
.......................................................................................................
....................................................................
.......................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 100 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) Chứng minh: (PMN )  (ABCD . )
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
c) Chứng minh: KI  (SCD).
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của S , A SD. S
a) Chứng minh: (OMN )  (SBC ).
...................................................................................................... ` M N
.......................................................................................................
.......................................................................................................
....................................................................................................... A D
....................................................................................................... O
....................................................................................................... B K C
.......................................................................................................
....................................................................
.......................................................................................................
....................................................................
.......................................................................................................
b) Gọi P, Q, R lần lượt là trung điểm của AB, ON , SB. Chứng minh: PQ  (SBC ).
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 101 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian c) Chứng minh: (MO ) R  (SCD).
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
4. Cho hai hình bình hành ABCD và ABEF a) Chứng minh: (ADF)  (BCE . )
có chung cạnh AB và không đồng phẳng. ...........................................................................................
Gọi I, J, K lần lượt là trung điểm các
cạnh AB, CD, EF. Chứng minh:
...........................................................................................
........................................................................................... F K E
...........................................................................................
...........................................................................................
...........................................................................................
........................................................................................... B A I
...........................................................................................
........................................................................................... D J C
...........................................................................................
b) Chứng minh: (DIK )  (JBE ).
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
5. Cho các hình bình hành ABCD, ABEF a) Chứng minh: MN  DE.
nằm trên hai mặt phẳng khác nhau. Trên ...........................................................................................
các đường chéo AC , BF lấy các điểm
M, N sao cho MC  2AM, NF  2BN . ...........................................................................................
Qua M, N lần lượt kẻ các đường thẳng ...........................................................................................
song song với cạnh AB, cắt các cạnh ...........................................................................................
AD, AF theo thứ tự tại M , N . 1 1
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 102 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
........................................................................................... F E
...........................................................................................
...........................................................................................
........................................................................................... N
........................................................................................... A B
........................................................................................... M
........................................................................................... D C
...........................................................................................
b) Chứng minh: M N  (DEF).
c) Chứng minh: (MNM N )  (DEF). 1 1 1 1
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
6. Cho hình chóp S.ABCD có đáy ABCD là a) Tìm giao tuyến của (SAD) và (MOP).
hình bình hành tâm O. Gọi M, N, P, E ...........................................................................................
lần lượt là trung điểm S ,
A BC, CD, SC
và I trên cạnh SA thỏa AI  3IS.
...........................................................................................
........................................................................................... S
...........................................................................................
........................................................................................... M
...........................................................................................
........................................................................................... A D
........................................................................................... P O B N C
...........................................................................................
b) Tìm K  IE  (ABC ), H  BC  (EIM )
c) Gọi G là trọng tâm SBC . Tìm thiết diện hình
và k với CH  k.CB.
chóp S .ABC bị cắt bởi (IMG).
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
................................................................................ ...........................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 103 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
7. Cho hình chóp S .ABC có G là trọng tâm của tam giác ABC . Trên đoạn SA lấy hai điểm M, N
sao cho SM  MN  N . A S
a) Chứng minh: GM  (SBC ).
....................................................................................................... ` M
.......................................................................................................
....................................................................................................... N
....................................................................................................... A C
....................................................................................................... G
....................................................................................................... B
.......................................................................................................
b) Gọi D là điểm đối xứng của A qua G. Chứng minh: (MCD)  (NBG).
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
c) Gọi H  DM  (SBC ). Chứng minh H là trọng tâm SBC .
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của SC, N
là điểm trên đường chéo BD sao cho BD  3BN . S
a) Xác định giao tuyến của (SDC ) và (SAB).
....................................................................................................... `
....................................................................................................... M
....................................................................................................... A
....................................................................................................... D
....................................................................................................... N O B C
.......................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 104 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian TM
b) Tìm giao điểm T của đường thẳng DM và (SAB). Tính tỉ số:  TD
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
c) Gọi K  AN  BC. Chứng minh rằng: MK  (SBD).
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. LS S
d) Gọi I  AN  DC , L  IM  SD. Tính tỉ số và IK  M  LD S IAL 
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 105 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
§ 5. BÀI TẬP ÔN CHƯƠNG 2 
BT 1. (THPT Bình Hưng Hòa – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy ABCD là hình
bình hành. Điểm M nằm trên cạnh SB sao cho SM  2MB. Gọi G là trọng tâm của tam giác SCD.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC ).
b) Chứng minh đường thẳng MG song song với mặt phẳng (ABCD).
c) Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (), biết rằng () chứa đường
thẳng MG và song song với đường thẳng S . A
BT 2. (THPT Bình Tân – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
gọi G là trọng tâm của tam giác SAB; I là trung điểm của AB.
a) Tìm giao tuyến của (SAB) và (SCD); (SID) và (SAC ).
b) Tìm giao điểm M  SA  (CDG).
c) Xác định thiết diện với hình chóp S.ABCD với (CDG). SN
d) Giả sử N  SB  (CDG). Tính tỉ số  SB
BT 3. (THPT Lê Quý Đôn – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có ABCD là hình bình hành.
Gọi M, N , P lần lượt là trung điểm S ,
A BC, CD; G là trọng tâm tam giác SCD và
E  AP  BD.
a) Tìm giao điểm F của MP và mặt phẳng (SBD).
b) Chứng minh: MN  (SCD) và GE  (SAC ). AH
c) Lấy điểm H thuộc cạnh AD sao cho
 n (0  n  1), mặt phẳng (P) qua H song song AD S ,
A CD cắt SD, SC, BC lần lượt tại K, , L .
R Tìm hình tính của thiết diện được tạo bởi
(P) với hình chóp S.ABCD. SA d) Cho
 k , Q  HR  AC . Tính n theo k để thiết diện HKLQ là hình thoi. CD BT 4.
(THPT Nguyễn Chí Thanh – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD đáy là hình thang,
AD  BC và AD  2BC . Gọi E, F lần lượt là trung điểm của SA và AD.
a) Xác định giao tuyến của hai mặt phẳng (BCE) và (SAD). Suy ra giao điểm I của (BCE) với SD.
b) Chứng minh CI  (BEF ).
c) Tìm giao diểm K của FI với (SBC ). Chứng minh: (SBF )  (KCD).
d) Gọi O là giao điểm của AC và BF; () là một mặt phẳng đi qua O và song song S , A BC .
Xác định thiết diện của () với hình chóp S.ABCD. BT 5.
(THPT Nguyễn Hiền – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy ABCD là một hình
thang AD  BC , biết AD  2BC . Gọi I và J lần lượt là trọng tâm các tam giác SAD và SBC .
a) Tìm giao tuyến của (ADJ ) và (SBC ); (BIC ) và (SAD).
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 106 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
b) Tìm giao điểm M, N của (ADJ ) và SB,SC , giao điểm P,Q của (BCI ) và S , A SD.
c) Chứng minh PM, NQ cùng song song (ABCD). EK
d) Cho AM cắt BP tại E; CQ cắt DN tại F và PC cắt EF tại K. Tính tỷ số  EF BT 6.
(THPT Nguyễn Hữu Cảnh – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy ABCD là hình
bình hành. Gọi E, F lần lượt là trung điểm của cạnh AB và SC .
a) Tìm giao tuyến của hai mặt phẳng (SDE ) với (SBC ), (SAB) với (SCD).
b) Gọi G là trọng tâm tam giác SAB, K là điểm trên cạnh SD sao cho SK  2KD. Chứng
minh GK song song với mặt phẳng (ABCD). EI
c) Gọi I là giao điểm của đường thẳng EF và (SBD). Tính tỉ số  EF BT 7.
(THPT Nguyễn Thị Minh Khai v– Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có mặt đáy
ABCD là hình thang, cạnh đáy lớn AD  2BC . Gọi I,K lần lượt là trung điểm AD và SI .
Trên cạnh AB lấy điểm M sao cho AM  2MB.
a) Tìm giao tuyến của 2 mặt phẳng (SAD) và (KBC ).
b) Tìm giao điểm J của đường thẳng BC và mặt phẳng (SKM ).
c) Gọi G là trọng tâm SAD. Chứng minh rằng JK  (GMC ).
d) Chứng minh thiết diện tạo bởi (KBC ) với hình chóp S.ABCD là 1 hình bình hành. BT 8.
(THPT Nguyễn Thượng Hiền – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy ABCD là
hình bình hành tâm O. Gọi E, I, N lần lượt là trung điểm của S ,
A BC, CD.
a) Tìm giao tuyến của hai mặt phẳng (ECD) và (SAB). Suy ra giao điểm F của đường thẳng
SB và mặt phẳng (ECD).
b) Chứng minh: (OEI )  (SCD). Tìm giao tuyến của hai mặt phẳng (EIN ) và (SCD).
c) Lấy điểm H thuộc cạnh SB sao cho BH  2SH, gọi M là trung điểm của AB, G là trọng
tâm của tam giác SBC . Chứng minh rằng: AH  (MNG). BT 9.
(THPT Bình Hưng Hòa – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy ABCD là hình
bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, BC , CD.
a) Tìm giao tuyến của hai mặt phẳng (MNP) và (SBD).
b) Chứng minh mặt phẳng (OMN ) song song với mặt phẳng (SCD).
c) Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (P ) đi qua điểm O, song song
với AB và SC . Thiết diện là hình gì ?
BT 10. (THPT Lê Trọng Tấn – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy là hình bình hành.
Gọi I, G lần lượt là trọng tâm của tam giác SAD, ACD.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Chứng minh rằng IG song song với mặt phẳng (SBC ).
c) Tìm giao điểm của SD và mặt phẳng (IBC ).
d) Thiết diện của hình chóp bị cắt bởi mặt phẳng (IBC ) là hình gì ? Giải thích.
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 107 -
§iÖn tho¹i ghi danh: 0933.755.607 (ThÇy §oµn) – 0983.047.188 (ThÇy Nam)
Ch¬ng 1. §êng & mÆt trong kh«ng gian
BT 11. (THPT Trần Phú – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy ABCD là hình thang có
đáy là AB và C .
D Biết đáy lớn AB  3C .
D Gọi E, F và I lần lượt là các điểm trên các cạnh
AB, SB và AD sao cho: EB  2E ,
A FB  2FS và IA  2ID.
a) Chứng minh EF  (SAD) và (CEF )  (SAD).
b) Chứng minh FI  (SCD).
c) Tìm giao điểm G của EF và mặt phẳng (SCD). Chứng minh GC  SD.
BT 12. (THPT Tân Bình – Tp. Hồ Chí Minh) Cho hình chóp S.ABC có G là trọng tâm S  AB và M 2
trên SC thỏa SM  SC . 3
a) Tìm giao tuyến của mặt phẳng (ABC ) và mặt phẳng (BMG ). b) Gọi ( )
 là mặt phẳng chứa MG và mp ()  S .
A Nêu cách vẽ thiết diện tạo bởi mặt phẳng ( )
 và hình chóp S.ABC. Thiết diện là hình gì ?
BT 13. (THPT Tây Thạnh – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy ABCD là hình thang
(đáy lớn AB ), AB  2AD. Gọi E là giao điểm của hai đường thẳng AD và BC; M, N lần
lượt là trung điểm của các cạnh S , A AB.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC ).
b) Tìm giao điểm P của đường thẳng SD với mặt phẳng (MBC ).
c) Gọi O  AC  DN. Chứng minh rằng: NC  AD, SC  (OMN ).
BT 14. (THPT Nguyễn Thượng Hiền – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy ABCD là
hình bình hành tâm O. Gọi I, J lần lượt là trung điểm của S ,
A SB và G là trọng tâm tam giác SCD.
a) Tìm giao tuyến của (IOJ ) và (ABCD), suy ra giao điểm N của BC và (IOJ ).
b) Gọi H là trung điểm của CD. Chứng minh rằng (IOH )  (SBC ).
c) Gọi M là điểm thuộc cạnh BC . Mặt phẳng () qua MG và song song CD cắt AD, SD, SC
lần lượt tại P, Q, .
R Xác định thiết diện tạo thành bởi mặt phẳng () và hình chóp. Thiết diện là hình gì ?
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 108 -
§iÖn tho¹i ghi danh: 0983.047.188 (ThÇy Nam) – 0933.755.607 (ThÇy §oµn) MỤC LỤC Trang
Chương 1. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG ...................................................... 1
§ 1. MỞ ĐẦU VỀ PHÉP BIẾN HÌNH .......................................................................................... 1
§ 2. PHÉP TỊNH TIẾN .................................................................................................................... 2
§ 3. PHÉP ĐỐI XỨNG TRỤC ..................................................................................................... 11
§ 4. PHÉP ĐỐI XỨNG TÂM ....................................................................................................... 15
§ 5. PHÉP QUAY ........................................................................................................................... 17
§ 6. PHÉP VỊ TỰ VÀ PHÉP ĐỒNG DẠNG ............................................................................. 25
ÔN TẬP CHƯƠNG 1 ............................................................................................................ 33
Chương 2. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN ........... 41
§ 1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG ............................................... 41
Dạng toán 1. Tìm giao tuyến của hai mặt phẳng ............................................................... 43
Dạng toán 2. Tìm giao điểm của đường thẳng và mặt phẳng ......................................... 52
Dạng toán 3. Tìm thiết diện .................................................................................................. 61
Dạng toán 4. Chứng minh ba điểm thẳng hàng ................................................................ 65
Dạng toán 5. Chứng minh ba điểm đồng quy ................................................................... 71
§ 2. HAI ĐƯỜNG THẲNG SONG SONG .............................................................................. 73
Dạng toán 1. Chứng minh đường thẳng song song mặt phẳng ...................................... 74
Dạng toán 2. Giao tuyến song song ..................................................................................... 77
§ 3. ĐƯỜNG THẲNG SONG SONG MẶT PHẲNG ............................................................ 81
Dạng toán 1. Chứng minh đường thẳng song song mặt phẳng ....................................... 81
Dạng toán 2. Tìm thiết diện song song ................................................................................ 87
§ 4. HAI MẶT PHẲNG SONG SONG ..................................................................................... 99
§ 5. ÔN TẬP CHƯƠNG 2 .......................................................................................................... 106 ĐỊA CHỈ GHI DANH
 TRUNG TÂM THẾ VINH – 45A LÊ THÚC HOẠCH – Q. TÂN PHÚ (ĐỐI DIỆN TRƯỜNG THPT TRẦN PHÚ).
 TRUNG TÂM HOÀNG GIA – 56 PHỐ CHỢ – P. TÂN THÀNH – Q. TÂN PHÚ (SAU CHỢ TÂN PHÚ).
 71/25/10 PHÚ THỌ HÒA – P. PHÚ THỌ HÒA – Q. TÂN PHÚ – TP. HỒ CHÍ MINH.
ĐIỆN THOẠI GHI DANH
 0983.047.188 – Zalo (Thầy Nguyễn Đức Nam) – Face: https://www.facebook.com/marion.zack/
 0933.755.607 – Zalo (Thầy Lê Văn Đoàn) – 0929.031.789 – Face: https://www.facebook.com/levan.doan.902
NHÓM TOÁN THẦY LÊ VĂN ĐOÀN
Ths. Lê Văn Đoàn – Ths. Trương Huy Hoàng – Ths. Nguyễn Tiến Hà – Thầy Bùi Sỹ Khanh – Thầy Nguyễn
Đức Nam – Thầy Đỗ Minh Tiến – Thầy Nguyễn Duy Tùng – Thầy Trần Nguyễn Vĩnh Nghi – Thầy Hoàng
Minh Thiện – Thầy Trần Quốc Tuấn.
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn
§iÖn tho¹i ghi danh: 0983.047.188 (ThÇy Nam) – 0933.755.607 (ThÇy §oµn)
THỜI KHÓA BIỂU CÁC LỚP TOÁN ĐANG HỌC KHỐI 6 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật 19’15 – 21’15 T6A T6A Giải đề KHỐI 7 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật 17’30 -19’30 T7A T7A Giải đề KHỐI 8 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật 19’15 – 21’15 T8A T8A Giải đề KHỐI 9 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật 17’30 -19’30 T9A T9B T9A T9B Giải đề KHỐI 10 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật 17’45 -19’15 T10C T10C 19’30 – 21’00 T10A1 T10B T10A1 T10B T10A1 T10B Giải đề T10A2 T10A2 T10A2 10HG 10HG 10HG KHỐI 11 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật 17’45 -19’15 T11A T11B1 T11A T11B1 T11A T11B1 Giải đề T11B2 T11B2 T11B2 19’30 – 21’00 T11-C T11-C T11-C KHỐI 12 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật T12A1 T12C T12A1 T12C T12A1 T12C Lớp 17’45 -19’15 T12A2 T12A2 T12A2 T12HG2 chuyên đề VD và T12HG1 T12HG1 T12HG1 VDC 19’30 – 21’00 T12B T12B T12HG2 T12B T12HG2
Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn

Đề cương học kì 1 Hình học 11 – Lê Văn Đoàn

Thông tin :

Tài liệu liên quan:

Ma trận đề thi học kì 1 lớp 11 năm 2023 - 2024 sách Cánh diều

Đề thi học kì 1 môn Toán 11 năm 2023 - 2024 sách Cánh diều | đề 3

Đề thi học kì 1 môn Toán 11 năm 2023 - 2024 sách Cánh diều | đề 2

Đề thi học kì 1 môn Toán 11 năm 2023 - 2024 sách Cánh diều | đề 1

Đề thi học kì 1 môn Toán 11 sách Chân trời sáng tạo | đề 1