















Preview text:
TRƯỜNG THPT YÊN HÒA
ĐỀ CƯƠNG ÔN TẬP HỌC KỲ I BỘ MÔN: TOÁN
NĂM HỌC 2024 - 2025 MÔN: TOÁN - KHỐI 11 CẤU TRÚC PHẦN TT NỘI DUNG CÁC DẠNG TOÁN 1. Góc lượng giác
2. Giá trị lượng giác của góc lượng giác
3. Áp dụng tính chất của GTLG
Hàm số lượng giác
4. GTLG của các góc có liên quan đặc biệt 1 và phương trình lượng giác
5. Tính giá trị biểu thức sử dụng các phép biến đổi lượng giác.
6. TXĐ; tính chẵn lẻ, tính đồng biến nghịch biến của hàm số. GTLN, GTNN của hàm số.
7. Giải phương trình lượng giác.
1. Xác định số hạng dãy số
2. Xét tính tăng giảm, bị chặn của dãy số ĐẠI SỐ Dãy số.
3. Xác định số hạng, công sai của CSC 2 Cấp số cộng và
4. Tính tổng n số hạng đầu tiên của CSC cấp số nhân
5. Xác định số hạng, công bội của CSN
6. Tính tổng n số hạng đầu tiên của CSN
Các số đặc trưng đo
1. Lập bảng mẫu số liệu ghép nhóm 3
xu thế trung tâm của
2. Xác định số TB, trung vị, tứ phân vị, mốt của MSL ghép MSL ghép nhóm nhóm.
1. Tính giới hạn của dãy số và ứng dụng Giới hạn. 4
2. Tính giới hạn của hàm số và ứng dụng Hàm số liên tục
3. Xét tính liên tục tại một điểm, trên một khoảng, đoạn.
1. Tìm giao tuyến của hai mặt phẳng.
2. Tìm giao điểm của đường thẳng và mặt phẳng.
Đường thẳng và mặt
3. Chứng minh ba điểm thẳng hàng, ba đường thẳng đồng qui. HÌNH phẳng trong không 5 HỌC gian.
4. Chứng minh hai đường thẳng song song. Quan hệ song song
5. Chứng minh đường thẳng song song với mặt phẳng.
6. Chứng minh hai mặt phẳng song song
PHẦN I: ĐẠI SỐ VÀ GIẢI TÍCH
CHƯƠNG 1: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
A. TRẮC NGHIỆM 4 LỰA CHỌN
Bài 1.GTLG của góc lượng giác Câu 1: Góc có số đo o 108 đổi ra radian là 3 3 A. . B. . C. . D. . 5 10 2 4 Câu 2:
Biết một số đo của góc (Ox Oy) 3 , =
+ 2001 . Giá trị tổng quát của góc (Ox,Oy) là 2 A. (Ox Oy) 3 , = + k .
B. (Ox,Oy) = + k2 . 2
C. (Ox,Oy) = + k .
D. (Ox,Oy) = + k2 . 2 2 Câu 3:
Góc có số đo 2 đổi sang độ là 5 A. o 240 . B. o 135 . C. o 72 . D. o 270 . Câu 4: Cho (Ox Oy) o o ,
= 22 30'+ k360 . Với k bằng bao nhiêu thì (Ox Oy) o , =1822 30'? A. k . B. k = 3. C. k = −5. D. k = 5. Câu 5:
Giá trị k để góc =
+ k2 thỏa mãn 10 11 là 2 A. k = 4. B. k = 6. C. k = 7. D. k = 5. Câu 6:
Xét góc lượng giác (O ;
A OM ) = , trong đó M là điểm không làm trên các trục tọa độ Ox và
Oy . Khi đó M thuộc góc phần tư nào để sin và cos cùng dấu
A. I và ( II ) . B. I và (III) . C. I và (IV) . D. (II) và (III) . Câu 7:
Cho là góc tù. Điều khẳng định nào sau đây đúng? A. sin 0 . B. cos 0 . C. tan 0 . D. cot 0 . Câu 8: Cho a =
+ k2 (k ). Để a(19;27) thì giá trị của k là 3
A. k = 2 , k = 3 .
B. k = 3 , k = 4 .
C. k = 4 , k = 5 .
D. k = 5 , k = 6 . Câu 9:
Cho góc lượng giác (O ,
A OB) có số đo bằng
. Hỏi trong các số sau, số nào là số đo của một 5
góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác (O , A OB) ? 6 11 9 31 A. . B. − . C. . D. . 5 5 5 5
Câu 10: Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 10 răng là A. o 30 . B. o 40 . C. o 50 . D. o 60 .
Câu 11: Trong 20 giây bánh xe của xe gắn máy quay được 60 vòng.Tính độ dài quãng đường xe gắn
máy đã đi được trong vòng 3 phút, biết rằng bán kính bánh xe gắn máy bằng 6,5 cm (lấy = 3,1416 ). A. 22054 cm . B. 22063 cm . C. 22054 mm . D. 22044 cm .
Câu 12: Trong mặt phẳng định hướng cho ba tia Ou, Ov,Ox . Xét các hệ thức sau: 1
(I). sđ (Ou,Ov) = sđ (Ou,Ox)+ đ s (O , x v
O ) + k2 , k .
(II). sđ (Ou,Ov) = sđ (O ,xOv)+ đ s (O , x u
O ) + k2 , k .
(III). sđ (Ou,Ov) = sđ (O ,vOx)+ sđ (O ,xOu)+ k2,k .
Hệ thức nào là hệ thức Sa- lơ về số đo các góc: A. Chỉ (I) . B. Chỉ (II) . C. Chỉ (III) .
D. Chỉ (I) và (III) .
Câu 13: Nếu góc lượng giác có sđ (Ox Oz) 63 , = −
thì hai tia Ox và Oz 2 A. Trùng nhau. B. Vuông góc. 3
C. Tạo với nhau một góc bằng . D. Đối nhau. 4 k
Câu 14: Có bao nhiêu điểm M trên đường tròn định hướng gốc A thoả mãn sđ AM = + , k 3 3 A. 6. B. 4. C. 3. D. 12.
Câu 15: Xét góc lượng giác
, trong đó M là điểm biểu diễn của góc lượng giác. Khi đó M thuộc góc 4 phần tư nào? A. I . B. II . C. III . D. IV . 89 Câu 16: Giá trị cot là 6 3 A. 3 . B. − 3 . C. . D. – 3 . 3 3 Câu 17: Cho
a . Kết quả đúng là 2
A. sin a 0 , cos a 0 .
B. sin a 0 , cos a 0 .
C. sin a 0 , cos a 0 .
D. sin a 0 , cos a 0 . 5
Câu 18: Cho 2 a
. Kết quả đúng là 2
A. tan a 0 , cot a 0 .
B. tan a 0 , cot a 0 .
C. tan a 0 , cot a 0 .
D. tan a 0 , cot a 0 .
Câu 19: Chọn đẳng thức sai trong các đẳng thức sau A. sin − x = cos x . B. sin + x = cos x . 2 2 C. tan − x = cot x . D. tan + x = cot x . 2 2
Câu 20: Đơn giản biểu thức A = cos − + sin − − cos + − sin + , ta có: 2 2 2 2
A. A = 2 sin a .
B. A = 2 cos a .
C. A = sin a – cos a .
D. A = 0 .
Câu 21: Trong các giá trị sau, sin có thể nhận giá trị nào? 4 5 A. 0 − ,7 . B. . C. − 2 . D. . 3 2
Câu 22: Trong các công thức sau, công thức nào sai? 2 1 A. 2 2 sin + cos = 1. B. 2 1+ tan =
+ k,k . 2 cos 2 1 k C. 2 1+ cot =
k,k .
D. tan + cot = 1 , k . 2 ( ) sin 2 Câu 23: Cho biết 1 tan = . Tính cot 2 1 1 A. cot = 2 . B. cot = . C. cot = . D. cot = 2 . 4 2 3 Câu 24: Cho sin = và
. Giá trị của cos là: 5 2 4 4 4 16 A. . B. − . C. . D. . 5 5 5 25 +
Câu 25: Cho tan = 2 . Giá trị của 3sin cos A = là: sin − cos 5 7 A. 5 . B. . C. 7 . D. . 3 3
Câu 26: Các cặp đẳng thức nào sau đây đồng thời xảy ra? 1 3
A. sin = 1 và cos = 1 . B. sin = và cos = − . 2 2 1 1 C. sin = và cos = − .
D. sin = 3 và cos = 0 . 2 2
Câu 27: Cho tam giác ABC. Hãy tìm mệnh đề sai A + C B A + C B A. sin = cos . B. cos = sin . 2 2 2 2
C. sin ( A + B) = sin C .
D. cos ( A + B) = cosC .
Câu 28: Đơn giản biểu thức A = cos − + sin ( − ) , ta có 2
A. A = cos a + sin a .
B. A = 2 sin a .
C. A = sin a – o c s a . D. A = 0 .
Câu 29: Cho cos = – 12 và
. Giá trị của sin và tan lần lượt là 3 1 2 5 2 2 5 5 5 5 5 A. − ; . B. ; − . C. − ; . D. ; − . 13 3 3 12 13 12 13 12 4
Câu 30: Cho tan = −
với 3 2 . Khi đó 5 2 4 5 4 5 A. sin = − , cos = − . B. sin = , cos = . 41 41 41 41 4 4 5 C. sin = − 5 cos = . D. sin = , cos = − . 41 41 41 41
Bài 2. Công thức lượng giác Câu 1:
Trong các công thức sau, công thức nào sai? A. 2 2
cos 2a = cos a – sin . a B. 2 2
cos 2a = cos a + sin . a C. 2
cos 2a = 2cos a –1. D. 2 cos 2a =1– 2sin . a 3 Câu 2:
Trong các công thức sau, công thức nào đúng?
A. cos (a – b) = cos . a cos b + sin . a sin . b
B. cos (a + b) = cos . a cos b + sin . a sin . b
C. sin (a – b) = sin . a cos b + cos . a sin . b
D. sin (a + b) = sin .
a cos b − cos.sin . b Câu 3:
Trong các công thức sau, công thức nào đúng? a + b A. (a −b) tan tan tan = .
B. tan (a – b) = tan a − tan . b 1− tan a tan b a + b C. (a +b) tan tan tan = .
D. tan (a + b) = tan a + tan . b 1− tan a tan b Câu 4:
Trong các công thức sau, công thức nào sai? 1 1
A. cos a cos b = cos
(a – b)+cos(a +b). B. sinasinb = cos
(a – b) – cos(a +b). 2 2 1 1
C. sin a cos b = sin
(a – b)+sin(a +b).
D. sin a cos b = sin
(a −b)−cos(a +b). 2 2 Câu 5:
Trong các công thức sau, công thức nào sai? a + b a − b a + b a − b
A. cos a + cos b = 2 cos .cos .
B. cos a – cos b = 2sin .sin . 2 2 2 2 a + b a − b a + b a − b
C. sin a + sin b = 2sin .cos .
D. sin a – sin b = 2 cos .sin . 2 2 2 2 Câu 6:
Rút gọn biểu thức: sin (a –17).cos(a +13) – sin (a +13).cos(a –17) , ta được: 1 1 A. sin 2 . a B. cos 2 . a C. − . D. . 2 2 Câu 7:
Rút gọn biểu thức: cos 54 . cos 4 – cos36 . cos86, ta được: A. cos 50 . B. cos 58 . C. sin 50 . D. sin 58 . 1 3 Câu 8:
Cho hai góc nhọn a và b với tan a = và tan b = . Tính a + b . 7 4 2 A. . B. . C. . D. . 3 4 6 3 Câu 9:
Cho A , B , C là ba góc của một tam giác. Hãy chỉ ra hệ thức SAI.
A + B + 3C A. sin = cosC.
B. cos ( A + B – C ) = – cos 2C. 2
A + B − 2C 3C
A + B + 2C C C. tan = cot . D. cot = tan . 2 2 2 2
Câu 10: Cho A , B , C là ba góc của một tam giác. Hãy chỉ ra hệ thức SAI. A + B C A. cos = sin .
B. cos ( A + B + 2C ) = – cosC. 2 2
C. sin ( A + C ) = – sin . B
D. cos ( A + B) = – cosC. 3 3
Câu 11: Cho sin a =
; cos a 0 ; cos b =
; sin b 0 . Giá trị sin (a − b) bằng: 5 4 1 9 1 9 1 9 1 9 A. − 7 + . B. − 7 − . C. 7 + . D. 7 − . 5 4 5 4 5 4 5 4 4
Bài 3. Hàm số lượng giác Câu 1:
Trong các hàm số sau, hàm số nào là hàm chẵn?
A. y = cos x +
B. y = sin x
C. y = 1− sin x
D. y = sin x + cos x 3 Câu 2:
Chọn phát biểu đúng:
A. Các hàm số y = sin x , y = cos x , y = cot x đều là hàm số chẵn.
B. Các hàm số y = sin x , y = cos x , y = cot x đều là hàm số lẻ.
C. Các hàm số y = sin x , y = cot x , y = tan x đều là hàm số chẵn
D. Các hàm số y = sin x , y = cot x , y = tan x đều là hàm số lẻ. Câu 3:
Khẳng định nào dưới đây là sai?
A. Hàm số y = cos x là hàm số lẻ.
B. Hàm số y = cot x là hàm số lẻ.
C. Hàm số y = sin x là hàm số lẻ.
D. Hàm số y = tan x là hàm số lẻ. Câu 4:
Hàm số nào sau đây là hàm số chẵn? A. y = 2 − cos x . B. y = 2 − sin x .
C. y = 2sin (−x) .
D. y = sin x − cos x . sin 2x Câu 5:
Xét tính chẵn lẻ của hàm số y =
thì y = f ( x) là 2 cos x − 3 A. Hàm số chẵn. B. Hàm số lẻ.
C. Không chẵn không lẻ.
D. Vừa chẵn vừa lẻ. Câu 6:
Cho các hàm số: y = sin 2x , y = cos x , y = tan x , y = cot x . Có bao nhiêu hàm số tuần hoàn với chu kỳ T = . A. 1 B. 2 C. 3 D. 4 Câu 7:
Trong các hàm số y = tan x ; y = sin 2x ; y = sin x ; y = cot x , có bao nhiêu hàm số thỏa mãn tính
chất f ( x + k ) = f ( x) , x , k . A. 3 . B. 2 . C. 1. D. 4 . Câu 8:
Trong bốn hàm số: (1) y = cos 2x , (2) y = sin x ; (3) y = tan 2x ; (4) y = cot 4x có mấy hàm số
tuần hoàn với chu kỳ ? A. 1. B. 0 . C. 2 . D. 3 . Câu 9:
Hàm số y = sin x đồng biến trên mỗi khoảng nào dưới đây. 3 A. − + k2; + k2 , k . B. + k2 ; + k2 , k . 2 2 2 2 C. (
− + k2;k2 ), k .
D. (k2 ; + k2 ) , k .
Câu 10: Khẳng định nào sau đây sai?
A. y = tan x nghịch biến trong 0; .
B. y = cos x đồng biến trong − ; 0 . 2 2
C. y = sin x đồng biến trong − ; 0 .
D. y = cot x nghịch biến trong 0; . 2 2
Câu 11: Tìm mệnh đề đúng trong các mệnh đề sau?
A. Hàm số y = cot x đồng biến trên khoảng (0; ) .
B. Hàm số y = sin x nghịch biến trên khoảng ( ; 2 ) . 5
C. Hàm số y = cos x nghịch biến trên khoảng − ; . 2 2
D. Hàm số y = sin x đồng biến trên khoảng 3 5 ; . 2 2
Câu 12: Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số y = tan x tuần hoàn với chu kì 2 .
B. Hàm số y = cos x tuần hoàn với chu kì .
C. Hàm số y = sin x đồng biến trên khoảng 0; . 2
D. Hàm số y = cot x nghịch biến trên .
Câu 13: Với x 0;
, mệnh đề nào sau đây là đúng? 4
A. Cả hai hàm số y = − sin 2x và y = 1
− + cos 2x đều nghịch biến.
B. Cả hai hàm số y = − sin 2x và y = 1
− + cos 2x đều đồng biến.
C. Hàm số y = − sin 2x nghịch biến, hàm số y = 1
− + cos 2x đồng biến.
D. Hàm số y = − sin 2x đồng biến, hàm số y = 1
− + cos 2x nghịch biến.
Câu 14: Hàm số nào sau đây nghịch biến trên khoảng 0; ? 2
A. y = sin x .
B. y = cos x .
C. y = tan x .
D. y = − cot x .
Câu 15: Hàm số nào đồng biến trên khoảng − ; : 3 6
A. y = cos x .
B. y = cot 2x .
C. y = sin x .
D. y = cos2x . 3
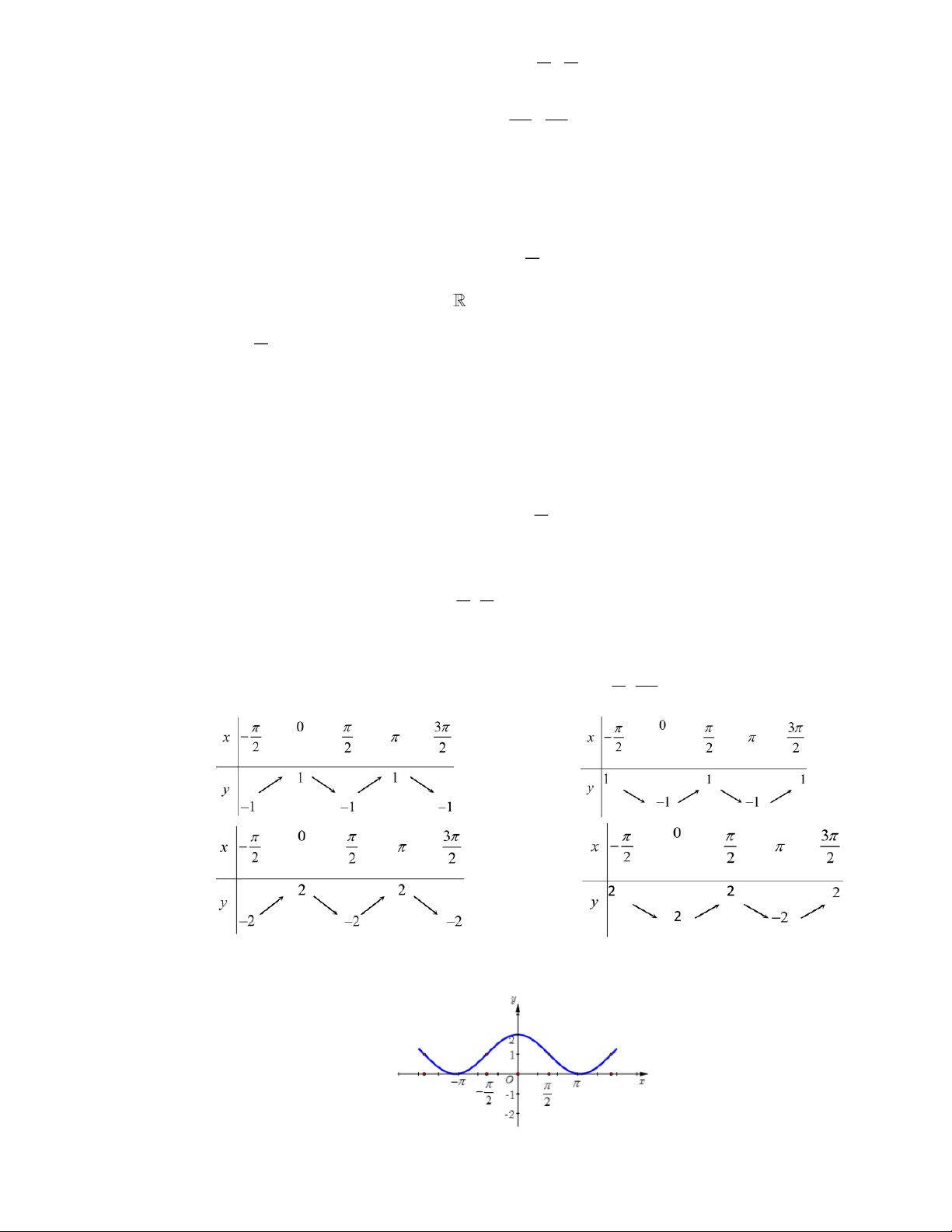
Câu 16: Bảng biến thiên của hàm số y = f (x) = cos 2x trên đoạn − ; là: 2 2 A. B. C. D.
Câu 17: Đường cong trong hình vẽ bên dưới là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A. y = cos x +1 .
B. y = 2 − sin x .
C. y = 2 cos x .D. 2 y = cos x +1. 6
Câu 18: Đường cong trong hình dưới là đồ thị của hàm số nào trong các hàm số sau đây?
A. y = 1+ sin 2x .
B. y = cos x .
C. y = − sin x .
D. y = − cos x .
Câu 19: Tập xác định của hàm số y = 2sin x là A. 0; 2 . B. 1 − ; 1 . C. . D. 2 − ;2.
Câu 20: Tìm tập xác định D của hàm số y = cot x + sin 5x + cos x
A. D = R\ + k , k Z
B. D = R\ + k2 , k Z 2 2
C. D = R\k , k Z
D. D = R\k2 , k Z
Câu 21: Chọn khẳng định sai?
A. Tập xác định của hàm số y = cot x là
\ + k , k . 2
B. Tập xác định của hàm số y = sin x là .
C. Tập xác định của hàm số y = cos x là .
D. Tập xác định của hàm số y = tan x là
\ + k , k . 2
Câu 22: Tập xác định của hàm số y = cot x là: A.
\ k2 , k . B.
\ + k , k . 2 C.
\ k , k . D.
\ + k2 , k . 2
Câu 23: Tập xác định của hàm số y = − tan x là: A. D =
\ + k , k . B. D =
\ k , k . 2 C. D =
\ k2 , k . D. D =
\ + k2 , k . 2 k
Câu 24: Tập D = \
k là tập xác định của hàm số nào sau đây? 2
A. y = cot x .
B. y = cot 2x .
C. y = tan x .
D. y = tan 2x 2sin x +1
Câu 25: Hàm số y = xác định khi 1− cos x A. x + k2
B. x k
C. x k 2 D. x + k 2 2 1− 3cos x
Câu 26: Tìm điều kiện xác định của hàm số y = sin x k
A. x k 2 . B. x . C. x + k .
D. x k . 2 2 7 +
Câu 27: Tập xác định của hàm số s inx 1 y = là s inx − 2 A. ( 2; − + ) B. (2; + ) C. \ 2 . D. . 1− cos x
Câu 28: Tập xác định của hàm số y = là: sin x −1 A. \ + k B. \ k C. \ k2 . D. \ + k2 2 2
Câu 29: Giá trị lớn nhất của hàm số y = 2sin x +1 là 1 A. −1. B. 1. C. − . D. 3 . 2
Câu 30: Tập giá trị của hàm số y = sin 2x là: A. 2 − ;2. B. 0; 2 . C. 1 − ; 1 . D. 0 ;1 .
Câu 31: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 − sin x . Khẳng định nào sau đây đúng?
A. M = 1 ; m = −1.
B. M = 2 ; m = 1.
C. M = 3 ; m = 0 .
D. M = 3 ; m = 1.
Câu 32: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 3sin 2x − 5 lần lượt là: A. 3 ; −5 . B. −2 ; −8 . C. 2 ; −5 . D. 8 ; 2 .
Câu 33: Gọi m là giá trị lớn nhất của hàm số y = 3 + 2sin 2x trên đoạn ;
. Giá trị m thỏa mãn hệ 6 2
thức nào dưới đây?
A. 3 m 6. B. 2 m = 16.
C. 4 m 5. D. m = 3 + 3. 5 7
Câu 34: Khi x thay đổi trong khoảng ;
thì y = sin x lấy mọi giá trị thuộc 4 4 2 2 2 A. 1 − ;− . B. − ; 0 C. 1 − ; 1 . D. ;1 . 2 2 2
Bài 4. Phương trình lượng giác cơ bản Câu 1: Phương trình 3 sin x = có nghiệm là: 2 x = + k x = + k2 6 3 A. x = + k2 . B. x = + k . C. . D. . 3 3 5 2 x = + k x = + k2 6 3 Câu 2:
Tập nghiệm của phương trình sin x = sin 30 là
A. S = 30 + k2 | k 150 + k2 | k .B. S = 3
0 + k2 | k . C. S = 3
0 + k360 | k .
D. S = 30 + 360 | k 150 + 360 | k . Câu 3:
Nghiệm của phương trình cos x = −1 là: A. x =
+ k , k .
B. x = k2 , k . 2
C. x = + k2 , k .
D. x = k , k . 8 Câu 4:
Phương trình lượng giác: 2cos x + 2 = 0 có nghiệm là 3 7 x = + k2 x = + k2 x = + k2 x = + k2 4 4 4 4 A. . B. . C. . D. . 3 3 7 x = − + k2 = − + = + = − + x k 2 x k 2 x k 2 4 4 4 4 Câu 5:
Phương trình tan x = 3 có tập nghiệm là
A. + k2 , k . B. .
C. + k , k . D. + k , k . 3 3 6 Câu 6:
Nghiệm của phương trình tan 3x = tan x là k k A. x = , k .
B. x = k , k .
C. x = k 2 , k . D. x = , k . 2 6 Câu 7: Giải phương trình: 2
tan x = 3 có nghiệm là: A. x = + k . B. x = − + k . C. x = + k .
D. vô nghiệm. 3 3 3 Câu 8:
Nghiệm của phương trình 3 + 3tan x = 0 là: A. x = − + k . B. x = + k . C. x = + k . D. x = + k2 . 6 2 3 2 Câu 9:
Giải phương trình 3 tan 2x − 3 = 0 . A. x =
+ k (k ) . B. x = + k (k ). 6 3 2 C. x =
+ k (k ) . D. x = + k (k ). 3 6 2
B. CÂU HỎI ĐÚNG, SAI 1
Câu 1: Cho biết sin x = và 0 x
.Các mệnh đề sau đúng hay sai? 3 2 Mệnh đề Đúng Sai
a) cos x 0 b) 6 cos x = 3 c) 3 tan x = 3 d) 6 − 3 cos x + = . 3 8 1
Câu 2: Biết: sin = và 0
. Các mệnh đề sau đúng hay sai? 3 2 Mệnh đề Đúng Sai a) 2 sin 2 = 9 b) 7 cos 2 = 9 9 c) 2 tan 2 = 7 d) 7 2 cot 2 = 2 1
Câu 3: Cho phương trình lượng giác sin 2x = −
(*).Các mệnh đề sau đúng hay sai? 2 Mệnh đề Đúng Sai a)
Phương trình (*) tương đương sin 2x = sin 6
b) Trong khoảng (0; ) phương trình có 3 nghiệm c)
Tổng các nghiệm của phương trình trong khoảng ( 0; ) bằng 3 2 d) Trong khoảng (
0; ) phương trình có nghiệm lớn nhất bằng 11 12 C. TỰ LUẬN
Bài 1. Cho biết một GTLG, tính các GTLG còn lại, với: 4 2 a) 0 0 cos a = , 270 a 360 b) cos = , − 0 5 5 2 5 1 c) sin a = , a d) 0 0
sin = − , 180 270 13 2 3 3
e) tan a = 3, a f) tan = 2 − , 2 2 3 g) 0 cot15 = 2 + 3
h) cot = 3, 2 3 − Bài 2. Cho sin = và 0 0
90 180 . Tính giá trị của biểu thức cot 2 tan E = . 5 tan + 3cot
Bài 3. Cho biết một GTLG, tính giá trị của biểu thức, với: 2
8 tan a + 3cot a −1 1 a) 0 0 B = khi sin a = , 90 a 180 tan a + cot a 3 2 2 sin a + 2sin .
a cos a − 2 cos a b) C = khi cot a = 3 − 2 2 2sin a − 3sin . a cos a + 4 cos a
Bài 4. Đơn giản biểu thức A = ( 2 x) 2 t x + ( 2 1– sin .co 1– cot x).
Bài 5. Chứng minh biểu thức 2 2 2 2 2 D = cos .
x cot x + 3cos x – cot x + 2sin x không phụ thuộc x . 2 2 cos x −1
Bài 6. Đơn giản biểu thức A = . sin x + cos x
Bài 7. Tính giá trị của biểu thức M = cos ( –53).sin ( –337) + sin 307 . sin113 5
Bài 8. Cho sin a + cos a =
. Tính giá trị các biểu thức sau: 4 a) A = sin . a cos a
b) B = sin a − cos a c) 3 3
C = sin a − cos a
Bài 9. Cho tan a − cot a = 3 . Tính giá trị các biểu thức sau: 10 a) 2 2
A = tan a + cot a
b) B = tan a + cot a c) 4 4
C = tan a − cot a
Bài 10. Rút gọn các biểu thức sau: a) B co ( = − x) 3 3 s + sin x − − t g + x cotg − x 2 2 2 sin( 4 − ,8 ).sin( 5 − ,7 ) cos( 6 − ,7 ).cos( 5 − ,8 ) b) C = + cot g ( 5 − , 2 ) t g ( 6 − , 2 )
Bài 11. Tính giá trị các biểu thức sau: 0 0 0 0 sin( 3 − 28 ).sin 958 cos( 5 − 08 ).cos( 1 − 022 ) a) A = − 0 0 cot 572 tan( 2 − 12 ) cos ( 288 − ).cot 72 b) A = ( − ) − tan18 tan 162 .sin108 c) 0 0 0 0 0 0 A = sin160 .co 1
s 10 + sin 250 .co 3 s 40 + t 1 g 10 .tg340
Bài 12. CMR biểu thức 2 2 2 A = cos x + cos + x + cos − x
không phụ thuộc x 3 3
Bài 13. Chứng minh các đẳng thức sau: tan a + tan b sin a cos a 1+ cot a a) tan . a tan b = b) − = cot a + cot b sin a − cos a cos a − sin a 1− cot a 2 2 sin a cos a 2 sin a sin a + cos a c) 1− − = sin . a cos a − = sin a + cos a 1+ cot a 1+ d) tan a 2 sin a − cos a tan a − 1
Bài 14. Tính giá trị của biểu thức lượng giác, khi biết: 3 a) tan + khi sin = , 3 5 2 12 3 b) cos
− khi sin = − , 2 3 13 2
Bài 15. Rút gọn biểu thức:
sin x + sin 2x + sin 3x
a) A = cos (120 – x) + cos(120 + x) – cos x . b) B =
cos x + cos 2x + cos 3x
Bài 16. Tính giá trị của các biểu thức lượng giác sau: a) A = 2 o 2 o 2 sin 20 sin 100 sin 140o + + b) B = 2 o o 2 cos 10 cos110 cos 130o + +
Bài 17. Tính giá trị của biểu thức lượng giác, khi biết: 5 3
a) cos 2, sin 2, tan 2 khi cos = − , 13 2
b) cos 2, sin 2, tan 2 khi tan = 2
Bài 18. Tính giá trị của biểu thức sau: a) cos 20 . o cos 40 . o cos 60 . o cos80o A = b) sin10 . o sin 50 . o sin 70o B =
Bài 19. Bài Rút gọn biểu thức 1+ cos x x 1) 2 2 A = .tg − cos x 1− cos x 2 sin 3 .
x cos5x − sin 5 . x cos3x 2) B = cos x 11 2 3) C = − cot g2x sin 4x 2 2
sin 2x − 4sin x 4) D = 2 2
sin 2x + 4sin x − 4 a a cotg + tg 5) 2 2 E = a a cotg − tg 2 2 2 2cos a −1 6) H = 2 2tg − a .sin + a 4 4
Bài 20. Chứng minh đẳng thức 1 3 1) 4
4.cos x − 2cos2x − cos4x = 2 2 sin 4x 2) 3 3 cos . x sin x − sin . x cosx = 4 1 3 3) 4 4 sin x + cos x = .cos4x + 4 4 1+ sin x x 4) = cot g − cos x 4 2
Bài 21. Xét tính chẵn lẻ của các hàm số sau
a) y = 2 cos 3x b) y = x + sinx c) y = .
x cot x + cos x d) 2
y = x + tan | x |
Bài 22. Xét tính chẵn lẻ của các hàm số sau a) y = 2x sin . x
b) y = cos x + sin 2 . x cos 2x c) y = . d) 7 y = tan 2 . x sin 5 . x x
Bài 23. Xét tính tuần hoàn và tìm chu kì (nếu có) của các hàm số sau: a) y = 1− sin 5 . x b) 2
y = cos x −1 .
Bài 24. Khảo sát sự biến thiên của các hàm số sau 3 a) y = sinx trên − ;
b) y = cos x trên ; 4 3 3 2 3 c) y = cot x − trên − ; − d) y = tan x + trên − ; 6 4 2 3 4 2
Bài 25. Tìm tập xác định của các hàm số sau? 1+ tan x
a) y = cos x + sin x b, y = sin x c, y = cot + x d) y = tan x + 2 4
Bài 26. Tìm giá trị lớn nhất và giá trị nhỏ nhất
a) y = 2sin 3x − −3 b) 2 y = 5 − + 2cos 2x − 2 3 12 2 sin (3x)
c) y = 2 cos 3x −1 d) 2 y = − 3cos (3x) 2
e) y = 4 − 2 cos 2x . f) 2018 y = 3 + sin x .
Bài 27. Giải các phương trình sau: x 3 a) sin − = −
b) sin (3x −30 ) = sin 45 2 3 4 3 c) sin 3x − = sin − x d) sin 4x − = 0 4 6 3 7 e) cos −x + = 1 f) cos 5x − = sin − 2x 3 3 4 1 g) ( x+ ) 2 cos 2 25 = − h) cos − 2x = − 2 6 4
Bài 28. Giải các phương trình sau: a) tan (2x − ) 1 = tan −x + b) tan (3x −10 ) = 3 3 c) 3 tan 3x + = 1 − d) cot 2x − =1 6 3 e) 2 cot (3x) = 3 f) cot x + = cot 2 − x + 3 6
Bài 29. Trong Vật lí, phương trình tổng quát của một vật dao động điều hoà cho bởi công thức x (t ) = c A os ( t
+) , trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời điểm t, A là
biên độ dao động (A 0) và
− ; là pha ban đầu của dao động. Xét hai dao động điều hoà có phương trình: x t = 2cos t + cm , 1 ( ) ( ) 3 6 x t = 2cos t − cm . 2 ( ) ( ) 3 3
Tìm dao động tổng hợp x(t) = x t + x t và sử dụng công thức biến đổi tổng thành tích để tìm biên 1 ( ) 2 ( )
độ và pha ban đầu của dao động tổng hợp này.
Bài 30. Một chất điểm dao động điều hoà theo phương trình s = 3sin t
với s tính bằng cm và t tính 2 3
bằng giây. Dựa vào đồ thị của hàm số sin, hãy xác định ở các thời điểm t nào trong 4 giây đầu thì s − 2
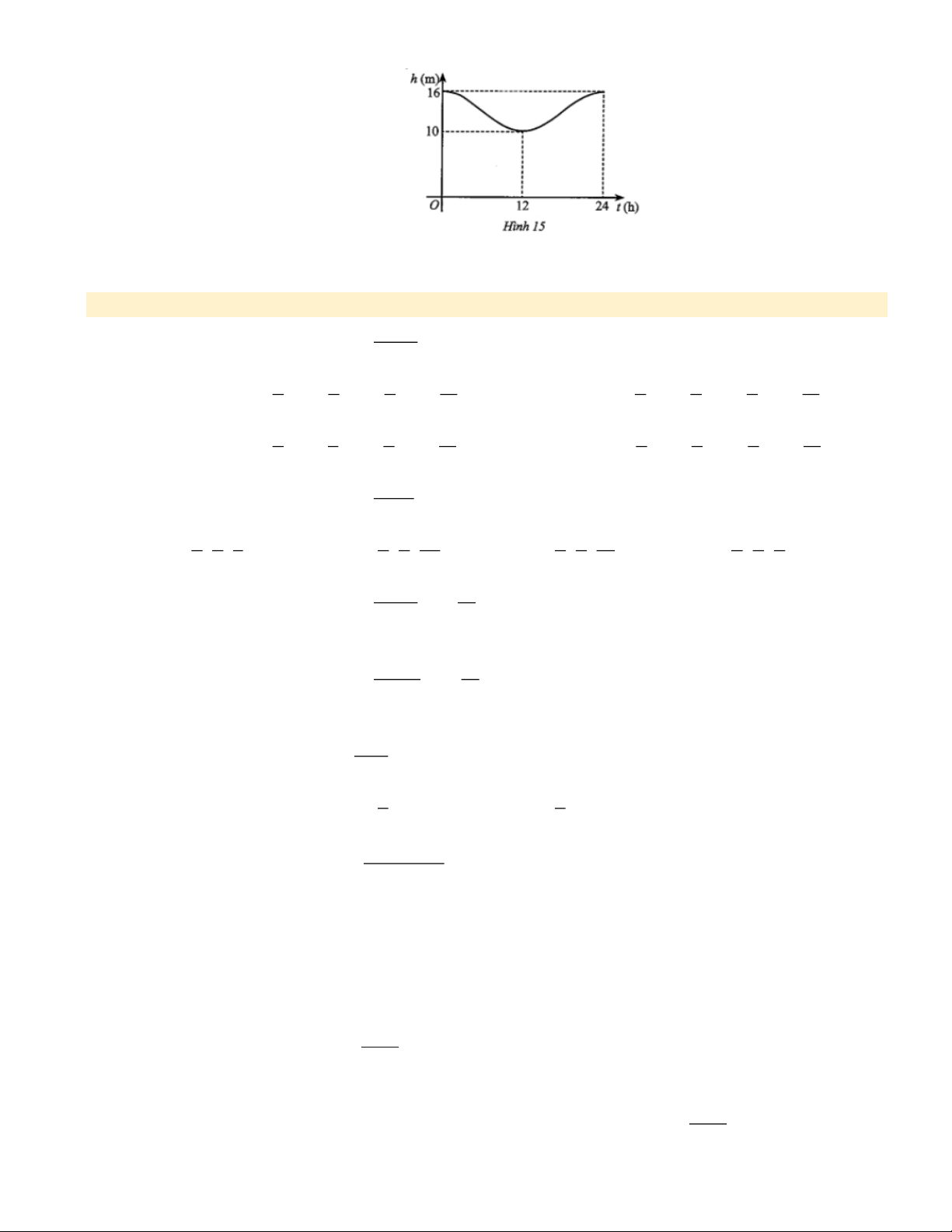
Bài 31. Mực nước cao nhất tại một cảng biển là 16 m khi thủy triều lên cao và sau 12 giờ khi thủy triều
xuống thấp thì mực nước thấp nhất là 10 m . Đồ thị ở Hình 15 mô tả sự thay đổi chiều cao của mực nước
tại cảng trong vòng 24 giờ tính từ lúc nửa đêm. Biết chiều cao của mực nước h ( m) theo thời gian
t ( h)(0 t 24) được cho bởi công thức h = m + c a os t
với m, a là các số thực dương cho trước. 12 a) Tìm m, a . 13
b) Tìm thời điềm trong ngày khi chiều cao của mực nước là 11,5 m .
CHƯƠNG 2: DÃY SỐ. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN A. TRẮC NGHIỆM Bài 5. Dãy số n + Câu 1:
Cho dãy số (u ), biết 2 1 u =
. Viết năm số hạng đầu của dãy số. n n n + 2 3 7 3 11 5 7 3 11
A. u = 1,u = ,u = ,u = ,u = .
B. u = 1,u = ,u = ,u = ,u = . 1 2 3 4 5 4 5 2 7 1 2 3 4 5 4 5 2 7 5 8 3 11 5 7 7 11
C. u = 1, u = , u = , u = , u =
D. u = 1,u = ,u = ,u = ,u = . 1 2 3 4 5 4 5 2 7 1 2 3 4 5 4 5 2 3 n Câu 2:
Cho dãy số (u ), biết u =
. Ba số hạng đầu tiên của dãy số đó là n n 3n −1 1 1 1 1 1 3 1 1 1 1 2 3 A. ; ; . B. ; ; . C. ; ; . D. ; ; . 2 4 8 2 4 26 2 4 16 2 3 4 n + Câu 3:
Cho dãy số (u ), biết 1 u =
. Số 8 là số hạng thứ mấy của dãy số? n n 2n +1 15 A. 8. B. 6. C. 5. D. 7. n + Câu 4:
Cho dãy số (u ), biết 2 5 u =
. Số 7 là số hạng thứ mấy của dãy số? n n 5n − 4 12 A. 6. B. 8. C. 9. D. 10. n +1 Câu 5:
Cho dãy số (u với u = . Tính u . n ) n 5 n 6 5 A. 5. B. . C. . 5 6 D. 1. 2 n + 3n + 7 Câu 6:
Cho dãy số (u với u = n ) n n + . 1
Hỏi dãy số trên có bao nhiêu số hạng nhận giá trị nguyên. A. 2. B. 4. C. 1. D. Không có. Câu 7:
Cho dãy số (u ) biết u = 3n + 6 . Mệnh đề nào sau đây đúng? n n A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm
D. Cả A, B, C đều sai n + Câu 8:
Cho dãy số (u ) biết 5 u =
. Mệnh đề nào sau đây đúng? n n n + 2 A. Dãy số tăng B. Dãy số giảm n + 5
C. Dãy số không tăng, không giảm
D. Có số hạng u = +1 n 1 + n + 2 14 Câu 9:
Trong các dãy số (u cho bởi số hạng tổng quát u sau, dãy số nào tăng? n ) n n n 2 n +1 A. u = . B. u = . C. u = . n u = − n − n 2n n 2 2n +1 n 3n + D. 2 ( 2) 1. 2 n
Câu 10: Cho dãy số (u ) biết u = 5n + 2 . Mệnh đề nào sau đây đúng? n n A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm
D. Cả A, B, C đều sai 1
Câu 11: Cho dãy số (u ) biết u =
. Mệnh đề nào sau đây đúng? n n 3n + 2 A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng, không giảm
D. Cả A, B, C đều đúng −
Câu 12: Cho dãy số (u ) biết 1 u =
. Mệnh đề nào sau đây đúng ? n n 2n + 3
A. Dãy số bị chặn.
B. Dãy số bị chặn trên.
C. Dãy số bị chặn dưới. D. Không bị chặn n +
Câu 13: Cho dãy số (u ) biết 4 5 u =
. Mệnh đề nào sau đây đúng ? n n n +1
A. Dãy số bị chặn.
B. Dãy số bị chặn trên.
C. Dãy số bị chặn dưới. D. Không bị chặn 3 n
Câu 14: Cho dãy số (u ) biết u =
. Mệnh đề nào sau đây đúng ? n n 2 n +1
A. Dãy số bị chặn.
B. Dãy số bị chặn trên.
C. Dãy số bị chặn dưới. D. Không bị chặn
Câu 15: Trong các dãy số sau dãy số nào bị chặn ? 1
A. Dãy (a , với 3
a = n + n, n *.
B. Dãy (b , với 2 b = n + , n * . n ) n ) n n 2n 3n
C. Dãy (c , với c = ( 2 − )n + 3, n *.
D. Dãy (d , với d = , n *. n ) n ) n n 3 n + 2
Bài 6. Cấp số cộng Câu 1:
Dãy số nào sau đây là một cấp số cộng? u = 1 u = 3 A. (u . B. (u . n ) 1 : n ) 1
: u = u + 2, n 1 u = 2u +1, n 1 n 1 + n n 1+ n
C. (u ) : 1; 3 ; 6 ; 10 ; 15 ; . D. (u −1; 1; −1; 1; −1; . n ) : n Câu 2:
Trong các dãy số sau, có bao nhiêu dãy số là cấp số cộng?
a) Dãy số (u với u = 4n . b) Dãy số (v với 2 v = 2n +1. n ) n ) n n b) Dãy số ( n w với w =
− 7 . d) Dãy số (t với t = 5 −5n . n ) n ) n 3 n A. 4 . B. 2 . C. 1. D. 3 . Câu 3:
Xác định a để 3 số 2 1+ 2 ; a 2a −1; 2
− a theo thứ tự thành lập một cấp số cộng? 3
A. Không có giá trị nào của a . B. a = . 4 15 3 C. a = 3 . D. a = . 2 Câu 4:
Các dãy số có số hạng tổng quát u . Trong các dãy số sau, dãy số nào không phải là cấp số cộng? n
A. u = 2n + 5 .
B. 49 , 43 , 37 , 31, 25 .C. u = 1+ 3n .
D. u = n + − n . n ( )2 2 3 n n Câu 5:
Biết bốn số 5 ; x ; 15 ; y theo thứ tự lập thành cấp số cộng. Giá trị của biểu thức 3x + 2 y bằng. A. 50 . B. 70 . C. 30 . D. 80 . Câu 6:
Cho cấp số cộng (u với u = 7 công sai d = 2 . Giá trị u bằng n ) 1 2 7 A. 14 . B. 9 . C. . D. 5 2 1 Câu 7:
Cho một cấp số cộng (u có u = , u = 26. Tìm công sai d n ) 1 3 8 11 10 3 3 A. d = . B. d = . C. d = . D. d = . 3 3 10 11 Câu 8:
Cho dãy số (u là một cấp số cộng có u = 3 và công sai d = 4 . Biết tổng n số hạng đầu của n ) 1
dãy số (u là S = 253 . Tìm n . n ) n A. 9 . B. 11. C. 12 . D. 10 . Câu 9:
Cho dãy số vô hạn u là cấp số cộng có công sai d , số hạng đầu u . Hãy chọn khẳng định sai? n 1 u + u A. 1 9 u = . B. u = u
+ d , n 2 . 5 − 2 n n 1 n C. S = 2u +11d .
D. u = u + (n −1).d , * n . 12 ( 1 ) 2 n 1
Câu 10: Cho một cấp số cộng (u có u = 5 và tổng của 50 số hạng đầu bằng 5150 . Tìm công thức của n ) 1
số hạng tổng quát u . n
A. u = 1+ 4n .
B. u = 5n .
C. u = 3 + 2n .
D. u = 2 + 3n . n n n n
Câu 11: Cho cấp số cộng (u có u = −12 , u =18 . Tính tổng 16 số hạng đầu tiên của cấp số cộng này. n ) 4 14 A. S = 24 − . B. S = 26 . C. S = 25 − . D. S = 24 . 16 16 16 16
Câu 12: Viết ba số xen giữa 2 và 22 để ta được một cấp số cộng có 5 số hạng? A. 6 , 12 , 18 . B. 8 , 13 , 18 . C. 7 , 12 , 17 . D. 6 , 10 , 14 .
Câu 13: Một đồng hồ đánh giờ, khi kim giờ chỉ số n (từ 1 đến 12) thì đồng hồ đánh đúng n tiếng. Hỏi
trong một ngày (24 giờ) đồng hồ đánh được bao nhiêu tiếng? A. 156. B. 152. C. 148. D. 160.
Câu 14: Sinh nhật lần thứ 17 của An vào ngày 01 tháng 5 năm 2018 . Bạn An muốn mua một chiếc máy
ảnh giá 3850000 đồng để làm quà sinh nhật cho chính mình nên An quyết định bỏ ống heo 1000
đồng vào ngày 01 tháng 02 năm 2018 . Trong các ngày tiếp theo, ngày sau bỏ ống nhiều hơn
ngày trước 1000 đồng. Hỏi đến ngày sinh nhật của mình, An có bao nhiêu tiền (tính đến ngày 30 tháng 4 năm 2018 )?
A. 4095000 đồng. B. 89000 đồng.
C. 4005000 đồng. D. 3960000 đồng. 16
Câu 15: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78 .
Câu 16: Trong sân vận động có tất cả 30 dãy ghế, dãy đầu tiên có 15 ghế, các dãy liền sau nhiều hơn dãy
trước 4 ghế, hỏi sân vận động đó có tất cả bao nhiêu ghế? A. 2250 . B. 1740 . C. 4380 . D. 2190 .
Bài 7. Cấp số nhân Câu 1:
Trong các dãy số sau, dãy số nào là một cấp số nhân?
A. 128; − 64; 32; −16; 8; ...
B. 2; 2; 4; 4 2; .... 1
C. 5; 6; 7; 8; ...
D. 15; 5; 1; ; ... 5 Câu 2:
Trong các dãy số sau, dãy số nào không phải là một cấp số nhân? A. 2; 4; 8; 16; B. 1; −1; 1; −1; C. 2 2 2 2 1 ; 2 ; 3 ; 4 ; D. 3 5 7 ;
a a ; a ; a ; (a 0). Câu 3:
Cho cấp số nhân (u với u = −2 và q = 5.
− Viết bốn số hạng đầu tiên của cấp số nhân. n ) 1 A. 2 − ; 10; 50; − 250. B. 2 − ; 10; − 50; 250. C. 2
− ; −10; − 50; − 250. D. 2 − ; 10; 50; 250. Câu 4:
Trong các dãy số (u cho bởi số hạng tổng quát u sau, dãy số nào là một cấp số nhân? n ) n 1 1 1 1 A. u = . B. u = −1.
C. u = n + . D. 2 u = n − . n n−2 3 n 3n n 3 n 3 Câu 5:
Trong các dãy số (u cho bởi số hạng tổng quát u sau, dãy số nào là một cấp số nhân? n ) n 7 A. u = 7 − 3 . n B. u = 7 − 3 . n C. u = . D. u = 7.3 . n n n n 3n n Câu 6:
Trong các phát biểu sau, phát biểu nào là sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Một cấp số cộng có công sai dương là một dãy số dương. Câu 7:
Xác định x dương để 2x − 3 ; x ; 2x + 3 lập thành cấp số nhân. A. x = 3 . B. x = 3 .
C. x = 3 .
D. không có giá trị nào của x . Câu 8:
Với giá trị x nào dưới đây thì các số 4 − ; ;
x − 9 theo thứ tự đó lập thành một cấp số nhân? 13 A. x = 36. B. x = − . C. x = 6. D. x = −36. 2 1 Câu 9:
Tìm b 0 để các số
; b; 2 theo thứ tự đó lập thành một cấp số nhân. 2 A. b = −1. B. b = 1. C. b = 2. D. b = −2.
Câu 10: Cho cấp số nhân (a có a = 3 và a = −6 . Tìm số hạng thứ năm của cấp số nhân đã cho. n ) 1 2 A. a = −24 . B. a = 48 . C. a = −48 .
D. a = 24 . 5 5 5 5 17
Câu 11: Một khu rừng có trữ lượng gỗ là 5
4.10 mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng
đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ A. ( )5 5 4.10 . 0, 05 . B. ( )5 5 4.10 . 1, 4 . C. ( )5 5 4.10 . 1, 04 . D. ( )5 4. 10, 4 .
Câu 12: Bài toán “Lãi kép”: Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất 7%
/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi được nhập
vào vốn ban đầu (người ta gọi đó là lãi kép). Giả sử trong khoảng thời gian gửi người gửi không
rút tiền ra và lãi suất không thay đổi, hỏi sau 10 năm thì tổng số tiền cả vốn lẫn lãi mà người gửi
nhận được gần với số tiền nào trong các số tiền dưới đây? A. 196715000 đồng.
B. 196716000 đồng. C. 183845000 đồng. D. 183846000 đồng.
Câu 13: Một người gửi ngân hàng 150 triệu đồng theo thể thức lãi kép, lãi suất 0,58% một tháng (kể từ
tháng thứ 2 , tiền lãi được tính theo phần trăm của tổng tiền lãi tháng trước đó và tiền gốc của
tháng trước đó). Sau ít nhất bao nhiêu tháng, người đó có 180 triệu đồng? A. 34 tháng. B. 32 tháng. C. 31 tháng. D. 30 tháng.
B. CÂU HỎI ĐÚNG, SAI n +1 Câu 1:
Cho dãy số (u có số hạng tổng quát u =
. Các mệnh đề sau đúng hay sai? n ) n n + 2 Mệnh đề Đúng Sai a) 1 u − u = n 1 + n (n + 3)(n + 2) b) * u u , n n 1 + n
c) Dãy số (u là dãy số giảm n )
d) Dãy (u là dãy số bị chặn n ) 3 1 Câu 2:
Cho cấp số cộng (u có số hạng đầu u = , công sai d =
. Các mệnh đề sau đúng hay sai? n ) 1 2 2 Mệnh đề Đúng Sai
a) Công thức cho số hạng tổng quát n u = 1+ n 3
b) 5 là số hạng thứ 8 của cấp số cộng đã cho c) 15
một số hạng của cấp số cộng đã cho 4
d) Tổng 100 số hạng đầu của cấp số cộng (u bằng 2620 n ) u − u = 54
Câu 3: Cho cấp số nhân (u có công bội nguyên và các số hạng thoả mãn 4 2 n ) u − u = 108 5 3
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Số hạng đầu của cấp số nhân bằng 9
b) Công bội của cấp số nhân q = 3
c) Tổng của 9 số hạng đầu tiên bằng 4599
d) Số 576 là số hạng thứ 6 của cấp số nhân 18 C. TỰ LUẬN Bài 1.
Xét tính tăng giảm của các dãy số sau:
1). Dãy số (u với 3
u = 2n − 5n +1
2). Dãy số (u với u = 3n − . n n ) n ) n n 3). Dãy số ( n n u với u = .
4). Dãy số (u với u = n ) n ) n 2 n +1 n 2n Bài 2.
Xét tính bị chặn của các dãy số sau 1 nx a) u = . b) u = 3.cos . c) 3 u = 2n +1. n 2 2n −1 n 3 n 2 n + 2n 1 d) u = . e) u = n + . n 2 n + n +1 n n Bài 4.
Xét tính bị chặn của các dãy số sau: 1 1 1 1 1 1 1 a). u = + +...+ b). u = + + +...+ n 1.2 2.3 n (n + ) 1 n 2 2 2 2 1 2 3 n 1 1 1 1 1 1 c). u = + +...+ d). u = + +...+ n 1.3 2.5 (2n − ) 1 (2n + ) 1 n 1.4 2.5 n (n + 3) Bài 5.
Trong các dãy số sau, dãy nào là cấp số cộng. Tìm số hạng đầu và công sai của cấp số cộng đó:
a). Dãy số (u với u =19n −5
b). Dãy số (u với u = 3 − n +1 n ) n ) n n c). Dãy số ( n u với 2
u = n + n +1
d). Dãy số (u với u = − + n n ( ) 1 10 n ) n ) n Bài 6. Định x để 3 số 2 10 − 3 ,
x 2x + 3, 7 − 4x theo thứ tự đó lập thành 1 cấp số cộng. Bài 7.
Một tam giác vuông có chu vi bằng 3a, và 3 cạnh lập thành một CSC. Tính độ dài ba cạnh của tam giác theo a. Bài 8.
Ba góc của một tam giác vuông lập thành một CSC. Tìm số đo các góc đó. Bài 9.
Tìm số hạng đầu tiên, công sai, số hạng thứ 20 và tổng của 20 số hạng đầu tiên của các cấp số cộng sau, biết rằng: u = 19 u
− u + u = 10 u + u = 14 a) 5 b) 2 3 5 c) 3 5 u = 35 u + u = 26 s = 129 9 4 6 12 u + u = 51 Bài 10.
Cho CSN (u có các số hạng thỏa: 1 5 n ) u + u = 102 2 6
a). Tìm số hạng đầu và công bội của CSN.
b). Hỏi tổng bao nhiêu số hạng đầu tiên bằng 3069?
c). Số 12288 là số hạng thứ mấy? Bài 11.
Tìm số hạng đầu của CSN biết công bội bằng 3, tổng số các số hạng là 728 và số hạng cuối bằng 486. Bài 12.
Cho 3 số tạo thành một cấp số cộng có tổng 21. Nếu thêm 2, 3, 9 lần lượt vào số thứ nhất, số thứ
hai, số thứ ba tạo thành một cấp số nhân. Tìm 3 số đó. Bài 13.
Cho 3 số dương có tổng là 65 lập thành một cấp số nhân tăng, nếu bớt một đơn vị ở số hạng thứ
nhất và 19 đơn vị ở số hạng thứ ba ta được một cấp số cộng. Tìm 3 số đó. Bài 14.
Cho x, 3, y theo thứ tự lập thành cấp số nhân và 4
x = y 3. Tìm x, y.
Bài 15. Một cầu thang bằng gạch có tổng cộng 30 bậc. Bậc dưới cùng cần 100 viên gạch. Mỗi bậc tiếp theo
cẩn ít hơn hai viên gạch so với bậc ngay trước nó. 19




