Đề cương ôn tập cuối học kì 1 Toán 11 Kết Nối Tri Thức Với Cuộc Sống

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 tài liệu đề cương hướng dẫn ôn tập kiểm tra cuối học kì 1 môn Toán 11 bộ sách Kết Nối Tri Thức Với Cuộc Sống.

43 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 11

Môn: Toán 11

Thông tin:

56 trang 6 tháng trước

Tác giả:

Profile Kim Oanh
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
MỤC LỤC
ChươngI. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 3
AA BÀI TẬP TRẮC NGHIỆM........... . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. 3
} Mức độ Nhận biết, Thông hiểu. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 3
} Mức độ Vận dụng. . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... 4
BB BÀI TẬP TỰ LUẬN. . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .4
ChươngII. DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN 5
AA BÀI TẬP TRẮC NGHIỆM.. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. 5
} Mức độ Nhận biết, Thông hiểu. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 5
} Mức độ Vận dụng. . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... 5
BB BÀI TẬP TỰ LUẬN. . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .6
ChươngIII. CÁCSỐĐẶCTRƯNGĐOXUTHẾTRUNGTÂMCỦAMẪUSỐLIỆUGHÉP
NHÓM 7
AA BÀI TẬP TRẮC NGHIỆM.. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. 7
} Mức độ Nhận biết, Thông hiểu. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 7
} Mức độ Vận dụng. . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... 8
BB BÀI TẬP TỰ LUẬN. . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .8
ChươngIV. QUAN HỆ SONG SONG SONG TRONG KHÔNG GIAN 10
AA BÀI TẬP TRẮC NGHIỆM.. . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . .10
} Mức độ Cơ bản.. . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . .10
} Mức độ Vận dụng. . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . 13
BB BÀI TẬP TỰ LUẬN.. . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 14
ChươngV. GIỚI HẠN. HÀM SỐ LIÊN TỤC 16
AA BÀI TẬP TRẮC NGHIỆM.. . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . .16
} Mức độ Nhận biết, Thông hiểu. . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . .16
} Mức độ Vận dụng. . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . 17
BB BÀI TẬP TỰ LUẬN.. . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 17
1
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chương I.
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH
LƯỢNG GIÁC
A. BÀI TẬP TRẮC NGHIỆM
1 Mức độ Nhận biết, Thông hiểu
Câu 1. Góc có số đo
π
12
đổi sang độ là
A. 15
◦
. B. 16
◦
.
C. 14
◦
. D. 17
◦
30
0
.
Câu 2. Góc có số đo 108
◦
đổi sang radian là
A.
3π
2
. B.
5π
2
. C.
5π
3
. D.
3π
5
.
Câu 3. Giá trị cot
89π
6
bằng
A.
p
3
3
. B. −
p
3. C. −
p
3
3
. D.
p
3.
Câu 4. Xác định số đo của góc lượng giác
(Ou, Ov) được biểu diễn trong hình bên dưới.
O
u
v
150
◦
A. 410
◦
. B. 510
◦
. C. 150
◦
. D. 420
◦
.
Câu 5. Xác định số đo của góc lượng giác
(Ou, Ov) được biểu diễn trong hình bên dưới
O
u
v
60
◦
A. −300
◦
. B. 510
◦
.
C. 60
◦
. D. −420
◦
.
Câu 6. Chọn khẳng định đúng trong các khẳng
định sau:
A. tan(π −α) =tan α. B. cot(π −α) =cot α.
C. cos(π −α) =−cos α. D. sin(π −α) =−sin α.
Câu 7. Cho sinα =
1
3
, với 90
◦
< α < 180
◦
. Tính
cosα.
A. cosα =−
2
3
. B. cosα =−
2
p
2
3
.
C. cosα =
2
p
2
3
. D. cos α =
2
3
.
Câu 8. Trong các mệnh đề sau, mệnh đề nào là
mệnh đề đúng?
A. sin2a =sin a +cos a.
B. sin2a =2sin a.
C. sin2a =cos
2
a −sin
2
a.
D. sin2a =2sin acos a.
Câu 9. Trong các mệnh đề sau, mệnh đề nào là
mệnh đề sai?
A. sin a +sin b =2 sin
a +b
2
cos
a −b
2
.
B. cos a −cos b =2 sin
a +b
2
sin
a −b
2
.
C. cos a +cos b =2 cos
a +b
2
cos
a −b
2
.
D. sin a −sin b =2 cos
a +b
2
sin
a −b
2
.
Câu 10. Chu kỳ của hàm số y = cot x là
A. kπ, k ∈Z. B. 2π.
C. π. D.
π
2
.
Câu 11. Chu kỳ của hàm số y = cos x là
A.
2π
3
. B. 2π. C. π. D. k2π.
Câu 12. Tập giá trị của hàm số y = cos x là tập
hợp nào sau đây?
A. [0;+∞]. B. R.
C. (−∞;0]. D. [−1; 1].
Câu 13. Giá trị nhỏ nhất m và giá trị lớn nhất
M của hàm số y =3 sin2x −5 lần lượt là
A. m =2, M = 8. B. m =−8, M = −2.
C. m =−5, M =−2. D. m =−8, M =−5.
Câu 14. Phương trình cos x = a có nghiệm khi
và chỉ khi
A. |a|≤1. B. |a|> 1.
C. |a|< 1. D. |a| ≥1.
Câu 15. Giải phương trình sin x =
p
3
2
.
A. x =±
π
3
+k2π. B. x =
π
3
+kπ.
C.
x =
π
6
+kπ
x =
5π
6
+kπ
. D.
x =
π
3
+k2π
x =
2π
3
+k2π
.
3
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 16. Phương trình cos 3x =cos
π
15
có nghiệm
là
A. x =±
π
15
+k2π. B. x =±
π
45
+
k2π
3
.
C. x =−
π
45
+
k2π
3
. D. x =
π
45
+
k2π
3
.
Câu 17. Giải phương trình tan x =
p
3 ta được
tập nghiệm là
A.
n
π
3
+k2π, k ∈Z
o
. B. ∅.
C.
n
π
3
+kπ, k ∈Z
o
. D.
n
π
6
+kπ, k ∈Z
o
.
2 Mức độ Vận dụng
Câu 18. Cho hai dao động điều hòa cùng
phương có phương trình lần lượt là x
1
=
5cos(100πt +π)(cm) và x
2
= 5cos(100πt −π/2)(cm).
Phương trình dao động tổng hợp của hai dao
động trên là
A. x =5
p
2cos
100πt +
3π
4
(cm).
B. x =5
p
2cos
100πt −
3π
4
(cm).
C. x =10 cos
100πt −
3π
4
(cm).
D. x =10 cos
100πt +
3π
4
(cm).
Câu 19. Cho hình vuông
ABCD như hình vẽ. Tính
giá trị của tanα.
A.
4
13
. B.
6
13
.
C.
9
13
. D.
7
17
.
α
5
7
A
B
C
D
E
Câu 20. Nhiệt độ ngoài trời ở một thành phố
vào các thời điểm khác nhau trong ngày có thể
được mô phỏng bởi công thức
h(t) =29 +3sin
h
π
12
(t −9)
i
với h tính bằng độ C và t là thời gian trong ngày
tính bằng giờ. Nhiệt độ thấp nhất trong ngày
vào lúc mấy giờ?
A. 5 giờ . B. 0 giờ . C. 3 giờ. D. 4 giờ.
B. BÀI TẬP TỰ LUẬN
BÀI 1. Giải các phương trình lượng giác sau:
sin x = −
p
2
2
;a) sin
3x +
π
6
=
p
3
2
;b)
cos2x =
p
3
2
;c) cos(2x −30
◦
) =−1;d)
tan3x =tan
π
7
;e) cot
2x −
π
5
=
p
3.f)
BÀI 2. Số giờ có ánh nắng mặt trời của một thành phố A trong ngày thứ t (ở đây t là số ngày tính từ
ngày 1 tháng Giêng) của một năm không nhuận được mô hình hóa bởi hàm số
L(t) =12 +2,83sin
h
2π
365
(t −80)
i
với t ∈Z và 0 < t ≤365.
a) Vào ngày nào trong năm thì thành phố A có ít giờ ánh sáng mặt trời nhất?
b) Vào ngày nào trong năm thì thành phố A có nhiều giờ ánh sáng mặt trời nhất?
c) Vào ngày nào trong năm thì thành phố A có khoảng 10 giờ ánh sáng mặt trời?
BÀI 3. Chiều cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển
động được cho bởi công thức h(t) =30 +20 sin
π
25
t +
π
3
.
a) Cabin đạt độ cao tối đa là bao nhiêu?
b) Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên?
4
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chương II.
DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN
A. BÀI TẬP TRẮC NGHIỆM
1 Mức độ Nhận biết, Thông hiểu
Câu 1. Cho dãy số (u
n
) có u
n
=
2n −1
n +1
. Tính
u
8
.
A. u
8
=
5
3
. B. u
8
=
11
9
.
C. u
8
=
17
9
. D. u
8
=1.
Câu 2. Cho dãy số (u
n
) xác định bởi
®
u
1
=3
u
n+1
= u
n
+5
. Ba số hạng đầu tiên của dãy
số đó là
A. −3;6;9. B. 3;8;13.
C. 3;5;7. D. 3; −2; −7.
Câu 3. Dãy nào sau đây là cấp số cộng?
A. 1; 5; 9; 5; 1. B. 1; 3; 5; 7; 11.
C. 2; 5; 8; 11. D. 3; 7; 3; 7.
Câu 4. Cho cấp số cộng 1, 8, 15, 22, 29, . ... Công
sai của cấp số cộng này là
A. 9. B. 1. C. 8. D. 7.
Câu 5. Cho cấp số cộng
(
u
n
)
có số hạng đầu
u
1
= 3 và d = 2. Số hạng thứ 2 của cấp số cộng
đã cho là
A. 3. B. 6. C. 1. D. 5.
Câu 6. Cho cấp số cộng (u
n
) có số hạng đầu
u
1
= 4 và d = 2. Số hạng thứ 50 của cấp số cộng
đó là
A. u
50
=100. B. u
50
=102.
C. u
50
=104. D. u
50
=198.
Câu 7. Cho cấp số cộng (u
n
) có số hạng đầu
u
1
= 3 và d = −2. Tổng của 20 số hạng đầu của
cấp số cộng đó là
A. S
20
=−380. B. S
20
=−214.
C. S
20
=−640. D. S
20
=−320.
Câu 8. Dãy số nào sau đây không phải là cấp
số nhân?
A. 1,−1,1, −1, 1. B. 1,2,3, 4, 5.
C. 1,−2,4, −8, 16. D. 1, 2, 4,8, 16.
Câu 9. Cho cấp số nhân (u
n
), biết u
1
= −9, u
2
=
3. Công bội q là
A. q =
1
3
. B. q =−3.
C. q =3. D. q =−
1
3
.
Câu 10. Cho cấp số nhân (u
n
), biết u
1
= 3 và
công bội q =−2. Tìm u
3
.
A. u
3
=16. B. u
3
=14.
C. u
3
=12. D. u
3
=11.
Câu 11. Cho cấp số nhân (u
n
) với u
1
= 2 và
q =−3. Khi đó, số hạng u
6
bằng
A. −3 ·2
5
. B. 2 ·(−3)
5
.
C. −3 ·2
6
. D. 2 ·(−3)
6
.
Câu 12. Cho cấp số nhân (u
n
) có số hạng đầu
u
1
=3 và công bội q =2. Tổng S
10
= u
1
+u
2
+u
3
+
···+u
10
bằng
A.
1023
2
. B. 1023. C. 1536. D. 3069.
2 Mức độ Vận dụng
Câu 13. Một người muốn chia 1000 ·000 đồng
cho bốn người con, đứa lớn hơn đứa nhỏ kế tiếp
100 ·000 đồng. Hỏi đứa con lớn nhất được bao
nhiêu tiền.
A. 400 ·000 đồng. B. 200 ·000 đồng.
C. 100 ·000 đồng. D. 300 ·000 đồng.
Câu 14. Một du khách vào trường đua ngựa
xem đua ngựa và đặt cược chọn con thắng cuộc.
Nếu chọn đúng con thắng cuộc thì sẽ nhận được
số tiền gấp đôi số tiền đặt cuộc, còn nếu chọn sai
thì sẽ mất số tiền đặt cuộc. Người du khách đó
lần đầu tiên đặt 20000 đồng, mỗi lần sau tiền
đặt gấp đôi tiền đặt lần trước. Người đó thua
9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du
khách đó thắng hay thua bao nhiêu?
A. Thắng 20000 đồng.
B. Hoà vốn.
C. Thua 20000 đồng.
D. Thua 40 000 đồng.
Câu 15. Một gia đình cần khoan một cái giếng
để lấy nước. Họ thuê một đội khoan giếng nước
đến để khoang giếng. Biết giá của mét khoan
đầu tiên là 80 000 đồng, kể từ mét khoan thứ hai
giá của mỗi mét khoan tăng thêm 5000 đồng so
với giá của mét khoan trước đó. Biết cần phải
khoan sâu xuống 50 m mới có nước. Hỏi phải
trả bao nhiêu tiền để khoan cái giếng đó?
A. 4245000 đồng. B. 5250000 đồng.
C. 4000000 đồng. D. 10 125 000 đồng.
5
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 16. Chu kì bán rã của nguyên tố phóng
xạ Poloni 210 là 138 ngày (nghĩa là sau 138
ngày khối lượng của nguyên tố đó chỉ còn một
nửa). Tính (chính xác đến hàng phần trăm)
khối lượng còn lại của 20 gam Poloni 210 sau
7314 ngày (khoảng 20 năm).
A. 3,22 ·10
−15
. B. 3,52 ·10
−15
.
C. 2,52 ·10
−15
. D. 2,22 ·10
−15
.
Câu 17. Tế bào E.Coli trong điều kiện nuôi cấy
thích hợp cứ 20 phút lại nhân đôi một lần. Nếu
lúc đầu có 10
12
tế bào thì sau 3 giờ sẽ phân chia
thành bao nhiêu tế bào?
A. 256 ·10
12
tế bào. B. 1024 ·10
12
tế bào.
C. 512 ·10
13
tế bào. D. 512 ·10
12
tế bào.
Câu 18. Ông Trung có 100 triệu đồng gửi tiết
kiệm vào ngân hàng theo thể thức lãi kép kì
hạn 6 tháng với lãi suất 8% cho một kì hạn. Giả
sử lãi suất không thay đổi. Hỏi sau 3 năm số
tiền trong tài khoản tiết kiệm của ông Trung
gần nhất với số nào sau đây?
A. 126532000 đồng. B. 158687 000 đồng.
C. 125971000 đồng. D. 112486 000 đồng.
Câu 19. Ba số phân biệt có tổng là 217 có thể
coi là các số hạng liên tiếp của một cấp số nhân,
cũng có thể coi là số hạng thứ 2, thứ 9, thứ 44
của một cấp số cộng. Hỏi phải lấy bao nhiêu số
hạng đầu của cấp số cộng này để tổng của chúng
bằng 210?
A. 40. B. 30. C. 20. D. 10.
Câu 20. Một đa giác có n cạnh và có chu vi
bằng 158 cm. Biết số đo các cạnh của đa giác
lập thành một cấp số cộng và công sai d = 3 cm
và cạnh lớn nhất có độ dài là 44 cm. Đa giác có
số cạnh n bằng
A. n =6. B. n =7. C. n =5. D. n =4.
B. BÀI TẬP TỰ LUẬN
BÀI 1. Tìm công sai của cấp số cộng (u
n
), biết
u
1
=−21 và u
14
=18;a) u
5
=−15 và u
20
=60;b)
u
1
=2 và u
2
+u
3
=5;c) u
2
+u
4
=16 và u
3
+u
7
=−4.d)
BÀI 2. Xác định công bội của một cấp số nhân (u
n
), biết
u
1
=
1
2
và u
6
=16;a) u
1
=−
1
2
và u
7
=−32;b)
u
3
=9 và u
6
=243;c) u
2
=
1
4
và u
5
=16.d)
BÀI 3. Có bao nhiêu hàng ghế trong một góc khán đài của một sân vận động, biết rằng góc khán
đài đó có 2040 chỗ ngồi, hàng ghế đầu tiên có 10 chỗ ngồi và mỗi hàng ghế sau có thêm 4 chỗ ngồi so
với hàng ghế ngay trước nó?
BÀI 4. Nếu anh Nam nhận được lời mời làm việc cho một công ty nước ngoài với mức lương khởi
điểm là 35000 đô la mỗi năm và được tăng thêm 1400 đô la lương mỗi năm, thì sẽ mất bao nhiêu
năm làm việc để tổng lương mà anh Nam nhận được là 319200 đô la?
6
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chương III.
CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA
MẪU SỐ LIỆU GHÉP NHÓM
A. BÀI TẬP TRẮC NGHIỆM
1 Mức độ Nhận biết, Thông hiểu
Câu 21. Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT A, ta được kết quả
Chiều
cao (cm)
[150;152) [152;154) [154;156) [156;158) [158;160) [160; 162) [162; 168)
Số học
sinh
5 18 40 25 8 3 1
a) Mẫu số liệu trên có bao nhiêu nhóm
A. 5. B. 6. C. 7. D. 8.
b) Số học sinh có chiều cao trong khoảng [154;156) là
A. 40. B. 18. C. 5. D. 8.
Câu 22. Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số
liệu ghép nhóm sau
Thời gian ( phút) [0;20) [20;40) [40;60) [60;80) [80;100)
Số học sinh 5 9 12 10 6
a) Giá trị đại diện của nhóm [60; 80) là
A. 40. B. 70. C. 60. D. 30.
b) Nhóm [20; 40) có tần số là
A. 5. B. 9. C. 12. D. 10.
c) Nhóm chứa mốt của mẫu số liệu này là
A. [80;100). B. [20;40). C. [40;60). D. [60;80).
d) Nhóm chứa trung vị là
A. [0;20). B. [20;40). C. [40;60). D. [60;80).
e) Nhóm chứa tứ phân vị thứ nhất là
A. [0;20). B. [20;40). C. [40;60). D. [60;80).
7
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
2 Mức độ Vận dụng
Câu 23. Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một số học sinh thu được kết
quả sau
Thời gian ( phút) [0;4) [4;8) [8;12) [12;16) [16;20)
Số học sinh 2 4 7 4 3
Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là
A. 7. B. 11,3. C. 10,4. D. 12,5.
Câu 24. Cho mẫu số liệu ghép nhóm về chiều cao của 25 cây dừa giống như sau
Chiều cao ( cm) [0;10) [10;20) [20;30) [30;40) [40;50)
Số cây 4 6 7 5 3
a) Mốt của mẫu số liệu ghép nhóm này là
A. M
o
=
70
3
. B. M
o
=
50
3
. C. M
o
=
70
2
. D. M
o
=
80
3
.
b) Trung vị của mẫu số liệu ghép nhóm này là
A. M
e
=
175
7
. B. M
e
=
165
5
. C. M
e
=
165
7
. D. M
e
=
165
3
.
c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm này là
A. Q
1
=13,5. B. Q
1
=13,9. C. Q
1
=15,75. D. Q
1
=13,75.
Câu 25. Cho mẫu số liệu ghép nhóm về khối lượng (đơn vị: gram) của 30 củ khoai tây như sau
Khối lượng [70;80) [80;90) [90;100) [100;110) [110;120)
Tần số 3 6 12 6 3
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là
A. Q
3
=133. B. Q
3
=134. C. Q
3
=132. D. Q
3
=102,5.
B. BÀI TẬP TỰ LUẬN
BÀI 5. Người ta ghi lại tốc độ cua 40 xe đạp đi qua một vị trí trên đường. Mẫu số liệu dưới đây ghi
lại tốc độ của 40 xe đó (đơn vị: km/h)
10 10,4 11 16 12 13 15,8 12,7 16,8 19
17 15,1 14 12,3 17,2 10,5 13,2 18,1 19,6 17,4
11,8 13,6 12,7 15,9 14,2 12,6 11,6 10,4 14,1 15,1
12,3 15,2 11,9 16,3 18,4 17,1 14,2 12,1 13,7 13,2
a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có năm nhóm ứng với sáu nửa khoảng
[
10;12
)
,
[
12;14
)
,
[
14;16
)
,
[
16;18
)
,
[
18;20
)
.
b) Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.
BÀI 6. Một công ty bảo hiểm thống kê lại độ tuổi các khách hàng mua bảo hiểm xe ô tô ở bảng sau:
Độ tuổi [25;30) [30;35) [35; 40) [40; 45) [45; 50) [50; 55)
Số khách hàng 25 38 62 42 37 29
8
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.
BÀI 7. Các bạn học sinh một lớp thống kê số túi nhựa mà gia đình bạn đó sử dụng trong một tuần.
Kết quả được tổng hợp lại ở bảng sau:
Số tuổi [5;9] [10;14] [15;19] [20; 24] [25; 29]
Số gia đình 8 15 12 7 2
a) Hãy ước lượng số trung bình và mốt của mẫu số liệu trên.
b) Cô giáo dự định trao danh hiệu “Gia đình xanh” cho 25% gia đình các bạn sử dụng ít túi nhựa
nhất. Cô giáo nên trao danh hiệu cho các gia đình dùng không quá bao nhiêu túi nhựa?
BÀI 8. Bảng sau thống kê doanh số bán hàng của các nhân viên một trung tâm thương mại trong
một ngày.
Doanh số
(triệu đồng)
[20;30) [30;40) [40; 50) [50; 60) [60; 70)
Số nhân viên 4 8 12 7 5
a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên.
b) Trung tâm thương mại dự định sẽ thưởng cho 25% số nhân viên có doanh số bán hàng cao nhất.
Theo mẫu số liệu trên, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán
hàng ít nhất là bao nhiêu?
—HẾT—
9
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chương IV.
QUAN HỆ SONG SONG SONG TRONG KHÔNG
GIAN
A. BÀI TẬP TRẮC NGHIỆM
1 Mức độ Cơ bản
Câu 26. Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Bốn điểm phân biệt. B. Một điểm và một đường thẳng.
C. Ba điểm phân biệt. D. Hai đường thẳng cắt nhau.
Câu 27. Cho tứ diện ABCD như hình bên. Mệnh đề nào sau đây đúng?
A. AB và CD cắt nhau. B. BD và AC cắt nhau.
C. BD và AC chéo nhau. D. BC và AD song song.
A
C
B D
Câu 28. Hình chóp tứ giác có tất cả bao nhiêu mặt là tam giác?
A. 5. B. 3. C. 6. D. 4.
Câu 29. Trong các hình sau
(I)
A
B
C
D
(II)
A
B
C
D
(III)
A
B
C
D
(VI)
A
B
C
D
Hình nào có thể là hình biểu diễn của một hình tứ diện?
A. (I). B. (I), (II). C. (I), (II), (IV). D. (I), (II), (III), (IV).
Câu 30. Trong không gian, hai đường thẳng không có điểm chung thì
A. cắt nhau. B. chéo nhau hoặc song song.
C. chéo nhau. D. song song.
Câu 31. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai đường thẳng phân biệt không song song thì chéo nhau.
B. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
C. Hai đường thẳng không có điểm chung thì chéo nhau .
D. Hai đường thẳng chéo nhau thì không có điểm chung.
Câu 32. Trong không gian cho hai đường thẳng cắt nhau a và b. Nếu c là một đường thẳng song
song với a thì
A. c và b song song với nhau. B. c và b cắt nhau.
C. c và b chéo nhau. D. c và b không song song với nhau.
10
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 33. Cho hình chóp S.ABCD có điểm O là giao điểm của hai đường chéo. Giao điểm của đường
thẳng AC với mặt phẳng (SBD) là điểm nào?
A. Điểm B. B. Điểm A. C. Điểm O. D. Điểm S.
Câu 34. Cho hình chóp S.ABCD đáy là tứ giác lồi ABCD, giao tuyến của mặt (S AD) và (SBD) là
A. SB. B. SA. C. SD. D. SC.
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm
AD và BC. Giao tuyến của hai mặt phẳng (SMN) và (S AC) là
A. SF ( F là trung điểm CD). B. SO (O là tâm hình bình hành ABCD).
C. SG (G là trung điểm AB) . D. SD.
Câu 36. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và
BC. Trên đoạn BD lấy P sao cho BP =2PD. Khi đó giao điểm của đường
thẳng CD với mặt phẳng (MNP) là
A. giao điểm của NP và CD. B. giao điểm của MN và CD.
C. trung điểm của CD. D. giao điểm của MP và CD.
A
C
B D
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi
I, J,E,F lần lượt là trung điểm S A, SB , SC, SD. Trong các đường thẳng
sau, đường thẳng nào không song song với I J?
A. EF. B. DC. C. AB. D. AD.
S
A
B
C
D
Câu 38. Cho hai đường thẳng song song a, b và mặt phẳng (P). Mệnh đề nào dưới đây đúng?
A. Nếu a ∥ (P) thì b ∥ (P) . B. Nếu a cắt (P) thì b cắt (P).
C. Nếu a nằm trên (P) thì b ∥ (P). D. Nếu a nằm trên (P) thì b nằm trên (P).
Câu 39. Cho hai mặt phẳng (P) và điểm A nằm ngoài mặt phẳng (P). Khẳng định nào sau đây
đúng?
A. Qua A có vô số mặt phẳng song song với (P).
B. Qua A có đúng một mặt phẳng song song với (P).
C. Qua A không có mặt phẳng nào song song với (P).
D. Qua A có đúng hai mặt phẳng song song với (P).
Câu 40. Cho hình chóp S.AB CD có đáy ABCD là hình bình hành. Đường thẳng AD song song với
mặt phẳng nào trong các mặt phẳng dưới đây?
A. (SBC). B. (ABCD). C. (S AC). D. (S AB).
11
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 41. Cho hình chóp tứ giác S.ABCD. Gọi M, N lần lượt là trung
điểm của S A và SC. Khẳng định nào sau đây đúng?
A. MN ∥ (ABCD). B. M N ∥ (S AB).
C. MN ∥ (SBC). D. MN ∥ (SCD).
M
A
N
B
S
D
C
Câu 42. Nếu mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) lần lượt theo hai giao tuyến a
và b thì vị trí tương đối giữa hai đường thẳng a và b là
A. song song. B. chéo nhau. C. trùng nhau. D. cắt nhau.
Câu 43. Cho đường thẳng a nằm trong mặt phẳng (α) và đường thẳng b nằm trong mặt phẳng (β).
Biết (α) ∥ (β). Trong các khẳng định sau, khẳng định nào sai?
A. a ∥ (β).
B. b ∥ (α).
C. a ∥ b.
D. Nếu có một mặt phẳng (γ) chứa a và b thì a ∥ b.
Câu 44. Khẳng định nào sau đây là sai khi nói về hình lăng trụ?
A. Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.
B. Các mặt bên của hình lăng trụ là các hình bình hành.
C. Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.
D. Hai đáy của hình lăng trụ là hai đa giác đều.
Câu 45. Cho hình hộp ABCD.A
0
B
0
C
0
D
0
. Hình chiếu song song của A
trên mặt phẳng (CDD
0
C
0
) theo phương BC
0
là
A. D
0
. B. D.
C. B . D. C
0
.
A
0
D
0
A
B
C
B
0
C
0
D
Câu 46. Cho hình lăng trụ ABC.A
0
B
0
C
0
, gọi I, I
0
lần lượt là trung
điểm của AB, A
0
B
0
. Qua phép chiếu song song đường thẳng AI
0
,
hình chiếu của điểm I lên mặt phẳng chiếu (A
0
B
0
C
0
) là điểm nào
sau đây?
A. A
0
. B. I
0
.
C. B
0
. D. C
0
.
B
0
C
0
I
0
A
A
0
C
B
I
Câu 47. Cho hình lăng trụ ABC.A
1
B
1
C
1
. Trong các khẳng định sau, khẳng định nào sai?
A. (ABC) ∥ (A
1
B
1
C
1
). B. AA
1
∥ (BCC
1
).
C. AB ∥ (A
1
B
1
C
1
). D. A A
1
B
1
B là hình chữ nhật.
12
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành
tâm O. Gọi M, N lần lượt là trung điểm của SA, AD. Hỏi mặt phẳng
(MNO) song song với mặt phẳng nào sau đây?
A. (S AB). B. (SBC). C. (SCD). D. (S AD).
S
N
B
C
O
D
M
A
Câu 49. Cho hình hộp ABCD.A
0
B
0
C
0
D
0
. Mặt phẳng (AB
0
D
0
) song song
với mặt phẳng nào sau đây?
A. (BC A
0
). B. (BD A
0
). C. (A
0
C
0
C). D. (BDC
0
).
A
0
D
0
A
B
C
B
0
C
0
D
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng
(S AB) và (SCD) là đường thẳng song song với đường thẳng nào sau đây?
A. BD . B. SC. C. AC. D. AB.
Câu 51. Cho hình chóp S.ABCD có AC cắt BD tại M, AB cắt
CD tại N. Trong các đường thẳng sau đây, đường thẳng nào là
giao tuyến của (S AC) và (SBD) ?
A. SM. B. SN. C. SB. D. SC.
S
A
B
C
D
M
N
2 Mức độ Vận dụng
Câu 52. Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng d cắt các mặt
phẳng (P),(Q),(R) lần lượt tại A, B, C. Đường thẳng d
0
cắt các mặt phẳng (P),(Q) ,(R) lần lượt tại
A
0
, B
0
, C
0
. Biết rằng
AB
AC
=
2
3
, tỷ số
A
0
B
0
A
0
C
0
bằng
A.
1
3
. B.
2
3
. C.
3
2
. D.
1
2
.
Câu 53. Cho tứ diện ABCD. Gọi E và F lần lượt là tr ung điểm của
AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường
thẳng EG và mặt phẳng (ACD) là
A. điểm F.
B. giao điểm của đường thẳng EG và CD.
C. giao điểm của đường thẳng EG và AF.
D. giao điểm của đường thẳng EG và AC.
A
D
C
B
F
E
G
13
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 54. Cho hình chóp S.ABCD có đáy ABCD là hình bình
hành. Gọi M, N, K lần lượt là trung điểm các cạnh DC, BC, S A.
Giao tuyến của (MNK) với (S AB) là đường thẳng KT, với T
được xác định theo một trong bốn phương án được liệt kê dưới
đây. Khẳng định nào sau đây đúng.
A. T là giao điểm của MN với SB.
B. T là giao điểm của MN với AB.
C. T là giao điểm của K N với AB.
D. T là giao điểm của K N với SB.
S
A
B
C
N
M
D
K
Câu 55. Cho hình chóp S.ABCD có đáy là hình bình hành. Trên
cạnh SA lấy điểm M sao cho M A =2MS. Mặt phẳng (CDM) cắt
SB tại N. Tỉ số
SN
SB
bằng
A.
1
2
. B.
1
3
.
C.
2
3
. D.
3
4
.
S
A
B
C
D
M
B. BÀI TẬP TỰ LUẬN
BÀI 9. Cho tứ diện ABCD. Gọi E, F lần lượt là các điểm thuộc các cạnh AB, AC sao cho AE =
1
2
BE
và AF = 2CF. Gọi O là một điểm nằm trong tam giác BCD.
a) Xác định giao tuyến của hai mặt phẳng (OEF) và (ABD).
b) Xác định giao điểm (nếu có) của đường thẳng AD và mặt phẳng (OEF).
BÀI 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là các
trung điểm của đoạn thẳng SC, S A và AB.
a) Tìm giao tuyến hai mặt phẳng (S AC) và (SBD).
b) Tìm tọa độ giao điểm của đường thẳng AM và mp(SBD).
c) Chứng minh MN song song với mặt phẳng (ABCD).
d) Chứng minh đường thẳng K N song song với mặt phẳng (SOD).
e) Chứng minh (KOM) song song với mặt phẳng (S AB).
f) Chứng minh K M song song với mặt phẳng (S AB).
BÀI 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao
cho AD =3AM. Gọi G, N lần lượt là trọng tâm của các tam giác S AB, ABC. Chứng minh
Đường thẳng MN song song với mặt phẳng (SCD).a)
Đường thẳng GN song song với mặt phẳng (S AC).b)
Đường thẳng GM song song với mặt phẳng (SCD).c)
BÀI 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi hai điểm M, N lần lượt
trên các cạnh SB, SC sao cho
SN
SC
=
1
2
và
SM
SB
=
2
3
.
14
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
a) Chứng minh rằng BC song song mặt phẳng (S AD).
b) Xác định giao tuyến ∆ của hai mặt phẳng (AMN) và (ABCD).
c) Chứng minh rằng BD song song mặt phẳng (AMN).
d) Gọi P là giao điểm của SD và (AMN). Tính tỷ số
SP
SD
.
e) Chứng minh rằng ba đường thẳng ∆, P N và CD đồng quy.
BÀI 13. Cho hình hộp ABCD A
0
B
0
C
0
D
0
. Gọi M, N, P lần lượt là trung điểm của AD, B
0
C
0
, DD
0
a) Chứng minh rằng ADC
0
B là hình bình hành.
b) Chứng minh rằng BD ∥
AB
0
D
0
, MN ∥
AB
0
D
0
.
c) Chứng minh rằng (MNP) ∥
AB
0
D
0
và BD ∥ (MNP).
d) Xác định giao tuyến của mặt phẳng (MNP) với các mặt của hình hộp.
e) Lấy một đường thẳng cắt ba mặt phẳng
AB
0
D
0
, (MNP),
C
0
BD
lần lượt tại I, J, H. Tính tỉ
số
I J
JH
.
BÀI 14. Cho hình lăng tr ụ tam giác ABC.A
0
B
0
C
0
. Gọi M, N, P lần lượt là trung điểm của các cạnh
A A
0
, AB, AC.
a) Chứng minh rằng BC ∥ (M N P).
b) Xác đinh giao tuyến d của hai mặt phẳng (MNP) và (A
0
B
0
C
0
).
c) Chứng minh rằng d ∥ NP.
—HẾT—
15
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chương V.
GIỚI HẠN. HÀM SỐ LIÊN TỤC
A. BÀI TẬP TRẮC NGHIỆM
1 Mức độ Nhận biết, Thông hiểu
Câu 56. Cho hai dãy số (u
n
) và (v
n
), biết
lim u
n
= a và lim v
n
= b. Trong các kết luận sau,
kết luận nào sai?
A. lim(u
n
+v
n
) = a +b.
B. lim(u
n
−v
n
) = a −b.
C. lim(u
n
v
n
) = ab.
D. lim
u
n
v
n
=
a
b
.
Câu 57. Cho các dãy số (u
n
), (v
n
) và lim u
n
= a,
lim v
n
=+∞ thì lim
u
n
v
n
bằng
A. +∞. B. 0. C. 1. D. −∞.
Câu 58. lim
n→+∞
3
n
bằng
A. +∞. B. 0. C. −∞. D. 2.
Câu 59. Tính lim
2020
n
.
A. +∞. B. −∞. C. 2020. D. 0.
Câu 60. Tính lim
2n −3
1 −3n
.
A. −
2
3
. B. 2. C.
1
3
. D. 1.
Câu 61. Cho dãy số
(
u
n
)
có lim u
n
=2. Tính giới
hạn lim
3u
n
−1
2u
n
+5
.
A. +∞. B.
3
2
. C.
−1
5
. D.
5
9
.
Câu 62. Biết lim
x→1
f (x) = 3 và lim
x→1
g(x) = −2. Tính
lim
x→1
[f (x) +2g(x)].
A. −1. B. 1. C. 5. D. −6.
Câu 63. Biết lim
x→1
f (x) = 4 và lim
x→1
g
(
x
)
= 1. Tính
lim
x→1
[
4f (x) +3g
(
x
)
]
.
A. 11. B. 19. C. 10. D. 9.
Câu 64. Cho lim
x→2
f (x) = 3. T ìm khẳng định
sai.
A. lim
x→2
[f (x) +3] =6. B. lim
x→2
p
f (x) +1 = 2.
C. lim
x→2
[f (x) −2x] =−1. D. lim
x→2
f (x) −x
2
=1.
Câu 65. lim
x→2
3x
2
+7x +11
có kết quả là
A. 37. B. 38. C. 39. D. 40.
Câu 66. Giá trị của lim
x→−1
x
2
−3
x
3
+2
là
A. 1. B. −2. C. 2. D. −
3
2
.
Câu 67. Cho c là hằng số, k là số nguyên
dương. Khẳng định nào sau đây sai?
A. lim
x→x
0
x = x
0
. B. lim
x→x
0
c = c.
C. lim
x→+∞
c
x
k
=0. D. lim
x→+∞
c =+∞.
Câu 68. Cho lim
x→a
f (x) =−∞, kết quả của lim
x→a
(−3·
f (x)) bằng
A. −∞. B. 0. C. +∞. D. 3.
Câu 69. Tính tổng S =9+3+1+
1
3
+
1
9
+···+
1
3
n−3
+
···.
A. S =
27
2
. B. S =14.
C. S =16. D. S =15.
Câu 70. Tổng của một cấp số nhân lùi vô hạn
bằng 2, tổng của ba số hạng đầu tiên của cấp số
nhân bằng
9
4
. Số hạng đầu u
1
của cấp số nhân
đó là
A. u
1
=3. B. u
1
=4.
C. u
1
=
9
2
. D. u
1
=5.
Câu 71. Cho hàm số y = f (x) có đồ thị như hình
vẽ bên dưới.
x
y
O
1
2
3
3
1
Tính lim
x→1
+
f (x) + lim
x→3
−
f (x).
A. 5. B. 4 . C. 2. D. 0.
Câu 72. Cho hàm số y = f (x) có đồ thị như hình
vẽ bên dưới.
x
y
O
1
2
3
3
1
Tính lim
x→0
f (x) + lim
x→1
−
f (x).
A. 5. B. 4 . C. 2. D. 0.
16
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 73. Tính lim
x→1
+
x
3
−2x +1
.
A. 1. B. 0. C. +∞. D. −∞.
Câu 74. Tính lim
x→3
−
p
x −3 −3x +x
2
.
A. Không tồn tại. B. −∞.
C. 0. D. +∞.
Câu 75. Trong các giới hạn sau đây, giới hạn
nào bằng 0?
A. lim
3 +2n
3
2n
2
−1
. B. lim
2n
2
−3
−2n
3
−4
.
C. lim
2n −3n
3
−2n
2
−1
. D. lim
2n
2
−3n
4
−2n
4
+n
2
.
Câu 76. Dãy số nào sau đây có giới hạn là
+∞?
A. u
n
=
1 +n
2
5n +5
. B. u
n
=
n
2
−2
5n +5n
3
.
C. u
n
=
n
2
−2n
5n +5n
2
. D.
1 +2n
5n +5n
2
.
Câu 77. Dãy số nào sau đây có giới hạn là
−∞?
A.
1 +2n
5n +5n
2
. B. u
n
=
n
3
+2n −1
−n +2n
3
.
C. u
n
=
2n
2
−3n
4
n
2
+2n
3
. D. u
n
=
n
2
−2n
5n +1
.
Câu 78. Giá trị lim
Ä
n −
p
n
2
−4n
ä
bằng
A. 3. B. 1. C. 2. D. 4.
Câu 79. Tính lim
x→1
x
2
−3x +2
x −1
.
A. 1. B. −∞. C. −1. D. +∞.
Câu 80. Tìm lim
x→−∞
(4x
4
−3x
2
+2).
A. +∞. B. −∞. C. 4. D. 2.
2 Mức độ Vận dụng
Câu 81. Cho dãy số
(
u
n
)
với u
n
=
an +4
5n +3
, với a
là tham số thực. Để dãy số
(
u
n
)
có giới hạn bằng
2 thì giá trị của a là
A. a =10. B. a =8.
C. a =6. D. a =4 .
Câu 82. Cho số thực a thỏa mãn
lim
x→+∞
a
p
2x
2
+3 +2017
2x +2018
=
1
2
. Khi đó giá trị của
a là
A. a =
−
p
2
2
. B. a =
1
2
.
C. a =
−1
2
. D. a =
p
2
2
.
Câu 83. Cho hàm số f (x) =
x
2
+1
1 −x
với x < 1
p
2x −2 với x > 1
.
Khi đó lim
x→1
−
f (x) là
A. +∞. B. −1. C. 0. D. 1.
Câu 84. Cho lim
x→−∞
p
x
2
+6 −x
p
3
x
p
2 −
p
x
2
+3
= a
p
2 + b
p
3 +
c
p
6 +d,
(
a, b, c, d ∈Q
)
. Tính ab +cd.
A. 1. B. 0. C. −2. D. 2.
Câu 85. Tìm tất cả các giá trị thực của tham
số m để hàm số f (x) =
x
2
+x −12
x +4
khi x 6=−4
mx +1 khi x =−4
liên tục tại điểm x
0
=−4.
A. m =4. B. m =2. C. m =3. D. m =5.
B. BÀI TẬP TỰ LUẬN
BÀI 15. Tính các giới hạn sau
lim
n→+∞
n
2
+1
2n
2
+n +2
.a) lim
n→+∞
2
n
+3
1 +3
n
.b)
lim
Ä
p
n
2
+2n −n
ä
.c) lim
2n
3
+2n −1
.d)
BÀI 16. Tính các giới hạn sau:
lim
x→3
x
2
+2x −15
x −3
.a) lim
x→2
2x
2
−5x +2
x
2
−4
.b)
lim
x→0
p
1 +2x −1
2x
.c) lim
x→1
+
x −2
x −1
.d)
lim
x→+∞
Ä
p
x
2
+x −x
ä
.e) lim
x→+∞
−x
3
−x
2
+4x +2
.f)
BÀI 17. Xét tính liên tục của mỗi hàm số sau tại điểm x =2.
a) f (x) =
®
6 −2x khi x ≥2
2x
2
−6 khi x < 2;
b) f (x) =
x
2
−4
x −2
khi x 6=2
0 khi x =2.
17
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
BÀI 18. Chứng minh rằng phương trình
a) x
3
+2x −1 =0 có nghiệm thuộc khoảng (−1; 1).
b)
p
x
2
+x +x
2
=1 có nghiệm thuộc khoảng (0;1).
BÀI 19. Trong hồ có chứa 6000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít
vào hồ với tốc độ 15 lít/phút.
a) Chứng tỏ rằng nồng độ muối của nước trong hồ sau t phút kể từ khi bắt đầu bơm là
C(t) =
30t
400 +t
(gam/lít).
b) Nồng độ muối trong hồ như thế nào nếu t →+∞.
BÀI 20. Từ độ cao 100 m, người ta thả một quả bóng cao su xuống đất. Giả sử cứ sau mỗi lần chạm
đất, quả bóng nảy lên một độ cao bằng
1
4
độ cao mà quả bóng đạt được trước đó. Gọi h
n
là độ cao quả
bóng đạt được ở lần nảy thứ n.
a) Tìm số hạng tổng quát của dãy số
(
h
n
)
.
b) Tính giới hạn của dãy số
(
h
n
)
và nêu ý nghĩa giới hạn của dãy số
(
h
n
)
.
c) Gọi S
n
là tổng độ dài quãng đường đi được của quả bóng từ lúc bắt đầu thả quả bóng đến khi
quả bóng chạm đất lần thứ n. Tính S
n
, nếu quá trình này cứ tiếp tục diễn ra mãi thì tổng
quãng đường quả bóng di chuyển được là bao nhiêu?
—HẾT—
18
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
MỤC LỤC
ChươngI. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 3
AA BÀI TẬP TRẮC NGHIỆM.. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. 3
} Mức độ Nhận biết, Thông hiểu.. . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 3
} Mức độ Vận dụng.. . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . 4
BB BÀI TẬP TỰ LUẬN. . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .5
ChươngII. DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN 8
AA BÀI TẬP TRẮC NGHIỆM.. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. 8
} Mức độ Nhận biết, Thông hiểu.. . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 8
} Mức độ Vận dụng.. . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . 9
BB BÀI TẬP TỰ LUẬN.. . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 10
ChươngIII. CÁCSỐĐẶCTRƯNGĐOXUTHẾTRUNGTÂMCỦAMẪUSỐLIỆUGHÉP
NHÓM 13
AA BÀI TẬP TRẮC NGHIỆM.. . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . .13
} Mức độ Nhận biết, Thông hiểu.. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . .13
} Mức độ Vận dụng.. . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . 14
BB BÀI TẬP TỰ LUẬN.. . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 15
ChươngIV. QUAN HỆ SONG SONG SONG TRONG KHÔNG GIAN 19
AA BÀI TẬP TRẮC NGHIỆM.. . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . .19
} Mức độ Cơ bản.. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . ..19
} Mức độ Vận dụng.. . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . 26
BB BÀI TẬP TỰ LUẬN.. . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 28
ChươngV. GIỚI HẠN. HÀM SỐ LIÊN TỤC 32
AA BÀI TẬP TRẮC NGHIỆM.. . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . .32
} Mức độ Nhận biết, Thông hiểu.. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . .32
} Mức độ Vận dụng.. . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . 34
BB BÀI TẬP TỰ LUẬN.. . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . 35
ĐÁP ÁN CÁC TRẮC NGHIỆM 38
} Trắc nghiệm chương I. . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . 38
} Trắc nghiệm chương II.. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . .38
} Trắc nghiệm chương III. . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . . . ... . . . . 38
} Trắc nghiệm chương IV. . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . 38
} Trắc nghiệm chương V. .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . . . . . .. . . . 38
1
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chương I.
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH
LƯỢNG GIÁC
A. BÀI TẬP TRẮC NGHIỆM
1 Mức độ Nhận biết, Thông hiểu
Câu 1. Góc có số đo
π
12
đổi sang độ là
A 15
◦
. B. 16
◦
.
C. 14
◦
. D. 17
◦
30
0
.
Ê Lời giải.
Ta có: α =
π
12
rađian, suy ra α =
π
12
·
180
π
◦
=
15
◦
.
Chọn đáp án A
Câu 2. Góc có số đo 108
◦
đổi sang radian là
A.
3π
2
. B.
5π
2
. C.
5π
3
. D
3π
5
.
Ê Lời giải.
Ta có: 108
◦
·
π
180
◦
=
3π
5
.
Chọn đáp án D
Câu 3. Giá trị cot
89π
6
bằng
A.
p
3
3
. B −
p
3. C. −
p
3
3
. D.
p
3.
Ê Lời giải.
Ta có cot
89π
6
=cot
14π +
5π
6
=cot
5π
6
=−
p
3.
Chọn đáp án B
Câu 4. Xác định số đo của góc lượng giác
(Ou, Ov) được biểu diễn trong hình bên dưới.
O
u
v
150
◦
A. 410
◦
. B 510
◦
. C. 150
◦
. D. 420
◦
.
Câu 5. Xác định số đo của góc lượng giác
(Ou, Ov) được biểu diễn trong hình bên dưới
O
u
v
60
◦
A −300
◦
. B. 510
◦
.
C. 60
◦
. D. −420
◦
.
Câu 6. Chọn khẳng định đúng trong các khẳng
định sau:
A. tan(π −α) =tanα. B. cot(π −α) =cot α.
C cos(π −α) =−cos α. D. sin(π −α) =−sin α.
Ê Lời giải.
Theo công thức về cung liên kết, ta có cos(π−α) =
−cosα.
Chọn đáp án C
Câu 7. Cho sin α =
1
3
, với 90
◦
< α < 180
◦
. Tính
cosα.
A. cosα =−
2
3
. B cos α =−
2
p
2
3
.
C. cosα =
2
p
2
3
. D. cos α =
2
3
.
Ê Lời giải.
Ta có sinα =
1
3
⇒cos
2
α =1 −
1
9
=
8
9
.
Vì 90
◦
< α < 180
◦
nên cos α < 0 do đó cos α =−
2
p
2
3
.
Chọn đáp án B
Câu 8. Trong các mệnh đề sau, mệnh đề nào là
mệnh đề đúng?
A. sin2a =sin a +cosa .
B. sin2a =2sin a.
C. sin 2a =cos
2
a −sin
2
a.
D sin2a =2sin acos a.
Ê Lời giải.
Hiển nhiên, sin 2a =2sin acos a là đúng.
Chọn đáp án D
Câu 9. Trong các mệnh đề sau, mệnh đề nào là
mệnh đề sai?
A. sina +sin b =2sin
a +b
2
cos
a −b
2
.
B cos a −cos b =2sin
a +b
2
sin
a −b
2
.
C. cos a +cos b =2 cos
a +b
2
cos
a −b
2
.
D. sin a −sin b =2 cos
a +b
2
sin
a −b
2
.
Ê Lời giải.
Công thức đúng là cos a−cos b =−2sin
a +b
2
sin
a −b
2
.
3
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chọn đáp án B
Câu 10. Chu kỳ của hàm số y = cot x là
A. kπ, k ∈Z. B. 2π.
C π. D.
π
2
.
Ê Lời giải.
Tập xác định của hàm số: D =R\
{
kπ, k ∈Z
}
.
Với mọi x ∈D , k ∈Z ta có x−kπ ∈D và x+kπ ∈D ,
cot(x +kπ) =cot x.
Vậy y =cot x là hàm số tuần hoàn với chu kì π là
số dương nhỏ nhất thỏa cot(x +kπ) =cot x.
Chọn đáp án C
Câu 11. Chu kỳ của hàm số y = cos x là
A.
2π
3
. B 2π. C. π. D. k2π.
Ê Lời giải.
Tập xác định của hàm số: D = R.
Với mọi x ∈ D, k ∈ Z ta có x −k2π ∈ D và x +k2π ∈
D, cos(x +k2π) =cos x.
Vậy y = cos xlà hàm số tuần hoàn với chu kì
2π(ứng với k = 1) là số dương nhỏ nhất thỏa
cos(x +k2π) =cos x.
Chọn đáp án B
Câu 12. Tập giá trị của hàm số y = cos x là tập
hợp nào sau đây?
A. [0;+∞]. B. R.
C. (−∞;0]. D [−1; 1].
Ê Lời giải.
Với mọi x ∈R thì −1 ≤cos x ≤1.
Chọn đáp án D
Câu 13. Giá trị nhỏ nhất m và giá trị lớn nhất
M của hàm số y =3 sin2x −5 lần lượt là
A. m =2, M = 8. B m =−8, M =−2.
C. m =−5, M =−2. D. m =−8, M =−5.
Ê Lời giải.
Ta có: −1 ≤sin 2x ≤1 ⇔−3 ≤3 sin 2x ≤3.
⇔−3−5 ≤3 sin2x−5 ≤3−5 ⇔−8 ≤ y =3sin 2x−5 ≤−2.
Vậy giá trị nhỏ nhất và giá trị lớn nhất của hàm
số đã cho lần lượt là −8 và −2.
Chọn đáp án
B
Câu 14. Phương trình cos x = a có nghiệm khi
và chỉ khi
A |a|≤1. B. |a|> 1.
C. |a|< 1. D. |a| ≥1.
Ê Lời giải.
Vì |cos x|≤1, ∀x ∈R nên phương trình cos x = a có
nghiệm khi và chỉ khi |a|≤1.
Chọn đáp án A
Câu 15. Giải phương trình sin x =
p
3
2
.
A. x =±
π
3
+k2π. B. x =
π
3
+kπ.
C.
x =
π
6
+kπ
x =
5π
6
+kπ
. D
x =
π
3
+k2π
x =
2π
3
+k2π
.
Ê Lời giải.
Ta có sin x =
p
3
2
⇔ sin x = sin
π
3
⇔
x =
π
3
+k2π
x =
2π
3
+k2π
(k ∈Z).
Chọn đáp án D
Câu 16. Phương trình cos 3x =cos
π
15
có nghiệm
là
A. x =±
π
15
+k2π. B x =±
π
45
+
k2π
3
.
C. x =−
π
45
+
k2π
3
. D. x =
π
45
+
k2π
3
.
Ê Lời giải.
Ta có
cos3x =cos
π
15
⇔3x =±
π
15
+k2π ⇔ x = ±
π
45
+
k2π
3
(k ∈Z).
Chọn đáp án B
Câu 17. Giải phương trình tan x =
p
3 ta được
tập nghiệm là
A.
n
π
3
+k2π, k ∈Z
o
. B. ∅.
C
n
π
3
+kπ, k ∈Z
o
. D.
n
π
6
+kπ, k ∈Z
o
.
Ê Lời giải.
Ta có tan x =
p
3 ⇔ tan x = tan
π
3
⇔ x =
π
3
+ kπ,
(k ∈Z).
Chọn đáp án C
2 Mức độ Vận dụng
Câu 18. Cho hai dao động điều hòa cùng
phương có phương trình lần lượt là x
1
=
5cos(100πt +π)(cm) và x
2
= 5cos(100πt −π/2)(cm).
Phương trình dao động tổng hợp của hai dao
động trên là
A. x =5
p
2cos
100πt +
3π
4
(cm).
B x = 5
p
2cos
100πt −
3π
4
(cm).
C. x =10 cos
100πt −
3π
4
(cm).
D. x =10 cos
100πt +
3π
4
(cm).
Ê Lời giải.
4
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Ta có
x = x
1
+x
2
= 5 cos(100πt +π) +5cos(100πt −π/2)
= 5
[
cos(100πt +π) +cos(100πt −π/2)
]
= 5 ·2cos
100πt +
π
4
cos
3π
4
= −5
p
2cos
100πt +
π
4
= 5
p
2cos
100πt −
3π
4
.
Chọn đáp án B
Câu 19. Cho hình vuông
ABCD như hình vẽ. Tính
giá trị của tanα.
A.
4
13
. B.
6
13
.
C.
9
13
. D
7
17
.
α
5
7
A
B
C
D
E
Ê Lời giải.
Đặt
BAE = β,
suy ra tan β =
BE
AB
=
5
12
và α =
45
◦
−β. Ta có
tanα =tan
45
◦
−β
=
1 −tan β
1 +tan β
=
1 −
5
12
1 +
5
12
=
7
17
.
α
β
5
7
A
B
C
D
E
Chọn đáp án D
Câu 20. Nhiệt độ ngoài trời ở một thành phố
vào các thời điểm khác nhau trong ngày có thể
được mô phỏng bởi công thức
h(t) =29 +3sin
h
π
12
(t −9)
i
với h tính bằng độ C và t là thời gian trong ngày
tính bằng giờ. Nhiệt độ thấp nhất trong ngày
vào lúc mấy giờ?
A. 5 giờ . B. 0 giờ . C 3 giờ. D. 4 giờ.
Ê Lời giải.
Nhiệt độ thấp nhất trong ngày là 26
◦
, xảy ra khi
sin
h
π
12
(t −9)
i
=−1 ⇔
π
12
(t−9) =
−π
2
+k2π ⇔ t =3+24k, k ∈Z
Do t là thời gian trong ngày tính bằng giờ nên
0 ≤ t ≤24. Suy ra: t =3
Chọn đáp án C
B. BÀI TẬP TỰ LUẬN
BÀI 1. Giải các phương trình lượng giác sau:
sin x = −
p
2
2
;a) sin
3x +
π
6
=
p
3
2
;b)
cos2x =
p
3
2
;c) cos(2x −30
◦
) =−1;d)
tan3x =tan
π
7
;e) cot
2x −
π
5
=
p
3.f)
Ê Lời giải.
sin x =−
p
2
2
⇔sin x =sin
−
π
4
⇔
x =−
π
4
+k2π
x =π −
−
π
4
+k2π
⇔
x =−
π
4
+k2π
x =
5π
4
+k2π
, k ∈Z.
Vậy phương trình có các nghiệm là x =−
π
4
+k2π và x =
5π
4
+k2π với k ∈Z.
sin
3x +
π
6
=
p
3
2
⇔sin
3x +
π
6
=sin
π
3
⇔
3x +
π
6
=
π
3
+k2π
3x +
π
6
=π −
π
3
+k2π
x =
π
18
+k
2π
3
x =
π
6
+k
2π
3
, k ∈Z.
cos2x =
p
3
2
⇔cos2x =cos
π
6
⇔ x =±
π
6
+kπ, k ∈Z.
Vậy phương trình có nghiệm là x =±
π
6
+kπ, k ∈Z.
5
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
cos(2x −30
◦
) =−1 ⇔2x −30
◦
=180
◦
+k360
◦
⇔ x =105
◦
+k180
◦
, k ∈Z
tan3x =tan
π
7
⇔3x =
π
7
+kπ ⇔ x =
π
21
+k
π
3
, k ∈Z.
Vậy phương trình có nghiệm là x =
π
21
+k
π
3
, k ∈Z.
cot
2x −
π
5
=
p
3 ⇔cot
2x −
π
5
=cot
π
6
⇔2x −
π
5
=
π
6
+kπ ⇔ x =
11π
60
+k
π
2
, k ∈Z.
Vậy phương trình có nghiệm là x =
11π
60
+k
π
2
, k ∈Z.
BÀI 2. Số giờ có ánh nắng mặt trời của một thành phố A trong ngày thứ t (ở đây t là số ngày tính từ
ngày 1 tháng Giêng) của một năm không nhuận được mô hình hóa bởi hàm số
L(t) =12 +2,83sin
h
2π
365
(t −80)
i
với t ∈Z và 0 < t ≤365.
a) Vào ngày nào trong năm thì thành phố A có ít giờ ánh sáng mặt trời nhất?
b) Vào ngày nào trong năm thì thành phố A có nhiều giờ ánh sáng mặt trời nhất?
c) Vào ngày nào trong năm thì thành phố A có khoảng 10 giờ ánh sáng mặt trời?
Ê Lời giải.
a) Với mọi x ∈R, ta có
−1 ≤sin
h
2π
365
(t −80)
i
≤1 ⇔ −2,83 ≤2,83 sin
h
2π
365
(t −80)
i
≤2,83
⇔ 9,17 ≤12 +2,83sin
h
2π
365
(t −80)
i
≤14,83.
Ngày thành phố A có ít giờ ánh sáng mặt trời nhất ứng với
sin
h
2π
365
(t −80)
i
=−1 ⇔
2π
365
(t −80) =−
π
2
+k2π ⇔ t =−
45
4
+365k, (k ∈Z).
Vì 0 < t ≤365 nên k =1, suy ra t =−
45
4
+365 =353,75.
Như vậy, vào ngày thứ 353 của năm, tức là khoảng ngày 20 tháng 12 thì thành phố A sẽ có ít
giờ ánh sáng mặt trời nhất.
b) Ngày thành phố A có nhiều giờ ánh sáng mặt trời nhất ứng với
sin
h
2π
365
(t −80)
i
=1 ⇔
2π
365
(t −80) =
π
2
+k2π ⇔ t =171,25 +365k, (k ∈Z).
Vì 0 < t ≤365 nên k =0, suy ra t =171,25.
Như vậy, vào ngày thứ 171 của năm, tức là khoảng ngày 20 tháng 6 thì thành phố A sẽ có nhiều
giờ ánh sáng mặt trời nhất.
c) Ngày thành phố A có 10 giờ ánh sáng mặt trời nhất ứng với
12 +2,83 sin
h
2π
365
(t −80)
i
=10 ⇔ sin
h
2π
365
(t −80)
i
=−
200
283
⇔
2π
365
(t −80) ≈−0,78 +k2π
2π
365
(t −80) ≈3,93 +k2π
⇔
ñ
t ≈34,69 +365k
t ≈308,30 +365k
(k ∈Z).
Vì 0 < t ≤365 nên k =0, suy ra t ≈34,69 hoặc t ≈308,30.
Như vậy, vào ngày thứ 34 của năm, tức là khoảng ngày 3 tháng 2 và ngày thứ 308 của năm,
tức là ngày 4 tháng 11 thì thành phố A sẽ có 10 giờ ánh sáng mặt trời.
6
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
BÀI 3. Chiều cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển
động được cho bởi công thức h(t) =30 +20 sin
π
25
t +
π
3
.
a) Cabin đạt độ cao tối đa là bao nhiêu?
b) Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên?
Ê Lời giải.
a) Vì sin
π
25
t +
π
3
≤1,∀t nên h(t) =30 +20sin
π
25
t +
π
3
≤50 (m).
b) Để cabin đạt độ cao 40 m thì
h(t) =40 ⇔20 sin
π
25
t +
π
3
=10 ⇔sin
π
25
t +
π
3
=
1
2
⇔
π
25
t +
π
3
=
π
6
+k2π
π
25
t +
π
3
=
5π
6
+k2π
⇔
t =−
25
6
+50k
t =
25
2
+50k
, k ∈Z.
Dễ thấy, giá trị t > 0 nhỏ nhất thoả mãn là t =12, 5 (giây).
7
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chương II.
DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN
A. BÀI TẬP TRẮC NGHIỆM
1 Mức độ Nhận biết, Thông hiểu
Câu 1. Cho dãy số (u
n
) có u
n
=
2n −1
n +1
. Tính
u
8
.
A u
8
=
5
3
. B. u
8
=
11
9
.
C. u
8
=
17
9
. D. u
8
=1.
Ê Lời giải.
Ta có u
8
=
2 ·8 −1
8 +1
=
5
3
.
Chọn đáp án A
Câu 2. Cho dãy số (u
n
) xác định bởi
®
u
1
=3
u
n+1
= u
n
+5
. Ba số hạng đầu tiên của dãy
số đó là
A. −3;6;9. B 3;8; 13.
C. 3;5;7. D. 3; −2; −7.
Ê Lời giải.
Ta có u
1
=3, u
2
=3 +5 =8, u
3
=8 +5 =13.
Chọn đáp án B
Câu 3. Dãy nào sau đây là cấp số cộng?
A. 1; 5; 9; 5; 1. B. 1; 3; 5; 7; 11.
C 2; 5; 8; 11. D. 3; 7; 3; 7.
Ê Lời giải.
Dãy số là cấp số cộng là 2; 5; 8; 11.
Chọn đáp án C
Câu 4. Cho cấp số cộng 1, 8, 15, 22, 29, . ... Công
sai của cấp số cộng này là
A. 9. B. 1. C. 8. D 7.
Ê Lời giải.
Công sai d = u
2
−u
1
=8 −1 =7.
Chọn đáp án D
Câu 5. Cho cấp số cộng
(
u
n
)
có số hạng đầu
u
1
= 3 và d = 2. Số hạng thứ 2 của cấp số cộng
đã cho là
A. 3. B. 6. C. 1. D 5.
Ê Lời giải.
Ta có u
2
= u
1
+d =3 +2 =5.
Chọn đáp án D
Câu 6. Cho cấp số cộng (u
n
) có số hạng đầu
u
1
= 4 và d = 2. Số hạng thứ 50 của cấp số cộng
đó là
A. u
50
=100. B u
50
=102.
C. u
50
=104. D. u
50
=198.
Ê Lời giải.
Ta có u
50
= u
1
+49d =4 +49 ·2 =102.
Chọn đáp án B
Câu 7. Cho cấp số cộng (u
n
) có số hạng đầu
u
1
= 3 và d = −2. Tổng của 20 số hạng đầu của
cấp số cộng đó là
A. S
20
=−380. B. S
20
=−214.
C. S
20
=−640. D S
20
=−320.
Ê Lời giải.
Ta có u
20
= u
1
+19d =3 +19 ·(−2) =−35.
Vậy S
20
=
20
(
u
1
+u
20
)
2
=
20(3 −35)
2
=−320.
Chọn đáp án D
Câu 8. Dãy số nào sau đây không phải là cấp
số nhân?
A. 1,−1,1, −1, 1. B 1,2,3, 4, 5.
C. 1,−2,4, −8, 16. D. 1, 2, 4,8, 16.
Ê Lời giải.
Dãy 1,2, 4, 8,16 là CSN với công bội q =2.
Dãy 1,−1, 1, −1,1 là CSN với công bội q = −1.
Dãy 1,−2, 4, −8,16 là CSN với công bội q = −2.
Dãy 1,2, 3, 4,5 là CSC với công sai d =1.
Chọn đáp án B
Câu 9. Cho cấp số nhân (u
n
), biết u
1
= −9, u
2
=
3. Công bội q là
A. q =
1
3
. B. q =−3.
C. q =3. D q =−
1
3
.
Ê Lời giải.
Ta có q =
u
2
u
1
=
3
−9
=−
1
3
.
Chọn đáp án D
Câu 10. Cho cấp số nhân (u
n
), biết u
1
= 3 và
công bội q =−2. Tìm u
3
.
A. u
3
=16. B. u
3
=14.
C u
3
=12. D. u
3
=11.
Ê Lời giải.
Ta có u
3
= u
1
·q
2
=3 ·(−2)
2
=12.
Chọn đáp án C
Câu 11. Cho cấp số nhân (u
n
) với u
1
= 2 và
q =−3. Khi đó, số hạng u
6
bằng
A. −3 ·2
5
. B 2 ·(−3)
5
.
8
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
C. −3 ·2
6
. D. 2 ·(−3)
6
.
Ê Lời giải.
Ta có u
6
= u
1
·q
5
=2 ·
(
−3
)
5
.
Chọn đáp án B
Câu 12. Cho cấp số nhân (u
n
) có số hạng đầu
u
1
=3 và công bội q =2. Tổng S
10
= u
1
+u
2
+u
3
+
···+u
10
bằng
A.
1023
2
. B. 1023. C. 1536. D 3069.
Ê Lời giải.
S
10
= u
1
·
q
10
−1
q −1
=3(2
10
−1) =3069.
Chọn đáp án D
2 Mức độ Vận dụng
Câu 13. Một người muốn chia 1000 ·000 đồng
cho bốn người con, đứa lớn hơn đứa nhỏ kế tiếp
100 ·000 đồng. Hỏi đứa con lớn nhất được bao
nhiêu tiền.
A 400 ·000 đồng. B. 200 ·000 đồng.
C. 100 ·000 đồng. D. 300 ·000 đồng.
Ê Lời giải.
Số tiền của bốn người con theo thứ tự từ đứa
lớn nhất đến đứa nhỏ nhất lập thành cấp số
cộng với công sai d = −100 ·000 đồng. Tổng số
tiền 4 người con là 1000 ·000 đồng.
Gọi số tiền của đứa con lớn nhất là x, ta có
4
2
(2x +3 d) = 1000 ·000 ⇔ 2(2x −300 ·000) = 1000 ·
000 ⇔ x =400 ·000.
Vậy đứa con lớn nhất được 400 ·000 đồng.
Chọn đáp án A
Câu 14. Một du khách vào trường đua ngựa
xem đua ngựa và đặt cược chọn con thắng cuộc.
Nếu chọn đúng con thắng cuộc thì sẽ nhận được
số tiền gấp đôi số tiền đặt cuộc, còn nếu chọn sai
thì sẽ mất số tiền đặt cuộc. Người du khách đó
lần đầu tiên đặt 20000 đồng, mỗi lần sau tiền
đặt gấp đôi tiền đặt lần trước. Người đó thua
9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du
khách đó thắng hay thua bao nhiêu?
A Thắng 20000 đồng.
B. Hoà vốn.
C. Thua 20000 đồng.
D. Thua 40 000 đồng.
Ê Lời giải.
Du khách đó lần đầu đặt 20 000 đồng, mỗi lần
sau tiền đặt gấp đôi tiền đặt lần trước. Vậy số
tiền đặt cược của du khách ở các lần khác nhau
tạo thành một cấp số nhân với số hạng đầu tiên
là u
1
=20000 và công bội là q =2.
Người đó thua 9 lần liên tiếp nên số tiền người
đó đã bỏ ra và mất trong 9 lần đầu là
S
9
=20000 ·
1 −2
9
1 −2
=10220 000 (đồng).
Số tiền người đó bỏ ra ở lần thứ 10 là
u
10
=20000 ·2
10−1
=10240 000 (đồng).
Du khách thắng ở lần thứ 10. Người đó bỏ ra
và nhận lại gấp đôi nghĩa là người đó lãi được
10240000 (đồng).
Vậy thì người đó đã thắng 20000 đồng.
Chọn đáp án A
Câu 15. Một gia đình cần khoan một cái giếng
để lấy nước. Họ thuê một đội khoan giếng nước
đến để khoang giếng. Biết giá của mét khoan
đầu tiên là 80 000 đồng, kể từ mét khoan thứ hai
giá của mỗi mét khoan tăng thêm 5000 đồng so
với giá của mét khoan trước đó. Biết cần phải
khoan sâu xuống 50 m mới có nước. Hỏi phải
trả bao nhiêu tiền để khoan cái giếng đó?
A. 4245000 đồng. B. 5250000 đồng.
C. 4000000 đồng. D 10125 000 đồng.
Ê Lời giải.
Số tiền phải trả ở mỗi mét khoan tạo thành một
cấp số cộng có số hạng đầu u
1
= 80 000 và công
sai d =5000.
Như vậy, tổng số tiền khi khoan đến mét thứ n
được tính theo công thức
S
n
=
n
2
[
2u
1
+(n −1)d
]
.
Vậy tổng số tiền phải trả là
S
50
=25 ·
(
2 ·80 000 +49 ·5000
)
=10125 000.
Chọn đáp án D
Câu 16. Chu kì bán rã của nguyên tố phóng
xạ Poloni 210 là 138 ngày (nghĩa là sau 138
ngày khối lượng của nguyên tố đó chỉ còn một
nửa). Tính (chính xác đến hàng phần trăm)
khối lượng còn lại của 20 gam Poloni 210 sau
7314 ngày (khoảng 20 năm).
A. 3,22 ·10
−15
. B. 3,52 ·10
−15
.
C. 2,52 ·10
−15
. D 2,22 ·10
−15
.
Ê Lời giải.
Kí hiệu u
n
(gam) là khối lượng còn lại của 20
gam Poloni 210 sau n chu kì bán rã.
Ta có 7314 ngày gồm 53 chu kì bán rã. Suy ra
theo đề bài ta cần tính u
53
.
Từ giả thiết suy ra dãy
(
u
n
)
là một cấp số nhân
với số hạng đầu là u
1
=
20
2
= 10 và công bội
q =0,5.
Khi đó u
53
=10 ·
1
2
52
≈2,22 ·10
−15
.
Chọn đáp án D
9
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 17. Tế bào E.Coli trong điều kiện nuôi cấy
thích hợp cứ 20 phút lại nhân đôi một lần. Nếu
lúc đầu có 10
12
tế bào thì sau 3 giờ sẽ phân chia
thành bao nhiêu tế bào?
A. 256 ·10
12
tế bào. B. 1024 ·10
12
tế bào.
C. 512 ·10
13
tế bào. D 512 ·10
12
tế bào.
Ê Lời giải.
Lúc đầu có 10
22
tế bào và mỗi lần phân chia thì
một tế bào tách thành hai tế bào nên ta có cấp
số nhân với u
1
=10
22
và công bội q =2.
Do cứ 20 phút phân đôi một lần nên sau 3 giờ
sẽ có 9 lần phân chia tế bào. Ta có u
10
là số tế
bào nhận được sau 3 giờ.
Vậy số tế bào nhận được sau 3 giờ là u
10
= u
1
q
9
=
512 ·10
12
.
Chọn đáp án D
Câu 18. Ông Trung có 100 triệu đồng gửi tiết
kiệm vào ngân hàng theo thể thức lãi kép kì
hạn 6 tháng với lãi suất 8% cho một kì hạn. Giả
sử lãi suất không thay đổi. Hỏi sau 3 năm số
tiền trong tài khoản tiết kiệm của ông Trung
gần nhất với số nào sau đây?
A. 126532000 đồng. B 158687 000 đồng.
C. 125971000 đồng. D. 112486 000 đồng.
Ê Lời giải.
3 năm tương ứng với 6 kì lãi của ông Trung.
Vậy sau ba năm, số tiền trong tài khoản tiết
kiệm của ông Trung khoảng
S =100000000 ·
1 +
8
100
6
≈158687 432.
Số tiền trong tài khoản tiết kiệm của ông Trung
gần nhất với số 158687 000 đồng.
Chọn đáp án B
Câu 19. Ba số phân biệt có tổng là 217 có thể
coi là các số hạng liên tiếp của một cấp số nhân,
cũng có thể coi là số hạng thứ 2, thứ 9, thứ 44
của một cấp số cộng. Hỏi phải lấy bao nhiêu số
hạng đầu của cấp số cộng này để tổng của chúng
bằng 210?
A. 40. B. 30. C. 20. D 10.
Ê Lời giải.
Gọi số hạng thứ 2, thứ 9, thứ 44 của cấp số cộng
này là u
2
, u
9
, u
44
.
Ta có
○ u
2
= u
1
+d;
○ u
9
= u
1
+8d =
(
u
1
+d
)
+7d = u
2
+7d;
○ u
44
= u
1
+43d =
(
u
1
+d
)
+42d = u
2
+42d.
Vì ba số hạng này là các số hạng liên tiếp của
một cấp số nhân nên ta có u
2
·u
44
= u
2
9
.
Tổng của ba số hạng đó bằng 217 nên u
2
+u
9
+
u
44
=217.
Do đó ta có hệ phương trình
®
u
2
+u
9
+u
44
=217
u
2
·u
44
= u
2
9
⇔
®
u
2
+u
2
+7d +u
2
+42d =217
u
2
·
(
u
2
+42d
)
=
(
u
2
+7d
)
2
⇔
®
u
2
=7
d =4
(do d 6= 0).
Do đó u
1
= u
2
−d =3 và S
n
=
n
2
·
[
2u
1
+(n −1) ·d
]
=
n ·(2n +1).
Tổng của n số hạng đầu bằng 210 nên
210 = n ·(2n +1) ⇔ n =10.
Vậy phải lấy 10 số hạng đầu của cấp số cộng
này.
Chọn đáp án D
Câu 20. Một đa giác có n cạnh và có chu vi
bằng 158 cm. Biết số đo các cạnh của đa giác
lập thành một cấp số cộng và công sai d = 3 cm
và cạnh lớn nhất có độ dài là 44 cm. Đa giác có
số cạnh n bằng
A. n =6. B. n =7. C. n = 5. D n =4.
Ê Lời giải.
Gọi u
i
(1 6 i 6 n) là độ dài cạnh thứ i trong cấp
số cộng tạo bởi đồ dài các cạnh của đa giác.
Ta có u
n
= 44, d = 3 nên u
1
= u
n
−(n − 1)d =
44 −(n −1) ·3 =47 −3n.
Chu vi của đa giác là tổng các cạnh của đa giác
và bằng
n(u
1
+u
n
)
2
=158 ⇔ n(91−3n) =316 ⇔3n
2
−91n+316 = 0 ⇔
n =4
n =
79
3
(loại).
Vậy n =4 thỏa mãn yêu cầu bài toán.
Chọn đáp án D
B. BÀI TẬP TỰ LUẬN
BÀI 1. Tìm công sai của cấp số cộng (u
n
), biết
u
1
=−21 và u
14
=18;a) u
5
=−15 và u
20
=60;b)
u
1
=2 và u
2
+u
3
=5;c) u
2
+u
4
=16 và u
3
+u
7
=−4.d)
Ê Lời giải.
10
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Gọi d là công sai của cấp số cộng u
n
, ta có
u
n
= u
1
+(n −1) ·d ⇒ u
14
= u
1
+13d ⇔18 =−21 +13d ⇔ d = 3.
Vậy công sai của cấp số cộng là d =3.
Ta có :
®
u
5
= u
1
+4d
u
20
= u
1
+19d
⇔
®
u
1
+4d =−15
u
1
+19d =60
⇔
®
d =5
u
1
=−35.
Ta có u
2
+u
3
= u
1
+d +u
1
+2d =2u
1
+3d =4 +3d.
Theo đề bài ta có u
2
+u
3
=5 nên 4 +3d =5, do đó d =
1
3
.
Ta có
®
u
2
+u
4
=16
u
3
+u
7
=−4
⇔
®
2u
1
+4d =16
2u
1
+8d =−4
⇔
®
u
1
=18
d =−5.
BÀI 2. Xác định công bội của một cấp số nhân (u
n
), biết
u
1
=
1
2
và u
6
=16;a) u
1
=−
1
2
và u
7
=−32;b)
u
3
=9 và u
6
=243;c) u
2
=
1
4
và u
5
=16.d)
Ê Lời giải.
Ta có u
6
= u
1
·q
5
⇒ q
5
=
u
6
u
1
=
16
1
2
=32. Suy ra q =2.
Áp dụng công thức số hạng tổng quát cấp số nhân ta có u
n
= u
1
q
n−1
⇒ u
7
= u
1
.q
6
⇒ q
6
= 64 ⇒
ñ
q =2
q =−2
.
Gọi q là công bội của cấp số nhân đã cho, ta có:
®
u
3
= u
1
.q
2
u
6
= u
1
.q
5
⇒ q
3
=
u
6
u
3
=27 ⇒ q =3.
Ta có: u
2
= u
1
.q ⇔
1
4
= u
1
.q; u
5
= u
1
.q
4
⇔16 = u
1
.q
4
.
Suy ra: q
3
=64 ⇔ q =4.
BÀI 3. Có bao nhiêu hàng ghế trong một góc khán đài của một sân vận động, biết rằng góc khán
đài đó có 2040 chỗ ngồi, hàng ghế đầu tiên có 10 chỗ ngồi và mỗi hàng ghế sau có thêm 4 chỗ ngồi so
với hàng ghế ngay trước nó?
Ê Lời giải.
Số ghế ở mỗi hàng của góc khán đài lập thành một cấp số cộng với số hạng đầu u
1
=10 và công sai
d =4.
Áp dụng công thức tính tổng n số hạng đầu của cấp số cộng với S
n
=2040, u
1
=10, d = 4 để tìm n, ta
có
2040 = S
n
=
n
2
[2 ·10 +(n −1) ·4]
⇔ n(16 +4n) =4080
⇔ 4n
2
+16n −4080 =0
⇔
ñ
n =30
n =−34 (loại).
Suy ra n =30, tức là góc khán đài đó có 30 hàng ghế.
11
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
BÀI 4. Nếu anh Nam nhận được lời mời làm việc cho một công ty nước ngoài với mức lương khởi
điểm là 35000 đô la mỗi năm và được tăng thêm 1400 đô la lương mỗi năm, thì sẽ mất bao nhiêu
năm làm việc để tổng lương mà anh Nam nhận được là 319200 đô la?
Ê Lời giải.
Lương mỗi năm của anh Nam lập thành một cấp số cộng với số hạng đầu u
1
= 35000 và công sai
d =1400, ta có
319200 = S
n
=
n
2
[2 ·35000 +(n −1) ·1400]
⇔ n(68600 +1400n) =638400
⇔ 1400n
2
+68600n −638400 =0
⇔
ñ
n =8
n =−57 (loại).
Vậy sau 8 năm làm việc thì tổng lương mà anh Nam nhận được là 319200 đô la.
12
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chương III.
CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA
MẪU SỐ LIỆU GHÉP NHÓM
A. BÀI TẬP TRẮC NGHIỆM
1 Mức độ Nhận biết, Thông hiểu
Câu 21. Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT A, ta được kết quả
Chiều
cao (cm)
[150;152) [152;154) [154;156) [156;158) [158;160) [160; 162) [162; 168)
Số học
sinh
5 18 40 25 8 3 1
a) Mẫu số liệu trên có bao nhiêu nhóm
A. 5. B. 6. C 7. D. 8.
Ê Lời giải.
Chọn đáp án C
b) Số học sinh có chiều cao trong khoảng [154;156) là
A 40. B. 18. C. 5. D. 8.
Ê Lời giải.
Chọn đáp án A
Câu 22. Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số
liệu ghép nhóm sau
Thời gian ( phút) [0;20) [20; 40) [40; 60) [60; 80) [80; 100)
Số học sinh 5 9 12 10 6
a) Giá trị đại diện của nhóm [60; 80) là
A. 40. B 70. C. 60. D. 30.
Ê Lời giải.
Chọn đáp án B
b) Nhóm [20; 40) có tần số là
A. 5. B 9. C. 12. D. 10.
Ê Lời giải.
Chọn đáp án B
13
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
c) Nhóm chứa mốt của mẫu số liệu này là
A. [80;100). B. [20;40). C [40;60). D. [60;80).
Ê Lời giải.
Chọn đáp án C
d) Nhóm chứa trung vị là
A. [0;20). B. [20;40). C [40;60). D. [60;80).
Ê Lời giải.
Gọi x
1
, x
2
,.. . , x
42
là thời gian xem tivi của các học sinh được xếp theo thứ tự không giảm.
Khi đó trung vị là
x
21
+x
22
2
, do hai giá trị x
21
, x
22
thuộc nhóm [40; 60) nên nhóm này chứa trung
vị.
Chọn đáp án C
e) Nhóm chứa tứ phân vị thứ nhất là
A. [0;20). B [20;40). C. [40; 60). D. [60; 80).
Ê Lời giải.
Cỡ mẫu là n =44.
Tứ phân vị thứ nhất là x
11
. Giá trị này thuộc nhóm [20;40).
Chọn đáp án B
2 Mức độ Vận dụng
Câu 23. Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một số học sinh thu được kết
quả sau
Thời gian ( phút) [0;4) [4; 8) [8; 12) [12; 16) [16; 20)
Số học sinh 2 4 7 4 3
Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là
A. 7. B. 11,3. C 10,4. D. 12,5.
Ê Lời giải.
Ta có bảng chứa giá trị đại diện như sau:
Thời gian ( phút) 2 6 10 14 18
Số học sinh 2 4 7 4 3
Thời gian trung bình để hoàn thành bài tập là
x =
2 ·2 +4 ·6+7 ·10 +4 ·14 +3 ·18
20
=10,4.
Chọn đáp án C
Câu 24. Cho mẫu số liệu ghép nhóm về chiều cao của 25 cây dừa giống như sau
Chiều cao ( cm) [0;10) [10; 20) [20; 30) [30; 40) [40; 50)
Số cây 4 6 7 5 3
14
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
a) Mốt của mẫu số liệu ghép nhóm này là
A M
o
=
70
3
. B. M
o
=
50
3
. C. M
o
=
70
2
. D. M
o
=
80
3
.
Ê Lời giải.
Tần số lớn nhất là 7 nên nhóm chứa mốt là [20; 30).
Do đó M
o
=20 +
7 −6
(7 −6) +(7 −5)
·10 =
70
3
.
Chọn đáp án A
b) Trung vị của mẫu số liệu ghép nhóm này là
A. M
e
=
175
7
. B. M
e
=
165
5
. C M
e
=
165
7
. D. M
e
=
165
3
.
Ê Lời giải.
Cỡ mẫu là n =25.
Gọi x
1
, x
2
,.. . , x
25
là chiều cao của 25 cây dừa giống xếp theo thứ tự không giảm.
Khi đó trung vị là x
13
. Giá trị này thuộc nhóm [20;30).
Do đó M
e
=20 +
25
2
−(4 +6)
7
·(30 −20) =
165
7
.
Chọn đáp án C
c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm này là
A. Q
1
=13,5. B. Q
1
=13,9. C. Q
1
=15,75.
D Q
1
=13,75.
Ê Lời giải.
Tứ phân vị thứ nhất là
x
6
+x
7
2
, hai giá trị này thuộc nhóm [10; 20).
Do đó Q
1
=10 +
25
4
−4
6
·(20 −10) =13,75.
Chọn đáp án D
Câu 25. Cho mẫu số liệu ghép nhóm về khối lượng (đơn vị: gram) của 30 củ khoai tây như sau
Khối lượng [70; 80) [80; 90) [90; 100) [100; 110) [110; 120)
Tần số 3 6 12 6 3
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là
A. Q
3
=133. B. Q
3
=134. C. Q
3
=132. D Q
3
=102,5.
Ê Lời giải.
Cỡ mẫu n =30.
Tứ phân vị thứ ba là x
23
, giá trị này thuộc nhóm [100;110).
Do đó Q
3
=100 +
3 ·30
4
−(3 +6 +12)
6
·(110 −100) =102,5.
Chọn đáp án D
B. BÀI TẬP TỰ LUẬN
BÀI 5. Người ta ghi lại tốc độ cua 40 xe đạp đi qua một vị trí trên đường. Mẫu số liệu dưới đây ghi
lại tốc độ của 40 xe đó (đơn vị: km/h)
10 10,4 11 16 12 13 15,8 12,7 16,8 19
17 15,1 14 12,3 17,2 10,5 13,2 18,1 19,6 17,4
11,8 13,6 12,7 15,9 14,2 12,6 11,6 10,4 14,1 15,1
12,3 15,2 11,9 16,3 18,4 17,1 14,2 12,1 13,7 13,2
15
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có năm nhóm ứng với sáu nửa khoảng
[
10;12
)
,
[
12;14
)
,
[
14;16
)
,
[
16;18
)
,
[
18;20
)
.
b) Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.
Ê Lời giải.
a) Bảng tần số ghép nhóm bao gồm cả tần số tích lũy được cho như ở bảng sau
Nhóm Tần số Tần số tích lũy
[10;12) 8 8
[12;14) 12 20
[14;16) 9 29
[16;18) 7 36
[18;20) 4 40
n =40
b) Ta có
n
20
=2,
n
4
=10,
3n
4
=30. Vì 8 < 20 ≤20 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn
hơn hoặc bằng 20.
Suy ra trung vị là M
e
=12 +
20 −8
12
·2 =14.
Tứ phân vị thứ hai là Q
2
= M
2
=14.
Vì 8 < 10 < 20 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10. Suy ra tứ
phân vị thứ nhất là Q
1
=12 +
10 −8
12
·2 ≈12,3.
Vì 29 < 30 < 36 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30. Suy ra tứ
phân vị thứ ba là Q
3
=16 +
30 −29
7
·2 ≈16,3.
Trong các nhóm, nhóm 2 có tần số lớn nhất, suy ra mốt là M
O
=12 +
12 −8
2 ·12 −8 −9
·2 ≈13,1.
BÀI 6. Một công ty bảo hiểm thống kê lại độ tuổi các khách hàng mua bảo hiểm xe ô tô ở bảng sau:
Độ tuổi [25;30) [30;35) [35; 40) [40; 45) [45; 50) [50; 55)
Số khách hàng 25 38 62 42 37 29
Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.
Ê Lời giải.
Độ tuổi [25;30) [30;35) [35;40) [40; 45) [45; 50) [50; 55)
Độ tuổi đại diện 27,5 32,5 37,5 42,5 47,5 52,5
Số khách hàng 25 38 62 42 37 29
Cỡ mẫu n =233.
Số trung bình của mẫu số liệu ghêp nhớm trên là
x =
27,5 ·25 +32,5 ·38 +37,5 ·62 +42,5 ·42 +47,5 ·37 +52,5 ·29
233
≈39,97.
Nhóm chứa mốt của mẫu số liệu trên là nhóm [35;40). Do đó: u
m
=35; n
m
=62, n
m−1
=38; n
m+1
=42;
u
m+1
=40.
Vậy mốt của mẩu số liệu ghép nhóm là
M
0
=35 +
62 −38
(62 −38) +(62 −42)
·(40 −35) =
415
11
.
Gọ x
1
; x
2
; . . . ; x
233
là mẫu số liệu được xếp theo thứ tự không giảm.
Tứ phân vị thứ hai của dãy số liệu x
1
; x
2
; . . . ; x
233
là x
117
.
16
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Do x
117
thuộc nhóm [35; 40) nên Q
2
=35 +
233
2
−63
62
·(40 −35) =
4875
124
.
Tứ phân vị thứ nhất của dãy số liệu x
1
; x
2
; . . . ; x
233
là
1
2
(
x
58
+x
59
)
.
Do x
58
và x
59
thuộc nhóm [30; 35) nên Q
1
=30 +
1·233
4
−25
38
·(35 −30) =
275
8
.
Tứ phân vị thứ ba của dãy số liệu x
1
; x
2
; . . . ; x
233
là
1
2
(
x
175
+x
176
)
.
Do x
175
và x
176
thuộc nhóm [45; 50) nên Q
3
=45 +
3·233
4
−167
37
·(50 −45) =
6815
148
.
BÀI 7. Các bạn học sinh một lớp thống kê số túi nhựa mà gia đình bạn đó sử dụng trong một tuần.
Kết quả được tổng hợp lại ở bảng sau:
Số tuổi [5;9] [10;14] [15;19] [20; 24] [25; 29]
Số gia đình 8 15 12 7 2
a) Hãy ước lượng số trung bình và mốt của mẫu số liệu trên.
b) Cô giáo dự định trao danh hiệu “Gia đình xanh” cho 25% gia đình các bạn sử dụng ít túi nhựa
nhất. Cô giáo nên trao danh hiệu cho các gia đình dùng không quá bao nhiêu túi nhựa?
Ê Lời giải.
Do số tuổi là số nguyên nên ta hiệu chỉnh lại như sau:
Số tuổi [4,5;9,5) [9,5;14, 5) [14,5; 19,5) [19, 5;24,5) [24,5; 29,5)
Số tuổi đại diện 7 12 17 22 27
Số gia đình 8 15 12 7 2
Cỡ mẫu n =44.
a) Số trung bình của mẫu số liệu ghép nhóm là
x =
7 ·8 +12 ·15+17 ·12 +22 ·7 +27 ·2
44
≈14,73.
Nhóm chứa mốt của mẫu số liệu trên là nhóm [9,5;14, 5). Do đó: u
m
= 9,5; n
m
= 15, n
m−1
= 8 ;
n
m+1
=12 ; u
m+1
=14,5.
Vậy mốt của mẩu số liệu ghép nhóm là
M
0
=9,5 +
15 −8
(15 −8) +(15 −12)
·(14,5 −9,5) =13.
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là Q
1
=
21
2
=10,5.
Do đó, cô giáo nên trao danh hiệu cho gia đình các bạn dùng không quá 10 túi nhựa.
BÀI 8. Bảng sau thống kê doanh số bán hàng của các nhân viên một trung tâm thương mại trong
một ngày.
Doanh số
(triệu đồng)
[20;30) [30;40) [40; 50) [50; 60) [60; 70)
Số nhân viên 4 8 12 7 5
a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên.
b) Trung tâm thương mại dự định sẽ thưởng cho 25% số nhân viên có doanh số bán hàng cao nhất.
Theo mẫu số liệu trên, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán
hàng ít nhất là bao nhiêu?
Ê Lời giải.
17
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Doanh số
(triệu đồng)
[20;30) [30;40) [40; 50) [50; 60) [60; 70)
Doanh số đại diện 25 35 45 55 65
Số nhân viên 4 8 12 7 5
a) x =
815
18
; M
0
=
400
9
; M
e
=45.
b) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là Q
3
=
380
7
≈54,29.
Do đó, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán hàng một ngày ít
nhất là 54, 29 triệu đồng.
—HẾT—
18
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chương IV.
QUAN HỆ SONG SONG SONG TRONG KHÔNG
GIAN
A. BÀI TẬP TRẮC NGHIỆM
1 Mức độ Cơ bản
Câu 26. Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Bốn điểm phân biệt. B. Một điểm và một đường thẳng.
C. Ba điểm phân biệt. D Hai đường thẳng cắt nhau.
Ê Lời giải.
○ A sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì sẽ có vô số mặt phẳng chứa 3 điểm
thẳng hàng đã cho.
○ B sai. T rong trường hợp điểm thuộc đường thẳng đã cho, khi đó ta chỉ có 1 đường thẳng, có vô
số mặt phẳng đi qua đường thẳng đó.
○ D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì có vô số mặt phẳng đi qua 4 điểm
đó hoặc trong trường hợp 4 điểm mặt phẳng không đồng phẳng thì sẽ tạo không tạo được mặt
phẳng nào đi qua cả 4 điểm.
Chọn đáp án D
Câu 27. Cho tứ diện ABCD như hình bên. Mệnh đề nào sau đây đúng?
A. AB và CD cắt nhau. B. BD và AC cắt nhau.
C BD và AC chéo nhau. D. BC và AD song song.
A
C
B D
Ê Lời giải.
Theo định nghĩa của tứ diện ABCD thì mệnh đề đúng là BD và AC là hai đường thẳng chéo nhau.
Chọn đáp án C
Câu 28. Hình chóp tứ giác có tất cả bao nhiêu mặt là tam giác?
A. 5. B. 3. C. 6. D 4.
Ê Lời giải.
Hình chóp tứ giác có tất cả 4 mặt là tam giác.
Chọn đáp án D
Câu 29. Trong các hình sau
(I)
A
B
C
D
(II)
A
B
C
D
(III)
A
B
C
D
(VI)
A
B
C
D
19
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Hình nào có thể là hình biểu diễn của một hình tứ diện?
A. (I). B. (I), (II). C. (I), (II), (IV). D (I), (II), (III), (IV).
Ê Lời giải.
Chọn đáp án D
Câu 30. Trong không gian, hai đường thẳng không có điểm chung thì
A. cắt nhau. B chéo nhau hoặc song song.
C. chéo nhau. D. song song.
Ê Lời giải.
Chọn đáp án B
Câu 31. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai đường thẳng phân biệt không song song thì chéo nhau.
B. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
C. Hai đường thẳng không có điểm chung thì chéo nhau .
D Hai đường thẳng chéo nhau thì không có điểm chung.
Ê Lời giải.
Hai đường thẳng chéo nhau không có điểm chung.
Chọn đáp án D
Câu 32. Trong không gian cho hai đường thẳng cắt nhau a và b. Nếu c là một đường thẳng song
song với a thì
A. c và b song song với nhau. B. c và b cắt nhau.
C. c và b chéo nhau. D c và b không song song với nhau.
Ê Lời giải.
Chọn đáp án D
Câu 33. Cho hình chóp S.ABCD có điểm O là giao điểm của hai đường chéo. Giao điểm của đường
thẳng AC với mặt phẳng (SBD) là điểm nào?
A. Điểm B. B. Điểm A. C Điểm O. D. Điểm S.
Ê Lời giải.
Ta thấy A ∉(SB D) và AC ∩BD = O nên AC ∩(SBD) ={O}.
A
B
C
D
S
O
Chọn đáp án C
Câu 34. Cho hình chóp S.ABCD đáy là tứ giác lồi ABCD, giao tuyến của mặt (S AD) và (SBD) là
A. SB. B. S A. C SD. D. SC.
Ê Lời giải.
Ta có (S AD) ∩(SBD) =SD.
S
A
B
D
C
20
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chọn đáp án C
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm
AD và BC. Giao tuyến của hai mặt phẳng (SMN) và (S AC) là
A. SF ( F là trung điểm CD). B SO (O là tâm hình bình hành ABCD).
C. SG (G là trung điểm AB). D. SD.
Ê Lời giải.
Dễ thấy S ∈(S AC)∩( SMN).
Gọi O là tâm của hình bình hành.
Khi đó, O = AC ∩M N ⇒ O ∈(S AC) ∩(SM N).
Vậy (S AC) ∩(SMN) = SO.
S
A
B
M
N
C
D
O
Chọn đáp án B
Câu 36. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và
BC. Trên đoạn BD lấy P sao cho BP =2PD. Khi đó giao điểm của đường
thẳng CD với mặt phẳng (MNP) là
A giao điểm của NP và CD. B. giao điểm của MN và CD.
C. trung điểm của CD. D. giao điểm của MP và CD.
A
C
B D
Ê Lời giải.
Trong mặt phẳng (BCD) kéo dài NP cắt CD tại I.
Ta có
I ∈ CD
I ∈ NP
NP ⊂ (MNP)
⇒{I} =CD ∩(MNP).
A
P
C
D
B
N
M
I
Chọn đáp án A
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi
I, J,E,F lần lượt là trung điểm S A, SB , SC, SD. Trong các đường thẳng
sau, đường thẳng nào không song song với I J?
A. EF. B. DC. C. AB. D AD.
S
A
B
C
D
Ê Lời giải.
21
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Ta có I J ∥ AB (tính chất đường trung bình trong tam giác S AB) và
EF ∥ CD (tính chất đường trung bình trong tam giác SCD).
Mà CD ∥ AB (đáy là hình bình hành) ⇒CD ∥ AB ∥ EF ∥ I J.
A
B
C
D
I
J
S
E
F
Chọn đáp án D
Câu 38. Cho hai đường thẳng song song a, b và mặt phẳng (P). Mệnh đề nào dưới đây đúng?
A. Nếu a ∥ (P) thì b ∥ (P) . B Nếu a cắt (P) thì b cắt (P).
C. Nếu a nằm trên (P) thì b ∥ (P). D. Nếu a nằm trên (P) thì b nằm trên (P).
Ê Lời giải.
Chọn đáp án B
Câu 39. Cho hai mặt phẳng (P) và điểm A nằm ngoài mặt phẳng (P). Khẳng định nào sau đây
đúng?
A. Qua A có vô số mặt phẳng song song với (P).
B Qua A có đúng một mặt phẳng song song với (P).
C. Qua A không có mặt phẳng nào song song với (P).
D. Qua A có đúng hai mặt phẳng song song với (P).
Ê Lời giải.
Chọn đáp án B
Câu 40. Cho hình chóp S.AB CD có đáy ABCD là hình bình hành. Đường thẳng AD song song với
mặt phẳng nào trong các mặt phẳng dưới đây?
A (SBC). B. (ABCD). C. (S AC). D. (S AB).
Ê Lời giải.
Do AD ∥ BC, AD 6⊂(SBC) và BC ⊂(SBC) nên AD ∥ (SBC).
S
D
B
C
A
Chọn đáp án A
Câu 41. Cho hình chóp tứ giác S.ABCD. Gọi M, N lần lượt là trung
điểm của S A và SC. Khẳng định nào sau đây đúng?
A M N ∥ (ABCD). B. MN ∥ (S AB).
C. MN ∥ (SBC). D. MN ∥ (SCD).
M
A
N
B
S
D
C
Ê Lời giải.
22
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Xét 4S AC có M, N lần lượt là trung điểm S A, SC
⇒ M N là đường trung bình của 4S AC
⇒ M N ∥ AC, mà AC ⊂(ABCD) ⇒ MN ∥ (ABCD).
M
A
N
B
S
D
C
Chọn đáp án A
Câu 42. Nếu mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) lần lượt theo hai giao tuyến a
và b thì vị trí tương đối giữa hai đường thẳng a và b là
A song song. B. chéo nhau. C. trùng nhau. D. cắt nhau.
Ê Lời giải.
Chọn đáp án A
Câu 43. Cho đường thẳng a nằm trong mặt phẳng (α) và đường thẳng b nằm trong mặt phẳng (β).
Biết (α) ∥ (β). Trong các khẳng định sau, khẳng định nào sai?
A. a ∥ (β).
B. b ∥ (α).
C a ∥ b.
D. Nếu có một mặt phẳng (γ) chứa a và b thì a ∥ b.
Ê Lời giải.
Chọn đáp án C
Câu 44. Khẳng định nào sau đây là sai khi nói về hình lăng trụ?
A. Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.
B. Các mặt bên của hình lăng trụ là các hình bình hành.
C. Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.
D Hai đáy của hình lăng tr ụ là hai đa giác đều.
Ê Lời giải.
Hai đáy của hình lăng trụ là hai đa giác bằng nhau.
Chọn đáp án D
Câu 45. Cho hình hộp ABCD.A
0
B
0
C
0
D
0
. Hình chiếu song song của A
trên mặt phẳng (CDD
0
C
0
) theo phương BC
0
là
A D
0
. B. D.
C. B . D C
0
.
A
0
D
0
A
B
C
B
0
C
0
D
Ê Lời giải.
Chọn đáp án D
23
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 46. Cho hình lăng trụ ABC.A
0
B
0
C
0
, gọi I, I
0
lần lượt là trung
điểm của AB, A
0
B
0
. Qua phép chiếu song song đường thẳng AI
0
,
hình chiếu của điểm I lên mặt phẳng chiếu (A
0
B
0
C
0
) là điểm nào
sau đây?
A. A
0
. B. I
0
.
C B
0
. D. C
0
.
B
0
C
0
I
0
A
A
0
C
B
I
Ê Lời giải.
Ta có
®
AI ∥ B
0
I
0
AI = B
0
I
0
⇒ AIB
0
I
0
là hình bình hành.
Suy ra qua phép chiếu song song đường thẳng A I
0
, mặt phẳng
chiếu (A
0
B
0
C
0
) biến điểm I thành điểm B
0
.
B
0
C
0
I
0
A
A
0
C
B
I
Chọn đáp án C
Câu 47. Cho hình lăng trụ ABC.A
1
B
1
C
1
. Trong các khẳng định sau, khẳng định nào sai?
A. (ABC) ∥ (A
1
B
1
C
1
). B. A A
1
∥ (BCC
1
).
C. AB ∥ (A
1
B
1
C
1
). D A A
1
B
1
B là hình chữ nhật.
Ê Lời giải.
Vì mặt bên A A
1
B
1
B là hình bình hành, còn nó là hình chữ nhật nếu ABC.A
1
B
1
C
1
là hình lăng trụ
đứng.
Chọn đáp án D
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành
tâm O. Gọi M, N lần lượt là trung điểm của SA, AD. Hỏi mặt phẳng
(MNO) song song với mặt phẳng nào sau đây?
A. (S AB). B. (SBC). C (SCD). D. (S AD).
S
N
B
C
O
D
M
A
Ê Lời giải.
Áp dụng tính chất đường trung bình, suy ra MN ∥ SD và ON ∥ CD.
Mà SD ∈(SCD) và CD ∈(SCD), do đó (MNO) ∥ (SCD).
Chọn đáp án C
24
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 49. Cho hình hộp ABCD.A
0
B
0
C
0
D
0
. Mặt phẳng (AB
0
D
0
) song song
với mặt phẳng nào sau đây?
A. (BC A
0
). B. (BD A
0
). C. (A
0
C
0
C). D (BDC
0
).
A
0
D
0
A
B
C
B
0
C
0
D
Ê Lời giải.
Mặt phẳng (AB
0
D
0
) song song với mặt phẳng (BDC
0
).
Thật vậy, ta có AB
0
∥ DC
0
và AD
0
∥ BC
0
, có điều cần chứng
minh.
D
C
D
0
C
0
B
B
0
A
A
0
Chọn đáp án D
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng
(S AB) và (SCD) là đường thẳng song song với đường thẳng nào sau đây?
A. BD . B. SC. C. AC. D AB.
Ê Lời giải.
Ta có mặt phẳng (S AB) và (SCD) có chứa hai cạnh AB và CD
song song nhau. Nên hai mặt phẳng (S AB) và (SCD) có giao
tuyến là đường thẳng qua S và song song với AB.
x
S
A
B
C
D
Chọn đáp án D
Câu 51. Cho hình chóp S.ABCD có AC cắt BD tại M, AB cắt
CD tại N. Trong các đường thẳng sau đây, đường thẳng nào là
giao tuyến của (S AC) và (SBD) ?
A SM. B. SN. C. SB. D. SC.
S
A
B
C
D
M
N
Ê Lời giải.
25
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Xét hai mặt phẳng (S AC) và (SBD) Ta có S là điểm chung thứ
nhất.
M là điểm chung thứ hai.
Nên giao tuyến của hai mặt phẳng (S AC) và (SBD) là SM.
S
A
B
C
D
M
N
Chọn đáp án A
2 Mức độ Vận dụng
Câu 52. Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng d cắt các mặt
phẳng (P),(Q),(R) lần lượt tại A, B, C. Đường thẳng d
0
cắt các mặt phẳng (P),(Q) ,(R) lần lượt tại
A
0
, B
0
, C
0
. Biết rằng
AB
AC
=
2
3
, tỷ số
A
0
B
0
A
0
C
0
bằng
A.
1
3
. B
2
3
. C.
3
2
. D.
1
2
.
Ê Lời giải.
Chọn đáp án B
Câu 53. Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của
AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường
thẳng EG và mặt phẳng (ACD) là
A. điểm F.
B. giao điểm của đường thẳng EG và CD.
C giao điểm của đường thẳng EG và AF.
D. giao điểm của đường thẳng EG và AC.
A
D
C
B
F
E
G
Ê Lời giải.
• Chọn mặt phẳng phụ (ABF) chứa EG. • Ta có (ABF) ∩
(ACD) = AF.
• Gọi M = EG ∩AF ⇒
®
M ∈ EG
M ∈ AF ⊂(ACD)
⇒ M = EG ∩(ACD).
Vậy giao điểm cần tìm giao điểm của đường thẳng EG và AF.
A
D
C
B
F
E
G
M
Chọn đáp án C
26
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 54. Cho hình chóp S.ABCD có đáy ABCD là hình bình
hành. Gọi M, N, K lần lượt là trung điểm các cạnh DC, BC, S A.
Giao tuyến của (MNK) với (S AB) là đường thẳng KT, với T
được xác định theo một trong bốn phương án được liệt kê dưới
đây. Khẳng định nào sau đây đúng.
A. T là giao điểm của MN với SB.
B T là giao điểm của MN với AB.
C. T là giao điểm của K N với AB.
D. T là giao điểm của K N với SB.
S
A
B
C
N
M
D
K
Ê Lời giải.
Ta có K là điểm chung thứ nhất của (S AB) và (K MN).
Ta sẽ tìm điểm chung thứ hai T.
Nhận thấy, trong mặt phẳng (S AB) và (K MN) có đường
thẳng AB và M N cùng nằm trong mặt phẳng (ABCD)
nên nếu T là giao điểm của AB và MN thì T là điểm
chung thứ hai của (S AB) và (K MN).
Suy ra, K T là giao tuyến của (S AB) và (K MN).
S
M
D
K
A
T
C
NB
Chọn đáp án B
Câu 55. Cho hình chóp S.ABCD có đáy là hình bình hành. Trên
cạnh SA lấy điểm M sao cho M A =2MS. Mặt phẳng (CDM) cắt
SB tại N. Tỉ số
SN
SB
bằng
A.
1
2
. B
1
3
.
C.
2
3
. D.
3
4
.
S
A
B
C
D
M
Ê Lời giải.
Xét hai mặt phẳng (MCD) và (S AB) có M là điểm chung, AB ∥
CD. Do đó giao tuyến của hai mặt phẳng (MCD) và (S AD) là
MN ∥ AB (với N thuộc SB).
Do đó
SN
SB
=
SM
S A
=
1
3
.
S
A
B
C
D
M
N
Chọn đáp án B
27
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
B. BÀI TẬP TỰ LUẬN
BÀI 9. Cho tứ diện ABCD. Gọi E, F lần lượt là các điểm thuộc các cạnh AB, AC sao cho AE =
1
2
BE
và AF = 2CF. Gọi O là một điểm nằm trong tam giác BCD.
a) Xác định giao tuyến của hai mặt phẳng (OEF) và (ABD).
b) Xác định giao điểm (nếu có) của đường thẳng AD và mặt phẳng (OEF).
Ê Lời giải.
a) Trong mặt phẳng (ABC), gọi G là giao điểm của EF và BC.
Trong mặt phẳng (BCD), gọi H là giao điểm của OG và BD.
Khi đó H là điểm chung của hai mặt phẳng (OEF) và (ABD),
suy ra EH là giao tuyến của hai mặt phẳng đó.
b) Trong mặt phẳng (ABD), gọi I là giao điểm (nếu có) của EH và
AD. Khi đó I là giao điểm của AD và mặt phẳng (OEF).
A
B
C
D
E
F
G
H
O
BÀI 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là các
trung điểm của đoạn thẳng SC, S A và AB.
a) Tìm giao tuyến hai mặt phẳng (S AC) và (SBD).
b) Tìm tọa độ giao điểm của đường thẳng AM và mp(SBD).
c) Chứng minh MN song song với mặt phẳng (ABCD).
d) Chứng minh đường thẳng K N song song với mặt phẳng (SOD).
e) Chứng minh (KOM) song song với mặt phẳng (S AB).
f) Chứng minh K M song song với mặt phẳng (S AB).
Ê Lời giải.
BÀI 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao
cho AD =3AM. Gọi G, N lần lượt là trọng tâm của các tam giác S AB, ABC. Chứng minh
Đường thẳng MN song song với mặt phẳng (SCD).a)
Đường thẳng GN song song với mặt phẳng (S AC).b)
Đường thẳng GM song song với mặt phẳng (SCD).c)
Ê Lời giải.
BÀI 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi hai điểm M, N lần lượt
trên các cạnh SB, SC sao cho
SN
SC
=
1
2
và
SM
SB
=
2
3
.
a) Chứng minh rằng BC song song mặt phẳng (S AD).
b) Xác định giao tuyến ∆ của hai mặt phẳng (AMN) và (ABCD).
28
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
c) Chứng minh rằng BD song song mặt phẳng (AMN).
d) Gọi P là giao điểm của SD và (AMN). Tính tỷ số
SP
SD
.
e) Chứng minh rằng ba đường thẳng ∆, P N và CD đồng quy.
Ê Lời giải.
S
B
C
M
N
I
O
P
A
D
K
H
a) Ta có BC ∥ AD,BC 6⊂(S AD) và AD ⊂(S AD) nên BC ∥ (S AD). ...... . . . . . . ...... . . . . . . . 1,0 điểm.
b) Ta có A ∈(AMN) ∩(ABCD). . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . . ......0,25 điểm.
Trong mp(SBC), gọi I là giao điểm MN và BC.
Ta có I ∈ (AMN) ∩(ABCD). . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . . ...... . 0,5 điểm.
Do đó AI là giao tuyến ∆ của (AMN) và (ABCD). ..... . . . . . . ...... . . . . . . ...... . . . . . . 0,25 điểm.
c) Tam giác SIC có IN là trung tuyến và
SM
SB
=
2
3
nên M là trọng tâm tam giác. . . . . . .. 0,5 điểm.
Do đó B là trung điểm IC, suy ra IBD A là hình bình hành, nên BD ∥ I A ⊂ (AM N). Vậy BD ∥
(AMN). . ...... . . . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . . ...... 0,5 điểm.
d) Trong mp(S AC), gọi K =SO ∩ AN. . . . ...... . . . . . . ...... . . . . . ...... . . . . . . ...... . . . . . . .. 0,5 điểm.
Trong mp(SBD), gọi P = SD ∩MK . Lúc đó P = SD ∩(AMN). . . . . . . . ...... . . . . . . ...... . 0,5 điểm.
Tam giác S AC có AN và SO là hai đường trung tuyến nên K là trọng tâm tam giác S AC. Suy
ra
SK
SO
=
2
3
. ..... . . . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . ...... . . . . . . ...... . . . . . . ...... 0,5 điểm.
Mà
SM
SB
=
2
3
nên K M song song BO. . ...... . . . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . . 0,25 điểm.
Do đó
SP
SD
=
2
3
. . . ...... . . . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . . ...... . . . . . ...... . . . . 0,25 điểm.
e) Trong mặt phẳng (SCD), vì
SP
SD
6=
SN
SC
nên P N và CD cắt nhau. . . . . . ...... . . . . . . .....0,5 điểm.
Gọi H = P N ∩CD.
Ta có (AMN) ∩(ABCD) = A I, (AMN) ∩(SCD) = P N và (SCD) ∩(ABCD) = CD nên AI đi qua H,
hay AI, PN, CD đồng quy tại H. ..... . . . . . . ...... . . . . . . ...... . . . . . ...... . . . . . . ...... . . 0,5 điểm.
BÀI 13. Cho hình hộp ABCD A
0
B
0
C
0
D
0
. Gọi M, N, P lần lượt là trung điểm của AD, B
0
C
0
, DD
0
29
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
a) Chứng minh rằng ADC
0
B là hình bình hành.
b) Chứng minh rằng BD ∥
AB
0
D
0
, MN ∥
AB
0
D
0
.
c) Chứng minh rằng (MNP) ∥
AB
0
D
0
và BD ∥ (MNP).
d) Xác định giao tuyến của mặt phẳng (MNP) với các mặt của hình hộp.
e) Lấy một đường thẳng cắt ba mặt phẳng
AB
0
D
0
, (MNP),
C
0
BD
lần lượt tại I, J, H. Tính tỉ
số
I J
JH
.
Ê Lời giải.
a)
Vì ABCD và BCC
0
B
0
là các hình bình hành nên AD ∥ BC,
AD = BC và BC ∥ B
0
C
0
, B C = B
0
C
0
. Suy ra AD ∥ B
0
C
0
, AD =
B
0
C
0
. Vậy ADC
0
B
0
là hình bình hành.
A
B
C
D
A
0
B
0
C
0
D
0
M
N
P
K
E
F
O
b) Vì BB
0
∥ DD
0
, BB
0
= DD
0
nên BDD
0
B
0
là hình bình hành. Do đó, BD ∥ B
0
D
0
. Suy ra BD ∥
AB
0
D
0
.
Ta có AMNB
0
’ là hình bình hành, suy ra MN ∥ AB
0
nên MN ∥
AB
0
D
0
.
c) Vì MP ∥ AD
0
nên MP ∥
AB
0
D
0
, cùng với kết quả câu b ta có (M NP) ∥
AB
0
D
0
. Vì BD ∥ B
0
D
0
nên
BD ∥
AB
0
D
0
, suy ra BD ∥ (MNP).
d) Gọi E, F, K lần lượt là trung điểm của C
0
D
0
, B
0
B, BA. Khi đó, PE ∥ MN, NF ∥ MP, K F ∥ MN
nên các điểm E, F, K đều thuộc mặt phẳng (MNP). Do đó giao tuyến của (MNP) với các mặt
ADD
0
A
0
,
DCC
0
D
0
,
A
0
B
0
C
0
D
0
,
BCC
0
B
0
,
ABB
0
A
0
và (ABCD) lần lượt là MP, PE, EN, NF,
FK, K M.
e)
Theo câu d, ta có (M NP) trùng với (MKF NEP).
Gọi R, O lần lượt là giao điểm của AC với MK,
BD. Khi đó, ta có
AR
RO
=1 và đường thẳng AC cắt
ba mặt phẳng
AB
0
D
0
, (M NP),
C
0
BD
lần lượt
tại A, R, O.
Áp dụng định lí Thalès trong không gian, ta có
AR
I J
=
RO
JH
=
AO
IH
.
Từ đó suy ra
I J
JH
=
AR
RO
=1.
A
R
O
B
C
D
A
0
B
0
C
0
D
0
M
N
P
K
E
F
I
H
J
d
BÀI 14. Cho hình lăng tr ụ tam giác ABC.A
0
B
0
C
0
. Gọi M, N, P lần lượt là trung điểm của các cạnh
A A
0
, AB, AC.
a) Chứng minh rằng BC ∥ (M N P).
b) Xác đinh giao tuyến d của hai mặt phẳng (MNP) và (A
0
B
0
C
0
).
30
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
c) Chứng minh rằng d ∥ NP.
Ê Lời giải.
A
B
C
A
0
B
0
C
0
M
N
P
E
F
a) Vì NP là đường trung bình của tam giác ABC nên BC ∥ NP, suy ra BC ∥ (MNP)
b) Trong mặt phẳng (ABB
0
A
0
) gọi E là giao điểm của MN và A
0
B
0
. Trong mặt phẳng (ACC
0
A
0
) gọi F
là giao điểm của MP và A
0
C
0
. Khi đó EF là giao tuyến của hai mặt phẳng (MNP) và (A
0
B
0
C
0
).
c) Vì NP ∥ BC và BC ∥ B
0
C
0
nên N P ∥ B
0
C
0
, suy ra NP ∥ (A
0
B
0
C
0
) Mặt phẳng (MNP) chứa đường
thẳng NP song song với mặt phẳng (A
0
B
0
C
0
) nên giao tuyến d của hai mặt phẳng đó song song
với B
0
C
0
, suy ra d ∥ NP.
—HẾT—
31
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Chương V.
GIỚI HẠN. HÀM SỐ LIÊN TỤC
A. BÀI TẬP TRẮC NGHIỆM
1 Mức độ Nhận biết, Thông hiểu
Câu 56. Cho hai dãy số (u
n
) và (v
n
), biết
lim u
n
= a và lim v
n
= b. Trong các kết luận sau,
kết luận nào sai?
A. lim(u
n
+v
n
) = a +b.
B. lim(u
n
−v
n
) = a −b.
C. lim(u
n
v
n
) = ab.
D lim
u
n
v
n
=
a
b
.
Câu 57. Cho các dãy số (u
n
), (v
n
) và lim u
n
= a,
lim v
n
=+∞ thì lim
u
n
v
n
bằng
A. +∞. B 0. C. 1. D. −∞.
Ê Lời giải.
Ta có lim u
n
=a, lim v
n
=+∞ thì lim
u
n
v
n
=0.
Chọn đáp án B
Câu 58. lim
n→+∞
3
n
bằng
A +∞. B. 0. C. −∞. D. 2.
Ê Lời giải.
Ta có lim
n→+∞
q
n
= +∞ nếu q > 1. Do đó, lim
n→+∞
3
n
=
+∞.
Chọn đáp án
A
Câu 59. Tính lim
2020
n
.
A. +∞. B. −∞. C. 2020. D 0.
Ê Lời giải.
Theo định nghĩa suy ra lim
x→+∞
2020
n
= 2020 ·
lim
x→+∞
1
n
=2020 ·0 =0.
Chọn đáp án D
Câu 60. Tính lim
2n −3
1 −3n
.
A −
2
3
. B. 2. C.
1
3
. D. 1.
Câu 61. Cho dãy số
(
u
n
)
có lim u
n
=2. Tính giới
hạn lim
3u
n
−1
2u
n
+5
.
A. +∞. B.
3
2
. C.
−1
5
. D
5
9
.
Ê Lời giải.
Ta có lim
3u
n
−1
2u
n
+5
=
3 ·2 −1
2 ·2 +5
=
5
9
.
Chọn đáp án D
Câu 62. Biết lim
x→1
f (x) = 3 và lim
x→1
g(x) = −2. Tính
lim
x→1
[f (x) +2g(x)].
A −1. B. 1. C. 5. D. −6.
Ê Lời giải.
Ta có lim
x→1
[f (x) +2g(x)] = lim
x→1
f (x) +2 lim
x→1
g(x) = 3 +
2(−2) =−1.
Chọn đáp án A
Câu 63. Biết lim
x→1
f (x) = 4 và lim
x→1
g
(
x
)
= 1. Tính
lim
x→1
[
4f (x) +3g
(
x
)
]
.
A. 11. B 19. C. 10. D. 9.
Câu 64. Cho lim
x→2
f (x) = 3. T ìm khẳng định
sai.
A. lim
x→2
[f (x) +3] =6. B. lim
x→2
p
f (x) +1 = 2.
C. lim
x→2
[f (x) −2x] =−1. D lim
x→2
f (x) −x
2
=1.
Ê Lời giải.
Ta có
lim
x→2
f (x) −x
2
=−1 = lim
x→2
f (x) −lim
x→2
x
2
=3 −4 =−1.
Vậy lim
x→2
f (x) −x
2
=1 sai.
Chọn đáp án D
Câu 65. lim
x→2
3x
2
+7x +11
có kết quả là
A 37. B. 38. C. 39. D. 40.
Ê Lời giải.
lim
x→2
3x
2
+7x +11
=3 ·2
2
+7 ·2 +11 =37.
Chọn đáp án A
Câu 66. Giá trị của lim
x→−1
x
2
−3
x
3
+2
là
A. 1. B −2. C. 2. D. −
3
2
.
Ê Lời giải.
lim
x→−1
x
2
−3
x
3
+2
=
(
−1
)
2
−3
(
−1
)
3
+2
=−2.
Chọn đáp án B
Câu 67. Cho c là hằng số, k là số nguyên
dương. Khẳng định nào sau đây sai?
A. lim
x→x
0
x = x
0
. B. lim
x→x
0
c = c.
C. lim
x→+∞
c
x
k
=0. D lim
x→+∞
c =+∞.
Ê Lời giải.
32
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Theo định lý về giới hạn, khẳng định sai là
lim
x→+∞
c =+∞.
Chọn đáp án D
Câu 68. Cho lim
x→a
f (x) =−∞, kết quả của lim
x→a
(−3·
f (x)) bằng
A. −∞. B. 0.
C +∞. D. 3.
Ê Lời giải.
Có lim
x→a
(−3 · f (x)) =−3 ·lim
x→a
f (x) =+∞.
Chọn đáp án C
Câu 69. Tính tổng S =9+3+1+
1
3
+
1
9
+···+
1
3
n−3
+
···.
A S =
27
2
. B. S =14.
C. S =16. D. S =15.
Ê Lời giải.
Ta có S = 9 + 3 + 1 +
1
3
+ ··· +
1
3
n−3
+ ··· =
9
1 +
1
3
+
1
3
2
+···+
1
3
n−1
+···
| {z }
CSN: u
1
=1, q=
1
3
= 9
Ö
1
1 −
1
3
è
=
27
2
.
Chọn đáp án A
Câu 70. Tổng của một cấp số nhân lùi vô hạn
bằng 2, tổng của ba số hạng đầu tiên của cấp số
nhân bằng
9
4
. Số hạng đầu u
1
của cấp số nhân
đó là
A u
1
=3. B. u
1
=4.
C. u
1
=
9
2
. D. u
1
=5.
Ê Lời giải.
Gọi q là công bội của cấp số nhân, ta có:
u
1
1 −q
=2
S
3
= u
1
·
1 −q
3
1 −q
=
9
4
⇔
u
1
=2
(
1 −q
)
2
1 −q
3
=
9
4
⇔
q =−
1
2
u
1
=2
1 +
1
2
=3.
Chọn đáp án A
Câu 71. Cho hàm số y = f (x) có đồ thị như hình
vẽ bên dưới.
x
y
O
1
2
3
3
1
Tính lim
x→1
+
f (x) + lim
x→3
−
f (x).
A. 5. B 4 . C. 2. D. 0.
Ê Lời giải.
Theo hình vẽ thì lim
x→1
+
f (x) = 1 và lim
x→3
−
f (x) = 3.
Suy ra lim
x→1
+
f (x) + lim
x→3
−
f (x) =4.
Chọn đáp án B
Câu 72. Cho hàm số y = f (x) có đồ thị như hình
vẽ bên dưới.
x
y
O
1
2
3
3
1
Tính lim
x→0
f (x) + lim
x→1
−
f (x).
A 5. B. 4 . C. 2. D. 0.
Ê Lời giải.
Theo hình vẽ thì lim
x→0
f (x) =3 và lim
x→1
−
f (x) =2. Suy
ra lim
x→0
f (x) + lim
x→1
−
f (x) =5.
Chọn đáp án A
Câu 73. Tính lim
x→1
+
x
3
−2x +1
.
A. 1. B 0. C. +∞. D. −∞.
Câu 74. Tính lim
x→3
−
p
x −3 −3x +x
2
.
A Không tồn tại. B. −∞.
C. 0. D. +∞.
Câu 75. Trong các giới hạn sau đây, giới hạn
nào bằng 0?
A. lim
3 +2n
3
2n
2
−1
. B lim
2n
2
−3
−2n
3
−4
.
C. lim
2n −3n
3
−2n
2
−1
. D. lim
2n
2
−3n
4
−2n
4
+n
2
.
Ê Lời giải.
lim
3 +2n
3
2n
2
−1
= +∞ : « bậc tử » > « bậc mẫu » và
a
m
b
k
=2 ·2 =4 > 0.
lim
2n
2
−3
−2n
3
−4
=0 : « bậc tử » < « bậc mẫu ».
lim
2n −3n
3
−2n
2
−1
= +∞ : « bậc tử » > « bậc mẫu » và
a
n
b
k
=
(
−3
)
·
(
−2
)
> 0.
lim
2n
2
−3n
4
−2n
4
+n
2
=
−3
−2
=
3
2
: « bậc tử » = « bậc mẫu »
và
a
m
b
k
=
−3
−2
=
3
2
.
Chọn đáp án B
Câu 76. Dãy số nào sau đây có giới hạn là
+∞?
A u
n
=
1 +n
2
5n +5
. B. u
n
=
n
2
−2
5n +5n
3
.
C. u
n
=
n
2
−2n
5n +5n
2
. D.
1 +2n
5n +5n
2
.
33
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Ê Lời giải.
lim u
n
= lim
1 +n
2
5n +5
= lim n ·
1
n
2
+1
5 +
5
n
= +∞ vì
lim n =+∞
lim
1
n
2
+1
5 +
5
n
=
a
m
b
k
=
1
5
> 0.
Chọn đáp án A
Câu 77. Dãy số nào sau đây có giới hạn là
−∞?
A.
1 +2n
5n +5n
2
. B. u
n
=
n
3
+2n −1
−n +2n
3
.
C u
n
=
2n
2
−3n
4
n
2
+2n
3
. D. u
n
=
n
2
−2n
5n +1
.
Ê Lời giải.
u
n
=
2n
2
−3n
4
n
2
+2n
3
: « bậc tử » > « bậc mẫu » và
a
m
b
k
=−3.2 =−6 < 0 ⇒lim u
n
=−∞.
Chọn đáp án C
Câu 78. Giá trị lim
Ä
n −
p
n
2
−4n
ä
bằng
A. 3. B. 1. C 2. D. 4.
Ê Lời giải.
Ta có lim
Ä
n −
p
n
2
−4n
ä
= lim
4n
n +
p
n
2
−4n
=
lim
4
1 +
…
1 −
4
n
=2.
Chọn đáp án C
Câu 79. Tính lim
x→1
x
2
−3x +2
x −1
.
A. 1. B. −∞. C −1. D. +∞.
Ê Lời giải.
Ta có L = lim
x→1
x
2
−3x +2
x −1
= lim
x→1
(x −1)(x −2)
(x −1)
=
lim
x→1
(x −2) =−1.
Chọn đáp án
C
Câu 80. Tìm lim
x→−∞
(4x
4
−3x
2
+2).
A +∞. B. −∞. C. 4. D. 2.
Ê Lời giải.
lim
x→−∞
(4x
4
−3x
2
+2) = lim
x→−∞
x
4
4 −
3
x
2
+
2
x
4
=+∞.
Chọn đáp án A
2 Mức độ Vận dụng
Câu 81. Cho dãy số
(
u
n
)
với u
n
=
an +4
5n +3
, với a
là tham số thực. Để dãy số
(
u
n
)
có giới hạn bằng
2 thì giá trị của a là
A a =10. B. a =8.
C. a =6. D. a =4 .
Ê Lời giải.
Ta có lim u
n
= lim
an +4
5n +3
= lim
a +
4
n
5 +
3
n
=
a
5
. Khi đó
lim u
n
=2 ⇔
a
5
=2 ⇔ a =10.
Chọn đáp án A
Câu 82. Cho số thực a thỏa mãn
lim
x→+∞
a
p
2x
2
+3 +2017
2x +2018
=
1
2
. Khi đó giá trị của
a là
A. a =
−
p
2
2
. B. a =
1
2
.
C. a =
−1
2
. D a =
p
2
2
.
Ê Lời giải.
Ta có
lim
x→+∞
a
p
2x
2
+3 +2017
2x +2018
= lim
x→+∞
ax
…
2 +
3
x
2
+2017
x
2 +
2018
x
= lim
x→+∞
a
…
2 +
3
x
2
+
2017
x
2 +
2018
x
=
a
p
2
2
.
Khi đó:
a
p
2
2
=
1
2
⇔a =
p
2
2
.
Chọn đáp án D
Câu 83. Cho hàm số f (x) =
x
2
+1
1 −x
với x < 1
p
2x −2 với x > 1
.
Khi đó lim
x→1
−
f (x) là
A +∞. B. −1. C. 0. D. 1.
Ê Lời giải.
lim
x→1
−
f (x) = lim
x→1
−
x
2
+1
1 −x
=+∞ vì
lim
x→1
−
x
2
+1
=2
lim
x→1
−
(
1 −x
)
=0 & 1 −x > 0
(
∀x < 1
)
.
Chọn đáp án A
Câu 84. Cho lim
x→−∞
p
x
2
+6 −x
p
3
x
p
2 −
p
x
2
+3
= a
p
2 + b
p
3 +
c
p
6 +d,
(
a, b, c, d ∈Q
)
. Tính ab +cd.
A. 1. B. 0. C −2. D. 2.
Câu 85. Tìm tất cả các giá trị thực của tham
số m để hàm số f (x) =
x
2
+x −12
x +4
khi x 6=−4
mx +1 khi x =−4
liên tục tại điểm x
0
=−4.
A. m =4. B m =2. C. m =3. D. m =5.
Ê Lời giải.
Ta có
lim
x→−4
f (x) = lim
x→−4
x
2
+x −12
x +4
= lim
x→−4
(x −3)(x +4)
x +4
=−7.
Hàm số đã cho liên tục khi và chỉ khi
lim
x→−4
f (x) = f (−4) ⇔−4m +1 =−7 ⇔ m = 2.
Vậy m =2 là giá trị cần tìm.
Chọn đáp án B
34
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
B. BÀI TẬP TỰ LUẬN
BÀI 15. Tính các giới hạn sau
lim
n→+∞
n
2
+1
2n
2
+n +2
.a) lim
n→+∞
2
n
+3
1 +3
n
.b)
lim
Ä
p
n
2
+2n −n
ä
.c) lim
2n
3
+2n −1
.d)
Ê Lời giải.
BÀI 16. Tính các giới hạn sau:
lim
x→3
x
2
+2x −15
x −3
.a) lim
x→2
2x
2
−5x +2
x
2
−4
.b)
lim
x→0
p
1 +2x −1
2x
.c) lim
x→1
+
x −2
x −1
.d)
lim
x→+∞
Ä
p
x
2
+x −x
ä
.e) lim
x→+∞
−x
3
−x
2
+4x +2
.f)
Ê Lời giải.
BÀI 17. Xét tính liên tục của mỗi hàm số sau tại điểm x =2.
a) f (x) =
®
6 −2x khi x ≥2
2x
2
−6 khi x < 2;
b) f (x) =
x
2
−4
x −2
khi x 6=2
0 khi x =2.
Ê Lời giải.
a) Tập xác định của hàm số là D =R, chứa điểm 2. Ta có
○ f (2) =6 −2 ·2 =2;
○ lim
x→2
+
f (x) = lim
x→2
+
(6 −2x) =6 −2 ·2 =2;
○ lim
x→2
−
f (x) = lim
x→2
−
(2x
2
−6) =2 ·2
2
−6 =2.
Do lim
x→2
+
f (x) = lim
x→2
−
f (x) =2 nên lim
x→2
f (x) =2.
Khi đó lim
x→2
f (x) = f (2) nên hàm số f (x) liên tục tại x = 2.
b) Tập xác định của hàm số là D =R, chứa điểm 2.
Ta có f (2) = 0 và lim
x→2
f (x) = lim
x→2
x
2
−4
x −2
= lim
x→2
(x −2)(x +2)
x −2
= lim
x→2
(x +2) =4.
Vì lim
x→2
f (x) 6= f (2) nên hàm số không liên tục tại x =2.
BÀI 18. Chứng minh rằng phương trình
a) x
3
+2x −1 =0 có nghiệm thuộc khoảng (−1; 1).
b)
p
x
2
+x +x
2
=1 có nghiệm thuộc khoảng (0;1).
Ê Lời giải.
a) Xét hàm số f (x) = x
3
+2x −1 là hàm số liên tục trên đoạn [−1;1].
Ta có f (−1) · f (1) =(−4) ·2 =−8 < 0 suy ra tồn tại c ∈(−1; 1) để f (c) =0.
Từ đó suy ra phương trình x
3
+2x −1 =0 có nghiệm thuộc khoảng (−1; 1) (đcpm).
35
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
b) Ta có
p
x
2
+x +x
2
=1 ⇔
p
x
2
+x +x
2
−1 =0.
Xét hàm số g (x) =
p
x
2
+x +x
2
−1 là hàm số liên tục trên đoạn [0;1].
Ta có g(0) · g(1) = (−1) ·
p
2 =−
p
2 < 0 suy ra tồn tại c ∈(0; 1) để g(c) =0.
Từ đó suy ra phương trình
p
x
2
+x+x
2
=1 có nghiệm thuộc khoảng (0; 1) có nghiệm trên khoảng
(0;1) (đpcm).
BÀI 19. Trong hồ có chứa 6000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít
vào hồ với tốc độ 15 lít/phút.
a) Chứng tỏ rằng nồng độ muối của nước trong hồ sau t phút kể từ khi bắt đầu bơm là
C(t) =
30t
400 +t
(gam/lít).
b) Nồng độ muối trong hồ như thế nào nếu t →+∞.
Ê Lời giải.
a) Sau thời gian t phút, số lít nước trong hồ là 6000 +15t (lít).
Số gam muối trong số lít nước bơm vào là 30 ·15t =450t (gam).
Nồng độ muối của nước trong hồ sau t phút khi bắt đầu bơm là
C(t) =
450t
6000 +15t
=
30t
400 +t
(gam/lít).
b) Khi t →+∞, ta xét giới hạn
lim
t→+∞
C(t) = lim
t→+∞
30t
400 +t
= lim
t→+∞
30
400
t
+1
=30.
Vậy khi bơm nước biểm vào hồ chứa, không giới hạn thời gian thì nồng độ muối trong hồ chứa
chính là nồng độ muối của nước biển.
BÀI 20. Từ độ cao 100 m, người ta thả một quả bóng cao su xuống đất. Giả sử cứ sau mỗi lần chạm
đất, quả bóng nảy lên một độ cao bằng
1
4
độ cao mà quả bóng đạt được trước đó. Gọi h
n
là độ cao quả
bóng đạt được ở lần nảy thứ n.
a) Tìm số hạng tổng quát của dãy số
(
h
n
)
.
b) Tính giới hạn của dãy số
(
h
n
)
và nêu ý nghĩa giới hạn của dãy số
(
h
n
)
.
c) Gọi S
n
là tổng độ dài quãng đường đi được của quả bóng từ lúc bắt đầu thả quả bóng đến khi
quả bóng chạm đất lần thứ n. Tính S
n
, nếu quá trình này cứ tiếp tục diễn ra mãi thì tổng
quãng đường quả bóng di chuyển được là bao nhiêu?
Ê Lời giải.
a) Vì sau mỗi lần chạm đất, quả bóng nảy lên một độ cao bằng
1
4
độ cao mà quả bóng đạt được
trước đó nên độ cao của quả bóng nảy lên lần thứ n là một cấp số nhân
(
h
n
)
có u
1
= 100, công
bội q =
1
4
. Khi đó số hạng tổng quát của dãy số
(
h
n
)
là h
n
=100 ·
1
4
n
b) Ta có lim h
n
=lim
ï
100 ·
1
4
n
ò
=100lim
1
4
n
=0.
Ý nghĩa của giới hạn là khi n tiến dần ra vô cực thì độ nảy của quả bóng càng dần về 0, có
nghĩa là sau khoảng thời gian đủ dài thì độ nảy của quả bóng không đáng kể.
36
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
c) Ta thấy tổng S
n
là tổng của cấp số nhân lùi vô hạn có u
1
=100, công bội q =
1
4
.
Ta có S
n
=100 +100 ·
1
4
+100 ·
1
4
2
+.. . +100 ·
1
4
n
+.. . =100 ·
1
1 −
1
4
=
400
3
m.
—HẾT—
37
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
ĐÁP ÁN CÁC TRẮC NGHIỆM
1 Trắc nghiệm chương I
1. A
2. D 3. B
4. B 5. A
6. C
7. B
8. D 9. B
10. C
11. B
12. D 13. B
14. A 15. D
16. B
17. C
18. B 19. D
20. C
2 Trắc nghiệm chương II
1. A
2. B
3. C
4. D 5. D
6. B
7. D
8. B 9. D
10. C
11. B
12. D 13. A
14. A 15. D
16. D
17. D
18. B 19. D 20. D
3 Trắc nghiệm chương III
21. A 22. B
23. C
24. D 25. D
4 Trắc nghiệm chương IV
26. D
27. C
28. D 29. D 30. B 31. D 32. D
33. C 34. C
35. B
36. A 37. D 38. B 39. B 40. A
41. A
42. A
43. C
44. D 45. D
46. C
47. D
48. C
49. D 50. D
51. A
52. B
53. C
54. B 55. B
5 Trắc nghiệm chương V
56. D
57. B
58. A 59. D 60. A 61. D 62. A 63. B 64. D 65. A
66. B 67. D
68. C
69. A 70. A
71. B
72. A 73. B
74. A 75. B
76. A
77. C 78. C 79. C
80. A 81. A 82. D 83. A
84. C
85. B
38
| 1/56
| | Tải xuống

Có thể bạn quan tâm:

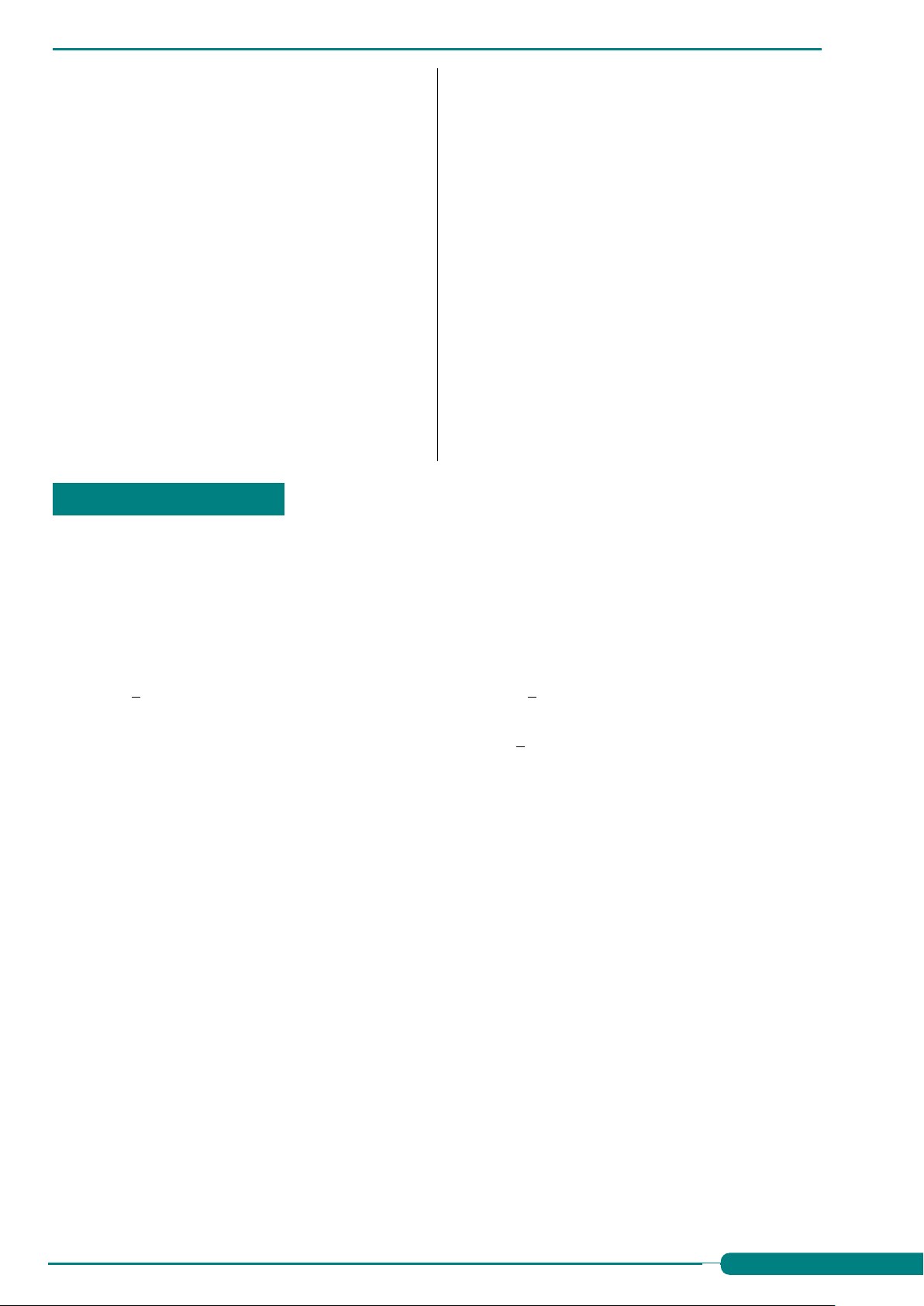
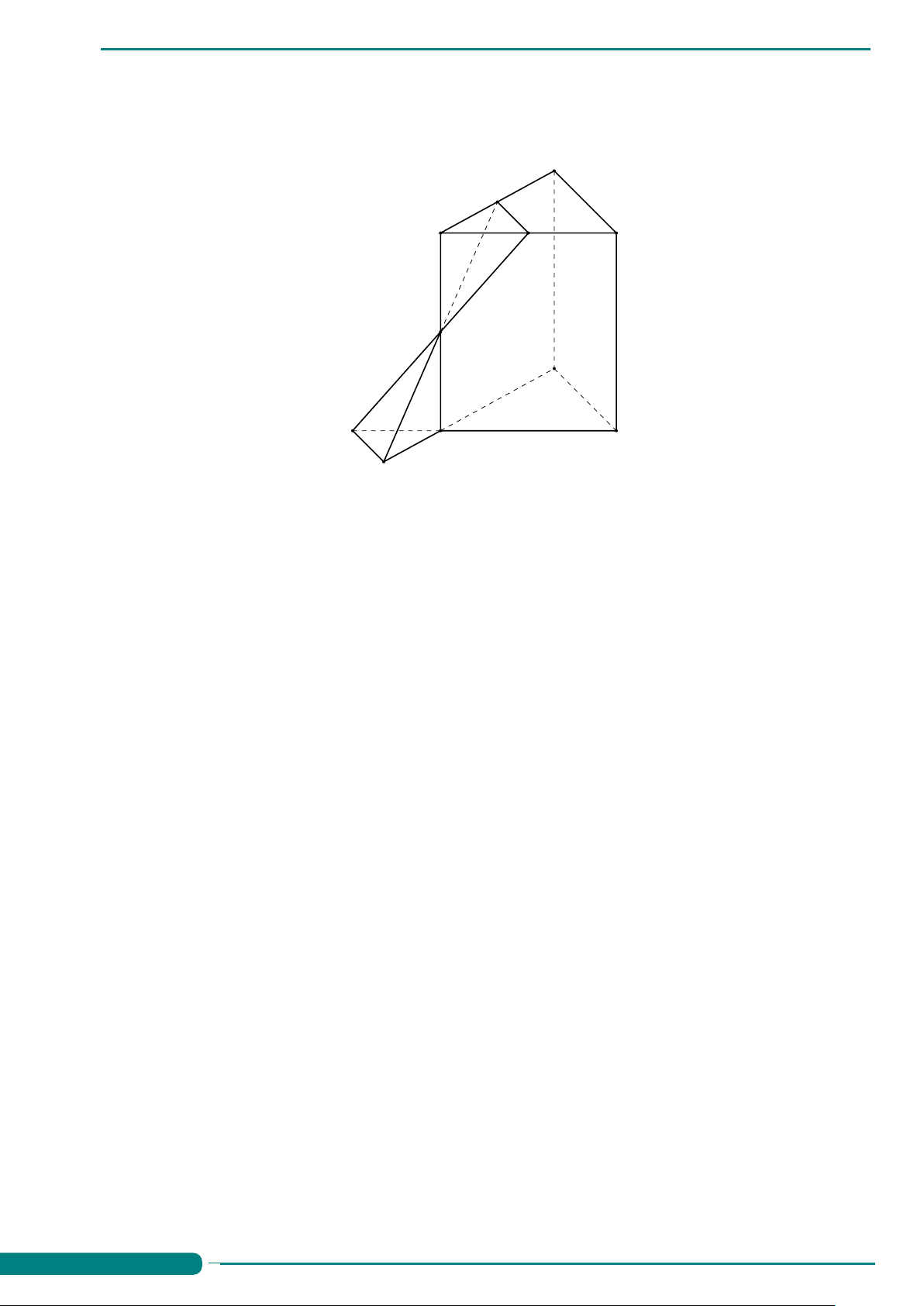
Preview text:

½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC MỤC LỤC Chương I.
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 3 A
BÀI TẬP TRẮC NGHIỆM............................................................................................3
} Mức độ Nhận biết, Thông hiểu .......................................................................... 3
} Mức độ Vận dụng .................................................................................................. 4 B
BÀI TẬP TỰ LUẬN.......................................................................................................4 Chương II.
DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN 5 A
BÀI TẬP TRẮC NGHIỆM............................................................................................5
} Mức độ Nhận biết, Thông hiểu .......................................................................... 5
} Mức độ Vận dụng .................................................................................................. 5 B
BÀI TẬP TỰ LUẬN.......................................................................................................6
Chương III. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU GHÉP NHÓM 7 A
BÀI TẬP TRẮC NGHIỆM............................................................................................7
} Mức độ Nhận biết, Thông hiểu .......................................................................... 7
} Mức độ Vận dụng .................................................................................................. 8 B
BÀI TẬP TỰ LUẬN.......................................................................................................8
Chương IV. QUAN HỆ SONG SONG SONG TRONG KHÔNG GIAN 10 A
BÀI TẬP TRẮC NGHIỆM..........................................................................................10
} Mức độ Cơ bản.....................................................................................................10
} Mức độ Vận dụng ................................................................................................ 13 B
BÀI TẬP TỰ LUẬN .................................................................................................... 14 Chương V.
GIỚI HẠN. HÀM SỐ LIÊN TỤC 16 A
BÀI TẬP TRẮC NGHIỆM..........................................................................................16
} Mức độ Nhận biết, Thông hiểu........................................................................16
} Mức độ Vận dụng ................................................................................................ 17 B
BÀI TẬP TỰ LUẬN .................................................................................................... 17 1
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chương I.
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
A. BÀI TẬP TRẮC NGHIỆM 1
Mức độ Nhận biết, Thông hiểu
Câu 8. Trong các mệnh đề sau, mệnh đề nào là π mệnh đề đúng?
Câu 1. Góc có số đo đổi sang độ là A. sin 2a 12 = sin a + cos a. A. 15◦. B. 16◦. B. sin 2a = 2sin a. C. 14◦. D. 17◦300. C. sin 2a = cos2 a − sin2 a.
Câu 2. Góc có số đo 108◦ đổi sang radian là D. sin 2a = 2sin a cos a. 3π 5π 5π 3π A. . B. . C. . D. .
Câu 9. Trong các mệnh đề sau, mệnh đề nào là 2 2 3 5 mệnh đề sai? 89π Câu 3. Giá trị cot bằng a + b a − b 6 A. sin a cos . p p + sin b = 2 sin 2 2 3 p 3 p A. a a . B. − 3. C. − . D. 3. + b − b B. cos a sin . 3 3 − cos b = 2 sin 2 2 a a
Câu 4. Xác định số đo của góc lượng giác + b − b C. cos a + cos b = 2cos cos .
(Ou, Ov) được biểu diễn trong hình bên dưới. 2 2 a + b a − b D. sin a sin . v − sin b = 2 cos 2 2
Câu 10. Chu kỳ của hàm số y = cot x là 150◦ A. kπ, k ∈ Z. B. 2π. π O u C. π. D. . 2
Câu 11. Chu kỳ của hàm số y A. = cos x là 410◦. B. 510◦. C. 150◦. D. 420◦. 2π A. . B. 2π. C. π. D. k2π.
Câu 5. Xác định số đo của góc lượng giác 3
(Ou, Ov) được biểu diễn trong hình bên dưới
Câu 12. Tập giá trị của hàm số y = cos x là tập v hợp nào sau đây? A. [0; +∞]. B. R. C. (−∞;0]. D. [−1;1].
Câu 13. Giá trị nhỏ nhất m và giá trị lớn nhất 60◦
M của hàm số y = 3sin2x − 5 lần lượt là O u A. m = 2, M = 8. B. m = −8, M = −2. C. m = −5, M = −2. D. m = −8, M = −5. A. −300◦. B. 510◦. C. 60◦. D. −420◦.
Câu 14. Phương trình cos x = a có nghiệm khi
Câu 6. Chọn khẳng định đúng trong các khẳng và chỉ khi định sau: A. |a| ≤ 1. B. |a| > 1.
A. tan(π − α) = tanα.
B. cot(π − α) = cotα. C. |a| < 1. D. |a| ≥ 1. C. cos(π p
− α) = −cos α. D. sin(π − α) = −sin α. 3 1
Câu 15. Giải phương trình sin x = .
Câu 7. Cho sin α =
, với 90◦ < α < 180◦. Tính 2 3 π π cos α. A. x p = ± + k2π. B. x = + kπ. 3 3 2 2 2  ππ A. cos α = − . B. cos α = − . x = + kπ x = + k2π 3 3 p 6 3 C.  . D.  . 2 2 2  5π  2π C. cos α = . D. cos α = . x = + kπ x = + k2π 3 3 6 3 3
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC π 3π
Câu 16. Phương trình cos 3x = cos có nghiệm C. x 100πt (cm). 15 = 10 cos − 4 là 3π π π k2π D. x = 10cos 100πt + (cm). A. x = ± + k2π. B. x = ± + . 4 15 45 3 π k2π π k2π C. x = − + . D. x = + . 45 3 45 3
Câu 19. Cho hình vuông D C p ABCD như hình vẽ. Tính
Câu 17. Giải phương trình tan x = 3 ta được
giá trị của tan α. tập nghiệm là 7 4 6 n π o A. A. . B. . + k2π, k ∈ Z . B. ∅. 13 13 E 3 9 7 n π o n π o C. + kπ, k ∈ Z . D. + kπ, k ∈ Z . C. . D. . α 5 3 6 13 17 A B
Câu 20. Nhiệt độ ngoài trời ở một thành phố 2
Mức độ Vận dụng
vào các thời điểm khác nhau trong ngày có thể
Câu 18. Cho hai dao động điều hòa cùng
được mô phỏng bởi công thức
phương có phương trình lần lượt là x1 = h π i
5 cos(100πt + π)(cm) và x h(t) = 29 + 3sin (t − 9)
2 = 5 cos(100πt − π/2)(cm). 12
Phương trình dao động tổng hợp của hai dao động trên là
với h tính bằng độ C và t là thời gian trong ngày p 3π A. x = 5 2cos 100πt + (cm).
tính bằng giờ. Nhiệt độ thấp nhất trong ngày 4 p vào lúc mấy giờ? 3π
B. x = 5 2cos 100πt − (cm).
A. 5 giờ . B. 0 giờ . C. 3 giờ. D. 4 giờ. 4
B. BÀI TẬP TỰ LUẬN
BÀI 1. Giải các phương trình lượng giác sau: p p 2 π 3 a) sin x = − ; b) sin 3x + = ; 2 6 2 p3 c) cos 2x = ; d) cos(2x − 30◦) = −1; 2 π π p e) tan 3x = tan ; f) cot 2x − = 3. 7 5
BÀI 2. Số giờ có ánh nắng mặt trời của một thành phố A trong ngày thứ t (ở đây t là số ngày tính từ
ngày 1 tháng Giêng) của một năm không nhuận được mô hình hóa bởi hàm số h 2π i L(t) = 12 + 2,83sin
(t − 80) với t ∈ Z và 0 < t ≤ 365. 365
a) Vào ngày nào trong năm thì thành phố A có ít giờ ánh sáng mặt trời nhất?
b) Vào ngày nào trong năm thì thành phố A có nhiều giờ ánh sáng mặt trời nhất?
c) Vào ngày nào trong năm thì thành phố A có khoảng 10 giờ ánh sáng mặt trời?
BÀI 3. Chiều cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển π π
động được cho bởi công thức h(t) = 30 + 20sin t + . 25 3
a) Cabin đạt độ cao tối đa là bao nhiêu?
b) Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên? 4
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chương II.
DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN
A. BÀI TẬP TRẮC NGHIỆM 1
Mức độ Nhận biết, Thông hiểu
Câu 10. Cho cấp số nhân (un), biết u1 = 3 và công bội q = −2. Tìm u3. 2n − 1
Câu 1. Cho dãy số (un) có un = . Tính A. u3 = 16. B. u3 = 14. n + 1 u8. C. u3 = 12. D. u3 = 11. 5 11 A. u8 = . B. u8 = .
Câu 11. Cho cấp số nhân (u 3 9 n) với u1 = 2 và 17
q = −3. Khi đó, số hạng u6 bằng C. u8 = . D. u8 = 1. 9 A. −3 · 25. B. 2 · (−3)5. C. −3 · 26. D. 2 · (−3)6. Câu 2. Cho dãy số (un) xác định bởi ®u1 = 3
Câu 12. Cho cấp số nhân (un) có số hạng đầu
. Ba số hạng đầu tiên của dãy u u n+1 = un + 5
1 = 3 và công bội q = 2. Tổng S10 = u1 + u2 + u3 + số đó là · · · + u10 bằng 1023 A. −3;6;9. B. 3; 8; 13. A. . B. 1023. C. 1536. D. 3069. 2 C. 3; 5; 7. D. 3; −2;−7.
Câu 3. Dãy nào sau đây là cấp số cộng? 2
Mức độ Vận dụng A. 1; 5; 9; 5; 1. B. 1; 3; 5; 7; 11. C. 2; 5; 8; 11. D. 3; 7; 3; 7.
Câu 13. Một người muốn chia 1000 · 000 đồng
cho bốn người con, đứa lớn hơn đứa nhỏ kế tiếp
Câu 4. Cho cấp số cộng 1, 8, 15, 22, 29, . . .. Công
100 · 000 đồng. Hỏi đứa con lớn nhất được bao
sai của cấp số cộng này là nhiêu tiền. A. 9. B. 1. C. 8. D. 7. A. 400 · 000 đồng. B. 200 · 000 đồng.
Câu 5. Cho cấp số cộng (u C. 100 · 000 đồng. D. 300 · 000 đồng. n) có số hạng đầu
u1 = 3 và d = 2. Số hạng thứ 2 của cấp số cộng
Câu 14. Một du khách vào trường đua ngựa đã cho là
xem đua ngựa và đặt cược chọn con thắng cuộc. A. 3. B. 6. C. 1. D. 5.
Nếu chọn đúng con thắng cuộc thì sẽ nhận được
Câu 6. Cho cấp số cộng (u
số tiền gấp đôi số tiền đặt cuộc, còn nếu chọn sai n) có số hạng đầu u
thì sẽ mất số tiền đặt cuộc. Người du khách đó
1 = 4 và d = 2. Số hạng thứ 50 của cấp số cộng đó là
lần đầu tiên đặt 20 000 đồng, mỗi lần sau tiền A. u
đặt gấp đôi tiền đặt lần trước. Người đó thua 50 = 100. B. u50 = 102. C. u
9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du 50 = 104. D. u50 = 198.
khách đó thắng hay thua bao nhiêu?
Câu 7. Cho cấp số cộng (un) có số hạng đầu A. Thắng 20 000 đồng.
u1 = 3 và d = −2. Tổng của 20 số hạng đầu của B. Hoà vốn. cấp số cộng đó là C. Thua 20 000 đồng. A. S20 = −380. B. S20 = −214. D. Thua 40 000 đồng. C. S20 = −640. D. S20 = −320.
Câu 15. Một gia đình cần khoan một cái giếng
Câu 8. Dãy số nào sau đây không phải là cấp
để lấy nước. Họ thuê một đội khoan giếng nước số nhân?
đến để khoang giếng. Biết giá của mét khoan A. 1, −1,1,−1,1. B. 1, 2, 3, 4, 5.
đầu tiên là 80 000 đồng, kể từ mét khoan thứ hai C. 1, −2,4,−8,16. D. 1, 2, 4, 8, 16.
giá của mỗi mét khoan tăng thêm 5000 đồng so
Câu 9. Cho cấp số nhân (un), biết u1 = −9, u2 =
với giá của mét khoan trước đó. Biết cần phải 3. Công bội q là
khoan sâu xuống 50 m mới có nước. Hỏi phải 1 A. q = . B. q = −3.
trả bao nhiêu tiền để khoan cái giếng đó? 3 1 A. 4 245 000 đồng. B. 5 250 000 đồng. C. q = 3. D. q = − . C. 4 000 000 đồng. D. 10 125 000 đồng. 3 5
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 16. Chu kì bán rã của nguyên tố phóng
tiền trong tài khoản tiết kiệm của ông Trung
xạ Poloni 210 là 138 ngày (nghĩa là sau 138
gần nhất với số nào sau đây?
ngày khối lượng của nguyên tố đó chỉ còn một A. 126 532 000 đồng. B. 158 687 000 đồng.
nửa). Tính (chính xác đến hàng phần trăm) C. 125 971 000 đồng. D. 112 486 000 đồng.
khối lượng còn lại của 20 gam Poloni 210 sau 7314 ngày (khoảng 20 năm).
Câu 19. Ba số phân biệt có tổng là 217 có thể A. 3,22 · 10−15. B. 3,52 · 10−15.
coi là các số hạng liên tiếp của một cấp số nhân, C. 2,52 · 10−15. D. 2,22 · 10−15.
cũng có thể coi là số hạng thứ 2, thứ 9, thứ 44
của một cấp số cộng. Hỏi phải lấy bao nhiêu số
Câu 17. Tế bào E.Coli trong điều kiện nuôi cấy
hạng đầu của cấp số cộng này để tổng của chúng
thích hợp cứ 20 phút lại nhân đôi một lần. Nếu bằng 210?
lúc đầu có 1012 tế bào thì sau 3 giờ sẽ phân chia A. 40. B. 30. C. 20. D. 10. thành bao nhiêu tế bào? A. 256 · 1012 tế bào. B. 1024 · 1012 tế bào.
Câu 20. Một đa giác có n cạnh và có chu vi C. 512 · 1013 tế bào. D. 512 · 1012 tế bào.
bằng 158 cm. Biết số đo các cạnh của đa giác
Câu 18. Ông Trung có 100 triệu đồng gửi tiết
lập thành một cấp số cộng và công sai d = 3 cm
kiệm vào ngân hàng theo thể thức lãi kép kì
và cạnh lớn nhất có độ dài là 44 cm. Đa giác có
hạn 6 tháng với lãi suất 8% cho một kì hạn. Giả số cạnh n bằng
sử lãi suất không thay đổi. Hỏi sau 3 năm số A. n = 6. B. n = 7. C. n = 5. D. n = 4.
B. BÀI TẬP TỰ LUẬN
BÀI 1. Tìm công sai của cấp số cộng (un), biết a) u1 = −21 và u14 = 18; b) u5 = −15 và u20 = 60; c) u1 = 2 và u2 + u3 = 5;
d) u2 + u4 = 16 và u3 + u7 = −4.
BÀI 2. Xác định công bội của một cấp số nhân (un), biết 1 1 a) u1 = và u6 = 16; b) u1 = − và u7 = −32; 2 2 1 c) u3 = 9 và u6 = 243; d) u2 = và u5 = 16. 4
BÀI 3. Có bao nhiêu hàng ghế trong một góc khán đài của một sân vận động, biết rằng góc khán
đài đó có 2040 chỗ ngồi, hàng ghế đầu tiên có 10 chỗ ngồi và mỗi hàng ghế sau có thêm 4 chỗ ngồi so
với hàng ghế ngay trước nó?
BÀI 4. Nếu anh Nam nhận được lời mời làm việc cho một công ty nước ngoài với mức lương khởi
điểm là 35000 đô la mỗi năm và được tăng thêm 1400 đô la lương mỗi năm, thì sẽ mất bao nhiêu
năm làm việc để tổng lương mà anh Nam nhận được là 319200 đô la? 6
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chương III.
CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA
MẪU SỐ LIỆU GHÉP NHÓM
A. BÀI TẬP TRẮC NGHIỆM 1
Mức độ Nhận biết, Thông hiểu
Câu 21. Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT A, ta được kết quả Chiều [150; 152) [152; 154) [154; 156) [156; 158) [158; 160) [160; 162) [162; 168) cao (cm) Số học 5 18 40 25 8 3 1 sinh
a) Mẫu số liệu trên có bao nhiêu nhóm A. 5. B. 6. C. 7. D. 8.
b) Số học sinh có chiều cao trong khoảng [154;156) là A. 40. B. 18. C. 5. D. 8.
Câu 22. Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau Thời gian ( phút) [0; 20) [20; 40) [40; 60) [60; 80) [80; 100) Số học sinh 5 9 12 10 6
a) Giá trị đại diện của nhóm [60; 80) là A. 40. B. 70. C. 60. D. 30.
b) Nhóm [20; 40) có tần số là A. 5. B. 9. C. 12. D. 10.
c) Nhóm chứa mốt của mẫu số liệu này là A. [80; 100). B. [20; 40). C. [40; 60). D. [60; 80). d) Nhóm chứa trung vị là A. [0; 20). B. [20; 40). C. [40; 60). D. [60; 80).
e) Nhóm chứa tứ phân vị thứ nhất là A. [0; 20). B. [20; 40). C. [40; 60). D. [60; 80). 7
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC 2
Mức độ Vận dụng
Câu 23. Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một số học sinh thu được kết quả sau Thời gian ( phút) [0; 4) [4; 8) [8; 12) [12; 16) [16; 20) Số học sinh 2 4 7 4 3
Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là A. 7. B. 11,3. C. 10,4. D. 12,5.
Câu 24. Cho mẫu số liệu ghép nhóm về chiều cao của 25 cây dừa giống như sau Chiều cao ( cm) [0; 10) [10; 20) [20; 30) [30; 40) [40; 50) Số cây 4 6 7 5 3
a) Mốt của mẫu số liệu ghép nhóm này là 70 50 70 80 A. Mo = . B. Mo = . C. Mo = . D. Mo = . 3 3 2 3
b) Trung vị của mẫu số liệu ghép nhóm này là 175 165 165 165 A. Me = . B. Me = . C. Me = . D. Me = . 7 5 7 3
c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm này là A. Q1 = 13,5. B. Q1 = 13,9. C. Q1 = 15,75. D. Q1 = 13,75.
Câu 25. Cho mẫu số liệu ghép nhóm về khối lượng (đơn vị: gram) của 30 củ khoai tây như sau Khối lượng [70; 80) [80; 90) [90; 100) [100; 110) [110; 120) Tần số 3 6 12 6 3
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là A. Q3 = 133. B. Q3 = 134. C. Q3 = 132. D. Q3 = 102,5.
B. BÀI TẬP TỰ LUẬN
BÀI 5. Người ta ghi lại tốc độ cua 40 xe đạp đi qua một vị trí trên đường. Mẫu số liệu dưới đây ghi
lại tốc độ của 40 xe đó (đơn vị: km/h) 10 10,4 11 16 12 13 15,8 12,7 16,8 19 17 15,1 14 12,3 17,2 10,5 13,2 18,1 19,6 17,4 11,8 13,6 12,7 15,9 14,2 12,6 11,6 10,4 14,1 15,1 12,3 15,2 11,9 16,3 18,4 17,1 14,2 12,1 13,7 13,2
a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có năm nhóm ứng với sáu nửa khoảng
[10; 12), [12; 14), [14; 16), [16; 18), [18; 20).
b) Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.
BÀI 6. Một công ty bảo hiểm thống kê lại độ tuổi các khách hàng mua bảo hiểm xe ô tô ở bảng sau: Độ tuổi [25; 30) [30; 35) [35; 40) [40; 45) [45; 50) [50; 55) Số khách hàng 25 38 62 42 37 29 8
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.
BÀI 7. Các bạn học sinh một lớp thống kê số túi nhựa mà gia đình bạn đó sử dụng trong một tuần.
Kết quả được tổng hợp lại ở bảng sau: Số tuổi [5; 9] [10; 14] [15; 19] [20; 24] [25; 29] Số gia đình 8 15 12 7 2
a) Hãy ước lượng số trung bình và mốt của mẫu số liệu trên.
b) Cô giáo dự định trao danh hiệu “Gia đình xanh” cho 25% gia đình các bạn sử dụng ít túi nhựa
nhất. Cô giáo nên trao danh hiệu cho các gia đình dùng không quá bao nhiêu túi nhựa?
BÀI 8. Bảng sau thống kê doanh số bán hàng của các nhân viên một trung tâm thương mại trong một ngày. Doanh số [20; 30) [30; 40) [40; 50) [50; 60) [60; 70) (triệu đồng) Số nhân viên 4 8 12 7 5
a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên.
b) Trung tâm thương mại dự định sẽ thưởng cho 25% số nhân viên có doanh số bán hàng cao nhất.
Theo mẫu số liệu trên, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán
hàng ít nhất là bao nhiêu? —HẾT— 9
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chương IV.
QUAN HỆ SONG SONG SONG TRONG KHÔNG GIAN
A. BÀI TẬP TRẮC NGHIỆM 1 Mức độ Cơ bản
Câu 26. Các yếu tố nào sau đây xác định một mặt phẳng duy nhất? A. Bốn điểm phân biệt.
B. Một điểm và một đường thẳng. C. Ba điểm phân biệt.
D. Hai đường thẳng cắt nhau.
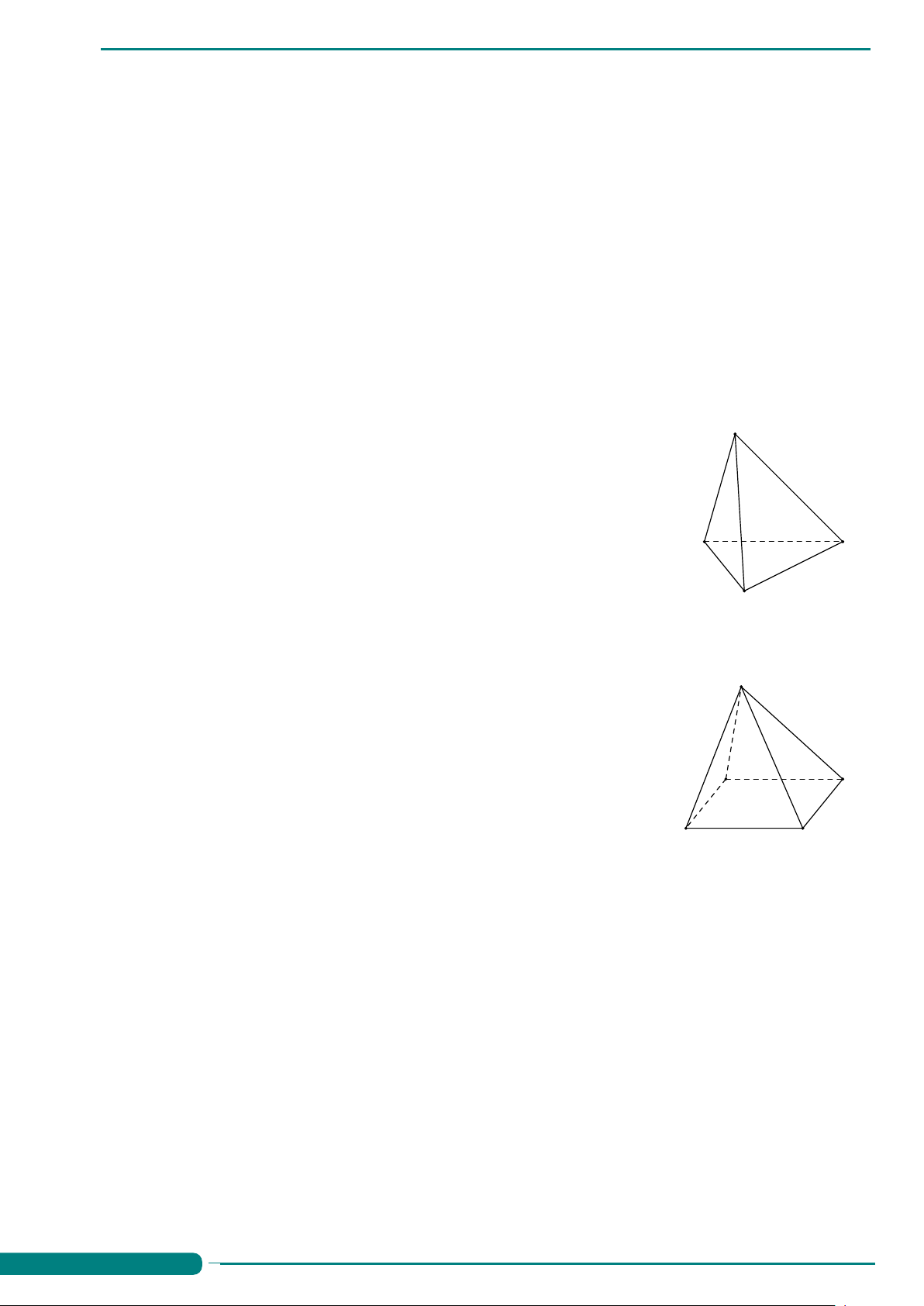
Câu 27. Cho tứ diện ABCD như hình bên. Mệnh đề nào sau đây đúng? A A. AB và CD cắt nhau. B. BD và AC cắt nhau. C. BD và AC chéo nhau. D. BC và AD song song. B D C
Câu 28. Hình chóp tứ giác có tất cả bao nhiêu mặt là tam giác? A. 5. B. 3. C. 6. D. 4.
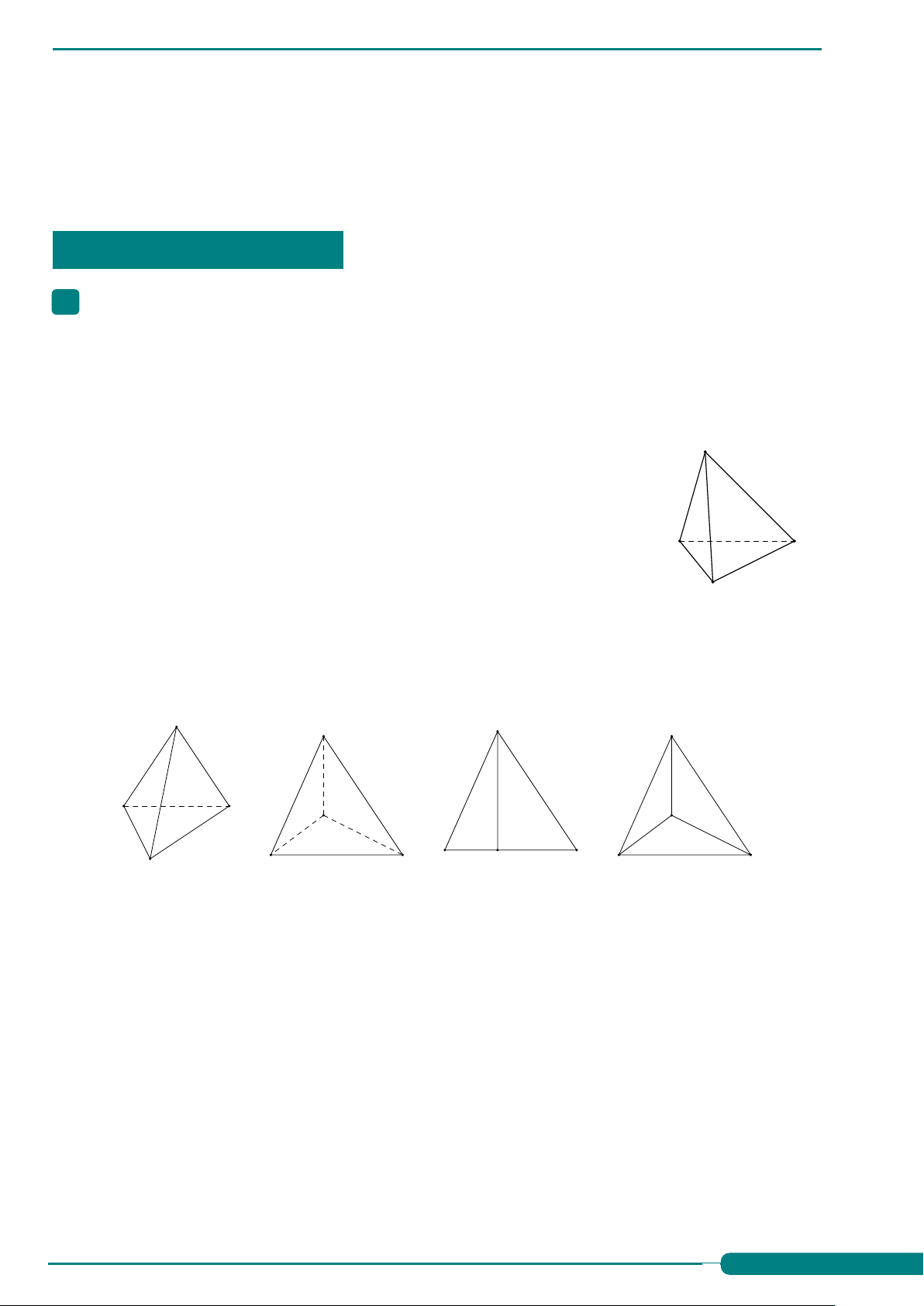
Câu 29. Trong các hình sau A A A A D B C C B D B D C B D (I) C (II) (III) (VI)
Hình nào có thể là hình biểu diễn của một hình tứ diện? A. (I). B. (I), (II). C. (I), (II), (IV). D. (I), (II), (III), (IV).
Câu 30. Trong không gian, hai đường thẳng không có điểm chung thì A. cắt nhau.
B. chéo nhau hoặc song song. C. chéo nhau. D. song song.
Câu 31. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai đường thẳng phân biệt không song song thì chéo nhau.
B. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
C. Hai đường thẳng không có điểm chung thì chéo nhau .
D. Hai đường thẳng chéo nhau thì không có điểm chung.
Câu 32. Trong không gian cho hai đường thẳng cắt nhau a và b. Nếu c là một đường thẳng song song với a thì
A. c và b song song với nhau. B. c và b cắt nhau. C. c và b chéo nhau.
D. c và b không song song với nhau. 10
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 33. Cho hình chóp S.ABCD có điểm O là giao điểm của hai đường chéo. Giao điểm của đường
thẳng AC với mặt phẳng (SBD) là điểm nào? A. Điểm B. B. Điểm A. C. Điểm O. D. Điểm S.
Câu 34. Cho hình chóp S.ABCD đáy là tứ giác lồi ABCD, giao tuyến của mặt (S AD) và (SBD) là A. SB. B. S A. C. SD. D. SC.
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm
AD và BC. Giao tuyến của hai mặt phẳng (SM N) và (S AC) là
A. SF (F là trung điểm CD).
B. SO (O là tâm hình bình hành ABCD).
C. SG (G là trung điểm AB). D. SD.
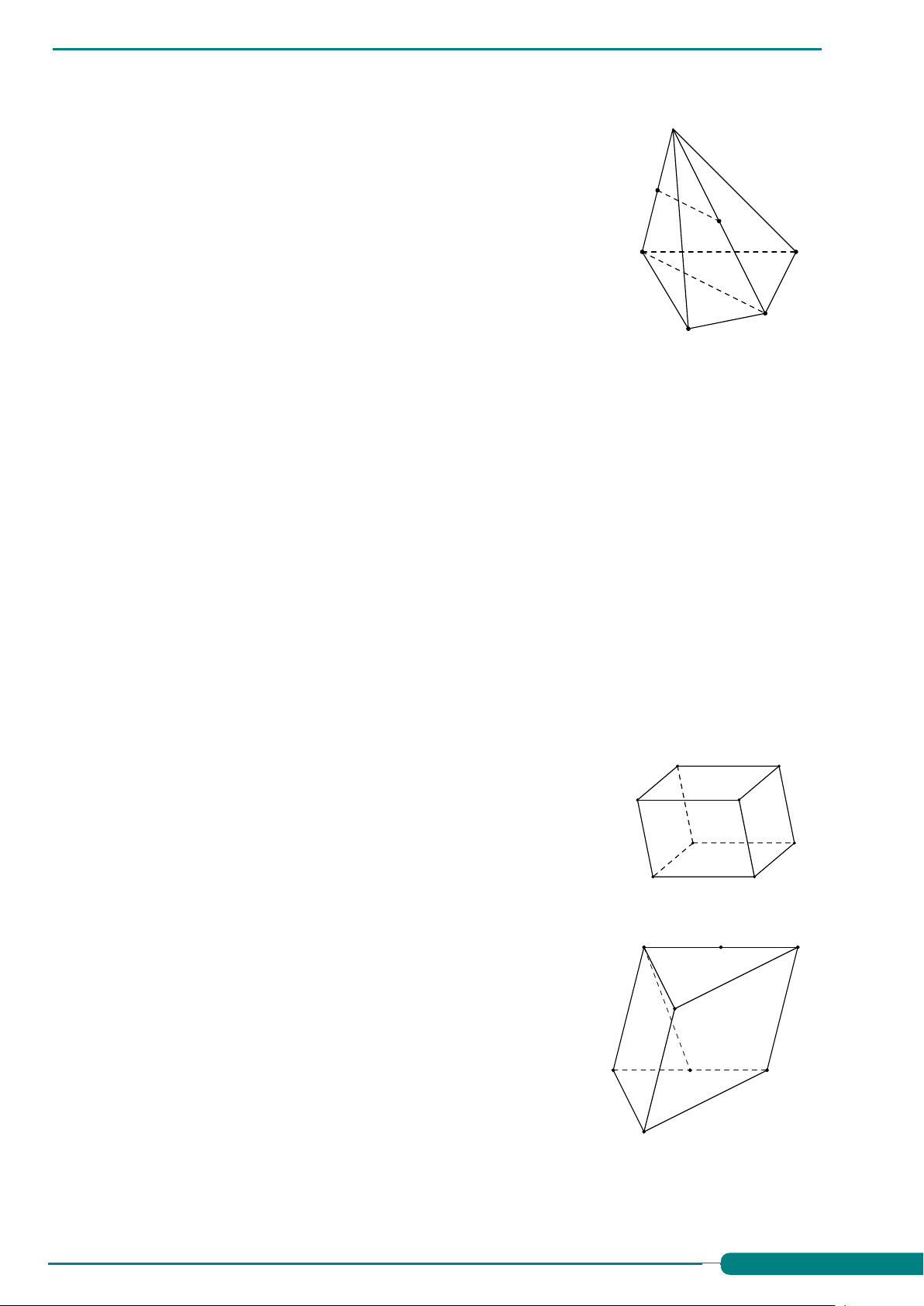
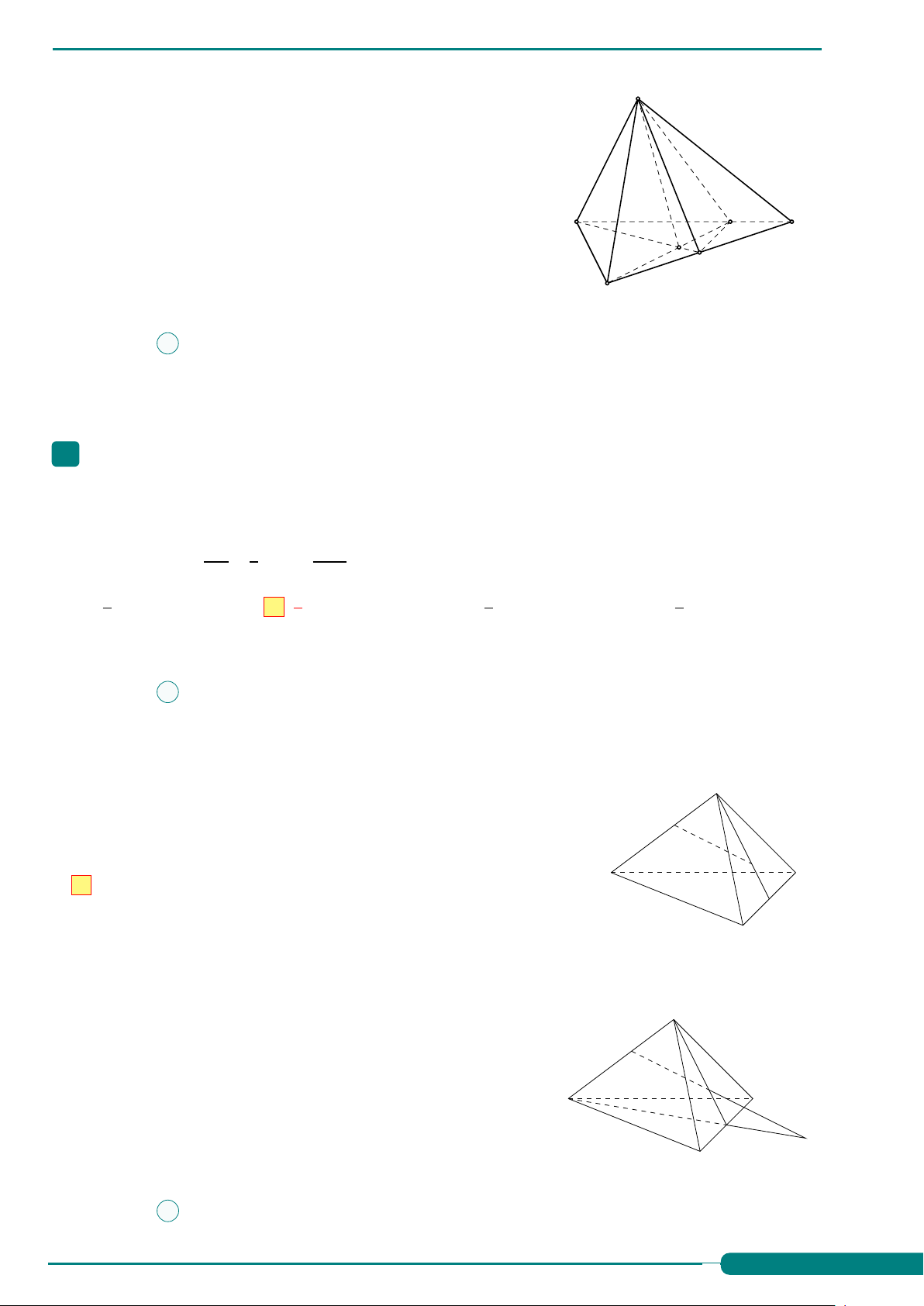
Câu 36. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và A
BC. Trên đoạn BD lấy P sao cho BP = 2PD. Khi đó giao điểm của đường
thẳng CD với mặt phẳng (MNP) là
A. giao điểm của NP và CD.
B. giao điểm của MN và CD. C. trung điểm của CD.
D. giao điểm của MP và CD. B D C
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi S
I, J, E, F lần lượt là trung điểm S A, SB, SC, SD. Trong các đường thẳng
sau, đường thẳng nào không song song với I J? A. EF. B. DC. C. AB. D. AD. D A B C
Câu 38. Cho hai đường thẳng song song a, b và mặt phẳng (P). Mệnh đề nào dưới đây đúng?
A. Nếu a ∥ (P) thì b ∥ (P) .
B. Nếu a cắt (P) thì b cắt (P).
C. Nếu a nằm trên (P) thì b ∥ (P).
D. Nếu a nằm trên (P) thì b nằm trên (P).
Câu 39. Cho hai mặt phẳng (P) và điểm A nằm ngoài mặt phẳng (P). Khẳng định nào sau đây đúng?
A. Qua A có vô số mặt phẳng song song với (P).
B. Qua A có đúng một mặt phẳng song song với (P).
C. Qua A không có mặt phẳng nào song song với (P).
D. Qua A có đúng hai mặt phẳng song song với (P).
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đường thẳng AD song song với
mặt phẳng nào trong các mặt phẳng dưới đây? A. (SBC). B. (ABCD). C. (S AC). D. (S AB). 11
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 41. Cho hình chóp tứ giác S.ABCD. Gọi M, N lần lượt là trung
điểm của S A và SC. Khẳng định nào sau đây đúng? S A. M N ∥ (ABCD). B. M N ∥ (S AB). C. M N ∥ (SBC). D. M N ∥ (SCD). M N A B C D
Câu 42. Nếu mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) lần lượt theo hai giao tuyến a
và b thì vị trí tương đối giữa hai đường thẳng a và b là A. song song. B. chéo nhau. C. trùng nhau. D. cắt nhau.
Câu 43. Cho đường thẳng a nằm trong mặt phẳng (α) và đường thẳng b nằm trong mặt phẳng (β).
Biết (α) ∥ (β). Trong các khẳng định sau, khẳng định nào sai? A. a ∥ (β). B. b ∥ (α). C. a ∥ b.
D. Nếu có một mặt phẳng (γ) chứa a và b thì a ∥ b.
Câu 44. Khẳng định nào sau đây là sai khi nói về hình lăng trụ?
A. Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.
B. Các mặt bên của hình lăng trụ là các hình bình hành.
C. Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.
D. Hai đáy của hình lăng trụ là hai đa giác đều.
Câu 45. Cho hình hộp ABCD.A0B0C0D0. Hình chiếu song song của A A0 D0
trên mặt phẳng (CDD0C0) theo phương BC0 là A. D0. B. D. B0 C0 C. B . D. C0. D A B C
Câu 46. Cho hình lăng trụ ABC.A0B0C0, gọi I, I0 lần lượt là trung I
điểm của AB, A0B0. Qua phép chiếu song song đường thẳng AI0, A B
hình chiếu của điểm I lên mặt phẳng chiếu (A0B0C0) là điểm nào sau đây? A. A0. B. I0. C C. B0. D. C0. A0 I0 B0 C0
Câu 47. Cho hình lăng trụ ABC.A1B1C1. Trong các khẳng định sau, khẳng định nào sai? A. (ABC) ∥ (A1B1C1). B. A A1 ∥ (BCC1). C. AB ∥ (A1B1C1).
D. A A1B1B là hình chữ nhật. 12
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
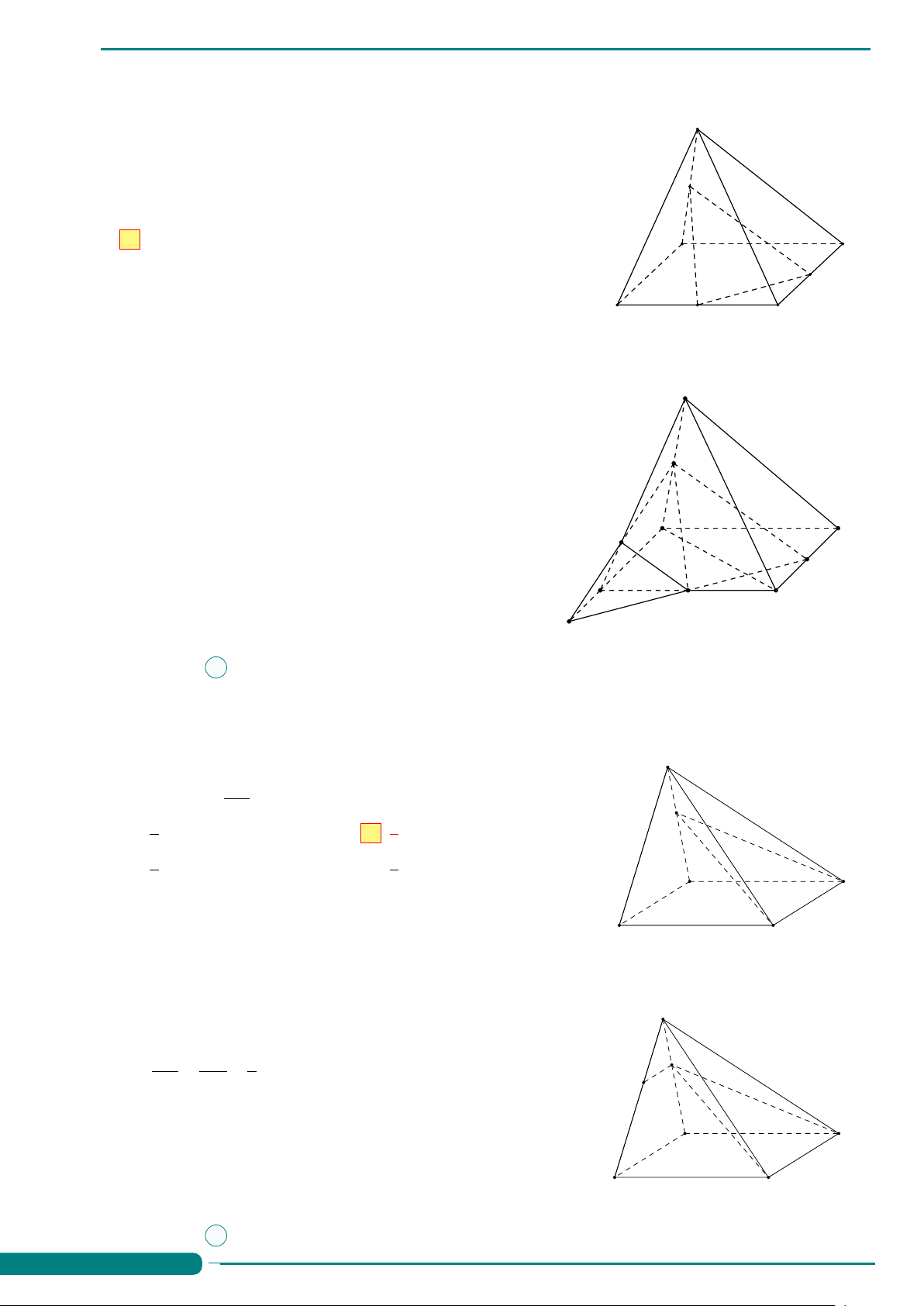
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành S
tâm O. Gọi M, N lần lượt là trung điểm của S A, AD. Hỏi mặt phẳng
(M NO) song song với mặt phẳng nào sau đây? A. (S AB). B. (SBC). C. (SCD). D. (S AD). M N A D O B C
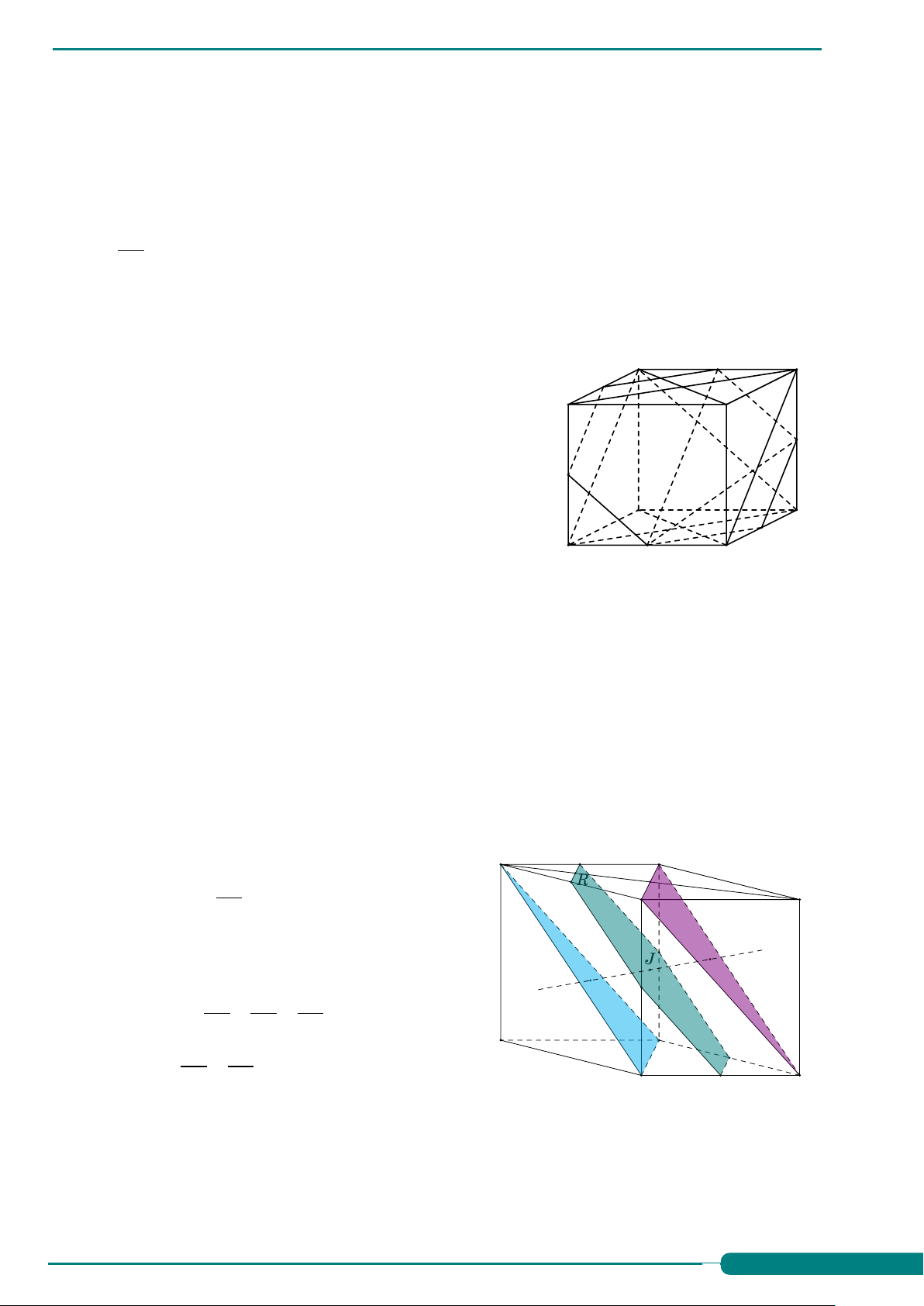
Câu 49. Cho hình hộp ABCD.A0B0C0D0. Mặt phẳng (AB0D0) song song A0 D0
với mặt phẳng nào sau đây? A. (BC A0). B. (BD A0). C. (A0C0C). D. (BDC0). B0 C0 D A B C
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng
(S AB) và (SCD) là đường thẳng song song với đường thẳng nào sau đây? A. BD . B. SC. C. AC. D. AB.
Câu 51. Cho hình chóp S.ABCD có AC cắt BD tại M, AB cắt S
CD tại N. Trong các đường thẳng sau đây, đường thẳng nào là
giao tuyến của (S AC) và (SBD) ? A. SM. B. SN. C. SB. D. SC. B A N M C D 2
Mức độ Vận dụng
Câu 52. Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng d cắt các mặt
phẳng (P),(Q),(R) lần lượt tại A, B, C. Đường thẳng d0 cắt các mặt phẳng (P),(Q),(R) lần lượt tại AB 2 A0B0 A0, B0, C0. Biết rằng = , tỷ số bằng AC 3 A0C0 1 2 3 1 A. . B. . C. . D. . 3 3 2 2
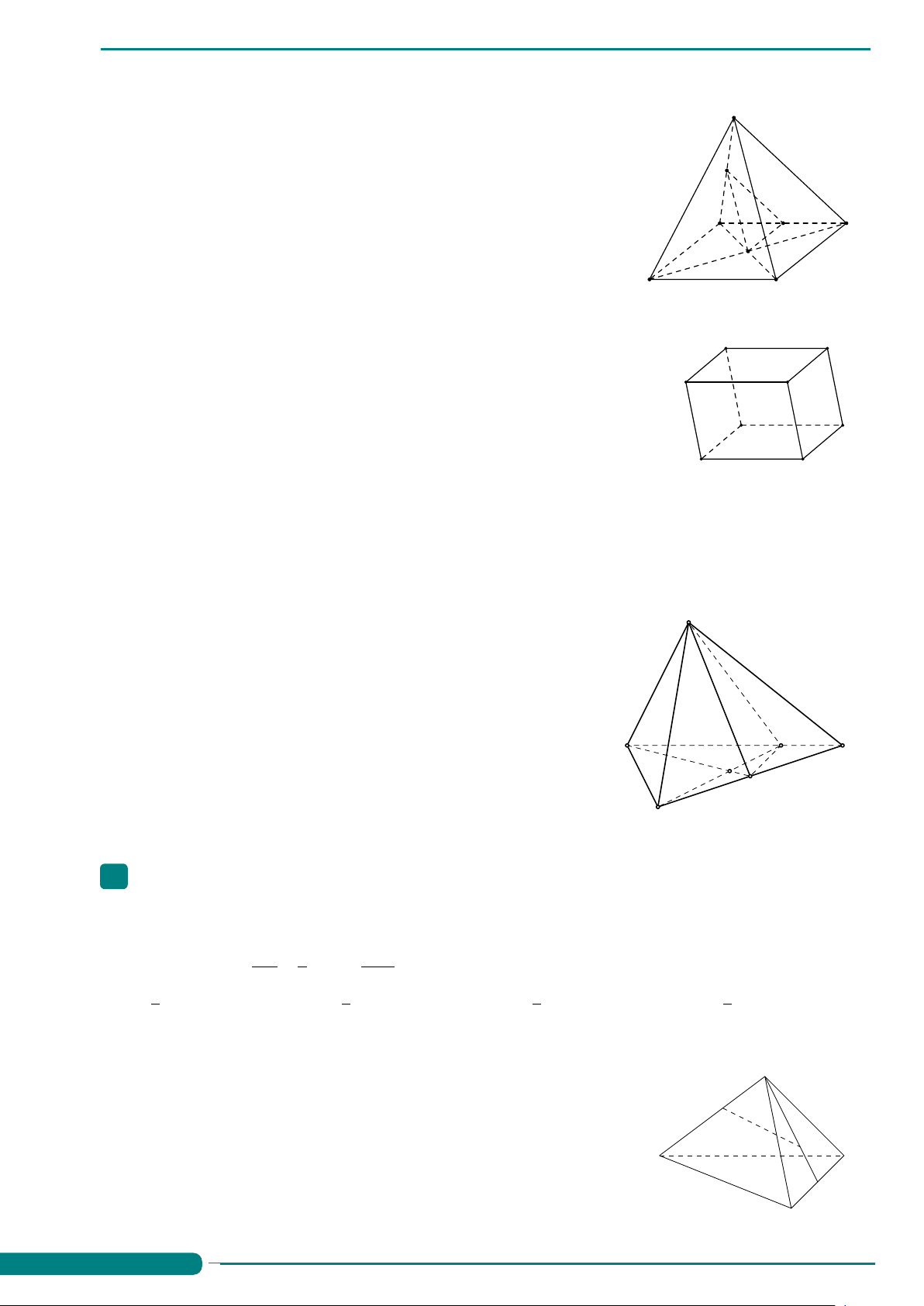
Câu 53. Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của B
AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường
thẳng EG và mặt phẳng (ACD) là E A. điểm F. G
B. giao điểm của đường thẳng EG và CD. A C
C. giao điểm của đường thẳng EG và AF.
D. giao điểm của đường thẳng EG và AC. F D 13
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
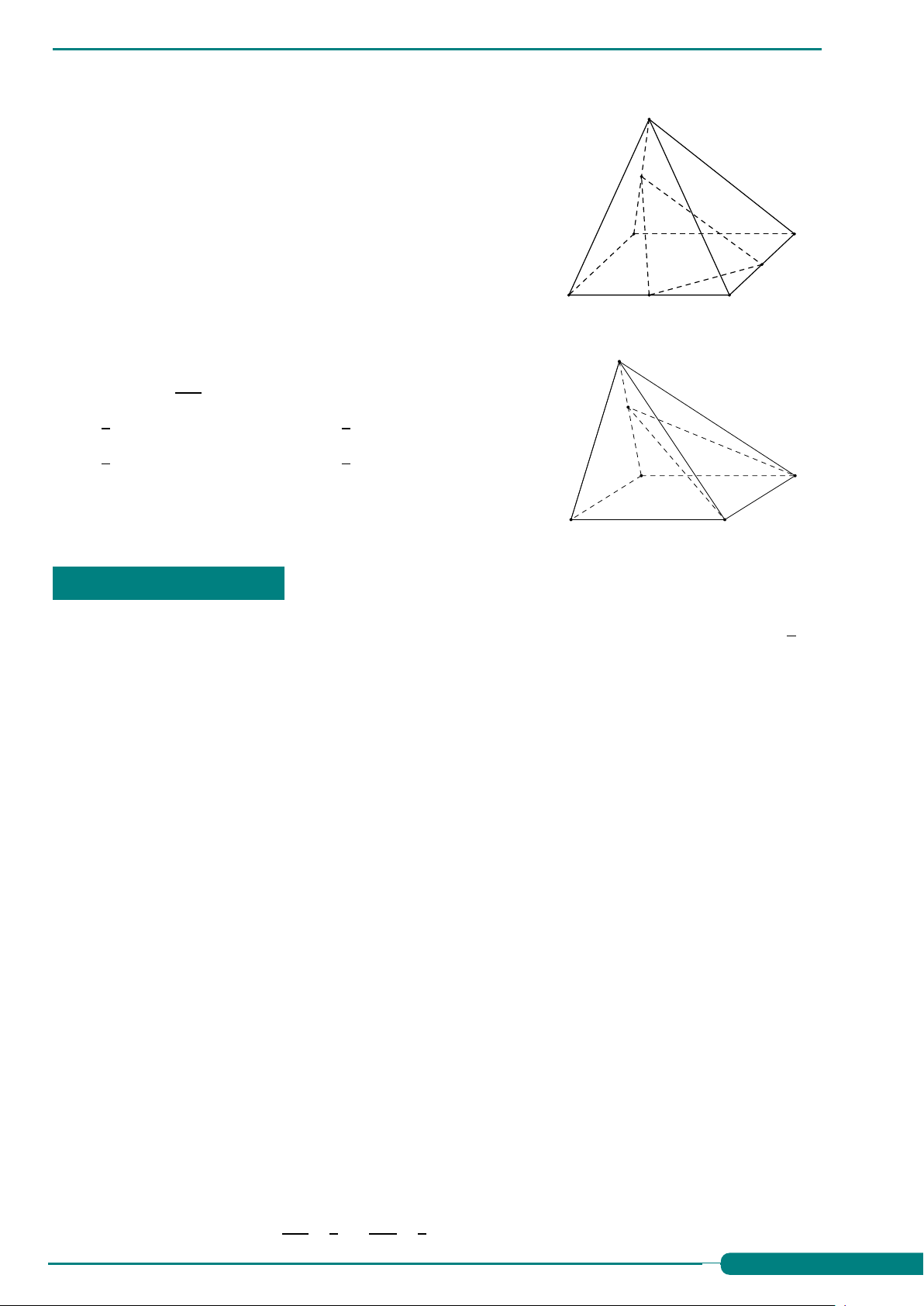
Câu 54. Cho hình chóp S.ABCD có đáy ABCD là hình bình S
hành. Gọi M, N, K lần lượt là trung điểm các cạnh DC, BC, S A.
Giao tuyến của (MNK) với (S AB) là đường thẳng K T, với T
được xác định theo một trong bốn phương án được liệt kê dưới K
đây. Khẳng định nào sau đây đúng.
A. T là giao điểm của MN với SB.
B. T là giao điểm của MN với AB. D
C. T là giao điểm của K N với AB. A
D. T là giao điểm của K N với SB. M B N C
Câu 55. Cho hình chóp S.ABCD có đáy là hình bình hành. Trên S
cạnh S A lấy điểm M sao cho M A = 2MS. Mặt phẳng (CDM) cắt SN SB tại N. Tỉ số bằng SB M 1 1 A. . B. . 2 3 2 3 C. . D. . 3 4 D A B C
B. BÀI TẬP TỰ LUẬN 1
BÀI 9. Cho tứ diện ABCD. Gọi E, F lần lượt là các điểm thuộc các cạnh AB, AC sao cho AE = BE 2
và AF = 2CF. Gọi O là một điểm nằm trong tam giác BCD.
a) Xác định giao tuyến của hai mặt phẳng (OEF) và (ABD).
b) Xác định giao điểm (nếu có) của đường thẳng AD và mặt phẳng (OEF).
BÀI 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là các
trung điểm của đoạn thẳng SC, S A và AB.
a) Tìm giao tuyến hai mặt phẳng (S AC) và (SBD).
b) Tìm tọa độ giao điểm của đường thẳng AM và mp(SBD).
c) Chứng minh MN song song với mặt phẳng (ABCD).
d) Chứng minh đường thẳng K N song song với mặt phẳng (SOD).
e) Chứng minh (KOM) song song với mặt phẳng (S AB).
f) Chứng minh K M song song với mặt phẳng (S AB).
BÀI 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao
cho AD = 3AM. Gọi G, N lần lượt là trọng tâm của các tam giác S AB, ABC. Chứng minh
a) Đường thẳng MN song song với mặt phẳng (SCD).
b) Đường thẳng GN song song với mặt phẳng (S AC).
c) Đường thẳng GM song song với mặt phẳng (SCD).
BÀI 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi hai điểm M, N lần lượt SN 1 SM 2
trên các cạnh SB, SC sao cho = và = . SC 2 SB 3 14
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
a) Chứng minh rằng BC song song mặt phẳng (S AD).
b) Xác định giao tuyến ∆ của hai mặt phẳng (AMN) và (ABCD).
c) Chứng minh rằng BD song song mặt phẳng (AMN). SP
d) Gọi P là giao điểm của SD và (AMN). Tính tỷ số . SD
e) Chứng minh rằng ba đường thẳng ∆, P N và CD đồng quy.
BÀI 13. Cho hình hộp ABCD A0B0C0D0. Gọi M, N, P lần lượt là trung điểm của AD, B0C0, DD0
a) Chứng minh rằng ADC0B là hình bình hành.
b) Chứng minh rằng BD ∥ AB0D0, MN ∥ AB0D0.
c) Chứng minh rằng (MNP) ∥ AB0D0 và BD ∥ (MNP).
d) Xác định giao tuyến của mặt phẳng (MNP) với các mặt của hình hộp.
e) Lấy một đường thẳng cắt ba mặt phẳng AB0D0, (MNP), C0BD lần lượt tại I, J, H. Tính tỉ I J số . J H
BÀI 14. Cho hình lăng trụ tam giác ABC.A0B0C0. Gọi M, N, P lần lượt là trung điểm của các cạnh A A0, AB, AC.
a) Chứng minh rằng BC ∥ (MNP).
b) Xác đinh giao tuyến d của hai mặt phẳng (MNP) và (A0B0C0).
c) Chứng minh rằng d ∥ NP. —HẾT— 15
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chương V.
GIỚI HẠN. HÀM SỐ LIÊN TỤC
A. BÀI TẬP TRẮC NGHIỆM 1
Mức độ Nhận biết, Thông hiểu
Câu 67. Cho c là hằng số, k là số nguyên
dương. Khẳng định nào sau đây sai?
Câu 56. Cho hai dãy số (un) và (vn), biết A. lim x = x0. B. lim c = c. lim u x x
n = a và lim vn = b. Trong các kết luận sau, →x0 →x0 c kết luận nào sai? C. lim = 0. D. lim c = +∞. x→+∞ xk x→+∞ A. lim(un + vn) = a + b. B. lim(u
Câu 68. Cho lim f (x) = −∞, kết quả của lim(−3· n − vn) = a − b. x→a x→a C. lim(unvn) = ab. f (x)) bằng un a D. lim = . A. −∞. B. 0. C. +∞. D. 3. vn b 1 1 1
Câu 69. Tính tổng S = 9+3+1+ + +···+ +
Câu 57. Cho các dãy số (un), (vn) và lim un = a, 3 9 3n−3 un · · · . lim v 27 n = +∞ thì lim bằng v A. S . B. S n = = 14. A. 2 +∞. B. 0. C. 1. D. −∞. C. S = 16. D. S = 15. Câu 58. lim 3n bằng n→+∞
Câu 70. Tổng của một cấp số nhân lùi vô hạn A. +∞. B. 0. C. −∞. D. 2.
bằng 2, tổng của ba số hạng đầu tiên của cấp số 2020 9 Câu 59. Tính lim . nhân bằng
. Số hạng đầu u1 của cấp số nhân n 4 A. +∞. B. −∞. C. 2020. D. 0. đó là 2n − 3 A. u1 = 3. B. u1 = 4. Câu 60. Tính lim . 9 1 − 3n C. u1 = . D. u1 = 5. 2 1 2 A. − . B. 2. C. . D. 1. 3 3
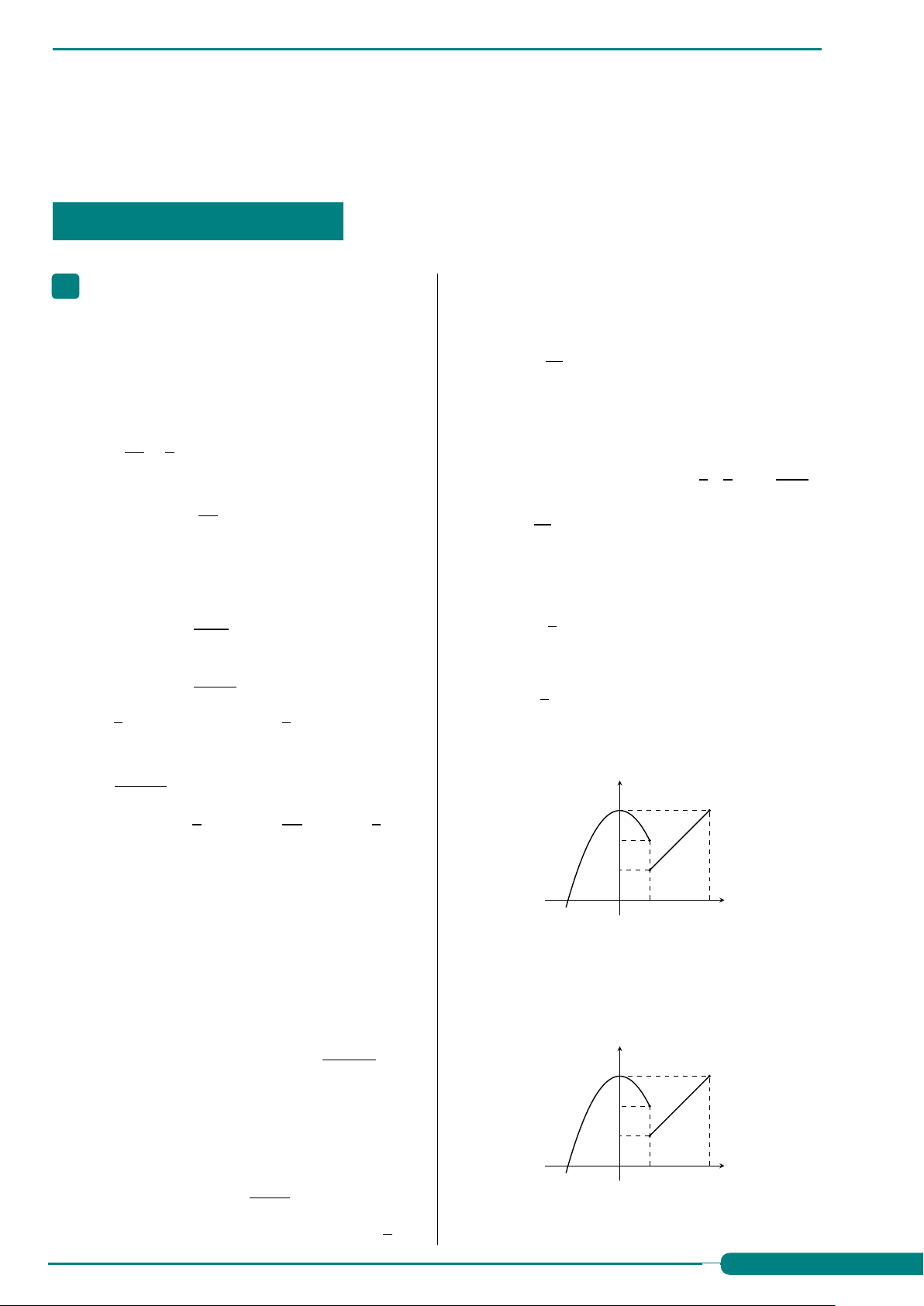
Câu 71. Cho hàm số y = f (x) có đồ thị như hình
Câu 61. Cho dãy số (u vẽ bên dưới.
n) có lim un = 2. Tính giới 3un − 1 y hạn lim . 2un + 5 3 3 −1 5 A. +∞. B. . C. . D. . 2 5 9 2
Câu 62. Biết lim f (x) = 3 và lim g(x) = −2. Tính x→1 x→1 1 lim[ f (x) + 2g(x)]. O x→1A. −1. B. 1. C. 5. D. −6. x 1 3
Câu 63. Biết lim f (x) = 4 và lim g (x) = 1. Tính Tính lim f (x) + lim f (x). x→1 x→1 x→1+ x→3− lim [4 f (x) + 3g (x)]. A. 5. B. 4 . C. 2. D. 0. x→1A. 11. B. 19. C. 10. D. 9.
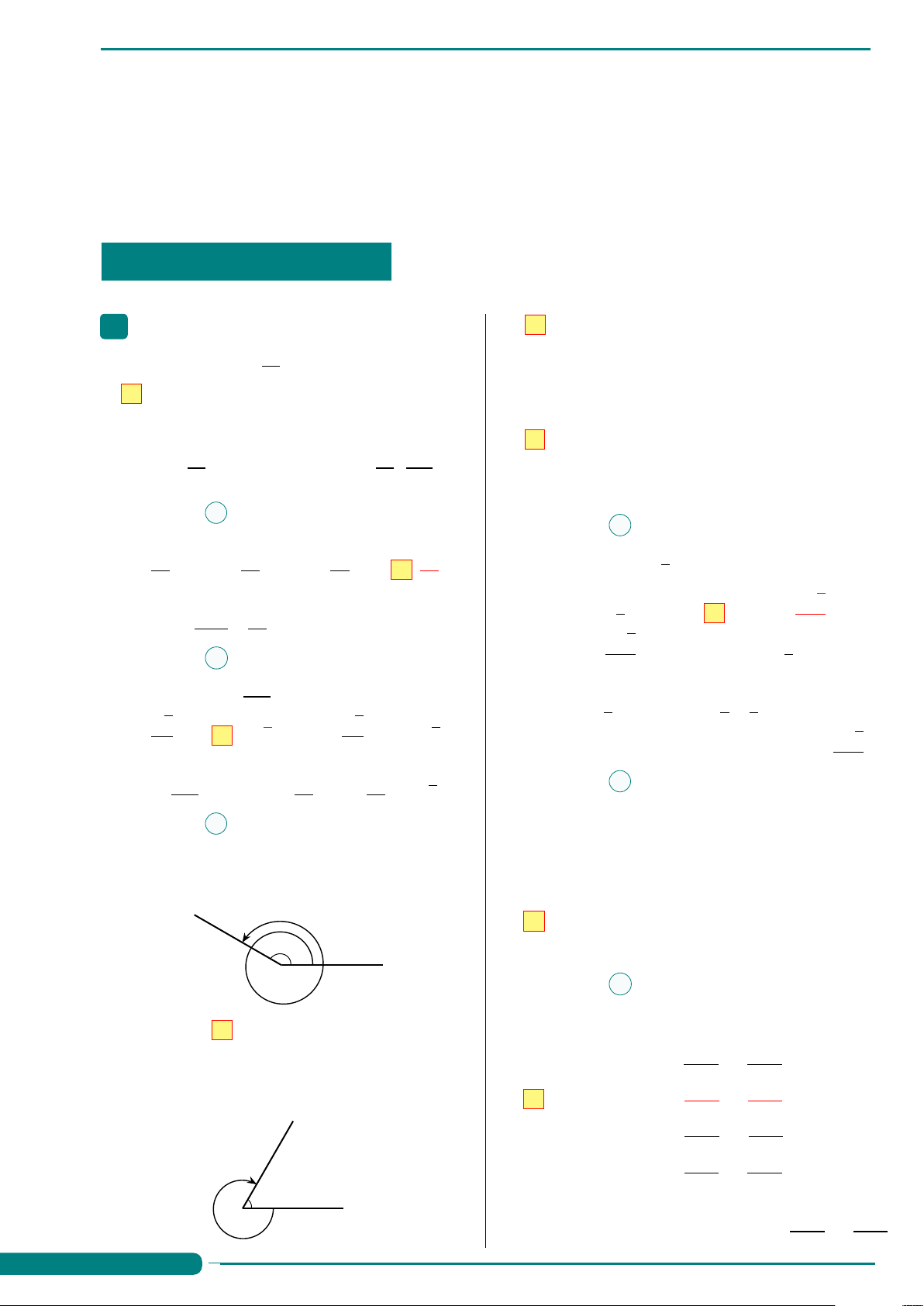
Câu 72. Cho hàm số y = f (x) có đồ thị như hình
Câu 64. Cho lim f (x) = 3. Tìm khẳng định vẽ bên dưới. x→2 sai. y A. lim[ f (x) p + 3] = 6. B. lim f (x) + 1 = 2. 3 x→2 x→2
C. lim[ f (x) − 2x] = −1. D. lim f (x) − x2 = 1. x→2 x→2 2
Câu 65. lim 3x2 + 7x + 11 có kết quả là 1 x→2 A. 37. B. 38. C. 39. D. 40. O x 1 3 x2 − 3
Câu 66. Giá trị của lim là x→−1 x3 + 2 Tính lim f (x) + lim f (x). 3 x→0 x→1− A. 1. B. −2. C. 2. D. − . A. 5. B. 4 . C. 2. D. 0. 2 16
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 73. Tính lim x3 − 2x + 1. 2
Mức độ Vận dụng x→1+ A. 1. B. 0. C. +∞. D. −∞. an + 4 p
Câu 81. Cho dãy số (un) với un = , với a Câu 74. Tính lim x − 3 − 3x + x2. 5n + 3 x→3−
là tham số thực. Để dãy số (un) có giới hạn bằng A. Không tồn tại. B. −∞. 2 thì giá trị của a là C. 0. D. +∞. A. a = 10. B. a = 8.
Câu 75. Trong các giới hạn sau đây, giới hạn C. a = 6. D. a = 4 . nào bằng 0? Câu 82. Cho số thực a thỏa mãn 3 + 2n3 2n2 − 3 p A. lim . B. lim . a 2x2 + 3 + 2017 1 2n2 − 1 −2n3 − 4 lim = . Khi đó giá trị của 2n − 3n3 2n2 − 3n4 x→+∞ 2x + 2018 2 C. lim . D. lim . a là p −2n2 − 1 −2n4 + n2 − 2 1 A. a = . B. a = .
Câu 76. Dãy số nào sau đây có giới hạn là 2 2 p +∞? −1 2 1 C. a . D. a . + n2 n2 − 2 = = A. u 2 2 n = . B. un = . 5n + 5 5n + 5n3  x2 + 1 n2 − 2n 1 + 2n  với x < 1 C. un = . D. .
Câu 83. Cho hàm số f (x) = 1 − x . 5n + 5n2 5n + 5n2 p  2x − 2 với x > 1
Câu 77. Dãy số nào sau đây có giới hạn là Khi đó lim f (x) là −∞? x→1− 1 + 2n n3 + 2n − 1 A. +∞. B. −1. C. 0. D. 1. A. . B. un = . p p 5n + 5n2 −n + 2n3 x2 + 6 − x 3 p p 2n2 − 3n4 n2 − 2n Câu 84. Cho lim p p = a 2 + b 3 + C. u x→−∞ n = . D. un = . x 2 − x2 + 3 n2 + 2n3 5n + 1 p
c 6 + d, (a, b, c, d ∈ Q). Tính ab + cd. Ä p ä
Câu 78. Giá trị lim n − n2 − 4n bằng A. 1. B. 0. C. −2. D. 2. A. 3. B. 1. C. 2. D. 4.
Câu 85. Tìm tất cả các giá trị thực của tham x2 − 3x + 2  x2 Câu 79. Tính lim . + x − 12  khi x 6= −4 x→1 x − 1 số m để hàm số f (x) = x + 4 A. 1. B. −∞. C. −1. D. +∞. mx + 1 khi x = −4
Câu 80. Tìm lim (4x4 − 3x2 + 2). liên tục tại điểm x x→−∞ 0 = −4. A. +∞. B. −∞. C. 4. D. 2.
A. m = 4. B. m = 2. C. m = 3. D. m = 5.
B. BÀI TẬP TỰ LUẬN
BÀI 15. Tính các giới hạn sau n2 + 1 2n + 3 a) lim . b) lim . n→+∞ 2n2 + n + 2 n→+∞ 1 + 3n Äp ä c) lim n2 + 2n − n . d) lim 2n3 + 2n − 1.
BÀI 16. Tính các giới hạn sau: x2 + 2x − 15 2x2 − 5x + 2 a) lim . b) lim . x→3 x − 3 x→2 x2 − 4 p1+2x−1 x − 2 c) lim . d) lim . x→0 2x x→1+ x − 1 Äp ä e) lim x2 + x − x . f) lim −x3 − x2 + 4x + 2. x→+∞ x→+∞
BÀI 17. Xét tính liên tục của mỗi hàm số sau tại điểm x = 2. ®6 − 2x khi x ≥ 2  x2 − 4 a) f (x) =  khi x 6= 2 2x2 − 6 khi x < 2; b) f (x) = x − 2 0 khi x = 2. 17
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
BÀI 18. Chứng minh rằng phương trình
a) x3 + 2x − 1 = 0 có nghiệm thuộc khoảng (−1;1). p b)
x2 + x + x2 = 1 có nghiệm thuộc khoảng (0;1).
BÀI 19. Trong hồ có chứa 6000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít
vào hồ với tốc độ 15 lít/phút.
a) Chứng tỏ rằng nồng độ muối của nước trong hồ sau t phút kể từ khi bắt đầu bơm là 30t C(t) = (gam/lít). 400 + t
b) Nồng độ muối trong hồ như thế nào nếu t → +∞.
BÀI 20. Từ độ cao 100 m, người ta thả một quả bóng cao su xuống đất. Giả sử cứ sau mỗi lần chạm 1
đất, quả bóng nảy lên một độ cao bằng
độ cao mà quả bóng đạt được trước đó. Gọi hn là độ cao quả 4
bóng đạt được ở lần nảy thứ n.
a) Tìm số hạng tổng quát của dãy số (hn).
b) Tính giới hạn của dãy số (hn) và nêu ý nghĩa giới hạn của dãy số (hn).
c) Gọi Sn là tổng độ dài quãng đường đi được của quả bóng từ lúc bắt đầu thả quả bóng đến khi
quả bóng chạm đất lần thứ n. Tính Sn, nếu quá trình này cứ tiếp tục diễn ra mãi thì tổng
quãng đường quả bóng di chuyển được là bao nhiêu? —HẾT— 18
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC MỤC LỤC Chương I.
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 3 A
BÀI TẬP TRẮC NGHIỆM............................................................................................3
} Mức độ Nhận biết, Thông hiểu..........................................................................3
} Mức độ Vận dụng .................................................................................................. 4 B
BÀI TẬP TỰ LUẬN.......................................................................................................5 Chương II.
DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN 8 A
BÀI TẬP TRẮC NGHIỆM............................................................................................8
} Mức độ Nhận biết, Thông hiểu..........................................................................8
} Mức độ Vận dụng .................................................................................................. 9 B
BÀI TẬP TỰ LUẬN .................................................................................................... 10
Chương III. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU GHÉP NHÓM 13 A
BÀI TẬP TRẮC NGHIỆM..........................................................................................13
} Mức độ Nhận biết, Thông hiểu........................................................................13
} Mức độ Vận dụng................................................................................................14 B
BÀI TẬP TỰ LUẬN .................................................................................................... 15
Chương IV. QUAN HỆ SONG SONG SONG TRONG KHÔNG GIAN 19 A
BÀI TẬP TRẮC NGHIỆM..........................................................................................19
} Mức độ Cơ bản.....................................................................................................19
} Mức độ Vận dụng................................................................................................26 B
BÀI TẬP TỰ LUẬN .................................................................................................... 28 Chương V.
GIỚI HẠN. HÀM SỐ LIÊN TỤC 32 A
BÀI TẬP TRẮC NGHIỆM..........................................................................................32
} Mức độ Nhận biết, Thông hiểu........................................................................32
} Mức độ Vận dụng................................................................................................34 B
BÀI TẬP TỰ LUẬN .................................................................................................... 35 ĐÁP ÁN CÁC TRẮC NGHIỆM 38
} Trắc nghiệm chương I.........................................................................................38
} Trắc nghiệm chương II........................................................................................38
} Trắc nghiệm chương III ...................................................................................... 38
} Trắc nghiệm chương IV......................................................................................38
} Trắc nghiệm chương V ....................................................................................... 38 1
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chương I.
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
A. BÀI TẬP TRẮC NGHIỆM 1
Mức độ Nhận biết, Thông hiểu A −300◦. B. 510◦. π C. 60◦. D. −420◦.
Câu 1. Góc có số đo đổi sang độ là 12
Câu 6. Chọn khẳng định đúng trong các khẳng A 15◦. B. 16◦. định sau: C. 14◦. D. 17◦300.
A. tan(π − α) = tanα.
B. cot(π − α) = cotα. Ê Lời giải.
C cos(π − α) = −cosα. D. sin(π − α) = −sinα. π π 180 ◦ Ê Ta có: α = rađian, suy ra α = · = Lời giải. 12 12 π
Theo công thức về cung liên kết, ta có cos(π 15◦. −α) = Chọn đáp án A − cos α. Chọn đáp án C
Câu 2. Góc có số đo 108◦ đổi sang radian là 3π 5π 5π 3π 1 A. . B. . C. . D .
Câu 7. Cho sin α =
, với 90◦ < α < 180◦. Tính 2 2 3 5 3 cos α. Ê p Lời giải. 2 2 2 π 3π A. cos α = − . B cos α = − . Ta có: 108◦ · = . 3 3 p 180◦ 5 2 2 2 Chọn đáp án D C. cos α = . D. cos α = . 3 3 89π Ê Lời giải. Câu 3. Giá trị cot bằng 1 1 8 6 p p Ta có sin α = ⇒ cos2 α = 1 − = . 3 p 3 p 3 9 9 A. . B p − 3. C. − . D. 3. 3 3 2 2
Vì 90◦ < α < 180◦ nên cosα < 0 do đó cosα = − . Ê Lời giải. 3 89π 5π 5π p Chọn đáp án B Ta có cot = cot 14π + = cot = − 3. 6 6 6
Câu 8. Trong các mệnh đề sau, mệnh đề nào là Chọn đáp án B mệnh đề đúng?
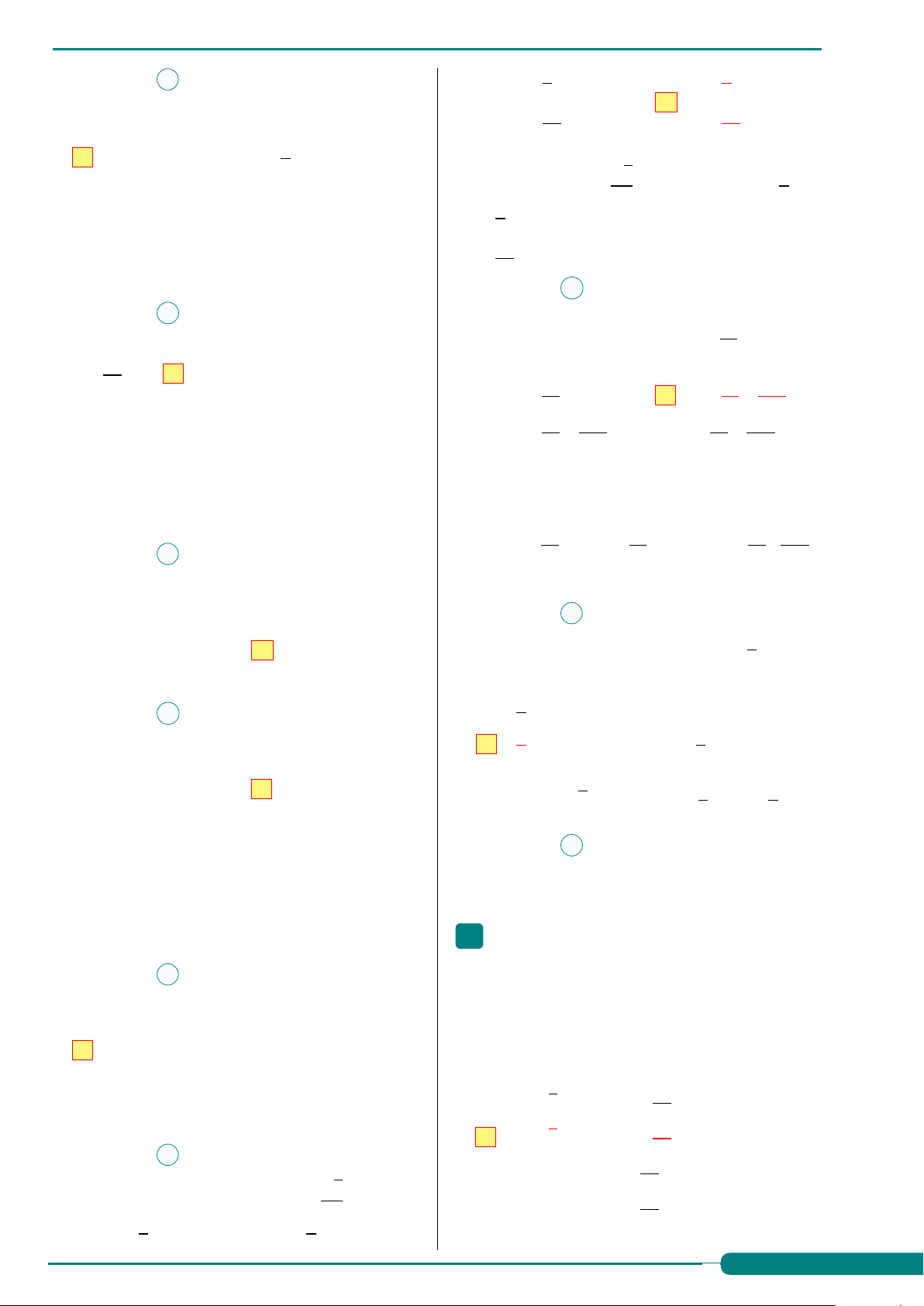
Câu 4. Xác định số đo của góc lượng giác A. sin 2a = sin a + cos a.
(Ou, Ov) được biểu diễn trong hình bên dưới. B. sin 2a = 2sin a. v C. sin 2a = cos2 a − sin2 a. D sin 2a = 2sin a cos a. 150◦ Ê Lời giải.
Hiển nhiên, sin 2a = 2sin a cos a là đúng. O u Chọn đáp án D
Câu 9. Trong các mệnh đề sau, mệnh đề nào là A. 410◦. B 510◦. C. 150◦. D. 420◦. mệnh đề sai?
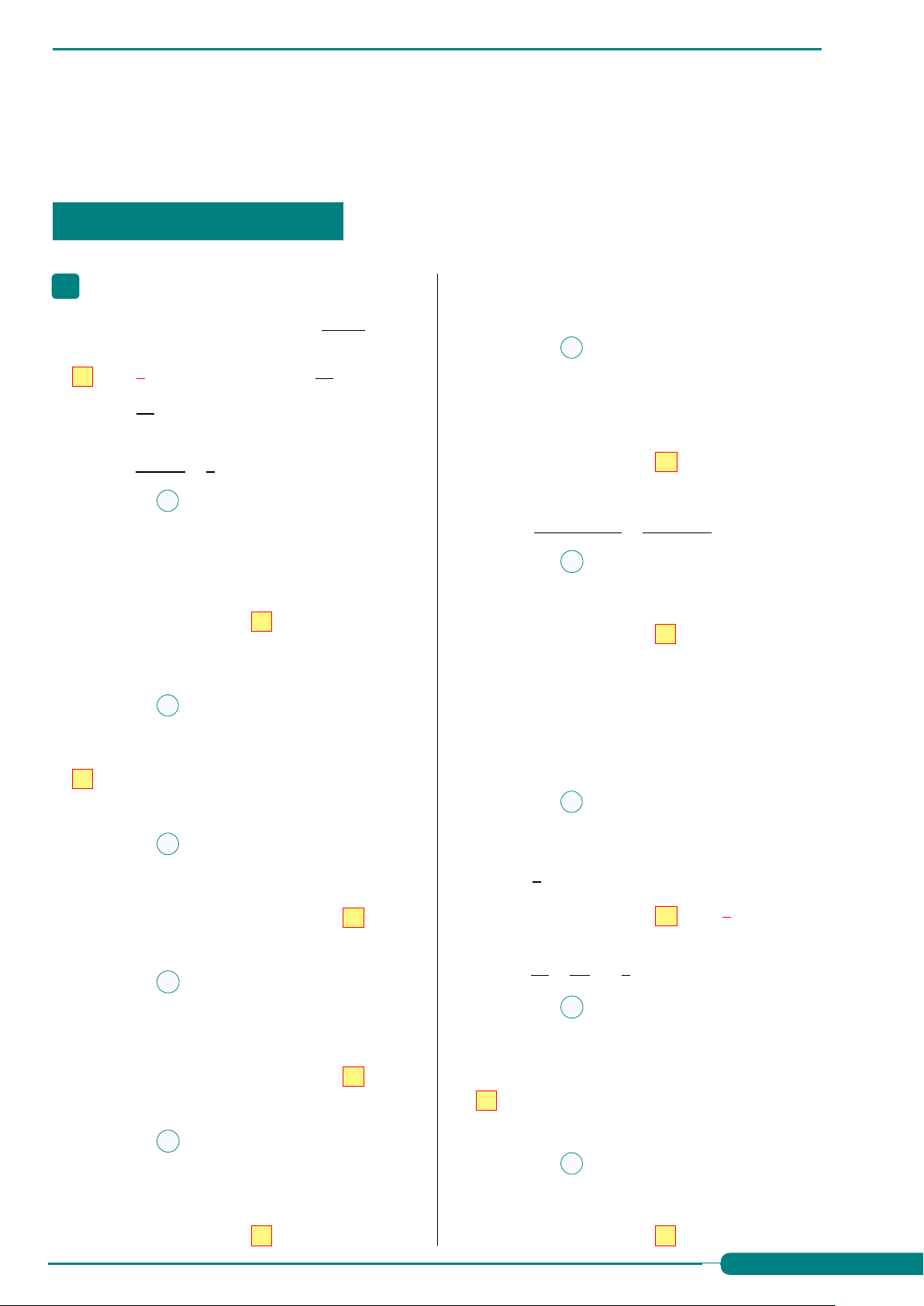
Câu 5. Xác định số đo của góc lượng giác a + b a − b A. sin a + sin b = 2sin cos .
(Ou, Ov) được biểu diễn trong hình bên dưới 2 2 a + b a − b B cos a − cos b = 2sin sin . v 2 2 a + b a − b C. cos a + cos b = 2cos cos . 2 2 a + b a − b D. sin a − sin b = 2cos sin . 2 2 60◦ Ê Lời giải. O u a + b a − b
Công thức đúng là cos a−cos b = −2sin sin . 2 2 3
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC  ππ Chọn đáp án B x = + kπ x = + k2π 6 3 C.  . D  .
Câu 10. Chu kỳ của hàm số y = cot x là  5π  2π x = + kπ x = + k2π A. kπ, k ∈ Z. B. 2π. 6 3 π Ê C π. D. . Lời giải. p 2 3 π Ê Lời giải. Ta có sin x = ⇔ sin x = sin ⇔ 2 3
Tập xác định của hàm số: D = R\{kπ, k ∈ Z}.  π x = + k2π
Với mọi x ∈ D, k ∈ Z ta có x− kπ ∈ D và x+ kπ ∈ D, 3  (k ∈ Z). cot(x + kπ) = cot x.  2π x = + k2π
Vậy y = cot x là hàm số tuần hoàn với chu kì π là 3
số dương nhỏ nhất thỏa cot(x + kπ) = cot x. Chọn đáp án D Chọn đáp án C π có nghiệm
Câu 11. Chu kỳ của hàm số
Câu 16. Phương trình cos 3x y = cos x là = cos 15 2π là A. . B 2π. C. π. D. k2π. 3 π π k2π Ê A. x . Lời giải. = ± + k2π. B x = ± + 15 45 3
Tập xác định của hàm số: D π k2π π k2π = R. C. x = − + . D. x = + .
Với mọi x ∈ D, k ∈ Z ta có x − k2π ∈ D và x + k2π ∈ 45 3 45 3 Ê Lời giải.
D, cos(x + k2π) = cos x. Ta có
Vậy y = cos xlà hàm số tuần hoàn với chu kì
2π(ứng với k = 1) là số dương nhỏ nhất thỏa cos(x + k2π) = cos x. π π π k2π cos3x = cos ⇔ 3x = ± +k2π ⇔ x = ± + (k ∈ Z). Chọn đáp án B 15 15 45 3
Câu 12. Tập giá trị của hàm số y = cos x là tập hợp nào sau đây? Chọn đáp án B A. [0; +∞]. B. R. C. (−∞;0]. D [−1;1]. p
Câu 17. Giải phương trình tan x = 3 ta được Ê Lời giải. tập nghiệm là
Với mọi x ∈ R thì −1 ≤ cos x ≤ 1. n π o Chọn đáp án D A. + k2π, k ∈ Z . B. ∅. 3 n π o n π o
Câu 13. Giá trị nhỏ nhất m và giá trị lớn nhất C + kπ, k ∈ Z . D. + kπ, k ∈ Z . 3 6
M của hàm số y = 3sin2x − 5 lần lượt là Ê Lời giải. A. m = 2, M = 8. B m = −8, M = −2. p π π Ta có tan x = 3 ⇔ tan x = tan ⇔ x = + kπ, C. m = −5, M = −2. D. m = −8, M = −5. 3 3 Ê Lời giải. (k ∈ Z).
Ta có: −1 ≤ sin2x ≤ 1 ⇔ −3 ≤ 3sin2x ≤ 3. Chọn đáp án C
⇔ −3−5 ≤ 3 sin 2x−5 ≤ 3−5 ⇔ −8 ≤ y = 3 sin 2x−5 ≤ −2.
Vậy giá trị nhỏ nhất và giá trị lớn nhất của hàm 2
Mức độ Vận dụng
số đã cho lần lượt là −8 và −2. Chọn đáp án B
Câu 18. Cho hai dao động điều hòa cùng
Câu 14. Phương trình cos x = a có nghiệm khi
phương có phương trình lần lượt là x1 = và chỉ khi
5 cos(100πt + π)(cm) và x2 = 5cos(100πt − π/2)(cm). A |a| ≤ 1. B. |a| > 1.
Phương trình dao động tổng hợp của hai dao C. |a| < 1. D. |a| ≥ 1. động trên là Ê Lời giải. p 3π A. x = 5 2cos 100πt + (cm).
Vì |cos x| ≤ 1,∀x ∈ R nên phương trình cos x = a có 4 p 3π
nghiệm khi và chỉ khi |a| ≤ 1. B x = 5 2cos 100πt − (cm). Chọn đáp án A 4 3π p C. x = 10cos 100πt − (cm). 3 4
Câu 15. Giải phương trình sin x = . 3π 2 D. x = 10cos 100πt + (cm). π π 4 A. x = ± + k2π. B. x = + kπ. Ê Lời giải. 3 3 4
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Ta có Chọn đáp án D x = x 1 + x2
= 5 cos(100πt + π) + 5 cos(100πt − π/2)
= 5 [cos(100πt + π) + cos(100πt − π/2)]
Câu 20. Nhiệt độ ngoài trời ở một thành phố π 3π
vào các thời điểm khác nhau trong ngày có thể = 5 · 2cos 100πt + cos 4 4
được mô phỏng bởi công thức p π = −5 2 cos 100πt + h π i 4 h(t) = 29 + 3sin (t − 9) p 12 3π = 5 2 cos 100πt − . 4
với h tính bằng độ C và t là thời gian trong ngày
tính bằng giờ. Nhiệt độ thấp nhất trong ngày Chọn đáp án B vào lúc mấy giờ? A. 5 giờ . B. 0 giờ . C 3 giờ. D. 4 giờ.
Câu 19. Cho hình vuông D C Ê Lời giải. ABCD như hình vẽ. Tính
Nhiệt độ thấp nhất trong ngày là 26◦, xảy ra khi
giá trị của tan α. 7 4 6 h π i π −π A. . B. . sin (t − 9) = −1 ⇔ (t−9) =
+k2π ⇔ t = 3+24k, k ∈ Z 13 13 E 12 12 2 9 7 C. . D . α 5 13 17 A B
Do t là thời gian trong ngày tính bằng giờ nên Ê Lời giải. 0 ≤ t ≤ 24. Suy ra: t = 3 Đặt Chọn đáp án C B AE = β, D C suy ra tan β = BE 5 = và α = AB 12 45◦ − β. Ta có 7 5 1 E 1 − tanβ − 12 7
tan α = tan 45◦ − β = = . 1 + tanβ = 5 17 α 5 1 + β 12 A B
B. BÀI TẬP TỰ LUẬN
BÀI 1. Giải các phương trình lượng giác sau: p p 2 π 3 a) sin x = − ; b) sin 3x + = ; 2 6 2 p3 c) cos 2x = ; d) cos(2x − 30◦) = −1; 2 π π p e) tan 3x = tan ; f) cot 2x − = 3. 7 5 Ê Lời giải. π p π  x x = − + k2π 2 = − + k2π π 4 4 sin x = − ⇔ sin x = sin − ⇔   ⇔ , k ∈ Z. 2 4 π  5π x = π − − + k2π x = + k2π 4 4 π 5π
Vậy phương trình có các nghiệm là x = − + k2π và x = + k2π với k ∈ Z. 4 4  p π π π 2π 3x + = + k2π x = + k π 3 π π 6 3 18 3 sin 3x + = ⇔ sin 3x + = sin ⇔   , k ∈ Z. 6 2 6 3 π ππ 2π 3x + = π − + k2π x 6 3 = + k 6 3 p3 π π cos2x = ⇔ cos 2x = cos
⇔ x = ± + kπ, k ∈ Z. 2 6 6 π
Vậy phương trình có nghiệm là x = ± + kπ, k ∈ Z. 6 5
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
cos(2x − 30◦) = −1 ⇔ 2x − 30◦ = 180◦ + k360◦ ⇔ x = 105◦ + k180◦, k ∈ Z π π π π
tan3x = tan ⇔ 3x = + kπ ⇔ x = + k , k ∈ Z. 7 7 21 3 π π
Vậy phương trình có nghiệm là x = + k , k ∈ Z. 21 3 π p π π π π 11π π cot 2x − = 3 ⇔ cot 2x − = cot ⇔ 2x − = + kπ ⇔ x = + k , k ∈ Z. 5 5 6 5 6 60 2 11π π
Vậy phương trình có nghiệm là x = + k , k ∈ Z. 60 2
BÀI 2. Số giờ có ánh nắng mặt trời của một thành phố A trong ngày thứ t (ở đây t là số ngày tính từ
ngày 1 tháng Giêng) của một năm không nhuận được mô hình hóa bởi hàm số h 2π i L(t) = 12 + 2,83sin
(t − 80) với t ∈ Z và 0 < t ≤ 365. 365
a) Vào ngày nào trong năm thì thành phố A có ít giờ ánh sáng mặt trời nhất?
b) Vào ngày nào trong năm thì thành phố A có nhiều giờ ánh sáng mặt trời nhất?
c) Vào ngày nào trong năm thì thành phố A có khoảng 10 giờ ánh sáng mặt trời? Ê Lời giải. a) Với mọi x ∈ R, ta có h 2π i h 2π i −1 ≤ sin
(t − 80) ≤ 1 ⇔ −2,83 ≤ 2,83sin (t − 80) ≤ 2,83 365 365 h 2π i ⇔ 9,17 ≤ 12 + 2,83 sin (t − 80) ≤ 14,83. 365
Ngày thành phố A có ít giờ ánh sáng mặt trời nhất ứng với h 2π i 2π π 45 sin (t − 80) = −1 ⇔
(t − 80) = − + k2π ⇔ t = − + 365k, (k ∈ Z). 365 365 2 4 45
Vì 0 < t ≤ 365 nên k = 1, suy ra t = − + 365 = 353,75. 4
Như vậy, vào ngày thứ 353 của năm, tức là khoảng ngày 20 tháng 12 thì thành phố A sẽ có ít
giờ ánh sáng mặt trời nhất.
b) Ngày thành phố A có nhiều giờ ánh sáng mặt trời nhất ứng với h 2π i 2π π sin (t − 80) = 1 ⇔ (t − 80) =
+ k2π ⇔ t = 171,25 + 365k, (k ∈ Z). 365 365 2
Vì 0 < t ≤ 365 nên k = 0, suy ra t = 171,25.
Như vậy, vào ngày thứ 171 của năm, tức là khoảng ngày 20 tháng 6 thì thành phố A sẽ có nhiều
giờ ánh sáng mặt trời nhất.
c) Ngày thành phố A có 10 giờ ánh sáng mặt trời nhất ứng với h 2π i h 2π i 200 12 + 2,83sin (t − 80) = 10 ⇔ sin (t − 80) = − 365 365 283
 2π (t−80) ≈ −0,78+k2π 365 ⇔ 
 2π (t−80) ≈ 3,93+k2π 365 ñt ≈ 34,69 + 365k ⇔ (k ∈ Z). t ≈ 308,30 + 365k
Vì 0 < t ≤ 365 nên k = 0, suy ra t ≈ 34,69 hoặc t ≈ 308,30.
Như vậy, vào ngày thứ 34 của năm, tức là khoảng ngày 3 tháng 2 và ngày thứ 308 của năm,
tức là ngày 4 tháng 11 thì thành phố A sẽ có 10 giờ ánh sáng mặt trời. 6
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
BÀI 3. Chiều cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển π π
động được cho bởi công thức h(t) = 30 + 20sin t + . 25 3
a) Cabin đạt độ cao tối đa là bao nhiêu?
b) Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên? Ê Lời giải. π π π π a) Vì sin t +
≤ 1, ∀t nên h(t) = 30 + 20 sin t + ≤ 50 (m). 25 3 25 3
b) Để cabin đạt độ cao 40 m thì  π π π  25 t + = + k2π t = − + 50k π π π π 1 25 3 6 6 h(t) = 40 ⇔ 20sin t + = 10 ⇔ sin t + = ⇔  ⇔  , k ∈ Z. 25 3 25 3 2  π π 5π  25 t + = + k2π t = + 50k 25 3 6 2
Dễ thấy, giá trị t > 0 nhỏ nhất thoả mãn là t = 12,5 (giây). 7
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chương II.
DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN
A. BÀI TẬP TRẮC NGHIỆM 1
Mức độ Nhận biết, Thông hiểu C. u50 = 104. D. u50 = 198. Ê Lời giải. 2n − 1
Câu 1. Cho dãy số (u Ta có u n) có un = . Tính
50 = u1 + 49d = 4 + 49 · 2 = 102. n + 1 u Chọn đáp án B 8. 5 11 A u8 = . B. u8 = .
Câu 7. Cho cấp số cộng (u 3 9 n) có số hạng đầu 17
u1 = 3 và d = −2. Tổng của 20 số hạng đầu của C. u8 = . D. u8 = 1. 9 cấp số cộng đó là Ê Lời giải. A. S20 = −380. B. S20 = −214. 2 · 8 − 1 5 C. S Ta có u 20 = −640. D S20 = −320. 8 = = . 8 + 1 3 Ê Lời giải. Chọn đáp án A
Ta có u20 = u1 + 19d = 3 + 19 · (−2) = −35. 20 (u1 + u20) 20(3 − 35) Câu 2. Cho dãy số (un) xác định bởi Vậy S20 = = = −320. ® 2 2 u1 = 3
. Ba số hạng đầu tiên của dãy Chọn đáp án D un+1 = un + 5
Câu 8. Dãy số nào sau đây không phải là cấp số đó là số nhân? A. −3;6;9. B 3; 8; 13. A. 1, C. 3; 5; 7. D. 3; −1, 1, −1, 1. B 1, 2, 3, 4, 5. −2; −7. Ê C. 1, Lời giải. −2, 4, −8, 16. D. 1, 2, 4, 8, 16. Ê Lời giải.
Ta có u1 = 3, u2 = 3 + 5 = 8, u3 = 8 + 5 = 13.
Dãy 1, 2, 4, 8, 16 là CSN với công bội q Chọn đáp án B = 2.
Dãy 1, −1,1,−1,1 là CSN với công bội q = −1.
Câu 3. Dãy nào sau đây là cấp số cộng?
Dãy 1, −2,4,−8,16 là CSN với công bội q = −2. A. 1; 5; 9; 5; 1. B. 1; 3; 5; 7; 11.
Dãy 1, 2, 3, 4, 5 là CSC với công sai d = 1. C 2; 5; 8; 11. D. 3; 7; 3; 7. Ê Lời giải. Chọn đáp án B
Dãy số là cấp số cộng là 2; 5; 8; 11.
Câu 9. Cho cấp số nhân (un), biết u1 = −9, u2 = Chọn đáp án C 3. Công bội q là
Câu 4. Cho cấp số cộng 1, 8, 15, 22, 29, . . .. Công 1 A. q = . B. q = −3.
sai của cấp số cộng này là 3 1 A. 9. B. 1. C. 8. D 7. C. q = 3. D q = − . 3 Ê Lời giải. Ê Lời giải.
Công sai d = u2 − u1 = 8 − 1 = 7. u2 3 1 Ta có q . Chọn đáp án D = = = − u1 −9 3
Câu 5. Cho cấp số cộng (u Chọn đáp án D n) có số hạng đầu
u1 = 3 và d = 2. Số hạng thứ 2 của cấp số cộng
Câu 10. Cho cấp số nhân (un), biết u1 = 3 và đã cho là công bội q = −2. Tìm u3. A. 3. B. 6. C. 1. D 5. A. u3 = 16. B. u3 = 14. Ê Lời giải. C u3 = 12. D. u3 = 11.
Ta có u2 = u1 + d = 3 + 2 = 5. Ê Lời giải. Chọn đáp án D
Ta có u3 = u1 · q2 = 3 · (−2)2 = 12. Chọn đáp án C
Câu 6. Cho cấp số cộng (u n) có số hạng đầu
u1 = 4 và d = 2. Số hạng thứ 50 của cấp số cộng
Câu 11. Cho cấp số nhân (un) với u1 = 2 và đó là
q = −3. Khi đó, số hạng u6 bằng A. u50 = 100. B u50 = 102. A. −3 · 25. B 2 · (−3)5. 8
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC C. −3 · 26. D. 2 · (−3)6.
đó đã bỏ ra và mất trong 9 lần đầu là Ê Lời giải. 1 Ta có u − 29 6 = u1 · q5 = 2 · (−3)5. S9 = 20000 · = 10 220 000 (đồng). Chọn đáp án B 1 − 2
Số tiền người đó bỏ ra ở lần thứ 10 là
Câu 12. Cho cấp số nhân (un) có số hạng đầu
u1 = 3 và công bội q = 2. Tổng S10 = u1 + u2 + u3 +
u10 = 20000 · 210−1 = 10240000 (đồng). · · · + u10 bằng 1023
Du khách thắng ở lần thứ 10. Người đó bỏ ra A. . B. 1023. C. 1536. D 3069. 2
và nhận lại gấp đôi nghĩa là người đó lãi được Ê Lời giải. 10 240 000 (đồng). q10 − 1
Vậy thì người đó đã thắng 20 000 đồng. S10 = u1 · = 3(210 − 1) = 3069. Chọn đáp án A q − 1 Chọn đáp án D
Câu 15. Một gia đình cần khoan một cái giếng
để lấy nước. Họ thuê một đội khoan giếng nước
đến để khoang giếng. Biết giá của mét khoan 2
Mức độ Vận dụng
đầu tiên là 80 000 đồng, kể từ mét khoan thứ hai
giá của mỗi mét khoan tăng thêm 5000 đồng so
Câu 13. Một người muốn chia 1000 · 000 đồng
với giá của mét khoan trước đó. Biết cần phải
cho bốn người con, đứa lớn hơn đứa nhỏ kế tiếp
khoan sâu xuống 50 m mới có nước. Hỏi phải
100 · 000 đồng. Hỏi đứa con lớn nhất được bao
trả bao nhiêu tiền để khoan cái giếng đó? nhiêu tiền. A. 4 245 000 đồng. B. 5 250 000 đồng. C. 4 000 000 đồng. D 10 125 000 đồng. A 400 · 000 đồng. B. 200 · 000 đồng. Ê Lời giải. C. 100 · 000 đồng. D. 300 · 000 đồng. Ê Lời giải.
Số tiền phải trả ở mỗi mét khoan tạo thành một
cấp số cộng có số hạng đầu u
Số tiền của bốn người con theo thứ tự từ đứa 1 = 80 000 và công sai d
lớn nhất đến đứa nhỏ nhất lập thành cấp số = 5000.
Như vậy, tổng số tiền khi khoan đến mét thứ n
cộng với công sai d = −100 · 000 đồng. Tổng số
được tính theo công thức
tiền 4 người con là 1000 · 000 đồng.
Gọi số tiền của đứa con lớn nhất là x, ta có n 4 Sn = [2u1 + (n − 1)d].
(2x + 3d) = 1000 · 000 ⇔ 2(2x − 300 · 000) = 1000 · 2 2 000 ⇔ x = 400 · 000.
Vậy tổng số tiền phải trả là
Vậy đứa con lớn nhất được 400 · 000 đồng. Chọn đáp án A
S50 = 25 · (2 · 80000 + 49 · 5000) = 10125000.
Câu 14. Một du khách vào trường đua ngựa Chọn đáp án D
xem đua ngựa và đặt cược chọn con thắng cuộc.
Câu 16. Chu kì bán rã của nguyên tố phóng
Nếu chọn đúng con thắng cuộc thì sẽ nhận được
xạ Poloni 210 là 138 ngày (nghĩa là sau 138
số tiền gấp đôi số tiền đặt cuộc, còn nếu chọn sai
ngày khối lượng của nguyên tố đó chỉ còn một
thì sẽ mất số tiền đặt cuộc. Người du khách đó
nửa). Tính (chính xác đến hàng phần trăm)
lần đầu tiên đặt 20 000 đồng, mỗi lần sau tiền
khối lượng còn lại của 20 gam Poloni 210 sau
đặt gấp đôi tiền đặt lần trước. Người đó thua 7314 ngày (khoảng 20 năm).
9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du A. 3,22 · 10−15. B. 3,52 · 10−15.
khách đó thắng hay thua bao nhiêu? C. 2,52 · 10−15. D 2,22 · 10−15. A Thắng 20 000 đồng. Ê Lời giải. B. Hoà vốn.
Kí hiệu un (gam) là khối lượng còn lại của 20 C. Thua 20 000 đồng.
gam Poloni 210 sau n chu kì bán rã. D. Thua 40 000 đồng.
Ta có 7314 ngày gồm 53 chu kì bán rã. Suy ra Ê Lời giải.
theo đề bài ta cần tính u53.
Du khách đó lần đầu đặt 20 000 đồng, mỗi lần
Từ giả thiết suy ra dãy (un) là một cấp số nhân 20
sau tiền đặt gấp đôi tiền đặt lần trước. Vậy số
với số hạng đầu là u1 = = 10 và công bội 2
tiền đặt cược của du khách ở các lần khác nhau q = 0,5.
tạo thành một cấp số nhân với số hạng đầu tiên 52 1 Khi đó u ≈ 2,22 · 10−15. là u 53 = 10 ·
1 = 20 000 và công bội là q = 2. 2
Người đó thua 9 lần liên tiếp nên số tiền người Chọn đáp án D 9
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 17. Tế bào E.Coli trong điều kiện nuôi cấy Ta có
thích hợp cứ 20 phút lại nhân đôi một lần. Nếu ○
lúc đầu có 1012 tế bào thì sau 3 giờ sẽ phân chia u2 = u1 + d; thành bao nhiêu tế bào?
○ u9 = u1 + 8d = (u1 + d) + 7d = u2 + 7d; A. 256 · 1012 tế bào. B. 1024 · 1012 tế bào. C. 512 · 1013 tế bào. D 512 · 1012 tế bào.
○ u44 = u1 + 43d = (u1 + d) + 42d = u2 + 42d. Ê Lời giải.
Lúc đầu có 1022 tế bào và mỗi lần phân chia thì
Vì ba số hạng này là các số hạng liên tiếp của
một tế bào tách thành hai tế bào nên ta có cấp
một cấp số nhân nên ta có u2 · u44 = u2. 9 số nhân với u
Tổng của ba số hạng đó bằng 217 nên u
1 = 1022 và công bội q = 2. 2 + u9 +
Do cứ 20 phút phân đôi một lần nên sau 3 giờ u44 = 217.
sẽ có 9 lần phân chia tế bào. Ta có u
Do đó ta có hệ phương trình 10 là số tế
bào nhận được sau 3 giờ. ®u ®u ®u
Vậy số tế bào nhận được sau 3 giờ là u 2 + u9 + u44 = 217 2 + u2 + 7d + u2 + 42d = 217 2 = 7 10 = u1 q9 = ⇔ ⇔ (do d 6= 0). 512 · 1012. u2 · u44 = u2 u d 9 2 · (u2 + 42d) = (u2 + 7d)2 = 4 Chọn đáp án D n Do đó u ·[2u
Câu 18. Ông Trung có 100 triệu đồng gửi tiết 1 = u2 − d = 3 và Sn = 1 + (n − 1) · d] = 2
kiệm vào ngân hàng theo thể thức lãi kép kì n · (2n + 1).
hạn 6 tháng với lãi suất 8% cho một kì hạn. Giả
Tổng của n số hạng đầu bằng 210 nên
sử lãi suất không thay đổi. Hỏi sau 3 năm số
210 = n · (2n + 1) ⇔ n = 10.
tiền trong tài khoản tiết kiệm của ông Trung
gần nhất với số nào sau đây?
Vậy phải lấy 10 số hạng đầu của cấp số cộng A. 126 532 000 đồng. B 158 687 000 đồng. này. C. 125 971 000 đồng. D. 112 486 000 đồng. Chọn đáp án D Ê Lời giải.
3 năm tương ứng với 6 kì lãi của ông Trung.
Câu 20. Một đa giác có n cạnh và có chu vi
Vậy sau ba năm, số tiền trong tài khoản tiết
bằng 158 cm. Biết số đo các cạnh của đa giác
kiệm của ông Trung khoảng
lập thành một cấp số cộng và công sai d = 3 cm
và cạnh lớn nhất có độ dài là 44 cm. Đa giác có 6 8 S = 100000000 · 1 + ≈ 158 687 432. số cạnh n bằng 100 A. n = 6. B. n = 7. C. n = 5. D n = 4.
Số tiền trong tài khoản tiết kiệm của ông Trung Ê Lời giải.
gần nhất với số 158 687 000 đồng.
Gọi ui (1 6 i 6 n) là độ dài cạnh thứ i trong cấp Chọn đáp án B
số cộng tạo bởi đồ dài các cạnh của đa giác.
Ta có un = 44, d = 3 nên u1 = un − (n − 1)d =
Câu 19. Ba số phân biệt có tổng là 217 có thể
44 − (n − 1) · 3 = 47 − 3n.
coi là các số hạng liên tiếp của một cấp số nhân,
Chu vi của đa giác là tổng các cạnh của đa giác
cũng có thể coi là số hạng thứ 2, thứ 9, thứ 44 và bằng
của một cấp số cộng. Hỏi phải lấy bao nhiêu số
hạng đầu của cấp số cộng này để tổng của chúng n = 4 bằng 210?
n(u1 + un) = 158 ⇔ n(91−3n) = 316 ⇔ 3n2−91n+316 = 0 ⇔  79 A. 40. B. 30. C. 20. D 10. 2 n = (loại). 3 Ê Lời giải.
Gọi số hạng thứ 2, thứ 9, thứ 44 của cấp số cộng
Vậy n = 4 thỏa mãn yêu cầu bài toán. này là u2, u9, u44. Chọn đáp án D
B. BÀI TẬP TỰ LUẬN
BÀI 1. Tìm công sai của cấp số cộng (un), biết a) u1 = −21 và u14 = 18; b) u5 = −15 và u20 = 60; c) u1 = 2 và u2 + u3 = 5;
d) u2 + u4 = 16 và u3 + u7 = −4. Ê Lời giải. 10
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Gọi d là công sai của cấp số cộng un, ta có
un = u1 + (n − 1) · d ⇒ u14 = u1 + 13d ⇔ 18 = −21 + 13d ⇔ d = 3.
Vậy công sai của cấp số cộng là d = 3. ®u ®u ®d = 5 5 = u1 + 4d 1 + 4d = −15 Ta có : ⇔ ⇔ u20 = u1 + 19d u1 + 19d = 60 u1 = −35.
Ta có u2 + u3 = u1 + d + u1 + 2d = 2u1 + 3d = 4 + 3d. 1
Theo đề bài ta có u2 + u3 = 5 nên 4 + 3d = 5, do đó d = . 3 ®u ®2u ®u 2 + u4 = 16 1 + 4d = 16 1 = 18 Ta có ⇔ ⇔ u3 + u7 = −4 2u1 + 8d = −4 d = −5.
BÀI 2. Xác định công bội của một cấp số nhân (un), biết 1 1 a) u1 = và u6 = 16; b) u1 = − và u7 = −32; 2 2 1 c) u3 = 9 và u6 = 243; d) u2 = và u5 = 16. 4 Ê Lời giải. u 16 6 Ta có u6 = u1 · q5 ⇒ q5 = = = 32. Suy ra q = 2. u 1 1 2
Áp dụng công thức số hạng tổng quát cấp số nhân ta có un = u1qn−1 ⇒ u7 = u1.q6 ⇒ q6 = 64 ⇒ ñ q = 2 . q = −2 ®u3 = u1.q2 u 6
Gọi q là công bội của cấp số nhân đã cho, ta có: ⇒ q3 = = 27 ⇒ q = 3. u u 6 = u1.q5 3 1
Ta có: u2 = u1.q ⇔ = u1.q; u5 = u1.q4 ⇔ 16 = u1.q4. 4 Suy ra: q3 = 64 ⇔ q = 4.
BÀI 3. Có bao nhiêu hàng ghế trong một góc khán đài của một sân vận động, biết rằng góc khán
đài đó có 2040 chỗ ngồi, hàng ghế đầu tiên có 10 chỗ ngồi và mỗi hàng ghế sau có thêm 4 chỗ ngồi so
với hàng ghế ngay trước nó? Ê Lời giải.
Số ghế ở mỗi hàng của góc khán đài lập thành một cấp số cộng với số hạng đầu u1 = 10 và công sai d = 4.
Áp dụng công thức tính tổng n số hạng đầu của cấp số cộng với Sn = 2040, u1 = 10, d = 4 để tìm n, ta có n
2040 = Sn = [2 · 10 + (n − 1) · 4] 2 ⇔ n(16 + 4n) = 4080 ⇔ 4n2 + 16n − 4080 = 0 ñn = 30 ⇔ n = −34 (loại).
Suy ra n = 30, tức là góc khán đài đó có 30 hàng ghế. 11
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
BÀI 4. Nếu anh Nam nhận được lời mời làm việc cho một công ty nước ngoài với mức lương khởi
điểm là 35000 đô la mỗi năm và được tăng thêm 1400 đô la lương mỗi năm, thì sẽ mất bao nhiêu
năm làm việc để tổng lương mà anh Nam nhận được là 319200 đô la? Ê Lời giải.
Lương mỗi năm của anh Nam lập thành một cấp số cộng với số hạng đầu u1 = 35000 và công sai d = 1400, ta có n
319200 = Sn = [2 · 35000 + (n − 1) · 1400] 2 ⇔ n(68600 + 1400n) = 638400
⇔ 1400n2 + 68600n − 638400 = 0 ñn = 8 ⇔ n = −57 (loại).
Vậy sau 8 năm làm việc thì tổng lương mà anh Nam nhận được là 319200 đô la. 12
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chương III.
CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA
MẪU SỐ LIỆU GHÉP NHÓM
A. BÀI TẬP TRẮC NGHIỆM 1
Mức độ Nhận biết, Thông hiểu
Câu 21. Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT A, ta được kết quả Chiều [150; 152) [152; 154) [154; 156) [156; 158) [158; 160) [160; 162) [162; 168) cao (cm) Số học 5 18 40 25 8 3 1 sinh
a) Mẫu số liệu trên có bao nhiêu nhóm A. 5. B. 6. C 7. D. 8. Ê Lời giải. Chọn đáp án C
b) Số học sinh có chiều cao trong khoảng [154;156) là A 40. B. 18. C. 5. D. 8. Ê Lời giải. Chọn đáp án A
Câu 22. Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau Thời gian ( phút) [0; 20) [20; 40) [40; 60) [60; 80) [80; 100) Số học sinh 5 9 12 10 6
a) Giá trị đại diện của nhóm [60; 80) là A. 40. B 70. C. 60. D. 30. Ê Lời giải. Chọn đáp án B
b) Nhóm [20; 40) có tần số là A. 5. B 9. C. 12. D. 10. Ê Lời giải. Chọn đáp án B 13
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
c) Nhóm chứa mốt của mẫu số liệu này là A. [80; 100). B. [20; 40). C [40; 60). D. [60; 80). Ê Lời giải. Chọn đáp án C d) Nhóm chứa trung vị là A. [0; 20). B. [20; 40). C [40; 60). D. [60; 80). Ê Lời giải.
Gọi x1, x2,..., x42 là thời gian xem tivi của các học sinh được xếp theo thứ tự không giảm. x21 + x22 Khi đó trung vị là
, do hai giá trị x21, x22 thuộc nhóm [40;60) nên nhóm này chứa trung 2 vị. Chọn đáp án C
e) Nhóm chứa tứ phân vị thứ nhất là A. [0; 20). B [20; 40). C. [40; 60). D. [60; 80). Ê Lời giải. Cỡ mẫu là n = 44.
Tứ phân vị thứ nhất là x11. Giá trị này thuộc nhóm [20;40). Chọn đáp án B 2
Mức độ Vận dụng
Câu 23. Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một số học sinh thu được kết quả sau Thời gian ( phút) [0; 4) [4; 8) [8; 12) [12; 16) [16; 20) Số học sinh 2 4 7 4 3
Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là A. 7. B. 11,3. C 10,4. D. 12,5. Ê Lời giải.
Ta có bảng chứa giá trị đại diện như sau: Thời gian ( phút) 2 6 10 14 18 Số học sinh 2 4 7 4 3
Thời gian trung bình để hoàn thành bài tập là
2 · 2 + 4 · 6 + 7 · 10 + 4 · 14 + 3 · 18 x = = 10,4. 20 Chọn đáp án C
Câu 24. Cho mẫu số liệu ghép nhóm về chiều cao của 25 cây dừa giống như sau Chiều cao ( cm) [0; 10) [10; 20) [20; 30) [30; 40) [40; 50) Số cây 4 6 7 5 3 14
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
a) Mốt của mẫu số liệu ghép nhóm này là 70 50 70 80 A Mo = . B. Mo = . C. Mo = . D. Mo = . 3 3 2 3 Ê Lời giải.
Tần số lớn nhất là 7 nên nhóm chứa mốt là [20; 30). 7 − 6 70 Do đó Mo = 20 + · 10 = . (7 − 6) + (7 − 5) 3 Chọn đáp án A
b) Trung vị của mẫu số liệu ghép nhóm này là 175 165 165 165 A. Me = . B. Me = . C Me = . D. Me = . 7 5 7 3 Ê Lời giải. Cỡ mẫu là n = 25.
Gọi x1, x2,..., x25 là chiều cao của 25 cây dừa giống xếp theo thứ tự không giảm.
Khi đó trung vị là x13. Giá trị này thuộc nhóm [20;30). 25 −(4+6) 165 Do đó 2 Me = 20 + · (30 − 20) = . 7 7 Chọn đáp án C
c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm này là A. Q1 = 13,5. B. Q1 = 13,9. C. Q1 = 15,75. D Q1 = 13,75. Ê Lời giải. x6 + x7
Tứ phân vị thứ nhất là
, hai giá trị này thuộc nhóm [10; 20). 2 25 −4 Do đó 4 Q1 = 10 + · (20 − 10) = 13,75. 6 Chọn đáp án D
Câu 25. Cho mẫu số liệu ghép nhóm về khối lượng (đơn vị: gram) của 30 củ khoai tây như sau Khối lượng [70; 80) [80; 90) [90; 100) [100; 110) [110; 120) Tần số 3 6 12 6 3
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là A. Q3 = 133. B. Q3 = 134. C. Q3 = 132. D Q3 = 102,5. Ê Lời giải. Cỡ mẫu n = 30.
Tứ phân vị thứ ba là x23, giá trị này thuộc nhóm [100;110). 3 · 30 −(3+6+12) Do đó 4 Q3 = 100 + · (110 − 100) = 102,5. 6 Chọn đáp án D
B. BÀI TẬP TỰ LUẬN
BÀI 5. Người ta ghi lại tốc độ cua 40 xe đạp đi qua một vị trí trên đường. Mẫu số liệu dưới đây ghi
lại tốc độ của 40 xe đó (đơn vị: km/h) 10 10,4 11 16 12 13 15,8 12,7 16,8 19 17 15,1 14 12,3 17,2 10,5 13,2 18,1 19,6 17,4 11,8 13,6 12,7 15,9 14,2 12,6 11,6 10,4 14,1 15,1 12,3 15,2 11,9 16,3 18,4 17,1 14,2 12,1 13,7 13,2 15
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có năm nhóm ứng với sáu nửa khoảng
[10; 12), [12; 14), [14; 16), [16; 18), [18; 20).
b) Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên. Ê Lời giải.
a) Bảng tần số ghép nhóm bao gồm cả tần số tích lũy được cho như ở bảng sau Nhóm Tần số Tần số tích lũy [10; 12) 8 8 [12; 14) 12 20 [14; 16) 9 29 [16; 18) 7 36 [18; 20) 4 40 n = 40 n n 3n b) Ta có = 2, = 10,
= 30. Vì 8 < 20 ≤ 20 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn 20 4 4 hơn hoặc bằng 20. 20 − 8
Suy ra trung vị là Me = 12 + · 2 = 14. 12
Tứ phân vị thứ hai là Q2 = M2 = 14.
Vì 8 < 10 < 20 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10. Suy ra tứ 10 − 8
phân vị thứ nhất là Q1 = 12 + · 2 ≈ 12, 3. 12
Vì 29 < 30 < 36 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30. Suy ra tứ 30 − 29
phân vị thứ ba là Q3 = 16 + · 2 ≈ 16, 3. 7 12 − 8
Trong các nhóm, nhóm 2 có tần số lớn nhất, suy ra mốt là MO = 12 + · 2 ≈ 13, 1. 2 · 12 − 8 − 9
BÀI 6. Một công ty bảo hiểm thống kê lại độ tuổi các khách hàng mua bảo hiểm xe ô tô ở bảng sau: Độ tuổi [25; 30) [30; 35) [35; 40) [40; 45) [45; 50) [50; 55) Số khách hàng 25 38 62 42 37 29
Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên. Ê Lời giải. Độ tuổi [25; 30) [30; 35) [35; 40) [40; 45) [45; 50) [50; 55) Độ tuổi đại diện 27,5 32,5 37,5 42,5 47,5 52,5 Số khách hàng 25 38 62 42 37 29 Cỡ mẫu n = 233.
Số trung bình của mẫu số liệu ghêp nhớm trên là
27,5 · 25 + 32,5 · 38 + 37,5 · 62 + 42,5 · 42 + 47,5 · 37 + 52,5 · 29 x = ≈ 39,97. 233
Nhóm chứa mốt của mẫu số liệu trên là nhóm [35; 40). Do đó: um = 35; nm = 62, nm−1 = 38; nm+1 = 42; um+1 = 40.
Vậy mốt của mẩu số liệu ghép nhóm là 62 − 38 415 M0 = 35 + · (40 − 35) = . (62 − 38) + (62 − 42) 11
Gọ x1; x2; ... ; x233 là mẫu số liệu được xếp theo thứ tự không giảm.
Tứ phân vị thứ hai của dãy số liệu x1; x2 ; ... ; x233 là x117. 16
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC 233 4875 Do x 2 − 63
117 thuộc nhóm [35; 40) nên Q2 = 35 + · (40 − 35) = . 62 124 1
Tứ phân vị thứ nhất của dãy số liệu x1 ; x2 ; ... ; x233 là (x58 + x59). 2 1·233 275 Do x 4 − 25
58 và x59 thuộc nhóm [30; 35) nên Q1 = 30 + · (35 − 30) = . 38 8 1
Tứ phân vị thứ ba của dãy số liệu x1 ; x2 ; ... ; x233 là (x175 + x176). 2 3·233 6815 Do x 4 − 167
175 và x176 thuộc nhóm [45; 50) nên Q3 = 45 + · (50 − 45) = . 37 148
BÀI 7. Các bạn học sinh một lớp thống kê số túi nhựa mà gia đình bạn đó sử dụng trong một tuần.
Kết quả được tổng hợp lại ở bảng sau: Số tuổi [5; 9] [10; 14] [15; 19] [20; 24] [25; 29] Số gia đình 8 15 12 7 2
a) Hãy ước lượng số trung bình và mốt của mẫu số liệu trên.
b) Cô giáo dự định trao danh hiệu “Gia đình xanh” cho 25% gia đình các bạn sử dụng ít túi nhựa
nhất. Cô giáo nên trao danh hiệu cho các gia đình dùng không quá bao nhiêu túi nhựa? Ê Lời giải.
Do số tuổi là số nguyên nên ta hiệu chỉnh lại như sau: Số tuổi [4,5; 9,5) [9,5; 14, 5) [14,5; 19,5) [19, 5; 24,5) [24,5; 29,5) Số tuổi đại diện 7 12 17 22 27 Số gia đình 8 15 12 7 2 Cỡ mẫu n = 44.
a) Số trung bình của mẫu số liệu ghép nhóm là
7 · 8 + 12 · 15 + 17 · 12 + 22 · 7 + 27 · 2 x = ≈ 14,73. 44
Nhóm chứa mốt của mẫu số liệu trên là nhóm [9,5; 14, 5). Do đó: um = 9,5; nm = 15, nm−1 = 8 ; nm+1 = 12 ; um+1 = 14,5.
Vậy mốt của mẩu số liệu ghép nhóm là 15 − 8 M0 = 9,5 + · (14,5 − 9,5) = 13. (15 − 8) + (15 − 12) 21
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là Q1 = = 10,5. 2
Do đó, cô giáo nên trao danh hiệu cho gia đình các bạn dùng không quá 10 túi nhựa.
BÀI 8. Bảng sau thống kê doanh số bán hàng của các nhân viên một trung tâm thương mại trong một ngày. Doanh số [20; 30) [30; 40) [40; 50) [50; 60) [60; 70) (triệu đồng) Số nhân viên 4 8 12 7 5
a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên.
b) Trung tâm thương mại dự định sẽ thưởng cho 25% số nhân viên có doanh số bán hàng cao nhất.
Theo mẫu số liệu trên, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán
hàng ít nhất là bao nhiêu? Ê Lời giải. 17
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Doanh số [20; 30) [30; 40) [40; 50) [50; 60) [60; 70) (triệu đồng) Doanh số đại diện 25 35 45 55 65 Số nhân viên 4 8 12 7 5 815 400 a) x = ; M0 = ; Me = 45. 18 9 380
b) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là Q3 = ≈ 54,29. 7
Do đó, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán hàng một ngày ít
nhất là 54,29 triệu đồng. —HẾT— 18
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chương IV.
QUAN HỆ SONG SONG SONG TRONG KHÔNG GIAN
A. BÀI TẬP TRẮC NGHIỆM 1 Mức độ Cơ bản
Câu 26. Các yếu tố nào sau đây xác định một mặt phẳng duy nhất? A. Bốn điểm phân biệt.
B. Một điểm và một đường thẳng. C. Ba điểm phân biệt.
D Hai đường thẳng cắt nhau. Ê Lời giải.
○ A sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì sẽ có vô số mặt phẳng chứa 3 điểm thẳng hàng đã cho.
○ B sai. Trong trường hợp điểm thuộc đường thẳng đã cho, khi đó ta chỉ có 1 đường thẳng, có vô
số mặt phẳng đi qua đường thẳng đó.
○ D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì có vô số mặt phẳng đi qua 4 điểm
đó hoặc trong trường hợp 4 điểm mặt phẳng không đồng phẳng thì sẽ tạo không tạo được mặt
phẳng nào đi qua cả 4 điểm. Chọn đáp án D
Câu 27. Cho tứ diện ABCD như hình bên. Mệnh đề nào sau đây đúng? A A. AB và CD cắt nhau. B. BD và AC cắt nhau. C BD và AC chéo nhau. D. BC và AD song song. B D C Ê Lời giải.
Theo định nghĩa của tứ diện ABCD thì mệnh đề đúng là BD và AC là hai đường thẳng chéo nhau. Chọn đáp án C
Câu 28. Hình chóp tứ giác có tất cả bao nhiêu mặt là tam giác? A. 5. B. 3. C. 6. D 4. Ê Lời giải.
Hình chóp tứ giác có tất cả 4 mặt là tam giác. Chọn đáp án D
Câu 29. Trong các hình sau A A A A D B C C B D B D C B D (I) C (II) (III) (VI) 19
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Hình nào có thể là hình biểu diễn của một hình tứ diện? A. (I). B. (I), (II). C. (I), (II), (IV). D (I), (II), (III), (IV). Ê Lời giải. Chọn đáp án D
Câu 30. Trong không gian, hai đường thẳng không có điểm chung thì A. cắt nhau. B chéo nhau hoặc song song. C. chéo nhau. D. song song. Ê Lời giải. Chọn đáp án B
Câu 31. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai đường thẳng phân biệt không song song thì chéo nhau.
B. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
C. Hai đường thẳng không có điểm chung thì chéo nhau .
D Hai đường thẳng chéo nhau thì không có điểm chung. Ê Lời giải.
Hai đường thẳng chéo nhau không có điểm chung. Chọn đáp án D
Câu 32. Trong không gian cho hai đường thẳng cắt nhau a và b. Nếu c là một đường thẳng song song với a thì
A. c và b song song với nhau. B. c và b cắt nhau. C. c và b chéo nhau.
D c và b không song song với nhau. Ê Lời giải. Chọn đáp án D
Câu 33. Cho hình chóp S.ABCD có điểm O là giao điểm của hai đường chéo. Giao điểm của đường
thẳng AC với mặt phẳng (SBD) là điểm nào? A. Điểm B. B. Điểm A. C Điểm O. D. Điểm S. Ê Lời giải.
Ta thấy A ∉ (SBD) và AC ∩ BD = O nên AC ∩ (SBD) = {O}. S A D O C B Chọn đáp án C
Câu 34. Cho hình chóp S.ABCD đáy là tứ giác lồi ABCD, giao tuyến của mặt (S AD) và (SBD) là A. SB. B. S A. C SD. D. SC. Ê Lời giải.
Ta có (S AD) ∩ (SBD) = SD. S A D C B 20
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chọn đáp án C
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm
AD và BC. Giao tuyến của hai mặt phẳng (SM N) và (S AC) là
A. SF (F là trung điểm CD).
B SO (O là tâm hình bình hành ABCD).
C. SG (G là trung điểm AB). D. SD. Ê Lời giải.
Dễ thấy S ∈ (S AC) ∩ (SMN). S
Gọi O là tâm của hình bình hành.
Khi đó, O = AC ∩ MN ⇒ O ∈ (S AC) ∩ (SMN). Vậy (S AC) ∩ (SMN) = SO. A B M N O D C Chọn đáp án B
Câu 36. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và A
BC. Trên đoạn BD lấy P sao cho BP = 2PD. Khi đó giao điểm của đường
thẳng CD với mặt phẳng (MNP) là
A giao điểm của NP và CD.
B. giao điểm của MN và CD. C. trung điểm của CD.
D. giao điểm của MP và CD. B D C Ê Lời giải.
Trong mặt phẳng (BCD) kéo dài NP cắt CD tại I. A  I ∈ CD   Ta có I ∈ NP  N P ⊂ (MNP) I ⇒ {I} = CD ∩ (MNP). M P B D N C Chọn đáp án A
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi S
I, J, E, F lần lượt là trung điểm S A, SB, SC, SD. Trong các đường thẳng
sau, đường thẳng nào không song song với I J? A. EF. B. DC. C. AB. D AD. D A B C Ê Lời giải. 21
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Ta có I J ∥ AB (tính chất đường trung bình trong tam giác S AB) và S
EF ∥ CD (tính chất đường trung bình trong tam giác SCD).
Mà CD ∥ AB (đáy là hình bình hành) ⇒ CD ∥ AB ∥ EF ∥ I J. I F J E A D B C Chọn đáp án D
Câu 38. Cho hai đường thẳng song song a, b và mặt phẳng (P). Mệnh đề nào dưới đây đúng?
A. Nếu a ∥ (P) thì b ∥ (P) .
B Nếu a cắt (P) thì b cắt (P).
C. Nếu a nằm trên (P) thì b ∥ (P).
D. Nếu a nằm trên (P) thì b nằm trên (P). Ê Lời giải. Chọn đáp án B
Câu 39. Cho hai mặt phẳng (P) và điểm A nằm ngoài mặt phẳng (P). Khẳng định nào sau đây đúng?
A. Qua A có vô số mặt phẳng song song với (P).
B Qua A có đúng một mặt phẳng song song với (P).
C. Qua A không có mặt phẳng nào song song với (P).
D. Qua A có đúng hai mặt phẳng song song với (P). Ê Lời giải. Chọn đáp án B
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đường thẳng AD song song với
mặt phẳng nào trong các mặt phẳng dưới đây? A (SBC). B. (ABCD). C. (S AC). D. (S AB). Ê Lời giải.
Do AD ∥ BC, AD 6⊂ (SBC) và BC ⊂ (SBC) nên AD ∥ (SBC). S A B D C Chọn đáp án A
Câu 41. Cho hình chóp tứ giác S.ABCD. Gọi M, N lần lượt là trung
điểm của S A và SC. Khẳng định nào sau đây đúng? S A M N ∥ (ABCD). B. M N ∥ (S AB). C. M N ∥ (SBC). D. M N ∥ (SCD). M N A B C D Ê Lời giải. 22
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Xét 4S AC có M, N lần lượt là trung điểm S A, SC S
⇒ MN là đường trung bình của 4S AC
⇒ MN ∥ AC, mà AC ⊂ (ABCD) ⇒ MN ∥ (ABCD). M N A B C D Chọn đáp án A
Câu 42. Nếu mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) lần lượt theo hai giao tuyến a
và b thì vị trí tương đối giữa hai đường thẳng a và b là A song song. B. chéo nhau. C. trùng nhau. D. cắt nhau. Ê Lời giải. Chọn đáp án A
Câu 43. Cho đường thẳng a nằm trong mặt phẳng (α) và đường thẳng b nằm trong mặt phẳng (β).
Biết (α) ∥ (β). Trong các khẳng định sau, khẳng định nào sai? A. a ∥ (β). B. b ∥ (α). C a ∥ b.
D. Nếu có một mặt phẳng (γ) chứa a và b thì a ∥ b. Ê Lời giải. Chọn đáp án C
Câu 44. Khẳng định nào sau đây là sai khi nói về hình lăng trụ?
A. Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.
B. Các mặt bên của hình lăng trụ là các hình bình hành.
C. Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.
D Hai đáy của hình lăng trụ là hai đa giác đều. Ê Lời giải.
Hai đáy của hình lăng trụ là hai đa giác bằng nhau. Chọn đáp án D
Câu 45. Cho hình hộp ABCD.A0B0C0D0. Hình chiếu song song của A A0 D0
trên mặt phẳng (CDD0C0) theo phương BC0 là A D0. B. D. B0 C0 C. B . D C0. D A B C Ê Lời giải. Chọn đáp án D 23
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 46. Cho hình lăng trụ ABC.A0B0C0, gọi I, I0 lần lượt là trung I
điểm của AB, A0B0. Qua phép chiếu song song đường thẳng AI0, A B
hình chiếu của điểm I lên mặt phẳng chiếu (A0B0C0) là điểm nào sau đây? A. A0. B. I0. C C B0. D. C0. A0 I0 B0 C0 Ê Lời giải. ® AI ∥ B0I0 Ta có
⇒ AIB0I0 là hình bình hành. I A I = B0I0 A B
Suy ra qua phép chiếu song song đường thẳng AI0, mặt phẳng
chiếu (A0B0C0) biến điểm I thành điểm B0. C A0 I0 B0 C0 Chọn đáp án C
Câu 47. Cho hình lăng trụ ABC.A1B1C1. Trong các khẳng định sau, khẳng định nào sai? A. (ABC) ∥ (A1B1C1). B. A A1 ∥ (BCC1). C. AB ∥ (A1B1C1).
D A A1B1B là hình chữ nhật. Ê Lời giải.
Vì mặt bên A A1B1B là hình bình hành, còn nó là hình chữ nhật nếu ABC.A1B1C1 là hình lăng trụ đứng. Chọn đáp án D
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành S
tâm O. Gọi M, N lần lượt là trung điểm của S A, AD. Hỏi mặt phẳng
(M NO) song song với mặt phẳng nào sau đây? A. (S AB). B. (SBC). C (SCD). D. (S AD). M N A D O B C Ê Lời giải.
Áp dụng tính chất đường trung bình, suy ra MN ∥ SD và ON ∥ CD.
Mà SD ∈ (SCD) và CD ∈ (SCD), do đó (MNO) ∥ (SCD). Chọn đáp án C 24
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 49. Cho hình hộp ABCD.A0B0C0D0. Mặt phẳng (AB0D0) song song A0 D0
với mặt phẳng nào sau đây? A. (BC A0). B. (BD A0). C. (A0C0C). D (BDC0). B0 C0 D A B C Ê Lời giải.
Mặt phẳng (AB0D0) song song với mặt phẳng (BDC0).
Thật vậy, ta có AB0 ∥ DC0 và AD0 ∥ BC0, có điều cần chứng minh. B0 C0 A0 D0 B C A D Chọn đáp án D
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng
(S AB) và (SCD) là đường thẳng song song với đường thẳng nào sau đây? A. BD . B. SC. C. AC. D AB. Ê Lời giải.
Ta có mặt phẳng (S AB) và (SCD) có chứa hai cạnh AB và CD S
song song nhau. Nên hai mặt phẳng (S AB) và (SCD) có giao x
tuyến là đường thẳng qua S và song song với AB. A B D C Chọn đáp án D
Câu 51. Cho hình chóp S.ABCD có AC cắt BD tại M, AB cắt S
CD tại N. Trong các đường thẳng sau đây, đường thẳng nào là
giao tuyến của (S AC) và (SBD) ? A SM. B. SN. C. SB. D. SC. B A N M C D Ê Lời giải. 25
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Xét hai mặt phẳng (S AC) và (SBD) Ta có S là điểm chung thứ S nhất. M là điểm chung thứ hai.
Nên giao tuyến của hai mặt phẳng (S AC) và (SBD) là SM. B A N M C D Chọn đáp án A 2
Mức độ Vận dụng
Câu 52. Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng d cắt các mặt
phẳng (P),(Q),(R) lần lượt tại A, B, C. Đường thẳng d0 cắt các mặt phẳng (P),(Q),(R) lần lượt tại AB 2 A0B0 A0, B0, C0. Biết rằng = , tỷ số bằng AC 3 A0C0 1 2 3 1 A. . B . C. . D. . 3 3 2 2 Ê Lời giải. Chọn đáp án B
Câu 53. Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của B
AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường
thẳng EG và mặt phẳng (ACD) là E A. điểm F. G
B. giao điểm của đường thẳng EG và CD. A C
C giao điểm của đường thẳng EG và AF.
D. giao điểm của đường thẳng EG và AC. F D Ê Lời giải.
• Chọn mặt phẳng phụ (ABF) chứa EG. • Ta có (ABF) ∩ B (ACD) = AF. ®M ∈ EG E
• Gọi M = EG ∩ AF ⇒ M ∈ AF ⊂(ACD) G ⇒ M = EG ∩ (ACD). A C
Vậy giao điểm cần tìm giao điểm của đường thẳng EG và AF. F M D Chọn đáp án C 26
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Câu 54. Cho hình chóp S.ABCD có đáy ABCD là hình bình S
hành. Gọi M, N, K lần lượt là trung điểm các cạnh DC, BC, S A.
Giao tuyến của (MNK) với (S AB) là đường thẳng K T, với T
được xác định theo một trong bốn phương án được liệt kê dưới K
đây. Khẳng định nào sau đây đúng.
A. T là giao điểm của MN với SB.
B T là giao điểm của MN với AB. D
C. T là giao điểm của K N với AB. A
D. T là giao điểm của K N với SB. M B N C Ê Lời giải.
Ta có K là điểm chung thứ nhất của (S AB) và (K MN). S
Ta sẽ tìm điểm chung thứ hai T.
Nhận thấy, trong mặt phẳng (S AB) và (K MN) có đường
thẳng AB và MN cùng nằm trong mặt phẳng (ABCD)
nên nếu T là giao điểm của AB và MN thì T là điểm K
chung thứ hai của (S AB) và (K MN).
Suy ra, K T là giao tuyến của (S AB) và (K MN). A D M B N C T Chọn đáp án B
Câu 55. Cho hình chóp S.ABCD có đáy là hình bình hành. Trên S
cạnh S A lấy điểm M sao cho M A = 2MS. Mặt phẳng (CDM) cắt SN SB tại N. Tỉ số bằng SB M 1 1 A. . B . 2 3 2 3 C. . D. . 3 4 D A B C Ê Lời giải.
Xét hai mặt phẳng (MCD) và (S AB) có M là điểm chung, AB ∥ S
CD. Do đó giao tuyến của hai mặt phẳng (MCD) và (S AD) là
M N ∥ AB (với N thuộc SB). SN SM 1 M Do đó = = . SB S A 3 N D A B C Chọn đáp án B 27
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
B. BÀI TẬP TỰ LUẬN 1
BÀI 9. Cho tứ diện ABCD. Gọi E, F lần lượt là các điểm thuộc các cạnh AB, AC sao cho AE = BE 2
và AF = 2CF. Gọi O là một điểm nằm trong tam giác BCD.
a) Xác định giao tuyến của hai mặt phẳng (OEF) và (ABD).
b) Xác định giao điểm (nếu có) của đường thẳng AD và mặt phẳng (OEF). Ê Lời giải. A
a) Trong mặt phẳng (ABC), gọi G là giao điểm của EF và BC.
Trong mặt phẳng (BCD), gọi H là giao điểm của OG và BD.
Khi đó H là điểm chung của hai mặt phẳng (OEF) và (ABD), E
suy ra EH là giao tuyến của hai mặt phẳng đó.
b) Trong mặt phẳng (ABD), gọi I là giao điểm (nếu có) của EH và
AD. Khi đó I là giao điểm của AD và mặt phẳng (OEF). F H B D O C G
BÀI 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là các
trung điểm của đoạn thẳng SC, S A và AB.
a) Tìm giao tuyến hai mặt phẳng (S AC) và (SBD).
b) Tìm tọa độ giao điểm của đường thẳng AM và mp(SBD).
c) Chứng minh MN song song với mặt phẳng (ABCD).
d) Chứng minh đường thẳng K N song song với mặt phẳng (SOD).
e) Chứng minh (KOM) song song với mặt phẳng (S AB).
f) Chứng minh K M song song với mặt phẳng (S AB). Ê Lời giải.
BÀI 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao
cho AD = 3AM. Gọi G, N lần lượt là trọng tâm của các tam giác S AB, ABC. Chứng minh
a) Đường thẳng MN song song với mặt phẳng (SCD).
b) Đường thẳng GN song song với mặt phẳng (S AC).
c) Đường thẳng GM song song với mặt phẳng (SCD). Ê Lời giải.
BÀI 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi hai điểm M, N lần lượt SN 1 SM 2
trên các cạnh SB, SC sao cho = và = . SC 2 SB 3
a) Chứng minh rằng BC song song mặt phẳng (S AD).
b) Xác định giao tuyến ∆ của hai mặt phẳng (AMN) và (ABCD). 28
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
c) Chứng minh rằng BD song song mặt phẳng (AMN). SP
d) Gọi P là giao điểm của SD và (AMN). Tính tỷ số . SD
e) Chứng minh rằng ba đường thẳng ∆, P N và CD đồng quy. Ê Lời giải. S N M K P I B C O A D H
a) Ta có BC ∥ AD, BC 6⊂ (S AD) và AD ⊂ (S AD) nên BC ∥ (S AD). . . . . . . . . . . . . . . . . . . . . . . . . . 1,0 điểm.
b) Ta có A ∈ (AMN) ∩ (ABCD). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .0,25 điểm.
Trong mp(SBC), gọi I là giao điểm MN và BC.
Ta có I ∈ (AMN) ∩ (ABCD). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,5 điểm.
Do đó AI là giao tuyến ∆ của (AMN) và (ABCD). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,25 điểm. SM 2
c) Tam giác SIC có I N là trung tuyến và =
nên M là trọng tâm tam giác. . . . . . . . 0,5 điểm. SB 3
Do đó B là trung điểm IC, suy ra IBD A là hình bình hành, nên BD ∥ I A ⊂ (AMN). Vậy BD ∥
(AM N). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,5 điểm.
d) Trong mp(S AC), gọi K = SO ∩ AN. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,5 điểm.
Trong mp(SBD), gọi P = SD ∩ MK. Lúc đó P = SD ∩ (AMN). . . . . . . . . . . . . . . . . . . . . . . . . . . 0,5 điểm.
Tam giác S AC có AN và SO là hai đường trung tuyến nên K là trọng tâm tam giác S AC. Suy SK 2 ra
= . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,5 điểm. SO 3 SM 2 Mà =
nên K M song song BO. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,25 điểm. SB 3 SP 2 Do đó
= . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,25 điểm. SD 3 SP SN
e) Trong mặt phẳng (SCD), vì 6=
nên P N và CD cắt nhau. . . . . . . . . . . . . . . . . . . . . . . 0,5 điểm. SD SC Gọi H = P N ∩ CD.
Ta có (AMN) ∩ (ABCD) = AI,(AMN) ∩ (SCD) = P N và (SCD) ∩ (ABCD) = CD nên AI đi qua H,
hay AI, P N, CD đồng quy tại H. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,5 điểm.
BÀI 13. Cho hình hộp ABCD A0B0C0D0. Gọi M, N, P lần lượt là trung điểm của AD, B0C0, DD0 29
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
a) Chứng minh rằng ADC0B là hình bình hành.
b) Chứng minh rằng BD ∥ AB0D0, MN ∥ AB0D0.
c) Chứng minh rằng (MNP) ∥ AB0D0 và BD ∥ (MNP).
d) Xác định giao tuyến của mặt phẳng (MNP) với các mặt của hình hộp.
e) Lấy một đường thẳng cắt ba mặt phẳng AB0D0, (MNP), C0BD lần lượt tại I, J, H. Tính tỉ I J số . J H Ê Lời giải. a)
Vì ABCD và BCC0B0 là các hình bình hành nên AD ∥ BC, A M AD = BC và BC D
∥ B0C0, BC = B0C0. Suy ra AD ∥ B0C0, AD = K
B0C0. Vậy ADC0B0 là hình bình hành. B O C P F A0 D0 E B0 N C0
b) Vì BB0 ∥ DD0, BB0 = DD0 nên BDD0B0 là hình bình hành. Do đó, BD ∥ B0D0. Suy ra BD ∥ AB0D0.
Ta có AMNB0 ’ là hình bình hành, suy ra MN ∥ AB0 nên MN ∥ AB0D0.
c) Vì MP ∥ AD0 nên MP ∥ AB0D0, cùng với kết quả câu b ta có (MNP) ∥ AB0D0. Vì BD ∥ B0D0 nên
BD ∥ AB0D0, suy ra BD ∥ (MNP).
d) Gọi E, F, K lần lượt là trung điểm của C0D0, B0B, BA. Khi đó, PE ∥ MN, NF ∥ MP, K F ∥ MN
nên các điểm E, F, K đều thuộc mặt phẳng (MNP). Do đó giao tuyến của (MNP) với các mặt
ADD0 A0, DCC0D0, A0B0C0D0, BCC0B0, ABB0 A0 và (ABCD) lần lượt là MP, PE, EN, NF, F K , K M. e)
Theo câu d, ta có (MNP) trùng với (MK F NEP). A M D
Gọi R, O lần lượt là giao điểm của AC với MK, AR R O BD. Khi đó, ta có
= 1 và đường thẳng AC cắt K B RO C
ba mặt phẳng AB0D0, (MNP), C0BD lần lượt d tại A, R, O. P H J
Áp dụng định lí Thalès trong không gian, ta có I F AR RO AO = = . I J J H I H A0 D0 I J AR E Từ đó suy ra = = 1. J H RO B0 N C0
BÀI 14. Cho hình lăng trụ tam giác ABC.A0B0C0. Gọi M, N, P lần lượt là trung điểm của các cạnh A A0, AB, AC.
a) Chứng minh rằng BC ∥ (MNP).
b) Xác đinh giao tuyến d của hai mặt phẳng (MNP) và (A0B0C0). 30
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
c) Chứng minh rằng d ∥ NP. Ê Lời giải. B N P A C M B0 F C0 A0 E
a) Vì NP là đường trung bình của tam giác ABC nên BC ∥ NP, suy ra BC ∥ (MNP)
b) Trong mặt phẳng (ABB0 A0) gọi E là giao điểm của MN và A0B0. Trong mặt phẳng (ACC0 A0) gọi F
là giao điểm của MP và A0C0. Khi đó EF là giao tuyến của hai mặt phẳng (MNP) và (A0B0C0).
c) Vì NP ∥ BC và BC ∥ B0C0 nên NP ∥ B0C0, suy ra NP ∥ (A0B0C0) Mặt phẳng (MNP) chứa đường
thẳng NP song song với mặt phẳng (A0B0C0) nên giao tuyến d của hai mặt phẳng đó song song với B0C0, suy ra d ∥ NP. —HẾT— 31
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Chương V.
GIỚI HẠN. HÀM SỐ LIÊN TỤC
A. BÀI TẬP TRẮC NGHIỆM 1
Mức độ Nhận biết, Thông hiểu
Câu 62. Biết lim f (x) = 3 và lim g(x) = −2. Tính x→1 x→1 lim[ f (x) + 2g(x)].
Câu 56. Cho hai dãy số (un) và (vn), biết x→1
lim un = a và lim vn = b. Trong các kết luận sau, A −1. B. 1. C. 5. D. −6. kết luận nào sai? Ê Lời giải. A. lim(un + vn) = a + b.
Ta có lim[ f (x) + 2g(x)] = lim f (x) + 2 lim g(x) = 3 + x→1 x→1 x→1 B. lim(un − vn) = a − b. 2(−2) = −1. C. lim(unvn) = ab. Chọn đáp án A un a D lim = . v
Câu 63. Biết lim f (x) g (x) n b = 4 và lim = 1. Tính x→1 x→1
Câu 57. Cho các dãy số (u lim [4 f (x) + 3g (x)]. n), (vn) và lim un = a, u x→1 n lim vn = +∞ thì lim bằng A. 11. B 19. C. 10. D. 9. vn A. +∞. B 0. C. 1. D. −∞.
Câu 64. Cho lim f (x) = 3. Tìm khẳng định x→2 Ê Lời giải. sai. un p Ta có lim u A. lim[ f (x) f (x) n = a, lim vn = +∞ thì lim = 0. + 3] = 6. B. lim + 1 = 2. v x x n →2 →2 Chọn đáp án B
C. lim[ f (x) − 2x] = −1. D lim f (x) − x2 = 1. x→2 x→2 Ê Lời giải. Câu 58. lim 3n bằng n→+∞ Ta có A +∞. B. 0. C. −∞. D. 2. Ê Lời giải.
lim f (x) − x2 = −1 = lim f (x) − lim x2 = 3 − 4 = −1. x→2 x→2 x→2
Ta có lim qn = +∞ nếu q > 1. Do đó, lim 3n = n→+∞ n→+∞ +∞.
Vậy lim f (x) − x2 = 1 sai. Chọn đáp án A x→2 Chọn đáp án D 2020 Câu 59. Tính lim . n
Câu 65. lim 3x2 + 7x + 11 có kết quả là x→2 A. +∞. B. −∞. C. 2020. D 0. A 37. B. 38. C. 39. D. 40. Ê Lời giải. Ê Lời giải. 2020 Theo định nghĩa suy ra lim = 2020 ·
lim 3x2 + 7x + 11 = 3 · 22 + 7 · 2 + 11 = 37. x→+∞ n x→2 1 lim Chọn đáp án A = 2020 · 0 = 0. x→+∞ n x2 Chọn đáp án D − 3
Câu 66. Giá trị của lim là x→−1 x3 + 2 2n − 3 3 Câu 60. Tính lim . A. 1. B −2. C. 2. D. − . 1 − 3n 2 2 1 Ê A − . B. 2. C. . D. 1. Lời giải. 3 3 x2 − 3 (−1)2 − 3 lim = = −2.
Câu 61. Cho dãy số (un) có lim un = 2. Tính giới x→−1 x3 + 2 (−1)3 + 2 3un − 1 hạn lim . Chọn đáp án B 2un + 5 3 −1 5
Câu 67. Cho c là hằng số, k là số nguyên A. +∞. B. . C. . D . 2 5 9
dương. Khẳng định nào sau đây sai? Ê Lời giải. A. lim x = x0. B. lim c = c. 3u x→x0 x→x0 n − 1 3 · 2 − 1 5 Ta có lim c = = . 2u C. lim = 0. D lim c = +∞. n + 5 2 · 2 + 5 9 x→+∞ xk x→+∞ Chọn đáp án D Ê Lời giải. 32
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
Theo định lý về giới hạn, khẳng định sai là Tính lim f (x) + lim f (x). x→1+ x→3− lim c = +∞. x→+∞ A. 5. B 4 . C. 2. D. 0. Chọn đáp án D Ê Lời giải.
Theo hình vẽ thì lim f (x) f (x) Câu 68. Cho lim f (x) = 1 và lim = 3.
= −∞, kết quả của lim(−3· x x→3− x →1+ →a x→a
Suy ra lim f (x) + lim f (x) = 4. f (x)) bằng x→1+ x→3− A. −∞. B. 0. C +∞. D. 3. Chọn đáp án B Ê Lời giải.
Câu 72. Cho hàm số y = f (x) có đồ thị như hình
Có lim(−3 · f (x)) = −3 · lim f (x) = +∞. x→a x→a vẽ bên dưới. Chọn đáp án C y 1 1 1 3
Câu 69. Tính tổng S = 9+3+1+ + +···+ + 3 9 3n−3 · · · . 2 27 A S = . B. S = 14. 2 1 C. S = 16. D. S = 15. O Ê Lời giải. x 1 3 1 1 Ta có S = 9 + 3 + 1 + + · · · + + · · · = 3 3n−3 Tính lim f (x) + lim f (x).   x→0 x→1− A 5. B. 4 . C. 2. D. 0.   Ö è Ê   Lời giải.  1 1 1  1 9 1 + + + · · · + + · · · = 9 =
Theo hình vẽ thì lim f (x) = 3 và lim f (x) = 2. Suy  3 32 3n−1  1 x→0 x→1−   1 − ra lim f (x) f (x) | {z } + lim = 5. 3 x x  1  →0 →1− CSN: u1=1, q= 3 Chọn đáp án A 27 .
Câu 73. Tính lim x3 − 2x + 1. 2 x→1+ Chọn đáp án A A. 1. B 0. C. +∞. D. −∞. p
Câu 70. Tổng của một cấp số nhân lùi vô hạn Câu 74. Tính lim x − 3 − 3x + x2. x→3−
bằng 2, tổng của ba số hạng đầu tiên của cấp số A Không tồn tại. B. −∞. 9 nhân bằng
. Số hạng đầu u1 của cấp số nhân C. 0. D. +∞. 4 đó là
Câu 75. Trong các giới hạn sau đây, giới hạn A u1 = 3. B. u1 = 4. nào bằng 0? 9 C. u 3 + 2n3 2n2 − 3 1 = . D. u1 = 5. 2 A. lim . B lim . 2n2 Ê − 1 −2n3 − 4 Lời giải. 2n − 3n3 2n2 − 3n4
Gọi q là công bội của cấp số nhân, ta có: C. lim . D. lim . −2n2 − 1 −2n4 + n2  u1  Ê Lời giải.  = 2  u1 = 2(1 − q)  1 − q  ⇔ ⇔ 3 + 2n3 1 − q3 9 9 lim
= +∞ : « bậc tử » > « bậc mẫu » và  2 1 − q3 = 2n2 − 1 S =  3 = u1 · 1− q 4 4 ambk = 2 · 2 = 4 > 0.  1 2n2 − 3  q = − lim
= 0 : « bậc tử » < « bậc mẫu ».  2 −2n3 − 4 1 2n − 3n3  u1 = 2 1 + = 3. lim
= +∞ : « bậc tử » > « bậc mẫu » và 2 −2n2 − 1 Chọn đáp án A
anbk = (−3) · (−2) > 0. 2n2 − 3n4 −3 3
Câu 71. Cho hàm số y = f (x) có đồ thị như hình lim = =
: « bậc tử » = « bậc mẫu » −2n4 + n2 −2 2 vẽ bên dưới. am −3 3 và = = . y bk −2 2 3 Chọn đáp án B
Câu 76. Dãy số nào sau đây có giới hạn là 2 +∞? 1 + n2 n2 − 2 1 A un = . B. un = . O 5n + 5 5n + 5n3 n2 1 x − 2n + 2n 1 3 C. un = . D. . 5n + 5n2 5n + 5n2 33
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC Ê Lời giải. 4 a + 1 an + 4 n a Ta có lim un = lim = lim = . Khi đó 1 + n2 + 1 3 n2 5n + 3 5 lim u 5 + n = lim = lim n · = +∞ vì 5n + 5 5 n 5 + a n lim un = 2 ⇔ = 2 ⇔ a = 10.  5 lim n = +∞  Chọn đáp án A    1  + 1 Câu 82. Cho số thực a thỏa mãn n2 am 1 p lim > 0.  = = a 2x2 1  5 + 3 + 2017  bk 5  lim = . Khi đó giá trị của  5 + n x→+∞ 2x + 2018 2 a là Chọn đáp án A p − 2 1 A. a = . B. a = .
Câu 77. Dãy số nào sau đây có giới hạn là 2 2 p −∞? −1 2 1 C. + 2n n3 + 2n − 1 a = . D a = . A. . B. u 2 2 n = . 5n + 5n2 −n + 2n3 Ê Lời giải. 2n2 − 3n4 n2 − 2n Ta có C un = . D. un = . n2 + 2n3 5n + 1 … … Ê 3 3 2017 Lời giải. p ax 2 + + 2017 a 2 + + p a 2x2 + 3 + 2017 x2 x2 x a 2 2n2 − 3n4 lim = lim = lim = . un =
: « bậc tử » > « bậc mẫu » và x→+∞ 2x + 2018 x→+∞ 2018 x→+∞ 2018 2 n2 + 2n3 x 2 + 2 + a x x
m bk = −3.2 = −6 < 0 ⇒ lim un = −∞. Chọn đáp án C p p a 2 1 2 Khi đó: = ⇔ a = . Ä p ä
Câu 78. Giá trị lim n − n2 − 4n bằng 2 2 2 Chọn đáp án D A. 3. B. 1. C 2. D. 4. Ê Lời giải.  x2 + 1  với x < 1 Ä p ä 4n
Câu 83. Cho hàm số f (x) = 1 − x . Ta có lim n − n2 − 4n = lim p = p n + n2 − 4n  2x − 2 với x > 1 4 lim = 2. Khi đó lim f (x) là … x 4 →1− 1 + 1 − A +∞. B. −1. C. 0. D. 1. n Ê Lời giải. Chọn đáp án C  lim x2 x2 + 1 = 2 + 1  x2 − 3x + 2 x lim f (x) →1− = lim = +∞ vì Câu 79. Tính lim . x→1− x→1− 1 − x
lim (1 − x) = 0 & 1 − x > 0(∀x < 1). x→1 x − 1  x→1− A. 1. B. −∞. C −1. D. +∞. Chọn đáp án A Ê Lời giải. p p p p x2 x2 3 − 3x + 2 (x − 1)(x − 2) + 6 − x Ta có L Câu 84. Cho lim 2 3 = lim = lim = p p = a + b + x→−∞ x→1 x − 1 x→1 (x − 1) x 2 − x2 + 3 p lim(x − 2) = −1.
c 6 + d, (a, b, c, d ∈ Q). Tính ab + cd. x→1 A. 1. B. 0. C −2. D. 2. Chọn đáp án C
Câu 85. Tìm tất cả các giá trị thực của tham
Câu 80. Tìm lim (4x4 − 3x2 + 2).  x→−∞ x2 + x − 12  A khi x +∞. B. −∞. C. 4. D. 2. 6= −4 số m để hàm số f (x) = x + 4 Ê Lời giải. mx + 1 khi x = −4 3 2
lim (4x4 − 3x2 + 2) = lim x4 4 − + = +∞.
liên tục tại điểm x0 = −4. x→−∞ x→−∞ x2 x4 A. m = 4. B m = 2. C. m = 3. D. m = 5. Chọn đáp án A Ê Lời giải. Ta có 2
Mức độ Vận dụng x2 + x − 12 (x − 3)(x + 4) lim f (x) = lim = lim = −7. an + 4 x→−4 x→−4 x + 4 x→−4 x + 4
Câu 81. Cho dãy số (un) với un = , với a 5n + 3
Hàm số đã cho liên tục khi và chỉ khi
là tham số thực. Để dãy số (un) có giới hạn bằng 2 thì giá trị của a là
lim f (x) = f (−4) ⇔ −4m + 1 = −7 ⇔ m = 2. x A a = 10. B. a = 8. →−4 C. a = 6. D. a = 4 .
Vậy m = 2 là giá trị cần tìm. Ê Lời giải. Chọn đáp án B 34
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
B. BÀI TẬP TỰ LUẬN
BÀI 15. Tính các giới hạn sau n2 + 1 2n + 3 a) lim . b) lim . n→+∞ 2n2 + n + 2 n→+∞ 1 + 3n Äp ä c) lim n2 + 2n − n . d) lim 2n3 + 2n − 1. Ê Lời giải.
BÀI 16. Tính các giới hạn sau: x2 + 2x − 15 2x2 − 5x + 2 a) lim . b) lim . x→3 x − 3 x→2 x2 − 4 p1+2x−1 x − 2 c) lim . d) lim . x→0 2x x→1+ x − 1 Äp ä e) lim x2 + x − x . f) lim −x3 − x2 + 4x + 2. x→+∞ x→+∞ Ê Lời giải.
BÀI 17. Xét tính liên tục của mỗi hàm số sau tại điểm x = 2. ®6 − 2x khi x ≥ 2  x2 − 4 a) f (x) =  khi x 6= 2 2x2 − 6 khi x < 2; b) f (x) = x − 2 0 khi x = 2. Ê Lời giải.
a) Tập xác định của hàm số là D = R, chứa điểm 2. Ta có ○ f (2) = 6 − 2 · 2 = 2;
○ lim f (x) = lim (6 − 2x) = 6 − 2 · 2 = 2; x→2+ x→2+
○ lim f (x) = lim (2x2 − 6) = 2 · 22 − 6 = 2. x→2− x→2−
Do lim f (x) = lim f (x) = 2 nên lim f (x) = 2. x→2+ x→2− x→2
Khi đó lim f (x) = f (2) nên hàm số f (x) liên tục tại x = 2. x→2
b) Tập xác định của hàm số là D = R, chứa điểm 2. x2 − 4 (x − 2)(x + 2)
Ta có f (2) = 0 và lim f (x) = lim = lim = lim(x + 2) = 4. x→2 x→2 x − 2 x→2 x − 2 x→2
Vì lim f (x) 6= f (2) nên hàm số không liên tục tại x = 2. x→2
BÀI 18. Chứng minh rằng phương trình
a) x3 + 2x − 1 = 0 có nghiệm thuộc khoảng (−1;1). p b)
x2 + x + x2 = 1 có nghiệm thuộc khoảng (0;1). Ê Lời giải.
a) Xét hàm số f (x) = x3 + 2x − 1 là hàm số liên tục trên đoạn [−1;1].
Ta có f (−1) · f (1) = (−4) · 2 = −8 < 0 suy ra tồn tại c ∈ (−1;1) để f (c) = 0.
Từ đó suy ra phương trình x3 + 2x − 1 = 0 có nghiệm thuộc khoảng (−1;1) (đcpm). 35
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC p p b) Ta có
x2 + x + x2 = 1 ⇔ x2 + x + x2 − 1 = 0. p
Xét hàm số g(x) = x2 + x + x2 − 1 là hàm số liên tục trên đoạn [0;1]. p p
Ta có g(0) · g(1) = (−1) · 2 = − 2 < 0 suy ra tồn tại c ∈ (0;1) để g(c) = 0. p
Từ đó suy ra phương trình
x2 + x+x2 = 1 có nghiệm thuộc khoảng (0;1) có nghiệm trên khoảng (0; 1) (đpcm).
BÀI 19. Trong hồ có chứa 6000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít
vào hồ với tốc độ 15 lít/phút.
a) Chứng tỏ rằng nồng độ muối của nước trong hồ sau t phút kể từ khi bắt đầu bơm là 30t C(t) = (gam/lít). 400 + t
b) Nồng độ muối trong hồ như thế nào nếu t → +∞. Ê Lời giải.
a) Sau thời gian t phút, số lít nước trong hồ là 6000 + 15t (lít).
Số gam muối trong số lít nước bơm vào là 30 · 15t = 450t (gam).
Nồng độ muối của nước trong hồ sau t phút khi bắt đầu bơm là 450t 30t C(t) = = (gam/lít). 6000 + 15t 400 + t
b) Khi t → +∞, ta xét giới hạn 30t 30 lim C(t) = lim = lim = 30. t→+∞ t→+∞ 400 + t t→+∞ 400 +1 t
Vậy khi bơm nước biểm vào hồ chứa, không giới hạn thời gian thì nồng độ muối trong hồ chứa
chính là nồng độ muối của nước biển.
BÀI 20. Từ độ cao 100 m, người ta thả một quả bóng cao su xuống đất. Giả sử cứ sau mỗi lần chạm 1
đất, quả bóng nảy lên một độ cao bằng
độ cao mà quả bóng đạt được trước đó. Gọi hn là độ cao quả 4
bóng đạt được ở lần nảy thứ n.
a) Tìm số hạng tổng quát của dãy số (hn).
b) Tính giới hạn của dãy số (hn) và nêu ý nghĩa giới hạn của dãy số (hn).
c) Gọi Sn là tổng độ dài quãng đường đi được của quả bóng từ lúc bắt đầu thả quả bóng đến khi
quả bóng chạm đất lần thứ n. Tính Sn, nếu quá trình này cứ tiếp tục diễn ra mãi thì tổng
quãng đường quả bóng di chuyển được là bao nhiêu? Ê Lời giải. 1
a) Vì sau mỗi lần chạm đất, quả bóng nảy lên một độ cao bằng
độ cao mà quả bóng đạt được 4
trước đó nên độ cao của quả bóng nảy lên lần thứ n là một cấp số nhân (hn) có u1 = 100, công 1 n 1
bội q = . Khi đó số hạng tổng quát của dãy số (hn) là hn = 100 · 4 4 ï nò n 1 1 b) Ta có lim hn = lim 100 · = 100 lim = 0. 4 4
Ý nghĩa của giới hạn là khi n tiến dần ra vô cực thì độ nảy của quả bóng càng dần về 0, có
nghĩa là sau khoảng thời gian đủ dài thì độ nảy của quả bóng không đáng kể. 36
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC 1
c) Ta thấy tổng Sn là tổng của cấp số nhân lùi vô hạn có u1 = 100, công bội q = . 4 1 2 n 1 1 1 400
Ta có Sn = 100 + 100 · + 100 · + . . . + 100 · + . . . = 100 · = m. 4 4 4 1 3 1 − 4 —HẾT— 37
½ ĐỀ CƯƠNG ÔN TẬP HKI - Năm học 2023 – 2024 ½
TOÁN 11 – KẾT NỐI TRI THỨC
ĐÁP ÁN CÁC TRẮC NGHIỆM 1
Trắc nghiệm chương I 1. A 2. D 3. B 4. B 5. A 6. C 7. B 8. D 9. B 10. C 11. B 12. D 13. B 14. A 15. D 16. B 17. C 18. B 19. D 20. C 2
Trắc nghiệm chương II 1. A 2. B 3. C 4. D 5. D 6. B 7. D 8. B 9. D 10. C 11. B 12. D 13. A 14. A 15. D 16. D 17. D 18. B 19. D 20. D 3
Trắc nghiệm chương III 21. A 22. B 23. C 24. D 25. D 4
Trắc nghiệm chương IV 26. D 27. C 28. D 29. D 30. B 31. D 32. D 33. C 34. C 35. B 36. A 37. D 38. B 39. B 40. A 41. A 42. A 43. C 44. D 45. D 46. C 47. D 48. C 49. D 50. D 51. A 52. B 53. C 54. B 55. B 5
Trắc nghiệm chương V 56. D 57. B 58. A 59. D 60. A 61. D 62. A 63. B 64. D 65. A 66. B 67. D 68. C 69. A 70. A 71. B 72. A 73. B 74. A 75. B 76. A 77. C 78. C 79. C 80. A 81. A 82. D 83. A 84. C 85. B 38
Document Outline

  • DE CUONG 11-HKI
    • HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
      • BÀI TẬP TRẮC NGHIỆM
        • Mức độ Nhận biết, Thông hiểu
          • Mức độ Vận dụng
        • BÀI TẬP TỰ LUẬN
    • DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN
      • BÀI TẬP TRẮC NGHIỆM
        • Mức độ Nhận biết, Thông hiểu
          • Mức độ Vận dụng
        • BÀI TẬP TỰ LUẬN
    • CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU GHÉP NHÓM
      • BÀI TẬP TRẮC NGHIỆM
        • Mức độ Nhận biết, Thông hiểu
          • Mức độ Vận dụng
        • BÀI TẬP TỰ LUẬN
    • QUAN HỆ SONG SONG SONG TRONG KHÔNG GIAN
      • BÀI TẬP TRẮC NGHIỆM
        • Mức độ Cơ bản
          • Mức độ Vận dụng
        • BÀI TẬP TỰ LUẬN
    • GIỚI HẠN. HÀM SỐ LIÊN TỤC
      • BÀI TẬP TRẮC NGHIỆM
        • Mức độ Nhận biết, Thông hiểu
          • Mức độ Vận dụng
        • BÀI TẬP TỰ LUẬN
  • DE CUONG 11-HKI-giai
    • HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
      • BÀI TẬP TRẮC NGHIỆM
        • Mức độ Nhận biết, Thông hiểu
          • Mức độ Vận dụng
        • BÀI TẬP TỰ LUẬN
    • DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN
      • BÀI TẬP TRẮC NGHIỆM
        • Mức độ Nhận biết, Thông hiểu
          • Mức độ Vận dụng
        • BÀI TẬP TỰ LUẬN
    • CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU GHÉP NHÓM
      • BÀI TẬP TRẮC NGHIỆM
        • Mức độ Nhận biết, Thông hiểu
          • Mức độ Vận dụng
        • BÀI TẬP TỰ LUẬN
    • QUAN HỆ SONG SONG SONG TRONG KHÔNG GIAN
      • BÀI TẬP TRẮC NGHIỆM
        • Mức độ Cơ bản
          • Mức độ Vận dụng
        • BÀI TẬP TỰ LUẬN
    • GIỚI HẠN. HÀM SỐ LIÊN TỤC
      • BÀI TẬP TRẮC NGHIỆM
        • Mức độ Nhận biết, Thông hiểu
          • Mức độ Vận dụng
        • BÀI TẬP TỰ LUẬN
      • myblue ĐÁP ÁN CÁC TRẮC NGHIỆM
        • Trắc nghiệm chương I
          • Trắc nghiệm chương II
          • Trắc nghiệm chương III
          • Trắc nghiệm chương IV
          • Trắc nghiệm chương V