

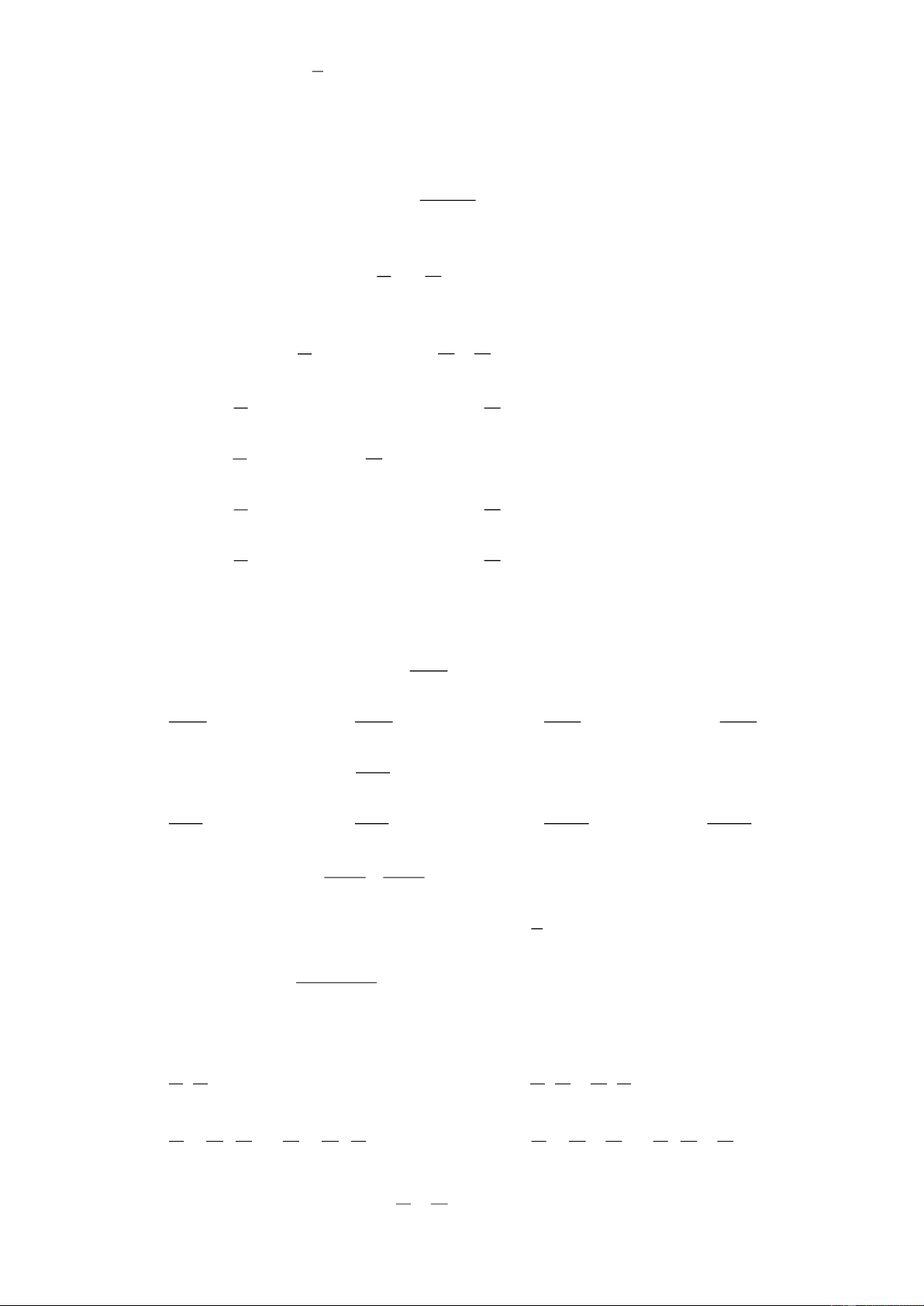

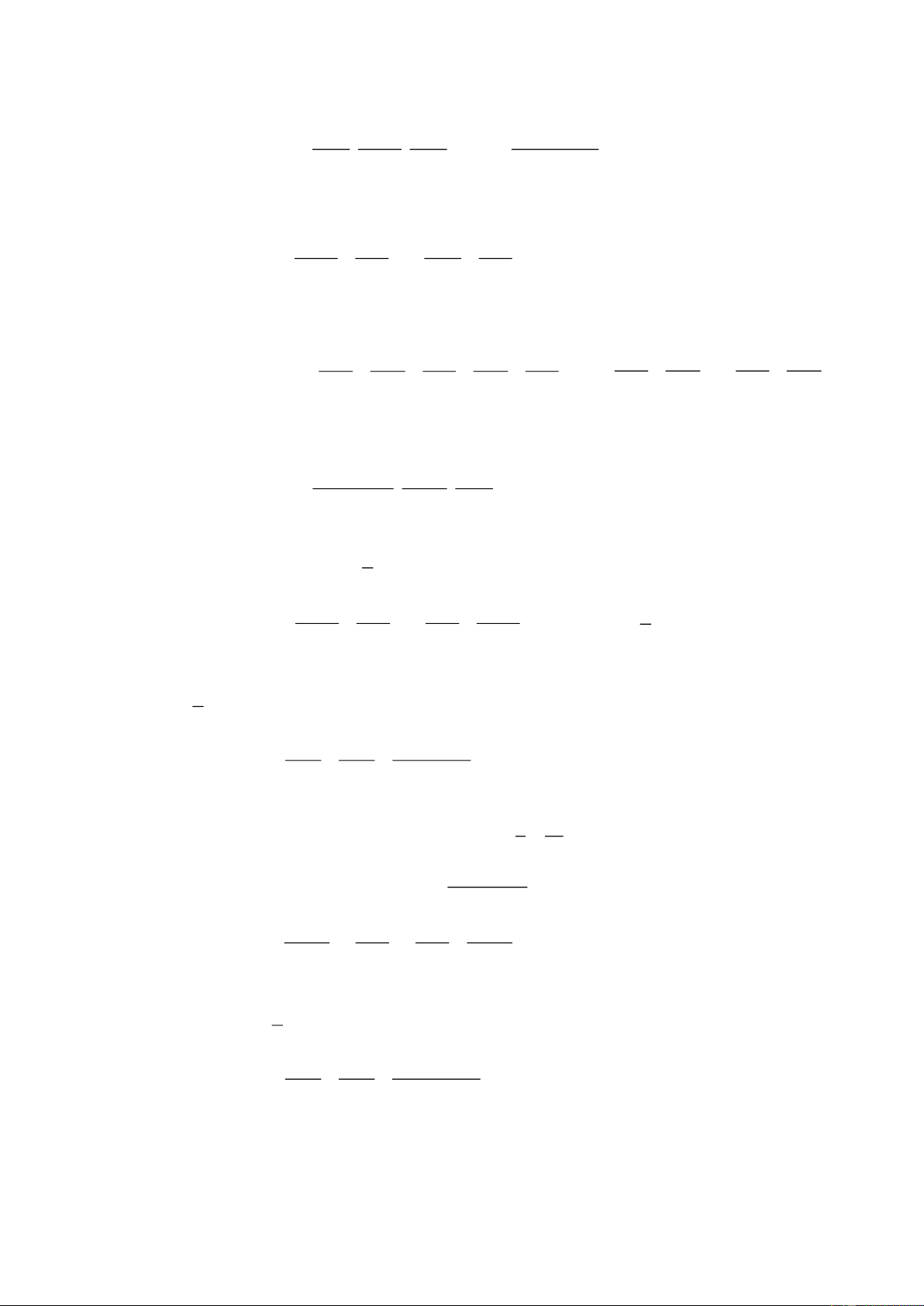



Preview text:
ĐỀ CƯƠNG HỌC KÌ I MÔN TOÁN 8
I. PHẦN TRẮC NGHIỆM Câu 1. Phân tích đa thức 3 3 2 2
x y − 6x y +12xy + 8 thành nhân tử, ta được? A. 3 xy + 2 . B. ( xy + )3 2 . C. 3 3 x y + 8 . D. 3 3 3 x y + 2 . 3 x Câu 2. Phân tích đa thức 3
+ 8y thành nhân tử, ta được? 8 2 x x 2 x x A. 2 + 2y + xy + 2y . B. 2 + 2y
− xy + 4y . 2 2 2 4 2 x x 2 x x C. 2 + 2y
− xy + 4y . D. 2 + 2y
− 2xy + 4y . 2 2 2 4 9 Câu 3. Phân tích đa thức 2 16x −12x +
thành nhân tử, ta được? 4 2 2 2 3 3 3 A. x − . B. 2 4x − 3 . C. 2x + . D. 4x − . 4 4 2 Câu 4. Phân tích đa thức 2 2 3
2x y −12xy +18y − 2 y thành nhân tử, ta được? A. 2
2 yx − 3y −1. B. 3 2 yx − 3y .
C. 2 y ( x − 3y + )
1 ( x − 3y − ) 1 .
D. ( x − y)2 2 3 −1 . Câu 5.
Biết rằng 2x+y=0. Biểu thức A = ( x + y)3 3 2 2 9
+ x − 2x y − xy thành nhân tử, ta được? 1 A. 0 . B. −1. C. . D. −1. 2 1010 Câu 6.
Giá trị của biểu thức 2 2
3x − 4 y + 4x − 3y tại x = 2020 2 và y = 4 là? A. 0 . B. 1. C. 2 . D. 3 . Câu 7.
Giá trị của biểu thức 2 9
− x − 6x + 5 là? 1 1 − A. . B. . C. 6 . D. 6 − . 3 3 Câu 8.
Giá trị nhỏ nhất của biểu thức 2
x +10x + 22 là? A. 3 − . B. 3 . C. 22 . D. −22 . Câu 9. Cho các công thức 2 y − 3 = ; x − 2 y = ;
x y = x . Có bao nhiêu công thức chứng tỏ rằng y là hàm số của x? A. 0 . B. 1. C. 2 . D. 3 . 15
Câu 10. Hàm số y = f (x) = 2x − được xác định khi nào? 4 A. x 4 . B. x = 4 . C. x 2 . D. x = 2 .
Câu 11. Cho hàm số được cho bởi công thức 2
y = f (x) = x tính giá trị của f ( 5
− ) + f (5) , ta được? A. 0 . B. 25 . C. 50 . D. 10 . 1
Câu 12. Cho hàm số được cho bởi công thức y = f (x) = −
x nhận giá trị âm thì dấu của x là? 2 A. x 0 . B. x 0 . C. x = 0 .
D. chưa biết dấu của x.
Câu 13. Viết biểu thức 2 2 3
2x y −12xy +18y − 2 y dưới dạng hiệu hai lập phương, ta được?
A. x + ( y)3 3 3 .
B. x + ( y)3 3 9 .
C. x − ( y)3 3 3 .
D. x − ( y)3 3 9 . Trang 1 1 −
Câu 14. Cho hàm số y = f (x) = 5x trong các điểm (
A 1; 2); B(2; 10);C( 2
− ;10); D( ;1) , có bao nhiêu điểm 5
thuộc đồ thị hàm số trên? A. 1. B. 2 . C. 3 . D. 4 .
Câu 15. Điền vào chỗ chấm trong đẳng thức ( x − y)( 2 2 2
x + 2xy + 4 y ) = ........ ta được? A. 3 3 x − 8 y . B. 3 3 x − y . C. 3 3 8x − y . D. 3 3 x + 8 y .
Câu 16. Cho hàm số y = 3
− x +1 và điểm C thuộc đồ thị của hàm số đó. Nếu tung độ của điểm C là 1 thì tọa độ của điểm C là? A. C( 1 − ;1) . B. C(0; 0) . C. C(0;1) . D. C(1; 0) .
Câu 17. Chọn khẳng định đúng về đồ thị của hàm số y = ax + b (a 0) ?
A. là đường thẳng đi qua gốc tọa độ.
B. là đường thẳng song song với trục hoành. b −
C. là đường thẳng đi qua hai điểm (
A 0; b) và B( ; 0) với a 0 . a
D. là đường cong đi qua gốc tọa độ.
Câu 18. Cho đường thẳng d : y = 2x + 6 , giao điểm của d với trục hoành là? 1 A. P 0; . B. N (6; 0) . C. M ( 3 − ; 0) .
D. D (0; − 6) . 6
Câu 19. Chọn khẳng định đúng về đồ thị của hàm số y = ax + b (a 0; b = 0) ?
A. là đường thẳng đi qua gốc tọa độ.
B. là đường thẳng song song với trục hoành. b −
C. là đường thẳng đi qua hai điểm (
A 0; b) và B( ; 0) với a 0 . a
D. là đường cong đi qua gốc tọa độ.
Câu 20. Trong các hàm số sau hàm số nào là hàm số bậc nhất? x − 3 x + 5 A. y = 4 . B. y = x + 3 . C. y = . D. y = . 4 x − 6
Câu 21. Đường thẳng y = 3
− x +1 có hệ số góc là? 1 1 − A. a = . B. a = 1. C. a = 3 − . D. a = . 3 3 m +1
Câu 22. Tìm m để hàm số y = x + 2m − 3 m − là hàm số bậc nhất? 2 A. m 1 − . B. m 1 − .
C. m { −1; 2} . D. m 2 .
Câu 23. Cho bảng giá trị sau: x -3 -2 -1 0 1 2 y 6 4 1 6 2 5 Chọn câu đúng
A. Đại lượng y là hàm số của đại lượng x.
B. Đại lượng y không là hàm số của đại lượng x.
C. Đại lượng y tỉ lệ thuận với đại lượng x.
D. Đại lượng y tỉ lệ nghịch với đại lượng x. 2
Câu 24. Đồ thị hàm số y = 5x −
đi qua điểm nào dưới đây? 5 22 1 3 2 − 3 − A. A 1; B. B ; C. C ; D. D(2;10) 5 5 5 5 5 Trang 2 1
Câu 25. Cho hàm số y = f (x) =
x + 2 . Tìm x, biết f (x) = − 6 . Câu nào sau đây đúng: 4 A. x = 28 − B. x = 30 C. x = 32 − D. x = 36
Câu 26. Tìm x biết 3 2
x + 3x + 3x +1 = 0 A. x = 1 − . B. x = 1. C. x = 2 − .
D. x = 0 . 3 −
Câu 27. Với điều kiện nào của x thì phân thức có nghĩa? 6x + 24 A. x 4 − . B. x 3. C. x 4 .
D. x 2 . A C
Câu 28. Với B 0, D 0 , hai phân thức và bằng nhau khi? B D
A. AB = CD .
B. AC = BD .
C. AD = BC .
D. AC BD . A C C
Câu 29. Muốn chia phân thức cho phân thức 0 B D D A D A. Ta nhân
với phân thức nghịch đảo của . B C A C B. Ta nhân với phân thức . B D A C C. Ta nhân
với phân thức nghịch đảo của . B D A C D. Ta cộng
với phân thức nghịch đảo của . B D
Câu 30. Giá trị của biểu thức 3 3
Q = a + b biết a + b = 5và ab = 3 − . A. Q = 170 . B. Q = 140 . C. Q = 80 . D. Q = 170 − . x
Câu 31. Phân thức nghịch đảo của phân thức
với x 0, x 2 − là: x + 2 x x + 2 x x A. . B. C. − . D. − . x + 2 x x + 2 x + 2 −x
Câu 32. Phân thức đối của phân thức là? x −1 x x −1 x x A. . B. . C. − . D. . x −1 −x −x −1 −x +1 3 x x
Câu 33. Thực hiện phép tính sau: + 2 2 x +1 x +1 x A. −x B. 2x C. . D. x 2 2 x − 4x + 4
Câu 34. Giá trị của phân thức khi x = 2020 x − 2 A. 2018 B. 2022 C. 2016 D. 2024
Câu 35. Chọn câu sai: A B A C C A A. = 1 B. = B A B D D B A C E E C A A C E A C E C. = D. + = + B D F F D B B D F B D F A C
Câu 36. Với B 0 kết quả của phép cộng + là B D Trang 3 . A C A + C A + C A + C A. B. C. D. B B 2 B 2B 3 x −16x
Câu 37. Giá trị của x để phân thức 3 2 x − 3x − bằng 0 4x A. x 4 B. x 1. C. x = 4 − . D. x = 1 − . 3 4 2x y
Câu 38. Trong các phân thức sau, phân thức nào bằng phân thức 2 3 8x y 2 4xy 2 2 x y 2 xy 3 2 2x y A. . B. . C. . D. . xy 4xy xy 8xy 1 1 1
Câu 39. Tính một cách hợp lí biểu thức A = − −
được kết quả là: x + 1 y + 1 x + 1 1 1 −1 −1 A. y + . B. 1 x + . C. 1 x + . D. 1 y + . 1
2x + 1 x −1 3y −1
Câu 40. Tính nhanh biểu thức B =
3y −1 x + 1 2x + được kết quả là? 1 x −1 1− x 3y −1 x −1 A. B. C. D. x +1 x +1 x +1 3y −1
Câu 41. Sử dụng tính chất phân phối của phép nhân đối với phép cộng rút gọn biểu thức 1 1 2 C = (x − 4).( − ) được kết quả là x − 2 x + 2 1 1 A. B.4 C.-4 D. x − 2 x − 2 x 2x x 4 −
Câu 42. Tính một cách hợp lý biểu thức D = . + . được kết quả là x − 2 x +1 x − 2 x +1 x 2 − x 2x −x A. B. C. D. x +1 x +1 x +1 x +1 x x x
Câu 43. Sử dụng quy tắc dấu ngoặc để rút gọn biểu thức 2 2 E = + − − được kết quả là
y x +1 y x +1 x 2x A. B. C.-2 D.2 y x +1
Câu 44. Một mảnh vườn hình chữ nhật có kích thước là 10 m và 7 m. Biết chu vi của mảnh vườn hình
chữ nhật này sau khi tăng chiều dài và chiều rộng thêm x (m) là một hàm số bậc nhất y theo biến
số x. Hệ số a,b của hàm số này là
A. a = 4;b = 34 B. a = 7;b = 10
C. a = 2;b = 17 D. a = 4;b = 17
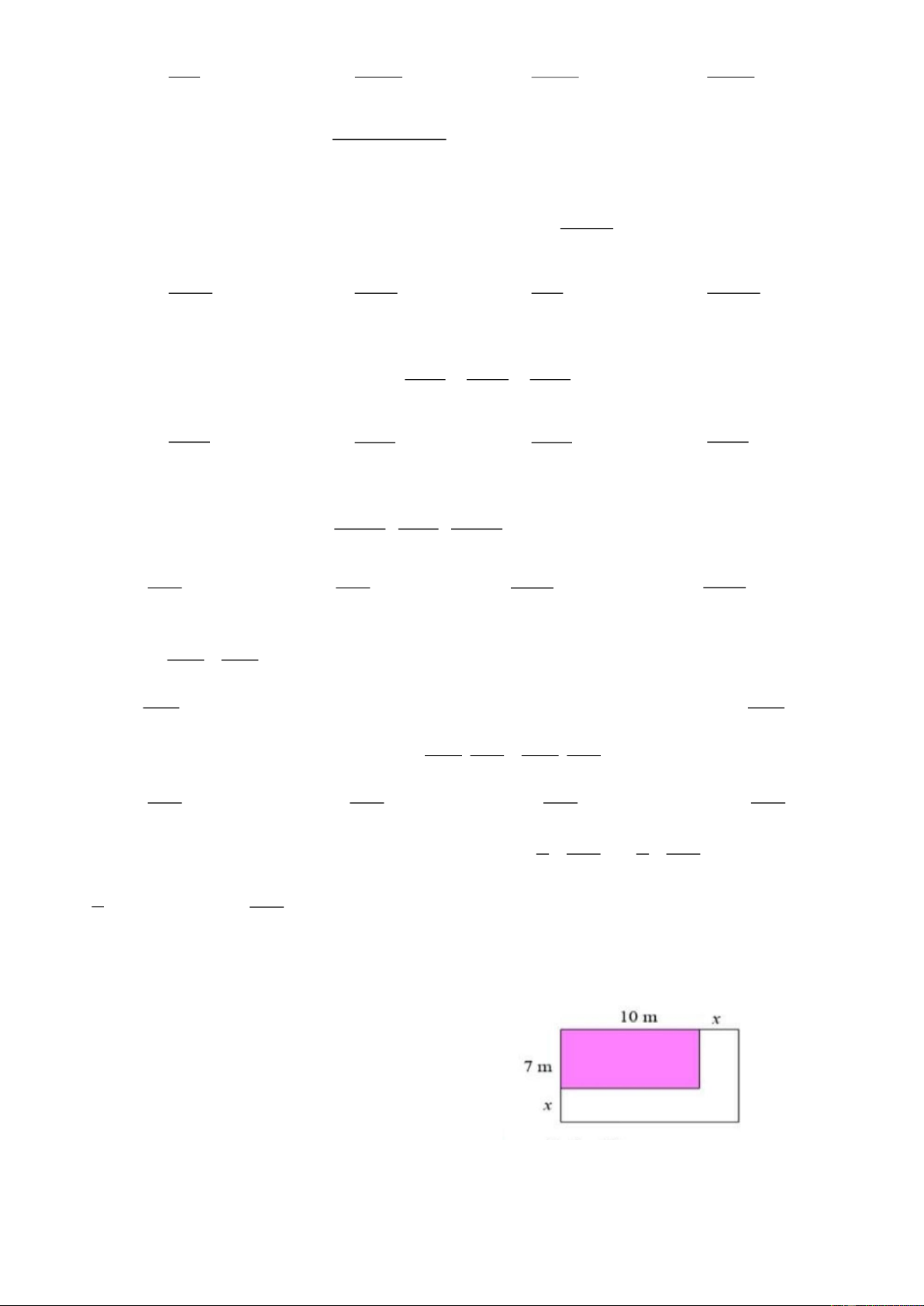
Câu 45. Hai ô tô khởi hành cùng lúc và đi cùng chiều về phía D
một ô tô bắt đầu đi từ B với vận tốc 40 km/h, một ô tô
bắt đầu đi từ C với vận tốc 50 km/h. Khoảng cách từ
A đến mỗi xe sau x giờ là một hàm số. Đồ thị của hai hàm số trên là hai đường thẳng Trang 4
A.Trùng nhau B.Cắt nhau C.Song song D.Phân biệt
Câu 46. Tuần này mẹ đi chợ hai lần để mua thịt heo với tổng số tiền mang theo là 500 000đ và đi bằng xe
máy. Biết 1 kg thịt heo có giá trị 150 000đ phí gửi xe máy là 5000đ. Công thức biểu thị số tiền còn
lại y (đồng) của mẹ sau khi gửi xe và mua x (kg) thịt của tuần này là
A. 150000.x −10000 B. 490000 +150000.x
C. 150000.x +10000 D. 490000 −150000.x
Câu 47. Bạn An đi đến nhà sách để mua x quyển vở, giá
mỗi quyển vở là a (nghìn đồng). Gọi b (nghìn
đồng) là phí gửi xe. Hàm số bậc nhất y biểu diễn
tổng số tiền bạn An cần khi đi mua vở ở nhà sách
như hình dưới. Nếu tổng số tiền mua vở y (nghìn
đồng) là 87(nghìn đồng) thì bạn An mua được bao nhiêu cuốn vở ? A.5 B.10 C.8 D.12
Câu 48. Hình chóp tứ giác đều có các mặt bên là hình
A.Tam giác cân B. Tam giác
đều C.Tam giác vuông D.Tam giác vuông cân
Câu 49. Hình chóp tam giác đều có bao nhiêu mặt ?
A.3 B.4 C.5 D.6
Câu 50. Diện tích xung quanh của hình chóp tam giác đều có độ dài trung đoạn 12 cm, cạnh đáy 5cm là
A.180 cm2 B.60 cm2 C.90 cm2 D.360 cm2
Câu 51. Thể tích của hình chóp tứ giác đều có chiều cao 6 cm, cạnh đáy 4 cm là
A.32 cm B.24 cm C.144 cm D.96 cm
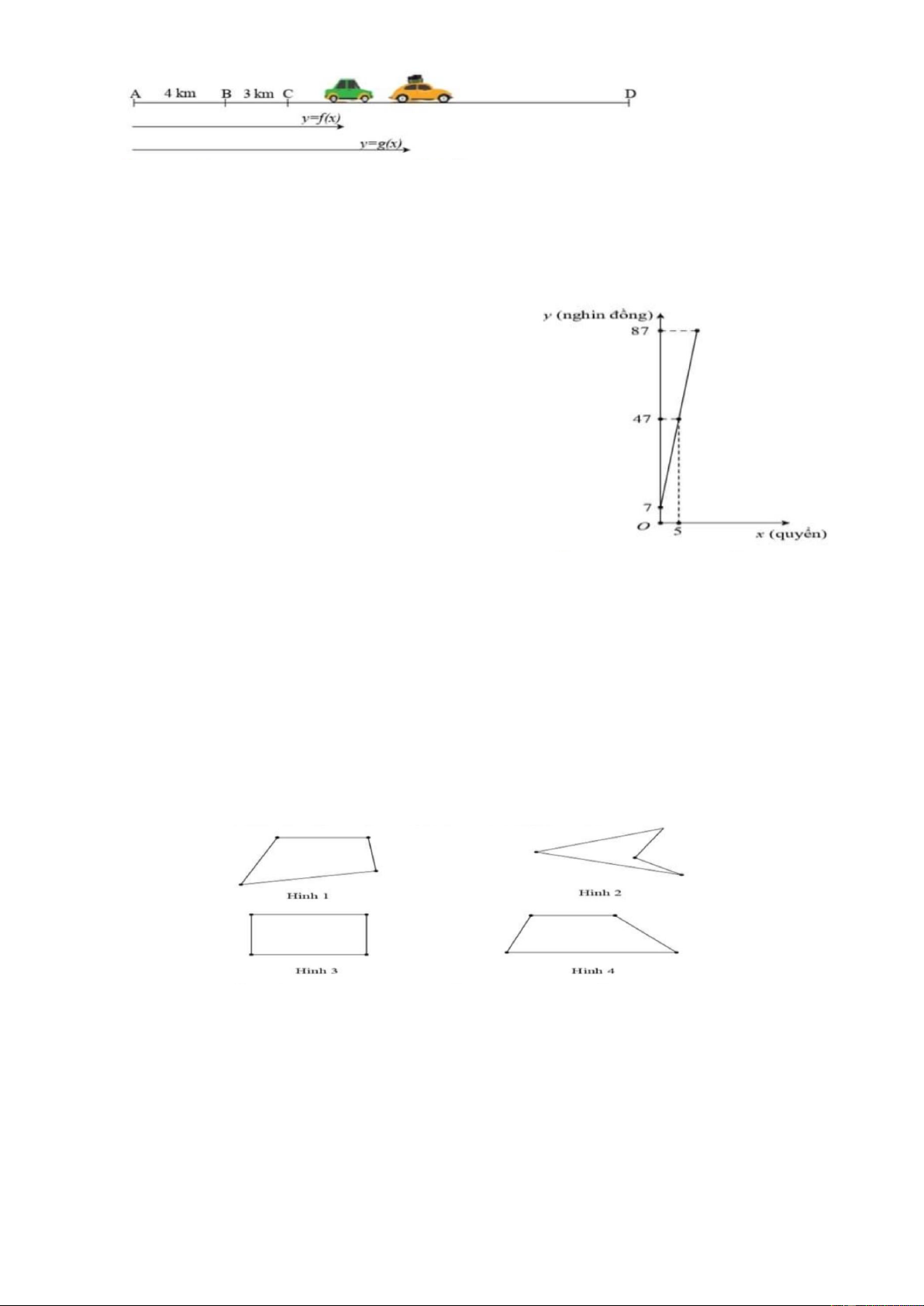
Câu 52. Tổng các góc của một tứ giác bằng
A.00 B.900 C.1800 D.3600
Câu 53. Trong các tứ giác sau, tứ giác nào không là tứ giác lồi ?
A.Hình 1 B.Hình 2 C.Hình 3 D.Hình 4
Câu 54. Cho tứ giác ABCD có 0 0 0
A = 58 ; B = 65 ;C = 102 Số đo góc D là
A.1220 B.780 C.1350 D.1150
Câu 55. Cho tam giác ABC vuông tại B, khi đó A. 2 2 2
AB = BC + AC B. 2 2 2
AC = AB + BC C. 2 2 2
BC = AB + AC D. 2
AC = AB + AC
Câu 56. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau ?
A.15cm, 8cm, 18cm B.2m, 3m, 4m
C.5cm, 2cm, 6cm D.5dm, 12dm, 13dm
Câu 57. Cho tam giác ABC vuông tại A có BC = 15 cm, AC = 12 cm độ dài đoạn thẳng AB bằng
A.4 cm B.27 cm C.81 cm D.9 cm Trang 5
Câu 58. Cho tam giác MNP vuông cân tại M. Tính độ dài NP, biết MN = MP = 3 dm
A.6 dm B.18 dm C. 18 dm D.3 dm
Câu 59. Cho hình thang cân ABCD (AB//CD) có 0
A = 70 . Khẳng định nào dưới đây là đúng ? A. 𝐶̂ = 1100. B. 𝐴̂ = 1100. C. 𝐶̂ = 700. D. 𝐵 ̂ = 700.
Câu 60. Cho hình thang cân ABCD (AB//CD) có 𝐶̂ – 𝐴̂ = 400. Khẳng định nào dưới đây là đúng? A. 𝐶̂ = 1100. B. 𝐴̂ = 1100. C. 𝐶̂ = 700. D. 𝐵 ̂ = 700.
Câu 61. Cho hình thang cân ABCD (AB//CD) có 𝐶̂ – 2.𝐴̂ = 900. Khẳng định nào dưới đây là đúng? A. 𝐴̂ = 300. B. 𝐴̂ = 1500. C. 𝐶̂ = 300. D. 𝐶̂ = 1500.
Câu 62. Cho hình thang cân ABCD (AB//CD). Vẽ tia Cx là tia đối của tia CD. Tính số đo góc BCx, biết 𝐴̂ = 300. A. 𝐵𝐶𝑥 ̂ = 300. B. 𝐵𝐶𝑥 ̂ = 1500. C. 𝐵𝐶𝑥 ̂ = 600. D. 𝐵𝐶𝑥 ̂ = 1400.
Câu 63. Cho hình thang cân MNED (MN//ED) có 𝐸̂ = 550. Khẳng định nào dưới đây là đúng? A. 𝑀 ̂ = 550. B. 𝑁 ̂ = 550. C. 𝑀 ̂ = 1250. D. 𝐷 ̂ = 1250.
Câu 64. Cho tam giác ABC cân tại A. Qua điểm M trên cạnh AB kẻ đường thẳng song song với BC cắt
cạnh AC tại N. So sánh CM và BN. A. CM > BN. B. CM = BN. C. CM < BN. D. CM ≠ BN.
Câu 65. Cho hình thang cân ABCD (AB//CD) có 𝐷
̂ = 750. Góc C có số đo bằng A. 750. B. 150. C. 1050. D. 1500.
Câu 66. Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đáy lớn CD = 15cm, cạnh bên BC = 10cm.
Chu vi hình thang cân ABCD là A. 18cm. B. 38cm. C. 28cm. D. 90cm.
Câu 67. Cho hình thang ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O sao cho OA
= OB, OC = OD. Tìm khẳng định sai trong các khẳng định sau?
A. ABCD là hình thang cân. B. AC = BD. C. BC = AD.
D. Tam giác BOC là tam giác cân tại O.
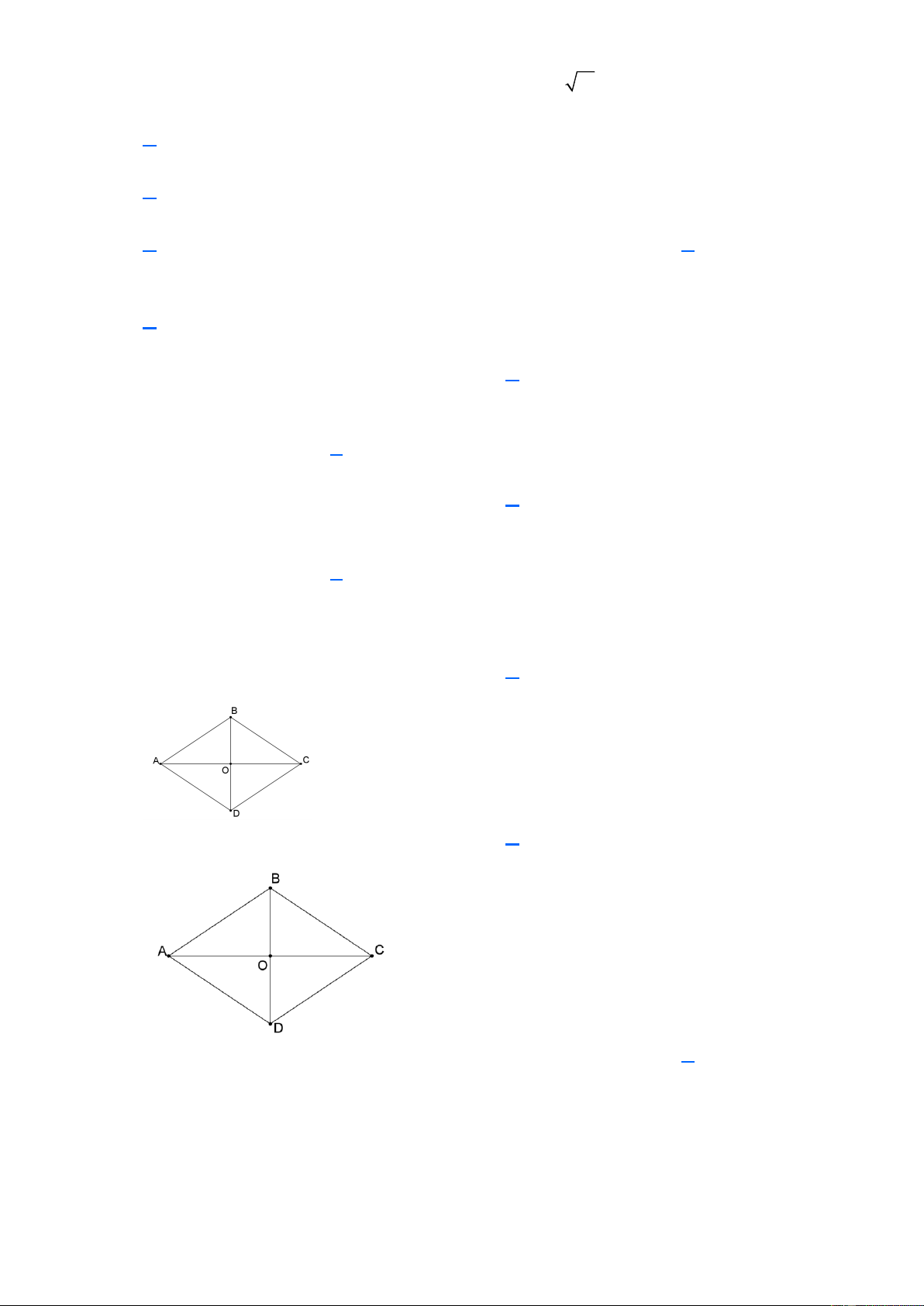
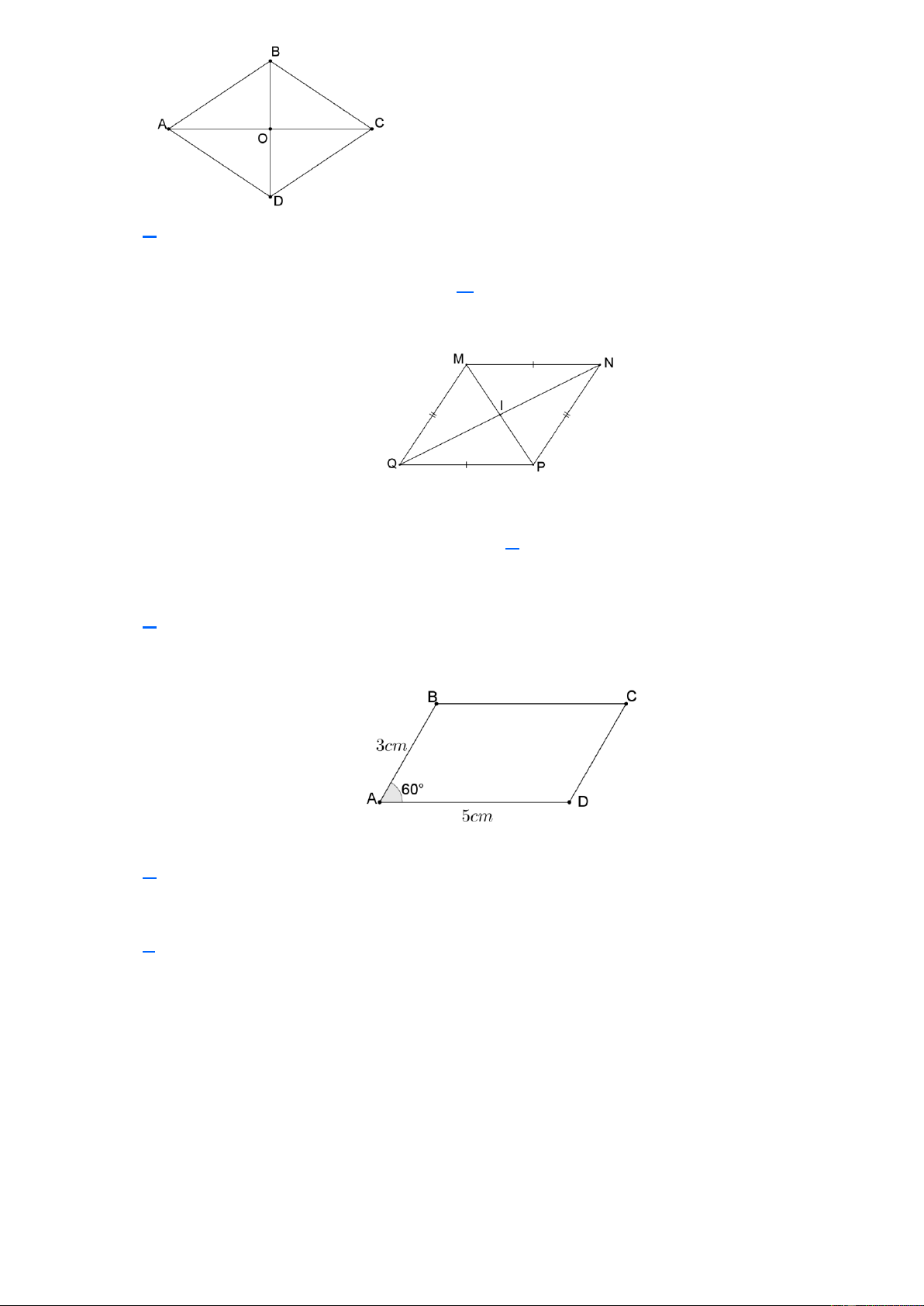
Câu 68. Cho hình thoi ABCD như hình vẽ sau, có OA = 8cm. Khi đó độ dài đường chéo AC là A. AC = 4cm. B. AC = 2cm. C. AC = 16cm. D. AC = 8cm.
Câu 69. Cho hình thoi ABCD như hình vẽ sau, có BD = 20cm. Khi đó độ dài OB là A. OB = 40cm. B. OB = 20cm. C. OB = 5cm. D. OB = 10cm.
Câu 70. Cho hình thoi ABCD như hình vẽ sau, có 𝐵𝐴𝐷
̂ = 600. Khi đó số đo 𝐵𝐴𝐶 ̂ là Trang 6 A. 𝐵𝐴𝐶 ̂ = 300. B. 𝐵𝐴𝐶 ̂ = 600. C. 𝐵𝐴𝐶 ̂ = 150. D. 𝐵𝐴𝐶 ̂ = 1200.
Câu 71. Hãy chọn câu đúng. Tứ giác ABCD là hình bình hành nếu: A. A = C B. AB=CD; BC=AD C. AB//CD D. BC=AD
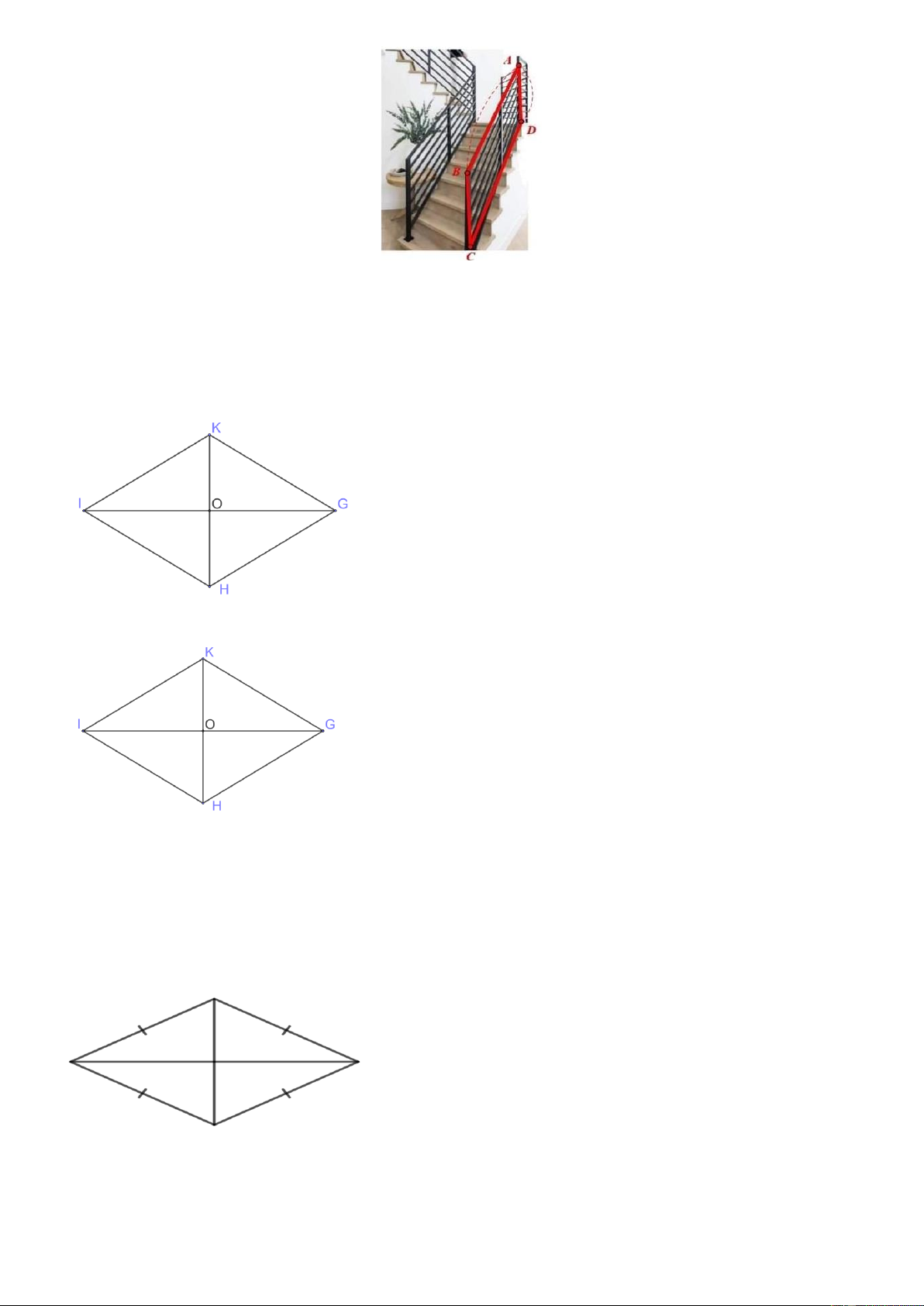
Câu 72. Cho hình vẽ
Chọn câu khẳng định sai. A. MQ // PN.
B. I là trung điểm của MP. C. MN // PQ.
D. MNPQ là hình thoi.
Câu 73. Hình bình hành ABCD có 𝐵
̂ = 700. Các góc còn lại của hình bình hành ABCD là A. 𝐶̂ = 𝐷 ̂ = 1100, 𝐴̂ = 700. B. 𝐴̂ = 𝐷 ̂ = 1100, 𝐶̂ = 700.
C. 𝐴̂ = 𝐶̂ = 1100, 𝐷 ̂ = 700.
D. 𝐴̂ = 𝐶̂ = 𝐷 ̂ = 700.
Câu 74. Cho hình bình hành ABCD biết AB = 3cm, AD = 5cm, 𝐵𝐴𝐷
̂ = 600. Độ dài cạnh BC và số đo 𝐵𝐶𝐷 ̂ là:
A. BC = 3cm và 𝐵𝐶𝐷 ̂ = 600.
B. BC = 3cm và 𝐵𝐶𝐷 ̂ = 1200.
C. BC = 5cm và 𝐵𝐶𝐷 ̂ = 600.
D. BC = 5cm và 𝐵𝐶𝐷 ̂ = 1200.
Câu 75. Hình chữ nhật không có tính chất nào sau đây?
A. Trong hình chữ nhật có hai đường chéo bằng nhau.
B. Trong hình chữ nhật có hai cạnh kề bằng nhau.
C. Trong hình chữ nhật có bốn góc vuông.
D. Trong hình chữ nhật có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Câu 76. Bạn An dự định lắp đèn Led để trang trí cầu thang nhà mình theo dạng hình bình hành ABCD
như hình vẽ, An đo được AB = 5cm, AD = 1,2cm, độ dài dây đèn Led bạn An cần dùng là Trang 7
A. 6, 2m
B.12, 4m C. 6m D.10m
Câu 77. Cho tam giác vuông có cạnh huyền bằng 12cm. Độ dài đường trung tuyến ứng với cạnh huyền
của tam giác vuông đó là A.12cm B. 6cm C. 24cm D. 4cm
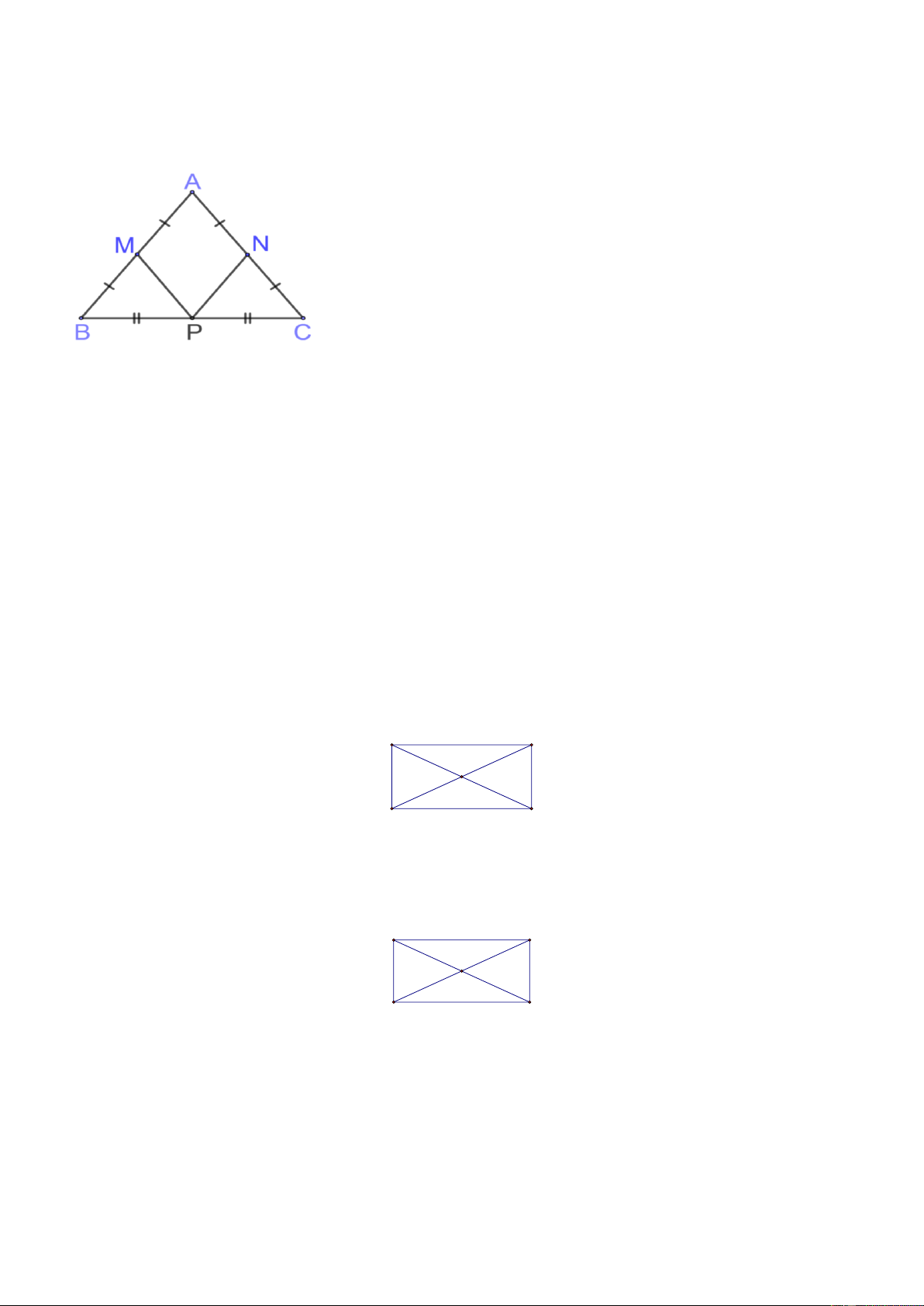
Câu 78. Cho hình thoi IKGH như hình vẽ sau, có IK = 10cm ; 0I = 8cm . Khi đó độ dài KH là
A. KH = 18cm
B. KH = 2cm
C. KH = 6cm
D. KH = 12cm
Câu 79. Cho hình thoi IKGH như hình vẽ sau, có IG = 48cm ; KH = 14cm . Khi đó độ dài IK là
A. IK = 25cm
B. IK = 50cm
C. IK = 62cm
D. IK = 34cm
Câu 80. Chọn câu sai. Cho ABCD là hình chữ nhật có O là giao điểm hai đường chéo. Khi đó
A. AC = BD
B. AB = C ;
D BC = AD
C. OA = OB
D. OC OD
Câu 81. Khẳng định sai. Trong hình thoi có:
A. Hai đường chéo cắt nhau tại trung điểm của mỗi đường
B. Hai đường chéo la các đường phân giác của các góc của hình thoi.
C. Hai đường chéo bằng nhau.
D. Hai đường chéo vuông góc với nhau
Câu 82. Tứ giác dưới đây là hình thoi theo dấu hiệu nào?
A. Tứ giác có 4 cạnh bằng nhau
B. Tứ giác có hai đường chéo vuông góc
C. Tứ giác có hai đường chéo bằng nhau
D. Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường. Trang 8
Câu 83. Hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O , AC = 5cm ; BD = 10cm . Độ dài
cạnh OC,OD lần lượt là:
A.10cm và 5cm
B.10cm và 20cm
C. 2,5cm và 5cm
D. 5cm và 10cm
Câu 84. Cho tam giác ABC gọi M , N, P lần lượt là trung điểm của AB, AC, BC . Biết AB = AC . Hỏi tứ
giác ANPM là hình gì? A.Hình vuông B.Hình chữ nhật C.Hình thoi D.Hình bình hành
Câu 85. Tìm câu nói đúng khi nói về hình vuông?
A.Hình vuông vừa là hình thang cân, vừa là hình thoi
B.Hình thang cân có hai đường chéo vuông góc là hình vuông.
C.Hình thoi có hai đường chéo bằng nhau là hình vuông
D.Tứ giác có bốn góc vuông là hình vuông.
Câu 86. Hình bình hành MNPQ có 0
M = 90 , MP = NQ . Khi đó MNPQ là: A.Hình thang cân B.Hình chữ nhật C.Hình thoi D.Hình vuông
Câu 87. Hình chữ nhật MNPQ . Đoạn thẳng MN bằng đoạn thẳng: A. NQ B. NP C. PQ D. QM
Câu 88. Cho tứ giác HKIB là hình vuông. Số đo góc KHI bằng: A. 0 45 B. 0 90 C. 0 25 D. 0 120
Câu 89. Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Biết 0
AOD = 50 , tính số đo ABO A. 0 50 B. 0 25 C. 0 90 D. 0 130
Câu 90. Cho hình chữ nhật ABCD có AB = 12c ; m AD = 5c .
m Độ dài đường trung tuyến AO = 6,5cm . Độ
dài đường chéo BD của hình chữ nhật là: A B O D C
A. 13cm . B. 10cm . C. 24cm . D. 6,5cm .
Câu 91. Cho hình chữ nhật ABCD có AB = 12c , m AD = 5c .
m Độ dài đường chéo BD = 13cm . Độ dài
đường trung tuyến AO là A B O D C
A. 5cm . B. 6,5cm . C. 2,5cm . D. 26cm .
Câu 92. Cho hình vuông MNPQ có hai đường chéo MP và NQ cắt nhau tại O . Chọn khẳng định đúng
trong các khẳng định sau: A. 0
MNO + OPQ = 45 . B. 0
MNO + OPQ = 60 . C. 0
MNO + OPQ = 90 . D. 0
MNO + OPQ = 135 .
Câu 93. Cho hình vuông HKPQ trên cạnh HK vẽ ra phía ngoài của hình vuông tam giác đều IHK . Số đo của IHP là Trang 9 A. 0 150 . B. 0 120 . C. 0 105 . D. 0 100 .
Câu 94. Cho hình vuông ABCD trên cạnh AB vẽ ra phía trong của hình vuông tam giác đều EAB . Số đo của EAC là A. 0 15 . B. 0 45 . C. 0 30 . D. 0 60 .
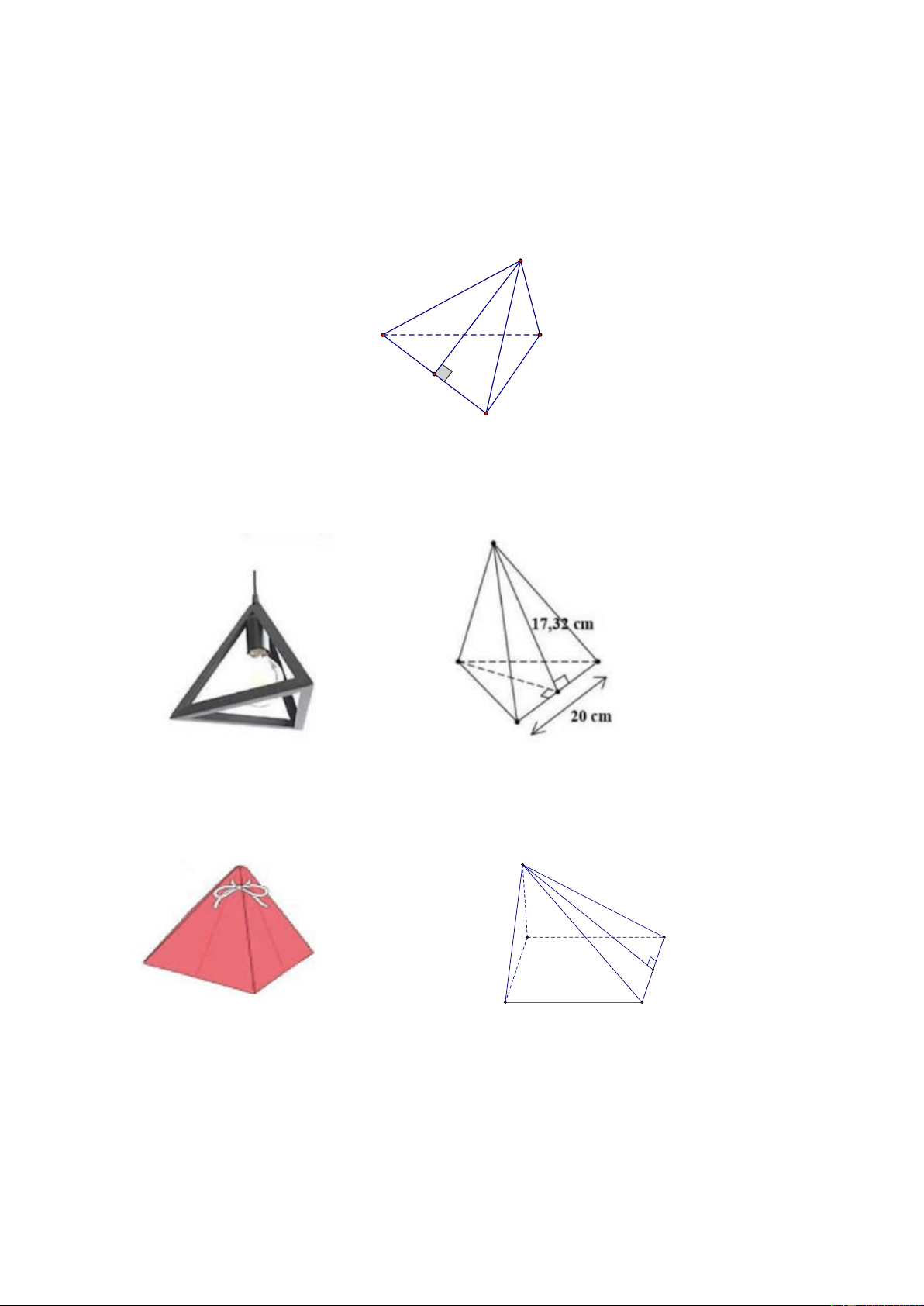
Câu 95. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy AC = 6(cm) , chiều cao của tam giác
cân SM = 9(cm) .Tính diện tích xung quanh của hình chóp tam giác đều S.ABC ? S 9cm A B M 6cm C A. ( 2 81 cm ) . B. ( 2 18 cm ) . C. ( 2 162 cm ) . D. ( 2 54 cm ) .
Câu 96. Một chiếc đèn thả trần có dạng hình chóp tam giác đều có tất cả các cạnh đều khoảng 20cm. Độ
dài trung đoạn 17,32cm. Tính diện tích xung quanh của chiếc đèn thả trần đó. A. ( 2 173, 2 cm ) . B. ( 2 519, 6 cm ) . C. ( 2 60 cm ) . D. ( 2 346, 4 cm ) .
Câu 97. Một túi quà có dạng hình chóp tứ giác đều (như hình bên) có độ dài cạnh đáy bằng 12(cm) , độ
dài trung đoạn bằng 8(cm) . Tính diện tích xung quanh của túi quà đó? 8cm 12cm A. 192 ( 2 cm ) B. 384 ( 2 cm ) C. 16 ( 2 cm ) D. 48 ( 2 cm )
Câu 98. Một khối Rubic có dạng hình chóp tam giác đều. Biết chiều cao khoảng 5,88cm , thể tích khối Rubic là 3
44, 002cm . Diện tích mặt đáy của khối Rubic là: Trang 10 A. khoảng 2 7, 4cm . B. 2
7, 5cm . C. khoảng 2 7, 5cm D. khoảng 2 22, 5cm
Câu 99. Nhân dịp tết Trung thu, Bảo và các bạn dự định làm 10 cái đèn lồng có dạng hình chóp tứ giác
đều có độ dài cạnh đáy là 30cm, đường cao của mặt bên kẻ từ đỉnh của hình chóp là 40cm để tặng các
bạn có hoàn cảnh khó khăn vui tết Trung thu. Số mét vuông giấy màu mà bạn Bảo phải dùng để dán tất cả
các mặt bên của chiếc đèn lồng (biết rằng các nếp gấp không đáng kể) là: A. 2 4800m . B. 2 2, 4m . C. 2 24m D. 2 2400m
Câu 100. Mô hình kim tự tháp có dạng hình chóp tứ giác đều đáy hình vuông có cạnh bằng 7cm. Thể tích của mô hình là 3
151, 9cm . Chiều cao của mô hình kim tự tháp là: A.Khoảng 9, 5 cm B. 5, 425 cm. C. 3,1cm D. 9, 3 cm.
Câu 101. Một khối Rubik có dạng hình chóp tam giác đều với chiều cao 6 cm. Biết thể tích khối Rubik
bằng 44 cm3, hãy tính diện tích mỗi mặt của Rubik đó? 22 22 A. cm2. B. 22 cm. C. 22 cm2. D. cm. 3 3
Câu 102. Nhân dịp Trung Thu, Nam dự định làm một chiếc đèn lồng hình chóp tam giác đều có độ dài
cạnh đáy là 30 cm, đường cao của một mặt bên là 40 cm. Hãy tính xem Nam cần bao nhiêu mét
vuông giấy vừa đủ để dán tất cả mặt xung quanh của chiếc đèn lồng? Biết rằng phải tốn 20% diện
tích giấy cho các mép giấy và diện tích dấy bị bỏ đi. A. 0,36 m2. B. 0,216 m2. C. 0,12 m2. D. 0,18 m2. Trang 11
Câu 103. Khu bảo tồn Muttart là một phần biểu tượng của cảnh quan thành phố Edmonton – Canada với
bốn nhà kính hình dạng kim tự tháp. Mỗi tòa nhà đều có từng chủ đề riêng. Hai nhà kính lớn đều
có dạng hình chóp tứ giác đều với chiều cao 24 m và thể tích của mỗi nhà kính là 5280 m3. Tính
tổng diện tích mặt đáy của hai nhà này? A. 360 m2. B. 120 m2. C. 90 m2. D. 180 m2.
Câu 104. Nhân Đỉnh Fansipan (Lào Cai) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi này, người ta
đặt một chóp làm bằng inox có dạng hình chóp tam giác đều, chiều cao bằng 90 cm, thể tích khối
chóp vào khoảng 46440 cm3,. Tính diện tích đáy của khối chóp? A. 516 cm2. B. 1548 cm2. C. 172 cm2. D. 258 cm2.
II. PHẦN TỰ LUẬN
Câu 105. Phân tích đa thức sau thành nhân tử 𝑥3 + 27𝑥 + (𝑥 + 3)(𝑥 − 9) a) 2 2
2x − 4x + 2 − 2 y ; c) 3
x + 27 + ( x + 3)( x − 9); b) 3 2
x − 6x +11x − 6; d) 3 3 2 2
2x y + 2xy + 4x y − 2x . y 1
Câu 106. Tính giá trị của biểu thức 3 2 2 3
M = x + 9x y + 27xy + 27 y + 27 biết rằng x + y +1 = 0. 3
Câu 107. Tìm giá trị của x để biểu thức 2
A = x + x − ( + x)( 2 − x + x ) 3 2 2 4 2
+ x đạt giá trị nhỏ nhất. 3 3
Câu 108. Tìm giá trị lớn nhất biểu thức M = ( x − 3) + (−x − ) 1 .
Câu 109. Tìm nghiệm của đa thức M = ( x + x − )2 2 2 1 + 4x + 4x .
Câu 110. Tính giá trị của biểu thức 2 2 2 2
M = x − 4xy + 4 y − 4m − 4mn − n biết rằng x + n = 2( y − m).
Câu 111. Phân tích đa thức sau thành nhân tử a) 2 2 2 2
5x + 5 y − x z + 2xyz − y z −10xy ; b) 2 2 2 3 3
x y + xy + x z + y + x .
Câu 112. Tính giá trị của biểu thức bằng cách hợp lý: a) 2
P = x ( x − )
1 − 4x ( x − ) 1 + 4( x − ) 1 tại x = 12. b) 3 2
Q = x + 3x + 3x với x = 999 .
Câu 113. Cho hai đa thức 3 2
A = 2x + 5x − 2x + ; a 2
B = 2x − x +1. Trang 12
a) Tính giá trị biểu thức B khi x = 1 − .
b) Tính giá trị của a để đa thức A chia hết cho đa thức B .
Câu 114. Tìm giá trị nhỏ nhất biểu thức 2 2
P = 8x + 3y − 8xy − 6 y + 21.
Câu 115. Tìm x biết: 2 a) ( x − ) − ( 2 3 1 9x + 7) = 0 .
b) ( − x)( + x) + ( x − )2 3 3 5 =14 . c) ( x − )2 2 2
21 − 25x = 0 .
Câu 116. Thực hiện phép tính (hợp lý nếu có thể) 2 2 − x x −1 5 4x − 8 a) + b) − ; x − x ( x − ) ; 2 1 2 1 2 x + 2 x − 4 x +1 x −1 6x − 6 3x + 2 x − 6 c) + + ; + 2 x − 3 x + 3 x − d) 9 x −1 x − . 1
Câu 117. Rút gọn các biểu thức sau 2
x − 3 x − 3x + 2 a) với ( x 4
− ; x 1; x 3). 2
x −1 x + x −12 3 2 − x x +1 b) với ( x 1
− ; x 1; x 2). 2 x −1 x − 2 2 2 x 5 − x x 2x − 6 c) + với ( x 1 − ; x ) 1 . x −1 x +1 x −1 x +1 2 2
x − 3x + 2 x − 2x − 3 d) với ( x 1
− ; x 1; x 2). 2 x − x − 2 (x − )2 1
Câu 118. Thực hiện phép tính 3x + 9 x + 3 2 x +10xy x + 2 y a) : ; : ; 2 x − 4 x − b) 2 2 2 3 3
x + 2xy + 4 y x − 8y
x +1 x + 2 x + 3 2 4x +1 c) : : ; : 1− 2x ..
x − 3 x + 3 x + d) ( ) 1 x 3x − 2 x − 7 10
Câu 119. Cho biểu thức A = − − x 0; x 5 2 ( ) x x − 5 x − 5x
a) Rút gọn biểu thức A x +1
b) Tìm các giá trị nguyên của x để B = . A có giá trị nguyên. x −1 2x x +1 3 −11x
Câu 120. Cho biểu thức P = + + với x 3 . 2 x + 3 x − 3 9 − x
a) Rút gọn biểu thức P .
b) Tính giá trị của P khi x − 2 = 1.
c) Tìm các giá trị nguyên của x để P có giá trị nguyên dương. 2x 3x 2x 3 − 2x 3x
Câu 121. Cho hai biểu thức A = . + . và B = . x + 3 x −1 x + 3 x −1 2x − 2
a) Sử dụng tính chất phân phối của phép nhân đối với phép cộng để rút gọn biểu thức A .
b) Rút gọn biểu thức P = A : B . 2 1 2x
1 x − 4x + 4
Câu 122. Cho biểu thức A = − + . 2
x + 2 4 − x x − 2 4x Trang 13
a) Tìm điều kiện của x để A xác định.
b) Rút gọn biểu thức A .
c) Tìm các giá trị nguyên của x để A có giá trị nguyên. x + 2 x −1 2 y 2 4x + 4x +1
Câu 123. Cho hai biểu thức A = . . và B = . 2 y 2x +1 x + 2 2x − 2
a) Sử dụng tính chất kết hợp để rút gọn biểu thức A .
b) Rút gọn biểu thức M = . A B . 2
2x −1 3x x − 2 3
Câu 124. Cho biểu thức E = − − − . x +1
x −1 x +1 x −1
a) Sử dụng quy tắc dấu ngoặc để rút gọn biểu thức E . b) Với x 1
, tìm x để biểu thức E có giá trị là 2. 1 1 1 1 1 2 2 2 x y 1 y
Câu 125. Cho hai biểu thức M = + + − − ; N = − − − x +1 y +1 z +1 y +1 z +1
x −1 y −1 x −1 y −1
a) Rút gọn một cách hợp lý M ; N .
b) Chứng tỏ biểu thức Q = M .N không phụ thuộc vào giá trị của biến. 2 y + 5 x − 4 x − 2
Câu 126. Cho hai biểu thức A = . . . 2
x − 4x + 4 x +1 y + 5
a) Sử dụng tính chất kết hợp để rút gọn biểu thức A . 1
b) Tính giá trị của biểu thức A khi x =
; y = 2023 với x 1 − ; x 2 − ; y 5 − . 2 2 2 4x x 1 4x +1 1
Câu 127. Cho biểu thức G = + − −
với x 1; x .
2x +1 x −1 x −1 2x +1 2
a) Sử dụng quy tắc dấu ngoặc để rút gọn biểu thức G 1
b) Với x 1; x
, tìm x để biểu thức có giá trị là -4 2 2 x 2x 9 − 3x − 4
Câu 128. Cho biểu thức A = + + với x 3 . 2 x + 3 x − 3 x − 9
a) Rút gọn biểu thức A . 1 10
b) Tính giá trị của biểu thức A tại x = 1 và x thỏa mãn x + = . 3 3 x − 3
c) Tìm giá trị lớn nhất của biểu thức B biết B = . A . 2 x − 4x + 5 2 2 9x x 1 4
Câu 129. Cho biểu thức T = + − + . 3x − 2
x −1 x −1 3x − 2
a) Tính một cách hợp lý để rút gọn biểu thức T . 2
b) Tìm x để T = 3 với x ; x 1 . 3 2 5 2 3x − 2x − 9
Câu 130. Cho biểu thức P = + − x . 2 x + 3 x − 3 x − với 3 9
a) Rút gọn biểu thức P .
b) Tìm x để P = 4 .
c) Tìm số nguyên x lớn nhất để biểu thức P có giá trị nguyên. Trang 14
Câu 131. Bạn Dương mang theo 100000 đồng và đạp xe đi nhà sách để mua vở. Biết giá mỗi quyển vở là
7000 đồng và phí gửi xe đạp là 3000 đồng.
a) Viết công thức biểu thị tổng số tiền y (đồng) bạn Dương cần phải trả cho việc gửi xe đạp và mua x
quyển vở. Hỏi y có phải là hàm số bậc nhất của x hay không?
b) Tính số tiền bạn Dương phải trả khi gửi xe và mua 12 quyển vở.
c) Viết công thức biểu thị số tiền còn lại t (đồng) bạn Dương còn lại sau khi gửi xe và mua x quyển vở.
d) Với số tiền trên, bạn Dương có thể mua được 15 quyển vở hay không? Vì sao? 3
Câu 132. Cho hàm số y = f (x) = x − 2 . Tính: 2 1
a) f (−6); f ( 4); − f ( 1 − ); f (0); f ; 2 1
b) Cho hàm số y = f (x) =
x − 4 . Tìm x biết y = 2 . 2
Câu 133. Tìm m để các hàm số sau là hàm số bậc nhất. a) 2
y = (2m − 6)x − m − 5 b) 2
y = (2 + m)x − 8x + 7 x m +1 + 5 c) y = 2 m + m − 2
d) y = ( k − 3 − ) 1 x + 5 3 − k 7k e) y = x − k + 2 3 k + 2 f) y = x + 2017 k − 2 1 − 1 −
Câu 134. Vẽ đồ thị của các hàm số y = 3 ;
x y = 3x + 4; y = x + 3; y =
x trên cùng mặt phẳng tọa độ. 2 2
Câu 135. Tìm m để đường thẳng (d ) : 2
y = (m +1)x − 3m + 2 có hệ số góc nhỏ nhất. 4
Câu 136. Tìm hệ số góc của mỗi đường thẳng y = m + 3 x − 7
và y = (3m −17) x + 3 khi chúng song 3 song với nhau.
Câu 137. Tìm hàm số bậc nhất y = ax + b (a 0) trong mỗi trường hợp sau:
a) Đồ thị hàm số đi qua điểm M (1;3) và có hệ số góc bằng -2.
b) Đồ thị hàm số đi qua điểm N( 1
− ;4) và song song với đường thẳng y = 3 − x −1.
Câu 138. Cho đường thẳng (d ) : y = x −1. Gọi A ; B lần lượt là giao điểm của đường thẳng (d ) với
hai trục tọa độ Ox ; Oy . Tính chu vi của tam giác OAB .
Câu 139. Bảng giá cước của một hãng Taxi được cho như sau:
a) Gọi y (đồng) là số tiền khách hàng phải trả sau khi đi x (km) . Lập hàm số y theo x .
b) Một khách hàng muốn đi quãng đường 35 km thì phải trả số tiền là bao nhiêu? Trang 15
Câu 140. Giá cước điện thoại cố định của hãng viễn thông A bao gồm cước thuê bao mỗi tháng là b
(đồng/tháng) và cước gọi là a (đồng/phút). Xem y là đại lượng biểu thị cho cước điện thoại cố
định mỗi tháng (chưa tính thuế VAT) và x là đại lượng biểu thị cho số phút gọi trong mỗi tháng.
a) Chứng tỏ rằng y là hàm số bậc nhất của biến x , tức là y = ax + b (a 0) .
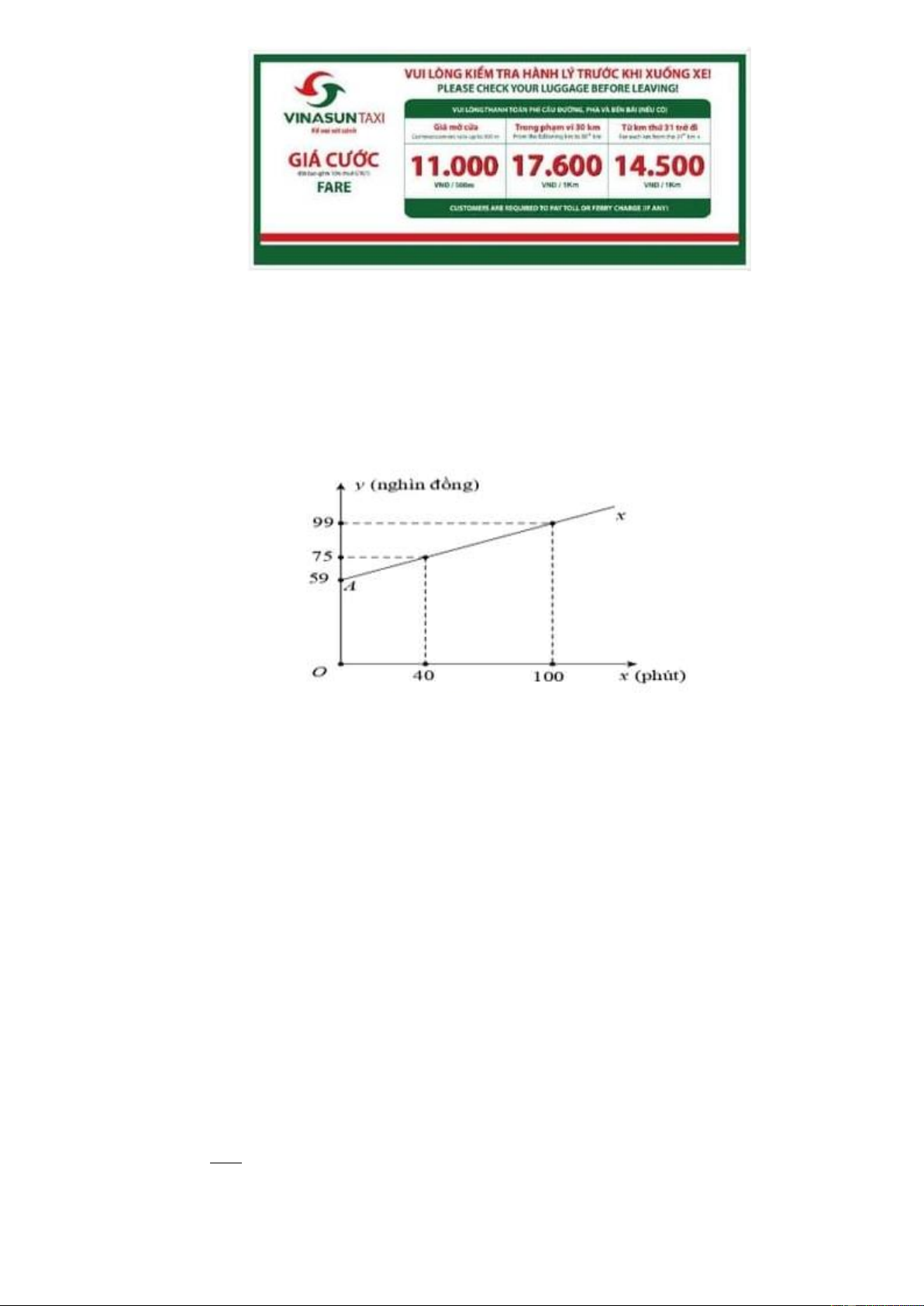
b) Trong hình dưới, tia Ax là một phần đường thẳng biểu diễn số tiền cước điện thoại cố định
của nhà bạn An. Tìm a và b . Từ đó hãy cho biết cước điện thoại cố định mà bạn An phải trả
trong tháng đó nếu nhà bạn đã sử dụng 60 phút gọi.
Câu 141. Nguyên đang muốn mua một bộ lego với giá 1 000 000 đồng. Mẹ đã cho nguyên 100 000
đồng. Mỗi ngày Nguyên để dành được 20 000 đồng.
a) Viết công thức tính số tiền y (đồng) Nguyên có được sau x (ngày) tiết kiệm (kể cả tiền mẹ cho).
b) Hỏi sau bao nhiêu ngày thì Nguyên có thể mua được bộ lego đấy?
Câu 142. Một nhà máy sản xuất lô áo gồm 300 chiếc áo với giá vốn là 45 000 000 (đồng) và giá bán
mỗi chiếc áo sẽ là 250 000 (đồng). Khi đó gọi K (đồng) là số tiền lời (hoặc lỗ) của nhà may thu
được khi bán t chiếc áo.
a) Thiết lập hàm số K theo t .
b) Hỏi cần phải bán bao nhiêu chiếc áo mới có thể thu hồi được vốn ban đầu?
c) Để lời được 6 000 000 đồng thì cần phải bán bao nhiêu chiếc áo?
Câu 143. Cho tam giác ABC vuông cân tại A , đường cao AH . Kẻ phân giác của các góc AHB , AHC
cắt AB , AC lần lượt tại D , E . Chứng minh:
a) DE là phân giác của HDA . b) DE // BC .
Câu 144. Cho hình chữ nhật ABCD có AB = 2.BC . Gọi I là trung điểm của AB và K là trung điểm
của DC . Chứng minh:
a) AIKD và BIKC là hình vuông. DC b) IK = và DIC = 90 . 2
Câu 145. Cho hình bình hành ABCD có BC = 2AB , A = 60 . Gọi E , F theo thứ tự là trung điểm
của BC , AD . Vẽ I đối xứng với A qua B . Trang 16
a) Tứ giác ABEF là hình gi? Vì sao?
b) Chứng minh tứ giác AIEF là hình thang cân.
c) Chứng minh BICD là hình chữ nhật. d) Tính góc AED.
Câu 146. Cho hình thang cân ABCD. Gọi M, N theo thứ tự là trung điểm của AB và CD.
a) Chứng minh tứ giác BMDN là hình bình hành. b) Chứng minh: AMD = BNC.
c) Gọi I là trung điểm của AC, Chứng minh M, I, N thẳng hàng.
Câu 147. Cho hình thang cân ABCD (AB//CD, AB.CD), Các đường cao AH, BK.
a) Tứ giác ABKH là hình gì? Vì sao? b) Chứng minh DH = CK.
c) Gọi E là điểm đối xứng với D qua H. Các điểm D và E đối xứng với nhau qua đường nào?
d) Tứ giác ABCE là hình gì?
Câu 148. Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Từ M kẻ ME, MF lần lượt vuông góc với AB, AC.
1) Chứng minh tứ giác AEMF là hình chữ nhật.
2) Gọi O là giao điểm của AM và È. K là điểm đối xứng của M qua AC. Chứng minh 3 điểm B, O, K thẳng hàng.
3) Tìm điều kiện của tam giác ABC để tứ giác ABCK là hình thang cân. Biết AM = 5cm, Tính diện tích tam giác
ABC trong trường hợp này.
Câu 149: Cho tam giác ABC vuông tại A, Đường cao AH. Gọi M và N lần lượt là hình chiếu của H trân AB và AC.
a) Tứ giác AMHN là hình gì? Vì sao?
b) Tam giác ABC cần thêm điều kiện gì để tứ giác AMHN là hình vuông?
c) Gọi E là điểm đối xứng của H qua M, F là điểm đối xứng của H qua N. Chứng minh rằng E đối xứng với F qua A. 1 1 1 = + 2 2 2 d) Chứng minh AH AB AC
Câu 150. Cho tam giác ABC vuông tại A, Gọi M và P theo thứ tự là trung điểm của BC và AC. Lấy điểm
Q đối xứng với P qua M.
a) Tứ giác BPCQ là hình gì? Vì sao? b) Chứng minh AQ = BP.
c) Gọi O là giao điểm của AQ và BP. Chứng minh S =12S . ABPQ OMP BI 1
d) Tia CI cắt BA tại I. Chứng minh = . PQ 3
Câu 151. Cho tam giác ABC vuông tại A. Đường cao AH, trung tuyến AM (H, M thuộc BC). Gọi D, E
theo thứ tự là hình chiếu của điểm H trân AB, AC.
a) Chứng minh rằng: Tứ giác ADHE là hình chữ nhật.
b) Chứng minh: AM vuông góc với DE.
c) Biết AB = 6cm, AC = 8cm. Tính DE?
d) Gọi N là giao điểm của AM và HE, K là hình chiếu của điểm M trên AB. Chứng minh rằng: 3 đường thẳng MK,BN,AH đồng quy.
Câu 152. Cho tam giác ABC vuông tại A (AB,AC), đường cao AH. Lấy K thuộc đoạn HC sao cho H là
trung điểm của BK, gọi F là điểm đối xứng với A qua H.
a) Chứng minh tứ giác ABFK là hình thoi.
b) FK cắt AC tại M ,qua K kẻ đường thẳng song song với AC và cắt AB tại N .Tứ giác ANKM là hình gì? Vì sao ?
c) Qua M kẻ đường thẳng vuông góc với MH và cắt KC tại P . Chứng minh HMF = HFM và P là
trung điểm của KC
d) Tam giác ABC ban đầu cần thêm điều kiện gì để tứ giác NHKM là hình bình hành.
Câu 153. Cho tam giác ABC vuông ở A , gọi E và M theo thứ tự là trung điểm của AC và BC . Lấy
điểm D đối xứng với E qua M
a) Chứng minh tứ giác BECD là hình bình hành.
b) Tứ giác ABDE là hình gì ? c) Gọi IK
I , K lần lượt là giao điểm của AD, AM với BE . Tính ? DC Trang 17
Câu 154. Cho tam giác ABC nhọn có trực tâm H . Các đường vuông góc với AB tại B và vuông góc với
AC tại C cắt nhau tại D .
1) Chứng minh tứ giác BDCH là hình bình hành.
2) Gọi M là trung điểm của BC . Chứng minh ba điểm H , M , D thẳng hàng 3) Chứng minh 4 điểm ,
A B, D, C cách đều một điểm
4) Tìm điều kiện của tam giác để tứ giác BDCH là hình thoi.
Câu 155. Cho hình vuông ABCD , E là điểm trên cạnh DC , F là điểm trên tia đối của tia BC sao cho
hình vuông BF = DE
a) Chứng minh tam giác AEF vuông cân.
b) Gọi I là trung điểm của EF . Chứng minh I thuộc BD
c) Lấy điểm K đối xứng A qua I . Chứng minh tứ giác AEKF là hình vuông.
Câu 156. Một nền nhà hình chữ nhật có chiều dài 8 m chiều rộng 6 m .
a) Tính diện tích nền nhà.
b) Lát nền nhà bằng gạch hình vuông cạnh 20cm , thì cần bao nhiêu viên gạch. Nếu giá mỗi viên gạch là
5500 đồng thì cần ít nhất số tiền là bao nhiêu để mua đủ gạch lát nền ?
Câu 157. Một khối rubik có dạng hình chóp tam giác đều ( các mặt khối rubik là các tam giác đều bằng
nhau), có chu vi đáy bằng C = 234 (m )
m , đường cao của mặt bên hình chóp là 67, 5( ) mm
a) Tính diện tích xung quanh của khối rubik đó.
b) Biết chiều cao của khối rubik là 63,7 ( )
mm . Tính thể tích của khối rubik đó.
Câu 159. Một hộp gỗ xông trầm dùng cho các loại nhang thơm, nhang trầm nụ có dạng như hình vẽ. Phần
dưới của hộp có dạng hình hộp chữ nhật có đáy là hình vuông có cạnh 7,5cm , chiều cao 5cm . Phần trên
của hộp có dạng hình chóp tứ giác đều có chiều cao là 8cm . Tính thể tích của hộp gỗ đó ( làm tròn đến hàng chục)
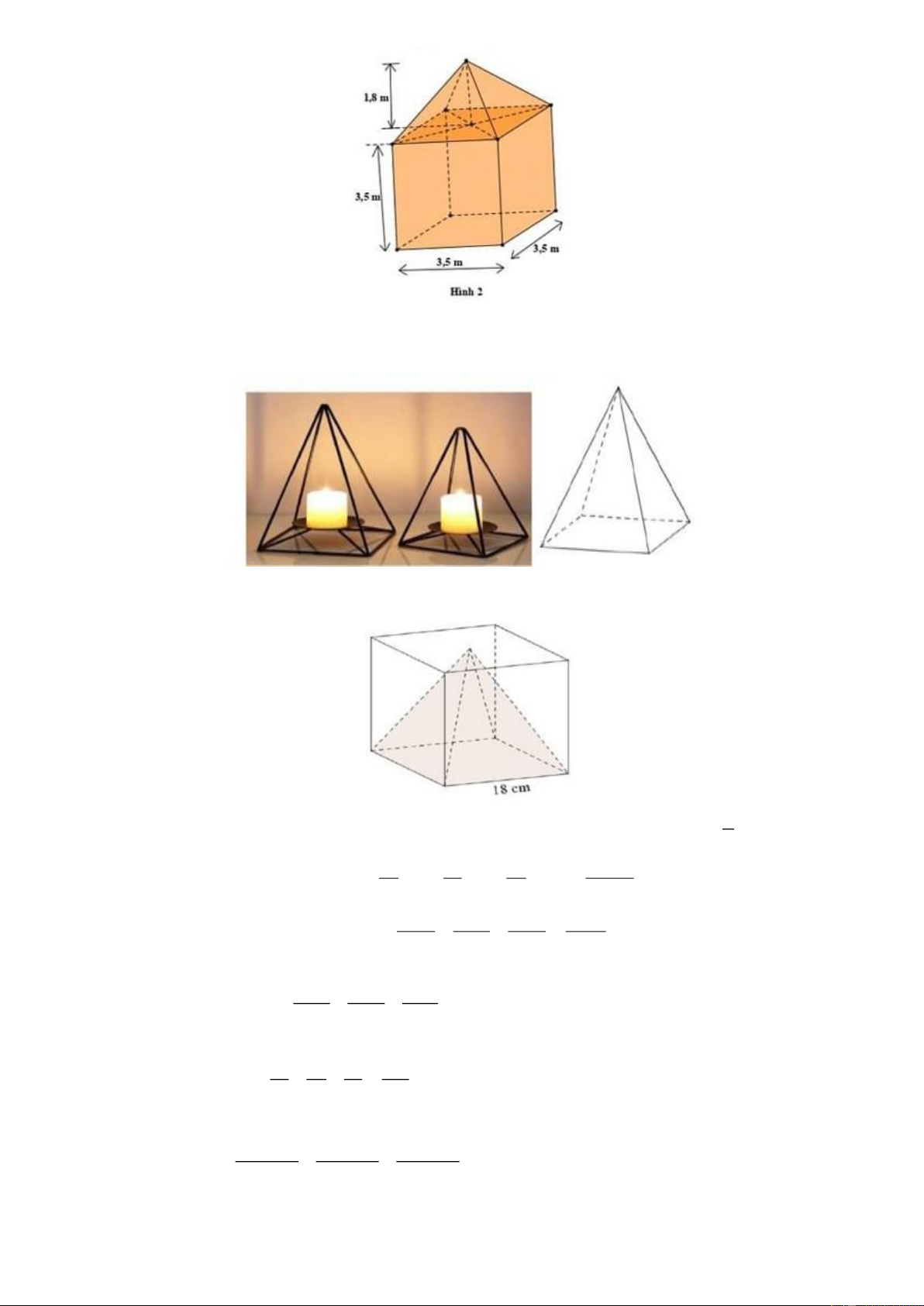
Câu 159. Hình 2 mô tả một lều tại gồm hai phần: Phần trên có dạng là một hình chóp tứ giác đều có chiều cao là 1,8( )
m . Phần dưới có dạng là một hình lập phương có cạnh là 3, 5(m) . Tính thể tích của lều trại đó. Trang 18
Câu 160. Một giá đèn cầy có dạng hình chóp tứ giác đều như hình bên có dộ dài cạnh đáy là 14 cm chiều
cao của giá đèn cầy là 22cm .Mặt bên có chiều cao kẻ từ đỉnh của hình chóp là 23cm.Tính diện tích xung
quanh và thể tích của giá đèn cầy ( kết quả làm tròn đến hàng đơn vị).
Câu 161. Một khối gỗ hình lập phương có cạnh 18 cm . Người ta muốn tạo ra một hình chóp tứ giác đều
như hình vẽ. Tính thể tích phần gỗ bị cắt đi. 5
Câu 162. Cho x và y là hai số thực thỏa mãn 3x − y = 1 . Chứng minh rằng 2 2 5x − y . 4 1 1 1 1
Câu 163. Tính giá trị của biểu thức : 1− 1− 1− ... 1− 2 2 2 2 2 3 4 2017 2 2 2 a b c 2020
Câu 164. Cho ba số dương a, , b c thỏa mãn + + = a + b b + c c + a 2021 2 2 2 a b c
Tính giá trị của biểu thức P = + + . a + c b + a c + b
Câu 165. Cho x, y, z là 3 số khác 0 thỏa mãn: 2 2 2 2
(x + y + z) = x + y + z 1 1 1 3 Chứng minh rằng + + = 3 3 3 x y z xyz
Câu 166. Cho a, ,
b c là ba số đôi một khác nhau thỏa mãn: 2 2 2 2
(x + y + z) = x + y + z . Tính giá trị của 2 2 2 a b c biểu thức: P = + + 2 2 2 a + 2bc b + 2ac c + 2ab
Câu 167. Cho các số 𝑥, 𝑦 thoả mãn đẳng thức 2 2
5x + 5 y + 8xy − 2x + 2 y + 2 = 0 . Tính giá trị của biểu thức: 2015 2016 2017
M = (x + y) + (x − 2) + (y +1) Trang 19
Câu 168. Tìm giá trị nhỏ nhất của biểu thức 4 2 2 2
B = 2x + 4 y + 4x y −10x − 4 y + 2037
Câu 169. Cho biểu thức 4 4
P = (x +1)( y +1) , với x, y là các số dương thỏa mãn: x + y = 10
Tính giá trị nhỏ nhất của biểu thức 𝑃
Câu 170. Cho 𝑎, 𝑏 là các số dương và 3 3
a + b = 3ab −1 . Chứng minh: 2020 2021 a + b = 2
Câu 171. Chứng minh rằng: Nếu 𝑚 và 𝑛 là hai số chính phương lẻ liên tiếp thì
P = mn − m − n +1 chia hết cho 192 .
Câu 172. Cho 𝑛 là số nguyên không chia hết cho 3. Chứng minh rằng 2 3 n 3n P = + +1 chia hết cho 13 .
Câu 173. Chứng minh rằng có vô số số tự nhiên 𝑎 sao cho 4
n + a không phải là số nguyên tố với mọi số tự nhiên 𝑛.
Câu 174. Cho các số nguyên m, n, p thỏa mãn 3 3 3
m − 2n = 4 p và biểu thức S = m + n − p . Chứng minh rằng S chia hết cho 3.
Câu 175. Tìm tất cả các số nguyên dương 𝑎, 𝑏 sao cho 2
a + b chia hết cho 2 a b −1 Trang 20




