











Preview text:
ĐỀ CƯƠNG TOÁN 11 HỌC KÌ 1 NĂM HỌC 2023-2024
A. Trắc nghiệm (7,0 điểm) (Gồm có 140 câu TNKQ)
Câu 1 [NB]. Đổi độ sang radian hoặc radian sang độ.
Câu 1.1. Khẳng định nào sau đây là đúng? 0 180 æ ö A. 0 p rad = 1 . B. 0 p rad = 60 . C. 0 p rad = 180 . D. p rad ç ÷ = ç ÷ . ç ÷ è p ø
Câu 1.2. Khẳng định nào sau đây là đúng? 0 180 æ ö A. 0 1 rad = 1 . B. 0 1 rad = 60 . C. 0 1 rad = 180 . D. 1 rad ç ÷ = ç ÷ . ç ÷ è p ø
Câu 1.3. Đổi số đo của góc 0 70 sang đơn vị radian. 70 7 7 7 A. . B. . C. p . D. . p 18 18 18p
Câu 1.4. Đổi số đo của góc p rad sang đơn vị độ, phút, giây. 12 A. 0 15 . B. 0 10 . C. 0 6 . D. 0 5 .
Câu 2 [NB]. Kiểm tra công thức giá trị lượng giác của các góc liên quan.
Câu 2.1. Chọn khẳng định đúng? A. tan ( − ) = tan . B. sin ( − ) = −sin . C. cot ( − ) = cot . D. cos ( − ) = −cos .
Câu 2.2. Chọn khẳng định đúng?
A. tan ( − ) = tan .
B. sin ( − ) = −sin .
C. cot ( − ) = cot .
D. cos ( − ) = − cos .
Câu 2.3. Chọn khẳng định đúng? A. tan − = co t . B. sin − = sin . 2 2 C. cot − = cot . D. cos − = cos . 2 2
Câu 2.4. Chọn khẳng định đúng?
A. tan ( + ) = − tan .
B. sin ( + ) = sin .
C. cot ( + ) = cot .
D. cos ( + ) = cos .
Câu 3 [NB]. Tìm tập xác định của các hàm số lượng giác cơ bản.
Câu 3.1. Tìm điều kiện của x để hàm số sau có nghĩa: y = 2tan x . A. x k (k ) . B. x + k (k ) . 2
C. x k 2 (k ) .
D. x + k 2 (k ) .
Câu 3.2. Tập xác định của hàm số y = 2 cot x − 3 là: 3 A.
\ k , k . B.
\ + k , k . C. \ 0; ; ;
. D. \k,k . 2 2 2 2 2cosx
Câu 3.3. Tìm điều kiện của x để hàm số sau có nghĩa: y = . sin x −1
A. x + k
2 (k ) . B. x
k (k ) . C. x k
2 (k ) .D. x + k 2 (k ) . 2 2cosx
Câu 3.4. Tìm điều kiện của x để hàm số sau có nghĩa: y = . cosx −1
A. x + k
2 (k ) . B. x k
2 (k ) . C. x
k (k ) .D. x + k 2 (k ) . 2
Câu 4 [NB]. Cho công thức số hạng tổng quát của dãy số (u tìm số hạng thứ i . n )
Câu 4.1. Cho dãy số (u được xác định bởi u = 2n −1 với n 1. Số hạng u bằng n ) n 5 A. 9. B. 10. C. 5. D. 4.
Câu 4.2. Cho dãy số (u được xác định bởi 2
u = n −1 với n 1. Số hạng u bằng n ) n 2 A. -3. B. -1. C. 3. D. 1.
Câu 4.3. Cho dãy số (u được xác định bởi u = 3n với . Tính u . n ) n n 1 3 A. u = 9. u = 27. u = 3. u = 81. 3 B. 3 C. 3 D. 3 1
Câu 4.4. Cho dãy số (u được xác định bởi u = u . n ) n n . Tính n + với 1 1 4 1 1 1 1 A. u = . u = . u = . u = . 3 B. C. D. 2 3 3 3 4 3 5
Câu 5 [NB]. Tìm cấp số cộng hoặc cấp số nhân trong các dãy số hữu hạn đã cho.
Câu 5.1. Dãy số nào sau đây không phải là cấp số cộng? A 1; 2; 3; 4; 5 .
B. 1; 0; −1; − 2; − 3. C. 2 2 2 2 2 1 ; 2 ;3 ; 4 ;5 . D. 0; 2; 4; 6; 8.
Câu 5.2. Trong các dãy số sau, dãy số nào là một cấp số cộng? A. 0; 2 − ; 4 − ; 6 − ; 8 − .
B. 3; 3; 3 3; 9. 1
C. 5;− 6;7;− 8;9. D. 15; 3; 1 ; . 3
Câu 5.3. Dãy số nào sau đây không phải là cấp số nhân? A. 1; 2; 3; 4; 5 .
B. 1; 2; 4; 8; 16 .
C. 1; −1; 1; −1; 1.
D. 1; − 2; 4; − 8; 16 .
Câu 5.4. Trong các dãy số sau, dãy số nào là một cấp số nhân?
A. 128; − 64; 32; −16; 8.
B. 2; 2; 4; 4 2. 1
C. 5;6;7;8;9.
D. 15; 5; 1 ; . 5
Câu 6 [NB]. Tìm số trung bình cộng hoặc giá trị đại diện của một nhóm trong điều tra ghép lớp.
Câu 6.1. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian(phút) 0;20) 20;40) 40;60) 60;80) 80 1;00) Số học sinh 5 9 12 10 6
Giá trị đại diện của nhóm [20; 40) là: A. 10. B. 20. C. 30. D. 40.
Câu 6.2. Người ta ghi lại tuổi thọ của một số con ong cho kết quả như sau: Tuổi thọ (ngày) 0;20) 20;40) 40;60) 60;80) 80 1;00) Số lượng 5 12 23 31 29
Giá trị đại diện của nhóm [40;60) là: A. 60. B. 20. C. 50. D. 40.
Câu 6.3. Tìm cân nặng trung bình của học sinh lớp 11 cho trong bảng sau Cân nặng 40 5 , ;45 5 , ) 45 5 , ;50 5 , ) 50 5 , ;55 5 , ) 55 5 , ;60 5 , ) 40 5 , ;45 5 , ) 40 5 , ;45 5 , ) Số học 10 7 16 4 2 3 sinh A. 51,81. B. 50,61. C. 51,91 D. 51,71.
Câu 6.4. Tìm hiểu thời gian xem ti vi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau: Thời gian(giờ) 0;5) 5 1;0) 10 1;5) 15;20) 20;25) Số học sinh 8 16 4 2 2
Tính thời gian xem ti vi trung bình trong tuần trước của các bạn học sinh này. A. 8,44. B. 8,54. C. 8,64. D. 8,34.
Câu 7 [NB]. Tìm nhóm chứa trung vị hoặc nhóm chứa mốt của mẫu số liệu.
Câu 7.1. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau: Thời gian(giờ)
9 5, 1;2 5,)
12,5 1;5,5) 15,5 1;8,5)
18,5;21,5) 21 5,;24 5,) Số học sinh 3 12 15 24 2 Tìm nhóm chứa trung vị. A. Nhóm 1. B. Nhóm 2. C. Nhóm 3. D. Nhóm 4.
Câu 7.2. Ghi lại tốc độ bóng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết quả
như bảng bên. Tính trung vị của mẫu số liệu ghép nhóm này. Tốc độ(km/h)
150 1;55) 155 1;60) 160 1;65) 165 1;70) 170 1;75) 175 1;80) Số lần 18 28 35 43 41 35 Tìm nhóm chứa trung vị. A. Nhóm 1. B. Nhóm 2. C. Nhóm 3. D. Nhóm 4.
Câu 7.3. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A. Khoảng chiều 145 1;50) 150 1;55) 155 1;60) 160 1;65) 165 1;70) cao(cm) Số học sinh 7 14 10 10 9
Tìm nhóm chứa mốt của mẫu số liệu trên. A. Nhóm 1. B. Nhóm 2. C. Nhóm 3. D. Nhóm 4.
Câu 7.4. Thời gian (phút) đề học sinh hoàn thành một câu hỏi thi được cho như sau: Thời gian(phút)
0 5, 1;0 5,) 10 5,;20 5,) 20 5,;30 5,) 30 5,;40 5,) 40 5,;50 5,) Số học sinh 8 16 4 2 2
Tìm nhóm chứa mốt của mẫu số liệu trên. A. Nhóm 1. B. Nhóm 2. C. Nhóm 3. D. Nhóm 4.
Câu 8 [NB]. Hỏi về số cách xác định một mặt phẳng hoặc đếm số mặt phẳng xác định thỏa mãn giả thiết cho trước.
Câu 8.1. Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
A. Một đường thẳng và một điểm thuộc nó.
B. Ba điểm mà nó đi qua.
C. Hai đường thẳng phân biệt
D. Hai đường thẳng song song.
Câu 8.2. Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
A. Một đường thẳng và một điểm thuộc nó.
B. Ba điểm mà nó đi qua.
C. Ba điểm không thẳng hàng.
D. Hai đường thẳng phân biệt
Câu 8.3. Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
A. Một đường thẳng và một điểm không thuộc đường thẳng đó. B. Ba điểm mà nó đi qua.
C. Ba điểm phân biệt.
D. Hai đường thẳng phân biệt.
Câu 8.4. Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
A. Một đường thẳng và một điểm thuộc nó.
B. Ba điểm mà nó đi qua.
C. Hai đường thẳng phân biệt.
D. Hai đường thẳng cắt nhau.
Câu 9. [NB] Đếm số mặt của hình chóp.
Câu 9.1. Một hình chóp có đáy là tam giác có số mặt là:
A. 4. B. 3. C. 6. D. 5.
Câu 9.2. Một hình chóp có đáy là tứ giác có số mặt là:
A. 4. B. 3. C. 6. D. 5.
Câu 9.3. Một hình chóp có đáy là ngũ giác có số mặt là:
A. 4. B. 3. C. 6. D. 5.
Câu 9.4. Một hình chóp có đáy là lục giác có số mặt là:
A. 4. B. 3. C. 6. D. 7.
Câu 10 [NB]. Hỏi về vị trí tương đối 2 đường thẳng (giả thiết có hình vẽ đi kèm).
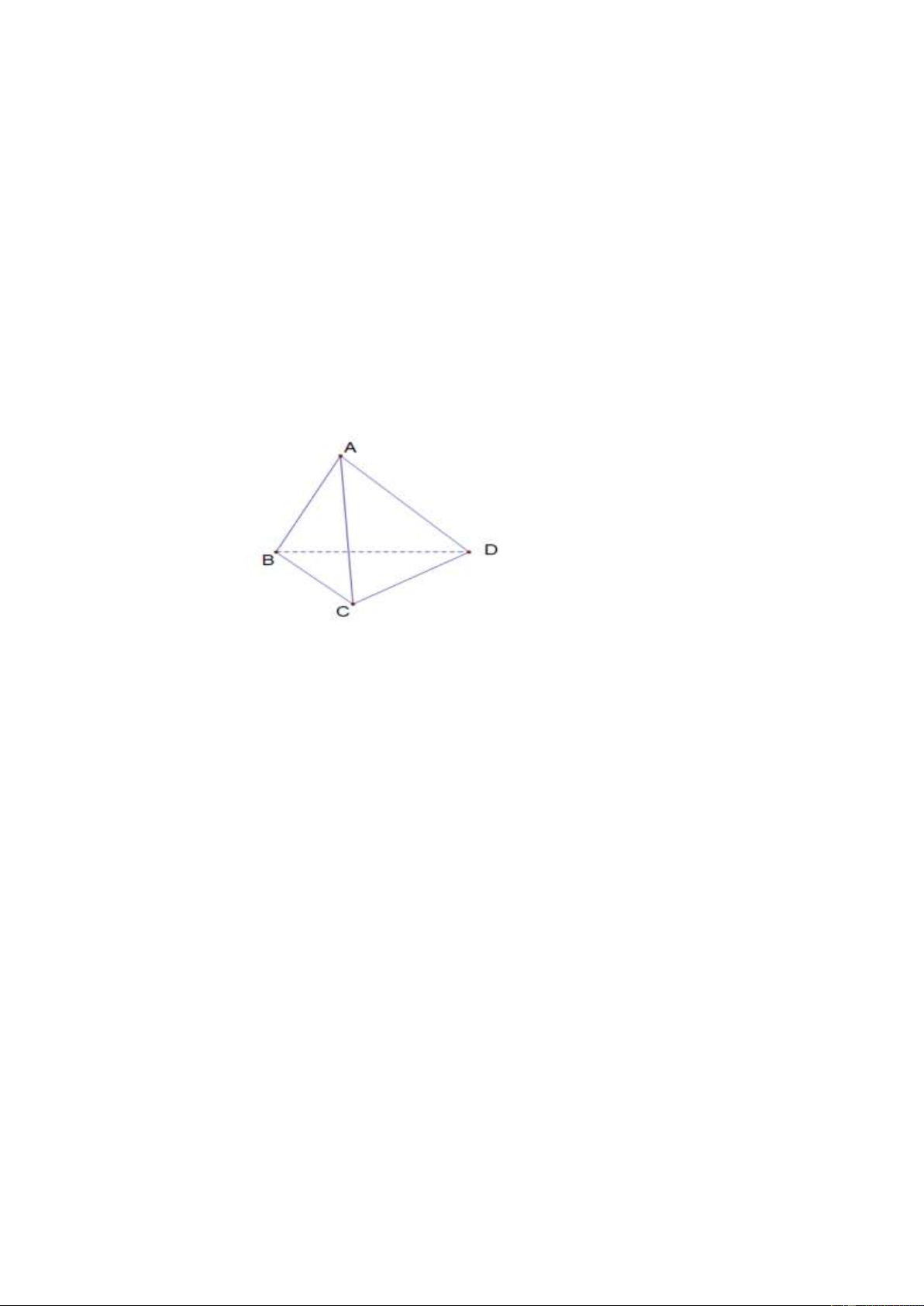
Câu 10.1. Cho tứ diện ABCD (hình vẽ)
Chọn khẳng định đúng trong các khẳng định sau:
A. AD và BC chéo nhau.
C. AD và BC song song.
C. AD và BC cắt nhau.
D. AB và CD chéo nhau; AC và BD cắt nhau.
Câu 10.2. Khẳng định nào sau đây đúng?
A. Hai đường thẳng chéo nhau thì chúng không có điểm chung.
B. Hai đường thẳng không có điểm chung là hai đường thẳng chéo nhau.
C. Hai đường thẳng song song nhau khi chúng ở trên cùng một mặt phẳng.
D. Khi hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
Câu 10.3. Cho hai đường thẳng chéo nhau a và b. Lấy hai điểm phân biệt A, B thuộc a và hai điểm phân
biệt C, D thuộc b. Khẳng định nào sau đây đúng khi nói về hai đường thẳng AD và BC?
A. Có thể song song hoặc cắt nhau. B. Cắt nhau. C. Song song nhau. D. Chéo nhau.
Câu 10.4. Trong không gian, cho ba đường thẳng phân biệt a, b, c trong đó a // b. Khẳng định nào sau đây không đúng?
A. Nếu a//c thì b//c.
B. Nếu c cắt a thì c cắt b.
C. Nếu A a và B b thì ba đường thẳng a, b, AB cùng ở trên một mặt phẳng.
D. Tồn tại duy nhất một mặt phẳng qua a và b.
Câu 11 [NB]. Hỏi về vị trí tương đối đường thẳng và mặt phẳng song song (giả thiết có hình vẽ đi kèm).
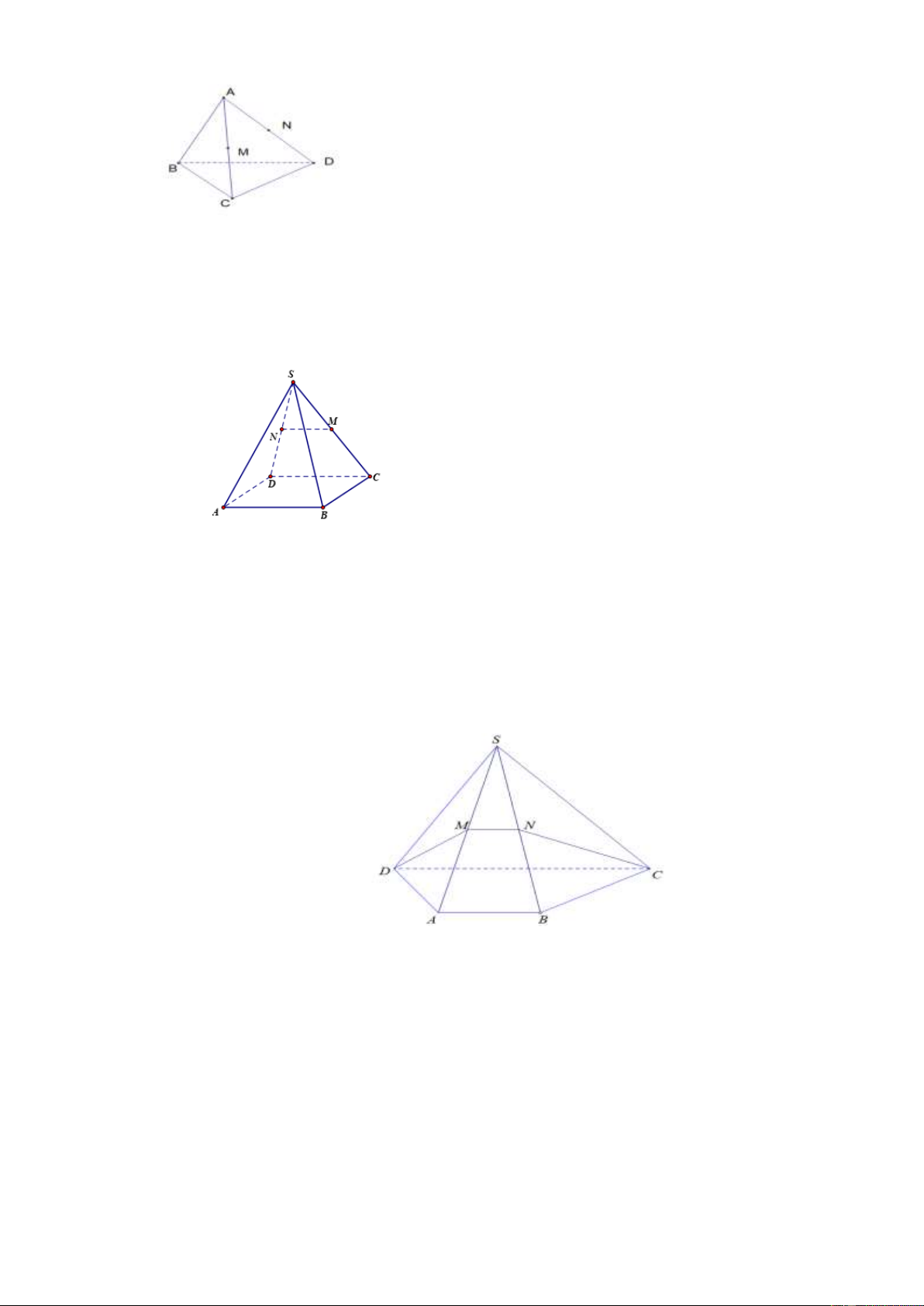
Câu 11.1. Cho 4 điểm A,B,C,D không đồng phẳng. Gọi M, N lần lượt là trung điểm của AC, AD (hình vẽ)
Chọn khẳng định đúng trong các khẳng định sau:
A. MN song song với (BCD). B. MN cắt (BCD).
C. MN song song với (BCD) và cắt (ACD).
D. MN cắt (BCD) chứa trong (ACD).
Câu 11.2. Cho hình chóp SABCD có đáy là hình bình hành . Gọi M , N lần lượt là trung điểm của SC
và SD . Mệnh đề nào sau đây là đúng?
A. MN / / (SBD) .
B. MN / / (SAB) .
C. MN / / (SAC)
D. MN / / (SCD) .
Câu 11.3. Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b? A. 0. B. 1. C. 2. D. Vô số.
Câu 11.4. Cho hình chóp S.ABCD có đáy là hình thang đáy lớn là CD . Gọi M là trung điểm của cạnh
SA , N là giao điểm của cạnh SB và mặt phẳng (MCD) . Mệnh đề nào sau đây là mệnh đề đúng?
A. MN và SD cắt nhau. B. MN // CD . C. MN và SC cắt nhau. D. MN và CD chéo nhau.
Câu 12 [NB]. Tìm giao tuyến dựa vào giả thiết đường thẳng song song mặt phẳng.
Câu 12.1. Cho đường thẳng a song song với mặt phẳng ( ) . Nếu mặt phẳng ( ) chứa a và cắt ( )
theo giao tuyến b thì b và a là hai đường thẳng:
A. Song song với nhau. B. Cắt nhau. C. Trùng nhau.
D. Chéo nhau. .
Câu 12.2. Cho hình chóp tứ giác S.ABCD có đáy là hình bình hành. Gọi a là giao tuyến của hai mặt
phẳng (SAB) và (SCD). Khẳng định nào sau đây là sai?
A. a // AD B. a // AB. C. a // CD. D. a // mp(ABCD).
Câu 12.3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi là giao tuyến của hai mặt
phẳng (SAD) và (SBC). Đường thẳng song song với đường thẳng nào dưới đây? A. Đường thẳng .
AD B. Đường thẳng . AB C. Đường thẳng .
AC D. Đường thẳng . SA
Câu 12.4. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M , N lần lượt là trung điểm của SA
và AB . Khẳng định nào sau đây đúng?
A. MN / / (SAB) .
B. MN / /BD . MN / / (SBC) C. .
D. MN cắt BC .
Câu 13 [NB]. Hỏi về số điểm chung của hai mặt phẳng trong mỗi vị trí tương đối.
Câu 13.1. Trong không gian cho hai mặt phẳng ( P) và (Q) song song. Số điểm chung của hai mặt
phẳng ( P) và (Q) là A. 0. B. 1. C. Vô số. D. 2.
Câu 13.2. Chọn khẳng định sai trong các khẳng định sau:
A. Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
D. Nếu ba điểm phân biệt M, N, P cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
Câu 13.3. Cho 4 điểm A, B, C, D không đồng phẳng. Gọi I, K lần lượt là trung điểm của hai đoạn thẳng
AD và BC. Hỏi K, I là điểm chung của hai mặt phẳng nào sau đây?
A. (IBC) và (KAD).
B. (IBC) và (KBD).
C. (ABI) và (KAD).
D. (IBC) và (KCD).
Câu 13.4. Tìm khẳng định đúng trong các khẳng định sau:
A. Nếu hai mặt phẳng cùng song song với một mặt phẳng khác thì chúng song song với nhau.
B. Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến thì ba giao tuyến đó đồng quy.
C. Nếu đường thẳng a song song với mặt phẳng ( P) thì a song song với một đường thẳng nào đó nằm trong (P) .
D. Cho hai đường thẳng a , b nằm trong mặt phẳng ( P) và hai đường thẳng a , b nằm trong
mặt phẳng (Q). Khi đó, nếu a // a ; b // b thì ( P) // (Q) .
Câu 14 [NB]. Hỏi về tính chất bắt cầu của hai mặt phẳng song song.
Câu 14.1. Trong các khẳng định sau khẳng định nào sai?
A. Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì chúng song song với nhau.
B. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì nó cắt mặt phẳng còn lại.
C. Nếu hai đường thẳng song song thì chúng cùng nằm trên một mặt phẳng.
D. Nếu một đường thẳng song song với một trong hai mặt phẳng song song thì nó song song hoặc
nằm trong mặt phẳng còn lại.
Câu 14.2. Cho hình hộp ABC .
D A' B 'C ' D ' . Tìm mệnh đề sai trong các mệnh đề sau
A. mp ( AA' B ' B) song song với mp(CC ' D ' D) .
B. Diện tích hai mặt bên bất kì bằng nhau.
C. AA ' song song với CC ' . D. Hai mặt phẳng đáy song song với nhau.
Câu 14.3. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai mặt phẳng song song thì không có điểm chung.
B. Hai mặt phẳng cùng song song với một mặt phẳng thì song song với nhau.
C. Hai mặt phẳng song song với nhau thì mọi đường thẳng nằm trong mặt phẳng này đều song
song với mặt phẳng kia.
D. Một mặt phẳng cắt hai mặt phẳng song song cho trước theo hai giao tuyến thì hai giao tuyến song song với nhau.
Câu 14.4. Trong không gian cho hai mặt phẳng ( P) và (Q) song song với nhau. Khẳng định nào sau đây sai?
A. Nếu d (P) và d ' (Q) thì d // d’.
B. Mọi đường thẳng đi qua điểm A (P) và song song với (Q) đều nằm trong ( P) .
C. Nếu đường thẳng a nằm trong ( P) thì a // (Q) .
D. Nếu đường thẳng cắt ( P) thì cắt (Q) .
Câu 15 [NB]. Hỏi về điều kiện để hai mặt phẳng song song.
Câu 15.1. Trong không gian cho ba mặt phẳng phân biệt ( P) , (Q) và ( R) . Xét các mệnh đề sau
I. Nếu mặt phẳng ( P) chứa một đường thẳng song song với (Q) thì ( P) song song với (Q) .
II. Nếu mặt phẳng ( P) chứa hai đường thẳng song song với (Q) thì ( P) song song với (Q) .
III. Nếu hai mặt phẳng (P) và (Q) cùng song song với mặt phẳng (R ) thì ( P) song song với (Q) .
IV. Nếu hai mặt phẳng (P) chứa hai đường thẳng cắt nhau cùng song song với mặt phẳng (Q) thì
hai mặt phẳng ấy song song. Số mệnh đề đúng là: A. 1. B. 0. C. 3. D. 2.
Câu 15.2. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hai mặt phẳng ( ) và ( ) song song với nhau thì mọi đường thẳng nằm trong ( )
đều song song với ( ).
B. Nếu hai mặt phẳng ( ) và ( ) song song với nhau thì bất kì đường thẳng nào nằm trong
() cũng song song với bất kì đường thẳng nào nằm trong ( ).
C. Nếu hai đường thẳng phân biệt a và b song song lần lượt nằm trong hai mặt phẳng ( )
và ( ) phân biệt thì (a) P ( ).
D. Nếu đường thẳng d song song với mp ( ) thì nó song song với mọi đường thẳng nằm trong mp ( ).
Câu 15.3. Cho hình chóp S.ABC . Gọi M, N, P lần lượt là trung điểm của SA, SB và SC . Mặt phẳng
(MNP) song song với mặt phẳng nào sau đây? A. (ABC). B. (SAB). C. (SBC). D. (MAC).
Câu 15.4. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M , N lần lượt là trung điểm
của SA và SB . Mặt phẳng (MNO) song song với mặt phẳng nào sau đây? A. (SCD). B. (SAB). C. (ABCD). D. (SBD).
Câu 16 [NB]. Tìm ảnh của điểm qua phép chiếu song song.
Câu 16.1. Phép chiếu song song biến ABC thành A B C
theo thứ tự đó. Vậy phép chiếu song song
nói trên, sẽ biến trung điểm M của cạnh BC thành
A. trung điểm M của cạnh B C .
B. trung điểm M của cạnh A C .
C. trung điểm M của cạnh AB .
D. trung điểm M của cạnh BC .
Câu 16.2. Cho hình chóp S.ABCD có đáy là hình bình hành. Hình chiếu song song của điểm A theo
phương AB lên mặt phẳng (SBC) là điểm nào sau đây? A. S .
B. Trung điểm của BC . C. B . D. C .
Câu 16.3: Cho lăng trụ AB . C A B C
. Gọi M là trung điểm của AC . Khi đó hình chiếu song song của
điểm M lên ( AA B
) theo phương chiếu CB là
A. Trung điểm BC .
B. Trung điểm AB .
C. Điểm A . D. Điểm B .
Câu 16.4: Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC . Hình chiếu
song song của điểm M theo phương AB lên mặt phẳng (SAD) là điểm nào sau đây? A. S .
B. Trung điểm của SD . C. A . D. D .
Câu 17 [NB]. Tìm giới hạn dãy số (công thức số hạng tổng quát dạng đa thức).
Câu 17.1. Giới hạn ( 3
lim n − 2023n + 2024) bằng A. + B. 2024 . C. − . D. 0.
Câu 17.2. Giới hạn ( 3 lim 2
− n − 3n + 4) bằng A. + B. 4 . C. − . D. 0.
Câu 17.3. Giới hạn ( 2 lim n − 3n + ) 1 bằng A. − B. 1. C. + . D. −2 .
Câu 17.4. Giới hạn 2 4
lim(2 − 3n − 4n ) bằng A. + . B. 4 . C. − . D. 2 .
Câu 18 [NB]. Tính giới hạn hàm số tại điểm không có dạng vô định. x − 3
Câu 18.1. Tính giới hạn L = lim . x→3 x + 3
A. L = 0
B. L = −
C. L = + D. L = 1 3x
Câu 18.2. Tính giới hạn L = lim . x→3 x + 3 3 9 2 A. L = B. L = C. L = D. L = 1 2 2 3 x + 3
Câu 18.3. Tính giới hạn L = lim . x 1 → x + 1
A. L = 1
B. L = 2
C. L = + D. L = 2 x − 4
Câu 18.4. Tính giới hạn L = lim . 2 x 2 →− x 3 − 3 3 A. L = .
B. L = 2 . C. L = . D. L = . 2 4 2
Câu 19 [NB]. Kiểm tra định lí giới hạn hữu hạn hàm số tại điểm.
Câu 19.1. Cho biết lim f ( x) = 2 và lim g ( x) = 3 . Hãy tính giới hạn I = lim 3 f
(x)−4g(x). x→x x→x x→x 0 0 0 A. I = 5. B. I = 2. C. I = 6. − D. I = 3. x − 3
Câu 19.2. Tính giới hạn L = lim L = . C. L = + . D. x 3 → x + . A. L = − . B. 0 3 L = 1 .
Câu 19.3. Giới hạn lim ( 2
x − x + 7) bằng? A. 5 . B. 9 . C. 0 . D. 7 . x 1 →− 2 x − 2x + 3
Câu 19.4. Giới hạn lim x 1 → x + bằng? A. 1. B. 0 . C. 3 . D. 2 . 1
Câu 20 [NB]. Chỉ ra điểm gián đoạn của hàm số dạng phân thức.
Câu 20.1. Hàm số nào dưới đây gián đoạn tại điểm x = −1 ? 0 2x −1 x x +1
A. y = ( x + )( 2
1 x + 2) . B. y = y = y = x + . C. 1 x − . D. 1 2 x + . 1 5 −
Câu 20.2. Hàm số y =
liên tục tại điểm nào dưới đây? x ( 2 x − 4)
A. x = 0 .
B. x = 2 .
C. x = 1. D. x = 2 − .
Câu 20.3. Hàm số nào sau đây gián đoạn tại điểm x = 1? 0 2x −1 x x +1 A. y = B. y = . C. 2
y = (x +1)(x + 2) . D. y = . x +1 x −1 2 x +1 1
Câu 20.4. Hàm số y =
gián đoạn tại điểm nào dưới đây? 2x − 4 A. x = 1. B. x = 0 . C. x = 2 . D. x = 1 − .
Câu 21 [TH]. Vận dụng công thức tính độ dài cung tròn vào tính toán.
Câu 21.1. Trên đường tròn bán kính 7 cm , lấy cung có số đo 54 . Độ dài l của cung tròn bằng 21 11 63 20 A. (cm). B. (cm) . C. (cm) . D. (cm) . 10 20 20 11
Câu 21.2. Trên đường tròn đường kính 8cm, tính độ dài cung tròn có số đo bằng 1,5 rad . A. 12cm. B. 4cm. C. 6cm. D. 15cm.
Câu 21.3. Một đường tròn có bán kính 15(cm) . Tìm độ dài cung tròn có góc ở tâm bằng 30 là: 5 5 2 A. . B. . C. . D. . 2 3 5 3
Câu 21.4. Một đường tròn có bán kính 10, độ dài cung tròn 40 trên đường tròn gần bằng A. 7. B. 9. C. 11. D. 13.
Câu 22 [TH]. Giải phương trình lượng giác cơ bản.
Câu 22.1. Biết các nghiệm của phương trình 1 cos 2x = − có dạng x =
+ k và x = − + k , k ; 2 m n với ,
m n là các số nguyên dương. Khi đó m + n bằng A. 4. B. 3. C. 5. D. 6.
Câu 22.2. Số nghiệm của phương trình sin x + = 1
với x 5 là 4 A. 1. B. 0 . C. 2 . D. 3 . 2
Câu 22.3. Có bao nhiêu nghiệm phương trình sin 2x = − trong khoảng (0; ) 2 A. 4 . B. 3 . C. 2 . D. 1.
Câu 22.4. Số nghiệm của phương trình 2cos x = 1 thuộc đoạn 2 − ;2 là? A. 4 . B. 2 . C. 3 . D. 1.
Câu 23 [TH]. Cho cấp số cộng có số hạng đầu và công sai, tìm tổng hữu hạn.
Câu 23.1. Cho cấp số cộng (u
với số hạng đầu u = 6
− và công sai d = 4. Tính tổng S n ) 1 của 14 số hạng
đầu tiên của cấp số cộng đó. A. S = 46 . B. S = 308. C. S = 644 . D. S = 280 .
Câu 23.2. Cho cấp số cộng (u
với số hạng đầu u = 1 và công sai d = 2 . Tính tổng S n ) 1 của 10 số hạng
đầu tiên của cấp số cộng đó. A. 100 . B. 110 . C. 10 . D. 90 .
Câu 23.3. Cho cấp số cộng (u
với số hạng đầu u = 21 −
và công sai d = 3. Tính tổng S n ) 1 của 16 số
hạng đầu tiên của cấp số cộng đó. A. S = 24 . B. S = 25 − . C. S = 24
− . D. S = 26 .
Câu 23.4. Cho cấp số cộng (u
với số hạng đầu u = 1 và công sai d = 2 − . Tính tổng S n ) 1 của 60 số hạng
đầu tiên của cấp số cộng đó. A. 6960 − . B. 117 − . C. 3840 − . D. 116 − .
Câu 24 [TH]. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành vận dụng định lí giao
tuyến của hai mặt phẳng chứa hai đường thẳng song song để tìm giao tuyến (không cho hình vẽ).
Câu 24.1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của SB, .
SD Khi đó giao tuyến của hai mặt phẳng (CMN ) và ( ABCD) là
A. đường thẳng CI , với I = MN BD .
B. đường thẳng MN .
C. đường thẳng BD .
D. đường thẳng d đi qua C và d //BD .
Câu 24.2. Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là
A. Đường thẳng qua S và song song với AD . B. Đường thẳng qua S và song song với CD .
C. Đường SO với O là tâm hình bình hành.
D. Đường thẳng qua S và cắt AB .
Câu 24.3. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I , J lần lượt là trung điểm của AB
và CB . Khi đó giao tuyến của 2 mặt phẳng (SAB) và (SCD) là đường thẳng song song với A. AD . B. IJ . C. BJ . D. BI .
Câu 24.4. Cho hình chóp S.ABCD có mặt đáy ( ABCD) là hình bình hành. Gọi đường thẳng d là giao
tuyến của hai mặt phẳng (SAD) và (SBC ) . Khẳng định nào sau đây đúng?
A. Đường thẳng d đi qua S và song song với AB .
B. Đường thẳng d đi qua S và song song với DC .
C. Đường thẳng d đi qua S và song song với BC .
D. Đường thẳng d đi qua S và song song với BD .
Câu 25 [TH]. Cho tứ diện ABCD chọn khẳng định đúng về vị trí tương đối hai đường thẳng (không cho hình vẽ).
Câu 25.1. Cho hình tứ diện ABCD . Khẳng định nào sau đây đúng?
A. AB và CD cắt nhau.
B. AB và CD chéo nhau.
C. AB và CD song song.
D. Tồn tại một mặt phẳng chứa AB và CD .
Câu 25.2. Cho tứ diện ABCD . Gọi I và J lần lượt là trọng tâm ABC
và ABD . Mệnh đề nào dưới đây đúng?
A. IJ song song với CD .
B. IJ song song với AB .
C. IJ chéo nhau với CD .
D. IJ cắt AB .
Câu 25.3. Cho tứ diện ABCD . Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC . Mệnh đề nào dưới đây đúng?
A. GE và CD chéo nhau. B. GE//CD . C. GE cắt AD .
D. GE cắt CD .
Câu 25.4. Cho tứ diện ABCD . Gọi I , J lần lượt là trọng tâm của các tam giác ABC, ABD . Đường
thẳng IJ song song với đường thẳng:
A. CM , trong đó M là trung điểm BD .
B. AC . C. DB . D. CD .
Câu 26 [TH]. Cho hình chóp tam giác hoặc hình chóp tứ giác có đáy là hình bình hành. Chọn kết luận
đúng về đường thẳng song song mặt phẳng (không cho trước hình vẽ).
Câu 26.1. Cho hình chóp S.ABC . Gọi M , N lần lượt là trung điểm của các cạnh SB, SC . Trong các
khẳng định sau, khẳng định nào đúng?
A. MN //( ABC) .
B. MN // (SAB) .
C. MN // (SAC) .
D. MN // (SBC) .
Câu 26.2. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I và J lần lượt là trung điểm của SC
và BC . Chọn khẳng định đúng trong các khẳng định sau:
A. JI // (SAC) .
B. JI // (SAB) .
C. JI // (SBC) .
D. JI // (SAD) .
Câu 26.3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O , M là trung điểm SA .
Khẳng định nào sau đây là đúng?
A. OM // (S D C ) .
B. OM // (S D B ) .
C. OM // (SAB) .
D. OM // (S D A ) .
Câu 26.4. Cho hình chóp SABCD có đáy là hình bình hành. M , N lần lượt là trung điểm của SC và
SD . Mệnh đề nào sau đây là đúng?
A. MN / / (SBD) .
B. MN / / (SAB) .
C. MN / / (SAC) .
D. MN / / (SCD) .
Câu 27 [TH]. Cho hình lăng trụ AB . C A B C
hoặc hình hộp ABC . D A B C D
'. Tìm khẳng định đúng về
hai mặt phẳng song song (không cho hình vẽ).
Câu 27.1. Cho hình lăng trụ AB . C A B C
. Gọi I , J , K lần lượt là trọng tâm tam giác ABC , ACC, AB C
.Mặt phẳng nào sau đây song song với (IJK ) ? A. ( BC A ). B. ( AA B ) . C. ( BB C ) . D. (CC A ).
Câu 27.2. Cho hình hộp ABC . D A B C D
. Mặt phẳng ( AB D
) song song với mặt phẳng nào trong các mặt phẳng sau đây?
A. ( BCA) . B. ( BC D ). C. ( A C C ). D. (BDA) .
Câu 27.3. Cho hình lăng trụ AB . C A B C
. Gọi H là trung điểm của AB . Mặt phẳng ( AHC) song
song với đường thẳng nào sau đây?
A. BA .
B. BB . C. BC .
D. CB .
Câu 27.4. Cho hình hộp ABC . D A B C D . Gọi ,
O O ' lần lượt là tâm của hình bình hành ABCD và
A' B 'C ' D ' . Biết K là trung điểm AD . Mặt phẳng (OKO ') song song với mặt phẳng nào trong các mặt phẳng sau?
A. ( BCC ' B ') .
B. ( DCC ' D ') . C. (
A CCA) . D. (BDA) .
Câu 28 [TH]. Tìm kết quả giới hạn dãy số có dạng vô định − .
Câu 28.1. Cho dãy số u = n ( 2 n +1 − n . n ) 1 Khi đó lim u bằng A. + . B. 1. C. . n 0 . D. 2 Câu 28.2. ( 2 lim
n − 3n +1 − n) bằng 3 A. 3 − . B. + . C. 0 . D. − . 2
Câu 28.3. Cho dãy số (u với 2 2
u = n + an − 3 − n + n , với a là tham số thực. Tìm a để n ) n lim u = 3 . A. 7 . B. 4 . C. 5 . D. 6 . n
Câu 28.4. Tính giới hạn ( 2 lim
n +18n − n). A. 9 . B. + . C. 18 . D. 0 . 0
Câu 29 [TH]. Tính giới hạn hàm số tại điểm có dạng vô định dạng . 0 x + 2 − 2
Câu 29.1. Tính giới hạn lim . x→2 x − 2 1 1 A. . B. . C. 0 . D. 1. 2 4 1 − x
Câu 29.2. Tính gới hạn L = lim . x 1 → 2 − x −1 A. L = 6 − . B. L = −4 . C. L = 2 . D. L = −2 . 2 2x − 6 Câu 29.3. Tính lim
= a b ( a , b nguyên). Khi đó giá trị của P = a + b bằng x→ 3 x − 3 A. 7 . B. 10 . C. 5 . D. 6 . 3x +1 −1 a Câu 29.4. Biết lim
= , trong đó a , b là các số nguyên dương và phân số a tối giản. Tính x→0 x b b giá trị biểu thức 2 2
P = a + b . A. P = 13. B. P = 0 . C. P = 5 . D. P = 40 .
Câu 30. [TH] Xét tính liên tục tại điểm của hàm số cho nhiều công thức. 2
x − 2x + 3 khi x 1
Câu 30.1. Cho hàm số f ( x) = 3
x + m −1 khi x =1.
Tìm m để hàm số liên tục tại x = 1. 0 A. m = 1. B. m = 3 . C. m = 0 . D. m = 2 . 2 x − 3x + 2 khi x 2
Câu 30.2. Cho hàm số f (x) = x − 2
a khi x = 2.
Hàm số liên tục tại x = 2 khi a bằng A. 1. B. 0 . C. 2 . D. −1. 2 x −16 khi x 4
Câu 30.3. Tìm tham số m để hàm số f ( x) = x − 4
liên tục tại điểm x = 4 .
mx +1 khi x 4 7 7 A. m = . B. m = 8 . C. m = − . D. m = 8 − . 4 4
Câu 30.4. Tìm tất cả các giá trị của tham số m để hàm số
liên tục tại x = 2 .
A. m = 3 . B. m = 2 . C. m = 2 − .
D. Không tồn tại m .
Câu 31. [VDT] Tìm tính chất của đa giác tạo bởi các giao tuyến của mặt phẳng ( ) với các mặt hình
chóp. Biết ( ) qua điểm M cho trước và song song với mặt phẳng nào đó của hình chóp (không cho hình vẽ).
Câu 31.1. Cho tứ diện ABCD có tất cả các cạnh đều bằng nhau. Gọi I là trung điểm đoạn CD , M là
điểm nằm trên đoạn BC ( M khác B và C ). Gọi ( ) là mặt phẳng qua M và song song với mặt phẳng
(ABI) , khi đó đa giác tạo bởi các giao tuyến của mặt phẳng () với các mặt của tứ diện là
A. Một tam giác vuông cân.
B. Một tam giác đều.
C. Một hình bình hành.
D. Một tam giác cân.
Câu 31.2. Cho tứ diện đều SABC cạnh bằng .
a Gọi I là trung điểm của đoạn AB , M là điểm di
động trên đoạn AI . Qua M vẽ mặt phẳng ( ) song song với (SIC) . Tính chu vi của đa giác tạo bởi
các giao tuyến của mặt phẳng ( ) với các mặt của tứ diện SABC , biết AM = x .
A. 2x (1+ 3).
B. 3x (1+ 3) .
C. Không tính được.
D. x (1+ 3) .
Câu 31.3. Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là
điểm di động trên đoạn .
AB Qua M vẽ mặt phẳng ( ) song song với ( SBC ) . Đa giác tạo bởi các giao
tuyến của mặt phẳng ( ) với các mặt của hình chóp S.ABCD là hình gì?
A. Hình tam giác.
B. Hình bình hành. C. Hình thang. D. Hình vuông.
Câu 31.4. Cho hình chóp SABC .
D Biết tứ giác ABCD là hình bình hành tâm O và có AC = 3 3;
BD = 3 . Tam giác SBD là tam giác đều. Mặt phẳng ( ) di động song song với (SBD) và đi qua điểm
I thuộc đoạn OC sao cho AI = 2 3 . Khi đó diện tích đa giác tạo bởi các giao tuyến của mặt phẳng
( ) với các mặt của hình chóp là: 25 A. 2 . B. 25 3 . C. . D. 3 . 3
Câu 32. [VDT] Vận dụng tính chất phép chiếu song song để xác định ảnh của một điểm qua phép chiếu song song.
Câu 32.1. Cho hình lăng trụ AB . C A B C
, gọi I , I lần lượt là trung điểm của AB , AB . Qua phép
chiếu song song đường thẳng AI , mặt phẳng chiếu ( AB C
) biến I thành? A. A . B. B . C. C . D. I .
Câu 32.2. Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC . Hình chiếu
song song của điểm M theo phương AB lên mặt phẳng (SAD) là điểm nào sau đây? A. S .
B. Trung điểm của SD . C. A . D. D .
Câu 32.3. Cho hình chóp S.ABCD có đáy là hình bình hành. Hình chiếu song song của điểm A theo
phương AB lên mặt phẳng (SBC) là điểm nào sau đây? A. S .
B. Trung điểm của BC . C. B . D. C .
Câu 32.4. Cho lăng trụ AB . C A B C
. Gọi M là trung điểm của AC . Khi đó hình chiếu song song của
điểm M lên ( AA B
) theo phương chiếu CB là
A. Trung điểm BC .
B. Trung điểm AB . C. Điểm A . D. Điểm B .
Câu 33. [VDT] Tìm tổng tất cả các nghiệm của phương trình lượng giác.
Câu 33.1. Tổng các nghiệm của phương trình 2sin ( x + 40) = 3 trên khoảng ( 1 − 80;180) là A. 20. B. 100 . C. 80 . D. 120 .
Câu 33.2. Tìm tổng các nghiệm của phương trình cos 5x − = cos 2x − trên 0; . 6 3 47 4 45 7 A. . B. . C. . D. . 18 18 18 18
Câu 33.3. Cho phương trình 3 sin 2x − = sin x +
. Tính tổng các nghiệm thuộc khoảng (0; ) 4 4 7 3
của phương trình trên. A. . B. . C. . D. . 2 2 4 2 3
Câu 33.4. Tổng các nghiệm của phương trình cos x + = − trong khoảng − ; là 5 2 3 2 21 8 13 A. . B. . C. . D. . 20 2 5 20
Câu 34. [VDT]. Cho kết quả giới hạn tại điểm của hàm phân thức còn chứa tham số, tìm tham số đó. 3
x − ax + a −1 Câu 34.1. Biết lim = 2
M = a + a . x 1 → x − . Tính 2 2 1 A. M = 3 . B. M = 1 . C. M = −1 . D. M = 8 . 2
x + ax + b 1 − Câu 34.2. Cho lim = a, b . 2 ( ) x 1 → x − 1 2 Tổng 2 2
S = a + b bằng A. S = 13. B. S = 9. C. S = 4. D. S = 1. 2 ax + bx − 5
Câu 34.3. Cho a, b là số nguyên và lim = 7 x 1 → x − . 1 Tính 2 2
a + b + a + b . A. 18 . B. 1. C. 15 . D. 5 . 2
x + ax + b
Câu 34.4. Cặp số (a;b) thỏa mãn lim
= 3 a b là các tham số) là x→3 x − ( , 3 A. a = 3 − , b = 0.
B. a = 3, b = 0 .
C. a = 0 , b = 9 − .
D. không tồn tại cặp số (a;b) thỏa mãn như vậy.
Câu 35. [VDT]. Xét tính liên tục tại điểm của hàm số cho nhiều công thức trên tập xác định. 2 x −1 khi x 1
Câu 35.1. Cho hàm số f ( x) = x −1 2 khi x = 1.
Khẳng định nào sau đây đúng?
A. Hàm số liên tục tại mọi điểm x 1 và gián đoạn tại x = 1.
B. Hàm số liên tục trên .
C. Hàm số không liên tục trên (1; +) .
D. Hàm số gián đoạn tại điểm x = 1. 2
2mx − 4 khi x 3
Câu 35.2. Cho hàm số f (x) =
( m là tham số). Tìm giá trị của m để hàm số liên 5 khi x 3 tục trên . 1 1 A. . B. . C. 18 . D. 2 . 2 18 2
ax + bx − 4 khi x 1
Câu 35.3. Biết hàm số f ( x) =
( a, b là các tham số) liên tục trên R. Tính giá trị 2ax − 2b khi x 1
của biểu thức P = a − 3b A. P = −4 . B. P = 5 . C. P = 4 . D. P = 5 − . 3 x − 7x + 6
, khi x 1vµx 2 2 x − 3x + 2
Câu 35.4. Biết hàm số f ( x) = 2a, khi x = 1
( a, b là các tham số) liên tục trên R . b −3, khi x = 2 Tính 2 2
P = a + b . A. P = 68.
B. P = 45 .
C. P = 41 . D. P =10 . B. Tự luận
Bài 1 (TH-1,0 điểm): Chứng minh đường thẳng song song mặt phẳng.
Bài 2 (VDT-1,0 điểm): Tính giới hạn hàm số bằng cách khử dạng vô định − .
Bài 3 (VDC-1,0 điểm): Vận dụng cấp số, giới hạn dãy số, giới hạn hàm số vào giải toán.
----------------------------------------------HẾT---------------------------------------------------




