Đề cương ôn tập Toán 11 HK2 năm 2022

ĐỀ CƯƠNG ÔN TẬP TOÁN 11 HỌC KỲ II NĂM HỌC 2021-2022
A. NỘI DUNG, PHẠM VI KIỂM TRA Phân môn
Chương trình từ đầu học kì II đến hết bài Đại số-Giải tích Quy tắc tính đạo hàm Hình học Khoảng cách B. KIẾN THỨC TRỌNG TÂM GIẢI TÍCH
I. GIỚI HẠN CỦA DÃY SỐ
1. Một vài giới hạn đặc biệt
2. Một số định lý về giới hạn của dãy số.
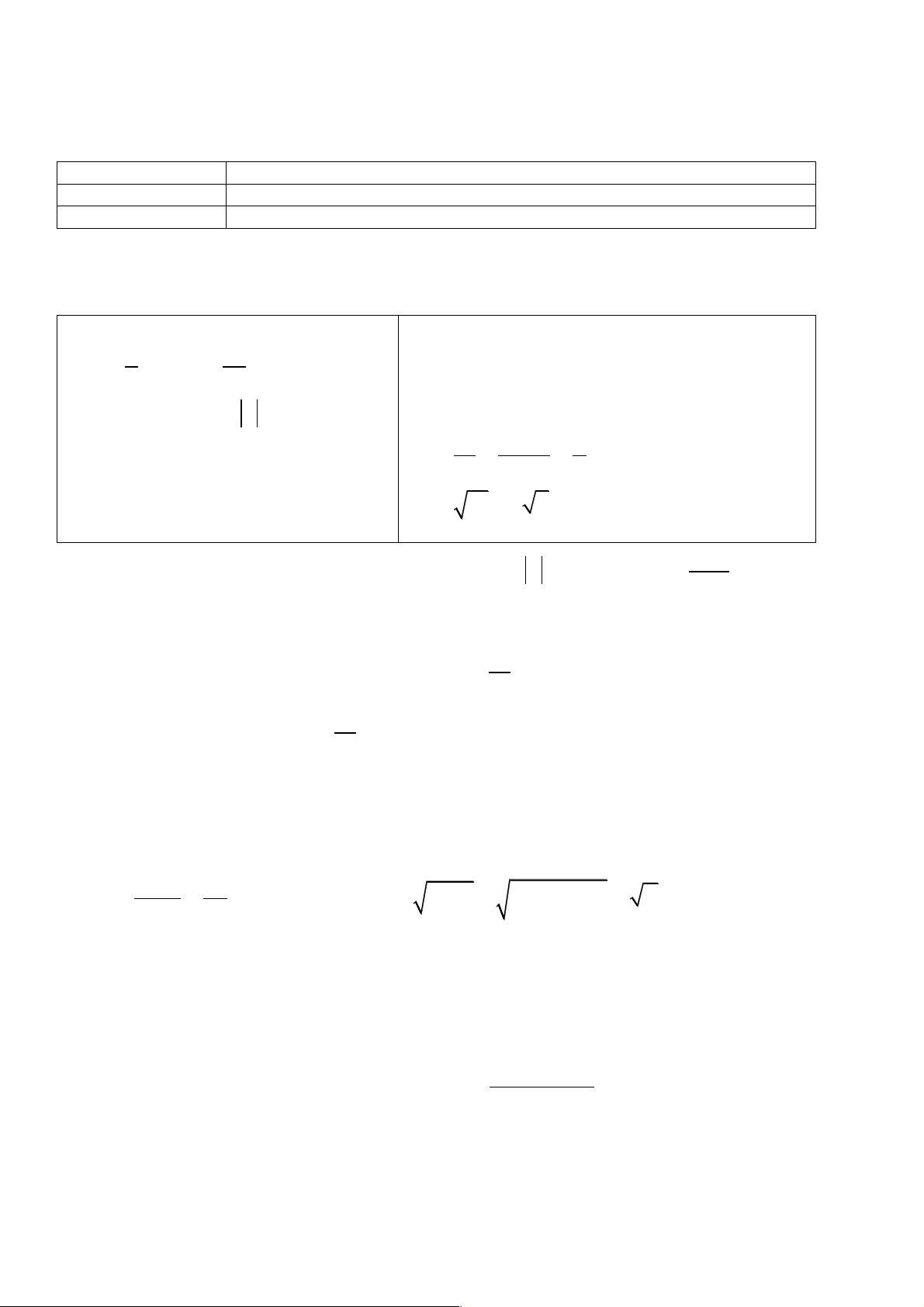
Định lý 2: Nếu lim(un) = a , lim(vn)= b thì: 1 1 a) * lim = 0 , lim = 0 , n Î N . k
lim(u ± v == a ± b n n ) . n n b) lim( n
q ) = 0 với q < .1
lim(u .v = a b n n ) . . c) lim C= C. u limu a lim n n = = ,( * v ¹ 0 n " Î N ;b ¹ 0 n ) v limv b n n
lim u == a ,(u ³ 0 ,a ³ 0 n n ). u
3. Tổng của cấp số nhân lùi vô hạn có công bội q ,với q < 1: 1 lim S = lim . n 1- q
4. Dãy số dần tới vô cực Định lý: lim(u ) = 0 ( * u ¹ 0 , n " Î 1 N lim = . ¥ n n ) Þ . un lim(u = ¥ 1 lim = 0 n ) Þ . un
II. GIỚI HẠN CỦA HÀM SỐ
Định lý 2: Nếu các giới hạn: lim é f
ë (x)ù = L , limég û
ë (x)ù = M thì û x®a x®a lim é f
ë ( x) ± g (x)ù = L ± M .
lim é f x .g x ù = . L M . û ë ( ) ( )û x®a x®a f ( x) L lim = , M ¹ 0.
lim f (x) = limé f
ë (x)ù = L ; f û
(x) ³ 0,L ³ 0.
x®a g ( x) M x a ® x a ®
III. HÀM SỐ LIÊN TỤC
ĐN hàm số liên tục tại một điểm: Hàm số liên tục tại x = x0 Û lim f (x) = f (x . 0 ) x® 0 x
Hệ quả: Nếu f(x) liên tục trên [a;b] và f(a).f(b) < 0 thì tồn tại ít nhất một điểm cÎ(a;b), f(c) = 0. IV. ĐẠO HÀM f x - f x
Định nghĩa đạo hàm tại một điểm: f '( 0 x ) ( ) ( 0) = lim . x® x x - x 0 0
1. Ý nghĩa của đạo hàm
Ý nghĩa hình học: Cho hàm số y = f (x) có đồ thị (C) • f '( (C) y = f (x) M0 ( 0 x , 0 y )Î(C) 0
x ) là hệ số góc của tiếp tuyến đồ thị của hàm số tại . Trang 1
• Phương trình tiếp tuyến của đồ thị hàm số y = f (x)tại điểm M0 ( 0 x , 0 y )Î(C)là : y = f '( 0 x )×(x - 0
x ) + y . 0
Ý nghĩa vật lí :
• Vận tốc tức thời của chuyển động thẳng xác định bởi phương trình : s = s(t) tại thời điểm t 0
là v( 0t) = s'( 0t).
• Cường độ tức thời của điện lượng Q = Q(t)tại thời điểm t là : I ( 0t) = Q'( 0t). 0
2. Qui tắc tính đạo hàm và công thức tính đạo hàm
• (u ± v)' = u'± v' • ( .
u v)' = u '.v + v'.u
Þ (C.u)¢ = C.u¢ , ¢ æ ö - æ ö ¢ • u
u '.v v '.u C C.u = , ç ÷ (v ¹ 0) Þ = - 2 ç ÷ 2 è v ø v è u ø u
• y = f (u), u = u(x) Þ y¢ = y¢ .u¢ . x u x
Các công thức
• (C)¢ 0 ; (x)¢ = =1 • ¢ ¢ n n 1 - n n 1 x = . n x Þ u = .
n u - .u¢ , nΕ , n ³ 2 ( ) ( ) ( ) ¢ 1 ¢ u¢ • ( x) =
, (x > 0) Þ ( u ) = , (u > 0) 2 x 2 u
• (sin x)¢ = cos x Þ (sin u)¢ = . u ¢cosu
• (cos x)¢ = -sin x Þ (cosu)¢ = u - .¢sin u ¢ • 1 u (tan x)¢ 2 = =1+ tan x Þ (tan u)¢ = = ( 2 1+ tan u .u¢ 2 2 ) cos x cos u ¢ • 1 u (cot x)¢ = - = -( 2 1+ cot x) Þ Þ (cot u)¢ = - = -u¢( 2 1+ cot u 2 2 ). sin x sin u HÌNH HỌC
1. Tích vô hướng của hai vectơ u v
. = u v cos(u, v .)
2. Góc giữa 2 đường thẳng a và b là góc giữa hai đường thẳng cùng đi qua một điểm và lần lượt song song với a và b.
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và hình chiếu a’ của a trên (P).
Góc giữa 2 mặt phẳng cắt nhau (P) và (Q) theo tuyến d là góc giữa đường thẳng a và b lần
lượt nằm trên (P) và (Q) cùng vuông góc giao tuyến c.
3. Cách chứng minh đường thẳng a vuông góc với mặt phẳng (a)
Chứng minh a vuông góc với hai đường thẳng cắt nhau nằm trong (a).
4. Cách chứng minh hai mặt phẳng vuông góc với nhau
Chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
5. Khoảng cách từ điểm O đến mặt phẳng (a) là khoảng cách giữa hai điểm O và H, với H là
hình chiếu vuông góc của O trên (a).
Khoảng cách giữa hai đường thẳng chéo nhau a và b
+ là độ dài đoạn thẳng vuông góc chung của a và b.
+ bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó chứa đường thẳng kia.
+ bằng khoảng cách giữa hai mặt phẳng song song và lần lượt chứa hai đường thẳng đó.
6. Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với các mặt đáy.
Hình hộp chữ nhật là hình lăng trụ đứng có đáy là hình chữ nhật. Trang 2
Hình lập phương là hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông.
7. Hình chóp đều là hình chóp có đáy là một đa giác đều và chân đường cao trùng với tâm của đa giác đáy.
C. MA TRẬN ĐỀ KIỂM TRA
Mức độ nhận thức Tổng Nội dung Số CH % TT
Đơn vị kiến thức VD VDC kiến thức NB TH tổng
(TL) (TL) TN TL điểm Giới hạn của dãy số 1 Giới hạn Giới hạn của hàm số 5 2 1 Hàm số liên tục
Định nghĩa và ý nghĩa của đạo 1 23 3 66 1 1 1 hàm 2 Đạo hàm Quy tắc tính đạo hàm 6 2
Đạo hàm của hàm số lượng giác 3 3 Đạo hàm cấp hai 2 2 4
Vectơ trong Vectơ trong không gian 1
không gian. Hai đường thẳng vuông góc 1 1 Quan hệ
Đường thẳng vuông góc với mặt 3 1 2 1 10 1 30 vuông góc phẳng
trong không Hai mặt phẳng vuông góc 1 1 gian. Khoảng cách 1 1 Tổng 20 15 2 2 35 4
Tỉ lệ % từng mức độ nhận thức 40 30 20 10 D. ĐỀ MINH HỌA
ĐỀ KIỂM TRA CUỐI KÌ II - NĂM HỌC 2021 – 2022 Môn: Toán, Lớp 11
Thời gian làm bài: 90 phút, không tính thời gian phát đề
PHẦN TRẮC NGHIỆM (7 điểm)
Câu 1: Cho hai dãy (u (v limu = 2 limv = 3. lim(u + v n n ) n ) n ) và thỏa mãn và Giá trị của bằng n n A. 5. B. 6. C. 1. - D. 1. 1 Câu 2: lim bằng 2n +1 1 A. 0. B. . C. 1. D. + . ¥ 2 1 n æ ö Câu 3: lim bằng ç ÷ è 3 ø 1 A. 0. B. . C. 1. D. + . ¥ 3 Câu 4: lim ( 2 x - ) 1 bằng x®2 A. 3. B. 1. - C. 1. D. + . ¥
Câu 5: lim (2x + 3) bằng x®+¥ A. + . ¥ B. 2. C. 3. D. . -¥
Câu 6: Cho hàm số y = f (x) có đồ thị (C) và đạo hàm f (2
¢ ) = 6. Hệ số góc của tiếp tuyến của (C) tại
điểm M (2; f (2)) bằng A. 6. B. 3. C. 2. D. 12.
Câu 7: Đạo hàm của hàm số 2
y = x tại điểm x = 3 bằng Trang 3 A. 6. B. 12. C. 3. D. 9.
Câu 8: Đạo hàm của hàm số 2
y = x + x là A. 2x +1. B. 2 . x C. 2 2x +1. D. 2 2x + . x
Câu 9: Đạo hàm của hàm số 3
y = x - 2x là A. 2 3x - 2. B. 2 3x . C. 3 3x - 2. D. 2 2x - 2.
Câu 10: Cho hai hàm số f (x) và g (x) có f ¢( ) 1 = 2 và g¢( )
1 = 3 .Đạo hàm của hàm số f (x) + g (x)
tại điểm x = 1 bằng A. 5. B. 6. C. 1. D. 1. -
Câu 11: Cho hai hàm số f (x) và g (x) có f ¢( ) 1 = 3 và g¢( )
1 =1. Đạo hàm của hàm số f (x) - g (x)
tại điểm x = 1 bằng A. 2. B. 3. C. 4. D. 2. -
Câu 12: Cho hàm số f (x) có đạo hàm f ¢(x) = 2x + 4 với mọi x Î ! . Hàm số 2 f ( x) có đạo hàm là A. 4x + 8. B. 4x + 4. C. x + 2. D. 2x + 6.
Câu 13: Đạo hàm của hàm số y = cos x là A. -sin . x B. sin . x C. - cos . x D. cos . x sin x Câu 14: lim bằng x®0 x A. 1. B. 1. - C. 0. D. + . ¥
Câu 15: Đạo hàm của hàm số y = x + sin x là A. 1+ cos . x B. 1- cos . x C. cos . x D. - cos . x !!!" !!!"
Câu 16: Trong không gian, cho hình bình hành ABC .
D Vectơ AB + AD bằng !!!" !!!" !!!" !!!" A. AC B. BC. C. BD D. . CA ! ! !
Câu 17: Trong không gian, với a,b,c là ba vectơ bất kỳ, mệnh đề nào dưới đây đúng ? ! ! ! ! ! ! ! ! ! ! ! ! ! !
A. a (b + c) = a.b + a.c.
B. a (b - c) = a.b + a.c. ! ! ! ! ! ! ! ! ! ! ! ! ! !
C. a (b + c) = a.b - a.c.
D. a (b + c) = a.b + b.c.
Câu 18: Trong không gian cho điểm A và mặt phẳng (P) .Mệnh đề nào dưới đây đúng ?
A. Có đúng một đường thẳng đi qua A và vuông góc với (P) .
B. Có đúng hai đường thẳng đi qua A và vuông góc với (P) .
C. Có vô số đường thẳng đi qua A và vuông góc với (P) .
D. Không tồn tại đường thẳng đi qua A và vuông góc với (P) .
Câu 19: Hình lăng trụ đứng tam giác có bao nhiêu mặt là hình chữ nhật ? A. 3. B. 1. C. 5. D. 2.
Câu 20: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ có cạnh bằng .
a Khoảng cách từ A¢ đến mặt phẳng (ABCD) bằng a A. . a B. 2 . a C. 3 . a D. . 2 1 Câu 21: Cho (u u = 3 q = . S n
n ) là cấp số nhân với và công bội Gọi
là tổng của số hạng đầu tiên 1 2 n
của cấp số nhân đã cho. Ta có lim S bằng n 3 1 A. 6. B. . C. 3. D. . 2 2 ì x + x ³
Câu 22: Giá trị thực của tham số m để hàm số f ( x) 2 1 khi 2 = í
liên tục tại x = 2 bằng î m khi x < 2 A. 5. B. 2. C. 3. D. 1.
Câu 23: Tiếp tuyến của đồ thị hàm số 3 2
y = x - 2x tại điểm M (1;- ) 1 có hệ số góc bằng Trang 4 A. 1. - B. 1. C. 7. D. 5.
Câu 24: Đạo hàm của hàm số y = ( x + )2 2 1 là
A. y¢ = 8x + 4.
B. y¢ = 2x +1.
C. y¢ = 4x + 2.
D. y = 4x +1.
Câu 25: Đạo hàm của hàm số 2
y = 3x + x là 1 A. 6x + 1 . B. 6x - 1 . C. 3x + 1 . D. 6x + . 2 x 2 x 2 x x
Câu 26: Đạo hàm của hàm số y = tan (2x + ) 1 là 2 2 1 2 A. . B. - . C. . D. . 2 cos (2x + ) 1 2 cos (2x + ) 1 2 cos (2x + ) 1 2 sin (2x + ) 1
Câu 27: Đạo hàm của hàm số y = xsin x là
A. sin x + x cos . x
B. sin x - x cos . x C. sin x + cos . x
D. cos x + x sin . x
Câu 28: Đạo hàm của hàm số y = sin 2x là A. 2cos 2 . x B. 2 - cos 2 . x C. cos 2 . x D. - cos 2 . x
Câu 29: Đạo hàm cấp hai của hàm số 3
y = x + 2x là A. 6 . x B. 6x + 2. C. 3 . x D. 3x + 2.
Câu 30: Cho hàm số f (x) = (x + )3
1 . Giá trị của f ¢ ( ) 1 bằng A. 12. B. 6. C. 24. D. 4. ! ! ! !
Câu 31: Trong không gian cho hai vectơ u,v tạo với nhau một góc 60° , u = 2 và v = 3. Tích vô ! !
hướng u.v bằng A. 3. B. 6. C. 2. D. 3 3.
Câu 32: Cho hình chóp S.ABCD có ABCD là hình chữ nhật và SA ^ (ABCD). Mệnh đề nào dưới đây đúng ?
A. AB ^ (SAD).
B. BC ^ (SAD).
C. AC ^ (SAD).
D. BD ^ (SAD).
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ^ (ABCD) và SA = . a Góc
giữa đường thẳng SB và mặt phẳng (ABCD) bằng A. 45 . ° B. 90 . ° C. 30 . ° D. 60 . °
Câu 34: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy. Mặt phẳng ( ABCD) vuông góc
với mặt phẳng nào dưới đây ? A. (SAC). B. (SBD). C. (SCD). D. (SBC).
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ^ (ABCD), AB = a và SB = 2 .
a Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng A. . a B. 2 . a C. 2 . a D. 3 . a PHẦN TỰ LUẬN (3điểm)
Câu 1: Tính đạo hàm các hàm số a) f (x) 3 2
= x - 4x -10x + 2022.
b) f (x) = sin3x + cos2 . x . x + 2
Câu 2: Cho hàm số y =
có đồ thị (C). Tìm điểm M thuộc (C) sao cho tiếp tuyến của (C) tại x +1
M tạo với hai trục tọa độ một tam giác vuông cân.
Câu 3: Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 .
° Tính độ dài đường cao của hình chóp đã cho. Trang 5