Đề giữa học kỳ 2 Toán 11 năm 2022 – 2023 trường THPT Núi Thành – Quảng Nam

SỞ GD-ĐT QUẢNG NAM
KIỂM TRA GIỮA KỲ 2, NĂM HỌC 2022-2023
TRƯỜNG THPT NÚI THÀNH
Môn: TOÁN – Lớp: 11 ĐỀ CHÍNH THỨC
Thời gian: 60 phút (không kể thời gian giao đề)
(Đề gồm có 02 trang) MÃ ĐỀ 101
A/ TRẮC NGHIỆM. (5.0 điểm)
Câu 1. Trong không gian, cho tứ diện ABCD có G là trọng tâm tam giác ACD. Mệnh đề nào sau đây là
đúng?    
   
A. GA + GC + GD = 0.
B. GA + CG + DG = 0.
   
   
C. GA + GB + GC = 0.
D. GA + GC + DG = 0. Câu 2. lim ( 3
2x − 5x + 3) bằng x 2 →− A. 3 − . B. −∞. C. +∞ . D. 9 .
Câu 3. Cho hình hộp ABC .
D A'B'C 'D'. Mệnh đề nào sau đây đúng?
  
  
A. BD + BB' = D' . B
B. BD + BB' = BD'.
  
  
C. BD + BB' = B'D'.
D. BD + BB' = B' . D
Câu 4. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, SB vuông góc với đáy.
Đường thẳng AC vuông góc với mặt phẳng nào sau đây? A. (SAC) . B. (ABC) . C. (SAB) . D. (SBC) .
Câu 5. Cho hàm số y = f (x) xác định trên khoảng K và 3∈ K . Hàm số y = f (x) được gọi là liên tục tại x = 3 nếu
A. lim f (x) = f (3) .
B. lim f (x) = f (3) . x 3− → x→3
C. lim f (x) = f (3) .
D. lim f (x) = lim f (x) . x 3+ → x 3− x 3+ → →
Câu 6. Cho các dãy số (u
v có limu = , limv = −∞ . Mệnh đề nào sau đây là đúng? n 3 n ), ( n ) n A. − lim( u u u v = −∞ . B. n 1 lim = .
C. lim n = −∞ .
D. lim(u v = − . n. n ) 3 n. n ) v v n 3 n  
Câu 7. Trong không gian, cho hai đường thẳng a,b có vectơ chỉ phương lần lượt là u và v . Biết rằng (  u v) 0
, =135 . Góc giữa hai đường thẳng a và b bằng A. 0 45 . B. 0 135 . C. 0 55 . D. 0 60 .
Câu 8. Mệnh đề nào sau đây sai? A. 5 lim x = −∞ .
B. lim x = +∞ . C. 2 lim x = −∞ . D. 2 lim x = +∞ . x→−∞ x→+∞ x→−∞ x→+∞
Câu 9. Mệnh đề nào sau đây là đúng? n n n A. lim2n = 0. B.  1 lim  =     0. C. lim( 2) = 0. D. 3 lim =   0.  2   2 
Câu 10. Khẳng định nào sau đây đúng ?
A. Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai vec tơ chỉ phương của hai đường thẳng đó.
B. Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a' và b' cùng đi qua một điểm.
C. Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a' và b'lần
lượt vuông góc với a và b.
D. Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a' và b'
cùng đi qua một điểm và lần lượt song song với a và b. Trang 1/2 – Mã đề 101 2 x − 3 Câu 11. Biết lim
= a b với a,b∈ và b <10. Tính giá trị biểu thức 2
T = b − a . x→ 3 x − 3 A. T =1. B. T = 7 − . C. T = 7 . D. T = 1 − .
Câu 12. Khẳng định nào sau đây đúng ?
A. Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với hai đường thẳng song
song cùng thuộc mặt phẳng đó.
B. Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với hai đường thẳng phân
biệt cùng thuộc mặt phẳng đó.
C. Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với một đường thẳng nằm trong mặt phẳng đó.
D. Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với hai đường thẳng cắt
nhau cùng thuộc mặt phẳng đó.
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SB ⊥ (ABCD). Gọi BH là đường cao
của tam giác SAB . Chọn khẳng định đúng trong các khẳng định sau ?
A. BH ⊥ (SAC).
B. BH ⊥ (SBC).
C. BH ⊥ (SCD).
D. BH ⊥ (SAD).
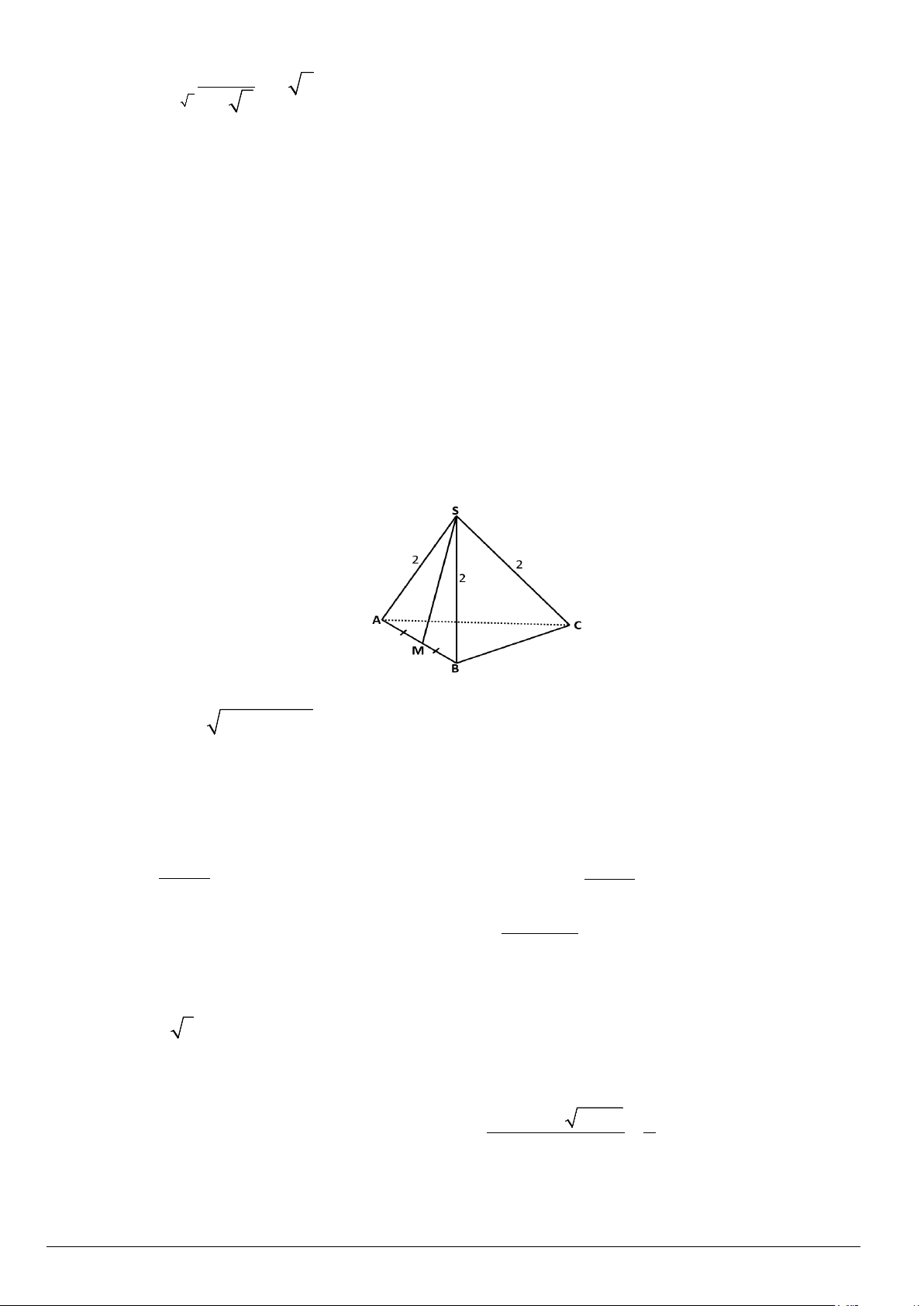
Câu 14. Cho hình chóp S.ABC có ,
SA SB,SC đôi một vuông góc và SA = SB = SC = 2 . Gọi M là trung
điểm AB ( tham khảo hình vẽ). Số đo góc giữa hai đường thẳng BC và SM bằng A. 0 120 . B. 0 45 . C. 0 60 . D. 0 30 . Câu 15. Biết ( 2 lim
x − mx + 3 − nx = với ,
m n∈ . Tính giá trị biểu thức P = m + n. →+∞ ) 5 x A. P = 11 − . B. P = 9 − . C. P =11. D. P = 9.
B/ TỰ LUẬN. (5,0 điểm)
Câu 1 (1,0 điểm). Tính các giới hạn sau. 5n + 3 2 x + 3 a) lim lim 2n −1 . b) . x 3 → x −1 2  x +3x −10
Câu 2 (1,0 điểm). Xét tính liên tục của hàm số  ≠ f (x) khi x 2 =  x − 2 tại điểm x = 2. 3  x+1 khi x = 2
Câu 3 (2,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ⊥ (ABCD) và SA = a 3 .
a) Chứng minh: BC ⊥ (SAB) .
b) Gọi ϕ góc giữa đường thẳng AC và mặt phẳng (SBC) . Tính sinϕ . 2
Câu 4. (1,0 điểm) Tìm hai số thực + − +
a và b sao cho ax bx 5x 4 1 lim = . 3 x 1 → x −1 2
================= HẾT ================= Trang 2/2 – Mã đề 101 SỞ GD-ĐT QUẢNG NAM
KIỂM TRA GIỮA KỲ 2, NĂM HỌC 2022-2023
TRƯỜNG THPT NÚI THÀNH
Môn: TOÁN – Lớp: 11 ĐỀ CHÍNH THỨC
Thời gian: 60 phút (không kể thời gian giao đề)
(Đề gồm có 02 trang) MÃ ĐỀ 102
A/ TRẮC NGHIỆM. (5.0 điểm)
Câu 1. Mệnh đề nào sau đây sai? A. 5 lim x = +∞ . B. 3 lim x = +∞ . C. 4 lim x = +∞ .
D. lim x = −∞ . x→+∞ x→−∞ x→−∞ x→−∞
Câu 2. Khẳng định nào sau đây đúng ?
A. Góc giữa hai đường thẳng d và ∆ trong không gian là góc giữa hai đường thẳng d ' và ∆'
lần lượt vuông góc với d và ∆ .
B. Góc giữa hai đường thẳng d và ∆ trong không gian là góc giữa hai đường thẳng d ' và ∆' cùng đi qua một điểm.
C. Góc giữa hai đường thẳng d và ∆ trong không gian là góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
D. Góc giữa hai đường thẳng d và ∆ trong không gian là góc giữa hai đường thẳng d ' và ∆'
cùng đi qua một điểm và lần lượt song song với d và ∆ .
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SC vuông góc với đáy.
Đường thẳng AB vuông góc với mặt phẳng nào sau đây? A. (SBC) . B. (SAB) . C. (SAC) . D. (ABC) .  
Câu 4. Trong không gian, cho hai đường thẳng a,b có vectơ chỉ phương lần lượt là u và v . Biết rằng (  u v) 0
, =150 . Góc giữa hai đường thẳng a và b bằng A. 0 30 . B. 0 60 . C. 0 35 . D. 0 150 .
Câu 5. Cho các dãy số (u
v có limu = , limv = +∞ . Mệnh đề nào sau đây là đúng? n 2 n ), ( n ) n A. lim u u n = +∞ . B. lim n = 0 . C. lim(u v = .
D. lim(u v = −∞. n. n ) n. n ) 2 v v n n
Câu 6. Mệnh đề nào sau đây là đúng? n n A.  2 lim  =   0. B. lim5n = 0 . C. lim( 3) = 0. D. lim3n = 0 .  5 
Câu 7. Cho hàm số y = f (x) xác định trên khoảng K và 4∈ K . Hàm số y = f (x) được gọi là liên tục tại x = 4 nếu
A. lim f (x) = f (4).
B. lim f (x) = f (4). x 4− → x 4+ →
C. lim f (x) = f (4) .
D. lim f (x) = lim f (x). x→4 x 4− x 4+ → → Câu 8. lim( 3
x + 4x − 2) bằng x→2 A. 2 − . B. −∞. C. 14. D. +∞ .
Câu 9. Cho hình hộp ABC .
D A'B'C 'D'. Mệnh đề nào sau đây đúng?
  
  
A. AC + AA' = CC '.
B. AC + AA' = C ' . A
  
  
C. AC + AA' = AC '.
D. AC + AA' = A'C.
Câu 10. Trong không gian, cho tứ diện ABCD có G là trọng tâm tam giác BCD. Mệnh đề nào sau đây
là đúng?    
   
A. GA + GB + GC = 0 .
B. GB + CG + DG = 0 .
   
   
C. GB + GC + DG = 0.
D. GB + GC + GD = 0. Trang 1/2 – Mã đề 102
Câu 11. Khẳng định nào sau đây đúng ?
A. Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với hai đường thẳng song
song cùng thuộc mặt phẳng đó.
B. Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với một đường thẳng trong mặt phẳng đó.
C. Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với hai đường thẳng cắt
nhau cùng thuộc mặt phẳng đó.
D. Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với hai đường thẳng phân
biệt cùng thuộc mặt phẳng đó. 2 x − 5 Câu 12. Biết lim
= a b với a,b∈ và b < 9 . Tính giá trị biểu thức 2
T = b + a . x→ 5 x − 5 A. T = 7 . B. T = 27 . C. T = 9 . D. T = 3.
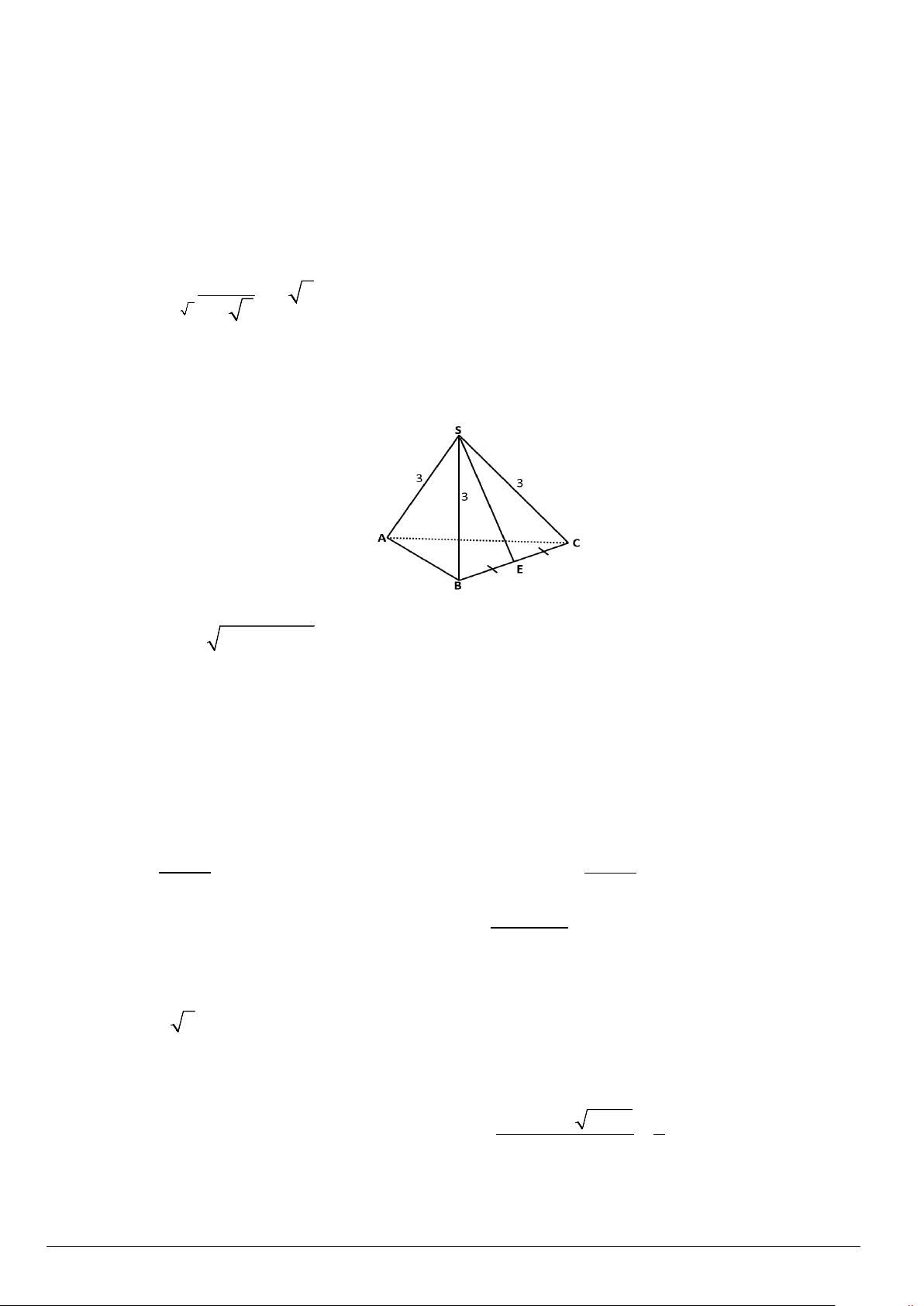
Câu 13. Cho hình chóp S.ABC có ,
SA SB,SC đôi một vuông góc và SA = SB = SC = 3. Gọi E là trung
điểm BC ( tham khảo hình vẽ). Số đo góc giữa hai đường thẳng SE và AC bằng A. 0 90 . B. 0 45 . C. 0 30 . D. 0 60 . Câu 14. Biết ( 2 lim
x + mx + 2 − nx = với ,
m n∈ . Tính giá trị biểu thức P = m + n. →+∞ ) 6 x A. P = 13 − . B. P =13. C. P = 12 − . D. P =12 .
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SC ⊥ (ABCD). Gọi CK là đường cao
của tam giác SBC . Chọn khẳng định đúng trong các khẳng định sau ?
A. CK ⊥ (SCD).
B. CK ⊥ (SBD).
C. CK ⊥ (SAB).
D. CK ⊥ (SAD).
B/ TỰ LUẬN. (5,0 điểm)
Câu 1 (1,0 điểm). Tính các giới hạn sau. 4n − 5 2 x + 2 a) lim lim 3n + 7 . b) . x→4 x − 2 2  x −7x +12
Câu 2 (1,0 điểm). Xét tính liên tục của hàm số  ≠ f (x) khi x 3 =  x −3 tại điểm x = 3. 2x−7 khi x = 3
Câu 3(2,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ⊥ (ABCD) và
SA = a 2 .
a) Chứng minh: CD ⊥ (SAD).
b) Gọi ϕ góc giữa đường thẳng AC và mặt phẳng (SCD) . Tính sinϕ . 2
Câu 4 (1,0 điểm). Tìm hai số thực + + +
a và b sao cho ax bx 3x 7 2 lim = . 3 x 1 →− x +1 3
================= HẾT ================= Trang 2/2 – Mã đề 102
TRƯỜNG THPT NÚI THÀNH
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HỌC KỲ II
MÔN: TOÁN 11 – NĂM HỌC 2022-2023
A. Phần trắc nghiệm: (5,0 điểm)
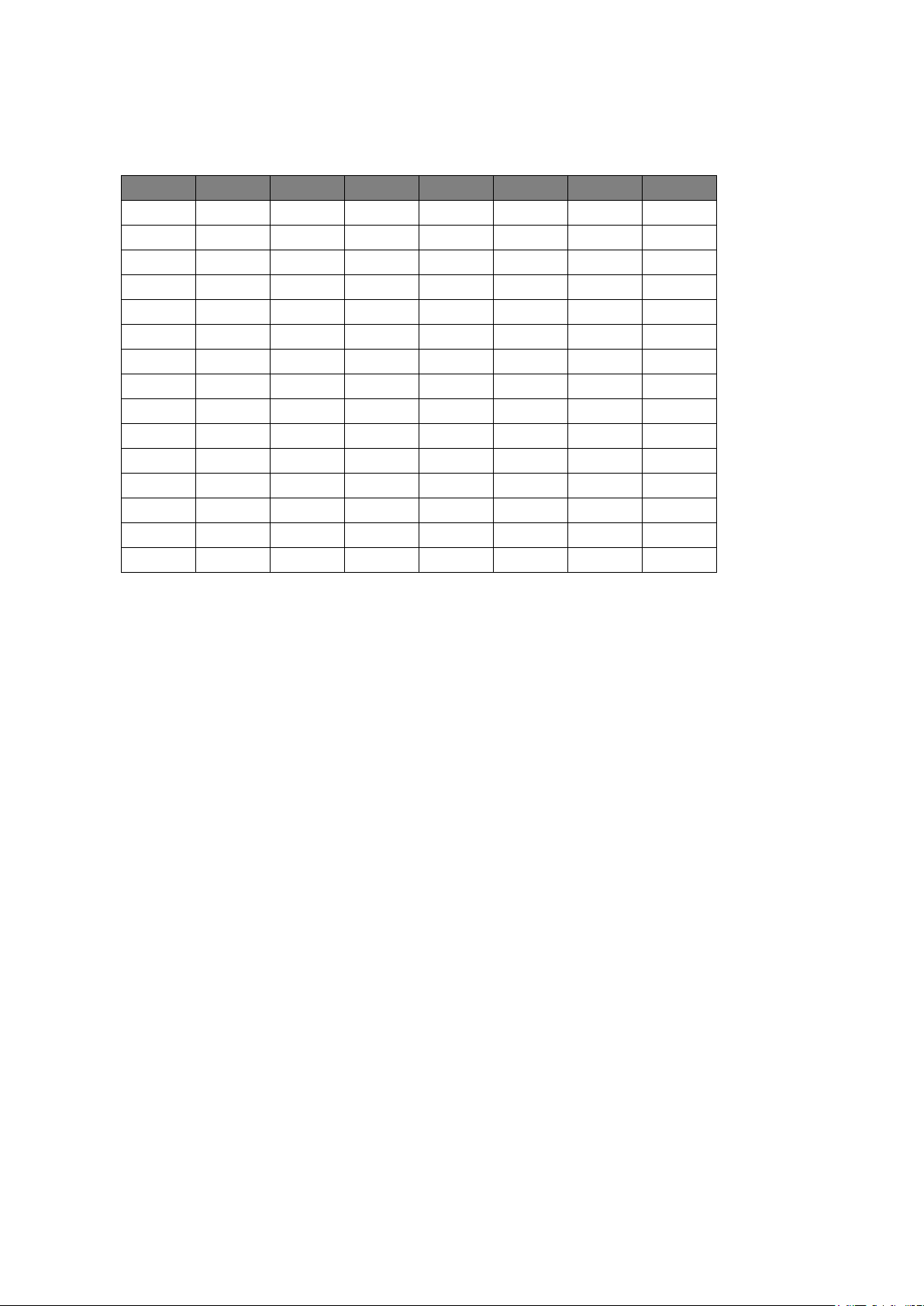
Đề 101 Đề 102 Đề 103 Đề 104 Đề 105 Đề 106 Đề 107 Đề 108 1. A 1. B 1. A 1. B 1. C 1. C 1. C 1. B 2. A 2. D 2. A 2. B 2. C 2. C 2. A 2. D 3. B 3. A 3. B 3. A 3. A 3. D 3. B 3. C 4. D 4. A 4. B 4. C 4. C 4. C 4. B 4. B 5. B 5. B 5. B 5. A 5. B 5. C 5. C 5. C 6. A 6. A 6. A 6. C 6. D 6. B 6. D 6. D 7. A 7. C 7. B 7. C 7. B 7. D 7. B 7. C 8. C 8. C 8. D 8. D 8. D 8. D 8. D 8. A 9. B 9. C 9. C 9. C 9. B 9. A 9. A 9. D
10. D 10. D 10. A 10. D 10. B 10. D 10. A 10. A
11. C 11. C 11. C 11. A 11. B 11. B 11. D 11. B
12. D 12. B 12. D 12. B 12. D 12. C 12. D 12. A
13. D 13. D 13. A 13. D 13. A 13. B 13. C 13. A
14. C 14. B 14. D 14. D 14. A 14. A 14. A 14. C
15. B 15. C 15. C 15. B 15. A 15. A 15. C 15. B
B. Phần tự luận: (5,0 điểm) CÂU
NỘI DUNG 101; 103; 105; 107
Điểm NỘI DUNG 102; 104; 106; 108  3   5  n 5 +  n4 − n      n  5n + 3 4n − 5 a) lim = lim 0,25 lim  1 a) lim =  7 2n −1 n 2  −    3n + 7 n 3 +    n   n  3 5 + 5 4 − lim n 5 0,25 lim n 4 = 1 = = = 2 − 2 7 3+ 3 Câu 1 n n (1điểm) 2 x + 3 2 3 + 3 2 x + 2 2 4 + 2 b) lim = 0,25 b) lim = x 3 → x −1 3−1 0,25 x→4 x − 2 4 − 2 = 6 =9
Xét tính liên tục của hàm số
Xét tính liên tục của hàm số 2  x +3x −10 2  x −7x +12  ≠ f (x) khi x 2 =  khi x ≠ 3  x − 2
tại điểm x = 2.
f (x) =  x −3
tại điểm x = 3. 3  x+1 khi x = 2 2x−7 khi x = 3 Ta có: Ta có: + f (2) = 7 0,25 + f (3) = 1 − 2 + − − + + x 3x 10 (x 2)(x 5) lim f (x) = lim = lim 0,25 2 + x −7x +12
(x − 4)(x −3) lim f (x) = lim = lim Câu 2 x→2 x→2 x→2 x − 2 x − 2 x 3 → x 3 → x 3 x −3 → x −3 (1điểm) = lim(x + 5) = 7 = lim(x − 4) = 1 − x→2 0,25 x 3 →
+ Vì lim f (x) = f (2) = 7 nên hàm số liên
+ Vì lim f (x) = f (3) = 1
− nên hàm số liên tục x→2 0,25 x 3 →
tục tại x = 2 . tại x = 3.
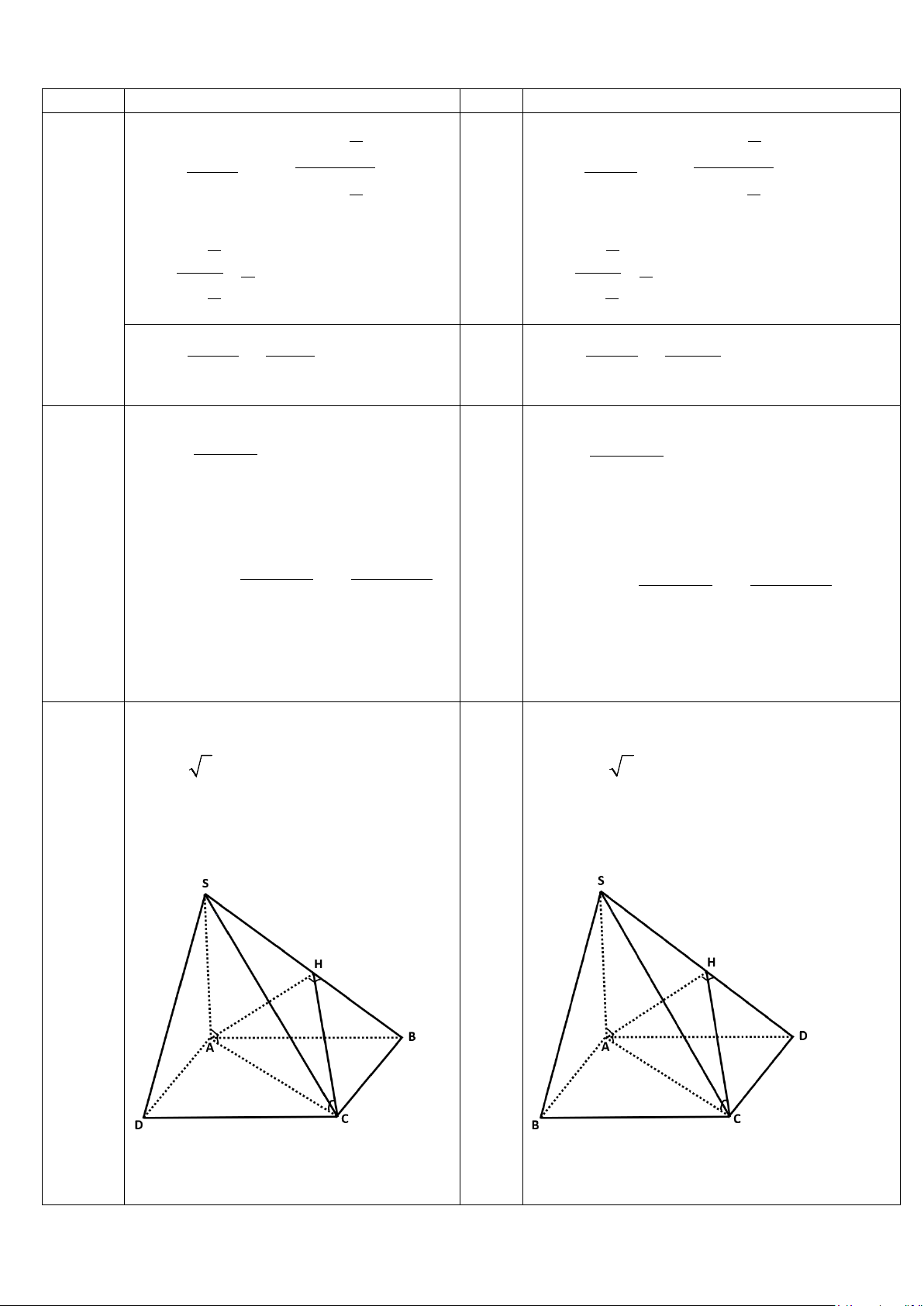
Cho hình chóp S.ABCD có đáy ABCD
Cho hình chóp S.ABCD có đáy ABCD là
là hình vuông cạnh a , SA ⊥ (ABCD) và
hình vuông cạnh a , SA ⊥ (ABCD)
SA = a 3 .
và SA = a 2 . ⊥
a) Chứng minh: CD ⊥ (SAD) .
a) Chứng minh: BC (SAB) .
b) Gọi ϕ góc giữa đường thẳng AC và
b) Gọi ϕ góc giữa đường thẳng AC và mặt
mặt phẳng (SBC) . Tính sinϕ .
phẳng (SCD) . Tính sinϕ . Câu 3 (2điểm)
(Hình vẽ phục vụ câu a, đúng)
0,25 (Hình vẽ phục vụ câu a, đúng)
a) Chứng minh: BC ⊥ (SAB) .
a) Chứng minh: CD ⊥ (SAD) .
Có: BC ⊥ SA
0,25 Có: CD ⊥ SA
BC ⊥ AB
0,25 CD ⊥ AD
Suy ra: BC ⊥ (SAB)
0,25 Suy ra: CD ⊥ (SAD)
b) Gọi ϕ góc giữa đường thẳng AC và
b) Gọi ϕ góc giữa đường thẳng AC và mặt
mặt phẳng (SBC) . Tính sinϕ .
phẳng (SCD) . Tính sinϕ .
+Dựng AH ⊥ SB ( với H ∈ SB )
+Dựng AH ⊥ SD ( với H ∈ SD )
Có: BC ⊥ (SAB) ⇒ AH ⊥ BC
Có: CD ⊥ (SAD) ⇒ AH ⊥ CD
⇒ AH ⊥ (SBC)
0,25 ⇒ AH ⊥ (SCD)
Suy ra hình chiếu của AC lên (SBC) là
Suy ra hình chiếu của AC lên (SCD) là HC HC = Nên 
ACH = ϕ là góc giữa đường thẳng Nên 
ACH ϕ là góc giữa đường thẳng AC và
AC và mặt phẳng (SBC) .
0,25 mặt phẳng (SCD) . S . A AB a 3 S . A AD a 6 + AH = = 0,25 + AH = = SB 2 SD 3
+ AC = a 2
+ AC = a 2 AH 6 AH 3 Suy ra sinϕ = = 0,25 Suy ra sinϕ = = AC 4 AC 3
Tìm hai số thực a và b sao cho
Tìm hai số thực a và b sao cho 2
ax + bx − 5x + 4 1 2
ax + bx + 3x + 7 2 lim = lim = . 3 x 1 → x −1 2 3 x 1 →− x +1 3 GIẢI GIẢI 2
ax + bx − 5x + 4 1 2
ax + bx + 3x + 7 2 Vì lim = hữu hạn Vì lim = hữu hạn 3 3 x 1 → x −1 2 x 1 →− x +1 3 Câu 4 nên .1 a + .1
b − 5.1+ 4 = 0 ⇔ b = 3− a.
0,25 nên a(− )2
1 +b(− )1+ 3(− )1+7 = 0 ⇔ b = a + 2. (1điểm) 2
ax + bx − 5x + 4 2
ax + bx + 3x + 7 Khi đó: lim 3 x 1 → x −1 Khi đó: lim 3 x 1 →− x +1 2
ax + (3− a) x − 5x + 4 = lim 2
ax + (a + 2) x + 3x + 7 3 x 1 → x −1 = lim 3 x 1 →− x +1 ax(x − ) 1 − +  3x 5x 4 = lim  + ax(x + ) 1 2x + 3x + 7  3 3  x 1 → =  +  x −1 x −1  0,25 lim 3 3  x 1 →−  x +1 x +1      ax 9x + 4 lim   = + ax 4x − 7  2  
x→ x + x +1 (3x+ 5x+4)( 2 1 x + x + = lim +  2  )1
x→− x − x +1 (2x − 3x +7)( 2 1 x − x +  ) 1  a 13 = + 0,25 a 3 18 11 = − + 3 12 2 2 Theo đề:
ax + bx − 5x + 4 1 lim =
ax + bx + 3x + 7 2 3 Theo đề: lim = x 1 → x −1 2 3 x 1 →− x +1 3 a 13 1 2 ⇔ + = ⇔ a = − a 3 18 2 3 11 2 3 ⇔ − + = ⇔ a = 3 12 3 4 Với 2 a = − ta có 2 11
b = 3− a = 3+ = . 3 3 3 0,25 Với 3 a = ta có 3 11
b = a + 2 = + 2 = . 4 4 4 Vậy 2 a = − và 11 b = . 3 3 Vậy 3 a = và 11 b = . 4 4
Document Outline

• 101
• 102
• HDC TOAN GK2- K11_2023