SỞ GD & ĐT TỈNH ĐỒNG THÁP
ĐỀ KIỂM TRA GIỮA HỌC KÌ II TRƯỜNG THPT CHUYÊN
Năm học : 2024 – 2025
NGUYỄN ĐÌNH CHIỂU Môn: TOÁN – Khối 11 ĐỀ CHÍNH THỨC Thời gian: 90 phút
(không kể thời gian phát đề) (Đề gồm có 02 trang ) Ngày kiểm tra: 12/03/2025 MÃ ĐỀ: 123
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. (3 điểm)
Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1. Cho các số thực x và y . Khẳng định nào dưới đây là khẳng định sai? x
A. 2x.2y = 2x+y . B. (2 )y x 2xy 2 = . C.
= 2x−y .
D. 2x.3x 5x = . 2y 1
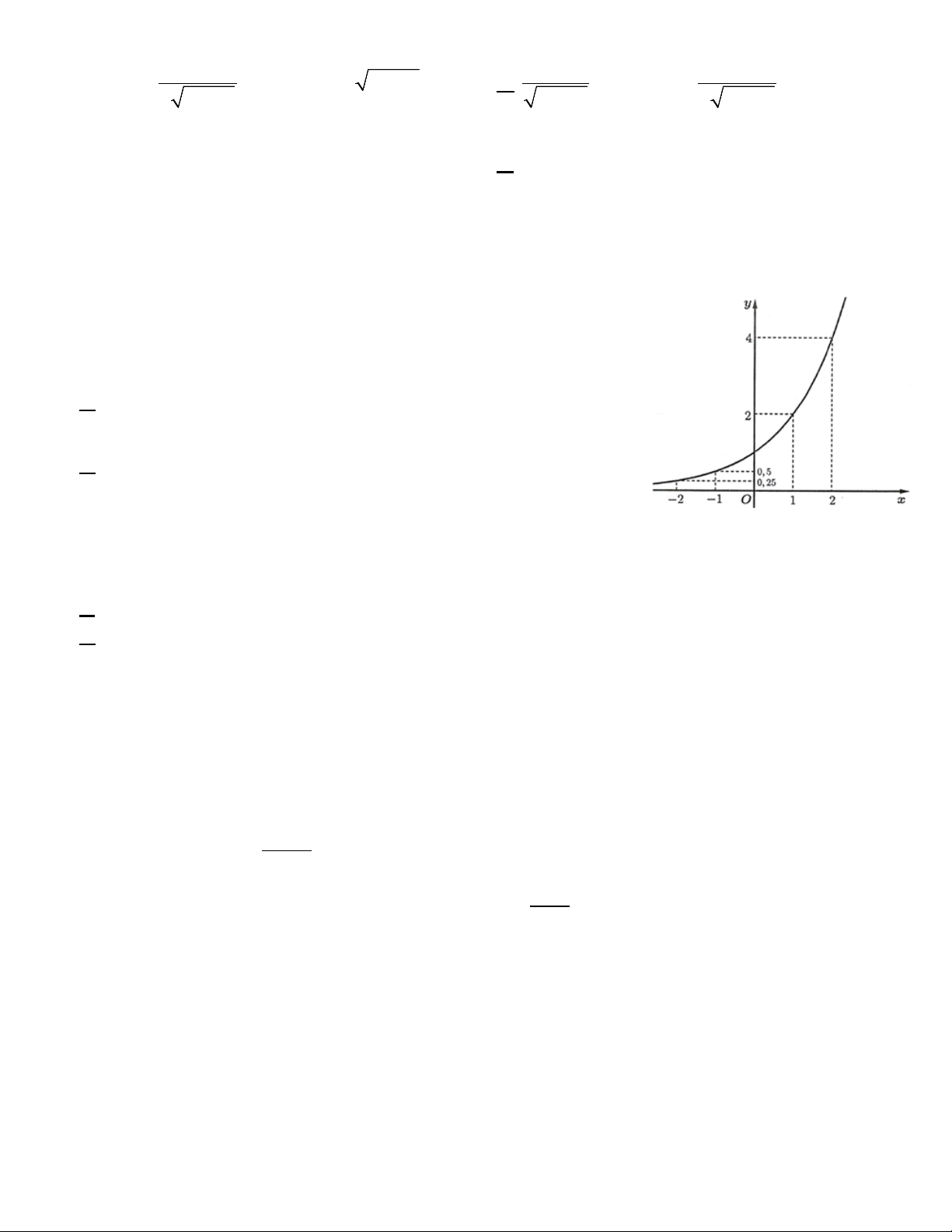
Câu 2. Rút gọn biểu thức 6 3
P = x ⋅ x với x > 0 . 1 2 A. 8 P = x .
B. P = x. C. 9 P = x . D. 2 P = x .
Câu 3. Cho các số thực dương a,b khác 1. Khẳng định nào sau đây sai? 1 A. b =
b . B. log b = − a log b = log b a = a log . C.
b . D. loga .logb 1. a ( 2 log ) 2loga b 3 a 3 a Câu 4. a
Với mọi số thực a dương, log bằng 5 25 1 A. log a .
B. log a +1.
C. log a − 2 . D. log a + 2 . 5 25 5 5 5
Câu 5. Với b,c là hai số thực dương tuỳ ý thoả mãn log b ≥ log c 5
5 , khẳng định nào dưới đây đúng?
A. b ≥ c .
B. b ≤ c .
C. b > c .
D. b < c .
Câu 6. Tập xác định của hàm số y = ( 2
ln −x + 7x −10) là A. (2;+ ∞) . B. (5;+∞) . C. [2;5]. D. (2;5) .
Câu 7. Nghiệm của phương trình 1−5 10 x =1000000 là A. x = 1 − . B. x =1. C. x = 2 − . D. x = 6 .
Câu 8. Tập nghiệm của bất phương trình log x −1 >1 là 0,5 ( )  3  3  3  3 A. ;  −∞ −     . B. 1; . C.  ;+ ∞ . D. 1; . 2         2   2   2 
f (x) − f (6)
Câu 9. Cho hàm số y = f (x) có đạo hàm thỏa mãn f ′(6) = 2. Giá trị của biểu thức lim x→6 x − 6 bằng A. 12. B. 2 . C. 1. D. 1 . 3 2
Câu 10. Hệ số góc tiếp tuyến của đồ thị hàm số 3
y = x + 2 tại điểm trên đồ thị có hoành độ x =1 0 là: A. k = 3 − .
B. k = 2.
C. k = 3. D. k = 2 − .
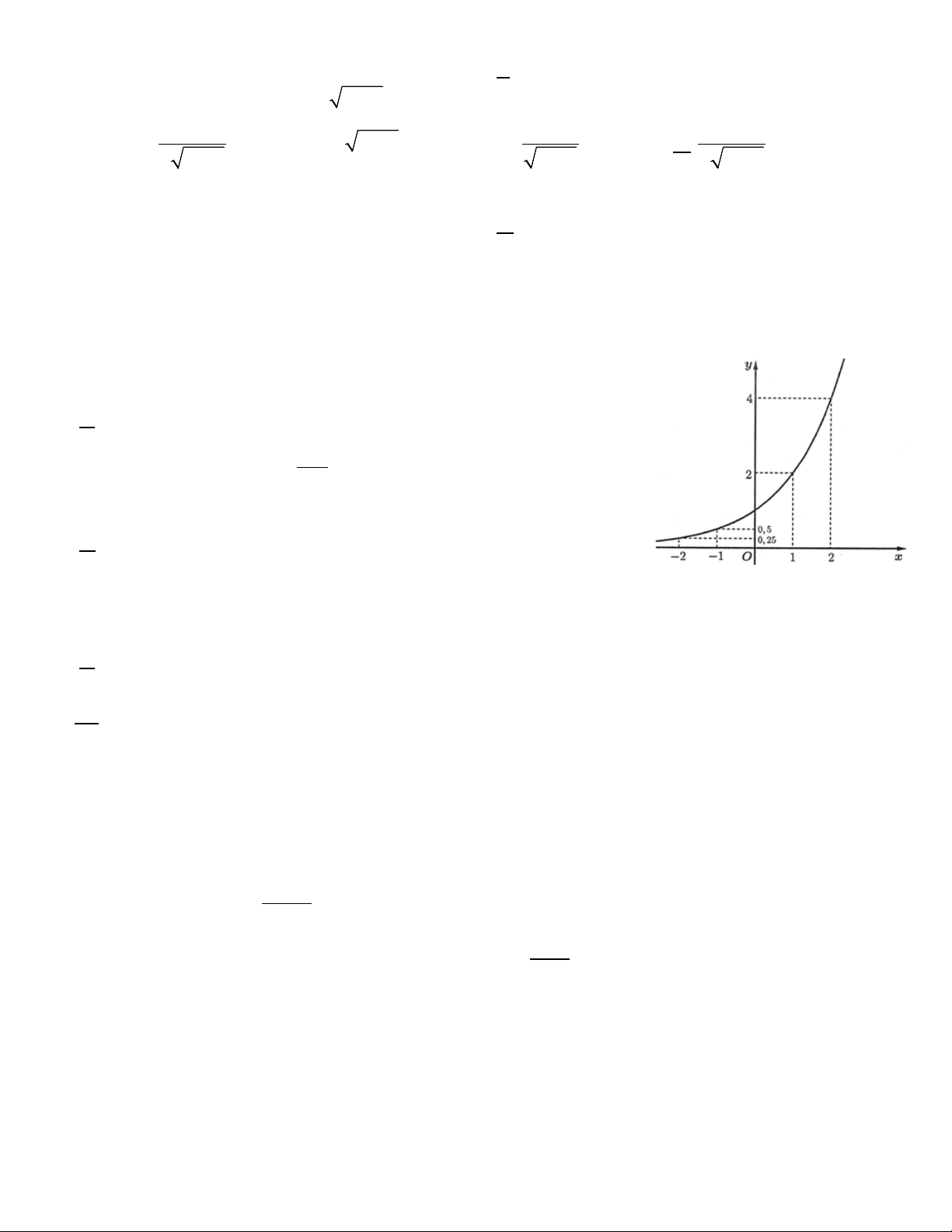
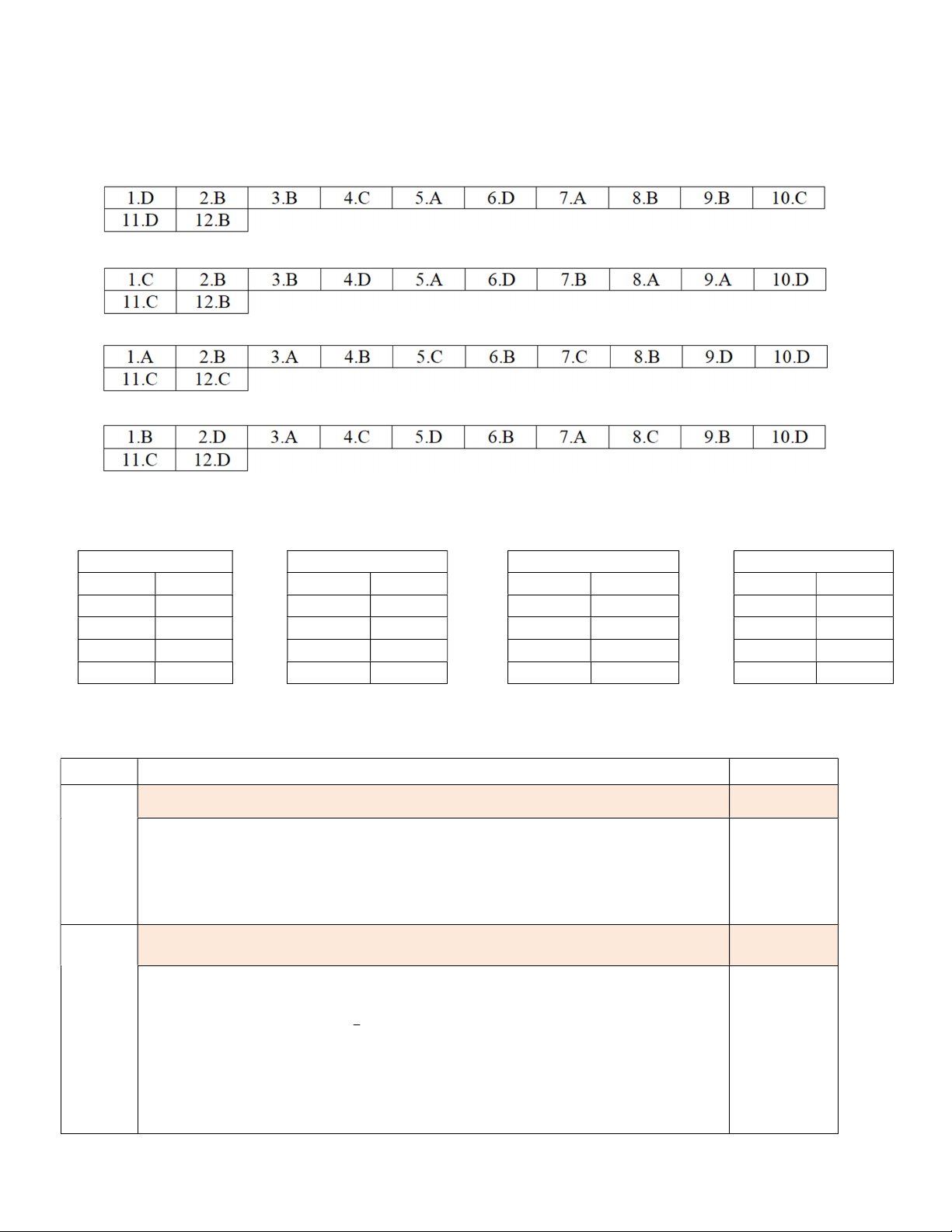
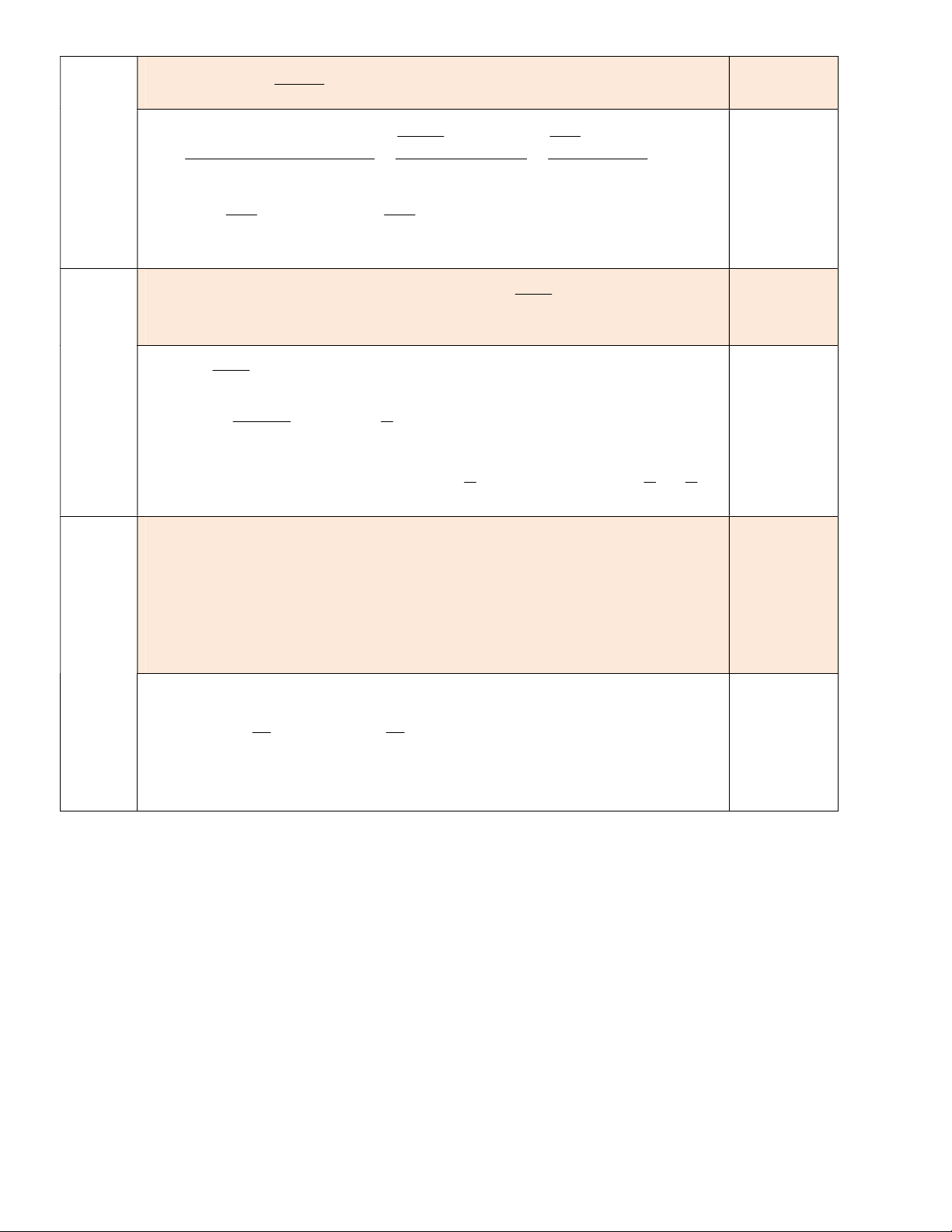
Câu 11. Đạo hàm của hàm số y = 4 − x (với x < 4 ) là 1 1 − 1 − A. . B. 4 − x . C. . D. . 2 4 − x 4 − x 2 4 − x
Câu 12. Đạo hàm cấp hai của hàm số 6 3
y = x − 4x + 2x + 2025 với x ∈ R là A. 4
y′ = 30x − 24x + 2 . B. 4
y′ = 30x − 24x. C. 5 2
y′ = 6x −12x + 2. D. 5 2
y′ = 6x −12x .
PHẦN 2. Trắc nghiệm đúng sai. (2 điểm)
Học sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Câu 13. Xét hàm số 2x y =
a) Hàm số có tập giá trị là (0;+∞). 2x
b) Hàm số có đạo hàm y′ = . ln 2
c) Phương trình 2x = m luôn có nghiệm x = log m 2 với mọi số thực . m
d) Hình bên là đồ thị của hàm số đã cho.
Câu 14. Có một vật chuyển động với vận tốc ban đầu là v (m / s) 0
sau đó dừng lại, phương trình quãng đường của vật là 3 2
s = f (t) = t
− + 6t +15t , trong đó t tính bằng giây và s tính bằng mét.
a) Phương trình vận tốc của vật là 2 v(t) = 3
− t +12t +15 ( tính theo đơn vị m / s ).
b) Vật dừng lại sau khoảng thời gian kể từ lúc bắt đầu chuyển động là t = 4 giây.
c) Vận tốc lớn nhất mà vật đạt được trong quá trình chuyển động là 27 m / .s .
d) Quãng đường vật đi được từ lúc bắt đầu chuyển động đến lúc đạt vận tốc lớn nhất là 45 m .
PHẦN 3. Tự luận. (5 điểm)
Câu 15. Tính đạo hàm của hàm số 2 y = sin 2 . x
Câu 16. Giải phương trình log ( 2 x − 2x + log 2x − 3 = 0. 5 ) 0,2 ( ) log Câu 17. x Cho hàm số 2 y =
với x > 0. Giải phương trình: y ' = 0 . x
Câu 18. Viết phương trình tiếp tuyến của đồ thị (C) x − 3 : y =
tại giao điểm của (C) với trục hoành. x +1
Câu 19. Giả sử giá trị còn lại (tính theo triệu đồng) của một chiếc ô tô sau t năm sử dụng được mô hình hoá
bằng công thức: ( ) = .(0,905)t V t A
, trong đó A là giá xe (tính theo triệu đồng) lúc mới mua. Hỏi nếu theo mô
hình này, sau bao nhiêu năm sử dụng thì giá trị của chiếc xe đó còn lại không quá 300 triệu đồng? (Làm tròn kết
quả đến hàng đơn vị). Biết giá xe lúc mới mua là 780 (triệu đồng). HẾT.
SỞ GD & ĐT TỈNH ĐỒNG THÁP
ĐỀ KIỂM TRA GIỮA HỌC KÌ II TRƯỜNG THPT CHUYÊN
Năm học : 2024 – 2025
NGUYỄN ĐÌNH CHIỂU Môn: TOÁN – Khối 11 ĐỀ CHÍNH THỨC Thời gian: 90 phút
(không kể thời gian phát đề) (Đề gồm có 02 trang ) Ngày kiểm tra: 12/03/2025 MÃ ĐỀ: 234
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. (3 điểm)
Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án. Câu 1. a
Với mọi số thực a dương, log bằng 5 125 1
A. log a .
B. log a + 5 .
C. log a − 3. D. log a + 3. 5 3 5 5 5
Câu 2. Cho các số thực dương a,b khác 1. Khẳng định nào sau đây sai? 1 A. b =
b . B. log b = − a log b = log b a = a log . C.
b . D. loga .logb 1. a ( 2 log ) 2loga b 3 a 3 a
Câu 3. Với b,c là hai số thực dương tuỳ ý thoả mãn log b ≤ log c 5
5 , khẳng định nào dưới đây đúng?
A. b ≥ c .
B. b ≤ c .
C. b > c .
D. b < c .
Câu 4. Cho các số thực x và y . Khẳng định nào dưới đây là khẳng định sai? x
A. 2x.2y = 2x+y . B. (2 )y x 2xy 2 = . C.
= 2x−y .
D. 2x.3x 5x = . 2y 1
Câu 5. Rút gọn biểu thức 6 3
P = x ⋅ x với x > 0 . 1 2
A. P = x. B. 8 P = x . C. 9 P = x . D. 2 P = x .
Câu 6. Tập xác định của hàm số y = ( 2
ln −x + 5x + 6) là A. ( 1; − + ∞) . B. (6;+∞) . C. [ 1; − 6]. D. ( 1; − 6) .
Câu 7. Nghiệm của phương trình 1+5 10 x =1000000 là A. x = 1 − .
B. x = 1. C. x = 2 − . D. x = 6 .
Câu 8. Tập nghiệm của bất phương trình log x −1 >1 là 0,5 ( ) A.  3 1;         . B. 3  ; −∞ − . C. 3  ;+ ∞ . D. 3 1; . 2         2   2   2 
f (x) − f (6)
Câu 9. Cho hàm số y = f (x) có đạo hàm thỏa mãn f ′(6) =12. Giá trị của biểu thức lim bằng x→6 x − 6 A. 12. B. 2 . C. 1. D. 1 . 3 2
Câu 10. Hệ số góc tiếp tuyến của đồ thị hàm số 3
y = x − 2x tại điểm trên đồ thị có hoành độ x =1 0 là: A. k = 1 − . B. k = 2 − .
C. k = 2. D. k =1.
Câu 11. Đạo hàm của hàm số y = 4 − 2x (với x < 2 ) là 1 1 − 1 − A. . B. 2 4 − 2x . C. . D. . 2 4 − 2x 4 − 2x 2 4 − 2x
Câu 12. Đạo hàm cấp hai của hàm số 6 3
y = x − 4x + 2x + 2025 với x ∈ R là A. 4
y′ = 30x − 24x + 2 . B. 4
y′ = 30x − 24x. C. 5 2
y′ = 6x −12x + 2. D. 5 2
y′ = 6x −12x .
PHẦN 2. Trắc nghiệm đúng sai. (2 điểm)
Học sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Câu 13. Xét hàm số 2x y =
a) Hàm số có tập xác định là (0;+∞).
b) Hàm số có đạo hàm 2 .x y′ = ln 2.
c) Phương trình 2x = m luôn có nghiệm x = log m 2 với mọi số thực . m
d) Hình bên là đồ thị của hàm số đã cho.
Câu 14. Có một vật chuyển động với vận tốc ban đầu là v (m / s) 0
sau đó dừng lại, phương trình quãng đường của vật là 3 2
s = f (t) = t
− + 6t +15t trong đó t tính bằng giây và s tính bằng mét.
a) Phương trình vận tốc của vật là 2 v(t) = 3
− t +12t +15 ( tính theo đơn vị m / s ).
b) Vật dừng lại sau khoảng thời gian kể từ lúc bắt đầu chuyển động là t = 5 giây.
c) Vận tốc lớn nhất mà vật đạt được trong quá trình chuyển động là 24 / m s .
d) Quãng đường vật đi được từ lúc bắt đầu chuyển động đến lúc đạt vận tốc lớn nhất là 45 m .
PHẦN 3. Tự luận. (5 điểm)
Câu 15. Tính đạo hàm của hàm số 2 y = sin 2 . x
Câu 16. Giải phương trình log ( 2 x − 2x + log 2x − 3 = 0. 5 ) 0,2 ( ) log Câu 17. x Cho hàm số 2 y =
với x > 0. Giải phương trình: y ' = 0 . x
Câu 18. Viết phương trình tiếp tuyến của đồ thị (C) x − 3 : y =
tại giao điểm của (C) với trục hoành. x +1
Câu 19. Giả sử giá trị còn lại (tính theo triệu đồng) của một chiếc ô tô sau t năm sử dụng được mô hình hoá
bằng công thức: ( ) = .(0,905)t V t A
, trong đó A là giá xe (tính theo triệu đồng) lúc mới mua. Hỏi nếu theo mô
hình này, sau bao nhiêu năm sử dụng thì giá trị của chiếc xe đó còn lại không quá 300 triệu đồng? (Làm tròn kết
quả đến hàng đơn vị). Biết giá xe lúc mới mua là 780 (triệu đồng). HẾT.
HƯỚNG DẪN CHẤM - BÀI KIỂM TRA GIỮA HỌC KỲ II - KHỐI 11 PHẦN 1. ĐỀ 123 ĐỀ 234 ĐỀ 345 ĐỀ 456 PHẦN 2. ĐỀ 123 ĐỀ 234 ĐỀ 345 ĐỀ 456 Câu 13 Câu 14 Câu 13 Câu 14 Câu 13 Câu 14 Câu 13 Câu 14 a) Đ a) Đ a) S a) Đ a) Đ a) Đ a) S a) Đ b) S b) S b) Đ b) Đ b) S b) S b) Đ b) Đ c) S c) Đ c) S c) S c) S c) Đ c) S c) S d) Đ d) S d) Đ d) S d) Đ d) S d) Đ d) S PHẦN 3. Câu Đáp án Điểm số
Câu 15 Tính đạo hàm của hàm số 2 y  sin 2 . x 1 đ y ' 2.sin 2 . x sin 2x  0.5 đ 2.sin 2 . x cos 2 . x 2x  0.25 đ 0.25 đ  4.sin 2 . x cos 2 . x
Câu 16 Giải phương trình log  2x  2x  log 2x 3  0. 1 đ 5  0,2   Điều kiện x  2 0.25 đ pt  log  2
x  2x  log 2x  3  0  log  2 x  2x  log 2x  3 5 1 5  5   0.25 đ 5 x  1 2 2
 x  2x  2x  3  x  4x  3  0  0.25 đ  x  3 0.25 đ Vậy x  3 Câu 17 log x 1 đ Cho hàm số 2 y 
với x  0. Giải phương trình : y '  0 . x 1 1
log x.x  log .xx .x  log x  log x 2 2 2 2 . x ln 2 ln 2 y    2 2 2 0.5 đ x x x 1 1 y  0   log x  0   log x  x  . e 2 2 ln 2 ln 2 0.5 đ
Vậy phương trình có nghiệm x  . e Câu 18 x 3
Viết phương trình tiếp tuyến của đồ thị C  : y  tại giao điểm của (C) x 1 1 đ với trục hoành. x  3 0.25 đ Cho y 
 0  x  3 . Ta có giao điểm là M 3;0 . x 1 4 Ta có: y   y3  1  0.5 đ x  2 1 4 1 1 3
Phương trình tiếp tuyến tại M là d : y   x  3  0  d : y  x  . 4 4 4 0.25 đ
Câu 19 Giả sử giá trị còn lại (tính theo triệu đồng) của một chiếc ô tô sau t năm sử
dụng được mô hình hoá bằng công thức: ( )  .(0,905)t V t A , trong đó A là
giá xe (tính theo triệu đồng) lúc mới mua. Hỏi nếu theo mô hình này, sau 1 đ
bao nhiêu năm sử dụng thì giá trị của chiếc xe đó còn lại không quá 300
triệu đồng? (Làm tròn kết quả đến hàng đơn vị). Biết giá xe lúc mới mua là 780 (triệu đồng). Ta có: ( ) 300 780.(0,905)t V t    300 0.25 đ t 5  5   (0,905)   t  log  9,57. 0.5 đ 0,905   13 13 
Kết luận: Sau khoảng 10 năm sử dụng thì giá trị của chiếc xe đó còn lại 0.25 đ
không quá 300 triệu đồng.
Xem thêm: ĐỀ THI GIỮA HK2 TOÁN 11
https://toanmath.com/de-thi-giua-hk2-toan-11
Document Outline

• ĐỀ 1
  • TRƯỜNG THPT CHUYÊN
• ĐỀ 2
  • TRƯỜNG THPT CHUYÊN
• ĐÁP ÁN GK2-K11
• GK2 - 11