Đề giữa kỳ 2 Toán 11 năm 2022 – 2023 trường THPT Lương Thế Vinh – Quảng Nam

SỞ GD & ĐT QUẢNG NAM
KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2022-2023
TRƯỜNG THPT LƯƠNG THẾ VINH
Môn: Toán – Lớp :11 ĐỀ CHÍNH TH
Thời gian: 60 phút (không kể thời gian giao đề) ỨC
(Đề gồm có 02 trang) MÃ ĐỀ 101
Họ và tên học sinh:……………………………………Số báo danh:………………......Lớp…….
A/ TRẮC NGHIỆM: (5.0 điểm).
Câu 1: Trong không gian cho hình hộp ABC .
D A' B 'C ' D' . Khẳng định nào sau đây đúng? A. CB CD CC ' CA . B. CB CD CC ' CB ' . C. CB CD CC ' CD '. D. CB CD CC ' CA'.
Câu 2: Cho hàm số f  x thỏa mãn lim f (x)  21 và lim f (x)  21
 . Khẳng định nào sau đây đúng?   x 1  x 1 
A. lim f (x) Không tồn tại. B. lim f (x) = -21
C. lim f (x) = 21. D. lim f (x) = 0 x 1  x 1  x 1  x 1 
Câu 3: Cho tứ diện ABCD có G là trọng tâm tam giác BCD . Đặt x  AB ; y  AC ; z  AD . Khẳng định nào sau đây đúng? 1 2 1 2
A. AG   x  y  z  B. AG    x  y  z  C. AG    x  y  z  D. AG   x  y  z  3 3 3 3
Câu 4: Dãy số nào sau đây có giới hạn bằng 0 ? n  n n n 2   5   4   3  A.   . B.   . C.   D.   .  3   4   3   2 
Câu 5: Trong không gian cho hình lập phương ABC .
D A' B 'C ' D' , số đo góc giữa AC và B ' D 'bằng bao nhiêu? A. 0 60 . B. 0 0 . C. 0 90 . D. 0 45 .
Câu 6: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). Khẳng định nào sau đây Sai ?
A. SA  SC .
B. BC  SA .
C. SA  AB .
D. AC  SA. u 
Câu 7: Cho dãy số u lim u  3 1 2 lim n n  có . Tính giới hạn . n 2u  5 n 3 1 A. B.  5 C. D. 2 9 5 2 x 1
Câu 8: Cho hàm số f x
, f x gián đoạn tại điểm nào sau đây? 2 x A. x 1. B. x 2 . C. x 1. D. x 2. n 1 1   1 1
Câu 9: Gọi S    ...
.... Giá trị của S bằng: 3 9 3n 1 1 3 A. B. C. . D. 1 2 4 4
Câu 10: Cho các giới hạn: lim f  x  5 ; lim g  x  4 .Tính lim 2 f  x  3g  x   . x   0 x x 0 x x 0 x A. 9  . B. 2 . C. 23. D. 22  .
Trang 1/2 - Mã đề thi 101 f (x)
Câu 11: Biết lim f (x)  L  0 , lim g(x)  0 và g(x)  0 với mọi x  x . Khi đó lim bằng: 0 xx xx xx 0 0 0 g ( x) A.  . B. 0 . C.  . D. L.
Câu 12: Cho tứ diện ABCD có tất cả các cạnh đều bằng a .Tính A . B AD . 2 a 3 2 a 3 2 a 2 a A.  . B. . C.  . D. . 2 2 2 2
Câu 13: Khẳng định nào sau đây Sai ? a / /b (P) / /(Q) A.   b  (P) B.   a  (Q) a  (P) a  (P) a  (P)  (P)  a C. b
  (P)  a / /b D.   (P) / /(Q)  (Q)  a a  b 
Câu 14: Hàm số nào sau đây liên tục trên R ? 2 x  2x 1
A. f (x)  . B. 2
f (x)  x  x  3 .
C. f (x)  tan x . D. f (x)  co x t . x  2
Câu 15: Phương trình nào sau đây có nghiệm trong khoảng ( 1  ;0) ? A. 5
x  2x  2  0 . B. 5
x  x  2  0 . C. 5
x  x  2  0 . D. 5
x  3x  2  0 .
B/ TỰ LUẬN ( 5.0 điểm).
Bài 1 (2,0 điểm) . Tính các giới hạn sau: 4n  3 a. lim
x  x   x 2n  b. 2 lim ( 2 3 ) 1 x
Bài 2 (1,0 điểm). Tìm tất cả các giá trị của tham số m để hàm số 2
3x 10x  3  khi x  3
f (x)   x  3
liên tục tại x  3 3
 m  2 khi x  3
Bài 3 ( 2,0 điểm). Cho hình chóp .
S ABCD có đáy ABCD là hình vuông tâm O và SO  ( ABCD) .
a. Chứng minh đường thẳng BD vuông góc với mặt phẳng (SAC)
b. Gọi E là điểm đối xứng với điểm D qua trung điểm P của cạnh SA. Gọi M, N lần lượt là
trung điểm của AE, BC. Chứng minh MN  BD ----------- HẾT ----------
Trang 2/2 - Mã đề thi 101
SỞ GD & ĐT QUẢNG NAM
KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2022-2023
TRƯỜNG THPT LƯƠNG THẾ VINH
Môn: Toán – Lớp :11
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH TH ỨC
(Đề gồm có 02 trang) MÃ ĐỀ 102
Họ và tên học sinh:……………………………………Số báo danh:………………......Lớp…….
A/ TRẮC NGHIỆM: (5.0 điểm).
Câu 1: Cho tứ diện ABCD có G là trọng tâm tam giác BCD . Đặt x  AB ; y  AC ; z  AD . Khẳng
định nào sau đây đúng? 1 2 2 1
A. AG    x  y  z  B. AG    x  y  z  C. AG   x  y  z  D. AG   x  y  z  3 3 3 3
Câu 2: Hàm số nào sau đây liên tục trên R ? 2 x  2x 1 A. 2
f (x)  x  x  3 . B. f (x)  tan x .
C. f (x)  co x
t . D. f (x)  . x  2
Câu 3: Khẳng định nào sau đây Sai ? a / /b (P) / /(Q) A.   b  (P) B.   a  (Q) a  (P) a  (P) a  (P)  (P)  a C. b
  (P)  a / /b D.   (P) / /(Q)  (Q)  a a  b 
Câu 4: Cho hàm số f  x thỏa mãn lim f (x)  21 và lim f (x)  21
 . Khẳng định nào sau đây đúng?   x 1  x 1 
A. lim f (x) = 21. B. lim f (x) = 0 C. lim f (x) Không tồn tại. D. lim f (x) = -21 x 1  x 1  x 1  x 1 
Câu 5: Trong không gian cho hình hộp ABC .
D A' B 'C ' D' . Khẳng định nào sau đây đúng? A. CB CD CC ' CA . B. CB CD CC ' CD '. C. CB CD CC ' CB ' . D. CB CD CC ' CA'. n 1 1   1 1
Câu 6: Gọi S    ...
.... Giá trị của S bằng: 3 9 3n 1 1 3 A. B. C. . D. 1 2 4 4 u 
Câu 7: Cho dãy số u lim u  3 1 2 lim n n  có . Tính giới hạn . n 2u  5 n 5 1 3 A. B. C. D.  9 5 2
Câu 8: Dãy số nào sau đây có giới hạn bằng 0 ? n   n n n 5   2   3   4  A.   . B.   . C.   . D.    4   3   2   3 
Câu 9: Trong không gian cho hình lập phương ABC .
D A' B 'C ' D' , số đo góc giữa AC và B ' D 'bằng bao nhiêu? A. 0 90 . B. 0 60 . C. 0 45 . D. 0 0 .
Trang 1/2 - Mã đề thi 102
Câu 10: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). Khẳng định nào sau đây Sai ?
A. AC  SA.
B. SA  AB .
C. BC  SA .
D. SA  SC .
Câu 11: Cho tứ diện ABCD có tất cả các cạnh đều bằng a .Tính A . B AD . 2 a 3 2 a 3 2 a 2 a A.  . B. . C.  . D. . 2 2 2 2 2 x 1
Câu 12: Cho hàm số f x
, f x gián đoạn tại điểm nào sau đây? 2 x A. x 1. B. x 2. C. x 2 . D. x 1.
Câu 13: Phương trình nào sau đây có nghiệm trong khoảng ( 1  ;0) ? A. 5
x  2x  2  0 . B. 5
x  x  2  0 . C. 5
x  x  2  0 . D. 5
x  3x  2  0 .
Câu 14: Cho các giới hạn: lim f  x  5 ; lim g  x  4 .Tính lim 2 f  x  3g  x   . x   0 x x 0 x x 0 x A. 9  . B. 22  . C. 2 . D. 23. f (x)
Câu 15: Biết lim f (x)  L  0 , lim g(x)  0 và g(x)  0 với mọi x  x . Khi đó lim bằng: 0 xx xx xx 0 0 0 g ( x) A.  . B. 0 . C.  . D. L.
B/ TỰ LUẬN ( 5.0 điểm).
Bài 1 (2,0 điểm) . Tính các giới hạn sau: 3n  2 a. lim
x  x   x 2n  b. 2 lim ( 4 5 ) 1 x
Bài 2 (1,0 điểm). Tìm tất cả các giá trị của tham số m để hàm số 2
2x  3x  2  khi x  2
f (x)   x  2
liên tục tại x  2
2m1 khi x  2
Bài 3 ( 2,0 điểm). Cho hình chóp .
S ABCD có đáy ABCD là hình vuông tâm O và SO  ( ABCD) .
a. Chứng minh đường thẳng AC vuông góc với mặt phẳng (SBD)
b. Gọi F là điểm đối xứng với điểm C qua trung điểm P của cạnh SB. Gọi H, K lần lượt là
trung điểm của BF, AD. Chứng minh HK  AC ----------- HẾT ----------
Trang 2/2 - Mã đề thi 102
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA KỲ II
MÔN: TOÁN 11 – NĂM HỌC 2022-2023
A. Phần trắc nghiệm: (5,0 điểm) Mã đề 101 102 103 104 Câu 1 D D D D 2 A A C A 3 A D C D 4 A C B C 5 C D A C 6 A B B D 7 C A A A 8 B B A C 9 B A C B 10 D D D C 11 C D C B 12 D C D C 13 D D C B 14 B B B D 15 D C C A
B. Phần tự luận: (5,0 điểm)
ĐỀ LẺ. (101,103) Câu Nội dung Điểm 4n  3
. Tính các giới hạn sau: a. lim
x  x   x 2n  b. 2 lim ( 2 3 ) 1 x 3 3 n(4  ) 4  4n  3 a. lim  lim n  lim n 2n 1 1 1 0,5 n(2  ) 2  n n 4  0 0,5   2 2  0 Câu 1 2 2
( x  2x  3  x)( x  2x  3  x)
(2,0 điểm) b. 2
lim ( x  2x  3  x)  lim 0.25 x x 2
( x  2x  3  x) 2  x  3  lim 0.25 x 2
( x  2x  3  x) 3 2    lim x x 2 3 0.25 1  1 2 x x  0.25 1  Câu 2
Tìm tất cả các giá trị của tham số m để hàm số (1,0 điểm) 2
3x 10x  3  khi x  3
f (x)   x  3
liên tục tại x  3 3
 m  2 khi x  3 TXĐ: D  1   2 3(x )(x 3) 3x 10x  3 +) 3
lim f (x)  lim  lim
 lim(3x 1)  8 (1) 0,25 x 3  x 3  x 3  x 3 x  3 x  3  0,25
+) f (3)  3m  2
Để hàm số liên tục tại x  3 thì lim f (x)  f (3) x 3  0,25
 3m  2  8  m  2 0.25 Câu 3 Cho hình chóp .
S ABCD có đáy ABCD là hình vuông tâm O và SO  ( ABCD) 1.0
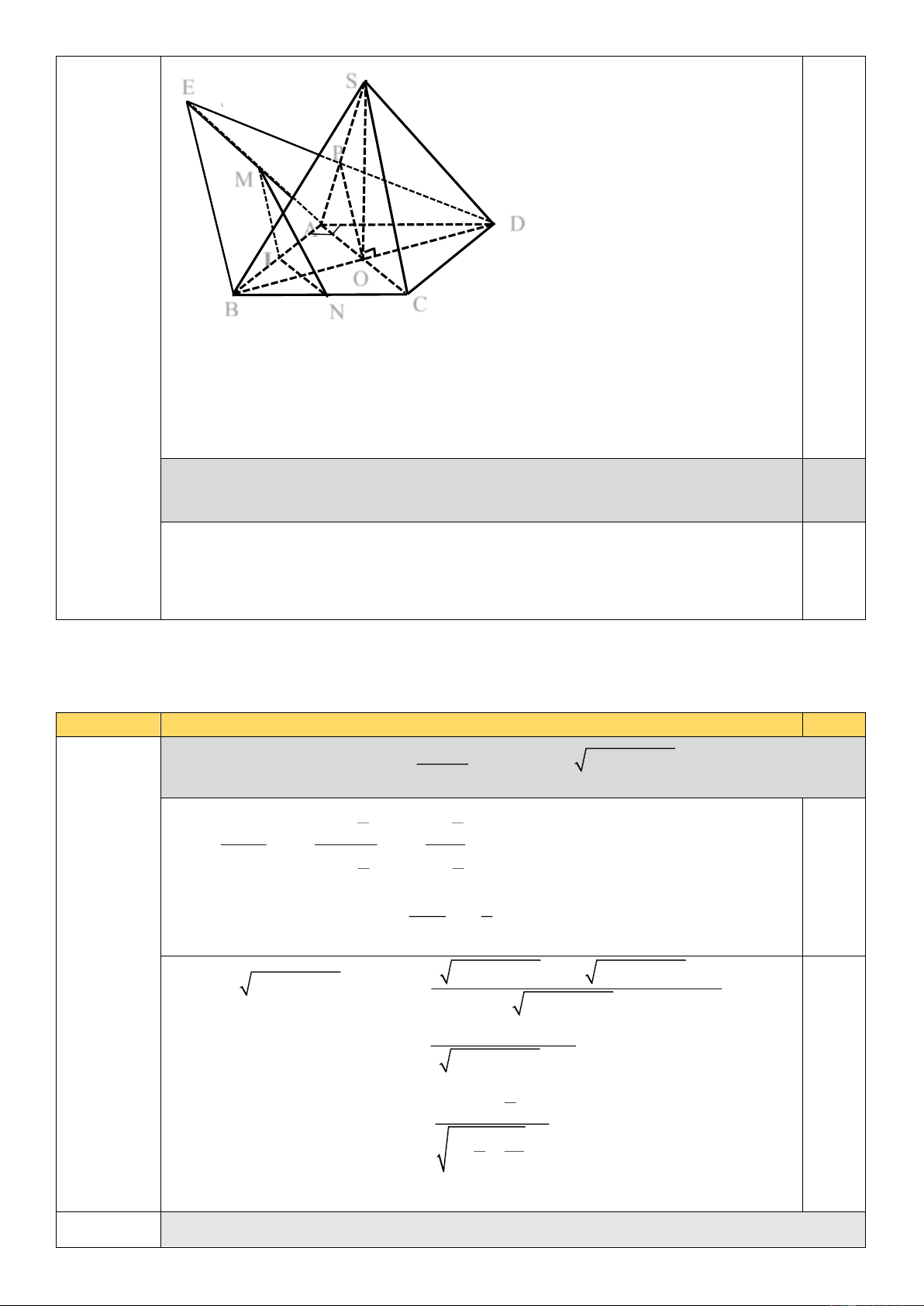
(2,0 điểm) . a. Chứng minh đường thẳng BD vuông góc với mặt phẳng (SAC) S E P M 0,25 A D I O C B N
(Học sinh vẽ đúng hình phục vụ cho câu a/.thì được điểm hình vẽ 0.25)
BD  AC (ABCD là hình vuông) (1) 0,25
SO  ( ABCD)  SO  BD và SO  AC  O (2) 0,25
Từ (1) và (2)  BD  (SAC) 0.25
( Nói BD  SO mà không giải thích thì trừ 0.25đ)
b. Gọi E là điểm đối xứng với điểm D qua trung điểm P của cạnh SA. Gọi 1.0
M, N lần lượt là trung điểm của AE, BC. Chứng minh MN  BD
+ Gọi I là trung điểm của AB, chứng minh IN  BD(1) 0,25 + chứng minh IM//BE//OP 0,25
+ chứng minh BD  OP  BD  IM (2) 0.25
+ từ (1) và (2)  BD  (MNI )  BD  MN 0.25 ĐỀ CHẴN (102,104) Câu Nội dung Điểm 3n  2
. Tính các giới hạn sau: a. lim
x  x   x 2n  b. 2 lim ( 4 5 ) 1 x 2 2 n(3  ) 3  3n  2 0,5 a. lim  lim n  lim n 2n 1 1 1 n(2  ) 2  n n 3  0 3 0,5   2  0 2 Câu 1 2 2
( x  4x  5  x)( x  4x  5  x) 0.25
(2,0 điểm) b. 2
lim ( x  4x  5  x)  lim x x 2
( x  4x  5  x) 4  x  5  lim 0.25 x 2
( x  4x  5  x) 5 4    lim x 0.25 x 4 5 1  1 2 x x  0.25 2 
Tìm tất cả các giá trị của tham số m để hàm số Câu 2 2
2x  3x  2 (1,0 điểm)   khi x 2
f (x)   x  2
liên tục tại x  2
2m1 khi x  2 TXĐ: D  1   2 2(x )(x 2) 2x  3x  2 +) 2
lim f (x)  lim  lim
 lim(2x 1)  5 (1) 0,25 x2 x 3  x 3  x2 x  2 x  2 0,25
+) f (3)  2m 1
Để hàm số liên tục tại x  2 thì lim f (x)  f (2) x2 0,25
 2m 1  5  m  3 0.25 Cho hình chóp .
S ABCD có đáy ABCD là hình vuông tâm O và SO  ( ABCD) 1.0
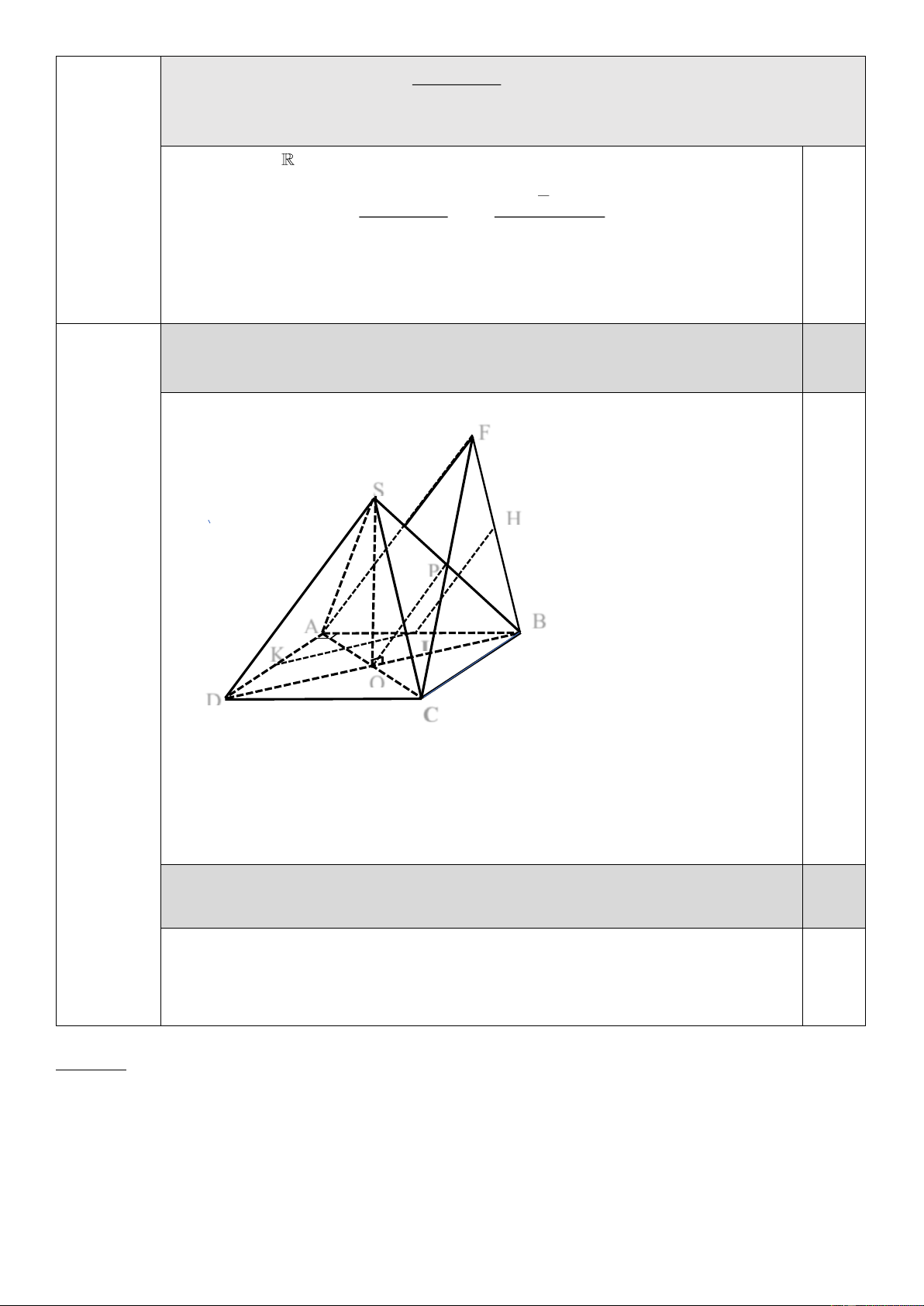
a. Chứng minh đường thẳng AC vuông góc với mặt phẳng (SBD) F S H 0,25 P A B I K Câu 3 (2,0 điểm) O D C
(Học sinh vẽ đúng hình phục vụ cho câu a/.thì được điểm hình vẽ 0.25)
AC  BD (ABCD là hình vuông) (1) 0,25
SO  ( ABCD)  SO  AC và SO  BD  O (2) 0,25
Từ (1) và (2)  AC  (SBD) 0.25
( Nói AC  SO mà không giải thích thì trừ 0.25đ)
b. Gọi F là điểm đối xứng với điểm C qua trung điểm P của cạnh SB. Gọi H, 1.0
K lần lượt là trung điểm của BF, AD. Chứng minh HK  AC
+ Gọi I là trung điểm của AB, chứng minh IK  AC (1) 0,25 + chứng minh IH//AF//OP 0,25
+ chứng minh AC  OP  AC  IH (2) 0.25
+ từ (1) và (2)  AC  (IHK)  AC  HK 0.25 Ghi chú:
Học sinh giải cách khác, giáo viên chia điểm tương tự HDC.
Document Outline

• ĐỀ 101
• ĐỀ 102.docx
• HDC TOAN K11_2022_2023 (tu luan).docx