Đề học kỳ 1 Toán 11 năm 2022 – 2023 trường THPT Nguyễn Thị Minh Khai – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra cuối học kỳ 1 môn Toán 11 năm học 2022 – 2023 trường THPT Nguyễn Thị Minh Khai, thành phố Hồ Chí Minh;

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 11

Môn: Toán 11

Thông tin:

3 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Họ và tên học sinh: ……………………………………………………………. SBD: ……………………………
Bài 1 (2,0 điểm): Giải các phương trình
a)
cos sin 1.
x x
(1,0 điểm)
b)
cos5 3
2sin tan 2cos5 6.
cos
x
x x x
x
(1,0 điểm)
Bài 2 (1,0 điểm): Chọn ngẫu nhiên hai số nguyên dương phân biệt thuộc đoạn
1913;2023
. Tính xác
suất để tích của chúng là một số chẵn.
Bài 3 (1,0 điểm): Tìm hệ số của số hạng chứa
10
x
trong khai triển Newton của
15
(2 3) .
x
Bài 4 (1,0 điểm): Dùng phương pháp qui nạp toán học, chứng minh rằng với mọi số nguyên dương
n
ta
luôn có:
1
3 3
3 9 ... 3 .
2
n
n
Bài 5 (1,0 điểm): Tìm số hạng đầu tiên
1
u
và công sai
d
của cấp số cộng
n
u
biết:
1 2
5
4
.
2 6
u u
u d
Bài 6 (4,0 điểm): Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi
M
là trung
điểm của
SO
.
a) Tìm giao tuyến của hai mặt phẳng
( )
MAD
và
( )
MBC
. (1,0 điểm)
b) Gọi
N
là điểm thuộc cạnh
BD
thỏa
3
BN ND
. Chứng minh rằng:
/ /( ).
MN SAD
(1,0 điểm)
c) Gọi
P
là trung điểm của cạnh
OB
,
Q
là điểm thuộc cạnh
SB
thỏa
3
SQ QB
. Chứng minh rằng:
( ) / /( ).
AMN CPQ
(1,0 điểm)
d) Gọi
I
là giao điểm của
SD
và
CMQ
. Tính tỉ số
.
SI
ID
(1,0 điểm)
HẾT
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Đề kiểm tra gồm có 01 trang
ĐỀ KIỂM TRA HỌC KỲ I
Năm học: 2022 – 2023
Môn TOÁN – Khối: 11
Thời gian: 90 phút
(Không kể thời gian phát đề)
Đề 1
ĐÁP ÁN & BIỂU ĐIỂM ĐỀ 1-Toán 11
Bài 1a:
cos sin 1
x x
(1)
1đ
2
1 1 1 1
(1) cos sin cos .
4
2
2 2 2 2
2
x k
x x x k
x k
0.25x4
Bài 1b:
cos5 3
2sin tan 2cos5 6.
cos
x
x x x
x
(1)
1đ
ĐK:
cos 0.
x
0
(1) 2cos 1 . sin cos 5 3 0 2 ( )
3
x x x x k n

.
0.25x4
Bài 2: Chọn ngẫu nhiên hai số nguyên dương phân biệt thuộc đoạn
1913;2023
. Tính xác suất
để tích của chúng là một số chẵn.
1đ
| |
2
111
6105.
C
2 2
111 56
4565.
A
C C
83
.
111
P A
0.25x4
Bài 3: Tìm hệ số của số hạng chứa
10
x
trong khai triển Newton của
15
(2 3)
x
.
1đ
Số hạng tổng quát của khai triển:
15 15
15 15
2 .3 .2 .3 ( , 15)
k
k k k k k k
C x C x k k
.
Số hạng chứa
10
x
ứng với k = 10. Hệ số cần tìm là:
10 10 5
15
.2 .3 747 242 496.
C
0.25x4
Bài 4:
1
3 3
3 9 ..... 3 .
2
n
n
(1)
1đ
n = 1:
2
3 3
3
2
VT VP
(Đúng).
Giả sử mệnh đề (1) đúng với n = k (
*
k
):
1
3 3
3 9 ... 3 .
2
k
k
Chứng minh mệnh đề (1) đúng với n = k + 1:
2
1
3 3
3 9 ... 3 3 .
2
k
k k
(2)
Theo nguyên lí qui nạp, ta có: VT (2) =
1 1 1 2
1
3 3 3 3 2.3 3 3
3
2 2 2
k k k k
k
= VP (2).
Vậy (1) đúng với mọi số nguyên dương n.
0.25x4
Bài 5: Tìm
1
u
và
d
biết:
1 2
5
4
.
2 6
u u
u d
1đ
1 2
5
4
2 6
u u
u d
1 1
1
1
4
4
.
15
2 4 6
u u d
d
u
u d d
0.25x4
Câu 6a: Tìm giao tuyến của hai mặt phẳng
( )
MAD
và
( )
MBC
.
1đ
( ) ( )
( ) ( ) , , / / / / .
/ /
M MAD MBC
MAD MBC d d qua M d AD BC
AD BC
0.25x4
Câu 6b:
N
là điểm thuộc cạnh
BD
thỏa
3
BN ND
. Chứng minh:
/ /( )
MN SAD
.
1đ
3BN ND
N là trung điểm của OD.
Mà M là trung điểm của SO nên MN là đường trung bình của tam giác SOD.
Suy ra: MN//SD.
Vậy:
/ /( )
MN SAD
0.25x4
Câu 6c:
P
trung điểm
OB
,
Q
thuộc cạnh
SB
thỏa
3
SQ QB
. Chứng minh:
( ) / /( ).
AMN CPQ
1đ
Hai đường chéo AC và PN cắt nhau tại trung điểm O của mỗi đường nên tứ giác ANCP là hình
bình hành
/ /
PC AN
(1)
1
/ / / /
4
BQ BP
PQ SD MN
BS BD
(2)
Từ (1), (2) suy ra
( ) / /( ).
AMN CPQ
0.25x4
Câu 6d:
I
là giao điểm của
SD
và
CMQ
. Tính tỉ số
.
SI
ID
1đ
Trong (SBD), gọi I là giao điểm của SD và QM. Suy ra: I là giao điểm của SD và (CMQ).
Trong (SBD), dựng BL//QI, OK//QI (K, L thuộc SD).
1 3
3 3 ; 5
1 2
SI SM
IK SI IL
SI SQ
IK MO
SI IL DI IL
DK DO
IL QB
DK KL IL
KL OB
. Vậy
.
SI
ID
3
5
0.5x2
Hình vẽ
HẾT
(d)
K
L
I
Q
M
O
D
I
Q
P
N
M
O
D
S
A
C
B
B
S
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Đề 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI Năm học: 2022 – 2023 Môn TOÁN – Khối: 11
Đề kiểm tra gồm có 01 trang Thời gian: 90 phút
(Không kể thời gian phát đề)
Họ và tên học sinh: ……………………………………………………………. SBD: ……………………………
Bài 1 (2,0 điểm): Giải các phương trình
a) cos x  sin x  1. (1,0 điểm) cos 5x  3 b)
 2sin x  tan x  2cos5x  6. (1,0 điểm) cos x
Bài 2 (1,0 điểm): Chọn ngẫu nhiên hai số nguyên dương phân biệt thuộc đoạn 1913;202  3 . Tính xác
suất để tích của chúng là một số chẵn.
Bài 3 (1,0 điểm): Tìm hệ số của số hạng chứa 10
x trong khai triển Newton của 15 (2x  3) .
Bài 4 (1,0 điểm): Dùng phương pháp qui nạp toán học, chứng minh rằng với mọi số nguyên dương n ta n 1  n 3  3
luôn có: 3  9  ...  3  . 2 u  u  4
Bài 5 (1,0 điểm): Tìm số hạng đầu tiên u và công sai d của cấp số cộng u biết: 1 2  . n  1 2u  d  6   5
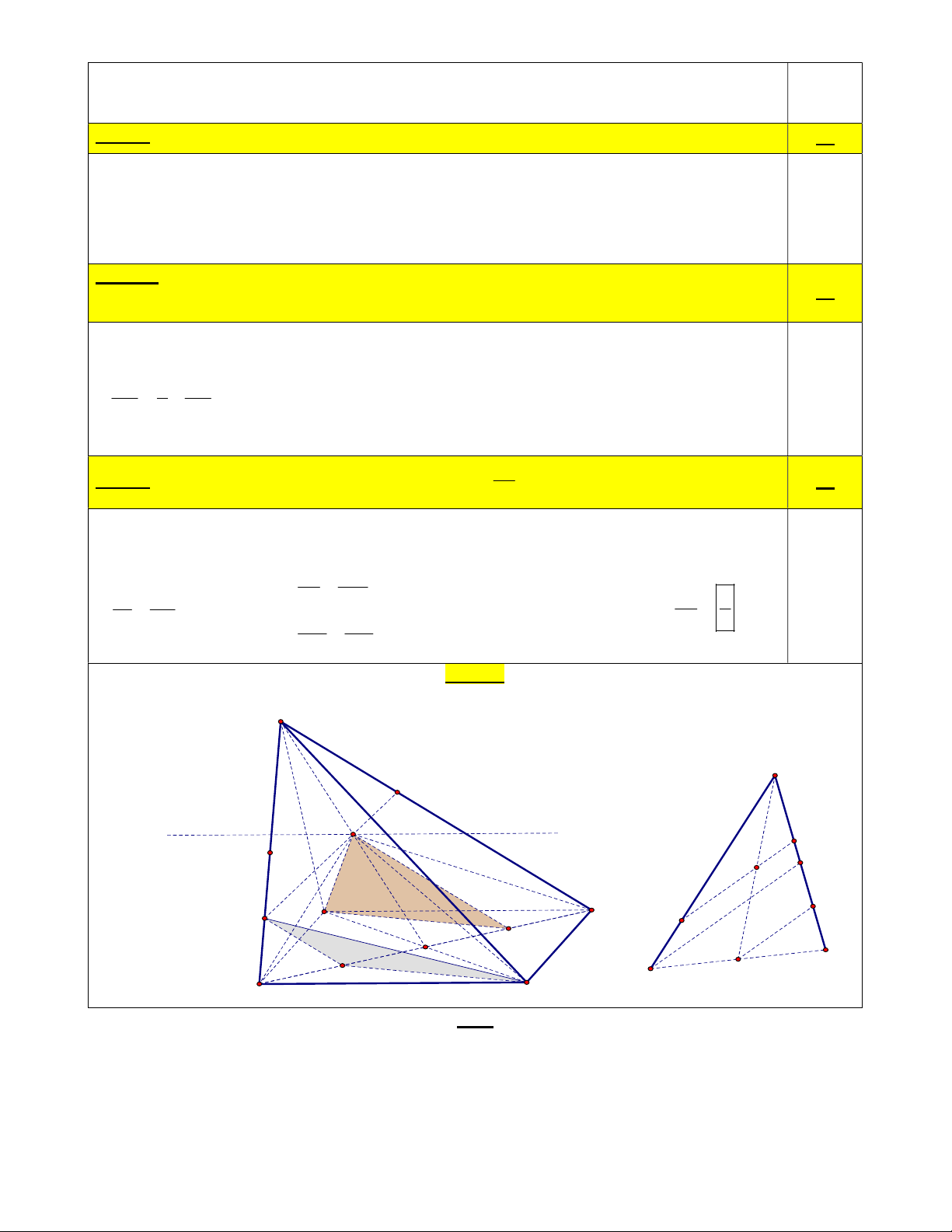
Bài 6 (4,0 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M là trung điểm của SO .
a) Tìm giao tuyến của hai mặt phẳng (MA ) D và (MBC) . (1,0 điểm)
b) Gọi N là điểm thuộc cạnh BD thỏa BN  3ND . Chứng minh rằng: MN / /(SAD). (1,0 điểm)
c) Gọi P là trung điểm của cạnh OB , Q là điểm thuộc cạnh SB thỏa SQ  3QB . Chứng minh rằng: (AMN) / /(CPQ). (1,0 điểm) SI
d) Gọi I là giao điểm của SD và CMQ . Tính tỉ số . (1,0 điểm) ID HẾT
ĐÁP ÁN & BIỂU ĐIỂM ĐỀ 1-Toán 11
Bài 1a: cos x  sin x  1 (1) 1 đ x  k2 1 1 1    1 (1) cos x sin x cos x             k . 0.25x4 2 2 2  4  2 x   k2  2 cos 5x  3 Bài 1b:
 2sin x  tan x  2 cos 5x  6. (1) 1đ cos x ĐK: cos x  0.    0.25x4 (1)  2 cos x  
1 . sin x  cos 5x  3  0  x    k2 (n)    .   0 3 
Bài 2: Chọn ngẫu nhiên hai số nguyên dương phân biệt thuộc đoạn 1913;202  3 . Tính xác suất 1đ
để tích của chúng là một số chẵn.  |  | 2 C  6105. 111  2 2   C  C  4565. A 111 56 0.25x4  P A 83  . 111
Bài 3: Tìm hệ số của số hạng chứa 10
x trong khai triển Newton của 15 (2x  3) . 1đ
Số hạng tổng quát của khai triển: 2 k k 15k k k 15 .3  .2 .3 k k C x C x (k  ,k  15) . 15 15 0.25x4 10
Số hạng chứa x ứng với k = 10. Hệ số cần tìm là: 10 10 5 C .2 .3  747 242 496. 15 n 1  n 3  3
Bài 4: 3  9  .....  3  . (1) 1đ 2 2 3  3  n = 1:    VT 3 VP (Đúng). 2 k 1   k 3 3
 Giả sử mệnh đề (1) đúng với n = k ( *
k   ): 3 9 ... 3  . 2 k 2  0.25x4 k k  3 3
Chứng minh mệnh đề (1) đúng với n = k + 1: 1 3  9  ... 3  3  . 2 (2) k 1  k 1  k 1  k 2      3 3 k  3 3 2.3 3 3
Theo nguyên lí qui nạp, ta có: VT (2) = 1  3   = VP (2). 2 2 2
Vậy (1) đúng với mọi số nguyên dương n. u  u  4 Bài 5: Tìm u và d biết: 1 2  . 1đ 1 2u  d  6   5 u  u  4 u   u  d  4     1  1  d 4 1 2      . 0.25x4 2u  d  6  2  u  4d  d  6 u  15 1  5  1
Câu 6a: Tìm giao tuyến của hai mặt phẳng (MA ) D và (MBC) . 1đ M (MA ) D  (MBC) 0.25x4   (MA )
D  (MBC)  d, d qua M,d / / AD / /B . C AD / /BC 
Câu 6b: N là điểm thuộc cạnh BD thỏa BN  3ND . Chứng minh: MN / /(SA ) D . 1đ
 BN  3ND  N là trung điểm của OD.
 Mà M là trung điểm của SO nên MN là đường trung bình của tam giác SOD. 0.25x4  Suy ra: MN//SD.  Vậy: MN / /(SA ) D
Câu 6c: P trung điểm OB , Q thuộc cạnh SB thỏa SQ  3QB . Chứng minh: 1đ (AMN) / /(CPQ).
 Hai đường chéo AC và PN cắt nhau tại trung điểm O của mỗi đường nên tứ giác ANCP là hình
bình hành  PC / / AN (1)  BQ 1 BP 0.25x4    PQ / /SD / /MN (2) BS 4 BD
 Từ (1), (2) suy ra (AMN) / /(CPQ). SI
Câu 6d: I là giao điểm của SD và CMQ . Tính tỉ số . 1đ ID
 Trong (SBD), gọi I là giao điểm của SD và QM. Suy ra: I là giao điểm của SD và (CMQ).
 Trong (SBD), dựng BL//QI, OK//QI (K, L thuộc SD). SI SM    1 IK  SI  3IL  0.5x2 SI SI SQ    3   3 ; IK MO SI IL   DI  5IL . Vậy  3 . IL QB DK DO ID 5 1 DK KL 2IL      KL OB  Hình vẽ S S I M I (d) M L K Q A D Q N D O O P B B C HẾT