Đề học kỳ 1 Toán 11 năm 2023 – 2024 trường Nguyễn Thị Minh Khai – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra cuối học kỳ 1 môn Toán 11 năm học 2023 – 2024 trường THPT Nguyễn Thị Minh Khai, thành phố Hà Nội; đề thi có đáp án và hướng dẫn chấm điểm.

57 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 11

Môn: Toán 11

Thông tin:

18 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
(Đề thi có 4 trang)
ĐỀ KIỂM TRA HỌC KỲ I
Môn: Toán 11, năm học 2023-2024
Thời gian làm bài 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 001
A. PHẦN TRẮC NGHIỆM
Câu 1. Nghiệm của phương trình cos x = −
1
2
là
A. x = ±
π
6
+ kπ, k ∈ Z. B. x = ±
2π
3
+ k2π, k ∈ Z.
C. x = ±
π
6
+ k2π, k ∈ Z. D. x = ±
π
3
+ k2π, k ∈ Z.
Câu 2. Tìm khẳng định sai.
A. sin(a − b) = sin a · cos b −sin b · cos a. B. sin(a + b) = sin a · cos b + sin b · cos a.
C. cos(a −b) = cos a · cos b − sin a · sin b. D. cos(a + b) = cos a · cos b − sin a · sin b.
Câu 3. Trong không gian, cho hai đường thẳng chéo nhau a và b. Có tất cả bao nhiêu mặt phẳng
chứa a và song song với b?
A. 1. B. 2. C. Vô số. D. 0.
Câu 4. Trong các mệnh đề sau, mệnh đề nào là sai?
A. lim
n→+∞
1
n
k
= 0, k là số nguyên dương.
B. Nếu lim
n→+∞
u
n
= a, lim
n→+∞
v
n
= b thì lim
n→+∞
u
n
v
n
=
a
b
.
C. lim
n→+∞
n
5
= +∞.
D. Nếu lim
n→+∞
u
n
= a, lim
n→+∞
v
n
= +∞ thì lim
n→+∞
u
n
v
n
= 0.
Câu 5. Cho các giới hạn lim
x→x
0
f(x) = 2, lim
x→x
0
g(x) = −3. Tính lim
x→x
0
[3f(x) + 4g(x)].
A. −6. B. −12. C. −2. D. 18.
Câu 6. Tập xác định của hàm số y =
1
sin 2x
là
A. R \ {kπ; k ∈ Z}. B. R \
n
π
2
+ kπ; k ∈ Z
o
.
C. R \
kπ
2
; k ∈ Z
. D. R \ {k2π; k ∈ Z}.
Câu 7. Người ta tiến hành phỏng vấn 40 người về điện thoại Iphone 15 Pro-Max. Người điều tra
yêu cầu cho điểm mẫu Iphone theo thang điểm là 100. Kết quả được trình bày trong bảng dưới.
Nhóm [50;60) [60;70) [70;80) [80;90) [90;100)
Tần số 4 5 23 6 2
Mốt của mẫu số liệu ghép nhóm trên (làm tròn đến kết quả hàng đơn vị) là
A. 74. B. 76. C. 75. D. 73.
Câu 8. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, BC. Trên đoạn BD lấy
điểm P sao cho BP = 3P D. Giao điểm của đường thẳng CD và mặt phẳng (MN P ) là
A. điểm S, với S là giao điểm của CD và M P .
B. điểm S, với S là giao điểm của CD và MN.
C. điểm S, với S là giao điểm của CD và M C.
D. điểm S, với S là giao điểm của CD và NP .
Câu 9. Cho hình lăng trụ có đáy là hình lục giác. Có bao nhiêu mặt của hình lăng trụ là hình
bình hành?
A. 5 mặt. B. 7 mặt. C. 6 mặt. D. 8 mặt.
Trang 1/4 − Mã đề 001
Câu 10. Giới hạn lim
n→+∞
2n
2
− 3n + 1
n + 1
bằng
A. −3. B. −∞. C. 3. D. +∞.
Câu 11. Giá trị lim
x→1
−
3x + 1
−1 + x
bằng
A. 2. B. −∞. C. +∞. D. −2.
Câu 12. Cho hình chóp tứ giác S.ABCD, gọi M và N lần lượt là trung điểm của SA và SC.
Trong các khẳng định sau, khẳng định đúng là
A. MN ∥ (SAB). B. M N ∥ (SCD). C. M N ∥ (SBC). D. M N ∥ (ABCD).
Câu 13. Một cấp số cộng có 15 số hạng, biết tổng các số hạng của cấp số cộng bằng 225, số hạng
cuối bằng 29. Tìm số hạng đầu u
1
của cấp số cộng đó.
A. u
1
= 5. B. u
1
= 3. C. u
1
= 1. D. u
1
= 2.
Câu 14. Giá trị lim
x→−∞
2x + 3
√
5x
2
− 4x + 2 + x
bằng
A. 0. B.
−2
√
5 − 1
. C.
2
√
5
. D.
2
√
5 + 1
.
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J, E, F lần lượt là
trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song
với IJ?
A. EF . B. CD. C. AD. D. AB.
Câu 16. Cho cos α =
3
4
với α ∈
3π
2
; 2π
. Khẳng định nào sau đây là sai?
A. tan 2α = −3
√
7. B. cot 2α = −
√
7
21
. C. cos 2α =
1
8
. D. sin 2α =
3
√
7
8
.
Câu 17. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì (P ) song song với mọi đường thẳng
nằm trong (Q).
B. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì mọi đường thẳng nằm trong (P ) đều
song song với mọi đường thẳng nằm trong (Q).
C. Nếu mặt phẳng (P ) và mặt phẳng (Q) cùng song song với mặt phẳng (R) thì mặt phẳng
(P ) và mặt phẳng (Q) song song với nhau.
D. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) và đường thẳng a song song với mặt phẳng
(Q) thì đường thẳng a song song với mặt phẳng (P ).
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, I theo thứ
tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
A. (NOM ) ∥ (OP M). B. (P ON) ∥ (SAC).
C. (MON) ∥ (SBC). D. (N M P ) ∥ (SBD).
Câu 19. Biết lim
x→0
3
√
7x + 1 − 1
x
=
a
b
, trong đó a, b là các số nguyên dương và phân số
a
b
tối giản.
Tính giá trị của biểu thức P = ab.
A.
7
3
. B.
3
7
. C. 21. D. 10.
Câu 20. Cho cấp số nhân (u
n
) có u
1
= −3 và q =
2
3
. Số −
32
81
là số hạng thứ bao nhiêu của cấp
số nhân?
A. Số hạng thứ 7. B. Số hạng thứ 8. C. Số hạng thứ 5. D. Số hạng thứ 6.
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Giao tuyến của
(SAC) và (SBD) là
A. SA. B. SC. C. SO. D. SB.
Trang 2/4 − Mã đề 001
Câu 22. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được
ghi lại ở bảng sau (đơn vị: triệu đồng):
Doanh thu [5; 7) [7; 9) [9; 11) [11; 13) [13; 15)
Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A. [9; 11). B. [11; 13). C. [7; 9). D. [13; 15).
Câu 23. Cho dãy số (u
n
) có
(
u
1
= 2
u
n+1
= 2u
n
− 3
, ∀n ∈ N
∗
. Tính u
6
.
A. u
6
= 7. B. u
6
= −13. C. u
6
= −61. D. u
6
= −29.
Câu 24. Giả sử lim
x→1
2x − 2
x
2
+ 7x − 8
=
a
b
2
, (với
a
b
2
là phân số tối giản và b là số nguyên dương). Tính
giá trị 2a + 3b.
A.
2
9
. B. 7. C. 11. D. 13.
Câu 25.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm BC và CD.
Gọi d là giao tuyến của hai mặt phẳng (AMN ) và (ABD) (tham
khảo hình vẽ). Khẳng định nào sau đây đúng?
A. d đi qua A và song song với NB.
B. d đi qua A và song song với MD.
C. d đi qua A và song song với BD.
D. d đi qua A và song song với BC.
A
B
C
M
D
N
Câu 26. Trong các dãy số (u
n
) cho bởi công thức số hạng tổng quát u
n
, dãy số nào là dãy số
tăng?
A. u
n
=
1
2
n
. B. u
n
=
2n − 1
n + 1
. C. u
n
=
n + 5
3n + 1
. D. u
n
=
1
n
.
Câu 27.
Các số hạng được viết trong các ô vuông tạo thành một cấp số
nhân từ trên xuống dưới và một cấp số cộng từ trái sang phải
(tham khảo hình vẽ). Số x được viết trong hình vuông dưới đây là
bao nhiêu?
A. 243. B. 768. C. 405. D. 45.
3
5
87
x
Câu 28.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J
lần lượt là trọng tâm của các tam giác SAB và SAD, P là trung
điểm của BC (tham khảo hình vẽ bên). Gọi E là giao điểm của SA
và (IJP ). Tính tỉ số
SE
SA
.
A.
SE
SA
=
3
5
. B.
SE
SA
=
2
3
. C.
SE
SA
=
4
7
. D.
SE
SA
=
5
8
.
S
I
D
J
B
C
P
A
Trang 3/4 − Mã đề 001
Câu 29. Cho các số thực a, b, c thỏa mãn a + c
2
= 18 và lim
x→+∞
√
ax
2
+ bx − cx
= −4. Tính
P = a
2
+ b
2
+ c
2
.
A. P = 777. B. P = 555. C. P = 666. D. P = 888.
Câu 30. Cho dãy số (u
n
) thỏa mãn
(
u
1
= 9
u
n+1
= 3u
n
+ 2.5
n
− 4, ∀n ∈ N
∗
. Tính giới hạn lim
n→+∞
u
n
3.4
n
+ 4.5
n
.
A. 0. B.
2
3
. C.
1
4
. D. +∞.
B. PHẦN TỰ LUẬN
Câu 1 (1,0 điểm). Tính các giới hạn sau:
1. lim
x→1
−2x
2
+ 5x − 3
x
2
− 4x + 3
.
2. lim
x→+∞
√
x
2
− x + 1 − x
.
Câu 2 (1,0 điểm). Cho hàm số f (x) =
√
x + 2 − 2
x
2
− 2x
nếu x > 2
mx + 1 nếu x ≤ 2
. Tìm m để hàm số có giới
hạn tại x
0
= 2.
Câu 3 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD ∥ BC và
AD = 2BC. Gọi N là trung điểm của SA; G, I lần lượt là trọng tâm của △SAB và △ABD.
1. Chứng minh rằng GI ∥ (SBD) và (BGI) ∥ (SCD).
2. Tìm giao điểm F của DN và mặt phẳng (SBC).
Câu 4 (0,5 điểm). Vườn bưởi Diễn nhà bà Hiền đang vào mua thu hoạch, các thương lái tấp
nập đến mua bưởi. Biết rằng bà Hiền đã bán cho người thứ nhất nửa số bưởi thu hoạch được và
tặng thêm 1 quả, bán cho người thứ hai nửa số bưởi còn lại và tặng thêm 1 quả. Bà Hiền cứ tiếp
tục cách bán như trên thì đến người thứ 15 số bưởi của bà được bán hết. Tính số bưởi mà bà Hiền
thu hoạch được.
HẾT
Trang 4/4 − Mã đề 001
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
(Đề thi có 4 trang)
ĐỀ KIỂM TRA HỌC KỲ I
Môn: Toán 11, năm học 2023-2024
Thời gian làm bài 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 002
A. PHẦN TRẮC NGHIỆM
Câu 1. Trong không gian, cho hai đường thẳng chéo nhau a và b. Có tất cả bao nhiêu mặt phẳng
chứa a và song song với b?
A. 1. B. 2. C. 0. D. Vô số.
Câu 2. Cho các giới hạn lim
x→x
0
f(x) = 2, lim
x→x
0
g(x) = −3. Tính lim
x→x
0
[3f(x) + 4g(x)].
A. 18. B. −6. C. −12. D. −2.
Câu 3. Tập xác định của hàm số y =
1
sin 2x
là
A. R \ {k2π; k ∈ Z}. B. R \ {kπ; k ∈ Z}.
C. R \
kπ
2
; k ∈ Z
. D. R \
n
π
2
+ kπ; k ∈ Z
o
.
Câu 4. Nghiệm của phương trình cos x = −
1
2
là
A. x = ±
π
6
+ k2π, k ∈ Z. B. x = ±
2π
3
+ k2π, k ∈ Z.
C. x = ±
π
3
+ k2π, k ∈ Z. D. x = ±
π
6
+ kπ, k ∈ Z.
Câu 5. Trong các mệnh đề sau, mệnh đề nào là sai?
A. Nếu lim
n→+∞
u
n
= a, lim
n→+∞
v
n
= +∞ thì lim
n→+∞
u
n
v
n
= 0.
B. Nếu lim
n→+∞
u
n
= a, lim
n→+∞
v
n
= b thì lim
n→+∞
u
n
v
n
=
a
b
.
C. lim
n→+∞
1
n
k
= 0, k là số nguyên dương.
D. lim
n→+∞
n
5
= +∞.
Câu 6. Tìm khẳng định sai.
A. cos(a + b) = cos a · cos b − sin a · sin b. B. cos(a − b) = cos a · cos b − sin a · sin b.
C. sin(a + b) = sin a · cos b + sin b · cos a. D. sin(a − b) = sin a · cos b − sin b · cos a.
Câu 7. Cho cos α =
3
4
với α ∈
3π
2
; 2π
. Khẳng định nào sau đây là sai?
A. cos 2α =
1
8
. B. sin 2α =
3
√
7
8
. C. tan 2α = −3
√
7. D. cot 2α = −
√
7
21
.
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, I theo thứ
tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
A. (NM P ) ∥ (SBD). B. (P ON) ∥ (SAC).
C. (NOM) ∥ (OP M). D. (MON) ∥ (SBC).
Câu 9. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì mọi đường thẳng nằm trong (P ) đều
song song với mọi đường thẳng nằm trong (Q).
B. Nếu mặt phẳng (P ) và mặt phẳng (Q) cùng song song với mặt phẳng (R) thì mặt phẳng
(P ) và mặt phẳng (Q) song song với nhau.
C. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì (P ) song song với mọi đường thẳng
nằm trong (Q).
D. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) và đường thẳng a song song với mặt phẳng
(Q) thì đường thẳng a song song với mặt phẳng (P ).
Trang 1/4 − Mã đề 002
Câu 10. Giá trị lim
x→1
−
3x + 1
−1 + x
bằng
A. −∞. B. +∞. C. −2. D. 2.
Câu 11. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được
ghi lại ở bảng sau (đơn vị: triệu đồng):
Doanh thu [5; 7) [7; 9) [9; 11) [11; 13) [13; 15)
Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A. [9; 11). B. [13; 15). C. [11; 13). D. [7; 9).
Câu 12. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, BC. Trên đoạn BD lấy
điểm P sao cho BP = 3P D. Giao điểm của đường thẳng CD và mặt phẳng (MN P ) là
A. điểm S, với S là giao điểm của CD và M C.
B. điểm S, với S là giao điểm của CD và MP .
C. điểm S, với S là giao điểm của CD và M N .
D. điểm S, với S là giao điểm của CD và NP .
Câu 13. Cho hình chóp tứ giác S.ABCD, gọi M và N lần lượt là trung điểm của SA và SC.
Trong các khẳng định sau, khẳng định đúng là
A. MN ∥ (SBC). B. M N ∥ (ABCD). C. M N ∥ (SCD). D. MN ∥ (SAB).
Câu 14. Cho dãy số (u
n
) có
(
u
1
= 2
u
n+1
= 2u
n
− 3
, ∀n ∈ N
∗
. Tính u
6
.
A. u
6
= −61. B. u
6
= 7. C. u
6
= −29. D. u
6
= −13.
Câu 15. Biết lim
x→0
3
√
7x + 1 − 1
x
=
a
b
, trong đó a, b là các số nguyên dương và phân số
a
b
tối giản.
Tính giá trị của biểu thức P = ab.
A. 10. B. 21. C.
7
3
. D.
3
7
.
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Giao tuyến của
(SAC) và (SBD) là
A. SO. B. SC. C. SB. D. SA.
Câu 17. Người ta tiến hành phỏng vấn 40 người về điện thoại Iphone 15 Pro-Max. Người điều
tra yêu cầu cho điểm mẫu Iphone theo thang điểm là 100. Kết quả được trình bày trong bảng
dưới.
Nhóm [50;60) [60;70) [70;80) [80;90) [90;100)
Tần số 4 5 23 6 2
Mốt của mẫu số liệu ghép nhóm trên (làm tròn đến kết quả hàng đơn vị) là
A. 75. B. 73. C. 74. D. 76.
Câu 18. Trong các dãy số (u
n
) cho bởi công thức số hạng tổng quát u
n
, dãy số nào là dãy số
tăng?
A. u
n
=
2n − 1
n + 1
. B. u
n
=
1
2
n
. C. u
n
=
n + 5
3n + 1
. D. u
n
=
1
n
.
Câu 19. Giới hạn lim
n→+∞
2n
2
− 3n + 1
n + 1
bằng
A. −∞. B. 3. C. −3. D. +∞.
Câu 20. Cho hình lăng trụ có đáy là hình lục giác. Có bao nhiêu mặt của hình lăng trụ là hình
bình hành?
A. 8 mặt. B. 6 mặt. C. 5 mặt. D. 7 mặt.
Trang 2/4 − Mã đề 002
Câu 21. Giả sử lim
x→1
2x − 2
x
2
+ 7x − 8
=
a
b
2
, (với
a
b
2
là phân số tối giản và b là số nguyên dương). Tính
giá trị 2a + 3b.
A. 11. B.
2
9
. C. 7. D. 13.
Câu 22. Cho cấp số nhân (u
n
) có u
1
= −3 và q =
2
3
. Số −
32
81
là số hạng thứ bao nhiêu của cấp
số nhân?
A. Số hạng thứ 8. B. Số hạng thứ 6. C. Số hạng thứ 5. D. Số hạng thứ 7.
Câu 23. Một cấp số cộng có 15 số hạng, biết tổng các số hạng của cấp số cộng bằng 225, số hạng
cuối bằng 29. Tìm số hạng đầu u
1
của cấp số cộng đó.
A. u
1
= 1. B. u
1
= 5. C. u
1
= 3. D. u
1
= 2.
Câu 24. Giá trị lim
x→−∞
2x + 3
√
5x
2
− 4x + 2 + x
bằng
A.
2
√
5 + 1
. B.
−2
√
5 − 1
. C.
2
√
5
. D. 0.
Câu 25.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm BC và CD.
Gọi d là giao tuyến của hai mặt phẳng (AMN ) và (ABD) (tham
khảo hình vẽ). Khẳng định nào sau đây đúng?
A. d đi qua A và song song với BD.
B. d đi qua A và song song với NB.
C. d đi qua A và song song với M D.
D. d đi qua A và song song với BC.
A
B
C
M
D
N
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J, E, F lần lượt là
trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song
với IJ?
A. EF . B. AD. C. CD. D. AB.
Câu 27.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J
lần lượt là trọng tâm của các tam giác SAB và SAD, P là trung
điểm của BC (tham khảo hình vẽ bên). Gọi E là giao điểm của SA
và (IJP ). Tính tỉ số
SE
SA
.
A.
SE
SA
=
3
5
. B.
SE
SA
=
5
8
. C.
SE
SA
=
2
3
. D.
SE
SA
=
4
7
.
S
I
D
J
B
C
P
A
Câu 28.
Các số hạng được viết trong các ô vuông tạo thành một cấp số
nhân từ trên xuống dưới và một cấp số cộng từ trái sang phải
(tham khảo hình vẽ). Số x được viết trong hình vuông dưới đây là
bao nhiêu?
A. 45. B. 768. C. 243. D. 405.
3
5
87
x
Trang 3/4 − Mã đề 002
Câu 29. Cho dãy số (u
n
) thỏa mãn
(
u
1
= 9
u
n+1
= 3u
n
+ 2.5
n
− 4, ∀n ∈ N
∗
. Tính giới hạn lim
n→+∞
u
n
3.4
n
+ 4.5
n
.
A. 0. B.
2
3
. C.
1
4
. D. +∞.
Câu 30. Cho các số thực a, b, c thỏa mãn a + c
2
= 18 và lim
x→+∞
√
ax
2
+ bx − cx
= −4. Tính
P = a
2
+ b
2
+ c
2
.
A. P = 666. B. P = 888. C. P = 777. D. P = 555.
B. PHẦN TỰ LUẬN
Câu 1 (1,0 điểm). Tính các giới hạn sau:
1. lim
x→1
−2x
2
+ 5x − 3
x
2
− 4x + 3
.
2. lim
x→+∞
√
x
2
− x + 1 − x
.
Câu 2 (1,0 điểm). Cho hàm số f (x) =
√
x + 2 − 2
x
2
− 2x
nếu x > 2
mx + 1 nếu x ≤ 2
. Tìm m để hàm số có giới
hạn tại x
0
= 2.
Câu 3 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD ∥ BC và
AD = 2BC. Gọi N là trung điểm của SA; G, I lần lượt là trọng tâm của △SAB và △ABD.
1. Chứng minh rằng GI ∥ (SBD) và (BGI) ∥ (SCD).
2. Tìm giao điểm F của DN và mặt phẳng (SBC).
Câu 4 (0,5 điểm). Vườn bưởi Diễn nhà bà Hiền đang vào mua thu hoạch, các thương lái tấp
nập đến mua bưởi. Biết rằng bà Hiền đã bán cho người thứ nhất nửa số bưởi thu hoạch được và
tặng thêm 1 quả, bán cho người thứ hai nửa số bưởi còn lại và tặng thêm 1 quả. Bà Hiền cứ tiếp
tục cách bán như trên thì đến người thứ 15 số bưởi của bà được bán hết. Tính số bưởi mà bà Hiền
thu hoạch được.
HẾT
Trang 4/4 − Mã đề 002
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
(Đề thi có 4 trang)
ĐỀ KIỂM TRA HỌC KỲ I
Môn: Toán 11, năm học 2023-2024
Thời gian làm bài 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 003
A. PHẦN TRẮC NGHIỆM
Câu 1. Trong các mệnh đề sau, mệnh đề nào là sai?
A. Nếu lim
n→+∞
u
n
= a, lim
n→+∞
v
n
= +∞ thì lim
n→+∞
u
n
v
n
= 0.
B. lim
n→+∞
1
n
k
= 0, k là số nguyên dương.
C. Nếu lim
n→+∞
u
n
= a, lim
n→+∞
v
n
= b thì lim
n→+∞
u
n
v
n
=
a
b
.
D. lim
n→+∞
n
5
= +∞.
Câu 2. Tìm khẳng định sai.
A. cos(a + b) = cos a · cos b − sin a · sin b. B. cos(a − b) = cos a · cos b − sin a · sin b.
C. sin(a −b) = sin a · cos b − sin b · cos a. D. sin(a + b) = sin a · cos b + sin b · cos a.
Câu 3. Trong không gian, cho hai đường thẳng chéo nhau a và b. Có tất cả bao nhiêu mặt phẳng
chứa a và song song với b?
A. Vô số. B. 2. C. 1. D. 0.
Câu 4. Cho các giới hạn lim
x→x
0
f(x) = 2, lim
x→x
0
g(x) = −3. Tính lim
x→x
0
[3f(x) + 4g(x)].
A. 18. B. −6. C. −2. D. −12.
Câu 5. Nghiệm của phương trình cos x = −
1
2
là
A. x = ±
2π
3
+ k2π, k ∈ Z. B. x = ±
π
6
+ k2π, k ∈ Z.
C. x = ±
π
3
+ k2π, k ∈ Z. D. x = ±
π
6
+ kπ, k ∈ Z.
Câu 6. Tập xác định của hàm số y =
1
sin 2x
là
A. R \
kπ
2
; k ∈ Z
. B. R \ {kπ; k ∈ Z}.
C. R \
n
π
2
+ kπ; k ∈ Z
o
. D. R \ {k2π; k ∈ Z}.
Câu 7. Biết lim
x→0
3
√
7x + 1 − 1
x
=
a
b
, trong đó a, b là các số nguyên dương và phân số
a
b
tối giản.
Tính giá trị của biểu thức P = ab.
A.
3
7
. B.
7
3
. C. 10. D. 21.
Câu 8. Giới hạn lim
n→+∞
2n
2
− 3n + 1
n + 1
bằng
A. −3. B. 3. C. +∞. D. −∞.
Câu 9. Giả sử lim
x→1
2x − 2
x
2
+ 7x − 8
=
a
b
2
, (với
a
b
2
là phân số tối giản và b là số nguyên dương). Tính
giá trị 2a + 3b.
A. 7. B. 11. C. 13. D.
2
9
.
Câu 10. Người ta tiến hành phỏng vấn 40 người về điện thoại Iphone 15 Pro-Max. Người điều
tra yêu cầu cho điểm mẫu Iphone theo thang điểm là 100. Kết quả được trình bày trong bảng
dưới.
Trang 1/4 − Mã đề 003
Nhóm [50;60) [60;70) [70;80) [80;90) [90;100)
Tần số 4 5 23 6 2
Mốt của mẫu số liệu ghép nhóm trên (làm tròn đến kết quả hàng đơn vị) là
A. 74. B. 75. C. 76. D. 73.
Câu 11. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được
ghi lại ở bảng sau (đơn vị: triệu đồng):
Doanh thu [5; 7) [7; 9) [9; 11) [11; 13) [13; 15)
Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A. [11; 13). B. [9; 11). C. [7; 9). D. [13; 15).
Câu 12. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu mặt phẳng (P ) và mặt phẳng (Q) cùng song song với mặt phẳng (R) thì mặt phẳng
(P ) và mặt phẳng (Q) song song với nhau.
B. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) và đường thẳng a song song với mặt phẳng
(Q) thì đường thẳng a song song với mặt phẳng (P ).
C. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì (P ) song song với mọi đường thẳng
nằm trong (Q).
D. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì mọi đường thẳng nằm trong (P ) đều
song song với mọi đường thẳng nằm trong (Q).
Câu 13. Một cấp số cộng có 15 số hạng, biết tổng các số hạng của cấp số cộng bằng 225, số hạng
cuối bằng 29. Tìm số hạng đầu u
1
của cấp số cộng đó.
A. u
1
= 3. B. u
1
= 1. C. u
1
= 2. D. u
1
= 5.
Câu 14.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm BC và CD.
Gọi d là giao tuyến của hai mặt phẳng (AMN ) và (ABD) (tham
khảo hình vẽ). Khẳng định nào sau đây đúng?
A. d đi qua A và song song với MD.
B. d đi qua A và song song với BD.
C. d đi qua A và song song với BC.
D. d đi qua A và song song với NB.
A
B
C
M
D
N
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Giao tuyến của
(SAC) và (SBD) là
A. SO. B. SC. C. SA. D. SB.
Câu 16. Giá trị lim
x→1
−
3x + 1
−1 + x
bằng
A. −2. B. −∞. C. 2. D. +∞.
Câu 17. Cho hình lăng trụ có đáy là hình lục giác. Có bao nhiêu mặt của hình lăng trụ là hình
bình hành?
A. 8 mặt. B. 5 mặt. C. 6 mặt. D. 7 mặt.
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J, E, F lần lượt là
trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song
với IJ?
A. CD. B. EF . C. AD. D. AB.
Trang 2/4 − Mã đề 003
Câu 19. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, BC. Trên đoạn BD lấy
điểm P sao cho BP = 3P D. Giao điểm của đường thẳng CD và mặt phẳng (MN P ) là
A. điểm S, với S là giao điểm của CD và M P .
B. điểm S, với S là giao điểm của CD và MC.
C. điểm S, với S là giao điểm của CD và M N .
D. điểm S, với S là giao điểm của CD và NP .
Câu 20. Cho cos α =
3
4
với α ∈
3π
2
; 2π
. Khẳng định nào sau đây là sai?
A. sin 2α =
3
√
7
8
. B. tan 2α = −3
√
7. C. cos 2α =
1
8
. D. cot 2α = −
√
7
21
.
Câu 21. Cho hình chóp tứ giác S.ABCD, gọi M và N lần lượt là trung điểm của SA và SC.
Trong các khẳng định sau, khẳng định đúng là
A. MN ∥ (SCD). B. M N ∥ (ABCD). C. MN ∥ (SAB). D. MN ∥ (SBC).
Câu 22. Giá trị lim
x→−∞
2x + 3
√
5x
2
− 4x + 2 + x
bằng
A.
2
√
5
. B.
2
√
5 + 1
. C.
−2
√
5 − 1
. D. 0.
Câu 23. Cho cấp số nhân (u
n
) có u
1
= −3 và q =
2
3
. Số −
32
81
là số hạng thứ bao nhiêu của cấp
số nhân?
A. Số hạng thứ 8. B. Số hạng thứ 6. C. Số hạng thứ 7. D. Số hạng thứ 5.
Câu 24. Cho dãy số (u
n
) có
(
u
1
= 2
u
n+1
= 2u
n
− 3
, ∀n ∈ N
∗
. Tính u
6
.
A. u
6
= −61. B. u
6
= −13. C. u
6
= −29. D. u
6
= 7.
Câu 25. Trong các dãy số (u
n
) cho bởi công thức số hạng tổng quát u
n
, dãy số nào là dãy số
tăng?
A. u
n
=
1
n
. B. u
n
=
n + 5
3n + 1
. C. u
n
=
2n − 1
n + 1
. D. u
n
=
1
2
n
.
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, I theo thứ
tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
A. (MON ) ∥ (SBC). B. (P ON ) ∥ (SAC).
C. (NMP ) ∥ (SBD). D. (NOM ) ∥ (OP M).
Câu 27.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J
lần lượt là trọng tâm của các tam giác SAB và SAD, P là trung
điểm của BC (tham khảo hình vẽ bên). Gọi E là giao điểm của SA
và (IJP ). Tính tỉ số
SE
SA
.
A.
SE
SA
=
4
7
. B.
SE
SA
=
2
3
. C.
SE
SA
=
3
5
. D.
SE
SA
=
5
8
.
S
I
D
J
B
C
P
A
Câu 28.
Trang 3/4 − Mã đề 003
Các số hạng được viết trong các ô vuông tạo thành một cấp số
nhân từ trên xuống dưới và một cấp số cộng từ trái sang phải
(tham khảo hình vẽ). Số x được viết trong hình vuông dưới đây là
bao nhiêu?
A. 768. B. 243. C. 45. D. 405.
3
5
87
x
Câu 29. Cho dãy số (u
n
) thỏa mãn
(
u
1
= 9
u
n+1
= 3u
n
+ 2.5
n
− 4, ∀n ∈ N
∗
. Tính giới hạn lim
n→+∞
u
n
3.4
n
+ 4.5
n
.
A.
2
3
. B.
1
4
. C. +∞. D. 0.
Câu 30. Cho các số thực a, b, c thỏa mãn a + c
2
= 18 và lim
x→+∞
√
ax
2
+ bx − cx
= −4. Tính
P = a
2
+ b
2
+ c
2
.
A. P = 888. B. P = 666. C. P = 555. D. P = 777.
B. PHẦN TỰ LUẬN
Câu 1 (1,0 điểm). Tính các giới hạn sau:
1. lim
x→1
−2x
2
+ 5x − 3
x
2
− 4x + 3
.
2. lim
x→+∞
√
x
2
− x + 1 − x
.
Câu 2 (1,0 điểm). Cho hàm số f (x) =
√
x + 2 − 2
x
2
− 2x
nếu x > 2
mx + 1 nếu x ≤ 2
. Tìm m để hàm số có giới
hạn tại x
0
= 2.
Câu 3 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD ∥ BC và
AD = 2BC. Gọi N là trung điểm của SA; G, I lần lượt là trọng tâm của △SAB và △ABD.
1. Chứng minh rằng GI ∥ (SBD) và (BGI) ∥ (SCD).
2. Tìm giao điểm F của DN và mặt phẳng (SBC).
Câu 4 (0,5 điểm). Vườn bưởi Diễn nhà bà Hiền đang vào mua thu hoạch, các thương lái tấp
nập đến mua bưởi. Biết rằng bà Hiền đã bán cho người thứ nhất nửa số bưởi thu hoạch được và
tặng thêm 1 quả, bán cho người thứ hai nửa số bưởi còn lại và tặng thêm 1 quả. Bà Hiền cứ tiếp
tục cách bán như trên thì đến người thứ 15 số bưởi của bà được bán hết. Tính số bưởi mà bà Hiền
thu hoạch được.
HẾT
Trang 4/4 − Mã đề 003
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
(Đề thi có 4 trang)
ĐỀ KIỂM TRA HỌC KỲ I
Môn: Toán 11, năm học 2023-2024
Thời gian làm bài 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 004
A. PHẦN TRẮC NGHIỆM
Câu 1. Tập xác định của hàm số y =
1
sin 2x
là
A. R \ {kπ; k ∈ Z}. B. R \
n
π
2
+ kπ; k ∈ Z
o
.
C. R \{k2π; k ∈ Z}. D. R \
kπ
2
; k ∈ Z
.
Câu 2. Trong các mệnh đề sau, mệnh đề nào là sai?
A. lim
n→+∞
n
5
= +∞.
B. Nếu lim
n→+∞
u
n
= a, lim
n→+∞
v
n
= +∞ thì lim
n→+∞
u
n
v
n
= 0.
C. lim
n→+∞
1
n
k
= 0, k là số nguyên dương.
D. Nếu lim
n→+∞
u
n
= a, lim
n→+∞
v
n
= b thì lim
n→+∞
u
n
v
n
=
a
b
.
Câu 3. Nghiệm của phương trình cos x = −
1
2
là
A. x = ±
π
6
+ kπ, k ∈ Z. B. x = ±
2π
3
+ k2π, k ∈ Z.
C. x = ±
π
6
+ k2π, k ∈ Z. D. x = ±
π
3
+ k2π, k ∈ Z.
Câu 4. Tìm khẳng định sai.
A. sin(a − b) = sin a · cos b − sin b · cos a. B. sin(a + b) = sin a · cos b + sin b · cos a.
C. cos(a −b) = cos a · cos b − sin a · sin b. D. cos(a + b) = cos a · cos b − sin a · sin b.
Câu 5. Trong không gian, cho hai đường thẳng chéo nhau a và b. Có tất cả bao nhiêu mặt phẳng
chứa a và song song với b?
A. 1. B. 0. C. 2. D. Vô số.
Câu 6. Cho các giới hạn lim
x→x
0
f(x) = 2, lim
x→x
0
g(x) = −3. Tính lim
x→x
0
[3f(x) + 4g(x)].
A. −2. B. −12. C. −6. D. 18.
Câu 7.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm BC và CD.
Gọi d là giao tuyến của hai mặt phẳng (AMN ) và (ABD) (tham
khảo hình vẽ). Khẳng định nào sau đây đúng?
A. d đi qua A và song song với MD.
B. d đi qua A và song song với BC.
C. d đi qua A và song song với BD.
D. d đi qua A và song song với NB.
A
B
C
M
D
N
Câu 8. Giá trị lim
x→−∞
2x + 3
√
5x
2
− 4x + 2 + x
bằng
A. 0. B.
2
√
5
. C.
−2
√
5 − 1
. D.
2
√
5 + 1
.
Câu 9. Trong các dãy số (u
n
) cho bởi công thức số hạng tổng quát u
n
, dãy số nào là dãy số
tăng?
A. u
n
=
n + 5
3n + 1
. B. u
n
=
1
n
. C. u
n
=
2n − 1
n + 1
. D. u
n
=
1
2
n
.
Trang 1/4 − Mã đề 004
Câu 10. Cho dãy số (u
n
) có
(
u
1
= 2
u
n+1
= 2u
n
− 3
, ∀n ∈ N
∗
. Tính u
6
.
A. u
6
= −61. B. u
6
= 7. C. u
6
= −13. D. u
6
= −29.
Câu 11. Cho hình lăng trụ có đáy là hình lục giác. Có bao nhiêu mặt của hình lăng trụ là hình
bình hành?
A. 8 mặt. B. 5 mặt. C. 7 mặt. D. 6 mặt.
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J, E, F lần lượt là
trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song
với IJ?
A. AB. B. EF . C. CD. D. AD.
Câu 13. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được
ghi lại ở bảng sau (đơn vị: triệu đồng):
Doanh thu [5; 7) [7; 9) [9; 11) [11; 13) [13; 15)
Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A. [11; 13). B. [9; 11). C. [13; 15). D. [7; 9).
Câu 14. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì mọi đường thẳng nằm trong (P ) đều
song song với mọi đường thẳng nằm trong (Q).
B. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) và đường thẳng a song song với mặt phẳng
(Q) thì đường thẳng a song song với mặt phẳng (P ).
C. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì (P ) song song với mọi đường thẳng
nằm trong (Q).
D. Nếu mặt phẳng (P ) và mặt phẳng (Q) cùng song song với mặt phẳng (R) thì mặt phẳng
(P ) và mặt phẳng (Q) song song với nhau.
Câu 15. Giá trị lim
x→1
−
3x + 1
−1 + x
bằng
A. 2. B. −∞. C. +∞. D. −2.
Câu 16. Cho hình chóp tứ giác S.ABCD, gọi M và N lần lượt là trung điểm của SA và SC.
Trong các khẳng định sau, khẳng định đúng là
A. MN ∥ (SAB). B. M N ∥ (SCD). C. M N ∥ (SBC). D. M N ∥ (ABCD).
Câu 17. Người ta tiến hành phỏng vấn 40 người về điện thoại Iphone 15 Pro-Max. Người điều
tra yêu cầu cho điểm mẫu Iphone theo thang điểm là 100. Kết quả được trình bày trong bảng
dưới.
Nhóm [50;60) [60;70) [70;80) [80;90) [90;100)
Tần số 4 5 23 6 2
Mốt của mẫu số liệu ghép nhóm trên (làm tròn đến kết quả hàng đơn vị) là
A. 75. B. 76. C. 74. D. 73.
Câu 18. Giả sử lim
x→1
2x − 2
x
2
+ 7x − 8
=
a
b
2
, (với
a
b
2
là phân số tối giản và b là số nguyên dương). Tính
giá trị 2a + 3b.
A.
2
9
. B. 11. C. 7. D. 13.
Câu 19. Giới hạn lim
n→+∞
2n
2
− 3n + 1
n + 1
bằng
A. −∞. B. +∞. C. 3. D. −3.
Trang 2/4 − Mã đề 004
Câu 20. Một cấp số cộng có 15 số hạng, biết tổng các số hạng của cấp số cộng bằng 225, số hạng
cuối bằng 29. Tìm số hạng đầu u
1
của cấp số cộng đó.
A. u
1
= 3. B. u
1
= 1. C. u
1
= 5. D. u
1
= 2.
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, I theo thứ
tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
A. (NM P ) ∥ (SBD). B. (P ON) ∥ (SAC).
C. (MON) ∥ (SBC). D. (N OM) ∥ (OP M).
Câu 22. Cho cos α =
3
4
với α ∈
3π
2
; 2π
. Khẳng định nào sau đây là sai?
A. tan 2α = −3
√
7. B. cos 2α =
1
8
. C. cot 2α = −
√
7
21
. D. sin 2α =
3
√
7
8
.
Câu 23. Cho cấp số nhân (u
n
) có u
1
= −3 và q =
2
3
. Số −
32
81
là số hạng thứ bao nhiêu của cấp
số nhân?
A. Số hạng thứ 6. B. Số hạng thứ 5. C. Số hạng thứ 7. D. Số hạng thứ 8.
Câu 24. Biết lim
x→0
3
√
7x + 1 − 1
x
=
a
b
, trong đó a, b là các số nguyên dương và phân số
a
b
tối giản.
Tính giá trị của biểu thức P = ab.
A. 21. B.
3
7
. C.
7
3
. D. 10.
Câu 25. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, BC. Trên đoạn BD lấy
điểm P sao cho BP = 3P D. Giao điểm của đường thẳng CD và mặt phẳng (MN P ) là
A. điểm S, với S là giao điểm của CD và M N.
B. điểm S, với S là giao điểm của CD và NP .
C. điểm S, với S là giao điểm của CD và M C.
D. điểm S, với S là giao điểm của CD và MP .
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Giao tuyến của
(SAC) và (SBD) là
A. SA. B. SO. C. SB. D. SC.
Câu 27.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J
lần lượt là trọng tâm của các tam giác SAB và SAD, P là trung
điểm của BC (tham khảo hình vẽ bên). Gọi E là giao điểm của SA
và (IJP ). Tính tỉ số
SE
SA
.
A.
SE
SA
=
4
7
. B.
SE
SA
=
3
5
. C.
SE
SA
=
5
8
. D.
SE
SA
=
2
3
.
S
I
D
J
B
C
P
A
Câu 28.
Các số hạng được viết trong các ô vuông tạo thành một cấp số
nhân từ trên xuống dưới và một cấp số cộng từ trái sang phải
(tham khảo hình vẽ). Số x được viết trong hình vuông dưới đây là
bao nhiêu?
A. 768. B. 243. C. 405. D. 45.
3
5
87
x
Trang 3/4 − Mã đề 004
Câu 29. Cho dãy số (u
n
) thỏa mãn
(
u
1
= 9
u
n+1
= 3u
n
+ 2.5
n
− 4, ∀n ∈ N
∗
. Tính giới hạn lim
n→+∞
u
n
3.4
n
+ 4.5
n
.
A. +∞. B.
1
4
. C.
2
3
. D. 0.
Câu 30. Cho các số thực a, b, c thỏa mãn a + c
2
= 18 và lim
x→+∞
√
ax
2
+ bx − cx
= −4. Tính
P = a
2
+ b
2
+ c
2
.
A. P = 777. B. P = 555. C. P = 666. D. P = 888.
B. PHẦN TỰ LUẬN
Câu 1 (1,0 điểm). Tính các giới hạn sau:
1. lim
x→1
−2x
2
+ 5x − 3
x
2
− 4x + 3
.
2. lim
x→+∞
√
x
2
− x + 1 − x
.
Câu 2 (1,0 điểm). Cho hàm số f (x) =
√
x + 2 − 2
x
2
− 2x
nếu x > 2
mx + 1 nếu x ≤ 2
. Tìm m để hàm số có giới
hạn tại x
0
= 2.
Câu 3 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD ∥ BC và
AD = 2BC. Gọi N là trung điểm của SA; G, I lần lượt là trọng tâm của △SAB và △ABD.
1. Chứng minh rằng GI ∥ (SBD) và (BGI) ∥ (SCD).
2. Tìm giao điểm F của DN và mặt phẳng (SBC).
Câu 4 (0,5 điểm). Vườn bưởi Diễn nhà bà Hiền đang vào mua thu hoạch, các thương lái tấp
nập đến mua bưởi. Biết rằng bà Hiền đã bán cho người thứ nhất nửa số bưởi thu hoạch được và
tặng thêm 1 quả, bán cho người thứ hai nửa số bưởi còn lại và tặng thêm 1 quả. Bà Hiền cứ tiếp
tục cách bán như trên thì đến người thứ 15 số bưởi của bà được bán hết. Tính số bưởi mà bà Hiền
thu hoạch được.
HẾT
Trang 4/4 − Mã đề 004
1
Sở GD & ĐT Hà Nội
Trường THPT Nguyễn Thị Minh Khai
ĐÁP ÁN − THANG ĐIỂM
ĐỀ KIỂM TRA HỌC KÌ I LỚP 11
Môn: Toán; Năm học: 2023-2024
(Đáp án − Thang điểm gồm 02 trang)
Câu Đáp án Điểm
1 1. (0,5 điểm) lim
x→1
−2x
2
+ 5x − 3
x
2
− 4x + 3
(1,0đ) Ta có lim
x→1
−2x
2
+ 5x − 3
x
2
− 4x + 3
= lim
x→1
(x −1)(−2x + 3)
(x −1)(x −3)
0,25
= lim
x→1
−2x + 3
x −3
= −
1
2
0,25
2. (0,5 điểm) lim
x→+∞
√
x
2
− x + 1 − x
Ta có:
lim
x→+∞
√
x
2
− x + 1 − x
= lim
x→+∞
h
√
x
2
− x + 1 + x
ih
√
x
2
− x + 1 − x
i
√
x
2
− x + 1 + x
= lim
x→+∞
−x + 1
√
x
2
− x + 1 + x
0,25
= lim
x→−∞
−x + 1
x
r
1 −
1
x
+
1
x
2
+ x
= lim
x→+∞
−1 +
1
x
r
1 −
1
x
+
1
x
2
+ 1
= −
1
2
. 0,25
2 Cho hàm số f (x) =
√
x + 2 −2
x
2
− 2x
nếu x > 2
mx + 1 nếu x ≤ 2
. Tìm m để hàm số có giới hạn tại x
0
= 2.
(1,0đ) lim
x→2
−
f(x) = lim
x→2
−
(mx + 1) = 2m + 1. 0,25
lim
x→2
+
f(x) = lim
x→2
+
√
x + 2 −2
x
2
− 2x
= lim
x→2
+
x −2
x(x −2)
√
x + 2 + 2
0,25
= lim
x→2
+
1
x
√
x + 2 + 2
=
1
8
Hàm số có giới hạn tại x
0
= 2 khi và chỉ khi lim
x→2
+
f(x) = lim
x→2
−
f(x) 0,25
⇔ 2m + 1 =
1
8
⇔ m = −
7
16
. 0,25
3
(1,5đ)
Hình vẽ:
∆
B C
S
N
D
F
A
G
I
H
M
2
Câu Đáp án Điểm
1. Gọi M , H lần lượt là trung điểm các cạnh AB và AD. Ta có
MG
GS
=
MI
ID
=
1
2
⇒
GI ∥ SD ⇒ GI ∥ (SBD)
0,5
Vì HD = BC và HD ∥ BC nên tứ giác BCHD là hình bình hành ⇒ BH ∥ DC. Mặt
khác GI ∥ SD ⇒ (BGI) ∥ (SCD).
0,5
2. Qua S kẻ đường thẳng ∆ ∥ AD. Ta có ∆ = (SBC) ∩ (SAD). 0,25
Do đó F là giao điểm của ND và ∆. 0,25
4
(0,5đ)
Gọi x là số bưởi bà Hiền thu hoạch được (x ∈ N
∗
). Khi đó:
• Số quả bưởi người thứ nhất mua và được tặng là:
x
2
+ 1 =
x + 2
2
.
• Số quả bưởi người thứ hai mua và được tặng là:
1
2
x −
x + 2
2
+ 1 =
x + 2
2
2
.
• Số quả bưởi người thứ ba mua và được tặng là:
1
2
x −
x + 2
2
−
x + 2
2
2
+ 1 =
x + 2
2
3
.
... • Số quả bưởi người thứ 15 mua và được tặng là:
x + 2
2
15
.
0,25
Ta có:
x + 2
2
+
x + 2
2
2
+ ··· +
x + 2
2
15
= x ⇔ (x + 2)
1
2
+
1
2
2
+ ... +
1
2
15
= x
⇔ (x + 2)
1
2
.
1 −
1
2
15
1 −
1
2
= x ⇔
32767
32768
(x + 2) = x ⇔ x = 65534. 0,25
——Hết——
Chú ý: Học sinh làm cách khác ra kết quả đúng vẫn cho điểm tuyệt đối.
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

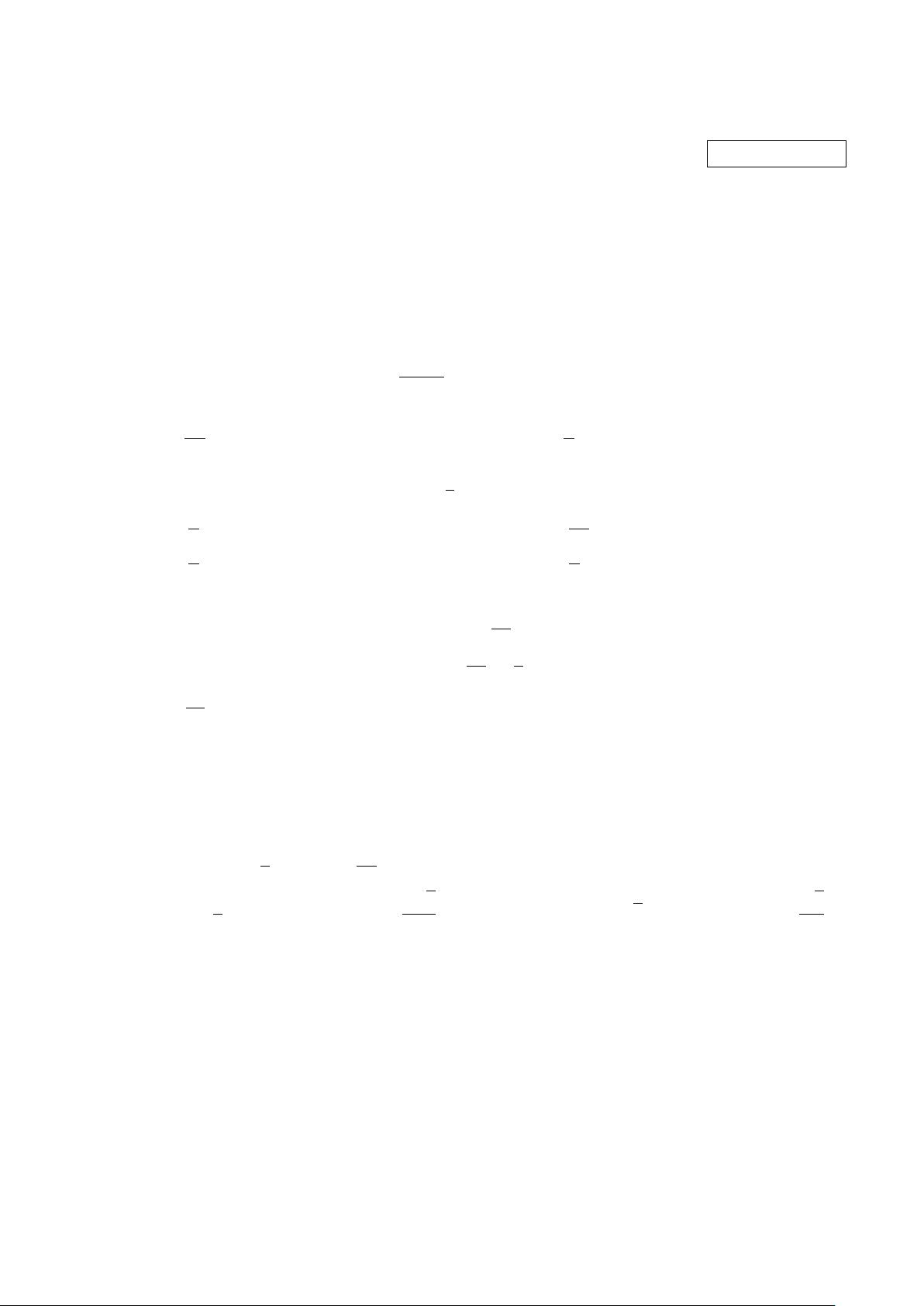
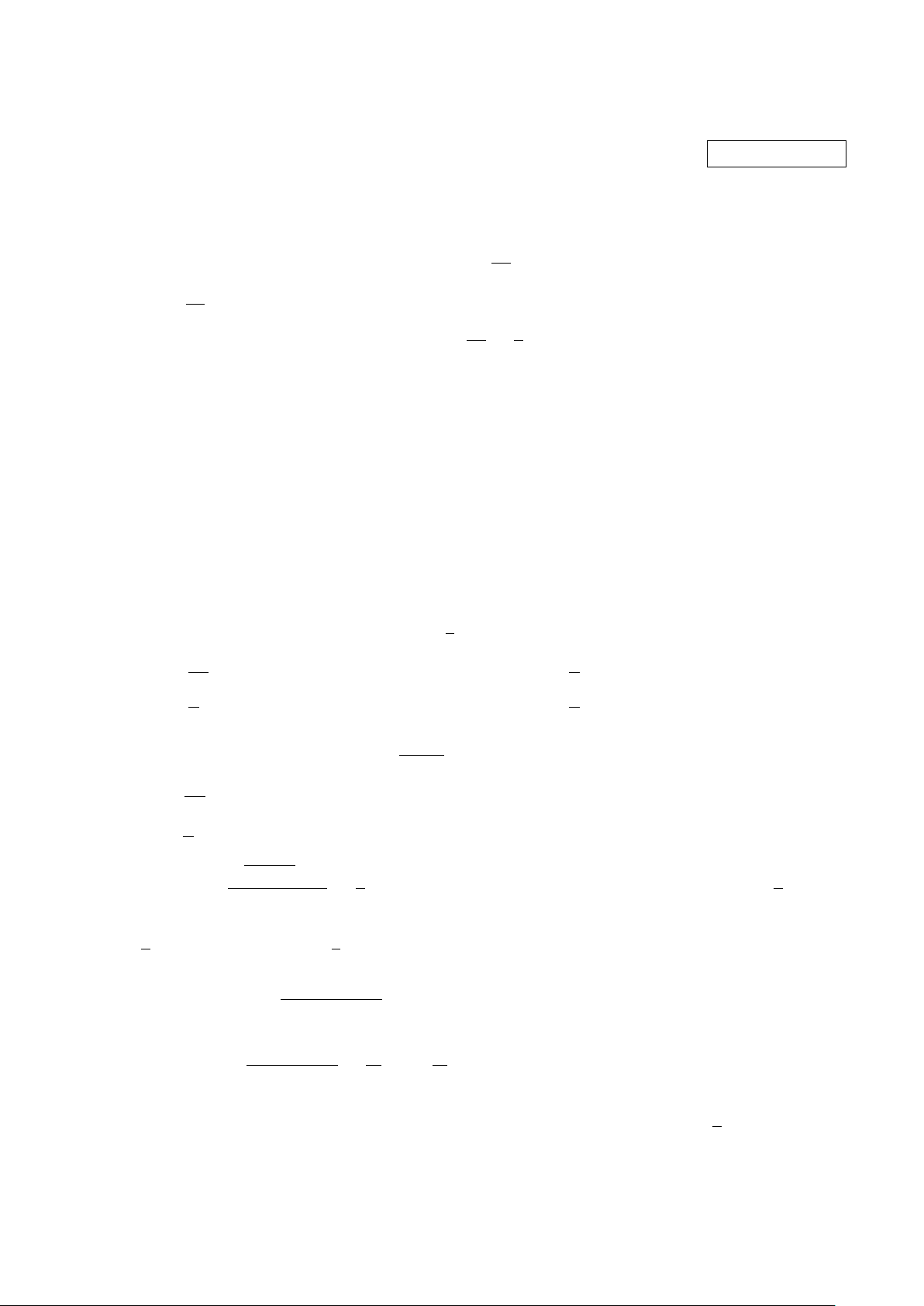
Preview text:

SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Môn: Toán 11, năm học 2023-2024 (Đề thi có 4 trang) Thời gian làm bài 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 001 A. PHẦN TRẮC NGHIỆM 1
Câu 1. Nghiệm của phương trình cos x = − là 2 π 2π A. x = ± + kπ, k ∈ Z. B. x = ± + k2π, k ∈ Z. 6 3 π π C. x = ± + k2π, k ∈ Z. D. x = ± + k2π, k ∈ Z. 6 3
Câu 2. Tìm khẳng định sai.
A. sin(a − b) = sin a · cos b − sin b · cos a.
B. sin(a + b) = sin a · cos b + sin b · cos a.
C. cos(a − b) = cos a · cos b − sin a · sin b.
D. cos(a + b) = cos a · cos b − sin a · sin b.
Câu 3. Trong không gian, cho hai đường thẳng chéo nhau a và b. Có tất cả bao nhiêu mặt phẳng
chứa a và song song với b? A. 1. B. 2. C. Vô số. D. 0.
Câu 4. Trong các mệnh đề sau, mệnh đề nào là sai? 1 A. lim
= 0, k là số nguyên dương. n→+∞ nk un a
B. Nếu lim un = a, lim vn = b thì lim = . n→+∞ n→+∞ n→+∞ vn b C. lim n5 = +∞. n→+∞ un
D. Nếu lim un = a, lim vn = +∞ thì lim = 0. n→+∞ n→+∞ n→+∞ vn
Câu 5. Cho các giới hạn lim f (x) = 2, lim g(x) = −3. Tính lim [3f (x) + 4g(x)]. x→x0 x→x0 x→x0 A. −6. B. −12. C. −2. D. 18. 1
Câu 6. Tập xác định của hàm số y = là sin 2x n π o A. R \ {kπ; k ∈ Z}. B. R \ + kπ; k ∈ Z . 2 kπ C. R \ ; k ∈ Z . D. R \ {k2π; k ∈ Z}. 2
Câu 7. Người ta tiến hành phỏng vấn 40 người về điện thoại Iphone 15 Pro-Max. Người điều tra
yêu cầu cho điểm mẫu Iphone theo thang điểm là 100. Kết quả được trình bày trong bảng dưới. Nhóm [50;60) [60;70) [70;80) [80;90) [90;100) Tần số 4 5 23 6 2
Mốt của mẫu số liệu ghép nhóm trên (làm tròn đến kết quả hàng đơn vị) là A. 74. B. 76. C. 75. D. 73.
Câu 8. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, BC. Trên đoạn BD lấy
điểm P sao cho BP = 3P D. Giao điểm của đường thẳng CD và mặt phẳng (M N P ) là
A. điểm S, với S là giao điểm của CD và M P .
B. điểm S, với S là giao điểm của CD và M N .
C. điểm S, với S là giao điểm của CD và M C.
D. điểm S, với S là giao điểm của CD và N P .
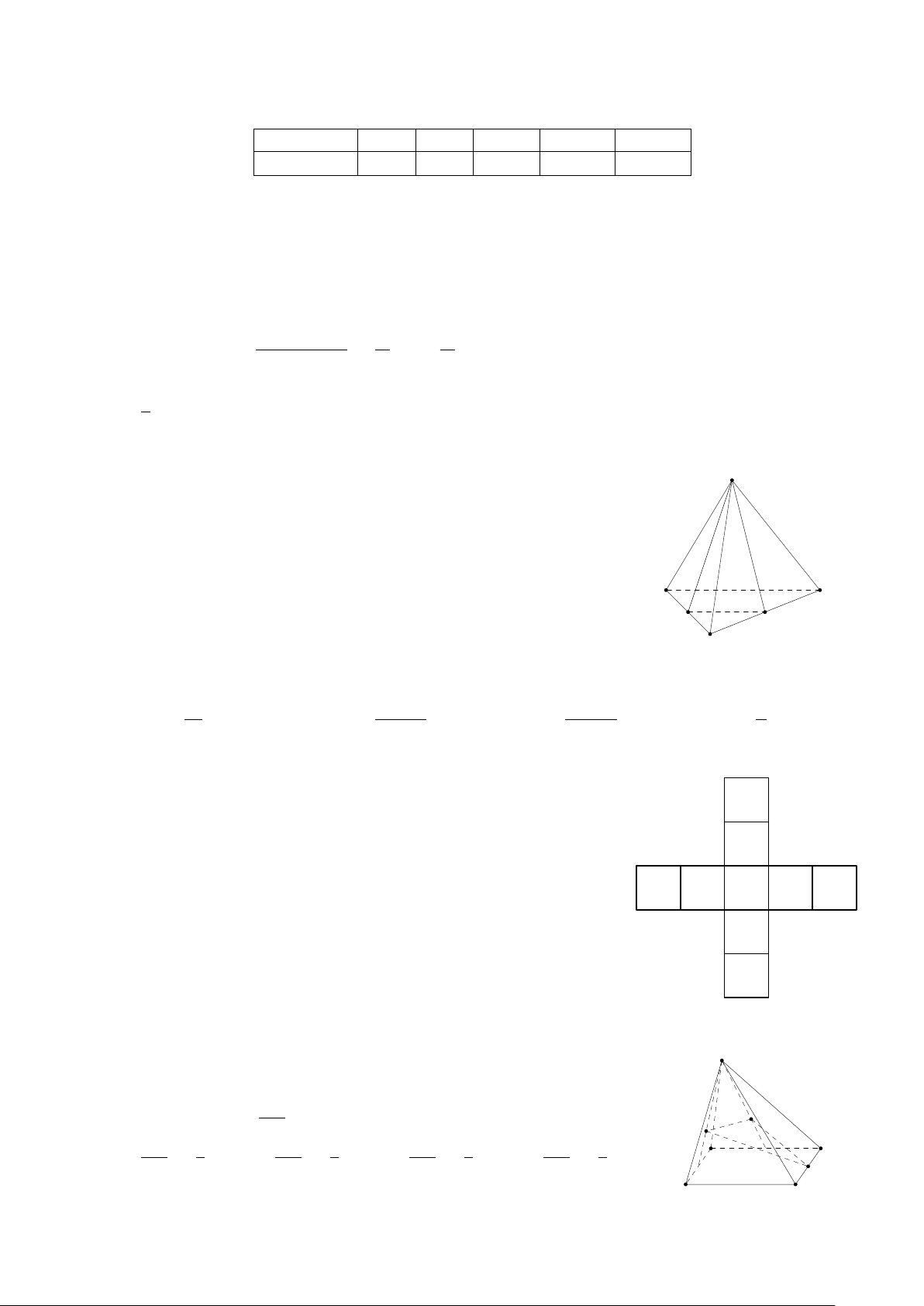
Câu 9. Cho hình lăng trụ có đáy là hình lục giác. Có bao nhiêu mặt của hình lăng trụ là hình bình hành? A. 5 mặt. B. 7 mặt. C. 6 mặt. D. 8 mặt. Trang 1/4 − Mã đề 001 2n2 − 3n + 1 Câu 10. Giới hạn lim bằng n→+∞ n + 1 A. −3. B. −∞. C. 3. D. +∞. 3x + 1 Câu 11. Giá trị lim bằng x→1− −1 + x A. 2. B. −∞. C. +∞. D. −2.
Câu 12. Cho hình chóp tứ giác S.ABCD, gọi M và N lần lượt là trung điểm của SA và SC.
Trong các khẳng định sau, khẳng định đúng là A. M N ∥ (SAB). B. M N ∥ (SCD). C. M N ∥ (SBC). D. M N ∥ (ABCD).
Câu 13. Một cấp số cộng có 15 số hạng, biết tổng các số hạng của cấp số cộng bằng 225, số hạng
cuối bằng 29. Tìm số hạng đầu u1 của cấp số cộng đó. A. u1 = 5. B. u1 = 3. C. u1 = 1. D. u1 = 2. 2x + 3 Câu 14. Giá trị lim √ bằng x→−∞ 5x2 − 4x + 2 + x −2 2 2 A. 0. B. √ . C. √ . D. √ . 5 − 1 5 5 + 1
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J , E, F lần lượt là
trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song với IJ ? A. EF . B. CD. C. AD. D. AB. 3 3π Câu 16. Cho cos α = với α ∈
; 2π . Khẳng định nào sau đây là sai? 4 2 √ √ √ 7 1 3 7 A. tan 2α = −3 7. B. cot 2α = − . C. cos 2α = . D. sin 2α = . 21 8 8
Câu 17. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì (P ) song song với mọi đường thẳng nằm trong (Q).
B. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì mọi đường thẳng nằm trong (P ) đều
song song với mọi đường thẳng nằm trong (Q).
C. Nếu mặt phẳng (P ) và mặt phẳng (Q) cùng song song với mặt phẳng (R) thì mặt phẳng
(P ) và mặt phẳng (Q) song song với nhau.
D. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) và đường thẳng a song song với mặt phẳng
(Q) thì đường thẳng a song song với mặt phẳng (P ).
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, I theo thứ
tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng? A. (N OM ) ∥ (OP M ). B. (P ON ) ∥ (SAC). C. (M ON ) ∥ (SBC). D. (N M P ) ∥ (SBD). √ 3 7x + 1 − 1 a a Câu 19. Biết lim =
, trong đó a, b là các số nguyên dương và phân số tối giản. x→0 x b b
Tính giá trị của biểu thức P = ab. 7 3 A. . B. . C. 21. D. 10. 3 7 2 32
Câu 20. Cho cấp số nhân (un) có u1 = −3 và q = . Số −
là số hạng thứ bao nhiêu của cấp 3 81 số nhân? A. Số hạng thứ 7. B. Số hạng thứ 8. C. Số hạng thứ 5. D. Số hạng thứ 6.
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Giao tuyến của (SAC) và (SBD) là A. SA. B. SC. C. SO. D. SB. Trang 2/4 − Mã đề 001
Câu 22. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được
ghi lại ở bảng sau (đơn vị: triệu đồng): Doanh thu [5; 7) [7; 9) [9; 11) [11; 13) [13; 15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [9; 11). B. [11; 13). C. [7; 9). D. [13; 15). (u1 = 2 Câu 23. Cho dãy số (u ∗ n) có , ∀n ∈ N . Tính u6. un+1 = 2un − 3 A. u6 = 7. B. u6 = −13. C. u6 = −61. D. u6 = −29. 2x − 2 a a Câu 24. Giả sử lim = , (với
là phân số tối giản và b là số nguyên dương). Tính x→1 x2 + 7x − 8 b2 b2 giá trị 2a + 3b. 2 A. . B. 7. C. 11. D. 13. 9 Câu 25.
Cho tứ diện ABCD. Gọi M , N lần lượt là trung điểm BC và CD. A
Gọi d là giao tuyến của hai mặt phẳng (AM N ) và (ABD) (tham
khảo hình vẽ). Khẳng định nào sau đây đúng?
A. d đi qua A và song song với N B.
B. d đi qua A và song song với M D.
C. d đi qua A và song song với BD. B D
D. d đi qua A và song song với BC. M N C
Câu 26. Trong các dãy số (un) cho bởi công thức số hạng tổng quát un, dãy số nào là dãy số tăng? 1 2n − 1 n + 5 1 A. un = . B. un = . C. un = . D. un = . 2n n + 1 3n + 1 n Câu 27.
Các số hạng được viết trong các ô vuông tạo thành một cấp số
nhân từ trên xuống dưới và một cấp số cộng từ trái sang phải 5
(tham khảo hình vẽ). Số x được viết trong hình vuông dưới đây là bao nhiêu? A. 243. B. 768. C. 405. D. 45. 3 87 x Câu 28.
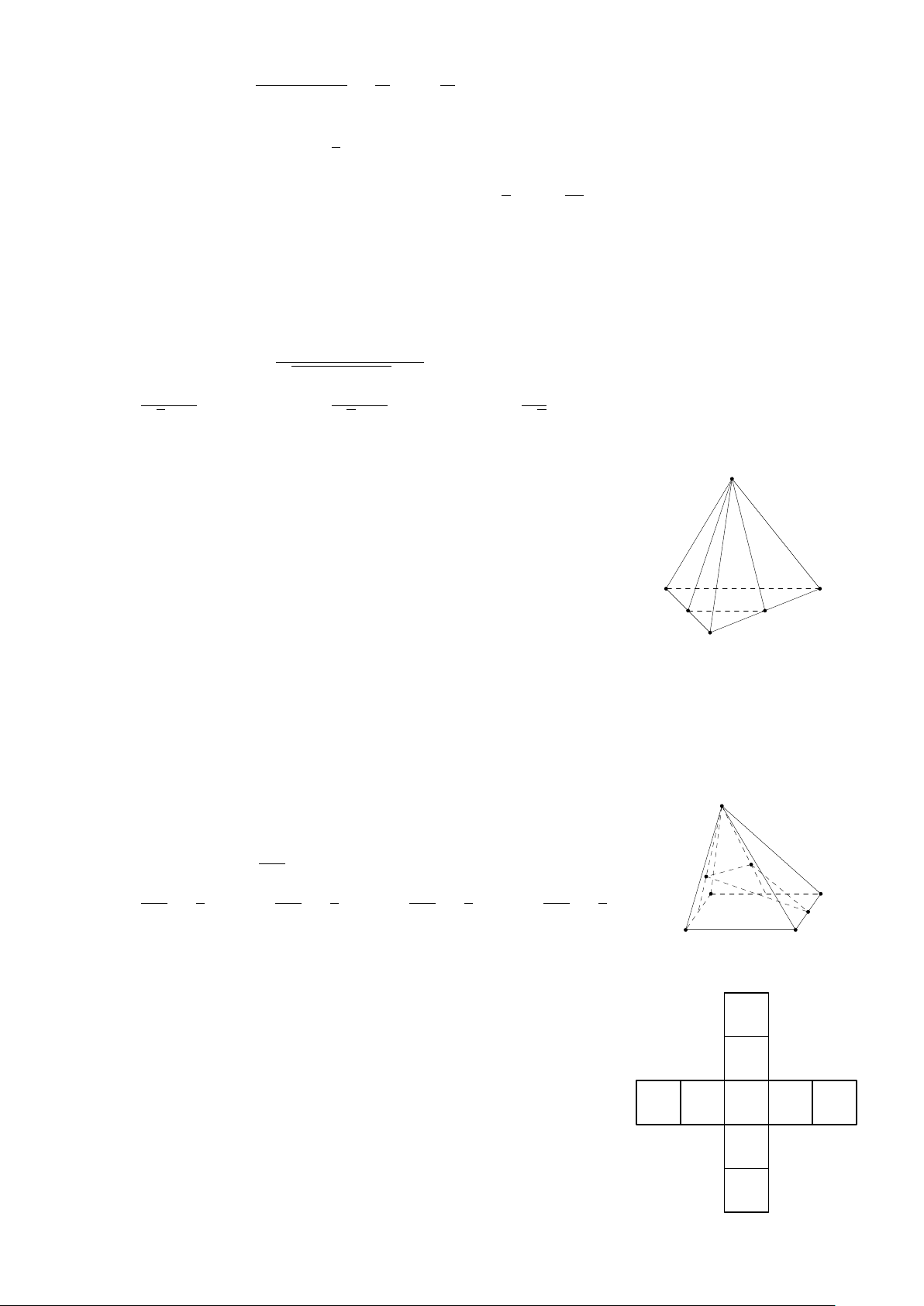
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J S
lần lượt là trọng tâm của các tam giác SAB và SAD, P là trung
điểm của BC (tham khảo hình vẽ bên). Gọi E là giao điểm của SA SE I và (IJ P ). Tính tỉ số . SA J SE 3 SE 2 SE 4 SE 5 A. = . B. = . C. = . D. = . SA 5 SA 3 SA 7 SA 8 A B D P C Trang 3/4 − Mã đề 001 √
Câu 29. Cho các số thực a, b, c thỏa mãn a + c2 = 18 và lim ax2 + bx − cx = −4. Tính x→+∞ P = a2 + b2 + c2. A. P = 777. B. P = 555. C. P = 666. D. P = 888. (u1 = 9 un
Câu 30. Cho dãy số (un) thỏa mãn . Tính giới hạn lim . u ∗
n+1 = 3un + 2.5n − 4, ∀n ∈ N n→+∞ 3.4n + 4.5n 2 1 A. 0. B. . C. . D. +∞. 3 4 B. PHẦN TỰ LUẬN
Câu 1 (1,0 điểm). Tính các giới hạn sau: −2x2 + 5x − 3 1. lim . x→1 x2 − 4x + 3 √ 2. lim x2 − x + 1 − x. x→+∞ √  x + 2 − 2  nếu x > 2
Câu 2 (1,0 điểm). Cho hàm số f (x) = x2 − 2x
. Tìm m để hàm số có giới mx + 1 nếu x ≤ 2 hạn tại x0 = 2.
Câu 3 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD ∥ BC và
AD = 2BC. Gọi N là trung điểm của SA; G, I lần lượt là trọng tâm của △SAB và △ABD.
1. Chứng minh rằng GI ∥ (SBD) và (BGI) ∥ (SCD).
2. Tìm giao điểm F của DN và mặt phẳng (SBC).
Câu 4 (0,5 điểm). Vườn bưởi Diễn nhà bà Hiền đang vào mua thu hoạch, các thương lái tấp
nập đến mua bưởi. Biết rằng bà Hiền đã bán cho người thứ nhất nửa số bưởi thu hoạch được và
tặng thêm 1 quả, bán cho người thứ hai nửa số bưởi còn lại và tặng thêm 1 quả. Bà Hiền cứ tiếp
tục cách bán như trên thì đến người thứ 15 số bưởi của bà được bán hết. Tính số bưởi mà bà Hiền thu hoạch được. HẾT Trang 4/4 − Mã đề 001
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Môn: Toán 11, năm học 2023-2024 (Đề thi có 4 trang) Thời gian làm bài 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 002 A. PHẦN TRẮC NGHIỆM
Câu 1. Trong không gian, cho hai đường thẳng chéo nhau a và b. Có tất cả bao nhiêu mặt phẳng
chứa a và song song với b? A. 1. B. 2. C. 0. D. Vô số.
Câu 2. Cho các giới hạn lim f (x) = 2, lim g(x) = −3. Tính lim [3f (x) + 4g(x)]. x→x0 x→x0 x→x0 A. 18. B. −6. C. −12. D. −2. 1
Câu 3. Tập xác định của hàm số y = là sin 2x A. R \ {k2π; k ∈ Z}. B. R \ {kπ; k ∈ Z}. kπ n π o C. R \ ; k ∈ Z . D. R \ + kπ; k ∈ Z . 2 2 1
Câu 4. Nghiệm của phương trình cos x = − là 2 π 2π A. x = ± + k2π, k ∈ Z. B. x = ± + k2π, k ∈ Z. 6 3 π π C. x = ± + k2π, k ∈ Z. D. x = ± + kπ, k ∈ Z. 3 6
Câu 5. Trong các mệnh đề sau, mệnh đề nào là sai? un
A. Nếu lim un = a, lim vn = +∞ thì lim = 0. n→+∞ n→+∞ n→+∞ vn un a
B. Nếu lim un = a, lim vn = b thì lim = . n→+∞ n→+∞ n→+∞ vn b 1 C. lim
= 0, k là số nguyên dương. n→+∞ nk D. lim n5 = +∞. n→+∞
Câu 6. Tìm khẳng định sai.
A. cos(a + b) = cos a · cos b − sin a · sin b.
B. cos(a − b) = cos a · cos b − sin a · sin b.
C. sin(a + b) = sin a · cos b + sin b · cos a.
D. sin(a − b) = sin a · cos b − sin b · cos a. 3 3π Câu 7. Cho cos α = với α ∈
; 2π . Khẳng định nào sau đây là sai? 4 2 √ √ 1 3 7 √ 7 A. cos 2α = . B. sin 2α = . C. tan 2α = −3 7. D. cot 2α = − . 8 8 21
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, I theo thứ
tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng? A. (N M P ) ∥ (SBD). B. (P ON ) ∥ (SAC). C. (N OM ) ∥ (OP M ). D. (M ON ) ∥ (SBC).
Câu 9. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì mọi đường thẳng nằm trong (P ) đều
song song với mọi đường thẳng nằm trong (Q).
B. Nếu mặt phẳng (P ) và mặt phẳng (Q) cùng song song với mặt phẳng (R) thì mặt phẳng
(P ) và mặt phẳng (Q) song song với nhau.
C. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì (P ) song song với mọi đường thẳng nằm trong (Q).
D. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) và đường thẳng a song song với mặt phẳng
(Q) thì đường thẳng a song song với mặt phẳng (P ). Trang 1/4 − Mã đề 002 3x + 1 Câu 10. Giá trị lim bằng x→1− −1 + x A. −∞. B. +∞. C. −2. D. 2.
Câu 11. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được
ghi lại ở bảng sau (đơn vị: triệu đồng): Doanh thu [5; 7) [7; 9) [9; 11) [11; 13) [13; 15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [9; 11). B. [13; 15). C. [11; 13). D. [7; 9).
Câu 12. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, BC. Trên đoạn BD lấy
điểm P sao cho BP = 3P D. Giao điểm của đường thẳng CD và mặt phẳng (M N P ) là
A. điểm S, với S là giao điểm của CD và M C.
B. điểm S, với S là giao điểm của CD và M P .
C. điểm S, với S là giao điểm của CD và M N .
D. điểm S, với S là giao điểm của CD và N P .
Câu 13. Cho hình chóp tứ giác S.ABCD, gọi M và N lần lượt là trung điểm của SA và SC.
Trong các khẳng định sau, khẳng định đúng là A. M N ∥ (SBC). B. M N ∥ (ABCD). C. M N ∥ (SCD). D. M N ∥ (SAB). (u1 = 2 Câu 14. Cho dãy số (u ∗ n) có , ∀n ∈ N . Tính u6. un+1 = 2un − 3 A. u6 = −61. B. u6 = 7. C. u6 = −29. D. u6 = −13. √ 3 7x + 1 − 1 a a Câu 15. Biết lim =
, trong đó a, b là các số nguyên dương và phân số tối giản. x→0 x b b
Tính giá trị của biểu thức P = ab. 7 3 A. 10. B. 21. C. . D. . 3 7
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Giao tuyến của (SAC) và (SBD) là A. SO. B. SC. C. SB. D. SA.
Câu 17. Người ta tiến hành phỏng vấn 40 người về điện thoại Iphone 15 Pro-Max. Người điều
tra yêu cầu cho điểm mẫu Iphone theo thang điểm là 100. Kết quả được trình bày trong bảng dưới. Nhóm [50;60) [60;70) [70;80) [80;90) [90;100) Tần số 4 5 23 6 2
Mốt của mẫu số liệu ghép nhóm trên (làm tròn đến kết quả hàng đơn vị) là A. 75. B. 73. C. 74. D. 76.
Câu 18. Trong các dãy số (un) cho bởi công thức số hạng tổng quát un, dãy số nào là dãy số tăng? 2n − 1 1 n + 5 1 A. un = . B. un = . C. un = . D. un = . n + 1 2n 3n + 1 n 2n2 − 3n + 1 Câu 19. Giới hạn lim bằng n→+∞ n + 1 A. −∞. B. 3. C. −3. D. +∞.
Câu 20. Cho hình lăng trụ có đáy là hình lục giác. Có bao nhiêu mặt của hình lăng trụ là hình bình hành? A. 8 mặt. B. 6 mặt. C. 5 mặt. D. 7 mặt. Trang 2/4 − Mã đề 002 2x − 2 a a Câu 21. Giả sử lim = , (với
là phân số tối giản và b là số nguyên dương). Tính x→1 x2 + 7x − 8 b2 b2 giá trị 2a + 3b. 2 A. 11. B. . C. 7. D. 13. 9 2 32
Câu 22. Cho cấp số nhân (un) có u1 = −3 và q = . Số −
là số hạng thứ bao nhiêu của cấp 3 81 số nhân? A. Số hạng thứ 8. B. Số hạng thứ 6. C. Số hạng thứ 5. D. Số hạng thứ 7.
Câu 23. Một cấp số cộng có 15 số hạng, biết tổng các số hạng của cấp số cộng bằng 225, số hạng
cuối bằng 29. Tìm số hạng đầu u1 của cấp số cộng đó. A. u1 = 1. B. u1 = 5. C. u1 = 3. D. u1 = 2. 2x + 3 Câu 24. Giá trị lim √ bằng x→−∞ 5x2 − 4x + 2 + x 2 −2 2 A. √ . B. √ . C. √ . D. 0. 5 + 1 5 − 1 5 Câu 25.
Cho tứ diện ABCD. Gọi M , N lần lượt là trung điểm BC và CD. A
Gọi d là giao tuyến của hai mặt phẳng (AM N ) và (ABD) (tham
khảo hình vẽ). Khẳng định nào sau đây đúng?
A. d đi qua A và song song với BD.
B. d đi qua A và song song với N B.
C. d đi qua A và song song với M D. B D
D. d đi qua A và song song với BC. M N C
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J , E, F lần lượt là
trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song với IJ ? A. EF . B. AD. C. CD. D. AB. Câu 27.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J S
lần lượt là trọng tâm của các tam giác SAB và SAD, P là trung
điểm của BC (tham khảo hình vẽ bên). Gọi E là giao điểm của SA SE I và (IJ P ). Tính tỉ số . SA J SE 3 SE 5 SE 2 SE 4 A. = . B. = . C. = . D. = . SA 5 SA 8 SA 3 SA 7 A B D P C Câu 28.
Các số hạng được viết trong các ô vuông tạo thành một cấp số
nhân từ trên xuống dưới và một cấp số cộng từ trái sang phải 5
(tham khảo hình vẽ). Số x được viết trong hình vuông dưới đây là bao nhiêu? A. 45. B. 768. C. 243. D. 405. 3 87 x Trang 3/4 − Mã đề 002 (u1 = 9 un
Câu 29. Cho dãy số (un) thỏa mãn . Tính giới hạn lim . u ∗
n+1 = 3un + 2.5n − 4, ∀n ∈ N n→+∞ 3.4n + 4.5n 2 1 A. 0. B. . C. . D. +∞. 3 4 √
Câu 30. Cho các số thực a, b, c thỏa mãn a + c2 = 18 và lim ax2 + bx − cx = −4. Tính x→+∞ P = a2 + b2 + c2. A. P = 666. B. P = 888. C. P = 777. D. P = 555. B. PHẦN TỰ LUẬN
Câu 1 (1,0 điểm). Tính các giới hạn sau: −2x2 + 5x − 3 1. lim . x→1 x2 − 4x + 3 √ 2. lim x2 − x + 1 − x. x→+∞ √  x + 2 − 2  nếu x > 2
Câu 2 (1,0 điểm). Cho hàm số f (x) = x2 − 2x
. Tìm m để hàm số có giới mx + 1 nếu x ≤ 2 hạn tại x0 = 2.
Câu 3 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD ∥ BC và
AD = 2BC. Gọi N là trung điểm của SA; G, I lần lượt là trọng tâm của △SAB và △ABD.
1. Chứng minh rằng GI ∥ (SBD) và (BGI) ∥ (SCD).
2. Tìm giao điểm F của DN và mặt phẳng (SBC).
Câu 4 (0,5 điểm). Vườn bưởi Diễn nhà bà Hiền đang vào mua thu hoạch, các thương lái tấp
nập đến mua bưởi. Biết rằng bà Hiền đã bán cho người thứ nhất nửa số bưởi thu hoạch được và
tặng thêm 1 quả, bán cho người thứ hai nửa số bưởi còn lại và tặng thêm 1 quả. Bà Hiền cứ tiếp
tục cách bán như trên thì đến người thứ 15 số bưởi của bà được bán hết. Tính số bưởi mà bà Hiền thu hoạch được. HẾT Trang 4/4 − Mã đề 002
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Môn: Toán 11, năm học 2023-2024 (Đề thi có 4 trang) Thời gian làm bài 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 003 A. PHẦN TRẮC NGHIỆM
Câu 1. Trong các mệnh đề sau, mệnh đề nào là sai? un
A. Nếu lim un = a, lim vn = +∞ thì lim = 0. n→+∞ n→+∞ n→+∞ vn 1 B. lim
= 0, k là số nguyên dương. n→+∞ nk un a
C. Nếu lim un = a, lim vn = b thì lim = . n→+∞ n→+∞ n→+∞ vn b D. lim n5 = +∞. n→+∞
Câu 2. Tìm khẳng định sai.
A. cos(a + b) = cos a · cos b − sin a · sin b.
B. cos(a − b) = cos a · cos b − sin a · sin b.
C. sin(a − b) = sin a · cos b − sin b · cos a.
D. sin(a + b) = sin a · cos b + sin b · cos a.
Câu 3. Trong không gian, cho hai đường thẳng chéo nhau a và b. Có tất cả bao nhiêu mặt phẳng
chứa a và song song với b? A. Vô số. B. 2. C. 1. D. 0.
Câu 4. Cho các giới hạn lim f (x) = 2, lim g(x) = −3. Tính lim [3f (x) + 4g(x)]. x→x0 x→x0 x→x0 A. 18. B. −6. C. −2. D. −12. 1
Câu 5. Nghiệm của phương trình cos x = − là 2 2π π A. x = ± + k2π, k ∈ Z. B. x = ± + k2π, k ∈ Z. 3 6 π π C. x = ± + k2π, k ∈ Z. D. x = ± + kπ, k ∈ Z. 3 6 1
Câu 6. Tập xác định của hàm số y = là sin 2x kπ A. R \ ; k ∈ Z . B. R \ {kπ; k ∈ Z}. 2 n π o C. R \ + kπ; k ∈ Z . D. R \ {k2π; k ∈ Z}. 2 √ 3 7x + 1 − 1 a a Câu 7. Biết lim =
, trong đó a, b là các số nguyên dương và phân số tối giản. x→0 x b b
Tính giá trị của biểu thức P = ab. 3 7 A. . B. . C. 10. D. 21. 7 3 2n2 − 3n + 1 Câu 8. Giới hạn lim bằng n→+∞ n + 1 A. −3. B. 3. C. +∞. D. −∞. 2x − 2 a a Câu 9. Giả sử lim = , (với
là phân số tối giản và b là số nguyên dương). Tính x→1 x2 + 7x − 8 b2 b2 giá trị 2a + 3b. 2 A. 7. B. 11. C. 13. D. . 9
Câu 10. Người ta tiến hành phỏng vấn 40 người về điện thoại Iphone 15 Pro-Max. Người điều
tra yêu cầu cho điểm mẫu Iphone theo thang điểm là 100. Kết quả được trình bày trong bảng dưới. Trang 1/4 − Mã đề 003 Nhóm [50;60) [60;70) [70;80) [80;90) [90;100) Tần số 4 5 23 6 2
Mốt của mẫu số liệu ghép nhóm trên (làm tròn đến kết quả hàng đơn vị) là A. 74. B. 75. C. 76. D. 73.
Câu 11. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được
ghi lại ở bảng sau (đơn vị: triệu đồng): Doanh thu [5; 7) [7; 9) [9; 11) [11; 13) [13; 15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [11; 13). B. [9; 11). C. [7; 9). D. [13; 15).
Câu 12. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu mặt phẳng (P ) và mặt phẳng (Q) cùng song song với mặt phẳng (R) thì mặt phẳng
(P ) và mặt phẳng (Q) song song với nhau.
B. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) và đường thẳng a song song với mặt phẳng
(Q) thì đường thẳng a song song với mặt phẳng (P ).
C. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì (P ) song song với mọi đường thẳng nằm trong (Q).
D. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì mọi đường thẳng nằm trong (P ) đều
song song với mọi đường thẳng nằm trong (Q).
Câu 13. Một cấp số cộng có 15 số hạng, biết tổng các số hạng của cấp số cộng bằng 225, số hạng
cuối bằng 29. Tìm số hạng đầu u1 của cấp số cộng đó. A. u1 = 3. B. u1 = 1. C. u1 = 2. D. u1 = 5. Câu 14.
Cho tứ diện ABCD. Gọi M , N lần lượt là trung điểm BC và CD. A
Gọi d là giao tuyến của hai mặt phẳng (AM N ) và (ABD) (tham
khảo hình vẽ). Khẳng định nào sau đây đúng?
A. d đi qua A và song song với M D.
B. d đi qua A và song song với BD.
C. d đi qua A và song song với BC. B D
D. d đi qua A và song song với N B. M N C
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Giao tuyến của (SAC) và (SBD) là A. SO. B. SC. C. SA. D. SB. 3x + 1 Câu 16. Giá trị lim bằng x→1− −1 + x A. −2. B. −∞. C. 2. D. +∞.
Câu 17. Cho hình lăng trụ có đáy là hình lục giác. Có bao nhiêu mặt của hình lăng trụ là hình bình hành? A. 8 mặt. B. 5 mặt. C. 6 mặt. D. 7 mặt.
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J , E, F lần lượt là
trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song với IJ ? A. CD. B. EF . C. AD. D. AB. Trang 2/4 − Mã đề 003
Câu 19. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, BC. Trên đoạn BD lấy
điểm P sao cho BP = 3P D. Giao điểm của đường thẳng CD và mặt phẳng (M N P ) là
A. điểm S, với S là giao điểm của CD và M P .
B. điểm S, với S là giao điểm của CD và M C.
C. điểm S, với S là giao điểm của CD và M N .
D. điểm S, với S là giao điểm của CD và N P . 3 3π Câu 20. Cho cos α = với α ∈
; 2π . Khẳng định nào sau đây là sai? 4 2 √ √ 3 7 √ 1 7 A. sin 2α = . B. tan 2α = −3 7. C. cos 2α = . D. cot 2α = − . 8 8 21
Câu 21. Cho hình chóp tứ giác S.ABCD, gọi M và N lần lượt là trung điểm của SA và SC.
Trong các khẳng định sau, khẳng định đúng là A. M N ∥ (SCD). B. M N ∥ (ABCD). C. M N ∥ (SAB). D. M N ∥ (SBC). 2x + 3 Câu 22. Giá trị lim √ bằng x→−∞ 5x2 − 4x + 2 + x 2 2 −2 A. √ . B. √ . C. √ . D. 0. 5 5 + 1 5 − 1 2 32
Câu 23. Cho cấp số nhân (un) có u1 = −3 và q = . Số −
là số hạng thứ bao nhiêu của cấp 3 81 số nhân? A. Số hạng thứ 8. B. Số hạng thứ 6. C. Số hạng thứ 7. D. Số hạng thứ 5. (u1 = 2 Câu 24. Cho dãy số (u ∗ n) có , ∀n ∈ N . Tính u6. un+1 = 2un − 3 A. u6 = −61. B. u6 = −13. C. u6 = −29. D. u6 = 7.
Câu 25. Trong các dãy số (un) cho bởi công thức số hạng tổng quát un, dãy số nào là dãy số tăng? 1 n + 5 2n − 1 1 A. un = . B. un = . C. un = . D. un = . n 3n + 1 n + 1 2n
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, I theo thứ
tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng? A. (M ON ) ∥ (SBC). B. (P ON ) ∥ (SAC). C. (N M P ) ∥ (SBD). D. (N OM ) ∥ (OP M ). Câu 27.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J S
lần lượt là trọng tâm của các tam giác SAB và SAD, P là trung
điểm của BC (tham khảo hình vẽ bên). Gọi E là giao điểm của SA SE I và (IJ P ). Tính tỉ số . SA J SE 4 SE 2 SE 3 SE 5 A. = . B. = . C. = . D. = . SA 7 SA 3 SA 5 SA 8 A B D P C Câu 28. Trang 3/4 − Mã đề 003
Các số hạng được viết trong các ô vuông tạo thành một cấp số
nhân từ trên xuống dưới và một cấp số cộng từ trái sang phải 5
(tham khảo hình vẽ). Số x được viết trong hình vuông dưới đây là bao nhiêu? A. 768. B. 243. C. 45. D. 405. 3 87 x (u1 = 9 un
Câu 29. Cho dãy số (un) thỏa mãn . Tính giới hạn lim . u ∗
n+1 = 3un + 2.5n − 4, ∀n ∈ N n→+∞ 3.4n + 4.5n 2 1 A. . B. . C. +∞. D. 0. 3 4 √
Câu 30. Cho các số thực a, b, c thỏa mãn a + c2 = 18 và lim ax2 + bx − cx = −4. Tính x→+∞ P = a2 + b2 + c2. A. P = 888. B. P = 666. C. P = 555. D. P = 777. B. PHẦN TỰ LUẬN
Câu 1 (1,0 điểm). Tính các giới hạn sau: −2x2 + 5x − 3 1. lim . x→1 x2 − 4x + 3 √ 2. lim x2 − x + 1 − x. x→+∞ √  x + 2 − 2  nếu x > 2
Câu 2 (1,0 điểm). Cho hàm số f (x) = x2 − 2x
. Tìm m để hàm số có giới mx + 1 nếu x ≤ 2 hạn tại x0 = 2.
Câu 3 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD ∥ BC và
AD = 2BC. Gọi N là trung điểm của SA; G, I lần lượt là trọng tâm của △SAB và △ABD.
1. Chứng minh rằng GI ∥ (SBD) và (BGI) ∥ (SCD).
2. Tìm giao điểm F của DN và mặt phẳng (SBC).
Câu 4 (0,5 điểm). Vườn bưởi Diễn nhà bà Hiền đang vào mua thu hoạch, các thương lái tấp
nập đến mua bưởi. Biết rằng bà Hiền đã bán cho người thứ nhất nửa số bưởi thu hoạch được và
tặng thêm 1 quả, bán cho người thứ hai nửa số bưởi còn lại và tặng thêm 1 quả. Bà Hiền cứ tiếp
tục cách bán như trên thì đến người thứ 15 số bưởi của bà được bán hết. Tính số bưởi mà bà Hiền thu hoạch được. HẾT Trang 4/4 − Mã đề 003
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Môn: Toán 11, năm học 2023-2024 (Đề thi có 4 trang) Thời gian làm bài 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 004 A. PHẦN TRẮC NGHIỆM 1
Câu 1. Tập xác định của hàm số y = là sin 2x n π o A. R \ {kπ; k ∈ Z}. B. R \ + kπ; k ∈ Z . 2 kπ C. R \ {k2π; k ∈ Z}. D. R \ ; k ∈ Z . 2
Câu 2. Trong các mệnh đề sau, mệnh đề nào là sai? A. lim n5 = +∞. n→+∞ un
B. Nếu lim un = a, lim vn = +∞ thì lim = 0. n→+∞ n→+∞ n→+∞ vn 1 C. lim
= 0, k là số nguyên dương. n→+∞ nk un a
D. Nếu lim un = a, lim vn = b thì lim = . n→+∞ n→+∞ n→+∞ vn b 1
Câu 3. Nghiệm của phương trình cos x = − là 2 π 2π A. x = ± + kπ, k ∈ Z. B. x = ± + k2π, k ∈ Z. 6 3 π π C. x = ± + k2π, k ∈ Z. D. x = ± + k2π, k ∈ Z. 6 3
Câu 4. Tìm khẳng định sai.
A. sin(a − b) = sin a · cos b − sin b · cos a.
B. sin(a + b) = sin a · cos b + sin b · cos a.
C. cos(a − b) = cos a · cos b − sin a · sin b.
D. cos(a + b) = cos a · cos b − sin a · sin b.
Câu 5. Trong không gian, cho hai đường thẳng chéo nhau a và b. Có tất cả bao nhiêu mặt phẳng
chứa a và song song với b? A. 1. B. 0. C. 2. D. Vô số.
Câu 6. Cho các giới hạn lim f (x) = 2, lim g(x) = −3. Tính lim [3f (x) + 4g(x)]. x→x0 x→x0 x→x0 A. −2. B. −12. C. −6. D. 18. Câu 7.
Cho tứ diện ABCD. Gọi M , N lần lượt là trung điểm BC và CD. A
Gọi d là giao tuyến của hai mặt phẳng (AM N ) và (ABD) (tham
khảo hình vẽ). Khẳng định nào sau đây đúng?
A. d đi qua A và song song với M D.
B. d đi qua A và song song với BC.
C. d đi qua A và song song với BD. B D
D. d đi qua A và song song với N B. M N C 2x + 3 Câu 8. Giá trị lim √ bằng x→−∞ 5x2 − 4x + 2 + x 2 −2 2 A. 0. B. √ . C. √ . D. √ . 5 5 − 1 5 + 1
Câu 9. Trong các dãy số (un) cho bởi công thức số hạng tổng quát un, dãy số nào là dãy số tăng? n + 5 1 2n − 1 1 A. un = . B. un = . C. un = . D. un = . 3n + 1 n n + 1 2n Trang 1/4 − Mã đề 004 (u1 = 2 Câu 10. Cho dãy số (u ∗ n) có , ∀n ∈ N . Tính u6. un+1 = 2un − 3 A. u6 = −61. B. u6 = 7. C. u6 = −13. D. u6 = −29.
Câu 11. Cho hình lăng trụ có đáy là hình lục giác. Có bao nhiêu mặt của hình lăng trụ là hình bình hành? A. 8 mặt. B. 5 mặt. C. 7 mặt. D. 6 mặt.
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J , E, F lần lượt là
trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song với IJ ? A. AB. B. EF . C. CD. D. AD.
Câu 13. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được
ghi lại ở bảng sau (đơn vị: triệu đồng): Doanh thu [5; 7) [7; 9) [9; 11) [11; 13) [13; 15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [11; 13). B. [9; 11). C. [13; 15). D. [7; 9).
Câu 14. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì mọi đường thẳng nằm trong (P ) đều
song song với mọi đường thẳng nằm trong (Q).
B. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) và đường thẳng a song song với mặt phẳng
(Q) thì đường thẳng a song song với mặt phẳng (P ).
C. Nếu mặt phẳng (P ) song song với mặt phẳng (Q) thì (P ) song song với mọi đường thẳng nằm trong (Q).
D. Nếu mặt phẳng (P ) và mặt phẳng (Q) cùng song song với mặt phẳng (R) thì mặt phẳng
(P ) và mặt phẳng (Q) song song với nhau. 3x + 1 Câu 15. Giá trị lim bằng x→1− −1 + x A. 2. B. −∞. C. +∞. D. −2.
Câu 16. Cho hình chóp tứ giác S.ABCD, gọi M và N lần lượt là trung điểm của SA và SC.
Trong các khẳng định sau, khẳng định đúng là A. M N ∥ (SAB). B. M N ∥ (SCD). C. M N ∥ (SBC). D. M N ∥ (ABCD).
Câu 17. Người ta tiến hành phỏng vấn 40 người về điện thoại Iphone 15 Pro-Max. Người điều
tra yêu cầu cho điểm mẫu Iphone theo thang điểm là 100. Kết quả được trình bày trong bảng dưới. Nhóm [50;60) [60;70) [70;80) [80;90) [90;100) Tần số 4 5 23 6 2
Mốt của mẫu số liệu ghép nhóm trên (làm tròn đến kết quả hàng đơn vị) là A. 75. B. 76. C. 74. D. 73. 2x − 2 a a Câu 18. Giả sử lim = , (với
là phân số tối giản và b là số nguyên dương). Tính x→1 x2 + 7x − 8 b2 b2 giá trị 2a + 3b. 2 A. . B. 11. C. 7. D. 13. 9 2n2 − 3n + 1 Câu 19. Giới hạn lim bằng n→+∞ n + 1 A. −∞. B. +∞. C. 3. D. −3. Trang 2/4 − Mã đề 004
Câu 20. Một cấp số cộng có 15 số hạng, biết tổng các số hạng của cấp số cộng bằng 225, số hạng
cuối bằng 29. Tìm số hạng đầu u1 của cấp số cộng đó. A. u1 = 3. B. u1 = 1. C. u1 = 5. D. u1 = 2.
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, I theo thứ
tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng? A. (N M P ) ∥ (SBD). B. (P ON ) ∥ (SAC). C. (M ON ) ∥ (SBC). D. (N OM ) ∥ (OP M ). 3 3π Câu 22. Cho cos α = với α ∈
; 2π . Khẳng định nào sau đây là sai? 4 2 √ √ √ 1 7 3 7 A. tan 2α = −3 7. B. cos 2α = . C. cot 2α = − . D. sin 2α = . 8 21 8 2 32
Câu 23. Cho cấp số nhân (un) có u1 = −3 và q = . Số −
là số hạng thứ bao nhiêu của cấp 3 81 số nhân? A. Số hạng thứ 6. B. Số hạng thứ 5. C. Số hạng thứ 7. D. Số hạng thứ 8. √ 3 7x + 1 − 1 a a Câu 24. Biết lim =
, trong đó a, b là các số nguyên dương và phân số tối giản. x→0 x b b
Tính giá trị của biểu thức P = ab. 3 7 A. 21. B. . C. . D. 10. 7 3
Câu 25. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, BC. Trên đoạn BD lấy
điểm P sao cho BP = 3P D. Giao điểm của đường thẳng CD và mặt phẳng (M N P ) là
A. điểm S, với S là giao điểm của CD và M N .
B. điểm S, với S là giao điểm của CD và N P .
C. điểm S, với S là giao điểm của CD và M C.
D. điểm S, với S là giao điểm của CD và M P .
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Giao tuyến của (SAC) và (SBD) là A. SA. B. SO. C. SB. D. SC. Câu 27.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J S
lần lượt là trọng tâm của các tam giác SAB và SAD, P là trung
điểm của BC (tham khảo hình vẽ bên). Gọi E là giao điểm của SA SE I và (IJ P ). Tính tỉ số . SA J SE 4 SE 3 SE 5 SE 2 A. = . B. = . C. = . D. = . SA 7 SA 5 SA 8 SA 3 A B D P C Câu 28.
Các số hạng được viết trong các ô vuông tạo thành một cấp số
nhân từ trên xuống dưới và một cấp số cộng từ trái sang phải 5
(tham khảo hình vẽ). Số x được viết trong hình vuông dưới đây là bao nhiêu? A. 768. B. 243. C. 405. D. 45. 3 87 x Trang 3/4 − Mã đề 004 (u1 = 9 un
Câu 29. Cho dãy số (un) thỏa mãn . Tính giới hạn lim . u ∗
n+1 = 3un + 2.5n − 4, ∀n ∈ N n→+∞ 3.4n + 4.5n 1 2 A. +∞. B. . C. . D. 0. 4 3 √
Câu 30. Cho các số thực a, b, c thỏa mãn a + c2 = 18 và lim ax2 + bx − cx = −4. Tính x→+∞ P = a2 + b2 + c2. A. P = 777. B. P = 555. C. P = 666. D. P = 888. B. PHẦN TỰ LUẬN
Câu 1 (1,0 điểm). Tính các giới hạn sau: −2x2 + 5x − 3 1. lim . x→1 x2 − 4x + 3 √ 2. lim x2 − x + 1 − x. x→+∞ √  x + 2 − 2  nếu x > 2
Câu 2 (1,0 điểm). Cho hàm số f (x) = x2 − 2x
. Tìm m để hàm số có giới mx + 1 nếu x ≤ 2 hạn tại x0 = 2.
Câu 3 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD ∥ BC và
AD = 2BC. Gọi N là trung điểm của SA; G, I lần lượt là trọng tâm của △SAB và △ABD.
1. Chứng minh rằng GI ∥ (SBD) và (BGI) ∥ (SCD).
2. Tìm giao điểm F của DN và mặt phẳng (SBC).
Câu 4 (0,5 điểm). Vườn bưởi Diễn nhà bà Hiền đang vào mua thu hoạch, các thương lái tấp
nập đến mua bưởi. Biết rằng bà Hiền đã bán cho người thứ nhất nửa số bưởi thu hoạch được và
tặng thêm 1 quả, bán cho người thứ hai nửa số bưởi còn lại và tặng thêm 1 quả. Bà Hiền cứ tiếp
tục cách bán như trên thì đến người thứ 15 số bưởi của bà được bán hết. Tính số bưởi mà bà Hiền thu hoạch được. HẾT Trang 4/4 − Mã đề 004 1 Sở GD & ĐT Hà Nội ĐÁP ÁN − THANG ĐIỂM
Trường THPT Nguyễn Thị Minh Khai
ĐỀ KIỂM TRA HỌC KÌ I LỚP 11
Môn: Toán; Năm học: 2023-2024
(Đáp án − Thang điểm gồm 02 trang) Câu Đáp án Điểm −2x2 + 5x − 3 1 1. (0,5 điểm) lim x→1 x2 − 4x + 3 −2x2 + 5x − 3 (x − 1)(−2x + 3) (1,0đ) Ta có lim = lim 0,25 x→1 x2 − 4x + 3 x→1 (x − 1)(x − 3) −2x + 3 1 = lim = − 0,25 x→1 x − 3 2 √ 2. (0,5 điểm) lim x2 − x + 1 − x x→+∞ Ta có: h√ i h√ i x2 − x + 1 + x x2 − x + 1 − x √ lim x2 − x + 1 − x = lim √ x→+∞ x→+∞ x2 − x + 1 + x 0,25 −x + 1 = lim √ x→+∞ x2 − x + 1 + x 1 −x + 1 −1 + 1 = lim = lim x = − . 0,25 x→−∞ r 1 1 x→+∞ r 1 1 2 x 1 − + + x 1 − + + 1 x x2 x x2 √  x + 2 − 2  nếu x > 2 2 Cho hàm số f (x) = x2 − 2x
. Tìm m để hàm số có giới hạn tại x0 = 2. mx + 1 nếu x ≤ 2 (1,0đ)
lim f (x) = lim (mx + 1) = 2m + 1. 0,25 x→2− x→2− √x + 2 − 2 x − 2 lim f (x) = lim = lim √ 0,25 x→2+ x→2+ x2 − 2x x→2+ x(x − 2) x + 2 + 2 1 1 = lim √ = x→2+ x x + 2 + 2 8
Hàm số có giới hạn tại x0 = 2 khi và chỉ khi lim f (x) = lim f (x) 0,25 x→2+ x→2− 1 7 ⇔ 2m + 1 = ⇔ m = − . 0,25 8 16 3 Hình vẽ: (1,5đ) S F ∆ N G A D H I M B C 2 Câu Đáp án Điểm M G M I 1
1. Gọi M , H lần lượt là trung điểm các cạnh AB và AD. Ta có = = ⇒ 0,5 GS ID 2 GI ∥ SD ⇒ GI ∥ (SBD)
Vì HD = BC và HD ∥ BC nên tứ giác BCHD là hình bình hành ⇒ BH ∥ DC. Mặt 0,5
khác GI ∥ SD ⇒ (BGI) ∥ (SCD).
2. Qua S kẻ đường thẳng ∆ ∥ AD. Ta có ∆ = (SBC) ∩ (SAD). 0,25
Do đó F là giao điểm của N D và ∆. 0,25 4
Gọi x là số bưởi bà Hiền thu hoạch được (x ∈ ∗). Khi đó: (0,5đ) N x x + 2
• Số quả bưởi người thứ nhất mua và được tặng là: + 1 = . 2 2 1 x + 2 x + 2
• Số quả bưởi người thứ hai mua và được tặng là: x − + 1 = . 2 2 22
• Số quả bưởi người thứ ba mua và được tặng là: 0,25 1 x + 2 x + 2 x + 2 x − − + 1 = . 2 2 22 23 x + 2 ...
• Số quả bưởi người thứ 15 mua và được tặng là: . 215 Ta có: x + 2 x + 2 x + 2 1 1 1 + + · · · + = x ⇔ (x + 2) + + ... + = x 2 22 215 2 22 215 1 15 1 − 1 2 32767 ⇔ (x + 2) . = x ⇔ (x + 2) = x ⇔ x = 65534. 0,25 2 1 32768 1 − 2 ——Hết——
Chú ý: Học sinh làm cách khác ra kết quả đúng vẫn cho điểm tuyệt đối.
Document Outline

  • ĐỀ HK1-11-NTMK-2023
  • ĐA-HK1-11-2023