SỞ GD VÀ ĐT HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT PHÙNG KHẮC
NĂM HỌC 2020 – 2021 KHOAN-THẠCH THẤT MÔN THI: TOÁN 11 ĐỀ CHÍ NH THỨC
Thời gian làm bài: 150 phút
(Không kể thời gian phát đề)
Đề thi gồm: 01 trang
Câu 1. (2,5 điểm) Giải phương trình 2
cos 2x = 2sin x + 4 cos x
Câu 2. (4,5 điểm) 2 2
 xy + x + y = x − 2y 
a. Giải hệ phương trình : 
x 2y − y x −1 = 2x − 2y  2 − − b. Tính giới hạn 2020(2021 x ) 2020 I = lim x 1 → x −1
Câu 3. (3,0 điểm) 15  3  a. Tìm hệ số của 9
x trong khai triển nhị thức Niu-tơn 2 2x −    x 
b. Cho một đa giác lồi (H ) có 30 đỉnh A A ...A . Gọi X là tập hợp các tam giác có 3 1 2 30
đỉnh là 3 đỉnh của (H ) . Chọn ngẫu nhiên 2 tam giác trong X . Tính xác suất để chọn được 2
tam giác là các tam giác có 1 cạnh là cạnh của đa giác (H ) .  7 u = 1  2
Câu 4. (3,0 điểm) Cho dãy số (u xác định bởi:  (n   ) n ) 7u + 4 n u  = n 1 +  2u + 5  n − a. Gọi ( u 2 v
là dãy số xác định bởi n v =
. Chứng minh rằng dãy số (v là một n ) n ) n u +1 n
cấp số nhân lùi vô hạn.
b. Tính giới hạn của dãy số (u n )
Câu 5. (5,0 điểm)
a. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, ( ) là mặt phẳng thay đổi
qua AB và cắt các cạnh SC, SD lần lượt tại M , N ( M khác S,C và N khác S, D . Gọi K là
giao điểm của hai đường thẳng AN và BM . Chứng minh rằng biểu thức AB BC T = − có MN SK
giá trị không đổi.
b.Cho hình lăng trụ tam giác ABC.A' B 'C ' có đáy là tam giác đều cạnh a, các mặt bên
đều là hình vuông. Gọi M , N , E lần lượt là trung điểm của các cạnh AB, AA', A'C '. Tính
diện tích thiết diện khi cắt lăng trụ ABC.A'B 'C ' bởi mặt phẳng (MNE) .
Câu 6. (2,0 điểm) ). Cho x, y, z là 3 số thực dương thỏa mãn x + y + z = 2 . Tìm giá trị lớn nhất của biểu thức: xy yz zx P = + + xy + 2z yz + 2x zx + 2 y
------------------ Hết ------------------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh: ………………………………….....… Số báo danh:……………
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI
ĐÁP ÁN ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG KHỐI 11
TRƯỜNG THPT PHÙNG KHẮC NĂM HỌC: 2020-2021 KHOAN MÔN: TOÁN - THẠCH THẤT -
Thời gian làm bài: 150 phút Câ Nội dung Điể u m
Giải phương trình sau: 2
cos 2x = 2sin x + 4 cos x 1 2.5 2
cos 2x = 2sin x + 4 cos x 2 2
 2cos x −1 = 2(1− cos x) + 4cos x 2
 4cos x − 4cos x − 3 = 0  3 1.5 cos x =  2   1 cos x = −  2 3 + cos x = (vô nghiệm) 2 1 2 + cos x = −  x =  + k2 , k  1.0 2 3 
KL: Vậy phương trình có nghiệm 2 x =  + k2 , k  3 2 2
xy + x + y = x − 2y  ( ) 2.a 1
a. Giải hệ phương trình :  2.0
x 2y − y x −1 = 2x − 2y  (2)
ĐK: x  1; y  0 ( ) 2 2 2
1  xy + y + x + y = x − y  + + + = − + 0.5 y(x y) (x y) (x y)(x y)
 (x + y)(y +1− x + y) = 0  x + y = 0  0.5  x = 2y +1
+) x + y = 0 (Loại do x  1; y  0 )
+) x = 2 y +1 thế vào (2) ta được
(2 y +1) 2 y − y 2 y = 4 y + 2 − 2 y
 2y(y +1) = 2y + 2 0.5
 ( y +1)( 2 y − 2) = 0  y = 1 −  
 2y = 2  y = 2  +) Với y = 1 − (L)
+) Với y = 2  x = 5 (TM ) 0.5
Vậy hệ phương trình có 1 nghiệm ( ; x y ) = (5;2) 2
2020(2021− x ) − 2020 2.b
Tính giới hạn I = lim 2,5 x 1 → x −1
2020(2021 − x ) − 2020 2020( 2 2021 − x ) 2 2 − 2020 1.0 I = lim = lim x 1 → x 1 x −1 → (x − ) 1 ( 2
2020(2021 − x ) + 2020) 2020( 2 1 − x ) 2020( 1 − − x) 2 − 1.5 = lim = lim = = 1 − x 1 → ( → x − )( 2 − x + ) x 1 ( 2 − x + ) 2 1 2020(2021 ) 2020 2020(2021 ) 2020 15  3  2 3.a Tìm hệ số của 9
x trong khai triển nhị thức Niutơn 2x −    1.5 x  15 k 15  3 − k    2 k x − = C .(2x )15 3 2 2 −     15  x  k =0  x  15 15 k k
= C .2 −k.( 3 − ) 30−3 . k x 0.5 15 k =0 Hệ số của 9
x trong khai triển tương ứng với k thỏa mãn: 30 − 3k = 9  k = 7 0.5 15  3  Hệ số của 9
x trong khai triển 2 2x −   là: 7 8 7 7 8 7 C .2 .( 3 − ) = C − .2 .3 0.5  x  15 15
Cho một đa giác lồi (H ) có 30 đỉnh A A ...A . Gọi X là tập hợp các tam 1.5 1 2 30 3.b
giác có 3 đỉnh là 3 đỉnh của (H ) . Chọn ngẫu nhiên 2 tam giác trong X .
Tính xác suất để chọn được 2 tam giác là các tam giác có 1 cạnh là cạnh của
đa giác (H ) .
Số tam giác có 3 đỉnh là 3 đỉnh của đa giác (H ) là: 3 C = 4060 30
Số phần tử của không gian mẫu 2 n() = C 4060 0.5
Gọi A là biến cố: ’’Hai tam giác được chọn là các tam giác có 1 cạnh là cạnh của đa giác (H ) ”.
+)Số tam giác có 1 cạnh là cạnh của (H ) :
- Chọn ra một cạnh của đa giác (H ) có 1 C 30
- Chọn ra 1 trong 26 đỉnh không kề với đỉnh thuộc cạnh đã chọn của (H ) có 1 C 26
 Số tam giác có 1 cạnh là cạnh của (H ) là 1 1
C .C = 780 0.5 30 26 2  n( ) A = C 780 0.5 2 C 247 780  P( ) A = = 2 C 6699 4060
KL: Vậy xác suất để chọn được 2 tam giác là tam giác có 1 cạnh là cạnh của đa giác 247 (H ) là 6699  7 4 u = 3.0 1  Cho dãy số ( 2 u
xác định bởi:  (n   ) n ) 7u + 4 n u  = n 1 +  2u + 5  n u −
a. Gọi (v là dãy số xác định bởi 2 n v =
. Chứng minh rằng dãy số n ) n u +1 n
(v là một cấp số nhân lùi vô hạn. n )
b. Tính giới hạn của dãy số (u n ) Ta có: 7u + 4 1.0 n − 2 u − 2 2u + 5 3u − 6 1 u − 2 1 n 1 + n n v = = = = . n = v n 1 + u +1 7u + 4 + + n 9u 9 3 u 1 3 n n 1 + +1 n n 2u + 5 n 1 1 u − 2 1 Suy ra v
= v . Vậy (v là một cấp số nhân với công bội 1 q = , v = = 1.0 n ) n 1 + 3 n 1 3 u +1 3 1
Vì q  1 nên (v là một cấp số nhân lùi vô hạn. n ) n 1 − n     n− 1 1 1 +) 1 v = v .q = =  lim v = 0 0.5 n 1     n 3  3   3  u − 2 2 + v n n Ta có v =  u = 0.5 n u +1 n 1− v n n + Do đó 2 v limu = lim n = 2 n 1− vn 5a
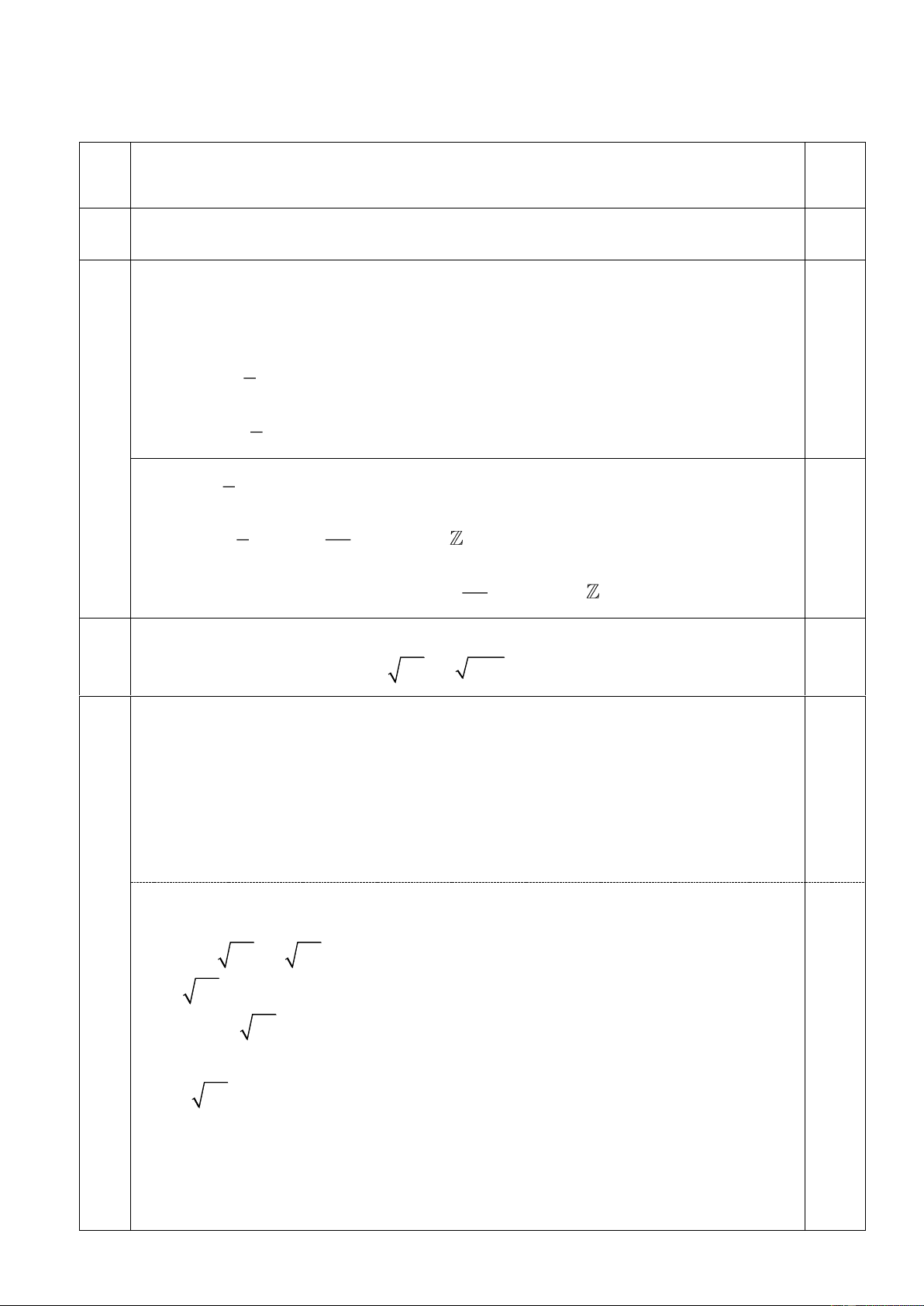
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, ( ) là mặt 2.0
phẳng thay đổi qua AB và cắt các cạnh SC, SD lần lượt tại M , N . Gọi K là
giao điểm của hai đường thẳng AN và BM . Chứng minh rằng biểu thức AB BC T = −
có giá trị không đổi. MN SK K S N M A D C Ta có B ( )  AB 
+) MN = ( )  (SCD)  MN AB CD  0.5 AB CD 
SK = (SAD) (SBC) +)   SK AD BC 0.5  AD BC Từ đó suy ra: AB CD CS = = 0.5 MN MN MS BC CM = SK SM 0.5 AB BC CS CM MS  − = − = =1 MN SK MS SM MS 5b
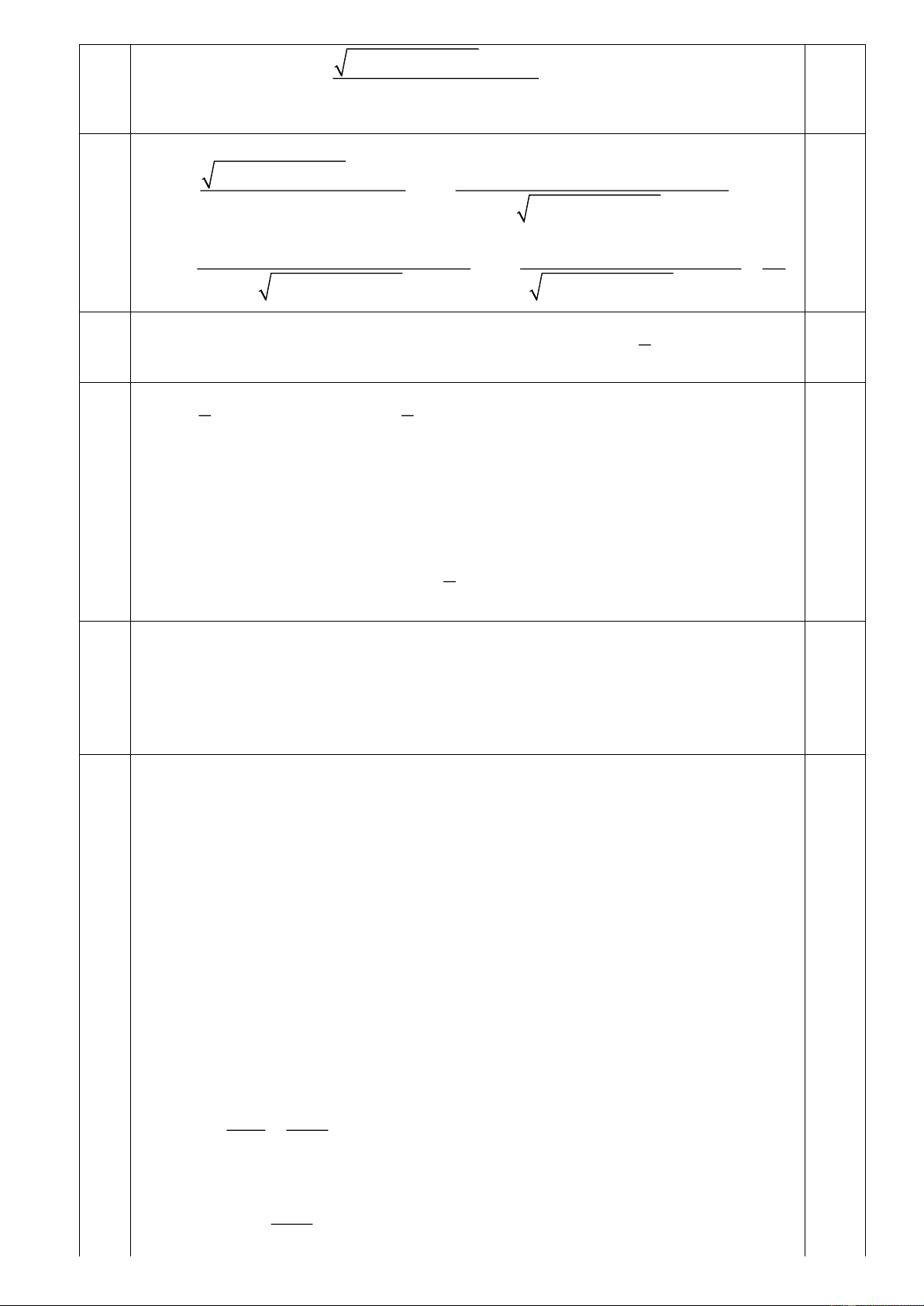
Cho hình lăng trụ tam giác ABC.A' B 'C ' có đáy là tam giác đều cạnh a, các 3.0
mặt bên đều là hình vuông. Gọi M , N , E lần lượt là trung điểm của các
cạnh AB, AA', A'C '. Tính diện tích thiết diện khi cắt lăng trụ ABC.A'B 'C '
bởi mặt phẳng (MNE) .
*) Dựng thiết diện I A C M H B N 0.5 E C' A' F B' J a
Trên ( ACC ' A') gọi NE  AC = I; NE  CC ' = J  AI=C'J= 2 a 1.0
Trên ( ABC ) gọi IM  BC = H  BH = 4 a
Trên ( BCC 'B ') gọi HJ  B 'C ' = F  FC '= 4 
Thiết diện là ngũ giác MNEFH 0.5
Tính diện tích thiết diện 2 a 3 3a 3 3a 3a 3a 5 18a 2 2 2 IH = 3MH = 3 = ; HJ = ( ) + ( ) = ; IJ = 4 4 4 2 4 4  HI  J vuông tại H 0.5 S IM .IN 2 1 2 S JE.JF 1 1 1 MNI EFJ = = . = ; = = . = S IH .IJ 3 3 9 S JI.JH 3 3 9 IHJ HIJ 2 2 1 3a 3 3a 5 3a 15  S = S − S − S = S = . . = 0.5 MNEFH IHJ MNI JEF I H J 3 3 4 4 16 6 2.0
Cho x, y, z là 3 số thực dương thỏa mãn x + y + z = 2 . Tìm giá trị lớn nhất của biểu thức: xy yz zx P = + + xy + 2z yz + 2x zx + 2 y Ta có: xy xy xy 1  x y  = =  +   0.5 xy + 2z
xy + z ( x + y + z )
(x + z)( y + z) 2 x + z y + z  Đẳng thức xảy ra x y  =  x = y x + z y + z   Tương tự yz 1 y z :  + 
 Đẳng thức xảy ra  y = z yz + 2x 2  y + x z + x  0.5 zx 1  z x   + 
 Đẳng thức xảy ra  z = x zx + 2 y 2  z + y x + y  xy yz zx 1  x + y y + z z + x  3  P = + +  + + =   0.5 xy + 2z yz + 2x zx + 2 y 2  x + y y + z z + x  2 Dấu bằng xảy ra khi 2
x = y = z = 3 Vậy 3 2 P
= khi x = y = z = 0.5 max 2 3
Nếu học sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì
vẫn cho đủ số điểm từng phần như hướng dẫn quy định.