Đề học sinh giỏi Toán 11 năm 2022 – 2023 trường THPT Phùng Khắc Khoan – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT PHÙNG KHẮC KHOAN -
CÁC MÔN VĂN HÓA KHỐI 10, 11 THẠCH THẤT NĂM HỌC 2022-2023
ĐỀ THI MÔN: TOÁN-LỚP 11 ĐỀ CHÍNH THỨC
Thời gian làm bài 150 phút, không kể thời gian giao đề (Đề thi gồm 2 trang)
Số báo danh:..................... Họ và tên .............................................................................
Câu 1 (2,5 điểm): cos 2x 1 Giải phương trình
+ (sin 2x + sin x −1) = 0 1+ tan x 2
Câu 2 (4,5 điểm):
a. Giải phương trình : ( x + )( x + ) 2 1
4 − 3 x + 5x + 2 = 6 5n  2 
b. Tìm số hạng không chứa x trong khai triển nhị thức Niu-tơn 3 x + , x  0   2  x 
biết n là số nguyên dương thỏa mãn: 2 2 3C + . n P = 4 A n 1 + 2 n
Câu 3 (3,0 điểm):
Từ các chữ số 0,1,3,5,7,8 có thể lập được bao nhiêu số có tám chữ số mà trong đó
chữ số 8 có mặt đúng 3 lần còn các chữ số khác xuất hiện đúng một lần?
Câu 4 (3,0 điểm): 2 3
(x + 2023) 1− 5x − 2023
a. Tính giới hạn I = lim x 0 → x u  = 2022; u = 2023 1 2 
b. Cho dãy số (u xác định bởi:  2u + u
(n  2, n ) n ) n n 1 u − =  n 1 +  3
Tính giới hạn của dãy số (u n )
Câu 5 (5,0 điểm):
1. Cho tứ diện ABCD gọi I , J lần lượt là trung điểm của AC, BC trên đoạn BD lấy
điểm K sao cho BK = 2KD ; Gọi E, F lần lượt là giao điểm của CD và AD với mặt
phẳng (IJK ) . Chứng minh rằng FK song song với IJ .
Đề thi môn Toán Lớp 11 Trang 1/ 2 trang
2. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D biết
AD = DC = a , AB = 2a ; SD = b . Trên đoạn AD lấy điểm M sao cho AM = x (0  x  a) .
Mặt phẳng ( ) qua M song song với AB và SD cắt BC,SB,SA lần lượt tại N, P,Q .
a. Chứng minh rằng NP luôn song song với một mặt phẳng cố định
b. Khi MN vuông góc với MQ , tìm x để tứ giác MNPQ có diện tích lớn nhất.
Câu 6 (2,0 điểm):
Cho các số thực không âm a,b,c thỏa mãn 2 2 2
a + b + c − 3b  0 . 1 4 8 Chứng minh rằng: + + 1 2 2 2 (a +1) (b + 2) (c + 3)
------------- HẾT -------------
(Thí sinh không dùng tài liệu, cán bộ coi thi không giải thích gì thêm)
Đề thi môn Toán Lớp 11 Trang 2/ 2 trang
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CẤP
TRƯỜNG THPT PHÙNG KHẮC
TRƯỜNG CÁC MÔN VĂN HÓA KHỐI 10, 11 KHOAN - THẠCH THẤT NĂM HỌC 2022-2023
ĐÁP ÁN ĐỀ THI MÔN: TOÁN. LỚP 11
Thời gian làm bài 150 phút, không kể thời gian giao đề Câ Nội dung Điể u m cos 2x 1 1
Giải phương trình sau:
+ (sin 2x + sin x −1) = 0 2.5 1+ tan x 2    x  + k  cos x  0  ĐK: 2    (k  ) tan x  1 −    0.5 x  − + k   4 cos 2x 1
+ (sin 2x + sin x −1) = 0 1 + tan x 2 2 2
2(cos x − sin x)cos x 
+ (sin 2x + sin x −1) = 0 1.0 cos x + sin x 2
 2cos x − 2sin xcos x + 2sin xcos x + sin x −1 = 0 2  2
− sin x + sin x +1 = 0  
sin x = 1  x = + k2  2      0.5 x = − + k2  1  6 sin x = −   2 7   x = + k2     6  7
Kết hợp đk pt có nghiệm: x = − + k2 , x =
+ k2 (k  ) 0.5 6 6 2.a
a. Giải phương trình : ( x + )( x + ) 2 1
4 − 3 x + 5x + 2 = 6 2.0 ( x + )( x + ) 2 2 2 1
4 − 3 x + 5x + 2 = 6  x + 5x + 2 − 3 x + 5x + 2 − 4 = 0 0.5 Đặt 2 t =
x + 5x + 2 (t  0)  0.5 t = 1 − (L) Ta được pt: 2
t − 3t − 4 = 0   t = 4 (TM )
Đề thi môn Toán Lớp 11 Trang 1/ 6 trang  x = 2 + Với 2 2 t = 4 
x + 5x + 2 = 4  x + 5x −14 = 0   x = 7 − 1.0
KL: PT có 2 nghiệm x = 2; x = 7 − 2b
Tìm số hạng không chứa x trong khai triển nhị thức Niu-tơn 5n  2  3 2.5 x + , x  0  
biết n là số nguyên dương thỏa mãn: 2 2 3C + .
n P = 4 A 2  + x  n 1 2 n
ĐK n  2, n  n +1 ! n! (n +1) 2 2 ( ) 3C + . n P = 4A  3. + 2n = 4.  3.
+ 2 = 4(n −1)  n = 3 1.0 n 1 + 2 n 2!(n −1)! (n − 2)! 2 +Với n = 3 5n 15 15 15  2   2  3 3 k 3(15−k ) k 2 − k k k 45 5 x + = x + = C x .2 .x =C 2 − k x     2 2 15 15  0.5 x   x  k =0 k =0
Số hạng không chứa x tương ứng với 45 − 5k = 0  k = 9 0.5
Số hạng không chứa x trong khai triển là 9 9 C 2 0.5 15 3
Từ các chữ số 0,1,3,5,7,8 có thể lập được bao nhiêu số có tám chữ số mà
trong đó chữ số 8 có mặt đúng 3 lần còn các chữ số khác xuất hiện đúng 3.0 một lần?
+ Xét các số có tám chữ số (kể cả chữ số 0 đứng đầu) Có 3
C = 56 cách chọn 3 vị trí cho chữ số 8 8 1.0
5 vị trí còn lại có 5! = 120 cách xếp các chữ số 0,1,3,5,7 Vậy có 56.120 = 6720 số
+ Xét các số có 8 chữ số có chữ số không đứng đầu Có 3
C = 35 cách chọn 3 vị trí cho chữ số 8 7 1.5
4 vị trí còn lại có 4! = 24 cách xếp các chữ số 1,3,5,7 Vậy có 35.24 = 840 số
Vậy số các số cần tìm là: 6720 − 840 = 5880 số 0.5 2 3
(x + 2023) 1− 5x − 2023 4a
Tính giới hạn I = lim 1.0 x 0 → x
Đề thi môn Toán Lớp 11 Trang 2/ 6 trang 2 3 3 x 1 − 5x 2023( 1 − 5x −1) = + I lim lim x→0 x→0 x x 0.5 2023( 5 − x) 3
= lim x 1− 5x + lim x→0 x→0 x( 2 3 3
(1 − 5x) + 1 − 5x + ) 1 0.25 2023( 5 − ) 10115 = 0 + lim = − 0.25 x→0 ( 2 3 3 − x + − x + ) 3 (1 5 ) 1 5 1 u  = 2022; u = 2023 4b 1 2  2.0
Cho dãy số (u xác định bởi:  2u + u
(n  2, n ) n ) n n 1 u − =  n 1 +  3
Tính giới hạn của dãy số (u n )
+ Với mọi n  2 ta có 2u + u 1 0.5 n n 1 u − =
 3u = 2u + u  3u − 3u = u
− + u  (u − u ) = − (u − u ) n 1 + n 1 + n n 1 − n 1 + n n n 1 − n 1 + n n n 1 − 3 3 (*)
Xét dãy số (v với v = u − u n ) n n 1 + n 1 1
Từ (*)  v = − v
 (v ) là một cấp số nhân với v = u − u =1; q = − n n 1 − 3 n 1 2 1 3 Ta có:
u = u − u
+ u − u + ...+ u − u + u = v + v + ...+ v + u n n n 1 − n 1 − n−2 2 1 1 n 1 − n−2 1 1 1.0 n 1 −  1  1 − − n 1 − n 1 −   n 1 1− q −  3  3   1   3 3  1  = v + u =1. + 2022 = 1  − −    + 2022 = + 2022 − −   1 1 1− q 1 4   3  +   4 4  3  1  3 n 1 −   3 8091 1 Ta có lim − = 0   . Vậy limu = 2022 + = 0.5 n  3  4 4 5.1
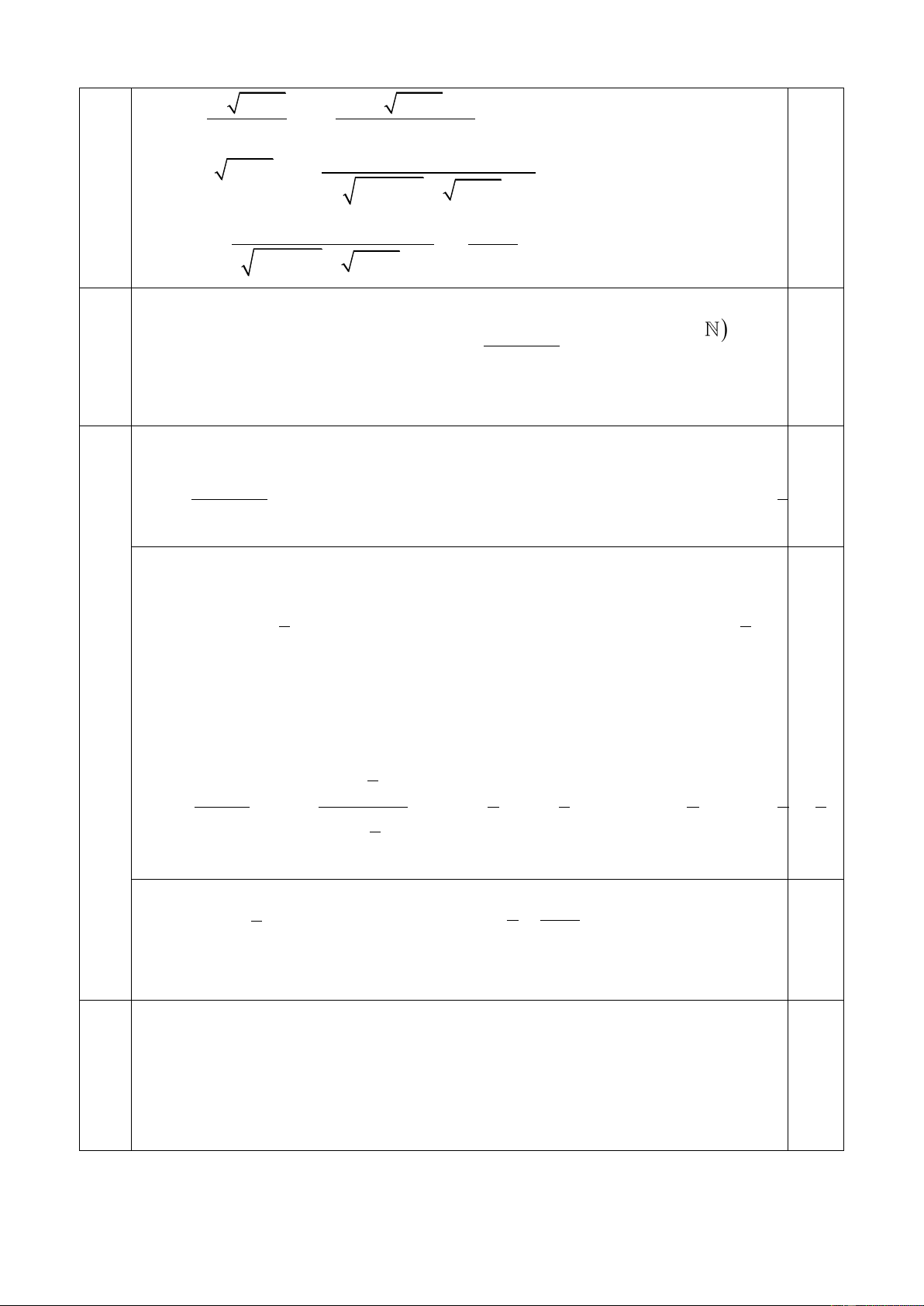
Cho tứ diện ABCD , gọi I , J lần lượt là trung điểm của AC, BC trên đoạn 1.0
BD lấy điểm K sao cho BK = 2KD ; Gọi E, F lần lượt là giao điểm của
CD và AD với mặt phẳng ( IJK ) . Chứng minh rằng FK song song với IJ .
Đề thi môn Toán Lớp 11 Trang 3/ 6 trang Vẽ hình: A F E I B K D 0.5 J C
Trong (IJK ) nối JK cắt CD tại E , nối EI cắt AD tại F . Ta có:
IJ  ( IJK ); AB  ( ABD), IJ / / AB, ( IJK )  ( ABD) = FK ; FK , IJ phân biệt 0.5
Suy ra FK / / IJ 5.2
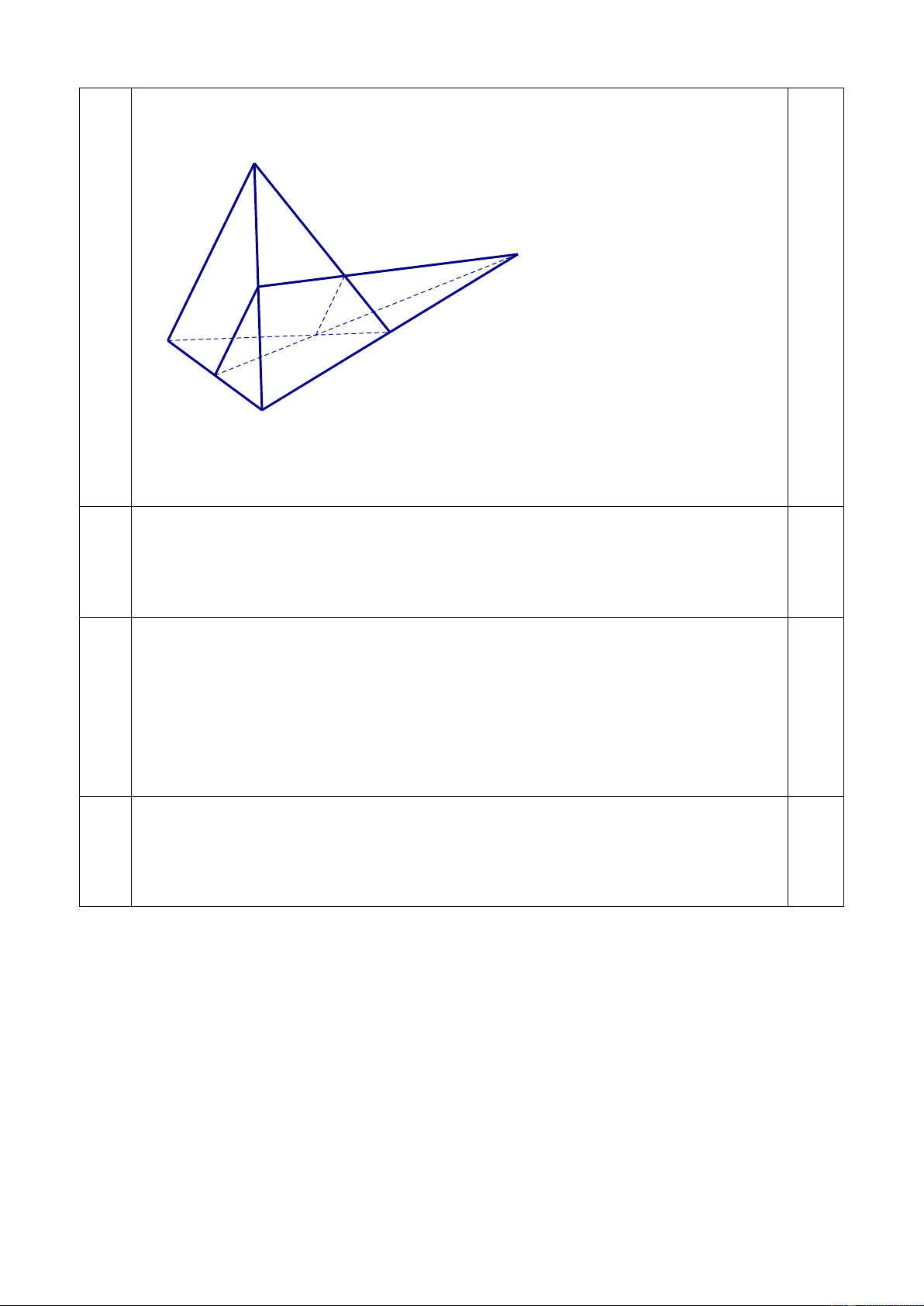
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D ; 4.0
AD = DC = a biết AB = 2a ; SD = b . Trên đoạn AD lấy điểm M sao cho
AM = x (0  x  a) . Mặt phẳng ( ) qua M song song với AB và SD cắt
BC, SB, SA lần lượt tại N , P,Q .
a. Chứng minh rằng NP luôn song song với một mặt phẳng cố định
b. Khi MN vuông góc với MQ , tìm x để tứ giác MNPQ có diện tích lớn nhất. 5.2.
Chứng minh rằng NP luôn song song với một mặt phẳng cố định 2.0 a
Đề thi môn Toán Lớp 11 Trang 4/ 6 trang 5.2. a S P Q 0.5 A B M N D C
+ Từ M kẻ đường thẳng song song với AB và SD lần lượt cắt BC tại N, SA tại Q
+ Từ Q kẻ đường thẳng song song với AB cắt SB tại P Ta có: AM AQ MQ / /SD  = AD AS 0.5 AM BN MN / / AB  = AD BC AQ BP PQ / / AB  = AS BS BN BP  =  NP / /SC mà
SC  (SCD), NP  (SCD). Do đó BC BS 1.0
NP / / (SCD) cố định 5.2.
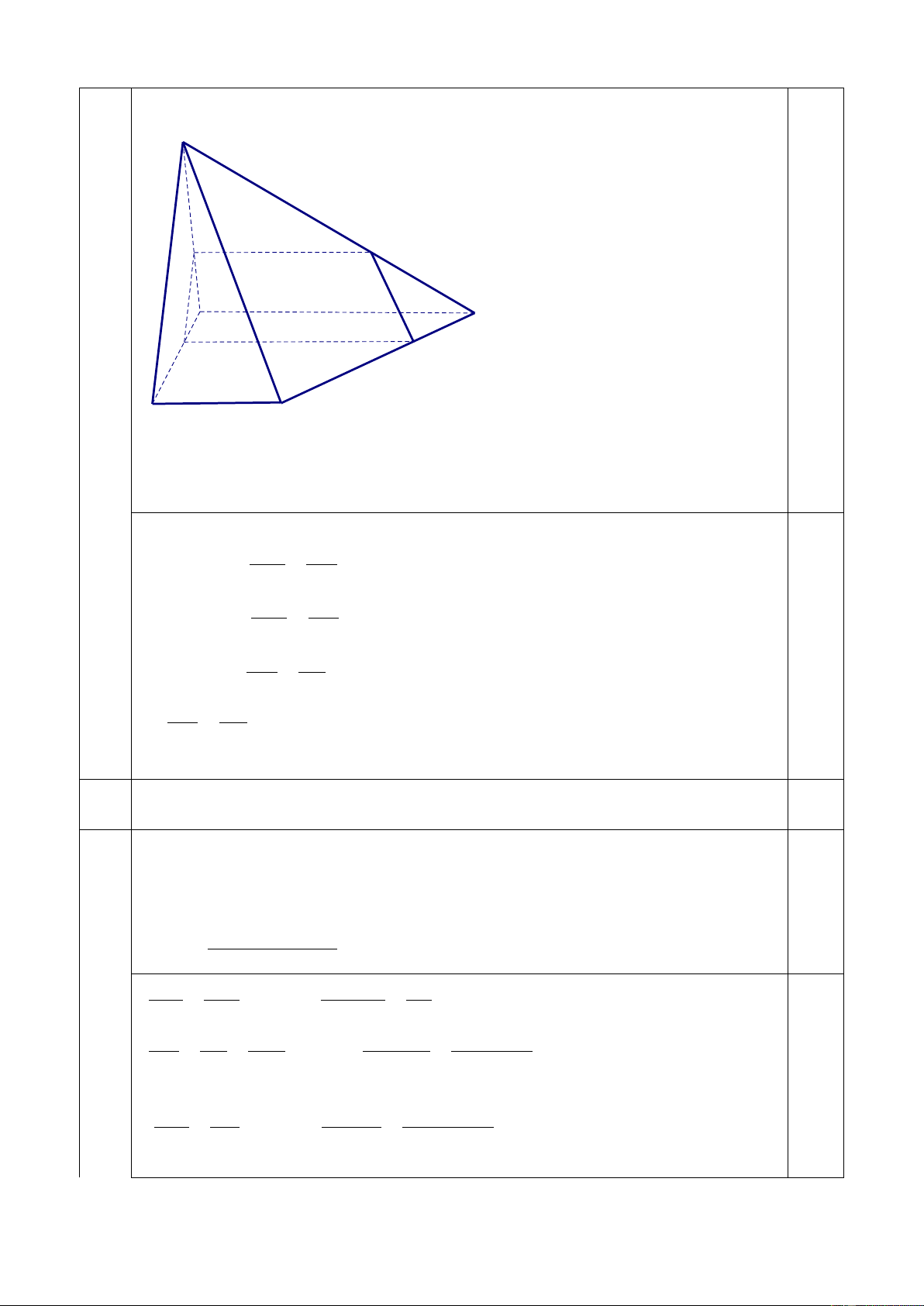
b. Khi MN vuông góc với MQ , tìm x để tứ giác MNPQ có diện tích lớn 2.0 b nhất.  PQ / / AB 
 PQ / /MN . Theo giả thiết MN ⊥ MQ . Tứ giác MNPQ là  MN / / AB 0.5
hình thang vuông tại M , Q
(MN + PQ)MQ S = MNPQ 2 MQ AM AM .SD . b x =  MQ = = SD AD AD a PQ SQ DM DM .AB
(a − x).2a = =  PQ = = = 2(a − x) AB SA AD AD a 0.75
Gọi I = AD  BC MN IM A . B IM 2 .
a (2a − x) =  MN = = = 2a − x AB IA IA 2a
Đề thi môn Toán Lớp 11 Trang 5/ 6 trang
(MN + PQ)MQ ( a − x + a − x) 2 2 2 2 bx b
b  a − x + x  0.5 S = = = a − x x  = ab   MNPQ ( ) 4 3 3 2 4 3 .3 2 2a 6a 6a  2  3 Dấu bằng xảy ra khi 2a
4a − 3x = 3x  x = 0.25 3
Vậy tứ giác MNPQ có diện tích lớn nhất khi 2a x = 3 6
Cho các số thực không âm a,b,c thỏa mãn 2 2 2
a + b + c − 3b  0 . 2.0 1 4 8 Chứng minh rằng: + + 1 2 2 2 (a +1) (b + 2) (c + 3)
+ Với 2 số thực dương x  0, y  0 ta có 2 2
 x + y  2xy  0.5 1 1 8   x + y x + y  8xy  +  . 2 ( )( )2 2 2 (  x + y  ) 2 2  4xy x y (x + y)2 + Áp dụng: 1 4 8 8 +  = 2 2 2 2 (a +1) (b + 2)  b   b  a +1+ +1 a + + 2      2   2  1 1 8 +  2 2 2  b  (c + 3)  b  0.75 a + + 2 a + + c + 5      2   2  2 8 8 8 16 P  +  8. = 2 2 2  b  (c + 3)  b 
(2a + b + 2c +10)2 a + + 2 a + + c + 5      2   2  Ta có: 2 2 2 2 2 2
(a −1) + (b − 2) + (c −1)  0  a + b + c  2a + 4b + 2c − 6 0.5 Theo giả thiết: 2 2 2
3b  a + b + c
 3b  2a + 4b + 2c − 6 hay 2a + b + 2c  6 0.25
Do 0  2a + b + 2c + 10  16  P  1
Dấu bằng xảy ra khi a = 1, b = 2, c = 1
Nếu học sinh làm bài không theo cách nêu trong đáp án nhưng đúng
thì vẫn cho đủ số điểm từng phần như hướng dẫn quy định.
Đề thi môn Toán Lớp 11 Trang 6/ 6 trang