


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO THÁI NGUYÊN
ĐỀ THI CHỌN HỌC SINH GIỎI
TRƯỜNG THPT LƯƠNG NGỌC QUYẾN CẤP TRƯỜNG NĂM HỌC 2023-2024 MÔN TOÁN 11
(Thời gian làm bài: 150 phút)
Câu 1. (6 điểm) Giải các phương trình sau
a. 3 cos 2x − sin 2x − 2cos x = 0; b. cos 2x 1
+ (sin 2x + sin x − ) 1 = 0 . 1+ tan x 2
Câu 2. (2 điểm) Biết ( 2 lim
4x + ax +1 + bx = − . Tính giá trị biểu thức 2 3
P = a − 3b . →−∞ ) 1 x
Câu 3. (4 điểm) Cho tập hợp S = {1;2;3;...;39; }
40 gồm 40 số tự nhiên từ 1 đến 40.
Lấy ngẫu nhiên ba số thuộc tập S. Tính xác suất để ba số lấy được lập thành cấp số cộng. 3 u =
Câu 4. (3 điểm) Dãy số (u 1 * 2 ,n∈ N
n ) được cho như sau: ( n +3)u = + nu n 3 1 n
Tìm công thức số hạng tổng quát của dãy số trên.
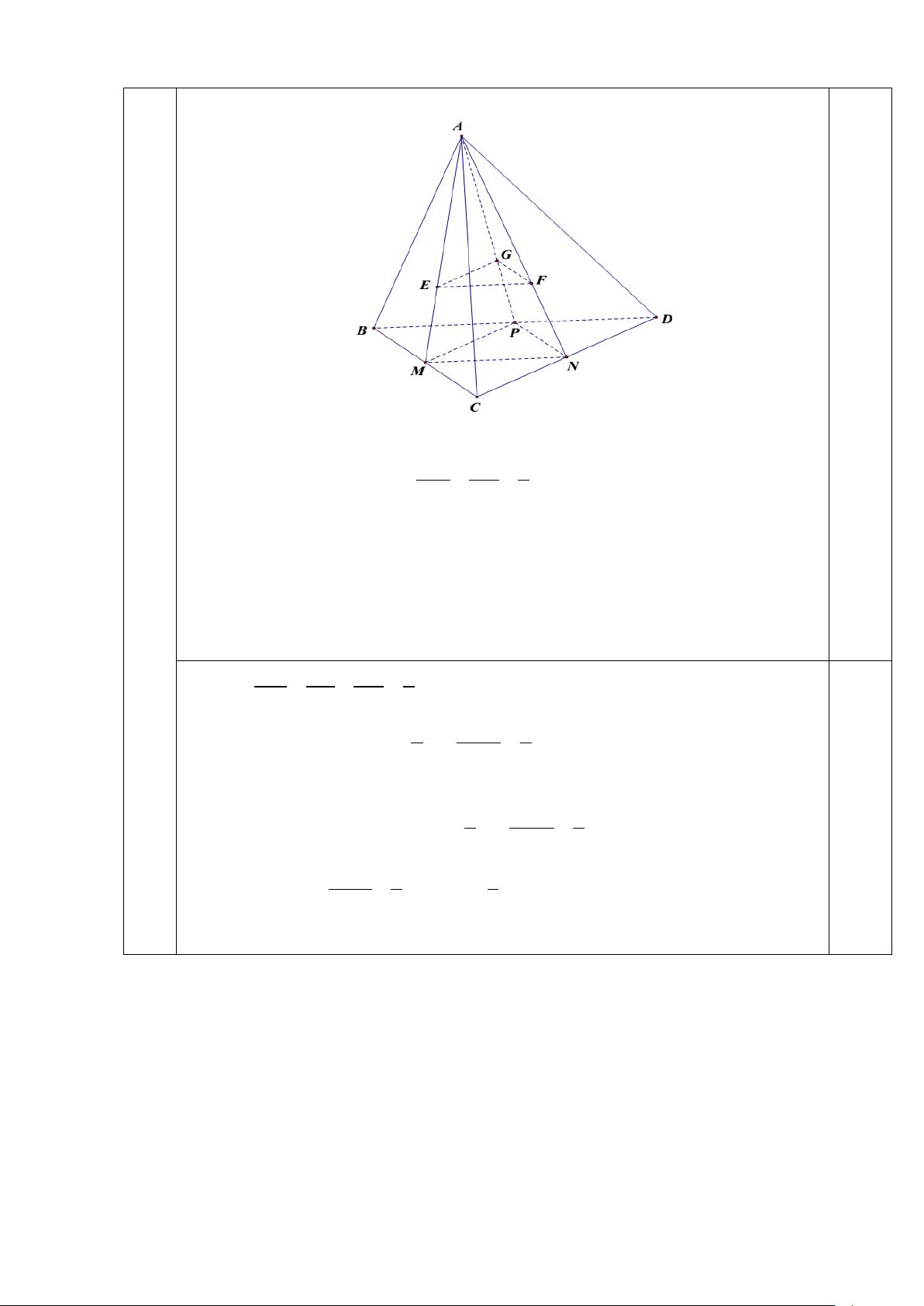
Câu 5. (5 điểm) Cho tứ diện ABCD
1) Gọi E, F,G lần lượt là trọng tâm của tam giác ABC, ACD, ABD .
a) Chứng minh (EFG) / /(BCD) .
b) Tính diện tích tam giác EFG theo diện tích tam giác BCD.
2) Gọi M là điểm thuộc miền trong của tam giác BCD. Kẻ qua M đường thẳng d / / AB .
a) Xác định giao điểm B' của đường thẳng d và mặt phẳng ( ACD).
b) Kẻ qua M các đường thẳng lần lượt song song với AC và AD cắt các mặt phẳng
( ABD) và ( ABC) theo thứ tự tại MB MC MD
C ', D ' . Chứng minh rằng ' ' ' + + = 1. AB AC AD
-----------------------Hết-----------------------
(Thí sinh không được sử dụng tài liệu)
Họ và tên thí sinh: ………………………………….Số báo danh……………………
SỞ GD&ĐT THÁI NGUYÊN
HƯỚNG DẪN CHẤM THI HSG
TRƯỜNG THPT LƯƠNG NGỌC QUYẾN MÔN: TOÁN 11 NĂM HỌC 2023-2024 Câu Nội dung Điểm
Giải các phương trình sau
a. 3 cos 2x − sin 2x − 2cos x = 0; b. cos 2x 1
+ (sin 2x + sin x − ) 1 = 0 . 1+ tan x 2 1
3 cos 2x − sin 2x − 2cos x = 0 a. 3 1
⇔ 3 cos 2x − sin 2x = 2cos x ⇔
cos 2x − sin 2x = cos x 1,5 2 2 π π
2x + = x + k2π x = − + k2π π 6 6 ⇔ cos2x + = cos x ⇔ ⇔ ,k ∈ 6 π π 2π
2x + = −x + k2π x = − + k 6 8 1 3 1,5 π π 2π
x = − + k2π; x = − + k (k ∈) Vậy PT có nghiệm là 6 18 3 π cos ≠ 0 x ≠ + k x π 2 ⇔ ,k ∈ 0,5 b. ĐK: tan x ≠ 1 − π
x ≠ − + kπ 4 cos 2x 1 ( 2 2
2 cos x − sin x) + ( x
sin 2x + sin x − ) cos 1 = 0 ⇔
+ sin 2x + sin x −1 = 0 1+ tan x 2 cos x + sin x 1,0 2
⇔ 2cos x − 2sin x cos x + 2sin x cos x + sin x −1 = 0 0,5 2 2
⇔ 2cos x + sin x −1 = 0 ⇔ 2
− sin x + sin x +1 = 0 π x = + k2π 2 sin x =1 0,5 π ⇔ 1
⇔ x = − + k2π ,k ∈ sin x = − 6 2 7π x = + k2π 6 π 7π
x = − + k2π; x =
+ k2π ,k ∈ 0,5
Kết hợp với điều kiện, PT có nghiệm là 6 6 Biết
x + ax + + bx = − . Tính giá trị biểu thức 2 3
P = a − 3b . x→−∞ ( 2 lim 4 1 ) 1 TH1: b =2 ax x ax bx x ax x + + + + = + + + = 0,5 x→−∞ ( 2 ) x→−∞( 2 ) 1 lim 4 1 lim 4 1 2 lim x→−∞ 2
4x + ax +1 − 2x 1 a + 0,5 = lim x a = − = 1 − ⇒ a = 4 x→−∞ 1 1 4 − 4 + a + − 2 2 x x 2 2 3 ⇒ P = 4 − 3.2 = 8 − 0,5 TH2: b ≠ 2 0,5 a +∞ b < lim
x + ax + + bx = x − + + + b = (không thỏa x→−∞ ( 1 , 2 2 4 1 ) lim 4 2 x→−∞ x x
−∞,b > 2 mãn đầu bài ( 2 lim
4x + ax +1 + bx = − ) →−∞ ) 1 x 3
Cho tập hợp S = {1;2;3;...;39; }
40 gồm 40 số tự nhiên từ 1 đến 40. Lấy ngẫu
nhiên ba số thuộc tập S. Tính xác suất để ba số lấy được lập thành cấp số cộng. 3
Ta có n(Ω) = C 0,5 40
Gọi A là biến cố: “Ba số lấy được lập thành cấp số cộng”
Giả sử ba số a, b, c theo thứ tự đó lập thành cấp số cộng, khi đó ta có 2,0
a + c = 2b . Hay a + c là một số chẵn và mỗi cách chọn 2 số a và c thỏa mãn
a + c là số chẵn sẽ có duy nhất cách chọn b . Số cách chọn hai số có tổng chẵn
sẽ là số cách chọn ba số tạo thành cấp số cộng. 2
TH1: Hai số a, b lấy được đều là chẵn có C 1,0 20 cách lấy 2
TH2: Hai số a, b lấy được đều là lẻ có C20 cách lấy 2 2 0,5 2 2 C + C 1
Suy ra n( A) = C + C ⇒ p( A) 20 20 = = 20 20 3 C 26 . 40 3 u = 1 * Dãy số (u 2 ,n∈ N
n ) được cho như sau: ( n +3)u = + nu n 3 4 1 n
Tìm công thức số hạng tổng quát của dãy số trên. 1,0
Ta có (n + 3)u = ⇔ + + + = + + + nu n n n u + n n nu n 3 n 3 2 1 n 2 1 1 ( )( )( ) 1 ( )( ) n v = 9 0,5 Đặt v = n + n + nu v ,n∈ N n ( 2)(
)1 n ta được dãy ( n ) xác định bởi 1 * v = + v n 3 1 n n n
Đây là cấp số nhân có công bội q = 3. Suy ra 1 1 v − + = = n 3 9. 3 0,5 n 1 v + 1,0 n 3 Do đó u = = n
(n + 2)(n + )1n (n + 2)(n + )1n Cho tứ diện ABCD
1) Gọi E, F,G lần lượt là trọng tâm của tam giác ABC, ACD, ABD .
a) Chứng minh (EFG) / / (BCD) .
b) Tính diện tích tam giác EFG theo diện tích tam giác BCD .
2) Gọi M là điểm thuộc miền trong của tam giác BCD . Kẻ qua M đường thẳng d / / AB .
a) Xác định giao điểm B ' của đường thẳng d và mặt phẳng ( ACD).
b) Kẻ qua M các đường thẳng lần lượt song song với AC và AD cắt các mặt phẳng
( ABD) và ( ABC) theo thứ tự tại MB MC MD
C ', D ' . Chứng minh rằng ' ' ' + + =1. AB AC AD 1)
a) Gọi M , N, P lần lượt là trung điểm của BC,CD, DB .
Theo tính chất trọng tâm ta có AE AF 2 =
= ⇒ EF / /MN . AM AN 3
Ta có MN ⊂ (BCD) nên EF / / (BCD). (1) 2đ
Chứng minh tương tự ta có EG / / (BCD) . (2)
EF, EG ⊂ (EFG) Từ (1) và (2) ta có
⇒ (EFG) / / (BCD). EF / /
(BCD),EG / /(BCD) b) Ta có EF FG EG 2 = = = theo định lý Talet. MN NP MP 3 ⇒ E ∆ FG S M
∆ NP theo tỉ số 2 EFG ∆ 4 ⇒
= (3) (Do tỉ số diện tích của hai tam 3 S 1đ MN ∆ P 9
giác đồng dạng bằng bình phương tỉ số đồng dạng) Mặt khác MN ∆ P S D
∆ BC theo tỉ số 1 MN ∆ P 1 ⇒ = . (4) 2 S DB ∆ C 4
Từ (3) và (4) ta có S EFG ∆ 1 1 = ⇒ S = . ∆ S S∆ 9 EFG 9 BD ∆ C DBC 2)
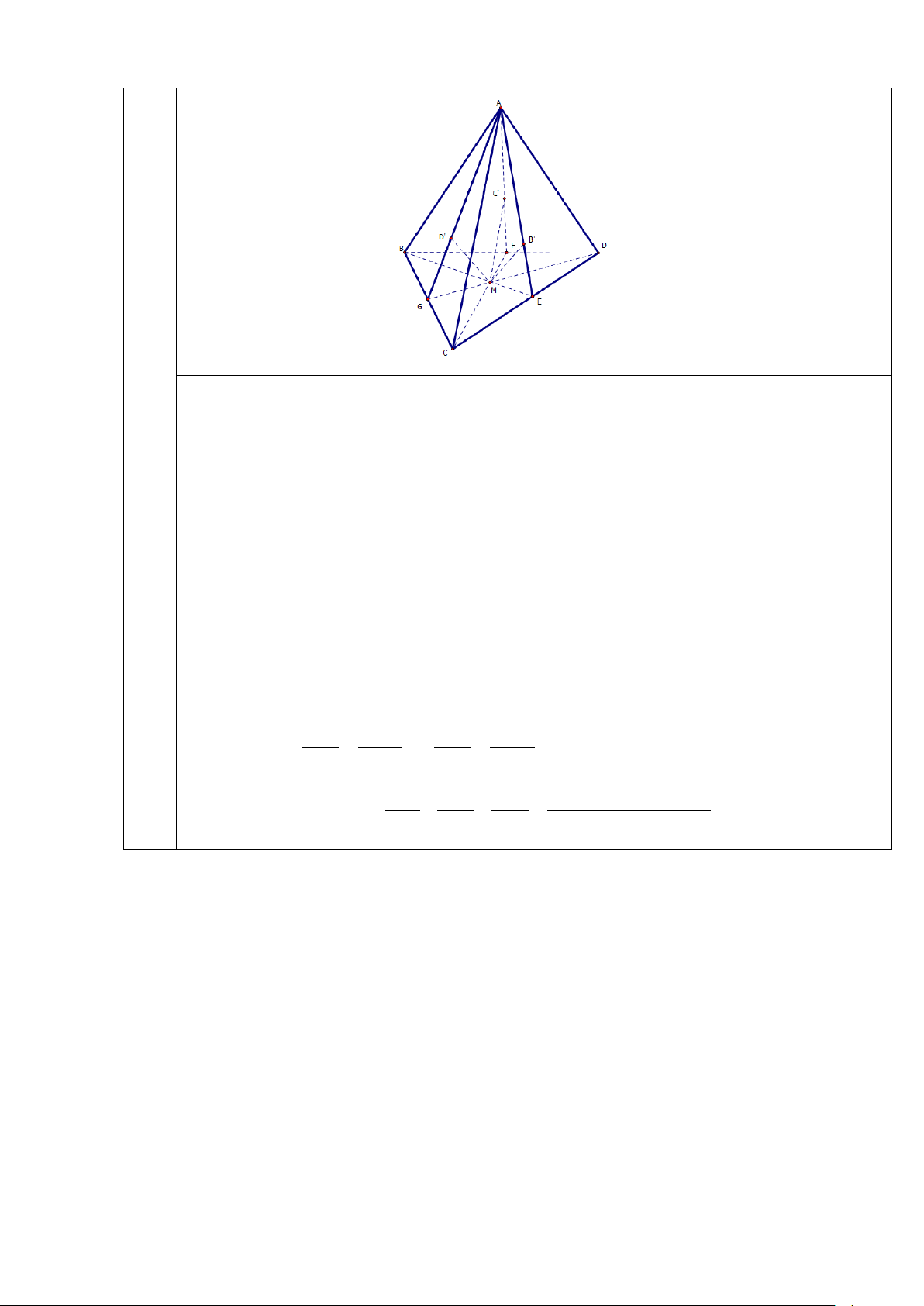
a) Trong mặt phẳng (BCD) gọi BM ∩CD = {E} .
Trong mặt phẳng ( ABE) kẻ MB'/ / AB(B'∈ AE) ⇒ d ≡ MB'. 0,5đ B '∈d Ta có ⇒ ∩ = B ∈ AE ⊂
( ACD) d ( ACD) {B }' '
b) Trong mặt phẳng (BCD) gọi CM ∩ BD = {F}, DM ∩ BC = { } G .
Trong mặt phẳng ( ACF ) kẻ MC '/ / AC (C '∈ AF ). 1,5đ
Trong mặt phẳng ( ADG) kẻ MD'/ / AD(D'∈ AG). Ta có MB ' MB '/ / ME S MC ∆ D AB ⇒ = = (1). AB BE S BC ∆ D
Tương tự ta có MC ' S∆ MD S MBD ' = (2); MB ∆ C = (3) . AC S∆ AD S BCD BC ∆ D Từ + + (1) , (2) và (3) MB MC MD S∆ S∆ S Suy ra ' ' ' MCD MBD MB ∆ C + + = = 1 AB AC AD S BC ∆ D
Document Outline
- ĐỀ THI HSG 11 MÔN TOÁN
- ĐÁP ÁN ĐỀ THI HSG 11 MÔN TOÁN




