Đề học sinh giỏi Toán 11 năm 2023 – 2024 trường THPT Ngô Gia Tự – Phú Yên

SỞ GD&ĐT PHÚ YÊN
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT NGÔ GIA TỰ NĂM HỌC 2023-2024
(Đề thi có 01 trang) Môn thi: TOÁN
Thời gian làm bài: 150 phút (không kể thời gian phát đề) Câu 1. (5,0 điểm)
a) Giải phương trình: sin 2x + 3sin 6x = − sin10 . x u =1
b) Cho dãy số (un) xác định như sau: 1  (n  N*). 2 u = 2023u + u  n 1+ n n  u u u u  Tìm 1 2 3 n lim + + + ... + . u u u u  2 3 4 n 1 +  Câu 2. (6,0 điểm)
a) Giải phương trình: 3x +1 + 5x + 4 = x + 4. 2 2
x + 2y − 3xy + y −1 = 0 
b) Giải hệ phương trình:  . 2 2
 x + y − y +1 = 0 
Câu 3. (2,0 điểm) Cho tam giác ABC có BC = , a CA = ,
b AB = c và có diện tích là S. Kí hiệu m , m , m a b c
lần lượt là độ dài của các đường trung tuyến kẻ từ các đỉnh A, B, C. Biết rằng 2 2 2
2m  m + m . Chứng minh a b c 2 a 4S.cot . A
Câu 4. (3,0 điểm) Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có phương trình đường thẳng chứa đường
cao kẻ từ các đỉnh A, B, C lần lượt có phương trình là x − 2 y = 0, x − 2 = 0, x + y − 3 = 0 . Tìm tọa độ các đỉnh 12
A, B, C biết độ dài đường cao đỉnh A của tam giác ABC bằng
và đỉnh A có hoành độ âm. 5
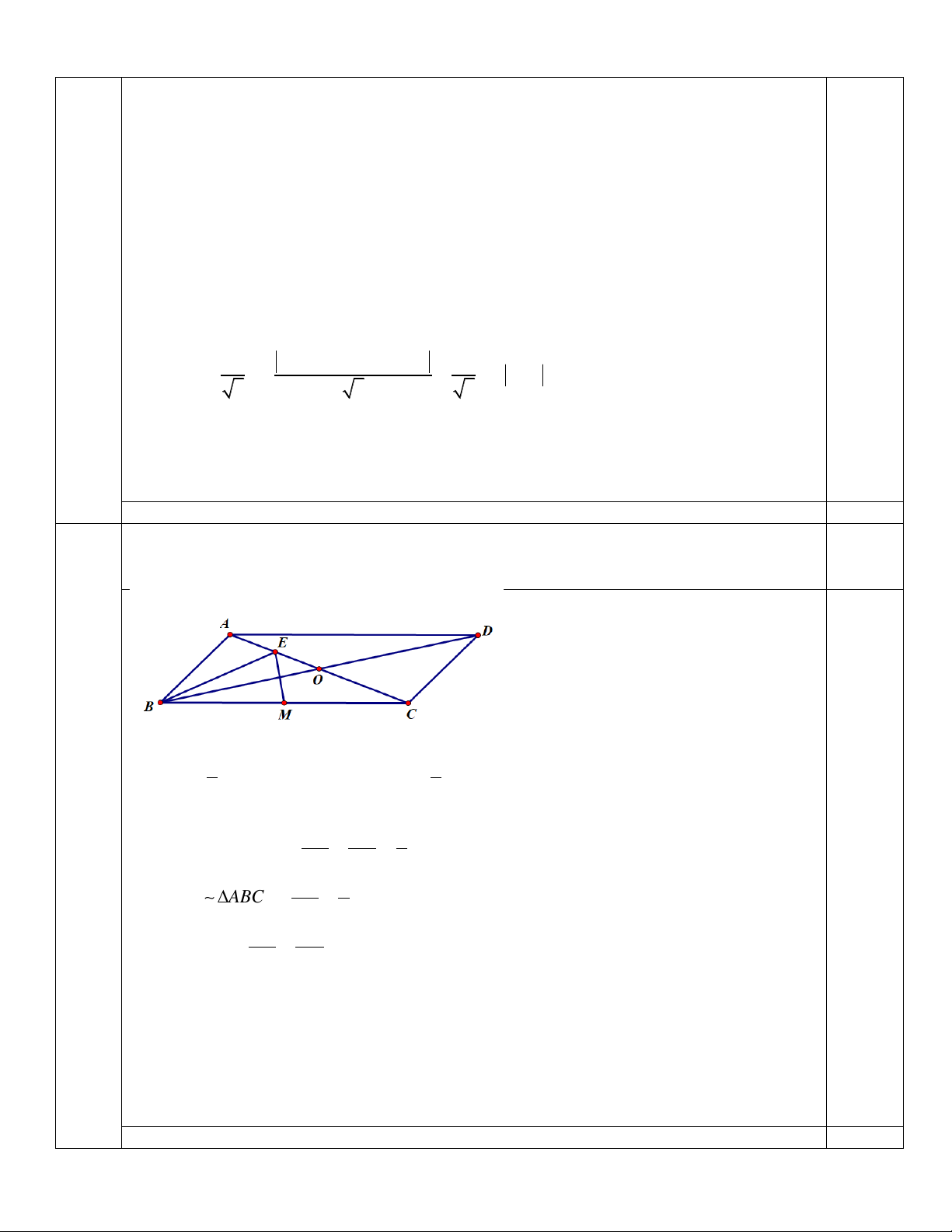
Câu 5. (2,0 điểm) Cho hình bình hành ABCD tâm O và AC = 2A .
B Gọi BE là trung tuyến của tam giác ABO
và M là trung điểm của BC. Chứng minh EM vuông góc với BD.
Câu 6. (2,0 điểm) Cho ba số thực dương a, b, c thỏa mãn ac = 4b + c . Tìm giá trị nhỏ nhất của biểu thức: 2 2  a 3c  225 2 P =  + c + 3b + .  3 4 
(b+c)(c +3b)
-------------------- Hết ------------------- SỞ GD&ĐT PHÚ YÊN
ĐÁP ÁN ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT NGÔ GIA TỰ NĂM HỌC 2023-2024 Môn: TOÁN Câu Nội dung Điểm
a) Giải phương trình: sin 2x + 3sin 6x = − sin10x 2,5
sin 2x + 3sin 6x = − sin10x  sin 2x + sin10x + 3sin 6x = 0 0,5  2sin 6 .
x cos 4x + 3sin 6x = 0 0,5
 sin 6x(2cos 4x + 3) = 0 0,5 sin 6x = 0  0,5 
2cos 4x + 3 = 0 (vn)   x = k (k  ). 0,5 1 6 u =1
b) Cho dãy số (un) xác định như sau: 1  (n  N*). 2 u = 2023u + u  n 1+ n n  u u u u  2,5 Tìm 1 2 3 n lim  + + + ... + . u u u u  2 3 4 n 1 +  Ta có: 2 u − u = 2023u  0, n   * (u  u 1, n   *. 0,5 n 1 + n n n ) tăng n Giả sử dãy (u  = +  = 
n ) có giới hạn là a 2 a 2023a a a 0 1 (vô lý) 0,5 nên limu = + n 2 u u (u − u ) 1  1 1  Ta có : n n n 1 + n = = =  −  0,5 u u u 2023u u 2023 u u n 1 + n 1 + n n 1 + n  n n 1 +  u u u u 1  1 1  1  1  1 2 3 n  + + + ... + =  −  = 1− . 0,5 u u u u 2023 u u 2023 u 2 3 4 n 1 +  1 n 1 +   n 1 +   u u u u  1  1  1 Vậy: 1 2 3 n lim + + + ... +  = lim 1−  = . 0,5 u u u u 2023 u 2023  2 3 4 n 1 +   n 1 + 
a) Giải phương trình: 2x + 2 + 3x + 6 = x + 4 (1) 3,0 ĐK: x  1 − 0,5
(1)  ( 2x + 2 −2)+( 3x +6 −3) = x −1 0,5 2(x −1) 3(x −1)  + = x −1 2x + 2 + 2 3x + 6 + 3 0,5 x =1 (nhan)   2 3  + =1 (*)  0,5 2x + 2 + 2 3x + 6 + 3 x = 2 Với 1 thì VT(*) = 1.
Với x 1 thì VT(*) < 1. 0,5 Với 1
−  x 1 thì VT(*) > 1.
Phương trình (*) có nghiệm duy nhất x =1.
Vậy phương trình đã cho có nghiệm duy nhất x = 1. 0,5 2 2
x + 2y − 3xy + y −1 = 0  ( ) 1
b) Giải hệ phương trình:  3,0 2 2
 x + y − y +1 = 0  (2) ĐK: y  1 − 0,5 ( ) 2 2
1  x − 3yx + 2y + y −1 = 0 , 0,5 2 2 2  = ( 3
− y) − 4(2y + y −1) = ( y − 2) x x = y +1 0,5 (1)   x = 2y −1
Với x = y +1 thay vào (2) ta được
 y = 0  x =1 2 2 2 ( y 1) y y 1 0 2 y y 0  + + − + =  + =  1 1 0,5  (thoả ĐK) y = −  x =  2 2
Với x = 2 y −1 thay vào (2) ta được
 y = 0  x = 1 − 2 2 2
(2 y −1) + y −
y +1 = 0  5y − 5y = 0   (thoả ĐK)  0,5 y = 1  x = 1  
Vậy hệ có 4 nghiệm là: ( ) (− ) ( ) 1 1 1; 0 , 1; 0 , 1;1 , ; − .    2 2  0,5
Cho tam giác ABC có BC = , a CA = ,
b AB = c và có diện tích là S. Kí hiệu 2,0
m , m , m lần lượt là độ dài của các đường trung tuyến kẻ từ các đỉnh A, B, C. a b c Biết rằng 2 2 2
2m  m + m . Chứng minh 2 a 4S.cot . A a b c 3 cos A Ta có 4S.cot A 2b . c sin . A 2 2 2 2b . c cos A b c a (1) 0,5 sin A 2 2 2
2m  m + m a b c 2 2 2 2 2 2 2 a c + a b a + b c 2 2  b + c −  − + − 0,5 2 2 4 2 4 2 2 2 2 2 2 2
 b + c  2a  b + c − a  a (2) 0,5 2
Từ (1) và (2) suy ra 4S.cotA a . 0,5
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có phương trình đường thẳng
chứa đường cao kẻ từ các đỉnh A, B, C lần lượt có phương trình là x − 2 y = 0,
x − 2 = 0, x + y − 3 = 0. Tìm tọa độ các đỉnh A, B, C biết độ dài đường cao đỉnh A 3,0 12
của tam giác ABC bằng
và đỉnh A có hoành độ âm. 5 4
Do BC vuông góc với đường cao kẻ từ A nên pt BC có dạng 2x + y + c = 0 . 0,5
Tọa độ đỉnh B là nghiệm của hệ
2x + y + c = 0 x = 2   
 B(2;− c − 4). 0,5 x − 2 = 0
y = −c − 4
Tọa độ đỉnh C là nghiệm của hệ
2x + y + c = 0
x = −c − 3 0,5   
 C (−c −3;c + 6) .
x + y − 3 = 0 y = c + 6
Phương trình của cạnh AB:
1.( x − 2) −1.( y + c + 4) = 0  x − y − c − 6 = 0.
Tọa độ đỉnh A là nghiệm của hệ
x − y − c − 6 = 0 x = 2c +12     0,5
A(2c +12;c + 6) . x − 2y = 0 y = c + 6 Theo giả thiết 0,5 12
2(2c +12) + c + 6 + c 12 c = 3 − d ( , A BC) =  =  c + 5 = 2   5 5 5 c = 7 − Nếu c = 3 −  A(6; )
3 không thỏa mãn hoành độ A âm. Nếu c = 7 −  A( 2 − ;− ) 1 , B(2; ) 3 ,C (4;− ) 1 . 0,5 Vậy A( 2 − ;− ) 1 , B(2; ) 3 ,C (4;− ) 1 .
Cho hình bình hành ABCD tâm O và AC = 2AB . Gọi BE là trung tuyến của tam 2,0
giác ABO, M là trung điểm của BC. Chứng minh EM vuông góc với BD. = 0,5 5
Vì ABCD hình bình hành nên OA O . C 1 1 Mà AE =
AO và AC = 2AB  AE = A . B 2 2
Xét hai tam giác AEB và ABC, ta có AE AB 1 0,5
BAE là góc chung và = = AB AC 2 EB 1  A  EB A  BC 
=  BE = BM  B
 EM cân tại B. 0,5 BC 2 BE OE Xét BEC  có =
 BO là phân giác của góc EBM BC OC
BEM cân tại B có BO là phân giác nên BO cũng là đường cao. 0,5 Vậy EM ⊥ . BD
(Học sinh có thể chứng minh BO là đường trung trực của đoạn EM hoặc sử dụng phương pháp vecto).
Cho ba số thực dương a, b, c thỏa mãn ac = 4b + c . Tìm giá trị nhỏ nhất của biểu thức: 2 2  2,0 a 3c  225 2 P =  + c + 3b + .  3 4 
(b+c)(c +3b) 2 2 2 2 a 3c a 3c
Áp dụng bất đẳng thức Cauchy cho hai số: +  2 . = ac 3 4 3 4 2 6 15 2 2
P  ac + 3b +
(b + c)(c + 3b) 0,5
Từ giả thiết: ac = 4b + c  ac − 3b = b + c 2 2 2 2
 ac +3b = ac −3bc +3b +3bc = (ac −3b)c +3b(b +c) 0,5
= (b + c)c + 3b(b + c) = (b + c)(c + 3b)
P  (b + c)(c + b) 2 15 3 +
(b + c)(c + 3b)
Sử dụng Cauchy cho hai số: 0,5 ( 2 15
b + c)(c + b) 2 15 3 + (
 2 (b + c)(c +3b) = 30
b + c)(c + 3b)
(b+c)(c +3b)  P  30 . 2 2 a 3c =  3 4   a = 3 2  15 
Dấu " = " xảy ra khi và chỉ khi (
 b + c)(c + 3b) =  b  =1 . 
(b + c)(c +3b)   c = 2 
ac = 4b + c   0,5
Vậy min P = 30 khi a = 3, b = 1, c = 2.
-------------------- Hết -------------------