


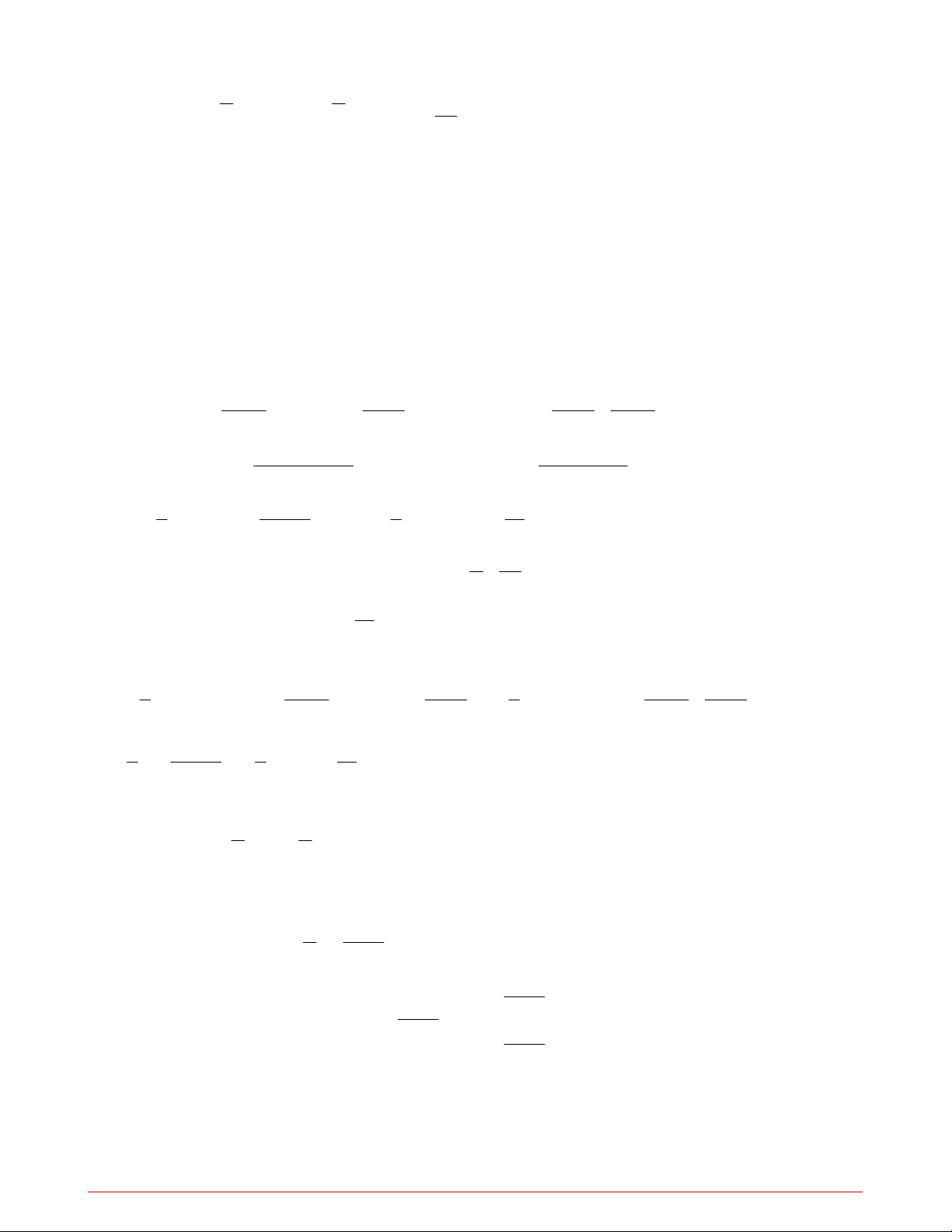
Preview text:
SỞ GD & ĐT THỪA THIÊN HUẾ
KIỂM TRA ĐỊNH KÌ HỌC KÌ 1 NĂM HỌC 2017 - 2018
TRƯỜNG THPT HAI BÀ TRƯNG Môn: Toán 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 45 phút (không kể thời gian phát đề)
Hoàng Đức Vương – 0948.573.074 – Tp Huế
Họ và tên thí sinh: ......................................................................... Số báo danh: ............................... Mã đề thi 132 Câu 1. 3
Tích tất cả các nghiệm của phương trình sin 2x cos x 0 trên 0; là: 4 2 23 3 2 13 3 11 A. . B. . C. . D. . 48 6 25 64
Câu 2. Hàm số nào sau đây nhận giá trị 1 khi x 2
A. y sin 2x .
B. y sin x .
C. y cosx .
D. y cos 2x . Câu 3.
Tìm giá trị nhỏ nhất m của hàm số y 3 cos 2x trên đoạn ; . 4 2 A. m 3 . B. m 4 . C. m 2 . D. m 1.
Câu 4. Hàm số nào sau đây là hàm số tuần hoàn và có chu kì bằng : x x A. y tan .
B. y tan x . C. y sin .
D. y sin x . 2 2
Câu 5. Trong mặt phẳng Oxy , cho vectơ v 1
;1 và hai điểm A0; 2 , B 2 ;
1 . Nếu T A A v ,
T B B v
thì đoạn A B có độ dài bằng: A. 10 . B. 13 . C. 11 . D. 12 . Câu 6. 2 2
Trong mặt phẳng Oxy , cho đường tròn C : x
1 y 2 4 . Phép tịnh tiến theo vectơ v 1; 3
biến đường tròn C thành đường tròn nào sau đây: 2 2 2 2 A. x 1 y 1
4 . B. x y 2 2 1 4 . C. x 1 y 1
4 . D. x y 2 2 1 4 .
Câu 7. Trong mặt phẳng Oxy , cho đường thẳng d : 2x 3y 1 0 và d : 2x 3y 5 0 . Phép tịnh tiến theo
vectơ v có tọa độ nào sau đây không biến d thành d : A. 0;2 . B. 3 ; 0 . C. 3; 4 . D. 1; 1 .
Câu 8. Phương trình 5 tan 5x 1 0 có tất cả các nghiệm là: k 1 k 1 1 k 1 A. x . B. x arctan . C. x arctan . D. x arctan k . 20 5 25 5 5 5 5 5
Câu 9. Tìm giá trị lớn nhất M của hàm số y 5sin x 2 . A. M 5 . B. M 7 . C. M 3 . D. M 1. Câu 10. 1
Tập xác định của hàm số y là: tan x k
A. D \ , k .
B. D \ k , k . 2 C. D .
D. D \ k , k . 2
Câu 11. Cho A , B cố định. Phép tịnh tiến theo vectơ AB biến điểm M thành điểm M . Đẳng thức nào sau đây đúng
A. AB MM .
B. BM AM . C. M M AB .
D. AM M B .
Câu 12. Tổng các nghiệm của phương trình cossinx 1 trên 0;2 là: A. 0 . B. . C. 2 . D. 3 . 2 2 Câu 13. 1 1
Tìm giá trị nhỏ nhất m của hàm số 2 2 y cos x sin x . 2 2 cos x sin x 25 50
A. m 11 4 2 . B. m 8 . C. m . D. m . 2 3
Hoàng Đức Vương (0948.573.074) – BDKT & Luyện thi THPT – Tp Huế
Trang 1 - Mã đề thi 132
Câu 14. Phương trình tan x tan
có tất cả các nghiệm là: 6 x k 6 A. x
k k . B. x
k 2 k . C.
k . D. x
k k . 6 6 x 3 k 6 Câu 15.
Tìm các giá trị nguyên của m để phương trình m sin x m 2 0 có nghiệm 4 A. 5 . B. 4 . C. 6 . D. 7 . Câu 16. 1
Tập xác định của hàm số y là: 1 cos x
A. D . B. D \ k 2 , k .
C. D \ k , k .
D. D \ k 2 , k . 2
Câu 17. Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số y sin 2x là hàm số chẵn.
B. Hàm số y sin 2x tuần hoàn với chu kì T 2 .
C. Đồ thị hàm số y sin 2x nhận trục Oy làm trục đối xứng.
D. Hàm số y sin 2x tuần hoàn với chu kì T . Câu 18. 2
Phương trình cos x 30
có tất cả các nghiệm là: 2 x 1 05 k360 x
75 k360 A. k . B. k .
x 165 k360
x 165 k360 x 10 5 k180 x 15 k360 C. k . D. k .
x 165 k180
x 75 k360
Câu 19. Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số y cos x nghịch biến trên khoảng ; . 2
B. Hàm số y cos x luôn có giá trị dương với mọi x ; . 2 1
C. Không có một giá trị nào của x ; để cos x . 2 2
D. Hàm số y cos x đồng biến trên khoảng ; . 2 x Câu 20. sin 3
Số nghiệm của phương trình
0 thuộc đoạn 2 ; 4 là: cos x 1 A. 5 . B. 6 . C. 7 . D. 4 .
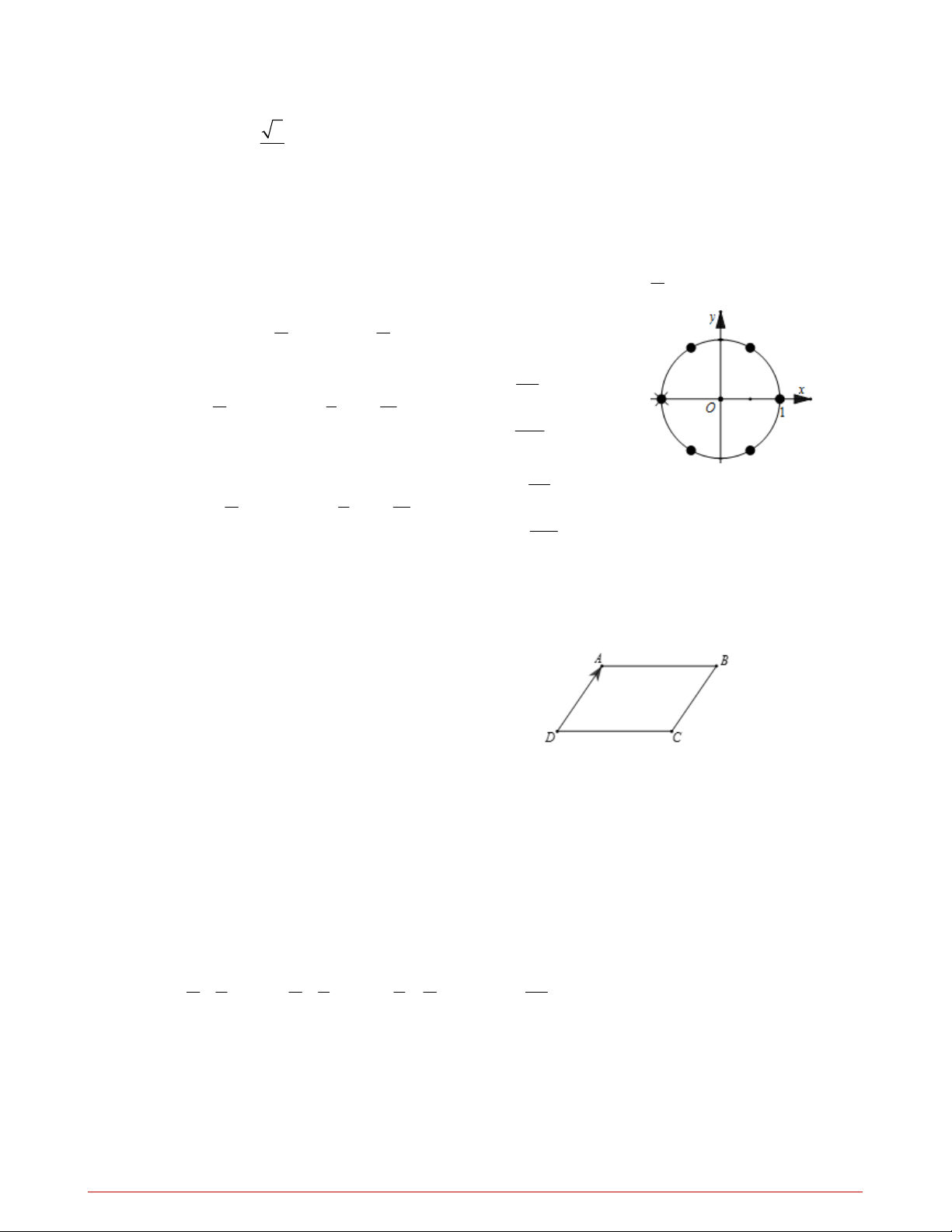
Câu 21. Cho hình bình hành ABCD , phép tịnh tiến theo vectơ DA biến:
A. C thành A .
B. B thành C .
C. C thành B .
D. A thành D .
Câu 22. Trong mặt phẳng Oxy cho điểm A2;5 . Phép tịnh tiến theo vectơ v 1;2 biến điểm A thành
điểm nào trong các điểm sau:
A. N 1;7 .
B. M 3; 7 .
C. Q 3; 3 .
D. P 1; 3 .
Câu 23. Cho đường thẳng a cắt hai đường thẳng song song b và b . Có bao nhiêu phép tịnh tiến biến đường
thẳng a thành chính nó và biến đường thẳng b thành b : A. 0 . B. 1. C. 2 . D. Vô số.
Hoàng Đức Vương (0948.573.074) – BDKT & Luyện thi THPT – Tp Huế
Trang 2 - Mã đề thi 132 Câu 24. x Phương trình sin 0
có tất cả các nghiệm là: 3 2 2 2 A. x k
k . B. x k k . C. x
k 2 k . D. x
k k . 6 2 6 3 3 Câu 25.
Trong mặt phẳng Oxy cho v 1;3 , phép tịnh tiến theo vectơ v biến đường thẳng
d : 3x 5y 8 0 thành đường thẳng nào sau đây?
A. 3x 2y 0 .
B. 3x 5y 9 0 .
C. 3x 5y 26 0 .
D. 5x 3y 10 0 .
----------------------HẾT----------------------
Hoàng Đức Vương (0948.573.074) – BDKT & Luyện thi THPT – Tp Huế
Trang 3 - Mã đề thi 132
HƯỚNG DẪN GIẢI VÀ ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 D D A B B B D C C A A D C A A
16 17 18 19 20 21 22 23 24 25 B D D A B C A B C C Câu 1. Đáp án D. 3 3 Ta có sin 2x
cosx 0 sin 2x sin x 4 4 2 3 5 2x x k 2 x k 2 4 2 4 k . 3 k 2 2x x k 2 x 4 2 4 3 5 5 9 3 Khi đó 0 k 2 k
k 1 x . 1 4 8 8 4 k 0 x 2 k 2 3 9 4 0 k . 4 3 4 8 11 k 1 x 3 12 3 3 11 11 Do đó x x x . . . 1 2 3 4 4 12 64 Câu 2. Đáp án D. Với x
, ta có cos 2x cos 1 . 2 Câu 3. Đáp án A. Ta có x 2x 1
cos 2x 0 3 3 cos 2x 4 . Do đó m 3 . 4 2 2 Câu 4. Đáp án B.
Ta có hàm số y tan x có chu kì T . x x
Các hàm số còn lại: y tan
chu kì 2 , y sin
chu kì 4 , y sin x chu kì 2 . 2 2 Câu 5. Đáp án B.
Ta có T A A T B B
AB AB v , v suy ra 13 . Câu 6. Đáp án B.
Ta có C có tâm I 1
; 2 , bán kính R 2 . T C C T I I 0; 1 C v v là tâm của .
Vậy C x y 2 2 : 1 4 . Câu 7. Đáp án D. Lấy M 2 ;1 d . Khi đó
Với v 0;2 , ta có T M N 2;3 d v
T M P d v .
Với 3;0 , ta có 1 ;1 v .
Với v 3; 4 , ta có T M Q 5;5 d v
T M R d v . Với 1; 1 , ta có 3;0 v . Câu 8. Đáp án C. 1 1 1 1 k
Ta có 5 tan 5x 1 0 tan 5x 5x arctan
k x arctan k . 5 5 5 5 5 Câu 9. Đáp án C.
Hoàng Đức Vương (0948.573.074) – BDKT & Luyện thi THPT – Tp Huế
Trang 4 - Mã đề thi 132
Ta có 1 sin x 1 5 5sin x 5 7
5sin x 2 3 . Do đó M 3 . Câu 10. Đáp án A. x k x k k HSXĐ 2 2 x k . 2 tan x 0 x k Câu 11. Đáp án A.
Ta có T M M MM AB . AB Câu 12. Đáp án D. x 0
Ta có cos sin x 1 sin x k 2 sin x 0 1 sin x
1 x k 02 x . x 2
Vậy tổng các nghiệm là 3 . Câu 13. Đáp án C. 2 2 1 1 1 1 Ta có 2 2 4 4 cos x sin x
sin x cos x 4 2 2 4 4 cos x sin x sin x cos x 4 4 x x sin cos 1 4 4
sin x cos x 4 4 4 sin x cos x 1 4 4 4 4 4 sin x.cos x sin x.cos x 1 16 1 25 2 1 sin 2x 1 4 1 116 4 (Do 2 0 sin 2x 1). 4 2 sin 2x 2 2 k
Dấu “ ” xảy ra khi 2
sin 2x 1 cos 2x 0 x k . 4 2 25
Vậy giá trị nhỏ nhất của hàm số là . 2
Cách khác: Áp dụng BĐT Bunnhia-Copski ta có 2 2 2 1 y 1 1 1 1 1 2 2 1 1 2 2 2 2 cos x sin x
cos x sin x 2 2 2 2 2 cos x sin x 2 cos x sin x 2 1 4 1 25 1 1 42 . 2 2 sin 2x 2 2 Câu 14. Đáp án A. Ta có tan x tan x
k k . 6 6 Câu 15. Đáp án A.
Với m 0 , ta có 2 0 (vô lí). 2 m
Với m 0 , ta có sin x . 4 m 2 m m 0 1 0 2 m m
Phương trình đã cho có nghiệm 1 1 m 1 m 0 . m 2 m 1 0 m 0 m
Do m nguyên và m 1 ;
5 nên m 1;2;3; 4; 5 . Câu 16. Đáp án B.
HSXĐ 1 cos x 0 cos x 1 x k 2 k . Câu 17. Đáp án D.
Hoàng Đức Vương (0948.573.074) – BDKT & Luyện thi THPT – Tp Huế
Trang 5 - Mã đề thi 132
Ta có hàm số y sin 2x là hàm số lẻ, nhận gốc tọa độ làm tâm đối xứng.
sin 2x sin 2x 2 sin 2x . Do đó hàm số y sin 2x tuần hoàn với chu kì T . Câu 18. Đáp án D. 2
x 30 45 k 360
x 75 k 360
Ta có cos x 30 k . 2
x 30 45 k360 x 1 5 k 360 Câu 19. Đáp án A.
Ta có hàm số y cosx nghịch biến trên 0; . Câu 20. Đáp án B.
ĐK: cosx 1 x k 2 k . PT sin 3x 0 3x k x k k . 3
Đối chiếu ta được: x
k ; x
k , x k 2 k . 3 3 7 k 2 x 5 11 3 Khi đó 2 k 4 k . 3 3 3 10 k 3 x 3 8 k 3 x 7 13 3 2 k 4 k . 3 3 3 11 k 4 x 3 k
1 x 2
2 k 2 4 1 k 2 . k
2 x 4
Vậy phương trình có 6 nghiệm trên 2 ;4 . Câu 21. Đáp án C.
Ta có DA CB T C B . DA Câu 22. Đáp án A. x 2 1 1
Ta có T A A x y A v ; 1 ; 7 . y 2 5 7 Câu 23. Đáp án B.
Đường thẳng a cắt b và b lần lượt ta A và B . Khi đó T a a , T b b . AB AB
Giả sử có AC thỏa mãn bài toán. Khi đó T a a suy ra AC cùng phương với AB , T b b suy AC AC
ra C b. Do đó C B .
Vậy có duy nhất phép tịnh tiến theo vectơ v AB thỏa mãn bài toán. Câu 24. Đáp án C. x x x 2 Ta có sin 0 k
k x
k 2 k . 3 2 3 2 2 3 2 Câu 25. Đáp án C.
Ta có T d d
x y c v
nên phương trình d có dạng: 3 5 0 . Lấy M 1
;1 d . Khi đó T M M 2;4 d
d x y v . Do đó phương trình : 3 5 26 0 .
Hoàng Đức Vương (0948.573.074) – BDKT & Luyện thi THPT – Tp Huế
Trang 6 - Mã đề thi 132




