Đề khảo sát chất lượng môn Toán lớp 11 trường chuyên Vĩnh Phúc lần 1

Đề kiểm tra chất lượng Toán 11 lần 1 năm học 2017 – 2018 trường THPT Hàn Thuyên – Bắc Ninh gồm 5 trang với 50 câu hỏi trắc nghiệm, thời gian làm bài 90 phút, đề thi có đáp án.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
SỞ GIÁO DỤC VÀ ĐÀO TẠO
Trường THPT Chuyên Vĩnh Phúc
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LẦN THỨ NHẤT
NĂM HỌC 2016 – 2017
(Đề thi có 01 trang)
Môn: Toán 11
Thời gian: 180 phút (Không kể giao đề)
Câu 1 (1,0 điểm).
a) Cho
2
1
cos
3
x
. Tính
cos2 .x
b) Cho
0;
2



thỏa mãn
2
sin
3
. Tính giá trị của biểu thức
Câu 2 (1,0 điểm). Giải phương trình
sin3 2cos2 sin 0.x x x
Câu 3 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho parabol
2
( ): 3P y x x
và đường
thẳng
: 6.d y x
Tìm tọa độ giao điểm
,AB
của d và
()P
. Tính diện tích tam giác OAB.
Câu 4 (1,0 điểm). Một tấm tôn hình vuông có cạnh bằng 30cm.
Người ta cắt ở bốn góc bốn hình vuông bằng nhau rồi gấp tấm tôn
lại (theo đường nét đứt) để được một cái hộp không nắp. Tính cạnh
các hình vuông bị cắt sao cho thể tích khối hộp bằng
3
2000 cm .
(Thể tích của một khối hộp bằng tích độ dài ba cạnh của nó)
Câu 5 (1,0 điểm). Giải hệ phương trình
2
2 2 0
, .
1 2 2
y xy x y
xy
xy
R
Câu 6 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho điểm
1;3M
và đường tròn
22
( ): 2 4 4 0.C x y x y
Tìm ảnh của điểm M và ảnh của đường tròn
C
qua phép tịnh
tiến theo véc tơ
1;2 .u 
Câu 7 (1,0 điểm). Trong mặt phẳng toạ độ Oxy, cho đường tròn
22
( ): 2 6 6 0C x y x y
và điểm
3;1 .M
Viết phương trình tiếp tuyến kẻ từ M đến
( ).C
Câu 8 (1,0 điểm). Trong mặt phẳng toạ độ Oxy, cho tam giác ABC vuông cân tại A, D là
trung điểm AC. Đường thẳng đi qua A và vuông góc với BD cắt đường thẳng BC tại
3;2E
.
Tìm tọa độ các đỉnh của tam giác ABC, biết đường thẳng AB có phương trình
30xy
và
hoành độ điểm B âm.
Câu 9 ( 1,0 điểm). Giải phương trình
2 2 2
2 2 1 2 1 8 8 1 0.x x x x x x x
Câu 10 (1,0 điểm). Cho
,xy
là hai số thực thỏa mãn
3
4 2.x y xy
a) Chứng minh rằng
1.xy
b) Tìm giá trị nhỏ nhất của
4 4 2 2 2 2
3 2 1.P x y x y xy x y
------Hết------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
ĐÁP ÁN-THANG ĐIỂM
ĐỀ THI KHẢO SÁT LẦN I- NĂM HỌC 2016-2017
MÔN: TOÁN 11
(Đáp án- thang điểm gồm 3 trang)
Câu
Đáp án
Điểm
1
(1,0 điểm)
a. ( 0,5 điểm)
Ta có
2
1 1 cos2 1
cos
3 2 3
x
x
0,25
Do đó
1
cos2 .
3
x 
0,25
b. ( 0,5 điểm)
Ta có
sin cos .
2
P




0,25
22
55
cos 1 sin cos
93
(do
0;
2



). Vậy
5
.
3
P
0,25
2
(1,0 điểm)
Ta có
sin3 2cos2 sin 0 2cos2 sin 2cos2x x x x x x
0,25
cos2 0x
hoặc
sin 1x
.
0,25
cos2 0
42
k
xx

;
sin 1 2 .
2
x x k
0,25
Vậy nghiệm của pt cần tìm là
;
42
k
x


2.
2
xk

0,25
3
(1,0 điểm)
PT hoành độ giao điểm:
22
3 6 2 3 0x x x x x
0,25
Từ đó tìm được
1;5A
;
3;9 .B
0,25
Ta có
42AB
và
; ; 3 2.d O AB d O d
0,25
Vậy
1
. ; 12
2
OAB
S AB d O AB
(đvdt).
0,25
4
(1,0 điểm)
Gọi x (cm) là độ dài cạnh hv bị cắt thì các cạnh của hình hộp tạo thành là
,30 2 ,30 2xxx
,
trong đó
0 15x
.
0,25
Thể tích khối hộp tạo thành là
22
30 2 4 15 .V x x x x
0,25
Ta có
2
32
2000 4 15 2000 30 225 500 0 5; 20.V x x x x x x x
0,25
Vậy
5x
(cm)
0,25
5
(1,0 điểm)
ĐKXĐ:
1; 2xy
.
PT (1) tương đương:
2 1 0y y x
0,25
Với
2y
, thay vào (2) ta được
5.x
0,25
Với
1yx
, thay vào (2) ta được:
1 3 2 2 2 ( 1)(3 ) 4x x x x
2
4 4 0 2x x x
, suy ra
1.y
Vậy hệ đã cho có hai nghiệm là
; 5;2 ; 2;1 .xy
6
(1,0 điểm)
Gọi
'
u
T M M
thì
'MM u
0,25
Từ đó tìm ra
' 0;5M
0,25
(C) có tâm
1;2I
và bán kính
3R
. Gọi
'
u
T I I
thì
' ' 0;4II u I
0,25
Gọi (C’) là ảnh của (C) cần tìm thì (C’) có tâm
' 0;4I
và bán kính
' 3.RR
Do đó
2
2
' : 4 9.C x y
0,25
7
(1,0 điểm)
Đường tròn (C) có tâm
1;3I
, bán kính
2.R
Tiếp tuyến kẻ từ M có dạng
22
: 3 1 0 3 0 ( 0).d a x b y ax by a b a b
0,25
Ta có
22
22
33
; 2 2
a b a b
d I d R a b a b
ab
2
3 4 0a ab
0,25
Với
0a
ta được
: 1 0.dy
Với
3 4 0ab
ta được
:4 3 15 0.d x y
0,25
Vậy có hai tiếp tuyến kẻ từ M là
10y 
và
4 3 15 0.xy
0,25
8
(1,0 điểm)
Vẽ đường cao AH của tam giác ABC. Gọi G là giao của BD và AH thì G là trọng tâm tam giác
ABC và G cũng là trực tâm tam giác ABE; GE cắt AB tại F thì EF
AB.
Suy ra
||EF AC
, và tam giác GEH vuông cân tại H, suy ra HE=HG. Từ đó HB=
3
4
BE.
0,25
Ta có
; 2 2EF d E AB
. Tam giác BFE vuông cân nên BE = 4 .
Gọi
;3B t t
. Ta có BE = 4
22
3 1 16tt
2
2 4 6 0tt
.
Do
0
B
x
nên
1t 
, suy ra
1;2 .B
0,25
Từ
3
4
BH BE
, suy ra
2;2 5;2HC
.
0,25
Phương trình
: 2 0AH x
, từ đó
2;5 .A
Vậy
2;5 ,A
1;2 ,B
5;2 .C
0,25
9
(1,0 điểm)
ĐKXĐ:
01x
.
PT
2 2 2
1 2( ) 2 1 2(2 1) 1 0.x x x x x x
0,25
Đặt
2
2 1;a x b x x
ta được:
22
1 2 2 1 0 ( )(2 1) 0.b a a b a b ab
0,25
Với
ab
, ta có
2
21x x x
, giải ra được
55
.
10
x
0,25
Với
2 1 0ab 
, ta được
22
2(2 1) 1 0 2(1 2 ) 1x x x x x x
(1)
Từ (1) suy ra
1
0 0 1 2 1.
2
xx
Mặt khác
2
2 2 1 1 1.x x x x x x
Suy ra
2
2(1 2 ) 1x x x
nên (1) vô
nghiệm. Vậy pt đã cho có nghiệm là
55
.
10
x
0,25
10
(1,0 điểm)
a. (0,25 điểm)
Ta có
2
4xy x y
, suy ra
32
2x y x y
.
2
1 2 2 0x y x y x y


. Do đó
1.xy
0,25
b. (0,75 điểm)
Ta có
4 4 2 2 2 2
3 2 1 3P x y x y x y xy
2
2 2 4 4 2 2
33
2 1 3
22
P x y x y x y xy
22
2 2 2 2 2 2
33
2 1 3
24
x y x y x y xy
.
0,25
Đặt
22
t x y
thì
2
11
22
t x y
. Ta có
2
9
2 1 3
4
P t t xy
Dễ thấy
1
41
4
xy xy
, nên
2
91
2
44
P t t
.
0,25
Ta thấy hàm số
2
91
( ) 2
44
f t t t
đồng biến trên
1
;
2



nên
13
( ) .
2 16
f t f



Vậy
3
.
16
P 
Đẳng thức xảy ra khi
1
.
2
xy
Vậy GTNN của P bằng
3
.
16
0,25
--------Hết-------
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LẦN THỨ NHẤT
Trường THPT Chuyên Vĩnh Phúc
NĂM HỌC 2016 – 2017
(Đề thi có 01 trang) Môn: Toán 11
Thời gian: 180 phút (Không kể giao đề)
Câu 1 (1,0 điểm). 1 a) Cho 2 cos x  . Tính cos 2 . x 3     b) Cho     0;   thỏa mãn 2 sin 
. Tính giá trị của biểu thức P  sin  .    2  3  2 
Câu 2 (1,0 điểm). Giải phương trình sin 3x  2cos 2x  sin x  0.
Câu 3 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho parabol 2
(P) : y x x  3 và đường
thẳng d : y x  6. Tìm tọa độ giao điểm ,
A B của d và (P) . Tính diện tích tam giác OAB.
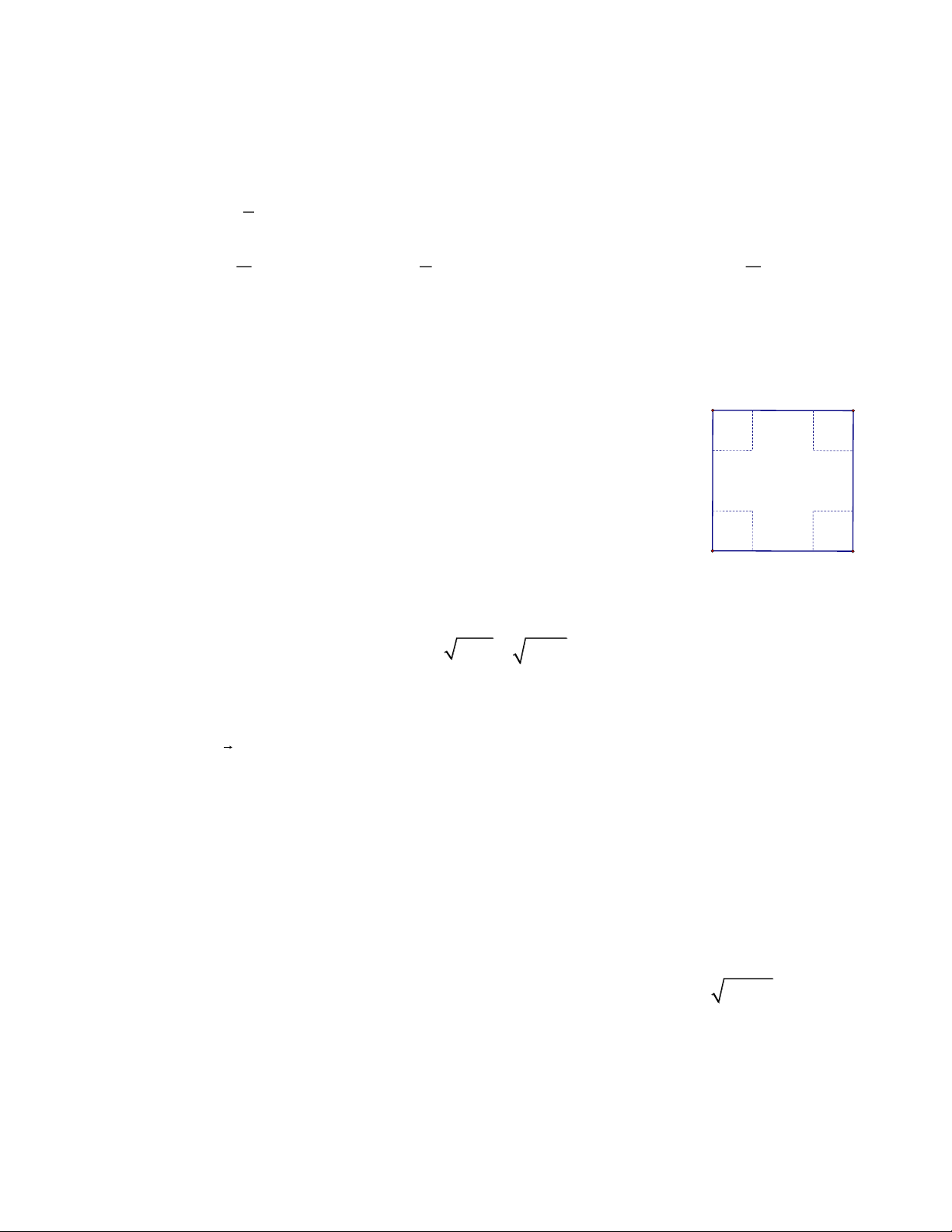
Câu 4 (1,0 điểm). Một tấm tôn hình vuông có cạnh bằng 30cm.
Người ta cắt ở bốn góc bốn hình vuông bằng nhau rồi gấp tấm tôn
lại (theo đường nét đứt) để được một cái hộp không nắp. Tính cạnh
các hình vuông bị cắt sao cho thể tích khối hộp bằng 3 2000 cm .
(Thể tích của một khối hộp bằng tích độ dài ba cạnh của nó) 2
y xy  2x y  2  0
Câu 5 (1,0 điểm). Giải hệ phương trình 
x, y R.
x 1  2  y  2 
Câu 6 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho điểm M 1;  3 và đường tròn 2 2
(C) : x y  2x  4 y  4  0. Tìm ảnh của điểm M và ảnh của đường tròn C  qua phép tịnh
tiến theo véc tơ u   1  ;2.
Câu 7 (1,0 điểm). Trong mặt phẳng toạ độ Oxy, cho đường tròn 2 2
(C) : x y  2x  6 y  6  0 và điểm M  3  ; 
1 . Viết phương trình tiếp tuyến kẻ từ M đến (C).
Câu 8 (1,0 điểm). Trong mặt phẳng toạ độ Oxy, cho tam giác ABC vuông cân tại A, D là
trung điểm AC. Đường thẳng đi qua A và vuông góc với BD cắt đường thẳng BC tại E 3;2.
Tìm tọa độ các đỉnh của tam giác ABC, biết đường thẳng AB có phương trình x y  3  0 và
hoành độ điểm B âm.
Câu 9 ( 1,0 điểm). Giải phương trình  2
x x   x     2 x x   2 2 2 1 2 1 8 8 1 x x  0.
Câu 10 (1,0 điểm). Cho x, y là hai số thực thỏa mãn  x y3  4xy  2.
a) Chứng minh rằng x y  1.
b) Tìm giá trị nhỏ nhất của P   4 4 2 2
x y x y xy   2 2 3
2 x y  1. ------Hết------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
ĐÁP ÁN-THANG ĐIỂM
ĐỀ THI KHẢO SÁT LẦN I- NĂM HỌC 2016-2017 MÔN: TOÁN 11
(Đáp án- thang điểm gồm 3 trang) Câu Đáp án Điểm 1
a. ( 0,5 điểm) (1,0 điểm) 1 1 cos 2x 1 Ta có 2 cos x    0,25 3 2 3 Do đó 1 cos 2x   . 0,25 3
b. ( 0,5 điểm)    Ta có P  sin   cos.   0,25 2  5 5  2 2 cos   1 sin    cos  (do     0;   ). Vậy 5 P  . 0,25 9 3  2  3 2
Ta có sin 3x  2cos 2x  sin x  0  2cos 2xsin x  2cos 2x 0,25 (1,0 điểm)
cos 2x  0 hoặc sin x  1. 0,25 k 
cos 2x  0  x  
; sin x  1  x   k2. 0,25 4 2 2  k 
Vậy nghiệm của pt cần tìm là x   ; x   k2. 0,25 4 2 2 3
(1,0 điểm) PT hoành độ giao điểm: 2 2
x x  3  x  6  x  2x  3  0 0,25
Từ đó tìm được A 1
 ;5 ; B3;9. 0,25
Ta có AB  4 2 và d  ;
O AB  d  ; O d   3 2. 0,25 Vậy 1 S  . AB d O AB  (đvdt). 0,25 OAB  ;  12 2 4
Gọi x (cm) là độ dài cạnh hv bị cắt thì các cạnh của hình hộp tạo thành là x,30  2x,30  2x , (1,0 điểm) 0,25
trong đó 0  x 15.
Thể tích khối hộp tạo thành là V x   x2  x  x2 30 2 4 15 . 0,25 Ta có V
x  x2 3 2 2000 4 15
 2000  x  30x  225x  500  0  x  5; x  20. 0,25 Vậy x  5 (cm) 0,25 5
ĐKXĐ: x  1; y  2 .
(1,0 điểm) PT (1) tương đương:  0,25
y  2 y x   1  0
Với y  2 , thay vào (2) ta được x  5. 0,25
Với y x 1, thay vào (2) ta được: x 1  3 x  2  2  2 (x 1)(3 ) x  4 2
x  4x  4  0  x  2 , suy ra y  1.
Vậy hệ đã cho có hai nghiệm là  ;
x y  5;2;2;  1 . 6  
(1,0 điểm) Gọi T M M ' thì MM ' u 0,25 u
Từ đó tìm ra M '0;5 0,25
(C) có tâm I 1;2 và bán kính R  3. Gọi T I   I ' thì II '  u I '0;4 0,25 u
Gọi (C’) là ảnh của (C) cần tìm thì (C’) có tâm I '0;4 và bán kính R'  R  3. 0,25
Do đó C x   y  2 2 ' : 4  9. 7
Đường tròn (C) có tâm I 1; 
3 , bán kính R  2. (1,0 điểm) 0,25
Tiếp tuyến kẻ từ M có dạng d ax   by   2 2 : 3
1  0  ax by  3a b  0 (a b  0).
a  3b  3a b
Ta có d I;d  2 2  R
 2  2a b a b 2
 3a  4ab  0 0,25 2 2 a b
Với a  0 ta được d : y 1  0. Với 3a  4b  0 ta được d : 4x  3y 15  0. 0,25
Vậy có hai tiếp tuyến kẻ từ M là y 1  0 và 4x  3y 15  0. 0,25 8 (1,0 điểm)
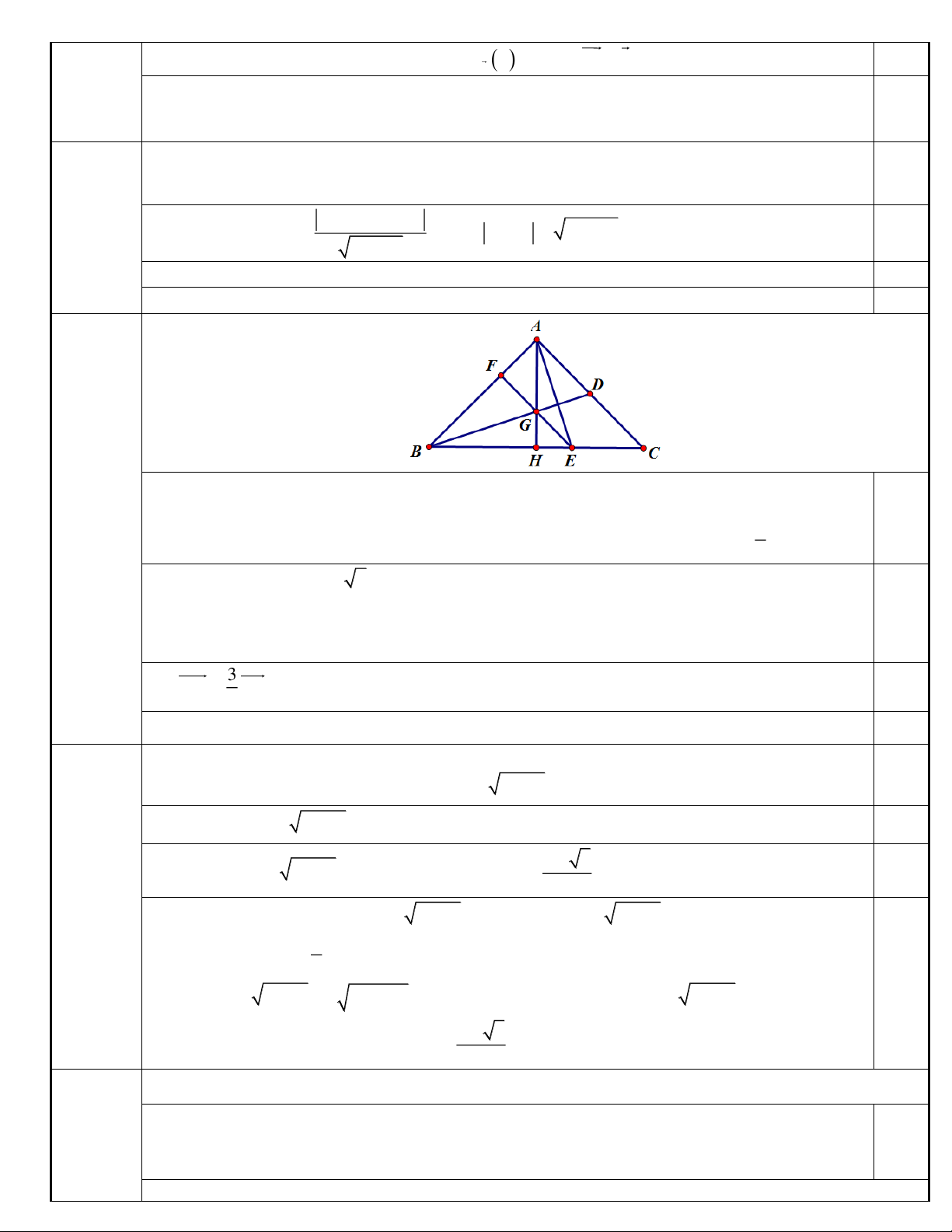
Vẽ đường cao AH của tam giác ABC. Gọi G là giao của BD và AH thì G là trọng tâm tam giác
ABC và G cũng là trực tâm tam giác ABE; GE cắt AB tại F thì EF AB. 0,25 3
Suy ra EF || AC , và tam giác GEH vuông cân tại H, suy ra HE=HG. Từ đó HB= BE. 4
Ta có EF d E; AB  2 2 . Tam giác BFE vuông cân nên BE = 4 . 2 2
Gọi B t;t  3 . Ta có BE = 4  t  3  t   1  16 2
 2t  4t  6  0 . 0,25
Do x  0 nên t  1  , suy ra B 1  ;2. B Từ 3 BH
BE , suy ra H 2;2  C 5;2 . 0,25 4
Phương trình AH : x  2  0 , từ đó A2;5. Vậy A2;5, B 1  ;2, C5;2. 0,25 9 ĐKXĐ: 0  x 1. (1,0 điểm) 0,25 PT   2
x x  x   2 x    2 1 2( ) 2 1 2(2 1) 1 x x  0. Đặt 2
a  2x 1;b
x x ta được:  2
b a   2 1 2 2a  
1 b  0  (a b)(2ab 1)  0. 0,25
Với a b , ta có 2
x x  2x 1, giải ra được 5 5 x  . 0,25 10
Với 2ab 1 0, ta được 2 2
2(2x 1) x x 1  0  2(1 2x) x x  1 (1) Từ (1) suy ra 1 0  x   0 1 2x 1. 2 0,25 Mặt khác 2
2 x x  2 x 1 x  x  1 x  1. Suy ra 2
2(1 2x) x x  1 nên (1) vô 
nghiệm. Vậy pt đã cho có nghiệm là 5 5 x  . 10 10
a. (0,25 điểm) (1,0 điểm) 3 2 Ta có    2 4xy x y
, suy ra  x y   x y  2 . 0,25
 x y     x y2 1
 2x y  2  0  
. Do đó x y  1.
b. (0,75 điểm) Ta có P   4 4 2 2
x y x y    2 2 3
2 x y  1 3xy 3 P
x y 2 3 2 2   4 4
x y   2 2 2
x y  1 3xy 2 2 0,25 2 2 3 3   2 2
x y    2 2
x y   2 2 2
x y  1 3xy . 2 4 Đặt 1 1 9 2 2
t x y thì t
x y2  . Ta có 2 P
t  2t 1 3xy 2 2 4 0,25 Dễ thấy 1 9 1
4xy  1  xy  , nên 2 P t  2t  . 4 4 4     Ta thấy hàm số 9 1 1 3 2 f (t)  t  2t
đồng biến trên 1 ;  
 nên f (t)  f   .   4 4  2   2  16 0,25 Vậy 3 P   . Đẳng thức xảy ra khi 1 x y  . Vậy GTNN của P bằng 3  . 16 2 16 --------Hết-------