Đề khảo sát đội tuyển Toán 11 lần 2 năm 2021 – 2022 trường THPT Trần Phú – Vĩnh Phúc

SỞ GD&ĐT VĨNH PHÚC
ĐỀ THI KSCL ĐỘI TUYỂN NĂM HỌC 2021-2022
TRƯỜNG THPT TRẦN PHÚ
Môn: TOÁN - Lớp 11 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 180 phút (Không kể thời gian phát đề)
(Đề này có 1 trang)
Câu 1. Giải phương trình: sin x  2sin 3x   sin 5x
Câu 2. Trong dãy số : 0 1 13
C ;C ;;C tồn tại 3 số hạng liên tiếp tạo thành cấp số cộng, tìm tổng ba số hạng 23 23 23 đó. 2
2x 1  2x  3
Câu 3. Tìm giới hạn lim 2 x 1  5x  6x 1
Câu 4. Từ các số 1, 2,3 ,4, 5, 6, 7, 8, 9 lập các số tự nhiên gồm bốn chữ số đôi một khác nhau. Lấy ngẫu
nhiên một số vừa lập. Tính xác suất để lấy được số chia hết cho 5.
Câu 5. Cho bất phương trình: 2
x  4  x  4x  x  m  3 . Xác định m để bất phương trình nghiệm đúng
với mọi x 0;4. 2x  n 2022 1
Câu 6. Cho dãy số  x được xác định bởi: x  1; x 
 x .Với n là số nguyên dương. n  1 n 1  2022 n 2021 2021 2021 2021 (2x 1) (2x 1) (2x 1) (2x 1) Đặt 1 2 3 u     ... n  . Tìm lim u . n 2x 1 2x 1 2x 1 2x 1  n n 2 3 3 n 1 
Câu 7. Giả sử 1 x  x  x ... x 11 2 3 10 2 3 110
 a  a x  a x  a x ... a x , với a , a , a ,..., a là các hệ 0 1 2 3 110 0 1 2 110
số. Tính giá trị của tổng 0 1 2 3 10 11
T  C a  C a  C a  C a  ...  C a  C a 11 11 11 10 11 9 11 8 11 1 11 0
Câu 8. Cho hình hộp ABC . D A B  C  D
  . Gọi G là trọng tâm BC  D  .
a. Xác định thiết diện của hình hộp ABC . D A B  C  D
  khi cắt bởi mặt phẳng  ABG . Thiết diện là hình gì?
b. Hai điểm M , N lần lượt thuộc hai đoạn thẳng AD , AC sao cho MN song song với mặt phẳng  BC D  , biết 1 CN AM  AD . Tính tỉ số 4 CA . x 1 y  2
Câu 9. Trong mặt phẳng tọa độ O xy , cho hai điểm A 1;  2, B3;  1 và đường thẳng  :  . Tìm tọa 1 1
độ điểm C thuộc  để tam giác ACB cân tại C .
Câu 10. Với ba số thực dương a, b, c thỏa mãn ac  4b  c . Tìm giá trị nhỏ nhất của 2 2 2  a 3c  15 2 P    c   3b  .  3 4 
b  cc  3b
-------------------------Hết---------------------------
(Giám thị coi thi không giải thích gì thêm)
Họ và tên thí sinh:...............................................
Chữ ký của giám thị:………………………
Số báo danh:………………………………………..
Phòng thi số:………………………………. ĐÁP ÁN Câu Nội dung Điểm pt 1,0 1 0,25 0,5 0,25 Giả sử 3 số n n 1  n2 C ;C ;C
theo thứ tự đó lập thành một cấp số cộng khi 23 23 23 n n n và chỉ khi 1 2 2C  C  C , n
  11, n   . 23 23 23 1,0 n 1
 4C    n n 1
C  C     n 1 n2 C  C 23 23 23 23 23  . n 1  n 1  n2 n2  4C  C  C  C 23 24 24 25
n  8 tm
 n  223 n 150   . 0,5 2 n  13  l Vậy 8 9 10
C  C  C  2451570 . 23 23 23 0,5 2
2x 1  2x  3 Tìm giới hạn lim 2 1,0 x 1    5x 6x 1 3 2 2 2x 1 x 0,5  3(x 1) 2 2x 1  lim x x 1 
(x 1)(5x 1) x 1 0,5  3 2 2x 1   lim x =1 x 1  5x 1
Từ các số 1, 2,3 ,4, 5, 6, 7, 8, 9 lập các số tự nhiên gồm bốn chữ số đôi 1,0
một khác nhau. Lấy ngẫu nhiên một số vừa lập. Tính xác suất để lấy
được số chia hết cho 5.
. Gọi số cần lập là a a a a , trong đó các a ,i  1, 4 đôi một khác nhau. 1 2 3 4 i
Số có 4 chữ số đôi một khác nhau là: 4 A  3024 (số). 9 0,25 4
Do số cần lập chia hết cho 5 nên a  5 có 1 cách chọn. 4 a có 8 cách chọn 1 a có 7 cách chọn 2 a có 6 cách chọn 0,5 3
Vậy số số có 4 chữ số chia hết cho 5 là: 8.7.6=336 (số)
Vậy xác suất để lấy được số chia hết cho 5 là: 0,25 336 1 P   3024 9 Cho bất phương trình: 1,0 2
x  4  x  4x  x  m  3
Xác định m để bất phương trình nghiệm đúng với mọi x 0;4. Lời giải 0  x  4 0  x  4 Điều kiện    2 2
4x  x  m  3  0(2)
m  x  4x  3(2) 0,5
Điều kiện cần để bpt (1) nghiệm đúng với x  0;4 thì (2) nghiệm đúng x  0;4 Xét f(x)= x2-4x-3 Bảng biến thiên x 0 2 4 f(x) -3 -3 -7
Từ bảng biến thiên (2) đúng với x  0;4 5
 m  max f (x)  m  3  [0;4] PT  2 2
4  2 4x  x  4x  x  m  3 Đặt 2 2 2
t  4x  x ,t  0  t  4x  x Bảng biến thiên x 0 2 4 4 2 t 0 0
Dựa vào bảng biến thiên suy ra 2 0  t  4
Bất phương trình trở thành g(t)=-t2+2t+1  m (3)
Để bất phương trình đầu nghiệm đúng với x  0;4 thì 0,5
(3) có nghiệm đúng với t
 0;2.  m  max g(t) [0;2] t 0 1 2 2 g(t) 1 1
Từ BBT suy ra m  2 .
Kết luân m  2 thì bpt (1) nghiệm đúng x  0;4 . 2x  n 2022 1 1,0
Cho dãy số  x được xác định bởi: x  1; x   x . n  1 n 1  2022 n
Với n là số nguyên dương. Đặt 2021 2021 2021 2021 (2x 1) (2x 1) (2x 1) (2x 1) 1 2 3 u     ... n  n 2x 1 2x 1 2x 1 2x 1 2 3 3 n 1  Tìm lim u .  n n 2022 (2x 1) Ta có n x  x  , n  1 n 1  n 2022 Suy ra 2021 1 1 2(x  x ) (2x 1) n 1  n n    0,5 6 2x 1 2x
1 (2x 1)(2x 1) 1011(2x 1) n n 1  n n 1  n 1   n 2021 (2x 1  ) n    i 1 1 1 1 u    1011    1011  n     i 1  2x 1   x x x x i i 2 1 2 1 2 1 2 1 1  i i 1    1 n 1  2022 (2x 1) Mặt khác: n x  x 
 0 nên dãy x là dãy số n  n 1  n 2022
tăng n  1 . Nếu  x bị chặn thì lim x tồn tại. n  n 2022 (2a 1) 0,5
Đặt lim x  a  a  1 và a 
 a (vô lý). Suy ra n 2022
x không bị chặn trên hay limx   suy ra n  n 1 lim  0 2x 1 n 1  1011 Suy ra lim u  . n n 3 7
Giả sử 1 x  x  x ... x 11 2 3 10 2 3 110
 a  a x  a x  a x ... a x , 1,0 0 1 2 3 110
với a , a , a ,..., a là các hệ số. Tính giá trị của tổng 0 1 2 110 0 1 2 3 10 11
T  C a  C a  C a  C a  ...  C a  C a 11 11 11 10 11 9 11 8 11 1 11 0 Ta có   x  
1 x  x  x  ... x  1.  11 11 11 1 2 3 10     x 1     x  11 1
 a  a x  a x  a x ... a x x  11 11 2 3 110 1 0 1 2 3 110   x   11 k k 1    1 .C .x  11 11 11 11 11   k k k 121 1  1 1 .C . k x . 11 11 k 0 k 0 Số hạng chứa 11
x trong khai triển trên ứng với 12111k  11  k  10 . 0,5
Hệ số của số hạng chứa 11
x trong khai triển x  11 11 1 là  10 10 1 .C  11 11 (1). 11
Mặt khác  x  11 1   k k 11 1 .C . k x  . 11 k 0
Hệ số của số hạng chứa 11 x trong khai triển 
a  a x  a x  a x  ... a x x  11 2 3 110 1 là 0 1 2 3 110 0,5 a . 0
1 .C  a . 1
1 .C  a . 2
1 .C  ... a . 11 0 1 2 11 1 .C 0 11 1 11 2 11 11 11 0 1 2 11
 a C  a C  a C ... a C  T  (2). 0 11 1 11 2 11 11 11
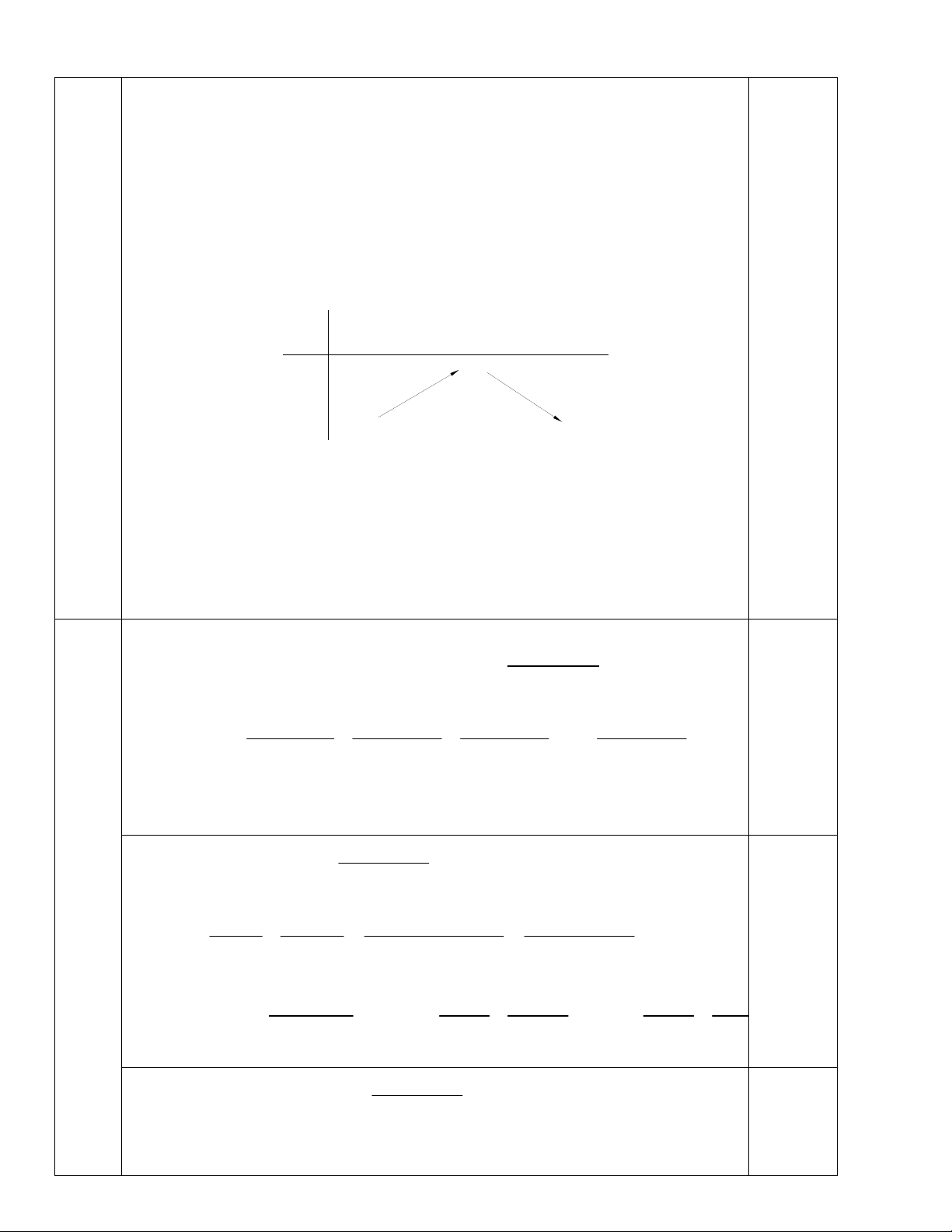
Từ (1) và (2) suy ra T  11  T  11  . Cho hình hộp ABC . D A B  C  D
  . Gọi G là trọng tâm BC  D  . 1,5
a. Xác định thiết diện của hình hộp ABC . D A B  C  D   khi cắt bởi mặt
phẳng  ABG . Thiết diện là hình gì?
b. Hai điểm M , N lần lượt thuộc hai đoạn thẳng AD , AC sao cho 1
MN song song với mặt phẳng BC D
 , biết AM  AD . Tính tỉ số 4 CN . CA 8 Lời giải D' C' B' A' 0,5 I E F G D C O A B a. Trong BC D
  kéo dài BG cắt C D  tại . I 
 ABG CDD C    Ix  Khi đó:
AB   ABG,CD  CDD C
   Ix // CD . AB//CD 
Từ đó, trong CDD C
  , kẻ đường thẳng
Ix // CD cắt ,
CC DD lần lượt tại E và F .
Vậy thiết diện cần tìm là hình bình hành ABEF (vì EF  CD  AB và EF // AB )
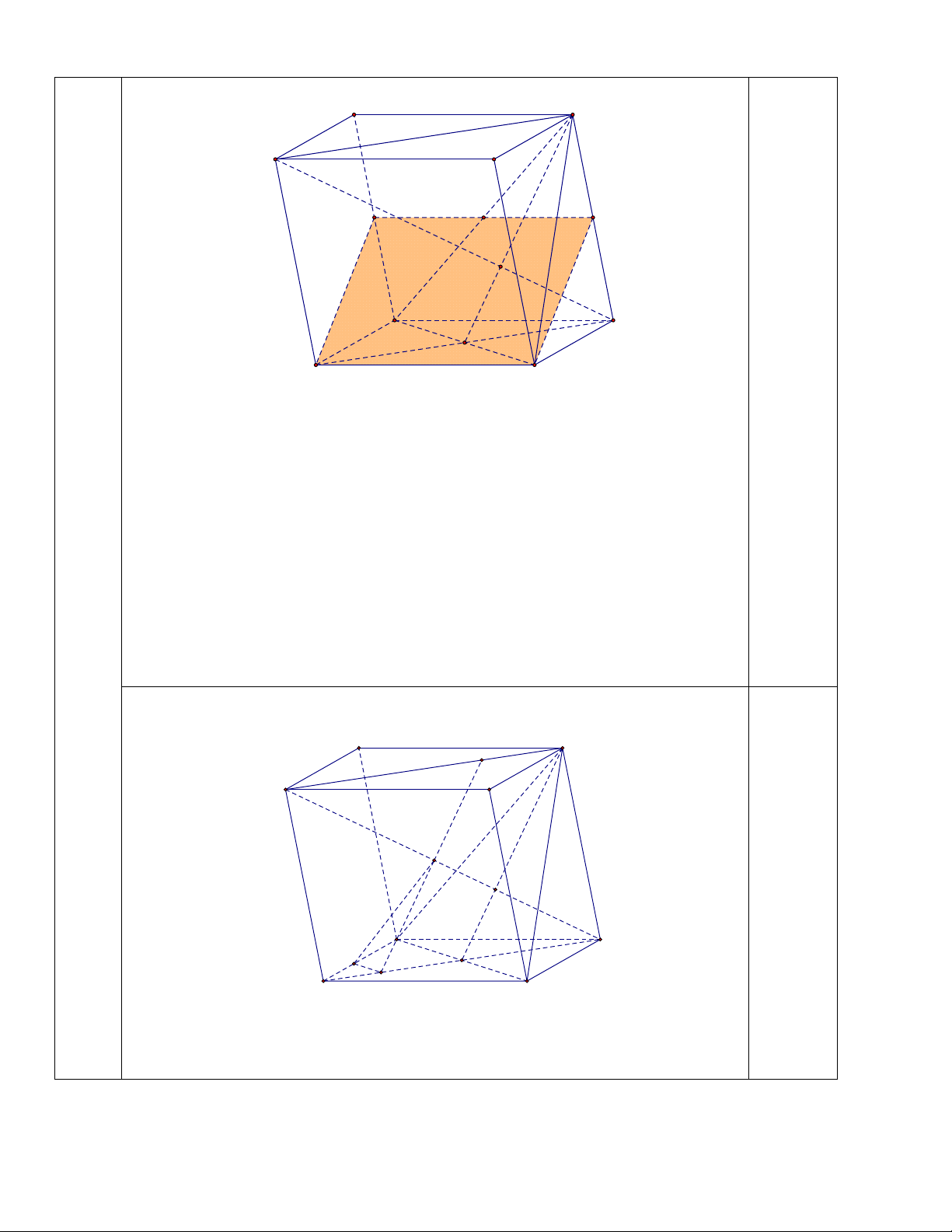
b. Gọi O là giao điểm của AC và BD . Dễ thấy . G  A C  D' C' L 1,0 A' B' N G D C M K O A B
Khi đó, qua M kẻ đường thẳng song song với BD và cắt AC tại . K Trong mặt phẳng ,
 ACC A gọi L  KN  A C   , ta có: MN //  BC D   
 MNK  // BC D   MK // BC D   
 KN // BC D
   KN //OC . AK AM 1 KO KO
Mặt khác, theo giả thiết, ta có:   3   3   và AO MD 4 AO 4 AC 8 KC 7  . AC 8 LC 3 AL 5 Vì ,
KO  LC AC  A C   nên    . AC 8 AC 8 AL AL AC 5 8 5 AN 5 Mà .  .  .    KC
AC KC 8 7 7 NC 7 CN 7 Vậy .  CA 12
Trong mặt phẳng tọa độ O xy , cho hai điểm A 1;  2, B3;  1 và đường x 1 y  2 thẳng  : 
. Tìm tọa độ điểm C thuộc  để tam giác ACB cân 0,5 1 1 tại C .  x 1 t
Phương trình tham số của  :  y  2  t  CA    2   t; t   
Ta có C    C 1 t, 2  t   CB    2t; 1   t Ta có AC  B cân tại C 2 2 2 2 1 2 2
 CA  CB   2
  t   t
   2 t   1
  t  t  6  7 13  Suy ra C ;   0,5  6 6  9
Với ba số thực dương a, b, c thỏa mãn ac  4b  c . Tìm giá trị nhỏ nhất của 1,0 2 2 2  a 3c  15 2 P    c   3b  .  3 4 
b  cc  3b 2 2 2 2 a 3c a 3c
Áp dụng bất đẳng thức Cauchy 2 số:   2 .  ac 3 4 3 4 2 15 2 2
P  ac  3b 
bcc 3b 0,5
Từ giả thiết: ac  4b  c  ac 3b  b  c Ta lại có: 2 2
ac  3b  ac  3bc  3bb  c  b  cc  3bb  c  b  c3b  c 2 15
P  b  c3b  c  
b  cc  3b 2 15
Sử dụng Cauchy cho 2 số: b  c3b  c  bcc3b 0,25 2
 2 b  c3b  c 15   30
b  cc  3b 10 Do vậy: P  30 . 2 2 a 3c   3 4  2  15
Dấu "  " xảy ra khi và chỉ khi 
 b  c3b  c   
b  cc 3b
ac  4b  c   a  3 0,25 b  1 . c   2  a  3 2 2 2  a 3c  15  Vậy min 2 P    c   3b   , khi b   1 .  3 4 
b  cc  3b 30 c   2 