Đề khảo sát HSG Toán 11 lần 1 năm 2019 – 2020 trường Hậu Lộc 4 – Thanh Hóa

TRƯỜNG THPT HẬU LỘC 4
KỲ THI KHẢO SÁT HỌC SINH GIỎI CẤP TỈNH LẦN 1 TỔ TOÁN Năm học: 2019 - 2020
Môn thi: TOÁN - Lớp 11 THPT
Thời gian: 180 phút (không kể thời gian giao đề) Số báo danh
Đề thi có 01 trang - gồm 05 câu ……………………… Câu I (4,0 điểm)
1. Lập bảng biến thiên và vẽ đồ thị P của hàm số 2
y  x  (m  2)x  m 1 ,biết rằng P đi qua điểm M(3;0) .  1   1 
2. Giải phương trình: x  1 x  x  1 x  x.      2   2  Câu II (4,0 điểm)
2 cos x  2 sin 2x  2 sin x 1
1. Giải phương trình: cos 2x  3 1 sin x  . 2 cos x 1 
 x  y  3 
 x  3  y 1
2. Giải hệ phương trình: 
 x, y  R . 
 x  y  3 2 x 
y  2x 1  x  y  0  Câu III (4,0 điểm)
1. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng: a b c 3 2    .  2  2  2 2 ab b bc c ca a
2. Gọi S là tập hợp các số tự nhiên có 6 chữ số khác nhau được thành lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8 .
Chọn ngẫu nhiên một số từ tập S . Tính Xác suất để số được chọn không có hai chữ số chẵn đứng cạnh nhau. Câu IV (4,0 điểm)
1. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC cân tại A 1;3 . Gọi D là một điểm trên cạnh AB  1 3 
sao cho AB  3 AD và H là hình chiếu vuông góc của B trên CD. Điểm M ;  
 là trung điểm đoạn HC.  2 2 
Xác định tọa độ điểm C, biết điểm B nằm trên đường thẳng x  y  7  0.
2. Trong mặt phẳng với trục toạ độ Oxy cho hình thang cân ABCD  AB / /CD . Gọi H, I lần lượt là hình chiếu
vuông góc của B trên các đường thẳng AC,CD . Giả sử M, N lần lượt là trung điểm của A ,
D HI . Viết phương
trình đường thẳng AB biết M 1;2, N 3;4 và đỉnh B nằm trên đường thẳng x  y  9  0 ,  2 cos ABM  . 5 Câu V (4,0 điểm)  1 
1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A là điểm trên SA sao cho - AA  AS . 2
Mặt phẳng   qua A cắt các cạnh SB , SC , SD lần lượt tại B, C , D . Tính giá trị của biểu thức SB SD SC T    . SB SD SC
2. Cho hình chóp S.ABCD đáy là hình thang, đáy lớn BC  2a , AD  a , AB  b . Mặt bên (SAD) là tam giác
đều. Mặt phẳng () qua điểm M trên cạnh AB và song song với các cạnh SA , BC . () cắt C , D SC, SB lần
lượt tại N , P, Q . Đặt x  AM (0  x  b) . Tính giá trị lớn nhất của diện tích thiết diện tạo bởi () và hình chóp S.ABCD .
................. HẾT ................. ĐÁP ÁN - THANG ĐIỂM Câu NỘI DUNG Điểm I
1. Lập bảng biến thiên và vẽ đồ thị P của hàm số 2
y  x  (m  2)x  m 1 , biết rằng 2.0
P đi qua điểm M(3;0) . 4,0
Do P đi qua điểm M(3;0) nên ta có 9 - 3(m  2)  m 1  0  2
 m  4  0  m  2 0.50 điểm Khi đó ta có hàm số 2
y  x  4x  3 x  2 Ta có đỉnh I :   I(2;1) 0.50 y  1  Bảng biến thiên x -∞ +∞ 2 +∞ +∞ y 0.50 -1 0.50  1   1 
2. Giải phương trình sau x  1 x  x  1 x  x.     2.0  2   2  Điều kiện 1   x  1.
Phương trình đã cho tương đương với: 0.50
2x  1 x  1 x  
1   1 x  1 x   0
Đặt a  1 x ; b  1 x , a, b  0 2 2  2x  a  b .
Phương trình dã cho trở thành:  2 2
a  b a  b  
1  a  b  0  a  b a  ba  b   1 1  0   0.50 a  b a  b     1 5 
a  b2  a  b 1  0  a  b   2
+ Với: a  b  1 x  1 x  x  0 0.50 1 5 1 5 5  5 + Với: a  b   1 x  1 x   x   2 2 8 0.50 5  5
- Kết luận. Phương trình có các nghiệm x  0; x   . 8 II
2 cos x  2 sin 2x  2 sin x 1 2.0
1. Giải phương trình: cos 2x  3 1 sin x  2 cos x 1 4,0 1 
Điều kiện: 2 cos x 1  0  cos x   x  
 k 2 ,k  Z . điểm 2 3 2cos x  
1  2 sin x 2 cos x   1 0.50
Pt  cos 2x  3 1 sin x  2 cos x 1 2cos x   1 1 2sin x
 cos 2x  3 1 sin x  2 cos x 1 0.50 2
 1 2 sin x  3  3 sin x  1 2sin x 3 2
 2 sin x  2  3sin x  3  0  sin x 
hoặc sin x  1. 2 3   2 Với sin x   sin x  sin  x 
 k 2 hoặc x 
 k 2 ,k  Z  2 3 3 3 0.50  Với sin x  1   x  
 k 2 ,k  Z  2 2  0.50
So với điều kiện nghiệm của phương trình: x 
 k 2 ; x  
 k 2 , k  Z . 3 2 
 x  y  3 2.0 
 x  3  y 1
2. Giải hệ phương trình:  
 x  y  3 2 x 
y  2x 1  x  y  0  x  0  Điều kiện: y  1  0 .  y  2x  1  0  0.50
Phương trình thứ nhất trong hệ được biến đổi thành phương trình :
x  y  3 x  3  y 1  x  y  2 x  3  y 1  x  3 y  x  2  1 
 x  y  2 x  3 
  x  y  2 x  3    0   1 y 1  x  3  y 1 x 3       0.50 1
Với điều kiện x  0, y  1 ta có : x  3   0 . y 1  x  3 Nên từ  
1 ta có : x  y  2  0  y  x  2 .
Thay vào phương trình thứ nhất trong hệ ta được phương trình : 2
x  3  x  x  x  2 *
Điều kiện 0  x  3 . Vì VT  0  VP  0  x 2;  3 . 0.50
Với mọi x 2; 
3 ta có:     x    x   x   2 1 1
2  3  x  x  3x 1  0 2 2 x  3x 1 x  3x 1 2  
 x  3x 1  0  x   1  x
 x  2  3  x   3  5   1 1 2 x  3x   1   1  0 2
 x  3x 1  0  x  0.50   x  1 x  x 2 3 x         2 7  5  3  5 7  5   y 
(tmđk). Vậy hệ phương trình đã cho có nghiệm  x; y   ;  . 2  2 2    III
1. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng: 2.0 a b c 3 2     2  2  2 2 ab b bc c ca a 4,0
Áp dụng bất đẳng thức Cauchy ta có điểm 2b  a  b    a  3b 2b. a b   2 2 0.50
Áp dụng tương tự ta được a b c 2a 2 2b 2 2c 2      . 2 2 2 a  3b b  3c c     3a ab b bc c ca a 2a 2 2b 2 2c 2 3 2 Ta cần chứng minh    a  3b b  3c c  3a 2 a b c 3 Hay    . a  3b b  3c c  3a 4 0.50
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được a  b  c a b c 2    . 2 2 2 a  3b b  3c c  3a
a  b  c  3ab  3bc  3ca
Mặt khác, từ một đánh giá quen thuộc ta có    2
a b c  3 ab  bc  ca Do đó ta được 0.50 2 2 2
a  b  c  3 ab  bc  ca 2 2 2
 a  b  c  2 ab  bc  ca  ab  bc  ca     2 1     2 4 a b c a b c  a  b  c2 3 3 a  b  c a b c 2 3 Từ đó suy ra     a  3b b  3c c  3a 4 0.50    2 4 a b c 3
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi a  b  c . 2.0
2. Gọi S là tập hợp các số tự nhiên có 6 chữ số khác nhau được thành lập từ các chữ số
0; 1; 2; 3; 4; 5; 6; 7; 8 . Chọn ngẫu nhiên một số từ tập S . Tính Xác suất để số được
chọn không có hai chữ số chẵn đứng cạnh nhau.
Số phần tử của S là 5
8.A  53760 . Do đó, chọn ngẫu nhiên một số từ tập S có 53760 0.50 8 (cách).
Vì số được chọn có 6 chữ số nên ít nhất phải có hai chữ số chẵn, và vì không có hai chữ
số chẵn đứng cạnh nhau nên số được chọn có tối đa 3 chữ số chẵn.
TH1: Số được chọn có đúng 2 chữ số chẵn, khi đó gọi số cần tìm là abcdef 0.50
Xếp 4 số lẻ trước ta có 4! cách. lẻ lẻ lẻ lẻ Xếp 2 số ch
ẵn vào 5 khe trống của các số lẻ có 2 2 1
C .A  4.C cách. 5 5 4
Trong trường hợp này có 4  2 2 1
! C .A  4.C  4416 (số). 5 5 4 
TH2: Số được chọn có đúng 3 chữ số chẵn, khi đó gọi số cần tìm là abcdef
Xếp 3 chữ số lẻ trước ta có 3 A cách. 4 lẻ lẻ lẻ 0.50
Xếp 3 chữ số chẵn vào 4 khe trống của các số lẻ có 3 3 2 2
C .A  C .A cách. 4 5 3 4
Trong trường hợp này có 3 A . 3 3 2 2
C .A  C .A  4896 (số). 4 4 5 3 4 
Vậy có tất cả 9312 số có 6 chữ số sao cho không có hai chữ số chẵn đứng cạnh nhau. 0.50 9312 97 Xác suất cần tìm là  . 53760 560 IV
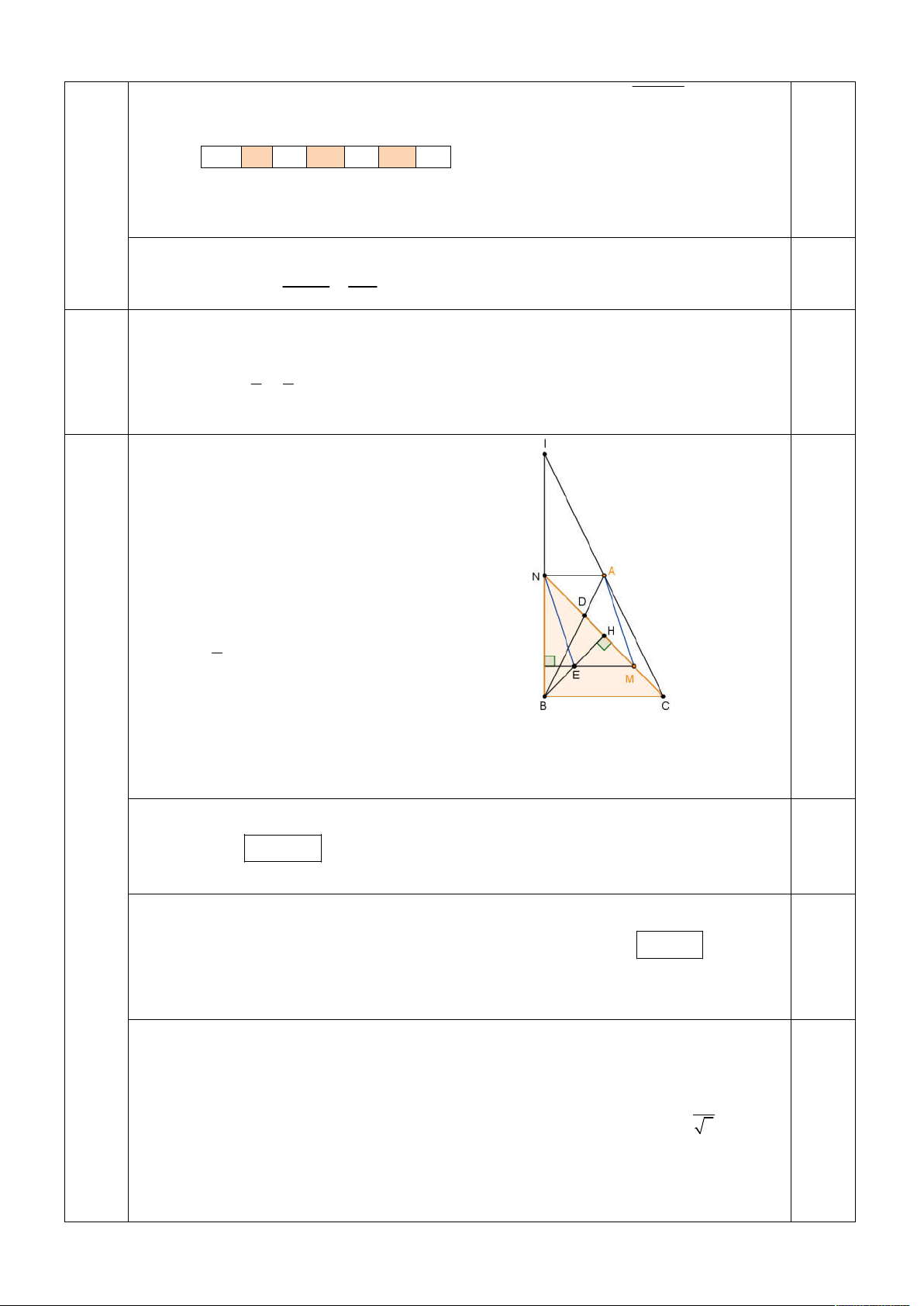
1. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC cân tại A 1;3 . Gọi D là
một điểm trên cạnh AB sao cho AB  3 AD và H là hình chiếu vuông góc của B trên 2.0  1 3  CD. Điểm M ;  
 là trung điểm đoạn HC. Xác định tọa độ điểm C, biết điểm B  2 2 
nằm trên đường thẳng x  y  7  0. 4,0 điểm
Gọi N, I là giao điểm của đường thẳng qua
B vuông góc với BC với các đường thẳng CD và CA .
Do tam giác IBC vuông tại B và 1.0
AB  AC  A là trung điểm của đoạn IC ,
suy ra D là trọng tâm tam giác IBC . Do đó 1 AN / /  B . C 2
Gọi E là trung điểm BH , khi đó E là trực
tâm tam giác NBM và tứ giác NAME là hình bình hành nên từ
NE  BM  AM  BM.
Đường thẳng BM có phương trình x  3 y  5 . Tọa độ điểm B là nghiệm của hệ
x  y  7 0.50   B 4; 3 x  3 y   5  
Từ AB  3 AD  D 2;1 . Lúc đó ta có phương trình các đường thẳng
CD : x  y  1; BH : x  y  1 . Suy ra tọa độ điểm H 1;0 .Suy ra C 2; 3 0.50
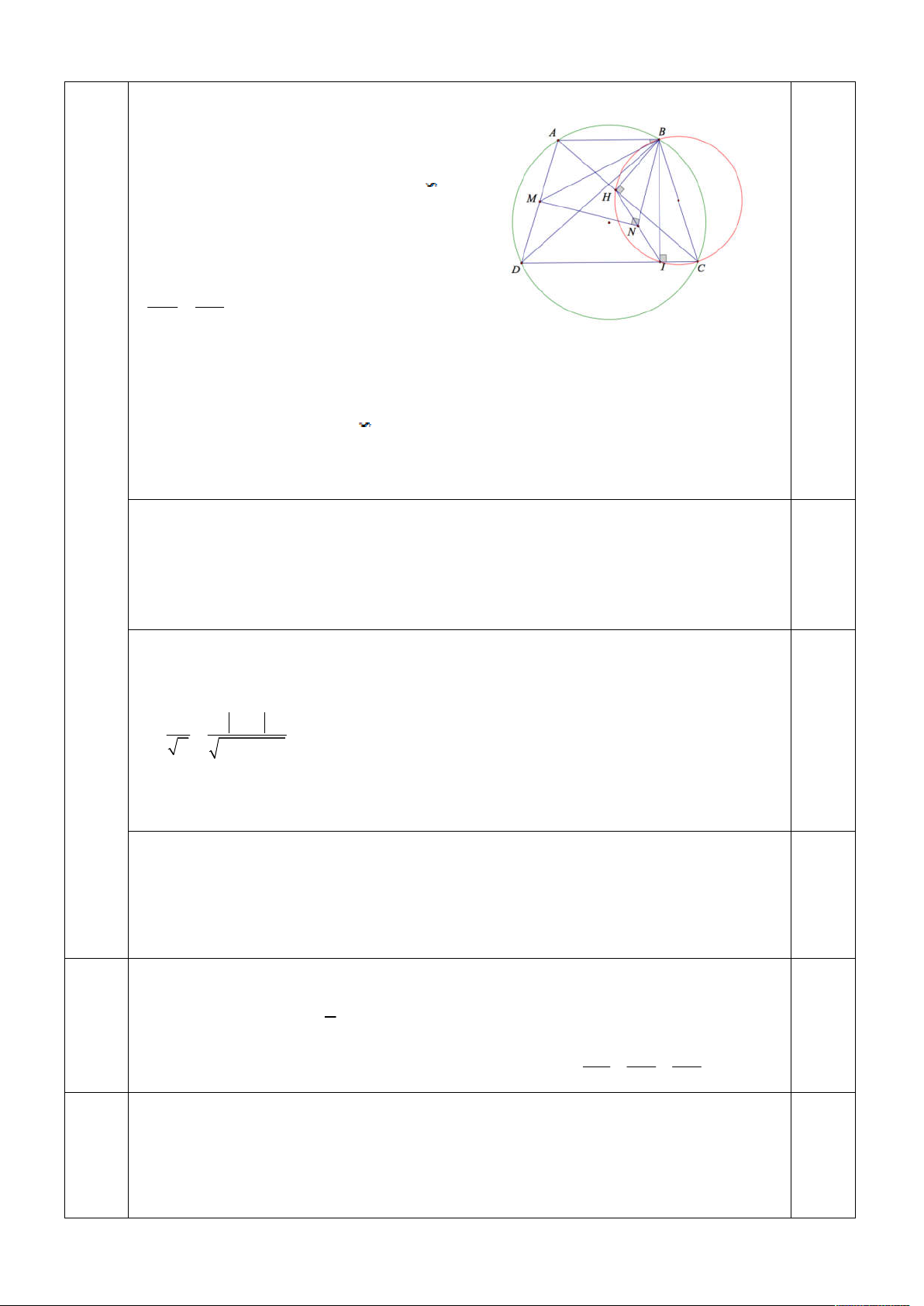
2. Trong mặt phẳng với trục toạ độ Oxy cho hình thang cân ABCD  AB / /CD . Gọi
H, I lần lượt là hình chiếu vuông góc của B trên các đường thẳng AC,CD . Giả sử 2.0
M, N lần lượt là trung điểm của A ,
D HI . Viết phương trình đường thẳng AB biết M 1; 2
 , N 3;4 và đỉnh B nằm trên đường thẳng x  y  9  0 ,  2 cos ABM  . 5
Xét tam giác ABD và HBI có:   
ABD  HCI  HBI . Và   
ADB  ACB  HIB . Suy ra  ABD HBI 0.50
Ta có BM, BN lần lượt là hai trung tuyến của tam giác A , BD HBI do đó: BM BA  (1) . BN BH Lại có   ABM  HBN    MBN  ABH (2) .
Từ (1) và (2) suy ra  ABH MBN . Do đó  
MNB  AHB  90 hay MN  NB
Đường thẳng BN đi qua N và vuông góc với MN nên có phương trình là : x  3 y  15  0 .
x  y  9  0 x  6 0.50
Toạ độ điểm B thoả mãn    . Suy ra ( B 6; 3) .
x  3 y  15  0 y  3   
Gọi na b  2 2 ;
a  b  0 là một vec tơ chỉ phương của đường thẳng AB .  
Ta có MB5; 5 cùng phương với vec tơ u 1;1 . Theo bài ra ta có: MB  2 a  b 2 2 2 2 2 2 0.50 
 8( a  b )  5( a  2ab  b )  3a  10ab  3b  0 2 2 5 2( a  b a  3b   3a  b 
Với a  3b , chọn b  1  a  3 ta có phương trình 3x  y  21  0
Với b  3a chọn a  1  b  3 ta có phương trình x  3 y  15  0 (loại do trùng với BN ) 0.50
Vậy phương trình đường thẳng AB là: 3x  y  21  0 . V
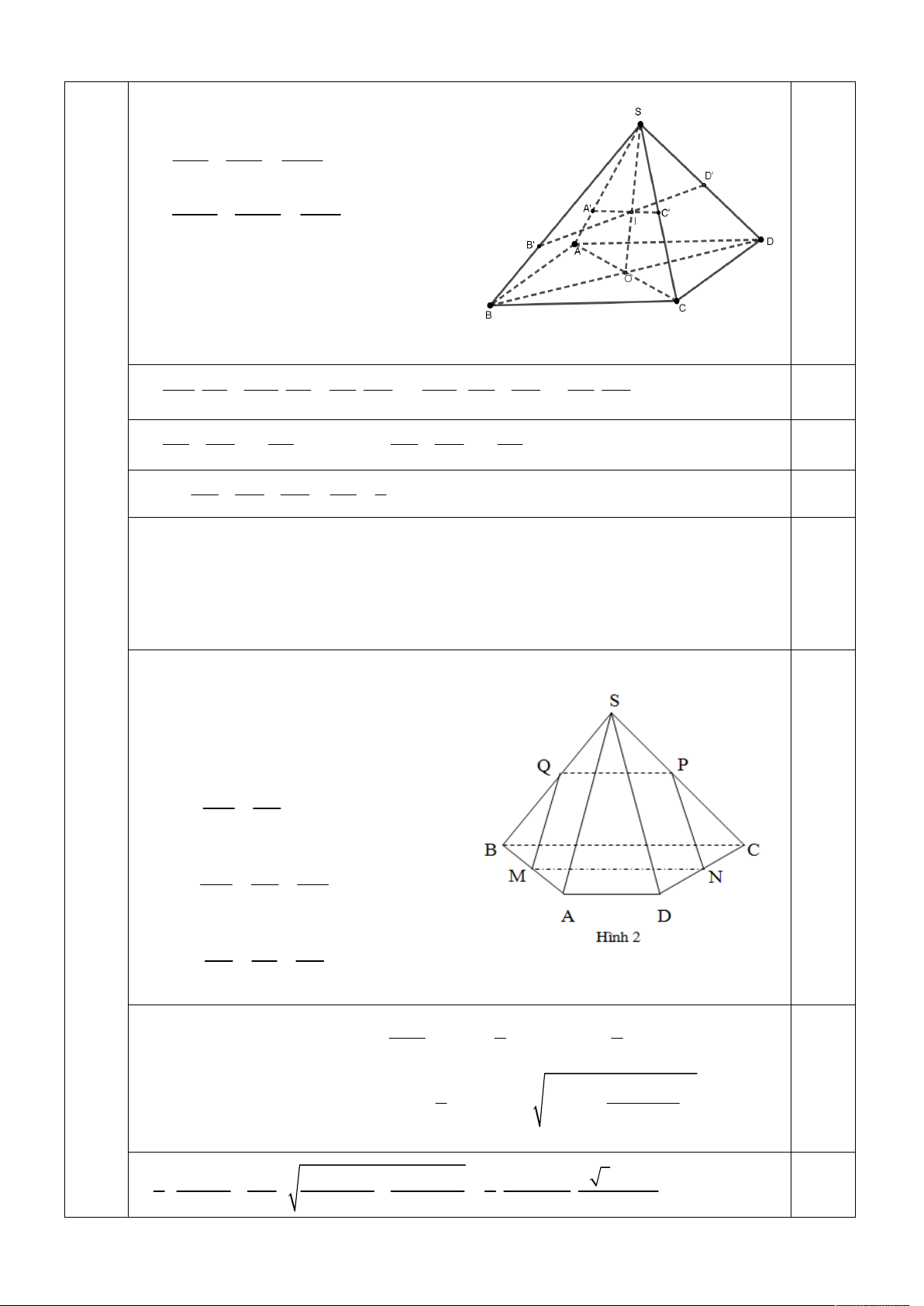
1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A là điểm trên SA  1 
sao cho - AA 
AS . Mặt phẳng   qua A cắt các cạnh SB , 2 SC , SD lần 2.0 SB SD SC
lượt tại B , C , D . Tính giá trị của biểu thức T    . SB SD SC 4,0 điểm
Gọi O là giao của AC và BD . Ta có O
là trung điểm của đoạn thẳng AC , BD .
Các đoạn thẳng SO , AC , B D   đồng quy tại I . Ta có: S  S  S 0.50 SA' I SC I  SAC S S S SAI SC I  SAC    S S S SAC SAC SAC S S S SAI SC I  SA C      2S 2S S SAO SCO SAC SA SI SC SI SA SC SI  SA SC  SA SC  .  .  .    .   . 2SA SO 2SC SO SA SC 2SO 0.50  SA SC  SA SC SA SC SO SB SD SO 0.50    2. ; Tương tự:   2. SA SC SI SB SD SI SB SD SC SA 3 Suy ra:     . SB SD SC SA 2 0.50
2. Cho hình chóp S.ABCD đáy là hình thang, đáy lớn BC  2a , AD  a , AB  b . Mặt
bên (SAD) là tam giác đều. Mặt phẳng () qua điểm M trên cạnh AB và song song 2.0
với các cạnh SA , BC . () cắt C ,
D SC, SB lần lượt tại N, P, Q . Đặt x  AM (0  x  )
b . Tính giá trị lớn nhất của diện tích thiết diện tạo bởi () và hình chóp S.ABCD .
( )  SA vµ BC nªn
( )  (SAD)  MQ  S ,
A NP  SD Ta có
MN  PQ  AD  BC
Theo ĐL Talét trong hình thang BM CN ABCD:  (1) BA CD 0.50 Theo ĐL Talét trong BM BQ MQ SAB :   (2) BA BS SA Theo ĐL Talét trong CN CP PN SCD :   (3) CD CS SD b  x x x
Từ (1), (2), (3) suy ra MQ  NP  a; PQ 
2a; MN  a  a b b b 2 0.50 1
 MN  PQ 
 Thiết diện là hình thang cân và 2 S 
(MN  PQ) MQ  td   2  2  2 2 2 2 1  ab  ax
2ax  a (b  x)
a (b  x)
1 a(b  3x) a 3(b  x)     . .   2 2 2  b b  b 4b 2 b 2b 0.50 2 2 2 a 3 a
3  3x  b  3b  3x  a 3 
(3x  b)(3b  3x)   2 2   12b 12b  2  3 2 a 3 b
Vậy diện tích lớn nhất của thiết diện là khi x  . 0.50 3 3
................ HẾT ................