Đề kiểm tra 1 tiết chương 1 Hình học 11 NC năm 2018 – 2019 trường Thị Xã Quảng Trị

TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 11 NC
TỔ TOÁN Thời gian làm bài : 45 phút ĐỀ 1 ( Khối sáng)
Câu 1: (7 điểm) Trong mp(Oxy) cho điểm 2 2
A 2;5 đường tròn (C):  x  2   y  3  16
và đường thẳng  : 5x  4 y  2  0 . 
a) Tìm tọa độ ảnh của điểm A qua phép tịnh tiến theo vectơ u  (1;  3) .
b) Lập phương trình đường thẳng  ' là ảnh của  qua phép đối xứng trục Ox.
c) Lập phương trình đường tròn (C ) là ảnh của (C) qua phép  0 Q O; 90   . 1
d) Lập phương trình đường tròn (C ) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện 2
liên tiếp phép đối xứng tâm O và phép vị tự tâm H(2;1) tỉ số k=-3. Câu 2: (2 điểm)
a) Trong mp(Oxy), xét phép biến hình F : M  ;
x y   M '3  4 ;
x y  2 . Cho điểm A(3;-2), tìm toạ độ
điểm B sao cho F  A  B .
b) Cho hình chữ nhật ABCD , gọi P,F,Q,E lần lượt trung điểm AB, BC, CD, DA. Gọi O là giao điểm
PQ và EF , I là giao điểm PO và EB. Gọi M,N,K lần lượt trung điểm PB, IB, FC. Chứng minh
rằng hình thang MPIN và hình thang CQOK đồng dạng với nhau. Câu 3: ( 1 điểm)
Về phía ngoài tứ giác lồi ABCD dựng các hình vuông có cạnh AB, BC,CD,DA. Chứng minh rằng
tâm của bốn hình vuông lập thành tứ giác có hai đường chéo vuông góc với nhau.
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 11 NC
TỔ TOÁN Thời gian làm bài : 45 phút ĐỀ 2 ( Khối sáng)
Câu 1: (7 điểm) Trong mp(Oxy) cho điểm 2 2 A  2
 ;3 đường tròn (C):  x   1
  y  4  16
và đường thẳng  : 3x  6 y  2  0 . 
a) Tìm tòa độ ảnh của điểm A qua phép tịnh tiến theo vectơ u  (2; 1) .
b) Lập phương trình đường thẳng  ' là ảnh của  qua phép đối xứng trục Oy.
c) Lập phương trình đường tròn (C ) là ảnh của (C) qua phép  0 Q O;90  . 1
d) Lập phương trình đường tròn (C ) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện 2
liên tiếp phép đối xứng tâm O và phép vị tự tâm H(3; 2) tỉ số k=-2. Câu 2: (2 điểm)
a) Trong mp(Oxy), xét phép biến hình F : M  ;
x y   M '2 ;1
x  3y  . Cho điểm A(2;-5), tìm toạ độ
điểm B sao cho F  A  B .
b) Cho hình chữ nhật ABCD , gọi P,F,Q,E lần lượt trung điểm AB, BC, CD, DA. Gọi O là giao điểm
PQ và EF , I là giao điểm PO và AF. Gọi M,N,K lần lượt trung điểm AP, IA, ED. Chứng minh
rằng hình thang MPIN đồng dạng với hình thang DQOK . Câu 3: ( 1 điểm)
Về phía ngoài tứ giác lồi ABCD dựng các hình vuông có cạnh AB, BC,CD,DA. Chứng minh rằng
tâm của bốn hình vuông lập thành tứ giác có hai đường chéo vuông góc với nhau.
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 11 NC
TỔ TOÁN Thời gian làm bài : 45 phút ĐỀ 1 ( Khối chiều)
Câu 1: (7 điểm) Trong mp(Oxy) cho điểm 2 2 A  2
 ; 4 đường tròn (C):  x   1
  y  3  25
và đường thẳng  : 3x  2 y  4  0 . 
a) Tìm tọa độ ảnh của điểm A qua phép tịnh tiến theo vectơ u  (2;3) .
b) Lập phương trình đường thẳng  ' là ảnh của  qua phép đối xứng trục Oy.
c) Lập phương trình đường tròn (C ) là ảnh của (C) qua phép  0 Q O;90  . 1
d) Lập phương trình đường tròn (C ) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện 2 
liên tiếp phép tịnh tiến u  (2;3) và phép vị tự tâm H(1; 2) tỉ số k=-4. Câu 2: (2 điểm)
a) Trong mp(Oxy), xét phép biến hình F : M  ;
x y  M '3  ;
x 2 y  2 . Cho điểm B(3;-4), tìm toạ độ
điểm A sao cho F  A  B .
b) Cho hình vuông ABCD có tâm O. Gọi E, F, N, M lần lượt là trung điểm AB, AD, OB, EB. Chứng
minh rằng hình thang MNOE đồng dạng với hình thang FOCD. Câu 3: ( 1 điểm)
Về phía ngoài hình bình hành ABCD dựng các hình vuông có cạnh AB, BC,CD,DA. Chứng minh
rằng bốn tâm của hình vuông đó là đỉnh của một hình vuông.
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 11 NC
TỔ TOÁN Thời gian làm bài : 45 phút ĐỀ 2 ( Khối chiều)
Câu 1: (7 điểm) Trong mp(Oxy) cho điểm 2 2 A  5
 ; 2 đường tròn (C):  x  
1   y  2  9
và đường thẳng  : 4x  3y  6  0 . 
a)Tìm tọa độ ảnh của điểm A qua phép tịnh tiến theo vectơ u  (5;  3) .
b) Lập phương trình đường thẳng  ' là ảnh của  qua phép đối xứng trục Ox.
c) Lập phương trình đường tròn (C ) là ảnh của (C) qua phép  0 Q O; 9  0  . 1
d) Lập phương trình đường tròn (C ) là ảnh của (C) qua phép đồng dạng có được bằng cách thực 2 
hiện liên tiếp phép tịnh tiến u  (2;  3) và phép vị tự tâm H(2; 1) tỉ số k=-2. Câu 2: (2 điểm)
a) Trong mp(Oxy), xét phép biến hình F : M  ;
x y   M '1 2 ;
x y  3 . Cho điểm B(3;-4), tìm toạ độ
điểm A sao cho F  A  B .
b) Cho hình vuông ABCD có tâm O. Gọi E, F, N, M lần lượt là trung điểm DC, AD, OC, EC. Chứng
minh rằng hình thang MNOE đồng dạng với hình thang OFAB. Câu 3: ( 1 điểm)
Về phía ngoài hình bình hành ABCD dựng các hình vuông có cạnh AB, BC,CD,DA. Chứng minh
rằng bốn tâm của hình vuông đó là đỉnh của một hình vuông.
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ 1 ( Sáng ) CÂU Nội dung ĐIỂM  1.a
a) Tìm ảnh của điểm A qua phép tịnh tiến theo vectơ u  (1;  3) . 2điểm
x '  x  a x '  2 1  3 0.5-0.5
Gọi A' x '; y '  T ( ) A   A '(3;2) . V   
y '  y  b y '  5  3  2   0.5-0.5
b) Lập pt đường thẳng  ' là ảnh của  qua phép đối xứng trục Ox. 2điểm
Lấy M = (x;y) tùy ý thuộc ∆. Khi đó § ()   Ox ' § (M)  M '(x ';y ') . Ox 0.5 x '  x x  x ' Thì   
V× M    5x ' 4(y ')  2  0  5x ' 4y ' 2  0 0.5-0.5 y '  y y  y '  
 ( ') : 5x  4y  2  0 0.5
c) Lập pt đường tròn (C ) là ảnh của (C) qua phép 0 Q(O; 90 ) . 1 điểm 1 t©m I(2;-3) Ta có : C : 0 0  . Q(O; 9
 0 ) C  C  Q(O; 90  ) I  I 3  ; 2  1    1   0.5 bk R = 4 t©m I (-3;-2) 1 2 2 Vậy : C :
pt C : (x  3)  (y  2)  16 . 1  1   bk R =R = 4 0.5 1
d) Lập phương trình đt C là ảnh của C  qua phép đồng dạng có được bằng cách 2  2 điểm
thực hiện liên tiếp phép đối xứng tâm O và phép vị tự tâm H(2;1) tỉ số k=-3 . t©m I(2;-3) C :  § (C)  C '  0.5 O § (I)  I '( O 2;3) bk R = 4 x '  a  k(x  a) x '  14 0.5-0.5 V H, 3
 C '  C  V H, 3  I '  I x '; y '   2     2   thì  y '  b  k(x  b) y '  5   t©m I (14;-5)  0.5 C : pt C :  2   2 (x 14) (y 5)  144 . 2  2   2 bk R = k R    12 2 . Câu 2 x '  3  4x x '  9
a) Ta có F(A)  Bx '; y '    
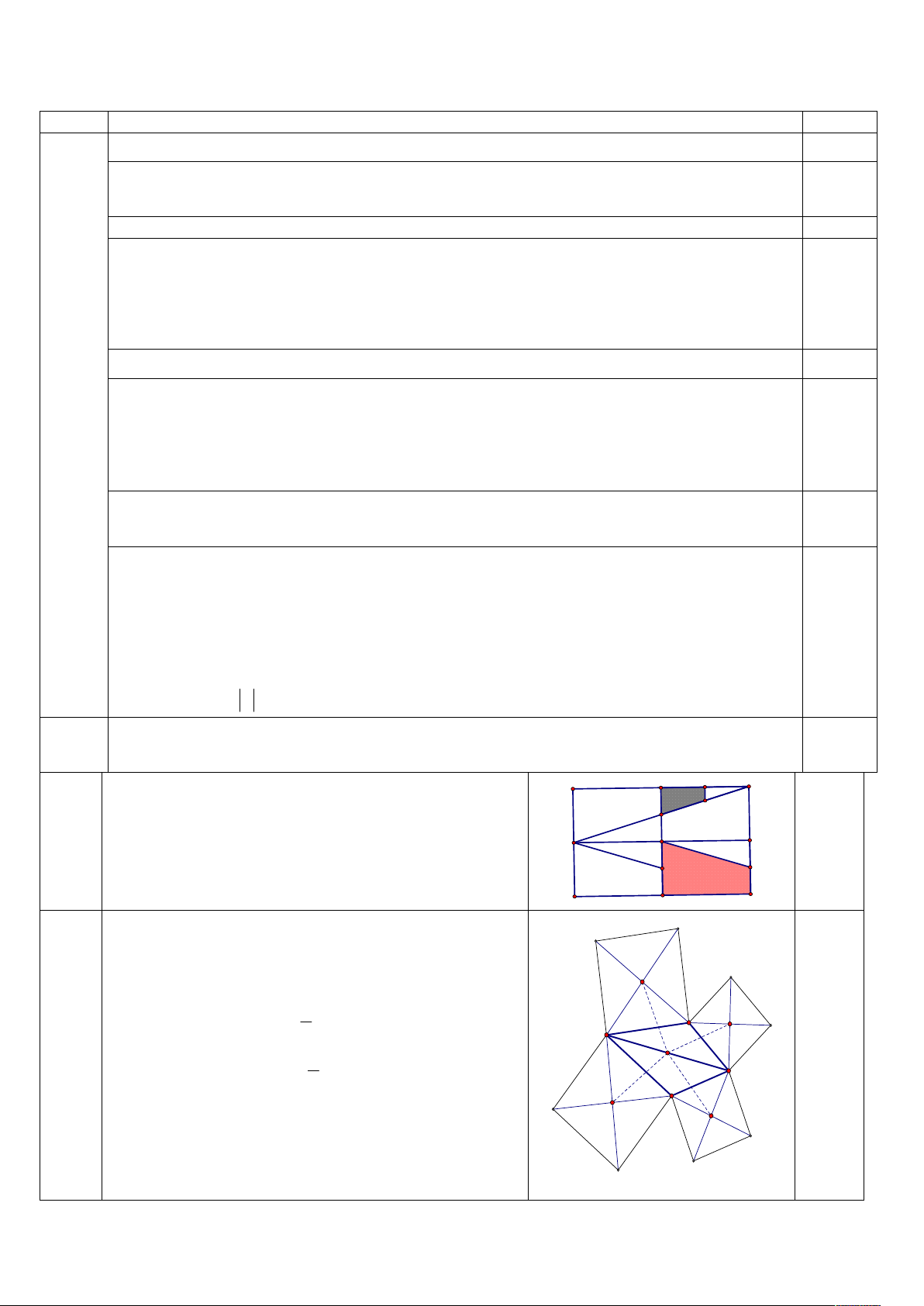
. Vậy A( -9 ;-4) 0.5-0.5 y '  y  2 y '  4    V ( M  NIP)  A P M B 0.25 (B,2) PIEA N 0.25 §  
OE ( PIEA)  QI ' ED (I’ là trung điểm OQ) I T O  ( Q
 I ' ED)  C  KOQ F 0.25 DQ E K
Vậy hình thang MPIN và hình thang CQOK đồng I' dạng với nhau 0.25 D C Q
Câu 3 Đặt   BC;BE , gọi I là trung điểm AC. H CH  EA
Khi đó Q B;CH  EA   E CH  EA  M  1 IN / /AE; IN  AE   0.5 2 N A B Mặt khác  . Suy ra I  NM vuông 1  I IM / /CH; IM  HC C   2 D
cân tại I. Tương tự tam giác IQP vuông cân tại I Q Xét P Q
 I;   N  M 0.5 
 Q I; NQ  MP  NQ  QN Q  I;  Q  P 
Ghi chú: Học sinh có cách làm khác đúng vẫn cho điểm tối đa.
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ 2 ( Sáng ) CÂU Nội dung ĐIỂM 
a) Tìm ảnh của điểm A qua phép tịnh tiến theo vectơ u  (1;  3) . 2điểm
x '  x  a x '  2   2  0 0.5-0.5
Gọi A' x '; y '  T ( ) A   A '(0;2) . V   
y '  y  b y '  3 1  2   0.5-0.5
b) Lập pt đường thẳng  ' là ảnh của  qua phép đối xứng trục Oy. 2điểm § ()   0.5 Oy
' Lấy M = (x;y) tùy ý thuộc ∆. Khi đó § (M)  M '(x ';y ') . Oy x '  x x  x ' Thì   
V× M    3x ' 6y ' 2  0  ( ') : 3x  6y  2  0 0.5-0.5 y '  y y  y '   0.5
c) Lập pt đường tròn (C ) là ảnh của (C) qua phép 0 Q(O;90 ) . 1 điểm 1 t©m I(-1;4) Ta có : C : 0 0 
. Q(O;90 ) C  C  Q(O;90 ) I  I 4  ; 1  1    1   bk R = 4 0.5  t©m I (-4;-1) Vậy : C  1 : pt C :  2   2 (x 4) (y 1)  16 . 1  1 bk R =R = 4  1 0.5
d) Lập phương trình đt C là ảnh của C  qua phép đồng dạng có được bằng cách 2  2 điểm
thực hiện liên tiếp phép đối xứng tâm O và phép vị tự tâm H(2;1) tỉ số k=-2 . t©m I(-1;4) C :  § (C)  C '  O § (I)  I '( O 2;3) 0.5 bk R = 4 Ta có  . x '  a  k(x  a) x '  14 0.5-0.5 V H, 3
 C '  C  V H, 3  I '  I x '; y '   2     2   thì  y '  b  k(x  b) y '  5   t©m I (14;-5) 0.5 C   2 : pt C :  2   2 (x 14) (y 5)  144 . 2  2 bk R' = k R    12 . Câu 2 x '  2x x '  4
a) Ta có F(A)  Bx '; y '    
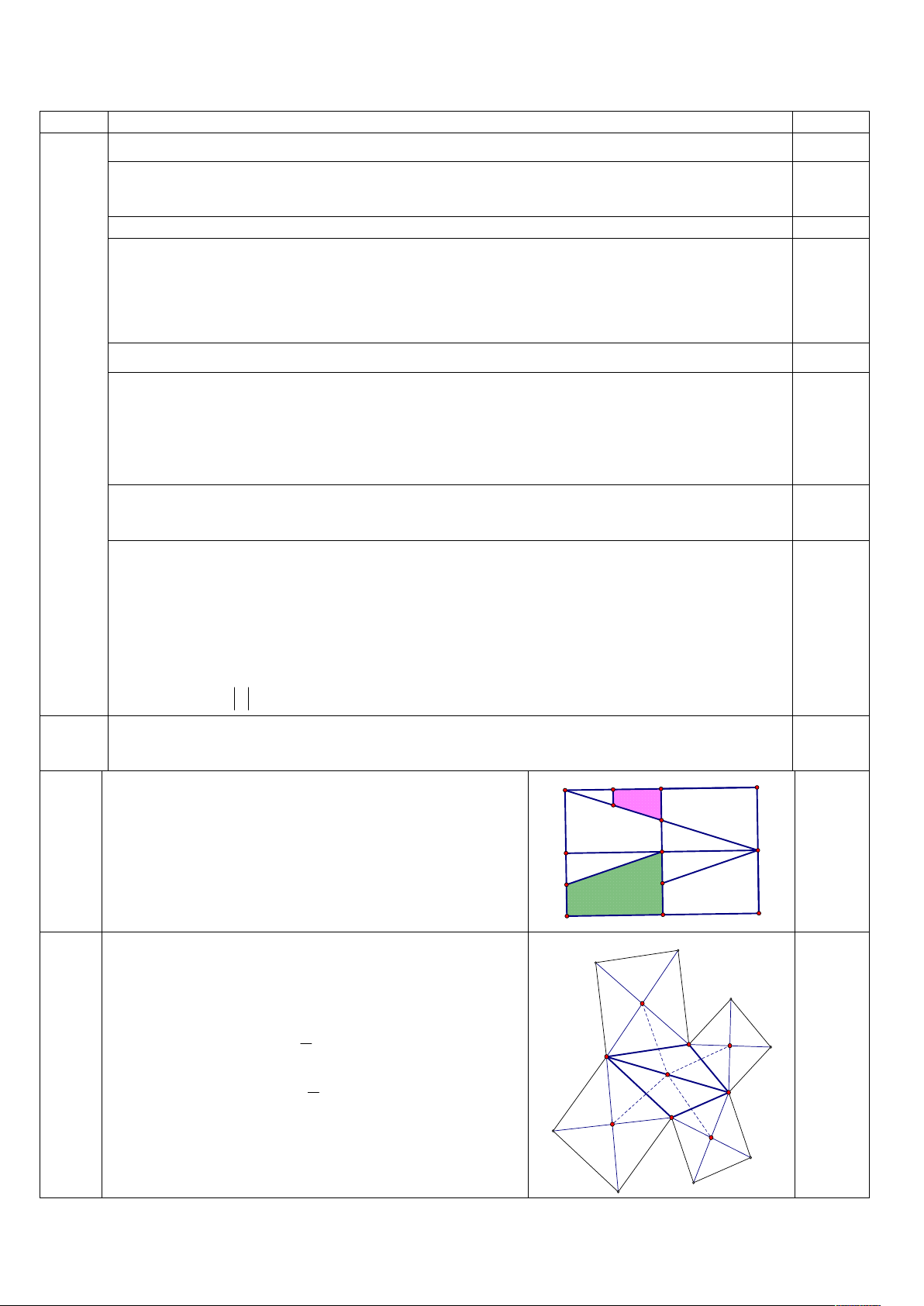
. Vậy B( 4 ;16) 0.5-0.5 (2 đ) y '  1 3y y '  16   V ( M  NIP)  M A P B 0.25 (A,2) PIFB 0.25 §   N
OF ( PIFB)  QI ' FC (I’ là trung điểm OQ) I
T ( Q
 I ' FC) DKOQ F 0.25 QD O E
Vậy hình thang MPIN và hình thang DQOK đồng dạng với nhau 0.25 K I' D C Q
Câu 3 Đặt   BC;BE , gọi I là trung điểm AC. H CH  EA
Khi đó Q B;CH  EA   E CH  EA  M  1 IN / /AE; IN  AE   0.5 2 N A B Mặt khác 
. Suy ra INM vuôn 1  I IM / /CH; IM  HC C   2 D
cân tại I. Tương tự tam giác IQP vuông cân tại I Q Xét P 0.5 Q
 I;   N  M 
 Q I; NQ  MP  NQ  QN Q  I;  Q  P 
Ghi chú: Học sinh có cách làm khác đúng vẫn cho điểm tối đa.
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ 1 ( Chiều ) CÂU Nội dung ĐIỂM 
a) Tìm ảnh của điểm A qua phép tịnh tiến theo vectơ u  (2;3) . 2điểm
x '  x  a x '  2   2  4  0.5-0.5
Gọi A' x '; y '  T ( ) A   A '(4;7) . V   
y '  y  b y '  4  3  7   0.5-0.5
b) Lập pt đường thẳng  ' là ảnh của  qua phép đối xứng trục Oy. 2điểm § ()   0.5 Oy
' Lấy M = (x;y) tùy ý thuộc ∆. Khi đó § (M)  M '(x ';y ') . Oy x '  x x  x ' Thì   
V× M    3x ' 2y ' 4  0  ( ') : 3x  2y  4  0 0.5-0.5 y '  y y  y '   0.5
c) Lập pt đường tròn (C ) là ảnh của (C) qua phép 0 Q(O;90 ) . 1 điểm 1 t©m I(-1;3) Ta có : C  : 0 0 
. Q(O;90 ) C  C  Q(O;90 ) I  I 3  ; 1  1    1   bk R = 5 0.5  t©m I (-3;-1) Vậy : C  1 : pt C :  2   2 (x 3) (y 1)  25 . 1  1 bk R =R = 5  1 0.5
d) Lập phương trình đt C là ảnh của C  qua phép đồng dạng có được bằng cách 2   2 điểm
thực hiện liên tiếp phép tịnh tiến u  (2;3) và phép vị tự tâm H(1; 2) tỉ số k=-4 . t©m I(-1;3)
x '  x  a x '  1   2  3  C : 
T (C)  C '  I ' x '; y '  T (I )   I '(3;6) 0.5 V    u bk R = 5
y '  y  b y '  3  3  6   x '  a  k(x  a) x '  9 0.5-0.5 V H, 3
 C '  C  V H, 3  I '  I x '; y '   2     2   thì  y '  b  k(x  b) y '  26    t©m I (9;-26)  0.5 C   2 : pt C :  2   2 (x 9) (y 26)  400 . 2  2 bk R' = k R    20 . Câu 2 x '  3  x x  0
a) Ta có F(A)  Bx '; y '    
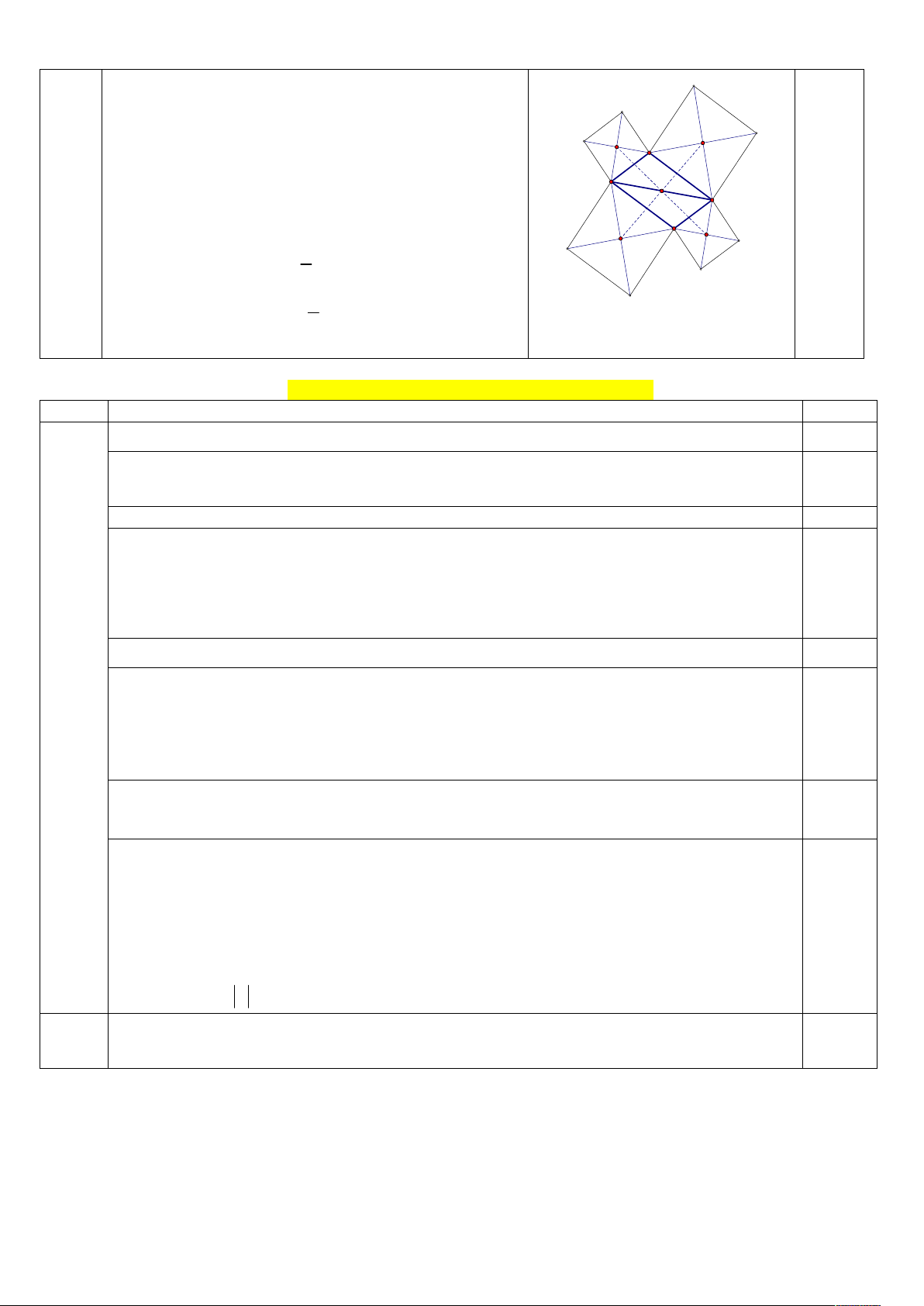
. Vậy B( 0 ;-1) (2 đ) y '  2y  2 y  1   V ( M  NOE)  A B 0.25 (B,2) EODA M E 0.25 §   OE ( EODA)  EOCB N §   AC ( EOCB)  FOCD 0.25 F
Vậy hình thang MNOE và hình thang FOCD đồng O dạng với nhau 0.25 D C
Câu 3 Gọi I là trung điểm AC. Suy ra I là tâm đối xứng của E
hình gồm hình bình hành và bốn hình vuông đã cho. H
Vậy I là trung điểm MP và QN. Hay tứ giác MNPQ là hình bình hành. N M
Đặt   BC; BE ,. B A 0.5 CH  EA I C
Khi đó Q B;CH  EA   CH  EA  D Q P  1 IN / /AE; IN  AE   IN  IM 2 Mặt khác    1 IN  IM IM / /CH;IM  HC  0.5   2
Vậy tứ giác MNPQ là hình vuông.
Ghi chú: Học sinh có cách làm khác đúng vẫn cho điểm tối đa.
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ 2 ( Chiều ) CÂU Nội dung ĐIỂM 
a) Tìm ảnh của điểm A qua phép tịnh tiến theo vectơ u  (5;  3) . 2điểm
x '  x  a x '  5   5  0 0.5-0.5
Gọi A' x '; y '  T ( ) A   A '(0;1) . V   
y '  y  b y '  2  3  1    0.5-0.5
b) Lập pt đường thẳng  ' là ảnh của  qua phép đối xứng trục Ox. 2điểm § ()   Ox
' Lấy M = (x;y) tùy ý thuộc ∆. Khi đó § (M)  M '(x ';y ') . Ox 0.5 x '  x x  x ' Thì   
V× M    5x ' 3(y ')  6  0  5x ' y ' 6  0 0.5-0.5 y '  y y  y '  
 ( ') : 5x  y  6  0 0.5
c) Lập pt đường tròn (C ) là ảnh của (C) qua phép 0 Q(O;90 ) . 1 điểm 1 t©m I(1;-2) Ta có : C : 0 0  . Q(O; 9
 0 ) C  C  Q(O; 90  ) I  I 2  ; 1  1    1   bk R = 3 0.5  t©m I (-2;-1) Vậy : C  1 : pt C :  2   2 (x 2) (y 1)  9 . 1  1 bk R =R = 3  1 0.5
d) Lập phương trình đt C là ảnh của C  qua phép đồng dạng có được bằng cách 2   2 điểm
thực hiện liên tiếp phép tịnh tiến u  (2;  3) và phép vị tự tâm H(2; 1  ) tỉ số k=-2 . t©m I(1;-2)
x '  x  a x '  1 2  3 C : 
T (C)  C '  I ' x '; y '  T (I )      I '(3;5) 0.5 u u bk R = 3
y '  y  b y '  2   3  5  .   x '  a  k(x  a) x '  0 0.5-0.5
V H, 2C '  C  V H, 2  I '  I x '; y '   2     2   thì  y '  b  k(x  b) y '  1   t©m I (0;1) 0.5 C   2 : pt C : 2   2 x (y 1)  36 . 2  2 bk R' = k R    6 . Câu 2 x '  1 2x x  1 
a) Ta có F(A)  Bx '; y '    
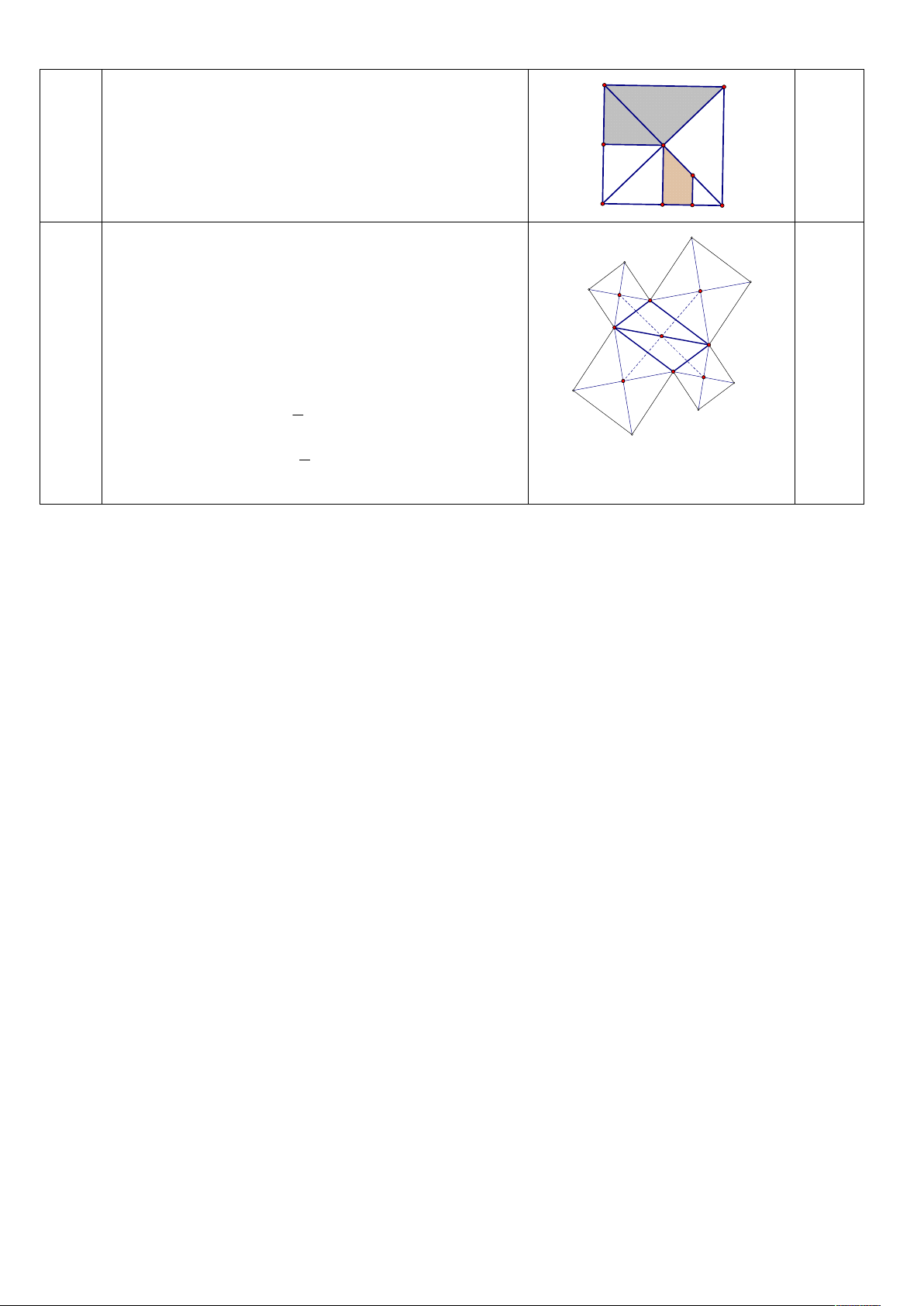
. Vậy A( -1 ;-7) 1 điểm (2 đ) y '  y  3 y  7   V ( M  NEO)  A B 0.25 (C,2) OEDA 0.25 §   OE ( OEDA)  OECB §   OF ( OECB)  OFAB F O 0.25
Vậy hình thang MNOE và hình thang FOBA đồng N dạng với nhau 0.25 D E M C
Câu 3 Gọi I là trung điểm AC. Suy ra I là tâm đối xứng của E
hình gồm hình bình hành và bốn hình vuông đã cho. H
Vậy I là trung điểm MP và QN. Hay tứ giác MNPQ là hình bình hành. N M B
Đặt   BC; BE , A 0.5 CH  EA I C
Khi đó Q B;CH  EA   D CH  EA  Q P  1 IN / /AE; IN  AE   IN  IM Mặt khác 2    1 IN  IM IM / /CH; IM  HC   0.5  2
Vậy tứ giác MNPQ là hình vuông.
Ghi chú: Học sinh có cách làm khác đúng vẫn cho điểm tối đa