Đề kiểm tra 1 tiết Đại số và Giải tích 11 chương 1 năm 2018 – 2019 trường THPT Đô Lương 4 – Nghệ An

Đề kiểm tra 1 tiết Đại số và Giải tích 11 chương 1 năm 2018 – 2019 trường THPT Đô Lương 4 – Nghệ An mã đề 01 gôm 2 trang với 20 câu hỏi trắc nghiệm khách quan

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

12 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
SỞ GIÁO DỤC & ĐÀO TẠO NGHỆ AN
TRƯỜNG THPT ĐÔ LƯƠNG 4
ĐỀ KIỂM TRA 1 TIẾT
Môn: Đại số và giải tích 11
Thời gian làm bài: 45 phút;
(20 câu trắc nghiệm)
Mã đề thi 01
Họ và tên:..................................................................... Lớp: ...........................
Câu
1
2
3
4
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Đáp án
Câu 1: Tất cả các nghiệm của phương trình
3
sinx + cosx = 0 là:
A.
6
xk
= − +
B.
3
xk
= − +
C.
3
xk
=+
D.
6
xk
=+
Câu 2: Với giá trị nào của m thì phương trình
sin 1xm−=
có nghiệm
A.
20m−
B.
0m
C.
01m
D.
1m
Câu 3: Số nghiệm thuộc
0;


của phương trình
22
sin cos 3 0xx−=
là:
A. 4. B. 6. C. 2 D. 8.
Câu 4: Phương trình lượng giác:
2cos 2 0x +=
có tất cả họ nghiệm là:
A.
5
2
4
5
2
4
xk
xk
=+
−
=+
B.
3
2
4
3
2
4
xk
xk
=+
−
=+
C.
2
4
3
2
4
xk
xk
=+
=+
D.
x2
4
2
4
k
xk
=+
−
=+
Câu 5: Số nghiệm của phương trình
sin cos 1xx+=
trên khoảng
( )
0;
là
A. 0 B. 1 C. 2 D. 3
Câu 6: Tất cả các nghiệm của phương trình cos
2
x – sinx cosx = 0 là:
A.
;
42
x k x k


= + = +
B.
4
xk
=+
C.
2
xk
=+
D.
57
;
66
x k x k


= + = +
Câu 7: Tất cả các nghiệm của phương trình: sin
2
x + sin2x – 3cos
2
x = 1 là
A. x = , B.
C. x = D. x =
Câu 8: Trong các phương trình sau phương trình nào vô nghiệm:
(I) cosx =
53−
(II) sinx = 1–
2
(III) sinx + cosx = 2
A. (I) B. (I) và (II) C. (II) D. (III)
Câu 9: Điều kiện xác định của hàm số
cot
cos
x
y
x
=
là:
A.
x k
B.
x
2
k
+
C.
x2k
D.
x
2
k
Câu 10: Phương trình
cos sinxx=
có số nghiệm thuộc đoạn
;

−
là:
A.
4
B.
5
C.
6
D.
2
Câu 11: Nghiệm của phương trình lượng giác:
2
2sin 3sin 1 0xx− + =
thõa điều kiện
0
2
x

là:
A.
3
x
=
B.
2
x
=
C.
6
x
=
D.
5
6
x
=
Câu 12. Tìm tập xác định của hàm số :
A. B.
C. D.
Câu 13: Điều kiện xác định của hàm số
tan
cos 1
x
y
x
=
−
là:
A.
2
3
xk
+
B.
x
2
2
k
xk
+
C.
x2k
D.
x
2
3
k
xk
+
+
Câu 14: . phương trình tương đương với phương trình:
A. B. C. D .
Câu 15: Giá trị lớn nhất và nhỏ nhất của hàm số
2sin3 3yx=−
là:
A. 1 và -5 B.
1−
và -5 C. 5 và -1 D. 3 và -3
Câu 16: Phương trình
2tan 2cot 3 0xx− − =
có số nghiệm thuộc khoảng
;
2

−


là:
A.
1
B.
2
C.
3
D.
4
Câu 17: Nghiệm âm lớn nhất của phương trình
2
2tan 5tan 3 0xx+ + =
là:
A.
3
arctan
2
−
B.
4
−
C.
6
−
D.
3
−
Câu 18: . Phương trình có nghiệm là:
A. B. C. D.
Câu 19: Phương trình lượng giác:
2
sin 3cos 4 0xx− − =
có nghiệm là:
A.
x2k

= − +
B.
x2
2
k
= − +
C.
x
6
k
=+
D. Vô nghiệm
Câu 20: Các họ nghiệm của phương trình:
0sin32sin =− xx
là:
A.
6
xk
xk
=
= +
B.
2
6
xk
= +
C.
2
6
xk
xk
=
= +
D.
2
2
3
xk
xk
=
= +
-----------------------------------------------
----------- HẾT ----------
SỞ GIÁO DỤC & ĐÀO TẠO NGHỆ AN
TRƯỜNG THPT ĐÔ LƯƠNG 4
ĐỀ KIỂM TRA 1 TIẾT
Môn: Đại số và giải tích 11
Thời gian làm bài: 45 phút;
(20 câu trắc nghiệm)
Mã đề thi 01
Họ và tên:..................................................................... Lớp: ...........................
Câu
1
2
3
4
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Đáp án
Câu 1: Tất cả các nghiệm của phương trình
3
sinx + cosx = 0 là:
A.
6
xk
= − +
B.
3
xk
= − +
C.
3
xk
=+
D.
6
xk
=+
Câu 2: Với giá trị nào của m thì phương trình
sin 1xm−=
có nghiệm
A.
20m−
B.
0m
C.
01m
D.
1m
Câu 3: Số nghiệm thuộc
0;


của phương trình
22
sin cos 3 0xx−=
là:
A. 4. B. 6. C. 2 D. 8.
Câu 4: Phương trình lượng giác:
2cos 2 0x +=
có tất cả họ nghiệm là:
A.
5
2
4
5
2
4
xk
xk
=+
−
=+
B.
3
2
4
3
2
4
xk
xk
=+
−
=+
C.
2
4
3
2
4
xk
xk
=+
=+
D.
x2
4
2
4
k
xk
=+
−
=+
Câu 5: Số nghiệm của phương trình
sin cos 1xx+=
trên khoảng
( )
0;
là
A. 0 B. 1 C. 2 D. 3
Câu 6: Tất cả các nghiệm của phương trình cos
2
x – sinx cosx = 0 là:
A.
;
42
x k x k


= + = +
B.
4
xk
=+
C.
2
xk
=+
D.
57
;
66
x k x k


= + = +
Câu 7: Tất cả các nghiệm của phương trình: sin
2
x + sin2x – 3cos
2
x = 1 là
A. x = , B.
C. x = D. x =
Câu 8: Trong các phương trình sau phương trình nào vô nghiệm:
(I) cosx =
53−
(II) sinx = 1–
2
(III) sinx + cosx = 2
A. (I) B. (I) và (II) C. (II) D. (III)
Câu 9: Điều kiện xác định của hàm số
cot
cos
x
y
x
=
là:
A.
x k
B.
x
2
k
+
C.
x2k
D.
x
2
k
Câu 10: Phương trình
cos sinxx=
có số nghiệm thuộc đoạn
;

−
là:
A.
4
B.
5
C.
6
D.
2
Câu 11: Nghiệm của phương trình lượng giác:
2
2sin 3sin 1 0xx− + =
thõa điều kiện
0
2
x

là:
A.
3
x
=
B.
2
x
=
C.
6
x
=
D.
5
6
x
=
Câu 12. Tìm tập xác định của hàm số :
A. B.
C. D.
Câu 13: Điều kiện xác định của hàm số
tan
cos 1
x
y
x
=
−
là:
A.
2
3
xk
+
B.
x
2
2
k
xk
+
C.
x2k
D.
x
2
3
k
xk
+
+
Câu 14: . phương trình tương đương với phương trình:
A. B. C. D .
Câu 15: Giá trị lớn nhất và nhỏ nhất của hàm số
2sin3 3yx=−
là:
A. 1 và -5 B.
1−
và -5 C. 5 và -1 D. 3 và -3
Câu 16: Phương trình
2tan 2cot 3 0xx− − =
có số nghiệm thuộc khoảng
;
2

−


là:
A.
1
B.
2
C.
3
D.
4
Câu 17: Nghiệm âm lớn nhất của phương trình
2
2tan 5tan 3 0xx+ + =
là:
A.
3
arctan
2
−
B.
4
−
C.
6
−
D.
3
−
Câu 18: . Phương trình có nghiệm là:
A. B. C. D.
Câu 19: Phương trình lượng giác:
2
sin 3cos 4 0xx− − =
có nghiệm là:
A.
x2k

= − +
B.
x2
2
k
= − +
C.
x
6
k
=+
D. Vô nghiệm
Câu 20: Các họ nghiệm của phương trình:
0sin32sin =− xx
là:
A.
6
xk
xk
=
= +
B.
2
6
xk
= +
C.
2
6
xk
xk
=
= +
D.
2
2
3
xk
xk
=
= +
-----------------------------------------------
----------- HẾT ----------
Tra
ng 4/11 – Diễn đàn giáo viên Toán
BẢNG ĐÁP ÁN
1.A
2.A
3.B
4.B
5.B
6.A
7.D
8.D
9.D
10.D
11.C
12.D 13.B 14.C 15.B 16.C 17.B 18.A 19.D 20.C
LỜI
GIẢI CHI TIẾT
Câu 1. Tất cả các nghiệm của phương trình
3s
in cos 0
x x
là:
A.
,
6
x k
k
. B.
,
3
x k
k
. C.
,
3
x k
k
. D.
,
6
x k
k
.
Lời
giải
Chọn A
Ta có:
3s
in cos 0
x x
3 1
sin cos 0
2 2
x x
si
n 0
6
x
,
6
x k
k
,
6
x k
k
.
Vậy phư
ơng trình có họ nghiệm là
,
6
x k
k
.
Câu
2. Với giá trị nào của
m
thì
phương trình
si
n 1
x m
có
nghiệm?
A.
2 0
m
. B.
0
m
. C.
0 1
m
. D.
1
m
.
Lời
giải
Chọn A
Ta c
ó:
sin 1
x m
sin 1
x m
.
Để phương trình đã cho có nghiệm thì
1 1
1 2 0
m m
.
Câu
3. Số nghiệm thuộc
0;
của phương trình
2 2
si
n cos 3 0
x x
.
A.
4
. B.
6
. C.
2
. D.
8
.
Lời
giải
Chọn B
2 2
cos3
cos 1
sinx cos3
2
sin cos 3 0
sinx cos3
cos3
cos 2
2
x x
x
x x
x
x x
.
Giải phương trình
1
ta
được:
8 2
c
os3 cos ,
2
4
x k
x x k
x k
.
T
rang 5/11 - WordToan
+
5
0
; 0;1 ;
8
2 8 8
x
k k x
.
+
3
0
; 1
4
4
x
k k x
.
Giải phươ
ng trình
2
t
a được:
4
c
os3 cos ,
2
8 2
x k
x x k
x k
.
+
0
; 0
4
4
x
k k x
.
+
3
7
0
; 1;2 ;
8
2 8 8
x
k k x
.
Vậy
có 6 nghiệm thỏa mãn yêu cầu.
Câu 4. Phương trình lượng giác
2
cos 2 0
x
c
ó tất cả họ nghiệm là
A.
5
2
4
,
5
2
4
x
k
k
x k
. B.
3
2
4
,
3
2
4
x
k
k
x k
.
C.
2
4
,
3
2
4
x
k
k
x k
. D.
2
4
,
2
4
x
k
k
x k
.
Lờ
i giải
Chọn
B
3
2
2
4
2
cos 2 0 cos ,
3
2
2
4
x k
x x k
x k
.
C
âu 5. Sô nghiêm cua phương trinh
si
n cos 1x x
t
rên khoang
(0
; )
l
a:
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta co:
sin
cos 1 2 cos 1
4
x
x x
1
cos
4
2
x
2
2
4
4
,
2
2
2
4 4
x k
x k
k
x k
x k
.
Tra
ng 6/11 – Diễn đàn giáo viên Toán
Đê
(0
; )
x
thi:
0 2
0
2
2
k
k x
k
.
0 2k
k
k
.
Vây, phương trinh
sin cos 1x x
co
đung
1
ng
hiêm trên khoang
(0; )
.
Câu
6. Tât ca cac nghiêm cua phương trinh
2
co
s sin cos 0
x x
x
la
:
A.
;
4 2
x
k x k
. B.
4
x k
.
C.
2
x k
. D.
5 7
;
6 6
x
k x k
.
Lời
giải
Chọn A
T
a co:
2
cos
0 cos 0
cos sin cos 0 cos (cos sin ) 0
cos
sin 0 cos sin
x x
x
x x x x x
x x
x x
cos
0
2
,
tan 1
4
x k
x
k
x
x k
.
Câu 7. Tất cả các nghiệm của phương trình:
2 2
si
n sin 2 3cos 1x x x
A.
; arctan 2
x k x k
. B.
ar
ctan 2
x k
.
C.
2
x k
. D.
; arct
an 2
2
x k
x k
.
Lời giải
Chọn D
Ta có:
2 2 2 2 2 2
si
n sin 2 3cos 1 sin 2sin .cos 3cos sin cosx x x x x x x x x
2
2sin .cos 4 cos 0
x x x
2cos (sin 2cos ) 0
x x x
2c
os 0
sin 2
cos 0
x
x x
2
ta
n 2
x k
x
2
ar
ctan 2
x k
x k
.
Câu 8. Trong các phương trình sau phương trình nào vô nghiệm:
(I)
co
s 5 3
x
(II)
sin
1 2
x
(III
)
si
n cos 2
x x
T
rang 7/11 - WordToan
A. (I
).
B. (I
) và (II).
C. (I
I). D
. (I
II)
Lời
giải
Chọn
D
Phương trình (I)
c
os 5 3
x
có nghiệm vì
5
3 1;1
.
Phư
ơng trình (II)
sin 1 2
x
có
nghiệm vì
1
2 1;1
.
Phư
ơng trình (III)
s
in cos 2 sin 2
4
x
x x
vô nghiệm vì
2
1;1
.
Câu 9. Điều kiện xác định của hàm số
c
ot
cos
x
y
x
l
à:
A.
x
k
. B.
2
x
k
. C.
2x
k
. D.
2
x
k
.
Lờ
i giải
Chọn
D
Điều kiện:
s
in 0
, , ,
cos 0
2
2
x m
x
m n x k m n k
x
x n
.
C
âu 10. Phương trình
co
s sinx x
có số nghiệm thuộc đoạn
;
là:
A.
4
. B.
5
. C.
6
. D.
2
.
Lờ
i giải
Chọn
D
Phương trình:
c
os sin sin cos 0 2 sin 0
4 4 4
x
x x x x x k x k
k
.
Vì n
ghiệm thuộc đoạn
;
n
ên nghiệm của phương trình là:
3
;
4 4
x
x
.
C
âu 11. Nghiệm của phương trình lượng giác
2
2
sin 3sin 1 0
x
x
t
hỏa điều kiện
0
2
x
là:
A.
3
x
. B.
2
x
. C.
6
x
. D.
5
6
x
Lờ
i giải
Chọn
C
Ta có
2
2sin 3sin 1 0
x x
s
inx 1
1
s
inx
2
2
2
2
( )
6
5
2
6
x
k
x k k
x k
.
Vì điều
kiện nghiệm của phương trình là
0
2
x
nên ứng
với k = 0
thì
6
x
thỏa
.
Vậy chọn đáp án là C.
T
rang 8/11 – Diễn đàn giáo viên Toán
C
âu 12. Tìm tập xác định của hàm số
ta
n(2 )
3
y
x
A.
D
\
,
3
k
k
B.
D
\
,
3
2
k k
.
C.
D

\
,
1
2
k k
. D.
D

\
,
1
2 2
k k
.
Lời giải
Chọn
D
Hàm số
ta
n(2 )
3
y
x
có
nghĩa khi và chỉ khi:
2
3
2
x
k
2
6
12 2
x k
x k
C
âu 13. Điều kiện xác định của hàm số
1
t
an
cos
x
y
x
l
à
A.
2
3
x k
. B.
2
2
x
k
x
k
. C.
2
x
k
. D.
2
3
x
k
x k
.
Lờ
i giải
Chọn
B
Hàm số
1
t
an
cos
x
y
x
xác định khi và chỉ khi
t
an x
xác định và
1
0cosx
.
Hay
0
2
1
2
cos
,
cos
x
x k
k
x
x k
.
Do
đó ta chọn phương án B
Câu 14. Phương trình
s
in 3 cos 2 1 2sin cos 2x x x x
tương
đương với phương trình:
A.
sin
0
sin 1
x
x
. B.
sin
0
sin 1
x
x
. C.
sin
0
1
sin
2
x
x
. D.
sin
0
1
sin
2
x
x
.
Lờ
i giải
Chọn
C
Ta có:
s
in 3 cos 2 1 2sin cos 2x x x x
3
2 2
3
sin 4sin 1 2sin 1 2sin 1 2sin
x
x x x x
3 2 3
3sin 4sin 2sin 2sin 4sinx x x x x
Tra
ng 9/11 - WordToan
2
2sin sin 0
x x
sin
0
1
sin
2
x
x
.
Câu
15. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2sin 3 3y x
là
A.
1
và
5.
B.
1
và
5.
C.
5
và
1.
D.
3
và
3.
Lời
giải
Chọn B
Ta c
ó:
1 si
n3 1, 2 2sin 3 2,x x x x
2 3
2sin 3 3 2 3, 5 1, .
x x y
x
.
Vậy hà
m số đã cho có giá trị lớn nhất bằng
1
và
giá trị nhỏ nhất bằng
5.
Câu
16. Phương trình
2 t
an 2cot 3 0
x x
có
số nghiệm thuộc khoảng
;
2
là
A.
1.
B.
2.
C.
3.
D.
4.
Lời
giải
Chọn C
Điều
kiện:
sin 0
.
cos
0
2
x
π
x k
x
Phư
ơng trình đã cho tương đương với:
2
ta
n 2
2 t
an 3tan 2 0
1
tan
2
x
x x
x
tan 2 arctan 2x x k
π
1 1
ta
n arctan
2 2
x x k
π
Với
1
arc
tan , arctan 2 ;
2 2 2
π π
ta
có các nghiệm của phương trình đã cho thuộc khoảng
;
2
là
1 2
1 1
ar
ctan , arctan
2 2
x x
π
và
3
arct
an 2.
x
Câu
17. Nghiệm âm lớn nhất của phương trình
2
2t
an 5 tan 3 0
x x
là
:
A.
3
arctan
.
2
B.
.
4
C.
.
6
D.
.
3
Lời giải
Chọn B
Điều kiện:
,
2
x k k
.
Đặt
tan x t
phương
trình trở thành
2
2 5 3 0
t t
.
1
4
,
3
3
arc
tan
2
2
t
x k
k
t
x k
.
Khi
biểu diễn các nghiệm trên đường tròn lượng giác ta được:
T
rang 10/11 – Diễn đàn giáo viên Toán
Dễ thấy, nghiệm âm lớn nhất sẽ thuộc họ nghiệm
,
4
x
k k
.
Các nghiệm âm khi và chỉ khi
1
0
, , .
4 4
k
k k k
Ng
hiệm âm lớn nhất
k
lớn
nhất
0
4
k
x
.
Vậy
nghiệm âm lớn nhất của phương trình là
4
x
.
Câu 18. Phương trình
2
2
3sin cos 2cos 3 1
8 8 8
x x x
có
nghiệm là:
A.
3
8
,
.
5
2
4
x k
k
x k
B.
3
4
;
.
5
12
x k
k
x k
C.
5
4
, .
5
16
x k
k
x k
D.
5
8
, .
7
24
x
k
k
x k
Lời giải
Chọn
A
2
2
3sin cos 2cos 3 1
8
8 8
x x x
.
3
sin 2 1 cos 2 3 1
4
4
x x
.
3
sin 2 cos 2 3
4
4
x x
.
3
1 3
sin
2 cos 2
2
4 2 4 2
x
x
.
s
in 2 sin
4 6 3
x
.
2
2
12 3
sin 2 sin ,
12 3
2 2
12 3
x k
x k
x k
.
T
rang 11/11 - WordToan
5
24
,
3
8
x k
k
x k
.
C
âu 19. Phương trình lượng giác
2
s
in 3cos 4 0
x
x
có
nghiệm là:
A.
2x
k
. B.
2
2
x
k
. C.
6
x k
. D. vô nghiệm.
Lờ
i giải
Chọn D
Ta có
2 2
sin 3cos 4 0 cos 3cos 3 0.
x x x x
Phư
ong trình vô nghiệm.
Câu 20. Các họ nghiệm của phương trình
si
n 2 3 sin 0
x
x
l
à:
A.
6
x
k
x
k
. B.
6
x k
. C.
2
6
x
k
x
k
. D.
2
2
3
x
k
x
k
.
Lờ
i giải
Chọn
C
Ta có
sin
2 3 sin 0 sin 2cos 3 0
x
x x x
sin
0
3
2
c
os
6
2
x
x k
x
k
x
.
| 1/12
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC & ĐÀO TẠO NGHỆ AN
ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT ĐÔ LƯƠNG 4
Môn: Đại số và giải tích 11
Thời gian làm bài: 45 phút;
(20 câu trắc nghiệm) Mã đề thi 01
Họ và tên:..................................................................... Lớp: ........................... Câu 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 Đáp án
Câu 1: Tất cả các nghiệm của phương trình 3 sinx + cosx = 0 là:     x = − + kx = − + kx = + kx = + kA. 6 B. 3 C. 3 D. 6
Câu 2: Với giá trị nào của m thì phương trình sin x − m = 1 có nghiệm A. 2 −  m  0 B. m  0 C. 0  m 1 D. m 1
Câu 3: Số nghiệm thuộc 0;    của phương trình 2 2
sin x − cos 3x = 0 là: A. 4. B. 6. C. 2 D. 8.
Câu 4: Phương trình lượng giác: 2 cos x + 2 = 0 có tất cả họ nghiệm là:  5  3     x = + k2  x = + k2  x = + k2  x = + k2  A. 4  B. 4  C. 4  D. 4  −5  −3  3   −  x = + k2 = +  = +  = +   x k 2 x k 2 x k 2  4  4  4  4
Câu 5: Số nghiệm của phương trình sin x + cos x =1 trên khoảng (0; ) là A. 0 B. 1 C. 2 D. 3
Câu 6: Tất cả các nghiệm của phương trình cos2x – sinx cosx = 0 là:    x =
+ k ; x = + kx = + k A. 4 2 B. 4  5 7 x = + kx = + k; x = + kC. 2 D. 6 6
Câu 7: Tất cả các nghiệm của phương trình: sin2x + sin2x – 3cos2x = 1 là A. x = , B. C. x = D. x =
Câu 8: Trong các phương trình sau phương trình nào vô nghiệm: (I) cosx = 5 − 3 (II) sinx = 1– 2 (III) sinx + cosx = 2 A. (I) B. (I) và (II) C. (II) D. (III) x
Câu 9: Điều kiện xác định của hàm số cot y = là: cos x   A. x  kB. x  + kC. x  k2 D. x  k 2 2
Câu 10: Phương trình cos x = sin x có số nghiệm thuộc đoạn   − ;  là: A. 4 B. 5 C. 6 D. 2
Câu 11: Nghiệm của phương trình lượng giác: 2
2 sin x − 3sin x +1 = 0 thõa điều kiện  0  x  là: 2    5 A. x = B. x = C. x = D. x = 3 2 6 6
Câu 12. Tìm tập xác định của hàm số : A. B. C. D. x
Câu 13: Điều kiện xác định của hàm số tan y = là: cos x −1      +    x k x  + k  2 x  + k2  2 C. x  k2  A. 3        +  B. x k2 x kD.  3
Câu 14: . phương trình
tương đương với phương trình: A. B. C. D .
Câu 15: Giá trị lớn nhất và nhỏ nhất của hàm số y = 2sin 3x − 3 là: A. 1 và -5 B. −1 và -5 C. 5 và -1 D. 3 và -3   
Câu 16: Phương trình 2tan x − 2cot x −3 = 0 có số nghiệm thuộc khoảng − ;   là:  2  A. 1 B. 2 C. 3 D. 4
Câu 17: Nghiệm âm lớn nhất của phương trình 2
2 tan x + 5 tan x + 3 = 0 là: 3 −    A. arctan B. − C. − D. − 2 4 6 3
Câu 18: . Phương trình có nghiệm là: A. B. C. D.
Câu 19: Phương trình lượng giác: 2
sin x − 3cos x − 4 = 0 có nghiệm là:   A. x =  − + k2 B. x = − + k2 C. x = + kD. Vô nghiệm 2 6
Câu 20: Các họ nghiệm của phương trình: sin 2x − 3 sin x = 0 là: x = k  =   =   x k x k 2 A.   =  +     B. x k 2 C. D. x =  + k 6
x =  + k2
x =  + k2  6  6  3
----------------------------------------------- ----------- HẾT ----------
SỞ GIÁO DỤC & ĐÀO TẠO NGHỆ AN
ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT ĐÔ LƯƠNG 4
Môn: Đại số và giải tích 11
Thời gian làm bài: 45 phút;
(20 câu trắc nghiệm) Mã đề thi 01
Họ và tên:..................................................................... Lớp: ........................... Câu 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 Đáp án
Câu 1: Tất cả các nghiệm của phương trình 3 sinx + cosx = 0 là:     x = − + kx = − + kx = + kx = + kA. 6 B. 3 C. 3 D. 6
Câu 2: Với giá trị nào của m thì phương trình sin x − m = 1 có nghiệm A. 2 −  m  0 B. m  0 C. 0  m 1 D. m 1
Câu 3: Số nghiệm thuộc 0;    của phương trình 2 2
sin x − cos 3x = 0 là: A. 4. B. 6. C. 2 D. 8.
Câu 4: Phương trình lượng giác: 2 cos x + 2 = 0 có tất cả họ nghiệm là:  5  3     x = + k2  x = + k2  x = + k2  x = + k2  A. 4  B. 4  C. 4  D. 4  −5  −3  3   −  x = + k2 = +  = +  = +   x k 2 x k 2 x k 2  4  4  4  4
Câu 5: Số nghiệm của phương trình sin x + cos x =1 trên khoảng (0; ) là A. 0 B. 1 C. 2 D. 3
Câu 6: Tất cả các nghiệm của phương trình cos2x – sinx cosx = 0 là:    x =
+ k ; x = + kx = + k A. 4 2 B. 4  5 7 x = + kx = + k; x = + kC. 2 D. 6 6
Câu 7: Tất cả các nghiệm của phương trình: sin2x + sin2x – 3cos2x = 1 là A. x = , B. C. x = D. x =
Câu 8: Trong các phương trình sau phương trình nào vô nghiệm: (I) cosx = 5 − 3 (II) sinx = 1– 2 (III) sinx + cosx = 2 A. (I) B. (I) và (II) C. (II) D. (III) x
Câu 9: Điều kiện xác định của hàm số cot y = là: cos x   A. x  kB. x  + kC. x  k2 D. x  k 2 2
Câu 10: Phương trình cos x = sin x có số nghiệm thuộc đoạn   − ;  là: A. 4 B. 5 C. 6 D. 2
Câu 11: Nghiệm của phương trình lượng giác: 2
2 sin x − 3sin x +1 = 0 thõa điều kiện  0  x  là: 2    5 A. x = B. x = C. x = D. x = 3 2 6 6
Câu 12. Tìm tập xác định của hàm số : A. B. C. D. x
Câu 13: Điều kiện xác định của hàm số tan y = là: cos x −1      +    x k x  + k  2 x  + k2  2 C. x  k2  A. 3        +  B. x k2 x kD.  3
Câu 14: . phương trình
tương đương với phương trình: A. B. C. D .
Câu 15: Giá trị lớn nhất và nhỏ nhất của hàm số y = 2sin 3x − 3 là: A. 1 và -5 B. −1 và -5 C. 5 và -1 D. 3 và -3   
Câu 16: Phương trình 2tan x − 2cot x −3 = 0 có số nghiệm thuộc khoảng − ;   là:  2  A. 1 B. 2 C. 3 D. 4
Câu 17: Nghiệm âm lớn nhất của phương trình 2
2 tan x + 5 tan x + 3 = 0 là: 3 −    A. arctan B. − C. − D. − 2 4 6 3
Câu 18: . Phương trình có nghiệm là: A. B. C. D.
Câu 19: Phương trình lượng giác: 2
sin x − 3cos x − 4 = 0 có nghiệm là:   A. x =  − + k2 B. x = − + k2 C. x = + kD. Vô nghiệm 2 6
Câu 20: Các họ nghiệm của phương trình: sin 2x − 3 sin x = 0 là: x = k  =   =   x k x k 2 A.   =  +     B. x k 2 C. D. x =  + k 6
x =  + k2
x =  + k2  6  6  3
----------------------------------------------- ----------- HẾT ---------- BẢNG ĐÁP ÁN 1.A 2.A 3.B 4.B 5.B 6.A 7.D 8.D 9.D 10.D 11.C 12.D 13.B 14.C 15.B 16.C 17.B 18.A 19.D 20.C
LỜI GIẢI CHI TIẾT Câu 1.
Tất cả các nghiệm của phương trình 3 sin x  cos x  0 là:     A. x  
k , k   . B. x  
k , k   . C. x
k , k   . D. x
k , k   . 6 3 3 6 Lời giải Chọn A Ta có: 3 1    
3 sin x  cos x  0  sin x
cos x  0  sin x   0    x
k , k   2 2  6  6   x  
k , k   . 6 
Vậy phương trình có họ nghiệm là x  
k , k   . 6 Câu 2.
Với giá trị nào của m thì phương trình sin x m  1 có nghiệm?
A. 2  m  0 . B. m  0 .
C. 0  m  1 . D. m  1. Lời giải Chọn A
Ta có: sin x m  1  sin x m 1.
Để phương trình đã cho có nghiệm thì 1  m 1  1  2  m  0 . Câu 3.
Số nghiệm thuộc 0;  của phương trình 2 2
sin x  cos 3x  0 . A. 4 . B. 6 . C. 2 . D. 8 . Lời giải Chọn B     cos 3x  cos  x      1 s inx  cos 3x  2 2 2  sin x cos 3x 0       . s inx   cos 3x      cos 3x  cos  x    2   2     x   k     8 2 Giải phương trình  
1 ta được: cos 3x  cos  x   , k    .  2  
x    k  4
Trang 4/11 – Diễn đàn giáo viên Toán    5  + x   k
0;   k 0  ;1  x   ;  . 8 2  8 8   3 + x  
k 0;   k  1 x  . 4 4   x   k     4
Giải phương trình 2 ta được: cos 3x  cos  x   , k    .  2   
x    k  8 2   + x
k 0;   k  0  x  . 4 4   3 7  + x    k
0;   k 1;  2  x   ;  . 8 2  8 8 
Vậy có 6 nghiệm thỏa mãn yêu cầu. Câu 4.
Phương trình lượng giác 2 cos x  2  0 có tất cả họ nghiệm là  5  3 x   k 2  x   k 2 4  4 A.  , k . B.  , k . 5  3 x    k 2 x    k 2  4  4     x   k 2  x   k 2 4  4 C.  , k . D.  , k . 3   x   k 2
x    k2  4  4 Lời giải Chọn B  3 x   k 2 2  4
2 cos x  2  0  cos x    
, k . 2 3  x    k 2  4 Câu 5.
Số nghiệm của phương trình sin x  cos x  1 trên khoảng (0; ) là: A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn B   
Ta có: sin x  cos x  1  2 cos x   1    4     x    2k      1  x   2 4 4 k  cos x         2 , k   .  4  2   
x     2kx  2k   4 4 Trang 5/11 - WordToan
Để x  (0; ) thì:   0   2k     2
k  0  x . 2 k    0  2k     k  . k   
Vậy, phương trình sin x  cos x  1 có đúng 1 nghiệm trên khoảng (0; ) . Câu 6.
Tất cả các nghiệm của phương trình 2
cos x  sin x cos x  0 là:    A. x   k ; x   k . B. x   k . 4 2 4  5 7 C. x   k . D. x   k ; x   k . 2 6 6 Lời giải Chọn A cos x  0 cos x  0 Ta có: 2
cos x  sin x cos x  0  cos x(cos x  sin x)  0    
cos x  sin x  0 cos x  sin x     x   k cos x  0  2    , k    . tan x  1  
x   k  4 2 2 Câu 7.
Tất cả các nghiệm của phương trình: sin x  sin 2x  3 cos x  1
A. x k ; x  arctan 2  k .
B. x  arctan 2  k .   x   kx
k ; x  arctan 2  kC. 2 . D. 2 . Lời giải Chọn D 2 2 2 2 2 2
Ta có: sin x  sin 2x  3cos x  1  sin x  2 sin .
x cos x  3cos x  sin x  cos x 2  2 sin .
x cos x  4 cos x  0
 2 cos x(sin x  2 cos x)  0 2 cos x  0
 sin x  2cos x  0    x   k   2 tan x  2    x   k   2
x  arctan 2 k  . Câu 8.
Trong các phương trình sau phương trình nào vô nghiệm:
(I) cos x  5  3 (II) sin x  1 2 (III) sin x  cos x  2
Trang 6/11 – Diễn đàn giáo viên Toán A. (I). B. (I) và (II). C. (II). D. (III) Lời giải Chọn D 5  3  1  ;  1
Phương trình (I) cos x  5  3 có nghiệm vì . 1 2  1   ;1
Phương trình (II) sin x  1 2 có nghiệm vì .   
sin x  cos x  2  sin x   2   2  1  ;  1 Phương trình (III)  4  vô nghiệm vì . cot x Câu 9.
Điều kiện xác định của hàm số y  là: cos x  
A. x k . B. x   k .
C. x k 2 .
D. x k . 2 2 Lời giải Chọn D x m s  in x  0   Điều kiện:    
m, n    x k  , m , n k   . cos x  0 x   n 2    2
Câu 10. Phương trình cos x  sin x có số nghiệm thuộc đoạn  ;   là: A. 4 . B. 5 . C. 6 . D. 2 . Lời giải Chọn D Phương trình:     
cos x  sin x  sin x  cos x  0  2 sin x   0  x
k  x   k   k   .  4  4 4  3
Vì nghiệm thuộc đoạn  ;
  nên nghiệm của phương trình là: x  ; x   . 4 4 
Câu 11. Nghiệm của phương trình lượng giác 2
2sin x  3sin x  1  0 thỏa điều kiện 0  x  là: 2    5 A. x  . B. x  . C. x  . D. x  3 2 6 6 Lời giải Chọn C   x   k2  2 sinx  1    Ta có 2
2sin x  3sin x  1  0   1  x
k2 (k ) . sinx   6  2  5  x   k2  6   
Vì điều kiện nghiệm của phương trình là 0  x
nên ứng với k = 0 thì x  thỏa. 2 6
Vậy chọn đáp án là C. Trang 7/11 - WordToan
Câu 12. Tìm tập xác định của hàm số y  tan(2x  ) 3     
A. D \   k ,k
B. D \   k ,k  . 3   3 2         
C. D \ 
k ,k  .
D. D \   k ,k . 12   12 2   Lời giải Chọn D
Hàm số y  tan(2x
) có nghĩa khi và chỉ khi: 3   2x    k 3 2   2x   k 6    x   k 12 2 tan x
Câu 13. Điều kiện xác định của hàm số y  là cosx 1     x    k  x   k   2 A. x   k 2 . B.  2 .
C. x k 2 . D.  . 3   x k 2   x    k   3 Lời giải Chọn B tan x Hàm số y
xác định khi và chỉ khi tan x xác định và cosx 1  0 . cosx 1   cosx  0 x   k Hay    2 , k   . cosx  1  x k2 
Do đó ta chọn phương án B
Câu 14. Phương trình sin 3x  cos 2x  1 2 sin x cos 2x tương đương với phương trình: sin x  0 sin x  0 sin x  0 sin x  0 A.    . B.  . C. 1 . D. 1 . sin x  1  sin x  1   sin x  sin x    2  2 Lời giải Chọn C Ta có:
sin 3x  cos 2x  1 2 sin x cos 2x 3 2  x x   x   x  2 3sin 4 sin 1 2 sin 1 2 sin 1 2 sin x 3 2 3
 3sin x  4sin x  2sin x  2sin x  4sin x
Trang 8/11 – Diễn đàn giáo viên Toán sin x  0 2
 2sin x  sin x  0   1 . sin x   2
Câu 15. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2sin 3x  3 là A. 1 và 5  . B. 1 và 5  . C. 5 và 1  . D. 3 và 3.  Lời giải Chọn B Ta có: 1
  sin 3x  1, x     2
  2sin 3x  2, x   
 2  3  2 sin 3x  3  2  3, x    5  y  1, x  .  .
Vậy hàm số đã cho có giá trị lớn nhất bằng 1
 và giá trị nhỏ nhất bằng 5  .   
Câu 16. Phương trình 2 tan x  2 cot x  3  0 có số nghiệm thuộc khoảng  ;    là  2  A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C sin  x  0 π Điều kiện:   x k . cos x  0 2  tan x  2
Phương trình đã cho tương đương với: 2
2 tan x 3 tan x 2 0      1 tan x    2
tan x  2  x  arctan 2  kπ 1  1  tan x    x  arctan   kπ   2  2   1   π π  Với arctan  , arctan 2   ;   
 ta có các nghiệm của phương trình đã cho thuộc khoảng  2   2 2      1   1   ; 
  là x  arctan  , x  arctan 
π và x  arctan 2. 1   2   3  2   2   2 
Câu 17. Nghiệm âm lớn nhất của phương trình 2
2 tan x  5 tan x  3  0 là: 3    A. arctan . B.  . C.  . D.  . 2 4 6 3 Lời giải Chọn B  Điều kiện: x
k , k   . 2
Đặt tan x t  phương trình trở thành 2
2t  5t  3  0 .   t  1  x    k  4   3   , k   . t   3  x  arctan  2  k  2
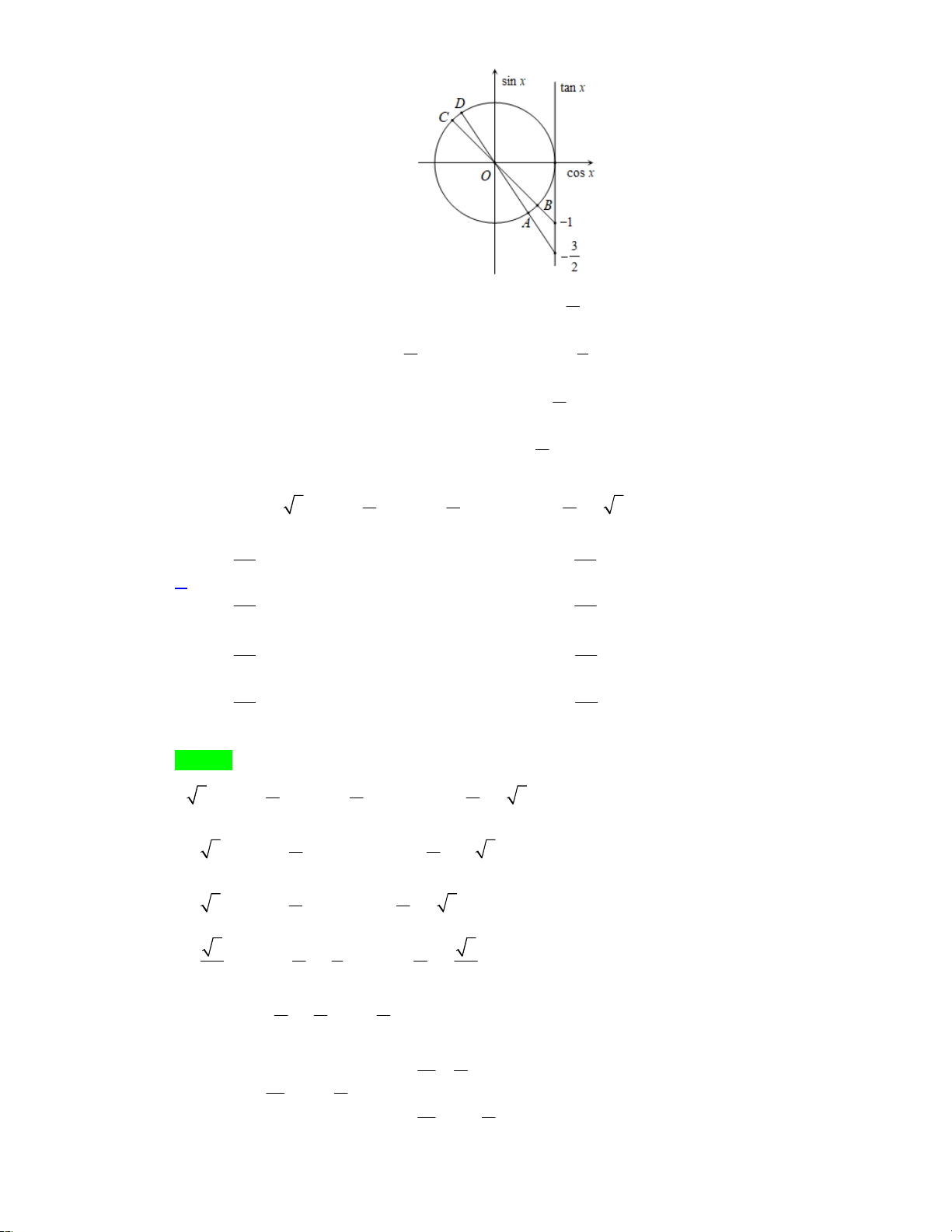
Khi biểu diễn các nghiệm trên đường tròn lượng giác ta được: Trang 9/11 - WordToan
Dễ thấy, nghiệm âm lớn nhất sẽ thuộc họ nghiệm x  
k , k   . 4  1
Các nghiệm âm khi và chỉ khi 
k  0, k    k  , k  .  4 4 
Nghiệm âm lớn nhất  k lớn nhất  k  0  x   . 4 
Vậy nghiệm âm lớn nhất của phương trình là x   . 4         
Câu 18. Phương trình 2 2 3 sin x  cos x   2cos x   3  1       có nghiệm là:  8   8   8   3  3 x   k  x   k 8  4 A.  , k  .  B.  ; k  .  5  5 x   k x   k  24  12  5  5 x   k  x   k 4  8 C.  , k  .  D.  , k  .  5  7 x   k x   k  16  24 Lời giải Chọn A         2  2 3 sin x  cos x   2 cos x   3  1       .  8   8   8          3 sin 2x   1  cos 2x   3  1      . 4 4              3 sin 2x   cos 2x   3     .  4   4  3    1    3  sin 2x   cos 2x       . 2  4  2  4  2        sin 2x    sin   . 4 6    3     2x    k 2      12 3  sin 2x   sin     , k   .  12  3   2x      k 2  12 3
Trang 10/11 – Diễn đàn giáo viên Toán  5 x   k  24   , k   . 3  x   k  8
Câu 19. Phương trình lượng giác 2
sin x  3cos x  4  0 có nghiệm là:   A. x     k 2 . B. x    k 2 . C. x   k. D. vô nghiệm. 2 6 Lời giải Chọn D Ta có 2 2
sin x  3cos x  4  0   cos x  3cos x  3  0. Phưong trình vô nghiệm.
Câu 20. Các họ nghiệm của phương trình sin 2x  3 sin x  0 là: x k x k x k 2  A.   . B. x    k . C.   . D.   . x    k 6 x    k 2 x    k 2  6  6  3 Lời giải Chọn C
Ta có sin 2x  3 sin x  0  sin x 2cos x  3  0 sin x  0  x k    3   .  cos x   x    k 2  2  6 Trang 11/11 - WordToan
Document Outline

  • 263203
    • Kiem tra 1 tiet chuong 1 GT 11 Moi em mot ma de00-converted
    • Kiem tra 1 tiet chuong 1 GT 11 Moi em mot ma de-converted
  • 1568691885_WT33-ĐS11-C1-KIỂM TRA 45 PHÚT-HSLG_PT LG-ĐẠI SỐ-11-THPT ĐÔ LƯƠNG 4-NGHỆ AN