Đề kiểm tra 1 tiết ĐS&GT 11 chương 1 năm 2019 – 2020 trường Nguyễn Trãi – Đà Nẵng

TRƯỜNG THPT NGUYỄN TRÃI
KIỂM TRA 1 TIẾT NĂM HỌC 2019 – 2020 TỔ TOÁN - TIN
Môn: Toán - Lớp 11 - Chương trình chuẩn
Thời gian: 45 phút (không kể thời gian phát đề) Mã đề thi
Họ và tên: …………………………………. Lớp: ……………… SBD: ………..…… Gốc
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1.
Tập xác định của hàm số f  x  tan x là:
A.  \ k | k    .
B.  \ k2 | k    .    C.  \   2k   1  | k    .
D.  \ 2k   1 | k   .  2  Lời giải Chọn D 
f  x xác định khi và chỉ khi cos x  0  x 
 k k  . 2 Câu 2.
Khẳng định nào sau đây đúng?      
A. y  tan x nghịch biến trong 0;   .
B. y  cos x đồng biến trong 0;   .  2   2       
C. y  sin x đồng biến trong 0;   .
D. y  cot x đồng biến trong 0;   .  2   2  Lời giải Chọn C    Trên khoảng 0; 
 thì hàm số y  sin x đồng biến.  2  Câu 3.
Cho các hàm số y  cos x , y  sin x , y  tan x , y  cot x . Trong các hàm số trên, có bao nhiêu hàm số lẻ? A. 2 . B. 1. C. 3 . D. 4 . Lời giải Chọn C
 y  f  x  cos x là hàm số chẵn vì:
Tập xác định D   , nên x
  D  x  D và f x  cosx  cos x  f  x .
 y  g  x  sin x là hàm số lẻ vì:
Tập xác định D   , nên x
  D  x  D và g x  sin x  sin x  g  x .
 y  h  x  tan x là hàm số lẻ vì:  
Tập xác định D   \   k | k  , nên  2  x
  D  x  D và h x  tan x   tan x  h x .
 y  k  x  cot x là hàm số lẻ vì:
Tập xác định D   \ k | k    , nên x
  D  x  D và k x  cot x   cot x  k  x . Câu 4.
Chu kỳ của hàm số y  3sin 2x là số nào sau đây? A. 0 . B. 2 . C. 4 . D.  . Lời giải Chọn D Trang 1/7 - Mã đề thi 188 2
Chu kì của hàm số T    . 2 Câu 5.
Hàm số y  2 cos 3x  3sin 3x  2 có tất cả bao nhiêu giá trị nguyên dương? A. 7 . B. 3 . C. 5 . D. 6 . Lời giải Chọn B TXD: D    2 3 
y  2 cos 3x  3sin 3x  2  13 cos 3x  sin 3x  2    13 13   3 
 y  13 sin 3x  arccos  2    13   3 
Để hàm số y có giá trị nguyên  13 sin 3x  arccos   nguyên  13   3  n  sin 3x  arccos   
( với n là một số nguyên)  13  13  3  Mà: sin 3x  arccos     1  ;  1  13  n  1  
 1   13  n  13 13 Mà: n    n  0; 1  ; 2    3
 y có 3 giá trị nguyên dương. Câu 6.
Phương án nào sau đây là sai với mọi k   ?   A. sin x  1   x    k 2 .
B. sin x  0  x   k . 2 2 
C. sin x  0  x  k .
D. sin x  1  x   k 2 . 2 Lời giải Chọn B
Ta có sin x  0  x  k , k   . Do đó đáp án B sai. Câu 7.
Phương trình nào sau đây luôn vô nghiệm?
A. 2020 cos x  2019 .
B. 2019sin x  2020 . C. 2 tan x  3  0 .
D. 2019 cot x  2020 . Lời giải Chọn B 2020
2019sin x  2020  cos x 
, phương trình vô nghiệm. 2019 2 Câu 8.
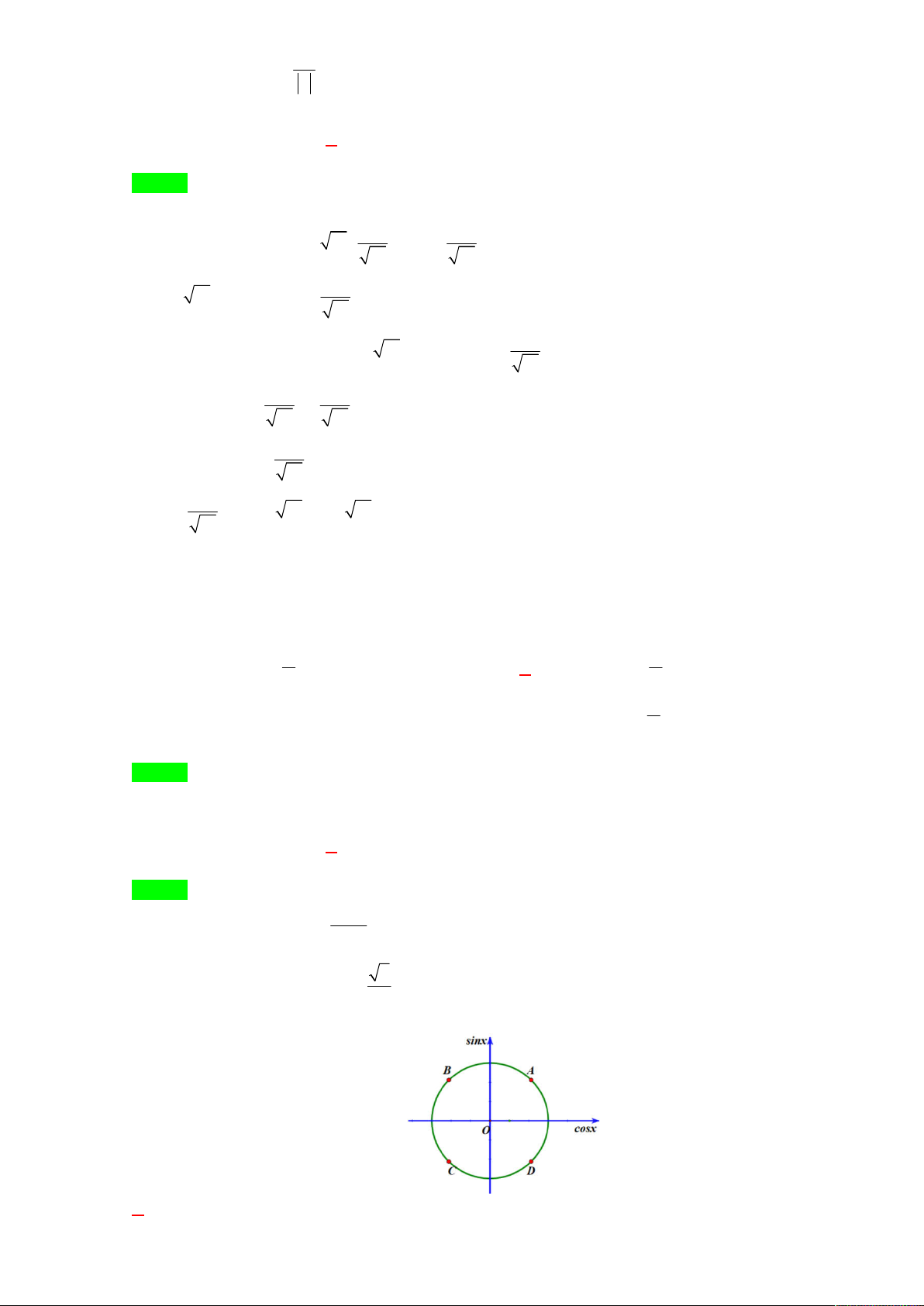
Nghiệm của phương trình cos x 
được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm 2 nào?
A. Điểm A , điểm D .
B. Điểm C , điểm B .
C. Điểm D , điểm C .
D. Điểm A , điểm B . Trang 2/7 - Mã đề thi 188 Lời giải Chọn A   x    k 2 2  4 sin x     . 2 5  x   k 2  4 Câu 9.
Phương trình sin 2x  3cos x  0 có bao nhiêu nghiệm trong khoảng 0;2018 ? A. 642 . B. 643 . C. 641. D. 1. Lời giải. Chọn A
sin 2x  3cos x  0  2sin .
x cos x  3cos x  0  cos .
x 2sin x  3  0  
cos x  0  x   k k   2   3 sin x  
loai vì sin x 1  ;  1   2  1
Theo đề: x 0;2018  0 
 k  2018    k  641,849... 2 2 Suy ra: k 0;  641 .
Vậy phương trình có 642 nghiệm.  5  Câu 10. Trên đoạn 2   ; 
, đồ thị hai hàm số y  tan x và y  1 cắt nhau tại bao nhiêu điểm? 2    A. 2 . B. 5 . C. 4 . D. 3 . Lời giải Chọn B 
Phương trình hoành độ giao điểm của hai đồ thị hàm số là: tan x  1  x 
 k k  . 4   5   5 9 9 Do x   k  2   ; nên 2     k     k   k  2  ; 1;0;1;  2 . 4  2    4 2 4 4  5 
Vậy đồ thị hai hàm số đã cho cắt nhau tại 5 điểm trên đoạn 2   ;  . 2   
Câu 11. Tổng tất cả các nghiệm của phương trình cos sin x  1 trên đoạn 0;2  bằng: A. 0. B.  . C. 2 . D. 3 . Lời giải Chọn B
Phương trình tương đương với sin x  k 2 , k  .  Vì 1
  sin x  1 nên suy ra k  0 , khi đó phương trình trở thành sin x  0  x     .
Vì x 0;2  
 x 0;. Suy ra tổng các nghiệm 0     . Câu 12. Phương trình  x   2 3 tan 1 sin x  
1  0 có tổng các nghiệm trên 0;  bằng: 2   5 A.  B.  . C. . D. . 3 6 6 6 Lời giải Chọn C 
Điều kiện cos x  0  x 
 k , k   . 2 Trang 3/7 - Mã đề thi 188 Do 2
sin x  1  0, x
   nên phương trình đã cho tương đương với 1    
3 tan x 1  0  tan x 
 tan x  tan    x 
 k , k   . 3  6  6 Vì x 0;   Suy ra: x  6
Câu 13. Tập nghiệm của phương trình 2 tan x  3  0 là:         A. S   . B. S    . C. S    . D. S    .  3   3   3  Lời giải Chọn A Ta có: 2 tan x  3  3
Suy ra: phương trình vô nghiệm.
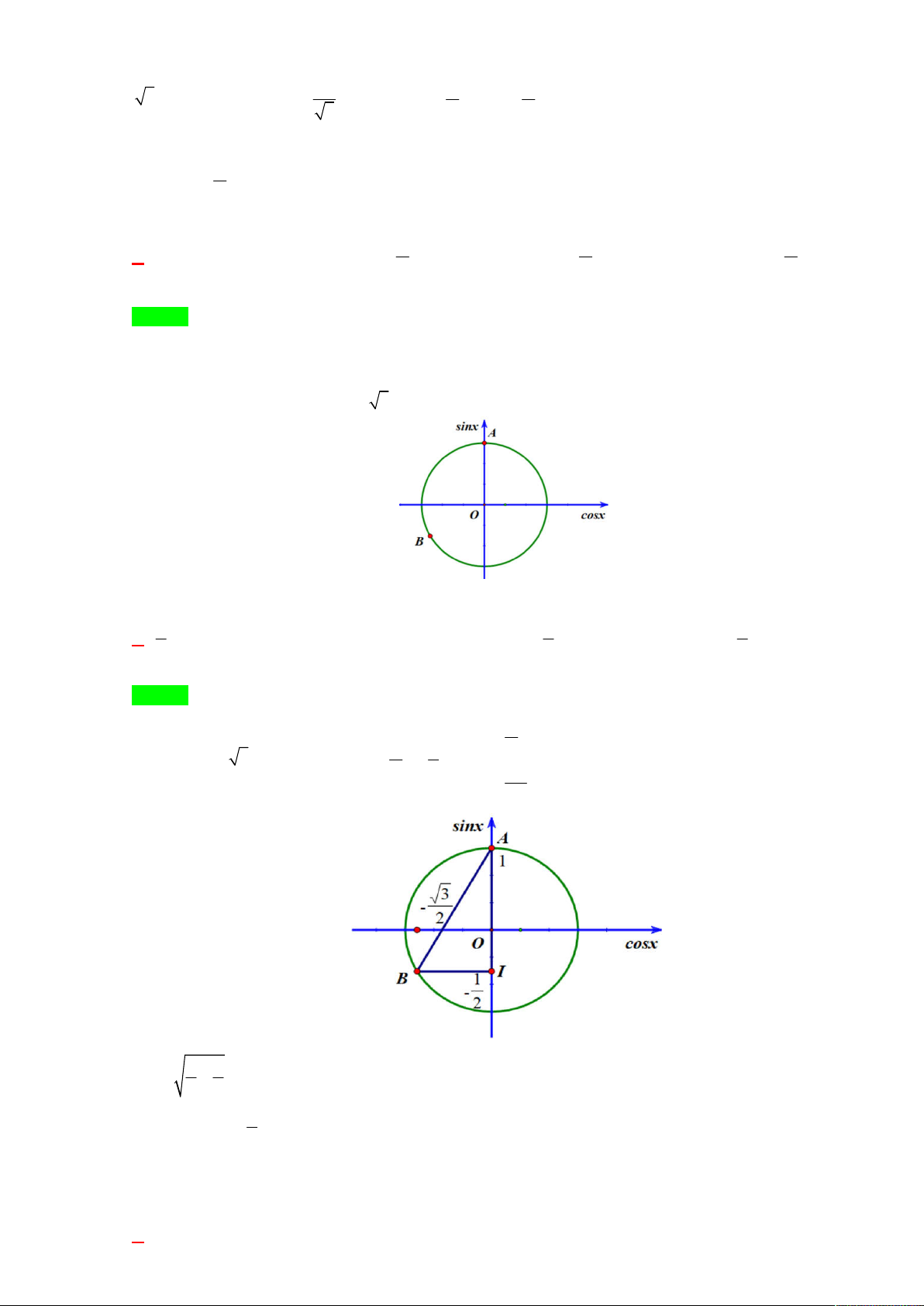
Câu 14. Biết hai nghiệm của phương trình 3 cos x  sin x  1
 được biểu diễn trên đường tròn lượng giác là:
Tính AB  OI với I là hình chiếu vuông góc của B trên OA bằng: 3 1 5 A. B. 3 C. D. 2 2 2 Lời giải Chọn A   x   k 2    1  2
Ta có: sin x  3 cos x  1  sin x       .  3  2 7 x   k 2  6 9 3 AB    3 . 4 4 3
Vậy: AB  OI  . 2 Câu 15. Phương trình 2 2
2sin x  4sin x cos x  4cos x  1 tương đương với phương trình nào trong các phương trình sau?
A. cos 2x  2sin 2x  2.
B. sin 2x  2 cos 2x  2.
C. cos 2x  2sin 2x  2. 
D. sin 2x  2 cos 2x  2.  Trang 4/7 - Mã đề thi 188 Lời giải Chọn C
Phương trình tương đương với  2 2 x  x  x x   2 2sin 2cos 2.2sin cos 2cos x   1  0
 2  2sin 2x  cos 2x  0  cos 2x  2sin 2x  2. 
Câu 16. Cho phương trình: 3cosx  cos2x  cos3x  1  2sin .
x sin 2x . Gọi  là nghiệm nhỏ nhất thuộc khoảng    
0; 2  của phương trình. Tính sin     .  4  2 2 A.  . B. . C. 0 . D. 1. 2 2 Lời giải Chọn B
Phương trình tương đương: 3cosx  cos2x  cos3x  1  cosx  cos3x  2cosx  cos2x  1  0   cosx  0 x   k 2
 cos x  cosx  0     2 . cosx  1  
x   k2   3  
Vì x 0;2  nên x   ; ,
 . Nghiệm lớn nhất của phương là   .  2 2  2         2 Vậy sin      sin     sin  .  4   2 4  4 2 Câu 17. Cho phương trình: 2
3cos 4x  sin 2x  cos 2x  2  0 . Nếu đặt u  cos 2x thì phương trình đã cho trở thành phương trình có dạng 2
au  bu  c  0 , a,b,c   và a  0 . Tính P  a  b  c . A. P  1. B. P  2 . C. P  0 . D. P  3 . Lời giải Chọn B Ta có 2 x  x  x     2 x   2 3cos 4 sin 2 cos 2 2 0 3 2cos 2
1  sin 2x  cos 2x  2  0
Do đó phương trình tương đương với 2
7 cos 2x  cos 2x  6  0
Nếu đặt u  cos 2x thì phương trình trở thành 2
7u  u  6  0 .
sin x  2cos x  1
Câu 18. Giá trị lớn nhất của hàm số y 
tại điểm là nghiệm của phương trình:
sin x  cos x  2
A. 3sin x  4 cos x  5 .
B. 3sin x  4 cos x  5  . C. cos x 1  0 . D. cos x  1  0 . Lời giải Chọn D
sin x  2cos x  1 Ta có y    y  
1 sin x   y  2cos x  1 2 y *
sin x  cos x  2 2 2 2
Phương trình * có nghiệm   y     y      y 2 1 2 1 2
 y  y  2  0  2   y  1.
Vậy giá trị lớn nhất của hàm số bằng 1 lúc đó  cos x  1  .
Câu 19. Tính diện tích của đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các nghiệm của phương   
trình tan x  tan x   1.    4  3 10 3 10 A. . B. . C. 2. D. 3. 10 5 Lời giải Chọn B Trang 5/7 - Mã đề thi 188 y 3 T 1 M H x O B A N -1   cos x  0 x   k    2 Điều kiện:       k  . cos x   0       4 x   k    4    tan x  1
Ta có tan x  tan x   1  tan x   1    4  1 tan x 2
 tan x  tan x  tan x  1  1  tan x tan x  0 x  k 2
 tan x  3tan x  0   k    . tan x  3
x  arctan 3  k  
 Nghiệm x  k biểu diễn trên đường tròn lượng giác là hai điểm , A B .
 Nghiệm x  arctan 3  k biểu diễn trên đường tròn lượng giác là hai điểm M , N . 1 1 A . O AT 3 10 3 10 Ta có S  MN.AH  .MN.    S  . AMN AMBN 2 2 2 2 10 5 AO  AT 1 1 1 1 k 2
Câu 20. Biết rằng phương trình     
 0 có nghiệm dạng x  với k   và 2018 sin x sin 2x sin 4x sin 2 x 2a  b a, b 
  , b  2018. Tính S  a  . b A. S  2017. B. S  2018. C. S  2019. D. S  2020. Lời giải Chọn B Điều kiện: 2018 sin 2 x  0. 2 cos a cos 2a
2cos a  cos 2a 1
Ta có cot a  cot 2a     . sin a sin 2a sin 2a sin 2a  x  Do đó phương trình   x     x  x    2017 2018 cot cot cot cot 2 ... cot 2 x  cot 2 x  0  2  x 2018  cot  cot 2 x  0 2 x x k 2 2018 2018  cot 2 x  cot  2 x 
 k  x  k   2019   2 2 2 1 a  2019    
 S  a  b  2018. b  1  Trang 6/7 - Mã đề thi 188 PHẦN II: TỰ LUẬN
Câu 21. Câu 25. (0,75 điểm) Giải phương trình: 1  2sin x  0 .
Câu 22. (0,75 điểm) Giải phương trình: 3 cos 2019x  sin 2019x  2cos 2020x .
Câu 23. (0,5 điểm) Giải phương trình: 2 3 sin x  3 3 tan x  2cos x  3 .
------------- HẾT ------------- ĐÁP ÁN PHẦN TỰ LUẬN   x   k 2 (0, 25) 1  6
Câu 21. 1  2sin x  0  sin x  (0, 25)   . 2 5  x   k 2 (0, 25)  6 3 1
Câu 22. 3 cos 2019x  sin 2019x  2 cos 2020x  cos 2019x  sin 2019x  cos 2020 2 2   2019x 
 2020x  k 2     6 cos 2019x 
 cos 2020x (0, 25)     (0,5).  6   2019x   20  20x  k 2  6 Câu 23.
Điều kiện: cos x  0 .
Đưa về phương trình tích: 2cos x  3 3 sin x  cos x  0 . (0,25)
Giải ra kết quả kết luận đúng. (0,25).
THỐNG KÊ ĐIỂM KIỂM TRA 0 1 2 3 4 5 6 7 8 9 10 >5 <5 Trang 7/7 - Mã đề thi 188