Đề kiểm tra 45 phút Đại số và Giải tích 11 chương 4 trường THPT Tứ Sơn – Bắc Giang

Đề kiểm tra 45 phút Đại số và Giải tích 11 chương 4 trường THPT Tứ Sơn – Bắc Giang mã đề 101 được biên soạn theo hình thức trắc nghiệm khách quan kết hợp với tự luận theo tỉ lệ điểm số 50 : 50

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1/3 - Mã đề 001
SỞ GD&ĐT CÀ MAU
(Đề có 3 trang)
KIỂM TRA ĐSGT 11 - NĂM HỌC 2017 - 2018
MÔN TOÁN HỌC
Thời gian làm bài: 45 Phút; (Đề có 25 câu)
Họ tên :.................................................................. Số báo danh : ...............
Câu 1: Cho hàm số
23
()
x
fx
mx
−
=
−
( 2)
( 2)
x
x
>
≤
. Tìm tất cả các giá trị thực của tham số
m
để hàm số
()fx
liên
tục tại
.
A.
5.m =
B.
2.m =
C.
3.m =
D.
4.m =
Câu 2: Cho hàm số
( )
4 13
2
x
fx
x
+−
=
−
. Tính
( )
2
lim .
x
fx
→
A.
( )
2
2
lim .
3
x
fx
→
= −
B.
( )
2
3
lim .
2
x
fx
→
= −
C.
( )
2
2
lim .
3
x
fx
→
=
D.
( )
2
3
lim .
2
x
fx
→
=
Câu 3: Cho cấp số cộng (u
n
) thỏa :
14
35
7
14
+=
−=
uu
uu
. Tìm số hạng đầu
1
u
và công sai d.
A.
1
7, 7=−=ud
. B.
1
14, 7ud 
. C.
1
14, 7=−=ud
. D.
1
7, 7= = −ud
.
Câu 4: Cho cấp số nhân
,
n
u
biết
6
7
192
.
384
u
u
Tìm số hạng đầu
1
u
và công bội
q
của cấp số nhân.
A.
1
5
.
3
u
q
B.
1
5
.
2
u
q
C.
1
6
.
3
u
q
D.
1
6
.
2
u
q
Câu 5: Tính giới hạn
2
1
lim .
32
nn
n
+−
+
A.
.−∞
B.
0.
C.
.+∞
D.
1
.
3
Câu 6: Cho hàm số
()y fx=
xác định trên khoảng
K
và
0
x
thuộc
K
. Giả sử hàm số
()y fx=
liên tục tại
0
x
. Khẳng định nào sau đây đúng ?
A.
0
0
lim ( ) ( )
xx
fx fx
→
=
. B. .
0
lim () ()
xx
fx fx
→
=
C.
0
lim ( ) ( )fx fx=
. D.
1
lim ( ) (1)
x
fx f
→
=
.
Câu 7: Tính giới hạn
2
22
lim .
32
n nn
n
+−
−
A.
.+∞
B.
2
.
3
−
C.
1.
D.
1
.
3
−
Câu 8: Cho hàm số
( )
22
32xaa
fx a
xa
+−
= +
−
, (với
0,aa>
là tham số). Tính
( )
lim .
xa
fx
→
A.
( )
21
lim .
2
xa
a
fx
→
−
=
B.
( )
21
lim .
2
xa
a
fx
→
+
=
C.
( )
2
lim .
21
xa
fx
a
→
=
+
D.
( )
2
lim .
21
xa
fx
a
→
=
−
Mã đề 001
Trang 2/3 - Mã đề 001
Câu 9: Cho cấp số nhân có
1
3u = −
,
2
3
q
=
. Tính
5
.u
A.
5
27
.
16
u
−
=
B.
5
16
.
27
u
=
C.
5
16
.
27
u
−
=
D.
5
27
.
16
u =
Câu 10: Tính giới hạn
21
lim .
32
n
n
−
+
A.
2
.
3
B.
1.
C.
1
.
2
−
D.
1
.
3
−
Câu 11: Cho cấp số cộng (u
n
) có u
1
= 1, d = 4. Tìm số hạng
12
.u
A.
12
31=u
. B.
12
13=u
. C.
12
45=u
. D.
12
17=u
.
Câu 12: Cho các hàm số
5
1
() 1fx x= +
,
3
2
2
2018
()
1
xx
fx
x
−+
=
+
,
3
2
1
()
7 12
x
fx
xx
−
=
−+
,
4
() 1fx x= −
. Có bao
nhiêu hàm số liên tục trên khoảng
(
)
0;2
.
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 13: Cho
(
)
3
33 2 22
2
lim 2 2018
x
ac
x x xx
bd
ππ
ππ
→−∞
+ + −+ = +
(
,
ac
bd
tối giản). Tính giá trị biểu thức
2
...
P a bcd=
.
A.
24
. B.
26−
. C.
26
. D.
24−
.
Câu 14: Cho cấp số cộng (u
n
) xác định bởi :
1
1
10
7
+
= −
= +
nn
u
uu
. Hỏi 690 là số hạng thứ mấy của cấp số cộng ?
A. Thứ 100. B. Thứ 102. C. Thứ 99. D. Thứ 101.
Câu 15: Cho phương trình
432
120 26 25 2 1 0x x xx− − + +=
. Chọn khẳng định đúng trong các khẳng định
sau.
A. Phương trình có đúng 1 nghiệm. B. Phương trình có đúng 3 nghiệm.
C. Phương trình có đúng 4 nghiệm. D. Phương trình có đúng 2 nghiệm.
Câu 16: Tính giới hạn:
( )
11 1
lim .... .
1.3 2.4 2
nn

+ ++

+

A.
3
.
4
B.
1.
C.
2
3
. D.
0.
Câu 17: Tính giới hạn :
2
lim ( x 1 ).
x
xx
→−∞
−+−
A. 0 . B.
+∞
. C.
1
.
2
D.
.−∞
Câu 18: Tính giới hạn sau:
3
2
1
2
81
lim
6 51
x
x
xx
→
−
−+
.
A. 6. B. 8. C. 1. D. 10.
Câu 19: Cho hàm số
( )
22
11f x x ax x= − +−−
, (với
a
là tham số). Tính
( )
lim .
x
fx
→+∞
A.
( )
2
lim 1 .
2
x
a
fx
→+∞
= −
B.
( )
2
lim 1.
2
x
a
fx
→+∞
= −
C.
( )
2
lim 1.
2
x
a
fx
→+∞
=−−
D.
( )
2
lim 1.
2
x
a
fx
→+∞
= +
Trang 3/3 - Mã đề 001
Câu 20: Cho hàm số
()fx
có đồ thị như hình vẽ. Chọn khẳng định đúng trong các khẳng định sau?
A. Hàm số
()fx
liên tục tại
1.x =
B. Hàm số
()fx
liên tục trên
.
C. Hàm số
()fx
liên tục trên khoảng
( 3;1).−
D. Hàm số
()fx
liên tục tại
1.x = −
Câu 21: Tính
( )
33
27
lim lim .
3
xx
x
fx
x
−−
→− →−
+
=
+
A.
( )
3
lim .
x
fx
−
→−
= −∞
B.
( )
3
7
lim .
3
x
fx
−
→−
=
C.
( )
3
lim 2.
x
fx
−
→−
=
D.
( )
3
lim .
x
fx
−
→−
= +∞
Câu 22: Tính giới hạn:
2
0
lim(2 3 5)
x
xx
→
+−
.
A. 0. B. 3. C. 2. D. -5.
Câu 23: Tính giới hạn
2
21
lim .
2 32
n
nn
−−
−−
A.
1
.
2
B.
1.−
C.
.−∞
D.
0.
Câu 24: Tính giới hạn
32
lim( 2 1).
nn− −+
A.
2.
−
B.
.+∞
C.
.−∞
D.
0.
Câu 25: Biết rằng tồn tại đúng hai giá trị của tham số
m
để phương trình
( )
32 2
7 2 6 80x x m mx− + + −=
có
ba nghiệm phân biệt lập thành một cấp số nhân. Tính tổng lập phương của hai giá trị đó.
A.
216.−
B.
342.−
C.
344.
D.
216.
--HẾT--
1
SỞ GD&ĐT CÀ MAU
()
KIỂM TRA ĐSGT 11 - ĐÁP ÁN NĂM HỌC 2017 -
2018
MÔN TOÁN HỌC – 11
Thời gian làm bài : 45 Phút
Phần đáp án câu trắc nghiệm:
001 002 003 004 005 006
1
C
A
C
A
C
C
2
C
C
A
C
A
C
3
B
D
D
B
C
D
4
D
D
A
B
C
C
5
C
D
B
A
B
A
6
A
D
D
D
C
D
7
D
D
A
D
B
A
8
B
B
A
D
B
C
9
C
D
C
D
D
D
10
A
C
D
C
B
A
11
C
A
C
D
B
B
12
B
B
A
A
C
C
13
A
A
A
D
D
A
14
D
D
B
D
B
D
15
C
D
C
B
B
C
16
A
B
B
C
D
C
17
B
C
B
C
C
A
18
A
D
C
A
B
B
19
C
B
D
C
D
D
20
A
D
D
A
D
A
21
A
C
B
A
D
C
22
D
C
B
A
A
B
23
D
C
C
C
B
A
24
C
D
C
B
A
C
25
B
A
A
D
B
D
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT CÀ MAU
KIỂM TRA ĐSGT 11 - NĂM HỌC 2017 - 2018 MÔN TOÁN HỌC
Thời gian làm bài: 45 Phút; (Đề có 25 câu) (Đề có 3 trang)
Họ tên :.................................................................. Số báo danh : ............... Mã đề 001
2x − 3 (x > 2)
Câu 1: Cho hàm số f (x) =  f x liên
m − x (x ≤
. Tìm tất cả các giá trị thực của tham số m để hàm số ( ) 2) tục tại x = 2 . A. m = 5. B. m = 2. C. m = 3. D. m = 4. x + −
Câu 2: Cho hàm số f ( x) 4 1 3 =
. Tính lim f ( x). x − 2 x→2 2 3 2 3
A. lim f ( x) = − .
B. lim f ( x) = − .
C. lim f ( x) = .
D. lim f ( x) = . x→2 3 x→2 2 x→2 3 x→2 2  u + u = 7
Câu 3: Cho cấp số cộng (un) thỏa : 1 4 
. Tìm số hạng đầu u và công sai d. u − u = 14  1 3 5 A. u = 7, − d = 7 .
B. u  14, d  7 . C. u = 1 − 4,d = 7 .
D. u = 7, d = 7 − . 1 1 1 1 u  192 
Câu 4: Cho cấp số nhân u , biết 6 
. Tìm số hạng đầu u và công bội q của cấp số nhân. n u   384  1  7 u   5  u   5  u   6  u   6  A. 1  .  B. 1  . C. 1  . D. 1  . q  3  q  2  q  3  q  2  2 n + n −1
Câu 5: Tính giới hạn lim . 3n + 2 1 A. . −∞ B. 0. C. . +∞ D. . 3
Câu 6: Cho hàm số y = f (x) xác định trên khoảng K và x thuộc K . Giả sử hàm số y = f (x) liên tục tại 0
x . Khẳng định nào sau đây đúng ? 0
A. lim f (x) = f (x ) .
B. . lim f (x) = f (x)
C. lim f (x) = f (x ) .
D. lim f (x) = f (1) . 0 0 x→ → → 0 x x 0 x x 1 2
n + 2n − 2n
Câu 7: Tính giới hạn lim . 3n − 2 2 1 A. . +∞ B. − . C. 1. D. − . 3 3
x + a − a
Câu 8: Cho hàm số f ( x) 2 2 3 2 =
+ a , (với a > 0, a là tham số). Tính lim f (x). x − a x→a a − a + A. f ( x) 2 1 lim = . B. f ( x) 2 1 lim = . C. f ( x) 2 lim = . D. f ( x) 2 lim = . x→a 2 x→a 2 x→a 2a +1 x→a 2a −1 Trang 1/3 - Mã đề 001 2
Câu 9: Cho cấp số nhân có u = 3
− , q = . Tính u . 1 3 5 27 − 16 16 − 27 A. u = . B. u = . C. u = . D. u = . 5 16 5 27 5 27 5 16 2n −1
Câu 10: Tính giới hạn lim . 3n + 2 2 1 1 A. . B. 1. C. − . D. − . 3 2 3
Câu 11: Cho cấp số cộng (un) có u1 = 1, d = 4. Tìm số hạng u . 12 A. u = 31. B. u = 13. C. u = 45 . D. u = 17 . 12 12 12 12 3 x − x + 2018 x −1
Câu 12: Cho các hàm số 5
f (x) = x +1, f (x) = , f (x) = , f (x) = x −1 . Có bao 1 2 2 x +1 3 2 x − 7x +12 4
nhiêu hàm số liên tục trên khoảng (0; 2) . A. 4 . B. 3 . C. 2 . D. 1. a c a c Câu 13: Cho lim + + − + = + ( ,
tối giản). Tính giá trị biểu thức →−∞ ( 3 3 3 2 2 2 π x 2x π x x 2018 x ) 2 bπ dπ b d 2 P = a . . b . c d . A. 24 . B. 26 − . C. 26 . D. 24 − .  u = 10 −
Câu 14: Cho cấp số cộng (un) xác định bởi : 1 
. Hỏi 690 là số hạng thứ mấy của cấp số cộng ? u = u + 7  n 1+ n A. Thứ 100. B. Thứ 102. C. Thứ 99. D. Thứ 101.
Câu 15: Cho phương trình 4 3 2
120x − 26x − 25x + 2x +1 = 0 . Chọn khẳng định đúng trong các khẳng định sau.
A. Phương trình có đúng 1 nghiệm.
B. Phương trình có đúng 3 nghiệm.
C. Phương trình có đúng 4 nghiệm.
D. Phương trình có đúng 2 nghiệm.  1 1 1 
Câu 16: Tính giới hạn: lim  + + ....+  n (n +  ) . 1.3 2.4 2  3 2 A. . B. 1. C. . D. 0. 4 3
Câu 17: Tính giới hạn : 2
lim ( x − x + 1 − x). x→− ∞ 1 A. 0 . B. +∞ . C. . D. . −∞ 2 3 8x − 1
Câu 18: Tính giới hạn sau: lim 2 1 − + . x→ 6x 5x 1 2 A. 6. B. 8. C. 1. D. 10.
Câu 19: Cho hàm số f ( x) 2 2
= x − a x +1 − x −1, (với a là tham số). Tính lim f (x). x→+∞ a a a a A. f ( x) 2 lim = 1− . B. f ( x) 2 lim = −1. C. f ( x) 2 lim = − −1. D. f ( x) 2 lim = +1. x→+∞ 2 x→+∞ 2 x→+∞ 2 x→+∞ 2 Trang 2/3 - Mã đề 001
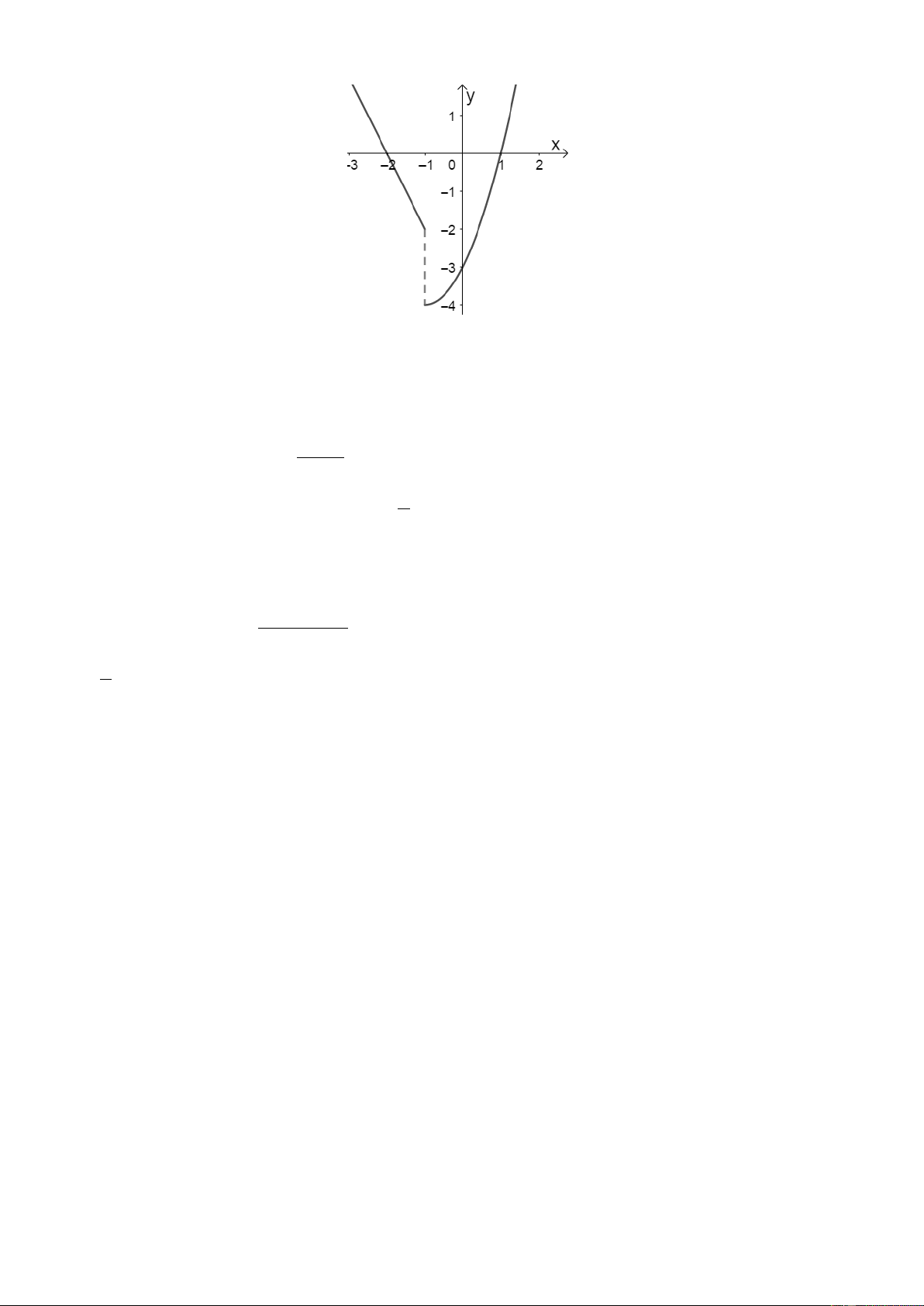
Câu 20: Cho hàm số f (x) có đồ thị như hình vẽ. Chọn khẳng định đúng trong các khẳng định sau?
A. Hàm số f (x) liên tục tại x = 1.
B. Hàm số f (x) liên tục trên . 
C. Hàm số f (x) liên tục trên khoảng ( 3 − ;1).
D. Hàm số f (x) liên tục tại x = 1. − 2x + 7
Câu 21: Tính lim f ( x) = lim . − − x 3 →− x 3 →− x + 3 7
A. lim f ( x) = . −∞
B. lim f ( x) = .
C. lim f ( x) = 2.
D. lim f ( x) = . +∞ − − − − x 3 →− x 3 →− 3 x 3 →− x 3 →−
Câu 22: Tính giới hạn: 2
lim(2x + 3x − 5) . x→0 A. 0. B. 3. C. 2. D. -5. 2 − n −1
Câu 23: Tính giới hạn lim . 2 2n − 3n − 2 1 A. . B. 1. − C. . −∞ D. 0. 2
Câu 24: Tính giới hạn 3 2 lim( 2
− n − n +1). A. 2. − B. . +∞ C. . −∞ D. 0.
Câu 25: Biết rằng tồn tại đúng hai giá trị của tham số m để phương trình 3 2 x − x + ( 2 7
2 m + 6m) x − 8 = 0 có
ba nghiệm phân biệt lập thành một cấp số nhân. Tính tổng lập phương của hai giá trị đó. A. 216. − B. 342. − C. 344. D. 216. --HẾT-- Trang 3/3 - Mã đề 001
SỞ GD&ĐT CÀ MAU
KIỂM TRA ĐSGT 11 - ĐÁP ÁN NĂM HỌC 2017 - 2018
MÔN TOÁN HỌC – 11
Thời gian làm bài ()
: 45 Phút
Phần đáp án câu trắc nghiệm: 001 002 003 004 005 006 1 C A C A C C 2 C C A C A C 3 B D D B C D 4 D D A B C C 5 C D B A B A 6 A D D D C D 7 D D A D B A 8 B B A D B C 9 C D C D D D 10 A C D C B A 11 C A C D B B 12 B B A A C C 13 A A A D D A 14 D D B D B D 15 C D C B B C 16 A B B C D C 17 B C B C C A 18 A D C A B B 19 C B D C D D 20 A D D A D A 21 A C B A D C 22 D C B A A B 23 D C C C B A 24 C D C B A C 25 B A A D B D 1
Document Outline

  • de 001
  • Phieu soi dap an