Đề kiểm tra chương 1 Hình học 11 cơ bản trường THPT Hải Lăng – Quảng Trị

Đề kiểm tra chương 1 Hình học 11 cơ bản trường THPT Hải Lăng – Quảng Trị gồm 4 mã đề, mỗi mã đề gồm 25 câu hỏi trắc nghiệm, thời gian làm bài 1 tiết (45 phút), nội dung kiểm tra thuộc chủ đề phép biến hình: phép dời hình và phép đồng dạng trong mặt phẳng, đề kiểm tra có đáp án.

96 48 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

19 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1/2 - Mã đề thi 132
SỞ GD-ĐT QUẢNG TRỊ ĐỀ KIỂM TRA CHƯƠNG I
TRƯỜNG THPT HẢI LĂNG Môn: Hình học - Lớp: 11– Ban: Cơ bản
Thời gian làm bài: 45 phút (25 câu trắc nghiệm)
Họ, tên thí sinh:......................................................Lớp.......... Mã đề thi 132
PHẦN TRẢ LỜI: Học sinh lựa chọn câu trả lời và điền vào bảng sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Câu 1: Trong mặt phẳng
Oxy
, cho đường tròn
. Phép đồng dạng có được bằng
cách thực hiện liên tiếp phép vị tự tâm
O
tỉ số
1
2
k =
và phép tịnh tiến theo
(
)
1; 2
u = −
sẽ biến
(
)
C
thành
đường tròn
( )
,.C IR
′ ′′
Khẳng định nào đúng ?
A.
( )
1; 4
I
′
và
2.R
′
=
B.
(
)
2;2I
′
và
2.R
′
=
C.
(
)
0;3
I
′
và
2.R
′
=
D.
( )
1;1I
′
và
4.R
′
=
Câu 2: Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
B. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
C. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho.
D. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
Câu 3: Cho đường tròn
( ) ( )
2
2
: 1 ( 2) 9Cx y+ +− =
. Phép tịnh tiến theo
( )
1; 2v = −
biến đường tròn
( )
C
thành đường tròn
( )
,.C IR
′ ′′
Khẳng định nào dưới đây đúng ?
A.
( )
2; 4I
′
−
và
3.R
′
=
B.
( )
0;0I
′
và
9.R
′
=
C.
( )
0; 4I
′
−
và
3.R
′
=
D.
( )
0;0I
′
và
3.R
′
=
Câu 4: Tính chất nào sau đây không phải là tính chất của phép đồng dạng ?
A. Biến tam giác thành tam giác đồng dạng với nó.
B. Biến đường tròn thành đường tròn bằng nó.
C. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.
D. Biến đoạn thẳng thành đoạn thẳng.
Câu 5: Cho đường tròn
22
( ): 2 8 0Cx y x
+ − −=
.
( , 2)
() ( )
O
V CC
−
′
=
. Tính diện tích hình tròn
()C
′
A.
36
π
. B.
64
π
. C.
9
π
. D.
4
π
.
Câu 6: Trong mặt phẳng
Oxy
, cho tam giác
ABC
có
( ) ( ) ( )
1; 2 , 1; 6 , 6; 2ABC−− −
. Phép vị tự tâm
O
tỉ số
1
2
k = −
biến tam giác
ABC
thành tam giác
ABC
′′′
. Tìm trọng tâm của tam giác
ABC
′′′
.
A.
( )
1; 1 .G
′
−−
B.
( )
1;1 .G
′
C.
( )
1;1 .G
′
−
D.
( )
1; 1 .G
′
−
Câu 7: Trong mặt phẳng tọa độ
Oxy
, cho đường hai thẳng
: 3 30dx y− +=
và
': 3 6 0dx y− +=
. Tìm tọa
độ
v
có phương vuông góc với
d
để
( )
'
v
Td d=
.
A.
39
;
10 10
v

=


B.
( )
3;1v =
C.
39
;
10 10
v

= −


D.
( )
3; 1v = −
Câu 8: Cho đường thẳng
:2 3 1 0dx y− +=
. Xét
( )
( )
,90O
Q dd
°
′
=
. Tìm vec tơ chỉ phương
u
của đg thẳng
d
′
.
A.
( )
2; 3u = −
. B.
( )
3;2u =
. C.
( )
3; 2u = −
. D.
( )
2; 3u =−−
.
Câu 9: Hãy tìm khẳng định sai ?
A. Phép quay là phép dời hình. B. Phép tịnh tiến là phép dời hình.
C. Phép vị tự là phép dời hình. D. Phép đồng nhất là phép dời hình.
Câu 10: Cho phép vị tự tâm
A
tỉ số
2k =
biến điểm M thành
'M
. Đẳng thức nào sau đây đúng ?
A.
'2AM AM=
 
. B.
1
'
3
AM AM=
 
. C.
1
'
2
AM AM=
 
. D.
3'AM AM=
 
.
Trang 2/2 - Mã đề thi 132
Câu 11: Trong mặt phẳng
Oxy
, cho
( ) ( )
1;5 , 3;3 .
AB
Phép đồng dạng tỉ số
1
2
k =
biến điểm
A
thành
,
A
′
biến điểm
B
thành
.
B
′
Khi đó độ dài
AB
′′
là:
A.
5
B.
25
C. .
2
.
D.
22
Câu 12: Cho đường tròn
()
C
:
22
( 1) 8xy+− =
. Ảnh của
()
C
qua phép quay tâm
O
góc
90
o
−
là.
A.
22
( 1) 8xy−+=
. B.
22
( 1) 8
xy++=
.
C.
22
( 1) 8xy+− =
. D.
22
( 1) 8xy++ =
.
Câu 13: Cho đường thẳng
: 2 30xy∆ − +=
và
( )
2; 1u = −
.
( )
'
u
T ∆=∆
có phương trình là:
A.
2 10xy+ +=
. B.
2 10xy− −=
. C.
2 10xy− +=
. D.
2 30xy− −=
.
Câu 14: Cho điểm
( )
2; 2M −
. Tìm điểm
M
′
là ảnh của điểm M qua phép quay tâm
O
, góc quay
90
o
.
A.
( )
2; 2M
′
−−
. B.
( )
2;2
M
′
−
. C.
( )
2; 2M
′
−
. D.
( )
2;2M
′
.
Câu 15: Trong măt phẳng
Oxy
, cho điểm
( )
5; 6A −
. Tìm ảnh của A qua phép dời hình có được bằng cách
thực hiện liên tiếp phép tịnh tiến theo
( )
3;4u = −
và phép quay tâm
O
góc quay bằng
0
90
?
A.
( )
2;2A
′
. B.
( )
2; 2A
′
−
. C.
( )
2;2A
′
−
. D.
( )
2; 2A
′
−−
.
Câu 16: Phép tịnh tiến theo vec tơ
u
biến hai điểm
,MN
thành điểm
,MN
′′
Chọn khẳng định đúng ?
A.
.M N u MN
′′
=
 
. B.
.M N MN
′′
=
 
C.
'..OM u OM=
 
D.
..M N u MN
′′
=
 
Câu 17: Cho tam giác đều tâm
O
. Hỏi có bao nhiêu phép quay tâm
O
góc quay
α
,
02
απ
<≤
biến tam
giác trên thành chính nó?
A. Một. B. Hai. C. Bốn. D. Ba.
Câu 18: Trong măt phẳng
Oxy
cho điểm
( 2;2)M −
. Phép vị tự tâm
O
tỉ số
2k
= −
biến điểm
M
thành
điểm nào trong các điểm sau?
A.
( 4;4)−
. B.
(4;4)
. C.
(4; 4)
−
. D.
( 4; 4)−−
.
Câu 19: Cho điểm
( )
1; 2M
. Tìm điểm
M
′
là ảnh của điểm M qua phép tịnh tiến theo véc tơ
( )
2; 1v = −
.
A.
( )
' 3; 3M −
. B.
(
)
' 3;1
M
. C.
( )
' 1; 3M −
. D.
( )
' 3;3M −
.
Câu 20: Cho hai điểm
(3;1)M
và
(2; 1)M
′
−
nếu
( )
'
v
TM M=
thì
v
T
biến điểm
( 2;2)A −
thành điểm
A
′
?
A.
( 3;2)
A
′
−
. B.
( 3;4)
A
′
−
. C.
( 1; 0)A
′
−
. D.
( 3;0)
A
′
−
.
Câu 21: Cho hình vuông
ABCD
tâm
O
cạnh bằng
2
.
Phép đồng dạng tỉ số
k
biến tam giác
AOD
thành tam giác
ABC
. Tính
k
.
A.
2.
k =
B.
2.k
=
C.
2
.
2
k
=
D.
4.k
=
Câu 22: Trong mặt phẳng
Oxy
cho đường thẳng
d
có phương trình
2 30
xy+−=
. Phép vị tự tâm
O
tỉ số
2k =
biến
d
thành đường thẳng nào trong các đường thẳng có phương trình sau?
A.
2 30
xy++=
. B.
2 60xy+−=
. C.
4 2 50xy+ −=
. D.
4 2 30xy− −=
.
Câu 23: Trong các mệnh đề nào sau đây mệnh đề nào đúng?
A. Phép quay là một phép đồng dạng. B. Phép vị tự là một phép dời hình.
C. Phép đồng dạng là một phép dời hình. D. Phép tịnh tiến không phải là phép đồng dạng.
Câu 24: Cho lục giác đều
ABCDEF
tâm
O
như hình vẽ.
Phép quay nào biến
EOD∆
thành
AOF∆
.
A.
( )
;120
.
O
Q
°
B.
( )
; 60
.
O
Q
−°
C.
( )
; 120
.
O
Q
−°
D.
( )
;60
.
O
Q
°
Câu 25: Tam giác
ABC
có diện tích
S
. Phép vị tự tỉ số
1
2
k = −
biến tam giác
ABC
thành tam giác
ABC
′′′
. Gọi
S
′
là diện tích tam giác
ABC
′′′
. Khẳng định nào sau đây đúng
A.
1
4
SS
′
=
B.
2SS
′
=
. C.
1
2
SS
′
=
. D.
4SS
′
=
.
-----------------------------------------------
----------- HẾT ----------
E
D
C
B
F
O
A
Trang 1/2 - Mã đề thi 209
SỞ GD-ĐT QUẢNG TRỊ ĐỀ KIỂM TRA CHƯƠNG I
TRƯỜNG THPT HẢI LĂNG Môn: Hình học - Lớp: 11– Ban: Cơ bản
Thời gian làm bài: 45 phút (25 câu trắc nghiệm)
Họ, tên thí sinh:......................................................Lớp.......... Mã đề thi 209
PHẦN TRẢ LỜI: Học sinh lựa chọn câu trả lời và điền vào bảng sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Câu 1: Trong mặt phẳng
Oxy
, cho
( ) ( )
1;5 , 3;3 .AB
Phép đồng dạng tỉ số
1
2
k =
biến điểm
A
thành
,A
′
biến điểm
B
thành
.B
′
Khi đó độ dài
AB
′′
là:
A.
25
B.
5
C.
22
D.
2
Câu 2: Cho đường thẳng
: 2 30xy∆ − +=
và
(
)
2; 1
u
= −
.
( )
'
u
T ∆=∆
có phương trình là:
A.
2 10xy+ +=
. B.
2 10xy− +=
. C.
2 30
xy
− −=
. D.
2 10xy− −=
.
Câu 3: Cho điểm
( )
2; 2M −
. Tìm điểm
M
′
là ảnh của điểm M qua phép quay tâm
O
, góc quay
90
o
.
A.
( )
2; 2M
′
−−
. B.
( )
2; 2M
′
−
. C.
( )
2;2M
′
−
. D.
(
)
2;2M
′
.
Câu 4: Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
B. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
C. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho.
D. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
Câu 5: Trong mặt phẳng
Oxy
, cho đường tròn
( )
C
có phương trình
( )
( )
22
2 2 16xy
− +− =
. Phép đồng
dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm
O
tỉ số
1
2
k =
và phép tịnh tiến theo
( )
1; 2
u = −
sẽ biến
( )
C
thành đường tròn
( )
,.C IR
′ ′′
Khẳng định nào đúng ?
A.
( )
1;1I
′
và
4.R
′
=
B.
( )
0;3I
′
và
2.R
′
=
C.
( )
1; 4I
′
và
2.R
′
=
D.
( )
2;2I
′
và
2.R
′
=
Câu 6: Trong mặt phẳng tọa độ
Oxy
, cho đường hai thẳng
: 3 30dx y− +=
và
': 3 6 0dx y− +=
. Tìm tọa
độ
v
có phương vuông góc với
d
để
( )
'
v
Td d=
.
A.
39
;
10 10
v

=


B.
( )
3;1v =
C.
39
;
10 10
v

= −


D.
( )
3; 1
v = −
Câu 7: Tính chất nào sau đây không phải là tính chất của phép đồng dạng ?
A. Biến tam giác thành tam giác đồng dạng với nó.
B. Biến đoạn thẳng thành đoạn thẳng.
C. Biến đường tròn thành đường tròn bằng nó.
D. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.
Câu 8: Hãy tìm khẳng định sai ?
A. Phép quay là phép dời hình. B. Phép tịnh tiến là phép dời hình.
C. Phép vị tự là phép dời hình. D. Phép đồng nhất là phép dời hình.
Câu 9: Trong mặt phẳng Oxy, cho đường tròn
( ) ( )
2
2
: 1 ( 2) 9Cx y+ +− =
. Phép tịnh tiến theo
( )
1; 2v = −
biến đường tròn
( )
C
thành đường tròn
( )
,.C IR
′ ′′
Khẳng định nào dưới đây đúng ?
A.
( )
2; 4I
′
−
và
3.R
′
=
B.
( )
0;0I
′
và
3.R
′
=
C.
( )
0; 4I
′
−
và
3.R
′
=
D.
( )
0;0I
′
và
9.R
′
=
Câu 10: Cho phép vị tự tâm
A
tỉ số
2k =
biến điểm M thành
'M
. Đẳng thức nào sau đây đúng ?
A.
1
'
3
AM AM=
 
. B.
'2AM AM=
 
. C.
1
'
2
AM AM=
 
.
D.
3'AM AM=
 
.
Trang 2/2 - Mã đề thi 209
Câu 11: Trong măt phẳng
Oxy
, cho điểm
( )
5; 6
A −
. Tìm ảnh của A qua phép dời hình có được bằng cách
thực hiện liên tiếp phép tịnh tiến theo
( )
3;4
u = −
và phép quay tâm
O
góc quay bằng
0
90
?
A.
( )
2;2A
′
. B.
( )
2; 2
A
′
−−
. C.
( )
2;2A
′
−
. D.
( )
2; 2
A
′
−
.
Câu 12: Tam giác
ABC
có diện tích
S
. Phép vị tự tỉ số
1
2
k = −
biến tam giác
ABC
thành tam giác
ABC
′′′
.
Gọi
S
′
là diện tích tam giác
ABC
′′′
. Khẳng định nào sau đây đúng
A.
1
2
SS
′
=
. B.
2SS
′
=
. C.
1
4
SS
′
=
D.
4
SS
′
=
.
Câu 13: Trong mặt phẳng
Oxy
cho đường tròn
()
C
có phương trình
22
2 80xy x+ − −=
. Phép vị tự tâm
O
tỉ số
2k = −
biến
()C
thành đường tròn
()C
′
. Tính diện tích hình tròn
()C
′
A.
36
π
. B.
4
π
. C.
64
π
. D.
9
π
.
Câu 14: Cho đường thẳng
:2 3 1 0dx y
− +=
. Xét
( )
( )
,90O
Q dd
°
′
=
. Tìm vec tơ chỉ phương
u
của
d
′
.
A.
(
)
2; 3
u
= −
. B.
( )
2; 3u =−−
. C.
( )
3;2u =
. D.
(
)
3; 2
u = −
.
Câu 15: Cho tam giác đều tâm
O
. Hỏi có bao nhiêu phép quay tâm
O
góc quay
α
,
02
απ
<≤
biến tam
giác trên thành chính nó?
A. Ba. B. Bốn. C. Một. D. Hai.
Câu 16: Trong mặt phẳng
Oxy
cho đường thẳng
d
có phương trình
2 30xy
+−=
. Phép vị tự tâm
O
tỉ số
2k =
biến
d
thành đường thẳng nào trong các đường thẳng có phương trình sau?
A.
2 60
xy+−=
. B.
4 2 50xy+ −=
. C.
2 30xy++=
. D.
4 2 30
xy− −=
.
Câu 17: Trong măt phẳng
Oxy
cho điểm
( 2;2)M −
.
( , 2)
()
O
V MM
−
′
=
.Tìm điểm
'.M
A.
( 4;4)−
. B.
(4;4)
. C.
(4; 4)−
. D.
( 4; 4)−−
.
Câu 18: Cho điểm
( )
1; 2
M
. Tìm điểm
M
′
là ảnh của điểm M qua phép tịnh tiến theo véc tơ
( )
2; 1v = −
.
A.
( )
' 3; 3M −
. B.
( )
' 3;1M
. C.
( )
' 1; 3M −
. D.
( )
' 3;3M −
.
Câu 19: Cho hai điểm
(3;1)M
và
(2; 1)M
′
−
nếu
( )
'
v
TM M=
thì
v
T
biến điểm
( 2;2)A −
thành điểm
A
′
?
A.
( 3;2)A
′
−
. B.
( 3;4)A
′
−
. C.
( 1; 0)A
′
−
. D.
( 3;0)A
′
−
.
Câu 20: Cho hình vuông
ABCD
tâm
O
cạnh bằng
2
.
Phép đồng dạng tỉ số
k
biến tam giác
AOD
thành tam giác
ABC
. Tính
k
.
A.
2.k =
B.
2.
k =
C.
2
.
2
k =
D.
4.
k
=
Câu 21: Cho đường tròn
()C
:
22
( 1) 8xy
+− =
. Ảnh của
()C
qua phép quay tâm
O
góc
90
o
−
là.
A.
22
( 1) 8xy++=
. B.
22
( 1) 8xy
++ =
.
C.
22
( 1) 8xy+− =
. D.
22
( 1) 8xy−+=
.
Câu 22: Trong các mệnh đề nào sau đây mệnh đề nào đúng?
A. Phép quay là một phép đồng dạng. B. Phép vị tự là một phép dời hình.
C. Phép đồng dạng là một phép dời hình. D. Phép tịnh tiến không phải là phép đồng dạng.
Câu 23: Cho lục giác đều
ABCDEF
tâm
O
như hình vẽ.
Phép quay nào biến
EOD∆
thành
AOF∆
.
A.
( )
;120
.
O
Q
°
B.
( )
; 60
.
O
Q
−°
C.
( )
; 120
.
O
Q
−°
D.
( )
;60
.
O
Q
°
Câu 24: Trong mặt phẳng
Oxy
, cho tam giác
ABC
có
( )
( ) ( )
1; 2 , 1; 6 , 6; 2ABC−− −
.
1
(, )
2
()
O
V ABC A B C
−
′′′
∆=∆
. Tìm trọng tâm của tam giác
ABC
′′′
.
A.
( )
1; 1 .G
′
−−
B.
( )
1;1 .G
′
C.
( )
1;1 .G
′
−
D.
( )
1; 1 .G
′
−
Câu 25: Phép tịnh tiến theo vec tơ
u
biến hai điểm
,MN
thành điểm
,MN
′′
Chọn khẳng định đúng ?
A.
.M N u MN
′′
=
 
. B.
.M N MN
′′
=
 
C.
'..OM u OM=
 
D.
..M N u MN
′′
=
 
-----------------------------------------------
----------- HẾT ----------
E
D
C
B
F
O
A
Trang 1/2 - Mã đề thi 357
SỞ GD-ĐT QUẢNG TRỊ ĐỀ KIỂM TRA CHƯƠNG I
TRƯỜNG THPT HẢI LĂNG Môn: Hình học - Lớp: 11– Ban: Cơ bản
Thời gian làm bài: 45 phút (25 câu trắc nghiệm)
Họ, tên thí sinh:......................................................Lớp.......... Mã đề thi 357
PHẦN TRẢ LỜI: Học sinh lựa chọn câu trả lời và điền vào bảng sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Câu 1: Tính chất nào sau đây không phải là tính chất của phép đồng dạng ?
A. Biến tam giác thành tam giác đồng dạng với nó.
B. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.
C. Biến đoạn thẳng thành đoạn thẳng.
D. Biến đường tròn thành đường tròn bằng nó.
Câu 2: Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho.
B. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
C. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
D. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
Câu 3: Cho đường thẳng
: 2 30xy∆ − +=
và
( )
2; 1u = −
.
( )
'
u
T ∆=∆
có phương trình là:
A.
2 10xy− −=
. B.
2 10xy+ +=
. C.
2 10xy− +=
. D.
2 30
xy− −=
.
Câu 4: Trong mặt phẳng
Oxy
, cho đường tròn
( )
C
có phương trình
(
)
(
)
22
2 2 16
xy− +− =
. Phép đồng dạng
có được bằng cách thực hiện liên tiếp phép vị tự tâm
O
tỉ số
1
2
k =
và phép tịnh tiến theo
(
)
1; 2u
= −
sẽ
biến
( )
C
thành đường tròn
( )
,.C IR
′ ′′
Khẳng định nào đúng ?
A.
( )
1;1
I
′
và
4.R
′
=
B.
( )
0;3I
′
và
2.R
′
=
C.
(
)
1; 4
I
′
và
2.R
′
=
D.
( )
2;2I
′
và
2.R
′
=
Câu 5: Cho hai điểm
(3;1)
M
và
(2; 1)M
′
−
nếu
( )
'
v
TM M=
thì
v
T
biến điểm
( 2;2)A −
thành điểm
A
′
?
A.
( 3;0)A
′
−
. B.
( 3;2)A
′
−
. C.
( 1; 0)A
′
−
. D.
( 3;4)
A
′
−
.
Câu 6: cho đường thẳng
:2 3 1 0dx y− +=
. Xét
(
)
( )
,90O
Q dd
°
′
=
. Tìm vec tơ chỉ phương
u
của
d
′
.
A.
( )
2; 3u =−−
. B.
( )
3; 2
u = −
. C.
( )
2; 3u = −
. D.
( )
3;2u =
.
Câu 7: Cho điểm
( )
1; 2
M
. Tìm điểm
M
′
là ảnh của điểm M qua phép tịnh tiến theo véc tơ
( )
2; 1v = −
.
A.
( )
' 3; 3M −
. B.
( )
' 3;1M
. C.
( )
' 1; 3M −
. D.
( )
' 3;3M −
.
Câu 8: Trong mặt phẳng Oxy, cho đường tròn
( ) ( )
2
2
: 1 ( 2) 9Cx y+ +− =
. Phép tịnh tiến theo
( )
1; 2v = −
biến
đường tròn
( )
C
thành đường tròn
( )
,.C IR
′ ′′
Khẳng định nào dưới đây đúng ?
A.
( )
2; 4I
′
−
và
3.R
′
=
B.
( )
0;0I
′
và
3.R
′
=
C.
( )
0; 4I
′
−
và
3.R
′
=
D.
( )
0;0I
′
và
9.R
′
=
Câu 9: Cho phép vị tự tâm
A
tỉ số
2k =
biến điểm M thành
'M
. Đẳng thức nào sau đây đúng ?
A.
'2AM AM=
 
. B.
1
'
3
AM AM=
 
. C.
1
'
2
AM AM=
 
.
D.
3'AM AM=
 
.
Câu 10: Trong mặt phẳng
Oxy
, cho tam giác
ABC
có
( ) ( ) ( )
1; 2 , 1; 6 , 6; 2ABC−− −
. Phép vị tự tâm
O
tỉ số
1
2
k = −
biến tam giác
ABC
thành tam giác
ABC
′′′
. Tìm trọng tâm của tam giác
ABC
′′′
.
A.
(
)
1; 1 .G
′
−
B.
( )
1;1 .G
′
−
C.
( )
1;1 .G
′
D.
( )
1; 1 .G
′
−−
Câu 11: Cho đường tròn
()C
:
22
( 1) 8xy+− =
. Ảnh của
()C
qua phép quay tâm
O
góc
90
o
−
là.
A.
22
( 1) 8xy++=
. B.
22
( 1) 8xy++ =
. C.
22
( 1) 8xy+− =
. D.
22
( 1) 8xy−+=
.
Trang 2/2 - Mã đề thi 357
Câu 12: Trong mặt phẳng tọa độ
Oxy
, cho đường hai thẳng
: 3 30dx y− +=
và
': 3 6 0dx y− +=
. Tìm tọa
độ
v
có phương vuông góc với
d
để
( )
'
v
Td d
=
.
A.
( )
3;1
v =
B.
( )
3; 1
v = −
C.
39
;
10 10
v

=


D.
39
;
10 10
v

= −


Câu 13: Trong mặt phẳng
Oxy
cho đường tròn
()
C
có phương trình
22
2 80xy x+ − −=
. Phép vị tự tâm
O
tỉ
số
2k = −
biến
()C
thành đường tròn
()
C
′
. Tính diện tích hình tròn
()C
′
A.
64
π
. B.
9
π
. C.
36
π
. D.
4
π
.
Câu 14: Cho hình vuông
ABCD
tâm
O
cạnh bằng
2
.
Phép đồng dạng tỉ số
k
biến tam giác
AOD
thành tam giác
ABC
. Tính
k
.
A.
2.k =
B.
2.k =
C.
2
.
2
k =
D.
4.k =
Câu 15: Tam giác
ABC
có diện tích
S
. Phép vị tự tỉ số
1
2
k = −
biến tam giác
ABC
thành tam giác
ABC
′′′
.
Gọi
S
′
là diện tích tam giác
ABC
′′′
. Khẳng định nào sau đây đúng
A.
4SS
′
=
. B.
1
2
SS
′
=
. C.
1
4
SS
′
=
D.
2SS
′
=
.
Câu 16: Trong măt phẳng
Oxy
, cho điểm
( )
5; 6A −
. Tìm ảnh của A qua phép dời hình có được bằng cách thực
hiện liên tiếp phép tịnh tiến theo
( )
3;4u = −
và phép quay tâm
O
góc quay bằng
0
90
?
A.
( )
2;2A
′
. B.
( )
2; 2A
′
−
. C.
( )
2;2A
′
−
. D.
( )
2; 2A
′
−−
.
Câu 17: Cho tam giác đều tâm
O
. Hỏi có bao nhiêu phép quay tâm
O
góc quay
α
,
02
απ
<≤
biến tam giác
trên thành chính nó?
A. Bốn. B. Hai. C. Ba. D. Một.
Câu 18: Trong mặt phẳng
Oxy
, cho
( ) ( )
1;5 , 3;3 .AB
Phép đồng dạng tỉ số
1
2
k =
biến điểm
A
thành
,A
′
biến
điểm
B
thành
.B
′
Khi đó độ dài
AB
′′
là:
A.
25
B.
2
C.
22
D.
5
Câu 19: Cho điểm
( )
2; 2M
−
. Tìm điểm
M
′
là ảnh của điểm M qua phép quay tâm
O
, góc quay
90
o
.
A.
( )
2; 2M
′
−
. B.
( )
2; 2
M
′
−−
. C.
( )
2;2M
′
−
. D.
(
)
2;2M
′
.
Câu 20: Trong các mệnh đề nào sau đây mệnh đề nào đúng?
A. Phép đồng dạng là một phép dời hình. B. Phép tịnh tiến không phải là phép đồng dạng.
C. Phép quay là một phép đồng dạng. D. Phép vị tự là một phép dời hình.
Câu 21: Trong mặt phẳng
Oxy
cho đường thẳng
d
có phương trình
2 30xy+−=
. Phép vị tự tâm
O
tỉ số
2k =
biến
d
thành đường thẳng nào trong các đường thẳng có phương trình sau?
A.
4 2 50xy+ −=
. B.
4 2 30
xy− −=
. C.
2 60xy+−=
. D.
2 30xy
++=
.
Câu 22: Cho lục giác đều
ABCDEF
tâm
O
như hình vẽ.
Phép quay nào biến
EOD∆
thành
AOF∆
.
A.
( )
;120
.
O
Q
°
B.
( )
; 60
.
O
Q
−°
C.
(
)
; 120
.
O
Q
−°
D.
( )
;60
.
O
Q
°
Câu 23: Phép tịnh tiến theo vec tơ
u
biến hai điểm
,MN
thành điểm
,MN
′′
Chọn khẳng định
đúng ?
A.
.M N u MN
′′
=
 
. B.
.M N MN
′′
=
 
C.
'..OM u OM=
 
D.
..M N u MN
′′
=
 
Câu 24: Trong măt phẳng
Oxy
cho điểm
( 2;2)M −
.
( , 2)
()
O
V MM
−
′
=
.Tìm điểm
'.M
A.
(4;4)
. B.
( 4; 4)−−
. C.
( 4;4)−
. D.
(4; 4)−
.
Câu 25: Hãy tìm khẳng định sai ?
A. Phép tịnh tiến là phép dời hình. B. Phép quay là phép dời hình.
C. Phép vị tự là phép dời hình. D. Phép đồng nhất là phép dời hình.
-----------------------------------------------
----------- HẾT ----------
E
D
C
B
F
O
A
Trang 1/2 - Mã đề thi 485
SỞ GD-ĐT QUẢNG TRỊ ĐỀ KIỂM TRA CHƯƠNG I
TRƯỜNG THPT HẢI LĂNG Môn: Hình học - Lớp: 11– Ban: Cơ bản
Thời gian làm bài: 45 phút (25 câu trắc nghiệm)
Họ, tên thí sinh:......................................................Lớp.......... Mã đề thi 485
PHẦN TRẢ LỜI: Học sinh lựa chọn câu trả lời và điền vào bảng sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Câu 1: Trong mặt phẳng tọa độ
Oxy
, cho đường hai thẳng
: 3 30dx y− +=
và
': 3 6 0dx y− +=
. Tìm
tọa độ
v
có phương vuông góc với
d
để
( )
'
v
Td d=
.
A.
( )
3;1v =
B.
( )
3; 1v = −
C.
39
;
10 10
v

=


D.
39
;
10 10
v

= −


Câu 2: Tam giác
ABC
có diện tích
S
. Phép vị tự tỉ số
1
2
k = −
biến tam giác
ABC
thành tam giác
ABC
′′′
.
Gọi
S
′
là diện tích tam giác
ABC
′′′
. Khẳng định nào sau đây đúng
A.
4SS
′
=
. B.
1
2
SS
′
=
. C.
2SS
′
=
. D.
1
4
SS
′
=
Câu 3: Phép tịnh tiến theo vec tơ
u
biến hai điểm
,MN
thành điểm
,
MN
′′
Chọn khẳng định đúng ?
A.
'..
OM u OM
=
 
B.
.
M N u MN
′′
=
 
. C.
.M N MN
′′
=
 
D.
..M N u MN
′′
=
 
Câu 4: Cho hình vuông
ABCD
tâm
O
cạnh bằng
2
.
Phép đồng dạng tỉ số
k
biến tam giác
AOD
thành tam giác
ABC
. Tính
k
.
A.
4.
k
=
B.
2
.
2
k =
C.
2.k =
D.
2.
k =
Câu 5: Hãy tìm khẳng định sai ?
A. Phép tịnh tiến là phép dời hình. B. Phép quay là phép dời hình.
C. Phép vị tự là phép dời hình. D. Phép đồng nhất là phép dời hình.
Câu 6: Cho điểm
( )
1; 2M
. Tìm điểm
M
′
là ảnh của điểm M qua phép tịnh tiến theo véc tơ
( )
2; 1v = −
.
A.
( )
' 3; 3M −
. B.
( )
' 3;1M
. C.
( )
' 1; 3M −
. D.
(
)
' 3;3M −
.
Câu 7: Trong các mệnh đề nào sau đây mệnh đề nào đúng?
A. Phép tịnh tiến không phải là phép đồng dạng. B. Phép đồng dạng là một phép dời hình.
C. Phép vị tự là một phép dời hình. D. Phép quay là một phép đồng dạng.
Câu 8: Cho đường thẳng
:2 3 1 0dx y− +=
. Xét
(
)
( )
,90
O
Q dd
°
′
=
. Tìm vec tơ chỉ phương
u
của
d
′
.
A.
( )
3; 2
u = −
. B.
( )
3;2u =
. C.
( )
2; 3u = −
. D.
( )
2; 3u =−−
.
Câu 9: Trong măt phẳng
Oxy
, cho điểm
( )
5; 6A −
. Tìm ảnh của A qua phép dời hình có được bằng cách
thực hiện liên tiếp phép tịnh tiến theo
( )
3;4u = −
và phép quay tâm
O
góc quay bằng
0
90
?
A.
( )
2;2A
′
. B.
( )
2; 2A
′
−−
. C.
( )
2; 2A
′
−
. D.
( )
2;2A
′
−
.
Câu 10: Cho tam giác đều tâm
O
. Hỏi có bao nhiêu phép quay tâm
O
góc quay
α
,
02
απ
<≤
biến tam
giác trên thành chính nó?
A. Bốn. B. Ba. C. Hai. D. Một.
Câu 11: Tính chất nào sau đây không phải là tính chất của phép đồng dạng ?
A. Biến đoạn thẳng thành đoạn thẳng.
B. Biến đường tròn thành đường tròn bằng nó.
C. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.
D. Biến tam giác thành tam giác đồng dạng với nó.
Câu 12: Cho đường tròn
22
( ): 2 8 0
Cx y x+ − −=
.
( , 2)
() ( )
O
V CC
−
′
=
. Tính diện tích hình tròn
()C
′
A.
64
π
. B.
9
π
. C.
36
π
. D.
4
π
.
Trang 2/2 - Mã đề thi 485
Câu 13: Cho đường tròn
()C
:
22
( 1) 8xy+− =
. Ảnh của
()C
qua phép quay tâm
O
góc
90
o
−
là.
A.
22
( 1) 8xy++ =
. B.
22
( 1) 8
xy
−+=
. C.
22
( 1) 8
xy
++=
. D.
22
( 1) 8xy+− =
.
Câu 14: Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho.
B. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
C. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
D. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
Câu 15: Cho phép vị tự tâm
A
tỉ số
2k =
biến điểm M thành
'M
. Đẳng thức nào sau đây đúng ?
A.
'2AM AM=
 
. B.
1
'
2
AM AM=
 
. C.
3'AM AM=
 
. D.
1
'
3
AM AM=
 
.
Câu 16: Trong mặt phẳng
Oxy
, cho tam giác
ABC
có
( ) ( ) ( )
1; 2 , 1; 6 , 6; 2ABC−− −
. Phép vị tự tâm
O
tỉ
số
1
2
k = −
biến tam giác
ABC
thành tam giác
ABC
′′′
. Tìm trọng tâm của tam giác
ABC
′′′
.
A.
( )
1;1 .G
′
−
B.
(
)
1;1 .
G
′
C.
( )
1; 1 .G
′
−
D.
( )
1; 1 .G
′
−−
Câu 17: Trong mặt phẳng
Oxy
, cho
( ) ( )
1;5 , 3;3 .AB
Phép đồng dạng tỉ số
1
2
k =
biến điểm
A
thành
,A
′
biến điểm
B
thành
.B
′
Khi đó độ dài
AB
′′
là:
A.
25
B.
5
C.
22
D.
2
Câu 18: Cho đường thẳng
: 2 30xy∆ − +=
và
( )
2; 1u
= −
.
( )
'
u
T ∆=∆
có phương trình là:
A.
2 10
xy− −=
. B.
2 10xy− +=
. C.
2 30xy− −=
. D.
2 10xy+ +=
.
Câu 19: Cho điểm
( )
2; 2M −
. Tìm điểm
M
′
là ảnh của điểm M qua phép quay tâm
O
, góc quay
90
o
.
A.
(
)
2;2M
′
−
. B.
( )
2; 2M
′
−
. C.
( )
2; 2
M
′
−−
. D.
( )
2;2M
′
.
Câu 20: Cho lục giác đều
ABCDEF
tâm
O
như hình vẽ.
Phép quay nào biến
EOD∆
thành
AOF∆
.
A.
( )
;120
.
O
Q
°
B.
( )
; 60
.
O
Q
−°
C.
( )
;60
.
O
Q
°
D.
( )
; 120
.
O
Q
−°
Câu 21: Cho đường thẳng
:2 3 0d xy+−=
.
( ,2)
()
O
V dd
′
=
.Tìm điểm
'.d
A.
4 2 30
xy− −=
. B.
2 60xy+−=
. C.
2 30xy++=
. D.
4 2 50xy+ −=
.
Câu 22: Trong mặt phẳng Oxy, cho đường tròn
( ) ( )
2
2
: 1 ( 2) 9Cx y+ +− =
và
( )
1; 2v = −
.
( )
'( , )
v
TC CIR
′′
=
. Khẳng định nào dưới đây đúng ?
A.
( )
0;0I
′
và
3.R
′
=
B.
( )
2; 4I
′
−
và
3.R
′
=
C.
( )
0; 4I
′
−
và
3.R
′
=
D.
( )
0;0I
′
và
9.R
′
=
Câu 23: Cho hai điểm
(3;1)
M
và
(2; 1)M
′
−
nếu
( )
'
v
TM M=
thì
v
T
biến điểm
( 2;2)A −
thành điểm
A
′
?
A.
( 3;2)A
′
−
. B.
( 1; 0)
A
′
−
. C.
( 3;0)A
′
−
. D.
( 3;4)A
′
−
.
Câu 24: Trong mặt phẳng
Oxy
, cho đường tròn
( )
C
có phương trình
( ) ( )
22
2 2 16xy− +− =
. Phép đồng
dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm
O
tỉ số
1
2
k =
và phép tịnh tiến theo
( )
1; 2u = −
sẽ biến
( )
C
thành đường tròn
( )
,.C IR
′ ′′
Khẳng định nào đúng ?
A.
( )
0;3I
′
và
2.
R
′
=
B.
( )
1; 4
I
′
và
2.R
′
=
C.
( )
1;1I
′
và
4.R
′
=
D.
( )
2;2I
′
và
2.R
′
=
Câu 25: Trong măt phẳng
Oxy
cho điểm
( 2;2)M −
.
( , 2)
()
O
V MM
−
′
=
.Tìm điểm
'.M
A.
( 4;4)−
. B.
(4; 4)
−
. C.
(4;4)
. D.
( 4; 4)−−
.
-----------------------------------------------
----------- HẾT ----------
E
D
C
B
F
O
A
PHIẾU ĐÁP ÁN TRẮC NGHIỆM
MÔN HÌNH HỌC CHƯƠNG I
Mã đề: 132
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
21
22
23
24
25
A
B
C
D
Mã đề: 209
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
21
22
23
24
25
A
B
C
D
Mã đề: 357
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
21
22
23
24
25
A
B
C
D
Mã đề: 485
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
21
22
23
24
25
A
B
C
D
Tra
ng 4/12 – Diễn đàn giáo viên Toán
BẢNG ĐÁP ÁN
1.C
2.C
3.C.C
4.C.C
5.A
6.D
7.C
8.A
9.C
10.A
11.C
12.A 13.B 14.D 15.A 16.B 17.D 18.C 19.B 20.D
21.B
22.B 23.A 24.C 25.A
LỜI
GIẢI CHI TIẾT
Câu 1. Trong mặt phẳng
Oxy
, c
ho đường tròn
2 2
: 2 2 16
C x y
. Phép
đồng dạng có được
bằng cách thực hiện liên tiếp phép vị tự tâm
O
tỉ số
1
2
k
và
phép tịnh tiến theo
1;
2
u
sẽ
biến
C
thành đ
ường tròn
,C I
R
. Kh
ẳng định nào đúng?
A.
1;4
I
và
2R
. B.
2;
2
I
và
2R
. C.
0;
3
I
và
2R
. D.
1;1
I
và
4R
.
Lời
giải
Chọn C
Đư
ờng tròn
C
có
tâm
2;
2
I
,
bán kính
4R
.
Xét
phép vị tự
1 1
1
1
,
2
: ,
,
O
V C
I R C I R
. Khi
đó:
1 1
1
1;1
2
OI O
I I
và
1
1
2
2
R R
.
Xét phép tịnh tiến
1 1
1
: , ,
u
T C I R C I R
. K
hi đó
1
0;
3
I I
u I
và
1
2
R R
.
Do đó
, ta chọn đáp án C.
Câu 2. Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
B. Phép tịnh tiến biến tam giác thành tam giác bằng nó.
C. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với nó.
D. Phép
tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kỳ.
Lời giải
Chọn C
Câ
u C là mệnh đề sai vì “Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc
trùng với nó”.
Câu 3. Cho đường tròn.
2 2
1 2
9
x y
. Phép tịnh tiến theo véc tơ
1;
2
v
biến đường tròn
C
thà
nh đường tròn
' '
; 'C I R
. K
hẳng định nào sau đây đúng?
A.
' 2
; 4
I
và
' 3
R
. B.
' 0
;0
I
và
' 9
R
.
C.
' 0
; 4
I
và
' 3
R
. D.
' 0
;0
I
và
' 3
R
.
Lời giả
i
Chọn A
2 2
: 1
2 9
C x
y
Tâm
1;
2
I
Banh
kính
3
R
Theo
tính chất của phé tịnh tiến nên ta có:
Trang
5/12 - WordToan
Phép tịnh tiế
n theo véc tơ
1; 2
v
biến đườ
ng tròn
C
thành
đường tròn
' ';
'C I R
.
Nên
' 3
R R
.
Tâm
'I
là
ảnh của
I
qua ph
ép tịnh tiến nên
' 2;
4
I
.
Câu 4. Tính ch
ất nào sau đây không phải là tính chất của phép đồng dạng ?
A. Biến tam giác thành tam giác đồng dạng với nó.
B. Biến đường tròn thành đường tròn bằng nó.
C. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.
D. Biến đoạn thẳng thành đoạn thẳng.
Lời giải
Chọn B
Phép đồng d
ạng với tỷ số
k
biến đường tròn bán kính
R
thành đường tròn bán kính
.k R
.
Nên 2 đường tròn không băng nhau.
Câu 5. Cho đường tròn
2 2
: 2 8 0
C x y x
. G
ọi
'
C
là ả
nh của
C
qua phé
p vị tự tâm
O
tỉ số
2
k
. Tính
diện tích hình tròn
'
.C
A.
36
. B.
64
. C.
9
. D.
18
.
Lời giải
Chọn A
Ta có
C
có
3.
R
Bán
kính của
'
C
là
'
2.3
6.
R k R
Vậy diệ
n tích hình tròn
'
C
là
2
' 2
.6 3
6 .
S R
Câu 6. Tr
ong mặt phẳng tọa độ
,Oxy
cho tam
giác
ABC
có
1; 2
, 1;6 , 6;2 .
A B C
Phép vị
tự
tâm
O
tỉ số
1
2
k
biến tam
giác
ABC
thành tam
giác
' ' '
.A BC
Tìm tr
ọng tâm
'
G
của ta
m giác
' ' '
.A BC
A.
'
1; 1
G
. B.
'
1;1
G
. C.
'
1;1
G
. D.
'
1; 1
G
.
Lời giải
Chọn D
Gọi
G
là
trọng tâm của tam giác
ABC
, ta có
2
3
2;2
2
3
A B C
G
A
B C
G
x x x
x
G
y
y y
y
.
T
rang 6/12 – Diễn đàn giáo viên Toán
Ta c
ó
'
G
là
ảnh của
G
qua
phép vị tự tâm
O
tỉ số
1
.
2
k
S
uy ra
'
1
2
O
G OG
'
'
'
'
'
1
1
2
1
; 1 .
1
1
2
G
G
G
G
G
G
x
x
x
G
y
y y
Vậy trọng tâm của tam giác
'
' '
A BC
là
'
1
; 1 .
G
Câu 7. Trong mặt phẳng tọa độ
O
xy
,
cho hai đường thẳng
:
3 3 0
d
x y
v
à
:
3 6 0
d
x y
.
Tìm
tọa độ vectơ
v
v
uông góc với
d
để
v
T
d d
.
A
.
3
9
;
10
10
v
. B.
3
;1
v
. C.
3
9
;
10
10
v
. D.
3
; 1
v
.
Lờ
i giải
Chọn
C
Đặt
;v
a b
,
vì
v
v
uông góc với
: 3 3 0
d x y
n
ên
3 0
a b
(1).
Lấ
y điểm
(
3;0)
M
d
,
gọi
M
l
à ảnh của
M
qua
v
T
,
suy ra
(
3; )M a b
.
Điểm
M
d
nên
ta có:
3
3 6 0 3 3 0
a
b a b
(2)
.
Giải hệ (1), (2) ta được
3
10
9
10
a
b
.
C
âu 8. Cho đường thẳng
: 2 3 1 0
d x y
, xé
t
;
90O
Q d d
. Tìm
vectơ chỉ phương
u
của
đường
thăng
d
.
A.
2
; 3
u
. B.
3
;2
u
. C.
3
; 2
u
. D.
2
; 3
u
.
Lờ
i giải
Chọn A
;
90O
Q
d d d d d
có
dạng:
3
2 0
x
y m
.
d
có
vectơ pháp tuyến
3
;2
n
nên
vectơ chỉ phương
2
; 3
u
.
C
âu 9. Hãy tìm khẳng định sai?
A
. P
hép quay là phép dời hình. B. Phép tịnh tiến là phép dời hình.
C
. P
hép vị tự là phép dời hình. D. Phép đồng nhất là phép dời hình.
Lờ
i giải
Chọn
C
Theo định nghĩa phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
Vì vậy phép vị tự không phải là phép dời hình.
Câu 10. Cho phép vị tự tâm
A
tỉ
số
2
k
biến
điểm
M
thành
M
.
Đẳng thức nào sau đây đúng?
A
.
2AM
AM
. B.
1
3
A
M AM
. C.
1
2
A
M AM
. D.
3
AM AM
.
Lờ
i giải
T
rang 7/12 - WordToan
Chọn A
Theo định nghĩa phép vị tự ta có
, 2A
V
M M
2
A
M AM
.
Vậy
chọn đáp án A.
Câu 11. Trong mặt phẳng
O
xy
, cho
1
;5 , 3; 3A B
. Phép đồng dạng tỷ số
1
2
k
biến điểm
A
thành
/
A
,
biến điểm
B
thà
nh
/
B
.
Khi đó độ dài
/
/
A
B
là
A
.
5
. B.
2 5
. C.
2
. D.
2 2
.
Lời gi
ải
Chọn
C
Ta có:
2
2
2; 2 2 2 2 2
AB AB
.
/
/
1
. .2 2 2
2
A B k AB
.
Chọn C.
Câu 12. Cho đường tròn
2
2
: 1 8
C x y
. Ảnh
của
C
qua
phép quay tâm
O
g
óc
0
90
l
à:
A
.
2
2
1
8
x
y
. B.
2
2
1
8
x
y
. C.
2
2
1
8
x
y
. D.
2
2
1
8
x
y
.
Lờ
i giải
Chọn
A
Đường tròn
C
c
ó tâm
0;1I
,
bán kính
2 2R
.
Vì
0
;1I Oy
v
à
1O
I
nên ảnh
của
I
qua
phép quay tâm
O
g
óc
0
90
là
điểm
/
1
;0I
.
Gọi
/
C
l
à ảnh của
C
qua
phép quay tâm
O
g
óc
0
90
/
C
có
tâm là điểm
/
1
;0I
v
à
bán kính
/
2
2 R R
.
phư
ơng trình
2
/ 2
:
1 8
C
x y
.
Chọn
A
Câu 13. Cho đương thăng
:
2 3 0
x
y
v
a
2
; 1
u
.
'
u
T
c
o phương trinh la:
A.
2 1 0
x y
. B.
2 1 0
x y
. C.
2 1 0
x y
. D.
2 3 0
x y
.
Lơ
i giai
Ch
on B
Cach 1:
+
'
u
T
khi
đo
v
a
'
s
ong song hoăc trung.
Suy ra:
'
: 2 0
x
y m
.
T
rang 8/12 – Diễn đàn giáo viên Toán
+ Lâ
y
1
;1A
.
'
1 2 1
' '; '
'
1 1 0
u
x
T
A A x y
y
.
+
'
'A
suy
ra
1 2.0 0 1
m m
.
Vâ
y phương trinh đương thăng
'
l
a
2
1 0
x
y
.
Cach
2:
+
Goi
;M
x y
.
+
'
'; '
u
T
M M x y
,
'
u
T
K
hi đo:
' 2 2 ' 1 3 0
2
3 0 2 3 0 ' 2 ' 1 0
'
2 ' 2 ' 2 ' 2
' 1 ' 1 ' 1 ' 1
x y
x y x y x y
x x x x x x x x
y y y y y y y y
.
Vi
'
'M
nê
n phương trinh đương thăng
'
l
a
2
1 0
x
y
.
C
âu 14. Cho điêm
2
; 2
M
. Ti
m điêm
'M
l
a anh cua điêm
M
qua
phep quay tâm
O
g
oc quay
9
0
.
A.
'
2; 2
M
. B.
'
2;2
M
. C.
'
2; 2
M
. D.
'
2;2
M
.
Lơ
i giai
Ch
on D
;
90
'
2
'
'; '
' 2
M
O
M
x
y
Q M M x y
y x
.
Vâ
y:
'
2;2
M
.
C
âu 15. Trong mặt phẳng
Ox
y
, cho điểm
(
5; 6)
A
. Tìm ảnh của
A
qua phép dời hình có được bằng
cách thực hiện liên tiếp phép tịnh tiến theo
(
3; 4)
u
và phép quay tâm
O
góc quay
9
0
?
A
.
'
(2;2)
A
. B.
'
(2; 2)
A
. C.
'
( 2; 2)
A
. D.
'
( 2; 2)
A
.
Lờ
i giải
Chọn
A
Gọi
''( ''; y '')
A x
là
ảnh của
(5; 6)
A
qua
phép tịnh tiến theo
(
3; 4)
u
.
Ta c
ó:
'
' 5 ( 3) 2
'' 6 4 2
x
y
'
'(2; 2)
A
Gọi
'
( '; y ')
A
x
là ả
nh của
'
'(2; 2)
A
qua
phép phép quay tâm
O
g
óc quay
9
0
.
Ta c
ó:
'
'' 2
'
(2; 2)
'
'' 2
x y
A
y x
Tr
ang 9/12 - WordToan
Vậy
'(
2;2)A
chính là ảnh của
A
qua phép dời hình có được bằng cách thực hiện liên tiếp
phép tịnh tiến theo
( 3
;4)u
và phép quay tâm
O
góc quay
90
.
Câu 16. Phép tịnh tiến theo vectơ
u
biến hai điểm
,M N
thành điểm
',
'M N
. Chọn khẳng định đúng?
A.
' '
.M N u MN
 
. B.
' 'M
N MN

. C.
' .O
M u OM
 
. D.
' '
.M N u MN
 
.
Lời giải
Chọn B
Dựa v
ào tính chất của phép tịnh tiến.
Câu 17. Cho tam giác đều tâm
O
. Hỏi có bao nhiêu phép quay tâm
O
góc quay
,0 2
biến tam
giác trên thành chính nó?
A. Một. B. Hai. C. Bốn. D. Ba.
Lời giả
i
Chọn D
Gọi
ABC
là
tam giác đều đã cho.
Vì
O
là
tâm của tam giác đều nên ta có:
2
,
3
2
, ,
,
3
.
O
OA OB OC
OA OB OB OC OC OA
Q ABC BCA
4
,
3
4
, ,
,
3
.
O
OA OB
OC
OA OC OB OA OC OB
Q ABC CAB
,2
, ,
, 2
.
O
OA
OB OC
OA OA OB OB OC OC
Q ABC ABC
Do g
óc quay
0
2
nên
có ba phép quay thỏa mãn bài toán.
Câu 18. Trong mặt phẳng
Oxy
cho
điểm
2 ;
2M
. P
hép vị tự tâm
O
, t
ỉ số
2k
biến
điểm
M
thành
điểm nào trong các điểm sau đây?
A.
4 ; 4
. B.
4 ; 4
. C.
4 ; -4
. D.
4 ; -4
.
Lời giải
Chọn C
O
C
B
A
Tr
ang 10/12 – Diễn đàn giáo viên Toán
Giả sử
,
2O
V
M M
.
Khi đó
2
4
2 4 ; 4 .
2 4
M
M
M M
x
x
OM OM M
y y
Vậy
4
; 4 .M
Câu 19. Cho điểm
1
;2M
. Tìm điểm
M
là ảnh của điểm
M
qua phép tịnh tiến theo véctơ
2; 1v
A
.
3; 3M
. B.
3;1M
. C.
1;3M
. D.
3;3M
.
Lời
giải
Chọn
B
Gọi
;M
x y
Ta
có:
v
T
M M
1
2 3
3;1
2 1 1
x
x x a
M
y
y y b
.
Câu
20. Cho hai điểm
3
;1M
v
à
2
; 1M
nếu
v
T
M M
t
hì
v
T
biến
điểm
2
;2A
thành
điểm
A
?
A.
3
;2A
. B.
3
;4A
. C.
1
;0A
. D.
3
;0A
.
Lời
giải
Chọn
D
Gọi
;A x y
.
Ta
có:
1
v
T M M MM v
.
2
v
T
A A AA v
.
Từ
1
v
à
2
2
1 3
2 2 ' 0
x x
AA MM
y y
.
Vậy
3
;0A
.
Câu
21. Cho hình vuông
A
BCD
tâ
m
O
cạn
h bằng
2
.
Phép đồng dạng tỉ số
k
biế
n tam giác
A
OD
thà
nh
tam giác
ABC
. Tính
k
.
A
.
2k
. B.
2k
. C.
2
2
k
. D.
4k
.
Lời
giải
Chọn B
Tr
ang 11/12 - WordToan
Theo
đề có phép đồng dạng tỉ số
k
bi
ến tam giác
AOD
thành
tam giác
ABC
nên
có
AO
D
đồng
dạng với
AB
C
, k
hi đó có tỉ số
1
2
AO AD OD
k
AB AC BC k
.
(Tron
g đó
2;AC 2 2AO OD
)
Câu 22. Trong
mặt phẳng
Oxy
cho
đường thẳng
d
có phương
trình
2 3 0x y
. Ph
ép vị tự tâm
O
tỉ
s
ố
2k
biến
d
thành đường thẳng
nào trong các đường thẳng có phương trình sau?
A.
2 3
0x y
. B.
2 6
0x y
. C.
4 2
5 0x y
. D.
4 2
3 0x y
.
Lời giả
i
Chọn B
Gọi
'd
là
ảnh của
d
qua phép v
ị tự tâm
O
tỉ số
2k
khi đó
đường thẳng
'd
có phương
trình
2 0x
y c
( Phé
p vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó).
Lấy
(0
;3)A d
;2
( ) ' O ' 2 (0;6)
A'(0;6) d'
O
V A A A OA
Thay
'(
0;6)A
vào
( '
) : 2 0 6d x y c c
.
Vậy
'd
có
phương trình là
2 6
0x y
.
Câu 23. Trong
các mệnh đề sau đây mệnh đề nào đúng?
A. Phép quay là một phép đồng dạng. B. Phép vị tự là một phép dời hình.
C. Phép
đồng dạng là một phép dời hình. D. Phép tịnh tiến không phải là phép đồng
dạng.
Lời giải
Chọn A
Ta có:
Phép quay là một phép dời hình nên nó là phép đồng dạng với tỉ số
1k
.
Vậy
mệnh đề A đúng.
Câu 24. Cho lục giác đều
AB
CDEF
tâ
m
O
như h
ình vẽ.
Phép quay nào biến
EOD
thành
AO
F
.
A.
0
,1
20O
Q
. B.
0
, 6
0O
Q
. C.
0
, 1
20O
Q
. D.
0
,60O
Q
.
Lời giả
i
Chọn C
T
rang 12/12 – Diễn đàn giáo viên Toán
Do
AB
CDEF
l
à lục giác đều
0
120 ; .AOE DOF OA OD OF OE
0
,
120
:
O
Q
EOD AOF
C
âu 25. Cho tam giác
ABC
có
diện tích
S
. Phép
vị tự tỉ số
1
2
k
biế
n tam giác
ABC
t
hành tam giác
'
' 'A B C
.
Gọi
'S
l
à diện tích tam giác
'
' 'A B C
.
Khẳng định nào sau đây đúng
A.
1
'
4
S S
. B.
' 2S S
. C.
1
'
2
S S
. D.
' 4S S
.
Lờ
i giải
Chọn
A
Gọi
, , ,a b c p
là
độ dài 3 cạnh và nửa chu vi của tam giác
A
BC
.
Gọi
', ', ', 'a b c p
là
độ dài 3
cạnh và nửa chu vi của tam giác
'
' 'A B C
.
Theo tính chất của phép vị tự với tỉ số
1
2
k
suy
ra
2
', 2 ', 2 ' 2 'a a b b c c p p
.
The
o công thức Hê rông

 
 
2
' 2 ' 2 ' 2 ' 2 ' 2 ' 2 '
4 ' ' ' ' ' ' ' 4 '
S
p p a p b p c
p
p a p b p c
p p a p b p c S
.
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD-ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA CHƯƠNG I
TRƯỜNG THPT HẢI LĂNG Môn: Hình học - Lớp: 11– Ban: Cơ bản
Thời gian làm bài: 45 phút (25 câu trắc nghiệm)
Họ, tên thí sinh:......................................................Lớp.......... Mã đề thi 132
PHẦN TRẢ LỜI: Học sinh lựa chọn câu trả lời và điền vào bảng sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 2 2
Câu 1: Trong mặt phẳng Oxy , cho đường tròn (C) : ( x − 2) + ( y − 2) = 16 . Phép đồng dạng có được bằng 
cách thực hiện liên tiếp phép vị tự tâm O tỉ số 1 k =
và phép tịnh tiến theo u = ( 1
− ;2) sẽ biến (C)thành 2
đường tròn C′(I ,′R′). Khẳng định nào đúng ?
A. I ′(1;4) và R′ = 2.
B. I ′(2;2) và R′ = 2.
C. I ′(0;3) và R′ = 2. D. I ′(1; ) 1 và R′ = 4.
Câu 2: Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
B. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
C. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho.
D. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì. 
Câu 3: Cho đường tròn (C ) ( x + )2 2 : 1
+ (y − 2) = 9 . Phép tịnh tiến theo v = (1; 2
− ) biến đường tròn (C)
thành đường trònC′(I ,′R′).Khẳng định nào dưới đây đúng ? A. I ′(2; 4
− ) và R′ = 3. B. I′(0;0) và R′ = 9. C. I′(0; 4
− ) và R′ = 3. D. I′(0;0) và R′ = 3.
Câu 4: Tính chất nào sau đây không phải là tính chất của phép đồng dạng ?
A. Biến tam giác thành tam giác đồng dạng với nó.
B. Biến đường tròn thành đường tròn bằng nó.
C. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.
D. Biến đoạn thẳng thành đoạn thẳng.
Câu 5: Cho đường tròn 2 2
(C) : x + y − 2x − 8 = 0 . V (C) = (C )
′ . Tính diện tích hình tròn (C )′ (O, 2) − A. 36π . B. 64π . C. 9π . D. 4π .
Câu 6: Trong mặt phẳng Oxy , cho tam giác ABC có A(1; 2 − ), B( 1 − ;6), C ( 6
− ;2) . Phép vị tự tâm O tỉ số 1 k = −
biến tam giác ABC thành tam giác A′B C
′ ′ . Tìm trọng tâm của tam giác A′B C ′ ′ . 2 A. G′( 1 − ;− ) 1 . B. G′(1; ) 1 . C. G′( 1 − ; ) 1 . D. G′(1;− ) 1 .
Câu 7: Trong mặt phẳng tọa độ Oxy , cho đường hai thẳng d : x − 3y + 3 = 0 và d ' : x − 3y + 6 = 0 . Tìm tọa 
độ v có phương vuông góc với d để T (d ) = d '. v   3 9     3 9   A. v = ;   B. v = (3; ) 1 C. v = − ;   D. v = (3;− ) 1 10 10   10 10  
Câu 8: Cho đường thẳng d : 2x − 3y + 1 = 0 . Xét Q
d = d′ . Tìm vec tơ chỉ phương u của đg thẳng d′ . O,90° ( ) ( )     A. u = (2; 3 − ) . B. u = (3;2) . C. u = (3; 2 − ) . D. u = ( 2; − 3 − ) .
Câu 9: Hãy tìm khẳng định sai ?
A. Phép quay là phép dời hình.
B. Phép tịnh tiến là phép dời hình.
C. Phép vị tự là phép dời hình.
D. Phép đồng nhất là phép dời hình.
Câu 10: Cho phép vị tự tâm A tỉ số k = 2 biến điểm M thành M ' . Đẳng thức nào sau đây đúng ?  
 1 
 1   
A. AM ' = 2 AM . B. AM ' = AM . C. AM ' = AM .
D. AM = 3AM ' . 3 2
Trang 1/2 - Mã đề thi 132
Câu 11: Trong mặt phẳng Oxy , cho A(1;5), B(3;3). Phép đồng dạng tỉ số 1 k =
biến điểm A thành A ,′ 2
biến điểm B thành B .′ Khi đó độ dài A′B′ là: A. 5 B. 2 5 C. . 2 D. 2 2 .
Câu 12: Cho đường tròn (C) : 2 2
x + ( y − 1) = 8 . Ảnh của (C) qua phép quay tâm O góc 90o − là. A. 2 2
(x − 1) + y = 8 . B. 2 2
(x + 1) + y = 8 . 2 2 + − = + + = C. x ( y 1) 8 . D. 2 2 x ( y 1) 8 . 
Câu 13: Cho đường thẳng ∆ : x − 2 y + 3 = 0 và u = (2;− )
1 . T (∆) = ∆ ' có phương trình là: u
A. 2x + y + 1 = 0 .
B. x − 2 y − 1 = 0 .
C. x − 2 y + 1 = 0 .
D. x − 2 y − 3 = 0 .
Câu 14: Cho điểm M (2;− 2) . Tìm điểm M ′ là ảnh của điểm M qua phép quay tâm O , góc quay 90o . A. M ′( 2; − 2 − ) . B. M ′( 2; − 2). C. M ′(2; 2 − ). D. M ′(2;2) .
Câu 15: Trong măt phẳng Oxy , cho điểm A(5; 6
− ) . Tìm ảnh của A qua phép dời hình có được bằng cách 
thực hiện liên tiếp phép tịnh tiến theo u = ( 3
− ;4) và phép quay tâm O góc quay bằng 0 90 ? A. A′(2;2) . B. A′(2; 2 − ). C. A′( 2; − 2). D. A′( 2; − 2 − ) . 
Câu 16: Phép tịnh tiến theo vec tơ u biến hai điểm M , N thành điểm M ,′ N′ Chọn khẳng định đúng ?  
 
  
  A. M N
′ ′ = u.MN . B. M N ′ ′ = MN. C. OM ' = . u OM . D. M N ′ ′ = u.MN.
Câu 17: Cho tam giác đều tâm O . Hỏi có bao nhiêu phép quay tâm O góc quay α , 0 < α ≤ 2π biến tam
giác trên thành chính nó? A. Một. B. Hai. C. Bốn. D. Ba.
Câu 18: Trong măt phẳng Oxy cho điểm M ( 2;
− 2) . Phép vị tự tâm O tỉ số k = 2
− biến điểm M thành
điểm nào trong các điểm sau? A. ( 4; − 4) . B. (4; 4) . C. (4; 4 − ) . D. ( 4; − 4 − ) . 
Câu 19: Cho điểm M (1;2) . Tìm điểm M ′ là ảnh của điểm M qua phép tịnh tiến theo véc tơ v = (2;− ) 1 . A. M '(3; 3 − ) . B. M '(3; ) 1 . C. M '( 1 − ;3) . D. M '( 3 − ;3) .
Câu 20: Cho hai điểm M (3;1) và M ( ′ 2; 1)
− nếu T (M ) = M ' thì T biến điểm ( A 2;
− 2) thành điểm A′? v v A. A ( ′ 3 − ;2) . B. A ( ′ 3 − ;4) . C. A ( ′ 1 − ;0) . D. A ( ′ 3 − ;0) .
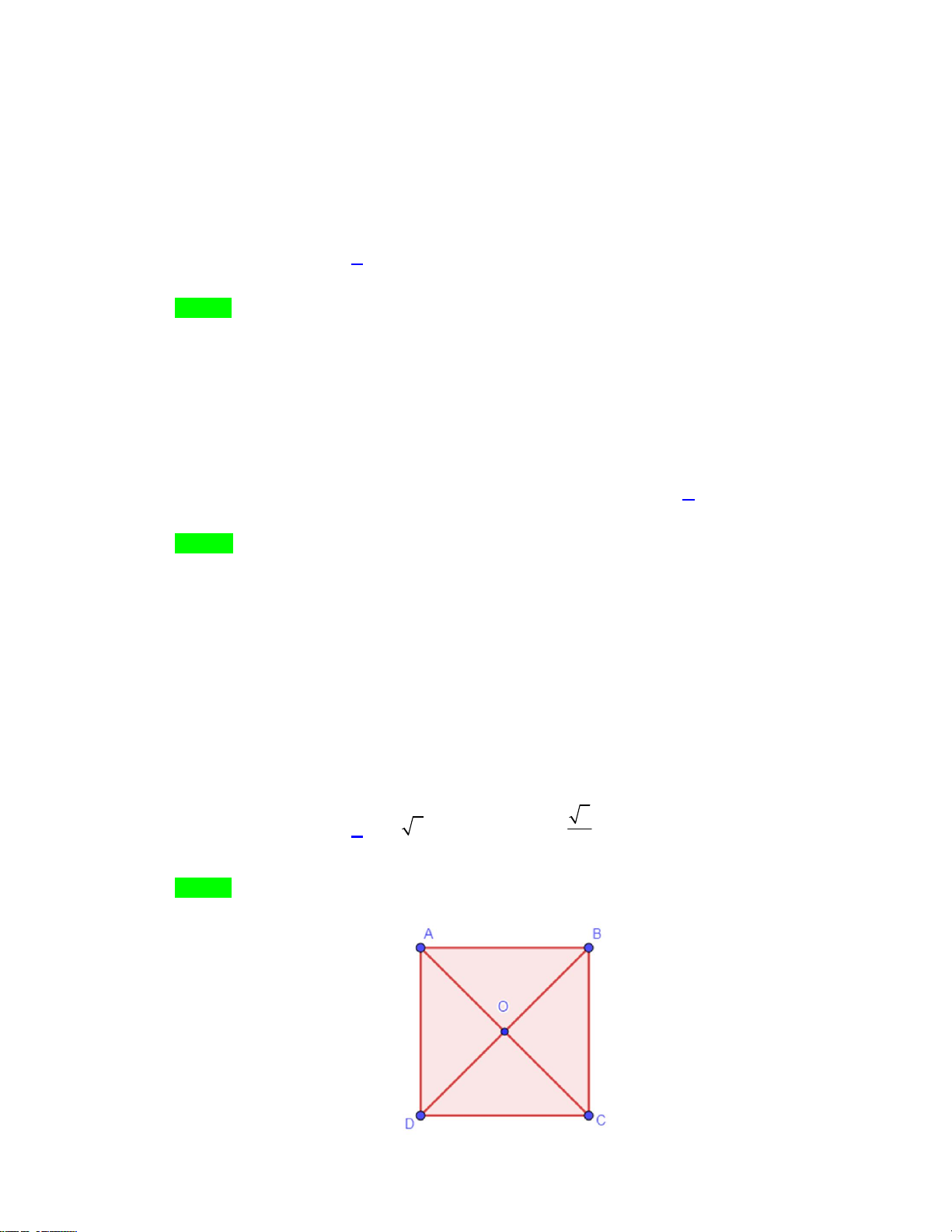
Câu 21: Cho hình vuông ABCD tâm O cạnh bằng 2 .
Phép đồng dạng tỉ số k biến tam giác AOD thành tam giác ABC . Tính k . 2 A. k = 2. B. k = 2. C. k = . D. k = 4. 2
Câu 22: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + y − 3 = 0 . Phép vị tự tâm O tỉ số
k = 2 biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?
A. 2x + y + 3 = 0 .
B. 2x + y − 6 = 0 .
C. 4x + 2 y − 5 = 0 .
D. 4x − 2 y − 3 = 0 .
Câu 23: Trong các mệnh đề nào sau đây mệnh đề nào đúng?
A. Phép quay là một phép đồng dạng.
B. Phép vị tự là một phép dời hình.
C. Phép đồng dạng là một phép dời hình.
D. Phép tịnh tiến không phải là phép đồng dạng.
Câu 24: Cho lục giác đều ABCDEF tâm O như hình vẽ. B A
Phép quay nào biến E ∆ OD thành A ∆ OF . A. ( Q . B. Q . C. Q . D. Q . F C O;120°) (O; 60 − °) (O; 120 − °) (O;60°) O
Câu 25: Tam giác ABC có diện tích S . Phép vị tự tỉ số 1 k = − biến tam giác ABC E D 2
thành tam giác A′B C
′ ′. Gọi S′ là diện tích tam giác A′B C
′ ′. Khẳng định nào sau đây đúng 1 1 A. S′ = S
B. S′ = 2S . C. S′ = S .
D. S′ = 4S . 4 2
----------------------------------------------- ----------- HẾT ----------
Trang 2/2 - Mã đề thi 132
SỞ GD-ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA CHƯƠNG I
TRƯỜNG THPT HẢI LĂNG Môn: Hình học - Lớp: 11– Ban: Cơ bản
Thời gian làm bài: 45 phút (25 câu trắc nghiệm)
Họ, tên thí sinh:......................................................Lớp.......... Mã đề thi 209
PHẦN TRẢ LỜI: Học sinh lựa chọn câu trả lời và điền vào bảng sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Câu 1: Trong mặt phẳng Oxy , cho A(1;5), B(3;3). Phép đồng dạng tỉ số 1 k =
biến điểm A thành A ,′ 2
biến điểm B thành B .′ Khi đó độ dài A′B′ là: A. 2 5 B. 5 C. 2 2 D. 2 
Câu 2: Cho đường thẳng ∆ : x − 2 y + 3 = 0 và u = (2;− )
1 . T (∆) = ∆ ' có phương trình là: u
A. 2x + y + 1 = 0 .
B. x − 2 y + 1 = 0 .
C. x − 2 y − 3 = 0 .
D. x − 2 y − 1 = 0 .
Câu 3: Cho điểm M (2;− 2) . Tìm điểm M ′ là ảnh của điểm M qua phép quay tâm O , góc quay 90o . A. M ′( 2; − 2 − ) . B. M ′(2; 2 − ). C. M ′( 2; − 2). D. M ′(2;2) .
Câu 4: Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
B. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
C. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho.
D. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì. 2 2
Câu 5: Trong mặt phẳng Oxy , cho đường tròn (C ) có phương trình ( x − 2) + ( y − 2) = 16 . Phép đồng
dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 1 k = và phép tịnh tiến theo 2
u = ( 1−;2) sẽ biến (C)thành đường tròn C′(I ,′R′). Khẳng định nào đúng ? A. I ′(1; ) 1 và R′ = 4.
B. I ′(0;3) và R′ = 2.
C. I ′(1;4) và R′ = 2.
I ′(2;2) và R′ = 2. D.
Câu 6: Trong mặt phẳng tọa độ Oxy , cho đường hai thẳng d : x − 3y + 3 = 0 và d ' : x − 3y + 6 = 0 . Tìm tọa 
độ v có phương vuông góc với d để T (d ) = d '. v   3 9     3 9   A. v = ;   B. v = (3; ) 1 C. v = − ;   D. v = (3;− ) 1 10 10   10 10 
Câu 7: Tính chất nào sau đây không phải là tính chất của phép đồng dạng ?
A. Biến tam giác thành tam giác đồng dạng với nó.
B. Biến đoạn thẳng thành đoạn thẳng.
C. Biến đường tròn thành đường tròn bằng nó.
D. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.
Câu 8: Hãy tìm khẳng định sai ?
A. Phép quay là phép dời hình.
B. Phép tịnh tiến là phép dời hình.
C. Phép vị tự là phép dời hình.
D. Phép đồng nhất là phép dời hình.
Câu 9: Trong mặt phẳng Oxy, cho đường tròn (C ) ( x + )2 2 : 1
+ (y − 2) = 9 . Phép tịnh tiến theo  v = (1; 2
− ) biến đường tròn (C) thành đường trònC′(I ,′R′).Khẳng định nào dưới đây đúng ? A. I ′(2; 4
− ) và R′ = 3. B. I′(0;0) và R′ = 3. C. I′(0; 4
− ) và R′ = 3. D. I′(0;0) và R′ = 9.
Câu 10: Cho phép vị tự tâm A tỉ số k = 2 biến điểm M thành M ' . Đẳng thức nào sau đây đúng ?
 1   
 1    A. AM ' = AM .
B. AM ' = 2 AM . C. AM ' = AM .
D. AM = 3AM ' . 3 2
Trang 1/2 - Mã đề thi 209
Câu 11: Trong măt phẳng Oxy , cho điểm A(5; 6
− ) . Tìm ảnh của A qua phép dời hình có được bằng cách 
thực hiện liên tiếp phép tịnh tiến theo u = ( 3
− ;4) và phép quay tâm O góc quay bằng 0 90 ? A. A′(2;2) . B. A′( 2; − 2 − ) . C. A′( 2; − 2). D. A′(2; 2 − ).
Câu 12: Tam giác ABC có diện tích S . Phép vị tự tỉ số 1 k = −
biến tam giác ABC thành tam giác A′B C ′ ′. 2
Gọi S′ là diện tích tam giác A′B C
′ ′. Khẳng định nào sau đây đúng 1 1 A. S′ = S .
B. S′ = 2S . C. S′ = S
D. S′ = 4S . 2 4
Câu 13: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình 2 2
x + y − 2x − 8 = 0 . Phép vị tự tâm O tỉ số k = 2
− biến (C) thành đường tròn (C )′ . Tính diện tích hình tròn (C )′ A. 36π . B. 4π . C. 64π . D. 9π . 
Câu 14: Cho đường thẳng d : 2x − 3y + 1 = 0 . Xét Q
d = d′ . Tìm vec tơ chỉ phương u của d′ . O,90° ( ) ( )     A. u = (2; 3 − ) . B. u = ( 2; − 3 − ) . C. u = (3;2) . D. u = (3; 2 − ) .
Câu 15: Cho tam giác đều tâm O . Hỏi có bao nhiêu phép quay tâm O góc quay α , 0 < α ≤ 2π biến tam
giác trên thành chính nó? A. Ba. B. Bốn. C. Một. D. Hai.
Câu 16: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + y − 3 = 0 . Phép vị tự tâm O tỉ số
k = 2 biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?
A. 2x + y − 6 = 0 .
B. 4x + 2 y − 5 = 0 .
C. 2x + y + 3 = 0 .
D. 4x − 2 y − 3 = 0 .
Câu 17: Trong măt phẳng Oxy cho điểm M ( 2; − 2) . V
(M ) = M ′ .Tìm điểm M '. (O, 2) − A. ( 4; − 4) . B. (4; 4) . C. (4; 4 − ) . D. ( 4; − 4 − ) . 
Câu 18: Cho điểm M (1;2) . Tìm điểm M ′ là ảnh của điểm M qua phép tịnh tiến theo véc tơ v = (2;− ) 1 . A. M '(3; 3 − ) . B. M '(3; ) 1 . C. M '( 1 − ;3) . D. M '( 3 − ;3) .
Câu 19: Cho hai điểm M (3;1) và M ( ′ 2; 1)
− nếu T (M ) = M ' thì T biến điểm ( A 2;
− 2) thành điểm A′? v v A. A ( ′ 3 − ;2) . B. A ( ′ 3 − ;4) . C. A ( ′ 1 − ;0) . D. A ( ′ 3 − ;0) .
Câu 20: Cho hình vuông ABCD tâm O cạnh bằng 2 .
Phép đồng dạng tỉ số k biến tam giác AOD thành tam giác ABC . Tính k . 2 A. k = 2. B. k = 2. C. k = . D. k = 4. 2
Câu 21: Cho đường tròn (C) : 2 2
x + ( y − 1) = 8 . Ảnh của (C) qua phép quay tâm O góc 90o − là. A. 2 2
(x + 1) + y = 8 . B. 2 2
x + ( y + 1) = 8 . 2 2 + − = − + = C. x ( y 1) 8 . D. 2 2 (x 1) y 8 .
Câu 22: Trong các mệnh đề nào sau đây mệnh đề nào đúng?
A. Phép quay là một phép đồng dạng.
B. Phép vị tự là một phép dời hình.
C. Phép đồng dạng là một phép dời hình.
D. Phép tịnh tiến không phải là phép đồng dạng.
Câu 23: Cho lục giác đều ABCDEF tâm O như hình vẽ. B A
Phép quay nào biến E ∆ OD thành A ∆ OF . A. ( Q . B. Q . C. Q . D. Q . F C O O;120°) (O; 60 − °) (O; 120 − °) (O;60°)
Câu 24: Trong mặt phẳng Oxy , cho tam giác ABC có A(1; 2 − ), B( 1 − ;6), C ( 6 − ;2) . E D V ( A ∆ BC) = A ∆ ′B C
′ ′ . Tìm trọng tâm của tam giác A′B C ′ ′ . 1 (O,− ) 2 A. G′( 1 − ;− ) 1 . B. G′(1; ) 1 . C. G′( 1 − ; ) 1 . D. G′(1;− ) 1 . 
Câu 25: Phép tịnh tiến theo vec tơ u biến hai điểm M , N thành điểm M ,′ N′ Chọn khẳng định đúng ?  
 
  
  A. M N
′ ′ = u.MN . B. M N ′ ′ = MN. C. OM ' = . u OM . D. M N ′ ′ = u.MN.
----------------------------------------------- ----------- HẾT ----------
Trang 2/2 - Mã đề thi 209
SỞ GD-ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA CHƯƠNG I
TRƯỜNG THPT HẢI LĂNG Môn: Hình học - Lớp: 11– Ban: Cơ bản
Thời gian làm bài: 45 phút (25 câu trắc nghiệm)
Họ, tên thí sinh:......................................................Lớp.......... Mã đề thi 357
PHẦN TRẢ LỜI: Học sinh lựa chọn câu trả lời và điền vào bảng sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Câu 1: Tính chất nào sau đây không phải là tính chất của phép đồng dạng ?
A. Biến tam giác thành tam giác đồng dạng với nó.
B. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.
C. Biến đoạn thẳng thành đoạn thẳng.
D. Biến đường tròn thành đường tròn bằng nó.
Câu 2: Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho.
B. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
C. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
D. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì. 
Câu 3: Cho đường thẳng ∆ : x − 2 y + 3 = 0 và u = (2;− )
1 . T (∆) = ∆ ' có phương trình là: u
A. x − 2 y − 1 = 0 .
B. 2x + y + 1 = 0 .
C. x − 2 y + 1 = 0 .
D. x − 2 y − 3 = 0 . 2 2
Câu 4: Trong mặt phẳng Oxy , cho đường tròn (C ) có phương trình ( x − 2) + ( y − 2) = 16 . Phép đồng dạng 
có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 1 k =
và phép tịnh tiến theo u = ( 1 − ;2) sẽ 2
biến (C)thành đường tròn C′(I ,′R′). Khẳng định nào đúng ? A. I ′(1; ) 1 và R′ = 4.
B. I ′(0;3) và R′ = 2.
C. I ′(1;4) và R′ = 2.
I ′(2;2) và R′ = 2. D.
Câu 5: Cho hai điểm M (3;1) và M ( ′ 2; 1)
− nếu T (M ) = M ' thì T biến điểm ( A 2;
− 2) thành điểm A′? v v A. A ( ′ 3 − ;0) . B. A ( ′ 3 − ;2) . C. A ( ′ 1 − ;0) . D. A ( ′ 3 − ;4) . 
Câu 6: cho đường thẳng d : 2x − 3y + 1 = 0 . Xét Q
d = d′ . Tìm vec tơ chỉ phương u của d′ . O,90° ( ) ( )     A. u = ( 2; − 3 − ) . B. u = (3; 2 − ) . C. u = (2; 3 − ) . D. u = (3;2) . 
Câu 7: Cho điểm M (1;2) . Tìm điểm M ′ là ảnh của điểm M qua phép tịnh tiến theo véc tơ v = (2;− ) 1 . A. M '(3; 3 − ) . B. M '(3; ) 1 . C. M '( 1 − ;3) . D. M '( 3 − ;3) . 
Câu 8: Trong mặt phẳng Oxy, cho đường tròn (C ) ( x + )2 2 : 1
+ (y − 2) = 9 . Phép tịnh tiến theo v = (1; 2 − ) biến
đường tròn (C) thành đường trònC′(I ,′R′).Khẳng định nào dưới đây đúng ? I ′(2; 4
− ) và R′ = 3. B. I′(0;0) và R′ = 3. C. I′(0; 4
− ) và R′ = 3. D. I′(0;0) và R′ = 9. A.
Câu 9: Cho phép vị tự tâm A tỉ số k = 2 biến điểm M thành M ' . Đẳng thức nào sau đây đúng ?  
 1 
 1   
A. AM ' = 2 AM . B. AM ' = AM . C. AM ' = AM .
D. AM = 3AM ' . 3 2
Câu 10: Trong mặt phẳng Oxy , cho tam giác ABC có A(1; 2 − ), B( 1 − ;6), C ( 6
− ;2) . Phép vị tự tâm O tỉ số 1 k = −
biến tam giác ABC thành tam giác A′B C
′ ′ . Tìm trọng tâm của tam giác A′B C ′ ′ . 2 A. G′(1;− ) 1 . B. G′( 1 − ; ) 1 . C. G′(1; ) 1 . D. G′( 1 − ;− ) 1 .
Câu 11: Cho đường tròn (C) : 2 2
x + ( y − 1) = 8 . Ảnh của (C) qua phép quay tâm O góc 90o − là. A. 2 2
(x + 1) + y = 8 . B. 2 2
x + ( y + 1) = 8 . C. 2 2
x + ( y − 1) = 8 . D. 2 2
(x − 1) + y = 8 .
Trang 1/2 - Mã đề thi 357
Câu 12: Trong mặt phẳng tọa độ Oxy , cho đường hai thẳng d : x − 3y + 3 = 0 và d ' : x − 3y + 6 = 0 . Tìm tọa 
độ v có phương vuông góc với d để T (d ) = d '. v     3 9    3 9  A. v = (3; ) 1 B. v = (3;− ) 1 C. v = ;   D. v = − ;   10 10   10 10 
Câu 13: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình 2 2
x + y − 2x − 8 = 0 . Phép vị tự tâm O tỉ số k = 2
− biến (C) thành đường tròn (C )′ . Tính diện tích hình tròn (C )′ A. 64π . B. 9π . C. 36π . D. 4π .
Câu 14: Cho hình vuông ABCD tâm O cạnh bằng 2 .
Phép đồng dạng tỉ số k biến tam giác AOD thành tam giác ABC . Tính k . 2 A. k = 2. B. k = 2. C. k = . D. k = 4. 2
Câu 15: Tam giác ABC có diện tích S . Phép vị tự tỉ số 1 k = −
biến tam giác ABC thành tam giác A′B C ′ ′. 2
Gọi S′ là diện tích tam giác A′B C
′ ′. Khẳng định nào sau đây đúng 1 1
A. S′ = 4S . B. S′ = S . C. S′ = S
D. S′ = 2S . 2 4
Câu 16: Trong măt phẳng Oxy , cho điểm A(5; 6
− ) . Tìm ảnh của A qua phép dời hình có được bằng cách thực 
hiện liên tiếp phép tịnh tiến theo u = ( 3
− ;4) và phép quay tâm O góc quay bằng 0 90 ? A. A′(2;2) . B. A′(2; 2 − ). C. A′( 2; − 2). D. A′( 2; − 2 − ) .
Câu 17: Cho tam giác đều tâm O . Hỏi có bao nhiêu phép quay tâm O góc quay α , 0 < α ≤ 2π biến tam giác trên thành chính nó? A. Bốn. B. Hai. C. Ba. D. Một.
Câu 18: Trong mặt phẳng Oxy , cho A(1;5), B(3;3). Phép đồng dạng tỉ số 1 k =
biến điểm A thành A ,′ biến 2
điểm B thành B .′ Khi đó độ dài A′B′ là: A. B. C. D. 2 5 2 2 2 5
Câu 19: Cho điểm M (2;− 2) . Tìm điểm M ′ là ảnh của điểm M qua phép quay tâm O , góc quay 90o . A. M ′(2; 2 − ). B. M ′( 2; − 2 − ) . C. M ′( 2; − 2). D. M ′(2;2) .
Câu 20: Trong các mệnh đề nào sau đây mệnh đề nào đúng?
A. Phép đồng dạng là một phép dời hình.
B. Phép tịnh tiến không phải là phép đồng dạng.
C. Phép quay là một phép đồng dạng.
D. Phép vị tự là một phép dời hình.
Câu 21: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + y − 3 = 0 . Phép vị tự tâm O tỉ số
k = 2 biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?
A. 4x + 2 y − 5 = 0 .
B. 4x − 2 y − 3 = 0 .
C. 2x + y − 6 = 0 .
D. 2x + y + 3 = 0 . B A
Câu 22: Cho lục giác đều ABCDEF tâm O như hình vẽ.
Phép quay nào biến E ∆ OD thành A ∆ OF . F C O A. ( Q . B. Q . C. Q . D. Q . O;120°) (O; 60 − °) (O; 120 − °) (O;60°)  E D
Câu 23: Phép tịnh tiến theo vec tơ u biến hai điểm M , N thành điểm M ,′ N′ Chọn khẳng định đúng ?  
 
  
  A. M N
′ ′ = u.MN . B. M N ′ ′ = MN. C. OM ' = . u OM . D. M N ′ ′ = u.MN.
Câu 24: Trong măt phẳng Oxy cho điểm M ( 2; − 2) . V
(M ) = M ′ .Tìm điểm M '. (O, 2) − A. (4; 4) . B. ( 4; − 4 − ) . C. ( 4; − 4) . D. (4; 4 − ) .
Câu 25: Hãy tìm khẳng định sai ?
A. Phép tịnh tiến là phép dời hình.
B. Phép quay là phép dời hình.
C. Phép vị tự là phép dời hình.
D. Phép đồng nhất là phép dời hình.
----------------------------------------------- ----------- HẾT ----------
Trang 2/2 - Mã đề thi 357
SỞ GD-ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA CHƯƠNG I
TRƯỜNG THPT HẢI LĂNG Môn: Hình học - Lớp: 11– Ban: Cơ bản
Thời gian làm bài: 45 phút (25 câu trắc nghiệm)
Họ, tên thí sinh:......................................................Lớp.......... Mã đề thi 485
PHẦN TRẢ LỜI: Học sinh lựa chọn câu trả lời và điền vào bảng sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Câu 1: Trong mặt phẳng tọa độ Oxy , cho đường hai thẳng d : x − 3y + 3 = 0 và d ' : x − 3y + 6 = 0 . Tìm 
tọa độ v có phương vuông góc với d để T (d ) = d '. v     3 9    3 9  A. v = (3; ) 1 B. v = (3;− ) 1 C. v = ;   D. v = − ;   10 10   10 10 
Câu 2: Tam giác ABC có diện tích S . Phép vị tự tỉ số 1 k = −
biến tam giác ABC thành tam giác A′B C ′ ′. 2
Gọi S′ là diện tích tam giác A′B C
′ ′. Khẳng định nào sau đây đúng 1 1
A. S′ = 4S . B. S′ = S .
C. S′ = 2S . D. S′ = S 2 4 
Câu 3: Phép tịnh tiến theo vec tơ u biến hai điểm M , N thành điểm M ,′ N′ Chọn khẳng định đúng ?
    
 
  A. OM ' = . u OM . B. M N
′ ′ = u.MN . C. M N ′ ′ = MN. D. M N ′ ′ = u.MN.
Câu 4: Cho hình vuông ABCD tâm O cạnh bằng 2 .
Phép đồng dạng tỉ số k biến tam giác AOD thành tam giác ABC . Tính k . 2 A. k = 4. B. k = . C. k = 2. D. k = 2. 2
Câu 5: Hãy tìm khẳng định sai ?
A. Phép tịnh tiến là phép dời hình.
B. Phép quay là phép dời hình.
C. Phép vị tự là phép dời hình.
D. Phép đồng nhất là phép dời hình. 
Câu 6: Cho điểm M (1;2) . Tìm điểm M ′ là ảnh của điểm M qua phép tịnh tiến theo véc tơ v = (2;− ) 1 . A. M '(3; 3 − ) . B. M '(3; ) 1 . C. M '( 1 − ;3) . D. M '( 3 − ;3) .
Câu 7: Trong các mệnh đề nào sau đây mệnh đề nào đúng?
A. Phép tịnh tiến không phải là phép đồng dạng. B. Phép đồng dạng là một phép dời hình.
C. Phép vị tự là một phép dời hình.
D. Phép quay là một phép đồng dạng. 
Câu 8: Cho đường thẳng d : 2x − 3y + 1 = 0 . Xét Q
d = d′ . Tìm vec tơ chỉ phương u của d′ . O,90° ( ) ( )     A. u = (3; 2 − ) . B. u = (3;2) . C. u = (2; 3 − ) . D. u = ( 2; − 3 − ) .
Câu 9: Trong măt phẳng Oxy , cho điểm A(5; 6
− ) . Tìm ảnh của A qua phép dời hình có được bằng cách 
thực hiện liên tiếp phép tịnh tiến theo u = ( 3
− ;4) và phép quay tâm O góc quay bằng 0 90 ? A. A′(2;2) . B. A′( 2; − 2 − ) . C. A′(2; 2 − ). D. A′( 2; − 2).
Câu 10: Cho tam giác đều tâm O . Hỏi có bao nhiêu phép quay tâm O góc quay α , 0 < α ≤ 2π biến tam
giác trên thành chính nó? A. Bốn. B. Ba. C. Hai. D. Một.
Câu 11: Tính chất nào sau đây không phải là tính chất của phép đồng dạng ?
A. Biến đoạn thẳng thành đoạn thẳng.
B. Biến đường tròn thành đường tròn bằng nó.
C. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.
D. Biến tam giác thành tam giác đồng dạng với nó.
Câu 12: Cho đường tròn 2 2
(C) : x + y − 2x − 8 = 0 . V (C) = (C ) ′ ′ (O, 2) −
. Tính diện tích hình tròn (C ) A. 64π . B. 9π . C. 36π . D. 4π .
Trang 1/2 - Mã đề thi 485
Câu 13: Cho đường tròn (C) : 2 2
x + ( y − 1) = 8 . Ảnh của (C) qua phép quay tâm O góc 90o − là. A. 2 2
x + ( y + 1) = 8 . B. 2 2
(x − 1) + y = 8 . C. 2 2
(x + 1) + y = 8 . D. 2 2
x + ( y − 1) = 8 .
Câu 14: Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho.
B. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
C. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
D. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
Câu 15: Cho phép vị tự tâm A tỉ số k = 2 biến điểm M thành M ' . Đẳng thức nào sau đây đúng ?  
 1   
 1 
A. AM ' = 2 AM . B. AM ' = AM .
C. AM = 3AM ' . D. AM ' = AM . 2 3
Câu 16: Trong mặt phẳng Oxy , cho tam giác ABC có A(1; 2 − ), B( 1 − ;6), C ( 6
− ;2) . Phép vị tự tâm O tỉ số 1 k = −
biến tam giác ABC thành tam giác A′B C
′ ′ . Tìm trọng tâm của tam giác A′B C ′ ′ . 2 A. G′( 1 − ; ) 1 . B. G′(1; ) 1 . C. G′(1;− ) 1 . D. G′( 1 − ;− ) 1 .
Câu 17: Trong mặt phẳng Oxy , cho A(1;5), B(3;3). Phép đồng dạng tỉ số 1 k =
biến điểm A thành A ,′ 2
biến điểm B thành B .′ Khi đó độ dài A′B′ là: A. 2 5 B. 5 C. 2 2 D. 2 
Câu 18: Cho đường thẳng ∆ : x − 2 y + 3 = 0 và u = (2;− )
1 . T (∆) = ∆ ' có phương trình là: u
A. x − 2 y − 1 = 0 .
B. x − 2 y + 1 = 0 .
C. x − 2 y − 3 = 0 .
D. 2x + y + 1 = 0 .
Câu 19: Cho điểm M (2;− 2) . Tìm điểm M ′ là ảnh của điểm M qua phép quay tâm O , góc quay 90o . A. M ′( 2; − 2). B. M ′(2; 2 − ). C. M ′( 2; − 2 − ) . D. M ′(2;2) . B A
Câu 20: Cho lục giác đều ABCDEF tâm O như hình vẽ.
Phép quay nào biến E ∆ OD thành A ∆ OF . F C O A. ( Q . B. Q . C. Q . D. Q . O;120°) (O; 60 − °) (O;60°) (O; 120 − °)
Câu 21: Cho đường thẳng d : 2x + y − 3 = 0 . V
(d ) = d′ .Tìm điểm d '. E D (O,2)
A. 4x − 2 y − 3 = 0 .
B. 2x + y − 6 = 0 .
C. 2x + y + 3 = 0 .
D. 4x + 2 y − 5 = 0 . 
Câu 22: Trong mặt phẳng Oxy, cho đường tròn (C ) ( x + )2 2 : 1
+ (y − 2) = 9 và v = (1; 2 − ) .
T (C ) = C '(I ,′ R )
′ . Khẳng định nào dưới đây đúng ? v
A. I ′(0;0) và R′ = 3. B. I ′(2; 4
− ) và R′ = 3. C. I′(0; 4
− ) và R′ = 3. D. I′(0;0) và R′ = 9.
Câu 23: Cho hai điểm M (3;1) và M ( ′ 2; 1)
− nếu T (M ) = M ' thì T biến điểm ( A 2;
− 2) thành điểm A′? v v A. A ( ′ 3 − ;2) . B. A ( ′ 1 − ;0) . C. A ( ′ 3 − ;0) . D. A ( ′ 3 − ;4) . 2 2
Câu 24: Trong mặt phẳng Oxy , cho đường tròn (C ) có phương trình ( x − 2) + ( y − 2) = 16 . Phép đồng
dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 1 k = và phép tịnh tiến theo 2
u = ( 1−;2) sẽ biến (C)thành đường tròn C′(I ,′R′). Khẳng định nào đúng ?
A. I ′(0;3) và R′ = 2.
B. I ′(1;4) và R′ = 2. C. I ′(1; ) 1 và R′ = 4.
I ′(2;2) và R′ = 2. D.
Câu 25: Trong măt phẳng Oxy cho điểm M ( 2; − 2) . V
(M ) = M ′ .Tìm điểm M '. (O, 2) − A. ( 4; − 4) . B. (4; 4 − ) . C. (4; 4) . D. ( 4; − 4 − ) .
----------------------------------------------- ----------- HẾT ----------
Trang 2/2 - Mã đề thi 485
PHIẾU ĐÁP ÁN TRẮC NGHIỆM MÔN HÌNH HỌC CHƯƠNG I Mã đề: 132 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 A B C D Mã đề: 209 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 A B C D Mã đề: 357 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 A B C D Mã đề: 485 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 A B C D BẢNG ĐÁP ÁN 1.C 2.C 3.C.C 4.C.C 5.A 6.D 7.C 8.A 9.C 10.A 11.C 12.A 13.B 14.D 15.A 16.B 17.D 18.C 19.B 20.D 21.B 22.B 23.A 24.C 25.A
LỜI GIẢI CHI TIẾT 2 2 Câu 1.
Trong mặt phẳng Oxy , cho đường tròn C  :  x  2   y  2  16 . Phép đồng dạng có được 1 
bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k
và phép tịnh tiến theo u   1  ; 2 sẽ 2
biến C  thành đường tròn C I , R . Khẳng định nào đúng?
A. I 1; 4 và R  2 . B. I 2; 2 và R  2 . C. I 0;3 và R  2 . D. I   1;1 và R  4 . Lời giải Chọn C
Đường tròn C  có tâm I 2; 2 , bán kính R  4 .  1  1 Xét phép vị tự V
: C I , R C I , R . Khi đó: OI
OI I 1;1 và R R  2 . 1 1    1    1  1 1  1 O ,   2 2  2   
Xét phép tịnh tiến T : C I , R CI , R . Khi đó I I   u I  0;3 và R  R  2 . 1   u 1  1 1    1 Do đó, ta chọn đáp án C. Câu 2.
Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
B. Phép tịnh tiến biến tam giác thành tam giác bằng nó.
C. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với nó.
D. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kỳ. Lời giải Chọn C
Câu C là mệnh đề sai vì “Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó”.  2 2 Câu 3.
Cho đường tròn.  x  
1   y  2  9 . Phép tịnh tiến theo véc tơ v  1;  2 biến đường tròn
C thành đường tròn C 'I '; R ' . Khẳng định nào sau đây đúng?
A. I '2;  4 và R '  3.
B. I '0;0 và R '  9 .
C. I '0;  4 và R '  3.
D. I '0;0 và R '  3. Lời giải Chọn A
C   x  2   y  2 : 1 2
 9  Tâm I 1;  2 Banh kính R  3
Theo tính chất của phé tịnh tiến nên ta có:
Trang 4/12 – Diễn đàn giáo viên Toán
Phép tịnh tiến theo véc tơ v  1;  2 biến đường tròn C  thành đường tròn C ' I '; R ' .
Nên R R '  3.
Tâm I ' là ảnh của I qua phép tịnh tiến nên I '2;  4 . Câu 4.
Tính chất nào sau đây không phải là tính chất của phép đồng dạng ?
A. Biến tam giác thành tam giác đồng dạng với nó.
B. Biến đường tròn thành đường tròn bằng nó.
C. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.
D. Biến đoạn thẳng thành đoạn thẳng. Lời giải Chọn B
Phép đồng dạng với tỷ số k biến đường tròn bán kính R thành đường tròn bán kính k .R .
Nên 2 đường tròn không băng nhau. Câu 5.
Cho đường tròn C  2 2
: x y  2x  8  0 . Gọi  '
C  là ảnh của C qua phép vị tự tâm O tỉ số k  2
 . Tính diện tích hình tròn  ' C . A. 36 . B. 64 . C. 9 . D. 18 . Lời giải Chọn A
Ta có C có R  3. Bán kính của  ' C  là '
R k R  2.3  6.
Vậy diện tích hình tròn  '
C  là S   R 2 ' 2   .6  36 . Câu 6.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A1; 2, B 1  ;6,C  6  ; 2. Phép vị tự 1
tâm O tỉ số k   biến tam giác ABC thành tam giác ' ' '
A B C . Tìm trọng tâm ' G của tam giác 2 ' ' ' A B C . A. ' G  1  ;   1 . B. ' G 1  ;1 . C. ' G 1  ;1 . D. ' G 1;   1 . Lời giải Chọn D
Gọi G là trọng tâm của tam giác ABC , ta có 
x x x A B C x   2 G   3   G 2; 2 .
y y y A B Cy   2 G   3 Trang 5/12 - WordToan  1 1  Ta có '
G là ảnh của G qua phép vị tự tâm O tỉ số k   . Suy ra ' OG   OG 2 2  1 x   x ' GGx  1 ' '  2  G      G 1;   1 . 1 y  1 '    G y   y '   2 G G '
Vậy trọng tâm của tam giác ' ' '
A B C là G 1;   1 . Câu 7.
Trong mặt phẳng tọa độ Oxy , cho hai đường thẳng d : x  3 y  3  0 và d  : x  3 y  6  0 . Tìm 
tọa độ vectơ v vuông góc với d để T d   d. v     3 9    3 9  A. v  ;   .
B. v  3;  1 . C. v   ;   .
D. v  3;   1 .  10 10   10 10  Lời giải Chọn C  
Đặt v  a;b , vì v vuông góc với d : x  3y  3  0 nên 3a b  0 (1).
Lấy điểm M (3; 0)  d , gọi M  là ảnh của M qua T , suy ra M (
a  3;b) . v
Điểm M   d  nên ta có: a  3  3b  6  0  a  3b  3  0 (2).  3  a    10
Giải hệ (1), (2) ta được  . 9 b     10  Câu 8.
Cho đường thẳng d : 2x  3y 1  0 , xét Q
d d  . Tìm vectơ chỉ phương u của đường O;90     thăng d .    
A. u  2; 3 .
B. u  3; 2 .
C. u  3; 2 . D. u   2  ; 3   . Lời giải Chọn A Q
d d   d   d d  có dạng: 3x  2 y m  0 . O ; 90      
d  có vectơ pháp tuyến n  3; 2 nên vectơ chỉ phương u  2; 3 . Câu 9.
Hãy tìm khẳng định sai?
A. Phép quay là phép dời hình.
B. Phép tịnh tiến là phép dời hình.
C. Phép vị tự là phép dời hình.
D. Phép đồng nhất là phép dời hình. Lời giải Chọn C
Theo định nghĩa phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
Vì vậy phép vị tự không phải là phép dời hình.
Câu 10. Cho phép vị tự tâm A tỉ số k  2 biến điểm M thành M  . Đẳng thức nào sau đây đúng?  
 1   1   
A. AM   2 AM . B. AM   AM . C. AM   AM .
D. AM  3AM  . 3 2 Lời giải
Trang 6/12 – Diễn đàn giáo viên Toán Chọn A  
Theo định nghĩa phép vị tự ta có V
M M   AM   2AM . A, 2    
Vậy chọn đáp án A. 1
Câu 11. Trong mặt phẳng Oxy , cho A1; 5 , B  3; 3  . Phép đồng dạng tỷ số k
biến điểm A thành 2 /
A , biến điểm B thành /
B . Khi đó độ dài / / A B là A. 5 . B. 2 5 . C. 2 . D. 2 2 . Lời giải Chọn C  Ta có: AB     2 2 2; 2  AB  2  2  2 2 . 1 / /
A B k.AB  .2 2  2 . 2  Chọn C.
Câu 12. Cho đường tròn C x   y  2 2 : 1
 8 . Ảnh của C  qua phép quay tâm O góc 0 90 là:
A. x  2 2 1  y  8 .
B. x  2 2 1  y  8 .
C. x   y  2 2 1  8 .
D. x   y  2 2 1  8 . Lời giải Chọn A
Đường tròn C  có tâm I  0;1, bán kính R  2 2 .
Vì I  0;1  Oy và OI  1 nên ảnh của I qua phép quay tâm O góc 0 90 là điểm / I 1; 0 . Gọi  /
C là ảnh của C qua phép quay tâm O góc 0 90    /
C  có tâm là điểm / I 1; 0 và bán kính /
R R  2 2 .
 phương trình C   x  2 / 2 : 1  y  8 .  Chọn A 
Câu 13. Cho đường thẳng  : x  2 y  3  0 và u  2;  
1 . T    ' có phương trình là: u
A. 2x y 1  0 .
B. x  2 y 1  0 .
C. x  2 y 1  0 .
D. x  2 y  3  0 . Lời giải Chọn B Cách 1:
+ T    ' khi đó  và  ' song song hoặc trùng. u
Suy ra:  ' : x  2 y m  0 . Trang 7/12 - WordToan + Lấy A1  ;1   .
x '  1 2  1
T  A  A' x '; y '   . u y '  11  0 
+ A '  ' suy ra 1 2.0  m  0  m  1  .
Vậy phương trình đường thẳng  ' là x  2 y 1  0 . Cách 2:
+ Gọi M x; y   .
+ T  M   M ' x '; y ' , T    ' u u
x  2 y  3  0
x  2 y  3  0 
x ' 2  2 y '  1  3  0
x ' 2 y '1  0    
Khi đó: x '  x  2
 x x ' 2
 x x ' 2
 x x ' 2 .  y ' y 1  y y ' 1  y y ' 1        y y '1    
Vì M '  ' nên phương trình đường thẳng  ' là x  2 y 1  0 .
Câu 14. Cho điểm M 2;  2 . Tìm điểm M ' là ảnh của điểm M qua phép quay tâm O góc quay 90 . A. M ' 2  ;  2 .
B. M '2; 2 .
C. M '2;  2 .
D. M '2; 2 . Lời giải Chọn D x '   y  2 Q
M M ' x '; y ' M. O;90      
y'  x  2  M
Vậy: M '2; 2 .
Câu 15. Trong mặt phẳng Oxy , cho điểm A(5; 6) . Tìm ảnh của A qua phép dời hình có được bằng 
cách thực hiện liên tiếp phép tịnh tiến theo u  (3; 4) và phép quay tâm O góc quay 90 ? A. A '(2; 2) .
B. A '(2; 2) .
C. A '(2; 2) .
D. A '(2; 2) . Lời giải Chọn A
Gọi A ' ( x ' ; y ' ) là ảnh của A(5; 6) qua phép tịnh tiến theo u  (3; 4) .
x '  5  (3)  2
Ta có:  y'  6  4  2   A ' (2; 2)
Gọi A '(x '; y ') là ảnh của A ' (2; 2) qua phép phép quay tâm O góc quay 90 .
x '   y '  2 Ta có:   A '(2; 2)
y '  x '  2 
Trang 8/12 – Diễn đàn giáo viên Toán
Vậy A '(2; 2) chính là ảnh của A qua phép dời hình có được bằng cách thực hiện liên tiếp 
phép tịnh tiến theo u  (3; 4) và phép quay tâm O góc quay 90 . 
Câu 16. Phép tịnh tiến theo vectơ u biến hai điểm M , N thành điểm M ', N ' . Chọn khẳng định đúng?          
A. M ' N '  u.MN .
B. M ' N '  MN .
C. OM '  u.OM .
D. M ' N '  u.MN . Lời giải Chọn B
Dựa vào tính chất của phép tịnh tiến.
Câu 17. Cho tam giác đều tâm O . Hỏi có bao nhiêu phép quay tâm O góc quay  , 0    2 biến tam
giác trên thành chính nó? A. Một. B. Hai. C. Bốn. D. Ba. Lời giải Chọn D A O B C
Gọi ABC là tam giác đều đã cho.
Vì O là tâm của tam giác đều nên ta có: OA   OB OC   2  ,
OA OB  OB,OC   OC,OA    3  Q ABC  . BCA  2    O,    3  OA   OB OC   4  ,
OA OC   OB,OA  OC,OB    3  Q ABC  . CAB  4    O,    3  O
A OB OC   O , A OA
  OB,OB  OC,OC  2   Q ABC ABC. O,2    
Do góc quay 0    2 nên có ba phép quay thỏa mãn bài toán.
Câu 18. Trong mặt phẳng Oxy cho điểm M  2
 ; 2 . Phép vị tự tâm O , tỉ số k  2 biến điểm M
thành điểm nào trong các điểm sau đây? A.  4  ; 4 . B. 4 ; 4 . C. 4 ; -4 . D.  4  ; -4 . Lời giải Chọn C Trang 9/12 - WordToan   x  2x  4 Giả sử V
M M  . Khi đó OM   2 M MOM    M 4 ; 4  . O, 2      y  2 y  4   M M Vậy M 4 ; 4  .
Câu 19. Cho điểm M 1; 2 . Tìm điểm M  là ảnh của điểm M qua phép tịnh tiến theo véctơ  v  2;   1 A. M 3; 3   .
B. M 3;  1 . C. M  1  ;3 . D. M  3  ;3 . Lời giải Chọn B
Gọi M  x ; y
x  x a
x  1 2  3 
Ta có:T  M   M       M 3  ;1 . v
y  y b y  2      1  1 
Câu 20. Cho hai điểm M 3; 
1 và M 2;  
1 nếu T  M   M  thì T biến điểm A2; 2 thành điểm v v A ? A. A 3  ; 2 . B. A 3  ; 4 . C. A 1  ; 0 . D. A 3  ; 0 . Lời giải Chọn D
Gọi A x ; y .  
Ta có: T  M   M   MM   v   1 . v  
T  A  A  AA  v 2 . v
  x  2  1 x  3 Từ  
1 và 2  AA  MM      . y  2  2  y '  0   Vậy A 3  ; 0 .
Câu 21. Cho hình vuông ABCD tâm O cạnh bằng 2 . Phép đồng dạng tỉ số k biến tam giác AOD thành
tam giác ABC . Tính k . 2 A. k  2 . B. k  2 . C. k  . D. k  4 . 2 Lời giải Chọn B
Trang 10/12 – Diễn đàn giáo viên Toán
Theo đề có phép đồng dạng tỉ số k biến tam giác AOD thành tam giác ABC AO AD OD 1 nên có A
OD đồng dạng với A
BC , khi đó có tỉ số     k  2 . AB AC BC k
(Trong đó AO OD  2; AC  2 2 )
Câu 22. Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x y  3  0 . Phép vị tự tâm O tỉ
số k  2 biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?
A. 2x y  3  0 .
B. 2x y  6  0 .
C. 4x  2 y  5  0 .
D. 4x  2 y  3  0 . Lời giải Chọn B
Gọi d ' là ảnh của d qua phép vị tự tâm O tỉ số k  2 khi đó đường thẳng d ' có phương trình
2x y c  0 ( Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó). Lấy ( A 0;3)  d   V ( )
A A'  O A'  2OA  (0;6) O;2  A'(0;6)  d'
Thay A '(0;6) vào (d ') : 2x y c  0  c  6  .
Vậy d ' có phương trình là 2x y  6  0 .
Câu 23. Trong các mệnh đề sau đây mệnh đề nào đúng?
A. Phép quay là một phép đồng dạng.
B. Phép vị tự là một phép dời hình.
C. Phép đồng dạng là một phép dời hình.
D. Phép tịnh tiến không phải là phép đồng dạng. Lời giải Chọn A
Ta có: Phép quay là một phép dời hình nên nó là phép đồng dạng với tỉ số k  1 . Vậy mệnh đề A đúng.
Câu 24. Cho lục giác đều ABCDEF tâm O như hình vẽ.
Phép quay nào biến EOD thành AOF . A. Q . B. Q . C. Q . D. Q .  0 O,120   0 O, 6  0   0 O, 1  20   0 O ,60  Lời giải Chọn C Trang 11/12 - WordToan
Do ABCDEF là lục giác đều   0
AOE DOF  120 ;OA OD OF OE.  Q : EOD AOF  0 O,120  1 
Câu 25. Cho tam giác ABC có diện tích S. Phép vị tự tỉ số k
biến tam giác ABC thành tam giác 2
A' B'C' . Gọi '
S là diện tích tam giác A' B'C' . Khẳng định nào sau đây đúng 1 1 A. S '  S .
B. S '  2S . C. S '  S .
D. S '  4S . 4 2 Lời giải Chọn A Gọi , a , b ,
c p là độ dài 3 cạnh và nửa chu vi của tam giác ABC . Gọi a',b',c', p' là độ dài 3
cạnh và nửa chu vi của tam giác A' B'C' . 1 
Theo tính chất của phép vị tự với tỉ số k
suy ra a  2a',b  2b',c  2c'  p  2p' . 2 Theo công thức Hê rông S  p p  a p  b p  c
 2p'2p'2a '2p'2b '2p'2c ' .
 4 p'p'a 'p'b 'p'c '  4 ' S
Trang 12/12 – Diễn đàn giáo viên Toán
Document Outline

  • 65156
    • 132.pdf
    • 209.pdf
    • 357.pdf
    • 485.pdf
    • phieudapan.pdf
  • 1568691641_WT39-H11-C1-PHÉP DỜI HÍNH_PHÉP ĐỒNG DẠNG-THPT THPT HẢI LĂNG-QUẢNG TRỊ